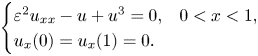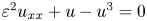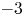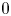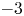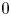1. Introduction and main results
We are concerned with the Neumann problem of a reaction–diffusion equation

and its linearized eigenvalue problem associated with a positive solution $u(x)$![]()

where $\varepsilon >0$![]() is a parameter and $f$
is a parameter and $f$![]() is smooth enough. We denote $F(u)$
is smooth enough. We denote $F(u)$![]() by
by
Precise information of eigenvalues is crucial not only in a stability analysis of a stationary solution of the associated parabolic problem but also in a study of dynamics. The goal of the present paper is to obtain a rather explicit expression of all the eigenvalues of (1.2) in the case
The equation $\varepsilon ^2u_{xx}-u+u^p=0$![]() , $p>1$
, $p>1$![]() , is called the scalar field equation which appears in the study of a standing wave of a nonlinear Schrödinger equation [Reference Berestycki and Lions2], of elastic curves in differential geometry [Reference Langer and Singer6] and of the Gierer–Meinhardt model in mathematical biology [Reference Gierer and Meinhardt5]. This equation has attracted much attention for these three decades. A complete bifurcation diagram of the positive solutions for (1.1) with $f(u)=-u+u^p$
, is called the scalar field equation which appears in the study of a standing wave of a nonlinear Schrödinger equation [Reference Berestycki and Lions2], of elastic curves in differential geometry [Reference Langer and Singer6] and of the Gierer–Meinhardt model in mathematical biology [Reference Gierer and Meinhardt5]. This equation has attracted much attention for these three decades. A complete bifurcation diagram of the positive solutions for (1.1) with $f(u)=-u+u^p$![]() , $p>1$
, $p>1$![]() , was obtained in [Reference Miyamoto and Yagasaki7, Reference Yagasaki16]. See Fig. 1. Let $p>1$
, was obtained in [Reference Miyamoto and Yagasaki7, Reference Yagasaki16]. See Fig. 1. Let $p>1$![]() and $\varepsilon _n:=\sqrt {p-1}/n\pi$
and $\varepsilon _n:=\sqrt {p-1}/n\pi$![]() . For each $n\ge 1$
. For each $n\ge 1$![]() , (1.1) has exactly two $n$
, (1.1) has exactly two $n$![]() -mode solutions $u^{\pm }_{n,\varepsilon }$
-mode solutions $u^{\pm }_{n,\varepsilon }$![]() if $0<\varepsilon <\varepsilon _n$
if $0<\varepsilon <\varepsilon _n$![]() . Here,
. Here,
In particular, if $n=2k+1$![]() , then both $u^+_{n,\varepsilon }$
, then both $u^+_{n,\varepsilon }$![]() and $u^-_{u,\varepsilon }$
and $u^-_{u,\varepsilon }$![]() have $k$
have $k$![]() interior peaks and $1$
interior peaks and $1$![]() boundary peak. On the other hand, if $n=2k$
boundary peak. On the other hand, if $n=2k$![]() , then $u^+_{n,\varepsilon }$
, then $u^+_{n,\varepsilon }$![]() (resp. $u^-_{n,\varepsilon }$
(resp. $u^-_{n,\varepsilon }$![]() ) has $k$
) has $k$![]() interior peaks and no boundary peak (resp. $k-1$
interior peaks and no boundary peak (resp. $k-1$![]() interior peaks and $2$
interior peaks and $2$![]() boundary peaks). Each peak becomes sharp as $\varepsilon \to 0$
boundary peaks). Each peak becomes sharp as $\varepsilon \to 0$![]() .
.

Figure 1. The complete bifurcation diagram for (1.1) with $f(u)=-u+u^3$![]() .
.
Hereafter, we consider the case $f(u)=-u+u^3$![]() . Then
. Then
All the solutions of (1.1) can be written in terms of elliptic functions:
Proposition 1.1 Let $n\ge 1$![]() be fixed and let $0<\varepsilon <\varepsilon _n$
be fixed and let $0<\varepsilon <\varepsilon _n$![]() . Let $k_{\varepsilon }=k_{n,\varepsilon }\in (0,1)$
. Let $k_{\varepsilon }=k_{n,\varepsilon }\in (0,1)$![]() be a solution of
be a solution of
Note that $k_{\varepsilon }$![]() is uniquely determined. Then ${u^+_{n,\varepsilon }}$
is uniquely determined. Then ${u^+_{n,\varepsilon }}$![]() and ${u^-_{n,\varepsilon }}$
and ${u^-_{n,\varepsilon }}$![]() can be written as follows:
can be written as follows:

where
The proof of proposition 1.1 is given in §2.
In this paper, we frequently use Jacobi's elliptic functions ${\rm sn}(x,k)$![]() and ${\rm dn}(x,k)$
and ${\rm dn}(x,k)$![]() and complete elliptic integrals $K(k)$
and complete elliptic integrals $K(k)$![]() , $E(k)$
, $E(k)$![]() and $\Pi (\nu,k)$
and $\Pi (\nu,k)$![]() . The definitions and various properties are summarized in Appendix A of the present paper.
. The definitions and various properties are summarized in Appendix A of the present paper.
The linearized eigenvalue problem (1.2) associated with $u^{\pm }_{n,\varepsilon }$![]() is as follows:
is as follows:

Hereafter, $\lambda ^{\pm }_{j,\varepsilon }$![]() , $j\ge 0$
, $j\ge 0$![]() denotes the $j+1$
denotes the $j+1$![]() -th eigenvalue of (LP±) and $\varphi ^{\pm }_{j,\varepsilon }$
-th eigenvalue of (LP±) and $\varphi ^{\pm }_{j,\varepsilon }$![]() denotes an associated eigenfunction. It is well known that each eigenvalue $\lambda ^{\pm }_{j,\varepsilon }$
denotes an associated eigenfunction. It is well known that each eigenvalue $\lambda ^{\pm }_{j,\varepsilon }$![]() is simple.
is simple.
The following three exact eigenvalues of (LP±) were obtained in the previous paper of the third author [Reference Wakasa11]:
Proposition 1.2 Let $n\ge 1$![]() ,
,

The following hold$:$![]()
(i) The problem (${\rm LP}_+$
 ) has the following two pairs of eigenvalues and eigenfunctions$:$
) has the following two pairs of eigenvalues and eigenfunctions$:$ $$\begin{align*} & \lambda^+_{0,\varepsilon}={-}1-\frac{2\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}}{2-k_{\varepsilon}^2},\quad \varphi^+_{0,\varepsilon}(x)=1\\& \quad -\left(1+k_{\varepsilon}^2-\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}\right){\rm SN}_n^+(x,k_{\varepsilon})^2,\\ & \lambda^+_{n,\varepsilon}={-}1+\frac{2\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}}{2-k_{\varepsilon}^2},\quad \varphi^+_{n,\varepsilon}(x)={-}1\\& \quad +\left(1+k_{\varepsilon}^2+\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}\right){\rm SN}_n^+(x,k_{\varepsilon})^2. \end{align*}$$Moreover, if $n$
$$\begin{align*} & \lambda^+_{0,\varepsilon}={-}1-\frac{2\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}}{2-k_{\varepsilon}^2},\quad \varphi^+_{0,\varepsilon}(x)=1\\& \quad -\left(1+k_{\varepsilon}^2-\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}\right){\rm SN}_n^+(x,k_{\varepsilon})^2,\\ & \lambda^+_{n,\varepsilon}={-}1+\frac{2\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}}{2-k_{\varepsilon}^2},\quad \varphi^+_{n,\varepsilon}(x)={-}1\\& \quad +\left(1+k_{\varepsilon}^2+\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}\right){\rm SN}_n^+(x,k_{\varepsilon})^2. \end{align*}$$Moreover, if $n$
 is even, then (LP$_+$
is even, then (LP$_+$ ) has one more pair$:$
) has one more pair$:$ \[ \lambda^+_{n/2,\varepsilon}={-}\frac{3(1-k_{\varepsilon}^2)}{2-k_{\varepsilon}^2},\quad \varphi^+_{n/2,\varepsilon}(x)={\rm SN}_n^+(x,k_{\varepsilon}){\rm DN}_n^+(x,k_{\varepsilon}). \]
\[ \lambda^+_{n/2,\varepsilon}={-}\frac{3(1-k_{\varepsilon}^2)}{2-k_{\varepsilon}^2},\quad \varphi^+_{n/2,\varepsilon}(x)={\rm SN}_n^+(x,k_{\varepsilon}){\rm DN}_n^+(x,k_{\varepsilon}). \]
(ii) The problem (${\rm LP}_-$
 ) has the following pairs of eigenvalues and eigenfunctions$:$
) has the following pairs of eigenvalues and eigenfunctions$:$ $$\begin{align*} & \lambda^-_{0,\varepsilon}={-}1-\frac{2\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}}{2-k_{\varepsilon}^2},\quad \varphi^-_{0,\varepsilon}(x)=1\\& \quad-\left(1+k_{\varepsilon}^2-\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}\right){\rm SN}_n^-(x,k_{\varepsilon})^2,\\ & \lambda^-_{n,\varepsilon}={-}1+\frac{2\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}}{2-k_{\varepsilon}^2},\quad \varphi^-_{n,\varepsilon}(x)={-}1\\& \quad +\left(1+k_{\varepsilon}^2+\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}\right){\rm SN}_n^-(x,k_{\varepsilon})^2. \end{align*}$$Moreover, if $n$
$$\begin{align*} & \lambda^-_{0,\varepsilon}={-}1-\frac{2\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}}{2-k_{\varepsilon}^2},\quad \varphi^-_{0,\varepsilon}(x)=1\\& \quad-\left(1+k_{\varepsilon}^2-\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}\right){\rm SN}_n^-(x,k_{\varepsilon})^2,\\ & \lambda^-_{n,\varepsilon}={-}1+\frac{2\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}}{2-k_{\varepsilon}^2},\quad \varphi^-_{n,\varepsilon}(x)={-}1\\& \quad +\left(1+k_{\varepsilon}^2+\sqrt{1-k_{\varepsilon}^2+k_{\varepsilon}^4}\right){\rm SN}_n^-(x,k_{\varepsilon})^2. \end{align*}$$Moreover, if $n$
 is even, then (LP$_-$
is even, then (LP$_-$ ) has one more pair$:$
) has one more pair$:$ \[ \lambda^-_{n/2,\varepsilon}={-}\frac{3}{2-k_{\varepsilon}^2},\quad \varphi^-_{n/2,\varepsilon}(x)={\rm CN}_n^-(x,k_{\varepsilon}){\rm DN}_n^-(x,k_{\varepsilon}). \]
\[ \lambda^-_{n/2,\varepsilon}={-}\frac{3}{2-k_{\varepsilon}^2},\quad \varphi^-_{n/2,\varepsilon}(x)={\rm CN}_n^-(x,k_{\varepsilon}){\rm DN}_n^-(x,k_{\varepsilon}). \]
Singularly perturbed problems have attracted great attention, because of a wide variety of applications. It follows from (1.3) that a singularly perturbed problem corresponds to the case where $k$![]() is close to $1$
is close to $1$![]() . The main result of the paper is the following asymptotic formula of the other eigenvalues as $k\to 1:$
. The main result of the paper is the following asymptotic formula of the other eigenvalues as $k\to 1:$![]()
Theorem 1.3 Let $n\ge 1$![]() and $j>0$
and $j>0$![]() be fixed. Let $k_{\varepsilon }$
be fixed. Let $k_{\varepsilon }$![]() be as in proposition 1.1. The following hold for (${\rm LP}_{\pm }$
be as in proposition 1.1. The following hold for (${\rm LP}_{\pm }$![]() )$:$
)$:$![]()
(i) For $0< j< n/2$
 ,
\[ \lambda_{j,\varepsilon}^{{\pm}}={-}3+3(1-k_{\varepsilon}^2)+\frac{3}{4}\left(\sin^2\frac{j\pi}{n}-5\right)(1-k_{\varepsilon}^2)^2\!+\!o\left((1-k_{\varepsilon}^2)^2\right)\ \textrm{as}\ k_{\varepsilon}\!\to\! 1. \]
,
\[ \lambda_{j,\varepsilon}^{{\pm}}={-}3+3(1-k_{\varepsilon}^2)+\frac{3}{4}\left(\sin^2\frac{j\pi}{n}-5\right)(1-k_{\varepsilon}^2)^2\!+\!o\left((1-k_{\varepsilon}^2)^2\right)\ \textrm{as}\ k_{\varepsilon}\!\to\! 1. \]
(ii) For $n/2< j< n$
 ,
\[ \lambda_{j,\varepsilon}^{{\pm}}={-}3\left(\sin^2\frac{j\pi}{n}\right)(1-k_{\varepsilon}^2)+o(1-k_{\varepsilon}^2)\ \textrm{as}\ k_{\varepsilon}\to 1. \]
,
\[ \lambda_{j,\varepsilon}^{{\pm}}={-}3\left(\sin^2\frac{j\pi}{n}\right)(1-k_{\varepsilon}^2)+o(1-k_{\varepsilon}^2)\ \textrm{as}\ k_{\varepsilon}\to 1. \]
(iii) For $j>n$
 ,
\[ \lambda_{j,\varepsilon}^{{\pm}}=1+\frac{(j-n)^2\pi^2}{n^2}\frac{1}{K(k_{\varepsilon})^2}+o\left(\frac{1}{K(k_{\varepsilon})^2}\right)\ \textrm{as}\ k_{\varepsilon}\to 1, \]where $K(k_{\varepsilon })\to \infty$
,
\[ \lambda_{j,\varepsilon}^{{\pm}}=1+\frac{(j-n)^2\pi^2}{n^2}\frac{1}{K(k_{\varepsilon})^2}+o\left(\frac{1}{K(k_{\varepsilon})^2}\right)\ \textrm{as}\ k_{\varepsilon}\to 1, \]where $K(k_{\varepsilon })\to \infty$
 as $k_{\varepsilon }\to 1$
as $k_{\varepsilon }\to 1$ .
.
Combining proposition 1.2 and theorem 1.3, we can relate locations of eigenvalues with the number of the peaks of $u^{\pm }_{n,\varepsilon }$![]() as follows: All the eigenvalues can be classified into three categories, i.e.,
as follows: All the eigenvalues can be classified into three categories, i.e.,

The number of the near $-3$![]() eigenvalues is equal to the number of the interior and boundary peaks of $u^{\pm }_{n,\varepsilon }$
eigenvalues is equal to the number of the interior and boundary peaks of $u^{\pm }_{n,\varepsilon }$![]() . The number of the near $0$
. The number of the near $0$![]() eigenvalues is equal to the number of the interior peaks of $u^{\pm }_{n,\varepsilon }$
eigenvalues is equal to the number of the interior peaks of $u^{\pm }_{n,\varepsilon }$![]() .
.
Example 1.4
(i) The solution $u^+_{10,\varepsilon }$
 has $5$
has $5$ interior peaks and no boundary peak. Hence, (${\rm LP}_+$
interior peaks and no boundary peak. Hence, (${\rm LP}_+$ ) has $5$
) has $5$ eigenvalues near $-3$
eigenvalues near $-3$ and $5$
and $5$ eigenvalues near $0$
eigenvalues near $0$ when $\varepsilon >0$
when $\varepsilon >0$ is small. On the other hand, $u^-_{10,\varepsilon }$
is small. On the other hand, $u^-_{10,\varepsilon }$ has $4$
has $4$ interior peaks and 2 boundary peaks. Hence (${\rm LP}_-$
interior peaks and 2 boundary peaks. Hence (${\rm LP}_-$ ) has 6 eigenvalues near $-3$
) has 6 eigenvalues near $-3$ and 4 eigenvalues near $0$
and 4 eigenvalues near $0$ when $\varepsilon >0$
when $\varepsilon >0$ is small.
is small.(ii) Each of $u^+_{11,\varepsilon }$
 and $u^-_{11,\varepsilon }$
and $u^-_{11,\varepsilon }$ has $5$
has $5$ interior peaks and 1 boundary peak. Hence, (${\rm LP}_{\pm }$
interior peaks and 1 boundary peak. Hence, (${\rm LP}_{\pm }$ ) has 6 eigenvalues near $-3$
) has 6 eigenvalues near $-3$ and 5 eigenvalues near $0$
and 5 eigenvalues near $0$ when $\varepsilon >0$
when $\varepsilon >0$ is small.
is small.In figures 2–4 profiles of eigenfunctions on (${\rm LP}_\pm$
 ) with $u^\pm _{10,\varepsilon }$
) with $u^\pm _{10,\varepsilon }$ and profiles of eigenfunctions on (${\rm LP}_+$
and profiles of eigenfunctions on (${\rm LP}_+$ ) with $u^+_{11,\varepsilon }$
) with $u^+_{11,\varepsilon }$ are shown. In each figure (a-0), (a-1) and (a-2) belong to category (a) in (LP±), and so on.
are shown. In each figure (a-0), (a-1) and (a-2) belong to category (a) in (LP±), and so on.

Figure 2. Profiles of eigenfunctions for (${\rm LP}_+$![]() ) with $u_{10,\varepsilon }^+(x)$
) with $u_{10,\varepsilon }^+(x)$![]() ; (a-0) $\varphi ^+_0$
; (a-0) $\varphi ^+_0$![]() , (a-1) $\varphi ^+_1$
, (a-1) $\varphi ^+_1$![]() , (a-2) $\varphi ^+_2$
, (a-2) $\varphi ^+_2$![]() , (b-0) $\varphi ^+_5$
, (b-0) $\varphi ^+_5$![]() , (b-1) $\varphi ^+_6$
, (b-1) $\varphi ^+_6$![]() , (b-2) $\varphi ^+_7$
, (b-2) $\varphi ^+_7$![]() , (c-0) $\varphi ^+_{10}$
, (c-0) $\varphi ^+_{10}$![]() , (c-1) $\varphi ^+_{11}$
, (c-1) $\varphi ^+_{11}$![]() and (c-2) $\varphi ^+_{12}$
and (c-2) $\varphi ^+_{12}$![]() .
.

Figure 3. Profiles of eigenfunctions for (LP$_-$![]() ) with $u_{10,\varepsilon }^-(x)$
) with $u_{10,\varepsilon }^-(x)$![]() ; (a-0) $\varphi ^-_0$
; (a-0) $\varphi ^-_0$![]() , (a-1) $\varphi ^-_1$
, (a-1) $\varphi ^-_1$![]() , (a-2) $\varphi ^-_2$
, (a-2) $\varphi ^-_2$![]() , (a-5) $\varphi ^-_5$
, (a-5) $\varphi ^-_5$![]() , (b-1) $\varphi ^-_6$
, (b-1) $\varphi ^-_6$![]() , (b-2) $\varphi ^-_7$
, (b-2) $\varphi ^-_7$![]() , (c-0) $\varphi ^-_{10}$
, (c-0) $\varphi ^-_{10}$![]() , (c-1) $\varphi ^-_{11}$
, (c-1) $\varphi ^-_{11}$![]() and (c-2) $\varphi ^-_{12}$
and (c-2) $\varphi ^-_{12}$![]() .
.

Figure 4. Profiles of eigenfunctions for (${\rm LP}_+$![]() ) with $u_{11,\varepsilon }^+(x)$
) with $u_{11,\varepsilon }^+(x)$![]() ; (a-0) $\varphi ^+_0$
; (a-0) $\varphi ^+_0$![]() , (a-1) $\varphi ^+_1$
, (a-1) $\varphi ^+_1$![]() , (a-2) $\varphi ^+_2$
, (a-2) $\varphi ^+_2$![]() , (a-5) $\varphi ^+_5$
, (a-5) $\varphi ^+_5$![]() , (b-1) $\varphi ^+_6$
, (b-1) $\varphi ^+_6$![]() , (b-2) $\varphi ^+_7$
, (b-2) $\varphi ^+_7$![]() , (c-0) $\varphi ^+_{11}$
, (c-0) $\varphi ^+_{11}$![]() , (c-1) $\varphi ^+_{12}$
, (c-1) $\varphi ^+_{12}$![]() and (c-2) $\varphi ^+_{13}$
and (c-2) $\varphi ^+_{13}$![]() .
.
Let us consider the stretched problem

and the limit problem

Here $\tilde {u}(y):=u(x)$![]() , $y:=(x-x_{\ell,\varepsilon })/\varepsilon$
, $y:=(x-x_{\ell,\varepsilon })/\varepsilon$![]() and $x_{\ell,\varepsilon }\in (0,1)$
and $x_{\ell,\varepsilon }\in (0,1)$![]() is a position of an $\ell$
is a position of an $\ell$![]() -th interior peak. Then $\bar {u}(y)=\frac {\sqrt {2}}{\cosh (y)}$
-th interior peak. Then $\bar {u}(y)=\frac {\sqrt {2}}{\cosh (y)}$![]() is a solution of (1.6) which has a one-peak at $y=0$
is a solution of (1.6) which has a one-peak at $y=0$![]() . The associated eigenvalue problem is as follows:
. The associated eigenvalue problem is as follows:

It is known that the spectral set consists of two eigenvalues $-3$![]() and $0$
and $0$![]() and the continuous spectrum $[1,\infty )$
and the continuous spectrum $[1,\infty )$![]() . The near $-3$
. The near $-3$![]() eigenvalues of (LP$_{\pm }$
eigenvalues of (LP$_{\pm }$![]() ) come from the $-3$
) come from the $-3$![]() eigenvalue of (1.7). Figures 2–4 indicate that an eigenfunction in category (a) can be approximated by a linear combination of translations of a compressed first eigenfunction of (1.7). The near $0$
eigenvalue of (1.7). Figures 2–4 indicate that an eigenfunction in category (a) can be approximated by a linear combination of translations of a compressed first eigenfunction of (1.7). The near $0$![]() eigenvalues of (LP$_{\pm }$
eigenvalues of (LP$_{\pm }$![]() ) come from a translation invariance of the one-peak solution $\bar {u}(y)$
) come from a translation invariance of the one-peak solution $\bar {u}(y)$![]() , which is indicated by a shape of an eigenfunction of category (b), e.g., (b-0), (b-1) and (b-2) of figure 2. Specifically, an eigenfunction is close to $cu'(x)$
, which is indicated by a shape of an eigenfunction of category (b), e.g., (b-0), (b-1) and (b-2) of figure 2. Specifically, an eigenfunction is close to $cu'(x)$![]() , $c\in \mathbb {R}$
, $c\in \mathbb {R}$![]() , near each peak of $u(x)$
, near each peak of $u(x)$![]() . The other eigenvalues converge to $1$
. The other eigenvalues converge to $1$![]() which is an end point of $[1,\infty )$
which is an end point of $[1,\infty )$![]() . The spectrum $1$
. The spectrum $1$![]() of (1.7) is not an eigenvalue, since a corresponding eigenfunction is not in $H^1(\mathbb {R})$
of (1.7) is not an eigenvalue, since a corresponding eigenfunction is not in $H^1(\mathbb {R})$![]() . Indeed, a graph of an eigenfunction of category (c) in figures 2–4 is close to $\cos (m\pi x)$
. Indeed, a graph of an eigenfunction of category (c) in figures 2–4 is close to $\cos (m\pi x)$![]() for most $x\in (0,1)$
for most $x\in (0,1)$![]() , and hence its stretched function is not in $H^1(\mathbb {R})$
, and hence its stretched function is not in $H^1(\mathbb {R})$![]() or $0$
or $0$![]() .
.
Remark 1.5 If $n$![]() is odd, then the eigenvalue sets of (${\rm LP}_+$
is odd, then the eigenvalue sets of (${\rm LP}_+$![]() ) and (${\rm LP}_-$
) and (${\rm LP}_-$![]() ) are the same, i.e., $\lambda ^+_{j,\varepsilon }=\lambda ^-_{j,\varepsilon }$
) are the same, i.e., $\lambda ^+_{j,\varepsilon }=\lambda ^-_{j,\varepsilon }$![]() for all $j\ge 0$
for all $j\ge 0$![]() , since $u^-_{n,\varepsilon }(x)=u^+_{n,\varepsilon }(1-x)$
, since $u^-_{n,\varepsilon }(x)=u^+_{n,\varepsilon }(1-x)$![]() . However, if $n$
. However, if $n$![]() is even, then $\lambda ^+_{j,\varepsilon }=\lambda ^-_{j,\varepsilon }$
is even, then $\lambda ^+_{j,\varepsilon }=\lambda ^-_{j,\varepsilon }$![]() for $j\neq n/2$
for $j\neq n/2$![]() , but $\lambda ^+_{n/2,\varepsilon }\neq \lambda ^-_{n/2,\varepsilon }$
, but $\lambda ^+_{n/2,\varepsilon }\neq \lambda ^-_{n/2,\varepsilon }$![]() . In the even case the number of all the peaks of $u_{n,\varepsilon }^+$
. In the even case the number of all the peaks of $u_{n,\varepsilon }^+$![]() is different from that of $u_{n,\varepsilon }^-$
is different from that of $u_{n,\varepsilon }^-$![]() .
.
Corollaries 1.6 and 1.7 are asymptotic formulas with respect to ${\rm e}^{-2/n\varepsilon }$![]() .
.
Corollary 1.6 Let $n\ge 1$![]() be fixed. The following hold for (LP±):
be fixed. The following hold for (LP±):
(i) $\displaystyle \lambda ^{\pm }_{0,\varepsilon }=-3+48\,{\rm e}^{-\frac {2}{n\varepsilon }}+o({\rm e}^{-\frac {2}{n\varepsilon }})$
 as $\varepsilon \to 0$
as $\varepsilon \to 0$ .
.(ii) If $n$
 is even, then as $\varepsilon \to 0$
is even, then as $\varepsilon \to 0$ ,
\[ \lambda^+_{n/2,\varepsilon}={-}48\,{\rm e}^{-\frac{2}{n\varepsilon}}+o({\rm e}^{-\frac{2}{n\varepsilon}}),\quad \lambda^-_{n/2,\varepsilon}={-}3+48\,{\rm e}^{-\frac{2}{n\varepsilon}}+o({\rm e}^{-\frac{2}{n\varepsilon}}). \]
,
\[ \lambda^+_{n/2,\varepsilon}={-}48\,{\rm e}^{-\frac{2}{n\varepsilon}}+o({\rm e}^{-\frac{2}{n\varepsilon}}),\quad \lambda^-_{n/2,\varepsilon}={-}3+48\,{\rm e}^{-\frac{2}{n\varepsilon}}+o({\rm e}^{-\frac{2}{n\varepsilon}}). \]
(iii) $\displaystyle \lambda ^{\pm }_{n,\varepsilon }=1-48\,{\rm e}^{-\frac {2}{n\varepsilon }}+o({\rm e}^{-\frac {2}{n\varepsilon }})$
 as $\varepsilon \to 0$
as $\varepsilon \to 0$ .
.
Corollary 1.7 Let $n\ge 1$![]() and $j\ge 0$
and $j\ge 0$![]() be fixed. The following hold for (${\rm LP}_{\pm }$
be fixed. The following hold for (${\rm LP}_{\pm }$![]() ):
):
(i) For $0< j< n/2$
 ,
\[ \lambda_{j,\varepsilon}^{{\pm}}={-}3+\left\{1+4\left(\sin^2\frac{j\pi}{n}\right){\rm e}^{-\frac{2}{n\varepsilon}}+o({\rm e}^{-\frac{2}{n\varepsilon}})\right\}(\lambda^{{\pm}}_{0,\varepsilon}+3) \ \textrm{as}\ \varepsilon\to 0. \]
,
\[ \lambda_{j,\varepsilon}^{{\pm}}={-}3+\left\{1+4\left(\sin^2\frac{j\pi}{n}\right){\rm e}^{-\frac{2}{n\varepsilon}}+o({\rm e}^{-\frac{2}{n\varepsilon}})\right\}(\lambda^{{\pm}}_{0,\varepsilon}+3) \ \textrm{as}\ \varepsilon\to 0. \]
(ii) For $n/2< j< n$
 ,
\[ \lambda_{j,\varepsilon}^{{\pm}}={-}48\left(\sin^2\frac{j\pi}{n}\right){\rm e}^{-\frac{2}{n\varepsilon}}+o({\rm e}^{-\frac{2}{n\varepsilon}})\ \textrm{as}\ \ \varepsilon\to 0. \]
,
\[ \lambda_{j,\varepsilon}^{{\pm}}={-}48\left(\sin^2\frac{j\pi}{n}\right){\rm e}^{-\frac{2}{n\varepsilon}}+o({\rm e}^{-\frac{2}{n\varepsilon}})\ \textrm{as}\ \ \varepsilon\to 0. \]
(iii) For $j>n$
 ,
\[ \lambda_{j,\varepsilon}^{{\pm}}=1+(j-n)^2\pi^2\varepsilon^2+o(\varepsilon^2) \ \textrm{as}\ \varepsilon\to 0. \]
,
\[ \lambda_{j,\varepsilon}^{{\pm}}=1+(j-n)^2\pi^2\varepsilon^2+o(\varepsilon^2) \ \textrm{as}\ \varepsilon\to 0. \]
It follows from corollary 1.7 (i) that $\lambda ^{\pm }_{j,\varepsilon }$![]() , $0< j< n/2$
, $0< j< n/2$![]() , can be also written as follows:
, can be also written as follows:
However a $j$![]() -dependence does not appear in the first two terms.
-dependence does not appear in the first two terms.
Let us recall known results. It is difficult to obtain exact expressions of eigenvalues of an elliptic differential operator even if a domain is a finite interval. Only few examples are known for elliptic differential operators with variable coefficients. A model case is the linearization problem for the Allen–Cahn equation (1.1) with $f(u)=u-u^3$![]() . The problem (1.1) with $f(u)=u-u^3$
. The problem (1.1) with $f(u)=u-u^3$![]() has $n$
has $n$![]() -mode solutions $u^{\pm }_{n,\varepsilon }$
-mode solutions $u^{\pm }_{n,\varepsilon }$![]() for small $\varepsilon >0$
for small $\varepsilon >0$![]() which has $n$
which has $n$![]() transition layers in the interval. In [Reference Carr and Pego4] the so-called very slow dynamics of a transition layer solution of an associated parabolic problem were studied. Then the first $n$
transition layers in the interval. In [Reference Carr and Pego4] the so-called very slow dynamics of a transition layer solution of an associated parabolic problem were studied. Then the first $n$![]() eigenvalues of (LP±), $\{\lambda ^{\pm }_{j,\varepsilon }\}_{j=0}^{n-1}$
eigenvalues of (LP±), $\{\lambda ^{\pm }_{j,\varepsilon }\}_{j=0}^{n-1}$![]() , play a crucial role. It was shown in [Reference Carr and Pego4, Corollary 4.2] that for $0\le j< n$
, play a crucial role. It was shown in [Reference Carr and Pego4, Corollary 4.2] that for $0\le j< n$![]() ,
,
These near $0$![]() eigenvalues come from translation invariance of each transition layer. Later exact expressions of three special eigenvalues $\lambda ^{\pm }_{j,\varepsilon }$
eigenvalues come from translation invariance of each transition layer. Later exact expressions of three special eigenvalues $\lambda ^{\pm }_{j,\varepsilon }$![]() , $j=0,n,2n$
, $j=0,n,2n$![]() , were obtained in [Reference Wakasa9]. Using these three exact eigenvalues, one can obtain
, were obtained in [Reference Wakasa9]. Using these three exact eigenvalues, one can obtain

Note that these three eigenvalues correspond to $\lambda ^{\pm }_{j,\varepsilon }$![]() , $j=0,n/2,n$
, $j=0,n/2,n$![]() , in our case $f(u)=-u+u^3$
, in our case $f(u)=-u+u^3$![]() . Then an exact representation formula of eigenvalues for general $f$
. Then an exact representation formula of eigenvalues for general $f$![]() , which is lemma 2.2 in our case, was obtained in [Reference Wakasa and Yotsutani12]. The authors of [Reference Wakasa and Yotsutani12] applied it to the case $f(u)=\sin u$
, which is lemma 2.2 in our case, was obtained in [Reference Wakasa and Yotsutani12]. The authors of [Reference Wakasa and Yotsutani12] applied it to the case $f(u)=\sin u$![]() and obtained an asymptotic formula for every eigenvalue. After that in [Reference Wakasa and Yotsutani14] asymptotic formulas of all the eigenvalues for the Allen–Cahn case $f(u)=u-u^3$
and obtained an asymptotic formula for every eigenvalue. After that in [Reference Wakasa and Yotsutani14] asymptotic formulas of all the eigenvalues for the Allen–Cahn case $f(u)=u-u^3$![]() were established. Specifically,
were established. Specifically,

These formulas show that (1.8) holds for $0\le j< n$![]() .
.
Detailed studies of all the eigenfunctions were made for the case $f(u)=\sin u$![]() in [Reference Wakasa and Yotsutani13] and for the case $f(u)=u-u^3$
in [Reference Wakasa and Yotsutani13] and for the case $f(u)=u-u^3$![]() in [Reference Wakasa and Yotsutani15]. The authors of [Reference Miyamoto and Wakasa8] obtained exact eigenvalues and eigenfunctions of a one-dimensional Gel'fand problem $f(u)=e^u$
in [Reference Wakasa and Yotsutani15]. The authors of [Reference Miyamoto and Wakasa8] obtained exact eigenvalues and eigenfunctions of a one-dimensional Gel'fand problem $f(u)=e^u$![]() , using the method developed in [Reference Wakasa and Yotsutani12]. In this paper, we apply the method developed in [Reference Wakasa and Yotsutani14] to the scalar field equation (1.1) with $f(u)=-u+u^3$
, using the method developed in [Reference Wakasa and Yotsutani12]. In this paper, we apply the method developed in [Reference Wakasa and Yotsutani14] to the scalar field equation (1.1) with $f(u)=-u+u^3$![]() to establish asymptotic formulas. This method seems to work for other nonlinearities and other boundary conditions. They may be future works.
to establish asymptotic formulas. This method seems to work for other nonlinearities and other boundary conditions. They may be future works.
The paper consists of five sections. In §2 we prove proposition 1.1. We obtain asymptotic formulas for three special eigenvalues $\lambda ^{\pm }_{0,\varepsilon }$![]() , $\lambda ^{\pm }_{n/2,\varepsilon }$
, $\lambda ^{\pm }_{n/2,\varepsilon }$![]() and $\lambda ^{\pm }_{n,\varepsilon }$
and $\lambda ^{\pm }_{n,\varepsilon }$![]() (corollary 1.6). We recall an exact representation formulas for the case $f(u)=-u+u^3$
(corollary 1.6). We recall an exact representation formulas for the case $f(u)=-u+u^3$![]() in lemma 2.2. In particular, the other eigenvalues are given by a unique solution of
in lemma 2.2. In particular, the other eigenvalues are given by a unique solution of
where $\mathcal {A}_0$![]() is given in lemma 2.2. Let $\mu :=(2-k^2)\lambda$
is given in lemma 2.2. Let $\mu :=(2-k^2)\lambda$![]() . We use $\mu$
. We use $\mu$![]() instead of $\lambda$
instead of $\lambda$![]() , since various formulas becomes simple. We define $\mathcal {A}(k,\mu ):=A_0(k,\lambda )$
, since various formulas becomes simple. We define $\mathcal {A}(k,\mu ):=A_0(k,\lambda )$![]() . We see in lemma 2.3 that the characteristic function $\mathcal {A}(k,\mu )$
. We see in lemma 2.3 that the characteristic function $\mathcal {A}(k,\mu )$![]() can be written in terms of the complete elliptic integral of the third kind. In § 3 we study the shape of the graph of $\mathcal {A}(k,\mu )$
can be written in terms of the complete elliptic integral of the third kind. In § 3 we study the shape of the graph of $\mathcal {A}(k,\mu )$![]() , since the graph of $\mathcal {A}(k,\mu )$
, since the graph of $\mathcal {A}(k,\mu )$![]() is directly related to the $j+1$
is directly related to the $j+1$![]() -th eigenvalue by the equation
-th eigenvalue by the equation
Specifically, we show that $\mathcal {A}(k,\mu )$![]() is increasing in $\mu$
is increasing in $\mu$![]() and that for each $j$
and that for each $j$![]() , (1.9) has a unique solution. See figure 5 in § 2 for a graph of $\mathcal {A}(k,\mu )$
, (1.9) has a unique solution. See figure 5 in § 2 for a graph of $\mathcal {A}(k,\mu )$![]() . In § 4 we prove theorem 1.3 and corollary 1.7, using results proved in § 3. In Appendix A we recall definitions and basic properties of Jacobi's elliptic functions ${\rm sn}(x,k)$
. In § 4 we prove theorem 1.3 and corollary 1.7, using results proved in § 3. In Appendix A we recall definitions and basic properties of Jacobi's elliptic functions ${\rm sn}(x,k)$![]() , ${\rm cn}(x,k)$
, ${\rm cn}(x,k)$![]() and ${\rm dn}(x,k)$
and ${\rm dn}(x,k)$![]() . Then we recall basic properties of the complete elliptic integrals $K(k)$
. Then we recall basic properties of the complete elliptic integrals $K(k)$![]() , $E(k)$
, $E(k)$![]() and $\Pi (\nu,k)$
and $\Pi (\nu,k)$![]() . We also recall various asymptotic formulas for $K(k)$
. We also recall various asymptotic formulas for $K(k)$![]() and $\Pi (\nu,k)$
and $\Pi (\nu,k)$![]() which are used in proofs of lemmas in § 3 and theorem 1.3.
which are used in proofs of lemmas in § 3 and theorem 1.3.

Figure 5. A graph of $\mathcal {A}(k,\mu )$![]() with $k=3/4$
with $k=3/4$![]() . $\mathcal {A}(k,\mu )$
. $\mathcal {A}(k,\mu )$![]() is defined on $\Sigma$
is defined on $\Sigma$![]() and monotone increasing in $\mu$
and monotone increasing in $\mu$![]() .
.
2. Preliminaries
2.1 Exact solutions of the nonlinear problem
Proof of proposition 1.1 Let $y={\rm dn}(x,k)$![]() . Then, $y(x)$
. Then, $y(x)$![]() satisfies $y''-(2-k^2)y+2y^3=0$
satisfies $y''-(2-k^2)y+2y^3=0$![]() . We can find a solution, assuming $u(x)=c_0y(c_1x)$
. We can find a solution, assuming $u(x)=c_0y(c_1x)$![]() and fixing $c_0$
and fixing $c_0$![]() and $c_1$
and $c_1$![]() . However, we take a different approach here.
. However, we take a different approach here.
We apply a change of variables $\tau =\sqrt {1-k^2s^2}$![]() to (A.1). We have
to (A.1). We have

where (A.2) is used. Let ${\rm dn}^{-1}(y,k)$![]() denote the inverse function of $y={\rm dn}(x,k)$
denote the inverse function of $y={\rm dn}(x,k)$![]() . Substituting $x={\rm dn}^{-1}(y,k)$
. Substituting $x={\rm dn}^{-1}(y,k)$![]() into (2.1), we obtain
into (2.1), we obtain

We consider only the case $u^-_{n,\varepsilon }(x)$![]() , since the case $u^+_{n,\varepsilon }(x)$
, since the case $u^+_{n,\varepsilon }(x)$![]() is similar. For simplicity, $u$
is similar. For simplicity, $u$![]() stands for $u^-_{n,\varepsilon }$
stands for $u^-_{n,\varepsilon }$![]() . By (1.1) we have
. By (1.1) we have
where
Since $2\varepsilon ^2u'^2=(\alpha ^2-u^2)(\alpha ^2-2+u^2)$![]() , we have
, we have
where we use the fact that $u'(x)<0$![]() for $0< x<1/n$
for $0< x<1/n$![]() . Let $k$
. Let $k$![]() be defined by the relation
be defined by the relation
Using a change of variables $\tau :=u/\alpha$![]() , we have
, we have

where (2.2) is used in the last equality. Thus,
Since $K(k)$![]() is a half-period of ${\rm dn}(x,k)$
is a half-period of ${\rm dn}(x,k)$![]() and $1/n$
and $1/n$![]() is a half-period of $u(x)$
is a half-period of $u(x)$![]() , we have
, we have
and hence (1.3) is obtained. Substituting $\varepsilon =1/\sqrt {2-k^2}nK(k)$![]() into (2.3), we have (1.4).
into (2.3), we have (1.4).
2.2 Three special eigenvalues
Proposition 1.2 says that there are three (resp. two) exact eigenvalues of (LP±) if $n$![]() is even (resp. odd). These three or two eigenvalues are special and play a key role in this paper. Proposition 1.2 can be proved by direct calculation. We define $\lambda _{\pm }(k)$
is even (resp. odd). These three or two eigenvalues are special and play a key role in this paper. Proposition 1.2 can be proved by direct calculation. We define $\lambda _{\pm }(k)$![]() by
by
Then it is obvious that $\lambda ^{\pm }_{0,\varepsilon }=\lambda _-$![]() and $\lambda ^{\pm }_{n,\varepsilon }=\lambda _+$
and $\lambda ^{\pm }_{n,\varepsilon }=\lambda _+$![]() .
.
Lemma 2.1 Let $k_{n,\varepsilon }$![]() be the unique solution of (1.3). Then,
be the unique solution of (1.3). Then,
Proof. By lemma A.3 we have
and hence $(1-k^2)K(k)\to 0$![]() as $k\to 1$
as $k\to 1$![]() . By (1.3) we have
. By (1.3) we have
Using $K(k)=1/\sqrt {2-k^2}n\varepsilon$![]() , we have
, we have

We obtain the desired result.
Using lemma 2.1, we obtain asymptotic expansions of three special eigenvalues.
Proof of corollary 1.6 First we prove (i) and (iii). By lemma 2.1 we have
Then

Next we prove (ii). If $n$![]() is even, then
is even, then

2.3 Exact representation of the other eigenvalues
Before we consider the scalar field equation, let us briefly explain a theory for a general nonlinear term developed in Wakasa–Yotsutani [Reference Wakasa and Yotsutani12].
Let $u(x)$![]() be a solution of (1.1), and let $\alpha$
be a solution of (1.1), and let $\alpha$![]() denote the maximum value of $u(x)$
denote the maximum value of $u(x)$![]() . Substituting $\varphi (x)=\sqrt {\psi (x)}$
. Substituting $\varphi (x)=\sqrt {\psi (x)}$![]() into the equation in (1.2), we see that $\psi (x)$
into the equation in (1.2), we see that $\psi (x)$![]() satisfies
satisfies
Let us consider the following function:
We have
We look for a solution of the equation
of the form $\psi (x)=h(u(x))$![]() , where $h(\,\cdot \,)$
, where $h(\,\cdot \,)$![]() is an unknown positive function. Substituting $\psi (x)=h(u(x))$
is an unknown positive function. Substituting $\psi (x)=h(u(x))$![]() into (2.6), we obtain a key equation
into (2.6), we obtain a key equation
where we use the following relations:
We assume that an exact expression $h(u)$![]() of a positive solution of (2.7) can be obtained. Then, $h(u)$
of a positive solution of (2.7) can be obtained. Then, $h(u)$![]() is also a solution of (2.6). Thus, $\Psi '(x)\equiv 0$
is also a solution of (2.6). Thus, $\Psi '(x)\equiv 0$![]() and $\Psi$
and $\Psi$![]() is constant. Substituting $h(u)$
is constant. Substituting $h(u)$![]() into (2.5), we see that there exists $\rho \in \mathbb {R}$
into (2.5), we see that there exists $\rho \in \mathbb {R}$![]() such that
such that
Now, we construct an eigenfunction of the form
using a solution $h(u)$![]() of (2.7). Here, $W(\,\cdot \,)$
of (2.7). Here, $W(\,\cdot \,)$![]() and $\theta (x)$
and $\theta (x)$![]() are defined later. Using (2.8), we have
are defined later. Using (2.8), we have

Substituting (2.9) into (1.2), we have

where (2.10) is used in the last equality. We assume that $\rho >0$![]() . We define $\theta (x)$
. We define $\theta (x)$![]() by a solution of
by a solution of
Specifically, the following function is a solution of (2.12):
Moreover, it follows from (2.11) that $W''(\theta )+W(\theta )=0$![]() , and hence $W(\theta )=C \cos (\theta +\theta _1)$
, and hence $W(\theta )=C \cos (\theta +\theta _1)$![]() . By (2.9) we obtain
. By (2.9) we obtain
where $x_0:=\theta _0+\theta _1$![]() . In other words, a general solution of $\varepsilon ^2\varphi ''+f'(u)\varphi +\lambda \varphi =0$
. In other words, a general solution of $\varepsilon ^2\varphi ''+f'(u)\varphi +\lambda \varphi =0$![]() can be written in terms of a solution $u(x)$
can be written in terms of a solution $u(x)$![]() of the nonlinear problem (1.1). Readers can find more details of (2.7) and (2.13) in [Reference Miyamoto and Wakasa8, Reference Wakasa and Yotsutani12, Reference Wakasa and Yotsutani14].
of the nonlinear problem (1.1). Readers can find more details of (2.7) and (2.13) in [Reference Miyamoto and Wakasa8, Reference Wakasa and Yotsutani12, Reference Wakasa and Yotsutani14].
In our case the maximum value of $u^{\pm }_{n,\varepsilon }(x)$![]() , which is denoted by $\alpha$
, which is denoted by $\alpha$![]() , is given by
, is given by
and (2.7) becomes
There seems to be no solution formula of (2.7) for general nonlinearities. In the case (2.15) every coefficient is a polynomial of $u$![]() . We substitute $h(u)=u^p$
. We substitute $h(u)=u^p$![]() into (2.15). Then it does not vanish, and the top term becomes
into (2.15). Then it does not vanish, and the top term becomes
This suggests that a bi-quadratic polynomial is a candidate of a solution, since (2.16) vanishes for $p=4$![]() . Actually, $h$
. Actually, $h$![]() defined by (2.19) is a solution of (2.15). We evaluate (2.8) at a maximum point of $u$
defined by (2.19) is a solution of (2.15). We evaluate (2.8) at a maximum point of $u$![]() . Then,
. Then,
which yields (2.18). Using $h(u)$![]() and $\rho _0$
and $\rho _0$![]() , we can construct a general solution of $\varepsilon ^2\varphi ''+f(u)\varphi +\lambda \varphi =0$
, we can construct a general solution of $\varepsilon ^2\varphi ''+f(u)\varphi +\lambda \varphi =0$![]() . We take the Neumann boundary condition into account. Let $x_0=0$
. We take the Neumann boundary condition into account. Let $x_0=0$![]() in (2.13). Since $1/n$
in (2.13). Since $1/n$![]() is a half-period of $u^{\pm }_{n,\varepsilon }(x)$
is a half-period of $u^{\pm }_{n,\varepsilon }(x)$![]() , the following holds:
, the following holds:

Eigenvalues can be found by solving the above equation.
Finding a solution of (2.7) is key in this theory. A solution for (2.7) was found for

We summarize these results in the following lemma:
Lemma 2.2 Let $j\neq 0,n$![]() and $j\neq n/2$
and $j\neq n/2$![]() if $n$
if $n$![]() is even. Let $k_{\varepsilon }$
is even. Let $k_{\varepsilon }$![]() be the unique solution of (1.3). We define $\mathcal {A}_0$
be the unique solution of (1.3). We define $\mathcal {A}_0$![]() by
by

for $\lambda \in \{\lambda \in \mathbb {R};\ \rho _0(\lambda,k)>0\}$![]() , where
, where
(i) Let $\alpha$
 be defined by (2.14). If $\rho _0(\lambda,k)>0$
be defined by (2.14). If $\rho _0(\lambda,k)>0$ , then either $h(u,\lambda,k)>0$
, then either $h(u,\lambda,k)>0$ or $h(u,\lambda,k)<0$
or $h(u,\lambda,k)<0$ for $u\in \left [\sqrt {2-\alpha ^2},\alpha \right ]$
for $u\in \left [\sqrt {2-\alpha ^2},\alpha \right ]$ .
.(ii) If the equation for $\lambda$
 (2.20)$$ \mathcal{A}_0(k_{\varepsilon},\lambda)=\frac{j\pi}{n} $$has a solution $\lambda \in \{\lambda \in \mathbb {R}|\ \rho _0(\lambda,k)>0\}$
(2.20)$$ \mathcal{A}_0(k_{\varepsilon},\lambda)=\frac{j\pi}{n} $$has a solution $\lambda \in \{\lambda \in \mathbb {R}|\ \rho _0(\lambda,k)>0\}$
 , then $\lambda$
, then $\lambda$ is a $j+1$
is a $j+1$ -th eigenvalue of $({\rm LP}_{\pm })$
-th eigenvalue of $({\rm LP}_{\pm })$ and
\[ \varphi^{{\pm}}_{j,\varepsilon}(x)=\sqrt{|h(u^{{\pm}}_{n,\varepsilon}(x),\lambda,k_{\varepsilon})|}\cos\left(\frac{1}{\varepsilon}\int_0^x\frac{\sqrt{\rho_0(\lambda,k_{\varepsilon})}\,{\rm d}\xi}{|h(u^{{\pm}}_{n,\varepsilon}(\xi),\lambda,k_{\varepsilon})|}\right) \]is an associated eigenfunction.
and
\[ \varphi^{{\pm}}_{j,\varepsilon}(x)=\sqrt{|h(u^{{\pm}}_{n,\varepsilon}(x),\lambda,k_{\varepsilon})|}\cos\left(\frac{1}{\varepsilon}\int_0^x\frac{\sqrt{\rho_0(\lambda,k_{\varepsilon})}\,{\rm d}\xi}{|h(u^{{\pm}}_{n,\varepsilon}(\xi),\lambda,k_{\varepsilon})|}\right) \]is an associated eigenfunction.
Proof. Here, we directly prove the lemma.
(i) By direct calculation we can check that $h(u)$
 satisfies
(2.21)$$ (F(\alpha)-F(u))(2hh''-h'^2)-f(u)hh'+2(f'(u)+\lambda)h^2=2\rho_0. $$Suppose the contrary, i.e., there exists $\bar {u}\in [\sqrt {2-\alpha ^2},\alpha ]$
satisfies
(2.21)$$ (F(\alpha)-F(u))(2hh''-h'^2)-f(u)hh'+2(f'(u)+\lambda)h^2=2\rho_0. $$Suppose the contrary, i.e., there exists $\bar {u}\in [\sqrt {2-\alpha ^2},\alpha ]$
 such that $h(\bar {u})=0$
such that $h(\bar {u})=0$ . Since $F(\alpha )-F(\bar {u})\ge 0$
. Since $F(\alpha )-F(\bar {u})\ge 0$ , it follows from (2.21) that
\[ 0\ge -(F(\alpha)-F(\bar{u}))h'^2=2\rho_0>0, \]which is a contradiction. This contradiction leads to the assertion (i).
, it follows from (2.21) that
\[ 0\ge -(F(\alpha)-F(\bar{u}))h'^2=2\rho_0>0, \]which is a contradiction. This contradiction leads to the assertion (i).
(ii) Without loss of generality, we can assume that $h(u^{\pm }_{n,\varepsilon }(x))>0$
 for $x\in [0,1]$
for $x\in [0,1]$ . Let
\[ \varphi(x):=\sqrt{h(u^{{\pm}}_{n,\varepsilon}(x))}\cos\left(\frac{1}{\varepsilon}\int_0^x\frac{\sqrt{\rho_0}\,{\rm d}\xi}{h(u^{{\pm}}_{n,\varepsilon}(\xi))}\right). \]For simplicity, we write $u^{\pm }_{n,\varepsilon }$
. Let
\[ \varphi(x):=\sqrt{h(u^{{\pm}}_{n,\varepsilon}(x))}\cos\left(\frac{1}{\varepsilon}\int_0^x\frac{\sqrt{\rho_0}\,{\rm d}\xi}{h(u^{{\pm}}_{n,\varepsilon}(\xi))}\right). \]For simplicity, we write $u^{\pm }_{n,\varepsilon }$
 and $h(u^{\pm }_{n,\varepsilon })$
and $h(u^{\pm }_{n,\varepsilon })$ as $u$
as $u$ and $h$
and $h$ , respectively. Then,
$$\begin{align*} & \varepsilon^2\varphi_{xx}+f'(u)\varphi+\lambda\varphi\\ & =\frac{1}{2h^{3/2}}\left\{\frac{\varepsilon^2u'^2}{2}(2hh''-h'^2)+\varepsilon^2u''hh'-2\rho_0+2f'(u)h^2+2\lambda h^2 \right\}\\& \quad \cos\left(\frac{1}{\varepsilon}\int_0^x\frac{\sqrt{\rho_0}\,{\rm d}\xi}{h(u(\xi))}\right)\\ & =\frac{1}{2h^{3/2}}\left\{ (F(\alpha)-F(u))(2hh''-h'^2)-f(u)hh'-2\rho_0+2f'(u)h^2+2\lambda h^2 \right\}\\& \quad\cos\left(\frac{1}{\varepsilon}\int_0^x\frac{\sqrt{\rho_0}\,{\rm d}\xi}{h(u(\xi))}\right)=0. \end{align*}$$By (2.20) we see that $\varphi (x)$
, respectively. Then,
$$\begin{align*} & \varepsilon^2\varphi_{xx}+f'(u)\varphi+\lambda\varphi\\ & =\frac{1}{2h^{3/2}}\left\{\frac{\varepsilon^2u'^2}{2}(2hh''-h'^2)+\varepsilon^2u''hh'-2\rho_0+2f'(u)h^2+2\lambda h^2 \right\}\\& \quad \cos\left(\frac{1}{\varepsilon}\int_0^x\frac{\sqrt{\rho_0}\,{\rm d}\xi}{h(u(\xi))}\right)\\ & =\frac{1}{2h^{3/2}}\left\{ (F(\alpha)-F(u))(2hh''-h'^2)-f(u)hh'-2\rho_0+2f'(u)h^2+2\lambda h^2 \right\}\\& \quad\cos\left(\frac{1}{\varepsilon}\int_0^x\frac{\sqrt{\rho_0}\,{\rm d}\xi}{h(u(\xi))}\right)=0. \end{align*}$$By (2.20) we see that $\varphi (x)$
 has exactly $j$
has exactly $j$ zero(s) in $0\le x\le 1$
zero(s) in $0\le x\le 1$ . It follows from Sturm–Liouville theory that $\varphi (x)$
. It follows from Sturm–Liouville theory that $\varphi (x)$ is a $j+1$
is a $j+1$ -th eigenfunction and $\lambda$
-th eigenfunction and $\lambda$ is the associated eigenvalue.
is the associated eigenvalue.
Since $\sqrt {2-\alpha ^2}\le u^{\pm }_{n,\varepsilon }(x)\le \alpha$![]() for $0\le\! x\le\! 1$
for $0\le\! x\le\! 1$![]() (proposition 1.1), either $h(u^{\pm }_{n,\varepsilon }(x))\!>\!0$
(proposition 1.1), either $h(u^{\pm }_{n,\varepsilon }(x))\!>\!0$![]() or $h(u^{\pm }_{n,\varepsilon }(x))<0$
or $h(u^{\pm }_{n,\varepsilon }(x))<0$![]() holds in the case $\rho _0(\lambda,k)>0$
holds in the case $\rho _0(\lambda,k)>0$![]() . Hence, $\mathcal {A}_0(k,\lambda )$
. Hence, $\mathcal {A}_0(k,\lambda )$![]() is well defined. It follows from lemma 2.2 that the $j+1$
is well defined. It follows from lemma 2.2 that the $j+1$![]() -th eigenvalue is determined by (2.20) and that the other eigenvalues are on $\{\rho _0>0\}$
-th eigenvalue is determined by (2.20) and that the other eigenvalues are on $\{\rho _0>0\}$![]() . Hence, it is important to study the function $\mathcal {A}_0(k,\lambda )$
. Hence, it is important to study the function $\mathcal {A}_0(k,\lambda )$![]() .
.
Let
We sometimes use $\mu$![]() instead of $\lambda$
instead of $\lambda$![]() , since various formulas become simple. We define
, since various formulas become simple. We define

We will show that the other eigenvalues are on $\{\lambda \in \mathbb {R}|\ \rho _0(\lambda,k)>0\}$![]() . The set $\{(k,\lambda )|\ k\in (0,1), \rho _0(\lambda,k)>0\}$
. The set $\{(k,\lambda )|\ k\in (0,1), \rho _0(\lambda,k)>0\}$![]() corresponds to
corresponds to
The set $\Sigma$![]() is split into three components, i.e., $\Sigma =\Sigma _0\cup \Sigma _1\cup \Sigma _2$
is split into three components, i.e., $\Sigma =\Sigma _0\cup \Sigma _1\cup \Sigma _2$![]() , where
, where

Let
where $\mathcal {A}_0$![]() is defined by (2.17). Then the characteristic equation (2.20) becomes
is defined by (2.17). Then the characteristic equation (2.20) becomes
Figure 5 shows the graph of $\mathcal {A}(k,\,\cdot \,)$![]() . In § 3 we rigorously study the graph of $\mathcal {A}(k,\,\cdot \,)$
. In § 3 we rigorously study the graph of $\mathcal {A}(k,\,\cdot \,)$![]() . Specifically, end points of $\mathcal {A}(k,\,\cdot \,)$
. Specifically, end points of $\mathcal {A}(k,\,\cdot \,)$![]() are obtained in lemma 3.1 and the monotone increase of $\mathcal {A}(k,\mu )$
are obtained in lemma 3.1 and the monotone increase of $\mathcal {A}(k,\mu )$![]() in $\mu$
in $\mu$![]() is proved in lemma 3.4.
is proved in lemma 3.4.
We would like to obtain a more simple expression of $\mathcal {A}(k,\mu )$![]() . The following lemma indicates that $\mathcal {A}(k,\mu )$
. The following lemma indicates that $\mathcal {A}(k,\mu )$![]() can be decomposed into two complete elliptic integrals of the third kind.
can be decomposed into two complete elliptic integrals of the third kind.
Lemma 2.3 Suppose that the assumptions of lemma 2.2 hold. Then the following hold$:$![]()
(i) If $(k,\mu )\in \Sigma _0\cup \Sigma _1$
 , then
(2.26)$$ \mathcal{A}(k,\mu)=|{\rm sgn}(\nu_+)\mathcal{M}(\nu_+,k)-{\rm sgn}(\nu_-)\mathcal{M}(\nu_-,k)|, $$where ${\rm sgn}(\,\cdot \,)$
, then
(2.26)$$ \mathcal{A}(k,\mu)=|{\rm sgn}(\nu_+)\mathcal{M}(\nu_+,k)-{\rm sgn}(\nu_-)\mathcal{M}(\nu_-,k)|, $$where ${\rm sgn}(\,\cdot \,)$
 denotes the sign function,
(2.27)$$\begin{align} \mathcal{M}(\nu,k)& :=\sqrt{\frac{(1+\nu)(k^2+\nu)}{\nu}}\Pi(\nu,k),\quad \Pi(\nu,k)\nonumber\\ & :=\int_0^1\frac{{\rm d}s}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)}}, \end{align}$$
denotes the sign function,
(2.27)$$\begin{align} \mathcal{M}(\nu,k)& :=\sqrt{\frac{(1+\nu)(k^2+\nu)}{\nu}}\Pi(\nu,k),\quad \Pi(\nu,k)\nonumber\\ & :=\int_0^1\frac{{\rm d}s}{(1+\nu s^2)\sqrt{(1-s^2)(1-k^2s^2)}}, \end{align}$$ (2.28)$$ \nu_{{\pm}}(k,\mu):=\frac{3k^2}{2}\frac{\mu-3k^2\pm\sqrt{-3\mu^2+6(k^2-2)\mu+9k^4}}{\mu(\mu+3-3k^2)}. $$
(2.28)$$ \nu_{{\pm}}(k,\mu):=\frac{3k^2}{2}\frac{\mu-3k^2\pm\sqrt{-3\mu^2+6(k^2-2)\mu+9k^4}}{\mu(\mu+3-3k^2)}. $$
(ii) If $(k,\mu )\in \Sigma _2$
 , then
\[ \mathcal{A}(k,\mu)=\frac{1}{9k^4}\sqrt{\mu(\mu+3)(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}\tilde{\Pi}(a,b,k), \]where
, then
\[ \mathcal{A}(k,\mu)=\frac{1}{9k^4}\sqrt{\mu(\mu+3)(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}\tilde{\Pi}(a,b,k), \]where (2.29)$$\begin{align} \tilde{\Pi}(a,b,k):=\int_0^1\frac{{\rm d}s}{\sqrt{(1-s^2)(1-k^2s^2)}\{a+(b-s^2)^2\}}, \end{align}$$
(2.29)$$\begin{align} \tilde{\Pi}(a,b,k):=\int_0^1\frac{{\rm d}s}{\sqrt{(1-s^2)(1-k^2s^2)}\{a+(b-s^2)^2\}}, \end{align}$$ (2.30)$$\begin{align} a(k,\mu):=\frac{1}{12k^2}(\mu-\mu_+)(\mu-\mu_-),\quad b(k,\mu):=\frac{3k^2-\mu}{6k^2}. \end{align}$$
(2.30)$$\begin{align} a(k,\mu):=\frac{1}{12k^2}(\mu-\mu_+)(\mu-\mu_-),\quad b(k,\mu):=\frac{3k^2-\mu}{6k^2}. \end{align}$$
Proof. (i) We consider the case $h(u^{\pm }_{n,\varepsilon }(x))>0$![]() for $x\in [0,1]$
for $x\in [0,1]$![]() . In both cases ${u^+_{n,\varepsilon }}$
. In both cases ${u^+_{n,\varepsilon }}$![]() and ${u^-_{n,\varepsilon }}$
and ${u^-_{n,\varepsilon }}$![]() by lemma 2.2 we see that
by lemma 2.2 we see that

because

Using the change of variables $w={u^-_{n,\varepsilon }}(\xi )$![]() , we have
, we have

where we use

In order to bring the integral closer to the expression of the complete elliptic integral of the third kind, we let $s=w/\alpha$![]() . Since
. Since
we have

We define $\sigma _{\pm }$![]() by
by

Then

Note that $-(\lambda -\lambda _+)(\lambda -\lambda _-)>0$![]() for $(k,\mu )\in \Sigma _0\cup \Sigma _1$
for $(k,\mu )\in \Sigma _0\cup \Sigma _1$![]() . Using (2.33), we have
. Using (2.33), we have

Using (2.18), which is the definition of $\rho _0$![]() , and
, and
we have

where

Using the change of variables $s:=\sqrt {1-k^2\tau ^2}$![]() , we have
, we have

Therefore,

Since $\lambda =\mu /(2-k^2)$![]() , we can check that
, we can check that
Here $\sigma _{\pm }$![]() are given by (2.32) and $\nu _{\pm }$
are given by (2.32) and $\nu _{\pm }$![]() are given by (2.28). Using
are given by (2.28). Using
by lemma 2.4 below we have

Here $\mathcal {M}$![]() and $\Pi$
and $\Pi$![]() are defined by (2.27). When $h({u^-_{n,\varepsilon }}(x))<0$
are defined by (2.27). When $h({u^-_{n,\varepsilon }}(x))<0$![]() for $x\in [0,1]$
for $x\in [0,1]$![]() , we have
, we have

We obtain (2.26).
(ii) We can check that if $(k,\mu )\in \Sigma _2$![]() , then $h(u^{\pm }_{n,\varepsilon }(x))>0$
, then $h(u^{\pm }_{n,\varepsilon }(x))>0$![]() for $x\in [0,1]$
for $x\in [0,1]$![]() . By the same way as in (i) we have (2.31). Using the change of variables $s:=\sqrt {1-k^2\tau ^2}$
. By the same way as in (i) we have (2.31). Using the change of variables $s:=\sqrt {1-k^2\tau ^2}$![]() , we have
, we have

where

In this case the polynomial $a+(b-\tau ^2)^2$![]() cannot be factored into two real quadratic polynomials. We have
cannot be factored into two real quadratic polynomials. We have
The proof of (ii) is complete.
The following equality, which is somewhat nontrivial, is left in the proof of lemma 2.3.
Lemma 2.4 Let $\sigma _{\pm }$![]() and $\nu _{\pm }$
and $\nu _{\pm }$![]() be defined by (2.32) and (2.28), respectively. If $(k,\mu )\in \Sigma _0\cup \Sigma _1$
be defined by (2.32) and (2.28), respectively. If $(k,\mu )\in \Sigma _0\cup \Sigma _1$![]() , then
, then

Proof. By (2.28) we can check that
Using (2.37), we have

On the other hand, we consider the right-hand side of (2.36). Let $\gamma _{\pm }:=\alpha ^2/\sigma _{\pm }$![]() . Then $\gamma _{\pm }$
. Then $\gamma _{\pm }$![]() satisfies
satisfies
Since
we have

By (2.39) we have

It follows from (2.40) and (2.38) that
Multiplying both sides by $\nu _{\pm }^2$![]() , we have
, we have
The assertion holds.
Now the proof of lemma 2.3 is complete.
3. Fundamental properties of $\mathcal {A}$
Let $\mathcal {A}(k,\mu )$![]() be defined by (2.25), and let $\Sigma$
be defined by (2.25), and let $\Sigma$![]() be defined by (2.23).
be defined by (2.23).
Lemma 3.1 Let $k\in (0,1)$![]() be fixed and $(k,\mu )\in \Sigma$
be fixed and $(k,\mu )\in \Sigma$![]() , and let $\mu _{\pm }$
, and let $\mu _{\pm }$![]() be defined by (2.22). Then the following hold$:$
be defined by (2.22). Then the following hold$:$![]()
(i) $\mathcal {A}(k,\mu )\to 0$
 as $\mu \to \mu _-$
as $\mu \to \mu _-$ .
.(ii) $\mathcal {A}(k,\mu )\to {\pi }/{2}$
 as $\mu \to -3$
as $\mu \to -3$ .
.(iii) $\mathcal {A}(k,\mu )\to {\pi }/{2}$
 as $\mu \to -3+3k^2$
as $\mu \to -3+3k^2$ .
.(iv) $\mathcal {A}(k,\mu )\to \pi$
 as $\mu \to 0$
as $\mu \to 0$ .
.(v) $\mathcal {A}(k,\mu )\to \pi$
 as $\mu \to \mu _+$
as $\mu \to \mu _+$ .
.(vi) $\mathcal {A}(k,\mu )\to \infty$
 as $\mu \to \infty$
as $\mu \to \infty$ .
.
Proof.
(i) In this case we can check that $h(u^{\pm }_{n,\varepsilon }(x))>0$
 for $x\in [0,1]$
for $x\in [0,1]$ . Let $\nu _{\pm }$
. Let $\nu _{\pm }$ be defined by (2.28). We see that there exists $\nu _*$
be defined by (2.28). We see that there exists $\nu _*$ such that
\[ \lim_{\mu\to\mu_-}\nu_+{=}\nu_*,\quad \lim_{\mu\to\mu_-}\nu_-{=}\nu_*. \]By direct calculation we can check that $-1<\nu _*<0$
such that
\[ \lim_{\mu\to\mu_-}\nu_+{=}\nu_*,\quad \lim_{\mu\to\mu_-}\nu_-{=}\nu_*. \]By direct calculation we can check that $-1<\nu _*<0$
 . Let $\mathcal {M}$
. Let $\mathcal {M}$ be defined by (2.27). Since
\[ \lim_{\nu_+\to\nu_*}\mathcal{M}(\nu_+,k)=\mathcal{M}(\nu_*,k),\quad \lim_{\nu_-\to\nu_*}\mathcal{M}(\nu_-,k)=\mathcal{M}(\nu_*,k), \]we have
be defined by (2.27). Since
\[ \lim_{\nu_+\to\nu_*}\mathcal{M}(\nu_+,k)=\mathcal{M}(\nu_*,k),\quad \lim_{\nu_-\to\nu_*}\mathcal{M}(\nu_-,k)=\mathcal{M}(\nu_*,k), \]we have \[ \lim_{\mu\to\mu_-}\mathcal{A}(k,\mu)=0. \]
\[ \lim_{\mu\to\mu_-}\mathcal{A}(k,\mu)=0. \]
(ii) In this case we can check that $h(u^{\pm }_{n,\varepsilon }(x))>0$
 for $x\in [0,1]$
for $x\in [0,1]$ . We see that $\nu _+\to -k^2$
. We see that $\nu _+\to -k^2$ ($\mu \to -3$
($\mu \to -3$ ) and $\nu _-\to -1$
) and $\nu _-\to -1$ ($\mu \to -3$
($\mu \to -3$ ). By lemma A.9 we have
\[ \lim_{\nu_+\to -k^2}{\rm sgn}(\nu_+)\mathcal{M}(\nu_+,k)=0,\quad \lim_{\nu_-\to-1}{\rm sgn}(\nu_-)\mathcal{M}(\nu_-,k)={-}\frac{\pi}{2}. \]Then,
). By lemma A.9 we have
\[ \lim_{\nu_+\to -k^2}{\rm sgn}(\nu_+)\mathcal{M}(\nu_+,k)=0,\quad \lim_{\nu_-\to-1}{\rm sgn}(\nu_-)\mathcal{M}(\nu_-,k)={-}\frac{\pi}{2}. \]Then, \[ \lim_{\mu\to -3}\mathcal{A}(k,\mu)=0-\left(-\frac{\pi}{2}\right)=\frac{\pi}{2}. \]
\[ \lim_{\mu\to -3}\mathcal{A}(k,\mu)=0-\left(-\frac{\pi}{2}\right)=\frac{\pi}{2}. \]
(iii) In this case we can check that $h(u^{\pm }_{n,\varepsilon }(x))<0$
 for $x\in [0,1]$
for $x\in [0,1]$ . We see that $\nu _+\to -k^2$
. We see that $\nu _+\to -k^2$ $(\mu \to -3+3k^2)$
$(\mu \to -3+3k^2)$ and $\nu _-\to \infty$
and $\nu _-\to \infty$ ($\mu \to -3+3k^2$
($\mu \to -3+3k^2$ ). By lemma A.9 we have
\[ \lim_{\nu_+\to -k^2}{\rm sgn}(\nu_+)\mathcal{M}(\nu_+,k)=0,\quad \lim_{\nu_-\to\infty}{\rm sgn}(\nu_-)\mathcal{M}(\nu_-,k)=\frac{\pi}{2}. \]Then,
). By lemma A.9 we have
\[ \lim_{\nu_+\to -k^2}{\rm sgn}(\nu_+)\mathcal{M}(\nu_+,k)=0,\quad \lim_{\nu_-\to\infty}{\rm sgn}(\nu_-)\mathcal{M}(\nu_-,k)=\frac{\pi}{2}. \]Then, \[ \lim_{\mu\to -3+3k^2}\mathcal{A}(k,\mu)={-}\left(0-\frac{\pi}{2}\right)=\frac{\pi}{2}. \]
\[ \lim_{\mu\to -3+3k^2}\mathcal{A}(k,\mu)={-}\left(0-\frac{\pi}{2}\right)=\frac{\pi}{2}. \]
(iv) In this case we can check that $h(u^{\pm }_{n,\varepsilon }(x))<0$
 for $x\in [0,1]$
for $x\in [0,1]$ . We see that $\nu _+\to -1$
. We see that $\nu _+\to -1$ ($\mu \to 0$
($\mu \to 0$ ) and $\nu _-\to \infty$
) and $\nu _-\to \infty$ ($\mu \to 0$
($\mu \to 0$ ). By lemma A.9 we have
\[ \lim_{\nu_+\to -1}{\rm sgn}(\nu_+)\mathcal{M}(\nu_+,k)={-}\frac{\pi}{2},\quad \lim_{\nu_-\to\infty}{\rm sgn}(\nu_-)\mathcal{M}(\nu_-,k)=\frac{\pi}{2}. \]Then,
). By lemma A.9 we have
\[ \lim_{\nu_+\to -1}{\rm sgn}(\nu_+)\mathcal{M}(\nu_+,k)={-}\frac{\pi}{2},\quad \lim_{\nu_-\to\infty}{\rm sgn}(\nu_-)\mathcal{M}(\nu_-,k)=\frac{\pi}{2}. \]Then, \[ \lim_{\mu\to 0}\mathcal{A}(k,\mu)={-}\left(-\frac{\pi}{2}-\frac{\pi}{2}\right)=\pi. \]
\[ \lim_{\mu\to 0}\mathcal{A}(k,\mu)={-}\left(-\frac{\pi}{2}-\frac{\pi}{2}\right)=\pi. \]
(v) In this case we can check that $h(u^{\pm }_{n,\varepsilon }(x))>0$
 for $x\in [0,1]$
for $x\in [0,1]$ . Let $a,b$
. Let $a,b$ be defined by (2.30). By lemmas 2.3 and A.7 we have
$$\begin{align*} \mathcal{A}(k,\mu) & =\frac{1}{9k^4}\sqrt{\mu(\mu+3)(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}\tilde{\Pi}(a,b,k)\\ & =\frac{2}{3\sqrt{3}k^2}\sqrt{\mu(\mu+3)(\mu+3-3k^2)}\sqrt{a}\tilde{\Pi}(a,b,k)\\ & \to \frac{2}{3\sqrt{3}k^2}\sqrt{\mu_+(\mu_+{+}3)(\mu_+{+}3-3k^2)}\\ & \qquad \frac{\pi}{2\sqrt{b_0(1-b_0)(1-k^2b_0)}}\ \ \textrm{as}\ \ \mu\to\mu_+. \end{align*}$$Here, $b_0:=(3k^2-\mu _+)/6k^2$
be defined by (2.30). By lemmas 2.3 and A.7 we have
$$\begin{align*} \mathcal{A}(k,\mu) & =\frac{1}{9k^4}\sqrt{\mu(\mu+3)(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}\tilde{\Pi}(a,b,k)\\ & =\frac{2}{3\sqrt{3}k^2}\sqrt{\mu(\mu+3)(\mu+3-3k^2)}\sqrt{a}\tilde{\Pi}(a,b,k)\\ & \to \frac{2}{3\sqrt{3}k^2}\sqrt{\mu_+(\mu_+{+}3)(\mu_+{+}3-3k^2)}\\ & \qquad \frac{\pi}{2\sqrt{b_0(1-b_0)(1-k^2b_0)}}\ \ \textrm{as}\ \ \mu\to\mu_+. \end{align*}$$Here, $b_0:=(3k^2-\mu _+)/6k^2$
 . Since
\[ \frac{2}{3\sqrt{3}k^2}\sqrt{\mu_+(\mu_+{+}3)(\mu_+{+}3-3k^2)} =\frac{2}{3\sqrt{3}k^2}\sqrt{(1-k^2+k^4)\mu_+{+}3k^4(2-k^2)}, \]
. Since
\[ \frac{2}{3\sqrt{3}k^2}\sqrt{\mu_+(\mu_+{+}3)(\mu_+{+}3-3k^2)} =\frac{2}{3\sqrt{3}k^2}\sqrt{(1-k^2+k^4)\mu_+{+}3k^4(2-k^2)}, \] \[ \frac{\pi}{2\sqrt{b_0(1-b_0)(1-k^2b_0)}} =\frac{3\sqrt{3}\pi k^2}{2\sqrt{(1-k^2+k^4)\mu_+{+}3k^4(2-k^2)}}, \]we have
\[ \frac{\pi}{2\sqrt{b_0(1-b_0)(1-k^2b_0)}} =\frac{3\sqrt{3}\pi k^2}{2\sqrt{(1-k^2+k^4)\mu_+{+}3k^4(2-k^2)}}, \]we have \[ \lim_{\mu\to\mu_+}\mathcal{A}(k,\mu)=\pi. \]
\[ \lim_{\mu\to\mu_+}\mathcal{A}(k,\mu)=\pi. \]
(vi) Let $\lambda _{\pm }$
 be defined by (2.4). We see that $\lambda _+:(0,1)\to \mathbb {R}$
be defined by (2.4). We see that $\lambda _+:(0,1)\to \mathbb {R}$ is increasing in $k$
is increasing in $k$ ,
\[ \lim_{k\to 0}\lambda_+(k)=0,\ \ \lim_{k\to 1}\lambda_+(k)=1. \]Hence, $0<\lambda _+<1$
,
\[ \lim_{k\to 0}\lambda_+(k)=0,\ \ \lim_{k\to 1}\lambda_+(k)=1. \]Hence, $0<\lambda _+<1$
 for $k\in (0,1)$
for $k\in (0,1)$ .
.
Let $a(k,\mu )$
 , $b(k,\mu )$
, $b(k,\mu )$ be defined by (2.30). Since $\lambda >\lambda _+>0$
be defined by (2.30). Since $\lambda >\lambda _+>0$ , we have see $\mu >\mu _+>0$
, we have see $\mu >\mu _+>0$ and
\[ (b(k,\mu)-1)^2-b(k,\mu)^2=\frac{\mu}{3k^2}>0. \]Hence,
and
\[ (b(k,\mu)-1)^2-b(k,\mu)^2=\frac{\mu}{3k^2}>0. \]Hence, \[ 0< a(k,\mu)+b(k,\mu)^2< a(k,\mu)+(b(k,\mu)-1)^2. \]Using the inequality
\[ 0< a(k,\mu)+b(k,\mu)^2< a(k,\mu)+(b(k,\mu)-1)^2. \]Using the inequality \[ \tilde{\Pi}(a,b,k)\ge\min\left\{\frac{1}{a+b^2},\frac{1}{a+(b-1)^2}\right\}K(k) \]for any $a>0$
\[ \tilde{\Pi}(a,b,k)\ge\min\left\{\frac{1}{a+b^2},\frac{1}{a+(b-1)^2}\right\}K(k) \]for any $a>0$
 , $b\in (0,1)$
, $b\in (0,1)$ , $k\in (0,1)$
, $k\in (0,1)$ , we have
$$\begin{align*} \mathcal{A}(k,\mu) & =\frac{1}{9k^4}\sqrt{\mu(\mu+3)(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}\tilde{\Pi}(a(k,\mu),b(k,\mu),k)\\ & \ge\frac{1}{9k^4}\sqrt{\mu(\mu+3)(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}\\ & \qquad\frac{K(k)}{a(k,\mu)+(b(k,\mu)-1)^2}\\ & =\sqrt{\frac{(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}{\mu(\mu+3)}}K(k)\\ & \ge c\sqrt{\mu-\mu_+}K(k), \end{align*}$$because there exists $c>0$
, we have
$$\begin{align*} \mathcal{A}(k,\mu) & =\frac{1}{9k^4}\sqrt{\mu(\mu+3)(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}\tilde{\Pi}(a(k,\mu),b(k,\mu),k)\\ & \ge\frac{1}{9k^4}\sqrt{\mu(\mu+3)(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}\\ & \qquad\frac{K(k)}{a(k,\mu)+(b(k,\mu)-1)^2}\\ & =\sqrt{\frac{(\mu+3-3k^2)(\mu-\mu_+)(\mu-\mu_-)}{\mu(\mu+3)}}K(k)\\ & \ge c\sqrt{\mu-\mu_+}K(k), \end{align*}$$because there exists $c>0$
 such that $\sqrt {\frac {(\mu +3-3k^2)(\mu -\mu _-)}{\mu (\mu +3)}}>c$
such that $\sqrt {\frac {(\mu +3-3k^2)(\mu -\mu _-)}{\mu (\mu +3)}}>c$ for $\mu >\mu _+$
for $\mu >\mu _+$ . Since
\[ \mathcal{A}(k,\mu)\ge c\sqrt{\mu-\mu_+}K(k)\to \infty\ \ \textrm{as}\ \ \mu\to\infty, \]the assertion (vi) holds.
. Since
\[ \mathcal{A}(k,\mu)\ge c\sqrt{\mu-\mu_+}K(k)\to \infty\ \ \textrm{as}\ \ \mu\to\infty, \]the assertion (vi) holds.
Let $\nu _{\pm }$![]() be defined by (2.28). We need two lemmas to prove a monotonicity of $\mathcal {A}(k,\mu )$
be defined by (2.28). We need two lemmas to prove a monotonicity of $\mathcal {A}(k,\mu )$![]() in $\mu$
in $\mu$![]() .
.
Lemma 3.2 Let $\nu _{\pm }$![]() be defined by (2.28). Then the following hold$:$
be defined by (2.28). Then the following hold$:$![]()

Proof. By (2.28) we can check that
Then by direct calculation we obtain the conclusion. We omit details.
We define
since a sign of $\mathcal {B}(k,\mu )$![]() is important in the study of ${\partial \mathcal {A}}/{\partial \mu }$
is important in the study of ${\partial \mathcal {A}}/{\partial \mu }$![]() .
.
Lemma 3.3 The following holds$:$![]()
Proof. It is obvious that $\mathcal {B}(0,0)=0$![]() . By lemma A.1 (i) and (ii) we have
. By lemma A.1 (i) and (ii) we have

for $k\in (0,1)$![]() . Thus, the assertion holds.
. Thus, the assertion holds.
Lemma 3.4 Let $\Sigma _i$![]() , $i=0,1,2$
, $i=0,1,2$![]() , be defined by (2.24). For each $i=0,1,2$
, be defined by (2.24). For each $i=0,1,2$![]() ,
,
Proof. We consider the case $(k,\mu )\in \Sigma _0$![]() . Let $\nu _{\pm }$
. Let $\nu _{\pm }$![]() be defined by (2.28). By (2.37) and (2.40) we can see that
be defined by (2.28). By (2.37) and (2.40) we can see that
Then, $\mathcal {A}(k,\mu )=-\mathcal {M}(\nu _+,k)+\mathcal {M}(\nu _-,k)$![]() . By lemma A.1(iv) we have
. By lemma A.1(iv) we have

By (3.3) we have

By (2.40) we have
Then,

By lemma 3.2 we have
where $\mathcal {B}(k,\mu )$![]() is defined by (3.1). Since $(k,\mu )\in \Sigma _0$
is defined by (3.1). Since $(k,\mu )\in \Sigma _0$![]() , we see that $-3(\mu -k^2+2)>0$
, we see that $-3(\mu -k^2+2)>0$![]() . By lemma A.2 we have
. By lemma A.2 we have

Thus, (3.2) holds for $(k,\mu )\in \Sigma _0$![]() .
.
We consider the case $(k,\mu )\in \Sigma _1$![]() . By (2.37) and (2.40) we can see that
. By (2.37) and (2.40) we can see that
Then, $\mathcal {A}(k,\mu )=\mathcal {M}(\nu _-,k)+\mathcal {M}(\nu _+,k)$![]() . By a similar calculation as in (i) we have
. By a similar calculation as in (i) we have

We show that $\mathcal {B}(k,\mu )<0$![]() for $(k,\mu )\in \Sigma _1$
for $(k,\mu )\in \Sigma _1$![]() . Since $\mathcal {B}(k,\mu )$
. Since $\mathcal {B}(k,\mu )$![]() is convex in $\mu$
is convex in $\mu$![]() , it is enough to show that $\mathcal {B}(k,-3+3k^2)<0$
, it is enough to show that $\mathcal {B}(k,-3+3k^2)<0$![]() and $\mathcal {B}(k,0)<0$
and $\mathcal {B}(k,0)<0$![]() . By lemma A.2 we have
. By lemma A.2 we have

for $k\in (0,1)$![]() . By lemma 3.3 we see that $\mathcal {B}(k,0)<0$
. By lemma 3.3 we see that $\mathcal {B}(k,0)<0$![]() for $k\in (0,1)$
for $k\in (0,1)$![]() . Thus, (3.2) holds for $(k,\mu )\in \Sigma _1$
. Thus, (3.2) holds for $(k,\mu )\in \Sigma _1$![]() .
.
We consider the case $(k,\mu )\in \Sigma _2$![]() . In this case by (2.35) we see that $\mathcal {A}(k,\mu )=\mathcal {M}(\nu _+,k)-\mathcal {M}(\nu _-,k)$
. In this case by (2.35) we see that $\mathcal {A}(k,\mu )=\mathcal {M}(\nu _+,k)-\mathcal {M}(\nu _-,k)$![]() , where we consider $\mathcal {M}(\nu _+,k)$
, where we consider $\mathcal {M}(\nu _+,k)$![]() and $\mathcal {M}(\nu _-,k)$
and $\mathcal {M}(\nu _-,k)$![]() as complex-valued functions. Then by a similar calculation as in (i) we obtain
as complex-valued functions. Then by a similar calculation as in (i) we obtain
Since $\mathcal {R}<0$![]() and $-\mu ^2+(2k^2-4)\mu +3k^4<0$
and $-\mu ^2+(2k^2-4)\mu +3k^4<0$![]() , we have
, we have
Thus, we show that $\mathcal {B}(k,\mu )>0$![]() for $\mu >\mu _+$
for $\mu >\mu _+$![]() . Since $\mu -k^2+2>0$
. Since $\mu -k^2+2>0$![]() for $\mu >\mu _+$
for $\mu >\mu _+$![]() , by lemma A.2 we have
, by lemma A.2 we have

Thus, (3.2) holds for $(k,\mu )\in \Sigma _2$![]() .
.
4. Asymptotic formulas
In this section let $\lambda _j(k)$![]() , $j\ge 0$
, $j\ge 0$![]() , denote the $j+1$
, denote the $j+1$![]() -th eigenvalue of (LP$_{\pm }$
-th eigenvalue of (LP$_{\pm }$![]() ) and let $\mu _j(k):=(2-k^2)\lambda _j(k)$
) and let $\mu _j(k):=(2-k^2)\lambda _j(k)$![]() .
.
We know the following:
• $\mathcal {A}(k,\mu )$
 is defined on $\Sigma _0\cup \Sigma _1\cup \Sigma _2$
is defined on $\Sigma _0\cup \Sigma _1\cup \Sigma _2$ (lemma 2.2),
(lemma 2.2),• $\mathcal {A}(k,\mu )$
 is increasing in $\mu$
is increasing in $\mu$ (lemma 3.4),
(lemma 3.4),• the range of $\mathcal {A}(k,\,\cdot \,)$
 is $\mathbb {R}_{+}\setminus \{\pi /2,\pi \}$
is $\mathbb {R}_{+}\setminus \{\pi /2,\pi \}$ , where $\mathbb {R}_{+}:=\{x|\ x>0\}$
, where $\mathbb {R}_{+}:=\{x|\ x>0\}$ (lemma 3.1).
(lemma 3.1).
The equation
has a unique solution $\mu _j$![]() in $\Sigma _0$
in $\Sigma _0$![]() for $0< j< n/2$
for $0< j< n/2$![]() , in $\Sigma _1$
, in $\Sigma _1$![]() for $n/2< j< n$
for $n/2< j< n$![]() and in $\Sigma _2$
and in $\Sigma _2$![]() for $j>n$
for $j>n$![]() . Then, $\lambda _j=\mu _j/(2-k^2)$
. Then, $\lambda _j=\mu _j/(2-k^2)$![]() is the $j+1$
is the $j+1$![]() -th eigenvalue for $j\neq 0,n/2,n$
-th eigenvalue for $j\neq 0,n/2,n$![]() . In this section we obtain an asymptotic expansion of $\lambda _j$
. In this section we obtain an asymptotic expansion of $\lambda _j$![]() as $k\to 1$
as $k\to 1$![]() for $j\neq 0,n/2,n$
for $j\neq 0,n/2,n$![]() .
.
Proof of theorem 1.3(i) Let $\lambda _{\pm }$![]() be defined by (2.4). We consider the case $\lambda _-<\lambda _j<-3/(2-k^2)$
be defined by (2.4). We consider the case $\lambda _-<\lambda _j<-3/(2-k^2)$![]() , which corresponds to the case $0< j< n/2$
, which corresponds to the case $0< j< n/2$![]() . Because of the definition of $\lambda _-$
. Because of the definition of $\lambda _-$![]() we have
we have

and hence
We define $r_j(k)$![]() by
by
It follows from corollary 1.6(i) that $\lambda _-+3>0$![]() for $k$
for $k$![]() close to $1$
close to $1$![]() . Since $r_j={(\lambda _j-\lambda _-)}/{(\lambda _-+3)}>0$
. Since $r_j={(\lambda _j-\lambda _-)}/{(\lambda _-+3)}>0$![]() , We have
, We have

Therefore,
Then there exists $r^*_j\in [0,{1}/{4}]$![]() such that
such that
with a suitable monotonically increasing sequence $\{k_m\}_{m=1}^{\infty }$![]() satisfying $k_m\to 1$
satisfying $k_m\to 1$![]() as $m\to \infty$
as $m\to \infty$![]() .
.
Let $\sigma _{\pm }(k_m)$![]() be defined by (2.32) with $k_m$
be defined by (2.32) with $k_m$![]() and $\lambda _j(k_m)$
and $\lambda _j(k_m)$![]() . Let $\nu _{\pm }(k_m)$
. Let $\nu _{\pm }(k_m)$![]() be defined by (2.28) with $k_m$
be defined by (2.28) with $k_m$![]() and $\mu _j(k_m)$
and $\mu _j(k_m)$![]() . Next we calculate the limit $\lim _{m\to \infty }{(1+\nu _{\pm })}/{(1-k_m^2)}$
. Next we calculate the limit $\lim _{m\to \infty }{(1+\nu _{\pm })}/{(1-k_m^2)}$![]() . By (2.4) we see that
. By (2.4) we see that
Using (4.2), we have

Since

Moreover,

Thus, by (4.5), (4.4) and (2.34) we have

Similarly we have

By lemma A.5 with (4.6) and (4.7) we have

Solving the equation

with respect to $r^*_j$![]() , we have $r^*_j=\frac {1}{4}\sin ^2(\frac {j\pi }{n})$
, we have $r^*_j=\frac {1}{4}\sin ^2(\frac {j\pi }{n})$![]() , which implies
, which implies
By (4.2) we have

Proof of theorem 1.3(ii) We consider the case $(-3+3k^2)/(2-k^2)<\lambda _j<0$![]() , which corresponds to the case $n/2< j< n$
, which corresponds to the case $n/2< j< n$![]() . We define $r_j(k)$
. We define $r_j(k)$![]() by
by
It is obvious that $\lambda _j\to 0$![]() as $k\to 1$
as $k\to 1$![]() . Since
. Since
there exists $r_j^*\in [-3,0]$![]() such that
such that
with a suitable monotonically increasing sequence $\{k_m\}_{m=1}^{\infty }$![]() satisfying $k_m\to 1$
satisfying $k_m\to 1$![]() as $m\to \infty$
as $m\to \infty$![]() .
.
Let $\sigma _{\pm }(k_m)$![]() be defined by (2.32) with $k_m$
be defined by (2.32) with $k_m$![]() and $\lambda _j(k_m)$
and $\lambda _j(k_m)$![]() . Let $\nu _{\pm }(k_m)$
. Let $\nu _{\pm }(k_m)$![]() be defined by (2.28) with $k_m$
be defined by (2.28) with $k_m$![]() and $\mu _j(k_m)$
and $\mu _j(k_m)$![]() . We calculate the limit $\lim _{m\to \infty }{(1+\nu _+)}/{(1-k_m^2)}$
. We calculate the limit $\lim _{m\to \infty }{(1+\nu _+)}/{(1-k_m^2)}$![]() . Since
. Since
we have

Moreover,
Hence, by (4.10), (4.9) and (2.34) we have

Since
and $\sigma _+<1$![]() , we have
, we have
Since

by lemma A.3 we have

Let $\mathcal {A}$![]() and $\mathcal {M}$
and $\mathcal {M}$![]() be given in lemma 2.3. By lemma A.5 with (4.11) and lemma A.6 we have
be given in lemma 2.3. By lemma A.5 with (4.11) and lemma A.6 we have

Solving the equation

with respect to $r^*_j$![]() , we have $r^*_j=-3\sin ^2(\frac {j\pi }{n})$
, we have $r^*_j=-3\sin ^2(\frac {j\pi }{n})$![]() , which implies
, which implies
Since $\lambda _j/(1-k^2)=r^*_j+o(1)$![]() , we have
, we have
Proof of theorem 1.3(iii) Let $\lambda _{\pm }$![]() be defined by (2.4). We consider the case $\lambda _j>\lambda _+$
be defined by (2.4). We consider the case $\lambda _j>\lambda _+$![]() , which corresponds to the case $j>n$
, which corresponds to the case $j>n$![]() . Let $\mathcal {A}$
. Let $\mathcal {A}$![]() be given in lemma 2.3 and let $\mu _{\pm }$
be given in lemma 2.3 and let $\mu _{\pm }$![]() be defined by (2.22). By the same argument as in the proof of lemma 3.1(vi) we have
be defined by (2.22). By the same argument as in the proof of lemma 3.1(vi) we have
This implies that
and in particular $\lim _{k\to 1 }\mu _j(k)=1$![]() ,
,
where $a(k,\mu _j)$![]() and $b(k,\mu _j)$
and $b(k,\mu _j)$![]() are defined by (2.30). Using
are defined by (2.30). Using
by lemma A.8 we have

Here we used


By lemmas 2.1 and (1.3) we see that $1-k^2=16\,{\rm e}^{-2/n\varepsilon }(1+o(1))$![]() and $K(k)=1/(1+o(1))n\varepsilon$
and $K(k)=1/(1+o(1))n\varepsilon$![]() . Hence,
. Hence,
Using this relation, we have

Proof of corollary 1.7 (i) By (4.8) and lemma 2.1 we have

(ii) By theorem 1.3(ii) and lemma 2.1 we have
(iii) By theorem 1.3(iii), corollary 1.6(iii) and (1.3) we have

Acknowledgements
The authors are grateful to referees for helpful comments which improve the presentation of the paper.
Y. M. was supported by JSPS KAKENHI Grant Numbers 19H01797, 19H05599.
T. W. was supported by JSPS KAKENHI Grant Numbers 18K03374, 21H00993.
A Appendix A. Elliptic integrals and functions
A.1 Elliptic functions
Let $k\in (0,1)$![]() . We denote the complete elliptic integrals of the first kind by
. We denote the complete elliptic integrals of the first kind by

Jacobi's elliptic function ${\rm sn}(x,k)$![]() is an odd, periodic and analytic function with the period $4K(k)$
is an odd, periodic and analytic function with the period $4K(k)$![]() as a function for the real domain, and is defined locally by
as a function for the real domain, and is defined locally by

for $x\in [0,K(k)]$![]() . The function ${\rm cn}(x,k)$
. The function ${\rm cn}(x,k)$![]() is an even and $4K(k)$
is an even and $4K(k)$![]() -periodic function defined locally by
-periodic function defined locally by
for $x\in [0,K(k)]$![]() and ${\rm dn}(x,k)$
and ${\rm dn}(x,k)$![]() is an even and $2K(k)$
is an even and $2K(k)$![]() -periodic function defined by
-periodic function defined by
In particular,
for $x\in \mathbb {R}$![]() and $k\in (0,1)$
and $k\in (0,1)$![]() .
.
A.2 Complete elliptic integrals
Let $k\in [0,1)$![]() and $\nu \in \mathbb {C}\setminus (-\infty,-1]$
and $\nu \in \mathbb {C}\setminus (-\infty,-1]$![]() . The complete elliptic integrals of the second and third kind are defined by
. The complete elliptic integrals of the second and third kind are defined by

respectively. The function $K(k)$![]() is monotonically increasing in $k$
is monotonically increasing in $k$![]() ,
,
and $E$![]() is monotonically decreasing in $k$
is monotonically decreasing in $k$![]() ,
,
In [Reference Wakasa10] the following modified complete integral of the third kind was introduced
for $k\in (0,1)$![]() and $\nu \in \mathbb {C}\setminus ((-\infty,-1]\cup [-k^2,0])$
and $\nu \in \mathbb {C}\setminus ((-\infty,-1]\cup [-k^2,0])$![]() . The function $\mathcal {M}$
. The function $\mathcal {M}$![]() appears in (2.27).
appears in (2.27).
We give standard formulas for $K(k)$![]() , $E(k)$
, $E(k)$![]() and $\Pi (\nu,k)$
and $\Pi (\nu,k)$![]() in lemmas A.1–A.3 without proofs. See [Reference Byrd and Friedman3] for details.
in lemmas A.1–A.3 without proofs. See [Reference Byrd and Friedman3] for details.
Lemma A.1 Let $k\in (0,1)$![]() and $\nu \neq 0,-1,-k^2$
and $\nu \neq 0,-1,-k^2$![]() . Then,
. Then,
(i) $\displaystyle \frac {{\rm d}E}{{\rm d}k}(k)=\frac {E(k)-K(k)}{k}$
 .
.(ii) $\displaystyle \frac {{\rm d}K}{{\rm d}k}(k)=\frac {E(k)-(1-k^2)K(k)}{k(1-k^2)}$
 .
.(iii) $\displaystyle \frac {\partial \Pi }{\partial k}(\nu,k)=\frac {k(E(k)-(1-k-2)\Pi (\nu,k))}{(k^2+\nu )(1-k^2)}$
 .
.(iv) $\displaystyle \frac {\partial \Pi }{\partial \nu }(\nu,k)=-\frac {K(k)}{2\nu (1+\nu )}+\frac {E(k)}{2(1+\nu )(k^2+\nu )}+\frac {(k^2-\nu ^2)\Pi (\nu,k)}{2\nu (1+\nu )(k^2+\nu )}$
 .
.
Lemma A.2 Let $k\in (0,1)$![]() . Then
. Then
Lemma A.3 Let $k\in (0,1)$![]() . Then
. Then
Lemmas A.4–A.6 are formulas for $\Pi (\nu,k)$![]() . Proofs can be found in [Reference Wakasa and Yotsutani14].
. Proofs can be found in [Reference Wakasa and Yotsutani14].
Lemma A.4 Let $k\in (0,1)$![]() and $\nu >-1$
and $\nu >-1$![]() . Then,
. Then,
(i) $\displaystyle \lim _{\nu \to -1}\sqrt {1+\nu }\Pi (\nu,k)=\frac {\pi }{2\sqrt {1-k^2}}$
 .
.(ii) $\displaystyle \lim _{\nu \to \infty }\sqrt {1+\nu }\Pi (\nu,k)=\frac {\pi }{2}$
 .
.
Lemma A.5 Let $k\in (0,1)$![]() . Suppose that $\nu$
. Suppose that $\nu$![]() is a continuous function on $(0,1)$
is a continuous function on $(0,1)$![]() with $-1<\nu (k)<-k^2$
with $-1<\nu (k)<-k^2$![]() for $k\in (0,1)$
for $k\in (0,1)$![]() . Assume that there exists $\nu ^*\in [0,1]$
. Assume that there exists $\nu ^*\in [0,1]$![]() such that
such that
Then, for each $\nu ^*\in [0,1]$![]() ,
,
and
Lemma A.6 Let $J(\nu,k):=\sqrt {1+\nu }\Pi (\nu,k)-\frac {1}{\sqrt {1+\nu }}K(k)$![]() . Then,
. Then,
In [Reference Wakasa and Yotsutani14] a kind of a complete elliptic integral $\tilde {\Pi }(a,b,k)$![]() defined by (2.29) was introduced. Lemmas A.7 and A.8 are formulas for $\tilde {\Pi }$
defined by (2.29) was introduced. Lemmas A.7 and A.8 are formulas for $\tilde {\Pi }$![]() and proofs can be found in [Reference Wakasa and Yotsutani14].
and proofs can be found in [Reference Wakasa and Yotsutani14].
Lemma A.7 Suppose that $a>0$![]() and $b,b_0\in (0,1)$
and $b,b_0\in (0,1)$![]() . Then for each $k\in (0,1)$
. Then for each $k\in (0,1)$![]() ,
,
Lemma A.8 Suppose that $a>0,\ b,\ b_0\in (0,1)$![]() and $k\in (0,1)$
and $k\in (0,1)$![]() . Let
. Let
Then,
Lemma A.9 is a formula for $\mathcal {M}(\nu,k)$![]() .
.
Lemma A.9 Let $k\in (0,1)$![]() and $\nu \in (-1,-k^2)\cup (0,\infty )$
and $\nu \in (-1,-k^2)\cup (0,\infty )$![]() . Then,
. Then,
(i) $\displaystyle \lim _{\nu \to -1}\mathcal {M}(\nu,k)=\frac {\pi }{2}$
 .
.(ii) $\displaystyle \lim _{\nu \to -k^2}\mathcal {M}(\nu,k)=0$
 .
.(iii) $\displaystyle \lim _{\nu \to \infty }\mathcal {M}(\nu,k)=\frac {\pi }{2}$
 .
.
Lemma A.9(i) (resp. (iii)) follows from Lemma A.4(i) (resp. (ii)). Lemma A.9(ii) is trivial.