Introduction
Maize shows great diversity in canopy architecture (Maddonni et al., Reference Maddonni, Otegui and Cirilo2001; Stewart et al., Reference Stewart, Costa, Dwyer, Smith, Hamilton and Ma2003); the arrangements of leaves in space and time affects light distribution and the way in which plants make use of the intercepted light for photosynthesis (Ellsworth and Reich, Reference Ellsworth and Reich1993; Wang et al., Reference Wang, Li and Su2007). Leaf architecture traits include leaf size and leaf orientation, specifically, the number of leaves, leaf shape, leaf area, leaf angle and leaf azimuth in maize canopy (Perez et al., Reference Perez, Fournier, Cabrera-Bosquet, Artzet, Pradal, Brichet, Chen, Chapuis, Welcker and Tardieu2019). The vertical distribution of leaf area is an important factor to influence light capture in canopy, which is an essential part of the development of plant and crop models (Fournier and Andrieu, Reference Fournier and Andrieu2000; Vos et al., Reference Vos, Evers, Buck-Sorlin, Andrieu, Chelle and De Visser2010).
Several approaches have been used to describe the distribution of leaf area of a maize plant. A direct method is to measure individual leaf area by an electronic planimeter (LI-COR, Lincoln, USA) or by calculating leaf area based on leaf length and maximum leaf width (Stewart and Dwyer, Reference Stewart and Dwyer1999; Zhu et al., Reference Zhu, Chang, Tang, Jiang, Zhang and Cao2009). However, these direct methods are usually time-consuming, labour-intensive and may cause canopy damage. Indirect methods are gap-fraction estimation, remote sensing or three-dimensional point clouds of plants, but they are less precise because indirect methods always use the top of canopy foliar samples to represent the whole plant architecture (Tang et al., Reference Tang, Dubayah, Brolly, Ganguly and Zhang2014; Jiang et al., Reference Jiang, Wang, Zhuang, Li, Li and Gong2018). Non-destructive and mathematical approaches of modelling present a potential alternative for describing the vertical profile of leaf size that may avoid these issues.
Previous studies used discontinuous equations to describe the relationship between leaf rank and leaf area, but the results were unsatisfactory because the area of leaves above the 12th leaf is often underestimated (Carberry et al., Reference Carberry, Hammer and Muchow1993). Another approach used a continuous equation to predict leaf area by using a skewed, bell-shaped function and its deformation equations (Stewart and Dwyer, Reference Stewart and Dwyer1999; Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018). The bell-shaped function is more generally applicable because it needs fewer parameters than the discontinuous equations and gives good predictions of leaf area for a large of hybrids with modified parameters (Dwyer and Stewart, Reference Dwyer and Stewart1986; Valentinuz and Tollenaar, Reference Valentinuz and Tollenaar2006). The equation of the original bell-shaped function is
where y is the fully expanded leaf area of each individual leaf, x is the leaf rank (leaves are numbered from bottom to top), y 0 is the maximum individual leaf area, x 0 is the leaf rank that corresponds to the maximum of leaf area and a and b are dimensionless empirical constants (Dwyer and Stewart, Reference Dwyer and Stewart1986). Studies focused on parameters of the original bell-shaped function (Eqn (1)). Specifically, y 0 and x 0 could be simply estimated from total leaf number (Muchow and Carberry, Reference Muchow and Carberry1989). In addition, nonlinear relationships were also found to exist between total leaf number and the parameters a and b (Eqn (1)) (Keating and Wafula, Reference Keating and Wafula1992). However, the regression functions are developed by using plants varying in total leaf number from 12 to 17 with the maize hybrids released before 1990 (Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018). The average total leaf number of modern high yielding maize hybrids is beyond the scope of the original leaf area model, and is strongly affected by genetic improvement and environmental conditions (Liu et al., Reference Liu, Xie, Hou, Li, Zhang, Ming, Long and Liang2013). Although the coefficients of determination (R 2) were too low to justify the use of total leaf number to estimate the function parameters (Valentinuz and Tollenaar, Reference Valentinuz and Tollenaar2006; Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018), the original bell-shaped function (Eqn (1)) is still a robust way to predict the fully-expanded leaf area of maize with modified parameters and fitted empirical constants (Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018).
The common equation of estimating maize fully-expanded leaf area was calculated as length × maximum width × coefficient (Stewart and Dwyer, Reference Stewart and Dwyer1999; Bosi and Struikl, Reference Bos and Struik2000). This equation is still widely used, although there is a slight modification of the constant coefficient (Keating and Wafula, Reference Keating and Wafula1992; Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018). Research of leaf length and width could lead to a better understanding of the distribution of leaf area. In addition, these geometrical variables of leaf length and width determine leaf shape, and leaf shape is of critical important in mathematically characterizing the two-dimensional structure of maize. Modelling the morphology of leaves is helpful for designing optimal plant shape and modelling plant growth (Fournier and Andrieu, Reference Fournier and Andrieu1999; Zhu et al., Reference Zhu, Chang, Tang, Jiang, Zhang and Cao2009; Archontoulis et al., Reference Archontoulis, Vos, Yin, Bastiaans, Danalatos and Struik2011).
The first objective was to develop and test a new equation that captures vertical leaf area distribution and describe the morphology of the various leaves of maize based on a series of observations and analyses of the length and width of leaves at individual leaf ranks. The second objective was to find the key leaf ranks based on the constitutive equations, which could simplify the field measurement process.
Materials and methods
Experimental site and design
The field experiments were conducted during the growing seasons (from 1 April to 30 September) from 2015 to 2018 at the Gongzhuling Experimental Station, Jilin province, China (43°30N, 124°50E). This area is typical of the rain-fed spring maize regions in Northeast China. We used maize hybrids ZD958 and XY335 in the same field for this 4 years, and this two hybrids were the most widely cultivated in China at the time of the current study. Maize hybrid ZD958 was developed by the Luohe Academy of Agricultural Science of Henan province, and XY335 was developed by the Tieling Pioneer Limited Company. Normally, the total leaf number of ZD958 is 22 and the rank of ear leaf is 16. The total leaf number of XY335 is 21 and the rank of ear leaf is 14 (Ma et al., Reference Ma, Xie, Niu, Li, Long and Liu2014; Huang et al., Reference Huang, Gao, Li, Xu, Tao and Wang2017). Maize seeds were sown by hand on 1 May 2015, 29 April 2016, 27 April 2017 and 29 April 2018. Prior to sowing, the plots were fertilized with 150 kg N/ha (urea), 42.5 kg/ha P2O5 (super phosphate) and 42.5 kg/ha K2O (potassium sulphate). Row orientation was east-west, row spacing was 65 cm and population density was 6.75 plants/m2. Individual plots measured about 45.5 m2, comprised of seven rows and 10 m long. The experiments were arranged in a randomized design with three replications. Plots were kept free of weeds, insects and diseases with chemicals based on standard practices. Monthly meteorological data of mean air temperature and total precipitation during the maize growing seasons in the years from 2015 to 2018 at the experimental site are shown in Table 1. Total precipitation during 2015 growing season was significantly lower than that in other years, particularly during June and July.
Table 1. Monthly mean air temperature and total precipitation during the maize growing seasons in the years from 2015 to 2018 at the Gongzhuling experimental station

Measurements of morphological traits
In the emergence period, ten successive plants were tagged in the central row of each plot. Red paint spray was applied on leaves 4, 8 and 12, which ensured the identification of leaf ranks (Fig. 1(a)). For each tagged plant, the rank of the ear leaf was noted as soon as it was identified. The appearance of the leaf collar at the base of a leaf signalled the termination of individual leaf area growth, which means the leaf was fully expanded (Fournier and Andrieu, Reference Fournier and Andrieu1998). The length and width of each leaf were manually measured in tagged plants using a non-destructive method by using a ruler when a leaf was considered fully expanded. The leaf length was defined as the distance from the base of the ligula to the tip of the leaf, and the leaf width was defined as the widest part of the leaf (Fig. 1(b)). The fully expanded leaf area was calculated as leaf length × leaf width × 0.75, and length–width ratio was calculated as length divided by width (Keating and Wafula, Reference Keating and Wafula1992; Stewart and Dwyer, Reference Stewart and Dwyer1999).
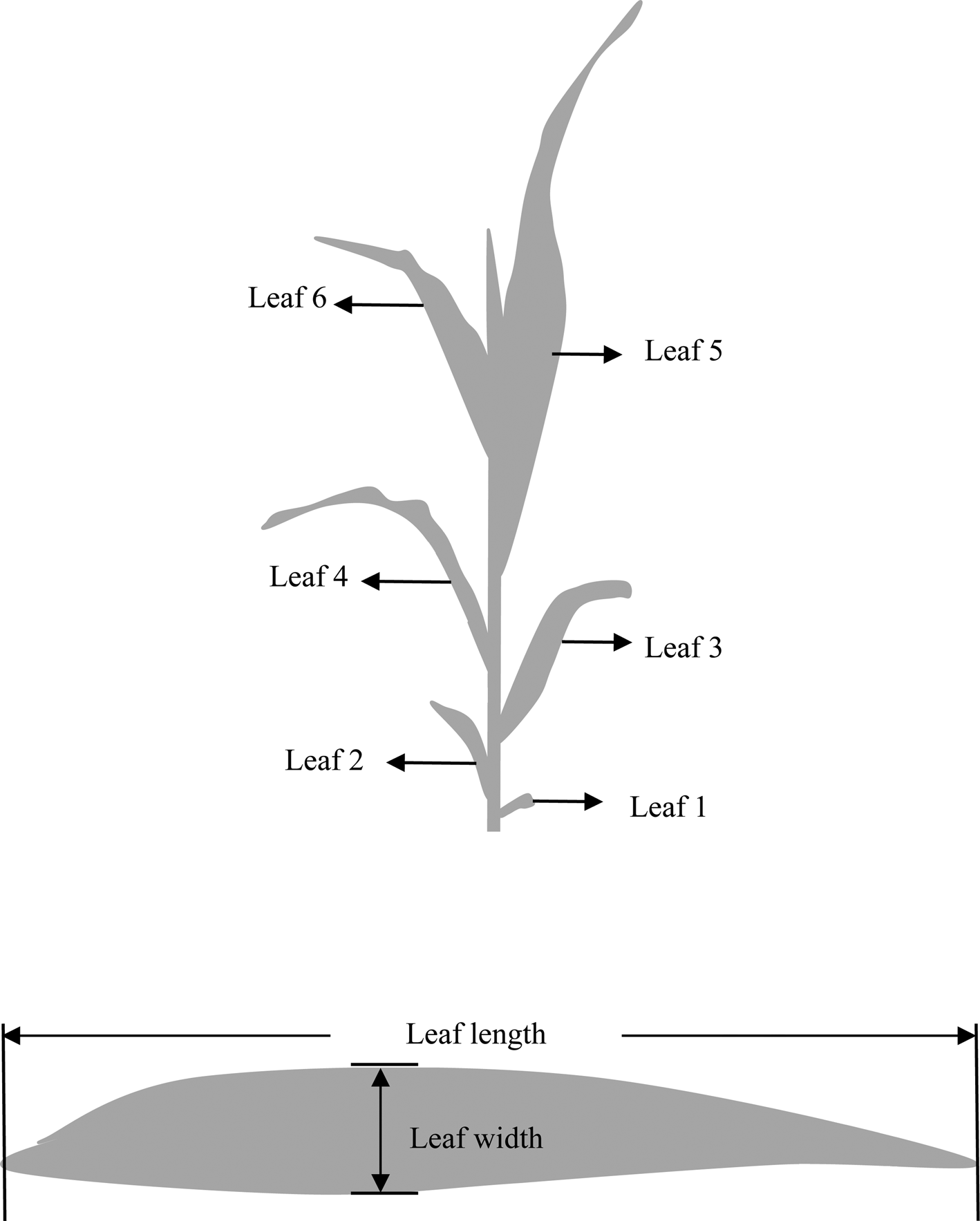
Fig. 1. Diagram of (a) leaf rank and (b) leaf morphological traits of leaf length and width.
New empirical equation of leaf size distribution
Bell-shaped functions are widely used in mathematical models, for example, in crop growth models (Yin et al., Reference Yin, Goudriaan, Lantinga, Vos and Spiertz2003) and plant morphology models (Zhu et al., Reference Zhu, Chang, Tang, Jiang, Zhang and Cao2009). The original equation used to describe the vertical distribution of leaf area (Dwyer and Stewart, Reference Dwyer and Stewart1986) is Eqn (1). Factoring out (x − x 0)2 gives
The parameter b that controls the degree of skewness ranges from −0.007 to 0.001 and varies little with total leaf number (Keating and Wafula, Reference Keating and Wafula1992; Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018). In other words, the polynomial b(x − x 0) is small and has little effect on the output of the equation. Removing the polynomial factor in the exponent results in:
The parameter a is a dimensionless empirical constant. Then the form of this equation also can be expressed as:
where y 0 is the maximum value of y, which is reached at leaf rank x 0. The new empirical equation (Eqn (4)) in this study was thus a simplified form of the original bell-shaped function (Eqn (1)) by omitting the limited effect from parameter b. An advantage of the simplicity of this new equation is that it can be easily evaluated because it only has three parameters, one parameter less than previous bell-shaped function.
The shape of the new empirical equation (Eqn (4)) is similar to the normal distribution which is widely used in plant modelling (Lizaso et al., Reference Lizaso, Batchelor and Westgate2003; Matsunaga et al., Reference Matsunaga, Tosti, Androcioli-Filho, Brancher, Costes and Rakocevic2016), and it has three parameters. The effects of different parameters on the output are shown by varying the parameter values (Fig. 2). Parameter y 0 determines the height of the curve and gives the maximum value y max of the curve (Fig. 2(a)). Parameter x 0 is the centre of symmetry on the x axis and corresponds to y max (Fig. 2(b)). Parameter a is the width of the curve and low values of a result in a curve that rise sharply and fall sharply (Fig. 2(c)).

Fig. 2. Characteristics of variations in parameters of the new empirical equation (Eqn (4)). Parameters are common to all curves unless stated below: y 0 = 20, x 0 = 10, a = 5. (a) Effects of varying y 0: y 0 = 15 ……; 20 ——; 25 ----. (b) Effects of varying x 0: x 0 = 8 ……; 10 ——; 12 ----. (c) Effects of varying a: a = 4 ……; 5 ——; 6 ----.
Comparison with existing bell-shaped function
The leaf morphological data (leaf length, width and area) obtained from 2015 to 2017 of all leaf ranks were used to fit the new equation (Eqn (4)) and the original bell-shaped function (Eqn (1)) to determine parameters using the nonlinear least squares algorithm. The independent data from 2018 of all leaf ranks were used to evaluate these two equations.
Derivatives of the new empirical equation
To obtain the key leaf ranks determining the shape of the curve, the first, second and third derivative equations of this new equation were derived (Table 2). The key points were obtained when these derivatives were set to zero. The first derivative is the slope of a tangent line through a given point on the curve, and the point where the first derivative is zero is the maximum of the primitive of the new equation (Figs 3(a) and (b)). The point where the second derivative is zero is the extreme point of the first derivative, also the inflection point of the primitive new equation (Fig. 3(c)). Finally, the point where the third derivative is zero is the extreme point of the second derivative (Fig. 3(d)).
Table 2. Derivative equations and key points of the new equation


Fig. 3. Shape of the new equation (a) and its first (b), second (c) and third (d) derivatives. The key points were obtained when these derivatives were set to zero.
Five key points are obtained in total by the derivatives equations of the new equation, and they are determined by parameters x 0 and a (Table 2). When the derivative equations are equal to zero, the number of key point is one, two and three, respectively, but one of the points obtained by the third derivative is the same with the results of first derivative (Fig. 3). Therefore, key leaf ranks are selected among these five key points (Table 2).
Data analysis
The key leaf ranks were obtained by substituting the value of parameters x 0 and a into the derivative equations of this new equation. The obtained key leaf ranks were rounded value of calculated key points of this new equation because leaf rank is an integer number, and the rounded key points were deleted if they are beyond the scope of the leaf rank of ZD958 and XY335. Leaf area was calculated by leaf length and width in this study, then the rounded average values of leaf length and width were assigned as the key leaf ranks of the entire leaf morphological traits distribution. The data from 2015 to 2017 of the key leaf ranks were used to establish the same equation, and the data from the remaining leaf ranks (except for the key leaf ranks) were used to test the feasibility of the simplified approach.
The root mean square error (RMSE), normalized root mean square error (NRMSE) and coefficient of determination R 2 were used to verify the accuracy of fit between observed values and estimated values (Zhu et al., Reference Zhu, Chang, Tang, Jiang, Zhang and Cao2009; Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018).
Results
Leaf morphological traits based on individual leaf rank
The relationship between leaf morphology (length, width and area) and leaf rank can be described quantitatively by the new empirical equation (Eqn (4); Fig. 4). The length and width of individual leaves increased with leaf rank up to leaf 14 and then decreased for leaf 15 and above (see Figs 4(a–d)). The maximum length and width all occurred around leaf 14 in both ZD958 and XY335. The distribution of individual leaf area was similar to that of leaf length and width (Figs 4 (e and f)), whereas the distribution of the length–width ratio differed because the changes from the bottom leaf to the top leaf were small (Figs 4 (g and h)). The relationships between leaf length, width, area and length–width ratio and leaf rank were the same for maize hybrids ZD958 and XY335 (Fig. 4). The results showed a high consistency between the estimated and observed values (Fig. 5). Overall, the predictability of the new equation (Eqn (4)) in estimating the changes in leaf morphological traits (leaf length, width and area) at different leaf ranks was good.

Fig. 4. Leaf length (a and b), leaf width (c and d) and leaf area (e and f) of ZD958 and XY335 were simulated by the new empirical equation. The length–width ratio at individual leaf rank of ZD958 (g) and XY335 (h).

Fig. 5. Estimated v. observed leaf length (a and b), leaf width (c and d) and leaf area (e and f) for hybrids ZD958 and XY335 at individual leaf rank. The observed data from 2015 to 2017 were used to fit the new equation (Eqn (4)), and independent data in 2018 were used to test.
Each parameter of the new equation (Eqn (4)) can be interpreted in a biologically meaningful way (Fig. 2). The parameter y 0 was defined as the maximum length, maximum width or maximum area of one plant (Fig. 2(a)). For ZD958, it was 103.2 cm, 11.3 cm or 855.0cm2, respectively, and for of XY335, it was 94.7 cm, 11.9 cm or 811.6 cm2, respectively (Table 3). The parameter x 0 was defined as the leaf rank corresponding to these maximum leaf morphological traits, and the leaf ranks of both ZD958 and XY335 were all around leaf 14. From the bottom leaf to the top leaf, the changes in leaf length were greater than the changes in leaf width, and the change in leaf area was the highest because it had the smallest value for the parameter a (Fig. 2(c)).
Table 3. Values of parameters y 0, x 0 and a of the new equation

Comparison with original bell-shaped function
The new equation (Eqn (4)) was evaluated by comparing with original bell-shaped function (Eqn (1)). The observed leaf morphological data (leaf length, width and area) from 2015 to 2017 were used to fit the new equation (Eqn (4)) and original bell-shaped function (Eqn (1)), respectively, and the parameter values of ZD958 and XY335 are listed in Tables 3 and 4. Equations (1) and (4) along with their parameter values were estimated using the independent data from 2018. The R 2 values of both ZD958 and XY335 for leaf length, width and area using Eqn (4) were higher than those using Eqn (1), especially for leaf width (Table 5). The RMSE and NRMSE of ZD958 using Eqn (4) were similar to that using Eqn (1), but the RMSE and NRMSE of XY335 using Eqn (1) were much smaller. Therefore, leaf length and leaf area were simulated well by using both Eqns (1) and (4), but Eqn (4) gave the better estimations for leaf width compared to Eqn (1) (Table 5).
Table 4. Values of parameters y 0, x 0, a and b of original bell-shaped function

Key leaf ranks of the new empirical equation for leaf morphological traits
The rounded average values of key leaf ranks of leaf length and width were assigned as the key ranks of the entire leaf morphological traits distribution (Table 6). The leaf area was ignored in this study because it was calculated by individual leaf length and width instead of being observed. Finally, the ranks of leaves 4, 8, 14 and 20 were defined as the key leaf ranks for the new Eqn (4) and the key leaf ranks of ZD958 and XY335 were the same (Table 6).
Table 6. Key leaf ranks of the new equation

The data were obtained by substituting the fitted parameter values of Table 3 into the first, second and third derivative formulas of key points of Table 2, respectively, and they were rounded because they represent leaf ranks (from bottom to top). The results beyond the scope of leaf rank were deleted.
The relationships between leaf morphological traits (i.e. length, width and area) and leaf rank were established based on the four key leaf ranks (leaves 4, 8, 14 and 20) instead of on all leaf ranks (Fig. 6). The new Eqn (4) was validated by using the data in the remaining leaf ranks except for the four key leaf ranks from the years 2015–2017, and the estimated fit observed the data well (Fig. 7). The NRMSE values of ZD958 for leaf length, leaf width and leaf area were 0.075, 0.092 and 0.137, respectively, and the NRMSE values of XY335 were 0.084, 0.111 and 0.132, respectively (Fig. 7). Therefore, the morphological data of the four key ranks (leaves 4, 8, 14 and 20) were used to estimate leaf length, width and area at individual leaf rank were acceptable.

Fig. 6. New empirical equations for leaf length (a and b), leaf width (c and d) and leaf area (e and f) for hybrids ZD958 and XY335. Estimated leaf length, width and area based on four key leaf ranks (leaves 4, 8, 12 and 20) from 2015 to 2017. The vertical dotted line gives the position of the ear leaf and is rounded average over 3 years.

Fig. 7. Estimated v. observed leaf length (a and b), leaf width (c and d) and leaf area (e and f) for hybrids ZD958 and XY335 at individual leaf rank. The observed data from key leaf ranks (4, 8, 12 and 20) from 2015 to 2017 were used to fit the new equation (Eqn (4)), and remaining leaf ranks (except for key leaf ranks) were used to test.
Discussion
Leaf sizes together with leaf orientation are important components of leaf architecture, influencing the leaf morphological trait distribution in maize canopy (Fournier and Andrieu, Reference Fournier and Andrieu1999; Maddonni et al., Reference Maddonni, Otegui and Cirilo2001; Huang et al., Reference Huang, Gao, Li, Xu, Tao and Wang2017). However, most previous studies focused only on leaf area of fully-expanded leaves as a function of leaf rank and neglect the more fundamental measurements of leaf length and width (Muchow and Carberry, Reference Muchow and Carberry1989; Keating and Wafula, Reference Keating and Wafula1992; Su et al., Reference Su, Zhu, Huang and Guo2018). The new empirical Eqn (4) describes the distribution of leaf length, width and area in a quantitative way that remain similar in shape from year to year (Fig. 4). Specifically, the individual leaf length and width of ZD958 and XY335 for the year 2015 were smaller than that for the years 2016 and 2017, mainly because the year 2015 had the least precipitation, particularly during June and July (Table 1). Water shortage limited elongation and expansion growth, moisture content and photosynthesis of leaves, which influences on the growth and development of maize plant (Duvick and Cassman, Reference Duvick and Cassman1999; Zhang et al., Reference Zhang, Wang, Wang, Ning, Wang, Wen, Li, Dong, Xu, Zhang and Li2019).
The morphological changes are observed in maize hybrids released over different generations in American (Duvick and Cassman, Reference Duvick and Cassman1999), European (Perez et al., Reference Perez, Fournier, Cabrera-Bosquet, Artzet, Pradal, Brichet, Chen, Chapuis, Welcker and Tardieu2019) and Chinese (Ma et al., Reference Ma, Xie, Niu, Li, Long and Liu2014) projects. The number of leaves per plant increased and the leaf area index tend to be higher for modern hybrids than older ones. The leaf orientation became more upright, the length of the middle leaves increase, and modern hybrids have a lower ear and ear leaf position than old hybrids (Ma et al., Reference Ma, Xie, Niu, Li, Long and Liu2014; Perez et al., Reference Perez, Fournier, Cabrera-Bosquet, Artzet, Pradal, Brichet, Chen, Chapuis, Welcker and Tardieu2019). These changes affect the light interception in maize canopy, and also lead to the different architecture of modern maize hybrids, especially for high-yielding modern maize hybrids (Liu et al., Reference Liu, Hou, Xie, Ming, Wang, Xu, Liu, Yang and Li2017). Therefore, the previous mathematical models need to be modified (Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018).
A great deal of effort has been devoted to measuring and characterizing leaf morphology (Fournier and Andrieu, Reference Fournier and Andrieu1998; Sher et al., Reference Sher, Khan, Cai, Ahmad, Asharf and Jamoro2017). Mathematical approaches with modelling can thus be very convenient and useful for estimating plant growth. The original bell-shaped function (Eqn (1)) is still a robust way to predict the fully-expanded leaf area of maize with modified parameters (Keating and Wafula, Reference Keating and Wafula1992; Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018), and the empirical constants parameters (a and b) were simply estimated from total leaf number (Keating and Wafula, Reference Keating and Wafula1992), but the total leaf number of modern hybrids were still beyond the scope of equations calibrated and affected by climate factors, such as thermal time and photoperiod duration of vegetative growth (Muchow and Carberry, Reference Muchow and Carberry1989). For instance, field experiments are conducted across 34 sites in seven provinces located in China, using maize hybrid ZD958, the total leaf number increased from 18.7 to 23.7 with an average of 21.0 (Liu et al., Reference Liu, Xie, Hou, Li, Zhang, Ming, Long and Liang2013). The values of parameter b in Eqn (1) were small enough, ranging from 1.9 × 10−5 to 2.7 × 10−4 (Table 4) in this study. Previous studies also clarified parameter b had fewer effects on the output of the function (Keating and Wafula, Reference Keating and Wafula1992; Zhen et al., Reference Zhen, Shao, Zhang, Huo, Batchelor, Hou, Wang, Mi, Miao, Li and Zhang2018). Then, Eqn (4) was a simplified form of Eqn (1) by removing the parameters b (see Eqns (1)–(4)). There are some advantages that using the new equation (Eqn (4)) to describe the vertical leaf distribution profile of maize, for example, the prediction accuracy, the number of parameters, the computational complexity and the speed of computer programming. Therefore, the new equation would contribute to more accurate simulation of light capture in relation to phenotype and management, and also lay a foundation for further research into comprehensive simulation systems to produce virtual expressions of leaf growth for maize. Since the morphological characteristics of leaves are complex and difficult to obtain in the field, four key leaf ranks were found by the a method of using derivation equations, because the morphology of any leaf is strongly influenced by the morphology of previously emitted leaves (Stewart and Dwyer, Reference Stewart and Dwyer1993; Fournier and Andrieu, Reference Fournier and Andrieu1999).
This study only focused on the geometrical properties of fully expanded leaf morphology and simplifies field measurements by four key leaf ranks. Further research is needed to test the flexibility of the new equation and the stability of this derivation method with more independent dataset from different hybrids, ecological sites and growing conditions.
Conclusions
The relationships between leaf length, width and area and leaf ranks were established by a new empirical equation and the biological meaning of each parameter in this equation is valuable. The use of the new equation reduces the number of parameters required to characterize the leaf morphology, and reduces the workload of computer program. According to the characteristics of this new equation, a method of using derivation formulas to determine key leaf ranks to simplify mathematical equations was proposed in this study. The four key leaf ranks (4th, 8th, 14th and 20th) were identified using maize hybrids ZD958 and XY335, that could simplify the process of data acquisition in the field.
Acknowledgements
We are grateful to Dr Niels Anten of Wageningen University & Research and anonymous reviewers for their constructive comments and suggestions to improve this manuscript.
Financial support
This study was supported by the National Key Research and Development Program of China (2017YFD0300302), the earmarked fund for China Agriculture Research System (CARS-02-25) and the Agricultural Science and Technology Innovation Project of Chinese Academy of Agricultural Sciences for their support.
Conflict of interest
The authors declare there are no conflicts of interest.
Ethical standards
Not applicable.

















