Introduction
In their ground-breaking work on turn-taking norms, “A Simplest Systematics for the Organization of Turn-Taking,” conversation analysts Sacks, et al. (Reference Sacks, Schegloff and Jefferson1978) offered an understanding of the deep structure of conversational rules that still shapes how we think about conversation. Using qualitative, ethnomethodological analysis of natural interactions, these researchers identified abstract, universal rules of conversational turn-taking. For example, speakers exchange turns commanding the floor; overwhelmingly, one party talks at a time; actors use techniques (e.g., addressing questions, interrupting) to allocate turns to self and others. Group processes researchers in the expectation states tradition also sometimes use conversations as a site for studying basic structures of interaction. This formal quantitative tradition attempts to explain how larger societal structures of status and power “get into” local social interactions (Fişek et al. Reference Fişek, Berger and Norman1991; Skvoretz & Fararo Reference Skvoretz and Fararo1996). A process referred to by Gibson (Reference Gibson2008) as permeation. However, work examining permeation within open interaction groups within the expectation states tradition has often failed to address conversational deep structure in a meaningful way, instead focusing on the development of a stable status structure and primarily attending to aggregated participation outcome distributions (Fişek et al. Reference Fişek, Berger and Norman1991; Skvoretz & Fararo Reference Skvoretz and Fararo1996). While some researchers have long advocated for group processes theorists to incorporate conversation analytic insights into improved models of power-and-prestige in conversational interactions (Cannon et al. Reference Cannon, Robinson and Smith-Lovin2019; Gibson Reference Gibson2003, Reference Gibson2005, Reference Gibson2008; Okamoto & Smith-Lovin Reference Okamoto and Smith-Lovin2001; Robinson & Smith-Lovin Reference Robinson and Smith-Lovin1990, Reference Robinson and Smith-Lovin2001) success has been limited (Gibson Reference Gibson2008).
This paper proposes that relational event models (Butts Reference Butts2008) provide the integral missing piece needed to integrate these two approaches while contributing to the overarching questions behind current research on both permeation and conversational deep structure in unique ways. Relational event models offer a quantitative, dynamic approach to the analysis of conversation, allowing for the analysis of deep structure as well as the emergence of socially significant patterns of interaction from conversational acts (Schecter et al. Reference Schecter, Pilny, Leung, Poole and Contractor2018). Gibson formalized some of the deep structural rules identified by conversation analysts into his formulation of participation shifts (Gibson Reference Gibson2003). Participation shifts, codifications of the moment-to-moment movement of individuals between the positions of speaker, target, and everyone else now serve as a central measure in the toolkit of relational event models (Butts Reference Butts2008), providing a degree of extant integration between conversation analysis and relational event modeling. To our knowledge, however, the major insights of expectations states theory have not been systematically incorporated into a relational event model framework. A major advantage of doing so would be to provide a set of tools and theoretical resources to address permeation in a formal and precise way alongside deep structure and emergence. We begin this integration by illustrating a formal process focused proto-theoretical extension to the expectation states theoretical program designed to operate within the relational event model framework that incorporates conversation analytic insights. We compare this formalized proto-theory with a traditional status model as a first point of comparison using 55 task group interactions from an experiment that systematically varied informal status, formal authority, and legitimacy of that authority. In doing so, we illustrate the benefits of combining insights from these approaches and lay the groundwork for future theoretical development. We begin by describing the operations of a specific theory within expectations states theory, status characteristics theory.
2. Hierarchy and social structure in interaction
Imagine a newly-formed work group in a creative organization. Anne, Charlie, and Fabian are charged with accomplishing some of the group’s most important tasks collaboratively – bouncing ideas off one another and collectively creating solutions. Anne serves as the team leader, but because of the newness of the group, her position is not yet legitimated. How do members of this group orient toward one another? Who speaks first? Who speaks most? How do they organize their participation to maximize their joint accomplishments? How much of these decisions are influenced by the status of the group members – leader/subordinate positions, gender, race, age? How much of these decisions are influenced by interaction style, content of contributions, or the happenstance of who speaks first?
One factor determining how much Anne’s authority as team leader might influence the course of the team’s interactions would be the degree of legitimacy associated with that authority. We define authority as the ability of an actor to direct, regulate or evaluate others’ behavior; and we define the legitimacy of that authority as the beliefs about whether the authority is appropriate (Dornbusch et al. Reference Dornbusch, Scott and Busching1975; Suchman Reference Suchman1995). Dornbusch et al. (Reference Dornbusch, Scott and Busching1975) also distinguish between two different sources of legitimacy, the degree to which external, higher status others lend their support to the legitimacy of the authority (authorization) and the extent to which peer and lower status group members support the legitimacy of the authority (endorsement). The way in which Fabian and Charlie interact with Anne will, in part, be determined by how much they endorse her position as team leader. Other less formal features of Anne, Charlie, and Fabian will also undoubtedly shape who contributes most to their conversations, who speaks to whom, who hangs back and listens. It is, in part, the impact of both formal and informal status structures on the conversational outcomes (read: permeation) that the expectation states research program family of theories aims to address.
Early laboratory observations noted that highly patterned participation hierarchies form in homogeneous task group conversations (Bales et al. Reference Bales, Strodtbeck, Mills and Roseborough1951). Leaders emerge and participation curves tend to roughly follow a harmonic distribution. These observations led to the development of the expectation states theoretical research program (Berger et al. Reference Berger, Conner and Fişek1974), which extended its attention to heterogeneous groups with the development of status characteristics theory, and provided a formalized theory for examining how social structure permeates interaction.
Status characteristics theory is part of the expectations states theory family that attempts to understand how societal structures shape local interactions when people come together to work on joint tasks in groups like juries, committees, judicial panels, creative teams, and other problem-solving task groups. This approach describes how social structural inequalities shape interaction through the concept of the status characteristic. Status refers to “a position in a set of things that are rank-ordered by a standard of value” (Ridgeway & Walker Reference Ridgeway and Walker1995:281). Status characteristics are features of individuals that may differentiate group members and carry societally imbued expectations for competence (e.g., educational attainment). These characteristics include specific characteristics, which carry expectations for specific tasks (e.g., mathematical ability, athleticism) and become salient, or activated in the interaction, when an associated task is present. Other status characteristics are diffuse, carrying general expectations of competence that become salient when they distinguish actors engaged in a task (e.g., gender in a mixed-gender setting; Berger & Webster Reference Berger and Webster2018). Status characteristics theory argues that socially significant characteristics come to organize performance expectations, creating a “power and prestige” order, with those higher in power and prestige having more influence in the group. The status beliefs tied to these characteristics are not necessarily those held by an individual actor (first-order beliefs), but rather cultural constructions regarding what the actor likely believes “most people” believe within a given group or culture (third-order beliefs; Ridgeway Reference Ridgeway2019). Past research has shown that actors’ status evaluations and behaviors are often not based on first-order beliefs, but rather those beliefs attributed to their interaction partners (second-order beliefs; see Ridgeway Reference Ridgeway2019; Troyer et al. Reference Troyer, Younts and Kalkhoff2001; Troyer & Younts Reference Troyer and Younts1997). The theory operates within a specific scope, when: (1) A group is working on a valued task (task-orientation); (2) There is an ability (C*) instrumental to the task on which people can vary (task ability); and (3) Actors believe it legitimate to take each other’s contributions into account to accomplish the task (collective-orientation). Five propositions contain the core arguments of the theory:
1. Expectation advantage leads to power and prestige ordering (expectation advantage)
The theory argues that actors whose task expectations are higher than others’ will be given more opportunities to contribute (action opportunities), produce more task-focused actions (performance outputs), will be given more praise for their contributions (reward actions), and their contributions will have more influence (others more likely to change opinions).
2. To affect expectations, characteristics must be salient (salience).
There are two routes to salience (or activation) in the theory – differentiation and relevance. Diffuse status characteristics (e.g., gender, attractiveness) become salient whenever they differentiate people in the group. Specific status characteristics (e.g., mathematical ability, athleticism) become salient whenever those characteristics are relevant to the task.
3. Once salient, characteristics will affect expectations, unless proved irrelevant (burden of proof)
Characteristics that get activated through differentiation or relevance stay activated, unless there is specific intervention.
4. When new factors become salient, they connect to all other factors already salient, strengthening or contradicting their implications for expectations (structure completion)
This assumption says that we take into account all salient information and integrate it into a connected understanding of status expectations.
5. Negative factors are weighted by relevance and combined; then they are subtracted from the weighted and combined positive elements (combined subsets)
This assumption implements an attenuation principle. It proposes that we combine all negative information and all positive information separately, with each successive piece of similarly valenced information being attenuated. This means that the first piece of positive status information has a bigger effect on our perceptions than the second piece of positive information. Likewise, the first piece of negative status information has a larger impact than the second piece of negative information. When our newly formed creative work group learns that Anne is the supervisor, this information contributes to a higher value of task expectation (status advantage) for Anne. When group members also learn that Anne is the only member with an advanced degree, that information also contributes positively to expected task competence. However, each subsequent high status characteristic after the first will contribute less than the prior piece of high status information. If our work group is a mixed-gender group, the theory would predict that being a woman would lead to lower expectation advantage for Anne. Every subsequent piece of evidence that is directly or indirectly negatively associated with task ability would contribute slightly less information than it otherwise would.
To examine the basic processes articulated by the theory, considerable research in this tradition relies on a standard experimental setting (Berger Reference Berger2014) that isolates theoretical factors to reduce other factors’ influence on status processes. In it, participants interact with unseen partners on a joint decision-making task. Participants usually work with a fictitious partner on a series of fixed choice decisions that require both accuracy and consensus in order to be rewarded. The key measure of position in the “power and prestige order” is how many times the participant changes an answer to match that of their partner. This is a measure of social influence and provides a clean platform to study how status processes operate to shape interpersonal influence. Importantly, however, a key element regulated by this paradigm is the opportunity structure, with actors’ opportunities to contribute to the joint task being highly prescribed within pre-determined pairs of behavior choices. Under the theory, expectation advantage should also lead to receiving more opportunities to contribute, taking more opportunities to contribute, and receiving more praise for contributions. Fully investigating the theory’s core arguments requires studying open interaction, where trading the speaking floor is an interactional accomplishment.
Early research applying expectations states theory outside the standard setting to open interaction tended to aggregate across group types and roles and study distributions of conversational behaviors, like speaker participation (e.g., Balkwell Reference Balkwell1991; Fişek et al. Reference Fişek, Berger and Norman1991). While some research in this tradition addressed process concerns (recognizing that actor behaviors shape the development of interactional hierarchies), this work still often aimed to understand the development of a stable hierarchy through behavioral patterns (called behavior interchange patterns; Fisek et al. Reference Fisek, Berger and Norman1991) or how these exchanges may lead to further status structure completion through observation (Skvoretz & Fararo Reference Skvoretz and Fararo1996) while ultimately comparing the structure with aggregated outcomes. Other group processes researchers called for greater integration of insights from conversation analysis about the regularity of certain forms of conversational exchange and used event history approaches to preserve the sequential nature of conversational actions and the influence of conversational histories while examining status processes (e.g., Cannon et al. Reference Cannon, Robinson and Smith-Lovin2019; Okamoto & Smith-Lovin Reference Okamoto and Smith-Lovin2001; Robinson & Smith-Lovin Reference Robinson and Smith-Lovin1990, Reference Robinson and Smith-Lovin2001). These approaches, however, faced new challenges (Gibson Reference Gibson2008) – (1) the methodological difficulty of examining nested sequential data and (2) the relatively limited theoretical integration of conversation analytic insights into quantitative research on small group interactions. These are challenges that can be addressed with relational event modeling.
The challenge to researchers interested in integrating deep structure, emergence, and permeation lies now at the level of theoretical construction. We argue that the ingredients for constructing such a theoretical model are available at the intersection of the expectation states research program’s formal theoretical structure, relational events’ network theory insights and modeling techniques, and conversation analysis’ in-depth insights into the process of open interaction. From here, we introduce central components of the relational event approach and construct the initial conceptual bridges needed to integrate these different approaches to conversational interactions.
3. Relational events as resource, challenge, and bridge
Relational event models (Butts Reference Butts2008; Butts & Marcum Reference Butts and Marcum2017; DuBois et al. Reference DuBois, Butts, McFarland and Smyth2013) focus on the connections between events and actors within an interaction at the event level and as a sequence providing a solution to many historical difficulties of studying open group interaction. The relational event framework views interaction as a series of discrete interactional events involving a sender, receiver, type of action, and timing of the event and situates theory as informing the set of possible events and the hazards relating to these events (Butts and Marcum Reference Butts and Marcum2017). Factors impacting these events are often referred to as Sequential Structural Signatures (SSS) and include the impacts of past relational events (e.g., inertia, reciprocation), actor attributes (e.g., qualities of senders/receivers), and exogenous factors (e.g., friendship, trust between particular members; Pilny et al. Reference Pilny, Schecter, Poole and Contractor2016). Relational event researchers often focus on the endogenous processes that shape the moment-to-moment structure of the interaction and how these processes further relate to actor attributes and exogenous factors – with the outcomes often highlighting how these factors collectively impact the event level likelihoods of sender/receiver ties.
With teams often serving as the subject of study for researchers using relational event models (e.g., Butts Reference Butts2008; Leenders et al. Reference Leenders, Contractor and DeChurch2016; Pilny et al. Reference Pilny, Schecter, Poole and Contractor2016; Quintane et al. Reference Quintane, Conaldi, Tonellato and Lomi2014; Schecter et al. Reference Schecter, Pilny, Leung, Poole and Contractor2018), researchers implementing relational event models have highlighted issues with other theoretical traditions that echo the challenges facing expectation states researchers working in open-interaction groups, our current interest in further theory development, and the goal of extending current frameworks to account for event-level processes. Leenders et al. (Reference Leenders, Contractor and DeChurch2016) provide a critique of existing theories on team effectiveness highlighting issues like the implicit assumptions of homogeneity over time within theories with the consequence that “variance across time is collapsed into a static summary indicator…” (pp. 95) and the limitations this can place on hypothesis construction that involves evolution or the emergence of structures. Schecter et al. (Reference Schecter, Pilny, Leung, Poole and Contractor2018) argue that relational events allow for the development of new theory for understanding team dynamics and that the basis of such theory should be at the level of the interactional event. Schecter and colleagues operationalized behaviors leading to hierarchy and centralization and examined how processual indicators of these factors influenced coordination and information sharing in a game scenario involving group interactions. This work demonstrated the strengths of process-focused theorizing about emergent states. They concluded by pointing out that theoretical formulations at the process level can help guide interventions that shape norms of behavior at the process level within groups and teams. Both Leenders et al. (Reference Leenders, Contractor and DeChurch2016) and Schecter et al. (Reference Schecter, Pilny, Leung, Poole and Contractor2018) also noted that a central place to look for theory application may involve the coding of different types of action (like Bales’ IPA Coding; Bales Reference Bales1950) relevant to the theory. We explore potential implications of making such distinctions for the utilization of Expectation States and Status Characteristics Theory in relational event models in our proposed theoretical integration.
Expectation States Theory driven examinations of permeation have been conducted by scholars in the tradition as well. Ben Gibson and colleagues (Gibson et al. Reference Gibson, Hoffman, La Fleur and Buchler2021) highlighted the effects of permeation and its relationship with endogenous effects (local impacts of past interactional processes) in email communications. The study included markers of formal positions (like military rank and experience) and examined how these markers impact the sending, receiving, and speed of communications. They found support for permeation effects in the likelihood of higher ranked individuals both sending and receiving emails from others and a small increase in the speed of response. Notably, the effects of endogenous processes far outweighed the permeation effects. While this finding is not particularly surprising given other research in the paradigm has found similar results, the difference in effect sizes may be partly due to the nature of the relationship exogenous processes (permeation) and endogenous processes (deep structure) in the interaction identified by researchers using an expectation states focused approach.
Using longitudinal mixed-model logistic regressions, Cannon et al. (Reference Cannon, Robinson and Smith-Lovin2019) found that gender differences in the odds of interruption events would disappear when cumulative effects of past interruptions (endogenous effects) were included, but also found that the history of being interrupted or overlapped in the interaction mediated the effect of gender on interruptions. This illustrates how the influence of actor attributes (like gender or rank) may be reproduced through endogenous patterns, so that structures brought into interactions then emerge as state-based manifestations after interaction like the processes described by Schecter, et al., 2017. However, this relationship remains undertheorized. In the following section, we outline a general perspective on interactional events and use the general structure of a relational event (sender, receiver, type of action, and time) to construct a theoretical bridge for researchers interested in including status processes in relational event models and provide a base-line construct for formalized modeling of status as a process in open interaction groups.
4. Reconciling and expanding insights on conversational structures
Like the theories discussed by Leenders et al. (Reference Leenders, Contractor and DeChurch2016) and Schecter et al. (Reference Schecter, Pilny, Leung, Poole and Contractor2018), expectations states theory and status characteristics theory operate as state-focused theories. Expectations states theory provides a basic outcome state structure for homogeneous groups and provides a formalized theoretical explanation for how some actor attribute SSS’s get “into” and emerge from interactions in the form of status characteristics theory – while not fully addressing the interactional processes between permeation and emergence. We propose the first steps toward theoretical integration with a theoretical extension to the expectation states theoretical research program that allows for direct examination of permeation and emergence in open interaction processes at the event level – accounting for the consequential nature of the deep structure of interaction itself.
4.1 Elaborating the structure of conversational events
We begin by incorporating Butts’ (Reference Butts2008) components of a relational event (sender, receiver, type of action, and timing) and behavioral patterns from expectation states research (e.g., Fisek et al. Reference Fisek, Berger and Norman1991) into a common distinction between forms of interactional structures found in conversation analysis and related work (see Gibson Reference Gibson2000, Reference Gibson2008; Hutchby & Wooffitt Reference Hutchby and Wooffitt2008; Schegloff Reference Schegloff2007b; Zimmerman Reference Zimmerman, Antaki and Widdicombe1998) to construct an elaborated description of the event space within interaction. We begin with an example interaction: Returning to our working example introduced at the beginning of the paper, Anne, Charlie, and Fabian are meeting face-to-face to make decisions about a component of their project. Anna (sender) opens the meeting by directing the group (receiver) to provide reports of their work thus far (type of action). Charlie (sender) takes up the floor and provides a report (type of action) directing his speech to Anna (receiver). Anna retakes the floor (sender) asking Charlie (receiver) a question (type of action) and Charlie (sender) answers (type of action) Anna (receiver) directly. Anna (sender) then asks Fabian (receiver) for his thoughts on Charlie’s answer (type of action) and Fabian (sender) replies to the group (receiver) with an alternative suggested answer (type of action). Charlie (sender) replies to Fabian (receiver) asking for clarification on the suggestion (type of action). Fabian (sender) clarifies his suggestion (type of action) directly to Charlie (receiver). Charlie (sender) then asks an additional question (type of action) to Fabian (receiver) which Fabian (sender) answers (type of action) directly to Charlie (receiver). Charlie (sender) then amends his original response (type of action) directing the turn to Anna (receiver). Anna (sender) then directs (type of action) Fabian (receiver) to provide his report.
In the interaction described, the group is coordinating the content of their work through performance outputs (task-focused types of actions) like providing information, asking for information, evaluating suggestions and answers, etc. These actions were likely influenced by the status positions of the three group members (e.g., Anna providing directives and receiving compliance). The group members were also, however, coordinating the transitions between turns - with Anna speaking to the group, receiving turns back from Charlie, and shifting the attention from Charlie to Fabian. When Charlie took the floor after Fabian’s group-directed turn, Anne waits until the repeated direct exchanges between the other two are complete to reenter the conversation having received a turn from Charlie. The turn structure did not provide Anne privileged floor access over the course of the interaction (e.g., few turns due to sequence of reciprocal turns between Charlie and Fabian despite high initial participation opportunities) though once an opportunity to act emerged, Anne performed a high-status action (giving direction to Fabian). Conversational norm structures like turn-taking norms (Sacks et al. Reference Sacks, Schegloff and Jefferson1978), conversational sequencing (Schegloff Reference Schegloff2007), past relational events/endogenous effects (e.g., Gibson et al. Reference Gibson, Hoffman, La Fleur and Buchler2021; Pilny et al. Reference Pilny, Schecter, Poole and Contractor2016), and interactional roles (e.g., Cannon et al. Reference Cannon, Robinson and Smith-Lovin2019; Gibson Reference Gibson2003) constrained opportunities to participate (see Gibson Reference Gibson2000 for a comprehensive discussion of this topic). Successfully working on their collective project required coordinating the relational structure (sender, receiver) and organizing the content of the interaction to accomplish group goals (task-oriented types of action like providing/assessing suggestions and information, etc.). The effects of status on these two dimensions of the interaction process are likely different: with status (and potentially other forms of actor attributes) primarily shaping the content dimension of the interaction involving types of action like performance outputs while interactional norms, past relational events, and endogenous processes involving the determination of senders and receivers. The question is how do these two processes intersect and influence one another in ways that begin with permeation and end with emergent inequalities that reflect that permeation process? We now turn our attention to a proposed theoretical system that incorporates both dimensions of conversation organization.
4.2 Theorizing expectations for turn structure
For the purposes of describing a theoretical process parallel to the status organizing process in Status Characteristics Theory, we divide the event space of a relational event formation process into our two separate, though interconnected dimensions: a coordination dimension and a content dimension (depicted in Figure 1). Understanding where these dimensions come together and diverge provides opportunities to articulate how deep conversational structure intersects with social structure (permeation) and is reproduced within interactional settings (emergence). We depict the two dimensions (content and coordination) as separate regions of the figure with event inputs (downward arrows) connecting to potential events from organizing/prioritizing processes and event outputs (upward arrows) connecting the realized event back to the organizing/prioritizing processes which then inform the inputs for the next potential events to demonstrate the relationship between our theoretical extension and relational events. We conceive this basic two-part interaction structure (content and coordination) to be more general than our present usage (applicable to other theoretical processes), as noted earlier, but narrow our focus here to our proposed status and turn organization theory in Figure 1 for the purposes of coherence.

Figure 1. Conceptualization of interaction process.
We situate Status Characteristics Theory and the status organizing process in the Content Dimension of our diagram, focusing on the accomplishment of group tasks through performance outputs (action types related to the completion of the task). This process involves the combination of status characteristics (actor attributes that carry cultural expectations for competence at task completion that become salient in the situation based upon either differentiation or relevance as described in our overview) as well as status related behaviors (like behavior interchange patterns) within the situation itself that further differentiate the status structure. New status information from such sources can be incorporated into the extant power structure once introduced (status completion).
The Coordination Dimension presents our parallel construct, focusing on the maintenance of the interaction. We argue that event formulations (sender and receiver combinations maintaining a cohesive interaction process) involve the development of a hierarchy of potential senders and receivers (an interaction priority order to build from Goffman’s (Reference Goffman1983) term) produced through an event prioritization process that incorporates expectations for the interactional structure based on the current interaction history in a way that mirrors the status organizing process from Status Characteristics Theory.
Event Formulation relies on what we, following past research (e.g., Cannon et al. Reference Cannon, Robinson and Smith-Lovin2019; Gibson Reference Gibson2003; see Zimmerman Reference Zimmerman, Antaki and Widdicombe1998 for a similar concept in "Discourse Identities") call interactional role positions: relational positions (e.g., current sender or current receiver) situated within the ongoing events (endogenous processes) of an interaction that carry with them normative expectations about the structural organization of subsequent events. Interactional role positions can carry expectations relating to subsequent senders, receivers, or both. Position shifts occurring through the realization of relational events provide input that updates the relational positions of actors - event to event. An interactional role position is possessed by a given actor so long as the position differentiates between two or more actors and the actor remains in the relational position tied to the normative expectations. The event prioritization process is influenced indirectly by the status organizing process through a general prioritization of actors perceived to contribute more to successful task completion (performance output prioritization).
Figure 1 provides a general presentation of the parallel processes. We begin with the inputs for initial potential events. The initial status organizing process incorporating information from status characteristics provides potential performance outputs (types of action) and an initial event prioritization process (not shown due to space) provides event formulations (senders and receivers) for the initial potential events, incorporating information from the status organizing process through performance output prioritization (permeation). The realized event then provides relevant output for both the status organizing process (status related behaviors) and the event prioritization process (position shifts) which is incorporated into the subsequent inputs provided through these processes for the next potential events.
This formulation provides a description of the process of permeation and accounts for the impacts of actor attributes and (potentially) exogeneous effects on relational events. We distinguish between factors that impact specific types of actions performed and the determination of sender and receiver pairings. Status Characteristics Theory primarily takes as its point of focus the performance of task-relevant types of actions. We reflect this in the positioning of the status organizing process within the Content Dimension of our structure. We further argue that interactional role positions tied to prior relational events/endogenous processes are the central driving focus in the organizing of sender and receiver pairings with status processes, providing for a limited impact of status through a general performance output prioritization contribution to the event prioritization process operating through the enactment of normative rules and interactional processes.
We formulate our theoretical process in a structure that operates in conjunction with the status organizing process of Status Characteristics Theory to describe how status characteristics permeate the interactional setting. Our process-focused extension to the Expectation States theoretical program involves two interconnected interaction systems, one centering on the content of the interaction (where status processes directly tie to performance outputs) and a coordination process (involving the interaction of status characteristics with systems of conversational norms that more directly guide the flow of the interaction itself). With our baseline two-dimensional construction of the interaction defined, we describe how these new concepts fit into the formalized graph models found in Expectation States Theory.
5. Formalizing a processual model of status and permeation
Expectation states theory uses graph-theoretic mathematical models (called S-graphs) to represent the logic of the status organizing process (Berger et al. Reference Berger, Fişek, Norman and Zelditch1977). The status organizing process is the process of moving from observations of features and actions of individuals in a group to assessments of their competence (or status expectations). These graphs are combined with empirically grounded path weights from prior research (Fişek et al. Reference Fişek, Norman and Nelson-Kilger1992) and conventions about how different types of status characteristics, behavior patterns, and other features of the interaction are represented to generate predictions about the outcomes of interactions within a given group structure. We utilize the logic of the status organizing process to encompass the organization of the event prioritization process and interaction priority order. The extension can be visualized in the graph-theoretic modeling component of expectation states theory as seen in the three graphs included in Figure 2. Graph 1 provides an example of a simple S-graph in the state-based form of the theory while Graphs 2 (sender) and 3 (receiver) present graphs that account for the event prioritization process and the construction of event formulations. For the sake of simplicity of interpretation and explanation, we limit the information provided to single characteristics in the demonstration graphs.

Figure 2. Example of graph models for event sequence.
Figure 2 (Graph 1) depicts the status organizing process in a three-person task interaction between a man and two women. Imagine a man (
![]() $a_{1}$
) and two women (
$a_{1}$
) and two women (
![]() $a_{2}$
and
$a_{2}$
and
![]() $a_{3}$
) working together on a committee report in a culture that generally deems men as higher status than women.
$a_{3}$
) working together on a committee report in a culture that generally deems men as higher status than women.
Expectation states are expectations for task success
![]() $T(\!+\!)$
or failure
$T(\!+\!)$
or failure
![]() $T(\!-\!)$
. According to the theory, diffuse status characteristics
$T(\!-\!)$
. According to the theory, diffuse status characteristics
![]() $D(\!\pm\!)$
, such as gender, lead to generalized impressions of competence
$D(\!\pm\!)$
, such as gender, lead to generalized impressions of competence
![]() ${\unicode[Arial]{x0393}} (\!\pm\!)$
, which in turn lead to expectations about ability at the immediate task
${\unicode[Arial]{x0393}} (\!\pm\!)$
, which in turn lead to expectations about ability at the immediate task
![]() $C*(\!\pm\!)$
, which lead to expectations for successful performance on the task
$C*(\!\pm\!)$
, which lead to expectations for successful performance on the task
![]() $T(\!\pm\!)$
. So, if ‘writing a committee report’ is understood as a gender-neutral task, we would not expect the actors to automatically presume a direct relationship between gender and task performance. Rather, we might expect that the actors may associate higher general competence with the man which then would translate into higher expectations for quality/important contributions on the joint task. Following this process in Figure 2 (Graph 1), we would say that the actors
$T(\!\pm\!)$
. So, if ‘writing a committee report’ is understood as a gender-neutral task, we would not expect the actors to automatically presume a direct relationship between gender and task performance. Rather, we might expect that the actors may associate higher general competence with the man which then would translate into higher expectations for quality/important contributions on the joint task. Following this process in Figure 2 (Graph 1), we would say that the actors
![]() $a_{1}$
,
$a_{1}$
,
![]() $a_{2}$
and
$a_{2}$
and
![]() $a_{3}$
possess differentially valued states of diffuse characteristic D (gender), with the value of man
$a_{3}$
possess differentially valued states of diffuse characteristic D (gender), with the value of man
![]() $D(\!+\!)$
being positively related to a generalized expectation state
$D(\!+\!)$
being positively related to a generalized expectation state
![]() and the value of woman
and the value of woman
![]() $D(\!-\!)$
being positively related to
$D(\!-\!)$
being positively related to
![]() ${\unicode[Arial]{x0393}} (\!-\!)$
through the salience assumption, because both men and women are present in the interaction. By convention, these diffuse states of D also negatively connect to each other – possession of one state (being a man) negatively relates to possession of the other (being a woman). Generalized expectation states
${\unicode[Arial]{x0393}} (\!-\!)$
through the salience assumption, because both men and women are present in the interaction. By convention, these diffuse states of D also negatively connect to each other – possession of one state (being a man) negatively relates to possession of the other (being a woman). Generalized expectation states
![]() $(\!\pm\!)$
are automatically linked to instrumental task ability C* unless something in the situation interferes with that link (the burden of proof assumption). The logic behind this graph serves as our baseline for the coordination dimension graphs for determining senders and receivers of turns depicted in Graphs 2 and 3 of Figure 1.
$(\!\pm\!)$
are automatically linked to instrumental task ability C* unless something in the situation interferes with that link (the burden of proof assumption). The logic behind this graph serves as our baseline for the coordination dimension graphs for determining senders and receivers of turns depicted in Graphs 2 and 3 of Figure 1.
5.1 Expanded graphical representation for events
As a graph model, we can represent the interaction priority order and its relationship with the power and prestige order as a nested structure of S-graphs that are tied to a particular relational event. This includes a standard S-graph for performance outcome expectations
![]() $T(\!\pm\!)$
and a pair of graphs representing expectations for sending an action or receiving an action during the next relational event. These two new graphs account for the impact of factors influencing performance outcome expectations
$T(\!\pm\!)$
and a pair of graphs representing expectations for sending an action or receiving an action during the next relational event. These two new graphs account for the impact of factors influencing performance outcome expectations
![]() $T(\!\pm\!)$
in their structure, but do not directly tie to
$T(\!\pm\!)$
in their structure, but do not directly tie to
![]() $T(\!\pm\!)$
in the graph structure (subsequently not directly impacting performance outcome expectations). Thus, for a given relational event, we produce three separate expectation sets: performance expectations following status characteristics and expectation states theory (graph connecting to
$T(\!\pm\!)$
in the graph structure (subsequently not directly impacting performance outcome expectations). Thus, for a given relational event, we produce three separate expectation sets: performance expectations following status characteristics and expectation states theory (graph connecting to
![]() $T(\!\pm\!)$
), an action priority structure representing expectations for taking the floor or acting next in the interactional sequence (graph connecting to
$T(\!\pm\!)$
), an action priority structure representing expectations for taking the floor or acting next in the interactional sequence (graph connecting to
![]() $A(\!\pm\!)$
), and a receiving priority structure for potential receivers of events (graph connecting to
$A(\!\pm\!)$
), and a receiving priority structure for potential receivers of events (graph connecting to
![]() $R(\!\pm\!)$
). We can consider the graph connecting to
$R(\!\pm\!)$
). We can consider the graph connecting to
![]() $T(\!\pm\!)$
as predictive of task-focused types of actions while the graphs connecting to
$T(\!\pm\!)$
as predictive of task-focused types of actions while the graphs connecting to
![]() $A(\!\pm\!)$
and
$A(\!\pm\!)$
and
![]() $R(\!\pm\!)$
are predictive of the senders and receivers of relational events respectively.
$R(\!\pm\!)$
are predictive of the senders and receivers of relational events respectively.
The full set of graphic models presented in Figure 2 represent the interaction priority structure for a single turn transition – specifically, Actor 2 (
![]() $a_{2}$
) just directed a turn to Actor 1 (
$a_{2}$
) just directed a turn to Actor 1 (
![]() $a_{1}$
) while Actor 3 (
$a_{1}$
) while Actor 3 (
![]() $a_{3}$
) served as only an observer of the previous turn. Subsequent events would require a reformulated structure that accounts for changes in interactional role positions and any changes to the expectation structure due to the actions occurring during the relational event for which the present graphs were constructed.
$a_{3}$
) served as only an observer of the previous turn. Subsequent events would require a reformulated structure that accounts for changes in interactional role positions and any changes to the expectation structure due to the actions occurring during the relational event for which the present graphs were constructed.
5.2 Expectation states graph structure (graph 1)
Figure 2’s first graph was described in the previous section, presenting the three-person status structure with a single diffuse characteristic (
![]() $D$
) present. Recalculation of this structure after each event allows us to account for potential changes and shifts in the expectation structure that then also impact the interaction priority order for subsequent relational events.
$D$
) present. Recalculation of this structure after each event allows us to account for potential changes and shifts in the expectation structure that then also impact the interaction priority order for subsequent relational events.
5.3 Action priority structure (graph 2)
The second graph presents the interaction priority order structure for potential senders - the action priority expectations for a given event
![]() $A(\!\pm\!)$
. We present a single interaction role position
$A(\!\pm\!)$
. We present a single interaction role position
![]() $O$
in the graph representing “current speaker’s target” with subsequent possession of “rights” to take the floor once the current speaker finishes their utterance. Since the previous turn involved Actor 2 (
$O$
in the graph representing “current speaker’s target” with subsequent possession of “rights” to take the floor once the current speaker finishes their utterance. Since the previous turn involved Actor 2 (
![]() $a_{2})$
directing speech to Actor 1 (
$a_{2})$
directing speech to Actor 1 (
![]() $a_{1}$
),
$a_{1}$
),
![]() $a_{1}$
has a line connecting them to
$a_{1}$
has a line connecting them to
![]() $O(\!+\!)$
. The role position provides direct expectation for who will take the following turn at talk (thus the next path line directly connects
$O(\!+\!)$
. The role position provides direct expectation for who will take the following turn at talk (thus the next path line directly connects
![]() $O$
to
$O$
to
![]() $A$
) leading to a much shorter path construction than seen for the diffuse status characteristic in the breakdown of Graph 1 (Fişek et al. Reference Fişek, Norman and Nelson-Kilger1992; describes the logic of path length construction: Paths of shorter lengths (2 or 3) involve more direct inferences where longer path lengths involve indirect inferences moving through more generalized expectations like the example of gender as a diffuse status characteristic described previously). Like for the diffuse status characteristic in Graph 1, a dimensionality relation connects
$A$
) leading to a much shorter path construction than seen for the diffuse status characteristic in the breakdown of Graph 1 (Fişek et al. Reference Fişek, Norman and Nelson-Kilger1992; describes the logic of path length construction: Paths of shorter lengths (2 or 3) involve more direct inferences where longer path lengths involve indirect inferences moving through more generalized expectations like the example of gender as a diffuse status characteristic described previously). Like for the diffuse status characteristic in Graph 1, a dimensionality relation connects
![]() $O(\!+\!)$
and
$O(\!+\!)$
and
![]() $O(\!-\!)$
meaning that
$O(\!-\!)$
meaning that
![]() $a_{1}$
would have positive paths of lengths 2 and 3 while
$a_{1}$
would have positive paths of lengths 2 and 3 while
![]() $a_{2}$
and
$a_{2}$
and
![]() $a_{3}$
(as non-targets), would have negative paths of lengths 2 and 3. We incorporate the expectation states structure (Graph 1) as well, with
$a_{3}$
(as non-targets), would have negative paths of lengths 2 and 3. We incorporate the expectation states structure (Graph 1) as well, with
![]() $C^{*}$
connecting to
$C^{*}$
connecting to
![]() $E$
which then connects to
$E$
which then connects to
![]() $A(\!\pm\!)$
, providing a path for status structures to influence the interaction priority order.
$A(\!\pm\!)$
, providing a path for status structures to influence the interaction priority order.
![]() $E$
represents performance output prioritization from Figure 1 – generalized expectations that those estimated to provide more through their contributions are given greater priority in the turn structure, in essence representing permeation in these structures. This path through
$E$
represents performance output prioritization from Figure 1 – generalized expectations that those estimated to provide more through their contributions are given greater priority in the turn structure, in essence representing permeation in these structures. This path through
![]() $E$
also means that the path lengths for status characteristics and similar constructs will be one step longer (path lengths of 5 and 6) than when estimating expectations for task contributions (path lengths of 4 and 5). It is also important to note that
$E$
also means that the path lengths for status characteristics and similar constructs will be one step longer (path lengths of 5 and 6) than when estimating expectations for task contributions (path lengths of 4 and 5). It is also important to note that
![]() $A(\!\pm\!)$
does not directly connect to
$A(\!\pm\!)$
does not directly connect to
![]() $T(\!\pm\!)$
, which we leave in the graph via the dotted line for demonstration. This represents the previous assertion that interactional role positions and the interaction priority order do not directly impact the power and prestige order.
$T(\!\pm\!)$
, which we leave in the graph via the dotted line for demonstration. This represents the previous assertion that interactional role positions and the interaction priority order do not directly impact the power and prestige order.
5.4 Receiving priority structure (graph 3)
Figure 2’s final graph provides a similar representation to Graph 2, but instead of including expectations regarding senders, (
![]() $O(\!\pm\!))$
represents the example interactional role position “involved actor” seen in our meeting between Anna, Charlie, and Fabian. Thus, the Receiving Priority structure provides positive paths to O for
$O(\!\pm\!))$
represents the example interactional role position “involved actor” seen in our meeting between Anna, Charlie, and Fabian. Thus, the Receiving Priority structure provides positive paths to O for
![]() $a_{1}$
(previous turn’s target) and
$a_{1}$
(previous turn’s target) and
![]() $a_{2}$
(previous turn’s speaker) while
$a_{2}$
(previous turn’s speaker) while
![]() $a_{3}$
(uninvolved in previous turn) possesses negative paths. We retain the impact of the status structure through performance output prioritization (E) like we saw in our formulation for
$a_{3}$
(uninvolved in previous turn) possesses negative paths. We retain the impact of the status structure through performance output prioritization (E) like we saw in our formulation for
![]() $A(\!\pm\!)$
and combine this with interactional role positions relating to who one “should” speak to rather than who “should” take the floor. In all, this structure presents the priorities for subsequent potential receivers for the upcoming event, accounting for interactional role positions and the relative impact of the existing status structure.
$A(\!\pm\!)$
and combine this with interactional role positions relating to who one “should” speak to rather than who “should” take the floor. In all, this structure presents the priorities for subsequent potential receivers for the upcoming event, accounting for interactional role positions and the relative impact of the existing status structure.
6. Calculating expectations
The diagrams presented in Figure 2 can be used to calculate aggregated expectation states for each actor using empirically grounded strength values assigned to each path and multiplied along the path by the sign of the relation. Accordingly, the path length determines the degree of relative influence the characteristic will have on one’s aggregated expectations for self and alter, with longer paths having a smaller impact on the aggregated expectation state compared to a shorter path (Berger et al. Reference Berger, Fişek, Norman and Zelditch1977). Table 1 presents path strength values for paths of different lengths (Fişek et al. Reference Fişek, Norman and Nelson-Kilger1992). We will introduce the calculations by demonstrating the original expectation states calculations before discussing how these may be adapted for use at the event level.
Table 1. Path strength by graph model path length

According to the basic expectation assumption, the relative position of the actors in the power-and-prestige order is directly related to their expectation advantage, or the difference between their aggregated expectation states and those of a given alter. To calculate aggregated expectation states, we use S-graphs to diagram the involvement of all characteristics (diffuse and specific) salient in the interaction (through relevance or differentiation respectively) as seen in Figure 2 Graph 1. Equations 1 through 3 are used to calculate aggregated expectations (
![]() $e_{x})$
for actor
$e_{x})$
for actor
![]() $x$
where
$x$
where
![]() $f(i)$
is a function representing the strength of a path of length
$f(i)$
is a function representing the strength of a path of length
![]() $i$
(see Table 1 for values from Fişek et. al. Reference Fişek, Norman and Nelson-Kilger1992). Following the combined subsets assumption, we separately aggregate the expectations states from the positive paths and from the negative paths included in the graph model for the given actor (
$i$
(see Table 1 for values from Fişek et. al. Reference Fişek, Norman and Nelson-Kilger1992). Following the combined subsets assumption, we separately aggregate the expectations states from the positive paths and from the negative paths included in the graph model for the given actor (
![]() $x$
). Positively valued paths (paths connecting
$x$
). Positively valued paths (paths connecting
![]() $x$
positively to T(+) or negatively to T(−)) are first combined with other positive paths (
$x$
positively to T(+) or negatively to T(−)) are first combined with other positive paths (
![]() $e_x^+$
) and likewise negative paths (paths connecting
$e_x^+$
) and likewise negative paths (paths connecting
![]() $x$
positively to T(−) or negatively to T(+)) with other negative paths (
$x$
positively to T(−) or negatively to T(+)) with other negative paths (
![]() $e_{x}^{-})$
. The actors’ aggregated expectations (
$e_{x}^{-})$
. The actors’ aggregated expectations (
![]() $e_{x})$
are equal to the sum of the positive and negative path values.
$e_{x})$
are equal to the sum of the positive and negative path values.
For example, following Figure 2 (Graph 1),
![]() $a_{1}$
possesses two positively valued paths through
$a_{1}$
possesses two positively valued paths through
![]() $D$
(one of length 4 and one of length 5, the latter due to the negative connection between D(+) and D(−)) and no negatively valued paths. To calculate
$D$
(one of length 4 and one of length 5, the latter due to the negative connection between D(+) and D(−)) and no negatively valued paths. To calculate
![]() $a_{1}$
’s aggregated expectations, we would utilize the path strengths for paths of length 4 and 5 from Table 1 (0.1358 and 0.0542 respectively) when calculating
$a_{1}$
’s aggregated expectations, we would utilize the path strengths for paths of length 4 and 5 from Table 1 (0.1358 and 0.0542 respectively) when calculating
![]() $e_{x}^{+}$
for an outcome of
$e_{x}^{+}$
for an outcome of
![]() $e_{x}^{+}$
= 0.1826 and
$e_{x}^{+}$
= 0.1826 and
![]() $e_{x}^{-}$
would equal 0 (as
$e_{x}^{-}$
would equal 0 (as
![]() $a_{1}$
possesses no negatively valued paths) meaning that
$a_{1}$
possesses no negatively valued paths) meaning that
![]() $e_{x}$
= 0.1826. For
$e_{x}$
= 0.1826. For
![]() $a_{2}$
and
$a_{2}$
and
![]() $a_{3}$
, the situation is reversed, as both possess no positive paths for calculating
$a_{3}$
, the situation is reversed, as both possess no positive paths for calculating
![]() $e_{x}^{+}$
(
$e_{x}^{+}$
(
![]() $e_{x}^{+}=0)$
but possess negative paths of length 4 and 5 which would be included when calculating
$e_{x}^{+}=0)$
but possess negative paths of length 4 and 5 which would be included when calculating
![]() $e_{x}^{-}$
(
$e_{x}^{-}$
(
![]() $e_{x}^{-}$
= −0.1826) meaning
$e_{x}^{-}$
= −0.1826) meaning
![]() $e_{x}$
for both both
$e_{x}$
for both both
![]() $a_{2}$
and
$a_{2}$
and
![]() $a_{3}$
would be (−0.1826). An actor’s expectation advantage or disadvantage is simply the difference between the actor’s and an alter’s aggregated expectations.
$a_{3}$
would be (−0.1826). An actor’s expectation advantage or disadvantage is simply the difference between the actor’s and an alter’s aggregated expectations.
Fişek, Berger, and Norman (Fişek et al. Reference Fişek, Berger and Norman1991) introduced a standardized version of expectation advantage for groups of greater than two, referred to as expectation standing (
![]() $s_{i})$
that normalizes the aggregated expectations as a value between 0 and 1 for each group member, with the expectation standings of all members of the group summing to 1.
$s_{i})$
that normalizes the aggregated expectations as a value between 0 and 1 for each group member, with the expectation standings of all members of the group summing to 1.
Equation (4) calculates the expectation standing (
![]() $s_{i})$
for actor
$s_{i})$
for actor
![]() $i$
where
$i$
where
![]() $e_{i}$
represents aggregate expectations (
$e_{i}$
represents aggregate expectations (
![]() $e_{x})$
for actor
$e_{x})$
for actor
![]() $i$
and
$i$
and
![]() $e_{j}$
represents the aggregate expectations (
$e_{j}$
represents the aggregate expectations (
![]() $e_{x})$
for actor
$e_{x})$
for actor
![]() $j$
and
$j$
and
![]() $n$
is equal to the number of interactants. Fişek, Berger, and Norman used expectation standings to predict the distribution of speech acts in open task-group interactions based on the status structure of the group with
$n$
is equal to the number of interactants. Fişek, Berger, and Norman used expectation standings to predict the distribution of speech acts in open task-group interactions based on the status structure of the group with
![]() $s_{i}$
being the predicted proportion of turns taken. Below we generalize these two measures (aggregate expectation states and expectation standing) to predict sending and receiving at the event level.
$s_{i}$
being the predicted proportion of turns taken. Below we generalize these two measures (aggregate expectation states and expectation standing) to predict sending and receiving at the event level.
6.1 Constructing turn-level expectations
To move from making predictions about emergent states at the encounter level to situated predictions at the event level, we distinguish between predictions for sending and predictions for receiving a turn. We can straightforwardly adapt Fişek et al.’s (Reference Fişek, Berger and Norman1991) formulation to construct turn-level predictions for sending a turn by simply adjusting the path lengths included in the (
![]() $e_{x}$
) calculations to reflect Graph 2’s paths to
$e_{x}$
) calculations to reflect Graph 2’s paths to
![]() $A(\!\pm\!)$
then following the formula for
$A(\!\pm\!)$
then following the formula for
![]() $s_{i}$
and limiting
$s_{i}$
and limiting
![]() $n$
in equation (4) to the set of possible senders to calculate a parallel 0 to 1 value of Action Priority Standing. The same process can be performed for Receiving Priority by adjusting path lengths for (
$n$
in equation (4) to the set of possible senders to calculate a parallel 0 to 1 value of Action Priority Standing. The same process can be performed for Receiving Priority by adjusting path lengths for (
![]() $e_{x}$
) to those reflecting in Graph 3’s paths to
$e_{x}$
) to those reflecting in Graph 3’s paths to
![]() $R(\!\pm\!)$
and limiting
$R(\!\pm\!)$
and limiting
![]() $n$
to the set of possible receivers in equation (4) to create a Receiving Priority Standing.
$n$
to the set of possible receivers in equation (4) to create a Receiving Priority Standing.
For the purposes of an initial test of our formalized construction of this proto-theory, we will construct two sets of values using S-Graphs, one set will straightforwardly translate the traditional S-Graphs (representing expectation states’ power and prestige order) into a set of expectation standing values for senders and receivers without incorporating the subgraph design (essentially, we take a path model like Figure 2 Graph 1 and only adjust expectation standings (
![]() $s_{i}$
) for senders and receivers by limiting the potential sets of actors
$s_{i}$
) for senders and receivers by limiting the potential sets of actors
![]() $n$
to those who may take this position at a given time). This model is intended to represent a simple translation of expectation states’ state-based formulation to a process-level analysis – in essence a formalized version of including only status-related actor attributes (and their aggregation based on the theory’s assumptions) in a relational event model. We will compare this with a set of values reflecting the entirety of our proposed model for the construction of an interaction priority order, incorporating a basic set of interactional role positions based on Gibson’s (Reference Gibson2003) observed propensities regarding participation shifts.
$n$
to those who may take this position at a given time). This model is intended to represent a simple translation of expectation states’ state-based formulation to a process-level analysis – in essence a formalized version of including only status-related actor attributes (and their aggregation based on the theory’s assumptions) in a relational event model. We will compare this with a set of values reflecting the entirety of our proposed model for the construction of an interaction priority order, incorporating a basic set of interactional role positions based on Gibson’s (Reference Gibson2003) observed propensities regarding participation shifts.
6.2 Initial test of the model
To test this theoretical construction, we use a set of data involving task-focused triads including either single or mixed sex groups. We focus on turn-taking structures (sender and receiver) and implement the interaction priority order model using interactional role positions for “speaker” and “target” of the concluding event for the calculation of action priority and the “involved actor” position for receiving priority. We compare this model with a standard expectation standing (Fişek et al. Reference Fişek, Berger and Norman1991) model adjusting both models’ possible set of senders and receivers for a given event at time
![]() $t$
based on the following modeling assumptions:
$t$
based on the following modeling assumptions:
1. Only one actor can send an event at a given time (one speaker rule)
2. An event transition occurs when either the sender or the receiver change (events cannot immediately follow themselves; two consecutive utterances from Actor 1 to Actor 2, like replying to a question then following up with one of their own, are treated as a single event as neither the sender nor the receiver have changed)
3. The group (as a unit) may not be the sender of an event, but may be the receiver of events (except when excluded based on assumption 2)Footnote 1
4. An actor may not be both the sender and receiver of the same event (no self-talk)
5. There are no restrictions on possible dyad combinations at the beginning of the interactions or during an event following an exogeneous event (e.g., an actor other than the participants enters the task space and converses with the group momentarily).
6.2.1 Data
The data for this study come from a larger study of authority and interaction in which 72 three-person groups of undergraduates participated in a thirty-minute discussion as a mock-organization. In a design adapted from Johnson (Reference Johnson1993), in each group, there was a randomly-assigned "Supervisor" (male or female) and two same-gender "Assistants" (male or female). Students from introductory sociology courses at a large university in the southern United States volunteered to participate a laboratory study on social creativity. Upon arrival, all participants completed a pretest questionnaire that asked about grade history, work history, and other leadership positions. The questionnaire also contained a brief creativity measure. An experimenter collected the completed questionnaires and left the room for a few minutes. Upon returning, the experimenter explained that past research indicated that the task they would be working on together would benefit if the group had a good leader. In half of the groups, the experimenter went on to say that, “Of course, we have no way of knowing which of you would make the best leader, so we have randomly assigned ____ to be the Supervisor, and ____ and ____ to be Assistants.” This was the low legitimacy manipulation. In the high legitimacy condition, after the same initial explanation, the experimenter went on to say that “Therefore, we have assigned ____ to be Supervisor for this group and ____ and ____ to be Assistants.” Without explaining why, the experimenter told the group that ____ [the assigned supervisor] was the “best suited” for the job. This constituted our authorization of the legitimacy of the Supervisor role. At this point, the experimenter handed badges to the participants and escorted them into the New Ideas Advertising, Inc “board room” that would serve as the site for the rest of the experiment.
We told participants that they were a small, fairly new advertising team that had recently been hired to conduct an advertising campaign for the university. Their task was to write a radio commercial to recruit out-of-state students to the university. To reinforce their assigned roles and the situational context, Supervisors and Assistants were given different “Supervisor” or “Assistant” badges, seated at identity-labeled chairs in the "board room", and worked from separate "Supervisor’s Manual" and "Assistant’s Manual" instruction booklets, respectively. The content of the Supervisor’s Manual and the Assistant’s Manual differed only in that the Supervisor’s Manual informed them that their job was to ensure that their team wrote the best possible commercial and the Assistant’s Manual informed them that they were to assist their Supervisor in creating the best possible commercial. Further, all experimental materials, including a sign affixed to the board room door, scratch paper, ad copy paper, and a sample radio commercial script, were emblazoned with the New Ideas mock company logo. The groups had 20 minutes to write a 15 s commercial. The group discussion during that twenty minutes was videotaped and transcribed. Study procedures were approved by the Institutional Review Board at the second author’s institution. The authors assert that all procedures contributing to this work comply with the ethical standards of the relevant national and institutional committees on human experimentation and with the Helsinki Declaration of 1975, as revised in 2008.
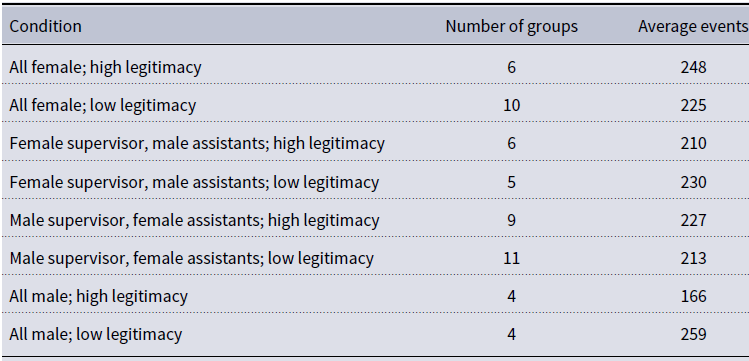
For our initial examination of this theoretical extension, we test the formulation on the 55 three-person experimental task who met the following conditions (a) group members were age 18–26 (4 group exclusions), (b) group members all identified as White or all identified as Black/African American (11 exclusions of mixed race groups), and (c) group members did not already know each other (two group exclusions). These exclusions reduce salient exogenous sources of status other than gender and formal position. Table 2 below shows the number of groups included from each of the eight conditions produced by the experiment’s structure and provides the average number of events per group for each condition.
Table 2. Number of groups per condition and average number of events
6.3 Computed variables
For this initial test of the proposed model, we develop two sets of sender/receiver values. The first set of sender and receiver values only include information from the status organizing process (like Figure 2 Graph 1) to determine path lengths and expectation standing calculations (with turn-level exclusions based on the assumptions stated previously) for senders and receivers. This reflects the relative impact of performance expectations as described in expectation states theory at the turn level with minimal adjustments to the initial state-based theory.
The second set of sender/receiver values represent participant prioritization expectations informing our proposed event formulations as described previously and implement the path models for event prioritization processes for sender (Figure 2 Graph 2) and receiver expectations (Figure 2 Graph 3) and include a base set of interactional role positions based on Gibson’s (Reference Gibson2003) termination, receiving, and targeting propensities to demonstrate basic incorporation of expectations based on previous relational events.
6.4 Status characteristics included in the computations
Based on the eight experimental conditions included in the study, we include the following status characteristics in the calculations of sender expectation standing, receiver expectation standing, sending priority standing, and receiving priority standing.
• Gender: Gender is included in the path models as a diffuse status characteristic in mixed-sex groups where it meets the differentiation salience requirement for diffuse status characteristics. The paths tied to this characteristic when salient are of lengths 4 and 5.
• Formal Position: We also include a status distinction based on the assigned formal group positions of Supervisor or Assistant in all models with Supervisors possessing positive paths and Assistants possessing corresponding negative paths. Such formal positions are treated as diffuse characteristics with paths of lengths 4 and 5 (positive paths for supervisors) in low legitimacy conditions. In the high legitimacy condition (authorization), we assume the experimental procedure removes the indirect link path between the diffuse characteristic (D) and generalized competence (Γ), since our manipulation directly linked the position with competence. This is the same as treating legitimate authority as a specific status characteristic with paths of lengths 3 and 4 connecting them to the task outcome states in high legitimacy conditions.
6.5 Interactional roles
For our initial set of interactional role positions, we build on the three turn-taking patterns described by Gibson (Reference Gibson2000, Reference Gibson2003): the termination propensity, receiving propensity, and targeting propensity. In short, these reflect the following:
1. Termination Propensity: An actor tends to secede the floor at a transition relevant place.
2. Receiving Propensity: An actor targeted by the previous turn will often take the floor.
3. Targeting Propensity: The target of a turn is often an actor involved in the previous event.
Given the central position of these patterns in classic conversation analytic work on turn-taking (Sacks et al. Reference Sacks, Schegloff and Jefferson1978), we assume that these expectations represent instrumental task expectations connected directly to
![]() $A(\!\pm\!)$
or
$A(\!\pm\!)$
or
![]() $R(\!\pm\!)$
. We connect these interactional role positions by paths of 2 and 3 to their respective outcomes.
$R(\!\pm\!)$
. We connect these interactional role positions by paths of 2 and 3 to their respective outcomes.
When determining who speaks next (sender), the termination propensity and receiving propensity (Gibson Reference Gibson2003) reflect two interactional role positions involved in the concluding turn: the concluding speaker and their target. If an actor is the “concluding speaker”, the termination propensity reflects an expectation that the actor will give up the floor after their turn. This provides the “concluding speaker” with negative paths of lengths 2 and 3 and provides “non-speakers” positive paths of equal length. The receiving propensity reflects expectations that the “target” of the concluding turn has priority in taking the floor (sending) during the next turn at talk. Subsequently, the “concluding speaker’s target” (if specified) possesses positive paths of lengths 2 and 3 and “non-targets” possess negative paths of equal length.
To construct the receiving priority for an event, we reference David Gibson’s (Reference Gibson2003) “targeting propensity” to construct another interactional role position: involved actor. We define an “involved actor” as any actor specifically involved in the event concluding at the turn transition. Thus, a targeted (specific receiver) previous turn would provide positive paths to both the sender and receiver of the concluding event (with the “non-targeted actor” possessing negative paths) while an undirected turn would provide these positive paths to only the sender of the concluding event (with both other group members possessing negative paths). We again treat these paths as having lengths of 2 and 3.
6.6 Turn level calculations
Table 3 provides a breakdown of the paths included in each expectation standing, action priority, and receiving priority path model for each relational event. Path models are updated for each event transition over the course of the group interactions. For example, in an all-female group with high authorization, the supervisor sent an undirected turn to the group: the supervisor’s Action Priority structure (Graph 2) for the next event would include positive paths with lengths 4 and 5 due to her formal position as a supervisor and negative paths of length 2 and 3 because she is just completing a turn. However, her Receiving Priority structure (Graph 3) for the upcoming event would include her status advantage positive paths of length 4 and 5 from her supervisor position along with positive paths of lengths 2 and 3 having been the only distinctly “involved” actor in the event presently ending. Both assistants would possess negative paths of lengths 4 and 5 based on their subordinate formal position (applied to both Graph 2 and Graph 3), positive paths as non-speakers during the previous turn of lengths 2 and 3 for expectations of sending the next event and negative paths of lengths 2 and 3 for receiving the next event (as they were not directly involved in the previous turn’s event). This means the supervisor is unlikely to send a second event but is very likely to be the recipient of the next turn.
These aggregated measures include information about actor attributes and past relational events in a single measure and are not as informative as breaking the variables apart for a substantive interpretation of the analysis outcomes. We use these aggregate values here for the purposes of comparing the formalized models from the two theoretical formulations of event level turn structure expectation states. Much like with Expectation States and Status Characteristics Theory, it is not necessary to utilize the formalized aggregated states to work with the theory or generate substantive hypotheses. The discursive structure of the theory could readily inform work with discrete Sequential Structural Signatures and hypotheses based on those variables (a simple example would be considering how actor attributes that are status characteristics mediate or moderate different endogenous processes). The formal theory structure, however, may provide a mechanism for precise hypothesis construction at the event level and could be utilized to construct agent-based simulations.
6.7 Group as receiver
Since we assume the group can receive events, we account for the group’s aggregate expectations
![]() $(e_{x})$
using the mean aggregate expectations of all group members. In essence, we conceptualize the group expectations as a reflection of the performance expectations for the group as a unit. For the performance expectations model (Model 1) this means we include the aggregate expectations based on performance expectations (Figure 2 Graph 1). For the participation priority model, we take the mean aggregate expectations of all group members for
$(e_{x})$
using the mean aggregate expectations of all group members. In essence, we conceptualize the group expectations as a reflection of the performance expectations for the group as a unit. For the performance expectations model (Model 1) this means we include the aggregate expectations based on performance expectations (Figure 2 Graph 1). For the participation priority model, we take the mean aggregate expectations of all group members for
![]() $R(\!\pm\!)$
when no interactional role positions are present (only including the base performance expectation paths found in the top region of the table under “Event Formulations”).
$R(\!\pm\!)$
when no interactional role positions are present (only including the base performance expectation paths found in the top region of the table under “Event Formulations”).
Table 3. Path lengths per condition for performance expectations and event formation models

6.7.1 Analysis
Our analysis compares two models:
• Performance Expectations Model: Model 1 examines the effects of performance expectations (expectation standings) for speakers and receivers given model assumption constraints on possible senders and receivers.
• Event Formulation Model: Model 2 examines the effects of action priority and receiving priority as predictors following our proposed theoretical formulation given model assumption constraints on possible senders and receivers.
For the purposes of parity, we will begin by comparing the two models’ (performance expectations and event formulations) predictions for participation outcomes (proportion of events sent by each actor over the full sequence of events). We then compare the performance expectations-based sender and receiver model to the event formulation sender and receiver model using relational event models.
Table 4 presents the average proportion of turns taken (sender) by Supervisors and Assistants (average of both Assistants) from the data across the eight experimental conditions and predictions based on the sender expectation standings calculations used in the Performance Expectations Model and Event Formulations Model. We use this to examine roughly how the two sets of calculations perform at the level of emergent outcome states. For performance expectations, this is simply the expectation standings of each member. For event formulations, we take the average Action Priority Standing of each member across all possible two-event (
![]() $t-1$
to
$t-1$
to
![]() $t$
) sequences (since our included interactional role positions involved only positions related to
$t$
) sequences (since our included interactional role positions involved only positions related to
![]() $t-1$
). In most cases, the average of the Action Priority Standing values for each actor is closer to the mean proportion of participation observed in each of the conditions. The action priority standing calculations also consistently anticipate less differentiation between the group members, something observed in most conditions of the study. The calculations also reveal a relative level of consistency in overall outcomes despite the inclusion of relatively strong interactional role position paths and the relatively weak path strengths for the status expectations in the Action Priority Standing calculations. Having examined the emergent outcomes as an initial parity test, we move on to the event level examinations.
$t-1$
). In most cases, the average of the Action Priority Standing values for each actor is closer to the mean proportion of participation observed in each of the conditions. The action priority standing calculations also consistently anticipate less differentiation between the group members, something observed in most conditions of the study. The calculations also reveal a relative level of consistency in overall outcomes despite the inclusion of relatively strong interactional role position paths and the relatively weak path strengths for the status expectations in the Action Priority Standing calculations. Having examined the emergent outcomes as an initial parity test, we move on to the event level examinations.
Table 4. Average proportion of turns taken by actor, performance expectation model, and event formation model by experimental condition

6.8 Relational event models
We use the rem command in the relevent package in R (Butts Reference Butts2008) to compare the full set of groups with the full set of nine possible dyadic pairings as the set of possible events. We also provide rem with a supplist file that excludes the event occurring at
![]() $t-1$
(as the coding of events precludes the possibility of repeating the same event without a different event occurring in between). We compare the model fit for these two models. We then model each of the 55 groups individually using rem.dyad (Butts Reference Butts2008) to further assess goodness of fit. Covariates for these models are the same as for the rem models with a structural zero matrix included for each turn to account for the inability of the group to be a “sender” in the model and to exclude the possibility of an event repeating itself without an intervening event of a different type.
$t-1$
(as the coding of events precludes the possibility of repeating the same event without a different event occurring in between). We compare the model fit for these two models. We then model each of the 55 groups individually using rem.dyad (Butts Reference Butts2008) to further assess goodness of fit. Covariates for these models are the same as for the rem models with a structural zero matrix included for each turn to account for the inability of the group to be a “sender” in the model and to exclude the possibility of an event repeating itself without an intervening event of a different type.
The edge lists each included four possible actors (Person 1, Person 2, Person 3, and the group). On a given turn, eight different events were possible, excepting turn 1 or the turn after an exogenous event where nine dyad combinations were possible.
6.8.1 Relational event models
Table 5 contains the results of the two relational event models. Model 1 uses Speaker Expectation Standing (Sender) and Receiver Expectation Standing (Receiver) as predictors. Model 2 uses the event-level Action Priority Standing (Sender) and Receiver Priority Standing (Receiver) as predictors. In addition, for ease of interpretation, we rescale these values to range from 0 to 100 rather than 0 to 1. These models allow us to see the relative efficacy of the event formulation model compared to a model based on performance expectations.
Table 5. Relational event models of performance expectations and event formation
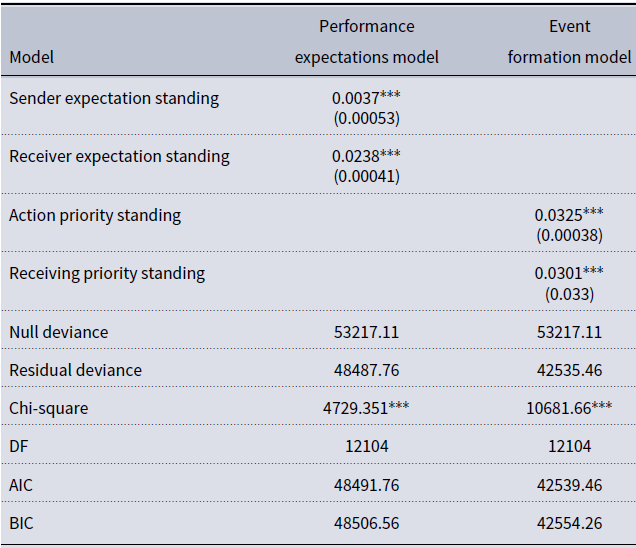
As expected, we find that the models using performance expectations alone provide a poorer fit than models calculated with situated participation priorities for sender and receiver (event formulation model). The coefficients are consistently significant in both models, though the differences between the strength of predictions is notable in the coefficients. These can be translated into likelihood changes per 0.01 change in the original standing values (ranging from 0 to 1) for interpretation (
![]() $e^{(coef.)}$
). The first model shows a weak performance expectation effect for the sender (0.0037; s.d. = 0.00054) and a considerably stronger receiver effect (0.0238; s.d. = 0.00041). Given a baseline set of standings for three actors with the high-status actor having an expectation standing of 0.42 and the subordinates each having equal relative standing at 0.29, this translates to the high-status actor having a 5% greater likelihood of taking the floor and a 72% greater likelihood of receiving a turn. For both senders and receivers, higher relative performance expectations for the actor translates to a higher likelihood of taking (the respective) position in the new relational event. Interestingly, the effect of performance expectations is much stronger for the receiver of the event action than the sender. Status, by itself, may have more of an effect on who someone acts toward than who acts in general (a pattern noted elsewhere as well). This contrasts with the event formulation model where both speaker priority (0.0325; s.d. = 0.00038) and target priority (0.0301; s.d. = 0.00033) are strong predictors with roughly equal effects. Returning to our previous values (0.42, 0.29, 0.29), the higher priority actor would be 135% more likely to take the floor and 115% more likely to receive a turn respectively. The inclusion of interactional role positions and adjustments to the relative weight of status included in the sender and receiver priority standings provides a stronger predictor that is also more consistent across the senders and receivers. Goodness-of-fit values indicate a better overall fit for the event formulation model (Model 2 BIC = 42554.26) compared to the performance expectations model (BIC = 48506.56).
$e^{(coef.)}$
). The first model shows a weak performance expectation effect for the sender (0.0037; s.d. = 0.00054) and a considerably stronger receiver effect (0.0238; s.d. = 0.00041). Given a baseline set of standings for three actors with the high-status actor having an expectation standing of 0.42 and the subordinates each having equal relative standing at 0.29, this translates to the high-status actor having a 5% greater likelihood of taking the floor and a 72% greater likelihood of receiving a turn. For both senders and receivers, higher relative performance expectations for the actor translates to a higher likelihood of taking (the respective) position in the new relational event. Interestingly, the effect of performance expectations is much stronger for the receiver of the event action than the sender. Status, by itself, may have more of an effect on who someone acts toward than who acts in general (a pattern noted elsewhere as well). This contrasts with the event formulation model where both speaker priority (0.0325; s.d. = 0.00038) and target priority (0.0301; s.d. = 0.00033) are strong predictors with roughly equal effects. Returning to our previous values (0.42, 0.29, 0.29), the higher priority actor would be 135% more likely to take the floor and 115% more likely to receive a turn respectively. The inclusion of interactional role positions and adjustments to the relative weight of status included in the sender and receiver priority standings provides a stronger predictor that is also more consistent across the senders and receivers. Goodness-of-fit values indicate a better overall fit for the event formulation model (Model 2 BIC = 42554.26) compared to the performance expectations model (BIC = 48506.56).
To further examine the turn-level accuracy of these models, we analyze each group independently with the same fit method and mirror the present model parameters. Table 6 shows the misclassification rate for both models.
Table 6. Goodness-of-fit statistics for null, performance expectations, and event formation models

The misclassification rate at baseline for eight possible events (as most turns will exclude the event occurring at t-1) would be 87.5%. The performance expectations model improves on this only slightly at 86.2%, revealing that knowing the performance expectations for a given actor actually does little to inform the turn-by-turn structure of the interaction as a whole. The event formulation model improves on this considerably, with a misclassification rate of 66.0%. Figure 3 provides a broader look at the accuracy of the different models. The plot shows the empirical cumulative distribution function for the rank ordering of predicted outcomes by the cumulative percentage of actual events predicted by that point in the rank ordering for each of the 55 groups.

Figure 3. Comparison of model accuracy.
At each speaker-transition, the relational event model rank orders each of the potential state transitions. Figure 3 reveals that the event formulation model predicted the top ranked state at higher rates than the performance expectations model and had a higher cumulative accuracy past the 5th place out of eight possible outcomes. Furthermore, the distribution of cumulative rank values is much tighter across groups for the event formulation model revealing greater consistency in predictions across different groups and group compositions. Of note, the lines for the performance expectations model predictions for low legitimacy groups with a female supervisor and male assistants (L-FMM). In these groups, the performance expectation values across all possible members are equal, leading to more ties between predictions of the different speaker-follower pairings which may truncate the ratings as the rank is determined at the point where a tie between potential outcomes begins. The event formulation model’s values “tie” on fewer occasions overall, which means that ties may differentially inflate the performance expectation model’s ranks. Table 7 provides an aggregated view of these same cumulative ranks, showing the overall trend seen in the graph, with both models performing better than the null model, and the event formulation model outperforming the early rankings of the performance expectations model.
Table 7. Cumulative number and percent of events predicted by models by rank of observed event
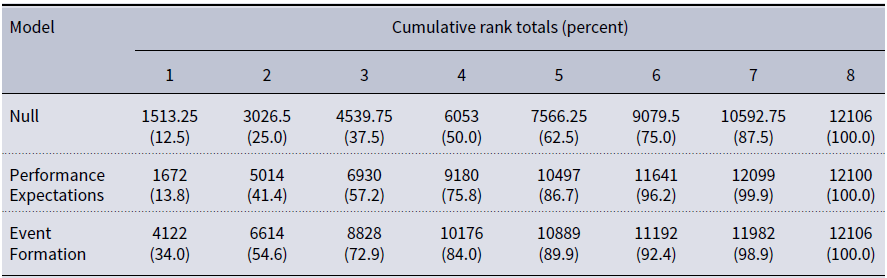
While not overwhelmingly accurate on its own, our initial event formulation model suggests the overall promise for this baseline construction of a process theory extension of expectation states theory. The present model only represents a simple model for turn-taking, not yet accounting for a full array of sequencing processes studied by conversation analysts and relational event researchers, nor the full complement of behavior-based status differentiations studied by group process theorists; both of which are compatible with the theoretical construction and offer opportunities for further theoretical development.
7. Discussion
In pursuit of better explaining the relationship between permeation, the deep structure of conversation, and the emergence of inequalities through the interaction process, we proposed and tested a preliminary theoretical extension for the Expectation States theoretical research program (Berger & Webster Reference Berger and Webster2018) designed to account for the distribution of action opportunities and the turn-taking structure of open interaction groups. We find that constructing a secondary theoretical model centering on the coordination of relational pairings at the event level provides a dynamic structure that can account for shifts in normative speaking rights and targeting preferences amongst members of a task group while maintaining the emergent status inequalities in participation outcomes. The model pulls from relational event and conversation analysis literature to develop a broader model of participation distributions within open interaction settings. The hope is that this model, in its simplest form, can serve as a framework for further work on open interaction groups.
For group processes researchers working with (or interested in working with) open interaction groups, a formal way to account for the intersection of status and process allows for more complex explorations of the interaction setting. For example, noting how the timing of a behavior interchange pattern (Fişek et al. Reference Fişek, Berger and Norman1991) or a status cue (Fişek et al. Reference Fişek, Berger and Norman2005) impacts later accumulation of further behavioral status markers or how the deference shown by other interlocutors in a group may shift given one’s early opportunity structures. Taking the example of the timing of a status cue – one could consider that an early claim to a higher status position would likely lead to higher likelihoods of being targeted by other actors, which then provides additional opportunities for strengthening the claim. It would also be possible to investigate how indicating possession of valued characteristics or possible changes to behavior patterns early during an interaction may serve to challenge status-based inequalities through shaping the normative structures of the interaction itself in ways that favor providing action opportunities to group members in lower status positions.
For researchers studying different Sequential Sequencing Signatures in relational event models, we provide further insight into the relationship between actor attributes (like status characteristics) and sender/receiver dyad outcomes (and types of actions involving coordination like interruptions or specific participation shifts). We argue that examining actor attributes like status characteristics in relational processes may require a greater focus on mediating or moderating processes as well as early events during interaction. For example, under the model we described, the event prioritization process would have included only the status differences between Anna, Charlie, and Fabian for the first relational event. As different endogenous effect patterns accumulate and replicate over the course of the interaction, the effect of Anna initializing the first turn at talk or being slightly more likely to receive the floor early provides the opportunities necessary for, say, a pattern of reciprocity between herself and Charlie to develop. In addition, following extant work discussing process theories in relational events (Leenders et al. Reference Leenders, Contractor and DeChurch2016; Schecter et al. Reference Schecter, Pilny, Leung, Poole and Contractor2018) we believe broader considerations of types of action (Butts Reference Butts2008; Butts & Marcum Reference Butts and Marcum2017) may be a key step forward. We presented the example of expectation states theory’s focus on expectations for performance outputs. If data included content related task coding (like data including sender, receiver, and Bales’ (Reference Bales1950) Interaction Process Analysis Coding or a similar coding system) we may anticipate stronger effects from status characteristics predicting task-focused event types (performance outputs) while sender and receiver pairings remain more closely linked with prior relational events/endogenous process variables with actor attributes primarily impacting sender/receivers through mediating or moderating effects. Further research will be necessary to fully test these expectations and directions.
Relational event modeling (Butts Reference Butts2008) provides researchers examining open interaction with a method that can account for the ongoing, shifting patterns that occur over the course of these types of groups. Accounting for these shifting patterns in theoretical models can provide new avenues for investigation and offers new directions for future research questions (Leenders et al. Reference Leenders, Contractor and DeChurch2016; Schecter et al. Reference Schecter, Pilny, Leung, Poole and Contractor2018). The formalized structure and mathematical framework provided by the expectation states tradition (Berger et al. Reference Berger, Fişek, Norman and Zelditch1977) offers a theoretical toolkit that, if expanded further into a process theory as we begin to here, could serve to construct highly nuanced process hypotheses as the relative impact of a given status position changes or shifts. Echoing Schecter et al.’s (Reference Schecter, Pilny, Leung, Poole and Contractor2018) call for “intervention” focused studies, potential behavioral interventions and their timings could be modeled theoretically and then examined in empirical data. Specifically, by further incorporating interactional role positions tied to interactional patterns into the sender and receiver priority models and incorporating status-relevant behaviors into the expectation states structure in a dynamic way, researchers can better theorize how permeation occurs through interactions between normative interactional structures (endogenous effects) and status characteristics (actor attributes).
We see this work primarily as a starting point, one arguing for further cross-theoretical integration between group processes theories, conversation analysis, and relational events. Expanding the theoretical model presented here will necessarily involve such cross-theoretical work. Potential next steps include incorporating additional status information into the model would be to replicate Fişek, et al. (Reference Fişek, Berger and Norman1991) behavior interchange patterns to differentiate between the two assistants or constructing an evolving status cue pattern using a graded status marker (Melamed Reference Melamed2011) accounting for accumulated participation. Data coded for conversational sequencing (Schegloff Reference Schegloff2007) - the pairing of related conversational behaviors like question/answer, summons/reply, etc. – even into generic first pair-parts (like questions) and second pair-parts (like answers) could provide additional interactional role positions, particularly those whose presence relates directly to the endogenous effects identified by relational event researchers.
Acknowledgements
The authors would like to thank Christopher D. Moore, Toby Ten Eyck, Kris Hutchinson, Alan Boxberger, April Douet, Brenda Bishop, and Kelly Vicknair for help with the data collection and processing. We also thank Ben Gibson for his help to the first author when first learning Relational Event Models. Finally, we are grateful for the thoughtful comments of two anonymous reviewers and the special editors for this issue.
Competing interests
None.
Funding statement
This work was partially supported by Army Research Office Grant W911NF1710509 and W911NF1510180.
Data availability statement
The data and code for replicating the analyses presented here are publicly available here: Cannon, B. C., & Robinson, D. T. (2022, November 23). A Simplest Mathematics of Turn-Taking Replication Materials. Retrieved from osf.io/8hmzj. That OSF project also links to the replication materials for the original data collection: Robinson, D. T. (2022, November 23). Open Group Interaction in a Mock Advertising Agency. Retrieved from osf.io/s5trn.












