Evolution of the cold gas fraction and the star formation history: Prospects with current and future radio facilities

Abstract

It has recently been shown that the abundance of cold neutral gas may follow a similar evolution as the star formation history. This is physically motivated, since stars form out of this component of the neutral gas and if the case, would resolve the long-standing issue that there is a clear disparity between the total abundance of neutral gas and star-forming activity over the history of the Universe. Radio-band 21-cm absorption traces the cold gas and comparison with the Lyman-α absorption, which traces all of the gas, provides a measure of the cold gas fraction, or the spin temperature, T_spin. The recent study has shown that the spin temperature (degenerate with the ratio of the absorber/emitter extent) appears to be anti-correlated with the star formation density, ψ_*, with 1/T_spin undergoing a similar steep evolution as ψ_* over redshifts of 0 ≲ z ≲ 3, whereas the total neutral hydrogen exhibits little evolution. Above z ∼ 3, where ψ_* shows a steep decline with redshift, there are insufficient 21-cm data to determine whether 1/T_spin continues to follow ψ_*. Knowing this is paramount in ascertaining whether the cold neutral gas does trace the star formation over the Universe’s history. We explore the feasibility of resolving this with 21-cm observations of the largest contemporary sample of reliable damped Lyman-α absorption systems and conclude that, while today’s largest radio interferometers can reach the required sensitivity at z ≲ 3.5, the Square Kilometre Array is required to probe higher redshifts.

1. Introduction

Neutral hydrogen (HI) provides the raw material for the formation of stars and so the abundance of this at various redshifts should closely trace the star-forming activity over the history of the Universe. Specifically, the star formation rate density, ψ _*, exhibits a steep climb from z = 0 before peaking at z ∼ 2.5, followed by a steep decline at higher redshifts (Hopkins & Beacom 2006; Burgarella et al. 2013; Sobral et al. 2013; Lagos et al. 2014; Madau & Dickinson 2014; Zwart et al. 2014). However, the mass density of the neutral gas exhibits very little redshift evolution: Over 0 ≲ z ≲ 0.5, where HI 21-cm can be detected in emission (e.g. Fernández et al. 2016), the mass density is Ω_HI ≈ 0.5 × 10⁻³ (Zwaan et al. 2005; Lah et al. 2007; Braun 2012; Delhaize et al. 2013; Rhee et al. 2013; Hoppmann et al. 2015). At higher redshift, where the HI column density is obtained from either space (z ≲ 1.7) or ground (z ≳ 1.7) based observations of damped Lyman-α systems (DLAs, where N _HI ≥ 2 × 10²⁰ cm⁻²),^a the mass density rises to Ω_HI ≈ 1 × 10⁻³, remaining constant up to at least z ∼ 5 (Rao & Turnshek 2000; Prochaska & Herbert-Fort 2004; Rao, Turnshek & Nestor 2006; Curran 2010; Prochaska & Wolfe 2009; Noterdaeme et al. 2012; Crighton et al. 2015; Neeleman et al. 2016). Thus, there is a clear disparity between the star formation density and the neutral gas available to fuel it.

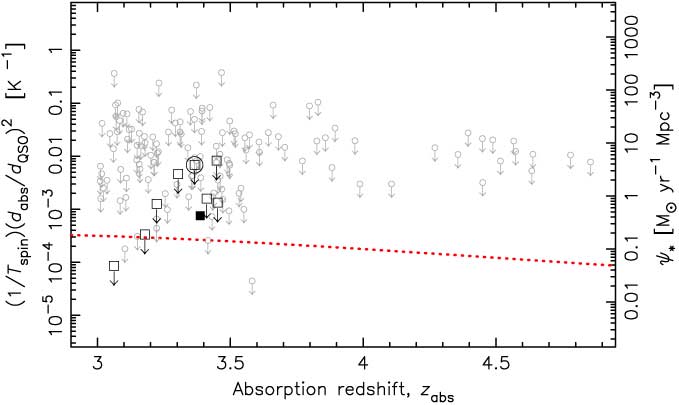
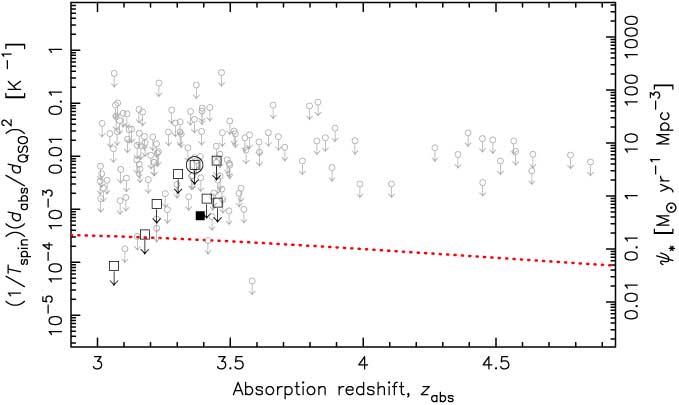
The Lyman-α (λ = 1215.67 Å) transition traces all of the neutral gas, specifically both the cold (CNM, where T ∼ 150 K and n ∼ 10 cm⁻³) and warm neutral media (WNM, where T ∼ 10 000 K and n ∼ 0.2 cm⁻³, Field, Goldsmith & Habing 1969; Wolfire et al. 1995). Given that only the gas clouds which are cool enough to collapse under their own gravity are expected to initiate star formation, we may only expect the cool component, the CNM, to follow the star formation history. Radio-band 21-cm absorption traces this component of the hydrogen, and the comparison of this with the total column density provides a temperature measure of the gas. Using this method, Curran (2017a) showed that the spin temperature and the star formation density may be inversely related (Figure 1). As seen from the figure, however, while 1/T _spin (degenerate with the ratio of the absorber and emitter extents, d _abs/d _QSO) does follow a similar increase as ψ _* up to the z ∼ 2.5 peak, what happens beyond this is as yet unknown. In this paper, we explore the feasibility of obtaining the required data with current state-of-the-art radio telescopes, in addition to exploring the prospects with the Square Kilometre Array (SKA).

Figure 1. The cosmological mass density of neutral hydrogen (solid trace, Crighton et al. 2017) and the star formation density (dotted trace, Hopkins & Beacom 2006) versus redshift. The error bars show the binned (n = 50 per bin) ±1σ values of (1/T _spin)(d _abs/d _QSO)², normalised on the ordinate by 500 M_⊙ yr⁻¹ Mpc⁻³ K (Curran, 2017b).

2. The sample

From Figure 1 it is clear that higher redshift (z _abs ≳ 3) data are required in order to determine whether the spin temperature, degenerate with the ratio of the absorber/emitter extent, is anti-correlated with the star formation density, or whether it just (coincidentally) increases by the same approximate factor out to the peak ψ _*. Since we wish to find the typical sensitivity limits attainable by current and future facilities, we require a large readily available sample of DLAs. Such a sample is provided by the spectra of quasi-stellar objects (QSOs) in the Sloan Digital Sky Survey (SDSS), which provides the largest catalogue of DLAs (Prochaska & Herbert-Fort 2004; Prochaska et al. 2005; Noterdaeme et al. 2009), with the SDSS-III DR9 DLA (Noterdaeme et al. 2012) being the most recently published catalogue of reliable absorbers.^b This contains 12 081 DLAs and sub-DLAs (all with N _HI ≥ 1 × 10²⁰ cm⁻²), over redshifts of 1.951 ≤ z _abs ≤ 5.343.

We match each QSO to the nearest radio source (within 10 arcsec) in each of the NRAO VLA Sky Survey (NVSS, Condon et al. 1998), the Very Large Array’s Faint Images of the Radio Sky at Twenty-Centimeters (FIRST, White et al. 1997), and the Sydney University Molonglo Sky Survey (SUMSS, Mauch et al. 2003). This yields 336 radio-loud sight-lines, containing a total of 414 absorbers (Figure 2). For each of the large radio interferometers, the Murchison Widefield Array (MWA), the Low-Frequency Array (LOFAR), the Giant Metrewave Radio Telescope (GMRT), the Very Large Array (VLA), as well as the forthcoming SKA, we determine which of the DLAs occulting a radio-loud source would have the 21-cm transition redshifted into an available band. From an estimate of the flux density, we then determine the best expected sensitivity of the instrument and whether this is sufficient to detect the putative high redshift downturn in 1/T _spin (Figure 1). Note that we do not include large single dish instruments (e.g. the Green Bank Telescope, GBT) due to the restrictions in mitigating the radio frequency interference (RFI) at these frequencies (e.g. Curran et al. 2016a).

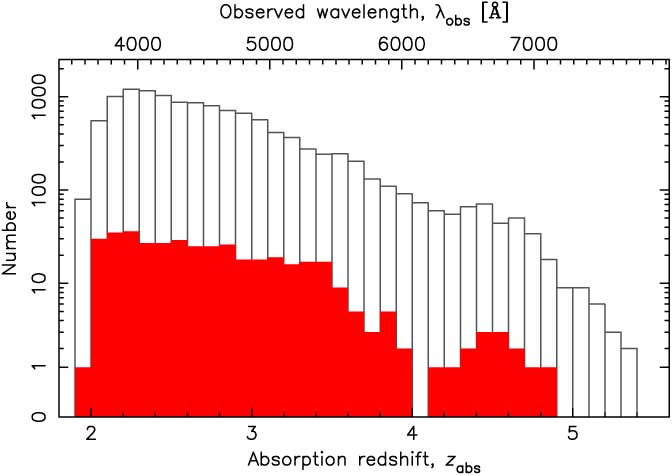
Figure 2. The redshift distribution of the DR9 DLAs (unfilled histogram) overlaid with those occulting a known radio source (filled histogram).

3. Analysis

3.1. Attainable limits

From the radiometer equation (e.g. Rohlfs & Wilson 2000), the r.m.s. noise level obtained after an integration time of t _int is given by

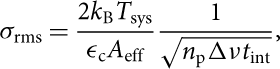(1) $${\sigma _{{\rm{rms}}}} = {{2{k_{\rm{B}}}{T_{{\rm{sys}}}}} \over {{\epsilon_{\rm{c}}}{A_{{\rm{eff}}}}}}{1 \over {\sqrt{{n_{\rm{p}}}\Delta \nu {t_{{\rm{int}}}}} }},$$

where k _B is the Boltzmann constant, T _sys the system temperature, ɛ_c the correlator efficiency, A _eff the effective collecting area of the telescope, n _p the number of polarisations, and Δv is the channel bandwidth. This is related to the velocity resolution, Δv, via Δv = (Δv/c)v _obs, where c is the speed of light and v _obs is the observed frequency.

The observed optical depth, τ _obs, of the absorption is given by the ratio of the line depth, ΔS, to the observed background flux, S, and is related to the intrinsic optical depth, τ, via

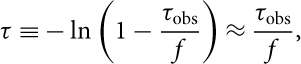(2) $$\tau \equiv - \ln\left( {1 - {{{\tau _{{\rm{obs}}}}} \over f}} \right) \approx {{{\tau _{{\rm{obs}}}}} \over f},$$

in the optically thin regime (ΔS/S ≲ 0.3), where the covering factor, f, is the fraction of S intercepted by the absorber. In the case of a 3σ upper limit, the optical depth is thus given by τ _obs ≲ 3σ _rms/S.

Using the flux density (see 3.2), we can therefore estimate the upper limits to the observed velocity-integrated optical depth. Inserting ∫τ _obs dv ≤ (3σ _rms/S) Δv per Δv channel (see Curran 2012) into N _Hi = 1.823 × 10¹⁸ T _spin ∫τ dv (Wolfe & Burbidge 1975) gives

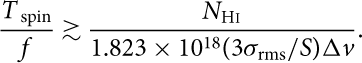(3) $$\frac{T_\textrm{ spin}}{f} \gtrsim \frac{N_\textrm{H\textsc{i}}}{1.823\times10^{18} (3\sigma_\textrm{rms}/S)\Delta v}.$$

Providing that the Lyman-α and 21-cm absorption arise along the same sight-line, Equation (3) yields the limit to the spin temperature of the gas attainable by each instrument. T _spin is a measure of the excitation of the gas by 21-cm absorption (Purcell & Field 1956), excitation above ground state by Lyman-α absorption (Field 1959), and collisional excitation (Bahcall & Ekers 1969). This provides a thermometer—allowing a measure of the fraction of the CNM—the cool gas in which star formation occurs. The spin temperature is, however, degenerate with the covering factor (Equation (3)), whose value requires knowledge of the relative extents of the absorber–frame 1 420 MHz absorption and emission cross-sections (d _abs/d _QSO). This can, however, be expressed as

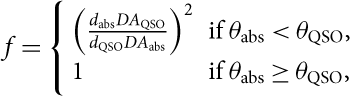(4) $$f = \left\{{\matrix{{{{\left( {{{{d_{{\rm{abs}}}}D{A_{{\rm{QSO}}}}} \over {{d_{{\rm{QSO}}}}D{A_{{\rm{abs}}}}}}} \right)}^2}} \hfill& {\;{\rm{if}}\;{\theta _{{\rm{abs}}}} \lt {\theta _{{\rm{QSO}}}},} \hfill\cr \\ 1 \hfill& {{\rm{if}}\;{\theta _{{\rm{abs}}}} \ge{\theta _{{\rm{QSO}}}},} \hfill\cr} }\right.$$

where DA _abs and DA _QSO are the angular diameter distances and θ _abs and θ _QSO the angular extents of the absorbers and emitter, respectively (Curran 2012).

The angular diameter distance is obtained from line-of-sight co-moving distance, DC, (e.g. Peacock 1999),

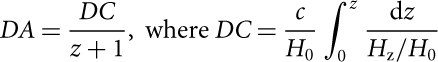$$DA = {{DC} \over {z + 1}} ,\ {\rm {where}}\;DC = {c \over {{H_0}}}\int_0^z {{{\rm {d}}z} \over {{H_{\rm {z}}}/{H_0}}}$$

in which c is the speed of light, H ₀ the Hubble constant, H _z the Hubble parameter at redshift z, and

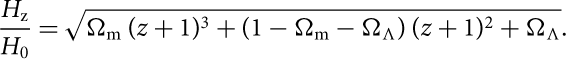$${{{H_{\rm {z}}}} \over {{H_0}}} = \sqrt {{\Omega _{\rm {m}}}{\kern 1pt} {{(z + 1)}^3} + (1 - {\Omega _{\rm {m}}} - {\Omega _\Lambda }){\kern 1pt} {{(z + 1)}^2} + {\Omega _\Lambda }}.$$

For a standard Λ cosmology, with H ₀ = 71 km s ⁻¹ Mpc⁻¹, Ω_m = 0.27 and, Ω_Λ = 0.73, this gives a range of possible values of DA _abs/DA _QSO at, z _abs ≲ 1.6 whereas above this redshift the ratio of angular diameter distances is always close to unity, i.e. DA _abs/DA _QSO ∼ 1, ∀z _abs ≳ 1.6. If left uncorrected, this will introduce a bias to the covering factors between low and high redshift DLAs (Curran & Webb 2006). Correcting for this, by inserting Equation (4) into Equation (3), gives

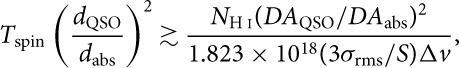(5) $$T_\textrm{spin}\left(\frac{d_\textrm{QSO}}{d_\textrm{abs}}\right)^2 \gtrsim\frac{N_\textrm{H \textsc{i}}(DA_\textrm{QSO}/DA_\textrm{abs})^2}{1.823\times10^{18} (3\sigma_\textrm{rms}/S)\Delta v},$$

for f < 1, which is expected for the high redshift absorbers (Curran 2017a).

Binning the current 21-cm absorption data, the spin temperature degenerate with the ratio of the emitter–absorber extent, (1/T _spin)(d _abs/d _QSO)², traces the star formation density up to the redshift limit of the data (Figure 1) and reproduces the observed CNM fractions in DLAs for a mean 〈d _QSO/d _qbs〉 ∼ 4 (Curran 2017b). With Equation (5), we can estimate the attainable limit for each radio-illuminated DLA in the SDSS DR9 and whether its addition to the current data could help determine if (1/T _spin)(d _abs/d _QSO)² follows the ψ _* downturn at z _abs ≳ 3.

3.2. Radio fluxes

For each of the 336 radio-loud sight-lines (Section 2), we obtain the radio photometry from NASA/IPAC Extragalactic Database (NED) and estimate the flux density from the background source at the redshifted 21-cm frequency of each DLA, via a fit in logarithm space:

• – for at least four radio-band photometry points, a second-order polynomial, according to the prescription of Curran et al. (2013),

• – for two or three radio-band photometry points, a first-order polynomial (a power law),

• – for a single radio-band photometry point, we assume a spectral index. Values of α ≈ −1 are typical of z ≳ 3 radio sources (e.g. De Breuck et al. 2002; Curran et al. 2013), although there may be a redshift dependence (Athreya & Kapahi 1998).

There are 14 sources which are fit by the second-order polynomial and 58 fit by a power law, leaving 264 requiring an estimate of the spectral index. In Figure 3 we show how the spectral indices of the 58 power law fits vary with redshift. From this, it is clear that, since the measured flux is generally at a higher frequency than the redshifted 21-cm absorption (Figure 4), assuming too steep a spectral index could significantly overestimate the flux density. Rather than assuming α = −1, we therefore use a redshift-dependent spectral index, where α = −0.087 z _QSO – 0.175 (Figure 3). The resulting flux density distribution is shown in Figure 5.

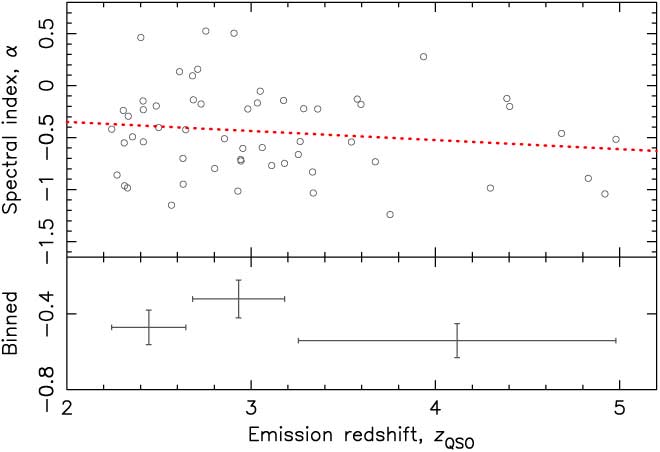
Figure 3. The radio-band spectral index versus redshift for the 58 SED (spectral energy distribution) fit by a power law, where the dotted line shows the least-squares fit. The bottom panel shows the binned values in equally sized bins, where the horizontal error bars show the range of points in the bin and the vertical error bars the error in the mean value.

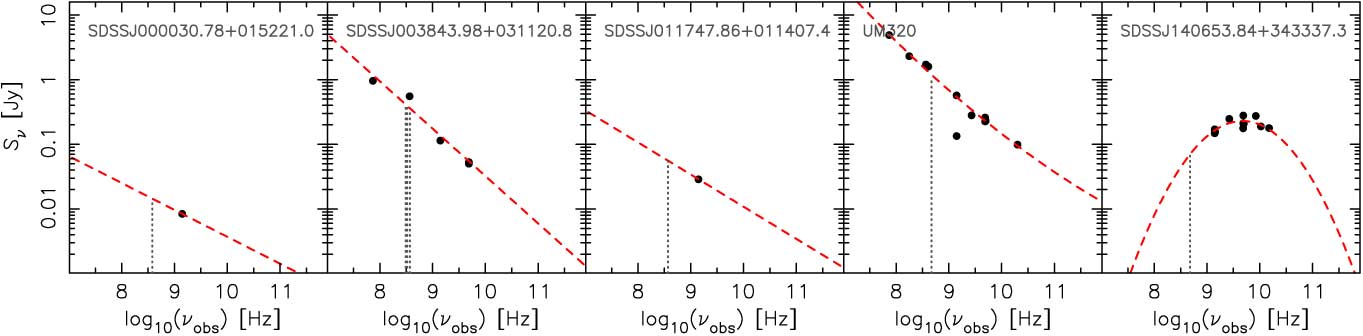
Figure 4. Examples of SED fits to the radio photometry of the background sources. The vertical dotted lines show the frequency of the 21-cm transition at the absorber redshift (the second source has four intervening absorbers).

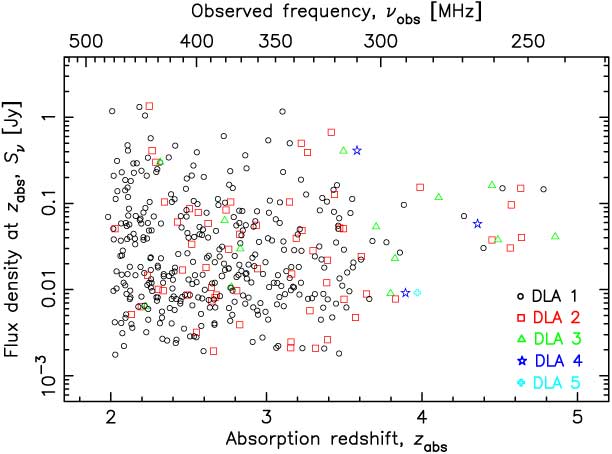
Figure 5. The flux density estimated at the absorption redshift. The colour/shape of the symbol indicates which absorber, since some sight-lines have multiple DLAs—48 sight-lines with a second DLA, ten with a third, two with a fourth and one with a fifth.

3.3. Prospects with current instruments

3.3.1. Murchison Widefield Array

The MWA (Tingay et al. 2013) has a coverage of 80–300 MHz, which spans HI 21-cm at redshifts of z _abs > 3.735. For declinations of δ < 33°, this range gives 15 DLAs illuminated by a radio source observable by the MWA. The spectrometer is limited to a channel spacing of ≥ 10 kHz, which corresponds to a spectral resolution of Δv ≥ 10 km s⁻¹ at v _obs ≤ 300 MHz.^c At v _obs = 200 MHz and T _sys = 195 K, using all 128 tiles (A _eff = 2 534 m²) gives a theoretical r.m.s. noise level of σ _rms = 11 mJy per 10 kHz channel after t _int = 10 h per sight-line (Equation (1)).^d From a search for Hi 21-cm absorption within the hosts of high redshift radio sources,^e a multiplicative (fudge) factor of ≈2 is found, i.e. we should expect an r.m.s. noise level of σ _rms ≈ 22 mJy per 10 kHz channel. Combining this with the estimated flux densities, we obtain limits of (1/T _spin)(d _abs/d _QSO)² ≳ 0.01 K⁻¹, which are insufficient to confirm the putative downturn in (1/T _spin)(d _abs/d _QSO)² at z ≳ 3 (Figure 6).

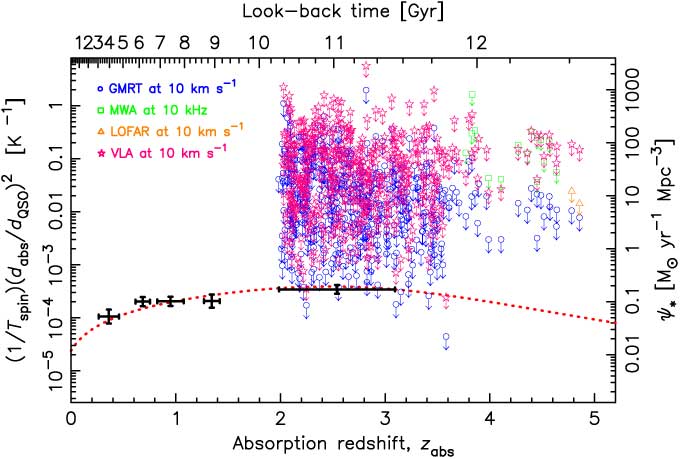
Figure 6. As Figure 1, but showing the 3σ limits in (1/T _spin)(d _abs/d _QSO)² reached after 10 h of integration at a spectral resolution of 10 km s⁻¹ per channel for the current instruments.

3.3.2. Low-Frequency Array

LOFAR (van Haarlem et al. 2013) has a frequency range of 10–250 MHz, which covers the 21-cm transition for only two of the DR9 DLAs, with the δ > −7° declination limit imposing no additional cut. From the point source sensitivity (Figure 7), t _int = 10 h gives an r.m.s. noise level of σ _rms = 11 − 13 mJy per 10 km s⁻¹ channel, cf. the theoretical 1.5 mJy using all stations (24 core, 14 remote, and 13 international). A fudge factor of ≲ 10 in the noise level is expected,^f giving the values in Figure 7, although spectral line observations suggest that this should be 3–5 (e.g. Oonk et al. 2014). Applying a factor of 4 gives σ _rms = 5.4 – 6.5 mJy per 10 km s⁻¹ channel and limits of (1/T _spin)(d _abs/d _QSO)² ∼ 0.01 K⁻¹, which are, again, insufficient to detect the downturn (Figure 6).

Figure 7. Polynomial fits to the system equivalent flux density of LOFAR (van Haarlem et al. 2013).

3.3.3. (Upgraded) Giant Metrewave Radio Telescope

For the GMRT (Ananthakrishnan 1995), there are two bands available which can detect 21-cm over the redshift range of the DR9 DLAs—the 230–250 and 250–500 MHz bands, the latter of which is currently being commissioned as part of the upgraded GMRT (uGMRT). Combining these gives 414 sight-lines towards a radio-loud source for which 21-cm is redshifted to 230–500 MHz and is at a declination observable with the GMRT (δ ≳ −40°). In order to calculate the telescope sensitivity, we estimate the system temperature by interpolating the values quoted for the 151, 235, and 325 MHz bands,^g giving T _sys = 0.0175v _obs² – 11.2v _obs + 1915, where v _obs is in MHz, resulting in T _sys = 106 – 215 K for the sample. For a t _int = 10 h integration using all 30 antennas (A _eff = 26 508 m²) and a fudge factor of 5 in the time estimate,^h we reach σ _rms = 1.3 − 16 mJy per 10 km s⁻¹ channel.

The radiometer equation Equation (1) gives the theoretical noise level, which can be significantly lower than the actual value obtained in the production of an image (e.g. 3.3.2). The fudge factor is intended to correct for this and, in order to check the validity of the value used, we show actual measured sensitivities (Table 1) in comparison to our predicted limits (Figure 8). From this we see that the predicted values are close to those observed and that the fudge factor may even overcompensate the correction somewhat. Using these conservative estimates, however, we see that sufficiently sensitive limits, (1/T _spin)(d _abs/d _QSO)² ∼ 10⁻⁴ K⁻¹, are attainable, although only at redshifts of z _abs ≲ 3.5 (Figure 6).

Table 1. The z _abs > 3 DLAs searched for HI 21-cm absorption

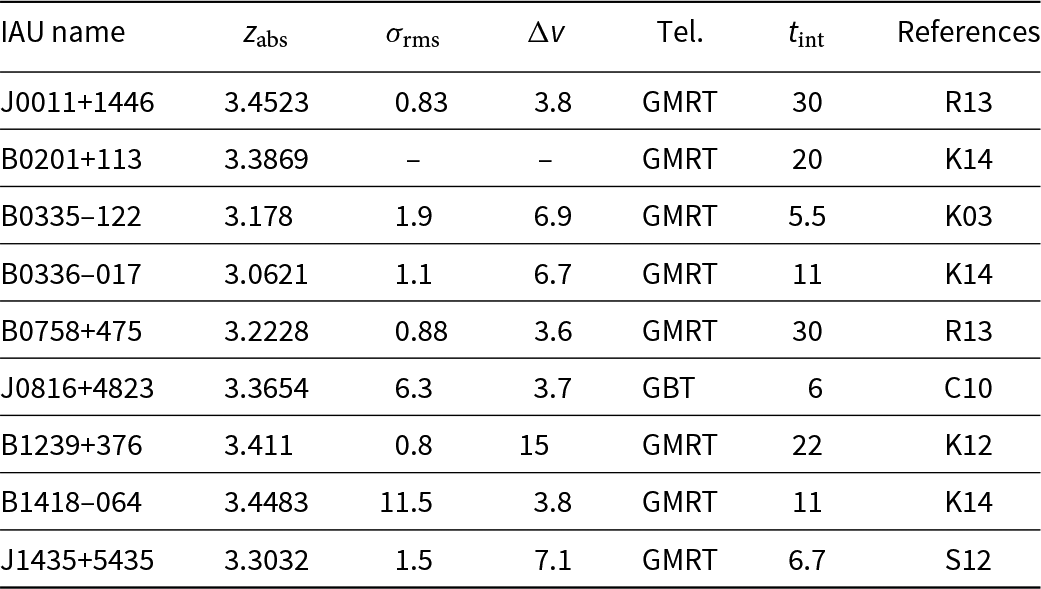
σ _rms [mJy] is the r.m.s. noise level per Δv [km s⁻¹] channel after t _int [hours] obtained with the listed telescope. The absorber towards B0201+113 is detected in 21-cm absorption with ∫ τ _obs dv = 0.71 km s⁻¹

References: K03—Kanekar & Chengalur (2003), C10—Curran et al. (2010), K12—Kanekar et al. (2013), S12—Srianand et al. (2012), R13—Roy et al. (2013), K14—Kanekar et al. (2014).

Figure 8. A detail of Figure 6 showing the current z _abs > 3 results (Table 1), re-sampled to a 10 km s⁻¹ spectral resolution and a 10-h integration, overlain upon the predicted GMRT limits. The filled square signifies the 21-cm detection and the circled square the only non-GMRT observation.

3.3.4. (Expanded) Very Large Array

The VLA P-band spans 230–470 MHz and so is suitable for 21-cm searches at the redshifts of interest, yielding 408 DR9 DLAs at declinations of δ ≳ −30°. Using the improved sensitivity of the Expanded Very Large Array (EVLA) upgrade (Figure 9), with 27 antennas, giving 351 baseline pairs, a correlator efficiency of ϵ _c = 0.93, assuming a fudge factor of 2 in the time estimate,ⁱ in dual polarisation, gives σ _rms = 4.7 – 55 mJy per 10 km s⁻¹, after 10 h of integration. As per the GMRT, limits of (1/T _spin)(d _abs/d _QSO)² ∼ 10⁻⁴ K⁻¹ are attainable, but again only at z _abs ≲ 3.5 (Figure 6).

Figure 9. Two-component (above and below 405 MHz) polynomial fits to the system equivalent flux density of the EVLA P-band.

3.4. Prospects with the SKA

It is therefore apparent that current instruments are unlikely to be able to provide sufficiently sensitive limits to determine whether (1/T _spin)(d _abs/d _QSO)² exhibits the same downturn as the star formation density at high redshift. Surveys for 21-cm absorption with the SKA pathfinders, the APERture Tile Array In Focus (APERTIF), the Australian Square Kilometre Array Pathfinder (ASKAP) and MeerKAT (Karoo Array Telescope) will be limited to z ≲ 0.26, z ≲ 1.0 and z ≲ 1.4, respectively (see Maccagni et al. 2017). Therefore, if (1/T _spin)(d _abs/d _QSO)² does trace the star formation density, i.e. this is not ruled out by a number of z _abs ≳ 3 detections with (1/T _spin)(d _abs/d _QSO)² ≳ 10 K⁻¹ (Figure 6), the SKA will be required to verify this. The first phase of the SKA is expected to be complete in 2020, comprising 125 000 low-frequency (50–350 MHz) antennas, located in Australia, and 300 mid-frequency (350 MHz–14 GHz) dishes, located in South Africa. Phase-2, expected around 2028, is planned to comprise one million low-frequency antennas and 2 000 dishes. The natural weighted sensitivity for each phase is shown in Figure 10. However, again this represents an ideal and so in Figure 11 we show the expected sensitivity, at least for the SKA phase-1, where this is available (Braun 2017). From this, we see that the fudge factor is expected to remain close to 2 for both phase-1 low- and mid-frequency apertures, which we assume to be the case for the SKA phase-2.

Figure 10. Polynomial fits to the point source sensitivity of the SKA (Braun 2017).

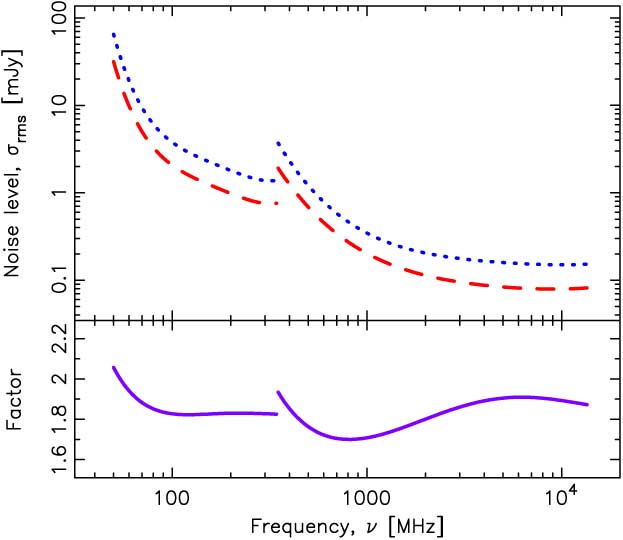
Figure 11. The noise level per each 10 km s⁻¹ channel after 1 h of integration with the SKA1. The dotted curve shows the natural weighted array sensitivities (Figure 10) and the broken curve the expected sensitivities (Tables 1 and 2 of Braun 2017). The bottom panel shows the ratio, i.e. the fudge factor in the noise level.

Inserting the values for A _eff/T _sys into Equation (1) and scaling by the fudge factor gives σ _rms = 0.5 – 1.2 and 0.03 – 0.06 mJy per 10 km s⁻¹ for phase-1 and phase-2, respectively. For the estimated flux densities, these result in (1/T _spin)(d _abs/d _QSO)² ∼ 10⁻³ K⁻¹ and (1/T _spin)(d _abs/d _QSO)² ∼ 10⁻⁴ K⁻¹ at z _abs ≳ 3.5, respectively (Figure 12). We see that these limits approach those required to confirm the downturn in (1/T _spin)(d _abs/d _QSO)², particularly for the SKA phase-2. Examining this in detail, in Figure 13 we show the integration times required to reach the necessary sensitivities at z ≳ 3.5. From this, we see that most of the absorbers can be searched to sufficiently deep limits within a total of ∼ 1 000 h. Since we used the longest integration required along the sight-lines with multiple absorbers, we expect a number of observations to be significantly more sensitive than required. Furthermore, if the fraction of cool gas, as traced by (1/T _spin)(d _abs/d _QSO)², does not follow the same steep decline as the star formation density (Figure 1) at high redshift, we may expect detections within much shorter integration times. The wide SKA-low field-of-view will allow this time to be cut further by observing multiple sight-lines simultaneously (Figure 14), which, given the high sky density of DLAs (figure inset), will yield radio flux measurements (rather than estimates, 3.2), at 7″ resolution (Dewdney 2015), and, possibly, unexpected 21-cm absorption.

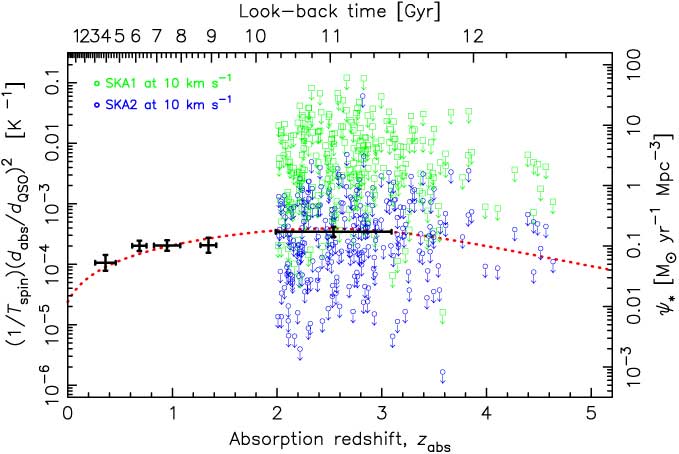
Figure 12. As Figure 6, but showing the limits reached by the SKA after 10 h of integration at 10 km s⁻¹ per channel for sight-lines at δ < 29° (where 237 absorbers reach elevations of > 30°).

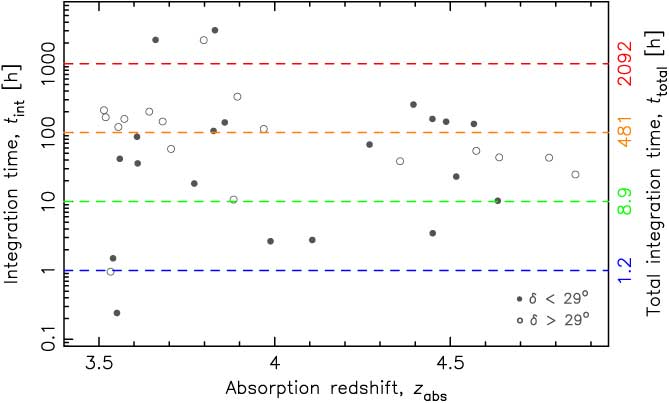
Figure 13. The integration times expected by the SKA2-low to obtain a 3σ detection if ψ _* T _spin (d _QSO/d _abs)² = 500 M_⊙ yr⁻¹ Mpc⁻³ K (e.g. the dotted trace in Figure 12). The filled symbols show the sources at declinations of δ < 29° and the unfilled those with δ > 29°, although all of the targets have δ ≤ 41.8°. The right axis shows the total integration time required on the basis of the longest single integration for that sight-line. For example, restricting all targets to t _int < 100 h gives 21 absorbers along 16 sight-lines with z _abs > 3.5, for a total observing time of 481 h.

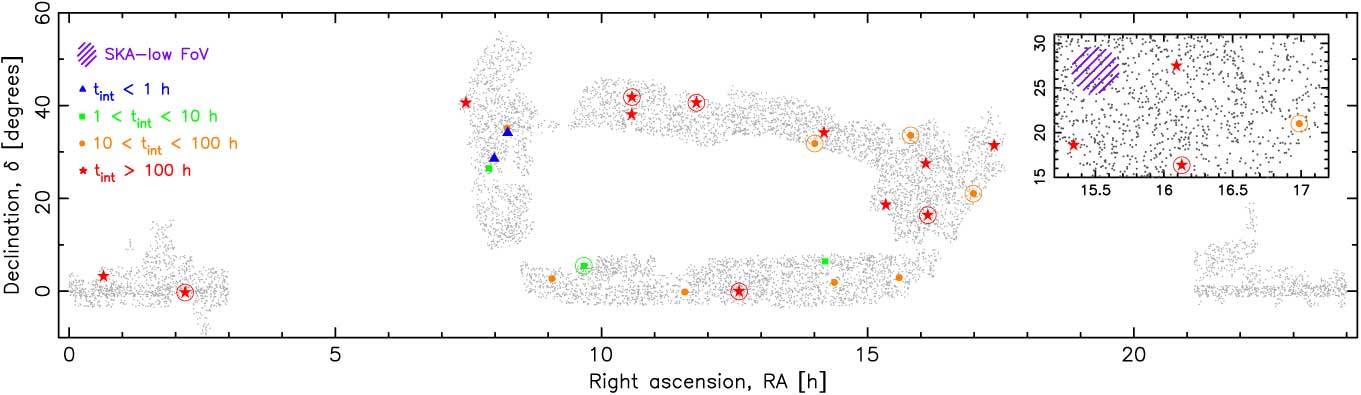
Figure 14. The sky distribution of the known radio-illuminated z _abs > 3.5 absorbers. The shapes designate the maximum required integration time (see Figure 13) with those circled having more than one absorber at z _abs > 3.5 along the sight-line. The small markers show the positions of the DR9 DLAs and the hatched region the SKA-low field-of-view (21 deg², Dewdney 2015). The inset shows a region of relatively high DLA density.

Looking further, several thousand 21-cm absorbers are expected to be detected with the SKA phase-1 at z _abs ≲ 3, with no estimate for the numbers at high redshift (Morganti, Sadler & Curran 2015; Allison et al. 2016). Even in the absence of further large DLA catalogues, blind surveys with the SKA are expected to yield a large number of redshifted absorption systems which are dust reddened (Webster et al. 1995; Carilli et al. 1998; Curran et al. 2017) and thus missed by those pre-selected based upon their optical/UV spectrum. The lack of an optical spectrum does, of course, prevent the nature of the absorber being determined—whether it arises in a quiescent galaxy, intervening a more distant continuum source (as per the DLAs), or is associated with the host of the background continuum source itself. Machine learning techniques do, however, offer the possibility of determining the nature of the absorber purely from its 21-cm absorption profile (Curran et al. 2016b). The other issue with avoiding optical pre-selection is the lack of a Lyman-α spectrum from which to determine the total neutral hydrogen column density. A statistical value for use in Equation (5) may, however, be derived from the cosmological HI density (Curran 2017b).

4. Discussion and summary

It is now well established that the evolution of the mass density of neutral hydrogen is in stark disagreement to that of the star formation density. There is, however, recent compelling evidence that the fraction of cool gas, as traced through the HI 21-cm absorption strength normalised by the total column density, could trace ψ _*. However, the paucity of 21-cm absorption searches at z _abs ≳ 3.5 prevents us from confirming whether the cold gas fraction follows the same downturn as the star formation density. In this paper, we examine the possibility of testing this through observations of a large sample of damped Lyman-α absorption systems, the SDSS SDSS-III DR9 catalogue (Noterdaeme et al. 2012). For each of the 12 081 N _HI ≥ 1 ×10²⁰ cm⁻² absorption systems,

• We search each sight-line in the NVSS, FIRST, and SUMSS for background radio emission. This yields 336 radio-loud sight-lines, containing a total of 414 absorbers. For each of these we obtain all of the available radio photometry and use this to estimate the flux density at the redshifted 21-cm frequency of each absorber.

• For each of the current large radio interferometers, we determine which absorbers are redshifted into an available band and is visible from the telescope location.

• From the instrument specifications, we calculate the sensitivity after a 10-h integration which we combine with the flux density and the neutral hydrogen column density, as well as removing line-of-sight geometry effects, to estimate the best expected limit to the spin temperature (degenerate with the ratio of the emitter–absorption extents) obtainable for each absorber.

From this, we find that none of the current instruments are of sufficient sensitivity to place useful limits on (1/T _spin)(d _abs/d _QSO)² at z _abs ≳ 3.5, although both the upgraded (u)GMRT and (E)VLA may be sufficiently sensitive at 3 ≲ z _abs ≲ 3.5. This, of course, does not preclude the possibility that a number of detections at these redshifts could rule out the hypothesis that ψ _* is traced by(1/T _spin)(d _abs/d _QSO)², a possibility which can only be addressed through observation.

With the SKA, the required sensitivity is achievable at z _abs ≳ 3.5, but only for a small number (≈ 10) of absorbers. This is due to the sensitivity function of the SDSS, exhibiting a steep decline in the number of sight-lines at z _abs ≳ 3 (λ_obs ≳ 5000 Å, Noterdaeme et al. 2009, 2012), above which the Lyman-α transition is shifted out of the optical and into the near-infrared band (at z _abs ≳ 5.5). If our derived radio fluxes are representative at these redshifts, in addition to new DLAs found through further optical surveys over the next decade, we expect an increased number of absorbers to be detected through the wide instantaneous bandwidth and field-of-view of the SKA. The detection of new absorption systems in radio surveys would not be subject to the same dust obscuration as their optical counterparts. In the absence of an optical spectrum, it may be possible to determine whether the absorption is intervening or associated, through machine learning techniques (Curran et al. 2016b), and apply a statistical column density in order to yield a statistical (1/T _spin)(d _abs/d _QSO)² (Curran 2017b).

Radio selection may also uncover intervening absorbers rich in molecular gas: although molecular absorption has been detected in 26 DLAs, through H₂ vibrational transitions redshifted into the optical band at z _abs ≳ 1.7 (compiled in Srianand et al. 2010 with the addition of Reimers et al. 2003; Fynbo et al. 2011; Guimarães et al. 2012; Srianand et al. 2012; Noterdaeme et al. 2015, 2017; Balashev et al. 2017), extensive millimetre-wave observations have yet to detect absorption from any rotational transition (e.g. Curran et al. 2004b). Since the DLAs in which H₂ has been detected have molecular fractions ${\cal F} \equiv 2{N_{{{\rm {H}}_2}}}/(2{N_{{{\rm {H}}_2}}} + {N_{{\rm {H1}}}}) \sim {10^{ - 7}} - 0.3$ and optical—near-infrared colours of V – K ≲ 4 (Curran et al. 2011), compared to the five known redshifted radio-band absorbers, where ℱ ≈ 0.7 – 1.1 and V – K ≥ 4.80 (Curran et al. 2006), we suspect that the selection of optically bright objects selects against dusty environments, which are more likely to harbour molecules in abundance. Thus, radio-selected surveys offer the possibility of finally detecting dust obscured DLAs which have similarly high molecular fractions (ℱ ∼ 1). Comparison of the atomic and molecular line strengths will provide an invaluable probe of the conditions in the highest redshift galaxies. Furthermore, comparison of the relative shifts of the atomic and molecular transitions in the radio-band offers a measure of the fundamental constants of nature at large-look back times to much greater precision than optical spectroscopy (e.g. Murphy, Webb & Flambaum 2003; Tzanavaris et al. 2007), making the SKA ideal in resolving this contentious issue (Curran, Kanekar & Darling 2004).