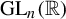Random and mean Lyapunov exponents for $\operatorname {\mathrm {GL}}_n(\mathbb {R})$

Abstract

We consider orthogonally invariant probability measures on $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ and compare the mean of the logs of the moduli of eigenvalues of the matrices with the Lyapunov exponents of random matrix products independently drawn with respect to the measure. We give a lower bound for the former in terms of the latter. The results are motivated by Dedieu and Shub [On random and mean exponents for unitarily invariant probability measures on $\operatorname {\mathrm {GL}}_n(\mathbb {C})$. Astérisque 287 (2003), xvii, 1–18]. A novel feature of our treatment is the use of the theory of spherical polynomials in the proof of our main result.

1 Introduction and main result

In this paper, we investigate bounds for the mean Lyapunov exponents for a measure on $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ in terms of random Lyapunov exponents. To explain this further, fix a probability measure $\mu $ on $G=\operatorname {\mathrm {GL}}_n(\mathbb {R})$ or $\operatorname {\mathrm {GL}}_n(\mathbb {C})$ . If $\mu $ satisfies a mild integrability condition, Oseledets theorem guarantees the existence of n real numbers,

$$ \begin{align*}r_1\geq r_2\geq \cdots \geq r_n, \end{align*} $$

such that for almost every sequence $A_1, A_2, \ldots $ of independent and identically distributed (i.i.d.) matrices drawn from the measure $\mu $ , the limit

(1.1) $$ \begin{align} \lim_m\frac 1m \log\|A_m\cdots A_1v\| \end{align} $$

exists for every non-zero vector v and is equal to one of the $r_i$ . We call these $r_i$ the random Lyapunov exponents associated to the measure $\mu $ . If the measure $\mu $ is concentrated on a single matrix $A\in G$ , the $r_i$ are simply

for $\unicode{x3bb} _i(A)$ , the eigenvalues of A written according to their algebraic multiplicity.

For a measure $\mu $ on $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ (or $\operatorname {\mathrm {GL}}_n(\mathbb {C})$ ), we say that $\mu $ is orthogonally (or unitarily) invariant if for any measurable set $\mathscr {V}$ in $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ (or $\operatorname {\mathrm {GL}}_n(\mathbb {C})$ ) and orthogonal (or unitary) linear map U, we have $\mu (U(\mathscr {V}))=\mu (V)$ , where $U(\mathscr {V})=\{Uv:\, v\in \mathscr {V}\}$ .

In the complex case, the main theorem of Dedieu and Shub [DS03] is as follows.

Theorem. [DS03, Theorem 1]

If $\mu $ is a unitarily invariant probability measure on $\operatorname {\mathrm {GL}}_n(\mathbb {C})$ satisfying the integrability condition

$$ \begin{align*} A\in\operatorname{\mathrm{GL}}_n(\mathbb{C})\mapsto \log^{+}(\|A\|)\quad\mbox{and}\quad \log^{+}(\|A^{-1}\|)\mbox{ are } \mu\mbox{-integrable}, \end{align*} $$

then

We note that we use the same symbol $\|\cdot \|$ for both the operator norm $\|A\|$ of a matrix and for the euclidean norm of a vector, as in equation (1.1). We hope no confusion will arise. In Theorem 1, we have also introduced the notation $f^+(x)=\max \{f(x), 0\}$ for a real-valued function f.

In [BPSW01, DS03], it is asked if a similar theorem holds for $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ and ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ perhaps with a constant $c_n$ depending on n. Here we prove that it does. Our main theorem is the following.

Theorem 1. For any $n\geq 0$ , if $\mu $ is an orthogonally probability invariant measure on $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ satisfying the integrability condition $A\in \operatorname {\mathrm {GL}}_n(\mathbb {R}) \mapsto \log ^{+}(\|A\|)\;\mbox {and} \log ^{+}(\|A^{-1}\|)\in L^1(\operatorname {\mathrm {GL}}_n(\mathbb {R}),\mu )$ , then

for any $k, 1\leq k\leq n.$

Let $SL_n(\mathbb {R})$ be the special linear group of $n\times n$ matrices with determinant $1$ . Then we have the following result.

Corollary 1. For any $n\geq 0$ , if $\mu$ is an orthogonally invariant probability measure on $SL_n(\mathbb{R})$ satisfying the integrability condition $A\in SL_n(\mathbb{R}) \mapsto \log^{+}(\|A\|)\;\mbox{and} \log^{+}(\|A^{-1}\|)\in L^1(SL_n(\mathbb{R}),\mu)$ , then

$$ \begin{align*} \int_{A\in SL_n(\mathbb{R})} \sum_{i=1}^k\log|\lambda_i(A)| \,d\mu(A)\geq \frac{1}{\binom nk}\left(\sum_{i=1}^k r_i\right)^+, \end{align*} $$

for any $k, 1\leq k\leq n$ .

The proof of the corollary follows immediately since for all $A\in SL(n,\mathbb {R})$ , $\prod _{j=1}^k|\unicode{x3bb} _j(A)|\geq 1 (k=1,\ldots ,n)$ .

Some special cases of our main result in Theorem 1 have been previously established. For $n=2$ , the result is proved in [DS03] and by Avila and Bochi [AB02]. Rivin [Riv05] proves the case $n>2, k=1$ . (Both [AB02, Riv05] prove more general results in these restricted settings, from which the stated results can be derived.)

1.1 Motivation

We place our results in a more general setting to provide motivation, which originates with the study of the entropy of diffeomorphisms of closed manifolds. Let $\pi :\mathcal {V}\to X$ be a finite dimensional vector bundle. The basic object of interest is the iteration of fiberwise linear maps $\mathcal A$ of $\pi $ which cover a map $f:X\to X$ of the base. The cocycle is described in the following diagram by the bundle map $\mathcal A:\mathcal {V}\to \mathcal {V}$ which satisfies $\pi \circ \mathcal A=f\circ \pi $ :

(1.2)

See Ruelle [Rue79], Mañe [Mn87], and Viana [Via14] for extensions. We give four basic examples of this setup.

Example 1.1. The base X is one point. (This is the object of our paper.)

Example 1.2. X is a closed manifold M, $\mathcal {V}$ is the tangent bundle $TM$ of M, f is a smooth (at least $C^{1+\alpha }$ ) endomorphism of M, and $\mathcal A=Tf$ is the derivative of f. This is the derivative cocycle. Note that the kth iterate of $Tf$ is given by

$$ \begin{align*} (Tf)^k(x,v)=(f^k(x),Tf(f^{k-1}(x))\cdots Tf(x)v),\quad (x,v)\in TM. \end{align*} $$

Example 1.3. Let $\mathcal {V}\xrightarrow []{\pi }X$ be a fixed vector bundle and $\mathscr F$ a family of bundle maps $(\mathcal A,f)$ as in equation (1.2), with $\mathcal A:\mathcal {V}\to \mathcal {V}$ fiberwise linear and $f:X\to X$ a base map. Assume given a finite measure $\mu $ on $\mathscr F$ .

Then random products of independent elements of $\mathscr F$ , drawn with respect to the measure $\mu $ , are described by the following cocycle. Let ${\mathcal {G}} =\mathscr F^{\mathbb {N}}$ with the product measure $\mu ^{\mathbb {N}}$ . Writing elements of ${\mathcal {G}}$ as

$$ \begin{align*}(\mathcal{A}_i,f_i)_{i}=(\ldots,(\mathcal{A}_{n}, f_n) ,\ldots,(\mathcal{A}_0,f_0)),\end{align*} $$

we define $\sigma :{\mathcal {G}}\to {\mathcal {G}}$ by $\sigma ((\mathcal {A}_i,f_i)_{i})=(\mathcal {A}_{i+1},f_{i+1})_{i}$ , that is, shift to the right and delete the first term. Then, the map $\mathcal H:{\mathcal {G}}\times \mathcal {V} \to {\mathcal {G}}\times \mathcal {V}$ , given by

$$ \begin{align*} \mathcal H((\mathcal{A}_i,f_i)_i,v)= (\sigma((\mathcal A_i,f_i)_i),\mathcal{A}_0(v)), \quad ((\mathcal A_i,f_i)_i,v)\in{\mathcal{G}}\times \mathcal{V} \end{align*} $$

defines the cocycle

where the base map $h:{\mathcal {G}}\times X\to {\mathcal {G}}\times X$ is given by $h((\mathcal {A}_i,f_i)_i,x)=(\sigma ((\mathcal A_i,f_i)_i), f_0(x))$ , where $\pi (v)=x$ .

The kth iterate of the cocycle $\mathcal H$ is given by

$$ \begin{align*} \mathcal{H}^k((\mathcal{A}_i,f_i)_i,v)= (\sigma^k((\mathcal{A}_i,f_i)_i),\mathcal{A}_{k-1}\cdots\mathcal{A}_{0}(v)),\quad ((\mathcal A_i,f_i)_i,v) \in {\mathcal{G}}\times\mathcal{V}, \end{align*} $$

which yields the products of random i.i.d. elements of the measure space $(\mathscr F,\mu )$ .

Example 1.4. Let $f:X\to X$ and $\phi :X\to \operatorname {\mathrm {GL}}_n(\mathbb {R})$ . Let

(1.3)

be defined by $\mathcal {A}(x,v)=(f(x),\phi (x)v)$ . The functions f and $\phi $ are frequently called linear cocyles in the literature, and $\mathcal A$ the associated linear extension. Here we use linear cocycle (or just cocycle) for both. In this case, the kth iterate of $\mathcal A$ is given by

$$ \begin{align*} \mathcal {A}^k(x,v)=(f^{k}(x),\phi(f^{k-1}(x)) \cdots\phi(f(x)) \phi(x)v),\quad (x,v)\in X\times \mathbb{R}^n. \end{align*} $$

We now return to the general setting of a finite dimensional vector bundle $\mathcal {V}\xrightarrow []{\pi }X$ and cocycle as in equation (1.2). Assume that $\pi $ has a Finsler structure, that is, a norm on each fiber of $\mathcal {V}.$ Consider the limit

(1.4) $$ \begin{align} \lim_n \frac1n \log \frac{\|\mathcal{A}^n(v)\|}{\|v\|} \end{align} $$

for a given non-zero vector $v\in \mathcal {V}$ . If the limit in equation (1.4) exists, we call it a Lyapunov exponent of $\mathcal A$ . We refer the reader to the expository article of Wilkinson [Wil17] for an introduction to Lyapunov exponents.

When X is a finite measure space, subject to various measurability and integrability conditions, the Oseledets theorem [Ose68] says that for all $v\in \mathcal {V}$ , the limit in equation (1.4) exists almost surely and coincides with one of the real numbers

(See also Gol’dsheid and Margulis [GdM89], Guivarc’h and Raugi [GR89], Ruelle [Rue79], and Viana [Via14].)

Recall that we have set $\psi ^+(x)=\max (0,\psi (x))$ for a real-valued function $\psi .$ Then the theorem of Pesin [Pes77] and Ruelle [Rue78] implies that in the setting of Example 1.2, if $f:M\to M$ preserves a measure $\mu $ , absolutely continuous with respect to Lebesgue, and $\mathcal A$ is the derivative cocycle, we have

(1.5)

where $h_\mu (f)$ is the entropy of f with respect to $\mu .$ From a dynamical systems perspective, knowing when $h_\mu (f)$ is positive and how large it may be is of great interest. However, the Lyapunov exponents of the derivative cocycle are generally difficult to compute, even to show positivity of the integral in equation (1.5). Nevertheless, the Lyapunov exponents of a random product are frequently easy to be shown as positive.

One attempt to approach the problem is to consider diffeomorphisms or, more generally, cocycles that belong to rich families $\mathscr F$ , and to prove that $\int _M\sum _i \unicode{x3bb} ^+(x,f)\,d\mu (x)$ is positive for at least some elements of the family by comparing with Lyapunov exponents of random products. It is not clear what the notion of rich should be to carry out this program of bounding the average Lyapunov exponents by those of random products.

There is some success reported by Pujals, Robert, and Shub [PRS06], Pujals and Shub [PS08], de la Llave, Shub, and Simó [dlLSS08], and Dedieu and Shub [DS03], and an extensive discussion by Burns et al [BPSW01] for derivative cocycles. A notion of rich which comes close for the circle and two spheres is ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ invariance. The theorem of [DS03] for unitarily invariant measures on $\operatorname {\mathrm {GL}}_n(\mathbb {C})$ was important in this direction.

1.2 Outline of paper

We conclude this introduction with an outline of the remainder of the paper and a sketch of the ideas used in the proof of Theorem 1. The sums $\sum _{i\leq k} r_i$ of the random Lyapunov exponents appearing in Theorem 1 admit a geometric interpretation relating them to an integral over the Grassmannian manifold $\mathbb {G}_{n,k}$ of k-dimensional subspaces of $\mathbb {R}^n.$ We use this relation in §2 to reduce the proof of Theorem 1 to a comparison of an integral on the the orthogonal group to an integral on the Grassmannian. This comparison is effected by applying the coarea formula to the two projections $\Pi _1,\Pi _2$ of the manifold ${\mathbb V}_A$ of fixed k-dimensional subspaces

$$ \begin{align*}{\mathbb V}_A=\{(U,g)\in {\operatorname{\mathrm{O}}_n(\mathbb{R})}\times \mathbb{G}_{n,k}: (UA)_{\#}g=g \}\quad \mbox{for fixed } A\in\operatorname{\mathrm{GL}}_n(\mathbb{R}). \end{align*} $$

This use of the coarea formula, presented in §§3 and 4, is similar to the approach of [DS03]. Our main point of departure from the earlier paper comes in §5 in our treatment of bounding an integral of the normal Jacobian of the projection $\Pi _1.$ We use the theory of spherical polynomials for the symmetric space $G/K$ for $G=\operatorname {\mathrm {GL}}_n(\mathbb {R})$ and $K=\operatorname {\mathrm {O}}_N(\mathbb {R}).$ Our Theorem 4 is a consequence of a positivity result for Jack polynomials due to Knop and Sahi [KS97]. This approach highlights a difficulty in extending the results of [DS03] to our setting. In the case of $G=\operatorname {\mathrm {GL}}_n(\mathbb {C}), K=\operatorname {\mathrm {U}}_n(\mathbb {C}),$ the associated spherical polynomials are simply Schur polynomials, thus permitting a more direct treatment in the earlier work using the Vandermonde determinant, see [DS03, §4.5].

We hope that the results and techniques of this paper stimulate further interactions between the ergodic theory of cocycles and harmonic analyses on symmetric spaces. One appealing direction is the investigations of families of cocycles which have elements with $\int _{x\in X}\sum _i\unicode{x3bb} _i^+(x)\,d\mu (x)$ positive. Especially interesting would be more rich families of dynamical systems which must have some elements of positive entropy. One approach for measure-preserving families of dynamical systems would be to compare the Lyapunov exponents of the derivative cocycles of the family to the Lyapunov exponents of the random products of the cocycles of the family.

For these reasons, our main interest in establishing Theorem 1 is to bound from below the mean Lyapunov exponents of an orthogonally invariant measure by random Lyapunov exponents. One of the reviewers sees interest in the other direction: the mean Lyapunov exponents provide an upper bound for the random exponents. The reviewer points to the recent paper of Hanin and Nica [HN20] and suggests the possible application of exponents of orthogonally invariant measures to stochastic gradient descent. We thank the reviewer for bringing this work to our attention.

2 Proof of Theorem 1

Let $\mathbb {G}_{n,k}$ be the Grassmannian of k-dimensional subspaces of $\mathbb {R}^n$ . Given $g\in \mathbb {G}_{n,k}$ , let $\operatorname {\mathrm {O}}(g)$ be the subgroup of ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ that fixes g. For $A\in \operatorname {\mathrm {GL}}_n(\mathbb {R})$ , we denote by $A_\#$ the mapping corresponding to the natural induced action on $\mathbb {G}_{n,k}$ and by $A|_g$ the restriction of A to the subspace g. Choose orthonormal bases for g and the image of g under A and let $\det A|_g$ denote the determinant of the matrix representing A with respect to these bases. It is easy to see that the absolute value $|{\det}\ A|_g|$ is independent of the choice of bases.

Consider the Riemannian metric on ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ coming from its embedding in the space of $n\times n$ matrices with the natural inner product $\langle A,B\rangle =\operatorname {\mathrm {tr}}(A\,{\vphantom {B}}^{t}\!{B}).$ As a Lie group, this Riemannian structure on ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ is left and right invariant and it induces a Riemannian structure on $\mathbb {G}_{n,k}$ as an homogeneous space of ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ . We denote by $\mathrm {vol} \operatorname {\mathrm {O}}_n(\mathbb {R})$ and $\mathrm {vol} \, \mathbb {G}_{n,k}$ the Riemannian volumes of the orthogonal group and Grassmannian, respectively, and note the relation

(2.1) $$ \begin{align} \mathrm{vol} \,\mathbb{G}_{n,k}=\frac{\mathrm{vol} \operatorname{\mathrm{O}}_n(\mathbb{R})}{\mathrm{vol} \operatorname{\mathrm{O}}_{k}(\mathbb{R})\cdot\mathrm{vol} \operatorname{\mathrm{O}}_{n-k}(\mathbb{R})}. \end{align} $$

Define the constant

(2.2) $$ \begin{align} c_{n,k}=\frac{\mathrm{vol} \operatorname{\mathrm{O}}_{k}(\mathbb{R})\cdot\mathrm{vol} \operatorname{\mathrm{O}}_{n-k}(\mathbb{R})}{\binom nk}. \end{align} $$

Theorem 2. For any $A\in \operatorname {\mathrm {GL}}_n(\mathbb {R})$ , we have

$$ \begin{align*} \int_{U\in{\operatorname{\mathrm{O}}_n(\mathbb{R})}} \Big[\!\!\sup_{\substack{g\in\mathbb{G}_{n,k}:\\ (UA)_\#g=g}}(\log^+|{\det}\ UA|_g|)\Big]d{\operatorname{\mathrm{O}}_n(\mathbb{R})} \geq c_{n,k}\int_{g\in\mathbb{G}_{n,k}}\log^+|{\det}\ A|_g|\,d\mathbb{G}_{n,k}. \end{align*} $$

If we integrate instead with respect to the Haar measure $dU$ on $\operatorname {\mathrm {O}}_n(\mathbb {R})$ and the invariant probability measure $dg$ on $\mathbb {G}_{n,k}$ , which is just $d\mathbb {G}_{n,k}$ normalized to have volume one, we get

(2.3) $$ \begin{align} \int_{U\in{\operatorname{\mathrm{O}}_n(\mathbb{R})}} \bigg[\sup_{\substack{g\in\mathbb{G}_{n,k}:\\ (UA)_\#g=g}}(\log^+|{\det}\ UA|_g|)\bigg]dU \geq \frac{1}{\binom nk} \int_{g\in\mathbb{G}_{n,k}}\log^+|{\det}\ A|_g|\,dg. \end{align} $$

This follows immediately from Theorem 2 and equation (2.1). The proof of Theorem 2 is given in §§2 and 5.

Note that Theorem 2 implies a slightly more general result.

Theorem 3. If $\mu $ is an orthogonally invariant probability measure on $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ , then

$$ \begin{align*} \int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})} \Big[\sup_{\substack{g\in \mathbb{G}_{n,k}:\\A_{\#}g=g}}\log^{+}|{\det}\ A|_g|\Big]d\mu \geq \frac{1}{\binom{n}{k}}\int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})} \int_{g\in \mathbb{G}_{n,k}} \log^{+}|{\det}\ A|_g|\,dg\,d\mu. \end{align*} $$

Proof. Since $\mu $ is an orthogonally invariant probability measure on $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ , for every integrable function $\eta :\operatorname {\mathrm {GL}}_n(\mathbb {R})\to \mathbb {R}$ , we have

(2.4) $$ \begin{align} \int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})} \eta(UA)\,d\mu = \int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})} \eta (A)\,d\mu. \end{align} $$

(This is just the change of variable formula of measure theory for the transformation $T_U:\operatorname {\mathrm {GL}}_n(\mathbb {R})\to \operatorname {\mathrm {GL}}_n(\mathbb {R})$ given by $T_U(A)=UA$ . Then, by the ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ -invariance of $\mu $ , we have that the pushforward measure $(T_U)_*\mu $ coincides with $\mu $ .)

For short, let us define $\varphi :\operatorname {\mathrm {GL}}_n(\mathbb {R})\to \mathbb {R}$ by

$$ \begin{align*} \varphi(B)=\sup_{\substack{g\in\mathbb{G}_{n,k}:\\ (B)_\#g=g}}(\log^+|{\det}\ B|_g|). \end{align*} $$

Then integrating over $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ , with respect to $\mu $ , on both sides of the inequality of Theorem 2, we obtain

$$ \begin{align*} &\int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})}\bigg\{\! \int_{U\in{\operatorname{\mathrm{O}}_n(\mathbb{R})}} \varphi(UA) d{\operatorname{\mathrm{O}}_n(\mathbb{R})} \bigg\}\,d\mu\\&\quad\geq c_{n,k}\int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})}\int_{g\in\mathbb{G}_{n,k}}\log^+|{\det}\ A|_g|\,d\mathbb{G}_{n,k}\,d\mu. \end{align*} $$

Applying Fubini on the left-hand side,

$$ \begin{align*} \int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})}\bigg\{\! \int_{U\in{\operatorname{\mathrm{O}}_n(\mathbb{R})}} \varphi(UA) d{\operatorname{\mathrm{O}}_n(\mathbb{R})} \bigg\}\,d\mu &= \int_{U\in{\operatorname{\mathrm{O}}_n(\mathbb{R})}}\bigg\{\! \int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})} \varphi(UA)d\mu \bigg\}\,d{\operatorname{\mathrm{O}}_n(\mathbb{R})} \\ & =\mathrm{vol} \,{\operatorname{\mathrm{O}}_n(\mathbb{R})} \int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})}\varphi(A) \,d\mu, \end{align*} $$

where the last equality follows from the ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ -invariance of $\mu $ as in equation (2.4). Using the facts that

$$ \begin{align*} \frac{c_{n,k}}{\mathrm{vol} \,{\operatorname{\mathrm{O}}_n(\mathbb{R})}}=\frac{1}{\binom nk\mathrm{vol} \, \mathbb{G}_{n,k}} \quad\mbox{and}\quad d\mathbb{G}_{n,k}=\mathrm{vol} \,\mathbb{G}_{n,k}\cdot dg \end{align*} $$

completes the proof.

Proof of Theorem 1

Pointwise, we have

where the supremum on the right-hand side is defined to be $0$ if the set of $g\in \mathbb {G}_{n,k}$ such that $A_\#g=g$ is empty.

Then, for finishing the proof of Theorem 1, it suffices to identify the right-hand side of the expression in Theorem 3 in terms of $(\sum _{i=1}^kr_i)^+$ . As in the proof of [DS03, Theorem 3],

$$ \begin{align*} \sum_{i=1}^k r_i =\int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})}\int_{g\in \mathbb{G}_{n,k}}\log |{\det}\ A|_g|\, dg\,d\mu, \end{align*} $$

so

$$ \begin{align*} \bigg(\!\sum_{i=1}^k r_i\bigg)^+ &= \bigg(\!\int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})}\int_{g\in \mathbb{G}_{n,k}}\log |{\det}\ A|_g|\, dg\,d\mu\bigg)^+\\ & \leq \int_{A\in\operatorname{\mathrm{GL}}_n(\mathbb{R})}\int_{g\in \mathbb{G}_{n,k}}\log^+ |{\det}\ A|_g|\, dg\,d\mu.\\[-3.6pc] \end{align*} $$

We will give the proof of Theorem 2 in §§2 and 5 after some preparations in the next section.

3 Manifold of fixed subspaces

Let $A\in \operatorname {\mathrm {GL}}_n(\mathbb {R})$ , and define the manifold of fixed k-dimensional subspaces

$$ \begin{align*} {\mathbb V}_A:=\{(U,g)\in {\operatorname{\mathrm{O}}_n(\mathbb{R})}\times \mathbb{G}_{n,k}: (UA)_{\#}g=g \}. \end{align*} $$

Let $\Pi _1:{\mathbb V}_A\to {\operatorname {\mathrm {O}}_n(\mathbb {R})}$ and $\Pi _2:{\mathbb V}_A\to \mathbb {G}_{n,k}$ be the associated projections.

Given $g\in \mathbb {G}_{n,k}$ , one has

$$ \begin{align*} \Pi_2^{-1}(g)=\{(U,g): U\in {\operatorname{\mathrm{O}}_n(\mathbb{R})},\, A_{\#}g=(U^{-1})_{\#}g\}. \end{align*} $$

By abusing notation, we identify $\Pi _2^{-1}(g)$ with $\Pi _1\Pi _2^{-1}(g)$ , which we in turn identify with $\operatorname {\mathrm {O}}(k)\times \operatorname {\mathrm {O}}(n-k)$ . Similarly, given $U\in {\operatorname {\mathrm {O}}_n(\mathbb {R})}$ , we identify $ \Pi _1^{-1}(U)$ with

$$ \begin{align*}\{g\in \mathbb{G}_{n,k}:\mbox{fixed by } (UA)_\#\}. \end{align*} $$

Remark 2. Note that on a set of full measure in ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ , the fiber $\Pi _1^{-1}(U)$ is finite and $\#\Pi _1^{-1}(U)$ is bounded above by $\binom nk$ . This follows from the fact that the set of $U\in {\operatorname {\mathrm {O}}_n(\mathbb {R})}$ , such that $UA$ has repeated eigenvalues, is a proper subvariety of ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ defined by the discriminant of the characteristic polynomial of $UA$ . Therefore, a k-dimensional invariant subspace for $UA$ , where U lies in the complement of the algebraic subvariety described above, corresponds to a choice of k-eigenvalues for $UA$ , and corresponding eigenspaces.

The tangent space to the Grassmannian $\mathbb {G}_{n,k}$ at g can be identified in a natural way with the set of linear maps $\mathrm {Hom}(g,g^\perp )$ , that is, any subspace $g'\in \mathbb {G}_{n,k}$ in a neighborhood of g can be represented as the graph of a unique map in $\mathrm {Hom}(g,g^\perp )$ . More precisely, if we denote by $\pi _g$ and $\pi _{g^\perp }$ the orthogonal projections of $\mathbb {R}^n=g\oplus g^\perp $ into g and $g^\perp $ , respectively, then $g'\in \mathbb {G}_{n,k}$ such that $g'\cap g^\perp =\{0\}$ is the graph of the linear map $\pi _{g^\perp }\circ ((\pi _{g})|_{g'})^{-1}$ .

Lemma 3. Let $B\in \operatorname {\mathrm {GL}}_n(\mathbb {R})$ and $g\in \mathbb {G}_{n,k}$ such that $B_\#g=g$ . Then, the induced map $\mathcal {L}_B:\mathrm {Hom}(g,g^\perp )\to \mathrm {Hom}(g,g^\perp )$ , on local charts, is given by

$$ \begin{align*} \mathcal{L}_B(\varphi)= [\pi_{g^\perp}(B|_{g^\perp})]\circ \varphi\circ ([\pi_{g}(B|_{g})]+ [\pi_{g}(B|_{g^\perp})]\circ \varphi) )^{-1}. \end{align*} $$

Furthermore, its derivative at g, represented by $0\in \mathrm {Hom}(g,g^\perp )$ , is given by

$$ \begin{align*} D\mathcal{L}_B(0)\dot\varphi= [\pi_{g^\perp}(B|_{g^\perp})]\circ\dot\varphi\circ [\pi_{g}(B|_{g})]^{-1}. \end{align*} $$

Let us denote by $\mathrm {NJ}_{\Pi _1}$ and $\mathrm {NJ}_{\Pi _2}$ the normal Jacobians of the maps $\Pi _1$ and $\Pi _2$ , respectively, where the normal Jacobian of a surjective linear map $L:V_1\to V_2$ of finite dimensional real vector spaces with inner product is the absolute value of the determinant of the linear map L restricted to the orthogonal complement of the kernel of L in $V_1$ . (See [DS03, §3.1].)

Lemma 4. [DS03, §3.2]

Given $(U,g)\in \mathbb V_A$ , one has:

• • ${\mathrm {NJ}}_{\Pi _1}(U,g)= |{\det}\ \mathrm {Id} -D\mathcal {L}_{UA}(g)|$ ;

• • $\mathrm {NJ}_{\Pi _2}(U,g)=1$ .

In §5, we will need the normal Jacobian written more explicitly. To this end, choose bases $v_1, \ldots , v_k$ for g and $v_{k+1}, \ldots , v_n$ for its orthogonal complement $g^\perp $ . In terms of the basis $v_1,\ldots , v_n$ of $\mathbb {R}^n$ , a linear map $B:\mathbb {R}^n\to \mathbb {R}^n$ which satisfies $Bg=g$ is represented by a matrix of the form

$$ \begin{align*} \left(\begin{array}{ c | c } B_1 & * \\ \hline 0 & B_2 \end{array}\right)\hspace{-1.5pt}. \end{align*} $$

By Lemma 3, if X is the matrix representing $\dot \varphi $ in this basis, then $D\mathcal {L}_B(0)\dot \varphi $ is represented by the matrix $B_2XB_1^{-1}$ .

Lemma 5. Let $(U,g)\in \mathbb V_A$ and let

$$ \begin{align*} \left(\begin{array}{ c | c } B_1 & * \\ \hline 0 & B_2 \end{array}\right) \end{align*} $$

represent the map $UA$ in the basis $v_1,\ldots , v_n$ defined above. Then,

$$ \begin{align*}\det (\mathrm{Id} -D\mathcal{L}_{UA}(g))= \det(\mathrm{Id}-B_2\otimes \,{\vphantom{B}}^{t}\!{B}_1^{-1}). \end{align*} $$

4 Proof of Theorem 2

Let $\phi :\mathbb {G}_{n,k}\to \mathbb {R}$ be an integrable function, and let $\hat \phi :\mathbb {V}_A\to \mathbb {R}$ be its lift to $\mathbb V_A$ , that is, $\hat \phi $ is given by $\hat \phi :=\phi \circ \Pi _2$ . (Note that given $g\in \mathbb {G}_{n,k}$ , $\hat \phi $ is constant in the fiber $\Pi _2^{-1}(g)$ , and its value coincides with the value of $\phi $ at g.)

For a set of full measure of $U\in {\operatorname {\mathrm {O}}_n(\mathbb {R})}$ (cf. Remark 2), we have

(4.1) $$ \begin{align} \binom{n}{k}\sup_{g\in\Pi_1^{-1}(U)}(\phi(g))\geq \#\Pi_1^{-1}(U)\sup_{g\in\Pi_1^{-1}(U)}(\phi(g))\geq \sum_{g\in\Pi_1^{-1}(U)}\phi(g). \end{align} $$

By the coarea formula applied to $\Pi _1$ , we get

(4.2) $$ \begin{align} \int_{U\in{\operatorname{\mathrm{O}}_n(\mathbb{R})}}\bigg(\!\sum_{g\in\Pi_1^{-1}(U)}\phi(g)\bigg)\,d{\operatorname{\mathrm{O}}_n(\mathbb{R})}= \int_{{\mathbb V}_A}\hat\phi(U,g)\, \mathrm{NJ}_{\Pi_1}(U,g)\, d{\mathbb V}_A. \end{align} $$

However, applying the coarea formula to the projection $\Pi _2$ ,

(4.3) $$ \begin{align} &\int_{{\mathbb V}_A}\hat\phi(U,g)\, \mathrm{NJ}_{\Pi_1}(U,g)\, d{\mathbb V}_A \\& \quad =\int_{g\in\mathbb{G}_{n,k}}\bigg(\!\int_{U\in \Pi_2^{-1}(g)} \phi(g)\, \mathrm{NJ}_{\Pi_1}(U,g)\, d\Pi_2^{-1}(g) \bigg)\,d\mathbb{G}_{n,k},\nonumber \end{align} $$

where we have used the fact that $\mathrm {NJ}_{\Pi _2}=1$ , and $d\Pi _2^{-1}(g)$ is the volume form on $\Pi _2^{-1}(g)$ induced by the restriction of the Riemannian metric on ${\mathbb V}_A$ to $\Pi _2^{-1}(g)$ .

Then from equations (4.1), (4.2), (4.3), and Lemma 4, we have

(4.4) $$ \begin{align} & \int_{U\in{\operatorname{\mathrm{O}}_n(\mathbb{R})}} \Big(\sup_{g\in\Pi_1^{-1}(U)}(\phi(g))\Big)\,d{\operatorname{\mathrm{O}}_n(\mathbb{R})}\nonumber\\ \nonumber & \quad \geq \binom nk^{-1} \int_{g\in\mathbb{G}_{n,k}}\phi(g)\bigg[\!\int_{U\in \Pi_2^{-1}(g)} {\mathrm{NJ}_{\Pi_1}(U,g)}\, d\Pi_2^{-1}(g) \bigg]\,d\mathbb{G}_{n,k}\\ & \quad =\binom nk^{-1} \int_{g\in\mathbb{G}_{n,k}}\phi(g)\bigg[\!\int_{U\in \Pi_2^{-1}(g)}|{\det}\ \mathrm{Id} -D\mathcal{L}_{UA}(g)| \, d\Pi_2^{-1}(g) \bigg]\,d\mathbb{G}_{n,k}. \end{align} $$

Specialize now to $\phi :\mathbb {G}_{n,k}\to \mathbb {R}$ given by

$$ \begin{align*} \phi(g):=\log^+ |{\det}\ A|_g|,\quad g\in \mathbb{G}_{n,k}. \end{align*} $$

In particular,

$$ \begin{align*}\sup_{g\in{\Pi}_1^{-1}(U)}\phi(g) = \sup_{\substack{g\in{\mathbb{G}}_{n,k}:\\(UA)_\#g=g}}\log^+ |{\det}\ (UA)|_g|. \end{align*} $$

Now, the proof of Theorem 2 follows from Theorem 4 below which is used to bound the bracketed inner integral in equation (4.4); this together with the non-negativity of $\phi $ proves Theorem 2.

Theorem 4. Given $g\in \mathbb {G}_{n,k}$ , one has

$$ \begin{align*} \int_{U\in \Pi_2^{-1}(g)} ( \det \mathrm{Id} -D\mathcal{L}_{UA}(g))\, d\Pi_2^{-1}(g)(U) \geq \mathrm{vol} \operatorname{\mathrm{O}}_k(\mathbb{R})\cdot\mathrm{vol} \operatorname{\mathrm{O}}_{n-k}(\mathbb{R}). \end{align*} $$

The proof is given in the following section.

5 Proof of Theorem 4

For fixed $g\in \mathbb {G}_{n,k}$ , choose $U_0\in {\operatorname {\mathrm {O}}_n(\mathbb {R})}$ such that $U_0Ag=g$ . Then,

$$ \begin{align*}\Pi_2^{-1}(g)=\{VU_0:V\in{\operatorname{\mathrm{O}}_k(\mathbb{R})}\times{\operatorname{\mathrm{O}}_{n-k}(\mathbb{R})} \},\end{align*} $$

where we continue to identify ${\operatorname {\mathrm {O}}_k(\mathbb {R})}\times {\operatorname {\mathrm {O}}_{n-k}(\mathbb {R})}$ with $\operatorname {\mathrm {O}}(g)\times \operatorname {\mathrm {O}}(g^\perp ) $ . We have

$$ \begin{align*} &\int_{U\in \Pi_2^{-1}(g)} \det( \mathrm{Id} -D\mathcal{L}_{UA}(g))\, d\Pi_2^{-1}(g)(U) \\ &\quad= \int_{V\in{\operatorname{\mathrm{O}}_k(\mathbb{R})}\times{\operatorname{\mathrm{O}}_{n-k}(\mathbb{R})}}\det(\mathrm{Id}-D\mathcal{L}_{VU_0A}(g))\, d\Pi_2^{-1}(g)(VU_0)\\ &\quad=\mathrm{vol} \operatorname{\mathrm{O}}_k(\mathbb{R})\cdot\mathrm{vol} \operatorname{\mathrm{O}}_{n-k}(\mathbb{R})\\ & \qquad\times\int_{\psi_1\in{\operatorname{\mathrm{O}}_k(\mathbb{R})}}\int_{\psi_2\in{\operatorname{\mathrm{O}}_{n-k}(\mathbb{R})}} \det(\mathrm{Id}-(\psi_2B_2)\otimes\,{\vphantom{(}}^{t}\!{(}\psi_1B_1)^{-1})\, d\psi_2\,d\psi_1, \end{align*} $$

where $d\psi _1,d\psi _2$ are the Haar measures on ${\operatorname {\mathrm {O}}_k(\mathbb {R})}$ and ${\operatorname {\mathrm {O}}_{n-k}(\mathbb {R})}$ . The last equality follows from Lemma 5, with

$$ \begin{align*} B_1=\pi_g((U_0A)|_g)\quad\mbox{and}\quad B_2=\pi_{g^\perp}((U_0A)|_{g^\perp}). \end{align*} $$

More generally, for $B_1\in \operatorname {\mathrm {GL}}_k(\mathbb {R}), B_2\in \operatorname {\mathrm {GL}}_{n-k}(\mathbb {R})$ , we consider the integral of the characteristic polynomial expressed in the real variable u:

(5.1) $$ \begin{align} {\mathcal {J}}(B_1,B_2;u)=\int_{\psi_1\in {\operatorname{\mathrm{O}}_k(\mathbb{R})}}\int_{\psi_2\in {\operatorname{\mathrm{O}}_{n-k}(\mathbb{R})}} \det(\mathrm{Id}-u(\psi_2B_2)\otimes\,{\vphantom{(\psi_1 B_1)^{-1}}}^{t}\!{(\psi_1 B_1)^{-1}})\,d\psi_2\,d\psi_1. \end{align} $$

Therefore, Theorem 4 is equivalent to

(5.2) $$ \begin{align} {\mathcal {J}}(B_1,B_2;1)\geq 1. \end{align} $$

In fact, we will prove an explicit formula for the integral, expressing the coefficients of the characteristic polynomial ${\mathcal {J}}(B_1,B_2;u)$ as polynomials in the squares of the singular values of $B_1$ and $B_2^{-1}$ with positive integer coefficients.

We complete the proof of Theorem 4 and the inequality in equation (5.2) in several steps. First, we use the representation theory of the general linear group to decompose the double integral into a linear combination of a product of two integrals over ${\operatorname {\mathrm {O}}_n(\mathbb {R})}$ and ${\operatorname {\mathrm {O}}_{n-k}(\mathbb {R})}$ , respectively. Next, each orthogonal group integral is identified with a spherical polynomial. Finally, the theorem follows from an identity between spherical polynomials and Jack polynomials, and a positivity result for the latter due to Knop and Sahi [KS97]. We first review some notation and terminology from combinatorics and representation theory.

5.1 Preliminaries

Let $\unicode{x3bb} =(\unicode{x3bb} _1, \unicode{x3bb} _2,\ldots , \unicode{x3bb} _k)$ be an integer partition of n with k parts:

(5.3)

Associated with the partition $\unicode{x3bb} $ is a Young diagram which is a left justified arrangement of n boxes into k rows, with $\unicode{x3bb} _i$ boxes in the ith row. For example, for the partition $\unicode{x3bb} =(5,3,1)$ of 9 into three parts, the associated Young diagram is

The conjugate partition to $\unicode{x3bb} $ , denoted $\unicode{x3bb} '$ , is obtained by interchanging the rows and columns of the Young diagram of $\unicode{x3bb} $ . For the partition $\unicode{x3bb} =(5,3,1)$ depicted above, we have $\unicode{x3bb} '=(3,2,2,1,1).$

Partitions $\unicode{x3bb} $ with at most n-parts—or equivalently, Young diagrams with at most n rows—parameterize irreducible polynomial representations of $G=GL_n(\mathbb {R})$ . For example, letting $V_0$ be the standard n-dimensional representation of G, the partition $(r)$ corresponds to $\operatorname {\mathrm {sym}}^r(V_0)$ and $(1,1,\ldots , 1)$ (with r ones) corresponds to $\Lambda ^r(V_0).$ More generally, letting $a_i$ be the number of columns of length i in the Young diagram of $\unicode{x3bb} ,$ the irreducible representation corresponding to $\unicode{x3bb} $ can be identified with a subspace of

(5.4) $$ \begin{align} \operatorname{\mathrm{sym}}^{a_n}\Lambda^n (V_0)\otimes \operatorname{\mathrm{sym}}^{a_{n-1}}\Lambda^{n-1} (V_0)\otimes \cdots \otimes \operatorname{\mathrm{sym}}^{a_1} V_0. \end{align} $$

The precise definition of this irreducible representation is not relevant for our present concerns. However, we note that the representation corresponding to $\unicode{x3bb} $ has a vector fixed by the orthogonal group $\operatorname {\mathrm {O}}_n(\mathbb {R})$ if and only if every part of $\unicode{x3bb} $ is even. (See §5.5.2 for an example.) This observation, presented in Theorem 6 below, and the more explicit positivity statement of Theorem 5 are the key ideas in our proof of Theorem 4.

5.2 Orthogonal group integrals

We begin by expanding the characteristic polynomial in the integrand as a sum of traces:

$$ \begin{align*} \det(\mathrm{Id}-u(\psi_2 B_2)\otimes\,{\vphantom{(\psi_1 B_1)^{-1}}}^{t}\!{(\psi_1 B_1)^{-1}}) =\sum_{j=0}^{k(n-k)} (-u)^j \operatorname{\mathrm{tr}}\bigwedge\nolimits^j(\psi_2 B_2\otimes \,{\vphantom{(}}^{t}\!{(}\psi_1 B_1)^{-1}). \end{align*} $$

Next, decompose the exterior powers of the tensor product as

(5.5) $$ \begin{align} \bigwedge\nolimits^j(\psi_2 B_2\otimes \,{\vphantom{(}}^{t}\!{(}\psi_1 B_1)^{-1}) = \sum_{\unicode{x3bb}:|\unicode{x3bb}|=j} \rho_{\unicode{x3bb}'}(\psi_2 B_2)\otimes \rho_{\unicode{x3bb}}(\,{\vphantom{(}}^{t}\!{(}\psi_1 B_1)^{-1}), \end{align} $$

where:

• • the sum is over all partitions $\unicode{x3bb} $ of j with at most k rows and $n-k$ columns;

• • $\unicode{x3bb} '$ is the partition conjugate to $\unicode{x3bb} $ ; and

• • $\rho _\unicode{x3bb} , \rho _{\unicode{x3bb} '}$ are the irreducible representations of $\operatorname {\mathrm {GL}}_k(\mathbb {R})$ and $\operatorname {\mathrm {GL}}_{n-k}(\mathbb {R})$ associated to the partitions $\unicode{x3bb} ,\unicode{x3bb} ',$ respectively.

See, for example, [FH91, Exercise 6.11]. Since the trace of a tensor product of two matrices is the product of the two traces, we may write

$$ \begin{align*} \det(\mathrm{Id}-u(\psi_2 B_2)\otimes\,{\vphantom{(\psi_1 B_1)^{-1}}}^{t}\!{(\psi_1 B_1)^{-1}}) =\sum_{j=0}^{k(n-k)} (-u)^j\sum_{|\unicode{x3bb}|=j} \operatorname{\mathrm{tr}}\rho_{\unicode{x3bb}'}(\psi_2 B_2)\cdot\operatorname{\mathrm{tr}}\rho_\unicode{x3bb} (\psi_1 B_1). \end{align*} $$

Integrating over $\operatorname {\mathrm {O}}_k(\mathbb {R})\times \operatorname {\mathrm {O}}_{n-k}(\mathbb {R})$ , we find that ${\mathcal {J}}(B_1,B_2;u)$ is equal to

(5.6) $$ \begin{align} &\sum_{j=0}^{k(n-k)}(-u)^j \sum_{|\unicode{x3bb}|=j} \bigg(\!\int_{\psi_2\in \operatorname{\mathrm{O}}_{n-k}(\mathbb{R})}\operatorname{\mathrm{tr}}\rho_{\unicode{x3bb}'}(\psi_2 B_2)\,d\psi_2\bigg)\cdot \bigg(\!\int_{\psi_1\in \operatorname{\mathrm{O}}_{k}(\mathbb{R})} \operatorname{\mathrm{tr}}\rho_{\unicode{x3bb}}(\psi_1 B_1)\,d\psi_1\bigg) \nonumber\\ &\qquad= 1+ \sum_{\substack{1\leq j\leq k(n-k)\\ |\unicode{x3bb}| = j}} (-u)^j F_{\unicode{x3bb}'}(B_2)F_{\unicode{x3bb}}(B_1) , \end{align} $$

where for $M\in \operatorname {\mathrm {GL}}_N(\mathbb {R})$ and $\mu $ a partition of j with at most N parts, we define

(5.7) $$ \begin{align} F_\mu(M)=\int_{\psi\in \operatorname{\mathrm{O}}_N(\mathbb{R})}\operatorname{\mathrm{tr}}\rho_\mu(\psi M)\,d\psi. \end{align} $$

Theorem 4 follows from the following more explicit result.

Theorem 5. Let $M\in \operatorname {\mathrm {GL}}_N(\mathbb {R})$ and $\mu =(\mu _1, \ldots , \mu _r)$ with $\mu _1\geq \mu _2\geq \cdots \geq \mu _r>0$ be a partition of k of at most N parts.

1. (1) If any of the parts $\mu _i$ is odd, then $F_\mu (M)=0.$

2. (2) If all the parts $\mu _i$ are even, then $F_\mu (M)$ is an even polynomial in the singular values of M with positive coefficients.

5.3 Spherical polynomials

The proof of Theorem 5 involves the theory of spherical polynomials for the symmetric space $G/K$ , where $G=\operatorname {\mathrm {GL}}_N(\mathbb {R})$ and $K=\operatorname {\mathrm {O}}_N(\mathbb {R})$ , and Jack polynomials. We recall these briefly.

Let ${\mathcal {P}}_N$ be the set of partitions with at most N parts, thus

$$ \begin{align*} {\mathcal {P}}_N=\{\mu \in \mathbb Z^N\mid \mu_1\ge \mu_2\ge \cdots\ \geq\mu_N\ge 0\}. \end{align*} $$

For $\mu \in {\mathcal {P}}_N$ , let $(\rho _\mu , V_\mu )$ be the corresponding representation of G, and let $(\rho _\mu ^\prime ,V_\mu ^*)$ be the contragredient representation. That is, G acts on the dual vector space $V_\mu ^*$ by

$$ \begin{align*}\langle\rho'(g)u,v\rangle=\langle u, \rho(g)^{-1}v\rangle, \end{align*} $$

where $\langle u,v\rangle $ is the evaluation pairing between $u\in V_{\mu }^*$ and $u\in V_\mu .$ A matrix coefficient of $V_\mu $ is a function on G of the form

$$ \begin{align*} \phi_{u,v}(M) =\langle u, \rho_\mu(M)v \rangle, \end{align*} $$

where $u\in V_\mu ^*$ and $v\in V_\mu $ . We write ${\mathcal {F}}_\mu $ for the span of matrix coefficients of $V_\mu $ . Then ${\mathcal {F}}_\mu $ is stable under left and right multiplication by G, and one has a $G\times G$ -module isomorphism

$$ \begin{align*} V_\mu^*\otimes V_\mu \approx {\mathcal {F}}_\mu,\quad u\otimes v\mapsto \phi_{u,v}.\end{align*} $$

Theorem 6. Let $\mu $ be a partition in ${\mathcal {P}}_N$ . Then the following are equivalent:

1. (1) $\mu $ is even, that is, $\mu _i\in 2\mathbb Z$ for all i;

2. (2) $V_\mu $ has a spherical vector, that is, a vector fixed by K;

3. (3) $V_\mu ^*$ has a spherical vector;

4. (4) ${\mathcal {F}}_\mu $ contains a spherical polynomial $\phi _\mu $ , that is, a function satisfying

   $$ \begin{align*} \phi_\mu(kgk')=\phi_\mu(g), \; g\in G,\; k,k'\in K.\end{align*} $$

The spherical vector $v_\mu $ and spherical polynomial $\phi _\mu $ are unique up to scalar multiple, and the latter is usually normalized by the requirement $\phi _\mu (e)=1$ , which fixes it uniquely.

Proof. This follows from the Cartan–Helgason theory of spherical representations [Hel84, Theorem V.4.1].

We now connect the polynomial $F_\mu $ to $\phi _\mu $ .

Theorem 7. Let $F_\mu (M)$ be as in equation (5.7). If $\mu $ is even, then $F_\mu =\phi _\mu $ , otherwise $F_\mu =0$ .

Proof. If $\{v_i\},\{u_i\}$ are dual bases for $V_\unicode{x3bb} ,V_\unicode{x3bb} ^*$ , then $\operatorname {\mathrm {tr}} \rho _\mu (M)=\sum _i\phi _{u_i,v_i}(M)$ , thus the character $\chi _\mu (M) = \operatorname {\mathrm {tr}} \rho _\mu (M)$ is an element of ${\mathcal {F}}_\mu $ . Since ${\mathcal {F}}_\mu $ is stable under the left action of K, it follows that $F_\mu (M)=\int _K\chi _\mu (k M)\,dk$ is in ${\mathcal {F}}_\mu $ as well.

We next argue that $F_\mu $ is $K\times K$ invariant. For this, we compute as follows:

$$ \begin{align*} F_\mu(k_1Mk_2)=\int_K\chi_\mu(kk_1Mk_2)\,dk = \int_K\chi_\mu(k_2kk_1M)\,dk = F_\mu(M).\end{align*} $$

Here, the first equality holds by definition, the second is a consequence the invariance of the trace character, $\chi _\mu (AB)=\chi _\mu (BA)$ , and the final equality follows from the $K\times K$ invariance of the Haar measure $dk$ .

By Theorem 6, this proves that $F_\mu $ is a multiple of $\phi _\mu $ if $\mu $ is even, and $F_\mu =0$ otherwise. To determine the precise multiple, we need to compute the following integral for even $\mu $ :

$$ \begin{align*} F_\mu(e)=\int_K\chi_\mu(k)\,dk.\end{align*} $$

By Schur orthogonality, this integral is the multiplicity of the trivial representation in the restriction of $V_\mu $ to K, which is $1$ if $\mu $ is even. Thus, we get $F_\mu =\phi _\mu $ , as desired.

5.4 Jack polynomials

Jack polynomials $J_\unicode{x3bb} ^{(\alpha )}(x_1,\ldots ,x_N)$ are a family of symmetric polynomials in N variables whose coefficients depend on a parameter $\alpha $ . The main result of [KS97] is that these coefficients are themselves positive integral polynomials in the parameter $\alpha $ .

Spherical functions correspond to Jack polynomials with $\alpha =2$ . More precisely, we have

(5.8) $$ \begin{align} \phi_\mu(g)= \frac{J_\unicode{x3bb}^{(2)}(a_1,\ldots, a_N)}{J_\unicode{x3bb}^{(2)}(1,\ldots, 1)}, \quad \mu=2\unicode{x3bb}, \end{align} $$

where $a_1,\ldots ,a_N$ are the eigenvalues of the symmetric matrix $\,{\vphantom {g}}^{t}\!{g}g$ ; in other words, the $a_i$ are the squares of the singular values of g.

We can now finish the proof of Theorem 5.

Proof of Theorem 5

Part (1) follows from Theorem 7. Part (2) follows from equation (5.8) and the positivity of Jack polynomials as proved in [KS97].

5.5 Examples

We conclude this section with two low rank examples of the characteristic polynomials ${\mathcal {J}}(A,B;u)$ for $A\in \operatorname {\mathrm {GL}}_k(\mathbb {R}), B\in \operatorname {\mathrm {GL}}_{n-k}(\mathbb {R}).$ As we may assume A and B are diagonal, let us write

$$ \begin{align*}A=\operatorname{\mathrm{diag}}(a_1,\ldots, a_k)\quad\mbox{and}\quad B=\operatorname{\mathrm{diag}}(b_1, \ldots, b_{n-k}). \end{align*} $$

5.5.1 The case $n=4,k=2$

Here we consider the integral

(5.9) $$ \begin{align} {\mathcal {J}}(A,B;u)=\int_{\psi_1\in \operatorname{\mathrm{O}}_2(\mathbb{R})}\int_{\psi_2\in \operatorname{\mathrm{O}}_2(\mathbb{R})} \det(\mathrm{Id}-u(\psi_2B)\otimes\,{\vphantom{(\psi_1 A)^{-1}}}^{t}\!{(\psi_1 A)^{-1}})\,d\psi_2\,d\psi_1. \end{align} $$

As we are essentially integrating over the circle, it is easy to compute this directly and see that

(5.10) $$ \begin{align} {\mathcal {J}}(A,B;u)=1+\frac{\det(B)^2}{\det(A)^2}u^4=1+\frac{b_1^2b_2^2}{a_1^2a_2^2}u^4. \end{align} $$

5.5.2 The case $n=6,k=2$

In this case, we use equation (5.6) to compute

$$\begin{align*}{\mathcal {J}}(A,B;u)=\int_{\psi_1\in \operatorname{\mathrm{O}}_2(\mathbb{R})}\int_{\psi_2\in \operatorname{\mathrm{O}}_4(\mathbb{R})} \det(\mathrm{Id}-u(\psi_2B)\otimes\,{\vphantom{(\psi_1 A)^{-1}}}^{t}\!{(\psi_1 A)^{-1}})\,d\psi_2\,d\psi_1 \end{align*}$$

for $A\in \operatorname {\mathrm {GL}}_2(\mathbb {R}),B\in \operatorname {\mathrm {GL}}_4(\mathbb {R}).$ Write

$$ \begin{align*}{\mathcal {J}}(A,B;u)=1+c_2u^2+c_4u^4+c_6u^6+c_8u^8. \end{align*} $$

By part (1) of Theorem 5, we immediately see that $c_2=c_6=0$ because there are no partitions $\unicode{x3bb} $ of $2$ or $6$ for which both $\unicode{x3bb} $ and its conjugate $\unicode{x3bb} '$ have only even parts. The only even partition of $k=8$ with at most two parts and with even conjugate is $\unicode{x3bb} =(4,4).$ For V, the standard two-dimensional representation of $\operatorname {\mathrm {GL}}_2(\mathbb {R})$ , we have that $\rho _\unicode{x3bb} (V)=\operatorname {\mathrm {sym}}^4(\Lambda ^2 V)$ is the fourth power of the determinant representation. Hence,

$$ \begin{align*}F_\unicode{x3bb}(A^{-1})=\det A^{-4}.\end{align*} $$

Similarly for W, the standard four-dimensional representation of $\operatorname {\mathrm {GL}}_4(\mathbb {R})$ , the conjugate $\unicode{x3bb} '=(2,2,2,2)$ and $\rho _{\unicode{x3bb} '}(W)=\operatorname {\mathrm {sym}}^2(\Lambda ^4(W))$ is the square of the determinant. Hence, $F_{\unicode{x3bb} '}(B)=\det B^{2}$ and

$$ \begin{align*}c_8=\frac{\det(B)^2}{\det(A)^4}.\end{align*} $$

The only even partition of $k=4$ with even conjugate is $\unicode{x3bb} =\unicode{x3bb} '=(2,2).$ In this case, $\rho _\unicode{x3bb} (V)$ is the square of the determinant representation. The dimension 20 representation $\rho _\unicode{x3bb} (W)$ is a quotient of $\operatorname {\mathrm {sym}}^2(\Lambda ^2(W))$ with a unique $\operatorname {\mathrm {O}}_4(\mathbb {R})$ -fixed vector, namely, the image of

$$ \begin{align*}v=(e_1\wedge e_2)^2+(e_1\wedge e_3)^2+(e_1\wedge e_4)^2+(e_2\wedge e_3)^2+(e_2\wedge e_4)^2+(e_3\wedge e_4)^2. \end{align*} $$

It is readily seen that the trace $\rho _\unicode{x3bb} (B)$ restricted to the span of v is

$$ \begin{align*}\sum_{1\leq i< j\leq 4} b_i^2b_j^2. \end{align*} $$

Then, including the normalizing factor of $1/J^{(2)}_{(1,1)}(1,1,1,1)=1/6$ , we conclude that

$$ \begin{align*}c_4=\frac{1/6 (b_1^2b_2^2+b_1^2b_3^2+b_1^2b_4^2+b_2^2b_3^2+b_2^2b_4^2+b_3^2b_4^2)} {a_1^2a_2^2}.\end{align*} $$