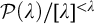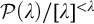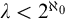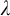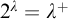1. Introduction
We investigate automorphisms of Boolean algebras of the form
The instance
![]() $P^{\omega }_{\omega }$
, i.e.,
$P^{\omega }_{\omega }$
, i.e.,
![]() ${\mathcal {P}}(\omega )/\mathrm {FIN}$
, has been studied extensively for many years.Footnote
1
One can study variants for uncountable cardinals
${\mathcal {P}}(\omega )/\mathrm {FIN}$
, has been studied extensively for many years.Footnote
1
One can study variants for uncountable cardinals
![]() $\lambda $
. Unsurprisingly, the behaviour here tends to be quite different to the countable case. One moderately popularFootnote
2
such generalisation is
$\lambda $
. Unsurprisingly, the behaviour here tends to be quite different to the countable case. One moderately popularFootnote
2
such generalisation is
![]() $P^\lambda _{\omega }$
. Here, we study another obvious generalization of the countable case,
$P^\lambda _{\omega }$
. Here, we study another obvious generalization of the countable case,
![]() $P^\lambda _{\lambda }$
. Some results for general
$P^\lambda _{\lambda }$
. Some results for general
![]() $P^\lambda _\kappa $
can be found in [Reference Larson and McKenney5].
$P^\lambda _\kappa $
can be found in [Reference Larson and McKenney5].
The main result of the paper is:
 $$ \begin{align} \nonumber & \mathit{The\ following\ is\ equiconsistent\ with\ an\ inaccessible}{:}\ \lambda\ \mathit{is\ inaccessible}, 2^\lambda\ \mathit{is } \\& \nonumber \lambda^{++},\ \mathit{and\ all\ automorphisms\ of}\ P^\lambda_{\lambda}\ \mathit{are\ densely\ trivial.} \\ \end{align} $$
$$ \begin{align} \nonumber & \mathit{The\ following\ is\ equiconsistent\ with\ an\ inaccessible}{:}\ \lambda\ \mathit{is\ inaccessible}, 2^\lambda\ \mathit{is } \\& \nonumber \lambda^{++},\ \mathit{and\ all\ automorphisms\ of}\ P^\lambda_{\lambda}\ \mathit{are\ densely\ trivial.} \\ \end{align} $$
Here,
![]() $2^\lambda>\lambda ^{+}$
is necessary, at least for measurables:
$2^\lambda>\lambda ^{+}$
is necessary, at least for measurables:
Remark 1.1. From [Reference Shelah and Steprāns12, Lemma 3.2] it would follow that Theorem B holds even when “measurable” is replaced by just “inaccessible.” However, the proof there turned out to be incorrect.Footnote 3
For
![]() $\lambda $
below the continuum we get the following result under Martin’s Axiom (MA). More explicitly, MA
$\lambda $
below the continuum we get the following result under Martin’s Axiom (MA). More explicitly, MA
![]() $_{=\lambda }(\sigma \text{-centered})$
is sufficient, which is the statement that for any
$_{=\lambda }(\sigma \text{-centered})$
is sufficient, which is the statement that for any
![]() $\sigma $
-centered poset P and
$\sigma $
-centered poset P and
![]() ${\le }\lambda $
many open dense sets in P there is a filter G meeting all these open sets:
${\le }\lambda $
many open dense sets in P there is a filter G meeting all these open sets:
 $$ \begin{align} \nonumber & \mathit{For}\ \aleph_0<\kappa\le\lambda<2^{\aleph_0}\ \mathit{and}\ \kappa\ \mathit{regular},\ MA_{=\lambda}(\sigma\mathit{-centered})\ \mathit{implies\ that\ every}\\\nonumber & \mathit{automorphism\ of}\ P^\lambda_{\kappa}\ \mathit{is\ trivial.}\\ \end{align} $$
$$ \begin{align} \nonumber & \mathit{For}\ \aleph_0<\kappa\le\lambda<2^{\aleph_0}\ \mathit{and}\ \kappa\ \mathit{regular},\ MA_{=\lambda}(\sigma\mathit{-centered})\ \mathit{implies\ that\ every}\\\nonumber & \mathit{automorphism\ of}\ P^\lambda_{\kappa}\ \mathit{is\ trivial.}\\ \end{align} $$
Larson and McKenney [Reference Larson and McKenney5] showed the same under MA
![]() $_{\aleph _1}$
for the case
$_{\aleph _1}$
for the case
![]() $\lambda =2^{\aleph _0}$
and
$\lambda =2^{\aleph _0}$
and
![]() $\kappa =\aleph _1$
.
$\kappa =\aleph _1$
.
Contrast this to the case
![]() $\lambda =\kappa =\omega $
: Due to results of Veličković, Steprāns, and the second author, “Every automorphisms of
$\lambda =\kappa =\omega $
: Due to results of Veličković, Steprāns, and the second author, “Every automorphisms of
![]() ${\mathcal {P}}(\omega )/[\omega ]^{<\omega }$
is trivial” is implied by PFA [Reference Shelah and Steprāns10], in fact even by MA+OCA [Reference Veličković15], but not by MA alone [Reference Veličković15] (not even for “somewhere trivial” [Reference Shelah and Steprāns11]).
${\mathcal {P}}(\omega )/[\omega ]^{<\omega }$
is trivial” is implied by PFA [Reference Shelah and Steprāns10], in fact even by MA+OCA [Reference Veličković15], but not by MA alone [Reference Veličković15] (not even for “somewhere trivial” [Reference Shelah and Steprāns11]).
Contents
We start by introducing some notation and basic results in Section 2 (page 2).
The following sections are independent of each other:
In Section 3 (page 3) we show Theorem C, which we state as Theorem 3.1; in Section 4 (page 6), we show Theorem B, i.e., Theorem 4.1; and finally in the main part, Section 5 (page 7) we develop some forcing notions to prove Theorem A, i.e., Theorem 5.2.
2. Definitions
We always assume that
![]() $\lambda $
is a cardinal and
$\lambda $
is a cardinal and
![]() $\kappa \le \lambda $
is regular.
$\kappa \le \lambda $
is regular.
-
• The case
 $\kappa =\aleph _0$
or
$\kappa =\aleph _0$
or
 $\lambda =\aleph _0$
is included only for completeness sake in the following definitions.
$\lambda =\aleph _0$
is included only for completeness sake in the following definitions. -
• In Section 3 we will assume that
 $\aleph _1\le \kappa \le \lambda < 2^{\aleph _0}$
.
$\aleph _1\le \kappa \le \lambda < 2^{\aleph _0}$
. -
• In Section 4 we assume that
 $\lambda $
is measurable and
$\lambda $
is measurable and
 $\kappa =\lambda $
.
$\kappa =\lambda $
. -
• In Section 5 we assume that
 $\lambda $
is inaccessible and
$\lambda $
is inaccessible and
 $\kappa =\lambda $
.
$\kappa =\lambda $
.
Notation:
-
• We investigate the Boolean algebra (BA)
 $P^\lambda _\kappa :={\mathcal {P}}(\lambda )/[\lambda ]^{{<}\kappa }$
, i.e., the power set of
$P^\lambda _\kappa :={\mathcal {P}}(\lambda )/[\lambda ]^{{<}\kappa }$
, i.e., the power set of
 $\lambda $
factored by the ideal of sets of size
$\lambda $
factored by the ideal of sets of size
 ${<}\kappa $
.
${<}\kappa $
. -
• For
 $A\subseteq \lambda $
, we denote the equivalence class of A with
$A\subseteq \lambda $
, we denote the equivalence class of A with
 $[A]$
. We set
$[A]$
. We set
 $\mathbb 0:=[\emptyset ]$
.
$\mathbb 0:=[\emptyset ]$
. -
•
 $A\subseteq ^* B$
means
$A\subseteq ^* B$
means
 $|B\setminus A|<\kappa $
, analogously for
$|B\setminus A|<\kappa $
, analogously for
 $A=^*B$
; and “for almost all
$A=^*B$
; and “for almost all
 $\alpha \in A$
” means for all but
$\alpha \in A$
” means for all but
 ${<}\kappa $
many in A. In particular,
${<}\kappa $
many in A. In particular,
 $A=^*\lambda $
means
$A=^*\lambda $
means
 $A\subseteq \lambda $
and
$A\subseteq \lambda $
and
 $|\lambda \setminus A|<\kappa $
.
$|\lambda \setminus A|<\kappa $
. -
• We denote the BA-operations in
 $P^\lambda _\kappa $
with
$P^\lambda _\kappa $
with
 $x \vee y$
,
$x \vee y$
,
 $x \wedge y $
and
$x \wedge y $
and
 $x^c$
(for the complement). So we have
$x^c$
(for the complement). So we have
 $[A]\vee [B]=[A\cup B]$
,
$[A]\vee [B]=[A\cup B]$
,
 $[A]\wedge [B]=[A\cap B]$
, and
$[A]\wedge [B]=[A\cap B]$
, and
 $[A]^c=[\lambda \setminus A]$
.
$[A]^c=[\lambda \setminus A]$
. -
• A function
 $\phi : P^\lambda _\kappa \to P^\lambda _\kappa $
is a BA-automorphism (which we will just call automorphism), if it is bijective, compatible with
$\phi : P^\lambda _\kappa \to P^\lambda _\kappa $
is a BA-automorphism (which we will just call automorphism), if it is bijective, compatible with
 $\wedge $
and the complement, and satisfies
$\wedge $
and the complement, and satisfies
 $\phi (\mathbb 0)=\mathbb 0$
.
$\phi (\mathbb 0)=\mathbb 0$
. -
• Preimages of a function f are denoted by
 $f^{-1}x$
, images by
$f^{-1}x$
, images by
 $f"x$
.
$f"x$
. -
• We sometimes identify
 $\eta \in 2^\lambda $
with
$\eta \in 2^\lambda $
with
 $\eta ^{-1}\{1\}\subseteq \lambda $
without explicitly mentioning it, by referring to
$\eta ^{-1}\{1\}\subseteq \lambda $
without explicitly mentioning it, by referring to
 $\eta $
as element of
$\eta $
as element of
 $2^\lambda $
or of
$2^\lambda $
or of
 $P(\lambda )$
.
$P(\lambda )$
.
Let us note that
![]() $P^\lambda _\kappa $
is
$P^\lambda _\kappa $
is
![]() ${<}\kappa $
-completeFootnote
4
and
${<}\kappa $
-completeFootnote
4
and
![]() $\lambda ^+$
-cc. Also, any automorphism
$\lambda ^+$
-cc. Also, any automorphism
![]() $\phi $
is closed under
$\phi $
is closed under
![]() ${<}\kappa $
unions:
${<}\kappa $
unions:
![]() $\phi (\bigvee _{i\in I}[A_i])= \bigvee _{i\in I}\phi ([A_i])$
.
$\phi (\bigvee _{i\in I}[A_i])= \bigvee _{i\in I}\phi ([A_i])$
.
An automorphism is trivial if it is induced by a function on
![]() $\lambda $
. A standard definition to capture this concept is the following:
$\lambda $
. A standard definition to capture this concept is the following:
Definition 2.1. An automorphism
![]() $\phi :P^\lambda _\kappa \to P^\lambda _\kappa $
is trivial, if there is a
$\phi :P^\lambda _\kappa \to P^\lambda _\kappa $
is trivial, if there is a
![]() $g:\lambda \to \lambda $
such that
$g:\lambda \to \lambda $
such that
![]() $\phi ([A])=[g^{-1}A]$
for all
$\phi ([A])=[g^{-1}A]$
for all
![]() $A\subseteq \lambda $
.
$A\subseteq \lambda $
.
However, we prefer to use forward images instead of inverse images, which can easily be seen to be equivalent:
Definition 2.2.
-
• For
 $f:A_0 \to \lambda $
with
$f:A_0 \to \lambda $
with
 $A_0=^* \lambda $
, define
$A_0=^* \lambda $
, define
 $\pi _f:P^\lambda _\kappa \to P^\lambda _\kappa $
by
$\pi _f:P^\lambda _\kappa \to P^\lambda _\kappa $
by
 $\pi _f([B]):=[f"(B\cap A_0)]$
for all
$\pi _f([B]):=[f"(B\cap A_0)]$
for all
 $B\subseteq \lambda $
.
$B\subseteq \lambda $
. -
• f is an almost permutation, if there are
 $A_0=^*\lambda $
and
$A_0=^*\lambda $
and
 $B_0=^*\lambda $
with
$B_0=^*\lambda $
with
 $f:A_0\to B_0$
bijective.
$f:A_0\to B_0$
bijective.
(Such a
![]() $\pi _f$
is always a well-defined function.)
$\pi _f$
is always a well-defined function.)
Lemma 2.3. Let
![]() $\phi :P^\lambda _\kappa \to P^\lambda _\kappa $
be a function. The following are equivalent
$\phi :P^\lambda _\kappa \to P^\lambda _\kappa $
be a function. The following are equivalent
![]() $:$
$:$
-
(1)
 $\phi $
is a trivial automorphism.
$\phi $
is a trivial automorphism. -
(2) There is an almost permutation f such that
 $\phi =\pi _f$
.
$\phi =\pi _f$
. -
(3) (Assuming
 $\kappa>\aleph _0$
.) There is a bijection
$\kappa>\aleph _0$
.) There is a bijection
 $f:\lambda \to \lambda $
such that
$f:\lambda \to \lambda $
such that
 $\phi =\pi _f$
.
$\phi =\pi _f$
.
Proof (1) implies (2): Assume
![]() $\phi $
is a trivial automorphism, witnessed by g.
$\phi $
is a trivial automorphism, witnessed by g.
Then
![]() $X:=g"\lambda =^*\lambda $
(as
$X:=g"\lambda =^*\lambda $
(as
![]() $\phi ([X])=[g^{-1}X]= [\lambda ]$
), and
$\phi ([X])=[g^{-1}X]= [\lambda ]$
), and
![]() $Y:=\{\alpha \in X:\, |g^{-1}\{\alpha \}|\ne 1\}=^*\emptyset $
: Otherwise, pick
$Y:=\{\alpha \in X:\, |g^{-1}\{\alpha \}|\ne 1\}=^*\emptyset $
: Otherwise, pick
![]() $y^0_\alpha \ne y^1_\alpha $
for each
$y^0_\alpha \ne y^1_\alpha $
for each
![]() $\alpha \in Y$
with
$\alpha \in Y$
with
![]() $g(y^0_\alpha )=g(y^1_\alpha )=\alpha $
. So
$g(y^0_\alpha )=g(y^1_\alpha )=\alpha $
. So
![]() $y^0_\alpha \in g^{-1}C$
iff
$y^0_\alpha \in g^{-1}C$
iff
![]() $y^1_\alpha \in g^{-1}C$
for any
$y^1_\alpha \in g^{-1}C$
for any
![]() $C\subseteq \lambda $
. Set
$C\subseteq \lambda $
. Set
![]() $B^i:=\{y^i_\alpha :\, \alpha \in Y\}$
for
$B^i:=\{y^i_\alpha :\, \alpha \in Y\}$
for
![]() $i=0,1$
and let
$i=0,1$
and let
![]() $[C]=\phi ^{-1}([B^0])$
. So
$[C]=\phi ^{-1}([B^0])$
. So
![]() $\phi ([C])=[g^{-1}C]=[B^0]$
, i.e., almost all
$\phi ([C])=[g^{-1}C]=[B^0]$
, i.e., almost all
![]() $y^0_\alpha $
are in
$y^0_\alpha $
are in
![]() $g^{-1}C$
, but then almost all
$g^{-1}C$
, but then almost all
![]() $y^1_\alpha $
are in
$y^1_\alpha $
are in
![]() $g^{-1}C$
as well, i.e.,
$g^{-1}C$
as well, i.e.,
![]() $[B^0]=\phi ([C])\ge [B^1]$
, a contradiction as
$[B^0]=\phi ([C])\ge [B^1]$
, a contradiction as
![]() $B^0\cap B^1=\emptyset $
.
$B^0\cap B^1=\emptyset $
.
Set
![]() $A_0:=X\setminus Y$
, and
$A_0:=X\setminus Y$
, and
![]() $B_0:=g^{-1}A_0$
. Note that
$B_0:=g^{-1}A_0$
. Note that
![]() $B_0=^*\lambda $
, as
$B_0=^*\lambda $
, as
![]() $\mathbb 0=\phi (\mathbb 0)=\phi ([Y])=[g^{-1}Y]$
. So
$\mathbb 0=\phi (\mathbb 0)=\phi ([Y])=[g^{-1}Y]$
. So
![]() $g\restriction B_0\to A_0$
is bijective, and we can set
$g\restriction B_0\to A_0$
is bijective, and we can set
![]() $f:A_0\to B_0$
the inverse. Then f is an almost permutation, and
$f:A_0\to B_0$
the inverse. Then f is an almost permutation, and
![]() $\pi =\pi _f$
.
$\pi =\pi _f$
.
(2) implies (1): Let
![]() $f:A_0\to B_0$
be an almost permutation, and
$f:A_0\to B_0$
be an almost permutation, and
![]() $g:B_0\to A_0$
the inverse (and let g be defined arbitrarily on
$g:B_0\to A_0$
the inverse (and let g be defined arbitrarily on
![]() $\lambda \setminus B_0$
). Then
$\lambda \setminus B_0$
). Then
![]() $\pi _f([X])=[f"(X\cap A_0)]=[g^{-1}(X)]$
. It remains to be shown that
$\pi _f([X])=[f"(X\cap A_0)]=[g^{-1}(X)]$
. It remains to be shown that
![]() $\pi _f$
is an automorphism:
$\pi _f$
is an automorphism:
![]() $\pi _f([\emptyset ])=[f"\emptyset ]=[\emptyset ]$
;
$\pi _f([\emptyset ])=[f"\emptyset ]=[\emptyset ]$
;
![]() $\pi _f([X\cap Y])= [f"(X\cap Y\cap A_0)]=[f"(X\cap A_0)\cap f"(Y\cap A_0)]$
; and
$\pi _f([X\cap Y])= [f"(X\cap Y\cap A_0)]=[f"(X\cap A_0)\cap f"(Y\cap A_0)]$
; and
![]() $\pi _f([\lambda \setminus X])= [f"(A_0\setminus X)]=[B_0\setminus f"X]$
.
$\pi _f([\lambda \setminus X])= [f"(A_0\setminus X)]=[B_0\setminus f"X]$
.
(2) implies (3) if
![]() $\operatorname {\mathrm {cf}}(\kappa )>\aleph _0$
: This follows from the following lemma.
$\operatorname {\mathrm {cf}}(\kappa )>\aleph _0$
: This follows from the following lemma.
Lemma 2.4 (
 $\kappa>\aleph _0$
).
$\kappa>\aleph _0$
).
Let f be a
![]() $\kappa $
-almost permutation. Then there is an
$\kappa $
-almost permutation. Then there is an
![]() $S=^*\lambda $
such that
$S=^*\lambda $
such that
![]() $f\restriction S:\, S\rightarrow S$
is bijective.
$f\restriction S:\, S\rightarrow S$
is bijective.
Proof Set
![]() $X_0:=A_0=\operatorname {\mathrm {dom}}(f)$
, and
$X_0:=A_0=\operatorname {\mathrm {dom}}(f)$
, and
![]() $X_{i+1}:= X_{i} \cap f" X_i \cap f^{-1}X_{i}$
, and
$X_{i+1}:= X_{i} \cap f" X_i \cap f^{-1}X_{i}$
, and
![]() $S:=\bigcap _{i\in \omega }X_i$
.
$S:=\bigcap _{i\in \omega }X_i$
.
The
![]() $X_n$
are decreasing, and
$X_n$
are decreasing, and
![]() $|\lambda \setminus X_n|<\kappa $
and thus
$|\lambda \setminus X_n|<\kappa $
and thus
![]() $|\lambda \setminus (f" X_n)|<\kappa $
for
$|\lambda \setminus (f" X_n)|<\kappa $
for
![]() $n<\omega $
. Accordingly,
$n<\omega $
. Accordingly,
![]() $|\lambda \setminus S|<\kappa $
. We claim that
$|\lambda \setminus S|<\kappa $
. We claim that
![]() $g:=f\restriction S$
is a permutation of S. Clearly it is injective. If
$g:=f\restriction S$
is a permutation of S. Clearly it is injective. If
![]() $\alpha \in S$
then
$\alpha \in S$
then
![]() $\alpha \in X_n$
for all
$\alpha \in X_n$
for all
![]() $n\in \omega $
, so
$n\in \omega $
, so
![]() $f(\alpha )\in X_{n+1}$
for all n. So
$f(\alpha )\in X_{n+1}$
for all n. So
![]() $g:S\to S$
. If
$g:S\to S$
. If
![]() $\alpha \in S$
, then
$\alpha \in S$
, then
![]() $\alpha \in X_{n+1}$
for all n, so
$\alpha \in X_{n+1}$
for all n, so
![]() $f^{-1}(\alpha )$
exists and is in
$f^{-1}(\alpha )$
exists and is in
![]() $X_n$
.
$X_n$
.
Remark: For
![]() $\kappa =\lambda =\omega $
, there are trivial automorphisms that are not induced by “proper” bijections
$\kappa =\lambda =\omega $
, there are trivial automorphisms that are not induced by “proper” bijections
![]() $f:\omega \to \omega $
, e.g., the automorphism
$f:\omega \to \omega $
, e.g., the automorphism
![]() $\phi $
induced by the almost permutation
$\phi $
induced by the almost permutation
![]() $n\mapsto n+1$
.Footnote
5
$n\mapsto n+1$
.Footnote
5
We will investigate somewhere and densely trivial automorphisms. To simplify notation, we assume
![]() $\kappa =\lambda>\aleph _0$
:
$\kappa =\lambda>\aleph _0$
:
Definition 2.5 (
 $\lambda>\aleph _0$
regular.).
$\lambda>\aleph _0$
regular.).
Let
![]() $\phi :P^\lambda _\lambda \to P^\lambda _\lambda $
be an automorphism.
$\phi :P^\lambda _\lambda \to P^\lambda _\lambda $
be an automorphism.
-
•
 $\phi $
is trivial on
$\phi $
is trivial on
 $A\in [\lambda ]^\lambda $
, if there is an
$A\in [\lambda ]^\lambda $
, if there is an
 $f:A\to \lambda $
with
$f:A\to \lambda $
with
 $\phi ([B])=[f"B]$
for all
$\phi ([B])=[f"B]$
for all
 $B\subseteq A$
.
$B\subseteq A$
. -
•
 $\phi $
is somewhere trivial, if it is trivial on some
$\phi $
is somewhere trivial, if it is trivial on some
 $A\in [\lambda ]^{\lambda }$
.
$A\in [\lambda ]^{\lambda }$
. -
•
 $\phi $
is densely trivial, if for all
$\phi $
is densely trivial, if for all
 $A\in [\lambda ]^{\lambda }$
there is a
$A\in [\lambda ]^{\lambda }$
there is a
 $B\subseteq A$
of size
$B\subseteq A$
of size
 $\lambda $
such that
$\lambda $
such that
 $\phi $
is trivial on B.
$\phi $
is trivial on B.
Just as before it is easy to see that we can assume f to be a full permutation:
Fact 2.6 (
 $\lambda>\aleph _0$
regular.).
$\lambda>\aleph _0$
regular.).
An automorphism
![]() $\phi :P^\lambda _\lambda \to P^\lambda _\lambda $
is trivial on
$\phi :P^\lambda _\lambda \to P^\lambda _\lambda $
is trivial on
![]() $A\in [\lambda ]^\lambda $
iff there is a bijection
$A\in [\lambda ]^\lambda $
iff there is a bijection
![]() $f:\lambda \to \lambda $
such that
$f:\lambda \to \lambda $
such that
![]() $\phi ([B])=[f"(B)]$
for all
$\phi ([B])=[f"(B)]$
for all
![]() $B\subseteq A$
.
$B\subseteq A$
.
Lemma 2.7 (
 $\lambda>\aleph _0$
regular.).
$\lambda>\aleph _0$
regular.).
If every automorphism of
![]() $P^\lambda _\lambda $
is somewhere trivial, then every automorphism of
$P^\lambda _\lambda $
is somewhere trivial, then every automorphism of
![]() $P^\lambda _\lambda $
is densely trivial.
$P^\lambda _\lambda $
is densely trivial.
Proof Assume
![]() $\pi $
is an automorphism of
$\pi $
is an automorphism of
![]() $P^\lambda _\lambda $
, and fix
$P^\lambda _\lambda $
, and fix
![]() $A\in [\lambda ]^\lambda $
. If
$A\in [\lambda ]^\lambda $
. If
![]() $A=^*\lambda $
and if
$A=^*\lambda $
and if
![]() $\pi $
is trivial on some B, then
$\pi $
is trivial on some B, then
![]() $\pi $
is trivial on
$\pi $
is trivial on
![]() $B\cap A\subseteq A$
, so we are done. So assume
$B\cap A\subseteq A$
, so we are done. So assume
![]() $A\ne ^*\lambda $
.
$A\ne ^*\lambda $
.
Pick some representative
![]() $\pi ^*:{\mathcal {P}}(\lambda ) \to {\mathcal {P}}(\lambda )$
of
$\pi ^*:{\mathcal {P}}(\lambda ) \to {\mathcal {P}}(\lambda )$
of
![]() $\pi $
such that
$\pi $
such that
![]() $\pi ^*(A)$
and
$\pi ^*(A)$
and
![]() $\pi ^*(\lambda \setminus A)$
partition
$\pi ^*(\lambda \setminus A)$
partition
![]() $\lambda $
, and such that
$\lambda $
, and such that
![]() $\pi ^*(C)\subseteq \pi ^*(A)$
for every
$\pi ^*(C)\subseteq \pi ^*(A)$
for every
![]() $C\subseteq A$
. Let
$C\subseteq A$
. Let
![]() $i: \lambda \setminus A \to A$
and
$i: \lambda \setminus A \to A$
and
![]() $j:\pi ^*(\lambda \setminus A)\to \pi ^*(A)$
both be bijective. Let
$j:\pi ^*(\lambda \setminus A)\to \pi ^*(A)$
both be bijective. Let
![]() $\pi '$
map
$\pi '$
map
![]() $[D]$
to
$[D]$
to
![]() $[\pi ^*(D\cap A)\cup j^{-1}\pi ^*(i"(D\setminus A))]$
. This is an automorphism of
$[\pi ^*(D\cap A)\cup j^{-1}\pi ^*(i"(D\setminus A))]$
. This is an automorphism of
![]() $P^\lambda _\lambda $
, so it is trivial on some
$P^\lambda _\lambda $
, so it is trivial on some
![]() $D_0$
. If
$D_0$
. If
![]() $|D_0\cap A|=\lambda $
, we are done, as
$|D_0\cap A|=\lambda $
, we are done, as
![]() $\pi '$
restricted to
$\pi '$
restricted to
![]() $D_0\cap A$
is the same as
$D_0\cap A$
is the same as
![]() $\pi $
and trivial. So assume otherwise. Then
$\pi $
and trivial. So assume otherwise. Then
![]() $\pi '$
is trivial on the large set
$\pi '$
is trivial on the large set
![]() $D_0\setminus A$
. Then
$D_0\setminus A$
. Then
![]() $\pi $
is trivial on
$\pi $
is trivial on
![]() $i"(D_0\setminus A)\subseteq A$
.
$i"(D_0\setminus A)\subseteq A$
.
3. Under MA, every automorphism is trivial for
 $\omega _1\le \lambda <2^{\aleph _0}$
$\omega _1\le \lambda <2^{\aleph _0}$
Theorem 3.1. Assume
![]() $\aleph _0<\kappa \leq \lambda <2^{\aleph _0}$
,
$\aleph _0<\kappa \leq \lambda <2^{\aleph _0}$
,
![]() $\kappa $
regular, and
$\kappa $
regular, and
![]() $ {\textrm {MA}}_{(=\lambda )}(\sigma {\textrm {-centered}})$
holds. Then every automorphism of
$ {\textrm {MA}}_{(=\lambda )}(\sigma {\textrm {-centered}})$
holds. Then every automorphism of
![]() $P^\lambda _\kappa $
is trivial.
$P^\lambda _\kappa $
is trivial.
For the proof we will use that we can separate certain sets by closed sets.
A tree T is a subset of
![]() $2^{<\omega }$
such that
$2^{<\omega }$
such that
![]() $s\in T\cap 2^n$
and
$s\in T\cap 2^n$
and
![]() $m\le n$
implies
$m\le n$
implies
![]() $s\restriction m\in T$
; for such a T we set
$s\restriction m\in T$
; for such a T we set
![]() $\lim (T)=\{\eta \in 2^\omega :\, (\forall n\in \omega )\, \eta \restriction n\in T\}$
. A subset of
$\lim (T)=\{\eta \in 2^\omega :\, (\forall n\in \omega )\, \eta \restriction n\in T\}$
. A subset of
![]() $2^\omega $
is closed iff it is of the form
$2^\omega $
is closed iff it is of the form
![]() $\lim (T)$
for some tree T.
$\lim (T)$
for some tree T.
Lemma 3.2. Assume
![]() $\aleph _0<\theta \leq \lambda <2^{\aleph _0}$
,
$\aleph _0<\theta \leq \lambda <2^{\aleph _0}$
,
![]() $\operatorname {\mathrm {cf}}(\theta )>\aleph _0$
, and
$\operatorname {\mathrm {cf}}(\theta )>\aleph _0$
, and
![]() $ {\textrm {MA}}_{(=\lambda )}(\sigma {\textrm {-centered}})$
holds. Assume
$ {\textrm {MA}}_{(=\lambda )}(\sigma {\textrm {-centered}})$
holds. Assume
![]() $A_0, A_1$
are disjoint subsets of
$A_0, A_1$
are disjoint subsets of
![]() $2^{\omega }$
of size
$2^{\omega }$
of size
![]() $\le \lambda $
;
$\le \lambda $
;
![]() $|A_0|\ge \theta $
. Then there is a tree
$|A_0|\ge \theta $
. Then there is a tree
![]() $T_0$
in
$T_0$
in
![]() $2^{<\omega }$
such that
$2^{<\omega }$
such that
![]() $|A_0\cap \lim (T_0)|\geq \theta $
and
$|A_0\cap \lim (T_0)|\geq \theta $
and
![]() $A_1\cap \lim (T_0)=\emptyset $
.
$A_1\cap \lim (T_0)=\emptyset $
.
If additionally
![]() $|A_1|\ge \theta $
, we get an additional tree
$|A_1|\ge \theta $
, we get an additional tree
![]() $T_1$
such that
$T_1$
such that
![]() $|A_1\cap \lim (T_1)|\geq \theta $
,
$|A_1\cap \lim (T_1)|\geq \theta $
,
![]() $A_0\cap \lim (T_1)=\emptyset $
, and
$A_0\cap \lim (T_1)=\emptyset $
, and
![]() $T_0\cap T_1\subseteq 2^n$
for some n.
$T_0\cap T_1\subseteq 2^n$
for some n.
Proof of the lemma
In the following we identify an
![]() $x\in 2^\omega $
with the according (infinite) branch b in the tree
$x\in 2^\omega $
with the according (infinite) branch b in the tree
![]() $2^{<\omega }$
. So a branch b can be in
$2^{<\omega }$
. So a branch b can be in
![]() $A_0$
or in
$A_0$
or in
![]() $A_1$
(or in neither; but not both, as
$A_1$
(or in neither; but not both, as
![]() $A_0$
and
$A_0$
and
![]() $A_1$
are disjoint).
$A_1$
are disjoint).
We define a poset Q as follows: A condition
![]() $q\in Q$
is a triple
$q\in Q$
is a triple
![]() $(n_q,S_q,f_q)$
, where:
$(n_q,S_q,f_q)$
, where:
-
•
 $n_q\in \omega $
,
$n_q\in \omega $
, -
•
 $S_q$
is a tree in
$S_q$
is a tree in
 $2^{<\omega }$
of the following form:
$2^{<\omega }$
of the following form:
 $S_q$
is the union of
$S_q$
is the union of
 $2^{\le n_q}$
and finitely many (infinite) branches
$2^{\le n_q}$
and finitely many (infinite) branches
 $\{b_j:\, j\in m\}$
for some
$\{b_j:\, j\in m\}$
for some
 $m\in \omega $
, each
$m\in \omega $
, each
 $b_j\in A_0\cup A_1$
, and
$b_j\in A_0\cup A_1$
, and
 $b_j\restriction n_q=b_k\restriction n_q$
implies (
$b_j\restriction n_q=b_k\restriction n_q$
implies (
 $b_j\in A_i$
iff
$b_j\in A_i$
iff
 $b_k\in A_i$
).
$b_k\in A_i$
).So every
 $s\in S_q$
with
$s\in S_q$
with
 $|s|> n_q$
is either “in
$|s|> n_q$
is either “in
 $A_0$
-branches” (i.e., there is one or more
$A_0$
-branches” (i.e., there is one or more
 $b_j\in A_0$
with
$b_j\in A_0$
with
 $s\in b_j$
), or “in
$s\in b_j$
), or “in
 $A_1$
-branches” (but not in both).
$A_1$
-branches” (but not in both).Note that an
 $s\in S_q$
of length
$s\in S_q$
of length
 $n_q$
is either in
$n_q$
is either in
 $A_0$
-branches, or in
$A_0$
-branches, or in
 $A_1$
-branches, or in neither (but not in both).
$A_1$
-branches, or in neither (but not in both). -
•
 $f_{q}: S_q\to 2$
such that, for
$f_{q}: S_q\to 2$
such that, for
 $i=0,1$
,
$i=0,1$
,
 $f_{q}(s)=i$
whenever
$f_{q}(s)=i$
whenever
 $s\in S_q$
,
$s\in S_q$
,
 $|s|\ge n_q$
and s is in
$|s|\ge n_q$
and s is in
 $A_i$
-branches.
$A_i$
-branches.
The order on Q is the natural one:
![]() $q\le p$
if
$q\le p$
if
![]() $n_q\ge n_p$
,
$n_q\ge n_p$
,
![]() $S_q\supseteq S_p$
, and
$S_q\supseteq S_p$
, and
![]() $f_q$
extends
$f_q$
extends
![]() $f_p$
.
$f_p$
.
Q is
![]() $\sigma $
-centered witnessed by
$\sigma $
-centered witnessed by
![]() $(n_q,S_q,f_q)\mapsto (n_q, f_q\restriction 2^{\le n_q})$
: If
$(n_q,S_q,f_q)\mapsto (n_q, f_q\restriction 2^{\le n_q})$
: If
![]() $p,q$
are in Q with
$p,q$
are in Q with
![]() $n_p=n_q=:n$
and
$n_p=n_q=:n$
and
![]() $f_p\restriction 2^{\le n}=f_q\restriction 2^{\le n}$
, then
$f_p\restriction 2^{\le n}=f_q\restriction 2^{\le n}$
, then
![]() $(n, S_p\cup S_q, f_p\cup f_q)$
is a valid condition stronger than both p and q.
$(n, S_p\cup S_q, f_p\cup f_q)$
is a valid condition stronger than both p and q.
For
![]() $x\in A_i$
, the set
$x\in A_i$
, the set
![]() $D_x$
of conditions containing x as branch is dense: Given
$D_x$
of conditions containing x as branch is dense: Given
![]() $p\in Q$
, let
$p\in Q$
, let
![]() $n_q\ge n_p$
be such that all
$n_q\ge n_p$
be such that all
![]() $A_{1-i}$
-branches in p split off x below
$A_{1-i}$
-branches in p split off x below
![]() $n_q$
; set
$n_q$
; set
![]() $S_q:=S_p\cup 2^{\le n_q}\cup x$
; and set
$S_q:=S_p\cup 2^{\le n_q}\cup x$
; and set
![]() $F_q(s)=i$
for
$F_q(s)=i$
for
![]() $s\in S_q\setminus S_p$
.
$s\in S_q\setminus S_p$
.
Similarly, for all
![]() $n\in \omega $
, the set
$n\in \omega $
, the set
![]() $D^*_n$
of conditions q with
$D^*_n$
of conditions q with
![]() $n_q\ge n$
is dense as well.
$n_q\ge n$
is dense as well.
By
![]() $\textrm {MA}_{(=\lambda )}(\sigma \text {-centered})$
and
$\textrm {MA}_{(=\lambda )}(\sigma \text {-centered})$
and
![]() $|A_i|\le \lambda $
, we can find a filter G which has nonempty intersection with each
$|A_i|\le \lambda $
, we can find a filter G which has nonempty intersection with each
![]() $D_x$
for
$D_x$
for
![]() $x\in A_0\cup A_1$
as well as for each
$x\in A_0\cup A_1$
as well as for each
![]() $D^*_n$
. So
$D^*_n$
. So
![]() $F:=\bigcup _{p\in G} f_p$
is a total function from
$F:=\bigcup _{p\in G} f_p$
is a total function from
![]() $2^{<\omega }$
to
$2^{<\omega }$
to
![]() $2$
; and for all
$2$
; and for all
![]() $x\in A_i$
there is an
$x\in A_i$
there is an
![]() $n_x\in \omega $
such that
$n_x\in \omega $
such that
![]() $m\ge n_x$
implies
$m\ge n_x$
implies
![]() $F(x\restriction m)=i$
.
$F(x\restriction m)=i$
.
As
![]() $|A_0|\geq \theta $
and
$|A_0|\geq \theta $
and
![]() $\operatorname {\mathrm {cf}}(\theta )>\aleph _0$
we can assume that there is an
$\operatorname {\mathrm {cf}}(\theta )>\aleph _0$
we can assume that there is an
![]() $n^*_0$
such that
$n^*_0$
such that
![]() $n_x=n^*_0$
for
$n_x=n^*_0$
for
![]() $\theta $
many
$\theta $
many
![]() $x\in A_0$
. If additionally
$x\in A_0$
. If additionally
![]() $|A_1|\geq \theta $
, we analogously get an
$|A_1|\geq \theta $
, we analogously get an
![]() $n^*_1$
and set
$n^*_1$
and set
![]() $n^*:=\max (n^*_0,n^*_1)$
; otherwise we set
$n^*:=\max (n^*_0,n^*_1)$
; otherwise we set
![]() $n^*:=n^*_0$
. We set
$n^*:=n^*_0$
. We set
![]() $T_i^*:=\{s\in 2^{<\omega }: |s|\ge n^*,\, (\forall n^*\le k\le |s|)\, F(s\restriction k)=i\}$
and generate a tree from it; i.e., we set
$T_i^*:=\{s\in 2^{<\omega }: |s|\ge n^*,\, (\forall n^*\le k\le |s|)\, F(s\restriction k)=i\}$
and generate a tree from it; i.e., we set
![]() $T_i:=T^*_i\cup \{s\restriction m:\, m<n^*, s\in T^*_i\}$
. As we have seen above,
$T_i:=T^*_i\cup \{s\restriction m:\, m<n^*, s\in T^*_i\}$
. As we have seen above,
![]() $\lim (T_i)\cap A_i\ge \theta $
for
$\lim (T_i)\cap A_i\ge \theta $
for
![]() $i=0$
(and, if
$i=0$
(and, if
![]() $|A_1|\ge \theta $
, for
$|A_1|\ge \theta $
, for
![]() $i=1$
as well). Clearly
$i=1$
as well). Clearly
![]() $T_0\cap T_1\subseteq 2^{n^*}$
; and
$T_0\cap T_1\subseteq 2^{n^*}$
; and
![]() $\lim (T_i)\cap A_{i-1}$
is empty, as for any
$\lim (T_i)\cap A_{i-1}$
is empty, as for any
![]() $x\in A_{i-1}$
, cofinally many n satisfy
$x\in A_{i-1}$
, cofinally many n satisfy
![]() $F(x\restriction n)=i-1$
.
$F(x\restriction n)=i-1$
.
Proof of the theorem
Fix an automorphism
![]() $\pi $
of
$\pi $
of
![]() $P^\lambda _\kappa $
represented by some
$P^\lambda _\kappa $
represented by some
![]() $\pi ^*:{\mathcal {P}}(\lambda )\to {\mathcal {P}}(\lambda )$
, and let
$\pi ^*:{\mathcal {P}}(\lambda )\to {\mathcal {P}}(\lambda )$
, and let
![]() $\pi ^{-1*}$
represent
$\pi ^{-1*}$
represent
![]() $\pi ^{-1}$
. We have to show that
$\pi ^{-1}$
. We have to show that
![]() $\pi $
is trivial.
$\pi $
is trivial.
Fix an injective function
![]() $\eta :\lambda \rightarrow 2^\omega $
. Set
$\eta :\lambda \rightarrow 2^\omega $
. Set
Define
![]() $\nu :\lambda \to 2^\omega $
by
$\nu :\lambda \to 2^\omega $
by
In the following, “large” means “of cardinality
![]() ${\ge }\kappa $
”, and “small” means not large. We will show:
${\ge }\kappa $
”, and “small” means not large. We will show:
-
(*1)
 $\pi ^*(\eta ^{-1}C) =^* \nu ^{-1}C$
for
$\pi ^*(\eta ^{-1}C) =^* \nu ^{-1}C$
for
 $C\subseteq 2^\omega $
closed.
$C\subseteq 2^\omega $
closed. -
(*2)
 $Y\subseteq \lambda \text { and }|Y|\ge \kappa $
implies
$Y\subseteq \lambda \text { and }|Y|\ge \kappa $
implies
 $|\nu "Y|\ge \kappa $
.
$|\nu "Y|\ge \kappa $
. -
(*3) If
 $A_0, A_1$
are disjoint subsets of
$A_0, A_1$
are disjoint subsets of
 $2^\omega $
,
$2^\omega $
,
 $A_0\subseteq \nu "\lambda $
large, then
$A_0\subseteq \nu "\lambda $
large, then
 $\pi ^{-1*}(\nu ^{-1}A_0)\setminus \eta ^{-1} A_1$
is large.
$\pi ^{-1*}(\nu ^{-1}A_0)\setminus \eta ^{-1} A_1$
is large. -
(*4) If
 $A_0, A_1$
are disjoint subsets of
$A_0, A_1$
are disjoint subsets of
 $2^\omega $
,
$2^\omega $
,
 $A_0\subseteq \eta "\lambda $
large, then
$A_0\subseteq \eta "\lambda $
large, then
 $\pi ^*(\eta ^{-1}A_0)\setminus \nu ^{-1} A_1$
is large.
$\pi ^*(\eta ^{-1}A_0)\setminus \nu ^{-1} A_1$
is large.
(Note that (
![]() $*_2$
) is the only place where we use that
$*_2$
) is the only place where we use that
![]() $\kappa $
is regular.)
$\kappa $
is regular.)
Proof:
-
(*1)
 $\pi ^*(\eta ^{-1}C_n) = \nu ^{-1}C_n$
holds by definition of
$\pi ^*(\eta ^{-1}C_n) = \nu ^{-1}C_n$
holds by definition of
 $\nu $
. As
$\nu $
. As
 $\pi $
honors
$\pi $
honors
 ${<}\kappa $
-unions and complements, and as the
${<}\kappa $
-unions and complements, and as the
 $C_n$
generate the open sets, this equation (with
$C_n$
generate the open sets, this equation (with
 $=^*$
) holds whenever C is generated by
$=^*$
) holds whenever C is generated by
 ${<}\kappa $
-unions and complements from the open sets, in particular, if C is closed.
${<}\kappa $
-unions and complements from the open sets, in particular, if C is closed. -
(*2) Fix
 $x\in 2^\omega $
. Then
$x\in 2^\omega $
. Then
 $\eta ^{-1}\{x\}$
has at most one element (as
$\eta ^{-1}\{x\}$
has at most one element (as
 $\eta $
is injective), and
$\eta $
is injective), and
 $\eta ^{-1} \{x\}=^* \pi ^{-1*}\nu ^{-1}\{x\}$
by (
$\eta ^{-1} \{x\}=^* \pi ^{-1*}\nu ^{-1}\{x\}$
by (
 $*_1$
). That is,
$*_1$
). That is,
 $\nu ^{-1}\{x\}$
is small. And
$\nu ^{-1}\{x\}$
is small. And
 $Y\subseteq \bigcup _{x\in \nu "Y}\nu ^{-1}\{x\}$
, so as
$Y\subseteq \bigcup _{x\in \nu "Y}\nu ^{-1}\{x\}$
, so as
 $\kappa $
is regular we get
$\kappa $
is regular we get
 $|\nu "Y|\ge \kappa $
.)
$|\nu "Y|\ge \kappa $
.) -
(*3) Using the previous lemma (with
 $\kappa $
as
$\kappa $
as
 $\theta $
) we get a tree
$\theta $
) we get a tree
 $T_0$
separating
$T_0$
separating
 $A_0$
and
$A_0$
and
 $A_1$
. That is,
$A_1$
. That is,
 $\lim (T_0)\cap A_1=\emptyset $
and
$\lim (T_0)\cap A_1=\emptyset $
and
 $X:=\lim (T_0)\cap A_0$
is large. As
$X:=\lim (T_0)\cap A_0$
is large. As
 $X\subseteq A_0\subseteq \nu "\lambda $
, we get that
$X\subseteq A_0\subseteq \nu "\lambda $
, we get that
 $\nu ^{-1} X$
is large. And
$\nu ^{-1} X$
is large. And
 $\nu ^{-1} X=\nu ^{-1}\lim (T_0)\cap \nu ^{-1}A_0=^*\pi ^*(\eta ^{-1}\lim (T_0))\cap \nu ^{-1}A_0$
, the last equation by (
$\nu ^{-1} X=\nu ^{-1}\lim (T_0)\cap \nu ^{-1}A_0=^*\pi ^*(\eta ^{-1}\lim (T_0))\cap \nu ^{-1}A_0$
, the last equation by (
 $*_1$
). This implies
$*_1$
). This implies
 $\eta ^{-1}\lim (T_0)\cap \pi ^{-1*}(\nu ^{-1}A_0)$
is large, and so
$\eta ^{-1}\lim (T_0)\cap \pi ^{-1*}(\nu ^{-1}A_0)$
is large, and so
 $\pi ^{-1*}(\nu ^{-1}A_0)\setminus \eta ^{-1} A_1$
is large.
$\pi ^{-1*}(\nu ^{-1}A_0)\setminus \eta ^{-1} A_1$
is large. -
(*4) We get an analogous result when interchanging
 $\nu $
and
$\nu $
and
 $\eta $
and using
$\eta $
and using
 $\pi ^*$
instead of
$\pi ^*$
instead of
 $\pi ^{-1*}$
.
$\pi ^{-1*}$
.
We claim that the following sets
![]() $N_i$
are all small:
$N_i$
are all small:
-
(1)
 $N_{1}:=\{\alpha \in \lambda :\, (\lnot \exists \beta \in \lambda ) \,\eta (\alpha )=\nu (\beta )\}$
.
$N_{1}:=\{\alpha \in \lambda :\, (\lnot \exists \beta \in \lambda ) \,\eta (\alpha )=\nu (\beta )\}$
. -
(2)
 $N_{2}:=\{\alpha \in \lambda :\, (\exists ^{(\geq 2)} \beta \in \lambda )\, \eta (\alpha )=\nu (\beta )\}$
.
$N_{2}:=\{\alpha \in \lambda :\, (\exists ^{(\geq 2)} \beta \in \lambda )\, \eta (\alpha )=\nu (\beta )\}$
. -
(3)
 $N_{3}:=\{\beta \in \lambda :\, (\lnot \exists \alpha \in \lambda )\, \eta (\alpha )=\nu (\beta )\}$
.
$N_{3}:=\{\beta \in \lambda :\, (\lnot \exists \alpha \in \lambda )\, \eta (\alpha )=\nu (\beta )\}$
.
Proof.
-
(3) Assume
 $N_{3}$
is large. Set
$N_{3}$
is large. Set
 $A_0:=\nu " N_{3}$
, which is large by (
$A_0:=\nu " N_{3}$
, which is large by (
 $*_2$
); and
$*_2$
); and
 $A_1:=\eta "\lambda $
. So
$A_1:=\eta "\lambda $
. So
 $A_0$
and
$A_0$
and
 $A_1$
are disjoint, and by (
$A_1$
are disjoint, and by (
 $*_3$
)
$*_3$
)
 $\pi ^{-1*}\nu ^{-1}A_0\setminus \eta ^{-1}A_1$
is large, but
$\pi ^{-1*}\nu ^{-1}A_0\setminus \eta ^{-1}A_1$
is large, but
 $\eta ^{-1}A_1=\lambda $
.
$\eta ^{-1}A_1=\lambda $
. -
(1) Assume
 $N_{1}$
is large. Set
$N_{1}$
is large. Set
 $A_0=\eta "N_{1}$
(large, as
$A_0=\eta "N_{1}$
(large, as  is injective) and
is injective) and
 $A_1:=\nu "\lambda $
. So
$A_1:=\nu "\lambda $
. So
 $A_0$
and
$A_0$
and
 $A_1$
are disjoint, and by (
$A_1$
are disjoint, and by (
 $*_4$
)
$*_4$
)
 $\pi ^*(\eta ^{-1}A_0)\setminus \nu ^{-1} A_1$
is large, but
$\pi ^*(\eta ^{-1}A_0)\setminus \nu ^{-1} A_1$
is large, but
 $\nu ^{-1} A_1=\lambda $
.
$\nu ^{-1} A_1=\lambda $
. -
(2) Assume that
 $N_{2}$
is large. For every
$N_{2}$
is large. For every
 $\alpha \in N_{2}$
, let
$\alpha \in N_{2}$
, let
 $\beta _\alpha ^0\neq \beta _\alpha ^1$
in
$\beta _\alpha ^0\neq \beta _\alpha ^1$
in
 $\lambda $
be such that
$\lambda $
be such that
 $\eta (\alpha )=\nu ({\beta _\alpha ^0})=\nu ({\beta _\alpha ^1})$
. For
$\eta (\alpha )=\nu ({\beta _\alpha ^0})=\nu ({\beta _\alpha ^1})$
. For
 $i\in \{0,1\}$
, set
$i\in \{0,1\}$
, set
 $Y_i:=\{ \beta _\alpha ^i:\ \alpha \in N_{2}\}$
and
$Y_i:=\{ \beta _\alpha ^i:\ \alpha \in N_{2}\}$
and
 $X_i:=\pi ^{-1*}(Y_i)$
(without loss of generality disjoint), and
$X_i:=\pi ^{-1*}(Y_i)$
(without loss of generality disjoint), and
 $A_i:=\eta " X_i$
. So the
$A_i:=\eta " X_i$
. So the
 $A_i$
are large and disjoint, and we can find a tree
$A_i$
are large and disjoint, and we can find a tree
 $T_0$
such that
$T_0$
such that
 $A_0\cap \lim (T_0)$
is large, and
$A_0\cap \lim (T_0)$
is large, and
 $A_1\cap \lim (T_0)$
is empty.
$A_1\cap \lim (T_0)$
is empty.As
 $A_0\subseteq \eta "\lambda $
, this implies that the inverse
$A_0\subseteq \eta "\lambda $
, this implies that the inverse
 $\eta $
-image of
$\eta $
-image of
 $A_0\cap \lim (T_0)$
is also large. That is,
$A_0\cap \lim (T_0)$
is also large. That is, $\eta ^{-1}(A_0\cap \lim (T_0))=\eta ^{-1}A_0\cap \eta ^{-1}\lim (T_0)=^* X_0\cap \pi ^{-1*}\nu ^{-1}\lim (T_0)$
is large (for the last equation we use (
$\eta ^{-1}(A_0\cap \lim (T_0))=\eta ^{-1}A_0\cap \eta ^{-1}\lim (T_0)=^* X_0\cap \pi ^{-1*}\nu ^{-1}\lim (T_0)$
is large (for the last equation we use (
 $*_1$
)). Therefore also
$*_1$
)). Therefore also
 $Y_0 \cap \nu ^{-1}\lim (T_0)$
is large, and so, by (
$Y_0 \cap \nu ^{-1}\lim (T_0)$
is large, and so, by (
 $*_2$
),
$*_2$
),
 $\nu "(Y_0 \cap \nu ^{-1}\lim (T_0))=\lim (T_0)\cap \nu " Y_0 $
is large as well.
$\nu "(Y_0 \cap \nu ^{-1}\lim (T_0))=\lim (T_0)\cap \nu " Y_0 $
is large as well.On the other hand,
 $\lim (T_0)\cap A_1$
is empty, so
$\lim (T_0)\cap A_1$
is empty, so
 $0=^*\pi ^*\eta ^{-1} (\lim (T_0)\cap A_1)=^* \pi ^*\eta ^{-1}\lim (T_0)\cap \pi ^*\eta ^{-1}A_1$
. Using (
$0=^*\pi ^*\eta ^{-1} (\lim (T_0)\cap A_1)=^* \pi ^*\eta ^{-1}\lim (T_0)\cap \pi ^*\eta ^{-1}A_1$
. Using (
 $*_1$
) for
$*_1$
) for
 $\lim (T_0)$
, and noting that
$\lim (T_0)$
, and noting that
 $\pi ^*\eta ^{-1}A_1=Y_1$
, this set is (almost) equal to
$\pi ^*\eta ^{-1}A_1=Y_1$
, this set is (almost) equal to
 $Y_1\cap \nu ^{-1}\lim (T_0)$
which therefore is also small, and so
$Y_1\cap \nu ^{-1}\lim (T_0)$
which therefore is also small, and so
 $ \lim (T_0)\cap \nu "Y_1$
is small.
$ \lim (T_0)\cap \nu "Y_1$
is small.So we know that
 $\lim (T_0)\cap \nu " Y_0$
is large and
$\lim (T_0)\cap \nu " Y_0$
is large and
 $ \lim (T_0)\cap \nu "Y_1$
is small, but
$ \lim (T_0)\cap \nu "Y_1$
is small, but
 $\nu " Y_0=\nu " Y_1$
, a contradiction.
$\nu " Y_0=\nu " Y_1$
, a contradiction.
Note that this implies:
-
(*5)
 $X\cap Y$
small implies
$X\cap Y$
small implies
 $\nu "X\cap \nu "Y$
small, for
$\nu "X\cap \nu "Y$
small, for
 $X,Y\subseteq \lambda $
.
$X,Y\subseteq \lambda $
. -
(*6)
 $\nu ^{-1}\nu " X=^*X$
for
$\nu ^{-1}\nu " X=^*X$
for
 $X\subseteq \lambda $
.
$X\subseteq \lambda $
.
Proof:
-
(*5) Assume otherwise. Without loss of generality we can assume that X and Y are disjoint, and by (3) that
 $\nu "X$
and
$\nu "X$
and
 $\nu " Y$
both are subsets of
$\nu " Y$
both are subsets of
 $\eta "\lambda $
. Then
$\eta "\lambda $
. Then
 $\nu "X\cap \nu "Y\subseteq \eta "N_{2}$
is small.
$\nu "X\cap \nu "Y\subseteq \eta "N_{2}$
is small. -
(*6) Set
 $Y:=\nu ^{-1}\nu "X\setminus X$
. Then
$Y:=\nu ^{-1}\nu "X\setminus X$
. Then
 $\nu "Y\subseteq N_2\cup N_3$
is small, and by (
$\nu "Y\subseteq N_2\cup N_3$
is small, and by (
 $*_2$
) Y is small.
$*_2$
) Y is small.
Set
![]() $D:=\lambda \setminus (N_{1}\cup N_{2})$
and define
$D:=\lambda \setminus (N_{1}\cup N_{2})$
and define
![]() $e:D\to \lambda $
such that
$e:D\to \lambda $
such that
![]() $e(\alpha )$
is the (unique)
$e(\alpha )$
is the (unique)
![]() $\beta \in \lambda $
with
$\beta \in \lambda $
with
![]() $\eta (\alpha )=\nu (\beta )$
. Clearly e is injective. We claim that e generates
$\eta (\alpha )=\nu (\beta )$
. Clearly e is injective. We claim that e generates
![]() $\pi $
, i.e., that the following are small (where we can assume
$\pi $
, i.e., that the following are small (where we can assume
![]() $X\subseteq D$
):
$X\subseteq D$
):
-
(4)
 $N_{4}:=\pi ^*(X)\setminus e"X$
.
$N_{4}:=\pi ^*(X)\setminus e"X$
. -
(5)
 $N_{5}:=e"X\setminus \pi ^*(X)$
.
$N_{5}:=e"X\setminus \pi ^*(X)$
.
Proof.
-
(4) Assume that
 $N_{4}$
is large. Set
$N_{4}$
is large. Set
 $Y=\pi ^{-1*}(N_{4})$
, without loss of generality
$Y=\pi ^{-1*}(N_{4})$
, without loss of generality
 $Y\subseteq X$
and
$Y\subseteq X$
and
 $\pi ^*(Y)=N_{4}$
. So
$\pi ^*(Y)=N_{4}$
. So
 $\pi ^*(Y)$
is disjoint from
$\pi ^*(Y)$
is disjoint from
 $e"Y$
(as it is even disjoint from
$e"Y$
(as it is even disjoint from
 $e"X$
). We set
$e"X$
). We set
 $A_0:=\nu "\pi ^*(Y)$
and
$A_0:=\nu "\pi ^*(Y)$
and
 $A_1:=\nu "e"Y$
, by (
$A_1:=\nu "e"Y$
, by (
 $*_5$
) we can assume they are disjoint, and by (
$*_5$
) we can assume they are disjoint, and by (
 $*_2$
) both are large (e is injective).
$*_2$
) both are large (e is injective).By (
 $*_3$
),
$*_3$
),
 $\pi ^{-1*}(\nu ^{-1}A_0)\setminus \eta ^{-1} A_1$
is large.
$\pi ^{-1*}(\nu ^{-1}A_0)\setminus \eta ^{-1} A_1$
is large. $\eta ^{-1}(A_1)=Y$
, as
$\eta ^{-1}(A_1)=Y$
, as
 $\nu (e(\alpha ))=\eta (\alpha )$
for all
$\nu (e(\alpha ))=\eta (\alpha )$
for all
 $\alpha \in D$
. And
$\alpha \in D$
. And
 $\pi ^{-1*}(\nu ^{-1}A_0)=^*Y$
by definition and (
$\pi ^{-1*}(\nu ^{-1}A_0)=^*Y$
by definition and (
 $*_6$
), a contradiction.
$*_6$
), a contradiction. -
(5) The same proof works: This time we set
 $Y=e^{-1}N_{5}$
; see that
$Y=e^{-1}N_{5}$
; see that
 $\pi ^*(Y)$
and
$\pi ^*(Y)$
and
 $e"Y$
are disjoint and large; set
$e"Y$
are disjoint and large; set
 $A_0:=\nu " \pi ^*(Y)$
and
$A_0:=\nu " \pi ^*(Y)$
and
 $A_1:=\nu " e" Y$
; use (
$A_1:=\nu " e" Y$
; use (
 $*_3$
) to see that
$*_3$
) to see that
 $Y\setminus \eta ^{-1}\nu " e"Y=Y\setminus Y$
is large, a contradiction.
$Y\setminus \eta ^{-1}\nu " e"Y=Y\setminus Y$
is large, a contradiction.
4. For measurables, GCH implies a nontrivial automorphism
Theorem 4.1. If
![]() $\lambda $
is measurable and
$\lambda $
is measurable and
![]() $2^\lambda =\lambda ^+$
, then there is a nontrivial automorphism of
$2^\lambda =\lambda ^+$
, then there is a nontrivial automorphism of
![]() $P^\lambda _\lambda $
.
$P^\lambda _\lambda $
.
Proof Let
![]() $\mathcal D$
be a normal ultrafilter on
$\mathcal D$
be a normal ultrafilter on
![]() $\lambda $
and denote by
$\lambda $
and denote by
![]() $\mathcal I:=[\lambda ]^\lambda \setminus \mathcal D$
its dual ideal restricted to sets of size
$\mathcal I:=[\lambda ]^\lambda \setminus \mathcal D$
its dual ideal restricted to sets of size
![]() $\lambda $
.
$\lambda $
.
Since
![]() $2^\lambda =\lambda ^+$
, we can list all permutations of
$2^\lambda =\lambda ^+$
, we can list all permutations of
![]() $\lambda $
as
$\lambda $
as
![]() $\{e_\alpha : \alpha <\lambda ^+\}$
; and analogously all elements of
$\{e_\alpha : \alpha <\lambda ^+\}$
; and analogously all elements of
![]() $\mathcal I $
as
$\mathcal I $
as
![]() $\{X_\alpha : \alpha <\lambda ^+\}$
.
$\{X_\alpha : \alpha <\lambda ^+\}$
.
We will construct, by induction on
![]() $\alpha <\lambda ^+$
a set
$\alpha <\lambda ^+$
a set
![]() $A_\alpha \in \mathcal I$
and a permutation
$A_\alpha \in \mathcal I$
and a permutation
![]() $f_\alpha $
of
$f_\alpha $
of
![]() $A_\alpha $
, such that for
$A_\alpha $
, such that for
![]() $\alpha <\beta $
:
$\alpha <\beta $
:
-
(1)
 $A_\alpha \subseteq ^*A_\beta $
.
$A_\alpha \subseteq ^*A_\beta $
. -
(2)
 $X_\alpha \subseteq A_{\alpha +1}$
.
$X_\alpha \subseteq A_{\alpha +1}$
. -
(3)
 $f_{\alpha }(x)=f_{\beta }(x)$
for almost all
$f_{\alpha }(x)=f_{\beta }(x)$
for almost all
 $x\in A_{\alpha }\cap A_{\beta }$
.
$x\in A_{\alpha }\cap A_{\beta }$
. -
(4) There is some
 $X\subseteq A_{\alpha +1}$
of size
$X\subseteq A_{\alpha +1}$
of size
 $\lambda $
such that
$\lambda $
such that
 $e_\alpha "X$
and
$e_\alpha "X$
and
 $f_{\alpha +1}"X$
are disjoint.
$f_{\alpha +1}"X$
are disjoint.
(Note that by
![]() $x\subseteq ^*y $
we mean
$x\subseteq ^*y $
we mean
![]() $|y\setminus x|=\lambda $
, not
$|y\setminus x|=\lambda $
, not
![]() $y\setminus x\in \mathcal I$
; and the same for ‘almost all”.)
$y\setminus x\in \mathcal I$
; and the same for ‘almost all”.)
The construction:
-
• Successor stages
 $\alpha +1$
: Fix any
$\alpha +1$
: Fix any
 $B\in \mathcal I$
disjoint to
$B\in \mathcal I$
disjoint to
 $A_\alpha $
such that
$A_\alpha $
such that
 $A_\alpha \cup B\supseteq X_\alpha $
. Set
$A_\alpha \cup B\supseteq X_\alpha $
. Set
 $C:=e_\alpha " B\cap A_\alpha $
.
$C:=e_\alpha " B\cap A_\alpha $
.First assume that
 $|C|=\lambda $
. Then set
$|C|=\lambda $
. Then set
 $A_{\alpha +1}=A_\alpha \cup B$
and let
$A_{\alpha +1}=A_\alpha \cup B$
and let
 $f_{\alpha +1}$
extend
$f_{\alpha +1}$
extend
 $f_\alpha $
by the identity on B. Then (4) is witnessed by
$f_\alpha $
by the identity on B. Then (4) is witnessed by
 $X:=e_\alpha ^{-1}C$
.So we assume
$X:=e_\alpha ^{-1}C$
.So we assume
 $|C|<\lambda $
. Partition B into large sets
$|C|<\lambda $
. Partition B into large sets
 $B_0,B_1,B_2$
such that
$B_0,B_1,B_2$
such that
 $e_\alpha "B_i$
is disjoint to
$e_\alpha "B_i$
is disjoint to
 $A_\alpha $
for
$A_\alpha $
for
 $i=0,1$
. Set
$i=0,1$
. Set
 $A_{\alpha +1}:=A_\alpha \cup B\cup e_\alpha " B$
, and define
$A_{\alpha +1}:=A_\alpha \cup B\cup e_\alpha " B$
, and define
 $f_{\alpha +1}$
on B such that the restriction to
$f_{\alpha +1}$
on B such that the restriction to
 $B_i$
is a bijection op
$B_i$
is a bijection op
 $e_\alpha " B_{1-i}$
for
$e_\alpha " B_{1-i}$
for
 $i=0,1$
, and the restriction to
$i=0,1$
, and the restriction to
 $B_2$
a bijection to
$B_2$
a bijection to
 $e"B_2\setminus A$
. Then (4) is witnessed by
$e"B_2\setminus A$
. Then (4) is witnessed by
 $X:=B_0$
.
$X:=B_0$
. -
• Limit stages
 $\delta $
of cofinality
$\delta $
of cofinality
 ${<}\lambda $
: Let
${<}\lambda $
: Let
 $\xi := \operatorname {\mathrm {cf}}(\delta )$
and choose
$\xi := \operatorname {\mathrm {cf}}(\delta )$
and choose
 $\langle \alpha _i: i<\xi \rangle $
a cofinal increasing sequence converging to
$\langle \alpha _i: i<\xi \rangle $
a cofinal increasing sequence converging to
 $\delta $
. The union
$\delta $
. The union
 $\bigcup _{i< \xi }A_{\alpha _i}$
is, by
$\bigcup _{i< \xi }A_{\alpha _i}$
is, by
 ${<}\lambda $
completeness, in
${<}\lambda $
completeness, in
 $\mathcal I$
. Remove
$\mathcal I$
. Remove
 $<\lambda $
many points to get a subset
$<\lambda $
many points to get a subset
 $A_\delta $
such that:
$A_\delta $
such that:-
– For all
 $i<j<\xi $
,
$i<j<\xi $
,
 $f_i$
and
$f_i$
and
 $f_j$
agree on
$f_j$
agree on
 $A_{\alpha _i}\cap A_\delta $
.
$A_{\alpha _i}\cap A_\delta $
. -
– For all
 $i<\xi $
,
$i<\xi $
,
 $f_i\restriction (A_{\alpha _i}\cap A_\delta )$
is a full permutation (we can do this as in Lemma 2.4).
$f_i\restriction (A_{\alpha _i}\cap A_\delta )$
is a full permutation (we can do this as in Lemma 2.4).
Then
 $f_\delta $
, defined as the union of the
$f_\delta $
, defined as the union of the
 $f_{\alpha _i}$
, is a permutation of
$f_{\alpha _i}$
, is a permutation of
 $A_\delta $
and almost extends each
$A_\delta $
and almost extends each
 $f_{\alpha _i}$
.
$f_{\alpha _i}$
. -
-
• Limit stages
 $\delta $
of cofinality
$\delta $
of cofinality
 $\lambda $
: We choose an increasing cofinal sequence
$\lambda $
: We choose an increasing cofinal sequence
 $\langle \alpha _i: i<\lambda \rangle $
converging to
$\langle \alpha _i: i<\lambda \rangle $
converging to
 $\delta $
. By induction on
$\delta $
. By induction on
 $i\in \lambda $
we construct
$i\in \lambda $
we construct
 $ A^{\prime }_i=^*A_{\alpha _i}$
, such that:
$ A^{\prime }_i=^*A_{\alpha _i}$
, such that:-
–
 $A^{\prime }_i\cap i=\emptyset $
.
$A^{\prime }_i\cap i=\emptyset $
. -
– The
 $f_{\alpha _i}$
’s fully extend each other on the
$f_{\alpha _i}$
’s fully extend each other on the
 $A^{\prime }_i$
’s, i.e., if
$A^{\prime }_i$
’s, i.e., if
 $x\in A^{\prime }_i\cap A^{\prime }_j$
then
$x\in A^{\prime }_i\cap A^{\prime }_j$
then
 $f_{\alpha _i}(x)=f_{\alpha _j}(x)$
.
$f_{\alpha _i}(x)=f_{\alpha _j}(x)$
. -
–
 $f_{\alpha _i}: A^{\prime }_i \rightarrow A^{\prime }_i$
is a “full” permutation.
$f_{\alpha _i}: A^{\prime }_i \rightarrow A^{\prime }_i$
is a “full” permutation.
We can do this by removing from
 $A_{\alpha _i}$
: the points less than i, the points where
$A_{\alpha _i}$
: the points less than i, the points where
 $f_{\alpha _i}$
disagrees with some previous
$f_{\alpha _i}$
disagrees with some previous
 $f_{\alpha _j}$
for any
$f_{\alpha _j}$
for any
 $j<i$
; and by removing
$j<i$
; and by removing
 ${<}\lambda $
many points to get a full permutation.
${<}\lambda $
many points to get a full permutation.Now we can set
 $A_\delta $
and
$A_\delta $
and
 $f_\delta $
to be the unions of
$f_\delta $
to be the unions of
 $A^{\prime }_{i}$
and
$A^{\prime }_{i}$
and
 $f_{\alpha _i}$
, respectively, for
$f_{\alpha _i}$
, respectively, for
 $i<\delta $
. Note that
$i<\delta $
. Note that
 $A_\delta $
is in
$A_\delta $
is in
 $\mathcal I$
(as it is a subset of the diagonal union); and
$\mathcal I$
(as it is a subset of the diagonal union); and
 $f_\delta $
is a permutation of
$f_\delta $
is a permutation of
 $A_\delta $
satisfying (3).
$A_\delta $
satisfying (3). -
Note that for all
![]() $X\subseteq \lambda $
, either
$X\subseteq \lambda $
, either
![]() $X\in \mathcal I$
or
$X\in \mathcal I$
or
![]() $\lambda \setminus X\in \mathcal I$
(but not both), i.e., either X or
$\lambda \setminus X\in \mathcal I$
(but not both), i.e., either X or
![]() $\lambda \setminus X$
is
$\lambda \setminus X$
is
![]() $\subseteq ^* A_\alpha $
for coboundedly many
$\subseteq ^* A_\alpha $
for coboundedly many
![]() $\alpha <\lambda $
.
$\alpha <\lambda $
.
This allows us to define the automorphism
![]() $\pi $
as follows: For
$\pi $
as follows: For
![]() $X\in [\lambda ]^\lambda $
,
$X\in [\lambda ]^\lambda $
,
 $$\begin{align*}\pi([X]):=\begin{cases} [f_\alpha"X], &\text{ if } X\in \mathcal I, X\subseteq^* A_\alpha \text{ for some }\alpha<\lambda^+\text{ (Case 1),}\\ [\lambda \setminus f_\alpha"(\lambda\setminus X) ],&\text{ if } X\notin \mathcal I,\lambda \setminus X\subseteq^* A_\alpha \text{ for some }\alpha<\lambda^+\text{ (Case 2)}.\end{cases}\end{align*}$$
$$\begin{align*}\pi([X]):=\begin{cases} [f_\alpha"X], &\text{ if } X\in \mathcal I, X\subseteq^* A_\alpha \text{ for some }\alpha<\lambda^+\text{ (Case 1),}\\ [\lambda \setminus f_\alpha"(\lambda\setminus X) ],&\text{ if } X\notin \mathcal I,\lambda \setminus X\subseteq^* A_\alpha \text{ for some }\alpha<\lambda^+\text{ (Case 2)}.\end{cases}\end{align*}$$
Note that in Case 2,
![]() $\pi ([X])=[(\lambda \setminus A_\alpha )\cup (A_\alpha \setminus f^{\prime \prime }_\alpha (A_\alpha \setminus X))]=[(\lambda \setminus A_\alpha )\cup f_\alpha "(X\cap A_\alpha )]$
, as
$\pi ([X])=[(\lambda \setminus A_\alpha )\cup (A_\alpha \setminus f^{\prime \prime }_\alpha (A_\alpha \setminus X))]=[(\lambda \setminus A_\alpha )\cup f_\alpha "(X\cap A_\alpha )]$
, as
![]() $f_\alpha "A_\alpha =^*A_\alpha $
.
$f_\alpha "A_\alpha =^*A_\alpha $
.
![]() $\pi $
is well defined on
$\pi $
is well defined on
![]() $[\lambda ]^\lambda $
, as exactly one of X or
$[\lambda ]^\lambda $
, as exactly one of X or
![]() $\lambda \setminus X$
will eventually be
$\lambda \setminus X$
will eventually be
![]() $\subseteq ^* A_\alpha $
.
$\subseteq ^* A_\alpha $
.
![]() $\pi $
is an automorphism:
$\pi $
is an automorphism:
![]() $\pi ([\emptyset ])=\emptyset $
.
$\pi ([\emptyset ])=\emptyset $
.
![]() $\pi $
honors complements: If X is Case 1, then
$\pi $
honors complements: If X is Case 1, then
![]() $\pi ([\lambda \setminus X])$
is by definition (Case 2)
$\pi ([\lambda \setminus X])$
is by definition (Case 2)
![]() $[\lambda \setminus f_\alpha "(X)]$
.
$[\lambda \setminus f_\alpha "(X)]$
.
![]() $\pi $
honors intersections
$\pi $
honors intersections
![]() $X\cap Y$
: This is clear if both sets are the same Case. Assume that X is Case 1 and Y Case 2. Then
$X\cap Y$
: This is clear if both sets are the same Case. Assume that X is Case 1 and Y Case 2. Then
![]() $X\cap Y\subseteq X$
is Case 1, and for any
$X\cap Y\subseteq X$
is Case 1, and for any
![]() $\alpha $
suitable for both X and Y we have
$\alpha $
suitable for both X and Y we have
 $$\begin{align*}\pi([X])\wedge \pi([Y])& = [f_\alpha" X\cap ((\lambda\setminus A_\alpha)\cup f_\alpha"(Y\cap A_\alpha))]\\ &= [f_\alpha" X \cap f^{\prime\prime}_\alpha(Y\cap A_\alpha)]= [f_\alpha" (X\cap Y))]. \end{align*}$$
$$\begin{align*}\pi([X])\wedge \pi([Y])& = [f_\alpha" X\cap ((\lambda\setminus A_\alpha)\cup f_\alpha"(Y\cap A_\alpha))]\\ &= [f_\alpha" X \cap f^{\prime\prime}_\alpha(Y\cap A_\alpha)]= [f_\alpha" (X\cap Y))]. \end{align*}$$
![]() $\pi $
is not trivial: Every automorphism e is an
$\pi $
is not trivial: Every automorphism e is an
![]() ${e_\alpha }$
for some
${e_\alpha }$
for some
![]() $\alpha \in \lambda ^+$
; and according to (4) there is some
$\alpha \in \lambda ^+$
; and according to (4) there is some
![]() $X_\alpha \subseteq A_{\alpha +1}$
(and therefore in
$X_\alpha \subseteq A_{\alpha +1}$
(and therefore in
![]() $\mathcal I$
) of size
$\mathcal I$
) of size
![]() $\lambda $
such that
$\lambda $
such that
![]() $e_\alpha "X_\alpha $
is disjoint to
$e_\alpha "X_\alpha $
is disjoint to
![]() $f_{\alpha +1}" X_\alpha $
, a representative of
$f_{\alpha +1}" X_\alpha $
, a representative of
![]() $\pi ([X_\alpha ])$
.
$\pi ([X_\alpha ])$
.
5. For inaccessible
 $\lambda $
, all automorphisms can be densely trivial
$\lambda $
, all automorphisms can be densely trivial
In this section, we always assume the following (in the ground model):
Assumption 5.1.
![]() $\lambda $
is inaccessible and
$\lambda $
is inaccessible and
![]() $2^\lambda =\lambda ^+$
. We set
$2^\lambda =\lambda ^+$
. We set
![]() $\mu :=\lambda ^{++}$
.
$\mu :=\lambda ^{++}$
.
In the rest of the paper, we will show the following:
Theorem 5.2.
![]() $(\lambda $
is inaccessible and
$(\lambda $
is inaccessible and
![]() $2^\lambda =\lambda ^+.)$
There is a
$2^\lambda =\lambda ^+.)$
There is a
![]() $\lambda $
-proper,
$\lambda $
-proper,
![]() ${<}\lambda $
-closed,
${<}\lambda $
-closed,
![]() $\lambda ^{++}$
-cc poset P (in particular, preserving all cofinalities) that forces:
$\lambda ^{++}$
-cc poset P (in particular, preserving all cofinalities) that forces:
![]() $2^{\lambda }=\lambda ^{++}$
, and every automorphism of
$2^{\lambda }=\lambda ^{++}$
, and every automorphism of
![]() $P^\lambda _\lambda $
is densely trivial.
$P^\lambda _\lambda $
is densely trivial.
By Lemma 2.7, it is enough to show that every automorphism is somewhere trivial.
5.1. The single forcing
 $\boldsymbol Q$
$\boldsymbol Q$
Definition 5.3. We fix a strictly increasing sequence
![]() $(\theta ^*_\zeta )_{\zeta <\lambda }$
with
$(\theta ^*_\zeta )_{\zeta <\lambda }$
with
![]() $\theta ^*_\zeta <\lambda $
regular and
$\theta ^*_\zeta <\lambda $
regular and
![]() $\theta ^*_\zeta>2^{|\zeta |}$
.
$\theta ^*_\zeta>2^{|\zeta |}$
.
-
• Let
 $(I^*_{\zeta })_{\zeta \in \lambda }$
be an increasing interval partition of
$(I^*_{\zeta })_{\zeta \in \lambda }$
be an increasing interval partition of
 $\lambda $
such that
$\lambda $
such that
 $I^*_\zeta $
has size
$I^*_\zeta $
has size
 $2^{\theta ^*_\zeta }$
; and fix a bijection of
$2^{\theta ^*_\zeta }$
; and fix a bijection of
 $I^*_\zeta $
and
$I^*_\zeta $
and
 $2^{\theta ^*_\zeta }$
. Using this (unnamed) bijection, we set
$2^{\theta ^*_\zeta }$
. Using this (unnamed) bijection, we set
 $[s]:=\{\ell \in I^*_\zeta : \ell>s\}$
for
$[s]:=\{\ell \in I^*_\zeta : \ell>s\}$
for
 $s\in 2^{<\theta ^*_\zeta }$
.
$s\in 2^{<\theta ^*_\zeta }$
.So the
 $[s]$
are cones, i.e., the set of all branches in
$[s]$
are cones, i.e., the set of all branches in
 $I^*_\zeta $
extending s.
$I^*_\zeta $
extending s.For
 $\zeta <\lambda $
, we set
$\zeta <\lambda $
, we set
 $I^*({<}\zeta ):=\bigcup _{\ell <\zeta } I^*_\ell $
, and analogously
$I^*({<}\zeta ):=\bigcup _{\ell <\zeta } I^*_\ell $
, and analogously
 $I^*({\le }\zeta ):=I^*({<}\zeta +1)$
,
$I^*({\le }\zeta ):=I^*({<}\zeta +1)$
,
 $I^*({\ge }\zeta ):=\lambda \setminus I^*({<}\zeta )$
, and
$I^*({\ge }\zeta ):=\lambda \setminus I^*({<}\zeta )$
, and
 $I^*({\ge }\zeta ,{<}\xi ):=I^*({\ge }\zeta )\cap I^*({<}\xi )$
.
$I^*({\ge }\zeta ,{<}\xi ):=I^*({\ge }\zeta )\cap I^*({<}\xi )$
. -
• A condition q of the forcing notion Q is a function with domain
 $\lambda $
such that, for all
$\lambda $
such that, for all
 $\zeta \in \lambda $
,
$\zeta \in \lambda $
,
 $q(\zeta )$
is a partial function from
$q(\zeta )$
is a partial function from
 $I^*_\zeta $
to
$I^*_\zeta $
to
 $2$
, and such that for a club-set
$2$
, and such that for a club-set
 $C^q\subseteq \lambda $
:
$C^q\subseteq \lambda $
:-
– if
 $\zeta \notin C^q$
, then
$\zeta \notin C^q$
, then
 $q(\zeta )$
is total,
$q(\zeta )$
is total, -
– otherwise, the domain of
 $q(\zeta )$
is
$q(\zeta )$
is
 $I^*_\zeta \setminus [s^q_\zeta ]$
for some
$I^*_\zeta \setminus [s^q_\zeta ]$
for some
 $s^q_\zeta \in 2^{<\theta ^*_\zeta }$
.
$s^q_\zeta \in 2^{<\theta ^*_\zeta }$
.
 $C^q$
and
$C^q$
and
 $s^q_\zeta $
are uniquely determined by q; and q is uniquely determined by the partial function
$s^q_\zeta $
are uniquely determined by q; and q is uniquely determined by the partial function
 $\eta ^q:\lambda \to 2$
defined as
$\eta ^q:\lambda \to 2$
defined as
 $\bigcup _{\zeta \in \lambda }q(\zeta )$
.
$\bigcup _{\zeta \in \lambda }q(\zeta )$
. -
-
• q is stronger than p if
 $\eta ^{q}$
extends
$\eta ^{q}$
extends
 $\eta ^p$
.
$\eta ^p$
.(This implies that
 $C^{q}\subseteq C^{p}$
, and that
$C^{q}\subseteq C^{p}$
, and that
 $s^{q}_\zeta $
extends
$s^{q}_\zeta $
extends
 $s^p_\zeta $
for all
$s^p_\zeta $
for all
 $\zeta \in C^{q}$
.)
$\zeta \in C^{q}$
.)
The following is straightforward:
Lemma 5.4. Q has size
![]() $2^{\lambda }$
, is
$2^{\lambda }$
, is
![]() ${<}\lambda $
-closed, and adds a generic real
${<}\lambda $
-closed, and adds a generic real ![]() in
in
![]() $2^\lambda $
.
$2^\lambda $
.
Proof
![]() ${<}\lambda $
-closure is obvious, but for later reference we would like to point out the “problematic cases”:
${<}\lambda $
-closure is obvious, but for later reference we would like to point out the “problematic cases”:
Let
![]() $(p_i)_{i<\delta }$
be decreasing for a limit ordinal
$(p_i)_{i<\delta }$
be decreasing for a limit ordinal
![]() $\delta <\lambda $
.
$\delta <\lambda $
.
As a first approximation, set
![]() $\eta ^*:=\bigcup _{i<\delta }\eta ^{p_i}$
(a partial function) and
$\eta ^*:=\bigcup _{i<\delta }\eta ^{p_i}$
(a partial function) and
![]() $C^*:=\bigcap _{i<\delta }C^{p_i}$
(a club set) and
$C^*:=\bigcap _{i<\delta }C^{p_i}$
(a club set) and
![]() $s^*_\zeta :=\bigcup _{i<\delta }s^{p_i}_\zeta \in 2^{\le \theta ^*_\zeta }$
for
$s^*_\zeta :=\bigcup _{i<\delta }s^{p_i}_\zeta \in 2^{\le \theta ^*_\zeta }$
for
![]() $s\in C^*$
. For
$s\in C^*$
. For
![]() $\zeta \notin C^*$
,
$\zeta \notin C^*$
,
![]() $\eta ^*$
is indeed total on
$\eta ^*$
is indeed total on
![]() $I^*_\zeta $
, and for
$I^*_\zeta $
, and for
![]() $\zeta \in C^*$
the domain in
$\zeta \in C^*$
the domain in
![]() $I^*_\zeta $
is
$I^*_\zeta $
is
![]() $I^*_\zeta \setminus [s^*_\zeta ]$
.
$I^*_\zeta \setminus [s^*_\zeta ]$
.
The problematic case is when
![]() $s^*_\zeta $
is unbounded in
$s^*_\zeta $
is unbounded in
![]() $\theta ^*_\zeta $
. (This can only happen if
$\theta ^*_\zeta $
. (This can only happen if
![]() $\operatorname {\mathrm {cf}}(\delta )= \theta ^*_\zeta $
, in particular for at most one
$\operatorname {\mathrm {cf}}(\delta )= \theta ^*_\zeta $
, in particular for at most one
![]() $\zeta $
.) In this case we can just pick any extension
$\zeta $
.) In this case we can just pick any extension
![]() $\eta ^q$
of
$\eta ^q$
of
![]() $\eta ^{*}$
by filling all values in
$\eta ^{*}$
by filling all values in
![]() $I^*_{\le \zeta }$
. This gives the desired q, with
$I^*_{\le \zeta }$
. This gives the desired q, with
![]() $C^{q_\delta }=C^*\setminus {\zeta +1}$
.
$C^{q_\delta }=C^*\setminus {\zeta +1}$
.
Remarks.
-
• The limits of
 ${<}\lambda $
-sequences of conditions are not “canonical” if there are problematic
${<}\lambda $
-sequences of conditions are not “canonical” if there are problematic
 $\zeta $
’s, as we have to fill in arbitrary values.
$\zeta $
’s, as we have to fill in arbitrary values. -
•
 determines the generic filter, by
determines the generic filter, by  . This follows from the following facts:
. This follows from the following facts:-
– p and q are compatible (as conditions in Q) iff
 $\eta ^p$
and
$\eta ^p$
and
 $\eta ^q$
are compatible as partial functions and
$\eta ^q$
are compatible as partial functions and
 $X_{p,q}:=\{\zeta \in C^p:\, s^p_\zeta \text { and }s^q_\zeta \text { are incomparable}\}$
is non-stationary.
$X_{p,q}:=\{\zeta \in C^p:\, s^p_\zeta \text { and }s^q_\zeta \text { are incomparable}\}$
is non-stationary. -
– If
 $p,q$
are such that
$p,q$
are such that
 $X_{p,q}$
is stationary, then the set of conditions r such that
$X_{p,q}$
is stationary, then the set of conditions r such that
 $\eta ^r$
and
$\eta ^r$
and
 $\eta ^q$
are incompatible (as partial functions) is dense below p.
$\eta ^q$
are incompatible (as partial functions) is dense below p.
-
5.2. Properness of
 $\boldsymbol Q$
: Fusion and pure decision
$\boldsymbol Q$
: Fusion and pure decision
Definition 5.5. We say
![]() $q\le _{\xi } p$
, if
$q\le _{\xi } p$
, if
![]() $q\le p$
,
$q\le p$
,
![]() $\xi \in C^q$
, and
$\xi \in C^q$
, and
![]() $q\restriction \xi =p\restriction \xi $
.
$q\restriction \xi =p\restriction \xi $
.
![]() $q\le ^+_{\xi } p$
means
$q\le ^+_{\xi } p$
means
![]() $q\le _\xi p$
and
$q\le _\xi p$
and
![]() $q(\xi )=p(\xi )$
.
$q(\xi )=p(\xi )$
.
(Note the difference between
![]() $q\le ^+_{\xi } p$
and
$q\le ^+_{\xi } p$
and
![]() $q\le _{\xi +1} p$
: The former does not require
$q\le _{\xi +1} p$
: The former does not require
![]() $\xi +1\in C^q$
.)
$\xi +1\in C^q$
.)
Lemma 5.6. Let
![]() $\delta \le \lambda $
be a limit ordinal,
$\delta \le \lambda $
be a limit ordinal,
![]() $\xi \in \lambda $
, and
$\xi \in \lambda $
, and
![]() $(q_i)_{i<\delta }$
a sequence in Q.
$(q_i)_{i<\delta }$
a sequence in Q.
-
(1) If
 $\delta <\lambda $
and
$\delta <\lambda $
and
 $q_{j}<^+_{\xi } q_i$
for all
$q_{j}<^+_{\xi } q_i$
for all
 $i<j<\delta $
, then there is a
$i<j<\delta $
, then there is a
 $q_\infty $
such that
$q_\infty $
such that
 $q_\infty <^+_{\xi }q_i$
for all i.
$q_\infty <^+_{\xi }q_i$
for all i. -
(2) If
 $q_{j}<_{\xi _i} q_i$
for
$q_{j}<_{\xi _i} q_i$
for
 $i<j<\delta $
, where
$i<j<\delta $
, where
 $(\xi _i)_{i\in \delta }$
is a strictly increasingFootnote
6
sequence in
$(\xi _i)_{i\in \delta }$
is a strictly increasingFootnote
6
sequence in
 $\lambda $
, then there is a
$\lambda $
, then there is a
 $($
canonical) limit
$($
canonical) limit
 $q_\infty $
such that
$q_\infty $
such that
 $q_\infty <_{\xi _i}q_i$
for all i.
$q_\infty <_{\xi _i}q_i$
for all i.
Proof (1): We perform the same construction as in the proof of Lemma 5.4. If there is a problematic case
![]() $\zeta $
, then
$\zeta $
, then
![]() $\zeta>\xi $
(as for
$\zeta>\xi $
(as for
![]() $\zeta '\le \xi $
the conditions
$\zeta '\le \xi $
the conditions
![]() $q_i(\zeta ')$
are constant). We can then make
$q_i(\zeta ')$
are constant). We can then make
![]() $\eta ^*$
total on
$\eta ^*$
total on
![]() $I^*(>\xi ,\le \zeta )$
. (It may not be enough to make it total on
$I^*(>\xi ,\le \zeta )$
. (It may not be enough to make it total on
![]() $I^*_\zeta $
, as
$I^*_\zeta $
, as
![]() $C^*\setminus \{\zeta \}$
might not be club.)
$C^*\setminus \{\zeta \}$
might not be club.)
(2): Define
![]() $q_\infty (\zeta ):= \bigcup _{i\in \delta } q_i(\zeta )$
for
$q_\infty (\zeta ):= \bigcup _{i\in \delta } q_i(\zeta )$
for
![]() $\zeta \in \lambda $
.
$\zeta \in \lambda $
.
This is a non-total function (on
![]() $I^*_\zeta $
) iff
$I^*_\zeta $
) iff
![]() $\zeta \in C^{q_\infty }:=\bigcap _{i<\delta } C^{q_i}$
, which is closed as intersection of closed sets, and also unbounded: If
$\zeta \in C^{q_\infty }:=\bigcap _{i<\delta } C^{q_i}$
, which is closed as intersection of closed sets, and also unbounded: If
![]() $\delta <\lambda $
because we have a small intersections of clubs, if
$\delta <\lambda $
because we have a small intersections of clubs, if
![]() $\delta =\lambda $
as it contains each
$\delta =\lambda $
as it contains each
![]() $\xi _i$
.
$\xi _i$
.
There are no problematic cases: If
![]() $\zeta $
is below some
$\zeta $
is below some
![]() $\xi _i$
, then
$\xi _i$
, then
![]() $q_j(\zeta )$
is eventually constant. If
$q_j(\zeta )$
is eventually constant. If
![]() $\zeta $
is above all
$\zeta $
is above all
![]() $\xi _i$
, which can only happen if
$\xi _i$
, which can only happen if
![]() $\delta <\lambda $
, then
$\delta <\lambda $
, then
![]() $\operatorname {\mathrm {cf}}(\delta )\le \delta \le \sup (\xi _i) \le \zeta < \theta ^*_\zeta $
.
$\operatorname {\mathrm {cf}}(\delta )\le \delta \le \sup (\xi _i) \le \zeta < \theta ^*_\zeta $
.
So Q satisfies fusion; and we will now show that it also satisfies “pure decision”; standard arguments then imply that Q is
![]() $\lambda $
-proper and
$\lambda $
-proper and
![]() $\lambda ^\lambda $
-bounding.
$\lambda ^\lambda $
-bounding.
Definition 5.7. Let
![]() $\xi \in \lambda $
,
$\xi \in \lambda $
,
![]() $q\in Q$
.
$q\in Q$
.
-
•
 $\operatorname {\mathrm {POSS}}^{Q}(\xi ):=2^{I^*({<}\xi )}$
. So in the extension
$\operatorname {\mathrm {POSS}}^{Q}(\xi ):=2^{I^*({<}\xi )}$
. So in the extension
 $V[G]$
, for each
$V[G]$
, for each
 $\xi $
there will be exactly one
$\xi $
there will be exactly one
 $x\in \operatorname {\mathrm {POSS}}^{Q}(\xi )$
compatible with (or equivalently: an initial segment of) the generic real
$x\in \operatorname {\mathrm {POSS}}^{Q}(\xi )$
compatible with (or equivalently: an initial segment of) the generic real  . We write “
. We write “ ” or “G chooses x” for this x.
” or “G chooses x” for this x. -
•
 $\operatorname {\mathrm {poss}}(q,\xi )$
is the set of
$\operatorname {\mathrm {poss}}(q,\xi )$
is the set of
 $x\in \operatorname {\mathrm {POSS}}^{Q}(\xi )$
compatible with
$x\in \operatorname {\mathrm {POSS}}^{Q}(\xi )$
compatible with
 $ \eta ^q$
(as partial functions), or equivalently:
$ \eta ^q$
(as partial functions), or equivalently:
 $x\in \operatorname {\mathrm {poss}}(q,\xi )$
iff
$x\in \operatorname {\mathrm {poss}}(q,\xi )$
iff  . So q forces that exactly one
. So q forces that exactly one
 $x\in \operatorname {\mathrm {poss}}(q,\xi )$
is chosen by G.
$x\in \operatorname {\mathrm {poss}}(q,\xi )$
is chosen by G. -
• Let
 be a name for an ordinal. We say that
be a name for an ordinal. We say that
 $q \xi $
-decides
$q \xi $
-decides  , if there is for all
, if there is for all
 $x\in \operatorname {\mathrm {poss}}(q,\xi )$
an ordinal
$x\in \operatorname {\mathrm {poss}}(q,\xi )$
an ordinal
 $\tau ^x$
such that q forces
$\tau ^x$
such that q forces  .
.
Note that for
![]() $p\in Q$
and
$p\in Q$
and
![]() $\zeta \in C^p$
,
$\zeta \in C^p$
,
![]() $q\le ^+_{\zeta } p$
is equivalent to
$q\le ^+_{\zeta } p$
is equivalent to
![]() $\operatorname {\mathrm {poss}}(q,\zeta +1)=\operatorname {\mathrm {poss}}(p,\zeta +1)$
, while
$\operatorname {\mathrm {poss}}(q,\zeta +1)=\operatorname {\mathrm {poss}}(p,\zeta +1)$
, while
![]() $q\le _\zeta p$
is equivalent to
$q\le _\zeta p$
is equivalent to
![]() $\zeta \in C^q$
and
$\zeta \in C^q$
and
![]() $\operatorname {\mathrm {poss}}(q,\zeta )=\operatorname {\mathrm {poss}}(p,\zeta )$
.
$\operatorname {\mathrm {poss}}(q,\zeta )=\operatorname {\mathrm {poss}}(p,\zeta )$
.
Lemma 5.8. Assume
![]() $p\in Q$
,
$p\in Q$
,
![]() $\zeta \in C^p$
,
$\zeta \in C^p$
,
![]() $x\in \operatorname {\mathrm {poss}}(p,\zeta +1)$
, and
$x\in \operatorname {\mathrm {poss}}(p,\zeta +1)$
, and
![]() $r\le p$
extendsFootnote
7
x. Then there is a
$r\le p$
extendsFootnote
7
x. Then there is a
![]() $q\le ^+_\zeta p$
forcing:
$q\le ^+_\zeta p$
forcing: ![]() . This condition is denoted by
. This condition is denoted by
![]() $r\vee (p\restriction \zeta +1)$
.
$r\vee (p\restriction \zeta +1)$
.
Proof We set
![]() $q(\ell )$
to be
$q(\ell )$
to be
![]() $p(\ell )$
for
$p(\ell )$
for
![]() $\ell \le \zeta $
, and
$\ell \le \zeta $
, and
![]() $r(\ell )$
otherwise. If
$r(\ell )$
otherwise. If
![]() $q'\le q$
forces
$q'\le q$
forces ![]() then
then
![]() $q'$
extends x and thus
$q'$
extends x and thus
![]() $q'\le r$
.
$q'\le r$
.
Corollary 5.9.
![]() $($
“Pure decision”) Let
$($
“Pure decision”) Let ![]() be a name for an ordinal,
be a name for an ordinal,
![]() $p\in Q$
, and
$p\in Q$
, and
![]() $\zeta \in C^p$
. Then there is a
$\zeta \in C^p$
. Then there is a
![]() $q\le ^+_\zeta p$
which
$q\le ^+_\zeta p$
which
![]() $(\zeta +1)$
-decides
$(\zeta +1)$
-decides ![]() .
.
Proof Let
![]() $(x_i)_{i\in \delta }$
enumerate
$(x_i)_{i\in \delta }$
enumerate
![]() $\operatorname {\mathrm {poss}}(p,\zeta +1)$
, for some
$\operatorname {\mathrm {poss}}(p,\zeta +1)$
, for some
![]() $\delta <\lambda $
. Set
$\delta <\lambda $
. Set
![]() $p_0=p$
, and define a
$p_0=p$
, and define a
![]() $\le ^+_\zeta $
-decreasing sequence
$\le ^+_\zeta $
-decreasing sequence
![]() $p_j$
by induction on
$p_j$
by induction on
![]() $j\le \delta $
: For limits use Lemma 5.6(1), and for successors choose some
$j\le \delta $
: For limits use Lemma 5.6(1), and for successors choose some
![]() $r\le p_i$
deciding
$r\le p_i$
deciding ![]() with a stem extending
with a stem extending
![]() $x_i$
and set
$x_i$
and set
![]() $p_{i+1}$
to
$p_{i+1}$
to
![]() $r\vee p_i\restriction (\zeta +1)$
.
$r\vee p_i\restriction (\zeta +1)$
.
From fusion and pure decision we get bounding and
![]() $\lambda $
-proper, via “continuous reading of names.” This is a standard argument, and we will not give it here; we will anyway prove a more “general” variant (for an iteration of Q’s), in Lemmas 5.25 and 5.27.
$\lambda $
-proper, via “continuous reading of names.” This is a standard argument, and we will not give it here; we will anyway prove a more “general” variant (for an iteration of Q’s), in Lemmas 5.25 and 5.27.
Fact 5.10.
-
• Q has continuous reading of names: If
 is a Q-name for a
is a Q-name for a
 $\lambda $
-sequence of ordinals, and
$\lambda $
-sequence of ordinals, and
 $p\in Q$
, then there is a
$p\in Q$
, then there is a
 $q\le p$
and there are
$q\le p$
and there are
 $\xi _i\in \lambda $
such that
$\xi _i\in \lambda $
such that
 $q \xi _i$
-decides
$q \xi _i$
-decides  for all
for all
 $i\in \lambda $
.
$i\in \lambda $
. -
• Q is
 $\lambda ^\lambda $
-bounding. That is, for every name
$\lambda ^\lambda $
-bounding. That is, for every name  and
and
 $p\in Q$
there is an
$p\in Q$
there is an
 $f\in \lambda ^\lambda $
and
$f\in \lambda ^\lambda $
and
 $q\le p$
such that q forces
$q\le p$
such that q forces  for all
for all
 $i\in \lambda $
.
$i\in \lambda $
. -
• Q is
 $\lambda $
-proper. This means: If N is a
$\lambda $
-proper. This means: If N is a
 ${<}\lambda $
-closed elementary submodel of
${<}\lambda $
-closed elementary submodel of
 $H(\chi )$
of size
$H(\chi )$
of size
 $\lambda $
containing Q, with
$\lambda $
containing Q, with
 $\chi $
sufficiently large and regular, and if
$\chi $
sufficiently large and regular, and if
 $p\in Q\cap N$
, then there is a
$p\in Q\cap N$
, then there is a
 $q\le p N$
-generic (i.e., forcing that each name of an ordinal which is in N is evaluated to an ordinal in N).
$q\le p N$
-generic (i.e., forcing that each name of an ordinal which is in N is evaluated to an ordinal in N).
For completeness, we also mention the following well-known fact (the proof is straightforward):
Fact 5.11. Assume
![]() $\kappa $
is regular, and that the forcing notion R is
$\kappa $
is regular, and that the forcing notion R is
![]() $\kappa ^\kappa $
-bounding. Then R preserves the regularity of
$\kappa ^\kappa $
-bounding. Then R preserves the regularity of
![]() $\kappa $
, and every club-subset of
$\kappa $
, and every club-subset of
![]() $\kappa $
in the extension contains a ground model club-set.
$\kappa $
in the extension contains a ground model club-set.
5.3. The iteration
 $\boldsymbol P$
$\boldsymbol P$
Let us first recall some well-known facts:
Facts 5.12. A
![]() ${<}\lambda $
-closed forcing preserves cofinalities
${<}\lambda $
-closed forcing preserves cofinalities
![]() ${\le }\lambda $
and also the inaccessibility of
${\le }\lambda $
and also the inaccessibility of
![]() $\lambda $
. The
$\lambda $
. The
![]() ${\le }\lambda $
-support iteration of
${\le }\lambda $
-support iteration of
![]() ${<}\lambda $
-closed forcings is
${<}\lambda $
-closed forcings is
![]() ${<}\lambda $
-closed.
${<}\lambda $
-closed.
We will iterate the forcings Q from the previous section in a
![]() ${<}\lambda $
-closed
${<}\lambda $
-closed
![]() ${\le }\lambda $
-support iteration of length
${\le }\lambda $
-support iteration of length
![]() $\mu :=\lambda ^{++}$
:
$\mu :=\lambda ^{++}$
:
Definition 5.13. Let
![]() $(P_\alpha ,Q_\alpha )_{\alpha < \mu }$
be the
$(P_\alpha ,Q_\alpha )_{\alpha < \mu }$
be the
![]() ${\le }\lambda $
-support iteration such that each
${\le }\lambda $
-support iteration such that each
![]() $Q_\alpha $
is the forcing Q (evaluated in the
$Q_\alpha $
is the forcing Q (evaluated in the
![]() $P_\alpha $
-extension). We will write P to denote the limit.
$P_\alpha $
-extension). We will write P to denote the limit.
Remark. One way to see that P is proper is to use the framework of [Reference Rosł anowski and Shelah6]. However, we will need an explicit form of continuous reading for P anyway, which in turn gives properness for free.
Definition 5.14. Assume that
![]() $w\in [\mu ]^{<\lambda }$
and
$w\in [\mu ]^{<\lambda }$
and
![]() $\xi \in \lambda $
.
$\xi \in \lambda $
.
-
•
 is the sequence of
is the sequence of
 $Q_\alpha $
-generic reals added by P.
$Q_\alpha $
-generic reals added by P. -
•
 $\operatorname {\mathrm {POSS}}(w,\xi ):=2^{w\times I^*({<}\xi )}$
. Exactly one
$\operatorname {\mathrm {POSS}}(w,\xi ):=2^{w\times I^*({<}\xi )}$
. Exactly one
 $x\in \operatorname {\mathrm {POSS}}(w,\xi )$
is extended by
$x\in \operatorname {\mathrm {POSS}}(w,\xi )$
is extended by  , we write “x is selected by G,” or “
, we write “x is selected by G,” or “
 $x\triangleleft G$
.”
$x\triangleleft G$
.” -
•
 $\operatorname {\mathrm {poss}}(p,w,\xi ):=\{x\in \operatorname {\mathrm {POSS}}(w,\xi ):\, \lnot p\Vdash \lnot x\triangleleft G\}$
.
$\operatorname {\mathrm {poss}}(p,w,\xi ):=\{x\in \operatorname {\mathrm {POSS}}(w,\xi ):\, \lnot p\Vdash \lnot x\triangleleft G\}$
. -
• Let
 be a name of an ordinal.
be a name of an ordinal.  is
is
 $(w,\xi )$
-decided by q, if there are
$(w,\xi )$
-decided by q, if there are
 $(\tau ^x)_{x\in \operatorname {\mathrm {poss}}(q,w,\xi )}$
such that q forces
$(\tau ^x)_{x\in \operatorname {\mathrm {poss}}(q,w,\xi )}$
such that q forces  .
.
Clearly, if ![]() is
is
![]() $(w,\xi )$
-decided by q, and if
$(w,\xi )$
-decided by q, and if
![]() $q'\le q$
,
$q'\le q$
,
![]() $w'\supseteq w$
and
$w'\supseteq w$
and
![]() $\xi '\ge \xi $
, then
$\xi '\ge \xi $
, then ![]() is
is
![]() $(w',\xi ')$
-decided by
$(w',\xi ')$
-decided by
![]() $q'$
.
$q'$
.
Remark. If
![]() $q\in P (w,\zeta )$
-decides some
$q\in P (w,\zeta )$
-decides some
![]() $P_\alpha $
-name
$P_\alpha $
-name ![]() , then the same q will generally not
, then the same q will generally not
![]() $(w\cap \alpha ,\xi )$
-decide
$(w\cap \alpha ,\xi )$
-decide ![]() for any
for any
![]() $\xi $
.Footnote
8
$\xi $
.Footnote
8
In the following, whenever we say that
![]() $q (w,\zeta )$
-decides something, we implicitly assume that
$q (w,\zeta )$
-decides something, we implicitly assume that
![]() $w\in [\mu ]^{<\lambda }$
and
$w\in [\mu ]^{<\lambda }$
and
![]() $\zeta \in \lambda $
.
$\zeta \in \lambda $
.
Definition 5.15. Let ![]() be a P-name for a
be a P-name for a
![]() $\lambda $
-sequence of ordinals.
$\lambda $
-sequence of ordinals.
-
• q continuously reads
 , if there are
, if there are
 $(w_i,\xi _i)_{i\in \lambda }$
such that
$(w_i,\xi _i)_{i\in \lambda }$
such that
 $q (w_i,\xi _i)$
-decides
$q (w_i,\xi _i)$
-decides  for each
for each
 $i\in \lambda $
.
$i\in \lambda $
. -
• P has continuous reading, if for each such
 and
and
 $p\in P$
there is some
$p\in P$
there is some
 $q\le p$
continuously reading
$q\le p$
continuously reading  .
.
The following is a straightforward standard argument:
Fact 5.16. If P has continuous reading, then it is
![]() $\lambda ^\lambda $
-bounding.
$\lambda ^\lambda $
-bounding.
As a first step towards pure decision, let us generalize the
![]() $\le _\zeta $
-notation we defined for Q:
$\le _\zeta $
-notation we defined for Q:
Definition 5.17. Let
![]() $p\in P$
,
$p\in P$
,
![]() $w\in [\mu ]^{<\lambda }$
, and
$w\in [\mu ]^{<\lambda }$
, and
![]() $\xi \in \lambda $
.
$\xi \in \lambda $
.
-
• p fits
 $(w,\xi )$
, if
$(w,\xi )$
, if
 $w\subseteq \operatorname {\mathrm {dom}}(p)$
and
$w\subseteq \operatorname {\mathrm {dom}}(p)$
and
 $p\restriction \alpha \Vdash \xi \in C^{p(\alpha )}$
for all
$p\restriction \alpha \Vdash \xi \in C^{p(\alpha )}$
for all
 $\alpha \in w$
.
$\alpha \in w$
. -
•
 $q\leq _{w,\xi } p$
means:
$q\leq _{w,\xi } p$
means:
 $q\leq p$
, and for all
$q\leq p$
, and for all
 $\alpha \in w$
,
$\alpha \in w$
,
 $q\restriction \alpha $
forces
$q\restriction \alpha $
forces
 $q(\alpha )<_\xi p(\alpha )$
.
$q(\alpha )<_\xi p(\alpha )$
. -
•
 $q\le ^+_{w,\xi } p$
is defined analogously using
$q\le ^+_{w,\xi } p$
is defined analogously using
 $<^+_\xi $
instead of
$<^+_\xi $
instead of
 $<_\xi $
.
$<_\xi $
.
Obviously
![]() $q\le ^+_{w,\xi } p$
implies
$q\le ^+_{w,\xi } p$
implies
![]() $q\leq _{w,\xi } p$
; and
$q\leq _{w,\xi } p$
; and
![]() $q\leq _{w,\xi } p$
implies that both p and q fit
$q\leq _{w,\xi } p$
implies that both p and q fit
![]() $(w,\xi )$
.
$(w,\xi )$
.
Remark. In contrast to the single forcing (or a product of such forcings),
![]() $q\le _{w,\xi }p$
(or
$q\le _{w,\xi }p$
(or
![]() $q\le ^+_{w,\xi }p$
) does not imply
$q\le ^+_{w,\xi }p$
) does not imply
![]() $\operatorname {\mathrm {poss}}(q,w,\xi )=\operatorname {\mathrm {poss}}(p,w,\xi )$
.Footnote
9
More explicitly, setting
$\operatorname {\mathrm {poss}}(q,w,\xi )=\operatorname {\mathrm {poss}}(p,w,\xi )$
.Footnote
9
More explicitly, setting
![]() $w=\{0,1\}$
, it is possible that
$w=\{0,1\}$
, it is possible that
![]() $x\in \operatorname {\mathrm {poss}}(p,w,\xi )$
but p does not force that
$x\in \operatorname {\mathrm {poss}}(p,w,\xi )$
but p does not force that ![]() implies
implies
![]() $x(1)\in \operatorname {\mathrm {poss}}(p(1),\xi )$
. (But see Section 5.5.)
$x(1)\in \operatorname {\mathrm {poss}}(p(1),\xi )$
. (But see Section 5.5.)
5.4. Continuous reading and properness of
 $\boldsymbol P$
$\boldsymbol P$
Lemma 5.18. If
![]() $q_i$
is a
$q_i$
is a
![]() $\leq ^+_{w,\zeta }$
-decreasing sequence of length
$\leq ^+_{w,\zeta }$
-decreasing sequence of length
![]() $\delta <\lambda $
, then there is an
$\delta <\lambda $
, then there is an
![]() $r\leq ^+_{w,\zeta }q_i$
for all
$r\leq ^+_{w,\zeta }q_i$
for all
![]() $i<\delta $
.
$i<\delta $
.
Proof Set
![]() $\operatorname {\mathrm {dom}}(r):=\bigcup _{i\in \delta }\operatorname {\mathrm {dom}}(q_i)$
, without loss of generality closed under limits. By induction on
$\operatorname {\mathrm {dom}}(r):=\bigcup _{i\in \delta }\operatorname {\mathrm {dom}}(q_i)$
, without loss of generality closed under limits. By induction on
![]() $\alpha \in \operatorname {\mathrm {dom}}(r)$
we know that
$\alpha \in \operatorname {\mathrm {dom}}(r)$
we know that
![]() $r\restriction \alpha \le q_i\restriction \alpha $
for all i, and define
$r\restriction \alpha \le q_i\restriction \alpha $
for all i, and define
![]() $r(\alpha )$
as follows: If
$r(\alpha )$
as follows: If
![]() $\alpha \in w$
, we know that the
$\alpha \in w$
, we know that the
![]() $q_i(\alpha )$
are
$q_i(\alpha )$
are
![]() $\le ^+_\zeta $
-increasing. Using Lemma 5.6(1), we pick some
$\le ^+_\zeta $
-increasing. Using Lemma 5.6(1), we pick some
![]() $r(\alpha )$
such that
$r(\alpha )$
such that
![]() $r(\alpha )\le ^+_\zeta q_i(\alpha )$
for all i. If
$r(\alpha )\le ^+_\zeta q_i(\alpha )$
for all i. If
![]() $\alpha \notin w$
, we just pick any
$\alpha \notin w$
, we just pick any
![]() $r(\alpha )\le q_i(\alpha )$
for all i.
$r(\alpha )\le q_i(\alpha )$
for all i.
It is easy to see that P satisfies a version of fusion:
Lemma 5.19. Assume
![]() $(p_i)_{i<\delta }$
is a sequence of length
$(p_i)_{i<\delta }$
is a sequence of length
![]() $\delta \le \lambda $
, such that
$\delta \le \lambda $
, such that
![]() $p_{j}\leq _{w_i,\xi _i} p_i$
for
$p_{j}\leq _{w_i,\xi _i} p_i$
for
![]() $i\leq j<\delta $
,
$i\leq j<\delta $
,
![]() $w_i\in [\mu ]^{<\lambda }$
increasing,
$w_i\in [\mu ]^{<\lambda }$
increasing,
![]() $\xi _i\in \lambda $
strictly increasing. Set
$\xi _i\in \lambda $
strictly increasing. Set
![]() $w_\infty :=\bigcup _{i<\delta } w_i$
,
$w_\infty :=\bigcup _{i<\delta } w_i$
,
![]() $\operatorname {\mathrm {dom}}_\infty :=\bigcup _{i<\delta }\operatorname {\mathrm {dom}}(p_i)$
, and
$\operatorname {\mathrm {dom}}_\infty :=\bigcup _{i<\delta }\operatorname {\mathrm {dom}}(p_i)$
, and
![]() $\xi _\infty :=\sup _{i<\delta }\xi _i$
. If
$\xi _\infty :=\sup _{i<\delta }\xi _i$
. If
![]() $\delta =\lambda $
, we additionally assume
$\delta =\lambda $
, we additionally assume
![]() $w_\infty =\operatorname {\mathrm {dom}}_\infty $
.
$w_\infty =\operatorname {\mathrm {dom}}_\infty $
.
Then there is a limit
![]() $q_\infty $
with
$q_\infty $
with
![]() $\operatorname {\mathrm {dom}}(q_\infty )=\operatorname {\mathrm {dom}}_\infty $
such that
$\operatorname {\mathrm {dom}}(q_\infty )=\operatorname {\mathrm {dom}}_\infty $
such that
![]() $q_\infty \le _{w_i,\xi _i} p_i$
for all
$q_\infty \le _{w_i,\xi _i} p_i$
for all
![]() $i<\delta $
.
$i<\delta $
.
If
![]() $\delta <\lambda $
, then
$\delta <\lambda $
, then
![]() $q_\infty $
fits
$q_\infty $
fits
![]() $(w_\infty ,\xi _\infty )$
.
$(w_\infty ,\xi _\infty )$
.
(If
![]() $w_\infty =\operatorname {\mathrm {dom}}_\infty $
, then the limit
$w_\infty =\operatorname {\mathrm {dom}}_\infty $
, then the limit
![]() $q_\infty $
is “canonical”.)
$q_\infty $
is “canonical”.)
Proof We define
![]() $q_\infty (\alpha )$
by induction on
$q_\infty (\alpha )$
by induction on
![]() $\operatorname {\mathrm {dom}}_\infty $
. We assume that we already have
$\operatorname {\mathrm {dom}}_\infty $
. We assume that we already have
![]() $q':=q_\infty \restriction \alpha $
which satisfies
$q':=q_\infty \restriction \alpha $
which satisfies
![]() $q'\le _{w_i\cap \alpha , \xi _i}p_i$
for all
$q'\le _{w_i\cap \alpha , \xi _i}p_i$
for all
![]() $i<\delta $
.
$i<\delta $
.
Case 1:
![]() $\alpha \notin w_\infty $
(this can only happen if
$\alpha \notin w_\infty $
(this can only happen if
![]() $\delta <\lambda $
): We know that
$\delta <\lambda $
): We know that
![]() $q'$
forces that
$q'$
forces that
![]() $(p_i(\alpha ))_{i<\delta }$
is a decreasing sequence, and we just pick some
$(p_i(\alpha ))_{i<\delta }$
is a decreasing sequence, and we just pick some
![]() $q_\infty (\alpha )$
stronger then all of them.
$q_\infty (\alpha )$
stronger then all of them.
Case 2:
![]() $\alpha \in w_\infty $
: Let
$\alpha \in w_\infty $
: Let
![]() $i^*$
be minimal such that
$i^*$
be minimal such that
![]() $\alpha \in w_{i^*}$
. We know that
$\alpha \in w_{i^*}$
. We know that
![]() $q'$
forces for all
$q'$
forces for all
![]() $i^*\le i<j<\delta $
that
$i^*\le i<j<\delta $
that
![]() $p_j(\alpha )<_{\xi _i}p_i(\alpha )$
, so according to Lemma 5.6(2) there is a limit
$p_j(\alpha )<_{\xi _i}p_i(\alpha )$
, so according to Lemma 5.6(2) there is a limit
![]() $q_\infty (\alpha )<_{\zeta _i}p_i(\alpha )$
(so in particular
$q_\infty (\alpha )<_{\zeta _i}p_i(\alpha )$
(so in particular
![]() $q'\Vdash \zeta _i\in C^{q_\infty (\alpha )}$
for all
$q'\Vdash \zeta _i\in C^{q_\infty (\alpha )}$
for all
![]() $i\ge i^*$
).
$i\ge i^*$
).
Now assume
![]() $\delta <\lambda $
. If
$\delta <\lambda $
. If
![]() $\alpha \in w_\infty $
, then it is in
$\alpha \in w_\infty $
, then it is in
![]() $w_i$
for coboundedly many
$w_i$
for coboundedly many
![]() $i<\delta $
. In other words,
$i<\delta $
. In other words,
![]() $p_j\restriction \alpha \Vdash \zeta _i\in C^{p_j(\alpha )}$
for coboundedly many
$p_j\restriction \alpha \Vdash \zeta _i\in C^{p_j(\alpha )}$
for coboundedly many
![]() $i\in \delta $
and all
$i\in \delta $
and all
![]() $j>i$
, which implies
$j>i$
, which implies
![]() $q_\infty \restriction \alpha \Vdash \xi _\infty \in C^{q_\infty (\alpha )}$
.
$q_\infty \restriction \alpha \Vdash \xi _\infty \in C^{q_\infty (\alpha )}$
.
Preliminary Lemma 5.20. Let p fit
![]() $(w,\zeta )$
,
$(w,\zeta )$
,
![]() $x\in \operatorname {\mathrm {poss}}(p,w,\zeta +1)$
, and let
$x\in \operatorname {\mathrm {poss}}(p,w,\zeta +1)$
, and let
![]() $r\le p$
extend x, i.e.,
$r\le p$
extend x, i.e.,
![]() $r\Vdash x\triangleleft G$
. Then there is a
$r\Vdash x\triangleleft G$
. Then there is a
![]() $q\le ^+_{w,\zeta } p$
forcing that
$q\le ^+_{w,\zeta } p$
forcing that
![]() $x\triangleleft G$
implies
$x\triangleleft G$
implies
![]() $r\in G$
.
$r\in G$
.
Proof Set
![]() $\operatorname {\mathrm {dom}}(q):=\operatorname {\mathrm {dom}}(r)$
. We define
$\operatorname {\mathrm {dom}}(q):=\operatorname {\mathrm {dom}}(r)$
. We define
![]() $q(\alpha )$
by induction on
$q(\alpha )$
by induction on
![]() $\alpha \in \operatorname {\mathrm {dom}}(q)$
and show inductively:
$\alpha \in \operatorname {\mathrm {dom}}(q)$
and show inductively:
-
•
 $q\restriction \alpha \le ^+_{w\cap \alpha ,\zeta }p\restriction \alpha $
.
$q\restriction \alpha \le ^+_{w\cap \alpha ,\zeta }p\restriction \alpha $
. -
•
 $q\restriction \alpha \Vdash (x\restriction \alpha \triangleleft G_\alpha \rightarrow r\restriction \alpha \in G_\alpha )$
.
$q\restriction \alpha \Vdash (x\restriction \alpha \triangleleft G_\alpha \rightarrow r\restriction \alpha \in G_\alpha )$
.
For notational convenience, we assume
![]() $\operatorname {\mathrm {dom}}(p)=\operatorname {\mathrm {dom}}(r)$
(by setting
$\operatorname {\mathrm {dom}}(p)=\operatorname {\mathrm {dom}}(r)$
(by setting
![]() $p(\alpha )=\mathbb {1}_Q$
for any
$p(\alpha )=\mathbb {1}_Q$
for any
![]() $\alpha $
outside the original domain of p).
$\alpha $
outside the original domain of p).
Assume we already have constructed
![]() $q_0=q\restriction \alpha $
. Work in the
$q_0=q\restriction \alpha $
. Work in the
![]() $P_\alpha $
-extension
$P_\alpha $
-extension
![]() $V[G_\alpha ]$
with
$V[G_\alpha ]$
with
![]() $q_0\in G$
.
$q_0\in G$
.
Case 1:
![]() $r\restriction \alpha \notin G_\alpha $
. Set
$r\restriction \alpha \notin G_\alpha $
. Set
![]() $q(\alpha ):=p(\alpha )$
.
$q(\alpha ):=p(\alpha )$
.
Case 2:
![]() $r\restriction \alpha \in G_\alpha $
. Then
$r\restriction \alpha \in G_\alpha $
. Then
![]() $r(\alpha )\le p(\alpha )$
. If
$r(\alpha )\le p(\alpha )$
. If
![]() $\alpha \notin w$
, we set
$\alpha \notin w$
, we set
![]() $q(\alpha ):=r(\alpha )$
; otherwise we set
$q(\alpha ):=r(\alpha )$
; otherwise we set
![]() $q(\alpha )$
to be
$q(\alpha )$
to be
![]() $r(\alpha )\vee (p(\alpha )\restriction \zeta +1)$
as in Lemma 5.8.
$r(\alpha )\vee (p(\alpha )\restriction \zeta +1)$
as in Lemma 5.8.
If
![]() $\alpha \in w$
, then in both cases we get
$\alpha \in w$
, then in both cases we get
![]() $q\restriction \alpha \vDash q(\alpha )\le ^+_\zeta p(\alpha )$
. Also, if
$q\restriction \alpha \vDash q(\alpha )\le ^+_\zeta p(\alpha )$
. Also, if
![]() $G_{\alpha +1}$
selects
$G_{\alpha +1}$
selects
![]() $x\restriction (\alpha +1)$
, then at stage
$x\restriction (\alpha +1)$
, then at stage
![]() $\alpha $
we used, by induction, Case 2; so then
$\alpha $
we used, by induction, Case 2; so then
![]() $r(\alpha )\in G(\alpha )$
as
$r(\alpha )\in G(\alpha )$
as ![]() .
.
We can iterate the construction for all elements of
![]() $\operatorname {\mathrm {poss}}(w, \zeta +1)$
, which gives us:
$\operatorname {\mathrm {poss}}(w, \zeta +1)$
, which gives us:
Lemma 5.21. If p fits
![]() $(w,\zeta )$
and
$(w,\zeta )$
and ![]() is a name for an ordinal, then there is a
is a name for an ordinal, then there is a
![]() $q\le ^+_{w,\zeta }p$
which
$q\le ^+_{w,\zeta }p$
which
![]() $(w,\zeta +1)$
-decides
$(w,\zeta +1)$
-decides ![]() .
.
Proof We enumerate
![]() $\operatorname {\mathrm {poss}}(p,w,\zeta +1)$
as
$\operatorname {\mathrm {poss}}(p,w,\zeta +1)$
as
![]() $(x_i)_{i\in \delta }$
. We start with
$(x_i)_{i\in \delta }$
. We start with
![]() $p_0:=p$
. Inductively we construct
$p_0:=p$
. Inductively we construct
![]() $p_\ell $
: If at step
$p_\ell $
: If at step
![]() $\ell $
, if
$\ell $
, if
![]() $x_\ell $
is not in
$x_\ell $
is not in
![]() $\operatorname {\mathrm {poss}}(p_\ell ,w,\zeta +1)$
any more, then we set
$\operatorname {\mathrm {poss}}(p_\ell ,w,\zeta +1)$
any more, then we set
![]() $p_{\ell +1}:=p_\ell $
. Otherwise, pick an
$p_{\ell +1}:=p_\ell $
. Otherwise, pick an
![]() $r\le p_\ell $
that decides
$r\le p_\ell $
that decides ![]() to be some
to be some
![]() $\tau ^{x_\ell }$
and extends
$\tau ^{x_\ell }$
and extends
![]() $x_\ell $
. Then apply 5.20 to get
$x_\ell $
. Then apply 5.20 to get
![]() $p_{\ell +1}\le ^+_{w,\zeta } p_\ell $
which forces that
$p_{\ell +1}\le ^+_{w,\zeta } p_\ell $
which forces that
![]() $x_\ell \triangleleft G$
implies
$x_\ell \triangleleft G$
implies ![]() . At limits use Lemma 5.18.
. At limits use Lemma 5.18.
For the proof of Lemma 5.23 we will need a variant where the “height”
![]() $\zeta $
is not the same for all elements of w, more specifically:
$\zeta $
is not the same for all elements of w, more specifically:
Preliminary Lemma 5.22. Assume that p fits
![]() $(w,\zeta )$
and
$(w,\zeta )$
and
![]() $p\restriction \alpha ^*\Vdash \zeta ^*\in C^{p(\alpha ^*)}$
, and that
$p\restriction \alpha ^*\Vdash \zeta ^*\in C^{p(\alpha ^*)}$
, and that ![]() is a name for an ordinal. Then there is a
is a name for an ordinal. Then there is a
![]() $q\le ^+_{w,\zeta }p$
such that
$q\le ^+_{w,\zeta }p$
such that
![]() $q\restriction \alpha ^*\Vdash q(\alpha ^*)\le ^+_{\zeta ^*}p(\alpha ^*)$
and there is a (ground model) set A of size
$q\restriction \alpha ^*\Vdash q(\alpha ^*)\le ^+_{\zeta ^*}p(\alpha ^*)$
and there is a (ground model) set A of size
![]() ${<}\lambda $
such that
${<}\lambda $
such that ![]() .
.
Proof This is just a notational variation of the previous proof. For notational simplicity we assume
![]() $\alpha ^*\notin w$
.
$\alpha ^*\notin w$
.
First we have to modify Preliminary Lemma 5.20: A candidate is a pair
![]() $(x,a)$
where
$(x,a)$
where
![]() $x\in \operatorname {\mathrm {POSS}}(w,\zeta )$
and
$x\in \operatorname {\mathrm {POSS}}(w,\zeta )$
and
![]() $a^*\in \operatorname {\mathrm {POSS}}^{Q}(\zeta ^*)$
. Assume that
$a^*\in \operatorname {\mathrm {POSS}}^{Q}(\zeta ^*)$
. Assume that
![]() $(x,a)$
is a candidate, that
$(x,a)$
is a candidate, that
![]() $p\in P$
fits
$p\in P$
fits
![]() $(w,\zeta )$
, and that
$(w,\zeta )$
, and that
![]() $p\restriction \alpha ^*\Vdash \zeta ^*\in C^{p(\alpha ^*)}$
, and assume that
$p\restriction \alpha ^*\Vdash \zeta ^*\in C^{p(\alpha ^*)}$
, and assume that
![]() $r\leq p$
extends
$r\leq p$
extends
![]() $(x,a)$
, i.e.,
$(x,a)$
, i.e., ![]() . Then there is a q such that
. Then there is a q such that
The same proof works, with the obvious modifications:
When defining
![]() $q(\alpha )$
, we inductively show:
$q(\alpha )$
, we inductively show:
-
•
 $q\restriction \alpha \le ^+_{w\cap \alpha ,\zeta }p\restriction \alpha $
and if
$q\restriction \alpha \le ^+_{w\cap \alpha ,\zeta }p\restriction \alpha $
and if
 $\alpha>\alpha ^*$
then
$\alpha>\alpha ^*$
then
 $q\restriction \alpha ^*\Vdash q(\alpha ^*)\le ^+_{\zeta ^*} p(\alpha ^*)$
,
$q\restriction \alpha ^*\Vdash q(\alpha ^*)\le ^+_{\zeta ^*} p(\alpha ^*)$
, -
•
 , unless
, unless
 $\alpha \le \alpha ^*$
in which case we omit the clause about
$\alpha \le \alpha ^*$
in which case we omit the clause about
 $\alpha ^*$
.
$\alpha ^*$
.
Again, in the
![]() $P_\alpha $
-extension we have:
$P_\alpha $
-extension we have:
Case 1:
![]() $r\restriction \alpha \notin G_\alpha $
. Set
$r\restriction \alpha \notin G_\alpha $
. Set
![]() $q(\alpha ):=p(\alpha )$
.
$q(\alpha ):=p(\alpha )$
.
Case 2:
![]() $r\restriction \alpha \in G_\alpha $
. Then
$r\restriction \alpha \in G_\alpha $
. Then
![]() $r(\alpha )\le p(\alpha )$
. If
$r(\alpha )\le p(\alpha )$
. If
![]() $\alpha \notin w\cup \{\alpha ^*\}$
, we set
$\alpha \notin w\cup \{\alpha ^*\}$
, we set
![]() $q(\alpha ):=r(\alpha )$
; otherwise we set
$q(\alpha ):=r(\alpha )$
; otherwise we set
![]() $q(\alpha )$
to be
$q(\alpha )$
to be
![]() $r(\alpha )\vee (p(\alpha )\restriction \zeta +1)$
as in Lemma 5.8.
$r(\alpha )\vee (p(\alpha )\restriction \zeta +1)$
as in Lemma 5.8.
Then we can show (*) as before.
We then enumerate all candidates (there are
![]() ${<}\lambda $
many) as
${<}\lambda $
many) as
![]() $(x_\ell ,a_\ell )$
, and at step
$(x_\ell ,a_\ell )$
, and at step
![]() $\ell $
, if
$\ell $
, if
![]() $(x_\ell ,a_\ell )$
is compatible with
$(x_\ell ,a_\ell )$
is compatible with
![]() $p_\ell $
, use (*) to decide
$p_\ell $
, use (*) to decide ![]() to be some
to be some ![]() .
.
We will now show that P is
![]() $\lambda ^\lambda $
-bounding and proper. We first give two preliminary lemmas that assume this is already the case for all
$\lambda ^\lambda $
-bounding and proper. We first give two preliminary lemmas that assume this is already the case for all
![]() $P_{\beta '}$
with
$P_{\beta '}$
with
![]() $\beta '<\beta $
.
$\beta '<\beta $
.
Preliminary Lemma 5.23. Let
![]() $\beta \le \mu $
, and assume that
$\beta \le \mu $
, and assume that
![]() $P_{\beta '}$
is
$P_{\beta '}$
is
![]() $\lambda ^\lambda $
-bounding for all
$\lambda ^\lambda $
-bounding for all
![]() $\beta '<\beta $
.
$\beta '<\beta $
.
Assume
![]() $p\in P_\beta $
fits
$p\in P_\beta $
fits
![]() $(w,\zeta )$
,
$(w,\zeta )$
,
![]() $\tilde C\subseteq \lambda $
is club, and
$\tilde C\subseteq \lambda $
is club, and
![]() $\alpha ^*<\beta $
.
$\alpha ^*<\beta $
.
Then there is a
![]() $q\le ^+_{w,\zeta } p$
and a
$q\le ^+_{w,\zeta } p$
and a
![]() $\xi \in \tilde C$
such that q fits
$\xi \in \tilde C$
such that q fits
![]() $(w\cup \{\alpha ^*\},\xi )$
.
$(w\cup \{\alpha ^*\},\xi )$
.
If additionally
![]() $\alpha ^*\in \operatorname {\mathrm {dom}}(p)$
and
$\alpha ^*\in \operatorname {\mathrm {dom}}(p)$
and
![]() $p\restriction \alpha ^*\Vdash \zeta ^*\in C^{p(\alpha ^*)}$
for some
$p\restriction \alpha ^*\Vdash \zeta ^*\in C^{p(\alpha ^*)}$
for some
![]() $\zeta ^*\in \lambda $
, then we can additionally get
$\zeta ^*\in \lambda $
, then we can additionally get
![]() $q\restriction \alpha ^*\Vdash q(\alpha ^*)\le ^+_{\zeta ^*} p(\alpha ^*)$
.
$q\restriction \alpha ^*\Vdash q(\alpha ^*)\le ^+_{\zeta ^*} p(\alpha ^*)$
.
Proof For notational simplicity assume
![]() $\alpha ^*\notin w$
and
$\alpha ^*\notin w$
and
![]() $\min (\tilde C)>\max (\zeta ,\zeta ^*)$
. By induction on
$\min (\tilde C)>\max (\zeta ,\zeta ^*)$
. By induction on
![]() $\alpha \le \beta $
we show that the result holds for all
$\alpha \le \beta $
we show that the result holds for all
![]() $w,\alpha ^*$
with
$w,\alpha ^*$
with
![]() $w\cup \{\alpha ^*\}\subseteq \alpha $
.
$w\cup \{\alpha ^*\}\subseteq \alpha $
.
Successor case
![]() $\alpha +1$
: Set
$\alpha +1$
: Set
![]() $w_0:=w\cap \alpha $
.
$w_0:=w\cap \alpha $
.
By our assumption
![]() $P_\alpha $
is
$P_\alpha $
is
![]() $\lambda ^\lambda $
-bounding, so every club-set in the
$\lambda ^\lambda $
-bounding, so every club-set in the
![]() $P_\alpha $
-extension contains a ground-model club (see Fact 5.11). In particular,
$P_\alpha $
-extension contains a ground-model club (see Fact 5.11). In particular,
![]() $C^{p(\alpha )}$
contains some ground-model
$C^{p(\alpha )}$
contains some ground-model
![]() $C^*$
. By Lemma 5.21 (or Preliminary Lemma 5.22, if
$C^*$
. By Lemma 5.21 (or Preliminary Lemma 5.22, if
![]() $\alpha ^*<\alpha $
) there is a
$\alpha ^*<\alpha $
) there is a
![]() $p'\le ^+_{w_0,\zeta }p\restriction \alpha $
(also dealing with
$p'\le ^+_{w_0,\zeta }p\restriction \alpha $
(also dealing with
![]() $\alpha ^*$
, if
$\alpha ^*$
, if
![]() $\alpha ^*<\alpha $
) leaving only
$\alpha ^*<\alpha $
) leaving only
![]() ${<}\lambda $
many possibilities for
${<}\lambda $
many possibilities for
![]() $C^*$
. So we can intersect them all, resulting in
$C^*$
. So we can intersect them all, resulting in
![]() $C'$
. Set
$C'$
. Set
![]() $C":=C'\cap \tilde C$
. Apply the induction hypothesis in
$C":=C'\cap \tilde C$
. Apply the induction hypothesis in
![]() $P_\alpha $
to get
$P_\alpha $
to get
![]() $q'\le ^+_{w_0,\zeta } p'$
and
$q'\le ^+_{w_0,\zeta } p'$
and
![]() $\xi $
in
$\xi $
in
![]() $C"$
such that
$C"$
such that
![]() $q'$
fits
$q'$
fits
![]() $(w_0,\xi )$
(and also
$(w_0,\xi )$
(and also
![]() $(\{\alpha ^*\},\xi )$
, if
$(\{\alpha ^*\},\xi )$
, if
![]() $\alpha ^*<\alpha $
). Set
$\alpha ^*<\alpha $
). Set
![]() $q:=q'\cup \{(\alpha , p(\alpha ))\}$
, so trivially
$q:=q'\cup \{(\alpha , p(\alpha ))\}$
, so trivially
![]() $q\le ^+_{w,\zeta } p$
(and, if
$q\le ^+_{w,\zeta } p$
(and, if
![]() $\alpha =\alpha ^*$
, then
$\alpha =\alpha ^*$
, then
![]() $q\restriction \alpha \Vdash q(\alpha )\le ^+_{\zeta ^*} p(\alpha )$
), and q fits
$q\restriction \alpha \Vdash q(\alpha )\le ^+_{\zeta ^*} p(\alpha )$
), and q fits
![]() $(w\cup \{\alpha \},\xi )$
.
$(w\cup \{\alpha \},\xi )$
.
Limit case: If w is bounded in
![]() $\alpha $
there is nothing to do. So assume w is cofinal.
$\alpha $
there is nothing to do. So assume w is cofinal.
Set
![]() $\alpha _0:=\min (w\setminus \alpha ^*)$
and
$\alpha _0:=\min (w\setminus \alpha ^*)$
and
![]() $w_0:=(w\cap \alpha _0)\cup \{\alpha ^*\}$
. Use the induction hypothesis in
$w_0:=(w\cap \alpha _0)\cup \{\alpha ^*\}$
. Use the induction hypothesis in
![]() $P_{\alpha _0}$
using
$P_{\alpha _0}$
using
![]() $(p\restriction \alpha _0,w_0,\zeta ,\alpha ^*,\zeta ^*)$
as
$(p\restriction \alpha _0,w_0,\zeta ,\alpha ^*,\zeta ^*)$
as
![]() $(p,w,\zeta ,\alpha ^*,\zeta ^*)$
. This gives us some
$(p,w,\zeta ,\alpha ^*,\zeta ^*)$
. This gives us some
![]() $p_0'\le ^+_{w\cap \alpha _0,\zeta } p\restriction \alpha _0$
fitting
$p_0'\le ^+_{w\cap \alpha _0,\zeta } p\restriction \alpha _0$
fitting
![]() $(w_0,\zeta _0)$
and dealing with
$(w_0,\zeta _0)$
and dealing with
![]() $\alpha ^*$
, for some
$\alpha ^*$
, for some
![]() $\zeta _0\in \tilde C$
. Set
$\zeta _0\in \tilde C$
. Set
![]() $p_0:=p'\wedge p$
.
$p_0:=p'\wedge p$
.
Enumerate
![]() $w\setminus w_0$
increasingly as
$w\setminus w_0$
increasingly as
![]() $(\alpha _i)_{i<\delta }$
, and set
$(\alpha _i)_{i<\delta }$
, and set
![]() $w_j:=w_0\cup \{\alpha _i:\ i<j\}$
for
$w_j:=w_0\cup \{\alpha _i:\ i<j\}$
for
![]() $j\le \delta $
.
$j\le \delta $
.
We will construct
![]() $p^{\prime }_i$
in
$p^{\prime }_i$
in
![]() $P_{\alpha _i}$
and
$P_{\alpha _i}$
and
![]() $(\zeta _i)_{i<\delta }$
a strictly increasing sequence in
$(\zeta _i)_{i<\delta }$
a strictly increasing sequence in
![]() $\tilde C$
, and we set
$\tilde C$
, and we set
![]() $p_j:=p^{\prime }_j\wedge p$
and will get:
$p_j:=p^{\prime }_j\wedge p$
and will get:
![]() $p_\ell $
fits
$p_\ell $
fits
![]() $(w_\ell ,\zeta _\ell )$
,and
$(w_\ell ,\zeta _\ell )$
,and
![]() $p_\ell \le ^+_{w_i,\zeta _i} p_i$
for all
$p_\ell \le ^+_{w_i,\zeta _i} p_i$
for all
![]() $i<\ell \le j$
.
$i<\ell \le j$
.
For successors
![]() $\ell =i+1$
, we use the induction hypothesis in
$\ell =i+1$
, we use the induction hypothesis in
![]() $P_{\alpha _{i+1}}$
, using
$P_{\alpha _{i+1}}$
, using
![]() $(p_i\restriction \alpha _{i+1},w_i,\zeta _i,\alpha _i,\zeta )$
as
$(p_i\restriction \alpha _{i+1},w_i,\zeta _i,\alpha _i,\zeta )$
as
![]() $(p,w,\zeta ,\alpha ^*,\zeta ^*)$
. This gives us
$(p,w,\zeta ,\alpha ^*,\zeta ^*)$
. This gives us
![]() $p^{\prime }_{i+1}\le ^+_{w_i,\zeta _i} p_i\restriction \alpha _{i+1}$
and some
$p^{\prime }_{i+1}\le ^+_{w_i,\zeta _i} p_i\restriction \alpha _{i+1}$
and some
![]() $\zeta _{i+1}>\zeta _i$
in
$\zeta _{i+1}>\zeta _i$
in
![]() $\tilde C$
such that
$\tilde C$
such that
![]() $p_{i+1}$
fits
$p_{i+1}$
fits
![]() $(w_{i+1},\zeta _{i+1})$
and
$(w_{i+1},\zeta _{i+1})$
and
![]() $p_{i+1}\restriction \alpha _i\Vdash p_{i+1}(\alpha _i)\le ^+_{\zeta } p_i(\alpha _i)$
.
$p_{i+1}\restriction \alpha _i\Vdash p_{i+1}(\alpha _i)\le ^+_{\zeta } p_i(\alpha _i)$
.
For j limit, we set
![]() $\zeta _j:=\sup _{i<j}\zeta _i$
(which is in
$\zeta _j:=\sup _{i<j}\zeta _i$
(which is in
![]() $\tilde C$
), and let
$\tilde C$
), and let
![]() $p_j$
be a limit of the
$p_j$
be a limit of the
![]() $(p_i)_{i<j}$
. That is,
$(p_i)_{i<j}$
. That is,
![]() $\operatorname {\mathrm {dom}}(p_j)=\bigcup _{i<j} \operatorname {\mathrm {dom}}(p_i)$
, and for
$\operatorname {\mathrm {dom}}(p_j)=\bigcup _{i<j} \operatorname {\mathrm {dom}}(p_i)$
, and for
![]() $\beta \in \operatorname {\mathrm {dom}}(p_j)$
let
$\beta \in \operatorname {\mathrm {dom}}(p_j)$
let
![]() $p_j(\beta )$
be as follows: If
$p_j(\beta )$
be as follows: If
![]() $\beta \notin w$
, fix some condition
$\beta \notin w$
, fix some condition
![]() $p_j(\beta )$
stronger than all
$p_j(\beta )$
stronger than all
![]() $p_i(\beta )$
. Otherwise, there is a minimal
$p_i(\beta )$
. Otherwise, there is a minimal
![]() $i_0<j$
such that
$i_0<j$
such that
![]() $\beta \in w_{i_0}$
, and
$\beta \in w_{i_0}$
, and
![]() $p_\ell (\beta )<^+_{\zeta _i} p_i(\beta )$
for all
$p_\ell (\beta )<^+_{\zeta _i} p_i(\beta )$
for all
![]() $i_0\le i<\ell <j$
. In that case let
$i_0\le i<\ell <j$
. In that case let
![]() $p_j(\beta )$
be the (canonical) limit of the
$p_j(\beta )$
be the (canonical) limit of the
![]() $(p_i(\beta ))_{i_0\le i<j}$
, and note that
$(p_i(\beta ))_{i_0\le i<j}$
, and note that
![]() $\zeta _j\in C^{p_j(\beta )}$
.
$\zeta _j\in C^{p_j(\beta )}$
.
Preliminary Lemma 5.24. Let
![]() $\beta \le \mu $
, and assume that
$\beta \le \mu $
, and assume that
![]() $P_{\beta '}$
is
$P_{\beta '}$
is
![]() $\lambda ^\lambda $
-bounding for all
$\lambda ^\lambda $
-bounding for all
![]() $\beta '<\beta $
.
$\beta '<\beta $
.
Assume that
![]() $p\in P_\beta $
fits
$p\in P_\beta $
fits
![]() $(w,\zeta )$
, and
$(w,\zeta )$
, and ![]() is a
is a
![]() $P_\beta $
-name for a
$P_\beta $
-name for a
![]() $\lambda $
-sequence of ordinals. Then there is a
$\lambda $
-sequence of ordinals. Then there is a
![]() $q\le ^+_{w,\zeta } p$
continuously reading
$q\le ^+_{w,\zeta } p$
continuously reading ![]() .
.
Proof Set
![]() $p_0:=p$
,
$p_0:=p$
,
![]() $\zeta _0:=\zeta $
,
$\zeta _0:=\zeta $
,
![]() $w_0:=w$
. We construct by induction on
$w_0:=w$
. We construct by induction on
![]() $i< \lambda p^{\prime }_i$
,
$i< \lambda p^{\prime }_i$
,
![]() $p_i$
,
$p_i$
,
![]() $\zeta _i$
,
$\zeta _i$
,
![]() $\alpha _i$
, and
$\alpha _i$
, and
![]() $w_i$
as follows:
$w_i$
as follows:
-
• Given
 $p_j$
,
$p_j$
,
 $w_j$
, and
$w_j$
, and
 $\zeta _j$
, pick
$\zeta _j$
, pick
 $\alpha _j\in \operatorname {\mathrm {dom}}(p_j)\setminus w_j$
by bookkeeping (so that in the end the domains of all conditions will be covered).
$\alpha _j\in \operatorname {\mathrm {dom}}(p_j)\setminus w_j$
by bookkeeping (so that in the end the domains of all conditions will be covered). -
• Successor
 $j=i+1$
: Set
$j=i+1$
: Set
 $w_{i+1}:=w_i\cup \{\alpha _i\}$
. Find
$w_{i+1}:=w_i\cup \{\alpha _i\}$
. Find
 $p^{\prime }_{i+1}\le ^+_{w_i,\zeta _i} p_i$
and
$p^{\prime }_{i+1}\le ^+_{w_i,\zeta _i} p_i$
and
 $\zeta _{i+1}>\zeta _i$
such that
$\zeta _{i+1}>\zeta _i$
such that
 $p^{\prime }_{i+1}$
fits
$p^{\prime }_{i+1}$
fits
 $(w_{i+1},\zeta _{i+1})$
(using the previous preliminary lemma).
$(w_{i+1},\zeta _{i+1})$
(using the previous preliminary lemma). -
• Limit j: Let
 $p^{\prime }_j$
be the canonical limit of the
$p^{\prime }_j$
be the canonical limit of the
 $(p_i)_{i<j}$
,
$(p_i)_{i<j}$
,
 $\zeta _j:=\sup _{i<j}(\zeta _i)$
, and
$\zeta _j:=\sup _{i<j}(\zeta _i)$
, and
 $w_j:=\bigcup _{i<j} w_i$
. Note that
$w_j:=\bigcup _{i<j} w_i$
. Note that
 $p^{\prime }_j$
fits
$p^{\prime }_j$
fits
 $(w_j,\zeta _j)$
.
$(w_j,\zeta _j)$
. -
• In any case, given
 $p^{\prime }_j$
we pick some
$p^{\prime }_j$
we pick some
 $p_j\le ^+_{w_j,\zeta _j} p^{\prime }_j$
which
$p_j\le ^+_{w_j,\zeta _j} p^{\prime }_j$
which
 $(w_j,\zeta _j+1)$
-decides
$(w_j,\zeta _j+1)$
-decides  .
.
Then the limit q of the
![]() $p_i$
continuously reads
$p_i$
continuously reads ![]() .
.
Lemma 5.25. P has continuous reading (and in particular is
![]() $\lambda ^\lambda $
-bounding).
$\lambda ^\lambda $
-bounding).
Proof Assume by induction that
![]() $P_{\beta '}$
is
$P_{\beta '}$
is
![]() $\lambda ^\lambda $
-bounding for all
$\lambda ^\lambda $
-bounding for all
![]() $\beta <\beta '$
. Then the previous lemma gives us that
$\beta <\beta '$
. Then the previous lemma gives us that
![]() $P_\beta $
has continuous reading of names, and thus is
$P_\beta $
has continuous reading of names, and thus is
![]() $\lambda ^\lambda $
-bounding.
$\lambda ^\lambda $
-bounding.
The same construction shows
![]() $\lambda $
-properness:
$\lambda $
-properness:
Definition 5.26. Let
![]() $\chi \gg \mu $
be sufficiently large and regular. An “elementary model” is an
$\chi \gg \mu $
be sufficiently large and regular. An “elementary model” is an
![]() $M\preceq H(\chi )$
of size
$M\preceq H(\chi )$
of size
![]() $\lambda $
which is
$\lambda $
which is
![]() ${<}\lambda $
-closed and contains
${<}\lambda $
-closed and contains
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
(and thus P).
$\mu $
(and thus P).
Lemma 5.27. If M is an elementary model containing
![]() $p\in P$
, then there is a
$p\in P$
, then there is a
![]() $q\le p$
which is strongly M-generic in the following sense
$q\le p$
which is strongly M-generic in the following sense
![]() $:$
For each P-name
$:$
For each P-name ![]() in M for an ordinal,
in M for an ordinal,
![]() $q (w,\zeta )$
-decides
$q (w,\zeta )$
-decides ![]() via a decision function in M (so in particular
via a decision function in M (so in particular ![]() ).
).
(The decision function being in M is equivalent to
![]() $w\subseteq M$
, as M is
$w\subseteq M$
, as M is
![]() ${<}\lambda $
closed.)
${<}\lambda $
closed.)
Proof Let ![]() be a sequence of all P-names for ordinals that are in M. Starting with
be a sequence of all P-names for ordinals that are in M. Starting with
![]() $p_0\in M$
, perform the successor step of the previous construction within M; as M is closed the limits at steps
$p_0\in M$
, perform the successor step of the previous construction within M; as M is closed the limits at steps
![]() ${<}\lambda $
are in M as well. Then the
${<}\lambda $
are in M as well. Then the
![]() $\lambda $
-limit is M-generic.
$\lambda $
-limit is M-generic.
5.5. Canonical conditions
We will use conditions that “continuously read themselves.”
Definition 5.28.
![]() $p\in P$
is
$p\in P$
is
![]() $(w,\zeta )$
-canonical if p fits
$(w,\zeta )$
-canonical if p fits
![]() $(w,\zeta )$
and
$(w,\zeta )$
and
![]() $p(\alpha )\restriction (\zeta +1)$
is
$p(\alpha )\restriction (\zeta +1)$
is
![]() $(w\cap \alpha ,\zeta +1)$
-decided by
$(w\cap \alpha ,\zeta +1)$
-decided by
![]() $p\restriction \alpha $
for all
$p\restriction \alpha $
for all
![]() $\alpha \in w$
.
$\alpha \in w$
.
Facts 5.29. Let p be canonical for
![]() $(w,\zeta )$
.
$(w,\zeta )$
.
-
(1) If
 $q\le ^+_{w,\zeta } p$
, then q is canonical for
$q\le ^+_{w,\zeta } p$
, then q is canonical for
 $(w,\zeta )$
and
$(w,\zeta )$
and
 $\operatorname {\mathrm {poss}}(p,w,\zeta +1)=\operatorname {\mathrm {poss}}(q,w,\zeta +1)$
.
$\operatorname {\mathrm {poss}}(p,w,\zeta +1)=\operatorname {\mathrm {poss}}(q,w,\zeta +1)$
. -
(2) Let
 $x\in \operatorname {\mathrm {poss}}(p,w,\zeta +1)$
. There is a naturally defined
$x\in \operatorname {\mathrm {poss}}(p,w,\zeta +1)$
. There is a naturally defined
 $p\wedge x\le p$
such that
$p\wedge x\le p$
such that
 $p\Vdash (p\wedge x\in G \leftrightarrow x\triangleleft G)$
.
$p\Vdash (p\wedge x\in G \leftrightarrow x\triangleleft G)$
.
 $\{p\wedge x:\, x\in \operatorname {\mathrm {poss}}(p,w,\zeta +1)\}$
is a maximal antichain below p.
$\{p\wedge x:\, x\in \operatorname {\mathrm {poss}}(p,w,\zeta +1)\}$
is a maximal antichain below p. -
(3) Let
 $x\in \operatorname {\mathrm {poss}}(p,w,\zeta +1)$
. In an intermediate
$x\in \operatorname {\mathrm {poss}}(p,w,\zeta +1)$
. In an intermediate
 $P_\alpha $
-extension
$P_\alpha $
-extension
 $V[G_\alpha ]$
with
$V[G_\alpha ]$
with
 $x\restriction \alpha \triangleleft G_\alpha $
the rest of x, i.e.,
$x\restriction \alpha \triangleleft G_\alpha $
the rest of x, i.e.,
 $x\restriction [\alpha ,\mu ]$
, is compatible with
$x\restriction [\alpha ,\mu ]$
, is compatible with
 $p/G_\alpha $
in the quotient forcing.
$p/G_\alpha $
in the quotient forcing.Or equivalently: If
 $r_0\leq p\restriction \alpha $
in
$r_0\leq p\restriction \alpha $
in
 $P_\alpha $
extends
$P_\alpha $
extends
 $x\restriction \alpha $
, then there is an
$x\restriction \alpha $
, then there is an
 $r\le r_0$
extending x.
$r\le r_0$
extending x.
Definition 5.30. Assume
![]() $p\in P$
, and
$p\in P$
, and ![]() is a P-name for a
is a P-name for a
![]() $\lambda $
-sequence of ordinals. Let
$\lambda $
-sequence of ordinals. Let
![]() $E\subseteq \lambda $
be a club-set and
$E\subseteq \lambda $
be a club-set and
![]() $\bar w=(w_\zeta )_{\zeta \in E}$
an increasing sequence in
$\bar w=(w_\zeta )_{\zeta \in E}$
an increasing sequence in
![]() $[\mu ]^{<\lambda }$
.
$[\mu ]^{<\lambda }$
.
p canonically reads ![]() as witnessed by
as witnessed by
![]() $\bar w$
if the following holds:
$\bar w$
if the following holds:
-
•
 $\operatorname {\mathrm {dom}}(p)=\bigcup _{\zeta \in E} w_\zeta $
.
$\operatorname {\mathrm {dom}}(p)=\bigcup _{\zeta \in E} w_\zeta $
. -
• p is
 $(w_\zeta ,\zeta )$
-canonical for all
$(w_\zeta ,\zeta )$
-canonical for all
 $\zeta \in E$
.
$\zeta \in E$
. -
•
 $p\restriction \alpha \Vdash C^{p(\alpha )}=E\setminus (\zeta ^{\prime }_\alpha )$
for some (ground model)
$p\restriction \alpha \Vdash C^{p(\alpha )}=E\setminus (\zeta ^{\prime }_\alpha )$
for some (ground model)
 $\zeta ^{\prime }_\alpha $
.
$\zeta ^{\prime }_\alpha $
. -
•
 is
is
 $(w_\zeta ,\zeta +1)$
-decided by p for all
$(w_\zeta ,\zeta +1)$
-decided by p for all
 $\zeta \in E$
.
$\zeta \in E$
.
If
![]() $\sigma $
is the constant
$\sigma $
is the constant
![]() $0$
sequence (or any sequence in V), we just say “p is canonical” (as witnessed by
$0$
sequence (or any sequence in V), we just say “p is canonical” (as witnessed by
![]() $\bar w$
).
$\bar w$
).
Lemma 5.31. For p, ![]() as above, there is a
as above, there is a
![]() $q\le p$
canonically reading
$q\le p$
canonically reading ![]() .
.
If
![]() $p\in P_\alpha $
and
$p\in P_\alpha $
and ![]() is a
is a
![]() $P_\alpha $
-name for some
$P_\alpha $
-name for some
![]() $\alpha <\mu $
, then
$\alpha <\mu $
, then
![]() $q\in P_\alpha $
.
$q\in P_\alpha $
.
Proof We just have to slightly modify the proof of Lemma 5.24.
We will construct
![]() $p_j$
,
$p_j$
,
![]() $\xi _j$
, and
$\xi _j$
, and
![]() $\alpha _j$
by induction on
$\alpha _j$
by induction on
![]() $j\in \lambda $
, setting
$j\in \lambda $
, setting
![]() $w_j:=\{\alpha _i:i<j\}$
, such that for
$w_j:=\{\alpha _i:i<j\}$
, such that for
![]() $0<j<k$
the following holds:
$0<j<k$
the following holds:
-
•
 $p_{k}\le ^+_{w_j,\xi _j} p_j$
.
$p_{k}\le ^+_{w_j,\xi _j} p_j$
. -
•
 $p_{j}$
is
$p_{j}$
is
 $(w_j,\xi _j)$
-canonical.
$(w_j,\xi _j)$
-canonical. -
•
 $p_{j} (w_j,\xi _j+1)$
-decides
$p_{j} (w_j,\xi _j+1)$
-decides  .
. -
• In
 $p_{k}$
, for
$p_{k}$
, for
 $\alpha _j\in w_k$
,
$\alpha _j\in w_k$
,
 $\{\zeta _i:\, j<i<k\}$
is (forced to be) an initial segment of
$\{\zeta _i:\, j<i<k\}$
is (forced to be) an initial segment of
 $C^{p_k(\alpha _j)}$
.
$C^{p_k(\alpha _j)}$
. -
• The
 $\alpha _j$
are chosen (by some book-keeping) so that
$\alpha _j$
are chosen (by some book-keeping) so that
 $\{\alpha _i:\, i\in \lambda \}=\bigcup _{i\in \lambda }\operatorname {\mathrm {dom}}(p_i)$
.
$\{\alpha _i:\, i\in \lambda \}=\bigcup _{i\in \lambda }\operatorname {\mathrm {dom}}(p_i)$
.
Then the limit of the
![]() $p_j$
is as required, with
$p_j$
is as required, with
![]() $E=\{\xi _i:\, i\in \lambda \}$
and, for
$E=\{\xi _i:\, i\in \lambda \}$
and, for
![]() $\zeta =\xi _j$
in E, we use
$\zeta =\xi _j$
in E, we use
![]() $w_j$
as
$w_j$
as
![]() $w_\zeta $
.
$w_\zeta $
.
Set
![]() $p_0\le p$
such that
$p_0\le p$
such that
![]() $|\operatorname {\mathrm {dom}}(p_0)|=\lambda $
, and set
$|\operatorname {\mathrm {dom}}(p_0)|=\lambda $
, and set
![]() $\xi _0:=0$
. Assume we already have
$\xi _0:=0$
. Assume we already have
![]() $p_i,\alpha _i$
for
$p_i,\alpha _i$
for
![]() $i<j$
(so we also have
$i<j$
(so we also have
![]() $w_j$
).
$w_j$
).
-
• For j limit, let s be a limit of
 $(p_i)_{i<j}$
, and set
$(p_i)_{i<j}$
, and set
 $\xi _j:= \sup _{i<j}\xi _i$
. Note that s fits
$\xi _j:= \sup _{i<j}\xi _i$
. Note that s fits
 $(w_j,\xi )$
.
$(w_j,\xi )$
. -
• Successor case
 $j=i+1$
: Find
$j=i+1$
: Find
 $s_0\le ^+_{w_i,\xi _i} p_i$
and
$s_0\le ^+_{w_i,\xi _i} p_i$
and
 $\xi _{j}>\xi _i$
such that s fits
$\xi _{j}>\xi _i$
such that s fits
 $(w_{j},\xi _{j})$
. (As in Lemma 5.23. Recall that
$(w_{j},\xi _{j})$
. (As in Lemma 5.23. Recall that
 $w_j=w_i\cup \{\alpha _i\}$
.)Strengthen
$w_j=w_i\cup \{\alpha _i\}$
.)Strengthen
 $s_0$
to
$s_0$
to
 $s\le ^+_{w_i,\xi _i}$
so that:
$s\le ^+_{w_i,\xi _i}$
so that:-
– s still fits
 $(w_{j},\xi _{j})$
,
$(w_{j},\xi _{j})$
, -
– the trunk at
 $\alpha _i$
has length
$\alpha _i$
has length
 $\xi _j$
, i.e.,
$\xi _j$
, i.e.,
 $s\restriction \alpha _i\Vdash \min (C^{s(\alpha _i)})=\xi _j$
),
$s\restriction \alpha _i\Vdash \min (C^{s(\alpha _i)})=\xi _j$
), -
– for
 $\alpha _{i'}$
,
$\alpha _{i'}$
,
 $i'<i$
, there are no elements in
$i'<i$
, there are no elements in
 $C^{s(\alpha _{i'})}$
between
$C^{s(\alpha _{i'})}$
between
 $\xi _i$
and
$\xi _i$
and
 $\xi _j$
.
$\xi _j$
.
-
-
• Construct
 $s^{*}\restriction \alpha $
by recursion on
$s^{*}\restriction \alpha $
by recursion on
 $\alpha \in w_j$
, such that
$\alpha \in w_j$
, such that
 $s^{*}\restriction \alpha \le ^+_{w_j\cap \alpha ,\xi _j} s\restriction \alpha $
and
$s^{*}\restriction \alpha \le ^+_{w_j\cap \alpha ,\xi _j} s\restriction \alpha $
and
 $s^{*}\restriction \alpha (w_j\cap \alpha ,\xi _j+1)$
-decides
$s^{*}\restriction \alpha (w_j\cap \alpha ,\xi _j+1)$
-decides
 $s(\alpha )\restriction (\xi _j+1)$
(which is the same as
$s(\alpha )\restriction (\xi _j+1)$
(which is the same as
 $s^*(\alpha )\restriction (\xi _j+1)$
). This gives
$s^*(\alpha )\restriction (\xi _j+1)$
). This gives
 $s^{*}\le ^+_{w_j,\xi _j} s$
.
$s^{*}\le ^+_{w_j,\xi _j} s$
. -
• Find
 $p_j\le ^+_{w_j,\xi _j} s^{*}$
which
$p_j\le ^+_{w_j,\xi _j} s^{*}$
which
 $(w_j,\xi _j+1)$
decides
$(w_j,\xi _j+1)$
decides  .
. -
• Choose
 $\alpha _j\in \operatorname {\mathrm {dom}}(p_j)\setminus w_j$
by bookkeeping.
$\alpha _j\in \operatorname {\mathrm {dom}}(p_j)\setminus w_j$
by bookkeeping.
Facts 5.32.
-
(1) If a
 $P_\beta $
-name
$P_\beta $
-name  is continuously read (by some
is continuously read (by some
 $P_\beta $
-condition p), and
$P_\beta $
-condition p), and
 $\operatorname {\mathrm {cf}}(\beta )>\lambda $
, then there is an
$\operatorname {\mathrm {cf}}(\beta )>\lambda $
, then there is an
 $\alpha <\beta $
such that:
$\alpha <\beta $
such that:
 $p\in P_\alpha $
, and
$p\in P_\alpha $
, and  is already a
is already a
 $P_\alpha $
-name (formally: there is a
$P_\alpha $
-name (formally: there is a
 $P_\alpha $
-name
$P_\alpha $
-name  such that
such that  ).
). -
(2) There are at most
 $|\alpha |^\lambda \le \lambda ^+$
many pairsFootnote
10
$|\alpha |^\lambda \le \lambda ^+$
many pairsFootnote
10
 such that p canonically reads
such that p canonically reads  in
in
 $P_\alpha $
.
$P_\alpha $
.
5.6.
 $\mathbf \Delta $
systems
$\mathbf \Delta $
systems
In this section we define
![]() $\Delta $
-systems and show that such systems exist, which we will in the indirect proofs of Lemmas 5.39 and 5.54.
$\Delta $
-systems and show that such systems exist, which we will in the indirect proofs of Lemmas 5.39 and 5.54.
In Section 5.10 we will then fix a specific
![]() $\Delta $
-system for the rest of the paper.
$\Delta $
-system for the rest of the paper.
From now on, we assume that
![]() $p_*$
forces
$p_*$
forces
and we set, for
![]() $\beta \in \mu $
,
$\beta \in \mu $
,
where, as usual, we identify ![]() with
with ![]() .
.
Note that, other than ![]() ,
, ![]() is a priori not a
is a priori not a
![]() $P_{\beta +1}$
-name (but see Section 5.9).
$P_{\beta +1}$
-name (but see Section 5.9).
We also fix a P-name for a representation of the inverse automorphism ![]() . Abusing notation, we call it
. Abusing notation, we call it ![]() .
.
With
![]() $S^\mu _{\lambda ^+}$
we denote the stationary subset of
$S^\mu _{\lambda ^+}$
we denote the stationary subset of
![]() $\mu $
consisting of ordinals with cofinality
$\mu $
consisting of ordinals with cofinality
![]() $\lambda ^+$
.
$\lambda ^+$
.
Definition 5.34. Let
![]() $S\subseteq S^{\mu }_{\lambda ^+}$
be stationary,
$S\subseteq S^{\mu }_{\lambda ^+}$
be stationary,
![]() $\chi \gg \mu $
sufficiently large, and regular, and
$\chi \gg \mu $
sufficiently large, and regular, and
![]() $z\in H(\chi )$
. “An elementary S-system” (using parameter z) is a sequence
$z\in H(\chi )$
. “An elementary S-system” (using parameter z) is a sequence
![]() $(M_\beta ,p_\beta )_{\beta \in S}$
such that, for each
$(M_\beta ,p_\beta )_{\beta \in S}$
such that, for each
![]() $\beta \in S$
,
$\beta \in S$
,
![]() $M_\beta $
is an elementary model (as in Definition 5.26) and contains z,
$M_\beta $
is an elementary model (as in Definition 5.26) and contains z,
![]() $\beta $
,
$\beta $
,
![]() $p_*$
,
$p_*$
, ![]() ,
, ![]() and
and ![]() , and
, and
![]() $p_\beta \in P\cap M_\beta $
canonically reads
$p_\beta \in P\cap M_\beta $
canonically reads ![]() witnessed by some
witnessed by some
![]() $(w^{p_\beta }_\zeta )_{\zeta \in E^{p_\beta }}$
, which
$(w^{p_\beta }_\zeta )_{\zeta \in E^{p_\beta }}$
, which
![]() $E^{p_\beta }\subseteq \lambda $
club (cf. Definition 5.30).
$E^{p_\beta }\subseteq \lambda $
club (cf. Definition 5.30).
By a simple
![]() $\Delta $
-system argument we can make an S-system homogeneous:
$\Delta $
-system argument we can make an S-system homogeneous:
Definition 5.35.
![]() $(M_\beta , p_\beta )_{\beta \in S}$
forms a “
$(M_\beta , p_\beta )_{\beta \in S}$
forms a “
![]() $\Delta $
-system,” if
$\Delta $
-system,” if
![]() $\bar M,\bar p$
is an elementary S-system with parameter z, and is homogeneous in the following sense: For
$\bar M,\bar p$
is an elementary S-system with parameter z, and is homogeneous in the following sense: For
![]() $\beta $
and
$\beta $
and
![]() $\beta _1< \beta _2$
in S, we get:
$\beta _1< \beta _2$
in S, we get:
-
(1)
 $M_{\beta _1}\cap M_{\beta _2}\cap \mu $
is constant. We call this set the “heart” and, abusing notation, denote it with
$M_{\beta _1}\cap M_{\beta _2}\cap \mu $
is constant. We call this set the “heart” and, abusing notation, denote it with
 $\Delta $
. Obviously
$\Delta $
. Obviously
 $\Delta \supseteq \lambda $
,
$\Delta \supseteq \lambda $
,
 $\Delta \supseteq \operatorname {\mathrm {dom}}(p_*)$
,
$\Delta \supseteq \operatorname {\mathrm {dom}}(p_*)$
,
 $\lambda ^+\in \Delta $
, etc.
$\lambda ^+\in \Delta $
, etc. -
(2)
 $M_{\beta }\cap {\beta }=\Delta $
. So in particular
$M_{\beta }\cap {\beta }=\Delta $
. So in particular
 $\beta $
is the minimal element of
$\beta $
is the minimal element of
 $M_\beta $
above
$M_\beta $
above
 $\Delta $
. All the non-heart elements of
$\Delta $
. All the non-heart elements of
 $M_{\beta _2}$
are above all elements of
$M_{\beta _2}$
are above all elements of
 $M_{\beta _1}$
. That is,
$M_{\beta _1}$
. That is,
 $\sup (M_{\beta _1}\cap \mu )<\beta _2$
.
$\sup (M_{\beta _1}\cap \mu )<\beta _2$
. -
(3) There is an
 $\in $
-isomorphism
$\in $
-isomorphism
 $h^*_{\beta _1,\beta _2}: M_{\beta _1}\to M_{\beta _2}$
, mapping
$h^*_{\beta _1,\beta _2}: M_{\beta _1}\to M_{\beta _2}$
, mapping
 $\beta _1$
to
$\beta _1$
to
 $\beta _2$
,
$\beta _2$
,
 $p_{\beta _1}$
to
$p_{\beta _1}$
to
 $p_{\beta _2}$
,
$p_{\beta _2}$
,  to
to  and fixing
and fixing  as well as each
as well as each
 $\alpha $
in
$\alpha $
in
 $\Delta $
.
$\Delta $
.
Note that this implies that the continuous reading of ![]() works the same way for all
works the same way for all
![]() $\beta $
. In particular the
$\beta $
. In particular the
![]() $E^{p_{\beta }}$
are that same E for all
$E^{p_{\beta }}$
are that same E for all
![]() $\beta $
; and if
$\beta $
; and if
![]() $F^\beta _\zeta $
is the function mapping
$F^\beta _\zeta $
is the function mapping
![]() $\operatorname {\mathrm {POSS}}(w^{p_\beta }_\zeta ,\zeta +1)$
to the value of
$\operatorname {\mathrm {POSS}}(w^{p_\beta }_\zeta ,\zeta +1)$
to the value of ![]() (for
(for
![]() $\zeta \in E$
), then
$\zeta \in E$
), then
![]() $h^*_{\beta _1,\beta _2}(F^{\beta _1}_\zeta )=F^{\beta _2}_\zeta $
and in particular
$h^*_{\beta _1,\beta _2}(F^{\beta _1}_\zeta )=F^{\beta _2}_\zeta $
and in particular
![]() $h^*_{\beta _1,\beta _2}(w^{p_{\beta _1}}_\zeta )=w^{p_{\beta _2}}_\zeta $
; i.e., they are the same apart from shifting coordinates above
$h^*_{\beta _1,\beta _2}(w^{p_{\beta _1}}_\zeta )=w^{p_{\beta _2}}_\zeta $
; i.e., they are the same apart from shifting coordinates above
![]() $\Delta $
.
$\Delta $
.
Lemma 5.36. Assume
![]() $S\subseteq S^\mu _{\lambda ^+}$
is stationary.
$S\subseteq S^\mu _{\lambda ^+}$
is stationary.
-
• For every
 $z\in H(\chi )$
and
$z\in H(\chi )$
and
 $(p^{\prime }_\beta )_{\beta \in S}$
there are
$(p^{\prime }_\beta )_{\beta \in S}$
there are
 $M_\beta $
and
$M_\beta $
and
 $p_\beta \le p^{\prime }_\beta $
such that
$p_\beta \le p^{\prime }_\beta $
such that
 $\bar M,\bar p$
is an S-system with parameter z.
$\bar M,\bar p$
is an S-system with parameter z. -
• If
 $\bar M,\bar p$
is an S-system then there is an
$\bar M,\bar p$
is an S-system then there is an
 $S'\subseteq S$
stationary such that
$S'\subseteq S$
stationary such that
 $(M_\beta ,p_\beta )_{\beta \in S'}$
is a
$(M_\beta ,p_\beta )_{\beta \in S'}$
is a
 $\Delta $
-system on
$\Delta $
-system on
 $S'$
.
$S'$
.
Proof The first item is trivial, using the fact that everything can be read canonically.
Using
![]() $2^\lambda =\lambda ^+$
, a standard
$2^\lambda =\lambda ^+$
, a standard
![]() $\Delta $
-system argument (or: Fodor’s Lemma argument) lets us thin out S to some
$\Delta $
-system argument (or: Fodor’s Lemma argument) lets us thin out S to some
![]() $S^2$
so that
$S^2$
so that
![]() $(M_\beta \cap \mu )_{\beta \in S^2}$
satisfies (1–3). For
$(M_\beta \cap \mu )_{\beta \in S^2}$
satisfies (1–3). For
![]() $\beta \in S^2$
let
$\beta \in S^2$
let
![]() $\iota _\beta :M_\beta \cup \{M_\beta \}\to H(\lambda ^+)$
be the transitive collapse, and assign to
$\iota _\beta :M_\beta \cup \{M_\beta \}\to H(\lambda ^+)$
be the transitive collapse, and assign to
![]() $\beta $
the tuple of the
$\beta $
the tuple of the
![]() $\iota _\beta $
-images of the following objects:
$\iota _\beta $
-images of the following objects:
-
•
 $M_\beta $
,
$M_\beta $
,
 $p_\beta $
,
$p_\beta $
,  ,
,
 $\mu $
,
$\mu $
,  ,
,  , and
, and
 $E^{p_\beta }$
.
$E^{p_\beta }$
. -
• For
 $\zeta \in E^{p_\beta }$
, the object
$\zeta \in E^{p_\beta }$
, the object
 $w^{p_\beta }_\zeta $
.
$w^{p_\beta }_\zeta $
. -
• For
 $\zeta \in E^{p_\beta }$
and
$\zeta \in E^{p_\beta }$
and
 $\gamma \in w^{p_\beta }_\zeta $
, the object
$\gamma \in w^{p_\beta }_\zeta $
, the object
 $F^{p_\beta }_\gamma $
.
$F^{p_\beta }_\gamma $
.
Again, there are
![]() $|H(\lambda ^+)|^\lambda <\mu $
many possibilities, so the objects are constant on a stationary
$|H(\lambda ^+)|^\lambda <\mu $
many possibilities, so the objects are constant on a stationary
![]() $S'\subseteq S^2$
.
$S'\subseteq S^2$
.
For
![]() $\alpha <\beta $
in
$\alpha <\beta $
in
![]() $S'$
, we define
$S'$
, we define
![]() $h^*_{\beta _1,\beta _2}:= \iota ^{-1}_{\beta _2}\circ \iota _{\beta _1}$
. (Note that
$h^*_{\beta _1,\beta _2}:= \iota ^{-1}_{\beta _2}\circ \iota _{\beta _1}$
. (Note that
![]() $\iota _{\beta _1}(\alpha )=\iota _{\beta _2}(\alpha )$
for
$\iota _{\beta _1}(\alpha )=\iota _{\beta _2}(\alpha )$
for
![]() $\alpha \in \Delta $
.)
$\alpha \in \Delta $
.)
So in particular if we have a
![]() $\Delta $
-system on S, then
$\Delta $
-system on S, then
![]() $p_\beta \restriction \sup (\Delta )=p_\beta \restriction \beta \in M_\beta $
is the same for all
$p_\beta \restriction \sup (\Delta )=p_\beta \restriction \beta \in M_\beta $
is the same for all
![]() $\beta \in S$
, and outside of
$\beta \in S$
, and outside of
![]() $\Delta $
the domains of the
$\Delta $
the domains of the
![]() $p_\beta $
are disjoint for
$p_\beta $
are disjoint for
![]() $\beta \in S$
. In particular we get:
$\beta \in S$
. In particular we get:
Fact 5.37. For a
![]() $\Delta $
-system with domain S, and
$\Delta $
-system with domain S, and
![]() $A\subseteq S$
of size
$A\subseteq S$
of size
![]() ${\le }\lambda $
, the union of the
${\le }\lambda $
, the union of the
![]() $(p_{\beta })_{\beta \in A}$
is a condition in P (and stronger than each
$(p_{\beta })_{\beta \in A}$
is a condition in P (and stronger than each
![]() $p_\beta $
).
$p_\beta $
).
Whenever
![]() $r \in P_\beta \cap M_\beta $
(as is the case for
$r \in P_\beta \cap M_\beta $
(as is the case for
![]() $r=p_\beta \restriction \beta $
), we know that
$r=p_\beta \restriction \beta $
), we know that
![]() $r\in P_\alpha $
for
$r\in P_\alpha $
for
![]() $\alpha \in \Delta $
(as
$\alpha \in \Delta $
(as
![]() $M_\beta $
knows that
$M_\beta $
knows that
![]() $\beta $
has cofinality
$\beta $
has cofinality
![]() $\lambda ^+$
).
$\lambda ^+$
).
Instead of “
![]() $r\in P_\alpha $
for some
$r\in P_\alpha $
for some
![]() $\alpha \in \Delta $
” we will sometimes just state the weaker but shorter
$\alpha \in \Delta $
” we will sometimes just state the weaker but shorter
![]() $r\in P_{\sup (\Delta )}$
.
$r\in P_{\sup (\Delta )}$
.
Remark. This is an important effect also for some names. Generally, a
![]() $P_\beta $
-name in
$P_\beta $
-name in
![]() $M_\beta $
is of course not a
$M_\beta $
is of course not a
![]() $P_\alpha $
-name for any
$P_\alpha $
-name for any
![]() $\alpha <\beta $
(just take the
$\alpha <\beta $
(just take the
![]() $P_\beta $
-generic filter
$P_\beta $
-generic filter
![]() $G_\beta $
). However, as we will explicitly state in Lemma 5.42, such names for subsets of
$G_\beta $
). However, as we will explicitly state in Lemma 5.42, such names for subsets of
![]() $\lambda $
are, modulo some condition,
$\lambda $
are, modulo some condition,
![]() $P_\alpha $
-names for some
$P_\alpha $
-names for some
![]() $\alpha \in \Delta $
and independent of
$\alpha \in \Delta $
and independent of
![]() $\beta $
. In the specific case of the
$\beta $
. In the specific case of the
![]() $P_\beta $
-name
$P_\beta $
-name
![]() $p_\beta (\beta )$
we do not have to increase the condition:
$p_\beta (\beta )$
we do not have to increase the condition:
Definition and Lemma 5.38.
![]() $\tilde p:=p_\beta (\beta )$
is a
$\tilde p:=p_\beta (\beta )$
is a
![]() $P_{\sup (\Delta )}$
-name independent of
$P_{\sup (\Delta )}$
-name independent of
![]() $\beta \in S$
.
$\beta \in S$
.
Proof
![]() $p_\beta (\beta )\restriction \zeta +1$
is
$p_\beta (\beta )\restriction \zeta +1$
is
![]() $(w^{p_\beta }_\zeta ,\zeta +1)$
-determined for cofinally many
$(w^{p_\beta }_\zeta ,\zeta +1)$
-determined for cofinally many
![]() $\zeta \in E$
, where
$\zeta \in E$
, where
![]() $w^{p_\beta }_\zeta \in [\beta ]^{<\lambda }$
is a subset of
$w^{p_\beta }_\zeta \in [\beta ]^{<\lambda }$
is a subset of
![]() $M_\beta $
. So
$M_\beta $
. So
![]() $w^{p_\beta }_\zeta \subseteq \Delta $
, and the isomorphisms between the
$w^{p_\beta }_\zeta \subseteq \Delta $
, and the isomorphisms between the
![]() $M_\beta $
guarantee that each
$M_\beta $
guarantee that each
![]() $w^{p_\beta }_\zeta $
is the same, and that
$w^{p_\beta }_\zeta $
is the same, and that
![]() $p_\beta (\beta )\restriction \zeta +1$
is decided the same way. So
$p_\beta (\beta )\restriction \zeta +1$
is decided the same way. So
![]() $\tilde p$
is a
$\tilde p$
is a
![]() $P_\gamma $
-name for
$P_\gamma $
-name for
![]() $\gamma =\sup (w^{p_\beta }_\zeta )_{\zeta \in E}$
. This
$\gamma =\sup (w^{p_\beta }_\zeta )_{\zeta \in E}$
. This
![]() $\gamma $
is independent of
$\gamma $
is independent of
![]() $\beta \in S$
, and is in
$\beta \in S$
, and is in
![]() $\Delta $
. So
$\Delta $
. So
![]() $\tilde p$
is actually a
$\tilde p$
is actually a
![]() $P_\alpha $
-name for some
$P_\alpha $
-name for some
![]() $\alpha \in \Delta $
; and certainly a
$\alpha \in \Delta $
; and certainly a
![]() $P_{\sup (\Delta )}$
-name.
$P_{\sup (\Delta )}$
-name.
For later reference we note:
Lemma 5.39. For all but non-stationary many
![]() $\beta $
,
$\beta $
,
![]() $p_*$
forces
$p_*$
forces ![]() .
.
(Here,
![]() $V_\beta $
denotes the
$V_\beta $
denotes the
![]() $P_\beta $
-extension of the ground model.)
$P_\beta $
-extension of the ground model.)
Proof Assume that
![]() $p_\beta \le p_*$
forces that
$p_\beta \le p_*$
forces that ![]() for a
for a
![]() $P_\beta $
-name
$P_\beta $
-name ![]() for all
for all
![]() $\beta \in S^*$
stationary. We can also assume that
$\beta \in S^*$
stationary. We can also assume that
![]() $p_\beta $
canonically reads
$p_\beta $
canonically reads ![]() . Pick
. Pick
![]() $M_\beta $
containing
$M_\beta $
containing
![]() $p_\beta $
and
$p_\beta $
and
![]() $S\subseteq S^*$
such that
$S\subseteq S^*$
such that
![]() $(M_\beta ,p_\beta )_{\beta \in S}$
is a
$(M_\beta ,p_\beta )_{\beta \in S}$
is a
![]() $\Delta $
-system, where we can assume (or get from homogeneity) that
$\Delta $
-system, where we can assume (or get from homogeneity) that ![]() . So the
. So the ![]() are
are
![]() $P_\beta $
-names in
$P_\beta $
-names in
![]() $M_\beta $
and therefore
$M_\beta $
and therefore
![]() $P_{\sup (\Delta )}$
-names, and are the same for all
$P_{\sup (\Delta )}$
-names, and are the same for all
![]() $\beta $
. Choose
$\beta $
. Choose
![]() $\beta _1>\beta _0$
in S. So
$\beta _1>\beta _0$
in S. So
![]() $p_{\beta _0}\wedge p_{\beta _1}$
force that
$p_{\beta _0}\wedge p_{\beta _1}$
force that ![]() , which contradicts the injectivity of
, which contradicts the injectivity of ![]() and the fact that
and the fact that ![]() .
.
5.7. Preservation of cofinalities, catching canonical names
Corollary 5.40. P is
![]() $\lambda ^{++}$
-cc and preserves all cofinalities.
$\lambda ^{++}$
-cc and preserves all cofinalities.
Proof Cofinalities
![]() ${\le }\lambda $
are preserved as P is
${\le }\lambda $
are preserved as P is
![]() ${<}\lambda $
-closed.
${<}\lambda $
-closed.
Cofinality
![]() $\lambda ^+$
is preserved by properness: Assume that it is forced by p that
$\lambda ^+$
is preserved by properness: Assume that it is forced by p that
![]() $\kappa $
has a cofinal
$\kappa $
has a cofinal
![]() $\lambda $
-sequence
$\lambda $
-sequence ![]() . Then there is an elementary model M containing p and
. Then there is an elementary model M containing p and ![]() . If
. If
![]() $q\le p$
is M-generic, and G a P-generic filter containing q, then
$q\le p$
is M-generic, and G a P-generic filter containing q, then ![]() for all
for all
![]() $i<\lambda $
, so
$i<\lambda $
, so
![]() $M\cap \kappa $
is a cofinal subset of
$M\cap \kappa $
is a cofinal subset of
![]() $\kappa $
of size
$\kappa $
of size
![]() $\lambda $
in the ground model.
$\lambda $
in the ground model.
Cofinality
![]() $\ge \lambda ^{++}$
is preserved as P has the
$\ge \lambda ^{++}$
is preserved as P has the
![]() $\lambda ^{++}$
-cc, which we have shown in a very roundabout way with the fact about
$\lambda ^{++}$
-cc, which we have shown in a very roundabout way with the fact about
![]() $\Delta $
-systems: If
$\Delta $
-systems: If
![]() $(p^{\prime }_\alpha )_{\alpha \in \mu }$
are arbitrary conditions, then
$(p^{\prime }_\alpha )_{\alpha \in \mu }$
are arbitrary conditions, then
![]() $(M_\beta ,p_\beta )$
form a
$(M_\beta ,p_\beta )$
form a
![]() $\Delta $
-system from some
$\Delta $
-system from some
![]() $p_\beta <p^{\prime }_\beta $
and stationary S, and any two (in fact,
$p_\beta <p^{\prime }_\beta $
and stationary S, and any two (in fact,
![]() ${\le }\lambda $
many)
${\le }\lambda $
many)
![]() $p_\beta $
are compatible for
$p_\beta $
are compatible for
![]() $\beta \in S$
.
$\beta \in S$
.
Remark 5.41. This shows that P is
![]() $(\mu ,\lambda )$
-Knaster, i.e., for every
$(\mu ,\lambda )$
-Knaster, i.e., for every
![]() $A\in [P]^\mu $
there is a
$A\in [P]^\mu $
there is a
![]() $B\in [A]^\mu $
which is
$B\in [A]^\mu $
which is
![]() $\lambda $
-linked.
$\lambda $
-linked.
The
![]() $\lambda ^{++}$
-cc also implies: For every name
$\lambda ^{++}$
-cc also implies: For every name ![]() for a subset of
for a subset of
![]() $\lambda $
(or of
$\lambda $
(or of
![]() $\lambda ^+$
) there is a
$\lambda ^+$
) there is a
![]() $\beta <\mu $
and a
$\beta <\mu $
and a
![]() $P_\beta $
-name
$P_\beta $
-name ![]() such that the empty condition forces that
such that the empty condition forces that ![]() .
.
Given
![]() $\alpha <\mu $
, there are
$\alpha <\mu $
, there are
![]() ${<}\mu $
many pairs
${<}\mu $
many pairs ![]() where p canonically reads
where p canonically reads ![]() in
in
![]() $P_\alpha $
(see Fact 5.32(2)). So there is a
$P_\alpha $
(see Fact 5.32(2)). So there is a
![]() $g(\alpha )<\mu $
such that for each such
$g(\alpha )<\mu $
such that for each such ![]() , both
, both ![]() and
and ![]() are equivalent (modulo the empty condition) to some
are equivalent (modulo the empty condition) to some
![]() $P_{g(\alpha )}$
-name. Let
$P_{g(\alpha )}$
-name. Let
![]() $C^*\subseteq \mu $
be the club set with
$C^*\subseteq \mu $
be the club set with
![]() $(\zeta \in C^*\, \&\, \alpha <\zeta )\ \rightarrow \ g(\alpha )<\zeta $
.
$(\zeta \in C^*\, \&\, \alpha <\zeta )\ \rightarrow \ g(\alpha )<\zeta $
.
Given a
![]() $\Delta $
-system on S we can restrict it to a
$\Delta $
-system on S we can restrict it to a
![]() $\Delta $
-system on
$\Delta $
-system on
![]() $S\cap C^*$
; so we will assume from now on that each
$S\cap C^*$
; so we will assume from now on that each
![]() $\Delta $
-system we consider satisfies
$\Delta $
-system we consider satisfies
![]() $S\subseteq C^*$
.
$S\subseteq C^*$
.
To summarize:
Lemma 5.42.
-
(1) If
 $\beta \in S$
,
$\beta \in S$
,
 $p\in P_\beta $
, and
$p\in P_\beta $
, and  a
a
 $P_\beta $
-name for a subset of
$P_\beta $
-name for a subset of
 $\lambda $
, then there is an
$\lambda $
, then there is an
 $\alpha <\beta $
and a
$\alpha <\beta $
and a
 $q\le p$
canonically reading
$q\le p$
canonically reading  ,
,  ,
,  as
as
 $P_\alpha $
-names.
$P_\alpha $
-names.More explicitly: There is a
 $P_\alpha $
-name
$P_\alpha $
-name  which is canonically read by q such that
which is canonically read by q such that  . (And analogously for
. (And analogously for  and
and  instead of
instead of  .)
.) -
(2) If additionally
 $p\le p_\beta \restriction \beta $
in
$p\le p_\beta \restriction \beta $
in
 $P_\beta $
and
$P_\beta $
and  , then we can additionally get:
, then we can additionally get:  ,
,  and
and  are
are
 $P_\alpha $
-names in
$P_\alpha $
-names in
 $M_\beta $
independent of
$M_\beta $
independent of
 $\beta \in S$
.
$\beta \in S$
.More explicitly: Let
 be as above (for
be as above (for  ). Then
). Then
 $\alpha \in \Delta $
, q and
$\alpha \in \Delta $
, q and  are in
are in
 $M_\beta $
, and if
$M_\beta $
, and if
 $\beta '\in S$
and
$\beta '\in S$
and
 $h:=h^*_{\beta ,\beta '}$
, then h acts as identity on
$h:=h^*_{\beta ,\beta '}$
, then h acts as identity on
 $\alpha $
, q, and
$\alpha $
, q, and  , and (
, and (
 $M_{\beta '}$
knows that)
$M_{\beta '}$
knows that)  . (And analogously for
. (And analogously for  and
and  instead of
instead of  )
)
Proof (1): Use Lemma 5.31 to get a
![]() $q_1\in P_\beta $
canonically reading
$q_1\in P_\beta $
canonically reading ![]() . And if
. And if
![]() $\beta \in S$
then
$\beta \in S$
then
![]() $\operatorname {\mathrm {cf}}(\beta )=\lambda ^+$
, so
$\operatorname {\mathrm {cf}}(\beta )=\lambda ^+$
, so
![]() $\operatorname {\mathrm {dom}}(p)$
is bounded by some
$\operatorname {\mathrm {dom}}(p)$
is bounded by some
![]() $\alpha '<\beta $
and, by Fact 5.32(1),
$\alpha '<\beta $
and, by Fact 5.32(1),
![]() $q_1\in P_{\alpha _1}$
for some
$q_1\in P_{\alpha _1}$
for some
![]() $\alpha '\le \alpha _1<\beta $
. As
$\alpha '\le \alpha _1<\beta $
. As
![]() $\beta \in C^*$
,
$\beta \in C^*$
, ![]() and
and ![]() are
are
![]() $P_\beta $
-names. So repeat the same argument to get
$P_\beta $
-names. So repeat the same argument to get
![]() $q\le q_1$
in
$q\le q_1$
in
![]() $P_\alpha $
canonically reading all three subsets of
$P_\alpha $
canonically reading all three subsets of
![]() $\lambda $
.
$\lambda $
.
(2): Apply (1) inside
![]() $M_\beta $
. As
$M_\beta $
. As
![]() $\alpha \in \beta \cap M_\beta $
, we get
$\alpha \in \beta \cap M_\beta $
, we get
![]() $\alpha \in \Delta $
. As q canonically reads itself as well as
$\alpha \in \Delta $
. As q canonically reads itself as well as ![]() , we know that h does not change q and
, we know that h does not change q and ![]() . As h is an isomorphism, we know that
. As h is an isomorphism, we know that
![]() $h(q)=q$
forces that
$h(q)=q$
forces that ![]() .
.
5.8. Majority decisions
For any
![]() $(a_1,a_2,a_3)$
with
$(a_1,a_2,a_3)$
with
![]() $a_i\in \{0,1\}$
there is a
$a_i\in \{0,1\}$
there is a
![]() $b\in \{0,1\}$
such that
$b\in \{0,1\}$
such that
![]() $b=a_i$
for at least two
$b=a_i$
for at least two
![]() $i\in \{1,2,3\}$
. We write
$i\in \{1,2,3\}$
. We write
![]() $b=\operatorname {\mathrm {major}}_{i=1,2,3}(a_i)$
.
$b=\operatorname {\mathrm {major}}_{i=1,2,3}(a_i)$
.
Similarly, if
![]() $f_1$
,
$f_1$
,
![]() $f_2$
,
$f_2$
,
![]() $f_3$
are functions
$f_3$
are functions
![]() $A\to 2$
we write
$A\to 2$
we write
![]() $\operatorname {\mathrm {major}}_{i=1,2,3}(f_i)$
for the function
$\operatorname {\mathrm {major}}_{i=1,2,3}(f_i)$
for the function
![]() $A\to 2$
that maps
$A\to 2$
that maps
![]() $\ell $
to
$\ell $
to
![]() $\operatorname {\mathrm {major}}_{i=1,2,3}(f_i(\ell ))$
.
$\operatorname {\mathrm {major}}_{i=1,2,3}(f_i(\ell ))$
.
The following is a central point of the whole construction:
Lemma 5.43. Let
![]() $(M_\alpha ,p_\alpha )_{\alpha \in S}$
be a
$(M_\alpha ,p_\alpha )_{\alpha \in S}$
be a
![]() $\Delta $
-system. Pick
$\Delta $
-system. Pick
![]() $\beta _0<\beta _1<\beta _2<\beta _3$
in S.
$\beta _0<\beta _1<\beta _2<\beta _3$
in S.
-
(1)
 $p_*$
forces: If
$p_*$
forces: If  , then
, then  .
. -
(2) Let
 $s=\bigwedge _{i<4} p_{\beta _i}$
. Recall that
$s=\bigwedge _{i<4} p_{\beta _i}$
. Recall that
 $s(\beta _i)$
is the same
$s(\beta _i)$
is the same
 $P_{\sup (\Delta )}$
-name called
$P_{\sup (\Delta )}$
-name called
 $\tilde p$
for all i. We can strengthen s by strengthening, for
$\tilde p$
for all i. We can strengthen s by strengthening, for
 $i=1,2,3$
, the condition
$i=1,2,3$
, the condition
 $s(\beta _i)=\tilde p$
to some
$s(\beta _i)=\tilde p$
to some
 $P_{\beta _0+1}$
-names
$P_{\beta _0+1}$
-names
 $r_i\le \tilde p$
(without changing
$r_i\le \tilde p$
(without changing
 $C^{\tilde p}$
) such that the resulting condition forces
$C^{\tilde p}$
) such that the resulting condition forces  .
.(We do not have to strengthen
 $s(\beta _0)$
for this, i.e., we can use
$s(\beta _0)$
for this, i.e., we can use
 $r_0:=\tilde p.$
)
$r_0:=\tilde p.$
)
We describe this by “
![]() $(r_i)_{i<4}$
honors majority.”
$(r_i)_{i<4}$
honors majority.”
Recall that
![]() $\nu _1=^*\nu _2$
denotes that
$\nu _1=^*\nu _2$
denotes that
![]() $\nu _1(\ell )=\nu _2(\ell )$
for all but
$\nu _1(\ell )=\nu _2(\ell )$
for all but
![]() ${<}\lambda $
many
${<}\lambda $
many
![]() $\ell \in \lambda $
.
$\ell \in \lambda $
.
Proof (1) Identifying
![]() $2^\lambda $
with
$2^\lambda $
with
![]() $P(\lambda )$
, we have
$P(\lambda )$
, we have
![]() $\operatorname {\mathrm {major}}_{i=1,2,3}{f_i}= (f_1\cap f_2)\cup (f_2\cap f_3)\cup (f_1\cap f_3)$
for any tuple
$\operatorname {\mathrm {major}}_{i=1,2,3}{f_i}= (f_1\cap f_2)\cup (f_2\cap f_3)\cup (f_1\cap f_3)$
for any tuple
![]() $(f_i)_{i=1,2,3}$
. As
$(f_i)_{i=1,2,3}$
. As ![]() represents an automorphism, we get
represents an automorphism, we get ![]() . Apply this to
. Apply this to ![]() .
.
(2) Work in the
![]() $P_{\beta _0+1}$
-extension. Recall
$P_{\beta _0+1}$
-extension. Recall
![]() $\tilde p:=p_{\beta _0}(\beta _0)$
. So both
$\tilde p:=p_{\beta _0}(\beta _0)$
. So both
![]() $\tilde p$
and
$\tilde p$
and ![]() are already determined, and
are already determined, and ![]() extends
extends
![]() $\eta ^{\tilde p}$
. Set
$\eta ^{\tilde p}$
. Set
![]() $r_0:=\tilde p$
.
$r_0:=\tilde p$
.
Set
![]() $s_1:=(0,0)$
,
$s_1:=(0,0)$
,
![]() $s_2:=(0,1)$
,
$s_2:=(0,1)$
,
![]() $s_3:=(1,0)$
. For
$s_3:=(1,0)$
. For
![]() $\zeta \in C^{\tilde p}$
and
$\zeta \in C^{\tilde p}$
and
![]() $i=1,2,3$
, we define
$i=1,2,3$
, we define
![]() $r_i(\zeta )\supseteq \tilde p(\zeta )$
as follows:
$r_i(\zeta )\supseteq \tilde p(\zeta )$
as follows:
So
![]() $\eta ^{r_i}$
agrees on its domain with
$\eta ^{r_i}$
agrees on its domain with ![]() , and each
, and each
![]() $\ell \in \lambda $
is in
$\ell \in \lambda $
is in
![]() $\operatorname {\mathrm {dom}}(\eta ^{r_i})$
for at least two
$\operatorname {\mathrm {dom}}(\eta ^{r_i})$
for at least two
![]() $i\in \{1,2,3\}$
. Accordingly, an extension by a generic filter G with
$i\in \{1,2,3\}$
. Accordingly, an extension by a generic filter G with
![]() $r_i\in G(\beta _i)$
for all
$r_i\in G(\beta _i)$
for all
![]() $i<4$
will satisfy
$i<4$
will satisfy ![]() . (We do not even have to assume that any
. (We do not even have to assume that any
![]() $p_\beta \in G$
.)
$p_\beta \in G$
.)
Remark 5.45. Let
![]() $p^{\prime }_{\beta _1}$
be the condition where we strengthen
$p^{\prime }_{\beta _1}$
be the condition where we strengthen
![]() $p_{\beta _1}(\beta _1)$
to
$p_{\beta _1}(\beta _1)$
to
![]() $r_1$
. Note that
$r_1$
. Note that
![]() $p^{\prime }_{\beta _1}$
is not in
$p^{\prime }_{\beta _1}$
is not in
![]() $M_{\beta _1}$
, as
$M_{\beta _1}$
, as
![]() $\beta _0\notin M_{\beta _1}$
and
$\beta _0\notin M_{\beta _1}$
and
![]() $r_1$
is defined using
$r_1$
is defined using ![]() . Similarly (basically the same):
. Similarly (basically the same):
![]() $r_1[G_{\beta _1}]\notin M_{\beta _1}[G_{\beta _1}]$
, even if we assume that
$r_1[G_{\beta _1}]\notin M_{\beta _1}[G_{\beta _1}]$
, even if we assume that
![]() $G_{\beta _1}$
is
$G_{\beta _1}$
is
![]() $M_{\beta _1}$
-generic. But generally we will not be interested in
$M_{\beta _1}$
-generic. But generally we will not be interested in
![]() $M_\beta $
-generic conditions or extensions (we needed generic conditions only in Lemma 5.27, which in turn is needed for Corollary 5.40). And while usually most conditions we consider can be constructed within (and therefore will be elements of) some
$M_\beta $
-generic conditions or extensions (we needed generic conditions only in Lemma 5.27, which in turn is needed for Corollary 5.40). And while usually most conditions we consider can be constructed within (and therefore will be elements of) some
![]() $M_\beta $
, this is generally not required (an example are the
$M_\beta $
, this is generally not required (an example are the
![]() $s_i$
’s in the following lemma).
$s_i$
’s in the following lemma).
The same proof works if we do not start with the
![]() $p_\beta $
but with any stronger conditions, as long as they still “cohere” in the way that the
$p_\beta $
but with any stronger conditions, as long as they still “cohere” in the way that the
![]() $p_{\beta _i}$
cohere:
$p_{\beta _i}$
cohere:
Lemma 5.46. Let
![]() $(M_\alpha ,p_\alpha )_{\alpha \in S}$
be a
$(M_\alpha ,p_\alpha )_{\alpha \in S}$
be a
![]() $\Delta $
-system,
$\Delta $
-system,
![]() $\beta _0<\beta _1<\beta _2<\beta _3$
in S, and
$\beta _0<\beta _1<\beta _2<\beta _3$
in S, and
![]() $s_{i}\le p_{\beta _i}$
for
$s_{i}\le p_{\beta _i}$
for
![]() $i=0,1,2,3$
such that
$i=0,1,2,3$
such that
![]() $:$
$:$
-
•
 $\operatorname {\mathrm {dom}}(s_i)\subseteq M_{\beta _i}$
.
$\operatorname {\mathrm {dom}}(s_i)\subseteq M_{\beta _i}$
. -
•
 $s^*:=s_i\restriction \beta _i$
is the same for all i.
$s^*:=s_i\restriction \beta _i$
is the same for all i. -
•
 $s^*$
forces that the
$s^*$
forces that the
 $s_{i}(\beta _i)$
are the same for all i.
$s_{i}(\beta _i)$
are the same for all i.(In the usual sense
 $:$
The
$:$
The
 $s_{i}(\beta _i)$
are continuously read from generics below
$s_{i}(\beta _i)$
are continuously read from generics below
 $\beta _0$
in the same way for each
$\beta _0$
in the same way for each
 $i<4$
.)
$i<4$
.)
Then there is condition stronger than all
![]() $s_{i}$
forcing that
$s_{i}$
forcing that ![]() and thus
and thus ![]() .
.
5.9.  is in the
is in the
 $\beta +1$
-extension
$\beta +1$
-extension
We now show that ![]() can be assumed to be a
can be assumed to be a
![]() $P_\beta $
-name.
$P_\beta $
-name.
The following definitions, in particular everything concerning the notion of coherence, is used only in this section. In the rest of the paper, we will use from this section only Lemma 5.54, i.e., the fact that ![]() .
.
Remark. Why do we introduce this (rather annoying) notion of coherence? Well, we would like to simultaneously construct something like
![]() $s_i\le p_{\beta _i}$
where each
$s_i\le p_{\beta _i}$
where each
![]() $s_i$
ends up in
$s_i$
ends up in
![]() $M_{\beta _i}$
. We cannot directly do this in
$M_{\beta _i}$
. We cannot directly do this in
![]() $M_{\beta _0}$
, as
$M_{\beta _0}$
, as
![]() $M_{\beta _0}$
does not know about, e.g.,
$M_{\beta _0}$
does not know about, e.g.,
![]() $\beta _1$
. So instead, we construct four different
$\beta _1$
. So instead, we construct four different
![]() $s_i'\le p_{\beta _0}$
in
$s_i'\le p_{\beta _0}$
in
![]() $M_{\beta _0}$
in such a way (a “coherent” way) and use
$M_{\beta _0}$
in such a way (a “coherent” way) and use
![]() $s_i:= h^*_{\beta _0,\beta _i}(s_i')$
.
$s_i:= h^*_{\beta _0,\beta _i}(s_i')$
.
Let us for now (until Lemma 5.54) fix an arbitrary
![]() $\Delta $
-system
$\Delta $
-system
![]() $(M_\beta ,p_\beta )_{\beta \in S}$
as well as
$(M_\beta ,p_\beta )_{\beta \in S}$
as well as
![]() $\beta _0<\beta _1<\beta _2<\beta _3$
in S. For notational convenience, set
$\beta _0<\beta _1<\beta _2<\beta _3$
in S. For notational convenience, set
Definition 5.47.
-
•
 $\bar q=(q_i)_{i<4}$
in
$\bar q=(q_i)_{i<4}$
in
 $M_\beta $
is called coherent, if each
$M_\beta $
is called coherent, if each
 $q_i$
is stronger than
$q_i$
is stronger than
 $p_{\beta }$
and
$p_{\beta }$
and
 $q_i\restriction (\beta +1)$
is the same for all
$q_i\restriction (\beta +1)$
is the same for all
 $i<4$
.
$i<4$
. -
• If
 $\bar q$
is coherent, then
$\bar q$
is coherent, then
 $\bigwedge _{i<4}h^*_{\beta ,\beta _i}(q_i)$
is a valid condition in P, and we call it
$\bigwedge _{i<4}h^*_{\beta ,\beta _i}(q_i)$
is a valid condition in P, and we call it
 $q^*$
.
$q^*$
.I.e.,
 $q^*$
is the union of the copies of
$q^*$
is the union of the copies of
 $q_i$
in
$q_i$
in
 $M_{\beta _i}$
; and the copy for
$M_{\beta _i}$
; and the copy for
 $q_0$
is just
$q_0$
is just
 $q_0$
.
$q_0$
. $r\in P$
is called coherent, if
$r\in P$
is called coherent, if
 $r=q^*$
for some coherent
$r=q^*$
for some coherent
 $\bar q\in M_{\beta }$
.
$\bar q\in M_{\beta }$
.
Facts.
-
• The
 $p_{\beta _i}$
are coherent, more correctly:
$p_{\beta _i}$
are coherent, more correctly:The condition
 $\bigwedge _{i\in 4}p_{\beta _i}$
is coherent; equivalently: The tuple
$\bigwedge _{i\in 4}p_{\beta _i}$
is coherent; equivalently: The tuple
 $\big (h^{*-1}_{\beta ,\beta _i}(p_{\beta _i})\big )_{i<4}$
is coherent.
$\big (h^{*-1}_{\beta ,\beta _i}(p_{\beta _i})\big )_{i<4}$
is coherent. -
• Any coherent r is stronger than
 $\bigwedge _{i<4}p_{\beta _i}$
.
$\bigwedge _{i<4}p_{\beta _i}$
. -
• If
 $\bar q$
is coherent,
$\bar q$
is coherent,
 $r_i\le q_i$
in
$r_i\le q_i$
in
 $M_{\beta }$
for
$M_{\beta }$
for
 $i<4$
, and
$i<4$
, and
 $r_i\restriction \beta _i$
is the same for all
$r_i\restriction \beta _i$
is the same for all
 $i<4$
, then
$i<4$
, then
 $\bigwedge _{i<4}h^*_{\beta ,\beta _i}(r_i)$
is (a valid condition and) compatible with
$\bigwedge _{i<4}h^*_{\beta ,\beta _i}(r_i)$
is (a valid condition and) compatible with
 $q^*$
.
$q^*$
. -
•
 $r\in P$
is coherent iff:
$r\in P$
is coherent iff:
 $\operatorname {\mathrm {dom}}(r)\subseteq \bigcup _{i<4} M_{\beta _i}$
,
$\operatorname {\mathrm {dom}}(r)\subseteq \bigcup _{i<4} M_{\beta _i}$
,
 $r\restriction (\mu \cap M_{\beta _i})\in M_{\beta _i}$
is stronger than
$r\restriction (\mu \cap M_{\beta _i})\in M_{\beta _i}$
is stronger than
 $p_{\beta _i}$
, and each
$p_{\beta _i}$
, and each
 $r(\beta _i)$
is forced to be the same condition.
$r(\beta _i)$
is forced to be the same condition.In that case,
 $r=q^*$
for
$r=q^*$
for
 $q_i:=h^{*-1}_{\beta ,\beta _i}(r_i)$
and
$q_i:=h^{*-1}_{\beta ,\beta _i}(r_i)$
and
 $r_i:=r\restriction (\mu \cap M_{\beta _i})$
.
$r_i:=r\restriction (\mu \cap M_{\beta _i})$
.
Lemma 5.48. If r is coherent, then it can be strengthenedFootnote
11
to forceFootnote
12
![]() .
.
Proof This follows from Lemma 5.46, using
![]() $s_i:=r\restriction (\mu \cap M_{\beta _i})$
.
$s_i:=r\restriction (\mu \cap M_{\beta _i})$
.
Definition 5.49.
-
•
 $\bar w=(w_i)_{i<4}$
is coherent, if
$\bar w=(w_i)_{i<4}$
is coherent, if
 $w_i\in [\mu ]^{<\lambda }$
is in
$w_i\in [\mu ]^{<\lambda }$
is in
 $M_{\beta }$
and
$M_{\beta }$
and
 $w_i\cap (\beta +1)$
is independent of i.
$w_i\cap (\beta +1)$
is independent of i.In the following we always assume that
 $\bar q$
and
$\bar q$
and
 $\bar w$
are coherent.
$\bar w$
are coherent. -
•
 $\bar q$
fits
$\bar q$
fits
 $(\bar w,\zeta )$
, if each
$(\bar w,\zeta )$
, if each
 $q_i$
fits
$q_i$
fits
 $(w_i,\zeta )$
.
$(w_i,\zeta )$
. -
•
 $\bar q$
is
$\bar q$
is
 $(\bar w,\zeta )$
-canonical, if each
$(\bar w,\zeta )$
-canonical, if each
 $q_i$
is
$q_i$
is
 $(w_i,\zeta )$
-canonical.
$(w_i,\zeta )$
-canonical. -
•
 $\bar r\le ^{+}_{\bar w,\zeta }\bar q$
means:
$\bar r\le ^{+}_{\bar w,\zeta }\bar q$
means:
 $\bar r$
is coherent, and
$\bar r$
is coherent, and
 $r_i\le ^+_{w_i,\zeta }q_i$
for all
$r_i\le ^+_{w_i,\zeta }q_i$
for all
 $i<4$
.
$i<4$
. -
•
 $\bar x=(x_i)_{i<4}$
is defined to be in
$\bar x=(x_i)_{i<4}$
is defined to be in
 $\operatorname {\mathrm {poss}}(\bar q,\bar w,\zeta )$
if
$\operatorname {\mathrm {poss}}(\bar q,\bar w,\zeta )$
if
 $x_i\in \operatorname {\mathrm {poss}}(q_i,w_i,\zeta )$
and
$x_i\in \operatorname {\mathrm {poss}}(q_i,w_i,\zeta )$
and
 $x_i\restriction \beta $
is independent of i. Such a
$x_i\restriction \beta $
is independent of i. Such a
 $\bar x$
will be called coherent possibility.
$\bar x$
will be called coherent possibility.(Note that the
 $x_i(\beta )$
in a coherent possibility can be different for different
$x_i(\beta )$
in a coherent possibility can be different for different
 $i<4$
. Also note that such an
$i<4$
. Also note that such an
 $\bar x$
is automatically in
$\bar x$
is automatically in
 $M_\beta $
, which is
$M_\beta $
, which is
 ${<}\lambda $
-closed.)
${<}\lambda $
-closed.)
Note that if
![]() $\bar r\le ^{+}_{\bar w,\zeta }\bar q$
and
$\bar r\le ^{+}_{\bar w,\zeta }\bar q$
and
![]() $\bar q$
is
$\bar q$
is
![]() $(\bar w,\zeta )$
-canonical, then
$(\bar w,\zeta )$
-canonical, then
![]() $\bar r$
and
$\bar r$
and
![]() $\bar q$
have the same coherent
$\bar q$
have the same coherent
![]() $(\bar w,\zeta +1)$
-possibilities (see Fact 5.29(1)).
$(\bar w,\zeta +1)$
-possibilities (see Fact 5.29(1)).
Several of the previous constructions result in coherent 4-tuples when applied to coherent 4-tuples. In particular:
Lemma 5.50.
-
(1) Assume
 $(\bar q^j)_{j\in \delta }$
is a sequence of coherent 4-tuples such that, for each
$(\bar q^j)_{j\in \delta }$
is a sequence of coherent 4-tuples such that, for each
 $i<4$
, the i-part
$i<4$
, the i-part
 $(q^j_i)_{j\in \delta }$
satisfies the assumptions of Lemma 5.18.
$(q^j_i)_{j\in \delta }$
satisfies the assumptions of Lemma 5.18.Then for each i, the lemma (in
 $M_\beta $
) gives us a limit r, which we call
$M_\beta $
) gives us a limit r, which we call
 $q^\delta _i$
.
$q^\delta _i$
.We can choose the
 $q^\delta _i$
so that they form a coherent 4-tuple.
$q^\delta _i$
so that they form a coherent 4-tuple. -
(2) The same applies to Lemma 5.19. That is, we can get a coherent fusion limit from a
 $\lambda $
-sequence of coherent tuples.
$\lambda $
-sequence of coherent tuples. -
(3) Assume
 $\bar p$
fits
$\bar p$
fits
 $(\bar w,\zeta )$
, and
$(\bar w,\zeta )$
, and
 $\alpha _i\in \mu $
such that
$\alpha _i\in \mu $
such that
 $w^{\prime }_i:=w_i\cup \{\alpha _i\}$
is coherent. Then there is a
$w^{\prime }_i:=w_i\cup \{\alpha _i\}$
is coherent. Then there is a
 $\xi>\zeta $
and a
$\xi>\zeta $
and a
 $\bar q\le ^+_{\bar w,\zeta }\bar p$
which fits
$\bar q\le ^+_{\bar w,\zeta }\bar p$
which fits
 $(\bar w',\xi )$
and is
$(\bar w',\xi )$
and is
 $(\bar w',\xi )$
-canonical.
$(\bar w',\xi )$
-canonical. -
(4) Assume
 $\bar q$
is coherent and (for simplicity)
$\bar q$
is coherent and (for simplicity)
 $(\bar w,\zeta )$
-canonical with
$(\bar w,\zeta )$
-canonical with
 $\beta \in w_i$
(which is independent of
$\beta \in w_i$
(which is independent of
 $i<4$
), and
$i<4$
), and  are names of ordinals. Then there is an
are names of ordinals. Then there is an
 $\bar r\le ^{+}_{\bar w,\zeta }\bar q$
such that
$\bar r\le ^{+}_{\bar w,\zeta }\bar q$
such that  is
is
 $(\bar w,\zeta +1)$
-decided by
$(\bar w,\zeta +1)$
-decided by
 $\bar r$
.
$\bar r$
.By this we mean that
 is
is
 $(w_i,\zeta +1)$
-decided by
$(w_i,\zeta +1)$
-decided by
 $r_i$
for all
$r_i$
for all
 $i<4$
.
$i<4$
.
Proof For the first items, we just have to look at the proofs of the according lemmas (For (3) this is Preliminary Lemmas 5.23 and 5.24) and note that coherent input gives us coherent output. In the following we will prove (4). We work in
![]() $M_\beta $
.
$M_\beta $
.
Enumerate all coherent possibilities as
![]() $(\bar x_k)_{k\in K}$
. Set
$(\bar x_k)_{k\in K}$
. Set
![]() $\bar r^0:=\bar q$
. We now construct
$\bar r^0:=\bar q$
. We now construct
![]() $\bar r^{k+1}$
from
$\bar r^{k+1}$
from
![]() $\bar r:=\bar r^k$
where we assume
$\bar r:=\bar r^k$
where we assume
![]() $\bar r^k\le ^{+}_{\bar w,\zeta }\bar q$
.
$\bar r^k\le ^{+}_{\bar w,\zeta }\bar q$
.
-
• Find
 $s_0$
stronger than
$s_0$
stronger than
 $r_0$
and extending
$r_0$
and extending
 $x_0$
, deciding
$x_0$
, deciding  .
. -
•
 $s^*:=(s_0\restriction \beta )\wedge r_1$
is stronger than
$s^*:=(s_0\restriction \beta )\wedge r_1$
is stronger than
 $r_1$
, as
$r_1$
, as
 $\bar r$
is coherent. Strengthen
$\bar r$
is coherent. Strengthen
 $s^*(\beta )=r_1(\beta )=r_0(\beta )$
to
$s^*(\beta )=r_1(\beta )=r_0(\beta )$
to
 $s_0(\beta )$
, but replace the trunk with
$s_0(\beta )$
, but replace the trunk with
 $x_1(\beta )$
. Then
$x_1(\beta )$
. Then
 $s^*\restriction \beta $
forces that
$s^*\restriction \beta $
forces that
 $s^*(\beta )\le r_1(\beta )$
, as
$s^*(\beta )\le r_1(\beta )$
, as
 $x_1\restriction \beta = x_0\restriction \beta $
and as
$x_1\restriction \beta = x_0\restriction \beta $
and as
 $x_1(\beta )$
is guaranteed to be possible, because
$x_1(\beta )$
is guaranteed to be possible, because
 $r_1$
is canonical. Further strengthen
$r_1$
is canonical. Further strengthen
 $s^*$
(above
$s^*$
(above
 $\beta $
) to extend (the rest of)
$\beta $
) to extend (the rest of)
 $x_1$
; and then strengthen the whole condition once more to decide
$x_1$
; and then strengthen the whole condition once more to decide  . Call the result
. Call the result
 $s_1$
.
$s_1$
. -
• Do the same for
 $i=2$
, starting with
$i=2$
, starting with
 $s_1$
, resulting in
$s_1$
, resulting in
 $s_2$
, and then for
$s_2$
, and then for
 $i=3$
, starting with
$i=3$
, starting with
 $s_2$
, resulting in some
$s_2$
, resulting in some
 $s_3$
.So
$s_3$
.So
 $s_i\le r_i$
extends
$s_i\le r_i$
extends
 $x_i$
and decides
$x_i$
and decides  , and
, and
 $s_3\restriction \beta \le s_i\restriction \beta $
and
$s_3\restriction \beta \le s_i\restriction \beta $
and
 $s_3(\beta )$
is stronger than
$s_3(\beta )$
is stronger than
 $s_i(\beta )$
“above
$s_i(\beta )$
“above
 $\zeta +1$
.”
$\zeta +1$
.” -
• We define
 $r^{\prime }_i\le r_i$
as follows:
$r^{\prime }_i\le r_i$
as follows:
 $\operatorname {\mathrm {dom}}(r^{\prime }_i)=(\operatorname {\mathrm {dom}}(s_3)\cap \beta )\cup \operatorname {\mathrm {dom}}(s_i)$
. We define
$\operatorname {\mathrm {dom}}(r^{\prime }_i)=(\operatorname {\mathrm {dom}}(s_3)\cap \beta )\cup \operatorname {\mathrm {dom}}(s_i)$
. We define
 $r^{\prime }_i(\alpha )$
inductively such that
$r^{\prime }_i(\alpha )$
inductively such that
 $r^{\prime }_i\restriction \alpha \le ^+_{w_i\cap \alpha ,\zeta } r_i$
forces that
$r^{\prime }_i\restriction \alpha \le ^+_{w_i\cap \alpha ,\zeta } r_i$
forces that
 $x_i\restriction \alpha \triangleleft G$
implies
$x_i\restriction \alpha \triangleleft G$
implies
 $s_i\restriction \alpha \in G$
.
$s_i\restriction \alpha \in G$
.-
– For
 $\alpha \le \beta $
:
$\alpha \le \beta $
:If
 $s_3\restriction \alpha \notin G_\alpha $
, set
$s_3\restriction \alpha \notin G_\alpha $
, set
 $r^{\prime }_i(\alpha )=r_i(\alpha )$
. Assume otherwise. So
$r^{\prime }_i(\alpha )=r_i(\alpha )$
. Assume otherwise. So
 $s_3(\alpha )$
is defined and stronger than
$s_3(\alpha )$
is defined and stronger than
 $r_i(\alpha )=r_3(\alpha )$
. If
$r_i(\alpha )=r_3(\alpha )$
. If
 $\alpha \notin w_i$
(which implies
$\alpha \notin w_i$
(which implies
 $\alpha <\beta $
), set
$\alpha <\beta $
), set
 $r^{\prime }_i(\alpha )=s_3(\alpha )$
. Otherwise, use
$r^{\prime }_i(\alpha )=s_3(\alpha )$
. Otherwise, use
 $s_3(\alpha )\vee (r_3(\alpha )\restriction \zeta +1)$
, as in Lemma 5.8.
$s_3(\alpha )\vee (r_3(\alpha )\restriction \zeta +1)$
, as in Lemma 5.8. -
– For
 $\alpha>\beta $
, we do the same but we use
$\alpha>\beta $
, we do the same but we use
 $s_i$
instead of
$s_i$
instead of
 $s_3$
. In more detail:
$s_3$
. In more detail:If
 $s_i\restriction \alpha \notin G_\alpha $
, set
$s_i\restriction \alpha \notin G_\alpha $
, set
 $r^{\prime }_i(\alpha )=r_i(\alpha )$
. Assume otherwise. If
$r^{\prime }_i(\alpha )=r_i(\alpha )$
. Assume otherwise. If
 $\alpha \notin w_i$
, set
$\alpha \notin w_i$
, set
 $r^{\prime }_i(\alpha )=s_i(\alpha )$
. Otherwise, use
$r^{\prime }_i(\alpha )=s_i(\alpha )$
. Otherwise, use
 $s_i(\alpha )\vee (r_i(\alpha )\restriction \zeta +1)$
.
$s_i(\alpha )\vee (r_i(\alpha )\restriction \zeta +1)$
.
We can use this
 $\bar r'$
as
$\bar r'$
as
 $\bar r^{k+1}$
: It is coherent,
$\bar r^{k+1}$
: It is coherent,
 $\bar r'\le ^{+}_{\bar w,\zeta }\bar r^k$
, and
$\bar r'\le ^{+}_{\bar w,\zeta }\bar r^k$
, and
 $r^{\prime }_i$
decides
$r^{\prime }_i$
decides  assuming
assuming
 $x_i\triangleleft G$
.
$x_i\triangleleft G$
. -
Coherent tuples
![]() $\bar q$
naturally define a P-condition
$\bar q$
naturally define a P-condition
![]() $q^*$
. However, we have to assume that
$q^*$
. However, we have to assume that
![]() $\bar q$
is canonical to guarantee that coherent
$\bar q$
is canonical to guarantee that coherent
![]() $\bar q$
possibilities correspond to
$\bar q$
possibilities correspond to
![]() $q^*$
-possibilities:
$q^*$
-possibilities:
Lemma 5.51. Assume
![]() $\bar q$
and
$\bar q$
and
![]() $\bar w$
coherent. We set
$\bar w$
coherent. We set
![]() $w^*:=\bigcup _{i<4}h^*_{\beta ,\beta _i}(w_i)$
. Let
$w^*:=\bigcup _{i<4}h^*_{\beta ,\beta _i}(w_i)$
. Let
![]() $\bar x$
be in
$\bar x$
be in
![]() $\operatorname {\mathrm {poss}}(\bar q,\bar w,\zeta +1)$
.
$\operatorname {\mathrm {poss}}(\bar q,\bar w,\zeta +1)$
.
-
(1)
 $\bar q$
fits
$\bar q$
fits
 $(\bar w,\zeta )$
iff
$(\bar w,\zeta )$
iff
 $q^*$
fits
$q^*$
fits
 $(w^*,\zeta )$
.
$(w^*,\zeta )$
. -
(2)
 $\bar r\le ^+_{\bar w,\zeta }\bar q$
iff
$\bar r\le ^+_{\bar w,\zeta }\bar q$
iff
 $r^*\le ^+_{w^*,\zeta } q^*$
.
$r^*\le ^+_{w^*,\zeta } q^*$
. -
(3) Assume
 $\bar q$
fits
$\bar q$
fits
 $(\bar w,\zeta )$
. Then
$(\bar w,\zeta )$
. Then
 $\bar q$
is
$\bar q$
is
 $(\bar w,\zeta )$
-canonical iff
$(\bar w,\zeta )$
-canonical iff
 $q^*$
is
$q^*$
is
 $(w^*,\zeta )$
-canonical.
$(w^*,\zeta )$
-canonical. -
(4) Assume that
 $\bar q$
is
$\bar q$
is
 $(\bar w,\zeta )$
-canonical. Let
$(\bar w,\zeta )$
-canonical. Let
 $x^*$
be the union of the
$x^*$
be the union of the
 $h^*_{\beta ,\beta _i}(x_i)$
. Then
$h^*_{\beta ,\beta _i}(x_i)$
. Then
 $x^*\in \operatorname {\mathrm {poss}}(q^*, w^*,\zeta +1)$
; and every element of
$x^*\in \operatorname {\mathrm {poss}}(q^*, w^*,\zeta +1)$
; and every element of
 $\operatorname {\mathrm {poss}}(q^*, w^*,\zeta +1)$
is such an
$\operatorname {\mathrm {poss}}(q^*, w^*,\zeta +1)$
is such an
 $x^*$
for some
$x^*$
for some
 $\bar x\in \operatorname {\mathrm {poss}}(\bar q,\bar w,\zeta +1)$
.
$\bar x\in \operatorname {\mathrm {poss}}(\bar q,\bar w,\zeta +1)$
. -
(5) Assume that
 $\bar q$
is
$\bar q$
is
 $(\bar w,\zeta )$
-canonical. Then
$(\bar w,\zeta )$
-canonical. Then
 $\bar q (\bar w,\zeta +1)$
-decides
$\bar q (\bar w,\zeta +1)$
-decides  iff
iff
 $q^* (w^*,\zeta +1)$
-decides all
$q^* (w^*,\zeta +1)$
-decides all  .
.
Proof Assume
![]() $\alpha \in w_i$
. Set
$\alpha \in w_i$
. Set
![]() $\alpha ':= h^*_{\beta ,\beta _i}(\alpha )\in w^*$
and
$\alpha ':= h^*_{\beta ,\beta _i}(\alpha )\in w^*$
and
![]() $q':=h^*_{\beta ,\beta _i}(q_i)$
.
$q':=h^*_{\beta ,\beta _i}(q_i)$
.
(1) Assume
![]() $q_i,\alpha $
satisfy
$q_i,\alpha $
satisfy
![]() $q_i\restriction \alpha \Vdash \zeta \in C^{q_i(\alpha )}$
. By absoluteness they satisfy it in
$q_i\restriction \alpha \Vdash \zeta \in C^{q_i(\alpha )}$
. By absoluteness they satisfy it in
![]() $M_{\beta }$
, so the
$M_{\beta }$
, so the
![]() $h^*_{\beta ,\beta _i}$
-images
$h^*_{\beta ,\beta _i}$
-images
![]() $q',\alpha '$
satisfy it in
$q',\alpha '$
satisfy it in
![]() $M_{\beta _i}$
, which again is absolute; and
$M_{\beta _i}$
, which again is absolute; and
![]() $q^*\restriction \alpha '\le q'\restriction \alpha '$
forces that
$q^*\restriction \alpha '\le q'\restriction \alpha '$
forces that
![]() $q^*(\alpha ')=q'(\alpha ')$
. For the other direction, assume (in
$q^*(\alpha ')=q'(\alpha ')$
. For the other direction, assume (in
![]() $M_{\beta }$
) some
$M_{\beta }$
) some
![]() $s\le q_i\restriction \alpha $
forces
$s\le q_i\restriction \alpha $
forces
![]() $\zeta \notin C^{q_i(\alpha )}$
. Then
$\zeta \notin C^{q_i(\alpha )}$
. Then
![]() $h^*_{\beta ,\beta _i}(s)$
is compatible with
$h^*_{\beta ,\beta _i}(s)$
is compatible with
![]() $q^*$
and forces
$q^*$
and forces
![]() $\zeta \notin C^{q^{\prime }_i(\alpha ')} =C^{q^*(\alpha ')}$
.
$\zeta \notin C^{q^{\prime }_i(\alpha ')} =C^{q^*(\alpha ')}$
.
In the same way we can show (2), as well as (5) and the trivial directions of (3) and (4). For example, if
![]() $\bar q$
is
$\bar q$
is
![]() $(\bar w,\zeta )$
-canonical, then
$(\bar w,\zeta )$
-canonical, then
![]() $q^*$
is
$q^*$
is
![]() $(w^*,\zeta )$
-canonical. For this, use the fact that every element
$(w^*,\zeta )$
-canonical. For this, use the fact that every element
![]() $y^*\in \operatorname {\mathrm {poss}}(q^*, w^*,\zeta +1)$
“induces” a coherent possibility
$y^*\in \operatorname {\mathrm {poss}}(q^*, w^*,\zeta +1)$
“induces” a coherent possibility
![]() $\bar y$
(which is true whether
$\bar y$
(which is true whether
![]() $\bar q$
is canonical or not). And if additionally
$\bar q$
is canonical or not). And if additionally
![]() $\bar x\in \operatorname {\mathrm {poss}}(\bar q, \bar w,\zeta +1)$
, then
$\bar x\in \operatorname {\mathrm {poss}}(\bar q, \bar w,\zeta +1)$
, then
![]() $x^*\in \operatorname {\mathrm {poss}}(q^*, w^*,\zeta +1)$
; and if each
$x^*\in \operatorname {\mathrm {poss}}(q^*, w^*,\zeta +1)$
; and if each
![]() $q_i$
forces that
$q_i$
forces that
![]() $x_i\triangleleft G$
implies
$x_i\triangleleft G$
implies ![]() , then
, then
![]() $q^*$
forces that
$q^*$
forces that
![]() $x^*\triangleleft G$
implies
$x^*\triangleleft G$
implies ![]() .
.
We omit the (also straightforward) proofs of the other directions of (3) and (4) (which we do not need in this paper).
In the following, whenever we mention
![]() $q^*$
or
$q^*$
or
![]() $w^*$
, we assume
$w^*$
, we assume
![]() $\bar w$
,
$\bar w$
,
![]() $\bar q$
to be coherent and in
$\bar q$
to be coherent and in
![]() $M_{\beta }$
. We will (and can) use
$M_{\beta }$
. We will (and can) use
![]() $x^*$
only if
$x^*$
only if
![]() $\bar q$
additionally is canonical (otherwise
$\bar q$
additionally is canonical (otherwise
![]() $x^*$
will generally not be a possibility for
$x^*$
will generally not be a possibility for
![]() $q^*$
). In this case, every P-generic filter containing
$q^*$
). In this case, every P-generic filter containing
![]() $q^*$
will select an
$q^*$
will select an
![]() $x^*$
for some coherent possibility
$x^*$
for some coherent possibility
![]() $\bar x$
.
$\bar x$
.
Lemma 5.52. Assume
![]() $\bar q$
is coherent,
$\bar q$
is coherent, ![]() are P-names in
are P-names in
![]() $M_\beta $
for elements of
$M_\beta $
for elements of
![]() $2^\lambda $
, andFootnote
13
$2^\lambda $
, andFootnote
13
![]() . Then there is a coherent
. Then there is a coherent
![]() $\bar r\le \bar q$
, and sequences
$\bar r\le \bar q$
, and sequences
![]() $(\zeta ^j)_{j\in \lambda }$
and
$(\zeta ^j)_{j\in \lambda }$
and
![]() $(\bar w^j)_{j\in \lambda }$
such that
$(\bar w^j)_{j\in \lambda }$
such that
![]() $\bar r$
is
$\bar r$
is
![]() $(\bar w^j,\zeta ^j)$
-canonical for all j, and for all
$(\bar w^j,\zeta ^j)$
-canonical for all j, and for all
![]() $\bar x\in \operatorname {\mathrm {poss}}(\bar r, \bar w^j,\zeta ^j+1)$
there is some
$\bar x\in \operatorname {\mathrm {poss}}(\bar r, \bar w^j,\zeta ^j+1)$
there is some
![]() $\ell \in I^*({>}\zeta ^j,{<}\zeta ^{j+1})$
and
$\ell \in I^*({>}\zeta ^j,{<}\zeta ^{j+1})$
and
![]() $\bar b=(b_i)_{i<4}$
, with
$\bar b=(b_i)_{i<4}$
, with
![]() $b_i\in 2$
, violating majorityFootnote
14
such that for all
$b_i\in 2$
, violating majorityFootnote
14
such that for all
![]() $i<4$
$i<4$
As the
![]() $p_{\beta _i}$
are coherent, we can apply the lemma to
$p_{\beta _i}$
are coherent, we can apply the lemma to ![]() (for all i) and get:
(for all i) and get:
Corollary 5.53. If ![]() , then there is a coherent
, then there is a coherent
![]() $r^*\le \bigwedge _{i<4}p_{\beta _i}$
forcing that
$r^*\le \bigwedge _{i<4}p_{\beta _i}$
forcing that
Proof of the lemma
We will construct (in
![]() $M_\beta $
), by induction on
$M_\beta $
), by induction on
![]() $j\in \lambda $
,
$j\in \lambda $
,
![]() $\zeta ^j$
,
$\zeta ^j$
,
![]() $\bar w^j$
and
$\bar w^j$
and
![]() $\bar r^j$
with
$\bar r^j$
with
![]() $r^0_i=q_i$
, such that the following holds:
$r^0_i=q_i$
, such that the following holds:
-
(1)
 $\bar r^j$
is coherent.
$\bar r^j$
is coherent. -
(2)
 $\bar w^j$
is coherent, for each
$\bar w^j$
is coherent, for each
 $i<4$
the
$i<4$
the
 $w_i^j$
are increasing with j, and their union covers
$w_i^j$
are increasing with j, and their union covers
 $\bigcup _{j\in \lambda }\operatorname {\mathrm {dom}}(r_i^j)$
.
$\bigcup _{j\in \lambda }\operatorname {\mathrm {dom}}(r_i^j)$
. -
(3)
 $\bar r^j$
is
$\bar r^j$
is
 $(\bar w^j,\zeta ^j)$
-canonical.
$(\bar w^j,\zeta ^j)$
-canonical. -
(4)
 $\bar r^k\le ^{+}_{\bar w^j,\zeta ^j} \bar r^j$
for
$\bar r^k\le ^{+}_{\bar w^j,\zeta ^j} \bar r^j$
for
 $j<k$
.
$j<k$
. -
(5) If
 $\bar x\in \operatorname {\mathrm {poss}}(\bar r^j,\bar w^j,\zeta ^j+1)$
, then there is an
$\bar x\in \operatorname {\mathrm {poss}}(\bar r^j,\bar w^j,\zeta ^j+1)$
, then there is an
 $\ell \in I^*({>}\zeta ^j,{<}\zeta ^{j+1})$
and a
$\ell \in I^*({>}\zeta ^j,{<}\zeta ^{j+1})$
and a
 $b\in 2$
such that for at least two
$b\in 2$
such that for at least two
 $i_1,i_2$
in
$i_1,i_2$
in
 $\{1,2,3\}$
,
$\{1,2,3\}$
,
 $r^{j+1}_i$
forces that
$r^{j+1}_i$
forces that
 $x_i\triangleleft G$
implies (*)
$x_i\triangleleft G$
implies (*)
Then we take the usual fusion limits, as in Lemma 5.50(2), and are done.
For limits j, let
![]() $\bar r'$
be a (coherent) limit of
$\bar r'$
be a (coherent) limit of
![]() $(\bar r^{j'})_{j'<j}$
, and set
$(\bar r^{j'})_{j'<j}$
, and set
![]() $\zeta ^*:=\sup _{j'<j}(\zeta ^{j'})$
and
$\zeta ^*:=\sup _{j'<j}(\zeta ^{j'})$
and
![]() $w^*_i:=\bigcup _{j'<j} w^{j'}_i$
for each
$w^*_i:=\bigcup _{j'<j} w^{j'}_i$
for each
![]() $i<4$
. Note that
$i<4$
. Note that
![]() $\bar r'$
fits
$\bar r'$
fits
![]() $(\bar w^*,\zeta ^*)$
. Then we can find coherent
$(\bar w^*,\zeta ^*)$
. Then we can find coherent
![]() $\bar r^*\le ^+_{\bar w^*,\zeta ^*} \bar r'$
which is
$\bar r^*\le ^+_{\bar w^*,\zeta ^*} \bar r'$
which is
![]() $(\bar w^*,\zeta ^*)$
-canonical, as in Lemma 5.50(3).
$(\bar w^*,\zeta ^*)$
-canonical, as in Lemma 5.50(3).
In successor cases
![]() $j=j'+1$
set
$j=j'+1$
set
![]() $(\bar r^*,\bar w^*,\zeta ^*):=(\bar r^{j'},\bar w^{j'},\zeta ^{j'})$
.
$(\bar r^*,\bar w^*,\zeta ^*):=(\bar r^{j'},\bar w^{j'},\zeta ^{j'})$
.
In any case we want to construct
![]() $\bar r^j$
,
$\bar r^j$
,
![]() $\bar w^j$
, and
$\bar w^j$
, and
![]() $\zeta ^j$
.
$\zeta ^j$
.
Enumerate
![]() $\operatorname {\mathrm {poss}}(\bar r^*,\bar w^*,\zeta ^*+1)$
as
$\operatorname {\mathrm {poss}}(\bar r^*,\bar w^*,\zeta ^*+1)$
as
![]() $(\bar x^k)_{k\in K}$
.
$(\bar x^k)_{k\in K}$
.
We define
![]() $\bar s^k$
for
$\bar s^k$
for
![]() $k\le K$
, with
$k\le K$
, with
![]() $\bar s^0:= \bar r^*$
and, as usual, taking (coherent) limits at limits, such that:
$\bar s^0:= \bar r^*$
and, as usual, taking (coherent) limits at limits, such that:
-
•
 $\bar s^k$
is coherent.
$\bar s^k$
is coherent. -
•
 $\bar s^\ell \le ^+_{\bar w^*,\zeta ^* } \bar s^k$
for
$\bar s^\ell \le ^+_{\bar w^*,\zeta ^* } \bar s^k$
for
 $k<\ell <K$
. (This implies that
$k<\ell <K$
. (This implies that
 $\bar s^k$
is
$\bar s^k$
is
 $(\bar w^*,\zeta ^*)$
-canonical.)
$(\bar w^*,\zeta ^*)$
-canonical.) -
• There is a
 $\xi ^k$
and an
$\xi ^k$
and an
 $\ell \in I^*({>}\zeta ^*,{<}\xi ^k)$
and a
$\ell \in I^*({>}\zeta ^*,{<}\xi ^k)$
and a
 $b\in 2$
such that (**)
$b\in 2$
such that (**)
Assume we can construct these
![]() $\bar s^k$
,
$\bar s^k$
,
![]() $\xi ^k$
for all
$\xi ^k$
for all
![]() $k\in K$
, then let
$k\in K$
, then let
![]() $\bar s^K$
be again a (coherent) limit. We set
$\bar s^K$
be again a (coherent) limit. We set
![]() $w^{j}_i:=w^*_i\cup \{\alpha _j\}$
such that
$w^{j}_i:=w^*_i\cup \{\alpha _j\}$
such that
![]() $\bar w^{j}$
is coherent (and such that, by bookkeeping, all elements of
$\bar w^{j}$
is coherent (and such that, by bookkeeping, all elements of
![]() $\operatorname {\mathrm {dom}}(p^j_i)$
will be eventually covered), and find some
$\operatorname {\mathrm {dom}}(p^j_i)$
will be eventually covered), and find some
![]() $\zeta ^{j}>\sup _{k\in K}(\xi ^k)$
and
$\zeta ^{j}>\sup _{k\in K}(\xi ^k)$
and
![]() $\bar r^{j}\le ^+_{\bar w^*,\zeta ^*} r^*$
which is
$\bar r^{j}\le ^+_{\bar w^*,\zeta ^*} r^*$
which is
![]() $(\bar w^{j},\zeta ^{j})$
-canonical, again as in Lemma 5.50(3). Then
$(\bar w^{j},\zeta ^{j})$
-canonical, again as in Lemma 5.50(3). Then
![]() $\bar r^{j}$
,
$\bar r^{j}$
,
![]() $\bar w^{j}$
and
$\bar w^{j}$
and
![]() $\zeta ^{j}$
are as required.
$\zeta ^{j}$
are as required.
So it remains to construct, for
![]() $k\in K$
,
$k\in K$
,
![]() $\bar s^{k+1}$
and
$\bar s^{k+1}$
and
![]() $\xi ^k$
, which we will do in the rest of the proof. Set
$\xi ^k$
, which we will do in the rest of the proof. Set
![]() $\bar s:= \bar s^k$
,
$\bar s:= \bar s^k$
,
![]() $\bar x:=\bar x^k$
,
$\bar x:=\bar x^k$
,
![]() $\bar w:=\bar w^*$
, and
$\bar w:=\bar w^*$
, and
![]() $\zeta :=\zeta ^*$
. Recall that
$\zeta :=\zeta ^*$
. Recall that
![]() $\bar s$
is
$\bar s$
is
![]() $(\bar w, \zeta )$
-canonical,
$(\bar w, \zeta )$
-canonical,
![]() $\bar x\in \operatorname {\mathrm {poss}}(\bar s,\bar w,\zeta )$
, and we are looking for
$\bar x\in \operatorname {\mathrm {poss}}(\bar s,\bar w,\zeta )$
, and we are looking for
![]() $\bar s^{k+1}\le ^+_{\bar w,\zeta }\bar s$
which satisfies (**) for
$\bar s^{k+1}\le ^+_{\bar w,\zeta }\bar s$
which satisfies (**) for
![]() $\bar x$
.
$\bar x$
.
Set
![]() $s^{\prime }_i:=s_i\wedge x_i$
. It is enough to construct
$s^{\prime }_i:=s_i\wedge x_i$
. It is enough to construct
![]() $t_i\le s^{\prime }_i$
such that:
$t_i\le s^{\prime }_i$
such that:
-
• Both
 $t_i\restriction \beta $
and
$t_i\restriction \beta $
and
 $t_i(\beta )\restriction (\lambda \setminus \zeta +1)$
are independent of i.
$t_i(\beta )\restriction (\lambda \setminus \zeta +1)$
are independent of i. -
•
 .
.
Then we can define
![]() $\bar s^{k+1}$
in the usual way:
$\bar s^{k+1}$
in the usual way:
![]() $\operatorname {\mathrm {dom}}(s_i^{k+1})=\operatorname {\mathrm {dom}}(t_i)$
(and we can assume
$\operatorname {\mathrm {dom}}(s_i^{k+1})=\operatorname {\mathrm {dom}}(t_i)$
(and we can assume
![]() $\operatorname {\mathrm {dom}}(s_i)=\operatorname {\mathrm {dom}}(t_i)$
, by using trivial conditions). For
$\operatorname {\mathrm {dom}}(s_i)=\operatorname {\mathrm {dom}}(t_i)$
, by using trivial conditions). For
![]() $\alpha \in \operatorname {\mathrm {dom}}(t_i)$
, if
$\alpha \in \operatorname {\mathrm {dom}}(t_i)$
, if
![]() $t_i\restriction \alpha \notin G_\alpha $
then set
$t_i\restriction \alpha \notin G_\alpha $
then set
![]() $s_i^{k+1}(\alpha )$
to be
$s_i^{k+1}(\alpha )$
to be
![]() $s_i(\alpha )$
, otherwise
$s_i(\alpha )$
, otherwise
![]() $t_i(\alpha )\vee (s_i(\alpha )\restriction \zeta +1)$
if
$t_i(\alpha )\vee (s_i(\alpha )\restriction \zeta +1)$
if
![]() $\alpha \in w_i$
and
$\alpha \in w_i$
and
![]() $t_i(\alpha )$
otherwise. The resulting
$t_i(\alpha )$
otherwise. The resulting
![]() $\bar s^{k+1}\le ^+_{\bar w,\zeta } \bar s$
is coherent and
$\bar s^{k+1}\le ^+_{\bar w,\zeta } \bar s$
is coherent and
![]() $s^{k+1}_i$
forces that
$s^{k+1}_i$
forces that
![]() $x_i\triangleleft G$
implies
$x_i\triangleleft G$
implies
![]() $t_i\in G$
.
$t_i\in G$
.
We have to introduce more notation: Fix
![]() $j\ne i$
, and
$j\ne i$
, and
![]() $a\le s^{\prime }_j$
and
$a\le s^{\prime }_j$
and
![]() $b\le s_i'\restriction \beta +1$
(in
$b\le s_i'\restriction \beta +1$
(in
![]() $P_{\beta +1}$
) such that
$P_{\beta +1}$
) such that
![]() $b\restriction \beta \le a$
and
$b\restriction \beta \le a$
and
![]() $b\restriction \beta $
forces that
$b\restriction \beta $
forces that
![]() $b(\beta )$
is stronger than
$b(\beta )$
is stronger than
![]() $a(\beta )$
above
$a(\beta )$
above
![]() $\zeta $
(i.e.,
$\zeta $
(i.e.,
![]() $b\restriction \beta \Vdash \, (\forall \xi>\zeta )\, b(\beta )(\xi )\supseteq a(\beta )(\xi )$
). Then we define
$b\restriction \beta \Vdash \, (\forall \xi>\zeta )\, b(\beta )(\xi )\supseteq a(\beta )(\xi )$
). Then we define
![]() $b^{[j]} \wedge a$
by
$b^{[j]} \wedge a$
by
 $$\begin{align*}(b^{[j]} \wedge a)(\alpha)(\xi)=\begin{cases} b(\alpha)(\xi), & \text{if }\alpha<\beta,\\ x_j(\beta)(\xi), & \text{if }\alpha=\beta\text{ and }\xi\le \zeta,\\ b(\beta)(\xi), & \text{if }\alpha=\beta\text{ and }\xi> \zeta,\\ a(\alpha)(\xi),& \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}(b^{[j]} \wedge a)(\alpha)(\xi)=\begin{cases} b(\alpha)(\xi), & \text{if }\alpha<\beta,\\ x_j(\beta)(\xi), & \text{if }\alpha=\beta\text{ and }\xi\le \zeta,\\ b(\beta)(\xi), & \text{if }\alpha=\beta\text{ and }\xi> \zeta,\\ a(\alpha)(\xi),& \text{otherwise.} \end{cases} \end{align*}$$
Note that
![]() $b^{[j]} \wedge a$
is stronger than a, but generally not stronger than b.
$b^{[j]} \wedge a$
is stronger than a, but generally not stronger than b.
By our assumption,
![]() $q_0$
and therefore
$q_0$
and therefore
![]() $s^{\prime }_0$
forces
$s^{\prime }_0$
forces ![]() . So in an intermediate model
. So in an intermediate model
![]() $V[G_{\beta +1}]$
, there is some
$V[G_{\beta +1}]$
, there is some
![]() $\ell \in I^*({>}\zeta )$
such that
$\ell \in I^*({>}\zeta )$
such that
![]() $s^{\prime }_0/G_{\beta +1}$
does not decide
$s^{\prime }_0/G_{\beta +1}$
does not decide ![]() . Back in V, fix some
. Back in V, fix some
![]() $b_0\le s^{\prime }_0\restriction (\beta +1)$
in
$b_0\le s^{\prime }_0\restriction (\beta +1)$
in
![]() $P_{\beta +1}$
which determines this
$P_{\beta +1}$
which determines this
![]() $\ell $
.
$\ell $
.
Find
![]() $r^{\prime }_1\le b_0^{[1]}\wedge s^{\prime }_1$
which determines
$r^{\prime }_1\le b_0^{[1]}\wedge s^{\prime }_1$
which determines ![]() to be
to be
![]() $j_1$
for some
$j_1$
for some
![]() $j_1\in 2$
. Find
$j_1\in 2$
. Find
![]() $r^{\prime }_2\le (r^{\prime }_1\restriction \beta +1)^{[2]}\wedge s^{\prime }_2$
which determines
$r^{\prime }_2\le (r^{\prime }_1\restriction \beta +1)^{[2]}\wedge s^{\prime }_2$
which determines ![]() to be
to be
![]() $j_2$
; analogously find
$j_2$
; analogously find
![]() $r^{\prime }_3\le (r^{\prime }_2\restriction \beta +1)^{[3]}\wedge s^{\prime }_3$
which determines
$r^{\prime }_3\le (r^{\prime }_2\restriction \beta +1)^{[3]}\wedge s^{\prime }_3$
which determines ![]() to be some
to be some
![]() $j_3$
. Let
$j_3$
. Let
![]() $j\in 2$
be equal to at least two of
$j\in 2$
be equal to at least two of
![]() $j_1,j_2,j_3$
.
$j_1,j_2,j_3$
.
Set
![]() $p:= (r^{\prime }_3\restriction \beta +1)^{[0]}\wedge s^{\prime }_0$
. In any
$p:= (r^{\prime }_3\restriction \beta +1)^{[0]}\wedge s^{\prime }_0$
. In any
![]() $P_{\beta +1}$
-extension honoring
$P_{\beta +1}$
-extension honoring
![]() $p\restriction \beta +1$
,
$p\restriction \beta +1$
, ![]() is not determined by
is not determined by
![]() $p/G_{\beta +1}$
, i.e., there is a
$p/G_{\beta +1}$
, i.e., there is a
![]() $t_0\le p$
forcing that
$t_0\le p$
forcing that ![]() .
.
We now set and
![]() $t_i:= (t_0\restriction \beta +1)^{[i]}\wedge r^{\prime }_i$
for
$t_i:= (t_0\restriction \beta +1)^{[i]}\wedge r^{\prime }_i$
for
![]() $i=1,2,3$
. Note that
$i=1,2,3$
. Note that
![]() $t_i\le r^{\prime }_i\le s^{\prime }_i$
extends
$t_i\le r^{\prime }_i\le s^{\prime }_i$
extends
![]() $x_i$
and forces
$x_i$
and forces ![]() to be
to be
![]() $1-j$
if
$1-j$
if
![]() $i=0$
and to be j for at least two i in
$i=0$
and to be j for at least two i in
![]() $\{1,2,3\}$
.
$\{1,2,3\}$
.
We can now easily show:
Lemma 5.54. For all but non-stationary many
![]() $\beta \in S^{\mu }_{\lambda ^+}$
$\beta \in S^{\mu }_{\lambda ^+}$
Proof We started in this section with an arbitrary
![]() $\Delta $
-system and showed that Corollary 5.53 and Lemma 5.48 hold for this system.
$\Delta $
-system and showed that Corollary 5.53 and Lemma 5.48 hold for this system.
We now use a specific
![]() $\Delta $
-system:
$\Delta $
-system:
Assume towards a contradiction that on a non-stationary set
![]() $S'$
there are
$S'$
there are
![]() $p_\beta \le p_*$
forcing
$p_\beta \le p_*$
forcing ![]() . By strengthening we can assume that
. By strengthening we can assume that
![]() $p_\beta $
canonically reads
$p_\beta $
canonically reads ![]() . Let
. Let
![]() $M_\beta $
contain
$M_\beta $
contain
![]() $p_\beta $
and let
$p_\beta $
and let
![]() $S\subseteq S'$
be such that
$S\subseteq S'$
be such that
![]() $(M_\beta ,p_\beta )_{\beta \in S}$
is a
$(M_\beta ,p_\beta )_{\beta \in S}$
is a
![]() $\Delta $
-system. Fix
$\Delta $
-system. Fix
![]() $\beta _0<\beta _1<\beta _2<\beta _3$
in S. By Corollary 5.53 we get a coherent
$\beta _0<\beta _1<\beta _2<\beta _3$
in S. By Corollary 5.53 we get a coherent
![]() $\bar r$
stronger than
$\bar r$
stronger than
![]() $\bar p$
such that
$\bar p$
such that ![]() . This contradicts Lemma 5.48.
. This contradicts Lemma 5.48.
5.10. Fixing the
 $\mathbf \Delta $
-system
$\mathbf \Delta $
-system
We now know that there is a stationary set
![]() $S^0\subseteq S^\mu _{\lambda ^+}$
such that for all
$S^0\subseteq S^\mu _{\lambda ^+}$
such that for all
![]() $\beta \in S^0$
,
$\beta \in S^0$
, ![]() is forced (by
is forced (by
![]() $p_*$
) to be in
$p_*$
) to be in
![]() $V_{\beta +1}$
but not in
$V_{\beta +1}$
but not in
![]() $V_{\beta }$
(see Lemmas 5.39 and 5.54).
$V_{\beta }$
(see Lemmas 5.39 and 5.54).
For each
![]() $\beta \in S^0$
there is a
$\beta \in S^0$
there is a
![]() $p^{\prime }_\beta \le p_*$
in P forcing that
$p^{\prime }_\beta \le p_*$
in P forcing that ![]() is equal to some
is equal to some
![]() $P_{\beta +1}$
-name, call it
$P_{\beta +1}$
-name, call it ![]() , and we choose
, and we choose
![]() $p_\beta \le p^{\prime }_\beta $
(we only have to strengthen the part below
$p_\beta \le p^{\prime }_\beta $
(we only have to strengthen the part below
![]() $\beta +1$
) which canonically reads
$\beta +1$
) which canonically reads ![]() .Footnote
15
.Footnote
15
We now fix, as usual, for each
![]() $\beta \in S^0$
, some elementary model
$\beta \in S^0$
, some elementary model
![]() $M_\beta $
containing
$M_\beta $
containing
![]() $p_\beta $
, and fix
$p_\beta $
, and fix
![]() $S\subseteq S^0$
such that
$S\subseteq S^0$
such that
![]() $(M_\beta ,p_\beta )_{\beta \in S}$
is a
$(M_\beta ,p_\beta )_{\beta \in S}$
is a
![]() $\Delta $
-system.
$\Delta $
-system.
So
![]() $p_{**}:=p_\beta \restriction \beta \le p_*$
is independent of
$p_{**}:=p_\beta \restriction \beta \le p_*$
is independent of
![]() $\beta \in S$
(it is a
$\beta \in S$
(it is a
![]() $P_\alpha $
-condition for some
$P_\alpha $
-condition for some
![]() $\alpha \in \Delta $
, independent of
$\alpha \in \Delta $
, independent of
![]() $\beta \in S$
); and
$\beta \in S$
); and ![]() is read continuously by
is read continuously by
![]() $p_\beta \restriction \beta +1$
via
$p_\beta \restriction \beta +1$
via
![]() $(w^{\prime }_\zeta )_{\zeta \in E'}$
for some
$(w^{\prime }_\zeta )_{\zeta \in E'}$
for some
![]() $E'\subseteq \lambda $
club, with
$E'\subseteq \lambda $
club, with
![]() $w^{\prime }_\zeta \subseteq \beta +1$
. As usual, due to homogeneity
$w^{\prime }_\zeta \subseteq \beta +1$
. As usual, due to homogeneity
![]() $E'$
is independent of
$E'$
is independent of
![]() $\beta \in S$
, and the
$\beta \in S$
, and the
![]() $w^{\prime }_\zeta $
are independent of
$w^{\prime }_\zeta $
are independent of
![]() $\beta $
apart from the shifting of the final coordinate
$\beta $
apart from the shifting of the final coordinate
![]() $\beta $
via the mapping
$\beta $
via the mapping
![]() $h^*_{\beta _0,\beta _1}$
; the same holds for the decision functions that map
$h^*_{\beta _0,\beta _1}$
; the same holds for the decision functions that map
![]() $\operatorname {\mathrm {poss}}(p_\zeta , w^{\prime }_\zeta ,\zeta +1)$
to
$\operatorname {\mathrm {poss}}(p_\zeta , w^{\prime }_\zeta ,\zeta +1)$
to ![]() .
.
Let E be the limit points of
![]() $E'$
, and set
$E'$
, and set
![]() $w_\zeta :=\bigcup _{\nu <\zeta }w^{\prime }_\nu $
. Then
$w_\zeta :=\bigcup _{\nu <\zeta }w^{\prime }_\nu $
. Then ![]() is
is
![]() $(w_\xi ,\xi )$
-determined by
$(w_\xi ,\xi )$
-determined by
![]() $p_\beta $
for all
$p_\beta $
for all
![]() $\xi \in E$
.
$\xi \in E$
.
In the
![]() $P_\beta $
-extension, only
$P_\beta $
-extension, only ![]() remains undetermined, i.e., there are
remains undetermined, i.e., there are
![]() $f_{\xi }$
for
$f_{\xi }$
for
![]() $\xi \in E$
such that
$\xi \in E$
such that
![]() $p_\beta /G_\beta $
forces
$p_\beta /G_\beta $
forces ![]() . The
. The
![]() $f_\xi $
are canonically read from
$f_\xi $
are canonically read from
![]() $p_\beta \restriction \beta $
in a way independent of
$p_\beta \restriction \beta $
in a way independent of
![]() $\beta $
(due to homogeneity).
$\beta $
(due to homogeneity).
Recall that
![]() $x\in \operatorname {\mathrm {poss}}(\tilde p,\xi )$
is equivalent to:
$x\in \operatorname {\mathrm {poss}}(\tilde p,\xi )$
is equivalent to:
![]() $x\in 2^{I^*({<}\xi )}$
and x extends
$x\in 2^{I^*({<}\xi )}$
and x extends
![]() $\eta ^{\tilde p}\restriction I^*({<}\xi )$
. So the domain of
$\eta ^{\tilde p}\restriction I^*({<}\xi )$
. So the domain of
![]() $f_\xi $
is
$f_\xi $
is
![]() $\operatorname {\mathrm {poss}}(\tilde p,\xi )$
.
$\operatorname {\mathrm {poss}}(\tilde p,\xi )$
.
To summarize:
Fact 5.55.
![]() $(M_\beta ,p_\beta )_{\beta \in S}$
satisfies:
$(M_\beta ,p_\beta )_{\beta \in S}$
satisfies:
-
•
 $p_\beta \restriction \beta =:p_{**}\le p_*$
is a
$p_\beta \restriction \beta =:p_{**}\le p_*$
is a
 $P_{\sup (\Delta )}$
-condition independent of
$P_{\sup (\Delta )}$
-condition independent of
 $\beta \in S$
.
$\beta \in S$
. -
•
 $p_\beta (\beta )=:\tilde p$
is a
$p_\beta (\beta )=:\tilde p$
is a
 $P_{\sup (\Delta )}$
-name independent of
$P_{\sup (\Delta )}$
-name independent of
 $\beta \in S$
.
$\beta \in S$
. -
• There is a club-set
 $E\subseteq \lambda $
and, for
$E\subseteq \lambda $
and, for
 $\xi \in E$
,
$\xi \in E$
,
 $P_{\sup (\Delta )}$
-names
$P_{\sup (\Delta )}$
-names  such that for all
such that for all
 $\beta \in S$
and
$\beta \in S$
and
 $\xi \in E$
$\xi \in E$

-
• If
 $\beta \in S$
,
$\beta \in S$
,  is a
is a
 $P_\beta $
-name,
$P_\beta $
-name,
 $q\le p_{**}$
in
$q\le p_{**}$
in
 $P_{\beta }$
, and
$P_{\beta }$
, and  are in
are in
 $M_\beta $
, then we can find
$M_\beta $
, then we can find
 $\alpha \in \Delta $
and
$\alpha \in \Delta $
and
 $p^{\prime }_{**}\le q$
in
$p^{\prime }_{**}\le q$
in
 $P_\alpha $
which continuously reads
$P_\alpha $
which continuously reads  ,
,  , and
, and  independentlyFootnote
16
of
independentlyFootnote
16
of
 $\beta $
.
$\beta $
.
The last item follows from Lemma 5.42; and we will use it several times: Before Corollary 5.59 we find
![]() $p^2_{**}\le p_{**}$
to get names for U,
$p^2_{**}\le p_{**}$
to get names for U,
![]() $F_\xi $
etc. that are independent of
$F_\xi $
etc. that are independent of
![]() $\beta $
; before Lemma 5.63 we get
$\beta $
; before Lemma 5.63 we get
![]() $p^3_{**}\le p^2_{**}$
to get independent names for some unions, intersections, and
$p^3_{**}\le p^2_{**}$
to get independent names for some unions, intersections, and ![]() -images; and finally after Corollary 5.70 we choose
-images; and finally after Corollary 5.70 we choose
![]() $q\le p^3_{**}$
to get an independent name for the generator
$q\le p^3_{**}$
to get an independent name for the generator
![]() $f_{\text {gen}}$
.
$f_{\text {gen}}$
.
5.11. Local reading
So we know that we can determine initial segments of ![]() from initial segments of
from initial segments of ![]() , more specifically, we can determine
, more specifically, we can determine ![]() from
from ![]() for
for
![]() $I:=I^*({<}\xi )$
.
$I:=I^*({<}\xi )$
.
In this section we show that on unboundedly many disjoint intervals of the form
![]() $A:=I^*(\ge \xi ,<\nu )$
, we can read
$A:=I^*(\ge \xi ,<\nu )$
, we can read ![]() from just
from just ![]() (without having to use the
(without having to use the ![]() -values below A).
-values below A).
The following definition (the notion of candidate) is only used in this section. In the rest of the paper we only need Corollary 5.59.
In the following, we work in
![]() $V_\beta $
, the
$V_\beta $
, the
![]() $P_\beta $
-extension
$P_\beta $
-extension
![]() $V[G_\beta ]$
where we assume
$V[G_\beta ]$
where we assume
![]() $\beta \in S$
and
$\beta \in S$
and
![]() $p_{**}\in G_\beta $
.
$p_{**}\in G_\beta $
.
Definition 5.56. (In
![]() $V_{\beta }$
)
$V_{\beta }$
)
-
• For
 $A\subseteq \lambda $
and
$A\subseteq \lambda $
and
 $\bar x=(x_i)_{i<4}$
,
$\bar x=(x_i)_{i<4}$
,
 $x_i:A\to 2$
, we say
$x_i:A\to 2$
, we say
 $\bar x$
honors majority above
$\bar x$
honors majority above
 $\zeta $
, if We say
$\zeta $
, if We say $$\begin{align*}x_0(\ell)=\operatorname{\mathrm{major}}_{i=1,2,3}x_i(\ell)\text{ for all } \ell\in A\cap I^*({\ge}\zeta). \end{align*}$$
$$\begin{align*}x_0(\ell)=\operatorname{\mathrm{major}}_{i=1,2,3}x_i(\ell)\text{ for all } \ell\in A\cap I^*({\ge}\zeta). \end{align*}$$
 $\bar x$
honors
$\bar x$
honors
 $\tilde p$
, if each
$\tilde p$
, if each
 $x_i$
is compatible with
$x_i$
is compatible with
 $\eta ^{\tilde p}$
(as partial functions).
$\eta ^{\tilde p}$
(as partial functions).
-
•
 $\bar x=(x_i)_{i<4}$
is a
$\bar x=(x_i)_{i<4}$
is a
 $(\zeta _0,\zeta _1)$
-candidate, (for
$(\zeta _0,\zeta _1)$
-candidate, (for
 $\zeta _0\le \zeta _1$
both in E) if the
$\zeta _0\le \zeta _1$
both in E) if the
 $x_i\in \operatorname {\mathrm {poss}}(\tilde p,\zeta _1)$
honor majority above
$x_i\in \operatorname {\mathrm {poss}}(\tilde p,\zeta _1)$
honor majority above
 $\zeta _0$
.
$\zeta _0$
.(As elements of
 $\operatorname {\mathrm {poss}}(\tilde p,\zeta _1)$
they automatically honor
$\operatorname {\mathrm {poss}}(\tilde p,\zeta _1)$
they automatically honor
 $\tilde p$
.)
$\tilde p$
.) -
• If
 $\bar x$
is a
$\bar x$
is a
 $(\zeta _0,\zeta _1)$
-candidate, we say “
$(\zeta _0,\zeta _1)$
-candidate, we say “
 $\bar y$
extends
$\bar y$
extends
 $\bar x$
” if
$\bar x$
” if
 $\bar y$
is a
$\bar y$
is a
 $(\zeta _1,\zeta _2)$
-candidateFootnote
17
for some
$(\zeta _1,\zeta _2)$
-candidateFootnote
17
for some
 $\zeta _2\ge \zeta _1$
and each
$\zeta _2\ge \zeta _1$
and each
 $y_i$
extends
$y_i$
extends
 $x_i$
.
$x_i$
.Equivalently,
 $\bar y=\bar x^\frown \bar b$
for some
$\bar y=\bar x^\frown \bar b$
for some
 $\bar b$
, with
$\bar b$
, with
 $b_i:I^*({\ge }\zeta _1,{<}\zeta _2)\to 2$
, which honors both majority and
$b_i:I^*({\ge }\zeta _1,{<}\zeta _2)\to 2$
, which honors both majority and
 $\tilde p$
.
$\tilde p$
. -
• A
 $(\zeta _0,\zeta _1)$
-candidate
$(\zeta _0,\zeta _1)$
-candidate
 $\bar y$
is “good,” if for every candidate
$\bar y$
is “good,” if for every candidate
 $\bar z$
of height
$\bar z$
of height
 $\xi>\zeta _1$
that extends
$\xi>\zeta _1$
that extends
 $\bar y$
we have: (*1)
$\bar y$
we have: (*1) $$\begin{align} f_\xi(z_0)(\ell) =\operatorname{\mathrm{major}}_{i=1,2,3}f_\xi(z_i)(\ell)\text{ for all }\ell\in I^*({\ge}\zeta_1,{<}\xi). \end{align} $$
$$\begin{align} f_\xi(z_0)(\ell) =\operatorname{\mathrm{major}}_{i=1,2,3}f_\xi(z_i)(\ell)\text{ for all }\ell\in I^*({\ge}\zeta_1,{<}\xi). \end{align} $$
Preliminary Lemma 5.57. (In
![]() $V_\beta $
.) Every candidate can be extended to a good candidate.
$V_\beta $
.) Every candidate can be extended to a good candidate.
Proof Assume otherwise, i.e., there is a
![]() $(\zeta ',\zeta _0)$
-candidate
$(\zeta ',\zeta _0)$
-candidate
![]() $\bar x$
which is a counterexample, which means:
$\bar x$
which is a counterexample, which means:
 $$\begin{align} \text{Whenever } \bar y \text{ is a } (\zeta_0,\zeta_1)\text{-candidate extending } \bar{x} \text{ then there is a}\\
\nonumber \xi>\zeta_1 \text{ and a } (\zeta_1,\xi)\text{-candidate } \bar{z} \text{ extending } \bar{y} \text{ which violates}~(*_{1}). \end{align} $$
$$\begin{align} \text{Whenever } \bar y \text{ is a } (\zeta_0,\zeta_1)\text{-candidate extending } \bar{x} \text{ then there is a}\\
\nonumber \xi>\zeta_1 \text{ and a } (\zeta_1,\xi)\text{-candidate } \bar{z} \text{ extending } \bar{y} \text{ which violates}~(*_{1}). \end{align} $$
We now construct
![]() $r_0\le \tilde p$
and, for
$r_0\le \tilde p$
and, for
![]() $i=1,2,3$
,
$i=1,2,3$
,
![]() $Q_\beta $
-names
$Q_\beta $
-names
![]() $r_i\le \tilde p$
. All these conditions live on the same
$r_i\le \tilde p$
. All these conditions live on the same
![]() $C^*\subseteq E$
with
$C^*\subseteq E$
with
![]() $\min (C^*)=\zeta _0$
. The trunk of
$\min (C^*)=\zeta _0$
. The trunk of
![]() $r_i$
is
$r_i$
is
![]() $x_i$
.
$x_i$
.
We now construct inductively
![]() $C^*\restriction \zeta $
and
$C^*\restriction \zeta $
and
![]() $r_i\restriction \zeta $
.
$r_i\restriction \zeta $
.
Assume we have determined that
![]() $\zeta \in C^*$
and we have constructed each
$\zeta \in C^*$
and we have constructed each
![]() $r_i$
below
$r_i$
below
![]() $\zeta $
. Set
$\zeta $
. Set
![]() $r_0(\zeta ):=\tilde p(\zeta )$
and pick
$r_0(\zeta ):=\tilde p(\zeta )$
and pick
![]() $r_i(\zeta )$
as in (5.44), i.e., they have majority
$r_i(\zeta )$
as in (5.44), i.e., they have majority ![]() and leave enough freedom to form a valid condition.
and leave enough freedom to form a valid condition.
We will now construct the
![]() $C^*$
-successor
$C^*$
-successor
![]() $\xi $
of
$\xi $
of
![]() $\zeta $
, together with
$\zeta $
, together with
![]() $r_i$
on
$r_i$
on
![]() $I^*({>}\zeta ,{<}\xi )$
.
$I^*({>}\zeta ,{<}\xi )$
.
Enumerate all
![]() $(\zeta _0,\zeta +1)$
-candidates extending
$(\zeta _0,\zeta +1)$
-candidates extending
![]() $\bar x$
as
$\bar x$
as
![]() $(\bar y^k)_{k\in K}$
.
$(\bar y^k)_{k\in K}$
.
Let
![]() $\bar a^0$
be the empty
$\bar a^0$
be the empty
![]() $4$
-tuple and set
$4$
-tuple and set
![]() $\xi _0:=\zeta +1$
. We will construct, for
$\xi _0:=\zeta +1$
. We will construct, for
![]() $k\in K$
,
$k\in K$
,
![]() $\xi _k$
and some
$\xi _k$
and some
![]() $\bar a^k$
that honors majority and
$\bar a^k$
that honors majority and
![]() $\tilde p$
, where
$\tilde p$
, where
![]() $a^k_i$
has domain
$a^k_i$
has domain
![]() $I^*({\ge }\zeta +1,{<}\xi _k)$
and extends
$I^*({\ge }\zeta +1,{<}\xi _k)$
and extends
![]() $a^j_i$
if
$a^j_i$
if
![]() $j<k$
.
$j<k$
.
If k is a limit, let
![]() $\bar a^x$
be the (pointwise) union of
$\bar a^x$
be the (pointwise) union of
![]() $\bar a^j$
with
$\bar a^j$
with
![]() $j<k$
, and set
$j<k$
, and set
![]() $\xi _k:=\sup _{j<k}(\xi _j)$
.
$\xi _k:=\sup _{j<k}(\xi _j)$
.
Assume we already have
![]() $\bar a^j$
. Extend
$\bar a^j$
. Extend
![]() ${{\bar y}^j}^\frown \bar a^j$
to some candidate
${{\bar y}^j}^\frown \bar a^j$
to some candidate
![]() ${{\bar y}^j}^\frown \bar a^{j+1}$
of some height
${{\bar y}^j}^\frown \bar a^{j+1}$
of some height
![]() $\xi _{j+1}$
in E such that
$\xi _{j+1}$
in E such that
We can do this due to (*2 ).
So in the end we get some
![]() $\xi>\zeta $
in E and
$\xi>\zeta $
in E and
![]() $\bar b^\zeta $
with domain
$\bar b^\zeta $
with domain
![]() $I^*({>}\zeta ,{<}\xi )$
honoring majority and
$I^*({>}\zeta ,{<}\xi )$
honoring majority and
![]() $\tilde p$
such that
$\tilde p$
such that
 $$\begin{align} & \text{for every } (\zeta_0,\zeta+1)-\text{candidate } \bar y \text{ extending } \bar x, \bar y^\frown \bar b^\zeta \text{ is a } (\zeta_0,\xi)-\text{candidate}\nonumber\\
&\text{violating } (*_{1}) \text{ for some } \ell\in I^*({>}\zeta,{<}\xi). \end{align} $$
$$\begin{align} & \text{for every } (\zeta_0,\zeta+1)-\text{candidate } \bar y \text{ extending } \bar x, \bar y^\frown \bar b^\zeta \text{ is a } (\zeta_0,\xi)-\text{candidate}\nonumber\\
&\text{violating } (*_{1}) \text{ for some } \ell\in I^*({>}\zeta,{<}\xi). \end{align} $$
We then define
![]() $C^*$
below
$C^*$
below
![]() $\xi +1$
by adding only
$\xi +1$
by adding only
![]() $\xi $
, i.e.,
$\xi $
, i.e.,
![]() $\xi $
is the
$\xi $
is the
![]() $C^*$
-successor of
$C^*$
-successor of
![]() $\zeta $
. We extend the conditions
$\zeta $
. We extend the conditions
![]() $r_i$
by
$r_i$
by
![]() $b^\zeta _i$
for
$b^\zeta _i$
for
![]() $i<4$
. That is, we have
$i<4$
. That is, we have
![]() $\eta ^{r_i}(\ell )=b^\zeta _i(\ell )$
. This ends the construction of
$\eta ^{r_i}(\ell )=b^\zeta _i(\ell )$
. This ends the construction of
![]() $r_i\le \tilde p$
.
$r_i\le \tilde p$
.
Back in V, assume that (*2
) is forced by some
![]() $q'\le p_\beta \restriction \beta $
. Pick an increasing sequence
$q'\le p_\beta \restriction \beta $
. Pick an increasing sequence
![]() $\beta _i$
(
$\beta _i$
(
![]() $i<4$
) in S. We take the union of
$i<4$
) in S. We take the union of
![]() $q'$
and the
$q'$
and the
![]() $p_{\beta _i}$
, call it s, and strengthen
$p_{\beta _i}$
, call it s, and strengthen
![]() $s(\beta _i)=\tilde p$
to
$s(\beta _i)=\tilde p$
to
![]() $r_i$
. The resulting condition
$r_i$
. The resulting condition
![]() $s'$
forces the following:
$s'$
forces the following:
-
•
 for all
for all
 $\xi \in C^*$
. This is because
$\xi \in C^*$
. This is because
 $s'\le p_{\beta _i}$
(cf. Fact 5.55).
$s'\le p_{\beta _i}$
(cf. Fact 5.55). -
• The
 honor majority above
honor majority above
 $\zeta _0$
. This is because for all
$\zeta _0$
. This is because for all
 $\zeta \in C^*$
, the
$\zeta \in C^*$
, the
 $r_i(\zeta )$
are chosen as in (5.44) and therefore honor majority; and for
$r_i(\zeta )$
are chosen as in (5.44) and therefore honor majority; and for
 $\zeta \in \lambda \setminus (C^*\cup \zeta _0)$
we use values
$\zeta \in \lambda \setminus (C^*\cup \zeta _0)$
we use values
 $\bar b$
which honor majority.
$\bar b$
which honor majority. -
• Accordingly, the
 honor majority above some
honor majority above some
 $\gamma <\lambda $
(cf. Lemma 5.43(1)). Pick
$\gamma <\lambda $
(cf. Lemma 5.43(1)). Pick
 $\zeta _1$
such that
$\zeta _1$
such that
 $\sup (I^*({<}\zeta _1))>\gamma $
.
$\sup (I^*({<}\zeta _1))>\gamma $
. -
• So for all
 $\xi>\zeta _1$
the
$\xi>\zeta _1$
the  honor majority above
honor majority above
 $\zeta _1$
.
$\zeta _1$
. -
• Pick some
 $\zeta>\zeta _0,\zeta _1$
in
$\zeta>\zeta _0,\zeta _1$
in
 $C^*$
with
$C^*$
with
 $C^*$
-successor
$C^*$
-successor
 $\xi $
. By construction of the
$\xi $
. By construction of the
 $r_i$
,
$r_i$
,  is
is
 $b^\zeta _i$
. As
$b^\zeta _i$
. As
 $r_i$
extends
$r_i$
extends
 $x_i$
,
$x_i$
,  is a
is a
 $(\zeta _0,\zeta +1)$
-candidate extending
$(\zeta _0,\zeta +1)$
-candidate extending
 $\bar x$
. So by (*4
), the
$\bar x$
. So by (*4
), the  violate (*1
) at some
violate (*1
) at some
 $\ell \in I^*({>\zeta },{<\xi })$
, a contradiction.
$\ell \in I^*({>\zeta },{<\xi })$
, a contradiction.
Let
![]() $U\subseteq \lambda $
be club. Set
$U\subseteq \lambda $
be club. Set
![]() to be the odd elementsFootnote
18
of U. For
to be the odd elementsFootnote
18
of U. For
![]() with U-successor
with U-successor
![]() $\nu $
, set
$\nu $
, set
Lemma 5.58. (In
![]() $V_{\beta }$
.) There is an
$V_{\beta }$
.) There is an
![]() $r_0\le \tilde p$
, a club
$r_0\le \tilde p$
, a club
![]() $U\subseteq C^{r_0}\subseteq E$
, and, for
$U\subseteq C^{r_0}\subseteq E$
, and, for
![]() , an
, an
![]() $F_\xi :2^{A^U_\xi }\to 2^{A^U_\xi }$
such that
$F_\xi :2^{A^U_\xi }\to 2^{A^U_\xi }$
such that
![]() $:$
$:$
-
•
 $r_0\wedge p_\beta /G_\beta $
forces that
$r_0\wedge p_\beta /G_\beta $
forces that  .
. -
•
 $F_\xi $
is not constant
$F_\xi $
is not constant
 $:$
There are, for
$:$
There are, for
 $k=0,1$
,
$k=0,1$
,
 $z_\xi ^k$
in
$z_\xi ^k$
in
 $\operatorname {\mathrm {poss}}(r_0,I^*({<}\nu ))$
and
$\operatorname {\mathrm {poss}}(r_0,I^*({<}\nu ))$
and
 $\ell _\xi \in A^U_\xi $
such that
$\ell _\xi \in A^U_\xi $
such that
 $F_\xi (z_\xi ^k\restriction A^U_\xi )(\ell _\xi )=k$
. (Again,
$F_\xi (z_\xi ^k\restriction A^U_\xi )(\ell _\xi )=k$
. (Again,
 $\nu $
is the U-successor of
$\nu $
is the U-successor of
 $\xi $
.)
$\xi $
.)
(Note: Only those elements of
![]() $2^{A^U_\xi }$
that are compatible with
$2^{A^U_\xi }$
that are compatible with
![]() $r_0$
are relevant as arguments for
$r_0$
are relevant as arguments for
![]() $F_\xi $
.)
$F_\xi $
.)
Proof We construct
![]() $r_i$
for
$r_i$
for
![]() $i<4$
and U iteratively;
$i<4$
and U iteratively;
![]() $C^{r_i}$
will be independent of i, call it C.
$C^{r_i}$
will be independent of i, call it C.
All
![]() $r_i$
have the same trunk as
$r_i$
have the same trunk as
![]() $\tilde p$
; i.e.,
$\tilde p$
; i.e.,
![]() $\min (C)=\min (C^{\tilde p})=:\zeta _0$
and
$\min (C)=\min (C^{\tilde p})=:\zeta _0$
and
![]() $r_i\restriction \zeta _0:=\tilde p\restriction \zeta _0$
. We also set
$r_i\restriction \zeta _0:=\tilde p\restriction \zeta _0$
. We also set
![]() $\min (U)=\zeta _0$
.
$\min (U)=\zeta _0$
.
For all
![]() $\zeta \in C$
, we choose some
$\zeta \in C$
, we choose some
![]() $r^*_i(\zeta )$
as in (5.44), i.e.,
$r^*_i(\zeta )$
as in (5.44), i.e.,
![]() $r^*_0(\zeta )=\tilde p(\zeta )$
, and the
$r^*_0(\zeta )=\tilde p(\zeta )$
, and the
![]() $r^*_i(\zeta )$
for
$r^*_i(\zeta )$
for
![]() $i=1,2,3$
are such that the majority of their generics would be the
$i=1,2,3$
are such that the majority of their generics would be the
![]() $r^*_0(\zeta )$
-generic.
$r^*_0(\zeta )$
-generic.
Assume that we already know that some
![]() $\zeta $
is in U (which is a subset of C), and that we know
$\zeta $
is in U (which is a subset of C), and that we know
![]() $r_i\restriction \zeta $
for
$r_i\restriction \zeta $
for
![]() $i<4$
.
$i<4$
.
We now construct the U-successor
![]() $\xi $
of
$\xi $
of
![]() $\zeta $
,
$\zeta $
,
![]() $C\restriction [\zeta ,\xi ]$
, and
$C\restriction [\zeta ,\xi ]$
, and
![]() $r_i(\nu )$
for
$r_i(\nu )$
for
![]() $i<4$
and
$i<4$
and
![]() $\nu \in [\zeta ,\xi )$
.
$\nu \in [\zeta ,\xi )$
.
-
• Even case: If
 $\zeta $
is an even element of U, we start with
$\zeta $
is an even element of U, we start with
 $r_i(\zeta ):=r_i^*(\zeta )$
, but then add a “shield,” or “isolator” above
$r_i(\zeta ):=r_i^*(\zeta )$
, but then add a “shield,” or “isolator” above
 $\zeta $
: As in the previous proof, we iterate over all
$\zeta $
: As in the previous proof, we iterate over all
 $\zeta +1$
-candidates
$\zeta +1$
-candidates
 $\bar y^j$
, but but in (*3
), instead of violating (*1
) for some
$\bar y^j$
, but but in (*3
), instead of violating (*1
) for some
 $\ell $
, we demand that
$\ell $
, we demand that
 ${\bar y^j}^\frown \bar z^{j+1}$
is good. (We already know that every candidate can be extended to a good one.) Accordingly, we get some
${\bar y^j}^\frown \bar z^{j+1}$
is good. (We already know that every candidate can be extended to a good one.) Accordingly, we get some
 $\xi>\zeta $
and
$\xi>\zeta $
and
 $\bar b^\zeta $
with domain
$\bar b^\zeta $
with domain
 $I^*({>}\zeta , {<}\xi )$
(and honoring majority and
$I^*({>}\zeta , {<}\xi )$
(and honoring majority and
 $\tilde p$
) such that
$\tilde p$
) such that
 $\bar y^\frown \bar b^\zeta $
is good for every candidate
$\bar y^\frown \bar b^\zeta $
is good for every candidate
 $\bar y$
of height
$\bar y$
of height
 $\zeta +1$
; i.e.: (*′ 4)We now let this
$\zeta +1$
; i.e.: (*′ 4)We now let this $$\begin{align} & \text{If } \bar z \text{ is a } (\zeta+1,\nu)\text{-candidate whose restriction to } I^*({>}\zeta, {<}\xi)\ \text{is}\ \bar b^\zeta, \text{ then the}\nonumber\\
& f_{\nu}(z_i) \text{ honor majority above } \xi. \end{align} $$
$$\begin{align} & \text{If } \bar z \text{ is a } (\zeta+1,\nu)\text{-candidate whose restriction to } I^*({>}\zeta, {<}\xi)\ \text{is}\ \bar b^\zeta, \text{ then the}\nonumber\\
& f_{\nu}(z_i) \text{ honor majority above } \xi. \end{align} $$
 $\xi $
be the successor of
$\xi $
be the successor of
 $\zeta $
in both C and U (and extend each
$\zeta $
in both C and U (and extend each
 $p_i(\zeta )$
by
$p_i(\zeta )$
by
 $b_i$
).
$b_i$
).
-
• Odd case: Now assume
 $\zeta $
is odd in U. Then we choose some
$\zeta $
is odd in U. Then we choose some
 $\xi>\zeta $
in
$\xi>\zeta $
in
 $C^{\tilde p}$
large enough such that there are, for
$C^{\tilde p}$
large enough such that there are, for
 $k=0,1$
,
$k=0,1$
,
 $z^k_\xi $
in
$z^k_\xi $
in
 $\operatorname {\mathrm {poss}}(\tilde p,\xi )$
compatible with all the
$\operatorname {\mathrm {poss}}(\tilde p,\xi )$
compatible with all the
 $r_0$
constructed so far, such that the
$r_0$
constructed so far, such that the
 $f_{\xi }(z^k_\xi )(\ell )=k$
for some
$f_{\xi }(z^k_\xi )(\ell )=k$
for some
 $\ell> I^*({<}\zeta )$
. (Such
$\ell> I^*({<}\zeta )$
. (Such
 $\xi $
and
$\xi $
and
 $\ell $
have to exist as
$\ell $
have to exist as  is not in
is not in
 $V_\beta $
.)
$V_\beta $
.)We let C restricted to
 $[\zeta ,\xi ]$
be the same as
$[\zeta ,\xi ]$
be the same as
 $C^{\tilde p}$
, and set
$C^{\tilde p}$
, and set
 $r_i(\nu ):=r_i^*(\nu )$
for
$r_i(\nu ):=r_i^*(\nu )$
for
 $\nu \in C\cap [\zeta ,\xi )$
. (For
$\nu \in C\cap [\zeta ,\xi )$
. (For
 $\zeta \in [\zeta ,\xi )\setminus C$
there is no freedom left, i.e.,
$\zeta \in [\zeta ,\xi )\setminus C$
there is no freedom left, i.e.,
 $\tilde p(\zeta )$
is already completely determined, so the only choice for any
$\tilde p(\zeta )$
is already completely determined, so the only choice for any
 $r\le \tilde p$
is
$r\le \tilde p$
is
 $r(\zeta )=\tilde p(\zeta )$
.)
$r(\zeta )=\tilde p(\zeta )$
.)
This ends the construction of U and of
![]() $r_i$
(for
$r_i$
(for
![]() $i<4$
).
$i<4$
).
Pick
![]() , let
, let
![]() $\zeta $
be the U-predecessor and
$\zeta $
be the U-predecessor and
![]() $\nu $
the U-successor. We have to show that we can determine (modulo
$\nu $
the U-successor. We have to show that we can determine (modulo
![]() $p_{\beta }$
)
$p_{\beta }$
) ![]() from
from ![]() alone. (We already know that we can determine it from
alone. (We already know that we can determine it from ![]() .)
.)
Fix any
![]() $z^\zeta _*\in \operatorname {\mathrm {poss}}(r_0,\zeta +1)$
. Let
$z^\zeta _*\in \operatorname {\mathrm {poss}}(r_0,\zeta +1)$
. Let
![]() $x_0\in \operatorname {\mathrm {poss}}(r_0,\nu )$
. In particular
$x_0\in \operatorname {\mathrm {poss}}(r_0,\nu )$
. In particular
![]() $x_0$
extends
$x_0$
extends
![]() $b_0^\zeta $
. For
$b_0^\zeta $
. For
![]() $i=1,2,3$
, let
$i=1,2,3$
, let
![]() $x_i$
be the copy of
$x_i$
be the copy of
![]() $x_0$
with the initial segment
$x_0$
with the initial segment
![]() $x_0\restriction \xi $
replaced by
$x_0\restriction \xi $
replaced by
![]() $z^\zeta _*{}^\frown b_i^\zeta $
. Note that
$z^\zeta _*{}^\frown b_i^\zeta $
. Note that
![]() $\bar x$
is a candidate extending
$\bar x$
is a candidate extending
![]() $\bar b^\zeta $
. Accordingly the
$\bar b^\zeta $
. Accordingly the
![]() $f_\nu (x_i)$
honor majority above
$f_\nu (x_i)$
honor majority above
![]() $\xi $
. So we can define
$\xi $
. So we can define
This is well-defined,Footnote
19
and
![]() $r_0\wedge p_\beta /G_\beta $
forces that
$r_0\wedge p_\beta /G_\beta $
forces that ![]() .
.
We now summarize this lemma, which was shown in
![]() $V_\beta $
for some
$V_\beta $
for some
![]() $\beta \in S$
, from the point of view of the ground model. The lemma only uses the parameters
$\beta \in S$
, from the point of view of the ground model. The lemma only uses the parameters ![]() and
and ![]() (and
(and
![]() $\tilde p$
, which is just
$\tilde p$
, which is just ![]() ), so by absoluteness
), so by absoluteness
![]() $M_\beta $
knows that the Lemma is forced by
$M_\beta $
knows that the Lemma is forced by
![]() $p_{**}$
. Accordingly, we can find
$p_{**}$
. Accordingly, we can find
![]() $P_\beta $
-names for U,
$P_\beta $
-names for U,
![]() $F_\xi $
, etc. in
$F_\xi $
, etc. in
![]() $M_\beta $
. Using the last item of Fact 5.55, we can strengthen
$M_\beta $
. Using the last item of Fact 5.55, we can strengthen
![]() $p_{**}$
to
$p_{**}$
to
![]() $p_{**}^2$
to canonically read these names:
$p_{**}^2$
to canonically read these names:
Corollary 5.59. There is an
![]() $\alpha \in \Delta $
, a
$\alpha \in \Delta $
, a
![]() $p_{**}^2\le p_{**}$
in
$p_{**}^2\le p_{**}$
in
![]() $P_\alpha $
and
$P_\alpha $
and
![]() $P_{\alpha }$
-names for
$P_{\alpha }$
-names for
![]() $:$
A condition
$:$
A condition
![]() $r_0\le \tilde p$
, a set U, and a sequence
$r_0\le \tilde p$
, a set U, and a sequence
![]() $(F_\xi , z^0_\xi , z^1_\xi ,\ell ^0_\xi , \ell ^1_\xi )_{\xi \in U}$
, such that the following holds for all
$(F_\xi , z^0_\xi , z^1_\xi ,\ell ^0_\xi , \ell ^1_\xi )_{\xi \in U}$
, such that the following holds for all
![]() $\beta \in S$
, where we set
$\beta \in S$
, where we set
-
(1)
 $\alpha $
, the condition
$\alpha $
, the condition
 $p^2_{**}$
and all the names are in
$p^2_{**}$
and all the names are in
 $M_\beta $
.
$M_\beta $
. -
(2)
 $p^2_{**}\Vdash U\subseteq C^{r_0}\subseteq \lambda $
club.
$p^2_{**}\Vdash U\subseteq C^{r_0}\subseteq \lambda $
club. -
(3) For
 $k=0,1$
:
$k=0,1$
:
 .
. -
(4)
 , where we define
, where we define  $$\begin{align*}A_\xi\text{ to be }I^*({\ge}\xi,{<}\nu)\text{ with } \nu \text{ the } U\text{-successor of } \xi. \end{align*}$$
$$\begin{align*}A_\xi\text{ to be }I^*({\ge}\xi,{<}\nu)\text{ with } \nu \text{ the } U\text{-successor of } \xi. \end{align*}$$
5.12. Finding the generator
In this section we use these
![]() $p^2_{**}$
,
$p^2_{**}$
,
![]() $r_0$
,
$r_0$
,
![]() $(F_\xi , z^0_\xi , z^1_\xi ,\ell ^0_\xi , \ell ^1_\xi )_{\xi \in U}$
.
$(F_\xi , z^0_\xi , z^1_\xi ,\ell ^0_\xi , \ell ^1_\xi )_{\xi \in U}$
.
We start working in
![]() $V_{\beta }=V[G_\beta ]$
, where we assume
$V_{\beta }=V[G_\beta ]$
, where we assume
![]() $p^2_{**}\in G_\beta $
.
$p^2_{**}\in G_\beta $
.
Let
![]() and
and
![]() $\nu $
its U-successor. Set
$\nu $
its U-successor. Set

For
![]() $F_\xi $
it is enough to use
$F_\xi $
it is enough to use ![]() as input (the part in
as input (the part in
![]() $A_\xi \setminus A^?_\xi $
is determined anyway by
$A_\xi \setminus A^?_\xi $
is determined anyway by
![]() $r_0$
), and every element of
$r_0$
), and every element of
![]() $2^{A^?_\xi }$
is compatible with
$2^{A^?_\xi }$
is compatible with
![]() $r_0$
(and thus a possible input for
$r_0$
(and thus a possible input for
![]() $F_\xi $
). Identifying
$F_\xi $
). Identifying
![]() $2^B$
and
$2^B$
and
![]() ${\mathcal {P}}(B)$
as usual, we get
${\mathcal {P}}(B)$
as usual, we get
is such that
![]() $p^+_\beta /G_\beta $
forces
$p^+_\beta /G_\beta $
forces
We now define
So in particular
![]() $p^+_\beta /G_\beta $
forces that
$p^+_\beta /G_\beta $
forces that
Note that for every
![]() (in
(in
![]() $V_\beta $
that is) there is an
$V_\beta $
that is) there is an
![]() $r'\le r_0$
forcing that
$r'\le r_0$
forcing that ![]() . (
. (
![]() is club, so it is enough to leave freedom at
is club, so it is enough to leave freedom at
![]() $C'$
and we may assign arbitrary values everywhere else.)
$C'$
and we may assign arbitrary values everywhere else.)
Back in the ground model V, using the last item of Fact 5.55 again, we can strengthen
![]() $p^2_{**}$
to
$p^2_{**}$
to
![]() $p^3_{**}$
so thatFootnote
20
$p^3_{**}$
so thatFootnote
20
-
•
 ,
,
 ,
,
 $r_0$
,
$r_0$
,
 ,
,
 (actually, these are already read by
(actually, these are already read by
 $r^2_{**}$
).
$r^2_{**}$
). -
• The closure of these sets under
 ,
,  , finite unions, and finite intersections.
, finite unions, and finite intersections.
In particular, the (names for) all these sets are independent of
![]() $\beta \in S$
, modulo
$\beta \in S$
, modulo
![]() $p^3_{**}$
.Footnote
21
$p^3_{**}$
.Footnote
21
Lemma 5.63. (In V) ![]() .
.
Proof Let
![]() $q\le p^3_{**}$
in
$q\le p^3_{**}$
in
![]() $P_\beta $
be arbitrary. We have to show that q does not force (in
$P_\beta $
be arbitrary. We have to show that q does not force (in
![]() $P_\beta $
)
$P_\beta $
) ![]() .
.
For
![]() and
and
![]() $k=0,1$
, use
$k=0,1$
, use
![]() $r_0$
,
$r_0$
,
![]() $p_\beta ^+$
,
$p_\beta ^+$
,
![]() $z^k_\xi $
and
$z^k_\xi $
and
![]() $\ell _\xi $
as in Corollary 5.59 and set
$\ell _\xi $
as in Corollary 5.59 and set
![]() $b^k_\xi := z^k_\xi \cap A_\xi ^?$
.
$b^k_\xi := z^k_\xi \cap A_\xi ^?$
.
For
![]() $k=0,1$
, set
$k=0,1$
, set
![]() . Note that
. Note that
![]() $F(B^1)\setminus F(B^0)$
contains
$F(B^1)\setminus F(B^0)$
contains
![]() , a set of size
, a set of size
![]() $\lambda $
.
$\lambda $
.
Pick increasing
![]() $(\beta _i)_{i< 4}$
in S with
$(\beta _i)_{i< 4}$
in S with
![]() $\beta _0=\beta $
. Set
$\beta _0=\beta $
. Set
![]() $s:=q\wedge \bigwedge _{i<4} p^+_{\beta _i}\in P$
.
$s:=q\wedge \bigwedge _{i<4} p^+_{\beta _i}\in P$
.
Now for each
![]() $i<4$
, strengthen
$i<4$
, strengthen
![]() $s(\beta _i)$
(i.e.,
$s(\beta _i)$
(i.e.,
![]() $r_0$
) as follows: At the even intervals in some way that together they honor majority; and at the odd intervals (where we do not have to leave freedom) to the value
$r_0$
) as follows: At the even intervals in some way that together they honor majority; and at the odd intervals (where we do not have to leave freedom) to the value
![]() $B^{\operatorname {\mathrm {sgn}}(i)}$
(where
$B^{\operatorname {\mathrm {sgn}}(i)}$
(where
![]() $\operatorname {\mathrm {sgn}}(k)=0$
for
$\operatorname {\mathrm {sgn}}(k)=0$
for
![]() $k=0$
and
$k=0$
and
![]() $1$
for
$1$
for
![]() $k=1,2,3$
).
$k=1,2,3$
).
Accordingly, we have
or, when we split ![]() into the parts in and out of
into the parts in and out of ![]() :
:

Now assume towards a contradiction that ![]() . Then we get
. Then we get
But on the other hand we have

Applying (5.64) to both sides of the last line, we get
![]() $F(B^0)=^*\operatorname {\mathrm {major}}_{i=1,2,3}F(B^{\operatorname {\mathrm {sgn}}(i)}) =F(B^1)$
, a contradiction.
$F(B^0)=^*\operatorname {\mathrm {major}}_{i=1,2,3}F(B^{\operatorname {\mathrm {sgn}}(i)}) =F(B^1)$
, a contradiction.
Set
By choice of
![]() $p^3_{**}$
,
$p^3_{**}$
, ![]() and
and ![]() are canonically read by
are canonically read by
![]() $p^3_{**}$
(and independent of
$p^3_{**}$
(and independent of
![]() $\beta $
).
$\beta $
).
We now show that ![]() for
for ![]() . Again, here we are talking about
. Again, here we are talking about
![]() $z\in V_\beta $
. To make that more explicit, let us formulate in the ground model V:
$z\in V_\beta $
. To make that more explicit, let us formulate in the ground model V:
Lemma 5.66. For
![]() $\beta \in S$
,
$\beta \in S$
, 
(Note that, other than
![]() $F(z)$
,
$F(z)$
, ![]() will generally not be in
will generally not be in
![]() $V_\beta $
, and we have to force with
$V_\beta $
, and we have to force with
![]() $p^{+}_\beta /G_\beta $
.)
$p^{+}_\beta /G_\beta $
.)
Proof Work in
![]() $V_\beta $
.
$V_\beta $
. ![]() follows from Lemma 5.63, as
follows from Lemma 5.63, as ![]() .
.
Set ![]() . So by (5.61),
. So by (5.61),
![]() $p^+_\beta /G_\beta \le r_0$
forces:
$p^+_\beta /G_\beta \le r_0$
forces: ![]() . As
. As ![]() , we get
, we get ![]() . Then
. Then ![]() (or equivalently,
(or equivalently, ![]() ) implies
) implies ![]() and thus
and thus ![]() . To summarize:
. To summarize:

Now back in V assume towards a contradiction that some
![]() $q\le p^+_\beta $
forces that the lemma fails, i.e., that
$q\le p^+_\beta $
forces that the lemma fails, i.e., that ![]() in
in
![]() $V_\beta $
is a counterexample (in the final extension). By absoluteness, we can assume that q and
$V_\beta $
is a counterexample (in the final extension). By absoluteness, we can assume that q and ![]() are in
are in
![]() $M_\beta $
, in particular
$M_\beta $
, in particular ![]() is a
is a
![]() $P_\beta $
-name in
$P_\beta $
-name in
![]() $M_\beta $
. Strengthen
$M_\beta $
. Strengthen
![]() $q\restriction \beta $
to canonically read
$q\restriction \beta $
to canonically read ![]() . So for every
. So for every
![]() $\beta '\in S$
,
$\beta '\in S$
, ![]() will be evaluated in
will be evaluated in
![]() $V_{\beta '}$
to the same
$V_{\beta '}$
to the same
![]() $z\subseteq \lambda $
as
$z\subseteq \lambda $
as ![]() in
in
![]() $V_\beta $
.
$V_\beta $
.
Chose a
![]() $\beta '$
above
$\beta '$
above
![]() $\operatorname {\mathrm {supp}}(q)$
. Then we can strengthen
$\operatorname {\mathrm {supp}}(q)$
. Then we can strengthen
![]() $q\wedge p_{\beta '}$
at index
$q\wedge p_{\beta '}$
at index
![]() $\beta '$
, i.e.,
$\beta '$
, i.e.,
![]() $r_0$
, to some
$r_0$
, to some
![]() $r_1$
that forces
$r_1$
that forces ![]() . (Recall that we can fix the values in the odd intervals, as the even intervals still form a club). Let G be P-generic containing
. (Recall that we can fix the values in the odd intervals, as the even intervals still form a club). Let G be P-generic containing
![]() $q\wedge p^+_{\beta '}\wedge r_1$
. Then we have:
$q\wedge p^+_{\beta '}\wedge r_1$
. Then we have:
-
• The evaluation of
 in
in
 $V_{\beta '}$
, is the same as the evaluation of
$V_{\beta '}$
, is the same as the evaluation of  in
in
 $V_\beta $
, call it z.
$V_\beta $
, call it z. -
• Also the evaluation of
 and F are the same
and F are the same
 $\beta $
and
$\beta $
and
 $\beta '$
(cf. (5.62)).
$\beta '$
(cf. (5.62)). -
•
 is a counterexample (as this is forced by q).
is a counterexample (as this is forced by q).In particular,
 and
and  in the final extension.
in the final extension. -
•
 $p_{\beta '}\wedge r_1$
forces in
$p_{\beta '}\wedge r_1$
forces in
 $V_{\beta '+1}$
that
$V_{\beta '+1}$
that  ; also we have just seen that
; also we have just seen that  ; and so
; and so  by (*), a contradiction.
by (*), a contradiction.
For
, we define the following
![]() $P_\beta $
-names (independent of
$P_\beta $
-names (independent of
![]() $\beta $
):Footnote
22
$\beta $
):Footnote
22

as well as

So the
![]() $p^3_{**}$
forces that for all
$p^3_{**}$
forces that for all
![]() $z \in V_\beta $
the following is forced by
$z \in V_\beta $
the following is forced by
![]() $p^{+}_\beta /G_\beta $
:
$p^{+}_\beta /G_\beta $
:

Lemma 5.68.
![]() $p^3_{**}$
forces: For almost all
$p^3_{**}$
forces: For almost all
![]() ,
,
![]() $F^{\prime }_\xi $
is a Boolean algebra isomorphism from
$F^{\prime }_\xi $
is a Boolean algebra isomorphism from ![]() to
to ![]() .
.
Proof All and nothing: We claim that for almost all
![]() $\zeta $
,
$\zeta $
, ![]() . Assume that
. Assume that ![]() . Then
. Then ![]() , and
, and
![]() $\ell $
is not in
$\ell $
is not in ![]() , so there cannot be many such
, so there cannot be many such
![]() $\ell $
. Similarly
$\ell $
. Similarly
![]() $F^{\prime }_\zeta (\emptyset )=\emptyset $
for almost all
$F^{\prime }_\zeta (\emptyset )=\emptyset $
for almost all
![]() $\zeta $
.
$\zeta $
.
Unions: We claim that for almost all
![]() $\zeta $
,
$\zeta $
,
![]() $F^{\prime }_\zeta (a)\cup F^{\prime }_\zeta (b)= F^{\prime }_\zeta (a\cup b)$
for all subsets
$F^{\prime }_\zeta (a)\cup F^{\prime }_\zeta (b)= F^{\prime }_\zeta (a\cup b)$
for all subsets
![]() $a,b$
of
$a,b$
of ![]() . Let
. Let
![]() $A\subseteq \lambda $
be the set of counterexamples, i.e., for
$A\subseteq \lambda $
be the set of counterexamples, i.e., for
![]() $\xi \in A$
there are
$\xi \in A$
there are ![]() , and
, and
![]() $a_\xi $
,
$a_\xi $
,
![]() $b_\xi $
subsets of
$b_\xi $
subsets of ![]() such that
such that
![]() $\ell _\xi \in \big (F^{\prime }_\xi (a_\xi )\cup F^{\prime }_\xi (b_\xi )\big )\Delta F^{\prime }_\xi (a_\xi \cup b_\xi )$
. Set
$\ell _\xi \in \big (F^{\prime }_\xi (a_\xi )\cup F^{\prime }_\xi (b_\xi )\big )\Delta F^{\prime }_\xi (a_\xi \cup b_\xi )$
. Set
![]() $x:=\bigcup _{\xi \in A}a_\xi $
and
$x:=\bigcup _{\xi \in A}a_\xi $
and
![]() $y:=\bigcup _{\xi \in A}b_\xi $
. Then
$y:=\bigcup _{\xi \in A}b_\xi $
. Then
![]() $\ell _\xi $
is in
$\ell _\xi $
is in
![]() $\big (F'(x)\cup F'(y)\big ) \Delta F'(x\cup y)=^*\emptyset $
, so A cannot be large.
$\big (F'(x)\cup F'(y)\big ) \Delta F'(x\cup y)=^*\emptyset $
, so A cannot be large.
Complements: We claim that for almost all
![]() $\xi $
,
$\xi $
, ![]() . Let A be the set of counterexamples, i.e., for
. Let A be the set of counterexamples, i.e., for
![]() $\xi \in A$
there is an
$\xi \in A$
there is an ![]() and
and ![]() such that
such that ![]() . Then
. Then
![]() $\ell _\xi $
is in
$\ell _\xi $
is in ![]() , so A cannot be large.
, so A cannot be large.
Injectivity: We already know that union and complements (and thus disjointness) are preserved, so it is enough to show that a nonempty set is mapped to a nonempty set.
Assume this fails often, then we get an ![]() of size
of size
![]() $\lambda $
such that
$\lambda $
such that ![]() , a contradiction.
, a contradiction.
Surjectivity: Assume surjectivity fails often; i.e., there are many ![]() not in the range of
not in the range of
![]() $F^{\prime }_\zeta $
. Let y be the union of those
$F^{\prime }_\zeta $
. Let y be the union of those
![]() $b_\zeta $
. Pick
$b_\zeta $
. Pick
![]() $x\subseteq \lambda $
such that
$x\subseteq \lambda $
such that ![]() . So we can assume
. So we can assume ![]() and so
and so
![]() $F'(x)=^*y$
, which implies that
$F'(x)=^*y$
, which implies that ![]() for almost all
for almost all
![]() $\zeta $
, a contradiction.
$\zeta $
, a contradiction.
Lemma 5.69. For each
![]() $\beta \in S$
:
$\beta \in S$
:
![]() $p^3_{**}$
forces (in
$p^3_{**}$
forces (in
![]() $P_\beta $
): There is a
$P_\beta $
): There is a ![]() bijective such that for all
bijective such that for all ![]() (in
(in
![]() $V_\beta $
),
$V_\beta $
),
![]() $p^{+}_\beta /G_\beta $
forces
$p^{+}_\beta /G_\beta $
forces ![]() .
.
Proof Every Boolean algebra isomorphism from
![]() $P(A)$
to
$P(A)$
to
![]() $P(B)$
is generated by a bijection from A to B (the restriction to the atoms). So there is a
$P(B)$
is generated by a bijection from A to B (the restriction to the atoms). So there is a
![]() with
with
![]() such that
such that
![]() $\zeta \in U'$
implies that
$\zeta \in U'$
implies that
![]() $F^{\prime }_\zeta $
is generated by some bijection
$F^{\prime }_\zeta $
is generated by some bijection ![]() . So
. So
![]() $F'$
is generated by
$F'$
is generated by
![]() $g:=\bigcup _{\zeta \in U'} g_\zeta $
; and we can change g into a bijection from
$g:=\bigcup _{\zeta \in U'} g_\zeta $
; and we can change g into a bijection from ![]() to
to ![]() by changing less than
by changing less than
![]() $\lambda $
many values.
$\lambda $
many values.
We now strengthen
![]() $p^3_{**}$
to some q to continuously read
$p^3_{**}$
to some q to continuously read
![]() $f_{\text {gen}}$
(independently of
$f_{\text {gen}}$
(independently of
![]() $\beta $
), again using Fact 5.55.
$\beta $
), again using Fact 5.55.
So to summarize, we have the following (where we start with the
![]() $\Delta $
-system
$\Delta $
-system
![]() $(M_\beta ,p_\beta )_{\beta \in S}$
of Section 5.10):
$(M_\beta ,p_\beta )_{\beta \in S}$
of Section 5.10):
Corollary 5.70. There is
![]() $\alpha \in \Delta $
,
$\alpha \in \Delta $
,
![]() $q\in P_\alpha $
stronger than all
$q\in P_\alpha $
stronger than all
![]() $p_\beta \restriction \beta $
and canonically reading
$p_\beta \restriction \beta $
and canonically reading
![]() $r_0\le \tilde p$
,
$r_0\le \tilde p$
, ![]() ,
,
![]() $f_{\text {gen}}$
, and
$f_{\text {gen}}$
, and ![]() , such that the following holds for all
, such that the following holds for all
![]() $\beta \in S$
:
$\beta \in S$
:
-
•
 $q\wedge p_\beta $
with the conditionFootnote
23
at index
$q\wedge p_\beta $
with the conditionFootnote
23
at index
 $\beta $
strengthened to
$\beta $
strengthened to
 $r_0$
is a valid condition, called
$r_0$
is a valid condition, called
 $p^{++}_\beta $
.
$p^{++}_\beta $
. -
•
 $\alpha $
,
$\alpha $
,
 $p^{++}_\beta $
and the names are in
$p^{++}_\beta $
and the names are in
 $M_\beta $
.
$M_\beta $
. -
• q forces in
 $P_\beta $
:
$P_\beta $
:  ,
,  is a bijection, and if
is a bijection, and if  is in
is in
 $V_\beta $
, then
$V_\beta $
, then  .
.
5.13. Putting everything together
Corollary 5.71. (Assuming
![]() $\lambda $
is inaccessible and
$\lambda $
is inaccessible and
![]() $2^\lambda =\lambda ^+.$
) P forces that every automorphism of
$2^\lambda =\lambda ^+.$
) P forces that every automorphism of
![]() $P^\lambda _\lambda $
is somewhere trivial.
$P^\lambda _\lambda $
is somewhere trivial.
Proof Assume towards a contradiction that some
![]() $p_*$
forces that
$p_*$
forces that ![]() is a nowhere trivial automorphism represented by
is a nowhere trivial automorphism represented by ![]() .
.
As described in Section 5.10 we find a
![]() $\Delta $
-system
$\Delta $
-system
![]() $(M_\beta ,p_\beta )_{\beta \in S}$
with
$(M_\beta ,p_\beta )_{\beta \in S}$
with
![]() $p_\beta \restriction \beta \le p_*$
for all
$p_\beta \restriction \beta \le p_*$
for all
![]() $\beta \in S$
, and we find q,
$\beta \in S$
, and we find q, ![]() ,
,
![]() $f_{\text {gen}}$
as in Corollary 5.70, so in particular:
$f_{\text {gen}}$
as in Corollary 5.70, so in particular:
![]() $q\le p_\beta \restriction \beta $
for all S; and q forces that
$q\le p_\beta \restriction \beta $
for all S; and q forces that ![]() and that
and that ![]() is a bijection.
is a bijection.
As ![]() is nowhere trivial,
is nowhere trivial,
![]() $f_{\text {gen}}$
cannot be a generator, i.e., there is some
$f_{\text {gen}}$
cannot be a generator, i.e., there is some ![]() with
with ![]() . Fix a name for this z and let
. Fix a name for this z and let
![]() $q^*\le q$
canonically read z.
$q^*\le q$
canonically read z.
Pick
![]() $\beta \in S$
above
$\beta \in S$
above
![]() $\operatorname {\mathrm {dom}}(q^*)$
. So
$\operatorname {\mathrm {dom}}(q^*)$
. So
![]() $q^*\wedge p^{++}_\beta $
is a valid condition, which forces that in the final extension
$q^*\wedge p^{++}_\beta $
is a valid condition, which forces that in the final extension
![]() $V[G]$
the following holds:
$V[G]$
the following holds:
-
•
 with
with  , as this is forced by
, as this is forced by
 $q^*$
.
$q^*$
. -
•
 $z\in V_\beta $
, as
$z\in V_\beta $
, as
 $q^*$
canonically reads z.
$q^*$
canonically reads z. -
• By Corollary 5.70 and as
 $p^{++}_\beta {\kern-1.5pt}\in{\kern-1.5pt} G$
, we get
$p^{++}_\beta {\kern-1.5pt}\in{\kern-1.5pt} G$
, we get  , a contradiction.
, a contradiction.
Acknowledgments
We thank an anonymous referee for numerous corrections. A variant of Sections 3 and 4, were included in the third author’s thesis.
Funding
Supported by Austrian Science Fund (FWF): grants [10.55776/P33420, 10.55776/P33895] (first author) and [10.55776/T1081] (third author); and Israel Science Foundation (ISF) grant 2320/23 (second author). For open access purposes, the authors have applied a CC BY public copyright license to any author accepted manuscript version arising from this submission.