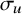1 Introduction
The ![]() is the parameter space of complete nestings
is the parameter space of complete nestings
of vector subspaces of
![]() $\mathbb {C}^n$
, where
$\mathbb {C}^n$
, where
![]() $\dim V_i = i$
. The Chow ring
$\dim V_i = i$
. The Chow ring
![]() $A(\mathsf {Flags}_n)$
of the flag variety has a basis of Schubert cycles
$A(\mathsf {Flags}_n)$
of the flag variety has a basis of Schubert cycles
![]() $\sigma _u$
indexed by permutations
$\sigma _u$
indexed by permutations
![]() $u \in S_n$
. One of the major open problems of algebraic combinatorics is to give a positive combinatorial formula for the structure coefficients defined by
$u \in S_n$
. One of the major open problems of algebraic combinatorics is to give a positive combinatorial formula for the structure coefficients defined by
Such rules are currently known only for special classes of permutations. For example, the Littlewood–Richardson rules compute the coefficients in the cases where
![]() $u,v,w$
are all p-Grassmannian for some common p; here, we say u is
$u,v,w$
are all p-Grassmannian for some common p; here, we say u is ![]() if
if
![]() $u(i) < u(i+1)$
whenever
$u(i) < u(i+1)$
whenever
![]() $i \neq p$
. For other special cases with known combinatorial rules; see, for example, [Reference MonkMon59, Reference SottileSot96, Reference Purbhoo and SottilePS09, Reference Knutson and PurbhooKP11, Reference WyserWys13, Reference Mészáros, Panova and PostnikovMPP14, Reference Buch, Kresch, Purbhoo and TamvakisBKPT16, Reference Knutson and Zinn-JustinKZ17, Reference HuangHua23, Reference Knutson and Zinn-JustinKZ23]. Much work has been done on extending the combinatorics of Littlewood–Richardson coefficients both to richer algebraic theories and to further families of analogous moduli spaces (see, e.g., [Reference BuchBuc02, Reference Knutson and TaoKT03, Reference Thomas and YongTY09, Reference BuchBuc15, Reference Buch and SamuelBS16, Reference Pechenik and YongPY17]). For discussion of the significance of positive combinatorial formulas for these and related numbers, see [Reference KnutsonKnu23].
$i \neq p$
. For other special cases with known combinatorial rules; see, for example, [Reference MonkMon59, Reference SottileSot96, Reference Purbhoo and SottilePS09, Reference Knutson and PurbhooKP11, Reference WyserWys13, Reference Mészáros, Panova and PostnikovMPP14, Reference Buch, Kresch, Purbhoo and TamvakisBKPT16, Reference Knutson and Zinn-JustinKZ17, Reference HuangHua23, Reference Knutson and Zinn-JustinKZ23]. Much work has been done on extending the combinatorics of Littlewood–Richardson coefficients both to richer algebraic theories and to further families of analogous moduli spaces (see, e.g., [Reference BuchBuc02, Reference Knutson and TaoKT03, Reference Thomas and YongTY09, Reference BuchBuc15, Reference Buch and SamuelBS16, Reference Pechenik and YongPY17]). For discussion of the significance of positive combinatorial formulas for these and related numbers, see [Reference KnutsonKnu23].
Building on work of B. Wyser [Reference WyserWys13], we present an inverse Grassmannian analogue of the Littlewood–Richardson rule. Specifically, we solve the problem of giving a positive combinatorial formula for multiplying the Schubert cycles
![]() $\sigma _{u^{-1}}$
and
$\sigma _{u^{-1}}$
and
![]() $\sigma _{v^{-1}}$
, where u is p-Grassmannian and v is q-Grassmannian. Wyser’s work solved many instances of these problems but required several additional technical hypotheses. We handle the remaining cases by embedding them into settings where these additional hypotheses hold. Wyser’s approach was to realize
$\sigma _{v^{-1}}$
, where u is p-Grassmannian and v is q-Grassmannian. Wyser’s work solved many instances of these problems but required several additional technical hypotheses. We handle the remaining cases by embedding them into settings where these additional hypotheses hold. Wyser’s approach was to realize
![]() $\sigma _{u^{-1}} \cdot \sigma _{v^{-1}}$
as the class of a Richardson variety in
$\sigma _{u^{-1}} \cdot \sigma _{v^{-1}}$
as the class of a Richardson variety in
![]() $\mathsf {Flags}_n$
and to show that under his hypotheses this variety is the closure of an orbit for the action of a
$\mathsf {Flags}_n$
and to show that under his hypotheses this variety is the closure of an orbit for the action of a
![]() $2$
-block Levi subgroup of
$2$
-block Levi subgroup of
![]() $\mathrm {GL}_n(\mathbb {C})$
; he then derives his formula from work of M. Brion [Reference BrionBri01] describing the classes of such orbit closures (K-orbits). Our extension of Wyser’s work, in contrast, involves purely combinatorial tools.
$\mathrm {GL}_n(\mathbb {C})$
; he then derives his formula from work of M. Brion [Reference BrionBri01] describing the classes of such orbit closures (K-orbits). Our extension of Wyser’s work, in contrast, involves purely combinatorial tools.
In sharp contrast to the Littlewood–Richardson case, these inverse Grassmannian products turn out to be ![]() , that is
, that is
![]() $c_{u^{-1}, v^{-1}}^w \in \{0,1\}$
for all w. Multiplicity-freeness has powerful geometric and combinatorial consequences (e.g., [Reference BrionBri03, Reference KnutsonKnu09, Reference Hamaker, Patrias, Pechenik and WilliamsHPPW20, Reference Pechenik and SatrianoPS24]); for instance, our results imply that the K-theory classes of the corresponding Richardson varieties are determined by their Chow classes.
$c_{u^{-1}, v^{-1}}^w \in \{0,1\}$
for all w. Multiplicity-freeness has powerful geometric and combinatorial consequences (e.g., [Reference BrionBri03, Reference KnutsonKnu09, Reference Hamaker, Patrias, Pechenik and WilliamsHPPW20, Reference Pechenik and SatrianoPS24]); for instance, our results imply that the K-theory classes of the corresponding Richardson varieties are determined by their Chow classes.
We now describe our first theorem in more detail. Say a permutation u is ![]() if
if
![]() $u^{-1}$
is p-Grassmannian and say u is
$u^{-1}$
is p-Grassmannian and say u is ![]() if it is p-inverse Grassmannian for some p. Our combinatorial rule extends the rule of Wyser [Reference WyserWys13, Theorem 3.10] based on combinatorial objects called clans, which were introduced by [Reference Matsuki and ŌshimaMO90, Reference YamamotoYam97] in the context of K-orbits. Wyser’s work provides a positive combinatorial formula for
if it is p-inverse Grassmannian for some p. Our combinatorial rule extends the rule of Wyser [Reference WyserWys13, Theorem 3.10] based on combinatorial objects called clans, which were introduced by [Reference Matsuki and ŌshimaMO90, Reference YamamotoYam97] in the context of K-orbits. Wyser’s work provides a positive combinatorial formula for
![]() $c_{u, v}^w$
when
$c_{u, v}^w$
when
-
• u and
 $v \in S_n$
are, respectively, p-inverse Grassmannian and q-inverse Grassmannian,
$v \in S_n$
are, respectively, p-inverse Grassmannian and q-inverse Grassmannian, -
•
 $p+q=n$
and
$p+q=n$
and -
•
 $u \leq w_0^{(n)}v$
(where
$u \leq w_0^{(n)}v$
(where
 $w_0^{(n)} \in S_n$
is the permutation of greatest Coxeter length and the comparison is with respect to the strong Bruhat order);
$w_0^{(n)} \in S_n$
is the permutation of greatest Coxeter length and the comparison is with respect to the strong Bruhat order);
see Theorem 3.1 for a precise statement of Wyser’s theorem. To eliminate these technical conditions, we introduce the notion of backstable clans by analogy with the backstable Schubert calculus of [Reference Lam, Lee and ShimozonoLLS21]. We believe that backstable clans will additionally be amenable to the study of backstabilized K-orbits in infinite flag varieties; however, we do not pursue that application here.
For inverse Grassmannian permutations
![]() $u,v$
, we associate a backstable clan
$u,v$
, we associate a backstable clan
![]() $\gamma _{u,v}$
. (When Wyser’s technical conditions hold, this backstable clan becomes the ordinary clan that he studies.) We also define a (backstable) rainbow clan
$\gamma _{u,v}$
. (When Wyser’s technical conditions hold, this backstable clan becomes the ordinary clan that he studies.) We also define a (backstable) rainbow clan
![]() $\Omega _{p,q}$
associated to any pair of integers
$\Omega _{p,q}$
associated to any pair of integers
![]() $p,q$
. Finally, we need an action of the
$p,q$
. Finally, we need an action of the
![]() $0$
-Hecke algebra on backstable clans, denoted by ‘
$0$
-Hecke algebra on backstable clans, denoted by ‘
![]() $\cdot $
’; we write
$\cdot $
’; we write
![]() $T_w$
for the element of the
$T_w$
for the element of the
![]() $0$
-Hecke algebra corresponding to the permutation w. All of these notions are defined precisely in Section 2. With these definitions, we have the following first main theorem, which we derive from Wyser’s formula via stabilization arguments.
$0$
-Hecke algebra corresponding to the permutation w. All of these notions are defined precisely in Section 2. With these definitions, we have the following first main theorem, which we derive from Wyser’s formula via stabilization arguments.
Theorem 1.1. Let
![]() $u,v \in S_n$
be permutations, where u is p-inverse Grassmannian and v is q-inverse Grassmannian. Then the product
$u,v \in S_n$
be permutations, where u is p-inverse Grassmannian and v is q-inverse Grassmannian. Then the product
![]() $\sigma _u \cdot \sigma _v \in A(\mathsf {Flags}_n)$
is a multiplicity-free sum of Schubert cycles. Precisely,
$\sigma _u \cdot \sigma _v \in A(\mathsf {Flags}_n)$
is a multiplicity-free sum of Schubert cycles. Precisely,
where
 $$\begin{align*}c_{u,v}^w = \begin{cases} 1, & \text{if and only if } \ell(w)=\ell(u)+\ell(v) \text{ and } T_w \cdot \gamma_{u,v} = \Omega_{p,q}; \\ 0, & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}c_{u,v}^w = \begin{cases} 1, & \text{if and only if } \ell(w)=\ell(u)+\ell(v) \text{ and } T_w \cdot \gamma_{u,v} = \Omega_{p,q}; \\ 0, & \text{otherwise}. \end{cases} \end{align*}$$
For illustrations of the use of Theorem 1.1, see Examples 3.4 and 3.5.
Our second main theorem uses analogous combinatorics to provide a positive combinatorial formula for a related class of products. Let
![]() $s_i \in S_n$
denote the permutation that transposes i and
$s_i \in S_n$
denote the permutation that transposes i and
![]() $i+1$
. Say that a permutation is
$i+1$
. Say that a permutation is ![]() if it is of the form
if it is of the form
![]() $s_p w$
for some p-inverse Grassmannian permutation
$s_p w$
for some p-inverse Grassmannian permutation
![]() $w \neq \mathrm {id}$
. Building on Theorem 1.1, we establish the following positive combinatorial rule for multiplying an inverse Grassmannian Schubert cycle by a subjacent Schubert cycle. Remarkably, such products are also multiplicity-free.
$w \neq \mathrm {id}$
. Building on Theorem 1.1, we establish the following positive combinatorial rule for multiplying an inverse Grassmannian Schubert cycle by a subjacent Schubert cycle. Remarkably, such products are also multiplicity-free.
Theorem 1.2. Let
![]() $u,v \in S_n$
be permutations, where
$u,v \in S_n$
be permutations, where
![]() $u\neq \mathrm {id}$
is p-inverse Grassmannian and v is q-inverse Grassmannian. Then the product
$u\neq \mathrm {id}$
is p-inverse Grassmannian and v is q-inverse Grassmannian. Then the product
![]() $\sigma _{s_p u} \cdot \sigma _v \in A(\mathsf {Flags}_n)$
is a multiplicity-free sum of Schubert cycles. Specifically,
$\sigma _{s_p u} \cdot \sigma _v \in A(\mathsf {Flags}_n)$
is a multiplicity-free sum of Schubert cycles. Specifically,
where
 $$\begin{align*}c_{s_p u,v}^w = \begin{cases} 1, & \text{if and only if } \ell(w)=\ell(u)+\ell(v)-1 \text{ and } T_w \cdot \gamma_{u,v} \in \Psi_{p,q}; \\ 0, & \text{otherwise}, \end{cases} \end{align*}$$
$$\begin{align*}c_{s_p u,v}^w = \begin{cases} 1, & \text{if and only if } \ell(w)=\ell(u)+\ell(v)-1 \text{ and } T_w \cdot \gamma_{u,v} \in \Psi_{p,q}; \\ 0, & \text{otherwise}, \end{cases} \end{align*}$$
where
![]() $\Psi _{p,q}$
denotes a set of almost rainbow clans defined precisely in Section 2.
$\Psi _{p,q}$
denotes a set of almost rainbow clans defined precisely in Section 2.
For an illustration of the use of Theorem 1.2, see Example 5.4. Note that the product of two subjacent Schubert cycles is not generally multiplicity-free (see Example 5.5), so the multiplicity-freeness of Theorems 1.1 and 1.2 does not generalize.
Our main tools for deriving Theorem 1.2 from Theorem 1.1 are new families of linear relations among Schubert structure coefficients that we establish in Propositions 4.2 and 4.10. We suspect that these linear relations have further consequences, which we briefly explore in Section 4.
This paper is organized as follows. In Section 2, we recall necessary background on permutations and Schubert polynomials, and we initiate a theory of backstable clans. In Section 3, we derive Theorem 1.1 from a theorem of Wyser, together with the new notion of backstable clans and a well-known stabilization technique. In Section 4, we establish new linear relations among Schubert structure coefficients, together with K-theoretic analogues and various corollaries. In particular, the families of linear relations from Propositions 4.2 and 4.10 will be key in our proof of Theorem 1.2. Section 5 contains the proof of Theorem 1.2 and related remarks.
2 Preliminaries
2.1 Permutations
We write
![]() $[n]$
for the set
$[n]$
for the set
![]() $\{1, 2, \dots , n\}$
.
$\{1, 2, \dots , n\}$
.
Let
![]() $S_{\mathbb {Z}}$
denote the group of permutations of
$S_{\mathbb {Z}}$
denote the group of permutations of
![]() $\mathbb {Z}$
that fix all but finitely many elements. For
$\mathbb {Z}$
that fix all but finitely many elements. For
![]() $i \in \mathbb {Z}$
, the
$i \in \mathbb {Z}$
, the ![]() is the involution that switches i and
is the involution that switches i and
![]() $i+1$
. Note that
$i+1$
. Note that
![]() $S_{\mathbb {Z}}$
is generated by
$S_{\mathbb {Z}}$
is generated by
![]() $\{s_i\}_{i \in \mathbb {Z}}$
. The
$\{s_i\}_{i \in \mathbb {Z}}$
. The ![]() of
of
![]() $w \in S_{\mathbb {Z}}$
is the length of a minimal expression for w as a product of simple transpositions.
$w \in S_{\mathbb {Z}}$
is the length of a minimal expression for w as a product of simple transpositions.
We write
![]() $S_+$
for the subgroup generated by
$S_+$
for the subgroup generated by
![]() $\{s_i\}_{i> 0}$
and write
$\{s_i\}_{i> 0}$
and write
![]() $S_n$
for the subgroup generated by
$S_n$
for the subgroup generated by
![]() $\{s_i\}_{0 < i < n}$
. For a permutation
$\{s_i\}_{0 < i < n}$
. For a permutation
![]() $w \in S_n$
, we often write w in one-line notation as
$w \in S_n$
, we often write w in one-line notation as
![]() $w(1)w(2) \dots w(n)$
. If we write w in one-line notation, then
$w(1)w(2) \dots w(n)$
. If we write w in one-line notation, then
![]() $ws_i$
is obtained by swapping the entries in positions i and
$ws_i$
is obtained by swapping the entries in positions i and
![]() $i+1$
;
$i+1$
;
![]() $s_iw$
is obtained by swapping the letters i and
$s_iw$
is obtained by swapping the letters i and
![]() $i+1$
. The
$i+1$
. The ![]() is
is
![]() $n (n-1) \dots 1$
. The inclusion map
$n (n-1) \dots 1$
. The inclusion map
![]() $\iota : S_n \to S_{n+1}$
sends w to
$\iota : S_n \to S_{n+1}$
sends w to
![]() $w(1)w(2)\cdots w(n)(n+1)$
.
$w(1)w(2)\cdots w(n)(n+1)$
.
![]() on permutations is defined by
on permutations is defined by
![]() $u \leq _L w$
if
$u \leq _L w$
if
![]() $w = vu$
for some permutation v with
$w = vu$
for some permutation v with
![]() $ \ell (u) + \ell (v) = \ell (w)$
. Similarly, in this case, we write
$ \ell (u) + \ell (v) = \ell (w)$
. Similarly, in this case, we write
![]() $v \leq _R w$
and call this the
$v \leq _R w$
and call this the ![]() . Let
. Let
![]() $t_{i,j} \in S_{\mathbb {Z}}$
denote the involution swapping i and j.
$t_{i,j} \in S_{\mathbb {Z}}$
denote the involution swapping i and j. ![]() is the transitive closure of the covering relations
is the transitive closure of the covering relations
![]() $wt_{i,j} \lessdot w$
for
$wt_{i,j} \lessdot w$
for
![]() $\ell (wt_{i,j}) = \ell (w) - 1$
. We write Bruhat order comparisons as
$\ell (wt_{i,j}) = \ell (w) - 1$
. We write Bruhat order comparisons as
![]() $u \leq w$
, without subscripts. The weak orders are weak in the sense that the corresponding relations are subsets of the Bruhat order relation.
$u \leq w$
, without subscripts. The weak orders are weak in the sense that the corresponding relations are subsets of the Bruhat order relation.
For a permutation
![]() $w \in S_{\mathbb {Z}}$
, say that i is a
$w \in S_{\mathbb {Z}}$
, say that i is a ![]() of w if
of w if
![]() $w(i)> w(i+1)$
, equivalently if
$w(i)> w(i+1)$
, equivalently if
![]() $ws_i < w$
. Say that i is a
$ws_i < w$
. Say that i is a ![]() of
of
![]() $w \in S_{\mathbb {Z}}$
if
$w \in S_{\mathbb {Z}}$
if
![]() $w^{-1}(i)> w^{-1}(i+1)$
, equivalently if
$w^{-1}(i)> w^{-1}(i+1)$
, equivalently if
![]() $s_i w < w$
. The
$s_i w < w$
. The ![]() of a permutation
of a permutation
![]() $w \in S_{\mathbb {Z}}$
is the function
$w \in S_{\mathbb {Z}}$
is the function
![]() $c(w) : \mathbb {Z} \to \mathbb {Z}_{\geq 0}$
such that
$c(w) : \mathbb {Z} \to \mathbb {Z}_{\geq 0}$
such that
![]() $c(w)(i)$
equals the number of
$c(w)(i)$
equals the number of
![]() $j> i$
such that
$j> i$
such that
![]() $w(j) < w(i)$
; as a shorthand, we often write
$w(j) < w(i)$
; as a shorthand, we often write
![]() $c_i(w) = c(w)(i)$
.
$c_i(w) = c(w)(i)$
.
A permutation
![]() $w \in S_{\mathbb {Z}}$
is
$w \in S_{\mathbb {Z}}$
is ![]() if k is its unique descent or if it has no descent. Note that the identity permutation is k-Grassmannian for all k. We say w is
if k is its unique descent or if it has no descent. Note that the identity permutation is k-Grassmannian for all k. We say w is ![]() if it is k-Grassmannian for some k. We say that w is
if it is k-Grassmannian for some k. We say that w is ![]() (resp.
(resp. ![]() ) if
) if
![]() $w^{-1}$
is k-Grassmannian (resp. Grassmannian).
$w^{-1}$
is k-Grassmannian (resp. Grassmannian).
The ![]() has generators
has generators
![]() $T_i$
for
$T_i$
for
![]() $i \in \mathbb {Z}$
satisfying
$i \in \mathbb {Z}$
satisfying
 $$ \begin{align} T_i^2 &= T_i, \nonumber\\ T_i T_j &= T_j T_i \quad \text{(if}\ |i-j|> 1\text{), and} \\ T_i T_{i+1} T_i &= T_{i+1} T_i T_{i+1}.\nonumber \end{align} $$
$$ \begin{align} T_i^2 &= T_i, \nonumber\\ T_i T_j &= T_j T_i \quad \text{(if}\ |i-j|> 1\text{), and} \\ T_i T_{i+1} T_i &= T_{i+1} T_i T_{i+1}.\nonumber \end{align} $$
For every
![]() $w \in S_{\mathbb {Z}}$
of length k, there is a corresponding element
$w \in S_{\mathbb {Z}}$
of length k, there is a corresponding element
![]() $T_w \in \mathcal {H}_{\mathbb {Z}}$
obtained by taking any reduced decomposition
$T_w \in \mathcal {H}_{\mathbb {Z}}$
obtained by taking any reduced decomposition
![]() $w = s_{i_1} \cdots s_{i_k}$
and setting
$w = s_{i_1} \cdots s_{i_k}$
and setting
![]() $T_w = T_{i_1} \cdots T_{i_k}$
. The elements
$T_w = T_{i_1} \cdots T_{i_k}$
. The elements
![]() $T_w$
for
$T_w$
for
![]() $w \in S_{\mathbb {Z}}$
are a linear basis of
$w \in S_{\mathbb {Z}}$
are a linear basis of
![]() $\mathcal {H}_{\mathbb {Z}}$
.
$\mathcal {H}_{\mathbb {Z}}$
.
2.2 Schubert polynomials
![]() are defined recursively as follows. For
are defined recursively as follows. For
![]() $w_0^{(n)} \in S_n$
, set the Schubert polynomial
$w_0^{(n)} \in S_n$
, set the Schubert polynomial
![]() $\mathfrak {S}_{w_0^{(n)}} = x_1^{n-1} x_2^{n-2} \cdots x_n^0$
. For w such that
$\mathfrak {S}_{w_0^{(n)}} = x_1^{n-1} x_2^{n-2} \cdots x_n^0$
. For w such that
![]() $ws_i < w$
, set
$ws_i < w$
, set
where
![]() $N_i$
is the
$N_i$
is the ![]() that acts on
that acts on
![]() $f \in \mathbb {Z}[x_1, \dots , x_n]$
by
$f \in \mathbb {Z}[x_1, \dots , x_n]$
by
Here,
![]() $s_i$
acts on a polynomial by swapping variables
$s_i$
acts on a polynomial by swapping variables
![]() $x_i$
and
$x_i$
and
![]() $x_{i+1}$
.
$x_{i+1}$
.
We have
![]() $\mathfrak {S}_w = \mathfrak {S}_{\iota (w)}$
, so we may treat Schubert polynomials as indexed by the elements of
$\mathfrak {S}_w = \mathfrak {S}_{\iota (w)}$
, so we may treat Schubert polynomials as indexed by the elements of
![]() $S_+$
. The set of Schubert polynomials
$S_+$
. The set of Schubert polynomials
![]() $\{\mathfrak {S}_w \}_{w \in S_+}$
is a linear basis of the free
$\{\mathfrak {S}_w \}_{w \in S_+}$
is a linear basis of the free
![]() $\mathbb {Z}$
-module
$\mathbb {Z}$
-module
![]() $\mathbb {Z}[x_1, x_2, x_3, \dots ]$
. In particular, there are structure coefficients defined by
$\mathbb {Z}[x_1, x_2, x_3, \dots ]$
. In particular, there are structure coefficients defined by
For
![]() $u,v,w \in S_n$
, these structure coefficients agree with the Schubert structure coefficients defined in Section 1, that is,
$u,v,w \in S_n$
, these structure coefficients agree with the Schubert structure coefficients defined in Section 1, that is,
![]() $c_{u,v}^w = d_{u,v}^w$
. Hence, we can study the structure coefficients
$c_{u,v}^w = d_{u,v}^w$
. Hence, we can study the structure coefficients
![]() $c_{u,v}^w$
by using Schubert polynomials in place of Schubert cycles. References for basic facts about Schubert polynomials include [Reference MacdonaldMac91, Reference Manivel and SwallowMan01].
$c_{u,v}^w$
by using Schubert polynomials in place of Schubert cycles. References for basic facts about Schubert polynomials include [Reference MacdonaldMac91, Reference Manivel and SwallowMan01].
2.3 Backstable clans
A ![]() is a partial matching of the integers such that there exist
is a partial matching of the integers such that there exist
![]() $i,j \in \mathbb {Z}$
such that
$i,j \in \mathbb {Z}$
such that
![]() $i - k$
is paired with
$i - k$
is paired with
![]() $j+k$
for all
$j+k$
for all
![]() $k> 0$
, together with an assignment of labels from
$k> 0$
, together with an assignment of labels from ![]() to the unmatched integers. We say that such a backstable clan
to the unmatched integers. We say that such a backstable clan
![]() $\gamma $
is
$\gamma $
is ![]() on
on
![]() $[i,j]$
and call
$[i,j]$
and call
![]() $\gamma $
an
$\gamma $
an ![]() . (Note that if
. (Note that if
![]() $\gamma $
is supported on
$\gamma $
is supported on
![]() $[i,j]$
, then
$[i,j]$
, then
![]() $\gamma $
is also supported on
$\gamma $
is also supported on
![]() $[i-a,j+a]$
for any
$[i-a,j+a]$
for any
![]() $a \geq 0$
.) When we draw diagrams to illustrate an
$a \geq 0$
.) When we draw diagrams to illustrate an
![]() $[i,j]$
-clan
$[i,j]$
-clan
![]() $\gamma $
, we often restrict to the interval
$\gamma $
, we often restrict to the interval
![]() $[i,j]$
since all information about
$[i,j]$
since all information about
![]() $\gamma $
can be extracted from this finite region. For examples of backstable clans, see Figures 1, 2 and 3.
$\gamma $
can be extracted from this finite region. For examples of backstable clans, see Figures 1, 2 and 3.

Figure 1 The rainbow clans
![]() $\Omega _{5,2}$
(left) and
$\Omega _{5,2}$
(left) and
![]() $\Omega _{0,1}$
(right).
$\Omega _{0,1}$
(right).

Figure 2 Some examples of the Hecke action on clans.

Figure 3 Some representative almost rainbow clans.
In the previous literature, ‘clans’ are restricted to the interval
![]() $[1,n]$
; we identify these objects with
$[1,n]$
; we identify these objects with
![]() $[1,n]$
-clans. Clans were introduced in [Reference Matsuki and ŌshimaMO90, Reference YamamotoYam97] in the context of K-orbits. For more recent work using clans in a related K-orbit context, see, for example, [Reference Wyser and YongWY14, Reference Woo and WyserWW15]. We believe that backstable clans will additionally be amenable to the study of backstabilized K-orbits, analogous to the backstable Schubert calculus of [Reference Lam, Lee and ShimozonoLLS21]; however, we do not pursue that application here. In this paper, backstable clans are a tool for explicating the Schubert calculus of
$[1,n]$
-clans. Clans were introduced in [Reference Matsuki and ŌshimaMO90, Reference YamamotoYam97] in the context of K-orbits. For more recent work using clans in a related K-orbit context, see, for example, [Reference Wyser and YongWY14, Reference Woo and WyserWW15]. We believe that backstable clans will additionally be amenable to the study of backstabilized K-orbits, analogous to the backstable Schubert calculus of [Reference Lam, Lee and ShimozonoLLS21]; however, we do not pursue that application here. In this paper, backstable clans are a tool for explicating the Schubert calculus of
![]() $\mathsf {Flags}_n$
.
$\mathsf {Flags}_n$
.
For a backstable clan
![]() $\gamma $
, let
$\gamma $
, let
![]() $\zeta (\gamma )$
denote the number of
$\zeta (\gamma )$
denote the number of ![]() labels minus the number of
labels minus the number of ![]() labels. If
labels. If
![]() $\gamma $
is supported on
$\gamma $
is supported on
![]() $[i,j]$
and
$[i,j]$
and
![]() $\zeta (\gamma ) = \zeta $
, we say that
$\zeta (\gamma ) = \zeta $
, we say that
![]() $\gamma $
is a
$\gamma $
is a ![]() , where
, where
![]() $p = \frac {1}{2} (i+j+\zeta -1)$
and
$p = \frac {1}{2} (i+j+\zeta -1)$
and
![]() $q = \frac {1}{2}(i+j - \zeta -1)$
. Note that
$q = \frac {1}{2}(i+j - \zeta -1)$
. Note that
![]() $\zeta = p-q$
and
$\zeta = p-q$
and
![]() $i+j-1 = p+q$
; moreover, a backstable clan
$i+j-1 = p+q$
; moreover, a backstable clan
![]() $\gamma $
supported on
$\gamma $
supported on
![]() $[i,j]$
with
$[i,j]$
with
![]() $\zeta (\gamma ) = p-q$
and
$\zeta (\gamma ) = p-q$
and
![]() $i+j-1 = p+q$
is a
$i+j-1 = p+q$
is a
![]() $(p,q)$
-clan.
$(p,q)$
-clan.
For a backstable clan
![]() $\gamma $
, we write
$\gamma $
, we write
![]() $\gamma (i) = j$
if i is matched with j in
$\gamma (i) = j$
if i is matched with j in
![]() $\gamma $
. Write
$\gamma $
. Write ![]() to denote an unspecified element of
to denote an unspecified element of ![]() . We write
. We write ![]() if i is unmatched in
if i is unmatched in
![]() $\gamma $
and labeled with
$\gamma $
and labeled with ![]() . If
. If
![]() $i \in \mathbb {Z}$
is matched, we say that i is
$i \in \mathbb {Z}$
is matched, we say that i is ![]() if
if
![]() $\gamma (i)> i$
and
$\gamma (i)> i$
and ![]() if
if
![]() $\gamma (i) < i$
. A backstable clan
$\gamma (i) < i$
. A backstable clan
![]() $\gamma $
is
$\gamma $
is ![]() if we never have
if we never have
![]() $a<b<c<d \in \mathbb {Z}$
with
$a<b<c<d \in \mathbb {Z}$
with
![]() $\gamma (a) = c$
and
$\gamma (a) = c$
and
![]() $\gamma (b) = d$
.
$\gamma (b) = d$
.
For each pair of integers
![]() $p,q \in \mathbb {Z}$
, the
$p,q \in \mathbb {Z}$
, the ![]() is the
is the
![]() $(p,q)$
-clan such that
$(p,q)$
-clan such that

See Figure 1 for some examples. Note that the rainbow clan is always noncrossing and never has both ![]() and
and ![]() appearing.
appearing.
For each generator
![]() $T_i$
of the
$T_i$
of the
![]() $0$
-Hecke algebra
$0$
-Hecke algebra
![]() $\mathcal {H}_{\mathbb {Z}}$
, we define an action of
$\mathcal {H}_{\mathbb {Z}}$
, we define an action of
![]() $T_i$
on
$T_i$
on
![]() $(p,q)$
-clans. This action is defined through various cases; however, all have the flavor of acting locally at the numbers i and
$(p,q)$
-clans. This action is defined through various cases; however, all have the flavor of acting locally at the numbers i and
![]() $i+1$
and of transforming the
$i+1$
and of transforming the
![]() $(p,q)$
-clan to more closely resemble the rainbow clan
$(p,q)$
-clan to more closely resemble the rainbow clan
![]() $\Omega _{p,q}$
. Precisely, for a clan
$\Omega _{p,q}$
. Precisely, for a clan
![]() $\gamma $
, we have:
$\gamma $
, we have:
-
• if
 and
and
 $i+1$
is initial, then
$i+1$
is initial, then 
-
• if i is final and
 , then
, then 
-
• if i and
 $i+1$
are both initial with
$i+1$
are both initial with
 $\gamma (i) < \gamma (i+1)$
, then
$\gamma (i) < \gamma (i+1)$
, then  $$\begin{align*}(T_i \cdot \gamma)(i) = \gamma(i +1), (T_i \cdot \gamma)(\gamma(i +1)) = i, (T_i \cdot \gamma)(i+1) = \gamma(i), \text{ and } (T_i \cdot \gamma)(\gamma(i)) = i+1; \end{align*}$$
$$\begin{align*}(T_i \cdot \gamma)(i) = \gamma(i +1), (T_i \cdot \gamma)(\gamma(i +1)) = i, (T_i \cdot \gamma)(i+1) = \gamma(i), \text{ and } (T_i \cdot \gamma)(\gamma(i)) = i+1; \end{align*}$$
-
• if i and
 $i+1$
are both final with
$i+1$
are both final with
 $\gamma (i) < \gamma (i+1)$
, then
$\gamma (i) < \gamma (i+1)$
, then  $$\begin{align*}(T_i \cdot \gamma)(i) = \gamma(i +1), (T_i \cdot \gamma)(\gamma(i +1)) = i, (T_i \cdot \gamma)(i+1) = \gamma(i), \text{ and } (T_i \cdot \gamma)(\gamma(i)) = i+1; \end{align*}$$
$$\begin{align*}(T_i \cdot \gamma)(i) = \gamma(i +1), (T_i \cdot \gamma)(\gamma(i +1)) = i, (T_i \cdot \gamma)(i+1) = \gamma(i), \text{ and } (T_i \cdot \gamma)(\gamma(i)) = i+1; \end{align*}$$
-
• if i is final and
 $i+1$
is initial, then
$i+1$
is initial, then  $$\begin{align*}(T_i \cdot \gamma)(i) = \gamma(i +1), (T_i \cdot \gamma)(\gamma(i +1)) = i, (T_i \cdot \gamma)(i+1) = \gamma(i), \text{ and } (T_i \cdot \gamma)(\gamma(i)) = i+1; \end{align*}$$
$$\begin{align*}(T_i \cdot \gamma)(i) = \gamma(i +1), (T_i \cdot \gamma)(\gamma(i +1)) = i, (T_i \cdot \gamma)(i+1) = \gamma(i), \text{ and } (T_i \cdot \gamma)(\gamma(i)) = i+1; \end{align*}$$
-
• if
 and
and  , then
, then
 $(T_i \cdot \gamma )(i) = i+1$
and
$(T_i \cdot \gamma )(i) = i+1$
and
 $(T_i \cdot \gamma )(i+1) = i$
;
$(T_i \cdot \gamma )(i+1) = i$
;
in all other cases,
![]() $T_i$
acts trivially. Since this action respects the braid relations of Equation (2.1) by [Reference WyserWys13, p. 839], we obtain an action of each
$T_i$
acts trivially. Since this action respects the braid relations of Equation (2.1) by [Reference WyserWys13, p. 839], we obtain an action of each
![]() $0$
-Hecke element
$0$
-Hecke element
![]() $T_w$
. (Wyser only considers
$T_w$
. (Wyser only considers
![]() $(p,q)$
-clans supported on
$(p,q)$
-clans supported on
![]() $[1,p+q]$
; however, by translating
$[1,p+q]$
; however, by translating
![]() $[i,j]$
-clans to be supported on
$[i,j]$
-clans to be supported on
![]() $[1,j-i+1]$
, the general result is immediate.) Examples of the
$[1,j-i+1]$
, the general result is immediate.) Examples of the
![]() $0$
-Hecke action on backstable clans are shown in Figure 2.
$0$
-Hecke action on backstable clans are shown in Figure 2.
We say that a
![]() $(p,q)$
-clan
$(p,q)$
-clan
![]() $\gamma $
is an
$\gamma $
is an ![]() if
if
![]() $T_i \cdot \gamma = \Omega _{p,q}$
for at least one
$T_i \cdot \gamma = \Omega _{p,q}$
for at least one
![]() $i \in \mathbb {Z}$
. Examples of almost rainbow clans are depicted in Figure 3. Write
$i \in \mathbb {Z}$
. Examples of almost rainbow clans are depicted in Figure 3. Write
![]() $\omega _{p}$
for the almost rainbow
$\omega _{p}$
for the almost rainbow
![]() $(p,p)$
-clan with
$(p,p)$
-clan with ![]() and
and ![]() . For example,
. For example,
![]() $\omega _3$
is illustrated in the center of Figure 3.
$\omega _3$
is illustrated in the center of Figure 3.
Suppose that
![]() $u \in S_{\mathbb {Z}}$
is p-inverse Grassmannian and
$u \in S_{\mathbb {Z}}$
is p-inverse Grassmannian and
![]() $v \in S_{\mathbb {Z}}$
is q-inverse Grassmannian. We define a noncrossing backstable clan
$v \in S_{\mathbb {Z}}$
is q-inverse Grassmannian. We define a noncrossing backstable clan
![]() $\gamma _{u,v}$
associated to the pair
$\gamma _{u,v}$
associated to the pair
![]() $(u,v)$
. Write
$(u,v)$
. Write
![]() $\hat {p} = p + \frac {1}{2}$
and
$\hat {p} = p + \frac {1}{2}$
and
![]() $\hat {q}=q + \frac {1}{2}$
. Then
$\hat {q}=q + \frac {1}{2}$
. Then
![]() $\gamma _{u,v}$
is the unique noncrossing
$\gamma _{u,v}$
is the unique noncrossing
![]() $(p,q)$
-clan such that
$(p,q)$
-clan such that
-
1. if
 $u(i) < \hat {p}$
and
$u(i) < \hat {p}$
and
 $v(i) < \hat {q}$
, then i is initial;
$v(i) < \hat {q}$
, then i is initial; -
2. if
 $u(i)> \hat {p}$
and
$u(i)> \hat {p}$
and
 $v(i)> \hat {q}$
, then i is final;
$v(i)> \hat {q}$
, then i is final; -
3. if
 $u(i) < \hat {p}$
and
$u(i) < \hat {p}$
and
 $v(i)> \hat {q}$
, then
$v(i)> \hat {q}$
, then  ; and
; and -
4. if
 $u(i)> \hat {p}$
and
$u(i)> \hat {p}$
and
 $v(i) < \hat {q}$
, then
$v(i) < \hat {q}$
, then  .
.
See Figure 4 for an example of this construction.

Figure 4 The clan
![]() $\gamma _{u,v}$
for
$\gamma _{u,v}$
for
![]() $u = 12435$
and
$u = 12435$
and
![]() $v = 13425$
. Here,
$v = 13425$
. Here,
![]() $p = 3$
,
$p = 3$
,
![]() $q = 2$
,
$q = 2$
,
![]() $\hat {p} = 3.5$
, and
$\hat {p} = 3.5$
, and
![]() $\hat {q} = 2.5$
.
$\hat {q} = 2.5$
.
Lemma 2.1. The backstable clan
![]() $\gamma _{u,v}$
is well defined.
$\gamma _{u,v}$
is well defined.
Proof. By assumption, there exists
![]() $N>0$
such that
$N>0$
such that
![]() $u(i) = i$
and
$u(i) = i$
and
![]() $v(i) = i$
for
$v(i) = i$
for
![]() $i \geq N$
and for
$i \geq N$
and for
![]() $i \leq -N$
. Therefore, all
$i \leq -N$
. Therefore, all
![]() $i<-N$
are initial and all
$i<-N$
are initial and all
![]() $i>N$
are final. Since these sets are then both countably infinite, there is a unique noncrossing way to pair them up. Thus,
$i>N$
are final. Since these sets are then both countably infinite, there is a unique noncrossing way to pair them up. Thus,
![]() $\gamma _{u,v}$
is a backstable clan; it remains to show that it is a
$\gamma _{u,v}$
is a backstable clan; it remains to show that it is a
![]() $(p,q)$
-clan.
$(p,q)$
-clan.
Choose an interval
![]() $[i,j]$
on which
$[i,j]$
on which
![]() $\gamma _{u,v}$
is supported. Suppose
$\gamma _{u,v}$
is supported. Suppose
![]() $p \geq q$
. By expanding the interval
$p \geq q$
. By expanding the interval
![]() $[i,j]$
as necessary, assume that
$[i,j]$
as necessary, assume that
![]() $i \leq q$
and
$i \leq q$
and
![]() $p \leq j$
.
$p \leq j$
.
On the interval
![]() $[i,j]$
, define
$[i,j]$
, define

and define
On the interval
![]() $[i,j]$
, both u and v take all of the values in
$[i,j]$
, both u and v take all of the values in
![]() $[i,j]$
. We see that the
$[i,j]$
. We see that the
![]() $z \in [i,j]$
with
$z \in [i,j]$
with
![]() $u(z) \in [i,p]$
are those
$u(z) \in [i,p]$
are those
![]() $z \in A \cup C$
, while those z with
$z \in A \cup C$
, while those z with
![]() $u(z) \in [p+1, j]$
are those
$u(z) \in [p+1, j]$
are those
![]() $z \in B \cup D$
. Therefore,
$z \in B \cup D$
. Therefore,
![]() $a+c = p-i+1$
and
$a+c = p-i+1$
and
![]() $b+d = j-p$
. Similarly, the
$b+d = j-p$
. Similarly, the
![]() $z \in [i,j]$
with
$z \in [i,j]$
with
![]() $v(z) \in [i,q]$
are those
$v(z) \in [i,q]$
are those
![]() $z \in A \cup D$
, while those z with
$z \in A \cup D$
, while those z with
![]() $v(z) \in [q+1,j]$
are those
$v(z) \in [q+1,j]$
are those
![]() $z \in B \cup C$
. Therefore,
$z \in B \cup C$
. Therefore,
![]() $a+d = q-i+1$
and
$a+d = q-i+1$
and
![]() $b+c = j-q$
.
$b+c = j-q$
.
By the definition of ‘supported’, the interval
![]() $[i,j]$
contains equal numbers of initial and of final elements, so
$[i,j]$
contains equal numbers of initial and of final elements, so
![]() $a=b$
. Thus,
$a=b$
. Thus,
![]() $\zeta (\gamma _{u,v}) = c-d = j-q-(j-p) = p-q$
, as desired for a
$\zeta (\gamma _{u,v}) = c-d = j-q-(j-p) = p-q$
, as desired for a
![]() $(p,q)$
-clan. Moreover, we have
$(p,q)$
-clan. Moreover, we have
![]() $p-i+1 - (j-q) = 0$
, so
$p-i+1 - (j-q) = 0$
, so
![]() $p+q = i+j-1$
, and so
$p+q = i+j-1$
, and so
![]() $\gamma _{u,v}$
is a
$\gamma _{u,v}$
is a
![]() $(p,q)$
-clan.
$(p,q)$
-clan.
The case
![]() $p < q$
is entirely analogous; we omit the details.
$p < q$
is entirely analogous; we omit the details.
In the case that p and q are positive,
![]() $u,v \in S_{p+q}$
, and
$u,v \in S_{p+q}$
, and
![]() $u \leq w_0^{(p+q)}v$
, Lemma 2.1 was previously established by Wyser [Reference WyserWys13, p. 840].
$u \leq w_0^{(p+q)}v$
, Lemma 2.1 was previously established by Wyser [Reference WyserWys13, p. 840].
For any positive integers
![]() $p,q \in \mathbb {Z}_{>0}$
, we define a set
$p,q \in \mathbb {Z}_{>0}$
, we define a set
![]() $\Psi _{p,q}$
of almost rainbow
$\Psi _{p,q}$
of almost rainbow
![]() $(p,q)$
-clans. Let
$(p,q)$
-clans. Let
 $$ \begin{align*} \Psi_{p,q} = \begin{cases} \{ \gamma : \gamma \text{ is almost rainbow and } T_i \cdot \gamma = \Omega_{p,q} \text{ for some } i \in \mathbb{Z}_{>0} \text{ with } i \neq q \}, & \!\!\!\text{if } p \neq q; \\ \{ \gamma : \gamma \text{ is almost rainbow and } T_i \cdot \gamma = \Omega_{p,q} \text{ for some } i \in \mathbb{Z}_{>0} \text{ with } i \neq q \} \cup \{\omega_p \}, & \!\!\! \text{if } p = q. \\ \end{cases} \end{align*} $$
$$ \begin{align*} \Psi_{p,q} = \begin{cases} \{ \gamma : \gamma \text{ is almost rainbow and } T_i \cdot \gamma = \Omega_{p,q} \text{ for some } i \in \mathbb{Z}_{>0} \text{ with } i \neq q \}, & \!\!\!\text{if } p \neq q; \\ \{ \gamma : \gamma \text{ is almost rainbow and } T_i \cdot \gamma = \Omega_{p,q} \text{ for some } i \in \mathbb{Z}_{>0} \text{ with } i \neq q \} \cup \{\omega_p \}, & \!\!\! \text{if } p = q. \\ \end{cases} \end{align*} $$
Note that in general
![]() $\Psi _{p,q} \neq \Psi _{q,p}$
. If we relax the conditions
$\Psi _{p,q} \neq \Psi _{q,p}$
. If we relax the conditions
![]() $i \in \mathbb {Z}_{>0}$
to
$i \in \mathbb {Z}_{>0}$
to
![]() $i \in \mathbb {Z}$
, then the enlarged set of almost rainbow
$i \in \mathbb {Z}$
, then the enlarged set of almost rainbow
![]() $(p,q)$
-clans can be used to compute backstable Schubert structure coefficients (introduced in [Reference Lam, Lee and ShimozonoLLS21]).
$(p,q)$
-clans can be used to compute backstable Schubert structure coefficients (introduced in [Reference Lam, Lee and ShimozonoLLS21]).
3 Discussion and proof of Theorem 1.1
First, we recall [Reference WyserWys13, Theorem 3.10], which establishes the case of Theorem 1.1 where
![]() $u,v,w \in S_{p+q}$
and
$u,v,w \in S_{p+q}$
and
![]() $u \leq w_0^{(p+q)}v$
. We will use Wyser’s result to prove Theorem 1.1. Theorem 1.1 will then be a major ingredient in our proof of Theorem 1.2 in Section 5.
$u \leq w_0^{(p+q)}v$
. We will use Wyser’s result to prove Theorem 1.1. Theorem 1.1 will then be a major ingredient in our proof of Theorem 1.2 in Section 5.
Theorem 3.1 [Reference WyserWys13, Theorem 3.10].
Let
![]() $u,v,w \in S_{p+q}$
be permutations, where u is p-inverse Grassmannian, v is q-inverse Grassmannian, and
$u,v,w \in S_{p+q}$
be permutations, where u is p-inverse Grassmannian, v is q-inverse Grassmannian, and
![]() $u \leq w_0^{(p+q)}v$
. Then
$u \leq w_0^{(p+q)}v$
. Then
![]() $c_{u,v}^w \in \{0,1\}$
. Moreover, we have
$c_{u,v}^w \in \{0,1\}$
. Moreover, we have
![]() $c_{u,v}^w = 1$
if and only if
$c_{u,v}^w = 1$
if and only if
![]() $\ell (w)=\ell (u)+\ell (v)$
and
$\ell (w)=\ell (u)+\ell (v)$
and
For a permutation
![]() $w \in S_n$
, let
$w \in S_n$
, let
![]() $1 \times w \in S_{n+1}$
denote the permutation such that
$1 \times w \in S_{n+1}$
denote the permutation such that
![]() $(1 \times w)(1) = 1$
and
$(1 \times w)(1) = 1$
and
![]() $(1 \times w)(i) = w(i-1)+1$
for
$(1 \times w)(i) = w(i-1)+1$
for
![]() $i>1$
. Iterating this operation gives rise to the notion of backstabilization of Schubert calculus; for further discussion, see [Reference Lam, Lee and ShimozonoLLS21, Reference NenashevNen20]. We will, however, only need to apply this operation once. The following fact is straightforward; moreover, it is a special case of Lemma 5.2, which we prove later.
$i>1$
. Iterating this operation gives rise to the notion of backstabilization of Schubert calculus; for further discussion, see [Reference Lam, Lee and ShimozonoLLS21, Reference NenashevNen20]. We will, however, only need to apply this operation once. The following fact is straightforward; moreover, it is a special case of Lemma 5.2, which we prove later.
Lemma 3.2. For any
![]() $u,v,w \in S_+$
, we have
$u,v,w \in S_+$
, we have
![]() $c_{u,v}^w=c_{1\times u,1\times v}^{1\times w}$
.
$c_{u,v}^w=c_{1\times u,1\times v}^{1\times w}$
.
Proof of Theorem 1.1.
Fix an interval
![]() $[i,j]$
on which
$[i,j]$
on which
![]() $\gamma _{u,v}$
is supported. If
$\gamma _{u,v}$
is supported. If
![]() $i>1$
, then
$i>1$
, then
![]() $\gamma _{u,v}$
is also supported on the interval
$\gamma _{u,v}$
is also supported on the interval
![]() $[1,p+q]$
. Therefore,
$[1,p+q]$
. Therefore,
![]() $\gamma _{u,v}$
is a noncrossing
$\gamma _{u,v}$
is a noncrossing
![]() $[1,p+q]$
-clan, so by [Reference WyserWys13, Remark 3.9], we have
$[1,p+q]$
-clan, so by [Reference WyserWys13, Remark 3.9], we have
![]() $u, v \in S_{p+q}$
and
$u, v \in S_{p+q}$
and
![]() $u \leq w_0^{(p+q)} v$
. We are then done in this case by Theorem 3.1.
$u \leq w_0^{(p+q)} v$
. We are then done in this case by Theorem 3.1.
Suppose instead that
![]() $i < 1$
. Then, let
$i < 1$
. Then, let
![]() $\tilde {\gamma }$
be the horizontal shift of
$\tilde {\gamma }$
be the horizontal shift of
![]() $\gamma _{u,v}$
to the right by
$\gamma _{u,v}$
to the right by
![]() $1-i$
. That is, let
$1-i$
. That is, let
so that
![]() $\tilde {\gamma }$
is supported on
$\tilde {\gamma }$
is supported on
![]() $[1, j-i+1]$
. Also, define
$[1, j-i+1]$
. Also, define
![]() $\tilde {u}$
and
$\tilde {u}$
and
![]() $\tilde {v}$
by
$\tilde {v}$
by
Then,
![]() $\tilde {u}$
is
$\tilde {u}$
is
![]() $\tilde {p}$
-inverse Grassmannian and
$\tilde {p}$
-inverse Grassmannian and
![]() $\tilde {v}$
is
$\tilde {v}$
is
![]() $\tilde {q}$
-inverse Grassmannian, where
$\tilde {q}$
-inverse Grassmannian, where
![]() $\tilde {p} = p+1-i$
and
$\tilde {p} = p+1-i$
and
![]() $\tilde {q} = q+1-i$
. Note that, since
$\tilde {q} = q+1-i$
. Note that, since
![]() $p+q = i+j-1$
, we have
$p+q = i+j-1$
, we have
![]() $\tilde {p} + \tilde {q} = j-i+1$
. Further, observe that
$\tilde {p} + \tilde {q} = j-i+1$
. Further, observe that
![]() $\gamma _{\tilde {u}, \tilde {v}} = \tilde {\gamma }$
by construction.
$\gamma _{\tilde {u}, \tilde {v}} = \tilde {\gamma }$
by construction.
The clan
![]() $\gamma _{\tilde {u}, \tilde {v}}$
is a noncrossing clan supported on
$\gamma _{\tilde {u}, \tilde {v}}$
is a noncrossing clan supported on
![]() $[1,\tilde {p} + \tilde {q}]$
. Therefore, by [Reference WyserWys13, Remark 3.9], we have
$[1,\tilde {p} + \tilde {q}]$
. Therefore, by [Reference WyserWys13, Remark 3.9], we have
![]() $\tilde {u}, \tilde {v} \in S_{\tilde {p} + \tilde {q}}$
and
$\tilde {u}, \tilde {v} \in S_{\tilde {p} + \tilde {q}}$
and
![]() $\tilde {u} \leq w_0^{(\tilde {p} + \tilde {q})} \tilde {v}$
.
$\tilde {u} \leq w_0^{(\tilde {p} + \tilde {q})} \tilde {v}$
.
Now, define
![]() $\tilde {w}$
by
$\tilde {w}$
by
Note that
for all z. This implies that
![]() $T_w \cdot \gamma _{u,v} = \Omega _{p,q}$
if and only if
$T_w \cdot \gamma _{u,v} = \Omega _{p,q}$
if and only if
![]() $T_{\tilde {w}} \cdot \gamma _{\tilde {u}, \tilde {v}} = \Omega _{\tilde {p}, \tilde {q}}$
.
$T_{\tilde {w}} \cdot \gamma _{\tilde {u}, \tilde {v}} = \Omega _{\tilde {p}, \tilde {q}}$
.
By Lemma 3.2, we have that
since
![]() $\tilde {u} = 1^{1-i} \times u$
,
$\tilde {u} = 1^{1-i} \times u$
,
![]() $\tilde {v} = 1^{1-i} \times v$
and
$\tilde {v} = 1^{1-i} \times v$
and
![]() $\tilde {w} = 1^{1-i} \times w$
. Thus, by Theorem 3.1, we have
$\tilde {w} = 1^{1-i} \times w$
. Thus, by Theorem 3.1, we have
![]() $c_{u,v}^w \in \{0,1\}$
. Also, note that
$c_{u,v}^w \in \{0,1\}$
. Also, note that
![]() $\ell (\tilde {u}) = \ell (u)$
,
$\ell (\tilde {u}) = \ell (u)$
,
![]() $\ell (\tilde {v}) = \ell (v)$
, and
$\ell (\tilde {v}) = \ell (v)$
, and
![]() $\ell (\tilde {w}) = \ell (w)$
. Thus, Theorem 3.1 additionally yields that
$\ell (\tilde {w}) = \ell (w)$
. Thus, Theorem 3.1 additionally yields that
![]() $c_{u,v}^w = 1$
if and only if
$c_{u,v}^w = 1$
if and only if
![]() $T_w \cdot \gamma _{u,v} = \Omega _{p,q}$
. This completes the proof of Theorem 1.1.
$T_w \cdot \gamma _{u,v} = \Omega _{p,q}$
. This completes the proof of Theorem 1.1.
Remark 3.3. Note that the hypotheses of Theorem 3.1 are somewhat restrictive. For instance, Theorem 3.1 is unable to compute any structure coefficient of the form
![]() $c_{231,231}^w$
since
$c_{231,231}^w$
since
![]() $231$
is
$231$
is
![]() $1$
-inverse Grassmannian but
$1$
-inverse Grassmannian but
![]() $231\not \in S_{1+1}$
. Example 3.4 demonstrates how we can instead compute these structure coefficients using backstable clans and Theorem 1.1.
$231\not \in S_{1+1}$
. Example 3.4 demonstrates how we can instead compute these structure coefficients using backstable clans and Theorem 1.1.
Similarly, Theorem 3.1 cannot compute any of the structure coefficients
![]() $c_{213,312}^w$
because
$c_{213,312}^w$
because
![]() $213\not \leq w_{0}^{(3)}312=132$
. See Example 3.5 for a demonstration of computing these structure coefficients through backstable clans and Theorem 1.1.
$213\not \leq w_{0}^{(3)}312=132$
. See Example 3.5 for a demonstration of computing these structure coefficients through backstable clans and Theorem 1.1.
We now show how Theorem 1.1 uses backstable clans to compute the Schubert structure coefficients described in Remark 3.3.
Example 3.4. Let
![]() $u = 231 \in S_3$
. The backstable clan
$u = 231 \in S_3$
. The backstable clan
![]() $\gamma _{u,u}$
looks like
$\gamma _{u,u}$
looks like

We consider all nontrivial actions of
![]() $0$
-Hecke generators
$0$
-Hecke generators
![]() $T_i$
on
$T_i$
on
![]() $\gamma _{u,u}$
until reaching the rainbow clan
$\gamma _{u,u}$
until reaching the rainbow clan
![]() $\Omega _{1,1}$
:
$\Omega _{1,1}$
:

There are two paths in this diagram from
![]() $\gamma _{u,u}$
to
$\gamma _{u,u}$
to
![]() $\Omega _{1,1}$
using only
$\Omega _{1,1}$
using only
![]() $T_i$
with
$T_i$
with
![]() $i>0$
; these paths are labeled by the sequences
$i>0$
; these paths are labeled by the sequences
![]() $(T_2,T_1,T_3,T_2)$
and
$(T_2,T_1,T_3,T_2)$
and
![]() $(T_2,T_3,T_1,T_2)$
, which both correspond to the permutation
$(T_2,T_3,T_1,T_2)$
, which both correspond to the permutation
![]() $3412 = s_2 s_3 s_1 s_2 = s_2 s_1 s_3 s_2$
. Thus, by Theorem 1.1, we have that
$3412 = s_2 s_3 s_1 s_2 = s_2 s_1 s_3 s_2$
. Thus, by Theorem 1.1, we have that
![]() $c_{u,u}^{3412} = 1$
, while
$c_{u,u}^{3412} = 1$
, while
![]() $c_{u,u}^w = 0$
for all
$c_{u,u}^w = 0$
for all
![]() $w \neq 3412$
.
$w \neq 3412$
.
Example 3.5. Let
![]() $u = 213$
and
$u = 213$
and
![]() $v = 312$
. Then the backstable clan
$v = 312$
. Then the backstable clan
![]() $\gamma _{u,v}$
looks like
$\gamma _{u,v}$
looks like

We consider all nontrivial actions of
![]() $0$
-Hecke generators
$0$
-Hecke generators
![]() $T_i$
on
$T_i$
on
![]() $\gamma _{u,v}$
, until reaching the rainbow clan
$\gamma _{u,v}$
, until reaching the rainbow clan
![]() $\Omega _{1,2}$
:
$\Omega _{1,2}$
:

There is a unique path in this diagram from
![]() $\gamma _{u,v}$
to
$\gamma _{u,v}$
to
![]() $\Omega _{1,2}$
using only
$\Omega _{1,2}$
using only
![]() $T_i$
with
$T_i$
with
![]() $i>0$
, namely that labeled by the sequence
$i>0$
, namely that labeled by the sequence
![]() $(T_1, T_2, T_3)$
. Note that
$(T_1, T_2, T_3)$
. Note that
![]() $s_3 s_2 s_1 = 4123$
. We conclude by Theorem 1.1 that
$s_3 s_2 s_1 = 4123$
. We conclude by Theorem 1.1 that
![]() $c_{u,v}^{4123} = 1$
, while
$c_{u,v}^{4123} = 1$
, while
![]() $c_{u,v}^w = 0$
for all
$c_{u,v}^w = 0$
for all
![]() $w \neq 4123$
.
$w \neq 4123$
.
4 Linear relations among Schubert structure coefficients
In this section, we establish new linear relations among Schubert structure coefficients. In the first subsection, we derive linear relations among cohomological structure coefficients; we will use these relations in Section 5 to prove Theorem 1.2. In the second subsection, we derive analogous linear relations among K-theoretic structure coefficients; these relations will not be explored further in the later sections of this paper. The third subsection studies stabilization phenomena to obtain additional linear relations among cohomological structure coefficients; these relations will also be important to the proof of Theorem 1.2 in Section 5. The fourth subsection considers relations obtained by iterating the technique of the first subsection; these relations will not be studied further in this paper.
4.1 Cohomology
We will need the differential operator
![]() $\nabla : \mathbb {Z}[x_1, x_2, \dots ] \to \mathbb {Z}[x_1, x_2, \dots ]$
defined by
$\nabla : \mathbb {Z}[x_1, x_2, \dots ] \to \mathbb {Z}[x_1, x_2, \dots ]$
defined by
 $$\begin{align*}\nabla = \sum_{i=1}^\infty \frac{\partial}{\partial x_i}. \end{align*}$$
$$\begin{align*}\nabla = \sum_{i=1}^\infty \frac{\partial}{\partial x_i}. \end{align*}$$
Our key tool will be the following, developed earlier in our joint work with Z. Hamaker and D. Speyer.
Proposition 4.1 [Reference Hamaker, Pechenik, Speyer and WeigandtHPSW20, Proposition 1.1].
For
![]() $w \in S_+$
, we have
$w \in S_+$
, we have
From this proposition, we can establish our primary family of linear relations.
Proposition 4.2. Let
![]() $u,v,w \in S_+$
. Then
$u,v,w \in S_+$
. Then
 $$ \begin{align} \sum_{s_iu < u} i c_{s_iu,v}^w + \sum_{s_jv < v} j c_{u,s_jv}^w = \sum_{s_kw> w} k c_{u,v}^{s_k w}. \end{align} $$
$$ \begin{align} \sum_{s_iu < u} i c_{s_iu,v}^w + \sum_{s_jv < v} j c_{u,s_jv}^w = \sum_{s_kw> w} k c_{u,v}^{s_k w}. \end{align} $$
Proposition 4.2 enables one to discern properties of an unknown
![]() $c_{u,v}^w$
from properties of other Schubert structure coefficients. In particular, our relations yield some new vanishing and nonvanishing conditions, as well as congruence conditions. We do not know how to relate our linear relations to the the nonpositive recurrence of [Reference KnutsonKnu03].
$c_{u,v}^w$
from properties of other Schubert structure coefficients. In particular, our relations yield some new vanishing and nonvanishing conditions, as well as congruence conditions. We do not know how to relate our linear relations to the the nonpositive recurrence of [Reference KnutsonKnu03].
Proof of Proposition 4.2.
Write
and apply the differential operator
![]() $\nabla $
to both sides to obtain
$\nabla $
to both sides to obtain
 $$ \begin{align} \sum_{s_i u < u} i \mathfrak{S}_{s_i u} \mathfrak{S}_v + \sum_{s_j v < v} j \mathfrak{S}_u \mathfrak{S}_{s_j v} = \sum_p \sum_{s_k p < p} k c_{u,v}^p \mathfrak{S}_{s_k p} \end{align} $$
$$ \begin{align} \sum_{s_i u < u} i \mathfrak{S}_{s_i u} \mathfrak{S}_v + \sum_{s_j v < v} j \mathfrak{S}_u \mathfrak{S}_{s_j v} = \sum_p \sum_{s_k p < p} k c_{u,v}^p \mathfrak{S}_{s_k p} \end{align} $$
by Proposition 4.1 and the Leibniz formula. Now, extract the coefficient of
![]() $\mathfrak {S}_w$
from both sides of Equation (4.2) to obtain
$\mathfrak {S}_w$
from both sides of Equation (4.2) to obtain
 $$\begin{align*}\sum_{s_i u < u} i c_{s_i u, v}^w + \sum_{s_jv < v} j c_{u,s_jv}^w = \sum_{s_k w> w} k c_{u,v}^{s_k w}, \end{align*}$$
$$\begin{align*}\sum_{s_i u < u} i c_{s_i u, v}^w + \sum_{s_jv < v} j c_{u,s_jv}^w = \sum_{s_k w> w} k c_{u,v}^{s_k w}, \end{align*}$$
as desired.
Proposition 4.2 has some surprising corollaries. The following result can be extracted straightforwardly from Monk’s formula [Reference MonkMon59], but we can alternatively derive it easily from Proposition 4.2.
Corollary 4.3. Let
![]() $v \in S_+$
, and let
$v \in S_+$
, and let
![]() $i \in \mathbb {Z}_+$
. Then there is some
$i \in \mathbb {Z}_+$
. Then there is some
![]() $k \in \mathbb {Z}_+$
such that
$k \in \mathbb {Z}_+$
such that
![]() $c_{s_i, v}^{s_k v}> 0$
.
$c_{s_i, v}^{s_k v}> 0$
.
Proof. Specialize Proposition 4.2 to the case
![]() $u = s_i$
and
$u = s_i$
and
![]() $w=v$
. Then we get
$w=v$
. Then we get
 $$\begin{align*}i + \sum_{s_j v < v} j c_{s_i, s_jv}^w = \sum_{s_k v> v} k c_{s_i, v}^{s_k v}. \end{align*}$$
$$\begin{align*}i + \sum_{s_j v < v} j c_{s_i, s_jv}^w = \sum_{s_k v> v} k c_{s_i, v}^{s_k v}. \end{align*}$$
Since the sum on the left is nonnegative and
![]() $i>0$
, we obtain
$i>0$
, we obtain
But then
so there is some k with
![]() $s_k v> v$
and
$s_k v> v$
and
![]() $c_{s_i, v}^{s_k v}> 0$
. By dimension counting, the second of these conditions implies the first, so the corollary follows.
$c_{s_i, v}^{s_k v}> 0$
. By dimension counting, the second of these conditions implies the first, so the corollary follows.
Proposition 4.2 also implies many congruence relations among Schubert structure coefficients.
Corollary 4.4. Suppose all left descents of u and v are multiples of
![]() $\alpha \in \mathbb Z_+$
. Then, for any
$\alpha \in \mathbb Z_+$
. Then, for any
![]() $w \in S_+$
, we have
$w \in S_+$
, we have
If moreover
![]() $u=v$
, then
$u=v$
, then
Proof. Under the hypotheses of the corollary, every term of each sum on the left of Equation (4.1) is a multiple of
![]() $\alpha $
. Hence, the sum on the right is as well. If also
$\alpha $
. Hence, the sum on the right is as well. If also
![]() $u=v$
, then the two sums on the left of Equation (4.1) are equal to each other.
$u=v$
, then the two sums on the left of Equation (4.1) are equal to each other.
What is remarkable about Corollary 4.4 is that although our sum is congruent to
![]() $0$
modulo
$0$
modulo
![]() $\alpha $
, the individual terms of the sum generally are not. For this reason, knowing some of the relevant Schubert structure coefficients imposes strong conditions on the remaining ones. Before giving an example of the application of Corollary 4.4, we need the following easy lemma.
$\alpha $
, the individual terms of the sum generally are not. For this reason, knowing some of the relevant Schubert structure coefficients imposes strong conditions on the remaining ones. Before giving an example of the application of Corollary 4.4, we need the following easy lemma.
Lemma 4.5. Suppose
![]() $u,v,a \in S_n$
, and let
$u,v,a \in S_n$
, and let
![]() $m>n$
. Then
$m>n$
. Then
![]() $c_{u,v}^{s_m a} = 0$
.
$c_{u,v}^{s_m a} = 0$
.
Proof. The Schubert polynomials
![]() $\mathfrak {S}_u$
,
$\mathfrak {S}_u$
,
![]() $\mathfrak {S}_v$
,
$\mathfrak {S}_v$
,
![]() $\mathfrak {S}_a$
all lie in
$\mathfrak {S}_a$
all lie in
![]() $\mathbb {Z}[x_1, \dots , x_{n-1}]$
. On the other hand, m is a (right) descent of
$\mathbb {Z}[x_1, \dots , x_{n-1}]$
. On the other hand, m is a (right) descent of
![]() $s_m a$
, so
$s_m a$
, so
![]() $\mathfrak {S}_{s_m a}$
involves the variable
$\mathfrak {S}_{s_m a}$
involves the variable
![]() $x_m$
, so
$x_m$
, so
![]() $\mathfrak {S}_{s_m a} \notin \mathbb {Z}[x_1, \dots , x_{n-1}]$
. Hence,
$\mathfrak {S}_{s_m a} \notin \mathbb {Z}[x_1, \dots , x_{n-1}]$
. Hence,
![]() $c_{u,v}^{s_m a} = 0$
.
$c_{u,v}^{s_m a} = 0$
.
Example 4.6. Suppose
![]() $u=13254$
, and note that it only has left descents
$u=13254$
, and note that it only has left descents
![]() $2$
and
$2$
and
![]() $4$
. Let
$4$
. Let
![]() $w = 231645$
, and suppose we have correctly computed already that
$w = 231645$
, and suppose we have correctly computed already that
![]() $c_{u,u}^w = 1$
.
$c_{u,u}^w = 1$
.
Now, let
![]() $a = s_1w = 132645$
. Corollary 4.4 gives that
$a = s_1w = 132645$
. Corollary 4.4 gives that
But we can expand this sum as
using Lemma 4.5 to see that the other potential terms vanish. Since we know the term with coefficient
![]() $1$
contributes
$1$
contributes
![]() $1$
, the sum of the other terms must be congruent to
$1$
, the sum of the other terms must be congruent to
![]() $3$
modulo
$3$
modulo
![]() $4$
. In particular, we learn for free that
$4$
. In particular, we learn for free that
![]() $c_{u,u}^{s_3 a} \neq 0$
. Even better, it is immediate without further computation that
$c_{u,u}^{s_3 a} \neq 0$
. Even better, it is immediate without further computation that
![]() $c_{u,u}^{s_3 a}$
is odd. In fact, it turns out that
$c_{u,u}^{s_3 a}$
is odd. In fact, it turns out that
![]() $c_{u,u}^{s_3 a} = 1$
.
$c_{u,u}^{s_3 a} = 1$
.
If we compute also that
![]() $c_{u,u}^{s_3 a} = 1$
, we learn then that
$c_{u,u}^{s_3 a} = 1$
, we learn then that
![]() $c_{u,u}^{s_6 a}$
must be even. In fact, it turns out that
$c_{u,u}^{s_6 a}$
must be even. In fact, it turns out that
![]() $c_{u,u}^{s_6 a} = 0$
.
$c_{u,u}^{s_6 a} = 0$
.
4.2 K-theory
The structure sheaves of Schubert varieties
![]() $X_w \subset \mathsf {Flags}_n$
give classes
$X_w \subset \mathsf {Flags}_n$
give classes
![]() $[\mathcal {O}_{X_w}]$
in the Grothendieck ring
$[\mathcal {O}_{X_w}]$
in the Grothendieck ring
![]() $K^0(\mathsf {Flags}_n)$
of algebraic vector bundles over
$K^0(\mathsf {Flags}_n)$
of algebraic vector bundles over
![]() $\mathsf {Flags}_n$
. These classes form an additive basis and give rise to K-theoretic Schubert structure coefficients
$\mathsf {Flags}_n$
. These classes form an additive basis and give rise to K-theoretic Schubert structure coefficients
![]() $K_{u,v}^w$
defined by
$K_{u,v}^w$
defined by
When
![]() $\ell (w) = \ell (u) + \ell (v)$
, we have
$\ell (w) = \ell (u) + \ell (v)$
, we have
![]() $K_{u,v}^w = c_{u,v}^w$
, but, unlike
$K_{u,v}^w = c_{u,v}^w$
, but, unlike
![]() $c_{u,v}^w$
,
$c_{u,v}^w$
,
![]() $K_{u,v}^w$
can be nonzero when
$K_{u,v}^w$
can be nonzero when
![]() $\ell (w)> \ell (u) + \ell (v)$
.
$\ell (w)> \ell (u) + \ell (v)$
.
![]() represent Schubert structure sheaf classes analogously to how Schubert polynomials represent Schubert cycles. We may also define Grothendieck polynomials recursively. For
represent Schubert structure sheaf classes analogously to how Schubert polynomials represent Schubert cycles. We may also define Grothendieck polynomials recursively. For
![]() $w_0^{(n)} \in S_n$
, we set
$w_0^{(n)} \in S_n$
, we set
![]() $\mathfrak {G}_{w_0^{(n)}} = \mathfrak {S}_{w_0^{(n)}} = x_1^{n-1}x_2^{n-2}\cdots x_n^0$
. For w such that
$\mathfrak {G}_{w_0^{(n)}} = \mathfrak {S}_{w_0^{(n)}} = x_1^{n-1}x_2^{n-2}\cdots x_n^0$
. For w such that
![]() $ws_i < w$
, set
$ws_i < w$
, set
where
![]() $\overline {N}_i(f) = N_i( (1-x_{i+1}) f)$
. We have
$\overline {N}_i(f) = N_i( (1-x_{i+1}) f)$
. We have
![]() $\mathfrak {G}_w = \mathfrak {G}_{\iota (w)}$
, so we think of Grothendieck polynomials as also being indexed by elements of
$\mathfrak {G}_w = \mathfrak {G}_{\iota (w)}$
, so we think of Grothendieck polynomials as also being indexed by elements of
![]() $S_+$
. The set of Grothendieck polynomials
$S_+$
. The set of Grothendieck polynomials
![]() $\{\mathfrak {G}_w \}_{w \in S_+}$
is another linear basis of
$\{\mathfrak {G}_w \}_{w \in S_+}$
is another linear basis of
![]() $\mathbb {Z}[x_1, x_2, x_3, \dots ]$
. The structure coefficients defined by
$\mathbb {Z}[x_1, x_2, x_3, \dots ]$
. The structure coefficients defined by
agree with the K-theoretic Schubert structure coefficients
![]() $K_{u,v}^w$
provided
$K_{u,v}^w$
provided
![]() $u,v,w \in S_n$
.
$u,v,w \in S_n$
.
Let
![]() $\beta $
be an indeterminate. Define the
$\beta $
be an indeterminate. Define the ![]() by
by
The
![]() $\beta $
-Grothendieck polynomials were introduced in [Reference Fomin and KirillovFK94] and represent classes in the connective K-theory of
$\beta $
-Grothendieck polynomials were introduced in [Reference Fomin and KirillovFK94] and represent classes in the connective K-theory of
![]() $\mathsf {Flags}_n$
[Reference HudsonHud14]. We will find the
$\mathsf {Flags}_n$
[Reference HudsonHud14]. We will find the
![]() $\beta $
-Grothendieck polynomials slightly easier to work with in our context. Let the structure coefficients for
$\beta $
-Grothendieck polynomials slightly easier to work with in our context. Let the structure coefficients for
![]() $\beta $
-Grothendieck polynomials be
$\beta $
-Grothendieck polynomials be
![]() $K_{u,v}^w(\beta )$
. We have
$K_{u,v}^w(\beta )$
. We have
![]() $K_{u,v}^w(-1) = K_{u,v}^w$
.
$K_{u,v}^w(-1) = K_{u,v}^w$
.
Let
![]() $\mathrm {Des}(w)$
denote the set of descents of the permutation w. The
$\mathrm {Des}(w)$
denote the set of descents of the permutation w. The ![]() of w is
of w is
We also need the following differential operators related to
![]() $\nabla $
:
$\nabla $
:
 $$\begin{align*}\nabla^\beta = \nabla + \beta^2 \frac{\partial}{\partial \beta} \quad \text{and} \quad E = \sum_{i=1}^\infty x_i \frac{\partial}{\partial x_i}. \end{align*}$$
$$\begin{align*}\nabla^\beta = \nabla + \beta^2 \frac{\partial}{\partial \beta} \quad \text{and} \quad E = \sum_{i=1}^\infty x_i \frac{\partial}{\partial x_i}. \end{align*}$$
We can now recall [Reference Pechenik, Speyer and WeigandtPSW24, Theorem A.1], as reformulated in [Reference Pechenik, Speyer and WeigandtPSW24, Corollary A.2], an analogue of Proposition 4.1 for Grothendieck polynomials and our key tool in this subsection.
Proposition 4.7 [Reference Pechenik, Speyer and WeigandtPSW24, Theorem A.1].
For
![]() $w \in S_+$
, we have
$w \in S_+$
, we have
and
Using essentially the same proof as for Proposition 4.2, but with [Reference Pechenik, Speyer and WeigandtPSW24, Theorem A.1] in place of [Reference Hamaker, Pechenik, Speyer and WeigandtHPSW20, Proposition 1.1], we obtain the following analogue of Proposition 4.2, giving linear relations among K-theoretic Schubert structure coefficients.
Proposition 4.8. Let
![]() $u,v,w \in S_+$
. Then
$u,v,w \in S_+$
. Then
 $$ \begin{align*} \beta K_{u,v}^w(\beta) \bigg( &\mathrm{maj}(u^{-1}) + \mathrm{maj}(v^{-1}) - \mathrm{maj}(w^{-1}) - \ell(u) - \ell(v) + \ell(w) \bigg) \\ &+ \sum_{s_iu < u} i K_{s_iu,v}^w(\beta) + \sum_{s_jv < v} j K_{u,s_jv}^w(\beta) = \sum_{s_kw> w} k K_{u,v}^{s_k w}(\beta). \end{align*} $$
$$ \begin{align*} \beta K_{u,v}^w(\beta) \bigg( &\mathrm{maj}(u^{-1}) + \mathrm{maj}(v^{-1}) - \mathrm{maj}(w^{-1}) - \ell(u) - \ell(v) + \ell(w) \bigg) \\ &+ \sum_{s_iu < u} i K_{s_iu,v}^w(\beta) + \sum_{s_jv < v} j K_{u,s_jv}^w(\beta) = \sum_{s_kw> w} k K_{u,v}^{s_k w}(\beta). \end{align*} $$
Proof. Write
and apply
![]() $\nabla ^\beta $
to both sides, using the first part of Proposition 4.7. Then on the left we have
$\nabla ^\beta $
to both sides, using the first part of Proposition 4.7. Then on the left we have
 $$ \begin{align*} \nabla^\beta \left( \sum_p K_{u,v}^p(\beta) \mathfrak{G}^{(\beta)}_p \right) &= \sum_p K_{u,v}^p(\beta) \nabla^\beta \mathfrak{G}^{(\beta)}_p \\ &= \sum_p K_{u,v}^p(\beta) \left( \beta \mathfrak{G}^{(\beta)}_p (\mathrm{maj}(p^{-1}) - \ell(p)) + \sum_{s_kp < p} k \mathfrak{G}^{(\beta)}_{s_k p} \right), \end{align*} $$
$$ \begin{align*} \nabla^\beta \left( \sum_p K_{u,v}^p(\beta) \mathfrak{G}^{(\beta)}_p \right) &= \sum_p K_{u,v}^p(\beta) \nabla^\beta \mathfrak{G}^{(\beta)}_p \\ &= \sum_p K_{u,v}^p(\beta) \left( \beta \mathfrak{G}^{(\beta)}_p (\mathrm{maj}(p^{-1}) - \ell(p)) + \sum_{s_kp < p} k \mathfrak{G}^{(\beta)}_{s_k p} \right), \end{align*} $$
while on the right we have
 $$ \begin{align*} \nabla^\beta ( \mathfrak{G}^{(\beta)}_u \cdot \mathfrak{G}^{(\beta)}_v) &= \nabla^\beta (\mathfrak{G}^{(\beta)}_u) \mathfrak{G}^{(\beta)}_v + \mathfrak{G}^{(\beta)}_u (\nabla^\beta \mathfrak{G}^{(\beta)}_v) \\&= \left( \beta \mathfrak{G}^{(\beta)}_u (\mathrm{maj}(u^{-1}) - \ell(u)) + \sum_{s_iu < u} i \mathfrak{G}^{(\beta)}_{s_i u} \right) \mathfrak{G}^{(\beta)}_v \\& \quad + \mathfrak{G}^{(\beta)}_u \left(\beta \mathfrak{G}^{(\beta)}_v (\mathrm{maj}(v^{-1}) - \ell(v)) + \sum_{s_j v < v} j \mathfrak{G}^{(\beta)}_{s_j v} \right). \end{align*} $$
$$ \begin{align*} \nabla^\beta ( \mathfrak{G}^{(\beta)}_u \cdot \mathfrak{G}^{(\beta)}_v) &= \nabla^\beta (\mathfrak{G}^{(\beta)}_u) \mathfrak{G}^{(\beta)}_v + \mathfrak{G}^{(\beta)}_u (\nabla^\beta \mathfrak{G}^{(\beta)}_v) \\&= \left( \beta \mathfrak{G}^{(\beta)}_u (\mathrm{maj}(u^{-1}) - \ell(u)) + \sum_{s_iu < u} i \mathfrak{G}^{(\beta)}_{s_i u} \right) \mathfrak{G}^{(\beta)}_v \\& \quad + \mathfrak{G}^{(\beta)}_u \left(\beta \mathfrak{G}^{(\beta)}_v (\mathrm{maj}(v^{-1}) - \ell(v)) + \sum_{s_j v < v} j \mathfrak{G}^{(\beta)}_{s_j v} \right). \end{align*} $$
Now, we can extract the coefficient of
![]() $\mathfrak {G}_w^{(\beta )}$
from both of these obtain
$\mathfrak {G}_w^{(\beta )}$
from both of these obtain
 $$ \begin{align*} \sum_{s_k w> w} k K_{u,v}^{s_k w}(\beta) + \beta (&\mathrm{maj}(w^{-1}) - \ell(w)) K_{u,v}^w(\beta) = \beta(\mathrm{maj}(v^{-1}) - \ell(v)) K_{u,v}^w(\beta)\\ & + \beta (\mathrm{maj}(u^{-1}) - \ell(u)) K_{u,v}^w(\beta) +\sum_{s_i u < u} i K_{s_i u, v}^w(\beta)+ \sum_{s_j v < v} j K_{u, s_jv}^w(\beta). \end{align*} $$
$$ \begin{align*} \sum_{s_k w> w} k K_{u,v}^{s_k w}(\beta) + \beta (&\mathrm{maj}(w^{-1}) - \ell(w)) K_{u,v}^w(\beta) = \beta(\mathrm{maj}(v^{-1}) - \ell(v)) K_{u,v}^w(\beta)\\ & + \beta (\mathrm{maj}(u^{-1}) - \ell(u)) K_{u,v}^w(\beta) +\sum_{s_i u < u} i K_{s_i u, v}^w(\beta)+ \sum_{s_j v < v} j K_{u, s_jv}^w(\beta). \end{align*} $$
The proposition follows by rearranging and collecting terms.
Let
![]() $\mathfrak {G}_w(\boldsymbol{1})$
denote the specialization of the Grothendieck polynomial
$\mathfrak {G}_w(\boldsymbol{1})$
denote the specialization of the Grothendieck polynomial
![]() $\mathfrak {G}_w$
obtained by setting all variables equal to
$\mathfrak {G}_w$
obtained by setting all variables equal to
![]() $1$
. It is well known to experts that
$1$
. It is well known to experts that
![]() $\mathfrak G_w( \boldsymbol{1})=1$
(see [Reference Yu. Smirnov and TutubalinaST21] for an explicit proof and [Reference Mészáros, Setiabrata and DizierMSS24] for further discussion). We present a new short proof using the second part of Proposition 4.7.
$\mathfrak G_w( \boldsymbol{1})=1$
(see [Reference Yu. Smirnov and TutubalinaST21] for an explicit proof and [Reference Mészáros, Setiabrata and DizierMSS24] for further discussion). We present a new short proof using the second part of Proposition 4.7.
Corollary 4.9. Given
![]() $w\in S_+$
,
$w\in S_+$
,
![]() $\mathfrak G_w( \boldsymbol{1})=1$
.
$\mathfrak G_w( \boldsymbol{1})=1$
.
Proof. We proceed by induction on Coxeter length. In the base case,
![]() $\mathfrak G_{\mathrm {id}}=1$
and there is nothing to show. Now, fix
$\mathfrak G_{\mathrm {id}}=1$
and there is nothing to show. Now, fix
![]() $w\in S_+$
with
$w\in S_+$
with
![]() $\ell (w) \geq 1$
, and assume the statement holds for all
$\ell (w) \geq 1$
, and assume the statement holds for all
![]() $v\in S_+$
with
$v\in S_+$
with
![]() $\ell (v)<\ell (w)$
.
$\ell (v)<\ell (w)$
.
First, note, for any
![]() $f\in \mathbb Z[x_1,x_2,\ldots ]$
, we have
$f\in \mathbb Z[x_1,x_2,\ldots ]$
, we have
![]() $(\nabla -E)(f)|_{\mathbf x=1}=0$
. Thus,
$(\nabla -E)(f)|_{\mathbf x=1}=0$
. Thus,
 $$ \begin{align*} \mathrm{maj}(w^{-1})\mathfrak G_w(\boldsymbol{1})&=\sum_{s_kw<w}k\mathfrak G_{s_kw}(\boldsymbol{1}) &\text{(by Proposition}\ {4.7})\\ &=\sum_{s_kw<w}k &\text{(by induction)}\\ &=\mathrm{maj}(w^{-1}). \end{align*} $$
$$ \begin{align*} \mathrm{maj}(w^{-1})\mathfrak G_w(\boldsymbol{1})&=\sum_{s_kw<w}k\mathfrak G_{s_kw}(\boldsymbol{1}) &\text{(by Proposition}\ {4.7})\\ &=\sum_{s_kw<w}k &\text{(by induction)}\\ &=\mathrm{maj}(w^{-1}). \end{align*} $$
Since
![]() $\ell (w)\geq 1$
,
$\ell (w)\geq 1$
,
![]() $\mathrm {maj}(w^{-1})\neq 0$
which implies
$\mathrm {maj}(w^{-1})\neq 0$
which implies
![]() $\mathfrak G_w(\boldsymbol{1})=1$
.
$\mathfrak G_w(\boldsymbol{1})=1$
.
4.3 Stabilization
Recall the stabilization operation from Section 3.
The following is an analogue of Proposition 4.2; we drop the coefficients on the linear relations at the expense of adding one extra term.
Proposition 4.10. Let
![]() $u,v,w \in S_+$
. Then
$u,v,w \in S_+$
. Then
 $$ \begin{align} \sum_{s_iu < u} c_{s_iu,v}^w + \sum_{s_jv < v} c_{u,s_jv}^w = c_{1\times u,1\times v}^{s_1(1\times w)}+\sum_{s_kw> w} c_{u,v}^{s_k w}. \end{align} $$
$$ \begin{align} \sum_{s_iu < u} c_{s_iu,v}^w + \sum_{s_jv < v} c_{u,s_jv}^w = c_{1\times u,1\times v}^{s_1(1\times w)}+\sum_{s_kw> w} c_{u,v}^{s_k w}. \end{align} $$
Proof. It follows easily from the pipe dream formula for Schubert polynomials (e.g., [Reference Fomin and KirillovFK96, Reference Bergeron and BilleyBB93, Reference Knutson and MillerKM05]) that
(Indeed, we will prove a stronger version of this statement as Lemma 5.1.) By Lemma 3.2,
![]() $c_{u,v}^w=c_{1\times u,1\times v}^{1\times w}$
.
$c_{u,v}^w=c_{1\times u,1\times v}^{1\times w}$
.
Apply Proposition 4.2 to
![]() $1 \times u$
,
$1 \times u$
,
![]() $1 \times v$
and
$1 \times v$
and
![]() $1\times w$
. Then we get
$1\times w$
. Then we get
 $$ \begin{align} \tiny \displaystyle \sum_{s_{i+1}(1\times u) < 1\times u} (i+1) c_{s_{i+1}(1\times u),1\times v}^{1\times w} + \sum_{s_{j+1} (1\times v) < 1\times v} (j+1) c_{1\times u,s_{j+1} (1\times v)}^{1\times w} = \sum_{s_{k+1}(1\times w)> 1\times w} (k+1) c_{1\times u,1\times v}^{s_{k+1} (1\times w)}. \end{align} $$
$$ \begin{align} \tiny \displaystyle \sum_{s_{i+1}(1\times u) < 1\times u} (i+1) c_{s_{i+1}(1\times u),1\times v}^{1\times w} + \sum_{s_{j+1} (1\times v) < 1\times v} (j+1) c_{1\times u,s_{j+1} (1\times v)}^{1\times w} = \sum_{s_{k+1}(1\times w)> 1\times w} (k+1) c_{1\times u,1\times v}^{s_{k+1} (1\times w)}. \end{align} $$
Thus,
 $$ \begin{align} \sum_{s_{i} u < u} (i+1) c_{s_{i} u, v}^{ w} + \sum_{s_{j}v < v} (j+1) c_{ u,s_{j} v}^{w} = c_{1\times u,1\times v}^{s_1 (1\times w)}+ \sum_{s_{k} w> w} (k+1) c_{ u, v}^{s_{k} w}. \end{align} $$
$$ \begin{align} \sum_{s_{i} u < u} (i+1) c_{s_{i} u, v}^{ w} + \sum_{s_{j}v < v} (j+1) c_{ u,s_{j} v}^{w} = c_{1\times u,1\times v}^{s_1 (1\times w)}+ \sum_{s_{k} w> w} (k+1) c_{ u, v}^{s_{k} w}. \end{align} $$
Furthermore, from applying Proposition 4.2 to u, v and w, we have
 $$ \begin{align} \sum_{s_iu < u} i c_{s_iu,v}^w + \sum_{s_jv < v} j c_{u,s_jv}^w = \sum_{s_kw> w} k c_{u,v}^{s_k w}. \end{align} $$
$$ \begin{align} \sum_{s_iu < u} i c_{s_iu,v}^w + \sum_{s_jv < v} j c_{u,s_jv}^w = \sum_{s_kw> w} k c_{u,v}^{s_k w}. \end{align} $$
Therefore, subtracting Equation (4.7) from Equation (4.6) yields
 $$ \begin{align*} \sum_{s_iu < u} c_{s_iu,v}^w + \sum_{s_jv < v} c_{u,s_jv}^w & = c_{1\times u,1\times v}^{s_1(1\times w)}+\sum_{s_kw> w} c_{u,v}^{s_k w}.\\[-50pt]\end{align*} $$
$$ \begin{align*} \sum_{s_iu < u} c_{s_iu,v}^w + \sum_{s_jv < v} c_{u,s_jv}^w & = c_{1\times u,1\times v}^{s_1(1\times w)}+\sum_{s_kw> w} c_{u,v}^{s_k w}.\\[-50pt]\end{align*} $$
Remark 4.11. The stabilization argument in the proof of Proposition 4.10 is essentially equivalent to the use of the operator
![]() $\xi $
developed in [Reference NenashevNen20].
$\xi $
developed in [Reference NenashevNen20].
In many cases, one can see that the extra term on the right side of Proposition 4.10 is in fact
![]() $0$
. In these situations, Proposition 4.10 becomes identical to Proposition 4.2, but with the coefficients dropped, yielding two linear relations among the same structure coefficients. In most cases, these relations are linearly independent.
$0$
. In these situations, Proposition 4.10 becomes identical to Proposition 4.2, but with the coefficients dropped, yielding two linear relations among the same structure coefficients. In most cases, these relations are linearly independent.
One can also do analogous analysis in K-theory; we omit the details since we will not use the K-theoretic analogue in what follows.
4.4 Iterations of differential operators
Iterating the application of
![]() $\nabla $
allows us to obtain additional linear relations among Schubert structure coefficients. These linear relations are somewhat more complicated to state, but the proof is analogous to that of Proposition 4.2.
$\nabla $
allows us to obtain additional linear relations among Schubert structure coefficients. These linear relations are somewhat more complicated to state, but the proof is analogous to that of Proposition 4.2.
Let
![]() $\mathfrak {S}_w(\boldsymbol{1})$
denote the specialization of the Schubert polynomial
$\mathfrak {S}_w(\boldsymbol{1})$
denote the specialization of the Schubert polynomial
![]() $\mathfrak {S}_w$
obtained by setting all variables equal to
$\mathfrak {S}_w$
obtained by setting all variables equal to
![]() $1$
. For w with
$1$
. For w with
![]() $\ell (w) = k$
, a
$\ell (w) = k$
, a ![]() for w is a sequence
for w is a sequence
![]() $(a_1, a_2, \dots , a_k)$
of positive integers such that
$(a_1, a_2, \dots , a_k)$
of positive integers such that
![]() $w = s_{a_1} s_{a_2} \cdots s_{a_k}$
. Let
$w = s_{a_1} s_{a_2} \cdots s_{a_k}$
. Let
![]() $R(w)$
denote the set of all reduced words for w. The Macdonald reduced word identity [Reference MacdonaldMac91, Eq. (6.11)] is the following.
$R(w)$
denote the set of all reduced words for w. The Macdonald reduced word identity [Reference MacdonaldMac91, Eq. (6.11)] is the following.
Proposition 4.12 [Reference MacdonaldMac91, Eq. (6.11)].
Let
![]() $w \in S_+$
have
$w \in S_+$
have
![]() $\ell (w) = k$
. Then
$\ell (w) = k$
. Then
We can use the Macdonald reduced word identity to obtain more linear relations.
Proposition 4.13. Let
![]() $u,v\in S_+$
, and fix
$u,v\in S_+$
, and fix
![]() $1\leq k\leq \ell (u)+\ell (v)$
. Let
$1\leq k\leq \ell (u)+\ell (v)$
. Let
![]() $w\in S_+$
with
$w\in S_+$
with
Then,
 $$ \begin{align} \sum_{\substack{\hat{w}\geq_Lw \\ \ell(\hat{w})=\ell(w)+k}} \!\! c_{u,v}^{\hat{w}}\cdot \mathfrak S_{\hat{w}w^{-1}}(\boldsymbol{1})=\sum_{i=0}^{k} \sum_{\substack{\hat{u}\leq_L u \\ \ell(\hat{u})=\ell(u)-i}} \;\;\sum_{\substack{\hat{v} \leq_L v \\ \ell(\hat{v})=\ell(v)-(k-i)}} \!\!\!\! c_{\hat{u},\hat{v}}^{w}\cdot\mathfrak S_{u\hat{u}^{-1}}(\boldsymbol{1}) \cdot \mathfrak S_{v\hat{v}^{-1}}(\boldsymbol{1}). \end{align} $$
$$ \begin{align} \sum_{\substack{\hat{w}\geq_Lw \\ \ell(\hat{w})=\ell(w)+k}} \!\! c_{u,v}^{\hat{w}}\cdot \mathfrak S_{\hat{w}w^{-1}}(\boldsymbol{1})=\sum_{i=0}^{k} \sum_{\substack{\hat{u}\leq_L u \\ \ell(\hat{u})=\ell(u)-i}} \;\;\sum_{\substack{\hat{v} \leq_L v \\ \ell(\hat{v})=\ell(v)-(k-i)}} \!\!\!\! c_{\hat{u},\hat{v}}^{w}\cdot\mathfrak S_{u\hat{u}^{-1}}(\boldsymbol{1}) \cdot \mathfrak S_{v\hat{v}^{-1}}(\boldsymbol{1}). \end{align} $$
Proof. First, note that
 $$ \begin{align*} \nabla^k(\mathfrak S_\pi)=\sum_{\substack{\hat{\pi}\leq_L \pi \\ \ell(\hat{\pi})=\ell(\pi)-k}} \left(\sum_{a \in R(\pi \hat{\pi}^{-1})} a_1a_2 \cdots a_k \right)\cdot \mathfrak S_{\hat{\pi}} \end{align*} $$
$$ \begin{align*} \nabla^k(\mathfrak S_\pi)=\sum_{\substack{\hat{\pi}\leq_L \pi \\ \ell(\hat{\pi})=\ell(\pi)-k}} \left(\sum_{a \in R(\pi \hat{\pi}^{-1})} a_1a_2 \cdots a_k \right)\cdot \mathfrak S_{\hat{\pi}} \end{align*} $$
by Proposition 4.1. By Proposition 4.12, we can replace the inner summation to obtain
 $$ \begin{align} \nabla^k(\mathfrak S_\pi)=\sum_{\substack{\hat{\pi}\leq_L \pi \\ \ell(\hat{\pi})=\ell(\pi)-k}} k!\mathfrak S_{\pi \hat{\pi}^{-1}}(\boldsymbol{1})\cdot \mathfrak S_{\hat{\pi}}. \end{align} $$
$$ \begin{align} \nabla^k(\mathfrak S_\pi)=\sum_{\substack{\hat{\pi}\leq_L \pi \\ \ell(\hat{\pi})=\ell(\pi)-k}} k!\mathfrak S_{\pi \hat{\pi}^{-1}}(\boldsymbol{1})\cdot \mathfrak S_{\hat{\pi}}. \end{align} $$
Write
Applying
![]() $\nabla ^k$
to both sides, we obtain
$\nabla ^k$
to both sides, we obtain
 $$ \begin{align*} \nabla^k\left(\sum_{\hat{p}} c_{u,v}^{\hat{p}} \mathfrak S_{\hat{p}} \right)=\nabla^k(\mathfrak S_u\cdot \mathfrak S_v) =\sum_{i=0}^{k} \binom{k}{i} \nabla^i(\mathfrak S_u)\nabla^{k-i}(\mathfrak S_v). \end{align*} $$
$$ \begin{align*} \nabla^k\left(\sum_{\hat{p}} c_{u,v}^{\hat{p}} \mathfrak S_{\hat{p}} \right)=\nabla^k(\mathfrak S_u\cdot \mathfrak S_v) =\sum_{i=0}^{k} \binom{k}{i} \nabla^i(\mathfrak S_u)\nabla^{k-i}(\mathfrak S_v). \end{align*} $$
Thus, Equation (4.9) yields
 $$ \begin{align*} \sum_{\hat{p}} c_{u,v}^{\hat{p}} & \sum_{\substack{p\leq_L \hat{p} \\ \ell(p)=\ell(\hat{p})-k}} k!\mathfrak S_{\hat{p}p^{-1}}(\boldsymbol{1}) \mathfrak S_p \\ &=\sum_{i=0}^{k} \binom{k}{i} \left(\sum_{\substack{\hat{u} \leq_Lu \\ \ell(\hat{u})=\ell(u)-i}} \! i!\mathfrak S_{u\hat{u}^{-1}}(\boldsymbol{1}) \mathfrak S_{\hat{u}}\right) \left (\sum_{\substack{\hat{v}\leq_L v \\ \ell(\hat{v})=\ell(v)-(k-i)}} \!\! \!(k-i)!\mathfrak S_{v\hat{v}^{-1}}(\boldsymbol{1}) \mathfrak S_{\hat{v}} \right )\\ &=\sum_{i=0}^{k} k! \sum_{\substack{\hat{u}\leq_L u \\ \ell(\hat{u})=\ell(u)-i}} \:\;\; \sum_{\substack{\hat{v} \leq_L v \\ \ell(\hat{v})= \ell(v)-(k-i)}} \mathfrak S_{u\hat{u}^{-1}}(\boldsymbol{1}) \mathfrak S_{v\hat{v}^{-1}}(\boldsymbol{1})\sum_q c_{\hat{u},\hat{v}}^q \mathfrak S_q. \end{align*} $$
$$ \begin{align*} \sum_{\hat{p}} c_{u,v}^{\hat{p}} & \sum_{\substack{p\leq_L \hat{p} \\ \ell(p)=\ell(\hat{p})-k}} k!\mathfrak S_{\hat{p}p^{-1}}(\boldsymbol{1}) \mathfrak S_p \\ &=\sum_{i=0}^{k} \binom{k}{i} \left(\sum_{\substack{\hat{u} \leq_Lu \\ \ell(\hat{u})=\ell(u)-i}} \! i!\mathfrak S_{u\hat{u}^{-1}}(\boldsymbol{1}) \mathfrak S_{\hat{u}}\right) \left (\sum_{\substack{\hat{v}\leq_L v \\ \ell(\hat{v})=\ell(v)-(k-i)}} \!\! \!(k-i)!\mathfrak S_{v\hat{v}^{-1}}(\boldsymbol{1}) \mathfrak S_{\hat{v}} \right )\\ &=\sum_{i=0}^{k} k! \sum_{\substack{\hat{u}\leq_L u \\ \ell(\hat{u})=\ell(u)-i}} \:\;\; \sum_{\substack{\hat{v} \leq_L v \\ \ell(\hat{v})= \ell(v)-(k-i)}} \mathfrak S_{u\hat{u}^{-1}}(\boldsymbol{1}) \mathfrak S_{v\hat{v}^{-1}}(\boldsymbol{1})\sum_q c_{\hat{u},\hat{v}}^q \mathfrak S_q. \end{align*} $$
Extract the coefficient of
![]() $\mathfrak S_w$
from each side to obtain
$\mathfrak S_w$
from each side to obtain
 $$ \begin{align*} k! \!\!\!\!\sum_{\substack{\hat{w}\geq_Lw \\ \ell(\hat{w})=\ell(w)+k}} \!\!\! c_{u,v}^{\hat{w}} \mathfrak S_{\hat{w}w^{-1}}(\boldsymbol{1})= k! \sum_{i=0}^{k} \sum_{\substack{\hat{u}\leq_Lu \\ \ell(\hat{u})=\ell(u)-i}} \;\;\;\sum_{\substack{\hat{v}\leq_Lv \\ \ell(\hat{v})=\ell(v)-(k-i)}} \!\!\!\! c_{\hat{u},\hat{v}}^{w}\mathfrak S_{u\hat{u}^{-1}}(\boldsymbol{1}) \mathfrak S_{v\hat{v}^{-1}}(\boldsymbol{1}). \end{align*} $$
$$ \begin{align*} k! \!\!\!\!\sum_{\substack{\hat{w}\geq_Lw \\ \ell(\hat{w})=\ell(w)+k}} \!\!\! c_{u,v}^{\hat{w}} \mathfrak S_{\hat{w}w^{-1}}(\boldsymbol{1})= k! \sum_{i=0}^{k} \sum_{\substack{\hat{u}\leq_Lu \\ \ell(\hat{u})=\ell(u)-i}} \;\;\;\sum_{\substack{\hat{v}\leq_Lv \\ \ell(\hat{v})=\ell(v)-(k-i)}} \!\!\!\! c_{\hat{u},\hat{v}}^{w}\mathfrak S_{u\hat{u}^{-1}}(\boldsymbol{1}) \mathfrak S_{v\hat{v}^{-1}}(\boldsymbol{1}). \end{align*} $$
The proposition follows by dividing out
![]() $k!$
.
$k!$
.
Proposition 4.2 may alternatively be proved as a corollary to Proposition 4.13 by setting
![]() $k=1$
. On the other extreme, we have the following corollary. Define
$k=1$
. On the other extreme, we have the following corollary. Define
 $$\begin{align*}\delta(w,i) = \begin{cases} 1, & \text{if}\ i \in \mathrm{Des}(w); \\ 0, & \text{if}\ i \notin \mathrm{Des}(w). \end{cases} \end{align*}$$
$$\begin{align*}\delta(w,i) = \begin{cases} 1, & \text{if}\ i \in \mathrm{Des}(w); \\ 0, & \text{if}\ i \notin \mathrm{Des}(w). \end{cases} \end{align*}$$
Corollary 4.14. Let
![]() $u,v\in S_+$
and fix
$u,v\in S_+$
and fix
![]() $i \in \mathbb {Z}_{>0}$
. Then,
$i \in \mathbb {Z}_{>0}$
. Then,
Proof. In Proposition 4.13, take
![]() $w=s_i$
and
$w=s_i$
and
![]() $k = \ell (u) + \ell (v) - 1$
. The left side of Equation (4.8) becomes the left side of Equation (4.10). Most of the terms on the right side of Equation (4.8) vanish by degree considerations. This leaves only the terms on the right side of Equation (4.10).
$k = \ell (u) + \ell (v) - 1$
. The left side of Equation (4.8) becomes the left side of Equation (4.10). Most of the terms on the right side of Equation (4.8) vanish by degree considerations. This leaves only the terms on the right side of Equation (4.10).
The following was observed as [Reference KnutsonKnu01, Lemma 1.1], where the phenomenon was referred to as dc-triviality. We obtain another easy proof of this fact.
Corollary 4.15 [Reference KnutsonKnu01, Lemma 1.1].
Let
![]() $u,v\in S_+$
, and suppose
$u,v\in S_+$
, and suppose
![]() $i \notin \mathrm {Des}(u) \cup \mathrm {Des}(v)$
. Then,
$i \notin \mathrm {Des}(u) \cup \mathrm {Des}(v)$
. Then,
![]() $c_{u,v}^p = 0$
for all
$c_{u,v}^p = 0$
for all
![]() $p \in S_+$
with
$p \in S_+$
with
![]() $i \in \mathrm {Des}(p)$
.
$i \in \mathrm {Des}(p)$
.
Proof. In Corollary 4.14, both terms on the right side vanish under these hypotheses. The left side is a sum of nonnegative integers, so all terms on the left side also vanish. Since each specialization
![]() $\mathfrak {S}_p(\boldsymbol{1})$
is strictly positive, all the relevant
$\mathfrak {S}_p(\boldsymbol{1})$
is strictly positive, all the relevant
![]() $c_{u,v}^p$
equal zero.
$c_{u,v}^p$
equal zero.
5 Discussion and proof of Theorem 1.2
For a permutation
![]() $w \in S_+$
and positive integer c, we define
$w \in S_+$
and positive integer c, we define
![]() $\tau _c^{-1}(w)$
to be
$\tau _c^{-1}(w)$
to be
![]() $s_{c} \cdots s_2s_1(1 \times w)$
. For a permutation
$s_{c} \cdots s_2s_1(1 \times w)$
. For a permutation
![]() $w \in S_+$
, we define the
$w \in S_+$
, we define the ![]() to be the permutation such that
to be the permutation such that
![]() $\tau _{c_1(w)}^{-1}(\tau (w)) = w$
. Note that
$\tau _{c_1(w)}^{-1}(\tau (w)) = w$
. Note that
![]() $\tau (w)$
is the unique element of
$\tau (w)$
is the unique element of
![]() $S_+$
such that
$S_+$
such that
 $$\begin{align*}c_i(\tau(w)) = \begin{cases} c_{i+1}(w), & \text{if } i>0; \\ 0, & \text{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}c_i(\tau(w)) = \begin{cases} c_{i+1}(w), & \text{if } i>0; \\ 0, & \text{otherwise}. \end{cases} \end{align*}$$
The following lemmas are closely related to ideas of [Reference Bergeron and SottileBS98, Reference Lenart, Robinson and SottileLRS06] and are known to experts; we include (sketches of) proofs for completeness.
Lemma 5.1. For any
![]() $w \in S_n$
, we have
$w \in S_n$
, we have
Proof. The Schubert polynomial
![]() $\mathfrak {S}_w$
can be written as a generating function for diagrams P called pipe dreams (cf. [Reference Bergeron and BilleyBB93, Reference Knutson and MillerKM05]), where each
$\mathfrak {S}_w$
can be written as a generating function for diagrams P called pipe dreams (cf. [Reference Bergeron and BilleyBB93, Reference Knutson and MillerKM05]), where each ![]() in row i of P contributes the variable
in row i of P contributes the variable
![]() $x_i$
to the weight of P. Under the specialization of the lemma, the highest-degree terms of
$x_i$
to the weight of P. Under the specialization of the lemma, the highest-degree terms of
![]() $\mathfrak {S}_w(1, x_1, x_2, \dots , x_{n-1})$
come from pipe dreams with as few
$\mathfrak {S}_w(1, x_1, x_2, \dots , x_{n-1})$
come from pipe dreams with as few ![]() ’s as possible in the first row.
’s as possible in the first row.
The ladder moves of [Reference Bergeron and BilleyBB93] describe a recursive algorithm to generate all pipe dreams for w. From this algorithm, it is straightforward that the pipe dreams for w with a minimum number of ![]() ’s in the first row are identical to the pipe dreams for
’s in the first row are identical to the pipe dreams for
![]() $\tau (w)$
after deleting their first row and shifting up.
$\tau (w)$
after deleting their first row and shifting up.
Lemma 5.2. Let
![]() $u,v,w \in S_n$
such that
$u,v,w \in S_n$
such that
![]() $c_1(w) = c_1(u) + c_1(v)$
. Then we have
$c_1(w) = c_1(u) + c_1(v)$
. Then we have
Proof. Write
Choose m sufficiently large so that
![]() $a \in S_m$
for all a such that
$a \in S_m$
for all a such that
![]() $c_{u,v}^a \neq 0$
. We may specialize all of the variables in this equation to obtain
$c_{u,v}^a \neq 0$
. We may specialize all of the variables in this equation to obtain
Now, by Lemma 5.1 applied to all of these Schubert polynomials, we find that
where
![]() $\deg f < \ell (\tau (u))$
,
$\deg f < \ell (\tau (u))$
,
![]() $\deg g < \ell (\tau (v))$
and
$\deg g < \ell (\tau (v))$
and
![]() $\deg h_a < \ell (\tau (a))$
for each a. Now, observe that
$\deg h_a < \ell (\tau (a))$
for each a. Now, observe that
![]() $\ell (\tau (a)) = \ell (\tau (u)) + \ell (\tau (v))$
if and only if we have
$\ell (\tau (a)) = \ell (\tau (u)) + \ell (\tau (v))$
if and only if we have
![]() $c_1(a) = c_1(u) + c_1(v)$
. Therefore, by extracting the top-degree terms on both sides of Equation (5.1), we obtain
$c_1(a) = c_1(u) + c_1(v)$
. Therefore, by extracting the top-degree terms on both sides of Equation (5.1), we obtain
On the other hand, by definition,
Now, observe that if
![]() $\tau (b_1) = \tau (b_2)$
and
$\tau (b_1) = \tau (b_2)$
and
![]() $c_1(b_1) = c_1(b_2)$
, then necessarily
$c_1(b_1) = c_1(b_2)$
, then necessarily
![]() $b_1 = b_2$
. Therefore, comparing Equations (5.2) and (5.3) yields
$b_1 = b_2$
. Therefore, comparing Equations (5.2) and (5.3) yields
as desired.
Note that Lemma 3.2 is a special case of Lemma 5.2. With these lemmas in hand, we are now prepared to finish the proof of Theorem 1.2.
Proof of Theorem 1.2.
Recall that
![]() $u,v,w \in S_+$
are permutations, where u is p-inverse Grassmannian and v is q-inverse Grassmannian. Note that this implies that
$u,v,w \in S_+$
are permutations, where u is p-inverse Grassmannian and v is q-inverse Grassmannian. Note that this implies that
![]() $p,q> 0$
. Let
$p,q> 0$
. Let
![]() $n = p+q$
. We consider a few cases in turn.
$n = p+q$
. We consider a few cases in turn.
We can assume that
![]() $\ell (w) = \ell (u) + \ell (v) - 1$
because otherwise we certainly have
$\ell (w) = \ell (u) + \ell (v) - 1$
because otherwise we certainly have
![]() $c_{s_pu, v}^w = 0$
.
$c_{s_pu, v}^w = 0$
.
(Case 1:
![]() $p\neq q$
): We first consider a technical special case, which we will then be able to extend.
$p\neq q$
): We first consider a technical special case, which we will then be able to extend.
(Case 1.1:
![]() $c_{1 \times u, 1 \times v}^{s_1(1 \times w)} = 0$
): In this case, we have by Proposition 4.10 that
$c_{1 \times u, 1 \times v}^{s_1(1 \times w)} = 0$
): In this case, we have by Proposition 4.10 that
and from Proposition 4.2 that
Thus, multiplying Equation (5.4) by q and subtracting from Equation (5.5), we find that
(Case 1.1.1:
![]() $T_w \cdot \gamma _{u,v}$
is not almost rainbow): By Theorem 1.1,
$T_w \cdot \gamma _{u,v}$
is not almost rainbow): By Theorem 1.1,
![]() $c_{u,v}^{s_k w}=0$
for all k such that
$c_{u,v}^{s_k w}=0$
for all k such that
![]() $s_k w> w$
. Therefore, the right side of Equation (5.6) is
$s_k w> w$
. Therefore, the right side of Equation (5.6) is
![]() $0$
. Since
$0$
. Since
![]() $p\neq q$
, this implies that
$p\neq q$
, this implies that
![]() $c_{s_p u, v}^w = 0$
.
$c_{s_p u, v}^w = 0$
.
(Case 1.1.2:
![]() $T_w \cdot \gamma _{u,v}$
is almost rainbow): Write
$T_w \cdot \gamma _{u,v}$
is almost rainbow): Write
![]() $\delta = T_w \cdot \gamma _{u,v}$
. We now break into cases according to what sort of almost rainbow clan
$\delta = T_w \cdot \gamma _{u,v}$
. We now break into cases according to what sort of almost rainbow clan
![]() $\delta $
is. Observe that
$\delta $
is. Observe that
![]() $\Omega _{p,q}$
has a nonzero number of signed unmatched numbers. If
$\Omega _{p,q}$
has a nonzero number of signed unmatched numbers. If
![]() $p < q$
, these signs are all
$p < q$
, these signs are all ![]() and appear in positions
and appear in positions
![]() $p+1, \dots , q$
; if
$p+1, \dots , q$
; if
![]() $p>q$
, these signs are all
$p>q$
, these signs are all ![]() and appear in positions
and appear in positions
![]() $q+1, \dots , p$
.
$q+1, \dots , p$
.
(Case 1.1.2.1:
![]() $T_{s_q} \cdot \delta = \Omega _{p,q}$
): We observe that
$T_{s_q} \cdot \delta = \Omega _{p,q}$
): We observe that
![]() $T_{s_q}$
must act on
$T_{s_q}$
must act on
![]() $\delta $
by moving a sign inside an arc (as in the
$\delta $
by moving a sign inside an arc (as in the
![]() $T_1$
or
$T_1$
or
![]() $T_6$
arrow of Figure 2). Therefore, we have
$T_6$
arrow of Figure 2). Therefore, we have
![]() $T_{s_r} \cdot \delta = \delta $
for all
$T_{s_r} \cdot \delta = \delta $
for all
![]() $r \neq q$
. So, in this case, Equation (5.6) simplifies to
$r \neq q$
. So, in this case, Equation (5.6) simplifies to
Since
![]() $p \neq q$
, we therefore have
$p \neq q$
, we therefore have
![]() $c_{s_p u, v}^w =0$
.
$c_{s_p u, v}^w =0$
.
(Case 1.1.2.2:
![]() $T_{s_p} \cdot \delta = \Omega _{p,q}$
): We observe that
$T_{s_p} \cdot \delta = \Omega _{p,q}$
): We observe that
![]() $T_{s_p}$
must again act on
$T_{s_p}$
must again act on
![]() $\delta $
by moving a sign inside an arc, as in the previous case. Therefore, we have
$\delta $
by moving a sign inside an arc, as in the previous case. Therefore, we have
![]() $T_{s_r} \cdot \delta = \delta $
for all
$T_{s_r} \cdot \delta = \delta $
for all
![]() $r \neq p$
. So, in this case, Equation (5.6) simplifies to
$r \neq p$
. So, in this case, Equation (5.6) simplifies to
Since
![]() $p \neq q$
, we therefore have
$p \neq q$
, we therefore have
![]() $c_{s_p u, v}^w = c_{u,v}^{s_p w} =1$
, where the last equality is by Theorem 1.1.
$c_{s_p u, v}^w = c_{u,v}^{s_p w} =1$
, where the last equality is by Theorem 1.1.
(Case 1.1.2.3:
![]() $T_{s_r} \cdot \delta = \Omega _{p,q}$
for some
$T_{s_r} \cdot \delta = \Omega _{p,q}$
for some
![]() $r \notin \{p,q \}$
): In this case,
$r \notin \{p,q \}$
): In this case,
![]() $T_{s_r}$
must act on
$T_{s_r}$
must act on
![]() $\delta $
by uncrossing a pair of adjacent arcs (as in the
$\delta $
by uncrossing a pair of adjacent arcs (as in the
![]() $T_2$
arrow of Figure 2). Recall that
$T_2$
arrow of Figure 2). Recall that
![]() $n-r$
and
$n-r$
and
![]() $n-r+1$
are the labels on the other ends of the crossing arcs from
$n-r+1$
are the labels on the other ends of the crossing arcs from
![]() $r, r+1$
.
$r, r+1$
.
(Case 1.1.2.3.1:
![]() $n-r> 0$
): In this case, we also have
$n-r> 0$
): In this case, we also have
![]() $T_{s_{n-r}} \cdot \delta = \Omega _{p,q}$
. Observe that
$T_{s_{n-r}} \cdot \delta = \Omega _{p,q}$
. Observe that
![]() $r \neq n-r$
. Moreover, we have
$r \neq n-r$
. Moreover, we have
![]() $T_{s_{t}} \cdot \delta = \delta $
for all
$T_{s_{t}} \cdot \delta = \delta $
for all
![]() $t \notin \{ r, n-r\}$
. By Theorem 1.1,
$t \notin \{ r, n-r\}$
. By Theorem 1.1,
Now, Equation (5.6) simplifies to
Thus,
![]() $c_{s_p u, v}^w=1$
.
$c_{s_p u, v}^w=1$
.
(Case 1.1.2.3.2:
![]() $n-r \leq 0$
): Define
$n-r \leq 0$
): Define
![]() $\tilde {u} = 1^{r-n+1} \times u$
,
$\tilde {u} = 1^{r-n+1} \times u$
,
![]() $\tilde {v} = 1^{r-n+1} \times v$
and
$\tilde {v} = 1^{r-n+1} \times v$
and
![]() $\tilde {w} = 1^{r-n+1} \times w$
. Then
$\tilde {w} = 1^{r-n+1} \times w$
. Then
![]() $\tilde {u}$
is
$\tilde {u}$
is
![]() $\tilde {p}$
-inverse Grassmannian, where
$\tilde {p}$
-inverse Grassmannian, where
![]() $\tilde {p} = p +r - n + 1$
. Also, let
$\tilde {p} = p +r - n + 1$
. Also, let
![]() $\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
, and notice that
$\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
, and notice that
![]() $\tilde {\gamma }$
is a horizontal shift of the backstable clan
$\tilde {\gamma }$
is a horizontal shift of the backstable clan
![]() $\gamma _{u,v}$
. Therefore,
$\gamma _{u,v}$
. Therefore,
![]() $T_{\tilde {w}} \cdot \tilde {\gamma }$
is a horizontal shift of
$T_{\tilde {w}} \cdot \tilde {\gamma }$
is a horizontal shift of
![]() $T_w \cdot \gamma _{u,v} = \delta $
. In particular,
$T_w \cdot \gamma _{u,v} = \delta $
. In particular,
![]() $T_{\tilde {w}} \cdot \tilde {\gamma }$
is almost rainbow with a pair of crossing arcs. Observe that
$T_{\tilde {w}} \cdot \tilde {\gamma }$
is almost rainbow with a pair of crossing arcs. Observe that
![]() $s_{\tilde {p}} \tilde {u} = 1^{r-n+1} \times s_p u$
. By the previous Case 1.1.2.3.1,
$s_{\tilde {p}} \tilde {u} = 1^{r-n+1} \times s_p u$
. By the previous Case 1.1.2.3.1,
Now, Lemma 3.2 gives that
so
![]() $c_{s_p u, v}^w = 1$
, as desired.
$c_{s_p u, v}^w = 1$
, as desired.
(Case 1.2:
![]() $c_{1 \times u, 1 \times v}^{s_1(1 \times w)}\neq 0$
): Define
$c_{1 \times u, 1 \times v}^{s_1(1 \times w)}\neq 0$
): Define
![]() $\tilde {u} = 1 \times u$
,
$\tilde {u} = 1 \times u$
,
![]() $\tilde {v} = 1 \times v$
, and
$\tilde {v} = 1 \times v$
, and
![]() $\tilde {w} = 1 \times w$
. Then
$\tilde {w} = 1 \times w$
. Then
![]() $\tilde {u}$
is
$\tilde {u}$
is
![]() $\tilde {p}$
-inverse Grassmannian and
$\tilde {p}$
-inverse Grassmannian and
![]() $\tilde {v}$
is
$\tilde {v}$
is
![]() $\tilde {q}$
-inverse Grassmannian, where
$\tilde {q}$
-inverse Grassmannian, where
![]() $\tilde {p} = p + 1$
and
$\tilde {p} = p + 1$
and
![]() $\tilde {q} = q+1$
. Also, let
$\tilde {q} = q+1$
. Also, let
![]() $\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
, and notice that
$\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
, and notice that
![]() $\tilde {\gamma }$
is a horizontal shift of
$\tilde {\gamma }$
is a horizontal shift of
![]() $\gamma _{u,v}$
.
$\gamma _{u,v}$
.
By Proposition 4.10, we have
and
By Lemma 3.2, we have
Thus, subtracting Equation (5.7) from Equation (5.8) yields that
![]() $c_{1 \times \tilde {u}, 1 \times \tilde {v}}^{s_1(1 \times \tilde {w})} = 0$
.
$c_{1 \times \tilde {u}, 1 \times \tilde {v}}^{s_1(1 \times \tilde {w})} = 0$
.
Now,
![]() $T_{\tilde {w}} \cdot \tilde {\gamma }$
is a horizontal shift of
$T_{\tilde {w}} \cdot \tilde {\gamma }$
is a horizontal shift of
![]() $T_w \cdot \gamma _{u,v}$
. Observe that
$T_w \cdot \gamma _{u,v}$
. Observe that
![]() $s_{\tilde {p}} \tilde {u} = 1 \times s_p u$
. Since Lemma 3.2 gives that
$s_{\tilde {p}} \tilde {u} = 1 \times s_p u$
. Since Lemma 3.2 gives that
![]() $c_{s_p u, v}^w = c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}}$
and the latter coefficient falls under Case 1.1, we are done.
$c_{s_p u, v}^w = c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}}$
and the latter coefficient falls under Case 1.1, we are done.
(Case 2:
![]() $p = q$
): We establish this case by reduction to Case 1 via stabilization. Choose an interval
$p = q$
): We establish this case by reduction to Case 1 via stabilization. Choose an interval
![]() $[i,j]$
on which
$[i,j]$
on which
![]() $\gamma _{u,v}$
is supported.
$\gamma _{u,v}$
is supported.
(Case 2.1:
![]() $i\geq 1$
): If
$i\geq 1$
): If
![]() $i>1$
, expand the interval
$i>1$
, expand the interval
![]() $[i,j]$
until
$[i,j]$
until
![]() $i=1$
.
$i=1$
.
Define
![]() $\tilde {u} = 1 \times u$
,
$\tilde {u} = 1 \times u$
,
![]() $\tilde {v} = \tau _p^{-1}(v)$
, and
$\tilde {v} = \tau _p^{-1}(v)$
, and
![]() $\tilde {w} = \tau _p^{-1}(w)$
. Then
$\tilde {w} = \tau _p^{-1}(w)$
. Then
![]() $\tilde {u}$
is
$\tilde {u}$
is
![]() $\tilde {p}$
-inverse Grassmannian, where
$\tilde {p}$
-inverse Grassmannian, where
![]() $\tilde {p} = p+1$
. On the other hand,
$\tilde {p} = p+1$
. On the other hand,
![]() $\tilde {v}$
is p-inverse Grassmannian.
$\tilde {v}$
is p-inverse Grassmannian.
By Lemma 5.2, we have
But also
![]() $1 \times (s_p u) = s_{\tilde {p}} \tilde {u}$
, so
$1 \times (s_p u) = s_{\tilde {p}} \tilde {u}$
, so
Since
![]() $\tilde {p} \neq p$
, the coefficient
$\tilde {p} \neq p$
, the coefficient
![]() $c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}}$
falls under Case 1. Note also that
$c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}}$
falls under Case 1. Note also that
![]() $\ell (\tilde {w}) = \ell (s_{\tilde {p}} \tilde {u}) + \ell (\tilde {v})$
.
$\ell (\tilde {w}) = \ell (s_{\tilde {p}} \tilde {u}) + \ell (\tilde {v})$
.
Let
![]() $\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
. Notice that
$\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
. Notice that
![]() $\tilde {\gamma }$
is supported on
$\tilde {\gamma }$
is supported on
![]() $[1,j+1]$
and is obtained from
$[1,j+1]$
and is obtained from
![]() $\gamma _{u,v}$
by placing a
$\gamma _{u,v}$
by placing a ![]() in position
in position
![]() $1$
and shifting the rest of
$1$
and shifting the rest of
![]() $\gamma _{u,v}$
horizontally one space to the right. That is,
$\gamma _{u,v}$
horizontally one space to the right. That is,

See Example 5.3 for an illustration of this construction.
Let
![]() $\delta = T_{w} \cdot \gamma _{u,v}$
, and let
$\delta = T_{w} \cdot \gamma _{u,v}$
, and let
![]() $\hat {\delta } = T_{1 \times w} \cdot \tilde {\gamma }$
. Notice that
$\hat {\delta } = T_{1 \times w} \cdot \tilde {\gamma }$
. Notice that
![]() $\hat {\delta }$
is similarly obtained from
$\hat {\delta }$
is similarly obtained from
![]() $\delta $
by placing a
$\delta $
by placing a ![]() in position
in position
![]() $1$
and shifting the rest of
$1$
and shifting the rest of
![]() $\delta $
horizontally one space to the right.
$\delta $
horizontally one space to the right.
Now, notice that
![]() $\tilde {w} = s_p s_{p-1} \cdots s_1(1\times w)$
, so
$\tilde {w} = s_p s_{p-1} \cdots s_1(1\times w)$
, so
(Case 2.1.1:
![]() $\delta $
is not almost rainbow): Let h be the least positive integer such that there is a permutation
$\delta $
is not almost rainbow): Let h be the least positive integer such that there is a permutation
![]() $\theta $
with
$\theta $
with
![]() $\ell (\theta ) = h$
and
$\ell (\theta ) = h$
and
![]() $T_\theta \cdot \delta = \Omega _{p,p}$
. Then, it is easy to see that any permutation
$T_\theta \cdot \delta = \Omega _{p,p}$
. Then, it is easy to see that any permutation
![]() $\sigma $
with
$\sigma $
with
![]() $T_\sigma \cdot \hat {\delta } = \Omega _{\tilde {p},p}$
must have
$T_\sigma \cdot \hat {\delta } = \Omega _{\tilde {p},p}$
must have
![]() $\ell (\sigma ) \geq h + p$
. In particular,
$\ell (\sigma ) \geq h + p$
. In particular,
![]() $T_{\tilde {w}} \cdot \tilde {\gamma } = T_p T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
is not almost rainbow. Therefore, by Case 1, we have
$T_{\tilde {w}} \cdot \tilde {\gamma } = T_p T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
is not almost rainbow. Therefore, by Case 1, we have
![]() $c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}} = 0$
. Therefore, Equation (5.9) gives that
$c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}} = 0$
. Therefore, Equation (5.9) gives that
![]() $c_{s_p u, v}^w = 0$
, as desired.
$c_{s_p u, v}^w = 0$
, as desired.
(Case 2.1.2:
![]() $\delta $
is almost rainbow): We break into cases according to what type of almost rainbow clan
$\delta $
is almost rainbow): We break into cases according to what type of almost rainbow clan
![]() $\delta $
is.
$\delta $
is.
(Case 2.1.2.1:
![]() $T_{s_p} \cdot \delta = \Omega _{p,p}$
): In this case,
$T_{s_p} \cdot \delta = \Omega _{p,p}$
): In this case,
![]() $T_{s_p}$
must act on
$T_{s_p}$
must act on
![]() $\delta $
by joining a
$\delta $
by joining a ![]() and a
and a ![]() into an arc (as in the
into an arc (as in the
![]() $T_4$
arrow of Figure 2). The action of
$T_4$
arrow of Figure 2). The action of
![]() $T_{p-1} T_{p-2} \cdots T_1$
on
$T_{p-1} T_{p-2} \cdots T_1$
on
![]() $\hat {\delta }$
is then to move another
$\hat {\delta }$
is then to move another ![]() from position
from position
![]() $1$
past
$1$
past
![]() $p-1$
initial nodes to land in position p.
$p-1$
initial nodes to land in position p.
(Case 2.1.2.1.1 ![]() ): Here,
): Here, ![]() and
and ![]() . Hence,
. Hence,
![]() $T_p T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta } = T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
and, in particular,
$T_p T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta } = T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
and, in particular,
![]() $T_p T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
is not an almost rainbow clan. Thus, by Case 1, we then have
$T_p T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
is not an almost rainbow clan. Thus, by Case 1, we then have
![]() $c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}} = 0$
. Therefore, Equation (5.9) gives that
$c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}} = 0$
. Therefore, Equation (5.9) gives that
![]() $c_{s_p u, v}^w = 0$
, as desired.
$c_{s_p u, v}^w = 0$
, as desired.
(Case 2.1.2.1.2 ![]() ): Here,
): Here, ![]() and
and ![]() . Hence,
. Hence,
![]() $T_p$
acts on
$T_p$
acts on
![]() $T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
by joining these
$T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
by joining these ![]() and
and ![]() into an arc. So
into an arc. So
![]() $T_p T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
is an almost rainbow clan in
$T_p T_{p-1} T_{p-2} \cdots T_1 \cdot \hat {\delta }$
is an almost rainbow clan in
![]() $\Psi _{\tilde {p}, p}$
. Thus, by Case 1, we then have
$\Psi _{\tilde {p}, p}$
. Thus, by Case 1, we then have
![]() $c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}} = 1$
. Therefore, Equation (5.9) gives that
$c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}} = 1$
. Therefore, Equation (5.9) gives that
![]() $c_{s_p u, v}^w = 1$
, as desired.
$c_{s_p u, v}^w = 1$
, as desired.
(Case 2.1.2.2:
![]() $T_{s_r} \cdot \delta = \Omega _{p,p}$
for some
$T_{s_r} \cdot \delta = \Omega _{p,p}$
for some
![]() $r \neq p$
): In this case,
$r \neq p$
): In this case,
![]() $T_{s_r}$
must act on
$T_{s_r}$
must act on
![]() $\delta $
by uncrossing a pair of adjacent arcs. Recall that
$\delta $
by uncrossing a pair of adjacent arcs. Recall that
![]() $n-r$
and
$n-r$
and
![]() $n-r+1$
are the labels on the other ends of the crossing arcs from
$n-r+1$
are the labels on the other ends of the crossing arcs from
![]() $r, r+1$
.
$r, r+1$
.
The action of
![]() $T_p T_{p-1} \cdots T_1$
on
$T_p T_{p-1} \cdots T_1$
on
![]() $\hat {\delta }$
is then to move the
$\hat {\delta }$
is then to move the ![]() from position
from position
![]() $1$
past p initial nodes to land in position
$1$
past p initial nodes to land in position
![]() $p+1$
. Thus,
$p+1$
. Thus,
![]() $T_{\tilde {w}} \cdot \tilde {\gamma } = T_p T_{p-1} \cdots T_1 \cdot \hat {\delta }$
is an almost rainbow clan in
$T_{\tilde {w}} \cdot \tilde {\gamma } = T_p T_{p-1} \cdots T_1 \cdot \hat {\delta }$
is an almost rainbow clan in
![]() $\Psi _{\tilde {p},p}$
. By Case 1, we then have
$\Psi _{\tilde {p},p}$
. By Case 1, we then have
![]() $c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}} = 1$
. Therefore, Equation (5.9) gives that
$c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}} = 1$
. Therefore, Equation (5.9) gives that
![]() $c_{s_p u, v}^w = 1$
, as desired.
$c_{s_p u, v}^w = 1$
, as desired.
(Case 2.2:
![]() $i < 1$
): Define
$i < 1$
): Define
![]() $\tilde {u} = 1^{1-i} \times u$
,
$\tilde {u} = 1^{1-i} \times u$
,
![]() $\tilde {v} = 1^{1-i} \times v$
, and
$\tilde {v} = 1^{1-i} \times v$
, and
![]() $\tilde {w} = 1^{1-i} \times w$
. Then
$\tilde {w} = 1^{1-i} \times w$
. Then
![]() $\tilde {u}$
and
$\tilde {u}$
and
![]() $\tilde {v}$
are
$\tilde {v}$
are
![]() $\tilde {p}$
-inverse Grassmannian, where
$\tilde {p}$
-inverse Grassmannian, where
![]() $\tilde {p} = p -i + 1$
.
$\tilde {p} = p -i + 1$
.
Also, let
![]() $\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
, and notice that
$\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
, and notice that
![]() $\tilde {\gamma }$
is a horizontal shift of
$\tilde {\gamma }$
is a horizontal shift of
![]() $\gamma _{u,v}$
. Therefore,
$\gamma _{u,v}$
. Therefore,
![]() $T_{\tilde {w}} \cdot \tilde {\gamma }$
is a horizontal shift of
$T_{\tilde {w}} \cdot \tilde {\gamma }$
is a horizontal shift of
![]() $T_w \cdot \gamma _{u,v} = \delta $
.
$T_w \cdot \gamma _{u,v} = \delta $
.
Observe that
![]() $s_{\tilde {p}} \tilde {u} = 1^{1-i} \times s_p u$
. Since Lemma 3.2 gives that
$s_{\tilde {p}} \tilde {u} = 1^{1-i} \times s_p u$
. Since Lemma 3.2 gives that
![]() $c_{s_p u, v}^w = c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}}$
and the latter coefficient falls under Case 2.1, we are done.
$c_{s_p u, v}^w = c_{s_{\tilde {p}} \tilde {u}, \tilde {v}}^{\tilde {w}}$
and the latter coefficient falls under Case 2.1, we are done.
Example 5.3. We illustrate part of the construction from Case 2.1. Let
![]() $u = 51236748$
and
$u = 51236748$
and
![]() $v = 12354678$
. Here,
$v = 12354678$
. Here,
![]() $p=q=4$
. The clan
$p=q=4$
. The clan
![]() $\gamma _{u,v}$
is
$\gamma _{u,v}$
is

Define
![]() $\tilde {u} = 1 \times u$
and
$\tilde {u} = 1 \times u$
and
![]() $\tilde {v} = \tau _p^{-1}(v)$
. In this case,
$\tilde {v} = \tau _p^{-1}(v)$
. In this case,
![]() $\tilde {u} = 162347859$
and
$\tilde {u} = 162347859$
and
![]() $\tilde {v} = 512364789$
. Note that
$\tilde {v} = 512364789$
. Note that
![]() $\tilde {u}$
is
$\tilde {u}$
is
![]() $5$
-inverse Grassmannian, while
$5$
-inverse Grassmannian, while
![]() $\tilde {v}$
is
$\tilde {v}$
is
![]() $4$
-inverse Grassmannian.
$4$
-inverse Grassmannian.
Let
![]() $\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
, which looks like
$\tilde {\gamma } = \gamma _{\tilde {u}, \tilde {v}}$
, which looks like

Notice that
![]() $\tilde {\gamma }$
is obtained from
$\tilde {\gamma }$
is obtained from
![]() $\gamma _{u,v}$
by placing a
$\gamma _{u,v}$
by placing a ![]() in position
in position
![]() $1$
and shifting the rest of
$1$
and shifting the rest of
![]() $\gamma _{u,v}$
to the right, as described in Case 2.1.
$\gamma _{u,v}$
to the right, as described in Case 2.1.
Example 5.4. Let
![]() $u = 3142$
. Note that u is
$u = 3142$
. Note that u is
![]() $2$
-inverse Grassmannian and that
$2$
-inverse Grassmannian and that
![]() $s_2 u = 2143$
. We use Theorem 1.2 to compute the Schubert structure coefficients
$s_2 u = 2143$
. We use Theorem 1.2 to compute the Schubert structure coefficients
![]() $c_{2143,3142}^w$
for all
$c_{2143,3142}^w$
for all
![]() $w \in S_+$
. We have that
$w \in S_+$
. We have that
![]() $\gamma _{u,u}$
looks like
$\gamma _{u,u}$
looks like

We consider all nontrivial actions of
![]() $0$
-Hecke generators
$0$
-Hecke generators
![]() $T_i$
on
$T_i$
on
![]() $\gamma _{u,u}$
, until reaching an almost rainbow clan:
$\gamma _{u,u}$
, until reaching an almost rainbow clan:

Here, we have drawn the arrows labeled only by
![]() $T_i$
with
$T_i$
with
![]() $i\leq 0$
in
$i\leq 0$
in ![]() to distinguish them from those that contribute in Theorem 1.2.
to distinguish them from those that contribute in Theorem 1.2.
First, observe that there are only two almost rainbow clans that we can reach, specifically the almost rainbow clans
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
at the bottom of the diagram above. Note that
$\psi _2$
at the bottom of the diagram above. Note that
![]() $\psi _1, \psi _2 \in \Psi _{2,2}$
. Using only
$\psi _1, \psi _2 \in \Psi _{2,2}$
. Using only
![]() $T_i$
with
$T_i$
with
![]() $i>0$
, there are exactly two paths from
$i>0$
, there are exactly two paths from
![]() $\gamma _{u,u}$
to
$\gamma _{u,u}$
to
![]() $\psi _1$
. These paths are labeled by the sequences
$\psi _1$
. These paths are labeled by the sequences
![]() $(T_1, T_2, T_3, T_2, T_4)$
and
$(T_1, T_2, T_3, T_2, T_4)$
and
![]() $(T_1, T_2, T_3, T_4, T_2)$
, both corresponding to the permutation
$(T_1, T_2, T_3, T_4, T_2)$
, both corresponding to the permutation
![]() $51324$
. Thus, by Theorem 1.2, we have computed that
$51324$
. Thus, by Theorem 1.2, we have computed that
![]() $c_{2143, 3142}^{51324} = 1$
.
$c_{2143, 3142}^{51324} = 1$
.
On the other hand, there are six paths from
![]() $\gamma _{u,u}$
to the almost rainbow clan
$\gamma _{u,u}$
to the almost rainbow clan
![]() $\psi _2$
. These six paths are labeled by the sequences
$\psi _2$
. These six paths are labeled by the sequences
![]() $\pi _1 = (T_1, T_3, T_2, T_4, T_3)$
,
$\pi _1 = (T_1, T_3, T_2, T_4, T_3)$
,
![]() $\pi _2 =(T_1, T_3, T_4, T_2, T_3)$
,
$\pi _2 =(T_1, T_3, T_4, T_2, T_3)$
,
![]() $\pi _3 = (T_3, T_1, T_2, T_4, T_3)$
,
$\pi _3 = (T_3, T_1, T_2, T_4, T_3)$
,
![]() $\pi _4 = (T_3, T_1, T_4, T_2, T_3)$
,
$\pi _4 = (T_3, T_1, T_4, T_2, T_3)$
,
![]() $\pi _5 = (T_3, T_2, T_1, T_2, T_3)$
, and
$\pi _5 = (T_3, T_2, T_1, T_2, T_3)$
, and
![]() $\pi _6 = (T_3, T_4, T_1, T_2, T_3)$
. The sequences
$\pi _6 = (T_3, T_4, T_1, T_2, T_3)$
. The sequences
![]() $\pi _1,\ \pi _2$
,
$\pi _1,\ \pi _2$
,
![]() $\pi _3$
,
$\pi _3$
,
![]() $\pi _4$
, and
$\pi _4$
, and
![]() $\pi _6$
all yield the permutation
$\pi _6$
all yield the permutation
![]() $41523$
. Thus, by Theorem 1.2, we have computed that
$41523$
. Thus, by Theorem 1.2, we have computed that
![]() $c_{2143,3142}^{41523} = 1$
. However,
$c_{2143,3142}^{41523} = 1$
. However,
![]() $\pi _5$
yields the permutation
$\pi _5$
yields the permutation
![]() $4231$
, so Theorem 1.2 also gives
$4231$
, so Theorem 1.2 also gives
![]() $c_{2143,3142}^{4231} = 1$
. Since these are the only paths from
$c_{2143,3142}^{4231} = 1$
. Since these are the only paths from
![]() $\gamma _{u,u}$
to almost rainbow clans in
$\gamma _{u,u}$
to almost rainbow clans in
![]() $\Psi _{2,2}$
, Theorem 1.2 finally computes that
$\Psi _{2,2}$
, Theorem 1.2 finally computes that
![]() $c_{2143,3142}^{w} = 0$
for all
$c_{2143,3142}^{w} = 0$
for all
![]() $w \notin \{51324, 41523, 4231 \}$
.
$w \notin \{51324, 41523, 4231 \}$
.
The fact that the products in Theorems 1.1 and 1.2 are multiplicity-free is remarkable. In contrast, for example, the Littlewood–Richardson rule shows that every nonnegative integer appears as a coefficient in some product of Grassmannian Schubert cycles. Indeed, the multiplicity-freeness of Theorems 1.1 and 1.2 does not extend to the product of subjacent Schubert cycles with each other, as illustrated by the following example.
Example 5.5. Let
![]() $u=142536$
and
$u=142536$
and
![]() $v=451236$
. Note that u and v are both
$v=451236$
. Note that u and v are both
![]() $3$
-inverse Grassmannian. We have that
$3$
-inverse Grassmannian. We have that
![]() $s_3u=132546$
and
$s_3u=132546$
and
![]() $s_3v=351246$
are subjacent. Furthermore, we have
$s_3v=351246$
are subjacent. Furthermore, we have
which is not multiplicity-free.
Acknowledgements
We are grateful for conversations with Zach Hamaker and David E Speyer. Many thanks to Alexander Yong for bringing the reference [Reference WyserWys13] to our attention. We are also very grateful to Christian Gaetz, Patricia Klein, Allen Knutson and Frank Sottile for many helpful comments on earlier drafts. In particular, we thank Frank Sottile for pointing out a derivation of Corollary 4.3 from Monk’s formula and providing useful remarks on [Reference Bergeron and SottileBS98, Reference Lenart, Robinson and SottileLRS06]. We also thank the anonymous referees for many helpful comments and suggestions.
Competing interest
The authors have no competing interest to declare.
Financial support
O.P. was partially supported by a Mathematical Sciences Postdoctoral Research Fellowship (#1703696) from the National Science Foundation, as well as by a Discovery Grant (RGPIN-2021-02391) and Launch Supplement (DGECR-2021-00010) from the Natural Sciences and Engineering Research Council of Canada. A.W. was partially supported by Bill Fulton’s Oscar Zariski Distinguished Professor Chair funds and by National Science Foundation grant DMS-2344764.