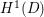EXTENSION AND RESTRICTION FOR BERGMAN SCALE OF SPACES AND ONE-DIMENSIONAL SUBVARIETIES ON CONVEX FINITE TYPE DOMAINS

Abstract

We prove that the extension problem from one-dimensional subvarieties with values in Bergman space $H^{1}(D)$ on convex finite type domains can be solved by means of appropriate measures. We obtain also almost optimal results concerning the extension problem for other Bergman spaces and one-dimensional varieties.

1 Introduction

In [15], Diederich and Mazzilli showed that there exists a pseudoconvex domain $D\subset \mathbb{C}^{3}$ with smooth polynomial boundary and a subvariety $A=\{z_{1}=0\}$ such that for any positive Borel measure ${\it\nu}$

$$\begin{eqnarray}R_{D\,\cap \,A}[H^{2}(D)]\neq H^{2}(D\cap A,d{\it\nu}).\end{eqnarray}$$

The symbol $R_{D\,\cap \,A}$ is the operator of restriction to the subvariety $D\cap A$, $H^{2}(D)$ stands for Bergman space

$$\begin{eqnarray}H^{2}(D)=\left\{f\in H(D):\int _{D}|f|^{2}\,dV<\infty \right\}\end{eqnarray}$$

and $H^{2}(D\cap A,d{\it\nu})$ is the space of all functions holomorphic in $D\cap A$ such that

$$\begin{eqnarray}\int _{D\,\cap \,A}|f|^{2}\,d{\it\nu}<\infty .\end{eqnarray}$$

It seems therefore interesting that there are domains $D$, essentially of the type considered in [15], and subvarieties $A$ such that the extension problem can be completely, or as we show almost completely, solved by means of measures. This is the subject of this paper. We investigate bounded convex domains of finite type with smooth boundary and linear affine subvarieties of $D$ of higher codimension. The class of domains that we consider includes, in particular, complex pseudoellipsoids which were studied in [15]. Our main results concern subvarieties of dimension one

$$\begin{eqnarray}A=A(l_{1},\ldots ,l_{n-1}):=\{z\in \mathbb{C}^{n}:l_{1}(z)=\cdots =l_{n-1}(z)=0\},\end{eqnarray}$$

where

$$\begin{eqnarray}l_{i}(z)=a_{i1}z_{1}+\cdots +a_{in}z_{n}+b_{i},\quad i=1,\ldots ,n-1,\end{eqnarray}$$

with $a_{ij},b_{i}\in \mathbb{C}$. We prove the following.

Theorem 1. Assume that $D$ is a bounded convex domain of finite type in $\mathbb{C}^{n},n>1$ with smooth boundary. Let $l_{1}\ldots ,l_{n-1}$ be linear affine maps such that $D\cap A(l_{1},\ldots ,l_{n-1})\neq \emptyset$ and $\dim A(l_{1},\ldots ,l_{n-1})=1$.

There exists a measure ${\it\omega}$ supported on $D\cap A(l_{1},\ldots ,l_{n-1})$ such that

$$\begin{eqnarray}R_{D\,\cap \,A}[H^{1}(D)]=H^{1}(D\cap A(l_{1},\ldots ,l_{n-1}),{\it\omega}).\end{eqnarray}$$

The measure ${\it\omega}$ is equal to

$$\begin{eqnarray}|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A}.\end{eqnarray}$$

Thus, the class of functions that admit a holomorphic extension in $H^{1}(D)$ is the space $H^{1}(D\cap A,{\it\omega})$. In other words, the extension and restriction problem for the space $H^{1}(D)$ and one-dimensional subvarieties can be completely solved by means of a measure.

The notation used in Theorem 1 requires explanation. The symbol

$$\begin{eqnarray}dV_{D\,\cap \,A}=dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}\end{eqnarray}$$

stands for the volume measure on the intersection $D\cap A(l_{1},\ldots ,l_{n-1})$. This is meaningful since $D$ is assumed to be equipped with the standard Hermitian metric and therefore the linear affine subspace $A(l_{1},\ldots ,l_{n-1})$ carries the natural metric, and, as a result, also the volume form. The symbol $|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}$ stands for a non-isotropic norm of the $(n-1,0)$-differential form $\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}$ (cf. Definition 1 below). It is important to notice that although $l_{i},i=1,\ldots ,n-1$ are affine linear the norm ${\it\zeta}\mapsto |\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}({\it\zeta})$ is not constant.

Theorem 1 provides a necessary and sufficient condition for extension from one-dimensional subvarieties with values in $H^{1}(D)$. It is natural to look for analogous results for other $H^{p}(D),1<p<\infty$ spaces. The result that we prove is ${\it\epsilon}$-optimal – there is an ${\it\epsilon}>0$ gap between the condition that is necessary for the extension and the one that is sufficient.

Theorem 2. Assume that $D$ is a bounded convex domain of finite type in $\mathbb{C}^{n},n>1$ with smooth boundary. Let $l_{1}\ldots ,l_{n-1}$ be linear affine maps such that $D\cap A(l_{1},\ldots ,l_{n-1})\neq \emptyset$ and $\dim A(l_{1},\ldots ,l_{n-1})=1$.

For any $1<p<\infty$ it holds that

$$\begin{eqnarray}\displaystyle & & \displaystyle R_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}[H^{p}(D)]\nonumber\\ \displaystyle & & \displaystyle \quad \subset H^{p}(D\cap A(l_{1},\ldots ,l_{n-1}),|\partial l_{1}\wedge \ldots \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}).\nonumber\end{eqnarray}$$

On the other hand, for any ${\it\epsilon}>0$ and $1<p<\infty$ there exists an operator $E_{D\,\cap \,A}$

$$\begin{eqnarray}E_{D\,\cap \,A}:H^{p}(D\cap A,|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2-{\it\epsilon}}\,dV_{D\,\cap \,A})\rightarrow H^{p}(D)\end{eqnarray}$$

such that

$$\begin{eqnarray}R_{D\,\cap \,A}\circ E_{D\,\cap \,A}=\text{id}.\end{eqnarray}$$

Another striking fact proved by Diederich and Mazzilli in [15] is that there exist pseudoconvex domains and subvarieties with no “regularity gain” in $H^{2}(D)$ space. This is in contrast to our results. Both Theorems 1 and 2 say that the class of holomorphic in $D\cap A$ functions that admit an extension in $H^{p}(D)$ is strictly larger than $H^{p}(D\cap A)$ when $A=A(l_{1},\ldots ,l_{n-1})$ is one-dimensional and $1\leqslant p<\infty$.

What is important in the proofs of Theorems 1 and 2 is the fact that the dimension of $A$ is equal to one. It is natural to seek analogous results for subvarieties of higher dimension. This was investigated by the author in [24] for subvarieties of codimension one. Here, we formulate a generalization of a different nature.

Theorem 3. Assume that $D$ is a bounded convex domain of finite type in $\mathbb{C}^{n},n>1$ with smooth boundary. Let $l_{1}\ldots ,l_{m},1\leqslant m\leqslant n-1$ be linear affine maps such that $D\cap A(l_{1},\ldots ,l_{m})\neq \emptyset$ and $\dim A(l_{1},\ldots ,l_{m})=n-m$.

Assume that there exists an open neighborhood ${\mathcal{U}}$ of $A(l_{1},\ldots ,l_{m})\cap bD$ and a constant $c>0$ such that for any $z\in {\mathcal{U}}$ there exists an $|r(z)|$-extremal basis $(u_{1},\ldots ,u_{n})$ at $z\in {\mathcal{U}}$ such that for any indices $1\leqslant j_{1}<\cdots <j_{m}\leqslant n$

$$\begin{eqnarray}(\partial l_{1}\wedge \cdots \wedge \partial l_{m})(u_{j_{1}},\ldots ,u_{j_{m}})\neq 0\Rightarrow |(\partial l_{1}\wedge \cdots \wedge \partial l_{m})(u_{j_{1}},\ldots ,u_{j_{m}})|\geqslant c.\end{eqnarray}$$

Then

$$\begin{eqnarray}R_{D\,\cap \,A}[H^{1}(D)]=H^{1}(D\cap A(l_{1},\ldots ,l_{m}),|\partial l_{1}\wedge \cdots \wedge \partial l_{m}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A}).\end{eqnarray}$$

Moreover, for any $1<p<\infty$ it holds that

$$\begin{eqnarray}\displaystyle & & \displaystyle R_{D\,\cap \,A(l_{1},\ldots ,l_{m})}[H^{p}(D)]\nonumber\\ \displaystyle & & \displaystyle \quad \subset H^{p}(D\cap A(l_{1},\ldots ,l_{m}),|\partial l_{1}\wedge \ldots \partial l_{m}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{m})}),\nonumber\end{eqnarray}$$

and for any ${\it\epsilon}>0$ and $1<p<\infty$ there exists an extension operator $E_{D\,\cap \,A}$ such that

$$\begin{eqnarray}E_{D\,\cap \,A}:H^{p}(D\cap A,|\partial l_{1}\wedge \cdots \wedge \partial l_{m}|_{{\mathcal{N}}}^{2-{\it\epsilon}}\,dV_{D\,\cap \,A})\rightarrow H^{p}(D).\end{eqnarray}$$

Our results suggest that the solution to the extension problem depends on the minimum of the dimension and the codimension of $A$. This seems to be consistent with the results in [15]. We pursued this observation further in [25].

Arguably the most important result concerning extension of holomorphic functions in several variables is Ohsawa–Takegoshi’s Theorem [32]. It concerns holomorphic $L^{2}$-extensions of holomorphic $L^{2}$-functions on general pseudoconvex domains. Compared with this result Theorem 2 says that under the additional assumption that $D$ is of finite type and convex the class of functions that admit an extension is strictly larger than $H^{2}(D\cap A(l_{1},\ldots ,l_{n-1}))$ (cf. [25] for more information in this direction). Similar results for strictly pseudoconvex domains were obtained by Cumenge in [11]. It is, however, a feature of the finite type case that the results are non-isotropic. This is reflected, for instance, in the definition of the measure $|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}$ and the estimates in Lemmas 2 and 3 below.

A convex domain $D=\{r<0\}$ with smooth boundary is of finite type if the maximal order of contact of $bD$ with complex lines is finite (cf. [6, 29, 33] for explanation of this equivalent definition). The finite type conditions were discovered in connection with the $\overline{\partial }$-Neumann problem (see the fundamental works of Kohn [26, 27] and Catlin [9, 10], see also [12] for more information on the type condition). The correct, from the viewpoint of complex analysis, geometric structure on convex finite type domains was introduced by Bruna et al. [8] and McNeal [29, 30]. In [7], Bruna et al. showed how to estimate integral kernels in terms of this geometric structure. Another important step was made by Diederich and Fornaess [14], who constructed support functions for this class of domains. This made it possible to answer many analytic questions such as the quantitative behavior of the $\overline{\partial }$-equation on $L^{p}$-spaces [18, 20, 21] and Hölder spaces [13, 19]. The extension problem for bounded holomorphic functions and linear subvarieties on convex finite type domains was studied by Diederich and Mazzilli in [16]. The case of non-linear subvarieties was investigated by Alexandre in [2]. This research generalizes the important results obtained by Henkin [22] and Amar [3] for strictly pseudoconvex domains. Other aspects of function theory on convex finite type domains such as duality problems were also studied (see [28] for example). We remark that recently Nikolov et al. [31] found a mistake in [29] and [30]. This, however, has no influence on our work since crucial estimates, in particular formula (6) below, remain valid.

In Section 2 we define the fundamental object in our study, that is the non-isotropic norm $|\cdot |_{{\mathcal{N}}}$. Section 3 is divided into two subsections. The first one contains the proof of the necessary condition for an extension with values in $H^{p}(D)$. This says that if a function $f\in H(D\cap A(l_{1},\ldots ,l_{n-1}))$ admits an extension to a function in $H^{p}(D)$, then it belongs to $H^{p}(D\cap A(l_{1},\ldots ,l_{n-1}),{\it\omega})$ for the measure ${\it\omega}$. Section 3.2 contains the construction of the extension operator $E_{D\,\cap \,A}$ following the method of Berndtsson [5], which is based on previous results by Berndtsson and Andersson [4] (we refer the reader to the monograph [1] for more information on integral formulas). In this subsection we also provide arguments that prove continuity of the operator $E_{D\,\cap \,A}$. It contains also the proof of Theorem 3.

2 Convex finite type domains and the non-isotropic norm

Let $D=\{r<0\}$ be a bounded convex domain with $C^{\infty }$-boundary. We may assume that $r$ has been chosen to be convex on $\mathbb{C}^{n}$ and smooth in $\mathbb{C}^{n}\setminus \{0\}$. Indeed, we may choose $r$ to be equal to $p_{D}-1$, where $p_{D}$ is the Minkowski functional of $D$

$$\begin{eqnarray}p_{D}(z):=\inf \{{\it\lambda}>0:z\in {\it\lambda}D\}.\end{eqnarray}$$

Such a defining function is everywhere convex (we may assume that $D$ contains $0$). It follows from the implicit function theorem that $r$ is also smooth close to $bD$, since it is defined by the equation $\tilde{r}(z/(1+r(z)))=0$, where $\tilde{r}$ is any defining function smooth near $bD$ (for instance the signed distance to $bD$). Since $p_{D}(tz)=tp_{D}(z)$ for $z\in \mathbb{C}^{n},t>0$, the function $r=p_{D}-1$ is smooth in $\mathbb{C}^{n}\setminus \{0\}$.

We assume that the domain $D$ is of type $M$. This means that the maximal order of contact of $bD$ with complex lines is equal to $M$.

We do not include separate background on the geometry of convex finite type domains. Such information can naturally be found in articles by McNeal [29, 30]. It was also given in many papers on convex finite type domains – we refer the reader, for instance, to [7] or [13]. What is important is the fact that some neighborhood $U$ of $\bar{D}$ is equipped with a geometric structure consisting of polydisks $P_{{\it\varepsilon}}({\it\zeta}),{\it\zeta}\in U,{\it\varepsilon}>0$. These polydisks are defined with respect to a distinguished basis, the so-called ${\it\varepsilon}$-extremal basis (cf. [29, 30] and [20, 21] for further generalizations). The choice of the basis is made in such a way that the polydisks reflect the shape of $bD$ and other level sets of the defining function. It is also important that the family of these polydisks furnish $U$ with a structure of a space of homogeneous type. This is crucial in the proof of Lemma 1 and Theorem 5.

The basic object in our study is the non-isotropic norm defined on covectors.

Definition 1. Assume that ${\rm\Omega}$ is an $(m,0)$-covector at ${\it\zeta}\in D$. Set

$$\begin{eqnarray}|{\rm\Omega}|_{{\mathcal{N}}}({\it\zeta}):=\sup \left\{|{\rm\Omega}(v_{1},\ldots ,v_{m})|\mathop{\prod }_{j=1}^{m}{\it\tau}({\it\zeta},v_{j},|r({\it\zeta})|):v_{1},\ldots ,v_{m}\neq 0\right\}.\end{eqnarray}$$

The function ${\it\tau}$ is a complex boundary distance

$$\begin{eqnarray}{\it\tau}({\it\zeta},v,{\it\varepsilon}):=\max \{c:|r({\it\zeta}+{\it\lambda}v)-r({\it\zeta})|<{\it\varepsilon}\hspace{2.22198pt}\forall \hspace{2.22198pt}{\it\lambda}\in \mathbb{C},|{\it\lambda}|<c\},\end{eqnarray}$$

${\it\zeta}\in D,v\in \mathbb{C}^{n},{\it\varepsilon}>0$ (cf. [29, 30] and [7, 13]).

3 Proofs

3.1 Necessary condition

We concentrate now on the necessity part of Theorems 1 and 2, that is we intend to show that for any $1\leqslant p<\infty$ it holds that

(1)$$\begin{eqnarray}R_{D\,\cap \,A}[H^{p}(D)]\subset H^{p}(D\cap A(l_{1},\ldots ,l_{n-1}),{\it\omega}),\end{eqnarray}$$

where

$$\begin{eqnarray}d{\it\omega}=|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A}.\end{eqnarray}$$

In order to prove (1) one shows first the following.

Theorem 4. Assume that $D$ is a bounded convex domain of finite type in $\mathbb{C}^{n},n>1$ with smooth boundary. Let $l_{1},\ldots ,l_{m},1\leqslant m\leqslant n-1$ be affine linear maps such that $D\cap A(l_{1},\ldots ,l_{m})\neq \emptyset$ and $\dim A(l_{1},\ldots ,l_{m})=n-m$.

Let ${\it\mu}$ be a positive Borel measure supported on $D\cap A(l_{1},\ldots ,l_{m})$. If for any sufficiently small $c>0$

(2)$$\begin{eqnarray}\sup \biggl\{\frac{{\it\mu}(P_{c|r(q)|}(q)\cap A(l_{1},\ldots ,l_{m}))}{V(P_{c|r(q)|}(q))}:q\in D\cap A(l_{1},\ldots ,l_{m})\biggr\}<\infty ,\end{eqnarray}$$

then for $1\leqslant p<\infty$

$$\begin{eqnarray}R_{D\,\cap \,A(l_{1},\ldots ,l_{m})}[H^{p}(D)]\subset H^{p}(D\cap A(l_{1},\ldots ,l_{m}),{\it\mu}).\end{eqnarray}$$

Observe that Theorem 4 holds true for $1\leqslant m\leqslant n-1$, not only for $n-1$.

Condition (2) in Theorem 4 is a Carleson type condition where instead of Carleson boxes one considers polydisks $P_{c|r(q)|}(q)$. It says that the measure ${\it\mu}$ behaves on the intersection $D\cap A(l_{1},\ldots ,l_{m})$ precisely like the volume measure $dV$ on the whole domain $D$.

The proof of Theorem 4 is similar to the corresponding result for subvarieties of codimension one. Therefore we only comment on it. In order to prove it one first establishes the existence of a Whitney type cover of $D\cap A(l_{1},\ldots ,l_{m})$ consisting of polydisks $P_{{\it\varepsilon}}(q)$ with ${\it\varepsilon}$ uniformly comparable with $|r(q)|$.

Lemma 1. Assume that $D$ is a bounded convex domain of finite type in $\mathbb{C}^{n},n>1$ with smooth boundary. Let $A(l_{1},\ldots ,l_{m})$ be the zero set of affine linear maps $l_{1},\ldots ,l_{m},1\leqslant m\leqslant n-1$ such that $D\cap A(l_{1},\ldots ,l_{m})\neq \emptyset$ and $\dim A(l_{1},\ldots ,l_{m})=n-m$.

For any $c_{1}>0$ sufficiently small there exist a constant $C_{2}>0$ and a family ${\mathcal{P}}=\{P_{{\it\varepsilon}_{1}}(q_{1}),P_{{\it\varepsilon}_{2}}(q_{2}),\ldots \,\}$ such that

1. (1) $p_{1},p_{2},\cdots \in D\cap A(l_{1},\ldots ,l_{m})$;

2. (2) the polydisks $P\in {\mathcal{P}}$ are disjoint;

3. (3)

   $$\begin{eqnarray}D\cap A(l_{1},\ldots ,l_{m})\subset \mathop{\bigcup }_{i=1}^{\infty }P_{C_{1}{\it\varepsilon}_{1}}(q_{i});\end{eqnarray}$$

4. (4) ${\it\varepsilon}_{i}=c_{1}|r(q_{i})|$, $i\in \mathbb{N}$;

5. (5)

   $$\begin{eqnarray}\sup _{q\in D}|\{P_{C_{1}^{2}{\it\varepsilon}_{i}}(q_{i})\in {\mathcal{P}}:q\in P_{C_{1}{\it\varepsilon}_{i}}(q_{i})\}|<C_{2}.\end{eqnarray}$$

The constant $C_{1}$ that appears in Lemma 1 is the constant from the engulfing property of the polydisks $P_{{\it\varepsilon}}(q)$:

$$\begin{eqnarray}P_{{\it\varepsilon}}(q_{1})\cap P_{{\it\varepsilon}}(q_{2})\neq \emptyset \Rightarrow P_{{\it\varepsilon}}(q_{1})\subset P_{C_{1}{\it\varepsilon}}(q_{2}).\end{eqnarray}$$

This property was established in [30]. The proof of Lemma 1 is standard. As we have already written, it relies on the fact that the polydisks $P_{{\it\varepsilon}}({\it\zeta})$ furnish $U\supset \bar{D}$ with the structure of a space of a homogeneous type.

Now, in order to prove Theorem 4 one uses the cover for Lemma 1 and the mean value property

$$\begin{eqnarray}|f(q)|^{p}\leqslant \frac{1}{V(P_{c|r(q)|})}\int _{P_{c|r(q)|}(q)}|f|^{p}\,dV.\end{eqnarray}$$

Since the argument is the same as in codimension one considered in [23], we omit the details. What remains to be proved is the fact that the measure $|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A}$ satisfies condition (2). Observe that here it is important that $m=n-1$.

Theorem 5. Assume that $D$ is a bounded convex domain of finite type in $\mathbb{C}^{n},n>1$ with smooth boundary. Let $l_{1},\ldots ,l_{n-1}$ be affine linear maps such that $D\cap V(l_{1},\ldots ,l_{n-1})\neq \emptyset$ and $\dim V(l_{1},\ldots ,l_{n-1})=1$. The measure

$$\begin{eqnarray}|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}\end{eqnarray}$$

satisfies condition (2). As a result, for any $1\leqslant p<\infty$

$$\begin{eqnarray}\displaystyle & & \displaystyle R_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}[H^{p}(D)]\nonumber\\ \displaystyle & & \displaystyle \quad \subset H^{p}(D\cap A(l_{1},\ldots ,l_{n-1}),|\partial l_{1}\wedge \ldots \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}).\nonumber\end{eqnarray}$$

Proof. We deal with the measure

$$\begin{eqnarray}d{\it\omega}({\it\zeta}):=|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}({\it\zeta})\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}({\it\zeta}),\end{eqnarray}$$

where $l_{1},\ldots ,l_{n-1}$ are affine linear. In order to have control on ${\it\omega}$ we use Wirtinger’s formula.

Consider a point $q\in D\cap A(l_{1},\ldots ,l_{n-1})$, and for a given small $c>0$ consider the $c|r(q)|$-extremal basis $(u_{1},\ldots ,u_{n})$ at $q$ (cf. [29, 30] or [20, 21] for the definition). Let $({\it\eta}_{1},\ldots ,{\it\eta}_{n})$ be the corresponding coordinates of a point ${\it\zeta}\in D$

$$\begin{eqnarray}{\it\zeta}=q+\mathop{\sum }_{j=1}^{n}{\it\eta}_{j}u_{j}.\end{eqnarray}$$

Let ${\rm\Phi}$ be a unitary transformation such that

$$\begin{eqnarray}{\it\eta}={\rm\Phi}^{-1}({\it\zeta}-q),\end{eqnarray}$$

and let ${\it\varphi}$ be defined by the relation

(3)$$\begin{eqnarray}{\it\zeta}={\rm\Phi}({\it\eta})+q={\it\varphi}({\it\eta}).\end{eqnarray}$$

By definition of $A(l_{1},\ldots ,l_{n-1})$, we have

$$\begin{eqnarray}l_{1}({\it\zeta})=\cdots =l_{n-1}({\it\zeta})=0,\end{eqnarray}$$

for ${\it\zeta}\in A(l_{1},\ldots ,l_{n-1})$. Thus, $l_{1}\circ {\it\varphi}({\it\eta})=\cdots =l_{n-1}\circ {\it\varphi}({\it\eta})=0$ when ${\it\eta}\in {\it\varphi}^{-1}(A(l_{1},\ldots ,l_{n-1}))$. Therefore,

$$\begin{eqnarray}0=d(l_{i}\circ {\it\varphi}({\it\eta}))=\mathop{\sum }_{j=1}^{n}\frac{\partial (l_{i}\circ {\it\varphi})}{\partial {\it\eta}_{j}}\,d{\it\eta}_{j},\quad i=1,\ldots ,n-1\end{eqnarray}$$

on ${\it\varphi}^{-1}(A(l_{1},\ldots ,l_{n-1}))$. Hence, for any permutation $j_{1},\ldots ,j_{n}$ of $1,\ldots ,n$

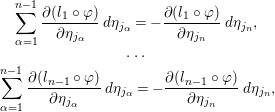$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{{\it\alpha}=1}^{n-1}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{{\it\alpha}}}}\,d{\it\eta}_{j_{{\it\alpha}}}=-\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n}}}\,d{\it\eta}_{j_{n}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \ldots & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{{\it\alpha}=1}^{n-1}\frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{{\it\alpha}}}}\,d{\it\eta}_{j_{{\it\alpha}}}=-\frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n}}}\,d{\it\eta}_{j_{n}}, & \displaystyle \nonumber\end{eqnarray}$$

and, as a result,

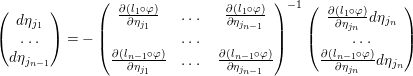(4)$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}d{\it\eta}_{j_{1}}\\ \ldots \\ d{\it\eta}_{j_{n-1}}\end{array}\right)=-\left(\begin{array}{@{}ccc@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\\ & \ldots \, & \\ \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\end{array}\right)^{-1}\left(\begin{array}{@{}c@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n}}}d{\it\eta}_{j_{n}}\\ \ldots \\ \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n}}}d{\it\eta}_{j_{n}}\end{array}\right)\end{eqnarray}$$

on ${\it\varphi}^{-1}A(l_{1},\ldots ,l_{n-1})$.

According to Wirtinger’s formula

$$\begin{eqnarray}dV_{D\,\cap \,A}=\frac{\sqrt{-1}}{2}(d{\it\zeta}_{1}\wedge d\bar{{\it\zeta}}_{1}+\cdots +d{\it\zeta}_{n}\wedge d\bar{{\it\zeta}}_{n})|_{D\,\cap \,A},\end{eqnarray}$$

and, as a result,

$$\begin{eqnarray}{\it\varphi}^{\ast }(dV_{D\,\cap \,A})=\frac{\sqrt{-1}}{2}(d{\it\eta}_{1}\wedge d\bar{{\it\eta}}_{1}+\cdots +d{\it\eta}_{n}\wedge d\bar{{\it\eta}}_{n})|_{{\it\varphi}^{-1}(D\cap A)},\end{eqnarray}$$

where ${\it\varphi}^{\ast }(dV_{D\,\cap \,A})$ denotes the pullback of the volume form $dV_{D\,\cap \,A}$.

We apply (4) and obtain the following estimate:

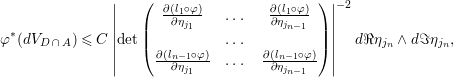(5)$$\begin{eqnarray}{\it\varphi}^{\ast }(dV_{D\,\cap \,A})\leqslant C\left|\det \left(\begin{array}{@{}ccc@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\\ & \ldots \, & \\ \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\end{array}\right)\right|^{-2}d\Re {\it\eta}_{j_{n}}\wedge d\Im {\it\eta}_{j_{n}},\end{eqnarray}$$

provided the determinant is non-zero.

In order to prove Theorem 5 we need to deal with the expression $|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}$. If ${\it\zeta}\in P_{{\it\varepsilon}}(q)$, then ${\it\tau}({\it\zeta},u,{\it\varepsilon})\sim {\it\tau}(q,u,{\it\varepsilon})$ for any unit vector $u$ with uniform constants [30, Proposition 2.3]. Moreover, if ${\it\zeta}\in P_{c|r(q)|}(q)$ with $c$ small enough, then $r({\it\zeta})\sim r(q)$. Furthermore, if $u=\sum _{j=1}^{n}{\it\alpha}_{j}u_{j}$, where $u_{1},\ldots ,u_{n}$ is the ${\it\varepsilon}$-extremal basis at $q$, then

(6)$$\begin{eqnarray}\frac{1}{{\it\tau}(q,u,{\it\varepsilon})}\sim \mathop{\sum }_{j=1}^{n}\frac{|{\it\alpha}_{j}|}{{\it\tau}_{j}(q,{\it\varepsilon})}.\end{eqnarray}$$

This is in [30, Proposition 2.2] (cf. also [31]). From these facts it is easy to deduce that there is a uniform constant $C$ such that if ${\it\zeta}\in P_{c|r(q)|}(q)$, then

(7)$$\begin{eqnarray}\displaystyle & & \displaystyle |\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}({\it\zeta})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\mathop{\sum }_{j_{1},\ldots ,j_{n-1}=1\atop j_{{\it\alpha}}\neq j_{{\it\beta}},{\it\alpha}\neq {\it\beta}}^{n}\left|\det \left(\begin{array}{@{}ccc@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\\ & \ldots \, & \\ \frac{\partial (l_{m}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\end{array}\right)\right|^{2}\mathop{\prod }_{i=1}^{n-1}{\it\tau}_{j_{i}}^{2}(q,|r(q)|).\end{eqnarray}$$

The map ${\it\varphi}$ is associated, as in (3), with the $c|r(q)|$-extremal basis at the point $q\in D$.

We briefly indicate how to prove inequality (7). Let $(u_{1},\ldots ,u_{n})$ be the $c|r(q)|$-extremal basis. For any vectors $v_{1},\ldots ,v_{n-1}$ we may write

$$\begin{eqnarray}v_{i}=\mathop{\sum }_{j=1}^{n}a_{ij}u_{j}\end{eqnarray}$$

for some $a_{ij}\in \mathbb{C}$, and, as a result,

$$\begin{eqnarray}\displaystyle & & \displaystyle (\partial l_{1}\wedge \cdots \wedge \partial l_{n-1})(v_{1},\ldots ,v_{n-1})\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{j_{1}=1}^{n}\ldots \mathop{\sum }_{j_{n-1}=1}^{n}a_{1j_{1}}\ldots a_{n-1j_{n-1}}(\partial l_{1}\wedge \cdots \wedge \partial l_{n-1})(u_{j_{1}},\ldots ,u_{j_{n-1}})\nonumber\\ \displaystyle & & \displaystyle =\mathop{\sum }_{j_{1},\ldots ,j_{n-1}=1\atop j_{{\it\alpha}}\neq j_{{\it\beta}},{\it\alpha}\neq {\it\beta}}^{n}a_{1j_{1}}\ldots a_{n-1j_{n-1}}\det \left(\begin{array}{@{}ccc@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\\ & \ldots \, & \\ \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\end{array}\right).\nonumber\end{eqnarray}$$

It follows from (6) that

(8)$$\begin{eqnarray}{\it\tau}(q,v_{i},|r(q)|)\leqslant C\frac{{\it\tau}(q,u_{j},|r(q)|)}{|a_{ij}|},\end{eqnarray}$$

if $a_{ij}\neq 0$, and we only have to take this case into account. Therefore, for any vectors $v_{1},\ldots ,v_{n-1}$

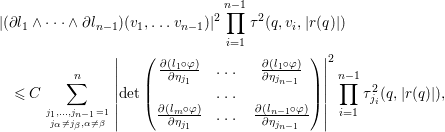$$\begin{eqnarray}\displaystyle & & \displaystyle |(\partial l_{1}\wedge \cdots \wedge \partial l_{n-1})(v_{1},\ldots v_{n-1})|^{2}\mathop{\prod }_{i=1}^{n-1}{\it\tau}^{2}(q,v_{i},|r(q)|)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\mathop{\sum }_{j_{1},\ldots ,j_{n-1}=1\atop j_{{\it\alpha}}\neq j_{{\it\beta}},{\it\alpha}\neq {\it\beta}}^{n}\left|\det \left(\begin{array}{@{}ccc@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\\ & \ldots \, & \\ \frac{\partial (l_{m}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\end{array}\right)\right|^{2}\mathop{\prod }_{i=1}^{n-1}{\it\tau}_{j_{i}}^{2}(q,|r(q)|),\nonumber\end{eqnarray}$$

since according to (8) coefficients $a_{ij}$ cancel out. The right-hand side does not depend on $v_{1},\ldots ,v_{n-1}$. This implies (7), since if ${\it\zeta}\in P_{{\it\varepsilon}}(q)$, then ${\it\tau}({\it\zeta},v,{\it\varepsilon})\sim {\it\tau}(q,v,{\it\varepsilon})$, and if ${\it\zeta}\in P_{c|r(q)|}(q)$, then $r({\it\zeta})\sim r(q)$. Obviously, since $l_{1},\ldots ,l_{n-1}$ are affine linear

$$\begin{eqnarray}(\partial l_{1}\wedge \cdots \wedge \partial l_{n-1})({\it\zeta})(v_{1},\ldots ,v_{n-1})=(\partial l_{1}\wedge \cdots \wedge \partial l_{n-1})(q)(v_{1},\ldots ,v_{n-1}).\end{eqnarray}$$

Finally, we can check condition (2). We have

$$\begin{eqnarray}\displaystyle & & \displaystyle {\it\omega}(A(l_{1},\ldots ,l_{n-1})\cap P_{c|r(q)|}(q))\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{A(l_{1},\ldots ,l_{n-1})\cap P_{c|r(q)|}(q)}|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}({\it\zeta})\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}({\it\zeta})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{{\it\varphi}^{-1}A(l_{1},\ldots ,l_{n-1})\cap \{|{\it\eta}_{j}|\leqslant {\it\tau}_{j}(q,c|r(q)|)\}}|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,({\it\varphi}({\it\eta})){\it\varphi}^{\ast }\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}.\nonumber\end{eqnarray}$$

It remains to estimate the last integral. We use (7) first and then apply for each set of indices $j_{1},\ldots ,j_{n-1}$, if the corresponding determinant is non-zero, estimate (5). In this way we obtain

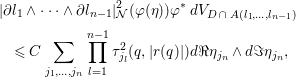$$\begin{eqnarray}\displaystyle & & \displaystyle |\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}({\it\varphi}({\it\eta})){\it\varphi}^{\ast }\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\mathop{\sum }_{j_{1},\ldots ,j_{n}}\mathop{\prod }_{l=1}^{n-1}{\it\tau}_{j_{l}}^{2}(q,|r(q)|)d\Re {\it\eta}_{j_{n}}\wedge d\Im {\it\eta}_{j_{n}},\nonumber\end{eqnarray}$$

when ${\it\zeta}={\it\varphi}({\it\eta})$ belongs to $P_{c|r(q)|}(q)$. Therefore,

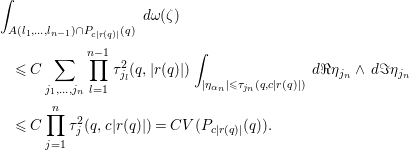$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{A(l_{1},\ldots ,l_{n-1})\cap P_{c|r(q)|}(q)}\,d{\it\omega}({\it\zeta})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\mathop{\sum }_{j_{1},\ldots ,j_{n}}\mathop{\prod }_{l=1}^{n-1}{\it\tau}_{j_{l}}^{2}(q,|r(q)|)\int _{|{\it\eta}_{{\it\alpha}_{n}}|\leqslant {\it\tau}_{j_{n}}(q,c|r(q)|)}\,d\Re {\it\eta}_{j_{n}}\wedge \,d\Im {\it\eta}_{j_{n}}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\mathop{\prod }_{j=1}^{n}{\it\tau}_{j}^{2}(q,c|r(q)|)=CV(P_{c|r(q)|}(q)).\nonumber\end{eqnarray}$$

This completes the proof of estimate (2). In view of Theorem 4 we immediately have

$$\begin{eqnarray}\displaystyle & & \displaystyle R_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}[H^{p}(D)]\nonumber\\ \displaystyle & & \displaystyle \quad \subset H^{p}(D\cap A(l_{1},\ldots ,l_{n-1}),|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A(l_{1},\ldots ,l_{n-1})}).\square\nonumber\end{eqnarray}$$

3.2 Sufficient conditions: the extension operator

We intend to complete the proofs of Theorems 1 and 2. In order to accomplish this task we need the extension operator $E_{D\,\cap \,A}$. We use the operator constructed by Berndtsson in [5]. The construction is based on methods worked out in [4] (we refer the reader also to [1] for detailed information concerning integral formulas). We write down the corresponding formulas for $z\in D$ sufficiently close to the boundary $bD$ – the corresponding estimates for $z$ in some relatively compact subset of $D$ become trivial. Let $A=A(l_{1},\ldots ,l_{m}),1\leqslant m\leqslant n-1$ be such that $D\cap A\neq 0$ and $\dim A=n-m$. As in [16] we obtain

(9)$$\begin{eqnarray}\displaystyle & & \displaystyle E_{D\,\cap \,A}^{N}f(z)\nonumber\\ \displaystyle & & \displaystyle \quad =C\int _{D\,\cap \,A}\left(dV^{\#}\rfloor \left(f({\it\zeta})\frac{r^{N+n-m}({\it\zeta})}{(r({\it\zeta})+S(z,{\it\zeta}))^{N+n-m}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left.(\overline{\partial }(\frac{1}{r({\it\zeta})}Q(z,{\it\zeta}))^{n-m})\wedge {\rm\Omega}[l_{1},\ldots ,l_{m}]\right)\right)\,dV_{D\,\cap \,A},\end{eqnarray}$$

where

$$\begin{eqnarray}{\rm\Omega}[l_{1},\ldots ,l_{m}]=\frac{\mathop{\sum }_{j=1}^{n}a_{1j}d{\it\zeta}_{j}\wedge \cdots \wedge \mathop{\sum }_{j=1}^{n}a_{mj}d{\it\zeta}_{j}\wedge \overline{\partial l_{1}}\wedge \cdots \wedge \overline{\partial l_{n-1}}}{\Vert \partial l_{1}\wedge \cdots \wedge \partial l_{m}\Vert }.\end{eqnarray}$$

The symbol $S$ stands for the support function constructed for convex finite type domains by Diederich and Fornaess in [14]. The coefficients $Q_{j}$ of the form

$$\begin{eqnarray}Q(z,{\it\zeta})=\mathop{\sum }_{j=1}^{n}Q_{j}(z,{\it\zeta})d{\it\zeta}_{j}\end{eqnarray}$$

satisfy the formula

$$\begin{eqnarray}S(z,{\it\zeta})=\mathop{\sum }_{j=1}^{n}Q_{j}(z,{\it\zeta})(z_{j}-{\it\zeta}_{j}).\end{eqnarray}$$

The form $Q$ was constructed in [13]. We use estimates of the form $Q$ proved in [18].

The symbol $\;\rfloor \;$ stands for the contraction between $(n,n)$-vectors and $(n,n)$-covectors. Thus, the operator $E_{D\,\cap \,A}^{N}$ is an integral operator of the form

$$\begin{eqnarray}E_{D\,\cap \,A}^{N}f(z)=\int _{D\,\cap \,A}f({\it\zeta})E_{D\,\cap \,A}^{N}({\it\zeta},z)\,dV_{D\,\cap \,A}({\it\zeta}).\end{eqnarray}$$

What is important in (9) is the functorial property of the contraction.

The proof of Theorem 1 follows from the following lemma, which we proved in [25].

Lemma 2. For sufficiently large $N$ there exists a constant $C$ such that

$$\begin{eqnarray}\int _{D}|E_{D\,\cap \,A}^{N}({\it\zeta},z)|\,dV(z)\leqslant C|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}({\it\zeta}).\end{eqnarray}$$

Proof of Theorem 1.

In view of Theorem 5 it suffices to show that

$$\begin{eqnarray}E_{D\,\cap \,A}^{N}:H^{1}(D\cap A,|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2}\,dV_{D\,\cap \,A})\rightarrow H^{1}(D).\end{eqnarray}$$

This follows from Fubini’s Theorem from Lemma 2. ◻

Proof of Theorem 2.

It is easy to prove the following modification of Schur’s test (we wrote the details in [24]).

Proposition 1. Let ${\it\mu},{\it\nu}$ be positive Borel measures on $X$, and let $W$ be a positive weight function. If there exist non-negative functions $h_{1},h_{2}$ such that

$$\begin{eqnarray}\displaystyle \int _{X}K(x,y)h_{1}(y)^{q}W^{-q/p}(y)\,d{\it\mu}(y) & {\leqslant} & \displaystyle C_{1}h_{2}(x)^{q},\nonumber\\ \displaystyle \int _{X}K(x,y)h_{2}(x)^{p}\,d{\it\nu}(x) & {\leqslant} & \displaystyle C_{2}h_{1}(y)^{p},\nonumber\end{eqnarray}$$

then the operator

$$\begin{eqnarray}Tf(x)=\int _{X}f(y)K(x,y)\,d{\it\mu}(y)\end{eqnarray}$$

is a bounded operator between $L^{p}(X,Wd{\it\mu})$ and $L^{p}(X,d{\it\nu})$.

We use Proposition 1 for the operator $E_{D\,\cap \,A}^{N}$. For this we choose $d{\it\nu}=dV$, $d{\it\mu}=dV_{D\,\cap \,A}$, $h_{2}\equiv 1$ and $h_{1}({\it\zeta})=|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{2/p}({\it\zeta})$ and $W({\it\zeta})=|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{(2-{\it\epsilon})}$ with small ${\it\epsilon}>0$. It follows from Proposition 1, in view of Theorem 5, that the proof of Theorem 2 will be completed once we show the following estimate for the kernel of the operator $E_{D\,\cap \,A}^{N}$.

Lemma 3. For any ${\it\epsilon}>0$ there exists a constant $C=C_{{\it\epsilon}}$ such that

$$\begin{eqnarray}\int _{D\,\cap \,A}|E_{D\,\cap \,A}^{N}({\it\zeta},z)||\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}^{{\it\epsilon}}({\it\zeta})\,dV_{D\,\cap \,A}({\it\zeta})\leqslant C.\end{eqnarray}$$

Proof. First of all observe that since $l_{1},\ldots ,l_{n-1}$ are affine linear we have

$$\begin{eqnarray}{\rm\Omega}[l_{1},\ldots ,l_{n-1}]=\frac{\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}\wedge \overline{\partial l}_{1}\wedge \cdots \wedge \overline{\partial l}_{n-1}}{\Vert \partial l_{1}\wedge \cdots \wedge \partial l_{n-1}\Vert }.\end{eqnarray}$$

This will be important when we change coordinates.

Since

$$\begin{eqnarray}{\it\tau}({\it\zeta},v,{\it\varepsilon})\lesssim {\it\varepsilon}^{1/M},\end{eqnarray}$$

uniformly for unit vectors $v$, where $M$ stands for the type of the domain, we have

(10)$$\begin{eqnarray}|\partial l_{1}\wedge \cdots \wedge \partial l_{n-1}|_{{\mathcal{N}}}({\it\zeta})\leqslant C(-r({\it\zeta}))^{(n-1)/M}.\end{eqnarray}$$

Only this property of the norm is used in the proof (note, however, that the non-isotropic nature of the estimates was crucial in the proof of Theorem 1).

Fix $z\in D$. We may assume that $z$ is close to the boundary. It is a consequence of (10) that it is sufficient to estimate the following integral:

$$\begin{eqnarray}\int _{D\,\cap \,A\,\cap \,P_{{\it\varepsilon}_{0}}(z)}|E_{D\,\cap \,A}^{N}({\it\zeta},z)|(-r({\it\zeta}))^{{\it\epsilon}((n-1)/M)}\,dV_{D\,\cap \,A}({\it\zeta}),\end{eqnarray}$$

where ${\it\varepsilon}_{0}$ is an appropriately chosen constant. The estimates uniformly far from $z$ follow easily from properties of the support function $S$. We consider a cover $P_{|r(z)|}(z),P_{|r(z)|}^{i}(z)$, where $P_{|r(z)|}^{i}(z)$ are polyannuli

$$\begin{eqnarray}P_{|r(z)|}^{i}(z):=CP_{2^{i}|r(z)|}(z)\setminus {\textstyle \frac{1}{2}}P_{2^{i}|r(z)|}(z).\end{eqnarray}$$

The constant $C$ is chosen to guarantee that $CP_{{\it\varepsilon}/2}({\it\zeta})\supset \frac{1}{2}P_{{\it\varepsilon}}({\it\zeta})$. We refer the reader to [13] for details. We will show that

(11)$$\begin{eqnarray}\int _{D\,\cap \,A\,\cap \,P_{|r(z)|}^{i}(z)}|E_{D\,\cap \,A}^{N}({\it\zeta},z)|(-r({\it\zeta}))^{{\it\epsilon}((n-1)/M)}\,dV_{D\,\cap \,A}\leqslant C(2^{i}|r(z)|)^{{\it\alpha}}\end{eqnarray}$$

for some constants $C>0$ and ${\it\alpha}>0$. From this we immediately have

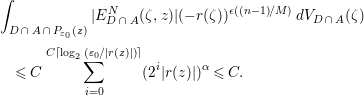$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{D\,\cap \,A\,\cap \,P_{{\it\varepsilon}_{0}}(z)}|E_{D\,\cap \,A}^{N}({\it\zeta},z)|(-r({\it\zeta}))^{{\it\epsilon}((n-1)/M)}\,dV_{D\,\cap \,A}({\it\zeta})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\mathop{\sum }_{i=0}^{C\lceil \log _{2}({\it\varepsilon}_{0}/|r(z)|)\rceil }(2^{i}|r(z)|)^{{\it\alpha}}\leqslant C.\nonumber\end{eqnarray}$$

We will estimate a typical term of $E_{D\,\cap \,A}^{N}$.

In order to show (11) we use the following.

Lemma 4. There exist an open cover $U\supset bD$ and a constant $c>0$ such that if $z,{\it\zeta}\in U$ and ${\it\zeta}\in P_{c}(z)\setminus P_{2^{i}|r(z)|}(z)$ with $2^{i}|r(z)|<c$, then

(12)$$\begin{eqnarray}|r({\it\zeta})+S(z,{\it\zeta})|\gtrsim 2^{i}|r(z)|.\end{eqnarray}$$

Lemma 4 can be proved in the same way as [13, Lemma 4.2] or [17, Lemma 3.3]. Therefore we omit the proof.

It can also be easily shown that for any $z,{\it\zeta}\in D$

(13)$$\begin{eqnarray}|r({\it\zeta})+S(z,{\it\zeta})|\gtrsim |r({\it\zeta})|.\end{eqnarray}$$

With (12) and (13) we obtain the following estimate of the integral:

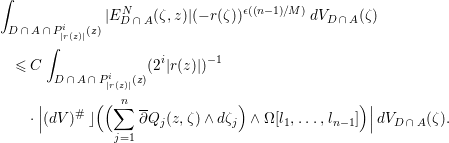$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{D\,\cap \,A\,\cap \,P_{|r(z)|}^{i}(z)}|E_{D\,\cap \,A}^{N}({\it\zeta},z)|(-r({\it\zeta}))^{{\it\epsilon}((n-1)/M)}\,dV_{D\,\cap \,A}({\it\zeta})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\int _{D\,\cap \,A\,\cap \,P_{|r(z)|}^{i}(z)}(2^{i}|r(z)|)^{-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \;|(dV)^{\#}\rfloor ((\mathop{\sum }_{j=1}^{n}\overline{\partial }Q_{j}(z,{\it\zeta})\wedge d{\it\zeta}_{j})\wedge {\rm\Omega}[l_{1},\ldots ,l_{n-1}])|\,dV_{D\,\cap \,A}({\it\zeta}).\nonumber\end{eqnarray}$$

We choose a $2^{i}|r(z)|$-extremal basis at $z$ and change coordinates. We use the notation from the proof of Theorem 5.

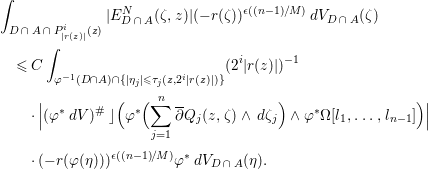$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{D\,\cap \,A\,\cap \,P_{|r(z)|}^{i}(z)}|E_{D\,\cap \,A}^{N}({\it\zeta},z)|(-r({\it\zeta}))^{{\it\epsilon}((n-1)/M)}\,dV_{D\,\cap \,A}({\it\zeta})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\int _{{\it\varphi}^{-1}(D\cap A)\cap \{|{\it\eta}_{j}|\leqslant {\it\tau}_{j}(z,2^{i}|r(z)|)\}}(2^{i}|r(z)|)^{-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \;|({\it\varphi}^{\ast }\,dV)^{\#}\rfloor ({\it\varphi}^{\ast }(\mathop{\sum }_{j=1}^{n}\overline{\partial }Q_{j}(z,{\it\zeta})\wedge \,d{\it\zeta}_{j})\wedge {\it\varphi}^{\ast }{\rm\Omega}[l_{1},\ldots ,l_{n-1}])|\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \;(-r({\it\varphi}({\it\eta})))^{{\it\epsilon}((n-1)/M)}{\it\varphi}^{\ast }\,dV_{D\,\cap \,A}({\it\eta}).\nonumber\end{eqnarray}$$

If ${\it\zeta}\in P_{2^{i}|r(z)|}(z)$, then $|r({\it\zeta})|\lesssim 2^{i}|r(z)|$. Therefore, it follows from [18, Lemma 3.3] and estimates of the form

$$\begin{eqnarray}{\it\varphi}^{\ast }{\rm\Omega}[l_{1},\ldots ,l_{n-1}]\end{eqnarray}$$

that

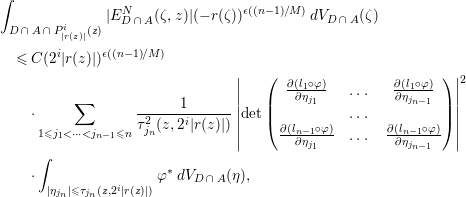$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{D\,\cap \,A\,\cap \,P_{|r(z)|}^{i}(z)}|E_{D\,\cap \,A}^{N}({\it\zeta},z)|(-r({\it\zeta}))^{{\it\epsilon}((n-1)/M)}\,dV_{D\,\cap \,A}({\it\zeta})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C(2^{i}|r(z)|)^{{\it\epsilon}((n-1)/M)}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \mathop{\sum }_{1\leqslant j_{1}<\cdots <j_{n-1}\leqslant n}\frac{1}{{\it\tau}_{j_{n}}^{2}(z,2^{i}|r(z)|)}\left|\det \left(\begin{array}{@{}ccc@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\\ & \ldots \, & \\ \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\end{array}\right)\right|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \int _{|{\it\eta}_{j_{n}}|\leqslant {\it\tau}_{j_{n}}(z,2^{i}|r(z)|)}{\it\varphi}^{\ast }\,dV_{D\,\cap \,A}({\it\eta}),\nonumber\end{eqnarray}$$

where $\{j_{1},\ldots ,j_{n}\}=\{1,\ldots ,n\}$.

Moreover, we showed in (4) that

$$\begin{eqnarray}{\it\varphi}^{\ast }(dV_{D\,\cap \,A})\leqslant C\left|\det \left(\begin{array}{@{}ccc@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\\ & \ldots \, & \\ \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{n-1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{n-1}}}\end{array}\right)\right|^{-2}d\Re {\it\eta}_{j_{n}}\wedge d\Im {\it\eta}_{j_{n}},\end{eqnarray}$$

provided that the determinant is non-zero. This argument completes the proof. ◻

This also proves Theorem 2. ◻

Proof of Theorem 3.

We now consider an affine linear subvariety $A(l_{1},\ldots ,l_{m})$ of codimension $m$. The proof is similar to the proofs of Theorems 1 and 2. Therefore we only sketch it. We use the same notation.

The main point is that under the assumption of the theorem

(14)$$\begin{eqnarray}{\it\varphi}^{\ast }(dV_{D\,\cap \,A})\leqslant Cd\Re {\it\eta}_{j_{m+1}}\wedge d\Im {\it\eta}_{j_{m+1}}\wedge \cdots \wedge d\Re {\it\eta}_{j_{n}}\wedge d\Im {\it\eta}_{j_{n}},\end{eqnarray}$$

with a uniform constant whenever

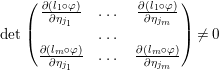(15)$$\begin{eqnarray}\det \left(\begin{array}{@{}ccc@{}}\frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{1}\circ {\it\varphi})}{\partial {\it\eta}_{j_{m}}}\\ & \ldots \, & \\ \frac{\partial (l_{m}\circ {\it\varphi})}{\partial {\it\eta}_{j_{1}}} & \ldots \, & \frac{\partial (l_{m}\circ {\it\varphi})}{\partial {\it\eta}_{j_{m}}}\end{array}\right)\neq 0\end{eqnarray}$$

and $\{j_{1},\ldots ,j_{n}\}=\{1,\ldots ,n\}$. This follows from the fact that

(16)$$\begin{eqnarray}{\it\varphi}^{\ast }\,dV_{D\,\cap \,A}=(\frac{\sqrt{-1}}{2(n-m)!})^{n-m}(\mathop{\sum }_{j=1}^{n}d{\it\eta}_{j}\wedge d\bar{{\it\eta}}_{j})^{n-m},\end{eqnarray}$$

which is a consequence of Wirtinger’s formula. Hence, we can again use the fact that $l_{1}\circ {\it\varphi}({\it\eta})=\cdots =l_{m}\circ {\it\varphi}({\it\eta})=0$ for ${\it\eta}\in {\it\varphi}^{-1}(D\cap A)$ to get rid of $d{\it\eta}_{j_{1}},\ldots ,d{\it\eta}_{j_{m}}$ and their conjugates in (16). Naturally, this is possible if condition (15) holds true. With (14) one immediately obtains that

$$\begin{eqnarray}{\it\omega}(A(l_{1},\ldots ,l_{m})\cap P_{c|r(q)|}(q))\leqslant CV(P_{c|r(q)|}(q)).\end{eqnarray}$$

The same estimates for the measure ${\it\varphi}^{\ast }\,dV_{D\,\cap \,A}$ show, as in the proof of Lemma 3, that

$$\begin{eqnarray}\int _{D\,\cap \,A}|E_{D\,\cap \,A}({\it\zeta},z)||\partial l_{1}\wedge \cdots \wedge \partial l_{m}|_{{\mathcal{N}}}^{{\it\epsilon}}({\it\zeta})\,dV_{D\,\cap \,A}({\it\zeta})\leqslant C.\end{eqnarray}$$

Lemma 2 and Proposition 1 complete the proof. ◻