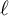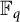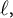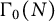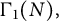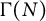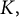1 Introduction
The set of isomorphism classes of elliptic curves over a finite field
![]() $\mathbb {F}_q$
can be viewed as vertices of a graph known as the isogeny graph. Vertices E and
$\mathbb {F}_q$
can be viewed as vertices of a graph known as the isogeny graph. Vertices E and
![]() $E'$
are connected by a directed edge
$E'$
are connected by a directed edge
![]() $(E, E')$
if and only if there exists an isogeny
$(E, E')$
if and only if there exists an isogeny
![]() $\varphi : E \to E'.$
Advancements in quantum computing have motivated the search for new cryptographic primitives which are resistant to quantum-style attacks. The search for problems which are computationally difficult for quantum adversaries gave birth to what is known as isogeny-based cryptography [Reference Charles, Lauter and Goren3]. Given two vertices E and
$\varphi : E \to E'.$
Advancements in quantum computing have motivated the search for new cryptographic primitives which are resistant to quantum-style attacks. The search for problems which are computationally difficult for quantum adversaries gave birth to what is known as isogeny-based cryptography [Reference Charles, Lauter and Goren3]. Given two vertices E and
![]() $E',$
the underlying hard problem of isogeny-based cryptography is that of finding a path from E to
$E',$
the underlying hard problem of isogeny-based cryptography is that of finding a path from E to
![]() $E'$
in the isogeny graph.
$E'$
in the isogeny graph.
Cryptographic applications of isogenies has attracted more attention to studying them. One such development in the field of isogenies has been to look at adding a level N structure to the isogeny graph. This graph consists of vertices of the form
![]() $(E, \gamma )$
where
$(E, \gamma )$
where
![]() $\gamma $
is some level N structure on
$\gamma $
is some level N structure on
![]() $E,$
and there is an edge between two vertices
$E,$
and there is an edge between two vertices
![]() $(E, \gamma )$
,
$(E, \gamma )$
,
![]() $(E', \gamma ')$
if and only if there exists an isogeny
$(E', \gamma ')$
if and only if there exists an isogeny
![]() $\varphi : E \to E'$
with the added condition that
$\varphi : E \to E'$
with the added condition that
![]() $\varphi (\gamma ) = \gamma '.$
Isogeny graphs with level N structure were first studied by Roda in [Reference Roda14] in which they looked at adding a full level N structure to the supersingular component of the
$\varphi (\gamma ) = \gamma '.$
Isogeny graphs with level N structure were first studied by Roda in [Reference Roda14] in which they looked at adding a full level N structure to the supersingular component of the
![]() $\ell $
-isogeny graph. Following Roda, further works have also studied adding level structure to the supersingular component; see [Reference Arpin1, Reference Levin12]. Additionally, during the writing of this article, Arpin, Castryck, Eriksen, Lorenzon, and Vercauteren [Reference Arpin, Castryck, Eriksen, Lorenzon and Vercauteren2] published results involving generalized class group actions on oriented elliptic curves with level structure. Prior to that, Colò [Reference Colò4] pointed out that the action of the ideals on elliptic curves with level structure factors through a ray class group.
$\ell $
-isogeny graph. Following Roda, further works have also studied adding level structure to the supersingular component; see [Reference Arpin1, Reference Levin12]. Additionally, during the writing of this article, Arpin, Castryck, Eriksen, Lorenzon, and Vercauteren [Reference Arpin, Castryck, Eriksen, Lorenzon and Vercauteren2] published results involving generalized class group actions on oriented elliptic curves with level structure. Prior to that, Colò [Reference Colò4] pointed out that the action of the ideals on elliptic curves with level structure factors through a ray class group.
Parallel to these developments, the isogeny graphs for ordinary elliptic curves was studied, motivated by problems in computational number theory. Kohel [Reference Kohel10] showed that the ordinary components have a nice “volcano” structure, where the term volcano was later coined by Fouquet and Morain [Reference Fouquet and Morain8] to describe the components due to their similarities to geological volcanoes. Sutherland [Reference Sutherland16] provides a summary of various algorithms, including computing the endomorphism ring of ordinary elliptic curves, which make use of volcanoes.
Due to their applications in cryptography, the supersingular setting has received more attention and the ordinary setting is not as well-studied. However, recent work by Lei and Müller [Reference Lei and Müller11] studies ordinary isogeny graphs with a
![]() $\Gamma _1(Np^m)$
-level structure. Our work differs as we will consider ordinary isogeny graphs with
$\Gamma _1(Np^m)$
-level structure. Our work differs as we will consider ordinary isogeny graphs with
![]() $\Gamma _0(N)$
,
$\Gamma _0(N)$
,
![]() $\Gamma _1(N),$
and
$\Gamma _1(N),$
and
![]() $\Gamma (N)$
-level structures.
$\Gamma (N)$
-level structures.
The viewpoint of our work is more mathematical in nature, and we will not discuss cryptographic applications here. For use of level structures in cryptography, the interested reader is recommended to look at [Reference De Feo, Fouotsa and Panny6, Reference Galbraith, Perrin and Voloch9]. This article aims to answer a question first raised by Levin [Reference Levin12], namely that of determining the crater size and number of components of the graphs constructed by adding various level structures to an ordinary component of the
![]() $\ell $
-isogeny graph.
$\ell $
-isogeny graph.
The theory of complex multiplication (CM) tells us that for an order
![]() $\mathcal {O}$
in an imaginary quadratic field
$\mathcal {O}$
in an imaginary quadratic field
![]() $K,$
the ideal class group
$K,$
the ideal class group
![]() $Cl(\mathcal {O})$
acts simply transitively on the set
$Cl(\mathcal {O})$
acts simply transitively on the set
of ordinary elliptic curves whose endomorphism rings are isomorphic to
![]() $\mathcal {O}$
modulo
$\mathcal {O}$
modulo
![]() $\overline {\mathbb {F}_q}$
-isomorphism. The main contribution of this work can be thought of as a generalization of this group action. We address Levin’s question by considering generalized ideal class groups acting on
$\overline {\mathbb {F}_q}$
-isomorphism. The main contribution of this work can be thought of as a generalization of this group action. We address Levin’s question by considering generalized ideal class groups acting on
![]() $\mathrm {Ell}_{\mathcal {O}}(\mathbb {F}_q)$
endowed with various level structures. For
$\mathrm {Ell}_{\mathcal {O}}(\mathbb {F}_q)$
endowed with various level structures. For
![]() $\mathfrak {l}$
a prime
$\mathfrak {l}$
a prime
![]() $\mathcal {O}$
-ideal above
$\mathcal {O}$
-ideal above
![]() $\ell ,$
we show that the crater size of components with a level structure is related to the order of the subgroup
$\ell ,$
we show that the crater size of components with a level structure is related to the order of the subgroup
![]() $\left\langle \mathfrak {l}, \overline {\mathfrak {l}} \right\rangle $
when viewed as a subgroup of a generalized class group. In Section 5, we give descriptions of these class groups for
$\left\langle \mathfrak {l}, \overline {\mathfrak {l}} \right\rangle $
when viewed as a subgroup of a generalized class group. In Section 5, we give descriptions of these class groups for
![]() $\Gamma _0(N)$
,
$\Gamma _0(N)$
,
![]() $\Gamma _1(N),$
and
$\Gamma _1(N),$
and
![]() $\Gamma (N)$
-level structures. We also show the role the prime factorization of N as an
$\Gamma (N)$
-level structures. We also show the role the prime factorization of N as an
![]() $\mathcal {O}$
-ideal plays in both the number and size of the components of these graphs with level structure. In Section 6, we conclude by showing several examples of adding
$\mathcal {O}$
-ideal plays in both the number and size of the components of these graphs with level structure. In Section 6, we conclude by showing several examples of adding
![]() $\Gamma _0(N)$
and
$\Gamma _0(N)$
and
![]() $\Gamma _1(N)$
-level structures to an isogeny volcano.
$\Gamma _1(N)$
-level structures to an isogeny volcano.
2 Background
Definition 2.1 Let
![]() $\mathbb {F}_q$
be a finite field of characteristic
$\mathbb {F}_q$
be a finite field of characteristic
![]() $p \neq 2,3$
and
$p \neq 2,3$
and
![]() $\ell $
a prime different from
$\ell $
a prime different from
![]() $p.$
Recall that the set of
$p.$
Recall that the set of
![]() $\overline {\mathbb {F}_q}$
-isomorphism classes of elliptic curves over
$\overline {\mathbb {F}_q}$
-isomorphism classes of elliptic curves over
![]() $\mathbb {F}_q$
can be identified with
$\mathbb {F}_q$
can be identified with
![]() $\mathbb {F}_q$
via the j-invariant. We let
$\mathbb {F}_q$
via the j-invariant. We let
![]() $X_{\ell }(\mathbb {F}_q)$
denote the
$X_{\ell }(\mathbb {F}_q)$
denote the
![]() $\ell $
-isogeny graph of
$\ell $
-isogeny graph of
![]() $\mathbb {F}_q$
where
$\mathbb {F}_q$
where
![]() $X_{\ell }(\mathbb {F}_q)$
has vertex set
$X_{\ell }(\mathbb {F}_q)$
has vertex set
![]() $\mathbb {F}_q.$
Each vertex represents an isomorphism class of elliptic curves defined over
$\mathbb {F}_q.$
Each vertex represents an isomorphism class of elliptic curves defined over
![]() $\mathbb {F}_q.$
The edge set of
$\mathbb {F}_q.$
The edge set of
![]() $X_{\ell }(\mathbb {F}_q)$
consists of pairs
$X_{\ell }(\mathbb {F}_q)$
consists of pairs
![]() $(j_1, j_2)$
where
$(j_1, j_2)$
where
![]() $j_1, j_2$
are j-invariants of elliptic curves which are
$j_1, j_2$
are j-invariants of elliptic curves which are
![]() $\overline {\mathbb {F}_q}$
-isogeneous via an isogeny of degree
$\overline {\mathbb {F}_q}$
-isogeneous via an isogeny of degree
![]() $\ell .$
$\ell .$
The field we work with will generally be understood to be
![]() $\mathbb {F}_q,$
so we will write
$\mathbb {F}_q,$
so we will write
![]() $X_{\ell }$
instead of
$X_{\ell }$
instead of
![]() $X_{\ell }(\mathbb {F}_q).$
Unless otherwise stated, we will treat
$X_{\ell }(\mathbb {F}_q).$
Unless otherwise stated, we will treat
![]() $X_{\ell }$
as an undirected graph since given an isogeny
$X_{\ell }$
as an undirected graph since given an isogeny
![]() $\varphi : E \to E'$
of degree
$\varphi : E \to E'$
of degree
![]() $\ell ,$
there exists a dual isogeny
$\ell ,$
there exists a dual isogeny
![]() $\hat {\varphi }: E' \to E$
of degree
$\hat {\varphi }: E' \to E$
of degree
![]() $\ell $
such that
$\ell $
such that
![]() $\varphi \circ \hat {\varphi } = \hat {\varphi } \circ \varphi = [\ell ].$
$\varphi \circ \hat {\varphi } = \hat {\varphi } \circ \varphi = [\ell ].$
For the purposes of this article, we will focus our attention on the ordinary components, volcanoes, of
![]() $X_{\ell }.$
$X_{\ell }.$
Definition 2.2 An
![]() $\ell $
-volcano is a connected, undirected graph whose vertices may be partitioned into one or more levels
$\ell $
-volcano is a connected, undirected graph whose vertices may be partitioned into one or more levels
![]() $V_0, \ldots , V_d$
such that:
$V_0, \ldots , V_d$
such that:
-
(i) The subgraph on
 $V_0$
is a regular connected graph of degree at most 2.
$V_0$
is a regular connected graph of degree at most 2. -
(ii) For each
 $i> 0,$
the vertices in
$i> 0,$
the vertices in
 $V_i$
have exactly one neighbour in
$V_i$
have exactly one neighbour in
 $V_{i-1}$
and the subgraph on
$V_{i-1}$
and the subgraph on
 $V_i$
is totally disconnected.
$V_i$
is totally disconnected. -
(iii) For each
 $i < d,$
the vertices in
$i < d,$
the vertices in
 $V_i$
have degree
$V_i$
have degree
 $\ell + 1.$
$\ell + 1.$
Definition 2.3 Let
![]() $G_{\ell }$
be an
$G_{\ell }$
be an
![]() $\ell $
-isogeny volcano of
$\ell $
-isogeny volcano of
![]() $X_{\ell }.$
The subgraph of level zero on
$X_{\ell }.$
The subgraph of level zero on
![]() $G_{\ell }$
is called the crater of
$G_{\ell }$
is called the crater of
![]() $G_{\ell }$
and is denoted
$G_{\ell }$
and is denoted
![]() $C_\ell $
and the subgraph of
$C_\ell $
and the subgraph of
![]() $X_{\ell }$
consisting of the craters of all ordinary components will be denoted
$X_{\ell }$
consisting of the craters of all ordinary components will be denoted
![]() $\mathcal {C}_{\ell }$
and is called the crater of
$\mathcal {C}_{\ell }$
and is called the crater of
![]() $X_{\ell }$
.
$X_{\ell }$
.
The term crater was introduced in [Reference Fouquet and Morain8] and strictly refers to the level zero subgraph of a single volcano. Some definitions of a volcano [Reference Fouquet, Miret and Valera7] require the crater to consist of a cycle, but we do not require this in our work and use a definition as in [Reference Sutherland16]. Many of the graphs we work with contain multiple components with a volcanic structure, so it makes sense to discuss the craters of all of
![]() $X_{\ell }.$
This terminology is consistent with what the authors of [Reference Lei and Müller11] use.
$X_{\ell }.$
This terminology is consistent with what the authors of [Reference Lei and Müller11] use.
We can now add an additional structure to the ordinary components of
![]() $X_{\ell }.$
The structure we impose is called a level structure and it is related to the N-torsion subgroup
$X_{\ell }.$
The structure we impose is called a level structure and it is related to the N-torsion subgroup
![]() $E[N]$
of an elliptic curve
$E[N]$
of an elliptic curve
![]() $E.$
$E.$
Definition 2.4 Let
![]() $E/\mathbb {F}_q$
be an elliptic curve, N an integer, and
$E/\mathbb {F}_q$
be an elliptic curve, N an integer, and
![]() $E[N]$
the group of N-torsion points of E. Then we call
$E[N]$
the group of N-torsion points of E. Then we call
-
(1) a
 $\Gamma _0(N)$
-level structure a cyclic subgroup
$\Gamma _0(N)$
-level structure a cyclic subgroup
 $\left\langle P \right\rangle \subseteq E[N]$
of order N;
$\left\langle P \right\rangle \subseteq E[N]$
of order N; -
(2) a
 $\Gamma _1(N)$
-level structure a point
$\Gamma _1(N)$
-level structure a point
 $P \in E[N]$
of order
$P \in E[N]$
of order
 $N;$
$N;$
-
(3) and a
 $\Gamma (N)$
-level structure, or full level structure, an ordered pair of points
$\Gamma (N)$
-level structure, or full level structure, an ordered pair of points
 $P, Q \in E[N]$
which are a basis for
$P, Q \in E[N]$
which are a basis for
 $E[N].$
$E[N].$
In this article, we will always assume N is an integer coprime to p and
![]() $\ell .$
$\ell .$
Definition 2.5 Consider the set of pairs
![]() $(E, \gamma )$
where E is an ordinary elliptic curve and
$(E, \gamma )$
where E is an ordinary elliptic curve and
![]() $\gamma $
is a level structure on
$\gamma $
is a level structure on
![]() $E.$
Then we may define an equivalence relation
$E.$
Then we may define an equivalence relation
![]() $\sim $
on pairs
$\sim $
on pairs
![]() $(E, \gamma ),$
where
$(E, \gamma ),$
where
![]() $(E, \gamma ) \sim (E', \gamma ')$
if and only if there exists an isomorphism
$(E, \gamma ) \sim (E', \gamma ')$
if and only if there exists an isomorphism
![]() $\varphi : E \to E'$
such that
$\varphi : E \to E'$
such that
![]() $\varphi (\gamma ) = \gamma '.$
$\varphi (\gamma ) = \gamma '.$
Note that if
![]() $\varphi \in \operatorname {\mathrm {Aut}}(E),$
then
$\varphi \in \operatorname {\mathrm {Aut}}(E),$
then
![]() $(E, \gamma )$
is equivalent to
$(E, \gamma )$
is equivalent to
![]() $(E, \varphi (\gamma )).$
In particular this applies to
$(E, \varphi (\gamma )).$
In particular this applies to
![]() $[-1].$
$[-1].$
We add a level structure to
![]() $X_{\ell }$
by adding the level structure to each vertex in
$X_{\ell }$
by adding the level structure to each vertex in
![]() $X_{\ell }$
up to the equivalence relation
$X_{\ell }$
up to the equivalence relation
![]() $\sim $
in Definition 2.5.
$\sim $
in Definition 2.5.
Definition 2.6 Let
![]() $G_{\ell }$
be an isogeny volcano with vertex set
$G_{\ell }$
be an isogeny volcano with vertex set
![]() $\mathbb {V} = {E_i}$
. Up to the equivalence relation in Definition 2.5, consider the set of tuples
$\mathbb {V} = {E_i}$
. Up to the equivalence relation in Definition 2.5, consider the set of tuples
and the set of tuples
 $$ \begin{align*} \mathbb{E}' = \big\{&((E_i, \gamma_i), (E_j, \gamma_j)) \text{ if } \exists \varphi: E_i \to E_j \text{ such that } \deg\varphi = \ell\\ & \text{ and } \varphi(\gamma_i) = \varphi(\gamma_j) \big\} \big/ \sim. \end{align*} $$
$$ \begin{align*} \mathbb{E}' = \big\{&((E_i, \gamma_i), (E_j, \gamma_j)) \text{ if } \exists \varphi: E_i \to E_j \text{ such that } \deg\varphi = \ell\\ & \text{ and } \varphi(\gamma_i) = \varphi(\gamma_j) \big\} \big/ \sim. \end{align*} $$
Then
-
(i) if the
 $\gamma _i$
are all
$\gamma _i$
are all
 $\Gamma _0(N)$
level structures on the
$\Gamma _0(N)$
level structures on the
 $E_i$
’s, we let
$E_i$
’s, we let
 $G_{\ell ,0}(N)$
denote the graph whose vertex set is
$G_{\ell ,0}(N)$
denote the graph whose vertex set is
 $\mathbb {V}'$
and edge set is
$\mathbb {V}'$
and edge set is
 $\mathbb {E}'$
;
$\mathbb {E}'$
; -
(ii) if the
 $\gamma _i$
are all
$\gamma _i$
are all
 $\Gamma _1(N)$
level structures on the
$\Gamma _1(N)$
level structures on the
 $E_i$
’s, we let
$E_i$
’s, we let
 $G_{\ell ,1}(N)$
denote the graph whose vertex set is
$G_{\ell ,1}(N)$
denote the graph whose vertex set is
 $\mathbb {V}'$
and edge set is
$\mathbb {V}'$
and edge set is
 $\mathbb {E}'$
;
$\mathbb {E}'$
; -
(iii) if the
 $\gamma _i$
are all
$\gamma _i$
are all
 $\Gamma (N)$
level structures on the
$\Gamma (N)$
level structures on the
 $E_i$
’s, we let
$E_i$
’s, we let
 $G_{\ell }(N)$
denote the graph whose vertex set is
$G_{\ell }(N)$
denote the graph whose vertex set is
 $\mathbb {V}'$
and edge set is
$\mathbb {V}'$
and edge set is
 $\mathbb {E}'$
.
$\mathbb {E}'$
.
We will say we add a
![]() $\gamma $
level structure to
$\gamma $
level structure to
![]() $G_{\ell }$
when we construct one of the graphs in Definition 2.6. We also remark that while
$G_{\ell }$
when we construct one of the graphs in Definition 2.6. We also remark that while
![]() $G_{\ell ,0}(N)$
remains undirected, the graphs
$G_{\ell ,0}(N)$
remains undirected, the graphs
![]() $G_{\ell ,1}(N)$
and
$G_{\ell ,1}(N)$
and
![]() $G_{\ell }(N)$
in Definition 2.6 are no longer undirected graphs.
$G_{\ell }(N)$
in Definition 2.6 are no longer undirected graphs.
3 Stabilizers of level structures
In this section, we will discuss the stabilizers of the
![]() $\Gamma _0(N)$
,
$\Gamma _0(N)$
,
![]() $\Gamma _1(N),$
and
$\Gamma _1(N),$
and
![]() $\Gamma (N)$
-level structures.
$\Gamma (N)$
-level structures.
We will let K be an imaginary quadratic field with ring of integers given by
![]() $\mathcal {O}_K.$
We are interested in ordinary elliptic curves with CM by an order
$\mathcal {O}_K.$
We are interested in ordinary elliptic curves with CM by an order
![]() $\mathcal {O} \subseteq \mathcal {O}_K$
where
$\mathcal {O} \subseteq \mathcal {O}_K$
where
![]() ${\mathcal {O} = \mathbb {Z}[\Phi ]}$
for some
${\mathcal {O} = \mathbb {Z}[\Phi ]}$
for some
![]() $\Phi \in \mathcal {O}_{K};$
in other words, their endomorphism ring is equal to
$\Phi \in \mathcal {O}_{K};$
in other words, their endomorphism ring is equal to
![]() $\mathcal {O}.$
We will restrict ourselves to the case of
$\mathcal {O}.$
We will restrict ourselves to the case of
![]() $(f, N) = 1$
where f is the conductor of
$(f, N) = 1$
where f is the conductor of
![]() $\mathcal {O}$
(i.e.,
$\mathcal {O}$
(i.e.,
![]() $f = [\mathcal {O}_K : \mathcal {O}]$
). Finally, we will assume that all elliptic curves we work with have j-invariant not equal to
$f = [\mathcal {O}_K : \mathcal {O}]$
). Finally, we will assume that all elliptic curves we work with have j-invariant not equal to
![]() $0, 1728.$
$0, 1728.$
Definition 3.1 Let
![]() $\gamma $
be a
$\gamma $
be a
![]() $\Gamma _0(N)$
,
$\Gamma _0(N)$
,
![]() $\Gamma _1(N),$
or
$\Gamma _1(N),$
or
![]() $\Gamma (N)$
-level structure on an ordinary elliptic curve
$\Gamma (N)$
-level structure on an ordinary elliptic curve
![]() $E.$
A stabilizer of
$E.$
A stabilizer of
![]() $\gamma $
is an element
$\gamma $
is an element
![]() $\alpha $
of
$\alpha $
of
![]() $\mathcal {O}/N \mathcal {O}$
where
$\mathcal {O}/N \mathcal {O}$
where
![]() $(E, \gamma ) \sim (E, \alpha (\gamma ))$
where
$(E, \gamma ) \sim (E, \alpha (\gamma ))$
where
![]() $\sim $
is the equivalence relation defined in Definition 2.5. The set
$\sim $
is the equivalence relation defined in Definition 2.5. The set
![]() $\operatorname {\mathrm {Stab}}(\gamma )$
of stabilizers of
$\operatorname {\mathrm {Stab}}(\gamma )$
of stabilizers of
![]() $\gamma $
form a subgroup of
$\gamma $
form a subgroup of
![]() $(\mathcal {O}/N \mathcal {O})^{\times }.$
$(\mathcal {O}/N \mathcal {O})^{\times }.$
Lemma 3.1 The N-torsion subgroup
![]() $E[N]$
and
$E[N]$
and
![]() $\mathcal {O}/N\mathcal {O}$
are isomorphic as
$\mathcal {O}/N\mathcal {O}$
are isomorphic as
![]() $\mathcal {O}/N\mathcal {O}$
-modules.
$\mathcal {O}/N\mathcal {O}$
-modules.
Proof A proof when
![]() $\mathcal {O} = \mathcal {O}_K$
is given in [Reference Silverman15, Proposition II.1.4]. For
$\mathcal {O} = \mathcal {O}_K$
is given in [Reference Silverman15, Proposition II.1.4]. For
![]() $\mathcal {O}$
a non-maximal order, a proof is given in [Reference Arpin, Castryck, Eriksen, Lorenzon and Vercauteren2, Section 3.1 Lemma 1 pg 7]
$\mathcal {O}$
a non-maximal order, a proof is given in [Reference Arpin, Castryck, Eriksen, Lorenzon and Vercauteren2, Section 3.1 Lemma 1 pg 7]
The importance of Theorem 3.1 is that it allows us to work with a somewhat simpler structure as we will shortly see. For the three level structures
![]() $\Gamma (N)$
,
$\Gamma (N)$
,
![]() $\Gamma _1(N),$
and
$\Gamma _1(N),$
and
![]() $\Gamma _0(N),$
we are interested in stabilizers of all of
$\Gamma _0(N),$
we are interested in stabilizers of all of
![]() $E[N],$
points
$E[N],$
points
![]() $P \in E[N]$
of order
$P \in E[N]$
of order
![]() $N,$
and cyclic subgroups
$N,$
and cyclic subgroups
![]() $\left\langle P \right\rangle \subseteq E[N]$
of order N respectively. The authors of [Reference Galbraith, Perrin and Voloch9] find the stabilizers of a
$\left\langle P \right\rangle \subseteq E[N]$
of order N respectively. The authors of [Reference Galbraith, Perrin and Voloch9] find the stabilizers of a
![]() $\Gamma (N)$
-level structure by considering subgroups of the kernel of an isogeny which fixes all of
$\Gamma (N)$
-level structure by considering subgroups of the kernel of an isogeny which fixes all of
![]() $E[N];$
this method can be adapted for
$E[N];$
this method can be adapted for
![]() $\Gamma _1(N)$
and
$\Gamma _1(N)$
and
![]() $\Gamma _0(N)$
-level structures, but one needs to take into consideration eigenvectors of
$\Gamma _0(N)$
-level structures, but one needs to take into consideration eigenvectors of
![]() $\Phi .$
We instead look at the equivalent problem of finding stabilizers for all of
$\Phi .$
We instead look at the equivalent problem of finding stabilizers for all of
![]() $\mathcal {O}/N\mathcal {O},$
elements
$\mathcal {O}/N\mathcal {O},$
elements
![]() $\alpha \in \mathcal {O}/N\mathcal {O}$
of order
$\alpha \in \mathcal {O}/N\mathcal {O}$
of order
![]() $N,$
and cyclic subgroups
$N,$
and cyclic subgroups
![]() $\left\langle \alpha \right\rangle \subseteq \mathcal {O}/N\mathcal {O}$
of order N respectively.
$\left\langle \alpha \right\rangle \subseteq \mathcal {O}/N\mathcal {O}$
of order N respectively.
Proposition 3.2 The stabilizers of a
![]() $\Gamma (N)$
-level structure are given by
$\Gamma (N)$
-level structure are given by
Proof Due to the equivalence relation in Definition 2.5, we trivially have
![]() $\alpha \equiv \pm 1 \mod N\mathcal {O}.$
$\alpha \equiv \pm 1 \mod N\mathcal {O}.$
Let
![]() $\tilde {P} \in E[N]$
be a
$\tilde {P} \in E[N]$
be a
![]() $\Gamma _1(N)$
-level structure. After choosing a generator of
$\Gamma _1(N)$
-level structure. After choosing a generator of
![]() $E[N]$
as an
$E[N]$
as an
![]() $\mathcal {O}/N \mathcal {O}$
-module, then by Theorem 3.1 we may identify
$\mathcal {O}/N \mathcal {O}$
-module, then by Theorem 3.1 we may identify
![]() $\tilde {P}$
with an element
$\tilde {P}$
with an element
![]() $P \in \mathcal {O}/N\mathcal {O}.$
In what follows, we will work with P instead of
$P \in \mathcal {O}/N\mathcal {O}.$
In what follows, we will work with P instead of
![]() $\tilde {P}.$
$\tilde {P}.$
Proposition 3.3 Given
![]() $P \in \mathcal {O}/N\mathcal {O}$
of order N and the ideal
$P \in \mathcal {O}/N\mathcal {O}$
of order N and the ideal
![]() $\mathfrak {a} = \langle P, N\mathcal {O} \rangle ,$
then
$\mathfrak {a} = \langle P, N\mathcal {O} \rangle ,$
then
Proof Let
![]() $\alpha \in \operatorname {\mathrm {Stab}}(P).$
Then
$\alpha \in \operatorname {\mathrm {Stab}}(P).$
Then
 $$ \begin{align*} \alpha P &\equiv \pm P \quad\mod N\mathcal{O} \\ (\alpha \pm 1)P &\equiv 0 \quad\mod N\mathcal{O}. \end{align*} $$
$$ \begin{align*} \alpha P &\equiv \pm P \quad\mod N\mathcal{O} \\ (\alpha \pm 1)P &\equiv 0 \quad\mod N\mathcal{O}. \end{align*} $$
Then
![]() $(\alpha \pm 1)P \in N \mathcal {O}.$
For any element
$(\alpha \pm 1)P \in N \mathcal {O}.$
For any element
![]() $\beta = aP + bN \in \mathfrak {a}$
for
$\beta = aP + bN \in \mathfrak {a}$
for
![]() $a,b \in \mathcal {O},$
consider the product
$a,b \in \mathcal {O},$
consider the product
 $$ \begin{align*} (\alpha \pm 1)\beta &= (\alpha \pm 1)(aP + bN) \\ &= a(\alpha \pm 1)P + b(\alpha \pm 1)N. \end{align*} $$
$$ \begin{align*} (\alpha \pm 1)\beta &= (\alpha \pm 1)(aP + bN) \\ &= a(\alpha \pm 1)P + b(\alpha \pm 1)N. \end{align*} $$
We have shown the first term is in
![]() $N \mathcal {O},$
and the second term is certainly in
$N \mathcal {O},$
and the second term is certainly in
![]() $N \mathcal {O},$
so their sum is in
$N \mathcal {O},$
so their sum is in
![]() $N \mathcal {O}.$
Then
$N \mathcal {O}.$
Then
![]() $(\alpha \pm 1)\mathfrak {a} \subseteq N \mathcal {O},$
and so
$(\alpha \pm 1)\mathfrak {a} \subseteq N \mathcal {O},$
and so
![]() $(\alpha \pm 1) \in \mathfrak {a}^{-1}N \mathcal {O},$
and
$(\alpha \pm 1) \in \mathfrak {a}^{-1}N \mathcal {O},$
and
![]() $\operatorname {\mathrm {Stab}}(P) \subseteq \left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod \mathfrak {a}^{-1}N \mathcal {O} \right\}.$
The reverse containment is clear.
$\operatorname {\mathrm {Stab}}(P) \subseteq \left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod \mathfrak {a}^{-1}N \mathcal {O} \right\}.$
The reverse containment is clear.
Proposition 3.4 Let
![]() $G = \left\langle P \right\rangle $
be a
$G = \left\langle P \right\rangle $
be a
![]() $\Gamma _0(N)$
-level structure and
$\Gamma _0(N)$
-level structure and
![]() $\mathfrak {a} = \left\langle P, N \mathcal {O} \right\rangle $
the smallest ideal containing P and
$\mathfrak {a} = \left\langle P, N \mathcal {O} \right\rangle $
the smallest ideal containing P and
![]() $N.$
Then
$N.$
Then
Proof Let
![]() $\alpha G = G.$
Then
$\alpha G = G.$
Then
![]() $\alpha P = P'$
where
$\alpha P = P'$
where
![]() $G = \left\langle P' \right\rangle .$
Since G is cyclic of order N, we must have
$G = \left\langle P' \right\rangle .$
Since G is cyclic of order N, we must have
![]() $P' = c P$
for some c coprime to
$P' = c P$
for some c coprime to
![]() $N.$
The rest of the proof follows as Theorem 3.3 but by replacing the requirement of
$N.$
The rest of the proof follows as Theorem 3.3 but by replacing the requirement of
![]() $\alpha \equiv \pm 1 \ \mod \mathfrak {a}^{-1}N \mathcal {O}$
with
$\alpha \equiv \pm 1 \ \mod \mathfrak {a}^{-1}N \mathcal {O}$
with
![]() $\alpha \equiv c \mod \mathfrak {a}^{-1}N \mathcal {O}$
where c is an integer coprime to
$\alpha \equiv c \mod \mathfrak {a}^{-1}N \mathcal {O}$
where c is an integer coprime to
![]() $N.$
$N.$
Remark 3.5 The above propositions can be modified to work for j-invariants
![]() $0$
and
$0$
and
![]() $1728$
by considering congruences modulo a
$1728$
by considering congruences modulo a
![]() $6^{\text {th}}$
or
$6^{\text {th}}$
or
![]() $4^{\text {th}}$
root of unity respectively.
$4^{\text {th}}$
root of unity respectively.
4 Adding level structure to isogeny graphs
This section will be organized into three subsections where we will look at ordinary
![]() $\ell $
-isogeny graphs with the three types of level structures. We are particularly interested in how the choice of N affects the size and number of components when adding level structure. In what follows, we will let
$\ell $
-isogeny graphs with the three types of level structures. We are particularly interested in how the choice of N affects the size and number of components when adding level structure. In what follows, we will let
![]() $\mathcal {O}$
be an order in an imaginary quadratic field
$\mathcal {O}$
be an order in an imaginary quadratic field
![]() $K.$
Rather than look at the entire isogeny graph, we will focus our attention on the connected components (i.e., volcanoes), and in particular, their craters. We will let
$K.$
Rather than look at the entire isogeny graph, we will focus our attention on the connected components (i.e., volcanoes), and in particular, their craters. We will let
![]() $G_{\ell }$
be such a component whose crater
$G_{\ell }$
be such a component whose crater
![]() $C_{\ell }$
consists of isomorphism classes of elliptic curves whose endomorphism rings are equal to
$C_{\ell }$
consists of isomorphism classes of elliptic curves whose endomorphism rings are equal to
![]() $\mathcal {O}.$
Further, we will restrict ourselves to only working with elliptic curves whose j-invariants are not
$\mathcal {O}.$
Further, we will restrict ourselves to only working with elliptic curves whose j-invariants are not
![]() $0$
or
$0$
or
![]() $1728$
to avoid automorphism groups different from
$1728$
to avoid automorphism groups different from
![]() $\left\{ \pm 1 \right\}.$
As usual, we will let N be a positive integer coprime to p,
$\left\{ \pm 1 \right\}.$
As usual, we will let N be a positive integer coprime to p,
![]() $\ell ,$
and the conductor of
$\ell ,$
and the conductor of
![]() $\mathcal {O}.$
$\mathcal {O}.$
Lemma 4.1 Let
![]() $G_{\ell }$
be an isogeny volcano with n vertices.
$G_{\ell }$
be an isogeny volcano with n vertices.
-
(i) The graph
 $G_{\ell ,0}(N)$
has vertices.
$G_{\ell ,0}(N)$
has vertices. $$\begin{align*}n N\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
$$\begin{align*}n N\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
-
(ii) If
 $N> 2,$
the graph
$N> 2,$
the graph
 $G_{\ell ,1}(N)$
has vertices and
$G_{\ell ,1}(N)$
has vertices and $$\begin{align*}\frac{nN\phi(N)}{2}\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
$$\begin{align*}\frac{nN\phi(N)}{2}\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
 $3n$
if
$3n$
if
 $N = 2$
.
$N = 2$
.
-
(iii) If
 $N> 2,$
the graph
$N> 2,$
the graph
 $G_{\ell }(N)$
has vertices and
$G_{\ell }(N)$
has vertices and $$\begin{align*}\frac{nN^2\phi(N)^2}{2} \prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
$$\begin{align*}\frac{nN^2\phi(N)^2}{2} \prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
 $6n$
if
$6n$
if
 $N = 2$
.
$N = 2$
.
where
![]() $\phi $
is Euler’s totient function.
$\phi $
is Euler’s totient function.
Proof For each case, we proceed by counting the number of level structures which can be added to each vertex in
![]() $G_{\ell }.$
$G_{\ell }.$
We begin by proving (ii). Since
![]() $E[N] \simeq \mathbb {Z}/N\mathbb {Z} \times \mathbb {Z}/N \mathbb {Z}$
and
$E[N] \simeq \mathbb {Z}/N\mathbb {Z} \times \mathbb {Z}/N \mathbb {Z}$
and
![]() $N = \prod p_i^{e_i},$
then by the Chinese remainder theorem we may write
$N = \prod p_i^{e_i},$
then by the Chinese remainder theorem we may write
An element P of
![]() $E[N]$
has maximal order N if and only if it has maximal order in each of factors on the right-hand side of (4.1), and so it is sufficient to find the number of elements of maximal order of each factor of
$E[N]$
has maximal order N if and only if it has maximal order in each of factors on the right-hand side of (4.1), and so it is sufficient to find the number of elements of maximal order of each factor of
![]() $E[N].$
An element
$E[N].$
An element
![]() $(a,b)$
of
$(a,b)$
of
![]() $(\mathbb {Z}/p_i^{e_i})^2$
is of maximal order if either
$(\mathbb {Z}/p_i^{e_i})^2$
is of maximal order if either
![]() $(a,p_i^{e_i}) = 1$
or
$(a,p_i^{e_i}) = 1$
or
![]() $(b, p_i^{e_i}) = 1.$
There are
$(b, p_i^{e_i}) = 1.$
There are
![]() $\phi (p_i^{e_i})p_i^{e_i}$
pairs where a is coprime to
$\phi (p_i^{e_i})p_i^{e_i}$
pairs where a is coprime to
![]() $p_i^{e_i}$
and
$p_i^{e_i}$
and
![]() $\phi (p_i^{e_i})(p_i^{e_i} - \phi (p_i^{e_i}))$
pairs where b is coprime to
$\phi (p_i^{e_i})(p_i^{e_i} - \phi (p_i^{e_i}))$
pairs where b is coprime to
![]() $p_i^{e_i}$
and a is not. Some algebraic manipulation shows there are a total of
$p_i^{e_i}$
and a is not. Some algebraic manipulation shows there are a total of
![]() $p_i^{2e_i} - p_i^{2(e_i-1)}$
such elements of maximal order in
$p_i^{2e_i} - p_i^{2(e_i-1)}$
such elements of maximal order in
![]() $(\mathbb {Z}/p_i^{e_i}\mathbb {Z})^2$
. We repeat this for each prime power factor of N and by the Chinese remainder theorem we may take their product to get
$(\mathbb {Z}/p_i^{e_i}\mathbb {Z})^2$
. We repeat this for each prime power factor of N and by the Chinese remainder theorem we may take their product to get
 $$ \begin{align} N \phi(N) \prod_{p \mid N}\left(1 + \frac{1}{p}\right) \end{align} $$
$$ \begin{align} N \phi(N) \prod_{p \mid N}\left(1 + \frac{1}{p}\right) \end{align} $$
total points of order
![]() $N.$
If
$N.$
If
![]() $N = 2,$
then
$N = 2,$
then
![]() $P = -P$
for any point P and so we may substitute
$P = -P$
for any point P and so we may substitute
![]() $N = 2$
into (4.2) to get a scaling factor of
$N = 2$
into (4.2) to get a scaling factor of
![]() $3.$
Otherwise, if
$3.$
Otherwise, if
![]() $N> 2,$
then we must divide the result of (4.2) by
$N> 2,$
then we must divide the result of (4.2) by
![]() $2$
due to identifying P with
$2$
due to identifying P with
![]() $-P.$
$-P.$
To prove (i), we use the fact that any cyclic subgroup
![]() $\left\langle P \right\rangle \subseteq E[N]$
of order N has
$\left\langle P \right\rangle \subseteq E[N]$
of order N has
![]() $\phi (N)$
elements with order
$\phi (N)$
elements with order
![]() $N.$
We may therefore partition the elements P of order N into equivalence classes where
$N.$
We may therefore partition the elements P of order N into equivalence classes where
![]() $P \sim P'$
if there exists an integer k such that
$P \sim P'$
if there exists an integer k such that
![]() $P' = kP.$
From (ii), we have that there are
$P' = kP.$
From (ii), we have that there are
 $$\begin{align*}N\phi(N)\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
$$\begin{align*}N\phi(N)\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
elements of order N in
![]() $E[N].$
Dividing by
$E[N].$
Dividing by
![]() $\phi (N)$
the size of each partition, we see there are
$\phi (N)$
the size of each partition, we see there are
 $$\begin{align*}N \prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
$$\begin{align*}N \prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
such equivalence classes, and therefore subgroups, of order
![]() $N.$
$N.$
To prove (iii), we first work with a factor
![]() $(\mathbb {Z}/p_i^{e_i}\mathbb {Z})^2$
of (4.1). The result of (ii) gives us the number of ways to choose a first basis point P. The restrictions on choosing a second basis point Q is that it must be of order
$(\mathbb {Z}/p_i^{e_i}\mathbb {Z})^2$
of (4.1). The result of (ii) gives us the number of ways to choose a first basis point P. The restrictions on choosing a second basis point Q is that it must be of order
![]() $p_i^{e_i}$
and it cannot be congruent to a scalar multiple of P modulo
$p_i^{e_i}$
and it cannot be congruent to a scalar multiple of P modulo
![]() $p_i.$
The congruence requirement arises from the fact that
$p_i.$
The congruence requirement arises from the fact that
![]() $\mathbb {Z}/p_i^{e_i} \mathbb {Z}$
is local at
$\mathbb {Z}/p_i^{e_i} \mathbb {Z}$
is local at
![]() $p_i.$
From (ii), we know there are
$p_i.$
From (ii), we know there are
![]() $\phi (p_i^{e_i})$
elements of order
$\phi (p_i^{e_i})$
elements of order
![]() $p_i^{e_i}$
in
$p_i^{e_i}$
in
![]() $\left\langle P \right\rangle $
and that each of those elements is congruent to
$\left\langle P \right\rangle $
and that each of those elements is congruent to
![]() $p_i^{e_i-1}$
distinct elements of order
$p_i^{e_i-1}$
distinct elements of order
![]() $p_i^{e_i}.$
This gives a total of
$p_i^{e_i}.$
This gives a total of
![]() $\phi (p_i^{e_i})(p_i^{e_i} + p_i^{e_i-1}) - \phi (p_i^{e_i})p_i^{e_i-1} = p_i^{e_i}\phi (p_i^{e_i})$
choices for
$\phi (p_i^{e_i})(p_i^{e_i} + p_i^{e_i-1}) - \phi (p_i^{e_i})p_i^{e_i-1} = p_i^{e_i}\phi (p_i^{e_i})$
choices for
![]() $Q.$
Taking the product over all
$Q.$
Taking the product over all
![]() $p_i$
by the Chinese remainder theorem gives
$p_i$
by the Chinese remainder theorem gives
 $$ \begin{align} N^2\phi(N)^2\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align} $$
$$ \begin{align} N^2\phi(N)^2\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align} $$
choices of bases. If
![]() $N = 2,$
then
$N = 2,$
then
![]() $P = -P$
and
$P = -P$
and
![]() $Q = -Q$
for any choice of
$Q = -Q$
for any choice of
![]() $P, Q,$
and so substituting
$P, Q,$
and so substituting
![]() $N = 2$
into (4.3) gives a scaling factor of
$N = 2$
into (4.3) gives a scaling factor of
![]() $6.$
If
$6.$
If
![]() $N> 2,$
we divide (4.3) by
$N> 2,$
we divide (4.3) by
![]() $2$
due to identifying the pair
$2$
due to identifying the pair
![]() $(P, Q)$
with
$(P, Q)$
with
![]() $(-P, -Q).$
$(-P, -Q).$
The graphs of Definition 2.6 consist of components which are each a covering graph of
![]() $G_{\ell }.$
The crater
$G_{\ell }.$
The crater
![]() $C_{\ell }$
is the defining characteristic of
$C_{\ell }$
is the defining characteristic of
![]() $G_{\ell },$
so the following work will only discuss craters unless otherwise stated.
$G_{\ell },$
so the following work will only discuss craters unless otherwise stated.
Definition 4.1 Let
![]() $G_{\ell }$
be an isogeny volcano and
$G_{\ell }$
be an isogeny volcano and
![]() $G_{\ell ,0}(N)$
,
$G_{\ell ,0}(N)$
,
![]() $G_{\ell ,1}(N),$
and
$G_{\ell ,1}(N),$
and
![]() $G_{\ell }(N)$
the graphs obtained as described in Definition 2.6. Then
$G_{\ell }(N)$
the graphs obtained as described in Definition 2.6. Then
-
(i)
 $C_{\ell ,0}(N)$
denotes the subgraph of
$C_{\ell ,0}(N)$
denotes the subgraph of
 $G_{\ell ,0}(N)$
whose components are obtained by adding a
$G_{\ell ,0}(N)$
whose components are obtained by adding a
 $\Gamma _0(N)$
-level structure to
$\Gamma _0(N)$
-level structure to
 $C_{\ell };$
$C_{\ell };$
-
(ii)
 $C_{\ell ,1}(N)$
denotes the subgraph of
$C_{\ell ,1}(N)$
denotes the subgraph of
 $G_{\ell ,1}(N)$
whose components are obtained by adding a
$G_{\ell ,1}(N)$
whose components are obtained by adding a
 $\Gamma _1(N)$
-level structure to
$\Gamma _1(N)$
-level structure to
 $C_{\ell };$
and,
$C_{\ell };$
and, -
(iii)
 $C_{\ell }(N)$
denotes the subgraph of
$C_{\ell }(N)$
denotes the subgraph of
 $G_{\ell }(N)$
whose are obtained by adding a
$G_{\ell }(N)$
whose are obtained by adding a
 $\Gamma (N)$
-level structure to
$\Gamma (N)$
-level structure to
 $C_{\ell }.$
$C_{\ell }.$
For lack of a better term, we will refer to the graphs
![]() $C_{\ell ,0}(N)$
,
$C_{\ell ,0}(N)$
,
![]() $C_{\ell ,1}(N)$
, and
$C_{\ell ,1}(N)$
, and
![]() $C_{\ell }(N)$
as the craters of
$C_{\ell }(N)$
as the craters of
![]() $G_{\ell ,0}(N)$
,
$G_{\ell ,0}(N)$
,
![]() $G_{\ell ,1}(N)$
, and
$G_{\ell ,1}(N)$
, and
![]() $G_{\ell }(N)$
respectively. The reader should note that since the graphs
$G_{\ell }(N)$
respectively. The reader should note that since the graphs
![]() $G_{\ell ,1}(N)$
and
$G_{\ell ,1}(N)$
and
![]() $G_{\ell }(N)$
are directed, their craters do not look like craters of standard isogeny volcanoes.
$G_{\ell }(N)$
are directed, their craters do not look like craters of standard isogeny volcanoes.
Let
![]() $\mathfrak {l}$
be a prime
$\mathfrak {l}$
be a prime
![]() $\mathcal {O}$
-ideal above
$\mathcal {O}$
-ideal above
![]() $\ell .$
If
$\ell .$
If
![]() $\ell $
is an inert prime, then
$\ell $
is an inert prime, then
![]() $\mathfrak {l}$
does not induce a degree
$\mathfrak {l}$
does not induce a degree
![]() $\ell $
isogeny and
$\ell $
isogeny and
![]() $C_{\ell }$
is totally disconnected. Adding a level structure does not change these craters. As such, for the remainder of this article we will only concern ourselves with primes
$C_{\ell }$
is totally disconnected. Adding a level structure does not change these craters. As such, for the remainder of this article we will only concern ourselves with primes
![]() $\ell $
which either split or ramify. From [Reference Kohel10], we know the size of
$\ell $
which either split or ramify. From [Reference Kohel10], we know the size of
![]() $C_{\ell }$
is equal to the order n of
$C_{\ell }$
is equal to the order n of
![]() $[\mathfrak {l}]$
in the class group
$[\mathfrak {l}]$
in the class group
![]() $Cl(\mathcal {O}).$
In particular, we have
$Cl(\mathcal {O}).$
In particular, we have
![]() $\mathfrak {l}^n = \lambda \mathcal {O}$
and
$\mathfrak {l}^n = \lambda \mathcal {O}$
and
![]() $\overline {\mathfrak {l}}^n = \overline {\lambda }\mathcal {O}$
for some
$\overline {\mathfrak {l}}^n = \overline {\lambda }\mathcal {O}$
for some
![]() $\lambda , \overline {\lambda } \in \mathcal {O}^{\times }$
where
$\lambda , \overline {\lambda } \in \mathcal {O}^{\times }$
where
![]() $\mathfrak {l} = \overline {\mathfrak {l}}$
if
$\mathfrak {l} = \overline {\mathfrak {l}}$
if
![]() $\ell $
is ramified.
$\ell $
is ramified.
4.1 Crater graphs
 $C_{\ell ,0}(N)$
$C_{\ell ,0}(N)$
We will begin by looking at the components with a
![]() $\Gamma _0(N)$
-level structure. Let E be an elliptic curve on a crater
$\Gamma _0(N)$
-level structure. Let E be an elliptic curve on a crater
![]() $C_{\ell }.$
$C_{\ell }.$
Definition 4.2 Let G be a
![]() $\Gamma _0(N)$
-level structure of
$\Gamma _0(N)$
-level structure of
![]() $E.$
Then
$E.$
Then
![]() $v = (E,G)$
is a vertex on some component
$v = (E,G)$
is a vertex on some component
![]() $\mathcal {C}_{\ell ,0}(N) \subseteq C_{\ell ,0}(N).$
We say a vertex
$\mathcal {C}_{\ell ,0}(N) \subseteq C_{\ell ,0}(N).$
We say a vertex
![]() $v' \in \mathcal {C}_{\ell ,0}(N)$
is a
$v' \in \mathcal {C}_{\ell ,0}(N)$
is a
![]() $\Gamma _0$
-principal vertex of v if
$\Gamma _0$
-principal vertex of v if
![]() $v'$
is of the form
$v'$
is of the form
![]() $(E, G')$
for some
$(E, G')$
for some
![]() $G' \subseteq E[N]$
of order
$G' \subseteq E[N]$
of order
![]() $N.$
$N.$
A crater
![]() $C_{\ell }$
can be described by the behavior of
$C_{\ell }$
can be described by the behavior of
![]() $\ell $
in its class group. If
$\ell $
in its class group. If
![]() $\ell $
splits as a product of non-principal ideals, the crater is a cycle of length equal to the order of a prime
$\ell $
splits as a product of non-principal ideals, the crater is a cycle of length equal to the order of a prime
![]() $\mathfrak {l}$
above
$\mathfrak {l}$
above
![]() $\ell $
in its class group. If
$\ell $
in its class group. If
![]() $\ell $
splits as a product of principal ideals, the crater consists of a single vertex with two loops. If
$\ell $
splits as a product of principal ideals, the crater consists of a single vertex with two loops. If
![]() $\ell $
ramifies as a non-principal ideal, then the crater consists of an edge, and if
$\ell $
ramifies as a non-principal ideal, then the crater consists of an edge, and if
![]() $\ell $
ramifies as a principal ideal, then the crater is a single vertex with a loop. The following lemma and theorem are independent of the behavior of
$\ell $
ramifies as a principal ideal, then the crater is a single vertex with a loop. The following lemma and theorem are independent of the behavior of
![]() $\ell $
in its class group.
$\ell $
in its class group.
Lemma 4.2 Let
![]() $v = (E,G)$
be a vertex on
$v = (E,G)$
be a vertex on
![]() $\mathcal {C}_{\ell ,0}(N) \subseteq C_{\ell ,0}(N).$
If
$\mathcal {C}_{\ell ,0}(N) \subseteq C_{\ell ,0}(N).$
If
![]() $v' = (E, G')$
is a
$v' = (E, G')$
is a
![]() $\Gamma _0$
-principal vertex of
$\Gamma _0$
-principal vertex of
![]() $v,$
then there exists an endomorphism
$v,$
then there exists an endomorphism
![]() $\alpha \in \operatorname {\mathrm {End}}(E)$
such that
$\alpha \in \operatorname {\mathrm {End}}(E)$
such that
![]() $\alpha (G) = G'$
. Furthermore, there exists some positive integer d such that
$\alpha (G) = G'$
. Furthermore, there exists some positive integer d such that
![]() $\mathfrak {l}^d = \alpha \mathcal {O}.$
$\mathfrak {l}^d = \alpha \mathcal {O}.$
Proof Any edge of
![]() $\mathcal {C}_{\ell ,0}(N)$
represents an isogeny induced by
$\mathcal {C}_{\ell ,0}(N)$
represents an isogeny induced by
![]() $\mathfrak {l}$
which has finite order n in
$\mathfrak {l}$
which has finite order n in
![]() $Cl(\mathcal {O}).$
Since
$Cl(\mathcal {O}).$
Since
![]() $v, v'$
are on the same component, the path connecting them is the isogeny
$v, v'$
are on the same component, the path connecting them is the isogeny
![]() $\varphi _{\mathfrak {l}^d}$
induced by
$\varphi _{\mathfrak {l}^d}$
induced by
![]() $\mathfrak {l}^d$
for some
$\mathfrak {l}^d$
for some
![]() $d.$
This isogeny must be induced by a principal ideal
$d.$
This isogeny must be induced by a principal ideal
![]() $\alpha \mathcal {O}$
since
$\alpha \mathcal {O}$
since
![]() $\varphi _{\mathfrak {l}^d}: E \to E,$
and so
$\varphi _{\mathfrak {l}^d}: E \to E,$
and so
![]() $\mathfrak {l}^d = \alpha \mathcal {O}$
where
$\mathfrak {l}^d = \alpha \mathcal {O}$
where
![]() $n \mid d.$
$n \mid d.$
It is now clear why we use the term principal vertex in Definition 4.2: paths from a vertex v to a principal vertex arise from principal ideals. Theorem 4.2 tells us the size of a component
![]() $\mathcal {C}_{\ell ,0}(N) \subseteq C_{\ell ,0}(N)$
is equal to the order n of
$\mathcal {C}_{\ell ,0}(N) \subseteq C_{\ell ,0}(N)$
is equal to the order n of
![]() $[\mathfrak {l}]$
in the class group scaled by the number of principal vertices for some fixed vertex
$[\mathfrak {l}]$
in the class group scaled by the number of principal vertices for some fixed vertex
![]() $v.$
$v.$
Given
![]() $\mathfrak {a}$
an
$\mathfrak {a}$
an
![]() $\mathcal {O}$
-ideal, we will let
$\mathcal {O}$
-ideal, we will let
![]() $\phi _{\mathcal {O}}(\mathfrak {a})$
denote the size of the residue ring
$\phi _{\mathcal {O}}(\mathfrak {a})$
denote the size of the residue ring
![]() $(\mathcal {O}/\mathfrak {a})^{\times }.$
This can be thought of as a generalized version of Euler’s totient function. A standard result [Reference Narkiewicz13, Theorem 1.19] gives
$(\mathcal {O}/\mathfrak {a})^{\times }.$
This can be thought of as a generalized version of Euler’s totient function. A standard result [Reference Narkiewicz13, Theorem 1.19] gives
 $$ \begin{align} \phi_{\mathcal{O}}(\mathfrak{a}) = \mathcal{N}(\mathfrak{a}) \prod_{\mathfrak{p} \mid \mathfrak{a}}\left( 1 - \frac{1}{\mathcal{N}(\mathfrak{p})} \right), \end{align} $$
$$ \begin{align} \phi_{\mathcal{O}}(\mathfrak{a}) = \mathcal{N}(\mathfrak{a}) \prod_{\mathfrak{p} \mid \mathfrak{a}}\left( 1 - \frac{1}{\mathcal{N}(\mathfrak{p})} \right), \end{align} $$
where
![]() $\mathcal {N}(\mathfrak {a})$
denotes the norm of
$\mathcal {N}(\mathfrak {a})$
denotes the norm of
![]() $\mathfrak {a}.$
We will let
$\mathfrak {a}.$
We will let
![]() $\phi _{\mathcal {O}}$
denote the totient function on
$\phi _{\mathcal {O}}$
denote the totient function on
![]() $\mathcal {O}$
-ideals and
$\mathcal {O}$
-ideals and
![]() $\phi $
denote the usual Euler totient function. We remark that
$\phi $
denote the usual Euler totient function. We remark that
![]() $\phi (N) \neq \phi _{\mathcal {O}}(N \mathcal {O})$
as the right-hand side depends on how the (rational) prime factors of N behave in
$\phi (N) \neq \phi _{\mathcal {O}}(N \mathcal {O})$
as the right-hand side depends on how the (rational) prime factors of N behave in
![]() $\mathcal {O}$
while the left-hand side only depends on the (rational) prime factorization of
$\mathcal {O}$
while the left-hand side only depends on the (rational) prime factorization of
![]() $N.$
$N.$
Theorem 4.3 Let
![]() $v = (E, G)$
be a vertex on a component
$v = (E, G)$
be a vertex on a component
![]() $\mathcal {C}_{\ell ,0}(N) \subseteq C_{\ell ,0}(N)$
where
$\mathcal {C}_{\ell ,0}(N) \subseteq C_{\ell ,0}(N)$
where
![]() $G = \left\langle P \right\rangle $
and let
$G = \left\langle P \right\rangle $
and let
![]() $\mathfrak {a} = (P, N)$
be the
$\mathfrak {a} = (P, N)$
be the
![]() $\mathcal {O}$
-ideal generated by P and
$\mathcal {O}$
-ideal generated by P and
![]() $N.$
Recall that
$N.$
Recall that
![]() $\lambda $
was defined by
$\lambda $
was defined by
![]() $\mathfrak {l}^n = \lambda \mathcal {O}.$
Then
$\mathfrak {l}^n = \lambda \mathcal {O}.$
Then
![]() $\#\mathcal {C}_{\ell ,0}(N) = nm_{\mathfrak {a}}$
where
$\#\mathcal {C}_{\ell ,0}(N) = nm_{\mathfrak {a}}$
where
![]() $m_{\mathfrak {a}}$
is the order of the natural projection of
$m_{\mathfrak {a}}$
is the order of the natural projection of
![]() $\lambda $
in
$\lambda $
in
![]() $(\mathcal {O}/NO)^{\times }/\operatorname {\mathrm {Stab}}(G).$
Further,
$(\mathcal {O}/NO)^{\times }/\operatorname {\mathrm {Stab}}(G).$
Further,
![]() $C_{\ell ,0}(N)$
contains
$C_{\ell ,0}(N)$
contains
![]() $\frac {\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})}{\phi (N)m_{\mathfrak {a}}}$
components isomorphic to
$\frac {\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})}{\phi (N)m_{\mathfrak {a}}}$
components isomorphic to
![]() $\mathcal {C}_{\ell ,0}(N).$
$\mathcal {C}_{\ell ,0}(N).$
Proof We first note that any component
![]() $\mathcal {C}_{\ell ,0}(N)$
of
$\mathcal {C}_{\ell ,0}(N)$
of
![]() $C_{\ell ,0}(N)$
will have a crater whose size is divisible by the order n of
$C_{\ell ,0}(N)$
will have a crater whose size is divisible by the order n of
![]() $\mathfrak {l}$
in
$\mathfrak {l}$
in
![]() $Cl(\mathcal {O}).$
Using this fact combined with Theorem 4.2, it suffices to know how many principal vertices exist for some fixed vertex
$Cl(\mathcal {O}).$
Using this fact combined with Theorem 4.2, it suffices to know how many principal vertices exist for some fixed vertex
![]() $v.$
Since paths between principal vertices correspond to principal ideals of the form
$v.$
Since paths between principal vertices correspond to principal ideals of the form
![]() $\lambda ^k \mathcal {O}$
for some
$\lambda ^k \mathcal {O}$
for some
![]() $k \in \mathbb {Z},$
we need to find the smallest k such that
$k \in \mathbb {Z},$
we need to find the smallest k such that
![]() $\lambda ^kG = G$
to determine the component sizes. Theorem 3.4 tells us the stabilizers of
$\lambda ^kG = G$
to determine the component sizes. Theorem 3.4 tells us the stabilizers of
![]() $G,$
and so the number of principal vertices of v is simply the order of the natural projection of
$G,$
and so the number of principal vertices of v is simply the order of the natural projection of
![]() $\lambda $
in
$\lambda $
in
![]() $(\mathcal {O}/N\mathcal {O})^{\times }/\operatorname {\mathrm {Stab}}(G).$
$(\mathcal {O}/N\mathcal {O})^{\times }/\operatorname {\mathrm {Stab}}(G).$
To prove the second claim, observe that
![]() $\mathfrak {a}$
is the smallest ideal containing P and
$\mathfrak {a}$
is the smallest ideal containing P and
![]() $N,$
so by the isomorphism in Theorem 3.1, the image of P under the natural projection is in
$N,$
so by the isomorphism in Theorem 3.1, the image of P under the natural projection is in
![]() $(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})^{\times }$
. By (4.4), the ring
$(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})^{\times }$
. By (4.4), the ring
![]() $(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})$
contains
$(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})$
contains
![]() $\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})$
such elements, one of which is the image of
$\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})$
such elements, one of which is the image of
![]() $P.$
For a cyclic group G of order
$P.$
For a cyclic group G of order
![]() $N,$
there are
$N,$
there are
![]() $\phi (N)$
elements of order
$\phi (N)$
elements of order
![]() $N,$
and so we may partition these
$N,$
and so we may partition these
![]() $\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})$
elements whereby two points are equivalent if and only if they generate the same cyclic group. The result follows since any component contains
$\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})$
elements whereby two points are equivalent if and only if they generate the same cyclic group. The result follows since any component contains
![]() $m_{\mathfrak {a}}$
such cyclic subgroups belonging to
$m_{\mathfrak {a}}$
such cyclic subgroups belonging to
![]() $E[N].$
$E[N].$
A consequence of Theorems 4.2 and 4.3 is that if
![]() $\ell $
decomposes as a product of principal ideals, then the crater may consist of a cycle rather than loops when adding a
$\ell $
decomposes as a product of principal ideals, then the crater may consist of a cycle rather than loops when adding a
![]() $\Gamma _{0}(N)$
level structure.
$\Gamma _{0}(N)$
level structure.
By Theorem 4.3, we can determine the components (and thus all) of
![]() $G_{\ell ,0}(N)$
by considering all ideals (including all of
$G_{\ell ,0}(N)$
by considering all ideals (including all of
![]() $\mathcal {O}$
)
$\mathcal {O}$
)
![]() $\mathfrak {a}$
dividing
$\mathfrak {a}$
dividing
![]() $N \mathcal {O}$
along with the condition that
$N \mathcal {O}$
along with the condition that
![]() $N \mid \mathcal {N}(\mathfrak {a}^{-1}N),$
and looking at the order
$N \mid \mathcal {N}(\mathfrak {a}^{-1}N),$
and looking at the order
![]() $m_{\mathfrak {a}}$
of the projection of
$m_{\mathfrak {a}}$
of the projection of
![]() $\lambda $
in
$\lambda $
in
![]() $(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})^{\times }$
divided by the index
$(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})^{\times }$
divided by the index
![]() $[(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})^{\times } : (\mathbb {Z}/N \mathbb {Z})^{\times }].$
The divisibility condition on
$[(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})^{\times } : (\mathbb {Z}/N \mathbb {Z})^{\times }].$
The divisibility condition on
![]() $\mathcal {N}(\mathfrak {a}^{-1}N)$
arises from the fact that P must generate a cyclic group of order
$\mathcal {N}(\mathfrak {a}^{-1}N)$
arises from the fact that P must generate a cyclic group of order
![]() $N.$
Equivalently, we can determine
$N.$
Equivalently, we can determine
![]() $G_{\ell ,0}(N)$
by considering each
$G_{\ell ,0}(N)$
by considering each
![]() $\Gamma _0(N)$
-level structure and applying Theorem 4.3 directly.
$\Gamma _0(N)$
-level structure and applying Theorem 4.3 directly.
If we only consider the case where N is a rational prime, the situation is simpler and we can describe component sizes of
![]() $C_{\ell ,0}(N).$
$C_{\ell ,0}(N).$
Corollary 4.4 Let N be a prime different from
![]() $\ell $
and p and let m denote the order of the natural projection of
$\ell $
and p and let m denote the order of the natural projection of
![]() $\lambda $
in
$\lambda $
in
![]() $(\mathcal {O}/N\mathcal {O})^{\times }/(\mathbb {Z}/N \mathbb {Z})^{\times }.$
Then
$(\mathcal {O}/N\mathcal {O})^{\times }/(\mathbb {Z}/N \mathbb {Z})^{\times }.$
Then
![]() $C_{\ell ,0}(N)$
consists of one of the following:
$C_{\ell ,0}(N)$
consists of one of the following:
-
(i) If N is inert, then
 $C_{\ell ,0}(N)$
contains
$C_{\ell ,0}(N)$
contains
 $\frac {N+1}{m}$
components each of size
$\frac {N+1}{m}$
components each of size
 $nm.$
$nm.$
-
(ii) If
 $N\mathcal {O} = \mathfrak {N}_1 \mathfrak {N}_2,$
then
$N\mathcal {O} = \mathfrak {N}_1 \mathfrak {N}_2,$
then
 $C_{\ell ,0}(N)$
contains
$C_{\ell ,0}(N)$
contains
 $\frac {N-1}{m}$
components each of size
$\frac {N-1}{m}$
components each of size
 $nm$
and two components of size
$nm$
and two components of size
 $n.$
$n.$
-
(iii) If
 $N\mathcal {O} = \mathfrak {N}^2,$
then
$N\mathcal {O} = \mathfrak {N}^2,$
then
 $C_{\ell ,0}(N)$
contains
$C_{\ell ,0}(N)$
contains
 $\frac {N}{m}$
components each of size
$\frac {N}{m}$
components each of size
 $nm$
and one component of size
$nm$
and one component of size
 $n.$
$n.$
Proof These are all special cases of Theorem 4.3.
To prove (i), observe that
![]() $\mathcal {O}/N \mathcal {O}$
is isomorphic to a finite field of order
$\mathcal {O}/N \mathcal {O}$
is isomorphic to a finite field of order
![]() $N^2,$
and so for any P of order
$N^2,$
and so for any P of order
![]() $N,$
we have
$N,$
we have
![]() $\mathfrak {a} = (P, N) = \mathcal {O}.$
Then
$\mathfrak {a} = (P, N) = \mathcal {O}.$
Then
![]() $\#(\mathcal {O}/N)^{\times } = N^2-1$
and
$\#(\mathcal {O}/N)^{\times } = N^2-1$
and
![]() $\operatorname {\mathrm {Stab}}(G) = (\mathbb {Z}/N \mathbb {Z})^{\times }$
for any
$\operatorname {\mathrm {Stab}}(G) = (\mathbb {Z}/N \mathbb {Z})^{\times }$
for any
![]() $G.$
By Theorem 4.3,
$G.$
By Theorem 4.3,
![]() $\mathcal {C}_{\ell ,0}(N),$
contains
$\mathcal {C}_{\ell ,0}(N),$
contains
![]() $\frac {N^2-1}{m(N-1)}$
components each of size
$\frac {N^2-1}{m(N-1)}$
components each of size
![]() $nm.$
To prove (ii), we first observe that
$nm.$
To prove (ii), we first observe that
![]() $\lvert (\mathcal {O}/N \mathcal {O})^{\times } \rvert = (N-1)^2$
and that
$\lvert (\mathcal {O}/N \mathcal {O})^{\times } \rvert = (N-1)^2$
and that
![]() $\mathfrak {a} \in \left\{ \mathfrak {N}_1, \mathfrak {N}_2, \mathcal {O} \right\}.$
If
$\mathfrak {a} \in \left\{ \mathfrak {N}_1, \mathfrak {N}_2, \mathcal {O} \right\}.$
If
![]() $\mathfrak {a} = \mathfrak {N}_1$
or
$\mathfrak {a} = \mathfrak {N}_1$
or
![]() $\mathfrak {N}_2,$
then by Theorem 4.3 we can determine the corresponding components by computing the order of the projection of
$\mathfrak {N}_2,$
then by Theorem 4.3 we can determine the corresponding components by computing the order of the projection of
![]() $\lambda $
in
$\lambda $
in
![]() $(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})^{\times }/(\mathbb {Z}/N \mathbb {Z})^{\times },$
but this is the trivial group, and so we obtain two components each of size
$(\mathcal {O}/\mathfrak {a}^{-1}N \mathcal {O})^{\times }/(\mathbb {Z}/N \mathbb {Z})^{\times },$
but this is the trivial group, and so we obtain two components each of size
![]() $n.$
If
$n.$
If
![]() $\mathfrak {a} = \mathcal {O},$
then G has a generator corresponding to an element of
$\mathfrak {a} = \mathcal {O},$
then G has a generator corresponding to an element of
![]() $(\mathcal {O}/N \mathcal {O})^{\times },$
and so there are
$(\mathcal {O}/N \mathcal {O})^{\times },$
and so there are
![]() $\frac {(N-1)^2}{m(N-1)}$
components each of size
$\frac {(N-1)^2}{m(N-1)}$
components each of size
![]() $nm.$
To prove (iii), we proceed as in the split case but set
$nm.$
To prove (iii), we proceed as in the split case but set
![]() $\mathfrak {N}_{1} = \mathfrak {N}_{2} = \mathfrak {N}$
and observe that
$\mathfrak {N}_{1} = \mathfrak {N}_{2} = \mathfrak {N}$
and observe that
![]() $\lvert (\mathcal {O} / N\mathcal {O})^{\times } \rvert = N^{2} - N.$
If
$\lvert (\mathcal {O} / N\mathcal {O})^{\times } \rvert = N^{2} - N.$
If
![]() $\mathfrak {a} = \mathfrak {N},$
then
$\mathfrak {a} = \mathfrak {N},$
then
![]() $(\mathcal {O}/\mathfrak {a}^{-1}N\mathcal {O})^{\times } = (\mathcal {O} / \mathfrak {N})^{\times } \simeq (\mathbb {Z} / N\mathbb {Z})^{\times }$
and so we obtain one component of size
$(\mathcal {O}/\mathfrak {a}^{-1}N\mathcal {O})^{\times } = (\mathcal {O} / \mathfrak {N})^{\times } \simeq (\mathbb {Z} / N\mathbb {Z})^{\times }$
and so we obtain one component of size
![]() $n.$
If
$n.$
If
![]() $\mathfrak {a} = \mathcal {O},$
then we obtain
$\mathfrak {a} = \mathcal {O},$
then we obtain
![]() $\frac {N^{2}-N}{m(N-1)} = \frac {N}{m}$
components of size
$\frac {N^{2}-N}{m(N-1)} = \frac {N}{m}$
components of size
![]() $nm.$
$nm.$
4.2 Crater graphs
 $C_{\ell ,1}(N)$
$C_{\ell ,1}(N)$
Definition 4.3 Let P be a
![]() $\Gamma _1(N)$
-level structure of
$\Gamma _1(N)$
-level structure of
![]() $E.$
Then
$E.$
Then
![]() $v = (E, P)$
is a vertex on some component
$v = (E, P)$
is a vertex on some component
![]() $\mathcal {C}_{\ell ,1}(N) \subseteq C_{\ell ,1}(N).$
We say a vertex
$\mathcal {C}_{\ell ,1}(N) \subseteq C_{\ell ,1}(N).$
We say a vertex
![]() $v' \in \mathcal {C}_{\ell ,1}(N)$
is a
$v' \in \mathcal {C}_{\ell ,1}(N)$
is a
![]() $\Gamma _1$
-principal vertex of v if it is of the form
$\Gamma _1$
-principal vertex of v if it is of the form
![]() $(E, P')$
for some
$(E, P')$
for some
![]() $P' \in E[N]$
of order
$P' \in E[N]$
of order
![]() $N.$
$N.$
Lemma 4.5 Let
![]() $v = (E,P)$
be a vertex on
$v = (E,P)$
be a vertex on
![]() $\mathcal {C}_{\ell ,1}(N) \subseteq C_{\ell ,1}(N).$
If
$\mathcal {C}_{\ell ,1}(N) \subseteq C_{\ell ,1}(N).$
If
![]() $v' = (E, P')$
is a
$v' = (E, P')$
is a
![]() $\Gamma _1$
-principal vertex of
$\Gamma _1$
-principal vertex of
![]() $v,$
then there exists an endomorphism
$v,$
then there exists an endomorphism
![]() $\alpha \in \operatorname {\mathrm {End}}(E)$
such that
$\alpha \in \operatorname {\mathrm {End}}(E)$
such that
![]() ${\alpha (P) = \pm P'}$
. Furthermore, there exists some ideal
${\alpha (P) = \pm P'}$
. Furthermore, there exists some ideal
![]() $\mathfrak {b}$
in the group
$\mathfrak {b}$
in the group
![]() $\left\langle \mathfrak {l}, \overline {\mathfrak {l}} \right\rangle $
such that
$\left\langle \mathfrak {l}, \overline {\mathfrak {l}} \right\rangle $
such that
![]() $\mathfrak {b} = \alpha \mathcal {O}.$
$\mathfrak {b} = \alpha \mathcal {O}.$
Proof Any edge of
![]() $\mathcal {C}_{\ell ,1}(N)$
arises from an isogeny induced by
$\mathcal {C}_{\ell ,1}(N)$
arises from an isogeny induced by
![]() $\mathfrak {l}$
or
$\mathfrak {l}$
or
![]() $\overline {\mathfrak {l}}.$
Since
$\overline {\mathfrak {l}}.$
Since
![]() $C_{\ell ,1}(N)$
is a directed graph, then an isogeny induced by
$C_{\ell ,1}(N)$
is a directed graph, then an isogeny induced by
![]() $\overline {\mathfrak {l}}$
does not necessarily represent a reverse edge to that arising from
$\overline {\mathfrak {l}}$
does not necessarily represent a reverse edge to that arising from
![]() $\mathfrak {l}$
as in the case of
$\mathfrak {l}$
as in the case of
![]() $G_{\ell }$
or
$G_{\ell }$
or
![]() $G_{\ell ,0}(N).$
Any isogeny mapping v to
$G_{\ell ,0}(N).$
Any isogeny mapping v to
![]() $v'$
must be an endomorphism since it maps a point P on E to a point
$v'$
must be an endomorphism since it maps a point P on E to a point
![]() $P'$
which also lies on E and thus proves the first claim.
$P'$
which also lies on E and thus proves the first claim.
![]() $\alpha $
be such an endomorphism.
$\alpha $
be such an endomorphism.
Any path between principal vertices is the result of an isogeny induced by some ideal
![]() $\mathfrak {b}$
belonging to the group
$\mathfrak {b}$
belonging to the group
![]() $\left\langle \mathfrak {l}, \overline {\mathfrak {l}} \right\rangle $
. Since v and
$\left\langle \mathfrak {l}, \overline {\mathfrak {l}} \right\rangle $
. Since v and
![]() $v'$
are on the same component, they are connected by a path arising from
$v'$
are on the same component, they are connected by a path arising from
![]() $\mathfrak {b}$
where
$\mathfrak {b}$
where
![]() $\mathfrak {b} = \alpha \mathcal {O}.$
$\mathfrak {b} = \alpha \mathcal {O}.$
Theorem 4.6 Let
![]() $v = (E, P)$
be a vertex on a component
$v = (E, P)$
be a vertex on a component
![]() $\mathcal {C}_{\ell ,1}(N) \subseteq C_{\ell ,1}(N)$
where
$\mathcal {C}_{\ell ,1}(N) \subseteq C_{\ell ,1}(N)$
where
![]() $P \in E[N]$
is of order
$P \in E[N]$
is of order
![]() $N,$
and let
$N,$
and let
![]() $\mathfrak {a} = (P, N)$
be the
$\mathfrak {a} = (P, N)$
be the
![]() $\mathcal {O}$
-ideal generated by P and
$\mathcal {O}$
-ideal generated by P and
![]() $N.$
Then
$N.$
Then
![]() $\#\mathcal {C}_{\ell ,1}(N) = nm_{\mathfrak {a}}$
where
$\#\mathcal {C}_{\ell ,1}(N) = nm_{\mathfrak {a}}$
where
![]() $m_{\mathfrak {a}}$
is the order of the group generated by the natural projections of
$m_{\mathfrak {a}}$
is the order of the group generated by the natural projections of
![]() $\lambda $
,
$\lambda $
,
![]() $\overline {\lambda }$
in
$\overline {\lambda }$
in
![]() $(\mathcal {O}/NO)^{\times }/\operatorname {\mathrm {Stab}}(P).$
Further,
$(\mathcal {O}/NO)^{\times }/\operatorname {\mathrm {Stab}}(P).$
Further,
![]() $C_{\ell ,1}(N)$
contains
$C_{\ell ,1}(N)$
contains
![]() $\frac {\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})}{2m_{\mathfrak {a}}}$
components isomorphic to
$\frac {\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})}{2m_{\mathfrak {a}}}$
components isomorphic to
![]() $\mathcal {C}_{\ell ,1}(N).$
$\mathcal {C}_{\ell ,1}(N).$
Proof The proof follows that of Theorem 4.3, but with making the necessary change in stabilizer subgroup and utilizing Theorem 4.5. As observed in Theorem 4.5, we must look at the group generated by the natural projections of
![]() $\lambda $
,
$\lambda $
,
![]() $\overline {\lambda }$
since
$\overline {\lambda }$
since
![]() $C_{\ell ,1}(N)$
is a directed graph. The difference in the second claim is that we instead partition
$C_{\ell ,1}(N)$
is a directed graph. The difference in the second claim is that we instead partition
![]() $\frac {\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})}{2}$
elements where the denominator of
$\frac {\phi _{\mathcal {O}}(\mathfrak {a}^{-1}N \mathcal {O})}{2}$
elements where the denominator of
![]() $2$
comes from the fact that elements are equivalent if and only if they differ by a factor of
$2$
comes from the fact that elements are equivalent if and only if they differ by a factor of
![]() $-1.$
$-1.$
As in Theorem 4.4, if we restrict ourselves to the case where N is prime, then we can describe the component sizes of
![]() $C_{\ell ,1}(N).$
$C_{\ell ,1}(N).$
Corollary 4.7 Let N be a prime different from
![]() $\ell $
and
$\ell $
and
![]() $p,$
and let m denote the order of the group generated by the natural projections of
$p,$
and let m denote the order of the group generated by the natural projections of
![]() $\lambda $
,
$\lambda $
,
![]() $\overline {\lambda }$
in
$\overline {\lambda }$
in
![]() $(\mathcal {O}/N \mathcal {O})^{\times }/\left\{ \pm 1 \right\}.$
Then the graph
$(\mathcal {O}/N \mathcal {O})^{\times }/\left\{ \pm 1 \right\}.$
Then the graph
![]() $G_{\ell ,1}(N)$
consists of one of the following:
$G_{\ell ,1}(N)$
consists of one of the following:
-
(i) If N is inert, then there are
 $\frac {N^2-1}{2m}$
components each of size
$\frac {N^2-1}{2m}$
components each of size
 $nm.$
$nm.$
-
(ii) If
 $N\mathcal {O} = \mathfrak {N}_1 \mathfrak {N}_2,$
then there are
$N\mathcal {O} = \mathfrak {N}_1 \mathfrak {N}_2,$
then there are
 $\frac {(N-1)^2}{2m}$
components each of size
$\frac {(N-1)^2}{2m}$
components each of size
 $nm$
,
$nm$
,
 $\frac {(N-1)}{2m_1}$
components each of size
$\frac {(N-1)}{2m_1}$
components each of size
 $nm_1$
and
$nm_1$
and
 $\frac {N-1}{2m_2}$
components each of size
$\frac {N-1}{2m_2}$
components each of size
 $nm_2$
where
$nm_2$
where
 $m_1$
,
$m_1$
,
 $m_2$
are the orders of the groups generated by the natural projections of
$m_2$
are the orders of the groups generated by the natural projections of
 $\lambda $
,
$\lambda $
,
 $\overline {\lambda }$
in
$\overline {\lambda }$
in
 $(\mathcal {O}/\mathfrak {N}_1)^{\times }$
and
$(\mathcal {O}/\mathfrak {N}_1)^{\times }$
and
 $(\mathcal {O}/\mathfrak {N}_2)^{\times }$
respectively.
$(\mathcal {O}/\mathfrak {N}_2)^{\times }$
respectively. -
(iii) If
 $N\mathcal {O} = \mathfrak {N}^2,$
then there are
$N\mathcal {O} = \mathfrak {N}^2,$
then there are
 $\frac {N^2-N}{2m}$
components each of size
$\frac {N^2-N}{2m}$
components each of size
 $nm$
and
$nm$
and
 $(N-1)/2m$
components each of size
$(N-1)/2m$
components each of size
 $nm_1$
where
$nm_1$
where
 $m_1$
is the order of the group generated by the natural projections of
$m_1$
is the order of the group generated by the natural projections of
 $\lambda $
,
$\lambda $
,
 $\overline {\lambda }$
in
$\overline {\lambda }$
in
 $(\mathcal {O}/\mathfrak {N})^{\times }/\left\{ \pm 1 \right\}.$
$(\mathcal {O}/\mathfrak {N})^{\times }/\left\{ \pm 1 \right\}.$
Proof The proof of (i) is similar to that of Theorem 4.4 (i), and so we will focus on (ii) and (iii).
As in Theorem 4.4, we fix a vertex
![]() $v = (E, P)$
where E is on
$v = (E, P)$
where E is on
![]() $C_{\ell }$
and P is an element of
$C_{\ell }$
and P is an element of
![]() $\mathcal {O}/N\mathcal {O}$
corresponding to a
$\mathcal {O}/N\mathcal {O}$
corresponding to a
![]() $\Gamma _1(N)$
-level structure of
$\Gamma _1(N)$
-level structure of
![]() $E.$
In the case where
$E.$
In the case where
![]() $N\mathcal {O} = \mathfrak {N}_1 \mathfrak {N}_2,$
if
$N\mathcal {O} = \mathfrak {N}_1 \mathfrak {N}_2,$
if
![]() $P \in (\mathcal {O}/N\mathcal {O})^{\times },$
then by Theorem 3.3 we have
$P \in (\mathcal {O}/N\mathcal {O})^{\times },$
then by Theorem 3.3 we have
![]() $\operatorname {\mathrm {Stab}}(P) = \left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod N \right\}.$
The component containing v will then be of size
$\operatorname {\mathrm {Stab}}(P) = \left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod N \right\}.$
The component containing v will then be of size
![]() $nm.$
As
$nm.$
As
![]() $\phi _{\mathcal {O}}(N \mathcal {O}) = (N-1)^2,$
and we identify P with
$\phi _{\mathcal {O}}(N \mathcal {O}) = (N-1)^2,$
and we identify P with
![]() $-P,$
we will have
$-P,$
we will have
![]() $\frac {(N-1)^2}{2m}$
components of size
$\frac {(N-1)^2}{2m}$
components of size
![]() $nm.$
If instead
$nm.$
If instead
![]() $P \in \mathfrak {N}_1$
(resp.
$P \in \mathfrak {N}_1$
(resp.
![]() $\mathfrak {N}_2$
), then by Theorem 3.3, we instead have
$\mathfrak {N}_2$
), then by Theorem 3.3, we instead have
![]() $\operatorname {\mathrm {Stab}}(P) = \left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod {\mathfrak {N}_2} \right\}$
(resp.
$\operatorname {\mathrm {Stab}}(P) = \left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod {\mathfrak {N}_2} \right\}$
(resp.
![]() $\left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod {\mathfrak {N}_1} \right\}$
). By the CRT,
$\left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod {\mathfrak {N}_1} \right\}$
). By the CRT,
![]() $(\mathcal {O}/N\mathcal {O})^{\times } \simeq (\mathcal {O}/\mathfrak {N}_1)^{\times } \times \mathcal {O}/(\mathfrak {N}_2)^{\times }$
and under this isomorphism P may be written as
$(\mathcal {O}/N\mathcal {O})^{\times } \simeq (\mathcal {O}/\mathfrak {N}_1)^{\times } \times \mathcal {O}/(\mathfrak {N}_2)^{\times }$
and under this isomorphism P may be written as
![]() $(0 \ \mod {\mathfrak {N}_{1}}, P \ \mod {\mathfrak {N}_2})$
(resp.
$(0 \ \mod {\mathfrak {N}_{1}}, P \ \mod {\mathfrak {N}_2})$
(resp.
![]() $(P \ \mod {\mathfrak {N}_1}, 0 \ \mod {\mathfrak {N}_{2}})$
). It follows that the component containing v will be of size
$(P \ \mod {\mathfrak {N}_1}, 0 \ \mod {\mathfrak {N}_{2}})$
). It follows that the component containing v will be of size
![]() $nm_2$
(resp.
$nm_2$
(resp.
![]() $nm_1$
). Since
$nm_1$
). Since
![]() $\# (\mathcal {O}/\mathfrak {N}_1)^{\times }/\left\{ \pm 1 \right\} = \#(\mathcal {O}/\mathfrak {N}_2)^{\times }/\left\{ \pm 1 \right\} = \frac {N-1}{2},$
it follows that there are
$\# (\mathcal {O}/\mathfrak {N}_1)^{\times }/\left\{ \pm 1 \right\} = \#(\mathcal {O}/\mathfrak {N}_2)^{\times }/\left\{ \pm 1 \right\} = \frac {N-1}{2},$
it follows that there are
![]() $\frac {N-1}{2m_2}$
(resp.
$\frac {N-1}{2m_2}$
(resp.
![]() $\frac {N-1}{2m_1}$
) components of size
$\frac {N-1}{2m_1}$
) components of size
![]() $nm_2$
(resp.
$nm_2$
(resp.
![]() $nm_1$
).
$nm_1$
).
The proof of (iii) is the same, but with the change that
![]() $\phi _{\mathcal {O}}(N \mathcal {O}) = N^2-N.$
$\phi _{\mathcal {O}}(N \mathcal {O}) = N^2-N.$
4.3 Crater graphs
 $C_{\ell }(N)$
$C_{\ell }(N)$
Definition 4.4 Let
![]() $(P, Q)$
be
$(P, Q)$
be
![]() $\Gamma (N)$
-level structure of
$\Gamma (N)$
-level structure of
![]() $E.$
Then the vertex
$E.$
Then the vertex
![]() ${v = (E, P, Q)}$
is on some component
${v = (E, P, Q)}$
is on some component
![]() $\mathcal {C}_{\ell }(N) \subseteq C_{\ell }(N).$
We say a vertex
$\mathcal {C}_{\ell }(N) \subseteq C_{\ell }(N).$
We say a vertex
![]() $v' \in \mathcal {C}_{\ell }(N)$
is a
$v' \in \mathcal {C}_{\ell }(N)$
is a
![]() $\Gamma $
-principal vertex of v if it is of the form
$\Gamma $
-principal vertex of v if it is of the form
![]() $(E, P', Q')$
for some
$(E, P', Q')$
for some
![]() $P', Q' \in E[N]$
which are a basis for
$P', Q' \in E[N]$
which are a basis for
![]() $E[N].$
$E[N].$
Lemma 4.8 Let
![]() $v = (E,P,Q)$
be a vertex on
$v = (E,P,Q)$
be a vertex on
![]() $\mathcal {C}_{\ell }(N) \subseteq C_{\ell }(N).$
If
$\mathcal {C}_{\ell }(N) \subseteq C_{\ell }(N).$
If
![]() $v' = (E, P',Q')$
is a
$v' = (E, P',Q')$
is a
![]() $\Gamma $
-principal vertex of
$\Gamma $
-principal vertex of
![]() $v,$
then there exists an endomorphism
$v,$
then there exists an endomorphism
![]() $\alpha \in \operatorname {\mathrm {End}}(E)$
such that
$\alpha \in \operatorname {\mathrm {End}}(E)$
such that
![]() $\alpha (P) = \pm P'$
and
$\alpha (P) = \pm P'$
and
![]() $\alpha (Q) = \pm Q'$
. Furthermore, there exists some ideal
$\alpha (Q) = \pm Q'$
. Furthermore, there exists some ideal
![]() $\mathfrak {b}$
in the group
$\mathfrak {b}$
in the group
![]() $\left\langle \mathfrak {l}, \overline {\mathfrak {l}} \right\rangle $
such that
$\left\langle \mathfrak {l}, \overline {\mathfrak {l}} \right\rangle $
such that
![]() $\mathfrak {b} = \alpha \mathcal {O}.$
$\mathfrak {b} = \alpha \mathcal {O}.$
Proof The proof is similar to that of Theorem 4.5.
As we will see shortly, the full level N structure case turns out to be the simplest of the three cases to describe.
Theorem 4.9 Let
![]() $v = (E, P, Q)$
be a vertex on a component
$v = (E, P, Q)$
be a vertex on a component
![]() $\mathcal {C}_{\ell }(N) \subseteq C_{\ell }(N)$
where
$\mathcal {C}_{\ell }(N) \subseteq C_{\ell }(N)$
where
![]() $P, Q$
are a
$P, Q$
are a
![]() $\mathbb {Z}$
-basis for
$\mathbb {Z}$
-basis for
![]() $E[N].$
Then
$E[N].$
Then
![]() $\# \mathcal {C}_{\ell }(N) = n m $
where m is the order of the group generated by the natural projections of
$\# \mathcal {C}_{\ell }(N) = n m $
where m is the order of the group generated by the natural projections of
![]() $\lambda $
,
$\lambda $
,
![]() $\overline {\lambda }$
in
$\overline {\lambda }$
in
![]() $(\mathcal {O}/N \mathcal {O})^{\times }/{\pm 1}.$
Further,
$(\mathcal {O}/N \mathcal {O})^{\times }/{\pm 1}.$
Further,
![]() $C_{\ell }(N)$
contains
$C_{\ell }(N)$
contains
 $$\begin{align*}\frac{N^2\phi(N)^2}{2m}\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
$$\begin{align*}\frac{N^2\phi(N)^2}{2m}\prod_{p \mid N}\left( 1 + \frac{1}{p} \right) \end{align*}$$
components isomorphic to
![]() $\mathcal {C}_{\ell }(N).$
$\mathcal {C}_{\ell }(N).$
Proof We first fix a vertex
![]() $v = (E, P, Q)$
where E is on
$v = (E, P, Q)$
where E is on
![]() $C_{\ell }$
and
$C_{\ell }$
and
![]() $P, Q$
are a
$P, Q$
are a
![]() $\mathbb {Z}$
-basis for
$\mathbb {Z}$
-basis for
![]() $E[N].$
From Theorem 3.2, we have that
$E[N].$
From Theorem 3.2, we have that
![]() $\operatorname {\mathrm {Stab}}((P,Q)) = \left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod N \mathcal {O} \right\}.$
The number of principal vertices of v is given by the order m of the group generated by the projections of
$\operatorname {\mathrm {Stab}}((P,Q)) = \left\{ \alpha \in \mathcal {O}/N \mathcal {O} \mid \alpha \equiv \pm 1 \ \mod N \mathcal {O} \right\}.$
The number of principal vertices of v is given by the order m of the group generated by the projections of
![]() $\lambda $
,
$\lambda $
,
![]() $\overline {\lambda }$
in
$\overline {\lambda }$
in
![]() $(\mathcal {O}/N\mathcal {O})^{\times }/\left\{ \pm 1 \right\}$
and so the component containing v is of size
$(\mathcal {O}/N\mathcal {O})^{\times }/\left\{ \pm 1 \right\}$
and so the component containing v is of size
![]() $nm.$
Theorem 4.1 (iii) gives us the number of vertices containing
$nm.$
Theorem 4.1 (iii) gives us the number of vertices containing
![]() $E,$
and division by m gives the desired result.
$E,$
and division by m gives the desired result.
We immediately see a difference between Theorem 4.9 and the theorems describing
![]() $G_{\ell ,0}(N)$
and
$G_{\ell ,0}(N)$
and
![]() $G_{\ell ,1}(N)$
graphs: the structure is independent of the prime ideal factorization of
$G_{\ell ,1}(N)$
graphs: the structure is independent of the prime ideal factorization of
![]() $N \mathcal {O}.$
However, given a vertex
$N \mathcal {O}.$
However, given a vertex
![]() $v = (E, P, Q),$
the factorization of
$v = (E, P, Q),$
the factorization of
![]() $N \mathcal {O}$
can place restrictions on the possible principal vertices of
$N \mathcal {O}$
can place restrictions on the possible principal vertices of
![]() $v.$
For example, if
$v.$
For example, if
![]() $N = \mathfrak {N}_1 \mathfrak {N}_2$
and
$N = \mathfrak {N}_1 \mathfrak {N}_2$
and
![]() $P \in \mathfrak {N}_1, Q \in (\mathcal {O}/N\mathcal {O})^{\times },$
then any principal vertex
$P \in \mathfrak {N}_1, Q \in (\mathcal {O}/N\mathcal {O})^{\times },$
then any principal vertex
![]() $v' = (E, P', Q')$
of v must have the same structure (i.e.,
$v' = (E, P', Q')$
of v must have the same structure (i.e.,
![]() $P' \in \mathfrak {N}_1, Q' \in (\mathcal {O}/N\mathcal {O})^{\times }$
).
$P' \in \mathfrak {N}_1, Q' \in (\mathcal {O}/N\mathcal {O})^{\times }$
).
5 Class field theory
We now extend these results and use the language of class field theory to describe a group action on the various level structures. We will begin by briefly discussing congruence subgroups. Much of the content we discuss here is covered in more detail in [Reference Cox5].
5.1 Generalized ideal class groups
Let K be an imaginary quadratic field and
![]() $\mathcal {O}$
an order in
$\mathcal {O}$
an order in
![]() $K.$
We will let
$K.$
We will let
![]() $\mathcal {I}_{\mathcal {O}}$
denote the group of proper fractional
$\mathcal {I}_{\mathcal {O}}$
denote the group of proper fractional
![]() $\mathcal {O}$
-ideals and
$\mathcal {O}$
-ideals and
![]() $\mathcal {P}_{\mathcal {O}} \subseteq \mathcal {I}_{\mathcal {O}}$
the subgroup of fractional principal
$\mathcal {P}_{\mathcal {O}} \subseteq \mathcal {I}_{\mathcal {O}}$
the subgroup of fractional principal
![]() $\mathcal {O}$
-ideals. In the imaginary quadratic settingFootnote
1
, a modulus
$\mathcal {O}$
-ideals. In the imaginary quadratic settingFootnote
1
, a modulus
![]() $\mathfrak {m} \subseteq \mathcal {O}$
is simply an
$\mathfrak {m} \subseteq \mathcal {O}$
is simply an
![]() $\mathcal {O}$
-ideal. For a modulus
$\mathcal {O}$
-ideal. For a modulus
![]() $\mathfrak {m},$
we let
$\mathfrak {m},$
we let
![]() $\mathcal {I}_{\mathcal {O}}(\mathfrak {m})$
denote the group of proper fractional
$\mathcal {I}_{\mathcal {O}}(\mathfrak {m})$
denote the group of proper fractional
![]() $\mathcal {O}$
-ideals which are coprime to
$\mathcal {O}$
-ideals which are coprime to
![]() $\mathfrak {m}$
,
$\mathfrak {m}$
,
![]() $\mathcal {P}_{\mathcal {O}}(\mathfrak {m}) \subseteq \mathcal {I}_{\mathcal {O}}(\mathfrak {m})$
denote the subgroup of principal ideals which are coprime to
$\mathcal {P}_{\mathcal {O}}(\mathfrak {m}) \subseteq \mathcal {I}_{\mathcal {O}}(\mathfrak {m})$
denote the subgroup of principal ideals which are coprime to
![]() $\mathfrak {m},$
and
$\mathfrak {m},$
and
![]() $\mathcal {P}_{\mathcal {O},1}(\mathfrak {m}) \subseteq \mathcal {P}_{\mathcal {O}}$
denote the subgroup of principal ideals generated by
$\mathcal {P}_{\mathcal {O},1}(\mathfrak {m}) \subseteq \mathcal {P}_{\mathcal {O}}$
denote the subgroup of principal ideals generated by
![]() $\alpha \in K^{\times }$
such that
$\alpha \in K^{\times }$
such that
![]() $\alpha \equiv 1 \ \mod \mathfrak {m}.$
A subgroup
$\alpha \equiv 1 \ \mod \mathfrak {m}.$
A subgroup
![]() $H \subseteq \mathcal {I}_{\mathcal {O}}(\mathfrak {m})$
satisfying
$H \subseteq \mathcal {I}_{\mathcal {O}}(\mathfrak {m})$
satisfying
![]() $\mathcal {P}_{\mathcal {O},1}(\mathfrak {m}) \subseteq H \subseteq \mathcal {I}_{\mathcal {O}}(\mathfrak {m})$
is called a congruence subgroup for
$\mathcal {P}_{\mathcal {O},1}(\mathfrak {m}) \subseteq H \subseteq \mathcal {I}_{\mathcal {O}}(\mathfrak {m})$
is called a congruence subgroup for
![]() $\mathfrak {m}.$
Given a congruence subgroup
$\mathfrak {m}.$
Given a congruence subgroup
![]() $H,$
we may form the quotient group
$H,$
we may form the quotient group
which we call a generalized ideal class group for
![]() $\mathfrak {m}.$
$\mathfrak {m}.$
A trivial example of a congruence subgroup we are familiar with is obtained by setting
![]() $\mathfrak {m} = 1.$
In this setting, any principal ideal
$\mathfrak {m} = 1.$
In this setting, any principal ideal
![]() $(\alpha )$
satisfies
$(\alpha )$
satisfies
![]() $\alpha \equiv 1 \ \mod \mathfrak {m}$
and so
$\alpha \equiv 1 \ \mod \mathfrak {m}$
and so
![]() $\mathcal {P}_{\mathcal {O},1} = \mathcal {P}_{\mathcal {O}}.$
Then the generalized ideal class group is the usual ideal class group
$\mathcal {P}_{\mathcal {O},1} = \mathcal {P}_{\mathcal {O}}.$
Then the generalized ideal class group is the usual ideal class group
![]() ${Cl_{\mathcal {O}} = \mathcal {I}_{\mathcal {O}}/\mathcal {P}_{\mathcal {O}}}$
we are familiar with.
${Cl_{\mathcal {O}} = \mathcal {I}_{\mathcal {O}}/\mathcal {P}_{\mathcal {O}}}$
we are familiar with.
In this article, we focus on the setting
![]() $\mathfrak {m} = N\mathcal {O}$
where N is defined as in the previous sections. The two congruence subgroups we are interested in are
$\mathfrak {m} = N\mathcal {O}$
where N is defined as in the previous sections. The two congruence subgroups we are interested in are
![]() $\mathcal {P}_{\mathcal {O},1}(N),$
and
$\mathcal {P}_{\mathcal {O},1}(N),$
and
The first of these congruence subgroups is generated by the elements which fix all of a
![]() $\Gamma _1(N)$
and
$\Gamma _1(N)$
and
![]() $\Gamma (N)$
-level structure, while the second fixes all of a
$\Gamma (N)$
-level structure, while the second fixes all of a
![]() $\Gamma _0(N)$
-level structure.
$\Gamma _0(N)$
-level structure.
Proposition 5.1 Let
![]() $\mathcal {O}, \mathcal {O}'$
be orders such that
$\mathcal {O}, \mathcal {O}'$
be orders such that
![]() $\mathcal {O}' \subseteq \mathcal {O}$
and
$\mathcal {O}' \subseteq \mathcal {O}$
and
![]() $[\mathcal {O}:\mathcal {O}'] = f.$
Then
$[\mathcal {O}:\mathcal {O}'] = f.$
Then
Proof As stated in [Reference Arpin, Castryck, Eriksen, Lorenzon and Vercauteren2, Theorem 2.3.1], the proof is the relative version of [Reference Cox5, Proposition 7.22].
We are now ready to discuss the group action on level structures. Given an ordinary elliptic curve E with
![]() $\operatorname {\mathrm {End}}(E) \simeq \mathcal {O}$
and a level structure
$\operatorname {\mathrm {End}}(E) \simeq \mathcal {O}$
and a level structure
![]() $\gamma (N)$
on E of type
$\gamma (N)$
on E of type
![]() $\Gamma _0(N)$
,
$\Gamma _0(N)$
,
![]() $\Gamma _1(N),$
or
$\Gamma _1(N),$
or
![]() $\Gamma (N),$
we may define a group action
$\Gamma (N),$
we may define a group action
where
![]() $\mathfrak {a} \in \mathcal {I}_{\mathcal {O}}(N)$
and
$\mathfrak {a} \in \mathcal {I}_{\mathcal {O}}(N)$
and
![]() $\varphi _{\mathfrak {a}}$
is the isogeny induced by
$\varphi _{\mathfrak {a}}$
is the isogeny induced by
![]() $\mathfrak {a}$
whose kernel is given by
$\mathfrak {a}$
whose kernel is given by
![]() $E[\mathfrak {a}].$
Up to the equivalence relation defined in Definition 2.5, if
$E[\mathfrak {a}].$
Up to the equivalence relation defined in Definition 2.5, if
![]() $\gamma (N)$
is a
$\gamma (N)$
is a
![]() $\Gamma _0(N)$
-level structure, then the common stabilizers among all
$\Gamma _0(N)$
-level structure, then the common stabilizers among all
![]() $\Gamma _0(N)$
-level structures is the set
$\Gamma _0(N)$
-level structures is the set
![]() $\mathcal {P}_{\mathcal {O},\mathbb {Z}}(N)$
of principal ideals which act as scalar multiplication on
$\mathcal {P}_{\mathcal {O},\mathbb {Z}}(N)$
of principal ideals which act as scalar multiplication on
![]() $\gamma (N)$
; if it is a
$\gamma (N)$
; if it is a
![]() $\Gamma _1(N)$
-level structure, then common stabilizers is the set
$\Gamma _1(N)$
-level structure, then common stabilizers is the set
![]() $\mathcal {P}_{\mathcal {O},1}(N)$
of principal ideals which act as multiplication by
$\mathcal {P}_{\mathcal {O},1}(N)$
of principal ideals which act as multiplication by
![]() $\pm 1$
on
$\pm 1$
on
![]() $\gamma (N);$
and if it is a
$\gamma (N);$
and if it is a
![]() $\Gamma (N)$
-level structure, its stabilizers is the set
$\Gamma (N)$
-level structure, its stabilizers is the set
![]() $\mathcal {P}_{\mathcal {O},1}(N)$
. We can then form quotient groups
$\mathcal {P}_{\mathcal {O},1}(N)$
. We can then form quotient groups
where (5.1) acts on isomorphism classes of
![]() $\Gamma _0(N)$
-level structures and (5.2) acts on isomorphism classes of
$\Gamma _0(N)$
-level structures and (5.2) acts on isomorphism classes of
![]() $\Gamma _1(N)$
and
$\Gamma _1(N)$
and
![]() $\Gamma (N)$
-level structures. The first of these two generalized ideal class groups is simply the ideal class group for the order of index N in
$\Gamma (N)$
-level structures. The first of these two generalized ideal class groups is simply the ideal class group for the order of index N in
![]() $\mathcal {O},$
while the second is known as the ray class group for modulus
$\mathcal {O},$
while the second is known as the ray class group for modulus
![]() $\mathfrak {m} = N.$
$\mathfrak {m} = N.$
6 Examples
We will now look at several examples. We will add various level structures to craters. The examples covered are computed using Sagemath [17]. The craters with level structure are constructed by explicitly computing
![]() $\ell $
-isogenies and applying them to the various level structures we are interested in. The examples we look at will all consider the case where
$\ell $
-isogenies and applying them to the various level structures we are interested in. The examples we look at will all consider the case where
![]() $\ell $
splits in
$\ell $
splits in
![]() $\mathcal {O}$
as
$\mathcal {O}$
as
![]() $\ell \mathcal {O} = \mathfrak {l}\cdot \overline {\mathfrak {l}}.$
We will lift
$\ell \mathcal {O} = \mathfrak {l}\cdot \overline {\mathfrak {l}}.$
We will lift
![]() $\mathfrak {l}$
to the various groups discussed in Section 5 and compute its order to show consistency with the craters we construct.
$\mathfrak {l}$
to the various groups discussed in Section 5 and compute its order to show consistency with the craters we construct.
Example 6.1 Let
![]() $p = 107$
,
$p = 107$
,
![]() $\ell = 5$
,
$\ell = 5$
,
![]() $N = 6,$
and
$N = 6,$
and
![]() $E/\mathbb {F}_p$
defined by
$E/\mathbb {F}_p$
defined by
![]() $y^2 = x^3 + 43x + 86$
where
$y^2 = x^3 + 43x + 86$
where
![]() $j(E) = 19.$
We have the discriminant of Frobenius
$j(E) = 19.$
We have the discriminant of Frobenius
![]() $\Delta _{\pi } = -284 = 2^2(-71)$
and so E has CM by an order
$\Delta _{\pi } = -284 = 2^2(-71)$
and so E has CM by an order
![]() $\mathcal {O}$
in
$\mathcal {O}$
in
![]() $K = \mathbb {Q}(\sqrt {-71}).$
One can check that
$K = \mathbb {Q}(\sqrt {-71}).$
One can check that
![]() $\operatorname {\mathrm {End}}(E) = \mathcal {O}_K = \mathbb {Z}[\Phi ] = \mathbb {Z}\left[\frac {1+\sqrt {-71}}{2}\right].$
Figure 1 shows the crater of the component of the
$\operatorname {\mathrm {End}}(E) = \mathcal {O}_K = \mathbb {Z}[\Phi ] = \mathbb {Z}\left[\frac {1+\sqrt {-71}}{2}\right].$
Figure 1 shows the crater of the component of the
![]() $\ell $
-isogeny graph containing E with the blue vertex highlighting the isomorphism class E belongs to while Figure 2 shows the crater graph
$\ell $
-isogeny graph containing E with the blue vertex highlighting the isomorphism class E belongs to while Figure 2 shows the crater graph
![]() $C_{5,0}(6)$
obtained by adding a
$C_{5,0}(6)$
obtained by adding a
![]() $\Gamma _0(5)$
-level structure to the graph in Figure 1.
$\Gamma _0(5)$
-level structure to the graph in Figure 1.
The factorization of
![]() $\ell $
and N into products of prime ideals is given by
$\ell $
and N into products of prime ideals is given by
 $$ \begin{align*} \ell\mathcal{O} &= (5) = \mathfrak{l} \cdot \overline{\mathfrak{l}} = (5, \Phi+1)(5, \Phi+3) \\ N\mathcal{O} &= (6) = \mathfrak{p}\cdot \overline{\mathfrak{p}} \cdot \mathfrak{q} \cdot \overline{\mathfrak{q}} = (2, \Phi)(2, \Phi + 1)(3,\Phi)(3,\Phi+2). \end{align*} $$
$$ \begin{align*} \ell\mathcal{O} &= (5) = \mathfrak{l} \cdot \overline{\mathfrak{l}} = (5, \Phi+1)(5, \Phi+3) \\ N\mathcal{O} &= (6) = \mathfrak{p}\cdot \overline{\mathfrak{p}} \cdot \mathfrak{q} \cdot \overline{\mathfrak{q}} = (2, \Phi)(2, \Phi + 1)(3,\Phi)(3,\Phi+2). \end{align*} $$
The ideal class
![]() $[\mathfrak {l}]$
has order
$[\mathfrak {l}]$
has order
![]() $7$
in
$7$
in
![]() $Cl_K$
which is consistent with the crater size seen in Figure 1. For the ideal
$Cl_K$
which is consistent with the crater size seen in Figure 1. For the ideal
![]() $\mathfrak {l},$
we have
$\mathfrak {l},$
we have
![]() $\mathfrak {l}^7 = \lambda \mathcal {O} = (-4\Phi + 281).$
If
$\mathfrak {l}^7 = \lambda \mathcal {O} = (-4\Phi + 281).$
If
![]() $\left\langle P \right\rangle $
is a
$\left\langle P \right\rangle $
is a
![]() $\Gamma _0(N)$
-level structure on
$\Gamma _0(N)$
-level structure on
![]() $E,$
we have three cases to consider:
$E,$
we have three cases to consider:
-
(i) P is identified with an element of
 $(\mathcal {O}/N\mathcal {O})^{\times };$
$(\mathcal {O}/N\mathcal {O})^{\times };$
-
(ii) P is identified with an element of exactly one of
 $\mathfrak {p}, \overline {\mathfrak {p}}, \mathfrak {q},$
or
$\mathfrak {p}, \overline {\mathfrak {p}}, \mathfrak {q},$
or
 $\overline {\mathfrak {q}}$
or;
$\overline {\mathfrak {q}}$
or; -
(iii) P is identified with an element of exactly one of
 $\mathfrak {p}, \overline {\mathfrak {p}}$
and exactly one of
$\mathfrak {p}, \overline {\mathfrak {p}}$
and exactly one of
 $\mathfrak {q}, \overline {\mathfrak {q}}.$
$\mathfrak {q}, \overline {\mathfrak {q}}.$

Figure 1 Crater of 5-volcano containing
![]() $j(E) = 19$
over
$j(E) = 19$
over
![]() $\mathbb {F}_{107}$
.
$\mathbb {F}_{107}$
.

Figure 2 Crater
![]() $C_{5,0}(6)$
corresponding to adding a
$C_{5,0}(6)$
corresponding to adding a
![]() $\Gamma _0(6)$
-level structure to the
$\Gamma _0(6)$
-level structure to the
![]() $5$
-isogeny graph containing
$5$
-isogeny graph containing
![]() $j(E) = 19.$
Blue vertices correspond to principal vertices of E.
$j(E) = 19.$
Blue vertices correspond to principal vertices of E.
For the first case, we can determine the size of the component containing
![]() $\left\langle P \right\rangle $
by considering the order of the projection of
$\left\langle P \right\rangle $
by considering the order of the projection of
![]() $\lambda $
in
$\lambda $
in
![]() $(\mathcal {O}/N\mathcal {O})^{\times }/(\mathbb {Z}/N \mathbb {Z})^{\times }.$
We have
$(\mathcal {O}/N\mathcal {O})^{\times }/(\mathbb {Z}/N \mathbb {Z})^{\times }.$
We have
![]() $\#({O}/N\mathcal {O})^{\times }/(\mathbb {Z}/N \mathbb {Z})^{\times } = 4/2 = 2$
and
$\#({O}/N\mathcal {O})^{\times }/(\mathbb {Z}/N \mathbb {Z})^{\times } = 4/2 = 2$
and
![]() $\lambda = -4\Phi + 281 \equiv 2\Phi + 5$
modulo
$\lambda = -4\Phi + 281 \equiv 2\Phi + 5$
modulo
![]() $6.$
This is clearly not congruent to an integer modulo
$6.$
This is clearly not congruent to an integer modulo
![]() $6,$
so
$6,$
so
![]() $\lvert \lambda \rvert = 2$
and so by Theorem 4.3 we have one component which is twice the size of our original volcano. For the second case, we need to consider the order of the projection of
$\lvert \lambda \rvert = 2$
and so by Theorem 4.3 we have one component which is twice the size of our original volcano. For the second case, we need to consider the order of the projection of
![]() $\lambda $
in each of
$\lambda $
in each of
 $$ \begin{align*} &(\mathcal{O}/\mathfrak{p}^{-1}N\mathcal{O})^{\times}/(\mathbb{Z}/N \mathbb{Z})^{\times}, \\ &(\mathcal{O}/\overline{\mathfrak{p}}^{-1}N\mathcal{O})^{\times}/(\mathbb{Z}/N \mathbb{Z})^{\times}, \\ &(\mathcal{O}/\mathfrak{q}^{-1}N\mathcal{O})^{\times}/(\mathbb{Z}/N \mathbb{Z})^{\times}; \text{ and} \\ &(\mathcal{O}/\overline{\mathfrak{q}}^{-1}N\mathcal{O})^{\times}/(\mathbb{Z}/N \mathbb{Z})^{\times}. \end{align*} $$
$$ \begin{align*} &(\mathcal{O}/\mathfrak{p}^{-1}N\mathcal{O})^{\times}/(\mathbb{Z}/N \mathbb{Z})^{\times}, \\ &(\mathcal{O}/\overline{\mathfrak{p}}^{-1}N\mathcal{O})^{\times}/(\mathbb{Z}/N \mathbb{Z})^{\times}, \\ &(\mathcal{O}/\mathfrak{q}^{-1}N\mathcal{O})^{\times}/(\mathbb{Z}/N \mathbb{Z})^{\times}; \text{ and} \\ &(\mathcal{O}/\overline{\mathfrak{q}}^{-1}N\mathcal{O})^{\times}/(\mathbb{Z}/N \mathbb{Z})^{\times}. \end{align*} $$
The last two of these rings has trivial order and so each corresponds to a component isomorphic to our original volcano. The first two rings are of size
![]() $2,$
and so it suffices to check the projection of
$2,$
and so it suffices to check the projection of
![]() $\lambda $
in
$\lambda $
in
![]() $(\mathcal {O}/\mathfrak {p}^{-1}N\mathcal {O})^{\times }$
and
$(\mathcal {O}/\mathfrak {p}^{-1}N\mathcal {O})^{\times }$
and
![]() $(\mathcal {O}/\overline {\mathfrak {p}}^{-1}N\mathcal {O})^{\times }.$
We compute these projections to be
$(\mathcal {O}/\overline {\mathfrak {p}}^{-1}N\mathcal {O})^{\times }.$
We compute these projections to be
![]() $2\Phi - 1$
and
$2\Phi - 1$
and
![]() $-\Phi - 1$
respectively which both square to the identity element in their respective rings. Therefore, we have an additional two components which are twice of our original volcano, giving a total of three components of this size. Finally, consider when
$-\Phi - 1$
respectively which both square to the identity element in their respective rings. Therefore, we have an additional two components which are twice of our original volcano, giving a total of three components of this size. Finally, consider when
![]() $P \in \mathfrak {p} \mathfrak {q}.$
Then
$P \in \mathfrak {p} \mathfrak {q}.$
Then
and so
![]() $\lambda $
always acts as an integer on
$\lambda $
always acts as an integer on
![]() $\left\langle P \right\rangle .$
The result holds for all possibilities in the third case, and so we have four additional components isomorphic to the original volcano for a total of six copies of the original volcano.
$\left\langle P \right\rangle .$
The result holds for all possibilities in the third case, and so we have four additional components isomorphic to the original volcano for a total of six copies of the original volcano.
Example 6.2 Let
![]() $p = 47$
,
$p = 47$
,
![]() $\ell = 5$
,
$\ell = 5$
,
![]() $N = 3$
and
$N = 3$
and
![]() $E/\mathbb {F}_p$
defined by
$E/\mathbb {F}_p$
defined by
![]() $y^2 = x^3 + 14x + 5$
where
$y^2 = x^3 + 14x + 5$
where
![]() $j(E) = 8.$
The discriminant of Frobenius is given by
$j(E) = 8.$
The discriminant of Frobenius is given by
![]() $\Delta _{\pi } = 2^2(-31).$
We compute the endomorphism ring of E to be
$\Delta _{\pi } = 2^2(-31).$
We compute the endomorphism ring of E to be
![]() $\operatorname {\mathrm {End}}(E) = \mathcal {O} = \mathbb {Z}[\pi ].$
Seen in Figure 3 is the crater containing the isomorphism class of E and Figure 4 shows the crater graph
$\operatorname {\mathrm {End}}(E) = \mathcal {O} = \mathbb {Z}[\pi ].$
Seen in Figure 3 is the crater containing the isomorphism class of E and Figure 4 shows the crater graph
![]() $C_{5,0}(3).$
A notable difference between the graph seen in Figure 4 and the one seen in Figure 2 of the previous example is the number of components. In this example,
$C_{5,0}(3).$
A notable difference between the graph seen in Figure 4 and the one seen in Figure 2 of the previous example is the number of components. In this example,
and N is an inert prime, so any
![]() $\Gamma _0(N)$
-level structure is generated by an element P which can be identified with an element of
$\Gamma _0(N)$
-level structure is generated by an element P which can be identified with an element of
![]() $(\mathcal {O}/N\mathcal {O})^{\times }.$
Consequently, the crater graph
$(\mathcal {O}/N\mathcal {O})^{\times }.$
Consequently, the crater graph
![]() $C_{5,0}(3)$
will consist of components all isomorphic to each other and by Theorem 5.1, they will have size equal to the order of
$C_{5,0}(3)$
will consist of components all isomorphic to each other and by Theorem 5.1, they will have size equal to the order of
![]() $[\mathfrak {l}]$
in
$[\mathfrak {l}]$
in
![]() $Cl(\mathcal {O}')$
where
$Cl(\mathcal {O}')$
where
![]() $\mathcal {O}' = \mathbb {Z} + 3 \mathcal {O} = \mathbb {Z} + 6 \mathcal {O}_K.$
We compute
$\mathcal {O}' = \mathbb {Z} + 3 \mathcal {O} = \mathbb {Z} + 6 \mathcal {O}_K.$
We compute
![]() $h(O') = 12,$
and so we simply need to check whether which of
$h(O') = 12,$
and so we simply need to check whether which of
![]() $\mathfrak {l}^3$
,
$\mathfrak {l}^3$
,
![]() $\mathfrak {l}^6,$
and
$\mathfrak {l}^6,$
and
![]() $\mathfrak {l}^{12}$
is principal when
$\mathfrak {l}^{12}$
is principal when
![]() $\mathfrak {l}$
is viewed as an
$\mathfrak {l}$
is viewed as an
![]() $\mathcal {O}'$
-ideal. We compute
$\mathcal {O}'$
-ideal. We compute
 $$ \begin{align*} \mathfrak{l} &= (5, 3\pi + 2) \\ \mathfrak{l}^3 &= (125, 3\pi + 52) \\ \mathfrak{l}^6 &= (15625, 3\pi + 3802) \end{align*} $$
$$ \begin{align*} \mathfrak{l} &= (5, 3\pi + 2) \\ \mathfrak{l}^3 &= (125, 3\pi + 52) \\ \mathfrak{l}^6 &= (15625, 3\pi + 3802) \end{align*} $$
none of which is principal, and so
![]() $[\mathfrak {l}]$
has order
$[\mathfrak {l}]$
has order
![]() $12$
in
$12$
in
![]() $Cl(\mathcal {O}).$
$Cl(\mathcal {O}).$

Figure 3 Crater of 5-volcano containing
![]() $j(E) = 8$
over
$j(E) = 8$
over
![]() $\mathbb {F}_{47}$
.
$\mathbb {F}_{47}$
.

Figure 4 Crater
![]() $C_{5,0}(3)$
corresponding to adding a
$C_{5,0}(3)$
corresponding to adding a
![]() $\Gamma _0(3)$
-level structure to the
$\Gamma _0(3)$
-level structure to the
![]() $5$
-isogeny graph containing
$5$
-isogeny graph containing
![]() $j(E) = 8.$
Blue vertices correspond to principal vertices of E.
$j(E) = 8.$
Blue vertices correspond to principal vertices of E.
We now look at our final example which is a graph obtained by adding a
![]() $\Gamma _1(N)$
-level structure.
$\Gamma _1(N)$
-level structure.
Example 6.3 Let
![]() $p = 53$
,
$p = 53$
,
![]() $\ell = 3$
,
$\ell = 3$
,
![]() $N = 5,$
and
$N = 5,$
and
![]() $E/\mathbb {F}_p$
be defined by
$E/\mathbb {F}_p$
be defined by
![]() $y^2 = x^3 + 46x + 6$
where
$y^2 = x^3 + 46x + 6$
where
![]() $j(E) = 8.$
The endomorphism ring of E is given by
$j(E) = 8.$
The endomorphism ring of E is given by
![]() $\operatorname {\mathrm {End}}(E) = \mathcal {O} = \mathbb {Z} + 2 \mathbb {Z}[\Phi ]$
where
$\operatorname {\mathrm {End}}(E) = \mathcal {O} = \mathbb {Z} + 2 \mathbb {Z}[\Phi ]$
where
![]() $\Phi = \left[ \frac {1+\sqrt {-11}}{2}\right].$
$\Phi = \left[ \frac {1+\sqrt {-11}}{2}\right].$
Figure 5 shows the crater containing the isomorphism class of
![]() $E,$
and Figure 6 shows the crater graph
$E,$
and Figure 6 shows the crater graph
![]() $C_{3,1}(5).$
$C_{3,1}(5).$

Figure 5 Crater of 3-volcano containing
![]() $j(E) = 8$
over
$j(E) = 8$
over
![]() $\mathbb {F}_{53}$
.
$\mathbb {F}_{53}$
.

Figure 6 Crater
![]() $C_{3,1}(5)$
corresponding to adding a
$C_{3,1}(5)$
corresponding to adding a
![]() $\Gamma _1(5)$
-level structure to the
$\Gamma _1(5)$
-level structure to the
![]() $3$
-isogeny graph containing
$3$
-isogeny graph containing
![]() $j(E) = 8.$
Blue vertices correspond to principal vertices of
$j(E) = 8.$
Blue vertices correspond to principal vertices of
![]() $E.$
Solid arrows represent isogenies induced by
$E.$
Solid arrows represent isogenies induced by
![]() $\mathfrak {l},$
and dashed lines represent isogenies induced by
$\mathfrak {l},$
and dashed lines represent isogenies induced by
![]() $\overline {\mathfrak {l}}$
.
$\overline {\mathfrak {l}}$
.
We factor
![]() $\ell , N$
into prime
$\ell , N$
into prime
![]() $\mathcal {O}$
-ideals as
$\mathcal {O}$
-ideals as
 $$ \begin{align*} \ell\mathcal{O} &= \mathfrak{l} \cdot \overline{\mathfrak{l}} = (3, 2\Phi + 1)(3, 2\Phi), \\ N\mathcal{O} &= \mathfrak{N} \cdot \overline{\mathfrak{N}} = (5, 2\Phi + 1)(5, 2\Phi + 2). \end{align*} $$
$$ \begin{align*} \ell\mathcal{O} &= \mathfrak{l} \cdot \overline{\mathfrak{l}} = (3, 2\Phi + 1)(3, 2\Phi), \\ N\mathcal{O} &= \mathfrak{N} \cdot \overline{\mathfrak{N}} = (5, 2\Phi + 1)(5, 2\Phi + 2). \end{align*} $$
In
![]() $Cl(K)$
,
$Cl(K)$
,
![]() $[\mathfrak {l}]$
has order
$[\mathfrak {l}]$
has order
![]() $3$
and
$3$
and
![]() $\mathfrak {l}^3 = \lambda \mathcal {O} = (-2\Phi + 5).$
For a
$\mathfrak {l}^3 = \lambda \mathcal {O} = (-2\Phi + 5).$
For a
![]() $\Gamma _1(N)$
-level structure
$\Gamma _1(N)$
-level structure
![]() $P,$
we have three cases to consider:
$P,$
we have three cases to consider:
-
(i) P is identified with an element of
 $(\mathcal {O}/N\mathcal {O})^{\times };$
$(\mathcal {O}/N\mathcal {O})^{\times };$
-
(ii) P is identified with an element of
 $\mathfrak {N}$
or;
$\mathfrak {N}$
or; -
(iii) P is identified with an element of
 $\overline {\mathfrak {N}}.$
$\overline {\mathfrak {N}}.$
For the first case, we have
![]() $\#(\mathcal {O}/N\mathcal {O})^{\times }/2 = 8.$
We let
$\#(\mathcal {O}/N\mathcal {O})^{\times }/2 = 8.$
We let
![]() $\tilde {\lambda }$
denote the equivalence class of
$\tilde {\lambda }$
denote the equivalence class of
![]() $(\mathcal {O}/N\mathcal {O})^{\times }$
containing
$(\mathcal {O}/N\mathcal {O})^{\times }$
containing
![]() $\lambda $
and compute
$\lambda $
and compute
 $$ \begin{align*} \tilde{\lambda} &= -2\Phi + 5 \equiv -2\Phi \quad\mod{N} \\ \tilde{\lambda}^2 &= -16\Phi + 13 \equiv -\Phi + 3 \quad\mod{N} \\ \tilde{\lambda}^4 &= -160\Phi - 599 \equiv 1 \quad\mod{N}, \end{align*} $$
$$ \begin{align*} \tilde{\lambda} &= -2\Phi + 5 \equiv -2\Phi \quad\mod{N} \\ \tilde{\lambda}^2 &= -16\Phi + 13 \equiv -\Phi + 3 \quad\mod{N} \\ \tilde{\lambda}^4 &= -160\Phi - 599 \equiv 1 \quad\mod{N}, \end{align*} $$
and so
![]() $\tilde {\lambda }$
has order
$\tilde {\lambda }$
has order
![]() $4$
and we get two components of size
$4$
and we get two components of size
![]() $12.$
Performing the same computations with
$12.$
Performing the same computations with
![]() $\overline {\mathfrak {l}}$
we find that the projection of
$\overline {\mathfrak {l}}$
we find that the projection of
![]() $\overline {\lambda }$
in
$\overline {\lambda }$
in
![]() $(\mathcal {O}/N\mathcal {O})^{\times }$
also has order
$(\mathcal {O}/N\mathcal {O})^{\times }$
also has order
![]() $4.$
One may also show that
$4.$
One may also show that
![]() $\overline {\mathfrak {l}} \equiv \mathfrak {l}^5 \ \mod N$
to construct the other half of the edges in Figure 6.
$\overline {\mathfrak {l}} \equiv \mathfrak {l}^5 \ \mod N$
to construct the other half of the edges in Figure 6.
The other two cases we need to consider are when P corresponds to an element of either
![]() $\mathfrak {N}$
or
$\mathfrak {N}$
or
![]() $\overline {\mathfrak {N}}.$
If P corresponds to an element of
$\overline {\mathfrak {N}}.$
If P corresponds to an element of
![]() $\mathfrak {N},$
then we need to consider the order of
$\mathfrak {N},$
then we need to consider the order of
![]() $\tilde {\lambda }$
in
$\tilde {\lambda }$
in
![]() $(\mathcal {O}/\overline {\mathfrak {N}})^{\times }.$
In the quotient ring
$(\mathcal {O}/\overline {\mathfrak {N}})^{\times }.$
In the quotient ring
![]() $(\mathcal {O}/\overline {\mathfrak {N}})^{\times }$
,
$(\mathcal {O}/\overline {\mathfrak {N}})^{\times }$
,
![]() $-2\Phi \equiv 3$
and so
$-2\Phi \equiv 3$
and so
![]() $\tilde {\lambda } \equiv 3$
which squares to
$\tilde {\lambda } \equiv 3$
which squares to
![]() $-1$
and stabilizes
$-1$
and stabilizes
![]() $P.$
This gives us one component of size six. In the quotient ring
$P.$
This gives us one component of size six. In the quotient ring
![]() $(\mathcal {O}/\mathfrak {N})^{\times }$
,
$(\mathcal {O}/\mathfrak {N})^{\times }$
,
![]() $-2\Phi \equiv 4$
and so
$-2\Phi \equiv 4$
and so
![]() $\tilde {\lambda } \equiv -1$
which gives two components of size
$\tilde {\lambda } \equiv -1$
which gives two components of size
![]() $3$
. To obtain the other half of the edges, we perform the same computations with
$3$
. To obtain the other half of the edges, we perform the same computations with
![]() $\overline {\mathfrak {l}}$
and find that the projection of
$\overline {\mathfrak {l}}$
and find that the projection of
![]() $\overline {\lambda }$
has order
$\overline {\lambda }$
has order
![]() $3$
and
$3$
and
![]() $6$
in
$6$
in
![]() $(\mathcal {O}/\mathfrak {N})^{\times }$
and
$(\mathcal {O}/\mathfrak {N})^{\times }$
and
![]() $(\mathcal {O}/\overline {\mathfrak {N}})^{\times }$
respectively and compute that
$(\mathcal {O}/\overline {\mathfrak {N}})^{\times }$
respectively and compute that
![]() $\mathfrak {l}^{2} \equiv \overline {\mathfrak {l}} \ \mod \mathfrak {N}$
and
$\mathfrak {l}^{2} \equiv \overline {\mathfrak {l}} \ \mod \mathfrak {N}$
and
![]() $\overline {\mathfrak {l}}^2 \equiv \mathfrak {l} \ \mod \overline {\mathfrak {N}}.$
$\overline {\mathfrak {l}}^2 \equiv \mathfrak {l} \ \mod \overline {\mathfrak {N}}.$
Acknowledgements
The authors thank W. Castryck, S. Galbraith, and the anonymous referee for comments and MBIE for support.