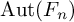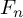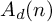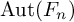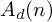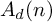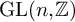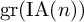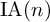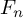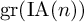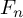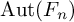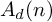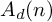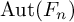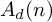1 Introduction
Jacobi diagrams are uni-trivalent graphs, which graphically encode the algebraic structures of Lie algebras and their representations. Jacobi diagrams were introduced for the Kontsevich integral, which is a universal finite type link invariant and unifies all quantum link invariants [Reference Bar-Natan2, Reference Kontsevich18, Reference Kassel15, Reference Ohtsuki19]. The associated graded vector space of finite type link invariants is isomorphic to the space of weight systems, which is the dual to the space of Jacobi diagrams.
Let
![]() $\Bbbk $
be a field of characteristic
$\Bbbk $
be a field of characteristic
![]() $0$
. We study the
$0$
. We study the
![]() $\Bbbk $
-vector space
$\Bbbk $
-vector space
![]() $A(n)$
of Jacobi diagrams on n-component oriented arcs, which is the target space of the Kontsevich integral for string links [Reference Habegger and Lin8, Reference Bar-Natan3] or bottom tangles [Reference Habiro9]. We consider the degree d part
$A(n)$
of Jacobi diagrams on n-component oriented arcs, which is the target space of the Kontsevich integral for string links [Reference Habegger and Lin8, Reference Bar-Natan3] or bottom tangles [Reference Habiro9]. We consider the degree d part
![]() $A_d(n)$
of
$A_d(n)$
of
![]() $A(n)$
, where the degree of a Jacobi diagram is determined by half the number of its vertices. The space
$A(n)$
, where the degree of a Jacobi diagram is determined by half the number of its vertices. The space
![]() $A_d(n)$
encodes the universal enveloping algebra
$A_d(n)$
encodes the universal enveloping algebra
![]() $U(\mathfrak {g})$
of any finite-dimensional semisimple Lie algebra
$U(\mathfrak {g})$
of any finite-dimensional semisimple Lie algebra
![]() $\mathfrak {g}$
. More precisely, the weight system maps
$\mathfrak {g}$
. More precisely, the weight system maps
![]() $A_d(n)$
to the
$A_d(n)$
to the
![]() $\mathfrak {g}$
-invariant part of
$\mathfrak {g}$
-invariant part of
![]() $U(\mathfrak {g})^{\otimes n}$
.
$U(\mathfrak {g})^{\otimes n}$
.
We consider a filtration for
![]() $A_d(n)$
defined by the number of trivalent vertices. The associated graded vector space of
$A_d(n)$
defined by the number of trivalent vertices. The associated graded vector space of
![]() $A_d(n)$
is identified via the PBW (Poincaré–Birkhoff–Witt) map [Reference Bar-Natan2, Reference Bar-Natan3] with a graded vector space
$A_d(n)$
is identified via the PBW (Poincaré–Birkhoff–Witt) map [Reference Bar-Natan2, Reference Bar-Natan3] with a graded vector space
![]() $B_d(n)$
of open Jacobi diagrams of degree d that are colored by elements of an n-dimensional
$B_d(n)$
of open Jacobi diagrams of degree d that are colored by elements of an n-dimensional
![]() $\Bbbk $
-vector space. For a finite-dimensional semisimple Lie algebra
$\Bbbk $
-vector space. For a finite-dimensional semisimple Lie algebra
![]() $\mathfrak {g}$
, the weight system maps
$\mathfrak {g}$
, the weight system maps
![]() $B_d(n)$
to the
$B_d(n)$
to the
![]() $\mathfrak {g}$
-invariant part of the tensor product
$\mathfrak {g}$
-invariant part of the tensor product
![]() $\mathfrak {S}(\mathfrak {g})^{\otimes n}$
of the symmetric algebra
$\mathfrak {S}(\mathfrak {g})^{\otimes n}$
of the symmetric algebra
![]() $\mathfrak {S}(\mathfrak {g})$
of
$\mathfrak {S}(\mathfrak {g})$
of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
In a previous paper [Reference Katada16], we proved that the vector spaces
![]() $A_d(n)$
define a functor
$A_d(n)$
define a functor
![]() $A_d:\mathbf {F}^{\mathrm {op}}\rightarrow \mathbf {fVect}$
from the opposite category
$A_d:\mathbf {F}^{\mathrm {op}}\rightarrow \mathbf {fVect}$
from the opposite category
![]() $\mathbf {F}^{\mathrm {op}}$
of the category
$\mathbf {F}^{\mathrm {op}}$
of the category
![]() $\mathbf {F}$
of finitely generated free groups to the category
$\mathbf {F}$
of finitely generated free groups to the category
![]() $\mathbf {fVect}$
of filtered vector spaces. By functoriality on
$\mathbf {fVect}$
of filtered vector spaces. By functoriality on
![]() $\mathbf {F}^{\mathrm {op}}$
,
$\mathbf {F}^{\mathrm {op}}$
,
![]() $A_d(n)$
inherits an action of the automorphism group
$A_d(n)$
inherits an action of the automorphism group
![]() $\operatorname {Aut}(F_n)$
and of the endomorphism monoid
$\operatorname {Aut}(F_n)$
and of the endomorphism monoid
![]() $\operatorname {End}(F_n)$
of the free group
$\operatorname {End}(F_n)$
of the free group
![]() $F_n$
of rank n. We proved in [Reference Katada16] that the action of
$F_n$
of rank n. We proved in [Reference Katada16] that the action of
![]() $\operatorname {Aut}(F_n)$
on
$\operatorname {Aut}(F_n)$
on
![]() $A_d(n)$
induces an action of the outer automorphism group
$A_d(n)$
induces an action of the outer automorphism group
![]() $\operatorname {Out}(F_n)$
of
$\operatorname {Out}(F_n)$
of
![]() $F_n$
on
$F_n$
on
![]() $A_d(n)$
and we observed that the
$A_d(n)$
and we observed that the
![]() $\operatorname {Aut}(F_n)$
-action on
$\operatorname {Aut}(F_n)$
-action on
![]() $A_d(n)$
induces two actions on
$A_d(n)$
induces two actions on
![]() $B_d(n)$
: an action of the general linear group
$B_d(n)$
: an action of the general linear group
![]() $\operatorname {GL}(n;\mathbb {Z})$
and an action of the graded Lie algebra
$\operatorname {GL}(n;\mathbb {Z})$
and an action of the graded Lie algebra
![]() $\mathrm {gr}(\operatorname {IA}(n))$
of the IA-automorphism group
$\mathrm {gr}(\operatorname {IA}(n))$
of the IA-automorphism group
![]() $\operatorname {IA}(n)$
of
$\operatorname {IA}(n)$
of
![]() $F_n$
associated with the lower central series. We used these two actions on
$F_n$
associated with the lower central series. We used these two actions on
![]() $B_d(n)$
to study the
$B_d(n)$
to study the
![]() $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
![]() $A_d(n)$
for
$A_d(n)$
for
![]() $d=2$
. However, it is rather difficult to compute the
$d=2$
. However, it is rather difficult to compute the
![]() $\mathrm {gr}(\operatorname {IA}(n))$
-action on
$\mathrm {gr}(\operatorname {IA}(n))$
-action on
![]() $B_d(n)$
directly for general d.
$B_d(n)$
directly for general d.
The aim of the present paper is to study the
![]() $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
![]() $A_d(n)$
for general d and especially
$A_d(n)$
for general d and especially
![]() $d=3$
in detail. We consider the Andreadakis filtration
$d=3$
in detail. We consider the Andreadakis filtration
![]() $\mathcal {E}_{\ast }(n)$
of the endomorphism monoid
$\mathcal {E}_{\ast }(n)$
of the endomorphism monoid
![]() $\operatorname {End}(F_n)$
of
$\operatorname {End}(F_n)$
of
![]() $F_n$
. We extend the action of the graded Lie algebra
$F_n$
. We extend the action of the graded Lie algebra
![]() $\mathrm {gr}(\operatorname {IA}(n))$
to an action of the associated graded Lie algebra
$\mathrm {gr}(\operatorname {IA}(n))$
to an action of the associated graded Lie algebra
![]() $\mathrm {gr}(\mathcal {E}_{\ast }(n))$
of the Andreadakis filtration. On the other hand, we construct a graphical version of the
$\mathrm {gr}(\mathcal {E}_{\ast }(n))$
of the Andreadakis filtration. On the other hand, we construct a graphical version of the
![]() $\mathrm {gr}(\mathcal {E}_{\ast }(n))$
-action on
$\mathrm {gr}(\mathcal {E}_{\ast }(n))$
-action on
![]() $B_d(n)$
. By using this graphical action, we study the
$B_d(n)$
. By using this graphical action, we study the
![]() $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
![]() $A_d(n)$
. We obtain an indecomposable decomposition of
$A_d(n)$
. We obtain an indecomposable decomposition of
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Aut}(F_n)$
-modules for
$\operatorname {Aut}(F_n)$
-modules for
![]() $n\geq 2d$
. Moreover, we obtain the radical filtration of
$n\geq 2d$
. Moreover, we obtain the radical filtration of
![]() $A_d(n)$
for
$A_d(n)$
for
![]() $n\geq 2d$
and the socle of
$n\geq 2d$
and the socle of
![]() $A_3(n)$
.
$A_3(n)$
.
1.1 Andreadakis filtration of
 $\operatorname {End}(F_n)$
$\operatorname {End}(F_n)$
Let
![]() $\Gamma _r:=\Gamma _r(F_n)$
denote the r-th term of the lower central series of the free group
$\Gamma _r:=\Gamma _r(F_n)$
denote the r-th term of the lower central series of the free group
![]() $F_n$
. Let
$F_n$
. Let
![]() $\mathcal {L}_r(n) :=\Gamma _r/\Gamma _{r+1}$
for
$\mathcal {L}_r(n) :=\Gamma _r/\Gamma _{r+1}$
for
![]() $r\geq 1$
, and set
$r\geq 1$
, and set
![]() $H:=\mathcal {L}_1(n)$
. Note that
$H:=\mathcal {L}_1(n)$
. Note that
![]() $\mathcal {L}_r(n)$
is the degree r part of the free Lie algebra
$\mathcal {L}_r(n)$
is the degree r part of the free Lie algebra
![]() $\mathcal {L}_{\ast }(n)$
on H.
$\mathcal {L}_{\ast }(n)$
on H.
Let
![]() $\operatorname {IA}(n)$
denote the IA-automorphism group of
$\operatorname {IA}(n)$
denote the IA-automorphism group of
![]() $F_n$
, which is the kernel of the canonical homomorphism
$F_n$
, which is the kernel of the canonical homomorphism
![]() $\operatorname {Aut}(F_n)\rightarrow \operatorname {GL}(n;\mathbb {Z})$
.
$\operatorname {Aut}(F_n)\rightarrow \operatorname {GL}(n;\mathbb {Z})$
.
The Andreadakis filtration
![]() $\mathcal {A}_{\ast }(n)$
of
$\mathcal {A}_{\ast }(n)$
of
![]() $\operatorname {Aut}(F_n)$
[Reference Andreadakis1, Reference Satoh22]
$\operatorname {Aut}(F_n)$
[Reference Andreadakis1, Reference Satoh22]
is defined by
For
![]() $r\geq 1$
, we have an injective homomorphism
$r\geq 1$
, we have an injective homomorphism
which is called the Johnson homomorphism. By Andreadakis [Reference Andreadakis1] and Kawazumi [Reference Kawazumi17], we have
![]() $\operatorname {gr}^1(\operatorname {IA}(n))\cong \operatorname {gr}^1(\mathcal {A}_{\ast }(n))\cong \operatorname {Hom}(H,\mathcal {L}_{2}(n))$
.
$\operatorname {gr}^1(\operatorname {IA}(n))\cong \operatorname {gr}^1(\mathcal {A}_{\ast }(n))\cong \operatorname {Hom}(H,\mathcal {L}_{2}(n))$
.
We construct the Andreadakis filtration
![]() $\mathcal {E}_{\ast }(n)$
of
$\mathcal {E}_{\ast }(n)$
of
![]() $\operatorname {End}(F_n)$
in a similar way by
$\operatorname {End}(F_n)$
in a similar way by
We define an equivalence relation on the monoid
![]() $\mathcal {E}_{r}(n)$
and consider the quotient group
$\mathcal {E}_{r}(n)$
and consider the quotient group
![]() $\operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
, which includes
$\operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
, which includes
![]() $\operatorname {gr}^r(\mathcal {A}_{\ast }(n))$
(see Section 3.3). We also construct the Johnson homomorphism
$\operatorname {gr}^r(\mathcal {A}_{\ast }(n))$
(see Section 3.3). We also construct the Johnson homomorphism
of
![]() $\operatorname {End}(F_n)$
, which turns out to be an abelian group isomorphism (see Proposition 3.8).
$\operatorname {End}(F_n)$
, which turns out to be an abelian group isomorphism (see Proposition 3.8).
The target group
![]() $\operatorname {Hom}(H,\mathcal {L}_{r+1}(n))\cong H^{\ast }\otimes \mathcal {L}_{r+1}(n)$
of the Johnson homomorphism is identified with the degree r part
$\operatorname {Hom}(H,\mathcal {L}_{r+1}(n))\cong H^{\ast }\otimes \mathcal {L}_{r+1}(n)$
of the Johnson homomorphism is identified with the degree r part
![]() $\operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
of the derivation Lie algebra
$\operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
of the derivation Lie algebra
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
of the free Lie algebra
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
of the free Lie algebra
![]() $\mathcal {L}_{\ast }(n)$
and with the tree module
$\mathcal {L}_{\ast }(n)$
and with the tree module
![]() $T_r(n)$
, which we define in Section 3.2. From the above, we have abelian group isomorphisms
$T_r(n)$
, which we define in Section 3.2. From the above, we have abelian group isomorphisms
Thus, we have
Moreover, we have isomorphisms of graded Lie algebras
(see Section 3.5). In what follows, we identify these three graded Lie algebras.
1.2 Actions of the derivation Lie algebra on
 $B_d(n)$
$B_d(n)$
Let
![]() $A_d(n)$
be the
$A_d(n)$
be the
![]() $\Bbbk $
-vector space spanned by Jacobi diagrams of degree d on n oriented arcs. We consider a filtration for
$\Bbbk $
-vector space spanned by Jacobi diagrams of degree d on n oriented arcs. We consider a filtration for
![]() $A_d(n)$
$A_d(n)$
where
![]() $A_{d,k}(n)$
is the subspace of
$A_{d,k}(n)$
is the subspace of
![]() $A_d(n)$
spanned by Jacobi diagrams with at least k trivalent vertices. By restricting the functor
$A_d(n)$
spanned by Jacobi diagrams with at least k trivalent vertices. By restricting the functor
![]() $A_d: \mathbf {F}^{\mathrm {op}}\to \mathbf {fVect}$
that we defined in [Reference Katada16] to the endomorphisms, we obtain an action of
$A_d: \mathbf {F}^{\mathrm {op}}\to \mathbf {fVect}$
that we defined in [Reference Katada16] to the endomorphisms, we obtain an action of
![]() $\operatorname {End}(F_n)$
on
$\operatorname {End}(F_n)$
on
![]() $A_d(n)$
. (See Section 2.3 and Section 4.)
$A_d(n)$
. (See Section 2.3 and Section 4.)
Let
![]() $V_n$
be an n-dimensional
$V_n$
be an n-dimensional
![]() $\Bbbk $
-vector space, which will be identified with the first cohomology of a handlebody of genus n. The associated graded vector space of
$\Bbbk $
-vector space, which will be identified with the first cohomology of a handlebody of genus n. The associated graded vector space of
![]() $A_d(n)$
is isomorphic via the PBW map [Reference Bar-Natan3] to a graded vector space
$A_d(n)$
is isomorphic via the PBW map [Reference Bar-Natan3] to a graded vector space
![]() $B_d(n)=\bigoplus _{k\geq 0}B_{d,k}(n)$
of
$B_d(n)=\bigoplus _{k\geq 0}B_{d,k}(n)$
of
![]() $V_n$
-colored open Jacobi diagrams of degree d, where
$V_n$
-colored open Jacobi diagrams of degree d, where
![]() $B_{d,k}(n)$
is the subspace of
$B_{d,k}(n)$
is the subspace of
![]() $B_d(n)$
spanned by open Jacobi diagrams with exactly k trivalent vertices.
$B_d(n)$
spanned by open Jacobi diagrams with exactly k trivalent vertices.
We defined in [Reference Katada16] a
![]() $\mathrm {gr}(\operatorname {IA}(n))$
-action on
$\mathrm {gr}(\operatorname {IA}(n))$
-action on
![]() $B_d(n)$
by using the bracket map
$B_d(n)$
by using the bracket map
We extend the
![]() $\mathrm {gr}(\operatorname {IA}(n))$
-action to an action of
$\mathrm {gr}(\operatorname {IA}(n))$
-action to an action of
![]() $\mathrm {gr}(\mathcal {E}_{\ast }(n))$
on
$\mathrm {gr}(\mathcal {E}_{\ast }(n))$
on
![]() $B_d(n)$
.
$B_d(n)$
.
We define a
![]() $\Bbbk $
-linear map
$\Bbbk $
-linear map
by using the following theorem.
Theorem 1.1 see Theorem 4.1
For any
![]() $r\geq 1$
, we have
$r\geq 1$
, we have
To prove this theorem, we introduce a category
![]() $\mathbf {A}^{L}$
, which includes as full subcategories the category
$\mathbf {A}^{L}$
, which includes as full subcategories the category
![]() $\mathbf {A}$
of Jacobi diagrams in handlebodies and the category isomorphic to the PROP for Casimir Lie algebras [Reference Hinich and Vaintrob13]. (See Section 4 and Appendix A).
$\mathbf {A}$
of Jacobi diagrams in handlebodies and the category isomorphic to the PROP for Casimir Lie algebras [Reference Hinich and Vaintrob13]. (See Section 4 and Appendix A).
By using the bracket maps, we obtain
![]() $\Bbbk $
-linear maps
$\Bbbk $
-linear maps
which form an action of the graded Lie algebra
![]() $\mathrm {gr}(\mathcal {E}_{\ast }(n))$
on the graded vector space
$\mathrm {gr}(\mathcal {E}_{\ast }(n))$
on the graded vector space
![]() $B_d(n)$
.
$B_d(n)$
.
We also define a
![]() $\Bbbk $
-linear map
$\Bbbk $
-linear map
which is an analogue of the contraction map for a vector space and its dual vector space (see Section 5). By using the map c, we obtain
![]() $\Bbbk $
-linear maps
$\Bbbk $
-linear maps
which form an action of the graded Lie algebra
![]() $\bigoplus _{r\geq 1}T_r(n)$
on the graded vector space
$\bigoplus _{r\geq 1}T_r(n)$
on the graded vector space
![]() $B_d(n)$
.
$B_d(n)$
.
Via the isomorphisms (1.1), these two actions of the derivation Lie algebra
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
![]() $B_d(n)$
coincide up to sign. (See Theorem 6.1.)
$B_d(n)$
coincide up to sign. (See Theorem 6.1.)
By using the linear map c for computation, we obtain the surjectivity of the bracket map.
Proposition 1.2 see Proposition 7.8
For
![]() $n\geq 2d-k$
, the bracket map
$n\geq 2d-k$
, the bracket map
is surjective.
1.3 The
 $\operatorname {GL}(n;\mathbb {Z})$
-module structure of
$\operatorname {GL}(n;\mathbb {Z})$
-module structure of
 $B_d(n)$
$B_d(n)$
The
![]() $\operatorname {GL}(n;\mathbb {Z})$
-action on
$\operatorname {GL}(n;\mathbb {Z})$
-action on
![]() $B_d(n)$
that is induced by the
$B_d(n)$
that is induced by the
![]() $\operatorname {Aut}(F_n)$
-action on
$\operatorname {Aut}(F_n)$
-action on
![]() $A_d(n)$
naturally extends to a polynomial
$A_d(n)$
naturally extends to a polynomial
![]() $\operatorname {GL}(V_n)$
-action on
$\operatorname {GL}(V_n)$
-action on
![]() $B_d(n)$
[Reference Katada16]. Therefore, the
$B_d(n)$
[Reference Katada16]. Therefore, the
![]() $\operatorname {GL}(V_n)$
-module
$\operatorname {GL}(V_n)$
-module
![]() $B_d(n)$
can be decomposed into the direct sum of images of the Schur functors. In general, however, it remains open to obtain an irreducible decomposition of
$B_d(n)$
can be decomposed into the direct sum of images of the Schur functors. In general, however, it remains open to obtain an irreducible decomposition of
![]() $B_d(n)$
as
$B_d(n)$
as
![]() $\operatorname {GL}(V_n)$
-modules. We can reduce this problem to the connected parts
$\operatorname {GL}(V_n)$
-modules. We can reduce this problem to the connected parts
![]() $B_{d,k}^c(n)\subset B_{d,k}(n)$
(see Theorem 7.2).
$B_{d,k}^c(n)\subset B_{d,k}(n)$
(see Theorem 7.2).
For a partition
![]() $\lambda \vdash N$
, let
$\lambda \vdash N$
, let
![]() $V_{\lambda }$
denote the image of
$V_{\lambda }$
denote the image of
![]() $V_n$
under the Schur functor
$V_n$
under the Schur functor
![]() $\mathbb {S}_{\lambda }$
. By using the results by Bar-Natan [Reference Bar-Natan4], we have isomorphisms of
$\mathbb {S}_{\lambda }$
. By using the results by Bar-Natan [Reference Bar-Natan4], we have isomorphisms of
![]() $\operatorname {GL}(V_n)$
-modules
$\operatorname {GL}(V_n)$
-modules
where
 $$ \begin{gather*} \begin{aligned} B_{3,0}(n)&\cong V_{(6)}\oplus V_{(4,2)}\oplus V_{(2^3)},\\ B_{3,1}(n)&\cong V_{(3,1^2)}\oplus V_{(2,1^3)},\\ B_{3,2}(n)&\cong V_{(4)}\oplus V_{(3,1)}\oplus (V_{(2^2)})^{\oplus 2},\\ B_{3,3}(n)&=B^c_{3,3}\cong V_{(1^3)},\\ B_{3,4}(n)&=B^c_{3,4}\cong V_{(2)} \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} B_{3,0}(n)&\cong V_{(6)}\oplus V_{(4,2)}\oplus V_{(2^3)},\\ B_{3,1}(n)&\cong V_{(3,1^2)}\oplus V_{(2,1^3)},\\ B_{3,2}(n)&\cong V_{(4)}\oplus V_{(3,1)}\oplus (V_{(2^2)})^{\oplus 2},\\ B_{3,3}(n)&=B^c_{3,3}\cong V_{(1^3)},\\ B_{3,4}(n)&=B^c_{3,4}\cong V_{(2)} \end{aligned} \end{gather*} $$
(see Proposition 7.6 for the cases
![]() $d=3,4,5$
).
$d=3,4,5$
).
In general degrees, we obtain irreducible decompositions of
![]() $B_{d,k}(n)$
as
$B_{d,k}(n)$
as
![]() $\operatorname {GL}(V_n)$
-modules for
$\operatorname {GL}(V_n)$
-modules for
![]() $k=0,1$
.
$k=0,1$
.
Proposition 1.3 see Proposition 7.7
For any
![]() $d\geq 1$
, we have
$d\geq 1$
, we have
where
![]() $2\lambda =(2\lambda _1,\cdots ,2\lambda _r)\vdash 2d$
for
$2\lambda =(2\lambda _1,\cdots ,2\lambda _r)\vdash 2d$
for
![]() $\lambda =(\lambda _1,\cdots ,\lambda _r)\vdash d$
. For any
$\lambda =(\lambda _1,\cdots ,\lambda _r)\vdash d$
. For any
![]() $d\geq 2$
, we have
$d\geq 2$
, we have
1.4 The
 $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
 $A_d(n)$
$A_d(n)$
We consider the
![]() $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
![]() $A_d(n)$
and give an indecomposable decomposition of
$A_d(n)$
and give an indecomposable decomposition of
![]() $A_d(n)$
. We have
$A_d(n)$
. We have
and we studied the cases where
![]() $d=1, 2$
in [Reference Katada16]. Thus, we mainly consider the cases where
$d=1, 2$
in [Reference Katada16]. Thus, we mainly consider the cases where
![]() $d\geq 3,n\geq 1$
.
$d\geq 3,n\geq 1$
.
For
![]() $X\in A_d(2d)$
, let
$X\in A_d(2d)$
, let
denote the subfunctor of
![]() $A_d$
generated by X. That is, for any
$A_d$
generated by X. That is, for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $A_d X(n)$
is the
$A_d X(n)$
is the
![]() $\operatorname {Aut}(F_n)$
-submodule of
$\operatorname {Aut}(F_n)$
-submodule of
![]() $A_d(n)$
defined by
$A_d(n)$
defined by
Set

Then, we have the following direct decomposition of
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Aut}(F_n)$
-modules, which is indecomposable for
$\operatorname {Aut}(F_n)$
-modules, which is indecomposable for
![]() $n\geq 2d$
.
$n\geq 2d$
.
Theorem 1.4 see Theorems 8.2, 8.9
We have
![]() $A_d(n)=A_d P(n)\oplus A_d Q(n)$
for any
$A_d(n)=A_d P(n)\oplus A_d Q(n)$
for any
![]() $d,n\geq 1$
. This direct decomposition is indecomposable for
$d,n\geq 1$
. This direct decomposition is indecomposable for
![]() $n\geq 2d$
.
$n\geq 2d$
.
In degree
![]() $1$
, we have
$1$
, we have
![]() $A_1 Q(n)=0$
and
$A_1 Q(n)=0$
and
![]() $A_1(n)\cong \operatorname {Sym}^2(V_n)$
is simple for
$A_1(n)\cong \operatorname {Sym}^2(V_n)$
is simple for
![]() $n\geq 1$
. In [Reference Katada16], we obtained that the direct decomposition of
$n\geq 1$
. In [Reference Katada16], we obtained that the direct decomposition of
![]() $A_2(n)$
is indecomposable for
$A_2(n)$
is indecomposable for
![]() $n\geq 3$
(see Theorem 6.9 of [Reference Katada16]). We improve Theorem 1.4 for
$n\geq 3$
(see Theorem 6.9 of [Reference Katada16]). We improve Theorem 1.4 for
![]() $d=3,4$
(see Theorems 8.12 and 8.17).
$d=3,4$
(see Theorems 8.12 and 8.17).
In general degree d, we obtain the radical of
![]() $A_{d,k}(n)$
for any
$A_{d,k}(n)$
for any
![]() $k\geq 0$
if
$k\geq 0$
if
![]() $n\geq 2d$
.
$n\geq 2d$
.
Theorem 1.5 see Theorem 8.6
Let
![]() $n\geq 2d$
. The filtration of
$n\geq 2d$
. The filtration of
![]() $A_d(n)$
by the number of trivalent vertices coincides with the radical filtration of
$A_d(n)$
by the number of trivalent vertices coincides with the radical filtration of
![]() $A_d(n)$
.
$A_d(n)$
.
In degree
![]() $3$
, we obtain the socle of
$3$
, we obtain the socle of
![]() $A_3(n)$
as well (see Proposition 8.15).
$A_3(n)$
as well (see Proposition 8.15).
1.5 Direct decomposition of the functor
 $A_d$
$A_d$
Lastly, we give an indecomposable decomposition of the functor
![]() $A_d$
.
$A_d$
.
By Theorem 1.4, we obtain an indecomposable decomposition of the functor
![]() $A_d$
.
$A_d$
.
Theorem 1.6 see Theorem 10.1
We have an indecomposable decomposition
in the functor category
![]() $\mathbf {fVect}^{\mathbf {F}^{\mathrm {op}}}$
.
$\mathbf {fVect}^{\mathbf {F}^{\mathrm {op}}}$
.
In degree
![]() $1$
, we have
$1$
, we have
![]() $A_1 Q=0$
and
$A_1 Q=0$
and
![]() $A_1=A_1 P$
. In [Reference Katada16], we obtained the direct decomposition (1.2) of the functor
$A_1=A_1 P$
. In [Reference Katada16], we obtained the direct decomposition (1.2) of the functor
![]() $A_2$
and proved that equation (1.2) is indecomposable (see Proposition 6.5 and Theorem 6.14 of [Reference Katada16]).
$A_2$
and proved that equation (1.2) is indecomposable (see Proposition 6.5 and Theorem 6.14 of [Reference Katada16]).
1.6 Organization of the paper
In Section 2, we recall the category
![]() $\mathbf {A}$
of Jacobi diagrams in handlebodies, N-series and graded Lie algebras, contents of the previous paper [Reference Katada16], Hopf algebras and Lie algebras in a linear symmetric strict monoidal category. In Section 3, we construct the Andreadakis filtration and the Johnson homomorphism of
$\mathbf {A}$
of Jacobi diagrams in handlebodies, N-series and graded Lie algebras, contents of the previous paper [Reference Katada16], Hopf algebras and Lie algebras in a linear symmetric strict monoidal category. In Section 3, we construct the Andreadakis filtration and the Johnson homomorphism of
![]() $\operatorname {End}(F_n)$
. In Section 4, we construct an action of the derivation Lie algebra
$\operatorname {End}(F_n)$
. In Section 4, we construct an action of the derivation Lie algebra
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
![]() $B_d(n)$
, which is defined by the bracket map. In preparation for the definition of the bracket map, we construct an extended category
$B_d(n)$
, which is defined by the bracket map. In preparation for the definition of the bracket map, we construct an extended category
![]() $\mathbf {A}^{L}$
of the category
$\mathbf {A}^{L}$
of the category
![]() $\mathbf {A}$
, which includes a Lie algebra structure. In Section 5, we define a contraction map, which forms another action of
$\mathbf {A}$
, which includes a Lie algebra structure. In Section 5, we define a contraction map, which forms another action of
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
![]() $B_d(n)$
. In Section 6, we prove that two actions of
$B_d(n)$
. In Section 6, we prove that two actions of
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
![]() $B_d(n)$
defined in Sections 4 and 5 coincide up to sign. In Section 7, we compute the
$B_d(n)$
defined in Sections 4 and 5 coincide up to sign. In Section 7, we compute the
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module structure of
$\operatorname {GL}(n;\mathbb {Z})$
-module structure of
![]() $B_d(n)$
. In Section 8, we study the
$B_d(n)$
. In Section 8, we study the
![]() $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
![]() $A_d(n)$
by using the
$A_d(n)$
by using the
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module structure of
$\operatorname {GL}(n;\mathbb {Z})$
-module structure of
![]() $B_d(n)$
and the action of
$B_d(n)$
and the action of
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on
![]() $B_d(n)$
. In Section 10, we give an indecomposable decomposition of the functor
$B_d(n)$
. In Section 10, we give an indecomposable decomposition of the functor
![]() $A_d$
. In Appendix A, we study an expected presentation of the category
$A_d$
. In Appendix A, we study an expected presentation of the category
![]() $\mathbf {A}^{L}$
.
$\mathbf {A}^{L}$
.
2 Preliminaries
In this section, we recall the contents of the previous paper [Reference Katada16] and definitions of the category
![]() $\mathbf {A}$
of Jacobi diagrams in handlebodies, Hopf algebras and Lie algebras in a symmetric strict monoidal category and an action of an N-series on a filtered vector space and that of a graded Lie algebra on a graded vector space.
$\mathbf {A}$
of Jacobi diagrams in handlebodies, Hopf algebras and Lie algebras in a symmetric strict monoidal category and an action of an N-series on a filtered vector space and that of a graded Lie algebra on a graded vector space.
In what follows, we work over a fixed field
![]() $\Bbbk $
of characteristic
$\Bbbk $
of characteristic
![]() $0$
. For a vector space V and an abelian group G, we just write
$0$
. For a vector space V and an abelian group G, we just write
![]() $V\otimes G$
instead of
$V\otimes G$
instead of
![]() $V\otimes _{\mathbb {Z}} G$
. For vector spaces V and W, we also write
$V\otimes _{\mathbb {Z}} G$
. For vector spaces V and W, we also write
![]() $V\otimes W$
instead of
$V\otimes W$
instead of
![]() $V\otimes _{\Bbbk } W$
.
$V\otimes _{\Bbbk } W$
.
For
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $[n]:=\{1,\cdots ,n\}$
.
$[n]:=\{1,\cdots ,n\}$
.
2.1 The category
 $\mathbf {A}$
of Jacobi diagrams in handlebodies
$\mathbf {A}$
of Jacobi diagrams in handlebodies
Here, we briefly review the category
![]() $\mathbf {A}$
of Jacobi diagrams in handlebodies defined in [Reference Habiro and Massuyeau11]. We use the same notations as in [Reference Katada16].
$\mathbf {A}$
of Jacobi diagrams in handlebodies defined in [Reference Habiro and Massuyeau11]. We use the same notations as in [Reference Katada16].
For
![]() $n\geq 0$
, let
$n\geq 0$
, let
 be the oriented
be the oriented
![]() $1$
-manifold consisting of n arc components.
$1$
-manifold consisting of n arc components.
Let
![]() $I=[-1,1]$
. For
$I=[-1,1]$
. For
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $U_n \subset \mathbb {R}^3$
denote the handlebody of genus n that is obtained from the cube
$U_n \subset \mathbb {R}^3$
denote the handlebody of genus n that is obtained from the cube
![]() $I^3$
by attaching n handles on the top square
$I^3$
by attaching n handles on the top square
![]() $I^2 \times \{1\}$
as depicted in Figure 1. We call
$I^2 \times \{1\}$
as depicted in Figure 1. We call
![]() $l := I \times \{0\} \times \{-1\}$
the bottom line of
$l := I \times \{0\} \times \{-1\}$
the bottom line of
![]() $U_n$
and
$U_n$
and
![]() $l':= I\times \{0\} \times \{1\}$
the upper line of
$l':= I\times \{0\} \times \{1\}$
the upper line of
![]() $U_n$
. We call
$U_n$
. We call
![]() $S := I^2 \times \{-1\}$
the bottom square of
$S := I^2 \times \{-1\}$
the bottom square of
![]() $U_n$
.
$U_n$
.

Figure 1 The handlebody
![]() $U_n$
.
$U_n$
.
For
![]() $i\in [n]$
, let
$i\in [n]$
, let
![]() $x_i$
be a loop which goes through only the i-th handle of the handlebody
$x_i$
be a loop which goes through only the i-th handle of the handlebody
![]() $U_n$
just once, and let
$U_n$
just once, and let
![]() $x_i$
denote its homotopy class as well. In what follows, for loops
$x_i$
denote its homotopy class as well. In what follows, for loops
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
with base points on l, let
$\gamma _2$
with base points on l, let
![]() $\gamma _2\gamma _1$
denote the loop that goes through
$\gamma _2\gamma _1$
denote the loop that goes through
![]() $\gamma _1$
first and then goes through
$\gamma _1$
first and then goes through
![]() $\gamma _2$
. That is, we write a product of elements of the fundamental group of
$\gamma _2$
. That is, we write a product of elements of the fundamental group of
![]() $U_n$
in the opposite order to the usual one. Let
$U_n$
in the opposite order to the usual one. Let
![]() $H=H_1(U_n;\mathbb {Z})$
, and let
$H=H_1(U_n;\mathbb {Z})$
, and let
![]() $\bar {x}_i\in H$
be the homology class of
$\bar {x}_i\in H$
be the homology class of
![]() $x_i$
. We have
$x_i$
. We have
![]() $H=\bigoplus _{i=1}^n \mathbb {Z}\bar {x}_i$
and
$H=\bigoplus _{i=1}^n \mathbb {Z}\bar {x}_i$
and
![]() $\pi _1(U_n)=\langle x_1,\cdots ,x_n\rangle $
. Let
$\pi _1(U_n)=\langle x_1,\cdots ,x_n\rangle $
. Let
and let
![]() $\{v_1,\cdots ,v_n\}$
be the dual basis of
$\{v_1,\cdots ,v_n\}$
be the dual basis of
![]() $\{\bar {x}_1,\cdots ,\bar {x}_n\}$
.
$\{\bar {x}_1,\cdots ,\bar {x}_n\}$
.
The objects in
![]() $\mathbf {A}$
are nonnegative integers.
$\mathbf {A}$
are nonnegative integers.
For
![]() $m,n\geq 0$
, the hom-set
$m,n\geq 0$
, the hom-set
![]() $\mathbf {A}(m,n)$
is the
$\mathbf {A}(m,n)$
is the
![]() $\Bbbk $
-vector space spanned by
$\Bbbk $
-vector space spanned by
![]() $(m,n)$
-Jacobi diagrams modulo the STU relation. An
$(m,n)$
-Jacobi diagrams modulo the STU relation. An
![]() $(m,n)$
-Jacobi diagram is a Jacobi diagram on
$(m,n)$
-Jacobi diagram is a Jacobi diagram on
![]() $X_n$
mapped into
$X_n$
mapped into
![]() $U_m$
in such a way that the endpoints of
$U_m$
in such a way that the endpoints of
![]() $X_n$
are uniformly distributed on the bottom line l of
$X_n$
are uniformly distributed on the bottom line l of
![]() $U_m$
(see [Reference Habiro and Massuyeau11, Reference Katada16] for further details). We usually depict
$U_m$
(see [Reference Habiro and Massuyeau11, Reference Katada16] for further details). We usually depict
![]() $(m,n)$
-Jacobi diagrams by drawing their images under the orthogonal projection of
$(m,n)$
-Jacobi diagrams by drawing their images under the orthogonal projection of
![]() $\mathbb {R}^3$
onto
$\mathbb {R}^3$
onto
![]() $\mathbb {R}\times \{0\}\times \mathbb {R}$
.
$\mathbb {R}\times \{0\}\times \mathbb {R}$
.
The degree of an
![]() $(m,n)$
-Jacobi diagram is the degree of its Jacobi diagram. Let
$(m,n)$
-Jacobi diagram is the degree of its Jacobi diagram. Let
![]() $\mathbf {A}_d(m,n)\subset \mathbf {A}(m,n)$
be the subspace spanned by
$\mathbf {A}_d(m,n)\subset \mathbf {A}(m,n)$
be the subspace spanned by
![]() $(m,n)$
-Jacobi diagrams of degree d. We have
$(m,n)$
-Jacobi diagrams of degree d. We have
![]() $\mathbf {A}(m,n)=\bigoplus _{d\geq 0} \mathbf {A}_d(m,n)$
.
$\mathbf {A}(m,n)=\bigoplus _{d\geq 0} \mathbf {A}_d(m,n)$
.
The category
![]() $\mathbf {A}$
has a structure of a linear symmetric strict monoidal category. The tensor product on objects is addition. The monoidal unit is
$\mathbf {A}$
has a structure of a linear symmetric strict monoidal category. The tensor product on objects is addition. The monoidal unit is
![]() $0$
. The tensor product on morphisms is juxtaposition followed by horizontal rescaling and relabelling of indices. The symmetry is determined by
$0$
. The tensor product on morphisms is juxtaposition followed by horizontal rescaling and relabelling of indices. The symmetry is determined by

2.2 N-series and graded Lie algebras
Here, we briefly review the definition of an action of an N-series on a filtered vector space and the induced action of the graded Lie algebra on the graded vector space (see [Reference Katada16] for details).
An N-series
![]() $K_{\ast }=(K_n)_{n\geq 1}$
of a group K is a descending series
$K_{\ast }=(K_n)_{n\geq 1}$
of a group K is a descending series
such that
![]() $[K_n,K_m]\subset K_{n+m}$
for all
$[K_n,K_m]\subset K_{n+m}$
for all
![]() $n,m\geq 1$
.
$n,m\geq 1$
.
A morphism
![]() $f: G_{\ast }\rightarrow K_{\ast }$
between N-series is a group homomorphism
$f: G_{\ast }\rightarrow K_{\ast }$
between N-series is a group homomorphism
![]() $f: G_1 \rightarrow K_1$
such that we have
$f: G_1 \rightarrow K_1$
such that we have
![]() $f(G_n)\subset K_n$
for all
$f(G_n)\subset K_n$
for all
![]() $n\geq 1.$
$n\geq 1.$
For a filtered vector space
![]() $W_{\ast }$
, set
$W_{\ast }$
, set
where
![]() $[\phi ,w]:=\phi (w)-w$
for
$[\phi ,w]:=\phi (w)-w$
for
![]() $w\in W_k$
. We can easily check that
$w\in W_k$
. We can easily check that
![]() $\operatorname {Aut}_{\ast }(W_{\ast }):=(\operatorname {Aut}_n(W_{\ast }))_{n\geq 1}$
is an N-series.
$\operatorname {Aut}_{\ast }(W_{\ast }):=(\operatorname {Aut}_n(W_{\ast }))_{n\geq 1}$
is an N-series.
Definition 2.1. (Action of N-series on filtered vector spaces) Let
![]() $K_{\ast }$
be an N-series and
$K_{\ast }$
be an N-series and
![]() $W_{\ast }$
be a filtered vector space. An action of
$W_{\ast }$
be a filtered vector space. An action of
![]() $K_{\ast }$
on
$K_{\ast }$
on
![]() $W_{\ast }$
is a morphism
$W_{\ast }$
is a morphism
![]() $f:K_{\ast }\rightarrow \operatorname {Aut}_{\ast }(W_{\ast })$
between N-series.
$f:K_{\ast }\rightarrow \operatorname {Aut}_{\ast }(W_{\ast })$
between N-series.
For an N-series
![]() $K_{\ast }$
, we have a graded Lie algebra
$K_{\ast }$
, we have a graded Lie algebra
![]() $\mathrm {gr}(K_{\ast })=\bigoplus _{n\geq 1} K_n/K_{n+1}$
, where the Lie bracket is defined by the commutator.
$\mathrm {gr}(K_{\ast })=\bigoplus _{n\geq 1} K_n/K_{n+1}$
, where the Lie bracket is defined by the commutator.
For a graded vector space
![]() $W=\bigoplus _{k\geq 0}W_k$
, set
$W=\bigoplus _{k\geq 0}W_k$
, set
We can check that
![]() $\operatorname {End}_{+}(W)=\bigoplus _{n\geq 1}\operatorname {End}_n(W)$
is a graded Lie algebra, where the Lie bracket is defined by
$\operatorname {End}_{+}(W)=\bigoplus _{n\geq 1}\operatorname {End}_n(W)$
is a graded Lie algebra, where the Lie bracket is defined by
Definition 2.2. (Action of graded Lie algebras on graded vector spaces) Let
![]() $L_{+}=\bigoplus _{n\geq 1}L_n$
be a graded Lie algebra and
$L_{+}=\bigoplus _{n\geq 1}L_n$
be a graded Lie algebra and
![]() $W=\bigoplus _{k\geq 0}W_k$
be a graded vector space. An action of
$W=\bigoplus _{k\geq 0}W_k$
be a graded vector space. An action of
![]() $L_{+}$
on W is a morphism
$L_{+}$
on W is a morphism
![]() $f:L_{+}\rightarrow \operatorname {End}_{+}(W)$
between graded Lie algebras.
$f:L_{+}\rightarrow \operatorname {End}_{+}(W)$
between graded Lie algebras.
Proposition 2.3. An action of an N-series
![]() $K_{\ast }$
on a filtered vector space
$K_{\ast }$
on a filtered vector space
![]() $W_{\ast }$
induces an action of the graded Lie algebra
$W_{\ast }$
induces an action of the graded Lie algebra
![]() $\mathrm {gr}(K_{\ast })$
on the graded vector space
$\mathrm {gr}(K_{\ast })$
on the graded vector space
![]() $\mathrm {gr}(W_{\ast })$
, which is a morphism
$\mathrm {gr}(W_{\ast })$
, which is a morphism
defined by
![]() $\rho _{+}(gK_{n+1})([v]_{W_{k+1}})=[[g,v]]_{W_{k+n+1}}$
for
$\rho _{+}(gK_{n+1})([v]_{W_{k+1}})=[[g,v]]_{W_{k+n+1}}$
for
![]() $gK_{n+1}\in \operatorname {gr}^n(K_{\ast })$
,
$gK_{n+1}\in \operatorname {gr}^n(K_{\ast })$
,
![]() $[v]_{W_{k+1}}\in \operatorname {gr}^k(W_{\ast })$
.
$[v]_{W_{k+1}}\in \operatorname {gr}^k(W_{\ast })$
.
The proof can be seen in Proposition 5.14 of [Reference Katada16].
2.3 Contents of the previous paper
Here, we briefly review the notations and contents of the previous paper [Reference Katada16]. Let
![]() $\operatorname {Aut}(F_n)$
denote the automorphism group of the free group
$\operatorname {Aut}(F_n)$
denote the automorphism group of the free group
![]() $F_n$
of rank n and
$F_n$
of rank n and
![]() $\operatorname {GL}(n;\mathbb {Z})$
the general linear group of degree n. Let
$\operatorname {GL}(n;\mathbb {Z})$
the general linear group of degree n. Let
![]() $\operatorname {IA}(n)$
denote the IA-automorphism group of
$\operatorname {IA}(n)$
denote the IA-automorphism group of
![]() $F_n$
, that is the kernel of the canonical surjection
$F_n$
, that is the kernel of the canonical surjection
Let
![]() $\Gamma _{\ast }(\operatorname {IA}(n))=(\Gamma _{r}(\operatorname {IA}(n)))_{r\geq 1}$
denote the lower central series of
$\Gamma _{\ast }(\operatorname {IA}(n))=(\Gamma _{r}(\operatorname {IA}(n)))_{r\geq 1}$
denote the lower central series of
![]() $\operatorname {IA}(n)$
, and
$\operatorname {IA}(n)$
, and
![]() $\mathrm {gr}(\operatorname {IA}(n))=\bigoplus _{r\geq 1}\operatorname {gr}^r(\operatorname {IA}(n))$
the associated graded Lie algebra, where
$\mathrm {gr}(\operatorname {IA}(n))=\bigoplus _{r\geq 1}\operatorname {gr}^r(\operatorname {IA}(n))$
the associated graded Lie algebra, where
![]() $\operatorname {gr}^r(\operatorname {IA}(n))=\Gamma _{r}(\operatorname {IA}(n))/\Gamma _{r+1}(\operatorname {IA}(n))$
.
$\operatorname {gr}^r(\operatorname {IA}(n))=\Gamma _{r}(\operatorname {IA}(n))/\Gamma _{r+1}(\operatorname {IA}(n))$
.
Let
![]() $A_d(n)=\mathbf {A}_d(0,n)$
denote the
$A_d(n)=\mathbf {A}_d(0,n)$
denote the
![]() $\Bbbk $
-vector space of Jacobi diagrams of degree d on
$\Bbbk $
-vector space of Jacobi diagrams of degree d on
![]() $X_n$
. We consider a filtration for
$X_n$
. We consider a filtration for
![]() $A_d(n)$
$A_d(n)$
such that
![]() $A_{d,k}(n)\subset A_d(n)$
is the subspace spanned by Jacobi diagrams with at least k trivalent vertices. Hence,
$A_{d,k}(n)\subset A_d(n)$
is the subspace spanned by Jacobi diagrams with at least k trivalent vertices. Hence,
![]() $A_d(n)$
is a filtered vector space.
$A_d(n)$
is a filtered vector space.
Let
![]() $\mathbf {F}$
denote the category of finitely generated free groups and
$\mathbf {F}$
denote the category of finitely generated free groups and
![]() $\mathbf {fVect}$
the category of filtered vector spaces over
$\mathbf {fVect}$
the category of filtered vector spaces over
![]() $\Bbbk $
.
$\Bbbk $
.
We have a
![]() $\Bbbk $
-vector space isomorphism
$\Bbbk $
-vector space isomorphism
from the hom-set
![]() $\Bbbk \mathbf {F}^{\mathrm {op}}(m,n)$
of the
$\Bbbk \mathbf {F}^{\mathrm {op}}(m,n)$
of the
![]() $\Bbbk $
-linearization of the opposite category of
$\Bbbk $
-linearization of the opposite category of
![]() $\mathbf {F}$
to the degree
$\mathbf {F}$
to the degree
![]() $0$
part of the hom-set
$0$
part of the hom-set
![]() $\mathbf {A}(m,n)$
[Reference Habiro and Massuyeau11]. We define a functor
$\mathbf {A}(m,n)$
[Reference Habiro and Massuyeau11]. We define a functor
by
![]() $A_d(n)=\mathbf {A}_d(0,n)$
for an object
$A_d(n)=\mathbf {A}_d(0,n)$
for an object
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $A_d(f)=Z(f)_{\ast }$
for a morphism
$A_d(f)=Z(f)_{\ast }$
for a morphism
![]() $f\in \mathbf {F}^{\mathrm {op}}(m,n)$
, where
$f\in \mathbf {F}^{\mathrm {op}}(m,n)$
, where
![]() $Z(f)_{\ast }$
denotes the post-composition with
$Z(f)_{\ast }$
denotes the post-composition with
![]() $Z(f)$
. The functor
$Z(f)$
. The functor
![]() $A_d$
is a polynomial functor of degree
$A_d$
is a polynomial functor of degree
![]() $2d$
in the sense of [Reference Hartl, Pirashvili and Vespa12, Reference Powell and Vespa20] (see Remark 3.1 of [Reference Katada16]). By restricting this functor to the automorphism group, we obtain an action of the opposite group
$2d$
in the sense of [Reference Hartl, Pirashvili and Vespa12, Reference Powell and Vespa20] (see Remark 3.1 of [Reference Katada16]). By restricting this functor to the automorphism group, we obtain an action of the opposite group
![]() $\operatorname {Aut}(F_n)^{\mathrm {op}}$
of
$\operatorname {Aut}(F_n)^{\mathrm {op}}$
of
![]() $\operatorname {Aut}(F_n)$
on
$\operatorname {Aut}(F_n)$
on
![]() $A_d(n)$
for each
$A_d(n)$
for each
![]() $n\geq 0$
. We consider this action as a right action of
$n\geq 0$
. We consider this action as a right action of
![]() $\operatorname {Aut}(F_n)$
on
$\operatorname {Aut}(F_n)$
on
![]() $A_d(n)$
. The
$A_d(n)$
. The
![]() $\operatorname {Aut}(F_n)$
-action on
$\operatorname {Aut}(F_n)$
-action on
![]() $A_d(n)$
induces an action on
$A_d(n)$
induces an action on
![]() $A_d(n)$
of the outer automorphism group
$A_d(n)$
of the outer automorphism group
![]() $\operatorname {Out}(F_n)$
of
$\operatorname {Out}(F_n)$
of
![]() $F_n$
(see Theorem 5.1 in [Reference Katada16]).
$F_n$
(see Theorem 5.1 in [Reference Katada16]).
On the other hand, the associated graded vector space
![]() $\mathrm {gr}(A_d(n))$
of
$\mathrm {gr}(A_d(n))$
of
![]() $A_d(n)$
is identified via the PBW map [Reference Bar-Natan2, Reference Bar-Natan3]
$A_d(n)$
is identified via the PBW map [Reference Bar-Natan2, Reference Bar-Natan3]
with the graded
![]() $\Bbbk $
-vector space
$\Bbbk $
-vector space
![]() $B_d(n)=\bigoplus _{k\geq 0}B_{d,k}(n)= \bigoplus _{k=0}^{2d-2}B_{d,k}(n)$
of
$B_d(n)=\bigoplus _{k\geq 0}B_{d,k}(n)= \bigoplus _{k=0}^{2d-2}B_{d,k}(n)$
of
![]() $V_n$
-colored open Jacobi diagrams of degree d, where the grading is determined by the number of trivalent vertices. Note that we have
$V_n$
-colored open Jacobi diagrams of degree d, where the grading is determined by the number of trivalent vertices. Note that we have
![]() $\theta _{d,n}=\bigoplus _{k}\theta _{d,n,k}$
, where
$\theta _{d,n}=\bigoplus _{k}\theta _{d,n,k}$
, where
Let
![]() $\mathbf {FAb}$
denote the category of finitely generated free abelian groups and
$\mathbf {FAb}$
denote the category of finitely generated free abelian groups and
![]() $\mathbf {gVect}$
the category of graded vector spaces over
$\mathbf {gVect}$
the category of graded vector spaces over
![]() $\Bbbk $
.
$\Bbbk $
.
We define a functor
by sending an object
![]() $n\in \mathbb {N}$
to the graded vector space
$n\in \mathbb {N}$
to the graded vector space
![]() $B_d(n)$
and a morphism
$B_d(n)$
and a morphism
![]() $f\in \mathbf {FAb}^{\mathrm {op}}(m,n)=\operatorname {Mat}(m,n;\mathbb {Z})$
to
$f\in \mathbf {FAb}^{\mathrm {op}}(m,n)=\operatorname {Mat}(m,n;\mathbb {Z})$
to
![]() $B_d(f)$
, which is a right action on each coloring, where we consider an element of
$B_d(f)$
, which is a right action on each coloring, where we consider an element of
![]() $V_n$
as a
$V_n$
as a
![]() $(1\times n)$
-matrix. By restricting this functor to the automorphism group, we obtain an action of the opposite group
$(1\times n)$
-matrix. By restricting this functor to the automorphism group, we obtain an action of the opposite group
![]() $\operatorname {GL}(n;\mathbb {Z})^{\mathrm {op}}$
of
$\operatorname {GL}(n;\mathbb {Z})^{\mathrm {op}}$
of
![]() $\operatorname {GL}(n;\mathbb {Z})$
on
$\operatorname {GL}(n;\mathbb {Z})$
on
![]() $B_d(n)$
for each
$B_d(n)$
for each
![]() $n\geq 0$
. We consider this action as a right action of
$n\geq 0$
. We consider this action as a right action of
![]() $\operatorname {GL}(n;\mathbb {Z})$
on
$\operatorname {GL}(n;\mathbb {Z})$
on
![]() $B_d(n)$
. Note that the
$B_d(n)$
. Note that the
![]() $\operatorname {GL}(n;\mathbb {Z})$
-action on
$\operatorname {GL}(n;\mathbb {Z})$
-action on
![]() $B_d(n)$
naturally extends to a
$B_d(n)$
naturally extends to a
![]() $\operatorname {GL}(V_n)$
-action on
$\operatorname {GL}(V_n)$
-action on
![]() $B_d(n)$
.
$B_d(n)$
.
Proposition 2.4 see Proposition 3.2 of [Reference Katada16]
For
![]() $d\geq 0$
, the PBW maps equation (2.1) give a natural isomorphism
$d\geq 0$
, the PBW maps equation (2.1) give a natural isomorphism
where
![]() $\mathrm {ab}^{\mathrm {op}}$
denotes the opposite functor of the abelianization functor and
$\mathrm {ab}^{\mathrm {op}}$
denotes the opposite functor of the abelianization functor and
![]() $\mathrm {gr}$
denote the functor that sends a filtered vector space to its associated graded vector space.
$\mathrm {gr}$
denote the functor that sends a filtered vector space to its associated graded vector space.
By this proposition, it turns out that the
![]() $\operatorname {Aut}(F_n)$
-action on
$\operatorname {Aut}(F_n)$
-action on
![]() $A_d(n)$
, which is an action of an extended N-series on a filtered vector space, induces two actions on
$A_d(n)$
, which is an action of an extended N-series on a filtered vector space, induces two actions on
![]() $B_d(n)$
, which form an action of an extended graded Lie algebra on a graded vector space (see Theorem 5.15 of [Reference Katada16] and [Reference Habiro and Massuyeau10] for extended N-series and extended graded Lie algebras). One of them is the
$B_d(n)$
, which form an action of an extended graded Lie algebra on a graded vector space (see Theorem 5.15 of [Reference Katada16] and [Reference Habiro and Massuyeau10] for extended N-series and extended graded Lie algebras). One of them is the
![]() $\operatorname {GL}(n;\mathbb {Z})$
-action, and the other of them is an action of the graded Lie algebra
$\operatorname {GL}(n;\mathbb {Z})$
-action, and the other of them is an action of the graded Lie algebra
![]() $\mathrm {gr}(\operatorname {IA}(n))$
on the graded vector space
$\mathrm {gr}(\operatorname {IA}(n))$
on the graded vector space
![]() $B_d(n)$
, which consists of
$B_d(n)$
, which consists of
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
$\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
for
![]() $k\geq 0, r\geq 1$
(see Proposition 5.10 and Theorem 5.15 of [Reference Katada16]). By using these two actions on
$k\geq 0, r\geq 1$
(see Proposition 5.10 and Theorem 5.15 of [Reference Katada16]). By using these two actions on
![]() $B_d(n)$
, we obtained an indecomposable decomposition of
$B_d(n)$
, we obtained an indecomposable decomposition of
![]() $A_2(n)$
as
$A_2(n)$
as
![]() $\operatorname {Aut}(F_n)$
-modules (see Theorem 6.9 of [Reference Katada16]).
$\operatorname {Aut}(F_n)$
-modules (see Theorem 6.9 of [Reference Katada16]).
2.4 Hopf algebra in a symmetric strict monoidal category
We review the definition of a Hopf algebra in a symmetric strict monoidal category. Let
![]() $\mathcal {C}=(\mathcal {C},\otimes ,I,P)$
be a symmetric strict monoidal category. A Hopf algebra in
$\mathcal {C}=(\mathcal {C},\otimes ,I,P)$
be a symmetric strict monoidal category. A Hopf algebra in
![]() $\mathcal {C}$
is an object H in
$\mathcal {C}$
is an object H in
![]() $\mathcal {C}$
equipped with morphisms
$\mathcal {C}$
equipped with morphisms
called the multiplication, unit, comultiplication, counit and antipode, respectively, satisfying
-
(1)
 $\mu (\mu \otimes \operatorname {id}_H)=\mu (\operatorname {id}_H \otimes \mu ),\quad \mu (\eta \otimes \operatorname {id}_H)=\operatorname {id}_H=\mu (\operatorname {id}_H\otimes \eta ),$
$\mu (\mu \otimes \operatorname {id}_H)=\mu (\operatorname {id}_H \otimes \mu ),\quad \mu (\eta \otimes \operatorname {id}_H)=\operatorname {id}_H=\mu (\operatorname {id}_H\otimes \eta ),$
-
(2)
 $(\Delta \otimes \operatorname {id}_H)\Delta =(\operatorname {id}_H\otimes \Delta )\Delta ,\quad (\epsilon \otimes \operatorname {id}_H)\Delta =\operatorname {id}_H=(\operatorname {id}_H\otimes \epsilon )\Delta ,$
$(\Delta \otimes \operatorname {id}_H)\Delta =(\operatorname {id}_H\otimes \Delta )\Delta ,\quad (\epsilon \otimes \operatorname {id}_H)\Delta =\operatorname {id}_H=(\operatorname {id}_H\otimes \epsilon )\Delta ,$
-
(3)
 $\epsilon \eta =\operatorname {id}_I, \quad \epsilon \mu =\epsilon \otimes \epsilon ,\quad \Delta \eta =\eta \otimes \eta ,$
$\epsilon \eta =\operatorname {id}_I, \quad \epsilon \mu =\epsilon \otimes \epsilon ,\quad \Delta \eta =\eta \otimes \eta ,$
-
(4)
 $\Delta \mu =(\mu \otimes \mu )(\operatorname {id}_H\otimes P_{H,H}\otimes \operatorname {id}_H)(\Delta \otimes \Delta ),$
$\Delta \mu =(\mu \otimes \mu )(\operatorname {id}_H\otimes P_{H,H}\otimes \operatorname {id}_H)(\Delta \otimes \Delta ),$
-
(5)
 $\mu (\operatorname {id}_H\otimes S)\Delta =\mu (S\otimes \operatorname {id}_H)\Delta =\eta \epsilon .$
$\mu (\operatorname {id}_H\otimes S)\Delta =\mu (S\otimes \operatorname {id}_H)\Delta =\eta \epsilon .$
A Hopf algebra H is said to be cocommutative if
![]() $P_{H,H}\Delta =\Delta .$
$P_{H,H}\Delta =\Delta .$
Define
![]() $\mu _n : H^{\otimes {n}} \otimes H^{\otimes {n}} \rightarrow H^{\otimes {n}}$
and
$\mu _n : H^{\otimes {n}} \otimes H^{\otimes {n}} \rightarrow H^{\otimes {n}}$
and
![]() $\Delta _m : H^{\otimes {m}} \rightarrow H^{\otimes {m}} \otimes H^{\otimes {m}}$
inductively by
$\Delta _m : H^{\otimes {m}} \rightarrow H^{\otimes {m}} \otimes H^{\otimes {m}}$
inductively by
for
![]() $n\geq 0$
and by
$n\geq 0$
and by
for
![]() $m\geq 0$
.
$m\geq 0$
.
For morphisms
![]() $f,\ f': H^{\otimes {m}} \rightarrow H^{\otimes {n}}$
,
$f,\ f': H^{\otimes {m}} \rightarrow H^{\otimes {n}}$
,
![]() $m,n\geq 0$
, the convolution
$m,n\geq 0$
, the convolution
![]() $f\ast f'$
of f and
$f\ast f'$
of f and
![]() $f'$
is defined by
$f'$
is defined by
The category
![]() $\mathbf {A}$
has a cocommutative Hopf algebra with the object
$\mathbf {A}$
has a cocommutative Hopf algebra with the object
![]() $1$
, where
$1$
, where

2.5 Lie algebra in a linear symmetric strict monoidal category
We review the definition of a Lie algebra in a linear symmetric strict monoidal category. Let
![]() $\mathcal {C}=(\mathcal {C},\otimes ,I,P)$
be a linear symmetric strict monoidal category. A Lie algebra in
$\mathcal {C}=(\mathcal {C},\otimes ,I,P)$
be a linear symmetric strict monoidal category. A Lie algebra in
![]() $\mathcal {C}$
is an object L in
$\mathcal {C}$
is an object L in
![]() $\mathcal {C}$
equipped with a morphism
$\mathcal {C}$
equipped with a morphism
satisfying
-
(1)
 $[\cdot ,\cdot ](\operatorname {id}_{L\otimes L}+P_{L,L})=0$
,
$[\cdot ,\cdot ](\operatorname {id}_{L\otimes L}+P_{L,L})=0$
, -
(2)
 $[\cdot ,\cdot ](\operatorname {id}_L\otimes [\cdot ,\cdot ])(\operatorname {id}_{L^{\otimes 3}}+\sigma +\sigma ^2)=0,$
where
$[\cdot ,\cdot ](\operatorname {id}_L\otimes [\cdot ,\cdot ])(\operatorname {id}_{L^{\otimes 3}}+\sigma +\sigma ^2)=0,$
where
 $\sigma =(1,2,3):L^{\otimes 3}\rightarrow L^{\otimes 3}$
.
$\sigma =(1,2,3):L^{\otimes 3}\rightarrow L^{\otimes 3}$
.
3 Andreadakis filtration
 $\mathcal {E}_{\ast }(n)$
of
$\mathcal {E}_{\ast }(n)$
of
 $\operatorname {End}(F_n)$
$\operatorname {End}(F_n)$
We briefly review the Andreadakis filtration and the Johnson homomorphism of
![]() $\operatorname {Aut}(F_n)$
. See [Reference Satoh22] for further details. Then we consider its extension to the endomorphism monoid
$\operatorname {Aut}(F_n)$
. See [Reference Satoh22] for further details. Then we consider its extension to the endomorphism monoid
![]() $\operatorname {End}(F_n)$
of
$\operatorname {End}(F_n)$
of
![]() $F_n$
.
$F_n$
.
3.1 Andreadakis filtration
 $\mathcal {A}_{\ast }(n)$
of
$\mathcal {A}_{\ast }(n)$
of
 $\operatorname {Aut}(F_n)$
$\operatorname {Aut}(F_n)$
In what follows, we consider the left action of
![]() $\operatorname {Aut}(F_n)$
on
$\operatorname {Aut}(F_n)$
on
![]() $F_n$
. Let
$F_n$
. Let
![]() $\Gamma _r:=\Gamma _r(F_n)$
denote the r-th term of the lower central series of the free group
$\Gamma _r:=\Gamma _r(F_n)$
denote the r-th term of the lower central series of the free group
![]() $F_n$
of rank n. Let
$F_n$
of rank n. Let
![]() $\mathcal {L}_r(n) :=\Gamma _r/\Gamma _{r+1}$
for
$\mathcal {L}_r(n) :=\Gamma _r/\Gamma _{r+1}$
for
![]() $r\geq 1$
. Note that
$r\geq 1$
. Note that
![]() $H=\mathcal {L}_1(n)$
and that
$H=\mathcal {L}_1(n)$
and that
![]() $\mathcal {L}_r(n)$
is the degree r part of the free Lie algebra
$\mathcal {L}_r(n)$
is the degree r part of the free Lie algebra
![]() $\mathcal {L}_{\ast }(n)$
on H.
$\mathcal {L}_{\ast }(n)$
on H.
For
![]() $r\geq 0$
, the left action of
$r\geq 0$
, the left action of
![]() $\operatorname {Aut}(F_n)$
on each nilpotent quotient
$\operatorname {Aut}(F_n)$
on each nilpotent quotient
![]() $F_n/\Gamma _{r+1}$
induces a group homomorphism
$F_n/\Gamma _{r+1}$
induces a group homomorphism
Set
Then we have a filtration, which is called the Andreadakis filtration of
![]() $\operatorname {Aut}(F_n)$
:
$\operatorname {Aut}(F_n)$
:
For
![]() $r\geq 1$
, the Johnson homomorphism
$r\geq 1$
, the Johnson homomorphism
is the injective homomorphism induced by the group homomorphism
defined by
3.2 The target group of the Johnson homomorphism
The target group
![]() $\operatorname {Hom}(H,\mathcal {L}_{r+1}(n))\cong H^{\ast }\otimes \mathcal {L}_{r+1}(n)$
of the Johnson homomorphism is identified with the degree r part
$\operatorname {Hom}(H,\mathcal {L}_{r+1}(n))\cong H^{\ast }\otimes \mathcal {L}_{r+1}(n)$
of the Johnson homomorphism is identified with the degree r part
![]() $\operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
of the derivation Lie algebra
$\operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
of the derivation Lie algebra
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
of the free Lie algebra
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
of the free Lie algebra
![]() $\mathcal {L}_{\ast }(n)$
and with the tree module
$\mathcal {L}_{\ast }(n)$
and with the tree module
![]() $T_r(n)$
via abelian group isomorphisms
$T_r(n)$
via abelian group isomorphisms
Here, we briefly review the derivation Lie algebra and the tree module. (See [Reference Satoh22] for details.)
A derivation f of
![]() $\mathcal {L}_{\ast }(n)$
is a
$\mathcal {L}_{\ast }(n)$
is a
![]() $\mathbb {Z}$
-linear map
$\mathbb {Z}$
-linear map
![]() $f:\mathcal {L}_{\ast }(n)\rightarrow \mathcal {L}_{\ast }(n)$
such that
$f:\mathcal {L}_{\ast }(n)\rightarrow \mathcal {L}_{\ast }(n)$
such that
![]() $f([a,b])=[f(a),b]+[a,f(b)]$
for any
$f([a,b])=[f(a),b]+[a,f(b)]$
for any
![]() $a,b\in \mathcal {L}_{\ast }(n)$
. The derivation Lie algebra
$a,b\in \mathcal {L}_{\ast }(n)$
. The derivation Lie algebra
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
of the Lie algebra
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
of the Lie algebra
![]() $\mathcal {L}_{\ast }(n)$
is the set of all derivations of
$\mathcal {L}_{\ast }(n)$
is the set of all derivations of
![]() $\mathcal {L}_{\ast }(n)$
. The degree r part
$\mathcal {L}_{\ast }(n)$
. The degree r part
![]() $\operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
of the derivation Lie algebra is defined to be
$\operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
of the derivation Lie algebra is defined to be
Then we have
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))=\bigoplus _{r\geq 0}\operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
and abelian group isomorphisms
$\operatorname {Der}(\mathcal {L}_{\ast }(n))=\bigoplus _{r\geq 0}\operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
and abelian group isomorphisms
We call a connected Jacobi diagram with no cycle a trivalent tree. For
![]() $r\geq 0$
, a trivalent tree is called a rooted trivalent tree of degree r if it has one univalent vertex (called the root) that is colored by an element of
$r\geq 0$
, a trivalent tree is called a rooted trivalent tree of degree r if it has one univalent vertex (called the root) that is colored by an element of
![]() $H^{\ast }$
and
$H^{\ast }$
and
![]() $r+1$
univalent vertices (called leaves) that are colored by elements of H. Let
$r+1$
univalent vertices (called leaves) that are colored by elements of H. Let
![]() $T_r(n)$
denote the
$T_r(n)$
denote the
![]() $\mathbb {Z}$
-module spanned by rooted trivalent trees of degree r modulo the AS, IHX and multilinearity relations. We have an abelian group isomorphism
$\mathbb {Z}$
-module spanned by rooted trivalent trees of degree r modulo the AS, IHX and multilinearity relations. We have an abelian group isomorphism
defined by

for
![]() $v_i\in H^{\ast }$
,
$v_i\in H^{\ast }$
,
![]() $[\bar {x}_{i_1},\cdots ,[\bar {x}_{i_r},\bar {x}_{i_{r+1}}]\cdots ]\in \mathcal {L}_{r+1}(n)$
.
$[\bar {x}_{i_1},\cdots ,[\bar {x}_{i_r},\bar {x}_{i_{r+1}}]\cdots ]\in \mathcal {L}_{r+1}(n)$
.
3.3 Andreadakis filtration
 $\mathcal {E}_{\ast }(n)$
of
$\mathcal {E}_{\ast }(n)$
of
 $\operatorname {End}(F_n)$
$\operatorname {End}(F_n)$
We extend the above construction to the endomorphism monoid
![]() $\operatorname {End}(F_n)$
of
$\operatorname {End}(F_n)$
of
![]() $F_n$
. For
$F_n$
. For
![]() $r\geq 0$
, consider the canonical map
$r\geq 0$
, consider the canonical map
and set
![]() $\mathcal {E}_r(n):=\ker (\rho _r)$
. Then we have a filtration of monoids
$\mathcal {E}_r(n):=\ker (\rho _r)$
. Then we have a filtration of monoids
and we call
![]() $\mathcal {E}_{\ast }(n)=(\mathcal {E}_{r}(n))_{r\geq 0}$
the Andreadakis filtration of
$\mathcal {E}_{\ast }(n)=(\mathcal {E}_{r}(n))_{r\geq 0}$
the Andreadakis filtration of
![]() $\operatorname {End}(F_n)$
.
$\operatorname {End}(F_n)$
.
For
![]() $f\in \operatorname {End}(F_n)$
and
$f\in \operatorname {End}(F_n)$
and
![]() $x,y\in F_n$
, set
$x,y\in F_n$
, set
and for a subset
![]() $T\subset F_n$
, set
$T\subset F_n$
, set
We can easily check the following lemma.
Lemma 3.1.
For subsets
![]() $S\subset \operatorname {End}(F_n)$
and
$S\subset \operatorname {End}(F_n)$
and
![]() $T\subset F_n$
, let
$T\subset F_n$
, let
![]() $[S,T]$
denote the subgroup of
$[S,T]$
denote the subgroup of
![]() $F_n$
generated by the elements
$F_n$
generated by the elements
![]() $[f,x]$
for
$[f,x]$
for
![]() $f\in S, x\in T$
.
$f\in S, x\in T$
.
Lemma 3.2. We have
for
![]() $r\geq 0, k\geq 1$
.
$r\geq 0, k\geq 1$
.
Proof. It is well known that
![]() $[\mathcal {A}_r(n),\Gamma _k]\subset \Gamma _{k+r}$
by Andreadakis [Reference Andreadakis1]. The same proof can be applied to
$[\mathcal {A}_r(n),\Gamma _k]\subset \Gamma _{k+r}$
by Andreadakis [Reference Andreadakis1]. The same proof can be applied to
![]() $\mathcal {E}_r(n)$
. We use induction on k. When
$\mathcal {E}_r(n)$
. We use induction on k. When
![]() $k=1$
, we have
$k=1$
, we have
![]() $[\mathcal {E}_r(n),F_n]\subset \Gamma _{r+1}$
by the definition of
$[\mathcal {E}_r(n),F_n]\subset \Gamma _{r+1}$
by the definition of
![]() $\mathcal {E}_r(n)$
. Suppose that
$\mathcal {E}_r(n)$
. Suppose that
![]() $[\mathcal {E}_r(n),\Gamma _{k-1}]\subset \Gamma _{k-1+r}$
. We will show that
$[\mathcal {E}_r(n),\Gamma _{k-1}]\subset \Gamma _{k-1+r}$
. We will show that
![]() $[\mathcal {E}_r(n),\Gamma _{k}]\subset \Gamma _{k+r}$
. Let
$[\mathcal {E}_r(n),\Gamma _{k}]\subset \Gamma _{k+r}$
. Let
![]() $f\in \mathcal {E}_r(n)$
. Recall that
$f\in \mathcal {E}_r(n)$
. Recall that
![]() $\Gamma _k$
is generated by the commutator
$\Gamma _k$
is generated by the commutator
![]() $[x,y]$
with
$[x,y]$
with
![]() $x\in \Gamma _{k-1},y\in F_n$
. We can check that for
$x\in \Gamma _{k-1},y\in F_n$
. We can check that for
![]() $x\in \Gamma _{k-1},y\in F_n$
, we have
$x\in \Gamma _{k-1},y\in F_n$
, we have
For
![]() $z,w\in \Gamma _k$
, we have
$z,w\in \Gamma _k$
, we have
and by letting
![]() $w=z^{-1}$
, we have
$w=z^{-1}$
, we have
Therefore, we have
![]() $[f,z]\in \Gamma _{k+r}$
for any
$[f,z]\in \Gamma _{k+r}$
for any
![]() $z\in \Gamma _k$
.
$z\in \Gamma _k$
.
Define a map
by
![]() $\sigma (f)=\tilde {f}$
for
$\sigma (f)=\tilde {f}$
for
![]() $f\in \operatorname {End}(F_n)$
, where
$f\in \operatorname {End}(F_n)$
, where
for
![]() $i\in [n]$
.
$i\in [n]$
.
Lemma 3.3. We have
Proof. We have equation (3.2) since for any
![]() $f\in \operatorname {End}(F_n)$
and
$f\in \operatorname {End}(F_n)$
and
![]() $i\in [n]$
, we have
$i\in [n]$
, we have
We have equation (3.3) since, for any
![]() $f\in \mathcal {E}_r(n)$
and
$f\in \mathcal {E}_r(n)$
and
![]() $i\in [n]$
, we have
$i\in [n]$
, we have
We prove equation (3.4). Let
![]() $f\in \mathcal {E}_r(n)$
. We have
$f\in \mathcal {E}_r(n)$
. We have
for any
![]() $i\in [n]$
. Thus, we have
$i\in [n]$
. Thus, we have
By equation (3.3), we have
![]() $\tilde {f}\in \mathcal {E}_r(n)$
, and by equations (3.2) and (3.5),
$\tilde {f}\in \mathcal {E}_r(n)$
, and by equations (3.2) and (3.5),
For
![]() $N\geq r\geq 0$
, we define an equivalence relation
$N\geq r\geq 0$
, we define an equivalence relation
![]() $\sim _{N}$
on the monoid
$\sim _{N}$
on the monoid
![]() $\mathcal {E}_r(n)$
by
$\mathcal {E}_r(n)$
by
for
![]() $f,g\in \mathcal {E}_r(n)$
. Thus, we have
$f,g\in \mathcal {E}_r(n)$
. Thus, we have
Lemma 3.4. Let
![]() $r\geq 1$
. For
$r\geq 1$
. For
![]() $f\in \mathcal {E}_r(n)$
, define
$f\in \mathcal {E}_r(n)$
, define
![]() $f^{R}_{N}$
and
$f^{R}_{N}$
and
![]() $f^{L}_{N}$
for
$f^{L}_{N}$
for
![]() $N\geq r+1$
inductively by
$N\geq r+1$
inductively by
 $$ \begin{align*}f^{R}_{N}= \begin{cases} \tilde{f} & (N=r+1)\\ f^{R}_{N-1}\widetilde{f f^{R}_{N-1}} & (N\geq r+2), \end{cases} \end{align*} $$
$$ \begin{align*}f^{R}_{N}= \begin{cases} \tilde{f} & (N=r+1)\\ f^{R}_{N-1}\widetilde{f f^{R}_{N-1}} & (N\geq r+2), \end{cases} \end{align*} $$
 $$ \begin{align*}f^{L}_{N}= \begin{cases} \tilde{f} & (N=r+1)\\ \widetilde{f^{L}_{N-1} f}f^{L}_{N-1} & (N\geq r+2). \end{cases} \end{align*} $$
$$ \begin{align*}f^{L}_{N}= \begin{cases} \tilde{f} & (N=r+1)\\ \widetilde{f^{L}_{N-1} f}f^{L}_{N-1} & (N\geq r+2). \end{cases} \end{align*} $$
Then we have
 $$ \begin{gather*} f^{R}_{N}\in \mathcal{E}_r(n),\quad f f^{R}_{N}\in \mathcal{E}_N(n),\quad f^{R}_{N}\sim_{N-1} f^{R}_{N-1},\\ f^{L}_{N}\in \mathcal{E}_r(n),\quad f^{L}_{N} f\in \mathcal{E}_N(n),\quad f^{L}_{N}\sim_{N-1} f^{L}_{N-1}. \end{gather*} $$
$$ \begin{gather*} f^{R}_{N}\in \mathcal{E}_r(n),\quad f f^{R}_{N}\in \mathcal{E}_N(n),\quad f^{R}_{N}\sim_{N-1} f^{R}_{N-1},\\ f^{L}_{N}\in \mathcal{E}_r(n),\quad f^{L}_{N} f\in \mathcal{E}_N(n),\quad f^{L}_{N}\sim_{N-1} f^{L}_{N-1}. \end{gather*} $$
Proof. We use induction on
![]() $N\geq r+1$
. When
$N\geq r+1$
. When
![]() $N=r+1$
, by Lemma 3.3, we have
$N=r+1$
, by Lemma 3.3, we have
![]() $\tilde {f}\in \mathcal {E}_r(n)$
and
$\tilde {f}\in \mathcal {E}_r(n)$
and
![]() $f \tilde {f}\in \mathcal {E}_{2r}(n)\subset \mathcal {E}_{r+1}(n)$
. Suppose that
$f \tilde {f}\in \mathcal {E}_{2r}(n)\subset \mathcal {E}_{r+1}(n)$
. Suppose that
![]() $f^{R}_{N-1}\in \mathcal {E}_r(n)$
satisfies
$f^{R}_{N-1}\in \mathcal {E}_r(n)$
satisfies
![]() $f f^{R}_{N-1}\in \mathcal {E}_{N-1}(n)$
. By Lemma 3.3, we have
$f f^{R}_{N-1}\in \mathcal {E}_{N-1}(n)$
. By Lemma 3.3, we have
![]() $\widetilde {f f^{R}_{N-1}}\in \mathcal {E}_{N-1}(n)$
and
$\widetilde {f f^{R}_{N-1}}\in \mathcal {E}_{N-1}(n)$
and
![]() $f f^{R}_{N-1} \widetilde {f f^{R}_{N-1}}\in \mathcal {E}_{2N-2}(n)\subset \mathcal {E}_{N}(n)$
. Then we have
$f f^{R}_{N-1} \widetilde {f f^{R}_{N-1}}\in \mathcal {E}_{2N-2}(n)\subset \mathcal {E}_{N}(n)$
. Then we have
![]() $f^{R}_N= f^{R}_{N-1}\widetilde {f f^{R}_{N-1}}\in \mathcal {E}_{r}(n)$
and
$f^{R}_N= f^{R}_{N-1}\widetilde {f f^{R}_{N-1}}\in \mathcal {E}_{r}(n)$
and
![]() $f f^{R}_N\in \mathcal {E}_{N}(n)$
. Since
$f f^{R}_N\in \mathcal {E}_{N}(n)$
. Since
![]() $\widetilde {f f^{R}_{N-1}}\in \mathcal {E}_{N-1}(n)$
, we have
$\widetilde {f f^{R}_{N-1}}\in \mathcal {E}_{N-1}(n)$
, we have
![]() $f^{R}_{N}\sim _{N-1} f^{R}_{N-1}$
. The case for
$f^{R}_{N}\sim _{N-1} f^{R}_{N-1}$
. The case for
![]() $f^{L}_N$
is similar.
$f^{L}_N$
is similar.
Proposition 3.5. For
![]() $N\geq 1$
, we have a filtration of groups
$N\geq 1$
, we have a filtration of groups
Moreover, this is an N-series.
Proof. Firstly, we show that
![]() $\mathcal {E}_r(n)/\sim _{N}$
is a group for each
$\mathcal {E}_r(n)/\sim _{N}$
is a group for each
![]() $r\geq 1$
. For
$r\geq 1$
. For
![]() $f,f',g\in \mathcal {E}_r(n)$
such that
$f,f',g\in \mathcal {E}_r(n)$
such that
![]() $f\sim _N f'$
, we can easily check that
$f\sim _N f'$
, we can easily check that
![]() $fg\sim _N f'g$
and
$fg\sim _N f'g$
and
![]() $gf\sim _N gf'$
. Thus, the composition makes the set
$gf\sim _N gf'$
. Thus, the composition makes the set
![]() $\mathcal {E}_r(n)/\sim _{N}$
a monoid. For
$\mathcal {E}_r(n)/\sim _{N}$
a monoid. For
![]() $[f]\in \mathcal {E}_r(n)/\sim _{N}$
, by Lemma 3.4, it follows that
$[f]\in \mathcal {E}_r(n)/\sim _{N}$
, by Lemma 3.4, it follows that
![]() $[f][f^{R}_N]=[f^{L}_N][f]=1 \in \mathcal {E}_r(n)/\sim _{N}$
. Since
$[f][f^{R}_N]=[f^{L}_N][f]=1 \in \mathcal {E}_r(n)/\sim _{N}$
. Since
![]() $\mathcal {E}_r(n)/\sim _{N}$
is a monoid, we have
$\mathcal {E}_r(n)/\sim _{N}$
is a monoid, we have
![]() $[f^{R}_N]=[f^{L}_N]$
, and this is the inverse of
$[f^{R}_N]=[f^{L}_N]$
, and this is the inverse of
![]() $[f]$
. Therefore,
$[f]$
. Therefore,
![]() $\mathcal {E}_r(n)/\sim _{N}$
is a group for each
$\mathcal {E}_r(n)/\sim _{N}$
is a group for each
![]() $r\geq 1$
.
$r\geq 1$
.
Since
![]() $\mathcal {E}_r(n)\supset \mathcal {E}_{r+1}(n)$
, we have
$\mathcal {E}_r(n)\supset \mathcal {E}_{r+1}(n)$
, we have
![]() $\mathcal {E}_r(n)/\sim _{N} \; \supset \mathcal {E}_{r+1}(n)/\sim _{N}$
. Secondly, we show that the descending series is an N-series. It suffices to show that, for
$\mathcal {E}_r(n)/\sim _{N} \; \supset \mathcal {E}_{r+1}(n)/\sim _{N}$
. Secondly, we show that the descending series is an N-series. It suffices to show that, for
![]() $f\in \mathcal {E}_r(n), g\in \mathcal {E}_s(n)$
, we have
$f\in \mathcal {E}_r(n), g\in \mathcal {E}_s(n)$
, we have
Note that, by Lemma 3.4, we can take
![]() $f^{R}_{N}, g^{R}_{N}\in \mathcal {E}_r(n)$
such that
$f^{R}_{N}, g^{R}_{N}\in \mathcal {E}_r(n)$
such that
![]() $ff^{R}_{N}, gg^{R}_{N}\in \mathcal {E}_{N}(n)\cap \mathcal {E}_{r+s}(n)$
. By commutator calculus, for
$ff^{R}_{N}, gg^{R}_{N}\in \mathcal {E}_{N}(n)\cap \mathcal {E}_{r+s}(n)$
. By commutator calculus, for
![]() $x\in F_n$
, we have
$x\in F_n$
, we have
Similarly, we have
Thus, we have
 $$ \begin{gather*} \begin{aligned} [fg,[f^{R}_{N} g^{R}_{N},x]]&\equiv [g,[f^{R}_{N} g^{R}_{N},x]]\;[f,[f^{R}_{N} g^{R}_{N},x]]\\ &\equiv [g,[g^{R}_{N},x]\;[f^{R}_{N},x]]\;[f,[g^{R}_{N},x]\;[f^{R}_{N},x]]\\ &\equiv [g,[g^{R}_{N},x]]\;[f,[f^{R}_{N},x]] \quad (\bmod\: \Gamma_{r+s+1}). \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} [fg,[f^{R}_{N} g^{R}_{N},x]]&\equiv [g,[f^{R}_{N} g^{R}_{N},x]]\;[f,[f^{R}_{N} g^{R}_{N},x]]\\ &\equiv [g,[g^{R}_{N},x]\;[f^{R}_{N},x]]\;[f,[g^{R}_{N},x]\;[f^{R}_{N},x]]\\ &\equiv [g,[g^{R}_{N},x]]\;[f,[f^{R}_{N},x]] \quad (\bmod\: \Gamma_{r+s+1}). \end{aligned} \end{gather*} $$
Therefore, we have
 $$ \begin{gather*} \begin{aligned} [f g f^{R}_{N} g^{R}_{N},x]&= [fg,[f^{R}_{N} g^{R}_{N},x]]\;[f^{R}_{N} g^{R}_{N},x]\;[fg,x]\\ &\equiv [g,[g^{R}_{N},x]]\;[f,[f^{R}_{N},x]]\;[g^{R}_{N},x]\;[f^{R}_{N},x]\;[g,x]\;[f,x]\\ &\equiv [g,[g^{R}_{N},x]]\;[g^{R}_{N},x]\;[g,x]\;[f,[f^{R}_{N},x]]\;[f^{R}_{N},x]\;[f,x]\\ &=[gg^{R}_{N},x]\;[ff^{R}_{N},x]\\ &\equiv 1 \quad (\bmod\: \Gamma_{r+s+1}), \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} [f g f^{R}_{N} g^{R}_{N},x]&= [fg,[f^{R}_{N} g^{R}_{N},x]]\;[f^{R}_{N} g^{R}_{N},x]\;[fg,x]\\ &\equiv [g,[g^{R}_{N},x]]\;[f,[f^{R}_{N},x]]\;[g^{R}_{N},x]\;[f^{R}_{N},x]\;[g,x]\;[f,x]\\ &\equiv [g,[g^{R}_{N},x]]\;[g^{R}_{N},x]\;[g,x]\;[f,[f^{R}_{N},x]]\;[f^{R}_{N},x]\;[f,x]\\ &=[gg^{R}_{N},x]\;[ff^{R}_{N},x]\\ &\equiv 1 \quad (\bmod\: \Gamma_{r+s+1}), \end{aligned} \end{gather*} $$
and the proof is complete.
For
![]() $N\geq r\geq 1$
, we have a canonical projection
$N\geq r\geq 1$
, we have a canonical projection
Let
![]() $\hat {\mathcal {E}}_r(n)$
denote the projective limit
$\hat {\mathcal {E}}_r(n)$
denote the projective limit
![]() $\underset {N}{\varprojlim } (\mathcal {E}_r(n)/\sim _N)$
and
$\underset {N}{\varprojlim } (\mathcal {E}_r(n)/\sim _N)$
and
denote the projection. By Proposition 3.5, we have a descending series of groups
satisfying
Proposition 3.6. The descending series
![]() $\hat {\mathcal {E}}_{\ast }(n):=(\hat {\mathcal {E}}_r(n))_{r\geq 1}$
is an N-series.
$\hat {\mathcal {E}}_{\ast }(n):=(\hat {\mathcal {E}}_r(n))_{r\geq 1}$
is an N-series.
Proof. By Proposition 3.5, we have
![]() $[\mathcal {E}_{r}(n)/\sim _{N},\mathcal {E}_{s}(n)/\sim _{N}]\subset \mathcal {E}_{r+s}(n)/\sim _{N}$
for each
$[\mathcal {E}_{r}(n)/\sim _{N},\mathcal {E}_{s}(n)/\sim _{N}]\subset \mathcal {E}_{r+s}(n)/\sim _{N}$
for each
![]() $N>r,s$
. By taking the projective limits, we have
$N>r,s$
. By taking the projective limits, we have
![]() $[\hat {\mathcal {E}}_{r}(n),\hat {\mathcal {E}}_{s}(n)]\subset \hat {\mathcal {E}}_{r+s}(n)$
.
$[\hat {\mathcal {E}}_{r}(n),\hat {\mathcal {E}}_{s}(n)]\subset \hat {\mathcal {E}}_{r+s}(n)$
.
We have a graded Lie algebra
![]() $\mathrm {gr}(\hat {\mathcal {E}}_{\ast }(n))$
associated to the N-series
$\mathrm {gr}(\hat {\mathcal {E}}_{\ast }(n))$
associated to the N-series
![]() $\hat {\mathcal {E}}_{\ast }(n)$
. Let
$\hat {\mathcal {E}}_{\ast }(n)$
. Let
![]() $\operatorname {gr}^r(\mathcal {E}_{\ast }(n)):=\mathcal {E}_r(n)/\sim _{r+1}$
for
$\operatorname {gr}^r(\mathcal {E}_{\ast }(n)):=\mathcal {E}_r(n)/\sim _{r+1}$
for
![]() $r\geq 1$
and
$r\geq 1$
and
![]() $\mathrm {gr}(\mathcal {E}_{\ast }(n)):=\bigoplus _{r\geq 1}\operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
.
$\mathrm {gr}(\mathcal {E}_{\ast }(n)):=\bigoplus _{r\geq 1}\operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
.
Proposition 3.7. We have a group isomorphism
induced by the projection
![]() $\pi _{r+1}:\hat {\mathcal {E}}_{r}(n)\rightarrow \operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
. Therefore,
$\pi _{r+1}:\hat {\mathcal {E}}_{r}(n)\rightarrow \operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
. Therefore,
![]() $\mathrm {gr}(\mathcal {E}_{\ast }(n))$
is a graded Lie algebra.
$\mathrm {gr}(\mathcal {E}_{\ast }(n))$
is a graded Lie algebra.
Proof. The projection
![]() $\pi _{r+1}$
induces
$\pi _{r+1}$
induces
![]() $\bar {\pi }_{r+1}$
since, for
$\bar {\pi }_{r+1}$
since, for
![]() $f\in \hat {\mathcal {E}}_{r+1}(n)$
, we have
$f\in \hat {\mathcal {E}}_{r+1}(n)$
, we have
![]() $\pi _{r+1}(f)\in \mathcal {E}_{r+1}(n)/\sim _{r+1}=1$
.
$\pi _{r+1}(f)\in \mathcal {E}_{r+1}(n)/\sim _{r+1}=1$
.
We will check that
![]() $\bar {\pi }_{r+1}$
is surjective. For any
$\bar {\pi }_{r+1}$
is surjective. For any
![]() $f\in \mathcal {E}_r(n)$
, let
$f\in \mathcal {E}_r(n)$
, let
![]() $\Phi (f)\in \hat {\mathcal {E}}_r(n)$
satisfy
$\Phi (f)\in \hat {\mathcal {E}}_r(n)$
satisfy
![]() $\pi _N(\Phi (f))=[f]\in \mathcal {E}_r(n)/\sim _{N}$
for each
$\pi _N(\Phi (f))=[f]\in \mathcal {E}_r(n)/\sim _{N}$
for each
![]() $N>r$
. We have
$N>r$
. We have
![]() $\bar {\pi }_{r+1}([\Phi (f)])=\pi _{r+1}(\Phi (f))=[f]\in \mathcal {E}_r(n)/\sim _{r+1}$
. Therefore,
$\bar {\pi }_{r+1}([\Phi (f)])=\pi _{r+1}(\Phi (f))=[f]\in \mathcal {E}_r(n)/\sim _{r+1}$
. Therefore,
![]() $\bar {\pi }_{r+1}$
is surjective.
$\bar {\pi }_{r+1}$
is surjective.
Finally, we show that
![]() $\bar {\pi }_{r+1}$
is injective. Let
$\bar {\pi }_{r+1}$
is injective. Let
![]() $f\in \hat {\mathcal {E}}_r(n)$
satisfy
$f\in \hat {\mathcal {E}}_r(n)$
satisfy
![]() $\bar {\pi }_{r+1}([f])=1\in \mathcal {E}_r(n)/\sim _{r+1}$
and
$\bar {\pi }_{r+1}([f])=1\in \mathcal {E}_r(n)/\sim _{r+1}$
and
![]() $\pi _{N}(f)=[f_N]\in \mathcal {E}_r(n)/\sim _{N}$
for
$\pi _{N}(f)=[f_N]\in \mathcal {E}_r(n)/\sim _{N}$
for
![]() $f_N\in \mathcal {E}_r(n)$
. Then, we have
$f_N\in \mathcal {E}_r(n)$
. Then, we have
![]() $f_{r+1}\in \mathcal {E}_{r+1}(n)$
and
$f_{r+1}\in \mathcal {E}_{r+1}(n)$
and
![]() $f_N\sim _{r+1}f_{r+1}$
for any
$f_N\sim _{r+1}f_{r+1}$
for any
![]() $N>r$
. Therefore, we have
$N>r$
. Therefore, we have
![]() $\pi _N(f)=[f_N]\in \mathcal {E}_{r+1}(n)/\sim _{N}$
for each
$\pi _N(f)=[f_N]\in \mathcal {E}_{r+1}(n)/\sim _{N}$
for each
![]() $N>r$
and thus
$N>r$
and thus
![]() $[f]=1\in \operatorname {gr}^r(\hat {\mathcal {E}}_{\ast }(n))$
. The proof is complete.
$[f]=1\in \operatorname {gr}^r(\hat {\mathcal {E}}_{\ast }(n))$
. The proof is complete.
3.4 Johnson homomorphism of
 $\operatorname {End}(F_n)$
$\operatorname {End}(F_n)$
For
![]() $r\geq 1$
, by using Lemma 3.2, we can define a monoid homomorphism
$r\geq 1$
, by using Lemma 3.2, we can define a monoid homomorphism
by
![]() $\tilde {\tau }^{\prime }_{r}(f)(x\Gamma _2):=[f,x]\Gamma _{r+2}$
for
$\tilde {\tau }^{\prime }_{r}(f)(x\Gamma _2):=[f,x]\Gamma _{r+2}$
for
![]() $f\in \mathcal {E}_r(n), x\in F_n$
. It is easily checked that the monoid homomorphism
$f\in \mathcal {E}_r(n), x\in F_n$
. It is easily checked that the monoid homomorphism
![]() $\tilde {\tau }^{\prime }_{r}$
induces an injective group homomorphism
$\tilde {\tau }^{\prime }_{r}$
induces an injective group homomorphism
We call it the r-th Johnson homomorphism of
![]() $\operatorname {End}(F_n)$
.
$\operatorname {End}(F_n)$
.
Proposition 3.8. The map
![]() $\tilde {\tau }_r:\operatorname {gr}^r(\mathcal {E}_{\ast }(n))\hookrightarrow \operatorname {Hom}(H, \mathcal {L}_{r+1}(n))$
is an abelian group isomorphism.
$\tilde {\tau }_r:\operatorname {gr}^r(\mathcal {E}_{\ast }(n))\hookrightarrow \operatorname {Hom}(H, \mathcal {L}_{r+1}(n))$
is an abelian group isomorphism.
Proof. It suffices to show that
![]() $\tilde {\tau }_r$
is surjective. For any
$\tilde {\tau }_r$
is surjective. For any
![]() $\varphi \in \operatorname {Hom}(H,\mathcal {L}_{r+1}(n))$
, we fix a representative of
$\varphi \in \operatorname {Hom}(H,\mathcal {L}_{r+1}(n))$
, we fix a representative of
![]() $\varphi (x_i\Gamma _2)\in \mathcal {L}_{r+1}(n)$
and write it
$\varphi (x_i\Gamma _2)\in \mathcal {L}_{r+1}(n)$
and write it
![]() $\varphi (x_i)\in \Gamma _{r+1},$
for
$\varphi (x_i)\in \Gamma _{r+1},$
for
![]() $i\in [n]$
. Define
$i\in [n]$
. Define
![]() $\psi \in \operatorname {End}(F_n)$
by
$\psi \in \operatorname {End}(F_n)$
by
It turns out that
![]() $[\psi ,x]\Gamma _{r+2}=\varphi (x\Gamma _{2})\in \mathcal {L}_{r+1}(n)$
for any
$[\psi ,x]\Gamma _{r+2}=\varphi (x\Gamma _{2})\in \mathcal {L}_{r+1}(n)$
for any
![]() $x\in F_n$
by induction on the word length of
$x\in F_n$
by induction on the word length of
![]() $x\in F_n$
. Therefore, we have
$x\in F_n$
. Therefore, we have
![]() $\tilde {\tau }_r(\psi )=\varphi $
, and thus the map
$\tilde {\tau }_r(\psi )=\varphi $
, and thus the map
![]() $\tilde {\tau }_r$
is surjective.
$\tilde {\tau }_r$
is surjective.
Then we obtain the following commutative diagram:

Remark 3.9. It is well known that the Andreadakis filtration
![]() $\mathcal {A}_{\ast }(n)$
of
$\mathcal {A}_{\ast }(n)$
of
![]() $\operatorname {Aut}(F_n)$
includes the lower central series of
$\operatorname {Aut}(F_n)$
includes the lower central series of
![]() $\operatorname {IA}(n)$
:
$\operatorname {IA}(n)$
:
We have
![]() $\mathcal {A}_1(n)=\operatorname {IA}(n)$
by definition. Andreadakis [Reference Andreadakis1] conjectured that
$\mathcal {A}_1(n)=\operatorname {IA}(n)$
by definition. Andreadakis [Reference Andreadakis1] conjectured that
for all
![]() $r\geq 2,n\geq 2$
. Andreadakis [Reference Andreadakis1] (
$r\geq 2,n\geq 2$
. Andreadakis [Reference Andreadakis1] (
![]() $n=3$
) and Kawazumi [Reference Kawazumi17] (for any n) showed that equation (3.6) holds for
$n=3$
) and Kawazumi [Reference Kawazumi17] (for any n) showed that equation (3.6) holds for
![]() $r=2$
. Moreover, Andreadakis [Reference Andreadakis1] showed that the first Johnson homomorphism
$r=2$
. Moreover, Andreadakis [Reference Andreadakis1] showed that the first Johnson homomorphism
![]() $\tau _1$
of
$\tau _1$
of
![]() $\operatorname {Aut}(F_n)$
is an isomorphism. Therefore, we have abelian group isomorphisms
$\operatorname {Aut}(F_n)$
is an isomorphism. Therefore, we have abelian group isomorphisms
Recently, Satoh [Reference Satoh23] showed that equation (3.6) holds for
![]() $r=3$
. On the other hand, Bartholdi [Reference Bartholdi5] showed that
$r=3$
. On the other hand, Bartholdi [Reference Bartholdi5] showed that
which is a counterexample of the Andreadakis conjecture. Now, the Andreadakis conjecture remains open for
![]() $n\gg r$
.
$n\gg r$
.
3.5 The derivation Lie algebra
By equation (3.1) and Proposition 3.8, we have abelian group isomorphisms
We write
![]() $\tilde {\tau }_r:\operatorname {gr}^r(\mathcal {E}_{\ast }(n))\xrightarrow {\cong } \operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
as well.
$\tilde {\tau }_r:\operatorname {gr}^r(\mathcal {E}_{\ast }(n))\xrightarrow {\cong } \operatorname {Der}_r(\mathcal {L}_{\ast }(n))$
as well.
Proposition 3.10. The abelian group isomorphism
is an isomorphism of graded Lie algebras.
Proof. We only need to check that the Lie bracket of
![]() $\mathrm {gr}(\mathcal {E}_{\ast }(n))$
is sent to the Lie bracket of
$\mathrm {gr}(\mathcal {E}_{\ast }(n))$
is sent to the Lie bracket of
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
. For
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
. For
![]() $f\in \hat {\mathcal {E}}_r(n),g\in \hat {\mathcal {E}}_s(n)$
and
$f\in \hat {\mathcal {E}}_r(n),g\in \hat {\mathcal {E}}_s(n)$
and
![]() $x\in F_n$
, we have
$x\in F_n$
, we have
 $$ \begin{gather*} \begin{aligned} [\tilde{\tau}_r([f]),\tilde{\tau}_s([g])](x\Gamma_2)&=\tilde{\tau}_r([f])\tilde{\tau}_s([g])(x\Gamma_2)-\tilde{\tau}_s([g])\tilde{\tau}_r([f])(x\Gamma_2)\\ &=[f,[g,x]]\;[g,[f,x]]^{-1}=[[f,g],x]\in \mathcal{L}_{r+s+1}(n). \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} [\tilde{\tau}_r([f]),\tilde{\tau}_s([g])](x\Gamma_2)&=\tilde{\tau}_r([f])\tilde{\tau}_s([g])(x\Gamma_2)-\tilde{\tau}_s([g])\tilde{\tau}_r([f])(x\Gamma_2)\\ &=[f,[g,x]]\;[g,[f,x]]^{-1}=[[f,g],x]\in \mathcal{L}_{r+s+1}(n). \end{aligned} \end{gather*} $$
On the other hand, we have
Therefore,
![]() $\tilde {\tau }$
is an isomorphism of graded Lie algebras.
$\tilde {\tau }$
is an isomorphism of graded Lie algebras.
Remark 3.11. The tree module
![]() $\bigoplus _{r\geq 1}T_r(n)$
also has a graded Lie algebra structure which is induced by the Lie algebra structure of
$\bigoplus _{r\geq 1}T_r(n)$
also has a graded Lie algebra structure which is induced by the Lie algebra structure of
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
. The Lie bracket
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
. The Lie bracket
is defined by the difference between two linear sums obtained by contracting the root of one of the trees and the leaves of the other tree

4 Action of
 $\mathrm {gr}(\mathcal {E}_{\ast }(n))$
on
$\mathrm {gr}(\mathcal {E}_{\ast }(n))$
on
 $B_{d}(n)$
$B_{d}(n)$
We defined the bracket maps (2.2) in [Reference Katada16]. In this section, we extend them to linear maps
In Section 4.1, we state Theorem 4.1, which we use to obtain the extended bracket map. In Section 4.2, we extend the category
![]() $\mathbf {A}$
to a category
$\mathbf {A}$
to a category
![]() $\mathbf {A}^{L}$
, which includes a Lie algebra structure besides the Hopf algebra structure in
$\mathbf {A}^{L}$
, which includes a Lie algebra structure besides the Hopf algebra structure in
![]() $\mathbf {A}$
. In Section 4.3, we observe some relations for morphisms of
$\mathbf {A}$
. In Section 4.3, we observe some relations for morphisms of
![]() $\mathbf {A}^{L}$
. By using these relations, we prove Theorem 4.1 in Section 4.4.
$\mathbf {A}^{L}$
. By using these relations, we prove Theorem 4.1 in Section 4.4.
4.1 Bracket map
 $[\cdot ,\cdot ]: B_{d,k}(n)\otimes \operatorname {gr}^r(\mathcal {E}_{\ast }(n))\rightarrow B_{d,k+r}(n)$
$[\cdot ,\cdot ]: B_{d,k}(n)\otimes \operatorname {gr}^r(\mathcal {E}_{\ast }(n))\rightarrow B_{d,k+r}(n)$
We have a right
![]() $\operatorname {End}(F_n)$
-action on
$\operatorname {End}(F_n)$
-action on
![]() $A_d(n)$
by letting
$A_d(n)$
by letting
for
![]() $u\in A_d(n), g\in \operatorname {End}(F_n)$
. We define
$u\in A_d(n), g\in \operatorname {End}(F_n)$
. We define
by
![]() $[u,g]:=u\cdot g -u$
for
$[u,g]:=u\cdot g -u$
for
![]() $u\in A_d(n),g\in \operatorname {End}(F_n)$
, which we call the bracket map.
$u\in A_d(n),g\in \operatorname {End}(F_n)$
, which we call the bracket map.
Theorem 4.1. The N-series
![]() $\hat {\mathcal {E}}_{\ast }(n)$
acts on the right on the filtered vector space
$\hat {\mathcal {E}}_{\ast }(n)$
acts on the right on the filtered vector space
![]() $A_d(n)$
. That is, we have
$A_d(n)$
. That is, we have
for any
![]() $r\geq 1$
.
$r\geq 1$
.
Note that we have
![]() $[A_{d,k}(n),\Gamma _{r}(\operatorname {IA}(n))]\subset A_{d,k+r}(n)$
(see Lemma 5.7 in [Reference Katada16]). We will prove Theorem 4.1 in Section 4.4.
$[A_{d,k}(n),\Gamma _{r}(\operatorname {IA}(n))]\subset A_{d,k+r}(n)$
(see Lemma 5.7 in [Reference Katada16]). We will prove Theorem 4.1 in Section 4.4.
By using Theorem 4.1, we can extend the bracket map
to
![]() $\operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
.
$\operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
.
Corollary 4.2. Let
![]() $r\geq 1$
. The bracket map (4.1) induces a
$r\geq 1$
. The bracket map (4.1) induces a
![]() $\Bbbk $
-linear map
$\Bbbk $
-linear map
We can also extend the
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module map
$\operatorname {GL}(n;\mathbb {Z})$
-module map
defined by
![]() $\beta _{d,k}^r(g)(u)=[u,g]$
for
$\beta _{d,k}^r(g)(u)=[u,g]$
for
![]() $g\in \operatorname {gr}^r(\operatorname {IA}(n)),u\in B_{d,k}(n)$
to a group homomorphism
$g\in \operatorname {gr}^r(\operatorname {IA}(n)),u\in B_{d,k}(n)$
to a group homomorphism
which
![]() $\beta _{d,k}^r$
factors through. That is, we have
$\beta _{d,k}^r$
factors through. That is, we have
![]() $\beta _{d,k}^r=\tilde {\beta }_{d,k}^r i$
, where the map
$\beta _{d,k}^r=\tilde {\beta }_{d,k}^r i$
, where the map
![]() $i:\operatorname {gr}^r(\operatorname {IA}(n))\rightarrow \operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
is induced by the inclusion map
$i:\operatorname {gr}^r(\operatorname {IA}(n))\rightarrow \operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
is induced by the inclusion map
![]() $\Gamma _{r}(\operatorname {IA}(n))\hookrightarrow \mathcal {E}_{r}(n)$
.
$\Gamma _{r}(\operatorname {IA}(n))\hookrightarrow \mathcal {E}_{r}(n)$
.
Remark 4.3. The right action of the N-series
![]() $\hat {\mathcal {E}}_{\ast }(n)$
on
$\hat {\mathcal {E}}_{\ast }(n)$
on
![]() $A_d(n)$
induces an action of the graded Lie algebra
$A_d(n)$
induces an action of the graded Lie algebra
![]() $\mathrm {gr}(\mathcal {E}_{\ast }(n))$
on the graded vector space
$\mathrm {gr}(\mathcal {E}_{\ast }(n))$
on the graded vector space
![]() $B_{d}(n)$
:
$B_{d}(n)$
:
which is given by the group homomorphisms
![]() $\tilde {\beta }_{d,k}^r$
. This induced action can be regarded as an action of the derivation Lie algebra
$\tilde {\beta }_{d,k}^r$
. This induced action can be regarded as an action of the derivation Lie algebra
![]() $\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on the graded vector space
$\operatorname {Der}(\mathcal {L}_{\ast }(n))$
on the graded vector space
![]() $B_d(n)$
by the identification in Section 3.5.
$B_d(n)$
by the identification in Section 3.5.
4.2 The category
 $\mathbf {A}^{L}$
of extended Jacobi diagrams in handlebodies
$\mathbf {A}^{L}$
of extended Jacobi diagrams in handlebodies
The category
![]() $\mathbf {A}$
has a cocommutative Hopf algebra with the underlying object
$\mathbf {A}$
has a cocommutative Hopf algebra with the underlying object
![]() $1$
, which we recalled in Section 2.4. Moreover, the morphisms of the category
$1$
, which we recalled in Section 2.4. Moreover, the morphisms of the category
![]() $\mathbf {A}$
have Jacobi diagrams, and the STU relations correspond to relations of Lie algebras. In a proof of Theorem 4.1, we use graphical computations which deal with the Hopf algebra structure and the Lie algebra structure. For this purpose, we extend the category
$\mathbf {A}$
have Jacobi diagrams, and the STU relations correspond to relations of Lie algebras. In a proof of Theorem 4.1, we use graphical computations which deal with the Hopf algebra structure and the Lie algebra structure. For this purpose, we extend the category
![]() $\mathbf {A}$
to another category
$\mathbf {A}$
to another category
![]() $\mathbf {A}^{L}$
which includes the Hopf algebra structure and the Lie algebra structure. In Appendix A, we give an expected presentation of the category
$\mathbf {A}^{L}$
which includes the Hopf algebra structure and the Lie algebra structure. In Appendix A, we give an expected presentation of the category
![]() $\mathbf {A}^{L}$
.
$\mathbf {A}^{L}$
.
Construct the category
![]() $\mathbf {A}^{L}$
as follows. The set of objects of
$\mathbf {A}^{L}$
as follows. The set of objects of
![]() $\mathbf {A}^{L}$
is the free monoid generated by two objects H and L, where multiplication is denoted by
$\mathbf {A}^{L}$
is the free monoid generated by two objects H and L, where multiplication is denoted by
![]() $\otimes $
. The category
$\otimes $
. The category
![]() $\mathbf {A}^{L}$
includes the category
$\mathbf {A}^{L}$
includes the category
![]() $\mathbf {A}$
as a full subcategory with the free monoid generated by H as the set of objects. (On the other hand, the full subcategory with the free monoid generated by L is isomorphic to a category in [Reference Hinich and Vaintrob13]. See Remark A.4.) In the category
$\mathbf {A}$
as a full subcategory with the free monoid generated by H as the set of objects. (On the other hand, the full subcategory with the free monoid generated by L is isomorphic to a category in [Reference Hinich and Vaintrob13]. See Remark A.4.) In the category
![]() $\mathbf {A}^{L}$
, we consider diagrams that are obtained from Jacobi diagrams in handlebodies by attaching univalent vertices of the Jacobi diagrams to the bottom line l and the upper line
$\mathbf {A}^{L}$
, we consider diagrams that are obtained from Jacobi diagrams in handlebodies by attaching univalent vertices of the Jacobi diagrams to the bottom line l and the upper line
![]() $l'$
.
$l'$
.
Example 4.4. Here is a morphism in
![]() $\mathbf {A}^{L}(H\otimes L\otimes H\otimes L\otimes H,H\otimes L^{\otimes 2}\otimes H)$
:
$\mathbf {A}^{L}(H\otimes L\otimes H\otimes L\otimes H,H\otimes L^{\otimes 2}\otimes H)$
:

As depicted in Figure 2, the objects H and L in the source of a morphism of
![]() $\mathbf {A}^{L}$
correspond to a handle of the handlebody and a univalent vertex attached to the upper line
$\mathbf {A}^{L}$
correspond to a handle of the handlebody and a univalent vertex attached to the upper line
![]() $l'$
, respectively.
$l'$
, respectively.

Figure 2 Source of a morphism
As depicted in Figure 3, the objects H and L in the target of a morphism of
![]() $\mathbf {A}^{L}$
correspond to an arc component mapped into the handlebody and a univalent vertex attached to the bottom line l, respectively.
$\mathbf {A}^{L}$
correspond to an arc component mapped into the handlebody and a univalent vertex attached to the bottom line l, respectively.

Figure 3 Target of a morphism
In the category
![]() $\mathbf {A}^{L}$
, the object H is considered as a Hopf algebra and L is considered as a Lie algebra. See Section 4.3 and Appendix A.
$\mathbf {A}^{L}$
, the object H is considered as a Hopf algebra and L is considered as a Lie algebra. See Section 4.3 and Appendix A.
To define morphisms of the category
![]() $\mathbf {A}^{L}$
precisely, we give the following definition.
$\mathbf {A}^{L}$
precisely, we give the following definition.
Definition 4.5. For a finite set T, an
![]() $(X_m,T)$
-diagram is a quadruple
$(X_m,T)$
-diagram is a quadruple
![]() $(D,V,f,g)$
, where
$(D,V,f,g)$
, where
-
• D is a vertex-oriented uni-trivalent graph such that each connected component has at least one univalent vertex,
-
• V is a subset of
 $\partial D=\{\text {univalent vertices of }D\}$
,
$\partial D=\{\text {univalent vertices of }D\}$
, -
• f is an embedding of V into the interior of
 $X_m$
,
$X_m$
, -
• g is a bijection from T to
 $\partial D\setminus V$
.
$\partial D\setminus V$
.
Note that an
![]() $(X_m,\emptyset )$
-diagram is a Jacobi diagram on
$(X_m,\emptyset )$
-diagram is a Jacobi diagram on
![]() $X_m$
.
$X_m$
.
For an object
![]() $w=H^{\otimes m_1}\otimes L^{\otimes n_1}\otimes \cdots \otimes H^{\otimes m_r}\otimes L^{\otimes n_r}\in \mathbf {A}^{L}$
, let
$w=H^{\otimes m_1}\otimes L^{\otimes n_1}\otimes \cdots \otimes H^{\otimes m_r}\otimes L^{\otimes n_r}\in \mathbf {A}^{L}$
, let
![]() $m:=\sum _{i=1}^r m_i$
and
$m:=\sum _{i=1}^r m_i$
and
![]() $n:=\sum _{i=1}^r n_i$
. For
$n:=\sum _{i=1}^r n_i$
. For
![]() $p\geq 0$
, let
$p\geq 0$
, let
![]() $[p]^{+}:=\{1^{+},\cdots ,p^{+}\}$
and
$[p]^{+}:=\{1^{+},\cdots ,p^{+}\}$
and
![]() $[p]^{-}:=\{1^{-},\cdots ,p^{-}\}$
be two copies of
$[p]^{-}:=\{1^{-},\cdots ,p^{-}\}$
be two copies of
![]() $[p]$
.
$[p]$
.
Definition 4.6. For objects
![]() $w=H^{\otimes m_1}\otimes L^{\otimes n_1}\otimes \cdots \otimes H^{\otimes m_r}\otimes L^{\otimes n_r}\in \mathbf {A}^{L}$
and
$w=H^{\otimes m_1}\otimes L^{\otimes n_1}\otimes \cdots \otimes H^{\otimes m_r}\otimes L^{\otimes n_r}\in \mathbf {A}^{L}$
and
![]() $w'=H^{\otimes m^{\prime }1}\otimes L^{\otimes n^{\prime }1}\otimes \cdots \otimes H^{\otimes m^{\prime }s}\otimes L^{\otimes n^{\prime }s}\in \mathbf {A}^{L}$
, a
$w'=H^{\otimes m^{\prime }1}\otimes L^{\otimes n^{\prime }1}\otimes \cdots \otimes H^{\otimes m^{\prime }s}\otimes L^{\otimes n^{\prime }s}\in \mathbf {A}^{L}$
, a
![]() $(w,w')$
-diagram consists of
$(w,w')$
-diagram consists of
-
• an
 $(X_{m'},[n]^{+}\sqcup [n']^{-})$
-diagram
$(X_{m'},[n]^{+}\sqcup [n']^{-})$
-diagram
 $(D,V,f,g)$
such that each connected component of D has at least one univalent vertex in
$(D,V,f,g)$
such that each connected component of D has at least one univalent vertex in
 $V\cup g([n']^{-})$
$V\cup g([n']^{-})$
-
• a map
 $\varphi :X_{m'}\cup D\rightarrow U_m$
such that
$\varphi :X_{m'}\cup D\rightarrow U_m$
such that-
(1) the pair (the empty set
 $\emptyset $
, the restriction
$\emptyset $
, the restriction
 $\varphi \mid _{X_{m'}}$
) is an
$\varphi \mid _{X_{m'}}$
) is an
 $(m,m')$
-Jacobi diagram; that is,
$(m,m')$
-Jacobi diagram; that is,
 $\varphi $
maps
$\varphi $
maps
 $X_m'$
into
$X_m'$
into
 $U_m$
in such a way that endpoints of
$U_m$
in such a way that endpoints of
 $X_m'$
are arranged in the bottom line l from left to right,
$X_m'$
are arranged in the bottom line l from left to right, -
(2)
 $g([n]^{+})$
is mapped into
$g([n]^{+})$
is mapped into
 $l'$
so that the corresponding object in
$l'$
so that the corresponding object in
 $\mathbf {A}^{L}$
with respect to Figure 2 will be w when we look at the top line
$\mathbf {A}^{L}$
with respect to Figure 2 will be w when we look at the top line
 $l'$
from left to right,
$l'$
from left to right, -
(3)
 $g([n']^{-})$
is mapped into l so that the corresponding object in
$g([n']^{-})$
is mapped into l so that the corresponding object in
 $\mathbf {A}^{L}$
with respect to Figure 3 will be
$\mathbf {A}^{L}$
with respect to Figure 3 will be
 $w'$
when we look at the bottom line l from left to right.
$w'$
when we look at the bottom line l from left to right.
-
We identify two
![]() $(w,w')$
-diagrams if they are homotopic in
$(w,w')$
-diagrams if they are homotopic in
![]() $U_m$
relative to the endpoints of
$U_m$
relative to the endpoints of
![]() $X_m'\cup D$
. In what follows, we simply write D for a
$X_m'\cup D$
. In what follows, we simply write D for a
![]() $(w,w')$
-diagram. For objects w and
$(w,w')$
-diagram. For objects w and
![]() $w'$
, the hom-set
$w'$
, the hom-set
![]() $\mathbf {A}^{L}(w,w')$
is the
$\mathbf {A}^{L}(w,w')$
is the
![]() $\Bbbk $
-vector space spanned by
$\Bbbk $
-vector space spanned by
![]() $(w,w')$
-diagrams modulo the STU, AS and IHX relations.
$(w,w')$
-diagrams modulo the STU, AS and IHX relations.
The composition of
![]() $\mathbf {A}^{L}$
is defined in a similar way to that of the category
$\mathbf {A}^{L}$
is defined in a similar way to that of the category
![]() $\mathbf {A}$
. We can define a square diagram for an
$\mathbf {A}$
. We can define a square diagram for an
![]() $(w,w')$
-diagram similarly. Let D be a diagram in
$(w,w')$
-diagram similarly. Let D be a diagram in
![]() $\mathbf {A}^{L}(w, w')$
and
$\mathbf {A}^{L}(w, w')$
and
![]() $D'$
a diagram in
$D'$
a diagram in
![]() $\mathbf {A}^{L}(w', w'')$
. Deform
$\mathbf {A}^{L}(w', w'')$
. Deform
![]() $D'$
to have only the parallel copies of the handle cores in each handle. Then the composition
$D'$
to have only the parallel copies of the handle cores in each handle. Then the composition
![]() $D'\circ D$
is a diagram obtained by stacking the cabling of D on top of the square presentation of
$D'\circ D$
is a diagram obtained by stacking the cabling of D on top of the square presentation of
![]() $D'$
.
$D'$
.
Example 4.7. For
 and
and
 , the composition
, the composition
![]() $D'\circ D$
is
$D'\circ D$
is
 , where the box notation represents a linear sum of Jacobi diagrams. (See [Reference Habiro and Massuyeau11] and [Reference Katada16] for the definition of the box notation.)
, where the box notation represents a linear sum of Jacobi diagrams. (See [Reference Habiro and Massuyeau11] and [Reference Katada16] for the definition of the box notation.)
The identity morphism
![]() $\operatorname {id}_{H^{\otimes m_1}\otimes L^{\otimes n_1}\otimes \cdots \otimes H^{\otimes m_r}\otimes L^{\otimes n_r}}$
is the following diagram:
$\operatorname {id}_{H^{\otimes m_1}\otimes L^{\otimes n_1}\otimes \cdots \otimes H^{\otimes m_r}\otimes L^{\otimes n_r}}$
is the following diagram:

We can naturally extend the linear symmetric strict monoidal structure of
![]() $\mathbf {A}$
to the category
$\mathbf {A}$
to the category
![]() $\mathbf {A}^{L}$
, where the tensor product is defined to be the juxtaposition of the handlebodies.
$\mathbf {A}^{L}$
, where the tensor product is defined to be the juxtaposition of the handlebodies.
Note that the symmetries in
![]() $\mathbf {A}^{L}$
are determined by
$\mathbf {A}^{L}$
are determined by

The degree of a
![]() $(w,w')$
-diagram is defined by
$(w,w')$
-diagram is defined by
Let
![]() $\mathbf {A}^{L}_{d}(w,w')\subset \mathbf {A}^{L}(w,w')$
be the subspace spanned by
$\mathbf {A}^{L}_{d}(w,w')\subset \mathbf {A}^{L}(w,w')$
be the subspace spanned by
![]() $(w,w')$
-diagrams of degree d. We have
$(w,w')$
-diagrams of degree d. We have
![]() $\mathbf {A}^{L}(w,w')=\bigoplus _{d\geq 0}\mathbf {A}^{L}_{d}(w,w')$
. Since we have
$\mathbf {A}^{L}(w,w')=\bigoplus _{d\geq 0}\mathbf {A}^{L}_{d}(w,w')$
. Since we have
and
for any
![]() $w,w',w'',z,z'\in \mathbf {A}^{L}$
, this grading is an
$w,w',w'',z,z'\in \mathbf {A}^{L}$
, this grading is an
![]() $\mathbb {N}$
-grading on
$\mathbb {N}$
-grading on
![]() $\mathbf {A}^{L}$
. Note that we have
$\mathbf {A}^{L}$
. Note that we have
![]() $\mathbf {A}_d(m,n)= \mathbf {A}^{L}_d(H^{\otimes m},H^{\otimes n})$
for
$\mathbf {A}_d(m,n)= \mathbf {A}^{L}_d(H^{\otimes m},H^{\otimes n})$
for
![]() $m,n\geq 0$
.
$m,n\geq 0$
.
4.3 Relations for morphisms in
 $\mathbf {A}^{L}$
$\mathbf {A}^{L}$
Here, we observe some relations for morphisms of
![]() $\mathbf {A}^{L}$
, which we use in the proof of Theorem 4.1.
$\mathbf {A}^{L}$
, which we use in the proof of Theorem 4.1.
The cocommutative Hopf algebra
![]() $(H,\mu ,\eta ,\Delta ,\epsilon ,S)$
in
$(H,\mu ,\eta ,\Delta ,\epsilon ,S)$
in
![]() $\mathbf {A}$
naturally induces a cocommutative Hopf algebra in
$\mathbf {A}$
naturally induces a cocommutative Hopf algebra in
![]() $\mathbf {A}^{L}$
such that
$\mathbf {A}^{L}$
such that

Additionally, the triple
![]() $(L,[\cdot ,\cdot ],c_{L})$
is a Lie algebra with a symmetric invariant
$(L,[\cdot ,\cdot ],c_{L})$
is a Lie algebra with a symmetric invariant
![]() $2$
-tensor in
$2$
-tensor in
![]() $\mathbf {A}^{L}$
(see Appendix A.2), where
$\mathbf {A}^{L}$
(see Appendix A.2), where

Moreover,
![]() $\mathbf {A}^{L}$
has two morphisms
$\mathbf {A}^{L}$
has two morphisms

The degree of the morphism
![]() $c_{L}$
is
$c_{L}$
is
![]() $1$
and that of the others of the above morphisms is
$1$
and that of the others of the above morphisms is
![]() $0$
.
$0$
.
The iterated multiplications
and the iterated comultiplications
for
![]() $q\geq 0$
are inductively defined by
$q\geq 0$
are inductively defined by
Let

which denotes the adjoint action, and

which denotes the commutator.
Lemma 4.8. We have
-
(1)
 $S\circ i =-i$
$S\circ i =-i$
-
(2)
 $\Delta \circ i=i\otimes \eta +\eta \otimes i$
$\Delta \circ i=i\otimes \eta +\eta \otimes i$
-
(3)
 $\epsilon \circ i=0$
$\epsilon \circ i=0$
-
(4)
 $ad_{H}(i\otimes i)=-i\circ [\cdot ,\cdot ]$
.
$ad_{H}(i\otimes i)=-i\circ [\cdot ,\cdot ]$
.
Proof. They can be checked by diagrammatic computation.
Let
![]() $\mathfrak {g}$
be a Lie algebra and
$\mathfrak {g}$
be a Lie algebra and
![]() $U=U(\mathfrak {g})$
be the universal enveloping algebra. We have a filtration
$U=U(\mathfrak {g})$
be the universal enveloping algebra. We have a filtration
![]() $F_{\ast }(U)$
of U induced by the usual filtration of the tensor algebra
$F_{\ast }(U)$
of U induced by the usual filtration of the tensor algebra
![]() $T(\mathfrak {g})$
of
$T(\mathfrak {g})$
of
![]() $\mathfrak {g}$
. Since U has a cocommutative Hopf algebra structure, we can define the commutator operator
$\mathfrak {g}$
. Since U has a cocommutative Hopf algebra structure, we can define the commutator operator
in a similar way as equation (4.2). For
![]() $x_1,\cdots ,x_m,y_1,\cdots ,y_n\in \mathfrak {g}$
, we have
$x_1,\cdots ,x_m,y_1,\cdots ,y_n\in \mathfrak {g}$
, we have
The following lemma is a diagrammatic version of this fact.
Lemma 4.9.
-
(1) Let
 $m,n\geq 1$
. We have where
$m,n\geq 1$
. We have where
 $c_\alpha ,c_\beta \in \mathbb {Z}$
, and where
$c_\alpha ,c_\beta \in \mathbb {Z}$
, and where
 $D_\alpha $
(resp.
$D_\alpha $
(resp.
 $D_\beta $
) is a union of trees with m (resp. n) trivalent vertices. Moreover, for
$D_\beta $
) is a union of trees with m (resp. n) trivalent vertices. Moreover, for
 $m=n=1$
, we have
$m=n=1$
, we have 
-
(2) Let
 $m\geq 1$
. We have
$m\geq 1$
. We have 
-
(3) We have

For example, we have

Proof of Lemma 4.9
By using Lemma 4.8 (2) and
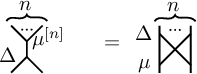
, we have

By Lemma 4.8 (1), it suffices to consider
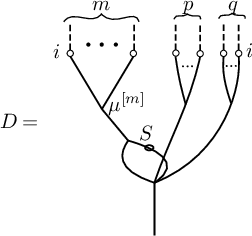
. By Lemma 4.8 (3), we have
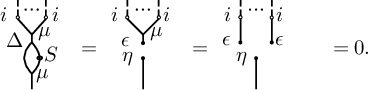
Thus, when
![]() $p=0$
, we have
$p=0$
, we have
![]() $D=0$
. When
$D=0$
. When
![]() $p\geq 1$
, by Lemma 4.8 (4), we have
$p\geq 1$
, by Lemma 4.8 (4), we have

Note that the last term is a
![]() $\mathbb {Z}$
-linear sum of unions of tree diagrams with m trivalent vertices. Therefore, the first equality of (1) follows. If
$\mathbb {Z}$
-linear sum of unions of tree diagrams with m trivalent vertices. Therefore, the first equality of (1) follows. If
![]() $m=n=1$
, then the equality follows from the case where
$m=n=1$
, then the equality follows from the case where
![]() $m=p=1, q=0$
. The second equality of (1) follows similarly.
$m=p=1, q=0$
. The second equality of (1) follows similarly.
The first equality of (2) follows from
 The second equality follows similarly.
The second equality follows similarly.
We have (3) because

4.4 Proof of Theorem 4.1
In this subsection, we prove Theorem 4.1.
For any
![]() $y_1,\cdots ,y_r\in F_n$
, we call
$y_1,\cdots ,y_r\in F_n$
, we call
![]() $[y_1,\cdots ,[y_{r-1},y_r]]\in \Gamma _r$
an r-fold commutator.
$[y_1,\cdots ,[y_{r-1},y_r]]\in \Gamma _r$
an r-fold commutator.
For
![]() $i\in [n]$
, define
$i\in [n]$
, define
![]() $d_i\in \operatorname {End}(F_n)=\mathbf {F}^{\mathrm {op}}(n,n)$
by
$d_i\in \operatorname {End}(F_n)=\mathbf {F}^{\mathrm {op}}(n,n)$
by
for
![]() $y_1,\cdots ,y_{r+1}\in F_n, \epsilon \in \{\pm 1\}$
, which we call an
$y_1,\cdots ,y_{r+1}\in F_n, \epsilon \in \{\pm 1\}$
, which we call an
![]() $(r+1)$
-fold commutator at i. Via the isomorphism
$(r+1)$
-fold commutator at i. Via the isomorphism
![]() $\Bbbk \mathbf {F}^{\mathrm {op}}(n,n)\cong \mathbf {A}_0(n,n)$
, we identify
$\Bbbk \mathbf {F}^{\mathrm {op}}(n,n)\cong \mathbf {A}_0(n,n)$
, we identify
![]() $d_i\in \mathbf {F}^{\mathrm {op}}(n,n)$
with a morphism of the following form
$d_i\in \mathbf {F}^{\mathrm {op}}(n,n)$
with a morphism of the following form

which we also call an
![]() $(r+1)$
-fold commutator at i, where each
$(r+1)$
-fold commutator at i, where each
depicts S or
![]() $\operatorname {id}_H$
, and
$\operatorname {id}_H$
, and
![]() $q_k,p_l\geq 0$
satisfy
$q_k,p_l\geq 0$
satisfy
![]() $\sum _{k=1}^{n}q_k=\sum _{l=1}^{r+1}p_l$
.
$\sum _{k=1}^{n}q_k=\sum _{l=1}^{r+1}p_l$
.
Claim 1. An element
![]() $g\in \mathcal {E}_r(n)$
can be written as a convolution product
$g\in \mathcal {E}_r(n)$
can be written as a convolution product
where
![]() $d_{i,j}$
is an
$d_{i,j}$
is an
![]() $(r+1)$
-fold commutator at i for
$(r+1)$
-fold commutator at i for
![]() $i\in [n]$
(
$i\in [n]$
(
![]() $l_i\geq 0, 1\leq j\leq l_i$
).
$l_i\geq 0, 1\leq j\leq l_i$
).
Proof. Let
![]() $g\in \mathcal {E}_r(n)$
. Since
$g\in \mathcal {E}_r(n)$
. Since
![]() $\Gamma _{r+1}$
is generated by
$\Gamma _{r+1}$
is generated by
![]() $(r+1)$
-fold commutators,
$(r+1)$
-fold commutators,
![]() $g(x_i)x_i^{-1}$
is a product of
$g(x_i)x_i^{-1}$
is a product of
![]() $(r+1)$
-fold commutators or their inverses for any
$(r+1)$
-fold commutators or their inverses for any
![]() $i\in [n]$
. Thus, we can decompose g into a convolution product of
$i\in [n]$
. Thus, we can decompose g into a convolution product of
![]() $(r+1)$
-fold commutators and
$(r+1)$
-fold commutators and
![]() $\operatorname {id}_{H^{\otimes n}}$
.
$\operatorname {id}_{H^{\otimes n}}$
.
Proof of Theorem 4.1
We show that
![]() $[A_{d,k}(n),\mathcal {E}_{r}(n)]\subset A_{d,k+r}(n)$
. We can write an element of
$[A_{d,k}(n),\mathcal {E}_{r}(n)]\subset A_{d,k+r}(n)$
. We can write an element of
![]() $A_{d,k}(n)\subset \mathbf {A}^{L}(I,H^{\otimes n})$
as a linear sum of the following diagrams:
$A_{d,k}(n)\subset \mathbf {A}^{L}(I,H^{\otimes n})$
as a linear sum of the following diagrams:

where D is a Jacobi diagram with at least k trivalent vertices. Let
![]() $g\in \mathcal {E}_{r}(n)$
. By Claim 1, we can write g as a convolution product
$g\in \mathcal {E}_{r}(n)$
. By Claim 1, we can write g as a convolution product
where
![]() $d_{i,j}\in \mathbf {A}_0(n,n)$
is an
$d_{i,j}\in \mathbf {A}_0(n,n)$
is an
![]() $(r+1)$
-fold commutator at i. Let
$(r+1)$
-fold commutator at i. Let
![]() $l=1+\sum _{i=1}^{n}{l_i}$
.
$l=1+\sum _{i=1}^{n}{l_i}$
.
By using
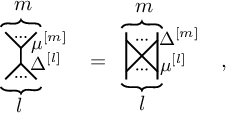
we have

Here, each
is once connected to all of the diagrams
![]() $d_{1,1}, \cdots , d_{n,l_n}$
and
$d_{1,1}, \cdots , d_{n,l_n}$
and
![]() $\operatorname {id}_{H^{\otimes n}}$
. Since we have
$\operatorname {id}_{H^{\otimes n}}$
. Since we have
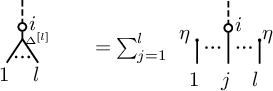
by Lemma 4.8 (2), the element
![]() $u\cdot g$
is a linear sum of diagrams of shape
$u\cdot g$
is a linear sum of diagrams of shape
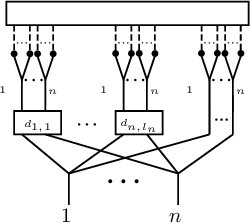
, where
denotes
or
. If all
that are connected to
![]() $\operatorname {id}_{H^{\otimes n}}$
are
$\operatorname {id}_{H^{\otimes n}}$
are
, then it is easily checked that the corresponding summand is just u by using Lemma 4.9 (3). Otherwise, at least one of
that are connected to diagrams
![]() $d_{1,1},\cdots ,d_{n,l_n}$
are
$d_{1,1},\cdots ,d_{n,l_n}$
are
. By using Lemma 4.9, it follows that each summand is a linear sum of diagrams with at least
![]() $k+r$
trivalent vertices. Therefore, we have
$k+r$
trivalent vertices. Therefore, we have
![]() $[u,g]=u\cdot g-u \in A_{d,k+r}(n)$
.
$[u,g]=u\cdot g-u \in A_{d,k+r}(n)$
.
5 Contraction map
Recall that
![]() $H=\mathcal {L}_1(n)= \bigoplus _{i=1}^n \mathbb {Z} \bar {x}_i$
and
$H=\mathcal {L}_1(n)= \bigoplus _{i=1}^n \mathbb {Z} \bar {x}_i$
and
![]() $H^{\ast }= \bigoplus _{i=1}^n \mathbb {Z} v_i$
. In what follows, we identify
$H^{\ast }= \bigoplus _{i=1}^n \mathbb {Z} v_i$
. In what follows, we identify
![]() $H^{\ast }\otimes \mathcal {L}_{r+1}(n)$
with
$H^{\ast }\otimes \mathcal {L}_{r+1}(n)$
with
![]() $T_{r}(n)$
as we remarked in Section 3.2.
$T_{r}(n)$
as we remarked in Section 3.2.
5.1 Preliminaries to computation
Let
![]() $N\geq 1$
. We briefly review the construction of the irreducible representations of the symmetric group
$N\geq 1$
. We briefly review the construction of the irreducible representations of the symmetric group
![]() $\mathfrak {S}_N$
. See Fulton–Harris [Reference Fulton6] and Sagan [Reference Sagan21] for basic facts of representation theory of
$\mathfrak {S}_N$
. See Fulton–Harris [Reference Fulton6] and Sagan [Reference Sagan21] for basic facts of representation theory of
![]() $\mathfrak {S}_N$
. Let
$\mathfrak {S}_N$
. Let
![]() $\lambda =(\lambda _1,\cdots ,\lambda _l)$
be a partition of N, and write
$\lambda =(\lambda _1,\cdots ,\lambda _l)$
be a partition of N, and write
![]() $\lambda \vdash N$
. A Young diagram of
$\lambda \vdash N$
. A Young diagram of
![]() $\lambda $
consists of
$\lambda $
consists of
![]() $\lambda _i$
boxes in the i-th row for
$\lambda _i$
boxes in the i-th row for
![]() $i\in [l]$
such that the rows of boxes are lined up on the left. A
$i\in [l]$
such that the rows of boxes are lined up on the left. A
![]() $\lambda $
-tableau is a numbering of the boxes by the integers in
$\lambda $
-tableau is a numbering of the boxes by the integers in
![]() $[N]$
. We call a
$[N]$
. We call a
![]() $\lambda $
-tableau standard if the numbering increases in each row and in each column. The canonical
$\lambda $
-tableau standard if the numbering increases in each row and in each column. The canonical
![]() $\lambda $
-tableau is a standard tableau whose numbering starts from the first row from left to right and then the second row from left to right and so on.
$\lambda $
-tableau is a standard tableau whose numbering starts from the first row from left to right and then the second row from left to right and so on.
Let
![]() $t_0$
be the canonical
$t_0$
be the canonical
![]() $\lambda $
-tableau. Define
$\lambda $
-tableau. Define
![]() $R_{t_0}$
(resp.
$R_{t_0}$
(resp.
![]() $C_{t_0}$
) to be the subgroup of
$C_{t_0}$
) to be the subgroup of
![]() $\mathfrak {S}_N$
that preserves each row (resp. column) of
$\mathfrak {S}_N$
that preserves each row (resp. column) of
![]() $t_0$
. We define
$t_0$
. We define
 $$ \begin{align*}a_{\lambda}:=\sum_{\sigma\in R_{t_0}}\sigma,\quad b_{\lambda}:=\sum_{\sigma\in C_{t_0}}\mathrm{sgn}(\sigma)\sigma\in\Bbbk\mathfrak{S}_N.\end{align*} $$
$$ \begin{align*}a_{\lambda}:=\sum_{\sigma\in R_{t_0}}\sigma,\quad b_{\lambda}:=\sum_{\sigma\in C_{t_0}}\mathrm{sgn}(\sigma)\sigma\in\Bbbk\mathfrak{S}_N.\end{align*} $$
For each
![]() $\lambda \vdash N$
, the Young symmetrizer
$\lambda \vdash N$
, the Young symmetrizer
![]() $c_{\lambda }$
is defined by
$c_{\lambda }$
is defined by
The Specht module
![]() $S^{\lambda }$
, which is an irreducible representation of
$S^{\lambda }$
, which is an irreducible representation of
![]() $\mathfrak {S}_N$
corresponding to
$\mathfrak {S}_N$
corresponding to
![]() $\lambda $
, can be constructed as
$\lambda $
, can be constructed as
Lemma 5.1. We have the following decomposition of
![]() $\Bbbk \mathfrak {S}_N$
-bimodules
$\Bbbk \mathfrak {S}_N$
-bimodules
Proof. This follows from basic facts of representation theory. The reader is referred to [Reference Fulton6] and [Reference Sagan21].
For
![]() $N',N''\geq 0$
, let
$N',N''\geq 0$
, let
![]() $N=N'+N''$
. For
$N=N'+N''$
. For
![]() $\mu \vdash N',\nu \vdash N''$
, let
$\mu \vdash N',\nu \vdash N''$
, let
![]() $S^{\mu }\diamond S^{\nu }$
denote the representation of
$S^{\mu }\diamond S^{\nu }$
denote the representation of
![]() $\mathfrak {S}_N$
induced from the tensor product representation
$\mathfrak {S}_N$
induced from the tensor product representation
![]() $S^{\mu }\boxtimes S^{\nu }$
of
$S^{\mu }\boxtimes S^{\nu }$
of
![]() $\mathfrak {S}_{N'}\times \mathfrak {S}_{N''}$
by the inclusion of
$\mathfrak {S}_{N'}\times \mathfrak {S}_{N''}$
by the inclusion of
![]() $\mathfrak {S}_{N'}\times \mathfrak {S}_{N''}$
in
$\mathfrak {S}_{N'}\times \mathfrak {S}_{N''}$
in
![]() $\mathfrak {S}_N$
. By the Littlewood–Richardson rule, we have
$\mathfrak {S}_N$
. By the Littlewood–Richardson rule, we have
where
![]() $LR_{\mu ,\nu }^{\lambda }$
denotes the Littlewood–Richardson coefficient. We have the following lemma by using basic facts of representation theory of
$LR_{\mu ,\nu }^{\lambda }$
denotes the Littlewood–Richardson coefficient. We have the following lemma by using basic facts of representation theory of
![]() $\mathfrak {S}_N$
.
$\mathfrak {S}_N$
.
Lemma 5.2. Let
![]() $N=N'+N''$
for
$N=N'+N''$
for
![]() $N',N''\geq 0$
. Let
$N',N''\geq 0$
. Let
![]() $\lambda \vdash N,\mu \vdash N',\nu \vdash N''$
, respectively. We have
$\lambda \vdash N,\mu \vdash N',\nu \vdash N''$
, respectively. We have
In particular, if the Littlewood–Richardson coefficient
![]() $LR_{\mu ,\nu }^{\lambda }=0$
, then we have
$LR_{\mu ,\nu }^{\lambda }=0$
, then we have
5.2 Contraction map
We have an isomorphism of
![]() $\operatorname {GL}(V_n)$
-modules
$\operatorname {GL}(V_n)$
-modules
where
![]() $D_{d,k}$
is the
$D_{d,k}$
is the
![]() $\Bbbk $
-vector space spanned by
$\Bbbk $
-vector space spanned by
![]() $[2d-k]$
-colored open Jacobi diagrams of degree d such that the map
$[2d-k]$
-colored open Jacobi diagrams of degree d such that the map
![]() $\{\text {univalent vertices of }D\}\rightarrow [2d-k]$
that gives the coloring of D is a bijection. Thus, any element of
$\{\text {univalent vertices of }D\}\rightarrow [2d-k]$
that gives the coloring of D is a bijection. Thus, any element of
![]() $B_{d,k}(n)$
can be written in the form
$B_{d,k}(n)$
can be written in the form
for
![]() $u\in D_{d,k}$
and
$u\in D_{d,k}$
and
![]() $w_1,\cdots , w_{2d-k}\in V_n$
.
$w_1,\cdots , w_{2d-k}\in V_n$
.
For
![]() $\lambda \vdash 2d-k$
, let
$\lambda \vdash 2d-k$
, let
![]() $B_{d,k}(n)_\lambda $
be the isotypic component of
$B_{d,k}(n)_\lambda $
be the isotypic component of
![]() $B_{d,k}(n)$
corresponding to
$B_{d,k}(n)$
corresponding to
![]() $\lambda $
; that is,
$\lambda $
; that is,
We have
![]() $B_{d,k}(n)=\bigoplus _{\lambda \vdash 2d-k}B_{d,k}(n)_{\lambda }$
.
$B_{d,k}(n)=\bigoplus _{\lambda \vdash 2d-k}B_{d,k}(n)_{\lambda }$
.
We define a contraction map
which is an analogue of the contraction map defined in Appendix B of [Reference Fulton6].
Let
![]() $p\geq q$
. For
$p\geq q$
. For
![]() $I=(i_1,\cdots ,i_{q})$
such that
$I=(i_1,\cdots ,i_{q})$
such that
![]() $i_1,\cdots ,i_{q}$
are distinct elements of
$i_1,\cdots ,i_{q}$
are distinct elements of
![]() $[p]$
, define a contraction map
$[p]$
, define a contraction map
by
 $$ \begin{align*}c^I((w_1\otimes\cdots\otimes w_p)\otimes(y_1\otimes\cdots\otimes y_q))= \left(\prod_{j=1}^{q}\langle w_{i_{j}},y_j\rangle\right) w_1\otimes\cdots\hat{w}_{i_1}\cdots\hat{w}_{i_q}\cdots\otimes w_{p}, \end{align*} $$
$$ \begin{align*}c^I((w_1\otimes\cdots\otimes w_p)\otimes(y_1\otimes\cdots\otimes y_q))= \left(\prod_{j=1}^{q}\langle w_{i_{j}},y_j\rangle\right) w_1\otimes\cdots\hat{w}_{i_1}\cdots\hat{w}_{i_q}\cdots\otimes w_{p}, \end{align*} $$
where
![]() $\hat {w}_{i_1}\cdots \hat {w}_{i_q}$
denotes the omission of
$\hat {w}_{i_1}\cdots \hat {w}_{i_q}$
denotes the omission of
![]() $w_{i_1},\cdots ,w_{i_q}$
and where
$w_{i_1},\cdots ,w_{i_q}$
and where
![]() $\langle -,-\rangle :V_n\otimes V_n^{\ast }\rightarrow \Bbbk $
denotes the dual pairing. (See [Reference Fulton6] for details.)
$\langle -,-\rangle :V_n\otimes V_n^{\ast }\rightarrow \Bbbk $
denotes the dual pairing. (See [Reference Fulton6] for details.)
We next consider a diagrammatic version of the above contraction map
![]() $c^I$
. Let
$c^I$
. Let
![]() $2d-k\geq r+1$
. For
$2d-k\geq r+1$
. For
![]() $I=(i_1,\cdots ,i_{r+1})\in [2d-k]^{r+1}$
such that
$I=(i_1,\cdots ,i_{r+1})\in [2d-k]^{r+1}$
such that
![]() $i_1,\cdots ,i_{r+1}$
are distinct, we define a linear map
$i_1,\cdots ,i_{r+1}$
are distinct, we define a linear map
by contracting colorings of a Jacobi diagram and leaves of a rooted trivalent tree; that is,

where
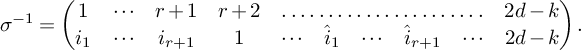
We define a contraction map
by
![]() $c=\sum _{I=(i_1,\cdots ,i_{r+1})\in [2d-k]^{r+1}:\text {distinct}}c^I$
. By using the contraction map c, we define a map
$c=\sum _{I=(i_1,\cdots ,i_{r+1})\in [2d-k]^{r+1}:\text {distinct}}c^I$
. By using the contraction map c, we define a map
by
![]() $\gamma _{d,k}^r(g)(u'):=c(u'\otimes g)$
for
$\gamma _{d,k}^r(g)(u'):=c(u'\otimes g)$
for
![]() $g\in T_r(n), u'=u(w_1,\cdots ,w_{2d-k})\in B_{d,k}(n)$
.
$g\in T_r(n), u'=u(w_1,\cdots ,w_{2d-k})\in B_{d,k}(n)$
.
5.3 Vanishing conditions for the contraction map
Here, we observe that the contraction map vanishes under certain specific conditions.
For
![]() $r\geq 0$
, a trivalent tree is called a based trivalent tree of degree r if it has one distinguished univalent vertex with no coloring (called a base) and
$r\geq 0$
, a trivalent tree is called a based trivalent tree of degree r if it has one distinguished univalent vertex with no coloring (called a base) and
![]() $r+1$
univalent vertices (called leaves) that are colored by distinct elements of
$r+1$
univalent vertices (called leaves) that are colored by distinct elements of
![]() $[r+1]$
. (Note that a based trivalent tree is different from a rooted trivalent tree.) Let
$[r+1]$
. (Note that a based trivalent tree is different from a rooted trivalent tree.) Let
![]() $L_{r}$
denote the
$L_{r}$
denote the
![]() $\mathbb {Z}$
-module spanned by based trivalent trees of degree r modulo the AS and IHX relations. The symmetric group
$\mathbb {Z}$
-module spanned by based trivalent trees of degree r modulo the AS and IHX relations. The symmetric group
![]() $\mathfrak {S}_{r+1}$
acts on the
$\mathfrak {S}_{r+1}$
acts on the
![]() $\mathbb {Z}$
-module
$\mathbb {Z}$
-module
![]() $L_{r}$
by the action on colorings of based trivalent trees. Then we have
$L_{r}$
by the action on colorings of based trivalent trees. Then we have
On the other hand,
![]() $\mathcal {L}_{r+1}(n)$
has a
$\mathcal {L}_{r+1}(n)$
has a
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module structure by the standard action on each factor. (See [Reference Fulton and Harris7] for representation theory of
$\operatorname {GL}(n;\mathbb {Z})$
-module structure by the standard action on each factor. (See [Reference Fulton and Harris7] for representation theory of
![]() $\operatorname {GL}(n;\mathbb {Z})$
.) For
$\operatorname {GL}(n;\mathbb {Z})$
.) For
![]() $\mu \vdash r+1$
, let
$\mu \vdash r+1$
, let
![]() $\mathcal {L}_{r+1}(n)_{\mu }$
denote the isotypic component of
$\mathcal {L}_{r+1}(n)_{\mu }$
denote the isotypic component of
![]() $\mathcal {L}_{r+1}(n)$
corresponding to
$\mathcal {L}_{r+1}(n)$
corresponding to
![]() $\mu $
; that is,
$\mu $
; that is,
We have
![]() $\mathcal {L}_{r+1}(n)=\bigoplus _{\mu \vdash r+1}\mathcal {L}_{r+1}(n)_{\mu }$
.
$\mathcal {L}_{r+1}(n)=\bigoplus _{\mu \vdash r+1}\mathcal {L}_{r+1}(n)_{\mu }$
.
For partitions
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
, we write
$\mu $
, we write
![]() $\lambda \nsupseteq \mu $
if the Young diagram of
$\lambda \nsupseteq \mu $
if the Young diagram of
![]() $\lambda $
does not contain that of
$\lambda $
does not contain that of
![]() $\mu $
.
$\mu $
.
Proposition 5.3. For
![]() $2d-k\geq r+1$
, let
$2d-k\geq r+1$
, let
![]() $\lambda \vdash 2d-k$
and
$\lambda \vdash 2d-k$
and
![]() $\mu \vdash r+1$
. We have
$\mu \vdash r+1$
. We have
 $$ \begin{align*}c(B_{d,k}(n)_{\lambda}\otimes (H^{\ast}\otimes \mathcal{L}_{r+1}(n)_{\mu})) \subset \bigoplus_{\rho:LR^{\lambda}_{\mu,\nu}LR^{\rho}_{\nu,(1)}\neq0 \text{ for some }\nu} B_{d,k+r}(n)_{\rho}. \end{align*} $$
$$ \begin{align*}c(B_{d,k}(n)_{\lambda}\otimes (H^{\ast}\otimes \mathcal{L}_{r+1}(n)_{\mu})) \subset \bigoplus_{\rho:LR^{\lambda}_{\mu,\nu}LR^{\rho}_{\nu,(1)}\neq0 \text{ for some }\nu} B_{d,k+r}(n)_{\rho}. \end{align*} $$
In particular, if
![]() $\lambda \nsupseteq \mu $
, then we have
$\lambda \nsupseteq \mu $
, then we have
Proof. Any element of
![]() $B_{d,k}(n)_{\lambda }$
is a linear sum of
$B_{d,k}(n)_{\lambda }$
is a linear sum of
![]() $(c_{\lambda }\cdot u)(w_1,\cdots ,w_{2d-k})$
, where
$(c_{\lambda }\cdot u)(w_1,\cdots ,w_{2d-k})$
, where
![]() $u(w_1,\cdots ,w_{2d-k})\in B_{d,k}(n)$
. Any element of
$u(w_1,\cdots ,w_{2d-k})\in B_{d,k}(n)$
. Any element of
![]() $L_{r}$
is a linear sum of
$L_{r}$
is a linear sum of

for
![]() $\pi \in \mathfrak {S}_{r+1}$
. Thus, any element of
$\pi \in \mathfrak {S}_{r+1}$
. Thus, any element of
![]() $H^{\ast }\otimes \mathcal {L}_{r+1}(n)_{\mu }$
is a linear sum of
$H^{\ast }\otimes \mathcal {L}_{r+1}(n)_{\mu }$
is a linear sum of
![]() $w\otimes ((y_1\otimes \cdots \otimes y_{r+1})\otimes c_{\mu }\cdot L)$
for
$w\otimes ((y_1\otimes \cdots \otimes y_{r+1})\otimes c_{\mu }\cdot L)$
for
![]() $w\in H^{\ast }, y_1,\cdots ,y_{r+1}\in H$
.
$w\in H^{\ast }, y_1,\cdots ,y_{r+1}\in H$
.
For any
![]() $I=(i_1,\cdots ,i_{r+1})\in [2d-k]^{r+1}$
such that
$I=(i_1,\cdots ,i_{r+1})\in [2d-k]^{r+1}$
such that
![]() $i_1,\cdots ,i_{r+1}$
are distinct, we have
$i_1,\cdots ,i_{r+1}$
are distinct, we have
 $$ \begin{align*}c^I((c_{\lambda}\cdot u)(w_1,\cdots,w_{2d-k})\otimes (w\otimes ((y_1 \otimes \cdots\otimes y_{r+1})\otimes c_{\mu}\cdot L))) =\prod_{j=1}^{r+1}\langle w_{i_j}, y_j \rangle D, \end{align*} $$
$$ \begin{align*}c^I((c_{\lambda}\cdot u)(w_1,\cdots,w_{2d-k})\otimes (w\otimes ((y_1 \otimes \cdots\otimes y_{r+1})\otimes c_{\mu}\cdot L))) =\prod_{j=1}^{r+1}\langle w_{i_j}, y_j \rangle D, \end{align*} $$
where


Let
![]() $l=2d-k-r-1$
. By Lemma 5.1, we have
$l=2d-k-r-1$
. By Lemma 5.1, we have
where
![]() $\tau _{i,1},\tau _{i,2}\in \Bbbk \mathfrak {S}_l$
. Thus, we have
$\tau _{i,1},\tau _{i,2}\in \Bbbk \mathfrak {S}_l$
. Thus, we have

If
![]() $LR^{\lambda }_{\mu ,\nu }=0$
for any
$LR^{\lambda }_{\mu ,\nu }=0$
for any
![]() $\nu \vdash l$
, then we have
$\nu \vdash l$
, then we have
![]() $D=0$
by Lemma 5.2. Otherwise, since we have
$D=0$
by Lemma 5.2. Otherwise, since we have
 $$ \begin{align*}\operatorname{id}_1\otimes c_{\nu}\in \bigoplus_{\rho\vdash l+1} (S^{\rho})^{LR^{\rho}_{\nu,(1)}}, \end{align*} $$
$$ \begin{align*}\operatorname{id}_1\otimes c_{\nu}\in \bigoplus_{\rho\vdash l+1} (S^{\rho})^{LR^{\rho}_{\nu,(1)}}, \end{align*} $$
by the Littlewood–Richardson rule, it follows that
 $$ \begin{align*}D\in\bigoplus_{\rho:LR^{\lambda}_{\mu,\nu}LR^{\rho}_{\nu,(1)}\neq0 \text{ for some }\nu}\left( B_{d,k+r}(n)\right)_{\rho}. \end{align*} $$
$$ \begin{align*}D\in\bigoplus_{\rho:LR^{\lambda}_{\mu,\nu}LR^{\rho}_{\nu,(1)}\neq0 \text{ for some }\nu}\left( B_{d,k+r}(n)\right)_{\rho}. \end{align*} $$
If
![]() $\lambda \nsupseteq \mu $
, then
$\lambda \nsupseteq \mu $
, then
![]() $LR_{\mu ,\nu }^{\lambda }=0$
for any
$LR_{\mu ,\nu }^{\lambda }=0$
for any
![]() $\nu \vdash l$
. Thus, we have
$\nu \vdash l$
. Thus, we have
Remark 5.4. Note that we have
![]() $\mathcal {L}_2(n)=\mathcal {L}_2(n)_{(1^2)}$
. Thus, the restriction
$\mathcal {L}_2(n)=\mathcal {L}_2(n)_{(1^2)}$
. Thus, the restriction
of the contraction map vanishes unless
![]() $\rho $
can be obtained from
$\rho $
can be obtained from
![]() $\lambda $
by taking away one box from each of two different rows of
$\lambda $
by taking away one box from each of two different rows of
![]() $\lambda $
and then by adding one box.
$\lambda $
and then by adding one box.
6 Correspondence between the map
 $\tilde {\beta }_{d,k}^r$
and the map
$\tilde {\beta }_{d,k}^r$
and the map
 $\gamma _{d,k}^r$
$\gamma _{d,k}^r$
In this section, we prove that the map
![]() $\tilde {\beta }_{d,k}^r$
defined in Section 4 can be identified with the map
$\tilde {\beta }_{d,k}^r$
defined in Section 4 can be identified with the map
![]() $\gamma _{d,k}^r$
defined in Section 5 via the Johnson homomorphism of
$\gamma _{d,k}^r$
defined in Section 5 via the Johnson homomorphism of
![]() $\operatorname {End}(F_n)$
defined in Section 3.
$\operatorname {End}(F_n)$
defined in Section 3.
Theorem 6.1. We have
![]() $\tilde {\beta }_{d,k}^r=(-1)^r\cdot \gamma _{d,k}^r\circ \tilde {\tau }_r$
. That is, we have the following commutative diagram (up to sign):
$\tilde {\beta }_{d,k}^r=(-1)^r\cdot \gamma _{d,k}^r\circ \tilde {\tau }_r$
. That is, we have the following commutative diagram (up to sign):

Proof. The
![]() $\mathbb {Z}$
-module
$\mathbb {Z}$
-module
![]() $H^{\ast }\otimes \mathcal {L}_{r+1}(n)$
is spanned by
$H^{\ast }\otimes \mathcal {L}_{r+1}(n)$
is spanned by
![]() $v_i\otimes [\bar {x}_{i_1},\cdots ,[\bar {x}_{i_r},\bar {x}_{i_{r+1}}]\cdots ]$
for
$v_i\otimes [\bar {x}_{i_1},\cdots ,[\bar {x}_{i_r},\bar {x}_{i_{r+1}}]\cdots ]$
for
![]() $i, i_1,\cdots ,i_{r+1}\in [n]$
. Define
$i, i_1,\cdots ,i_{r+1}\in [n]$
. Define
![]() $\phi \in \operatorname {End}(F_n)$
by
$\phi \in \operatorname {End}(F_n)$
by
It is easily checked that
![]() $\phi \in \mathcal {E}_{r}(n)$
and that
$\phi \in \mathcal {E}_{r}(n)$
and that
![]() $\tilde {\tau }_r([\phi ]_r)=v_i\otimes [\bar {x}_{i_1},\cdots ,[\bar {x}_{i_r},\bar {x}_{i_{r+1}}]\cdots ]$
, where
$\tilde {\tau }_r([\phi ]_r)=v_i\otimes [\bar {x}_{i_1},\cdots ,[\bar {x}_{i_r},\bar {x}_{i_{r+1}}]\cdots ]$
, where
![]() $[\phi ]_r\in \operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
denotes the image of
$[\phi ]_r\in \operatorname {gr}^r(\mathcal {E}_{\ast }(n))$
denotes the image of
![]() $\phi $
under the projection.
$\phi $
under the projection.
Any element of
![]() $B_{d,k}(n)$
can be written as a linear sum of
$B_{d,k}(n)$
can be written as a linear sum of
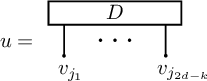
, where
![]() $1\leq j_1\leq \cdots \leq j_{2d-k}\leq n$
, by arranging the univalent vertices according to the order of indices of the colorings from left to right. We have
$1\leq j_1\leq \cdots \leq j_{2d-k}\leq n$
, by arranging the univalent vertices according to the order of indices of the colorings from left to right. We have

where
![]() $\tau ^{-1}\in \mathfrak {S}_{2d-k}$
is the
$\tau ^{-1}\in \mathfrak {S}_{2d-k}$
is the
![]() $(r+1,2d-k-r-1)$
-shuffle that maps
$(r+1,2d-k-r-1)$
-shuffle that maps
![]() $[r+1]\subset [2d-k]$
to
$[r+1]\subset [2d-k]$
to
![]() $\{\alpha _l\}$
, and
$\{\alpha _l\}$
, and
![]() $\sigma \in \mathfrak {S}_{r+1}$
satisfies
$\sigma \in \mathfrak {S}_{r+1}$
satisfies
![]() $\sigma ^{-1}(l)=\tau (\alpha _l)$
for any
$\sigma ^{-1}(l)=\tau (\alpha _l)$
for any
![]() $l\in [r+1]$
.
$l\in [r+1]$
.
Let
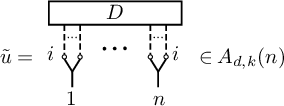
, which can be obtained from u by replacing univalent vertices with
and combining solid lines whose corresponding colorings of u are the same. Then
![]() $\tilde {u}$
is a lift of u; that is, we have
$\tilde {u}$
is a lift of u; that is, we have
![]() $\theta _{d,n,k}(\tilde {u})=u$
. By the definition of
$\theta _{d,n,k}(\tilde {u})=u$
. By the definition of
![]() $\tilde {\beta }_{d,k}^r$
, we have
$\tilde {\beta }_{d,k}^r$
, we have
We have

where
![]() $\rho ^{-1}\in \mathfrak {S}_{n}$
is the
$\rho ^{-1}\in \mathfrak {S}_{n}$
is the
![]() $(r+1,n-r-1)$
-shuffle that maps
$(r+1,n-r-1)$
-shuffle that maps
![]() $[r+1]\subset [n]$
to
$[r+1]\subset [n]$
to
![]() $\{i_1,\cdots ,i_{r+1}\}$
and
$\{i_1,\cdots ,i_{r+1}\}$
and
![]() $\pi \in \mathfrak {S}_{r+1}$
satisfies
$\pi \in \mathfrak {S}_{r+1}$
satisfies
![]() $\pi ^{-1}(j)=\rho (i_j)$
for any
$\pi ^{-1}(j)=\rho (i_j)$
for any
![]() $j\in [r+1]$
. By using Lemma 4.9, we have for
$j\in [r+1]$
. By using Lemma 4.9, we have for
![]() $\beta _1,\cdots ,\beta _{r+1}\geq 0$
,
$\beta _1,\cdots ,\beta _{r+1}\geq 0$
,

In the last case, the corresponding term of
![]() $[\tilde {u},\phi ]$
is included in
$[\tilde {u},\phi ]$
is included in
![]() $A_{d,k+r+1}(n)$
.
$A_{d,k+r+1}(n)$
.
Thus, by equation (6.1) and Lemma 4.8 (2), we have

7 The
 $\operatorname {GL}(V_n)$
-module structure of
$\operatorname {GL}(V_n)$
-module structure of
 $B_d(n)$
$B_d(n)$
In this section, we consider the
![]() $\operatorname {GL}(V_n)$
-module structure of
$\operatorname {GL}(V_n)$
-module structure of
![]() $B_d(n)$
and give a decomposition of
$B_d(n)$
and give a decomposition of
![]() $B_d(n)$
with respect to connected parts. Moreover, we compute the irreducible decomposition of
$B_d(n)$
with respect to connected parts. Moreover, we compute the irreducible decomposition of
![]() $B_d(n)$
for
$B_d(n)$
for
![]() $d=3,4,5$
and that of
$d=3,4,5$
and that of
![]() $B_{d,0}(n),B_{d,1}(n)$
for any d. Lastly, we show the surjectivity of the bracket map which we defined in Section 4.
$B_{d,0}(n),B_{d,1}(n)$
for any d. Lastly, we show the surjectivity of the bracket map which we defined in Section 4.
Let
![]() $B_{d,k}^c(n)\subset B_{d,k}(n)$
denote the connected part of
$B_{d,k}^c(n)\subset B_{d,k}(n)$
denote the connected part of
![]() $B_{d,k}(n)$
, which is spanned by connected
$B_{d,k}(n)$
, which is spanned by connected
![]() $V_n$
-colored open Jacobi diagrams. Let
$V_n$
-colored open Jacobi diagrams. Let
![]() $D_{d,k}^c\subset D_{d,k}$
denote the connected part of
$D_{d,k}^c\subset D_{d,k}$
denote the connected part of
![]() $D_{d,k}$
, which is spanned by connected
$D_{d,k}$
, which is spanned by connected
![]() $[2d-k]$
-colored open Jacobi diagrams. We have an isomorphism of
$[2d-k]$
-colored open Jacobi diagrams. We have an isomorphism of
![]() $\operatorname {GL}(V_n)$
-modules
$\operatorname {GL}(V_n)$
-modules
which is the connected version of equation (5.2).
The direct sum
![]() $\bigoplus _{d\geq 0}B_d(n)$
has the following coalgebra structure. This is an analogue of the coalgebra structure of the space of open Jacobi diagrams colored by one element [Reference Bar-Natan2]. Let
$\bigoplus _{d\geq 0}B_d(n)$
has the following coalgebra structure. This is an analogue of the coalgebra structure of the space of open Jacobi diagrams colored by one element [Reference Bar-Natan2]. Let
![]() $C=\bigcup _{i\in I}C_i$
be a presentation of a diagram
$C=\bigcup _{i\in I}C_i$
be a presentation of a diagram
![]() $C\in \bigoplus _{d\geq 0}B_d(n)$
as the disjoint union of its connected components. The comultiplication
$C\in \bigoplus _{d\geq 0}B_d(n)$
as the disjoint union of its connected components. The comultiplication
![]() $\Delta $
is defined by
$\Delta $
is defined by
 $$ \begin{align*}\Delta(C)=\sum_{J\subset I}\left(\bigcup_{i\in J}C_i\right)\otimes \left(\bigcup_{i\in I\setminus J}C_i\right).\end{align*} $$
$$ \begin{align*}\Delta(C)=\sum_{J\subset I}\left(\bigcup_{i\in J}C_i\right)\otimes \left(\bigcup_{i\in I\setminus J}C_i\right).\end{align*} $$
Note that the connected part
![]() $\bigoplus _{d,k\geq 0}B_{d,k}^c(n)$
coincides with the primitive part of the coalgebra
$\bigoplus _{d,k\geq 0}B_{d,k}^c(n)$
coincides with the primitive part of the coalgebra
![]() $\bigoplus _{d\geq 0}B_d(n)$
.
$\bigoplus _{d\geq 0}B_d(n)$
.
7.1 Decomposition of
 $B_d(n)$
with respect to connected parts
$B_d(n)$
with respect to connected parts
Note that
![]() $D_{d,k}^c\neq 0$
if and only if
$D_{d,k}^c\neq 0$
if and only if
![]() $d-1\leq k\leq 2d-2$
because each element of
$d-1\leq k\leq 2d-2$
because each element of
![]() $D_{d,k}^c$
has at least two univalent vertices and is connected. For
$D_{d,k}^c$
has at least two univalent vertices and is connected. For
![]() $d\geq 1,k\geq 0$
, the pair
$d\geq 1,k\geq 0$
, the pair
![]() $(d,k)$
is called a good pair if
$(d,k)$
is called a good pair if
![]() $d-1\leq k\leq 2d-2$
. We consider the following decomposition of a pair
$d-1\leq k\leq 2d-2$
. We consider the following decomposition of a pair
![]() $(d,k)$
to consider the decomposition of an element of
$(d,k)$
to consider the decomposition of an element of
![]() $D_{d,k}$
into the connected parts.
$D_{d,k}$
into the connected parts.
Definition 7.1. Let
![]() $d,\ k\geq 0$
. A decomposition of
$d,\ k\geq 0$
. A decomposition of
![]() $(d,k)$
into good pairs is a sequence of triples of integers
$(d,k)$
into good pairs is a sequence of triples of integers
such that
![]() $(d_i,k_i)$
are good pairs,
$(d_i,k_i)$
are good pairs,
![]() $a_i\geq 1$
,
$a_i\geq 1$
,
 $$ \begin{align*}\sum_{i=1}^l a_i d_i = d, \quad \sum_{i=1}^l a_i k_i = k, \end{align*} $$
$$ \begin{align*}\sum_{i=1}^l a_i d_i = d, \quad \sum_{i=1}^l a_i k_i = k, \end{align*} $$
and
in the lexicographical order.
Let
![]() $\Pi (d,k)$
be the set of all decompositions of
$\Pi (d,k)$
be the set of all decompositions of
![]() $(d,k)$
into good pairs.
$(d,k)$
into good pairs.
For example, we have
For any diagram
![]() $K\in D_{d,k}$
, we can assign a decomposition of
$K\in D_{d,k}$
, we can assign a decomposition of
![]() $(d,k)$
into good pairs such that
$(d,k)$
into good pairs such that
![]() $d_i$
and
$d_i$
and
![]() $k_i$
correspond to the degree and the number of trivalent vertices of each connected component of K, respectively, and
$k_i$
correspond to the degree and the number of trivalent vertices of each connected component of K, respectively, and
![]() $a_i$
corresponds to the multiplicity of
$a_i$
corresponds to the multiplicity of
![]() $(d_i,k_i)$
. We call a coloring of
$(d_i,k_i)$
. We call a coloring of
![]() $K=\bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}\in D_{d,k}$
standard if the set of colorings of
$K=\bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}\in D_{d,k}$
standard if the set of colorings of
![]() $K_{i}^{(j)}\in D_{d_i,k_i}^c$
is
$K_{i}^{(j)}\in D_{d_i,k_i}^c$
is
 $$ \begin{align*}\left\{\sum_{p=1}^{i-1}(2d_p-k_p)a_p +(j-1)(2d_i-k_i)+1 ,\cdots, \sum_{p=1}^{i-1}(2d_p-k_p)a_p +j(2d_i-k_i)\right\}\end{align*} $$
$$ \begin{align*}\left\{\sum_{p=1}^{i-1}(2d_p-k_p)a_p +(j-1)(2d_i-k_i)+1 ,\cdots, \sum_{p=1}^{i-1}(2d_p-k_p)a_p +j(2d_i-k_i)\right\}\end{align*} $$
for each
![]() $i\in [l],j\in [a_i]$
.
$i\in [l],j\in [a_i]$
.
Theorem 7.2. For
![]() $d,k,n\geq 0$
, we have an isomorphism of
$d,k,n\geq 0$
, we have an isomorphism of
![]() $\operatorname {GL}(V_n)$
-modules
$\operatorname {GL}(V_n)$
-modules
 $$ \begin{align} B_{d,k}(n) \cong \bigoplus_{\pi =((a_1,d_1, k_1),\cdots,(a_l,d_l, k_l))\in\Pi(d,k)} \left(\bigotimes_{i=1}^l \operatorname{Sym}^{a_i}(B_{d_i,k_i}^c(n))\right). \end{align} $$
$$ \begin{align} B_{d,k}(n) \cong \bigoplus_{\pi =((a_1,d_1, k_1),\cdots,(a_l,d_l, k_l))\in\Pi(d,k)} \left(\bigotimes_{i=1}^l \operatorname{Sym}^{a_i}(B_{d_i,k_i}^c(n))\right). \end{align} $$
To prove this, we need the following proposition.
Proposition 7.3. Let
![]() $d,k\geq 0$
. We have an isomorphism of
$d,k\geq 0$
. We have an isomorphism of
![]() $\mathfrak {S}_{2d-k}$
-modules
$\mathfrak {S}_{2d-k}$
-modules
 $$ \begin{align} D_{d,k}\cong \bigoplus_{\pi =((a_1,d_1,k_1),\cdots,(a_l,d_l,k_l))\in\Pi(d,k)} \operatorname{Ind}_{\prod_{i=1}^l(\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})}^{\mathfrak{S}_{2d-k}} (\bigotimes_{i=1}^l(D_{d_i,k_i}^c)^{\otimes a_i}), \end{align} $$
$$ \begin{align} D_{d,k}\cong \bigoplus_{\pi =((a_1,d_1,k_1),\cdots,(a_l,d_l,k_l))\in\Pi(d,k)} \operatorname{Ind}_{\prod_{i=1}^l(\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})}^{\mathfrak{S}_{2d-k}} (\bigotimes_{i=1}^l(D_{d_i,k_i}^c)^{\otimes a_i}), \end{align} $$
where
![]() $\mathfrak {S}_{2d_i-k_i}\wr \mathfrak {S}_{a_i}={\mathfrak {S}_{2d_i-k_i}}^{a_i}\rtimes \mathfrak {S}_{a_i}\subset \mathfrak {S}_{(2d_i-k_i)a_i}$
is the wreath product.
$\mathfrak {S}_{2d_i-k_i}\wr \mathfrak {S}_{a_i}={\mathfrak {S}_{2d_i-k_i}}^{a_i}\rtimes \mathfrak {S}_{a_i}\subset \mathfrak {S}_{(2d_i-k_i)a_i}$
is the wreath product.
For example, we have an isomorphism of
![]() $\mathfrak {S}_6$
-modules for
$\mathfrak {S}_6$
-modules for
![]() $(d,k)=(4,2)$
, which corresponds to equation (7.1),
$(d,k)=(4,2)$
, which corresponds to equation (7.1),
For example,
and
Via the above isomorphism, the element
corresponds to the element
Proof of Proposition 7.3 Let
![]() $D^{\prime }_{d,k}$
denote the right-hand side of equation (7.3).
$D^{\prime }_{d,k}$
denote the right-hand side of equation (7.3).
For any coset
![]() $\sigma \in \mathfrak {S}_{2d-k}/\prod _{i=1}^l (\mathfrak {S}_{2d_i-k_i}\wr \mathfrak {S}_{a_i})$
, we fix a representative
$\sigma \in \mathfrak {S}_{2d-k}/\prod _{i=1}^l (\mathfrak {S}_{2d_i-k_i}\wr \mathfrak {S}_{a_i})$
, we fix a representative
![]() $\tilde {\sigma }\in \mathfrak {S}_{2d-k}$
of
$\tilde {\sigma }\in \mathfrak {S}_{2d-k}$
of
![]() $\sigma $
.
$\sigma $
.
Any element of
![]() $D^{\prime }_{d,k}$
can be written uniquely as a linear sum of
$D^{\prime }_{d,k}$
can be written uniquely as a linear sum of
 $$ \begin{align*}K=\tilde{\sigma}\cdot\bigotimes_{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}, \end{align*} $$
$$ \begin{align*}K=\tilde{\sigma}\cdot\bigotimes_{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}, \end{align*} $$
where
![]() $K_{i}^{(j)}\in D_{d_i,k_i}^c$
. We assign
$K_{i}^{(j)}\in D_{d_i,k_i}^c$
. We assign
![]() $\bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i}K_{i}^{(j)}$
a standard coloring in
$\bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i}K_{i}^{(j)}$
a standard coloring in
![]() $[2d-k]$
according to the order of the colorings in
$[2d-k]$
according to the order of the colorings in
![]() $\bigsqcup _{i=1}^{l} [2d_i-k_i]^{a_i}$
of
$\bigsqcup _{i=1}^{l} [2d_i-k_i]^{a_i}$
of
![]() $\bigotimes _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}$
. For example, if
$\bigotimes _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}$
. For example, if

then the corresponding coloring of
![]() $\bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i}K_{i}^{(j)}$
is
$\bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i}K_{i}^{(j)}$
is

Define a map
![]() $\Psi :D^{\prime }_{d,k}\rightarrow D_{d,k}$
by
$\Psi :D^{\prime }_{d,k}\rightarrow D_{d,k}$
by
 $$ \begin{align*}\Psi(K)=\tilde{\sigma}\cdot \bigsqcup_{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}, \end{align*} $$
$$ \begin{align*}\Psi(K)=\tilde{\sigma}\cdot \bigsqcup_{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}, \end{align*} $$
where
![]() $\tilde {\sigma }\in \mathfrak {S}_{2d-k}$
acts on the colorings in
$\tilde {\sigma }\in \mathfrak {S}_{2d-k}$
acts on the colorings in
![]() $[2d-k]$
. We can check that the map
$[2d-k]$
. We can check that the map
![]() $\Psi $
is an
$\Psi $
is an
![]() $\mathfrak {S}_{2d-k}$
-module map.
$\mathfrak {S}_{2d-k}$
-module map.
We need to check that
![]() $\Psi $
is bijective. If we have
$\Psi $
is bijective. If we have
![]() $\Psi (K)=\Psi (L)$
for
$\Psi (K)=\Psi (L)$
for
![]() $K=\tilde {\sigma }\cdot \bigotimes _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}$
,
$K=\tilde {\sigma }\cdot \bigotimes _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}$
,
![]() $L=\tilde {\tau }\cdot \bigotimes _{1\leq i\leq l, 1\leq j\leq a_i} L_{i}^{(j)}$
, then we have
$L=\tilde {\tau }\cdot \bigotimes _{1\leq i\leq l, 1\leq j\leq a_i} L_{i}^{(j)}$
, then we have
![]() $\sigma =\tau $
by looking at the set of colorings of each connected component. Since we fix the representatives of cosets of
$\sigma =\tau $
by looking at the set of colorings of each connected component. Since we fix the representatives of cosets of
![]() $\mathfrak {S}_{2d-k}/\prod _{i=1}^l (\mathfrak {S}_{2d_i-k_i}\wr \mathfrak {S}_{a_i})$
, we have
$\mathfrak {S}_{2d-k}/\prod _{i=1}^l (\mathfrak {S}_{2d_i-k_i}\wr \mathfrak {S}_{a_i})$
, we have
![]() $\tilde {\sigma }=\tilde {\tau }$
. Thus, we have
$\tilde {\sigma }=\tilde {\tau }$
. Thus, we have
![]() $K=L$
and
$K=L$
and
![]() $\Psi $
is injective. For any element
$\Psi $
is injective. For any element
![]() $K\in D_{d,k}$
, we can take
$K\in D_{d,k}$
, we can take
![]() $\sigma \in \mathfrak {S}_{2d-k}/\prod _{i=1}^l (\mathfrak {S}_{2d_i-k_i}\wr \mathfrak {S}_{a_i})$
such that
$\sigma \in \mathfrak {S}_{2d-k}/\prod _{i=1}^l (\mathfrak {S}_{2d_i-k_i}\wr \mathfrak {S}_{a_i})$
such that
![]() $K=\tilde {\sigma }\cdot \bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}$
, where
$K=\tilde {\sigma }\cdot \bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}$
, where
![]() $K_{i}^{(j)}\in D_{(d_i,k_i)}^c$
and
$K_{i}^{(j)}\in D_{(d_i,k_i)}^c$
and
![]() $\bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}$
has a standard coloring. Therefore,
$\bigsqcup _{1\leq i\leq l, 1\leq j\leq a_i} K_{i}^{(j)}$
has a standard coloring. Therefore,
![]() $\Psi $
is surjective.
$\Psi $
is surjective.
Proof of Theorem 7.2 By Proposition 7.3, we have
 $$ \begin{gather*} \begin{aligned} B_{d,k}(n) &\cong V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}}D_{d,k} \\ &\cong\bigoplus_{\pi\in \Pi(d,k)} \left(V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}} \operatorname{Ind}_{\prod_{i=1}^l (\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})}^{\mathfrak{S}_{2d-k}} \left(\bigotimes_{i=1}^l(D_{d_i,k_i}^c)^{\otimes a_i} \right) \right). \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} B_{d,k}(n) &\cong V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}}D_{d,k} \\ &\cong\bigoplus_{\pi\in \Pi(d,k)} \left(V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}} \operatorname{Ind}_{\prod_{i=1}^l (\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})}^{\mathfrak{S}_{2d-k}} \left(\bigotimes_{i=1}^l(D_{d_i,k_i}^c)^{\otimes a_i} \right) \right). \end{aligned} \end{gather*} $$
Moreover, we can check equation (7.2) as follows.
 $$ \begin{gather*} \begin{aligned} &V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}} \operatorname{Ind}_{\prod_{i=1}^l (\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})}^{\mathfrak{S}_{2d-k}} \left(\bigotimes_{i=1}^l(D_{d_i,k_i}^c)^{\otimes a_i} \right)\\ &\cong V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}} \operatorname{Ind}_{\prod_{i=1}^l \mathfrak{S}_{a_i(2d_i-k_i)}}^{\mathfrak{S}_{2d-k}} \left( \operatorname{Ind}_{\prod_{i=1}^l (\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})}^{\prod_{i=1}^l \mathfrak{S}_{a_i(2d_i-k_i)}} \left(\bigotimes_{i=1}^l(D_{d_i,k_i}^c)^{\otimes a_i} \right) \right)\\ &\cong V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}} \operatorname{Ind}_{\prod_{i=1}^l \mathfrak{S}_{a_i(2d_i-k_i)}}^{\mathfrak{S}_{2d-k}} \left( \bigotimes_{i=1}^l \operatorname{Ind}_{\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i}}^{\mathfrak{S}_{a_i(2d_i-k_i)}} \left((D_{d_i,k_i}^c)^{\otimes a_i} \right) \right)\\ &\cong V_n^{\otimes 2d-k}\otimes_{\Bbbk(\prod_{i=1}^l \mathfrak{S}_{a_i(2d_i-k_i)})} \left( \bigotimes_{i=1}^l \operatorname{Ind}_{\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i}}^{\mathfrak{S}_{a_i(2d_i-k_i)}} \left((D_{d_i,k_i}^c)^{\otimes a_i} \right) \right)\\ &\cong \bigotimes_{i=1}^l \left( V_n^{\otimes a_i(2d_i-k_i)}\otimes_{\Bbbk\mathfrak{S}_{a_i(2d_i-k_i)}} \left( \operatorname{Ind}_{\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i}}^{\mathfrak{S}_{a_i(2d_i-k_i)}} \left((D_{d_i,k_i}^c)^{\otimes a_i} \right) \right) \right)\\ &\cong \bigotimes_{i=1}^l \left( V_n^{\otimes a_i(2d_i-k_i)}\otimes_{\Bbbk(\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})} \left((D_{d_i,k_i}^c)^{\otimes a_i} \right) \right)\\ &\cong \bigotimes_{i=1}^l \operatorname{Sym}^{a_i}\left( V_n^{\otimes(2d_i-k_i)}\otimes_{\Bbbk\mathfrak{S}_{2d_i-k_i}} D_{d_i,k_i}^c \right)\\ &\cong \bigotimes_{i=1}^l \operatorname{Sym}^{a_i}\left(B_{d_i,k_i}^c(n)\right). \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} &V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}} \operatorname{Ind}_{\prod_{i=1}^l (\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})}^{\mathfrak{S}_{2d-k}} \left(\bigotimes_{i=1}^l(D_{d_i,k_i}^c)^{\otimes a_i} \right)\\ &\cong V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}} \operatorname{Ind}_{\prod_{i=1}^l \mathfrak{S}_{a_i(2d_i-k_i)}}^{\mathfrak{S}_{2d-k}} \left( \operatorname{Ind}_{\prod_{i=1}^l (\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})}^{\prod_{i=1}^l \mathfrak{S}_{a_i(2d_i-k_i)}} \left(\bigotimes_{i=1}^l(D_{d_i,k_i}^c)^{\otimes a_i} \right) \right)\\ &\cong V_n^{\otimes 2d-k}\otimes_{\Bbbk\mathfrak{S}_{2d-k}} \operatorname{Ind}_{\prod_{i=1}^l \mathfrak{S}_{a_i(2d_i-k_i)}}^{\mathfrak{S}_{2d-k}} \left( \bigotimes_{i=1}^l \operatorname{Ind}_{\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i}}^{\mathfrak{S}_{a_i(2d_i-k_i)}} \left((D_{d_i,k_i}^c)^{\otimes a_i} \right) \right)\\ &\cong V_n^{\otimes 2d-k}\otimes_{\Bbbk(\prod_{i=1}^l \mathfrak{S}_{a_i(2d_i-k_i)})} \left( \bigotimes_{i=1}^l \operatorname{Ind}_{\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i}}^{\mathfrak{S}_{a_i(2d_i-k_i)}} \left((D_{d_i,k_i}^c)^{\otimes a_i} \right) \right)\\ &\cong \bigotimes_{i=1}^l \left( V_n^{\otimes a_i(2d_i-k_i)}\otimes_{\Bbbk\mathfrak{S}_{a_i(2d_i-k_i)}} \left( \operatorname{Ind}_{\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i}}^{\mathfrak{S}_{a_i(2d_i-k_i)}} \left((D_{d_i,k_i}^c)^{\otimes a_i} \right) \right) \right)\\ &\cong \bigotimes_{i=1}^l \left( V_n^{\otimes a_i(2d_i-k_i)}\otimes_{\Bbbk(\mathfrak{S}_{2d_i-k_i}\wr\mathfrak{S}_{a_i})} \left((D_{d_i,k_i}^c)^{\otimes a_i} \right) \right)\\ &\cong \bigotimes_{i=1}^l \operatorname{Sym}^{a_i}\left( V_n^{\otimes(2d_i-k_i)}\otimes_{\Bbbk\mathfrak{S}_{2d_i-k_i}} D_{d_i,k_i}^c \right)\\ &\cong \bigotimes_{i=1}^l \operatorname{Sym}^{a_i}\left(B_{d_i,k_i}^c(n)\right). \end{aligned} \end{gather*} $$
7.2 Irreducible decomposition of
 $B_d(n)$
as
$B_d(n)$
as
 $\operatorname {GL}(V_n)$
-modules
$\operatorname {GL}(V_n)$
-modules
In this subsection, for simplicity, we write
![]() $V=V_n$
,
$V=V_n$
,
![]() $B_{d,k}=B_{d,k}(n)$
and
$B_{d,k}=B_{d,k}(n)$
and
![]() $B_{d,k}^c=B_{d,k}^c(n)$
.
$B_{d,k}^c=B_{d,k}^c(n)$
.
Let N be a nonnegative integer and
![]() $\lambda \vdash N$
. Recall from Section 5.1 that
$\lambda \vdash N$
. Recall from Section 5.1 that
![]() $S^\lambda $
denotes the Specht module, which is an irreducible representation of
$S^\lambda $
denotes the Specht module, which is an irreducible representation of
![]() $\mathfrak {S}_N$
corresponding to
$\mathfrak {S}_N$
corresponding to
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $V_{\lambda }=\mathbb {S}_{\lambda }V$
denote the image of V under the Schur functor
$V_{\lambda }=\mathbb {S}_{\lambda }V$
denote the image of V under the Schur functor
![]() $\mathbb {S}_{\lambda }$
. Note that
$\mathbb {S}_{\lambda }$
. Note that
![]() $V_{\lambda }$
is a simple
$V_{\lambda }$
is a simple
![]() $\operatorname {GL}(V)$
-module if
$\operatorname {GL}(V)$
-module if
![]() $n\geq r(\lambda )$
and that
$n\geq r(\lambda )$
and that
![]() $V_{\lambda }=0$
if
$V_{\lambda }=0$
if
![]() $n<r(\lambda )$
, where
$n<r(\lambda )$
, where
![]() $r(\lambda )$
is the number of rows of
$r(\lambda )$
is the number of rows of
![]() $\lambda $
.
$\lambda $
.
We use the Littlewood–Richardson rule, plethysms and results by Bar-Natan [Reference Bar-Natan4] to compute the irreducible decompositions of the
![]() $\operatorname {GL}(V)$
-modules
$\operatorname {GL}(V)$
-modules
![]() $B_d$
.
$B_d$
.
Proposition 7.4 Bar-Natan [Reference Bar-Natan4]
As
![]() $\mathfrak {S}_{2d-k}$
-modules, we have isomorphisms
$\mathfrak {S}_{2d-k}$
-modules, we have isomorphisms
Lemma 7.5. We have the following isomorphisms of the
![]() $\operatorname {GL}(V)$
-modules:
$\operatorname {GL}(V)$
-modules:
Proof. These follow from Proposition 7.4.
Proposition 7.6. For
![]() $d=3,4,5$
, we have the following irreducible decompositions of the
$d=3,4,5$
, we have the following irreducible decompositions of the
![]() $\operatorname {GL}(V)$
-modules
$\operatorname {GL}(V)$
-modules
![]() $B_d$
.
$B_d$
.
-
(1) We have
 $B_3=B_{3,0}\oplus \cdots \oplus B_{3,4},$
where
$B_3=B_{3,0}\oplus \cdots \oplus B_{3,4},$
where  $$ \begin{gather*} \begin{aligned} B_{3,0}&\cong V_{(6)}\oplus V_{(4,2)}\oplus V_{(2^3)},\\ B_{3,1}&\cong V_{(3,1^2)}\oplus V_{(2,1^3)},\\ B_{3,2}&\cong V_{(4)}\oplus V_{(3,1)}\oplus (V_{(2^2)})^{\oplus 2},\\ B_{3,3}&=B^c_{3,3}\cong V_{(1^3)},\\ B_{3,4}&=B^c_{3,4}\cong V_{(2)}. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} B_{3,0}&\cong V_{(6)}\oplus V_{(4,2)}\oplus V_{(2^3)},\\ B_{3,1}&\cong V_{(3,1^2)}\oplus V_{(2,1^3)},\\ B_{3,2}&\cong V_{(4)}\oplus V_{(3,1)}\oplus (V_{(2^2)})^{\oplus 2},\\ B_{3,3}&=B^c_{3,3}\cong V_{(1^3)},\\ B_{3,4}&=B^c_{3,4}\cong V_{(2)}. \end{aligned} \end{gather*} $$
-
(2) We have
 $B_4=B_{4,0}\oplus \cdots \oplus B_{4,6},$
where
$B_4=B_{4,0}\oplus \cdots \oplus B_{4,6},$
where  $$ \begin{gather*} \begin{aligned} B_{4,0}&\cong V_{(8)}\oplus V_{(6,2)}\oplus V_{(4^2)}\oplus V_{(4,2^2)}\oplus V_{(2^4)},\\ B_{4,1}&\cong V_{(5,1^2)}\oplus V_{(4,1^3)}\oplus V_{(3^2,1)} \oplus V_{(3,2,1^2)}\oplus V_{(2^2,1^3)},\\ B_{4,2}&\cong V_{(6)}\oplus V_{(5,1)}\oplus(V_{(4,2)})^{\oplus 3}\oplus(V_{(3,2,1)})^{\oplus 2}\oplus(V_{(2^3)})^{\oplus 3}\oplus V_{(2,1^4)},\\ B_{4,3}&\cong(V_{(3,1^2)})^{\oplus 3}\oplus(V_{(2,1^3)})^{\oplus 2},\\ B_{4,4}&\cong(V_{(4)})^{\oplus 3}\oplus V_{(3,1)}\oplus(V_{(2^2)})^{\oplus 3},\\ B_{4,5}&\cong V_{(1^3)},\\ B_{4,6}&\cong V_{(2)}. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} B_{4,0}&\cong V_{(8)}\oplus V_{(6,2)}\oplus V_{(4^2)}\oplus V_{(4,2^2)}\oplus V_{(2^4)},\\ B_{4,1}&\cong V_{(5,1^2)}\oplus V_{(4,1^3)}\oplus V_{(3^2,1)} \oplus V_{(3,2,1^2)}\oplus V_{(2^2,1^3)},\\ B_{4,2}&\cong V_{(6)}\oplus V_{(5,1)}\oplus(V_{(4,2)})^{\oplus 3}\oplus(V_{(3,2,1)})^{\oplus 2}\oplus(V_{(2^3)})^{\oplus 3}\oplus V_{(2,1^4)},\\ B_{4,3}&\cong(V_{(3,1^2)})^{\oplus 3}\oplus(V_{(2,1^3)})^{\oplus 2},\\ B_{4,4}&\cong(V_{(4)})^{\oplus 3}\oplus V_{(3,1)}\oplus(V_{(2^2)})^{\oplus 3},\\ B_{4,5}&\cong V_{(1^3)},\\ B_{4,6}&\cong V_{(2)}. \end{aligned} \end{gather*} $$
-
(3) We have
 $B_5=B_{5,0}\oplus \cdots \oplus B_{5,8},$
where
$B_5=B_{5,0}\oplus \cdots \oplus B_{5,8},$
where  $$ \begin{gather*} \begin{aligned} B_{5,0}&\cong V_{(10)}\oplus V_{(8,2)}\oplus V_{(6,4)}\oplus V_{(6,2^2)}\oplus V_{(4^2,2)}\oplus V_{(4,2^3)} \oplus V_{(2^5)},\\ B_{5,1}&\cong V_{(7,1^2)}\oplus V_{(6,1^3)}\oplus V_{(5,3,1)}\oplus V_{(5,2,1^2)}\oplus V_{(4,3,1^2)}\oplus V_{(4,2,1^3)}\\ &\oplus V_{(3^3)}\oplus V_{(3^2,2,1)}\oplus V_{(3,2^2,1^2)}\oplus V_{(2^3,1^3)},\\ B_{5,2}&\cong V_{(8)}\oplus V_{(7,1)}\oplus(V_{(6,2)})^{\oplus 3}\oplus V_{(5,3)}\oplus(V_{(5,2,1)})^{\oplus 2}\oplus(V_{(4^2)})^{\oplus 2}\\ &\oplus(V_{(4,3,1)})^{\oplus 2}\oplus(V_{(4,2^2)})^{\oplus 5}\oplus V_{(4,1^4)}\oplus V_{(3^2,1^2)}\oplus(V_{(3,2^2,1)})^{\oplus 3}\\ &\oplus V_{(3,2,1^3)}\oplus V_{(3,1^5)}\oplus(V_{(2^4)})^{\oplus 3}\oplus V_{(2^2,1^4)},\\ B_{5,3}&\cong (V_{(5,1^2)})^{\oplus 3}\oplus(V_{(4,2,1)})^{\oplus 2}\oplus(V_{(4,1^3)})^{\oplus 4}\oplus(V_{(3^2,1)})^{\oplus 4}\oplus(V_{(3,2,1^2)})^{\oplus 5}\\ &\oplus V_{(3,1^4)}\oplus(V_{(2^2,1^3)})^{\oplus 3},\\ B_{5,4}&\cong (V_{(6)})^{\oplus 3}\oplus(V_{(5,1)})^{\oplus 3}\oplus(V_{(4,2)})^{\oplus 8}\oplus(V_{(3,2,1)})^{\oplus 4}\oplus V_{(3,1^3)}\oplus(V_{(2^3)})^{\oplus 6}\\ &\oplus V_{(2^2,1^2)}\oplus V_{(2,1^4)}\oplus V_{(1^6)},\\ B_{5,5}&\cong (V_{(3,1^2)})^{\oplus 5}\oplus(V_{(2,1^3)})^{\oplus 3},\\ B_{5,6}&\cong (V_{(4)})^{\oplus 3}\oplus(V_{(3,1)})^{\oplus 2}\oplus(V_{(2^2)})^{\oplus 4},\\ B_{5,7}&\cong (V_{(1^3)})^{\oplus 2},\\ B_{5,8}&\cong (V_{(2)})^{\oplus 2}. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} B_{5,0}&\cong V_{(10)}\oplus V_{(8,2)}\oplus V_{(6,4)}\oplus V_{(6,2^2)}\oplus V_{(4^2,2)}\oplus V_{(4,2^3)} \oplus V_{(2^5)},\\ B_{5,1}&\cong V_{(7,1^2)}\oplus V_{(6,1^3)}\oplus V_{(5,3,1)}\oplus V_{(5,2,1^2)}\oplus V_{(4,3,1^2)}\oplus V_{(4,2,1^3)}\\ &\oplus V_{(3^3)}\oplus V_{(3^2,2,1)}\oplus V_{(3,2^2,1^2)}\oplus V_{(2^3,1^3)},\\ B_{5,2}&\cong V_{(8)}\oplus V_{(7,1)}\oplus(V_{(6,2)})^{\oplus 3}\oplus V_{(5,3)}\oplus(V_{(5,2,1)})^{\oplus 2}\oplus(V_{(4^2)})^{\oplus 2}\\ &\oplus(V_{(4,3,1)})^{\oplus 2}\oplus(V_{(4,2^2)})^{\oplus 5}\oplus V_{(4,1^4)}\oplus V_{(3^2,1^2)}\oplus(V_{(3,2^2,1)})^{\oplus 3}\\ &\oplus V_{(3,2,1^3)}\oplus V_{(3,1^5)}\oplus(V_{(2^4)})^{\oplus 3}\oplus V_{(2^2,1^4)},\\ B_{5,3}&\cong (V_{(5,1^2)})^{\oplus 3}\oplus(V_{(4,2,1)})^{\oplus 2}\oplus(V_{(4,1^3)})^{\oplus 4}\oplus(V_{(3^2,1)})^{\oplus 4}\oplus(V_{(3,2,1^2)})^{\oplus 5}\\ &\oplus V_{(3,1^4)}\oplus(V_{(2^2,1^3)})^{\oplus 3},\\ B_{5,4}&\cong (V_{(6)})^{\oplus 3}\oplus(V_{(5,1)})^{\oplus 3}\oplus(V_{(4,2)})^{\oplus 8}\oplus(V_{(3,2,1)})^{\oplus 4}\oplus V_{(3,1^3)}\oplus(V_{(2^3)})^{\oplus 6}\\ &\oplus V_{(2^2,1^2)}\oplus V_{(2,1^4)}\oplus V_{(1^6)},\\ B_{5,5}&\cong (V_{(3,1^2)})^{\oplus 5}\oplus(V_{(2,1^3)})^{\oplus 3},\\ B_{5,6}&\cong (V_{(4)})^{\oplus 3}\oplus(V_{(3,1)})^{\oplus 2}\oplus(V_{(2^2)})^{\oplus 4},\\ B_{5,7}&\cong (V_{(1^3)})^{\oplus 2},\\ B_{5,8}&\cong (V_{(2)})^{\oplus 2}. \end{aligned} \end{gather*} $$
Proof. By using Theorem 7.2, Lemma 7.5 and plethysm, we have
By using Theorem 7.2, Lemma 7.5 and the Littlewood–Richardson rule, we have
and
The other isomorphisms of (1) follow from Lemma 7.5.
The irreducible decompositions (2) and (3) follow in a similar way.
We need the irreducible decompositions of
![]() $B_{d,0}$
and
$B_{d,0}$
and
![]() $B_{d,1}$
to study the
$B_{d,1}$
to study the
![]() $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
![]() $A_d(n)$
. For
$A_d(n)$
. For
![]() $\lambda =(\lambda _1,\cdots ,\lambda _r)\vdash N$
, let
$\lambda =(\lambda _1,\cdots ,\lambda _r)\vdash N$
, let
![]() $2\lambda $
denote the partition
$2\lambda $
denote the partition
![]() $(2\lambda _1,\cdots ,2\lambda _r)$
of
$(2\lambda _1,\cdots ,2\lambda _r)$
of
![]() $2N$
.
$2N$
.
Proposition 7.7. For any
![]() $d\geq 0$
, we have
$d\geq 0$
, we have
For any
![]() $d\geq 2$
, we have
$d\geq 2$
, we have
Proof. By Theorem 5.4.23 in [Reference James and Kerber14], we have
Therefore, by Theorem 7.2 and Lemma 7.5, we have
By Theorem 7.2, Lemma 7.5, plethysm and the Littlewood–Richardson rule, we have
7.3 Surjectivity of the bracket map
 $[\cdot ,\cdot ]:B_{d,k}(n)\otimes \operatorname {gr}^1(\operatorname {IA}(n))\rightarrow B_{d,k+1}(n)$
$[\cdot ,\cdot ]:B_{d,k}(n)\otimes \operatorname {gr}^1(\operatorname {IA}(n))\rightarrow B_{d,k+1}(n)$
Here, we show that the bracket map
![]() $[\cdot ,\cdot ]: B_{d,k}(n)\otimes \operatorname {gr}^1(\operatorname {IA}(n))\rightarrow B_{d,k+1}(n)$
is surjective for
$[\cdot ,\cdot ]: B_{d,k}(n)\otimes \operatorname {gr}^1(\operatorname {IA}(n))\rightarrow B_{d,k+1}(n)$
is surjective for
![]() $n\geq 2d$
. Since we have abelian group isomorphisms (3.7), the bracket map of
$n\geq 2d$
. Since we have abelian group isomorphisms (3.7), the bracket map of
![]() $\operatorname {gr}^1(\operatorname {IA}(n))$
coincides with that of
$\operatorname {gr}^1(\operatorname {IA}(n))$
coincides with that of
![]() $\operatorname {gr}^1(\mathcal {E}_{\ast }(n))$
. Thus, we can compute the bracket map by using the contraction map c defined in Section 5.
$\operatorname {gr}^1(\mathcal {E}_{\ast }(n))$
. Thus, we can compute the bracket map by using the contraction map c defined in Section 5.
Define
![]() $K_{i,j}, K_{i,j,k}\in \operatorname {IA}(n)$
by
$K_{i,j}, K_{i,j,k}\in \operatorname {IA}(n)$
by
Proposition 7.8. For
![]() $n\geq 2d-k$
, the bracket map
$n\geq 2d-k$
, the bracket map
is surjective.
Proof. Any element of
![]() $B_{d,k+1}(n)$
is a linear sum of
$B_{d,k+1}(n)$
is a linear sum of
 , where
, where
![]() $i_1,\cdots ,i_{2d-k-1}\in [n]$
. Since
$i_1,\cdots ,i_{2d-k-1}\in [n]$
. Since
![]() $n\geq 2d-k$
, we can take
$n\geq 2d-k$
, we can take
 , where
, where
![]() $i,j\in [n]\setminus \{i_2,\cdots ,i_{2d-k-1}\}$
are distinct. We have
$i,j\in [n]\setminus \{i_2,\cdots ,i_{2d-k-1}\}$
are distinct. We have
![]() $[\tilde {u},K_{i_1,j,i}]=u$
, and therefore, the bracket map is surjective.
$[\tilde {u},K_{i_1,j,i}]=u$
, and therefore, the bracket map is surjective.
As in Section 5.3, for
![]() $\lambda \vdash 2d-k$
, let
$\lambda \vdash 2d-k$
, let
![]() $B_{d,k}(n)_{\lambda }$
denote the isotypic component of
$B_{d,k}(n)_{\lambda }$
denote the isotypic component of
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module
$\operatorname {GL}(n;\mathbb {Z})$
-module
![]() $B_{d,k}(n)$
corresponding to
$B_{d,k}(n)$
corresponding to
![]() $\lambda $
.
$\lambda $
.
In Proposition 7.7, we computed a decomposition of
![]() $B_{d,0}(n)$
. Since the Young diagram of
$B_{d,0}(n)$
. Since the Young diagram of
![]() $(2d)$
does not contain that of
$(2d)$
does not contain that of
![]() $(1^2)$
, by Remark 5.4, we have the following corollary.
$(1^2)$
, by Remark 5.4, we have the following corollary.
Corollary 7.9. The restriction of the bracket map
 $$ \begin{align*}[\cdot,\cdot]:\bigoplus_{\lambda\vdash d,\lambda\neq (d)} B_{d,0}(n)_{2\lambda}\otimes \operatorname{gr}^1(\operatorname{IA}(n))\rightarrow B_{d,1}(n)\end{align*} $$
$$ \begin{align*}[\cdot,\cdot]:\bigoplus_{\lambda\vdash d,\lambda\neq (d)} B_{d,0}(n)_{2\lambda}\otimes \operatorname{gr}^1(\operatorname{IA}(n))\rightarrow B_{d,1}(n)\end{align*} $$
is surjective for
![]() $n\geq 2d$
.
$n\geq 2d$
.
Lastly, we consider the condition for
![]() $\lambda \vdash 2d-k$
that the isotypic component
$\lambda \vdash 2d-k$
that the isotypic component
![]() $B_{d,k}(n)_{\lambda }$
of
$B_{d,k}(n)_{\lambda }$
of
![]() $B_{d,k}(n)$
does not vanish. Let
$B_{d,k}(n)$
does not vanish. Let
![]() $o(\lambda )$
be the number of odd parts of
$o(\lambda )$
be the number of odd parts of
![]() $\lambda $
. We have
$\lambda $
. We have
In Proposition 7.7, we observed that
![]() $o(\lambda )=0\; (k=0)$
and
$o(\lambda )=0\; (k=0)$
and
![]() $o(\lambda )=3 \;(k=1)$
. Moreover, by Proposition 7.8 and Remark 5.4, we have
$o(\lambda )=3 \;(k=1)$
. Moreover, by Proposition 7.8 and Remark 5.4, we have
![]() $o(\lambda )\leq 3k$
if
$o(\lambda )\leq 3k$
if
![]() $B_{d,k}(n)_{\lambda }\neq 0$
.
$B_{d,k}(n)_{\lambda }\neq 0$
.
8 The
 $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
 $A_d(n)$
$A_d(n)$
In this section, we study the
![]() $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
![]() $A_d(n)$
. We have
$A_d(n)$
. We have
![]() $A_0(n)=\Bbbk $
for any
$A_0(n)=\Bbbk $
for any
![]() $n\geq 0$
, and we studied the cases where
$n\geq 0$
, and we studied the cases where
![]() $d=1, 2$
in [Reference Katada16]. Note that we have
$d=1, 2$
in [Reference Katada16]. Note that we have
![]() $A_d(0)=0$
for
$A_d(0)=0$
for
![]() $d\geq 1$
. Thus, we have only to consider
$d\geq 1$
. Thus, we have only to consider
![]() $n\geq 1$
. Here, we construct a direct decomposition of
$n\geq 1$
. Here, we construct a direct decomposition of
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Aut}(F_n)$
-modules for any
$\operatorname {Aut}(F_n)$
-modules for any
![]() $d\geq 3,n\geq 1$
, which is indecomposable for
$d\geq 3,n\geq 1$
, which is indecomposable for
![]() $n\geq 2d$
. Moreover, we study the degree
$n\geq 2d$
. Moreover, we study the degree
![]() $3$
case in detail.
$3$
case in detail.
8.1 A direct decomposition of
 $A_d(n)$
$A_d(n)$
Here, we give a direct decomposition of the
![]() $\operatorname {Aut}(F_n)$
-module
$\operatorname {Aut}(F_n)$
-module
![]() $A_d(n)$
.
$A_d(n)$
.
Let
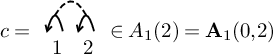
, and depict it as
Here, we use the same graphical notation of morphisms
![]() $\mu ,\eta ,\Delta ,\epsilon ,S$
in the category
$\mu ,\eta ,\Delta ,\epsilon ,S$
in the category
![]() $\mathbf {A}$
as in the category
$\mathbf {A}$
as in the category
![]() $\mathbf {A}^{L}$
. As in Section 4.3, we can define the iterated multiplications
$\mathbf {A}^{L}$
. As in Section 4.3, we can define the iterated multiplications
![]() $\mu ^{[q]}\in \mathbf {A}(q,1)$
for
$\mu ^{[q]}\in \mathbf {A}(q,1)$
for
![]() $q\geq 0$
. For
$q\geq 0$
. For
![]() $m\geq 0$
, there is a group homomorphism
$m\geq 0$
, there is a group homomorphism
where
![]() $P_{\sigma }$
is the symmetry in
$P_{\sigma }$
is the symmetry in
![]() $\mathbf {A}$
corresponding to
$\mathbf {A}$
corresponding to
![]() $\sigma $
. Set
$\sigma $
. Set

By Habiro–Massuyeau [Reference Habiro and Massuyeau11, Lemma 5.16], every element of
![]() $A_d(n)$
is a linear combination of morphisms of the form
$A_d(n)$
is a linear combination of morphisms of the form

for
![]() $\sigma \in \mathfrak {S}_{2d}$
and
$\sigma \in \mathfrak {S}_{2d}$
and
![]() $q_1,\cdots , q_n\geq 0$
such that
$q_1,\cdots , q_n\geq 0$
such that
![]() $q_1+\cdots +q_n=2d$
. The following lemma easily follows.
$q_1+\cdots +q_n=2d$
. The following lemma easily follows.
Lemma 8.1. For
![]() $n\geq 0$
, we have
$n\geq 0$
, we have
For
![]() $X\in A_d(m)$
, let
$X\in A_d(m)$
, let
denote the subfunctor of
![]() $A_d$
generated by X. That is, for any
$A_d$
generated by X. That is, for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $A_d X(n)$
is the
$A_d X(n)$
is the
![]() $\operatorname {Aut}(F_n)$
-submodule of
$\operatorname {Aut}(F_n)$
-submodule of
![]() $A_d(n)$
defined by
$A_d(n)$
defined by
Set

Note that we have
![]() $A_1 Q=0$
.
$A_1 Q=0$
.
Theorem 8.2. We have
Proof. By Lemma 8.1, any element of
![]() $A_d(n)$
is a linear sum of
$A_d(n)$
is a linear sum of
![]() $A_d(f)(c^{\otimes d})$
for
$A_d(f)(c^{\otimes d})$
for
![]() $f\in \mathbf {F}^{\mathrm {op}}(2d,n)$
. Define an
$f\in \mathbf {F}^{\mathrm {op}}(2d,n)$
. Define an
![]() $\operatorname {Aut}(F_n)$
-module map
$\operatorname {Aut}(F_n)$
-module map
by
![]() $e_n(A_d(f)(c^{\otimes d}))=\frac {1}{(2d)!} A_d(f)(P)$
for
$e_n(A_d(f)(c^{\otimes d}))=\frac {1}{(2d)!} A_d(f)(P)$
for
![]() $f\in \mathbf {F}^{\mathrm {op}}(2d,n)$
. This is well defined because the
$f\in \mathbf {F}^{\mathrm {op}}(2d,n)$
. This is well defined because the
![]() $4$
T relation is sent to
$4$
T relation is sent to
![]() $0$
. Since
$0$
. Since
![]() $A_d P$
is generated by P, we have
$A_d P$
is generated by P, we have
![]() $\operatorname {im}(e_n)=A_d P(n)$
.
$\operatorname {im}(e_n)=A_d P(n)$
.
Since we have
![]() $e_n(A_d(f)(P))=A_d(f)(P)$
for any
$e_n(A_d(f)(P))=A_d(f)(P)$
for any
![]() $f\in \mathbf {F}^{\mathrm {op}}(2d,n)$
, the
$f\in \mathbf {F}^{\mathrm {op}}(2d,n)$
, the
![]() $\operatorname {Aut}(F_n)$
-endomorphism
$\operatorname {Aut}(F_n)$
-endomorphism
![]() $e_n$
is an idempotent in
$e_n$
is an idempotent in
![]() $\operatorname {End}(A_d(n))$
, where we consider
$\operatorname {End}(A_d(n))$
, where we consider
![]() $A_d(n)$
as a right
$A_d(n)$
as a right
![]() $\operatorname {Aut}(F_n)$
-module. Therefore, we have
$\operatorname {Aut}(F_n)$
-module. Therefore, we have
Since
 , we have
, we have
![]() $A_d Q(n)\subset \ker (e_n)$
. Finally, we need to check that
$A_d Q(n)\subset \ker (e_n)$
. Finally, we need to check that
![]() $\operatorname {im}(1-e_n)\subset A_d Q(n)$
. Since we have for
$\operatorname {im}(1-e_n)\subset A_d Q(n)$
. Since we have for
![]() $f\in \mathbf {F}^{\mathrm {op}}(2d,n)$
,
$f\in \mathbf {F}^{\mathrm {op}}(2d,n)$
,
 $$ \begin{gather*} \begin{aligned} (1-e_n)(A_d(f)(c^{\otimes d}))&= A_d(f)(c^{\otimes d})-\frac{1}{(2d)!} A_d(f)(P)\\ &=\frac{1}{(2d)!}\sum_{\sigma\in\mathfrak{S}_{2d}}A_d(f)(c^{\otimes d}- \sigma c^{\otimes d}), \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} (1-e_n)(A_d(f)(c^{\otimes d}))&= A_d(f)(c^{\otimes d})-\frac{1}{(2d)!} A_d(f)(P)\\ &=\frac{1}{(2d)!}\sum_{\sigma\in\mathfrak{S}_{2d}}A_d(f)(c^{\otimes d}- \sigma c^{\otimes d}), \end{aligned} \end{gather*} $$
we need to show that, for any
![]() $\sigma \in \mathfrak {S}_{2d}$
, there exists
$\sigma \in \mathfrak {S}_{2d}$
, there exists
![]() $\tau \in \Bbbk \mathfrak {S}_{2d}$
such that
$\tau \in \Bbbk \mathfrak {S}_{2d}$
such that
It suffices to show the existence of
![]() $\tau $
satisfying equation (8.2) when
$\tau $
satisfying equation (8.2) when
![]() $\sigma $
is an adjacent transposition because any permutation is generated by adjacent transpositions, and we have such
$\sigma $
is an adjacent transposition because any permutation is generated by adjacent transpositions, and we have such
![]() $\tau $
by inductively using
$\tau $
by inductively using
If
![]() $\sigma $
is an adjacent transposition
$\sigma $
is an adjacent transposition
![]() $(2i,2i+1)$
for
$(2i,2i+1)$
for
![]() $i\in [n-1]$
, then we set
$i\in [n-1]$
, then we set
 $$ \begin{align*}\tau= \begin{pmatrix} 1&2&3&4&5&\cdots&2d\\ 2i-1&2i+2&2i+1&2i&1&\cdots \widehat{2i-1}\cdots \widehat{2i+2}\cdots&2d\\ \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\tau= \begin{pmatrix} 1&2&3&4&5&\cdots&2d\\ 2i-1&2i+2&2i+1&2i&1&\cdots \widehat{2i-1}\cdots \widehat{2i+2}\cdots&2d\\ \end{pmatrix}.\end{align*} $$
If
![]() $\sigma $
is an adjacent transposition
$\sigma $
is an adjacent transposition
![]() $(2i-1,2i)$
for
$(2i-1,2i)$
for
![]() $i\in [n]$
, then we set
$i\in [n]$
, then we set
![]() $\tau =0$
. The proof is complete.
$\tau =0$
. The proof is complete.
Lemma 8.3. The
![]() $\operatorname {Aut}(F_n)$
-module
$\operatorname {Aut}(F_n)$
-module
![]() $A_d P(n)$
is irreducible and thus indecomposable.
$A_d P(n)$
is irreducible and thus indecomposable.
Proof. Since
 , we have
, we have
![]() $\theta _{d,n}(A_d P(n))=B_{d,0}(n)_{(2d)}$
by the PBW map. Therefore,
$\theta _{d,n}(A_d P(n))=B_{d,0}(n)_{(2d)}$
by the PBW map. Therefore,
![]() $A_d P(n)$
is an irreducible
$A_d P(n)$
is an irreducible
![]() $\operatorname {Aut}(F_n)$
-module.
$\operatorname {Aut}(F_n)$
-module.
For
![]() $\lambda \vdash d$
, set
$\lambda \vdash d$
, set
 , where
, where
![]() $c_{2\lambda }\in \Bbbk \mathfrak {S}_{2d}$
is the Young symmetrizer. Note that we have
$c_{2\lambda }\in \Bbbk \mathfrak {S}_{2d}$
is the Young symmetrizer. Note that we have
![]() $Q_{(d)}=P$
.
$Q_{(d)}=P$
.
Lemma 8.4. For
![]() $\lambda \vdash d, \lambda \neq (d)$
, we have
$\lambda \vdash d, \lambda \neq (d)$
, we have
![]() $Q_{\lambda }\in A_d Q(2d)$
.
$Q_{\lambda }\in A_d Q(2d)$
.
Proof. For
![]() $\lambda =(\lambda _1,\cdots ,\lambda _r)\neq (d)$
, we have
$\lambda =(\lambda _1,\cdots ,\lambda _r)\neq (d)$
, we have
![]() $r\geq 2$
. By expanding
$r\geq 2$
. By expanding
![]() $a_{\lambda }$
and
$a_{\lambda }$
and
![]() $b_{\lambda }$
except for the first column, we can write
$b_{\lambda }$
except for the first column, we can write
![]() $Q_{\lambda }$
as a linear sum of
$Q_{\lambda }$
as a linear sum of

where
![]() $\sigma \in \mathfrak {S}_{2d-r}$
. The latter diagram is obtained from Q by composing a morphism of
$\sigma \in \mathfrak {S}_{2d-r}$
. The latter diagram is obtained from Q by composing a morphism of
![]() $\Bbbk \mathbf {F}^{\mathrm {op}}(2d,2d)$
, so is included in
$\Bbbk \mathbf {F}^{\mathrm {op}}(2d,2d)$
, so is included in
![]() $A_d Q(2d)$
.
$A_d Q(2d)$
.
By Lemma 8.4, we have
![]() $A_d Q(n)\supset \sum _{\lambda \vdash d, \lambda \neq (d)}A_d Q_{\lambda }(n)$
. Moreover, we have the following corollary.
$A_d Q(n)\supset \sum _{\lambda \vdash d, \lambda \neq (d)}A_d Q_{\lambda }(n)$
. Moreover, we have the following corollary.
Corollary 8.5. The
![]() $\operatorname {Aut}(F_n)$
-module
$\operatorname {Aut}(F_n)$
-module
![]() $A_d Q(n)$
is generated by
$A_d Q(n)$
is generated by
![]() $\{Q_{\lambda }\mid \lambda \vdash d, \lambda \neq (d)\}$
for
$\{Q_{\lambda }\mid \lambda \vdash d, \lambda \neq (d)\}$
for
![]() $n\geq 2d$
. That is, we have
$n\geq 2d$
. That is, we have
![]() $A_d Q(n)=\sum _{\lambda \vdash d, \lambda \neq (d)}A_d Q_{\lambda }(n)$
.
$A_d Q(n)=\sum _{\lambda \vdash d, \lambda \neq (d)}A_d Q_{\lambda }(n)$
.
Proof. For simplicity, let A denote
![]() $\sum _{\lambda \vdash d, \lambda \neq (d)}A_d Q_{\lambda }(n)$
. By Lemma 8.3, we have
$\sum _{\lambda \vdash d, \lambda \neq (d)}A_d Q_{\lambda }(n)$
. By Lemma 8.3, we have
![]() $\theta _{d,n}(A_d P(n))= B_{d,0}(n)_{(2d)}$
. Thus, by Theorem 8.2, we have
$\theta _{d,n}(A_d P(n))= B_{d,0}(n)_{(2d)}$
. Thus, by Theorem 8.2, we have
 $$ \begin{align*}\theta_{d,n}(A_d Q(n))= \left(\bigoplus_{\lambda\vdash d, \lambda\neq (d)}B_{d,0}(n)_{2\lambda}\right)\oplus \left(\bigoplus_{k\geq 1}B_{d,k}(n)\right).\end{align*} $$
$$ \begin{align*}\theta_{d,n}(A_d Q(n))= \left(\bigoplus_{\lambda\vdash d, \lambda\neq (d)}B_{d,0}(n)_{2\lambda}\right)\oplus \left(\bigoplus_{k\geq 1}B_{d,k}(n)\right).\end{align*} $$
On the other hand, by the PBW theorem, we have
 $$ \begin{align*}\theta_{d,n}(A)\supset \left(\bigoplus_{\lambda\vdash d, \lambda\neq (d)}B_{d,0}(n)_{2\lambda}\right).\end{align*} $$
$$ \begin{align*}\theta_{d,n}(A)\supset \left(\bigoplus_{\lambda\vdash d, \lambda\neq (d)}B_{d,0}(n)_{2\lambda}\right).\end{align*} $$
By Corollary 7.9 and Proposition 7.8, we have
 $$ \begin{align*}\theta_{d,n}(A)\supset \left(\bigoplus_{\lambda\vdash d, \lambda\neq (d)}B_{d,0}(n)_{2\lambda}\right)\oplus \left(\bigoplus_{k\geq 1}B_{d,k}(n)\right).\end{align*} $$
$$ \begin{align*}\theta_{d,n}(A)\supset \left(\bigoplus_{\lambda\vdash d, \lambda\neq (d)}B_{d,0}(n)_{2\lambda}\right)\oplus \left(\bigoplus_{k\geq 1}B_{d,k}(n)\right).\end{align*} $$
Therefore, we have
![]() $A_d Q(n)\subset A.$
Hence, we have
$A_d Q(n)\subset A.$
Hence, we have
![]() $A_d Q(n)= A$
.
$A_d Q(n)= A$
.
8.2 Radical filtration of
 $A_d(n)$
$A_d(n)$
For an
![]() $\operatorname {Aut}(F_n)$
-module M, let
$\operatorname {Aut}(F_n)$
-module M, let
![]() $\operatorname {Rad}(M)$
denote the radical of M; that is,
$\operatorname {Rad}(M)$
denote the radical of M; that is,
We have a radical filtration of
![]() $A_d(n)$
$A_d(n)$
Theorem 8.6. Let
![]() $n\geq 2d$
. Then, the filtration of
$n\geq 2d$
. Then, the filtration of
![]() $A_d(n)$
by the number of trivalent vertices coincides with the radical filtration. That is, we have
$A_d(n)$
by the number of trivalent vertices coincides with the radical filtration. That is, we have
![]() $\operatorname {Rad}(A_{d,k}(n))=A_{d,k+1}(n)$
for any
$\operatorname {Rad}(A_{d,k}(n))=A_{d,k+1}(n)$
for any
![]() $k\geq 0$
.
$k\geq 0$
.
Proof. For
![]() $\lambda \vdash 2d-k$
, we have
$\lambda \vdash 2d-k$
, we have
![]() $B_{d,k}(n)_{\lambda }\cong \bigoplus _{i=1}^{r_{\lambda }}(V_{\lambda })_{i}$
as
$B_{d,k}(n)_{\lambda }\cong \bigoplus _{i=1}^{r_{\lambda }}(V_{\lambda })_{i}$
as
![]() $\operatorname {GL}(n;\mathbb {Z})$
-modules. Let
$\operatorname {GL}(n;\mathbb {Z})$
-modules. Let
![]() $B_{d,k}(n)_{\lambda , i}\subset B_{d,k}(n)_{\lambda }$
be a
$B_{d,k}(n)_{\lambda , i}\subset B_{d,k}(n)_{\lambda }$
be a
![]() $\operatorname {GL}(n;\mathbb {Z})$
-submodule corresponding to
$\operatorname {GL}(n;\mathbb {Z})$
-submodule corresponding to
![]() $(V_{\lambda })_{i}$
. Let
$(V_{\lambda })_{i}$
. Let
![]() $A_{d,k}(n)_{\lambda , i}\subset A_{d,k}(n)$
be the
$A_{d,k}(n)_{\lambda , i}\subset A_{d,k}(n)$
be the
![]() $\operatorname {Aut}(F_n)$
-submodule generated by
$\operatorname {Aut}(F_n)$
-submodule generated by
![]() $\theta _{d,n}^{-1}(B_{d,k}(n)_{\lambda , i})$
. For each
$\theta _{d,n}^{-1}(B_{d,k}(n)_{\lambda , i})$
. For each
![]() $\lambda \vdash 2d-k, i\in [r_{\lambda }]$
, we have a maximal submodule
$\lambda \vdash 2d-k, i\in [r_{\lambda }]$
, we have a maximal submodule
 $$ \begin{align*}R_{\lambda, i}= \left(\sum_{(\mu,j)\neq (\lambda,i)} A_{d,k}(n)_{\mu, j}\right)+ A_{d,k+1}(n).\end{align*} $$
$$ \begin{align*}R_{\lambda, i}= \left(\sum_{(\mu,j)\neq (\lambda,i)} A_{d,k}(n)_{\mu, j}\right)+ A_{d,k+1}(n).\end{align*} $$
Since we have
![]() $\bigcap _{(\lambda ,i)} R_{\lambda , i}=A_{d,k+1}(n)$
, it follows that
$\bigcap _{(\lambda ,i)} R_{\lambda , i}=A_{d,k+1}(n)$
, it follows that
![]() $\operatorname {Rad}(A_{d,k}(n))\subset A_{d,k+1}(n)$
.
$\operatorname {Rad}(A_{d,k}(n))\subset A_{d,k+1}(n)$
.
For any maximal submodule K of
![]() $A_{d,k}(n)$
, the quotient
$A_{d,k}(n)$
, the quotient
![]() $A_{d,k}(n)/K$
is an irreducible
$A_{d,k}(n)/K$
is an irreducible
![]() $\operatorname {Aut}(F_n)$
-module, which factors through an irreducible polynomial
$\operatorname {Aut}(F_n)$
-module, which factors through an irreducible polynomial
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module. It follows that
$\operatorname {GL}(n;\mathbb {Z})$
-module. It follows that
![]() $\theta _{d,n}(A_{d,k}(n))/\theta _{d,n}(K)$
is isomorphic to one of the irreducible components of the
$\theta _{d,n}(A_{d,k}(n))/\theta _{d,n}(K)$
is isomorphic to one of the irreducible components of the
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module
$\operatorname {GL}(n;\mathbb {Z})$
-module
![]() $\bigoplus _{i\geq k}B_{d,i}(n)$
. If
$\bigoplus _{i\geq k}B_{d,i}(n)$
. If
![]() $B_{d,k}(n)\subset \theta _{d,n}(K)$
, then by Proposition 7.8, we have
$B_{d,k}(n)\subset \theta _{d,n}(K)$
, then by Proposition 7.8, we have
![]() $K= A_{d,k}(n)$
, which contradicts to the maximality of K. Therefore,
$K= A_{d,k}(n)$
, which contradicts to the maximality of K. Therefore,
![]() $\theta _{d,n}(A_{d,k}(n))/\theta _{d,n}(K)$
is isomorphic to one of the irreducible components of
$\theta _{d,n}(A_{d,k}(n))/\theta _{d,n}(K)$
is isomorphic to one of the irreducible components of
![]() $B_{d,k}(n)$
, and we have
$B_{d,k}(n)$
, and we have
![]() $K\supset A_{d,k+1}(n)$
. This implies that
$K\supset A_{d,k+1}(n)$
. This implies that
![]() $\operatorname {Rad}(A_{d,k}(n))\supset A_{d,k+1}(n)$
, and the proof is complete.
$\operatorname {Rad}(A_{d,k}(n))\supset A_{d,k+1}(n)$
, and the proof is complete.
It is possible that Theorem 8.6 holds for some
![]() $n<2d$
. However, it does not hold for all n. (See Remark 8.13.)
$n<2d$
. However, it does not hold for all n. (See Remark 8.13.)
8.3 Indecomposability of the decomposition of
 $A_d(n)$
$A_d(n)$
Here, we consider the indecomposability of the decomposition (8.1) of
![]() $A_d(n)$
.
$A_d(n)$
.
In Proposition 7.7, we observed that
In order to study the indecomposability of equation (8.1), we observe certain connectivity at the level of partitions.
Let
![]() $X_d=\{ 2\lambda \mid \lambda \vdash d, \lambda \neq (d)\}$
and
$X_d=\{ 2\lambda \mid \lambda \vdash d, \lambda \neq (d)\}$
and
![]() $Y_d=\{\mu \vdash 2d-1\mid \mu \text { has exactly }3\text { odd parts}\}$
. We consider the bipartite graph
$Y_d=\{\mu \vdash 2d-1\mid \mu \text { has exactly }3\text { odd parts}\}$
. We consider the bipartite graph
![]() $G_d$
with vertex sets
$G_d$
with vertex sets
![]() $X_d$
and
$X_d$
and
![]() $Y_d$
and with an edge between each pair of vertices
$Y_d$
and with an edge between each pair of vertices
![]() $2\lambda $
and
$2\lambda $
and
![]() $\mu $
if
$\mu $
if
![]() $\mu $
is obtained from
$\mu $
is obtained from
![]() $2\lambda $
by taking away one box from each of two different rows of
$2\lambda $
by taking away one box from each of two different rows of
![]() $2\lambda $
and then by adding one box to another row. For example,
$2\lambda $
and then by adding one box to another row. For example,
![]() $G_2$
is
$G_2$
is
![]() $G_3$
is
$G_3$
is

and
![]() $G_4$
is
$G_4$
is

Proposition 8.7. The graph
![]() $G_d$
is path-connected.
$G_d$
is path-connected.
Proof. For
![]() $\lambda \vdash d, \lambda \neq (d)$
, let
$\lambda \vdash d, \lambda \neq (d)$
, let
![]() $r(\lambda )$
be the number of rows of
$r(\lambda )$
be the number of rows of
![]() $\lambda $
. We write
$\lambda $
. We write
![]() $\lambda =(\lambda _1^{a_1},\lambda _2^{a_2},\cdots ,\lambda _l^{a_l})$
, where
$\lambda =(\lambda _1^{a_1},\lambda _2^{a_2},\cdots ,\lambda _l^{a_l})$
, where
![]() $\lambda _1>\lambda _2>\cdots >\lambda _l$
,
$\lambda _1>\lambda _2>\cdots >\lambda _l$
,
![]() $\sum _{i=1}^l a_i=r(\lambda )$
,
$\sum _{i=1}^l a_i=r(\lambda )$
,
![]() $a_i\geq 1$
.
$a_i\geq 1$
.
We show that for
![]() $\lambda \vdash d$
such that
$\lambda \vdash d$
such that
![]() $r(\lambda )<d$
, there is a path between
$r(\lambda )<d$
, there is a path between
![]() $2\lambda $
and some
$2\lambda $
and some
![]() $2\lambda '\in X_d$
such that
$2\lambda '\in X_d$
such that
![]() $r(\lambda ')=r(\lambda )+1$
. Then, since
$r(\lambda ')=r(\lambda )+1$
. Then, since
![]() $(2^d)$
is the only partition that has d rows, it follows by induction on
$(2^d)$
is the only partition that has d rows, it follows by induction on
![]() $k=r(\lambda )$
that all vertices in
$k=r(\lambda )$
that all vertices in
![]() $X_d$
are path-connected.
$X_d$
are path-connected.
If
![]() $a_1=k$
, then we have
$a_1=k$
, then we have
![]() $2\lambda =((2\lambda _1)^k)$
and
$2\lambda =((2\lambda _1)^k)$
and
![]() $2\lambda _1\geq 4$
because we assume that
$2\lambda _1\geq 4$
because we assume that
![]() $k<d$
. Thus, we have
$k<d$
. Thus, we have
where
![]() $\mu '=((2\lambda _1)^{k-2},(2\lambda _1-1)^2,1)$
is obtained from
$\mu '=((2\lambda _1)^{k-2},(2\lambda _1-1)^2,1)$
is obtained from
![]() $2\lambda $
by taking away a box from each of the
$2\lambda $
by taking away a box from each of the
![]() $(k-1)$
-st and k-th row and adding one box to the
$(k-1)$
-st and k-th row and adding one box to the
![]() $(k+1)$
-st row, and
$(k+1)$
-st row, and
where
![]() $2\lambda '=((2\lambda _1)^{k-1},2\lambda _1-2,2)$
is obtained from
$2\lambda '=((2\lambda _1)^{k-1},2\lambda _1-2,2)$
is obtained from
![]() $\mu '$
by taking away a box from the k-th row and adding a box to each of the
$\mu '$
by taking away a box from the k-th row and adding a box to each of the
![]() $(k-1)$
-st and
$(k-1)$
-st and
![]() $(k+1)$
-st row. Therefore, we have a path between
$(k+1)$
-st row. Therefore, we have a path between
![]() $2\lambda $
and
$2\lambda $
and
![]() $2\lambda '$
such that
$2\lambda '$
such that
![]() $r(\lambda ')=k+1$
.
$r(\lambda ')=k+1$
.
If
![]() $a_1< k$
, then we have
$a_1< k$
, then we have
where
![]() $\mu ''$
is obtained from
$\mu ''$
is obtained from
![]() $2\lambda $
by taking away a box from each of the
$2\lambda $
by taking away a box from each of the
![]() $a_1$
-th and
$a_1$
-th and
![]() $(a_1+a_2)$
-th row, and adding a box to the
$(a_1+a_2)$
-th row, and adding a box to the
![]() $(k+1)$
-st row, and
$(k+1)$
-st row, and
where
![]() $2\lambda ''$
is obtained from
$2\lambda ''$
is obtained from
![]() $\mu ''$
by taking away a box from the
$\mu ''$
by taking away a box from the
![]() $a_1$
-th row and adding a box to each of the
$a_1$
-th row and adding a box to each of the
![]() $(a_1+a_2)$
-th and
$(a_1+a_2)$
-th and
![]() $(k+1)$
-st row. Therefore, we have a path between
$(k+1)$
-st row. Therefore, we have a path between
![]() $2\lambda $
and
$2\lambda $
and
![]() $2\lambda ''$
such that
$2\lambda ''$
such that
![]() $r(\lambda '')=k+1$
.
$r(\lambda '')=k+1$
.
Lastly, we will show that each vertex of
![]() $Y_d$
is connected to a vertex of
$Y_d$
is connected to a vertex of
![]() $X_d$
. Any element
$X_d$
. Any element
![]() $\mu \in Y_d$
is a partition of
$\mu \in Y_d$
is a partition of
![]() $2d-1$
and has three odd parts. Therefore, by taking away a box from the last odd row and then adding one box to each of the other two odd rows, we obtain a partition of
$2d-1$
and has three odd parts. Therefore, by taking away a box from the last odd row and then adding one box to each of the other two odd rows, we obtain a partition of
![]() $2d$
with only even parts, which is a vertex of
$2d$
with only even parts, which is a vertex of
![]() $X_d$
. The proof is complete.
$X_d$
. The proof is complete.
If
![]() $n\geq d$
, then for any
$n\geq d$
, then for any
![]() $2\lambda \in X_d$
,
$2\lambda \in X_d$
,
![]() $B_{d,0}(n)_{2\lambda }$
is a nonzero
$B_{d,0}(n)_{2\lambda }$
is a nonzero
![]() $\operatorname {GL}(n;\mathbb {Z})$
-submodule of
$\operatorname {GL}(n;\mathbb {Z})$
-submodule of
![]() $B_d(n)$
. If
$B_d(n)$
. If
![]() $n\geq d$
, then for any
$n\geq d$
, then for any
![]() $\mu \in Y_d$
(except
$\mu \in Y_d$
(except
![]() $\mu =(2^{d-2},1^3)$
if
$\mu =(2^{d-2},1^3)$
if
![]() $n=d$
),
$n=d$
),
![]() $B_{d,1}(n)_{\mu }$
is a nonzero
$B_{d,1}(n)_{\mu }$
is a nonzero
![]() $\operatorname {GL}(n;\mathbb {Z})$
-submodule of
$\operatorname {GL}(n;\mathbb {Z})$
-submodule of
![]() $B_d(n)$
.
$B_d(n)$
.
Let
![]() $\pi _{\mu }:B_{d,1}(n)\twoheadrightarrow B_{d,1}(n)_{\mu }$
be the projection.
$\pi _{\mu }:B_{d,1}(n)\twoheadrightarrow B_{d,1}(n)_{\mu }$
be the projection.
Proposition 8.8. Let
![]() $n\geq 2d$
. Let
$n\geq 2d$
. Let
![]() $2\lambda \in X_d$
,
$2\lambda \in X_d$
,
![]() $\mu \in Y_d$
be two endpoints of an edge of the bipartite graph
$\mu \in Y_d$
be two endpoints of an edge of the bipartite graph
![]() $G_d$
. Then the composition of the bracket map and the projection
$G_d$
. Then the composition of the bracket map and the projection
![]() $\pi _{\mu }$
$\pi _{\mu }$
does not vanish.
Note that this proposition holds for
![]() $d=1,2$
because we have
$d=1,2$
because we have
![]() $X_1=Y_1=\emptyset , X_2=\{(2^2)\}, Y_2=\{(1^3)\}$
and by Lemma 6.7 in [Reference Katada16].
$X_1=Y_1=\emptyset , X_2=\{(2^2)\}, Y_2=\{(1^3)\}$
and by Lemma 6.7 in [Reference Katada16].
Recall that we have

and

What the bracket map does is to contract two of the univalent vertices of a diagram of an element of
![]() $B_{d,0}(n)$
with two leaves of a trivalent tree in
$B_{d,0}(n)$
with two leaves of a trivalent tree in
![]() $\operatorname {gr}^1(\operatorname {IA}(n))$
, which corresponds to the operation on partitions of taking away two boxes from different rows and then adding a box. Here, we introduce an intermediate vector space
$\operatorname {gr}^1(\operatorname {IA}(n))$
, which corresponds to the operation on partitions of taking away two boxes from different rows and then adding a box. Here, we introduce an intermediate vector space
![]() $B_d'(n)$
between
$B_d'(n)$
between
![]() $B_{d,0}(n)$
and
$B_{d,0}(n)$
and
![]() $B_{d,1}(n)$
, whose elements correspond to partitions which are obtained by the operation of taking away two boxes from different rows. Define
$B_{d,1}(n)$
, whose elements correspond to partitions which are obtained by the operation of taking away two boxes from different rows. Define
![]() $B_d'(n)$
by
$B_d'(n)$
by

where
is a based trivalent tree of degree
![]() $1$
. Then,
$1$
. Then,
![]() $B_d'(n)$
is a
$B_d'(n)$
is a
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module, and we have an irreducible decomposition
$\operatorname {GL}(n;\mathbb {Z})$
-module, and we have an irreducible decomposition
in a way similar to Proposition 7.7. Let
![]() $B_d'(n)_{\nu }$
be the isotypic component of
$B_d'(n)_{\nu }$
be the isotypic component of
![]() $B_d'(n)$
corresponding to
$B_d'(n)$
corresponding to
![]() $\nu $
.
$\nu $
.
Recall that
![]() $a_{\lambda }, b_{\lambda }$
and
$a_{\lambda }, b_{\lambda }$
and
![]() $\diamond $
are defined in Section 5.1. In the proof of Proposition 8.8, we use the following notation
$\diamond $
are defined in Section 5.1. In the proof of Proposition 8.8, we use the following notation

which represents the linear sum of permutations
![]() $a_{2\lambda }$
.
$a_{2\lambda }$
.
Proof of Proposition 8.8 Let
![]() $2\lambda =(2\lambda _1,\cdots ,2\lambda _r)\vdash 2d \in X_d$
. Any vertex
$2\lambda =(2\lambda _1,\cdots ,2\lambda _r)\vdash 2d \in X_d$
. Any vertex
![]() $\mu \in Y_d$
that is connected to
$\mu \in Y_d$
that is connected to
![]() $2\lambda $
by an edge of
$2\lambda $
by an edge of
![]() $G_d$
is obtained from
$G_d$
is obtained from
![]() $2\lambda $
by taking away a box from each of the i-th and j-th row of
$2\lambda $
by taking away a box from each of the i-th and j-th row of
![]() $2\lambda $
and adding a box to the k-th row of
$2\lambda $
and adding a box to the k-th row of
![]() $2\lambda $
for some
$2\lambda $
for some
![]() $i,j\in [r], i<j, k\in [r+1], k\neq i,j$
. We write
$i,j\in [r], i<j, k\in [r+1], k\neq i,j$
. We write
![]() $\mu =(\mu _1,\cdots ,\mu _s)$
. Then we have
$\mu =(\mu _1,\cdots ,\mu _s)$
. Then we have
![]() $\mu _i=2\lambda _i-1, \mu _j=2\lambda _j-1, \mu _k=2\lambda _k+1$
and
$\mu _i=2\lambda _i-1, \mu _j=2\lambda _j-1, \mu _k=2\lambda _k+1$
and
![]() $\mu _l=2\lambda _l$
for
$\mu _l=2\lambda _l$
for
![]() $l\in [s], l\neq i,j,k$
.
$l\in [s], l\neq i,j,k$
.
Since we have
![]() $\operatorname {gr}^1(\operatorname {IA}(n))\cong H^{\ast }\otimes \mathcal {L}_2(n)$
, we can write equation (8.3) by
$\operatorname {gr}^1(\operatorname {IA}(n))\cong H^{\ast }\otimes \mathcal {L}_2(n)$
, we can write equation (8.3) by
We will show that
![]() $h_{\lambda ,\mu }$
does not vanish.
$h_{\lambda ,\mu }$
does not vanish.
Let
![]() $\nu \vdash 2d-2$
be the partition that is obtained from
$\nu \vdash 2d-2$
be the partition that is obtained from
![]() $2\lambda $
by taking away a box from each of the i-th and j-th row of
$2\lambda $
by taking away a box from each of the i-th and j-th row of
![]() $2\lambda $
. We decompose
$2\lambda $
. We decompose
![]() $h_{\lambda ,\mu }$
into the composition
$h_{\lambda ,\mu }$
into the composition
where
![]() $h_{\nu ,\mu }$
and
$h_{\nu ,\mu }$
and
![]() $h_{\lambda ,\nu }$
are
$h_{\lambda ,\nu }$
are
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module maps defined as follows.
$\operatorname {GL}(n;\mathbb {Z})$
-module maps defined as follows.
Let
be a
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module map defined in a way similar to the contraction map in Section 5.2. Define
$\operatorname {GL}(n;\mathbb {Z})$
-module map defined in a way similar to the contraction map in Section 5.2. Define
by
![]() $h_{\lambda }(x\otimes y\otimes z)=h^{\prime }_{\lambda }(x\otimes z)\otimes y$
for
$h_{\lambda }(x\otimes y\otimes z)=h^{\prime }_{\lambda }(x\otimes z)\otimes y$
for
![]() $x\in B_{d,0}(n)_{2\lambda }, y\in H^{\ast }, z\in \mathcal {L}_2(n)$
. We also define a
$x\in B_{d,0}(n)_{2\lambda }, y\in H^{\ast }, z\in \mathcal {L}_2(n)$
. We also define a
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module map
$\operatorname {GL}(n;\mathbb {Z})$
-module map
by connecting two bases
![]() $\ast _1,\ast _2$
, that is, for
$\ast _1,\ast _2$
, that is, for
![]() $w_1,\cdots , w_{2d-2}\in V_n, v\in H^{\ast }$
,
$w_1,\cdots , w_{2d-2}\in V_n, v\in H^{\ast }$
,

Let
![]() $\pi _{\nu }: B_d'(n)\otimes H^{\ast }\rightarrow B_d'(n)_{\nu }\otimes H^{\ast }$
be the tensor product of the projection and
$\pi _{\nu }: B_d'(n)\otimes H^{\ast }\rightarrow B_d'(n)_{\nu }\otimes H^{\ast }$
be the tensor product of the projection and
![]() $\operatorname {id}_{H^{\ast }}$
. Then we have two
$\operatorname {id}_{H^{\ast }}$
. Then we have two
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module maps
$\operatorname {GL}(n;\mathbb {Z})$
-module maps
and
Since
![]() $h_{\lambda ,\nu }$
and
$h_{\lambda ,\nu }$
and
![]() $h_{\nu ,\mu }$
are
$h_{\nu ,\mu }$
are
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module maps and since
$\operatorname {GL}(n;\mathbb {Z})$
-module maps and since
![]() $B_{d,0}(n)_{2\lambda }$
and
$B_{d,0}(n)_{2\lambda }$
and
![]() $B_d'(n)_{\nu }$
are irreducible, it suffices to prove that
$B_d'(n)_{\nu }$
are irreducible, it suffices to prove that
![]() $h_{\lambda ,\nu }\neq 0$
and
$h_{\lambda ,\nu }\neq 0$
and
![]() $h_{\nu ,\mu }\neq 0$
.
$h_{\nu ,\mu }\neq 0$
.
We will prove that
![]() $h_{\lambda ,\nu }$
does not vanish. Let
$h_{\lambda ,\nu }$
does not vanish. Let

where
![]() $\bar {i}=\sum _{l=1}^{i}2\lambda _l-1, \bar {j}=\sum _{l=1}^{j}2\lambda _l-2$
. Since we have
$\bar {i}=\sum _{l=1}^{i}2\lambda _l-1, \bar {j}=\sum _{l=1}^{j}2\lambda _l-2$
. Since we have
 $$ \begin{align*}c_{\nu}\diamond c_{(1^2)}\in S^{\nu}\diamond S^{(1^2)}=\bigoplus_{\rho\vdash 2d}(S^{\rho})^{LR^{\rho}_{\nu,(1^2)}}\end{align*} $$
$$ \begin{align*}c_{\nu}\diamond c_{(1^2)}\in S^{\nu}\diamond S^{(1^2)}=\bigoplus_{\rho\vdash 2d}(S^{\rho})^{LR^{\rho}_{\nu,(1^2)}}\end{align*} $$
and
we have
![]() $u\in B_{d,0}(n)_{2\lambda }$
. Moreover, we have
$u\in B_{d,0}(n)_{2\lambda }$
. Moreover, we have

By the relation
![]() $b_{(1^2)}=\operatorname {id}-(1,2)$
and the AS relation, the right-hand side of equation (8.4) is
$b_{(1^2)}=\operatorname {id}-(1,2)$
and the AS relation, the right-hand side of equation (8.4) is

Since we have
locally, by pulling
![]() $\ast _1$
to the top, we have
$\ast _1$
to the top, we have

We will look at the coefficient in
![]() $u'$
of
$u'$
of
to show that
![]() $u'$
does not vanish. Note that the upper box corresponds to
$u'$
does not vanish. Note that the upper box corresponds to
![]() $a_{\nu }$
and that
$a_{\nu }$
and that
![]() $b_{\nu }a_{\nu }=\sum _{\tau \in C_{t_0},\rho \in R_{t_0}} \mathrm {sgn}(\tau )\tau \rho $
, where
$b_{\nu }a_{\nu }=\sum _{\tau \in C_{t_0},\rho \in R_{t_0}} \mathrm {sgn}(\tau )\tau \rho $
, where
![]() $t_0$
is the canonical
$t_0$
is the canonical
![]() $\nu $
-tableau. If
$\nu $
-tableau. If
![]() $\lambda _i\neq \lambda _j$
, then there is no
$\lambda _i\neq \lambda _j$
, then there is no
![]() $\tau \in C_{t_0}$
such that
$\tau \in C_{t_0}$
such that
![]() $\tau (\bar {i})=\bar {j}, \tau (\bar {j})=\bar {i}$
. Thus, the diagram
$\tau (\bar {i})=\bar {j}, \tau (\bar {j})=\bar {i}$
. Thus, the diagram
![]() $u_0$
appears only when
$u_0$
appears only when
![]() $\tau $
is an even permutation which fixes
$\tau $
is an even permutation which fixes
![]() $\bar {i}$
and
$\bar {i}$
and
![]() $\bar {j}$
. Then, the coefficient of
$\bar {j}$
. Then, the coefficient of
![]() $u_0$
in
$u_0$
in
![]() $u'$
is negative. If
$u'$
is negative. If
![]() $\lambda _i= \lambda _j$
, then the diagram
$\lambda _i= \lambda _j$
, then the diagram
![]() $u_0$
appears when
$u_0$
appears when
![]() $\tau $
preserves the subset
$\tau $
preserves the subset
![]() $\{\bar {i},\bar {j}\}$
and the parity of
$\{\bar {i},\bar {j}\}$
and the parity of
![]() $\tau $
coincides with that of the restriction of
$\tau $
coincides with that of the restriction of
![]() $\tau $
to
$\tau $
to
![]() $\{\bar {i},\bar {j}\}$
. Hence, by the AS relation, the coefficient of
$\{\bar {i},\bar {j}\}$
. Hence, by the AS relation, the coefficient of
![]() $u_0$
in
$u_0$
in
![]() $u'$
is negative. Therefore,
$u'$
is negative. Therefore,
![]() $h_{\lambda , \nu }$
does not vanish.
$h_{\lambda , \nu }$
does not vanish.
We will prove that
![]() $h_{\nu ,\mu }$
does not vanish. Let
$h_{\nu ,\mu }$
does not vanish. Let
![]() $N\in \mathbb {N}$
. Set
$N\in \mathbb {N}$
. Set
![]() $c^{\prime }_{\rho }=a_{\rho } b_{\rho }\in \Bbbk \mathfrak {S}_{N}$
for
$c^{\prime }_{\rho }=a_{\rho } b_{\rho }\in \Bbbk \mathfrak {S}_{N}$
for
![]() $\rho \vdash N$
. From basic facts of representation theory, we have an isomorphism of
$\rho \vdash N$
. From basic facts of representation theory, we have an isomorphism of
![]() $\Bbbk \mathfrak {S}_{N}$
-modules
$\Bbbk \mathfrak {S}_{N}$
-modules
In what follows, we use
![]() $c^{\prime }_{\rho }$
instead of
$c^{\prime }_{\rho }$
instead of
![]() $c_{\rho }$
as the Young symmetrizer. Let
$c_{\rho }$
as the Young symmetrizer. Let

where
![]() $\sigma \in \mathfrak {S}_{2d-1}$
is defined by
$\sigma \in \mathfrak {S}_{2d-1}$
is defined by
 $$ \begin{align*}\sigma= \begin{pmatrix} 1&\cdots &2d-3 &2d-2 & 2d-1\\ 1&\cdots &i' &j' & k' \end{pmatrix} \text{ for } i'=\sum_{l=1}^{i}\mu_{l},\: j'=\sum_{l=1}^{j} \mu_{l},\: k'=\sum_{l=1}^{k} \mu_{l}. \end{align*} $$
$$ \begin{align*}\sigma= \begin{pmatrix} 1&\cdots &2d-3 &2d-2 & 2d-1\\ 1&\cdots &i' &j' & k' \end{pmatrix} \text{ for } i'=\sum_{l=1}^{i}\mu_{l},\: j'=\sum_{l=1}^{j} \mu_{l},\: k'=\sum_{l=1}^{k} \mu_{l}. \end{align*} $$
We will show that
![]() $h(\pi _{\nu }(Z_{\mu }))\in B_{d,1}(n)_{\mu }$
and that
$h(\pi _{\nu }(Z_{\mu }))\in B_{d,1}(n)_{\mu }$
and that
![]() $h(\pi _{\nu }(Z_{\mu }))\neq 0$
.
$h(\pi _{\nu }(Z_{\mu }))\neq 0$
.
If the diagram that is obtained from
![]() $\mu $
by taking away a box from the i-th (resp. j-th) row of
$\mu $
by taking away a box from the i-th (resp. j-th) row of
![]() $\mu $
is a partition of
$\mu $
is a partition of
![]() $2d-2$
, then write it
$2d-2$
, then write it
![]() $\nu _i$
(resp.
$\nu _i$
(resp.
![]() $\nu _j$
). Since any partition
$\nu _j$
). Since any partition
![]() $\rho \vdash 2d-2$
with exactly two odd parts other than
$\rho \vdash 2d-2$
with exactly two odd parts other than
![]() $\nu ,\nu _i,\nu _j$
is not included in
$\nu ,\nu _i,\nu _j$
is not included in
![]() $\mu $
, it follows that
$\mu $
, it follows that
By using an argument similar to Proposition 5.3, we have
 $$ \begin{gather*} h(B_d'(n)_{\nu}\otimes H^{\ast})\subset \bigoplus_{\alpha=\nu\sqcup \square} B_{d,1}(n)_{\alpha},\quad h(B_d'(n)_{\nu_i}\otimes H^{\ast})\subset \bigoplus_{\alpha=\nu_i\sqcup \square} B_{d,1}(n)_{\alpha},\\ h(B_d'(n)_{\nu_j}\otimes H^{\ast})\subset \bigoplus_{\alpha=\nu_j\sqcup \square} B_{d,1}(n)_{\alpha}. \end{gather*} $$
$$ \begin{gather*} h(B_d'(n)_{\nu}\otimes H^{\ast})\subset \bigoplus_{\alpha=\nu\sqcup \square} B_{d,1}(n)_{\alpha},\quad h(B_d'(n)_{\nu_i}\otimes H^{\ast})\subset \bigoplus_{\alpha=\nu_i\sqcup \square} B_{d,1}(n)_{\alpha},\\ h(B_d'(n)_{\nu_j}\otimes H^{\ast})\subset \bigoplus_{\alpha=\nu_j\sqcup \square} B_{d,1}(n)_{\alpha}. \end{gather*} $$
Since
![]() $\{\nu \sqcup \square \}\cap \{\nu _i\sqcup \square \}\cap \{\nu _j\sqcup \square \}=\{\mu \}$
and since
$\{\nu \sqcup \square \}\cap \{\nu _i\sqcup \square \}\cap \{\nu _j\sqcup \square \}=\{\mu \}$
and since
![]() $h(Z_{\mu })\in B_{d,1}(n)_{\mu }$
, we have
$h(Z_{\mu })\in B_{d,1}(n)_{\mu }$
, we have
![]() $h(\pi _{\nu }(Z_{\mu }))\in B_{d,1}(n)_{\mu }$
.
$h(\pi _{\nu }(Z_{\mu }))\in B_{d,1}(n)_{\mu }$
.
In order to prove that
![]() $h(\pi _{\nu }(Z_{\mu }))\neq 0$
, we will look at the coefficient in
$h(\pi _{\nu }(Z_{\mu }))\neq 0$
, we will look at the coefficient in
![]() $h(\pi _{\nu }(Z_{\mu }))$
of
$h(\pi _{\nu }(Z_{\mu }))$
of

Note that
![]() $c^{\prime }_{\mu }=\sum _{\rho \in R_{s_0},\tau \in C_{s_0}} \mathrm {sgn}(\tau )\rho \tau $
, where
$c^{\prime }_{\mu }=\sum _{\rho \in R_{s_0},\tau \in C_{s_0}} \mathrm {sgn}(\tau )\rho \tau $
, where
![]() $s_0$
is the canonical
$s_0$
is the canonical
![]() $\mu $
-tableau.
$\mu $
-tableau.
Firstly, we consider the case where
![]() $\mu _i,\mu _j,\mu _k$
are distinct. Then z appears only when
$\mu _i,\mu _j,\mu _k$
are distinct. Then z appears only when
![]() $\tau $
is an even permutation which fixes
$\tau $
is an even permutation which fixes
![]() $i'$
,
$i'$
,
![]() $j'$
and
$j'$
and
![]() $k'$
. Therefore, the coefficient of z in
$k'$
. Therefore, the coefficient of z in
![]() $h(Z_{\mu })$
is positive. Moreover, the linear sum of terms in
$h(Z_{\mu })$
is positive. Moreover, the linear sum of terms in
![]() $Z_{\mu }$
such that
$Z_{\mu }$
such that
![]() $\ast _2$
is connected to
$\ast _2$
is connected to
![]() $v_k$
lies in
$v_k$
lies in
![]() $\pi _{\nu }(Z_{\mu })$
, so the coefficient of z in
$\pi _{\nu }(Z_{\mu })$
, so the coefficient of z in
![]() $h(\pi _{\nu }(Z_{\mu }))$
is equal to that of z in
$h(\pi _{\nu }(Z_{\mu }))$
is equal to that of z in
![]() $h(Z_{\mu })$
, which is nonzero.
$h(Z_{\mu })$
, which is nonzero.
The other cases, where at least two of
![]() $\mu _i,\mu _j$
and
$\mu _i,\mu _j$
and
![]() $\mu _k$
are equal, follow in a similar argument. The only thing that differs from the above case is that z appears when
$\mu _k$
are equal, follow in a similar argument. The only thing that differs from the above case is that z appears when
![]() $\tau $
preserves the subset
$\tau $
preserves the subset
![]() $\{i',j',k'\}\subset [2d-1]$
, and the parity of
$\{i',j',k'\}\subset [2d-1]$
, and the parity of
![]() $\tau $
coincides with that of the restriction of
$\tau $
coincides with that of the restriction of
![]() $\tau $
to
$\tau $
to
![]() $\{i',j',k'\}$
. Since we have the AS relation, the sign due to the permutation of
$\{i',j',k'\}$
. Since we have the AS relation, the sign due to the permutation of
![]() $\{i',j',k'\}$
is cancelled. Therefore, the coefficient of z in
$\{i',j',k'\}$
is cancelled. Therefore, the coefficient of z in
![]() $h(Z_{\mu })$
is positive in any case. The proof is complete.
$h(Z_{\mu })$
is positive in any case. The proof is complete.
Theorem 8.9. Let
![]() $d\geq 2$
. The direct decomposition
$d\geq 2$
. The direct decomposition
of
![]() $\operatorname {Aut}(F_n)$
-modules is indecomposable for
$\operatorname {Aut}(F_n)$
-modules is indecomposable for
![]() $n\geq 2d$
.
$n\geq 2d$
.
Proof. By Lemma 8.3, it suffices to show that
![]() $A_d Q(n)$
is indecomposable. Since the radical preserves the direct sum, we have only to show that
$A_d Q(n)$
is indecomposable. Since the radical preserves the direct sum, we have only to show that
![]() $A_d Q(n)/\operatorname {Rad}^2(A_d Q(n))$
is indecomposable. Suppose that we have a nontrivial decomposition of
$A_d Q(n)/\operatorname {Rad}^2(A_d Q(n))$
is indecomposable. Suppose that we have a nontrivial decomposition of
![]() $\operatorname {Aut}(F_n)$
-modules
$\operatorname {Aut}(F_n)$
-modules
 $$ \begin{gather*} \begin{aligned} A_d Q(n)/\operatorname{Rad}^2(A_d Q(n))&=A_d Q(n)/A_{d,2}(n)\\ &=(M_1+A_{d,2}(n))/ A_{d,2}(n)\oplus (M_2+A_{d,2}(n))/A_{d,2}(n), \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} A_d Q(n)/\operatorname{Rad}^2(A_d Q(n))&=A_d Q(n)/A_{d,2}(n)\\ &=(M_1+A_{d,2}(n))/ A_{d,2}(n)\oplus (M_2+A_{d,2}(n))/A_{d,2}(n), \end{aligned} \end{gather*} $$
where
![]() $M_i$
is an
$M_i$
is an
![]() $\operatorname {Aut}(F_n)$
-submodule of
$\operatorname {Aut}(F_n)$
-submodule of
![]() $A_d Q(n)$
for
$A_d Q(n)$
for
![]() $i=1,2$
. Let
$i=1,2$
. Let
for
![]() $i=1,2$
. We have
$i=1,2$
. We have
 $$ \begin{align*}N_1\oplus N_2=\theta_{d,n}(A_d Q(n))/\theta_{d,n}(A_{d,2}(n))=\left(\bigoplus_{\lambda\vdash d, \lambda\neq (d)} B_{d,0}(n)_{2\lambda}\right) \oplus B_{d,1}(n).\end{align*} $$
$$ \begin{align*}N_1\oplus N_2=\theta_{d,n}(A_d Q(n))/\theta_{d,n}(A_{d,2}(n))=\left(\bigoplus_{\lambda\vdash d, \lambda\neq (d)} B_{d,0}(n)_{2\lambda}\right) \oplus B_{d,1}(n).\end{align*} $$
For any
![]() $2\lambda \in X_d$
, there uniquely exists
$2\lambda \in X_d$
, there uniquely exists
![]() $i\in \{1,2\}$
such that
$i\in \{1,2\}$
such that
![]() $N_i$
includes a
$N_i$
includes a
![]() $\operatorname {GL}(n;\mathbb {Z})$
-submodule
$\operatorname {GL}(n;\mathbb {Z})$
-submodule
![]() $(N_i)_{2\lambda }\cong V_{2\lambda }$
. Let
$(N_i)_{2\lambda }\cong V_{2\lambda }$
. Let
![]() $x\in (N_i)_{2\lambda }$
be a generator of the irreducible
$x\in (N_i)_{2\lambda }$
be a generator of the irreducible
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module
$\operatorname {GL}(n;\mathbb {Z})$
-module
![]() $(N_i)_{2\lambda }$
. Then, the image
$(N_i)_{2\lambda }$
. Then, the image
![]() $x'$
of x under the composition of
$x'$
of x under the composition of
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module maps
$\operatorname {GL}(n;\mathbb {Z})$
-module maps
is an element of
![]() $B_{d,0}(n)_{2\lambda }$
. For any
$B_{d,0}(n)_{2\lambda }$
. For any
![]() $\mu \in Y_d$
that is connected to
$\mu \in Y_d$
that is connected to
![]() $2\lambda $
by an edge of
$2\lambda $
by an edge of
![]() $G_d$
, by Proposition 8.8, there exists
$G_d$
, by Proposition 8.8, there exists
![]() $g\in \operatorname {gr}^1(\operatorname {IA}(n))$
such that
$g\in \operatorname {gr}^1(\operatorname {IA}(n))$
such that
![]() $[x',g]\neq 0\in B_{d,1}(n)_{\mu }$
. Therefore, we have
$[x',g]\neq 0\in B_{d,1}(n)_{\mu }$
. Therefore, we have
It follows that
![]() $N_i$
includes a
$N_i$
includes a
![]() $\operatorname {GL}(n;\mathbb {Z})$
-submodule
$\operatorname {GL}(n;\mathbb {Z})$
-submodule
![]() $(N_i)_{\mu }$
that is isomorphic to
$(N_i)_{\mu }$
that is isomorphic to
![]() $V_{\mu }$
for any
$V_{\mu }$
for any
![]() $\mu \in Y_d$
that is connected to
$\mu \in Y_d$
that is connected to
![]() $2\lambda $
by an edge of
$2\lambda $
by an edge of
![]() $G_d$
. Hence, by Proposition 8.7, we have
$G_d$
. Hence, by Proposition 8.7, we have
![]() $N_1\cap N_2\neq \{0\}$
, a contradiction. Therefore,
$N_1\cap N_2\neq \{0\}$
, a contradiction. Therefore,
![]() $A_d Q(n)$
is indecomposable.
$A_d Q(n)$
is indecomposable.
Note that the assumption
![]() $n\geq 2d$
is needed for the surjectivity of the bracket map and the nontriviality of the bracket map for each pair of nonzero irreducible
$n\geq 2d$
is needed for the surjectivity of the bracket map and the nontriviality of the bracket map for each pair of nonzero irreducible
![]() $\operatorname {GL}(n;\mathbb {Z})$
-submodules. Thus, if we have the surjectivity and the nontriviality of the bracket map for some
$\operatorname {GL}(n;\mathbb {Z})$
-submodules. Thus, if we have the surjectivity and the nontriviality of the bracket map for some
![]() $n<2d$
, we can loose the assumption.
$n<2d$
, we can loose the assumption.
8.4 The
 $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
 $A_3(n)$
$A_3(n)$
Here, we consider the
![]() $\operatorname {Aut}(F_n)$
-module structure of
$\operatorname {Aut}(F_n)$
-module structure of
![]() $A_3(n)$
in detail.
$A_3(n)$
in detail.
In degree
![]() $3$
, the restrictions of the bracket map to each isotypic component induce
$3$
, the restrictions of the bracket map to each isotypic component induce
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
$\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
 $$ \begin{gather*} \begin{aligned} \rho_1:B_{3,0}(n)_{(4,2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{3,1}(n)_{(3,1^2)}),\\ \rho_2:B_{3,0}(n)_{(2^3)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{3,1}(n)_{(3,1^2)}),\\ \rho_3:B_{3,0}(n)_{(2^3)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{3,1}(n)_{(2,1^3)}). \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} \rho_1:B_{3,0}(n)_{(4,2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{3,1}(n)_{(3,1^2)}),\\ \rho_2:B_{3,0}(n)_{(2^3)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{3,1}(n)_{(3,1^2)}),\\ \rho_3:B_{3,0}(n)_{(2^3)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{3,1}(n)_{(2,1^3)}). \end{aligned} \end{gather*} $$
Proposition 8.10. The
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
$\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
are injective for
$\rho _2$
are injective for
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $\rho _3$
for
$\rho _3$
for
![]() $n\geq 4$
.
$n\geq 4$
.
Proof. Recall that
![]() $c_{\lambda }$
denotes the Young symmetrizer defined in equation (5.1) and that
$c_{\lambda }$
denotes the Young symmetrizer defined in equation (5.1) and that
![]() $K_{i,j,k}\in \operatorname {IA}(n)$
is defined by equation (7.4). For
$K_{i,j,k}\in \operatorname {IA}(n)$
is defined by equation (7.4). For
![]() $n\geq 3$
, we have
$n\geq 3$
, we have
where

and

Thus, we have
![]() $\rho _1\neq 0$
for
$\rho _1\neq 0$
for
![]() $n\geq 3$
. Since
$n\geq 3$
. Since
![]() $B_{3,0}(n)_{(4,2)}$
is irreducible,
$B_{3,0}(n)_{(4,2)}$
is irreducible,
![]() $\rho _1$
is injective.
$\rho _1$
is injective.
Let

We have
Thus, we have
![]() $\rho _2\neq 0$
for
$\rho _2\neq 0$
for
![]() $n\geq 3$
. Since
$n\geq 3$
. Since
![]() $B_{3,0}(n)_{(2^3)}$
is irreducible,
$B_{3,0}(n)_{(2^3)}$
is irreducible,
![]() $\rho _2$
is injective.
$\rho _2$
is injective.
For
![]() $n\geq 4$
, we have
$n\geq 4$
, we have
and thus,
where

and

Therefore, we have
![]() $\rho _3\neq 0$
for
$\rho _3\neq 0$
for
![]() $n\geq 4$
. Since
$n\geq 4$
. Since
![]() $B_{3,0}(n)_{(2^3)}$
is irreducible,
$B_{3,0}(n)_{(2^3)}$
is irreducible,
![]() $\rho _3$
is injective.
$\rho _3$
is injective.
Remark 8.11. We consider a restriction of the bracket map
for each irreducible
![]() $\operatorname {GL}(n;\mathbb {Z})$
-submodule
$\operatorname {GL}(n;\mathbb {Z})$
-submodule
![]() $V_{\lambda }$
(resp.
$V_{\lambda }$
(resp.
![]() $V_{\mu }$
) of
$V_{\mu }$
) of
![]() $B_{d,k}(n)$
(resp.
$B_{d,k}(n)$
(resp.
![]() $B_{d,k+1}(n)$
). We write a wavy arrow
$B_{d,k+1}(n)$
). We write a wavy arrow
if the restriction map (8.5) does not vanish. Then, we have the following diagram for
![]() $n\geq 4$
:
$n\geq 4$
:

where
![]() $B_{3,2}^{(i)}(n)_{(2^2)}$
is the irreducible component of
$B_{3,2}^{(i)}(n)_{(2^2)}$
is the irreducible component of
![]() $B_{3,2}(n)_{(2^2)}$
generated by
$B_{3,2}(n)_{(2^2)}$
generated by


respectively. Note that, for
![]() $n=3$
,
$n=3$
,
![]() $B_3(3)$
includes all of the above irreducible subrepresentations but
$B_3(3)$
includes all of the above irreducible subrepresentations but
![]() $B_{3,1}(3)_{(2,1^3)}=0$
, and there are all of the wavy arrows but the three wavy arrows that are directed to or coming from
$B_{3,1}(3)_{(2,1^3)}=0$
, and there are all of the wavy arrows but the three wavy arrows that are directed to or coming from
![]() $B_{3,1}(3)_{(2,1^3)}$
. For
$B_{3,1}(3)_{(2,1^3)}$
. For
![]() $n=2$
, we have
$n=2$
, we have
For
![]() $n=1$
, we have
$n=1$
, we have
For
![]() $n=1,2$
, there are no wavy arrows because
$n=1,2$
, there are no wavy arrows because
![]() $B_{3,1}(n)=B_{3,3}(n)=0$
.
$B_{3,1}(n)=B_{3,3}(n)=0$
.
By Proposition 8.10 and Remark 8.11, we have the surjectivity and the nontriviality of the bracket map for
![]() $n\geq 3$
. Thus, by Theorem 8.9, one can obtain the following theorem, which improves Theorem 8.9 for
$n\geq 3$
. Thus, by Theorem 8.9, one can obtain the following theorem, which improves Theorem 8.9 for
![]() $d=3$
.
$d=3$
.
Theorem 8.12. We have an indecomposable decomposition
of
![]() $\operatorname {Aut}(F_n)$
-modules for
$\operatorname {Aut}(F_n)$
-modules for
![]() $n\geq 3$
.
$n\geq 3$
.
For
![]() $\lambda \vdash 4$
, let
$\lambda \vdash 4$
, let
 , where
, where
![]() $c_{\lambda }$
is the Young symmetrizer. Let
$c_{\lambda }$
is the Young symmetrizer. Let
![]() and
and
 .
.
For
![]() $n=2$
, we can check that
$n=2$
, we can check that
![]() $A_{3,2}(2)$
is semisimple as
$A_{3,2}(2)$
is semisimple as
![]() $\operatorname {Aut}(F_2)$
-modules, that is,
$\operatorname {Aut}(F_2)$
-modules, that is,
where
 We do not know whether or not the
We do not know whether or not the
![]() $\operatorname {Aut}(F_2)$
-module
$\operatorname {Aut}(F_2)$
-module
![]() $A_3(2)$
is semisimple.
$A_3(2)$
is semisimple.
Remark 8.13. Since
![]() $A_{3,2}(2)$
is semisimple, we have
$A_{3,2}(2)$
is semisimple, we have
![]() $\operatorname {Rad}(A_{3,2}(2))=0$
. On the other hand, we have
$\operatorname {Rad}(A_{3,2}(2))=0$
. On the other hand, we have
![]() $A_{3,3}(2)=A_{3,4}(2)\cong B_{3,4}(2)\neq 0$
. Therefore, we have
$A_{3,3}(2)=A_{3,4}(2)\cong B_{3,4}(2)\neq 0$
. Therefore, we have
![]() $\operatorname {Rad}(A_{3,2}(2))\neq A_{3,3}(2)$
.
$\operatorname {Rad}(A_{3,2}(2))\neq A_{3,3}(2)$
.
For
![]() $n=1$
, we have
$n=1$
, we have
![]() $\operatorname {Aut}(F_1)=\mathbb {Z}/2\mathbb {Z}$
. We can easily check the following proposition.
$\operatorname {Aut}(F_1)=\mathbb {Z}/2\mathbb {Z}$
. We can easily check the following proposition.
Proposition 8.14. The
![]() $\operatorname {Aut}(F_1)$
-action on
$\operatorname {Aut}(F_1)$
-action on
![]() $A_3(1)$
is trivial. Therefore, we have
$A_3(1)$
is trivial. Therefore, we have
![]() $A_3(1)=A_3 P(1)\oplus A_3 R_{(4)}(1) \oplus A_3 T(1).$
$A_3(1)=A_3 P(1)\oplus A_3 R_{(4)}(1) \oplus A_3 T(1).$
8.5 The socle of
 $A_d(n)$
for small d
$A_d(n)$
for small d
For an
![]() $\operatorname {Aut}(F_n)$
-module M, let
$\operatorname {Aut}(F_n)$
-module M, let
![]() $\operatorname {Soc}(M)$
denote the socle of M; that is,
$\operatorname {Soc}(M)$
denote the socle of M; that is,
Let us consider the cases for small d. Since
![]() $A_1(n)\cong \operatorname {Sym}^2(V_n)$
is simple, we have
$A_1(n)\cong \operatorname {Sym}^2(V_n)$
is simple, we have
By Theorem 6.9 of [Reference Katada16], we have
where
Note that
![]() $A_2 \tilde {T}(n)=A_{2,2}(n)$
$A_2 \tilde {T}(n)=A_{2,2}(n)$
By Proposition 8.14, we have
![]() $\operatorname {Soc}(A_3(1))=A_3(1)$
.
$\operatorname {Soc}(A_3(1))=A_3(1)$
.
Proposition 8.15. For
![]() $n\geq 3$
, we have
$n\geq 3$
, we have
Proof. A simple
![]() $\operatorname {Aut}(F_n)$
-submodule
$\operatorname {Aut}(F_n)$
-submodule
![]() $K\subset A_3(n)$
corresponds to an irreducible component of
$K\subset A_3(n)$
corresponds to an irreducible component of
![]() $B_3(n)$
via the PBW map. Therefore, by Remark 8.11, we have
$B_3(n)$
via the PBW map. Therefore, by Remark 8.11, we have
Moreover, we can check that
 $$ \begin{gather*} A_3 P(n)\cong V_{(6)},\quad A_3 R_{(4)}(n)\cong V_{(4)},\quad A_3 R_{(3,1)}(n)\cong V_{(3,1)},\\ A_3 S(n)\cong V_{(2,2)},\quad A_3 T(n)\cong V_{(2)}. \end{gather*} $$
$$ \begin{gather*} A_3 P(n)\cong V_{(6)},\quad A_3 R_{(4)}(n)\cong V_{(4)},\quad A_3 R_{(3,1)}(n)\cong V_{(3,1)},\\ A_3 S(n)\cong V_{(2,2)},\quad A_3 T(n)\cong V_{(2)}. \end{gather*} $$
Hence, we have
and the proof is complete.
8.6 The indecomposable decomposition of
 $A_4(n)$
$A_4(n)$
Here, we consider the indecomposable decomposition of
![]() $A_4(n)$
.
$A_4(n)$
.
Similarly, in degree
![]() $4$
, we have
$4$
, we have
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
$\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
 $$ \begin{gather*} \begin{aligned} \rho_1:B_{4,0}(n)_{(6,2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(5,1^2)}),\\ \rho_2:B_{4,0}(n)_{(4^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(3^2,1)}),\\ \rho_3:B_{4,0}(n)_{(4,2^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(5,1^2)}),\\ \rho_4:B_{4,0}(n)_{(4,2^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(4,1^3)}),\\ \rho_5:B_{4,0}(n)_{(4,2^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(3^2,1)}),\\ \rho_6:B_{4,0}(n)_{(4,2^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(3,2,1^2)}),\\ \rho_7:B_{4,0}(n)_{(2^4)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(3,2,1^2)}),\\ \rho_8:B_{4,0}(n)_{(2^4)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(2^2,1^3)}). \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} \rho_1:B_{4,0}(n)_{(6,2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(5,1^2)}),\\ \rho_2:B_{4,0}(n)_{(4^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(3^2,1)}),\\ \rho_3:B_{4,0}(n)_{(4,2^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(5,1^2)}),\\ \rho_4:B_{4,0}(n)_{(4,2^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(4,1^3)}),\\ \rho_5:B_{4,0}(n)_{(4,2^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(3^2,1)}),\\ \rho_6:B_{4,0}(n)_{(4,2^2)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(3,2,1^2)}),\\ \rho_7:B_{4,0}(n)_{(2^4)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(3,2,1^2)}),\\ \rho_8:B_{4,0}(n)_{(2^4)}&\rightarrow \operatorname{Hom}(\operatorname{gr}^1(\operatorname{IA}(n)), B_{4,1}(n)_{(2^2,1^3)}). \end{aligned} \end{gather*} $$
Proposition 8.16. The
![]() $\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
$\operatorname {GL}(n;\mathbb {Z})$
-module homomorphisms
![]() $\rho _1, \rho _2,\rho _3$
and
$\rho _1, \rho _2,\rho _3$
and
![]() $\rho _5$
are injective for
$\rho _5$
are injective for
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $\rho _4,\rho _6$
and
$\rho _4,\rho _6$
and
![]() $\rho _7$
for
$\rho _7$
for
![]() $n\geq 4$
and
$n\geq 4$
and
![]() $\rho _8$
for
$\rho _8$
for
![]() $n\geq 5$
.
$n\geq 5$
.
Proof. As in the proof of Proposition 8.10 in degree
![]() $3$
, we will check that
$3$
, we will check that
![]() $\rho _1$
is injective for
$\rho _1$
is injective for
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $\rho _7$
for
$\rho _7$
for
![]() $n\geq 4$
and
$n\geq 4$
and
![]() $\rho _8$
for
$\rho _8$
for
![]() $n\geq 5$
. The others can be obtained in a similar way.
$n\geq 5$
. The others can be obtained in a similar way.
For
![]() $n\geq 3$
, we have
$n\geq 3$
, we have
where

and

Thus, we have
![]() $\rho _1\neq 0$
for
$\rho _1\neq 0$
for
![]() $n\geq 3$
. Since
$n\geq 3$
. Since
![]() $B_{4,0}(n)_{(6,2)}$
is irreducible,
$B_{4,0}(n)_{(6,2)}$
is irreducible,
![]() $\rho _1$
is injective.
$\rho _1$
is injective.
For
![]() $n\geq 4$
, we have
$n\geq 4$
, we have
where

and

Thus,
![]() $\rho _7$
is injective for
$\rho _7$
is injective for
![]() $n\geq 4$
.
$n\geq 4$
.
For
![]() $n\geq 5$
, we have
$n\geq 5$
, we have
where

and

Therefore, we have
and thus,
![]() $\rho _8$
is injective for
$\rho _8$
is injective for
![]() $n\geq 5$
.
$n\geq 5$
.
By using Theorem 8.9 and Proposition 8.16 carefully, one can obtain the following theorem, which improves Theorem 8.9 for
![]() $d=4$
.
$d=4$
.
Theorem 8.17. We have an indecomposable decomposition
of
![]() $\operatorname {Aut}(F_n)$
-modules for
$\operatorname {Aut}(F_n)$
-modules for
![]() $n\geq 7$
.
$n\geq 7$
.
We expect that Theorem 8.17 holds for
![]() $n\geq 3$
.
$n\geq 3$
.
9 The
 $\operatorname {Out}(F_n)$
-module structure of
$\operatorname {Out}(F_n)$
-module structure of
 $A_d(n)$
$A_d(n)$
In [Reference Katada16], we observed that the
![]() $\operatorname {Aut}(F_n)$
-action on
$\operatorname {Aut}(F_n)$
-action on
![]() $A_d(n)$
induces an action of
$A_d(n)$
induces an action of
![]() $\operatorname {Out}(F_n)$
on
$\operatorname {Out}(F_n)$
on
![]() $A_d(n)$
. In this section, we obtain some results for
$A_d(n)$
. In this section, we obtain some results for
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Out}(F_n)$
-modules, which is induced by the results in Section 8.
$\operatorname {Out}(F_n)$
-modules, which is induced by the results in Section 8.
Since the
![]() $\operatorname {Aut}(F_n)$
-action on
$\operatorname {Aut}(F_n)$
-action on
![]() $A_d(n)$
factors through
$A_d(n)$
factors through
![]() $\operatorname {Out}(F_n)$
, any submodule of
$\operatorname {Out}(F_n)$
, any submodule of
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Aut}(F_n)$
-modules is a submodule of
$\operatorname {Aut}(F_n)$
-modules is a submodule of
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Out}(F_n)$
-modules, and vice versa. By Theorem 8.6, we obtain the radical filtration of
$\operatorname {Out}(F_n)$
-modules, and vice versa. By Theorem 8.6, we obtain the radical filtration of
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Out}(F_n)$
-modules.
$\operatorname {Out}(F_n)$
-modules.
Theorem 9.1. Let
![]() $n\geq 2d$
. Then, the filtration of
$n\geq 2d$
. Then, the filtration of
![]() $A_d(n)$
by the number of trivalent vertices coincides with the radical filtration of
$A_d(n)$
by the number of trivalent vertices coincides with the radical filtration of
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Out}(F_n)$
-modules.
$\operatorname {Out}(F_n)$
-modules.
By Theorem 8.9, we obtain an indecomposable decomposition of
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Out}(F_n)$
-modules.
$\operatorname {Out}(F_n)$
-modules.
Theorem 9.2. Let
![]() $d\geq 2$
. We have a direct decomposition
$d\geq 2$
. We have a direct decomposition
of
![]() $\operatorname {Out}(F_n)$
-modules, which is indecomposable for
$\operatorname {Out}(F_n)$
-modules, which is indecomposable for
![]() $n\geq 2d$
.
$n\geq 2d$
.
Theorems 8.12, 8.17 also hold as
![]() $\operatorname {Out}(F_n)$
-modules. Other results for
$\operatorname {Out}(F_n)$
-modules. Other results for
![]() $A_d(n)$
as
$A_d(n)$
as
![]() $\operatorname {Aut}(F_n)$
-modules such as Proposition 8.15 also hold.
$\operatorname {Aut}(F_n)$
-modules such as Proposition 8.15 also hold.
10 Indecomposable decomposition of the functor
 $A_d$
$A_d$
In this section, we obtain an indecomposable decomposition of the functor
![]() $A_d$
by using results in Section 8.
$A_d$
by using results in Section 8.
By Theorem 8.2, we obtain the following direct decomposition of the functor
![]() $A_d$
.
$A_d$
.
Theorem 10.1. We have a direct decomposition
in the functor category
![]() $\mathbf {fVect}^{\mathbf {F}^{\mathrm {op}}}$
.
$\mathbf {fVect}^{\mathbf {F}^{\mathrm {op}}}$
.
For
![]() $d=1$
, we have
$d=1$
, we have
![]() $A_1 Q=0$
and the functor
$A_1 Q=0$
and the functor
![]() $A_1=A_1 P$
is simple. For
$A_1=A_1 P$
is simple. For
![]() $d=2$
, we obtained this direct decomposition in Theorem 6.5 of [Reference Katada16]. Moreover, we proved that this direct decomposition of the functor
$d=2$
, we obtained this direct decomposition in Theorem 6.5 of [Reference Katada16]. Moreover, we proved that this direct decomposition of the functor
![]() $A_2$
is indecomposable (see Theorem 6.14 of [Reference Katada16]).
$A_2$
is indecomposable (see Theorem 6.14 of [Reference Katada16]).
By Theorem 8.9, we obtain the indecomposability of the direct decomposition of the functor
![]() $A_d$
.
$A_d$
.
Proposition 10.2. Let
![]() $d\geq 2$
. The decomposition
$d\geq 2$
. The decomposition
of the functor
![]() $A_d$
is indecomposable in the functor category
$A_d$
is indecomposable in the functor category
![]() $\mathbf {fVect}^{\mathbf {F}^{\mathrm {op}}}$
.
$\mathbf {fVect}^{\mathbf {F}^{\mathrm {op}}}$
.
Proof. Suppose that we have a decomposition
Then we have
![]() $A_d Q(2d)=G(2d)\oplus G'(2d)$
as
$A_d Q(2d)=G(2d)\oplus G'(2d)$
as
![]() $\operatorname {Aut}(F_{2d})$
-modules. By Theorem 8.9, the
$\operatorname {Aut}(F_{2d})$
-modules. By Theorem 8.9, the
![]() $\operatorname {Aut}(F_{2d})$
-module
$\operatorname {Aut}(F_{2d})$
-module
![]() $A_d Q(2d)$
is indecomposable. Therefore, we can assume that
$A_d Q(2d)$
is indecomposable. Therefore, we can assume that
![]() $G'(2d)=0$
and
$G'(2d)=0$
and
![]() $A_d Q(2d)=G(2d)$
. Since the subfunctor
$A_d Q(2d)=G(2d)$
. Since the subfunctor
![]() $A_d Q$
is generated by
$A_d Q$
is generated by
![]() $Q\in A_d Q(2d)$
, we have
$Q\in A_d Q(2d)$
, we have
![]() $A_d Q=G$
. Hence, the subfunctor
$A_d Q=G$
. Hence, the subfunctor
![]() $A_d Q$
is also indecomposable. By Lemma 8.3,
$A_d Q$
is also indecomposable. By Lemma 8.3,
![]() $A_d P(2d)$
is also indecomposable. Therefore, by the similar argument, the subfunctor
$A_d P(2d)$
is also indecomposable. Therefore, by the similar argument, the subfunctor
![]() $A_d P$
is also indecomposable.
$A_d P$
is also indecomposable.
Appendix A Presentation of the category
 $\mathbf {A}^{L}$
$\mathbf {A}^{L}$
In this section, we construct a category
![]() $\widetilde {\mathbf {A}^{L}}$
and a full functor
$\widetilde {\mathbf {A}^{L}}$
and a full functor
![]() $F: \widetilde {\mathbf {A}^{L}}\rightarrow \mathbf {A}^{L}$
to study a presentation of the category
$F: \widetilde {\mathbf {A}^{L}}\rightarrow \mathbf {A}^{L}$
to study a presentation of the category
![]() $\mathbf {A}^{L}$
, which we construct in Section 4.2.
$\mathbf {A}^{L}$
, which we construct in Section 4.2.
A.1 The category
 $\widetilde {\mathbf {A}^{L}}$
$\widetilde {\mathbf {A}^{L}}$
In this section, we construct a category
![]() $\widetilde {\mathbf {A}^{L}}$
, which has a generating set and some relations of the category
$\widetilde {\mathbf {A}^{L}}$
, which has a generating set and some relations of the category
![]() $\mathbf {A}^{L}$
.
$\mathbf {A}^{L}$
.
In a linear symmetric strict monoidal category
![]() $\mathcal {C}$
, let H be a Hopf algebra and L a Lie algebra. Define the adjoint action
$\mathcal {C}$
, let H be a Hopf algebra and L a Lie algebra. Define the adjoint action
![]() $ad_H:H\otimes H\rightarrow H$
by
$ad_H:H\otimes H\rightarrow H$
by
We call a morphism
![]() $c:I\rightarrow L^{\otimes 2}$
a symmetric invariant
$c:I\rightarrow L^{\otimes 2}$
a symmetric invariant
![]() $2$
-tensor if c satisfies
$2$
-tensor if c satisfies
and
Define
![]() $\widetilde {\mathbf {A}^{L}}$
to be the category which is as a linear symmetric strict monoidal category, generated by
$\widetilde {\mathbf {A}^{L}}$
to be the category which is as a linear symmetric strict monoidal category, generated by
-
• a cocommutative Hopf algebra
 $(H,\mu ,\eta ,\Delta ,\epsilon ,S)$
$(H,\mu ,\eta ,\Delta ,\epsilon ,S)$
-
• a Lie algebra with a symmetric invariant 2-tensor
 $(L,[\cdot ,\cdot ],c)$
$(L,[\cdot ,\cdot ],c)$
-
• morphisms
 $i: L\rightarrow H$
and
$i: L\rightarrow H$
and
 $ad_{L}: H\otimes L \rightarrow L$
$ad_{L}: H\otimes L \rightarrow L$
with the following nine relations:
-
(
 $\widetilde {\mathbf {A}^{L}}$
.1)
$\widetilde {\mathbf {A}^{L}}$
.1)
 $i\; [\cdot ,\cdot ]=-\mu (i\otimes i)+\mu P_{H,H}(i\otimes i),$
$i\; [\cdot ,\cdot ]=-\mu (i\otimes i)+\mu P_{H,H}(i\otimes i),$
-
(
 $\widetilde {\mathbf {A}^{L}}$
.2)
$\widetilde {\mathbf {A}^{L}}$
.2)
 $\Delta i=i\otimes \eta +\eta \otimes i,$
$\Delta i=i\otimes \eta +\eta \otimes i,$
-
(
 $\widetilde {\mathbf {A}^{L}}$
.3)
$\widetilde {\mathbf {A}^{L}}$
.3)
 $\epsilon i=0,$
$\epsilon i=0,$
-
(
 $\widetilde {\mathbf {A}^{L}}$
.4)
$\widetilde {\mathbf {A}^{L}}$
.4)
 $ad_{L}(\mu \otimes \operatorname {id}_L)=ad_{L}(\operatorname {id}_H\otimes ad_{L}),$
$ad_{L}(\mu \otimes \operatorname {id}_L)=ad_{L}(\operatorname {id}_H\otimes ad_{L}),$
-
(
 $\widetilde {\mathbf {A}^{L}}$
.5)
$\widetilde {\mathbf {A}^{L}}$
.5)
 $ad_{L}(\eta \otimes \operatorname {id}_{L})=\operatorname {id}_{L},$
$ad_{L}(\eta \otimes \operatorname {id}_{L})=\operatorname {id}_{L},$
-
(
 $\widetilde {\mathbf {A}^{L}}$
.6)
$\widetilde {\mathbf {A}^{L}}$
.6)
 $(ad_{L}\otimes ad_{L}) (\operatorname {id}_{H}\otimes P_{H,L}\otimes \operatorname {id}_{L}) (\Delta \otimes c)=c\epsilon ,$
$(ad_{L}\otimes ad_{L}) (\operatorname {id}_{H}\otimes P_{H,L}\otimes \operatorname {id}_{L}) (\Delta \otimes c)=c\epsilon ,$
-
(
 $\widetilde {\mathbf {A}^{L}}$
.7)
$\widetilde {\mathbf {A}^{L}}$
.7)
 $ad_{L}(\operatorname {id}_{H}\otimes [\cdot ,\cdot ]) =[\cdot ,\cdot ](ad_{L}\otimes ad_{L}) (\operatorname {id}_{H}\otimes P_{H,L}\otimes \operatorname {id}_{L})(\Delta \otimes \operatorname {id}_{L^{\otimes 2}}),$
$ad_{L}(\operatorname {id}_{H}\otimes [\cdot ,\cdot ]) =[\cdot ,\cdot ](ad_{L}\otimes ad_{L}) (\operatorname {id}_{H}\otimes P_{H,L}\otimes \operatorname {id}_{L})(\Delta \otimes \operatorname {id}_{L^{\otimes 2}}),$
-
(
 $\widetilde {\mathbf {A}^{L}}$
.8)
$\widetilde {\mathbf {A}^{L}}$
.8)
 $i\; ad_{L}=ad_{H}\; i,$
$i\; ad_{L}=ad_{H}\; i,$
-
(
 $\widetilde {\mathbf {A}^{L}}$
.9)
$\widetilde {\mathbf {A}^{L}}$
.9)
 $ad_{L}(i\otimes \operatorname {id}_{L})=-[\cdot ,\cdot ].$
$ad_{L}(i\otimes \operatorname {id}_{L})=-[\cdot ,\cdot ].$
Lemma A.1. In the category
![]() $\widetilde {\mathbf {A}^{L}}$
, the following relations hold.
$\widetilde {\mathbf {A}^{L}}$
, the following relations hold.
-
(1)
 $S i=- i.$
$S i=- i.$
-
(2)
 $ad_{H}(i\otimes i)=-i\; [\cdot ,\cdot ].$
$ad_{H}(i\otimes i)=-i\; [\cdot ,\cdot ].$
Proof. By
![]() $(\widetilde {\mathbf {A}^{L}}.2)$
and
$(\widetilde {\mathbf {A}^{L}}.2)$
and
![]() $(\widetilde {\mathbf {A}^{L}}.3)$
of the category
$(\widetilde {\mathbf {A}^{L}}.3)$
of the category
![]() $\widetilde {\mathbf {A}^{L}}$
and relations of Hopf algebras, we have
$\widetilde {\mathbf {A}^{L}}$
and relations of Hopf algebras, we have
Thus, we have equation (1). By
![]() $(\widetilde {\mathbf {A}^{L}}.8), (\widetilde {\mathbf {A}^{L}}.9)$
, we have equation (2) as follows:
$(\widetilde {\mathbf {A}^{L}}.8), (\widetilde {\mathbf {A}^{L}}.9)$
, we have equation (2) as follows:
We review the definition of a Casimir Hopf algebra. Let
![]() $\mathcal {C}$
be a linear symmetric strict monoidal category and H be a cocommutative Hopf algebra in
$\mathcal {C}$
be a linear symmetric strict monoidal category and H be a cocommutative Hopf algebra in
![]() $\mathcal {C}$
. A Casimir 2-tensor for H is a morphism
$\mathcal {C}$
. A Casimir 2-tensor for H is a morphism
![]() $c:I\rightarrow H^{\otimes 2}$
which is primitive, symmetric and invariant:
$c:I\rightarrow H^{\otimes 2}$
which is primitive, symmetric and invariant:
where
![]() $c_{13}:=(\operatorname {id}\otimes \eta \otimes \operatorname {id})c$
and
$c_{13}:=(\operatorname {id}\otimes \eta \otimes \operatorname {id})c$
and
![]() $c_{23}:=\eta \otimes c$
. By a Casimir Hopf algebra, we mean a cocommutative Hopf algebra H equipped with a Casimir 2-tensor.
$c_{23}:=\eta \otimes c$
. By a Casimir Hopf algebra, we mean a cocommutative Hopf algebra H equipped with a Casimir 2-tensor.
Lemma A.2.
![]() $(H,\mu ,\eta ,\Delta ,\epsilon ,S,\tilde {c}:=(i\otimes i) c)$
is a Casimir Hopf algebra in
$(H,\mu ,\eta ,\Delta ,\epsilon ,S,\tilde {c}:=(i\otimes i) c)$
is a Casimir Hopf algebra in
![]() $\widetilde {\mathbf {A}^{L}}$
.
$\widetilde {\mathbf {A}^{L}}$
.
Proof. Since H is a cocommutative Hopf algebra in
![]() $\widetilde {\mathbf {A}^{L}}$
, it suffices to check that
$\widetilde {\mathbf {A}^{L}}$
, it suffices to check that
![]() $\tilde {c}$
is a Casimir 2-tensor. By (
$\tilde {c}$
is a Casimir 2-tensor. By (
![]() $\widetilde {\mathbf {A}^{L}}$
. 2), we have equation (A.1) because
$\widetilde {\mathbf {A}^{L}}$
. 2), we have equation (A.1) because
By the symmetricity of c, we have equation (A.2) because
By (
![]() $\widetilde {\mathbf {A}^{L}}$
. 6) and (
$\widetilde {\mathbf {A}^{L}}$
. 6) and (
![]() $\widetilde {\mathbf {A}^{L}}$
. 8), we have equation (A.3) because
$\widetilde {\mathbf {A}^{L}}$
. 8), we have equation (A.3) because
 $$ \begin{gather*} \begin{aligned} &(ad_H\otimes ad_H)(\operatorname{id}_H\otimes P_{H,H}\otimes\operatorname{id}_H)(\Delta\otimes \tilde{c})\\ &=(ad_H\otimes ad_H)(\operatorname{id}_H\otimes P_{H,H}\otimes\operatorname{id}_H)(\Delta\otimes (i\otimes i))(\operatorname{id}_H\otimes c)\\ &=(i\otimes i)(ad_L\otimes ad_L)(\operatorname{id}_H\otimes P_{H,L}\otimes\operatorname{id}_L)(\Delta\otimes c)\\ &=(i\otimes i)c\epsilon\\ &=\tilde{c}\epsilon. \end{aligned} \end{gather*} $$
$$ \begin{gather*} \begin{aligned} &(ad_H\otimes ad_H)(\operatorname{id}_H\otimes P_{H,H}\otimes\operatorname{id}_H)(\Delta\otimes \tilde{c})\\ &=(ad_H\otimes ad_H)(\operatorname{id}_H\otimes P_{H,H}\otimes\operatorname{id}_H)(\Delta\otimes (i\otimes i))(\operatorname{id}_H\otimes c)\\ &=(i\otimes i)(ad_L\otimes ad_L)(\operatorname{id}_H\otimes P_{H,L}\otimes\operatorname{id}_L)(\Delta\otimes c)\\ &=(i\otimes i)c\epsilon\\ &=\tilde{c}\epsilon. \end{aligned} \end{gather*} $$
The category
![]() $\mathbf {A}$
has a Casimir Hopf algebra
$\mathbf {A}$
has a Casimir Hopf algebra
![]() $(H,c)=(1,\mu ,\eta ,\Delta ,\epsilon , S, c)$
, where
$(H,c)=(1,\mu ,\eta ,\Delta ,\epsilon , S, c)$
, where
 Moreover, Theorem 5.11 in [Reference Habiro and Massuyeau11] implies that as a linear symmetric strict monoidal category, the category
Moreover, Theorem 5.11 in [Reference Habiro and Massuyeau11] implies that as a linear symmetric strict monoidal category, the category
![]() $\mathbf {A}$
is free on the Casimir Hopf algebra
$\mathbf {A}$
is free on the Casimir Hopf algebra
![]() $(H,c)$
. Therefore, we have a unique linear symmetric monoidal functor
$(H,c)$
. Therefore, we have a unique linear symmetric monoidal functor
![]() $F_{(H,\tilde {c})}:\mathbf {A} \rightarrow \widetilde {\mathbf {A}^{L}}$
.
$F_{(H,\tilde {c})}:\mathbf {A} \rightarrow \widetilde {\mathbf {A}^{L}}$
.
A.2 Structure of the category
 $\mathbf {A}^{L}$
$\mathbf {A}^{L}$
In Section 4.3, we observed that the category
![]() $\mathbf {A}^{L}$
has a cocommutative Hopf algebra
$\mathbf {A}^{L}$
has a cocommutative Hopf algebra
![]() $(H,\mu ,\eta ,\Delta ,\epsilon ,S)$
and morphisms
$(H,\mu ,\eta ,\Delta ,\epsilon ,S)$
and morphisms
Lemma A.3. In the category
![]() $\mathbf {A}^{L}$
,
$\mathbf {A}^{L}$
,
![]() $(L, [\cdot ,\cdot ], c_{L})$
is a Lie algebra with a symmetric invariant
$(L, [\cdot ,\cdot ], c_{L})$
is a Lie algebra with a symmetric invariant
![]() $2$
-tensor.
$2$
-tensor.
Proof. By the AS and IHX relations, it follows that
![]() $(L,[\cdot ,\cdot ])$
is a Lie algebra. Since we have
$(L,[\cdot ,\cdot ])$
is a Lie algebra. Since we have

and

it follows that
![]() $c_{L}$
is a symmetric invariant
$c_{L}$
is a symmetric invariant
![]() $2$
-tensor.
$2$
-tensor.
Remark A.4. The full subcategory of
![]() $\mathbf {A}^{L}$
with the free monoid generated by L as the set of objects is isomorphic to the PROP
$\mathbf {A}^{L}$
with the free monoid generated by L as the set of objects is isomorphic to the PROP
![]() $LIE^{c}$
for Casimir Lie algebras (see [Reference Hinich and Vaintrob13] for details).
$LIE^{c}$
for Casimir Lie algebras (see [Reference Hinich and Vaintrob13] for details).
For each
![]() $m\geq 1,n\in \mathbb {N}$
, the degree
$m\geq 1,n\in \mathbb {N}$
, the degree
![]() $0$
part
$0$
part
![]() $\mathbf {A}^{L}_0(L^{\otimes m}, H^{\otimes n})$
of the hom-set
$\mathbf {A}^{L}_0(L^{\otimes m}, H^{\otimes n})$
of the hom-set
![]() $\mathbf {A}^{L}(L^{\otimes m}, H^{\otimes n})$
has an
$\mathbf {A}^{L}(L^{\otimes m}, H^{\otimes n})$
has an
![]() $\operatorname {Aut}(F_n)$
-module structure which is defined in a way similar to that of
$\operatorname {Aut}(F_n)$
-module structure which is defined in a way similar to that of
![]() $A_d(n)$
. For general
$A_d(n)$
. For general
![]() $m,n$
, the
$m,n$
, the
![]() $\operatorname {Aut}(F_n)$
-action on
$\operatorname {Aut}(F_n)$
-action on
![]() $\mathbf {A}^{L}_0(L^{\otimes m}, H^{\otimes n})$
does not factors through the outer automorphism group
$\mathbf {A}^{L}_0(L^{\otimes m}, H^{\otimes n})$
does not factors through the outer automorphism group
![]() $\operatorname {Out}(F_n)$
.
$\operatorname {Out}(F_n)$
.
Proposition A.5. There exists a unique linear symmetric monoidal functor
![]() $F:\widetilde {\mathbf {A}^{L}} \rightarrow \mathbf {A}^{L}$
which maps
$F:\widetilde {\mathbf {A}^{L}} \rightarrow \mathbf {A}^{L}$
which maps
![]() $(L,[\cdot ,\cdot ],c_{L},i,ad_L)$
in
$(L,[\cdot ,\cdot ],c_{L},i,ad_L)$
in
![]() $\widetilde {\mathbf {A}^{L}}$
to
$\widetilde {\mathbf {A}^{L}}$
to
![]() $(L,[\cdot ,\cdot ],c,i,ad_L)$
in
$(L,[\cdot ,\cdot ],c,i,ad_L)$
in
![]() $\mathbf {A}^{L}$
and which makes the following diagram commutative
$\mathbf {A}^{L}$
and which makes the following diagram commutative

Proof. We can check that morphisms of
![]() $\mathbf {A}^{L}$
satisfy the relations
$\mathbf {A}^{L}$
satisfy the relations
![]() $(\widetilde {\mathbf {A}^{L}}.1),\cdots ,(\widetilde {\mathbf {A}^{L}}.9)$
by diagrammatic computation. Since
$(\widetilde {\mathbf {A}^{L}}.1),\cdots ,(\widetilde {\mathbf {A}^{L}}.9)$
by diagrammatic computation. Since
![]() $\widetilde {\mathbf {A}^{L}}$
is the linear symmetric strict monoidal category generated by H, L and morphisms
$\widetilde {\mathbf {A}^{L}}$
is the linear symmetric strict monoidal category generated by H, L and morphisms
![]() $i, ad_L$
with relations
$i, ad_L$
with relations
![]() $(\widetilde {\mathbf {A}^{L}}.1),\cdots ,(\widetilde {\mathbf {A}^{L}}.9)$
, we can construct a unique linear symmetric monoidal functor
$(\widetilde {\mathbf {A}^{L}}.1),\cdots ,(\widetilde {\mathbf {A}^{L}}.9)$
, we can construct a unique linear symmetric monoidal functor
![]() $F:\widetilde {\mathbf {A}^{L}} \rightarrow \mathbf {A}^{L}$
which maps
$F:\widetilde {\mathbf {A}^{L}} \rightarrow \mathbf {A}^{L}$
which maps
![]() $(H,L,c,i,ad_L)$
in
$(H,L,c,i,ad_L)$
in
![]() $\widetilde {\mathbf {A}^{L}}$
to
$\widetilde {\mathbf {A}^{L}}$
to
![]() $(H,L,c_{L},i,ad_L)$
in
$(H,L,c_{L},i,ad_L)$
in
![]() $\mathbf {A}^{L}$
.
$\mathbf {A}^{L}$
.
A.3 The full functor
 $F: \widetilde {\mathbf {A}^{L}} \rightarrow \mathbf {A}^{L}$
$F: \widetilde {\mathbf {A}^{L}} \rightarrow \mathbf {A}^{L}$
We prove that the functor F in Proposition A.5 is full.
Lemma A.6. A morphism in
![]() $\mathbf {A}^{L}$
can be written as a linear sum of the following diagrams:
$\mathbf {A}^{L}$
can be written as a linear sum of the following diagrams:

where
![]() denotes S or
denotes S or
![]() $\operatorname {id}_H$
and
$\operatorname {id}_H$
and
 .
.
Note that
![]() $c^{\ast }$
is not a morphism in
$c^{\ast }$
is not a morphism in
![]() $\mathbf {A}^{L}$
but just a diagram.
$\mathbf {A}^{L}$
but just a diagram.
Proof. By using symmetries
![]() $P_{H,L}, P_{L,H}$
, we can deform any diagram
$P_{H,L}, P_{L,H}$
, we can deform any diagram
![]() $f\in \mathbf {A}^{L}$
into a morphism in
$f\in \mathbf {A}^{L}$
into a morphism in
![]() $\mathbf {A}^{L}(H^{\otimes m}\otimes L^{\otimes n}, H^{\otimes m'}\otimes L^{\otimes n'})$
, so it suffices to consider a diagram f in
$\mathbf {A}^{L}(H^{\otimes m}\otimes L^{\otimes n}, H^{\otimes m'}\otimes L^{\otimes n'})$
, so it suffices to consider a diagram f in
![]() $\mathbf {A}^{L}(H^{\otimes m}\otimes L^{\otimes n}, H^{\otimes m'}\otimes L^{\otimes n'})$
.
$\mathbf {A}^{L}(H^{\otimes m}\otimes L^{\otimes n}, H^{\otimes m'}\otimes L^{\otimes n'})$
.
We can decompose f as follows:
![]() $f=f'\circ ((P\circ \Delta ^{[c_1,\cdots , c_m]})\otimes \operatorname {id}_{L^{\otimes n}}),$
where P is a tensor product of copies of
$f=f'\circ ((P\circ \Delta ^{[c_1,\cdots , c_m]})\otimes \operatorname {id}_{L^{\otimes n}}),$
where P is a tensor product of copies of
![]() $P_{H,H}$
and
$P_{H,H}$
and
![]() $\operatorname {id}_H$
,
$\operatorname {id}_H$
,
![]() $c_1,\cdots ,c_m\geq 0$
, and
$c_1,\cdots ,c_m\geq 0$
, and
![]() $f'$
is a diagram such that each handle has only one solid or dashed line. We can assume that handles of
$f'$
is a diagram such that each handle has only one solid or dashed line. We can assume that handles of
![]() $U_m$
which include a dashed line are arranged right-hand side of
$U_m$
which include a dashed line are arranged right-hand side of
![]() $U_m$
.
$U_m$
.
By pulling univalent vertices that are attached to the solid lines toward the upper right-hand side of
![]() $U_m$
, we can decompose
$U_m$
, we can decompose
![]() $f'$
as
$f'$
as
 (see Lemma 5.16 [Reference Habiro and Massuyeau11]).
(see Lemma 5.16 [Reference Habiro and Massuyeau11]).
Furthermore, any uni-trivalent graph can be obtained from morphisms
![]() $c_{L}$
,
$c_{L}$
,
![]() $P_{L,L}$
,
$P_{L,L}$
,
![]() $[\cdot ,\cdot ]$
,
$[\cdot ,\cdot ]$
,
![]() $\operatorname {id}_L\in \mathbf {A}^{L}$
and
$\operatorname {id}_L\in \mathbf {A}^{L}$
and
![]() $c^{\ast }$
by the tensor product and the composition, so the proof is complete.
$c^{\ast }$
by the tensor product and the composition, so the proof is complete.
Proposition A.7. The linear symmetric monoidal functor
![]() $F:\widetilde {\mathbf {A}^{L}} \rightarrow \mathbf {A}^{L}$
in Proposition A.5 is full.
$F:\widetilde {\mathbf {A}^{L}} \rightarrow \mathbf {A}^{L}$
in Proposition A.5 is full.
Proof. It suffices to show that morphisms of
![]() $\mathbf {A}^{L}$
are generated by
$\mathbf {A}^{L}$
are generated by
![]() $\mu ,\eta ,\Delta ,\epsilon ,S$
,
$\mu ,\eta ,\Delta ,\epsilon ,S$
,
![]() $[\cdot ,\cdot ],c_{L}$
, i,
$[\cdot ,\cdot ],c_{L}$
, i,
![]() $ad_{L}$
and symmetries. By Lemma A.6, we need to prove that we can eliminate
$ad_{L}$
and symmetries. By Lemma A.6, we need to prove that we can eliminate
![]() $c^{\ast }$
from the diagram (A.4) by using the above morphisms in
$c^{\ast }$
from the diagram (A.4) by using the above morphisms in
![]() $\mathbf {A}^{L}$
.
$\mathbf {A}^{L}$
.
By the definition of the category
![]() $\mathbf {A}^{L}$
, for any
$\mathbf {A}^{L}$
, for any
![]() $c^{\ast }$
in the diagram (A.4), if exists, either of the endpoints of
$c^{\ast }$
in the diagram (A.4), if exists, either of the endpoints of
![]() $c^{\ast }$
is finally attached to one of the lower dashed lines. Therefore, there is
$c^{\ast }$
is finally attached to one of the lower dashed lines. Therefore, there is
![]() $c_{L}$
between
$c_{L}$
between
![]() $c^{\ast }$
and the lower dashed line. If there are more than one such
$c^{\ast }$
and the lower dashed line. If there are more than one such
![]() $c_{L}$
, then we choose one such that there are the least trivalent vertices between
$c_{L}$
, then we choose one such that there are the least trivalent vertices between
![]() $c^{\ast }$
and itself. By the AS relation, we have only to consider the case where the neighborhood of the
$c^{\ast }$
and itself. By the AS relation, we have only to consider the case where the neighborhood of the
![]() $c_{L}$
and the
$c_{L}$
and the
![]() $c^{\ast }$
is either
$c^{\ast }$
is either

Hence, we can eliminate
![]() $c^{\ast }$
from the diagram (A.4) and the proof is complete.
$c^{\ast }$
from the diagram (A.4) and the proof is complete.
Acknowledgements
The author would like to thank Kazuo Habiro for careful reading and valuable advice.
Competing Interests
None.