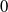1. Introduction
1.1. Étale gerbes
Let
![]() $X$
be a smooth projective variety over the complex numbers. An étale gerbe
$X$
be a smooth projective variety over the complex numbers. An étale gerbe
![]() $\mathcal{G}$
over
$\mathcal{G}$
over
![]() $X$
may be thought of as a fiber bundle over
$X$
may be thought of as a fiber bundle over
![]() $X$
whose fibers are the classifying stack
$X$
whose fibers are the classifying stack
![]() $BG$
of a certain finite group
$BG$
of a certain finite group
![]() $G$
. Geometric properties of
$G$
. Geometric properties of
![]() $\mathcal{G}$
are of purely stack-theoretic nature.
$\mathcal{G}$
are of purely stack-theoretic nature.
In ref. [Reference Hellerman, Henriques, Pantev and Sharpe17], physical theories on an étale gerbe
![]() $\mathcal{G}$
are considered, leading to the formulation of decomposition conjecture (also known as gerbe duality). Interpreted in mathematics, the decomposition conjecture for
$\mathcal{G}$
are considered, leading to the formulation of decomposition conjecture (also known as gerbe duality). Interpreted in mathematics, the decomposition conjecture for
![]() $\mathcal{G}$
asserts that the geometry of
$\mathcal{G}$
asserts that the geometry of
![]() $\mathcal{G}$
is equivalent to the geometry of a disconnected space
$\mathcal{G}$
is equivalent to the geometry of a disconnected space
![]() $\widehat{\mathcal{G}}$
equipped with a
$\widehat{\mathcal{G}}$
equipped with a
![]() $\mathbb{C}^*$
-gerbe. The decomposition conjecture has been proven in several mathematical aspects in ref. [Reference Tang and Tseng22].
$\mathbb{C}^*$
-gerbe. The decomposition conjecture has been proven in several mathematical aspects in ref. [Reference Tang and Tseng22].
1.2. Gromov-Witten theory
Gromov-Witten theory of a target
![]() $Z$
is defined using moduli stacks
$Z$
is defined using moduli stacks
![]() ${\mathcal{K}}_{g,n}(Z,d)$
of stable maps to
${\mathcal{K}}_{g,n}(Z,d)$
of stable maps to
![]() $Z$
. Gromov-Witten invariants of
$Z$
. Gromov-Witten invariants of
![]() $Z$
are integrals of natural cohomology classes on
$Z$
are integrals of natural cohomology classes on
![]() ${\mathcal{K}}_{g,n}(Z,d)$
against the virtual fundamental class of
${\mathcal{K}}_{g,n}(Z,d)$
against the virtual fundamental class of
![]() ${\mathcal{K}}_{g,n}(Z,d)$
.
${\mathcal{K}}_{g,n}(Z,d)$
.
The Gromov-Witten theory of an étale gerbe
![]() $\mathcal{G}$
has been studied, with a point of view toward the decomposition conjecture, in various generalities in refs. [Reference Andreini, Jiang and Tseng5], [Reference Andreini, Jiang and Tseng6], [Reference Johnson19], [Reference Tang and Tseng23], [Reference Tseng25].
$\mathcal{G}$
has been studied, with a point of view toward the decomposition conjecture, in various generalities in refs. [Reference Andreini, Jiang and Tseng5], [Reference Andreini, Jiang and Tseng6], [Reference Johnson19], [Reference Tang and Tseng23], [Reference Tseng25].
1.3. Quantum K-theory
Quantum K-theory, introduced in refs. [Reference Givental13], [Reference Lee20], is the K-theoretic counterpart of Gromov-Witten theory. K-theoretic Gromov-Witten invariants of a target
![]() $Z$
are Euler characteristics of natural K-theory classes on
$Z$
are Euler characteristics of natural K-theory classes on
![]() ${\mathcal{K}}_{g,n}(Z,d)$
tensored with the virtual structure sheaf
${\mathcal{K}}_{g,n}(Z,d)$
tensored with the virtual structure sheaf
![]() $\mathcal{O}_{{\mathcal{K}}_{g,n}(Z,d)}^{vir}$
. An extension of quantum K-theory to target Deligne-Mumford stacks is given in ref. [Reference Tonita and Tseng24].
$\mathcal{O}_{{\mathcal{K}}_{g,n}(Z,d)}^{vir}$
. An extension of quantum K-theory to target Deligne-Mumford stacks is given in ref. [Reference Tonita and Tseng24].
Quantum Hirzebruch-Riemann-Roch theorems [Reference Givental and Tonita16], [Reference Tonita and Tseng24], [Reference Givental14], [Reference Givental15] imply that quantum K-theory can be determined by (cohomological) Gromov-Witten theory. Since (cohomological) Gromov-Witten theory of étale gerbes has been shown to satisfy the decomposition conjecture in many cases, it is natural to ask if quantum K-theory of an étale gerbe
![]() $\mathcal{G}$
can be studied with a viewpoint toward the decomposition conjecture. This note contains an attempt to address this for root gerbes over
$\mathcal{G}$
can be studied with a viewpoint toward the decomposition conjecture. This note contains an attempt to address this for root gerbes over
![]() $X$
in genus
$X$
in genus
![]() $0$
.
$0$
.
1.4. Root gerbes
Given a line bundle
![]() $L\to X$
and an integer
$L\to X$
and an integer
![]() $r\gt 0$
, one can associate the stack
$r\gt 0$
, one can associate the stack
![]() $\sqrt [r]{L/X}$
of
$\sqrt [r]{L/X}$
of
![]() $r$
-th roots of
$r$
-th roots of
![]() $L$
, which is a smooth Deligne-Mumford stack whose points over an
$L$
, which is a smooth Deligne-Mumford stack whose points over an
![]() $X$
-scheme
$X$
-scheme
![]() $f\,:\, S\to X$
are
$f\,:\, S\to X$
are
The coarse moduli space of
![]() $\sqrt [r]{L/X}$
is
$\sqrt [r]{L/X}$
is
![]() $X$
. Furthermore, the natural map
$X$
. Furthermore, the natural map
![]() $\rho \,:\, \sqrt [r]{L/X}\to X$
has the structure of a
$\rho \,:\, \sqrt [r]{L/X}\to X$
has the structure of a
![]() $\mu _r$
-gerbe.
$\mu _r$
-gerbe.
The strategy employed to study quantum K-theory of
![]() $\sqrt [r]{L/X}$
in this note is the same as that of [Reference Andreini, Jiang and Tseng5]. Namely, we examine the structure of moduli stacks of genus
$\sqrt [r]{L/X}$
in this note is the same as that of [Reference Andreini, Jiang and Tseng5]. Namely, we examine the structure of moduli stacks of genus
![]() $0$
stable maps to
$0$
stable maps to
![]() $\sqrt [r]{L/X}$
and apply pushforward results for virtual structure sheaves. The main result of this note is Proposition 2.2.
$\sqrt [r]{L/X}$
and apply pushforward results for virtual structure sheaves. The main result of this note is Proposition 2.2.
1.5. Root stacks
Given a smooth irreducible divisor
![]() $D\subset X$
and an integer
$D\subset X$
and an integer
![]() $r\gt 0$
, one can associate the stack
$r\gt 0$
, one can associate the stack
![]() $X_{D,r}$
of
$X_{D,r}$
of
![]() $r$
-th roots of
$r$
-th roots of
![]() $X$
along
$X$
along
![]() $D$
. In [Reference Abramovich, Cadman and Wise1], genus
$D$
. In [Reference Abramovich, Cadman and Wise1], genus
![]() $0$
relative Gromov-Witten invariants of
$0$
relative Gromov-Witten invariants of
![]() $(X,D)$
and Gromov-Witten invariants of
$(X,D)$
and Gromov-Witten invariants of
![]() $X_{D,r}$
are shown to be the same when
$X_{D,r}$
are shown to be the same when
![]() $r$
is sufficiently large. Their proof uses pushforwards of virtual fundamental classes and an intermediate moduli space. In Section 2.6, we explain how to adapt their argument to obtain a similar result for genus
$r$
is sufficiently large. Their proof uses pushforwards of virtual fundamental classes and an intermediate moduli space. In Section 2.6, we explain how to adapt their argument to obtain a similar result for genus
![]() $0$
K-theoretic Gromov-Witten invariants, see (2.13).
$0$
K-theoretic Gromov-Witten invariants, see (2.13).
1.6. Outline
The rest of this note is organized as follows. Section 2.1 recalls notations used the definition of K-theoretic Gromov-Witten invariants of Deligne-Mumford stacks. In Section 2.2, we discuss properties of the structure morphism for moduli stacks of genus
![]() $0$
stable maps to a root gerbe. In Section 2.3, we discuss pushforwards of virtual structure sheaves. Section 2.4 contains the proof of our main result and Section 2.5 discusses an extension of the main result to a more general class of gerbes. In Section 2.6, we discuss a K-theoretic version of relative/orbifold correspondence. In Section 3, we discuss some related questions.
$0$
stable maps to a root gerbe. In Section 2.3, we discuss pushforwards of virtual structure sheaves. Section 2.4 contains the proof of our main result and Section 2.5 discusses an extension of the main result to a more general class of gerbes. In Section 2.6, we discuss a K-theoretic version of relative/orbifold correspondence. In Section 3, we discuss some related questions.
1.7. Acknowledgment
This note is inspired by the results on virtual pushforwards in K-theory in refs. [Reference Chou, Herr and Lee10] and [Reference Chou, Herr and Lee11]. It is a pleasure to thank the authors Y.-C. Chou, L. Herr, and Y.-P. Lee. The author also thanks E. Sharpe for discussions. The author is supported in part by Simons Foundation Collaboration Grant.
2. Results
2.1. Quantum K-theory of target stacks
We begin with recalling the definition of K-theoretic Gromov-Witten invariants of Deligne-Mumford stacks, as given in ref. [Reference Tonita and Tseng24]. Let
![]() $\mathcal{Z}$
be a smooth proper Deligne-Mumford stack with projective coarse moduli space
$\mathcal{Z}$
be a smooth proper Deligne-Mumford stack with projective coarse moduli space
![]() $Z$
. The moduli stack of
$Z$
. The moduli stack of
![]() $n$
-pointed genus
$n$
-pointed genus
![]() $g$
degree
$g$
degree
![]() $d$
stable maps to
$d$
stable maps to
![]() $\mathcal{Z}$
is denoted by
$\mathcal{Z}$
is denoted by
![]() ${\mathcal{K}}_{g,n}(\mathcal{Z},d)$
. The detailed definition can be found in [Reference Abramovich and Vistoli4]. It is known that
${\mathcal{K}}_{g,n}(\mathcal{Z},d)$
. The detailed definition can be found in [Reference Abramovich and Vistoli4]. It is known that
![]() ${\mathcal{K}}_{g,n}(\mathcal{Z},d)$
is a proper Deligne-Mumford stack equipped with a perfect obstruction theory, see [Reference Abramovich and Vistoli4], [Reference Abramovich, Graber and Vistoli3]. Applying the recipe of [Reference Lee20] to this perfect obstruction theory yields a virtual structure sheaf
${\mathcal{K}}_{g,n}(\mathcal{Z},d)$
is a proper Deligne-Mumford stack equipped with a perfect obstruction theory, see [Reference Abramovich and Vistoli4], [Reference Abramovich, Graber and Vistoli3]. Applying the recipe of [Reference Lee20] to this perfect obstruction theory yields a virtual structure sheaf
![]() ${\mathcal{O}}_{{\mathcal{K}}_{g,n}(\mathcal{Z},d)}^{vir}$
. There are evaluation maps
${\mathcal{O}}_{{\mathcal{K}}_{g,n}(\mathcal{Z},d)}^{vir}$
. There are evaluation maps
![]() $ev_i\,:\,{\mathcal{K}}_{g,n}(\mathcal{Z}, d)\to \bar{I}\mathcal{Z}$
, where
$ev_i\,:\,{\mathcal{K}}_{g,n}(\mathcal{Z}, d)\to \bar{I}\mathcal{Z}$
, where
![]() $\bar{I}\mathcal{Z}$
is the rigidified inertia stack of
$\bar{I}\mathcal{Z}$
is the rigidified inertia stack of
![]() $\mathcal{Z}$
. See [Reference Abramovich, Graber and Vistoli3] for more details on the construction of evaluation maps.
$\mathcal{Z}$
. See [Reference Abramovich, Graber and Vistoli3] for more details on the construction of evaluation maps.
K-theoretic Gromov-Witten invariants of
![]() $\mathcal{Z}$
are Euler characteristics of the following form:
$\mathcal{Z}$
are Euler characteristics of the following form:
 \begin{equation} \chi \!\left ({\mathcal{K}}_{g,n}(\mathcal{Z},d),{\mathcal{O}}_{{\mathcal{K}}_{g,n}(\mathcal{Z},d)}^{vir}\otimes \bigotimes _{i=1}^n ev_i^* \alpha _i\right )\in \mathbb{Z}, \quad \alpha _1,\ldots,\alpha _n\in K^*(\bar{I}\mathcal{Z}). \end{equation}
\begin{equation} \chi \!\left ({\mathcal{K}}_{g,n}(\mathcal{Z},d),{\mathcal{O}}_{{\mathcal{K}}_{g,n}(\mathcal{Z},d)}^{vir}\otimes \bigotimes _{i=1}^n ev_i^* \alpha _i\right )\in \mathbb{Z}, \quad \alpha _1,\ldots,\alpha _n\in K^*(\bar{I}\mathcal{Z}). \end{equation}
2.2. Structure morphism
Sending a stable map
![]() $f\,:\, \left({\mathcal{C}}, \{\Sigma _i\}_{i=1}^n\right)/S\to \mathcal{Z}$
to the induced map
$f\,:\, \left({\mathcal{C}}, \{\Sigma _i\}_{i=1}^n\right)/S\to \mathcal{Z}$
to the induced map
![]() $\bar{f}\,:\, \left(C, \{\bar{\Sigma }_i\}_{i=1}^n\right){/}S\to Z$
between coarse moduli spaces yields a morphism
$\bar{f}\,:\, \left(C, \{\bar{\Sigma }_i\}_{i=1}^n\right){/}S\to Z$
between coarse moduli spaces yields a morphism
We examine (2.2) in the special case
![]() $\mathcal{Z}=\sqrt [r]{L/X}$
and
$\mathcal{Z}=\sqrt [r]{L/X}$
and
![]() $g=0$
.
$g=0$
.
As explained in [Reference Andreini, Jiang and Tseng5, Section 3.1], the rigidified inertia stack of
![]() $\sqrt [r]{L/X}$
is a disjoint union of components
$\sqrt [r]{L/X}$
is a disjoint union of components
![]() $\bar{I}\!\left(\sqrt [r]{L/X}\right)_g$
indexed by
$\bar{I}\!\left(\sqrt [r]{L/X}\right)_g$
indexed by
![]() $g\in \mu _r$
. As in [Reference Andreini, Jiang and Tseng5, Definition 3.3], for
$g\in \mu _r$
. As in [Reference Andreini, Jiang and Tseng5, Definition 3.3], for
![]() $g_1,\ldots,g_n\in \mu _r$
, put
$g_1,\ldots,g_n\in \mu _r$
, put
In order for
![]() ${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
to be non-empty, the elements
${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
to be non-empty, the elements
![]() $g_1,\ldots,g_n$
are required to satisfy certain condition, see [Reference Andreini, Jiang and Tseng5, Section 3.1].
$g_1,\ldots,g_n$
are required to satisfy certain condition, see [Reference Andreini, Jiang and Tseng5, Section 3.1].
We consider the restriction of (2.2) to
![]() ${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
:
${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
:
The structure of the map
![]() $p$
has been analyzed in ref. [Reference Andreini, Jiang and Tseng5]. We reproduce [Reference Andreini, Jiang and Tseng5, Diagram (26)] as follows:
$p$
has been analyzed in ref. [Reference Andreini, Jiang and Tseng5]. We reproduce [Reference Andreini, Jiang and Tseng5, Diagram (26)] as follows:

Here,
![]() $\mathfrak{M}_{0,n}$
is the stack of
$\mathfrak{M}_{0,n}$
is the stack of
![]() $n$
-pointed genus
$n$
-pointed genus
![]() $0$
prestable curves (see e.g. [Reference Bae and Schmidt7] for a discussion), and
$0$
prestable curves (see e.g. [Reference Bae and Schmidt7] for a discussion), and
![]() $\mathfrak{M}_{0,n}^{tw}$
is the stack of
$\mathfrak{M}_{0,n}^{tw}$
is the stack of
![]() $n$
-pointed genus
$n$
-pointed genus
![]() $0$
prestable twisted curves (see [Reference Olsson21]).
$0$
prestable twisted curves (see [Reference Olsson21]).
![]() $\mathfrak{M}_{0,n,d}$
and
$\mathfrak{M}_{0,n,d}$
and
![]() $\mathfrak{M}_{0,n,d}^{tw}$
are variants of
$\mathfrak{M}_{0,n,d}^{tw}$
are variants of
![]() $\mathfrak{M}_{0,n}$
and
$\mathfrak{M}_{0,n}$
and
![]() $\mathfrak{M}_{0,n}^{tw}$
parametrizing prestable (twisted) curves weighted by
$\mathfrak{M}_{0,n}^{tw}$
parametrizing prestable (twisted) curves weighted by
![]() $d\in H^2(X,\mathbb{Z})$
, see [Reference Andreini, Jiang and Tseng5, Section 3.2] for an introduction and [Reference Bae and Schmidt7] and [Reference Tseng26] for further details.
$d\in H^2(X,\mathbb{Z})$
, see [Reference Andreini, Jiang and Tseng5, Section 3.2] for an introduction and [Reference Bae and Schmidt7] and [Reference Tseng26] for further details.
In (2.4), the stack
![]() $\mathfrak{Y}_{0,n,d}^{\vec{g}}$
is constructed in [Reference Andreini, Jiang and Tseng5, Definition 3.12] by applying the root construction to a certain divisor of
$\mathfrak{Y}_{0,n,d}^{\vec{g}}$
is constructed in [Reference Andreini, Jiang and Tseng5, Definition 3.12] by applying the root construction to a certain divisor of
![]() $\mathfrak{M}_{0,n,d}$
. It follows that the composition
$\mathfrak{M}_{0,n,d}$
. It follows that the composition
![]() $\mathfrak{Y}_{0,n,d}^{\vec{g}}\to \mathfrak{M}_{0,n,d}^{tw}\to \mathfrak{M}_{0,n,d}$
is proper and birational. The stacks
$\mathfrak{Y}_{0,n,d}^{\vec{g}}\to \mathfrak{M}_{0,n,d}^{tw}\to \mathfrak{M}_{0,n,d}$
is proper and birational. The stacks
![]() $P$
and
$P$
and
![]() $P_n^{\vec{g}}$
are defined by cartesian squares. The map
$P_n^{\vec{g}}$
are defined by cartesian squares. The map
![]() $s$
is defined by [Reference Andreini, Jiang and Tseng5, Lemma 3.18].
$s$
is defined by [Reference Andreini, Jiang and Tseng5, Lemma 3.18].
Example 2.1.
When
![]() $X$
is a point, the line bundle
$X$
is a point, the line bundle
![]() $L$
is necessarily trivial. In this case,
$L$
is necessarily trivial. In this case,
![]() $\sqrt [r]{L/X}=B\mu _r$
. The moduli stacks
$\sqrt [r]{L/X}=B\mu _r$
. The moduli stacks
![]() ${\mathcal{K}}_{0,n}(B\mu _r)^{\vec{g}}$
and
${\mathcal{K}}_{0,n}(B\mu _r)^{\vec{g}}$
and
![]() ${\mathcal{K}}_{0,n}(\text{pt})=\overline{\mathcal{M}}_{0,n}$
are smooth of expected dimensions. The morphism (
2.3
) in this case has been studied in [8]. It is shown in [8] that there is a factorization
${\mathcal{K}}_{0,n}(\text{pt})=\overline{\mathcal{M}}_{0,n}$
are smooth of expected dimensions. The morphism (
2.3
) in this case has been studied in [8]. It is shown in [8] that there is a factorization
![]() ${\mathcal{K}}_{0,n}(B\mu _r)^{\vec{g}}\to \mathcal{N}\to \overline{\mathcal{M}}_{0,n}$
, where
${\mathcal{K}}_{0,n}(B\mu _r)^{\vec{g}}\to \mathcal{N}\to \overline{\mathcal{M}}_{0,n}$
, where
![]() ${\mathcal{K}}_{0,n}(B\mu _r)^{\vec{g}}\to \mathcal{N}$
is the stack of
${\mathcal{K}}_{0,n}(B\mu _r)^{\vec{g}}\to \mathcal{N}$
is the stack of
![]() $r$
-th roots of certain line bundle, and
$r$
-th roots of certain line bundle, and
![]() $\mathcal{N}\to \overline{\mathcal{M}}_{0,n}$
is a root construction.
$\mathcal{N}\to \overline{\mathcal{M}}_{0,n}$
is a root construction.
2.3. Pushforward
We now examine obstruction theories. Since the map
![]() $s^{\prime\prime}$
is étale, the standard obstruction theory on
$s^{\prime\prime}$
is étale, the standard obstruction theory on
![]() ${\mathcal{K}}_{0,n}(X,d)$
relative to
${\mathcal{K}}_{0,n}(X,d)$
relative to
![]() $\mathfrak{M}_{0,n}$
can be viewed as a obstruction theory
$\mathfrak{M}_{0,n}$
can be viewed as a obstruction theory
![]() $E_{{\mathcal{K}}_{0,n}(X,d)}^\bullet \to L_q^\bullet$
on
$E_{{\mathcal{K}}_{0,n}(X,d)}^\bullet \to L_q^\bullet$
on
![]() ${\mathcal{K}}_{0,n}(X,d)$
relative to the morphism
${\mathcal{K}}_{0,n}(X,d)$
relative to the morphism
![]() $q$
. The stack
$q$
. The stack
![]() $P$
can be equipped with an obstruction theory relative to the morphism
$P$
can be equipped with an obstruction theory relative to the morphism
![]() $q^{\prime}$
by pulling back
$q^{\prime}$
by pulling back
![]() $E_{{\mathcal{K}}_{0,n}(X,d)}^\bullet$
. The stack
$E_{{\mathcal{K}}_{0,n}(X,d)}^\bullet$
. The stack
![]() $P_n^{\vec{g}}$
can be equipped with an obstruction theory relative to
$P_n^{\vec{g}}$
can be equipped with an obstruction theory relative to
![]() $\mathfrak{Y}_{0,n,d}^{\vec{g}}$
by pulling back the obstruction theory on
$\mathfrak{Y}_{0,n,d}^{\vec{g}}$
by pulling back the obstruction theory on
![]() $P$
.
$P$
.
Since both maps
![]() $s^{\prime}$
and
$s^{\prime}$
and
![]() $\mathfrak{Y}_{0,n,d}^{\vec{g}}\to \mathfrak{M}_{0,n,d}^{tw}$
are étale [Reference Andreini, Jiang and Tseng5, Lemma 3.15], the standard obstruction theory on
$\mathfrak{Y}_{0,n,d}^{\vec{g}}\to \mathfrak{M}_{0,n,d}^{tw}$
are étale [Reference Andreini, Jiang and Tseng5, Lemma 3.15], the standard obstruction theory on
![]() ${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
relative to
${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
relative to
![]() $\mathfrak{M}_{0,n}^{tw}$
can be viewed as an obstruction theory
$\mathfrak{M}_{0,n}^{tw}$
can be viewed as an obstruction theory
![]() $E_{{\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}}^\bullet \to L_s^\bullet$
on
$E_{{\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}}^\bullet \to L_s^\bullet$
on
![]() ${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
relative to the morphism
${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
relative to the morphism
![]() $s$
.
$s$
.
By [Reference Andreini, Jiang and Tseng5, Lemma 4.1],
![]() $E_{{\mathcal{K}}_{0,n}(X,d)}^\bullet$
pulls back to
$E_{{\mathcal{K}}_{0,n}(X,d)}^\bullet$
pulls back to
![]() $E_{{\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}}^\bullet$
. We then have the following results on virtual structure sheaves.
$E_{{\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}}^\bullet$
. We then have the following results on virtual structure sheaves.
-
1. Since
 $\mathfrak{Y}_{0,n,d}^{\vec{g}}\to \mathfrak{M}_{0,n,d}$
is proper and birational, by [Reference Chou, Herr and Lee11, Theorem 1.12], we have(2.5)
$\mathfrak{Y}_{0,n,d}^{\vec{g}}\to \mathfrak{M}_{0,n,d}$
is proper and birational, by [Reference Chou, Herr and Lee11, Theorem 1.12], we have(2.5) \begin{equation} (r\circ r^{\prime})_*\!\left[{\mathcal{O}}_{P_n^{\vec{g}}}^{vir}\right]=\left[{\mathcal{O}}_{{\mathcal{K}}_{0,n}(X,d)}^{vir}\right]. \end{equation}
\begin{equation} (r\circ r^{\prime})_*\!\left[{\mathcal{O}}_{P_n^{\vec{g}}}^{vir}\right]=\left[{\mathcal{O}}_{{\mathcal{K}}_{0,n}(X,d)}^{vir}\right]. \end{equation}
-
2. By [Reference Andreini, Jiang and Tseng5, Theorem 3.19], the map
 $t\,:\,{\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}\to P_n^{\vec{g}}$
is a
$t\,:\,{\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}\to P_n^{\vec{g}}$
is a
 $\mu _r$
-gerbe. Hence, by [Reference Chou, Herr and Lee11, Proposition 1.9], we have(2.6)
$\mu _r$
-gerbe. Hence, by [Reference Chou, Herr and Lee11, Proposition 1.9], we have(2.6) \begin{equation} t_*\!\left[{\mathcal{O}}_{{\mathcal{K}}_{0,n}\left(\sqrt [r]{L/X},d\right)^{\vec{g}}}^{vir}\right]=\left[{\mathcal{O}}_{P_n^{\vec{g}}}^{vir}\right]. \end{equation}
\begin{equation} t_*\!\left[{\mathcal{O}}_{{\mathcal{K}}_{0,n}\left(\sqrt [r]{L/X},d\right)^{\vec{g}}}^{vir}\right]=\left[{\mathcal{O}}_{P_n^{\vec{g}}}^{vir}\right]. \end{equation}
2.4. Invariants
The evaluation maps on
![]() ${\mathcal{K}}_{0,n}(X,d)$
and
${\mathcal{K}}_{0,n}(X,d)$
and
![]() ${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
fit into the following commutative diagram:
${\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}$
fit into the following commutative diagram:

Consider the descendant line bundles
![]() $L_1, \ldots, L_n\to{\mathcal{K}}_{0,n}(X,d)$
associated to the marked points. The following is the main result of this note:
$L_1, \ldots, L_n\to{\mathcal{K}}_{0,n}(X,d)$
associated to the marked points. The following is the main result of this note:
Proposition 2.2.
For
![]() $\alpha _1,\ldots,\alpha _n\in K^*(X)$
and
$\alpha _1,\ldots,\alpha _n\in K^*(X)$
and
![]() $k_1,\ldots,k_n\in \mathbb{Z}$
, we have
$k_1,\ldots,k_n\in \mathbb{Z}$
, we have
 \begin{align*} & \chi \!\left ({\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}},{\mathcal{O}}_{{\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}}^{vir}\otimes \bigotimes _{i=1}^n \!\left((p^*L_i)^{\otimes k_i}\otimes ev_i^*\left(\left(\bar{I}\rho \right)^*\alpha _i\right)\right) \right )\\ & \qquad =\chi \!\left ({\mathcal{K}}_{0,n}(X,d),{\mathcal{O}}_{{\mathcal{K}}_{0,n}(X,d)}^{vir}\otimes \bigotimes _{i=1}^n \left(L_i^{\otimes k_i}\otimes ev_i^*(\alpha _i)\right) \right ). \end{align*}
\begin{align*} & \chi \!\left ({\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}},{\mathcal{O}}_{{\mathcal{K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}}^{vir}\otimes \bigotimes _{i=1}^n \!\left((p^*L_i)^{\otimes k_i}\otimes ev_i^*\left(\left(\bar{I}\rho \right)^*\alpha _i\right)\right) \right )\\ & \qquad =\chi \!\left ({\mathcal{K}}_{0,n}(X,d),{\mathcal{O}}_{{\mathcal{K}}_{0,n}(X,d)}^{vir}\otimes \bigotimes _{i=1}^n \left(L_i^{\otimes k_i}\otimes ev_i^*(\alpha _i)\right) \right ). \end{align*}
Proof. Since
![]() $\bar{I}\rho \circ ev_i=ev_i\circ p$
, projection formula gives
$\bar{I}\rho \circ ev_i=ev_i\circ p$
, projection formula gives
 \begin{equation*} p_*\left ({\mathcal {O}}_{{\mathcal {K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec {g}}}^{vir}\otimes \bigotimes _{i=1}^n \left(\left(p^*L_i\right)^{\otimes k_i}\otimes ev_i^*\left(\left(\bar {I}\rho \right)^*\alpha _i\right)\right)\right )=p_*\left({\mathcal {O}}_{{\mathcal {K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec {g}}}^{vir}\right)\!\otimes\! \bigotimes _{i=1}^n \left(L_i^{\otimes k_i}\otimes ev_i^*(\alpha _i)\right). \end{equation*}
\begin{equation*} p_*\left ({\mathcal {O}}_{{\mathcal {K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec {g}}}^{vir}\otimes \bigotimes _{i=1}^n \left(\left(p^*L_i\right)^{\otimes k_i}\otimes ev_i^*\left(\left(\bar {I}\rho \right)^*\alpha _i\right)\right)\right )=p_*\left({\mathcal {O}}_{{\mathcal {K}}_{0,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec {g}}}^{vir}\right)\!\otimes\! \bigotimes _{i=1}^n \left(L_i^{\otimes k_i}\otimes ev_i^*(\alpha _i)\right). \end{equation*}
Since
![]() $p=r\circ r^{\prime}\circ t$
, the result follows from (2.5) and (2.6).
$p=r\circ r^{\prime}\circ t$
, the result follows from (2.5) and (2.6).
2.5. Banded abelian gerbes
Suppose
![]() $G$
is a finite abelian group. Suppose
$G$
is a finite abelian group. Suppose
![]() $\mathcal{G}\to X$
is a gerbe banded by
$\mathcal{G}\to X$
is a gerbe banded by
![]() $G$
. Then the isomorphism class of
$G$
. Then the isomorphism class of
![]() $\mathcal{G}\to X$
is classified by the cohomology group
$\mathcal{G}\to X$
is classified by the cohomology group
![]() $H^2(X, G)$
, where
$H^2(X, G)$
, where
![]() $G$
is viewed as a constant sheaf on
$G$
is viewed as a constant sheaf on
![]() $X$
. We say that
$X$
. We say that
![]() $\mathcal{G}\to X$
is essentially trivial if the image of its class is trivial for maps
$\mathcal{G}\to X$
is essentially trivial if the image of its class is trivial for maps
![]() $H^2(X,G)\to H^2(X,\mathbb{C}^*)$
induced by group homomorphisms
$H^2(X,G)\to H^2(X,\mathbb{C}^*)$
induced by group homomorphisms
![]() $G\to \mathbb{C}^*$
. Examples of essentially trivial gerbes include toric gerbes [Reference Tseng25].
$G\to \mathbb{C}^*$
. Examples of essentially trivial gerbes include toric gerbes [Reference Tseng25].
Let
![]() $\mathcal{G}\to X$
be an essentially trivial gerbe over
$\mathcal{G}\to X$
be an essentially trivial gerbe over
![]() $X$
. Then by [Reference Andreini, Jiang and Tseng5, Lemma A.2],
$X$
. Then by [Reference Andreini, Jiang and Tseng5, Lemma A.2],
![]() $\mathcal{G}$
is of the form
$\mathcal{G}$
is of the form
where
![]() $L_1,\ldots,L_k$
are line bundles over
$L_1,\ldots,L_k$
are line bundles over
![]() $X$
and
$X$
and
![]() $r_1,\ldots,r_k$
are natural numbers.
$r_1,\ldots,r_k$
are natural numbers.
Consider the morphism (2.2) in this case:
By the alaysis of [Reference Andreini, Jiang and Tseng5, Appendix A], (2.8) also fits into diagram like (2.4), with a factorization
Here,
![]() $\vec{g}$
is defined in [Reference Andreini, Jiang and Tseng5, Definition A.5].
$\vec{g}$
is defined in [Reference Andreini, Jiang and Tseng5, Definition A.5].
The map
![]() $P_n^{\vec{g}}\to{\mathcal{K}}_{0,n}(X,d)$
is by construction virtually birational, hence we can apply [Reference Chou, Herr and Lee11, Theorem 1.12] to it. By [Reference Andreini, Jiang and Tseng5, Theorem A.6], the map
$P_n^{\vec{g}}\to{\mathcal{K}}_{0,n}(X,d)$
is by construction virtually birational, hence we can apply [Reference Chou, Herr and Lee11, Theorem 1.12] to it. By [Reference Andreini, Jiang and Tseng5, Theorem A.6], the map
![]() ${\mathcal{K}}_{0,n}(\mathcal{G},d)^{\vec{g}}\to P_n^{\vec{g}}$
is also a gerbe, so we can apply [Reference Chou, Herr and Lee11, Proposition 1.9] to it. Therefore, we may repeat the arguments in Section 2.4 to extend Proposition 2.2 to essentially trivial banded abelian gerbes
${\mathcal{K}}_{0,n}(\mathcal{G},d)^{\vec{g}}\to P_n^{\vec{g}}$
is also a gerbe, so we can apply [Reference Chou, Herr and Lee11, Proposition 1.9] to it. Therefore, we may repeat the arguments in Section 2.4 to extend Proposition 2.2 to essentially trivial banded abelian gerbes
![]() $\mathcal{G}\to X$
.
$\mathcal{G}\to X$
.
2.6. Root stacks
Let
![]() $D\subset X$
be a smooth irreducible divisor. For an integer
$D\subset X$
be a smooth irreducible divisor. For an integer
![]() $r\gt 0$
, one can construct the stack
$r\gt 0$
, one can construct the stack
![]() $X_{D,r}$
of
$X_{D,r}$
of
![]() $r$
-th roots of
$r$
-th roots of
![]() $X$
along
$X$
along
![]() $D$
, see [Reference Cadman9] and [Reference Abramovich, Graber and Vistoli3, Appendix B]. The natural map
$D$
, see [Reference Cadman9] and [Reference Abramovich, Graber and Vistoli3, Appendix B]. The natural map
is an isomorphism over
![]() $X\setminus D$
and is a
$X\setminus D$
and is a
![]() $\mu _r$
-gerbe over
$\mu _r$
-gerbe over
![]() $D$
. Denote by
$D$
. Denote by
![]() $D_r\subset X_{D,r}$
the inverse image of
$D_r\subset X_{D,r}$
the inverse image of
![]() $D$
under (2.10).
$D$
under (2.10).
It is shown in ref. [Reference Abramovich, Cadman and Wise1] that genus
![]() $0$
relative Gromov-Witten invariants of the pair
$0$
relative Gromov-Witten invariants of the pair
![]() $(X,D)$
are the same as Gromov-Witten invariants of
$(X,D)$
are the same as Gromov-Witten invariants of
![]() $X_{D,r}$
for
$X_{D,r}$
for
![]() $r$
sufficiently large. Here we explain how their method can be adapted to K-theoretic Gromov-Witten theory.
$r$
sufficiently large. Here we explain how their method can be adapted to K-theoretic Gromov-Witten theory.
By [Reference Abramovich and Fantechi2], there is an isomorphism between moduli spacesFootnote 1 of stable relative maps,
see also [Reference Abramovich, Cadman and Wise1, Theorem 2.1]. This implies an identification of virtual structure sheaves,
There is a natural map that forgets the relative structure
Assume that
![]() $r$
is sufficiently large. The proof of [Reference Abramovich, Cadman and Wise1, Theorem 2.2] implies that
$r$
is sufficiently large. The proof of [Reference Abramovich, Cadman and Wise1, Theorem 2.2] implies that
![]() $\Phi$
is virtually birational. Hence, by [Reference Chou, Herr and Lee11, Theorem 1.12], we have
$\Phi$
is virtually birational. Hence, by [Reference Chou, Herr and Lee11, Theorem 1.12], we have
Evaluation maps of these moduli spaces are compatible with
![]() $\Psi$
and
$\Psi$
and
![]() $\Phi$
, see [Reference Abramovich, Cadman and Wise1, Section 2.2]. It follows from (2.11) and (2.12) that for
$\Phi$
, see [Reference Abramovich, Cadman and Wise1, Section 2.2]. It follows from (2.11) and (2.12) that for
![]() $\alpha _1,\ldots,\alpha _k\in K^*(X)$
,
$\alpha _1,\ldots,\alpha _k\in K^*(X)$
,
![]() $\gamma _1,\ldots,\gamma _l\in K^*(D)$
, and
$\gamma _1,\ldots,\gamma _l\in K^*(D)$
, and
![]() $r$
sufficiently large, we have
$r$
sufficiently large, we have
 \begin{align} &\chi \!\left (\overline{M}_{0,n}(X_{D,r}),\mathcal{O}_{\overline{M}_{0,n}(X_{D,r})}^{vir}\otimes \bigotimes _{i=1}^k L_i^{k_i}\otimes ev_i^*(\alpha _i)\otimes \bigotimes _{j=1}^l L_j^{m_j}\otimes ev_j^*(\beta _j) \right )\nonumber\\& \quad = \chi \!\left (\overline{M}_{0,n}(X,D),\mathcal{O}_{\overline{M}_{0,n}(X,D)}^{vir}\otimes \bigotimes _{i=1}^k L_i^{k_i}\otimes ev_i^*(\alpha _i)\otimes \bigotimes _{j=1}^l L_j^{m_j}\otimes ev_j^*(\beta _j) \right ). \end{align}
\begin{align} &\chi \!\left (\overline{M}_{0,n}(X_{D,r}),\mathcal{O}_{\overline{M}_{0,n}(X_{D,r})}^{vir}\otimes \bigotimes _{i=1}^k L_i^{k_i}\otimes ev_i^*(\alpha _i)\otimes \bigotimes _{j=1}^l L_j^{m_j}\otimes ev_j^*(\beta _j) \right )\nonumber\\& \quad = \chi \!\left (\overline{M}_{0,n}(X,D),\mathcal{O}_{\overline{M}_{0,n}(X,D)}^{vir}\otimes \bigotimes _{i=1}^k L_i^{k_i}\otimes ev_i^*(\alpha _i)\otimes \bigotimes _{j=1}^l L_j^{m_j}\otimes ev_j^*(\beta _j) \right ). \end{align}
We view (2.13) as a correspondence between genus
![]() $0$
K-theoretic Gromov-Witten invariants of
$0$
K-theoretic Gromov-Witten invariants of
![]() $(X,D)$
and
$(X,D)$
and
![]() $X_{D,r}$
.
$X_{D,r}$
.
3. Comments
3.1. On higher genus
3.1.1. Root gerbes
For
![]() $h\gt 0$
, the genus-
$h\gt 0$
, the genus-
![]() $h$
version of the morphism (2.3),
$h$
version of the morphism (2.3),
has been studied in ref. [Reference Andreini, Jiang and Tseng6]. The map (3.1) is understood well enough so that a result on the pushforward of virtual fundamental classes is proven in ref. [Reference Andreini, Jiang and Tseng6]. However, pushforward of virtual structure sheaves under (3.1) appears to be difficult. The key issue is that, in order to apply [Reference Chou, Herr and Lee11, Proposition 1.9, Theorem 1.12], we need (3.1) to be factored into virtual birational maps and gerbes. A factorization of (3.1) was obtained for more general banded gerbes in [Reference Andreini, Jiang and Tseng6, Diagram (41)]. In our setting, this gives
For a root gerbe
![]() $\sqrt [r]{L/X}\to X$
, one can check that
$\sqrt [r]{L/X}\to X$
, one can check that
![]() $P_{h,n}^{\vec{g}}\to{\mathcal{K}}_{h,n}(X,d)$
is also virtually birational. However, by the discussion of [Reference Andreini, Jiang and Tseng6, Section 6.2], the map
$P_{h,n}^{\vec{g}}\to{\mathcal{K}}_{h,n}(X,d)$
is also virtually birational. However, by the discussion of [Reference Andreini, Jiang and Tseng6, Section 6.2], the map
![]() ${\mathcal{K}}_{h,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}\to P_{h,n}^{\vec{g}}$
is a composition of two maps, one has degree
${\mathcal{K}}_{h,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}\to P_{h,n}^{\vec{g}}$
is a composition of two maps, one has degree
![]() $1/r$
and the other had degree
$1/r$
and the other had degree
![]() $r^{2h}\gt 1$
. The degree
$r^{2h}\gt 1$
. The degree
![]() $r^{2h}$
-map cannot possibly be a gerbe. Hence, [Reference Chou, Herr and Lee11, Proposition 1.9] is not applicable to
$r^{2h}$
-map cannot possibly be a gerbe. Hence, [Reference Chou, Herr and Lee11, Proposition 1.9] is not applicable to
![]() ${\mathcal{K}}_{h,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}\to P_{h,n}^{\vec{g}}$
. This prevents us from obtaining genus-
${\mathcal{K}}_{h,n}\!\left(\sqrt [r]{L/X},d\right)^{\vec{g}}\to P_{h,n}^{\vec{g}}$
. This prevents us from obtaining genus-
![]() $h$
version of Proposition 2.2.
$h$
version of Proposition 2.2.
3.1.2. Root stacks
The relative/orbifold correspondence in cohomological Gromov-Witten theory has been extended to higher genus in ref. [Reference Tseng and You27]. A K-theoretic relative/orbifold correspondence in higher genus is an interesting question. It is unlikely that virtual pushforwards used in genus
![]() $0$
will be enough in higher genus. Some foundational work in K-theoretic Gromov-Witten theory is required in order to follow the arguments in ref. [Reference Tseng and You27].
$0$
will be enough in higher genus. Some foundational work in K-theoretic Gromov-Witten theory is required in order to follow the arguments in ref. [Reference Tseng and You27].
3.2. On virtual pushforward
There are many situations in cohomological Gromov-Witten theory in which “virtually birational” maps occur, see [Reference Herr and Wise18] for a detailed list. In addition, we note that the morphism
![]() $u$
in [Reference Coates, Corti, Lee and Tseng12, Lemma 4.16] is virtually birational. Hence, we can apply [Reference Chou, Herr and Lee11, Theorem 1.12] to obtain a calculation of the K-theoretic
$u$
in [Reference Coates, Corti, Lee and Tseng12, Lemma 4.16] is virtually birational. Hence, we can apply [Reference Chou, Herr and Lee11, Theorem 1.12] to obtain a calculation of the K-theoretic
![]() $J$
-function of weighted projective spaces. Since such a result is a special case of the work [Reference Zhang28] on quantum K-theory of toric stacks, we do not pursue it in detail.
$J$
-function of weighted projective spaces. Since such a result is a special case of the work [Reference Zhang28] on quantum K-theory of toric stacks, we do not pursue it in detail.
3.3. On decomposition conjecture
Consider an étale gerbe
![]() ${\mathcal{G}}\to X$
. As defined in (2.1), K-theoretic Gromov-Witten invariants of
${\mathcal{G}}\to X$
. As defined in (2.1), K-theoretic Gromov-Witten invariants of
![]() $\mathcal{G}$
have insertions coming from the K-theory
$\mathcal{G}$
have insertions coming from the K-theory
![]() $K^*(\bar{I}{\mathcal{G}})$
of the rigidified inertia stack
$K^*(\bar{I}{\mathcal{G}})$
of the rigidified inertia stack
![]() $\bar{I}{\mathcal{G}}$
. Since
$\bar{I}{\mathcal{G}}$
. Since
![]() ${\mathcal{G}}\subset \bar{I}{\mathcal{G}}$
is a connected component, the K-theory
${\mathcal{G}}\subset \bar{I}{\mathcal{G}}$
is a connected component, the K-theory
![]() $K^*({\mathcal{G}})$
of
$K^*({\mathcal{G}})$
of
![]() $\mathcal{G}$
is a direct summand of
$\mathcal{G}$
is a direct summand of
![]() $K^*(\bar{I}{\mathcal{G}})$
. The proof of Proposition 2.2 only allows classes in
$K^*(\bar{I}{\mathcal{G}})$
. The proof of Proposition 2.2 only allows classes in
![]() $K^*(\bar{I}\sqrt [r]{L/X})$
pulled back from
$K^*(\bar{I}\sqrt [r]{L/X})$
pulled back from
![]() $X$
. Studying K-theoretic Gromov-Witten invariants of
$X$
. Studying K-theoretic Gromov-Witten invariants of
![]() $\sqrt [r]{L/X}$
with other kinds of insertions requires new ideas.
$\sqrt [r]{L/X}$
with other kinds of insertions requires new ideas.
For root gerbes
![]() ${\mathcal{G}}\to X$
arising in toric geometry, for example, weighted projective spaces and more general toric gerbes, it may be possible to study the decomposition conjecture by analyzing the K-theoretic
${\mathcal{G}}\to X$
arising in toric geometry, for example, weighted projective spaces and more general toric gerbes, it may be possible to study the decomposition conjecture by analyzing the K-theoretic
![]() $I$
-functions calculated in ref. [Reference Zhang28] in a manner similar to [Reference Tseng25]. An additive decomposition of the K-theory
$I$
-functions calculated in ref. [Reference Zhang28] in a manner similar to [Reference Tseng25]. An additive decomposition of the K-theory
![]() $K(\bar{I}{\mathcal{G}})$
is a basic question.
$K(\bar{I}{\mathcal{G}})$
is a basic question.