Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-26T22:50:24.134Z Has data issue: false hasContentIssue false
  • English
  • Français

Friction drag model for axial turbulent flow along the surface of a circular cylinder based on the universal characteristics of wall turbulence

Published online by Cambridge University Press:  25 November 2024

Takashi Ohta Open the ORCID record for Takashi Ohta [Opens in a new window]  and
Futaro Shirahata
Takashi Ohta*
Affiliation:
CFD Research Group, Department of Mechanical and System Engineering, University of Fukui, 3-9-1 Bunkyo, Fukui 910-8507, Japan
Futaro Shirahata
Affiliation:
CFD Research Group, Department of Mechanical and System Engineering, University of Fukui, 3-9-1 Bunkyo, Fukui 910-8507, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

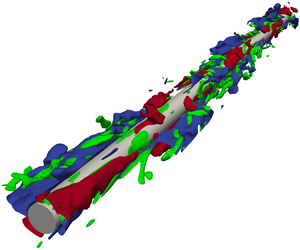
The friction drag of the axial flow along the outer surface of a cylinder varies with the cylinder radius and flow conditions. This study included direct numerical simulations of the axial turbulent flow along a circular cylinder under different conditions for obtaining the turbulence statistics and wall friction coefficient. Then the characteristics of velocity streaks were observed from a geometrical perspective of turbulence structures around the circular cylinder, and compared with the characteristics of the turbulence structures in a boundary layer on a flat plate. The results showed that the velocity streak spacing and the distance between the velocity streak and the cylinder surface in the viscous length scale do not vary substantively with the radius of the cylinder, and are the same as those of the turbulent flow along a flat plate. Therefore, they can be considered geometrical characteristics of the turbulence structure independent of the cylinder radius. Moreover, the friction coefficient per pair of high- and low-speed velocity streaks is the same as that of flat-plate turbulent flow, independent of the cylinder radius, and can be regarded as a dynamical characteristic for a pair of velocity streaks. Two equations were derived based on the characteristics of wall turbulence. The characteristics of the turbulence predicted by the two formulae were consistent with the simulation results. Consequently, we showed that the wall friction coefficient and number of the velocity streak pairs, which are statistical and structural characteristics of wall turbulence, can be predicted appropriately by specifying the radius Reynolds number.

JFM classification

Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A35
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alam, M.M. 2020 A review of transverse curvature effect on friction force and leading-edge flow. Ocean Engng 218, 107573.CrossRefGoogle Scholar
Bokde, A.L.W., Lueptow, R.M. & Abraham, B. 1999 Spanwise structure of wall pressure on a cylinder in axial flow. Phys. Fluids 11 (1), 151–161.CrossRefGoogle Scholar
Coles, D.E. 1962 The turbulent boundary layer in a compressible fluid. Tech. Rep. R–403–PR. RAND Corporation, Santa Monica.Google Scholar
Coles, D.E. 1964 The turbulent boundary layer in a compressible fluid. Phys. Fluids 7 (9), 1403–1423.CrossRefGoogle Scholar
Glauert, M.B. & Lighthill, M.J. 1955 The axisymmetric boundary layer on a long thin cylinder. Math. Phys. Sci. 230 (1181), 188–203.Google Scholar
Gould, J. & Smith, F.S. 1980 Air-drag on synthetic-fibre textile monofilaments and yarns in axial flow at speeds of up to 100 metres per second. J. Text. Inst. 71 (1), 38–49.CrossRefGoogle Scholar
Ishida, T., Duguet, Y. & Tsukahara, T. 2016 Transitional structures in annular Poiseuille flow depending on radius ratio. J. Fluid Mech. 794, R2.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jordan, S.A. 2011 a Axisymmetric turbulent statistics of long slender circular cylinders. Phys. Fluids 23, 075105.CrossRefGoogle Scholar
Jordan, S.A. 2011 b Near-wall turbulent characteristics along very long thin circular cylinders. J. Fluids Struct. 27 (3), 329–341.CrossRefGoogle Scholar
Kajishima, T., Ohta, T., Okazaki, K. & Miyake, Y. 1998 High-order finite-difference method for incompressible flows using collocated grid system. JSME Intl J. 41 (4), 830–839.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Liu, N.S. & Lu, X.Y. 2004 Large eddy simulation of turbulent concentric annular channel flows. Intl J. Numer. Meth. Fluids 45 (12), 1317–1338.CrossRefGoogle Scholar
Lueptow, R.M., Leehey, P. & Stellinger, T. 1985 The thick, axisymmetric turbulent boundary layer: mean and fluctuating velocities. Phys. Fluids 28, 3495–3505.CrossRefGoogle Scholar
Luxton, R.E., Bull, M.K. & Rajagopalan, S. 1984 The thick turbulent boundary layer on a long fine cylinder in axial flow. Aeronaut. J. 88 (875), 186–199.CrossRefGoogle Scholar
Moser, R.D., Kim, J. & Mansour, N.N. 1999 Direct numerical simulation of turbulent channel flow up to $Re_\tau = 590$. Phys. Fluids 11 (4), 943–945.CrossRefGoogle Scholar
Neves, J.C. & Moin, P. 1994 Effects of convex transverse curvature on wall-bounded turbulence. Part 2. The pressure fluctuations. J. Fluid Mech. 272, 383–406.CrossRefGoogle Scholar
Neves, J.C., Moin, P. & Moser, R.D. 1994 Effects of convex transverse curvature on wall-bounded turbulence. Part 1. The velocity and vorticity. J. Fluid Mech. 272, 349–382.CrossRefGoogle Scholar
Ohta, T. 2017 Turbulence structures in high-speed air flow along a thin cylinder. J. Turbul. 18 (6), 497–511.CrossRefGoogle Scholar
Ohta, T., Kajishima, T., Mizobata, K. & Nakamura, K. 2012 Influence of density fluctuation on DNS of turbulent channel flow in the presence of temperature stratification. Flow Turbul. Combust. 89 (3), 435–448.CrossRefGoogle Scholar
Potter, J.R., Delaory, E., Constantin, S. & Badiu, S. 2000 The ‘thinarray’; a lightweight, ultra-thin (8 mm OD) towed array for use from small vessels of opportunity. In Proceedings of the 2000 International Symposium on Underwater Technology (Cat. No. 00EX418), pp. 49–53. IEEE.CrossRefGoogle Scholar
Robinson, S.K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.CrossRefGoogle Scholar
Satake, S. & Kawamura, H. 1995 Large eddy simulation of turbulent flow in concentric annuli with a thin inner rod. In Turbulent Shear Flows 9 (ed. F. Durst, N. Kasagi, B.E. Launder, F.W. Schmidt, K. Suzuki & J.H. Whitelaw), pp. 259–281. Springer.CrossRefGoogle Scholar
Smith, C.R. & Metzler, W.G. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.CrossRefGoogle Scholar
Snarski, S.R. & Lueptow, R.M. 1995 Wall pressure and coherent structures in a turbulent boundary layer on a cylinder in axial flow. J. Fluid Mech. 286, 137–171.CrossRefGoogle Scholar
Tutty, O.R. 2008 Flow along a long thin cylinder. J. Fluid Mech. 602, 1–37.CrossRefGoogle Scholar
White, F.M. 1972 An analysis of axisymmetric turbulent flow past a long cylinder. Trans. ASME J. Basic Engng 94 (1), 200–204.CrossRefGoogle Scholar
Willmarth, W.W., Winkel, R.E., Sharma, L.K. & Bogar, T.J. 1976 Axially symmetric turbulent boundary layers on cylinders: mean velocity profiles and wall pressure fluctuations. J. Fluid Mech. 76, 35–64.CrossRefGoogle Scholar