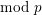1 Introduction
Let
![]() $K$
be a complete discrete valuation field whose residue field
$K$
be a complete discrete valuation field whose residue field
![]() $F$
is of characteristic
$F$
is of characteristic
![]() $p>0$
. The Swan conductor
$p>0$
. The Swan conductor
generalizing the classical perfect residue field case, the subgroups
of
![]() $H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
for
$H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
for
![]() $n\geqslant 0$
, and an injective homomorphism
$n\geqslant 0$
, and an injective homomorphism
called the refined Swan conductor for
![]() $n\geqslant 1$
, where
$n\geqslant 1$
, where
![]() $\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
is the module of differential forms with log poles, are defined in [Reference Kato20]. Let
$\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
is the module of differential forms with log poles, are defined in [Reference Kato20]. Let
![]() $m=\max (n-e_{K},[n/p])$
where
$m=\max (n-e_{K},[n/p])$
where
![]() $e_{K}$
denotes the absolute ramification index
$e_{K}$
denotes the absolute ramification index
![]() $\text{ord}_{K}(p)$
of
$\text{ord}_{K}(p)$
of
![]() $K$
(
$K$
(
![]() $e_{K}=\infty$
if
$e_{K}=\infty$
if
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
) and
$p$
) and
![]() $[n/p]=\max \{x\in \mathbb{Z}\mid x\leqslant n/p\}$
. In this paper, we define an injective homomorphism
$[n/p]=\max \{x\in \mathbb{Z}\mid x\leqslant n/p\}$
. In this paper, we define an injective homomorphism
which is a lifting of (3). Note that
![]() $\mathfrak{m}_{K}^{-m}=p\mathfrak{m}_{K}^{-n}+\mathfrak{m}_{K}^{-[n/p]}$
. We will call the homomorphism (3) the refined Swan conductor mod
$\mathfrak{m}_{K}^{-m}=p\mathfrak{m}_{K}^{-n}+\mathfrak{m}_{K}^{-[n/p]}$
. We will call the homomorphism (3) the refined Swan conductor mod
![]() $\mathfrak{m}_{K}$
and the homomorphism (4) the refined Swan conductor mod
$\mathfrak{m}_{K}$
and the homomorphism (4) the refined Swan conductor mod
![]() $p$
.
$p$
.
In the case
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
(in this case,
$p$
(in this case,
![]() $m=[n/p]$
), the homomorphism Rsw is defined by using Artin–Schreier–Witt theory and is already known [Reference Borger6, Reference Matsuda30]. In the mixed characteristic case, we define Rsw by using higher dimensional class field theory. See Section 3 for the definition of Rsw.
$m=[n/p]$
), the homomorphism Rsw is defined by using Artin–Schreier–Witt theory and is already known [Reference Borger6, Reference Matsuda30]. In the mixed characteristic case, we define Rsw by using higher dimensional class field theory. See Section 3 for the definition of Rsw.
In Section 4, we show that for a regular scheme
![]() $X$
of finite type over
$X$
of finite type over
![]() $\mathbb{Z}$
and for a divisor
$\mathbb{Z}$
and for a divisor
![]() $D$
on
$D$
on
![]() $X$
with simple normal crossings, and for
$X$
with simple normal crossings, and for
![]() $U=X\smallsetminus D$
and
$U=X\smallsetminus D$
and
![]() $\unicode[STIX]{x1D712}\in H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
, the refined Swan conductors mod
$\unicode[STIX]{x1D712}\in H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
, the refined Swan conductors mod
![]() $p$
of
$p$
of
![]() $\unicode[STIX]{x1D712}$
at generic points of
$\unicode[STIX]{x1D712}$
at generic points of
![]() $D$
defined in Section 3 glue to a global section of a certain sheaf of differential forms on
$D$
defined in Section 3 glue to a global section of a certain sheaf of differential forms on
![]() $X$
.
$X$
.
We will give applications 3.6.1, 3.6.3 and 4.3.13 of our theory. Theorem 3.6.1 (resp. 4.3.13) shows that the Swan conductor (1) is recovered from pullbacks of
![]() $\unicode[STIX]{x1D712}$
to the perfect residue field cases (resp. to one-dimensional subschemes in the situation of Section 4). Theorem 3.6.3 improves a result of the second author in [Reference Leal29] concerning the change of the Swan conductor (1) in a transcendental extension of local fields.
$\unicode[STIX]{x1D712}$
to the perfect residue field cases (resp. to one-dimensional subschemes in the situation of Section 4). Theorem 3.6.3 improves a result of the second author in [Reference Leal29] concerning the change of the Swan conductor (1) in a transcendental extension of local fields.
Shuji Saito played leading roles in the developments of higher dimensional class field theory and its applications. We dedicate this paper to him with admiration.
2 Preliminaries
2.1 Differential forms and discrete valuations
2.1.1. Let
![]() $K$
be a discrete valuation field with residue field
$K$
be a discrete valuation field with residue field
![]() $F$
, valuation ring
$F$
, valuation ring
![]() $O_{K}$
and maximal ideal
$O_{K}$
and maximal ideal
![]() $\mathfrak{m}_{K}$
. Assume
$\mathfrak{m}_{K}$
. Assume
![]() $F$
is of characteristic
$F$
is of characteristic
![]() $p>0$
.
$p>0$
.
Let
![]() $e_{K}=\text{ord}_{K}(p)$
be the absolute ramification index of
$e_{K}=\text{ord}_{K}(p)$
be the absolute ramification index of
![]() $K$
(
$K$
(
![]() $e_{K}=\infty$
if
$e_{K}=\infty$
if
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
).
$p$
).
2.1.2. Let
![]() $\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )=\unicode[STIX]{x1D6FA}_{O_{K}/\mathbb{Z}}^{1}(\log )$
be the module of differential forms with log poles of
$\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )=\unicode[STIX]{x1D6FA}_{O_{K}/\mathbb{Z}}^{1}(\log )$
be the module of differential forms with log poles of
![]() $O_{K}$
over
$O_{K}$
over
![]() $\mathbb{Z}$
with respect to the standard log structure of
$\mathbb{Z}$
with respect to the standard log structure of
![]() $O_{K}$
[Reference Kato21]. It is the
$O_{K}$
[Reference Kato21]. It is the
![]() $O_{K}$
-module defined by the following generators and relations.
$O_{K}$
-module defined by the following generators and relations.
Generators.
![]() $dx$
for
$dx$
for
![]() $x\in O_{K}$
and
$x\in O_{K}$
and
![]() $d\log (x)$
for
$d\log (x)$
for
![]() $x\in K^{\times }$
.
$x\in K^{\times }$
.
Relations.
![]() $d(x+y)=dx+dy$
and
$d(x+y)=dx+dy$
and
![]() $d(xy)=x\,dy+y\,dx$
for
$d(xy)=x\,dy+y\,dx$
for
![]() $x,y\in O_{K}$
.
$x,y\in O_{K}$
.
![]() $d\log (xy)=d\log (x)+d\log (y)$
for
$d\log (xy)=d\log (x)+d\log (y)$
for
![]() $x,y\in K^{\times }$
.
$x,y\in K^{\times }$
.
![]() $dx=x\,d\log (x)$
for
$dx=x\,d\log (x)$
for
![]() $x\in O_{K}\smallsetminus \{0\}$
.
$x\in O_{K}\smallsetminus \{0\}$
.
Let
Note that
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )/\mathfrak{m}_{K}^{n}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )=\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )/\mathfrak{m}_{K}^{n}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
for any
$\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )/\mathfrak{m}_{K}^{n}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )=\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )/\mathfrak{m}_{K}^{n}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
for any
![]() $n\geqslant 1$
[Reference Fujiwara and Kato9, Chapter 0, 7.2.8, 7.2.16].
$n\geqslant 1$
[Reference Fujiwara and Kato9, Chapter 0, 7.2.8, 7.2.16].
The following (2) of 2.1.3 is the log version of [Reference Kurihara27, Lemma 1.1] and the proof given below is essentially the same as that in [Reference Kurihara27, Lemma 1.1].
Lemma 2.1.3. Let
![]() $(b_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
be a
$(b_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
be a
![]() $p$
-base of
$p$
-base of
![]() $F$
[Reference Grothendieck12, Chapitre 0, 21.1.9] and let
$F$
[Reference Grothendieck12, Chapitre 0, 21.1.9] and let
![]() $\tilde{b}_{\unicode[STIX]{x1D706}}$
be a lifting of
$\tilde{b}_{\unicode[STIX]{x1D706}}$
be a lifting of
![]() $b_{\unicode[STIX]{x1D706}}$
to
$b_{\unicode[STIX]{x1D706}}$
to
![]() $O_{K}$
for each
$O_{K}$
for each
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
(1) Assume
 $K$
is of characteristic
$K$
is of characteristic
 $p$
, and let
$p$
, and let
 $\unicode[STIX]{x1D70B}$
be a prime element of
$\unicode[STIX]{x1D70B}$
be a prime element of
 $K$
. Then
$K$
. Then
 $\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )$
is the
$\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )$
is the
 $\mathfrak{m}_{K}$
-adic completion of the free
$\mathfrak{m}_{K}$
-adic completion of the free
 $O_{K}$
-module with base
$O_{K}$
-module with base
 $d\tilde{b}_{\unicode[STIX]{x1D706}}$
(
$d\tilde{b}_{\unicode[STIX]{x1D706}}$
(
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
) and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
) and
 $d\log (\unicode[STIX]{x1D70B})$
. If
$d\log (\unicode[STIX]{x1D70B})$
. If
 $K$
is complete and
$K$
is complete and
 $[F:F^{p}]<\infty$
, we have
$[F:F^{p}]<\infty$
, we have
 $\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )=\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
.
$\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )=\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
.(2) If
 $K$
is of mixed characteristic, we have an isomorphism of topological
$K$
is of mixed characteristic, we have an isomorphism of topological
 $O_{K}$
-modules for some integer
$O_{K}$
-modules for some integer $$\begin{eqnarray}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )\cong \left(\mathop{\{}_{\unicode[STIX]{x1D6EC}}O_{K}\right)\oplus O_{K}/\mathfrak{m}_{K}^{a},\end{eqnarray}$$
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )\cong \left(\mathop{\{}_{\unicode[STIX]{x1D6EC}}O_{K}\right)\oplus O_{K}/\mathfrak{m}_{K}^{a},\end{eqnarray}$$
 $a\geqslant 1$
, where
$a\geqslant 1$
, where
 $\hat{\bigoplus }_{\unicode[STIX]{x1D6EC}}O_{K}$
denotes the
$\hat{\bigoplus }_{\unicode[STIX]{x1D6EC}}O_{K}$
denotes the
 $\mathfrak{m}_{K}$
-adic completion of the free
$\mathfrak{m}_{K}$
-adic completion of the free
 $O_{K}$
-module
$O_{K}$
-module
 $\bigoplus _{\unicode[STIX]{x1D6EC}}O_{K}$
with base
$\bigoplus _{\unicode[STIX]{x1D6EC}}O_{K}$
with base
 $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.(3) If
 $K$
is of mixed characteristic,
$K$
is of mixed characteristic,
 $O_{K}/pO_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
is a free
$O_{K}/pO_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
is a free
 $O_{K}/pO_{K}$
-module with base
$O_{K}/pO_{K}$
-module with base
 $d\tilde{b}_{\unicode[STIX]{x1D706}}$
(
$d\tilde{b}_{\unicode[STIX]{x1D706}}$
(
 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
) and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
) and
 $d\log (\unicode[STIX]{x1D70B})$
.
$d\log (\unicode[STIX]{x1D70B})$
.
Proof. We may assume that
![]() $K$
is complete (and so we assume it).
$K$
is complete (and so we assume it).
(1) follows from the fact that
![]() $O_{K}\cong F[[T]]$
in this case.
$O_{K}\cong F[[T]]$
in this case.
Assume
![]() $K$
is of characteristic 0. Then
$K$
is of characteristic 0. Then
![]() $K$
is a finite extension of a complete discrete valuation field
$K$
is a finite extension of a complete discrete valuation field
![]() $K_{0}$
such that
$K_{0}$
such that
![]() $p$
is a prime element in
$p$
is a prime element in
![]() $K_{0}$
and the residue field of
$K_{0}$
and the residue field of
![]() $K_{0}$
coincides with that of
$K_{0}$
coincides with that of
![]() $K$
. We may assume
$K$
. We may assume
![]() $\tilde{b}_{\unicode[STIX]{x1D706}}\in O_{K_{0}}$
for all
$\tilde{b}_{\unicode[STIX]{x1D706}}\in O_{K_{0}}$
for all
![]() $\unicode[STIX]{x1D706}$
. As is easily seen, there is an isomorphism between the
$\unicode[STIX]{x1D706}$
. As is easily seen, there is an isomorphism between the
![]() $\mathfrak{m}_{K_{0}}$
-adic completion
$\mathfrak{m}_{K_{0}}$
-adic completion
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{K_{0}}}^{1}$
of the differential module
$\hat{\unicode[STIX]{x1D6FA}}_{O_{K_{0}}}^{1}$
of the differential module
![]() $\unicode[STIX]{x1D6FA}_{O_{K_{0}}/\mathbb{Z}}^{1}$
(without log) and
$\unicode[STIX]{x1D6FA}_{O_{K_{0}}/\mathbb{Z}}^{1}$
(without log) and
![]() $\hat{\bigoplus }_{\unicode[STIX]{x1D6EC}}O_{K_{0}}$
which sends the
$\hat{\bigoplus }_{\unicode[STIX]{x1D6EC}}O_{K_{0}}$
which sends the
![]() $\unicode[STIX]{x1D706}$
th base of
$\unicode[STIX]{x1D706}$
th base of
![]() $\bigoplus _{\unicode[STIX]{x1D6EC}}O_{K_{0}}$
to
$\bigoplus _{\unicode[STIX]{x1D6EC}}O_{K_{0}}$
to
![]() $d\tilde{b}_{\unicode[STIX]{x1D706}}$
. Let
$d\tilde{b}_{\unicode[STIX]{x1D706}}$
. Let
![]() $\unicode[STIX]{x1D70B}$
be a prime element of
$\unicode[STIX]{x1D70B}$
be a prime element of
![]() $K$
and let
$K$
and let
![]() $f(T)=\sum _{i=0}^{e}a_{i}T^{i}$
be the irreducible polynomial of
$f(T)=\sum _{i=0}^{e}a_{i}T^{i}$
be the irreducible polynomial of
![]() $\unicode[STIX]{x1D70B}$
over
$\unicode[STIX]{x1D70B}$
over
![]() $K$
such that
$K$
such that
![]() $a_{e}=1$
. Then
$a_{e}=1$
. Then
![]() $a_{0}$
is a prime element of
$a_{0}$
is a prime element of
![]() $K_{0}$
and
$K_{0}$
and
![]() $p|a_{i}$
for all
$p|a_{i}$
for all
![]() $0\leqslant i<e$
. We have
$0\leqslant i<e$
. We have
![]() $O_{K_{0}}[T]/(f(T))\overset{\cong }{\rightarrow }O_{K}\;;\;T\mapsto \unicode[STIX]{x1D70B}$
. From this, we see that
$O_{K_{0}}[T]/(f(T))\overset{\cong }{\rightarrow }O_{K}\;;\;T\mapsto \unicode[STIX]{x1D70B}$
. From this, we see that
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )$
has the presentation with generators the
$\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )$
has the presentation with generators the
![]() $O_{K}$
-module
$O_{K}$
-module
![]() $O_{K}\otimes _{O_{K_{0}}}\hat{\unicode[STIX]{x1D6FA}}_{O_{K_{0}}}^{1}$
and
$O_{K}\otimes _{O_{K_{0}}}\hat{\unicode[STIX]{x1D6FA}}_{O_{K_{0}}}^{1}$
and
![]() $d\log (\unicode[STIX]{x1D70B})$
and with the relation
$d\log (\unicode[STIX]{x1D70B})$
and with the relation
![]() $f^{\prime }(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}\,d\log (\unicode[STIX]{x1D70B})+\sum _{i=0}^{e-1}\unicode[STIX]{x1D70B}^{i}da_{i}=0$
. This proves (2).
$f^{\prime }(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}\,d\log (\unicode[STIX]{x1D70B})+\sum _{i=0}^{e-1}\unicode[STIX]{x1D70B}^{i}da_{i}=0$
. This proves (2).
We prove (3). The last relation is written as
which is trivial mod
![]() $p$
.◻
$p$
.◻
Remark 2.1.4. Note that the version of (3) of 2.1.3 without log poles is false. For example, if
![]() $F$
is perfect and
$F$
is perfect and
![]() $p$
is a prime element of
$p$
is a prime element of
![]() $K$
,
$K$
,
![]() $O_{K}/pO_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}=0$
whereas
$O_{K}/pO_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}=0$
whereas
![]() $O_{K}/pO_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\cong O_{K}/pO_{K}$
with base
$O_{K}/pO_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\cong O_{K}/pO_{K}$
with base
![]() $d\log (p)$
. Our theory will go well with log poles.
$d\log (p)$
. Our theory will go well with log poles.
Lemma 2.1.5. Let
![]() $L/K$
be a separable extension of complete discrete valuation fields. Assume that the residue field of
$L/K$
be a separable extension of complete discrete valuation fields. Assume that the residue field of
![]() $K$
is perfect. Then the map
$K$
is perfect. Then the map
![]() $O_{L}\otimes _{O_{K}}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )\rightarrow \hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
is injective.
$O_{L}\otimes _{O_{K}}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )\rightarrow \hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
is injective.
Proof. Assume first
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
. Let
$p$
. Let
![]() $\unicode[STIX]{x1D70B}_{K}$
be a prime element of
$\unicode[STIX]{x1D70B}_{K}$
be a prime element of
![]() $K$
. By (1) of 2.1.3,
$K$
. By (1) of 2.1.3,
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )$
is a free
$\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )$
is a free
![]() $O_{K}$
-module of rank 1 with base
$O_{K}$
-module of rank 1 with base
![]() $d\log (\unicode[STIX]{x1D70B}_{K})$
. As is easily seen, if
$d\log (\unicode[STIX]{x1D70B}_{K})$
. As is easily seen, if
![]() $f\in O_{L}$
and
$f\in O_{L}$
and
![]() $df=0$
in
$df=0$
in
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
, then
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
, then
![]() $f$
is a
$f$
is a
![]() $p$
th power in
$p$
th power in
![]() $O_{L}$
. Hence by the assumption that
$O_{L}$
. Hence by the assumption that
![]() $L/K$
is separable, we have
$L/K$
is separable, we have
![]() $d\unicode[STIX]{x1D70B}_{K}\neq 0$
in
$d\unicode[STIX]{x1D70B}_{K}\neq 0$
in
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
. By 2.1.3, this proves the injectivity in question.
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
. By 2.1.3, this proves the injectivity in question.
Assume next
![]() $K$
is of characteristic 0. We have
$K$
is of characteristic 0. We have
![]() $K\subset L^{\prime }\subset L$
where
$K\subset L^{\prime }\subset L$
where
![]() $L^{\prime }$
is a complete discrete valuation field such that
$L^{\prime }$
is a complete discrete valuation field such that
![]() $L$
is a finite extension of
$L$
is a finite extension of
![]() $L^{\prime }$
, the residue field of
$L^{\prime }$
, the residue field of
![]() $L^{\prime }$
coincides with that of
$L^{\prime }$
coincides with that of
![]() $L$
, and a prime element of
$L$
, and a prime element of
![]() $K$
is still a prime element of
$K$
is still a prime element of
![]() $L^{\prime }$
. Take a
$L^{\prime }$
. Take a
![]() $p$
-base
$p$
-base
![]() $(b_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
of the residue field of
$(b_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
of the residue field of
![]() $L$
and let
$L$
and let
![]() $\tilde{b}_{\unicode[STIX]{x1D706}}$
be a lifting of
$\tilde{b}_{\unicode[STIX]{x1D706}}$
be a lifting of
![]() $b_{\unicode[STIX]{x1D706}}$
to
$b_{\unicode[STIX]{x1D706}}$
to
![]() $O_{L^{\prime }}$
for each
$O_{L^{\prime }}$
for each
![]() $\unicode[STIX]{x1D706}$
. Then the proof of (2) of 2.1.3 shows that
$\unicode[STIX]{x1D706}$
. Then the proof of (2) of 2.1.3 shows that
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L^{\prime }}}^{1}(\log )=O_{L^{\prime }}\otimes _{O_{K}}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )\oplus (\hat{\bigoplus }_{\unicode[STIX]{x1D6EC}}O_{L^{\prime }})$
. Let
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L^{\prime }}}^{1}(\log )=O_{L^{\prime }}\otimes _{O_{K}}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )\oplus (\hat{\bigoplus }_{\unicode[STIX]{x1D6EC}}O_{L^{\prime }})$
. Let
![]() $\unicode[STIX]{x1D70B}$
be a prime element of
$\unicode[STIX]{x1D70B}$
be a prime element of
![]() $L$
and let
$L$
and let
![]() $f(T)=\sum _{i=0}^{e}a_{i}T^{i}$
be the irreducible polynomial of
$f(T)=\sum _{i=0}^{e}a_{i}T^{i}$
be the irreducible polynomial of
![]() $\unicode[STIX]{x1D70B}$
over
$\unicode[STIX]{x1D70B}$
over
![]() $L^{\prime }$
with
$L^{\prime }$
with
![]() $a_{e}=1$
. Then
$a_{e}=1$
. Then
![]() $a_{0}$
is a prime element of
$a_{0}$
is a prime element of
![]() $L^{\prime }$
and
$L^{\prime }$
and
![]() $a_{0}|a_{i}$
for
$a_{0}|a_{i}$
for
![]() $0\leqslant i\leqslant e-1$
. From the fact
$0\leqslant i\leqslant e-1$
. From the fact
![]() $O_{L^{\prime }}[T]/(f(T))\overset{\cong }{\rightarrow }O_{L}\;;\;T\mapsto \unicode[STIX]{x1D70B}$
, we have that
$O_{L^{\prime }}[T]/(f(T))\overset{\cong }{\rightarrow }O_{L}\;;\;T\mapsto \unicode[STIX]{x1D70B}$
, we have that
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
has a presentation with the generators the
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
has a presentation with the generators the
![]() $O_{L}$
-module
$O_{L}$
-module
![]() $O_{L}\otimes _{O_{L^{\prime }}}\hat{\unicode[STIX]{x1D6FA}}_{O_{L^{\prime }}}^{1}(\log )$
and
$O_{L}\otimes _{O_{L^{\prime }}}\hat{\unicode[STIX]{x1D6FA}}_{O_{L^{\prime }}}^{1}(\log )$
and
![]() $d\log (\unicode[STIX]{x1D70B})$
and with the relation
$d\log (\unicode[STIX]{x1D70B})$
and with the relation
(note
![]() $f^{\prime }(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}/a_{0}\in O_{L}\smallsetminus \{0\}$
). This proves 2.1.5.◻
$f^{\prime }(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}/a_{0}\in O_{L}\smallsetminus \{0\}$
). This proves 2.1.5.◻
2.1.6. Let
![]() $a$
be an integer such that
$a$
be an integer such that
![]() $0\leqslant a\leqslant e_{K}$
. Take a ring homomorphism
$0\leqslant a\leqslant e_{K}$
. Take a ring homomorphism
![]() $\unicode[STIX]{x1D704}:F\rightarrow O_{K}/\mathfrak{m}_{K}^{a}$
which lifts the identity map of
$\unicode[STIX]{x1D704}:F\rightarrow O_{K}/\mathfrak{m}_{K}^{a}$
which lifts the identity map of
![]() $F$
(
$F$
(
![]() $\unicode[STIX]{x1D704}$
exists by a theorem of Cohen [Reference Grothendieck12, Chapitre 0, 19.6.1] and a prime element
$\unicode[STIX]{x1D704}$
exists by a theorem of Cohen [Reference Grothendieck12, Chapitre 0, 19.6.1] and a prime element
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $K$
). Then we have an isomorphism
$K$
). Then we have an isomorphism
of rings with log structures given by
![]() $T$
and
$T$
and
![]() $\unicode[STIX]{x1D70B}$
, respectively, which sends
$\unicode[STIX]{x1D70B}$
, respectively, which sends
![]() $T$
to
$T$
to
![]() $\unicode[STIX]{x1D70B}$
in the log structures. (See [Reference Kato21] for log structures.) Since
$\unicode[STIX]{x1D70B}$
in the log structures. (See [Reference Kato21] for log structures.) Since
![]() $O_{K}/\mathfrak{m}_{K}^{a}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
coincides with the module of differential forms with log poles [Reference Kato21] of the ring
$O_{K}/\mathfrak{m}_{K}^{a}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
coincides with the module of differential forms with log poles [Reference Kato21] of the ring
![]() $O_{K}/\mathfrak{m}_{K}^{a}$
with the log structure given by
$O_{K}/\mathfrak{m}_{K}^{a}$
with the log structure given by
![]() $\unicode[STIX]{x1D70B}$
, it is isomorphic to the module of differential forms with log poles of the ring
$\unicode[STIX]{x1D70B}$
, it is isomorphic to the module of differential forms with log poles of the ring
![]() $F[T]/(T^{a})$
with the log structure given by
$F[T]/(T^{a})$
with the log structure given by
![]() $T$
. In the case
$T$
. In the case
![]() $K$
is of mixed characteristic and
$K$
is of mixed characteristic and
![]() $a=e_{K}$
, this gives another proof of (3) of 2.1.3.
$a=e_{K}$
, this gives another proof of (3) of 2.1.3.
In the rest of Section 2.1, we consider the case
![]() $[F:F^{p}]=p^{r}<\infty$
and consider a residue map whose target is the one-dimensional
$[F:F^{p}]=p^{r}<\infty$
and consider a residue map whose target is the one-dimensional
![]() $F$
-vector space
$F$
-vector space
![]() $\unicode[STIX]{x1D6FA}_{F}^{r}=\wedge _{F}^{r}\unicode[STIX]{x1D6FA}_{F}^{1}$
.
$\unicode[STIX]{x1D6FA}_{F}^{r}=\wedge _{F}^{r}\unicode[STIX]{x1D6FA}_{F}^{1}$
.
Proposition 2.1.7. Assume
![]() $K$
is complete and of characteristic
$K$
is complete and of characteristic
![]() $p$
, and that
$p$
, and that
![]() $[F:F^{p}]=p^{r}<\infty$
. Consider a prime element
$[F:F^{p}]=p^{r}<\infty$
. Consider a prime element
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $K$
, a ring homomorphism
$K$
, a ring homomorphism
![]() $\unicode[STIX]{x1D704}:F\rightarrow O_{K}$
which lifts the identity map of
$\unicode[STIX]{x1D704}:F\rightarrow O_{K}$
which lifts the identity map of
![]() $F$
, and the residue map
$F$
, and the residue map
Let
![]() $C:\unicode[STIX]{x1D6FA}_{F}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}$
be the Cartier operator [Reference Illusie16, Chapter 0, Section 2]. Then for integers
$C:\unicode[STIX]{x1D6FA}_{F}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}$
be the Cartier operator [Reference Illusie16, Chapter 0, Section 2]. Then for integers
![]() $a,b$
such that
$a,b$
such that
![]() $a\geqslant 1$
and
$a\geqslant 1$
and
![]() $p^{b}\geqslant a$
, the restriction of
$p^{b}\geqslant a$
, the restriction of
![]() $C^{b}\circ \text{Res}$
to
$C^{b}\circ \text{Res}$
to
![]() $\mathfrak{m}_{K}^{1-a}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )$
is independent of the choices of
$\mathfrak{m}_{K}^{1-a}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )$
is independent of the choices of
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D704}$
.
$\unicode[STIX]{x1D704}$
.
Proof. Note that the Cartier operator
![]() $C:\unicode[STIX]{x1D6FA}_{F}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}$
is characterized by the properties
$C:\unicode[STIX]{x1D6FA}_{F}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}$
is characterized by the properties
![]() $C(x^{p}\,d\log y_{1}\wedge \cdots \wedge d\log y_{r})=x\,d\log y_{1}\wedge \cdots \wedge d\log y_{r}$
for
$C(x^{p}\,d\log y_{1}\wedge \cdots \wedge d\log y_{r})=x\,d\log y_{1}\wedge \cdots \wedge d\log y_{r}$
for
![]() $x\in F$
and
$x\in F$
and
![]() $y_{i}\in F^{\times }$
and
$y_{i}\in F^{\times }$
and
![]() $C(d\unicode[STIX]{x1D714})=0$
for
$C(d\unicode[STIX]{x1D714})=0$
for
![]() $\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{F}^{r-1}$
. Using also the Cartier operator
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{F}^{r-1}$
. Using also the Cartier operator
![]() $C:\unicode[STIX]{x1D6FA}_{K}^{r+1}\rightarrow \unicode[STIX]{x1D6FA}_{K}^{r+1}$
, we have
$C:\unicode[STIX]{x1D6FA}_{K}^{r+1}\rightarrow \unicode[STIX]{x1D6FA}_{K}^{r+1}$
, we have
We have
![]() $C^{b}(\mathfrak{m}_{K}^{1-a}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log ))\subset \unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )$
. On
$C^{b}(\mathfrak{m}_{K}^{1-a}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log ))\subset \unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )$
. On
![]() $\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )$
, the residue map is the unique map which sends
$\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )$
, the residue map is the unique map which sends
![]() $\unicode[STIX]{x1D714}\wedge d\log (t)$
for any
$\unicode[STIX]{x1D714}\wedge d\log (t)$
for any
![]() $\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{r}$
and any
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{r}$
and any
![]() $t\in K^{\times }$
to
$t\in K^{\times }$
to
![]() $\text{ord}_{K}(t)\bar{\unicode[STIX]{x1D714}}$
where
$\text{ord}_{K}(t)\bar{\unicode[STIX]{x1D714}}$
where
![]() $\bar{\unicode[STIX]{x1D714}}$
is the image of
$\bar{\unicode[STIX]{x1D714}}$
is the image of
![]() $\unicode[STIX]{x1D714}$
in
$\unicode[STIX]{x1D714}$
in
![]() $\unicode[STIX]{x1D6FA}_{F}^{r}$
.◻
$\unicode[STIX]{x1D6FA}_{F}^{r}$
.◻
2.1.8. Assume
![]() $[F:F^{p}]=p^{r}<\infty$
. Let
$[F:F^{p}]=p^{r}<\infty$
. Let
![]() $a$
be an integer such that
$a$
be an integer such that
![]() $1\leqslant a\leqslant e_{K}$
.
$1\leqslant a\leqslant e_{K}$
.
Fix a ring homomorphism
![]() $\unicode[STIX]{x1D704}:F\rightarrow O_{K}/\mathfrak{m}_{K}^{a}$
which lifts the identity map of
$\unicode[STIX]{x1D704}:F\rightarrow O_{K}/\mathfrak{m}_{K}^{a}$
which lifts the identity map of
![]() $F$
. Fix a prime element
$F$
. Fix a prime element
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $K$
. Then by the isomorphism (5), we have an isomorphism
$K$
. Then by the isomorphism (5), we have an isomorphism
which sends
![]() $(\unicode[STIX]{x1D714}_{i})_{0\leqslant i\leqslant a-1}$
to
$(\unicode[STIX]{x1D714}_{i})_{0\leqslant i\leqslant a-1}$
to
![]() $\sum _{i=0}^{a-1}\unicode[STIX]{x1D70B}^{i}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D714}_{i})\wedge d\log (\unicode[STIX]{x1D70B})$
.
$\sum _{i=0}^{a-1}\unicode[STIX]{x1D70B}^{i}\unicode[STIX]{x1D704}(\unicode[STIX]{x1D714}_{i})\wedge d\log (\unicode[STIX]{x1D70B})$
.
Proposition 2.1.9. Assume
![]() $[F:F^{p}]=p^{r}<\infty$
. Let
$[F:F^{p}]=p^{r}<\infty$
. Let
![]() $a,b$
be integers such that
$a,b$
be integers such that
![]() $1\leqslant a\leqslant e_{K}$
and
$1\leqslant a\leqslant e_{K}$
and
![]() $p^{b}\geqslant a$
.
$p^{b}\geqslant a$
.
(1) The map
( $$\begin{eqnarray}\displaystyle & \displaystyle R_{b}:\mathfrak{m}_{K}^{1-a}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}\;; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{i=0}^{a-1}\unicode[STIX]{x1D70B}^{-i}\otimes \unicode[STIX]{x1D704}(\unicode[STIX]{x1D714}_{i})\wedge d\log (\unicode[STIX]{x1D70B})\mapsto C^{b}(\unicode[STIX]{x1D714}_{0}) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle R_{b}:\mathfrak{m}_{K}^{1-a}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}\;; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{i=0}^{a-1}\unicode[STIX]{x1D70B}^{-i}\otimes \unicode[STIX]{x1D704}(\unicode[STIX]{x1D714}_{i})\wedge d\log (\unicode[STIX]{x1D70B})\mapsto C^{b}(\unicode[STIX]{x1D714}_{0}) & \displaystyle \nonumber\end{eqnarray}$$
 $\unicode[STIX]{x1D714}_{i}\in \unicode[STIX]{x1D6FA}_{F}^{r}$
), which is defined by fixing
$\unicode[STIX]{x1D714}_{i}\in \unicode[STIX]{x1D6FA}_{F}^{r}$
), which is defined by fixing
 $\unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}$
and
 $\unicode[STIX]{x1D70B}$
as in 2.1.8 using the isomorphism (6), is independent of the choices of
$\unicode[STIX]{x1D70B}$
as in 2.1.8 using the isomorphism (6), is independent of the choices of
 $\unicode[STIX]{x1D704}$
and
$\unicode[STIX]{x1D704}$
and
 $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.(2) Let
 $\unicode[STIX]{x1D704}_{b}:F\rightarrow O_{K}/\mathfrak{m}_{K}^{a}$
be the ring homomorphism which sends
$\unicode[STIX]{x1D704}_{b}:F\rightarrow O_{K}/\mathfrak{m}_{K}^{a}$
be the ring homomorphism which sends
 $x\in F$
to
$x\in F$
to
 $(\tilde{x})^{p^{b}}$
where
$(\tilde{x})^{p^{b}}$
where
 $\tilde{x}$
is a lifting of
$\tilde{x}$
is a lifting of
 $x$
to
$x$
to
 $O_{K}/\mathfrak{m}_{K}^{a}$
. Then for integers
$O_{K}/\mathfrak{m}_{K}^{a}$
. Then for integers
 $i,j$
such that
$i,j$
such that
 $i\geqslant 0$
,
$i\geqslant 0$
,
 $j\geqslant 0$
and
$j\geqslant 0$
and
 $i+j=r+1$
and for integers
$i+j=r+1$
and for integers
 $m,n$
such that
$m,n$
such that
 $a=n-m$
, the pairing sending
$a=n-m$
, the pairing sending $$\begin{eqnarray}(\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{j}(\log ))\times (\mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{i}(\log ))\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}\end{eqnarray}$$
$$\begin{eqnarray}(\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{j}(\log ))\times (\mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{i}(\log ))\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}\end{eqnarray}$$
 $(x,y)$
to
$(x,y)$
to
 $R_{b}(x\wedge y)$
is a perfect duality of finite-dimensional
$R_{b}(x\wedge y)$
is a perfect duality of finite-dimensional
 $F$
-vector spaces, where
$F$
-vector spaces, where
 $F$
acts on the two
$F$
acts on the two
 $O_{K}/\mathfrak{m}_{K}^{a}$
-modules on the left hand side via
$O_{K}/\mathfrak{m}_{K}^{a}$
-modules on the left hand side via
 $\unicode[STIX]{x1D704}_{b}$
.
$\unicode[STIX]{x1D704}_{b}$
.
Proof. We prove (1). If
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
, this follows from 2.1.7. Using the isomorphism (5), the mixed characteristic case is reduced to the positive characteristic case.
$p$
, this follows from 2.1.7. Using the isomorphism (5), the mixed characteristic case is reduced to the positive characteristic case.
We prove (2). The pairing
![]() $(O_{K}/\mathfrak{m}_{K}^{a}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{j}(\log ))\times (O_{K}/\mathfrak{m}_{K}^{a}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{i}(\log ))\rightarrow O_{K}/\mathfrak{m}_{K}^{a}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )\;;\;(x,y)\mapsto x\wedge y$
is a perfect duality of finitely generated free
$(O_{K}/\mathfrak{m}_{K}^{a}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{j}(\log ))\times (O_{K}/\mathfrak{m}_{K}^{a}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{i}(\log ))\rightarrow O_{K}/\mathfrak{m}_{K}^{a}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )\;;\;(x,y)\mapsto x\wedge y$
is a perfect duality of finitely generated free
![]() $O_{K}/\mathfrak{m}_{K}^{a}$
-modules. Hence we are reduced to the case
$O_{K}/\mathfrak{m}_{K}^{a}$
-modules. Hence we are reduced to the case
![]() $i=0$
and
$i=0$
and
![]() $j=r+1$
. Then by induction on
$j=r+1$
. Then by induction on
![]() $a$
, we are reduced to the statement that
$a$
, we are reduced to the statement that
![]() $F\times \unicode[STIX]{x1D6FA}_{F}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}\;;\;(x,y)\mapsto C^{b}(xy)$
is a perfect duality of finite-dimensional vector spaces over
$F\times \unicode[STIX]{x1D6FA}_{F}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}\;;\;(x,y)\mapsto C^{b}(xy)$
is a perfect duality of finite-dimensional vector spaces over
![]() $F$
which acts on these three spaces as follows. An element
$F$
which acts on these three spaces as follows. An element
![]() $c$
of
$c$
of
![]() $F$
acts on
$F$
acts on
![]() $F$
(resp. on the first
$F$
(resp. on the first
![]() $\unicode[STIX]{x1D6FA}_{F}^{r}$
, resp. on the second
$\unicode[STIX]{x1D6FA}_{F}^{r}$
, resp. on the second
![]() $\unicode[STIX]{x1D6FA}_{F}^{r}$
) as
$\unicode[STIX]{x1D6FA}_{F}^{r}$
) as
![]() $c^{p^{b}}$
(resp.
$c^{p^{b}}$
(resp.
![]() $c^{p^{b}}$
, resp.
$c^{p^{b}}$
, resp.
![]() $c$
).◻
$c$
).◻
2.2 Truncated exponential maps for Milnor
 $K$
-groups
$K$
-groups
Kurihara [Reference Kurihara28] defined exponential maps of (completed) Milnor
![]() $K$
-groups of complete discrete valuation fields in mixed characteristic.
$K$
-groups of complete discrete valuation fields in mixed characteristic.
Proposition 2.2.4 is a truncated version of it but works also in the positive characteristic case and outside the area of the convergence of the usual exponential map.
2.2.1. Let
![]() $p$
be a prime number. Let
$p$
be a prime number. Let
The following 2.2.2 is well known. (In (2) of 2.2.2, note that for an integer
![]() $i\geqslant 1$
which is coprime to
$i\geqslant 1$
which is coprime to
![]() $p$
, the map
$p$
, the map
![]() $1+T\mathbb{Z}_{(p)}[[T]]\rightarrow 1+T\mathbb{Z}_{(p)}[[T]]$
;
$1+T\mathbb{Z}_{(p)}[[T]]\rightarrow 1+T\mathbb{Z}_{(p)}[[T]]$
;
![]() $x\mapsto x^{i}$
is bijective and hence the converse map
$x\mapsto x^{i}$
is bijective and hence the converse map
![]() $x\mapsto x^{1/i}$
is defined on
$x\mapsto x^{1/i}$
is defined on
![]() $1+T\mathbb{Z}_{(p)}[[T]]$
.)
$1+T\mathbb{Z}_{(p)}[[T]]$
.)
Lemma 2.2.2.
(1)
 $E(T_{1}+T_{2})\equiv E(T_{1})E(T_{2})\hspace{0.2em}{\rm mod}\hspace{0.2em}(T_{1},T_{2})^{p}\mathbb{Z}_{(p)}[T_{1},T_{2}]$
.
$E(T_{1}+T_{2})\equiv E(T_{1})E(T_{2})\hspace{0.2em}{\rm mod}\hspace{0.2em}(T_{1},T_{2})^{p}\mathbb{Z}_{(p)}[T_{1},T_{2}]$
.(2)
 $E(T)\equiv \prod _{i=1}^{p-1}(1-T^{i})^{-\unicode[STIX]{x1D707}(i)/i}~\text{mod}~T^{p}\mathbb{Z}_{(p)}[[T]]$
. Here
$E(T)\equiv \prod _{i=1}^{p-1}(1-T^{i})^{-\unicode[STIX]{x1D707}(i)/i}~\text{mod}~T^{p}\mathbb{Z}_{(p)}[[T]]$
. Here
 $\unicode[STIX]{x1D707}$
is the Möbius function.
$\unicode[STIX]{x1D707}$
is the Möbius function.(3)
 $(T/E(T))(dE(T)/dT)\equiv T~\text{mod}~T^{p}\mathbb{Z}_{(p)}[[T]]$
.
$(T/E(T))(dE(T)/dT)\equiv T~\text{mod}~T^{p}\mathbb{Z}_{(p)}[[T]]$
.
Proof. (1) (resp. (2)) follows from the property
![]() $\exp (T_{1}+T_{2})=\exp (T_{1})\cdot \exp (T_{2})$
in
$\exp (T_{1}+T_{2})=\exp (T_{1})\cdot \exp (T_{2})$
in
![]() $\mathbb{Q}[[T_{1},T_{2}]]$
(resp.
$\mathbb{Q}[[T_{1},T_{2}]]$
(resp.
![]() $\exp (\sum _{i\geqslant 0}(T^{p^{i}}/p^{i}))=\prod _{i\geqslant 1,(i,p)=1}(1-T^{i})^{-\unicode[STIX]{x1D707}(i)/i}$
in
$\exp (\sum _{i\geqslant 0}(T^{p^{i}}/p^{i}))=\prod _{i\geqslant 1,(i,p)=1}(1-T^{i})^{-\unicode[STIX]{x1D707}(i)/i}$
in
![]() $\mathbb{Q}[[T]]$
) of the usual exponential (resp. of Artin–Hasse exponential) and the injectivity of
$\mathbb{Q}[[T]]$
) of the usual exponential (resp. of Artin–Hasse exponential) and the injectivity of
![]() $\mathbb{Z}_{(p)}[T_{1},T_{2}]/(T_{1},T_{2})^{p}\rightarrow \mathbb{Q}[[T_{1},T_{2}]]/(T_{1},T_{2})^{p}$
(resp. of
$\mathbb{Z}_{(p)}[T_{1},T_{2}]/(T_{1},T_{2})^{p}\rightarrow \mathbb{Q}[[T_{1},T_{2}]]/(T_{1},T_{2})^{p}$
(resp. of
![]() $\mathbb{Z}_{(p)}[[T]]/(T^{p})\rightarrow \mathbb{Q}[[T]]/(T^{p})$
).
$\mathbb{Z}_{(p)}[[T]]/(T^{p})\rightarrow \mathbb{Q}[[T]]/(T^{p})$
).
(3) is straightforward. ◻
2.2.3. For a field
![]() $K$
, let
$K$
, let
![]() $K_{r}^{M}(K)$
be the
$K_{r}^{M}(K)$
be the
![]() $r$
th Milnor
$r$
th Milnor
![]() $K$
-group of
$K$
-group of
![]() $K$
. For a discrete valuation field
$K$
. For a discrete valuation field
![]() $K$
and for
$K$
and for
![]() $i\geqslant 1$
, we denote by
$i\geqslant 1$
, we denote by
![]() $U^{i}K_{r}^{M}(K)$
the subgroup of
$U^{i}K_{r}^{M}(K)$
the subgroup of
![]() $K_{r}^{M}(K)$
generated by elements of the form
$K_{r}^{M}(K)$
generated by elements of the form
![]() $\{u_{1},\ldots ,u_{r}\}$
where
$\{u_{1},\ldots ,u_{r}\}$
where
![]() $u_{i}\in K^{\times }$
(
$u_{i}\in K^{\times }$
(
![]() $1\leqslant i\leqslant r$
) and
$1\leqslant i\leqslant r$
) and
![]() $u_{1}\in \text{Ker}(O_{K}^{\times }\rightarrow (O_{K}/\mathfrak{m}_{K}^{i})^{\times })$
.
$u_{1}\in \text{Ker}(O_{K}^{\times }\rightarrow (O_{K}/\mathfrak{m}_{K}^{i})^{\times })$
.
Proposition 2.2.4. Let
![]() $K$
be a discrete valuation field whose residue field is of characteristic
$K$
be a discrete valuation field whose residue field is of characteristic
![]() $p>0$
and let
$p>0$
and let
![]() $r\geqslant 0$
,
$r\geqslant 0$
,
![]() $t\geqslant 1$
.
$t\geqslant 1$
.
(1) We have a well-defined homomorphism
( $$\begin{eqnarray}\displaystyle & E:\mathfrak{m}_{K}^{t}/\mathfrak{m}_{K}^{pt}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )\rightarrow U^{t}K_{r+1}^{M}(K)/U^{pt}K_{r+1}^{M}(K) & \displaystyle \nonumber\\ \displaystyle & x\otimes d\log (y_{1})\wedge \cdots \wedge d\log (y_{r})\mapsto \{E(x),y_{1},\ldots ,y_{r}\} & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & E:\mathfrak{m}_{K}^{t}/\mathfrak{m}_{K}^{pt}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )\rightarrow U^{t}K_{r+1}^{M}(K)/U^{pt}K_{r+1}^{M}(K) & \displaystyle \nonumber\\ \displaystyle & x\otimes d\log (y_{1})\wedge \cdots \wedge d\log (y_{r})\mapsto \{E(x),y_{1},\ldots ,y_{r}\} & \displaystyle \nonumber\end{eqnarray}$$
 $x\in \mathfrak{m}_{K}^{i}$
,
$x\in \mathfrak{m}_{K}^{i}$
,
 $y_{j}\in K^{\times }$
). Here
$y_{j}\in K^{\times }$
). Here
 $\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )=\wedge _{O_{K}}^{r}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
.
$\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )=\wedge _{O_{K}}^{r}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
.(2) This map
 $E$
is surjective.
$E$
is surjective.(3) This map
 $E$
kills the image of (7)
$E$
kills the image of (7) $$\begin{eqnarray}d:\mathfrak{m}_{K}^{t}/\mathfrak{m}_{K}^{pt}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r-1}(\log )\rightarrow \mathfrak{m}_{K}^{t}/\mathfrak{m}_{K}^{pt}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log ).\end{eqnarray}$$
$$\begin{eqnarray}d:\mathfrak{m}_{K}^{t}/\mathfrak{m}_{K}^{pt}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r-1}(\log )\rightarrow \mathfrak{m}_{K}^{t}/\mathfrak{m}_{K}^{pt}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log ).\end{eqnarray}$$
Proof. We prove (1). The
![]() $O_{K}$
-module
$O_{K}$
-module
![]() $\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
has the following presentation by generators and relations.
$\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
has the following presentation by generators and relations.
Generators.
![]() $d\log (x)$
for
$d\log (x)$
for
![]() $x\in O_{K}\smallsetminus \{0\}$
.
$x\in O_{K}\smallsetminus \{0\}$
.
Relations.
![]() $d\log (xy)=d\log (x)+d\log (y)$
for
$d\log (xy)=d\log (x)+d\log (y)$
for
![]() $x,y\in O_{K}\smallsetminus \{0\}$
.
$x,y\in O_{K}\smallsetminus \{0\}$
.
![]() $x_{0}\,d\log (x_{0})=\sum _{i=1}^{n}x_{i}\,d\log (x_{i})$
if
$x_{0}\,d\log (x_{0})=\sum _{i=1}^{n}x_{i}\,d\log (x_{i})$
if
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
![]() $x_{i}\in O_{K}\smallsetminus \{0\}$
, and
$x_{i}\in O_{K}\smallsetminus \{0\}$
, and
![]() $x_{0}=\sum _{i=1}^{n}x_{i}$
.
$x_{0}=\sum _{i=1}^{n}x_{i}$
.
Let
![]() $h$
be a generator of the ideal
$h$
be a generator of the ideal
![]() $\mathfrak{m}_{K}^{t}$
of
$\mathfrak{m}_{K}^{t}$
of
![]() $O_{K}$
. By the above presentation of
$O_{K}$
. By the above presentation of
![]() $\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
, in the case
$\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
, in the case
![]() $r=1$
, it is sufficient to prove that
$r=1$
, it is sufficient to prove that
![]() $\{E(hx_{0}),x_{0}\}\equiv \sum _{i=1}^{n}\{E(hx_{i}),x_{i}\}~\text{mod}~U^{pt}K_{2}^{M}(K)$
if
$\{E(hx_{0}),x_{0}\}\equiv \sum _{i=1}^{n}\{E(hx_{i}),x_{i}\}~\text{mod}~U^{pt}K_{2}^{M}(K)$
if
![]() $x_{i}\in O_{K}\smallsetminus \{0\}$
and
$x_{i}\in O_{K}\smallsetminus \{0\}$
and
![]() $x_{0}=\sum _{i=1}^{n}x_{i}$
. (Here we denote the group law of
$x_{0}=\sum _{i=1}^{n}x_{i}$
. (Here we denote the group law of
![]() $K_{2}^{M}(K)$
additively.) Since
$K_{2}^{M}(K)$
additively.) Since
![]() $\{E(hx_{i}),x_{i}\}=\{E(hx_{i}),hx_{i}\}-\{E(hx_{i}),h\}$
and since
$\{E(hx_{i}),x_{i}\}=\{E(hx_{i}),hx_{i}\}-\{E(hx_{i}),h\}$
and since
![]() $\{E(hx_{0}),h\}\equiv \sum _{i=1}^{n}\{E(hx_{i}),h\}$
by (1) of 2.2.2, it is sufficient to prove that
$\{E(hx_{0}),h\}\equiv \sum _{i=1}^{n}\{E(hx_{i}),h\}$
by (1) of 2.2.2, it is sufficient to prove that
From (2) of 2.2.2 we have, modulo
![]() $U^{pt}K_{2}^{M}(K)$
,
$U^{pt}K_{2}^{M}(K)$
,
 $$\begin{eqnarray}\displaystyle \{E(hx),hx\} & \equiv & \displaystyle \left\{\mathop{\prod }_{i=1}^{p-1}(1-(hx)^{i})^{-\unicode[STIX]{x1D707}(i)/i},hx\right\}\nonumber\\ \displaystyle & \equiv & \displaystyle -\mathop{\sum }_{i=1}^{p-1}\unicode[STIX]{x1D707}(i)i^{-2}\{1-(hx)^{i},(hx)^{i}\}=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{E(hx),hx\} & \equiv & \displaystyle \left\{\mathop{\prod }_{i=1}^{p-1}(1-(hx)^{i})^{-\unicode[STIX]{x1D707}(i)/i},hx\right\}\nonumber\\ \displaystyle & \equiv & \displaystyle -\mathop{\sum }_{i=1}^{p-1}\unicode[STIX]{x1D707}(i)i^{-2}\{1-(hx)^{i},(hx)^{i}\}=0.\nonumber\end{eqnarray}$$
The case
![]() $r\geqslant 2$
is reduced to the case
$r\geqslant 2$
is reduced to the case
![]() $r=1$
and to
$r=1$
and to
![]() $\{E(hx),y,y\}\equiv 0~\text{mod}~U^{pt}K_{3}^{M}(K)$
for
$\{E(hx),y,y\}\equiv 0~\text{mod}~U^{pt}K_{3}^{M}(K)$
for
![]() $x\in O_{K}$
and
$x\in O_{K}$
and
![]() $y\in K^{\times }$
. Since
$y\in K^{\times }$
. Since
![]() $\{y,y\}=\{-1,y\}$
in
$\{y,y\}=\{-1,y\}$
in
![]() $K_{2}^{M}(K)$
, it is sufficient to prove that
$K_{2}^{M}(K)$
, it is sufficient to prove that
![]() $\{E(hx),-1\}\in U^{pt}K_{2}^{M}(K)$
. But this follows from the case
$\{E(hx),-1\}\in U^{pt}K_{2}^{M}(K)$
. But this follows from the case
![]() $r=1$
because
$r=1$
because
![]() $d\log (-1)=0$
in
$d\log (-1)=0$
in
![]() $\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
.
$\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
.
(2) is clear.
We prove (3). For
![]() $x\in O_{K}\smallsetminus \{0\}$
and
$x\in O_{K}\smallsetminus \{0\}$
and
![]() $y_{1},\ldots ,y_{r-1}\in K^{\times }$
,
$y_{1},\ldots ,y_{r-1}\in K^{\times }$
,
![]() $E$
sends
$E$
sends
![]() $d(h\otimes x\,d\log (y_{1})\wedge \cdots \wedge d\log (y_{r-1}))$
to
$d(h\otimes x\,d\log (y_{1})\wedge \cdots \wedge d\log (y_{r-1}))$
to
![]() $\{E(hx),hx,y_{1},\ldots ,y_{r-1}\}$
. Hence (3) follows from (8).◻
$\{E(hx),hx,y_{1},\ldots ,y_{r-1}\}$
. Hence (3) follows from (8).◻
2.3 Cohomology of the highest degree
2.3.1. Let
![]() $X$
be a Noetherian scheme of dimension
$X$
be a Noetherian scheme of dimension
![]() $d<\infty$
. Let
$d<\infty$
. Let
![]() ${\mathcal{F}}$
be a sheaf of abelian groups on
${\mathcal{F}}$
be a sheaf of abelian groups on
![]() $X$
for Zariski topology. In 2.3.4 (resp. 2.3.5), for an abelian group
$X$
for Zariski topology. In 2.3.4 (resp. 2.3.5), for an abelian group
![]() $A$
, we give an elementary understanding of a homomorphism
$A$
, we give an elementary understanding of a homomorphism
![]() $H^{d}(X,{\mathcal{F}})\rightarrow A$
(resp.
$H^{d}(X,{\mathcal{F}})\rightarrow A$
(resp.
![]() $H_{x}^{d}(X,{\mathcal{F}})\rightarrow A$
for a closed point
$H_{x}^{d}(X,{\mathcal{F}})\rightarrow A$
for a closed point
![]() $x$
of
$x$
of
![]() $X$
), where
$X$
), where
![]() $H^{d}$
is the cohomology for Zariski topology and
$H^{d}$
is the cohomology for Zariski topology and
![]() $H_{x}^{d}$
is the cohomology with support in
$H_{x}^{d}$
is the cohomology with support in
![]() $x$
.
$x$
.
2.3.2. Let
![]() $P(X)$
be the set of all
$P(X)$
be the set of all
![]() $(d+1)$
-tuples
$(d+1)$
-tuples
![]() $\mathfrak{p}=(x_{0},\ldots ,x_{d})$
of points of
$\mathfrak{p}=(x_{0},\ldots ,x_{d})$
of points of
![]() $X$
such that
$X$
such that
![]() $\overline{\{x_{i}\}}\subsetneq \overline{\{x_{i+1}\}}$
for all
$\overline{\{x_{i}\}}\subsetneq \overline{\{x_{i+1}\}}$
for all
![]() $0\leqslant i\leqslant d-1$
.
$0\leqslant i\leqslant d-1$
.
For an integer
![]() $s$
such that
$s$
such that
![]() $0\leqslant s\leqslant d$
, let
$0\leqslant s\leqslant d$
, let
![]() $Q_{s}(X)$
be the set of all
$Q_{s}(X)$
be the set of all
![]() $d$
-tuples
$d$
-tuples
![]() $\mathfrak{q}=(x_{0},\ldots ,x_{s-1},x_{s+1},\ldots ,x_{d})$
of points of
$\mathfrak{q}=(x_{0},\ldots ,x_{s-1},x_{s+1},\ldots ,x_{d})$
of points of
![]() $X$
such that the set
$X$
such that the set
![]() $P_{\mathfrak{q}}(X):=\{(x_{i}^{\prime })_{i}\in P(X)\mid x_{i}^{\prime }=x_{i}\;\text{if}\;i\neq s\}$
is not empty.
$P_{\mathfrak{q}}(X):=\{(x_{i}^{\prime })_{i}\in P(X)\mid x_{i}^{\prime }=x_{i}\;\text{if}\;i\neq s\}$
is not empty.
2.3.3. For any
![]() $\mathfrak{p}=(x_{i})_{i}\in P(X)$
, we have a homomorphism
$\mathfrak{p}=(x_{i})_{i}\in P(X)$
, we have a homomorphism
![]() $\unicode[STIX]{x1D704}_{\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow H^{d}(X,{\mathcal{F}})$
with
$\unicode[STIX]{x1D704}_{\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow H^{d}(X,{\mathcal{F}})$
with
![]() $\unicode[STIX]{x1D702}(\mathfrak{p})=x_{d}$
defined as the composition
$\unicode[STIX]{x1D702}(\mathfrak{p})=x_{d}$
defined as the composition
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}=H_{x_{d}}^{0}(X,{\mathcal{F}})\rightarrow H_{x_{d-1}}^{1}(X,{\mathcal{F}})\rightarrow \cdots \rightarrow H_{x_{0}}^{d}(X,{\mathcal{F}})\rightarrow H^{d}(X,{\mathcal{F}})$
. (See [Reference Hartshorne13, Chapter IV] for these cohomology groups with support
${\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}=H_{x_{d}}^{0}(X,{\mathcal{F}})\rightarrow H_{x_{d-1}}^{1}(X,{\mathcal{F}})\rightarrow \cdots \rightarrow H_{x_{0}}^{d}(X,{\mathcal{F}})\rightarrow H^{d}(X,{\mathcal{F}})$
. (See [Reference Hartshorne13, Chapter IV] for these cohomology groups with support
![]() $\{x_{i}\}$
.)
$\{x_{i}\}$
.)
Hence for an abelian group
![]() $A$
, a homomorphism
$A$
, a homomorphism
![]() $h:H^{d}(X,{\mathcal{F}})\rightarrow A$
induces a homomorphism
$h:H^{d}(X,{\mathcal{F}})\rightarrow A$
induces a homomorphism
![]() $h_{\mathfrak{p}}=h\circ \unicode[STIX]{x1D704}_{\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow A$
for each
$h_{\mathfrak{p}}=h\circ \unicode[STIX]{x1D704}_{\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow A$
for each
![]() $\mathfrak{p}\in P(X)$
.
$\mathfrak{p}\in P(X)$
.
Lemma 2.3.4. Let the notation be as above. Then for an abelian group
![]() $A$
, the map
$A$
, the map
defined above is an injection and the image consists of all elements
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}\in P(X)}$
satisfying the following conditions
$(h_{\mathfrak{p}})_{\mathfrak{p}\in P(X)}$
satisfying the following conditions
![]() $\text{(i)}$
and
$\text{(i)}$
and
![]() $\text{(ii)}$
.
$\text{(ii)}$
.
(i) Let
 $0\leqslant s\leqslant d-1$
,
$0\leqslant s\leqslant d-1$
,
 $\mathfrak{q}=(x_{i})_{i}\in Q_{s}(X)$
, and let
$\mathfrak{q}=(x_{i})_{i}\in Q_{s}(X)$
, and let
 $a\in {\mathcal{F}}_{x_{d}}$
. Then
$a\in {\mathcal{F}}_{x_{d}}$
. Then
 $h_{\mathfrak{p}}(a)=0$
for almost all
$h_{\mathfrak{p}}(a)=0$
for almost all
 $\mathfrak{p}\in P_{\mathfrak{q}}(X)$
and
$\mathfrak{p}\in P_{\mathfrak{q}}(X)$
and
 $\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}\;h_{\mathfrak{p}}(a)=0$
.
$\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}\;h_{\mathfrak{p}}(a)=0$
.(ii) Let
 $\mathfrak{q}=(x_{i})_{i}\in Q_{d}(X)$
and let
$\mathfrak{q}=(x_{i})_{i}\in Q_{d}(X)$
and let
 $a\in {\mathcal{F}}_{x_{d-1}}$
. Then
$a\in {\mathcal{F}}_{x_{d-1}}$
. Then
 $\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}(a)=0$
. (Note that
$\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}(a)=0$
. (Note that
 $P_{\mathfrak{q}}(X)$
is a finite set in this situation.)
$P_{\mathfrak{q}}(X)$
is a finite set in this situation.)
A version of 2.3.4 for Nisnevich topology (not Zariski topology) is stated and proved in [Reference Kato and Saito23, Section 1.6].
Lemma 2.3.5. Let the notation be as above. Let
![]() $x$
be a closed point of
$x$
be a closed point of
![]() $X$
. Let
$X$
. Let
![]() $P_{x}(X)=\{\mathfrak{p}=(x_{i})_{i}\mid x_{0}=x\}$
and
$P_{x}(X)=\{\mathfrak{p}=(x_{i})_{i}\mid x_{0}=x\}$
and
![]() $Q_{s,x}(X)=\{\mathfrak{q}=(x_{i})_{i}\in Q_{s}(X)\mid x_{0}=x\}$
for
$Q_{s,x}(X)=\{\mathfrak{q}=(x_{i})_{i}\in Q_{s}(X)\mid x_{0}=x\}$
for
![]() $1\leqslant s\leqslant d$
. Then for an abelian group
$1\leqslant s\leqslant d$
. Then for an abelian group
![]() $A$
, the map
$A$
, the map
(
![]() $h_{\mathfrak{p}}=h\circ \unicode[STIX]{x1D704}_{x,\mathfrak{p}}$
where
$h_{\mathfrak{p}}=h\circ \unicode[STIX]{x1D704}_{x,\mathfrak{p}}$
where
![]() $\unicode[STIX]{x1D704}_{x,\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow H_{x}^{d}(X,{\mathcal{F}})$
is defined as in 2.3.3) is an injection and the image consists of all elements
$\unicode[STIX]{x1D704}_{x,\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow H_{x}^{d}(X,{\mathcal{F}})$
is defined as in 2.3.3) is an injection and the image consists of all elements
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}\in P_{x}(X)}$
satisfying the following conditions
$(h_{\mathfrak{p}})_{\mathfrak{p}\in P_{x}(X)}$
satisfying the following conditions
![]() $\text{(i)}$
and
$\text{(i)}$
and
![]() $\text{(ii)}$
.
$\text{(ii)}$
.
(i) Let
 $1\leqslant s\leqslant d-1$
,
$1\leqslant s\leqslant d-1$
,
 $\mathfrak{q}=(x_{i})_{i}\in Q_{s,x}(X)$
, and let
$\mathfrak{q}=(x_{i})_{i}\in Q_{s,x}(X)$
, and let
 $a\in {\mathcal{F}}_{x_{d}}$
. Then
$a\in {\mathcal{F}}_{x_{d}}$
. Then
 $h_{\mathfrak{p}}(a)=0$
for almost all
$h_{\mathfrak{p}}(a)=0$
for almost all
 $\mathfrak{p}\in P_{\mathfrak{q}}(X)$
and
$\mathfrak{p}\in P_{\mathfrak{q}}(X)$
and
 $\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}\;h_{\mathfrak{p}}(a)=0$
.
$\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}\;h_{\mathfrak{p}}(a)=0$
.(ii) Let
 $\mathfrak{q}=(x_{i})_{i}\in Q_{d,x}(X)$
, and let
$\mathfrak{q}=(x_{i})_{i}\in Q_{d,x}(X)$
, and let
 $a\in {\mathcal{F}}_{x_{d-1}}$
. Then
$a\in {\mathcal{F}}_{x_{d-1}}$
. Then
 $\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}(a)=0$
.
$\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}(a)=0$
.
2.3.6. Lemmas 2.3.4 and 2.3.5 are proved together by induction on
![]() $d=\dim (X)$
as follows, by using the localization theory of cohomology with supports explained in [Reference Hartshorne13, Chapter IV].
$d=\dim (X)$
as follows, by using the localization theory of cohomology with supports explained in [Reference Hartshorne13, Chapter IV].
Let
![]() $X_{i}$
be the set of all
$X_{i}$
be the set of all
![]() $x\in X$
such that
$x\in X$
such that
![]() $\dim (\overline{\{x\}})=i$
. Let
$\dim (\overline{\{x\}})=i$
. Let
![]() $X^{i}$
be the set of all
$X^{i}$
be the set of all
![]() $x\in X$
such that
$x\in X$
such that
![]() $\dim (\text{Spec}({\mathcal{O}}_{X,x}))=i$
. By using the spectral sequence
$\dim (\text{Spec}({\mathcal{O}}_{X,x}))=i$
. By using the spectral sequence
and using
![]() $H_{x}^{i}(X,{\mathcal{F}})=H_{x}^{i}(\text{Spec}({\mathcal{O}}_{X,x}),{\mathcal{F}})$
, where we denote the pullback of
$H_{x}^{i}(X,{\mathcal{F}})=H_{x}^{i}(\text{Spec}({\mathcal{O}}_{X,x}),{\mathcal{F}})$
, where we denote the pullback of
![]() ${\mathcal{F}}$
to
${\mathcal{F}}$
to
![]() $\text{Spec}({\mathcal{O}}_{X,x})$
also by
$\text{Spec}({\mathcal{O}}_{X,x})$
also by
![]() ${\mathcal{F}}$
, we obtain the following (1)–(5) by induction on
${\mathcal{F}}$
, we obtain the following (1)–(5) by induction on
![]() $\dim (X)$
.
$\dim (X)$
.
(1) If
 $i>d$
,
$i>d$
,
 $H^{i}(X,{\mathcal{F}})=0$
and
$H^{i}(X,{\mathcal{F}})=0$
and
 $H_{x}^{i}(X,{\mathcal{F}})=0$
for any
$H_{x}^{i}(X,{\mathcal{F}})=0$
for any
 $x\in X$
.
$x\in X$
.(2) We have an exact sequence
 $\bigoplus _{x\in X_{1}}H_{x}^{d-1}(X,{\mathcal{F}})\rightarrow \bigoplus _{x\in X_{0}}H_{x}^{d}(X,{\mathcal{F}})\rightarrow H^{d}(X,{\mathcal{F}})\rightarrow 0$
.
$\bigoplus _{x\in X_{1}}H_{x}^{d-1}(X,{\mathcal{F}})\rightarrow \bigoplus _{x\in X_{0}}H_{x}^{d}(X,{\mathcal{F}})\rightarrow H^{d}(X,{\mathcal{F}})\rightarrow 0$
.(3) If
 $x\in X^{i}$
and
$x\in X^{i}$
and
 $i\geqslant 2$
,
$i\geqslant 2$
,
 $H_{x}^{i}(X,{\mathcal{F}})\cong H^{i-1}(\text{Spec}({\mathcal{O}}_{X,x})\smallsetminus \{x\},{\mathcal{F}})$
and
$H_{x}^{i}(X,{\mathcal{F}})\cong H^{i-1}(\text{Spec}({\mathcal{O}}_{X,x})\smallsetminus \{x\},{\mathcal{F}})$
and
 $\text{Spec}({\mathcal{O}}_{X,x})\smallsetminus \{x\}$
is of dimension
$\text{Spec}({\mathcal{O}}_{X,x})\smallsetminus \{x\}$
is of dimension
 $i-1$
.
$i-1$
.(4) If
 $x\in X^{1}$
, we have an exact sequence
$x\in X^{1}$
, we have an exact sequence
 ${\mathcal{F}}_{x}\rightarrow \bigoplus _{\unicode[STIX]{x1D702}\in \text{Spec}({\mathcal{O}}_{X,x})\smallsetminus \{x\}}{\mathcal{F}}_{\unicode[STIX]{x1D702}}\rightarrow H_{x}^{1}(X,{\mathcal{F}})\rightarrow 0$
.
${\mathcal{F}}_{x}\rightarrow \bigoplus _{\unicode[STIX]{x1D702}\in \text{Spec}({\mathcal{O}}_{X,x})\smallsetminus \{x\}}{\mathcal{F}}_{\unicode[STIX]{x1D702}}\rightarrow H_{x}^{1}(X,{\mathcal{F}})\rightarrow 0$
.(5) If
 $x\in X^{0}$
,
$x\in X^{0}$
,
 $H_{x}^{0}(X,{\mathcal{F}})={\mathcal{F}}_{x}$
.
$H_{x}^{0}(X,{\mathcal{F}})={\mathcal{F}}_{x}$
.
By (1)–(5) and by induction on
![]() $d=\dim (X)$
, we have the map
$d=\dim (X)$
, we have the map
![]() $h\mapsto (h_{\mathfrak{p}})_{\mathfrak{p}}$
from the left hand side of 2.3.4 (resp. 2.3.5) to the right hand side of 2.3.4 (resp. 2.3.5), that
$h\mapsto (h_{\mathfrak{p}})_{\mathfrak{p}}$
from the left hand side of 2.3.4 (resp. 2.3.5) to the right hand side of 2.3.4 (resp. 2.3.5), that
![]() $H^{d}(X,{\mathcal{F}})$
(resp.
$H^{d}(X,{\mathcal{F}})$
(resp.
![]() $H_{x}^{d}(X,{\mathcal{F}})$
for
$H_{x}^{d}(X,{\mathcal{F}})$
for
![]() $x\in X_{0}$
) is generated by the images of
$x\in X_{0}$
) is generated by the images of
![]() $\unicode[STIX]{x1D704}_{\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow H^{d}(X,{\mathcal{F}})$
for
$\unicode[STIX]{x1D704}_{\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow H^{d}(X,{\mathcal{F}})$
for
![]() $\mathfrak{p}\in P(X)$
(resp.
$\mathfrak{p}\in P(X)$
(resp.
![]() $\unicode[STIX]{x1D704}_{x,\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow H_{x}^{d}(X,{\mathcal{F}})$
for
$\unicode[STIX]{x1D704}_{x,\mathfrak{p}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow H_{x}^{d}(X,{\mathcal{F}})$
for
![]() $\mathfrak{p}\in P_{x}(X)$
), and hence that this map
$\mathfrak{p}\in P_{x}(X)$
), and hence that this map
![]() $h\mapsto (h_{\mathfrak{p}})_{\mathfrak{p}}$
is injective. We give the proof of the surjectivity of this map.
$h\mapsto (h_{\mathfrak{p}})_{\mathfrak{p}}$
is injective. We give the proof of the surjectivity of this map.
Let
![]() $x\in X_{0}$
and let
$x\in X_{0}$
and let
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}}$
be an element of the set on the right hand side of 2.3.5. If
$(h_{\mathfrak{p}})_{\mathfrak{p}}$
be an element of the set on the right hand side of 2.3.5. If
![]() $x\in X^{i}$
with
$x\in X^{i}$
with
![]() $i<d$
,
$i<d$
,
![]() $P_{x}(X)$
is empty. So we may assume
$P_{x}(X)$
is empty. So we may assume
![]() $x\in X^{d}$
. Let
$x\in X^{d}$
. Let
![]() $U=\text{Spec}({\mathcal{O}}_{X,x})\smallsetminus \{x\}$
. We have the bijection
$U=\text{Spec}({\mathcal{O}}_{X,x})\smallsetminus \{x\}$
. We have the bijection
![]() $P_{x}(X)\rightarrow P(U)\;;\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d}\mapsto \mathfrak{p}^{\prime }=(x_{i+1})_{0\leqslant i\leqslant d-1}$
. By induction on
$P_{x}(X)\rightarrow P(U)\;;\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d}\mapsto \mathfrak{p}^{\prime }=(x_{i+1})_{0\leqslant i\leqslant d-1}$
. By induction on
![]() $d$
,
$d$
,
![]() $(h_{\mathfrak{p}^{\prime }})_{\mathfrak{p}^{\prime }\in P(U)}$
corresponds to a homomorphism
$(h_{\mathfrak{p}^{\prime }})_{\mathfrak{p}^{\prime }\in P(U)}$
corresponds to a homomorphism
![]() $H^{d-1}(U,{\mathcal{F}})\rightarrow A$
. If
$H^{d-1}(U,{\mathcal{F}})\rightarrow A$
. If
![]() $d\geqslant 2$
, by the above (3),
$d\geqslant 2$
, by the above (3),
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}}$
corresponds to a homomorphism
$(h_{\mathfrak{p}})_{\mathfrak{p}}$
corresponds to a homomorphism
![]() $h:H_{x}^{d}(X,{\mathcal{F}})\rightarrow A$
. The proof for the case
$h:H_{x}^{d}(X,{\mathcal{F}})\rightarrow A$
. The proof for the case
![]() $d=1$
(resp.
$d=1$
(resp.
![]() $d=0$
) is similar by using the above (4) (resp. (5)).
$d=0$
) is similar by using the above (4) (resp. (5)).
Next let
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}}$
be an element of the set on the right hand side of 2.3.4. The case
$(h_{\mathfrak{p}})_{\mathfrak{p}}$
be an element of the set on the right hand side of 2.3.4. The case
![]() $d=0$
is trivial and so assume
$d=0$
is trivial and so assume
![]() $d\geqslant 1$
. Since
$d\geqslant 1$
. Since
![]() $P(X)$
is the disjoint union of
$P(X)$
is the disjoint union of
![]() $P_{x}(X)$
for
$P_{x}(X)$
for
![]() $x\in X_{0}$
,
$x\in X_{0}$
,
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}}$
induces a homomorphism
$(h_{\mathfrak{p}})_{\mathfrak{p}}$
induces a homomorphism
![]() $\bigoplus _{x\in X_{0}}H_{x}^{d}(X,{\mathcal{F}})\rightarrow A$
. Consider the exact sequence in the above (2). For
$\bigoplus _{x\in X_{0}}H_{x}^{d}(X,{\mathcal{F}})\rightarrow A$
. Consider the exact sequence in the above (2). For
![]() $x\in X_{1}$
,
$x\in X_{1}$
,
![]() $H_{x}^{d-1}(X,{\mathcal{F}})$
is zero unless
$H_{x}^{d-1}(X,{\mathcal{F}})$
is zero unless
![]() $x\in X^{d-1}$
by the above (1), and is generated by the images of
$x\in X^{d-1}$
by the above (1), and is generated by the images of
![]() $h_{x,\mathfrak{q}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{q})}\rightarrow H_{x}^{d-1}(X,{\mathcal{F}})$
if
$h_{x,\mathfrak{q}}:{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{q})}\rightarrow H_{x}^{d-1}(X,{\mathcal{F}})$
if
![]() $x\in X^{d-1}$
where
$x\in X^{d-1}$
where
![]() $\mathfrak{q}$
ranges over all elements of
$\mathfrak{q}$
ranges over all elements of
![]() $P_{x}(\text{Spec}({\mathcal{O}}_{X,x}))$
. By this fact and by the fact
$P_{x}(\text{Spec}({\mathcal{O}}_{X,x}))$
. By this fact and by the fact
![]() $Q_{0}(X)$
is the disjoint union of
$Q_{0}(X)$
is the disjoint union of
![]() $P_{x}(\text{Spec}({\mathcal{O}}_{X,x}))$
for
$P_{x}(\text{Spec}({\mathcal{O}}_{X,x}))$
for
![]() $x\in X_{1}\cap X^{d-1}$
, the homomorphism
$x\in X_{1}\cap X^{d-1}$
, the homomorphism
![]() $\bigoplus _{x}H_{x}^{d}(X,{\mathcal{F}})\rightarrow A$
kills the image of
$\bigoplus _{x}H_{x}^{d}(X,{\mathcal{F}})\rightarrow A$
kills the image of
![]() $\bigoplus _{x\in X_{1}}H_{x}^{d-1}(X,{\mathcal{F}})$
by the property (i) with
$\bigoplus _{x\in X_{1}}H_{x}^{d-1}(X,{\mathcal{F}})$
by the property (i) with
![]() $s=0$
of
$s=0$
of
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}}$
in 2.3.4. Hence
$(h_{\mathfrak{p}})_{\mathfrak{p}}$
in 2.3.4. Hence
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}}$
corresponds to a homomorphism
$(h_{\mathfrak{p}})_{\mathfrak{p}}$
corresponds to a homomorphism
![]() $H^{d}(X,{\mathcal{F}})\rightarrow A$
.
$H^{d}(X,{\mathcal{F}})\rightarrow A$
.
2.4 Higher dimensional class field theory (review)
We review higher dimensional local class field theory in [Reference Parshin31], [Reference Kato17], etc. in 2.4.1–2.4.5 and higher dimensional global class field theory in [Reference Kato and Saito23], etc. in 2.4.10–2.4.12 briefly, giving complements 2.4.6–2.4.9 to the relation between local theory and global theory.
We first review the higher dimensional local class field theory.
2.4.1. Recall that the notion
![]() $d$
-dimensional local field is as follows. A 0-dimensional local field is a finite field. For
$d$
-dimensional local field is as follows. A 0-dimensional local field is a finite field. For
![]() $d\geqslant 1$
, a
$d\geqslant 1$
, a
![]() $d$
-dimensional local field is a complete discrete valuation field whose residue field is a
$d$
-dimensional local field is a complete discrete valuation field whose residue field is a
![]() $d-1$
-dimensional local field.
$d-1$
-dimensional local field.
2.4.2. The following remark is used in 2.4.8 later.
To give a
![]() $d$
-dimensional local field
$d$
-dimensional local field
![]() $K$
is equivalent to giving a valuation ring
$K$
is equivalent to giving a valuation ring
![]() $V$
having the following properties (i)–(iii). (i) The residue field of
$V$
having the following properties (i)–(iii). (i) The residue field of
![]() $V$
is a finite field. (ii) The value group of
$V$
is a finite field. (ii) The value group of
![]() $V$
is isomorphic to
$V$
is isomorphic to
![]() $\mathbb{Z}^{d}$
with the lexicographic order. (iii) If
$\mathbb{Z}^{d}$
with the lexicographic order. (iii) If
![]() $P_{0}\supsetneq \cdots \supsetneq P_{d}=(0)$
are all prime ideals of
$P_{0}\supsetneq \cdots \supsetneq P_{d}=(0)$
are all prime ideals of
![]() $V$
, for each
$V$
, for each
![]() $1\leqslant i\leqslant d$
, the local ring of
$1\leqslant i\leqslant d$
, the local ring of
![]() $V/P_{i}$
at the prime ideal
$V/P_{i}$
at the prime ideal
![]() $P_{i-1}/P_{i}$
(which is a discrete valuation ring) is complete.
$P_{i-1}/P_{i}$
(which is a discrete valuation ring) is complete.
In fact,
![]() $K$
is obtained from
$K$
is obtained from
![]() $V$
as the field of fractions of
$V$
as the field of fractions of
![]() $V$
.
$V$
.
![]() $V=V_{K}$
is a subring of
$V=V_{K}$
is a subring of
![]() $K$
defined by induction on
$K$
defined by induction on
![]() $d$
as follows. If
$d$
as follows. If
![]() $d=0$
, then
$d=0$
, then
![]() $V_{K}=K$
. If
$V_{K}=K$
. If
![]() $d\geqslant 1$
,
$d\geqslant 1$
,
![]() $V_{K}$
is the subring of the discrete valuation ring
$V_{K}$
is the subring of the discrete valuation ring
![]() $O_{K}$
consisting of all elements whose images in the residue field
$O_{K}$
consisting of all elements whose images in the residue field
![]() $F$
of
$F$
of
![]() $K$
belong to
$K$
belong to
![]() $V_{F}$
.
$V_{F}$
.
2.4.3. By higher dimensional local field theory (see [Reference Kato17, Reference Parshin31]), for a
![]() $d$
-dimensional local field
$d$
-dimensional local field
![]() $K$
, we have a canonical homomorphism
$K$
, we have a canonical homomorphism
![]() $K_{d}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)$
called the reciprocity map, where
$K_{d}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)$
called the reciprocity map, where
![]() $K^{\text{ab}}$
is the maximal abelian extension of
$K^{\text{ab}}$
is the maximal abelian extension of
![]() $K$
.
$K$
.
2.4.4. For
![]() $n\geqslant 0$
, define the category
$n\geqslant 0$
, define the category
![]() ${\mathcal{F}}_{n}$
inductively as follows.
${\mathcal{F}}_{n}$
inductively as follows.
![]() ${\mathcal{F}}_{0}$
is the category of finite sets. For
${\mathcal{F}}_{0}$
is the category of finite sets. For
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
![]() ${\mathcal{F}}_{n}=\text{ind}(\text{pro}({\mathcal{F}}_{n-1}))$
where
${\mathcal{F}}_{n}=\text{ind}(\text{pro}({\mathcal{F}}_{n-1}))$
where
![]() $\text{pro}(\;)$
is the category of pro-objects and
$\text{pro}(\;)$
is the category of pro-objects and
![]() $\text{ind}(\;)$
is the category of ind-objects. Let
$\text{ind}(\;)$
is the category of ind-objects. Let
![]() ${\mathcal{F}}_{\infty }=\bigcup _{n}{\mathcal{F}}_{n}$
.
${\mathcal{F}}_{\infty }=\bigcup _{n}{\mathcal{F}}_{n}$
.
2.4.5. For a
![]() $d$
-dimensional local field
$d$
-dimensional local field
![]() $K$
, we can regard
$K$
, we can regard
![]() $K$
and
$K$
and
![]() $K^{\times }$
as objects of
$K^{\times }$
as objects of
![]() ${\mathcal{F}}_{\infty }$
(actually of
${\mathcal{F}}_{\infty }$
(actually of
![]() ${\mathcal{F}}_{d}$
) canonically [Reference Kato22, Introduction]. A homomorphism
${\mathcal{F}}_{d}$
) canonically [Reference Kato22, Introduction]. A homomorphism
![]() $K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
is said to be continuous if the composition
$K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
is said to be continuous if the composition
![]() $K^{\times }\times \cdots \times K^{\times }\;(d~\text{times})\overset{\{\;\}}{\rightarrow }K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
is a morphism of
$K^{\times }\times \cdots \times K^{\times }\;(d~\text{times})\overset{\{\;\}}{\rightarrow }K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
is a morphism of
![]() ${\mathcal{F}}_{\infty }$
.
${\mathcal{F}}_{\infty }$
.
A main result of higher dimensional local class field theory formulated in [Reference Kato22, Theorem 2] is the following. Via the reciprocity map in 2.4.3,
![]() $H^{1}(K,\mathbb{Q}/\mathbb{Z})=\text{Hom}_{\text{cont}}(\text{Gal}(K^{\text{ab}}/K),\mathbb{Q}/\mathbb{Z})$
is isomorphic to the group of continuous homomorphisms
$H^{1}(K,\mathbb{Q}/\mathbb{Z})=\text{Hom}_{\text{cont}}(\text{Gal}(K^{\text{ab}}/K),\mathbb{Q}/\mathbb{Z})$
is isomorphic to the group of continuous homomorphisms
![]() $K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
of finite orders.
$K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
of finite orders.
We now consider the global theory. In the higher dimensional global class field theory in [Reference Kato and Saito23], “henselian variants of higher dimensional local fields” (the fields
![]() $K_{v}^{h}$
below) are used. But we use in this paper the higher dimensional local fields
$K_{v}^{h}$
below) are used. But we use in this paper the higher dimensional local fields
![]() $K_{v}$
(see below). We give complements to relate
$K_{v}$
(see below). We give complements to relate
![]() $K_{v}$
to the global class field theory in [Reference Kato and Saito23].
$K_{v}$
to the global class field theory in [Reference Kato and Saito23].
2.4.6. Let
![]() $X$
be an integral scheme of finite type over
$X$
be an integral scheme of finite type over
![]() $\mathbb{Z}$
of dimension
$\mathbb{Z}$
of dimension
![]() $d$
, and let
$d$
, and let
![]() $K$
be the function field of
$K$
be the function field of
![]() $X$
. By a place of
$X$
. By a place of
![]() $K$
along
$K$
along
![]() $X$
, we mean a subring
$X$
, we mean a subring
![]() $v$
of
$v$
of
![]() $K$
satisfying the following conditions (i)–(iii).
$K$
satisfying the following conditions (i)–(iii).
(i)
 $K$
is the field of fractions of
$K$
is the field of fractions of
 $v$
.
$v$
.(ii)
 $v$
is a valuation ring and the value group is isomorphic to
$v$
is a valuation ring and the value group is isomorphic to
 $\mathbb{Z}^{d}$
with the lexicographic order.
$\mathbb{Z}^{d}$
with the lexicographic order.(iii) There is an element
 $\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d}\in P(X)$
such that if
$\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d}\in P(X)$
such that if
 $P_{0}\supsetneq \cdots \supsetneq P_{d}$
denotes the set of all prime ideals of
$P_{0}\supsetneq \cdots \supsetneq P_{d}$
denotes the set of all prime ideals of
 $v$
, then for
$v$
, then for
 $0\leqslant i\leqslant d$
, the local ring of
$0\leqslant i\leqslant d$
, the local ring of
 $v$
at
$v$
at
 $P_{i}$
(which is a valuation ring) dominates
$P_{i}$
(which is a valuation ring) dominates
 $x_{i}$
.
$x_{i}$
.
Let
![]() $Pl(X)$
be the set of all places of
$Pl(X)$
be the set of all places of
![]() $K$
along
$K$
along
![]() $X$
. We have a canonical map
$X$
. We have a canonical map
![]() $Pl(X)\rightarrow P(X)$
which sends
$Pl(X)\rightarrow P(X)$
which sends
![]() $v\in Pl(X)$
to
$v\in Pl(X)$
to
![]() $\mathfrak{p}$
in (iii).
$\mathfrak{p}$
in (iii).
For
![]() $v\in Pl(X)$
, we will define a
$v\in Pl(X)$
, we will define a
![]() $d$
-dimensional local field
$d$
-dimensional local field
![]() $K_{v}\supset K$
called the local field of
$K_{v}\supset K$
called the local field of
![]() $K$
at
$K$
at
![]() $v$
. The class field theory of
$v$
. The class field theory of
![]() $K$
is related to the local class field theory of
$K$
is related to the local class field theory of
![]() $K_{v}$
as is explained below.
$K_{v}$
as is explained below.
2.4.7. To obtain local fields
![]() $K_{v}$
of
$K_{v}$
of
![]() $K$
for
$K$
for
![]() $v\in Pl(X)$
and their henselian versions
$v\in Pl(X)$
and their henselian versions
![]() $K_{v}^{h}$
, we use the following iterated completion and iterated henselization.
$K_{v}^{h}$
, we use the following iterated completion and iterated henselization.
For
![]() $0\leqslant i\leqslant d$
and for a sequence
$0\leqslant i\leqslant d$
and for a sequence
![]() $(x_{0},\ldots ,x_{i})$
of points of
$(x_{0},\ldots ,x_{i})$
of points of
![]() $X$
such that
$X$
such that
![]() $\overline{\{x_{0}\}}\subset \cdots \subset \overline{\{x_{i}\}}$
and such that
$\overline{\{x_{0}\}}\subset \cdots \subset \overline{\{x_{i}\}}$
and such that
![]() $\dim (\overline{\{x_{j}\}})=j$
for
$\dim (\overline{\{x_{j}\}})=j$
for
![]() $0\leqslant j\leqslant i$
, we define the rings
$0\leqslant j\leqslant i$
, we define the rings
![]() $\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{i}}$
and
$\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{i}}$
and
![]() ${\mathcal{O}}_{X,x_{0},\ldots ,x_{i}}^{h}$
over
${\mathcal{O}}_{X,x_{0},\ldots ,x_{i}}^{h}$
over
![]() ${\mathcal{O}}_{X,x_{i}}$
as follows, inductively.
${\mathcal{O}}_{X,x_{i}}$
as follows, inductively.
In the case
![]() $i=0$
,
$i=0$
,
![]() $\hat{{\mathcal{O}}}_{X,x_{0}}$
(resp.
$\hat{{\mathcal{O}}}_{X,x_{0}}$
(resp.
![]() ${\mathcal{O}}_{X,x_{0}}^{h}$
) is the completion (resp. henselization) of
${\mathcal{O}}_{X,x_{0}}^{h}$
) is the completion (resp. henselization) of
![]() ${\mathcal{O}}_{X,x_{0}}$
.
${\mathcal{O}}_{X,x_{0}}$
.
For
![]() $i\geqslant 1$
, let
$i\geqslant 1$
, let
where
![]() $P$
ranges over all prime ideals of
$P$
ranges over all prime ideals of
![]() $\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{i-1}}$
(resp.
$\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{i-1}}$
(resp.
![]() ${\mathcal{O}}_{X,x_{0},\ldots ,x_{i-1}}^{h}$
) lying over the prime ideal of
${\mathcal{O}}_{X,x_{0},\ldots ,x_{i-1}}^{h}$
) lying over the prime ideal of
![]() ${\mathcal{O}}_{X,x_{i-1}}$
corresponding to
${\mathcal{O}}_{X,x_{i-1}}$
corresponding to
![]() $x_{i}$
, and
$x_{i}$
, and
![]() $(\;)_{P}^{\wedge }$
(resp.
$(\;)_{P}^{\wedge }$
(resp.
![]() $(\;)_{P}^{h}$
) denotes the completion (resp. henselization) of the local ring
$(\;)_{P}^{h}$
) denotes the completion (resp. henselization) of the local ring
![]() $(\;)_{P}$
of the ring
$(\;)_{P}$
of the ring
![]() $(\;)$
at
$(\;)$
at
![]() $P$
. By induction on
$P$
. By induction on
![]() $i$
, we see that the set of such
$i$
, we see that the set of such
![]() $P$
is a nonempty finite set and that
$P$
is a nonempty finite set and that
![]() $\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{i}}$
and
$\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{i}}$
and
![]() ${\mathcal{O}}_{X,x_{0},\ldots ,x_{i}}^{h}$
are finite products of complete (resp. henselian) local integral domains of dimension
${\mathcal{O}}_{X,x_{0},\ldots ,x_{i}}^{h}$
are finite products of complete (resp. henselian) local integral domains of dimension
![]() $d-i$
.
$d-i$
.
For
![]() $\mathfrak{p}=(x_{i})_{i}\in P(X)$
, let
$\mathfrak{p}=(x_{i})_{i}\in P(X)$
, let
Then
![]() $K_{\mathfrak{p}}$
and
$K_{\mathfrak{p}}$
and
![]() $K_{\mathfrak{p}}^{h}$
are finite products of fields.
$K_{\mathfrak{p}}^{h}$
are finite products of fields.
2.4.8. Let
![]() $X$
and
$X$
and
![]() $K$
be as above. The following statements are proved in 2.4.9 by induction on
$K$
be as above. The following statements are proved in 2.4.9 by induction on
![]() $d$
.
$d$
.
(1) Let
 $\mathfrak{p}\in P(X)$
, and let
$\mathfrak{p}\in P(X)$
, and let
 $Pl(\mathfrak{p})=Pl(X,\mathfrak{p})$
be the inverse image of
$Pl(\mathfrak{p})=Pl(X,\mathfrak{p})$
be the inverse image of
 $\mathfrak{p}$
in
$\mathfrak{p}$
in
 $Pl(X)$
. Then each field factor of
$Pl(X)$
. Then each field factor of
 $K_{\mathfrak{p}}$
has canonically a structure of a
$K_{\mathfrak{p}}$
has canonically a structure of a
 $d$
-dimensional local field. We have a bijection
$d$
-dimensional local field. We have a bijection
 $\text{Spec}(K_{\mathfrak{p}})\rightarrow Pl(\mathfrak{p})$
which sends the point of
$\text{Spec}(K_{\mathfrak{p}})\rightarrow Pl(\mathfrak{p})$
which sends the point of
 $\text{Spec}(K_{\mathfrak{p}})$
corresponding to a field factor
$\text{Spec}(K_{\mathfrak{p}})$
corresponding to a field factor
 $L$
of
$L$
of
 $K_{\mathfrak{p}}$
to the valuation ring
$K_{\mathfrak{p}}$
to the valuation ring
 $V_{L}\cap K$
, where
$V_{L}\cap K$
, where
 $V_{L}\subset L$
is the valuation ring of rank
$V_{L}\subset L$
is the valuation ring of rank
 $d$
associated to
$d$
associated to
 $L$
by 2.4.2. In particular, the set
$L$
by 2.4.2. In particular, the set
 $Pl(\mathfrak{p})$
is a nonempty finite set.
$Pl(\mathfrak{p})$
is a nonempty finite set.(2) Let
 $\mathfrak{p}\in P(X)$
. Then the map
$\mathfrak{p}\in P(X)$
. Then the map
 $\text{Spec}(K_{\mathfrak{p}})\rightarrow \text{Spec}(K_{\mathfrak{p}}^{h})$
induced by the inclusion map
$\text{Spec}(K_{\mathfrak{p}})\rightarrow \text{Spec}(K_{\mathfrak{p}}^{h})$
induced by the inclusion map
 $K_{\mathfrak{p}}^{h}\rightarrow K_{\mathfrak{p}}$
is bijective.
$K_{\mathfrak{p}}^{h}\rightarrow K_{\mathfrak{p}}$
is bijective.(3) Let
 $X^{\prime }\rightarrow X$
be a finite surjective morphism of integral schemes of finite type over
$X^{\prime }\rightarrow X$
be a finite surjective morphism of integral schemes of finite type over
 $\mathbb{Z}$
and let
$\mathbb{Z}$
and let
 $K^{\prime }$
be the function field of
$K^{\prime }$
be the function field of
 $X^{\prime }$
. Then we have canonical isomorphisms where
$X^{\prime }$
. Then we have canonical isomorphisms where $$\begin{eqnarray}K^{\prime }\otimes _{K}K_{v}=\mathop{\prod }_{v^{\prime }|v}K_{v^{\prime }}^{\prime },\quad K^{\prime }\otimes _{K}K_{v}^{h}=\mathop{\prod }_{v^{\prime }}(K^{\prime })_{v^{\prime }}^{h}\end{eqnarray}$$
$$\begin{eqnarray}K^{\prime }\otimes _{K}K_{v}=\mathop{\prod }_{v^{\prime }|v}K_{v^{\prime }}^{\prime },\quad K^{\prime }\otimes _{K}K_{v}^{h}=\mathop{\prod }_{v^{\prime }}(K^{\prime })_{v^{\prime }}^{h}\end{eqnarray}$$
 $v^{\prime }|v$
means that
$v^{\prime }|v$
means that
 $v^{\prime }$
ranges over all elements of
$v^{\prime }$
ranges over all elements of
 $Pl(X^{\prime })$
such that
$Pl(X^{\prime })$
such that
 $v^{\prime }\cap K=v$
.
$v^{\prime }\cap K=v$
.
2.4.9. We prove statements in 2.4.8 by induction on
![]() $d$
.
$d$
.
We prove (1). Let
![]() $\mathfrak{p}=(x_{i})_{i}\in P(X)$
, and let
$\mathfrak{p}=(x_{i})_{i}\in P(X)$
, and let
![]() $Y\subset X$
be the closure of
$Y\subset X$
be the closure of
![]() $x_{d-1}$
in
$x_{d-1}$
in
![]() $X$
with the reduced scheme structure. Let
$X$
with the reduced scheme structure. Let
![]() $\mathfrak{q}=(x_{0},\ldots ,x_{d-1})\in P(Y)$
. Let
$\mathfrak{q}=(x_{0},\ldots ,x_{d-1})\in P(Y)$
. Let
![]() $F$
be the residue field of
$F$
be the residue field of
![]() $x_{d-1}$
, that is, the function field of
$x_{d-1}$
, that is, the function field of
![]() $Y$
. Let
$Y$
. Let
![]() $A$
be the normalization of
$A$
be the normalization of
![]() ${\mathcal{O}}_{X,x_{d-1}}$
and let
${\mathcal{O}}_{X,x_{d-1}}$
and let
![]() $\unicode[STIX]{x1D6E5}$
be the set of all maximal ideals of
$\unicode[STIX]{x1D6E5}$
be the set of all maximal ideals of
![]() $A$
. Then
$A$
. Then
![]() $\unicode[STIX]{x1D6E5}$
is finite. For
$\unicode[STIX]{x1D6E5}$
is finite. For
![]() $z\in \unicode[STIX]{x1D6E5}$
, let
$z\in \unicode[STIX]{x1D6E5}$
, let
![]() $\unicode[STIX]{x1D705}(z)$
be the residue field of
$\unicode[STIX]{x1D705}(z)$
be the residue field of
![]() $z$
which is a finite extension of
$z$
which is a finite extension of
![]() $F$
, let
$F$
, let
![]() $Y(z)$
be the integral closure of
$Y(z)$
be the integral closure of
![]() $Y$
in
$Y$
in
![]() $\unicode[STIX]{x1D705}(z)$
and let
$\unicode[STIX]{x1D705}(z)$
and let
![]() $Pl(Y(z),\mathfrak{q})\subset Pl(Y(z))$
be the inverse image of
$Pl(Y(z),\mathfrak{q})\subset Pl(Y(z))$
be the inverse image of
![]() $\mathfrak{q}$
under the map
$\mathfrak{q}$
under the map
![]() $Pl(Y(z))\rightarrow P(Y)$
. Then we have a bijection
$Pl(Y(z))\rightarrow P(Y)$
. Then we have a bijection
![]() $\coprod _{z\in \unicode[STIX]{x1D6E5}}Pl(Y(z),\mathfrak{q})\rightarrow Pl(\mathfrak{p})$
which sends
$\coprod _{z\in \unicode[STIX]{x1D6E5}}Pl(Y(z),\mathfrak{q})\rightarrow Pl(\mathfrak{p})$
which sends
![]() $w\in Pl(Y(z),\mathfrak{q})$
with
$w\in Pl(Y(z),\mathfrak{q})$
with
![]() $z\in \unicode[STIX]{x1D6E5}$
to the valuation ring consisting of all elements of the local ring of
$z\in \unicode[STIX]{x1D6E5}$
to the valuation ring consisting of all elements of the local ring of
![]() $A$
at
$A$
at
![]() $z$
whose residue classes in
$z$
whose residue classes in
![]() $\unicode[STIX]{x1D705}(z)$
belong to
$\unicode[STIX]{x1D705}(z)$
belong to
![]() $w$
. The ring
$w$
. The ring
![]() $A$
is Noetherian normal one-dimensional semilocal integral domain, and hence is a principal ideal domain. Let
$A$
is Noetherian normal one-dimensional semilocal integral domain, and hence is a principal ideal domain. Let
![]() $t$
be a generator of the intersection of all maximal ideals of
$t$
be a generator of the intersection of all maximal ideals of
![]() $A$
. Let
$A$
. Let
![]() $B=\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{d-1}}$
and let
$B=\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{d-1}}$
and let
![]() $C=A\otimes _{{\mathcal{O}}_{X,x_{d-1}}}B$
. Then
$C=A\otimes _{{\mathcal{O}}_{X,x_{d-1}}}B$
. Then
![]() $C$
is a finite product of one-dimensional local integral domains,
$C$
is a finite product of one-dimensional local integral domains,
![]() $C/tC=(\prod _{z\in \unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D705}(z))\otimes _{F}B/\mathfrak{m}B$
where
$C/tC=(\prod _{z\in \unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D705}(z))\otimes _{F}B/\mathfrak{m}B$
where
![]() $\mathfrak{m}$
is the maximal ideal of
$\mathfrak{m}$
is the maximal ideal of
![]() ${\mathcal{O}}_{X,x_{d-1}}$
, and
${\mathcal{O}}_{X,x_{d-1}}$
, and
![]() $B/\mathfrak{m}B=\hat{{\mathcal{O}}}_{Y,x_{0},\ldots ,x_{d-1}}=\prod _{\unicode[STIX]{x1D706}\in Pl(\mathfrak{q})}F_{\unicode[STIX]{x1D706}}$
where the last
$B/\mathfrak{m}B=\hat{{\mathcal{O}}}_{Y,x_{0},\ldots ,x_{d-1}}=\prod _{\unicode[STIX]{x1D706}\in Pl(\mathfrak{q})}F_{\unicode[STIX]{x1D706}}$
where the last
![]() $=$
is by the statement 1 for dimension
$=$
is by the statement 1 for dimension
![]() $d-1$
. Hence
$d-1$
. Hence
![]() $\unicode[STIX]{x1D705}(z)\otimes _{F}B/\mathfrak{m}B=\unicode[STIX]{x1D705}(z)\otimes _{F}\prod _{\unicode[STIX]{x1D706}\in Pl(\mathfrak{q})}F_{\unicode[STIX]{x1D706}}=\prod _{w\in Pl(Y(z),\mathfrak{q})}\unicode[STIX]{x1D705}(z)_{w}$
by the statement (3) for dimension
$\unicode[STIX]{x1D705}(z)\otimes _{F}B/\mathfrak{m}B=\unicode[STIX]{x1D705}(z)\otimes _{F}\prod _{\unicode[STIX]{x1D706}\in Pl(\mathfrak{q})}F_{\unicode[STIX]{x1D706}}=\prod _{w\in Pl(Y(z),\mathfrak{q})}\unicode[STIX]{x1D705}(z)_{w}$
by the statement (3) for dimension
![]() $d-1$
. This shows that
$d-1$
. This shows that
![]() $\text{Spec}(K_{\mathfrak{p}})$
is identified with
$\text{Spec}(K_{\mathfrak{p}})$
is identified with
![]() $\coprod _{z\in \unicode[STIX]{x1D6E5}}Pl(Y(z),\mathfrak{q})$
. Hence
$\coprod _{z\in \unicode[STIX]{x1D6E5}}Pl(Y(z),\mathfrak{q})$
. Hence
![]() $\text{Spec}(K_{\mathfrak{p}})$
is identified with
$\text{Spec}(K_{\mathfrak{p}})$
is identified with
![]() $Pl(\mathfrak{p})$
, and for
$Pl(\mathfrak{p})$
, and for
![]() $v\in Pl(\mathfrak{p})$
corresponding to
$v\in Pl(\mathfrak{p})$
corresponding to
![]() $w\in Pl(Y(z),\mathfrak{q})$
,
$w\in Pl(Y(z),\mathfrak{q})$
,
![]() $K_{v}$
is the field of fractions of a complete discrete valuation ring whose residue field is
$K_{v}$
is the field of fractions of a complete discrete valuation ring whose residue field is
![]() $\unicode[STIX]{x1D705}(z)_{w}$
. This proves (1).
$\unicode[STIX]{x1D705}(z)_{w}$
. This proves (1).
We prove (2). Replacing the iterated completion in the above arguments by the iterated henselization, and by using the induction on
![]() $d$
, we obtain similarly a bijection between
$d$
, we obtain similarly a bijection between
![]() $\text{Spec}(K_{\mathfrak{p}}^{h})$
and
$\text{Spec}(K_{\mathfrak{p}}^{h})$
and
![]() $Pl(\mathfrak{p})$
. This shows that the map
$Pl(\mathfrak{p})$
. This shows that the map
![]() $\text{Spec}(K_{\mathfrak{p}})\rightarrow \text{Spec}(K_{\mathfrak{p}}^{h})$
is bijective.
$\text{Spec}(K_{\mathfrak{p}})\rightarrow \text{Spec}(K_{\mathfrak{p}}^{h})$
is bijective.
We prove (3) for
![]() $K_{v}$
. Let
$K_{v}$
. Let
![]() $f$
be the morphism
$f$
be the morphism
![]() $X^{\prime }\rightarrow X$
. By induction on
$X^{\prime }\rightarrow X$
. By induction on
![]() $i$
, we have that
$i$
, we have that
![]() $(f_{\ast }{\mathcal{O}}_{X^{\prime }})_{x_{i}}\otimes _{{\mathcal{O}}_{X,x_{d-1}}}\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{i}}\overset{\cong }{\rightarrow }\prod _{x_{0}^{\prime },\ldots ,x_{i}^{\prime }}\hat{{\mathcal{O}}}_{X^{\prime },x_{0}^{\prime },\ldots ,x_{i}^{\prime }}$
where
$(f_{\ast }{\mathcal{O}}_{X^{\prime }})_{x_{i}}\otimes _{{\mathcal{O}}_{X,x_{d-1}}}\hat{{\mathcal{O}}}_{X,x_{0},\ldots ,x_{i}}\overset{\cong }{\rightarrow }\prod _{x_{0}^{\prime },\ldots ,x_{i}^{\prime }}\hat{{\mathcal{O}}}_{X^{\prime },x_{0}^{\prime },\ldots ,x_{i}^{\prime }}$
where
![]() $(x_{0}^{\prime },\ldots ,x_{i}^{\prime })$
ranges over all sequences of points of
$(x_{0}^{\prime },\ldots ,x_{i}^{\prime })$
ranges over all sequences of points of
![]() $X^{\prime }$
such that
$X^{\prime }$
such that
![]() $x_{j}^{\prime }$
lies over
$x_{j}^{\prime }$
lies over
![]() $x_{j}$
for
$x_{j}$
for
![]() $0\leqslant j\leqslant i$
and such that
$0\leqslant j\leqslant i$
and such that
![]() $\overline{\{x_{0}^{\prime }\}}\subset \cdots \subset \overline{\{x_{i}^{\prime }\}}$
. The case
$\overline{\{x_{0}^{\prime }\}}\subset \cdots \subset \overline{\{x_{i}^{\prime }\}}$
. The case
![]() $i=d$
gives an isomorphism
$i=d$
gives an isomorphism
![]() $K^{\prime }\otimes _{K}K_{\mathfrak{p}}\overset{\cong }{\rightarrow }\prod _{\mathfrak{p}^{\prime }}K_{\mathfrak{p}^{\prime }}^{\prime }$
where
$K^{\prime }\otimes _{K}K_{\mathfrak{p}}\overset{\cong }{\rightarrow }\prod _{\mathfrak{p}^{\prime }}K_{\mathfrak{p}^{\prime }}^{\prime }$
where
![]() $\mathfrak{p}^{\prime }$
ranges over all elements of
$\mathfrak{p}^{\prime }$
ranges over all elements of
![]() $P(X^{\prime })$
lying over
$P(X^{\prime })$
lying over
![]() $\mathfrak{p}$
. By looking at the
$\mathfrak{p}$
. By looking at the
![]() $v$
-factor of this isomorphism, we have (3) for
$v$
-factor of this isomorphism, we have (3) for
![]() $K_{v}$
.
$K_{v}$
.
The proof of (3) for
![]() $K_{v}^{h}$
is similar to that for
$K_{v}^{h}$
is similar to that for
![]() $K_{v}$
.
$K_{v}$
.
2.4.10. In 2.4.10–2.4.12, let
![]() $X$
be a proper normal integral scheme over
$X$
be a proper normal integral scheme over
![]() $\mathbb{Z}$
and let
$\mathbb{Z}$
and let
![]() $K$
be the function field of
$K$
be the function field of
![]() $X$
. We assume
$X$
. We assume
![]() $X(\mathbb{R})=\emptyset$
.
$X(\mathbb{R})=\emptyset$
.
The following is what we use in this paper from the higher dimensional global class field theory.
We have a unique continuous homomorphism
called the reciprocity map, where
![]() $I$
ranges over all nonzero coherent ideals of
$I$
ranges over all nonzero coherent ideals of
![]() ${\mathcal{O}}_{X}$
,
${\mathcal{O}}_{X}$
,
![]() $K_{d}^{M}({\mathcal{O}}_{X},I)$
denotes the kernel of
$K_{d}^{M}({\mathcal{O}}_{X},I)$
denotes the kernel of
![]() $K_{d}^{M}({\mathcal{O}}_{X})\rightarrow K_{d}^{M}({\mathcal{O}}_{X}/I)$
with
$K_{d}^{M}({\mathcal{O}}_{X})\rightarrow K_{d}^{M}({\mathcal{O}}_{X}/I)$
with
![]() $K_{d}^{M}$
the sheaf of
$K_{d}^{M}$
the sheaf of
![]() $d$
th Milnor
$d$
th Milnor
![]() $K$
-groups, the cohomology groups are the Zariski cohomology groups, and the left hand side is regarded as a topological space for the projective limit of the discrete topologies of
$K$
-groups, the cohomology groups are the Zariski cohomology groups, and the left hand side is regarded as a topological space for the projective limit of the discrete topologies of
![]() $H^{d}(X,K_{d}^{M}({\mathcal{O}}_{X},I))$
, which is characterized by the following property. For
$H^{d}(X,K_{d}^{M}({\mathcal{O}}_{X},I))$
, which is characterized by the following property. For
![]() $\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}/\mathbb{Z})=\text{Hom}_{\text{cont}}(\text{Gal}(K^{\text{ab}}/K),\mathbb{Q}/\mathbb{Z})$
, the homomorphism
$\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}/\mathbb{Z})=\text{Hom}_{\text{cont}}(\text{Gal}(K^{\text{ab}}/K),\mathbb{Q}/\mathbb{Z})$
, the homomorphism
induced by
![]() $\unicode[STIX]{x1D712}$
for some
$\unicode[STIX]{x1D712}$
for some
![]() $I$
corresponds to
$I$
corresponds to
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}\in P(X)}$
via 2.3.4 where
$(h_{\mathfrak{p}})_{\mathfrak{p}\in P(X)}$
via 2.3.4 where
![]() $h_{\mathfrak{p}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
is the composition
$h_{\mathfrak{p}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
is the composition
where
![]() $Pl(\mathfrak{p})$
is as in 2.4.8, the first arrow is the diagonal map, and the map
$Pl(\mathfrak{p})$
is as in 2.4.8, the first arrow is the diagonal map, and the map
![]() $K_{d}^{M}(K_{v})\rightarrow \mathbb{Q}/\mathbb{Z}$
is induced by the image of
$K_{d}^{M}(K_{v})\rightarrow \mathbb{Q}/\mathbb{Z}$
is induced by the image of
![]() $\unicode[STIX]{x1D712}$
in
$\unicode[STIX]{x1D712}$
in
![]() $H^{1}(K_{v},\mathbb{Q}/\mathbb{Z})$
and by the
$H^{1}(K_{v},\mathbb{Q}/\mathbb{Z})$
and by the
![]() $d$
-dimensional local class field theory of
$d$
-dimensional local class field theory of
![]() $K_{v}$
.
$K_{v}$
.
2.4.11. In [Reference Kato and Saito23], a continuous map
called the reciprocity map is defined, where the cohomology groups are Nisnevich cohomology, instead of Zariski cohomology, and the left hand side is endowed with the topology of the projective limit of the discrete sets.
The map (9) is induced from the map (10) and the canonical map
![]() $H^{d}(X,K_{d}^{M}({\mathcal{O}}_{X},I))\rightarrow H^{d}(X_{\text{Nis}},K_{d}^{M}({\mathcal{O}}_{X},I))$
.
$H^{d}(X,K_{d}^{M}({\mathcal{O}}_{X},I))\rightarrow H^{d}(X_{\text{Nis}},K_{d}^{M}({\mathcal{O}}_{X},I))$
.
In fact, by the definition of the reciprocity map (10) in [Reference Kato and Saito23], for
![]() $\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}/\mathbb{Z})$
, the induced homomorphism (9) corresponds to
$\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}/\mathbb{Z})$
, the induced homomorphism (9) corresponds to
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}\in P(X)}$
where
$(h_{\mathfrak{p}})_{\mathfrak{p}\in P(X)}$
where
![]() $h_{\mathfrak{p}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
is the composition
$h_{\mathfrak{p}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
is the composition
![]() $K_{d}^{M}(K)\rightarrow \bigoplus _{v\in Pl(\mathfrak{p})}K_{d}^{M}(K_{v}^{h})$
$K_{d}^{M}(K)\rightarrow \bigoplus _{v\in Pl(\mathfrak{p})}K_{d}^{M}(K_{v}^{h})$
![]() $\overset{\unicode[STIX]{x1D712}}{\rightarrow }\mathbb{Q}/\mathbb{Z}$
with
$\overset{\unicode[STIX]{x1D712}}{\rightarrow }\mathbb{Q}/\mathbb{Z}$
with
![]() $K_{d}^{M}(K_{v}^{h})\rightarrow \mathbb{Q}/\mathbb{Z}$
a homomorphism defined in [Reference Kato and Saito23]. This last homomorphism coincides with the composition
$K_{d}^{M}(K_{v}^{h})\rightarrow \mathbb{Q}/\mathbb{Z}$
a homomorphism defined in [Reference Kato and Saito23]. This last homomorphism coincides with the composition
![]() $K_{d}^{M}(K_{v}^{h})\rightarrow K_{d}^{M}(K_{v})\rightarrow \mathbb{Q}/\mathbb{Z}$
where the last map is that in 2.4.10.
$K_{d}^{M}(K_{v}^{h})\rightarrow K_{d}^{M}(K_{v})\rightarrow \mathbb{Q}/\mathbb{Z}$
where the last map is that in 2.4.10.
2.4.12. The main result of [Reference Kato and Saito23] concerning the class field theory of
![]() $K$
is as follows. (In [Reference Kato and Saito23], we do not need to assume
$K$
is as follows. (In [Reference Kato and Saito23], we do not need to assume
![]() $X(\mathbb{R})=\emptyset$
, but if we do not assuming
$X(\mathbb{R})=\emptyset$
, but if we do not assuming
![]() $X(\mathbb{R})=\emptyset$
, the left hand side of (10) should be modified by adding archimedean objects to have results below.)
$X(\mathbb{R})=\emptyset$
, the left hand side of (10) should be modified by adding archimedean objects to have results below.)
In the case
![]() $K$
is of characteristic 0, the map (10) is an isomorphism of topological groups.
$K$
is of characteristic 0, the map (10) is an isomorphism of topological groups.
In the case
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p>0$
, the map (10) induces an isomorphism of topological groups from the left hand side of (10) to the fiber product of
$p>0$
, the map (10) induces an isomorphism of topological groups from the left hand side of (10) to the fiber product of
![]() $\text{Gal}(K^{\text{ab}}/K)\rightarrow \text{Gal}(\mathbb{F}_{p}^{\text{ab}}/\mathbb{F}_{p})\leftarrow \mathbb{Z}$
, where
$\text{Gal}(K^{\text{ab}}/K)\rightarrow \text{Gal}(\mathbb{F}_{p}^{\text{ab}}/\mathbb{F}_{p})\leftarrow \mathbb{Z}$
, where
![]() $\mathbb{Z}$
is discrete and the right arrow sends
$\mathbb{Z}$
is discrete and the right arrow sends
![]() $1\in \mathbb{Z}$
to the Frobenius
$1\in \mathbb{Z}$
to the Frobenius
![]() $\mathbb{F}_{p}^{\text{ab}}\rightarrow \mathbb{F}_{p}^{\text{ab}}\;;\;x\mapsto x^{p}$
.
$\mathbb{F}_{p}^{\text{ab}}\rightarrow \mathbb{F}_{p}^{\text{ab}}\;;\;x\mapsto x^{p}$
.
By Raskind [Reference Raskind32] and Kerz and Saito [Reference Kerz and Saito26], these results on the class field theory of
![]() $K$
hold also for Zariski cohomology
$K$
hold also for Zariski cohomology
![]() $\mathop{\varprojlim }\nolimits_{I}H^{d}(X,K_{d}^{m}({\mathcal{O}}_{X},I))$
(replacing Nisnevich cohomology) if
$\mathop{\varprojlim }\nolimits_{I}H^{d}(X,K_{d}^{m}({\mathcal{O}}_{X},I))$
(replacing Nisnevich cohomology) if
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $\neq 2$
.
$\neq 2$
.
2.4.13. There is another formulation of higher dimensional class field theory due to Wiesend [Reference Wiesend34] which was studied more in [Reference Kerz and Saito26]. But we do not use it in this paper.
Remark 2.4.14. The first author would like to take this opportunity to express that the both authors of [Reference Kato and Saito23] regret that Nisnevich topology is called henselian topology in [Reference Kato and Saito23] due to their ignorance of the preceding works of Nisnevich.
3 Refined Swan conductors mod
 $p$
$p$
3.1 The subject
3.1.1. Let
![]() $K$
be a complete discrete valuation field with residue field
$K$
be a complete discrete valuation field with residue field
![]() $F$
, and assume
$F$
, and assume
![]() $F$
is of characteristic
$F$
is of characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $n\geqslant 1$
and let
$n\geqslant 1$
and let
![]() $m=\max (n-e_{K},[n/p])$
.
$m=\max (n-e_{K},[n/p])$
.
We define a homomorphism
which we call the refined Swan conductor modulo
![]() $p$
.
$p$
.
3.1.2. The homomorphism
![]() $\text{Rsw}$
in 3.1.1 is characterized by the following properties (i) and (ii).
$\text{Rsw}$
in 3.1.1 is characterized by the following properties (i) and (ii).
(i)
 $\text{Rsw}$
is compatible with any homomorphisms of cdvf. That is, the following diagram is commutative for an extension of complete discrete valuation fields
$\text{Rsw}$
is compatible with any homomorphisms of cdvf. That is, the following diagram is commutative for an extension of complete discrete valuation fields
 $K^{\prime }/K$
, where
$K^{\prime }/K$
, where
 $n^{\prime }=e(K^{\prime }/K)n$
with
$n^{\prime }=e(K^{\prime }/K)n$
with
 $e(K^{\prime }/K)$
the ramification index of the extension
$e(K^{\prime }/K)$
the ramification index of the extension
 $K^{\prime }/K$
and
$K^{\prime }/K$
and
 $m^{\prime }=\max (n^{\prime }-e_{K^{\prime }},[n^{\prime }/p])$
. (The fact
$m^{\prime }=\max (n^{\prime }-e_{K^{\prime }},[n^{\prime }/p])$
. (The fact $$\begin{eqnarray}\begin{array}{@{}ccc@{}}F_{n}H^{1}(K,\mathbb{Q}/\mathbb{Z}) & \rightarrow & \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\\ \downarrow & & \downarrow \\ F_{n^{\prime }}H^{1}(K^{\prime },\mathbb{Q}/\mathbb{Z}) & \rightarrow & \mathfrak{m}_{K^{\prime }}^{-n^{\prime }}/\mathfrak{m}_{K^{\prime }}^{-m^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{1}(\log )\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}F_{n}H^{1}(K,\mathbb{Q}/\mathbb{Z}) & \rightarrow & \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\\ \downarrow & & \downarrow \\ F_{n^{\prime }}H^{1}(K^{\prime },\mathbb{Q}/\mathbb{Z}) & \rightarrow & \mathfrak{m}_{K^{\prime }}^{-n^{\prime }}/\mathfrak{m}_{K^{\prime }}^{-m^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{1}(\log )\end{array}\end{eqnarray}$$
 $F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is sent to
$F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is sent to
 $F_{n^{\prime }}H^{1}(K^{\prime },\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is proved in [Reference Kato20].)
$F_{n^{\prime }}H^{1}(K^{\prime },\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is proved in [Reference Kato20].)(ii) If
 $F$
is an
$F$
is an
 $r$
-dimensional local field (
$r$
-dimensional local field (
 $r\geqslant 0$
), Rsw is characterized by the property for
$r\geqslant 0$
), Rsw is characterized by the property for $$\begin{eqnarray}\unicode[STIX]{x1D712}(E(\unicode[STIX]{x1D6FC}))=\text{Res}_{F}(R_{b}(\unicode[STIX]{x1D6FC}\wedge \text{Rsw}(\unicode[STIX]{x1D712})))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(E(\unicode[STIX]{x1D6FC}))=\text{Res}_{F}(R_{b}(\unicode[STIX]{x1D6FC}\wedge \text{Rsw}(\unicode[STIX]{x1D712})))\end{eqnarray}$$
 $\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
,
$\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
,
 $\unicode[STIX]{x1D6FC}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )$
. Here
$\unicode[STIX]{x1D6FC}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )$
. Here
 $E(\unicode[STIX]{x1D6FC})$
denotes the image of
$E(\unicode[STIX]{x1D6FC})$
denotes the image of
 $\unicode[STIX]{x1D6FC}$
under the truncated exponential map
$\unicode[STIX]{x1D6FC}$
under the truncated exponential map  $$\begin{eqnarray}\mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )\rightarrow U^{m+1}K_{r+1}^{M}(K)/U^{n+1}K_{r+1}^{M}(K),\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )\rightarrow U^{m+1}K_{r+1}^{M}(K)/U^{n+1}K_{r+1}^{M}(K),\end{eqnarray}$$
 $\unicode[STIX]{x1D712}(E(\unicode[STIX]{x1D6FC}))$
denotes the image of
$\unicode[STIX]{x1D712}(E(\unicode[STIX]{x1D6FC}))$
denotes the image of
 $E(\unicode[STIX]{x1D6FC})$
under the composition
$E(\unicode[STIX]{x1D6FC})$
under the composition
 $K_{r+1}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)\overset{\unicode[STIX]{x1D712}}{\rightarrow }\mathbb{Q}_{p}/\mathbb{Z}_{p}$
of the reciprocity map of the
$K_{r+1}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)\overset{\unicode[STIX]{x1D712}}{\rightarrow }\mathbb{Q}_{p}/\mathbb{Z}_{p}$
of the reciprocity map of the
 $r+1$
-dimensional local field
$r+1$
-dimensional local field
 $K$
and
$K$
and
 $\unicode[STIX]{x1D712}$
, which kills
$\unicode[STIX]{x1D712}$
, which kills
 $U^{n+1}K_{r+1}^{M}(K)$
by the condition
$U^{n+1}K_{r+1}^{M}(K)$
by the condition
 $\text{Sw}(\unicode[STIX]{x1D712})\leqslant n$
, and is the residue map (3.3.2). Note that
$\text{Sw}(\unicode[STIX]{x1D712})\leqslant n$
, and is the residue map (3.3.2). Note that $$\begin{eqnarray}\text{Res}_{F}:\unicode[STIX]{x1D6FA}_{F}^{r}\rightarrow \mathbb{F}_{p}\end{eqnarray}$$
$$\begin{eqnarray}\text{Res}_{F}:\unicode[STIX]{x1D6FA}_{F}^{r}\rightarrow \mathbb{F}_{p}\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}\wedge \text{Rsw}(\unicode[STIX]{x1D712})\in \mathfrak{m}_{K}^{m+1-n}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )$
and
$\unicode[STIX]{x1D6FC}\wedge \text{Rsw}(\unicode[STIX]{x1D712})\in \mathfrak{m}_{K}^{m+1-n}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r+1}(\log )$
and
 $n-m\leqslant e_{K}$
and hence its
$n-m\leqslant e_{K}$
and hence its
 $R_{b}$
is defined in
$R_{b}$
is defined in
 $\unicode[STIX]{x1D6FA}_{F}^{r}$
.
$\unicode[STIX]{x1D6FA}_{F}^{r}$
.
3.1.3. If
![]() $\text{char}(K)=p>0$
,
$\text{char}(K)=p>0$
,
is the homomorphism of Matsuda [Reference Matsuda30, Remark 3.2.2] and Borger [Reference Borger6, 3.6] defined by using Artin–Schreier–Witt theory. It was studied in [Reference Leal29, Section 2]. See Sections 3.2 and 3.5.9.
In the mixed characteristic case, we will construct
![]() $\text{Rsw}$
using higher dimensional local class field theory (Section 3.3) and also higher dimensional global class field theory (Section 3.4).
$\text{Rsw}$
using higher dimensional local class field theory (Section 3.3) and also higher dimensional global class field theory (Section 3.4).
3.1.4. It may seem strange that we use higher dimensional global class field theory for the local subject
![]() $\text{Rsw}$
. Our idea is that since any field is a union of finitely generated fields over a prime field and since each finitely generated field over a prime field has class field theory, any subject about one-dimensional Galois representations of any field can be studied by using higher dimensional global class field theory. Our method in 3.5.6 to define
$\text{Rsw}$
. Our idea is that since any field is a union of finitely generated fields over a prime field and since each finitely generated field over a prime field has class field theory, any subject about one-dimensional Galois representations of any field can be studied by using higher dimensional global class field theory. Our method in 3.5.6 to define
![]() $\text{Rsw}$
actually follows this idea.
$\text{Rsw}$
actually follows this idea.
A purely local method for the local subject
![]() $\text{Rsw}$
exists also in the mixed characteristic case as in 3.1.5.
$\text{Rsw}$
exists also in the mixed characteristic case as in 3.1.5.
3.1.5. In the case
![]() $F$
is perfect, our homomorphism Rsw can be defined also by using the local class field theory of Serre [Reference Serre33] and Hazewinkel [Reference Hazewinkel14].
$F$
is perfect, our homomorphism Rsw can be defined also by using the local class field theory of Serre [Reference Serre33] and Hazewinkel [Reference Hazewinkel14].
In the case
![]() $[F:F^{p}]=p^{r}<\infty$
, Rsw can be also defined by using the duality theory [Reference Kato and Suzuki25] which is a generalization of the local class field theory of Serre [Reference Serre33] and Hazewinkel [Reference Hazewinkel14] to the case
$[F:F^{p}]=p^{r}<\infty$
, Rsw can be also defined by using the duality theory [Reference Kato and Suzuki25] which is a generalization of the local class field theory of Serre [Reference Serre33] and Hazewinkel [Reference Hazewinkel14] to the case
![]() $[F:F^{p}]=p^{r}$
.
$[F:F^{p}]=p^{r}$
.
These things will be explained elsewhere.
3.1.6. The authors wonder whether Rsw in general can be obtained by the reduction to the perfect residue field case using the local class field theory of Serre [Reference Serre33] and Hazewinkel [Reference Hazewinkel14] and the work [Reference Borger5] of Borger.
3.1.7. The authors wonder whether our refined Swan conductor mod
![]() $p$
can be obtained from the relation of
$p$
can be obtained from the relation of
![]() $p$
-adic étale cohomology and de Rham–Witt complex in [Reference Geisser and Hesselholt11] or from the relation of
$p$
-adic étale cohomology and de Rham–Witt complex in [Reference Geisser and Hesselholt11] or from the relation of
![]() $p$
-adic étale cohomology and Hochschild homology in [Reference Bhatt, Morrow and Scholze4].
$p$
-adic étale cohomology and Hochschild homology in [Reference Bhatt, Morrow and Scholze4].
3.2 Positive characteristic case (review)
3.2.1. Let
![]() $K$
be a complete discrete valuation field of characteristic
$K$
be a complete discrete valuation field of characteristic
![]() $p>0$
. We briefly review the definition of
$p>0$
. We briefly review the definition of
For details, see [Reference Borger6, Reference Illusie16, Reference Matsuda30].
In 3.5.9, we will show that this Rsw has the properties (i) and (ii) in 3.1.2.
3.2.2. From Artin–Schreier–Witt theory, there are isomorphisms
where
![]() $W_{s}(K)$
denotes the ring of Witt vectors of length
$W_{s}(K)$
denotes the ring of Witt vectors of length
![]() $s$
, and
$s$
, and
![]() $\unicode[STIX]{x1D719}$
the endomorphism of Frobenius.
$\unicode[STIX]{x1D719}$
the endomorphism of Frobenius.
3.2.3. For a Witt vector
![]() $a=(a_{s-1},\ldots ,a_{0})\in W_{s}(K)$
, let
$a=(a_{s-1},\ldots ,a_{0})\in W_{s}(K)$
, let
![]() $\text{ord}_{K}(a)=\min _{i}\{p^{i}\text{ord}_{K}(a_{i})\}$
. In [Reference Brylinski7], Brylinski defined an increasing filtration of
$\text{ord}_{K}(a)=\min _{i}\{p^{i}\text{ord}_{K}(a_{i})\}$
. In [Reference Brylinski7], Brylinski defined an increasing filtration of
![]() $W_{s}(K)$
as
$W_{s}(K)$
as
for
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
. The filtration
$n\in \mathbb{Z}_{{\geqslant}0}$
. The filtration
![]() $F_{n}H^{1}(K,\mathbb{Z}/p^{s}\mathbb{Z})$
defined in [Reference Kato20] is the image of
$F_{n}H^{1}(K,\mathbb{Z}/p^{s}\mathbb{Z})$
defined in [Reference Kato20] is the image of
![]() $F_{n}W_{s}(K)$
under (11).
$F_{n}W_{s}(K)$
under (11).
3.2.4. The homomorphism
![]() $-d:W_{s}(K)\rightarrow \unicode[STIX]{x1D6FA}_{K}^{1}$
given by
$-d:W_{s}(K)\rightarrow \unicode[STIX]{x1D6FA}_{K}^{1}$
given by
![]() $a=(a_{s-1},\ldots ,a_{0})\mapsto -\sum _{i}a_{i}^{p^{i}-1}\,da_{i}$
produces a map
$a=(a_{s-1},\ldots ,a_{0})\mapsto -\sum _{i}a_{i}^{p^{i}-1}\,da_{i}$
produces a map
which factors through
inducing
Here the minus sign of the definition of
![]() $-d$
may seem strange, but we put it to have the compatibility with the refined Swan conductor mod
$-d$
may seem strange, but we put it to have the compatibility with the refined Swan conductor mod
![]() $\mathfrak{m}_{K}$
in [Reference Kato20]. The minus sign naturally appears in the argument in 3.5.11.
$\mathfrak{m}_{K}$
in [Reference Kato20]. The minus sign naturally appears in the argument in 3.5.11.
Remark 3.2.5. The second author was unaware of the unpublished work of Borger [Reference Borger6] when writing [Reference Leal29], and sincerely regrets not quoting it in [Reference Leal29].
3.3 Application of higher dimensional local class field theory
3.3.1. Let
![]() $K$
be a complete discrete valuation field with residue field
$K$
be a complete discrete valuation field with residue field
![]() $F$
. In the case
$F$
. In the case
![]() $F$
is an
$F$
is an
![]() $r$
-dimensional local field, we define Rsw by using higher dimensional local class field theory as below.
$r$
-dimensional local field, we define Rsw by using higher dimensional local class field theory as below.
We will use the continuity of
![]() $K_{r+1}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
induced by the reciprocity map of the
$K_{r+1}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
induced by the reciprocity map of the
![]() $r+1$
-dimensional local field
$r+1$
-dimensional local field
![]() $K$
and by
$K$
and by
![]() $\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}/\mathbb{Z})$
and we will use also the self-duality of the additive group
$\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}/\mathbb{Z})$
and we will use also the self-duality of the additive group
![]() $F$
. Here the continuity is the one defined in [Reference Kato22], and the duality is also treated by using such continuity. (In the case
$F$
. Here the continuity is the one defined in [Reference Kato22], and the duality is also treated by using such continuity. (In the case
![]() $r=1$
, this duality is the usual self-duality of the locally compact abelian group
$r=1$
, this duality is the usual self-duality of the locally compact abelian group
![]() $F$
.)
$F$
.)
3.3.2. Let
![]() $F$
be an
$F$
be an
![]() $r$
-dimensional local field of characteristic
$r$
-dimensional local field of characteristic
![]() $p>0$
. We have the residue map
$p>0$
. We have the residue map
defined as follows. (The following definition and properties of
![]() $\text{Res}_{F}$
are contained in [Reference Kato17, Chapter 2, Lemmas 12 and 14].) Let
$\text{Res}_{F}$
are contained in [Reference Kato17, Chapter 2, Lemmas 12 and 14].) Let
![]() $F_{r}=F$
and for
$F_{r}=F$
and for
![]() $1\leqslant i\leqslant r$
, define the field
$1\leqslant i\leqslant r$
, define the field
![]() $F_{i-1}$
to be the residue field of
$F_{i-1}$
to be the residue field of
![]() $F_{i}$
by downward induction on
$F_{i}$
by downward induction on
![]() $i$
. Then
$i$
. Then
![]() $\text{Res}_{F}$
is the composition
$\text{Res}_{F}$
is the composition
where each
![]() $\text{Res}:\unicode[STIX]{x1D6FA}_{F_{i}}^{i}\rightarrow \unicode[STIX]{x1D6FA}_{F_{i-1}}^{i-1}$
is the residue map in 2.1.7 defined by taking
$\text{Res}:\unicode[STIX]{x1D6FA}_{F_{i}}^{i}\rightarrow \unicode[STIX]{x1D6FA}_{F_{i-1}}^{i-1}$
is the residue map in 2.1.7 defined by taking
![]() $F_{i-1}\rightarrow O_{F_{i}}$
and a prime element
$F_{i-1}\rightarrow O_{F_{i}}$
and a prime element
![]() $\unicode[STIX]{x1D70B}_{i}$
of the discrete valuation field
$\unicode[STIX]{x1D70B}_{i}$
of the discrete valuation field
![]() $F_{i}$
as in 2.1.7. This composition
$F_{i}$
as in 2.1.7. This composition
![]() $\text{Res}_{F}$
is independent of the choices of
$\text{Res}_{F}$
is independent of the choices of
![]() $F_{i-1}\rightarrow O_{F_{i}}$
and
$F_{i-1}\rightarrow O_{F_{i}}$
and
![]() $\unicode[STIX]{x1D70B}_{i}$
.
$\unicode[STIX]{x1D70B}_{i}$
.
We have
where
![]() $C$
is the Cartier operator. For a finite extension
$C$
is the Cartier operator. For a finite extension
![]() $F^{\prime }$
of
$F^{\prime }$
of
![]() $F$
, we have
$F$
, we have
where
![]() $\text{Tr}_{F^{\prime }/F}$
is the trace map
$\text{Tr}_{F^{\prime }/F}$
is the trace map
![]() $\unicode[STIX]{x1D6FA}_{F^{\prime }}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}$
. (This trace map for differential forms is defined in [Reference Kato19] as
$\unicode[STIX]{x1D6FA}_{F^{\prime }}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{r}$
. (This trace map for differential forms is defined in [Reference Kato19] as
The trace map for differential forms in a more general setting is defined in [Reference Garel10]. The formula (13) contains the formula (12) because for a field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
such that
$p$
such that
![]() $[k:k^{p}]=p^{r}$
, the Cartier operator
$[k:k^{p}]=p^{r}$
, the Cartier operator
![]() $\unicode[STIX]{x1D6FA}_{k}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{k}^{r}$
is the trace map of the homomorphism
$\unicode[STIX]{x1D6FA}_{k}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{k}^{r}$
is the trace map of the homomorphism
![]() $k\rightarrow k\;;\;x\mapsto x^{p}$
.)
$k\rightarrow k\;;\;x\mapsto x^{p}$
.)
3.3.3. Let
![]() $F$
be as in 3.3.2 and let
$F$
be as in 3.3.2 and let
![]() $V$
be a finite-dimensional vector space over
$V$
be a finite-dimensional vector space over
![]() $F$
. Then
$F$
. Then
![]() $V$
is canonically regarded as an object of the category
$V$
is canonically regarded as an object of the category
![]() ${\mathcal{F}}_{r,\text{ab}}$
of abelian group objects of the category
${\mathcal{F}}_{r,\text{ab}}$
of abelian group objects of the category
![]() ${\mathcal{F}}_{r}$
(2.4.4).
${\mathcal{F}}_{r}$
(2.4.4).
Lemma 3.3.4. Let
![]() $F$
and
$F$
and
![]() $V$
be as in 3.3.3 and let
$V$
be as in 3.3.3 and let
![]() $V^{\ast }=\text{Hom}_{F}(V,\unicode[STIX]{x1D6FA}_{F}^{r})$
. Then we have the bijection
$V^{\ast }=\text{Hom}_{F}(V,\unicode[STIX]{x1D6FA}_{F}^{r})$
. Then we have the bijection
Here
![]() $\text{Hom}_{\text{cont}}$
is the set of homomorphisms in the category
$\text{Hom}_{\text{cont}}$
is the set of homomorphisms in the category
![]() ${\mathcal{F}}_{r,\text{ab}}$
.
${\mathcal{F}}_{r,\text{ab}}$
.
Proof. This follows from [Reference Kato22, Proposition 3]. ◻
3.3.5. Let
![]() $K$
be a complete discrete valuation field with residue field
$K$
be a complete discrete valuation field with residue field
![]() $F$
and assume that
$F$
and assume that
![]() $F$
is an
$F$
is an
![]() $r$
-dimensional local field of characteristic
$r$
-dimensional local field of characteristic
![]() $p>0$
. (Hence
$p>0$
. (Hence
![]() $K$
is an
$K$
is an
![]() $r+1$
-dimensional local field.)
$r+1$
-dimensional local field.)
Let
![]() $\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Then by [Reference Kato and Saito23],
$\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Then by [Reference Kato and Saito23],
![]() $\unicode[STIX]{x1D712}$
induces a continuous homomorphism
$\unicode[STIX]{x1D712}$
induces a continuous homomorphism
![]() $K_{r+1}^{M}(K)/U^{n+1}K_{r+1}^{M}(K)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
, where the continuity is that of [Reference Kato22]. Let
$K_{r+1}^{M}(K)/U^{n+1}K_{r+1}^{M}(K)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
, where the continuity is that of [Reference Kato22]. Let
![]() $m=\max (n-e_{K},[n/p])$
. Then via
$m=\max (n-e_{K},[n/p])$
. Then via
(2.2.4(1)), we obtain a continuous homomorphism
![]() $u_{\unicode[STIX]{x1D712}}:\mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )\rightarrow \mathbb{F}_{p}$
.
$u_{\unicode[STIX]{x1D712}}:\mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{r}(\log )\rightarrow \mathbb{F}_{p}$
.
Take an integer
![]() $b\geqslant 0$
such that
$b\geqslant 0$
such that
![]() $p^{b}\geqslant n-m$
. Then
$p^{b}\geqslant n-m$
. Then
![]() $(x,y)\mapsto R_{b}(x\wedge y)$
is a perfect duality of finite-dimensional
$(x,y)\mapsto R_{b}(x\wedge y)$
is a perfect duality of finite-dimensional
![]() $F$
-vector spaces where
$F$
-vector spaces where
![]() $F$
acts on the two
$F$
acts on the two
![]() $O_{K}/\mathfrak{m}_{K}^{n-m}$
-modules on the left hand side via
$O_{K}/\mathfrak{m}_{K}^{n-m}$
-modules on the left hand side via
![]() $\unicode[STIX]{x1D704}_{b}$
((2) of 2.1.9). Hence by 3.3.4,
$\unicode[STIX]{x1D704}_{b}$
((2) of 2.1.9). Hence by 3.3.4,
![]() $u_{\unicode[STIX]{x1D712}}$
corresponds to an element
$u_{\unicode[STIX]{x1D712}}$
corresponds to an element
![]() $\text{Rsw}_{K}(\unicode[STIX]{x1D712})\in \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
. This element is independent of the choice of
$\text{Rsw}_{K}(\unicode[STIX]{x1D712})\in \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
. This element is independent of the choice of
![]() $b$
.
$b$
.
The following lemma will be used in Section 3.5.
Lemma 3.3.6. Assume that
![]() $K$
is a
$K$
is a
![]() $d$
-dimensional local field whose residue field
$d$
-dimensional local field whose residue field
![]() $F$
is of characteristic
$F$
is of characteristic
![]() $p>0$
. Assume one of the following
$p>0$
. Assume one of the following
![]() $\text{(i)}$
and
$\text{(i)}$
and
![]() $\text{(ii)}$
.
$\text{(ii)}$
.
(i)
 $K^{\prime }$
is a finite extension of
$K^{\prime }$
is a finite extension of
 $K$
.
$K$
.(ii)
 $K^{\prime }$
is the field of fractions
$K^{\prime }$
is the field of fractions
 $K\{\{T\}\}$
of the completion of the local ring of
$K\{\{T\}\}$
of the completion of the local ring of
 $O_{K}[[T]]$
at the prime ideal generated by
$O_{K}[[T]]$
at the prime ideal generated by
 $\mathfrak{m}_{K}$
(then
$\mathfrak{m}_{K}$
(then
 $K^{\prime }$
is a
$K^{\prime }$
is a
 $d+1$
-dimensional local field with residue field
$d+1$
-dimensional local field with residue field
 $F((T))$
).
$F((T))$
).
Then
![]() $\text{Rsw}_{K}$
and
$\text{Rsw}_{K}$
and
![]() $\text{Rsw}_{K^{\prime }}$
are compatible.
$\text{Rsw}_{K^{\prime }}$
are compatible.
3.3.7. We prove the case (i) of 3.3.6. We have a commutative diagram
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}K_{d}^{M}(K^{\prime }) & \rightarrow & \text{Gal}((K^{\prime })^{\text{ab}}/K^{\prime })\\ \downarrow & & \downarrow \\ K_{d}^{M}(K) & \rightarrow & \text{Gal}(K^{\text{ab}}/K)\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}K_{d}^{M}(K^{\prime }) & \rightarrow & \text{Gal}((K^{\prime })^{\text{ab}}/K^{\prime })\\ \downarrow & & \downarrow \\ K_{d}^{M}(K) & \rightarrow & \text{Gal}(K^{\text{ab}}/K)\end{array}\end{eqnarray}$$
where the horizontal arrows are the reciprocity maps, the left vertical arrow is the norm map and the right vertical arrow is the natural one [Reference Kato17, Section 3.2, Corollary 1].
Let
![]() $R_{K}:\mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )\rightarrow \mathbb{F}_{p}$
be the composite map
$R_{K}:\mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )\rightarrow \mathbb{F}_{p}$
be the composite map
![]() $\text{Res}_{F}\circ R_{b}$
(
$\text{Res}_{F}\circ R_{b}$
(
![]() $p^{b}\geqslant n-m$
) which is independent of
$p^{b}\geqslant n-m$
) which is independent of
![]() $b$
, and let
$b$
, and let
![]() $R_{K^{\prime }}:\mathfrak{m}_{K^{\prime }}^{1-n^{\prime }+m^{\prime }}/\mathfrak{m}_{K^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d}(\log )\rightarrow \mathbb{F}_{p}$
(
$R_{K^{\prime }}:\mathfrak{m}_{K^{\prime }}^{1-n^{\prime }+m^{\prime }}/\mathfrak{m}_{K^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d}(\log )\rightarrow \mathbb{F}_{p}$
(
![]() $n^{\prime }=e(K^{\prime }/K)n$
,
$n^{\prime }=e(K^{\prime }/K)n$
,
![]() $m^{\prime }=\max (n^{\prime }-e_{K^{\prime }},[n^{\prime }/p])$
) be the corresponding map for
$m^{\prime }=\max (n^{\prime }-e_{K^{\prime }},[n^{\prime }/p])$
) be the corresponding map for
![]() $K^{\prime }$
.
$K^{\prime }$
.
Let
![]() $\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
, let
$\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
, let
![]() $\unicode[STIX]{x1D712}_{K^{\prime }}\in F_{n^{\prime }}H^{1}(K^{\prime },\mathbb{Q}_{p}/\mathbb{Z}_{p})$
be the image of
$\unicode[STIX]{x1D712}_{K^{\prime }}\in F_{n^{\prime }}H^{1}(K^{\prime },\mathbb{Q}_{p}/\mathbb{Z}_{p})$
be the image of
![]() $\unicode[STIX]{x1D712}$
, and let
$\unicode[STIX]{x1D712}$
, and let
![]() $\text{Rsw}(\unicode[STIX]{x1D712})_{K^{\prime }}\in \mathfrak{m}_{K^{\prime }}^{-n^{\prime }}/\mathfrak{m}_{K^{\prime }}^{-m^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{1}(\log )$
be the image of
$\text{Rsw}(\unicode[STIX]{x1D712})_{K^{\prime }}\in \mathfrak{m}_{K^{\prime }}^{-n^{\prime }}/\mathfrak{m}_{K^{\prime }}^{-m^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{1}(\log )$
be the image of
![]() $\text{Rsw}(\unicode[STIX]{x1D712})=\text{Rsw}_{K}(\unicode[STIX]{x1D712})\in \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
. Since any finite extension of
$\text{Rsw}(\unicode[STIX]{x1D712})=\text{Rsw}_{K}(\unicode[STIX]{x1D712})\in \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
. Since any finite extension of
![]() $K$
is a successive extension of a tame extension and extensions of degree
$K$
is a successive extension of a tame extension and extensions of degree
![]() $p$
, it is sufficient to prove
$p$
, it is sufficient to prove
![]() $\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})=\text{Rsw}(\unicode[STIX]{x1D712})_{K^{\prime }}$
in the case
$\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})=\text{Rsw}(\unicode[STIX]{x1D712})_{K^{\prime }}$
in the case
![]() $K^{\prime }/K$
is tame and in the case
$K^{\prime }/K$
is tame and in the case
![]() $[K^{\prime }:K]=p$
. It is sufficient to prove in these cases that
$[K^{\prime }:K]=p$
. It is sufficient to prove in these cases that
for any
![]() $\unicode[STIX]{x1D6FC}\in \mathfrak{m}_{K^{\prime }}^{m^{\prime }+1}/\mathfrak{m}_{K^{\prime }}^{n^{\prime }+1}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d-1}(\log )$
. In these cases, the last group is generated additively by elements of the following three forms.
$\unicode[STIX]{x1D6FC}\in \mathfrak{m}_{K^{\prime }}^{m^{\prime }+1}/\mathfrak{m}_{K^{\prime }}^{n^{\prime }+1}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d-1}(\log )$
. In these cases, the last group is generated additively by elements of the following three forms.
(a)
 $f\unicode[STIX]{x1D714}$
where
$f\unicode[STIX]{x1D714}$
where
 $f\in \mathfrak{m}_{K^{\prime }}^{m^{\prime }+1}$
and
$f\in \mathfrak{m}_{K^{\prime }}^{m^{\prime }+1}$
and
 $\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
.
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
.(b)
 $\unicode[STIX]{x1D714}\wedge df$
where
$\unicode[STIX]{x1D714}\wedge df$
where
 $f$
is as in (a) and
$f$
is as in (a) and
 $\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{d-2}(\log )$
.
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{d-2}(\log )$
.(c)
 $\unicode[STIX]{x1D714}\wedge d\log (f)$
where
$\unicode[STIX]{x1D714}\wedge d\log (f)$
where
 $\unicode[STIX]{x1D714}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-2}(\log )$
and
$\unicode[STIX]{x1D714}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-2}(\log )$
and
 $f\in (K^{\prime })^{\times }$
.
$f\in (K^{\prime })^{\times }$
.
(This generation is deduced from 2.1.3. If
![]() $K^{\prime }/K$
is tamely ramified,
$K^{\prime }/K$
is tamely ramified,
![]() $\mathfrak{m}_{K^{\prime }}^{m^{\prime }+1}/\mathfrak{m}_{K^{\prime }}^{n^{\prime }+1}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d-1}(\log )$
is additively generated by elements of the form (a). If the ramification index of
$\mathfrak{m}_{K^{\prime }}^{m^{\prime }+1}/\mathfrak{m}_{K^{\prime }}^{n^{\prime }+1}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d-1}(\log )$
is additively generated by elements of the form (a). If the ramification index of
![]() $K^{\prime }/K$
is one and if the residue field of
$K^{\prime }/K$
is one and if the residue field of
![]() $K^{\prime }$
is a purely inseparable extension of
$K^{\prime }$
is a purely inseparable extension of
![]() $K$
of degree
$K$
of degree
![]() $p$
generated by the residue class of an element
$p$
generated by the residue class of an element
![]() $g$
of
$g$
of
![]() $O_{K^{\prime }}$
, and if
$O_{K^{\prime }}$
, and if
![]() $\unicode[STIX]{x1D70B}$
denotes a prime element of
$\unicode[STIX]{x1D70B}$
denotes a prime element of
![]() $K$
, it is additively generated by elements of the form (a), elements of the form (b) with
$K$
, it is additively generated by elements of the form (a), elements of the form (b) with
![]() $f=\unicode[STIX]{x1D70B}^{j}g^{j}$
(
$f=\unicode[STIX]{x1D70B}^{j}g^{j}$
(
![]() $m+1\leqslant i\leqslant n$
,
$m+1\leqslant i\leqslant n$
,
![]() $1\leqslant j\leqslant p-1$
), and elements of the form (c) with
$1\leqslant j\leqslant p-1$
), and elements of the form (c) with
![]() $f=g$
. If the residue field of
$f=g$
. If the residue field of
![]() $K^{\prime }$
coincides with that of
$K^{\prime }$
coincides with that of
![]() $K$
and
$K$
and
![]() $[K^{\prime }:K]=p$
, and if
$[K^{\prime }:K]=p$
, and if
![]() $\unicode[STIX]{x1D70B}^{\prime }$
denotes a prime element of
$\unicode[STIX]{x1D70B}^{\prime }$
denotes a prime element of
![]() $K^{\prime }$
, it is additively generated by elements of the form (a), elements of the form (b) with
$K^{\prime }$
, it is additively generated by elements of the form (a), elements of the form (b) with
![]() $f=(\unicode[STIX]{x1D70B}^{\prime })^{i}$
(
$f=(\unicode[STIX]{x1D70B}^{\prime })^{i}$
(
![]() $m^{\prime }+1\leqslant i\leqslant n^{\prime }$
), and elements of the form (c) with
$m^{\prime }+1\leqslant i\leqslant n^{\prime }$
), and elements of the form (c) with
![]() $f=\unicode[STIX]{x1D70B}^{\prime }$
.)
$f=\unicode[STIX]{x1D70B}^{\prime }$
.)
Assume
![]() $\unicode[STIX]{x1D6FC}$
is an element as in (a) (resp. (b), resp. (c)), and let
$\unicode[STIX]{x1D6FC}$
is an element as in (a) (resp. (b), resp. (c)), and let
![]() $\unicode[STIX]{x1D6FD}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
be
$\unicode[STIX]{x1D6FD}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
be
![]() $\text{Tr}_{K^{\prime }/K}(f)\unicode[STIX]{x1D714}$
(resp.
$\text{Tr}_{K^{\prime }/K}(f)\unicode[STIX]{x1D714}$
(resp.
![]() $\unicode[STIX]{x1D714}\wedge d(\text{Tr}_{K^{\prime }/K}(f))$
, resp.
$\unicode[STIX]{x1D714}\wedge d(\text{Tr}_{K^{\prime }/K}(f))$
, resp.
![]() $\unicode[STIX]{x1D714}\wedge d\log (N(f))$
where
$\unicode[STIX]{x1D714}\wedge d\log (N(f))$
where
![]() $N$
is the norm map
$N$
is the norm map
![]() $(K^{\prime })^{\times }\rightarrow K^{\times }$
). Then
$(K^{\prime })^{\times }\rightarrow K^{\times }$
). Then
![]() $R_{K^{\prime }}(\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})\wedge \unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D712}_{K^{\prime }}(E(\unicode[STIX]{x1D6FC}))=\unicode[STIX]{x1D712}(N(E(\unicode[STIX]{x1D6FC})))$
(here
$R_{K^{\prime }}(\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})\wedge \unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D712}_{K^{\prime }}(E(\unicode[STIX]{x1D6FC}))=\unicode[STIX]{x1D712}(N(E(\unicode[STIX]{x1D6FC})))$
(here
![]() $E$
is as in 3.3.5 and
$E$
is as in 3.3.5 and
![]() $N$
is the norm map)
$N$
is the norm map)
![]() $=\unicode[STIX]{x1D712}(E(\unicode[STIX]{x1D6FD}))=R_{K}(\text{Rsw}(\unicode[STIX]{x1D712})\wedge \unicode[STIX]{x1D6FD})$
. Hence, for the proof of (14), it is sufficient to prove
$=\unicode[STIX]{x1D712}(E(\unicode[STIX]{x1D6FD}))=R_{K}(\text{Rsw}(\unicode[STIX]{x1D712})\wedge \unicode[STIX]{x1D6FD})$
. Hence, for the proof of (14), it is sufficient to prove
(A)
 $\!R_{K^{\prime }}(f\unicode[STIX]{x1D714})=R_{K}(\text{Tr}_{K^{\prime }/K}(f)\unicode[STIX]{x1D714})$
for
$\!R_{K^{\prime }}(f\unicode[STIX]{x1D714})=R_{K}(\text{Tr}_{K^{\prime }/K}(f)\unicode[STIX]{x1D714})$
for
 $f\in \mathfrak{m}_{K^{\prime }}^{1-n^{\prime }+m^{\prime }}$
and
$f\in \mathfrak{m}_{K^{\prime }}^{1-n^{\prime }+m^{\prime }}$
and
 $\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )$
;
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )$
;(B)
 $\!R_{K^{\prime }}(\unicode[STIX]{x1D714}\wedge df)=R_{K}(\unicode[STIX]{x1D714}\wedge d(\text{Tr}_{K^{\prime }/K}(f)))$
for
$\!R_{K^{\prime }}(\unicode[STIX]{x1D714}\wedge df)=R_{K}(\unicode[STIX]{x1D714}\wedge d(\text{Tr}_{K^{\prime }/K}(f)))$
for
 $f$
as in (A) and
$f$
as in (A) and
 $\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
;
$\unicode[STIX]{x1D714}\in \unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
;(C)
 $\!R_{K^{\prime }}(\unicode[STIX]{x1D714}\wedge d\log (f))=R_{K}(\unicode[STIX]{x1D714}\wedge d\log (N(f)))$
for
$\!R_{K^{\prime }}(\unicode[STIX]{x1D714}\wedge d\log (f))=R_{K}(\unicode[STIX]{x1D714}\wedge d\log (N(f)))$
for
 $\unicode[STIX]{x1D714}\in \mathfrak{m}_{K}^{1-n+m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
and for
$\unicode[STIX]{x1D714}\in \mathfrak{m}_{K}^{1-n+m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
and for
 $f\in (K^{\prime })^{\times }$
.
$f\in (K^{\prime })^{\times }$
.
If
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
,
$p$
,
![]() $\mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )$
is a subquotient of
$\mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )$
is a subquotient of
![]() $\unicode[STIX]{x1D6FA}_{K}^{d}$
and
$\unicode[STIX]{x1D6FA}_{K}^{d}$
and
![]() $R_{K}$
coincides with the map induced from
$R_{K}$
coincides with the map induced from
![]() $\text{Res}_{K}:\unicode[STIX]{x1D6FA}_{K}^{d}\rightarrow \mathbb{F}_{p}$
on the subquotient, and the same thing holds for
$\text{Res}_{K}:\unicode[STIX]{x1D6FA}_{K}^{d}\rightarrow \mathbb{F}_{p}$
on the subquotient, and the same thing holds for
![]() $K^{\prime }$
. Hence (A), (B), (C) follow from
$K^{\prime }$
. Hence (A), (B), (C) follow from
![]() $\text{Res}_{K^{\prime }}=\text{Res}_{K}\circ \text{Tr}_{K^{\prime }/K}$
(3.3.2).
$\text{Res}_{K^{\prime }}=\text{Res}_{K}\circ \text{Tr}_{K^{\prime }/K}$
(3.3.2).
Assume
![]() $K$
is of characteristic 0. Let
$K$
is of characteristic 0. Let
![]() $L=F((T))$
. Then via the isomorphism
$L=F((T))$
. Then via the isomorphism
![]() $F[T]/(T^{n-m})\overset{\cong }{\rightarrow }O_{K}/\mathfrak{m}_{K}^{n-m}$
of rings with log structures ((5) with
$F[T]/(T^{n-m})\overset{\cong }{\rightarrow }O_{K}/\mathfrak{m}_{K}^{n-m}$
of rings with log structures ((5) with
![]() $a=n-m$
),
$a=n-m$
),
![]() $\mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )$
is a subquotient of
$\mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )$
is a subquotient of
![]() $\unicode[STIX]{x1D6FA}_{L}^{d}$
and
$\unicode[STIX]{x1D6FA}_{L}^{d}$
and
![]() $R_{K}$
coincides with the map induced from
$R_{K}$
coincides with the map induced from
![]() $\text{Res}_{L}:\unicode[STIX]{x1D6FA}_{L}^{d}\rightarrow \mathbb{F}_{p}$
on the subquotient. As is easily seen, there is an extension
$\text{Res}_{L}:\unicode[STIX]{x1D6FA}_{L}^{d}\rightarrow \mathbb{F}_{p}$
on the subquotient. As is easily seen, there is an extension
![]() $L^{\prime }$
of
$L^{\prime }$
of
![]() $L$
of degree
$L$
of degree
![]() $[K^{\prime }:K]$
and an isomorphism
$[K^{\prime }:K]$
and an isomorphism
![]() $O_{K^{\prime }}/\mathfrak{m}_{K}^{n-m}O_{K^{\prime }}\cong O_{L^{\prime }}/\mathfrak{m}_{L}^{n-m}O_{L^{\prime }}$
of rings with log structures extending the isomorphism
$O_{K^{\prime }}/\mathfrak{m}_{K}^{n-m}O_{K^{\prime }}\cong O_{L^{\prime }}/\mathfrak{m}_{L}^{n-m}O_{L^{\prime }}$
of rings with log structures extending the isomorphism
![]() $O_{K}/\mathfrak{m}_{K}^{n-m}\cong O_{L}/\mathfrak{m}_{L}^{n-m}$
of rings with log structures, and
$O_{K}/\mathfrak{m}_{K}^{n-m}\cong O_{L}/\mathfrak{m}_{L}^{n-m}$
of rings with log structures, and
![]() $R_{K^{\prime }}:\mathfrak{m}_{K^{\prime }}^{1-n^{\prime }+m^{\prime }}/\mathfrak{m}_{K^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d}(\log )\rightarrow \mathbb{F}_{p}$
is identified with the map induced from
$R_{K^{\prime }}:\mathfrak{m}_{K^{\prime }}^{1-n^{\prime }+m^{\prime }}/\mathfrak{m}_{K^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d}(\log )\rightarrow \mathbb{F}_{p}$
is identified with the map induced from
![]() $\text{Res}_{L^{\prime }}:\unicode[STIX]{x1D6FA}_{L^{\prime }}^{d}\rightarrow \mathbb{F}_{p}$
on the subquotient. Hence (A), (B), (C) follow from
$\text{Res}_{L^{\prime }}:\unicode[STIX]{x1D6FA}_{L^{\prime }}^{d}\rightarrow \mathbb{F}_{p}$
on the subquotient. Hence (A), (B), (C) follow from
![]() $\text{Res}_{L^{\prime }}=\text{Res}_{L}\circ \text{Tr}_{L^{\prime }/L}$
(3.3.2).
$\text{Res}_{L^{\prime }}=\text{Res}_{L}\circ \text{Tr}_{L^{\prime }/L}$
(3.3.2).
3.3.8. We prove the case (ii) of 3.3.6. By [Reference Kato19, Theorem 2], we have a commutative diagram
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}\hat{K}_{d+1}^{M}(K^{\prime }) & \rightarrow & \text{Gal}((K^{\prime })^{\text{ab}}/K^{\prime })\\ \downarrow & & \downarrow \\ \hat{K}_{d}^{M}(K) & \rightarrow & \text{Gal}(K^{\text{ab}}/K)\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}\hat{K}_{d+1}^{M}(K^{\prime }) & \rightarrow & \text{Gal}((K^{\prime })^{\text{ab}}/K^{\prime })\\ \downarrow & & \downarrow \\ \hat{K}_{d}^{M}(K) & \rightarrow & \text{Gal}(K^{\text{ab}}/K)\end{array}\end{eqnarray}$$
where
![]() $\hat{K}_{d}^{M}(K)=\mathop{\varprojlim }\nolimits_{i}K_{d}^{M}(K)/U^{i}K_{d}^{M}(K)$
,
$\hat{K}_{d}^{M}(K)=\mathop{\varprojlim }\nolimits_{i}K_{d}^{M}(K)/U^{i}K_{d}^{M}(K)$
,
![]() $\hat{K}_{d+1}^{M}(K^{\prime })$
is defined similarly, the horizontal arrows are the reciprocity maps, the left vertical arrow is minus the residue homomorphism in [Reference Kato19] and the right vertical arrow is the natural one.
$\hat{K}_{d+1}^{M}(K^{\prime })$
is defined similarly, the horizontal arrows are the reciprocity maps, the left vertical arrow is minus the residue homomorphism in [Reference Kato19] and the right vertical arrow is the natural one.
Let
![]() $R_{K}:\mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )\rightarrow \mathbb{F}_{p}$
and
$R_{K}:\mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )\rightarrow \mathbb{F}_{p}$
and
![]() $R_{K^{\prime }}:\mathfrak{m}_{K^{\prime }}^{1-n+m}/\mathfrak{m}_{K^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d+1}(\log )\rightarrow \mathbb{F}_{p}$
be the maps defined as in 3.3.7.
$R_{K^{\prime }}:\mathfrak{m}_{K^{\prime }}^{1-n+m}/\mathfrak{m}_{K^{\prime }}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d+1}(\log )\rightarrow \mathbb{F}_{p}$
be the maps defined as in 3.3.7.
Let
![]() $\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. We prove
$\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. We prove
![]() $\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})=\text{Rsw}(\unicode[STIX]{x1D712})_{K^{\prime }}$
. For this, it is sufficient to prove that
$\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})=\text{Rsw}(\unicode[STIX]{x1D712})_{K^{\prime }}$
. For this, it is sufficient to prove that
![]() $R_{K^{\prime }}(\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})\wedge \unicode[STIX]{x1D6FC})=R_{K^{\prime }}(\text{Rsw}(\unicode[STIX]{x1D712})_{K^{\prime }}\wedge \unicode[STIX]{x1D6FC})$
for any
$R_{K^{\prime }}(\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})\wedge \unicode[STIX]{x1D6FC})=R_{K^{\prime }}(\text{Rsw}(\unicode[STIX]{x1D712})_{K^{\prime }}\wedge \unicode[STIX]{x1D6FC})$
for any
![]() $\unicode[STIX]{x1D6FC}\in \mathfrak{m}_{K^{\prime }}^{m+1}/\mathfrak{m}_{K^{\prime }}^{n+1}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d}(\log )$
. By 2.1.3, the last group is generated additively by elements as in the following (i)–(iii).
$\unicode[STIX]{x1D6FC}\in \mathfrak{m}_{K^{\prime }}^{m+1}/\mathfrak{m}_{K^{\prime }}^{n+1}\otimes _{O_{K^{\prime }}}\unicode[STIX]{x1D6FA}_{O_{K^{\prime }}}^{d}(\log )$
. By 2.1.3, the last group is generated additively by elements as in the following (i)–(iii).
(a) Elements in the image of
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\mathfrak{m}_{K^{\prime }}^{m+1}/\mathfrak{m}_{K^{\prime }}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log ))\nonumber\\ \displaystyle & & \displaystyle \quad \oplus \,(\mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}O_{K}[[T]]\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )\wedge dT).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\mathfrak{m}_{K^{\prime }}^{m+1}/\mathfrak{m}_{K^{\prime }}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log ))\nonumber\\ \displaystyle & & \displaystyle \quad \oplus \,(\mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}O_{K}[[T]]\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )\wedge dT).\nonumber\end{eqnarray}$$
(b)
 $\unicode[STIX]{x1D714}\otimes d\log (T)$
with
$\unicode[STIX]{x1D714}\otimes d\log (T)$
with
 $\unicode[STIX]{x1D714}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
.
$\unicode[STIX]{x1D714}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
.(c)
 $T^{-i}\unicode[STIX]{x1D714}\otimes d\log (T)$
with
$T^{-i}\unicode[STIX]{x1D714}\otimes d\log (T)$
with
 $\unicode[STIX]{x1D714}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
and with
$\unicode[STIX]{x1D714}\in \mathfrak{m}_{K}^{m+1}/\mathfrak{m}_{K}^{n+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d-1}(\log )$
and with
 $i\geqslant 1$
.
$i\geqslant 1$
.
Assume
![]() $\unicode[STIX]{x1D6FC}$
is an element as in (a) (resp. (b), resp. (c)). Let
$\unicode[STIX]{x1D6FC}$
is an element as in (a) (resp. (b), resp. (c)). Let
![]() $\text{Res}_{K^{\prime }/K}:\hat{K}_{d+1}^{M}(K^{\prime })\rightarrow \hat{K}_{d}^{M}(K)$
be the residue map. Then
$\text{Res}_{K^{\prime }/K}:\hat{K}_{d+1}^{M}(K^{\prime })\rightarrow \hat{K}_{d}^{M}(K)$
be the residue map. Then
![]() $R_{K^{\prime }}(\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})\wedge \unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D712}_{K^{\prime }}(E(\unicode[STIX]{x1D6FC}))=-\unicode[STIX]{x1D712}(\text{Res}_{K^{\prime }/K}(E(\unicode[STIX]{x1D6FC})))$
where
$R_{K^{\prime }}(\text{Rsw}(\unicode[STIX]{x1D712}_{K^{\prime }})\wedge \unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D712}_{K^{\prime }}(E(\unicode[STIX]{x1D6FC}))=-\unicode[STIX]{x1D712}(\text{Res}_{K^{\prime }/K}(E(\unicode[STIX]{x1D6FC})))$
where
![]() $E$
is as in 3.3.5. By (ii) of 2.2.2 and by the definition of
$E$
is as in 3.3.5. By (ii) of 2.2.2 and by the definition of
![]() $\text{Res}_{K^{\prime }/K}$
in [Reference Kato19], we have
$\text{Res}_{K^{\prime }/K}$
in [Reference Kato19], we have
![]() $\unicode[STIX]{x1D712}(\text{Res}_{K^{\prime }/K}(E(\unicode[STIX]{x1D6FC})))=\unicode[STIX]{x1D712}(E(\unicode[STIX]{x1D6FD}))=R_{K}(\text{Rsw}(\unicode[STIX]{x1D712})\wedge \unicode[STIX]{x1D6FD})$
where
$\unicode[STIX]{x1D712}(\text{Res}_{K^{\prime }/K}(E(\unicode[STIX]{x1D6FC})))=\unicode[STIX]{x1D712}(E(\unicode[STIX]{x1D6FD}))=R_{K}(\text{Rsw}(\unicode[STIX]{x1D712})\wedge \unicode[STIX]{x1D6FD})$
where
![]() $\unicode[STIX]{x1D6FD}=0$
in cases (a) and (c) and
$\unicode[STIX]{x1D6FD}=0$
in cases (a) and (c) and
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D714}$
in the case (b). Hence it is sufficient to prove
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D714}$
in the case (b). Hence it is sufficient to prove
 $$\begin{eqnarray}\displaystyle & & \displaystyle R_{K^{\prime }}\left(\mathop{\sum }_{i\gg -\infty }T^{i}\unicode[STIX]{x1D714}_{i}\wedge d\log (T)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-R_{K}(\unicode[STIX]{x1D714}_{0})\quad (\unicode[STIX]{x1D714}_{i}\in \mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle R_{K^{\prime }}\left(\mathop{\sum }_{i\gg -\infty }T^{i}\unicode[STIX]{x1D714}_{i}\wedge d\log (T)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-R_{K}(\unicode[STIX]{x1D714}_{0})\quad (\unicode[STIX]{x1D714}_{i}\in \mathfrak{m}_{K}^{1-n+m}/\mathfrak{m}_{K}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{d}(\log )).\end{eqnarray}$$
Take a lifting
![]() $\unicode[STIX]{x1D704}:F\rightarrow O_{K}/\mathfrak{m}_{K}^{n-m}$
and extend it to
$\unicode[STIX]{x1D704}:F\rightarrow O_{K}/\mathfrak{m}_{K}^{n-m}$
and extend it to
![]() $\unicode[STIX]{x1D704}:F((T))\rightarrow O_{K^{\prime }}/\mathfrak{m}_{K^{\prime }}^{n-m}$
;
$\unicode[STIX]{x1D704}:F((T))\rightarrow O_{K^{\prime }}/\mathfrak{m}_{K^{\prime }}^{n-m}$
;
![]() $\sum _{i\gg -\infty }a_{i}T^{i}\mapsto \sum _{i\gg -\infty }\unicode[STIX]{x1D704}(a_{i})T^{i}$
. Let
$\sum _{i\gg -\infty }a_{i}T^{i}\mapsto \sum _{i\gg -\infty }\unicode[STIX]{x1D704}(a_{i})T^{i}$
. Let
![]() $\unicode[STIX]{x1D70B}$
be a prime element of
$\unicode[STIX]{x1D70B}$
be a prime element of
![]() $K$
. Write
$K$
. Write
We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle R_{K^{\prime }}\left(\mathop{\sum }_{i\gg -\infty }T^{i}\unicode[STIX]{x1D714}_{i}\wedge d\log (T)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =R_{K^{\prime }}\left(\unicode[STIX]{x1D704}\left(\mathop{\sum }_{i,j}T^{i}\unicode[STIX]{x1D714}_{ij}\right)\unicode[STIX]{x1D70B}^{-j}\,d\log (\unicode[STIX]{x1D70B})\wedge d\log (T)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{Res}_{F((T))}\left(\mathop{\sum }_{i}T^{i}\unicode[STIX]{x1D714}_{i0}\wedge d\log (T)\right)=-\text{Res}_{F}(\unicode[STIX]{x1D714}_{00})=-R_{K}(\unicode[STIX]{x1D714}_{0}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle R_{K^{\prime }}\left(\mathop{\sum }_{i\gg -\infty }T^{i}\unicode[STIX]{x1D714}_{i}\wedge d\log (T)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =R_{K^{\prime }}\left(\unicode[STIX]{x1D704}\left(\mathop{\sum }_{i,j}T^{i}\unicode[STIX]{x1D714}_{ij}\right)\unicode[STIX]{x1D70B}^{-j}\,d\log (\unicode[STIX]{x1D70B})\wedge d\log (T)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{Res}_{F((T))}\left(\mathop{\sum }_{i}T^{i}\unicode[STIX]{x1D714}_{i0}\wedge d\log (T)\right)=-\text{Res}_{F}(\unicode[STIX]{x1D714}_{00})=-R_{K}(\unicode[STIX]{x1D714}_{0}).\nonumber\end{eqnarray}$$
This proves (15).
3.4 Application of higher dimensional global class field theory
3.4.1. Let
![]() $X$
be a proper normal integral scheme over
$X$
be a proper normal integral scheme over
![]() $\mathbb{Z}$
with function field
$\mathbb{Z}$
with function field
![]() $J$
and let
$J$
and let
![]() $\unicode[STIX]{x1D708}$
be a point of
$\unicode[STIX]{x1D708}$
be a point of
![]() $X$
of codimension one whose residue field is of characteristic
$X$
of codimension one whose residue field is of characteristic
![]() $p>0$
. We assume
$p>0$
. We assume
![]() $X(\mathbb{R})=\emptyset$
.
$X(\mathbb{R})=\emptyset$
.
Let
![]() $n\geqslant 1$
and let
$n\geqslant 1$
and let
![]() $F_{\unicode[STIX]{x1D708},n}H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})\subset H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
be the inverse image of
$F_{\unicode[STIX]{x1D708},n}H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})\subset H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
be the inverse image of
![]() $F_{n}H^{1}({\hat{J}}_{\unicode[STIX]{x1D708}},\mathbb{Q}_{p}/\mathbb{Z}_{p})\subset H^{1}({\hat{J}}_{\unicode[STIX]{x1D708}},\mathbb{Q}_{p}/\mathbb{Z}_{p})$
where
$F_{n}H^{1}({\hat{J}}_{\unicode[STIX]{x1D708}},\mathbb{Q}_{p}/\mathbb{Z}_{p})\subset H^{1}({\hat{J}}_{\unicode[STIX]{x1D708}},\mathbb{Q}_{p}/\mathbb{Z}_{p})$
where
![]() ${\hat{J}}_{\unicode[STIX]{x1D708}}$
denotes the field of fractions of the completion of the discrete valuation ring
${\hat{J}}_{\unicode[STIX]{x1D708}}$
denotes the field of fractions of the completion of the discrete valuation ring
![]() $O_{X,\unicode[STIX]{x1D708}}$
. Let
$O_{X,\unicode[STIX]{x1D708}}$
. Let
![]() $\mathfrak{m}_{\unicode[STIX]{x1D708}}$
be the maximal ideal of
$\mathfrak{m}_{\unicode[STIX]{x1D708}}$
be the maximal ideal of
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
. Let
${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
. Let
![]() $m=\max (n-e_{{\hat{J}}_{\unicode[STIX]{x1D708}}},[n/p])$
.
$m=\max (n-e_{{\hat{J}}_{\unicode[STIX]{x1D708}}},[n/p])$
.
We define a canonical homomorphism
by using the higher dimensional global class field theory in [Reference Kato and Saito23].
3.4.2. By the class field theory of
![]() $X$
[Reference Kato and Saito23], we have a canonical continuous homomorphism
$X$
[Reference Kato and Saito23], we have a canonical continuous homomorphism
where
![]() $d=\dim (X)$
, and hence
$d=\dim (X)$
, and hence
![]() $\unicode[STIX]{x1D712}\in H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
induces a homomorphism
$\unicode[STIX]{x1D712}\in H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
induces a homomorphism
![]() $C_{X}\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
which factors through
$C_{X}\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
which factors through
![]() $H^{d}(X,K_{d}^{M}({\mathcal{O}}_{X},I))$
for some
$H^{d}(X,K_{d}^{M}({\mathcal{O}}_{X},I))$
for some
![]() $I$
(2.4.10).
$I$
(2.4.10).
3.4.3. Let
![]() $Y$
be the closure of
$Y$
be the closure of
![]() $\unicode[STIX]{x1D708}$
in
$\unicode[STIX]{x1D708}$
in
![]() $X$
. We will identify an element
$X$
. We will identify an element
![]() $\mathfrak{p}=(y_{i})_{i}\in P(Y)$
with the element
$\mathfrak{p}=(y_{i})_{i}\in P(Y)$
with the element
![]() $(x_{i})_{i}\in P(X)$
where
$(x_{i})_{i}\in P(X)$
where
![]() $x_{i}=y_{i}$
for
$x_{i}=y_{i}$
for
![]() $0\leqslant i\leqslant d-1$
and
$0\leqslant i\leqslant d-1$
and
![]() $x_{d}$
is the generic point of
$x_{d}$
is the generic point of
![]() $X$
.
$X$
.
Let
![]() $\unicode[STIX]{x1D712}\in F_{\unicode[STIX]{x1D708},n}H^{1}(J,\mathbb{Q}_{p}/Z_{p})$
. For
$\unicode[STIX]{x1D712}\in F_{\unicode[STIX]{x1D708},n}H^{1}(J,\mathbb{Q}_{p}/Z_{p})$
. For
![]() $\mathfrak{p}\in P(X)$
, let
$\mathfrak{p}\in P(X)$
, let
![]() $h_{\mathfrak{p}}:K_{d}^{M}(J)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
be the homomorphism induced by
$h_{\mathfrak{p}}:K_{d}^{M}(J)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
be the homomorphism induced by
![]() $\unicode[STIX]{x1D712}:C_{X}\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
(2.3.3). Then if
$\unicode[STIX]{x1D712}:C_{X}\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
(2.3.3). Then if
![]() $\mathfrak{p}\in P(Y)$
,
$\mathfrak{p}\in P(Y)$
,
![]() $h_{\mathfrak{p}}$
kills
$h_{\mathfrak{p}}$
kills
![]() $U^{n+1}K_{d}^{M}(J)$
where
$U^{n+1}K_{d}^{M}(J)$
where
![]() $U^{\bullet }$
is defined with respect to the discrete valuation ring
$U^{\bullet }$
is defined with respect to the discrete valuation ring
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
. For
${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
. For
![]() $\mathfrak{p}\in P(Y)$
, let
$\mathfrak{p}\in P(Y)$
, let
![]() $s_{\mathfrak{p}}:\mathfrak{m}_{\unicode[STIX]{x1D708}}^{m+1}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{n+1}\otimes _{{\mathcal{O}}_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{d-1}(\log )\rightarrow \mathbb{F}_{p}$
be the homomorphism induced by
$s_{\mathfrak{p}}:\mathfrak{m}_{\unicode[STIX]{x1D708}}^{m+1}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{n+1}\otimes _{{\mathcal{O}}_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{d-1}(\log )\rightarrow \mathbb{F}_{p}$
be the homomorphism induced by
![]() $h_{\mathfrak{p}}$
and the truncated exponential map
$h_{\mathfrak{p}}$
and the truncated exponential map
![]() $E$
of 3.3.5.
$E$
of 3.3.5.
Lemma 3.4.4. There exists a sheaf
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() $Y$
satisfying the following
$Y$
satisfying the following
![]() $\text{(i)}$
and
$\text{(i)}$
and
![]() $\text{(ii)}$
.
$\text{(ii)}$
.
(i)
 ${\mathcal{F}}$
is a coherent
${\mathcal{F}}$
is a coherent
 ${\mathcal{O}}_{X}$
-submodule of the constant sheaf
${\mathcal{O}}_{X}$
-submodule of the constant sheaf
 $\mathfrak{m}_{\unicode[STIX]{x1D708}}^{m+1}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{n+1}\otimes _{{\mathcal{O}}_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{d-1}(\log )$
on
$\mathfrak{m}_{\unicode[STIX]{x1D708}}^{m+1}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{n+1}\otimes _{{\mathcal{O}}_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{d-1}(\log )$
on
 $Y$
and the map
$Y$
and the map
 ${\mathcal{F}}_{\unicode[STIX]{x1D708}}\rightarrow \mathfrak{m}_{\unicode[STIX]{x1D708}}^{m+1}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{n+1}\otimes _{{\mathcal{O}}_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{d-1}(\log )$
is an isomorphism.
${\mathcal{F}}_{\unicode[STIX]{x1D708}}\rightarrow \mathfrak{m}_{\unicode[STIX]{x1D708}}^{m+1}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{n+1}\otimes _{{\mathcal{O}}_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{d-1}(\log )$
is an isomorphism.(ii) Via the map in Lemma 2.3.4,
 $(s_{\mathfrak{p}})_{\mathfrak{p}\in P(Y)}$
defines a homomorphism
$(s_{\mathfrak{p}})_{\mathfrak{p}\in P(Y)}$
defines a homomorphism
 $H^{d-1}(Y,{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
.
$H^{d-1}(Y,{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
.
Proof. Let
![]() $U$
be a regular dense open subset of
$U$
be a regular dense open subset of
![]() $X$
such that
$X$
such that
![]() $D:=U\cap Y$
is also a regular dense open subset of
$D:=U\cap Y$
is also a regular dense open subset of
![]() $Y$
and that
$Y$
and that
![]() $\unicode[STIX]{x1D712}$
is unramified on
$\unicode[STIX]{x1D712}$
is unramified on
![]() $U\smallsetminus D$
. Let
$U\smallsetminus D$
. Let
![]() ${\mathcal{F}}_{U}$
be the coherent
${\mathcal{F}}_{U}$
be the coherent
![]() ${\mathcal{O}}_{U}$
-module
${\mathcal{O}}_{U}$
-module
![]() ${\mathcal{O}}_{U}(-(m+1)D)/{\mathcal{O}}_{U}(-(n+1)D)\otimes _{{\mathcal{O}}_{U}}\unicode[STIX]{x1D6FA}_{U}^{d-1}(\log D)$
. Note that
${\mathcal{O}}_{U}(-(m+1)D)/{\mathcal{O}}_{U}(-(n+1)D)\otimes _{{\mathcal{O}}_{U}}\unicode[STIX]{x1D6FA}_{U}^{d-1}(\log D)$
. Note that
![]() ${\mathcal{F}}_{U,\unicode[STIX]{x1D708}}$
equals
${\mathcal{F}}_{U,\unicode[STIX]{x1D708}}$
equals
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D708}}:=\mathfrak{m}_{\unicode[STIX]{x1D708}}^{m+1}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{n+1}\otimes _{{\mathcal{O}}_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{d-1}(\log )$
. We show that it is sufficient to prove the following (i) and (ii). Let
${\mathcal{F}}_{\unicode[STIX]{x1D708}}:=\mathfrak{m}_{\unicode[STIX]{x1D708}}^{m+1}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{n+1}\otimes _{{\mathcal{O}}_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{d-1}(\log )$
. We show that it is sufficient to prove the following (i) and (ii). Let
![]() $\unicode[STIX]{x1D709}\in Y$
be a point of codimension one.
$\unicode[STIX]{x1D709}\in Y$
be a point of codimension one.
(i) If
 $\unicode[STIX]{x1D709}\in U$
, then for any
$\unicode[STIX]{x1D709}\in U$
, then for any
 $\mathfrak{p}=(y_{i})_{i}\in P(Y)$
such that
$\mathfrak{p}=(y_{i})_{i}\in P(Y)$
such that
 $y_{d-2}=\unicode[STIX]{x1D709}$
,
$y_{d-2}=\unicode[STIX]{x1D709}$
,
 $s_{\mathfrak{p}}$
kills the image of
$s_{\mathfrak{p}}$
kills the image of
 ${\mathcal{F}}_{U,\unicode[STIX]{x1D709}}\rightarrow {\mathcal{F}}_{U,\unicode[STIX]{x1D708}}$
.
${\mathcal{F}}_{U,\unicode[STIX]{x1D709}}\rightarrow {\mathcal{F}}_{U,\unicode[STIX]{x1D708}}$
.(Note that there are only finitely many
 $\unicode[STIX]{x1D709}\in Y$
of codimension one such that
$\unicode[STIX]{x1D709}\in Y$
of codimension one such that
 $\unicode[STIX]{x1D709}\notin U$
.)
$\unicode[STIX]{x1D709}\notin U$
.)(ii) There is a finitely generated
 ${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
-submodule
${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
-submodule
 ${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
of
${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
of
 ${\mathcal{F}}_{\unicode[STIX]{x1D708}}$
which generates
${\mathcal{F}}_{\unicode[STIX]{x1D708}}$
which generates
 ${\mathcal{F}}_{\unicode[STIX]{x1D708}}$
over
${\mathcal{F}}_{\unicode[STIX]{x1D708}}$
over
 ${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
having the following property: For any
${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
having the following property: For any
 $\mathfrak{p}=(y_{i})_{i}\in P(Y)$
such that
$\mathfrak{p}=(y_{i})_{i}\in P(Y)$
such that
 $y_{d-2}=\unicode[STIX]{x1D709}$
,
$y_{d-2}=\unicode[STIX]{x1D709}$
,
 $s_{\mathfrak{p}}$
kills
$s_{\mathfrak{p}}$
kills
 ${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
.
${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
.
Let
![]() $j:U\rightarrow X$
be the open immersion and
$j:U\rightarrow X$
be the open immersion and
![]() ${\mathcal{F}}$
be a coherent
${\mathcal{F}}$
be a coherent
![]() ${\mathcal{O}}_{X}$
-module such that
${\mathcal{O}}_{X}$
-module such that
![]() ${\mathcal{F}}|_{U}={\mathcal{F}}_{U}$
and
${\mathcal{F}}|_{U}={\mathcal{F}}_{U}$
and
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
is given in (ii) for each codimension one point
${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
is given in (ii) for each codimension one point
![]() $\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D709}$
of
![]() $Y$
not contained in
$Y$
not contained in
![]() $U$
. Then,
$U$
. Then,
![]() $(s_{\mathfrak{p}})_{\mathfrak{p}\in P(Y)}$
satisfies the conditions (i) and (ii) in Lemma 2.3.4 for
$(s_{\mathfrak{p}})_{\mathfrak{p}\in P(Y)}$
satisfies the conditions (i) and (ii) in Lemma 2.3.4 for
![]() $H^{d-1}(Y,{\mathcal{F}})$
since the kernel of
$H^{d-1}(Y,{\mathcal{F}})$
since the kernel of
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D708}}=H_{\unicode[STIX]{x1D708}}^{0}(Y,{\mathcal{F}})\rightarrow H_{\unicode[STIX]{x1D709}}^{1}(Y,{\mathcal{F}})$
is
${\mathcal{F}}_{\unicode[STIX]{x1D708}}=H_{\unicode[STIX]{x1D708}}^{0}(Y,{\mathcal{F}})\rightarrow H_{\unicode[STIX]{x1D709}}^{1}(Y,{\mathcal{F}})$
is
![]() ${\mathcal{F}}_{U,\unicode[STIX]{x1D709}}$
(resp.
${\mathcal{F}}_{U,\unicode[STIX]{x1D709}}$
(resp.
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
) for codimension one point
${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
) for codimension one point
![]() $\unicode[STIX]{x1D709}$
in
$\unicode[STIX]{x1D709}$
in
![]() $U$
(resp. not contained in
$U$
(resp. not contained in
![]() $U$
).
$U$
).
Note that for any
![]() $\mathfrak{p}=(y_{i})_{i}\in P(Y)$
, we have
$\mathfrak{p}=(y_{i})_{i}\in P(Y)$
, we have
![]() $\sum _{\mathfrak{p}^{\prime }\in R(\mathfrak{p})}h_{\mathfrak{p}^{\prime }}=0$
on
$\sum _{\mathfrak{p}^{\prime }\in R(\mathfrak{p})}h_{\mathfrak{p}^{\prime }}=0$
on
![]() $K_{d}^{M}(J)$
where
$K_{d}^{M}(J)$
where
![]() $R(\mathfrak{p})$
denotes the set of
$R(\mathfrak{p})$
denotes the set of
![]() $\mathfrak{p}^{\prime }=(x_{i})_{i}\in P(X)$
such that
$\mathfrak{p}^{\prime }=(x_{i})_{i}\in P(X)$
such that
![]() $x_{i}=y_{i}$
for
$x_{i}=y_{i}$
for
![]() $0\leqslant i\leqslant d-2$
.
$0\leqslant i\leqslant d-2$
.
We prove (i). Let
![]() $\unicode[STIX]{x1D70B}$
be an element of
$\unicode[STIX]{x1D70B}$
be an element of
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
which defines
${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
which defines
![]() $Y$
at
$Y$
at
![]() $\unicode[STIX]{x1D709}$
. For
$\unicode[STIX]{x1D709}$
. For
![]() $\mathfrak{p}$
as in (i) and for
$\mathfrak{p}$
as in (i) and for
![]() $g\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
and
$g\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
and
![]() $u_{1},\ldots ,u_{d-1}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
, we have
$u_{1},\ldots ,u_{d-1}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
, we have
![]() $s_{\mathfrak{p}}(\unicode[STIX]{x1D70B}^{m+1}g\,d\log (u_{1})\wedge \cdots \wedge d\log (u_{d-1}))=h_{\mathfrak{p}}(\{E(\unicode[STIX]{x1D70B}^{m+1}g),u_{1},\ldots ,u_{d-1}\})$
. This element
$s_{\mathfrak{p}}(\unicode[STIX]{x1D70B}^{m+1}g\,d\log (u_{1})\wedge \cdots \wedge d\log (u_{d-1}))=h_{\mathfrak{p}}(\{E(\unicode[STIX]{x1D70B}^{m+1}g),u_{1},\ldots ,u_{d-1}\})$
. This element
![]() $\{E(\unicode[STIX]{x1D70B}^{m+1}g),u_{1},\ldots ,u_{d-1}\}\in K_{d}^{M}(J)/U^{n+1}K_{d}^{M}(J)$
belongs to the subgroup of
$\{E(\unicode[STIX]{x1D70B}^{m+1}g),u_{1},\ldots ,u_{d-1}\}\in K_{d}^{M}(J)/U^{n+1}K_{d}^{M}(J)$
belongs to the subgroup of
![]() $K_{d}^{M}(J)/U^{n+1}K_{d}^{M}(J)$
generated by all elements of the form
$K_{d}^{M}(J)/U^{n+1}K_{d}^{M}(J)$
generated by all elements of the form
![]() $\{u_{1},\ldots ,u_{d}\}\in K_{d}^{M}(J)$
such that
$\{u_{1},\ldots ,u_{d}\}\in K_{d}^{M}(J)$
such that
![]() $u_{1},\ldots ,u_{d}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
. For any
$u_{1},\ldots ,u_{d}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
. For any
![]() $\mathfrak{p}^{\prime }=(x_{i})_{i}\in R(\mathfrak{p})\smallsetminus \{\mathfrak{p}\}$
,
$\mathfrak{p}^{\prime }=(x_{i})_{i}\in R(\mathfrak{p})\smallsetminus \{\mathfrak{p}\}$
,
![]() $h_{\mathfrak{p}^{\prime }}:K_{d}^{M}(J)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
kills such
$h_{\mathfrak{p}^{\prime }}:K_{d}^{M}(J)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
kills such
![]() $\{u_{1},\ldots ,u_{d}\}$
because
$\{u_{1},\ldots ,u_{d}\}$
because
![]() $\unicode[STIX]{x1D712}$
is unramified at
$\unicode[STIX]{x1D712}$
is unramified at
![]() $x_{d-1}$
and hence
$x_{d-1}$
and hence
![]() $h_{\mathfrak{p}^{\prime }}$
factors through the boundary map
$h_{\mathfrak{p}^{\prime }}$
factors through the boundary map
![]() $K_{d}^{M}(J)\rightarrow K_{d-1}^{M}(\unicode[STIX]{x1D705}(x_{d-1}))$
(
$K_{d}^{M}(J)\rightarrow K_{d-1}^{M}(\unicode[STIX]{x1D705}(x_{d-1}))$
(
![]() $\unicode[STIX]{x1D705}$
denotes the residue field) which kills
$\unicode[STIX]{x1D705}$
denotes the residue field) which kills
![]() $\{u_{1},\ldots ,u_{d}\}$
. Hence
$\{u_{1},\ldots ,u_{d}\}$
. Hence
![]() $h_{\mathfrak{p}}(\{u_{1},\ldots ,u_{d}\})=0$
.
$h_{\mathfrak{p}}(\{u_{1},\ldots ,u_{d}\})=0$
.
We prove (ii). Take an element
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
which is a prime element of the discrete valuation ring
${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
which is a prime element of the discrete valuation ring
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
. Take an element
${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
. Take an element
![]() $f\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
having the following properties (a1) and (a2). (a1)
$f\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
having the following properties (a1) and (a2). (a1)
![]() $f$
is a unit in
$f$
is a unit in
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
. (a2)
${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
. (a2)
![]() $\text{ord}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70B}^{m+1}f)>\text{Sw}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D712})$
for any point
$\text{ord}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70B}^{m+1}f)>\text{Sw}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D712})$
for any point
![]() $\unicode[STIX]{x1D707}$
of
$\unicode[STIX]{x1D707}$
of
![]() $X$
of codimension one such that
$X$
of codimension one such that
![]() $\unicode[STIX]{x1D709}\in \overline{\{\unicode[STIX]{x1D707}\}}$
and
$\unicode[STIX]{x1D709}\in \overline{\{\unicode[STIX]{x1D707}\}}$
and
![]() $\unicode[STIX]{x1D707}\neq \unicode[STIX]{x1D708}$
and such that either
$\unicode[STIX]{x1D707}\neq \unicode[STIX]{x1D708}$
and such that either
![]() $\unicode[STIX]{x1D712}$
ramifies at
$\unicode[STIX]{x1D712}$
ramifies at
![]() $\unicode[STIX]{x1D707}$
or
$\unicode[STIX]{x1D707}$
or
![]() $\text{ord}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70B})>0$
. Let
$\text{ord}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70B})>0$
. Let
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
be the
${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
be the
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
-submodule of
${\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
-submodule of
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D708}}$
generated by the images of
${\mathcal{F}}_{\unicode[STIX]{x1D708}}$
generated by the images of
![]() $\unicode[STIX]{x1D70B}^{m+1}f\otimes \unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D709}}^{d-1}$
and
$\unicode[STIX]{x1D70B}^{m+1}f\otimes \unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D709}}^{d-1}$
and
![]() $\unicode[STIX]{x1D70B}^{m+1}f\otimes \unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D709}}^{d-2}\wedge d\log (\unicode[STIX]{x1D70B})$
. We prove that
$\unicode[STIX]{x1D70B}^{m+1}f\otimes \unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D709}}^{d-2}\wedge d\log (\unicode[STIX]{x1D70B})$
. We prove that
![]() $s_{\mathfrak{p}}$
kills
$s_{\mathfrak{p}}$
kills
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
. For
${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
. For
![]() $g\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
and
$g\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
and
![]() $u_{1},\ldots ,u_{d-1}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
,
$u_{1},\ldots ,u_{d-1}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
,
![]() $s_{\mathfrak{p}}(\unicode[STIX]{x1D70B}^{m+1}f\otimes g\,d\log (u_{1})\wedge \cdots \wedge d\log (u_{d-1}))=h_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})$
where
$s_{\mathfrak{p}}(\unicode[STIX]{x1D70B}^{m+1}f\otimes g\,d\log (u_{1})\wedge \cdots \wedge d\log (u_{d-1}))=h_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})$
where
![]() $\unicode[STIX]{x1D6FC}=\{E(\unicode[STIX]{x1D70B}^{m+1}fg),u_{1},\ldots ,u_{d-1}\}\in K_{d}^{M}(J)$
. To prove that
$\unicode[STIX]{x1D6FC}=\{E(\unicode[STIX]{x1D70B}^{m+1}fg),u_{1},\ldots ,u_{d-1}\}\in K_{d}^{M}(J)$
. To prove that
![]() $h_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})=0$
, it is enough to prove that
$h_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})=0$
, it is enough to prove that
![]() $h_{\mathfrak{p}^{\prime }}(\unicode[STIX]{x1D6FC})=0$
for any
$h_{\mathfrak{p}^{\prime }}(\unicode[STIX]{x1D6FC})=0$
for any
![]() $\mathfrak{p}^{\prime }=(x_{i})_{i}\in R(\mathfrak{p})\smallsetminus \{\mathfrak{p}\}$
. Let
$\mathfrak{p}^{\prime }=(x_{i})_{i}\in R(\mathfrak{p})\smallsetminus \{\mathfrak{p}\}$
. Let
![]() $\unicode[STIX]{x1D707}=x_{d-1}$
. Assume first that either
$\unicode[STIX]{x1D707}=x_{d-1}$
. Assume first that either
![]() $\unicode[STIX]{x1D712}$
ramifies at
$\unicode[STIX]{x1D712}$
ramifies at
![]() $\unicode[STIX]{x1D707}$
or
$\unicode[STIX]{x1D707}$
or
![]() $\text{ord}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70B})>0$
. Then
$\text{ord}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D70B})>0$
. Then
![]() $\unicode[STIX]{x1D6FC}\in U_{\unicode[STIX]{x1D707}}^{s+1}K_{d}^{M}(J)$
where
$\unicode[STIX]{x1D6FC}\in U_{\unicode[STIX]{x1D707}}^{s+1}K_{d}^{M}(J)$
where
![]() $s=\text{Sw}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D712})$
and
$s=\text{Sw}_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D712})$
and
![]() $U_{\unicode[STIX]{x1D707}}^{\bullet }$
is the filtration defined for the discrete valuation ring
$U_{\unicode[STIX]{x1D707}}^{\bullet }$
is the filtration defined for the discrete valuation ring
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D707}}$
. Hence
${\mathcal{O}}_{X,\unicode[STIX]{x1D707}}$
. Hence
![]() $h_{\mathfrak{p}^{\prime }}$
kills
$h_{\mathfrak{p}^{\prime }}$
kills
![]() $\unicode[STIX]{x1D6FC}$
. Assume next
$\unicode[STIX]{x1D6FC}$
. Assume next
![]() $\unicode[STIX]{x1D712}$
is unramified at
$\unicode[STIX]{x1D712}$
is unramified at
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\unicode[STIX]{x1D70B}$
is a unit at
$\unicode[STIX]{x1D70B}$
is a unit at
![]() $\unicode[STIX]{x1D707}$
. Then
$\unicode[STIX]{x1D707}$
. Then
![]() $h_{\mathfrak{p}^{\prime }}$
factors through the boundary map
$h_{\mathfrak{p}^{\prime }}$
factors through the boundary map
![]() $K_{d}^{M}(J)\rightarrow K_{d-1}^{M}(\unicode[STIX]{x1D705}(\unicode[STIX]{x1D707}))$
which kills
$K_{d}^{M}(J)\rightarrow K_{d-1}^{M}(\unicode[STIX]{x1D705}(\unicode[STIX]{x1D707}))$
which kills
![]() $\unicode[STIX]{x1D6FC}$
.◻
$\unicode[STIX]{x1D6FC}$
.◻
3.4.5. By Serre–Grothendieck duality of the cohomology of coherent sheaves [Reference Hartshorne13], we have a canonical isomorphism
where
![]() ${\mathcal{F}}$
ranges over coherent
${\mathcal{F}}$
ranges over coherent
![]() ${\mathcal{O}}_{X}$
-modules
${\mathcal{O}}_{X}$
-modules
![]() ${\mathcal{F}}$
as in (i) in 3.4.4. (The inductive system is given by making
${\mathcal{F}}$
as in (i) in 3.4.4. (The inductive system is given by making
![]() ${\mathcal{F}}$
smaller and smaller. If
${\mathcal{F}}$
smaller and smaller. If
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() ${\mathcal{F}}^{\prime }$
are as in (i) in 3.4.4 and
${\mathcal{F}}^{\prime }$
are as in (i) in 3.4.4 and
![]() ${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
, the canonical map
${\mathcal{F}}^{\prime }\subset {\mathcal{F}}$
, the canonical map
![]() $H^{d-1}(Y,{\mathcal{F}}^{\prime })\rightarrow H^{d-1}(Y,{\mathcal{F}})$
is a surjective map of finite abelian groups.) By 3.4.4,
$H^{d-1}(Y,{\mathcal{F}}^{\prime })\rightarrow H^{d-1}(Y,{\mathcal{F}})$
is a surjective map of finite abelian groups.) By 3.4.4,
![]() $\unicode[STIX]{x1D712}\in F_{\unicode[STIX]{x1D708},n}H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
gives an element of the left hand side of this isomorphism, and hence gives an element of
$\unicode[STIX]{x1D712}\in F_{\unicode[STIX]{x1D708},n}H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
gives an element of the left hand side of this isomorphism, and hence gives an element of
![]() $\mathfrak{m}_{\unicode[STIX]{x1D708}}^{-n}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{-m}\otimes _{O_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{1}(\log )$
. This is our
$\mathfrak{m}_{\unicode[STIX]{x1D708}}^{-n}/\mathfrak{m}_{\unicode[STIX]{x1D708}}^{-m}\otimes _{O_{X,\unicode[STIX]{x1D708}}}\unicode[STIX]{x1D6FA}_{X,\unicode[STIX]{x1D708}}^{1}(\log )$
. This is our
![]() $\text{Rsw}_{X,\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D712})$
.
$\text{Rsw}_{X,\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D712})$
.
3.5 Rsw in general
We prove our statements in 3.1.1 and 3.1.2.
Lemma 3.5.1. Let
![]() $K$
be a complete discrete valuation field whose residue field
$K$
be a complete discrete valuation field whose residue field
![]() $F$
is a finitely generated field over
$F$
is a finitely generated field over
![]() $\mathbb{F}_{p}$
, and let
$\mathbb{F}_{p}$
, and let
![]() $\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Then there exist a proper normal integral scheme
$\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Then there exist a proper normal integral scheme
![]() $X$
over
$X$
over
![]() $\mathbb{Z}$
such that
$\mathbb{Z}$
such that
![]() $X(\mathbb{R})=\emptyset$
, a point
$X(\mathbb{R})=\emptyset$
, a point
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $X$
of codimension one, and an isomorphism
$X$
of codimension one, and an isomorphism
![]() $\unicode[STIX]{x1D6FC}$
between
$\unicode[STIX]{x1D6FC}$
between
![]() $O_{K}$
and the completion of the local ring
$O_{K}$
and the completion of the local ring
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
such that if
${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
such that if
![]() $J$
denotes the function field of
$J$
denotes the function field of
![]() $X$
,
$X$
,
![]() $\unicode[STIX]{x1D712}$
comes from
$\unicode[STIX]{x1D712}$
comes from
![]() $H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
via
$H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
via
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Proof. If
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
, take a proper normal integral scheme
$p$
, take a proper normal integral scheme
![]() $Y$
over
$Y$
over
![]() $\mathbb{F}_{p}$
with function field
$\mathbb{F}_{p}$
with function field
![]() $F$
, let
$F$
, let
![]() $X=\mathbf{P}_{Y}^{1}$
, and let
$X=\mathbf{P}_{Y}^{1}$
, and let
![]() $\unicode[STIX]{x1D708}$
be the generic point of the image of any section
$\unicode[STIX]{x1D708}$
be the generic point of the image of any section
![]() $Y\rightarrow \mathbf{P}_{Y}^{1}$
. Next assume
$Y\rightarrow \mathbf{P}_{Y}^{1}$
. Next assume
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $0$
. Let
$0$
. Let
![]() $(t_{i})_{1\leqslant i\leqslant r}$
be a transcendental basis of
$(t_{i})_{1\leqslant i\leqslant r}$
be a transcendental basis of
![]() $F$
over
$F$
over
![]() $\mathbb{F}_{p}$
and let
$\mathbb{F}_{p}$
and let
![]() $(T_{i})_{1\leqslant i\leqslant r}$
be its lifting to
$(T_{i})_{1\leqslant i\leqslant r}$
be its lifting to
![]() $O_{K}$
. Let
$O_{K}$
. Let
![]() $J_{0}=\mathbb{Q}(T_{1},\ldots ,T_{r})$
. Then the algebraic closure
$J_{0}=\mathbb{Q}(T_{1},\ldots ,T_{r})$
. Then the algebraic closure
![]() $J_{\infty }$
of
$J_{\infty }$
of
![]() $J_{0}$
in
$J_{0}$
in
![]() $K$
is a henselian discrete valuation field whose completion is
$K$
is a henselian discrete valuation field whose completion is
![]() $K$
, and hence
$K$
, and hence
![]() $H^{1}(J_{\infty },\mathbb{Q}_{p}/\mathbb{Z}_{p})\overset{\cong }{\rightarrow }H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Hence
$H^{1}(J_{\infty },\mathbb{Q}_{p}/\mathbb{Z}_{p})\overset{\cong }{\rightarrow }H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Hence
![]() $\unicode[STIX]{x1D712}$
comes from
$\unicode[STIX]{x1D712}$
comes from
![]() $H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
for some finite extension
$H^{1}(J,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
for some finite extension
![]() $J$
of
$J$
of
![]() $J_{0}$
in
$J_{0}$
in
![]() $J_{\infty }$
such that
$J_{\infty }$
such that
![]() $J$
is dense in
$J$
is dense in
![]() $K$
. Let
$K$
. Let
![]() $X$
be the integral closure of
$X$
be the integral closure of
![]() $\mathbf{P}_{\mathbb{Z}}^{r}\supset \text{Spec}(\mathbb{Z}[T_{1},\ldots ,T_{r}])$
in
$\mathbf{P}_{\mathbb{Z}}^{r}\supset \text{Spec}(\mathbb{Z}[T_{1},\ldots ,T_{r}])$
in
![]() $J$
. By replacing
$J$
. By replacing
![]() $J$
by a bigger
$J$
by a bigger
![]() $J$
, we have
$J$
, we have
![]() $X(\mathbb{R})=\emptyset$
. (Indeed,
$X(\mathbb{R})=\emptyset$
. (Indeed,
![]() $K$
contains a purely imaginary algebraic number
$K$
contains a purely imaginary algebraic number
![]() $\unicode[STIX]{x1D6FD}$
, for example, a square root of
$\unicode[STIX]{x1D6FD}$
, for example, a square root of
![]() $1-p$
if
$1-p$
if
![]() $p\neq 2$
, and a square root of
$p\neq 2$
, and a square root of
![]() $-7=1-8$
in the case
$-7=1-8$
in the case
![]() $p=2$
. By replacing
$p=2$
. By replacing
![]() $J$
by
$J$
by
![]() $J(\unicode[STIX]{x1D6FD})\subset K$
, we have
$J(\unicode[STIX]{x1D6FD})\subset K$
, we have
![]() $\unicode[STIX]{x1D6FD}\in J$
. For such
$\unicode[STIX]{x1D6FD}\in J$
. For such
![]() $J$
,
$J$
,
![]() $X(\mathbb{R})=\emptyset$
.) Let
$X(\mathbb{R})=\emptyset$
.) Let
![]() $\unicode[STIX]{x1D708}$
be the image of the closed point of
$\unicode[STIX]{x1D708}$
be the image of the closed point of
![]() $\text{Spec}(O_{K})$
under
$\text{Spec}(O_{K})$
under
![]() $\text{Spec}(O_{K})\rightarrow X$
.◻
$\text{Spec}(O_{K})\rightarrow X$
.◻
Lemma 3.5.2. Let
![]() $K$
be a complete discrete valuation field whose residue field
$K$
be a complete discrete valuation field whose residue field
![]() $F$
is a function field in
$F$
is a function field in
![]() $r$
variables over
$r$
variables over
![]() $\mathbb{F}_{p}$
, and let
$\mathbb{F}_{p}$
, and let
![]() $\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Then there is a unique element
$\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Then there is a unique element
![]() $\text{Rsw}_{K}(\unicode[STIX]{x1D712})$
of
$\text{Rsw}_{K}(\unicode[STIX]{x1D712})$
of
![]() $\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
(
$\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
(
![]() $m=\max (n-e_{K},[n/p])$
) having the following property
$m=\max (n-e_{K},[n/p])$
) having the following property
![]() $\text{(i)}$
for any
$\text{(i)}$
for any
![]() $(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})$
as in 3.5.1.
$(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})$
as in 3.5.1.
![]() $\text{(i)}$
Let
$\text{(i)}$
Let
![]() $J$
be as in 3.5.1 and let
$J$
be as in 3.5.1 and let
![]() $Y\subset X$
be the closure of
$Y\subset X$
be the closure of
![]() $\unicode[STIX]{x1D708}$
. Then for any
$\unicode[STIX]{x1D708}$
. Then for any
![]() $v\in Pl(Y)\subset Pl(X)$
, the image of
$v\in Pl(Y)\subset Pl(X)$
, the image of
![]() $\text{Rsw}_{K}(\unicode[STIX]{x1D712})$
in
$\text{Rsw}_{K}(\unicode[STIX]{x1D712})$
in
![]() $\mathfrak{m}_{J_{v}}^{-n}/\mathfrak{m}_{J_{v}}^{-m}\otimes _{O_{J_{v}}}\unicode[STIX]{x1D6FA}_{O_{J_{v}}}^{1}(\log )$
coincides with the element
$\mathfrak{m}_{J_{v}}^{-n}/\mathfrak{m}_{J_{v}}^{-m}\otimes _{O_{J_{v}}}\unicode[STIX]{x1D6FA}_{O_{J_{v}}}^{1}(\log )$
coincides with the element
![]() $\text{Rsw}_{J_{v}}(\unicode[STIX]{x1D712}_{J_{v}})$
defined in Section 3.3. Here the inclusion map
$\text{Rsw}_{J_{v}}(\unicode[STIX]{x1D712}_{J_{v}})$
defined in Section 3.3. Here the inclusion map
![]() $Pl(Y)\subset Pl(X)$
sends
$Pl(Y)\subset Pl(X)$
sends
![]() $v\in Pl(Y)$
to the ring of all elements of
$v\in Pl(Y)$
to the ring of all elements of
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
whose residue classes belong to
${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
whose residue classes belong to
![]() $v$
, and we regard
$v$
, and we regard
![]() $K$
as a subfield of
$K$
as a subfield of
![]() $J_{v}$
via
$J_{v}$
via
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
The proof of 3.5.2 is given after preparations 3.5.3 and 3.5.4.
Lemma 3.5.3. Let
![]() $Y$
be an integral scheme over
$Y$
be an integral scheme over
![]() $\mathbb{F}_{p}$
of finite type, let
$\mathbb{F}_{p}$
of finite type, let
![]() $F$
be the function field of
$F$
be the function field of
![]() $Y$
, and let
$Y$
, and let
![]() $v\in Pl(Y)$
. Then we have an isomorphism
$v\in Pl(Y)$
. Then we have an isomorphism
where
![]() $F\rightarrow F$
in the tensor product is
$F\rightarrow F$
in the tensor product is
![]() $x\mapsto x^{p}$
.
$x\mapsto x^{p}$
.
Proof. This follows from (3) of 2.4.8. ◻
Lemma 3.5.4. Let
![]() $(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC},J)$
be as in 3.5.1 and let
$(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC},J)$
be as in 3.5.1 and let
![]() $Y\subset X$
be the closure of
$Y\subset X$
be the closure of
![]() $\unicode[STIX]{x1D708}$
. Then for any
$\unicode[STIX]{x1D708}$
. Then for any
![]() $v\in Pl(Y)\subset Pl(X)$
and for any integer
$v\in Pl(Y)\subset Pl(X)$
and for any integer
![]() $t$
such that
$t$
such that
![]() $1\leqslant t\leqslant e_{K}$
, the map
$1\leqslant t\leqslant e_{K}$
, the map
is injective. More precisely, the map
![]() $O_{J_{v}}\otimes _{O_{K}}(\text{l.h.s.})\rightarrow (\text{r.h.s.})$
is bijective.
$O_{J_{v}}\otimes _{O_{K}}(\text{l.h.s.})\rightarrow (\text{r.h.s.})$
is bijective.
Proof. If
![]() $F$
denotes the residue field of
$F$
denotes the residue field of
![]() $K$
, the residue field of
$K$
, the residue field of
![]() $J_{v}$
is identified with
$J_{v}$
is identified with
![]() $F_{v}$
. By 3.5.3, a
$F_{v}$
. By 3.5.3, a
![]() $p$
-base of
$p$
-base of
![]() $F$
is a
$F$
is a
![]() $p$
-base of
$p$
-base of
![]() $F_{v}$
. Hence 3.5.4 is reduced to 2.1.3.◻
$F_{v}$
. Hence 3.5.4 is reduced to 2.1.3.◻
3.5.5. We prove 3.5.2. Take
![]() $(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC},J)$
as in 3.5.1 and let
$(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC},J)$
as in 3.5.1 and let
![]() $Y\subset X$
be the closure of
$Y\subset X$
be the closure of
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
By Section 3.4,
![]() $\unicode[STIX]{x1D712}$
defines an element of
$\unicode[STIX]{x1D712}$
defines an element of
![]() $\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
which we denote by
$\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
which we denote by
![]() $\text{Rsw}_{K}(\unicode[STIX]{x1D712})$
. By the construction of this element in Section 3.4, it is sent to
$\text{Rsw}_{K}(\unicode[STIX]{x1D712})$
. By the construction of this element in Section 3.4, it is sent to
![]() $\text{Rsw}_{J_{v}}(\unicode[STIX]{x1D712}_{J_{v}})$
for any
$\text{Rsw}_{J_{v}}(\unicode[STIX]{x1D712}_{J_{v}})$
for any
![]() $v\in Pl(Y)\subset Pl(X)$
.
$v\in Pl(Y)\subset Pl(X)$
.
If we change
![]() $(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})$
by
$(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})$
by
![]() $(X^{\prime },\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
, since the associated
$(X^{\prime },\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
, since the associated
![]() $Y$
and
$Y$
and
![]() $Y^{\prime }$
are birational, there is
$Y^{\prime }$
are birational, there is
![]() $v\in Pl(Y)$
which belongs also to
$v\in Pl(Y)$
which belongs also to
![]() $Pl(Y^{\prime })$
. By [Reference Kato18, Lemma 1], there is a unique
$Pl(Y^{\prime })$
. By [Reference Kato18, Lemma 1], there is a unique
![]() $K$
-isomorphism of complete discrete valuation fields between
$K$
-isomorphism of complete discrete valuation fields between
![]() $J_{v}$
and
$J_{v}$
and
![]() $J_{v}^{\prime }$
which induces the identity map of the residue field
$J_{v}^{\prime }$
which induces the identity map of the residue field
![]() $F_{v}$
. By the injectivity 3.5.4, we have that
$F_{v}$
. By the injectivity 3.5.4, we have that
![]() $\text{Res}_{K}(\unicode[STIX]{x1D712})$
defined by using
$\text{Res}_{K}(\unicode[STIX]{x1D712})$
defined by using
![]() $(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})$
coincides with that defined by using
$(X,\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC})$
coincides with that defined by using
![]() $(X^{\prime },\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
.
$(X^{\prime },\unicode[STIX]{x1D708}^{\prime },\unicode[STIX]{x1D6FC}^{\prime })$
.
3.5.6. Now we prove the unique existence of the definition of
![]() $\text{Rsw}$
satisfying (i) and (ii) in 3.1.2.
$\text{Rsw}$
satisfying (i) and (ii) in 3.1.2.
Note that
![]() $K=\bigcup _{J}J$
where
$K=\bigcup _{J}J$
where
![]() $J$
ranges over subfields of
$J$
ranges over subfields of
![]() $K$
which are finitely generated over the prime field. For a sufficiently large such
$K$
which are finitely generated over the prime field. For a sufficiently large such
![]() $J$
,
$J$
,
![]() $J$
contains a prime element of
$J$
contains a prime element of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D712}$
comes from
$\unicode[STIX]{x1D712}$
comes from
![]() $F_{n}H^{1}({\hat{J}},\mathbb{Q}_{p}/\mathbb{Z}_{p})$
where
$F_{n}H^{1}({\hat{J}},\mathbb{Q}_{p}/\mathbb{Z}_{p})$
where
![]() ${\hat{J}}$
denotes the completion of
${\hat{J}}$
denotes the completion of
![]() $J$
for the restriction of the discrete valuation of
$J$
for the restriction of the discrete valuation of
![]() $K$
to
$K$
to
![]() $J$
. By 3.5.2 applied to
$J$
. By 3.5.2 applied to
![]() ${\hat{J}}$
, we get an element of
${\hat{J}}$
, we get an element of
![]() $\mathfrak{m}_{{\hat{J}}}^{-n}/\mathfrak{m}_{{\hat{J}}}^{-m}\otimes _{O_{{\hat{J}}}}\unicode[STIX]{x1D6FA}_{O_{{\hat{J}}}}^{1}(\log )$
, and hence an element
$\mathfrak{m}_{{\hat{J}}}^{-n}/\mathfrak{m}_{{\hat{J}}}^{-m}\otimes _{O_{{\hat{J}}}}\unicode[STIX]{x1D6FA}_{O_{{\hat{J}}}}^{1}(\log )$
, and hence an element
![]() $\text{Rsw}(\unicode[STIX]{x1D712})$
of
$\text{Rsw}(\unicode[STIX]{x1D712})$
of
![]() $\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
as the image of it.
$\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
as the image of it.
We show that this element
![]() $\text{Rsw}(\unicode[STIX]{x1D712})$
is independent of such
$\text{Rsw}(\unicode[STIX]{x1D712})$
is independent of such
![]() $J$
. Let
$J$
. Let
![]() $J$
and
$J$
and
![]() $J^{\prime }$
be two such fields. We may assume
$J^{\prime }$
be two such fields. We may assume
![]() $J\subset J^{\prime }$
. Then the residue field
$J\subset J^{\prime }$
. Then the residue field
![]() $E^{\prime }$
of
$E^{\prime }$
of
![]() $J^{\prime }$
is an extension of finite type of the residue field
$J^{\prime }$
is an extension of finite type of the residue field
![]() $E$
of
$E$
of
![]() $J$
. Choosing a transcendental basis of
$J$
. Choosing a transcendental basis of
![]() $E^{\prime }$
of
$E^{\prime }$
of
![]() $E$
, we find embeddings
$E$
, we find embeddings
![]() $J\rightarrow M$
and
$J\rightarrow M$
and
![]() $J^{\prime }\rightarrow M^{\prime }$
to higher dimensional local field such that
$J^{\prime }\rightarrow M^{\prime }$
to higher dimensional local field such that
![]() $M^{\prime }$
is a successive extension of those in 3.3.6. Thus it follows from the injectivity 3.5.4.
$M^{\prime }$
is a successive extension of those in 3.3.6. Thus it follows from the injectivity 3.5.4.
It is clear that this
![]() $\text{Rsw}$
has the properties (i) and (ii) in 3.1.2, and the uniqueness follows from 3.5.4.
$\text{Rsw}$
has the properties (i) and (ii) in 3.1.2, and the uniqueness follows from 3.5.4.
Lemma 3.5.7. Let
![]() $n$
and
$n$
and
![]() $m$
be as in 3.1.1. Then for an integer
$m$
be as in 3.1.1. Then for an integer
![]() $i$
such that
$i$
such that
![]() $m<i<n$
,
$m<i<n$
,
![]() $\text{Rsw}:F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
sends
$\text{Rsw}:F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
sends
![]() $F_{i}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
to
$F_{i}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
to
![]() $\mathfrak{m}_{K}^{-i}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
, and the induced homomorphism
$\mathfrak{m}_{K}^{-i}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
, and the induced homomorphism
![]() $F_{i}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})/F_{i-1}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow \mathfrak{m}_{K}^{-i}/\mathfrak{m}_{K}^{-i+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
coincides with the refined Swan conductor mod
$F_{i}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})/F_{i-1}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow \mathfrak{m}_{K}^{-i}/\mathfrak{m}_{K}^{-i+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
coincides with the refined Swan conductor mod
![]() $\mathfrak{m}_{K}$
(3).
$\mathfrak{m}_{K}$
(3).
Proof. If the residue field
![]() $F$
is an
$F$
is an
![]() $r$
-dimensional local field, then by [Reference Kato20, (6.5)], the refined Swan conductor
$r$
-dimensional local field, then by [Reference Kato20, (6.5)], the refined Swan conductor
![]() $\text{rsw}\unicode[STIX]{x1D712}$
mod
$\text{rsw}\unicode[STIX]{x1D712}$
mod
![]() $\mathfrak{m}_{K}$
is characterized by the property:
$\mathfrak{m}_{K}$
is characterized by the property:
![]() $\{\unicode[STIX]{x1D712},1+a\unicode[STIX]{x1D70B}^{n},u_{1},\ldots ,u_{r}\}=\text{Res}_{F}R_{b}(a\unicode[STIX]{x1D70B}^{n}\text{rsw}\unicode[STIX]{x1D712}\wedge d\log u_{1}\wedge \cdots \wedge d\log u_{r})$
for
$\{\unicode[STIX]{x1D712},1+a\unicode[STIX]{x1D70B}^{n},u_{1},\ldots ,u_{r}\}=\text{Res}_{F}R_{b}(a\unicode[STIX]{x1D70B}^{n}\text{rsw}\unicode[STIX]{x1D712}\wedge d\log u_{1}\wedge \cdots \wedge d\log u_{r})$
for
![]() $n=\text{sw}\unicode[STIX]{x1D712}$
,
$n=\text{sw}\unicode[STIX]{x1D712}$
,
![]() $a\in {\mathcal{O}}_{K},u_{1},\ldots ,u_{r-1}\in {\mathcal{O}}_{K}^{\times },u_{r}\in K^{\times }$
. Hence the assertion follows in this case. The general case follows by the injectivity 3.5.4.◻
$a\in {\mathcal{O}}_{K},u_{1},\ldots ,u_{r-1}\in {\mathcal{O}}_{K}^{\times },u_{r}\in K^{\times }$
. Hence the assertion follows in this case. The general case follows by the injectivity 3.5.4.◻
Proposition 3.5.8. Let
![]() $n$
and
$n$
and
![]() $m$
be as in 3.1.1.
$m$
be as in 3.1.1.
(1) The map
 $\text{Rsw}:F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})/F_{m}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
is injective.
$\text{Rsw}:F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})/F_{m}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
is injective.(2) Let
 $\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
and let
$\unicode[STIX]{x1D712}\in F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
and let
 $i$
be an integer such that
$i$
be an integer such that
 $m<i\leqslant n$
. Assume that
$m<i\leqslant n$
. Assume that
 $\text{Rsw}(\unicode[STIX]{x1D712})\in \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
belongs to the image of
$\text{Rsw}(\unicode[STIX]{x1D712})\in \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
belongs to the image of
 $\mathfrak{m}_{K}^{-i}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
but not to the image of
$\mathfrak{m}_{K}^{-i}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
but not to the image of
 $\mathfrak{m}_{K}^{-i+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
. Then
$\mathfrak{m}_{K}^{-i+1}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
. Then
 $\text{Sw}(\unicode[STIX]{x1D712})=i$
.
$\text{Sw}(\unicode[STIX]{x1D712})=i$
.(3) The image of
 $\text{Rsw}$
is contained in the kernel of (16)
$\text{Rsw}$
is contained in the kernel of (16) $$\begin{eqnarray}d:\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\rightarrow \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{2}(\log ).\end{eqnarray}$$
$$\begin{eqnarray}d:\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\rightarrow \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{2}(\log ).\end{eqnarray}$$
Proof. (1) and (2) follow from 3.5.7 and the injectivity of the refined Swan conductor mod
![]() $\mathfrak{m}_{K}$
(3).
$\mathfrak{m}_{K}$
(3).
(3) is reduced to the case
![]() $F$
is a higher dimensional local field. Then it is reduced to (3) of 2.2.4 by the fact that the map (16) is dual to the map (7) in (3) of 2.2.4.◻
$F$
is a higher dimensional local field. Then it is reduced to (3) of 2.2.4 by the fact that the map (16) is dual to the map (7) in (3) of 2.2.4.◻
In the case of characteristic
![]() $p$
, the two definitions of the refined Swan conductor mod
$p$
, the two definitions of the refined Swan conductor mod
![]() $p$
coincide:
$p$
coincide:
Proposition 3.5.9. In the case
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
, the refined Swan conductor mod
$p$
, the refined Swan conductor mod
![]() $p$
defined in Section 3.2 coincides with that defined in Sections 3.3–3.5.
$p$
defined in Section 3.2 coincides with that defined in Sections 3.3–3.5.
3.5.10. To prove 3.5.9, we review the definition of the reciprocity map
![]() $K_{d}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)$
of a
$K_{d}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)$
of a
![]() $d$
-dimensional local field of characteristic
$d$
-dimensional local field of characteristic
![]() $p$
.
$p$
.
Let
![]() $K$
be a field of characteristic
$K$
be a field of characteristic
![]() $p>0$
, let
$p>0$
, let
![]() $s\geqslant 1$
, and let
$s\geqslant 1$
, and let
![]() $P$
be a commutative ring over
$P$
be a commutative ring over
![]() $\mathbb{Z}/p^{s}\mathbb{Z}$
which is flat over
$\mathbb{Z}/p^{s}\mathbb{Z}$
which is flat over
![]() $\mathbb{Z}/p^{s}\mathbb{Z}$
such that
$\mathbb{Z}/p^{s}\mathbb{Z}$
such that
![]() $P/pP=K$
. We have a well-defined ring homomorphism
$P/pP=K$
. We have a well-defined ring homomorphism
where
![]() $\tilde{a}_{i}$
is a lifting of
$\tilde{a}_{i}$
is a lifting of
![]() $a_{i}$
to
$a_{i}$
to
![]() $P$
. In
$P$
. In
![]() $\unicode[STIX]{x1D6FA}_{P}^{1}$
, we have
$\unicode[STIX]{x1D6FA}_{P}^{1}$
, we have
Now let
![]() $K$
be a
$K$
be a
![]() $d$
-dimensional local field of characteristic
$d$
-dimensional local field of characteristic
![]() $p>0$
. The reciprocity map
$p>0$
. The reciprocity map
![]() $K_{d}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)$
is defined as follows [Reference Kato19, Chapter 3]. Take an isomorphism
$K_{d}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)$
is defined as follows [Reference Kato19, Chapter 3]. Take an isomorphism
of
![]() $d$
-dimensional local fields and identify them. Define rings
$d$
-dimensional local fields and identify them. Define rings
![]() $P_{i}$
(
$P_{i}$
(
![]() $0\leqslant i\leqslant d$
) inductively as
$0\leqslant i\leqslant d$
) inductively as
![]() $P_{0}=W_{s}(\mathbb{F}_{q})$
,
$P_{0}=W_{s}(\mathbb{F}_{q})$
,
![]() $P_{i}=P_{i-1}[[T_{i}]][T_{i}^{-1}]$
(
$P_{i}=P_{i-1}[[T_{i}]][T_{i}^{-1}]$
(
![]() $1\leqslant i\leqslant d$
). Let
$1\leqslant i\leqslant d$
). Let
![]() $P=P_{d}$
. So
$P=P_{d}$
. So
![]() $P$
is
$P$
is
![]() $\mathbb{Z}/p^{s}\mathbb{Z}$
-flat and
$\mathbb{Z}/p^{s}\mathbb{Z}$
-flat and
![]() $P/pP=K$
. Let
$P/pP=K$
. Let
![]() $\text{Res}_{P}:\unicode[STIX]{x1D6FA}_{P}^{d}\rightarrow \mathbb{Z}/p^{s}\mathbb{Z}$
be the composition
$\text{Res}_{P}:\unicode[STIX]{x1D6FA}_{P}^{d}\rightarrow \mathbb{Z}/p^{s}\mathbb{Z}$
be the composition
where
![]() $\unicode[STIX]{x1D6FA}_{P_{i}}^{i}\rightarrow \unicode[STIX]{x1D6FA}_{P_{i-1}}^{i-1}$
(
$\unicode[STIX]{x1D6FA}_{P_{i}}^{i}\rightarrow \unicode[STIX]{x1D6FA}_{P_{i-1}}^{i-1}$
(
![]() $1\leqslant i\leqslant d$
) is the map
$1\leqslant i\leqslant d$
) is the map
![]() $\text{Res}_{P}$
kills the image of
$\text{Res}_{P}$
kills the image of
![]() $d:\unicode[STIX]{x1D6FA}_{P}^{d-1}\rightarrow \unicode[STIX]{x1D6FA}_{P}^{d}$
.
$d:\unicode[STIX]{x1D6FA}_{P}^{d-1}\rightarrow \unicode[STIX]{x1D6FA}_{P}^{d}$
.
Then the reciprocity map
![]() $K_{d}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)$
(which is independent of the choice of the isomorphism (18)) is characterized by the following property: let
$K_{d}^{M}(K)\rightarrow \text{Gal}(K^{\text{ab}}/K)$
(which is independent of the choice of the isomorphism (18)) is characterized by the following property: let
![]() $\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Z}/p^{s}\mathbb{Z})$
and assume that
$\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Z}/p^{s}\mathbb{Z})$
and assume that
![]() $\unicode[STIX]{x1D712}$
is the image of
$\unicode[STIX]{x1D712}$
is the image of
![]() $f\in W_{s}(K)$
. Then
$f\in W_{s}(K)$
. Then
![]() $\unicode[STIX]{x1D712}$
sends the image of
$\unicode[STIX]{x1D712}$
sends the image of
![]() $\{y_{1},\ldots ,y_{d}\}\in K_{d}^{M}(K)$
(
$\{y_{1},\ldots ,y_{d}\}\in K_{d}^{M}(K)$
(
![]() $y_{i}\in K^{\times }$
) to
$y_{i}\in K^{\times }$
) to
![]() $\text{Res}_{P}(\unicode[STIX]{x1D703}(f)\,d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d}))$
where
$\text{Res}_{P}(\unicode[STIX]{x1D703}(f)\,d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d}))$
where
![]() ${\tilde{y}}_{i}$
is a lifting of
${\tilde{y}}_{i}$
is a lifting of
![]() $y_{i}$
to
$y_{i}$
to
![]() $P$
.
$P$
.
3.5.11. We prove 3.5.9. We may assume that
![]() $K$
is a
$K$
is a
![]() $d$
-dimensional local field of characteristic
$d$
-dimensional local field of characteristic
![]() $p$
with
$p$
with
![]() $d\geqslant 1$
.
$d\geqslant 1$
.
Let
![]() $m=\max (n-e_{K},[n/p])$
and let
$m=\max (n-e_{K},[n/p])$
and let
![]() $x\in \mathfrak{m}_{K}^{m+1}$
,
$x\in \mathfrak{m}_{K}^{m+1}$
,
![]() $y_{i}\in K^{\times }$
(
$y_{i}\in K^{\times }$
(
![]() $1\leqslant i\leqslant d-1$
). Let the notation be as in 3.5.10. We have
$1\leqslant i\leqslant d-1$
). Let the notation be as in 3.5.10. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}(\{E(x),y_{1},\ldots ,y_{d-1}\})\nonumber\\ \displaystyle & & \displaystyle \quad =\text{Res}_{P}(\unicode[STIX]{x1D703}(f)\,d\log E(\tilde{x})\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1}))\nonumber\\ \displaystyle & & \displaystyle \quad =\text{Res}_{P}(\unicode[STIX]{x1D703}(f)\,d\tilde{x}\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1}))\nonumber\\ \displaystyle & & \displaystyle \qquad (\text{here we used (3) of 2.2.2})\nonumber\\ \displaystyle & & \displaystyle \quad =\text{Res}_{P}(d(\unicode[STIX]{x1D703}(f)\tilde{x}\,d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1})))\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\text{Res}_{P}(\tilde{x}\,d\unicode[STIX]{x1D703}(f)\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1}))\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{Res}_{P}(\tilde{x}\,d\unicode[STIX]{x1D703}(f)\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1})).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}(\{E(x),y_{1},\ldots ,y_{d-1}\})\nonumber\\ \displaystyle & & \displaystyle \quad =\text{Res}_{P}(\unicode[STIX]{x1D703}(f)\,d\log E(\tilde{x})\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1}))\nonumber\\ \displaystyle & & \displaystyle \quad =\text{Res}_{P}(\unicode[STIX]{x1D703}(f)\,d\tilde{x}\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1}))\nonumber\\ \displaystyle & & \displaystyle \qquad (\text{here we used (3) of 2.2.2})\nonumber\\ \displaystyle & & \displaystyle \quad =\text{Res}_{P}(d(\unicode[STIX]{x1D703}(f)\tilde{x}\,d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1})))\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\text{Res}_{P}(\tilde{x}\,d\unicode[STIX]{x1D703}(f)\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1}))\nonumber\\ \displaystyle & & \displaystyle \quad =-\text{Res}_{P}(\tilde{x}\,d\unicode[STIX]{x1D703}(f)\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1})).\nonumber\end{eqnarray}$$
Write
![]() $f=(f_{s-1},\ldots ,f_{0})$
with
$f=(f_{s-1},\ldots ,f_{0})$
with
![]() $f_{i}\in K$
. By (17),
$f_{i}\in K$
. By (17),
![]() $\text{Res}_{P}(\tilde{x}\,d\unicode[STIX]{x1D703}(f)\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1}))$
is the image of
$\text{Res}_{P}(\tilde{x}\,d\unicode[STIX]{x1D703}(f)\wedge d\log ({\tilde{y}}_{1})\wedge \cdots \wedge d\log ({\tilde{y}}_{d-1}))$
is the image of
![]() $\text{Res}_{F}(x\cdot \sum _{i=0}^{s-1}f_{i}^{p^{i}-1}\,df_{i}\wedge d\log (y_{1})\wedge \cdots d\log (y_{d-1}))\in \mathbb{F}_{p}$
under the homomorphism
$\text{Res}_{F}(x\cdot \sum _{i=0}^{s-1}f_{i}^{p^{i}-1}\,df_{i}\wedge d\log (y_{1})\wedge \cdots d\log (y_{d-1}))\in \mathbb{F}_{p}$
under the homomorphism
![]() $\mathbb{F}_{p}\overset{\subset }{\rightarrow }\mathbb{Z}/p^{s}\mathbb{Z}$
which sends 1 to
$\mathbb{F}_{p}\overset{\subset }{\rightarrow }\mathbb{Z}/p^{s}\mathbb{Z}$
which sends 1 to
![]() $p^{s-1}$
. Hence
$p^{s-1}$
. Hence
![]() $\text{Rsw}\unicode[STIX]{x1D712}$
equals
$\text{Rsw}\unicode[STIX]{x1D712}$
equals
![]() $-\sum _{i=0}^{s-1}f_{i}^{p^{i}-1}df_{i}$
as in 3.2.4.
$-\sum _{i=0}^{s-1}f_{i}^{p^{i}-1}df_{i}$
as in 3.2.4.
3.6 Applications
A nonlogarithmic version of the following result is obtained in [Reference Borger6].
Theorem 3.6.1. Let
![]() $K$
be a complete discrete valuation field whose residue field is of characteristic
$K$
be a complete discrete valuation field whose residue field is of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Then
$\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Then
where
![]() $L$
ranges over cdvf over
$L$
ranges over cdvf over
![]() $K$
with perfect residue fields.
$K$
with perfect residue fields.
Proof. By the characterization of the Swan conductor in [Reference Kato20, Proposition (6.3)], we have
![]() $e(L/K)\cdot Sw(\unicode[STIX]{x1D712})\leqslant Sw(\unicode[STIX]{x1D712}_{L})$
in general.
$e(L/K)\cdot Sw(\unicode[STIX]{x1D712})\leqslant Sw(\unicode[STIX]{x1D712}_{L})$
in general.
Write
![]() $\text{Rsw}(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D70B}^{-n}\otimes (a+c\,d\log (\unicode[STIX]{x1D70B}))$
where
$\text{Rsw}(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D70B}^{-n}\otimes (a+c\,d\log (\unicode[STIX]{x1D70B}))$
where
![]() $\unicode[STIX]{x1D70B}$
is a prime element of
$\unicode[STIX]{x1D70B}$
is a prime element of
![]() $K$
,
$K$
,
![]() $n=\text{Sw}(\unicode[STIX]{x1D712})$
,
$n=\text{Sw}(\unicode[STIX]{x1D712})$
,
![]() $a\in \unicode[STIX]{x1D6FA}_{O_{K}}^{1}$
and
$a\in \unicode[STIX]{x1D6FA}_{O_{K}}^{1}$
and
![]() $c\in O_{K}$
. If
$c\in O_{K}$
. If
![]() $c$
is a unit, any
$c$
is a unit, any
![]() $L/K$
with
$L/K$
with
![]() $e(L/K)=1$
(the residue field of
$e(L/K)=1$
(the residue field of
![]() $L$
is perfect) satisfies
$L$
is perfect) satisfies
![]() $\text{Rsw}(\unicode[STIX]{x1D712}_{L})$
is the image of
$\text{Rsw}(\unicode[STIX]{x1D712}_{L})$
is the image of
![]() $\text{Rsw}(\unicode[STIX]{x1D712})$
and hence
$\text{Rsw}(\unicode[STIX]{x1D712})$
and hence
![]() $\text{Sw}(\unicode[STIX]{x1D712}_{L})=\text{Sw}(\unicode[STIX]{x1D712})$
. Assume
$\text{Sw}(\unicode[STIX]{x1D712}_{L})=\text{Sw}(\unicode[STIX]{x1D712})$
. Assume
![]() $c$
is not a unit. Write
$c$
is not a unit. Write
![]() $a=\sum _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}a_{\unicode[STIX]{x1D706}}\,db_{\unicode[STIX]{x1D706}}$
where
$a=\sum _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}a_{\unicode[STIX]{x1D706}}\,db_{\unicode[STIX]{x1D706}}$
where
![]() $(b_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
is a lifting of a
$(b_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$
is a lifting of a
![]() $p$
-base of
$p$
-base of
![]() $F$
to
$F$
to
![]() $O_{K}$
and
$O_{K}$
and
![]() $a_{\unicode[STIX]{x1D706}}\in O_{K}$
. Then
$a_{\unicode[STIX]{x1D706}}\in O_{K}$
. Then
![]() $a_{\unicode[STIX]{x1D707}}$
is a unit for some
$a_{\unicode[STIX]{x1D707}}$
is a unit for some
![]() $\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
. For an integer
$\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6EC}$
. For an integer
![]() $t\geqslant 2$
, let
$t\geqslant 2$
, let
![]() $L_{t}$
be the completion of the extension of
$L_{t}$
be the completion of the extension of
![]() $K$
obtained by adding a
$K$
obtained by adding a
![]() $t$
th root
$t$
th root
![]() $\unicode[STIX]{x1D70B}^{1/t}$
of
$\unicode[STIX]{x1D70B}^{1/t}$
of
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $b_{\unicode[STIX]{x1D706},n}$
(
$b_{\unicode[STIX]{x1D706},n}$
(
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
,
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
,
![]() $n\geqslant 0$
) such that
$n\geqslant 0$
) such that
![]() $b_{\unicode[STIX]{x1D706},n}=b_{\unicode[STIX]{x1D706},n+1}^{p}$
for any
$b_{\unicode[STIX]{x1D706},n}=b_{\unicode[STIX]{x1D706},n+1}^{p}$
for any
![]() $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$
and
![]() $n\geqslant 0$
,
$n\geqslant 0$
,
![]() $b_{0,\unicode[STIX]{x1D706}}=b_{\unicode[STIX]{x1D706}}$
for
$b_{0,\unicode[STIX]{x1D706}}=b_{\unicode[STIX]{x1D706}}$
for
![]() $\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D707}$
, and
$\unicode[STIX]{x1D706}\neq \unicode[STIX]{x1D707}$
, and
![]() $b_{\unicode[STIX]{x1D707},0}=b_{\unicode[STIX]{x1D707}}-\unicode[STIX]{x1D70B}^{1/t}$
. Then the residue field of
$b_{\unicode[STIX]{x1D707},0}=b_{\unicode[STIX]{x1D707}}-\unicode[STIX]{x1D70B}^{1/t}$
. Then the residue field of
![]() $L_{t}$
is perfect,
$L_{t}$
is perfect,
![]() $\unicode[STIX]{x1D70B}^{1/t}$
is a prime element in
$\unicode[STIX]{x1D70B}^{1/t}$
is a prime element in
![]() $L_{t}$
,
$L_{t}$
,
![]() $\text{Rsw}(\unicode[STIX]{x1D712}_{L_{t}})=\unicode[STIX]{x1D70B}^{-n}\otimes (a_{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D70B}^{1/t}+ct)\,d\log (\unicode[STIX]{x1D70B}^{1/t})$
, and hence we have
$\text{Rsw}(\unicode[STIX]{x1D712}_{L_{t}})=\unicode[STIX]{x1D70B}^{-n}\otimes (a_{\unicode[STIX]{x1D707}}\unicode[STIX]{x1D70B}^{1/t}+ct)\,d\log (\unicode[STIX]{x1D70B}^{1/t})$
, and hence we have
![]() $e(L_{t}/K)^{-1}\text{Sw}(\unicode[STIX]{x1D712}_{L_{t}})=\text{Sw}(\unicode[STIX]{x1D712})-t^{-1}$
.◻
$e(L_{t}/K)^{-1}\text{Sw}(\unicode[STIX]{x1D712}_{L_{t}})=\text{Sw}(\unicode[STIX]{x1D712})-t^{-1}$
.◻
We improve a previous result of the second author in [Reference Leal29].
3.6.2. Let
![]() $L/K$
be a separable extension of complete discrete valuation fields whose residue fields are of characteristic
$L/K$
be a separable extension of complete discrete valuation fields whose residue fields are of characteristic
![]() $p>0$
, and assume that
$p>0$
, and assume that
![]() $K$
has perfect residue field. (The extension
$K$
has perfect residue field. (The extension
![]() $L/K$
need not be a finite extension.)
$L/K$
need not be a finite extension.)
Let
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}/O_{K}}^{1}(\log )$
be the
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}/O_{K}}^{1}(\log )$
be the
![]() $\mathfrak{m}_{L}$
-adic completion of the cokernel of
$\mathfrak{m}_{L}$
-adic completion of the cokernel of
![]() $O_{L}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\rightarrow \unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
. Then by 2.1.3, the
$O_{L}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\rightarrow \unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
. Then by 2.1.3, the
![]() $O_{L}$
-torsion part
$O_{L}$
-torsion part
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}/O_{K}}^{1}(\log )_{\text{tor}}$
of
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}/O_{K}}^{1}(\log )_{\text{tor}}$
of
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}/O_{K}}^{1}(\log )$
is of finite length as an
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}/O_{K}}^{1}(\log )$
is of finite length as an
![]() $O_{L}$
-module. Let
$O_{L}$
-module. Let
![]() $\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)\in \mathbb{Z}_{{\geqslant}0}$
be the length of the
$\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)\in \mathbb{Z}_{{\geqslant}0}$
be the length of the
![]() $O_{L}$
-module
$O_{L}$
-module
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}/O_{K}}^{1}(\log )_{\text{tor}}$
.
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}/O_{K}}^{1}(\log )_{\text{tor}}$
.
Theorem 3.6.3. Let
![]() $L/K$
and
$L/K$
and
![]() $\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)$
be as in 3.6.2. Assume
$\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)$
be as in 3.6.2. Assume
If
![]() $\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is such that
$\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is such that
Then
Remark 3.6.4. In the case
![]() $K$
is of characteristic
$K$
is of characteristic
![]() $p$
, this result is proved in [Reference Leal29]. In [Reference Leal29], it is stated without assuming
$p$
, this result is proved in [Reference Leal29]. In [Reference Leal29], it is stated without assuming
![]() $L/K$
is separable, but this was a mistake.
$L/K$
is separable, but this was a mistake.
When
![]() $K$
is of mixed characteristic and
$K$
is of mixed characteristic and
![]() $\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)<e_{L}$
, Theorem 3.6.3 gives a stronger result than the following result obtained in [Reference Leal29].
$\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)<e_{L}$
, Theorem 3.6.3 gives a stronger result than the following result obtained in [Reference Leal29].
Theorem 3.6.5. [Reference Leal29]
Let
![]() $L/K$
be an extension of complete discrete valuation fields of mixed characteristic. Assume that
$L/K$
be an extension of complete discrete valuation fields of mixed characteristic. Assume that
![]() $K$
has perfect residue field of characteristic
$K$
has perfect residue field of characteristic
![]() $p>0$
and
$p>0$
and
![]() $\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is such that
$\unicode[STIX]{x1D712}\in H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is such that
Then
3.6.6. We prove 3.6.3. Write
![]() $n=\text{Sw}(\unicode[STIX]{x1D712})$
,
$n=\text{Sw}(\unicode[STIX]{x1D712})$
,
![]() $n^{\prime }=e(L/K)n$
,
$n^{\prime }=e(L/K)n$
,
![]() $m=\max (n-e_{K},[n/p])$
,
$m=\max (n-e_{K},[n/p])$
,
![]() $m^{\prime }=\max (n^{\prime }-e_{L},[n^{\prime }/p])$
and
$m^{\prime }=\max (n^{\prime }-e_{L},[n^{\prime }/p])$
and
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)$
. We prove first
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)$
. We prove first
By 2.1.3 and 2.1.5,
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )$
is a nonzero monogenic
$\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )$
is a nonzero monogenic
![]() $O_{K}$
-module of finite length,
$O_{K}$
-module of finite length,
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )_{\text{tor}}$
is a nonzero monogenic
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )_{\text{tor}}$
is a nonzero monogenic
![]() $O_{L}$
-module of finite length and it is a direct summand of
$O_{L}$
-module of finite length and it is a direct summand of
![]() $\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
, and the canonical map
$\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )$
, and the canonical map
![]() $\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\rightarrow \unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
induces an isomorphism
$\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )\rightarrow \unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
induces an isomorphism
![]() $O_{L}\otimes _{O_{K}}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )\overset{\cong }{\rightarrow }\mathfrak{m}_{L}^{\unicode[STIX]{x1D6FF}}\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )_{\text{tor}}$
. The map
$O_{L}\otimes _{O_{K}}\hat{\unicode[STIX]{x1D6FA}}_{O_{K}}^{1}(\log )\overset{\cong }{\rightarrow }\mathfrak{m}_{L}^{\unicode[STIX]{x1D6FF}}\hat{\unicode[STIX]{x1D6FA}}_{O_{L}}^{1}(\log )_{\text{tor}}$
. The map
![]() $\text{Rsw}:F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
sends
$\text{Rsw}:F_{n}H^{1}(K,\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow \mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
sends
![]() $\unicode[STIX]{x1D712}$
to a generator of the
$\unicode[STIX]{x1D712}$
to a generator of the
![]() $O_{K}$
-module
$O_{K}$
-module
![]() $\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
. Hence if
$\mathfrak{m}_{K}^{-n}/\mathfrak{m}_{K}^{-m}\otimes _{O_{K}}\unicode[STIX]{x1D6FA}_{O_{K}}^{1}(\log )$
. Hence if
![]() $n^{\prime }-\unicode[STIX]{x1D6FF}>m^{\prime }$
, the image of this generator in
$n^{\prime }-\unicode[STIX]{x1D6FF}>m^{\prime }$
, the image of this generator in
![]() $\mathfrak{m}_{L}^{-n^{\prime }}/\mathfrak{m}_{L}^{-m^{\prime }}\otimes _{O_{L}}\unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
belongs to the image of
$\mathfrak{m}_{L}^{-n^{\prime }}/\mathfrak{m}_{L}^{-m^{\prime }}\otimes _{O_{L}}\unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
belongs to the image of
![]() $\mathfrak{m}_{L}^{-n^{\prime }+\unicode[STIX]{x1D6FF}}/\mathfrak{m}_{L}^{-m^{\prime }}\otimes _{O_{L}}\unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
but does not belong to the image of
$\mathfrak{m}_{L}^{-n^{\prime }+\unicode[STIX]{x1D6FF}}/\mathfrak{m}_{L}^{-m^{\prime }}\otimes _{O_{L}}\unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
but does not belong to the image of
![]() $\mathfrak{m}_{L}^{-n^{\prime }+\unicode[STIX]{x1D6FF}+1}/\mathfrak{m}_{L}^{-m^{\prime }}\otimes _{O_{L}}\unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
. Hence by the compatibility with pullback ((i) of 3.1.2) and the relationship between
$\mathfrak{m}_{L}^{-n^{\prime }+\unicode[STIX]{x1D6FF}+1}/\mathfrak{m}_{L}^{-m^{\prime }}\otimes _{O_{L}}\unicode[STIX]{x1D6FA}_{O_{L}}^{1}(\log )$
. Hence by the compatibility with pullback ((i) of 3.1.2) and the relationship between
![]() $\text{Rsw}$
and
$\text{Rsw}$
and
![]() $\text{Sw}$
((2) of 3.5.8), we obtain (19).
$\text{Sw}$
((2) of 3.5.8), we obtain (19).
If
then
![]() $e(L/K)n-\unicode[STIX]{x1D6FF}>e(L/K)np^{-1}$
and hence
$e(L/K)n-\unicode[STIX]{x1D6FF}>e(L/K)np^{-1}$
and hence
![]() $n^{\prime }-\unicode[STIX]{x1D6FF}>[n^{\prime }/p]$
. Further, since
$n^{\prime }-\unicode[STIX]{x1D6FF}>[n^{\prime }/p]$
. Further, since
![]() $\unicode[STIX]{x1D6FF}<e_{L}$
, we have
$\unicode[STIX]{x1D6FF}<e_{L}$
, we have
![]() $n^{\prime }-\unicode[STIX]{x1D6FF}>n^{\prime }-e_{L}$
. It follows that
$n^{\prime }-\unicode[STIX]{x1D6FF}>n^{\prime }-e_{L}$
. It follows that
![]() $n^{\prime }-\unicode[STIX]{x1D6FF}>m^{\prime }$
and the formula holds.
$n^{\prime }-\unicode[STIX]{x1D6FF}>m^{\prime }$
and the formula holds.
3.6.7. In the case
![]() $\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)<e_{L}$
, 3.6.3 in the mixed characteristic case is stronger than 3.6.5. Indeed, we have that
$\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)<e_{L}$
, 3.6.3 in the mixed characteristic case is stronger than 3.6.5. Indeed, we have that
To see this, observe that
 $$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{2e_{K}}{p-1}}+{\displaystyle \frac{1}{e(L/K)}}+\left\lceil {\displaystyle \frac{\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)}{e(L/K)}}\right\rceil \nonumber\\ \displaystyle & & \displaystyle \quad >{\displaystyle \frac{e_{K}}{p-1}}+{\displaystyle \frac{1}{p-1}}{\displaystyle \frac{\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)}{e(L/K)}}+{\displaystyle \frac{\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)}{e(L/K)}}\nonumber\\ \displaystyle & & \displaystyle \quad >{\displaystyle \frac{p}{p-1}}{\displaystyle \frac{\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)}{e(L/K)}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\displaystyle \frac{2e_{K}}{p-1}}+{\displaystyle \frac{1}{e(L/K)}}+\left\lceil {\displaystyle \frac{\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)}{e(L/K)}}\right\rceil \nonumber\\ \displaystyle & & \displaystyle \quad >{\displaystyle \frac{e_{K}}{p-1}}+{\displaystyle \frac{1}{p-1}}{\displaystyle \frac{\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)}{e(L/K)}}+{\displaystyle \frac{\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)}{e(L/K)}}\nonumber\\ \displaystyle & & \displaystyle \quad >{\displaystyle \frac{p}{p-1}}{\displaystyle \frac{\unicode[STIX]{x1D6FF}_{\text{tor}}(L/K)}{e(L/K)}},\nonumber\end{eqnarray}$$
so we have an improvement.
4 Globalization
4.1 Module theoretic preparations
In this paper, a simple normal crossing divisor has no multiplicity (it is reduced as a scheme).
Proposition 4.1.1. Let
![]() $X$
be a regular scheme of finite type over
$X$
be a regular scheme of finite type over
![]() $\mathbb{Z}$
of dimension
$\mathbb{Z}$
of dimension
![]() $d$
, let
$d$
, let
![]() $D$
be a simple normal crossing divisor on
$D$
be a simple normal crossing divisor on
![]() $X$
, let
$X$
, let
![]() $p$
be a prime number, and let
$p$
be a prime number, and let
![]() $E$
be an effective divisor on
$E$
be an effective divisor on
![]() $X$
whose support is contained in
$X$
whose support is contained in
![]() $D$
such that the scheme
$D$
such that the scheme
![]() $E=\text{Spec}({\mathcal{O}}_{X}/{\mathcal{O}}_{X}(-E))\subset X$
is of characteristic
$E=\text{Spec}({\mathcal{O}}_{X}/{\mathcal{O}}_{X}(-E))\subset X$
is of characteristic
![]() $p$
.
$p$
.
(1) The
 ${\mathcal{O}}_{E}$
-module
${\mathcal{O}}_{E}$
-module
 ${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
is locally free of rank
${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
is locally free of rank
 $d$
.
$d$
.(2) The
 ${\mathcal{O}}_{E}$
-module
${\mathcal{O}}_{E}$
-module
 ${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(E-D)$
is the canonical dualizing module of
${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(E-D)$
is the canonical dualizing module of
 $E$
relative to
$E$
relative to
 $\mathbb{F}_{p}$
.
$\mathbb{F}_{p}$
.
Proof. We may assume either
![]() $X$
is a scheme over
$X$
is a scheme over
![]() $\mathbb{F}_{p}$
or
$\mathbb{F}_{p}$
or
![]() $X$
is flat over
$X$
is flat over
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Assume first that
![]() $X$
is over
$X$
is over
![]() $\mathbb{F}_{p}$
. Then
$\mathbb{F}_{p}$
. Then
![]() $X$
is smooth over
$X$
is smooth over
![]() $\mathbb{F}_{p}$
and hence
$\mathbb{F}_{p}$
and hence
![]() $\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
is locally free of rank
$\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
is locally free of rank
![]() $d$
and
$d$
and
![]() $\unicode[STIX]{x1D6FA}_{X}^{d}$
is a dualizing module of
$\unicode[STIX]{x1D6FA}_{X}^{d}$
is a dualizing module of
![]() $X$
relative to
$X$
relative to
![]() $\mathbb{F}_{p}$
. Hence the
$\mathbb{F}_{p}$
. Hence the
![]() ${\mathcal{O}}_{E}$
-module
${\mathcal{O}}_{E}$
-module
![]() ${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
is locally free of rank
${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
is locally free of rank
![]() $d$
and
$d$
and
![]() $R{\mathcal{H}}om_{{\mathcal{O}}_{X}}({\mathcal{O}}_{E},\unicode[STIX]{x1D6FA}_{X}^{d})[1]={\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(E)={\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(E-D)$
is the dualing module of
$R{\mathcal{H}}om_{{\mathcal{O}}_{X}}({\mathcal{O}}_{E},\unicode[STIX]{x1D6FA}_{X}^{d})[1]={\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(E)={\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(E-D)$
is the dualing module of
![]() $E$
relative to
$E$
relative to
![]() $\mathbb{F}_{p}$
.
$\mathbb{F}_{p}$
.
Assume
![]() $X$
is flat over
$X$
is flat over
![]() $\mathbb{Z}$
. This case is reduced to the case
$\mathbb{Z}$
. This case is reduced to the case
![]() $X$
is over
$X$
is over
![]() $\mathbb{F}_{p}$
as follows. Let
$\mathbb{F}_{p}$
as follows. Let
![]() $x$
be a closed point of
$x$
be a closed point of
![]() $X$
and let
$X$
and let
![]() $(t_{i})_{1\leqslant i\leqslant d}$
be a regular system of parameters of the regular local ring
$(t_{i})_{1\leqslant i\leqslant d}$
be a regular system of parameters of the regular local ring
![]() ${\mathcal{O}}_{X,x}$
such that
${\mathcal{O}}_{X,x}$
such that
![]() $D$
is defined at
$D$
is defined at
![]() $x$
by
$x$
by
![]() $t_{1}\ldots t_{r}$
for some
$t_{1}\ldots t_{r}$
for some
![]() $r$
(
$r$
(
![]() $0\leqslant r\leqslant d$
). Then
$0\leqslant r\leqslant d$
). Then
![]() $E$
is defined by
$E$
is defined by
![]() $t_{1}^{a(1)}\ldots t_{r}^{a(r)}$
at
$t_{1}^{a(1)}\ldots t_{r}^{a(r)}$
at
![]() $x$
for some
$x$
for some
![]() $a(i)\in \mathbb{Z}_{{\geqslant}0}$
and we have
$a(i)\in \mathbb{Z}_{{\geqslant}0}$
and we have
![]() $p=t_{1}^{e(1)}\ldots t_{r}^{e(r)}h$
for some
$p=t_{1}^{e(1)}\ldots t_{r}^{e(r)}h$
for some
![]() $e(i)\in \mathbb{Z}_{{\geqslant}0}$
such that
$e(i)\in \mathbb{Z}_{{\geqslant}0}$
such that
![]() $e(i)\geqslant a(i)$
(
$e(i)\geqslant a(i)$
(
![]() $1\leqslant i\leqslant r$
) and for some
$1\leqslant i\leqslant r$
) and for some
![]() $h\in {\mathcal{O}}_{X,x}$
. Replacing
$h\in {\mathcal{O}}_{X,x}$
. Replacing
![]() $X$
by an open neighborhood of
$X$
by an open neighborhood of
![]() $x$
in
$x$
in
![]() $X$
, we have an unramified morphism
$X$
, we have an unramified morphism
![]() $X\rightarrow \mathbf{A}_{\mathbb{Z}}^{d}$
given by
$X\rightarrow \mathbf{A}_{\mathbb{Z}}^{d}$
given by
![]() $(t_{i})_{1\leqslant i\leqslant d}$
. Replacing
$(t_{i})_{1\leqslant i\leqslant d}$
. Replacing
![]() $X$
by an open neighborhood of
$X$
by an open neighborhood of
![]() $x$
in
$x$
in
![]() $X$
, this morphism factors as
$X$
, this morphism factors as
![]() $X\overset{f}{\rightarrow }Z\overset{g}{\rightarrow }\mathbf{A}_{\mathbb{Z}}^{d}$
where
$X\overset{f}{\rightarrow }Z\overset{g}{\rightarrow }\mathbf{A}_{\mathbb{Z}}^{d}$
where
![]() $g$
is étale and
$g$
is étale and
![]() $f$
is a closed immersion [Reference Grothendieck12, 18.4.7] defined by a section
$f$
is a closed immersion [Reference Grothendieck12, 18.4.7] defined by a section
![]() $p-T_{1}^{e(1)}\ldots T_{r}^{e(r)}\tilde{h}$
of
$p-T_{1}^{e(1)}\ldots T_{r}^{e(r)}\tilde{h}$
of
![]() ${\mathcal{O}}_{Z}$
for some lifting
${\mathcal{O}}_{Z}$
for some lifting
![]() $\tilde{h}$
of
$\tilde{h}$
of
![]() $h$
to
$h$
to
![]() ${\mathcal{O}}_{Z}$
. Hence
${\mathcal{O}}_{Z}$
. Hence
![]() $E$
is defined in
$E$
is defined in
![]() $Z$
by
$Z$
by
![]() $T_{1}^{a(1)}\ldots T_{r}^{a(r)}$
and
$T_{1}^{a(1)}\ldots T_{r}^{a(r)}$
and
![]() $p$
. Hence we have an étale morphism from
$p$
. Hence we have an étale morphism from
![]() $E$
to
$E$
to
![]() $E^{\prime }:=\text{Spec}(\mathbb{F}_{p}[T_{1},\ldots ,T_{d}]/(T_{1}^{a(1)}\ldots T_{r}^{a(r)}))$
for which the pullback of
$E^{\prime }:=\text{Spec}(\mathbb{F}_{p}[T_{1},\ldots ,T_{d}]/(T_{1}^{a(1)}\ldots T_{r}^{a(r)}))$
for which the pullback of
![]() $T_{i}$
is
$T_{i}$
is
![]() $t_{i}$
. Let
$t_{i}$
. Let
![]() $X^{\prime }=\text{Spec}(\mathbb{F}_{p}[T_{1},\ldots ,T_{d}])$
and let
$X^{\prime }=\text{Spec}(\mathbb{F}_{p}[T_{1},\ldots ,T_{d}])$
and let
![]() $D^{\prime }$
be the divisor
$D^{\prime }$
be the divisor
![]() $T_{1}\ldots T_{r}=0$
on
$T_{1}\ldots T_{r}=0$
on
![]() $X^{\prime }$
with simple normal crossings. Then
$X^{\prime }$
with simple normal crossings. Then
![]() ${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
is the pullback of
${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
is the pullback of
![]() ${\mathcal{O}}_{E^{\prime }}\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime })$
. (1) follows from this. Since
${\mathcal{O}}_{E^{\prime }}\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime })$
. (1) follows from this. Since
![]() ${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(E-D)$
is the module theoretic pullback of
${\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(E-D)$
is the module theoretic pullback of
![]() ${\mathcal{O}}_{E^{\prime }}\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{d}(\log D^{\prime })(E^{\prime }-D^{\prime })$
which is the dualizing module of
${\mathcal{O}}_{E^{\prime }}\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{d}(\log D^{\prime })(E^{\prime }-D^{\prime })$
which is the dualizing module of
![]() $E^{\prime }$
relative to
$E^{\prime }$
relative to
![]() $\mathbb{F}_{p}$
by the étale morphism
$\mathbb{F}_{p}$
by the étale morphism
![]() $E\rightarrow E^{\prime }$
, it is the dualizing module of
$E\rightarrow E^{\prime }$
, it is the dualizing module of
![]() $E$
relative to
$E$
relative to
![]() $\mathbb{F}_{p}$
.◻
$\mathbb{F}_{p}$
.◻
4.1.2. Let the assumption and the notation be as in 4.1.1 and let
![]() ${\mathcal{H}}={\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(E-D)$
. By local duality of Grothendieck [Reference Hartshorne13, Chapter V, Section 6],
${\mathcal{H}}={\mathcal{O}}_{E}\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(E-D)$
. By local duality of Grothendieck [Reference Hartshorne13, Chapter V, Section 6],
![]() $\text{Hom}(H_{x}^{d-1}(E,{\mathcal{H}}),\mathbb{F}_{p})$
is isomorphic to the completion
$\text{Hom}(H_{x}^{d-1}(E,{\mathcal{H}}),\mathbb{F}_{p})$
is isomorphic to the completion
![]() $\hat{{\mathcal{O}}}_{E,x}$
of
$\hat{{\mathcal{O}}}_{E,x}$
of
![]() ${\mathcal{O}}_{E,x}$
, and in the correspondence 2.3.5 (we take
${\mathcal{O}}_{E,x}$
, and in the correspondence 2.3.5 (we take
![]() $E$
as
$E$
as
![]() $X$
in 2.3.5 and we take
$X$
in 2.3.5 and we take
![]() $d-1$
as
$d-1$
as
![]() $d$
in 2.3.5),
$d$
in 2.3.5),
![]() $f\in {\mathcal{O}}_{E,x}$
corresponds to
$f\in {\mathcal{O}}_{E,x}$
corresponds to
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}\in P_{x}(E)}$
with
$(h_{\mathfrak{p}})_{\mathfrak{p}\in P_{x}(E)}$
with
![]() $h_{\mathfrak{p}}(\unicode[STIX]{x1D714})=\text{Res}_{\mathfrak{p}}(f\unicode[STIX]{x1D714})$
where
$h_{\mathfrak{p}}(\unicode[STIX]{x1D714})=\text{Res}_{\mathfrak{p}}(f\unicode[STIX]{x1D714})$
where
![]() $\text{Res}_{\mathfrak{p}}:{\mathcal{H}}_{x_{d-1}}\rightarrow \mathbb{F}_{p}$
is as follows. Write
$\text{Res}_{\mathfrak{p}}:{\mathcal{H}}_{x_{d-1}}\rightarrow \mathbb{F}_{p}$
is as follows. Write
![]() $\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d-1}$
, let
$\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d-1}$
, let
![]() $Y\subset X$
be the closure of
$Y\subset X$
be the closure of
![]() $x_{d-1}$
, let
$x_{d-1}$
, let
![]() $F$
be the residue field of
$F$
be the residue field of
![]() $x_{d-1}$
, and take an integer
$x_{d-1}$
, and take an integer
![]() $b$
such that
$b$
such that
![]() $p^{b}\geqslant \text{ord}_{x_{d-1}}(E)$
. Then
$p^{b}\geqslant \text{ord}_{x_{d-1}}(E)$
. Then
Here
![]() $R_{b}:{\mathcal{H}}_{x_{d-1}}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{d-1}$
is as in 2.1.9,
$R_{b}:{\mathcal{H}}_{x_{d-1}}\rightarrow \unicode[STIX]{x1D6FA}_{F}^{d-1}$
is as in 2.1.9,
![]() $Pl(Y,\mathfrak{p})$
is as in 2.4.8, and
$Pl(Y,\mathfrak{p})$
is as in 2.4.8, and
![]() $\text{Res}_{F_{v}}$
is as in 3.3.2. Note that
$\text{Res}_{F_{v}}$
is as in 3.3.2. Note that
![]() $\text{Res}_{F_{v}}\circ R_{b}$
is independent of the choice of
$\text{Res}_{F_{v}}\circ R_{b}$
is independent of the choice of
![]() $b$
because
$b$
because
![]() $\text{Res}_{F_{v}}\circ C=\text{Res}_{F_{v}}$
where
$\text{Res}_{F_{v}}\circ C=\text{Res}_{F_{v}}$
where
![]() $C$
is the Cartier operator.
$C$
is the Cartier operator.
4.1.3. Let the assumption and the notation be as in 4.1.2. Let
![]() $\bar{E}$
be a proper scheme over
$\bar{E}$
be a proper scheme over
![]() $\mathbb{F}_{p}$
which contains
$\mathbb{F}_{p}$
which contains
![]() $E$
as a dense open subscheme. Let
$E$
as a dense open subscheme. Let
![]() ${\mathcal{F}}$
be a coherent
${\mathcal{F}}$
be a coherent
![]() ${\mathcal{O}}_{\bar{E}}$
-module whose restriction
${\mathcal{O}}_{\bar{E}}$
-module whose restriction
![]() ${\mathcal{F}}|_{E}$
to
${\mathcal{F}}|_{E}$
to
![]() $E$
is a vector bundle, and consider the vector bundle
$E$
is a vector bundle, and consider the vector bundle
![]() ${\mathcal{G}}:={\mathcal{H}}om_{{\mathcal{O}}_{E}}({\mathcal{F}}|_{E},{\mathcal{H}})$
on
${\mathcal{G}}:={\mathcal{H}}om_{{\mathcal{O}}_{E}}({\mathcal{F}}|_{E},{\mathcal{H}})$
on
![]() $E$
. Let
$E$
. Let
![]() $h:H^{d-1}(\bar{E},{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
be a homomorphism. Then we obtain an element
$h:H^{d-1}(\bar{E},{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
be a homomorphism. Then we obtain an element
![]() $g$
of
$g$
of
![]() ${\mathcal{G}}(E)$
associated to
${\mathcal{G}}(E)$
associated to
![]() $h$
as follows. By Grothendieck–Serre duality,
$h$
as follows. By Grothendieck–Serre duality,
![]() $h$
gives an element of
$h$
gives an element of
![]() $H^{1-d}(\bar{E},R{\mathcal{H}}om_{{\mathcal{O}}_{\bar{E}}}({\mathcal{F}},I))$
where
$H^{1-d}(\bar{E},R{\mathcal{H}}om_{{\mathcal{O}}_{\bar{E}}}({\mathcal{F}},I))$
where
![]() $I$
is the dualizing complex of
$I$
is the dualizing complex of
![]() $\bar{E}$
. Since the restriction of
$\bar{E}$
. Since the restriction of
![]() $I$
to
$I$
to
![]() $E$
is
$E$
is
![]() ${\mathcal{H}}[d-1]$
, we obtain an element
${\mathcal{H}}[d-1]$
, we obtain an element
![]() $g$
of
$g$
of
![]() $H^{1-d}(E,R{\mathcal{H}}om_{{\mathcal{O}}_{E}}({\mathcal{F}},I))=H^{0}(E,{\mathcal{H}}om_{{\mathcal{O}}_{E}}({\mathcal{F}},{\mathcal{H}}))={\mathcal{G}}(E)$
.
$H^{1-d}(E,R{\mathcal{H}}om_{{\mathcal{O}}_{E}}({\mathcal{F}},I))=H^{0}(E,{\mathcal{H}}om_{{\mathcal{O}}_{E}}({\mathcal{F}},{\mathcal{H}}))={\mathcal{G}}(E)$
.
This element
![]() $g$
is characterized by the following property. For any closed point
$g$
is characterized by the following property. For any closed point
![]() $x$
of
$x$
of
![]() $E$
, the homomorphism
$E$
, the homomorphism
![]() $H_{x}^{d-1}(E,{\mathcal{F}})=H_{x}^{d-1}(\bar{E},{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
induced by
$H_{x}^{d-1}(E,{\mathcal{F}})=H_{x}^{d-1}(\bar{E},{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
induced by
![]() $h$
corresponds by local duality
$h$
corresponds by local duality
![]() $\text{Hom}(H_{x}^{d-1}(E,{\mathcal{F}}),\mathbb{F}_{p})\cong \hat{{\mathcal{G}}}_{x}$
of Grothendieck to the image of
$\text{Hom}(H_{x}^{d-1}(E,{\mathcal{F}}),\mathbb{F}_{p})\cong \hat{{\mathcal{G}}}_{x}$
of Grothendieck to the image of
![]() $g$
in the completion
$g$
in the completion
![]() $\hat{{\mathcal{G}}}_{x}$
of
$\hat{{\mathcal{G}}}_{x}$
of
![]() ${\mathcal{G}}_{x}$
.
${\mathcal{G}}_{x}$
.
4.2 Global refined Swan conductor mod
 $p$
$p$
4.2.1. In this Section 4.2, let
![]() $X$
be a regular scheme of finite type over
$X$
be a regular scheme of finite type over
![]() $\mathbb{Z}$
, let
$\mathbb{Z}$
, let
![]() $D$
be a divisor on
$D$
be a divisor on
![]() $X$
with simple normal crossings, let
$X$
with simple normal crossings, let
![]() $j:U:=X\smallsetminus D\rightarrow X$
be the inclusion morphism, and let
$j:U:=X\smallsetminus D\rightarrow X$
be the inclusion morphism, and let
![]() $p$
be a prime number. Consider the sheaf
$p$
be a prime number. Consider the sheaf
![]() $R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
on the étale site of
$R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
on the étale site of
![]() $X$
, where
$X$
, where
![]() $j_{\ast }$
is the direct image functor for the étale topology.
$j_{\ast }$
is the direct image functor for the étale topology.
For an effective divisor
![]() $N$
on
$N$
on
![]() $X$
whose support is contained in
$X$
whose support is contained in
![]() $D$
, let
$D$
, let
![]() $F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
be the subsheaf of
$F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
be the subsheaf of
![]() $R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
consisting of local sections
$R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
consisting of local sections
![]() $\unicode[STIX]{x1D712}$
such that the Swan conductor
$\unicode[STIX]{x1D712}$
such that the Swan conductor
![]() $\text{Sw}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D712})$
at any point
$\text{Sw}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D712})$
at any point
![]() $\unicode[STIX]{x1D708}$
of codimension one satisfies
$\unicode[STIX]{x1D708}$
of codimension one satisfies
![]() $\text{Sw}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D712})\leqslant \text{ord}_{\unicode[STIX]{x1D708}}(N)$
, where
$\text{Sw}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D712})\leqslant \text{ord}_{\unicode[STIX]{x1D708}}(N)$
, where
![]() $\text{ord}_{\unicode[STIX]{x1D708}}(N)$
denotes the multiplicity of
$\text{ord}_{\unicode[STIX]{x1D708}}(N)$
denotes the multiplicity of
![]() $N$
at
$N$
at
![]() $\unicode[STIX]{x1D708}$
. Let
$\unicode[STIX]{x1D708}$
. Let
![]() $F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})\subset H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
be the inverse image of
$F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})\subset H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
be the inverse image of
![]() $H^{0}(X,F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p}))$
.
$H^{0}(X,F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p}))$
.
Theorem 4.2.2. Let
![]() $N$
be an effective divisor on
$N$
be an effective divisor on
![]() $X$
whose support is contained in
$X$
whose support is contained in
![]() $D$
. Write
$D$
. Write
![]() $N=\sum _{P}n(P)P$
(
$N=\sum _{P}n(P)P$
(
![]() $P$
ranges over all generic points of
$P$
ranges over all generic points of
![]() $D$
and
$D$
and
![]() $n(P)\in \mathbb{Z}_{{\geqslant}0}$
) and let
$n(P)\in \mathbb{Z}_{{\geqslant}0}$
) and let
![]() $M=\sum _{P}m(P)P$
where
$M=\sum _{P}m(P)P$
where
![]() $m(P)=\max (n(P)-\text{ord}_{P}(p),[n(P)/p])$
(so
$m(P)=\max (n(P)-\text{ord}_{P}(p),[n(P)/p])$
(so
![]() $M$
is an effective divisor on
$M$
is an effective divisor on
![]() $X$
such that
$X$
such that
![]() $M\leqslant N$
). Then there is a unique homomorphism
$M\leqslant N$
). Then there is a unique homomorphism
which is compatible with Rsw at all points of
![]() $X$
of codimension one in the support of
$X$
of codimension one in the support of
![]() $N-M$
.
$N-M$
.
Proof. By using étale localization of
![]() $X$
and then by taking a compactification of
$X$
and then by taking a compactification of
![]() $X$
, we may assume that
$X$
, we may assume that
![]() $X$
is a dense open subscheme of a proper normal
$X$
is a dense open subscheme of a proper normal
![]() $d$
-dimensional integral scheme
$d$
-dimensional integral scheme
![]() $\bar{X}$
over
$\bar{X}$
over
![]() $\mathbb{Z}$
such that
$\mathbb{Z}$
such that
![]() $\bar{X}(\mathbb{R})=\emptyset$
and
$\bar{X}(\mathbb{R})=\emptyset$
and
![]() $E=\text{Spec}({\mathcal{O}}_{X}/{\mathcal{O}}_{X}(M-N))$
is a dense open subscheme of a closed subscheme
$E=\text{Spec}({\mathcal{O}}_{X}/{\mathcal{O}}_{X}(M-N))$
is a dense open subscheme of a closed subscheme
![]() $\bar{E}$
of
$\bar{E}$
of
![]() $\bar{X}$
.
$\bar{X}$
.
We use the global class field theory of
![]() $\bar{X}$
. (Note that
$\bar{X}$
. (Note that
![]() $\bar{X}$
here is
$\bar{X}$
here is
![]() $X$
in Section 3.3.) Let
$X$
in Section 3.3.) Let
![]() $\unicode[STIX]{x1D712}\in F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Let
$\unicode[STIX]{x1D712}\in F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Let
![]() $K$
be the function field of
$K$
be the function field of
![]() $X$
and let
$X$
and let
![]() $h_{\mathfrak{p}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
for
$h_{\mathfrak{p}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
for
![]() $\mathfrak{p}\in P(\bar{X})$
be the homomorphism induced by
$\mathfrak{p}\in P(\bar{X})$
be the homomorphism induced by
![]() $\unicode[STIX]{x1D712}$
. We identify
$\unicode[STIX]{x1D712}$
. We identify
![]() $P(\bar{E})$
with the subset of
$P(\bar{E})$
with the subset of
![]() $P(\bar{X})$
consisting of all elements
$P(\bar{X})$
consisting of all elements
![]() $\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d}$
such that
$\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d}$
such that
![]() $x_{d-1}\in E$
. Let
$x_{d-1}\in E$
. Let
For a generic point
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
![]() $E$
, let
$E$
, let
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D708}}$
be the stalk of
${\mathcal{F}}_{\unicode[STIX]{x1D708}}$
be the stalk of
![]() ${\mathcal{F}}_{E}$
at
${\mathcal{F}}_{E}$
at
![]() $\unicode[STIX]{x1D708}$
. For
$\unicode[STIX]{x1D708}$
. For
![]() $\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d-1}\in P(\bar{E})$
, let
$\mathfrak{p}=(x_{i})_{0\leqslant i\leqslant d-1}\in P(\bar{E})$
, let
![]() $s_{\mathfrak{p}}:{\mathcal{F}}_{x_{d-1}}\rightarrow \mathbb{F}_{p}$
be the homomorphism induced by
$s_{\mathfrak{p}}:{\mathcal{F}}_{x_{d-1}}\rightarrow \mathbb{F}_{p}$
be the homomorphism induced by
![]() $h_{\mathfrak{p}}$
and the truncated exponential map.
$h_{\mathfrak{p}}$
and the truncated exponential map.
By using the arguments in the proof of 3.4.4, we can show that there is a coherent
![]() ${\mathcal{O}}_{\bar{E}}$
-module
${\mathcal{O}}_{\bar{E}}$
-module
![]() ${\mathcal{F}}$
such that
${\mathcal{F}}$
such that
![]() ${\mathcal{F}}|_{E}={\mathcal{F}}_{E}$
and such that for any
${\mathcal{F}}|_{E}={\mathcal{F}}_{E}$
and such that for any
![]() $\mathfrak{p}=(x_{i})_{i}\in P(\bar{E})$
such that
$\mathfrak{p}=(x_{i})_{i}\in P(\bar{E})$
such that
![]() $x_{d-2}\notin E$
,
$x_{d-2}\notin E$
,
![]() $s_{\mathfrak{p}}$
kills the image of
$s_{\mathfrak{p}}$
kills the image of
![]() ${\mathcal{F}}_{x_{d-2}}\rightarrow {\mathcal{F}}_{x_{d-1}}$
.
${\mathcal{F}}_{x_{d-2}}\rightarrow {\mathcal{F}}_{x_{d-1}}$
.
We prove that
![]() $(s_{\mathfrak{p}})_{\mathfrak{p}\in P(\bar{E})}$
comes from a homomorphism
$(s_{\mathfrak{p}})_{\mathfrak{p}\in P(\bar{E})}$
comes from a homomorphism
![]() $s:H^{d-1}(\bar{E},{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
. For this, by 2.3.4, it is sufficient to prove that for any point
$s:H^{d-1}(\bar{E},{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
. For this, by 2.3.4, it is sufficient to prove that for any point
![]() $\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D709}$
of
![]() $E$
of codimension one and for any
$E$
of codimension one and for any
![]() $\mathfrak{q}=(x_{i})_{i}\in Q_{d-1}(\bar{E})$
such that
$\mathfrak{q}=(x_{i})_{i}\in Q_{d-1}(\bar{E})$
such that
![]() $x_{d-2}=\unicode[STIX]{x1D709}$
, the map
$x_{d-2}=\unicode[STIX]{x1D709}$
, the map
![]() $(h_{\mathfrak{p}})_{\mathfrak{p}\in P_{\mathfrak{q}}(\bar{E})}:\bigoplus _{\mathfrak{p}\in P_{\mathfrak{q}}(\bar{E})}\;{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow \mathbb{F}_{p}$
kills the diagonal image of
$(h_{\mathfrak{p}})_{\mathfrak{p}\in P_{\mathfrak{q}}(\bar{E})}:\bigoplus _{\mathfrak{p}\in P_{\mathfrak{q}}(\bar{E})}\;{\mathcal{F}}_{\unicode[STIX]{x1D702}(\mathfrak{p})}\rightarrow \mathbb{F}_{p}$
kills the diagonal image of
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
. This is proved by the following Facts 1 and 2.
${\mathcal{F}}_{\unicode[STIX]{x1D709}}$
. This is proved by the following Facts 1 and 2.
Fact 1. We have
![]() $\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}=\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(\bar{X})}h_{\mathfrak{p}}=0$
on
$\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}=\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(\bar{X})}h_{\mathfrak{p}}=0$
on
![]() $K_{d}^{M}(K)$
, where
$K_{d}^{M}(K)$
, where
![]() $\mathfrak{q}$
is identified with an element of
$\mathfrak{q}$
is identified with an element of
![]() $Q_{d-1}(X)$
.
$Q_{d-1}(X)$
.
Fact 2. If
![]() $\mathfrak{p}=(x_{i})_{i}\in P_{\mathfrak{q}}(X)$
and
$\mathfrak{p}=(x_{i})_{i}\in P_{\mathfrak{q}}(X)$
and
![]() $\unicode[STIX]{x1D707}:=x_{d-1}$
does not belong to
$\unicode[STIX]{x1D707}:=x_{d-1}$
does not belong to
![]() $E$
,
$E$
,
![]() $h_{\mathfrak{p}}$
factors through the boundary map
$h_{\mathfrak{p}}$
factors through the boundary map
![]() $K_{d}^{M}(K)\rightarrow K_{d-1}^{M}(\unicode[STIX]{x1D705}(\unicode[STIX]{x1D707}))$
and
$K_{d}^{M}(K)\rightarrow K_{d-1}^{M}(\unicode[STIX]{x1D705}(\unicode[STIX]{x1D707}))$
and
![]() $s_{\mathfrak{p}}({\mathcal{F}}_{\unicode[STIX]{x1D709}})$
is generated by elements of the form
$s_{\mathfrak{p}}({\mathcal{F}}_{\unicode[STIX]{x1D709}})$
is generated by elements of the form
![]() $h_{\mathfrak{p}}(\{u_{1},\ldots ,u_{d}\})$
with
$h_{\mathfrak{p}}(\{u_{1},\ldots ,u_{d}\})$
with
![]() $u_{i}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }$
and such
$u_{i}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }$
and such
![]() $\{u_{1},\ldots ,u_{d}\}$
is killed by the boundary map.
$\{u_{1},\ldots ,u_{d}\}$
is killed by the boundary map.
Let
![]() ${\mathcal{H}}:={\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)$
as in 4.1.2, and let
${\mathcal{H}}:={\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{d}(\log D)$
as in 4.1.2, and let
![]() ${\mathcal{G}}:={\mathcal{H}}om_{{\mathcal{O}}_{E}}({\mathcal{F}},{\mathcal{H}})={\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
. Then
${\mathcal{G}}:={\mathcal{H}}om_{{\mathcal{O}}_{E}}({\mathcal{F}},{\mathcal{H}})={\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
. Then
![]() $s:H^{d-1}(\bar{E},{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
gives an element
$s:H^{d-1}(\bar{E},{\mathcal{F}})\rightarrow \mathbb{F}_{p}$
gives an element
![]() $\text{Rsw}(\unicode[STIX]{x1D712})\in {\mathcal{G}}(E)$
by 4.1.3. By 4.1.2 and 4.1.3, this element induces
$\text{Rsw}(\unicode[STIX]{x1D712})\in {\mathcal{G}}(E)$
by 4.1.3. By 4.1.2 and 4.1.3, this element induces
![]() $\text{Rsw}$
at any generic point of
$\text{Rsw}$
at any generic point of
![]() $E$
.◻
$E$
.◻
Proposition 4.2.3. Let the notation be as in 4.2.2. The map
is injective, and its image is contained in the kernel of
Proof. This follows from 3.5.8. ◻
4.3 Pullbacks
We prove that the global Rsw (4.2.2) commutes with the pullback maps.
Theorem 4.3.1. Let
![]() $f:X^{\prime }\rightarrow X$
be a morphism of regular schemes of finite type over
$f:X^{\prime }\rightarrow X$
be a morphism of regular schemes of finite type over
![]() $\mathbb{Z}$
, let
$\mathbb{Z}$
, let
![]() $D$
(resp.
$D$
(resp.
![]() $D^{\prime }$
) be a divisor on
$D^{\prime }$
) be a divisor on
![]() $X$
(resp.
$X$
(resp.
![]() $X^{\prime }$
) with simple normal crossings, and assume
$X^{\prime }$
) with simple normal crossings, and assume
![]() $f(U^{\prime })\subset U$
where
$f(U^{\prime })\subset U$
where
![]() $U=X\smallsetminus D$
,
$U=X\smallsetminus D$
,
![]() $U^{\prime }=X^{\prime }\smallsetminus D^{\prime }$
. Let
$U^{\prime }=X^{\prime }\smallsetminus D^{\prime }$
. Let
![]() $p$
be a prime number. Let
$p$
be a prime number. Let
![]() $N$
be an effective divisor on
$N$
be an effective divisor on
![]() $X$
whose support is contained in
$X$
whose support is contained in
![]() $D$
, let
$D$
, let
![]() $N^{\prime }$
be the pullback
$N^{\prime }$
be the pullback
![]() $f^{\ast }N$
of
$f^{\ast }N$
of
![]() $N$
on
$N$
on
![]() $X^{\prime }$
, define the effective divisor
$X^{\prime }$
, define the effective divisor
![]() $M\leqslant N$
on
$M\leqslant N$
on
![]() $X$
using
$X$
using
![]() $N$
as in 4.2.2 and define the effective divisor
$N$
as in 4.2.2 and define the effective divisor
![]() $M^{\prime }\leqslant N^{\prime }$
on
$M^{\prime }\leqslant N^{\prime }$
on
![]() $X^{\prime }$
using
$X^{\prime }$
using
![]() $N^{\prime }$
similarly. Let
$N^{\prime }$
similarly. Let
![]() $j^{\prime }:U^{\prime }\rightarrow X^{\prime }$
be the inclusion morphism.
$j^{\prime }:U^{\prime }\rightarrow X^{\prime }$
be the inclusion morphism.
(1) The map
 $f^{\ast }R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow R^{1}j_{\ast }^{\prime }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
sends
$f^{\ast }R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})\rightarrow R^{1}j_{\ast }^{\prime }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
sends
 $f^{\ast }F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
to
$f^{\ast }F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
to
 $F_{N^{\prime }}R^{1}j_{\ast }^{\prime }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
.
$F_{N^{\prime }}R^{1}j_{\ast }^{\prime }(\mathbb{Q}_{p}/\mathbb{Z}_{p})$
.(2) We have a commutative diagram
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}f^{\ast }F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p}) & \overset{\text{Rsw}}{\rightarrow } & f^{\ast }({\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))\\ \downarrow & & \downarrow \\ F_{N^{\prime }}R^{1}j_{\ast }^{\prime }(\mathbb{Q}_{p}/\mathbb{Z}_{p}) & \overset{\text{Rsw}}{\rightarrow } & {\mathcal{O}}_{X^{\prime }}(N^{\prime })/{\mathcal{O}}_{X}(M^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime }).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}f^{\ast }F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p}) & \overset{\text{Rsw}}{\rightarrow } & f^{\ast }({\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))\\ \downarrow & & \downarrow \\ F_{N^{\prime }}R^{1}j_{\ast }^{\prime }(\mathbb{Q}_{p}/\mathbb{Z}_{p}) & \overset{\text{Rsw}}{\rightarrow } & {\mathcal{O}}_{X^{\prime }}(N^{\prime })/{\mathcal{O}}_{X}(M^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime }).\end{array}\end{eqnarray}$$
We first prove Theorem 4.3.1 in special cases (4.3.2, 4.3.5, and 4.3.7).
Lemma 4.3.2. Theorem 4.3.1 is true if
![]() $X^{\prime }$
is the blowing-up of
$X^{\prime }$
is the blowing-up of
![]() $X$
at a closed point of
$X$
at a closed point of
![]() $D$
.
$D$
.
To prove 4.3.2, we use the following lemma.
Lemma 4.3.3. Let the notation be as in 4.2.2. Let
![]() $X^{\prime }$
be the blowing-up of
$X^{\prime }$
be the blowing-up of
![]() $X$
at a closed point
$X$
at a closed point
![]() $x$
of
$x$
of
![]() $D$
and let
$D$
and let
![]() $D^{\prime }$
be the support of the pullback of
$D^{\prime }$
be the support of the pullback of
![]() $D$
on
$D$
on
![]() $X^{\prime }$
. Assume
$X^{\prime }$
. Assume
![]() $\dim ({\mathcal{O}}_{X,x})\geqslant 2$
. Let
$\dim ({\mathcal{O}}_{X,x})\geqslant 2$
. Let
![]() $\unicode[STIX]{x1D706}:X\smallsetminus \{x\}\rightarrow X$
and
$\unicode[STIX]{x1D706}:X\smallsetminus \{x\}\rightarrow X$
and
![]() $\unicode[STIX]{x1D706}^{\prime }:X^{\prime }\smallsetminus f^{-1}(x)\rightarrow X^{\prime }$
be the inclusion maps. Then the composite map
$\unicode[STIX]{x1D706}^{\prime }:X^{\prime }\smallsetminus f^{-1}(x)\rightarrow X^{\prime }$
be the inclusion maps. Then the composite map
 $$\begin{eqnarray}\displaystyle & & \displaystyle f_{\ast }({\mathcal{O}}_{X^{\prime }}(N^{\prime })/{\mathcal{O}}_{X^{\prime }}(M^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow f_{\ast }\unicode[STIX]{x1D706}_{\ast }^{\prime }(\unicode[STIX]{x1D706}^{\prime })^{\ast }({\mathcal{O}}_{X^{\prime }}(N^{\prime })/{\mathcal{O}}_{X^{\prime }}(M^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad \cong \unicode[STIX]{x1D706}_{\ast }\unicode[STIX]{x1D706}^{\ast }({\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f_{\ast }({\mathcal{O}}_{X^{\prime }}(N^{\prime })/{\mathcal{O}}_{X^{\prime }}(M^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow f_{\ast }\unicode[STIX]{x1D706}_{\ast }^{\prime }(\unicode[STIX]{x1D706}^{\prime })^{\ast }({\mathcal{O}}_{X^{\prime }}(N^{\prime })/{\mathcal{O}}_{X^{\prime }}(M^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad \cong \unicode[STIX]{x1D706}_{\ast }\unicode[STIX]{x1D706}^{\ast }({\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))\end{eqnarray}$$
is injective.
Proof. Let
![]() $D_{i}$
(
$D_{i}$
(
![]() $1\leqslant i\leqslant r$
) be the irreducible components of
$1\leqslant i\leqslant r$
) be the irreducible components of
![]() $D$
which contain
$D$
which contain
![]() $x$
. Replacing
$x$
. Replacing
![]() $X$
by an open neighborhood of
$X$
by an open neighborhood of
![]() $x$
, we may assume that
$x$
, we may assume that
![]() $D=\bigcup _{i=1}^{r}D_{i}$
. Write
$D=\bigcup _{i=1}^{r}D_{i}$
. Write
![]() $N=\sum _{i=1}^{r}n_{i}D_{i}$
,
$N=\sum _{i=1}^{r}n_{i}D_{i}$
,
![]() $M=\sum _{i=1}^{r}m_{i}D_{i}$
(
$M=\sum _{i=1}^{r}m_{i}D_{i}$
(
![]() $n_{i},m_{i}\in \mathbb{Z}_{{\geqslant}0}$
). We have
$n_{i},m_{i}\in \mathbb{Z}_{{\geqslant}0}$
). We have
![]() $N^{\prime }=\sum _{i=1}^{r}n_{i}D_{i}^{\prime }+(\sum _{i=1}^{r}n_{i})P$
where
$N^{\prime }=\sum _{i=1}^{r}n_{i}D_{i}^{\prime }+(\sum _{i=1}^{r}n_{i})P$
where
![]() $D_{i}^{\prime }$
is the proper transformation of
$D_{i}^{\prime }$
is the proper transformation of
![]() $D_{i}$
in
$D_{i}$
in
![]() $X^{\prime }$
and
$X^{\prime }$
and
![]() $P$
is the inverse image of
$P$
is the inverse image of
![]() $x$
in
$x$
in
![]() $X^{\prime }$
. We have
$X^{\prime }$
. We have
![]() $M^{\prime }=\sum _{i=1}^{r}m_{i}D_{i}^{\prime }+m^{\prime }P$
for some integer
$M^{\prime }=\sum _{i=1}^{r}m_{i}D_{i}^{\prime }+m^{\prime }P$
for some integer
![]() $m^{\prime }$
such that
$m^{\prime }$
such that
![]() $\sum _{i=1}^{r}m_{i}\leqslant m^{\prime }\leqslant \sum _{i=1}^{r}n_{i}$
. Take integers
$\sum _{i=1}^{r}m_{i}\leqslant m^{\prime }\leqslant \sum _{i=1}^{r}n_{i}$
. Take integers
![]() $a_{i}$
(
$a_{i}$
(
![]() $1\leqslant i\leqslant r$
) such that
$1\leqslant i\leqslant r$
) such that
![]() $m_{i}\leqslant a_{i}\leqslant n_{i}$
and
$m_{i}\leqslant a_{i}\leqslant n_{i}$
and
![]() $\sum _{i=1}^{r}a_{i}=m^{\prime }$
, and let
$\sum _{i=1}^{r}a_{i}=m^{\prime }$
, and let
![]() $A$
be the divisor
$A$
be the divisor
![]() $\sum _{i=1}^{r}a_{i}D_{i}$
on
$\sum _{i=1}^{r}a_{i}D_{i}$
on
![]() $X$
. Then the pullback
$X$
. Then the pullback
![]() $A^{\prime }$
of
$A^{\prime }$
of
![]() $A$
on
$A$
on
![]() $X^{\prime }$
is
$X^{\prime }$
is
![]() $\sum _{i=1}^{r}a_{i}D_{i}^{\prime }+m^{\prime }P$
. It is sufficient to prove that the maps
$\sum _{i=1}^{r}a_{i}D_{i}^{\prime }+m^{\prime }P$
. It is sufficient to prove that the maps
are injective.
We first prove that the map (22) is injective. Regard the divisors
![]() $A-M$
and
$A-M$
and
![]() $A^{\prime }-M^{\prime }$
as schemes. Then
$A^{\prime }-M^{\prime }$
as schemes. Then
![]() $(A-M)\smallsetminus \{x\}$
is a dense open subscheme of
$(A-M)\smallsetminus \{x\}$
is a dense open subscheme of
![]() $A^{\prime }-M^{\prime }$
,
$A^{\prime }-M^{\prime }$
,
![]() ${\mathcal{F}}:={\mathcal{O}}_{X^{\prime }}(A^{\prime })/{\mathcal{O}}_{X^{\prime }}(M^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime })$
is a vector bundle on
${\mathcal{F}}:={\mathcal{O}}_{X^{\prime }}(A^{\prime })/{\mathcal{O}}_{X^{\prime }}(M^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime })$
is a vector bundle on
![]() $A^{\prime }-M^{\prime }$
, and the map (22) is the canonical map
$A^{\prime }-M^{\prime }$
, and the map (22) is the canonical map
![]() ${\mathcal{F}}\rightarrow \unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }{\mathcal{F}}$
for the inclusion map
${\mathcal{F}}\rightarrow \unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }{\mathcal{F}}$
for the inclusion map
![]() $\unicode[STIX]{x1D6FE}:(A-M)-\{x\}\rightarrow A-M$
and hence it is injective.
$\unicode[STIX]{x1D6FE}:(A-M)-\{x\}\rightarrow A-M$
and hence it is injective.
We next prove that the map (21) is injective. Take a sequence of divisors
![]() $A_{i}$
(
$A_{i}$
(
![]() $0\leqslant i\leqslant s$
) on
$0\leqslant i\leqslant s$
) on
![]() $X$
such that
$X$
such that
![]() $N=A_{s}\geqslant \cdots \geqslant A_{0}=A$
and such that for each
$N=A_{s}\geqslant \cdots \geqslant A_{0}=A$
and such that for each
![]() $1\leqslant i\leqslant s$
,
$1\leqslant i\leqslant s$
,
![]() $A_{i}-A_{i-1}$
coincides with the divisor
$A_{i}-A_{i-1}$
coincides with the divisor
![]() $D_{j}$
for some
$D_{j}$
for some
![]() $j$
(
$j$
(
![]() $1\leqslant j\leqslant r$
,
$1\leqslant j\leqslant r$
,
![]() $j$
can depend on
$j$
can depend on
![]() $i$
,
$i$
,
![]() $D_{j}$
is regarded as a reduced scheme), and let
$D_{j}$
is regarded as a reduced scheme), and let
![]() $A_{i}^{\prime }$
be the pullback of
$A_{i}^{\prime }$
be the pullback of
![]() $A_{i}$
to
$A_{i}$
to
![]() $X^{\prime }$
. It is sufficient to prove that the map
$X^{\prime }$
. It is sufficient to prove that the map
is injective for each
![]() $1\leqslant i\leqslant s$
. Since
$1\leqslant i\leqslant s$
. Since
![]() ${\mathcal{O}}_{X^{\prime }}(A_{i}^{\prime })/{\mathcal{O}}_{X^{\prime }}(A_{i-1}^{\prime })\cong {\mathcal{O}}_{Q}$
where
${\mathcal{O}}_{X^{\prime }}(A_{i}^{\prime })/{\mathcal{O}}_{X^{\prime }}(A_{i-1}^{\prime })\cong {\mathcal{O}}_{Q}$
where
![]() $Q=D_{j}^{\prime }\cup P$
with the reduced scheme structure for some
$Q=D_{j}^{\prime }\cup P$
with the reduced scheme structure for some
![]() $j$
, it is sufficient to prove that the map
$j$
, it is sufficient to prove that the map
is injective. We may assume that
![]() $r=d$
where
$r=d$
where
![]() $d$
is the dimension of
$d$
is the dimension of
![]() ${\mathcal{O}}_{X,x}$
. In fact, on an open neighborhood of
${\mathcal{O}}_{X,x}$
. In fact, on an open neighborhood of
![]() $x$
, we can enlarge
$x$
, we can enlarge
![]() $D$
to a simple normal crossing divisor
$D$
to a simple normal crossing divisor
![]() $D^{\ast }$
with
$D^{\ast }$
with
![]() $d$
irreducible components such that
$d$
irreducible components such that
![]() $x$
is contained in all irreducible components of
$x$
is contained in all irreducible components of
![]() $D^{\ast }$
, and we can replace
$D^{\ast }$
, and we can replace
![]() $D$
by
$D$
by
![]() $D^{\ast }$
because the map
$D^{\ast }$
because the map
![]() ${\mathcal{O}}_{Q}\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime })\rightarrow {\mathcal{O}}_{Q}\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log (D^{\ast })^{\prime })$
is injective where
${\mathcal{O}}_{Q}\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime })\rightarrow {\mathcal{O}}_{Q}\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log (D^{\ast })^{\prime })$
is injective where
![]() $(D^{\ast })^{\prime }$
is the support of the pullback of
$(D^{\ast })^{\prime }$
is the support of the pullback of
![]() $D^{\ast }$
to
$D^{\ast }$
to
![]() $X^{\prime }$
. In the case
$X^{\prime }$
. In the case
![]() $r=d$
,
$r=d$
,
![]() $\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime })$
is the module theoretic pullback of
$\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime })$
is the module theoretic pullback of
![]() $\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
, and hence the injectivity of (24) is reduced to the injectivity of
$\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
, and hence the injectivity of (24) is reduced to the injectivity of
Since
![]() $P$
is isomorphic to the
$P$
is isomorphic to the
![]() $d-1$
-dimensional projective space over the residue field of
$d-1$
-dimensional projective space over the residue field of
![]() $\unicode[STIX]{x1D705}(x)$
,
$\unicode[STIX]{x1D705}(x)$
,
![]() $f_{\ast }({\mathcal{O}}_{P})$
consists of constant functions. Hence (25) is injective.◻
$f_{\ast }({\mathcal{O}}_{P})$
consists of constant functions. Hence (25) is injective.◻
4.3.4. We prove 4.3.2. Let
![]() $U^{\prime }$
be the inverse image of
$U^{\prime }$
be the inverse image of
![]() $U$
in
$U$
in
![]() $X^{\prime }$
(so we have an isomorphism
$X^{\prime }$
(so we have an isomorphism
![]() $U^{\prime }\overset{\cong }{\rightarrow }U$
). Let
$U^{\prime }\overset{\cong }{\rightarrow }U$
). Let
![]() $\unicode[STIX]{x1D712}\in F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. By [Reference Kato20, Theorem 8.1], the Swan conductor divisor of
$\unicode[STIX]{x1D712}\in F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. By [Reference Kato20, Theorem 8.1], the Swan conductor divisor of
![]() $\unicode[STIX]{x1D712}_{U^{\prime }}$
on
$\unicode[STIX]{x1D712}_{U^{\prime }}$
on
![]() $X^{\prime }$
is
$X^{\prime }$
is
![]() ${\leqslant}N^{\prime }$
. Both
${\leqslant}N^{\prime }$
. Both
![]() $\text{Rsw}(\unicode[STIX]{x1D712}_{U^{\prime }})$
and the pullback of
$\text{Rsw}(\unicode[STIX]{x1D712}_{U^{\prime }})$
and the pullback of
![]() $\text{Rsw}(\unicode[STIX]{x1D712})$
on
$\text{Rsw}(\unicode[STIX]{x1D712})$
on
![]() $X^{\prime }$
are sections of the left hand side of (20) whose images in the right hand side of (20) coincide with the pullback of
$X^{\prime }$
are sections of the left hand side of (20) whose images in the right hand side of (20) coincide with the pullback of
![]() $\text{Rsw}(\unicode[STIX]{x1D712})$
. Hence by the injectivity 4.3.3, they coincide.
$\text{Rsw}(\unicode[STIX]{x1D712})$
. Hence by the injectivity 4.3.3, they coincide.
Lemma 4.3.5. Theorem 4.3.1 is true if
![]() $X^{\prime }$
is a (locally closed) subscheme of
$X^{\prime }$
is a (locally closed) subscheme of
![]() $X$
of codimension one,
$X$
of codimension one,
![]() $D$
is regular, and the scheme
$D$
is regular, and the scheme
![]() $D\times _{X}X^{\prime }$
is regular.
$D\times _{X}X^{\prime }$
is regular.
The following proof of 4.3.5 models on the method of Brylinski in [Reference Brylinski7] who studied the induced ramification on a curve
![]() $X^{\prime }\subset X$
for a surface
$X^{\prime }\subset X$
for a surface
![]() $X$
over a finite field by using the class field theory of
$X$
over a finite field by using the class field theory of
![]() $X$
.
$X$
.
Proof. Let
![]() $D^{\prime }=D\times _{X}X^{\prime }$
. We may assume that
$D^{\prime }=D\times _{X}X^{\prime }$
. We may assume that
![]() $X$
,
$X$
,
![]() $D$
,
$D$
,
![]() $X^{\prime }$
and
$X^{\prime }$
and
![]() $D^{\prime }$
are integral and that
$D^{\prime }$
are integral and that
![]() $D$
is of characteristic
$D$
is of characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $K$
(resp.
$K$
(resp.
![]() $F$
, resp.
$F$
, resp.
![]() $K^{\prime }$
, resp.
$K^{\prime }$
, resp.
![]() $F^{\prime }$
) be the function field of
$F^{\prime }$
) be the function field of
![]() $X$
(resp.
$X$
(resp.
![]() $D$
, resp.
$D$
, resp.
![]() $X^{\prime }$
, resp.
$X^{\prime }$
, resp.
![]() $D^{\prime }$
). Let
$D^{\prime }$
). Let
![]() $d$
be the dimension of
$d$
be the dimension of
![]() $X$
. Let
$X$
. Let
![]() $\unicode[STIX]{x1D709}$
be the generic point of
$\unicode[STIX]{x1D709}$
be the generic point of
![]() $D^{\prime }$
and let
$D^{\prime }$
and let
![]() $\unicode[STIX]{x1D708}$
be the generic point of
$\unicode[STIX]{x1D708}$
be the generic point of
![]() $D$
. Let
$D$
. Let
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
be an element which defines
$\unicode[STIX]{x1D70F}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
be an element which defines
![]() $X^{\prime }$
at
$X^{\prime }$
at
![]() $\unicode[STIX]{x1D709}$
and let
$\unicode[STIX]{x1D709}$
and let
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
be an element which defines
$\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
be an element which defines
![]() $D$
at
$D$
at
![]() $\unicode[STIX]{x1D709}$
. Let
$\unicode[STIX]{x1D709}$
. Let
![]() $\mathfrak{q}=(x_{i})_{i}\in Q_{d-1}(X)$
and assume
$\mathfrak{q}=(x_{i})_{i}\in Q_{d-1}(X)$
and assume
![]() $x_{d-2}=\unicode[STIX]{x1D709}$
. Let
$x_{d-2}=\unicode[STIX]{x1D709}$
. Let
![]() $\unicode[STIX]{x1D712}\in F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. For
$\unicode[STIX]{x1D712}\in F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. For
![]() $\mathfrak{p}\in P_{\mathfrak{q}}(X)$
, consider the homomorphism
$\mathfrak{p}\in P_{\mathfrak{q}}(X)$
, consider the homomorphism
![]() $h_{\mathfrak{p}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
induced by
$h_{\mathfrak{p}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}$
induced by
![]() $\unicode[STIX]{x1D712}$
. Then we have
$\unicode[STIX]{x1D712}$
. Then we have
![]() $\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}=0$
on
$\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}=0$
on
![]() $K_{d}^{M}(K)$
. Let
$K_{d}^{M}(K)$
. Let
![]() $\mathfrak{p}_{1}=(x_{i})_{i}\in P_{\mathfrak{q}}(X)$
be the unique element such that
$\mathfrak{p}_{1}=(x_{i})_{i}\in P_{\mathfrak{q}}(X)$
be the unique element such that
![]() $x_{d-1}$
is the generic point of
$x_{d-1}$
is the generic point of
![]() $D$
, and let
$D$
, and let
![]() $\mathfrak{p}_{2}=(x_{i}^{\prime })_{i}$
be the unique element of
$\mathfrak{p}_{2}=(x_{i}^{\prime })_{i}$
be the unique element of
![]() $P_{\mathfrak{q}}(X)$
such that
$P_{\mathfrak{q}}(X)$
such that
![]() $x_{d-1}^{\prime }$
is the generic point of
$x_{d-1}^{\prime }$
is the generic point of
![]() $X^{\prime }$
.
$X^{\prime }$
.
Write
![]() $N=nD$
,
$N=nD$
,
![]() $M=mD$
. We may assume
$M=mD$
. We may assume
![]() $n>0$
and hence
$n>0$
and hence
![]() $n>m$
. Let
$n>m$
. Let
![]() $g\in \unicode[STIX]{x1D70B}^{m+1}{\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
and
$g\in \unicode[STIX]{x1D70B}^{m+1}{\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
and
![]() $y_{1},\ldots ,y_{d-2}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
, and let
$y_{1},\ldots ,y_{d-2}\in {\mathcal{O}}_{X,\unicode[STIX]{x1D709}}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
, and let
![]() $\unicode[STIX]{x1D6FC}=\{E(g),y_{1},\ldots ,y_{d-2},\unicode[STIX]{x1D70F}\}$
$\unicode[STIX]{x1D6FC}=\{E(g),y_{1},\ldots ,y_{d-2},\unicode[STIX]{x1D70F}\}$
![]() $\in K_{d}^{M}(K)$
. Since
$\in K_{d}^{M}(K)$
. Since
![]() $\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})=0$
and
$\sum _{\mathfrak{p}\in P_{\mathfrak{q}}(X)}h_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})=0$
and
![]() $h_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})=0$
for
$h_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})=0$
for
![]() $\mathfrak{p}\in P_{\mathfrak{q}}(X)\smallsetminus \{\mathfrak{p}_{1},\mathfrak{p}_{2}\}$
, we have
$\mathfrak{p}\in P_{\mathfrak{q}}(X)\smallsetminus \{\mathfrak{p}_{1},\mathfrak{p}_{2}\}$
, we have
Let
![]() $\unicode[STIX]{x1D712}^{\prime }$
be the pullback of
$\unicode[STIX]{x1D712}^{\prime }$
be the pullback of
![]() $\unicode[STIX]{x1D712}$
to
$\unicode[STIX]{x1D712}$
to
![]() $X^{\prime }\cap U$
. Let
$X^{\prime }\cap U$
. Let
![]() $\mathfrak{p}_{1}(D)$
be
$\mathfrak{p}_{1}(D)$
be
![]() $\mathfrak{p}_{1}$
regarded as an element of
$\mathfrak{p}_{1}$
regarded as an element of
![]() $P(D)$
and define
$P(D)$
and define
![]() $\mathfrak{p}_{2}(X^{\prime })\in P(X^{\prime })$
and
$\mathfrak{p}_{2}(X^{\prime })\in P(X^{\prime })$
and
![]() $\mathfrak{q}(D^{\prime })\in P(D^{\prime })$
similarly. Let
$\mathfrak{q}(D^{\prime })\in P(D^{\prime })$
similarly. Let
![]() $h_{\mathfrak{p}_{2}(X^{\prime })}:K_{d-1}^{M}(K^{\prime })\rightarrow \mathbb{Q}/\mathbb{Z}$
be the homomorphism induced by
$h_{\mathfrak{p}_{2}(X^{\prime })}:K_{d-1}^{M}(K^{\prime })\rightarrow \mathbb{Q}/\mathbb{Z}$
be the homomorphism induced by
![]() $\unicode[STIX]{x1D712}^{\prime }$
. Then
$\unicode[STIX]{x1D712}^{\prime }$
. Then
![]() $h_{\mathfrak{p}_{2}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
coincides with the composition
$h_{\mathfrak{p}_{2}}:K_{d}^{M}(K)\rightarrow \mathbb{Q}/\mathbb{Z}$
coincides with the composition
![]() $K_{d}^{M}(K)\overset{\unicode[STIX]{x2202}}{\rightarrow }K_{d-1}^{M}(K^{\prime })\rightarrow \mathbb{Q}/\mathbb{Z}$
where the first arrow is the boundary map and the second arrow is
$K_{d}^{M}(K)\overset{\unicode[STIX]{x2202}}{\rightarrow }K_{d-1}^{M}(K^{\prime })\rightarrow \mathbb{Q}/\mathbb{Z}$
where the first arrow is the boundary map and the second arrow is
![]() $h_{\mathfrak{p}_{2}(X^{\prime })}$
.
$h_{\mathfrak{p}_{2}(X^{\prime })}$
.
We first prove
![]() $\text{Sw}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D712}^{\prime })\leqslant n$
. It is sufficient to prove that
$\text{Sw}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D712}^{\prime })\leqslant n$
. It is sufficient to prove that
![]() $h_{\mathfrak{p}_{2}(X^{\prime })}$
kills
$h_{\mathfrak{p}_{2}(X^{\prime })}$
kills
![]() $U^{n+1}K_{d-1}^{M}(K^{\prime })$
where
$U^{n+1}K_{d-1}^{M}(K^{\prime })$
where
![]() $U^{\bullet }$
is for the discrete valuation ring
$U^{\bullet }$
is for the discrete valuation ring
![]() ${\mathcal{O}}_{X^{\prime },\unicode[STIX]{x1D709}}$
. The group
${\mathcal{O}}_{X^{\prime },\unicode[STIX]{x1D709}}$
. The group
![]() $U^{n+1}K_{d-1}^{M}(K^{\prime })$
is generated by
$U^{n+1}K_{d-1}^{M}(K^{\prime })$
is generated by
![]() $\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FC})$
where
$\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FC})$
where
![]() $\unicode[STIX]{x1D6FC}=\{E(g),y_{1},\ldots ,y_{d-2},\unicode[STIX]{x1D70F}\}$
is as above such that
$\unicode[STIX]{x1D6FC}=\{E(g),y_{1},\ldots ,y_{d-2},\unicode[STIX]{x1D70F}\}$
is as above such that
![]() $g\in \unicode[STIX]{x1D70B}^{n+1}{\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
. For such
$g\in \unicode[STIX]{x1D70B}^{n+1}{\mathcal{O}}_{X,\unicode[STIX]{x1D709}}$
. For such
![]() $\unicode[STIX]{x1D6FC}$
, we have
$\unicode[STIX]{x1D6FC}$
, we have
![]() $h_{\mathfrak{p}_{2}(X^{\prime })}(\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FC}))=h_{\mathfrak{p}_{2}}(\unicode[STIX]{x1D6FC})=-h_{\mathfrak{p}_{1}}(\unicode[STIX]{x1D6FC})=0$
. Here we used (26) and the fact
$h_{\mathfrak{p}_{2}(X^{\prime })}(\unicode[STIX]{x2202}(\unicode[STIX]{x1D6FC}))=h_{\mathfrak{p}_{2}}(\unicode[STIX]{x1D6FC})=-h_{\mathfrak{p}_{1}}(\unicode[STIX]{x1D6FC})=0$
. Here we used (26) and the fact
![]() $\text{Sw}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D712})\leqslant n$
and hence
$\text{Sw}_{\unicode[STIX]{x1D708}}(\unicode[STIX]{x1D712})\leqslant n$
and hence
![]() $h_{\mathfrak{p}_{1}}$
kills
$h_{\mathfrak{p}_{1}}$
kills
![]() $\unicode[STIX]{x1D6FC}\in U^{n+1}K_{d}^{M}(K)$
where
$\unicode[STIX]{x1D6FC}\in U^{n+1}K_{d}^{M}(K)$
where
![]() $U^{\bullet }$
is for the discrete valuation ring
$U^{\bullet }$
is for the discrete valuation ring
![]() ${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
.
${\mathcal{O}}_{X,\unicode[STIX]{x1D708}}$
.
Let
![]() $E$
and
$E$
and
![]() $E^{\prime }$
be the schemes
$E^{\prime }$
be the schemes
![]() $(n-m)D$
and
$(n-m)D$
and
![]() $(n-m)D^{\prime }$
, respectively. Since
$(n-m)D^{\prime }$
, respectively. Since
![]() $\mathbb{F}_{p}[T]\rightarrow {\mathcal{O}}_{D,\unicode[STIX]{x1D709}}\;;\;T\mapsto \unicode[STIX]{x1D70F}$
is a localization of a smooth map, there is a ring homomorphism
$\mathbb{F}_{p}[T]\rightarrow {\mathcal{O}}_{D,\unicode[STIX]{x1D709}}\;;\;T\mapsto \unicode[STIX]{x1D70F}$
is a localization of a smooth map, there is a ring homomorphism
![]() $\unicode[STIX]{x1D704}:{\mathcal{O}}_{D,\unicode[STIX]{x1D709}}\rightarrow {\mathcal{O}}_{E,\unicode[STIX]{x1D709}}$
which lifts the identity map of
$\unicode[STIX]{x1D704}:{\mathcal{O}}_{D,\unicode[STIX]{x1D709}}\rightarrow {\mathcal{O}}_{E,\unicode[STIX]{x1D709}}$
which lifts the identity map of
![]() ${\mathcal{O}}_{D,\unicode[STIX]{x1D709}}$
and which sends the image of
${\mathcal{O}}_{D,\unicode[STIX]{x1D709}}$
and which sends the image of
![]() $\unicode[STIX]{x1D70F}$
to the image of
$\unicode[STIX]{x1D70F}$
to the image of
![]() $\unicode[STIX]{x1D70F}$
. Then
$\unicode[STIX]{x1D70F}$
. Then
![]() $\unicode[STIX]{x1D704}$
induces ring homomorphisms
$\unicode[STIX]{x1D704}$
induces ring homomorphisms
![]() $F\rightarrow {\mathcal{O}}_{E,\unicode[STIX]{x1D708}}$
and
$F\rightarrow {\mathcal{O}}_{E,\unicode[STIX]{x1D708}}$
and
![]() $F^{\prime }\rightarrow {\mathcal{O}}_{E^{\prime },\unicode[STIX]{x1D709}}$
which lift the identity maps of
$F^{\prime }\rightarrow {\mathcal{O}}_{E^{\prime },\unicode[STIX]{x1D709}}$
which lift the identity maps of
![]() $F$
and
$F$
and
![]() $F^{\prime }$
, respectively. Write
$F^{\prime }$
, respectively. Write
 $$\begin{eqnarray}\displaystyle \text{Rsw}(\unicode[STIX]{x1D712}) & = & \displaystyle \mathop{\sum }_{i=m+1}^{n}\unicode[STIX]{x1D70B}^{-i}\otimes (\unicode[STIX]{x1D704}(a_{i})\,d\log (\unicode[STIX]{x1D70B})+\unicode[STIX]{x1D704}(b_{i}))\nonumber\\ \displaystyle & \in & \displaystyle ({\mathcal{O}}_{X}(nD)/{\mathcal{O}}_{X}(mD)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))_{\unicode[STIX]{x1D709}},\nonumber\\ \displaystyle \text{Rsw}(\unicode[STIX]{x1D712}^{\prime }) & = & \displaystyle \mathop{\sum }_{i=m+1}^{n}\unicode[STIX]{x1D70B}^{-i}\otimes (\unicode[STIX]{x1D704}(a_{i}^{\prime })\,d\log (\unicode[STIX]{x1D70B})+\unicode[STIX]{x1D704}(b_{i}^{\prime }))\nonumber\\ \displaystyle & \in & \displaystyle ({\mathcal{O}}_{X^{\prime }}(nD^{\prime })/{\mathcal{O}}_{X^{\prime }}(mD^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime }))_{\unicode[STIX]{x1D709}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Rsw}(\unicode[STIX]{x1D712}) & = & \displaystyle \mathop{\sum }_{i=m+1}^{n}\unicode[STIX]{x1D70B}^{-i}\otimes (\unicode[STIX]{x1D704}(a_{i})\,d\log (\unicode[STIX]{x1D70B})+\unicode[STIX]{x1D704}(b_{i}))\nonumber\\ \displaystyle & \in & \displaystyle ({\mathcal{O}}_{X}(nD)/{\mathcal{O}}_{X}(mD)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))_{\unicode[STIX]{x1D709}},\nonumber\\ \displaystyle \text{Rsw}(\unicode[STIX]{x1D712}^{\prime }) & = & \displaystyle \mathop{\sum }_{i=m+1}^{n}\unicode[STIX]{x1D70B}^{-i}\otimes (\unicode[STIX]{x1D704}(a_{i}^{\prime })\,d\log (\unicode[STIX]{x1D70B})+\unicode[STIX]{x1D704}(b_{i}^{\prime }))\nonumber\\ \displaystyle & \in & \displaystyle ({\mathcal{O}}_{X^{\prime }}(nD^{\prime })/{\mathcal{O}}_{X^{\prime }}(mD^{\prime })\otimes _{{\mathcal{O}}_{X^{\prime }}}\unicode[STIX]{x1D6FA}_{X^{\prime }}^{1}(\log D^{\prime }))_{\unicode[STIX]{x1D709}},\nonumber\end{eqnarray}$$
where
![]() $a_{i}\in {\mathcal{O}}_{D,\unicode[STIX]{x1D709}},b_{i}\in \unicode[STIX]{x1D6FA}_{D,\unicode[STIX]{x1D709}}^{1},a_{i}^{\prime }\in F^{\prime },b_{i}^{\prime }\in \unicode[STIX]{x1D6FA}_{F^{\prime }}^{1}$
.
$a_{i}\in {\mathcal{O}}_{D,\unicode[STIX]{x1D709}},b_{i}\in \unicode[STIX]{x1D6FA}_{D,\unicode[STIX]{x1D709}}^{1},a_{i}^{\prime }\in F^{\prime },b_{i}^{\prime }\in \unicode[STIX]{x1D6FA}_{F^{\prime }}^{1}$
.
For
![]() $j\in \mathbb{Z}$
, let
$j\in \mathbb{Z}$
, let
![]() $\unicode[STIX]{x1D716}:\unicode[STIX]{x1D6FA}_{D,\unicode[STIX]{x1D709}}^{j}\rightarrow \unicode[STIX]{x1D6FA}_{F^{\prime }}^{j}$
be the canonical projection. It is sufficient to prove
$\unicode[STIX]{x1D716}:\unicode[STIX]{x1D6FA}_{D,\unicode[STIX]{x1D709}}^{j}\rightarrow \unicode[STIX]{x1D6FA}_{F^{\prime }}^{j}$
be the canonical projection. It is sufficient to prove
![]() $a_{i}^{\prime }=\unicode[STIX]{x1D716}(a_{i}),b_{i}^{\prime }=\unicode[STIX]{x1D716}(b_{i})$
for all
$a_{i}^{\prime }=\unicode[STIX]{x1D716}(a_{i}),b_{i}^{\prime }=\unicode[STIX]{x1D716}(b_{i})$
for all
![]() $i$
.
$i$
.
We prove
![]() $a_{i}^{\prime }=\unicode[STIX]{x1D716}(a_{i})$
. For any
$a_{i}^{\prime }=\unicode[STIX]{x1D716}(a_{i})$
. For any
![]() $c\in \unicode[STIX]{x1D6FA}_{D,\unicode[STIX]{x1D709}}^{d-2}$
, we have
$c\in \unicode[STIX]{x1D6FA}_{D,\unicode[STIX]{x1D709}}^{d-2}$
, we have
where
![]() $\text{Res}_{\mathfrak{p}_{1}(D)}=\sum _{v\in Pl(D,\mathfrak{p}_{1}(D))}\text{Res}_{F_{v}}$
,
$\text{Res}_{\mathfrak{p}_{1}(D)}=\sum _{v\in Pl(D,\mathfrak{p}_{1}(D))}\text{Res}_{F_{v}}$
,
![]() $\text{Res}_{\mathfrak{q}(D^{\prime })}=\sum _{v\in Pl(D^{\prime },\mathfrak{q}(D^{\prime }))}\text{Res}_{F_{v}^{\prime }}$
. On the other hand,
$\text{Res}_{\mathfrak{q}(D^{\prime })}=\sum _{v\in Pl(D^{\prime },\mathfrak{q}(D^{\prime }))}\text{Res}_{F_{v}^{\prime }}$
. On the other hand,
Hence by (26),
![]() $\text{Res}_{\mathfrak{q}(D^{\prime })}(\unicode[STIX]{x1D716}(a_{i})c)=\text{Res}_{\mathfrak{q}(D^{\prime })}(a_{i}^{\prime }c)$
for any
$\text{Res}_{\mathfrak{q}(D^{\prime })}(\unicode[STIX]{x1D716}(a_{i})c)=\text{Res}_{\mathfrak{q}(D^{\prime })}(a_{i}^{\prime }c)$
for any
![]() $c\in \unicode[STIX]{x1D6FA}_{F^{\prime }}^{d-2}$
. Hence we have
$c\in \unicode[STIX]{x1D6FA}_{F^{\prime }}^{d-2}$
. Hence we have
![]() $a_{i}=a_{i}^{\prime }$
.
$a_{i}=a_{i}^{\prime }$
.
We prove
![]() $b_{i}^{\prime }=\unicode[STIX]{x1D716}(b_{i})$
. For
$b_{i}^{\prime }=\unicode[STIX]{x1D716}(b_{i})$
. For
![]() $c\in \unicode[STIX]{x1D6FA}_{D,\unicode[STIX]{x1D709}}^{d-3}$
,
$c\in \unicode[STIX]{x1D6FA}_{D,\unicode[STIX]{x1D709}}^{d-3}$
,
On the other hand,
Hence by (26),
![]() $\text{Res}_{\mathfrak{q}(D^{\prime })}(\unicode[STIX]{x1D716}(b_{i})\wedge c)=\text{Res}_{\mathfrak{q}(D^{\prime })}(b_{i}^{\prime }\wedge c)$
for any
$\text{Res}_{\mathfrak{q}(D^{\prime })}(\unicode[STIX]{x1D716}(b_{i})\wedge c)=\text{Res}_{\mathfrak{q}(D^{\prime })}(b_{i}^{\prime }\wedge c)$
for any
![]() $c\in \unicode[STIX]{x1D6FA}_{F^{\prime }}^{d-3}$
. Hence we have
$c\in \unicode[STIX]{x1D6FA}_{F^{\prime }}^{d-3}$
. Hence we have
![]() $b_{i}=b_{i}^{\prime }$
.◻
$b_{i}=b_{i}^{\prime }$
.◻
Corollary 4.3.6. Theorem 4.3.1 is true in the case
![]() $X^{\prime }$
is a one-dimensional subscheme of
$X^{\prime }$
is a one-dimensional subscheme of
![]() $X$
such that
$X$
such that
![]() $X^{\prime }$
meets
$X^{\prime }$
meets
![]() $D$
only at regular points of
$D$
only at regular points of
![]() $D$
and the scheme
$D$
and the scheme
![]() $D\times _{X}X^{\prime }$
is regular.
$D\times _{X}X^{\prime }$
is regular.
Proof. This is because the morphism
![]() $X^{\prime }\rightarrow X$
is a composition of morphisms
$X^{\prime }\rightarrow X$
is a composition of morphisms
![]() $X^{\prime }\rightarrow X$
of the type of 4.3.5.◻
$X^{\prime }\rightarrow X$
of the type of 4.3.5.◻
Lemma 4.3.7. Theorem 4.3.1 is true if
![]() $X^{\prime }$
is one-dimensional.
$X^{\prime }$
is one-dimensional.
Proof. Let
![]() $C$
be the image of
$C$
be the image of
![]() $X^{\prime }\rightarrow X$
. We may assume that
$X^{\prime }\rightarrow X$
. We may assume that
![]() $C$
is one-dimensional. By repeating the blowing-up of
$C$
is one-dimensional. By repeating the blowing-up of
![]() $X$
at
$X$
at
![]() $C\cap D$
, we obtain the situation of 4.3.6 with
$C\cap D$
, we obtain the situation of 4.3.6 with
![]() $X^{\prime }=C$
. Hence in the composition
$X^{\prime }=C$
. Hence in the composition
![]() $X^{\prime }\rightarrow C\rightarrow X$
, 4.3.7 for the latter morphism is reduced to 4.3.2 and 4.3.6. Lemma 4.3.7 for the first morphism is reduced to (i) of 3.1.2.◻
$X^{\prime }\rightarrow C\rightarrow X$
, 4.3.7 for the latter morphism is reduced to 4.3.2 and 4.3.6. Lemma 4.3.7 for the first morphism is reduced to (i) of 3.1.2.◻
The following 4.3.8 is a preparation for 4.3.9 which is important to reduce Theorem 4.3.1 to 4.3.7.
Lemma 4.3.8. Let
![]() $D$
be a smooth scheme over a perfect field
$D$
be a smooth scheme over a perfect field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>0$
and let
$p>0$
and let
![]() $x$
be a closed point of
$x$
be a closed point of
![]() $D$
. Then we have an injection
$D$
. Then we have an injection
where
![]() $Z$
ranges over all closed integral subschemes of
$Z$
ranges over all closed integral subschemes of
![]() $D$
of dimension one which contain
$D$
of dimension one which contain
![]() $x$
and which are smooth at
$x$
and which are smooth at
![]() $x$
.
$x$
.
Proof. Let
![]() $\unicode[STIX]{x1D714}$
be a nonzero element of
$\unicode[STIX]{x1D714}$
be a nonzero element of
![]() $\unicode[STIX]{x1D6FA}_{D/k,x}^{1}$
. Let
$\unicode[STIX]{x1D6FA}_{D/k,x}^{1}$
. Let
![]() $(t_{i})_{1\leqslant i\leqslant d}$
be a regular system of parameters at
$(t_{i})_{1\leqslant i\leqslant d}$
be a regular system of parameters at
![]() $x$
. We prove by induction on
$x$
. We prove by induction on
![]() $d$
. Write
$d$
. Write
![]() $\unicode[STIX]{x1D714}=\sum _{i}g_{i}dt_{i}$
on an open neighborhood of
$\unicode[STIX]{x1D714}=\sum _{i}g_{i}dt_{i}$
on an open neighborhood of
![]() $x$
. We may assume
$x$
. We may assume
![]() $g_{1}\neq 0$
. Assume
$g_{1}\neq 0$
. Assume
![]() $d\geqslant 2$
. Since the ideals of
$d\geqslant 2$
. Since the ideals of
![]() $(t_{1}^{n}-t_{d})$
(
$(t_{1}^{n}-t_{d})$
(
![]() $n\geqslant 1$
) of
$n\geqslant 1$
) of
![]() ${\mathcal{O}}_{X,x}$
are distinct prime ideals of height one, there is
${\mathcal{O}}_{X,x}$
are distinct prime ideals of height one, there is
![]() $n\geqslant 1$
which is divisible by
$n\geqslant 1$
which is divisible by
![]() $p$
such that
$p$
such that
![]() $g_{1}\notin (t_{1}^{n}-t_{d})$
. Let
$g_{1}\notin (t_{1}^{n}-t_{d})$
. Let
![]() $Z$
be the closed integral subscheme of
$Z$
be the closed integral subscheme of
![]() $X$
containing
$X$
containing
![]() $x$
which is defined by
$x$
which is defined by
![]() $t_{1}^{n}-t_{d}$
at
$t_{1}^{n}-t_{d}$
at
![]() $x$
. Then
$x$
. Then
![]() $Z$
is smooth at
$Z$
is smooth at
![]() $x$
,
$x$
,
![]() $(dt_{i})_{1\leqslant i\leqslant d-1}$
is a base of
$(dt_{i})_{1\leqslant i\leqslant d-1}$
is a base of
![]() $\unicode[STIX]{x1D6FA}_{Z,x}^{1}$
, the image of
$\unicode[STIX]{x1D6FA}_{Z,x}^{1}$
, the image of
![]() $\unicode[STIX]{x1D714}$
in
$\unicode[STIX]{x1D714}$
in
![]() $\unicode[STIX]{x1D6FA}_{Z,x}^{1}$
is
$\unicode[STIX]{x1D6FA}_{Z,x}^{1}$
is
![]() $\sum _{i=1}^{d-1}g_{i}dt_{i}$
, and
$\sum _{i=1}^{d-1}g_{i}dt_{i}$
, and
![]() $g_{1}$
is nonzero in
$g_{1}$
is nonzero in
![]() ${\mathcal{O}}_{Z,x}$
.◻
${\mathcal{O}}_{Z,x}$
.◻
Lemma 4.3.9. Let the notation be as in 4.2.2. Let
![]() $x$
be a closed point of
$x$
be a closed point of
![]() $D$
at which
$D$
at which
![]() $D$
is regular. Then we have an injection
$D$
is regular. Then we have an injection
 $$\begin{eqnarray}\displaystyle & & \displaystyle ({\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))_{x}\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow \mathop{\prod }_{C}({\mathcal{O}}_{C}(N_{C}^{\prime })/{\mathcal{O}}_{C}(M_{C}^{\prime })\otimes _{{\mathcal{O}}_{C}}\unicode[STIX]{x1D6FA}_{C}^{1}(\log D_{C}^{\prime }))_{x}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle ({\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))_{x}\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow \mathop{\prod }_{C}({\mathcal{O}}_{C}(N_{C}^{\prime })/{\mathcal{O}}_{C}(M_{C}^{\prime })\otimes _{{\mathcal{O}}_{C}}\unicode[STIX]{x1D6FA}_{C}^{1}(\log D_{C}^{\prime }))_{x}\nonumber\end{eqnarray}$$
where
![]() $C$
ranges over all one-dimensional regular integral subschemes of
$C$
ranges over all one-dimensional regular integral subschemes of
![]() $X$
which contain
$X$
which contain
![]() $x$
and which are not contained in
$x$
and which are not contained in
![]() $D$
. Here
$D$
. Here
![]() $N_{C}^{\prime }$
is the pullback of
$N_{C}^{\prime }$
is the pullback of
![]() $N$
to
$N$
to
![]() $C$
,
$C$
,
![]() $M_{C}^{\prime }$
is the effective divisor on
$M_{C}^{\prime }$
is the effective divisor on
![]() $C$
defined using
$C$
defined using
![]() $N_{C}^{\prime }$
similarly to
$N_{C}^{\prime }$
similarly to
![]() $M$
, and
$M$
, and
![]() $D_{C}^{\prime }$
is the support of the pullback of
$D_{C}^{\prime }$
is the support of the pullback of
![]() $D$
to
$D$
to
![]() $C$
regarded as a divisor on
$C$
regarded as a divisor on
![]() $C$
with simple normal crossings.
$C$
with simple normal crossings.
Proof. We may assume that
![]() $D$
is regular and that
$D$
is regular and that
![]() $N=nD$
for some integer
$N=nD$
for some integer
![]() $n\geqslant 1$
. Let
$n\geqslant 1$
. Let
![]() $\unicode[STIX]{x1D714}$
be a nonzero element of
$\unicode[STIX]{x1D714}$
be a nonzero element of
![]() $({\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))_{x}$
. Let
$({\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(M)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D))_{x}$
. Let
![]() $\unicode[STIX]{x1D70B}$
be an element of
$\unicode[STIX]{x1D70B}$
be an element of
![]() ${\mathcal{O}}_{X,x}$
which defines
${\mathcal{O}}_{X,x}$
which defines
![]() $D$
at
$D$
at
![]() $x$
. Take a system of regular parameters
$x$
. Take a system of regular parameters
![]() $(t_{1},\ldots ,t_{d})$
of
$(t_{1},\ldots ,t_{d})$
of
![]() ${\mathcal{O}}_{X,x}$
such that
${\mathcal{O}}_{X,x}$
such that
![]() $t_{d}=\unicode[STIX]{x1D70B}$
. Write
$t_{d}=\unicode[STIX]{x1D70B}$
. Write
![]() $M=mD$
. Let
$M=mD$
. Let
![]() $h\geqslant 0$
be the largest integer such that
$h\geqslant 0$
be the largest integer such that
![]() $\unicode[STIX]{x1D714}$
is in the image of
$\unicode[STIX]{x1D714}$
is in the image of
![]() $\unicode[STIX]{x1D70B}^{h-n}\otimes \unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
. Then
$\unicode[STIX]{x1D70B}^{h-n}\otimes \unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
. Then
![]() $n-h>m$
. Write
$n-h>m$
. Write
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{h-n}\otimes (f\,d\log (\unicode[STIX]{x1D70B})+\sum _{i=1}^{d-1}g_{i}dt_{i})$
with
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{h-n}\otimes (f\,d\log (\unicode[STIX]{x1D70B})+\sum _{i=1}^{d-1}g_{i}dt_{i})$
with
![]() $f,g_{i}\in {\mathcal{O}}_{X,x}$
. Then the pullback of some of
$f,g_{i}\in {\mathcal{O}}_{X,x}$
. Then the pullback of some of
![]() $f$
and
$f$
and
![]() $g_{i}$
to
$g_{i}$
to
![]() $D$
is nonzero.
$D$
is nonzero.
There are two cases.
Case 1. The pullback of some
![]() $g_{i}$
to
$g_{i}$
to
![]() $D$
is nonzero.
$D$
is nonzero.
Case 2. The pullbacks of
![]() $g_{i}$
to
$g_{i}$
to
![]() $D$
are zero for all
$D$
are zero for all
![]() $i$
. In this case, the pullback of
$i$
. In this case, the pullback of
![]() $f$
to
$f$
to
![]() $D$
is nonzero.
$D$
is nonzero.
In Case 1 (resp. Case 2), there is a closed integral subscheme
![]() $Z$
of
$Z$
of
![]() $D$
of dimension one which contains
$D$
of dimension one which contains
![]() $x$
and which is smooth at
$x$
and which is smooth at
![]() $x$
such that the pullback of
$x$
such that the pullback of
![]() $\sum _{i=1}^{d-1}g_{i}dt_{i}$
(resp.
$\sum _{i=1}^{d-1}g_{i}dt_{i}$
(resp.
![]() $f$
) to
$f$
) to
![]() $Z$
is nonzero. (In Case 1, the existence of
$Z$
is nonzero. (In Case 1, the existence of
![]() $Z$
is by 4.3.8.) By changing the choice of
$Z$
is by 4.3.8.) By changing the choice of
![]() $(t_{i})_{1\leqslant i\leqslant d-1}$
, we may assume that
$(t_{i})_{1\leqslant i\leqslant d-1}$
, we may assume that
![]() $Z$
is defined at
$Z$
is defined at
![]() $x$
by
$x$
by
![]() $t_{2},\ldots ,t_{d-1}$
and
$t_{2},\ldots ,t_{d-1}$
and
![]() $\unicode[STIX]{x1D70B}$
. (In Case 1, the pullback of
$\unicode[STIX]{x1D70B}$
. (In Case 1, the pullback of
![]() $\sum _{i=1}^{d-1}g_{i}dt_{i}$
to
$\sum _{i=1}^{d-1}g_{i}dt_{i}$
to
![]() $Z$
becomes the pullback of
$Z$
becomes the pullback of
![]() $g_{1}dt_{1}$
.)
$g_{1}dt_{1}$
.)
Let
![]() $a$
be the order of the pullback of
$a$
be the order of the pullback of
![]() $g_{1}t_{1}$
(resp.
$g_{1}t_{1}$
(resp.
![]() $f$
) to
$f$
) to
![]() $Z$
at
$Z$
at
![]() $x$
.
$x$
.
Take an integer
![]() $e$
which is divisible by
$e$
which is divisible by
![]() $p$
(resp. is coprime to
$p$
(resp. is coprime to
![]() $p$
) such that
$p$
) such that
![]() $e\geqslant p(a+1)$
. Let
$e\geqslant p(a+1)$
. Let
![]() $C$
be a one-dimensional regular integral subscheme of
$C$
be a one-dimensional regular integral subscheme of
![]() $X$
containing
$X$
containing
![]() $x$
which is defined by
$x$
which is defined by
![]() $t_{2},\ldots ,t_{d-1},t_{1}^{e}-\unicode[STIX]{x1D70B}$
at
$t_{2},\ldots ,t_{d-1},t_{1}^{e}-\unicode[STIX]{x1D70B}$
at
![]() $x$
. Let
$x$
. Let
![]() $\unicode[STIX]{x1D714}^{\prime }$
be the pullback of
$\unicode[STIX]{x1D714}^{\prime }$
be the pullback of
![]() $\unicode[STIX]{x1D714}$
to
$\unicode[STIX]{x1D714}$
to
![]() $({\mathcal{O}}_{C}(N_{C}^{\prime })/{\mathcal{O}}_{C}(M_{C}^{\prime })\otimes _{{\mathcal{O}}_{C}}\unicode[STIX]{x1D6FA}_{C}^{1}(\log D_{C}^{\prime }))_{x}$
.
$({\mathcal{O}}_{C}(N_{C}^{\prime })/{\mathcal{O}}_{C}(M_{C}^{\prime })\otimes _{{\mathcal{O}}_{C}}\unicode[STIX]{x1D6FA}_{C}^{1}(\log D_{C}^{\prime }))_{x}$
.
In Case 1 (resp. Case 2), we have the following.
Claim 1.
![]() $N_{C}^{\prime }=enD_{C}^{\prime }$
,
$N_{C}^{\prime }=enD_{C}^{\prime }$
,
![]() $M_{C}^{\prime }=m^{\prime }D_{C}^{\prime }$
where
$M_{C}^{\prime }=m^{\prime }D_{C}^{\prime }$
where
![]() $m^{\prime }$
is an integer such that
$m^{\prime }$
is an integer such that
![]() $e^{-1}m^{\prime }\leqslant m+p^{-1}(p-1)$
.
$e^{-1}m^{\prime }\leqslant m+p^{-1}(p-1)$
.
![]() $t_{1}$
is a prime element of the discrete valuation ring
$t_{1}$
is a prime element of the discrete valuation ring
![]() ${\mathcal{O}}_{C,x}$
.
${\mathcal{O}}_{C,x}$
.
![]() $d\log (t_{1})$
is a generator of
$d\log (t_{1})$
is a generator of
![]() $\unicode[STIX]{x1D6FA}_{C}^{1}(\log D_{C}^{\prime })_{x}$
.
$\unicode[STIX]{x1D6FA}_{C}^{1}(\log D_{C}^{\prime })_{x}$
.
Claim 2.
![]() $\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D70B}^{h-n}\otimes g\,d\log (t_{1})$
, where
$\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D70B}^{h-n}\otimes g\,d\log (t_{1})$
, where
![]() $g$
is the pullback of
$g$
is the pullback of
![]() $g_{1}t_{1}$
(resp.
$g_{1}t_{1}$
(resp.
![]() $ef+g_{1}t_{1}$
) to
$ef+g_{1}t_{1}$
) to
![]() $C$
. The order of
$C$
. The order of
![]() $g$
at
$g$
at
![]() $x$
is
$x$
is
![]() $a$
.
$a$
.
The proofs of Claims 1 and 2 are straightforward.
Claim 3.
![]() $\unicode[STIX]{x1D714}^{\prime }\neq 0$
.
$\unicode[STIX]{x1D714}^{\prime }\neq 0$
.
To prove Claim 3, by Claims 1 and 2, it is sufficient to prove
![]() $e(n-h)-a>m^{\prime }$
. But
$e(n-h)-a>m^{\prime }$
. But
![]() $e^{-1}(e(n-h)-a-m^{\prime }-1)=(n-h-m-1)+m-e^{-1}m^{\prime }+1-e^{-1}(a+1)\geqslant (m-e^{-1}m^{\prime })+1-e^{-1}(a+1)\geqslant -p^{-1}(p-1)+1-p^{-1}=0$
.◻
$e^{-1}(e(n-h)-a-m^{\prime }-1)=(n-h-m-1)+m-e^{-1}m^{\prime }+1-e^{-1}(a+1)\geqslant (m-e^{-1}m^{\prime })+1-e^{-1}(a+1)\geqslant -p^{-1}(p-1)+1-p^{-1}=0$
.◻
4.3.10. Now we prove Theorem 4.3.1. By 4.3.9 which we apply by taking
![]() $X^{\prime }$
in 4.3.1 as
$X^{\prime }$
in 4.3.1 as
![]() $X$
in 4.3.9, we may assume that
$X$
in 4.3.9, we may assume that
![]() $X^{\prime }$
in 4.3.1 is one-dimensional. Then we are reduced to 4.3.7.
$X^{\prime }$
in 4.3.1 is one-dimensional. Then we are reduced to 4.3.7.
4.3.11. By 4.3.7 and 4.3.9, for
![]() $\unicode[STIX]{x1D712}\in F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
,
$\unicode[STIX]{x1D712}\in F_{N}H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
,
![]() $\text{Rsw}(\unicode[STIX]{x1D712})$
in Theorem 4.2.2 is determined by
$\text{Rsw}(\unicode[STIX]{x1D712})$
in Theorem 4.2.2 is determined by
![]() $\text{Rsw}$
of the pullbacks of
$\text{Rsw}$
of the pullbacks of
![]() $\unicode[STIX]{x1D712}$
to
$\unicode[STIX]{x1D712}$
to
![]() $F_{n(C,x)}H^{1}(K_{C,x},\mathbb{Q}_{p}/\mathbb{Z}_{p})$
, where
$F_{n(C,x)}H^{1}(K_{C,x},\mathbb{Q}_{p}/\mathbb{Z}_{p})$
, where
![]() $x$
ranges over regular points of
$x$
ranges over regular points of
![]() $D$
,
$D$
,
![]() $C$
ranges over one-dimensional regular integral subschemes of
$C$
ranges over one-dimensional regular integral subschemes of
![]() $X$
which contain
$X$
which contain
![]() $x$
and which are not contained in
$x$
and which are not contained in
![]() $D$
,
$D$
,
![]() $n(C,x)$
denotes the multiplicity of the pullback of
$n(C,x)$
denotes the multiplicity of the pullback of
![]() $N$
to
$N$
to
![]() $C$
at
$C$
at
![]() $x$
, and
$x$
, and
![]() $K_{C,x}$
denotes the local field of the function field of
$K_{C,x}$
denotes the local field of the function field of
![]() $C$
at
$C$
at
![]() $x$
.
$x$
.
4.3.12. In the case
![]() $X$
is of characteristic
$X$
is of characteristic
![]() $p$
, the proofs of the Theorems 4.2.2 and 4.3.1 can be given also by using Artin–Schreier–Witt theory.
$p$
, the proofs of the Theorems 4.2.2 and 4.3.1 can be given also by using Artin–Schreier–Witt theory.
We first consider 4.2.2. The exact sequence
![]() $0\rightarrow \mathbb{Z}/p^{s}\mathbb{Z}\rightarrow W_{s}({\mathcal{O}}_{U})\overset{\unicode[STIX]{x1D719}-1}{\rightarrow }W_{s}({\mathcal{O}}_{U})\rightarrow 0$
on
$0\rightarrow \mathbb{Z}/p^{s}\mathbb{Z}\rightarrow W_{s}({\mathcal{O}}_{U})\overset{\unicode[STIX]{x1D719}-1}{\rightarrow }W_{s}({\mathcal{O}}_{U})\rightarrow 0$
on
![]() $U_{et}$
, where
$U_{et}$
, where
![]() $\unicode[STIX]{x1D719}$
is the Frobenius, induces an exact sequence
$\unicode[STIX]{x1D719}$
is the Frobenius, induces an exact sequence
![]() $0\rightarrow \mathbb{Z}/p^{s}\mathbb{Z}\rightarrow j_{\ast }W_{s}({\mathcal{O}}_{U})\overset{\unicode[STIX]{x1D719}-1}{\rightarrow }j_{\ast }W_{s}({\mathcal{O}}_{U})\rightarrow R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})\rightarrow 0$
on
$0\rightarrow \mathbb{Z}/p^{s}\mathbb{Z}\rightarrow j_{\ast }W_{s}({\mathcal{O}}_{U})\overset{\unicode[STIX]{x1D719}-1}{\rightarrow }j_{\ast }W_{s}({\mathcal{O}}_{U})\rightarrow R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})\rightarrow 0$
on
![]() $X_{et}$
(this is because
$X_{et}$
(this is because
![]() $R^{1}j_{\ast }W_{s}({\mathcal{O}}_{U})=0$
by the fact
$R^{1}j_{\ast }W_{s}({\mathcal{O}}_{U})=0$
by the fact
![]() $j$
is an affine morphism). For an effective divisor
$j$
is an affine morphism). For an effective divisor
![]() $N$
whose support is contained in
$N$
whose support is contained in
![]() $D$
, let
$D$
, let
![]() $F_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})$
be the subsheaf of
$F_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})$
be the subsheaf of
![]() $j_{\ast }W_{s}({\mathcal{O}}_{U})$
consisting of local sections
$j_{\ast }W_{s}({\mathcal{O}}_{U})$
consisting of local sections
![]() $(f_{s-1},\ldots ,f_{0})$
satisfying
$(f_{s-1},\ldots ,f_{0})$
satisfying
![]() $p^{i}\text{div}(f_{i})\geqslant -N$
for all
$p^{i}\text{div}(f_{i})\geqslant -N$
for all
![]() $i$
. Similarly as [Reference Yatagawa35, Proposition 1.31(1)], the subsheaf
$i$
. Similarly as [Reference Yatagawa35, Proposition 1.31(1)], the subsheaf
![]() $F_{N}R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z}):=R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})\cap F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})\subset R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})$
where
$F_{N}R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z}):=R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})\cap F_{N}R^{1}j_{\ast }(\mathbb{Q}_{p}/\mathbb{Z}_{p})\subset R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})$
where
![]() $\mathbb{Z}/p^{s}\mathbb{Z}$
is embedded in
$\mathbb{Z}/p^{s}\mathbb{Z}$
is embedded in
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}$
in the canonical way equals the image of
$\mathbb{Q}_{p}/\mathbb{Z}_{p}$
in the canonical way equals the image of
![]() $F_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})$
.
$F_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})$
.
We have the homomorphism
 $$\begin{eqnarray}\displaystyle & \displaystyle F_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})\rightarrow {\mathcal{O}}_{X}(N)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D); & \displaystyle \nonumber\\ \displaystyle & \displaystyle (f_{s-1},\ldots ,f_{0})\mapsto -\mathop{\sum }_{i}f_{i}^{p^{i}-1}\,df_{i}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle F_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})\rightarrow {\mathcal{O}}_{X}(N)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D); & \displaystyle \nonumber\\ \displaystyle & \displaystyle (f_{s-1},\ldots ,f_{0})\mapsto -\mathop{\sum }_{i}f_{i}^{p^{i}-1}\,df_{i}. & \displaystyle \nonumber\end{eqnarray}$$
By the exact sequence
![]() $0\rightarrow \mathbb{Z}/p^{s}\mathbb{Z}\rightarrow F_{M}j_{\ast }W_{s}({\mathcal{O}}_{U})\overset{\unicode[STIX]{x1D719}-1}{\rightarrow }F_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})\rightarrow F_{N}^{\prime }R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})\rightarrow 0$
and by the surjectivity of
$0\rightarrow \mathbb{Z}/p^{s}\mathbb{Z}\rightarrow F_{M}j_{\ast }W_{s}({\mathcal{O}}_{U})\overset{\unicode[STIX]{x1D719}-1}{\rightarrow }F_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})\rightarrow F_{N}^{\prime }R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})\rightarrow 0$
and by the surjectivity of
![]() $\mathbb{F}_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})\rightarrow F_{N}R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})$
, this homomorphism induces a homomorphism
$\mathbb{F}_{N}j_{\ast }W_{s}({\mathcal{O}}_{U})\rightarrow F_{N}R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})$
, this homomorphism induces a homomorphism
which is
![]() $\text{Rsw}$
.
$\text{Rsw}$
.
The compatibility with pullbacks (4.3.1) is evident in this method.
The refined Swan conductor
![]() $F_{N}R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})\rightarrow {\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(N+D)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
defined in [Reference Yatagawa35, Definition 1.33] is induced by
$F_{N}R^{1}j_{\ast }(\mathbb{Z}/p^{s}\mathbb{Z})\rightarrow {\mathcal{O}}_{X}(N)/{\mathcal{O}}_{X}(N+D)\otimes _{{\mathcal{O}}_{X}}\unicode[STIX]{x1D6FA}_{X}^{1}(\log D)$
defined in [Reference Yatagawa35, Definition 1.33] is induced by
![]() $\text{Rsw}$
, by 3.5.7.
$\text{Rsw}$
, by 3.5.7.
As an application of our theory, we have the following theorem.
Theorem 4.3.13. Let
![]() $X$
be a regular scheme of finite type over
$X$
be a regular scheme of finite type over
![]() $\mathbb{Z}$
,
$\mathbb{Z}$
,
![]() $D$
a divisor on
$D$
a divisor on
![]() $X$
which is regular and integral,
$X$
which is regular and integral,
![]() $U=X\smallsetminus D$
,
$U=X\smallsetminus D$
,
![]() $p$
a prime number, and let
$p$
a prime number, and let
![]() $\unicode[STIX]{x1D712}\in H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Let
$\unicode[STIX]{x1D712}\in H_{et}^{1}(U,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
. Let
![]() $x$
be a closed point of
$x$
be a closed point of
![]() $D$
. Then
$D$
. Then
where
![]() $C$
ranges over all one-dimensional integral subschemes on
$C$
ranges over all one-dimensional integral subschemes on
![]() $X$
which contain
$X$
which contain
![]() $x$
, which are regular at
$x$
, which are regular at
![]() $x$
, and which are not contained
$x$
, and which are not contained
![]() $D$
. Here
$D$
. Here
![]() $\text{Sw}_{D}(\unicode[STIX]{x1D712})$
denotes the Swan conductor of
$\text{Sw}_{D}(\unicode[STIX]{x1D712})$
denotes the Swan conductor of
![]() $\unicode[STIX]{x1D712}$
at the generic point of
$\unicode[STIX]{x1D712}$
at the generic point of
![]() $D$
, and
$D$
, and
![]() $(C,D)_{x}$
denotes the intersection number of
$(C,D)_{x}$
denotes the intersection number of
![]() $C$
and
$C$
and
![]() $D$
at
$D$
at
![]() $x$
which is the multiplicity at
$x$
which is the multiplicity at
![]() $x$
of the pullback of the divisor
$x$
of the pullback of the divisor
![]() $D$
to
$D$
to
![]() $C$
.
$C$
.
The positive characteristic case of 4.3.13 is already proved by Barrientos [Reference Barrientos3, Theorem 5.2] without the assumption
![]() $X$
is of finite type over
$X$
is of finite type over
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
In the equal characteristic and geometric case, an analogue of 4.3.13 is proved in Hu [Reference Hu15] for the Swan conductor of a locally constant sheaf with ramification along a divisor defined by the logarithmic filtration by ramification groups [Reference Abbes and Saito1]. Conjecture A in [Reference Barrientos3] discussed in 4.3.15 is also studied in [Reference Hu15].
4.3.14. We prove 4.3.13. l.h.s
![]() ${\geqslant}$
r.h.s. follows from (1) of Theorem 4.3.1. To prove l.h.s.
${\geqslant}$
r.h.s. follows from (1) of Theorem 4.3.1. To prove l.h.s.
![]() ${\leqslant}$
r.h.s., we consider the
${\leqslant}$
r.h.s., we consider the
![]() $C$
in the proof of 4.3.9 with
$C$
in the proof of 4.3.9 with
![]() $n=\text{Sw}_{D}(\unicode[STIX]{x1D712})$
(so
$n=\text{Sw}_{D}(\unicode[STIX]{x1D712})$
(so
![]() $h=0$
). We have
$h=0$
). We have
![]() $\text{Sw}_{x}(\unicode[STIX]{x1D712}|_{C\cap U})=en-a$
,
$\text{Sw}_{x}(\unicode[STIX]{x1D712}|_{C\cap U})=en-a$
,
![]() $(C,D)_{x}=e$
, and hence
$(C,D)_{x}=e$
, and hence
![]() $\text{Sw}_{x}(\unicode[STIX]{x1D712}|_{C\cap U})/(C,D)_{x}=n-e^{-1}a$
.
$\text{Sw}_{x}(\unicode[STIX]{x1D712}|_{C\cap U})/(C,D)_{x}=n-e^{-1}a$
.
![]() $a$
can be fixed and
$a$
can be fixed and
![]() $e$
can become arbitrarily big.
$e$
can become arbitrarily big.
4.3.15. As is discussed in [Reference Barrientos3], 4.3.13 is related to the rank one case of Conjecture A in [Reference Barrientos3] on ramification of
![]() $\ell$
-adic sheaves on a scheme
$\ell$
-adic sheaves on a scheme
![]() $X$
(here
$X$
(here
![]() $\ell$
is a prime number which is invertible on
$\ell$
is a prime number which is invertible on
![]() $X$
). This conjecture was first formulated by Esnault and Kerz in the positive characteristic case at the end of Section 3 of [Reference Esnault and Kerz8]. Conjecture A is formulated by using the Swan conductor of a representation of
$X$
). This conjecture was first formulated by Esnault and Kerz in the positive characteristic case at the end of Section 3 of [Reference Esnault and Kerz8]. Conjecture A is formulated by using the Swan conductor of a representation of
![]() $\text{Gal}(\bar{K}/K)$
for a complete discrete valuation field
$\text{Gal}(\bar{K}/K)$
for a complete discrete valuation field
![]() $K$
defined by Abbes–Saito theory [Reference Abbes and Saito1]. For a one-dimensional Galois representation, the Swan conductor given by [Reference Kato20] and used in this paper coincides with that given by [Reference Abbes and Saito1] in the positive characteristic case [Reference Abbes and Saito2, Corollary 9.12], but this coincidence is not yet known in the mixed characteristic case.
$K$
defined by Abbes–Saito theory [Reference Abbes and Saito1]. For a one-dimensional Galois representation, the Swan conductor given by [Reference Kato20] and used in this paper coincides with that given by [Reference Abbes and Saito1] in the positive characteristic case [Reference Abbes and Saito2, Corollary 9.12], but this coincidence is not yet known in the mixed characteristic case.
If the last coincidence is true, then (1) of 4.3.1, 4.3.13 and the arguments in [Reference Barrientos3, Section 6] show that Conjecture A is true for rank one
![]() $\ell$
-adic sheaves on
$\ell$
-adic sheaves on
![]() $X$
in 4.2.1.
$X$
in 4.2.1.
(Two of the authors (K.K. and T.S.) are preparing an article [Reference Kato and Saito24] where the coincidence in the mixed characteristic case is proved. This should imply Conjecture A in the rank one and the mixed characteristic case.)
Acknowledgments
The authors are grateful to the referee for careful reading of the manuscript and valuable comments.