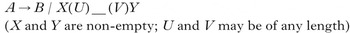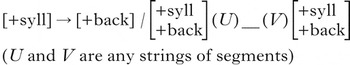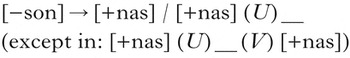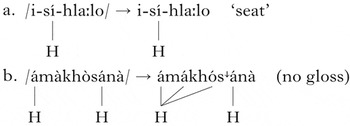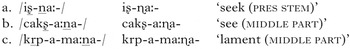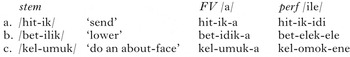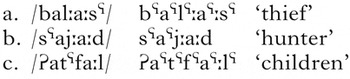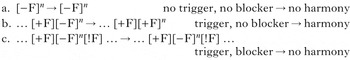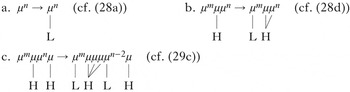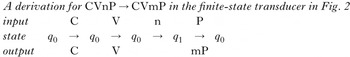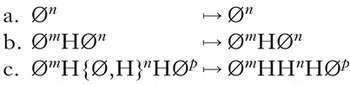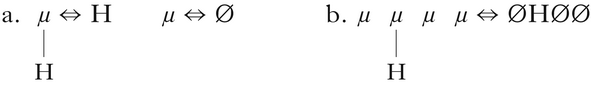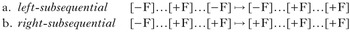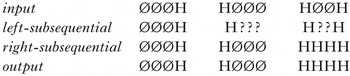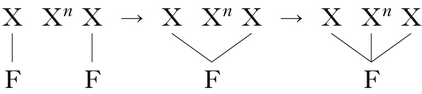1 Introduction
This paper establishes and characterises a typological difference between segmental and tonal phonology: unbounded circumambient processes are frequently attested in tonal phonology, but rare in segmental phonology. I define an unbounded circumambient process as one in which triggers or blockers appear on both sides of a target, and there is no bound, on either side, on the distance between these triggers or blockers and the target. This paper argues that these processes are more complex than those that are commonly attested in segmental phonology, and so the asymmetry can be characterised in a unified way by positing that tone is more computationally complex than segmental phonology.
A common unbounded circumambient process in tonal phonology is unbounded tonal plateauing (Kisseberth & Odden Reference Kisseberth, Odden, Nurse and Philippson2003, Hyman Reference Hyman, Goldsmith, Riggle and Yu2011; henceforth UTP), in which any number of tone-bearing units between two underlying high tones also become high. A simple example from Luganda (Hyman Reference Hyman, Goldsmith, Riggle and Yu2011: 231) is given in (1), where the plateau is underlined.
-
(1)

UTP is an unbounded circumambient process because the triggering H tones can be any distance away from the affected tone-bearing units. Hyman (Reference Hyman, Goldsmith, Riggle and Yu2011) observes that UTP is commonly attested in tonal phonology, but similar plateauing effects are, with one exception, unattested in segmental phonology.
The first contribution of this paper is to document this asymmetry in detail, and, by comparing UTP to the sour-grapes vowel-harmony pathology (Baković Reference Baković2000, Wilson Reference Wilson2003, McCarthy Reference McCarthy, Goldsmith, Hume and Wetzels2010, Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013), to show that it is part of a typological asymmetry that applies to unbounded circumambient processes in general. The second contribution is to show that UTP and the sour-grapes pattern, by virtue of being unbounded circumambient, are formally similar. This is because for these processes, each target must ‘look ahead’ in either direction to see crucial information in the environment. It is argued that this places unbounded circumambient processes outside the weakly deterministic class of maps, a complexity class in formal language theory defined in terms of finite-state transducers. The third contribution is to offer an account of the unbounded circumambient asymmetry in terms of such classes of maps. Previous work has found segmental processes to be at most weakly deterministic (Chandlee et al. Reference Chandlee, Athanasopoulou and Heinz2012, Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013, Chandlee Reference Chandlee2014, Payne Reference Payne2014). The unbounded circumambient asymmetry can thus be captured in terms of a complexity bound on segmental phonology: segmental phonology is restricted to weakly deterministic maps, but tonal phonology is not.
The structure of this paper is as follows. §2 establishes the unbounded circumambient asymmetry between tonal and segmental phonology. §3 introduces the formal language theory notions of complexity, and reviews previous work applying them to phonology. §4 shows that unbounded circumambient processes are not subsequential, and §5 argues that they are not weakly deterministic. This leads to the computational characterisation proposed in this paper: segmental processes are at most weakly deterministic, but tone is not restricted in this way. It is also discussed how two potential exceptions to this characterisation, Sanskrit n-retroflexion and Yaka vowel harmony, fit into this proposal. §6 discusses how Optimality Theory does not offer a unified way of characterising the typological asymmetry. §7 concludes, and mathematical definitions and a proof that UTP is neither left-nor right-subsequential are given in an online appendix.
2 The unbounded circumambient asymmetry
This section defines unbounded circumambient processes, and shows how they are common in tonal phonology, but extremely rare in segmental phonology. A circumambient process is one whose application is dependent on the existence of triggers or blockers on both sides of a target; an unbounded circumambient process is one in which there is no bound, on either side, on the distance between these triggers/blockers and the target. These terms are discussed in detail below in §2.1.
The bulk of the evidence for the asymmetry comes from unbounded tonal plateauing. §2.2 surveys attestations of UTP in the tonal literature, as a thorough documentation of Hyman's claim. §2.3 reviews two known segmental unbounded circumambient processes: mid-vowel harmony in Yaka and n-retroflexion in Sanskrit. §2.4 and §2.5 summarise related generalisations in other typological work which support the conclusion that unbounded circumambient processes are rare in segmental phonology, and discuss why Sanskrit and Yaka are exceptional for these generalisations as well. Thus the asymmetry is not confined to UTP but rather to the class of unbounded circumambient processes. This is highlighted in §2.5 by way of the sour-grapes vowel-harmony pathology, which in Copperbelt Bemba H-spreading (Bickmore & Kula Reference Bickmore and Kula2013, Kula & Bickmore Reference Kula and Bickmore2015) has an attested correlate in tone.
2.1 Unbounded circumambient processes
A precise definition of an unbounded circumambient process is given in (2). Crucially, this property is atheoretical, and thus agnostic to specific theories of representation and processes.
-
(2)

To illustrate the concept, a rewrite rule representation of this type of process is given in (3). In (3), X and Y are non-empty, they surround the target and there is no bound on the distance between them.
-
(3)

An example is the possible rule in (4).
-
(4)

In (4), whether a vowel becomes [+back] depends on the presence of [+back] vowels on both sides of the target. However, these [+back] vowels may be separated from the target by strings U and V. Because U and V can be of any length, the process must be able to ‘look back’ for a [+back] segment over any distance in the left context (i.e. over U) and ‘look ahead’ over any distance for a [+back] vowel in the right context (i.e. over V).
Importantly, X or Y might contain ‘blocking’ information which prevents the process from applying. A possible such rule is given in (5).
-
(5)

Here, the target will nasalise only when it is preceded by a [+nasal] segment and not followed by another [+nasal] segment. While (5) is given as a rule, such conditions are more intuitively expressed with Optimality Theory constraints (Prince & Smolensky Reference Prince and Smolensky1993).
Furthermore, the definition of unbounded circumambient applies also to autosegmental representations. From an autosegmental standpoint, the ‘target’ referred to in (2) is any unit affected by the changing of association lines, and the distance from the ‘trigger’ is measured on the timing tier. These choices will become clear in §4.4.
Because ‘unbounded’ is critical to the definition in (2), we must set the criteria for an unbounded process. Intuitively, an unbounded process is one which operates over multiple units, like segments or tone-bearing units (TBUs), for which the correct generalisation does not refer to a bound on how many units over which it may operate. As linguists may differ as to what constitutes evidence for a process being ‘unbounded’, I use the criteria in (6).
-
(6)

On its own, criterion (6a) does not constitute strong evidence for a process being unbounded, and thus no processes are included here which only meet (6a).
For some, (6b) is enough evidence that a process is unbounded, especially if there are examples of it operating over three or more units – as Kenstowicz (Reference Kenstowicz1994: 372) puts it, ‘phonological rules do not count past two’. In contrast, other researchers may consider only (6c) sufficient. However, the evidence presented here shows there is a typological asymmetry, regardless of which criterion one considers. By either (6b) or (6c), unbounded circumambient processes are far more common in tonal phonology than in segmental phonology.
2.2 Unbounded tonal plateauing
Having established the criteria for classifying a process as unbounded and circumambient, we can now discuss individual unbounded circumambient processes. This section surveys eight languages with some form of unbounded tonal plateauing, in which any number of L-toned or unspecified (Ø) TBUs (the TBU will be assumed to be the mora) surface as H if they are between two Hs, but as L otherwise.
Kisseberth & Odden (Reference Kisseberth, Odden, Nurse and Philippson2003: 67) motivate UTP as a repair for a constraint against ‘toneless moras between Hs’. Hyman & Katamba (Reference Hyman and Katamba2010) formalise UTP in Luganda (which they refer to as ‘H-tone plateauing’) as in (7).
-
(7)

UTP thus fits the definition in §2.1 of an unbounded circumambient process, because whether or not the process applies depends on two Hs that (a) are on both sides of the affected TBUs, and (b) can be arbitrarily far away from any one of the affected TBUs.Footnote 1
Using data from a number of sources, the following subsections confirm Hyman's (Reference Hyman, Goldsmith, Riggle and Yu2011) claim that UTP is a well-attested tonal process, and that by criterion (6b) it is unbounded in all cases and by (6c) in most.
2.2.1 Luganda
UTP occurs in Luganda (Bantu, Uganda; Hyman et al. Reference Hyman, Katamba and Walusimbi1987, Hyman & Katamba Reference Hyman and Katamba2010) both word-internally and in the phrasal phonology. Luganda TBUs can be either H or unspecified underlyingly. Lexically, a L tone is inserted after a H, causing a falling HL contour when the H is on a final syllable. In some cases, these intermediate L tones contrast with Ø, but not with regard to UTP (technically, they delete in the UTP environment), so they will not factor into the discussion. Luganda nouns are given in (8) (all Luganda forms in this section are taken from Hyman & Katamba Reference Hyman and Katamba2010).Footnote 2 Underlying and surface H tones are indicated; underlying unspecified and surface L tones are unmarked.
-
(8)

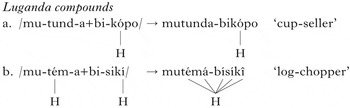
If a toneless noun and a noun with an underlying H tone form a compound, they are pronounced as in isolation, as in (9a). However, when both nouns have an underlying H, a H-tone plateau occurs between them, as in (9b). In compounds, the toneless plural /bi-/ is used for nouns from the /ki-/ noun class IV.
-
(9)

In (9b) there is a plateau over three unspecified TBUs. This shows target toneless TBUs three TBUs away from their triggers – the mora represented by /a/ in /mu-tém-a/ is two TBUs from its right trigger H /í/ in /bi-sikí/, and the second /i/ in /bi-sikí/ is three TBUs from its left trigger /é/ in /mu-tém-a/. Thus Luganda satisfies the ‘multiple unit’ criterion for unboundedness in (6b).
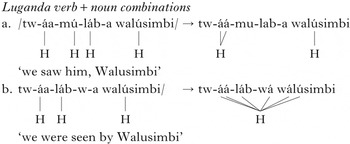
UTP operates over syntactic phrases as well, satisfying (6c). Under certain morphosyntactic conditions, noun–verb sequences can also form a domain for UTP. The noun in (10a) is an adjunct, and thus outside of the domain of plateauing. In (10b), however, the noun and verb form a phonological phrase, and plateauing occurs across all TBUs between the surviving Hs.
-
(10)

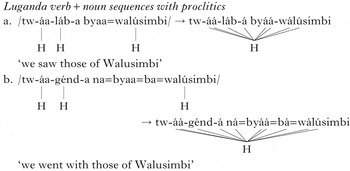
A more extreme example can be seen when proclitics are added to the noun. Proclitics generally do not have tone, as (11) shows.
-
(11)

Luganda UTP ‘sees’ over these as well, no matter how many are stacked on to the noun, as in (12).
-
(12)

These examples show UTP operating over a six-TBU span of toneless TBUs created by prefixation, illustrating triggers separated from their targets by five TBUs on each side. Thus Luganda UTP satisfies both criterion (6c), with respect to unboundedness, and criterion (6b), applying across five TBUs.
2.2.2 Digo
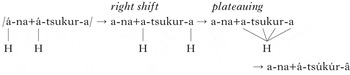
Verbs in Digo (Bantu, Kenya and Tanzania; Kisseberth Reference Kisseberth, Clements and Goldsmith1984) show complex interactions between underlying H tones, including UTP. Underlyingly, Digo has a privative H/Ø system. Both verb roots and affixes may carry a H tone, although this is not obligatory. A single H tone in a verbal H shifts to the end of the word, surfacing as a rising/falling pattern on the final two TBUs. This is illustrated with the addition of the 3rd person plural object prefix /á/ to the toneless root /tsukur/ ‘take’ in (13b) (the underlying position of the H is underlined).
-
(13)

An autosegmental analysis of (13b) is given in (14).
-
(14)

The forms in (13a, b) have the toneless 1st person prefix /ni/; if this is substituted for the H-toned 3rd person singular subject prefix /á/, a plateau occurs from the object prefix to the end of the root, as in (13c). Again, we see the presence of two H tones creating a long-distance plateau across the length of the root. The Digo example is complicated by tone shifting; Kisseberth analyses it as a two-step process, in which the first H shifts to the initial vowel of a ‘verbal complex’ (marked with ‘+’), the second H shifts to the end of the word (as in (14)) and then the first H triggers a plateau across the root between them. This analysis is illustrated with the derivation in (15).
-
(15)

The domain for both right shift and plateauing is larger than the verb – they also apply to verb + noun constructions. (16a) shows right shift applying when there is only one H in the verb, and (b) shows plateauing over the phrase resulting from two Hs associated with the verb.
-
(16)

The phrase in the final form in (16b) results in a plateau over six TBUs, which shows target TBUs three TBUs away from their triggers, and thus satisfies criterion (6b) for unboundedness. It also contains a plateau created over a syntactic domain, satisfying criterion (6c).
2.2.3 Other languages
Kisseberth & Odden (Reference Kisseberth, Odden, Nurse and Philippson2003) cite a plateauing process in Xhosa which is similar to that in Digo. In Xhosa, underlying H tones shift to the antepenult. A phrase with two H tones shows a plateau between the first and the second H, and shifted H on the antepenult, as in (17) (data from Kisseberth & Odden (Reference Kisseberth, Odden, Nurse and Philippson2003: 67–68).
-
(17)

The second H shifts to the third /o/ in /ú-ku-qononondis-a/, and becomes the right trigger for UTP; this shows triggers on both sides affecting targets four TBUs away. In Zulu, related to Xhosa (Laughren Reference Laughren, Clements and Goldsmith1984, Cassimjee & Kisseberth Reference Cassimjee, Kisseberth and Kaji2001, Downing Reference Downing2001), a single H shifts to the antepenult (if it originates on a prefix) or penult (if it originates on a stem). In forms with two Hs, a plateau forms between the Hs. In Zulu, the two H tones do not fuse; instead, as shown in (18), the first spreads up to the second, creating downstep.
-
(18)

Laughren (Reference Laughren, Clements and Goldsmith1984: 221) states that ‘the rule only applies to a H which is followed by a LH tonal sequence’ (Yip Reference Yip2002 represents the LH as a single H, which is then downstepped), and, while she only gives examples of the plateau operating over two TBUs, analyses the process as operating over an arbitrary number of TBUs.
Other examples of UTP can be found throughout Bantu. In Yaka (Kidima Reference Kidima1991), ‘all toneless syllables flanked by Hs become H by rightward spreading of the H to the left of the domain’ (Kidima Reference Kidima1991: 44). (19), from Kidima (Reference Kidima1991: 180), shows plateauing alternations. Kidima gives Yaka tonal assignment a complex accentual analysis; the underlying Hs marked in the following data result from a tonal assignment rule.Footnote 3 In the following examples, bakhoko is not assigned a tone, prompting the alternations.
-
(19)

(19c) shows two plateaus, each with their target TBUs separated from their triggers by two TBUs.
UTP also occurs outside of Bantu. In Saramaccan, a creole spoken in Suriname (Roundtree Reference Roundtree1972, Good Reference Good2004, McWhorter & Good Reference McWhorter and Good2012), a phrasal version of UTP occurs across words in certain syntactic configurations. This analysis follows Good (Reference Good2004), who posits an underlying H/L/Ø distinction, as in the nouns in (20).
-
(20)

According to Roundtree (Reference Roundtree1972: 314), ‘all changeable low tones [Good's Ø TBUs] between the highs in successive morphs in certain syntactic positions are changed to high’. One such syntactic position is an adjective–noun sequence. In the following, the final /o/ in /hánso/ is realised as low [ó] before /sὲmbὲ/ (21a), but as high before /wómi/ (21b) and /mujέE/ (21c). Relevant vowels are underlined.
-
(21)

Note that in (21b) the initial /u/ of /mujέE/ also surfaces as H, illustrating plateauing over two TBUs. In (e) a plateau occurs over four TBUs, the final /a/ of /taánga/ and the first three vowels of /amEEká/; Saramaccan UTP thus satisfies (6b), with its targets and triggers separated by three TBUs on each side.
Similar to the Saramaccan system, as noted by Good (Reference Good2004), is the intonational phonology of the Uto-Aztecan language Papago (Hale & Selkirk Reference Hale and Selkirk1987: 152), in which H tones are associated ‘to each stressed vowel and to all vowels in between’; they list examples of plateaus created in between stressed vowels three TBUs apart. Finally, Do & Kenstowicz (Reference Do and Kenstowicz2011) discuss plateauing between Hs in certain intonational phrases in South Kyungsang Korean, giving a spectrogram showing a plateau between the two H tones in [seccók khaliphonía] ‘Western California’ (2011: 3, 11), which shows unspecified TBUs affected by triggers two TBUs away (on either side).
2.3 Unbounded circumambient processes in segmental phonology
Turning to segmental phonology, there are the only two potential attestations of unbounded circumambient processes of which I am aware. One is Sanskrit n-retroflexion. The other is ‘plateauing harmony’ in Yaka, which also has UTP, as explained in §2.2. Both satisfy the unboundedness criterion in (6b), but neither satisfy (6c).
2.3.1 Sanskrit
In Sanskrit n-retroflexion (Whitney Reference Whitney1889, Macdonell Reference Macdonell1910, Schein & Steriade Reference Schein and Steriade1986, Hansson Reference Hansson2001, Graf Reference Graf2010, Ryan Reference Ryanforthcoming), an underlying alveolar /n/ becomes retroflex [ɳ] after retroflex /r ᶳ/, which can appear far to the left of the target /n/. Both trigger and target in (22), from Hansson (2011: 225), are underlined.
-
(22)

One restriction on n-retroflexion potentially gives the process an unbounded circumambient quality. Hansson (Reference Hansson2001: 230) states that retroflexion fails ‘when there is also an /ᶳ/ or /r/ later in the word’.Footnote 4 He cites the data in (23), from Macdonell (Reference Macdonell1910) and Monier-Williams (Reference Monier-Williams1899).Footnote 5
-
(23)

Given the data in (22), one would expect, for example, that the underlying /n/ in [pari-nakᶳati] would surface as [ɳ], as in (23b), because it follows a trigger /r/ for n- retroflexion. However, it instead surfaces as [n], which is attributed to the ‘blocking’ /ᶳ/ three segments to the right. Thus Sanskrit n-retroflexion fits the definition for circumambience in a slightly different way than UTP: the crucial context includes the presence of a trigger on the left side and a blocker on the right. The evidence in the examples here also fit criterion (6b) for unboundedness; (23g) shows a blocker three segments to the right of the target, and (22c) shows a trigger five segments to the left. Thus, by criterion (6b), Sanskrit n-retroflexion is an unbounded circumambient process. However, Ryan's (forthcoming) study of several Sanskrit corpora finds no examples of retroflexion being blocked when a long vowel or multiple syllables intervene between the target and blocker. Thus, whether or not it is truly unbounded is the subject of some doubt. Furthermore, there is no evidence satisfying (6c), i.e. that the distance this second blocker can be from the target may be extended by a morphological or syntactic process.
2.3.2 Yaka vowel harmony
The other attested unbounded circumambient segmental process is vowel-height harmony in Yaka (Hyman Reference Hyman1998, 2011). Hyman (Reference Hyman, Goldsmith, Riggle and Yu2011) cites Yaka as a unique example of vowel ‘plateauing’. In Yaka, the initial vowel of the perfective suffix /ile/ lowers to mid [e] when the vowel in the stem is also mid (24c, d). Otherwise, a progressive harmony converts the final /e/ to [i] ([l] and [d] alternate depending on the following vowel, and with [n] following a root nasal; hence the allomorph [ene] in (25c) below). The lowering of this middle /i to [e] does not happen in the applicative suffix /ila/, which does not end in a mid vowel. The examples in (24), from Hyman (Reference Hyman, Goldsmith, Riggle and Yu2011: 501), show this alternation.
-
(24)

That this is part of a more general process lowering high vowels to mid if and only if they are between two mid vowels can be seen in (25), from Hyman (Reference Hyman1998: 19). This process can take place over at least three vowels.
-
(25)

As in UTP, the mid-vowel plateau shows triggers on both sides of the target vowels. (25b) and (c) thus show triggers two vowels from the right and two vowels from the left from their targets. As such, Yaka vowel harmony satisfies criterion (6b) for an unbounded process. However, according to Hyman (Reference Hyman1998), plateauing alternations can only be seen with verb roots and the perfective /-ile/; it thus does not satisfy (6c).
2.4 Empirical summary
The preceding sections presented eight attestations of UTP, an unbounded circumambient process in tonal phonology, and two examples of separate unbounded circumambient processes in segmental phonology. All satisfied criterion (6b), with the greatest distance between target and trigger being five TBUs. Seven examples of UTP were shown to operate over domains extended by morphology or syntax, thus satisfying criterion (6c). Neither segmental process satisfied (6c), and in Yaka, the distribution of the process was quite limited. Both satisfied (6b), although in Yaka the greatest attested distance between trigger and target was three vowels, and in Sanskrit there was no evidence for blocking beyond the syllable following the target.
Most importantly, to the best of my knowledge, these are the only examples of such processes in segmental phonology. This is notable, given the wide attestation of long-distance segmental processes in general, as documented in the comprehensive surveys on feature-spreading harmony (Rose & Walker Reference Rose and Walker2004), vowel harmony (Baković Reference Baković2000, Nevins Reference Nevins2010), consonant harmony (Rose & Walker Reference Rose and Walker2004, Hansson Reference Hansson2001, Reference Hansson2010) and consonant disharmony (Suzuki Reference Suzuki1998, Bennett Reference Bennett2013). In fact, Wilson (Reference Wilson2003, Reference Wilson2006b), reviewing the typologies of nasal, emphasis and vowel harmonies, characterises segmental spreading processes as ‘myopic’. This means that even segmental spreading processes which affect multiple segments proceed in a local fashion, never ‘looking ahead’ beyond immediately adjacent segments. As unbounded circumambient processes by definition depend on information unboundedly far away from the target, any myopic process is not an unbounded circumambient process, and any unbounded circumambient spreading process is necessarily not myopic. Yaka vowel harmony and Sanskrit n-retroflexion are thus exceptions to the myopic spreading generalisation; this highlights how atypical these two processes are.Footnote 6
There is thus a typological asymmetry between tonal and segmental processes: unbounded circumambient patterns are extremely rare in segmental processes, but widely attested in tonal phonology, as evidenced by the variants of UTP discussed. A comparison between the proportions of circumambient unbounded processes found in typological surveys (such as those just mentioned) of segmental and tonal processes would be ideal, but comparable surveys of tonal processes, or even particular kinds of processes, do not exist (to the best of my knowledge). Regardless, the evidence reviewed in this paper clearly shows an asymmetry, despite the absence of such surveys for tone.
It should be noted that bidirectional spreading processes, in which a feature spreads outwards from a single trigger in two directions, are common in segmental harmony. An example is Arabic emphasis spreading, in which an emphatic gesture spreads in an unbounded fashion in both directions from an underlying emphatic segment. In the following example from Southern Palestinian Arabic (Al Khatib Reference Al Khatib2008: 2), emphasis spreads to the left (26a), to the right (b) and to both the left and right (c) (spreading is blocked by high front segments, such as /j/).Footnote 7
-
(26)

Other bidirectional processes are nasal spread in Capanahua and Southern Castillian (Safir Reference Safir1982) and cases of stem control in vowel harmony (Baković Reference Baković2000) and consonant harmony (Hansson Reference Hansson2001, Reference Hansson2010). While these processes apply in an unbounded fashion, and operate in two directions, they only have one trigger, and are thus not circumambient.
2.5 The sour-grapes pattern in tonal phonology
One final piece of evidence for the unbounded circumambient asymmetry involves the unattested ‘sour-grapes’ vowel-harmony pattern (Baković Reference Baković2000, Wilson Reference Wilson2003, McCarthy Reference McCarthy, Goldsmith, Hume and Wetzels2010, Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013).Footnote 8 The sour-grapes pattern is a non-myopic harmony pattern predicted to exist by ranking permutations of classic OT with Agree constraints, but not attested in segmental harmony. The sour-grapes pattern is also unbounded circumambient, and, as will be discussed momentarily, a sour-grapes-like process appears in tonal phonology.
Sour-grapes harmony works as follows. Given a spreading [+F] feature (which targets underlying [–F] segments) and a blocking feature [!F], [–F] segments become [+F] after another [+F], provided that there is no blocking feature following in the word, as shown in (27).
-
(27)

In other words, [+F] spreads if and only if it can spread all the way.Footnote 9 Note that sour-grapes spreading is not myopic: the spread of the [+F] has to ‘look ahead’ to see if there is a blocker before it can apply. As such, it is also an unbounded circumambient pattern, because the presence or absence of both [+F] and [!F] segments, which can be any distance apart, bears on the realisation of [–F] segments in between (this blocking aspect makes it circumambient in a similar way to Sanskrit n-retroflexion).
However, a sour-grapes-like pattern does exist in tonal phonology. In Copperbelt Bemba (Bickmore & Kula Reference Bickmore and Kula2013, Kula & Bickmore Reference Kula and Bickmore2015), underlying H tones undergo one of two spreading processes, bounded ternary spreading or unbounded spreading. The latter is blocked by the presence of another H tone, as shown in (28). In phrase-final forms, unbounded spreading applies to the rightmost H.
-
(28)

Bounded spreading occurs when another H appears to the right, as in (29). Bounded spreading obeys the Obligatory Contour Principle; it will spread up to two additional TBUs, maintaining at least one L TBU before the second H. All other intervening TBUs surface with a L tone.
-
(29)

The formalisations in (30) summarise the facts. When no Hs are present, as in (a), all TBUs surface as L (cf. (28a): [ù-kù-tùl-à]). When one H is present, it spreads to all remaining TBUs in the domain (and the rest surface as L, as in (28d): [tù-kà-páápáátík-á]). When two Hs are present, the first only spreads to the next two TBUs (cf. (29c): [tù-kà-bélééng-él-àn-à kó]).
-
(30)

Note that, modulo the bounded spreading, the formalisations in (30) are almost identical to the sour-grapes generalisations in (27). In other words, in Copperbelt Bemba the second H can be seen as a blocker for unbounded spread. This makes it an unbounded circumambient process, because the realisation of unspecified TBUs depends on the presence or absence of Hs on both sides which can be arbitrarily far away. As a tonal process, it does not seem particularly aberrant, in contrast to Sanskrit n-retroflexion and Yaka vowel harmony. Thus it provides more evidence for the unbounded circumambient asymmetry.
3 The computational complexity of phonological maps
A relevant measure of computational complexity can be found in formal language theory (FLT). This section introduces FLT, shows how it relates to phonology, and introduces properties of finite-state transducers that allow us to measure the relative complexity of phonological processes.
3.1 Formal language complexity and cognitive complexity
A formal language is a set of strings, and FLT studies the relationships between formal languages and the expressive power of grammars that describe them. FLT characterisations of natural language patterns have been argued to reflect domain-specific cognitive biases for and against patterns of a certain level of complexity. For example, the regular class of formal languages is insufficient to describe English syntax, and English syntax is at least context-free (Chomsky Reference Chomsky1956). Phonology, on the other hand, appears to be at most regular (Johnson Reference Johnson1972, Kaplan & Kay Reference Kaplan and Kay1994).Footnote 10 This notion of complexity has been explicitly linked to cognitive complexity (Folia et al. Reference Folia, Uddén, Vries, Forkstam and Petersson2010, Rogers & Hauser Reference Rogers, Hauser and Hulst2010, Rogers & Pullum Reference Rogers and Pullum2011), and results from artificial language learning experiments provide evidence in support of the psychological reality of the context-free/regular division between syntax and phonology (Lai Reference Lai2015).
The primary goal of this paper is to use this notion of complexity to characterise the unbounded circumambient asymmetry discussed in §2. Instead of formal languages, however, the following sections study the relationships between regular maps, where a map is a relation between strings in which an input string is paired with at most one output string.Footnote 11 Analogous to the regular/context-free distinction for formal languages, maps can be classified according to their complexity. The distinctions important for this paper centre around the property of subsequentiality (Mohri Reference Mohri1997), which can be defined in terms of finite-state transducers (FSTs). FSTs are idealised machines that match pairs of strings; they are described in more detail below. While FSTs in general can describe any regular map, subsequential FSTs describe a more restricted set of maps.
3.2 Overview: formal language complexity and phonology
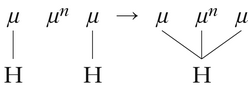
The classes of interest in this paper are left- and right-subsequential maps, weakly deterministic maps and regular maps. Figure 1 depicts the relationships between these classes as a nested hierarchy, in which more complex classes properly include lesser ones. Left- and right-subsequential maps are provably less complex than weakly deterministic maps (Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013) and regular maps (Mohri Reference Mohri1997), and weakly deterministic maps have been conjectured to be less complex than regular maps (Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013). Assuming this conjecture to be true (see further below), this means that all weakly deterministic maps are also regular maps, but not all regular maps are weakly deterministic. Regular maps conjectured not to be weakly deterministic can be referred to as fully regular.

Figure 1 Phonological processes in the subregular hierarchy.
Figure 1 also depicts where typological research examining segmental processes as maps place these processes in the complexity hierarchy. This work has found all of them to be within the weakly deterministic class, with most in the less complex left- and right-subsequential classes. This has led to the hypothesis that that the weakly deterministic class forms a bound on the complexity of phonology. As Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) discuss, this hypothesis is supported by the absence of sour-grapes patterns, which they prove to be neither left- nor right-subsequential, and conjecture to not be weakly deterministic.
In addition, Fig. 1 shows the other unbounded circumambient processes discussed in this paper belonging to the fully regular region. As will be explained in detail in §4, this is because UTP and other unbounded circumambient processes are, like sour-grapes harmony, neither left- nor right-subsequential, and there is no known weakly deterministic characterisation of them. By revising the above hypothesis, then, we have a characterisation for the typological asymmetry established earlier: segmental phonology, but not tonal phonology, is weakly deterministic. The existence of Sanskrit n-retroflexion and Yaka harmony are admittedly exceptions, but as already discussed in §2, they are not only rare, but also exceptions to Wilson's myopia generalisation. These exceptions will be discussed in §5.3.
3.3 Finite-state transducers, subsequentiality and determinism
This subsection gives an informal introduction to FSTs, and discusses subsequential transducers, a type of FST which is strictly less expressive than the fully regular non-deterministic transducers (Mohri Reference Mohri1997). As an example, consider the regressive assimilation generalisation ‘nasals become labial before a labial consonant’. A rule for this generalisation is given in (31).
-
(31)

To simplify the notation, let us abstract away from place features other than [labial] as follows. ‘C’ represents non-labial, non-nasal consonants and ‘P’ labial consonants. A FST corresponding to the generalisation in (31) is given in Fig. 2. It comprises a set of states (the circles labelled with a q) and transitions between the states (the labelled arrows). The FST can be interpreted as reading an input and writing an output as follows. Beginning from the start state (marked with the unlabelled arrow; q0 in Fig. 2), it traverses the transition for each symbol (indicated to the left of the colon in a transition label) in the input string, each time writing out the corresponding output (indicated to the right of each label).Footnote 12 At the end of the input string, it appends to the output the output for the current state (indicated to the right of the colon on the state label). The empty string λ indicates that there is no output. In this way, the transitions and states define which input/output string pairs are accepted by a machine. As an example, the derivation in (32) shows how an input CVnC corresponds to an output CVnC (i.e. no change occurs). The derivation highlights each state, input symbol and output as the machine reads CVnC.

Figure 2 A deterministic finite-state transducer for nasal place assimilation.
-
(32)

Note that, while on the initial C and V the FST simply loops on state q0, outputting C and V respectively, on the following ‘n’ it makes a transition to state q1, outputting nothing. This is because the machine cannot yet ‘decide’ the output for this ‘n’, as it could be ‘n’ or ‘m’, depending on whether or not the following input symbol is a P. Let us thus call state q1 a ‘wait’ state. As the next symbol is a C, the machine takes the C:nC transition from q1 to q0, outputting nC. If the input is instead CVnP, the derivation is similar, but in the last step the machine takes the P:mP transition from state q1, as in (33).
-
(33)

In this way, state q1 allows the machine to ‘look ahead’ one symbol in the input. The reader can verify that this machine will take any permutation of C, V, n and P as an input, outputting ‘n’ as ‘m’ only before a P. Thus Fig. 2 describes exactly the map as (31).Footnote 13
For all states in Fig. 2, there is only one possible transition, given a particular input symbol. This means the FST in Fig. 2 is deterministic. Not all FSTs are deterministic; it is possible to write a FST such that a state may have two separate transitions on a particular output. Figure 3 is such a machine. Here, there are no outputs specified for the states, and q2 is a ‘non-accepting’ state (indicated by the single, rather than double, circle), meaning that the machine rejects an input/output pair for which the input ends on that state.

Figure 3 A non-deterministic finite-state transducer for nasal place assimilation.
Non-deterministic FSTs are more powerful than deterministic FSTs: any map describable by a deterministic FST can be described by a non-deterministic FST, but not vice versa (Mohri Reference Mohri1997). The ability to be described by a deterministic FST is central to the definition of the classes of left- and right-subsequential maps (Mohri Reference Mohri1997). The regular class of maps are those maps which can be described by any non-deterministic FST. Thus the left- and right-subsequential maps form a strict subset of the regular class.
UTP is a concrete example of a map which cannot be described with a deterministic FST, and will be described in detail in §4. For now, the restriction which determinism places on the subsequential maps can be understood in terms of ‘wait’ states, as in Fig. 2, which allow deterministic FSTs to look ahead in the input. Because the number of states is finite, there can only ever be a finite number of wait states, and so a deterministic FST has bounded look-ahead. Non-determinism, in contrast, allows a FST to ‘postpone’ a decision about a particular input symbol indefinitely.
3.4 Subsequentiality and segmental phonology
Computational analyses of typologies of segmental processes have shown that they are describable with deterministic FSTs, with some variation regarding directionality. Mohri (Reference Mohri1997) described two kinds of subsequential maps: right-subsequential and left-subsequential, which are describable by deterministic FSTs reading an input string left-to-right and right-to-left respectively. Collectively, they can be referred to as subsequential maps.
The discussion in the previous section suggests how local processes are subsequential. For a thorough survey of the subsequentiality of local processes, including epenthesis, deletion, metathesis, substitution and partial reduplication, see Chandlee (Reference Chandlee2014). Work on long-distance segmental processes such as vowel harmony (Gainor et al. Reference Gainor, Lai and Heinz2012, Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013) and dissimilation (Payne Reference Payne2014) has also found them to be largely left- or right-subsequential. To see how, imagine a long-distance progressive consonantal harmony process in which a feature [–F] becomes [+F] after some other consonant specified [+F], no matter how early in the word this consonant appeared (an example is /l/ in Yaka becoming [n] in suffixes attaching to a root containing a nasal). Such a map, given in (34), is describable with the deterministic FST in Fig. 4 (the tailed arrow indicates an input/output pair that belongs to a map).

Figure 4 A deterministic finite-state transducer for progressive harmony (C = consonant, V = vowel segments not participating in harmony).
-
(34)

This is impossible for a regressive harmony process, in which [–F] becomes [+F] before some [+F] segment an unspecified distance later in the word, as in (35).
-
(35)

This requires unbounded look-ahead from left to right; in order to determine the output for a target [–F] in the input, a FST reading from left to right would have to wait indefinitely to see if a trigger [+F] appeared later in the string. However, this map is right-subsequential, because reading the input from right to left requires no look-ahead. Reading from right to left can be thought of as reversing the input, feeding it into the FST and then reversing the output (Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013). If we reverse the strings in the map in (35), we get the same map as in (34). We can thus describe the reverse of (35) with a deterministic FST, so it is right-subsequential.
Thus local processes and unidirectional long-distance processes are either left- or right-subsequential. However, there are two classes of phonological processes which are neither left- nor right-subsequential: unbounded circumambient processes and bidirectional spreading processes. These processes are the focus of the following two sections.
4 The non-subsequentiality of unbounded circumambient processes
This section provides proof that UTP is neither left- nor right-subsequential. This is compared to a similar result obtained for sour-grapes processes by Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013), and is then generalised to the class of unbounded circumambient processes. Additionally, §4.4 defends the use of a linear representation of UTP.
4.1 Unbounded tonal plateauing as a map
To analyse UTP using the computational framework for studying string maps outlined above, this section uses a string-based representation which marks associations to H tones on each TBU. The use of this representation will be discussed in §4.4. For now, we can say that if UTP is viewed with this kind of string-based representation, then it is neither left- nor right-subsequential.
The unbounded tonal plateauing generalisation was formalised in (7) in §2. Its string-based counterpart is given in (36), where H represents a TBU associated to a H tone, and Ø represents an unspecified TBU. Superscript m, n and p represent any natural number.
-
(36)

The linear map in (36) makes explicit every possible situation in UTP. In (a) and (b), in which there are fewer than two H-toned TBUs in the underlying form, no plateauing occurs. Plateauing occurs instead when there are two or more Hs in the input (e.g. (10b) above from Luganda). This is seen in (36c): all TBUs between the first and last H-toned TBUs surface as H. The notation {Ø,H}n denotes a string of n TBUs, either H or Ø.
4.2 The non-subsequentiality of unbounded tonal plateauing
The UTP map in (36) is neither left- nor right-subsequential. As §5.3 will discuss in detail, this holds for any unbounded circumambient process. This section presents an informal illustration of the proof; for the full proof, see the online appendix.
The UTP map in (36) is regular, as it can be modelled with a non-deterministic FST. This FST is given in Fig. 5, where underlying Ø TBUs are H in the output in state q1, from which a final state can only be reached if there is another input H following; one can think of q1 as the ‘plateau’ state.

Figure 5 A non-deterministic finite-state transducer for unbounded tonal plateauing.
This non-determinism is necessary, as there is no way to capture this map with a deterministic FST. Recall that a deterministic FST must have at most one transition per input symbol at every state. We cannot determinise the FST in Fig. 5. To see why not, let us adopt the ‘wait’ strategy employed in the FST in Fig. 2 in §3.3. There are many ways to try this; this discussion follows one. The proof in the appendix ensures that all will fail, but the discussion here is intended to give an intuition as to why.
In the deterministic FST in Fig. 6, q2 is a wait state representing the knowledge that a sequence HØ – which may be a plateauing environment – has been seen in the input. Here, it ‘waits’ one symbol to see whether the next symbol in the input is a H or a Ø. It will thus correctly transform ØHØH, with only one intervening Ø TBU, to ØHHH. However it incorrectly maps inputs for which the second H is further away; for example, the input ØHØØH would be mapped to ØHØØH (itself). Thus, because there is only one wait state, the machine in Fig. 6 can only describe plateaus of at most three Hs.

Figure 6 First attempt at a deterministic finite-state transducer for unbounded tonal plateauing.
The machine in Fig. 7 adds an additional wait state to try to remedy this situation. Here the FST is much like the one in Fig. 6, except that it has two wait states, q2 and q3, which represent the look-ahead necessary to capture the behaviour of one and two Øs following an input H. Thus, Fig. 7 correctly maps ØHØH↦ØHHH and ØHØØH↦ØHHHH.However, it incorrectly maps inputs like ØHØØØH, where two Hs are separated by three or more Øs, to themselves. By now it is perhaps obvious that we are on a wild-goose chase; any ‘wait n symbol’ strategy will fail for any mapping in the UTP relation whose input string includes the sequence HØn+1H. However, given the restriction of determinism, ‘wait n symbols’ is the best we can do. Simply reversing the string, in an attempt to create a right-subsequential transducer, will not help; the position of the first triggering H is just as arbitrarily far to the right as the second is to the left. Thus a deterministic FST representation of the UTP map is impossible, and so it lies outside both the left- and right-subsequential classes.

Figure 7 Second attempt at a deterministic finite-state transducer for unbounded tonal plateauing.
4.3 Unbounded circumambient processes in general
That UTP is neither left- nor right-subsequential follows from its unbounded circumambient nature: as triggers may lie any distance away on either side of a given target, a FST describing the map requires unbounded look-ahead in both directions.
Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) prove this is also true for sour-grapes harmony, for the same reasons. For these processes, the fate of an input segment that can potentially assimilate rests on whether or not a trigger appears to one side and whether or not a blocker appears to the other. They show that this means it cannot be described by a deterministic FST reading in either direction. We can then see why no unbounded circumambient process can be subsequential. For unbounded circumambient processes, it is definitional that crucial information may appear on either side of the target, unboundedly far away. This means any unbounded circumambient process will require unbounded look-ahead in both directions, and will not be subsequential. This result is then key to characterising the unbounded circumambient asymmetry in terms of computational complexity, as discussed further in §5.
As stated at the outset, this result depends on a particular kind of string-based representation. Before we compare unbounded circumambient processes with bidirectional spreading in §5, it is therefore necessary to address the potential objection that these results are invalid because they hinge on this string-based representation for UTP.
4.4 Autosegmental representations and linear representations
Tone has been widely analysed in terms of autosegmental representations (though for alternatives see Cassimjee & Kisseberth Reference Cassimjee, Kisseberth and Kaji2001 and Shih & Inkelas Reference Shih, Inkelas, Kingston, Moore-Cantwell, Pater and Staubs2014), while the notion of subsequentiality is defined in terms of strings. The preceding analysis used a string-based representation of UTP, even though it is a tonal process. This section explains and defends two interrelated facts about such string-based representations, formulated in (37).
-
(37)

(37a) is a common assumption about the relationship between string-based representations and autosegmental representations, and is the one implicit in the string-based representations used in the computational literature cited in §3.4. As for (37b), measuring distance on the timing tier as opposed to the melody tier is a representational choice. Indeed, Kornai (Reference Kornai1995) compares different ways of encoding string-based representations of autosegmental representations. The following sections explain and justify string-based representations based on (37).
4.4.1 Translating between string and autosegmental representations
Let us compare string and autosegmental representations of the sour-grapes map in (27). We have a number of options for autosegmentally representing the featural contrasts given by the symbols in (27). Some possible representations for the underlying form [+F][−F]n[!F] in (27c) are given in (38).
-
(38)

In (a) and (b), the target [–F] vowels in the string are represented as underlyingly associated to [–F] features in the autosegmental diagram. In (a), a single [–F] feature is associated to multiple vowels, whereas in (b), each [–F] vowel is associated to its own [–F] feature (in violation of the Obligatory Contour Principle; Leben Reference Leben1973, McCarthy Reference McCarthy1986). As above, [!F] is used as shorthand for some vowel which is also associated to some other feature [+G] which prevents [+F] from spreading to it (e.g. as in [+low] vowels in Akan (Clements Reference Clements1976), which block the spreading of a [+ATR] feature). In (c), the targets are analysed as underspecified on the [F] tier, and the blocker is analysed as underlyingly specified as [–F] (as in Clements’ analysis of [+low] vowels in Akan as underlyingly [–ATR]).
One property that all possible autosegmental analyses share is that each symbol in a string in (27a) corresponds to the featural associations of a particular timing tier unit in (38). As an explicit example of this, (39) is a translation between symbols in UR strings in (27) and the autosegmental information at each timing tier unit in (38a). The translation for each string symbol [+F], [–F] and [+F] is given in (39a), with an example of correspondence between the string [+F][–F][–F][!F] and an autosegmental representation in (b).
-
(39)

While simplified in the sense that it focuses on one feature, translations like in (39) are what phonologists commonly, if implicitly, use when moving back and forth between linear strings of feature bundles and autosegmental representations. Again, what is important is that each symbol in the string corresponds to a timing tier unit in the autosegmental representation – the property highlighted in (37a).
As (39) makes clear, information about the melody (or featural) tier units in the autosegmental representation is obscured in the string-based representation. In (39b), the string does not encode the multiple associations of the [–F] autosegment, and it also does not show that [+F] and [!F] are only separated by a single [–F] autosegment. This ambiguity is apparent in (38), in which different autosegmental interpretations of the same string-based representation have different information on their featural tiers.
4.4.2 Representational assumptions and look-ahead
As a result, when a FST reads a symbol in a string-based representation as in (27), it can be thought of in autosegmental terms as reading the featural information of a particular timing tier unit. Thus, because subsequentiality depends on look-ahead in terms of a FST reading such a string-based representation, the results regarding subsequentiality in the work of Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) and others are based on what translates in autosegmental terms to look-ahead on the timing tier, not the melody tier.
There are a number of arguments for this assumption. One is that locality on the melody tier depends on certain representational assumptions such as underspecification and the Obligatory Contour Principle, both of which have been argued against as phonological universals (see Inkelas Reference Inkelas1995 for the former, and Odden Reference Odden1986 for the latter). The string-based representation is agnostic about such assumptions.
More importantly, as detailed in this paper, it is measuring unboundedness on the timing tier which distinguishes UTP and sour-grapes harmony from common segmental processes via their non-subsequentiality. Thus, while this choice is an assumption on which the results in this and the literature cited in §3.4 is based, it appears to be correct, in that it helps us to characterise the unbounded circumambient asymmetry. How this relates to different representational assumptions will be discussed in a moment.
Returning to UTP, it is important to establish that the linearisation used in the previous section is indeed comparable to that of previous studies of subsequentiality, such as for the sour-grapes process (Heinz & Lai Reference Heinz, Lai, Kornai and Kuhlmann2013), in that it also measures look-ahead in terms of the timing tier. The linearisation in (35) can be made explicit with a map along the lines of the one in (39), as in (40a).
-
(40)

As can be seen in (40b), the string symbols H and Ø can encode both contrasts in association in the underlying representation and changes in these associations in the surface, as claimed in (37a). Additionally, the string-based representation in (40b) preserves the linear order of the TBU tier of the autosegmental representation, just as in (39). Look-ahead is thus measured in terms of the timing tier, as in (37b). Note again that, as they simply encode the associations to each timing tier unit, linearisations like in (39) and (40) are very general, and can be applied to any set of autosegmental representations for a particular process.
4.4.3 Representation and subsequentiality
This concludes the arguments for why this particular kind of representation is used in this paper. However, there remains an important open question: what if we don't use this particular representation? This is a valid direction for research, but any answers to this question will not change the result argued for in this paper. Formally, representation is related to expressive power (Medvedev Reference Medvedev and Moore1964, Rogers et al. Reference Rogers, Heinz, Fero, Hurst, Lambert, Wibel, Morrill and Nederhof2013). Work studying the computational properties of autosegmental representations (Bird & Ellison Reference Bird and Ellison1994, Kornai Reference Kornai1995, Yli-Jyrä Reference Yli-Jyrä2013) has not yet offered a hierarchy of complexity like the one presented in §3.4. Future research may use this work in computational autosegmental phonology as a starting point to study the relationship between representation and computational complexity of phonological processes.
It may even be possible to derive non-subsequentiality of unbounded circumambient processes from some aspect of representation (such as look-ahead on the melody tier). This requires, however, that if such representations were translated into the string-based representations according to (37), non-subsequentiality in the string-based representations would somehow emerge. Thus any such explanation based on representation would duplicate the computational results outlined here – it would not refute them. That is, it would have to maintain the result that much of segmental phonology, when viewed with string-based representations that obey the criteria in (37), is subsequential, while UTP and sour-grapes harmony are not.
5 Unbounded circumambient processes and weak determinism
Having shown that unbounded circumambient processes are not left- or right-subsequential, we must make one final distinction. This section argues that unbounded circumambient processes are computationally distinct from the bidirectional spreading processes introduced in §2.5. This leads to the characterisation of the unbounded circumambient asymmetry in terms of a weakly deterministic complexity bound on segmental phonology which is absent in tonal phonology.
5.1 Bidirectional spreading and the weakly deterministic class
The class of unbounded circumambient processes is not the only one which is not left- or right-subsequential. In patterns of stem-control harmony, or cases of bidirectional spreading, such as the Arabic emphasis spreading discussed in §2.5, a feature spreads outward both to the right and the left, as in (41).
-
(41)

Such a map requires unbounded look-ahead in either direction: a target may follow or precede the trigger, in any direction. Thus, as Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) also show, such cases (which will henceforth be referred to under the umbrella term bidirectional spreading) are not subsequential. However, there is a crucial difference between bidirectional spreading and unbounded circumambient processes. Bidirectional spreading hinges on a single trigger, whose influence spreads outward. In contrast, unbounded circumambient processes hinge on two triggers/blockers, whose targets lie between.
Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) observe that a bidirectional spreading process is essentially the same unidirectional map applied left-to-right and then right-to-left. They propose a superclass of the subsequential maps, called weakly deterministic maps, which includes this kind of process. A weakly deterministic map can be decomposed into a left- and right-subsequential map, such that the left-subsequential map is not allowed to change the alphabet or increase the length of the string.
The process in (41) can be decomposed into two left- and right-subsequential maps, describable by the consonant harmony FST in Fig. 4. First, the input string is read by the FST left-to-right (applying the left-subsequential map), then the resulting output is fed back into the FST right-to-left (applying the right-subsequential map to the output). This decomposition is schematised in (42).
-
(42)

This composition of the two maps is special, because it does not change the alphabet or increase the length of the string. Intuitively, this is because these bidirectional processes can be thought of as one unidirectional process operating in two directions. This is highlighted by the fact that both sub-maps use the same FST. Thus, bidirectional spreading is weakly deterministic, as first seen in Fig. 1.
The weakly deterministic class is defined as such by Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) as a restriction on Elgot & Mezei's (Reference Elgot and Mezei1965) result that any regular map can be decomposed into a left-subsequential and right-subsequential map, as long as the left-subsequential map is allowed to enlarge the alphabet. This result holds because the left-subsequential map can ‘mark up’ the string with extra symbols in the first map, and then erase them in the second.Footnote 14 However, no attested segmental maps studied in the literature cited above require such a mark-up.
5.2 Unbounded circumambient processes and the weakly deterministic class
In contrast to attested segmental processes, Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) argue that sour-grapes harmony requires such a mark-up, and thus is not weakly deterministic. This is because it is not simply the application of the same process in two directions. Because the sour-grapes pattern is unbounded circumambient, for any decomposition into two sub-maps the left-subsequential process must somehow encode whether or not a [+F] has been seen to the right of the [–F] targets. It is difficult to see how this can be done without intermediate mark-up, and thus Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) conjecture that sour-grapes harmony is not weakly deterministic. The exact same arguments apply to UTP.
UTP can be decomposed into two subsequential maps with an augmented alphabet, as in (43). First, the left-subsequential process marks all Ø following a H as ?, and then the right-subsequential process changes all ? preceding a H to H (and all ? not preceding a H to Ø).
-
(43)

Crucially, this decomposition relies on the intermediate ? symbols to ‘carry forward’ the information that a H appears to the left in the string. This allows the right-subsequential map to correctly apply without any unbounded look-ahead. However, as in the case of sour-grapes processes, it is hard to see how there could be a similar decomposition which uses only H and Ø, maintains string length in the left-subsequential sub-map and obtains the exact same map. This is because using the same alphabet to create an encoding will always lead to distinctions between input strings being lost, and so such an encoding is bound to fail.
Again, this is based on the unbounded circumambient nature of the process: because there is crucial information on either side of the targets, it is necessary to mark targets to the right of the left trigger in order for the right-subsequential function to correctly process them without unbounded look-ahead. Thus, Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013)’s conjecture applies not just to UTP, but also to any unbounded circumambient process.
An important implication of Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013)’s conjecture is that there exist fully regular maps outside of the weakly deterministic class, and thus that the weakly deterministic class of maps is a proper subclass of the regular class of maps, as depicted in Fig. 1. This section has argued that unbounded circumambient processes fall into this fully regular class, as in Fig. 1, and that this distinguishes them in complexity from bidirectional spreading.
5.3 The weakly deterministic hypothesis
The conjecture that the weakly deterministic class is a proper subclass of the regular class provides a way to capture the unbounded circumambient asymmetry. Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) propose that phonology is weakly deterministic. This hypothesis correctly predicts the absence of unbounded circumambient processes like the sour-grapes pattern in the typology of vowel harmony. However, this paper has shown that unbounded circumambient processes are widely attested in tonal phonology, and has proposed that the weakly deterministic bound only applies to segmental phonology. This accurately predicts that fully regular maps such as UTP and Copperbelt Bemba H-tone spreading exist in tonal phonology. Furthermore, the proposal that tone is more computationally complex than segmental phonology is in line with the assertion of Hyman (Reference Hyman, Goldsmith, Riggle and Yu2011) and others that tone can ‘do more’ than phonology.
An explanation for how the weakly deterministic bound is manifested in the phonological system will be left for future work, although it is possible to speculate on a few points. For example, formal language complexity correlates with an increase in the computational resources necessary for parsing and generation. It could be that tone has access to such resources because prosodic information more commonly interacts with syntax (see e.g. Hyman & Katamba Reference Hyman and Katamba2010), and thus requires more powerful computation. This issue of computational power can also be directly related to learning, as empirical work suggests that formal complexity constrains phonological learning (Moreton & Pater Reference Moreton and Pater2012, McMullin & Hansson Reference McMullin and Hansson2014, Lai Reference Lai2015).
5.4 Explaining the exceptions to the weakly deterministic hypothesis
The weakly deterministic hypothesis in its strongest form cannot account for the rare cases of unbounded circumambient segmental processes discussed in this paper, i.e. Sanskrit n-retroflexion and Yaka vowel harmony. There are a few ways to reconcile these exceptions with the weakly deterministic hypothesis.
One possibility is that the accounts of these processes in the literature are incorrect in classifying them as unbounded. As mentioned in §2.3, Ryan (forthcoming) observes that blocking of Sanskrit n-retroflexion may be bound to the adjacent syllable. In Yaka harmony, the greatest attested distance is only three vowels, and is restricted to a particular morphological context.
Another explanation comes from potentially interfering factors. For example, the presence of an unbounded circumambient process in the tonal phonology may license an unbounded circumambient process in segmental phonology. This may be the case for Yaka, which as noted in §2.2, also has UTP. It could be that Yaka speakers, having first internalised the plateauing process in tonal phonology, may then be able to generalise it to their segmental phonology.
Finally, it may simply be that the constraint against fully regular maps in segmental phonology is not categorical, but in some sense gradient, and thus can admit exceptions. One way in which this may be manifested is through a learning bias in which individuals are more receptive to some patterns than others (Wilson Reference Wilson2006a, Moreton Reference Moreton2008). Children may show a strong preference for weakly deterministic maps when learning segmental phonology, but change to a more general learner in the face of sufficient data. As Staubs (Reference Staubs2014) shows, gradient typological generalisations may also result from the transmission of patterns among multiple learning agents. It is likely that non-weakly deterministic patterns require more kinds of data to learn, and perhaps this data is only available in tonal phonology, which is known to operate over much larger domains than segmental phonology.
Hence there are a number of reasons why the cases of Sanskrit n-retroflexion and Yaka vowel harmony do not immediately invalidate the proposal offered here. Even if they cannot ultimately be explained away, they are exceptional with respect to other characterisations of segmental phonology, such as Wilson's (Reference Wilson2003, 2006b) myopia generalisation. Finally, Sanskrit n-retroflexion and Yaka vowel harmony appear to be the only such cases – Hyman (Reference Hyman, Goldsmith, Riggle and Yu2011: 218) states, for example, that Yaka harmony is the ‘only one example’ of such a process of which he is aware. As such, the development of the potential explanations above will be left to future research.
In sum, this paper has characterised the unbounded circumambient asymmetry in terms of computational complexity, and has identified the weakly deterministic boundary as the relevant difference between tonal and segmental phonology which captures this asymmetry.
6 The unbounded circumambient asymmetry in Optimality Theory
This paper has laid out a computational explanation for the unbounded circumambient asymmetry. Here I briefly outline why this explanation is superior to any possible explanation using current theories based on Optimality Theory (Prince & Smolensky Reference Prince and Smolensky1993) or its variants. This is because current theories of OT do not provide a unified characterisation of the unbounded circumambient processes, meaning that making OT empirically adequate with regards to the asymmetry runs into a ‘duplication of effort’ problem. Banning the particular non-local effects that generate segmental unbounded circumambient processes requires changes both to how OT manipulates segments autosegmentally and to how it compares candidates. Thus OT does not provide a unified characterisation of the asymmetry comparable to the one based on computational complexity put forward in the preceding sections.
Sour-grapes vowel harmony is an appropriate place to begin. It is unattested in segmental phonology, but predicted by parallel OT and local Agree constraints checking the agreement between features of adjacent segments. Given such constraints, candidates in which spreading is blocked still violate Agree (as the last segment to which the feature has spread still disagrees with the blocker) and are thus harmonically bounded by candidates in which no spreading occurs, as they also violate Agree but do not register any faithfulness violations incurred by the spreading feature (see McCarthy Reference McCarthy, Goldsmith, Hume and Wetzels2010 for how the sour-grapes pattern is generated in OT). Thus the nature of optimisation, which involves comparison of candidates with non-local changes to those with local ones, allows for unbounded behaviour with local constraints. In fact, this is exactly this type of behaviour that Hyman (Reference Hyman1998) harnesses to describe vowel harmony in Yaka.
One proposal for dealing with the sour-grapes problem is McCarthy's (Reference McCarthy, Goldsmith, Hume and Wetzels2010) Harmonic Serialism (HS) analysis of spreading, which restricts Gen to the production of candidates with a single change (with winning candidates fed back into the grammar until no changes produce a more optimal candidate). As only candidates with single changes are compared, global comparison cannot take place, and thus patterns such as sour-grapes harmony can no longer be generated with local Agree constraints. Of course, assuming a HS framework provides no explanation for the presence of a sour-grapes-like tone pattern in Copperbelt Bemba.
Furthermore, this solution is specific to sour-grapes vowel harmony resulting from Agree, and does not extend to autosegmental analyses of plateauing. Plateauing, tonal or otherwise, can be seen as two identical features adjacent on the tier merging to satisfy the OCP, with the intervening anchor units associating to the resulting fused feature in order to avoid a gapped structure. This can be schematised derivationally as in (44).
-
(44)

While (44) is a derivational sketch of the process, the intuition can be implemented in either serial or parallel versions of OT, given basic constraints governing the behaviour of autosegments proposed in the OT literature. Fusion of identical adjacent autosegments can be motivated by an OCP markedness constraint (Leben Reference Leben1973, McCarthy Reference McCarthy1986, Yip Reference Yip2002) ranking above a Uniformity faithfulness constraint militating against the fusion of autosegments (Myers Reference Myers1997, Pater Reference Pater and McCarthy2004). The ‘filling in’ of the associations to the intervening anchor units can then be motivated by ranking NoGap (Itô et al. Reference Itô, Mester and Padgett1995, Yip Reference Yip2002), a constraint against structures in which associations skip over potential anchors, above faithfulness constraints prohibiting the addition of association lines. Given such a ranking in classical OT, only a candidate featuring both fusion and filling in will satisfy both the OCP and NoGap markedness constraints. In HS, a candidate with fusion will represent an increase in harmony (as it satisfies the OCP), and then successive candidates representing a gradual filling in of the associations in the intervening anchor units will represent an increase in harmony with respect to NoGap. Thus, both fusion and filling in can be achieved straightforwardly either in parallel OT or in HS.
We therefore have a duplication of effort problem: in order to categorically remove segmental unbounded circumambient processes from the typology predicted by OT theories of phonology, it is necessary to adopt at least one of the changes proposed for sour-grapes harmony and to remove the segmental versions of the constraints above that achieve autosegmental plateauing. Thus, while it appears technically possible to have a theory of OT that is empirically adequate with regards to the unbounded circumambient asymmetry, it does not provide a unified explanation. In contrast, the FLT-based account presented here characterises the difference: segmental phonology is weakly deterministic, but tonal phonology is not.
7 Conclusion
This paper has made three contributions. First, it has documented the asymmetry in the attestation of unbounded circumambient processes in tonal phonology and segmental phonology. Second, it has shown that UTP is similar to sour-grapes harmony, in that they are both unbounded circumambient processes, and that this similarity has formal consequences. Third, it has characterised the asymmetry between segmental and tonal phonology by arguing that unbounded circumambient processes are fully regular, and thus more computationally complex than processes which do not require unbounded look-ahead in two directions. This was shown to be a superior characterisation than that offered in OT, which cannot account for the asymmetry in a unified way.
The conclusions in this paper raise a number of interesting questions for future research. What computational constraints are there on tone? In other words, is there a subregular class of maps which includes (or corresponds to) unbounded circumambient processes? How does this relate to Elgot & Mezei's (Reference Elgot and Mezei1965) result using intermediate mark-up to generate any regular map from two subsequential maps? As Heinz & Lai (Reference Heinz, Lai, Kornai and Kuhlmann2013) point out, this idea may be brought to bear on the question of how abstract intermediate representations are in phonology. The questions of representation raised at the end of §4.4 can be approached in a similar way – how do changes in representation correlate with changes in generative capacity? Finally, it remains to be seen how the FLT insight presented here can be incorporated into traditional phonological theory. One potential approach is to appeal to learning, as considered in §5.3.
Unfortunately, going into these concerns in detail is beyond the scope of this paper. Instead, its goal is similar to that of Kisseberth (Reference Kisseberth1970)’s prophetic work on conspiracies in Yawelmani. Kisseberth writes that he is not ‘principally interested in proposing detailed formalism; instead I would like to encourage phonologists to look at the phonological component of a grammar in a particular way’ (1970: 293). This work, too, aims to encourage phonologists to look at phonology in a new way. Regardless of how it is incorporated into our previous understanding of phonology, the unbounded circumambient asymmetry between tonal and segmental phonology is robust, and the best available characterisation of this generalisation comes from computational complexity.