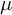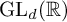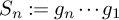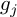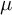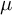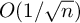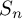BERRY–ESSEEN BOUND AND LOCAL LIMIT THEOREM FOR THE COEFFICIENTS OF PRODUCTS OF RANDOM MATRICES

Abstract

Let $\mu $ be a probability measure on $\mathrm {GL}_d(\mathbb {R})$, and denote by $S_n:= g_n \cdots g_1$ the associated random matrix product, where $g_j$ are i.i.d. with law $\mu $. Under the assumptions that $\mu $ has a finite exponential moment and generates a proximal and strongly irreducible semigroup, we prove a Berry–Esseen bound with the optimal rate $O(1/\sqrt n)$ for the coefficients of $S_n$, settling a long-standing question considered since the fundamental work of Guivarc’h and Raugi. The local limit theorem for the coefficients is also obtained, complementing a recent partial result of Grama, Quint and Xiao.

1 Introduction

Let $\mu $ be a probability measure on $G:=\mathrm {GL}_d(\mathbb {R})$ , $d \geq 2$ . Then, $\mu $ induces a random walk on G by letting

$$ \begin{align*}S_n: = g_n \cdots g_1,\end{align*} $$

where $n \geq 1$ and the $g_j$ ’s are independent and identically distributed random elements of G with law given by $\mu $ . The study of these random processes and associated limit theorems has a rich history, starting from seminal works of Furstenberg and Kesten [12, 13], leading to important progress since then. This topic is still very active, with important new results and techniques being recently discovered. We refer to [2, 3] for an overview. See also discussion below for some recent results.

We consider the standard linear action of G on $\mathbb {R}^d$ and the induced action on the real projective space ${\mathbb {P}}^{d-1}$ . Denote by $\| v \|$ the standard Euclidean norm of $v \in \mathbb {R}^d$ , and, for $g \in G$ , let $\|g\|$ be the associated operator norm.

In order to study the random matrices $S_n$ , it is useful to look at associated real-valued random variables. An important function in this setting is the norm cocycle, defined by

$$ \begin{align*}\sigma(g,x) := \log \frac{\lVert gv\rVert}{\lVert v\rVert}, \quad \text{for }\,\, v \in \mathbb{R}^d \setminus \{0\}, \, x = [v] \in \mathbb{P}^{d-1} \, \text{ and } g \in G.\end{align*} $$

The cocycle relation $\sigma (g_2g_1,x) = \sigma (g_2,g_1 x) + \sigma (g_1,x)$ can be used to effectively apply methods from the spectral theory of complex transfer operators (see Subsection 2.3) and martingale approximation [1]. Some other natural quantities that can be studied in this setting are: the norm $\|g\|$ , the spectral radius $\rho (g)$ and the coefficients of g, the latter being the object of this article.

The goal of this work is to obtain two new limit theorems for the coefficients of $S_n$ as n tends to infinity. For $v \in \mathbb {R}^d$ and $f \in (\mathbb {R}^d)^*$ , its dual space, we denote by $\langle f,v \rangle := f(v)$ their natural coupling. Observe that the $(i,j)$ -entry of a matrix g is given by $\langle e_i^* , g e_j \rangle $ , where $(e_k)_{1\leq k \leq d}$ (resp. $(e^*_k)_{1\leq k \leq d}$ ) denotes the canonical basis of $\mathbb {R}^d$ (resp. $(\mathbb {R}^d)^*$ ). Our results will apply, more generally, to the random variables of the form

$$ \begin{align*}\log{ |\langle f, S_n v\rangle | \over \lVert f\rVert \lVert v\rVert},\end{align*} $$

with $v \in \mathbb {R}^d \setminus \{0\}$ and $f \in (\mathbb {R}^d)^* \setminus \{0\}$ .

In order to obtain meaningful results, some standard assumptions on the measure $\mu $ need to be made. Recall that a matrix $g\in G$ is said to be proximal if it admits a unique eigenvalue of maximal modulus which is moreover of multiplicity one. Let $\Gamma _\mu $ be the smallest closed semigroup containing the support of $\mu $ . We assume that $\Gamma _\mu $ is proximal, that is, it contains a proximal matrix, and strongly irreducible, that is, the action of $\Gamma _\mu $ on $\mathbb {R}^d$ does not preserve a finite union of proper linear subspaces. It is well known that, under the above conditions, $\mu $ admits a unique stationary probability measure on $\mathbb {P}^{d-1}$ ; see Section 2.

We’ll also assume that $\mu $ has a finite exponential moment, that is, $\int _{G} N(g)^\varepsilon \mathrm {d}\mu (g) < \infty $ for some $\varepsilon>0$ , where $N(g):=\max \big ( \lVert g\rVert ,\lVert g^{-1}\rVert \big )$ .

It is now a classical result of Guivarc’h and Raugi that, under the above conditions, the variables $\log { |\langle f, S_n v\rangle | \over \lVert f\rVert \lVert v\rVert }$ satisfy the central limit theorem (CLT); see [16, 3] and also [2] for a modern treatment. Since their work, the corresponding Berry–Esseen bound has been considered and, apart from partial results, remained open. See below for more details on the known results. The aim of this article is to obtain such bound for general random walks with finite exponential moment. Our methods also give the local limit theorem (LLT) for the coefficients.

We now state our first result, namely, a Berry–Esseen bound with rate $O(1/ \sqrt n)$ for the coefficients. This is a quantitative version of the above-mentioned CLT. The first Lyapunov exponent of $\mu $ is, by definition, the number

$$ \begin{align*}\gamma := \lim_{n \to \infty} \frac1n \int \log\|g_n \cdots g_1\| \, \mathrm{d} \mu(g_1) \cdots \mathrm{d} \mu(g_n).\end{align*} $$

Theorem A. Let $\mu $ be a probability measure on $\mathrm {GL}_d(\mathbb {R})$ . Assume that $\mu $ has a finite exponential moment and that $\Gamma _\mu $ is proximal and strongly irreducible. Let $\gamma $ be the associated first Lyapunov exponent. Then, there is a constant $C>0$ and a real number $\varrho> 0$ such that, for any $v \in \mathbb {R}^d \setminus \{0\}, f \in (\mathbb {R}^d)^* \setminus \{0\}$ , any interval $J\subset \mathbb {R}$ , and all $n\geq 1$ , we have

$$ \begin{align*}\bigg| \mathbf P \Big( \log{ |\langle f, S_n v\rangle | \over \lVert f\rVert \lVert v\rVert} - n \gamma\in \sqrt n J \Big) - \frac{1}{\sqrt{2 \pi} \, \varrho} \int_{J} e^{-\frac{s^2}{2 \varrho^2}} \, \mathrm{d} s \bigg| \leq \frac{C}{\sqrt n}.\end{align*} $$

We observe that the rate $O(1/ \sqrt n)$ in the above theorem is optimal as this is also the case for sums of real-valued i.i.d.s. Many related bounds for the other random variables associated with $S_n$ mentioned above can be found in the recent literature. More details are given below.

Our second result is an LLT for the coefficients.

Theorem B. Let $\mu $ be a probability measure on $\mathrm {GL}_d(\mathbb {R})$ . Assume that $\mu $ has a finite exponential moment and that $\Gamma _\mu $ is proximal and strongly irreducible. Let $\gamma $ be the associated first Lyapunov exponent. Let $\varrho> 0$ be as in Theorem A. Then, for any $v \in \mathbb {R}^d \setminus \{0\}, f \in (\mathbb {R}^d)^* \setminus \{0\}$ and any $-\infty <a<b<\infty $ , we have

$$ \begin{align*}\lim_{n\to \infty}\sup_{t\in\mathbb{R}}\bigg| \sqrt{n} \, \mathbf P \Big( t+ \log{ |\langle f, S_n v\rangle | \over \lVert f\rVert \lVert v\rVert} - n \gamma\in [ a, b] \Big) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \bigg| =0.\end{align*} $$

Moreover, the convergence is uniform in $v \in \mathbb {R}^d \setminus \{0\}$ and $f \in (\mathbb {R}^d)^* \setminus \{0\}$ .

Theorem B contains a recent result of Grama, Quint and Xiao [14]. See the discussion below.

Related works. As mentioned before, the rate $O(1 / \sqrt n)$ in Theorem A is optimal. Under the assumptions of Theorem A, it has been known for a long time that one can obtain a Berry–Esseen bound for the norm cocycle $\sigma (S_n,x)$ with rate $O(1 / \sqrt n)$ ; see [3, 18] and [11] for a refined version. For the coefficients of $S_n$ the progress is more recent, and before our work, Berry–Esseen bounds were only known under strong positivity conditions on the matrices in the support of $\mu $ ; see [21]. After the appearance of the first version of this article on the arXiv, a weaker $O(\log n / \sqrt n)$ bound was announced by Cuny, Dedecker, Merlevède and Peligrad under the same hypothesis as ours; see [6]. The improvement from $O(\log n / \sqrt n)$ to $O(1 / \sqrt n)$ is a delicate matter and a challenging problem, even in the exponential moment case, cf. [21, p.8].

Concerning the variables $\log \|S_n \|$ and $\rho (S_n)$ , a Berry–Esseen bound with rate $O(1 / \sqrt n)$ is known under some positivity conditions and without such conditions an $O(\log n / \sqrt n)$ rate can be obtained; see [20, 21].

The exponential moment condition in Theorem A is stronger than what one should require. Parallel to the case of sums of i.i.d.s, one should expect to have the same result under a third moment condition, that is, $\int _G \big ( \log N(g) \big )^3 \, \mathrm {d} \mu (g) < + \infty $ . This is unknown, in general, for the coefficients. Under this condition, for the norm cocycle $\sigma (S_n,x)$ , the best-known rate is $O(n^{-1/4} \sqrt {\log n})$ obtained in [4] using martingale approximation methods in the spirit of [1]. This has been recently improved in [5] to an $O(1 / \sqrt n)$ (resp. $O((\log n)^{1/2}n^{-1/2})$ ) rate under a fourth (resp. third) moment condition. See also [17] for related results under low moment conditions. In the particular case where $d=2$ , the optimal $O(1 / \sqrt n)$ bound was obtained by the authors for the norm cocycle and the coefficients under a third moment condition [8]. In higher dimensions, an $O(1 / n^{(p-1)/2p})$ bound was recently announced in [6] under a $p^{th}$ moment condition, $p \geq 3$ .

Concerning the LLT, Theorem B above strengthens a recent result of Grama, Quint and Xiao [14], which holds under the same hypothesis as Theorem B, but only for the parameter $t = 0$ . See also [22] for related results. The aforementioned theorems allow us to estimate the probability that the random variables $ \frac {1}{\sqrt n} \big (\log { |\langle f, S_n v \rangle | \over \lVert f\rVert \lVert v\rVert } - n \gamma \big )$ fall on intervals of size $O(1 / \sqrt n)$ around the origin, while Theorem B works for intervals of size $O(1 / \sqrt n)$ around an arbitrary point on the real line. When $d=2$ , the same result can be proved under a third moment condition, see [8]. For the norm cocycle, the general LLT is due to Le Page [18] under an exponential moment condition. For $d=2$ and the optimal second moment condition, this was obtained by the authors in [8].

Overview of the proofs. When proving limit theorems for the coefficients, the first step is to compare them with the norm cocycle via the elementary identity

$$ \begin{align*} \log{ |\langle f, S_n v \rangle | \over \lVert f\rVert \lVert v\rVert} = \sigma(S_n,x) + \log \Delta(S_n x,y), \end{align*} $$

where $x:=[v]\in \mathbb {P}^{d-1}, y:=[f]\in (\mathbb {P}^{d-1})^*$ and $\Delta (x,y):= \frac { |\langle f, v \rangle |}{\lVert f\rVert \lVert v\rVert }$ , see [14]. One can check that $\Delta (x,y) = d (x,H_y)$ , where $H_y := \mathbb {P}(\ker f)$ is a hyperplane in $\mathbb {P}^{d-1}$ and d is a natural distance on $\mathbb {P}^{d-1}$ (see Section 2). Then, we can use the above formula and work with the random variable $\sigma (S_n,x) +\log d(S_n x, H_y)$ instead of $\log { |\langle f, S_n v \rangle | \over \lVert f\rVert \lVert v\rVert } $ . The behaviour of $\sigma (S_n,x)$ can be studied via the perturbed Markov operators (see Subsection 2.3). The term $\log d(S_n x, H_y)$ is handled using some large deviation estimates combined with a good partition of unity (see Lemmas 3.3 and 4.1). The introduction of such partition is one of our key arguments, applied to approximate the quantity $\sigma (S_n,x) + \log d(S_n x,H_y)$ by a sum of functions of two separate variables $\sigma (S_n,x)$ and $S_n x$ ; see also [14]. We use a partition of $\mathbb {P}^{d-1} \setminus H_y$ by functions $(\chi _k)_{k \geq 0}$ subordinated to ‘annuli’ around $H_y$ of the form $ \big \{ w \in \mathbb {P}^{d-1} :\, e^{-k-1} < d(w,H_y) < e^{-k+1} \big \}$ . This allows us to have good control on the errors in a ‘uniform’ manner. This key idea is responsible for the sharp bounds, in contrast with the weaker bounds from previous works described above. This is also what provides the necessary estimates for the general version of the LLT above. In particular, we don’t need to use the zero-one law for algebraic subsets of $\mathbb {P}^{d-1}$ obtained in [14], which is a main ingredient in the proof of their version of the LLT.

For most of our estimates, we strongly rely on the spectral analysis of the Markov operator and its perturbations on a Hölder space $\mathscr {C}^\alpha (\mathbb {P}^{d-1})$ (see Subsection 2.3). It is crucial to choose $\alpha $ small in order to reduce the impact of the norm of $\chi _k$ when k is large; see Lemmas 3.6 and 4.4. A main difficulty that appeared in our computations is how to handle the ‘tail’ of the approximation using $\chi _k$ . To overcome this problem, we introduce an auxiliary function

$$ \begin{align*}\Phi_{n}^{\star} (w):= 1 - \sum_{0\leq k\leq A\log n} \chi_k(w)\end{align*} $$

for some well-chosen $A>0$ , which has negligible impact on the estimates but whose presence is helpful in the computations; see, for example, Lemmas 3.8, 3.9 and 4.5. For Theorem A, it is also crucial to use a refinement of the classical Berry–Esseen lemma, which is of independent interest; see Lemma 3.1 below. In particular, this allows us to avoid the use of real perturbations of the Markov operator, which can be useful when only purely imaginary perturbations are allowed, as in [8].

Our approach can also be applied to the case of more general target functions. More precisely, we can replace the probabilities in Theorems A and B by the expectation of some good test functions on $\mathbb {R}\times \mathbb {P}^{d-1}$ . These questions are treated in the separate work [9] in order to keep the current article less technical. The results presented here can be extended to the case of matrices with entries in a local field; see [2] for local field versions of the results stated in Section 2.

Organization of the article. The article is organized as follows. In Section 2, we recall some standard result from the theory of random matrix products that will be used in the proofs, most notably: spectral gap results, large deviation estimates and regularity properties of the stationary measure. Theorem A is proved in Section 3, and Theorem B is proved in Section 4.

Notations. Throughout this article, the symbols $\lesssim $ and $\gtrsim $ stand for inequalities up to a multiplicative constant. The dependence of these constants on certain parameters (or lack thereof), if not explicitly stated, will be clear from the context. We denote by $\mathbf E$ the expectation and $\mathbf P$ the probability.

2 Preliminary results

We start with some basic results and notations. We refer to [2, 3] for the proofs of the results described here. See also [18].

2.1 Norm cocycle, first Lyapunov exponent and the stationary measure

Let $G:=\mathrm {GL}_d(\mathbb {R})$ . We consider its standard linear action on $\mathbb {R}^d$ and the induced action on the real projective space $\mathbb {P}^{d-1}$ . Let $\mu $ be a probability measure on G. For $n \geq 1$ , we define the convolution measure by $\mu ^{*n} := \mu * \cdots * \mu $ (n times) as the push-forward of the product measure $\mu ^{\otimes n}$ on $G^n$ by the map $(g_1, \ldots , g_n) \mapsto g_n \cdots g_1$ . If $g_j$ are i.i.d. random matrices with law $\mu $ , then $\mu ^{*n} $ is the law of $S_n := g_n \cdots g_1$ .

Denote by $\lVert g\rVert $ the operator norm of the matrix g, and define $N(g):=\max \big ( \lVert g\rVert ,\lVert g^{-1}\rVert \big )$ . We say that $\mu $ has a finite exponential moment if

$$ \begin{align*}\mathbf{E} \big( N(g)^\varepsilon \big) = \int_G N(g)^\varepsilon \, \mathrm{d} \mu(g) < \infty \quad \text{for some } \,\, \varepsilon> 0.\end{align*} $$

The first Lyapunov exponent is the number

$$ \begin{align*}\gamma := \lim_{n \to \infty} \frac1n \mathbf{E} \big( \log\|S_n\| \big)=\lim_{n \to \infty} \frac1n \int \log\|g_n \cdots g_1\| \, \mathrm{d} \mu(g_1) \cdots \mathrm{d} \mu(g_n).\end{align*} $$

The norm cocycle is the function $\sigma : G \times \mathbb {P}^{d-1} \to \mathbb {R}$ given by

$$ \begin{align*}\sigma(g,x) = \sigma_g(x):= \log \frac{\lVert gv\rVert}{\lVert v\rVert}, \quad \text{for }\,\, v \in \mathbb{R}^d \setminus \{0\}, \, x = [v] \in \mathbb{P}^{d-1} \, \text{ and } g \in G.\end{align*} $$

An element $g\in G$ is said to be proximal if it admits a unique eigenvalue of maximal modulus which is moreover of multiplicity one. A semigroup $\Gamma $ is said to be proximal if it contains a proximal element. We say that (the action of) $\Gamma $ is strongly irreducible if it does not preserve a finite union of proper linear subspaces of $\mathbb {R}^d$ .

Denote by $\Gamma _\mu $ the semigroup generated by the support of $\mu $ . If $\Gamma _\mu $ is proximal and strongly irreducible, then $\mu $ admits a unique stationary measure, that is, a probability measure $\nu $ on $\mathbb {P}^{d-1}$ satisfying

$$ \begin{align*}\int_G g_* \nu \, \mathrm{d} \mu(g)= \nu.\end{align*} $$

The above measure is also called the Furstenberg measure associated with $\mu $ .

2.2 Large deviation estimates and regularity

We equip $\mathbb {P}^{d-1}$ with a natural distance given by

$$ \begin{align*} d(x,w) : = \sqrt{1 - \bigg( \frac{\langle v_x,v_w \rangle}{\|v_x\| \|v_w\|} \bigg)^2}, \quad \text{where} \quad v_x,v_w \in \mathbb{R}^d \setminus \{0\}, \, x = [v_x], \,\, w = [v_w] \in \mathbb{P}^{d-1}. \end{align*} $$

Observe that $d(x,w)$ is the sine of the angle between the lines x and w in $\mathbb {R}^d$ . Then, $(\mathbb {P}^{d-1}, d)$ has diameter one on which the orthogonal group $\text {O}(d)$ acts transitively and isometrically. We will denote by $\mathbb {B}(x,r)$ the associated open ball of center x and radius r in $\mathbb {P}^{d-1}$ .

For $y\in (\mathbb {P}^{d-1})^*$ , the dual of $\mathbb {P}^{d-1}$ , we denote by $H_y$ the kernel of y, which is a (projective) hyperplane in $\mathbb {P}^{d-1}$ . We’ll need the following large deviation estimates. Recall that $\gamma $ denotes the first Lyapunov exponent of $\mu $ .

Proposition 2.1 ([2]—Theorem 12.1, Proposition 14.3 and Lemma 14.11)

Let $\mu $ be a probability measure on $G=\mathrm {GL}_d(\mathbb {R})$ . Assume that $\mu $ has a finite exponential moment and that $\Gamma _\mu $ is proximal and strongly irreducible. Then, for any $\epsilon>0$ there exist $c>0$ and $n_0 \in \mathbb {N}$ such that, for all $\ell \geq n\geq n_0$ , $x\in \mathbb {P}^{d-1}$ and $y\in (\mathbb {P}^{d-1})^*$ , one has

$$ \begin{align*}\mu^{*n} \big\{g\in G:\, |\sigma(g,x)-n\gamma| \geq n\epsilon \big\}\leq e^{-cn}\end{align*} $$

and

$$ \begin{align*}\mu^{*\ell} \big\{g\in G:\, d(gx, H_y) \leq e^{-\epsilon n} \big\} \leq e^{-cn}.\end{align*} $$

The next result gives a regularity property of the stationary measure $\nu $ . See also [1, 7] for the case where $\mu $ satisfies weaker moment conditions. For a hyperplane H in $\mathbb {P}^{d-1}$ and $r>0$ , we denote $\mathbb {B}(H,r) :=\{x \in \mathbb {P}^{d-1}: d(x,H) < r\}$ , which is a ‘tubular’ neighborhood of H.

Proposition 2.2 ([15], [2]–Theorem 14.1)

Let $\mu $ be a probability measure on $G=\mathrm {GL}_d(\mathbb {R})$ . Assume that $\mu $ has a finite exponential moment and that $\Gamma _\mu $ is proximal and strongly irreducible. Let $\nu $ be the associated stationary measure. Then, there are constants $C>0$ and $\eta>0$ such that

$$ \begin{align*}\nu\big(\mathbb{B}(H_y,r)\big)\leq C r^\eta \quad\text{for every} \quad y\in (\mathbb{P}^{d-1})^* \, \, \text{ and } \,\, 0 \leq r \leq 1.\end{align*} $$

2.3 The Markov operator and its perturbations

The Markov operator associated to $\mu $ is the operator

$$ \begin{align*}\mathcal{P} \varphi(x):=\int_{G} \varphi(gx) \,\mathrm{d}\mu(g),\end{align*} $$

acting on functions on $\mathbb {P}^{d-1}$ .

For $z\in \mathbb {C}$ , we consider the perturbation $\mathcal {P}_z$ of $\mathcal {P}$ given by

$$ \begin{align*}\mathcal{P}_z \varphi(x):=\int_{G} e^{z\sigma(g,x)}\varphi(gx) \,\mathrm{d}\mu(g),\end{align*} $$

where $\sigma (g,x)$ is the norm cocycle defined above. The operator $\mathcal {P}_z$ is often called the complex transfer operator. Notice that $\mathcal {P}_0= \mathcal {P}$ is the original Markov operator. A direct computation using the cocycle relation $\sigma (g_2g_1,x) = \sigma (g_2,g_1 x) + \sigma (g_1,x)$ gives that

(2.1) $$ \begin{align} \mathcal{P}^n_z \varphi (x) = \int_G e^{z \sigma(g,x)} \varphi(gx) \, \mathrm{d} \mu^{* n} (g). \end{align} $$

In other words, $\mathcal {P}^n_z$ corresponds to the perturbed Markov operator associated with the convolution power $\mu ^{\ast n}$ .

We recall some fundamental results of Le Page about the spectral properties of the above operators. For $0<\alpha <1$ , we denote by $\mathscr {C}^\alpha (\mathbb {P}^{d-1})$ the space of Hölder continuous functions on $\mathbb {P}^{d-1}$ equipped with the norm

$$ \begin{align*} \|\varphi\|_{\mathscr{C}^\alpha} := \|\varphi\|_\infty + \sup_{x \neq y \in \mathbb{P}^{d-1}} \frac{|\varphi(x)-\varphi(y)|}{d(x,y)^\alpha}. \end{align*} $$

Recall that the essential spectrum of an operator is the subset of the spectrum obtained by removing its isolated points corresponding to eigenvalues of finite multiplicity. The essential spectral radius $\rho _{\mathrm {ess}}$ is then the radius of the smallest disc centered at the origin which contains the essential spectrum.

Theorem 2.3 ([18] and [3]–V.2)

Let $\mu $ be a probability measure on $G=\mathrm {GL}_d(\mathbb {R})$ with a finite exponential moment such that $\Gamma _\mu $ is proximal and strongly irreducible. Then, there exists an $0<\alpha _0 <1$ such that, for all $0<\alpha \leq \alpha _0$ , the operator $\mathcal {P}$ acts continuously on $\mathscr {C}^\alpha (\mathbb {P}^{d-1})$ with a spectral gap. In other words, $\rho _{\mathrm {ess}}(\mathcal {P})<1$ and $\mathcal {P}$ has a single eigenvalue of modulus $\geq 1$ located at $1$ , which is isolated and of multiplicity one.

It follows directly from the above theorem that $\|\mathcal {P}^n - \mathcal {N}\|_{\mathscr {C}^\alpha } \leq C \lambda ^n$ for some constants $C> 0$ and $0<\lambda <1$ , where $\mathcal {N}$ is the projection $\varphi \mapsto \big ( \int _{\mathbb {P}^{d-1}} \varphi \, \mathrm {d} \nu \big ) \cdot \mathbf 1$ onto the space of constant functions. Here and in what follows, we denote by $\mathbf 1$ the constant function equal to $1$ on $\mathbb {P}^{d-1}$ .

The following result gives the regularity of the family of operators $z \mapsto \mathcal {P}_z$ . The second part follows from the general theory of perturbations of linear operators, which implies that the spectral properties of $\mathcal {P}_0$ persist for small values of z. For a proof, see, for example, [3, V.4].

Proposition 2.4. Let $\mu $ and $\alpha _0$ be as in Theorem 2.3. There exists $b> 0$ such that, for $|\mathop {\mathrm {Re}} z| < b$ , the operators $\mathcal {P}_z$ act continuously on $\mathscr {C}^\alpha (\mathbb {P}^{d-1})$ for all $0<\alpha \leq \alpha _0$ . Moreover, the family of operators $z \mapsto \mathcal {P}_z$ is analytic near $z=0$ .

In particular, there exists an $\epsilon _0> 0$ such that, for $|z|\leq \epsilon _0$ , one has a decomposition

$$ \begin{align*} \mathcal{P}_z = \lambda_z \mathcal{N}_z + \mathcal{Q}_z, \end{align*} $$

where $\lambda _z \in \mathbb {C}$ , $\mathcal {N}_z$ and $\mathcal {Q}_z$ are bounded operators on $\mathscr {C}^{\alpha }(\mathbb {P}^{d-1})$ and

1. 1. $\lambda _0 = 1$ and $\mathcal {N}_0 \varphi = \int _{\mathbb {P}^{d-1}} \varphi \, \mathrm {d} \nu $ , which is a constant function, where $\nu $ is the unique $\mu $ -stationary measure;

2. 2. $\rho := \displaystyle \lim _{n \to \infty } \|\mathcal {P}_0^n - \mathcal {N}_0\|_{\mathscr {C}^\alpha }^{1/n} < 1$ ;

3. 3. $\lambda _z$ is the unique eigenvalue of maximum modulus of $\mathcal {P}_z$ , $\mathcal {N}_z$ is a rank-one projection and $\mathcal {N}_z \mathcal {Q}_z = \mathcal {Q}_z \mathcal {N}_z = 0$ ;

4. 4. The maps $z \mapsto \lambda _z$ , $z \mapsto \mathcal {N}_z$ and $z \mapsto \mathcal {Q}_z$ are analytic;

5. 5. $|\lambda _z| \geq \frac {2 + \rho }{3}$ and for every $k\in \mathbb {N}$ , there exists a constant $c> 0$ such that

   $$ \begin{align*}\Big \| \frac{\mathrm{d}^k \mathcal{Q}_z^n}{\mathrm{d} z^k} \Big \|_{\mathscr{C}^\alpha} \leq c \Big( \frac{1 + 2 \rho}{3} \Big)^n \quad \text{ for every}\quad n \geq 0;\end{align*} $$

6. 6. for $z=i\xi \in i\mathbb {R}$ , we have

   $$ \begin{align*}\lambda_{i\xi} = 1 + i \gamma \xi - \frac{\varrho^2+\gamma^2}{2}\xi^2+O(|\xi|^3) \quad \text {as } \,\, \xi \to 0,\end{align*} $$

   where $\gamma $ is the first Lyapunov exponent of $\mu $ and $\varrho> 0$ is a constant.

The constant $\varrho ^2> 0$ appearing in the above expansion of $\lambda _{i\xi }$ coincides with the variance in the CLT for the norm cocycle; see [3, 2, 8]. As a consequence of the above proposition, we can derive the following estimates which will be crucial in the proof of our main theorems. For the proof, see [8, Lemma 4.10] and [18, Lemma 9].

Lemma 2.5. Let $\epsilon _0$ be as in Proposition 2.4. There exists $0 < \xi _0 < \epsilon _0$ such that, for all $n \in \mathbb {N}$ large enough, one has

$$ \begin{align*}\big|\lambda_{{i\xi\over \sqrt n}}^n\big|\leq e^{-{\varrho^2\xi^2\over 3}} \quad\text{for}\quad |\xi|\leq \xi_0\sqrt n,\end{align*} $$

$$ \begin{align*}\Big| e^{-i\xi\sqrt n \gamma}\lambda_{{i\xi\over \sqrt n}}^n-e ^{-{\varrho^2\xi^2\over 2}} \Big|\leq {c\over \sqrt n}|\xi|^3e^{-{\varrho^2\xi^2\over 2}} \quad\text{for}\quad |\xi|\leq \sqrt[6] n,\end{align*} $$

$$ \begin{align*}\Big| e^{-i\xi\sqrt n \gamma} \lambda_{{i\xi\over \sqrt n}}^n-e ^{-{\varrho^2\xi^2\over 2}} \Big|\leq {c\over \sqrt n}e^{-{\varrho^2\xi^2\over 4}} \quad\text{for}\quad \sqrt[6] n<|\xi|\leq \xi_0\sqrt n,\end{align*} $$

where $c>0$ is a constant independent of n.

The following important result describes the spectrum of $\mathcal {P}_{i\xi }$ for large real values of $\xi $ . It is one of the main tools in the proof of the LLT for the norm cocycle, and it will also be indispensable in our proof of Theorem B.

Proposition 2.6 ([18] and [2]–Chapter 15)

Let $\mu $ and $\alpha _0$ be as in Theorem 2.3. Let K be a compact subset of $\mathbb {R} \setminus \{0\}$ . Then, for every $0<\alpha \leq \alpha _0$ there exist constants $C_K>0$ and $0<\rho _K<1$ such that $\lVert \mathcal {P}^n_{i\xi }\rVert _{\mathscr {C}^\alpha }\leq C_K \rho _K^n$ for all $n\geq 1$ and $\xi \in K$ .

2.4 Fourier transform and characteristic function

Recall that the Fourier transform of an integrable function h on $\mathbb {R}$ , denoted by $\widehat h$ , is defined by

$$ \begin{align*}\widehat h(\xi):=\int_{-\infty}^{+\infty}h(u)e^{-i u\xi} \mathrm{d} u\end{align*} $$

and the inverse Fourier transform of h is

$$ \begin{align*}\mathcal{F}^{-1} h(u) :={1\over {2\pi}}\int_{-\infty}^{+\infty} h(\xi) e^{ i u\xi} \mathrm{d} \xi,\end{align*} $$

so that, when $\widehat h$ is integrable, one has $h = \mathcal {F}^{-1} \widehat h$ . With these definitions, the Fourier transform of $\widehat h(\xi )$ is $2\pi h(-u)$ and the convolution operator satisfies $\widehat {h_1*h_2}=\widehat h_1\cdot \widehat h_2$ .

Lemma 2.7 ([8]–Lemma 2.2)

There exists a smooth strictly positive even function $\vartheta $ on $\mathbb {R}$ with $\int _{\mathbb {R}} \vartheta (u) \mathrm {d} u=1$ such that its Fourier transform $\widehat \vartheta $ is a smooth even function supported by $[-1,1]$ . Moreover, for $0<\delta \leq 1$ and $\vartheta _\delta (u):=\delta ^{-2}\vartheta (u/\delta ^2)$ , the function $\widehat {\vartheta _\delta }$ is supported by $[-\delta ^{-2},\delta ^{-2}]$ , $|\widehat {\vartheta _\delta }|\leq 1$ and $\lVert \widehat {\vartheta _\delta }\rVert _{\mathscr {C}^1}\leq c$ for some constant $c>0$ independent of $\delta $ .

As a consequence, we have the following approximation lemma.

Lemma 2.8 ([8]–Lemma 2.4)

Let $\psi $ be a continuous real-valued function with support in a compact set K in $\mathbb {R}$ . Assume that $\|\psi \|_\infty \leq 1$ . Then, for every $0< \delta \leq 1$ there exist a smooth functions $\psi ^\pm _\delta $ such that $\widehat {\psi ^\pm _\delta }$ have support in $[-\delta ^{-2},\delta ^{-2}]$ ,

$$ \begin{align*}\psi^-_\delta \leq\psi\leq \psi^+_\delta,\quad \lim_{\delta \to 0} \psi^\pm_\delta =\psi \quad \text{and} \quad \lim_{\delta \to 0} \big \|\psi^\pm_\delta -\psi \big \|_{L^1} = 0.\end{align*} $$

Moreover, $\lVert \psi _\delta ^\pm \rVert _\infty $ , $\lVert \psi _\delta ^\pm \rVert _{L^1}$ and $\|\widehat {\psi ^\pm _\delta }\|_{\mathscr {C}^1}$ are bounded by a constant which only depends on K.

When proving limit theorems for random variables, we often resort to the associated characteristic functions. For notational convenience, we will also use their conjugates.

Definition 2.1. For a real random variable X with cumulative distribution function F (c.d.f. for short), we define its conjugate characteristic function by

$$ \begin{align*}\phi_F(\xi):=\mathbf E\big(e^{-i\xi X}\big).\end{align*} $$

Observe that $\mathrm {d} F$ is a probability measure on $\mathbb {R}$ and $\phi _F$ is its Fourier transform. In particular, when F is differentiable and $\phi _F$ is integrable, the following inversion formula holds

(2.2) $$ \begin{align} F'(u)={1\over 2\pi}\int_{-\infty}^\infty e^{iu\xi} \phi_F(\xi) \,\mathrm{d} \xi. \end{align} $$

3 Berry–Esseen bound for coefficients

This section is devoted to the proof of Theorem A. We begin with the following version of the Berry–Esseen lemma. See also [10, XVI.3].

Lemma 3.1. Let F be a c.d.f. of some real random variable, and let H be a differentiable real-valued function on $\mathbb {R}$ with derivative h such that $H(-\infty )=0,H(\infty )=1,|h(u)|\leq m$ for some constant $m>0$ . Let $D>0$ and $0<\delta <1$ be real numbers such that $\big |F(u)-H(u) \big |\leq D \delta ^2$ for $|u|\geq \delta ^{-2}$ . Then, there exist constants $C>0$ and $\kappa> 1$ independent of $F,H,\delta $ , such that

$$ \begin{align*}\sup_{u\in\mathbb{R}}\big|F(u)-H(u) \big|\leq 2\sup_{|u|\leq \kappa \delta^{-2}} \big|(F-H)*\vartheta_\delta(u)\big|+C \delta^2,\end{align*} $$

where $\vartheta _\delta $ is defined in Lemma 2.7.

Proof. We begin by noticing that, from the definition of $\vartheta _\delta $ , we have that, for any $d>0$ ,

(3.1) $$ \begin{align} \int_{|u|\geq d}\vartheta_\delta(u) \,\mathrm{d} u=\int_{|u|\geq d}{\vartheta(u/\delta^2)\over \delta^2}\,\mathrm{d} u=\int_{|u|\geq d\delta^{-2}} \vartheta(u)\,\mathrm{d} u\leq c\delta^2/d \end{align} $$

for some constant $c>0$ independent of d and $\delta $ . This is due to the fact that $\widehat {\vartheta }$ is smooth and compactly supported, hence $\vartheta $ has fast decay at infinity, say $|\vartheta (u)| \lesssim 1 / |u|^2$ .

Since the function $F(u)-H(u)$ vanishes at $\pm \infty $ , the maximum of $\big |F(u)-H(u) \big |$ exists. Let $u_0$ be a point where this maximum is attained. If $|u_0|\geq \delta ^{-2}$ , there is nothing to prove because $\sup _{|u|\geq \delta ^{-2}}\big |F(u)-H(u) \big |\leq D \delta ^2$ by hypothesis. So, we can assume $|u_0|\leq \delta ^{-2}$ and $M:=\big |F(u_0)-H(u_0) \big |\geq D \delta ^2$ . If $M\leq 12 mc\delta ^2$ , the lemma clearly follows, so we may assume $M>12 mc\delta ^2$ . We will use the fact that $F(-\infty )=0,F(\infty )=1$ and F is nondecreasing.

After replacing $F(u)$ and $H(u)$ by $1-F(-u)$ and $1-H(-u)$ if necessary, we may assume that $M=F(u_0)-H(u_0)>0$ . Let $d>0$ be a constant such that $M \geq 2 m d$ whose precise value will be determined later. Since F is nondecreasing and $h(u)\leq m$ by assumption, we have $F(u_0+r)-H(u_0+r)\geq M- mr$ for $r\geq 0$ . Thus,

(3.2) $$ \begin{align} F(u)-H(u)\geq M-2md \quad\text{for} \quad u_0\leq u\leq u_0+2d, \end{align} $$

and from the definition of M,

$$ \begin{align*}F(u)-H(u)\geq -M \quad\text{for all }\quad u \in \mathbb{R}.\end{align*} $$

Therefore, because $|u_0| \leq \delta ^{-2}$ , we obtain using equations (3.1) and (3.2) that

$$ \begin{align*} \sup_{|u|\leq \delta^{-2}+d} \big|(F-H)*\vartheta_\delta(u)\big| &\geq (F-H)*\vartheta_\delta(u_0+d)\\&=\Big(\int_{|u|< d}+ \int_{|u|\geq d}\Big) (F-H)(u_0+d-u) \cdot \vartheta_\delta (u)\,\mathrm{d} u\\[4pt]&\geq (M-2md)(1-c \delta^2 /d) - Mc \delta^2/d \\[4pt]&=(1-2c \delta^2/d)M-2md+2m c \delta^2. \end{align*} $$

By setting $d:=4c\delta ^2$ and recalling that $M>12 mc\delta ^2$ , we get that $M \geq 2md$ , and the last quantity above equals $M/2-6mc\delta ^2$ . Since $\delta ^{-2}+d \leq (1+4c) \delta ^{-2}$ , the lemma follows by setting $\kappa := 1+4c$ and $C:= 12 mc$ .

Corollary 3.2. Keep the notations and assumptions of Lemma 3.1. Assume moreover that $h\in L^1$ , $\widehat h\in \mathscr {C}^1$ and that $\phi _F$ is differentiable at zero (see Definition 2.1). Then,

$$ \begin{align*}\sup_{u\in\mathbb{R}}\big|F(u)-H(u) \big|\leq {1\over \pi} \sup_{|u|\leq \kappa \delta^{-2}} \Big|\int_{-\delta^{-2}}^{\delta^{-2}} {\Theta_u(\xi) \over \xi} \,\mathrm{d} \xi\Big| +C\delta^2,\end{align*} $$

where $\Theta _u(\xi ):=e^{iu\xi }\big (\phi _F(\xi )- \widehat {h}(\xi ) \big )\widehat {\vartheta _\delta }(\xi )$ .

Proof. Notice that, by the convolution formula, the function $\phi _F \cdot \widehat {\vartheta _\delta }$ is the conjugate characteristic function associated with the c.d.f. $F*\vartheta _\delta $ . Since $\mathrm {supp}(\widehat {\vartheta _\delta })\subset [-\delta ^{-2},\delta ^{-2}]$ , and $\phi _F$ is bounded by definition, it follows that $\phi _F \cdot \widehat {\vartheta _\delta }$ is integrable. Identity (2.2) gives that

$$ \begin{align*}(F*\vartheta_\delta)'(u) ={1\over 2\pi}\int_{-\infty}^\infty e^{iu\xi} \phi_F(\xi)\cdot\widehat{\vartheta_\delta}(\xi) \,\mathrm{d} \xi.\end{align*} $$

As the inverse Fourier transform of $\widehat {h} \cdot \widehat {\vartheta _\delta }$ is $h*\vartheta _\delta $ , we get

$$ \begin{align*}\big((F-H)*\vartheta_\delta\big)'(u)={1\over 2\pi}\int_{-\delta^{-2}}^{\delta^{-2}} e^{iu\xi} \big( \phi_F(\xi)-\widehat h(\xi)\big) \widehat{\vartheta_\delta}(\xi) \,\mathrm{d}\xi.\end{align*} $$

Observe that $\phi _F(0) = \mathbf {E}(\mathbf 1) = 1$ and $\widehat h(0) = H(\infty ) - H(-\infty ) = 1$ , so $\phi _F(0)-\widehat h(0)=0$ . Moreover, $\phi _F'(0)-\widehat h\,'(0)$ is finite by the assumptions on F and h. Integrating the above identity with respect to u yields

$$ \begin{align*}(F-H)*\vartheta_\delta (u)={1\over 2\pi}\int_{-\delta^{-2}}^{\delta^{-2}} {e^{iu\xi}\over i\xi} \big( \phi_F(\xi)-\widehat h(\xi)\big) \widehat{\vartheta_\delta}(\xi) \,\mathrm{d}\xi .\end{align*} $$

Here, the constant term is zero because, when $u\to \pm \infty $ , the left-hand side tends to zero and, by the above observations, the integrand is a bounded function, so the integral in the right-hand side also tends to zero as $u\to \pm \infty $ by the Riemann-–Lebesgue lemma. The desired result follows from Lemma 3.1.

Fix $v \in \mathbb {R}^d \setminus \{0\}, f \in (\mathbb {R}^d)^* \setminus \{0\}$ , and set $x:=[v]\in \mathbb {P}^{d-1}, y:=[f]\in (\mathbb {P}^{d-1})^*$ . Consider the pairing

$$ \begin{align*}\Delta(x,y):= \frac{ |\langle f, v \rangle |}{\lVert f\rVert \lVert v\rVert},\end{align*} $$

where $\langle \cdot , \cdot \rangle $ denotes the natural pairing between $\mathbb {R}^d$ and $(\mathbb {R}^d)^*$ . One can easily check that $\Delta (x,y) = d (x,H_y)$ , where $H_y := \mathbb {P}(\ker f)$ and d is the distance defined in Section 2. Using these definitions, it is not hard to see that

(3.3) $$ \begin{align} \log{ |\langle f, S_n v \rangle | \over \lVert f\rVert \lVert v\rVert} = \sigma(S_n,x) + \log d(S_n x, H_y). \end{align} $$

The strategy to prove Theorem A is to use the above formula and work with the random variable $\sigma (S_n,x) +\log d(S_n x, H_y)$ instead of $\log { |\langle f, S_n v \rangle | \over \lVert f\rVert \lVert v\rVert } $ . Then, the behaviour of $\sigma (S_n,x)$ can be studied via the perturbed Markov operators, and the term $\log d(S_n x, H_y)$ can be handled using the large deviation estimates from Section 2 combined with a good partition of unity that we now introduce.

For integers $k \geq 0$ , introduce

$$ \begin{align*} \mathscr{T}_k := \big\{ w \in \mathbb{P}^{d-1} :\, e^{-k-1} < d(w,H_y) < e^{-k+1} \big\} = \mathbb{B}(H_y,e^{-k+1}) \setminus \overline{\mathbb{B}(H_y,e^{-k-1})}. \end{align*} $$

Note that, since $\mathbb {P}^{d-1}$ has diameter one, these open sets cover $\mathbb {P}^{d-1}$ .

Lemma 3.3. There exist nonnegative smooth functions $\chi _k$ on $\mathbb {P}^{d-1}$ , $k \geq 0$ such that

1. 1. $\chi _k$ is supported by $\mathscr {T}_k$ ;

2. 2. If $w \in \mathbb {P}^{d-1} \setminus H_y$ , then $\chi _k(w) \neq 0$ for at most two values of k;

3. 3. $\sum _{k\geq 0} \chi _k=1$ on $\mathbb {P}^{d-1} \setminus H_y$ ;

4. 4. $\lVert \chi _k\rVert _{\mathscr {C}^1}\leq C e^{k}$ for some constant $C>0$ independent of k.

Proof. It is easy to find a smooth function $0 \leq \widetilde {\chi } \leq 1$ supported by $(-1,1)$ such that $\widetilde {\chi }(t) = 1$ for $|t|$ small, $\widetilde {\chi }(t) + \widetilde {\chi }(t-1)= 1$ for $0 \leq t\leq 1$ and $\lVert \widetilde {\chi }\rVert _{\mathscr {C}^1}\leq 4$ . Define $\widetilde {\chi }_k (t) := \widetilde {\chi }(t+k)$ . We see that $\widetilde {\chi }_k$ is supported by $(-k-1,-k+1)$ , $\sum _{k\geq 0} \widetilde {\chi }_k=1$ on $\mathbb {R}_{\leq 0}$ and $\lVert \widetilde {\chi }_k\rVert _{\mathscr {C}^1}\leq 4$ . Set $\chi _k(w):= \widetilde {\chi }_k \big ( \log d(w,H_y) \big )$ . One can easily check that the function $\Psi (w) := \log d(w,H_y)$ satisfies $\lVert \Psi |_{\mathscr {T}_k }\rVert _{\mathscr {C}^1} \lesssim e^{k}$ . It follows that $\chi _k$ satisfies (1)–(4).

We now begin the proof of Theorem A. It suffices to prove Theorem A for intervals of the type $J=(-\infty ,b]$ with $b \in \mathbb {R}$ , as the case of an arbitrary interval can be obtained as a consequence. For example, the case $(b,+\infty )$ follows directly by considering its complement. The case of $[b, +\infty )$ can be deduced by approximating it by $(b \pm \varepsilon , + \infty )$ and the case $(-\infty ,b)$ follows by taking the complement. The case of bounded intervals can be obtained by considering differences of the previous cases.

Let $A>0$ be a large constant. By Proposition 2.1 applied for $\epsilon = 1$ , there exists a constant $c>0$ such that with $\ell ,m$ large enough and $\ell \geq m$ , one has

$$ \begin{align*}\mu^{*\ell} \big\{g\in G:\, d(gx, H_y) \leq e^{- m} \big\} \leq e^{-cm}.\end{align*} $$

Setting $\ell :=n$ and $m:=\lfloor A \log n \rfloor $ with n big enough yields

$$ \begin{align*}\mu^{*n} \big\{g\in G:\,d(gx,H_y)\leq n^{-A} \big\}\leq e^{-c\lfloor A \log n \rfloor} \leq n^{-cA}e^c \leq e^c/\sqrt n\end{align*} $$

since A is large. It follows that $\log d(S_n x,H_y)\leq -A\log n $ with probability less than $e^c/\sqrt n$ . Hence, in order to prove Theorem A, it is enough to show that

(3.4) $$ \begin{align} \Big| \mathcal{L}_n(b) - \frac{1}{\sqrt{2 \pi} \,\varrho} \int_{-\infty}^b e^{-\frac{s^2}{2 \varrho^2}} \, \mathrm{d} s \Big| \lesssim \frac{1}{\sqrt n}, \end{align} $$

uniformly in b, where

$$ \begin{align*}\mathcal{L}_n(b):= \mathbf E \Big( \mathbf 1_{{\sigma(S_n,x) +\log d(S_n x, H_y) - n \gamma\over \sqrt n}\leq b} \mathbf 1_{ \log d(S_n x,H_y)> - A \log n } \Big),\end{align*} $$

where we use $\mathbf 1_\bigstar $ to denote the indicator function of a set defined by the property $\bigstar $ .

Let $\chi _k$ be as in Lemma 3.3. It is clear that

$$ \begin{align*}\sum_{0\leq k\leq A\log n - 1}\chi_k(w) \leq \mathbf 1_{ \log d(w,H_y)> - A \log n} \leq \sum_{0\leq k\leq A\log n+1}\chi_k(w)\end{align*} $$

as functions on $\mathbb {P}^{d-1}$ . Using that $\chi _k$ is supported by $\mathscr {T}_k$ , it follows that

(3.5) $$ \begin{align} \sum_{0\leq k\leq A\log n-1} \hspace{-7pt} \mathbf{E}\Big( \mathbf 1_{{\sigma(S_n,x) - n \gamma - k+1\over \sqrt n}\leq b} \, & \chi_k(S_n x) \Big) \leq \mathcal{L}_n(b) \\ \nonumber &\leq \hspace{-5pt} \sum_{0\leq k\leq A\log n+1} \hspace{-7pt} \mathbf E\Big( \mathbf 1_{{\sigma(S_n,x) - n \gamma - k-1\over \sqrt n}\leq b} \, \chi_k(S_n x) \Big). \end{align} $$

For $w \in \mathbb {P}^{d-1}$ , let

$$ \begin{align*}\Phi_{n}^{\star} (w):= 1 - \sum_{0\leq k\leq A\log n} \chi_k(w),\end{align*} $$

and define, for $b \in \mathbb {R}$ ,

$$ \begin{align*} F_n(b):&= \sum_{0\leq k\leq A\log n} \mathbf{E}\Big( \mathbf 1_{{\sigma(S_n,x) - n \gamma - k\over \sqrt n}\leq b} \chi_k (S_n x) \Big) + \mathbf{E} \Big( \mathbf 1_{{\sigma(S_n,x) - n \gamma \over \sqrt n}\leq b} \, \Phi_{n}^{\star} (S_n x) \Big). \end{align*} $$

Notice that $F_n$ is nondecreasing, right continuous, $F_n(-\infty )=0$ and $F_n(\infty )=1$ . Therefore, it is the c.d.f. of some probability distribution. We’ll see that the term involving $\Phi _{n}^{\star }$ has a negligible impact in our estimates. However, its presence is important and will be useful in our computations.

Lemma 3.4. Let $\mathcal {L}_n$ and $F_n$ be as above. Then, there exists a constant $C>0$ independent of n such that for all $n \geq 1$ and $b \in \mathbb {R}$ ,

$$ \begin{align*}F_n(b - 1 / \sqrt n) - C / \sqrt n \leq \mathcal{L}_n(b) \leq F_n(b + 1 / \sqrt n) + C / \sqrt n.\end{align*} $$

Proof. Notice first that $\Phi _{n}^{\star }$ is nonnegative, bounded by one and supported by a tubular neighborhood $\mathbf T_n$ of $H_y$ of radius $O(n^{-A})$ . As discussed above, the probability that $S_n x$ belongs to $\mathbf T_n$ is $\lesssim 1 / \sqrt n$ . This yields the following bounds for the second term in the definition of $F_n$ :

$$ \begin{align*}0 \leq \mathbf{E} \Big( \mathbf 1_{{\sigma(S_n,x) - n \gamma \over \sqrt n}\leq b} \, \Phi_{n}^{\star} (S_n x) \Big) \leq \mathbf{E} \Big(\Phi_{n}^{\star}(S_n x) \Big) \lesssim 1 / \sqrt n.\end{align*} $$

Therefore, in order to prove the lemma, we can replace $F_n$ by the function

(3.6) $$ \begin{align} \widetilde{F}_n(b) := \sum_{0\leq k\leq A\log n} \mathbf{E}\Big( \mathbf 1_{{\sigma(S_n,x) - n \gamma - k \over \sqrt n}\leq b} \chi_k (S_n x) \Big). \end{align} $$

Using the second inequality in equation (3.5), we have

$$ \begin{align*} \mathcal{L}_n(b) - \widetilde{F}_n(b + 1 / \sqrt n) \leq \mathbf{E}\Big( \mathbf 1_{{\sigma(S_n,x) - n \gamma - k^+-1\over \sqrt n}\leq b} \chi_{k^+} (S_n x) \Big) \leq \mathbf{E}\Big( \chi_{k^+} (S_n x) \Big), \end{align*} $$

where $k^+:= \lfloor A \log n \rfloor + 1$ . Since $\chi _k \leq \mathbf 1_{\mathbb {B}(H_y,e^{-k+1})}$ and $\log d(S_n x,H_y)\leq -A\log n +1 $ with probability $\lesssim 1/\sqrt n$ , the above quantity is $\lesssim 1/\sqrt n$ . This gives the second inequality in the lemma.

Using now the first inequality in equation (3.5) and letting $k^-:= \lfloor A \log n \rfloor $ , we obtain

$$ \begin{align*} \widetilde{F}_n(b - 1 /\sqrt n) - \mathcal{L}_n(b) \leq \mathbf{E}\Big( \mathbf 1_{{\sigma(S_n,x) - n \gamma - k^- +1\over \sqrt n}\leq b} \chi_{k^-} (S_n x) \Big) \leq \mathbf{E}\Big(\chi_{k^-} (S_n x) \Big), \end{align*} $$

which is $\lesssim 1/\sqrt n$ by the same arguments as before. The lemma follows.

Introduce

$$ \begin{align*}\Phi_{n,\xi} (w):= \sum_{0\leq k\leq A\log n} e^{i \xi{k \over \sqrt n}}\chi_k(w).\end{align*} $$

Lemma 3.5. The conjugate characteristic function of $F_n$ (cf. Definition 2.1) is given by

$$ \begin{align*}\phi_{F_n}(\xi)= e^{i\xi\sqrt n \gamma} \mathcal{P}_{-{i\xi\over \sqrt n}}^n \Phi_{n,\xi} (x) + e^{i\xi\sqrt n \gamma} \mathcal{P}_{-{i\xi\over \sqrt n}}^n \Phi_{n}^{\star} (x) = e^{i\xi\sqrt n \gamma} \mathcal{P}_{-{i\xi\over \sqrt n}}^n \big( \Phi_{n,\xi} + \Phi_{n}^{\star} \big) (x).\end{align*} $$

In particular, $\phi _{F_n}$ is differentiable near zero.

Proof. Recall that x is fixed. Let $c_{k,n}:= \int _G \chi _k(gx) \, \mathrm {d} \mu ^{\ast n} (g)$ and $\mu _{k,n}: = c^{-1}_{k,n} \, \chi _k(gx) \, \mu ^{\ast n}$ , which is a probability measure on G that is absolutely continuous with respect to $\mu ^{\ast n}$ . Let $Z_{n,k}$ be the measurable function ${\sigma (g,x) - n \gamma - k \over \sqrt n}$ on the probability space $(G,\mu _{k,n})$ . The corresponding c.d.f. is

$$ \begin{align*}F_{Z_{n,k}}(b) = c^{-1}_{k,n} \int_G \mathbf 1_{{\sigma(g,x) - n \gamma - k\over \sqrt n}\leq b} \chi_k(gx) \, \mathrm{d} \mu^{\ast n} (g),\end{align*} $$

and the associated conjugate characteristic function is

$$ \begin{align*}\phi_{F_{Z_{n,k}}}(\xi) = c^{-1}_{k,n} \int_G e^{-i \xi{\sigma(g,x) - n \gamma - k \over \sqrt n}} \chi_k(gx) \, \mathrm{d} \mu^{\ast n} (g) = c^{-1}_{k,n} e^{i\xi\sqrt n \gamma} \mathcal{P}_{-{i\xi\over \sqrt n}}^n \big(e^{i \xi{k\over \sqrt n}}\chi_k \big) (x),\end{align*} $$

where we have used equation (2.1).

Analogously, set $d_n:= \int _G \Phi _{n}^{\star }(gx) \, \mathrm {d} \mu ^{\ast n}(g)$ , consider the probability measure $\eta _{n}: = d^{-1}_{n} \, \Phi _{n}^{\star } (gx) \, \mu ^{\ast n}$ and let $W_{n}$ be the measurable function ${\sigma (g,x) - n \gamma \over \sqrt n}$ on the probability space $(G,\eta _{n})$ . Then, the corresponding c.d.f. is

$$ \begin{align*}F_{W_n}(b) = d^{-1}_{k} \int_G {\mathbf 1}_{{\sigma(g,x) - n \gamma \over \sqrt n}\leq b} \Phi_{n}^{\star}(gx) \, \mathrm{d} \mu^{\ast n} (g)\end{align*} $$

and the associated conjugate characteristic function is

$$ \begin{align*} \phi_{F_{W_n}}(\xi) = d^{-1}_{n} \int_G e^{-i \xi{\sigma(g,x) - n \gamma \over \sqrt n}} \Phi_{n}^{\star}(gx) \, \mathrm{d} \mu^{\ast n} (g) = d^{-1}_{n} e^{i\xi\sqrt n \gamma} \mathcal{P}_{-{i\xi\over \sqrt n}}^n \Phi_{n}^{\star} (x). \end{align*} $$

Notice that, by definition $F_n = \sum _{0\leq k\leq A\log n} c_{k,n} F_{Z_{n,k}} + d_n F_{W_n}$ so, by linearity, $\phi _{F_n} = \sum _{0\leq k\leq A\log n} c_{k,n} \phi _{F_{Z_{n,k}}} + d_n \phi _{F_{W_n}}$ . Using the definition of $\Phi _{n,\xi }$ , the lemma follows.

From now on, we fix the value of the constant $A>0$ used above. Fix a value of $\alpha>0$ such that

$$ \begin{align*}\alpha A\leq 1/6 \quad \text{ and } \quad \alpha \leq \alpha_0,\end{align*} $$

where $0<\alpha _0<1$ is the exponent appearing in Theorem 2.3. Then, from the results of Subsection 2.3, the family $\xi \mapsto \mathcal {P}_{i\xi }$ acting on $\mathscr {C}^\alpha (\mathbb {P}^{d-1})$ with $\xi \in \mathbb {R}$ is everywhere defined, analytic near $0$ and $\mathcal {P}_0$ has a spectral gap. The bound $\alpha A\leq 1/6$ is chosen so that we can control the impact of the Hölder norms of $\Phi _{n,\xi }$ and $\Phi _{n}^{\star }$ in our estimates, as shown in the following lemma.

Lemma 3.6. Let $\Phi _{n,\xi }, \Phi _{n}^{\star }$ be the functions on $\mathbb {P}^{d-1}$ defined above. Then, the following identity holds

(3.7) $$ \begin{align} \Phi_{n,\xi} + \Phi_{n}^{\star} = \mathbf 1 + \sum_{0\leq k\leq A\log n} \big( e^{i \xi{k \over \sqrt n}} - 1 \big) \chi_k. \end{align} $$

Moreover, $\lVert \Phi _{n,\xi } + \Phi _{n}^{\star }\rVert _\infty \leq 1$ and there is a constant $C>0$ independent of $\xi $ and n such that

(3.8) $$ \begin{align} \lVert\Phi_{n,\xi} \rVert_{\mathscr{C}^\alpha}\leq C \, n^{\alpha A} \quad\text{and}\quad \lVert\Phi_{n}^{\star} \rVert_{\mathscr{C}^\alpha} \leq C \, n^{\alpha A}, \end{align} $$

where $\alpha>0$ is the exponent fixed above. In addition, $\Phi _{n}^{\star } $ is supported by $\big \{w:\,\log d(w,H_y)\leq -A\log n + 1\big \}$ .

Proof. Identity (3.7) follows directly from the definition of $\Phi _{n,\xi }$ and $ \Phi _{n}^{\star }$ . Also from the definition, we have $|\Phi _{n,\xi } + \Phi _{n}^{\star } | \leq \Phi _{n,0} + \Phi _{n}^{\star }$ and the last function is identically equal to $1$ by equation (3.7). It follows that $\lVert \Phi _{n,\xi } + \Phi _{n}^{\star }\rVert _\infty \leq 1$ .

For the first inequality in equation (3.8), notice that $\big \| e^{i \xi {k \over \sqrt n}}\chi _k \big \|_{\mathscr {C}^\alpha } = \lVert \chi _k\rVert _{\mathscr {C}^\alpha }$ . From Lemma 3.3-(4), the fact that $\lVert \chi _k\rVert _{\mathscr {C}^0} \leq 1$ and the interpolation inequality $\lVert \, \cdot \,\rVert _{\mathscr {C}^\alpha } \leq c_\alpha \lVert \, \cdot \,\rVert _{\mathscr {C}^0}^{1-\alpha } \, \lVert \, \cdot \,\rVert _{\mathscr {C}^1}^\alpha $ (see [19, p. 202]), it follows that $\lVert \chi _k\rVert _{\mathscr {C}^\alpha } \leq C^\alpha c_\alpha e^{\alpha k}$ . The last inequality can also be checked by a direct computation. Then, the first inequality in equation (3.8) follows from the definition of $\Phi _{n,\xi }$ and the fact that at most two $\chi _k$ ’s are nonzero simultaneously. The second inequality in equation (3.8) follows from the first one and the identity $\Phi _{n,0} + \Phi _{n}^{\star } = \mathbf 1$ , after increasing the value of C if necessary.

In order to prove the last assertion, observe that, over $\mathbb {P}^{d-1} \setminus H_y$ , one has $\Phi _{n}^{\star } = \sum _{k> A\log n} \chi _k$ by Lemma 3.3-(3). Since $\chi _k$ is supported by $\mathscr {T}_k$ , the conclusion follows. This finishes the proof of the lemma.

Let

$$ \begin{align*}H(b): =\frac{1}{\sqrt{2 \pi} \,\varrho} \int_{-\infty}^b e^{-\frac{s^2}{2 \varrho^2}} \, \mathrm{d} s\end{align*} $$

be the c.d.f. of the normal distribution $\mathscr {N}(0;\varrho ^2)$ . In the notation of Lemma 3.1, we have $h(u): =\frac {1}{\sqrt {2 \pi } \,\varrho } e^{-\frac {u^2}{2 \varrho ^2}}$ and $\widehat h(\xi ) = e^{-{\varrho ^2 \xi ^2\over 2}}$ . Let $\xi _0$ be the constant in Lemma 2.5.

Lemma 3.7. Let $F_n$ and H be as above. Then, $\big |F_n(b)-H(b)\big |\lesssim 1/\sqrt n$ for $|b|\geq \xi _0 \sqrt n$ .

Proof. We only consider the case of $b\leq -\xi _0\sqrt n$ . The case $b \geq \xi _0\sqrt n$ can be treated similarly using $1-F_n$ and $1-H$ instead of $F_n$ and H. We can also assume that n is large enough. Clearly, $H(b)\lesssim 1/\sqrt n$ for $b\leq -\xi _0\sqrt n$ , so it is enough to bound $F_n(b)$ .

For $0\leq k\leq A\log n$ , we have

$$ \begin{align*} \mathbf P\Big( {\sigma(S_n,x) - n \gamma - k \over \sqrt n}\leq -\xi_0\sqrt n \Big)&=\mathbf P\Big(\sigma(S_n,x) - n \gamma \leq -\xi_0 n +k \Big)\\ &\leq \mathbf P\Big(\sigma(S_n,x) - n \gamma \leq - \xi_0 n / 2\Big) \end{align*} $$

since n is large. By Proposition 2.1 applied with $\epsilon = \xi _0 / 2$ , there exists a constant $c>0$ , independent of n, such that the last quantity is bounded by $e^{-cn}$ .

Using the definition of $F_n$ and the fact that $\mathbf {E} \big (\Phi _{n}^{\star }(S_n x) \big ) \lesssim 1 / \sqrt n$ (see the proof of Lemma 3.4), it follows that

$$ \begin{align*}F_n (-\xi_0\sqrt n)\lesssim \sum_{0\leq k\leq A\log n}e^{-cn} + 1/\sqrt n \leq (A \log n + 1) e^{-cn} + 1/\sqrt n \lesssim 1/\sqrt n.\end{align*} $$

As $F_n(b)$ is nondecreasing in b, one gets that $F_n(b) \lesssim 1 / \sqrt n$ for all $b\leq -\xi _0\sqrt n$ . The lemma follows.

Lemmas 3.5 and 3.7 imply that $F_n$ satisfies the conditions of Corollary 3.2 with $\delta _n:=(\xi _0 \sqrt n)^{-1/2}$ . Let $\kappa> 1$ be the constant appearing in that corollary. For simplicity, by taking a smaller $\xi _0$ is necessary, one can assume that $2\kappa \xi _0 \leq 1$ . Then, Corollary 3.2 gives that

(3.9) $$ \begin{align} \sup_{b \in\mathbb{R}}\big|F_n(b)-H(b)\big|\leq {1\over \pi} \sup_{|b|\leq \sqrt n} \Big| \int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {\Theta_b(\xi) \over \xi} \,\mathrm{d} \xi \Big|+{C\over \sqrt n}, \end{align} $$

where $C>0$ is a constant independent of n and

$$ \begin{align*}\Theta_b(\xi):=e^{ib\xi}\big( \phi_{F_n}(\xi)- \widehat {h}(\xi) \big)\widehat{\vartheta_{\delta_n}}(\xi).\end{align*} $$

We now estimate the integral in the right-hand side of equation (3.9). Define

$$ \begin{align*}\widetilde{h}_n(\xi):= \big(\mathcal{N}_0 \Phi_{n,\xi} \big) e^{-{\varrho^2 \xi^2\over 2}} + \big(\mathcal{N}_0 \Phi_{n}^{\star} \big) e^{-{\varrho^2 \xi^2\over 2}} = e^{-{\varrho^2 \xi^2\over 2}} \mathcal{N}_0 ( \Phi_{n,\xi} + \Phi_{n}^{\star} ).\end{align*} $$

In light of Lemma 3.5, we will use it to approximate $\phi _{F_n}$ (see Proposition 2.4 and Lemma 2.5). Notice that $\mathcal {N}_0 ( \Phi _{n,\xi } + \Phi _{n}^{\star } )$ is a constant independent of x. Define also

$$ \begin{align*}\Theta_b^{(1)}(\xi):= e^{ib\xi}\big( \phi_{F_n}(\xi)- \widetilde{h}_n(\xi) \big)\widehat{\vartheta_{\delta_n}}(\xi) \quad\text{and} \quad \Theta_b^{(2)}(\xi):= e^{ib\xi}\big( \widetilde{h}_n(\xi)-\widehat h(\xi) \big)\widehat{\vartheta_{\delta_n}}(\xi),\end{align*} $$

so that $\Theta _b = \Theta _b^{(1)} + \Theta _b^{(2)}$ .

Lemma 3.8. We have

$$ \begin{align*}\sup_{|b|\leq \sqrt n} \Big| \int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {\Theta_b^{(1)}(\xi) \over \xi} \,\mathrm{d} \xi \Big| \lesssim {1\over \sqrt n}.\end{align*} $$

Proof. Using Lemma 3.5 and the decomposition in Proposition 2.4, we write

$$ \begin{align*}\Theta_b^{(1)}=\Lambda_1+\Lambda_2+\Lambda_3,\end{align*} $$

where

$$ \begin{align*}\Lambda_1(\xi):= e^{ib\xi}\Big( e^{i\xi\sqrt n \gamma} \lambda_{-{i\xi\over \sqrt n}}^n \mathcal{N}_{-{i\xi\over \sqrt n}} (\Phi_{n,\xi} +\Phi_{n}^{\star} ) (x) - e^{-{\varrho^2 \xi^2\over 2}} \mathcal{N}_0 (\Phi_{n,\xi} +\Phi_{n}^{\star} ) (x) \Big) \widehat{\vartheta_{\delta_n}}(\xi),\end{align*} $$

$$ \begin{align*}\hspace{-28pt}\Lambda_2(\xi):=e^{ib\xi}\Big( e^{i\xi\sqrt n \gamma} \mathcal{Q}_{-{i\xi\over \sqrt n}}^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) -e^{i\xi\sqrt n \gamma}\mathcal{Q}_0^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \Big)\widehat{\vartheta_{\delta_n}}(\xi)\end{align*} $$

and

$$ \begin{align*}\Lambda_3(\xi):=e^{ib\xi}e^{i\xi\sqrt n \gamma}\mathcal{Q}_0^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \,\widehat{\vartheta_{\delta_n}}(\xi).\end{align*} $$

We will estimate the integral of $\Lambda _j(\xi ) / \xi $ , $j=1,2,3$ , separately. Notice that, from equation (3.7), we have that $\Phi _{n,0} + \Phi _{n}^{\star } = \mathbf 1 $ . Together with the fact that $\lambda _0=1$ , $\mathcal {N}_0 \mathbf 1 = \mathbf 1$ and $\mathcal {Q}_0 \mathbf 1 = 0$ , we get that $\Lambda _j(0) = 0$ for $j=1,2,3$ . In particular, $\Lambda _j(\xi ) / \xi $ is a smooth function of $\xi $ for $j=1,2,3$ . We see here the role of the auxiliary function $\Phi _{n}^{\star }$ .

In order to estimate $\Lambda _2$ , observe that, for z small, the norm of the operator $\mathcal {Q}^n_z - \mathcal {Q}^n_0$ is bounded by a constant times $|z| n \beta ^n$ for some $0<\beta <1$ . This can be seen by writing the last difference as $\sum _{\ell =0}^{n-1} \mathcal {Q}_z^{n-\ell -1}(\mathcal {Q}_z - \mathcal {Q}_0)\mathcal {Q}_0^\ell $ , applying Proposition 2.4-(5) and using the fact that $\lVert \mathcal {Q}_z - \mathcal {Q}_0\rVert _{\mathscr {C}^\alpha } \lesssim |z|$ . Therefore, we have

$$ \begin{align*}\Big| \mathcal{Q}_{-{i\xi\over \sqrt n}}^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) - \mathcal{Q}_0^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \Big| \lesssim {|\xi|\over \sqrt n} n \beta^n \lVert \Phi_{n,\xi} +\Phi_{n}^{\star} \rVert_{\mathscr{C}^\alpha}.\end{align*} $$

Using Lemma 3.6, this gives

$$ \begin{align*} \Big|\int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {\Lambda_2(\xi) \over \xi} \,\mathrm{d} \xi\Big| &\leq\int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {1\over |\xi|} \cdot \Big| \mathcal{Q}_{-{i\xi\over \sqrt n}}^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) - \mathcal{Q}_0^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \Big|\,\mathrm{d}\xi \\ &\lesssim \int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {1\over |\xi|} \cdot |\xi| \sqrt n \beta^n \lVert \Phi_{n,\xi} +\Phi_{n}^{\star} \rVert_{\mathscr{C}^\alpha} \,\mathrm{d}\xi \lesssim \beta^n n^{\alpha A + 1} \lesssim {1\over \sqrt n}. \end{align*} $$

We now estimate $\Lambda _3$ using its derivative $\Lambda ^{\prime }_3$ . Recall that $\lVert \widehat {\vartheta _{\delta _n}}\rVert _{\mathscr {C}^1}\lesssim 1,|b|\leq \sqrt n$ and $\big |\mathcal {Q}_0^n (\Phi _{n,\xi } +\Phi _{n}^{\star } )(x) \big |\lesssim \beta ^n\lVert \Phi _{n,\xi } +\Phi _{n}^{\star } \rVert _{\mathscr {C}^\alpha }$ , where $0<\beta <1$ is as before. A direct computation using the definition of $\Phi _{n,\xi } $ gives, for $|\xi | \leq \xi _0 \sqrt n$ ,

$$ \begin{align*} | \Lambda_3'(\xi)| &\leq \Big|b \mathcal{Q}_0^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x)\Big|+ \Big|\sqrt n \gamma \mathcal{Q}_0^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x)\Big| \\ & \quad \quad + \sum_{1 \leq k \leq A \log n} \Big|{k\over \sqrt n} e^{i \xi \frac{k}{\sqrt n}}\mathcal{Q}_0^n \chi_k (x) \Big| + \Big|\mathcal{Q}_0^n (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x)\Big| \cdot \lVert\widehat{\vartheta_{\delta_n}}\rVert_{\mathscr{C}^1} \\ &\lesssim \sqrt n \beta^n n^{\alpha A} + \frac{(\log n)^2}{\sqrt n} \beta^n n^{\alpha A} + \beta^n n^{\alpha A} \lesssim (1+\sqrt n) \beta^n n^{\alpha A}, \end{align*} $$

where we have used that $|b| \leq \sqrt n$ , $\lVert \chi _k\rVert _{\mathscr {C}^\alpha } \lesssim e^{\alpha k}$ and $\lVert \Phi _{n,\xi } +\Phi _{n}^{\star } \rVert _{\mathscr {C}^\alpha } \lesssim n^{\alpha A}$ ; see Lemma 3.6.

Applying the mean value theorem over the interval between $0$ and $\xi $ yields

$$ \begin{align*} \Big|\int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {\Lambda_3(\xi) \over \xi} \,\mathrm{d} \xi\Big|\leq 2\xi_0\sqrt n\sup_{|\xi|\leq \xi_0\sqrt n} | \Lambda_3'(\xi)|\lesssim \sqrt n (1+\sqrt n) n^{\alpha A} \beta^n \lesssim {1 \over \sqrt n}. \end{align*} $$

It remains to estimate the term involving $\Lambda _1$ . We have

$$ \begin{align*} \Big| & \int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {\Lambda_1(\xi) \over \xi} \mathrm{d} \xi\Big| \\ &\leq \int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {1\over |\xi|}\cdot \Big| e^{i\xi\sqrt n \gamma} \lambda_{-{i\xi\over \sqrt n}}^n \mathcal{N}_{-{i\xi\over \sqrt n}} (\Phi_{n,\xi} +\Phi_{n}^{\star} ) (x) - e^{-{\varrho^2 \xi^2\over 2}} \mathcal{N}_0 (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \Big| \mathrm{d} \xi. \end{align*} $$

We split the last integral into two integrals using

$$ \begin{align*}\Gamma_1(\xi):= e^{i\xi\sqrt n \gamma} \lambda_{-{i\xi\over \sqrt n}}^n \mathcal{N}_{-{i\xi\over \sqrt n}} (\Phi_{n,\xi} +\Phi_{n}^{\star} ) (x) - e^{i\xi\sqrt n \gamma} \lambda_{-{i\xi\over \sqrt n}}^n \mathcal{N}_0 (\Phi_{n,\xi} +\Phi_{n}^{\star} )(x)\end{align*} $$

and

$$ \begin{align*}\Gamma_2(\xi):= e^{i\xi\sqrt n \gamma} \lambda_{-{i\xi\over \sqrt n}}^n \mathcal{N}_0 (\Phi_{n,\xi} +\Phi_{n}^{\star} ) (x) - e^{-{\varrho^2 \xi^2\over 2}} \mathcal{N}_0 (\Phi_{n,\xi} +\Phi_{n}^{\star} ) (x) .\end{align*} $$

Case 1. $\sqrt [6] n<|\xi |\leq \xi _0\sqrt n$ . In this case, by Lemma 2.5, we have

(3.10) $$ \begin{align} \big|\lambda_{-{i\xi\over \sqrt n}}^n\big|\leq e^{-{\varrho^2\xi^2\over 3}} \quad \text{and}\quad \Big| e^{i\xi\sqrt n \gamma} \lambda_{-{i\xi\over \sqrt n}}^n-e ^{-{\varrho^2\xi^2\over 2}} \Big|\lesssim {1\over \sqrt n}e^{-{\varrho^2\xi^2\over 4}}. \end{align} $$

From the analyticity of $\xi \mapsto \mathcal {N}_{i\xi }$ (cf. Proposition 2.4), Lemma 3.6 and the fact that $\alpha A\leq 1/6$ , one has

$$ \begin{align*}\Big\|\big(\mathcal{N}_{-{i\xi\over \sqrt n}}-\mathcal{N}_0 \big) (\Phi_{n,\xi} +\Phi_{n}^{\star} ) \Big\|_\infty \lesssim {|\xi| \over \sqrt n} \lVert \Phi_{n,\xi} +\Phi_{n}^{\star} \rVert_{\mathscr{C}^\alpha}\lesssim {|\xi| \over \sqrt n}n^{\alpha A} \leq {|\xi| \over \sqrt n}\sqrt[6] n.\end{align*} $$

Hence, using equation (3.10), we get

$$ \begin{align*}\int_{\sqrt[6] n<|\xi|\leq \xi_0\sqrt n} {1\over |\xi|}\cdot \big| \Gamma_1(\xi) \big| \,\mathrm{d} \xi \lesssim \int_{- \infty}^{\infty} {1\over \sqrt[6] n} \cdot e^{-{\varrho^2\xi^2\over 3}} {|\xi| \over \sqrt n}\sqrt[6] n \,\mathrm{d} \xi \lesssim { 1\over \sqrt n}.\end{align*} $$

Recall that $ \lVert \Phi _{n,\xi } +\Phi _{n}^{\star }\rVert _\infty \leq 1$ by Lemma 3.6, so $\big |\mathcal {N}_0 (\Phi _{n,\xi } +\Phi _{n}^{\star } )\big | \leq 1$ . Therefore, using equation (3.10), we obtain

$$ \begin{align*}\int_{\sqrt[6] n<|\xi|\leq \xi_0\sqrt n} {1\over |\xi|}\cdot \big| \Gamma_2(\xi) \big| \,\mathrm{d} \xi \lesssim \int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {1\over \sqrt[6] n} \cdot{1\over \sqrt n} e^{-{\varrho^2\xi^2\over 4}} \,\mathrm{d} \xi \lesssim { 1\over \sqrt n}.\end{align*} $$

Case 2. $|\xi |\leq \sqrt [6] n$ . In this case, Lemma 2.5 gives that

(3.11) $$ \begin{align} \big|\lambda_{-{i\xi\over \sqrt n}}^n\big|\leq e^{-{\varrho^2\xi^2\over 3}} \quad \text{and}\quad \Big| e^{i\xi\sqrt n \gamma} \lambda_{-{i\xi\over \sqrt n}}^n-e ^{-{\varrho^2\xi^2\over 2}} \Big|\lesssim {1\over \sqrt n}|\xi|^3e^{-{\varrho^2\xi^2\over 2}}. \end{align} $$

From equation (3.7), it follows that $\lVert \Phi _{n,\xi } +\Phi _{n}^{\star }\rVert _{\mathscr {C}^\alpha }$ is bounded by

$$ \begin{align*}1 + \sum_{0\leq k\leq A\log n} \big| e^{i \xi{k \over \sqrt n}}-1 \big|\cdot \lVert\chi_k\rVert_{\mathscr{C}^\alpha}\lesssim 1 + \sum_{0\leq k\leq A\log n}|\xi|{k \over \sqrt n} e^{\alpha k} \lesssim 1 + {\sqrt[6] n (\log n)^2 n^{\alpha A}\over \sqrt n} \lesssim 1 ,\end{align*} $$

where in the last step we have used that $\alpha A\leq 1/6$ . It follows from the analyticity of $\xi \mapsto \mathcal {N}_{i\xi }$ that

$$ \begin{align*}\Big\|\big(\mathcal{N}_{-{i\xi\over \sqrt n}} -\mathcal{N}_0\big)(\Phi_{n,\xi} +\Phi_{n}^{\star} ) \Big\|_\infty \lesssim {|\xi|\over \sqrt n} .\end{align*} $$

We conclude, using equation (3.11), that

$$ \begin{align*}\int_{|\xi|\leq\sqrt[6] n} {1\over |\xi|}\cdot \big| \Gamma_1(\xi) \big| \,\mathrm{d} \xi \lesssim \int_{|\xi|\leq\sqrt[6] n} {1\over |\xi|} \cdot e^{-{\varrho^2\xi^2\over 3}} {|\xi|\over \sqrt n} \,\mathrm{d} \xi \lesssim {1 \over \sqrt n}.\end{align*} $$

For $\Gamma _2$ , using that $\big |\mathcal {N}_0 (\Phi _{n,\xi } +\Phi _{n}^{\star } )\big | \leq 1$ as before together with equation (3.11), gives

$$ \begin{align*}\int_{|\xi|\leq\sqrt[6] n} {1\over |\xi|}\cdot \big| \Gamma_2(\xi) \big| \,\mathrm{d} \xi \lesssim \int_{|\xi|\leq\sqrt[6] n} {1\over |\xi|}\cdot {1\over \sqrt n}|\xi|^3e^{-{\varrho^2\xi^2\over 2}} \,\mathrm{d} \xi\lesssim {1 \over \sqrt n}.\end{align*} $$

Together with Case 1, we deduce that

$$ \begin{align*}\Big|\int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {\Lambda_1(\xi) \over \xi} \,\mathrm{d} \xi\Big| \lesssim {1 \over \sqrt n},\end{align*} $$

which ends the proof of the lemma.

Lemma 3.9. We have

$$ \begin{align*}\sup_{|b|\leq \sqrt n} \Big| \int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {\Theta_b^{(2)}(\xi) \over \xi} \,\mathrm{d} \xi \Big| \lesssim { 1\over \sqrt n}.\end{align*} $$

Proof. Recall that $\chi _k$ is bounded by $1$ and is supported by $ \mathscr {T}_k \subset \mathbb {B}(H_y,e^{-k+1})$ . Therefore,

$$ \begin{align*}\mathcal{N}_0 \chi_k = \int_{\mathbb{P}^{d-1}} \chi_k \, \mathrm{d} \nu \leq \nu \big( \mathbb{B}(H_y,e^{-k+1}) \big) \lesssim e^{-k\eta},\end{align*} $$

where in the last step we have used Proposition 2.2.

Recall that $\widehat h(\xi ) = e^{-{\varrho ^2 \xi ^2\over 2}}$ and $\widetilde {h}_n(\xi )= e^{-{\varrho ^2 \xi ^2\over 2}} \mathcal {N}_0 (\Phi _{n,\xi } + \Phi _{n}^{\star })$ . Using equation (3.7) and $\mathcal {N}_0 \mathbf 1 = \mathbf 1$ , we get

$$ \begin{align*} \Theta_b^{(2)}(\xi) &= e^{ib \xi} e^{-{\varrho^2 \xi^2\over 2}} \big( \mathcal{N}_0 (\Phi_{n,\xi} + \Phi_{n}^{\star}) - 1 \big) \widehat{\vartheta_{\delta_n}}(\xi) \\ &= e^{ib \xi} e^{-{\varrho^2 \xi^2\over 2}} \sum_{0\leq k\leq A\log n} \big( e^{i \xi{k \over \sqrt n}}-1 \big) \big( \mathcal{N}_0 \chi_k \big) \cdot \widehat{\vartheta_{\delta_n}}(\xi). \end{align*} $$

As $\lVert \widehat {\vartheta _{\delta _n}}\rVert _\infty \leq 1$ , we obtain

$$ \begin{align*} \big|\Theta_b^{(2)}(\xi)\big| \leq e^{-{\varrho^2 \xi^2\over 2}} \sum_{0\leq k\leq A\log n} \big| e^{i \xi{k \over \sqrt n}}-1\big| \big( \mathcal{N}_0\chi_k \big) \lesssim e^{-{\varrho^2 \xi^2\over 2}}\sum_{k \geq 0} | \xi| {k \over \sqrt n} e^{-k\eta}\lesssim e^{-{\varrho^2 \xi^2\over 2}} {|\xi|\over \sqrt n}, \end{align*} $$

where the constants involved do not depend on b. Therefore,

$$ \begin{align*}\int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} \Big|{\Theta_b^{(2)}(\xi)\over \xi} \Big| \,\mathrm{d} \xi \lesssim \int_{-\xi_0\sqrt n}^{\xi_0\sqrt n} {1\over |\xi|} \cdot e^{-{\varrho^2 \xi^2\over 2}} {|\xi|\over \sqrt n} \,\mathrm{d} \xi \lesssim {1 \over \sqrt n},\end{align*} $$

thus proving the lemma.

Gathering the above estimates, we can finish the proof.

End of proof of Theorem A

Recall that our goal is to prove equation (3.4). Estimate (3.9) together with Lemmas 3.8 and 3.9 give that $\big |F_n(b)-H(b)\big | \leq C'/ \sqrt n$ for all $b \in \mathbb {R}$ , where $C'> 0$ is a constant. Recall that $H(b): =\frac {1}{\sqrt {2 \pi } \,\varrho } \int _{-\infty }^b e^{-\frac {s^2}{2 \varrho ^2}} \, \mathrm {d} s$ . Coupling the last estimate with Lemma 3.4 and the easy fact that $\sup _{b \in \mathbb {R}} \big |H(b)-H(b \pm 1/ \sqrt n)\big | \lesssim 1/ \sqrt n$ gives that $ \big |\mathcal {L}_n(b)-H(b)\big | \leq C" / \sqrt n$ for some constant $C"> 0$ . Therefore, equation (3.4) holds. Observe that all of our estimates are uniform in $x \in \mathbb {P}^{d-1}$ and $y\in (\mathbb {P}^{d-1})^*$ . The proof of the theorem is complete.

4 Local limit theorem for coefficients

This section is devoted to the proof of Theorem B. As in the previous section, we fix $x =[v]\in \mathbb {P}^{d-1}$ and $y=[f]\in (\mathbb {P}^{d-1})^*$ . Fix also $-\infty <a<b<\infty $ , and define

$$ \begin{align*} \mathcal{A}_n(t) := \sqrt{n} \, \mathbf P \Big( t+ \log{ |\langle f, S_n v \rangle | \over \lVert f\rVert \lVert v\rVert} - n \gamma\in [ a, b] \Big). \end{align*} $$

Our goal is to prove that

(4.1) $$ \begin{align} \lim_{n\to \infty}\sup_{t\in\mathbb{R}} \Big|\, \mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \, \Big| =0. \end{align} $$

Our strategy is similar to the one employed in the proof of Theorem A, that is, to replace $\log { |\langle f, S_n v \rangle | \over \lVert f\rVert \lVert v\rVert } $ by $\sigma (S_n,x) +\log d(S_n x, H_y)$ (see equation (3.3)) and use the perturbed Markov operator and large deviation estimates to handle $\sigma (S_n,x)$ and $\log d(S_n x, H_y)$ . Here, we are dealing with ‘local’ probabilities for $\sigma (S_n,x)$ , so the analysis is more involved. In particular, we need to use finer approximation results, such as the one in Lemma 2.8 and properties of the operator $\mathcal {P}_{i\xi }$ for large values of $\xi \in \mathbb {R}$ , as in Proposition 2.6.

Let $0<\zeta \leq 1$ be a constant. For integers $k \geq 0$ , introduce

$$ \begin{align*} \mathscr{T}_k^\zeta := \big\{ w \in \mathbb{P}^{d-1} :\, e^{-(k+1)\zeta} < d(w,H_y) < e^{-(k-1)\zeta} \big\} = \mathbb{B}(H_y,e^{-(k-1) \zeta}) \setminus \overline{\mathbb{B}(H_y,e^{-(k+1)\zeta})}. \end{align*} $$

We have the following version of Lemma 3.3. We’ll use the same notation to denote slightly different functions. This shouldn’t cause confusion. The functions from Lemma 3.3 correspond to the particular case $\zeta =1$ .

Lemma 4.1. Let $0<\zeta \leq 1$ . There exist nonnegative smooth functions $\chi _k$ on $\mathbb {P}^{d-1}$ , $k \geq 0$ , such that

1. 1. $\chi _k$ is supported by $\mathscr {T}_k^\zeta $ ;

2. 2. If $w \in \mathbb {P}^{d-1} \setminus H_y$ , then $\chi _k(w) \neq 0$ for at most two values of k;

3. 3. $\sum _{k\geq 0} \chi _k=1$ on $\mathbb {P}^{d-1} \setminus H_y$ ;

4. 4. $\lVert \chi _k\rVert _{\mathscr {C}^1}\leq C \zeta ^{-1} e^{k\zeta }$ .

Proof. Let $\widetilde {\chi }_k$ be as in Lemma 3.3, and set $\chi _k(w):= \widetilde {\chi }_k \big (\zeta ^{-1} \log d(w,H_y) \big )$ . Since the function $\Psi (w) := \log d(w,H_y)$ satisfies $\lVert \Psi |_{\mathscr {T}_k^\zeta }\rVert _{\mathscr {C}^1} \lesssim e^{k \zeta }$ , it follows that $\chi _k$ satisfies (1)–(4).

We will prove equation (4.1) by dealing separately with the upper and lower limit.

4.1 Upper bound

The upper bound in the limit (4.1) is handled by the following proposition.

Proposition 4.2. Let $\mathcal {A}_n(t)$ be as above. Then,

$$ \begin{align*}\limsup_{n\to \infty}\sup_{t\in\mathbb{R}}\bigg( \mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \bigg) \leq 0.\end{align*} $$

Let $0< \zeta \leq 1$ be a small constant, and define $\psi :\mathbb {R}\to \mathbb {R}_{\geq 0}$ by

$$ \begin{align*} \psi (u) := & \begin{cases} u/\zeta -(a-2\zeta)/\zeta & \text{for} \quad u\in[a-2\zeta,a-\zeta] \\ 1 & \text{for} \quad u\in[a-\zeta,b+\zeta] \\ -u/\zeta +(b+2\zeta)/\zeta & \text{for} \quad u\in [b+\zeta,b+2\zeta] \\ 0 & \text{for} \quad u\in \mathbb{R} \setminus [a-2\zeta,b+2\zeta]. \end{cases} \end{align*} $$

Notice that $\psi $ is Lipschitz and piecewise affine. Moreover, $0 \leq \psi \leq 1$ , its support is contained in $[a-2\zeta ,b+2\zeta ] \subset [a-2,b+2]$ and $\int _{\mathbb {R}} \psi (u)\,\mathrm {d} u = b-a+3\zeta $ .

For $t\in \mathbb {R}$ and $k\in \mathbb {N}$ , consider the translations

$$ \begin{align*}\psi_{t,k}(u):=\psi(u+t-k\zeta).\end{align*} $$

Observe that, for fixed $t,u\in \mathbb {R}$ , we have that $\psi _{t,k}(u)\neq 0$ for only finitely many k’s. By construction, we have $\psi _{t,k} \geq \mathbf 1_{[a-t+(k-1)\zeta , b-t+(k+1)\zeta ]}$ .

Let $B>0$ be a large constant. Arguing as in Section 3, we obtain that, for n large,

$$ \begin{align*}\mu^{*n} \big\{g\in G:\,d(gx,H_y)\leq e n^{-B} \big\}\leq e^{2c} \, n^{-c B},\end{align*} $$

for some constant $c> 0$ independent of n and B. Taking B large enough allows us to assume that $n^{-c B } \leq 1 / n$ for all $n \geq 1$ .

In order to simplify the notation, consider the linear functional

(4.2) $$ \begin{align} \mathcal{E}_n\big(\Psi\big):= \sqrt n \, \mathbf E\Big( \Psi\big( \sigma(S_n,x)-n\gamma ,S_n x \big) \Big), \end{align} $$

where $\Psi $ is a function of $(u,w) \in \mathbb {R} \times \mathbb {P}^{d-1}$ .

For $w \in \mathbb {P}^{d-1}$ , set

(4.3) $$ \begin{align} \Phi_n^\star (w):= 1 - \sum_{0\leq k\leq B\zeta^{-1}\log n} \chi_k(w), \end{align} $$

where $\chi _k$ are the functions in Lemma 4.1. We observe that we use the same notation as in Section 3 to denote slightly different functions. We recover the functions from last section by taking $\zeta = 1$ and $B=A$ . This shouldn’t cause any confusion.

Set

$$ \begin{align*}\mathcal{B}_n(t):= \sum_{0\leq k\leq B\zeta^{-1}\log n} \mathcal{E}_n\big(\psi_{t,k}\cdot\chi_k \big)+ \mathcal{E}_n\big(\psi_{t,0}\cdot \Phi_n^\star \big).\end{align*} $$

Lemma 4.3. There exists a constant $C_1>0$ , independent of n and $\zeta $ such that, for all $t \in \mathbb {R}$ ,

$$ \begin{align*}\mathcal{A}_n(t) \leq \mathcal{B}_n(t) + C_1 / \sqrt n.\end{align*} $$

Proof. Using the decomposition (3.3) and the fact that $\mathbf P \big ( d(S_n x,H_y)\leq n^{-B} \big ) \lesssim 1 / n$ , we obtain

$$ \begin{align*} \mathcal{A}_n(t) \leq \sqrt{n} \, \mathbf E \Big( \mathbf 1_{t+ \sigma(S_n,x) +\log d(S_n x, H_y) - n \gamma\in [a, b]} \mathbf 1_{\log d(S_n x, H_y)\geq -B\log n} \Big) + O \Big( {1 \over \sqrt n} \Big). \end{align*} $$

Observe that, when $S_n x \in \mathrm {supp}(\chi _k)$ , we have $-(k+1) \zeta \leq \log d(S_n x,H_y) \leq - (k-1) \zeta $ , so

$$ \begin{align*}\mathbf 1_{t+ \sigma(S_n,x) +\log d(S_n x, H_y) - n \gamma\in [a, b]}\leq \mathbf 1_{\sigma(S_n,x) - n \gamma\in [a-t+(k-1)\zeta, b-t+(k+1)\zeta]} \leq \psi_{t,k}\big(\sigma(S_n,x) - n \gamma\big).\end{align*} $$

Using that $\mathbf 1_{\log d(w, H_y)\geq -B\log n} \leq \sum _{0\leq k\leq B\zeta ^{-1}\log n + 1} \chi _k(w)$ and taking the expectation, it follows that

$$ \begin{align*} &\mathbf{E} \Big(\mathbf 1_{t+ \sigma(S_n,x) +\log d(S_n x, H_y) - n \gamma\in [a, b]} \mathbf 1_{\log d(S_n x, H_y)\geq -B\log n} \Big) \\ &\leq \sum_{0\leq k\leq B\zeta^{-1}\log n + 1} \mathbf{E} \Big( \psi_{t,k}\big(\sigma(S_n,x)-n\gamma\big)\chi_k(S_n x) \Big) \\ &\leq \sum_{0\leq k\leq B\zeta^{-1}\log n} \mathbf{E} \Big(\psi_{t,k}\big(\sigma(S_n,x)-n\gamma\big)\chi_k(S_n x) \Big) + \mathbf{E}\Big(\chi_{k_0}(S_n x) \Big), \end{align*} $$

where $k_0:= \lfloor B \zeta ^{-1} \log n \rfloor + 1$ .

From the fact that $\chi _{k_0} \leq \mathbf 1_{\mathbb {B}(H_y,e^{-(k_0-1)\zeta })}$ , we see that the last term above is bounded by $\mathbf P \big ( d(S_n x,H_y)\leq e n^{-B} \big ) \lesssim 1 / n$ . Hence, there is a constant $C_1>0$ such that

$$ \begin{align*} \mathcal{A}_n(t) \leq \sum_{0\leq k\leq B\zeta^{-1}\log n} \mathcal{E}_n\big(\psi_{t,k}\cdot\chi_k \big)+{C_1 \over \sqrt n} \leq \mathcal{B}_n(t) +{C_1 \over \sqrt n}, \end{align*} $$

proving the lemma.

By Lemma 2.8, for every $0<\delta \leq 1$ , there exists a smooth function $\psi ^+_{\delta }$ such that $\widehat {\psi ^+_{\delta }}$ has support in $[-\delta ^{-2},\delta ^{-2}]$ ,

$$ \begin{align*}\psi\leq \psi^+_\delta,\quad \lim_{\delta\to 0} \psi^+_{\delta} =\psi \quad \text{and} \quad \lim_{\delta\to 0} \big \|\psi^+_{\delta} -\psi \big \|_{L^1} = 0.\end{align*} $$

Moreover, $\lVert \psi _{\delta }^+\rVert _\infty $ , $\lVert \psi _{\delta }^+\rVert _{L^1}$ and $\|\widehat {\psi ^+_{\delta }}\|_{\mathscr {C}^1}$ are bounded by a constant independent of $\delta $ and $\zeta $ since the support of $\psi $ is contained in $[a-2,b+2]$ .

As above, for $t\in \mathbb {R}$ and $k\in \mathbb {N}$ , we consider the translations

$$ \begin{align*}\psi_{t,k}^+(u):=\psi_{\delta}^+(u+t-k\zeta) .\end{align*} $$

We omit the dependence on $\delta $ in order to ease the notation. Define also

(4.4) $$ \begin{align} \mathcal{R}_n(t):= \sum_{0\leq k\leq B\zeta^{-1}\log n } \mathcal{E}_n\big(\psi_{t,k}^+\cdot\chi_k \big)+ \mathcal{E}_n\big(\psi_{t,0}^+\cdot \Phi_n^\star \big). \end{align} $$

Clearly, we have $\mathcal {B}_n(t)\leq \mathcal {R}_n(t)$ . From the definition of $\mathcal {E}_n$ , Fourier inversion formula and Fubini’s theorem, we have

$$ \begin{align*} \mathcal{E}_n\big(\psi_{t,k}^+\cdot\chi_k \big)&=\sqrt n \, \int_{G} \psi_{\delta}^+\big(\sigma(g,x)-n\gamma+t-k\zeta\big) \cdot \chi_k(gx) \,\mathrm{d} \mu^{*n}(g)\\ &={\sqrt n\over 2\pi}\int_{G} \int_{-\infty}^\infty \widehat{\psi_{\delta}^+}(\xi) e^{i\xi(\sigma(g,x)-n\gamma+t-k\zeta )} \cdot \chi_k(gx) \,\mathrm{d} \xi\mathrm{d}\mu^{*n}(g)\\ &={\sqrt n\over 2\pi}\int_{-\infty}^\infty \widehat{\psi_{\delta}^+}(\xi) e^{i\xi(t-k\zeta)}\cdot e^{-i\xi n\gamma}\mathcal{P}^n_{i\xi}\chi_k(x) \,\mathrm{d} \xi, \end{align*} $$

where in the last step we have used equation (2.1).

Recall that $\mathrm {supp}\big ( \widehat {\psi _{\delta }^+} \big )\subset [-\delta ^{-2},\delta ^{-2}]$ . So, after the change of variables $\xi \mapsto \xi / \sqrt n$ , the above identity becomes

$$ \begin{align*} \mathcal{E}_n\big(\psi_{t,k}^+\cdot\chi_k \big) ={1\over 2\pi}\int_{-\delta^{-2} \sqrt n}^{\delta^{-2} \sqrt n} \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big) e^{i\xi{t-k\zeta\over \sqrt n}}\cdot e^{-i\xi \sqrt n\gamma}\mathcal{P}^n_{{i\xi\over \sqrt n}}\chi_k(x) \,\mathrm{d} \xi.\end{align*} $$

A similar computation yields

$$ \begin{align*}\mathcal{E}_n\big(\psi_{t,0}^+ \cdot \Phi_n^\star \big) = {1\over 2\pi}\int_{-\delta^{-2} \sqrt n}^{\delta^{-2} \sqrt n} \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big) e^{i\xi{t \over \sqrt n}}\cdot e^{-i\xi \sqrt n\gamma}\mathcal{P}^n_{{i\xi\over \sqrt n}}\Phi_{n}^{\star} (x) \,\mathrm{d} \xi.\end{align*} $$

Define

(4.5) $$ \begin{align} \Phi_{n,\xi} (w):= \sum_{0\leq k\leq B\zeta^{-1}\log n} e^{-i \xi{k\zeta\over \sqrt n}}\chi_k(w). \end{align} $$

We use again the same notation as in Section 3 to denote a slightly different function. The difference here is the factor $\zeta $ and the sign before $i\xi $ . Using this notation and the above computations, equation (4.4) becomes

(4.6) $$ \begin{align} \mathcal{R}_n(t)= {1\over 2\pi}\int_{-\delta^{-2} \sqrt n}^{\delta^{-2} \sqrt n} \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big) e^{i\xi{t\over \sqrt n}}\cdot e^{-i \xi \sqrt n\gamma}\mathcal{P}_{{i\xi\over \sqrt n}}^n(\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \,\mathrm{d} \xi. \end{align} $$

Fix $\alpha>0$ such that

$$ \begin{align*}\alpha B\leq 1/6 \quad \text{ and } \quad \alpha \leq \alpha_0,\end{align*} $$

where $0<\alpha _0<1$ is the exponent appearing in Theorem 2.3. Then, all the results of Subsection 2.3 apply to the operators $\xi \mapsto \mathcal {P}_{i\xi }$ acting on $\mathscr {C}^\alpha (\mathbb {P}^{d-1})$ .

The next lemma can be proved in the same way as Lemma 3.6.

Lemma 4.4. Let $0 < \zeta \leq 1$ , $\Phi _{n,\xi }, \Phi _{n}^{\star }$ and $\alpha> 0$ be as above. Then,

(4.7) $$ \begin{align} \Phi_{n,\xi} + \Phi_{n}^{\star} = \mathbf 1 + \sum_{0\leq k\leq B\zeta^{-1}\log n} \big(e^{-i \xi{k\zeta\over \sqrt n}} - 1 \big) \chi_k \end{align} $$

and there is a constant $C_\zeta>0$ independent of n and $\xi $ such that

$$ \begin{align*} \lVert\Phi_{n,\xi} \rVert_{\mathscr{C}^\alpha}\leq C_\zeta n^{\alpha B} \quad\text{and}\quad \lVert\Phi_{n}^{\star} \rVert_{\mathscr{C}^\alpha}\leq C_\zeta n^{\alpha B}. \end{align*} $$

Moreover, $\Phi _{n}^{\star } $ is supported by $\big \{w:\,\log d(w,H_y)\leq -B\log n + 1\big \}$ .

Define

(4.8) $$ \begin{align} \mathcal{S}_n(t):={1\over 2\pi}\widehat{\psi_{\delta}^+}(0) \int_{-\infty}^\infty e^{i\xi{t\over \sqrt n}} e^{-{ \varrho^2\xi^2 \over 2}} \,\mathrm{d} \xi ={1\over \sqrt{2\pi} \, \varrho} e^{-{t^2\over2\varrho^2 n}}\int_{\mathbb{R}} \psi_{\delta}^+ (u)\,\mathrm{d} u, \end{align} $$

where in the second equality we have used the fact that the inverse Fourier transform of $e^{-{ \varrho ^2\xi ^2 \over 2}}$ is $ {1\over \sqrt {2\pi } \, \varrho } e^{-{t^2\over 2\varrho ^2}}$ .

Lemma 4.5. Fix $0< \delta \leq 1$ and $0<\zeta \leq 1$ . Then, there exists a constant $C_{\zeta ,\delta }>0$ such that, for all $n \geq 1$ ,

$$ \begin{align*}\sup_{t\in\mathbb{R}}\big|\mathcal{R}_n(t)-\mathcal{S}_n(t) \big| \leq {C_{\zeta,\delta}\over \sqrt[3] n}.\end{align*} $$

Proof. Let $\xi _0>0$ be the constant in Lemma 2.5. In particular, the decomposition of $\mathcal {P}_z$ in Proposition 2.4 holds for $|z| \leq \xi _0$ . Using that decomposition, equation (4.6) and equation (4.8), we can write

$$ \begin{align*}\mathcal{R}_n(t)-\mathcal{S}_n(t) = \Lambda_n^1(t) + \Lambda_n^2(t) + \Lambda_n^3(t) + \Lambda_n^4(t) + \Lambda_n^5(t),\end{align*} $$

where

$$ \begin{align*}\Lambda_n^1(t):={1\over 2\pi}\int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} e^{i\xi{t\over \sqrt n}} \Big[ \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big)e^{-i \xi \sqrt n\gamma} \lambda_{{i\xi\over \sqrt n}}^n\mathcal{N}_0(\Phi_{n,\xi} +\Phi_{n}^{\star} )-\widehat{\psi_{\delta}^+}(0) e^{-{ \varrho^2\xi^2 \over 2}}\Big] \,\mathrm{ d} \xi ,\end{align*} $$

$$ \begin{align*}\Lambda_n^2(t):= {1\over 2\pi}\int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} e^{i\xi{t\over \sqrt n}}\Big[ \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big) e^{-i \xi \sqrt n\gamma} \lambda_{{i\xi\over \sqrt n}}^n\big(\mathcal{N}_{{i\xi\over \sqrt n}}-\mathcal{N}_0\big)(\Phi_{n,\xi} +\Phi_{n}^{\star} ) (x) \Big] \,\mathrm{d} \xi ,\end{align*} $$

$$ \begin{align*}\Lambda_n^3(t):= {1\over 2\pi}\int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} e^{i\xi{t\over \sqrt n}} \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big) e^{-i \xi \sqrt n\gamma} \mathcal{Q}_{{i\xi\over \sqrt n}}^n(\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \,\mathrm{d} \xi,\end{align*} $$

$$ \begin{align*}\Lambda_n^4(t):= {1\over 2\pi}\int_{\xi_0\sqrt n \leq|\xi|\leq\delta^{-2} \sqrt n}e^{i\xi{t\over \sqrt n}} \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big) e^{-i \xi \sqrt n\gamma} \mathcal{P}_{{i\xi\over \sqrt n}}^n(\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \,\mathrm{d} \xi\end{align*} $$

and

$$ \begin{align*}\Lambda_n^5(t):= - {1\over 2\pi}\widehat{\psi_{\delta}^+}(0) \int_{|\xi|\geq \xi_0 \sqrt n} e^{i\xi{t\over \sqrt n}} e^{-{ \varrho^2\xi^2 \over 2}} \,\mathrm{d} \xi.\end{align*} $$

We will bound each $\Lambda _n^j$ , $j=1,\ldots , 5$ , separately. We will use that

$$ \begin{align*}\lVert\Phi_{n,\xi} +\Phi_{n}^{\star} \rVert_{\mathscr{C}^\alpha}\leq 2C_\zeta n^{\alpha B} \leq 2C_\zeta n^{1 / 6}\end{align*} $$

for every $\xi $ , after Lemma 4.4 and the choice of $\alpha $ and B.

In order to bound $\Lambda _n^2$ , we have, using the analyticity of $\xi \mapsto \mathcal {N}_{i\xi }$ , that

$$ \begin{align*}\Big\| \big(\mathcal{N}_{{i\xi\over \sqrt n}}-\mathcal{N}_0\big)(\Phi_{n,\xi} +\Phi_{n}^{\star} ) \Big\|_\infty \lesssim {|\xi|\over \sqrt n} \lVert\Phi_{n,\xi} +\Phi_{n}^{\star} \rVert_{\mathscr{C}^\alpha}\leq { 2C_\zeta|\xi|\over \sqrt [3] n}.\end{align*} $$

Recall, from Lemma 2.5, that $\big |\lambda _{{i\xi \over \sqrt n}}^n\big |\leq e^{-{\varrho ^2\xi ^2\over 3}}$ for $|\xi |\leq \xi _0 \sqrt n$ . Since $\|\widehat {\psi ^\pm _{\delta }}\|_{\mathscr {C}^1}$ is bounded uniformly in $\delta $ and $\zeta $ , we get

$$ \begin{align*}\sup_{t\in\mathbb{R}} \big|\Lambda_n^2(t)\big|\lesssim \int_{-\infty}^{\infty} e^{-{\varrho^2\xi^2\over 3}} {2C_\zeta|\xi|\over \sqrt [3] n} \,\mathrm{d} \xi \lesssim {C_\zeta\over \sqrt[3] n}.\end{align*} $$

For $\Lambda _n^3$ , we use that $\lVert \mathcal {Q}^n_z\rVert _{\mathscr {C}^\alpha } \leq c \beta ^n$ for $|z| \leq \xi _0$ , where $c>0$ and $0<\beta <1$ are constants; see Proposition 2.4. Therefore, for $|\xi |\leq \xi _0\sqrt n$ ,

$$ \begin{align*}\Big\| \mathcal{Q}_{{i\xi\over \sqrt n}}^n(\Phi_{n,\xi} +\Phi_{n}^{\star} ) \Big\|_\infty \lesssim \beta^n\lVert\Phi_{n,\xi} +\Phi_{n}^{\star} \rVert_{\mathscr{C}^\alpha} \leq 2 C_\zeta \beta^n \sqrt[6] n,\end{align*} $$

which gives

$$ \begin{align*}\sup_{t\in\mathbb{R}} \big|\Lambda_n^3(t)\big|\lesssim \int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} 2 C_\zeta \beta^n \sqrt[6] n \,\mathrm{d} \xi = 4\xi_0 C_\zeta \sqrt n \beta^n \sqrt[6] n\lesssim \frac{C_\zeta}{\sqrt n}.\end{align*} $$

In order to bound $\Lambda _n^4$ , we use that, after Proposition 2.6, there are constants $C_\delta>0$ and $0<\rho _\delta <1$ such that $\lVert \mathcal {P}^n_{i\xi }\rVert _{\mathscr {C}^\alpha }\leq C_\delta \rho _\delta ^n$ for all $\xi _0\leq |\xi |\leq \delta ^{-2}$ and $n \geq 1$ . Therefore,

$$ \begin{align*}\sup_{t\in\mathbb{R}} \big|\Lambda_n^4(t)\big|\lesssim \int_{\xi_0\sqrt n \leq|\xi|\leq\delta^{-2} \sqrt n} C_\delta \rho_\delta^n \sqrt[6] n\,\mathrm{d} \xi\leq 2\delta^{-2}\sqrt n C_\delta \rho_\delta^n C_\zeta \sqrt[6] n\lesssim \frac{C_{\zeta,\delta}'}{\sqrt n},\end{align*} $$

for some constant $C_{\zeta ,\delta }'>0$ .

The modulus of the term $\Lambda _n^5$ is clearly $\lesssim 1/\sqrt n$ , so it only remains to estimate $\Lambda _n^1$ . For every $t \in \mathbb {R}$ , we have

$$ \begin{align*}\big| \Lambda_n^1(t) \big|\leq \Gamma_n^1+\Gamma_n^2+\Gamma_n^3,\end{align*} $$

where

$$ \begin{align*}\Gamma_n^1:= {1\over 2\pi}\int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} \Big| \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big) \Big| \, \big|\lambda_{{i\xi\over \sqrt n}}^n \big| \cdot\Big| \mathcal{N}_0(\Phi_{n,\xi} +\Phi_{n}^{\star} )- 1 \Big| \,\mathrm{d} \xi ,\end{align*} $$

$$ \begin{align*}\Gamma_n^2:= {1\over 2\pi}\int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} \big|\lambda_{{i\xi\over \sqrt n}}^n\big|\cdot \Big| \widehat{\psi_{\delta}^+}\Big({\xi\over \sqrt n}\Big) -\widehat{\psi_{\delta}^+}(0) \Big| \,\mathrm{d} \xi\end{align*} $$

and

$$ \begin{align*}\Gamma_n^3:= {1\over 2\pi}\int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} \big| \widehat{\psi_{\delta}^+}(0) \big| \cdot\Big| e^{-i \xi \sqrt n\gamma} \lambda_{{i\xi\over \sqrt n}}^n- e^{-{ \varrho^2\xi^2 \over 2}}\Big| \,\mathrm{d} \xi.\end{align*} $$

Recall that $\chi _k$ is bounded by $1$ and is supported by $ \mathscr {T}_k^\zeta \subset \mathbb {B}(H_y,e^{-(k-1)\zeta })$ . Therefore,

$$ \begin{align*}\mathcal{N}_0 \chi_k = \int_{\mathbb{P}^{d-1}} \chi_k \, \mathrm{d} \nu \leq \nu \big(\mathbb{B}(H_y,e^{-(k-1) \zeta})\big) \lesssim e^{-k\zeta \eta},\end{align*} $$

where in the last step we have used Proposition 2.2.

Using equation (4.7), we get

$$ \begin{align*} \Big| \mathcal{N}_0(\Phi_{n,\xi} +\Phi_{n}^{\star} )- 1 \Big| &= \Big| \mathcal{N}_0(\Phi_{n,\xi} +\Phi_{n}^{\star} )-\mathcal{N}_0 \mathbf 1\Big|\leq \sum_{0\leq k\leq B\zeta^{-1}\log n} \big| e^{-i \xi{k\zeta\over \sqrt n}}-1 \big|\mathcal{N}_0 \chi_k \\ &\lesssim \sum_{ k \geq 0} |\xi|{k\zeta\over \sqrt n}e^{-k \zeta\eta}\leq c_\zeta {|\xi|\over \sqrt n}, \end{align*} $$

for some constant $c_\zeta>0$ independent of n.

Using that $\big |\lambda _{{i\xi \over \sqrt n}}^n\big |\leq e^{-{\varrho ^2\xi ^2\over 3}}$ for $|\xi |\leq \xi _0 \sqrt n$ (Lemma 2.5) and that $\|\widehat {\psi ^+_{\delta }}\|_{\mathscr {C}^1}$ is uniformly bounded, we get that

$$ \begin{align*}\Gamma_n^1\lesssim \int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} \|\widehat{\psi^+_{\delta}}\|_{\infty} e^{-{\varrho^2\xi^2\over 3}} c_\zeta {|\xi|\over \sqrt n} \,\mathrm{d} \xi\lesssim {c_\zeta\over \sqrt n}\end{align*} $$

and

$$ \begin{align*}\Gamma_n^2\lesssim \int_{-\xi_0 \sqrt n}^{\xi_0 \sqrt n} e^{-{\varrho^2\xi^2\over 3}} {|\xi|\over \sqrt n} \|\widehat{\psi^+_{\delta}}\|_{\mathscr{C}^1} \,\mathrm{d} \xi\lesssim {1\over \sqrt n}.\end{align*} $$

The bound $\Gamma _n^3\lesssim 1/\sqrt n$ follows by splitting the integral along the intervals $|\xi |\leq \sqrt [6] n$ and $\sqrt [6] n< |\xi | \leq \xi _0\sqrt n$ and using Lemma 2.5.

We conclude that

$$ \begin{align*}\sup_{t\in\mathbb{R}} \big|\Lambda_n^1(t)\big|\lesssim \frac{c_\zeta'}{\sqrt n},\end{align*} $$

for some constant $c_\zeta '>0$ independent of n.

Gathering the above estimates, we obtain

$$ \begin{align*}\sup_{t\in\mathbb{R}}\big|\mathcal{R}_n(t)-\mathcal{S}_n(t) \big|\lesssim \frac{c_\zeta'}{\sqrt n} + {C_\zeta\over \sqrt[3] n} + \frac{C_\zeta}{\sqrt n} + \frac{C_{\zeta,\delta}'}{\sqrt n} + \frac{1}{\sqrt n}.\end{align*} $$

Hence, the above quantity is bounded by $C_{\zeta ,\delta } / \sqrt [3] n$ for some constant $C_{\zeta ,\delta }> 0$ . This finishes the proof of the lemma.

The above estimates are enough to obtain the desired upper bound.

Proof of Proposition 4.2

Fix $0<\delta \leq 1$ and $0 < \zeta \leq 1$ as in the beginning of this subsection. Lemmas 4.3 and 4.5 and the fact that $\mathcal {B}_n(t) \leq \mathcal {R}_n(t)$ give that

$$ \begin{align*}\mathcal{A}_n(t) \leq \mathcal{S}_n(t) + {C_{\zeta,\delta}\over \sqrt[3] n}+{C_1 \over \sqrt n} \quad \text{for all } \,\, t \in \mathbb{R}.\end{align*} $$

Recall, from equation (4.8), that $\mathcal {S}_n(t) = {1\over \sqrt {2\pi } \, \varrho } e^{-{t^2\over 2\varrho ^2 n}}\int _{\mathbb {R}} \psi _{\delta }^+ (u)\,\mathrm {d} u$ and $\int _{\mathbb {R}} \psi (u)\,\mathrm {d} u = b-a+3\zeta $ . Hence, for every fixed n and $\zeta $ ,

$$ \begin{align*}\Big| \mathcal{S}_n(t)- e^{-{t^2\over2\varrho^2 n}}{b-a+3\zeta\over \sqrt{2\pi} \, \varrho} \Big| \leq {1\over \sqrt{2\pi} \, \varrho} \big\| \psi_{\delta}^+ -\psi\big\|_{L^1}.\end{align*} $$

We deduce that

$$ \begin{align*}\mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \leq e^{-{t^2\over2\varrho^2 n}} {3\zeta\over \sqrt{2\pi} \, \varrho} + {1\over \sqrt{2\pi} \, \varrho} \big\| \psi_{\delta}^+ -\psi\big\|_{L^1} + {C_{\zeta,\delta}\over \sqrt[3] n}+{C_1 \over \sqrt n},\end{align*} $$

so

$$ \begin{align*}\limsup_{n\to \infty} \sup_{t\in\mathbb{R}} \bigg( \mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \bigg) \leq {3\zeta\over \sqrt{2\pi} \, \varrho} + {1\over \sqrt{2\pi} \, \varrho} \big\| \psi_{\delta}^+ -\psi\big\|_{L^1}.\end{align*} $$

Since $0<\delta \leq 1$ and $0 < \zeta \leq 1$ are arbitrary and $\big \| \psi _{\delta }^+ -\psi \big \|_{L^1}$ tends to zero as $\delta \to 0$ , the proposition follows.

4.2 Lower bound

We now deal with the lower bound for the limit in equation (4.1).

Proposition 4.6. Let $\mathcal {A}_n(t)$ be as above. Then,

$$ \begin{align*}\liminf_{n\to \infty}\inf_{t\in\mathbb{R}}\bigg( \mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \bigg) \geq 0.\end{align*} $$

The argument is a variation of the one used in the proof of Proposition 4.2, but the upper approximations used above will be replaced by analogous lower approximations. We now give the details.

Let $0< \zeta \leq 1$ be a small constant, and define $\widetilde {\psi }:\mathbb {R}\to \mathbb {R}_{\geq 0}$ by

$$ \begin{align*} \widetilde{\psi} (u)= & \begin{cases} u/\zeta -(a+\zeta)/\zeta & \text{for} \quad u\in[a+\zeta,a+2\zeta] \\ 1 & \text{for} \quad u\in[a+2\zeta,b-2\zeta] \\ -u/\zeta +(b-\zeta)/\zeta & \text{for} \quad u\in [b-2\zeta,b-\zeta] \\ 0 & \text{for} \quad u\in \mathbb{R} \setminus [a+\zeta,b-\zeta]. \end{cases} \end{align*} $$

The function $\widetilde {\psi }$ is Lipschitz and piecewise affine. Moreover, $0 \leq \widetilde {\psi } \leq 1$ , its support is contained in $[a+\zeta ,b-\zeta ] \subset [a,b]$ and $\int _{\mathbb {R}} \widetilde {\psi } (u)\,\mathrm {d} u = b-a - 3\zeta $ .

For $t\in \mathbb {R}$ and $k\in \mathbb {N}$ , consider the translations

$$ \begin{align*}\widetilde\psi_{t,k}(u):=\widetilde\psi(u+t-k\zeta).\end{align*} $$

Then, for fixed $t,u\in \mathbb {R}$ , we have that $\widetilde {\psi }_{t,k}(u)\neq 0$ for only finitely many k’s and $\mathbf 1_{[a-t+(k+1)\zeta , b-t+(k-1)\zeta ]} \geq \widetilde \psi _{t,k}$ .

Let $\chi _k$ be as in Lemma 4.1 and $\Phi _n^\star $ be the function defined in equation (4.3). Set

$$ \begin{align*}\widetilde{\mathcal{B}}_{n}(t):= \sum_{0\leq k\leq B\zeta^{-1}\log n} \mathcal{E}_n\big(\widetilde{\psi}_{t,k}\cdot\chi_k \big)+ \mathcal{E}_n\big(\widetilde{\psi}_{t,0}\cdot \Phi_n^\star \big),\end{align*} $$

where $\mathcal {E}_n$ is defined in equation (4.2).

Lemma 4.7. There exists a constant $C_2>0$ , independent of n and $\zeta $ , such that, for all $t \in \mathbb {R}$ ,

$$ \begin{align*}\mathcal{A}_n(t) \geq \widetilde{\mathcal{B}}_n(t) - C_2 / \sqrt n.\end{align*} $$

Proof. Using equation (3.3) and the definition of $\mathcal {A}_n(t)$ , it follows that

$$ \begin{align*} \mathcal{A}_n(t) \geq \sqrt{n} \, \mathbf E \Big( \mathbf 1_{t+ \sigma(S_n,x) +\log d(S_n x, H_y) - n \gamma\in [a, b]}\mathbf 1_{\log d(S_n x, H_y)\geq -B\log n} \Big).\end{align*} $$

Recall that when $S_n x\in \mathrm {supp}(\chi _k)$ , one has $-(k+1) \zeta \leq \log d(S_n x,H_y) \leq - (k-1) \zeta $ , so

$$ \begin{align*}\mathbf 1_{t+ \sigma(S_n,x) +\log d(S_n x, H_y) - n \gamma\in [a, b]}\geq \mathbf 1_{\sigma(S_n,x) - n \gamma\in [a-t+(k+1)\zeta, b-t+(k-1)\zeta]} \geq \widetilde\psi_{t,k}\big(\sigma(S_n,x) - n \gamma\big).\end{align*} $$

Using that $\mathbf 1_{\log d(w, H_y)\geq -B\log n} \geq \sum _{0\leq k\leq B\zeta ^{-1}\log n - 1} \chi _k(w)$ , it follows that

$$ \begin{align*} \mathbf 1_{t+ \sigma(S_n,x) +\log d(S_n x, H_y) - n \gamma\in [a, b]} & \mathbf 1_{\log d(S_n x, H_y)\geq -B\log n} \\ & \geq \sum_{0\leq k\leq B\zeta^{-1}\log n-1} \widetilde{\psi}_{t,k}\big(\sigma(S_n,x)-n\gamma\big)\chi_k(S_n x). \end{align*} $$

Therefore, if $k_0:= \lfloor B \zeta ^{-1} \log n \rfloor $ , then

$$ \begin{align*} \mathcal{A}_n(t) \geq \sum_{0\leq k\leq B\zeta^{-1}\log n-1} \mathcal{E}_n\big(\widetilde\psi_{t,k}\cdot\chi_k \big) = \widetilde{\mathcal{B}}_n(t) - \mathcal{E}_n\big(\widetilde{\psi}_{t,k_0}\cdot\chi_{k_0} \big) - \mathcal{E}_n\big(\widetilde{\psi}_{t,0}\cdot \Phi_n^\star \big). \end{align*} $$

Arguing as in the proof of Lemma 4.3, we see that the last two terms above are $\gtrsim - 1 / \sqrt n$ . The lemma follows.

Let $0<\delta \leq 1$ . By Lemma 2.8, there exists a smooth function $\widetilde {\psi }^-_{\delta }$ such that $\widehat {\widetilde {\psi }^-_{\delta }}$ has support in $[-\delta ^{-2},\delta ^{-2}]$ ,

$$ \begin{align*}\widetilde{\psi}^-_{\delta} \leq \widetilde\psi,\quad \lim_{\delta\to 0} \widetilde{\psi}^-_{\delta} =\widetilde{\psi} \quad \text{and} \quad \lim_{\delta\to 0} \big \|\widetilde{\psi}^-_{\delta} -\widetilde\psi \big \|_{L^1} = 0.\end{align*} $$

Moreover, $\lVert \widetilde {\psi }_{\delta }^-\rVert _\infty $ , $\lVert \widetilde \psi _{\delta }^-\rVert _{L^1}$ and $\|\widehat { \widetilde {\psi }^-_{\delta }}\|_{\mathscr {C}^1}$ are bounded by a constant independent of $\delta $ and $\zeta $ since the support of $\psi $ is contained in $[a,b]$ . We warn that, even if $\widetilde {\psi }$ is nonnegative, $\widetilde {\psi }^-_{\delta }$ might take negative values.

For $t\in \mathbb {R}$ and $k\in \mathbb {N}$ , consider the translations

$$ \begin{align*}\widetilde\psi_{t,k}^-(u):= \widetilde{\psi}_{\delta}^-(u+t-k\zeta)\end{align*} $$

and define

$$ \begin{align*}\widetilde{\mathcal{R}}_n(t):= \sum_{0\leq k\leq B\zeta^{-1}\log n} \mathcal{E}_n\big(\widetilde{\psi}_{t,k}^-\cdot\chi_k \big)+ \mathcal{E}_n\big(\widetilde{\psi}_{t,0}^-\cdot \Phi_n^\star \big)\end{align*} $$

and

$$ \begin{align*}\widetilde{\mathcal{S}}_n (t):={1\over 2\pi}\widehat{\widetilde{\psi}_{\delta}^-}(0) \int_{-\infty}^\infty e^{i\xi{t\over \sqrt n}} e^{-{ \varrho^2\xi^2 \over 2}} \,\mathrm{d} \xi={1\over \sqrt{2\pi} \, \varrho} e^{-{t^2\over2\varrho^2 n}}\int_{\mathbb{R}} \widetilde{\psi}_{\delta}^- (u)\,\mathrm{d} u.\end{align*} $$

Lemma 4.8. Fix $0< \delta \leq 1$ and $0<\zeta \leq 1$ small enough. Then, there exists a constant $\widetilde C_{\zeta ,\delta }>0$ such that, for all $n \geq 1$ ,

$$ \begin{align*}\sup_{t\in\mathbb{R}}\big| \widetilde{\mathcal{R}}_n(t)- \widetilde{\mathcal{S}}_n(t) \big| \leq {\widetilde C_{\zeta,\delta}\over \sqrt[3] n}.\end{align*} $$

Proof. By the same computations as the ones from Subsection 4.1, we obtain the identity

$$ \begin{align*}\widetilde{\mathcal{R}}_n(t)= {1\over 2\pi}\int_{-\delta^{-2} \sqrt n}^{\delta^{-2} \sqrt n} \widehat {\widetilde{\psi}^-_{\delta}} \Big({\xi\over \sqrt n}\Big) e^{i\xi{t\over \sqrt n}}\cdot e^{-i \xi \sqrt n\gamma} \mathcal{P}_{{i\xi\over \sqrt n}}^n(\Phi_{n,\xi} +\Phi_{n}^{\star} )(x) \,\mathrm{d} \xi,\end{align*} $$

where $\Phi _{n,\xi }$ and $\Phi _{n}^{\star }$ are defined in equations (4.3) and (4.5) respectively. The proof of Lemma 4.5 can be repeated by using ${\widetilde {\psi }^-_{\delta }}$ instead of $\psi _\delta ^+$ . This yields the desired estimate.

We can now obtain the lower bound.

Proof of Proposition 4.6

Lemmas 4.7 and 4.8 and the fact that $\widetilde {\mathcal {B}}_n(t) \geq \widetilde {\mathcal {R}}_n(t)$ give that

$$ \begin{align*}\mathcal{A}_n(t) \geq \widetilde{\mathcal{S}}_n(t) - {\widetilde C_{\zeta,\delta}\over \sqrt[3] n} - {C_2 \over \sqrt n} \quad \text{for all } \,\, t \in \mathbb{R}.\end{align*} $$

Arguing as in the proof of Proposition 4.2 and recalling that $\int _{\mathbb {R}} \widetilde {\psi } (u)\,\mathrm {d} u = b-a - 3\zeta $ , we get that, for every fixed n, $\delta $ and $\zeta $ ,

$$ \begin{align*}\Big| \widetilde{\mathcal{S}}_n(t)- e^{-{t^2\over2\varrho^2 n}}{b-a - 3\zeta\over \sqrt{2\pi} \, \varrho} \Big| \leq {1\over \sqrt{2\pi} \, \varrho} \big\| \widetilde{\psi}^-_{\delta} -\widetilde\psi \big \|_{L^1}.\end{align*} $$

Therefore,

$$ \begin{align*}\mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \geq - e^{-{t^2\over2\varrho^2 n}} {3\zeta\over \sqrt{2\pi} \, \varrho} - {1\over \sqrt{2\pi} \, \varrho} \big\| \widetilde{\psi}^-_{\delta} -\widetilde\psi \big \|_{L^1} - {\widetilde C_{\zeta,\delta}\over \sqrt[3] n} - {C_2 \over \sqrt n},\end{align*} $$

and

$$ \begin{align*}\liminf_{n\to \infty} \inf_{t\in\mathbb{R}} \bigg( \mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \bigg) \geq - {3\zeta\over \sqrt{2\pi} \, \varrho} - {1\over \sqrt{2\pi} \, \varrho} \big\| \widetilde{\psi}^-_{\delta} -\widetilde\psi \big \|_{L^1}.\end{align*} $$

Since $0<\delta \leq 1$ and $0 < \zeta \leq 1$ are arbitrary and $ \big \| \widetilde {\psi }^-_{\delta } -\widetilde \psi \big \|_{L^1}$ tends to zero as $\delta \to 0$ , the proposition follows.

Now, the proof of Theorem B can be concluded.

Proof of Theorem B

Recall that the conclusion of Theorem B is equivalent to the limit (4.1). Propositions 4.2 and 4.6 give that

$$ \begin{align*}\limsup_{n\to \infty}\sup_{t\in\mathbb{R}} \bigg( \mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \bigg) \leq 0 \quad \text{and} \quad \liminf_{n\to \infty} \inf_{t\in\mathbb{R}} \bigg( \mathcal{A}_n(t) - e^{-\frac{t^2}{2 \varrho^2 n}} {b-a\over \sqrt{2 \pi}\,\varrho} \bigg) \geq 0\end{align*} $$

respectively. This clearly implies equation (4.1). It is also clear that all of our estimates are uniform in $x \in \mathbb {P}^{d-1}$ and $y\in (\mathbb {P}^{d-1})^*$ . The proof of the theorem is finished.