Numerical simulations of Gurenhekou glacier on the Tibetan Plateau

Abstract

We investigate the impact of climate change on Gurenhekou glacier, southern Tibetan Plateau, which is representative of the tens of thousands of mountain glaciers in the region. We apply a three-dimensional, thermomechanically coupled full-Stokes model to simulate the evolution of the glacier. The steep and rugged bedrock geometry requires use of such a flow model. We parameterize the temperature and surface mass-balance (SMB) uncertainties using nearby automatic weather and meteorological stations, 6 year measured SMB data and an energy-balance model for a nearby glacier. Summer air temperature increased at 0.02 Ka⁻¹ over the past 50 years, and the glacier has retreated at an average rate of 8.3 m a⁻¹. Prognostic simulations suggest an accelerated annual average retreat rate of ~9.1 ma⁻¹ along the central flowline for the next 25 years under continued steady warming. However, regional climate models suggest a marked increase in warming rate over Tibet during the 21st century, and this rate causes about a 0.9 ± 0.3% a⁻¹ loss of glaciated area and 1.1 ± 0.6% a⁻¹ shrinkage of glacier volume. These results, the rather high warming rates predicted and the small sizes of most Tibetan glaciers, suggest that significant numbers of glaciers will be lost in the region during the 21st century.

1. Introduction

The Tibetan Plateau possesses tens of thousands of mountain glaciers which provide water for many large rivers (e.g. Brahmaputra, Ganges, Yellow, Yangtze, Indus and Mekong) and hence affect millions of people’s daily lives. Observations show that many glaciers on the Tibetan Plateau have retreated rapidly in the past 30 years (Ding and others, 2006; Ye and others, 2006; Xiao and others, 2007; Yao and others 2007a). However, there are significant regional differences in the ongoing response of Tibetan glaciers to climate change (Yao and others, 2007a, 2012; Bolch and others, 2012; Gardelle and others, 2012; Sorg and others, 2012). The magnitude of glacier retreat increases from the continental interior to the margin of the Tibetan Plateau, and reaches a maximum on the southern Tibetan Plateau, with relative stability or mass gain in the Karakoram. A lack of understanding of the processes affecting the glaciers, the various climatic conditions and extreme topography within the region make projections into the future problematic (Bolch and others, 2012). However, Shi and Liu (2000) estimated future shrinkage of glaciers in China using an empirical relationship between glacier and temperature rise since the Little Ice Age, finding that subcontinental glaciers would lose ~48% of their volume by 2100 under a 3^°C temperature rise scenario. However, little work has been done on projection of glacier mass change on the Tibetan Plateau using flow dynamics models. Here we consider a small but representative glacier in the southern Tibetan Plateau and simulate its evolution over the next 50 years under regional climate model forcing.

Few glaciers on the Tibetan Plateau and in the surrounding regions have detailed geophysical observations, making modeling of their further evolution problematic. Urumqi glacier No. 1 has been modeled with the widely used shallow-ice approximation (SIA) ice-dynamics models (Zhou and others, 2009; Li, 2010). In this paper, a model accounting for all stress components is applied to Gurenhekou glacier, southern Tibetan Plateau (30^°11’ N, 90^°28’ E), to simulate the coupled mechanical and thermodynamical ice dynamics in the present day and predict the evolution of this glacier over the next five decades. In general we would not expect that an approximation to the Stokes equations, such as the SIA, will introduce errors in the volume balance exceeding those caused by the large uncertainties in the climate forcing (Leysinger Vieli and Gudmundsson, 2004). However, Gurenhekou glacier in parts has steep and rugged slopes, which motivated the deployment of a model accounting for all stress components (e.g. Le Meur and others, 2004;Blatter and others, 2011) in order to exclude errors introduced by approximations in the first instance.

The open-source, finite-element method package Elmer/Ice (http://elmerice.elmerfem.org) solves the complete threedimensional (3-D), thermomechanically coupled ice- dynamics equations (a so-called ‘full-Stokes’ model (e.g. Gagliardini and others. 2013)). In this application we solve a coupled thermomechanical time-evolving system (Stokes and heat transfer equation) under the given parameters imposed by the forcing: surface mass balance (SMB), a given value for the surface temperature and the geothermal heat flux at the bedrock.

Gurenhekou glacier is a small, cold alpine-type valley glacier in the southeast part of the Nyainqentanglha range in the central part of the southern Tibetan Plateau (Fig. 1). The region is of special interest for glacio-climatological research as it is influenced by both the continental climate of central Asia and the Indian monsoon system, and is situated at the transition zone between temperate and subcontinental glaciers (Kang and others, 2009; Bolch and others, 2010). The glacier area is rectangular, with a length of 2.5 km, a width of 0.6 km and an area of 1.40 km² (Fig. 2), and the elevation ranges between about 5500 and 6000ma.s.l. (Pu and others, 2006; Ma and others, 2008). The slope of the glacier surface varies from 9.6^° to 14.5^° and has a mean value of 11.3^°. The glacier is smooth and flat at the surface, but steep at the tongue and along the mountain ridges at the sides of the glacier. Gurenhekou glacier is a summer- accumulation type glacier, like most glaciers on the Tibetan Plateau (Ageta and others, 1992; Fujita and others, 2000; Shi and others, 2000).

Fig. 1. The location of the Nyainqentanglha range, lake Nam Co, Gurenhekou glacier, Xibu glacier and Damxiong station. The small rectangle centred northwest of Lhasa in the map of China indicates the location of the study area.

Fig. 2. Image of Gurenhekou glacier from Google maps, with the boundary profile of the glacier (magenta) used in the flow modeling. Nine GPR and GPS tracks were surveyed in 2007, 2008, 2009 and 2011. Tracks in different years are denoted in different colors: red for 2007, cyan for 2008, blue for 2009, green for 2011. For instance, 1–2009 means the first track measured in the year 2009.

Ground-penetrating radar (GPR) and differential GPS measurements were taken during 2007, 2008, 2009 and 2011 (Ma and others, 2008; Fig. 2). The surface elevation was measured along all the tracks shown in Figure 2, and bed elevation only along tracks 2–2009, 3–2009, 1–2008, 2–2008, 1–2007 and 2–2007. Elevations above 5860 m were not surveyed due to terrain hazards, but the ice appears to be rather thin in those regions. The maximum thickness observed was 135 m ~550m down-glacier of the head of the glacier (ice thickness contours in Fig. 8 further below). The quality of measured surface and bedrock elevation is good; crossover analysis of radar lines shows differences in both surface and bed elevations were >4 m.

2. Surface Temperature and Surface Mass Balance on the Glacier

On decadal timescales, regional climate has strong control on glacier surface temperature and SMB, which in combination are the main driving force of the glacier dynamics and are important boundary conditions to the flow model. Therefore, correctly prescribing these two input fields is vital for accurate simulations and predictions.

2.1. Surface temperature

We constructed a surface and bedrock digital elevation model (DEM) for 2007. Surface temperature was estimated using the annual mean air temperature and lapse rates from nine automatic weather stations (AWS) set up on the southern slope of the Nyainqentanglha range (Xie and others, 2010). A temperature inversion exists below elevations of 4950 m, so we confine our data to four AWS above 4950 m to estimate the surface temperature as a function of elevation:

(1)

where T is temperature (K), z is elevation (m) and the lapse rate is –0.0075 Km⁻¹. This regression neglects the temperature offset due to the presence of the glacier influencing local climate, which may range from 0.2^°C to 3.5^°C (Shi and others, 2000). However, since the glacier is relatively small, and the ice-free slopes are extensive (Figs 1 and 2), we neglect this effect. Since the glacier is below pressuremelting point throughout (see the diagnostic model, Section 4), this offset would make little difference to the simulations in any event. Geothermal heat flux is approximated using a measured temperature profile in an ice-core borehole of Naimonanyi glacier, southwestern Tibetan Plateau (Yao and others, 2007b), and taken as 78.6 mW m⁻².

2.2. Surface mass balance

Little information on SMB is available for Gurenhekou glacier, due to the harsh climatic conditions and high altitude. Since there are no meteorological observations on the glacier, we could not use a tailored mass-balance model of the type shown to give excellent results for glaciers in the region (e.g. Mölg and others, 2012). Instead we decided to try three independent methods of estimating SMB. We use SMB terminology in this paper to mean ‘climatic mass balance’, i.e. the sum of the surface and internal mass balances as defined by Cogley and others (2011). Since the firn layer is thin and neglected in dynamics, we refer to SMB in ice equivalent units.

2.1.1. Observation-based SMB

We digitized the measured SMB of Gurenhekou glacier over the 6year period 2004–10 (from a figure published in Yao and others, 2012 supplementary information) and combined it with our surface elevation data to obtain the SMB-altitude profile for 6 years (Fig. 3a).

Fig. 3. (a) SMB of Gurenhekou glacier digitized from supplementary figure S7 in Yao and others (2012) for the 6year period 2004–10. (b) Linear regression of SMB at 5800ma.s.l. on the JJA mean temperature from Lhasa, for the 6year period 2004–10. The solid red curve shows the best-fit SMB, and the dashed curve gives the 1σ confidence interval. (c) The best-fit SMB (red curve) and its uncertainties (the region bounded by the dashed curves) as a function of altitude in 2012 based on JJA Lhasa temperatures, and the best fit for the same analysis using Damxiong station JJA temperatures (blue curve).

As the glacier is of summer accumulation type, the SMB is essentially determined only by the summer (mainly JuneAugust (JJA)) climate. Molg and others (2012) used a physically based energy-balance model to quantify the impact of the Indian summer monsoon (ISM) on Zhadang glacier (30^°28’ N, 90^°38’ E;2.5 km², length 2.7 km) which is located on the northeastern slope of the Nyainqentanglha range. They found that early (late) monsoon onset causes higher (lower) accumulation and reduces (increases) ablation, but has no direct ISM impact on the glacier in the main monsoon season. While it is clear that atmospheric circulation type and precipitation pattern influence SMB, we could not find a statistically significant relationship between variables other than summer temperature and SMB. This is consistent with the findings of Rupper and Roe (2008) who note that ablation in high-precipitation regions (such as the Nyainqentanglha range) is dominated by melt (rather than sublimation), and glacier sensitivity to climate is dominated by air temperature. We used observed JJA mean temperature from the two closest meteorological stations, Lhasa and Damxiong (Fig. 1), as a proxy for glacier temperature with a suitable lapse rate. For each altitude, we linearly regressed SMB on the JJA mean temperature at Lhasa station for the 6 years to produce SMB and its 1σ confidence interval as a function of temperature. As an example, the linear regression of SMB on the JJA mean temperature at 5800 m a.s.l. is shown in Figure 3b. Given the JJA mean temperature in a particular year, the modeled SMB in that year and its uncertainties as a function of altitude can be calculated (Fig. 3c). The regression results for Damxiong station are very close to those using Lhasa station, and well within the 1σ confidence interval (Fig. 3c).

2.2.2 Model-based SMB

Since the observations are over a relatively short period, we also tried computing the SMB by adapting a mass-balance model used on a nearby glacier. Caidong and Sorteberg (2010) used an energy-balance model to simulate the mass balance of Xibu glacier (30^°23’ N, 90^°36’ E), which is a large glacier (18.3 km², length 12.7 km) in the central part and on the southern slope of the Nyainqentanglha range and 25 km northeast of Gurenhekou glacier. Their model produces three distinct mass-balance regions as a function of altitude. The northern and the southern slopes of the Nyainqentanglha range have different local climates in terms of temperature, relative humidity and radiation (You and others, 2007). Since both Xibu and Gurenhekou glaciers are on the southern slope and face southeast, it is reasonable to suppose that both are subject to a similar local climate, which makes the SMB of Xibu glacier a better proxy than those of glaciers on the northern slope (e.g. Zhadang glacier). Therefore, we assume that Gurenhekou glacier exhibits a similar mass-balance profile to Xibu glacier, and we prescribe a mass-balance gradient and SMB for each of these three regions. We can test this hypothesis using the observed change in glacier surface elevation and the stake mass-balance measurements neglecting the ice dynamics (Fig. 4a). The annual SMB is a function of altitude (z) and equilibrium-line altitude (ELA)

(2)

The unit is m ice eq. a⁻¹.

The ELA of Gurenhekou glacier in 2008 is ~5800m (Yao and others, 2012). We can estimate the dependence of ELA on climate using the six balance years 2004–10 (Yao and others, 2012) and observed JJA temperature and JJA precipitation at Lhasa station during 2005–10 (Fig. 4b). We find that a 1 K air temperature rise results in a shift of ELA by 79 ± 30 m on Gurenhekou glacier. In contrast, the same analysis using the Damxiong temperature data gives an ELA temperature sensitivity of 135 ± 88 m for a 1 K warming. We evaluate how much these different ELA sensitivities affect the evolution of the glacier over time in Section 3.3.2. There is no statistically significant dependence of ELA on precipitation. Hence, ELA in the kth year starting from 2008 was estimated by

(3)

where ΔT is the net change of JJA temperature between 2008 and the kth year and α is the sensitivity of ELA to temperature change.

Fig. 4. (a) Annual SMB modeled by Eqn (2) with ELA = 5800 m (black curve). The grey region corresponds to the altitude outside the range of Gurenhekou glacier (5500~6000 m a.s.l.). The cyan curve is the rate of annual average surface change observed between 2007 and 2011. The magenta circles represent the median value of SMB from stake measurements (Yao and others, 2012), and the magenta bar widths show their variability. The vertical bars represent the change in ELA for a 1^°C change in summer temperature (a in Eqn (3)) calibrated using Lhasa JJA temperatures (red) and Damxiong JJA temperatures (blue). (b) The observed ELA and JJA mean temperature at Lhasa and linear regression line (red symbols and line) during the 6year period 2004–10, and the same for Damxiong values (blue).

2.2.3 PDD-based SMB

SMB is estimated as the difference between accumulation and ablation, which we parameterize as functions of local temperature and precipitation on the glacier. To simulate future climate impact on SMB we use the ‘delta’ approach which is commonly used in statistical downscaling climate simulations (e.g. Hay and others, 2000). The natural climate variability is better preserved in observational data than produced by climate models, We use the daily temperature and precipitation records for the period 2008–11 from Damxiong meteorological station to estimate variability as this is a higher-elevation station than Lhasa (4200 and 3650 m respectively). We use the temperature fluctuations over the 4year period (2008–11) added in a cyclic fashion to the temperature trend from regional model results and average temperature on the glacier from the AWS data as described in Section 2.1. We assume a precipitation/elevation (increase) lapse rate gradient of 5% (100 m)⁻¹ based on the observations and parameterizations in Li (1986) from the region.

Accumulation at elevation z, Acc(z), is estimated using snow precipitation p_snow(z):

Acc(z) = ρ_water/ρ_ice p_snow(z)

(4)

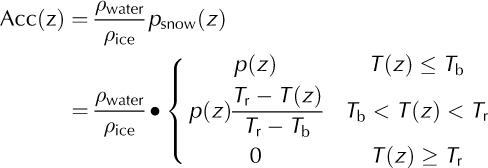
where p_water = 1000 kg m⁻³ and p_ice = 910 kg m⁻³ are the density of water and ice, respectively. T_b = –1^°C is a threshold air temperature below which all precipitation is snow, and T_r = 3^°C is a threshold air temperature above which all precipitation is rain (Caidong and Sorteberg, 2010). Ablation is parameterized by the positive degree-day (PDD) method (Braithwaite, 1984). Zhang and others (2006) note that the degree-day factor β_ice relating ice melt to temperatures increases from northwest to southeast on the Tibetan Plateau, reflecting higher values in warmer and wetter places. Their mean value was 7.1 mmd^{−1 °}C⁻¹, while Rupper and Roe (2008) suggest a value of 10mmd^{−1 °}C⁻¹ for their eastern region which covers Gurenhekou glacier. Kirchner and others (2011) explored the importance of 3ice with values of 12 and 7 mm d^{−1 °}C⁻¹ and found significant differences in paleo-glacier extent when using the two values in SIA simulations of Tibetan glaciation history. Here we ignore the firn layer and use a relatively low factor of 8mmd^{−1 °}C⁻¹, which we show in Section 3.3.2 still produces far too negative a mass balance. The modeled SMB variability in the 4 year period 2008–11 is shown in Figure 5, with only one of the four years having a net positive balance.

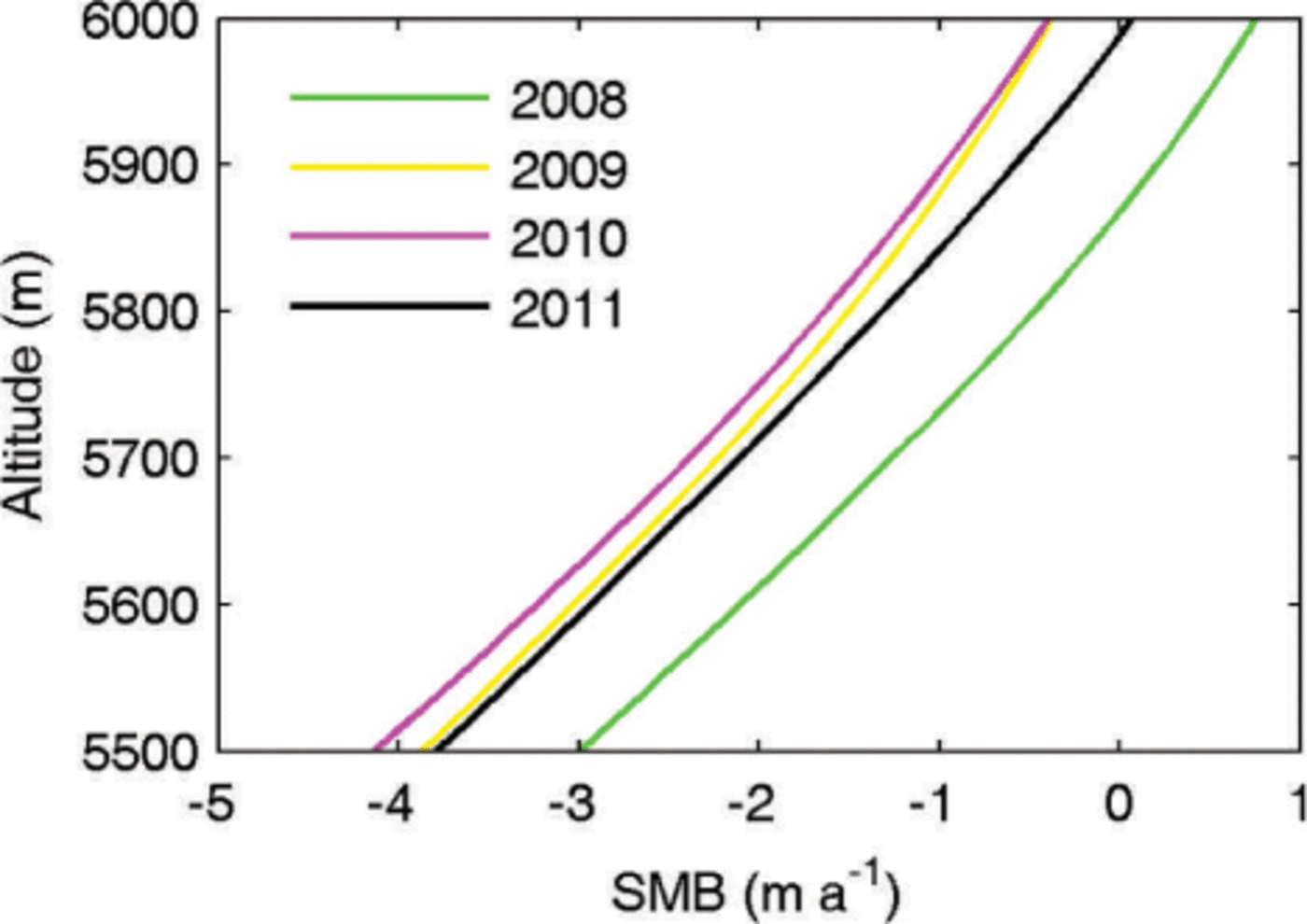
Fig. 5. The PDD-based SMB for the 4 year period 2008–11, using Eqn (4) and β_ice = 8mmd^{−1 °}C⁻¹.

3. Modelling Approach

3.1. Numerical ice flow model Elmer/Ice

The finite-element model Elmer/Ice can solve local and larger-scale ice flow problems of high mechanical and physical complexity, including the full-Stokes model. The equations implemented in the thermomechanically coupled full-Stokes model are well published (e.g. Zwinger and Moore, 2009). We prescribe a no-slip boundary condition for velocity at the bedrock, and a stress-free condition at the glacier surface. The temperature at the glacier surface is taken as a function of elevation (Eqn (1)). At the bedrock, a Neumann boundary condition for the temperature is set and the geothermal heat flux is taken as 78.6 mWm⁻², as described earlier. Equations in steady state (assuming all time derivatives vanish) are solved using a fixed point iteration scheme.

For the prognostic run, the kinematic boundary condition is applied at the surface because the surface elevation changes with time:

(5)

where h is the surface elevation and (u _x, u _y, u_z) denotes the ice flow velocity. The full-Stokes model and the kinematic boundary condition (Eqn (5)) were solved at each time-step. Consequently, the surface DEM evolved every year due to ice movement and SMB, and the resulting change of surface elevation changed the SMB.

3.2. Geometry set-up and meshing

We constructed a DEM of the surface and bedrock by interpolating the GPS and radar profiles (Fig. 2) on a twodimensional (2-D) footprint with mesh resolution of 30 m. Both the surface and bedrock profiles were smoothed in order to avoid artificial roughness introduced by the very limited points of the profiles, and were also smoothly extended to the boundary defined from satellite images. The smoothing has negligible impact on the simulation results. Using the surface and bedrock DEM and the boundary shape, the 3-D geometry of Gurenhekou glacier was built by extruding the 2-D footprint from the bedrock to the surface containing 15 terrain-following layers of varying thickness (Fig. 6). The bedrock slope is >16.7^° along the direction of the center line in the top part of the glacier, and has a large variation from 0^° to 38.7^° in the transverse direction since this glacier is located in a valley. We applied a refinement of layer thickness towards the bedrock to better capture the highest deformation rates.

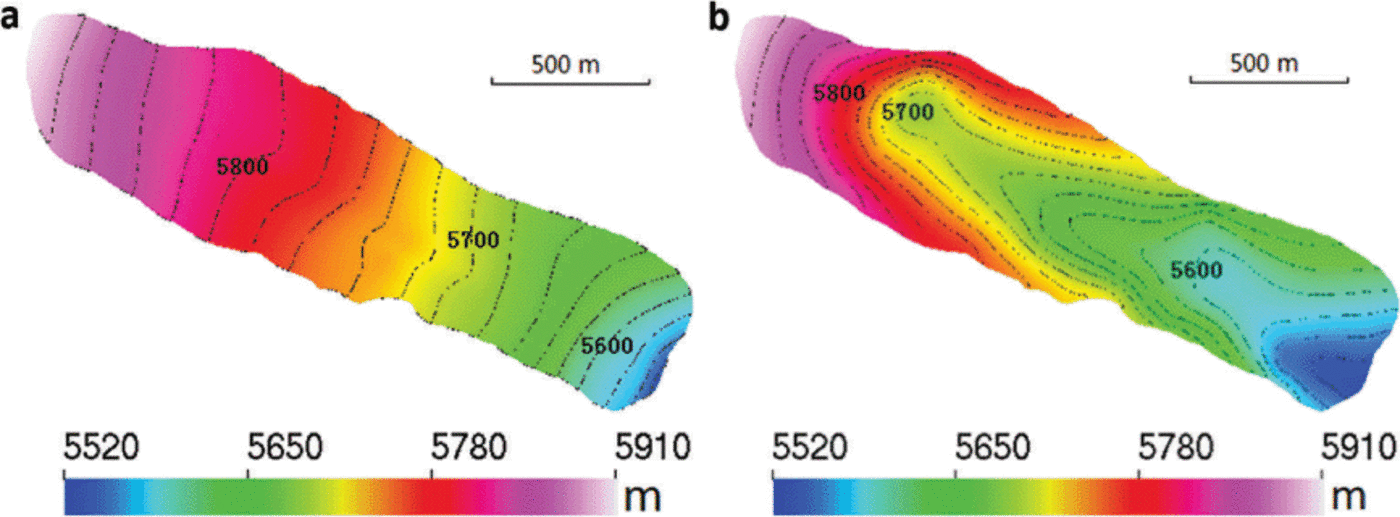
Fig. 6. The surface (a) and bedrock (b) geometry of Gurenhekou glacier. The contour interval is 20 m.

4. Model Experiments

We perform two kinds of simulations. The first is a diagnostic simulation, i.e. assuming steady state with constant surface elevation. We also perform prognostic simulations with differing 21st-century temperature increases to produce mass-balance uncertainties on the glacier as functions of elevation and time. To produce estimates of warming rate representative of the latter half of the 20th century and the first half of this century, we use results from the Regional Climate Model Version 3.0 (RegCM3). The horizontal grid spacing of RegCM3 is 25 km, and the model domain covers all of China and surrounding east Asian areas (Gao and others, 2012). RegCM3 reproduces the observed spatial distribution of surface air temperature and precipitation well, though there is cold bias of 1–2^°C between the modeled and observed surface air temperature on the Tibetan Plateau in JJA (Gao and others, 2012).

Since the glacier is of summer accumulation type, conditions in JJA are far more important than those in the rest of the year. Figure 7 shows summer surface temperature evolution from 1951 to 2100 for the nine 25 km × 25 km gridboxes centered on the cell containing Gurenhekou glacier. Since we are interested in climatic impacts rather than interannual variability in SMB caused by factors such as monsoon intensity, we focus on the smoothed response to temperature rises. Figure 7 shows that two simple linear rates (Ṫ) of temperature rise fit the past simulated temperature history and the simulated future temperature rise. The historical simulation rate for the period 1955–2005 is 2^°C(100a)⁻¹. This is also the observed temperature rise rate (Caidong and Sorteberg, 2010) at Lhasa station (the station was established in 1955), so we are confident that the regional model reproduces observed temperature trends well in this area, and that this rate represents the ongoing situation on the glacier. The slope of the RegCM3 result for the period 2005–2100 is 5^°C(100a)⁻¹. We use both warming scenarios for prognostic simulations.

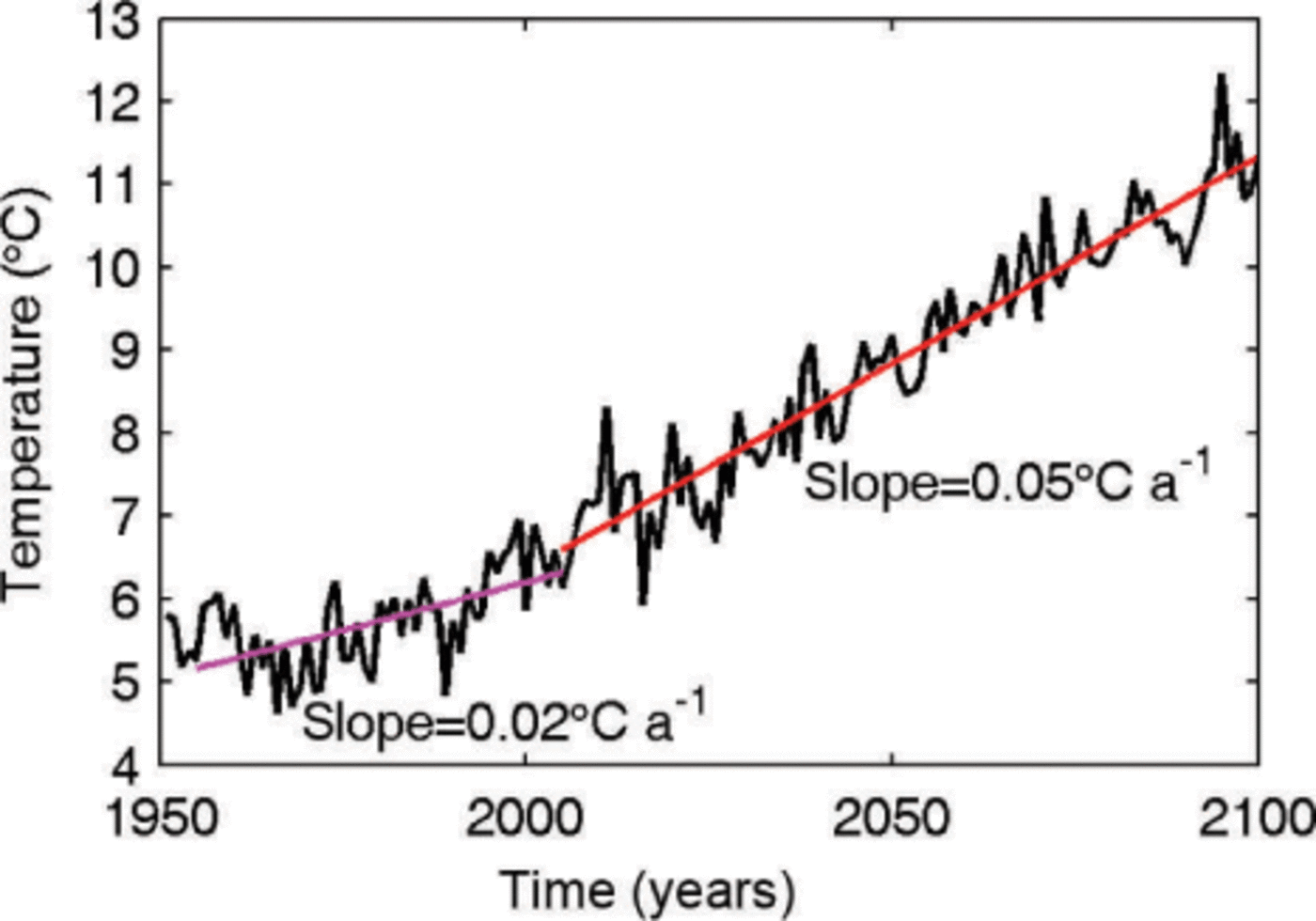
Fig. 7. JJA mean air temperature from RegCM 3.0 simulations for mean temperatures of the nine gridcells surrounding Gurenhekou glacier. The linear warming trends for the periods 1955–2005 and 2005–2100 are drawn in magenta and red, respectively.

4.1. Diagnostic simulation

The initial surface DEM was built for the year 2007. The surface was kept constant at the 2007 geometry. The thermomechanically coupled model then produces a ‘diagnostic’ simulation for this geometry. Figure 8 shows the simulated surface velocity. The maximum speed found is 1.9 m a⁻¹ around the middle of the glacier. The surface velocity in the southern terminus is ~0.4ma⁻¹ due to the steep surface slope there. The temperature distribution at the bedrock and along the center line in Figure 9 shows that the whole glacier is below the pressure-melting point. The highest temperature is about –1.6^°C, justifying the freeze-on condition we imposed in the model set-up. The computed components of the deviatoric stress tensor on both the surface and bedrock are shown in Figure 10. The shear stresses in the horizontal plane (τ _xz, τ _yz) and the normal stress deviators (τ _xx, τ _yy, τ _zz) are of a similar order of magnitude to the shear stress in the vertical plane (τ _xy), demonstrating the value of using a full-Stokes model. We also performed a ‘surface relaxation’ experiment (Zwinger and Moore, 2009) over 10 years without SMB forcing to determine if parts of the glacier exhibit unrealistic surface velocities that are likely caused by errors in the surface or bedrock DEMs. We find the maximum deviation of surface velocities is only 0.01 ma⁻¹. Thus, this procedure did not detect systematic errors in the DEMs and hence we chose to run on the initial glacier geometry.

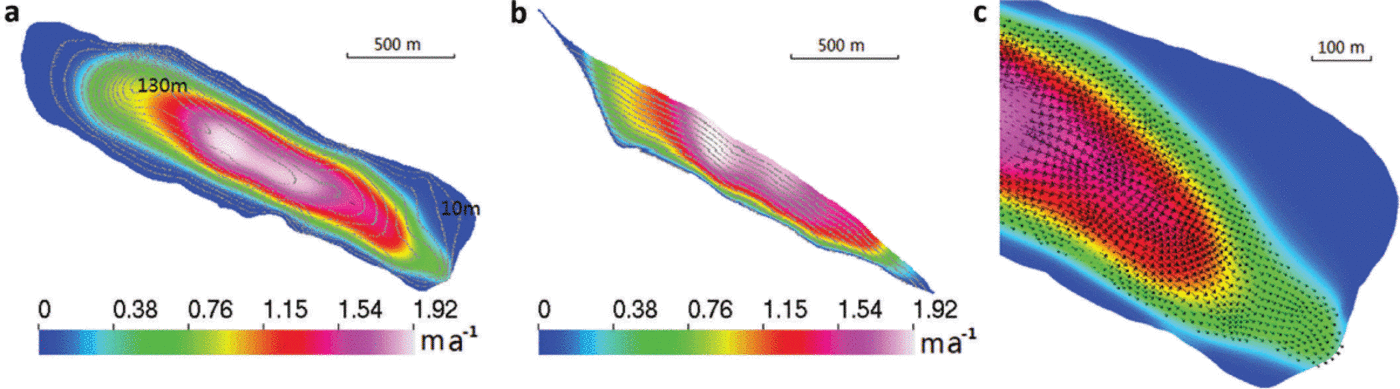
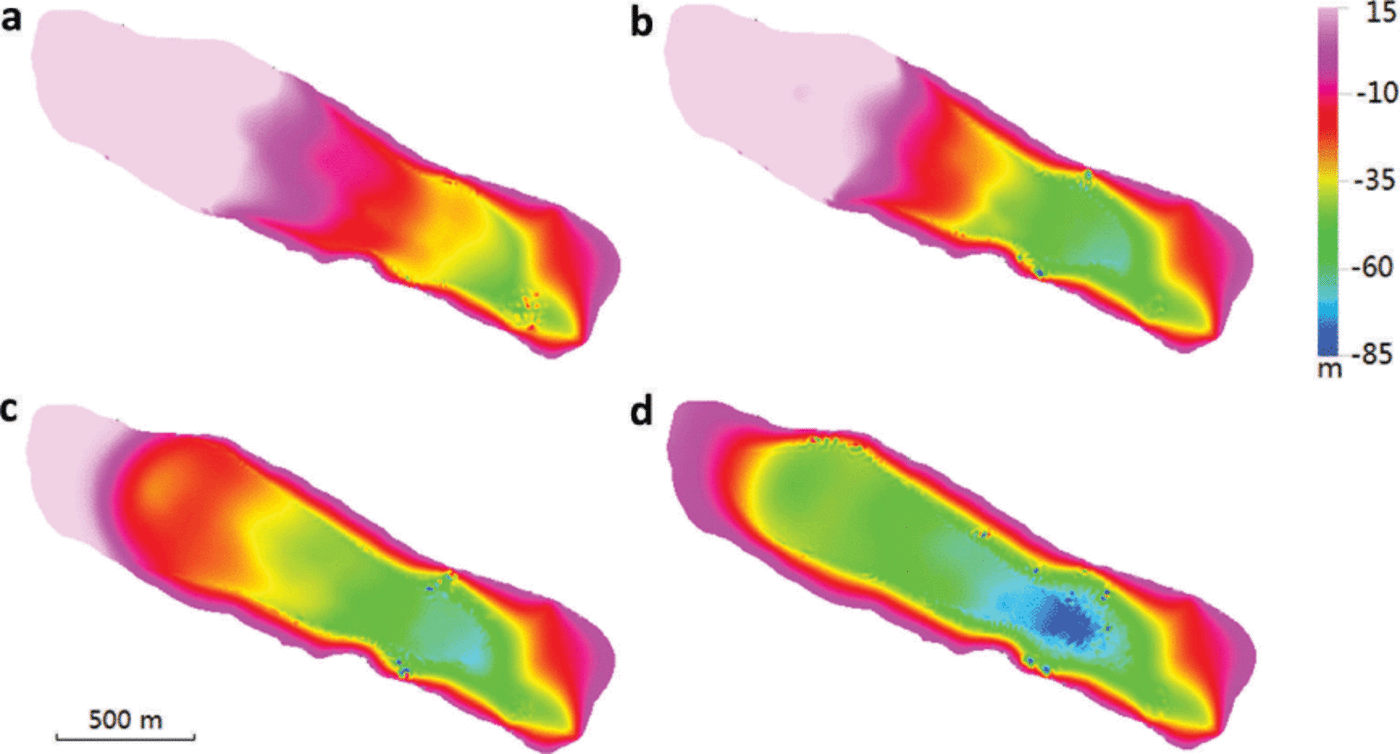
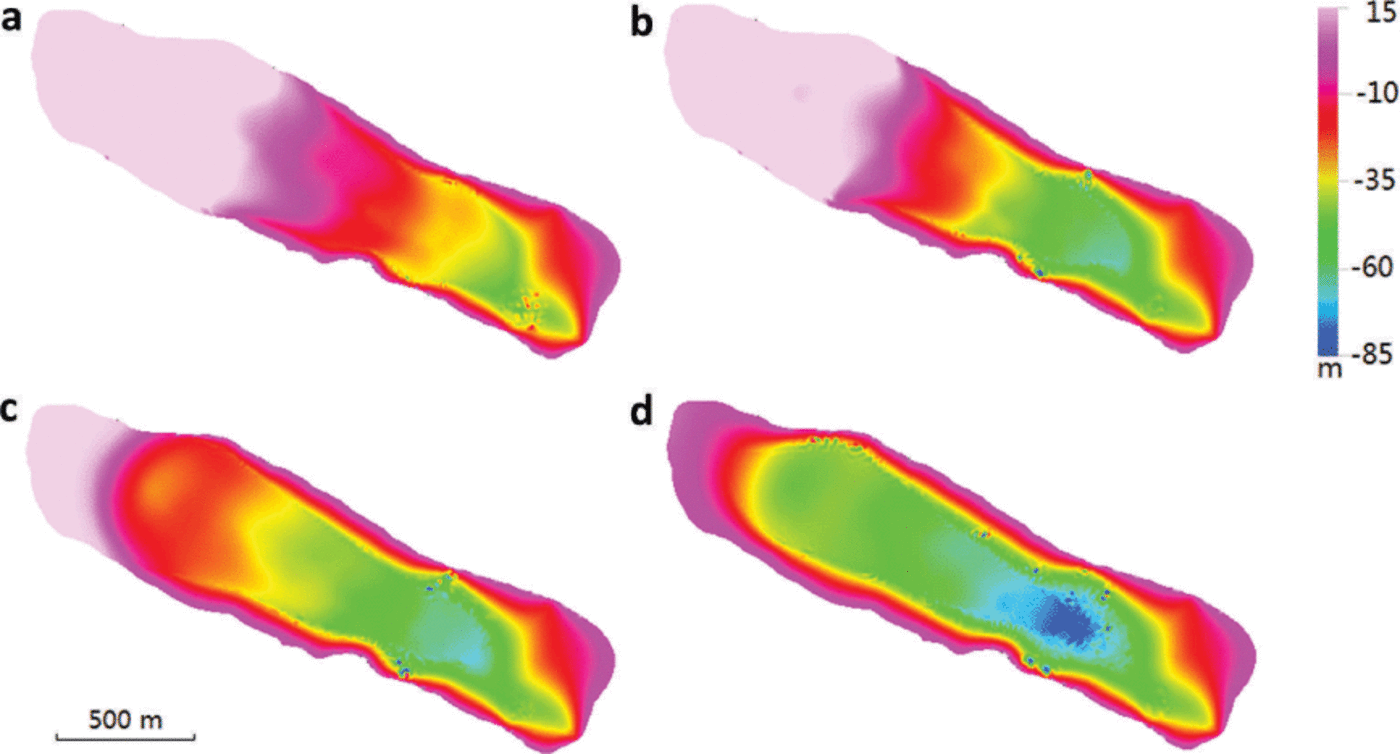
Fig. 8. The absolute value of ice flow velocity on the surface (a), on the transect along the central line (b), and enlarged flow vector map in the lower part of the glacier surface (c) of the diagnostic run (the vertical coordinate is stretched by 3). The contours indicate the ice thickness in 10 m intervals from 10 to 130 m.

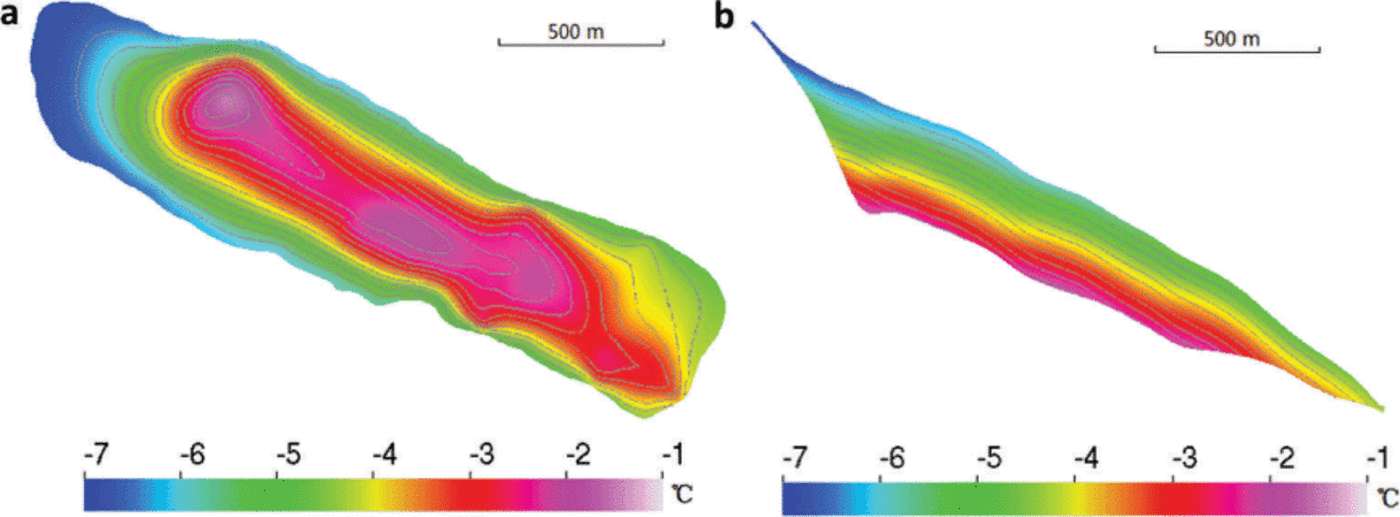
Fig. 9. Distribution of temperature relative to pressure-melting point at the bedrock (a) and along the center line (b) of the diagnostic run (the vertical coordinate is stretched by 3). The contours indicate the ice thickness in 10m intervals from 10 to 130m.

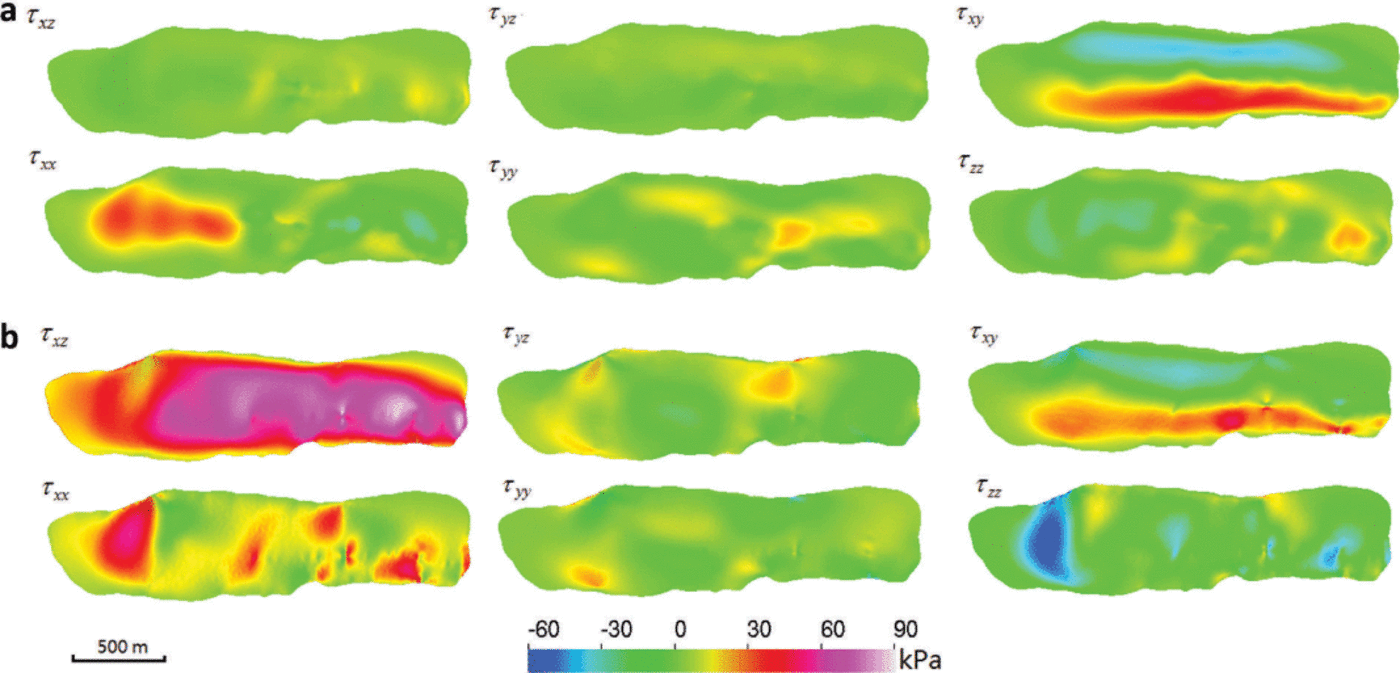
Fig. 10. The computed components of the deviatoric stress tensor at the surface (a) and bedrock (b) in the diagnostic run. These results indicate that longitudinal deviatoric stresses are of same order of magnitude as τ _xz and τ_yz, the only components accounted for in SIA models.

4.2. Prognostic simulations with Ṫ = 0.02 ka⁻¹ and Ṫ = 0.05 ka⁻¹

The evolution of the glacier is modeled by ‘prognostic’ simulations. The steady-state solution from the diagnostic run was taken as the starting point (initial condition) for the prognostic simulation from 2008 to 2057. Using the JJA mean temperature increase rate 0.02 or 0.05 Ka⁻¹, the observation-based SMB and its upper and lower 1σ confidence interval are obtained for the whole altitude range and for each year by using the SMB parameterization described in Section 2.2.1. Model-based SMB evolution using data at both Lhasa and Damxiong stations and PDD- based SMB evolution was also calculated separately as discussed in Sections 2.2.2 and 2.2.3. This makes six different SMB realizations we can drive with temperatureforcing scenarios. We investigate the uncertainties of glacier change over the next five decades based on the spread of the six SMB experiments in each warming scenario.

For both the 0.02 and 0.05 Ka⁻¹ warming scenarios the upper SMB calculated using the observation-based method in Section 2.2.1 leads to glacier growth (Fig. 11). This is unrealistic behavior since observational evidence proves that the glacier has shrunk in recent years (Pu and others, 2006; Yao and others, 2012). Hence we can reject those SMB formulations that produce a growing glacier in a warming climate.

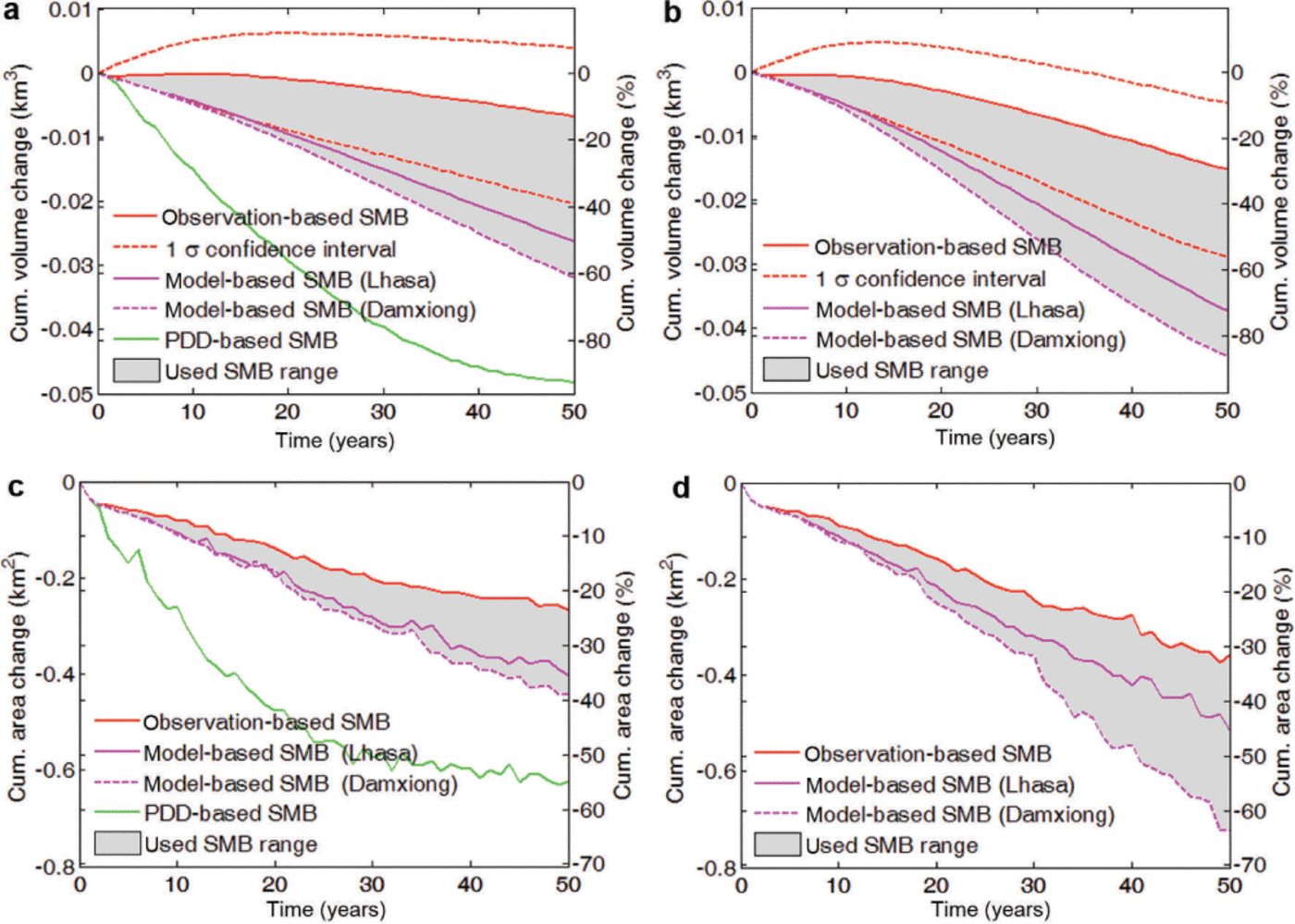
Fig. 11. Cumulative volume changes (a, b) and cumulative area changes (c, d) of Gurenhekou glacier as functions of time In the Ṫ = 0.02 Ka¹ (a, c) and Ṫ = 0.05 Ka⁻¹ (b, d) warming scenario based on different SMB formulations. Observation-based SMB (red curve) and 1σ margins (dotted) defined in Section 2.2.1; model-based SMB using data from Lhasa (magenta solid curve) and Damxiong (dotted) defined in Section 2.2.2; PDD-based SMB (green) defined in Section 2.2.3. Grey region denotes outcome from realistic SMB range.

Using topographic maps and aerial photographs (Pu and others, 2006), the annual average retreat rate of this glacier was ~7.0 m a⁻¹ from the end of the Little Ice Age to the 1970s, and 8.3 m a⁻¹ during 1974–2004. In situ observations showed that the glacier retreated at 9.5 ma⁻¹ from 2004 to 2005 and 17.0m a⁻¹ from 2005 to 2006 (Pu and others, 2006). The observed rapid retreat between 2005 and 2006 is likely due to interannual climate variability and stochastic variability in local ice thickness.

The computed glacier terminus using both the best-fit observation-based SMB and model-based SMB are very similar in the first 25 years (Fig. 12). The terminus of the glacier in the northeast retreats more intensively than that in the southwest due to thinner ice there (note the ice thickness contour in Fig. 8). The maximal retreat rate is ~13ma⁻¹ in the northeast of the tongue and 4.6 m a⁻¹ in the southwest for the period 2008–32. The annual averaged retreat rate along the central flowline is ~9.1 ma⁻¹ using a temperature rise rate of Ṫ = 0.02 Ka⁻¹, and 9.6 m a⁻¹ using Ṫ = 0.05 Ka⁻¹. This is consistent with the observed trend for Gurenhekou glacier over the past decade and also the retreat rates of ~10 m a⁻¹ for five glaciers in the Nyainqentanglha range from 1976 to 2009 (Bolch and others, 2010).

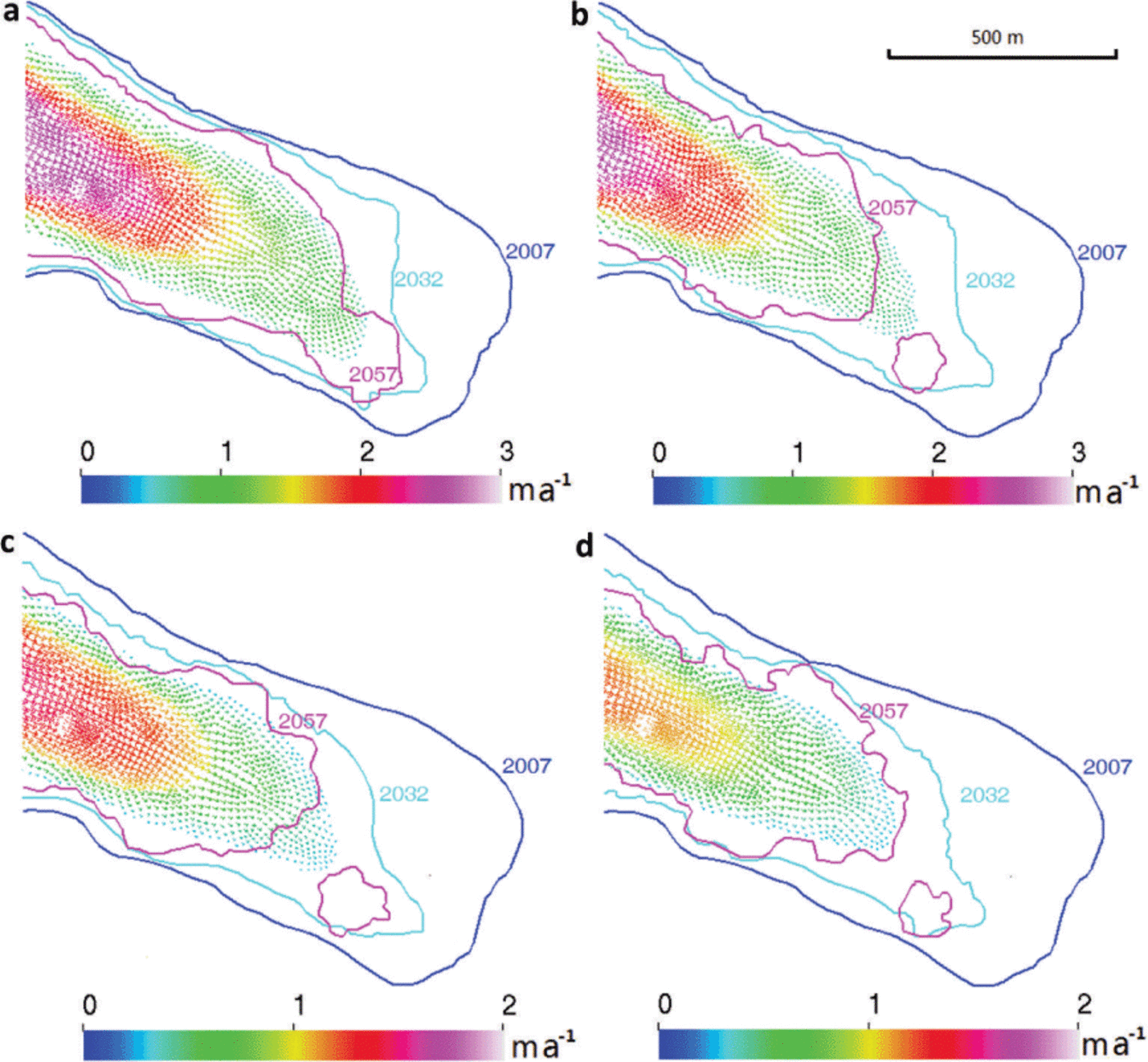
Fig. 12. flow velocity (colored vectors) In the year 2032 of prognostic simulations, outlines In 2007 (blue curve) and the computed position of outlines in 2032 (cyan) and 2057 (magenta) using (a, b) the best-fit observation-based SMB (red curve in Fig. 11a and b) and (c, d) the model-based SMB (magenta curve in Fig. 11c and d) with Ṫ = 0.02 Ka⁻¹ (a, c) and Ṫ = 0.05 Ka⁻¹ (b, d).

The modeled retreat rate using PDD-based SMB in the first 20 years is 18 m a⁻¹ along the central flowline, which is more than twice the observed rate over the past three decades. The PDD model also simulates much more ice volume and area loss (2% a⁻¹) than the other two SMB parameterizations (Fig. 11), and these losses are far larger than observed in glaciers in the region (up to 0.7% a⁻¹; see below and Section 5). Therefore, we judge that the PDD-based SMB formulation does not reproduce observed glacier behavior given past forcing, and hence reject this model as a reliable prognostic indicator of future glacier condition. Therefore, the credible SMB range we use in the following is assembled from the interval between the mean observation-based SMB derived in Section 2.2.1 and the modeled SMBs calculated in Section 2.2.2. This SMB range in turn produces glacier evolution defined by the region in Figure 11, and we take a mean between the upper and lower limits as our best estimate.

With the SMB range defined above, the annual averaged volume shrinkage rate is 0.7± 0.5%a⁻¹ with Ṫ = 0.02Ka⁻¹, and 1.1 ±0.6%a⁻¹ with Ṫ = 0.05 Ka⁻¹. Faster-rising temperatures cause greater surface thinning and thus more intensive volume loss (Fig. 11). The surface-elevation changes from 2008 to 2057 with two SMBs are illustrated in Figure 13. The maximum difference in surface elevation change over the SMB uncertainty range is 45 m with Ṫ = 0.02 K a⁻¹, and 65 m with Ṫ = 0.05 K a⁻¹.

Fig. 13. Surface elevation change from 2008 to 2057 of prognostic simulations with Ṫ = 0.02 Ka¹ (a, c) and Ṫ = 0.05 Ka¹ (b, d) and by using the best-fit observation-based SMB (red curve in Fig. 11a and b) and the model-based SMB (magenta curve in Fig. 11c and d).

The termini in 2007, 2032 and 2057 using two SMBs are shown in Figure 12. In the second 25 year period, the annual average retreat rate along the central flowline is ~4.8ma⁻¹ using Ṫ = 0.02 Ka⁻¹, and 6.7 m a⁻¹ using Ṫ = 0.05 Ka⁻¹.

The annual average area reduction rate is 0.6 ± 0.2% a⁻¹ with Ṫ = 0.02Ka⁻¹, and 0.9±0.3%a⁻¹ with Ṫ = 0.05Ka⁻¹. The model-based SMB results in more area loss than the observation-based SMB parameterization (Fig. 11), with the largest differences in the upper glacier. One reason for this difference is that the ELA variation is both very sensitive to air temperature and quite uncertain. In Eqn (3) we used a coefficient of 79 m K⁻¹ or 135 m K⁻¹, which leads to much of the glacier being subject to ablation by mid-century and quickly exposes bedrock in marginal regions. The SMB obtained in Section 2.2.2 has larger relative uncertainties at the upper glacier than in other parts due to lack of constraining data, but the region only makes up a small fraction of the whole surface. The area reduction estimates we derive are much greater than annual area change observed in the southeast Nyainqentanglha range. Over the period 1980–2001 Yao and others (2012) found a rate of –0.17% a⁻¹, and Bolch and others (2010) found –0.25% a⁻¹ during 1976–2001 based on remote-sensing images and maps. However, our estimates are similar to the –0.7%a⁻¹ from Frauenfelder and Kääb (2009) over a similar period. We discuss these differences further in Section 5.

The surface velocity pattern of the ice flow looks similar in each year. The surface velocity maximums increase when SMB models build the accumulation area and thin the ablation area, but velocities decrease when most of the glacier (except the thin top) is subject to ablation. Basal temperatures remain below the pressure-melting point throughout the period 2008–57.

In these simulations we limited the maximal surface increase at any point on the glacier to 15 m. We chose to do this because the valley glacier is physically constrained from growing above the level of the surrounding mountain ridge and side-walls. If the glacier did grow to that level, the flow geometry would change dramatically as overflow out of the valley would occur (with no geomorphological evidence of it having done so – a further reason to reject the upper SMB realization in Fig. 11). The new geometry would affect the snow accumulation pattern and effectively destroy the basic assumptions of the mass-balance model. Hence we make the physically realistic limitation that the glacier does not outgrow its restraining walls.

5. Discussion and Conclusion

Suites of prognostic simulations have been made for the period 2008–57 using a range of SMB formulations on the glacier for two warming scenarios rates of 0.02 and 0.05 Ka⁻¹. SMB is parameterized using three different methods and six years of observational data. We reject some SMB realizations that result in unrealistic glacier volume change.

For the first 25 year period 2008–32, the computed retreat rate along the central flowline of Gurenhekou glacier is 9.1 ± 1.0 m a⁻¹ using Ṫ = 0.02Ka⁻¹, and 9.6 ± 1.0 m a⁻¹ using Ṫ = 0.05 Ka⁻¹, which is consistent with the trend observed over the past decade. In both warming scenarios the retreat rate along the central flowline is slower in the second than in the first 25 year period, but the area change rate and volume shrinkage rate are almost the same over the whole five decades. Although there are only slight differences in terminus retreat rates, there are more noticeable differences in annual average area loss and volume change rates between the two warming scenarios. The annual average area reduction rate is 0.6± 0.2%a⁻¹ with Ṫ = 0.02 Ka⁻¹, and 0.9 ± 0.3% a⁻¹ with Ṫ = 0.05Ka⁻¹. The annual average volume shrinkage for the period 2008–57 is about 0.7±0.5%a⁻¹ using Ṫ = 0.02 Ka⁻¹, and 1.1 ±0.6%a⁻¹ using T = 0.05 Ka⁻¹.

In this paper, we have used a sophisticated flow model, but it is not practical to apply this model to many other glaciers in Tibet (or mountain regions in general) because of the difficulty in mapping bedrock topography. We showed in Section 3.3.1 and Figure 10 that the full-Stokes model is more appropriate and reliable than the SIA, but it is reasonable to ask how significant is the dynamic contribution to mass loss compared with shrinkage in situ that would result from changing climate without ice flow. We therefore made a prognostic simulation without ice dynamics for Gurenhekou glacier with temperature increasing at a rate of 0.02 Ka⁻¹. We find that the volume loss over 50 years is 13% with dynamics and 19% without dynamics by using observation- based SMB, and the volume loss with or without dynamics is almost the same using model-based SMB (Fig. 14). Therefore, for this small and thin glacier with low surface speed, the ice dynamics plays a much less significant role than SMB. However, this may not be the case for larger glaciers since flow velocity increases rapidly with increasing thickness (perhaps by the third or fourth power depending on geometry). But probably for many smaller glaciers, even on steep slopes, neglecting ice flow will not be a bad approximation for the purpose of mass and volume loss estimates.

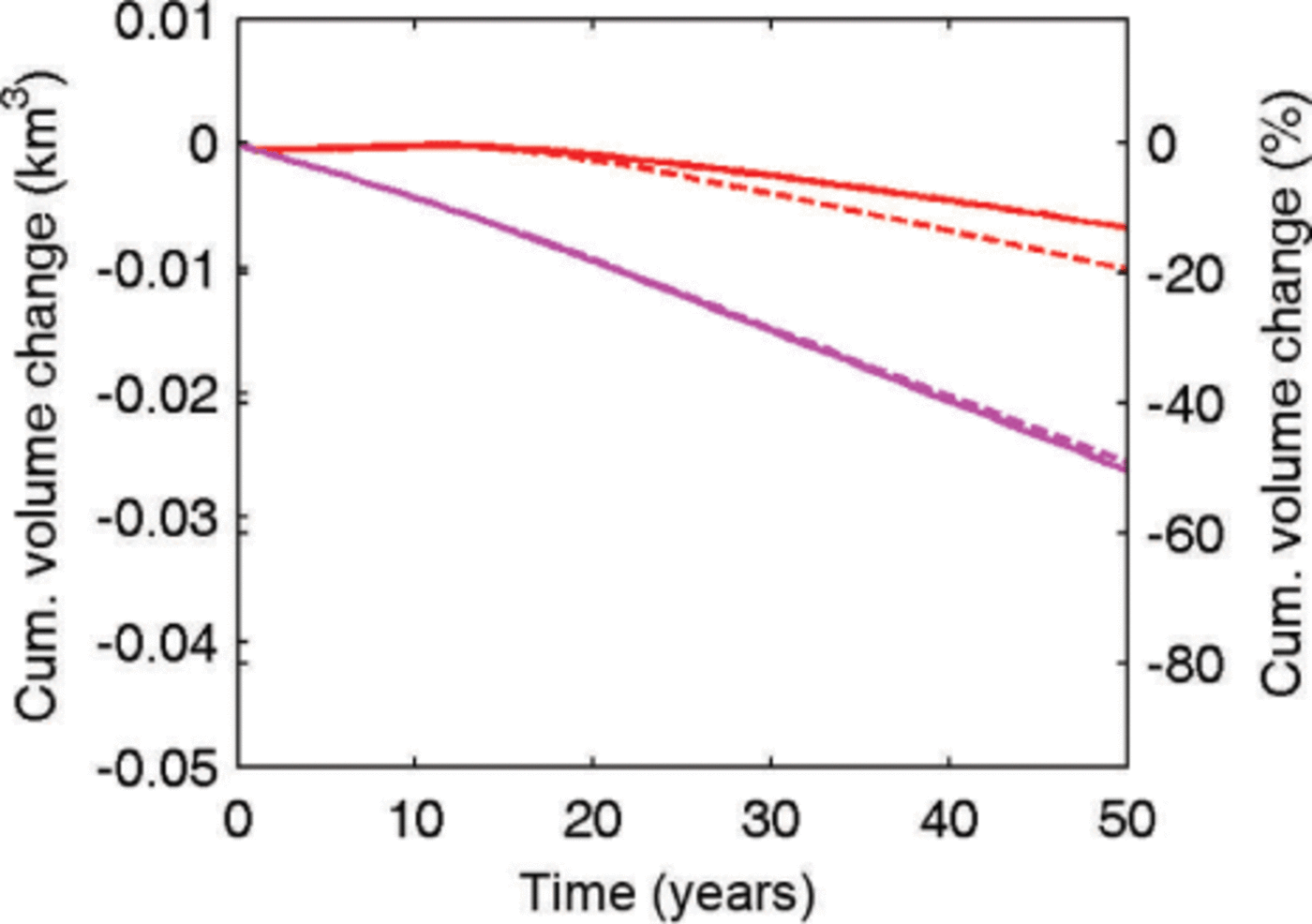
Fig. 14. Cumulative volume changes of Gurenhekou glacier as functions of time with ice dynamics (solid curves) and without (dashed curves) in the Ṫ = 0.02 Ka⁻¹ warming scenario. The red and magenta curves represent the cumulative volume changes using the best-fit SMB based on observations (red curve in Fig. 11) and the model-based SMB (magenta curve in Fig. 11), respectively.

Bolch and others (2010) report that only ~40 out of 960 glaciers in the Nyainqentanglha range are >1 km² in area, though they make up ~28% of the total glaciated area. Most glaciers of the Nyainqentanglha range are 0.1–0.5km² in extent, while glaciers between 0.5 and 1.0km² cover a larger area and most of them face east (Gurenhekou glacier faces southeast). The median elevation of the glaciers is ~5820m, and the majority of them terminate around 5600 m. Therefore, Gurenhekou glacier is typical in many respects of a large number of glaciers in the Nyainqen- tanglha region: in its size, aspect ratio and elevation range. Smaller glaciers will tend to react faster to climate warming than larger ones both because of their larger surface-area to volume ratio and their greater sensitivity to extreme years.

Bolch and others (2010) estimated that areal loss rates were ~0.25%a⁻¹ across the whole Nyainqentanglha range for the period 1976–2001. This rate is significantly lower than area loss rates of 0.7% a⁻¹ for the southeast Nyainqentanglha range (Frauenfelder and Kaab, 2009). It is clear that some of these differences arise in mapping glaciated area with inconsistencies in defining termini on debris-covered or seasonal-snow-obscured glaciers. Detailed analysis of five glaciers by Bolch and others (2010) showed an increased areal loss rate between 2001 and 2009 of 0.5% a⁻¹, but with large variations of 0.16–0.84% a⁻¹.

Reasons for differences in mass wastage estimates also include varying climate across the mountain range (Shang-guan and others, 2008), debris cover which provides insulating cover on small scales but can cause accelerated mass loss on larger scales (e.g. Benn and others, 2012), and general stochastic variability between glacier responses to climate forcing. In the Nyainqentanglha range, only ~29 glaciers have significant debris cover (Bolch and others, 2010), and recent observations of glacier thinning rates on the Tibetan Plateau indicate similar rates for both clean and debris-covered glaciers (Gardelle and others, 2012;Kaab and others, 2012). Hence, differences in debris cover do not seem to be the cause of different estimates of ongoing mass loss.

There is a difference in climate between the northeast and southwest sides of the Nyainqentanglha range (Shangguan and others, 2008), with the southeast side receiving more snowfall than the northwest side and also more direct radiation; at present the two sides have similar average areal loss rates (Shangguan and others, 2008;Bolch and others, 2010). For the future, regional climate models suggest only modest increases in precipitation, but large temperature rises. Hence, it is likely that direct radiation will lead to the southerly-facing glaciers suffering accelerated mass loss. Furthermore using the past as a guide to future change may not be reliable, as decreases in surface albedo from deposition of anthropogenic pollutants are becoming more significant (Ramanathan and Carmichael, 2008;Xu and others, 2009). Over Tibet as a whole, total volume is likely dominated by ice in large glaciers. These glaciers, being thicker, will suffer proportionally less ice wastage per year and will remain well past the end of this century.