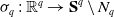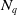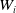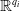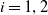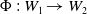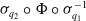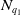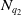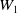1. Introduction
Any subset
![]() $S$
of
$S$
of
![]() ${\mathbb{R}}^q$
is equipped with the outer metric structure, where the distance between points of
${\mathbb{R}}^q$
is equipped with the outer metric structure, where the distance between points of
![]() $S$
is their distance in
$S$
is their distance in
![]() ${\mathbb{R}}^q$
. Thus, (outer) Lipschitz mappings
${\mathbb{R}}^q$
. Thus, (outer) Lipschitz mappings
![]() $S_1 \to S_2$
, for
$S_1 \to S_2$
, for
![]() $S_i$
a subset of
$S_i$
a subset of
![]() ${\mathbb{R}}^{q_i}$
, are well defined.
${\mathbb{R}}^{q_i}$
, are well defined.
The inverse of the stereographic projection of the unit sphere
![]() ${\textbf{S}}^q$
of
${\textbf{S}}^q$
of
![]() ${\mathbb{R}}^{q+1}$
onto
${\mathbb{R}}^{q+1}$
onto
![]() ${\mathbb{R}}^q$
with center the north pole
${\mathbb{R}}^q$
with center the north pole
![]() $N_q = (0,\ldots,0,1) \in{\mathbb{R}}^q\times{\mathbb{R}}$
is denoted
$N_q = (0,\ldots,0,1) \in{\mathbb{R}}^q\times{\mathbb{R}}$
is denoted
![]() $\sigma _q \,:\,{\mathbb{R}}^q \to{\textbf{S}}^q\setminus N_q$
. Let
$\sigma _q \,:\,{\mathbb{R}}^q \to{\textbf{S}}^q\setminus N_q$
. Let
![]() $\widetilde{S}$
be the closure in
$\widetilde{S}$
be the closure in
![]() ${\textbf{S}}^q$
of
${\textbf{S}}^q$
of
![]() $\sigma _q(S)$
where
$\sigma _q(S)$
where
![]() $S$
is a closed subset of
$S$
is a closed subset of
![]() ${\mathbb{R}}^q$
. For
${\mathbb{R}}^q$
. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $W_i$
be a closed subset of
$W_i$
be a closed subset of
![]() ${\mathbb{R}}^{q_i}$
. If
${\mathbb{R}}^{q_i}$
. If
![]() $\Phi \,:\,W_1 \to W_2$
is a homeomorphism, the stereographic pre-compactification of
$\Phi \,:\,W_1 \to W_2$
is a homeomorphism, the stereographic pre-compactification of
![]() $\Phi$
is the following homeomorphism:
$\Phi$
is the following homeomorphism:
Since
![]() $W_1,W_2$
are closed, the stereographic pre-compactification of
$W_1,W_2$
are closed, the stereographic pre-compactification of
![]() $\Phi$
extends as a homeomorphism
$\Phi$
extends as a homeomorphism
![]() $\widetilde{\Phi }\,:\,\widetilde{W}_1 \to \widetilde{W}_2$
mapping
$\widetilde{\Phi }\,:\,\widetilde{W}_1 \to \widetilde{W}_2$
mapping
![]() $N_{q_1}$
onto
$N_{q_1}$
onto
![]() $N_{q_2}$
whenever
$N_{q_2}$
whenever
![]() $W_1$
is unbounded. We call this extension the stereographic compactification of
$W_1$
is unbounded. We call this extension the stereographic compactification of
![]() $\Phi$
.
$\Phi$
.
The main result of this note is the following:
Theorem 10.
The mapping
![]() $\Phi$
is bi-Lipschitz if and only if its stereographic compactification
$\Phi$
is bi-Lipschitz if and only if its stereographic compactification
![]() $\widetilde{\Phi }$
is bi-Lipschitz.
$\widetilde{\Phi }$
is bi-Lipschitz.
The main result is a consequence of Lemma 9 presented below. We recall that the Euclidean inversion of
![]() ${\mathbb{R}}^q$
is the following mapping:
${\mathbb{R}}^q$
is the following mapping:
Let
![]() $\Phi \,:\,W_1 \to W_2$
be a homeomorphism between the closed subsets
$\Phi \,:\,W_1 \to W_2$
be a homeomorphism between the closed subsets
![]() $W_i$
of
$W_i$
of
![]() ${\mathbb{R}}^{q_i}$
,
${\mathbb{R}}^{q_i}$
,
![]() $i=1,2$
. The inversion of the mapping
$i=1,2$
. The inversion of the mapping
![]() $\Phi \,:\,W_1 \to W_2$
is defined as follows:
$\Phi \,:\,W_1 \to W_2$
is defined as follows:
The next result (so called the inversion lemma) is the main tool we use to obtain the main result. It is of interest on its own and can be applied in many different contexts.
Lemma 9.
Assume furthermore that, either
![]() $W_i$
contains the origin
$W_i$
contains the origin
![]() $\textbf{0}\in{\mathbb{R}}^{q_i}$
for
$\textbf{0}\in{\mathbb{R}}^{q_i}$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $\Phi (\textbf{0}) = \textbf{0}$
, or
$\Phi (\textbf{0}) = \textbf{0}$
, or
![]() $\textbf{0}\notin W_i$
for
$\textbf{0}\notin W_i$
for
![]() $i=1,2$
. The homeomorphism
$i=1,2$
. The homeomorphism
![]() $\iota (\Phi )$
is bi-Lipschitz if and only
$\iota (\Phi )$
is bi-Lipschitz if and only
![]() $\Phi$
is. Moreover, if
$\Phi$
is. Moreover, if
![]() $W_1$
is unbounded, then
$W_1$
is unbounded, then
![]() $\iota (\Phi )$
extends bi-Lipschitz-ly at
$\iota (\Phi )$
extends bi-Lipschitz-ly at
![]() $\textbf{0}$
taking the value
$\textbf{0}$
taking the value
![]() $\textbf{0}$
.
$\textbf{0}$
.
Our interest in this problem arose from results of the recent PhD Thesis of the second named author [Reference Oliveira10], where a bi-Lipschitz classification of local plane objects germs, at the origin, respectively, at infinity and in correspondence by the Euclidean inversion, presented strikingly similar properties, now explained by Lemma 9. The main result is mostly a convenient reformulation of the inversion lemma. It is also in tune with the joint works of the first named author [Reference Costa, Grandjean and Michalska2–Reference Costa, Grandjean and Michalska4] expanding the results of the recent PhD Thesis [Reference Costa1]. Last, we want to point out that the proofs of the inversion lemma and of the main result, presented here, are self-contained.
The paper is organized as follows: Section 2 introduces preliminary materials and notations. Section 3 presents the special case of a global bi-Lipschitz homeomorphism of
![]() ${\mathbb{R}}^q$
. Sections 4 and 5, respectively, show germ-ified versions of the inversion lemma, namely Lemma 7 at
${\mathbb{R}}^q$
. Sections 4 and 5, respectively, show germ-ified versions of the inversion lemma, namely Lemma 7 at
![]() $\infty$
and, respectively Lemma 8 at
$\infty$
and, respectively Lemma 8 at
![]() $\textbf{0}$
. Section 6 is the short proof of our main tool, the inversion Lemma 9. The main result is dealt with in Section 7. The last section presents two immediate applications, versions at infinity of two results about germs of definable subsets at the origin: Proposition 15 (tangent cone result [Reference Sampaio12]) and Proposition 17 (links preserving reparametrization of definable bi-Lipschitz homeomorphism [Reference Valette16]).
$\textbf{0}$
. Section 6 is the short proof of our main tool, the inversion Lemma 9. The main result is dealt with in Section 7. The last section presents two immediate applications, versions at infinity of two results about germs of definable subsets at the origin: Proposition 15 (tangent cone result [Reference Sampaio12]) and Proposition 17 (links preserving reparametrization of definable bi-Lipschitz homeomorphism [Reference Valette16]).
A few days after making public this result on ArXiv [Reference Grandjean and Oliveira7], the preprint [Reference Sampaio13] found independently (among other results) what we present here.
2. Preliminaries
2.1. Notations
The Euclidean space
![]() ${\mathbb{R}}^q$
is equipped with the Euclidean distance, denoted
${\mathbb{R}}^q$
is equipped with the Euclidean distance, denoted
![]() $|-|$
. We denote by
$|-|$
. We denote by
![]() $B_r^q$
the open ball of
$B_r^q$
the open ball of
![]() ${\mathbb{R}}^q$
of radius
${\mathbb{R}}^q$
of radius
![]() $r$
and centered at the origin
$r$
and centered at the origin
![]() $\textbf{0}$
, by
$\textbf{0}$
, by
![]() ${\textbf{B}}_r^q$
its closure and by
${\textbf{B}}_r^q$
its closure and by
![]() ${\textbf{S}}_r^{q-1}$
its boundary. The open ball of radius
${\textbf{S}}_r^{q-1}$
its boundary. The open ball of radius
![]() $r$
and with center
$r$
and with center
![]() ${\textbf{x}}_0\in{{\mathbb{R}}^q}$
is
${\textbf{x}}_0\in{{\mathbb{R}}^q}$
is
![]() $B^q({\textbf{x}}_0,r)$
, its closure is
$B^q({\textbf{x}}_0,r)$
, its closure is
![]() ${\textbf{B}}^q({\textbf{x}}_0,r)$
, and
${\textbf{B}}^q({\textbf{x}}_0,r)$
, and
![]() ${\textbf{S}}^{q-1}({\textbf{x}}_0,r)$
is its boundary. The unit sphere
${\textbf{S}}^{q-1}({\textbf{x}}_0,r)$
is its boundary. The unit sphere
![]() ${\textbf{S}}_1^{q-1}$
is simply denoted by
${\textbf{S}}_1^{q-1}$
is simply denoted by
![]() ${\textbf{S}}^{q-1}$
.
${\textbf{S}}^{q-1}$
.
If
![]() $S$
is any subset of
$S$
is any subset of
![]() ${\mathbb{R}}^q$
, its closure in
${\mathbb{R}}^q$
, its closure in
![]() ${\mathbb{R}}^q$
is
${\mathbb{R}}^q$
is
![]() $\textrm{clos}(S)$
, and
$\textrm{clos}(S)$
, and
![]() $S^*$
is
$S^*$
is
![]() $S\setminus \textbf{0}$
.
$S\setminus \textbf{0}$
.
Let
![]() ${\textbf{U}}_q$
be the punctured affine space
${\textbf{U}}_q$
be the punctured affine space
![]() ${{\mathbb{R}}^q}^*$
.
${{\mathbb{R}}^q}^*$
.
Compactifying the space
![]() ${\mathbb{R}}^q$
with the point
${\mathbb{R}}^q$
with the point
![]() $\infty$
at infinity as:
$\infty$
at infinity as:
yields a space that is smoothly diffeomorphic to the unit sphere
![]() ${\textbf{S}}^q$
of
${\textbf{S}}^q$
of
![]() ${\mathbb{R}}^{q+1}$
, using the stereographic projections centered at the “north” and “south” poles of
${\mathbb{R}}^{q+1}$
, using the stereographic projections centered at the “north” and “south” poles of
![]() ${\textbf{S}}^q$
. Under this correspondence, the points
${\textbf{S}}^q$
. Under this correspondence, the points
![]() $\textbf{0}$
and
$\textbf{0}$
and
![]() $\infty$
are antipodal.
$\infty$
are antipodal.
If
![]() $S$
is any subset of
$S$
is any subset of
![]() ${\mathbb{R}}^q$
its closure in
${\mathbb{R}}^q$
its closure in
![]() $\overline{{\mathbb{R}}^q}$
is
$\overline{{\mathbb{R}}^q}$
is
![]() $\overline{S}$
. Thus,
$\overline{S}$
. Thus,
![]() $S$
is unbounded if and only if
$S$
is unbounded if and only if
![]() $\overline{S} = \textrm{clos}(S) \cup \infty$
.
$\overline{S} = \textrm{clos}(S) \cup \infty$
.
The germ
![]() $({{\mathbb{R}}^q},\infty )$
of
$({{\mathbb{R}}^q},\infty )$
of
![]() ${\mathbb{R}}^q$
at infinity is well defined and can be considered as a germ in
${\mathbb{R}}^q$
at infinity is well defined and can be considered as a germ in
![]() ${\mathbb{R}}^q$
and in
${\mathbb{R}}^q$
and in
![]() $\overline{{\mathbb{R}}^q}$
.
$\overline{{\mathbb{R}}^q}$
.
Let
![]() $\gamma$
be a point of
$\gamma$
be a point of
![]() $\overline{{\mathbb{R}}^q}$
. Let
$\overline{{\mathbb{R}}^q}$
. Let
![]() $({\textbf{x}}_n)_n, (\textbf{y}_n)_n$
be two sequences of
$({\textbf{x}}_n)_n, (\textbf{y}_n)_n$
be two sequences of
![]() ${\mathbb{R}}^q$
converging to
${\mathbb{R}}^q$
converging to
![]() $\gamma$
in
$\gamma$
in
![]() $\overline{{\mathbb{R}}^q}$
. Let
$\overline{{\mathbb{R}}^q}$
. Let
![]() $\textbf{z}_n$
be
$\textbf{z}_n$
be
![]() ${\textbf{x}}_n$
or
${\textbf{x}}_n$
or
![]() $\textbf{y}_n$
and let
$\textbf{y}_n$
and let
 \begin{equation*} z_n \,:\!=\, \left \{ \begin {array}{r@{\quad}c@{\quad}l} |\textbf {z}_n - {\gamma }| & \textrm {if} & {\gamma } \in {{\mathbb {R}}^q} \\[4pt] |\textbf {z}_n| & \textrm {if} & {\gamma } = \infty \end {array} \right . \end{equation*}
\begin{equation*} z_n \,:\!=\, \left \{ \begin {array}{r@{\quad}c@{\quad}l} |\textbf {z}_n - {\gamma }| & \textrm {if} & {\gamma } \in {{\mathbb {R}}^q} \\[4pt] |\textbf {z}_n| & \textrm {if} & {\gamma } = \infty \end {array} \right . \end{equation*}
We will use the following notation:
as well as the next one
and the last one
2.2. On affine subsets
Any non-empty subset
![]() $S$
of
$S$
of
![]() ${\mathbb{R}}^q$
inherits from the ambient Euclidean structure of
${\mathbb{R}}^q$
inherits from the ambient Euclidean structure of
![]() ${\mathbb{R}}^q$
the outer metric space structure
${\mathbb{R}}^q$
the outer metric space structure
![]() $(S,d_S)$
, where
$(S,d_S)$
, where
for any pair of points
![]() ${\textbf{x}},{\textbf{x}}^{\prime}$
of
${\textbf{x}},{\textbf{x}}^{\prime}$
of
![]() $S$
. We recall that if a mapping
$S$
. We recall that if a mapping
![]() $\varphi \,:\, (S,d_S) \to{{\mathbb{R}}^p}$
is Lipschitz with Lipschitz constant
$\varphi \,:\, (S,d_S) \to{{\mathbb{R}}^p}$
is Lipschitz with Lipschitz constant
![]() $C$
, it extends as a Lipschitz mapping
$C$
, it extends as a Lipschitz mapping
![]() $(\textrm{clos}(S),d_{\textrm{clos}(S)}) \to{{\mathbb{R}}^p}$
with the same Lipschitz constant
$(\textrm{clos}(S),d_{\textrm{clos}(S)}) \to{{\mathbb{R}}^p}$
with the same Lipschitz constant
![]() $C$
. In practice, we can assume that
$C$
. In practice, we can assume that
![]() $S$
is closed in
$S$
is closed in
![]() ${\mathbb{R}}^q$
.
${\mathbb{R}}^q$
.
In order to ease the accumulation of hypotheses and notations, we introduce the following:
Definition 1.
A
![]() $q$
-affine subset is a non-empty closed subset of
$q$
-affine subset is a non-empty closed subset of
![]() ${\mathbb{R}}^q$
with
${\mathbb{R}}^q$
with
![]() $q\geq 1$
.
$q\geq 1$
.
An affine subset is a
![]() $q$
-affine subset for some positive integer
$q$
-affine subset for some positive integer
![]() $q$
.
$q$
.
Since any affine subset
![]() $S$
is equipped with the outer metric space structure
$S$
is equipped with the outer metric space structure
![]() $(S,d_S)$
described above, we introduce the following
$(S,d_S)$
described above, we introduce the following
Definition 2.
A Lipschitz mapping
![]() $S \to T$
between the affine subsets
$S \to T$
between the affine subsets
![]() $S,T$
is a Lipschitz mapping
$S,T$
is a Lipschitz mapping
![]() $(S,d_S) \to (T,d_T)$
.
$(S,d_S) \to (T,d_T)$
.
2.3. On the inversion
The inversion of the (punctured) affine space
![]() ${\mathbb{R}}^q$
, defined as:
${\mathbb{R}}^q$
, defined as:
is a
![]() $C^\infty$
(semi-algebraic) diffeomorphism and extends as a (semi-algebraic) homeomorphism (
$C^\infty$
(semi-algebraic) diffeomorphism and extends as a (semi-algebraic) homeomorphism (
![]() $C^\infty$
actually) over
$C^\infty$
actually) over
![]() $\overline{{\mathbb{R}}^q}$
exchanging the origin
$\overline{{\mathbb{R}}^q}$
exchanging the origin
![]() $\textbf{0}$
and the point at infinity
$\textbf{0}$
and the point at infinity
![]() $\infty$
.
$\infty$
.
Let
![]() $\textbf{x}$
be any point of
$\textbf{x}$
be any point of
![]() ${\textbf{U}}_q$
. Let
${\textbf{U}}_q$
. Let
be the real vector line through
![]() $\textbf{x}$
. The tangent space of
$\textbf{x}$
. The tangent space of
![]() ${\textbf{U}}_q$
at
${\textbf{U}}_q$
at
![]() $\textbf{x}$
decomposes as the Euclidean orthogonal sum:
$\textbf{x}$
decomposes as the Euclidean orthogonal sum:
Observe that
![]() ${\textbf{S}}(s{\textbf{x}}) ={\textbf{S}}({\textbf{x}})$
and
${\textbf{S}}(s{\textbf{x}}) ={\textbf{S}}({\textbf{x}})$
and
![]() $R(s{\textbf{x}}) = R({\textbf{x}})$
, as vector subspaces of
$R(s{\textbf{x}}) = R({\textbf{x}})$
, as vector subspaces of
![]() ${\mathbb{R}}^q$
, whenever
${\mathbb{R}}^q$
, whenever
![]() $s\neq 0$
. An elementary computation shows that in the previous orthogonal basis of
$s\neq 0$
. An elementary computation shows that in the previous orthogonal basis of
![]() $T_{\textbf{x}}{\textbf{U}}_q$
we obtain
$T_{\textbf{x}}{\textbf{U}}_q$
we obtain
In particular,
![]() $D_{\textbf{x}}\iota _q$
is an orthogonal mapping, since
$D_{\textbf{x}}\iota _q$
is an orthogonal mapping, since
![]() $|{\textbf{x}}|^2 D_{\textbf{x}}\iota _q$
is simply the orthogonal symmetry w.r.t. the hyperplane
$|{\textbf{x}}|^2 D_{\textbf{x}}\iota _q$
is simply the orthogonal symmetry w.r.t. the hyperplane
![]() ${\textbf{S}}({\textbf{x}})$
. We thus deduce the (Euclidean) norm of
${\textbf{S}}({\textbf{x}})$
. We thus deduce the (Euclidean) norm of
![]() $D_{\textbf{x}}\iota _q$
:
$D_{\textbf{x}}\iota _q$
:
2.4. Elementary, yet very useful, identities
We recall the following known estimates
Claim 3.
Let
![]() ${\textbf{x}},{\textbf{x}}^{\prime} \in{{\mathbb{R}}^q}$
and
${\textbf{x}},{\textbf{x}}^{\prime} \in{{\mathbb{R}}^q}$
and
![]() $C\gt 0$
such that
$C\gt 0$
such that
![]() $|{\textbf{x}}^{\prime}| \geq (1+C) |{\textbf{x}}|$
. Then,
$|{\textbf{x}}^{\prime}| \geq (1+C) |{\textbf{x}}|$
. Then,
Given
![]() ${\textbf{x}}_1,{\textbf{x}}_2 \in{\textbf{U}}_q$
, we define
${\textbf{x}}_1,{\textbf{x}}_2 \in{\textbf{U}}_q$
, we define
We assume that
![]() $r_1 = (1+C)r_2$
for some
$r_1 = (1+C)r_2$
for some
![]() $C\geq 0$
. Let
$C\geq 0$
. Let
![]() $2{\theta }\in [0,\pi ]$
be the angle between
$2{\theta }\in [0,\pi ]$
be the angle between
![]() ${\textbf{x}}_1,{\textbf{x}}_2$
(thus between
${\textbf{x}}_1,{\textbf{x}}_2$
(thus between
![]() $\textbf{y}_1,\textbf{y}_2$
as well). Let
$\textbf{y}_1,\textbf{y}_2$
as well). Let
![]() $r_1 -r_2 = Cr_2$
and
$r_1 -r_2 = Cr_2$
and
![]() $R_2 - R_1 = CR_1$
. We recall that the law of cosines is the following identity:
$R_2 - R_1 = CR_1$
. We recall that the law of cosines is the following identity:
The inversion and the law of cosines give the following identity:
3. Inversion mapping and global bi-Lipschitz homeomorphisms
We present a special occurrence of the inversion lemma. Although it is likely that it has already been written in a few books, we give a proof, following from elementary Lipschitz analysis.
Let
![]() $\mathcal{L}(a,b)$
be the space of
$\mathcal{L}(a,b)$
be the space of
![]() $\mathbb{R}$
-linear mappings
$\mathbb{R}$
-linear mappings
![]() ${\mathbb{R}}^a\to{\mathbb{R}}^b$
.
${\mathbb{R}}^a\to{\mathbb{R}}^b$
.
Let
![]() $\varphi \,:\,{{\mathbb{R}}^p} \to{{\mathbb{R}}^q}$
be a Lipschitz mapping with Lipschitz constant
$\varphi \,:\,{{\mathbb{R}}^p} \to{{\mathbb{R}}^q}$
be a Lipschitz mapping with Lipschitz constant
![]() $A_\varphi$
:
$A_\varphi$
:
Let
![]() $\mathcal{D}(\varphi )$
be the set of points where
$\mathcal{D}(\varphi )$
be the set of points where
![]() $\varphi$
is differentiable. Rademacher Theorem states that the complement
$\varphi$
is differentiable. Rademacher Theorem states that the complement
![]() ${{\mathbb{R}}^p}\setminus \mathcal{D}(\varphi )$
is of null measure [Reference Heinonen8, Reference Rademacher11]. We consider the following closed subset:
${{\mathbb{R}}^p}\setminus \mathcal{D}(\varphi )$
is of null measure [Reference Heinonen8, Reference Rademacher11]. We consider the following closed subset:
Let
![]() $\pi _{\mathcal{L}} \,:\,{{\mathbb{R}}^p}\times \mathcal{L}(p,q)\to \mathcal{L}(p,q)$
be the projection onto the second factor. Let
$\pi _{\mathcal{L}} \,:\,{{\mathbb{R}}^p}\times \mathcal{L}(p,q)\to \mathcal{L}(p,q)$
be the projection onto the second factor. Let
For any
![]() ${\textbf{x}}\in \mathcal{D} (\varphi )$
, the Lipschitz condition on
${\textbf{x}}\in \mathcal{D} (\varphi )$
, the Lipschitz condition on
![]() $\varphi$
yields the following estimate about the norm of
$\varphi$
yields the following estimate about the norm of
![]() $D_{\textbf{x}} \varphi$
:
$D_{\textbf{x}} \varphi$
:
Since the norm is continuous over
![]() $\mathcal{L}(q,p)$
, we deduce that
$\mathcal{L}(q,p)$
, we deduce that
Let
![]() $H\,:\,{{\mathbb{R}}^q} \to{{\mathbb{R}}^q}$
be a bi-Lipschitz homeomorphism mapping the origin onto itself, with Lipschitz constant
$H\,:\,{{\mathbb{R}}^q} \to{{\mathbb{R}}^q}$
be a bi-Lipschitz homeomorphism mapping the origin onto itself, with Lipschitz constant
![]() $A_H\gt 0$
:
$A_H\gt 0$
:
Therefore from Estimate (3.1), we get
The mapping
![]() $H$
extends as a homeomorphism of
$H$
extends as a homeomorphism of
![]() $\overline{{\mathbb{R}}^q}$
mapping
$\overline{{\mathbb{R}}^q}$
mapping
![]() $\infty$
onto
$\infty$
onto
![]() $\infty$
.
$\infty$
.
The inversion of
![]() $H$
is the mapping
$H$
is the mapping
![]() $\iota _q \circ H \circ \iota _q^{-1}$
. It is a homeomorphism of
$\iota _q \circ H \circ \iota _q^{-1}$
. It is a homeomorphism of
![]() ${\textbf{U}}_q$
which extends continuously to
${\textbf{U}}_q$
which extends continuously to
![]() $\textbf{0}$
, taking the value
$\textbf{0}$
, taking the value
![]() $\textbf{0}$
, as the homeomorphism
$\textbf{0}$
, as the homeomorphism
![]() $\iota (H) \,:\,{{\mathbb{R}}^q} \to{{\mathbb{R}}^q}$
. More precisely, the following holds true:
$\iota (H) \,:\,{{\mathbb{R}}^q} \to{{\mathbb{R}}^q}$
. More precisely, the following holds true:
Proposition 4.
The inversion
![]() $\iota (H)$
of
$\iota (H)$
of
![]() $H$
is bi-Lipschitz.
$H$
is bi-Lipschitz.
Proof. It is enough to show that
![]() $\iota (H)$
is Lipschitz, since
$\iota (H)$
is Lipschitz, since
![]() $\iota (H^{-1}) = \iota (H)^{-1}$
. Let
$\iota (H^{-1}) = \iota (H)^{-1}$
. Let
![]() $\textbf{y}\in{\textbf{U}}_q$
and let
$\textbf{y}\in{\textbf{U}}_q$
and let
![]() ${\textbf{x}} \,:\!=\, \iota _q^{-1}(\textbf{y})$
and
${\textbf{x}} \,:\!=\, \iota _q^{-1}(\textbf{y})$
and
![]() $\textbf{z} \,:\!=\, H ({\textbf{x}})$
. Since
$\textbf{z} \,:\!=\, H ({\textbf{x}})$
. Since
![]() $H(\textbf{0}) = \textbf{0}$
, we find
$H(\textbf{0}) = \textbf{0}$
, we find
If
![]() $\textbf{x}$
is a point of
$\textbf{x}$
is a point of
![]() ${\textbf{U}}_q$
at which
${\textbf{U}}_q$
at which
![]() $H$
is differentiable, we find the following estimate:
$H$
is differentiable, we find the following estimate:
Since
![]() $\iota _q$
is a
$\iota _q$
is a
![]() $C^\infty$
diffeomorphism, the subset
$C^\infty$
diffeomorphism, the subset
![]() $\iota _q({{\mathbb{R}}^q} \setminus \mathcal{D}(H))$
has null measure. Thus,
$\iota _q({{\mathbb{R}}^q} \setminus \mathcal{D}(H))$
has null measure. Thus,
![]() $\iota (H)$
is differentiable outside a subset of zero measure with uniformly bounded first derivatives. Thus, it is Lipschitz.
$\iota (H)$
is differentiable outside a subset of zero measure with uniformly bounded first derivatives. Thus, it is Lipschitz.
Let
![]() $\omega$
be either
$\omega$
be either
![]() $\textbf{0}$
or
$\textbf{0}$
or
![]() $\infty$
. Let
$\infty$
. Let
![]() $h \,:\,\big(\overline{{\mathbb{R}}^q},\omega \big) \to \big(\overline{{\mathbb{R}}^q},\omega \big)$
be a germ of homeomorphism which is bi-Lipschitz over
$h \,:\,\big(\overline{{\mathbb{R}}^q},\omega \big) \to \big(\overline{{\mathbb{R}}^q},\omega \big)$
be a germ of homeomorphism which is bi-Lipschitz over
![]() $({\textbf{U}}_q,\omega )$
. Let
$({\textbf{U}}_q,\omega )$
. Let
![]() $\omega ^*$
be the point of
$\omega ^*$
be the point of
![]() $\overline{{\mathbb{R}}^q}$
antipodal to
$\overline{{\mathbb{R}}^q}$
antipodal to
![]() $\omega$
, that is,
$\omega$
, that is,
The map germ
![]() $\iota _q\circ h \circ \iota _q^{-1} \,:\, \big({\textbf{U}}_q,\omega ^*\big) \to \big({\textbf{U}}_q,\omega ^*\big)$
extends as a homeomorphism germ
$\iota _q\circ h \circ \iota _q^{-1} \,:\, \big({\textbf{U}}_q,\omega ^*\big) \to \big({\textbf{U}}_q,\omega ^*\big)$
extends as a homeomorphism germ
![]() $\iota (h) \,:\, \big(\overline{{\mathbb{R}}^q}, \omega ^*\big) \to (\overline{{\mathbb{R}}^q},\omega ^*)$
. A consequence of Proposition 4 is the (now expected) following result, initial motivation of the paper:
$\iota (h) \,:\, \big(\overline{{\mathbb{R}}^q}, \omega ^*\big) \to (\overline{{\mathbb{R}}^q},\omega ^*)$
. A consequence of Proposition 4 is the (now expected) following result, initial motivation of the paper:
Corollary 5.
The germ of homeomorphism
![]() $\iota (h)$
is bi-Lipschitz over
$\iota (h)$
is bi-Lipschitz over
![]() $\big({\textbf{U}}_q,\omega ^*\big)$
.
$\big({\textbf{U}}_q,\omega ^*\big)$
.
4. Inversion and germs of bi-Lipschitz homeomorphisms at infinity
Let
![]() $\sigma$
be a point of
$\sigma$
be a point of
![]() $\overline{{\mathbb{R}}^q}$
. Following Definition 1, the notion of germ of
$\overline{{\mathbb{R}}^q}$
. Following Definition 1, the notion of germ of
![]() $q$
-affine subset at
$q$
-affine subset at
![]() $\sigma$
is well defined. If
$\sigma$
is well defined. If
![]() $\tau$
is a point of
$\tau$
is a point of
![]() $\overline{{\mathbb{R}}^p}$
, the notion of Lipschitz mapping of affine germs
$\overline{{\mathbb{R}}^p}$
, the notion of Lipschitz mapping of affine germs
![]() $(S,\sigma ) \to (T,\tau )$
is also well defined by Definition 2.
$(S,\sigma ) \to (T,\tau )$
is also well defined by Definition 2.
Let
![]() $\phi \,:\,(Y_1,\infty ) \to (Y_2,\infty )$
be a germ of bi-Lipschitz homeomorphism between
$\phi \,:\,(Y_1,\infty ) \to (Y_2,\infty )$
be a germ of bi-Lipschitz homeomorphism between
![]() $q_i$
-affine subsets germs
$q_i$
-affine subsets germs
![]() $(Y_i,\infty )$
with
$(Y_i,\infty )$
with
![]() $i=1,2$
. There exists a positive constant
$i=1,2$
. There exists a positive constant
![]() $A_\phi$
such that
$A_\phi$
such that
Thus, we can assume that the Lipschitz constant
![]() $A_\phi$
is such that the following estimates are also satisfied:
$A_\phi$
is such that the following estimates are also satisfied:
With the previous notation, we deduce
![]() $\phi (\textbf{y}) \sim \textbf{y}$
.
$\phi (\textbf{y}) \sim \textbf{y}$
.
For
![]() $i=1,2$
, we denote by
$i=1,2$
, we denote by
![]() $X_i$
the closure
$X_i$
the closure
![]() $\textrm{clos}(\iota _{q_i}(Y_i))$
of
$\textrm{clos}(\iota _{q_i}(Y_i))$
of
![]() $\iota _{q_i}(Y_i)$
in
$\iota _{q_i}(Y_i)$
in
![]() ${\mathbb{R}}^q$
. The inversion of
${\mathbb{R}}^q$
. The inversion of
![]() $\phi$
is the mapping defined as follows:
$\phi$
is the mapping defined as follows:
 \begin{equation*} {\iota (\phi )} \,:\, (X_1,\textbf {0}) \to (X_2,\textbf {0}), \;\; {\textbf {x}} \to {\iota (\phi )}({\textbf {x}}) \,:\!=\, \left \{ \begin {array}{r@{\quad}c@{\quad}l} \iota _{q_2} \circ \phi \circ \iota _{q_1}^{-1}({\textbf {x}}) & \textrm {if} & {\textbf {x}} \in X_1^* \\[4pt] \textbf {0} & \textrm {if} & {\textbf {x}} = \textbf {0} \end {array} \right . \end{equation*}
\begin{equation*} {\iota (\phi )} \,:\, (X_1,\textbf {0}) \to (X_2,\textbf {0}), \;\; {\textbf {x}} \to {\iota (\phi )}({\textbf {x}}) \,:\!=\, \left \{ \begin {array}{r@{\quad}c@{\quad}l} \iota _{q_2} \circ \phi \circ \iota _{q_1}^{-1}({\textbf {x}}) & \textrm {if} & {\textbf {x}} \in X_1^* \\[4pt] \textbf {0} & \textrm {if} & {\textbf {x}} = \textbf {0} \end {array} \right . \end{equation*}
It is a germ of homeomorphism which extends continuously at
![]() $\textbf{0}$
taking the value
$\textbf{0}$
taking the value
![]() $\textbf{0}$
at
$\textbf{0}$
at
![]() $\textbf{0}$
. The homogeneity of the Euclidean metric as well as the existence of the inversion mapping yield the following result.
$\textbf{0}$
. The homogeneity of the Euclidean metric as well as the existence of the inversion mapping yield the following result.
Lemma 7.
If
![]() $\phi :(Y_1,\infty ) \to (Y_2,\infty )$
is a bi-Lipschitz homeomorphism germ between
$\phi :(Y_1,\infty ) \to (Y_2,\infty )$
is a bi-Lipschitz homeomorphism germ between
![]() $q_i$
-affine subsets germs
$q_i$
-affine subsets germs
![]() $(Y_i,\infty )$
, for
$(Y_i,\infty )$
, for
![]() $i=1,2$
, then its inversion
$i=1,2$
, then its inversion
![]() ${\iota (\phi )} \,:\, (X_1,\textbf{0}) \to (X_2,\textbf{0})$
is bi-Lipschitz homeomorphism germ.
${\iota (\phi )} \,:\, (X_1,\textbf{0}) \to (X_2,\textbf{0})$
is bi-Lipschitz homeomorphism germ.
Proof. First, let us denote
![]() $h \,:\!=\, \phi \circ \iota _{q_1}^{-1}$
, that is
$h \,:\!=\, \phi \circ \iota _{q_1}^{-1}$
, that is
Therefore, we get that
Since
![]() $|h({\textbf{x}})| \sim |{\textbf{x}}^{-1}|$
, we observe that
$|h({\textbf{x}})| \sim |{\textbf{x}}^{-1}|$
, we observe that
![]() ${\iota (\phi )}({\textbf{x}}) \sim{\textbf{x}}$
, more precisely:
${\iota (\phi )}({\textbf{x}}) \sim{\textbf{x}}$
, more precisely:
It is sufficient to show that
![]() $\iota (\phi )$
is Lipschitz.
$\iota (\phi )$
is Lipschitz.
Assume that
![]() $\iota (\phi )$
is not Lipschitz. Therefore, there exist two sequences
$\iota (\phi )$
is not Lipschitz. Therefore, there exist two sequences
![]() $({\textbf{x}}_n)_n$
and
$({\textbf{x}}_n)_n$
and
![]() $({\textbf{x}}^{\prime}_n)_n$
of
$({\textbf{x}}^{\prime}_n)_n$
of
![]() ${\textbf{U}}_{q_1}$
such that
${\textbf{U}}_{q_1}$
such that
We work with a representative of
![]() $\phi$
outside a compact subset
$\phi$
outside a compact subset
![]() $C_1$
of
$C_1$
of
![]() ${\mathbb{R}}^{q_1}$
containing
${\mathbb{R}}^{q_1}$
containing
![]() $\textbf{0}$
and with the representative of
$\textbf{0}$
and with the representative of
![]() $\iota (\phi )$
over
$\iota (\phi )$
over
![]() $X_1$
, the closure
$X_1$
, the closure
![]() $\textrm{clos}(\iota _{q_1}(Y_1 \setminus C_1))$
. Thus,
$\textrm{clos}(\iota _{q_1}(Y_1 \setminus C_1))$
. Thus,
![]() $X_1$
is compact. For convenience sake let
$X_1$
is compact. For convenience sake let
We further define the following numbers:
Of course we have
![]() $s_n t_n = s^{\prime}_n t^{\prime}_n = 1$
.
$s_n t_n = s^{\prime}_n t^{\prime}_n = 1$
.
Without the loss of generality, we can assume that the sequence
![]() $({\textbf{x}}_n)_n$
converges to
$({\textbf{x}}_n)_n$
converges to
![]() $\chi \in X_1$
and
$\chi \in X_1$
and
![]() $({\textbf{x}}^{\prime}_n)_n$
converges to
$({\textbf{x}}^{\prime}_n)_n$
converges to
![]() $\chi ^{\prime}\in X_1$
.
$\chi ^{\prime}\in X_1$
.
-
Case 1.
 $\chi \neq \textbf{0}$
and
$\chi \neq \textbf{0}$
and
 $\chi ^{\prime} \neq \textbf{0}$
.
$\chi ^{\prime} \neq \textbf{0}$
.
In other words, there exists a compact subset
![]() $K_1$
of
$K_1$
of
![]() ${\textbf{U}}_{q_1}$
which contains
${\textbf{U}}_{q_1}$
which contains
![]() ${\textbf{x}}_n,{\textbf{x}}^{\prime}_n$
for all
${\textbf{x}}_n,{\textbf{x}}^{\prime}_n$
for all
![]() $n$
. Since the inversion
$n$
. Since the inversion
![]() $\iota _{q_1}$
is bi-Lipschitz over
$\iota _{q_1}$
is bi-Lipschitz over
![]() $K_1$
, so is the mapping
$K_1$
, so is the mapping
![]() $\iota (\phi )$
, contradicting the estimate (4.1). Therefore, this case cannot happen and we can assume that
$\iota (\phi )$
, contradicting the estimate (4.1). Therefore, this case cannot happen and we can assume that
![]() $\chi = \textbf{0}$
.
$\chi = \textbf{0}$
.
-
Case 2.
 $\chi = \textbf{0}$
and
$\chi = \textbf{0}$
and
 $\chi ^{\prime}\neq \textbf{0}$
.
$\chi ^{\prime}\neq \textbf{0}$
.
Observe that the following estimates hold true
for positive real numbers
![]() $b\gt a$
. Therefore, we deduce that
$b\gt a$
. Therefore, we deduce that
contradicting the estimate (4.1). Therefore, this case cannot happen and thus
![]() $\chi ^{\prime} = \textbf{0}$
as well.
$\chi ^{\prime} = \textbf{0}$
as well.
-
Case 3.
 $\chi = \chi ^{\prime} = \textbf{0}$
and there exists
$\chi = \chi ^{\prime} = \textbf{0}$
and there exists
 $B\gt 1$
such that
$B\gt 1$
such that
 $|{\textbf{x}}^{\prime}_n|\geq B|{\textbf{x}}_n|$
for
$|{\textbf{x}}^{\prime}_n|\geq B|{\textbf{x}}_n|$
for
 $n$
large enough.
$n$
large enough.
For
![]() $n$
large enough, Claim 3 yields
$n$
large enough, Claim 3 yields
Since
![]() ${\iota (\phi )}_n \leq (1+B) A_\phi ^3 t^{\prime}_n$
for large
${\iota (\phi )}_n \leq (1+B) A_\phi ^3 t^{\prime}_n$
for large
![]() $n$
, we produce again a contradiction to the estimate (4.1). This case does not occur and we can assume, up to taking a subsequence that
$n$
, we produce again a contradiction to the estimate (4.1). This case does not occur and we can assume, up to taking a subsequence that
![]() $\frac{t_n}{t^{\prime}_n} \to 1$
as
$\frac{t_n}{t^{\prime}_n} \to 1$
as
![]() $n$
goes to
$n$
goes to
![]() $\infty$
.
$\infty$
.
Let
![]() $2{\theta }_n\in [0,\pi ]$
be the angle between the vectors
$2{\theta }_n\in [0,\pi ]$
be the angle between the vectors
![]() ${\textbf{x}}_n$
and
${\textbf{x}}_n$
and
![]() ${\textbf{x}}^{\prime}_n$
.
${\textbf{x}}^{\prime}_n$
.
-
Case 4.
 $\lim _n\frac{|{\textbf{x}}_n|}{|{\textbf{x}}^{\prime}_n|} = 1$
and
$\lim _n\frac{|{\textbf{x}}_n|}{|{\textbf{x}}^{\prime}_n|} = 1$
and
 $\liminf _n 2{\theta }_n \in ]0,\pi ]$
.
$\liminf _n 2{\theta }_n \in ]0,\pi ]$
.
We can assume that
![]() $2{\theta }_n \geq 2{\theta } \in ]0,\pi ]$
. From Identity (2.2), we deduce that
$2{\theta }_n \geq 2{\theta } \in ]0,\pi ]$
. From Identity (2.2), we deduce that
Since
![]() ${\iota (\phi )}_n \leq A_\phi ^3(t_n+t^{\prime}_n)$
for
${\iota (\phi )}_n \leq A_\phi ^3(t_n+t^{\prime}_n)$
for
![]() $n$
large enough, estimate (4.1) cannot be satisfied and thus
$n$
large enough, estimate (4.1) cannot be satisfied and thus
![]() ${\theta } = 0$
.
${\theta } = 0$
.
Up to passing to subsequences, we can assume that
![]() $({\theta }_n)_n$
converges to
$({\theta }_n)_n$
converges to
![]() $0$
.
$0$
.
-
Case 5.
 $\lim _n\frac{|{\textbf{x}}_n|}{|{\textbf{x}}^{\prime}_n|} = 1$
and
$\lim _n\frac{|{\textbf{x}}_n|}{|{\textbf{x}}^{\prime}_n|} = 1$
and
 $\lim _n{\theta }_n =0$
.
$\lim _n{\theta }_n =0$
.
We can assume that
![]() $t^{\prime}_n \geq t_n$
and
$t^{\prime}_n \geq t_n$
and
![]() ${\textbf{x}}^{\prime}_n ={\textbf{x}}_n + \textbf{z}_n$
so that
${\textbf{x}}^{\prime}_n ={\textbf{x}}_n + \textbf{z}_n$
so that
Let
![]() $a_n \,:\!=\, \cos ({\theta }_n)$
,
$a_n \,:\!=\, \cos ({\theta }_n)$
,
![]() $b_n\,:\!=\, \sin ({\theta }_n)$
, and
$b_n\,:\!=\, \sin ({\theta }_n)$
, and
![]() ${\delta }_n t_n \,:\!=\, t^{\prime}_n - t_n$
. We get
${\delta }_n t_n \,:\!=\, t^{\prime}_n - t_n$
. We get
Since we can write
![]() $\textbf{y}_n = \textbf{y}^{\prime}_n + \textbf{w}_n$
, equation (2.3) yields
$\textbf{y}_n = \textbf{y}^{\prime}_n + \textbf{w}_n$
, equation (2.3) yields
and thus we deduce that
Since
![]() $\phi$
is bi-Lipschitz, we obtain the following estimate:
$\phi$
is bi-Lipschitz, we obtain the following estimate:
from which we deduce
Combining the various previous estimates yields the following one:
contradicting estimate (4.1).
5. Inversion and germs of bi-Lipschitz homeomorphism at
 $\textbf{0}$
$\textbf{0}$
This section is about the counterpart at the origin of the previous result at infinity Lemma 7, more precisely its converse.
Let
![]() $\psi \,:\,(X_1,\textbf{0}) \to (X_2,\textbf{0})$
be a germ of bi-Lipschitz homeomorphism between
$\psi \,:\,(X_1,\textbf{0}) \to (X_2,\textbf{0})$
be a germ of bi-Lipschitz homeomorphism between
![]() $q_i$
-affine subsets
$q_i$
-affine subsets
![]() $X_i$
, where
$X_i$
, where
![]() $i=1,2$
. Thus, there exists a positive constant
$i=1,2$
. Thus, there exists a positive constant
![]() $A_\psi$
such that
$A_\psi$
such that
Thus, the following estimates are also satisfied:
that is
![]() $\psi ({\textbf{x}}) \sim{\textbf{x}}$
, with the previous notation. Denoting
$\psi ({\textbf{x}}) \sim{\textbf{x}}$
, with the previous notation. Denoting
![]() $Y_i \,:\!=\, \iota _{q_i} (X_i^*)$
for
$Y_i \,:\!=\, \iota _{q_i} (X_i^*)$
for
![]() $i=1,2$
, the inversion of
$i=1,2$
, the inversion of
![]() $\psi$
is the germ of mapping defined as follows:
$\psi$
is the germ of mapping defined as follows:
It clearly extends as a germ of homeomorphism
![]() $(\overline{Y}_1,\infty ) \to (\overline{Y}_2,\infty )$
.
$(\overline{Y}_1,\infty ) \to (\overline{Y}_2,\infty )$
.
The converse of Lemma 7 is
Lemma 8.
If
![]() $\psi \,:\,(X_1,\textbf{0}) \to (X_2,\textbf{0})$
is a bi-Lipschitz homeomorphism germ between
$\psi \,:\,(X_1,\textbf{0}) \to (X_2,\textbf{0})$
is a bi-Lipschitz homeomorphism germ between
![]() $q_i$
-affine subset germs
$q_i$
-affine subset germs
![]() $(X_i,\textbf{0})$
, for
$(X_i,\textbf{0})$
, for
![]() $i=1,2$
, then its inversion
$i=1,2$
, then its inversion
![]() ${\iota (\psi )} \,:\, (Y_1,\infty ) \to (Y_2,\infty )$
is a bi-Lipschitz homeomorphism germ.
${\iota (\psi )} \,:\, (Y_1,\infty ) \to (Y_2,\infty )$
is a bi-Lipschitz homeomorphism germ.
The proof will be symmetric to that of Lemma 7 in the sense that arguments at
![]() $\textbf{0}$
are replaced by their exact analogs at
$\textbf{0}$
are replaced by their exact analogs at
![]() $\infty$
, as expected from such a statement.
$\infty$
, as expected from such a statement.
Proof. First, let
![]() $g \,:\!=\, \psi \circ \iota _{q_1}^{-1}$
, that is,
$g \,:\!=\, \psi \circ \iota _{q_1}^{-1}$
, that is,
Therefore, we get that
and since
![]() $|g(\textbf{y})| \sim |\textbf{y}|^{-1}$
we find that
$|g(\textbf{y})| \sim |\textbf{y}|^{-1}$
we find that
![]() ${\iota (\psi )}(\textbf{y}) \sim \textbf{y}$
, more precisely
${\iota (\psi )}(\textbf{y}) \sim \textbf{y}$
, more precisely
As in the previous section, it is enough to show that
![]() $\iota (\psi )$
is Lipschitz.
$\iota (\psi )$
is Lipschitz.
Assume that
![]() $\iota (\psi )$
is not Lipschitz. Therefore, there exist two sequences
$\iota (\psi )$
is not Lipschitz. Therefore, there exist two sequences
![]() $(\textbf{y}_n)_n$
and
$(\textbf{y}_n)_n$
and
![]() $(\textbf{y}^{\prime}_n)_n$
of
$(\textbf{y}^{\prime}_n)_n$
of
![]() ${\textbf{U}}_{q_1}$
such that
${\textbf{U}}_{q_1}$
such that
We work with a representative of
![]() $\psi$
within a compact subset
$\psi$
within a compact subset
![]() $K_1$
of
$K_1$
of
![]() ${\mathbb{R}}^{q_1}$
containing
${\mathbb{R}}^{q_1}$
containing
![]() $\textbf{0}$
. Let
$\textbf{0}$
. Let
In order to ease computations, we further define the following numbers:
Of course we find again that
![]() $s_n t_n = s^{\prime}_n t^{\prime}_n = 1$
.
$s_n t_n = s^{\prime}_n t^{\prime}_n = 1$
.
-
Case 1.
 $\limsup _n \max (|\textbf{y}_n|,|\textbf{y}^{\prime}_n|) \, \lt \infty$
.
$\limsup _n \max (|\textbf{y}_n|,|\textbf{y}^{\prime}_n|) \, \lt \infty$
.
In other words, there exists a compact subset
![]() $C_1$
of
$C_1$
of
![]() ${\textbf{U}}_{q_1}$
which contains
${\textbf{U}}_{q_1}$
which contains
![]() $\textbf{y}_n,\textbf{y}^{\prime}_n$
for all
$\textbf{y}_n,\textbf{y}^{\prime}_n$
for all
![]() $n$
. Since the inversion
$n$
. Since the inversion
![]() $\iota _{q_1}$
is bi-Lipschitz over
$\iota _{q_1}$
is bi-Lipschitz over
![]() $C_1$
, so is the mapping
$C_1$
, so is the mapping
![]() $\iota (\psi )$
, contradicting the estimate (5.1). Therefore, this case cannot happen and we can assume, after taking a subsequence, that
$\iota (\psi )$
, contradicting the estimate (5.1). Therefore, this case cannot happen and we can assume, after taking a subsequence, that
![]() $(\textbf{y}^{\prime}_n)_n$
converges to
$(\textbf{y}^{\prime}_n)_n$
converges to
![]() $\infty$
.
$\infty$
.
-
Case 2.
 $\textbf{y}^{\prime}_n \to \infty$
and
$\textbf{y}^{\prime}_n \to \infty$
and
 $\limsup _n|\textbf{y}_n|\lt \infty$
.
$\limsup _n|\textbf{y}_n|\lt \infty$
.
Observe that the following estimates hold true
for positive real numbers
![]() $b\gt a$
. Therefore, we deduce that
$b\gt a$
. Therefore, we deduce that
contradicting the estimate (5.1). This case cannot happen and therefore a subsequence of
![]() $(\textbf{y})_n$
converges to
$(\textbf{y})_n$
converges to
![]() $\infty$
as well.
$\infty$
as well.
-
Case 3.
 $\textbf{y}_n,\textbf{y}^{\prime}_n \to \infty$
and there exists
$\textbf{y}_n,\textbf{y}^{\prime}_n \to \infty$
and there exists
 $B\gt 1$
such that
$B\gt 1$
such that
 $|\textbf{y}^{\prime}_n|\geq B|\textbf{y}_n|$
for
$|\textbf{y}^{\prime}_n|\geq B|\textbf{y}_n|$
for
 $n$
large enough.
$n$
large enough.
For
![]() $n$
large enough, Claim 3 yields
$n$
large enough, Claim 3 yields
Since
![]() ${\iota (\psi )}_n \leq (1+B)A_\psi ^3 s^{\prime}_n$
, we produce again a contradiction to the estimate (5.1). This case does not occur and we can assume up to taking subsequences that
${\iota (\psi )}_n \leq (1+B)A_\psi ^3 s^{\prime}_n$
, we produce again a contradiction to the estimate (5.1). This case does not occur and we can assume up to taking subsequences that
![]() $\frac{s_n}{s^{\prime}_n} \to 1$
as
$\frac{s_n}{s^{\prime}_n} \to 1$
as
![]() $n$
goes to
$n$
goes to
![]() $\infty$
.
$\infty$
.
Let
![]() $2{\theta }_n\in [0,\pi ]$
be the angle between the vectors
$2{\theta }_n\in [0,\pi ]$
be the angle between the vectors
![]() $\textbf{y}_n$
and
$\textbf{y}_n$
and
![]() $\textbf{y}^{\prime}_n$
.
$\textbf{y}^{\prime}_n$
.
-
Case 4.
 $\lim _n\frac{|\textbf{y}_n|}{|\textbf{y}^{\prime}_n|} = 1$
and
$\lim _n\frac{|\textbf{y}_n|}{|\textbf{y}^{\prime}_n|} = 1$
and
 $\liminf _n 2{\theta }_n \in ]0,\pi ]$
.
$\liminf _n 2{\theta }_n \in ]0,\pi ]$
.
We can assume that
![]() $2{\theta }_n$
converges to
$2{\theta }_n$
converges to
![]() $2{\theta } \in ]0,\pi ]$
. We check that
$2{\theta } \in ]0,\pi ]$
. We check that
Since
![]() ${\iota (\psi )}_n \leq A_\psi ^3 (s_n+ s^{\prime}_n)$
for
${\iota (\psi )}_n \leq A_\psi ^3 (s_n+ s^{\prime}_n)$
for
![]() $n$
large enough, estimate (5.1) cannot be satisfied and thus
$n$
large enough, estimate (5.1) cannot be satisfied and thus
![]() ${\theta } = 0$
.
${\theta } = 0$
.
-
Case 5.
 $\lim _n\frac{|\textbf{y}_n|}{|\textbf{y}^{\prime}_n|} = 1$
and
$\lim _n\frac{|\textbf{y}_n|}{|\textbf{y}^{\prime}_n|} = 1$
and
 $\lim _n{\theta }_n =0$
.
$\lim _n{\theta }_n =0$
.
We can assume that
![]() $s_n \geq s^{\prime}_n$
and
$s_n \geq s^{\prime}_n$
and
![]() $\textbf{y}_n = \textbf{y}^{\prime}_n + \textbf{w}_n$
so that
$\textbf{y}_n = \textbf{y}^{\prime}_n + \textbf{w}_n$
so that
Let
![]() $a_n \,:\!=\, \cos ({\theta }_n)$
,
$a_n \,:\!=\, \cos ({\theta }_n)$
,
![]() $b_n\,:\!=\, \sin ({\theta }_n)$
, and
$b_n\,:\!=\, \sin ({\theta }_n)$
, and
![]() ${\delta }_n s^{\prime}_n \,:\!=\, s_n - s^{\prime}_n$
. We get
${\delta }_n s^{\prime}_n \,:\!=\, s_n - s^{\prime}_n$
. We get
Since we can write
![]() ${\textbf{x}}^{\prime}_n ={\textbf{x}}_n + \textbf{z}_n$
, equation (2.3) yields
${\textbf{x}}^{\prime}_n ={\textbf{x}}_n + \textbf{z}_n$
, equation (2.3) yields
and thus we deduce that
Since
![]() $\psi$
is bi-Lipschitz, we obtain the following estimate:
$\psi$
is bi-Lipschitz, we obtain the following estimate:
from which we deduce
Combining the various previous estimates yields the following one:
contradicting estimate (5.1).
6. Inversion and bi-Lipschitz homeomorphisms
This section presents the inversion lemma, that is, the main tool of this note. It is a rather straightforward consequence of Lemmas 8 and 7.
Lemma 9.
Let
![]() $\Phi \,:\,W_1 \to W_2$
be a homeomorphism between
$\Phi \,:\,W_1 \to W_2$
be a homeomorphism between
![]() $q_i$
-affine subsets
$q_i$
-affine subsets
![]() $W_i$
, for
$W_i$
, for
![]() $i=1,2$
. Assume furthermore that, either
$i=1,2$
. Assume furthermore that, either
![]() $W_i$
contains the origin
$W_i$
contains the origin
![]() $\textbf{0}\in{\mathbb{R}}^{q_i}$
for
$\textbf{0}\in{\mathbb{R}}^{q_i}$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $\Phi (\textbf{0}) = \textbf{0}$
, or
$\Phi (\textbf{0}) = \textbf{0}$
, or
![]() $\textbf{0}\notin W_i$
for
$\textbf{0}\notin W_i$
for
![]() $i=1,2$
. The mapping defined as
$i=1,2$
. The mapping defined as
is bi-Lipschitz if and only if
![]() $\Phi$
is. Moreover if
$\Phi$
is. Moreover if
![]() $W_1$
is unbounded, the mapping
$W_1$
is unbounded, the mapping
![]() $\iota (\Phi )$
extends bi-Lipschitz-ly at
$\iota (\Phi )$
extends bi-Lipschitz-ly at
![]() $\textbf{0}$
, taking the value
$\textbf{0}$
, taking the value
![]() $\textbf{0}$
.
$\textbf{0}$
.
Proof. Since
![]() $\iota ({\iota (\Phi )}) = \Phi$
, it is enough to show the result when
$\iota ({\iota (\Phi )}) = \Phi$
, it is enough to show the result when
![]() $\Phi$
is bi-Lipschitz. Since
$\Phi$
is bi-Lipschitz. Since
![]() ${\iota (\Phi )}^{-1} = \iota _{q_1} \circ \Phi ^{-1} \circ \iota _{q_2}^{-1}$
, we only need to show that
${\iota (\Phi )}^{-1} = \iota _{q_1} \circ \Phi ^{-1} \circ \iota _{q_2}^{-1}$
, we only need to show that
![]() $\iota (\Phi )$
is Lipschitz.
$\iota (\Phi )$
is Lipschitz.
By construction, we already know that
![]() $\iota (\Phi )$
is a homeomorphism of
$\iota (\Phi )$
is a homeomorphism of
![]() $\iota _{q_1}\big(W_1^*\big)\to \iota _{q_2}(W_2^*)$
which extends homeomorphically to
$\iota _{q_1}\big(W_1^*\big)\to \iota _{q_2}(W_2^*)$
which extends homeomorphically to
![]() $\overline{\iota _{q_1}\big(W_1^*\big)}\to \overline{\iota _{q_2}(W_2^*)}$
, mapping
$\overline{\iota _{q_1}\big(W_1^*\big)}\to \overline{\iota _{q_2}(W_2^*)}$
, mapping
![]() $\textbf{0}$
to
$\textbf{0}$
to
![]() $\textbf{0}$
whence
$\textbf{0}$
whence
![]() $W_1$
is unbounded.
$W_1$
is unbounded.
Let
![]() $0\lt r\lt R\lt \infty$
be radii. We define the following subsets:
$0\lt r\lt R\lt \infty$
be radii. We define the following subsets:
 \begin{eqnarray*} C_r^* & \,:\!=\, & \big\{\textbf{y} \in \iota _{q_1}\big(W_1^*\big) \,:\, 0 \lt |\textbf{y}| \leq r\big\} \\ C_r^R & \,:\!=\, & \big\{\textbf{y} \in \iota _{q_1}\big(W_1^*\big) \,:\, r\leq |\textbf{y}| \leq R\big\} \\ C^R & \,:\!=\, & \big\{\textbf{y} \in \iota _{q_1}\big(W_1^*\big) \,:\, R\leq |\textbf{y}|\big\} . \end{eqnarray*}
\begin{eqnarray*} C_r^* & \,:\!=\, & \big\{\textbf{y} \in \iota _{q_1}\big(W_1^*\big) \,:\, 0 \lt |\textbf{y}| \leq r\big\} \\ C_r^R & \,:\!=\, & \big\{\textbf{y} \in \iota _{q_1}\big(W_1^*\big) \,:\, r\leq |\textbf{y}| \leq R\big\} \\ C^R & \,:\!=\, & \big\{\textbf{y} \in \iota _{q_1}\big(W_1^*\big) \,:\, R\leq |\textbf{y}|\big\} . \end{eqnarray*}
The “annulus”
![]() $C_r^R$
is compact and does not contain the origin. We recall that the mapping
$C_r^R$
is compact and does not contain the origin. We recall that the mapping
![]() $\iota _q$
induces a bi-Lipschitz homeomorphism
$\iota _q$
induces a bi-Lipschitz homeomorphism
![]() $K \to \iota _q(K)$
over any compact subset
$K \to \iota _q(K)$
over any compact subset
![]() $K$
of
$K$
of
![]() ${\textbf{U}}_q$
. Thus,
${\textbf{U}}_q$
. Thus,
![]() $\iota (\Phi )$
induces a bi-Lipschitz homeomorphism from
$\iota (\Phi )$
induces a bi-Lipschitz homeomorphism from
![]() $C_r^R$
onto its image. By Lemma 8,
$C_r^R$
onto its image. By Lemma 8,
![]() $\iota (\Phi )$
is a bi-Lipschitz homeomorphism from
$\iota (\Phi )$
is a bi-Lipschitz homeomorphism from
![]() $C^R$
onto its image. If
$C^R$
onto its image. If
![]() $W_1$
is compact, we can take
$W_1$
is compact, we can take
![]() $r$
small enough so that
$r$
small enough so that
![]() $C_r^*$
is empty. If
$C_r^*$
is empty. If
![]() $W_1$
is unbounded, Lemma 7 implies that
$W_1$
is unbounded, Lemma 7 implies that
![]() $\iota (\Phi )$
is a bi-Lipschitz homeomorphism from
$\iota (\Phi )$
is a bi-Lipschitz homeomorphism from
![]() $C_r^*$
onto its image and extends bi-Lipschitz-ly at
$C_r^*$
onto its image and extends bi-Lipschitz-ly at
![]() $\textbf{0}$
.
$\textbf{0}$
.
Let
![]() $A,B \in \{C^R,C_r^R,C_r^*\}$
with
$A,B \in \{C^R,C_r^R,C_r^*\}$
with
![]() $A\neq B$
. If
$A\neq B$
. If
![]() $\iota (\Phi )$
is not Lipschitz in
$\iota (\Phi )$
is not Lipschitz in
![]() $A\cup B$
, then there exist a pair of sequences
$A\cup B$
, then there exist a pair of sequences
![]() $({\textbf{a}}_n)_n$
of
$({\textbf{a}}_n)_n$
of
![]() $A$
and
$A$
and
![]() $({\textbf{b}}_n)_n$
of
$({\textbf{b}}_n)_n$
of
![]() $B$
such that
$B$
such that
Up to taking some subsequences, we can further assume that each sequence
![]() $({\textbf{a}}_n)_n$
and
$({\textbf{a}}_n)_n$
and
![]() $({\textbf{b}}_n)_n$
either converges or goes to infinity. We check that the only scenario where such a pair of sequences could exist satisfying the required limit condition above is when both converge to a point
$({\textbf{b}}_n)_n$
either converges or goes to infinity. We check that the only scenario where such a pair of sequences could exist satisfying the required limit condition above is when both converge to a point
![]() $\textbf{c} \in A \cap B$
, thus
$\textbf{c} \in A \cap B$
, thus
![]() $\textbf{c} \neq \textbf{0}$
. Which is absurd since nearby the point
$\textbf{c} \neq \textbf{0}$
. Which is absurd since nearby the point
![]() $\textbf{c}$
the inversion
$\textbf{c}$
the inversion
![]() $\iota _{q_1}^{-1}$
is Lipschitz as is
$\iota _{q_1}^{-1}$
is Lipschitz as is
![]() $\iota _{q_2}$
near the point
$\iota _{q_2}$
near the point
![]() $\Phi (\iota _{q_1}^{-1}(\textbf{c}))$
.
$\Phi (\iota _{q_1}^{-1}(\textbf{c}))$
.
Thus,
![]() $\iota (\Phi )$
is Lipschitz over each
$\iota (\Phi )$
is Lipschitz over each
![]() $A\cup B$
with
$A\cup B$
with
![]() $A,B \in \{C^R,C_r^R,C_r^*\}$
with
$A,B \in \{C^R,C_r^R,C_r^*\}$
with
![]() $A\neq B$
. Let
$A\neq B$
. Let
![]() $C$
be the remaining subset among
$C$
be the remaining subset among
![]() $\{C^R,C_r^R,C_r^*\}$
so that
$\{C^R,C_r^R,C_r^*\}$
so that
![]() $A\cup B\cup C = \iota _{q_1}(W_1)$
. Working with
$A\cup B\cup C = \iota _{q_1}(W_1)$
. Working with
![]() $A^{\prime} = A\cup B$
and
$A^{\prime} = A\cup B$
and
![]() $B^{\prime} = C$
instead of
$B^{\prime} = C$
instead of
![]() $A,B$
as we did in the previous case, we conclude that
$A,B$
as we did in the previous case, we conclude that
![]() $\iota (\Phi )$
is Lipschitz.
$\iota (\Phi )$
is Lipschitz.
7. Main result
Let
![]() $N_q = (0,\ldots,0,1) \in{\mathbb{R}}^{q+1}$
be the north pole of the unit sphere
$N_q = (0,\ldots,0,1) \in{\mathbb{R}}^{q+1}$
be the north pole of the unit sphere
![]() ${\textbf{S}}^q$
. Let
${\textbf{S}}^q$
. Let
be the inverse of the stereographic projection with center
![]() $N_q$
. Given a subset of
$N_q$
. Given a subset of
![]() $S$
of
$S$
of
![]() ${\mathbb{R}}^q$
, let
${\mathbb{R}}^q$
, let
If
![]() $\Phi \,:\,W_1 \to W_2$
is a homeomorphism, where each subset
$\Phi \,:\,W_1 \to W_2$
is a homeomorphism, where each subset
![]() $W_i$
is
$W_i$
is
![]() $q_i$
-affine,
$q_i$
-affine,
![]() $i=1,2$
, its stereographic pre-compactification is the homeomorphism
$i=1,2$
, its stereographic pre-compactification is the homeomorphism
![]() $\sigma _{q_2}\circ \Phi \circ \sigma _{q_1}^{-1}$
. If
$\sigma _{q_2}\circ \Phi \circ \sigma _{q_1}^{-1}$
. If
![]() $W_1$
is unbounded, the stereographic compactification of
$W_1$
is unbounded, the stereographic compactification of
![]() $\Phi$
is the mapping
$\Phi$
is the mapping
![]() $\widetilde{\Phi }$
, extension of
$\widetilde{\Phi }$
, extension of
![]() $\sigma _{q_2}\circ \Phi \circ \sigma _{q_1}^{-1}$
to
$\sigma _{q_2}\circ \Phi \circ \sigma _{q_1}^{-1}$
to
![]() $\widetilde{W}_1$
.
$\widetilde{W}_1$
.
Theorem 10.
Let
![]() $W_i$
be
$W_i$
be
![]() $q_i$
-affine subsets,
$q_i$
-affine subsets,
![]() $i=1,2$
. A mapping
$i=1,2$
. A mapping
![]() $\Phi \,:\,W_1\to W_2$
is bi-Lipschitz, if and only if its stereographic compactification
$\Phi \,:\,W_1\to W_2$
is bi-Lipschitz, if and only if its stereographic compactification
![]() $\widetilde{\Phi }\,:\, \widetilde{W}_1 \to \widetilde{W}_2$
is bi-Lipschitz
$\widetilde{\Phi }\,:\, \widetilde{W}_1 \to \widetilde{W}_2$
is bi-Lipschitz
The rest of this section is devoted to the proof of this result.
We recall that the quotient space obtained from gluing two copies of
![]() ${\mathbb{R}}^q$
, when both
${\mathbb{R}}^q$
, when both
![]() ${\textbf{U}}_q$
are identified by the inversion
${\textbf{U}}_q$
are identified by the inversion
![]() $\iota _q$
is
$\iota _q$
is
![]() ${\textbf{S}}^q$
. Therefore, the next result, somehow tuned with [Reference Costa, Grandjean and Michalska3, Lemma 7.2], should not come as a surprise.
${\textbf{S}}^q$
. Therefore, the next result, somehow tuned with [Reference Costa, Grandjean and Michalska3, Lemma 7.2], should not come as a surprise.
Lemma 11.
Suppose that
![]() $W_1$
is unbounded. The mapping germ
$W_1$
is unbounded. The mapping germ
![]() $\Phi \,:\, (W_1,\infty ) \to (W_2,\infty )$
is bi-Lipschitz if and only if
$\Phi \,:\, (W_1,\infty ) \to (W_2,\infty )$
is bi-Lipschitz if and only if
![]() $\widetilde{\Phi } \,:\,\big(\widetilde{W}_1,N_{q_1}\big) \to \big(\widetilde{W}_2,N_{q_2}\big)$
is bi-Lipschitz.
$\widetilde{\Phi } \,:\,\big(\widetilde{W}_1,N_{q_1}\big) \to \big(\widetilde{W}_2,N_{q_2}\big)$
is bi-Lipschitz.
Proof. Let
![]() $\textbf{z} = (\textbf{z}^{\prime},t)$
be Euclidean coordinates on
$\textbf{z} = (\textbf{z}^{\prime},t)$
be Euclidean coordinates on
![]() ${\mathbb{R}}^{q+1} ={{\mathbb{R}}^q}\times{\mathbb{R}}$
. The following mapping
${\mathbb{R}}^{q+1} ={{\mathbb{R}}^q}\times{\mathbb{R}}$
. The following mapping
is a
![]() $C^\infty$
diffeomorphism; thus, it is a bi-Lipschitz homeomorphism mapping
$C^\infty$
diffeomorphism; thus, it is a bi-Lipschitz homeomorphism mapping
![]() $\textbf{0}$
onto
$\textbf{0}$
onto
![]() $N_q$
. We also check that
$N_q$
. We also check that
The lemma follows from Lemmas 8 and 7, and the fact that
![]() $\beta _q$
is bi-Lipschitz.
$\beta _q$
is bi-Lipschitz.
Proof of Theorem 10. We recall that
![]() $\sigma _q$
is bi-Lipschitz over any given compact subset of
$\sigma _q$
is bi-Lipschitz over any given compact subset of
![]() ${\mathbb{R}}^q$
. If
${\mathbb{R}}^q$
. If
![]() $W_1$
is compact, the result is thus obvious.
$W_1$
is compact, the result is thus obvious.
Assume that
![]() $W_1$
is unbounded. Let
$W_1$
is unbounded. Let
![]() $K_1 ={\textbf{B}}_{R_1}^{q_1}\cap W_1$
and
$K_1 ={\textbf{B}}_{R_1}^{q_1}\cap W_1$
and
![]() $K_2 = \Phi (K_1)$
with
$K_2 = \Phi (K_1)$
with
![]() $R_1\geq 2$
chosen so that
$R_1\geq 2$
chosen so that
![]() $W_i \setminus K_i$
is contained in
$W_i \setminus K_i$
is contained in
![]() ${\mathbb{R}}^{q_i}\setminus{\textbf{B}}_2^{q_i}$
, where
${\mathbb{R}}^{q_i}\setminus{\textbf{B}}_2^{q_i}$
, where
![]() $i=1,2$
. Thus, the mapping
$i=1,2$
. Thus, the mapping
is bi-Lipschitz, if and only if
![]() $\widetilde{\Phi }_b \,:\!=\, \widetilde{\Phi }|_{\widetilde{K}_1} \,:\, \widetilde{K}_1 \to \widetilde{K}_2$
is bi-Lipschitz.
$\widetilde{\Phi }_b \,:\!=\, \widetilde{\Phi }|_{\widetilde{K}_1} \,:\, \widetilde{K}_1 \to \widetilde{K}_2$
is bi-Lipschitz.
Up to increasing
![]() $R_1$
, following the proof of Lemma 11, we deduce that the mapping
$R_1$
, following the proof of Lemma 11, we deduce that the mapping
is bi-Lipschitz if and only if the mapping
![]() $\widetilde{\Phi }_u \,:\!=\, \widetilde{\Phi }|_{\widetilde{W}_1\setminus \widetilde{K}_1} \,:\, \widetilde{W}_1\setminus \widetilde{K}_1 \to \widetilde{W}_2\setminus \widetilde{K}_2$
is observe that
$\widetilde{\Phi }_u \,:\!=\, \widetilde{\Phi }|_{\widetilde{W}_1\setminus \widetilde{K}_1} \,:\, \widetilde{W}_1\setminus \widetilde{K}_1 \to \widetilde{W}_2\setminus \widetilde{K}_2$
is observe that
![]() $\Phi _u$
and
$\Phi _u$
and
![]() $\widetilde{\Phi }_u$
, respectively, extend bi-Lipschitz-ly on the closure of their domains when
$\widetilde{\Phi }_u$
, respectively, extend bi-Lipschitz-ly on the closure of their domains when
![]() $\Phi$
and
$\Phi$
and
![]() $\widetilde{\Phi }$
, respectively, are bi-Lipschitz.
$\widetilde{\Phi }$
, respectively, are bi-Lipschitz.
-
Assume that
 $\Phi$
is bi-Lipschitz. Thus,
$\Phi$
is bi-Lipschitz. Thus,
 $\widetilde{\Phi }$
is a homeomorphism and both
$\widetilde{\Phi }$
is a homeomorphism and both
 $\widetilde{\Phi }_b$
and
$\widetilde{\Phi }_b$
and
 $\widetilde{\Phi }_u$
are bi-Lipschitz. If
$\widetilde{\Phi }_u$
are bi-Lipschitz. If
 $\widetilde{\Phi }$
were not Lipschitz, there would exist two sequences
$\widetilde{\Phi }$
were not Lipschitz, there would exist two sequences
 $(\textbf{z}_n)_n$
,
$(\textbf{z}_n)_n$
,
 $(\textbf{z}^{\prime}_n)_n$
of
$(\textbf{z}^{\prime}_n)_n$
of
 $\widetilde{W}_1$
such thatSince
$\widetilde{W}_1$
such thatSince \begin{equation*} \lim _{n\to \infty }\frac {\big|\widetilde {\Phi }(\textbf {z}^{\prime}_n) - \widetilde {\Phi }(\textbf {z}_n)\big|}{|\textbf {z}^{\prime}_n - \textbf {z}_n|} = \infty . \end{equation*}
\begin{equation*} \lim _{n\to \infty }\frac {\big|\widetilde {\Phi }(\textbf {z}^{\prime}_n) - \widetilde {\Phi }(\textbf {z}_n)\big|}{|\textbf {z}^{\prime}_n - \textbf {z}_n|} = \infty . \end{equation*}
 $\widetilde{W}_1$
is compact, up to passing to subsequences we can assume that both sequences converge to
$\widetilde{W}_1$
is compact, up to passing to subsequences we can assume that both sequences converge to
 $\omega _1$
. Since
$\omega _1$
. Since
 $\Phi _u,\Phi _b$
are bi-Lipschitz and
$\Phi _u,\Phi _b$
are bi-Lipschitz and
 $\Phi _u$
extends bi-Lipschitz-ly onto
$\Phi _u$
extends bi-Lipschitz-ly onto
 $\textrm{clos}(\widetilde{W}_1\setminus \widetilde{K}_1)$
, necessarily one of the sequences is contained in
$\textrm{clos}(\widetilde{W}_1\setminus \widetilde{K}_1)$
, necessarily one of the sequences is contained in
 $\widetilde{K}_1$
and the other one in
$\widetilde{K}_1$
and the other one in
 $\widetilde{W}_1\setminus \widetilde{K}_1$
. Thus,
$\widetilde{W}_1\setminus \widetilde{K}_1$
. Thus,
 $\omega _1 \in \widetilde{K}_1$
and
$\omega _1 \in \widetilde{K}_1$
and
 $\omega _2 \,:\!=\, \widetilde{\Phi }(\omega _1) \in \widetilde{K}_2$
. Since
$\omega _2 \,:\!=\, \widetilde{\Phi }(\omega _1) \in \widetilde{K}_2$
. Since
 $\sigma _{q_1}^{-1}$
is bi-Lipschitz nearby
$\sigma _{q_1}^{-1}$
is bi-Lipschitz nearby
 $\omega _1$
and
$\omega _1$
and
 $\sigma _{q_2}^{-1}$
is bi-Lipschitz nearby
$\sigma _{q_2}^{-1}$
is bi-Lipschitz nearby
 $\omega _2$
, the mapping
$\omega _2$
, the mapping
 $\widetilde{\Phi }$
is Lipschitz nearby
$\widetilde{\Phi }$
is Lipschitz nearby
 $\omega _1$
, yielding a contradiction.
$\omega _1$
, yielding a contradiction.
-
Assume that
 $\widetilde{\Phi }$
is bi-Lipschitz. Thus,
$\widetilde{\Phi }$
is bi-Lipschitz. Thus,
 $\Phi$
is a homeomorphism and both
$\Phi$
is a homeomorphism and both
 $\Phi _b$
and
$\Phi _b$
and
 $\Phi _u$
are bi-Lipschitz. Moreover,
$\Phi _u$
are bi-Lipschitz. Moreover,
 $\Phi _u$
extends bi-Lipschitz-ly to
$\Phi _u$
extends bi-Lipschitz-ly to
 $\textrm{clos}(W_1\setminus K_1)$
. If
$\textrm{clos}(W_1\setminus K_1)$
. If
 $\Phi$
were not Lipschitz, there would exist two sequences
$\Phi$
were not Lipschitz, there would exist two sequences
 $({\textbf{x}}_n)_n$
and
$({\textbf{x}}_n)_n$
and
 $({\textbf{x}}^{\prime}_n)_n$
of
$({\textbf{x}}^{\prime}_n)_n$
of
 $\widetilde{W}_1$
such thatNecessarily one sequence belongs to
$\widetilde{W}_1$
such thatNecessarily one sequence belongs to \begin{equation*} \lim _{n\to \infty }\frac {\big|\Phi ({\textbf {x}}^{\prime}_n) - \widetilde {\Phi }({\textbf {x}}_n)\big|}{|{\textbf {x}}^{\prime}_n - {\textbf {x}}_n|} = \infty . \end{equation*}
\begin{equation*} \lim _{n\to \infty }\frac {\big|\Phi ({\textbf {x}}^{\prime}_n) - \widetilde {\Phi }({\textbf {x}}_n)\big|}{|{\textbf {x}}^{\prime}_n - {\textbf {x}}_n|} = \infty . \end{equation*}
 $K_1$
and the other one to
$K_1$
and the other one to
 $\textrm{clos}(W_1\setminus K_1)$
. Assume that
$\textrm{clos}(W_1\setminus K_1)$
. Assume that
 $({\textbf{x}}_n)_n$
is contained in
$({\textbf{x}}_n)_n$
is contained in
 $K_1$
. So, we can assume it converges to
$K_1$
. So, we can assume it converges to
 $\textbf{y}_1$
. If
$\textbf{y}_1$
. If
 $\textbf{y}_1$
does not lie in the compact set
$\textbf{y}_1$
does not lie in the compact set
 $L_1 = K_1\cap \textrm{clos}(W_1\setminus K_1)$
, thustherefore
$L_1 = K_1\cap \textrm{clos}(W_1\setminus K_1)$
, thustherefore \begin{equation*} \liminf _n |{\textbf {x}}^{\prime}_n - {\textbf {x}}_n| \in (0,\infty ] \end{equation*}
\begin{equation*} \liminf _n |{\textbf {x}}^{\prime}_n - {\textbf {x}}_n| \in (0,\infty ] \end{equation*}
 $\Phi ({\textbf{x}}^{\prime}_n)$
goes to
$\Phi ({\textbf{x}}^{\prime}_n)$
goes to
 $\infty$
, and using
$\infty$
, and using
 $\widetilde{\Phi }$
, we conclude that
$\widetilde{\Phi }$
, we conclude that
 ${\textbf{x}}^{\prime}_n \to \infty$
. Let
${\textbf{x}}^{\prime}_n \to \infty$
. Let
 $M$
be a Lipschitz constant common to
$M$
be a Lipschitz constant common to
 $\Phi _b$
and
$\Phi _b$
and
 $\Phi _u$
. Let
$\Phi _u$
. Let
 $\textbf{y}^{\prime}_1$
be a point of
$\textbf{y}^{\prime}_1$
be a point of
 $L_1$
. Thus,yielding a contradiction since
$L_1$
. Thus,yielding a contradiction since \begin{equation*} |\Phi ({\textbf {x}}^{\prime}_n) - \Phi ({\textbf {x}}_n)|\leq |\Phi _u({\textbf {x}}_n) - \Phi _u(\textbf {y}^{\prime}_1)| + |\Phi _b(\textbf {y}^{\prime}_1)-\Phi _b({\textbf {x}}_n)| \leq M|{\textbf {x}}_n - \textbf {y}^{\prime}_1| + M |\textbf {y}^{\prime}_1-{\textbf {x}}_n| \end{equation*}
\begin{equation*} |\Phi ({\textbf {x}}^{\prime}_n) - \Phi ({\textbf {x}}_n)|\leq |\Phi _u({\textbf {x}}_n) - \Phi _u(\textbf {y}^{\prime}_1)| + |\Phi _b(\textbf {y}^{\prime}_1)-\Phi _b({\textbf {x}}_n)| \leq M|{\textbf {x}}_n - \textbf {y}^{\prime}_1| + M |\textbf {y}^{\prime}_1-{\textbf {x}}_n| \end{equation*}
 $|{\textbf{x}}_n-\textbf{y}^{\prime}_1|\to \infty$
. Thus,
$|{\textbf{x}}_n-\textbf{y}^{\prime}_1|\to \infty$
. Thus,
 $\textbf{y}_1$
lies in
$\textbf{y}_1$
lies in
 $L_1$
.
$L_1$
.
The same argument involving the point
![]() $\textbf{y}^{\prime}_1 = \textbf{y}_1$
implies that
$\textbf{y}^{\prime}_1 = \textbf{y}_1$
implies that
![]() $\liminf _n |{\textbf{x}}^{\prime}_n -{\textbf{x}}_n| = 0$
, so we can assume that
$\liminf _n |{\textbf{x}}^{\prime}_n -{\textbf{x}}_n| = 0$
, so we can assume that
![]() $({\textbf{x}}^{\prime}_n)_n$
converges to
$({\textbf{x}}^{\prime}_n)_n$
converges to
![]() $\textbf{y}_1$
as well. Since
$\textbf{y}_1$
as well. Since
![]() $\sigma _{q_1}^{-1}$
is bi-Lipschitz nearby
$\sigma _{q_1}^{-1}$
is bi-Lipschitz nearby
![]() $\textbf{y}_1$
and
$\textbf{y}_1$
and
![]() $\sigma _{q_2}$
is bi-Lipschitz nearby
$\sigma _{q_2}$
is bi-Lipschitz nearby
![]() $\Phi (\textbf{y}_1)$
, the mapping
$\Phi (\textbf{y}_1)$
, the mapping
![]() $\Phi$
is Lipschitz nearby
$\Phi$
is Lipschitz nearby
![]() $\textbf{y}_1$
, yielding a contradiction.
$\textbf{y}_1$
, yielding a contradiction.
8. Geometry at infinity of tame sets
There are many possible applications of the inversion Lemma 9. In particular, any bi-Lipschitz classification problem of subsets at infinity is equivalent to a bi-Lipschitz classification problem at the origin.
There are quite a few questions of bi-Lipschitz definable geometry at infinity which now reduce to a problem at the origin by our main result. Many of them would require some specific preparations, that is why we present here only two such applications, which are immediate consequences of Lemma 9.
8.1. Bi-Lipschitz definable sets at infinity and their tangent cones
A non-negative cone
![]() $C$
of
$C$
of
![]() ${\mathbb{R}}^q$
is any subset of
${\mathbb{R}}^q$
is any subset of
![]() ${\mathbb{R}}^q$
stable by non-negative rescaling:
${\mathbb{R}}^q$
stable by non-negative rescaling:
For a given non-negative cone
![]() $C$
, the link of
$C$
, the link of
![]() $C$
is defined as;
$C$
is defined as;
Let
![]() $S$
be a non-empty subset of
$S$
be a non-empty subset of
![]() ${\mathbb{R}}^q$
. The non-negative cone over
${\mathbb{R}}^q$
. The non-negative cone over
![]() $S$
with vertex the origin
$S$
with vertex the origin
![]() $\textbf{0}$
is the subset of
$\textbf{0}$
is the subset of
![]() ${\mathbb{R}}^q$
defined as:
${\mathbb{R}}^q$
defined as:
In particular, a subset
![]() $C$
is a non-negative cone of
$C$
is a non-negative cone of
![]() ${\mathbb{R}}^q$
if and only if it is the non-negative cone over its link:
${\mathbb{R}}^q$
if and only if it is the non-negative cone over its link:
Definition 12.
Let
![]() $S$
be a subset of
$S$
be a subset of
![]() ${\mathbb{R}}^q$
.
${\mathbb{R}}^q$
.
-
(i) The asymptotic set of
 $S$
at
$S$
at
 $\textbf{0}$
is the closed subset of the unit sphere
$\textbf{0}$
is the closed subset of the unit sphere
 ${\textbf{S}}^{q-1}$
${\textbf{S}}^{q-1}$
 \begin{equation*} S^{\textbf {0}} \,:\!=\, \left \{{\textbf {u}} \in {\textbf {S}}^{q-1} \; : \; \exists \; ({\textbf {x}}_k)_k \in S^* \;\; \rm {such \, that} \;\; {\textbf {x}}_k\to \textbf {0} \;\;\textrm {and} \;\; \frac {{\textbf {x}}_k}{|{\textbf {x}}_k|} \to {\textbf {u}} \right \}. \end{equation*}
\begin{equation*} S^{\textbf {0}} \,:\!=\, \left \{{\textbf {u}} \in {\textbf {S}}^{q-1} \; : \; \exists \; ({\textbf {x}}_k)_k \in S^* \;\; \rm {such \, that} \;\; {\textbf {x}}_k\to \textbf {0} \;\;\textrm {and} \;\; \frac {{\textbf {x}}_k}{|{\textbf {x}}_k|} \to {\textbf {u}} \right \}. \end{equation*}
-
(ii) The asymptotic set of
 $S$
at
$S$
at
 $\infty$
is the closed subset of the unit sphere
$\infty$
is the closed subset of the unit sphere
 ${\textbf{S}}^{q-1}$
${\textbf{S}}^{q-1}$
 \begin{equation*} S^\infty \,:\!=\, \left \{{\textbf {u}} \in {\textbf {S}}^{q-1} \; : \; \exists \; ({\textbf {x}}_k)_k \in S \;\; \rm{such \, that} \;\; |{\textbf {x}}_k| \to \infty \;\;\textrm {and} \;\; \frac {{\textbf {x}}_k}{|{\textbf {x}}_k|} \to {\textbf {u}} \right \}. \end{equation*}
\begin{equation*} S^\infty \,:\!=\, \left \{{\textbf {u}} \in {\textbf {S}}^{q-1} \; : \; \exists \; ({\textbf {x}}_k)_k \in S \;\; \rm{such \, that} \;\; |{\textbf {x}}_k| \to \infty \;\;\textrm {and} \;\; \frac {{\textbf {x}}_k}{|{\textbf {x}}_k|} \to {\textbf {u}} \right \}. \end{equation*}
The subsets
![]() $S^{\textbf{0}}$
and
$S^{\textbf{0}}$
and
![]() $S^\infty$
are classical objects, with various names. We decided for a common denomination. The subset
$S^\infty$
are classical objects, with various names. We decided for a common denomination. The subset
![]() $S^\omega$
is often called, misleadingly, the tangent cone at
$S^\omega$
is often called, misleadingly, the tangent cone at
![]() $\omega$
. Note that
$\omega$
. Note that
![]() $S^{\textbf{0}}$
is call set of directions in [Reference Koike and Paunescu9]. The subset
$S^{\textbf{0}}$
is call set of directions in [Reference Koike and Paunescu9]. The subset
![]() $S^\omega$
is not empty if and only if
$S^\omega$
is not empty if and only if
![]() $\overline{S}$
contains
$\overline{S}$
contains
![]() $\omega$
, and observe that
$\omega$
, and observe that
where
![]() $\omega =\textbf{0}$
or
$\omega =\textbf{0}$
or
![]() $\infty$
. Since we are interested in the non-negative cones
$\infty$
. Since we are interested in the non-negative cones
![]() $\widehat{S^{\textbf{0}}}^+$
and
$\widehat{S^{\textbf{0}}}^+$
and
![]() $\widehat{S^\infty }^+$
, we will work only with closed subsets. The non-negative cone
$\widehat{S^\infty }^+$
, we will work only with closed subsets. The non-negative cone
![]() $\widehat{S^\omega }^+$
is also known as the tangent cone of
$\widehat{S^\omega }^+$
is also known as the tangent cone of
![]() $S$
at
$S$
at
![]() $\omega$
, for
$\omega$
, for
![]() $\omega = \textbf{0}$
or
$\omega = \textbf{0}$
or
![]() $\infty$
.
$\infty$
.
Given
![]() ${\textbf{x}} \in{\textbf{U}}_q$
, observe the following obvious fact
${\textbf{x}} \in{\textbf{U}}_q$
, observe the following obvious fact
Let
![]() $X$
be a closed subset of
$X$
be a closed subset of
![]() ${\mathbb{R}}^q$
and let
${\mathbb{R}}^q$
and let
![]() $\iota (X)$
be the closure
$\iota (X)$
be the closure
![]() $\textrm{clos}(\iota _q(X^*))$
. The following result is obvious from the definitions of asymptotic sets and the inversion.
$\textrm{clos}(\iota _q(X^*))$
. The following result is obvious from the definitions of asymptotic sets and the inversion.
Lemma 13. The following identities hold true:
From this lemma, we deduce
Let
![]() $\mathcal{M}$
be a polynomially bounded o-minimal structure expanding the real field
$\mathcal{M}$
be a polynomially bounded o-minimal structure expanding the real field
![]() $({\mathbb{R}},+,.,\geq )$
(see [Reference van den Dries5]). A subset of an Euclidean space
$({\mathbb{R}},+,.,\geq )$
(see [Reference van den Dries5]). A subset of an Euclidean space
![]() ${\mathbb{R}}^q$
is definable if it is definable in
${\mathbb{R}}^q$
is definable if it is definable in
![]() $\mathcal{M}$
. Let
$\mathcal{M}$
. Let
![]() $S$
be a subset of
$S$
be a subset of
![]() ${\mathbb{R}}^q$
. A mapping
${\mathbb{R}}^q$
. A mapping
![]() $S\to{{\mathbb{R}}^p}$
is definable if its graph is definable.
$S\to{{\mathbb{R}}^p}$
is definable if its graph is definable.
We recall the following result of Sampaio about tangent cones:
Theorem 14 ([Reference Sampaio12]). Let
![]() $(X_i,\textbf{0})$
be the germ of a definable set of
$(X_i,\textbf{0})$
be the germ of a definable set of
![]() ${\mathbb{R}}^{q_i}$
at the origin, i = 1,2. If there exists a bi-Lipschitz homeomorphism
${\mathbb{R}}^{q_i}$
at the origin, i = 1,2. If there exists a bi-Lipschitz homeomorphism
![]() $(X_1,\textbf{0}) \to (X_2,\textbf{0})$
, then there exists a bi-Lipschitz homeomorphism
$(X_1,\textbf{0}) \to (X_2,\textbf{0})$
, then there exists a bi-Lipschitz homeomorphism
![]() $\widehat{X_1^{\textbf{0}}}^+ \to \widehat{X_2^{\textbf{0}}}^+$
mapping
$\widehat{X_1^{\textbf{0}}}^+ \to \widehat{X_2^{\textbf{0}}}^+$
mapping
![]() $\textbf{0}$
onto
$\textbf{0}$
onto
![]() $\textbf{0}$
.
$\textbf{0}$
.
In truth [Reference Sampaio12] deals only with sub-analytic subsets, but the part of the demonstration using sub-analyticity goes through the definable context readily.
We recall that the inversion
![]() $\iota _q$
is a rational mapping, thus semi-algebraic, therefore definable in
$\iota _q$
is a rational mapping, thus semi-algebraic, therefore definable in
![]() $\mathcal{M}$
. As a corollary of this latter fact, of the inversion Lemma 9 and of identity (8.1), we deduce the following ([Reference Fernandes and Sampaio6, Theorem 2.19], [Reference Sampaio and Silva14, Theorem 3.1])
$\mathcal{M}$
. As a corollary of this latter fact, of the inversion Lemma 9 and of identity (8.1), we deduce the following ([Reference Fernandes and Sampaio6, Theorem 2.19], [Reference Sampaio and Silva14, Theorem 3.1])
Proposition 15.
Let
![]() $(W_i,\infty )$
be the germ of a closed definable set of
$(W_i,\infty )$
be the germ of a closed definable set of
![]() ${\mathbb{R}}^{q_i}$
at infinity, i = 1,2. If there exists a bi-Lipschitz homeomorphism
${\mathbb{R}}^{q_i}$
at infinity, i = 1,2. If there exists a bi-Lipschitz homeomorphism
![]() $(W_1,\infty ) \to (W_2,\infty )$
, then there exists a bi-Lipschitz homeomorphism
$(W_1,\infty ) \to (W_2,\infty )$
, then there exists a bi-Lipschitz homeomorphism
![]() $\widehat{W_1^\infty }^+ \to \widehat{W_2^\infty }^+$
mapping
$\widehat{W_1^\infty }^+ \to \widehat{W_2^\infty }^+$
mapping
![]() $\textbf{0}$
onto
$\textbf{0}$
onto
![]() $\textbf{0}$
.
$\textbf{0}$
.
8.2. On the link at infinity
Let
![]() $S$
be a subset of
$S$
be a subset of
![]() ${\mathbb{R}}^q$
. For any positive radius
${\mathbb{R}}^q$
. For any positive radius
![]() $R$
, we define the following subsets:
$R$
, we define the following subsets:
Let again denote
![]() $\iota (S)$
the closure of
$\iota (S)$
the closure of
![]() $\iota _q(S^*)$
. Thus, we get the obvious identifications:
$\iota _q(S^*)$
. Thus, we get the obvious identifications:
When
![]() $X$
is definable and contains the origin
$X$
is definable and contains the origin
![]() $\textbf{0}$
, the local conic structure theorem states that there exists
$\textbf{0}$
, the local conic structure theorem states that there exists
![]() $r_0$
such that for any radius
$r_0$
such that for any radius
![]() $r_0\geq r\gt 0$
, the definable subset
$r_0\geq r\gt 0$
, the definable subset
![]() $X_{\leq r}$
is definably homeomorphic with
$X_{\leq r}$
is definably homeomorphic with
![]() $( \widehat{X_r}^+ )_{\leq r}$
, the “non-negative cone over
$( \widehat{X_r}^+ )_{\leq r}$
, the “non-negative cone over
![]() $X_r$
” [Reference van den Dries5]. Moreover, such a definable homeomorphism can be found so that it preserves the distance to
$X_r$
” [Reference van den Dries5]. Moreover, such a definable homeomorphism can be found so that it preserves the distance to
![]() $\textbf{0}$
[Reference Valette15]. In particular,
$\textbf{0}$
[Reference Valette15]. In particular,
![]() $X_r$
has constant topological type for
$X_r$
has constant topological type for
![]() $r \leq r_0$
. It can also be shown that for any pair of radii
$r \leq r_0$
. It can also be shown that for any pair of radii
![]() $0\lt r\lt r^{\prime}\leq r_0$
, the links
$0\lt r\lt r^{\prime}\leq r_0$
, the links
![]() $X_r$
and
$X_r$
and
![]() $X_{r^{\prime}}$
are bi-Lipschitz definably homeomorphic [Reference Valette15, Reference Valette17, Reference Valette18], although the Lipschitz constant in general cannot be uniform over
$X_{r^{\prime}}$
are bi-Lipschitz definably homeomorphic [Reference Valette15, Reference Valette17, Reference Valette18], although the Lipschitz constant in general cannot be uniform over
![]() $]0,r_0]$
.
$]0,r_0]$
.
Let
![]() $W$
be a definable subset of
$W$
be a definable subset of
![]() ${\mathbb{R}}^q$
. Using the inversion and the local conicstructure theorem yield the locally conic structure theorem at infinity: there exists a positive radius
${\mathbb{R}}^q$
. Using the inversion and the local conicstructure theorem yield the locally conic structure theorem at infinity: there exists a positive radius
![]() $R_0$
such that for any
$R_0$
such that for any
![]() $R\geq R_0$
, the subset
$R\geq R_0$
, the subset
![]() $W_{\geq R}$
is definably homeomorphic to
$W_{\geq R}$
is definably homeomorphic to
![]() $\big(\widehat{W_R}^+\big)_{\geq R}$
, the “non-negative cone over
$\big(\widehat{W_R}^+\big)_{\geq R}$
, the “non-negative cone over
![]() $W_R$
” at infinity. Moreover, such a definable homeomorphism can be found so that it also preserves the distance to the origin. Last given any pair of radii
$W_R$
” at infinity. Moreover, such a definable homeomorphism can be found so that it also preserves the distance to the origin. Last given any pair of radii
![]() $R,R^{\prime}\geq R_0$
, the links
$R,R^{\prime}\geq R_0$
, the links
![]() $W_R$
and
$W_R$
and
![]() $W_{R^{\prime}}$
are definable and bi-Lipschitz homeomorphic.
$W_{R^{\prime}}$
are definable and bi-Lipschitz homeomorphic.
We have mentioned the local conic structure theorems and the bi-Lipschitz constancy of the links in light of the following result about links preserving reparametrization of definable bi-Lipschitz homeomorphism of Valette:
Theorem 16 ([Reference Valette16–Reference Valette18]). Let
![]() $(X_i,\textbf{0})$
be a closed definable germ of
$(X_i,\textbf{0})$
be a closed definable germ of
![]() ${\mathbb{R}}^{q_i}$
,
${\mathbb{R}}^{q_i}$
,
![]() $i=1,2$
. If there exists a definable bi-Lipschitz homeomorphism
$i=1,2$
. If there exists a definable bi-Lipschitz homeomorphism
![]() $(X_1,\textbf{0}) \to (X_2,\textbf{0})$
, then there exists a definable bi-Lipschitz homeomorphism
$(X_1,\textbf{0}) \to (X_2,\textbf{0})$
, then there exists a definable bi-Lipschitz homeomorphism
![]() $(X_1,\textbf{0}) \to (X_2,\textbf{0})$
preserving the distance to the origin.
$(X_1,\textbf{0}) \to (X_2,\textbf{0})$
preserving the distance to the origin.
Again as a corollary of our main result of Theorems 10 and 16 and the semi-algebraicity of the inversion, thus definable in
![]() $\mathcal{M}$
, we find the following
$\mathcal{M}$
, we find the following
Proposition 17.
Let
![]() $(W_i,\infty )$
be a closed definable germ of
$(W_i,\infty )$
be a closed definable germ of
![]() ${\mathbb{R}}^{q_i}$
,
${\mathbb{R}}^{q_i}$
,
![]() $i=1,2$
. If there exists a definable bi-Lipschitz homeomorphism
$i=1,2$
. If there exists a definable bi-Lipschitz homeomorphism
![]() $(W_1,\infty ) \to (W_2,\infty )$
, then there exists a definable bi-Lipschitz homeomorphism
$(W_1,\infty ) \to (W_2,\infty )$
, then there exists a definable bi-Lipschitz homeomorphism
![]() $(W_1,\infty ) \to (W_2,\infty )$
preserving the distance to the origin.
$(W_1,\infty ) \to (W_2,\infty )$
preserving the distance to the origin.
Acknowledgement
The authors are very grateful to André Costa and Maria Michalska for conversations, comments, and insight.