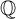1 Introduction
An algebraic variety Y over
![]() $\mathbb {Q}$
violates the Hasse principle if
$\mathbb {Q}$
violates the Hasse principle if
![]() $Y(\mathbb {Q}) = \emptyset $
despite the fact that
$Y(\mathbb {Q}) = \emptyset $
despite the fact that
![]() $Y(\mathbb {Q}_p) \neq \emptyset $
for all completions
$Y(\mathbb {Q}_p) \neq \emptyset $
for all completions
![]() $\mathbb {Q}_p$
of
$\mathbb {Q}_p$
of
![]() $\mathbb {Q}$
, including the archimedean completion
$\mathbb {Q}$
, including the archimedean completion
![]() $\mathbb {Q}_{\infty } = \mathbb {R}$
. The Hasse-Minkowski theorem shows that quadrics in
$\mathbb {Q}_{\infty } = \mathbb {R}$
. The Hasse-Minkowski theorem shows that quadrics in
![]() $\mathbb {P}^n$
never violate the Hasse principle, but violations do exist in higher degree. Some early examples include the hyperelliptic curve
$\mathbb {P}^n$
never violate the Hasse principle, but violations do exist in higher degree. Some early examples include the hyperelliptic curve
![]() $2y^2 = x^4 - 17$
studied by Lind and Reichardt [Reference Lind24, Reference Reichardt33] and Selmer’s plane cubic
$2y^2 = x^4 - 17$
studied by Lind and Reichardt [Reference Lind24, Reference Reichardt33] and Selmer’s plane cubic
![]() $3x^3 + 4y^3 + 5z^3 = 0$
[Reference Selmer35]. Each of these is a genus one curve C, and is therefore a torsor for its Jacobian, the elliptic curve
$3x^3 + 4y^3 + 5z^3 = 0$
[Reference Selmer35]. Each of these is a genus one curve C, and is therefore a torsor for its Jacobian, the elliptic curve
![]() $E = \mathrm {Pic}^0(C)$
. The fact that C violates the Hasse principle means that it represents a nontrivial element
$E = \mathrm {Pic}^0(C)$
. The fact that C violates the Hasse principle means that it represents a nontrivial element
![]() $[C]$
in the Tate-Shafarevich group
$[C]$
in the Tate-Shafarevich group ![]() parameterizing locally trivial E-torsors. The order of
parameterizing locally trivial E-torsors. The order of
![]() $[C]$
in
$[C]$
in ![]() is, in these cases, equal to the minimum positive degree of an effective
is, in these cases, equal to the minimum positive degree of an effective
![]() $0$
-cycle – hence
$0$
-cycle – hence
![]() $2$
in the first example and
$2$
in the first example and
![]() $3$
in the second.
$3$
in the second.
There are by now many other examples of nontrivial elements of Tate-Shafarevich groups of elliptic curves. However, it is an open question whether for every prime p there exists an elliptic curve
![]() $E/\mathbb {Q}$
with a class of order p in
$E/\mathbb {Q}$
with a class of order p in ![]() . Geometrically, such E-torsors are realized as genus one curves
. Geometrically, such E-torsors are realized as genus one curves
![]() $C \subset \mathbb {P}^{p-1}_{\mathbb {Q}}$
contained in no hyperplane, which violate the Hasse principle. The lack of a systematic construction of order p elements is somewhat surprising, since heuristics of Delaunay predict that for a given prime p, the probability that a random elliptic curve E satisfies
$C \subset \mathbb {P}^{p-1}_{\mathbb {Q}}$
contained in no hyperplane, which violate the Hasse principle. The lack of a systematic construction of order p elements is somewhat surprising, since heuristics of Delaunay predict that for a given prime p, the probability that a random elliptic curve E satisfies ![]() should be positive [Reference Delaunay11].
should be positive [Reference Delaunay11].
More generally, for any abelian variety
![]() $A/\mathbb {Q}$
, the group
$A/\mathbb {Q}$
, the group ![]() parameterizes A-torsors which violate the Hasse principle. Like the 1-dimensional case of elliptic curves, there are few examples with
parameterizes A-torsors which violate the Hasse principle. Like the 1-dimensional case of elliptic curves, there are few examples with ![]() for large primes p, beyond examples where
for large primes p, beyond examples where
![]() $A = \mathrm {Res}^F_{\mathbb {Q}} B$
is the Weil restriction of an abelian variety B over a number field F with
$A = \mathrm {Res}^F_{\mathbb {Q}} B$
is the Weil restriction of an abelian variety B over a number field F with ![]() (see, for example, [Reference Clark and Sharif9, Reference Kloosterman18, Reference Kloosterman and Schaefer19]). However, the second author and Weiss [Reference Shnidman and Weiss37] recently showed that for every prime p, there exist absolutely simple abelian varieties A over
(see, for example, [Reference Clark and Sharif9, Reference Kloosterman18, Reference Kloosterman and Schaefer19]). However, the second author and Weiss [Reference Shnidman and Weiss37] recently showed that for every prime p, there exist absolutely simple abelian varieties A over
![]() $\mathbb {Q}$
with
$\mathbb {Q}$
with ![]() . They prove such A exist among the quadratic twists of quotients of modular Jacobians
. They prove such A exist among the quadratic twists of quotients of modular Jacobians
![]() $J_0(N)$
with prime level
$J_0(N)$
with prime level
![]() $N \equiv 1\ \pmod {p}$
, but the proof does not yield explicit examples.
$N \equiv 1\ \pmod {p}$
, but the proof does not yield explicit examples.
1.1 Results
Our first main result is an explicit construction of A-torsors X which violate the Hasse principle. In our examples, both A and X have very simple equations. To state the theorem, recall the p-th power character
![]() $\left (\frac {q}{\ell }\right )_p$
, which satisfies
$\left (\frac {q}{\ell }\right )_p$
, which satisfies
![]() $\left (\frac {q}{\ell }\right )_p = 1$
if and only if q is a p-th power in
$\left (\frac {q}{\ell }\right )_p = 1$
if and only if q is a p-th power in
![]() $\mathbb {Q}_{\ell }^\times $
.
$\mathbb {Q}_{\ell }^\times $
.
Theorem 1.1. Let
![]() $p> 5$
be a prime and let
$p> 5$
be a prime and let
![]() $u,v$
be integers not divisible by
$u,v$
be integers not divisible by
![]() $3$
. Let U be the set of primes dividing
$3$
. Let U be the set of primes dividing
![]() $3puv(u-3v)$
. Let
$3puv(u-3v)$
. Let
![]() $t \geq 2$
, and let
$t \geq 2$
, and let
![]() $k = p_1 p_2 \cdots p_t$
, where each
$k = p_1 p_2 \cdots p_t$
, where each
![]() $p_i$
is a prime not in U satisfying
$p_i$
is a prime not in U satisfying
-
(1)
 $\left (\frac {p_i}{p_j}\right )_p = 1$
, for all
$\left (\frac {p_i}{p_j}\right )_p = 1$
, for all
 $i \neq j$
in
$i \neq j$
in
 $\{1,\ldots , t\}$
,
$\{1,\ldots , t\}$
, -
(2)
 $\left (\frac {p_i}{q}\right )_p = 1$
, for all
$\left (\frac {p_i}{q}\right )_p = 1$
, for all
 $i \in \{1, \ldots , t\}$
and all
$i \in \{1, \ldots , t\}$
and all
 $q \in U$
,
$q \in U$
, -
(3)
 $\left (\frac {q}{p_i}\right )_p = 1$
, for all
$\left (\frac {q}{p_i}\right )_p = 1$
, for all
 $i \in \{1, \ldots , t\}$
and all
$i \in \{1, \ldots , t\}$
and all
 $q \in U\backslash \{3\}$
,
$q \in U\backslash \{3\}$
, -
(4)
 $\left (\frac {3}{p_i}\right )_p \neq 1$
, for all
$\left (\frac {3}{p_i}\right )_p \neq 1$
, for all
 $i \in \{1, \ldots , t\}$
.
$i \in \{1, \ldots , t\}$
.
Let
![]() $g = p-1$
and consider the variety
$g = p-1$
and consider the variety
![]() $\tilde A \subset \mathbb {A}_{\mathbb {Q}}^{2g+1}$
defined by the equations
$\tilde A \subset \mathbb {A}_{\mathbb {Q}}^{2g+1}$
defined by the equations
 $$\begin{align*}y_i^p = x_i(x_i - 3uk)(x_i - 9vk),\mbox{ for } i = 1,\ldots ,g, \mbox{ and } z^p = \prod_{i = 1}^g x_i(x_i - 3uk).\end{align*}$$
$$\begin{align*}y_i^p = x_i(x_i - 3uk)(x_i - 9vk),\mbox{ for } i = 1,\ldots ,g, \mbox{ and } z^p = \prod_{i = 1}^g x_i(x_i - 3uk).\end{align*}$$
The symmetric group
![]() $S_g$
acts on
$S_g$
acts on
![]() $\tilde A$
, and the quotient
$\tilde A$
, and the quotient
![]() $\tilde A/S_g$
is birational to a unique g-dimensional abelian variety A over
$\tilde A/S_g$
is birational to a unique g-dimensional abelian variety A over
![]() $\mathbb {Q}$
. Let
$\mathbb {Q}$
. Let
![]() $I \subset \{1, \ldots , t\}$
be a proper nonempty subset, and let
$I \subset \{1, \ldots , t\}$
be a proper nonempty subset, and let
![]() $q = \prod _{i \in I} p_i$
. Let
$q = \prod _{i \in I} p_i$
. Let
![]() $\tilde X \subset \mathbb {A}_{\mathbb {Q}}^{2g+1}$
be defined by the equations
$\tilde X \subset \mathbb {A}_{\mathbb {Q}}^{2g+1}$
be defined by the equations
![]() $($
with
$($
with
![]() $i = 1,\ldots , g)$
$i = 1,\ldots , g)$
 $$\begin{align*}y_i^p = x_i(x_i - 3uk)(x_i - 9vk) \mbox{ and } qz^p = \prod_{i = 1}^g x_i(x_i - 3uk).\end{align*}$$
$$\begin{align*}y_i^p = x_i(x_i - 3uk)(x_i - 9vk) \mbox{ and } qz^p = \prod_{i = 1}^g x_i(x_i - 3uk).\end{align*}$$
Then
![]() $\tilde X/S_{g}$
is birational to an A-torsor X that violates the Hasse principle, and the class of X in
$\tilde X/S_{g}$
is birational to an A-torsor X that violates the Hasse principle, and the class of X in ![]() has order p.
has order p.
Remark 1.2. Both A and X are
![]() $\mu _p$
-covers of the Jacobian J of the genus
$\mu _p$
-covers of the Jacobian J of the genus
![]() $p-1$
superelliptic curve
$p-1$
superelliptic curve
![]() $C \colon y^p = x(x-3uk)(x-9vk)$
. Since J is birational to the symmetric power
$C \colon y^p = x(x-3uk)(x-9vk)$
. Since J is birational to the symmetric power
![]() $C^g/S_g$
, the
$C^g/S_g$
, the
![]() $\mu _p$
-covers can be seen from the equations above as well.
$\mu _p$
-covers can be seen from the equations above as well.
Using the Cebotarev density theorem, we show in Proposition 6.1 that there exist primes
![]() $p_1,\ldots , p_t$
satisfying the hypotheses of Theorem 1.1. Here is an example with
$p_1,\ldots , p_t$
satisfying the hypotheses of Theorem 1.1. Here is an example with
![]() $p = 29$
.
$p = 29$
.
Example 1.3. Let
![]() $\tilde X \subset \mathbb {A}_{\mathbb {Q}}^{28} \times \mathbb {A}_{\mathbb {Q}}^{28} \times \mathbb {A}_{\mathbb {Q}}^1$
be the variety defined by the
$\tilde X \subset \mathbb {A}_{\mathbb {Q}}^{28} \times \mathbb {A}_{\mathbb {Q}}^{28} \times \mathbb {A}_{\mathbb {Q}}^1$
be the variety defined by the
![]() $28$
equations
$28$
equations
for
![]() $i = 1, \ldots , 28$
, as well as the additional equation
$i = 1, \ldots , 28$
, as well as the additional equation
 $$\begin{align*}386029093 z^{29} = \prod_{i = 1}^{28} x_i(x_i - 3\cdot 386029093\cdot545622299).\end{align*}$$
$$\begin{align*}386029093 z^{29} = \prod_{i = 1}^{28} x_i(x_i - 3\cdot 386029093\cdot545622299).\end{align*}$$
Then
![]() $\tilde X/S_{g}$
is birational to a torsor X for a
$\tilde X/S_{g}$
is birational to a torsor X for a
![]() $28$
-dimensional abelian variety A over
$28$
-dimensional abelian variety A over
![]() $\mathbb {Q}$
. Moreover, X violates the Hasse principle and represents an order
$\mathbb {Q}$
. Moreover, X violates the Hasse principle and represents an order
![]() $29$
element of
$29$
element of ![]() .
.
Remark 1.4. As a point of comparison, work of Radičević [Reference Radičević32] gives a method to compute equations for order p torsors in the Tate-Shafarevich group of an elliptic curve E over
![]() $\mathbb {Q}$
. Even for
$\mathbb {Q}$
. Even for
![]() $p = 11$
, the equations for these torsors are not so easy for humans to write down. As p grows, the computations quickly become intractable even for computers.
$p = 11$
, the equations for these torsors are not so easy for humans to write down. As p grows, the computations quickly become intractable even for computers.
Since the hypotheses of Theorem 1.1 are always met, this gives a second proof of [Reference Shnidman and Weiss37, Thm. 1], and moreover gives explicit examples for any prime p. Moreover, the flexibility of the index set I allows us to prove our second main result, that ![]() can be arbitrarily large.
can be arbitrarily large.
Theorem 1.5. For every prime p and every integer
![]() $k \geq 1$
, there exists an absolutely simple abelian variety A over
$k \geq 1$
, there exists an absolutely simple abelian variety A over
![]() $\mathbb {Q}$
with
$\mathbb {Q}$
with ![]() .
.
The cases
![]() $p = 2,3,5$
not covered by Theorem 1.1 were proven by Bölling [Reference Bölling3], Cassels [Reference Cassels6] and Fisher [Reference Fisher12], respectively. Indeed, it was previously known that the p-part of the Tate-Shafarevich group of absolutely simple abelian varieties over
$p = 2,3,5$
not covered by Theorem 1.1 were proven by Bölling [Reference Bölling3], Cassels [Reference Cassels6] and Fisher [Reference Fisher12], respectively. Indeed, it was previously known that the p-part of the Tate-Shafarevich group of absolutely simple abelian varieties over
![]() $\mathbb {Q}$
can be arbitrarily large only for certain small primes p. Our examples are special since they arise as
$\mathbb {Q}$
can be arbitrarily large only for certain small primes p. Our examples are special since they arise as
![]() $\mu _p$
-covers of a specific type of Jacobian, so we leave open the question of existence of order p elements in
$\mu _p$
-covers of a specific type of Jacobian, so we leave open the question of existence of order p elements in ![]() for ‘generic’ abelian varieties over
for ‘generic’ abelian varieties over
![]() $\mathbb {Q}$
(i.e., those such that the Mumford-Tate group is
$\mathbb {Q}$
(i.e., those such that the Mumford-Tate group is
![]() $\mathrm {GSp}_{2g}$
and
$\mathrm {GSp}_{2g}$
and
![]() $A[p]$
is irreducible as a
$A[p]$
is irreducible as a
![]() $\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
-module). In both this paper and [Reference Shnidman and Weiss37], the abelian varieties are such that
$\mathrm {Gal}(\bar {\mathbb {Q}}/\mathbb {Q})$
-module). In both this paper and [Reference Shnidman and Weiss37], the abelian varieties are such that
![]() $\mathrm {rk}\, \mathrm {End}(A_{\bar {\mathbb {Q}}}) = \dim A$
and
$\mathrm {rk}\, \mathrm {End}(A_{\bar {\mathbb {Q}}}) = \dim A$
and
![]() $A[p]$
is reducible.
$A[p]$
is reducible.
Since we can control the dimension of our examples, we also conclude the following:
Corollary 1.6. Suppose
![]() $g = p-1$
for some prime
$g = p-1$
for some prime
![]() $p \geq 7$
. Then the Tate-Shafarevich groups of absolutely simple abelian varieties A over
$p \geq 7$
. Then the Tate-Shafarevich groups of absolutely simple abelian varieties A over
![]() $\mathbb {Q}$
of dimension g can be arbitrarily large. More precisely, the groups
$\mathbb {Q}$
of dimension g can be arbitrarily large. More precisely, the groups ![]() can be arbitrarily large.
can be arbitrarily large.
Our construction generalizes in an obvious way to any global field. We work over
![]() $\mathbb {Q}$
because it is the most interesting case and to keep the notation simple. The restriction
$\mathbb {Q}$
because it is the most interesting case and to keep the notation simple. The restriction
![]() $p \neq 5$
in our results is related to some quirky numerology (see Proposition A
$p \neq 5$
in our results is related to some quirky numerology (see Proposition A
![]() $(iii)$
in the Appendix) that could probably be removed by tweaking the construction slightly.
$(iii)$
in the Appendix) that could probably be removed by tweaking the construction slightly.
1.2 Previous work
Previous work on elliptic curves ([Reference Bhargava, Klagsbrun, Lemke Oliver and Shnidman2, Reference Bölling3, Reference Cassels6, Reference Fisher12, Reference Kloosterman18, Reference Kloosterman and Schaefer19, Reference Kramer20, Reference Lemmermeyer22, Reference Lemmermeyer and Mollin23, Reference Matsuno26]) has found arbitrarily large p-torsion part of the Tate-Shafarevich group for
![]() $p \leqslant 7$
and
$p \leqslant 7$
and
![]() $p=13$
. In higher dimension, Creutz [Reference Creutz10] has shown that for any principally polarized abelian variety A over a number field K, the p-torsion in the Tate-Shafarevich group can be arbitrarily large over a field extension L of degree which is bounded in terms of p and the dimension of A, generalizing work of Clark and Sharif [Reference Clark and Sharif9]. In higher dimension over
$p=13$
. In higher dimension, Creutz [Reference Creutz10] has shown that for any principally polarized abelian variety A over a number field K, the p-torsion in the Tate-Shafarevich group can be arbitrarily large over a field extension L of degree which is bounded in terms of p and the dimension of A, generalizing work of Clark and Sharif [Reference Clark and Sharif9]. In higher dimension over
![]() $\mathbb {Q}$
, the first author [Reference Flynn14] has recently shown that the 2-torsion subgroup of Tate-Shafarevich groups of absolutely simple Jacobians of genus
$\mathbb {Q}$
, the first author [Reference Flynn14] has recently shown that the 2-torsion subgroup of Tate-Shafarevich groups of absolutely simple Jacobians of genus
![]() $2$
curves over
$2$
curves over
![]() $\mathbb {Q}$
can be arbitrarily large, and then in [Reference Flynn15] that the
$\mathbb {Q}$
can be arbitrarily large, and then in [Reference Flynn15] that the
![]() $2$
-torsion of the Tate-Shafarevich groups of absolutely simple Jacobians of curves of any genus over
$2$
-torsion of the Tate-Shafarevich groups of absolutely simple Jacobians of curves of any genus over
![]() $\mathbb {Q}$
can be arbitrarily large. With Bruin, the authors recently showed in [Reference Bruin, Flynn and Shnidman5] that
$\mathbb {Q}$
can be arbitrarily large. With Bruin, the authors recently showed in [Reference Bruin, Flynn and Shnidman5] that ![]() can be arbitrarily large among certain abelian surfaces
can be arbitrarily large among certain abelian surfaces
![]() $A/\mathbb {Q}$
. Many of these works make use of Jacobians with an isogeny to another Jacobian, comparing the bound obtained using isogeny-descent against that of a complete p-descent.
$A/\mathbb {Q}$
. Many of these works make use of Jacobians with an isogeny to another Jacobian, comparing the bound obtained using isogeny-descent against that of a complete p-descent.
1.3 Approach
Our method makes use of Jacobians with two independent
![]() $\mathbb {Q}$
-rational p-torsion points, so we also make (implicit) use of isogenies. However, instead of bounding the Mordell-Weil rank, we construct locally soluble torsors and show directly that they have no rational points. Since our method does not require knowledge of L-functions nor any information related to the rank of
$\mathbb {Q}$
-rational p-torsion points, so we also make (implicit) use of isogenies. However, instead of bounding the Mordell-Weil rank, we construct locally soluble torsors and show directly that they have no rational points. Since our method does not require knowledge of L-functions nor any information related to the rank of
![]() $A(\mathbb {Q})$
, it is more widely applicable. Our technique is similar in spirit to that of Cassels in [Reference Cassels6] who used the Cassels-Tate pairing to show that the
$A(\mathbb {Q})$
, it is more widely applicable. Our technique is similar in spirit to that of Cassels in [Reference Cassels6] who used the Cassels-Tate pairing to show that the
![]() $3$
-part of the Tate-Shafarevich group of elliptic curves can be arbitrarily large. However, our approach is more direct. In the appendix by Tom Fisher, an alternative interpretation of our proof is given in terms of an appropriate Cassels-Tate pairing.
$3$
-part of the Tate-Shafarevich group of elliptic curves can be arbitrarily large. However, our approach is more direct. In the appendix by Tom Fisher, an alternative interpretation of our proof is given in terms of an appropriate Cassels-Tate pairing.
We construct our torsors purely geometrically, as
![]() $\mu _p$
-covers. In fact, we avoid the use of Galois cohomology in this paper, as a way of emphasizing the geometry. Experts will see that the proof can be interpreted cohomologically using standard descent techniques [Reference Cassels and Flynn8, Reference Schaefer34], but the geometric point of view is the most direct way to understand the construction and will perhaps be more accessible to those less familiar with Selmer groups (though we do assume familiarity with the basics of abelian varieties).
$\mu _p$
-covers. In fact, we avoid the use of Galois cohomology in this paper, as a way of emphasizing the geometry. Experts will see that the proof can be interpreted cohomologically using standard descent techniques [Reference Cassels and Flynn8, Reference Schaefer34], but the geometric point of view is the most direct way to understand the construction and will perhaps be more accessible to those less familiar with Selmer groups (though we do assume familiarity with the basics of abelian varieties).
1.4 Outline of proof
In Section 2 and 3, we prove some preliminary material on
![]() $\mu _p$
-covers and
$\mu _p$
-covers and
![]() $\mu _p$
-descent. Most of this will be well known to experts, but we have customized the discussion to our needs and made it fairly self-contained. In Section 4, we specialize the discussion to
$\mu _p$
-descent. Most of this will be well known to experts, but we have customized the discussion to our needs and made it fairly self-contained. In Section 4, we specialize the discussion to
![]() $\mu _p$
-covers of Jacobians of superelliptic curves. In Section 5, we prove Theorem 1.1. We must show that the torsors have local points everywhere and yet have no rational points. For most primes
$\mu _p$
-covers of Jacobians of superelliptic curves. In Section 5, we prove Theorem 1.1. We must show that the torsors have local points everywhere and yet have no rational points. For most primes
![]() $\ell $
, it is easy to see that the torsors have
$\ell $
, it is easy to see that the torsors have
![]() $\mathbb {Q}_{\ell }$
-points using the fact that almost all of the primes in the set
$\mathbb {Q}_{\ell }$
-points using the fact that almost all of the primes in the set
![]() $\{p_1,\cdots , p_t\} \cup U$
are p-th powers modulo each other. The subtle case is where
$\{p_1,\cdots , p_t\} \cup U$
are p-th powers modulo each other. The subtle case is where
![]() $\ell = p_i$
, and in this case, we construct points explicitly using the torsion points
$\ell = p_i$
, and in this case, we construct points explicitly using the torsion points
![]() $D_0 = (0,0) - \infty $
and
$D_0 = (0,0) - \infty $
and
![]() $D_1= (3uk,0) - \infty $
on J. The more interesting argument is the proof that the torsors have no global points. For this, we first show that the two global torsion divisors
$D_1= (3uk,0) - \infty $
on J. The more interesting argument is the proof that the torsors have no global points. For this, we first show that the two global torsion divisors
![]() $D_0$
and
$D_0$
and
![]() $D_1$
generate a certain quotient of
$D_1$
generate a certain quotient of
![]() $J(\mathbb {Q}_{p_i})$
, for each
$J(\mathbb {Q}_{p_i})$
, for each
![]() $p_i$
. The presence of the powers of
$p_i$
. The presence of the powers of
![]() $3$
in the model of the curve, and the fact that
$3$
in the model of the curve, and the fact that
![]() $3$
is not a p-th power locally, then ‘glues together’ the localizations of the torsors in a certain way that makes it impossible for them to have a global point unless the parameter q is divisible by either all or none of the primes
$3$
is not a p-th power locally, then ‘glues together’ the localizations of the torsors in a certain way that makes it impossible for them to have a global point unless the parameter q is divisible by either all or none of the primes
![]() $p_1, \ldots , p_t$
. The particular choice of the prime
$p_1, \ldots , p_t$
. The particular choice of the prime
![]() $3$
here is not special (we could replace it by
$3$
here is not special (we could replace it by
![]() $5$
or
$5$
or
![]() $7$
, etc.), but the presence of this ‘gluing prime’ plays the crucial role in the argument.
$7$
, etc.), but the presence of this ‘gluing prime’ plays the crucial role in the argument.
In Section 6, we deduce Theorem 1.5 from Theorem 1.1. First, we use a Cebotarev argument to show that given p, the set U, and any
![]() $t \geq 1$
, there exist primes
$t \geq 1$
, there exist primes
![]() $p_1, \ldots , p_t$
satisfying the conditions of Theorem 1.1. Second, the flexibility in the choice of q allows us to generate a subgroup of
$p_1, \ldots , p_t$
satisfying the conditions of Theorem 1.1. Second, the flexibility in the choice of q allows us to generate a subgroup of
![]() $\mathbb {F}_p$
-rank at least
$\mathbb {F}_p$
-rank at least
![]() $t - 1$
in
$t - 1$
in ![]() . Finally, we use a theorem of Masser to show that for
. Finally, we use a theorem of Masser to show that for
![]() $100\%$
of integers
$100\%$
of integers
![]() $u,v$
not divisible by
$u,v$
not divisible by
![]() $3$
, the corresponding abelian variety is geometrically simple. In the appendix, Tom Fisher recasts our proof in terms of a Cassels-Tate pairing.
$3$
, the corresponding abelian variety is geometrically simple. In the appendix, Tom Fisher recasts our proof in terms of a Cassels-Tate pairing.
2
 $\mu _p$
-covers
$\mu _p$
-covers
2.1 Classifying
 $\mu _p$
-covers
$\mu _p$
-covers
Let X be a proper variety over a field F. Let
![]() $\mu _p$
be the F-group scheme of p-th roots of unity. A
$\mu _p$
be the F-group scheme of p-th roots of unity. A
![]() $\mu _p$
-cover of Y (or more formally, a
$\mu _p$
-cover of Y (or more formally, a
![]() $\mu _p$
-torsor over Y in the fppf topology) is a Y-scheme X together with a
$\mu _p$
-torsor over Y in the fppf topology) is a Y-scheme X together with a
![]() $\mu _p$
-action that is simply transitive on fibers over Y. The
$\mu _p$
-action that is simply transitive on fibers over Y. The
![]() $\mu _p$
-covers of Y form a category
$\mu _p$
-covers of Y form a category
![]() $\mathcal {M}_p(Y)$
whose morphisms are
$\mathcal {M}_p(Y)$
whose morphisms are
![]() $\mu _p$
-equivariant isomorphisms. The following proposition gives a concrete way to think about
$\mu _p$
-equivariant isomorphisms. The following proposition gives a concrete way to think about
![]() $\mu _p$
-covers.
$\mu _p$
-covers.
Proposition 2.1. There is an equivalence of categories between
![]() $\mathcal {M}_p(Y)$
and the category of pairs
$\mathcal {M}_p(Y)$
and the category of pairs
![]() $(\mathcal {L}, \eta )$
where
$(\mathcal {L}, \eta )$
where
![]() $\mathcal {L}$
is an invertible sheaf on Y and
$\mathcal {L}$
is an invertible sheaf on Y and
![]() $\eta \colon \mathcal {L}^{\otimes p} \simeq \mathcal {O}_Y$
is an isomorphism. Here, the morphisms
$\eta \colon \mathcal {L}^{\otimes p} \simeq \mathcal {O}_Y$
is an isomorphism. Here, the morphisms
![]() $(\mathcal {L}, \eta ) \to (\mathcal {L}', \eta ')$
are isomorphisms
$(\mathcal {L}, \eta ) \to (\mathcal {L}', \eta ')$
are isomorphisms
![]() $g \colon \mathcal {L} \to \mathcal {L}'$
such that
$g \colon \mathcal {L} \to \mathcal {L}'$
such that
![]() $\eta ' \circ g^{\otimes p} = \eta $
.
$\eta ' \circ g^{\otimes p} = \eta $
.
Proof. This is well known (see [Reference Arsie and Vistoli1] or [Reference Mumford29, pg. 71]), so we just describe the functors in both directions. If
![]() $\pi \colon X \to Y$
is a
$\pi \colon X \to Y$
is a
![]() $\mu _p$
-cover, then there is a
$\mu _p$
-cover, then there is a
![]() $\mathbb {Z}/p\mathbb {Z}$
-grading on the
$\mathbb {Z}/p\mathbb {Z}$
-grading on the
![]() $\mathcal {O}_Y$
-module
$\mathcal {O}_Y$
-module
 $$\begin{align*}\pi_*\mathcal{O}_X = \mathcal{O}_Y \oplus \bigoplus_{i = 1}^{p-1} \mathcal{L}_i\end{align*}$$
$$\begin{align*}\pi_*\mathcal{O}_X = \mathcal{O}_Y \oplus \bigoplus_{i = 1}^{p-1} \mathcal{L}_i\end{align*}$$
where each
![]() $\mathcal {L}_i$
is the invertible subsheaf of
$\mathcal {L}_i$
is the invertible subsheaf of
![]() $\pi _*\mathcal {O}_X$
on which
$\pi _*\mathcal {O}_X$
on which
![]() $\mu _p$
acts by
$\mu _p$
acts by
![]() $\zeta \cdot s = \zeta ^i s$
. The algebra structure of
$\zeta \cdot s = \zeta ^i s$
. The algebra structure of
![]() $\pi _*\mathcal {O}_X$
gives isomorphisms
$\pi _*\mathcal {O}_X$
gives isomorphisms
![]() $\mathcal {L}_i \otimes \mathcal {L}_j \simeq \mathcal {L}_{i + j}$
, where indices are to be taken modulo p and where
$\mathcal {L}_i \otimes \mathcal {L}_j \simeq \mathcal {L}_{i + j}$
, where indices are to be taken modulo p and where
![]() $\mathcal {L}_0 = \mathcal {O}_Y$
. Thus, we obtain an isomorphism
$\mathcal {L}_0 = \mathcal {O}_Y$
. Thus, we obtain an isomorphism
![]() $\mathcal {L}_1^{\otimes p} \simeq \mathcal {O}_Y$
. Conversely, starting with a pair
$\mathcal {L}_1^{\otimes p} \simeq \mathcal {O}_Y$
. Conversely, starting with a pair
![]() $(\mathcal {L},\eta )$
, we can define a sheaf of
$(\mathcal {L},\eta )$
, we can define a sheaf of
![]() $\mathcal {O}_Y$
-algebras
$\mathcal {O}_Y$
-algebras
![]() $\mathcal {O}_Y \oplus \bigoplus _{i = 1}^{p-1} \mathcal {L}^i$
using the given isomorphism
$\mathcal {O}_Y \oplus \bigoplus _{i = 1}^{p-1} \mathcal {L}^i$
using the given isomorphism
![]() $\eta $
to define the multiplication
$\eta $
to define the multiplication
![]() $\mathcal {L}^i \otimes \mathcal {L}^j \simeq \mathcal {L}^{i+j} \simeq \mathcal {L}^{i+j - p}$
on the factors with
$\mathcal {L}^i \otimes \mathcal {L}^j \simeq \mathcal {L}^{i+j} \simeq \mathcal {L}^{i+j - p}$
on the factors with
![]() $i + j \geq p$
. The relative spectrum of this sheaf over Y is then naturally endowed with a
$i + j \geq p$
. The relative spectrum of this sheaf over Y is then naturally endowed with a
![]() $\mu _p$
-action making it a
$\mu _p$
-action making it a
![]() $\mu _p$
-cover.
$\mu _p$
-cover.
Remark 2.2. If
![]() $Y = \mathrm {Spec} \, F$
, this recovers Kummer theory.
$Y = \mathrm {Spec} \, F$
, this recovers Kummer theory.
2.2
 $\mu _p$
-covers of abelian varieties
$\mu _p$
-covers of abelian varieties
Let us now specialize to the case where Y is an abelian variety over a field F of characteristic not p. We will think of a
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $\pi \colon X \to Y$
in terms of the corresponding pair
$\pi \colon X \to Y$
in terms of the corresponding pair
![]() $(\mathcal {L}, \eta )$
. The isomorphism class of
$(\mathcal {L}, \eta )$
. The isomorphism class of
![]() $\mathcal {L}$
is a well-defined element of
$\mathcal {L}$
is a well-defined element of
![]() $\mathrm {Pic}(Y) = \mathrm {Pic}_Y(F)$
, called the Steinitz class of
$\mathrm {Pic}(Y) = \mathrm {Pic}_Y(F)$
, called the Steinitz class of
![]() $\pi $
. The existence of
$\pi $
. The existence of
![]() $\eta $
means that
$\eta $
means that
![]() $\mathcal {L}$
is p-torsion, so that
$\mathcal {L}$
is p-torsion, so that
![]() $\mathcal {L} \in \widehat {Y}[p](F)$
, where
$\mathcal {L} \in \widehat {Y}[p](F)$
, where
![]() $\widehat {Y} = \mathrm {Pic}^0_Y \subset \mathrm {Pic}_Y$
is the dual abelian variety parameterizing algebraically trivial line bundles on Y.
$\widehat {Y} = \mathrm {Pic}^0_Y \subset \mathrm {Pic}_Y$
is the dual abelian variety parameterizing algebraically trivial line bundles on Y.
From one
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $(\mathcal {L}, \eta )$
, we may construct many more, simply by scaling
$(\mathcal {L}, \eta )$
, we may construct many more, simply by scaling
![]() $\eta \colon \mathcal {L}^{\otimes p} \to \mathcal {O}_Y$
by any
$\eta \colon \mathcal {L}^{\otimes p} \to \mathcal {O}_Y$
by any
![]() $r \in F^*$
. Two
$r \in F^*$
. Two
![]() $\mu _p$
-covers
$\mu _p$
-covers
![]() $(\mathcal {L}, r\eta )$
and
$(\mathcal {L}, r\eta )$
and
![]() $(\mathcal {L}, s\eta )$
are isomorphic if and only if
$(\mathcal {L}, s\eta )$
are isomorphic if and only if
![]() $r/s\in F^{*p}$
. More generally, given two
$r/s\in F^{*p}$
. More generally, given two
![]() $\mu _p$
-covers
$\mu _p$
-covers
![]() $(\mathcal {L},\eta )$
and
$(\mathcal {L},\eta )$
and
![]() $(\mathcal {L}', \eta ')$
, the tensor product
$(\mathcal {L}', \eta ')$
, the tensor product
![]() $(\mathcal {L} \otimes \mathcal {L}', \eta \otimes \eta ')$
is another. Let
$(\mathcal {L} \otimes \mathcal {L}', \eta \otimes \eta ')$
is another. Let
![]() $H^1(Y, \mu _p)$
denote the set of isomorphism classes of
$H^1(Y, \mu _p)$
denote the set of isomorphism classes of
![]() $\mu _p$
-covers of Y.
$\mu _p$
-covers of Y.
Proposition 2.3. The set
![]() $H^1(Y, \mu _p)$
is naturally an abelian group and sits in a short exact sequence
$H^1(Y, \mu _p)$
is naturally an abelian group and sits in a short exact sequence
Proof. This follows from Proposition 2.1 and the discussion above.
Remark 2.4. We use the notation
![]() $H^1(Y, \mu _p)$
since the étale cohomology group
$H^1(Y, \mu _p)$
since the étale cohomology group
![]() $H^1_{\mathrm {et}}(Y, \mu _p)$
is also in bijection with isomorphism classes of
$H^1_{\mathrm {et}}(Y, \mu _p)$
is also in bijection with isomorphism classes of
![]() $\mu _p$
-covers. From this point of view, one obtains Proposition 2.3 by applying the long exact sequence in cohomology to the short sequence of sheaves
$\mu _p$
-covers. From this point of view, one obtains Proposition 2.3 by applying the long exact sequence in cohomology to the short sequence of sheaves
![]() $0 \to \mu _p \to \mathbb {G}_m \to \mathbb {G}_m \to 0$
.
$0 \to \mu _p \to \mathbb {G}_m \to \mathbb {G}_m \to 0$
.
Lemma 2.5. The
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $\pi \colon X \to Y$
corresponding to
$\pi \colon X \to Y$
corresponding to
![]() $(\mathcal {L}, \eta )$
is geometrically connected if and only if
$(\mathcal {L}, \eta )$
is geometrically connected if and only if
![]() $\mathcal {L}\not \simeq \mathcal {O}_X$
.
$\mathcal {L}\not \simeq \mathcal {O}_X$
.
Proof. If
![]() $\mathcal {L} \simeq \mathcal {O}_X$
, then
$\mathcal {L} \simeq \mathcal {O}_X$
, then
![]() $\eta $
is scalar multiplication by some
$\eta $
is scalar multiplication by some
![]() $r \in F^\times $
. In this case, X is isomorphic to
$r \in F^\times $
. In this case, X is isomorphic to
![]() $Y \times _F F(\sqrt [p]{r})$
as an F-scheme, which is not geometrically connected. Conversely, if X is not geometrically connected, then the
$Y \times _F F(\sqrt [p]{r})$
as an F-scheme, which is not geometrically connected. Conversely, if X is not geometrically connected, then the
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $X_{\bar F} \to Y_{\bar F}$
induces an isomorphism on connected components, forcing
$X_{\bar F} \to Y_{\bar F}$
induces an isomorphism on connected components, forcing
![]() $X_{\bar F}$
to be isomorphic to the trivial
$X_{\bar F}$
to be isomorphic to the trivial
![]() $\mu _p$
-torsor
$\mu _p$
-torsor
![]() $Y_{\bar F} \times _{\bar F} \mu _p$
. It follows that
$Y_{\bar F} \times _{\bar F} \mu _p$
. It follows that
![]() $\pi $
is in
$\pi $
is in
![]() $\ker (H^1(Y, \mu _p) \to H^1(Y_{\bar F}, \mu _p)) \simeq F^*/F^{*p}$
, and hence has trivial Steinitz class.
$\ker (H^1(Y, \mu _p) \to H^1(Y_{\bar F}, \mu _p)) \simeq F^*/F^{*p}$
, and hence has trivial Steinitz class.
Suppose now that
![]() $\pi \colon X \to Y$
is a geometrically connected
$\pi \colon X \to Y$
is a geometrically connected
![]() $\mu _p$
-cover corresponding to
$\mu _p$
-cover corresponding to
![]() $(\mathcal {L}, \eta )$
, so that
$(\mathcal {L}, \eta )$
, so that
![]() $\mathcal {L} \not \simeq \mathcal {O}_Y$
. Since every connected finite étale cover of the abelian variety
$\mathcal {L} \not \simeq \mathcal {O}_Y$
. Since every connected finite étale cover of the abelian variety
![]() $Y_{\bar F}$
is itself an abelian variety [Reference Mumford29, §18], X becomes an abelian variety over the algebraic closure
$Y_{\bar F}$
is itself an abelian variety [Reference Mumford29, §18], X becomes an abelian variety over the algebraic closure
![]() $\overline {F}$
. It follows that X is a torsor for a certain abelian variety, which we will now identify.
$\overline {F}$
. It follows that X is a torsor for a certain abelian variety, which we will now identify.
Let
![]() $ \widehat {\psi } \colon \widehat {Y} \to \widehat {Y}/\langle \mathcal {L} \rangle $
be the degree p isogeny obtained by modding out by
$ \widehat {\psi } \colon \widehat {Y} \to \widehat {Y}/\langle \mathcal {L} \rangle $
be the degree p isogeny obtained by modding out by
![]() $\mathcal {L}$
. Let
$\mathcal {L}$
. Let
![]() $\psi \colon A_{\mathcal {L}} \to Y$
be the dual isogeny, which is also of degree p. Then
$\psi \colon A_{\mathcal {L}} \to Y$
be the dual isogeny, which is also of degree p. Then
![]() $\psi $
can itself be given the structure of
$\psi $
can itself be given the structure of
![]() $\mu _p$
-cover. Indeed, we have
$\mu _p$
-cover. Indeed, we have
Note that there are
![]() $p-1$
different isomorphisms
$p-1$
different isomorphisms
![]() $\ker (\psi ) \simeq \mu _p$
, corresponding to the different
$\ker (\psi ) \simeq \mu _p$
, corresponding to the different
![]() $\mathbb {Z}/p\mathbb {Z}$
-gradings we can put on
$\mathbb {Z}/p\mathbb {Z}$
-gradings we can put on
![]() $\psi _*\mathcal {O}_{A_{\mathcal {L}}}$
. Exactly one of them will have the property that the corresponding
$\psi _*\mathcal {O}_{A_{\mathcal {L}}}$
. Exactly one of them will have the property that the corresponding
![]() $\mu _p$
-cover has Steinitz class
$\mu _p$
-cover has Steinitz class
![]() $\mathcal {L}_1 \subset \psi _*\mathcal {O}_{A_{\mathcal {L}}}$
isomorphic to
$\mathcal {L}_1 \subset \psi _*\mathcal {O}_{A_{\mathcal {L}}}$
isomorphic to
![]() $\mathcal {L}$
. We choose this
$\mathcal {L}$
. We choose this
![]() $\mu _p$
-cover structure for
$\mu _p$
-cover structure for
![]() $\psi $
.
$\psi $
.
Lemma 2.6. Let
![]() $\pi \colon X \to Y$
be a
$\pi \colon X \to Y$
be a
![]() $\mu _p$
-cover with nontrivial Steinitz class
$\mu _p$
-cover with nontrivial Steinitz class
![]() $\mathcal {L} \in \widehat {Y}[p](F)$
. Then
$\mathcal {L} \in \widehat {Y}[p](F)$
. Then
![]() $\pi $
is a twist of the
$\pi $
is a twist of the
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $\psi \colon A_{\mathcal {L}} \to Y$
and X is a torsor for
$\psi \colon A_{\mathcal {L}} \to Y$
and X is a torsor for
![]() $A_{\mathcal {L}}$
.
$A_{\mathcal {L}}$
.
Proof. If
![]() $\psi \colon A_{\mathcal {L}} \to Y$
corresponds to
$\psi \colon A_{\mathcal {L}} \to Y$
corresponds to
![]() $(\mathcal {L}, \eta )$
, then
$(\mathcal {L}, \eta )$
, then
![]() $\pi \colon X \to Y$
corresponds to
$\pi \colon X \to Y$
corresponds to
![]() $(\mathcal {L}, s \eta )$
for some scalar
$(\mathcal {L}, s \eta )$
for some scalar
![]() $s \in F^*$
. Over
$s \in F^*$
. Over
![]() $\bar {F}$
there is an isomorphism
$\bar {F}$
there is an isomorphism
![]() $\rho \colon (A_{\mathcal {L}})_{\bar {F}} \to X_{\bar {F}}$
of
$\rho \colon (A_{\mathcal {L}})_{\bar {F}} \to X_{\bar {F}}$
of
![]() $\mu _p$
-covers, which satisfies
$\mu _p$
-covers, which satisfies
for all
![]() $g \in \mathrm {Gal}(\bar F/F)$
and
$g \in \mathrm {Gal}(\bar F/F)$
and
![]() $P \in A_{\mathcal {L}}(\bar {F})$
; here,
$P \in A_{\mathcal {L}}(\bar {F})$
; here,
![]() $\sqrt [p]{s}^g/\sqrt [p]{s} \in \mu _p$
and
$\sqrt [p]{s}^g/\sqrt [p]{s} \in \mu _p$
and
![]() $+$
is the torsor action. The torsor structure
$+$
is the torsor action. The torsor structure
![]() $A_{\mathcal {L}} \times X \to X$
is given by
$A_{\mathcal {L}} \times X \to X$
is given by
![]() $(P, Q) \mapsto \rho (P + \rho ^{-1}(Q))$
. Using the formula for
$(P, Q) \mapsto \rho (P + \rho ^{-1}(Q))$
. Using the formula for
![]() $\rho ^g$
, we see that this torsor is indeed defined over F.
$\rho ^g$
, we see that this torsor is indeed defined over F.
We have seen that for each nonzero
![]() $\mathcal {L} \in \widehat {Y}[p](F)$
, there is, in fact, a distinguished
$\mathcal {L} \in \widehat {Y}[p](F)$
, there is, in fact, a distinguished
![]() $\mu _p$
-cover with Steinitz class
$\mu _p$
-cover with Steinitz class
![]() $\mathcal {L}$
– namely, the cover
$\mathcal {L}$
– namely, the cover
![]() $A_{\mathcal {L}} \to Y$
. This means there must be a distinguished isomorphism
$A_{\mathcal {L}} \to Y$
. This means there must be a distinguished isomorphism
![]() $\eta \colon \mathcal {L}^p \simeq \mathcal {O}_Y$
. We will describe this isomorphism
$\eta \colon \mathcal {L}^p \simeq \mathcal {O}_Y$
. We will describe this isomorphism
![]() $\eta $
in Lemma 3.6, in the context of rational points. For simplicity, we will specialize to the case where Y is a Jacobian, and in particular principally polarized (so that
$\eta $
in Lemma 3.6, in the context of rational points. For simplicity, we will specialize to the case where Y is a Jacobian, and in particular principally polarized (so that
![]() $\widehat {Y} \simeq Y$
). However, most of what we prove can be generalized to arbitrary abelian varieties in a straightforward way.
$\widehat {Y} \simeq Y$
). However, most of what we prove can be generalized to arbitrary abelian varieties in a straightforward way.
2.3
 $\mu _p$
-covers of Jacobians
$\mu _p$
-covers of Jacobians
Let C be a smooth projective geometrically integral curve over F, and let
![]() $J = \mathrm {Pic}^0(C)$
be its Jacobian. Let g be the genus of C, and hence also the dimension of the abelian variety J. Let
$J = \mathrm {Pic}^0(C)$
be its Jacobian. Let g be the genus of C, and hence also the dimension of the abelian variety J. Let
![]() $D \in J[p](F)$
be a divisor class of order p. Let
$D \in J[p](F)$
be a divisor class of order p. Let
![]() $J \to J/\langle D \rangle $
be the quotient and let
$J \to J/\langle D \rangle $
be the quotient and let
![]() $\psi \colon A_D\to \widehat {J}$
be the corresponding dual isogeny, where
$\psi \colon A_D\to \widehat {J}$
be the corresponding dual isogeny, where
![]() $A_D$
is the dual of
$A_D$
is the dual of
![]() $J/\langle D \rangle $
. Then
$J/\langle D \rangle $
. Then
![]() $\psi $
is a
$\psi $
is a
![]() $\mu _p$
-cover of
$\mu _p$
-cover of
![]() $\widehat {J}$
corresponding to a pair
$\widehat {J}$
corresponding to a pair
![]() $(\mathcal {L}, \eta )$
, as in the previous section.
$(\mathcal {L}, \eta )$
, as in the previous section.
Remark 2.7. As before, we may choose the
![]() $\mu _p$
-cover structure on
$\mu _p$
-cover structure on
![]() $\psi $
so that
$\psi $
so that
![]() $\mathcal {L} \in \mathrm {Pic}^0(\widehat {J})(F)$
is mapped to D under the isomorphism
$\mathcal {L} \in \mathrm {Pic}^0(\widehat {J})(F)$
is mapped to D under the isomorphism
![]() $\hat {\hat J} \simeq J$
.
$\hat {\hat J} \simeq J$
.
From now on, we identify J and
![]() $\widehat {J}$
via the principal polarization
$\widehat {J}$
via the principal polarization
![]() $\lambda \colon J \to \widehat J$
coming from the theta divisor of the curve C. To make this explicit, we assume that C contains a rational point
$\lambda \colon J \to \widehat J$
coming from the theta divisor of the curve C. To make this explicit, we assume that C contains a rational point
![]() $\infty \in C(F)$
. The theta divisor
$\infty \in C(F)$
. The theta divisor
![]() $\Theta \subset J$
is the subvariety of degree 0 divisor classes of the form
$\Theta \subset J$
is the subvariety of degree 0 divisor classes of the form
![]() $E - (g-1)\infty $
, where E is an effective divisor of degree
$E - (g-1)\infty $
, where E is an effective divisor of degree
![]() $g -1$
. The isomorphism
$g -1$
. The isomorphism
![]() $J \to \widehat {J}$
sends P to
$J \to \widehat {J}$
sends P to
![]() $t_P^*\mathcal {O}_J(\Theta ) \otimes \mathcal {O}_J(\Theta )^{-1}$
, where
$t_P^*\mathcal {O}_J(\Theta ) \otimes \mathcal {O}_J(\Theta )^{-1}$
, where
![]() $t_P \colon J \to J$
is translation by P. We can also describe
$t_P \colon J \to J$
is translation by P. We can also describe
![]() $\lambda (P)$
as the line bundle on J associated to the divisor
$\lambda (P)$
as the line bundle on J associated to the divisor
![]() $[\Theta - P] - [\Theta ]$
.
$[\Theta - P] - [\Theta ]$
.
After making the identification
![]() $J \simeq \widehat {J}$
, we may view
$J \simeq \widehat {J}$
, we may view
![]() $\psi $
as a
$\psi $
as a
![]() $\mu _p$
-cover of J and
$\mu _p$
-cover of J and
![]() $\eta $
as an isomorphism
$\eta $
as an isomorphism
![]() $\mathcal {L}^{\otimes p} \to \mathcal {O}_J$
. By Proposition 2.3, we have the exact sequence
$\mathcal {L}^{\otimes p} \to \mathcal {O}_J$
. By Proposition 2.3, we have the exact sequence
3
 $\mu _p$
-descent
$\mu _p$
-descent
We continue with our assumptions on
![]() $J = \mathrm {Pic}^0(C)$
. We have seen that to each
$J = \mathrm {Pic}^0(C)$
. We have seen that to each
![]() $D \in J[p](F)$
of order p, there is a corresponding
$D \in J[p](F)$
of order p, there is a corresponding
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $\psi \colon A_D \to J$
giving rise to the data
$\psi \colon A_D \to J$
giving rise to the data
![]() $(\mathcal {L}, \eta )$
. These particular
$(\mathcal {L}, \eta )$
. These particular
![]() $\mu _p$
-covers are by construction abelian varieties, but general
$\mu _p$
-covers are by construction abelian varieties, but general
![]() $\mu _p$
-covers corresponding to pairs
$\mu _p$
-covers corresponding to pairs
![]() $(\mathcal {L}, r\eta )$
, for
$(\mathcal {L}, r\eta )$
, for
![]() $r \in F^\times $
, may only be torsors for abelian varieties. We characterize those which are abelian varieties, or equivalently, those which have rational points.
$r \in F^\times $
, may only be torsors for abelian varieties. We characterize those which are abelian varieties, or equivalently, those which have rational points.
3.1 Descent over general fields
Fix
![]() $D \in J[p](F)$
and
$D \in J[p](F)$
and
![]() $(\mathcal {L}, \eta )$
, as above. Given
$(\mathcal {L}, \eta )$
, as above. Given
![]() $P \in J(F)$
, we may consider the
$P \in J(F)$
, we may consider the
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $\psi _P = t_P \circ \psi \colon A_D \to J$
, where
$\psi _P = t_P \circ \psi \colon A_D \to J$
, where
![]() $t_P \colon J \to J$
is translation by P. The
$t_P \colon J \to J$
is translation by P. The
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $\psi _P$
is endowed with the same
$\psi _P$
is endowed with the same
![]() $\mu _p$
-action as
$\mu _p$
-action as
![]() $\psi $
, but different structure map to J. Since the Steinitz class is in
$\psi $
, but different structure map to J. Since the Steinitz class is in
![]() $\mathrm {Pic}^0(J)$
, it is invariant under translation, and hence,
$\mathrm {Pic}^0(J)$
, it is invariant under translation, and hence,
![]() $\psi _P$
and
$\psi _P$
and
![]() $\psi $
have isomorphic Steinitz classes. If
$\psi $
have isomorphic Steinitz classes. If
![]() $\psi _P = (\mathcal {L}', \eta ')$
, then we can choose an isomorphism
$\psi _P = (\mathcal {L}', \eta ')$
, then we can choose an isomorphism
![]() $\mathcal {L}' \simeq \mathcal {L}$
, and under this isomorphism, we have
$\mathcal {L}' \simeq \mathcal {L}$
, and under this isomorphism, we have
![]() $\eta ' = r_P \eta $
for some
$\eta ' = r_P \eta $
for some
![]() $r_P \in F^*$
. Any other choice of isomorphism
$r_P \in F^*$
. Any other choice of isomorphism
![]() $\mathcal {L}' \simeq \mathcal {L}$
differs by a scalar, so the element
$\mathcal {L}' \simeq \mathcal {L}$
differs by a scalar, so the element
![]() $r_P$
is well defined up to
$r_P$
is well defined up to
![]() $F^{*p}$
.
$F^{*p}$
.
Lemma 3.1. The map
![]() $P \mapsto r_P$
induces an injective map
$P \mapsto r_P$
induces an injective map
![]() $\partial ^D \colon J(F)/\psi (A_D(F)) \to F^*/F^{*p}$
.
$\partial ^D \colon J(F)/\psi (A_D(F)) \to F^*/F^{*p}$
.
Proof. Note that
![]() $r_P\in F^{*p}$
if and only if
$r_P\in F^{*p}$
if and only if
![]() $\psi _P$
is isomorphic as a
$\psi _P$
is isomorphic as a
![]() $\mu _p$
-cover to
$\mu _p$
-cover to
![]() $\psi $
. But any isomorphism of
$\psi $
. But any isomorphism of
![]() $\mu _p$
-covers induces an isomorphism of
$\mu _p$
-covers induces an isomorphism of
![]() $A_D$
-torsors, and hence must be given by translation by Q for some
$A_D$
-torsors, and hence must be given by translation by Q for some
![]() $Q \in A_D(F)$
. Translation by Q gives an isomorphism between these two
$Q \in A_D(F)$
. Translation by Q gives an isomorphism between these two
![]() $\mu _p$
-covers if and only if
$\mu _p$
-covers if and only if
![]() $P = \psi (Q)$
.
$P = \psi (Q)$
.
For completeness, we state the following result, connecting the map
![]() $\partial ^D$
to a boundary map in Galois cohomology:
$\partial ^D$
to a boundary map in Galois cohomology:
Lemma 3.2. The map
![]() $\partial ^D$
is the boundary map
$\partial ^D$
is the boundary map
![]() $J(F) \to H^1(F, \mu _p) \simeq F^*/F^{*p}$
in the long exact sequence in group cohomology for the short exact sequence of
$J(F) \to H^1(F, \mu _p) \simeq F^*/F^{*p}$
in the long exact sequence in group cohomology for the short exact sequence of
![]() $\mathrm {Gal}(\bar F/F)$
-modules
$\mathrm {Gal}(\bar F/F)$
-modules
Proof. The boundary map
![]() $J(F) \to H^1(F, \mu _p)$
sends
$J(F) \to H^1(F, \mu _p)$
sends
![]() $P \in J(F)$
to the cocycle
$P \in J(F)$
to the cocycle
![]() $c \colon \mathrm {Gal}(\bar F/F) \to \mu _p \simeq A_D[\psi ]$
given by
$c \colon \mathrm {Gal}(\bar F/F) \to \mu _p \simeq A_D[\psi ]$
given by
![]() $g \mapsto Q^g - Q$
, where
$g \mapsto Q^g - Q$
, where
![]() $Q \in A_D$
is such that
$Q \in A_D$
is such that
![]() $\psi (Q) = P$
. We must show that this cocycle agrees with the cocycle
$\psi (Q) = P$
. We must show that this cocycle agrees with the cocycle
![]() $g \mapsto \sqrt [p]{r}^g/\sqrt [p]{r}$
, where
$g \mapsto \sqrt [p]{r}^g/\sqrt [p]{r}$
, where
![]() $r = r_P$
. From the proof of Lemma 2.6, we see that the
$r = r_P$
. From the proof of Lemma 2.6, we see that the
![]() $A_D$
-torsors
$A_D$
-torsors
![]() $(\mathcal {L}, r\eta )$
and
$(\mathcal {L}, r\eta )$
and
![]() $(\mathcal {L}, \eta )$
are isomorphic (over
$(\mathcal {L}, \eta )$
are isomorphic (over
![]() $\bar F$
) via translation by Q. By the explicit formula given there, this exactly means that
$\bar F$
) via translation by Q. By the explicit formula given there, this exactly means that
![]() $Q^g - Q$
is equal to the element
$Q^g - Q$
is equal to the element
![]() $\sqrt [p]{r}^g/\sqrt [p]{r} \in \mu _p$
.
$\sqrt [p]{r}^g/\sqrt [p]{r} \in \mu _p$
.
Lemma 3.3. The image of
![]() $\partial ^D$
is the set of
$\partial ^D$
is the set of
![]() $r \in F^*/F^{*p}$
such that the
$r \in F^*/F^{*p}$
such that the
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $(\mathcal {L}, r\eta )$
has a rational point.
$(\mathcal {L}, r\eta )$
has a rational point.
Proof. Every torsor in the image clearly has a rational point since it is isomorphic to
![]() $A_D$
as a variety. Conversely, if a
$A_D$
as a variety. Conversely, if a
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $X \to J$
of the form
$X \to J$
of the form
![]() $(\mathcal {L}, r\eta )$
has a rational point, then the underlying
$(\mathcal {L}, r\eta )$
has a rational point, then the underlying
![]() $A_D$
-torsor is isomorphic to the trivial
$A_D$
-torsor is isomorphic to the trivial
![]() $A_D$
-torsor up to translation by a point P. Hence,
$A_D$
-torsor up to translation by a point P. Hence,
![]() $\partial ^D(-P) = r$
.
$\partial ^D(-P) = r$
.
Remark 3.4. It follows that for a
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $\pi \colon X \to J$
with Steinitz class
$\pi \colon X \to J$
with Steinitz class
![]() $\mathcal {L}$
, X is isomorphic to
$\mathcal {L}$
, X is isomorphic to
![]() $A_D$
(as varieties) if and only if
$A_D$
(as varieties) if and only if
![]() $\pi $
corresponds to
$\pi $
corresponds to
![]() $(\mathcal {L}, r\eta )$
, with r in the image of
$(\mathcal {L}, r\eta )$
, with r in the image of
![]() $\partial ^D$
.
$\partial ^D$
.
The following lemma is immediate from the definitions and can be used to give an explicit formula for the homomorphism
![]() $\partial ^D$
.
$\partial ^D$
.
Lemma 3.5. Let
![]() $F(J)$
be the function field of J and view
$F(J)$
be the function field of J and view
![]() $\eta ^{-1} \colon \mathcal {O}_J \to \mathcal {L}^p$
as a global section of
$\eta ^{-1} \colon \mathcal {O}_J \to \mathcal {L}^p$
as a global section of
![]() $\mathcal {L}^p$
. Fix an embedding of
$\mathcal {L}^p$
. Fix an embedding of
![]() $\mathcal {L}$
as a subsheaf of
$\mathcal {L}$
as a subsheaf of
![]() $F(J)$
, so that
$F(J)$
, so that
![]() $\eta ^{-1}$
is a nonzero element f of
$\eta ^{-1}$
is a nonzero element f of
![]() $F(J)$
. Let Q be such that Q and
$F(J)$
. Let Q be such that Q and
![]() $Q + P$
are in a domain of definition for f. Then
$Q + P$
are in a domain of definition for f. Then
![]() $\partial ^D(P) = r_P = f(P+Q)/f(Q)$
, up to p-th powers.
$\partial ^D(P) = r_P = f(P+Q)/f(Q)$
, up to p-th powers.
Thinking of
![]() $\eta ^{-1}$
as a function on J allows us to distinguish the unique
$\eta ^{-1}$
as a function on J allows us to distinguish the unique
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $(\mathcal {L}, \eta )$
corresponding to
$(\mathcal {L}, \eta )$
corresponding to
![]() $\psi \colon A_D \to J$
among all
$\psi \colon A_D \to J$
among all
![]() $\mu _p$
-covers with Steinitz class
$\mu _p$
-covers with Steinitz class
![]() $\mathcal {L}$
, as promised.
$\mathcal {L}$
, as promised.
Lemma 3.6. The
![]() $\mu _p$
-cover corresponding to
$\mu _p$
-cover corresponding to
![]() $(\mathcal {L}, \eta )$
, which is isomorphic to the
$(\mathcal {L}, \eta )$
, which is isomorphic to the
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $A_{\mathcal {L}} = A_D \to J$
, is characterized among all
$A_{\mathcal {L}} = A_D \to J$
, is characterized among all
![]() $\mu _p$
-covers with Steinitz class
$\mu _p$
-covers with Steinitz class
![]() $\mathcal {L}$
by the fact that the value
$\mathcal {L}$
by the fact that the value
![]() $f(0_J)$
of the function
$f(0_J)$
of the function
![]() $f = \eta ^{-1} \in F(J)$
at
$f = \eta ^{-1} \in F(J)$
at
![]() $0_J$
is a p-th power in
$0_J$
is a p-th power in
![]() $F^*$
. (Here we assume that
$F^*$
. (Here we assume that
![]() $\mathcal {L}$
is chosen within its isomorphism class so that
$\mathcal {L}$
is chosen within its isomorphism class so that
![]() $f(0_J) \in F^\times $
.)
$f(0_J) \in F^\times $
.)
Proof. The
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $A_D \to J$
is distinguished among
$A_D \to J$
is distinguished among
![]() $\mu _p$
-covers with Steinitz class
$\mu _p$
-covers with Steinitz class
![]() $\mathcal {L}$
by the fact that the fiber above
$\mathcal {L}$
by the fact that the fiber above
![]() $0$
has a rational point. Indeed, if
$0$
has a rational point. Indeed, if
![]() $\pi \colon X \to J$
is a
$\pi \colon X \to J$
is a
![]() $\mu _p$
-cover of type
$\mu _p$
-cover of type
![]() $(\mathcal {L}, r\eta )$
with a rational point
$(\mathcal {L}, r\eta )$
with a rational point
![]() $Q \in X(F)$
above
$Q \in X(F)$
above
![]() $0 \in J(F)$
, then
$0 \in J(F)$
, then
![]() $\pi = \psi _P$
for some
$\pi = \psi _P$
for some
![]() $P \in J(F)$
, and
$P \in J(F)$
, and
![]() $\pi ^{-1}(0) = \psi ^{-1}(-P)$
. It follows that
$\pi ^{-1}(0) = \psi ^{-1}(-P)$
. It follows that
![]() $P \in \psi (A_D(F))$
, and hence, r is a p-th power, or in other words,
$P \in \psi (A_D(F))$
, and hence, r is a p-th power, or in other words,
![]() $\pi $
is isomorphic to
$\pi $
is isomorphic to
![]() $\psi $
as
$\psi $
as
![]() $\mu _p$
-covers.
$\mu _p$
-covers.
However, the pullback of the
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $(\mathcal {L}, \eta )$
on J to
$(\mathcal {L}, \eta )$
on J to
![]() $\mathrm {Spec}\, F$
, via the inclusion
$\mathrm {Spec}\, F$
, via the inclusion
![]() $\{0_J\} \hookrightarrow J$
, is
$\{0_J\} \hookrightarrow J$
, is
![]() $\mathrm {Spec}\, k[z]/(z^p - h)$
where
$\mathrm {Spec}\, k[z]/(z^p - h)$
where
![]() $h = f(0_J)$
. This has an F-rational point if and only if h is a p-th power.
$h = f(0_J)$
. This has an F-rational point if and only if h is a p-th power.
Let
![]() $\mathrm {Sym}^g C = C^g/S_g$
be the g-th symmetric power of C. Points of
$\mathrm {Sym}^g C = C^g/S_g$
be the g-th symmetric power of C. Points of
![]() $\mathrm {Sym}^g C$
correspond to effective degree g divisors E on C. Recall that the map
$\mathrm {Sym}^g C$
correspond to effective degree g divisors E on C. Recall that the map
![]() $\mathrm {Sym}^g C \to J$
sending
$\mathrm {Sym}^g C \to J$
sending
![]() $E \mapsto E - g\infty $
is birational [Reference Milne, Cornell and Silverman27, Thm. 5.1], and hence induces an isomorphism of function fields
$E \mapsto E - g\infty $
is birational [Reference Milne, Cornell and Silverman27, Thm. 5.1], and hence induces an isomorphism of function fields
![]() $F(\mathrm {Sym}^g C) \simeq F(J)$
.
$F(\mathrm {Sym}^g C) \simeq F(J)$
.
Lemma 3.7. Suppose
![]() $pD = \mathrm {div}(\tilde f)$
for some
$pD = \mathrm {div}(\tilde f)$
for some
![]() $\tilde f \in F(C)$
. Then
$\tilde f \in F(C)$
. Then
![]() $\mathcal {L}\simeq \mathcal {O}_J(\tilde D)$
for a divisor
$\mathcal {L}\simeq \mathcal {O}_J(\tilde D)$
for a divisor
![]() $\tilde D$
on J such that
$\tilde D$
on J such that
![]() $p\tilde D = \mathrm {div}(f)$
, where
$p\tilde D = \mathrm {div}(f)$
, where
![]() $f \in F(J) \simeq F(\mathrm {Sym}^g C)$
is the rational function
$f \in F(J) \simeq F(\mathrm {Sym}^g C)$
is the rational function
![]() $f(\sum _{i = 1}^g (x_i,y_i) - g\infty ) = \prod _{i = 1}^g \tilde f(x_i,y_i)$
.
$f(\sum _{i = 1}^g (x_i,y_i) - g\infty ) = \prod _{i = 1}^g \tilde f(x_i,y_i)$
.
Proof. Assume, for simplicity, that
![]() $D = \infty - Q$
for some
$D = \infty - Q$
for some
![]() $Q \in C(F)$
. Under the polarization
$Q \in C(F)$
. Under the polarization
![]() $J \to \widehat {J}$
, the point D gets sent to the divisor
$J \to \widehat {J}$
, the point D gets sent to the divisor
![]() $[\Theta - D] - [\Theta ]$
. Note that
$[\Theta - D] - [\Theta ]$
. Note that
is the locus of poles of the function f. Similarly,
![]() $\Theta $
is the zero locus. Taking into account multiplicities, the divisor of f is
$\Theta $
is the zero locus. Taking into account multiplicities, the divisor of f is
![]() $p[\Theta - D] - p[\Theta ]$
, as claimed. The general case where
$p[\Theta - D] - p[\Theta ]$
, as claimed. The general case where
![]() $D = \sum _j (\infty - Q_j)$
is similar.
$D = \sum _j (\infty - Q_j)$
is similar.
Finally, we will use a generalization of the map
![]() $\partial $
and Lemma 3.1. Let
$\partial $
and Lemma 3.1. Let
![]() $H = \{D_1, \ldots , D_m\} \subset J[p](F)$
be a subset of
$H = \{D_1, \ldots , D_m\} \subset J[p](F)$
be a subset of
![]() $\mathbb {F}_p$
-linearly independent elements. For each
$\mathbb {F}_p$
-linearly independent elements. For each
![]() $i = 1, \ldots , m$
, let
$i = 1, \ldots , m$
, let
![]() $\psi _i \colon A_i \to J$
be the
$\psi _i \colon A_i \to J$
be the
![]() $\mu _p$
-covers corresponding to
$\mu _p$
-covers corresponding to
![]() $D_i$
. Let
$D_i$
. Let
![]() $A_H = \widehat {J/\langle H\rangle }$
and let
$A_H = \widehat {J/\langle H\rangle }$
and let
![]() $\psi _H \colon A_H \to J$
be the isogeny dual to
$\psi _H \colon A_H \to J$
be the isogeny dual to
![]() $J \to J/\langle H\rangle $
. Then we have a homomorphism
$J \to J/\langle H\rangle $
. Then we have a homomorphism
 $$\begin{align*}\tilde \partial^H \colon J(F) \longrightarrow \prod_{i = 1}^m F^*/F^{*p}\end{align*}$$
$$\begin{align*}\tilde \partial^H \colon J(F) \longrightarrow \prod_{i = 1}^m F^*/F^{*p}\end{align*}$$
sending P to
![]() $(\partial ^{D_1}(P), \ldots , \partial ^{D_m}(P))$
.
$(\partial ^{D_1}(P), \ldots , \partial ^{D_m}(P))$
.
Lemma 3.8. The map
![]() $\tilde \partial ^H$
induces an injection
$\tilde \partial ^H$
induces an injection
![]() $\partial ^H \colon J(F)/\psi _H(A_H(F)) \hookrightarrow \bigoplus _{i = 1}^m F^*/F^{*p}$
.
$\partial ^H \colon J(F)/\psi _H(A_H(F)) \hookrightarrow \bigoplus _{i = 1}^m F^*/F^{*p}$
.
Proof. We prove this in the case
![]() $m = 2$
, which is the only case we will use. The general case follows by an inductive argument. Suppose
$m = 2$
, which is the only case we will use. The general case follows by an inductive argument. Suppose
![]() $\tilde \partial ^{D_1}(P) = 0$
and
$\tilde \partial ^{D_1}(P) = 0$
and
![]() $\tilde \partial ^{D_2}(P) = 0$
, so that
$\tilde \partial ^{D_2}(P) = 0$
, so that
![]() $P = \psi _i(Q_i)$
for some
$P = \psi _i(Q_i)$
for some
![]() $Q_i \in A_i(F)$
by Lemma 3.1. Let
$Q_i \in A_i(F)$
by Lemma 3.1. Let
![]() $g_i \colon A_H \to A_i$
be the natural maps, of degree p; note that
$g_i \colon A_H \to A_i$
be the natural maps, of degree p; note that
![]() $\psi _1 g_1 = \psi _2 g_2$
. The fiber diagram
$\psi _1 g_1 = \psi _2 g_2$
. The fiber diagram
 $$ \begin{align} \begin{array}{ccc} A_H &\longrightarrow&A_2 \\ \downarrow & &\downarrow \\ A_1& \longrightarrow&J\\ \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ccc} A_H &\longrightarrow&A_2 \\ \downarrow & &\downarrow \\ A_1& \longrightarrow&J\\ \end{array} \end{align} $$
shows that there is a unique point Q in
![]() $A_H(\bar F)$
such that
$A_H(\bar F)$
such that
![]() $g_i(Q) = Q_i$
for
$g_i(Q) = Q_i$
for
![]() $i = 1,2$
. The uniqueness of Q implies that it is
$i = 1,2$
. The uniqueness of Q implies that it is
![]() $\mathrm {Gal}(\bar F/F)$
-stable, and so we have
$\mathrm {Gal}(\bar F/F)$
-stable, and so we have
![]() $P = \psi _H(Q)$
with
$P = \psi _H(Q)$
with
![]() $Q \in A_H(F)$
. This shows that
$Q \in A_H(F)$
. This shows that
![]() $\partial ^H$
is injective.
$\partial ^H$
is injective.
3.2 Descent over global fields
Suppose now that C is a curve over
![]() $\mathbb {Q}$
. The preceding discussion applies for
$\mathbb {Q}$
. The preceding discussion applies for
![]() $F =\mathbb {Q}$
, but also for
$F =\mathbb {Q}$
, but also for
![]() $F =\mathbb {Q}_{\ell }$
for any prime
$F =\mathbb {Q}_{\ell }$
for any prime
![]() $\ell \leq \infty $
. Having fixed
$\ell \leq \infty $
. Having fixed
![]() $D \in J[p](\mathbb {Q})$
, let
$D \in J[p](\mathbb {Q})$
, let
be the subgroup of classes r with the property that for every prime
![]() $\ell $
, the class of r in
$\ell $
, the class of r in
![]() $\mathbb {Q}_{\ell }^*/\mathbb {Q}_{\ell }^{*p}$
is in the image of
$\mathbb {Q}_{\ell }^*/\mathbb {Q}_{\ell }^{*p}$
is in the image of
![]() $\partial ^D \colon J(\mathbb {Q}_{\ell })/\psi (A_D(\mathbb {Q}_{\ell })) \to \mathbb {Q}_{\ell }^*/\mathbb {Q}_{\ell }^{*p}$
. In other words, an element of
$\partial ^D \colon J(\mathbb {Q}_{\ell })/\psi (A_D(\mathbb {Q}_{\ell })) \to \mathbb {Q}_{\ell }^*/\mathbb {Q}_{\ell }^{*p}$
. In other words, an element of
![]() $\mathrm {Sel}(A_D)$
is a
$\mathrm {Sel}(A_D)$
is a
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $X \to J$
with Steinitz class D and such that
$X \to J$
with Steinitz class D and such that
![]() $X(\mathbb {Q}_{\ell }) \neq \emptyset $
for every prime
$X(\mathbb {Q}_{\ell }) \neq \emptyset $
for every prime
![]() $\ell $
.
$\ell $
.
Recall that if A is an abelian variety over
![]() $\mathbb {Q}$
, then
$\mathbb {Q}$
, then ![]() is the group of A-torsors which are trivial over
is the group of A-torsors which are trivial over
![]() $\mathbb {Q}_{\ell }$
, for all primes
$\mathbb {Q}_{\ell }$
, for all primes
![]() $\ell \leq \infty $
.
$\ell \leq \infty $
.
Proposition 3.9. Let ![]() be the Tate-Shafarevich group of
be the Tate-Shafarevich group of
![]() $A_D$
. There is an exact sequence
$A_D$
. There is an exact sequence
where ![]() is the kernel of the map
is the kernel of the map ![]() induced by
induced by
![]() $\psi $
.
$\psi $
.
Proof. The map ![]() sends the
sends the
![]() $\mu _p$
-cover
$\mu _p$
-cover
![]() $X \to J$
to the underlying
$X \to J$
to the underlying
![]() $A_D$
-torsor (c.f. Lemma 2.6). The cocycle
$A_D$
-torsor (c.f. Lemma 2.6). The cocycle
![]() $c \colon \mathrm {Gal}(\bar F/F) \to A_D(\bar F)$
with
$c \colon \mathrm {Gal}(\bar F/F) \to A_D(\bar F)$
with
![]() $c(g) = \sqrt [p]{s}^g/\sqrt [p]{s}$
determines this torsor and has image in
$c(g) = \sqrt [p]{s}^g/\sqrt [p]{s}$
determines this torsor and has image in
![]() $\mu _p \simeq \ker (\psi )$
, so the cocycle indeed becomes trivial in
$\mu _p \simeq \ker (\psi )$
, so the cocycle indeed becomes trivial in ![]() . The exactness of the sequence in the middle follows from Lemma 3.3. The exactness on the right can be proved using direct geometric arguments but is most easily seen using Lemma 3.2. Since we will not actually use the exactness on the right, we omit the proof.
. The exactness of the sequence in the middle follows from Lemma 3.3. The exactness on the right can be proved using direct geometric arguments but is most easily seen using Lemma 3.2. Since we will not actually use the exactness on the right, we omit the proof.
The group
![]() $\mathrm {Sel}(A_D)$
is isomorphic to the usual Selmer group
$\mathrm {Sel}(A_D)$
is isomorphic to the usual Selmer group
In particular, it is finite. This can also be seen from the following proposition.
Proposition 3.10. Suppose
![]() $\ell \neq p$
is a prime of good reduction for J. Then the image of
$\ell \neq p$
is a prime of good reduction for J. Then the image of
![]() $\partial ^D \colon J(\mathbb {Q}_{\ell }) \to \mathbb {Q}_{\ell }^*/\mathbb {Q}_{\ell }^{*p}$
is the subgroup
$\partial ^D \colon J(\mathbb {Q}_{\ell }) \to \mathbb {Q}_{\ell }^*/\mathbb {Q}_{\ell }^{*p}$
is the subgroup
![]() $\mathbb {Z}_{\ell }^*/\mathbb {Z}_{\ell }^{*p}$
.
$\mathbb {Z}_{\ell }^*/\mathbb {Z}_{\ell }^{*p}$
.
Proof. This well-known fact follows from [Reference Česnavičius7, Prop. 2.7(d)] if we grant Lemma 3.2, but we will give a more geometric proof in the spirit of this paper. The classes in
![]() $\mathbb {Z}_{\ell }^*/\mathbb {Z}_{\ell }^{*p}$
represent
$\mathbb {Z}_{\ell }^*/\mathbb {Z}_{\ell }^{*p}$
represent
![]() $\mu _p$
-covers
$\mu _p$
-covers
![]() $X \to J$
which are trivialized by an unramified field extension; hence, the corresponding
$X \to J$
which are trivialized by an unramified field extension; hence, the corresponding
![]() $A_D$
-torsor X is also trivialized by an unramified field extension. Since
$A_D$
-torsor X is also trivialized by an unramified field extension. Since
![]() $A_D$
has good reduction at
$A_D$
has good reduction at
![]() $\ell $
, the torsor X has a Néron model
$\ell $
, the torsor X has a Néron model
![]() $\mathcal {X}$
over
$\mathcal {X}$
over
![]() $\mathbb {Z}_{\ell }$
, which is a torsor for the Néron model
$\mathbb {Z}_{\ell }$
, which is a torsor for the Néron model
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $A_D$
[Reference Bosch4, Reference Cassels6.5. Cor. 4]. Since any torsor for a smooth proper group scheme over
$A_D$
[Reference Bosch4, Reference Cassels6.5. Cor. 4]. Since any torsor for a smooth proper group scheme over
![]() $\mathbb {Z}_{\ell }$
has a
$\mathbb {Z}_{\ell }$
has a
![]() $\mathbb {Z}_{\ell }$
-point, it follows that such classes are in the image of
$\mathbb {Z}_{\ell }$
-point, it follows that such classes are in the image of
![]() $\partial ^D$
by Lemma 3.3. Conversely, any element r in the image of
$\partial ^D$
by Lemma 3.3. Conversely, any element r in the image of
![]() $\partial ^D$
corresponds to a
$\partial ^D$
corresponds to a
![]() $\mu _p$
-cover (and
$\mu _p$
-cover (and
![]() $A_D$
-torsor) X which is abstractly isomorphic to
$A_D$
-torsor) X which is abstractly isomorphic to
![]() $A_D$
, and hence has good reduction over
$A_D$
, and hence has good reduction over
![]() $\mathbb {Q}_{\ell }$
. By the Néron mapping property, X extends to a
$\mathbb {Q}_{\ell }$
. By the Néron mapping property, X extends to a
![]() $\mu _p$
-cover and even an
$\mu _p$
-cover and even an
![]() $\mathcal {A}$
-torsor over
$\mathcal {A}$
-torsor over
![]() $\mathbb {Z}_{\ell }$
. It follows that
$\mathbb {Z}_{\ell }$
. It follows that
![]() $r \in \mathbb {Z}_{\ell }^*$
, since we can interpret this scalar as an automorphism of a line bundle on an abelian scheme
$r \in \mathbb {Z}_{\ell }^*$
, since we can interpret this scalar as an automorphism of a line bundle on an abelian scheme
![]() $\mathcal {J}$
over
$\mathcal {J}$
over
![]() $\mathbb {Z}_{\ell }$
(well-defined up to p-th powers).
$\mathbb {Z}_{\ell }$
(well-defined up to p-th powers).
We will also consider more general Selmer groups. Given a subset
![]() $H = \{D_1, \ldots , D_m\} \subset J[p](F)$
of linearly independent elements, we can define an analogous Selmer group
$H = \{D_1, \ldots , D_m\} \subset J[p](F)$
of linearly independent elements, we can define an analogous Selmer group
![]() $\mathrm {Sel}(A_H) \subset \prod _{i = 1}^m F^*/F^{*p}$
which sits in an exact sequence
$\mathrm {Sel}(A_H) \subset \prod _{i = 1}^m F^*/F^{*p}$
which sits in an exact sequence
and which is isomorphic to the usual Selmer group
![]() $\mathrm {Sel}_{\psi _H}(A_H)$
.
$\mathrm {Sel}_{\psi _H}(A_H)$
.
4 Jacobians of curves of the form
 $y^p = x(x-e_1)(x-e_2)$
$y^p = x(x-e_1)(x-e_2)$
4.1 A special family of curves
Let
![]() $p> 5$
be a prime and let
$p> 5$
be a prime and let
![]() $e_0, e_1,e_2$
be distinct integers. Let C be the smooth projective curve over
$e_0, e_1,e_2$
be distinct integers. Let C be the smooth projective curve over
![]() $\mathbb {Q}$
with affine model
$\mathbb {Q}$
with affine model
There is no loss in generality in assuming
![]() $e_0 = 0$
, so we will do so. The affine model is itself smooth, and its complement in C is a single rational point we call
$e_0 = 0$
, so we will do so. The affine model is itself smooth, and its complement in C is a single rational point we call
![]() $\infty $
. The genus of C is
$\infty $
. The genus of C is
![]() $g = p-1$
. For more details on such curves, see [Reference Poonen and Schaefer30].
$g = p-1$
. For more details on such curves, see [Reference Poonen and Schaefer30].
Let J be the Jacobian of C. Note that
![]() $J(\mathbb {Q})$
has p-torsion of rank at least
$J(\mathbb {Q})$
has p-torsion of rank at least
![]() $2$
, generated by the three divisor classes
$2$
, generated by the three divisor classes
![]() $D_i = [(e_i,0) - \infty ]$
, for
$D_i = [(e_i,0) - \infty ]$
, for
![]() $i \in \{0,1,2\}$
. The equality of divisors
$i \in \{0,1,2\}$
. The equality of divisors
![]() $D_0 + D_1 + D_2 = \mathrm {div}(y)$
means that
$D_0 + D_1 + D_2 = \mathrm {div}(y)$
means that
![]() $D_0 + D_1 + D_2 = 0$
in J. Let
$D_0 + D_1 + D_2 = 0$
in J. Let
![]() $D = D_0 + D_1$
and define the abelian varieties
$D = D_0 + D_1$
and define the abelian varieties
and the corresponding quotient isogenies
![]() ${\widehat \phi } : J \rightarrow {\widehat {A}}$
and
${\widehat \phi } : J \rightarrow {\widehat {A}}$
and
![]() ${\widehat \psi } \colon J \to {\widehat {B}}$
. As before, we identify J with its dual via the canonical principal polarization, so that we may write
${\widehat \psi } \colon J \to {\widehat {B}}$
. As before, we identify J with its dual via the canonical principal polarization, so that we may write
![]() $\phi : A \to J$
and
$\phi : A \to J$
and
![]() $\psi \colon B \to J$
for the dual isogenies. We also define
$\psi \colon B \to J$
for the dual isogenies. We also define
![]() $A_{D_i}$
to be the dual of
$A_{D_i}$
to be the dual of
![]() $J/\langle D_i\rangle $
for
$J/\langle D_i\rangle $
for
![]() $i = 0,1,2$
with isogenies
$i = 0,1,2$
with isogenies
![]() $\psi _i \colon A_{D_i} \to J$
. We have
$\psi _i \colon A_{D_i} \to J$
. We have
![]() $B \simeq A_{D_2}$
since
$B \simeq A_{D_2}$
since
![]() $D = -D_2$
.
$D = -D_2$
.
Let
![]() $H = \langle D_0, D_1\rangle $
, and define the map
$H = \langle D_0, D_1\rangle $
, and define the map
 $$ \begin{align} \begin{aligned} \partial^H : &J(\mathbb{Q})/\phi\bigl( A(\mathbb{Q}) \bigr) \longrightarrow {\mathbb{Q}}^*/\mathbb{Q}^{*p} \times {\mathbb{Q}}^*/\mathbb{Q}^{*p},\\ &\left[ \sum_{j=1}^g (x_j,y_j) - g \cdot \infty \right] \mapsto \Bigl( \prod_{j=1}^g x_j,\ \prod_{j=1}^g (x_j - e_1) \Bigr) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \partial^H : &J(\mathbb{Q})/\phi\bigl( A(\mathbb{Q}) \bigr) \longrightarrow {\mathbb{Q}}^*/\mathbb{Q}^{*p} \times {\mathbb{Q}}^*/\mathbb{Q}^{*p},\\ &\left[ \sum_{j=1}^g (x_j,y_j) - g \cdot \infty \right] \mapsto \Bigl( \prod_{j=1}^g x_j,\ \prod_{j=1}^g (x_j - e_1) \Bigr) \end{aligned} \end{align} $$
as in Lemmas 3.5 and 3.7 of Section 2.3. In the above definition, each
![]() $x_j,y_j \in \overline {\mathbb {Q}}$
, the divisor
$x_j,y_j \in \overline {\mathbb {Q}}$
, the divisor
![]() $\sum _{j=1}^g (x_j,y_j) - g \cdot \infty $
is Galois stable, and the left-hand side is its divisor class. That such representatives exist follows from the fact that
$\sum _{j=1}^g (x_j,y_j) - g \cdot \infty $
is Galois stable, and the left-hand side is its divisor class. That such representatives exist follows from the fact that
![]() $C(\mathbb {Q}) \neq \emptyset $
[Reference Schaefer34, Prop. 2.7]. The above description of
$C(\mathbb {Q}) \neq \emptyset $
[Reference Schaefer34, Prop. 2.7]. The above description of
![]() $\partial ^H$
applies whenever it makes sense – that is, when all
$\partial ^H$
applies whenever it makes sense – that is, when all
![]() $x_j$
and
$x_j$
and
![]() $x_j - e_1$
are nonzero. Every class in
$x_j - e_1$
are nonzero. Every class in
![]() $J(\mathbb {Q})/\phi \bigl ( A(\mathbb {Q}) \bigr )$
can be represented by such a divisor [Reference Lang21, pg.166].
$J(\mathbb {Q})/\phi \bigl ( A(\mathbb {Q}) \bigr )$
can be represented by such a divisor [Reference Lang21, pg.166].
For
![]() $i \in \{1,2,3\}$
, we have similar homomorphisms
$i \in \{1,2,3\}$
, we have similar homomorphisms
 $$ \begin{align} \begin{aligned} \partial^{D_i} :&J(\mathbb{Q})/\psi_i\bigl( A_{D_i}(\mathbb{Q}) \bigr) \longrightarrow {\mathbb{Q}}^*/\mathbb{Q}^{*p},\\ &\left[ \sum_{j=1}^g (x_j,y_j) - g \cdot \infty \right] \mapsto \prod_{j=1}^g \Bigl( x_j - e_i \Bigr), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \partial^{D_i} :&J(\mathbb{Q})/\psi_i\bigl( A_{D_i}(\mathbb{Q}) \bigr) \longrightarrow {\mathbb{Q}}^*/\mathbb{Q}^{*p},\\ &\left[ \sum_{j=1}^g (x_j,y_j) - g \cdot \infty \right] \mapsto \prod_{j=1}^g \Bigl( x_j - e_i \Bigr), \end{aligned} \end{align} $$
as well as the homomorphism
 $$ \begin{align} \begin{aligned} \partial^{D} :&J(\mathbb{Q})/\psi\bigl( B(\mathbb{Q}) \bigr) \longrightarrow {\mathbb{Q}}^*/\mathbb{Q}^{*p},\\ &\left[ \sum_{j=1}^g (x_j,y_j) - g \cdot \infty \right] \mapsto \prod_{j=1}^g \Bigl( x_j(x_j - e_1) \Bigr). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \partial^{D} :&J(\mathbb{Q})/\psi\bigl( B(\mathbb{Q}) \bigr) \longrightarrow {\mathbb{Q}}^*/\mathbb{Q}^{*p},\\ &\left[ \sum_{j=1}^g (x_j,y_j) - g \cdot \infty \right] \mapsto \prod_{j=1}^g \Bigl( x_j(x_j - e_1) \Bigr). \end{aligned} \end{align} $$
As before, the description of these maps is for representative divisors for which it makes sense. However, note that by the equation for the curve, we have
![]() $\partial ^{D_0} \cdot \partial ^{D_1} \cdot \partial ^{D_2} = 1$
. This allows us to describe the maps
$\partial ^{D_0} \cdot \partial ^{D_1} \cdot \partial ^{D_2} = 1$
. This allows us to describe the maps
![]() $\partial ^{D_i}$
even on points where the formula above is not well defined. For example,
$\partial ^{D_i}$
even on points where the formula above is not well defined. For example,
Lemma 4.1. We have
and
In the next section, we will make critical use of the following commutative diagram
 $$ \begin{align} \begin{array}{ccc} J(\mathbb{Q})/\phi\bigl( A(\mathbb{Q}) \bigr) &\overset{\partial^H}{\longrightarrow}&{\mathbb{Q}}^*/\mathbb{Q}^{*p}\times {\mathbb{Q}}^*/\mathbb{Q}^{*p}\\ \downarrow & &\downarrow \\ J(\mathbb{Q})/\psi\bigl(B(\mathbb{Q})\bigr)&\overset{\partial^D} {\longrightarrow}&{\mathbb{Q}}^*/\mathbb{Q}^{*p},\\ \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ccc} J(\mathbb{Q})/\phi\bigl( A(\mathbb{Q}) \bigr) &\overset{\partial^H}{\longrightarrow}&{\mathbb{Q}}^*/\mathbb{Q}^{*p}\times {\mathbb{Q}}^*/\mathbb{Q}^{*p}\\ \downarrow & &\downarrow \\ J(\mathbb{Q})/\psi\bigl(B(\mathbb{Q})\bigr)&\overset{\partial^D} {\longrightarrow}&{\mathbb{Q}}^*/\mathbb{Q}^{*p},\\ \end{array} \end{align} $$
whose right vertical map is
![]() $[r_1,r_2] \mapsto r_1r_2$
.
$[r_1,r_2] \mapsto r_1r_2$
.
4.2 Models
There are simple birational models for the
![]() $\mu _p$
-covers of J with a given Steinitz class. For concreteness, assume that the Steinitz class is
$\mu _p$
-covers of J with a given Steinitz class. For concreteness, assume that the Steinitz class is
![]() $D = D_0 + D_1$
. The distinguished
$D = D_0 + D_1$
. The distinguished
![]() $\mu _p$
-cover with this Steinitz class is the cover
$\mu _p$
-cover with this Steinitz class is the cover
![]() $B \to J$
. A birational model for J is given by the equations
$B \to J$
. A birational model for J is given by the equations
for
![]() $i = 1,\ldots , g$
, modulo the action of
$i = 1,\ldots , g$
, modulo the action of
![]() $S_g$
. By Lemmas 3.5, 3.6 and 3.7, a birational model for B is given by the same g equations above along with the additional equation
$S_g$
. By Lemmas 3.5, 3.6 and 3.7, a birational model for B is given by the same g equations above along with the additional equation
 $$\begin{align*}z^p = \prod_{i = 1}^g x_i(x_i - e_1),\end{align*}$$
$$\begin{align*}z^p = \prod_{i = 1}^g x_i(x_i - e_1),\end{align*}$$
all modulo the action of
![]() $S_g$
. Similarly, if
$S_g$
. Similarly, if
![]() $r \in \mathbb {Q}^\times $
, then the
$r \in \mathbb {Q}^\times $
, then the
![]() $\mu _p$
-cover corresponding to
$\mu _p$
-cover corresponding to
![]() $(\mathcal {L}, r\eta )$
is given by the same equations, with the last one twisted by r:
$(\mathcal {L}, r\eta )$
is given by the same equations, with the last one twisted by r:
for
![]() $i = 1,\ldots , g$
and
$i = 1,\ldots , g$
and
 $$\begin{align*}rz^p = \prod_{i = 1}^g x_i(x_i - e_1), \end{align*}$$
$$\begin{align*}rz^p = \prod_{i = 1}^g x_i(x_i - e_1), \end{align*}$$
again modulo the action of
![]() $S_g$
.
$S_g$
.
5 Arbitrarily large p-torsion part of the Tate-Shafarevich group
We wish to produce examples of arbitrarily large p-torsion subgroups in the Tate-Shafarevich group ![]() , by finding elements of
, by finding elements of
![]() $\mathrm {Sel}(B)$
which can be shown to violate the Hasse principle by using
$\mathrm {Sel}(B)$
which can be shown to violate the Hasse principle by using
![]() $\mathrm {Sel}(A)$
. We will choose fairly generic curves of the form
$\mathrm {Sel}(A)$
. We will choose fairly generic curves of the form
![]() $y^p = x(x-e_1)(x-e_2)$
, but then we will twist them in a carefully chosen way to produce our examples.
$y^p = x(x-e_1)(x-e_2)$
, but then we will twist them in a carefully chosen way to produce our examples.
Let
where
![]() $p> 5$
is prime and where
$p> 5$
is prime and where
![]() $u,v \in \mathbb {Z}$
are not divisible by
$u,v \in \mathbb {Z}$
are not divisible by
![]() $3$
. Let J be the Jacobian of C and let A be the isogenous abelian variety, as in the previous section.
$3$
. Let J be the Jacobian of C and let A be the isogenous abelian variety, as in the previous section.
Lemma 5.1. Suppose q is a prime such that
![]() $q \equiv 1\ \pmod p$
. Then
$q \equiv 1\ \pmod p$
. Then
![]() $J(\mathbb {Q}_q)/\phi \bigl (A(\mathbb {Q}_q)\bigr )$
has order
$J(\mathbb {Q}_q)/\phi \bigl (A(\mathbb {Q}_q)\bigr )$
has order
![]() $p^2$
.
$p^2$
.
Proof. The congruence condition on q implies
![]() $\mathbb {Q}_q^*$
contains a primitive p-th root of unity
$\mathbb {Q}_q^*$
contains a primitive p-th root of unity
![]() $\zeta $
. Over any field containing
$\zeta $
. Over any field containing
![]() $\zeta $
, the automorphism
$\zeta $
, the automorphism
![]() $(x,y) \mapsto (x, \zeta y)$
of C induces a ring embedding
$(x,y) \mapsto (x, \zeta y)$
of C induces a ring embedding
![]() $\iota \colon \mathbb {Z}[\zeta ] \hookrightarrow \mathrm {End}(J)$
. The degree of
$\iota \colon \mathbb {Z}[\zeta ] \hookrightarrow \mathrm {End}(J)$
. The degree of
![]() $\iota (\alpha )$
is equal to
$\iota (\alpha )$
is equal to
![]() $\mathrm {Nm}(\alpha )^2 = \#(\mathbb {Z}[\zeta ]/\alpha )^2$
. Indeed, the degree function restricted to
$\mathrm {Nm}(\alpha )^2 = \#(\mathbb {Z}[\zeta ]/\alpha )^2$
. Indeed, the degree function restricted to
![]() $\mathbb {Z}[\zeta ]$
is a power of the norm [Reference Mumford29, §19], and we have
$\mathbb {Z}[\zeta ]$
is a power of the norm [Reference Mumford29, §19], and we have
![]() $\deg ([n]) = n^{2g} = n^{2[\mathbb {Q}(\zeta ) \colon \mathbb {Q}]}$
, so it is the square of the norm in this case. The kernel of
$\deg ([n]) = n^{2g} = n^{2[\mathbb {Q}(\zeta ) \colon \mathbb {Q}]}$
, so it is the square of the norm in this case. The kernel of
![]() ${\widehat \phi } \colon J \to {\widehat {A}}$
is then equal to the kernel of the endomorphism
${\widehat \phi } \colon J \to {\widehat {A}}$
is then equal to the kernel of the endomorphism
![]() $1 - \iota (\zeta )$
. It follows that
$1 - \iota (\zeta )$
. It follows that
![]() ${\widehat \phi }$
agrees with
${\widehat \phi }$
agrees with
![]() $1 - \iota (\zeta )$
up to post-composition with an automorphism (since they have the same degree and one factors through the other); hence, the abelian varieties A and
$1 - \iota (\zeta )$
up to post-composition with an automorphism (since they have the same degree and one factors through the other); hence, the abelian varieties A and
![]() $\widehat {A}$
are isomorphic to J (over any field containing
$\widehat {A}$
are isomorphic to J (over any field containing
![]() $\zeta $
, and in particular over
$\zeta $
, and in particular over
![]() $\mathbb {Q}_{q}$
). However, we have [Reference Shnidman36, Cor. 3.2]
$\mathbb {Q}_{q}$
). However, we have [Reference Shnidman36, Cor. 3.2]
 $$\begin{align*}\dfrac{\#J( \mathbb{Q}_{q} )/ \phi\bigl(A(\mathbb{Q}_{q})\bigr)}{\#A( \mathbb{Q}_{q} )[\phi]} = c_{q}(J)/c_{q}(A),\end{align*}$$
$$\begin{align*}\dfrac{\#J( \mathbb{Q}_{q} )/ \phi\bigl(A(\mathbb{Q}_{q})\bigr)}{\#A( \mathbb{Q}_{q} )[\phi]} = c_{q}(J)/c_{q}(A),\end{align*}$$
where the right-hand side is the ratio of Tamagawa numbers over
![]() $\mathbb {Q}_{q}$
. Since
$\mathbb {Q}_{q}$
. Since
![]() $J \simeq A$
over
$J \simeq A$
over
![]() $\mathbb {Q}_{q}$
, this ratio is 1. We also have
$\mathbb {Q}_{q}$
, this ratio is 1. We also have
![]() $\#A(\mathbb {Q}_{q})[\phi ] = p^2$
, which shows that
$\#A(\mathbb {Q}_{q})[\phi ] = p^2$
, which shows that
![]() $\#J( \mathbb {Q}_{q} )/ \phi \bigl (A(\mathbb {Q}_{q})\bigr ) = p^2$
.
$\#J( \mathbb {Q}_{q} )/ \phi \bigl (A(\mathbb {Q}_{q})\bigr ) = p^2$
.
For each integer k, we will consider the curve
Another model for
![]() $C_k$
is
$C_k$
is
![]() $k^{-3} y^p = x(x-3u)(x-9v)$
, which shows that
$k^{-3} y^p = x(x-3u)(x-9v)$
, which shows that
![]() $C_k$
is a
$C_k$
is a
![]() $\mu _p$
-twist of the original curve
$\mu _p$
-twist of the original curve
![]() $C = C_{u,v}$
. Let
$C = C_{u,v}$
. Let
![]() $J_k$
,
$J_k$
,
![]() $A_k$
and
$A_k$
and
![]() $B_k$
be the corresponding abelian varieties for the curve
$B_k$
be the corresponding abelian varieties for the curve
![]() $C_k$
. These are
$C_k$
. These are
![]() $\mu _p$
-twists of
$\mu _p$
-twists of
![]() $J,A$
and B, respectively.
$J,A$
and B, respectively.
For two primes q and
![]() $\ell $
, set
$\ell $
, set
![]() $\left (\frac {q}{\ell }\right )_p = 1$
if and only if q is a p-th power in
$\left (\frac {q}{\ell }\right )_p = 1$
if and only if q is a p-th power in
![]() $\mathbb {Q}_{\ell }^\times $
. Recall the exact sequence
$\mathbb {Q}_{\ell }^\times $
. Recall the exact sequence
from Proposition 3.9.
Proposition 5.2. Let U be the set of primes that divide
![]() $3puv(u-3v)$
. Suppose k is a product of distinct primes
$3puv(u-3v)$
. Suppose k is a product of distinct primes
![]() $k = p_1 p_2 \cdot \ldots \cdot p_t$
, where
$k = p_1 p_2 \cdot \ldots \cdot p_t$
, where
![]() $t\geq 2$
and each prime
$t\geq 2$
and each prime
![]() $p_i$
is not in U, and satisfies
$p_i$
is not in U, and satisfies
-
(1)
 $\left (\frac {p_i}{p_j}\right )_p = 1$
, for all
$\left (\frac {p_i}{p_j}\right )_p = 1$
, for all
 $i \neq j$
in
$i \neq j$
in
 $\{1,\ldots , t\}$
,
$\{1,\ldots , t\}$
, -
(2)
 $\left (\frac {p_i}{q}\right )_p = 1$
, for all
$\left (\frac {p_i}{q}\right )_p = 1$
, for all
 $i \in \{1, \ldots , t\}$
and all
$i \in \{1, \ldots , t\}$
and all
 $q \in U$
,
$q \in U$
, -
(3)
 $\left (\frac {q}{p_i}\right )_p = 1$
, for all
$\left (\frac {q}{p_i}\right )_p = 1$
, for all
 $i \in \{1, \ldots , t\}$
and all
$i \in \{1, \ldots , t\}$
and all
 $q \in U\backslash \{3\}$
,
$q \in U\backslash \{3\}$
, -
(4)
 $\left (\frac {3}{p_i}\right )_p \neq 1$
, for all
$\left (\frac {3}{p_i}\right )_p \neq 1$
, for all
 $i \in \{1, \ldots , t\}$
.
$i \in \{1, \ldots , t\}$
.
Then, for all i, we have
![]() $p_i \in \mathrm {Sel}(B_k)$
but
$p_i \in \mathrm {Sel}(B_k)$
but
![]() $p_i \notin \partial ^D(J_k(\mathbb {Q}))$
. More generally, if
$p_i \notin \partial ^D(J_k(\mathbb {Q}))$
. More generally, if
![]() $q = \prod _{i \in I} p_i^{a_i}$
, where I is any nonempty proper subset of
$q = \prod _{i \in I} p_i^{a_i}$
, where I is any nonempty proper subset of
![]() $ \{1,\ldots , t\}$
and
$ \{1,\ldots , t\}$
and
![]() $1 \leq a_i \leq p-1$
, then
$1 \leq a_i \leq p-1$
, then
![]() $q \in \mathrm {Sel}(B_k)$
but
$q \in \mathrm {Sel}(B_k)$
but
![]() $q \notin \partial ^D(J_k(\mathbb {Q}))$
.
$q \notin \partial ^D(J_k(\mathbb {Q}))$
.
Note that condition
![]() $(4)$
implies that
$(4)$
implies that
![]() $p_i \equiv 1\ \pmod {p}$
for all i.
$p_i \equiv 1\ \pmod {p}$
for all i.
Proof. By Lemma 4.1, we have
and
For
![]() $i = 1,\ldots , t$
, the images of these two elements in
$i = 1,\ldots , t$
, the images of these two elements in
![]() $\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p \times \mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
are
$\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p \times \mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
are
![]() $[3^{-3}p_i^{-2},3p_i]$
and
$[3^{-3}p_i^{-2},3p_i]$
and
![]() $[3p_i,3^{-2}p_i^{-2}]$
, respectively, by our assumptions on the
$[3p_i,3^{-2}p_i^{-2}]$
, respectively, by our assumptions on the
![]() $p_i$
. These two elements are linearly independent, and hence generate all of
$p_i$
. These two elements are linearly independent, and hence generate all of
![]() $\partial ^H\bigl ( J_k(\mathbb {Q}_{p_i}) /\phi (A_k(\mathbb {Q}_{p_i})) \bigr )$
, by Lemma 5.1.
$\partial ^H\bigl ( J_k(\mathbb {Q}_{p_i}) /\phi (A_k(\mathbb {Q}_{p_i})) \bigr )$
, by Lemma 5.1.
Let
![]() $[r_1,r_2]$
be in
$[r_1,r_2]$
be in
![]() $\partial ^H\bigl ( J_k(\mathbb {Q})/\phi (A_k(\mathbb {Q})) \bigr )$
. We shall consider elements of
$\partial ^H\bigl ( J_k(\mathbb {Q})/\phi (A_k(\mathbb {Q})) \bigr )$
. We shall consider elements of
![]() $\mathbb {Q}^*/\mathbb {Q}^{*p}$
as pth-power-free integers. Note that by Proposition 3.10, the integers
$\mathbb {Q}^*/\mathbb {Q}^{*p}$
as pth-power-free integers. Note that by Proposition 3.10, the integers
![]() $r_1$
and
$r_1$
and
![]() $r_2$
can only be divisible by primes in the set
$r_2$
can only be divisible by primes in the set
![]() $\{p_1, \ldots , p_t\} \cup U$
.
$\{p_1, \ldots , p_t\} \cup U$
.
If there is no i such that
![]() $\mathrm {ord}_{p_i}(r_1) \equiv \mathrm {ord}_{p_i}(1/r_2)\ \pmod p$
, then
$\mathrm {ord}_{p_i}(r_1) \equiv \mathrm {ord}_{p_i}(1/r_2)\ \pmod p$
, then
![]() $\mathrm {ord}_{p_i}(r_1r_2) \not \equiv 0\ \pmod {p}$
for every
$\mathrm {ord}_{p_i}(r_1r_2) \not \equiv 0\ \pmod {p}$
for every
![]() $p_i$
, and so
$p_i$
, and so
![]() $r_1 r_2$
cannot be of the form
$r_1 r_2$
cannot be of the form
![]() $\prod _{i \in I} p_i^{a_i}$
, for a nonempty proper subset of indices I, and any tuple of exponents
$\prod _{i \in I} p_i^{a_i}$
, for a nonempty proper subset of indices I, and any tuple of exponents
![]() $a_i$
with
$a_i$
with
![]() $1 \leq a_i \leq p-1$
.
$1 \leq a_i \leq p-1$
.
Suppose there exists i such that
![]() $\mathrm {ord}_{p_i}(r_1) \equiv \mathrm {ord}_{p_i}(1/r_2)\ \pmod p$
. Since
$\mathrm {ord}_{p_i}(r_1) \equiv \mathrm {ord}_{p_i}(1/r_2)\ \pmod p$
. Since
![]() $[3^{-3}p_i^{-2},3p_i]$
and
$[3^{-3}p_i^{-2},3p_i]$
and
![]() $[3p_i,3^{-2}p_i^{-2}]$
generate all of
$[3p_i,3^{-2}p_i^{-2}]$
generate all of
![]() $\partial ^H\bigl ( J_k(\mathbb {Q}_{p_i})/ \phi (A_k(\mathbb {Q}_{p_i})) \bigr )$
, considering only the
$\partial ^H\bigl ( J_k(\mathbb {Q}_{p_i})/ \phi (A_k(\mathbb {Q}_{p_i})) \bigr )$
, considering only the
![]() $p_i$
-adic valuation, we have
$p_i$
-adic valuation, we have
for integers a and b. So
and we must have
![]() $b \equiv -a$
(mod
$b \equiv -a$
(mod
![]() $p_i$
). In other words, the image of
$p_i$
). In other words, the image of
![]() $[r_1,r_2]$
in
$[r_1,r_2]$
in
![]() $\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p \times \mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
must be a power of the quotient of these generators. Thus, in
$\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p \times \mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
must be a power of the quotient of these generators. Thus, in
![]() $\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p \times \mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
, we have
$\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p \times \mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
, we have
for some
![]() $0 \leq m < p$
. Thus, in
$0 \leq m < p$
. Thus, in
![]() $\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
, we have
$\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
, we have
Since
![]() $3$
is not a p-th power modulo
$3$
is not a p-th power modulo
![]() $p_i$
, this implies that
$p_i$
, this implies that
![]() $3$
divides
$3$
divides
![]() $r_1^3$
and
$r_1^3$
and
![]() $1/r_2^4$
to the same power. Since, for any j, the elements
$1/r_2^4$
to the same power. Since, for any j, the elements
![]() $[ 3^{-3} p_j^{-2}, 3 p_j ]$
and
$[ 3^{-3} p_j^{-2}, 3 p_j ]$
and
![]() $[ 3p_j, 3^{-2}p_j^{-2} ]$
generate all of
$[ 3p_j, 3^{-2}p_j^{-2} ]$
generate all of
![]() $\partial ^H(( J_k(\mathbb {Q}_{p_j})/\phi (A_k(\mathbb {Q}_{p_j}))))$
, and since we have already shown that
$\partial ^H(( J_k(\mathbb {Q}_{p_j})/\phi (A_k(\mathbb {Q}_{p_j}))))$
, and since we have already shown that
![]() $3$
divides
$3$
divides
![]() $r_1^3$
and
$r_1^3$
and
![]() $1/r_2^4$
to the same power, we deduce that the image of
$1/r_2^4$
to the same power, we deduce that the image of
![]() $[r_1,r_2]$
in
$[r_1,r_2]$
in
![]() $\mathbb {Q}_{p_j}^*/(\mathbb {Q}_{p_j}^*)^p \times \mathbb {Q}_{p_j}^*/(\mathbb {Q}_{p_j}^*)^p$
must be a power of the quotient of these generators, and so
$\mathbb {Q}_{p_j}^*/(\mathbb {Q}_{p_j}^*)^p \times \mathbb {Q}_{p_j}^*/(\mathbb {Q}_{p_j}^*)^p$
must be a power of the quotient of these generators, and so
![]() $p_j$
must divide
$p_j$
must divide
![]() $r_1$
and
$r_1$
and
![]() $1/r_2$
to the same power. This applies for all j; hence, no
$1/r_2$
to the same power. This applies for all j; hence, no
![]() $p_j$
will appear in
$p_j$
will appear in
![]() $r_1 r_2$
. So again we have that
$r_1 r_2$
. So again we have that
![]() $r_1 r_2$
cannot be of the form
$r_1 r_2$
cannot be of the form
![]() $\prod _{i \in I} p_i^{a_i}$
with
$\prod _{i \in I} p_i^{a_i}$
with
![]() $0 < \#I < t$
.
$0 < \#I < t$
.
Since
![]() $\partial ^H \bigl ( J_k(\mathbb {Q})/\phi (A_k(\mathbb {Q})) \bigr )$
maps surjectively onto
$\partial ^H \bigl ( J_k(\mathbb {Q})/\phi (A_k(\mathbb {Q})) \bigr )$
maps surjectively onto
![]() $\partial ^D \bigl ( J_k(\mathbb {Q})/\psi (B_k(\mathbb {Q})) \bigr )$
, it follows that each element of the form
$\partial ^D \bigl ( J_k(\mathbb {Q})/\psi (B_k(\mathbb {Q})) \bigr )$
, it follows that each element of the form
![]() $\prod _{i \in I} p_i^{a_i}$
with
$\prod _{i \in I} p_i^{a_i}$
with
![]() $0 < \#I < t$
and
$0 < \#I < t$
and
![]() $0 < a_i < p$
is not in
$0 < a_i < p$
is not in
![]() $\partial ^D \bigl ( J_k(\mathbb {Q})/\psi (B_k(\mathbb {Q})) \bigr )$
.
$\partial ^D \bigl ( J_k(\mathbb {Q})/\psi (B_k(\mathbb {Q})) \bigr )$
.
However, we show that each
![]() $p_i$
is in
$p_i$
is in
![]() $\partial ^D ( J_k(\mathbb {Q}_{\ell })/\psi (B_k(\mathbb {Q}_{\ell })) )$
for every prime
$\partial ^D ( J_k(\mathbb {Q}_{\ell })/\psi (B_k(\mathbb {Q}_{\ell })) )$
for every prime
![]() $\ell $
, as follows. First, note that for every prime
$\ell $
, as follows. First, note that for every prime
![]() $\ell \in U \cup \{p_1, \ldots , p_t\}$
except
$\ell \in U \cup \{p_1, \ldots , p_t\}$
except
![]() $p_i$
itself,
$p_i$
itself,
![]() $p_i$
is a pth power in
$p_i$
is a pth power in
![]() $\mathbb {Q}_{\ell }^*$
, and so
$\mathbb {Q}_{\ell }^*$
, and so
![]() $p_i$
is in
$p_i$
is in
![]() $\partial ^D\bigl ( J_k(\mathbb {Q}_{\ell })/\psi (B_k(\mathbb {Q}_{\ell })) \bigr )$
by virtue of being
$\partial ^D\bigl ( J_k(\mathbb {Q}_{\ell })/\psi (B_k(\mathbb {Q}_{\ell })) \bigr )$
by virtue of being
![]() $\partial ^D$
of the identity. If
$\partial ^D$
of the identity. If
![]() $\ell \notin U \cup \{p_1, \ldots , p_t\}$
, we have
$\ell \notin U \cup \{p_1, \ldots , p_t\}$
, we have
![]() $p_i \in \partial ^D ( J_k(\mathbb {Q}_{\ell })/\psi (B_k(\mathbb {Q}_{\ell })) )$
, by Proposition 3.10. For the remaining case
$p_i \in \partial ^D ( J_k(\mathbb {Q}_{\ell })/\psi (B_k(\mathbb {Q}_{\ell })) )$
, by Proposition 3.10. For the remaining case
![]() $\ell = p_i$
, note that
$\ell = p_i$
, note that
![]() $\partial ^D( [(0,0)-\infty ] )= [ -3^{-2} v^{-1} k^{-1} ]$
and
$\partial ^D( [(0,0)-\infty ] )= [ -3^{-2} v^{-1} k^{-1} ]$
and
![]() $\partial ^D([(3uk,0)-\infty ]) = [ 3^{-1} (u-3v)^{-1} k^{-1} ]$
, and so the first divided by the square of the second gives
$\partial ^D([(3uk,0)-\infty ]) = [ 3^{-1} (u-3v)^{-1} k^{-1} ]$
, and so the first divided by the square of the second gives
![]() $p_i$
, since all other factors are pth powers in
$p_i$
, since all other factors are pth powers in
![]() $\mathbb {Q}_{p_i}$
. Hence,
$\mathbb {Q}_{p_i}$
. Hence,
![]() $p_i$
is in the image everywhere locally.
$p_i$
is in the image everywhere locally.
As a corollary, we deduce the first theorem from the introduction.
Proof of Theorem 1.1.
The Theorem follows from Lemma 3.3 and Proposition 5.2, together with the discussion of models in Section 4.2.
As a second corollary, we have the following:
Corollary 5.3. Let
![]() $C_{u,v,k}$
be as in Proposition 5.2. Then
$C_{u,v,k}$
be as in Proposition 5.2. Then ![]() .
.
Proof. Let
![]() $B_k = B_{u,v,k}$
. We have the exact sequence
$B_k = B_{u,v,k}$
. We have the exact sequence
Moreover, we have seen that any element of the form
![]() $\prod _{i \in I} p_i^{a_i}$
, for some proper subset
$\prod _{i \in I} p_i^{a_i}$
, for some proper subset
![]() $I \subset \{1,\ldots , t\}$
is contained in
$I \subset \{1,\ldots , t\}$
is contained in
![]() $\mathrm {Sel}(B_k)$
but does not lie in the subgroup
$\mathrm {Sel}(B_k)$
but does not lie in the subgroup
![]() $J_k(\mathbb {Q})/\psi (B_k(\mathbb {Q})$
. Thus, these elements must map nontrivially to
$J_k(\mathbb {Q})/\psi (B_k(\mathbb {Q})$
. Thus, these elements must map nontrivially to ![]() . In fact, we see that the intersection of
. In fact, we see that the intersection of
![]() $J_k(\mathbb {Q})/\psi (B_k(\mathbb {Q}))$
with the subgroup of
$J_k(\mathbb {Q})/\psi (B_k(\mathbb {Q}))$
with the subgroup of
![]() $\mathrm {Sel}(B_k)$
generated by the elements
$\mathrm {Sel}(B_k)$
generated by the elements
![]() $p_1, \ldots , p_t$
is at most one dimensional as an
$p_1, \ldots , p_t$
is at most one dimensional as an
![]() $\mathbb {F}_p$
-vector space. Indeed, any two linearly independent elements in this subgroup can be scaled so that they are divisible exactly once by
$\mathbb {F}_p$
-vector space. Indeed, any two linearly independent elements in this subgroup can be scaled so that they are divisible exactly once by
![]() $p_1$
, and hence, their ratio is nonzero and not divisible by
$p_1$
, and hence, their ratio is nonzero and not divisible by
![]() $p_1$
, which would be a contradiction. It follows that the image of the subgroup
$p_1$
, which would be a contradiction. It follows that the image of the subgroup
![]() $\langle p_1, \ldots , p_t\rangle $
in
$\langle p_1, \ldots , p_t\rangle $
in ![]() has dimension at least
has dimension at least
![]() $t - 1$
. Since
$t - 1$
. Since
![]() $\deg (\psi ) = p$
, we have
$\deg (\psi ) = p$
, we have ![]() , which finishes the proof.
, which finishes the proof.
6 Proof of Theorem 1.5
To deduce Theorem 1.5 from the results of the previous section, we need two extra ingredients.
Proposition 6.1. For any
![]() $u,v$
as above, and for any
$u,v$
as above, and for any
![]() $t \geq 0$
, there are primes
$t \geq 0$
, there are primes
![]() $p_1,\dots , p_t$
satisfying the conditions of Proposition 5.2.
$p_1,\dots , p_t$
satisfying the conditions of Proposition 5.2.
Proof. Let
![]() $K = \mathbb {Q}(\zeta ) = \mathbb {Q}(\mu _p)$
. We prove this by induction on t. If
$K = \mathbb {Q}(\zeta ) = \mathbb {Q}(\mu _p)$
. We prove this by induction on t. If
![]() $t = 0$
, then there is nothing to prove.
$t = 0$
, then there is nothing to prove.
Now let
![]() $t> 0$
and suppose we have found primes
$t> 0$
and suppose we have found primes
![]() $p_1,\cdots , p_{t-1}$
satisfying the conditions. Let
$p_1,\cdots , p_{t-1}$
satisfying the conditions. Let
![]() $k = p_1 \cdots p_{t-1}$
. Let N be the product of the primes dividing
$k = p_1 \cdots p_{t-1}$
. Let N be the product of the primes dividing
![]() $puv(u-3v)k$
, and let
$puv(u-3v)k$
, and let
![]() $\zeta _{pN}$
be a primitive
$\zeta _{pN}$
be a primitive
![]() $pN$
-th root of unity. Let L be the compositum inside
$pN$
-th root of unity. Let L be the compositum inside
![]() $\bar {\mathbb {Q}}$
of
$\bar {\mathbb {Q}}$
of
![]() $\mathbb {Q}(\zeta _{pN})$
with all of the fields
$\mathbb {Q}(\zeta _{pN})$
with all of the fields
![]() $\mathbb {Q}(\sqrt [p]{q})$
, with q a prime dividing N. Then L is an abelian extension of K and a Galois extension of
$\mathbb {Q}(\sqrt [p]{q})$
, with q a prime dividing N. Then L is an abelian extension of K and a Galois extension of
![]() $\mathbb {Q}$
. Finally, let
$\mathbb {Q}$
. Finally, let
![]() $E = \mathbb {Q}(\sqrt [p]{3})$
and let
$E = \mathbb {Q}(\sqrt [p]{3})$
and let
![]() $F =EL$
be the compositum of E and L, which is again a Galois extension of
$F =EL$
be the compositum of E and L, which is again a Galois extension of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Note that the fields E and L are linearly disjoint over
![]() $\mathbb {Q}$
. Indeed,
$\mathbb {Q}$
. Indeed,
![]() $E/\mathbb {Q}$
is totally ramified at
$E/\mathbb {Q}$
is totally ramified at
![]() $3$
, whereas L is unramified at
$3$
, whereas L is unramified at
![]() $3$
. Thus, we have an exact sequence
$3$
. Thus, we have an exact sequence
By the Cebotarev density theorem, there exists a prime
![]() $p_t$
(in fact, infinitely many such primes) whose Frobenius conjugacy class in
$p_t$
(in fact, infinitely many such primes) whose Frobenius conjugacy class in
![]() $\mathrm {Gal}(F/\mathbb {Q})$
is not trivial but restricts to the trivial class in
$\mathrm {Gal}(F/\mathbb {Q})$
is not trivial but restricts to the trivial class in
![]() $\mathrm {Gal}(L/\mathbb {Q})$
. Let us check that
$\mathrm {Gal}(L/\mathbb {Q})$
. Let us check that
![]() $p_t$
satisfies all the desired properties.
$p_t$
satisfies all the desired properties.
By construction,
![]() $p_t$
splits completely in any subfield of L. In particular,
$p_t$
splits completely in any subfield of L. In particular,
![]() $p_t$
splits completely in
$p_t$
splits completely in
![]() $\mathbb {Q}(\zeta _{pN})$
and hence is a p-th power in
$\mathbb {Q}(\zeta _{pN})$
and hence is a p-th power in
![]() $\mathbb {Q}_q^*$
for any prime q dividing
$\mathbb {Q}_q^*$
for any prime q dividing
![]() $3pN$
. For
$3pN$
. For
![]() $q \nmid 3p$
, this is because
$q \nmid 3p$
, this is because
![]() $p_t \equiv 1\ \pmod q$
, and hence,
$p_t \equiv 1\ \pmod q$
, and hence,
![]() $p_t$
is a p-th power in
$p_t$
is a p-th power in
![]() $\mathbb {Q}_q^*$
by Hensel’s lemma. For
$\mathbb {Q}_q^*$
by Hensel’s lemma. For
![]() $q = p$
, this is because
$q = p$
, this is because
![]() $p^2 \mid pN$
, and hence
$p^2 \mid pN$
, and hence
![]() $p_t \equiv 1\ \pmod {p^2}$
, and hence is a p-th power, again by Hensel’s lemma. For
$p_t \equiv 1\ \pmod {p^2}$
, and hence is a p-th power, again by Hensel’s lemma. For
![]() $q = 3$
, this is because every unit in
$q = 3$
, this is because every unit in
![]() $\mathbb {Z}_3$
is a p-th power. Similarly,
$\mathbb {Z}_3$
is a p-th power. Similarly,
![]() $p_t$
splits completely in
$p_t$
splits completely in
![]() $\mathbb {Q}(\sqrt [p]{q})$
for all
$\mathbb {Q}(\sqrt [p]{q})$
for all
![]() $q \mid N$
, so all such primes q are p-th powers modulo
$q \mid N$
, so all such primes q are p-th powers modulo
![]() $p_t$
.
$p_t$
.
Finally, we check that 3 is not a p-th power in
![]() $\mathbb {Q}_{p_t}^*$
. It is enough to show that the prime
$\mathbb {Q}_{p_t}^*$
. It is enough to show that the prime
![]() $p_t$
does not have a degree 1 prime above it in E. If it did, then because
$p_t$
does not have a degree 1 prime above it in E. If it did, then because
![]() $\zeta \in \mathbb {Q}_{p_t}^*$
, once the polynomial
$\zeta \in \mathbb {Q}_{p_t}^*$
, once the polynomial
![]() $x^p - 3$
has one root in
$x^p - 3$
has one root in
![]() $\mathbb {Q}_{p_t}^*$
, it necessarily has all of its roots in
$\mathbb {Q}_{p_t}^*$
, it necessarily has all of its roots in
![]() $\mathbb {Q}_{p_t}^*$
. Therefore,
$\mathbb {Q}_{p_t}^*$
. Therefore,
![]() $p_t$
would split completely in E. Since
$p_t$
would split completely in E. Since
![]() $p_t$
splits completely in L, this would mean that
$p_t$
splits completely in L, this would mean that
![]() $p_t$
splits completely in
$p_t$
splits completely in
![]() $F = EL$
. But by construction, the Frobenius at
$F = EL$
. But by construction, the Frobenius at
![]() $p_t$
is nontrivial, so
$p_t$
is nontrivial, so
![]() $p_t$
does not split completely.
$p_t$
does not split completely.
It remains to show that, for each prime p, there exist examples for which
![]() $J_{u,v,k}$
is absolutely simple, and hence
$J_{u,v,k}$
is absolutely simple, and hence
![]() $B_{u,v,k}$
as well.
$B_{u,v,k}$
as well.
Lemma 6.2. For each
![]() $p> 5$
, there exist
$p> 5$
, there exist
![]() $u,v \in \mathbb {Z}$
as in Proposition 5.2 such that
$u,v \in \mathbb {Z}$
as in Proposition 5.2 such that
![]() $B_{u,v,k}$
is absolutely simple for all k.
$B_{u,v,k}$
is absolutely simple for all k.
Proof. The Jacobian of the curve
![]() $y^p = x(x-1)(x-t)$
over
$y^p = x(x-1)(x-t)$
over
![]() $\mathbb {Q}(t)$
is absolutely simple since there is a value of
$\mathbb {Q}(t)$
is absolutely simple since there is a value of
![]() $t\in \mathbb {C}$
– namely,
$t\in \mathbb {C}$
– namely,
![]() $t = \frac {1}{2} + \frac {\sqrt {3}}{2} i$
– which makes the curve isomorphic over
$t = \frac {1}{2} + \frac {\sqrt {3}}{2} i$
– which makes the curve isomorphic over
![]() $\mathbb {C}$
to
$\mathbb {C}$
to
![]() $y^p = x^3 - 1$
, and the Jacobian of the latter is known to be absolutely simple [Reference Hazama16, Reference Jedrzejak17]. By a result of Masser [Reference Masser25], for an abelian variety over
$y^p = x^3 - 1$
, and the Jacobian of the latter is known to be absolutely simple [Reference Hazama16, Reference Jedrzejak17]. By a result of Masser [Reference Masser25], for an abelian variety over
![]() $\mathbb {Q}(t)$
, the geometric endomorphism ring for 100% of specializations of
$\mathbb {Q}(t)$
, the geometric endomorphism ring for 100% of specializations of
![]() $t \in \mathbb {Q}$
(ordered by height) is the same as the generic geometric endomorphism ring. Since the generic abelian variety is geometrically simple, this endomorphism ring is a division ring, and hence,
$t \in \mathbb {Q}$
(ordered by height) is the same as the generic geometric endomorphism ring. Since the generic abelian variety is geometrically simple, this endomorphism ring is a division ring, and hence,
![]() $100\%$
of specializations are simple as well. But for
$100\%$
of specializations are simple as well. But for
![]() $t = a/b \in \mathbb {Q}$
, a positive proportion has
$t = a/b \in \mathbb {Q}$
, a positive proportion has
![]() $3$
exactly dividing a and
$3$
exactly dividing a and
![]() $3$
not dividing b. So, there are many curves
$3$
not dividing b. So, there are many curves
![]() $y^p = x(x-1)(x-3 v/u)$
with
$y^p = x(x-1)(x-3 v/u)$
with
![]() $u,v \in \mathbb {Z}$
, not divisible by
$u,v \in \mathbb {Z}$
, not divisible by
![]() $3$
, with absolutely simple Jacobian. This is a twist of the curve
$3$
, with absolutely simple Jacobian. This is a twist of the curve
![]() $\mathcal {C}_{u,v,1} : y^p = x(x-3u)(x-3^2v)$
, so there are curves of this form with absolutely simple Jacobian, giving that
$\mathcal {C}_{u,v,1} : y^p = x(x-3u)(x-3^2v)$
, so there are curves of this form with absolutely simple Jacobian, giving that
![]() $B_{u,v,1}$
is also absolutely simple. Since each
$B_{u,v,1}$
is also absolutely simple. Since each
![]() $B_{u,v,k}$
is a twist of
$B_{u,v,k}$
is a twist of
![]() $B_{u,v,1}$
, it follows that
$B_{u,v,1}$
, it follows that
![]() $B_{u,v,k}$
is absolutely simple for all k.
$B_{u,v,k}$
is absolutely simple for all k.
Appendix: The Cassels-Tate pairing for p-coverings of Jacobians
by Tom Fisher
The purpose of this appendix is to interpret the proof of Proposition 5.2 in terms of a certain Cassels-Tate pairing. Let
![]() $J/\mathbb {Q}$
be a Jacobian, and identify
$J/\mathbb {Q}$
be a Jacobian, and identify
![]() $J = \widehat {J}$
in the usual way.
$J = \widehat {J}$
in the usual way.
Let
![]() $p> 5$
be a prime. Suppose that
$p> 5$
be a prime. Suppose that
![]() $J(\mathbb {Q})$
contains subgroups
$J(\mathbb {Q})$
contains subgroups
![]() $\mathbb {Z}/p\mathbb {Z}$
and
$\mathbb {Z}/p\mathbb {Z}$
and
![]() $(\mathbb {Z}/p\mathbb {Z})^2$
that we take to be the kernels of isogenies
$(\mathbb {Z}/p\mathbb {Z})^2$
that we take to be the kernels of isogenies
![]() $\widehat {\psi } : J \to \widehat {B}$
and
$\widehat {\psi } : J \to \widehat {B}$
and
![]() $\widehat {\phi } : J \to \widehat {A}$
. We further suppose that
$\widehat {\phi } : J \to \widehat {A}$
. We further suppose that
![]() $\ker \widehat {\psi } \subset \ker \widehat {\phi }$
, so that
$\ker \widehat {\psi } \subset \ker \widehat {\phi }$
, so that
![]() $\widehat {\phi }$
factors via
$\widehat {\phi }$
factors via
![]() $\widehat {\psi }$
to give a commutative diagram
$\widehat {\psi }$
to give a commutative diagram

There is then a commutative diagram

where
![]() $\iota (s) = (s,s^{-1})$
and
$\iota (s) = (s,s^{-1})$
and
![]() $\pi (r_1,r_2) = r_1 r_2$
. We now give the Weil pairing definition of the Cassels-Tate pairing (see [Reference Milne28, Chapter 1, Proposition 6.9], [Reference Poonen and Stoll31, Section 12.2] or [Reference Fisher13]) simplified by the fact that
$\pi (r_1,r_2) = r_1 r_2$
. We now give the Weil pairing definition of the Cassels-Tate pairing (see [Reference Milne28, Chapter 1, Proposition 6.9], [Reference Poonen and Stoll31, Section 12.2] or [Reference Fisher13]) simplified by the fact that
![]() $\pi $
has an obvious section given by
$\pi $
has an obvious section given by
![]() $r \mapsto (r,1)$
. The Cassels-Tate pairing
$r \mapsto (r,1)$
. The Cassels-Tate pairing
is defined as follows. We start with
For each prime
![]() $\ell $
, we pick
$\ell $
, we pick
![]() $P_{\ell } \in J(\mathbb {Q}_{\ell })$
with
$P_{\ell } \in J(\mathbb {Q}_{\ell })$
with
![]() $\delta _{\psi ,\ell }(P_{\ell }) \equiv r\ \mod {(\mathbb {Q}_{\ell }^*)^p}$
. Then
$\delta _{\psi ,\ell }(P_{\ell }) \equiv r\ \mod {(\mathbb {Q}_{\ell }^*)^p}$
. Then
![]() $\delta _{\phi ,\ell }(P_{\ell }) = (r \xi _{\ell },\xi _{\ell }^{-1})$
for some
$\delta _{\phi ,\ell }(P_{\ell }) = (r \xi _{\ell },\xi _{\ell }^{-1})$
for some
![]() $\xi _{\ell } \in \mathbb {Q}_{\ell }^*/(\mathbb {Q}_{\ell }^*)^p$
. We define
$\xi _{\ell } \in \mathbb {Q}_{\ell }^*/(\mathbb {Q}_{\ell }^*)^p$
. We define
where
is the local pairing given by cup product and the local invariant map. Since the sum of the local invariants of an element in
![]() $H^2(\mathbb {Q}, \mu _p)$
is 0, we have
$H^2(\mathbb {Q}, \mu _p)$
is 0, we have
![]() $\langle r,s\rangle _{\operatorname {CT}}= 0$
for all
$\langle r,s\rangle _{\operatorname {CT}}= 0$
for all
![]() $r \in \delta _\psi (J(\mathbb {Q}))$
.
$r \in \delta _\psi (J(\mathbb {Q}))$
.
Proposition A. With the notation and assumptions of Proposition 5.2 (noting that
![]() $\delta _\phi $
,
$\delta _\phi $
,
![]() $\delta _\psi $
and
$\delta _\psi $
and
![]() $S^{(\psi )}(B/\mathbb {Q})$
are there called
$S^{(\psi )}(B/\mathbb {Q})$
are there called
![]() $\partial ^H$
,
$\partial ^H$
,
![]() $\partial ^D$
and
$\partial ^D$
and
![]() ${\operatorname {Sel}}(B_k)$
), we have
${\operatorname {Sel}}(B_k)$
), we have
-
(i)
 $p_i \in S^{(\psi )}(B/\mathbb {Q}) \subset \mathbb {Q}^*/(\mathbb {Q}^*)^p$
for all
$p_i \in S^{(\psi )}(B/\mathbb {Q}) \subset \mathbb {Q}^*/(\mathbb {Q}^*)^p$
for all
 $1 \leqslant i \leqslant t$
.
$1 \leqslant i \leqslant t$
. -
(ii) Let
 $\chi _i \in H^1(\mathbb {Q},\mathbb {Z}/p\mathbb {Z}) = \operatorname {Hom}(\operatorname {Gal}({\overline {\mathbb Q}}/\mathbb {Q}),\mathbb {Z}/p\mathbb {Z})$
be the unique continuous character that factors via
$\chi _i \in H^1(\mathbb {Q},\mathbb {Z}/p\mathbb {Z}) = \operatorname {Hom}(\operatorname {Gal}({\overline {\mathbb Q}}/\mathbb {Q}),\mathbb {Z}/p\mathbb {Z})$
be the unique continuous character that factors via
 $\operatorname {Gal}(\mathbb {Q}(\zeta _{p_i})/\mathbb {Q})$
and satisfies
$\operatorname {Gal}(\mathbb {Q}(\zeta _{p_i})/\mathbb {Q})$
and satisfies
 $\chi _i(\operatorname {Frob}_3) = 1$
(this is possible by assumption (4)). Then for all
$\chi _i(\operatorname {Frob}_3) = 1$
(this is possible by assumption (4)). Then for all $$\begin{align*}\chi_i - \chi_j \in S^{(\widehat{\nu})}(\widehat{B}/\mathbb{Q}) \subset H^1(\mathbb{Q},\mathbb{Z}/p\mathbb{Z}) \end{align*}$$
$$\begin{align*}\chi_i - \chi_j \in S^{(\widehat{\nu})}(\widehat{B}/\mathbb{Q}) \subset H^1(\mathbb{Q},\mathbb{Z}/p\mathbb{Z}) \end{align*}$$
 $1 \leqslant i,j, \leqslant t$
.
$1 \leqslant i,j, \leqslant t$
.
-
(iii) For
 $a_1,\ldots ,a_t,b_1, \ldots , b_t \in \{0,1, \ldots ,p-1\}$
with
$a_1,\ldots ,a_t,b_1, \ldots , b_t \in \{0,1, \ldots ,p-1\}$
with
 $\sum b_j \equiv 0\ \pmod {p}$
, we have In particular, since
$\sum b_j \equiv 0\ \pmod {p}$
, we have In particular, since $$\begin{align*}\left\langle \prod_{i=1}^t p_i^{a_i} , \sum_{j=1}^t b_j \chi_j \right\rangle_{\operatorname{CT}} = \frac{-5}{p} \sum_{i=1}^t a_i b_i. \end{align*}$$
$$\begin{align*}\left\langle \prod_{i=1}^t p_i^{a_i} , \sum_{j=1}^t b_j \chi_j \right\rangle_{\operatorname{CT}} = \frac{-5}{p} \sum_{i=1}^t a_i b_i. \end{align*}$$
 $p> 5$
, if
$p> 5$
, if
 $q = \prod _{i=1}^t p_i^{a_i}$
, and the
$q = \prod _{i=1}^t p_i^{a_i}$
, and the
 $a_i \in \{0,1, \ldots ,p-1\}$
are not all equal, then
$a_i \in \{0,1, \ldots ,p-1\}$
are not all equal, then
 $q \not \in \delta _\psi (J(\mathbb {Q}))$
.
$q \not \in \delta _\psi (J(\mathbb {Q}))$
.
Proof. (i) See the final paragraph of the proof of Proposition 5.2.
(ii) The restriction
![]() $\operatorname {res}_{\ell }(\chi _i)$
is unramified for all
$\operatorname {res}_{\ell }(\chi _i)$
is unramified for all
![]() $\ell \not = p_i$
, and trivial for all
$\ell \not = p_i$
, and trivial for all
![]() $\ell \in U \setminus \{3\}$
by assumption (3). So we only need to check the local conditions at
$\ell \in U \setminus \{3\}$
by assumption (3). So we only need to check the local conditions at
![]() $p_1, \ldots , p_t$
and
$p_1, \ldots , p_t$
and
![]() $3$
. By Lemmas 4.1 and 5.1, we know that
$3$
. By Lemmas 4.1 and 5.1, we know that
![]() $\operatorname {im} \delta _{\phi ,p_i}$
has order
$\operatorname {im} \delta _{\phi ,p_i}$
has order
![]() $p^2$
, and the natural map
$p^2$
, and the natural map
![]() $\operatorname {im} \delta _{\phi ,p_i} \to \operatorname {im} \delta _{\psi ,p_i}$
is an isomorphism. Chasing around (the local analogue of) the above diagram shows that
$\operatorname {im} \delta _{\phi ,p_i} \to \operatorname {im} \delta _{\psi ,p_i}$
is an isomorphism. Chasing around (the local analogue of) the above diagram shows that
![]() $\operatorname {im} \delta _{\nu ,p_i}$
is trivial. It follows by Tate local duality that
$\operatorname {im} \delta _{\nu ,p_i}$
is trivial. It follows by Tate local duality that
![]() $\operatorname {im} \delta _{\widehat {\nu },p_i}$
is all of
$\operatorname {im} \delta _{\widehat {\nu },p_i}$
is all of
![]() $H^1(\mathbb {Q}_{p_i},\mathbb {Z}/p\mathbb {Z})$
. In other words, in the definition of
$H^1(\mathbb {Q}_{p_i},\mathbb {Z}/p\mathbb {Z})$
. In other words, in the definition of
![]() $S^{(\widehat {\nu })} (\widehat {B}/\mathbb {Q})$
, there are no local conditions at
$S^{(\widehat {\nu })} (\widehat {B}/\mathbb {Q})$
, there are no local conditions at
![]() $p_1, \ldots , p_t$
. It is the local condition at
$p_1, \ldots , p_t$
. It is the local condition at
![]() $3$
that forces us to take differences.
$3$
that forces us to take differences.
(iii) We take
![]() $r = p_i$
in the above description of the pairing. The only primes
$r = p_i$
in the above description of the pairing. The only primes
![]() $\ell $
that can contribute to the pairing are those in
$\ell $
that can contribute to the pairing are those in
![]() $\{p_1, \ldots ,p_t\} \cup U$
. For all such primes
$\{p_1, \ldots ,p_t\} \cup U$
. For all such primes
![]() $\ell \not = p_i$
we have that r is trivial in
$\ell \not = p_i$
we have that r is trivial in
![]() $\mathbb {Q}_{\ell }^\times /(\mathbb {Q}_{\ell }^\times )^p$
by assumptions (1) and (2). Taking
$\mathbb {Q}_{\ell }^\times /(\mathbb {Q}_{\ell }^\times )^p$
by assumptions (1) and (2). Taking
![]() $P_{\ell } = 0$
and
$P_{\ell } = 0$
and
![]() $\xi _{\ell } = 1$
, we see that these primes make no contribution to the pairing. It remains to compute the contribution at
$\xi _{\ell } = 1$
, we see that these primes make no contribution to the pairing. It remains to compute the contribution at
![]() $\ell = p_i$
. By Lemma 4.1, we have
$\ell = p_i$
. By Lemma 4.1, we have
for some
![]() $a,b \in \mathbb {Z}/p\mathbb {Z}$
. We know that
$a,b \in \mathbb {Z}/p\mathbb {Z}$
. We know that
![]() $(r_1,r_2) \mapsto r_1 r_2$
maps this to
$(r_1,r_2) \mapsto r_1 r_2$
maps this to
![]() $r = p_i \in \mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
, and that
$r = p_i \in \mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
, and that
![]() $\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
is generated by
$\mathbb {Q}_{p_i}^*/(\mathbb {Q}_{p_i}^*)^p$
is generated by
![]() $3$
and
$3$
and
![]() $p_i$
. Therefore,
$p_i$
. Therefore,
![]() $-2a-b \equiv 0\ \pmod {p}$
and
$-2a-b \equiv 0\ \pmod {p}$
and
![]() $-a-b \equiv 1\ \pmod {p}$
. We solve these to give
$-a-b \equiv 1\ \pmod {p}$
. We solve these to give
![]() $a = 1$
and
$a = 1$
and
![]() $b=-2$
. Therefore,
$b=-2$
. Therefore,
and
![]() $\xi _{\ell } = 3^{-5} p_i^{-5}$
. Therefore,
$\xi _{\ell } = 3^{-5} p_i^{-5}$
. Therefore,
Notice that, since
![]() $p_i \equiv 1\ \pmod {p}$
, evaluating the local pairing (6.1) reduces to a computation of Hilbert symbols. The formula in the statement of the proposition follows by linearity in the first argument.
$p_i \equiv 1\ \pmod {p}$
, evaluating the local pairing (6.1) reduces to a computation of Hilbert symbols. The formula in the statement of the proposition follows by linearity in the first argument.
Acknowledgements
The authors thank Michael Stoll for his comments and for organizing Rational Points 2022, where they began working together on this problem. The second author was supported by the Israel Science Foundation (grant No. 2301/20). The authors also thank Ariyan Javanpeykar, Jef Laga and Ariel Weiss for comments on an earlier draft. Finally, we thank Tom Fisher for his suggestions and for letting us include his appendix.
Competing interest
The authors have no competing interest to declare.