Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T04:05:46.912Z Has data issue: false hasContentIssue false
  • English
  • Français

The Existence of Continuable Solutions of a Second Order Differential Equation

Published online by Cambridge University Press:  20 November 2018

G. J. Butler
G. J. Butler*
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A much-studied equation in recent years has been the second order nonlinear ordinary differential equation

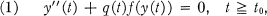
where q and f are continuous on the real line and, in addition, f is monotone increasing with yf(y) > 0 for y ≠ 0. Although the original interest in (1) lay largely with the case that q﹛t) ≧ 0 for all large values of t, a number of papers have recently appeared in which this sign restriction is removed.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 3 , 01 June 1977 , pp. 472 - 479
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Buckley, E. D. J., Studies in nonlinear oscillation, Ph.D. thesis, University of Alberta, 1971.Google Scholar
2. Burton, T. and Grimmer, R., On continuability of solutions of second order differential equations, Proc. Amer. Math. Soc. 29 (1971), 277–283.Google Scholar
3. Coffman, C. V. and Ullrich, D. F., On the continuability of solutions of a certain nonlinear differential equation, Monatsh. fur Math. 71 (1967), 385–392.Google Scholar
4. Hartman, P., Ordinary differential equations (Wiley & Sons, New York, 1964).Google Scholar
5. Jacobowitz, H., Periodic solutions of x” + f(t, x) = 0 via the Poincarê-Birkhoff theorem, J. Differential Equations 20 (1976), 37–52.Google Scholar
6. Kiguradze, I. T., A note on the oscillation of u” + a﹛t)\u\n sgn u = 0, Casopis Pest. Math. 92 (1967), 343–350 (Russian).Google Scholar