Introduction
Most avalanches in western Europe and North America that result in deaths and injury occur during skiing (or snowmobiling or snowboarding), with people themselves serving as the triggering agent. Therefore, understanding the problem of skier triggering of dry-snow slabs is very important.
Instead of the traditional view that stability can be described by a strength-to-load ratio, Reference McClungMcClung, (1977, Reference McClung1981, Reference McClung1987, Reference McClung1996) proposed an alternate view of dry-slab initiation: namely, that avalanche release depends crucially on both slab and weak layer, their interaction as a dependent mechanical system and the mechanical properties of both. The result is that deformation (and the energy needed to form cracks) is the key to understanding avalanche release. Slab avalanches initiate by propagation of shear fractures in a weak layer under a slab and there are macroscopic size effects associated with such fracture initiation (Reference Palmer and Rice.Palmer and Rice, 1973; Reference McClungMcClung, 1979, Reference McClung1981, Reference McClung1987, Reference McClung1996; Reference Bažant and Planas.Bažant and Planas, 1998). Reference Bažant and Planas.Bažant and Planas, 1998 show that when failures are described according to a strength or yield criterion alone (as with the traditional method), no such size effect is implied. The analysis in this paper includes for the first time a discussion of size effects in relation to skier triggering.
This paper is based on our experiences and field observations of snow temperatures and their effects on mechanical properties (including the slab) and skier triggering of avalanches. The influence of slab mechanical properties is overlooked in the traditional method of stability evaluation. As well as snow temperatures, we examine the stability index more generally with a simple stress analysis for skier loading on a snow slab. This analysis shows that if alpine snow is assumed to be a pressure-sensitive, Coulomb–Mohr material (the traditional assumption), the stability index may either increase or decrease under static skier loading, which conflicts with experience. The discrepancy is explained by showing that the static stability index does not account for deformation and macroscopic imperfections. We also emphasize the importance of dynamic effects for analysis of skier triggering by a comparison with the measurements of Reference Schweizer, Camponovo., Fierz., Föhn. and SivardièreSchweizer and others (1995a, Reference Schweizer, Camponovo., Fierz., Föhn. and Sivardièreb).
The fundamental argument in this paper is that macroscopic size effects and slab properties combined with dynamic effects are crucial in skier/human triggering, and that there are great variations in their combined effects. The result is to cast back-country avalanche forecasting as a risk analysis rather than a deterministic one based on an engineering stability index. We begin with a discussion of temperature effects on slab and failure properties in order to provide the link to slab properties, and conclude with a discussion of the stability index and size effects for skier triggering.
Effects of Snow Temperature on Hardness, Failure Toughnsss and Strength
The effects of snow temperature on hardness, failure toughness and shear strength have been described previously (Reference McClung and SivardièreMcClung, 1995, Reference McClung1996). Experience, field observations and measurements show that there are two important groups of competing effects: (1) metamorphism (depending on temperature, temperature gradient and other snow properties) and creep; (2) mechanical properties (excluding metamorphism effects), including snow hardness (initial tangent modulus in shear which we term stiffness), fracture propagation potential (fracture toughness which depends on stiffness) and strength. In this paper, we consider only the mechanical properties in group 2 for short time-scale changes in relation to skier triggering. Creep and metamorphism take more time to affect the temperature-dependent mechanical properties than the effects in group 2; the latter can be affected on time-scales of seconds or less.
Figure 1 shows a schematic of the effects and definitions of the terms based on our experimental results (Reference McClungMcClung, 1996, and unpublished data from more than 200 tests by McClung; Reference SchweizerSchweizer, 1998) from simple shear tests on alpine snow (for data description and experimental procedures see Reference McClungMcClung, 1977; Reference SchweizerSchweizer, 1998). The shear strain rates range from 103 to 106 s1 and the temperatures range from –2° to –15°C. The important effects sketched in Figure 1 from Reference SchweizerSchweizer, 1998) are:
(1) Initial tangent modulus in shear is highly temperature-dependent. The increase in initial tangent modulus is > 100% as the temperature decreases from –5° to –15°C. This is the most important temperature-depentent property of alpine snow. In this paper, we use the terms initial tangent modulus in shear test, hardness and stiffness as synonymous. In engineering mechanics, hardness is usually related to tensile strength, but in practical work with the snow slab the relationship to resistance to shear deformation is much more important. When the hand hardness test is used in field applications, people seek information about the relative relationship of shear properties of layers and the relation to shear strength.
(2) Failure strength (defined as peak on the stress–strain curve) can increase by >20% as temperature decreases over the range –5° to –15°C. Weak dependence of failure strength on temperature is a characteristic of most high-temperature materials (Reference PisarenkoPisarenko, 1969). The conventional explanation of temperature effects on stability is based only on the decrease in strength with increasing temperature. Our measurements and theoretical arguments lead to the conclusion that strength decrease is not the major effect, particularly for skier triggering.
(3) Failure toughness (work input needed to reach a peak on the stress–strain curve) increases slightly with increasing temperature. It is equivalent to the area under the stress strain curve until a peak is reached. The failure toughness is related to the failure strain and failure strength. Data (Reference SchweizerSchweizer, 1998) show that failure strain decreases, resulting in a failure toughness which decreases as the temperature decreases by about 30% over the range –5° to 15°C.

Fig. 1. Failure toughness and strength. (a) General concept with respect to stress (σ) and strain (ε). (b) Schematic for alpine snow in shear in relation to temperature and strength: toughness increases slightly with temperature increase whereas strength decreases. Figure 1b is drawn mainly from data in Reference SchweizerSchweizer, 1998).
Results by Reference SchweizerSchweizer, 1998) indicate that when temperature and strain rate are studied together in a multivariate sense, temperature effects are more significant than rate effects on initial tangent modulus. For peak strength and toughness, however, rate effects predominate over temperature effects. These results strengthen the argument that temperature effects are most significant with respect to their effect on effective stiffness (or initial tangent modulus) (Reference McClungMcClung, 1996).
Since the hardness (or initial shear modulus) is strongly temperature-dependent, it is likely that fracture toughness for the snow-slab problem increases as temperature decreases, since fracture toughness is proportional to the square root of the shear modulus (e.g. Reference McClungMcClung, 1996). Since peak strength increases as temperature decreases, and failure displacement decreases as temperature decreases, it is likely that the shear modulus controls the temperature dependence of fracture toughness. This expectation matches that for other high-temperature materials. Reference BroekBroek (1986) argues that alloy steels and other materials show an increase in fracture toughness as the temperature decreases similar to what we expect for alpine snow.
Field data (Reference PerlaPerla, 1977; see also Reference McClung and Schaerer.McClung and Schaerer, 1993) show that avalanche frequency is less when weak-layer failure temperatures are cold. We believe the decrease in frequency could be due in part to an increase in slab stiffness with decreasing temperature, because colder weak layers also imply colder slab temperatures. However, there are other complicating factors which prevent a direct correlation (Reference McClungMcClung, 1996).
Skier Triggering and Snow Temperatures
Consider now the case of skier triggering with the immediate effects of snow temperatures on stiffness and failure toughness. When a skier moves over a snowpack a dynamic load is applied to the snow cover and the stresses penetrate through the entire depth of the snow cover (see, e.g., Reference FöhnFöhn, 1987, for a static analysis). In order to generate propagating shear fractures in a weak layer, a skier will have to impart significant deformation energy to the layer. While crack initiation will depend on stresses, the formation and propagation of cracks requires deformation energy (Reference Bažant and Planas.Bažant and Planas, 1998). It is not possible to generate propagating fractures, even if stresses are very high, unless the required deformation energy is applied. Measurements of snow deformation imparted by skis Reference Schweizer, Camponovo., Fierz., Föhn. and SivardièreSchweizer and others (1995a, Reference Schweizer, Camponovo., Fierz., Föhn. and Sivardièreb) show that the most important variable with respect to the penetration of significant deformation is the snow hardness. Harder layers permit less deformation at depth than softer layers, thereby reducing the chance of failure. Furthermore, by the argument above, snow hardness increases rapidly with decreasing temperature.
Combining the above results, increasing snow temperatures can rapidly decrease snow-slab stability in two ways. (1) By decreasing the delayed elastic (or viscoelastic) stiffness of surface (slab) layers, significant deformation may penetrate deeper in the snow cover to increase weak-layer deformation and allow easier failure (more deformation) and propagation. (See Reference McClungMcClung, 1996 for a discussion of delayed elasticity and its relation to temperature dependence. The analysis shows that slab temperature effects reside in delayed elastic (viscoelastic) response rather than the time-independent elastic modulus.) (2) If warming temperatures also reach the weak layer, failure toughness is increased slightly (Reference SchweizerSchweizer, 1998), but peak strength is reduced to produce only small changes in the ease with which failure takes place. Of these two processes, we consider the first to be the more important, from our extensive failure data on snow.
A person on skis is directly in contact with the surface layers, and deformation energy to the weak layer must be communicated through the slab. Furthermore, surface layers are subject to great variations in temperature, and snow hardness is affected rapidly. Therefore, one can expect the stability to vary greatly when conditions are right, depending on the hardness of the surface layers and their fluctuating temperatures. For example, on a cold morning or northerly aspect (Northern Hemisphere) when surface layers are cold and hard, deformation under skis will not penetrate as far and as effectively as later on or at other places where surface layers are warmer. Furthermore, the effect on stability can be rapid when surface layers warm: metamorphism or significant creep (settlement) effects are not required since the viscoelastic (delayed elastic) properties are affected almost immediately on loading. Figure 2 shows a schematic of the expected snowpack deformation patterns for a person on skis. Further information on skier deformation is provided in the Appendix.
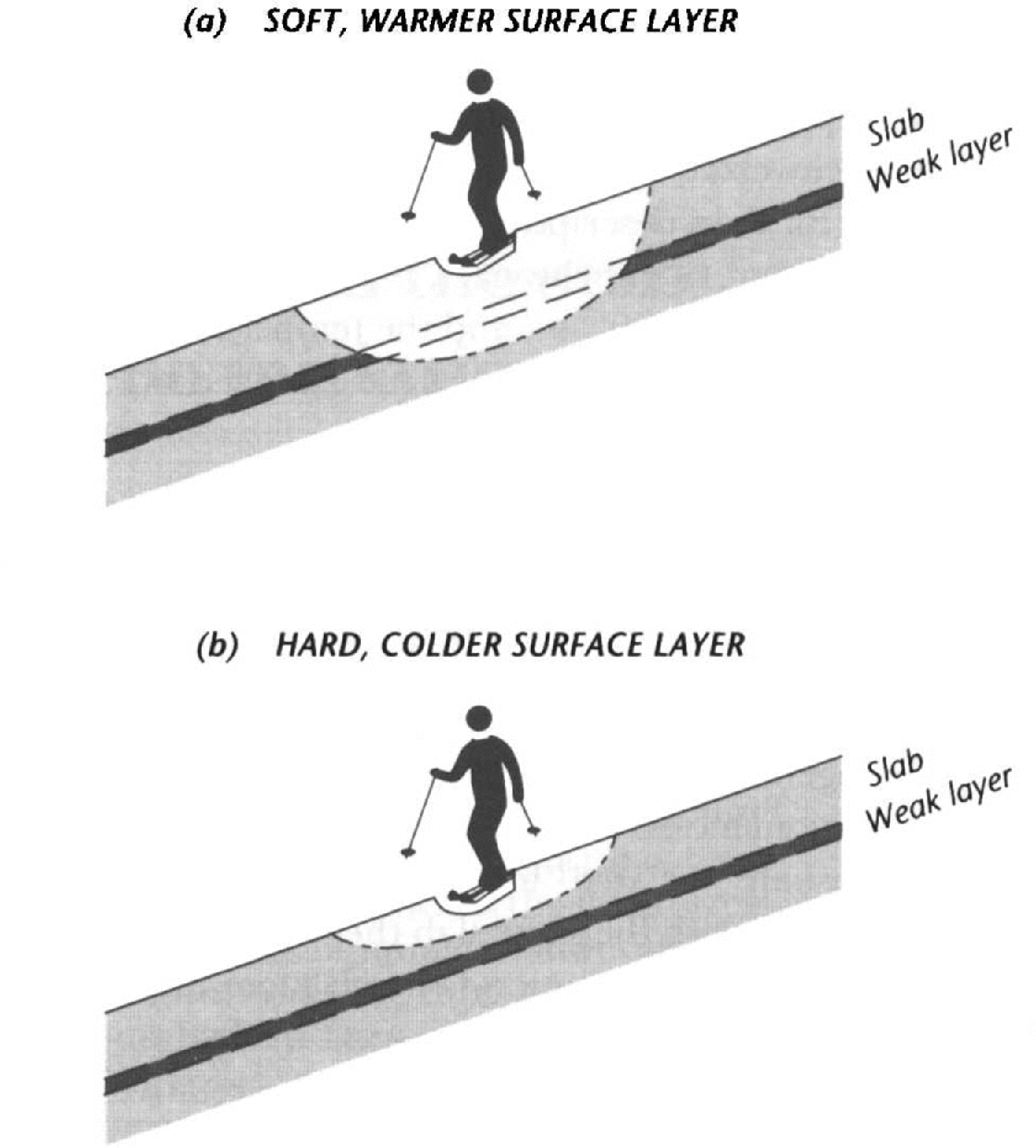
Fig. 2. Schematic of deformation patterns for a skier.
Stability Tests
(1) Rutschblock test
The suggestions above have important implications for interpretations of common stability tests used by skiers, particularly the Rutschblock test. (See Reference McClung and Schaerer.McClung and Schaerer (1993) for descriptions of the common stability tests.) The interpretation of the Rutschblock test is complicated since the results are highly dependent on the hardness of the surface layers. Since hardness of surface layers can vary considerably, not only spatially across a slope but also rapidly in the vertical directions with time as layer temperatures change, it may be expected that Rutschblock test results can vary significantly with snow-slab temperatures. At a location, it is possible to go from a condition indicating stability to one of instability as surface layers warm to allow deeper penetration of deformation energy. Therefore, the Rutschblock may sometimes only test the surface layer hardness and its propensity for deformation penetration rather than indicate instability at a location. The Rutschblock test measures primarily surface layer deformation, but if deformation penetrates deep enough with enough deformation energy to fail snow in a weak layer it indicates local instability. A great advantage of the test is that it includes provision for application of dynamic loads which can partially replicate skier loading. Thus, interpretation of the Rutschblock is not simple, and results may vary according to hardness variations of the surface layers (Reference Jamieson and Johnston.Jamieson and Johnston, 1995). Such highly variable results have been amply demonstrated (Reference FöhnFöhn, 1989). At a given location, the Rutschblock is a very good test, but extrapolation to other locations is complex if surface hardness conditions change, for example due to temperature or wind-packing variations.
(2) Shovel shear test
The shovel shear test also has limitations (Reference McClung and Schaerer.McClung and Schaerer, 1993) but it is simpler to interpret than the Rutschblock test, and variations in test results are due primarily to strength variations in the layer tested rather than a combination of surface hardness changes and weak-layer strength variations as in the Rutschblocktest. Once the weak layer is found, the shovel shear test gives a qualitative estimate of weak-layer strength (based on the applied force necessary to reveal a shear failure), as well as an indication of the quality of any shear-failure plane formed.
(3) Shear frame test
The shear frame test is similar to the shovel shear test in that it tests true variations in weak-layer strength. It gives a more quantitative index of weak-layer strength. As with the shovel shear test, the weak layer has to be found first. The method involves special techniques appropriate for special investigations and professional services. It is useful to follow the evolution of weak-layer strength in a relative sense, and combined with experience it can also be used to assess stability. Potential limitations of this method have been studied by Reference Perla and ColbeckPerla (1980), Reference FöhnFöhn (1987) and Reference JamiesonJamieson (1995).
Field experience shows that near-surface layer properties are very important for skier triggering, and the results of Reference Schweizer, Camponovo., Fierz., Föhn. and SivardièreSchweizer and others (1995a, Reference Schweizer, Camponovo., Fierz., Föhn. and Sivardièreb) confirm that deformation and stresses are sensitive to surface layer properties. For example, field practitioners apply the term “bridging” when slab material is hard (or stiff) and deformation energy at depth is reduced to lessen the chance of avalanche initiation by a skier. Our work provides experimental and theoretical evaluation of this important effect which practitioners have developed from experience. In order to be effective, stability tests must be supplanted with information about slab mechanical properties.
Stability Index and Skier Triggering
The stability index (also called a strength-to-load ratio) is normally defined as the ratio of shear strength in the weak layer to applied shear stress for describing the possibility of slab-avalanche initiation. The shear strength is normally defined by an index of weak-layer strength using the shear frame. The shear stress is defined from density measurements in the slab as the downslope component of body force per unit area applied to the weak layer. In practice, stability-index calculations are sometimes performed in places such as level study plots, and instead of shear stress in the calculations the summed product of density and snow depth is used for the load. Reference Perla and ColbeckPerla (1980) reviewed the difficulties and problems with the use of the shear frame, but he concluded, and it is still true, that there is nothing better to replace it for quantitative field estimates. Besides a multitude of disadvantages with the shear frame there are two additional drawbacks of the stability index for use on the skier-triggering problem: (1) the stability index does not include important slab properties such as hardness and the effects of snow temperatures on slab hardness; (2) measurements of shear strength using the shear frame do not encompass information about the effects of imperfections and macroscopic size effects, whereas such information likely plays a crucial role in avalanche initiation under skier triggering. Other common stability tests do not contain such information either. Below, we illustrate (mathematically) properties of the stability index (ratio) to further clarify its role in evaluating snow-slab stability and describing skier triggering with emphasis on size effects.
Stability-Index Stress Analysis
In this section, we investigate the properties of the stability index mathematically under two types of applied loading increments: loading increments from new snowfall and from a skier approximated as a line-source load (Reference FöhnFöhn, 1987). Figure 3 is a schematic of the geometry and applied load. Following the conventional approach (Reference Perla and ColbeckPerla, 1980; Reference FöhnFöhn, 1987; Reference Jamieson and Johnston.Jamieson and Johnston, 1998a), we approximate the shear strength, τs, most simply as a linear, pressure-dependent (frictional) Coulomb Mohr material with strength components: cohesion (C) and friction expressed as the product of a friction coefficient, μ, and applied normal stress, σ, with both μ and C taken constant:
In order to simplify the notation, we write σ = σ xx(H), the mean normal stress applied to the weak layer (in Cartesian coordinates) for a planar slab of depth H; and similarly τ = τ xy(H) is the mean shear stress. From Equation (1), the stability index, S 0, prior to new snow load or skier loading is given by:

Fig. 3. Geometry for line-source loading of a skier where P is load (kg) per unit length.
New Snowfall Loading
Consider now the additional loading by snowfall with mean density ρ, slope angle Ψ and incremental depth ΔH; then the incremental shear and normal load added are:
The new stability index,S ′, then becomes:
From Equation (4), the stability index increases under loading if
and the stability index decreases under loading if
From Equation (4) these conditions are (under snowfall loading):

However, given the definition of S 0 from Equation (2), it is easily shown that the stability always decreases when the cohesion C is greater than zero: a condition we take to be always fulfilled by alpine snow in buried weak layers. Mathematically, therefore, stability is implied to decrease for new snowfall loading assuming Equation (1). However, data for μ and S 0 might imply otherwise as we show below.
Consider typical values for the parameters in Expressions (5) from the perspective of data. Reference PerlaPerla (1977) analyzed data from 23 avalanche fracture lines combined with shear frame measurements and obtained a mean value of S 0 = 1.66. Reference FöhnFöhn (1987) obtained an average value of 2.3 for 18 natural slabs. Reference JamiesonJamieson (1995) determined higher values during natural avalanche release with the values taken from a study plot instead of at fracture lines, with most avalanche occurrences when S 0 was < 3.
We take the effective friction coefficient μ = tan ϕ (where ϕ is peak friction angle for the material at the weak layer). Measurements for homogeneous samples by Reference McClungMcClung,1987 give friction angles in the range 40–70° for direct simple shear: the expected strain and stress conditions prevailing in a thin, homogeneous weak layer. Reference RochRoch’s (1966) static friction angles varied from 37° to values exceeding 60°. Taking the simple shear values for μ = 0.75–2.75 for the left side of Expressions (5), in comparison with Ψ = 35°, the right side has the value 1.16 for Reference PerlaPerla’s 1977 average. We conclude that, from the perspective of data, any of the conditions of Expressions (5) might be fulfilled. This seems contradictory and we believe the explanation lies with the values of the friction angles. If we use Reference JamiesonJamieson’s (1995, p.38) values for S 0, stability would be implied to increase with loading.
The same problem occurs in explaining landslide releases (Reference BjerrumBjerrum, 1967): peak friction angles from small-sample-size testing machines are routinely higher than slope angles measured for the landslide occurrences. Our analysis above extends Bjerrum’s constant-load observation to that for new snowfall loading. The contradiction for the landslide problem was a major factor which led Palmer and Reference Rice and PalmerRice (1973) to introduce strain-softening properties and size effects into the landslide literature, and Reference McClungMcClung, 1977,Reference McClung1981) proceeded by analogy to apply similar theory for snow-slab failure. Our analysis provides further evidence that the shear frame provides an index property but does not account for macroscopic size effects. Below we provide an analysis of macroscopic size effects on fracture initiation to emphasize this point.
If friction angles are derived from shear frame measurements for very weak, anisotropic layers, different conclusions result. According to Reference Jamieson and Johnston.Jamieson and Johnston, 1998a, shear frame measurements show some persistent snow layers (e.g. surface hoar) to be nearly pressure-insensitive, and therefore μ ≈ 0 and from Expressions (5) new snow loading (or skier loading as shown below) always increases instability. We believe there is high uncertainty about the true values of friction angles for such layers and the analysis applying them. The shear frame has large stress concentrations around the fins that act as cross-members (e.g. Reference Irwin and FlüggeJamieson, 1995) to divide the frame. It seems likely that crystals like surface hoar or facets may display preferential deformation when sheared rapidly in the presence of stress concentrations. If the shear frame forces preferential deformation in shear near the fins, an underestimate of pressure sensitivity can result. Therefore, the imprecision in stress and strain conditions for shear frame might limit its usefulness in studying the effects of normal stresses on shear strength. Measurements (Reference McClungMcClung,1987) with the Norwegian Geo-technical Institute simple shear apparatus (with much better stress and strain conditions) consistently show higher friction angles than those estimated from shear frames, and such measurements include faceted snow which is an important avalanche-failure layer.
Static Skier Loading
In this section, we investigate the properties of the stability index for skier loading similar to Reference FöhnFöhn’s(1987) analysis (the original treatment of this problem is due to Boussinesq in 1892). Reference FöhnFöhn (1987) considered the stresses for this problem but did not include an analysis of the stability index. Reference Jamieson and Johnston.Jamieson and Johnston, 1998a considered refinements to the static stability index, but neither Föhn nor Jamieson and Johnston considered the mathematical analysis we present here. We neglect inertial effects and macroscopic weak-layer imperfections and approximate the load a skier applies to a snowpack as a line source over an elastic half-space. Even though our analysis is static, as a first approximation the dynamic problem might be examined by studying steady-state response to a moving line load at constant speed over an elastic half-space, but this is beyond the scope of the present paper. From Figure 3, we consider the load to be applied in the direction toward the centre of the Earth with magnitude P (kg m−1). It is convenient to write the applied stress in polar coordinates (r, θ) since then the only stress is in the radial direction (Reference Timoshenko and Goodier.Timoshenko and Goodier, 1970):
From Equation (6), we may write:
From Equation (7), the loading ratio is:
From Equation (8), repeating the analysis leading to Expressions (5) gives:

For typical parameters, the last condition is fulfilled if C > 0 and Ψ < θ: stability always decreases under skier loading. However, as with Expressions (5), we show below that this condition may appear to be violated if S 0 is evaluated from shear frame measurements combined with information known about peak friction angles to imply that stability increases under skier loading.
For a weak layer at a given depth, H, in polar coordinates, the depth may be expressed as H = r(H) cosθ. The expression for the perturbation shear stress load is:
From Equation (10), the angle θ at which the maximum shear stress loading is about 35° for Ψ is in the range 25–45° (the range of most slab-avalanche slope failure angles). Therefore, it may be justifiable to simplify Expressions (9) by approximating tan θ ≈ 0.7. From Perla’s (1977) average (S 0 = 1.66) and from Expressions (9) it is implied that stability is increased by skier loading if μ = tan ϕ > 1.16 or for friction angles of > 49°. Such a condition is often fulfilled if measurements of homogeneous, isotropic snow are used (40–70°) from the data of Reference RochRoch (1966) or Reference McClungMcClung,1987. Since Perla’s data are from natural releases, the mean value of S 0 may be higher for actual skier triggering, which reinforces the prediction of increased stability.
The number of accidents associated with skier triggering (e.g. Reference Jamieson and Geldsetzer.Jamieson and Geldsetzer, 1996) shows that skiing has a negative influence on stability. We believe that the static analysis above neglects two important effects: (1) the dynamic effects in skiing (see Appendix and the results of Reference Schweizer, Camponovo., Fierz., Föhn. and SivardièreSchweizer and others (1995a, Reference Schweizer, Camponovo., Fierz., Föhn. and Sivardièreb) are neglected, and (2) the measurements (shear frame or simple shear) do not take into account that macroscopic imperfections in weak layers and at their boundaries are the most likely genesis of avalanche formation. Most shear frame analyses yield results for S 0 > 1 when the snowpack can be highly unstable (e.g. Reference PerlaPerla, 1977). Clearly, if shear frame measurements contained the important information about imperfections, the measurements would show S 0 ≤ 1 when there is instability in the snow cover.Reference PerlaPerla’s 1977 fracture-line data are easily explainable from the view that the initial fractures propagated from weak fracture zones underneath the snow slabs with termination in stronger snow at the fracture lines.
Many attempts have been made to explain the discrepancy between the strength-to-load ratio (S 0 > 1) and observed instability by attributing size effects in a statistical sense to the shear frame using Weibull or Daniels statistics of micro-scale flaws (e.g. Reference SommerfeldSommerfeld, 1980; Reference FöhnFöhn, 1987; Reference Jamieson and Johnston.Jamieson and Johnston, 1998a). Reference Bažant and Planas.Bažant and Planas, 1998; see also Reference Freudenthal and LiebowitzFreudenthal, 1968, p.615) present a comprehensive summary of size effects for quasi-brittle (strain-softening) materials, and conclude that Weibull statistics are not applicable to this class of materials for explaining size effects of large-scale failures such as the snow slab. They show that statistical approaches such as the Weibull theory apply only to failures in which the material just before failure contains only microscopic cracks or other flaws such as for brittle materials. Materials which fail after macroscopic imperfection growth (the quasi-brittle or strain-softening materials) are governed by such macroscopic effects, and the emphasis is on stress redistributions which mitigate the effect of microscopic flaws.
The alternate view is that micro-scale statistical aspects of fracture (e.g. Daniels (or the bundle model) or Weibull statistics as discussed by Reference SommerfeldSommerfeld, 1980, can be used to reduce the strength measurements from shear frames to yield S 0 values that are ≤ 1 for most avalanche events (including skier triggering). With respect to application of a bundle model,Reference Freudenthal and LiebowitzFreudenthal, 1968,p. 609) states that such a model applies only to a description of fracture processes in materials for which bundles such as long-chain molecular filaments physically exist such as linear high polymers or elastomers which fail after chain orientation after large strain. We believe there are size effects associated with the shear frame, and, as such, the shear frame is only an index, but the size effects in avalanche fractures are macroscopic not micro-scale in size.
Static Stress Analysis of Skier Loading
It is interesting to compare the approximate load generated by a skier (Equation (10)) with the value of τ from the weight of the slab. From Equation (10), the non-dimensional ratio is:
For a skier of mass 70 kg, and length of ski 1.70 m, the value of P in the above equation representing the line source is P = 70/(1.70) = 41.2 kg m−1. For typical values θ = 35°, Ψ = 35° and average slab density ρ s = 200 kg m−3, the ratio above is given by 0.088/H 2 and it ranges from 0.35 at H = 0.5 m to 0.09 at H = 1.0 m and 0.02 at H = 2.0 m, as shown in Figure 4.
Application of values for cohesion of surface hoar (values range from 1.5 to 3.5 kPa corrected for statistical size effects) by Reference Jamieson and Johnston.Jamieson and Johnston, 1998a with μ assumed to be zero, as they recommend, shows that the unperturbed stability index given by Equation (2) predicts stability (S 0 > 1) for snow depths greater than 1.24 m (cohesion 1.5 kPa) and 2.90 m (cohesion 3.5 kPa). When the stability index includes static skier loading as calculated in Figure 4 these values are reduced to 1.18 and 2.86 m, nearly negligible differences.

Fig. 4. Stress ratio as a function of depth for a skier approximated as a line-source loading. Also shown is a comparison for a ski of width 0.1 m (see Appendix). The geometry is shown in Figure 6.
The actual stress values compared with typical strength values are also of interest. With the above values, Equation (10) gives Δτ = 99/H (Pa) where H is in meters (see Fig. 5). If H = 1 m then the stress added is about 100 Pa (200 Pa for 0.5 m) which, from field measurements, is close to the minimum for shear strength estimated from fracture lines for failure density 100 kg m−3 (see Reference McClung and Schaerer.McClung and Schaerer, 1993, p.71). Virtually all of Reference Irwin and FlüggeJamieson’s 1995strength estimates exceed these values by more than a factor of 3. The conclusion is that skier loading by such analysis (excluding imperfections and dynamic effects) is nearly insignificant below 1 m depth.

Fig. 5. Shear stress as a function of depth for a skier approximated as a line-source loading. Also shown is a comparison for a ski of width 0.1 m (see Appendix). The geometry is shown in Figure 6.
Even though the analysis shows nearly negligible stresses in comparison with slab values below about 1 m in the snow-pack, it is known that skiers can rarely trigger avalanches as deep as 1 m (see Reference Jamieson and Johnston.Jamieson and Johnston, 1998b, for data). Reference Jamieson and Geldsetzer.Jamieson and Geldsetzer, 1996 showed that about 11% (sample of 261) of recreational accidents (including snowmobile accidents) in Canada during 1984–96 involved average slab thicknesses of > 1 m. Reference Jamieson and Johnston.Jamieson and Johnston, 1998b compiled start-zone data on 1193 skier-triggered avalanches observed by helicopter skiing guides. These data showed that depth exceeded 40 cm in 25% of cases and 65 cm in 10% of cases, but maximum depth was 2 m. There is uncertainty in such data because all are related to fracture lines, not the actual position where fracture initiated. Field observations (personal communication from D. Fesler, 1998) often show that fractures propagate into deeper areas following skier triggering, so that fracture-line depths are often greater than slab depths at the initiation triggering point.
Static Analysis with Effect of Finite Ski Width
The analysis above is for a line-source loading of infinitesimal width. Reference FöhnFöhn (1987) considered a similar analysis to approximate snowcat loading, but he did not consider a ski of finite width. In the Appendix, we give an analysis for which skier loading is approximated near the centre of a ski of finite width on a slope as a plane-strain analysis. Figure 6 shows the loading situation. In order to compare with the line-source analysis above, we calculated the stress distribution for the same parameters as in Figures 4 and 5: Ψ = 35°, θ = 35°, for a ski of width 10 cm. Figures 4 and 5 show these calculations in comparison to calculations for the line source. The results show very little difference between this and our previous analysis.

Fig. 6. Geometry for loading by a skier with finite-width ski (w).
Simple Analysis with Imperfection in a Weak Layer
With an imperfection present in a weak layer, application of a load will result in amplification of stress and deformation conditions in the stress and strain concentrations associated with the imperfections analogous to the stress-intensity factor of fracture mechanics: the stress intensity at the tip of the imperfection is proportional to the intensity of stress applied remotely at the top of the snowpack. Reference Rice and LiebowitzRice (1968) gave an expression for the stress-intensity factor for slip band (or crack) of length 2a loaded in shear uniformly at the top of a slab. If τ ∞ is a uniform shear stress applied at the top of the slab and τ 0 is the friction stress (e.g. residual shear strength) along the imperfection, the stress-intensity factor for shear fracture (mode II) propagation is given by: K Π = (τ ∞ – τ 0) (πα)0.5. Such a solution, from small-scale yielding linear elastic fracture mechanics, is too simple for use in the problem here, but illustrates in principle how a remotely applied shear stress (at the slab surface) affects propagation of an imperfection; the stress-intensity factor is, then, a convenient measure of load applied to the crack (imperfection) tip region. For example, if a line-source solution is applied, the implied shear stress intensity added at the top of the slab to τ ∞ may be approximated as (Pg sin Ψ)/w where w is the width of a ski. If w = 0.1 m, P = 41.2 kg m−1 and Ψ = 35°, τ ∞ has the approximate value 2.3 kPa which represents an increase in “intensity” applied to a weak zone from the skier-loading remotely applied shear stress at the top of the slab; its value is more than ten times the values calculated from skier loading by Equations (10) and (11) at depths exceeding 1m.
Reference Rice and LiebowitzRice (1968) emphasizes that such an analysis (linear elastic) does not take into account the response of the material to the applied load but it does illustrate the stress-concentrating effect once imperfections are introduced. The stress and deformation state induced by skier loading is not uniform as required by K Π given above (such would be approximately the case for new snowfall loading). Furthermore, the driving energy for propagation of an imperfection from fracture mechanics is proportional to the stress-intensity factor squared, and inversely proportional to the modulus E′ = 2G/(1 - ν) where G is shear modulus and ν is Poisson ratio of the slab. Reference Rice and PalmerRice (1973) and Reference Bažant and Planas.Bažant and Planas, 1998show that for the assumption of linear viscoelasticity in the slab and small-scale yielding in the weak layer, the reciprocal of modulus may be replaced by the time-dependent compliance which contains the signified temperature dependence of alpine snow (Reference McClungMcClung, 1996). This simple analysis shows how one is implicitly forced toward consideration of slab mechanical properties once imperfections are introduced.
Virtually all modern work on the snow slab (Reference McClungMcClung, 1979, Reference McClung1981, Reference McClung1987; Reference Conway and Abrahamson.Conway and Abrahamson, 1988; Reference Bader and Salm.Bader and Salm, 1990; Reference ConwayConway, 1998) postulates that the size effects controlling avalanche release are macroscopic, with a size effect independent of statistical properties in agreement with the arguments of Bažant and Planas. The size effects associated with sample-size dependence as in the (brittle) shear frame test are microscopic and dependent on statistical properties. Microscopic flaws are present in abundance everywhere in alpine snow and there is evidence that such flaws are important for interpreting shear frame results. However, it is unlikely that such small flaws control avalanche release. If such small defects truly controlled avalanche release, avalanches would be present continuously. However, experience shows that avalanches are actually rare occurrences. In fact, the strength of snow would be virtually zero if micro-scale flaws controlled (see J. F. Nye in IAHS, 1975). In the light of new experimental information on shear strength by Reference SchweizerSchweizer, 1998) and information summarized by Reference Bažant and Planas.Bažant and Planas, 1998 it is imperative to revisit the question of size effects, which we do in the next section.
Two Estimates of Imperfection Size Effects
(1) Simple brittle size effect from scaling
If alpine snow behaved as a classical brittle material (as might occur under rapid loading such as for explosives), a simple method to estimate order-of-magnitude size effects could be as discussed by Reference Bader and Salm.Bader and Salm (1990). For a completely brittle material, the ratio of fracture strength to theoretical ultimate (uncracked) strength is given by σ f/σ th ≈ (b/a)1/2 (e.g. Reference Kanninen and Popelar.Kanninen and Popelar, 1985) where b is atomic bond size and a is critical crack length. Reference Bader and Salm.Bader and Salm (1990) pointed out that for brittle materials such as glass, typical atom bond sizes are 2–5 x 10−7 mm associated with minimum critical lengths of order 10−3 mm (Reference Lardner.Lardner, 1974). For snow grains, typical bond sizes are on the order of 0.1–1 mm. Simple proportions yield critical size effects of 0.2–5 m for snow. From Griffith’s experiments on glass (Reference Kanninen and Popelar.Kanninen and Popelar, 1985) the ratio σ f/σ th is 1/64 using the bulk strength of glass (large samples) for σ f, which (with b = 0.1–l mm for snow) gives critical-size estimates 0.4–4 m. The strength ratio for glass is of the same order as the ratio of typical avalanche failure strengths (about 1 kPa: Reference McClung and Schaerer.McClung and Schaerer, 1993, p. 71; Reference Jamieson and Johnston.Jamieson and Johnston, 1998b) to the yield stress of single ice crystals in shear (about 100 kPa: Reference Higashi, Koinuma. and Mae.Higashi and others, 1964; Reference FletcherFletcher, 1970; Reference HobbsHobbs, 1974) which approximates the fracture stress (Reference Lardner.Lardner, 1974). This analysis is very crude but it is a starting-point for estimating size effects. The implication is that imperfections much smaller than the order-of-magnitude range 0.1–1 m would not be energetically favourable for reaching a self-propagation condition.
(2) Estimate of size effects for constant gravitational loads
Snow cannot be approximated as a brittle material unless it is deformed very rapidly. The other limit, when snow displays strain-softening under constant load, was addressed by Palmer and Reference Rice and PalmerRice (1973). They gave a formalism to enable calculation of the size of the end zone (or plastic zone) at the end of a slip surface generated by strain-softening initiated at an imperfection in a weak layer with the slab assumed to be elastic. The estimate of the cohesive (or end) zone size, ω, in terms of peak shear stress, τ ρ, residual shear stress, τ τ, shear modulus, G, Poisson ratio, ν, and average shear displacement, δ, in the strain-softening regime from a simple shear experiment is:
Reference Bažant and Planas.Bažant and Planas, 1998 provide an analogous expression for strain-softening materials in tension, and point out that the non-linear end-zone size may be many times the estimates for metals as estimated by Irwin (1958).
From our simple shear experiments (data from Reference SchweizerSchweizer, 1998), and unpublished collection of more than 200 experiments by McClung) the ratio of peak to residual shear stress can be taken as 1.5. The G/τ ρ ratio increases as the temperature decreases, due to the temperature dependence of G, and increases with strain rate, again possibly due to the dominance of stiffness. The ratio is about 100 for slow rates (10−1 s−1), increasing to 300 for higher rates (103 s1). The average values of displacement in the strain-softening portion of the stress–strain curve range from 5 mm (slow rates) to 1 mm (fast rates). From these estimates the end-zone size is estimated to be about 1.5 m (fast rates) to 3 m (slow rates) in field situations from Equation (12). Since the critical length must be a multiple of the end-zone size, our estimate is somewhat higher than the one above based on scaling from bond sizes for brittle materials.
For reference,Reference Bažant and Planas.Bažant and Planas, 1998 estimate for concrete in tension a fully developed fracture-process-zone size range of 0.3–2 m for large concrete structures. Our two estimates have a certain consistency with respect to rate: smaller sizes are implied for more rapid loading and this is consistent with results for concrete described byReference Bažant and Planas.Bažant and Planas, 1998. These two limit estimates (brittle and strain-softening) are reasonably consistent and our best estimate for the important minimum critical-size effect for skier triggering is on the order of a significant fraction of a meter.
For skier triggering, once size effects for imperfections approach a significant fraction of a meter, the situation seems to be critical as the extra dynamic loading will feed deformation energy to the tip to cause extension and catastrophic fracture propagation. Furthermore, if a critical condition is not achieved by the first skier, passage of subsequent skiers can cause extension to a critical length. This explains some rare field observations (e.g. Reference LaChapelleLaChapelle, 1985) in which an avalanche releases after the passage of more than one skier. Our static analysis without imperfections implies that the applied loads are very small at depth, whereas field data (Reference Schweizer, Camponovo., Fierz., Föhn. and SivardièreSchweizer and others (1995a, Reference Schweizer, Camponovo., Fierz., Föhn. and Sivardièreb; see Appendix) show that dynamic loads are higher. The application of dynamic loads and the presence of partially formed (subcritical) imperfections to concentrate deformation provide a powerful combination to drive propagating shear fractures from imperfections which are subcritical before passage.
Our size-effect estimate is a significant fraction of a ski length, and from St Venant’s principle the slope distance for the zone of influence of significant stresses and deformation energy by passage of a skier will be a few ski lengths. If small (micro-scale) imperfections were responsible for avalanche release, a person on skis would influence huge numbers of them in skiing down a given slope, and skier triggering would be far more common than it is. Skiers sometimes term positions on snow slopes where avalanches initiate as “sweet spots”. We believe “sweet spots” are preferentially located where subcritical imperfections coincide with thin- and/or soft-snow slabs so that maximum deformation energy is communicated to the weak layer during skier passage.
Most snow-slab releases (either natural or human-triggered) occur under loading conditions. In fact, avalanche releases under constant gravitational loads (e.g. releases after storms without wind loading) are very rare in comparison, probably because bond formation may inhibit imperfection expansion if growth is too slow. Therefore, we believe subcritical imperfections and their growth under loading are of primary importance in the vast majority of cases. Furthermore, there is no requirement for a strain-softening process to have occurred in a weak layer over large distances (many meters) as envisioned by Reference Conway and Abrahamson.Conway and Abrahamson, 1988 to place the slab weak-layer system in a critical condition with respect to future load application. Reference Bader and Salm.Bader and Salm (1990) hypothesized that critical lengths for imperfections to start propagation are on the order of several meters, with brittle fracture starting at distances of tens of meters, but they did not consider the problem of skier triggering explicitly. Observations concerned with fracture propagation during skiing show that Bader and Salm’s distances (40 60 m) are unrealistic for skier triggering: shear fractures propagate rapidly within a few meters of initiation, implying very high stresses and deformation rates.
Once the minimum conditions for imperfection growth are approached, further load application can result in shear fracture (Reference Bažant and Planas.Bažant and Planas, 1998) essentially at peak stress if loading is progressive (load-controlled), as may be approximated by new snowfall loading Reference McClungMcClung, 1981 with no requirement for strain-softening.Reference Bažant and Planas.Bažant and Planas, 1998 show that instability may result from further application of load at any time after a peak has been reached for strain-softening material in the failure zone (weak layer), given that the critical fracture energy has been delivered and the size requirement is satisfied.
The fact that strain-softening is not required for fracture initiation under loading, along with our estimates of size effects, again points to critical imperfection size effects of a fraction of a meter for dynamic loading applied during skiing. The presence of an imperfection will concentrate stresses, deformation and deformation rates to help achieve a critical condition, with thin, soft slab material being of primary importance to deliver maximum deformation energy to the weak layer.
Summary
The immediate or nearly immediate effects of snow temperatures on snow-slab instability are influences which promote instability under warming, including reduced snow stiffness (or hardness), and strength with very short time delays to affect properties; failure toughness increases slightly with increasing temperature. However, we expect overall fracture toughness for snow-slab stability to decrease with increasing temperature since weak-layer failure toughness appears weakly temperature-dependent, while the slab stiffness should decrease with increasing temperature. Other temperature effects include metamorphism and long-term creep and they can affect skier triggering, but such effects are beyond the scope of this paper.
In order to include the effects of snow temperature in an analysis of instability, one must seek out information about slab hardness and think about the problem in regard to deformation energy rather than an analysis of stresses. Conventional stability evaluation (e.g. calculation of a strength-to-load ratio) will not contain much of the important information about slab-temperature dependence (or snow hardness) and instability.
For skier triggering, the most important immediate influence of snow temperatures is the decrease of hardness of the surface layers under warming. Secondary effects include decreased shear strength if the weak layer is warmed, with failure toughness being (apparently) only slightly temperature-dependent. Hardness estimates (e.g. the hand hardness test) implicitly include snow-temperature effects.
Mathematically, our static stress analysis indicates that new snow loading or skier loading should always decrease stability if snow is modelled as a linear Coulomb–Mohr material (the usual assumption, which we believe is unrealistic). However, when results from shear frame estimates of the stability index are combined with measured peak friction angles from simple shear tests for alpine snow, this mathematical condition may not always be fulfilled: it might be implied that stability increases with loading. We believe the discrepancy may be found in the imprecision of shear frame measurements combined with extrapolation of such results to the real situation where macroscopic imperfections will control avalanche initiation. Neither simple shear tests nor the shear frame will include the effects of macroscopic imperfections. Simple shear tests should provide peak friction angles closer to values for a homogeneous Coulomb–Mohr material compatible with the analysis leading to Expressions (5) and (9). The stress concentrations induced by the fins of the shear frame might produce artificially lower friction angles, but these should not be equated with the field situation in which macroscopic imperfections, perhaps larger in size than the shear frame, can initiate the failure process.
The Rutschblock test has the advantage that it implicitly includes dynamic effects, snow temperatures and slab hardness effects in an analysis of instability, whereas tests like the shovel shear test or the shear frame test do not. The drawback is that another source of variation is included that must be considered for extrapolation: the test results depend heavily on the surface layer stiffness. It is proposed to perform Rutschblock tests at places with relatively soft rather than hard surface layers for comparison and extrapolation. Furthermore, tests will have a better chance of revealing instability where the slab is thin.
The advantage of the shovel test and shear frame test is that they contain direct information about the strength and quality of weak-layer failures, and therefore their interpretation is less complicated than the Rutschbloek test. However, they do not contain the most important information about snow temperatures and hardness, and therefore supplementary information about the slab properties must be sought. This same comment applies to the calculated shear frame index. We propose that to complete a stability test, observations of hardness variations be made (e.g. with a profile), otherwise the information gained by the tests is too limited and cannot easily be used for extrapolation.
Field observations show that most skier-triggered avalanches occur during the act of skiing, which implies dynamic loading in which stresses and deformation will be higher than for a static analysis. Dynamic deformation measurements (Fig. 7; Reference Schweizer, Camponovo., Fierz., Föhn. and SivardièreSchweizer and others (1995a, Reference Schweizer, Camponovo., Fierz., Föhn. and Sivardièreb) compared with a static analysis show that a realistic treatment of the problem would require dynamic effects to be included.
Any information that helps to evaluate snow-slab instability is useful, and this includes calculation of the stability index from, for example, the shear frame and the other common stability tests. In this paper, we have addressed the problem of skier triggering in an attempt to place it in its true context: a forecasting problem on the micro-scale for terrain (the scale involving individual terrain features) in which a general stability index is only a good first step. Consideration should also be given to slab mechanical properties, the size effects associated with fracture propagation, and influences of terrain as primary factors for avalanche forecasting on individual terrain features. Reference McClung and Schaerer.McClung and Schaerer (1993) argued that stability tests constitute some of the most important information available for back-country avalanche forecasting. However, in this paper we provide analysis to show that some key information is often excluded by stability tests and that some of the key information such as location of subcritical imperfections can be virtually impossible to gauge. What we have done, then, is to indicate that the snow-stability evaluation problem is analogous to a probabilistic risk analysis in which the risk (uncertainty) is never zero. The fundamental problem in back-country avalanche forecasting is a knowledge of the temporal and spatial distribution of snow instability which cannot be known exactly. Risk management, then, becomes another term for back-country travel in avalanche terrain.
Acknowledgements
The support of the Natural Sciences and Engineering Research Council of Canada is gratefully acknowledged. This work was also supported by the Peter Wall Institute of Advanced Studies, University of British Columbia. The support of our industrial research partner, Canadian Mountain Holidays, has been essential to this work. Our simple shear experiments were performed at Glacier National Park, British Columbia. We are grateful to the Canadian Parks Service for their support.
Appendix Static Analysis for a Ski of Finite Width
In this Appendix, we relate the analysis accompanying Figures 4 and 5 in the text with the loading and geometry depicted in Figure 6. Pure shear loading is applied in the y direction of magnitude 2Bπ, and compressive loading is applied with magnitude 2Aπ in the x direction. Our analysis is a slight extension of that given by Reference Timoshenko and Goodier.Timoshenko and Goodier, 1970, so the solution methods we present are well known in engineering mechanics. The stress intensity in shear is q s = 2Bπ = Pgsin Ψ/w and in the normal direction is q n = –2Aπ = Pgcos Ψ/w where P is the skier mass divided by the ski length (kg m−1) and w is the ski width.
The stresses in the problem are then defined by the standard equations of elasticity in polar coordinates. From Reference DasDas (1983) and Reference FöhnFöhn (1987), it can be shown that:

The engineering shear strain is then:
so that hardness and temperature dependence is introduced through G. In Equation (A1), θ 1 is defined by tan θ 1 = (H tan θ + w)/H at any depth H.
For the calculations in Figure 6, we chose the same parameters as in Figures 4 and 5 (Ψ =35°, P = 41.2 kg m1, θ = 35°) and the width of the ski w = 0.1m. For the slab density in Figure 7 we took ρ s = 200 kg m−3. The calculations again show that stresses and strains decrease inversely-proportional to H and the stress ratio: Δτ/τ is then inversely proportional to H 2. Since the calculations depend on ski width and the value of θ, the results for finite ski width (Figs 4 and 5) are somewhat different than those for infinitesimal ski width. The stresses implied by any of these calculations for typical large slab depths are extremely small. The results indicate that dynamic effects coupled with imperfections and anisotropic deformations in weak layers appear to be important elements of the skier-triggering problem.

Fig. 7. Calculated force for a skier standing with 0.2 m combined width of skis (solid line) compared with static and dynamic measurements (Camponovo and Schweizer, 1996). Dynamic stresses during skiing would be closest to the data for jumping.
In order to compare with ski deformation experiments, we set Ψ = 0°, then B = 0, to yield (Reference Timoshenko and Goodier.Timoshenko and Goodier, 1970):
which represents a uniform compressive stress.
From Equation (A3) the displacements in plane strain below the ski are of the form:

with similar expressions following from Equation (A1) by replacing A with –A, r with r 1, and θ with θ 1 in Equation (A1). In Equation (A4), E * = E/(1 – v 2) and v * = v/(1 – v) with E and v being Young’s modulus and Poisson’s ratio, respectively. Figure 8 shows the downward deformation component (along the y axis) in the vicinity of the centre of the ski (near the foot) where –A = Pg/2πw from the work of Reference Timoshenko and Goodier.Timoshenko and Goodier, 1970. Again, temperature and hardness enter through E and v.

Fig. 8. Plane-strain deformation pattern for a skier with ski width w between O and O1 (adapted from Reference Timoshenko and Goodier.Timoshenko and Goodier, 1970).
At the midpoint below the ski, θ = –θ 1 and r = r 1 to yield the downward displacement:

where θ 1 = tan−1(w/2H) and r 1 = [H 2 + (w/2)2]0.5. Similarly, the vertical stress below the midpoint is:

Equations (A5) and (A6) may be used to compare with skier deformation measurements (Schweizer and others, 1995a, b). Figure 7 shows this comparison for vertical stress calculated from Equation (A6) for a combined ski width of 0.2 m and Pg = 500 N m−1. The loading plate has an area of 0.25 m2 for conversion of stresses to forces. Note that static loads are much lower than dynamic loads. Since the experimentally estimated forces on the plate are calculated from deformation measurements which are communicated through the snow, they depend on snow hardness which is not considered in the elastic analysis of Equation (A6). Therefore, the comparison of calculated forces from Equation (A6) in Figure 7 is an approximation.










