A multimethod dating study of ancient permafrost, Batagay megaslump, east Siberia

Abstract

Dating of ancient permafrost is essential for understanding long-term permafrost stability and interpreting palaeoenvironmental conditions but presents substantial challenges to geochronology. Here, we apply four methods to permafrost from the megaslump at Batagay, east Siberia: (1) optically stimulated luminescence (OSL) dating of quartz, (2) post-infrared infrared-stimulated luminescence (pIRIR) dating of K-feldspar, (3) radiocarbon dating of organic material, and (4) ³⁶Cl/Cl dating of ice wedges. All four chronometers produce stratigraphically consistent and comparable ages. However, OSL appears to date Marine Isotope Stage (MIS) 3 to MIS 2 deposits more reliably than pIRIR, whereas the latter is more consistent with ³⁶Cl/Cl ages for older deposits. The lower ice complex developed at least 650 ka, potentially during MIS 16, and represents the oldest dated permafrost in western Beringia and the second-oldest known ice in the Northern Hemisphere. It has survived multiple interglaciations, including the super-interglaciation MIS 11c, though a thaw unconformity and erosional surface indicate at least one episode of permafrost thaw and erosion occurred sometime between MIS 16 and 6. The upper ice complex formed from at least 60 to 30 ka during late MIS 4 to 3. The sand unit above the upper ice complex is dated to MIS 3–2, whereas the sand unit below formed at some time between MIS 4 and 16.

INTRODUCTION

Sedimentary deposits frozen continuously in permafrost since the Pleistocene preserve important evidence for climate and environmental change and for the interchange of flora and fauna between Eurasia and the Americas. They also help us to evaluate the stability of permafrost and its resilience to Earth system change over the course of the Pleistocene. Ancient permafrost, however, is difficult to date, because its components (mineral particles, ice, organic remains, and liquid water) experience complex histories of warming and cooling and deposition and freezing by different processes and at various depths and times and—in the case of organic remains—often preserve exceptionally well before reworking and refreezing, resulting in ages that are anomalously old relative to the depositional age of the sediment. Such complexities must be considered carefully when dating the time of permafrost formation or thaw or the minimum age of permafrost preserved in the geologic record.

Dating of Pleistocene permafrost beyond the range of radiocarbon dating is challenging, though several promising methods have been applied. Radiocarbon dating of organic material incrementally buried in aggrading sedimentary sequences has provided some relatively robust chronologies of up to ~40–50 ka for syngenetic (upward) permafrost growth (e.g., Wetterich et al., 2014; Murton et al., 2015). Beyond this age range, methods applied to date permafrost include optically and infrared-stimulated luminescence dating of sand and silt (e.g., Demuro et al., 2013; Opel et al., 2017) back to ~210 ka (Ashastina et al., 2017), radioisotope disequilibria (²³⁰Th/²³⁴U) of frozen peat to ~220 ka (Wetterich et al., 2016, 2019), uranium isotope (²³⁴U/²³⁸U) series of ground ice to ~200 ka (Ewing et al., 2015), and palaeomagnetic analysis of silty to sandy deposits to ~200 ka (Andreev et al., 2004). Still older ages of ~610 ka have been obtained from ³⁶Cl/Cl ratios of ground ice (Blinov et al., 2009), and ~740 ka from fission track dating of tephra above ground ice (e.g., Froese et al., 2008; Davies et al., 2016). Nonetheless, some of these applications of dating methods are in early stages of development, and calculated ages have large uncertainties. Moreover, increasingly old permafrost deposits are rare (due to erosion and/or thaw) or tend to be deeply buried. Overall, therefore, information about the age, nature, and distribution of permafrost preserved since before the last interglaciation (~132–117 ka)—that is, ancient permafrost—is scarce.

Here, we determine the age of ancient permafrost at the Batagay megaslump, east Siberia, in a multimethod dating study. The slump headwall exposes four generations of ice wedges and sand–ice (composite) wedges that formed synchronously with permafrost growth and two woody beds that represent the remains of two episodes of taiga forest development before the modern Holocene forest. Thus, the ancient permafrost at Batagay potentially provides one of the longest—but discontinuous—terrestrial records of Pleistocene environments in western Beringia (east Siberia). We report results from optically stimulated luminescence (OSL) dating of quartz grains and post-infrared infrared (pIRIR) luminescence dating of K-feldspar grains from aeolian sand that has remained continuously frozen since ice wedges formed concurrently with deposition (syngenetically). Additionally, we use radiocarbon methods to date organic macroremains from ice wedges and host sediments and provide a starting point (base age) for ³⁶Cl/Cl dating of the wedge ice itself. Both ³⁶Cl/Cl and radiocarbon dating methods take advantage of accelerator mass spectrometry (AMS). This study builds on earlier work at the Batagay megaslump (Ashastina et al., 2017; Murton et al., 2017b; Opel et al., 2019; Vasil'chuk and Vasil'chuk, 2019; Vasil'chuk et al., 2020) and integrates all available dating results for the permafrost sequence exposed there. The aims of this study are (1) to test several independent methods for dating of ancient permafrost, (2) to develop a suitable multimethod framework to date the ancient permafrost deposits at the Batagay megaslump, and (3) to improve the chronological constraints for the latter. Additionally, we provide the first application of ³⁶Cl/Cl dating of ground ice with independent testing of ages using other dating methods. Our study provides the framework for planning future, systematic dating of the site.

STUDY SITE

The Batagay megaslump (67.58°N, 134.77°E) is the largest known retrogressive thaw slump in the world, measuring ~1.8 km long and >0.8 km wide in 2019. The slump has developed over the past five decades and was first studied in 2011 (Kunitskiy et al., 2013). It is located on a hillslope at an elevation of ~330 m above sea level (for the highest part of the headwall), near the town of Batagay, in the Yana Highlands of northern Yakutia (Fig. 1). This region is characterized by a strongly continental climate and increasing temperature and precipitation since the mid-twentieth century. At Batagay, the mean annual air temperature over the period 1988–2017 was −12.4°C, with a mean winter (December to February) air temperature of −40.0°C and a mean summer (June to August) air temperature of 13.7°C (Murton et al., in press). About half of the mean annual precipitation of 203 mm (i.e., 106 mm) falls in summer. The permafrost is continuous and ~200 to 500 m thick (fig. 15.2 in Yershov, 1998), with mean annual ground temperatures of −8.0°C to −5.5°C and active-layer thicknesses between 0.2 and 1.2 m, depending on soil and vegetation types (Ivanova, 2003).

Figure 1. (a) Location map of Beringia. Red dashed box shows location of panel b. (b) Location map showing the topographic setting of the Batagay megaslump within the Yana River basin, northern Yakutia. Glacial limits during the last (Sartan) glaciation, according to Glushkova (2011), are indicated. Red dashed box shows location of panel c. (c) Topographic map of the Batagay region, showing the location of the megaslump on a northeast-facing hillslope. Contours at 20 m intervals; grid spacing at 4 km.

The vegetation near Batagay comprises mainly open woodlands dominated by Cajander larch (Larix cajanderi) with birch (Betula exilis or Betula divaricata) undergrowth and a lichen–green moss ground cover. Birch (Betula pendula) occurs in some burnt areas. Higher upland areas are typically covered by thickets of dwarf stone pine (Pinus pumila), mountain tundra, or stony debris. Permafrost podburs are the most common soil type beneath open woodlands of larch, and underdeveloped stony soils characterize rubbly mountain areas. Peaty and humus–gley soils underlie the bottoms of small river valleys, whereas the terraced floodplains of the Yana and Batagay rivers contain underdeveloped sandy soils and alluvial permafrost soils.

In palaeoenvironmental terms, the study region has probably remained unglaciated throughout the late Cenozoic (Batchelor et al., 2019) and belonged to the ice-free subcontinent of Beringia (Fig. 1a). A sequence of permafrost deposits about 60 m thick crops out in the slump and can be divided into seven stratigraphic units (Fig. 2; Table 1) and summarised as follows. Above slate bedrock is (1) a diamicton at least 0.5 m thick, containing abundant clasts of slate, that is interpreted as colluvium. The overlying (2) lower ice complex (~3–7 m thick) contains woody material—including in situ tree stumps as well as woody debris related to erosional features within the ice complex—and ice wedges at least 2–3 m high and 1 m wide truncated along their tops by a thaw unconformity. There are also traces of an erosional surface overlain by gravelly deposits along the top of this unit. The woody material is thought to represent the remains of a forest bed. Above the lower ice complex, (3) a lower sand unit (≤20 m thick) of pore-ice-cemented fine sand interpreted as aeolian sand-sheet deposits contains tall, narrow syngenetic ice wedges and composite wedges up to 0.5 m wide. In places, (4) prominent lenses of woody debris (≤3 m thick) sharply overlie the lower sand unit below a prominent disconformity (erosional surface). The woody debris is interpreted as a second forest bed and is overlain by few metres of sand at the base of (5) an upper ice complex (~20–25 m thick) dominated by large syngenetic ice wedges up to a few metres wide and at least several metres high set within silty and sandy deposits. The upper ice complex probably formed as a result of a substantial increase in snow meltwater supply into thermal contraction cracks relative to the limited water supply to the narrow wedges in the lower sand unit. The upper ice complex plunges downslope beneath and partly grades into (6) the upper sand unit (~20–30 m thick, and similar in nature and interpretation to the lower one), which is best exposed near the slump exit. Capping the sequence is (7) a near-surface layer of brown sand and modern soil (~1–3 m thick).

Figure 2. (a) Panoramic photograph of the Batagay megaslump showing the main stratigraphic units and locations of sections 1 and 2. (b) Schematic stratigraphic section of the exposed units along the slump headwall, with approximate positions of the studied sections. Numbers 2 to 6 represent cryostratigraphic units summarised in Table 1. Modified from Opel et al. (2019).

Table 1. Stratigraphic units of the permafrost sequence exposed in the Batagay megaslump.^a

^a Based on Ashastina et al. (2017), Murton et al. (2017b), Opel et al. (2019), Vasil'chuk and Vasil'chuk (2019), Vasil'chuk et al. (2020), and field observations in spring 2019.

^b IRSL, infrared-stimulated luminescence; OSL, optically stimulated luminescence; n/a, not analysed.

^c MIS, Marine Isotope Stage.

METHODS AND DATA

Fieldwork

Sediment and ground-ice samples for dating in the present study were taken during fieldwork in summer 2017 based on cryostratigraphic observations that largely confirm earlier interpretations (Ashastina et al., 2017, 2018; Murton et al., 2017b). We focused on sampling at two sections in different parts of the exposure (Fig. 2): (1) the contact of the lower ice complex to the lower sand in a gully of the icy badlands on the slump bottom (section 1, Fig. 3) and (2) the upper ice complex and the upper sand in a headwall slope in the southern part of the slump (section 2, Fig. 4).

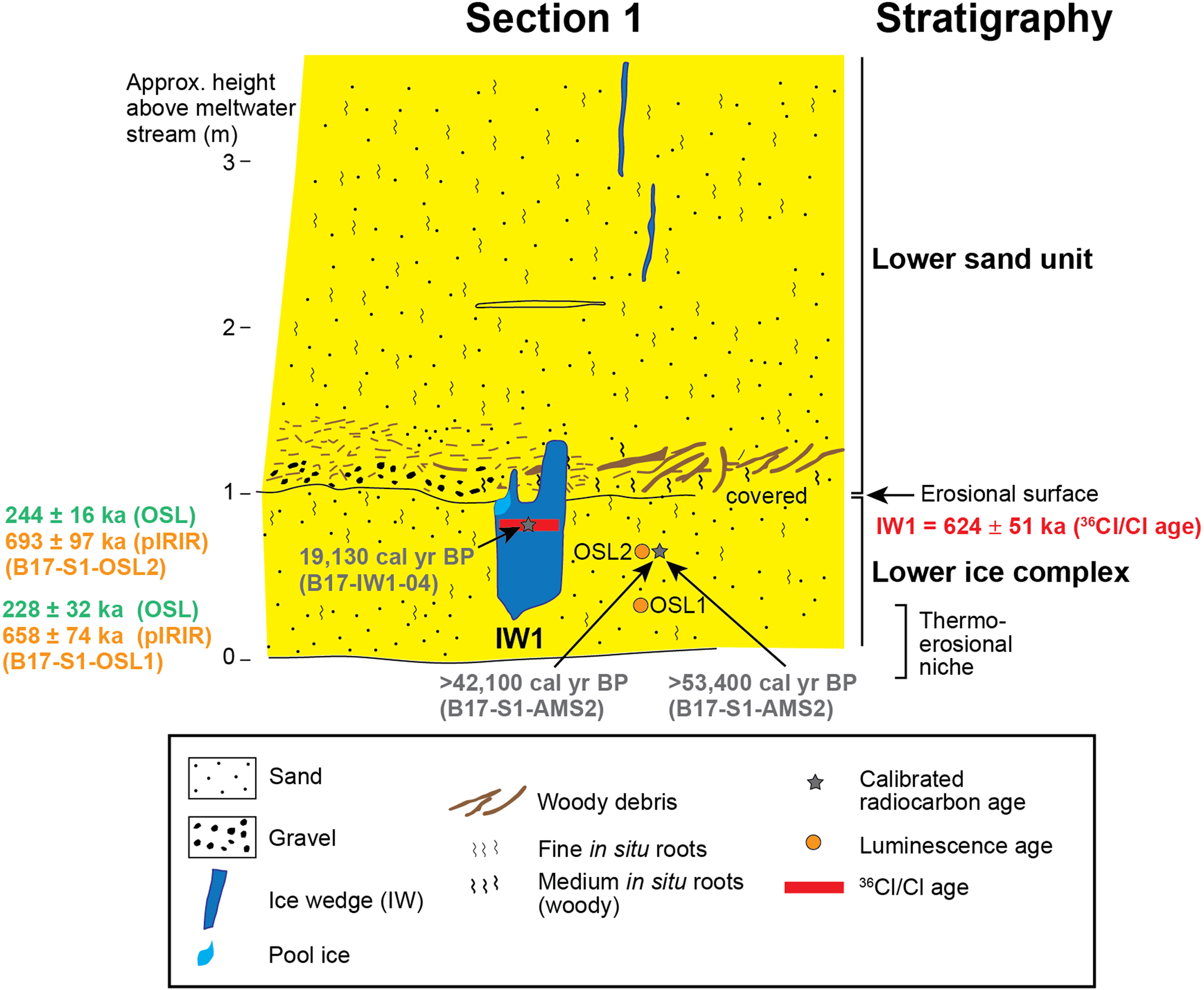
Figure 3. Schematic cryostratigraphic sketch of section 1, showing age estimates. Radiocarbon ages are given as calibrated median ages where available or otherwise as uncalibrated ages (see Table 5). The post-infrared infrared-stimulated luminescence (pIRIR) and optically stimulated luminescence (OSL) ages are associated with the orange circles labelled “OSL1” and “OSL2.”

Figure 4. Schematic cryostratigraphic sketch of section 2, showing age estimates. Radiocarbon ages are given as calibrated median ages where available or otherwise as uncalibrated ages (see Table 5). The post-infrared infrared-stimulated luminescence (pIRIR) and optically stimulated luminescence (OSL) ages are associated with the orange circles labelled “OSL3” to “OSL7.”

Samples for luminescence dating (n = 7) were taken from freshly thawed undisturbed sediments using a metal cylinder. The samples were immediately shielded from sunlight, tightly sealed, and stored cool until analysis. We additionally sampled the frozen sediments for analysis of radionuclide concentrations by gamma spectrometry and for measurements of ice content. We sampled ice wedges for ³⁶Cl/Cl dating (n = 4) by chainsaw. In total, we cut ~2 kg of ice and stored it cool in sample bags. After melting the ice, we filled two 1 L low-density polyethylene bottles with the meltwater and kept them cool until analysis. Organic macroremains were picked from sediment and wedge-ice samples for radiocarbon dating (n = 12; Opel et al., 2019; this study).

Luminescence dating

In luminescence dating, age estimates of the time of sedimentation (Huntley et al., 1985) are premised upon reduction of the time-dependent signal in minerals (OSL) to zero through exposure to sunlight. Once sediment is buried, the OSL signal accrues through exposure to natural litho- and cosmogenic radiation. The total burial dose related to the observed luminescence signal intensity is found by estimating the dose of laboratory radiation (equivalent dose) that produces luminescence equal to that measured from the sample of interest. Based on this dose-luminescence response relationship, the dosimeter (typically quartz and feldspar) can then be converted to a chronometer by estimating the rate of dose absorption. The luminescence age is generally defined by the quotient:

(Eq. 1)$$ \eqalign{ {\rm Age} = & \, {\rm equivalent\ dose\ }( {{\rm D}_{\rm e}, \;{\rm Gy}} ) / \cr& {\rm total\ environmental\ dose\ rate\ }( {{\rm D}_{{\rm r}, }{\rm Gy}/{\rm ka}} )} $$

General accounts of the method can be found in, for example, Aitken (1998) and Bøtter-Jensen et al. (2003). Quartz is typically the mineral of choice in OSL dating, owing principally to the temporal stability of its luminescence signal and rapid resetting of this signal by sunlight during sediment transport before deposition (e.g., Wallinga, 2008; Wintle, 2008). However, saturation of the quartz signal usually limits its application to samples with burial doses of <200 Gy (Wintle, 2008) and thus restricts the maximum datable age to 100–200 ka (assuming a D_r range of 2 to 1 Gy/ka, respectively). Feldspars saturate at higher doses compared with quartz, but anomalous fading of their infrared-stimulated luminescence (IRSL) signal (Wintle, 1973; Huntley and Lamothe, 2001) has complicated the use of these minerals due to the need for additional corrections (e.g., Auclair et al., 2003; Kars et al., 2008). Because the anomalous fading rate displayed dose-dependent behaviour (e.g., Li and Li, 2008), overestimation was reported for corrected ages, especially in older samples (e.g., Li and Li, 2011). However, the discovery of an IR signal with significantly reduced fading in K-feldspars (pIRIR; Thomsen et al., 2008) and the subsequent development of measurement protocols (e.g., Buylaert et al., 2009; Li et al., 2014b) have recently encouraged wider adoption of these minerals and provide the potential to date samples with burial doses of up to 1500 Gy (e.g., Wintle, 2008; Zhang and Li, 2020). Given the D_r values present at the site (~2–3 Gy/ka; Table 2) and the potential for quartz samples at depth to be close to saturation, we adopted a paired quartz OSL and K-feldspar pIRIR approach to luminescence dating.

Table 2. Dose-rate parameters from 125–180 μm quartz and K-feldspar isolates for luminescence dating.

^a Cosmic dose rate for ~68°N, 135°E, 300 m above sea level.

Sample preparation

Luminescence samples were prepared and measured in the Luminescence Dating Laboratory, University of Gloucestershire. To preclude optical erosion of the signal, the sediment samples were collected in opaque tubing and processed under controlled laboratory illumination provided by Encapsulite RB-10 (red) filters. The fine-sand fraction (125–180 μm) of six samples was segregated and subjected to acid and alkaline digestion (10% HCl, 15% H₂O₂) to remove carbonate and organic components, respectively. Density separations at 2.53 and 2.58 g/cm³ were undertaken to isolate the K-feldspar fraction. Minerals >2.58 g/cm³ were then subjected to an HF acid digestion (40%, 60 min) to etch the outer 10–15 μm layer affected by alpha radiation; 10% HCl was then added to remove acid-soluble fluorides, and the sample was then dried and resieved. Quartz was concentrated from the remaining heavy-mineral fraction using a density separation at 2.68 g/cm³. Sample mass proved a constraint in this study, with a dry mass of ~450 g yielding ~70 mg to, exceptionally, 250 mg of each mineral type within the modal sand fraction (125–180 μm). Depending on the mass remaining after sample preparation, up to 12 multigrain 8 mm aliquots of quartz and K-feldspar were mounted on stainless-steel cups and aluminium discs, respectively, to determine D_e values. Owing to limited quantities of quartz and K-feldspar, sample GL17121 was not progressed to D_e measurement. Given the magnitude of D_e values above 120 Gy, and thus the relatively old ages previously reported for the site by Ashastina et al. (2017), intergrain analysis using single-grain or small aliquots was not considered of utility in this study. In this it is assumed that intergrain D_e distribution is dominated by microdosimetric effects, with the passage of time serving to amplify the influence of spatial variations in dose rate over D_e variation forced by partial bleaching and pedoturbation. Bulk subsamples for D_r assessment were homogenized in a mill, with 50 g then placed in a polystyrene pot with a polyethylene lid and stored for 3 weeks to enable radon stabilisation.

Measurement

Quartz and feldspar naturally exhibit marked intersample variability in luminescence per unit dose (sensitivity). Therefore, the estimation of dose absorbed since burial requires calibration of the natural signal using known doses of laboratory radiation. D_e values were quantified using a single-aliquot regenerative-dose (SAR) protocol based on Murray and Wintle (2000, 2003) for quartz and Li et al. (2014b) for K-feldspar. In the case of quartz, this was facilitated by a Freiberg Instruments Lexsyg Smart irradiation-stimulation-detection system (Richter et al., 2015). The quartz was stimulated at 445 ± 3 nm and 80 mW/cm² by blue laser diodes combined with 3 mm Schott GG420 and HC448/20 filters in front of each diode. Quartz was held at ~125°C (105°C substrate temperature) during optical stimulation to preclude charge retrapping within the 110°C TL trap (Murray and Wintle, 2000, 2003). IR stimulation, provided by IR laser diodes stimulating at 850 ± 3 nm filtered by 3 mm RG 715 and delivering ~ 200 mW/cm² to the sample, was used to detect feldspar contamination (Hütt et al., 1988). The significance of such contamination was assessed using post-IR OSL ratios (Duller, 2003). Resulting photon emissions from quartz were divided from stimulating photons by 2.5 mm Hoya U-340 and 1 mm NG4 glass filters, and a Delta BP 365/50 interference filter, then detected by a Hamamatsu H7360-02 bi-alkaline cathode photomultiplier. The OSL signal was derived from the initial 0.1 s of stimulation, subtracting a background count based on the final 5 s of stimulation. Aliquot irradiation was conducted using a ⁹⁰Sr/⁹⁰Y β source delivering 0.11 Gy/s.

K-feldspars were analysed using a Risø TL-DA-15 irradiation-stimulation-detection system (Markey et al., 1997; Bøtter-Jensen et al., 1999). IR stimulation for K-feldspars was provided at 875 ± 80 nm (IR diodes, Telefunken TSHA 6203, ~40 mW/cm²). IR stimulation was performed at 50°C then 200°C in an attempt to minimise fading signals, with the pIRIR signal then measured at 250°C (pIRIR₂₅₀; Li et al., 2014b). K-feldspar emissions were filtered by 2 mm Schott BG-39 and 3 mm Schott BG-3 glass and detected by an EMI 9235QA photomultiplier fitted with a blue–green sensitive bi-alkaline photocathode. The pIRIR signal was determined from the initial 1.2 s of data, less a background count derived from the final 10 s of stimulation. Irradiation of K-feldspars was provided by a ⁹⁰Sr/⁹⁰Y β source conveying 0.07 Gy/s.

Sensitivity change was monitored using a test dose (5 Gy for quartz; 30 Gy for GL17171 quartz; 33 Gy for K-feldspar) and corrected by dividing the natural and regenerative-dose blue-OSL and pIRIR signals (Lx) by the test-dose signal response (Tx). Hot bleaches were applied after each SAR cycle, at 280°C for quartz (Murray and Wintle, 2003) and 320°C for K-feldspar (Li et al., 2014b).

Dose recovery tests help to assess whether a SAR protocol might accurately determine absorbed dose (Murray and Wintle, 2003). The dose recovery ratio (the quotient of an applied dose close in magnitude to the D_e value of a sample and recovered dose; Table 3) should be statistically concordant with unity. For the quartz fraction, dose recovery tests were performed for a range of preheats (180°C–280°C for 10 s). The thermal treatment resulting in a dose recovery ratio consistent with unity was then selected for the D_e measurement. For the K-feldspar fraction, the efficacy of a 300°C preheat for 60 s (Li et al., 2014b) was assessed from the average of dose recovery ratios of three aliquots. The limited quantity of K-feldspar in GL17117 (B17-S1-OSL2) precluded a dose recovery test for this sample.

Table 3. Luminescence parameters from 125–180 μm quartz and K-feldspar isolates for dating.

^a Lexsyg smart substrate temperature.

^b IR, infrared; OSL, optically stimulated luminescence.

^c Age estimates expressed relative to 2017. Uncertainties in age are quoted at 1σ confidence, are based on analytical errors, and reflect combined systematic and experimental variability.

Anomalous fading tests on K-feldspar were conducted for two samples, one from the upper ice complex (GL17121), the other from the lower ice complex (GL17171)(Table 4). Fading measurements were adapted from the procedure outlined by Auclair et al. (2003) to align with the pIRIR measurement protocol in this study. To minimise the influence of initial sensitivity change upon fading calculations, each aliquot was subjected to the first SAR cycle of the K-feldspar measurement protocol. Aliquots were then bleached for 4 h in a Hönle SOL2 solar simulator to minimise any residual, optically sensitive signals. Each aliquot was then given a 474 Gy dose and preheated at 300°C for 60 s before storage. For GL17121, storage intervals were 38, 214, 544, and 1259 h; those for GL17171 differed slightly: 39, 350, 1105, and 1265 h. Lx/Tx values were obtained for three aliquots per storage interval and g-values were calculated using the R Luminescence package (Kreutzer et al., 2012).

Table 4. K-feldspar IR₅₀, pIRIR₂₀₀, and pIRIR₂₅₀ g values calculated for samples GL17121 and GL17171.

D_e values were interpolated from regenerative dose response curves (DRCs) and fitted with a single saturating exponential, using Analyst (Duller, 2015). For samples GL17117 (B17-S1-OSL2) and GL17171 (B17-S1-OSL1), single exponential fits produced infinite estimates of D_e. In both instances, D_e values were based on exponential plus linear fits. Given the use of multigrain aliquots in this study, age estimates are based on measures of D_e centrality; weighted mean D_e values were calculated using the central age model (CAM; Galbraith et al., 1999) within the R Luminescence package (Kreutzer et al., 2012).

U, Th, and K concentrations and U disequilibrium (²²⁸Ra/²³⁸U) within the sediment were measured from subsamples using a laboratory-based Ortec GEM-S high-purity Ge coaxial detector spectrometer system, calibrated with certified reference materials supplied by CANMET (Table 2). Values of ²²⁸Ra/²³⁸U were, with the exception of GL17119 (B17-S2-OSL4) and GL17121 (B17-S2-OSL6), consistent with unity, suggesting negligible U disequilibrium. Using DRAC (Durcan et al., 2015), estimates of radionuclide concentration were converted into external, lithogenic D_r values (Adamiec and Aitken, 1998), accounting for D_r modulation forced by grain size (Mejdahl, 1979) and gravimetric moisture content (Zimmerman, 1971). Owing to the persistence of permafrost in the region, we assume gravimetric water content to be representative of the burial period. Nevertheless, the correction assumes liquid water instead of the in situ ice content, a distinction that is yet to be investigated in detail. Lithogenic radiation internal to K-feldspar grains was assumed to derive from a K content of 12.5% (Huntley and Baril, 1997). Cosmogenic D_r values were calculated on the basis of sample depth, geographic position, and matrix density (Prescott and Hutton, 1994). Luminescence ages are reported as thousands of years (ka) before the time of sampling. The difference between the year of sampling (e.g., 2017 in the present study) is considered negligible compared with the year AD 1950 datum for the Pleistocene ¹⁴C ages reported here.

¹⁴C dating

Organic remains from the samples of ice-wedge ice and the host sediment were picked for radiocarbon dating at the MICADAS ¹⁴C dating facility of the Alfred Wegener Institute, Bremerhaven. Detailed descriptions of the laboratory procedures are given in Opel et al. (2019). In addition to the previously published radiocarbon ages in Ashastina et al. (2017), Murton et al. (2017b), Opel et al. (2019), Vasil'chuk and Vasil'chuk (2019), and Vasil'chuk et al. (2020), two more sediment samples from the upper sand unit were newly dated (Table 5). Results are given as F¹⁴C values (Reimer et al., 2004). Conventional radiocarbon ages are presented in years before present (yr BP). Ages within the calibration range were calibrated to years before present (cal yr BP), that is, before AD 1950, using Calib 8.20 (Stuiver and Reimer, 1993) based on the IntCal20 data set (Reimer et al., 2020). Calibrated age values are rounded to the nearest 10 yr.

Table 5. Radiocarbon ages of organic remains in ice wedges and host sediments as well as respective sample depths.^a

^a The samples at the AWI MICADAS ¹⁴C dating facility were radiocarbon dated as gas targets (Lab ID ends with 1.1) or graphite targets (Lab ID ends with 2.1). The ages were calibrated using CALIB 8.2 (Stuiver and Reimer, 1993) and the IntCal20 calibration curves (Reimer et al., 2020). Calibrated age values are rounded to the nearest 10 yr. Calibrated finite radiocarbon ages are shown in Figure 8. n/r, not reported; n/a, not analysed; n/i, not identified; S, sediment; IW, ice wedge.

^b References: (1) Ashastina et al. (2017); (2) Murton et al. (2017b); (3) Opel et al. (2019); (4) Vasil'chuk and Vasil'chuk (2019); (5) Vasil'chuk et al. (2020); and (6) this study.

^c interpreted as relocated material by Vasil'chuk et al. (2020).

^d Interpreted as nonfinite date by Murton et al. (2017b).

^e Interpreted as relocated material by Opel et al. (2019).

^f The angular brackets [ ] indicate that the calibrated range impinges on end of calibration data set.

³⁶Cl/Cl dating

Background and age calculation

The ³⁶Cl/Cl dating method determines the difference in ages between distinctly different generations of ground ice within permafrost, based on measurements of ³⁶Cl/Cl ratios, that is, the radionuclide (³⁶Cl) relative to the two stable nuclides (³⁵Cl and ³⁷Cl). The ³⁶Cl/Cl method was first applied to permafrost samples from Cape Svyatoy Nos, northeastern Siberia (Gilichinsky et al., 2007). Dating of a more representative collection of ice samples from permafrost exposed along the coast of the Dmitry Laptev Strait (Blinov et al., 2009; Fig. 1a) showed the potential of the method and identified its limitations and uncertainties. As ¹⁰Be was previously found unsuitable and again confirmed (Merchel et al., 2019) for dating ground ice with substantial sediment inclusions, ³⁶Cl/Cl dating is, therefore, the radionuclide dating method of choice, and its basis is briefly described here.

The long-lived radioactive isotope of chlorine ³⁶Cl (half-life T _1/2 = 301 ± 2 ka; Endt, 1990; Firestone, 1996) forms mainly in nuclear reactions of galactic and solar cosmic ray particles on atmospheric argon. ³⁶Cl atoms generated in the stratosphere enter the troposphere and, after mixing with the tropospheric fraction, are deposited on the Earth's surface by wet precipitation and by dry sedimentation. The mean global cosmogenic production rate of ³⁶Cl in the atmosphere is about 24 atoms/m²/s (Masarik and Beer, 2009), which supports local surface fluxes, depending on geographic location and climatic conditions.

The stable isotopes of chlorine (³⁵Cl and ³⁷Cl), according to the well-established global chlorine cycle (Graedel and Keene, 1996), enter the troposphere by sea spray and return to the Earth's surface with atmospheric water. The local deposition flux of Cl depends on the distance to oceans and on the dominant local wind directions. In regions with permafrost, winter precipitation enters ice wedges mainly in spring as snow meltwater percolates and refreezes in thermal contraction cracks (Opel et al., 2018). Then, after an ice wedge ceases growing and becomes isolated from new atmospheric inputs of ³⁶Cl, the ³⁶Cl/Cl ratio decreases with time, following the law of radioactive decay. The time interval between the ages of two ice-wedge samples is determined by the difference in their residual ³⁶Cl/Cl ratio. Obviously, the validity of the dating rests on the assumption that the ³⁶Cl/Cl input into the atmospheric water cycle is constant and that the ice wedge is a closed system.

The directions of moisture fluxes, from west to east in northern Europe and Asia, indicate that most moisture presently reaching Siberian regions with longitudes <140°E originates from the relatively warm northern Atlantic Ocean (Kuznetsova, 1998). Moisture transport from the cold Arctic Ocean to Siberia can be considered negligible, particularly during winter, when the Arctic Ocean is covered by sea ice. Therefore, the change in distance of north Siberian regions to the Arctic Ocean is not expected to influence the deposition flux of stable chlorine.

Temporal and spatial variations in ³⁶Cl atmospheric flux reflect a combination of variations in production and transport. The production rate of ³⁶Cl has a strong latitudinal dependence caused by the shielding effect of the Earth's magnetic field. However, strong mixing of the stratospheric air masses (Heikkila et al., 2008) eliminates most of this effect. The production rate is also affected by temporal changes of solar activity and of the geomagnetic field intensity, which both modulate the cosmic ray flux in time. The corresponding decadal- to centennial-scale variations of ³⁶Cl concentration are well preserved in polar ice cores (Muscheler et al., 2007), but their resulting effect should cancel out when averaged on the geologic timescale.

The upper limit of age determination of wedge ice is defined by ³⁶Cl in situ production. Such production may occur at the place of fixation by thermal-neutron capture of stable ³⁵Cl contained in ice. These low-energy neutrons originate from cascades of cosmic ray interactions above and below the ground level, and from the decay of natural uranium and thorium. The dating limit is reached when the atmospheric concentrations in ice decay to the level of the in situ production and corresponds to an age limit of 3 Ma (Tikhomirov and Blinov, 2009). This limit likely exceeds the age of most terrestrial permafrost samples.

The ³⁶Cl/Cl method proposes that the time interval Δt between the formation of two ice-wedge horizons (1 and 2) is calculated from the corresponding ³⁶Cl/Cl ratios according to the formula:

(Eq. 2)$${\rm \Delta }t = t_2\;-\;t_1 = {\rm \tau }_{36}\;{\rm ln}\;\left[{\displaystyle{{( {^{36} {\rm Cl}/{\rm Cl}} ) \;t_1} \over {( {^{36} {\rm Cl}/{\rm Cl}} ) \;t_2}}} \right] $$

The mean lifetime of ³⁶Cl is τ₃₆ = T _1/2/ln 2 = (434 ± 3) ka. For the model base sample of known age, the equation gives the absolute age of the deeper sample. Thus, ³⁶Cl/Cl age estimates are reported as the age difference, in thousands of years (ka), between the younger and older ice wedges.

Sample processing and AMS measurements

Water melted from ice wedges was chemically treated in a dedicated ³⁶Cl (i.e., Cl- and S-free) chemistry laboratory at the Helmholtz-Zentrum Dresden-Rossendorf. The only suitable chemical form for ³⁶Cl AMS measurements is AgCl; hence, radiochemical separation needs to produce AgCl, preferably with high chemical yield and low isobar (³⁶S) abundance. Having experienced low chemical yield (20%–35%) for AgCl from large groundwater and ice samples during routine sample treatment, we split the four ice-wedge samples (Table 6) of this study into two halves and applied our routine method, as well as an alternative one with a preconcentration step using anion exchange. Details have been presented earlier (Merchel et al., 2019). Further sample processing followed routine protocols for calcite samples but without the use of isotopically enriched ³⁵Cl carrier (Merchel et al., 2013). Individual results of ³⁶Cl/³⁵Cl presented in Table 6 for the two aliquots of each sample can be interpreted as replicate measurements. Resulting AgCl was pressed into dedicated Cu sample holders (Pavetich et al., 2014) without taking any further precautions like AgBr backing for additional isobar suppression. A specialised ion source with lowest cross-contamination and long-term memory (Pavetich et al., 2014) attached to the 6 MV tandem accelerator (Rugel et al., 2016) was used for AMS measurements at the DREAMS (DREsden AMS) facility. All ³⁶Cl/Cl data are traceable to the primary-type standard material SM-Cl-11 with a nominal ratio of (1.079 ± 0.010) × 10⁻¹¹ (Merchel et al., 2011). The sequential age difference of the measured samples, calculated with Eq. 2, is presented in Table 6 (“Calculated Age Difference”). The given uncertainties are calculated formally from experimental results and do not include nonstatistical uncertainty of their interpretation.

Table 6. Sample information and results from accelerator mass spectrometry for ³⁶Cl/Cl dating.^a

^a The data are traceable to primary-type standard material SM-Cl-11 (Merchel et al., 2011). The given uncertainties include statistical measurement uncertainties, the given uncertainty of the standard used, and the uncertainty of the mean of the standard measurement.

^b Age difference between this sample and the one above.

RESULTS

Luminescence dating

D_e, D_r, and luminescence age data are presented in Tables 2 and 3; Figure 5 illustrates representative signal decays and DRCs, as well as inter-aliquot age distributions. The strong IRSL response (Fig. 5a and b) and post-IR OSL ratios (Table 3) for quartz suggest the presence of significant feldspar contamination. A 2-week, 35% H₂SiF₆ digestion was subsequently applied to one sample (GL17172) in an attempt to remove the contaminant (Jackson et al., 1976; Berger et al., 1980) without significantly altering quartz grain size. The SAR analysis was then repeated, producing a negligible IRSL signal, a post-IR OSL ratio consistent with unity (Table 3), and an OSL fast component more consistent with that of quartz (ca. 94% of the signal at t = 0), all suggesting removal of the contaminant.

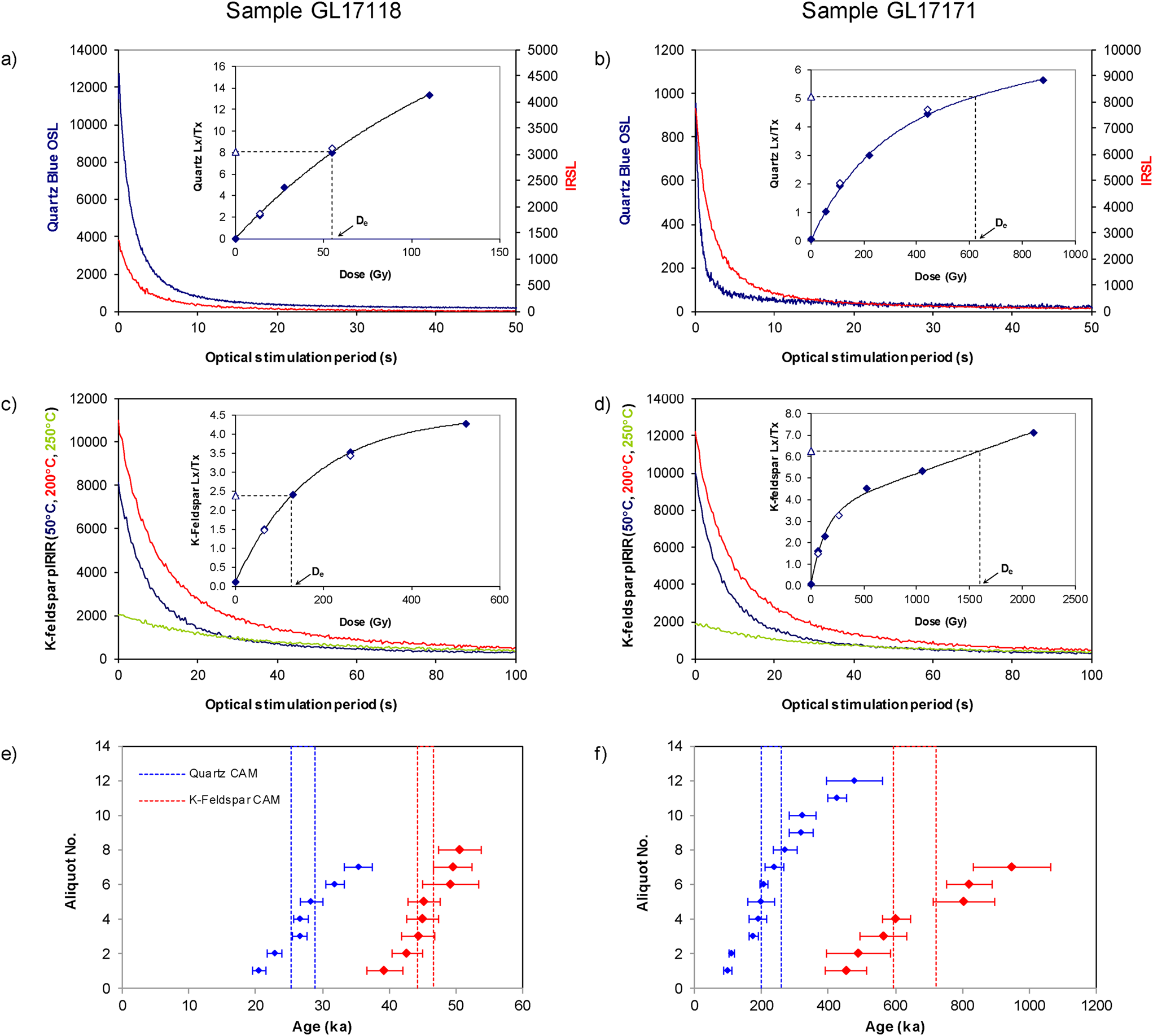
Figure 5. Dose–response curves (DRCs) and inter-aliquot age distributions for samples GL17118 (B17-S2-OSL3, left column) and GL17171 (B17-S1-OSL1, right column), representative of the sample suite; the top and bottom optically stimulated luminescence (OSL) samples from the Batagay megaslump sequence. (a and b) blue OSL and infrared-stimulated luminescence (IRSL) signal decays from quartz; (c and d) IR₅₀, pIRIR₂₀₀, and pIRIR₂₅₀ signal decays from K-feldspar; insets are the associated Lx/Tx DRCs (open triangle, natural signal; closed diamonds, regenerative-dose signals; open diamonds, repeat regenerative doses). (e and f) inter-aliquot age distributions and central age models (CAM) derived from quartz blue OSL and K-feldspar pIRIR₂₅₀.

Dose recovery ratios are, except for GL17119 (B17-S2-OSL4), consistent with unity for the majority of quartz samples, indicating accurate retrieval of applied laboratory doses (Table 3). For K-feldspar extracts, dose recovery ratios from pIRIR₂₅₀ generally produced overestimates of the applied dose by 10%–30% (Table 3). Figure 6 highlights that dose recovery ratios for IR₅₀ and pIRIR₂₀₀ demonstrate greater consistency with unity. Low and high dose repeat ratios (Table 3) for both quartz and K-feldspar are generally consistent with unity, which suggests adequate correction of any sensitivity change that progressed with laboratory measurement. In general, the variation in D_e beyond counting statistics (% overdispersion) increases with depth, most likely as a function of the proximity of absorbed dose to saturation. Overdispersion is generally higher for quartz than K-feldspar, which on a multigrain aliquot likely reflects a greater proportion of K-feldspar grains contributing to the luminescence signal relative to quartz.

Figure 6. Dose recovery ratios for IR₅₀, pIRIR₂₀₀, and pIRIR₂₅₀ of three aliquots from sample GL17171 (B17-S1-OSL1).

K-feldspar fading tests on GL17121 and GL17171 reveal a pattern consistent with previous studies of pIRIR signals (e.g., Thomsen et al., 2008), whereby the g-value depends on IRSL stimulation temperature (Fig. 7; Table 4). For both samples, the IR₅₀ signal displayed the greatest IRSL decay during storage. However, the g-value for GL17171 (8.30 ± 0.98%/decade) was much higher than that calculated for GL17121 (2.96 ± 0.98%/decade). GL17121 displayed negligible fading at elevated stimulation temperatures, with the pIRIR₂₀₀ and pIRIR₂₅₀ signals producing g-values statistically consistent with zero. For GL17171 the pIRIR₂₀₀ signal still observed significant decay (g = 3.44 ± 1.02%/decade), whereas the pIRIR₂₅₀ signal produced a g-value indistinguishable from zero.

Figure 7. Signal depletion as a function of storage time for the IR₅₀ (blue circles), pIRIR₂₀₀ (red crosses), and pIRIR₂₅₀ (green triangles) signals for samples GL17121 (a) and GL17171 (b). Storage times (t) and Lx/Tx ratios were normalised to the first/prompt measurements (t _c) at 38 and 39 h for panels a and b, respectively.

Six age estimates were produced from each of the quartz and K-feldspar fractions (Table 3). Samples from the same mineral produce ages that are in stratigraphic order. However, except for GL17120 (B17-S2-OSL5), all quartz ages are significantly younger than those from K-feldspar by 20%–65%. The lower ice complex, sampled at depths of ~50 and 49.5 m below the ground surface, yielded quartz OSL ages of 228 ± 32 ka and 244 ± 16 ka, and K-feldspar pIRIR ages of 658 ± 74 ka and 693 ± 97 ka (GL17171 and GL17117, B17-S1-OSL1 and B17-S1-OSL2, respectively). The upper ice complex, sampled ~5 m above its base (GL17172), yielded a quartz OSL age of 57.5 ± 5.8 ka and a K-feldspar pIRIR age of 90.5 ± 6.2 ka. The upper sand unit, sampled at depths of 11, 2.3, and 2.1 m below the ground surface, provided quartz OSL ages of 40.0 ± 3.9 ka, 41.0 ± 3.9 ka, and 27.1 ± 2.1 ka, and K-feldspar pIRIR ages of 61.0 ± 3.7 ka, 50.9 ± 3.5 ka, and 45.5 ± 2.9 ka (GL17120, GL17119, and GL17118 corresponding to B17-S2-OSL5, B17-S2-OSL4, and B17-S2-OSL3, respectively).

¹⁴C dating

Several radiocarbon ages yielded lower ¹⁴C intensities than the blanks included in the respective sequence. For these cases, data are given as F¹⁴C_sample < F¹⁴C_blank, resulting in minimum ages (Table 5). Based on all available radiocarbon ages from the Batagay megaslump, but excluding those considered as redeposited by the original authors (Ashastina et al., 2017; Murton et al., 2017b; Opel et al., 2019; Vasil'chuk and Vasil'chuk, 2019; Vasil'chuk et al., 2020), it is obvious that radiocarbon dating covers only the uppermost units of the stratigraphy, that is, the Holocene cover and the upper parts of the upper sand and the upper ice complex, whereas the respective lower parts of these units yield nonfinite radiocarbon ages. The Holocene cover deposits exhibit only one age of 0.39 cal ka BP. The upper sand unit has finite ages that range from 15.09 to 42.39 cal ka BP. The finite age range of the upper ice complex spans from 27.16 to 52.21 cal ka BP (Table 5). Nonfinite ages from both sediment and wedge ice of the upper ice complex are common and might suggest formation of this unit started well before 50 cal ka BP. The lowermost three units—the woody debris layer, the lower sand, and the lower ice complex—show nonfinite radiocarbon ages, with one exception from the woody debris layer (49,320 ± 3,150 yr BP interpreted as a nonfinite age by Murton et al., 2017b). It is notable that previous sampling in the megaslump at different accessible locations and uncertainties about exact sampling depth complicate the understanding of age–depth relations.

³⁶Cl/Cl dating

AMS results for ³⁶Cl/³⁵Cl measurements are presented as individual results for the two aliquots of each sample. Assuming natural ³⁵Cl/³⁷Cl, they can be transformed into ³⁶Cl/³⁵⁺³⁷Cl ratios if needed. ³⁶Cl/³⁵Cl sample values are two to three orders of magnitude above typical machine blank values, hence, no blank correction has been applied. Total uncertainties in the dating include those associated with the statistical measurement of the samples, the standard SM-Cl-11 used (Merchel et al., 2011), the mean of the standard measurement, and an additional 6% systematic uncertainty to account for unstable measurement conditions (Table 6).

Weighted mean ³⁶Cl/³⁵Cl ratios of the four studied ice wedges range from (2.79 ± 0.12) × 10⁻¹² for the stratigraphically youngest ice wedge B17-IW4 to (7.11 ± 0.34) × 10⁻¹³ for the stratigraphically oldest ice wedge B17-IW1 and decrease with depth (Table 6). The corresponding calculated ages are in correct stratigraphic order, that is, without age reversals. They show that the ice wedge B17-IW5 from the upper ice complex is 10 ± 19 ka older than ice wedge B17-IW4 from the upper sand. Ice wedge B17-IW6, also from the upper ice complex, is 11 ± 20 ka older than ice wedge B17-IW5. Ice wedge B17-IW1, from the lower ice complex, is 573 ± 42 ka older than ice wedge B17-IW6 (Table 6).

DISCUSSION

Methods of permafrost age determination

A major problem in determining the age of permafrost is that dating methods are generally not well established on frozen material and must be applied to differing constituents (i.e., organic remains, quartz, feldspar, ice) that may have different formation processes and ages. For example, ice wedges are—due to their downward-directed formation—younger (by up to many thousands of years or more) than their host sediments at the same altitude and may penetrate multiple layers of sediment, each of differing age. Some of these uncertainties relate to unknown influences of [1] freezing and thawing or warming and cooling and [2] temperature-gradient-induced migration of unfrozen water through porous media on chemical and physical parameters important to the four age-determination techniques applied at Batagay.

Luminescence dating

Based on the diagnostics deployed, issues of luminescence age reliability are fivefold. First, the mass of quartz and K-feldspar within the modal grain fraction is relatively small, which meant that after preliminary measurements as few as seven multigrain aliquots were available to produce a luminescence age. Future sampling should aim to retrieve twice the bulk mass from the site (~1 kg). Nonetheless, the luminescence ages are in stratigraphic order and distinct between units. Second, a nonstandard post-HF (H₂SiF₆) step is required to remove feldspar contamination from quartz sand samples in the Batagay sequence. For the single sample where this acid treatment was used (GL17172, B17-S2-OSL7), there was a modest though statistically insignificant increase in D_e relative to its untreated counterpart (Table 3). At this point, we consider the age estimates from quartz untreated with H₂SiF₆ as minima owing to the dominance and probable anomalous fading of the contaminating feldspar IRSL signal.

Third, for the K-feldspar samples, the mean dose recovery ratio for most samples indicates that the measured dose overestimates the applied laboratory dose by 10%–30% (Table 3). Of the five samples for which a dose recovery test was undertaken, only sample GL17172 (B17-S2-OSL7) returned a mean pIRIR₂₅₀-based dose recovery ratio consistent with unity. In contrast, the mean dose recovery ratios for IR₅₀ and pIRIR₂₀₀ approximate unity for each sample. The success of SAR dose recovery tests in previous studies using high-temperature K-feldspar pIRIR signals has varied, with measured doses overestimating (e.g., Thiel et al., 2011), underestimating (e.g., Li and Li, 2011), and consistent with (e.g., Li et al., 2014b) the applied dose. The proposed origins of this inconsistent performance can be summarised as an effect of residual signals, present before the initial laboratory dose is applied (e.g., Stevens et al., 2011) and/or remaining after each regenerative dose (e.g., Colarossi et al., 2018), and an effect of sensitivity changes within the first measurement cycle (e.g., Qin et al., 2018) and/or between the first and second cycles (Roberts, 2012). A poor high-temperature pIRIR dose recovery outcome does not necessarily translate directly to an inaccurate estimate of burial age (e.g., Thiel et al., 2011), but it is clear that the effects of residual signals and response to measurement conditions can vary between samples. It is therefore essential to compare high-temperature K-feldspar pIRIR SAR age estimates with independent chronological controls.

Fourth, despite varying degrees of IRSL decay for the lower stimulation temperatures, for both GL17121 and GL17171 the pIRIR₂₅₀ signal does not appear to significantly fade at room storage temperatures. It is acknowledged that the evaluation of fading is limited by laboratory time scales and precision. However, it is also noted that lower levels of anomalous fading in K-feldspar have previously been observed under frozen conditions (e.g., Krause et al., 1997; Preusser et al., 2001, 2003; Preusser and Schlüchter, 2004; Huntley and Lian, 2006; Thomsen et al., 2008; Fuchs et al., 2013).

Finally, the characteristic saturation point (D₀) for K-feldspar in these samples, derived from fitting a single exponential to DRCs, is broadly comparable to the “D₁” value (D₀ value for first of a double exponential fit; 142 ± 35 Gy) presented by Li et al. (2015) for pIRIR₂₅₀ Lx/Tx-based DRCs in their evaluation of standardised DRCs for K-feldspar. All but the two deepest samples, GL17117 and GL17171, produce D_e values that are lower than 2D₀ (86% saturation of a single exponential DRC), proposed by Wintle and Murray (2006) as the upper limit for quartz OSL age estimation. The D_e values for GL17117 (B17-S1-OSL2) and GL17171 (B17-S1-OSL1) also exceed 3D₀ (95% saturation of a single exponential DRC). Given this observation and that D_e values were derived from non-standard, exponential plus linear fits, the pIRIR₂₅₀ ages associated with GL17117 (B17-S1-OSL2) and GL17171 (B17-S1-OSL1) should be treated with caution if considered in isolation.

Given the range of uncertainties discussed, it is essential that the reliability of luminescence age estimates be considered through a comparison of quartz OSL, K-feldspar pIRIR₂₅₀, and independent age controls. The relative difference in ages between quartz OSL and K-feldspar pIRIR₂₅₀ increases with depth. Quartz ages are 20%–40% younger than those for K-feldspar through the upper sand and upper ice complex, whereas those for quartz within the lower ice complex are ~65% younger than those for K-feldspar. The removal of feldspar contamination in sample GL17172 (B17-S2-OSL7) reduces the discrepancy between quartz and K-feldspar ages from 36% to 25%, though this shift is not statistically significant. Given the relatively high preheat and cutheat temperatures (>200°C, substrate >160°C) used for quartz measurements in this study, any thermally unstable, ultrafast OSL component is unlikely to explain the age gap between quartz treated with H₂SiF₆ and K-feldspar (Jain et al., 2008). Further, it is the quartz age that remains consistent with the ³⁶Cl/Cl ages in the upper ice complex, with the K-feldspar age being significantly higher despite the relatively large uncertainties in the ³⁶Cl/Cl estimates (Fig. 8). For GL17172 at least, this might suggest that it is the K-feldspar that is overestimating age. Residual doses have frequently been observed in pIRIR studies. These are typically less than ~35 Gy but can range from ~17 to 145 Gy (Lowick et al., 2012; Li et al., 2014a). They appear sample dependent rather than driven by bleaching conditions (Li et al., 2014a), but when combined with the burial dose can produce age overestimates. In the case of GL17172, the K-feldspar age exceeds that of quartz by virtue of an additional 63 Gy (accounting for differences in D_r between quartz and K-feldspar). Although the aeolian nature of the sedimentary deposits from which the luminescence samples were extracted would have promoted bleaching, there was insufficient sample to estimate sample-specific residual dose through laboratory bleaching experiments. At this point, we assume 63 Gy to be the upper limit of residual dose. The lower sand was previously dated by Ashastina et al. (2017) using quartz OSL and K-feldspar IR₅₀ (Fig. 8) and ascribed to MIS 6. Though the age estimates are stratigraphically consistent, there is no independent chronological control in this unit, and there is again divergence between the quartz and K-feldspar age estimates, with the former 32% younger than the latter. The IR₅₀ signal is not corrected for anomalous fading and is considered here to be a minimum age estimate.

Figure 8. Schematic overview of all available chronostratigraphic data of the Batagay megaslump summarised from (1) Ashastina et al. (2017); (2) Murton et al. (2017b); (3) Opel et al. (2019); (4) Vasil'chuk and Vasil'chuk (2019); (5) Vasil'chuk et al. (2020); and (6) this study. Stratigraphy not to scale (see Table 1). Radiocarbon ages are shown as calibrated ages in ka BP. Note that this compilation is based on several sampling campaigns by different researchers working at different sections, which precludes placing the data in true vertical order. The positions of ³⁶Cl/Cl and ¹⁴C ages above luminescence age do not have depth significance and are solely to show the single data points clearly. Glacial–interglacial cycles shown in the lower graph derive from the marine isotope stages of the LR04 stack of benthic δ¹⁸O (Lisiecki and Raymo, 2005) and a current review of past interglaciations (Past Interglacials Working Group of PAGES, 2016), which are given here for chronologic orientation. MIS numbers above the curve indicate interglacial maxima (interstades of the Late Pleistocene are given in brackets). MIS numbers below the curve indicate glacial maxima. At the bottom of the plot, “H” stands for Holocene and “E P” for Early Pleistocene.

Within the lower ice complex, it is the K-feldspar pIRIR₂₅₀ age that is coeval with that from ³⁶Cl/Cl, with the quartz OSL age estimate significantly younger. It is unlikely that the difference here between quartz and K-feldspar ages relates to residual doses in the latter; it would require a residual of ~1100 Gy to explain the divergence, which is an order of magnitude higher than any previously reported residual dose. Although the Lx/Tx DRCs for the quartz OSL and K-feldspar pIRIR₂₅₀ signals in this unit have similar D₀ values (Table 3), it appears that quartz has crossed a threshold where it underestimates age. This may in part relate to anomalous fading driven by feldspar IRSL contamination of the quartz OSL signal. This underestimation also likely afflicts the quartz age from the lower sand unit (Ashastina et al. 2017), which is less than the IR₅₀ K-feldspar age estimate that in itself is probably an underestimate due to anomalous fading. The agreement in age between K-feldspar pIRIR₂₅₀ and ³⁶Cl/Cl is encouraging, but it is acknowledged that D_e values associated with the former exceed 3D₀ (95% saturation), and until further work is conducted pIRIR₂₅₀ indicates that the lower ice complex dates to at least 650 ka.

¹⁴C dating

The ¹⁴C dating of different organic materials has proven useful to varying degrees for determining the age of the upper part of the permafrost sequence at Batagay. Organic samples dated (n = 40) from the upper ice complex, the upper sand unit, and the cover layer comprise plant macrofossil remains (wood fragments, twigs, leaves, stems, in situ rootlets, charcoal), ground-squirrel droppings, insect remains, and unidentified microinclusions within ice wedges (Table 5). The calibrated ages range from 0.39 cal ka BP in the cover layer to 51.92 cal ka BP, and numerous ages are nonfinite (Table 5). Interpretation of the finite ¹⁴C ages, however, highlights a number of problems. First, some material, particularly wood fragments, is likely reworked—for example by thermal erosion from permafrost—and simply provides maximum ages of sediment deposition. Therefore, we compare ¹⁴C ages obtained only from in situ material with ages from other methods. Second, unidentified organic material in microinclusions in wedge ice (Vasil'chuk and Vasil'chuk, 2019; Vasil'chuk et al., 2020) makes interpretation of ages obtained by these authors difficult without knowing exactly how the material relates to the age of the host ice. Finally, depth measurements obtained from different parts of the large and topographically variable floor and headwall of the megaslump had to be integrated, and this introduced considerable error in determining the samples’ precise stratigraphic positions. This error is compounded by the downslope inclination of the stratigraphy and the variable thickness and geometry of the stratigraphic units (Fig. 2) and by local irregularities in the distribution of ice and mineral soil. Nonetheless, the age estimates suggest in broad terms that the cover layer is of Holocene age, the upper sand unit began forming sometime within MIS 3 (58–28 ka) and formation continued into MIS 2 (28–11.7 ka), and the upper ice complex developed during MIS 3, but the starting time of formation is not known, because the oldest ages are beyond the effective limit of ¹⁴C dating (~40–50 ka).

We recommend that the best material for ¹⁴C dating of syngenetic permafrost at Batagay is plant material that can be identified taxonomically and is in growth position within the stratigraphic sequence. Such material includes in situ roots and tree stumps. Where in situ material is not available, we recommend dating of fragile macrofossils— which are unlikely to have survived significant reworking and are likely representative of the palaeoecological conditions and therefore local environment —a strategy adopted in stringent ¹⁴C dating studies from other permafrost regions (e.g., Mann et al., 2010; Kennedy et al., 2010; Murton et al., 2015, 2017a).

³⁶Cl/Cl dating

As the ³⁶Cl/Cl method provides relative ages with respect to a starting point of known age, we need to use other available age information to constrain the age of the reference ice wedge. We decided not to select the youngest and uppermost ice wedge B17-IW4 from the upper sand as the reference ice wedge, because (1) it is located only about 2 m below the modern surface (Fig. 4) and (2) its stable-isotope composition is quite close to that of a Holocene ice wedge nearby (Opel et al., 2019). Hence, we cannot exclude that this ice wedge is an epigenetic Holocene ice wedge, that is, it developed substantially later than the time of deposition of its host sediments of MIS 3 to MIS 2 age (Fig. 4), as discussed in detail by Opel et al. (2019). Instead, we selected ice wedge B17-IW5 from the upper ice complex as the reference for the ³⁶Cl/Cl dating results. Based on the available ¹⁴C ages for this ice wedge (calibrated median age 29 cal ka BP) and its host sediments (> 50 cal ka BP), we estimate about 40 ± 10 cal ka BP as starting point (base age) for the ³⁶Cl/Cl ice-wedge age calculations.

The deduced ages for the ice wedges from older strata are 51 ± 30 ka for ice wedge B17-IW6 from the upper ice complex and 624 ± 51 ka for ice wedge B17-IW1 from the lower ice complex (Table 6, “Interpreted Absolute Age”). It is notable that under the present assumptions, the large uncertainty range of the ³⁶Cl/Cl age of B17-IW6 covers the OSL age estimate from the upper ice complex but is somewhat younger than the pIRIR age. The ³⁶Cl/Cl age of B17-IW1 from the lower ice complex is distinctly older than the OSL ages from the lower ice complex but falls well into the uncertainty range of both pIRIR ages (Fig. 7). These results support the earlier finding of Blinov et al. (2009) that the strength of the ³⁶Cl/Cl method is to get age estimates for ice on long (i.e., glacial–interglacial) time scales, whereas it is not able to sufficiently resolve shorter (i.e., multimillennial) age differences between ice wedges. Due to the long lifetime of ³⁶Cl (434 ka), the method is more applicable to old (Middle Pleistocene) ice wedges than to younger (Late Pleistocene) ones.

However, the method's critical assumption is that the ratio of concentrations of cosmogenic ³⁶Cl to stable chlorine at a given time corresponds to the mean atmospheric value, which remains constant during the period of stable climatic conditions. As the potential influence of climatic changes cannot be excluded or quantitatively estimated so far, the results of the ³⁶Cl/Cl method should not be used as the only source of information but as supplementary evidence in combination with other dating results.

Dating synthesis

The new age estimates obtained from the four dating methods can be compared with the full data set of ages (Tables 3, 5, and 6) to evaluate the likely age of the lower ice complex, the upper ice complex, and the upper sand (Fig. 8). The lower ice complex provides two pIRIR ages of 658 ± 74 ka and 693 ± 97 ka from sand that, within uncertainties, are indistinguishable not only from each other but also from a single deduced ³⁶Cl/Cl age of 624 ± 51 ka from ice wedge B17-IW1. Accepting the caveats of pIRIR₂₅₀ Lx/Tx saturation, this consistency provides reasonable confidence that the lower ice complex developed during the early Middle Pleistocene or earlier, and we provisionally suggest an age of about 650 ka (MIS 16) or earlier.

The upper ice complex shows reasonable agreement between ages from three of the four dating methods. Sixteen finite ¹⁴C ages of ~50 to 27 cal ka BP and seven nonfinite ¹⁴C ages from different sections within the slump, one deduced ³⁶Cl/Cl age of 51 ± 30 ka, and one OSL age of 67.6 ± 9.9 ka point to the development of the upper ice complex during MIS 3, possibly ceasing during the early part of MIS 2. Nonetheless, we suspect that some of the ¹⁴C ages near the effective limit of ¹⁴C dating (~40–50 ka) underestimate the true age of ice-complex development, which could have started earlier during MIS 4.

The upper sand unit also shows reasonable agreement between ages from two of the dating methods. Eight finite ¹⁴C ages of ~42 to 15 cal ka BP and two nonfinite ¹⁴C ages are fairly similar to the three quartz OSL ages of 40.0 ± 3.9 ka, 41.0 ± 3.9 ka, and 27.1 ± 2.1 ka. These OSL ages are affected by feldspar contamination, but removal of this contaminant from GL17172 suggests any shift in age would be statistically insignificant at these depths. The agreement is strengthened if we select only those organic samples that were demonstrably in situ (i.e., rootlets) or that included delicate organic material (e.g., Empetrum nigrum leaves) that is unlikely to have survived much reworking. This selection provides three finite ¹⁴C ages from in situ rootlets of ~27 and 22 cal ka BP from a depth of ~1 m below the ground surface and one age of ~41 ka BP from a depth of 18.5 m. Additionally, a single age of ~42 cal ka BP was obtained from a depth of ~11 m, though the sample is considered less reliable than the rootlets on account of its composite nature (leaf, twigs, and Cyperaceae remains). The three pIRIR ages of 61.0 ± 3.7 ka, 50.9 ± 3.5 ka, and 45.5 ± 2.9 ka are somewhat greater than the ¹⁴C and OSL ages, which we attribute to residual doses within the K-feldspars. No deduced age is available from the ³⁶Cl/Cl method, because we used ice wedge B17-IW5 from the upper ice complex as a reference and hence cannot calculate an age for ice wedge B17-IW4. Overall, we infer that the upper sand unit accumulated during MIS 3 and 2, though further dating is needed to corroborate this and to determine the time when deposition commenced.

Palaeoenvironmental significance

The dating results (Fig. 8) suggest that the lower ice complex formed during or before MIS 16 (~677–622 ka), a pronounced glacial period with substantial glaciations in the Northern Hemisphere (Batchelor et al., 2019). Direct dating of permafrost to ~650 ka represents the oldest known permafrost in western Beringia and the second-oldest known ice in the Northern Hemisphere. The ancient permafrost at Batagay dates from the early part of the Middle Pleistocene, which began ~774 ka, during MIS 19 (Head, 2019). Only permafrost from the Klondike, Yukon, in eastern Beringia, is known to be older than that at Batagay and dates to ~740 ka (Froese et al., 2008). The ancient permafrost at Batagay indicates that ice-rich permafrost has survived repeated episodes of climate warming, including multiple glacial terminations and even the exceptionally warm and wet conditions during a “super-interglaciation” at 420 ka (MIS 11c; Vaks et al., 2013, 2020; Wennrich et al., 2016), the warmer-than-present last interglaciation (MIS 5e; CAPE, 2006), and the warm climate of the Holocene thermal maximum (Kaufman et al., 2004; Renssen et al., 2009). Clearly, the remaining lower ice complex, buried under ~50 m of covering permafrost deposits, has been resilient to natural climate and environmental change over multiple glacial–interglacial cycles (Fig. 8), though it is vulnerable to anthropogenic disturbance and local thermokarst activity (Murton et al., in press). Additionally, the thaw unconformity and erosional surface at the top of the lower ice complex (Fig. 3) indicate that this ice complex experienced partial thaw and erosion before deposition of the lower sand unit; thaw and erosion of unknown magnitude occurred on one or more occasions between MIS 16 and 4.

The direct dating of permafrost at Batagay to ~650 ka or earlier can be compared with inferences about permafrost conditions based on indirect evidence from western Beringia. The onset of permafrost during the late Pliocene has been inferred from pollen spectra consistent with a change in vegetation toward tundra and cold-adapted larch–birch forest from samples in and near Lake El'gygytgyn in Chukotka, northeastern Russia (Glushkova and Smirnov, 2007; Andreev et al., 2014; Brigham-Grette et al., 2013; Fig. 1a) and from a reduction of Ca²⁺ flux into the lake, attributed to reduced chemical weathering in the catchment, after 3.3 Ma, during the M2 cooling event (Wennrich et al., 2014). The present study cannot confirm a late Pliocene onset of permafrost in western Beringia, because such permafrost may have thawed and re-formed multiple times during the late Pliocene and Early Pleistocene, but it does provide robust evidence that the permafrost of the lower ice complex has persisted at the Batagay site continuously since at least ~650 ka. Such persistence is consistent with the absence of observed speleothem growth—due to permafrost freezing up the karst vadose system in caves—since ~429 ka (MIS 11) in a Siberian cave (Ledyanaya Lenskaya) near the boundary between continuous and discontinuous permafrost (see Vaks et al., 2013, 2020).

Given its great age, the permafrost of the lower ice complex offers excellent potential for preservation of ancient flora and fauna, including remains of environmental DNA as well as palaeoclimate proxies (ice, sediments), back to the early Middle Pleistocene. However, some limitations must be considered. Most prominent are gaps in the stratigraphy (e.g., erosional surfaces) that complicate correlation of the stratigraphy at Batagay with those from other Beringian sites.

CONCLUSIONS AND OUTLOOK

Four conclusions are drawn from this study. First, good agreement of age estimates between two independent dating methods (pIRIR dating of K-feldspar from sand and ³⁶Cl/Cl dating of ice-wedge ice) provides a reasonable degree of confidence in dating ancient permafrost that has persisted since before the last interglaciation.

Second, the ³⁶Cl/Cl method provides a valuable means of dating ancient ground ice. The method is more applicable to old (Middle Pleistocene) ice wedges than to younger (Late Pleistocene) ones.

Third, if the pIRIR and ³⁶Cl/Cl dating are correct, ancient permafrost within the lower ice complex at Batagay megaslump has been preserved since the early Middle Pleistocene (~650 ka or earlier) and represents the oldest known permafrost that has been directly dated in western Beringia and the second-oldest known dated permafrost in the Northern Hemisphere.

Fourth, the ancient permafrost at Batagay has been resilient to multiple episodes of climate warming and environmental change but is vulnerable to local disturbance by anthropogenic and thermokarst activity.

In terms of outlook, multiple dating methods—including ¹⁴C, pIRIR, OSL, and ³⁶Cl/Cl—are needed to date ancient permafrost, and a future priority should be to apply them to silt-rich yedoma in western Beringia in which palaeomagnetic dating can be added to the methods used in the present study. Further sampling campaigns should seek to secure larger (~1 kg) sediment samples to expand the number of luminescence aliquots and range of measurements, including direct assessment of pIRIR₂₅₀ residual doses, post-H₂SiF₆ quartz analysis, and investigation of the quartz age barrier at Batagay through thermally transferred OSL dating (Duller and Wintle, 2012). Tephras or microtephras should also be sought in western Beringia, as they have proved invaluable in dating of permafrost sequences in eastern Beringia. Future permafrost dating studies at the Batagay megaslump are needed to confirm the obtained results and to shed light on the disconformities between the lower ice complex and the lower sand as well as the lower sand and the woody debris layer.