1. Introduction
Understanding the behaviour of microswimmers in flow environments has a wide range of applications; from upstream contamination by bacteria in medical devices (Figueroa-Morales et al. Reference Figueroa-Morales, Rivera, Soto, Lindner, Altshuler and Clement2020), to the vertical migration of phytoplankton in turbulence (Lovecchio et al. Reference Lovecchio, Climent, Stocker and Durham2019). To predict how a microswimmer moves through a flow environment, we need to track the swimmer's orientation and position; these are coupled because changes in orientation can depend on space if the flow field is non-uniform, and changes in position occur due to swimming, which depends on orientation, as well as advection by the fluid.
Because of their small size, microswimmers typically live in the world of low Reynolds numbers, where inertial effects can be neglected (Purcell Reference Purcell1977). In this Stokes flow limit, the motion of spheroidal particles in simple shear was first described by Jeffery (Reference Jeffery1922), and shown to be valid for all axisymmetric particles by Bretherton (Reference Bretherton1962). These results have been used to study hydrodynamic phenomena in microswimmer suspensions (e.g. Pedley & Kessler Reference Pedley and Kessler1992). In general, for a swimmer with orientation  $\boldsymbol {p}$, the change in orientation is governed by
$\boldsymbol {p}$, the change in orientation is governed by
where  $\boldsymbol {\varOmega }$ is the vorticity,
$\boldsymbol {\varOmega }$ is the vorticity,  $\boldsymbol{\mathsf{E}}$ is the rate-of-strain tensor and
$\boldsymbol{\mathsf{E}}$ is the rate-of-strain tensor and  $B$ is the Bretherton constant (which ranges from zero for a sphere to unity for an infinitely thin rod). Microswimmers can display interesting dynamics distinct from the dynamics exhibited by passive colloids, as highlighted by Zoettl & Stark (Reference Zoettl and Stark2013) who used a dynamical systems approach to identify that elongated swimmers in Poiseuille flow can undergo either tumbling or swinging behaviour.
$B$ is the Bretherton constant (which ranges from zero for a sphere to unity for an infinitely thin rod). Microswimmers can display interesting dynamics distinct from the dynamics exhibited by passive colloids, as highlighted by Zoettl & Stark (Reference Zoettl and Stark2013) who used a dynamical systems approach to identify that elongated swimmers in Poiseuille flow can undergo either tumbling or swinging behaviour.
Microswimmers typically propel themselves through fluid environments by changing their shape in a periodic manner, for example by the beating of long whip-like flagella, or shorter cilia which cover the surface of the swimmer (Elgeti, Winkler & Gompper Reference Elgeti, Winkler and Gompper2015). Walker et al. (Reference Walker, Ishimoto, Moreau, Gaffney and Dalwadi2022) (WIMGD) take a minimal model to account for shape changing; they use the model of Jeffery, (1.1), but allow the Bretherton constant,  $B$, and swimming speed to be an oscillatory function of time. WIMGD show that this simple model can capture the key long-time dynamics of swimmers, in particular they are able to identify a single shape parameter which captures whether swimmers undergo rheotaxis, that is that the swimmers stably orientate themselves to swim upstream.
$B$, and swimming speed to be an oscillatory function of time. WIMGD show that this simple model can capture the key long-time dynamics of swimmers, in particular they are able to identify a single shape parameter which captures whether swimmers undergo rheotaxis, that is that the swimmers stably orientate themselves to swim upstream.
2. Overview
Applying (1.1) to planar Poiseuille flow, Omori et al. (Reference Omori, Kikuchi, Schmitz, Pavlovic, Chuang and Ishikawa2021) introduced and numerically analysed the following system of ordinary differential equations describing the transverse coordinate  $y$ and swimmer orientation
$y$ and swimmer orientation  $\theta$, with
$\theta$, with  $\theta =0$ corresponding to the direction of flow and
$\theta =0$ corresponding to the direction of flow and  $y=0$ the centreline:
$y=0$ the centreline:
The shape-changing nature of the swimmers is captured here by allowing the swimming speed,  $u$, and Bretherton constant,
$u$, and Bretherton constant,  $B$, to be oscillatory functions, where
$B$, to be oscillatory functions, where  $\omega \gg 1$ is the high frequency period of the oscillations. The parameter
$\omega \gg 1$ is the high frequency period of the oscillations. The parameter  $\gamma$ is a fixed (positive) characteristic shear rate of the flow.
$\gamma$ is a fixed (positive) characteristic shear rate of the flow.
In order to understand the observed dynamics, WIMGD define  $z(t)=y(t)/w^{1/2}$ and, inspired by Zoettl & Stark (Reference Zoettl and Stark2013), introduce a Hamiltonian-like quantity
$z(t)=y(t)/w^{1/2}$ and, inspired by Zoettl & Stark (Reference Zoettl and Stark2013), introduce a Hamiltonian-like quantity
where  $g$ is a closed form analytic function that only depends on
$g$ is a closed form analytic function that only depends on  $B$, and
$B$, and  $\langle (\cdot ) \rangle$ denotes the average value over an oscillatory period.
$\langle (\cdot ) \rangle$ denotes the average value over an oscillatory period.
WIMGD introduce fast and intermediate time scales:  $T=\omega t; \tau =\omega ^{1/2}t$, and implement a multiple-scale analysis, formally defining
$T=\omega t; \tau =\omega ^{1/2}t$, and implement a multiple-scale analysis, formally defining  $z(t)=z(T,\tau,t)$ and
$z(t)=z(T,\tau,t)$ and  $\theta (t)= \theta (T,\tau,t)$, treating each time variable as independent. At leading order, WIMGD find that the intermediate time scale dynamics directly corresponds to the dynamics for a fixed shape particle,
$\theta (t)= \theta (T,\tau,t)$, treating each time variable as independent. At leading order, WIMGD find that the intermediate time scale dynamics directly corresponds to the dynamics for a fixed shape particle,
Over the intermediate time scale  $\tau$, this yields the result that the leading-order expression for the Hamiltonian-like quantity given by
$\tau$, this yields the result that the leading-order expression for the Hamiltonian-like quantity given by  $H_0(t)$ (equal to
$H_0(t)$ (equal to  $H(t)$ with
$H(t)$ with  $z=z_0$ and
$z=z_0$ and  $\theta =\theta _0$) is conserved. Now, on considering
$\theta =\theta _0$) is conserved. Now, on considering  $H_0$ as a fixed quantity, as identified by Zoettl & Stark (Reference Zoettl and Stark2013) and illustrated in figure 1, two types of behaviours are observed: if
$H_0$ as a fixed quantity, as identified by Zoettl & Stark (Reference Zoettl and Stark2013) and illustrated in figure 1, two types of behaviours are observed: if  $H_0>g(0)$ the swimmers tumble and there is monotonic evolution of
$H_0>g(0)$ the swimmers tumble and there is monotonic evolution of  $\theta _0$; else if
$\theta _0$; else if  $H_0< g(0)$, the swimmers exhibit a swinging motion with
$H_0< g(0)$, the swimmers exhibit a swinging motion with  $\theta _0$ oscillating between two values. Also note in figure 1 the existence of the unique equilibrium point (
$\theta _0$ oscillating between two values. Also note in figure 1 the existence of the unique equilibrium point ( $z_0,\theta _0)=(0,{\rm \pi} )$ which corresponds to rheotaxis and
$z_0,\theta _0)=(0,{\rm \pi} )$ which corresponds to rheotaxis and  $H_0$ taking its minimum value of
$H_0$ taking its minimum value of  $g({\rm \pi} )$.
$g({\rm \pi} )$.
In order to examine the long-time dynamics of the swimmers, WIMGD examine the full dynamics of  $H(t)$. Specifically, they introduce the function
$H(t)$. Specifically, they introduce the function  $h(T,\tau,t)=H_{2T}+H_{1\tau }+H_{0t}$ to represent the
$h(T,\tau,t)=H_{2T}+H_{1\tau }+H_{0t}$ to represent the  $O(1)$ terms in the full derivative
$O(1)$ terms in the full derivative  ${\rm d} H/{\rm d} t$. Averaging over a period in
${\rm d} H/{\rm d} t$. Averaging over a period in  $T$ and then period in
$T$ and then period in  $\tau$ yields the long-time evolution equation
$\tau$ yields the long-time evolution equation
where  $W$ is a constant that can be calculated purely from the shape properties of the swimmer. The quantity
$W$ is a constant that can be calculated purely from the shape properties of the swimmer. The quantity  $f(H_0)$ is shown to be negative for all
$f(H_0)$ is shown to be negative for all  $H_0$ and so the sign of
$H_0$ and so the sign of  ${{\rm d} H_0}/{{\rm d} t}$ is determined by the constant
${{\rm d} H_0}/{{\rm d} t}$ is determined by the constant  $W$. Specifically, the fixed point
$W$. Specifically, the fixed point  $H_0=g({\rm \pi} )$ corresponding to the rheotactic configuration (
$H_0=g({\rm \pi} )$ corresponding to the rheotactic configuration ( $z_0,\theta _0)=(0,{\rm \pi} )$ is globally stable if
$z_0,\theta _0)=(0,{\rm \pi} )$ is globally stable if  $W>0$ and unstable if
$W>0$ and unstable if  $W<0$.
$W<0$.
WIMGD illustrate the asymptotic calculations with the specific example of  ${u(T)=\alpha +\beta \sin T}$ and
${u(T)=\alpha +\beta \sin T}$ and  $B(T)=\delta +\mu \sin (T+\lambda )$. In this case, if
$B(T)=\delta +\mu \sin (T+\lambda )$. In this case, if  $\beta \mu >0$ then
$\beta \mu >0$ then  $\lambda \in (0,{\rm \pi} )$ corresponds to
$\lambda \in (0,{\rm \pi} )$ corresponds to  $W<0$ and tumbling, whereas
$W<0$ and tumbling, whereas  $\lambda \in ({\rm \pi},2{\rm \pi} )$ corresponds to
$\lambda \in ({\rm \pi},2{\rm \pi} )$ corresponds to  $W>0$ and rheotaxis, as illustrated in figure 2, which also demonstrates the good agreement between the full solutions of the dynamical system with the asymptotic approximation.
$W>0$ and rheotaxis, as illustrated in figure 2, which also demonstrates the good agreement between the full solutions of the dynamical system with the asymptotic approximation.
Figure 2. The value of  $H$ as computed from the full numerical solution (blue), (2.1)–(2.3) and approximate solution (black), (2.6), for three phase shifts
$H$ as computed from the full numerical solution (blue), (2.1)–(2.3) and approximate solution (black), (2.6), for three phase shifts  $\lambda \in \{4{\rm \pi} /5,{\rm \pi},6{\rm \pi} /5\}$ and parameters
$\lambda \in \{4{\rm \pi} /5,{\rm \pi},6{\rm \pi} /5\}$ and parameters  $(\alpha, \beta,\delta,\mu )= (1,0.5,0.32,0.3)$. Adapted from WIMGD.
$(\alpha, \beta,\delta,\mu )= (1,0.5,0.32,0.3)$. Adapted from WIMGD.
3. Future
The elegant analysis of WIMGD has the potential to be applied and extended to a wide range of topical questions in the field of active biofluids, and there are open questions to determine the range of applicability of the results. In particular, WIMGD assumed shape changing can be modelled through periodic oscillations in the Bretherton constant (valid for axisymmetric particles in steady Stokes flow) and swimming speed. When considering individual microswimmers, the detailed mechanisms of propulsion, for example gait, can affect the swimming speed, as demonstrated theoretically and recently experimentally by using dynamically similar robotic models (Diaz et al. Reference Diaz, Robinson, Aydin, Aydin, Goldman and Wan2021). Furthermore, swimmers can swim in chiral patterns when propulsive torque and propulsive force are not aligned, and the unsteady nature of Stokes flow and external fields can also affect their swimming velocity and rotation rate (Maity & Burada Reference Maity and Burada2022). The role of external fields, such as gravity, light or chemical gradients is also incorporated in recent work by Lauga, Dang & Ishikawa (Reference Lauga, Dang and Ishikawa2021), who identified a new instability in suspensions of biased microswimmers. Because of the ability of swimmers to cross streamlines, their dispersion is quite different to passive colloids, and current work aims to identify the correct population-level transport models for microswimmers (e.g. Fung, Bearon & Hwang Reference Fung, Bearon and Hwang2022); incorporating the shape-changing effects of WIMGD would be an interesting development in such population-level models.
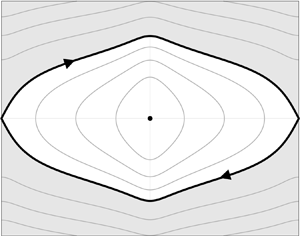

 $\tau$, showing contours of
$\tau$, showing contours of  $H_0$. Solutions in the shaded region where
$H_0$. Solutions in the shaded region where  $H_0>g(0)$ correspond to tumbling motion whereas trajectories with
$H_0>g(0)$ correspond to tumbling motion whereas trajectories with  $H_0< g(0)$ exhibit swinging motion. The stationary point
$H_0< g(0)$ exhibit swinging motion. The stationary point  $(z_0,\theta _0)=(0,{\rm \pi} )$ corresponds to upstream swimming, i.e. rheotaxis, with
$(z_0,\theta _0)=(0,{\rm \pi} )$ corresponds to upstream swimming, i.e. rheotaxis, with  ${H_0=g({\rm \pi})}$. Taken from WIMGD.
${H_0=g({\rm \pi})}$. Taken from WIMGD.
 $H$ as computed from the full numerical solution (blue), (2.1)–(2.3) and approximate solution (black), (2.6), for three phase shifts
$H$ as computed from the full numerical solution (blue), (2.1)–(2.3) and approximate solution (black), (2.6), for three phase shifts  $\lambda \in \{4{\rm \pi} /5,{\rm \pi},6{\rm \pi} /5\}$ and parameters
$\lambda \in \{4{\rm \pi} /5,{\rm \pi},6{\rm \pi} /5\}$ and parameters  $(\alpha, \beta,\delta,\mu )= (1,0.5,0.32,0.3)$. Adapted from WIMGD.
$(\alpha, \beta,\delta,\mu )= (1,0.5,0.32,0.3)$. Adapted from WIMGD.
1. Introduction
Understanding the behaviour of microswimmers in flow environments has a wide range of applications; from upstream contamination by bacteria in medical devices (Figueroa-Morales et al. Reference Figueroa-Morales, Rivera, Soto, Lindner, Altshuler and Clement2020), to the vertical migration of phytoplankton in turbulence (Lovecchio et al. Reference Lovecchio, Climent, Stocker and Durham2019). To predict how a microswimmer moves through a flow environment, we need to track the swimmer's orientation and position; these are coupled because changes in orientation can depend on space if the flow field is non-uniform, and changes in position occur due to swimming, which depends on orientation, as well as advection by the fluid.
Because of their small size, microswimmers typically live in the world of low Reynolds numbers, where inertial effects can be neglected (Purcell Reference Purcell1977). In this Stokes flow limit, the motion of spheroidal particles in simple shear was first described by Jeffery (Reference Jeffery1922), and shown to be valid for all axisymmetric particles by Bretherton (Reference Bretherton1962). These results have been used to study hydrodynamic phenomena in microswimmer suspensions (e.g. Pedley & Kessler Reference Pedley and Kessler1992). In general, for a swimmer with orientation $\boldsymbol {p}$, the change in orientation is governed by
$\boldsymbol {p}$, the change in orientation is governed by
where $\boldsymbol {\varOmega }$ is the vorticity,
$\boldsymbol {\varOmega }$ is the vorticity,  $\boldsymbol{\mathsf{E}}$ is the rate-of-strain tensor and
$\boldsymbol{\mathsf{E}}$ is the rate-of-strain tensor and  $B$ is the Bretherton constant (which ranges from zero for a sphere to unity for an infinitely thin rod). Microswimmers can display interesting dynamics distinct from the dynamics exhibited by passive colloids, as highlighted by Zoettl & Stark (Reference Zoettl and Stark2013) who used a dynamical systems approach to identify that elongated swimmers in Poiseuille flow can undergo either tumbling or swinging behaviour.
$B$ is the Bretherton constant (which ranges from zero for a sphere to unity for an infinitely thin rod). Microswimmers can display interesting dynamics distinct from the dynamics exhibited by passive colloids, as highlighted by Zoettl & Stark (Reference Zoettl and Stark2013) who used a dynamical systems approach to identify that elongated swimmers in Poiseuille flow can undergo either tumbling or swinging behaviour.
Microswimmers typically propel themselves through fluid environments by changing their shape in a periodic manner, for example by the beating of long whip-like flagella, or shorter cilia which cover the surface of the swimmer (Elgeti, Winkler & Gompper Reference Elgeti, Winkler and Gompper2015). Walker et al. (Reference Walker, Ishimoto, Moreau, Gaffney and Dalwadi2022) (WIMGD) take a minimal model to account for shape changing; they use the model of Jeffery, (1.1), but allow the Bretherton constant, $B$, and swimming speed to be an oscillatory function of time. WIMGD show that this simple model can capture the key long-time dynamics of swimmers, in particular they are able to identify a single shape parameter which captures whether swimmers undergo rheotaxis, that is that the swimmers stably orientate themselves to swim upstream.
$B$, and swimming speed to be an oscillatory function of time. WIMGD show that this simple model can capture the key long-time dynamics of swimmers, in particular they are able to identify a single shape parameter which captures whether swimmers undergo rheotaxis, that is that the swimmers stably orientate themselves to swim upstream.
2. Overview
Applying (1.1) to planar Poiseuille flow, Omori et al. (Reference Omori, Kikuchi, Schmitz, Pavlovic, Chuang and Ishikawa2021) introduced and numerically analysed the following system of ordinary differential equations describing the transverse coordinate $y$ and swimmer orientation
$y$ and swimmer orientation  $\theta$, with
$\theta$, with  $\theta =0$ corresponding to the direction of flow and
$\theta =0$ corresponding to the direction of flow and  $y=0$ the centreline:
$y=0$ the centreline:
The shape-changing nature of the swimmers is captured here by allowing the swimming speed, $u$, and Bretherton constant,
$u$, and Bretherton constant,  $B$, to be oscillatory functions, where
$B$, to be oscillatory functions, where  $\omega \gg 1$ is the high frequency period of the oscillations. The parameter
$\omega \gg 1$ is the high frequency period of the oscillations. The parameter  $\gamma$ is a fixed (positive) characteristic shear rate of the flow.
$\gamma$ is a fixed (positive) characteristic shear rate of the flow.
In order to understand the observed dynamics, WIMGD define $z(t)=y(t)/w^{1/2}$ and, inspired by Zoettl & Stark (Reference Zoettl and Stark2013), introduce a Hamiltonian-like quantity
$z(t)=y(t)/w^{1/2}$ and, inspired by Zoettl & Stark (Reference Zoettl and Stark2013), introduce a Hamiltonian-like quantity
where $g$ is a closed form analytic function that only depends on
$g$ is a closed form analytic function that only depends on  $B$, and
$B$, and  $\langle (\cdot ) \rangle$ denotes the average value over an oscillatory period.
$\langle (\cdot ) \rangle$ denotes the average value over an oscillatory period.
WIMGD introduce fast and intermediate time scales: $T=\omega t; \tau =\omega ^{1/2}t$, and implement a multiple-scale analysis, formally defining
$T=\omega t; \tau =\omega ^{1/2}t$, and implement a multiple-scale analysis, formally defining  $z(t)=z(T,\tau,t)$ and
$z(t)=z(T,\tau,t)$ and  $\theta (t)= \theta (T,\tau,t)$, treating each time variable as independent. At leading order, WIMGD find that the intermediate time scale dynamics directly corresponds to the dynamics for a fixed shape particle,
$\theta (t)= \theta (T,\tau,t)$, treating each time variable as independent. At leading order, WIMGD find that the intermediate time scale dynamics directly corresponds to the dynamics for a fixed shape particle,
Over the intermediate time scale $\tau$, this yields the result that the leading-order expression for the Hamiltonian-like quantity given by
$\tau$, this yields the result that the leading-order expression for the Hamiltonian-like quantity given by  $H_0(t)$ (equal to
$H_0(t)$ (equal to  $H(t)$ with
$H(t)$ with  $z=z_0$ and
$z=z_0$ and  $\theta =\theta _0$) is conserved. Now, on considering
$\theta =\theta _0$) is conserved. Now, on considering  $H_0$ as a fixed quantity, as identified by Zoettl & Stark (Reference Zoettl and Stark2013) and illustrated in figure 1, two types of behaviours are observed: if
$H_0$ as a fixed quantity, as identified by Zoettl & Stark (Reference Zoettl and Stark2013) and illustrated in figure 1, two types of behaviours are observed: if  $H_0>g(0)$ the swimmers tumble and there is monotonic evolution of
$H_0>g(0)$ the swimmers tumble and there is monotonic evolution of  $\theta _0$; else if
$\theta _0$; else if  $H_0< g(0)$, the swimmers exhibit a swinging motion with
$H_0< g(0)$, the swimmers exhibit a swinging motion with  $\theta _0$ oscillating between two values. Also note in figure 1 the existence of the unique equilibrium point (
$\theta _0$ oscillating between two values. Also note in figure 1 the existence of the unique equilibrium point ( $z_0,\theta _0)=(0,{\rm \pi} )$ which corresponds to rheotaxis and
$z_0,\theta _0)=(0,{\rm \pi} )$ which corresponds to rheotaxis and  $H_0$ taking its minimum value of
$H_0$ taking its minimum value of  $g({\rm \pi} )$.
$g({\rm \pi} )$.
Figure 1. Phase portrait on the intermediate time scale, $\tau$, showing contours of
$\tau$, showing contours of  $H_0$. Solutions in the shaded region where
$H_0$. Solutions in the shaded region where  $H_0>g(0)$ correspond to tumbling motion whereas trajectories with
$H_0>g(0)$ correspond to tumbling motion whereas trajectories with  $H_0< g(0)$ exhibit swinging motion. The stationary point
$H_0< g(0)$ exhibit swinging motion. The stationary point  $(z_0,\theta _0)=(0,{\rm \pi} )$ corresponds to upstream swimming, i.e. rheotaxis, with
$(z_0,\theta _0)=(0,{\rm \pi} )$ corresponds to upstream swimming, i.e. rheotaxis, with  ${H_0=g({\rm \pi})}$. Taken from WIMGD.
${H_0=g({\rm \pi})}$. Taken from WIMGD.
In order to examine the long-time dynamics of the swimmers, WIMGD examine the full dynamics of $H(t)$. Specifically, they introduce the function
$H(t)$. Specifically, they introduce the function  $h(T,\tau,t)=H_{2T}+H_{1\tau }+H_{0t}$ to represent the
$h(T,\tau,t)=H_{2T}+H_{1\tau }+H_{0t}$ to represent the  $O(1)$ terms in the full derivative
$O(1)$ terms in the full derivative  ${\rm d} H/{\rm d} t$. Averaging over a period in
${\rm d} H/{\rm d} t$. Averaging over a period in  $T$ and then period in
$T$ and then period in  $\tau$ yields the long-time evolution equation
$\tau$ yields the long-time evolution equation
where $W$ is a constant that can be calculated purely from the shape properties of the swimmer. The quantity
$W$ is a constant that can be calculated purely from the shape properties of the swimmer. The quantity  $f(H_0)$ is shown to be negative for all
$f(H_0)$ is shown to be negative for all  $H_0$ and so the sign of
$H_0$ and so the sign of  ${{\rm d} H_0}/{{\rm d} t}$ is determined by the constant
${{\rm d} H_0}/{{\rm d} t}$ is determined by the constant  $W$. Specifically, the fixed point
$W$. Specifically, the fixed point  $H_0=g({\rm \pi} )$ corresponding to the rheotactic configuration (
$H_0=g({\rm \pi} )$ corresponding to the rheotactic configuration ( $z_0,\theta _0)=(0,{\rm \pi} )$ is globally stable if
$z_0,\theta _0)=(0,{\rm \pi} )$ is globally stable if  $W>0$ and unstable if
$W>0$ and unstable if  $W<0$.
$W<0$.
WIMGD illustrate the asymptotic calculations with the specific example of ${u(T)=\alpha +\beta \sin T}$ and
${u(T)=\alpha +\beta \sin T}$ and  $B(T)=\delta +\mu \sin (T+\lambda )$. In this case, if
$B(T)=\delta +\mu \sin (T+\lambda )$. In this case, if  $\beta \mu >0$ then
$\beta \mu >0$ then  $\lambda \in (0,{\rm \pi} )$ corresponds to
$\lambda \in (0,{\rm \pi} )$ corresponds to  $W<0$ and tumbling, whereas
$W<0$ and tumbling, whereas  $\lambda \in ({\rm \pi},2{\rm \pi} )$ corresponds to
$\lambda \in ({\rm \pi},2{\rm \pi} )$ corresponds to  $W>0$ and rheotaxis, as illustrated in figure 2, which also demonstrates the good agreement between the full solutions of the dynamical system with the asymptotic approximation.
$W>0$ and rheotaxis, as illustrated in figure 2, which also demonstrates the good agreement between the full solutions of the dynamical system with the asymptotic approximation.
Figure 2. The value of $H$ as computed from the full numerical solution (blue), (2.1)–(2.3) and approximate solution (black), (2.6), for three phase shifts
$H$ as computed from the full numerical solution (blue), (2.1)–(2.3) and approximate solution (black), (2.6), for three phase shifts  $\lambda \in \{4{\rm \pi} /5,{\rm \pi},6{\rm \pi} /5\}$ and parameters
$\lambda \in \{4{\rm \pi} /5,{\rm \pi},6{\rm \pi} /5\}$ and parameters  $(\alpha, \beta,\delta,\mu )= (1,0.5,0.32,0.3)$. Adapted from WIMGD.
$(\alpha, \beta,\delta,\mu )= (1,0.5,0.32,0.3)$. Adapted from WIMGD.
3. Future
The elegant analysis of WIMGD has the potential to be applied and extended to a wide range of topical questions in the field of active biofluids, and there are open questions to determine the range of applicability of the results. In particular, WIMGD assumed shape changing can be modelled through periodic oscillations in the Bretherton constant (valid for axisymmetric particles in steady Stokes flow) and swimming speed. When considering individual microswimmers, the detailed mechanisms of propulsion, for example gait, can affect the swimming speed, as demonstrated theoretically and recently experimentally by using dynamically similar robotic models (Diaz et al. Reference Diaz, Robinson, Aydin, Aydin, Goldman and Wan2021). Furthermore, swimmers can swim in chiral patterns when propulsive torque and propulsive force are not aligned, and the unsteady nature of Stokes flow and external fields can also affect their swimming velocity and rotation rate (Maity & Burada Reference Maity and Burada2022). The role of external fields, such as gravity, light or chemical gradients is also incorporated in recent work by Lauga, Dang & Ishikawa (Reference Lauga, Dang and Ishikawa2021), who identified a new instability in suspensions of biased microswimmers. Because of the ability of swimmers to cross streamlines, their dispersion is quite different to passive colloids, and current work aims to identify the correct population-level transport models for microswimmers (e.g. Fung, Bearon & Hwang Reference Fung, Bearon and Hwang2022); incorporating the shape-changing effects of WIMGD would be an interesting development in such population-level models.
Declaration of interests
The author report no conflict of interest.