Voltage synchronisation for hybrid-electric aircraft propulsion systems

Abstract

Increasing demand for commercial air travel is projected to have additional environmental impact through increased emissions from fuel burn. This has necessitated the improvement of aircraft propulsion technologies and proposal of new concepts to mitigate this impact. The hybrid-electric aircraft propulsion system has been identified as a potential method to achieve this improvement. However, there are many challenges to overcome. One such challenges is the combination of electrical power sources and the best strategy to manage the power available in the propulsion system. Earlier methods reviewed did not quantify the mass and efficiency penalties incurred by each method, especially at system level. This work compares three power management approaches on the basis of feasibility, mass and efficiency. The focus is on voltage synchronisation and adaptation to the load rating. The three methods are the regulated rectification, the generator field flux variation and the buck-boost. This comparison was made using the propulsion system of the propulsive fuselage aircraft concept as the reference electrical configuration. Based on the findings, the generator field flux variation approach appeared to be the most promising, based on a balance of feasibility, mass and efficiency, for a 2.6MW system.

NOMENCLATURE

AVR

Automatic Voltage Regulator

BLI

Boundary Layer Ingestion

DPC

Direct Power Converter

EIS

Entry into Service

FAA

Federal Aviation Administration

PMSG

Permanent Magnet Synchronous Generator

SPSG

Salient Pole Synchronous Generator

TRL

Technology Readiness Level

ρ

Density

$\varphi$

Flux

λ

Flux linkage

1.0 INTRODUCTION

Increasing demand for commercial air travel is expected to cause additional environmental impact⁽¹⁾, as more flights will be required to meet this rising demand. Along with improvement in other sectors of aviation, far-reaching improvement of deployed aircrafts has become inevitable. Precisely, a need to reduce the propulsion system’s contribution to emissions has been identified.

Several concepts have been proposed to improve the performance of aircrafts in terms of efficiency and noise pollution^(2,3) . Much of the possible optimisation has relied on disruptive technologies⁽⁴⁾ that support distributed propulsion using electrical drive trains. Such a configuration offers not only the benefits of running individual components at their optimal operating conditions, but also a flexibility in positioning them around the aircraft.

A typical electrical drive train would compose an electrical power source, driving a motor through an electronic speed controller. In order to arrive at the most efficient and reliable configuration, the various combination of power sources and distribution systems have been researched. A comparison is made of architectures suitable for electric aircraft propulsion in⁽⁵⁾. These are composed of multiple generators and magnetic energy storage devices, interconnected for redundancy purpose, to drive multiple motors. There it is revealed that the weight of additional components, needed for power flow control and conversion between multiple sources, could constrain the design space. However, analysis of voltage stability conducted in⁽⁶⁾, for a DC bus with multiple power sources from a turbine revealed that they possess improved stability over single source configurations. Also, a system sourcing power from the low-pressure spool of the turbine has better stability than that sourcing from the high-pressure spool. In⁽⁷⁾, the feasibility of propelling a large hybrid aircraft using combined battery and generator power sources was investigated. This was conducted on the basis of viability and reliability. The sensitivity analysis revealed that there exists a point beyond which the weight of the batteries erode the benefits of such a propulsion system. Also, system failure caused by a battery or the generator was investigated. A review of technologies relating to on-board microgrids was performed in⁽⁸⁾ for more electric aircraft. Major aspects like voltage level disparity, alternating current (AC) and direct current (DC) interconnection and safety were considered. The outcome indicates that microgrids and their related technologies were an advantage in aircraft electrification; however, optimising their weight and performance prior to incorporation was an absolute need.

These earlier works reflect an advantage in deploying multiple power sources. They also indicate the need to achieve a balance between having multiple power sources and the weight penalty incurred by interconnecting them. In combining multiple power sources, voltage and phase balancing is required in order to effectively achieve load distribution and continued system health. This is especially so at a high-power level, such as is required for aircraft propulsion. Hence, an optimal power management approach is an important factor in the successful implementation of an electric propulsion system.

In⁽⁹⁾ a strategy was proposed for managing power sharing for multi-source electrical auxiliary power unit, by the inclusion of photovoltaic and other renewable energy sources. This strategy demonstrated the ability to achieve high-quality voltage profile during load fluctuations. However, weight considerations were not highlighted. Supercapacitors (SC) and fuel cell (FC) were used as auxiliary power units in⁽¹⁰⁾ to demonstrate a decentralised energy management strategy for more electric aircraft. The strategy splits the load power requirement into high and low frequency ranges and maps to the SC and FC, respectively. The weight profile of the proposed system was also not presented. In⁽¹¹⁾ a method was presented to help regain phase balance in aircraft electrical networks during the asymmetric utilisation of the power feeders’ phases. The aim was to demonstrate possible weight reduction of the electrical network, if balanced phase operation could be guaranteed. A weight saving of 19.7% was demonstrated but no propulsive load was considered. A review of power electronic converters in aircrafts like the Boeing 787 and Airbus A380 was done in⁽¹²⁾. These were for non-propulsive functions. A combination of AC/AC, DC/AC, AC/DC and DC/DC converters, were highlighted as viable candidates to be advanced into aircraft propulsion. Others like the Transformer Rectifier Unit (TRU) and Auto Transformer Rectifier Unit (ATRU) are considered for low power and low voltage ratio applications, respectively. A weight comparison of these electronic components was also not performed.

The reviewed literature proposes methods that could be used for voltage synchronisation and power management of electrical propulsion systems. However, the more critical aspect of overall system weight was not considered to the extent that the most viable options could be easily identified. Also, the potential of automatic voltage regulation using field voltage of synchronous generator has not been proven viable or otherwise.

This work presents a comparison between three methods of achieving voltage synchronisation between multiple sources on the basis of weight and efficiency. These are the regulated rectification, generator field flux variation and buck-boost converter methods. For this comparison, the propulsive fuselage aircraft concept⁽¹³⁾ is used as the reference electrical network.

2.0 BACKGROUND

This section covers the detailed architecture of the reference aircraft concept and the associated voltage synchronisation challenge that has inspired this work.

2.1 Reference aircraft model

In previous work⁽¹⁴⁾, the benefits of integrating a fan at the aft of a conventional tube and wing airframe was highlighted. Initial investigations assumed both mechanical and electrical power transmission to the fan. Both approaches offered promising expectations for entry into service (EIS) in 2035, based on a correlation between technology readiness level (TRL) and a clearly defined roadmap. Also, in⁽¹³⁾ a 12% less mission fuel was estimated for a 150-passenger capacity propulsive fuselage aircraft. This was for a total range of 3500nm. A total additional mass of 3,480kg compared with a conventional tube and wing aircraft was estimated. This was intended to be electrically driven.

Figure 1 shows a notional power system comprising the electrical components for driving the fuselage propulsor.

Figure 1. Notional electrical power system of the propulsive fuselage concept⁽¹⁵⁾.

In this electrically driven configuration, the sources of power are the two wing-mounted turbofans. It is expected that more shaft power is extracted from one of the spools to drive a three-phase alternating current (AC) generator, along with the turbine’s fan. The AC electrical power output from the driven generators is converted to direct current (DC) by the rectifier and then transmitted to an inverter. This conversion serves two purposes; more efficient transmission and enabling independent motor speed control by the inverter, irrespective of prime mover and generator speed. The inverter reverts DC back to AC, for driving the three-phase motor that is connected to a fan at the aft of the aircraft. Hence, the decoupling ambition of electrical propulsion is achieved. The described components are interconnected with high-voltage capacity cables.

Preliminary sizing of these components has been performed in⁽¹⁵⁾. An overall electrical system weight of 1394kg was estimated, for a 2.6MW electrical system. The added weight was assumed to be compatible with the main engines’ thrust capabilities as presented in⁽¹⁶⁾. However, further feasibility investigation was required, especially with regards to the structural and electrical systems integration.

The operational details of the electrical system need to be quantified and investigated to ensure the continued health of the system. This includes the power flow and optimal parameters selection. In⁽¹⁷⁾, the control of the entire propulsion system was modelled to investigate the ability of the proposed concept to meet the Federal Aviation Administration (FAA) transient response requirement. This included the electrical dynamics of the system. However, the performed investigation was reliant on the assumption that the two turbine spools were always at equal speed. This appears to be a scarce reality in practice. The consequence of a shaft speed difference between the two turbines is that the generators would generate voltages with different profiles. In this reference aircraft configuration, the output of the two generators has to be combined to drive a single load. The major power management challenge is the synchronisation of the different voltage profiles. This is a challenge because, unlike with land applications, the wing mounted turbofans are dedicated primarily for thrust generation in this case with electrical power generation being their secondary function. Hence, their speeds are varied for thrust rather than to maintain a specified output voltage profile. A lack of synchronisation makes the generator of lower voltage an additional electrical load to the one of higher voltage, upon interconnection. This is in addition to instability and possible failure of the electrical network.

2.2 Voltage synchronisation

Synchronisation for AC interconnections require that the voltages being combined from different sources should have the same profile. This means the same waveform, phase sequence, frequency, phase angle and voltage amplitude⁽¹⁸⁾. However, in this work, the voltage amplitude is the main focus, since the other requirements like the synchronisation of phase, can be achieved using intelligent rectifiers, with advanced control algorithms and more robust passive components. Using these methods, scenarios such as unbalanced loading can be sufficiently catered for. Hence, it is possible to achieve a DC output with the correct profile from both sources before interconnecting them.

3.0 ELECTRICAL NETWORK MODELLING

In order to compare the three approaches, a baseline electrical model is required. The target output is the voltage and current combination (power), required by the electrical network to produce the design thrust. This has a direct impact on the mass of the components. Figure 2 shows the procedure followed for the electrical network modelling.

Figure 2. Investigation approach.

3.1 Propulsor model

The propulsor is the component to be driven to produce the aircraft thrust. It comprises a fan and a duct. It is required to be modelled for a certain amount of thrust. Such a modelling should yield the optimised dimensions, rotational speed and the power required to rotate the fan. The derived power and rotations per minute (RPM) become the rating of the electrical motor to drive the fan. This implements the aerodynamic and electrical coupling. For a net thrust ${{T}}$ (N) given by Equation (1),

(1) \begin{equation}{\rm{T}} = \dot{\rm{m}}{V_e} - \dot{\rm{m}}{V_i}\end{equation}

Equation (2) gives the power $P$ (W) required by the fan to achieve ${{T}}$ .

(2) \begin{equation}P = \dot{\rm{m}}{C_p}{\rm{\Delta {\rm{t}}}}\end{equation}

With the change in temperature across the duct ${{\Delta t}}$ derived, it is possible to obtain the fan RPM using Equation (3)

(3) \begin{equation}RPM = \frac{{\sqrt {\frac{{{C_p}{\rm{\Delta t}}}}{{Load}}} {\rm{\;}} \times {\rm{\;}}60}}{{2\pi r}}\end{equation}

where, $\dot{m}$ (kg/s) is the mass flow rate of the air ingested by the fan, ${\rm{\;}}{C_p}$ is the isobaric specific heat capacity, ${V_i}$ (m/s) and ${V_e}$ (m/s) are the inlet and exit velocities respectively, and $Load$ is the fan stage loading coefficient.

The power and RPM derivation procedure was validated against previous works^(16,19) that gave values for the cruise stage. These are listed in Table 1.

Table 1 Design Input Validation

^*At take-off

A higher RPM value compared to existing literature⁽¹⁷⁾ is obtained, partly due to altitude difference (cruise altitude was used for the estimate). Also, because a low stage loading coefficient was selected for the fan, to mitigate the effects of lower RPM and higher torque on motor size. Typical loading coefficients can be assumed between 0.15 and 0.4, provided the RPM yields a fan tip speed below 0.9 Mach. It is important to also state that boundary layer ingestion was considered in the model presented above, since the aircraft concept capitalises on the reduced velocity air along the fuselage by ingesting it to obtain more thrust using same power, as compared to ingesting freestream air. A boundary layer length of 37m has been assumed to arrive at the estimated values presented in Table 1.

3.2 Voltage and current selection

From the propulsor modelling, the power and speed of the propulsor is known. The electrical system used to deliver this power must be operated at a combination of voltage and current, suitable to deliver the required torque and speed. At constant power, higher voltage implies higher cable insulation weight, while higher current implies higher conductor weight and ohmic (I²R) losses⁽²⁰⁾. The derivation of voltage and current presented here follows just the motor demands, since its performance has the most impact on the reliability of the propulsion system.

Electric motors currently deployed in small aircrafts are permanent magnet synchronous motors (PMSM). These have also been proposed for future medium and large aircraft due to their high specific power and minimal complexity, thus enabling them to be seamlessly deployed also as synchronous generators (SG), by the application of torque. Following this trend, a PMSM is considered in this work.

Equations describing the dynamic characteristics of the PMSM are presented in^(21,22) . However, the physical dimensions of the machines must be considered to correctly estimate the operational parameters. This is based on the close relationship between the required torque and the volume of the rotor. This can be derived using the power and volume (seen in Equations (4) and (5)) as presented in⁽²³⁾.

(4) \begin{equation}{P_m} = \frac{{{\pi ^2}}}{{\surd 2}}{K_w}{B_g}{A_L}{D^2}Ln\end{equation}

Where ${K_w}$ is the fundamental winding factor, ${B_g}$ is the airgap flux density (T), ${A_L}$ is the armature loading (A/m), $D$ and $L$ are the machine active diameter and length (m) respectively and $n$ is the machine speed (rev/s).

Existing methods for modelling motors, do not overcome the challenge of estimating the number and diameter of turns and also, the volume-flux correlation. Therefore, they could not be used to determine voltage and current in the motor equations.

The flow chart in Fig. 3 shows a procedure for the derivation of the architecture voltage based on the motor requirement, similar to that presented in⁽²⁴⁾.

Figure 3. Voltage and current selection procedure.

To obtain the machine airgap volume, Equation (4) becomes

(5) \begin{equation}{v_m} = {\rm{\;}}\frac{{{P_m}}}{{{\omega _R}{K_w}{B_g}{A_L}\surd 2}}\end{equation}

The airgap flux and flux linkage can be obtained using Equation (6) and (7) respectively.

(6) \begin{equation}\varphi = {B_g} \times {A_{AG}}\end{equation}

(7) \begin{equation}{\rm{\lambda }} = \frac{\varphi }{{{p_S}}}\end{equation}

where ${A_{AG}}$ is the airgap area, ${p_S}$ is the stator phase count and ${\omega _R}$ (rad/s) is the speed of the machine. The voltage of the motor and hence the electrical network can be obtained using Equation (8).

(8) \begin{equation}V = \frac{{{\omega _R}{\rm{\lambda }}}}{{\surd 2}}{\rm{\;}}\end{equation}

With known voltage, the current can be obtained using Equation (9).

(9) \begin{equation}I = \frac{{{P_m}}}{V}\end{equation}

The voltage and current selection approach presented is validated against published motor parameters for the EMRAX 268⁽²⁵⁾ and Siemens SP260D⁽²⁶⁾ as shown in Fig. 4. The machine mass has been obtained using the density of the existing machine and the obtained volume from the approach presented above.

Figure 4. Comparison published vs estimated machine parameters.

The obtained values are consistent, to the extent that this approach can be relied upon, in the selection of operational voltages and currents, provided the other propulsion system components size and efficiency are not greatly impacted by the imposition of the motor’s voltage and current.

3.3 Components mass estimation

The components considered in this work are shown in Fig. 1. Circuit protection devices have also been added. The mass estimation is done using an analytical approach. Details are presented in subsequent subsections.

3.3.1 Motor

The mass of the motor has been estimated together with the voltage and current selection in section 3.2. The specific power approach is not utilised because the investigated aircraft concept is a high torque application in which the motor speed would not operate anywhere near 14000RPM in the absence of a gearbox. The result of such an estimate would be too optimistic. This is in consideration of the relationship between rotating machines’ torque capability, volume and mass⁽²³⁾.

3.3.2 Generator

The mass of the generator is estimated using same relationship among speed, volume and mass as in the motor. The system voltage is imposed on the generator to derive the flux linkage and volume of the rotor from which the mass is estimated.

3.3.3 Power electronics

The power electronics include the inverter, rectifier, buck-boost converter and the circuit protection devices. Their mass estimation have been performed using the total mass of the required switches for each device, multiplied by a mass factor of 9.1⁽²⁴⁾. This mass factor accounts for the control circuitry and support elements. The selected switch has a rated voltage, current and maximum current of 1200V, 523A and 1280A, respectively. Also, the mass of the passive devices has been included.

3.3.4 Transmission

The transmission cable weight is estimated, considering the short circuit characteristics of the electrical network and the transmitted voltage. A regression has been performed from a collection of cable data to obtain a value relating the insulation thickness with the voltage magnitude. Equations (10) and (11)⁽²⁷⁾ were used to obtain the transmission mass,

(10) \begin{equation}{m_T} = {A_C}{L_T}{\rho _C}\left({0.0019V + 1} \right){\rm{\;}}\end{equation}

(11) \begin{equation}{A_C} = \frac{{{I_R}{K_{SC}}\sqrt {{t_{SC}}} {{10}^{ - 3}}}}{{0.143}}\end{equation}

where ${A_C}$ is the cross-sectional area of the conductor, ${L_T}$ is the total transmission length, ${\rho _C}$ is the density of the conductor material, ${I_R}$ is the rated system current (Equation 9) presented in kilo amperes, ${K_{SC}}$ is the short-circuit factor and ${t_{SC}}$ is the maximum estimated short-circuit duration.

Table 2 shows the components’ mass estimated versus published data in⁽¹⁵⁾ for a similar-rated (2.6MW) electrical network configuration.

Table 2 Components Initial Mass

^*Estimated for 75m total transmission length

The estimated generator mass is significantly more because in the referenced work, the model used for the electrical machine was based on specific power derived from a machine rated at 14000 RPM with much lower torque capability. The electric machines modelled here are rated close to the speed of the propulsor for the motor and that of the low-pressure compressor spool for the generator. A value of 3750 RPM and 4200RPM were used for the motor and generator, respectively. Also, the power electronics estimates presented have considered peak current handling requirements of each device, which have defined their size, based on the capability of the selected switch data. Such requirements were not considered in the referenced work and is accountable for the significant difference in protection device size.

4.0 POWER MANAGEMENT FOR THE PROPULSIVE FUSELAGE AIRFRAME CONCEPT

The peculiarity of power management in the investigated aircraft is the non-feasibility of continuously adjusting the turbine (prime mover) speed to balance the output voltages from two sources. Conventionally, a feedback system is used to control the prime mover speed, as shown in Fig. 5. However, such an arrangement is only feasible in applications where the turbines are dedicated for electrical power generation. In this case, they are turbofans, deployed in a flight critical propulsion configuration.

Figure 5. Typical grid voltage control scheme.

Hence, in this work, three voltage synchronisation approaches to solve this power management challenge are investigated and compared on the basis of incurred mass penalty, efficiency and feasibility. These are presented in the next subsections.

4.1. Investigated power management approaches

The three approaches investigated are the regulated rectification, generator field flux variation and the buck-boost converter. Figure 6 presents the layout of the electrical components in the investigated aircraft concept, indicating the location of the synchronisation equipment.

Figure 6. Electrical layout of the investigated aircraft concept (GEN-generator, TXN- transmission, REC-rectifier, B-B C-buck-boost converter, CB-circuit breaker, INV-inverter, MOT-motor).

The blue-, yellow- and green-coded components are the designated devices for the respective synchronisation approaches.

4.1.1 Regulated rectification

The first implementation of such approach was highlighted in⁽²⁸⁾. A two-stage direct power converter (DPC) was utilised for both voltage balancing and power loading of two or more grids. Such an arrangement was utilised to supply a single DC link from multiple power sources. The power is then distributed to one or more load centres. This approach was enabled by the replacement of diodes with switches for rectification. Figure 7 shows the setup of the DPC.

Figure 7. AC/AC direct power converter⁽²⁸⁾.

The proposed system is modified for the purpose of supply voltage synchronisation. The DPC is decomposed into two rectifier equipment (yellow-coded components in Fig. 6) with input connected to a generator and output combined on a DC link (bus bar in Fig. 6). To perform the synchronisation, the rectification is performed in such a way that the voltage output from each source rectifier is of equal value. This can be done using pulse width modulation switching technique with a feedback system from a comparator. The comparator circuit would track the voltage differences between the two generators and constantly adjust the pulse width modulation of both rectifiers and hence maintain the same voltage.

The limitation of this approach is that the value of the voltage fed into the bus bar is limited to the lower voltage of the two generators. Therefore, this is not suitable for a configuration where the motor requires a set voltage level to meet the required thrust. This implies that only a voltage synchronisation rather than a voltage amplification is achievable. Note that the buck-boost converter (green coded) is absent when this synchronisation strategy is employed.

4.1.2 Generator field flux variation (AVR excitation)

The generator field flux variation is implemented in the generator (blue-coded component). In the deployment of this voltage synchronisation strategy, the buck-boost converter (green coded) is absent in the electrical network system. This strategy is based on the relationship between generator excitation and voltage output. This is typically achieved using salient pole rotors. Salient pole rotors, unlike permanent magnet rotors, generate the rotor magnetic field flux by the application of a direct current to the rotor (field) windings. In principle, the magnitude of voltage output from a generator can be controlled by varying the magnitude of direct current input to the field winding and hence the flux. This principle is explored for the regulation of output voltage in most land-based grid applications. Hence, an adaptation to aircraft propulsion system is investigated. Figure 8 shows the schematic of the proposed method.

Details about generator excitation can be obtained from^(30)–(32). The main task here, is to size the salient pole synchronous generator (SPSG) in comparison with the permanent magnet synchronous generator (PMSG). The PMSG is preferred for aerospace propulsion because of the absence of an excitation system. This is easily replaced by the installation of permanent magnets on the rotor poles. Hence, eliminating the weight and complexity penalties of an excitation system. In⁽³³⁾ a study of cost, mass, efficiency and capacity is performed for the PMSG and SPSG. The outcome shows lesser cost and more power capacity for the SPSG while the PMSG has better mass and efficiency. However, the SPSG is considered here, not in comparison with the PMSG but for its potential for lesser weight penalty on the system, when compared to other voltage synchronisation methods.

A breakdown of mass comparison between the PMSG and the SPSG is utilised in the weight estimation of the SPSG to be investigated. Table 3 shows the weight computation for the SPSG by components contribution.

Table 3 Mass Computation for the SPSG vs PMSG⁽³³⁾

^*Assumed 25% rotor mass ^** Assumed 5% rotor mass

Figure 8. Schematic of a generator utilising salient pole rotor⁽²⁹⁾.

A 25% increase in rotor weight is assumed by the addition of an exciter generator based on inspection of Fig. 9. From Table 3, an estimate of the SPSG mass was derived to be 20.6% higher than a similar rated PMSG.

Figure 9. Salient pole rotor with exciter⁽³⁴⁾.

4.1.3 Buck-boost converter

Buck-boost converters are non-isolated transformers with the ability to step-up and step-down voltages. They are typically implemented in inverting and non-inverting output modes. Due to the complicated circuitry associated with an inverting output, a non-inverting topology is selected. Figure 10 shows a schematic of a buck-boost converter.

Figure 10. Buck-boost converter.

Each converter (green-coded component shown in Fig. 6) is proposed to take input from one rectifier’s circuit breaker and terminate its output at the bus bar. Ports 1 and 4 are the respective positive and negative inputs from the rectifier side while ports 2 and 3 are the respective positive and negative outputs. S1 and S2 are the switches for buck and boost operation respectively, while D1 and D2 are the corresponding diodes. I is the common inductor used for both buck and boost operations. Using the control signals G1 and G2, the step-down and step-up voltage adaptation can be achieved.

4.2 Comparison of power management approaches

The three approaches will be compared in this section, to give an outlook on the feasibility and viability of each approach. The comparison is based on efficiency and mass contribution of each employed strategy. The initial sizing has been done for a ±5% voltage change, which is a minimum requirement for voltage drop usually incorporated in power components design. The voltage change here refers to the difference between a generator’s output voltage and a set value. Figure 11 shows the individual mass comparison of the three synchronisation components, estimated over a range of voltages. These voltages were derived for fan speed between 1500RPM and 6000RPM at 750 RPM intervals.

The mass depicted is for the pair required for the propulsion power. The mass of the two generators is shown to be significantly higher at all investigated voltage ratings. Table 4 shows the variation tendencies of the component masses for each employed strategy.

Table 4 Component Mass Variation for the Synchronisation Approaches

Figure 11. Synchronisation components mass vs voltage.

The normal mass refers to the component’s mass in an ideal configuration where no synchronisation of power sources is required. In the generator field flux variation strategy, the generators’ mass is increased by a fraction compared to the normal configuration (using PMSG) to cover the added excitation system. The buck-boost converter is absent when any of the other two approaches is employed.

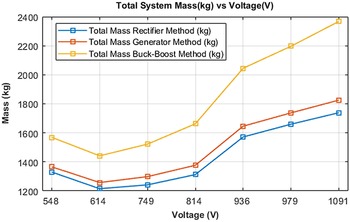
Figure 12 shows a comparison of the total electrical system mass when each of the synchronisation approaches are employed. A noticeable difference is observed when a buck-boost converter is deployed. This is seen to be more significant as voltage increases, due to the addition of magnetics and capacitors to support the voltage adaptation process.

Figure 12. Total Electrical system mass vs voltage.

Figure 13 shows the propulsion system efficiency and power loss for all three synchronisation approaches. The regulated rectification offers significantly more efficiency compared to the other two methods. This is mostly due to a fewer number of components.

Figure 13. Total electrical system efficiency and power loss vs voltage.

The results shown in Figs. 11–13 represent a system that accommodates only a ±5% voltage change. An extension of the investigation is performed for a range of ±20%. Figure 14 shows the trend for a system with a voltage rating of 814V. It can be seen that the rectifier can only perform the synchronisation function for input voltages from −5% and higher than the set value, for which it has been sized. This is mainly because the output voltage of the rectifier is inherently limited to the input voltage. Therefore, oversizing it for higher voltages would still not overcome this limitation.

Figure 14. Variation in component mass vs voltage change.

Figure 15. Variation in total electrical mass by vs voltage change.

The generator is able to function for all the investigated range of voltages, but the weight penalty increases slightly with more negative voltage change. This is a result of oversizing the excitation system. The buck-boost converter demonstrates the most significant mass sensitivity to voltage change compared to the other components.

Figure 15 depicts the total electrical system mass comparison when each of the synchronisation approach is employed. The buck-boost approach incurs a significantly higher mass penalty for the range of investigated voltage change. The total system mass when deploying the generator field flux variation and the regulated rectification approach showed little sensitivity to voltage change. However, the regulated rectification approach could only be used in a positive voltage change configuration.

In terms of efficiency, the performance shown by all three methods as presented in Fig. 13 has been maintained. As seen in Fig. 16, for the investigated range of voltage change, the generator approach appeared least efficient while the regulated rectification approach demonstrates the best efficiency. It is noticeable that the buck-boost approach is more efficient in the positive voltage change region, where it has significantly less power losses.

Figure 16. Variation in total electrical efficiency by voltage change.

4.3 Discussion

The regulated rectification is only able to perform voltage synchronisation, but cannot adapt by boosting lower input voltages to higher values. This limitation is likely to impact the feasibility of the intended electrical system when the voltage output of the generator is much lower than the rated system voltage. The viability of such an approach could be improved by operating the generator (PMSG) at significantly higher voltage than that required by the motor. Also, the rectifier and all the upstream components have to be oversized to handle higher voltages and power. A balanced comparison would have to be done to identify where the incurred mass penalty cancels out the benefits of such an approach.

In addition to added mass, the approach utilising the generator field flux variation adds an extra complexity to the generator configuration. This is a deviation from the current trend for future electrical propulsion, where a permanent magnet rotor is preferred for mass and complexity reduction. However, the approach meets the feasibility requirement sought for a configuration where a certain magnitude of voltage must be delivered to the motor for continued normal operation. Also, there exists a possibility to further optimise the approach using the pole count. This method is, however, subject to other operational parameters being satisfied, especially the limits of magnetic saturation of the machine core.

The buck-boost converter is absent when any of the other two approach is employed. It does not offer promising mass profiles on a system level. However, it meets the power management requirement for all the range of voltages investigated. Compared to the generator field flux variation, it offers more efficiency at the system level with about 20kW less losses.

5.0 CONCLUSION

In this paper, three approaches for power management in an electric aircraft propulsion system have been investigated. These were focused on their ability to synchronise the voltage difference between interconnecting power sources and adapt the input voltage magnitude to the load requirement.

Of the three approaches investigated, only two demonstrated the required robustness for an electrical propulsion system in terms of the ability to adapt input voltages lower than system rating. These were the generator field flux variation and the buck-boost approaches. The generator field flux variation approach offers the least mass penalty of the two. However, achieving a similar specific power for SPSG compared to PMSG appears to be a challenge. This offers more opportunities to the regulated rectification approach, which has better mass and efficiency profiles compared to the other two. The limitation of the regulated rectification approach is its inability to deliver voltages higher than the upstream (input) voltage.

The contribution of this work offers good insight into potential strategies that could be employed in electrical propulsion systems for optimal power management through voltage synchronisation and adaptation. On a balance of feasibility, mass and efficiency, the generator field flux approach appears to be the optimal choice. However, further investigation would be required to improve the efficiency of this approach.