1. Introduction
An important issue that threatens U.S. peanut production, particularly Runner peanuts, is the susceptibility of this crop to several types of fungal pathogens.Footnote 1 In particular, Aspergillus (flavus, fumigatus, and parasiticus), a group of fungi, are responsible for producing aflatoxins, which are carcinogenic mycotoxins. Specifically, A. flavus, the most dangerous hepatocarcinogen known to man, has been associated with an increased risk of liver cancer and is commonly found in peanuts (Hedayati et al., Reference Hedayati, Pasqualotto, Warn, Bowyer and Denning2007). Although the rates of primary liver cancer are highest in places where peanuts are a mainstay in the diet (e.g., Asia and Africa), each year more than 15,000 men and 6,000 women are found to have primary liver cancer in the United States (National Cancer Institute [NCI], 2011; Wu and Khlangwiset, Reference Wright, Porter, Powell and Ross2010). In 2011, the number of new cases of liver cancer was projected to reach over 26,000 persons along with approximately 20,000 deaths (NCI, 2011). To reduce the level of aflatoxin exposure and the risk of liver cancer, the U.S. Food and Drug Administration (FDA) maintains a tightly controlled screening program of the food supply including peanut products (FDA, 2015). To mitigate the presence of the A. flavus mold, peanut producers use large amounts of chemicals to prevent fungal growth.
The use of chemical factors therefore has a positive effect on social welfare by reducing the risk exposure to a human carcinogen that may be present in edible peanuts; on the other hand, the excessive use of pesticides may also have a negative effect on social welfare by degrading the quality of the ecosystems surrounding peanuts farms and by risking adverse impacts on human health. For example, Carsel et al. (Reference Carsel, Jones, Hanse, Lamb and Anderson1988) simulate the level of mass fluxes of aldicarb, an insecticide commonly used by peanut growers in North Carolina, to the groundwater, and they assessed a concentration level between 0.01 and 0.1 kg ha−1 within a radius of 120 m downgradientFootnote 2 from the application point. Pesticide residuals can be transported and can be a serious threat for public health when they reach water bodies that are sources of drinkable water.
1.1. Potential Benefits of a Biotech Solution
With the implications of chemical overuse in peanut production, this research provides analysis to test the hypothesis that peanut farmers overuse certain chemicals. With evidence of this overuse of chemical inputs, we exploit this information to identify the area of research that may generate the greatest benefit to farmers. Based on the input use, we suggest that a genetic manipulation that lowers the demand of the overused input may be one avenue to improve farmer welfare. For example, if farmers overuse herbicides, then the adoption of a new cultivar with enhanced traits that are more resistant to weeds, thus reducing the need for herbicides, will increase the welfare of farmers. The benefits will occur by lowering the cost of this chemical factor in addition to reducing the induced cost increase attributable to the allocative inefficient use of herbicides.
In the past decade, genetic engineering has offered a potential remedy to help peanut producers successfully defeat the problem of fungal pathogens. For example Jonnala, Dunford, and Chenault (Reference Jonnala, Dunford and Chenault2005) analyze the differences between three transgenic peanut lines (resistant to fungal pathogens) in the southwestern United States. From comparison with the parent line, they found that genetic modification did not cause substantial unintentional changes in the nutritional value of peanuts. Genetically engineered (GE) peanuts may provide fungal resistance without any significant difference in quality.
Price et al. (Reference Price, Lin, Falck-Zepeda and Fernandez-Cornejo2003) argue that the adoption of agricultural biotechnologies for cotton, soybean, and corn has increased the U.S. total welfare by US$750 million. The world benefit from adopting herbicide-tolerant cotton is shared by consumers (57%), U.S. farmers (4.1%), biotech firms (4.6%), seed firms (1.6%), and other producers from the rest of the world (32.6%). The use of GE crops in agriculture may have environmental benefits such as improved water-use efficiency through modification for arid climate crops or abatement of non-point-source pollutants through reduced input use (Godfray et al., Reference Godfray, Beddington, Crute, Haddad, Lawrence, Muir, Pretty, Robinson, Thomas and Toulmin2010). This is the case with GE crops that have a high resistance to pests and reduce the need for pesticides. GE peanuts, still in the development stage, may represent a promising alternative that may reduce the costs of inputs and increase crop yield and productivity (Fernandez-Cornejo and Caswell, Reference Fernandez-Cornejo and Caswell2006).
Holbrook and Stalker (Reference Holbrook, Stalker and Janick2002) provide a review of hybridization efforts that agronomic scientists have accomplished with Arachis hypogaea. The authors report several studies that addressed the issue of breeding peanuts with resistance to root-knot nematode, fungal pathogens, and drought. Despite the large qualitative and quantitative variation in genotypic variations of the cultivar in U.S. domesticated peanuts, only a few of their genetic traits have been studied (Knauft and Wynne, Reference Knauft and Wynne1995; Murthy and Reddy, Reference Murthy and Reddy1993; Wynne and Coffelt, Reference Wu and Khlangwiset1982).
Few studies reported the economic losses of peanut producers because of fungal pathogens or soil-borne diseases that could be mitigated if a GE cultivar was available to the farmers. For example, Lamb and Sternitzke (Reference Lamb and Sternitzke2001) argue that the average annual cost of aflatoxin borne by all segments of the southeast peanut industry is approximately US$25.8 million. Isleib, Holbrook, and Gorbet (Reference Isleib, Holbrook and Gorbet2001) report that breeding programs, which improved the resistance of domesticated peanuts to Sclerotinia blight, root-knot nematodes, and tomato spotted wilt virus, increased producer welfare by more than US$200 million over a 20-year period.
Although Lamb and Sternitzke (Reference Lamb and Sternitzke2001) present an accounting estimation of the costs of plant disease based on 4 years (1993–1996) within a single region, Isleib, Holbrook, and Gorbet (Reference Isleib, Holbrook and Gorbet2001) calculate farmers’ benefits by comparing the advantage of the increased yield obtained from the resistant cultivar with the old yield. Isleib, Holbrook, and Gorbet (Reference Isleib, Holbrook and Gorbet2001) also account for reduced costs of pesticides. None of the researchers use a neoclassical economic framework for estimating the potential benefit deriving from improved genetic traits, and they ignore climatic variability that may also affect the crop yield of both traditional and new cultivars. The current literature is missing a large-scale positive economic analysis of the potential benefits deriving from the use of GE peanuts.
In the current study of U.S. peanut production, we conduct an economic analysis of technical and allocative inefficiency of chemical inputs. From the analysis, we identify efficient chemical input use, and we suggest research priorities in agricultural biotechnology based on inefficient input use. To our knowledge, this is the first study that addresses this question in the peanut sector.
2. Theoretical Considerations
Hanson, Hite, and Bosworth (Reference Hanson, Hite and Bosworth2001) study the potential economic benefit of biotechnology in the fishery sector. The authors evaluate the value of various forms of farm-raised catfish in the attempt to help geneticists determine the inherited traits on which breeders should focus their research. They use a complete demand system to simulate different welfare scenarios from the potential genetic manipulations that increase the quantity and cut of catfish available in the market.
Replicating this methodology to estimate a complete demand system of chemical production factors used by peanut farmers may be economically sound, but the approach cannot take agronomic principles into account. For example, a grower would not substitute between nitrogen and fungicide because these two factors serve two very different tasks and thus belong to different branches of the purchasing decision tree. Furthermore, lack of substitution among chemical factors in agricultural economics is supported by several authors (Ackello-Ogutu, Paris, and Williams, Reference Ackello-Ogutu, Paris and Williams1985; Frank, Beattie, and Embleton, Reference Frank, Beattie and Embleton1990; Grimm et al., Reference Grimm, Paris and Williams1987; Paris, Reference Paris1992; Paris and Knapp, Reference Paris and Knapp1989). These researchers propose crop response functions to chemical factors that exhibit a plateau effect, which occurs after a threshold in the nutrient application rate. After this point, additional nutrient applications do not increase plant growth as hypothesized by von Liebig's law of minimum.
Frank, Beattie, and Embleton (Reference Frank, Beattie and Embleton1990) suggest the Mitscherlich-Baule (MB) response function as a way to address the plateau of chemical use in agricultural production. For example, an indirect profit function that accounts for production plateaus can be obtained by substituting the MB for peanut yieldFootnote 3 in a profit maximization problem as a function of chemical factors and then solving a simple optimization problem. From the first-order necessary condition and the implicit function theorem, the profit maximizing value of endogenous chemical factors, as functions of input and output prices, can be substituted into the profit function to derive an indirect profit function. The indirect specification may then be used to derive elasticities of substitution.
However, mathematical derivation of the indirect profit function based on the MB specification does not have a closed form. Although a second-order Taylor approximation reduces the production function to a quadratic form, the approximation consistently misspecifies the original MB form. The error approximation is relevant considering that we expand the Taylor series up to the second order as we are interested in finding elasticities of substitution in the current research. Therefore, estimating a demand system for chemical production factors, based on misspecified functional forms, would not be the appropriate strategy to make policy recommendations.
2.1. An Alternative Approach
Because direct estimation of the substitution elasticities of inputs (nutrients and pesticides) in peanut production is flawed, an alternative approach to study input use of peanut farmers is to assess their inefficient use. For example, producers may overuse labor in input application,Footnote 4 which is systematically tied to overuse of a particular chemical input, say herbicide, because they believe that using large quantities of this factor can help them eliminate unwanted weeds.
Schmidt and Lovell (Reference Schmidt and Lovell1979) define allocative inefficiency as a failure to allocate inputs in the right proportions given the input prices. In a production process that has allocative inefficiency, the marginal revenue product is not equal to the marginal resource cost. Technical inefficiency occurs when producers fail to maximize the output given a bundle of inputs. In reference to allocative efficiency, Kumbhakar and Lovell (Reference Kumbhakar and Lovell2000, p. 152) state that “in a wide variety of environments farmers use excessive amounts of fertilizers and pesticides relative to other inputs.”
Kumbhakar and Wang (Reference Kumbhakar and Wang2006) extend the primal system approach of Schmidt and Lovell (Reference Schmidt and Lovell1979) by using the more flexible transcendental logarithmic functional form of the stochastic frontier. The authors argue that if the input endogeneity is considered during the implementation of the econometric problem, then the output-oriented or input-oriented technical inefficiencies are the same.
The primal system technique consists of estimating simultaneously a parametric self-dual production function
and the first-order conditions of a cost-minimization problem that can be implicitly formulated as
where y is the level of production; x is a vector of inputs; v is a vector of unobserved farmers’ heterogeneities; u is the vector of technical inefficiencies; fj and f 1 are the marginal products of input j and input 1, respectively; wj and w 1 are prices of input j and input 1, respectively; and ηj is a vector of allocative inefficiencies.
The cost-minimizing condition for a profitable producer is that the marginal rate of technical substitution of input j with respect to input 1 should equal the price ratio wj and w 1. This condition occurs if the allocative inefficiency term equals zero (ηj = 0). However, this condition is violated if ηj ≠ 0. Assuming limited substitutability between chemical factors, if the allocative inefficiency for the input pair (j, 1) is ηj < 0, then wje ηj < wj that consists of an overuse of input j with respect to input 1. In other words, the farmer will reduce the use of input 1 in favor of input j. Cost analysis in a stochastic frontier framework would provide results that are less biased by including the inefficiency terms that raise the costs of production.
3. Econometric Model
The analytical expression that allows the econometric estimation of technical and allocative inefficiency using the primal approach is formulated assuming a cost function c(w, y) and using Shephard's lemma to derive the conditional demand of factor xj(wj, y). In logarithmic form, it follows that
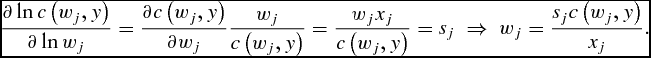 \begin{equation}
\frac{{\partial \ln c\left( {w_j ,y} \right)}}{{\partial \ln w_j }} = \frac{{\partial c\left( {w_j ,y} \right)}}{{\partial w_j }}\frac{{w_j }}{{c\left( {w_j ,y} \right)}} = \frac{{w_j x_j }}{{c\left( {w_j ,y} \right)}} = s_j \; \Rightarrow \; w_j = \frac{{s_j c\left( {w_j ,y} \right)}}{{x_j }}.\end{equation}
\begin{equation}
\frac{{\partial \ln c\left( {w_j ,y} \right)}}{{\partial \ln w_j }} = \frac{{\partial c\left( {w_j ,y} \right)}}{{\partial w_j }}\frac{{w_j }}{{c\left( {w_j ,y} \right)}} = \frac{{w_j x_j }}{{c\left( {w_j ,y} \right)}} = s_j \; \Rightarrow \; w_j = \frac{{s_j c\left( {w_j ,y} \right)}}{{x_j }}.\end{equation}
This result is used to substitute the new expression of wj in equation (2) to obtain
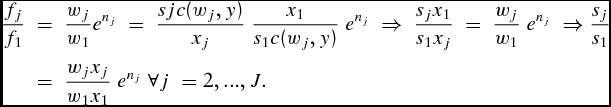 \begin{eqnarray}
\frac{{f_j }}{{f_1 }}\; &=& \;\frac{{w_j }}{{w_1 }}e^{n_j } \; = \;\frac{{sjc(w_j ,y)}}{{x_j }}\;\frac{{x_1 }}{{s_1 c(w_j ,y)}}\;e^{n_j } \; \Rightarrow \;\frac{{s_j x_1 }}{{s_1 x_j }}\; = \;\frac{{w_j }}{{w_1 }}\;e^{n_j } \; \Rightarrow \frac{{s_j }}{{s_1 }}\nonumber\\
&=& \;\frac{{w_j x_j }}{{w_1 x_1 }}\;e^{n_j } \;\forall j\; = 2,...,J.\end{eqnarray}
\begin{eqnarray}
\frac{{f_j }}{{f_1 }}\; &=& \;\frac{{w_j }}{{w_1 }}e^{n_j } \; = \;\frac{{sjc(w_j ,y)}}{{x_j }}\;\frac{{x_1 }}{{s_1 c(w_j ,y)}}\;e^{n_j } \; \Rightarrow \;\frac{{s_j x_1 }}{{s_1 x_j }}\; = \;\frac{{w_j }}{{w_1 }}\;e^{n_j } \; \Rightarrow \frac{{s_j }}{{s_1 }}\nonumber\\
&=& \;\frac{{w_j x_j }}{{w_1 x_1 }}\;e^{n_j } \;\forall j\; = 2,...,J.\end{eqnarray}
Taking the logarithm of equation (4), we get
where sj are cost shares of the input xj given the input price wj.
Econometric estimation of the primal system described by equations (1) and (5) can be performed under the assumption that the error components have the following distributions as suggested by Kumbhakar and Lovell (Reference Kumbhakar and Lovell2000): v ~ N(0, σ2ν) is a vector of normally distributed random noises that capture specific heterogeneities of peanut farmers; u ~ N + (0, σ2u) is the vector of technical inefficiencies half-normally distributed; η = (η2i, η3i, …, ηJi, ) ~ N(0, Σ) is the vector of allocative inefficiencies for the ith peanut farmer; and ηj is assumed to be independent of v and u for simplicity.
The joint density function of the three error components is calculated by multiplying their probability density functions. Consequently, the log-likelihood function for the ith peanut farmer is
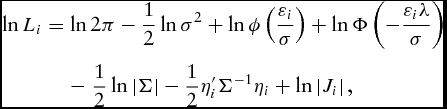 \begin{eqnarray}
\ln L_i &=& \ln 2{\rm \pi } - \frac{1}{2}\ln {\rm \sigma }^2 + \ln \phi \left(\frac{{{\rm \varepsilon }_i }}{{\rm \sigma }}\right) + \ln {\rm \Phi }\left( { - \frac{{{\rm \varepsilon }_i {\rm \lambda }}}{{\rm \sigma }}} \right) \nonumber\\
&& -\; \frac{1}{2}\ln \left| {\rm \Sigma } \right| - \frac{1}{2}{\rm \eta }'_i {\rm \Sigma }^{ - 1} {\rm \eta }_i + \ln \left| {J_i } \right|,\end{eqnarray}
\begin{eqnarray}
\ln L_i &=& \ln 2{\rm \pi } - \frac{1}{2}\ln {\rm \sigma }^2 + \ln \phi \left(\frac{{{\rm \varepsilon }_i }}{{\rm \sigma }}\right) + \ln {\rm \Phi }\left( { - \frac{{{\rm \varepsilon }_i {\rm \lambda }}}{{\rm \sigma }}} \right) \nonumber\\
&& -\; \frac{1}{2}\ln \left| {\rm \Sigma } \right| - \frac{1}{2}{\rm \eta }'_i {\rm \Sigma }^{ - 1} {\rm \eta }_i + \ln \left| {J_i } \right|,\end{eqnarray}
where the error components v and u and the related standard deviations are reparameterized as ε = v − u, σ = σ2u + σν2, and λ = σu/σν, and ϕ( · ) and Φ( · ), which are probability density and cumulative density functions of a standard normal variable, respectively. Note that the |J| is the determinant of the Jacobian matrix of the transformation from ![]() $\left( {{\rm \varepsilon },{\bf \eta }} \right)$ to (lnx 1, lnx 2, …, lnxj) that serves to address the endogeneity of input x under the cost-minimization assumption. In other words, the determinant of the Jacobian is the degree of homogeneity or the return to scale that may lower the production costs if the producers adopt economies of scale.
$\left( {{\rm \varepsilon },{\bf \eta }} \right)$ to (lnx 1, lnx 2, …, lnxj) that serves to address the endogeneity of input x under the cost-minimization assumption. In other words, the determinant of the Jacobian is the degree of homogeneity or the return to scale that may lower the production costs if the producers adopt economies of scale.
The number of parameters to be estimated can be reduced if equation (6) is concentrated with respect to Σ. Schmidt and Lovell (Reference Schmidt and Lovell1979) show that the element σjk of Σ, when equation (6) reaches its maximum, can be expressed as follows:
Substituting equation (8) into equation (6) leads to the concentrated log-likelihood function LLi(yi|xji, βj, σ, λ) as a function of the technical parameters βj and the parameters σ and λ that allow one to recover the vector of technical inefficiencies. In particular, technical efficiency can be calculated by the exponential of the negative of the point estimates of ui, that is, TE = exp( − ui). The components of this vector can be recovered using the formula suggested by Jondrow et al. (Reference Jondrow, Lovell, Materov and Schmidt1982), which is
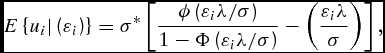 \begin{equation}
E\left\{ {u_i {\rm |}\left( {{\rm \varepsilon }_i } \right)} \right\} = {\rm \sigma }^* \left[ {\frac{{\phi \left( {{\rm \varepsilon }_i {\rm \lambda }/{\rm \sigma }} \right)}}{{1 - {\rm \Phi }\left( {{\rm \varepsilon }_i {\rm \lambda }/{\rm \sigma }} \right)}} - \left( {\frac{{{\rm \varepsilon }_i {\rm \lambda }}}{{\rm \sigma }}} \right)} \right],\end{equation}
\begin{equation}
E\left\{ {u_i {\rm |}\left( {{\rm \varepsilon }_i } \right)} \right\} = {\rm \sigma }^* \left[ {\frac{{\phi \left( {{\rm \varepsilon }_i {\rm \lambda }/{\rm \sigma }} \right)}}{{1 - {\rm \Phi }\left( {{\rm \varepsilon }_i {\rm \lambda }/{\rm \sigma }} \right)}} - \left( {\frac{{{\rm \varepsilon }_i {\rm \lambda }}}{{\rm \sigma }}} \right)} \right],\end{equation}
where σ* = σuσν/σ, and the allocative inefficiencies ηj for the input bundle (j, 1) can be calculated from the residuals of the First Order Conditions (FOC) in equation (5).
Knowing the allocative inefficiency would be enough to address the research priority in biotechnology to produce a crop that has resistant traits that would reduce the (over)use of the chemical input that is applied inefficiently. However, to quantify the economic and environmental impact of the allocative inefficiency, Kumbhakar and Wang (Reference Kumbhakar and Wang2006) suggest placing the estimated η into the input demand equations. The demand equations can be derived by the simultaneous solution of the primal system composed of equations (1) and (5). These equations can be used to simulate the actual input demand increase attributable to the inefficient use of inputs. That information can then be used to calculate the potential welfare change for the farmers who adopt genetically modified peanuts. The welfare change is the result of the elimination of the inefficiently used chemical factor. An additional welfare change derives from a readjustment in the use of the other inputs once the inefficient input is eliminated.
Overuse of chemical factors can occur systematically, and such systematically inefficient farming behavior can be modeled by assuming the following multivariate normal distribution of the allocative inefficiencies: η ~ N(ρ, Σ), where ![]() ${\rm \rho }_j = {\rm \bar \eta }_j = \frac{1}{n}\mathop \sum \nolimits_{i = 1}^n {\rm \eta }_{ji} {\rm }\forall j = 2, \ldots ,J \ {\rm and} \ i = 1,2, \ldots ,n.$
${\rm \rho }_j = {\rm \bar \eta }_j = \frac{1}{n}\mathop \sum \nolimits_{i = 1}^n {\rm \eta }_{ji} {\rm }\forall j = 2, \ldots ,J \ {\rm and} \ i = 1,2, \ldots ,n.$
4. Data and Empirical Model
The Economic Research Service (ERS) and the National Agricultural Statistical Service (NASS) collect data on cost and returns on peanut production as part of the U.S. Department of Agricultural (USDA) Agricultural Resource Management Survey (ARMS). In 2004, NASS collected data regarding peanut farming operations in three phases. A screening phase (Phase I) conducted in summer 2004 served to identify peanut farmers in operation. In Phase II (fall 2004 and winter 2004–2005), NASS randomly selected a sample of peanut farmers from Phase I and interviewed them concerning their production practices and chemical use. Finally, in Phase III (spring 2005), a nationally representative sample of peanut farmers provided information on costs and returns during the crop year 2004. We merged the ARMS data with climate data such as average temperature, average precipitation, and average dew point temperature (air moisture less humidity) of each farm in the 2004 growing period. We calculated these through a geospatial analysis on gridded data from the National Oceanic and Atmospheric Administration, USDA, and PRISM Climate Group at Oregon State University. The final data set consisted of 389 observations. The climate data serve as exogenous frontier shifters in the following model:
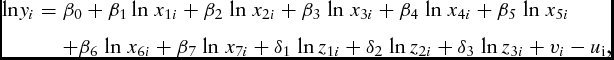 \begin{eqnarray}
{\rm ln }y_i &=& {\rm \beta }_{\rm 0} + {\rm \beta }_{\rm 1} \,{\rm ln}\ x_{1i} + {\rm \beta }_{\rm 2} \ {\rm ln}\ x_{2i} + {\rm \beta }_{\rm 3}\ {\rm ln}\ x_{3i} + {\rm \beta }_{\rm 4} \ {\rm ln}\ x_{4i} + {\rm \beta }_{\rm 5}\ {\rm ln}\ x_{5i} \nonumber\\
&& + {\rm \beta }_{\rm 6}\ {\rm ln}\ x_{6i} + {\rm \beta }_{\rm 7}\ {\rm ln}\ x_{7i} + {\rm \delta }_{\rm 1} \ {\rm ln}\,z_{1i} + {\rm \delta }_{\rm 2} \ {\rm ln}\,z_{2i} + {\rm \delta }_{\rm 3} \ {\rm ln}\,z_{3i} + v_i - u_{\rm i} ,
\end{eqnarray}
\begin{eqnarray}
{\rm ln }y_i &=& {\rm \beta }_{\rm 0} + {\rm \beta }_{\rm 1} \,{\rm ln}\ x_{1i} + {\rm \beta }_{\rm 2} \ {\rm ln}\ x_{2i} + {\rm \beta }_{\rm 3}\ {\rm ln}\ x_{3i} + {\rm \beta }_{\rm 4} \ {\rm ln}\ x_{4i} + {\rm \beta }_{\rm 5}\ {\rm ln}\ x_{5i} \nonumber\\
&& + {\rm \beta }_{\rm 6}\ {\rm ln}\ x_{6i} + {\rm \beta }_{\rm 7}\ {\rm ln}\ x_{7i} + {\rm \delta }_{\rm 1} \ {\rm ln}\,z_{1i} + {\rm \delta }_{\rm 2} \ {\rm ln}\,z_{2i} + {\rm \delta }_{\rm 3} \ {\rm ln}\,z_{3i} + v_i - u_{\rm i} ,
\end{eqnarray}
where yi is the total physical production of peanuts expressed in pounds and x 1i is hired labor expressed in hours on farm i. Nitrogen, phosphate, potash, insecticide, herbicide, and fungicide expressed in pounds correspond with x 2i, x 3i, x 4i, x 5i, x 6i, and x 7i for each farm. The variables z 1i, z 2i, and z 3i are rainfall, temperature, and relative humidity (dew point) expressed in millimeters and degrees Celsius. The Cobb-Douglas production function is the most parsimonious first-order approximation of the true production function; thus, we use it in our analysis.Footnote 5 With labor (x 1) as the numeraire, the first-order condition of the cost-minimization problem produces the column vector of allocative inefficiencies with wj, j = 1, 2, ..., 7 as prices of production factors expressed in US$/lb.
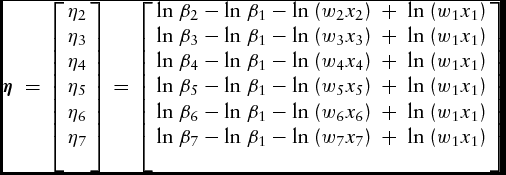 \begin{equation}
{\bf \eta}\;{\rm = }\;\left[ \begin{array}{l}
{\eta}_{\rm 2} \\
{\eta}_{\rm 3} \\
{\eta}_{\rm 4} \\
{\eta}_{\rm 5} \\
{\eta}_{\rm 6} \\
{\eta}_{\rm 7} \\
\end{array} \right]\;{\rm = }\;\left[ \begin{array}{l}
{\rm ln}\;{\rm \beta }_{\rm 2} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_2 x_2 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 3} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_3 x_3 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 4} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_4 x_4 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 5} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_5 x_5 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 6} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_6 x_6 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 7} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_7 x_7 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
\end{array} \right]\end{equation}
\begin{equation}
{\bf \eta}\;{\rm = }\;\left[ \begin{array}{l}
{\eta}_{\rm 2} \\
{\eta}_{\rm 3} \\
{\eta}_{\rm 4} \\
{\eta}_{\rm 5} \\
{\eta}_{\rm 6} \\
{\eta}_{\rm 7} \\
\end{array} \right]\;{\rm = }\;\left[ \begin{array}{l}
{\rm ln}\;{\rm \beta }_{\rm 2} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_2 x_2 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 3} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_3 x_3 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 4} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_4 x_4 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 5} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_5 x_5 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 6} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_6 x_6 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
{\rm ln}\;{\rm \beta }_{\rm 7} - {\rm ln}\;{\rm \beta }_{\rm 1} - {\rm ln}\;(w_7 x_7 )\; + \;{\rm ln}\;(w_1 x_1 ) \\
\end{array} \right]\end{equation}
The determinant of the Jacobian matrix of the transformation from ![]() $\left( {v - u,{\bf \eta }} \right)$ to (lnx 1, lnx 2, …, lnx 7) will be
$\left( {v - u,{\bf \eta }} \right)$ to (lnx 1, lnx 2, …, lnx 7) will be
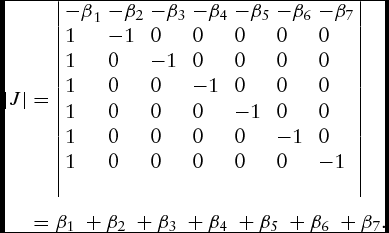 \begin{eqnarray}
\left| J \right|
&=& \left| \begin{array}{lllllll}
- {\rm \beta }_{\rm 1} & - {\rm \beta }_{\rm 2} & - {\rm \beta }_{\rm 3} & - {\rm \beta }_{\rm 4} & - {\rm \beta }_{\rm 5} & - {\rm \beta }_{\rm 6} & - {\rm \beta }_{\rm 7} \\
1 & - 1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & - 1 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & - 1 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & - 1 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & - 1 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 & - 1 \\
\end{array} \right| \nonumber\\
&=& {\rm \beta }_{\rm 1} \; + {\rm \beta }_{\rm 2} \; + {\rm \beta }_{\rm 3} \; + {\rm \beta }_{\rm 4} \; + {\rm \beta }_{\rm 5} \; + {\rm \beta }_{\rm 6} \; + {\rm \beta }_{\rm 7} .\end{eqnarray}
\begin{eqnarray}
\left| J \right|
&=& \left| \begin{array}{lllllll}
- {\rm \beta }_{\rm 1} & - {\rm \beta }_{\rm 2} & - {\rm \beta }_{\rm 3} & - {\rm \beta }_{\rm 4} & - {\rm \beta }_{\rm 5} & - {\rm \beta }_{\rm 6} & - {\rm \beta }_{\rm 7} \\
1 & - 1 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & - 1 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & - 1 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & - 1 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & - 1 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 & - 1 \\
\end{array} \right| \nonumber\\
&=& {\rm \beta }_{\rm 1} \; + {\rm \beta }_{\rm 2} \; + {\rm \beta }_{\rm 3} \; + {\rm \beta }_{\rm 4} \; + {\rm \beta }_{\rm 5} \; + {\rm \beta }_{\rm 6} \; + {\rm \beta }_{\rm 7} .\end{eqnarray}
The NASS survey design is a stratified sample frame based on characteristics of farms (USDA-ERS, 2014). For each observation, the data set includes sampling weights or expansion factors (Qi = 1/πi) that are based on the probability (πi) of the farmers being selected within a stratum. Therefore, in order to provide unbiased estimators, we use the weighted exogenous sampling estimator (WESML) (Manski and Lerman, Reference Manski and Lerman1977). According to the authors, with reference to this study, the quasi-log-likelihood function will be
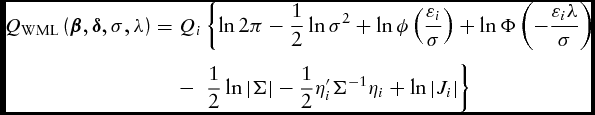 \begin{eqnarray}
Q_{{\rm WML}} \left( {{\bf \beta },{\bf \delta },{\rm \sigma },{\rm \lambda }} \right)& =& Q_i \left\{ \ln 2{\rm \pi } - \frac{1}{2}\ln {\rm \sigma }^2 + \ln \phi \left(\frac{{{\rm \varepsilon }_i }}{{\rm \sigma }}\right) + \ln {\rm \Phi }\left( { - \frac{{{\rm \varepsilon }_i {\rm \lambda }}}{{\rm \sigma }}} \right)\right. \nonumber\\
&& -\; \left.\frac{1}{2}\ln \left| {\rm \Sigma } \right| - \frac{1}{2}{\rm \eta }'_i {\rm \Sigma }^{ - 1} {\rm \eta }_i + \ln | {J_i } |\right\}\end{eqnarray}
\begin{eqnarray}
Q_{{\rm WML}} \left( {{\bf \beta },{\bf \delta },{\rm \sigma },{\rm \lambda }} \right)& =& Q_i \left\{ \ln 2{\rm \pi } - \frac{1}{2}\ln {\rm \sigma }^2 + \ln \phi \left(\frac{{{\rm \varepsilon }_i }}{{\rm \sigma }}\right) + \ln {\rm \Phi }\left( { - \frac{{{\rm \varepsilon }_i {\rm \lambda }}}{{\rm \sigma }}} \right)\right. \nonumber\\
&& -\; \left.\frac{1}{2}\ln \left| {\rm \Sigma } \right| - \frac{1}{2}{\rm \eta }'_i {\rm \Sigma }^{ - 1} {\rm \eta }_i + \ln | {J_i } |\right\}\end{eqnarray}
with i = 1, 2, …, n.
Cameron and Trivedi (Reference Cameron and Trivedi2005) show that even if the sampling process is affected by endogeneities, the WESML is still consistent. Because the information matrix does not hold for the quasi-maximum likelihood estimator (Q WML), the asymptotic variance-covariance matrix can be calculated using the sandwich estimator ![]() $n^{ - 1} \mathop \sum \nolimits_{i = 1}^n \left( {{\bf Q}_i \odot {\bf H}_i } \right)^{ - 1} \left( {{\bf Q}_i ^2 \odot {\bf G}_i {\bf G}_i^\prime } \right)\left( {{\bf Q}_i \odot {\bf H}_i } \right)^{ - 1} $ where n is the sample size; G and H are the gradient and the Hessian of equation (13), respectively; Qi is the sampling weight associated with each observation; and ⊙ is the element-wise Hadamard product (Cameron and Trivedi, Reference Cameron and Trivedi2005, p. 828).
$n^{ - 1} \mathop \sum \nolimits_{i = 1}^n \left( {{\bf Q}_i \odot {\bf H}_i } \right)^{ - 1} \left( {{\bf Q}_i ^2 \odot {\bf G}_i {\bf G}_i^\prime } \right)\left( {{\bf Q}_i \odot {\bf H}_i } \right)^{ - 1} $ where n is the sample size; G and H are the gradient and the Hessian of equation (13), respectively; Qi is the sampling weight associated with each observation; and ⊙ is the element-wise Hadamard product (Cameron and Trivedi, Reference Cameron and Trivedi2005, p. 828).
ARMS does not report the price of single nutrients applied by the respondents; therefore, we derived these data from ARMS: We thus projected the prices of nutrients based on an ordinary least square model based on (1) total cost of commercial fertilizer (nitrogen, phosphorus, and potash; N-P-K) applied, (2) total acres treated with these products, (3) quantity applied per acre, and (4) percentage analysis of plant nutrients applied per acre. We regressed fertilizer expenditure (E) per unit of land (US$/acre) on the actual acreage treatedFootnote 6 with the chemical components producing the estimates as reported in Table 1.Footnote 7
Table 1. Estimated Nutrient Expenditures

Notes: Dependent variable is expenditure per unit of land (E). Asterisks ***, **, and * indicate 99%, 95%, and 90% confidence interval, respectively. Standard errors are in parentheses.
Based on the Ordinary Least Squares (OLS) model, we project the expenditure of each nutrient per acre by setting the use of the other inputs (A N, A P, or A K) to zero. For example, phosphorus expenditure per acre is E P = 41.014 – 0.085A P. Finally, the nutrient price for each farmer is the ratio of the total nutrient expenditure (US$) to the total pounds of nutrient applied; for example, the price of phosphorus (US$/pound) for each farmer is calculated as PriceP = (E P × A P)/P, where P is total pounds of phosphorus. Descriptive Statistics are reported in Table 2.
Table 2. Descriptive Statistics

Notes: Nutrients and pesticides refer to the actual weight of the active chemical component. The actual active component of the commercial pesticides has been calculated using the specific gravity of each chemical component as reported by the “AccuStandard Pesticde Standards Reference Guide.” Prices of nitrogen, phosphate, and potash have been simulated through an OLS model.
5. Results
The quasi-log-likelihood function (equation 13) is optimized using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method for nonlinear optimization available in the optimization library of the Ox Matrix language (Doornik and Ooms, Reference Doornik and Ooms2006). The BFGS algorithm is widely used to numerically solve very complex unconstrained problems such as equation (13) using a limited amount of computer memory. Furthermore, this algorithm numerically approximates the Hessian matrix of equation (13) with a positive-semidefinite matrix that is updated at each step by an iterative procedure based on gradient evaluation. Consequently, the cumbersome computation of the analytical Hessian matrix (equation 13) can be avoided while ensuring a convergent solution of the numerical optimization problem.
Table 3 presents the parameter estimates of the production function with and without systematic errors in allocation. The parameter λ is statistically different from zero at the 10% confidence level; therefore, the peanut production frontier is stochastic as also previously found by Nadolnyak, Fletcher, and Hartarska (Reference Nadolnyak, Fletcher and Hartarska2006).Footnote 8
Table 3. Stochastic Frontier Analysis

Notes: Asterisks ***, **, and * indicate 99%, 95%, and 90% confidence level, respectively. Standard errors are in parentheses.
In terms of the magnitude of the parameters, no substantial differences exist between the model that includes systematic error in allocation and the model that disregards them. However, given the lower Akaike information criteria, the model representing the production function that accounts for systematic errors better represents reality with minimum information loss. Additionally, given the hypothesis that agricultural producers systematically overuse chemical inputs, the model with systematic errors is a better choice.
Table 4 reports the model statistics also in case of systematic error in allocation. On average, peanut farmers have a technical efficiency that is 65.3%. Thus, output is below the optimum output level given the input use. The hypothesis of overuse of chemical production factors is confirmed by the negative sign of all the allocative inefficiency terms, η ’s. In particular, fungicides, by the magnitude of their mean allocative inefficiency, appear to be the chemical factor that is used in the least efficient way. In fact, at the mean value, wFexp(ηF) = 0.38 < wF = 60.39, and the labor/fungicide ratio is lower than the cost-minimizing condition.
Table 4. Model Statistics

Notes: There were 389 observations. Technical efficiency and cost increases are expressed in percentages. Subscripts N, P, K, I, H, and F refer to nitrogen, phosphate, potash, insecticides, herbicides, and fungicides, respectively.
The overuse of fungicides with respect to all the other inputs is also confirmed by the fact that (wF/wi)exp(ηF/ηi) < wF/wi∀i = N, P, K, I, H and (wF/wL)exp(ηF) < wF/wL. Table 5 reports these inequalities evaluated at their mean values.
Table 5. Overuse of Fungicide with Respect to Other Inputs

Note: Input price ratios are evaluated at the mean value of the variables.
A comparison of the results in Table 5 indicates that the price ratio of fungicide to other input prices is on average always lower than the cost-minimizing ratios.
We derive input demand equations by solving simultaneously the estimated system of equations (10) and (11) for each input. The input demand equations in logarithmic form are
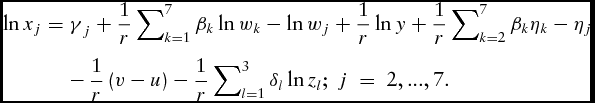 \begin{eqnarray}
\ln x_j & =& {\rm \gamma }_j + \frac{1}{r} \sum \nolimits_{k = 1}^7 {\rm \beta }_k \ln w_k - \ln w_j + \frac{1}{r}\ln y + \frac{1}{r} \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k - {\rm \eta }_j \nonumber\\
&& -\, \frac{1}{r}\left( {v - u} \right) - \frac{1}{r} \sum \nolimits_{l = 1}^3 {\rm \delta }_l \ln z_l; j = 2,...,7.\end{eqnarray}
\begin{eqnarray}
\ln x_j & =& {\rm \gamma }_j + \frac{1}{r} \sum \nolimits_{k = 1}^7 {\rm \beta }_k \ln w_k - \ln w_j + \frac{1}{r}\ln y + \frac{1}{r} \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k - {\rm \eta }_j \nonumber\\
&& -\, \frac{1}{r}\left( {v - u} \right) - \frac{1}{r} \sum \nolimits_{l = 1}^3 {\rm \delta }_l \ln z_l; j = 2,...,7.\end{eqnarray}
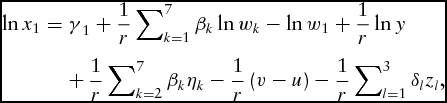 \begin{eqnarray}
\ln x_1 & =& {\rm \gamma }_1 + \frac{1}{r}\mathop \sum \nolimits_{k = 1}^7 {\rm \beta }_k \ln w_k - \ln w_1 + \frac{1}{r}\ln y\nonumber\\
&& +\, \frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k - \frac{1}{r}\left( {v - u} \right) - \frac{1}{r}\mathop \sum \nolimits_{l = 1}^3 {\rm \delta }_l z_l ,\end{eqnarray}
\begin{eqnarray}
\ln x_1 & =& {\rm \gamma }_1 + \frac{1}{r}\mathop \sum \nolimits_{k = 1}^7 {\rm \beta }_k \ln w_k - \ln w_1 + \frac{1}{r}\ln y\nonumber\\
&& +\, \frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k - \frac{1}{r}\left( {v - u} \right) - \frac{1}{r}\mathop \sum \nolimits_{l = 1}^3 {\rm \delta }_l z_l ,\end{eqnarray}
The actual demand change attributable to allocative inefficiency is given by ![]() $\left[ {\ln x_j {\rm |\eta } = {\rm \hat \eta ]} - } \right[\ln x_j {\rm |\eta } = 0{\rm ]} = \frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k - \widehat{{\rm \eta }_j }$ percent increase for the chemical input xj and
$\left[ {\ln x_j {\rm |\eta } = {\rm \hat \eta ]} - } \right[\ln x_j {\rm |\eta } = 0{\rm ]} = \frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k - \widehat{{\rm \eta }_j }$ percent increase for the chemical input xj and ![]() $\frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k $ percent for labor ( x 1). The change in demand can be positive or negative depending on the magnitudes and signs of the estimated allocative inefficiencies
$\frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k $ percent for labor ( x 1). The change in demand can be positive or negative depending on the magnitudes and signs of the estimated allocative inefficiencies ![]() $(\widehat{{\rm \eta }_j }$). For the inputs, the change in demand from the technical inefficiency is a demand increase that is equal to
$(\widehat{{\rm \eta }_j }$). For the inputs, the change in demand from the technical inefficiency is a demand increase that is equal to ![]() $\frac{u}{r} \% = 0.21\% $ in this study. Behind the econometric assumption, there is also an economic explanation for the demand increase attributable to the technical inefficiency. This is related to the self-duality property of the functional form that was chosen to model the production frontier. In fact, self-dual production functions allow us to convert the output-oriented technical inefficiency ( − u) in equation (10) into input-oriented technical inefficiency
$\frac{u}{r} \% = 0.21\% $ in this study. Behind the econometric assumption, there is also an economic explanation for the demand increase attributable to the technical inefficiency. This is related to the self-duality property of the functional form that was chosen to model the production frontier. In fact, self-dual production functions allow us to convert the output-oriented technical inefficiency ( − u) in equation (10) into input-oriented technical inefficiency ![]() $\frac{u}{r}$ in equations (14) and (15) by using
$\frac{u}{r}$ in equations (14) and (15) by using ![]() $\frac{1}{r}$ as a conversion factor. The change of sign is consistent with the equivalence of these two statements: “producing less than optimal output” and “using more than minimum inputs.” In addition, economies of scale can mitigate the input demand increase attributable to technical inefficiency because an inverse relationship between such an input demand increase and the degree of homogeneity exists.
$\frac{1}{r}$ as a conversion factor. The change of sign is consistent with the equivalence of these two statements: “producing less than optimal output” and “using more than minimum inputs.” In addition, economies of scale can mitigate the input demand increase attributable to technical inefficiency because an inverse relationship between such an input demand increase and the degree of homogeneity exists.
Another important result is that of the input demand equations also being functions of the exogenous environmental factors, z, as is clearly demonstrated by the last terms in equations (14) and (15). It is clear that these environmental factors refer to climatic conditions of each farm during the growing period; therefore, these are frontier shifters that exogenously affect the input demand. Consequently, as for the output-oriented technical inefficiency, there exists a dual role of the climatic factors as production frontier and input demand shifters. As a result, it is possible to derive for each climatic variable the corresponding demand elasticity from equations (14) and (15), that is, ![]() $\frac{{\partial \ln x_{j} }}{{\partial \ln z_{l} }} = - \frac{{\delta _l }}{r} $; j = 1,…,7 and l = 1,…,3. The effects of the allocative inefficiencies and climatic conditions on input demand are reported in Table 6.
$\frac{{\partial \ln x_{j} }}{{\partial \ln z_{l} }} = - \frac{{\delta _l }}{r} $; j = 1,…,7 and l = 1,…,3. The effects of the allocative inefficiencies and climatic conditions on input demand are reported in Table 6.
Table 6. Allocative Inefficiency, Climate Conditions, and Input Demand

Notes: The change in demand for input j attributable to the allocative inefficiencies ηj = 2,…,7 is ![]() $\frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k - \widehat{{\rm \eta }_j }$, and the change in demand for labor (x 1) is
$\frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k - \widehat{{\rm \eta }_j }$, and the change in demand for labor (x 1) is ![]() $\frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k $. The increased demand attributable to technical inefficiency is
$\frac{1}{r}\mathop \sum \nolimits_{k = 2}^7 {\rm \beta }_k {\rm \eta }_k $. The increased demand attributable to technical inefficiency is ![]() $\frac{u}{r}$ = 0.21% for each input. For each climatic variable, the corresponding elasticity of demand for each input is calculated from equations (16) and (17) as
$\frac{u}{r}$ = 0.21% for each input. For each climatic variable, the corresponding elasticity of demand for each input is calculated from equations (16) and (17) as ![]() $\partial \ln x_j / \partial \ln z_l = - \frac{{{\rm \delta }_l }}{r}$; j = 1,…,7 and l = 1,…,3.
$\partial \ln x_j / \partial \ln z_l = - \frac{{{\rm \delta }_l }}{r}$; j = 1,…,7 and l = 1,…,3.
Because of allocative inefficiencies, demand for production factors increased between 0.71% and 2.15% except for labor (x 1) and insecticides (x 5), whose demands decreased potentially by 2.91% and 1%, respectively. It also appears that, holding other factors constant, farmers from relatively humid and rainy areas would increase the use of each input by 1.2% and 8.3% per 10% increase in rainfall and relative humidity, respectively. In contrast, farmers from warmer areas potentially used 19% less inputs if the temperature during the growing period was 10% higher than average.
In addition, following Kumbhakar and Lovell (Reference Kumbhakar and Lovell2000, p. 149), from equations (14) and (15) we derive an expression for the total costs of peanut production, ![]() $C = \mathop \sum \nolimits_{j = 1}^7 w_j x_j $. This expression includes the cost of technical and allocative inefficiency as well as the impact of climate on production costs. The cost function in logarithmic notation, after algebraic manipulation, is given by
$C = \mathop \sum \nolimits_{j = 1}^7 w_j x_j $. This expression includes the cost of technical and allocative inefficiency as well as the impact of climate on production costs. The cost function in logarithmic notation, after algebraic manipulation, is given by
where ![]() ${\rm \Psi } = \ln r - \frac{{{\rm \beta }_0 }}{r} - \frac{1}{r}\mathop \sum \nolimits_{j = 1}^7 {\rm \beta }_j \ln {\rm \beta }_j $ and
${\rm \Psi } = \ln r - \frac{{{\rm \beta }_0 }}{r} - \frac{1}{r}\mathop \sum \nolimits_{j = 1}^7 {\rm \beta }_j \ln {\rm \beta }_j $ and
The derivation of the cost increase attributable to both technical and allocative inefficiency is the percentage cost increase of allocative inefficiency,
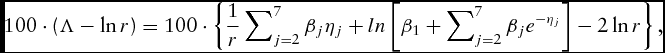 \begin{eqnarray}
100 \cdot ({\rm \Lambda } - \ln r) = 100 \cdot \left\{ {\frac{1}{r}\mathop \sum \nolimits_{j = 2}^7 {\rm \beta }_j {\rm \eta }_j + ln\left[ {{\rm \beta }_1 + \mathop \sum \nolimits_{j = 2}^7 {\rm \beta }_j e^{ - {\rm \eta }_j } } \right] - 2\ln r} \right\},\nonumber\\
\end{eqnarray}
\begin{eqnarray}
100 \cdot ({\rm \Lambda } - \ln r) = 100 \cdot \left\{ {\frac{1}{r}\mathop \sum \nolimits_{j = 2}^7 {\rm \beta }_j {\rm \eta }_j + ln\left[ {{\rm \beta }_1 + \mathop \sum \nolimits_{j = 2}^7 {\rm \beta }_j e^{ - {\rm \eta }_j } } \right] - 2\ln r} \right\},\nonumber\\
\end{eqnarray}
and the percentage cost increase of technical inefficiency is 100 × ![]() $\frac{u}{r}$ % (Kumbhakar and Wang, Reference Kumbhakar and Wang2006, pp. 435–36).
$\frac{u}{r}$ % (Kumbhakar and Wang, Reference Kumbhakar and Wang2006, pp. 435–36).
In the current study, peanut farmers face a cost increase of 21.4% because of technical inefficiency on average, and 50% of farmers see their costs increase by 70.3% because of allocative inefficiency. Those cost increases could be reduced if peanut farmers appropriately reduced chemical input use. For example, Nadolnyak, Fletcher, and Hartarska (Reference Nadolnyak, Fletcher and Hartarska2006) found that the experience and managerial skill (proxied by education) of the peanut farmer increase technical efficiency and reduce the associated costs.
Isolating the effect of fungicides, if peanut farmers could cultivate an engineered crop that would avoid the use of this factor, then they would have potentially reduced the total cost of chemical inputs up to 36.2%.
5.1. Environmental and Public Health Implications
Climate variables have a significant impact on the productivity of peanuts. In particular, temperature appears to be an important growth factor as also confirmed by field experiments conducted by Cox (Reference Cox1979). Farmers whose farms are located in areas that had on average a temperature of 2°C higher could expand their production by 250,000 pounds in the 2004 growing period, ceteris paribus. Farms located in wet areas appear to be less productive. Based on the results of this study, a 10% increase in rainfall would decrease on average the production of peanuts by 2.4%. A similar negative impact of water was found by Wright et al. (1986) in Virginia. These authors attributed the decrease in peanut yield to the excess of water that may increase the proliferation of soil-borne disease. In line with the previous result, but to a different extent, this research also finds a negative and more severe impact of an increase in relative humidity (dew point). Cotty and Jaime-Garcia (Reference Cotty and Jaime-Garcia2007) found evidence that warm and humid climates are particularly favorable for Aspergillus infections and aflatoxin contamination that may explain the decline in productivity of those areas.
According to USDA-NASS (2015), the most common fungicides used in 2004 by peanut farmers from Alabama, Florida, Georgia, North Carolina, and Texas were chlorothalonil and tubeconazole. In particular, the first was used in a range of between 54% and 90% of the total fungicides used, the latter between 2% and 21%. Both these active ingredients have been classified as potential carcinogens by U.S. Environmental Protection Agency, Office of Pesticide Programs (2013). Therefore, we further investigate the potential harm of these classes of fungicides by computing their environmental impact using the environmental impact quotient (EIQ) equation developed by Kovach et al. (Reference Kovach, Petzoldt, Degni and Tette1992). The authors derived a measure called field use environmental impact quotient (FUEIQ), which is based on application rates and percentage of active ingredients and allows one to perform an accurate comparison of pesticides and pest management strategies. Disregarding the FUEIQ of tubeconazole, which is in the safe zone between 10.1 and 20.2,Footnote 9 in Table 7 we report the environmental impact analysis of chlorothalonil, which is also the most used fungicide by U.S. peanut producers.
Table 7. Chlorothalonil Use in U.S. Peanut Production and Environmental Impact Quotient (EIQ)
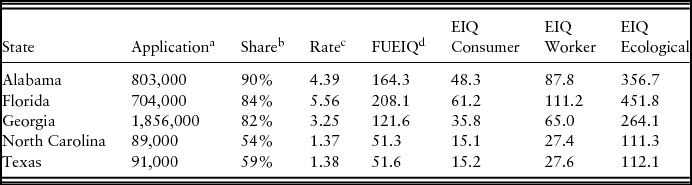
a Total application of chlorothalonil in pounds.
b Percentage share of chlorothalonil of the total use of fungicides.
c Average application rate expressed in pounds/acres.
d Field use EIQ (FUEIQ).
Notes: FUEIQ has been calculated by the authors using the EIQ online calculator of New York State Integrated Pest Management (http://www.nysipm.cornell.edu/EIQCalc/input.php). An FUEIQ >100 poses high risk to applicators and the environment.
Source: USDA-NASS (2015).
From the EIQ analysis, it appears that in Alabama, Florida, and Georgia, which are also particularly humid areas, the application rate of chlorothalonil is more than twice that of North Carolina and Texas. As a consequence, the excessive use of chlorothalonil should raise some concerns for the environmental quality of the agroecological areas of those states (FUEIQ >100).
The results of this research are clear: U.S. peanut farmers overused fungicides based on 2004 data. The impact of allocative inefficiency of fungicide on the demand for other inputs was derived from equations (16) and (17). This analysis shows that the inefficient use of fungicides would also increase in general the demand for other chemical factors (except for insecticides) between 0.70% and 2.15% per farmer. Furthermore, in humid areas the use of chemical factors can potentially increase by 5.14% per farmer for each degree Celsius increase in dew point temperature.Footnote 10 Therefore, in general, the overuse of chemical factors can be seen as an environmental externality that is connected to the inefficient use of fungicides.
The magnitude of this finding is not extremely severe for the case of non-point-source pollution derived by the induced overuse of fertilizer; however, considering also the potential for increased use of chemical inputs in more humid areas, the cumulative effect of some pesticides released in the environment over time, and the aggregate contribution of all peanut farmers in the United States, the inefficient use of fungicides can have a significant negative impact on the quality of ecosystems. Between 1992 and 2001, pesticides and their degradates were found in 4,380 water samples derived from agricultural, urban, and mixed-use land streams across the nation (Gilliom et al., Reference Gilliom, Barbash, Crawford, Hamilton, Martin, Nakagaki and Nowell2007).
Agricultural biotechnological research should pay attention to genetic traits of peanuts to make this cultivar resistant to fungal pathogens. In addition to farmers’ welfare improving by cutting the cost of fungicide, an increase in social welfare would be derived by reducing the usage of other chemicals that may affect the soil and water quality of those areas in proximity of peanuts farms. A cultivar that is genetically manipulated to be resistant to fungal pathogens would also induce the farmers to reduce the usage of other chemicals, thereby decreasing environmental contamination.
5.2. Limitations to the Study
It should be made clear that the current study considers the entire aggregate class of fungicides. Peanuts are known to be affected by more than 40 fungal diseases (Podile and Kishore, Reference Podile, Kishore and Gnanamanickam2002, pp. 131–60); therefore, the potential costs savings attributable to the adoption of a GE cultivar reflects an aggregation of the total cost of fungicide control of a consistent number of fungal diseases. Therefore, the cost estimates of allocative inefficiency should be considered as an upper boundary of damage control for fungal diseases. Furthermore, GE technologies may be effective for controlling only damage associated with a specific event (e.g., diseases, pests, droughts, etc.). Therefore, the real value of genetic modification depends on the relative share of the total economic injury of each fungal disease that could be avoided if an engineered crop could be adopted. Given these limitations, we recommend that a future disaggregated productivity analysis in the U.S. peanut sector should be restricted only to the chemical class of fungicides to study the overuse of a particular active ingredient with respect to the others. Such an analysis will allow understanding of precisely the particular class of fungal pathogen that should be the research focus of geneticists. A more detailed analysis that also includes the ecotoxicological impact deriving from the overuse of a specific class of fungicides in the peanut sector is a future research avenue that can be explored in an interdisciplinary effort.
Admittedly, the data for this study are from 2004. An ideal data set would be panel data of the cost of production of peanut farmers to capture yearly fluctuations, but these data do not exist. Despite this, the completeness of the ARMS data makes use of these data ideal for our analysis, and these data reflect peanut production and costs after the elimination of the peanut quota. Our main hypothesis is that producers overuse fungicides. It should thus be noted that annual fungicide use by U.S. farmers has not changed significantly in the past 50 years (Fernandez-Conejo et al., Reference Fernandez-Cornejo, Nehring, Osteen, Wechsler, Martin and Vialou2014), and there have been no additional restrictions on fungicide use since the amendments to the Federal Insecticide, Fungicide, and Rodenticide Act, which date back to 1972 (Federal Environmental Pesticide Control Act) and 1996 (Food Quality Protection Act). Hence, we believe that our hypothesis of systematic overuse of fungicides among U.S. peanut farmers is still a valid concern.
6. Conclusions
A consistent amount of agricultural output is known to be lost every year to insects, weeds, and other plant pathogens. The use of pesticides is a common agricultural practice that, combined with other inorganic chemical factors such as nutrients, produces environmental externalities. Furthermore, Kumbhakar and Lovell (Reference Kumbhakar and Lovell2000, p. 152) suggest that farmers overuse chemical inputs. Thus, technologies that lower this input use could produce benefits to farmers and the environment. In particular, appropriate genetic engineering may lower production costs, mitigate output loss, increase productivity, and lessen environmental externalities. For example, Falck-Zepeda, Traxler, and Nelson (Reference Falck-Zepeda, Traxler and Nelson2000) provide evidence that biotechnology indeed increased the economic welfare of producers and consumers. By extension, advances in genetic engineering in the peanut sector, which are in their infancy, may yield similar benefits.
This study is the first to suggest that innovations in peanut cultivars, for example through genetic engineering, could yield economic and environmental benefits. The benefits derive from a reallocation of input use. Our analysis suggests that peanut farmers overuse chemical inputs, specifically fungicides, so that targeted genetic traits to lower the need for fungicides could generate economic and environmental benefits. In particular, in this research we used a cross-sectional sample of U.S. peanut farmers to test the hypothesis of overuse of chemical factors with respect to labor.
A primal system approach of a stochastic frontier analysis revealed that U.S. peanut farmers overused fungicides more than any other input. The overuse of fungicide could be a particular need of peanut farmers to defeat crop infestations from mycotoxin-producing fungi. Although this research does not explain the overuse of fungicides, future research could be directed toward understanding the reasons for the overuse. Additionally, future analysis may help explain how the misuse of fungicides also induces an increase in demand for other chemical factors.
If peanut farmers could have adopted a GE cultivar resistant to the fungal pathogens that produce the largest economic damage, they could have potentially reduced on average the total cost of chemicals up to 36.2% and the demand for all other factors up to 2.15%. Given the evidence of systematic overuse of fungicides in U.S. peanut production, we recommend that future genetic research should focus primarily on the class of fungal pathogens. Considering the cumulative effect of pesticides in the environment, reducing the use of these factors can be a further contribution toward the increase in social welfare by improving the quality of ecosystems in proximity to the farming areas.









