A comparison of empirical and physically based glacier surface melt models for long-term simulations of glacier response

Abstract

We investigate the performance of five glacier melt models over a multi-decadal period in order to assess their ability to model future glacier response. The models range from a simple degree-day model, based solely on air temperature, to more-sophisticated models, including the full shortwave radiation balance. In addition to the empirical models, the performance of a physically based energy-balance (EB) model is examined. The melt models are coupled to an accumulation and a surface evolution model and applied in a distributed manner to Rhonegletscher, Switzerland, over the period 1929–2012 at hourly resolution. For calibration, seasonal mass-balance measurements (2006–12) are used. Decadal ice volume changes for six periods in the years 1929–2012 serve for model validation. Over the period 2006–12, there are almost no differences in performance between the models, except for EB, which is less consistent with observations, likely due to lack of meteorological in situ data. However, simulations over the long term (1929–2012) reveal that models which include a separate term for shortwave radiation agree best with the observed ice volume changes, indicating that their melt relationships are robust in time and thus suitable for long-term modelling, in contrast to more empirical approaches that are oversensitive to temperature fluctuations.

Introduction

Several studies have demonstrated the impact of the expected 21st-century climate change on glacier mass balance at the regional and global scale (Le Meur and others, 2007; Huss and others, 2008a; Farinotti and others, 2012; Radić and others, 2014). Model simulations depend, however, on the type of model used (Pellicciotti and others, 2013; Huss and others, 2014). Approaches to computing melt range from empirical models (e.g. simple temperature-index models) to more-sophisticated physically based energy-balance models. Temperature-index models require only temperature as input and are based on an assumed linear relationship between this variable and melt rates, whereas energy-balance models are based on the computation of all relevant energy fluxes at the glacier surface, and thus require extrapolation of numerous meteorological and surface input variables at the glacier scale. There is great variety in the degree of sophistication of the approaches incorporating more or fewer meteorological input variables (Jóhannesson and others, 1995; Cazorzi and Dalla Fontana, 1996; Hock, 1999; Hock and Holmgren, 2005; Anslow and others, 2008). Advances over the simple dependence of melt on air temperature by addition of radiation terms have been suggested recently (Cazorzi and Dalla Fontana, 1996; Hock, 1999; Pellicciotti and others, 2005), and are called enhanced temperature-index models. In contrast to simple temperature-index models, enhanced temperature-index models provide a better representation of the spatial and temporal variability of melt controlled by solar radiation. Some of these approaches also cope better with the physical character of the melt process and provide a promising approach to modelling melt at the glacier-wide scale with fewer input data than energy-balance models, but with a higher accuracy than standard temperature-index models. Pellicciotti and others (2005) presented such an enhanced temperature-index melt model and showed that the performance, compared with conventional temperature-index models, was significantly better. The authors suggested that simpler models that are directly dependent on air temperature might be oversensitive to temperature fluctuations. The model comparison was performed at the point scale with measured input data from five automatic weather stations operated over one ablation season at Haut Glacier d’Arolla, Switzerland. Carenzo and others (2009) tested the transferability of the enhanced temperature-index model and showed that model parameters calibrated over one season could be applied to another year or another site with only a small decrease in model performance. The stronger physical basis might imply that the model parameters are less dependent on meteorological conditions and thus more robust in time. In contrast, there are indications that the parameters of simple temperature-index models are not stable over decadal periods, and thus require recalibration for individual subperiods (Huss and others, 2009a), calling into question their suitability for future glacier projections. Physically based energy-balance models provide accurate point melt rates when high-quality, in situ records of meteorological variables are available (Pellicciotti and others, 2013). However, their performance declines when forced with data recorded outside the glacier boundary layer, where the equations of the energy fluxes are valid. As a result, it might be questioned whether they continue to represent the best model approach for spatially distributed simulations and long-term modelling when meteorological input variables need to be extrapolated from off-glacier stations. Despite this, several studies have applied distributed energy-balance models forced with data from off-glacier weather stations (e.g. Klok and Oerlemans, 2002; Gerbaux and others, 2005).

The aim of this study is to examine the performance of five different melt models, (1) a classical temperature-index (TI) model, (2) the temperature-index model of Hock (1999) (HTI), (3) an enhanced temperature-index (ETI) model, (4) a simplified energy-balance (SEB) model and (5) an energy-balance (EB) model, over multiple decades (1929–2012), to study the performance of the different approaches for long-term modelling studies. The selected models range from using the most simple (empirical) to the most complex (physically based) form of melt equation, but they are all well-established and widely used melt models commonly applied in mass-balance studies. The robustness of the parameters of the empirical models (TI, HTI, ETI, SEB) over a period of several years (2006–12) is investigated using repeated mass-balance measurements. In order to test the multi-seasonal glacier mass-balance evolution, the melt models are coupled to an accumulation and a mass-balance redistribution model and are applied to Rhonegletscher, Swiss Alps, in a distributed manner. Meteorological data from the nearby weather station at Grimsel Hospiz (hereafter referred to as Grimsel) are used to force the models. The simple TI model is based on few input data and requires only air temperature and precipitation, while the HTI model needs, in addition, an index of potential clear-sky solar radiation. The ETI and SEB models require, instead of the potential radiation, the full shortwave radiation balance, i.e. the actual incoming and outgoing shortwave radiation, the latter being defined by the surface albedo. Solar radiation is calculated on the basis of a radiation model for clear-sky conditions and a cloud factor. The EB model is the most data-demanding approach, as it requires (in addition to air temperature, precipitation and incoming and reflected shortwave radiation) the longwave radiation flux, wind speed and relative humidity, and a knowledge of surface characteristics (e.g. surface roughness).

Rhonegletscher has a long history of measurements and has been investigated intensively, particularly in recent years. A comprehensive set of sub-seasonal mass-balance and accumulation measurements for the period 2006–12 provides extensive mass-balance data and serves as the basis for the calibration of the model parameters. For each year of the period 2006–12, individual model parameters are calibrated by minimizing the difference between simulated and observed sub-seasonal mass-balance measurements. Furthermore, a mean parameter set calculated from all available mass-balance measurements for the years 2006–12 is determined and adopted for the long-term modelling (1929–2012). The performance of the five models is validated against decadal ice volume changes derived by seven digital elevation models (DEMs) covering the period 1929–2012. Based on the insights gained, we attempt to determine which model is best suited for mass-balance modelling over decadal periods and for glacier projections into the 21st century.

Study Site and Data

The study site is located in the central Swiss Alps and forms the headwaters of the Rhone river (Fig. 1a). Rhonegletscher is a medium-sized valley glacier and covers an area of ~16 km². It has approximately north–south orientation and an altitude range of 2200–3600 m a.s.l.

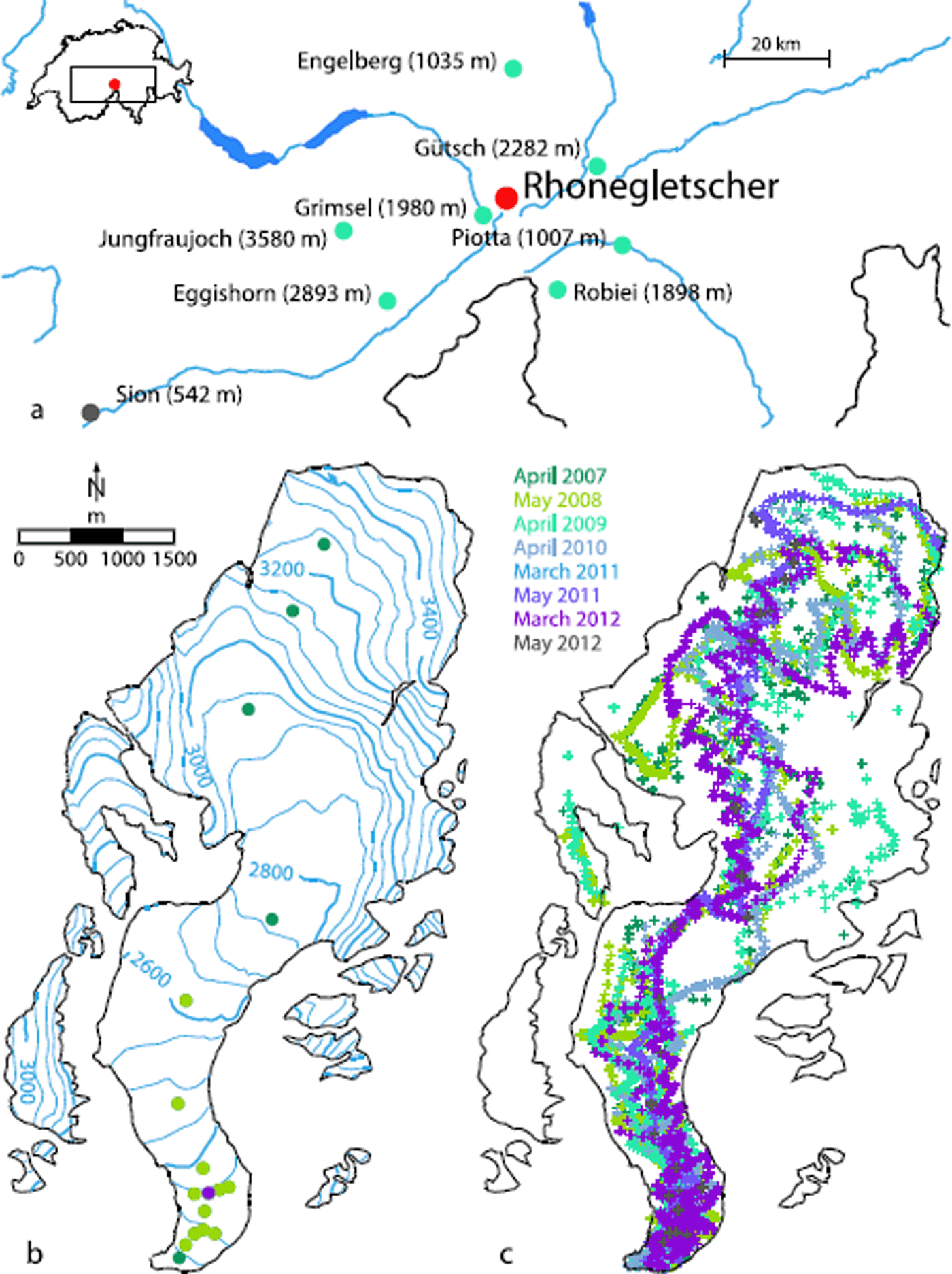
Fig. 1. (a) The location of Rhonegletscher (red dot) and of the weather station Grimsel, Sion and the six additional weather stations used to derive temperature lapse rates (green dots), with elevations given in parentheses. (b) Overview of the study site with the location of the ablation stakes (all dots) and of the fixed pyranometer (violet dot). Light green dots show the location of the albedo measurements carried out every second to third week in summer 2011. (c) Position of the snow depth measurements for the years 2007–12.

Meteorological data are taken from the nearest weather station, Grimsel (1980 m a.s.l.), operated by MeteoSwiss and located ~4 km west of the glacier tongue of Rhonegletscher (Fig. 1a). This weather station has recorded air temperature, precipitation, global radiation, humidity, wind speed and wind direction at daily resolution since the beginning of 1959 and at hourly resolution since spring 1989.

Air temperature measured at Grimsel is extrapolated by means of seasonal temperature lapse rates with a daily cycle. Recent studies have shown that temperature lapse rates in high-elevation catchments exhibit a distinct variability during the day (Petersen and Pellicciotti, 2011; Carenzo, 2012) and that this needs to be taken into account when forcing melt models to avoid modelling errors (Petersen and Pellicciotti, 2011; Immerzeel and others, 2014). Neglecting a daily cycle could result in an overestimation of air temperatures during the central hours of the day and an underestimation during the night. Air temperature data from seven weather stations within a 32 km radius of Rhonegletscher, ranging between 1007 and 3580 m a.s.l. (Grimsel, Gütsch, Robiei, Piotta, Engelberg, Eggishorn and Jungfraujoch), covering the period 1994–2012 are used to derive hourly lapse rates. Data from the Ulrichen weather station are not considered, because air temperatures at Ulrichen are strongly affected by cold air drainage, particularly during winter months (Scherrer, 2014). Air temperature lapse rates show a persistent daily cycle with maximum absolute values around noon (Fig. 2). Steepest temperature lapse rates of –0.0063°C m> 1 occur in spring and summer and shallower gradients (–0.0045°C m> 1) in winter, probably due to inversion of air temperatures during the cold season (Rolland, 2003). Coefficients of determination for the temperature gradient analysis are overall high (r ² > 0.96).

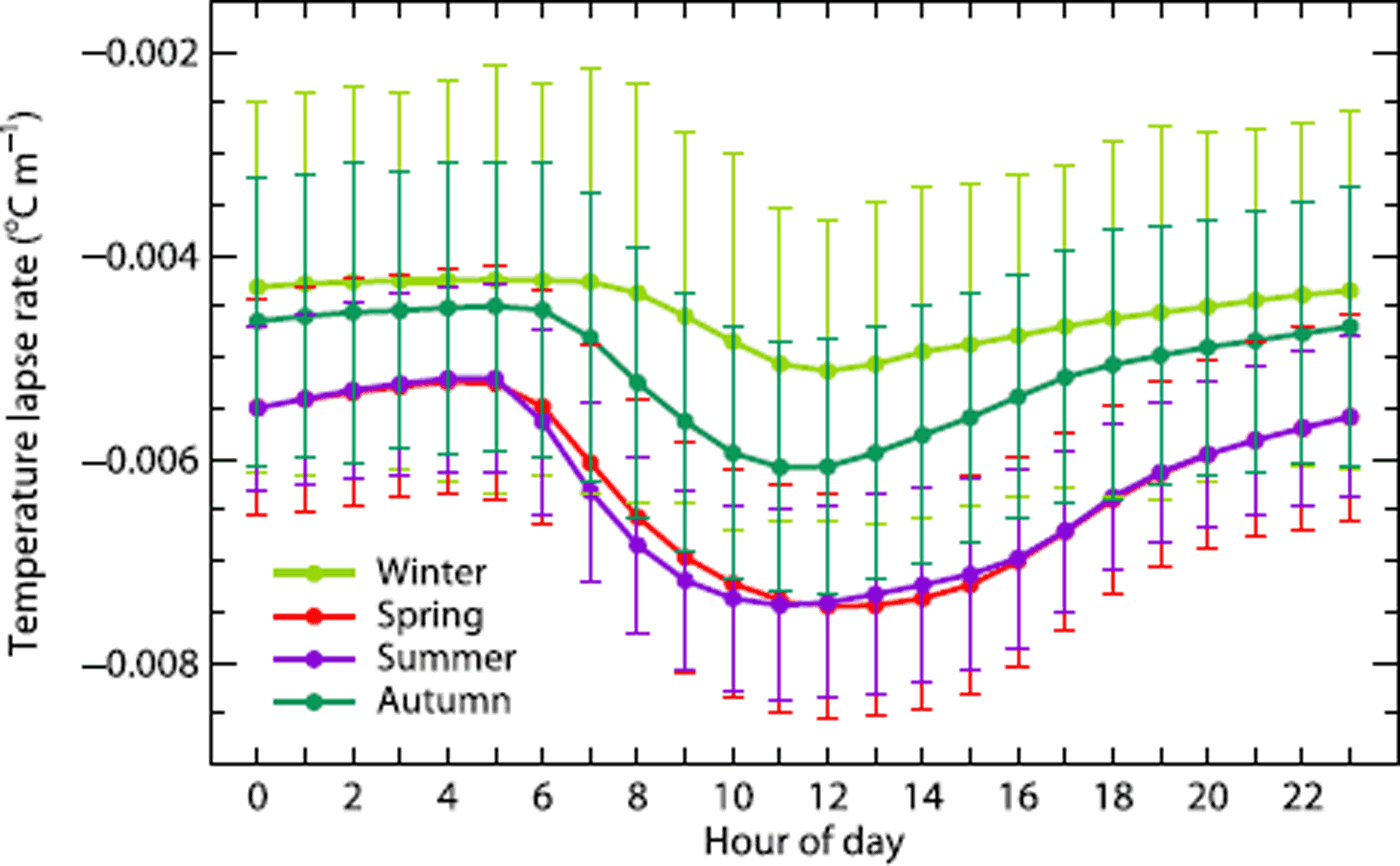
Fig. 2. Hourly temperature lapse rates and the corresponding standard deviations for each season, computed by linear regression of hourly temperatures on altitude, for the period 1994–2012, recorded at seven weather stations around Rhonegletscher.

The mass-balance model is run on an hourly basis. For this reason, the daily temperature records of the period 1959–89 are converted into hourly data by superimposing diurnal variations on the mean daily temperatures. Measured minimum and maximum daily temperatures are employed to constrain daily temperature fluctuations. In an iterative procedure, hourly temperature values are generated by taking the daily temperature fluctuations within a day in the period 1989–2012 which exhibited as similar as possible distribution of minimum, maximum and average temperature. Only days of the same month are considered. Hourly precipitation time series were derived in a similar manner, except that only information about the total daily precipitation and not about peak values was available.

For the period 1929–59 no climate records exist for Grimsel weather station. Instead air temperature data from Jungfraujoch (operating since the beginning of the 1933) are used. Jungfraujoch was chosen because it shows the best correlation with temperature measured at Grimsel, of all the stations in the surrounding area with a long recording history (r ² = 0.92). The temperature measured at Jungfraujoch is extrapolated to the altitude of Grimsel weather station by seasonal lapse rates, determined by evaluating temperature deviations between the two stations in the overlapping measuring period (1959–2012). For the first three years, 1930–32, temperatures measured at Sion weather station are used. In the case of precipitation, data from the Sion weather station are employed and shifted according to seasonal lapse rates to the location of Grimsel. The daily values are then converted to hourly values, as described above. The generation of distributed precipitation fields from station measurements is described in the ‘Accumulation model’ subsection in Methods.

Repeated mass-balance measurements were carried out in the period 2006–12 (1 October 2006 to 30 September 2012). Between 11 and 17 stakes were installed in the ablation and accumulation area of Rhonegletscher (Fig. 1b). In 2010 and 2011, additional stakes were installed in the tongue area. The mass balance was usually measured at the beginning and end of the accumulation period and several times (9–14 times) during the ablation period. In total, >1000 stake readings are available. The uncertainty of mass-balance measurements is estimated as ±0.2 m w.e. a^-1 (Dyurgerov, 2002).

Snow depth measurements were carried out at the end of the accumulation season of each year 2007–12 (Fig. 1c). Two additional surveys were performed in 2011 and 2012 at the beginning of March. Simultaneously, snow density profiles were measured between one and five locations during the snow depth surveys.

Six DEMs derived from a historic topographic map and aerial photographs from the years 1929, 1959, 1980, 1991, 2000 and 2007, with a spatial resolution of 25 m, exist for Rhonegletscher (Bauder and others, 2007). For 2012 a partial DEM of the ablation area of Rhonegletscher exists. The 1929 DEM serves as input for the modelling; the other six DEMs are used for validation of the model outputs by deriving decadal ice volume changes. Geodetically determined ice volume changes are affected by an error of about ±5% (Bauder and others, 2007). The total volume change for the period 2007–12 is obtained by scaling the observed ice volume change of the partial DEM according to the proportion of ice volume changes of previous periods which fall within this zone (47–61%).

In summer 2011 and 2012, the albedo of the glacier surface was recorded continuously at one site and in 2011 also every second to third week at 12 additional locations within the ablation area (Fig. 1b), providing the mean ice albedo (α _ice = 0. 24 ± 0.06) for Rhonegletscher.

The topography of the glacier bed, and hence the ice volume distribution is known (Farinotti and others, 2009).

Methods

For the melt model comparison, we consider five distributed melt models of varying complexity, which are described in the following subsections.

Classical temperature-index (TI) melt model

The classical TI melt model is solely based on air temperature and linearly relates melt rates to air temperature by a melt factor differing for snow and ice surfaces:

(1)

where DDF_ice/snow is the degree-day factor for ice or snow (mm d^{−1 °}C⁻¹), T _a is the air temperature (°C), n is the number of time steps per day (here n = 24) and T _T the threshold temperature distinguishing between melt and no melt (T _T = 1°C; Pellicciotti and others, 2005). T _T accounts for the fact that melt is controlled by the energy budget at the surface and can also occur at air temperatures below and above the melting point of snow and ice (Kuhn, 1987). The model keeps track of the snow water equivalent in each gridcell of the modelling domain, and, when this is zero, ice melt is calculated.

Temperature-index melt model of Hock (HTI)

In contrast to the classical TI model, where melt varies in space only as a function of elevation (given by temperature lapse rates), the HTI (Hock, 1999) includes a term for clear-sky potential solar radiation, in order to account for topographic effects (e.g. exposition, slope and shading) on the spatial distribution of melt but without the need for additional meteorological variables (e.g. radiation and cloud data). Melt rates (mm h⁻¹) are obtained as

(2)

where MF is the melt factor (mm h^{−1 °}C⁻¹), R _{ice/ snow} is the radiation factor for ice or snow (mm m² h⁻¹ W^-1 °C⁻¹) and I _pot is the potential clear-sky direct solar radiation (W m⁻²). Radiation factors are different for snow and ice surfaces, in order to account for differences in the surface characteristics (e.g. the albedo). The potential, clear-sky direct solar radiation is calculated (Hock, 1999) as a function of solar geometry, topography and atmospheric transmissivity, assuming a constant clear-sky atmospheric transmissivity in space and time:

(3)

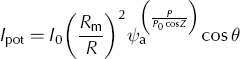
where I ₀ is the solar constant, R _m and R are the mean and actual Sun–Earth distance, ψ _a is the atmospheric transmissivity, P is the atmospheric pressure and P ₀ is the pressure at sea level, Z is the solar zenith angle and θ is the incidence angle of the Sun on the surface.

Enhanced temperature-index (ETI) melt model

The ETI melt model of Pellicciotti and others (2005) has a more physical basis, through the inclusion of the shortwave radiation balance, and distinguishes between melt induced by solar radiation and melt induced by other heat fluxes (temperature-induced melt). Melt is calculated according to

(4)

where TF is the temperature factor (mm h^{−1 °}C⁻¹), SRF is the shortwave radiation factor (mm m² h⁻¹ W⁻¹), α is the surface albedo and I is the incoming shortwave radiation (W m⁻²).

The actual incoming shortwave radiation, I, is computed as a product of clear-sky incoming shortwave radiation (Iqbal, 1983; Corripio, 2003) and a cloud transmission factor, cf, representing the attenuation of solar radiation by clouds. The clear-sky incoming shortwave radiation is calculated as the sum of direct, diffuse and reflected shortwave radiation and requires knowledge of the exact position of the Sun and its interaction with the surface topography, as well as the transmissivity of the atmosphere. The transmittance of Rayleigh scattering, ozone, uniformly mixed gases, water vapor and aerosols, as well as the altitude dependency, is accounted for and is computed on the basis of the concept of the relative optical air mass (Bird and Hulstrom, 1981). Cloud transmissivity factors (i.e. the ratio of observed to simulated clear-sky incoming shortwave radiation) are derived (Pellicciotti and others, 2011) as a function of daily temperature ranges. The cloud-factor parameterization is recalibrated against measured global radiation and daily temperature ranges, ΔT, at the Grimsel weather station, resulting in the relationship

(5)

For the ice albedo a value of 0.24 is assumed. The albedo of snow is calculated (Brock and others, 2000) as a function of the accumulated daily maximum positive air temperature since the last snowfall, T _acc. The associated parameters are adopted from Pellicciotti and others (2005):

(6)

where a ₁ = 0.86 and a ₂ = 0.155. The recalibration of the parameterization against albedo measurements during summer snowfall events by the pyranometer on the tongue of Rhonegletscher (summer 2011 and 2012) yields the same value for parameter a ₂, describing the decline of the albedo after a snowfall event, as proposed by Pellicciotti and others (2005). For a ₁ a different value is obtained, likely because after a summer snowfall event the albedo drops back rapidly to the albedo of the underlying ice, which is lower than the albedo of snow.

Simplified energy-balance (SEB) melt model

The SEB model of Oerlemans (2001) is very close to the ETI model of Pellicciotti and others (2005), but instead of using a threshold temperature for the onset of melt, the available melt energy is calculated and converted to melt rates by the latent heat of fusion. The melt energy, Q _M (W m⁻²), is obtained as

(7)

where C ₀ (W m⁻²) and C ₁ (W m⁻² K⁻¹) are empirical factors that describe the temperature-dependent energy fluxes. The incoming shortwave radiation, I, and the albedo, α, are calculated as in the ETI model. Melt rates, M (m s⁻¹), are obtained by dividing the melt energy by the latent heat of fusion, L _f (333 700 J kg⁻¹), and the density of water, ρ _w (1000 kg m^-3):

(8)

where Δt (s) is the time step. Melt occurs only when the melt energy is larger than zero.

Energy-balance (EB) melt model

The EB model used in this work is described in detail by Carenzo (2012). Here we only recall its main characteristics. The energy balance at the glacier/atmosphere interface is given by

(9)

where Q _M is the melt energy, α is the albedo, SW↓ is the incoming shortwave radiation, LW↓ and LW↑ are the incoming and outgoing longwave radiation, Q _H is the turbulent sensible heat flux, Q _L is the turbulent latent heat flux and Q _S is the heat conduction into the snow/ice pack. Melt rates are computed using Eqn (8).

Ablation is the sum of melt and sublimation minus resublimation. sublimation, S (m s⁻¹), is computed as

(10)

where L _s is the latent heat of sublimation (2 834 000 J kg⁻¹).

The measured incoming shortwave radiation is distributed over the glacier based on the spatially varying incident Sun angle, the sky-view fraction and the surface property (i.e. albedo; Corripio, 2002). Albedo of snow and ice is modelled in the same way as in the ETI.

The incoming longwave radiation, LW↓, is calculated according to the Stefan–Boltzmann relationship, and depends on the absolute air temperature, the percentage of cloud cover and the cloud type (Brock and Arnold, 2000). The outgoing longwave radiation, LW↑, is computed following the Stefan–Boltzmann relationship, as a function of surface temperature (calculated at each time step as a function of the energy penetrating into the snow/ice pack with a heat conduction scheme (Pellicciotti and others, 2009) and surface emissivity (snow and ice surface emissivity is set to 1, assuming that the surface radiates as a black body; Oke, 1987).

The turbulent sensible and latent heat fluxes are calculated according to the bulk aerodynamic method, as a function of air temperature, humidity and wind speed (e.g. Munro, 1989). In contrast to the profile aerodynamic method, the meteorological variables are required only for one height above ground level. In addition, the scaling lengths for aerodynamic roughness, z ₀, temperature, z _t, and humidity, z _e, the stability-correction factors for momentum, the heat and humidity and the Monin–Obukhov length scale have to be known. Different values for z ₀ are assigned to fresh snow (z ₀ = 0. 1 mm), snow after snowfall when melting has taken place (z ₀ = 1. 0 mm) and ice (z ₀ = 2. 0 mm), as proposed by Pellicciotti and others (2005). Scaling lengths z _t and z _e are calculated from the roughness Reynolds number and z₀. Due to a lack of additional measurements and the complexity of wind and humidity fields, wind speed and relative humidity are assumed to be constant in space over the modelling domain and equal to those measured at Grimsel weather station.

Accumulation model

The repeated snow depth measurements are utilized to derive precipitation fields. The first step was to calculate precipitation fields using valley precipitation lapse rates, determined from precipitation data from six weather stations located in the Rhone valley and from Grimsel weather station. However, comparisons with snow depth measurements showed that, particularly at high altitudes, snow water equivalents (SWEs) are underestimated, revealing that valley lapse rates are too flat. The snow depth measurements show a consistent pattern of moderate, nearly constant snow depths below 2600–2700 m a.s.l. and a stronger increase in the upper area (Fig. 3). The uniform snow depths in the lower part of the glacier might be a result of enhanced wind redistribution, due to a wind-tunnel effect in the narrow valley at the glacier tongue. To account for the observed increase with altitude, elevation-dependent lapse rates are determined for elevation bands of 100 m, by comparing measured SWE (corrected for snowmelt and snow redistribution) with SWE at Grimsel weather station inferred from precipitation measurements by applying a threshold temperature of 1°C to distinguish between solid and liquid precipitation. For the years 2007–12, for which snow depth surveys are available, individual lapse rates are derived, whereas for the other years a mean set of lapse rates is used. Annual elevation-dependent lapse rates are in the range 0.024–0.096% m⁻¹ and mean gradients of the period 2007–12 are 0.038–0.069% m⁻¹. The correlation between modelled and measured SWEs for all years reveals a coefficient of determination r ² = 0. 71. For individual years r ² is in the range 0.51–0.85 (Fig. 3).

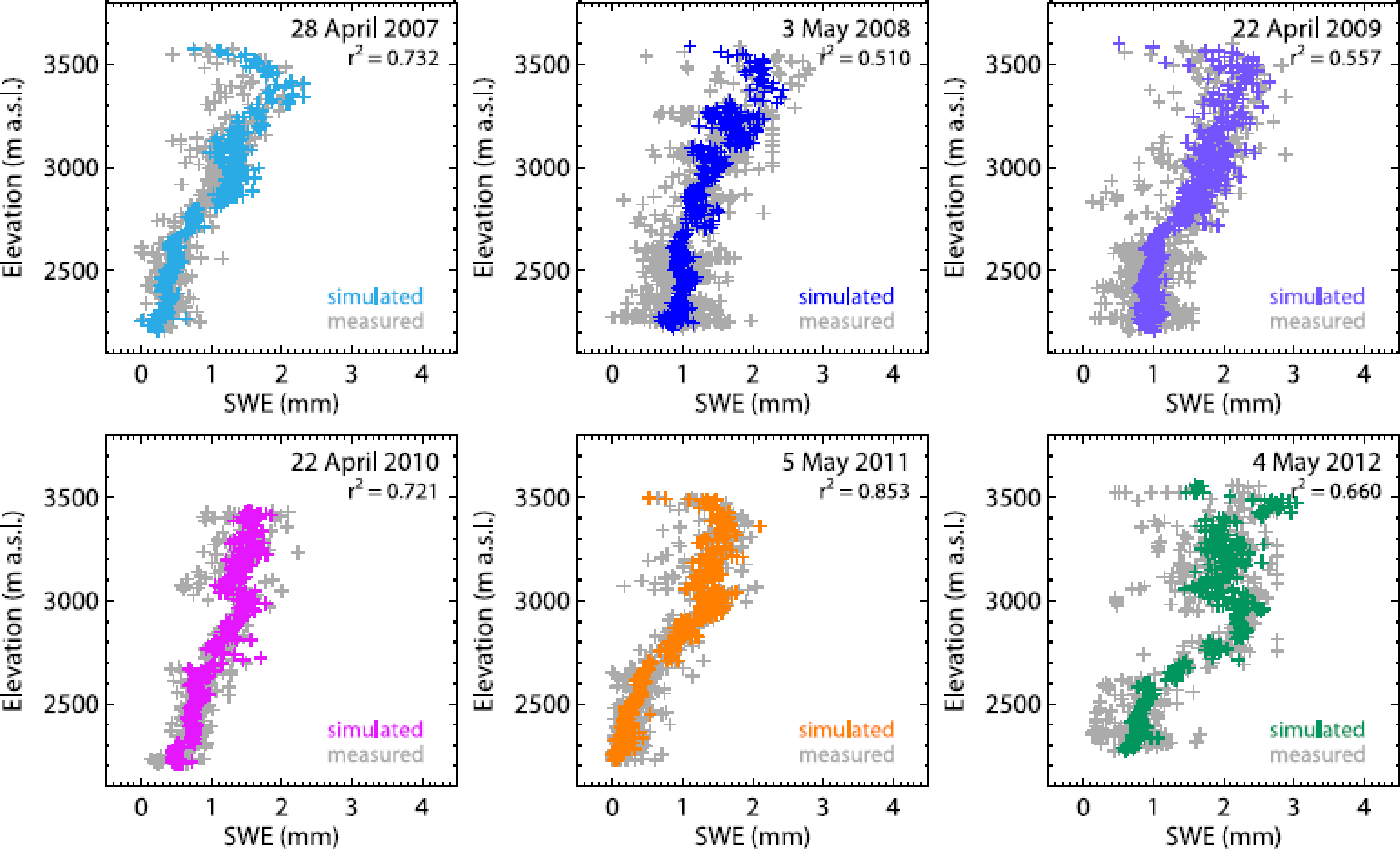
Fig. 3. Measured and simulated snow water equivalents (SWE) versus elevation for each snow depth survey (at the end of the accumulation period). The coefficients of determination, r ², of measured and modelled SWEs are indicated.

Precipitation fields are computed by applying these precipitation lapse rates to the hourly precipitation sums measured at Grimsel weather station. A threshold temperature set to 1^°C is used to distinguish between liquid and solid precipitation (MacDougall and Flowers, 2011). The spatial redistribution of snow by snowdrift and avalanches is accounted for with the approach proposed by Huss and others (2008b), in which accumulation is redistributed according to the curvature and slope of the terrain.

Mass-balance redistribution model

The melt and accumulation models are forced by hourly temperature and precipitation data for the period 1 October 1929 to 31 December 2012. The mass balance is evaluated on a DEM with an extent of 7.5 km × 12.5 km and a grid spacing of 25 m. The mass-balance model is coupled to a mass-balance redistribution model that updates the geometry of the glacier surface in annual time steps. A simplified approach that redistributes the annual mass balance according to the pattern of historic ice-thickness changes with elevation is used (Huss and others, 2010). For this purpose the relationship between altitude and ice volume changes of Rhonegletscher (given by the six DEMs) is determined and employed to update the surface topography. In comparison with an ice-flow model, this approach requires less computation time. In order to test the influence of the chosen parameterization for glacier surface geometry changes, we force the five mass-balance models with prescribed glacier surface geometries, which are obtained by linear interpolation of the glacier surface between two successive DEMs (Huss and others, 2008b), ensuring consistency in glacier elevation and extent among the five models. Results of this test showed that the employed approach only marginally affects model results.

Model calibration and validation

The empirical character of the temperature-index models and the SEB model requires calibration of the model parameters. The two coefficients of the TI (DDF_ice, DDF_snow), ETI (TF, SRF) and SEB (C ₀, C ₁) models and the three coefficients of the HTI model (MF, R _snow, R _ice) are calibrated using the weekly to monthly mass-balance measurements from the period 2006–12. Only measurements during the ablation period are considered (April–October). In a first step, the optimal parameter sets are systematically searched in parameter ranges determined from previous studies (e.g. Farinotti and others, 2012; Pellicciotti and others, 2012), and in a later step parameter ranges are extended, where necessary, in order to find the optimum. The parameter ranges and increments employed for the calibration of the different models are listed in Table 1. Model performance is determined by calculating the efficiency criteria, R ², (Nash and Sutcliffe, 1970) of the observed and simulated mass balances, MB_obs/sim:

(11)

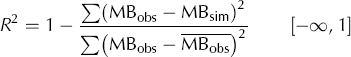
Table 1. Parameter ranges and the corresponding increments, Δ, employed for the model calibration of the four empirical models

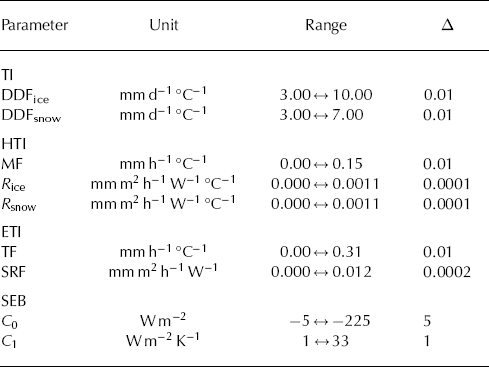
An R ² of 1 indicates perfect fit; R ² < 0 indicates that the average value of all observations is a better predictor than the model itself. The parameter combinations with the highest R ² are chosen. Different parameter sets with highest Nash–Sutcliffe efficiency are determined (1) for each individual year during 2006–12 (yearly calibrated), taking only ablation measurements for the current year, and (2) for the entire period (multi-yearly calibrated), incorporating all measurements from 2006–12, in order to analyze the variability of the model parameters over several years and to investigate the difference in performance between yearly and multi-yearly calibrated parameter sets.

For model validation, simulated and observed ice volume changes of the six subperiods (1929–59, 1959–80, 1980– 91, 1991–2000, 2000–07, 2007–12) and the entire period 1929–2012 are compared. For calibration and validation two independent datasets were used to confirm the overlap of the calibration period with the validation period.

Multi-yearly calibrated parameters are used to force the models over the long-term period. Observed ice volume changes (10⁶ m³) are converted to cumulative mass balances (m w.e.) assuming an ice density of 900 kg m⁻³. As a measure for model performance the absolute and percentage differences of modelled versus measured cumulative mass balances are employed.

Results

Parameter variability

The yearly calibrated parameters of the ETI and HTI models vary from year to year (Figs 4 and 5a). The temperature factors of ETI fluctuate in the range 0.00–0.25, and the shortwave radiation factors between 0.0012 and 0.0100. The melt factors of HTI are in the range 0.02–0.14 and the radiation factors for snow and ice are 0.0002–0.0006 and 0.0004–0.0008, respectively (Table 2). Variations in the yearly calibrated parameter values are of similar magnitude for both melt models. The temperature factors of ETI and HTI, TF and MF vary in a range of about ±100% compared with the mean over all years. The variations in the radiation factors, SRF and R _snow/ice, are smaller and range between 80 and +60% for SRF and between –50 and +50% for R _snow/ice. In the case of SEB, variations are also high, with coefficients of variation of 0: 64 and 0.42, but the parameters seem to be more robust for the years 2009–12, for which they are identical or very close to the multi-yearly calibrated parameter values of C ₀ = –75 and C ₁ = 15. In 2007, a higher C ₁ compensates for a lower C ₀ value compared with the mean and in 2008 the opposite is true, with a lower C ₁ balanced by a higher C ₀. Due to the two deviating years, the variations of C ₀ and C ₁ are in the order of –80 to –115% (C ₀: –80 ↔ 115%; C ₁: –79 ↔ 50%), comparable with the variations of the parameters of ETI and HTI. The yearly calibrated degree-day factors of the TI model demonstrate clearly lower variations, i.e. the coefficients of variation are 0.09 and 0.16 for DDF_ice and DD_snow, respectively, as there is no possibility for compensation. The multi-yearly calibrated parameters of TI, ETI and SEB are close to the mean of all yearly calibrated parameters (Fig. 4). In the case of HTI, the multi-yearly calibrated temperature factor, MF, is higher and the radiation factors, R _snow and R _ice, are lower than the mean. In general, years with high temperature factors are accompanied by low radiation factors and vice versa.

Fig. 4. The yearly calibrated model parameters of the (a) TI, (b) HTI, (c) ETI and (d) SEB models for the years 2007–12. The horizontal lines show the multi-yearly calibrated parameter values.

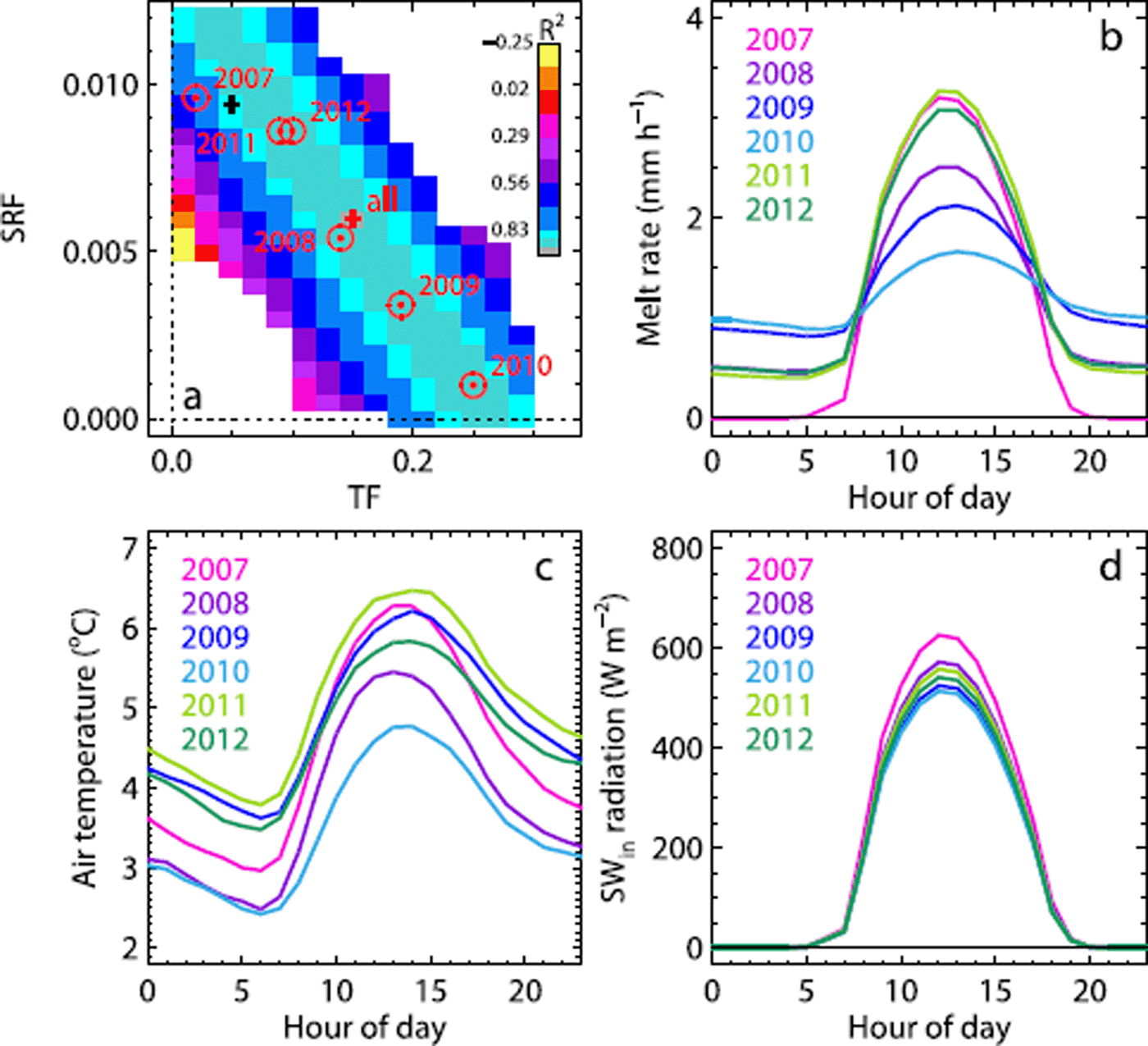
Fig. 5. (a) The Nash–Sutcliffe efficiency criteria corresponding to the combinations of the two parameters, TF and SRF, of the ETI model around the optimum. The colors indicate the magnitude of the efficiency criteria of the calibration over the 6 year period. The red circles and the red cross show the optimal parameter set for the individual years and the entire period, 2007–12. The black cross refers to the parameter set proposed by Pellicciotti and others (2005). (b–d) The mean daily cycle of surface melt (b), air temperature (c) and incoming solar radiation (d) over the ablation seasons of the individual years, obtained by yearly calibrated parameter values.

Table 2. Yearly and multi-yearly calibrated parameters of TI, HTI, ETI and SEB models and the corresponding coefficient of variation, cv, which is defined as the ratio of the standard deviation to the mean and indicates the variability of the model parameters

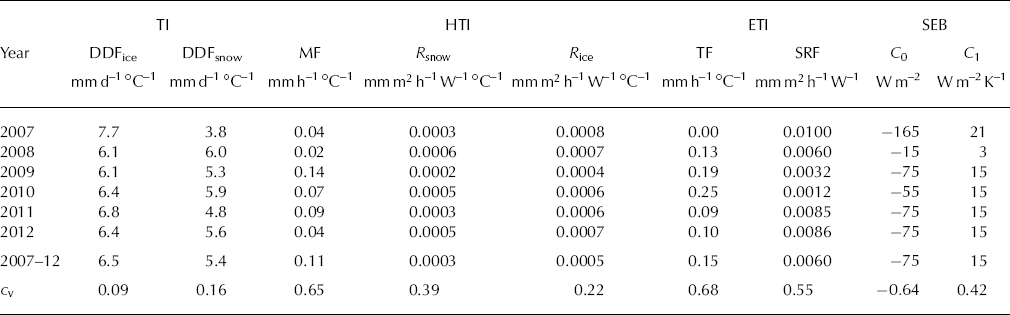
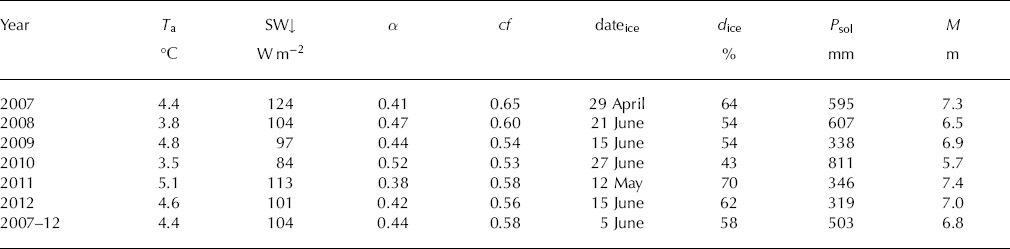
Meteorological conditions for the multi-year period are listed in Table 3. Years with high temperature factors (e.g. 2010; Fig. 5a) are correlated with low incoming solar radiation, and thus predominately overcast conditions, whereas years with low temperature factors (e.g. 2007) are related to clear-sky conditions. This observation agrees with the results of Carenzo and others (2009), who concluded that parameter variations are induced by the changing contribution of the individual fluxes to the energy balance, i.e. on cloudy days the shortwave radiation flux is reduced, whereas the longwave radiation flux and the turbulent heat fluxes are enhanced, leading to higher temperature factors and lower radiation factors. Furthermore, we observe that years with low temperature factors (e.g. 2007) are generally associated with an earlier depletion of the snow cover, whereas years with a long-lasting winter snow cover (e.g. 2010) correspond to high temperature factors (Table 3).

Table 3. Mean air temperature, T _a, mean incoming shortwave radiation, SW↓, mean albedo, α, mean cloud cover, cf, the date when the glacier surface becomes snow-free, date_ice, numbers of days with ice melt, d _ice, total solid precipitation, P _sol, and total melt, M, in the ablation periods 2007–12 at the central stake (indicated by the violet dot in Fig. 1b)

The calibration of the melt models reveals a strong correlation between the temperature factor and the radiation factor of the ETI model, as well as between C ₀ and C ₁ of SEB, indicated by the elongated area with similarly high efficiency criteria (Fig. 5a; shown for the example of ETI). This has been termed an equifinality problem, by which several combinations of model parameters result in the same model performance (e.g. Finger and others, 2011). However, the difference between the parameter combinations is evident in the diurnal variations of melt rates (Fig. 5b; shown for the example of ETI), where higher temperature factors yield shallower daily melt cycles than higher solar radiation factors. Daily fluctuations of air temperature and solar radiation only secondarily influence the daily melt cycle (Fig. 5c and d). The coarse temporal resolution of the mass-balance measurements (available at intervals of several days) does not allow us to determine the true proportions of temperature-and solar-radiation-induced melt, and data at higher time resolution (hourly data) would be required to obtain more realistic daily melt cycles. Particularly with regard to the climate-change-related temperature increase, it is important to assess the effective ratio between temperature-and solar-radiation-induced melt.

The threshold temperature for melt to occur, T _T, is kept constant and not recalibrated, following a commonly used approach (e.g. Hock, 1999; Pellicciotti and others, 2005). This parameter might also vary from year to year, but Pellicciotti and others (2012) have shown that for a number of sites and seasons in the Swiss Alps the recalibrated T _T of the ETI model did not vary significantly, indicating that T _T values around 0 or 1°C (values commonly assumed) are reasonable.

Multi-year modelling: 2006–12

Melt model comparison

The yearly calibration of the model parameters reveals the four empirical melt models, TI, HTI, ETI and SEB, have very similar performances (Fig. 6). The Nash–Sutcliffe efficiency criteria of the observed and simulated mass balances calculated with the yearly calibrated parameters vary between 0.80 and 0.98 for all four models. In contrast, the EB model shows a weaker performance, particularly in 2007 and 2008, with corresponding Nash–Sutcliffe efficiency criteria in the range 0.46–0.98. In 2010 and 2012, the EB model shows higher performance, similar to that of the other melt models. Exceptionally high performance and almost no variations among the different melt models is obtained for 2012, with R ² of 0.97–0.98. Reasons for the good agreement with measurements in 2012 might be related to the fact that the ablation season was not affected by summer snowfall events until mid-September. A sustained period of ice melt favors high performance, as models have been shown to perform worse during periods of transition from snow to ice or of frequent snowfalls (Pellicciotti and others, 2005).

Fig. 6. Comparison of the performance of the five melt models. The Nash–Sutcliffe efficiency criteria of observed and simulated mass balances of the ablation period for each year and the entire period are shown. Blue bars represent the efficiency criteria of TI and HTI, green bars of ETI and SEB and orange bars of EB. White numbers refer to the corresponding efficiency criteria, red numbers to the bias (mm) and blue numbers to the number of stake measurements available.

The modelling over the entire period, 2006–12, with the best parameters for each year reveals no significant differences between TI, HTI, ETI and SEB (R ² = 0.90–0.92) and a lower performance of the EB model, with a Nash–Sutcliffe efficiency criterion of 0.85. In general, HTI has the highest Nash–Sutcliffe efficiency criterion in the different years and over the entire period, although the differences are negligibly small (except for EB). The same conclusion can also be drawn for the calibration of the period 2006–12 (Fig. 7).

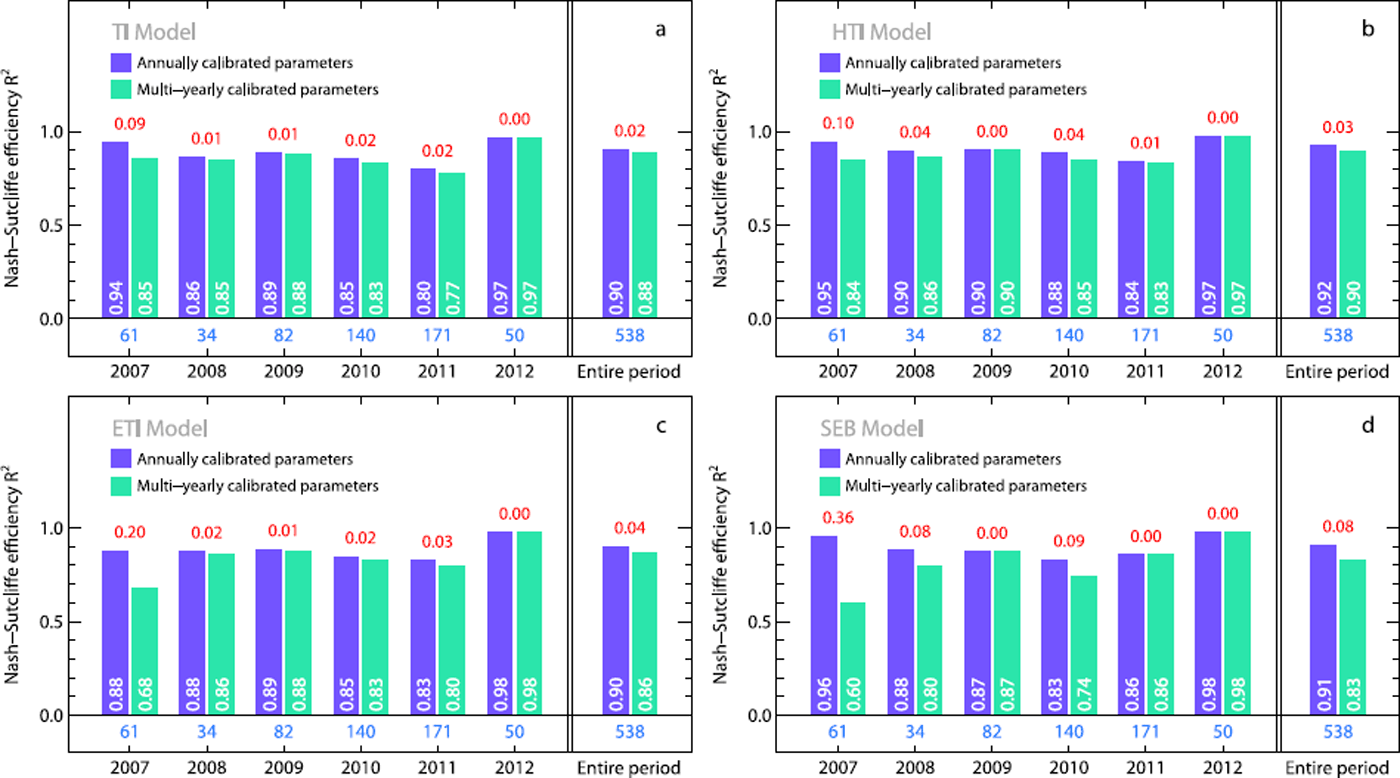
Fig. 7. Differences in model performance using either annually or multi-yearly calibrated model parameters for the (a) TI, (b) HTI, (c) ETI and (d) SEB models. The Nash–Sutcliffe efficiency criteria of observed and simulated mass balances of the ablation period for each year and the entire period are shown. Bars represent the efficiency criteria of annually (violet) and of multi-yearly (green) calibrated model parameters. White numbers refer to the corresponding efficiency criteria, blue numbers to the number of stake measurements available and red numbers to the differences in R ² between annually and multi-yearly calibrated parameters.

The analysis of the model performances over several years indicates that all four models, TI, HTI, ETI and SEB, are appropriate for melt simulations when parameters are calibrated every year or over a period of several years. Despite their simplicity, the TI and HTI approaches compare well with other melt models. In contrast to the empirical melt models, the EB model was not calibrated. It does not achieve the same high performance as the other approaches, and a possible reason for this might be the forcing of the EB model with data from an off-glacier weather station (see Discussion).

Annual vs multi-year calibrated parameters

In general, the performance of TI, HTI, ETI and SEB with multi-yearly calibrated parameters is slightly lower than when using yearly calibrated parameters (Fig. 7). However, differences in the efficiency criteria are generally low (ΔR ² ≤ 0.04). An exception is the year 2007 in which the decline of performance is substantial (ΔR ² = 0.09–0.36), especially for SEB and ETI. Another significant performance drop is observed in the case of SEB in 2008 and 2010 (dominated by low air temperatures and long-lasting snow cover; Table 3), with a decrease in model efficiency of 0.08 and 0.09, respectively. Over the entire period, the differences are < 0.04 for TI, HTI and ETI and not significant. In the case of SEB, the difference in R ² is larger, ΔR ² = 0.08, and thus not negligible. Hence, despite the large variability of the model parameters from year to year (Fig. 4), it seems that only a small decrease in model performance is associated with the use of multi-yearly calibrated parameters.

Multi-decadal modelling: 1929–2012

In order to validate the long-term performance of the different melt models and to assess differences in their reaction to variable climatic conditions, simulated ice volume changes are compared with observations. Differencing of DEMs of the historical glacier surface provides ice volume changes of six subperiods within 1929–2012. The absolute difference between modelled and measured ice volume changes and the difference in percentage are chosen to compare observed and simulated values. The DEMs provide an integrated picture of past glacier changes over that period. The first period (1929–59) is characterized by a general ice volume loss (Fig. 8a). The climate over the analysis period showed both higher and lower air temperatures compared with the mean (results not shown). In the second period (1959–80), the ice volume has stabilized and in total a slight increase in the ice volume is observed, likely resulting from decreasing air temperatures towards the early 1980s and augmented precipitation volumes. The last four DEM periods are characterized by a persistent loss of ice mass, as a consequence of rising air temperatures towards the present and decreasing precipitation in the past decade.

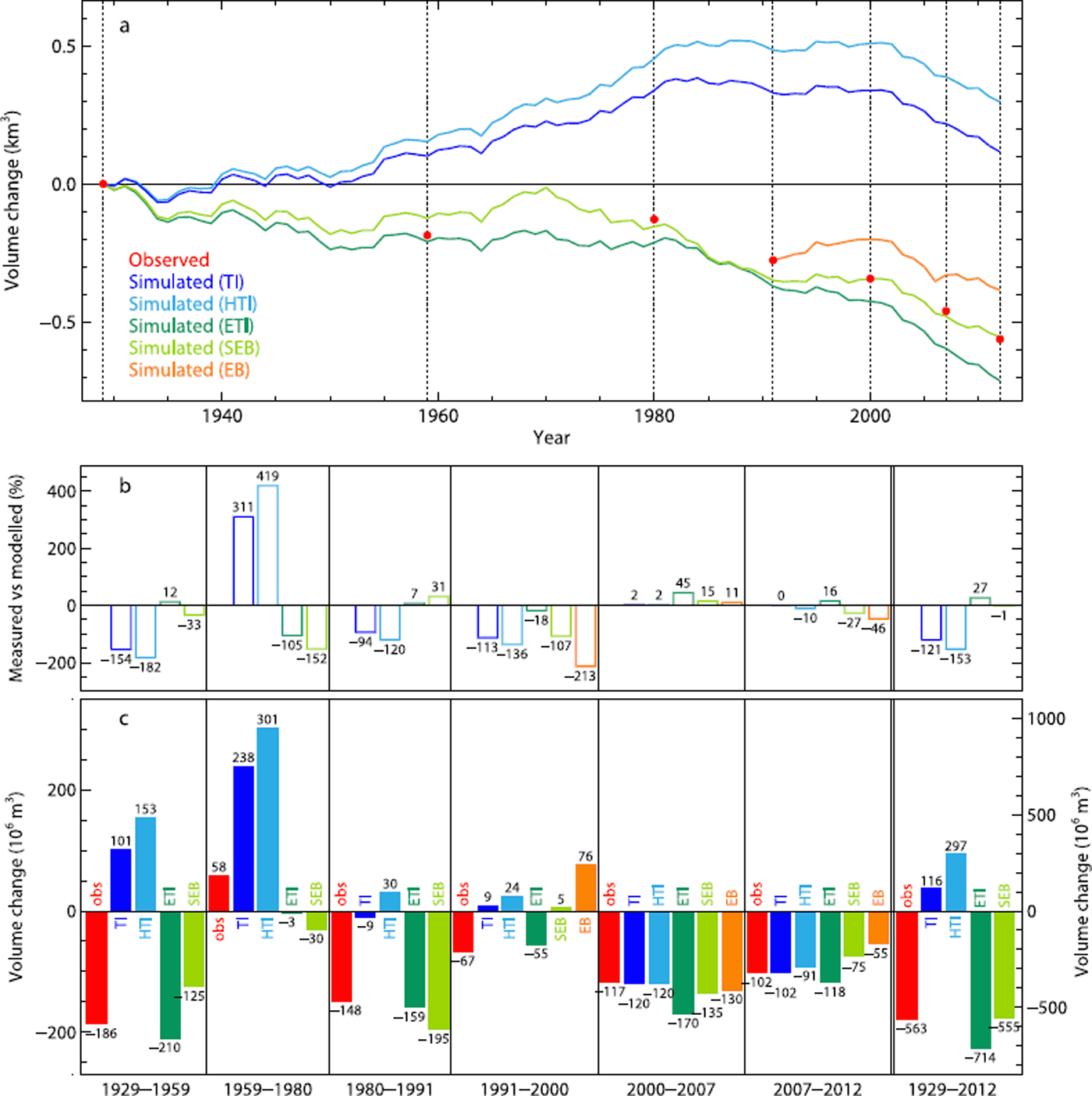
Fig. 8. (a) The evolution of the ice volume changes over 1929–2012. The solid blue and green curves show the simulated volume changes derived by TI, HTI, ETI and SEB. The medium and light green dotted lines correspond to the ice volume changes of ETI and SEB with the original parameter values (see Discussion). The red dots indicate the inferred ice volume changes from available DEMs. (b) Differences in percentage of modelled compared with measured ice volume changes. The orange bars refer to the ice volume changes derived by EB, and are limited to last three subperiods. (c) The observed (red) and modelled (blue/green) ice volume changes for the six DEM subperiods and the entire period, 1929–2012. Black numbers indicate the ice volume change (10⁶ m³). The axis on the right extends over a larger range and refers to the ice volume change over the entire period, 1929–2012.

The validation of the simulated ice volume changes over the long-term period reveals that the TI and the HTI model perform poorly in comparison with ETI and SEB, and clearly differ from the general trend of ice volume evolution indicated by the DEMs (Fig. 8). Instead of a glacier retreat, the TI and HTI yield an almost continuous ice volume increase of 116 and 297 × 10⁶ m³, respectively, in the period 1929–2012, in contrast to an actual ice volume loss of 563 × 10⁶ m³. Particularly in the first and second periods, they deviate from the common trend by predicting a strong mass gain. In the first period (1929–59), the models simulate a substantial volume growth of 101 and 153 × 10⁶ m³, compared with an observed ice volume loss of 186 × 10⁶ m³ in the same period. In the second period, measurements indeed show an ice mass gain, but the increase of TI and HTI is four to five times larger than observations show. During the subsequent two periods, they show an almost constant ice volume, whereas measurements indicate a total ice volume decrease of >200 × 10⁶ m³. The only period in which the TI and HTI modelled volume changes are very close to measurements are the calibration period and the six following years, with differences of ~0–10% (Fig. 8b and c).

In contrast to TI and HTI, the ETI and SEB models are able to reproduce the general trend of past ice volume changes. Looking at the entire period (1929–2012), the ETI results in a total ice volume loss of 714 × 10⁶ m³, and the measured volume loss is 563 × 10⁶ m³, corresponding to a misfit of 27%. SEB is closer to the observations, with a total modelled volume decrease of 555 × 10⁶ m³, which is equivalent to a difference of only 1%. However, when considering the individual subperiods, it is evident that deviations from observations are generally smaller for ETI than SEB and that the SEB agreement with observations over the entire period results partly from compensations of over-and underestimations (Fig. 8b). Percentage differences for ETI are <18%, with the exception of 1959–80 (where ETI underestimates the glacier growth by 105%) and the 2000–07 period, where ETI predicts an enhanced ice volume loss (+45%). SEB leads, in general, to larger deviations from periodic observations than ETI, ranging between 15 and 152%. Only in the second to last period, 2000–07, is the ice volume change modelled by SEB closer to measurements than ETI, differing by only ~15%.

The marked differences between the persistent positive mass balances of the TI and HTI models and the mostly negative or only partly positive mass balances of the ETI and SEB models over the first and second DEM subperiods are a result of the different model structures. While melt rates of the TI and HTI models are dominated by air temperature fluctuations and experience a decrease of ~20–25% under the colder climate of the first and second DEM subperiods compared with the calibration period, the melt rates of the ETI model are only reduced by ~12–16%. The reason for the weaker reduction of melt rates in the case of the ETI and SEB models is that in these models melt is controlled in approximately equal shares by temperature and incoming solar radiation. While the mean air temperatures of the first two subperiods are ~0.9–1.0°C lower than in the calibration period, the mean net shortwave radiation fluxes are approximately the same (±5 W m⁻²). As a result, the temperature-induced melt component of ETI decreases by ~22–25% (as in the case of the TI and HTI models), whereas the radiation-induced melt component is comparable (±2%) to the values of the calibration period, and thus leads to generally higher melt rates under colder climate conditions than the TI and HTI models and, thus, to more negative mass balances.

The performance of the EB model could only be investigated in the period 1991–2012, because the data-intense character of the EB approach requires numerous meteorological hourly input data points, in addition to temperature and precipitation, which could not be reconstructed for the years prior to 1989. In comparison to the other approaches, the EB model performs significantly worse and yields an ice volume change of only –109 × 10⁶ m³ from 1991 to 2012, corresponding to 38% of the observed ice volume change of –286 × 10⁶ m³ (Fig. 8). This misfit originates particularly during the first subperiod (1991– 2000), where EB simulates an ice volume increase of 76 × 10⁶ m³, while observations show an ice volume loss of 67 × 10⁶ m³. In the second period, 2000–07, the EB agrees quite well with the observed ice volume changes (misfit 11%), whereas in the last subperiod the EB model again underestimates melt (misfit –46%). The lower melt rates of the first and last subperiods are primarily the result of less intense turbulent heat fluxes, due to generally lower wind speeds compared with the intermediate period.

The largest differences between EB and the other melt models are found in the accumulation area, where EB simulates a more positive mass balance, due to lower melt rates compared with the empirical models, as demonstrated by the elevation distribution of the mass balance (results not shown).

Temperature sensitivity

In the future an increase in the average global air temperature is expected (Stocker and others, 2013). Depending on the region and the season, an average temperature increase of 3.4 ± 0.7^°C by the end of the 21st century is projected for Switzerland under the A1B emission scenario (CH2011, 2011). In order to test the temperature sensitivity of the different melt models we forced them with a fictive raise in air temperature of 2^°C increasing linearly in the period 1929–2012.

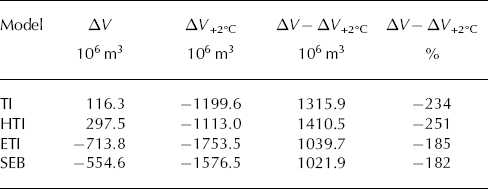
Results show that the simple and HTI models, directly relating melt rate to temperature through a proportionality factor, react in the strongest manner to a temperature increase (Table 4). This oversensitivity to temperature has been suggested earlier, but only at the point scale (Pellicciotti and others, 2005). The simple TI model yields a 2.3 × larger ice volume change from 1929 to 2012 than the observed ice volume change in response to the changed temperature regime, whereas HTI shows a 2.5 × larger ice volume change. ETI and SEB show less strong reactions to the temperature alterations, with volume losses that are 1.8 × higher than the present. However, the temperature sensitivity of ETI and SEB depends on the choice of the melt model parameters controlling the proportion of temperature-and solar-radiation-induced melt.

Table 4. Ice volume changes over the period 1929–2012 for the different melt models, with an unaltered temperature forcing (ΔV) and superimposing a temperature rise of 2°C (ΔV _+2°C), and the absolute and relative difference compared with the observed ice volume change (ΔV – ΔV _+2°C)

Discussion

Model performance over the multi-year period

During the 6 years of the calibration period, all models perform in a similar manner in comparison with the mass-balance measurements. The HTI has marginally higher efficiency criteria than TI, ETI and SEB. In contrast to the other models, the HTI model contains three adjustable parameters, which might favor its performance compared with the other models. These findings contradict the results of Pellicciotti and others (2005), who found the enhanced model performed better than the standard temperature-index models. The reason for this disagreement might be found in the different model set-ups. While Pellicciotti and others (2005) performed the analysis at the point scale with measured meteorological data and compared model results against hourly melt rates, we used extrapolated data from a weather station outside the glacier and calibrated to weekly–monthly mass-balance measurements. Hence, uncertainties in the model input data and the coarser resolution of the calibration data might blur differences in performance between HTI and ETI over the multi-year period.

Choosing multi-yearly calibrated rather than yearly calibrated parameter values results in only a small drop in model performance over the multi-year period, except in 2007, in particular for ETI and SEB. A possible reason for these discrepancies might be a failure of the cloud-factor parameterization. According to our model, days with clear-sky conditions (cf > 0.8) prevail in 2007, compared with the other years. If modelled incoming solar radiation is compared with measurements, it is evident that the cloud-factor parameterization results in erroneously high incoming solar radiation. Consequently, smaller melt coefficients are obtained in order to compensate the overestimated radiation flux and, thus, the application of multi-yearly calibrated parameters leads to melt rates that are too high and, therefore, to a larger disagreement.

The analysis of the climatic conditions shows that parameter variations over the 6 year periods are not arbitrary, but are controlled by the characteristics of the ablation season. The 6 year periods cover a wide range of climatic conditions and provide us with a selection of distinct climate conditions. Hence, it seems to be important that the calibration of melt parameters is based on several years of mass-balance data, in order to balance the characteristics of single years and obtain reasonable simulations for long-term modelling.

Model performance over decadal periods

There is general agreement that physically based energy-balance models represent best melt processes and, thus, should provide the best simulations of melt rates. While this has been established at the point scale (Pellicciotti and others, 2005, 2008; Andreassen and others, 2008), it is less clear for applications at the glacier and catchment scales. Our study has shown that the EB model performance is inferior to that of the simpler ETI and SEB models, when validated against mass-balance observations over several years. The model performs well for ice volume changes in the years 2000–07, but not in the period 1991–2000. The reason for the poor results of the EB model over the long term, despite the physical basis of the model, might be found in the input data. The EB model was forced with data from an off-glacier weather station, due to a lack of on-glacier data. However, fluxes at the glacier/atmosphere interface refer to the exchange of heat in the glacier boundary layer, i.e. the layer of atmosphere affected by the presence of a cold surface at 0°C and the presence of katabatic flow. Air temperature, wind speed and relative humidity measured at an off-glacier site might therefore not be appropriate to represent those in the glacier boundary layer. In our study, the different components of the energy balance are either extrapolated from the weather station or parameterized. Air temperature, in particular, was extrapolated from the off-glacier Grimsel weather station. Recent studies have suggested that the temperature regime over glaciers may substantially differ from that on-glacier (e.g. Petersen and others, 2013), so that such extrapolation might not be accurate enough for energy-balance modelling. In the same way, the TI and HTI models, being strongly and solely dependent on air temperature, might be more affected by errors in this variable.

The difficulties experienced by TI and HTI in modelling long-term glacier evolution indicate that the relationship between temperature and melt is not constant with time, and depends on the prevailing climate conditions. In particular, the positive ice volume changes of the first two periods (1929–59 and 1959–80), when air temperatures were lower than in the subsequent periods, demonstrate that the parameters calibrated to present conditions are not valid in a colder climate. This is further supported by the fact that TI and HTI give reliable ice volume changes only in the two most recent periods (2000–07 and 2007–12), one being the calibration period. Our findings are in agreement with the results of Huss and others (2009a), who showed that degree-day factors are not stable in the long term and were clearly higher in the 1920s–70s than their present values. These results confirm that recalibration of model parameters to individual subperiods is essential (as already shown by Huss and others, 2009b) to reconstruct long-term mass-balance time series and support our findings of an overly positive mass budget in the first two periods.

The separation of temperature- and solar-radiation-induced melt leads to major improvements in the stability of the model parameters. This is reflected in the considerably better performance of ETI and SEB over the long term. Our results suggest that the relationship between air temperature, solar radiation and melt rates remains constant over time, in the face of climate variations. Nonetheless, certain deviations from measurements remain. While the SEB model fits better to the overall ice volume change over the period 1929–2012, ETI comes closer to the ice volume changes of the individual subperiods.

A major difference between the TI and SEB models (and the only one between the ETI and SEB models) is the use of a threshold temperature for melt to occur: while the TI models employ a threshold temperature, in the SEB melt occurs only when the sum of the terms is positive. This leads to situations in which the SEB model simulates melt at air temperature below the threshold temperature, which occurs particularly during days in winter or spring with high incident solar radiation. In contrast to this, in other cases the SEB model simulates no melt while air temperatures are above the threshold, which is generally observed during warm nights in summer. The effect of these two phenomena on total melt is in the range of a few percent, with the latter effect slightly outweighing the former. Thus, this difference in model structure does not seem to have a significant impact on the mass balance. It is rather the separation of solar-radiation-and temperature-induced melt that leads to improvements in long-term simulations by reducing the oversensitivity to temperature.

Parameter robustness

The poor performance of ETI with the original parameter values (Fig. 5) proposed by Pellicciotti and others (2005) indicates that site-specific recalibration of model parameters is required for applications over several decades. Despite a relatively small drop in model performance over the multi-year period (ΔR ² = 0.06; results not shown), the effect on the long-term modelling is not negligible and results in a misfit between simulated and observed ice volume changes of 59% (Fig. 8a). Similar considerations apply to the SEB model. Assuming the parameter C ₁ equal to 10 W m⁻² K⁻¹, as suggested by Oerlemans (2001), and adjusting only parameter C ₀ by means of the mass-balance measurements of the multi-year period (C ₀ = –39 W m⁻²) reveals that a parameter combination with a fixed C ₁ value leads to mass balances that are too negative on average, with a difference in the total ice volume change (1929–2012) of 87% compared with observations (Fig. 8a). Hence, our results suggest that recalibration of both the ETI and SEB model parameters to local conditions is required in order to correctly reproduce the observed ice volume evolution over multi-decadal periods. However, once the parameters are recalibrated for a specific site they seem to be robust over the long term. These results do not rule out the possibility that for settings where meteorological conditions are better known (data from an on-glacier weather station) the original parameters might lead to better agreement with observed glacier changes, even over the long term.

Other model comparison studies

Few studies have compared the performance of melt models of different complexity and assessed their transferability in space and time. The analyses are generally carried out at the point scale and are, to our knowledge, all limited to a few ablation seasons. Pellicciotti and others (2005) compared the performance of the ETI model with three temperature-index models at the point scale, and showed that the ETI model performed better than the other models. The study of Essery and others (2013), which applies a snow model in 1701 different configurations to a well-instrumented site over four ablation seasons, supports this finding, concluding that well-established empirical models achieve similarly good performance to more physically based models. At the glacier scale, results are less clear. Pellicciotti and others (2013) showed that there were small differences in performance between the ETI model and an EB model when applied in a distributed manner to a glacier in the Chilean Andes in the ablation area. However, differences were substantial in the upper sections of the glacier, where lack of data prevented a sound assessment of which model best reproduced ablation rates. MacDougall and others (2011) applied a distributed EB model and four empirical models to two glaciers and two seasons in the St Elias Mountains, North America, and came to a similar conclusion, but showed, in addition, that energy-balance models have the highest transferability in time. Our study is the first attempt to evaluate the long-term performance of several melt model approaches with different complexities and to have compared their performance over a period of >80 years. We have shown that comparison over short periods might not provide enough insight into reasons for model failures, such as parameter instability. Particularly with regard to glacier projections into the future, the results presented here are likely important, since recent studies have shown that the type of melt model affects runoff projections (Kobierska and others, 2013; Huss and others, 2014).

Conclusions

This study has examined the long-term performance of five well-established melt models: (1) a classical TI model, (2) the HTI model (Hock, 1999), (3) an ETI model, (4) a SEB model and (5) a full EB model. The melt models were coupled to an accumulation model and a model for the evolution of the glacier surface geometry, in order to simulate in a distributed manner the ice volume evolution of Rhonegletscher over the period 1929–2012. Meteorological time series from a nearby weather station were used to force the mass-balance models. sub-seasonal mass-balance measurements for 2006–12 were used to calibrate the parameters of the empirical melt models. Observed ice volume changes of six subperiods between 1929 and 2012 served for model validation.

From our comparative study the following conclusions can be drawn:

1. 1. The performance of the different melt models over the multi-year period (2006–12) is very similar when parameters are calibrated to the prevailing climate settings and the local conditions, except for the EB model, which shows less consistency with the stake readings than the other approaches.

2. 2. The calibration of model parameters to each single year of the multi-year period showed that the parameters strongly fluctuate from year to year, independently of the model type (except TI). These variations originate from an equifinality problem, i.e. different parameter sets leading to equally good model performance. Discrepancies among the parameter combinations emerge only in the daily cycle of melt rates. However, despite the high parameter variability from year to year, using multi-year calibrated parameter values results in only a small decrease in model performance over the multi-year period, in comparison with yearly calibrated parameters.

3. 3. Model results over the multi-decade period (1929–2012) suggest that only the ETI and SEB models can reproduce the observed ice volume changes. This implies that the melt relationship of these two models remains stable over time. It is interesting to note that, under the conditions of our study, the models of intermediate sophistication seem to perform better over the long term and be better suited to long-term simulations than either the EB model or the conventional temperature-index models, TI and HTI.

4. 4. The TI and HTI models are only able to reproduce the ice volume changes of the most recent (calibration) sub-periods with sufficient accuracy. In the earlier periods, the models simulate too-positive mass balances and a sustained glacier growth. This result indicates that the relationship between melt and temperature changes over time, in response to changes in the magnitude of the energy fluxes that temperature can only partially account for. This implies that the parameters of the temperature-index models are not robust in time and require recalibration for distinct climate conditions (Huss and others, 2009a).

5. 5. The EB model shows the poorest performance of all our melt models, despite its physical character. It predicts a too-positive mass budget. The reason for the failure might be found in the forcing of the model with data from an off-glacier weather station, while the energy balance is based on knowledge of heat fluxes exchanged in the glacier boundary layer, that are therefore likely to be poorly predicted by variables measured far away on non-glacierized ground. Inadequate input data could thus result in erroneous melt simulations.

The separation of temperature- and solar-radiation-induced melt seems to lead to reasonably stable model parameters over time, and to make these models suitable for long-term modelling in the future. Particularly with regard to future projections, the use of appropriate melt approaches is crucial to provide reliable glacier projections. The results obtained for Rhonegletscher should be confirmed with comparable studies on other glaciers for which the necessary data are available.