1. Introduction
Many fluids of importance to human life or activity flow through canals or pipes, and so they attracted attention early in the development of the science. As early as 1775, Antoine de Chézy established a link between the mean velocity in a water channel, the hydraulic radius and the channel slope, and showed that this link could depend on the state of the surface via algae growth or decline, for example. This equation proved very robust, and was used to build many canals in the 19th century. While the Chézy equation can be obtained by simple balance arguments for linear momentum, it hides subtleties of the pipe or channel flow physics, some of which may be connected to a famous conjecture by Onsager (Eyink Reference Eyink2024).
The mean flow rate in parallel flows is obtained by a balance between the work done by the applied force (gravity or pressure gradient) and the energy loss due to friction against the surface. The frictional process is very subtle as it depends both on the state of the surface and of the fluid state itself, i.e. whether the flow is laminar or turbulent. In general, frictional losses are characterized by a skin friction coefficient which is proportional to the ratio of the applied shear stress at the surface,  $\tau _w$, divided by the pressure in the free stream. In straight, smooth circular pipe flows, for which the pressure gradient balances the shear stress, the friction coefficient is simply given by the formula
$\tau _w$, divided by the pressure in the free stream. In straight, smooth circular pipe flows, for which the pressure gradient balances the shear stress, the friction coefficient is simply given by the formula
where  $\partial _x P$ is the pressure drop per unit length,
$\partial _x P$ is the pressure drop per unit length,  $D$ is the pipe diameter,
$D$ is the pipe diameter,  $\rho$ is the fluid density,
$\rho$ is the fluid density,  $\bar {U}$ is the velocity averaged over the pipe cross-sectional area and
$\bar {U}$ is the velocity averaged over the pipe cross-sectional area and  $u_\tau =\sqrt {\tau _w/\rho }$ is the skin friction velocity. This formula shows that the friction depends on the velocity profile at the wall (via
$u_\tau =\sqrt {\tau _w/\rho }$ is the skin friction velocity. This formula shows that the friction depends on the velocity profile at the wall (via  $\bar {U}$) and on the viscosity
$\bar {U}$) and on the viscosity  $\nu$ (through
$\nu$ (through  $\tau_w$). Experimental measurements indicate in fact that they only depend on these two ingredients, provided one normalizes the viscosity by
$\tau_w$). Experimental measurements indicate in fact that they only depend on these two ingredients, provided one normalizes the viscosity by  $D \bar {U}$ to form the Reynolds number
$D \bar {U}$ to form the Reynolds number  $Re=D \bar {U}/\nu$.
$Re=D \bar {U}/\nu$.
In the laminar state, where  $Re<10^3$, the velocity profile close to the wall (
$Re<10^3$, the velocity profile close to the wall ( $y=0$) is linear in the coordinate normal to the wall,
$y=0$) is linear in the coordinate normal to the wall,  $U(y)=Sy$, with
$U(y)=Sy$, with  $\tau _w=\rho \nu S$, so that
$\tau _w=\rho \nu S$, so that  $\bar {U}^2/u_\tau ^2\propto Re$, meaning that the friction coefficient simply decreases like
$\bar {U}^2/u_\tau ^2\propto Re$, meaning that the friction coefficient simply decreases like  $\lambda \sim 1/Re$. As soon as the flow becomes turbulent, however, the velocity profile displays a more complex behaviour, and the drag exhibits a transition towards a milder decrease with
$\lambda \sim 1/Re$. As soon as the flow becomes turbulent, however, the velocity profile displays a more complex behaviour, and the drag exhibits a transition towards a milder decrease with  $Re$. For economical and theoretical reasons, prediction of this decrease has been the topic of active research since 1945. A search using ‘Web of Science’ for papers including ‘skin friction’ in the title displays 1120 papers since 1945, cited 17 485 times, following an exponential curve.
$Re$. For economical and theoretical reasons, prediction of this decrease has been the topic of active research since 1945. A search using ‘Web of Science’ for papers including ‘skin friction’ in the title displays 1120 papers since 1945, cited 17 485 times, following an exponential curve.
From a theoretical point of view, two large categories of laws can be found, depending on whether one assumes that the turbulent velocity profile is logarithmic,  $U(y)\sim \kappa ^{-1} u_\tau \log (y_++a_+)+B_*$, or algebraic,
$U(y)\sim \kappa ^{-1} u_\tau \log (y_++a_+)+B_*$, or algebraic,  $U(y)=A_* u_\tau (y_++a_+)^{\alpha }$, with
$U(y)=A_* u_\tau (y_++a_+)^{\alpha }$, with  $y_+=yu_\tau /\nu$;
$y_+=yu_\tau /\nu$;  $\kappa$ is the Kármán constant, and
$\kappa$ is the Kármán constant, and  $a_+$,
$a_+$,  $A_*$ and
$A_*$ and  $B_*$ are constants. By continuity of the velocity profile, we can write
$B_*$ are constants. By continuity of the velocity profile, we can write  $\bar {U}=U(\beta D)$, where
$\bar {U}=U(\beta D)$, where  $\beta \in [0, 1]$ is a constant that depends on the profile shape. Taking
$\beta \in [0, 1]$ is a constant that depends on the profile shape. Taking  $a_+=0$ for simplicity, we are thus led to implicit equations for the drag coefficient for the two cases
$a_+=0$ for simplicity, we are thus led to implicit equations for the drag coefficient for the two cases
respectively, where  $A$ and
$A$ and  $B$ are new constants depending on the choice of
$B$ are new constants depending on the choice of  $\beta$. Equation (1.2) encompasses, for example, the Blasius formula (Blasius Reference Blasius1913) with
$\beta$. Equation (1.2) encompasses, for example, the Blasius formula (Blasius Reference Blasius1913) with  $\lambda _B\sim 0.3164 Re^{-1/4}$ corresponding to
$\lambda _B\sim 0.3164 Re^{-1/4}$ corresponding to  $\alpha =1/7$, while (1.3) corresponds to the Prandtl formula (Prandtl Reference Prandtl1932) with
$\alpha =1/7$, while (1.3) corresponds to the Prandtl formula (Prandtl Reference Prandtl1932) with  $\kappa =0.407$ and
$\kappa =0.407$ and  $B=-0.8$. In the limit
$B=-0.8$. In the limit  $Re\to \infty$, it is easy to solve the implicit equations to obtain the asymptotic decay of the drag as
$Re\to \infty$, it is easy to solve the implicit equations to obtain the asymptotic decay of the drag as  $\lambda _{alg}\sim Re^{-2\alpha /(1+\alpha )}$ and
$\lambda _{alg}\sim Re^{-2\alpha /(1+\alpha )}$ and  $\lambda _{log}\sim 1/\log (Re)^2$.
$\lambda _{log}\sim 1/\log (Re)^2$.
Blasius and Prandtl theories basically provide the same value of friction for  $Re\in [10^3, 10^5]$, see figure 1. However, they markedly differ in the large Reynolds limit. Reaching this limit numerically or experimentally is challenging, as both the computational burden, or the inaccuracy of experimental measurements increase with Reynolds due to the thinning of the boundary layers at the wall. In this respect McKeon, Zagarola & Smits (Reference McKeon, Zagarola and Smits2005) set up a benchmark by analysing results obtained from high-performance measurement devices installed in a large Reynolds number facility, the Princeton SuperPipe.
$Re\in [10^3, 10^5]$, see figure 1. However, they markedly differ in the large Reynolds limit. Reaching this limit numerically or experimentally is challenging, as both the computational burden, or the inaccuracy of experimental measurements increase with Reynolds due to the thinning of the boundary layers at the wall. In this respect McKeon, Zagarola & Smits (Reference McKeon, Zagarola and Smits2005) set up a benchmark by analysing results obtained from high-performance measurement devices installed in a large Reynolds number facility, the Princeton SuperPipe.
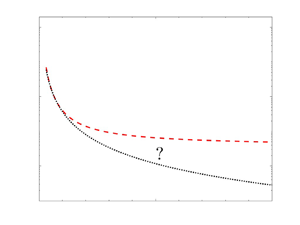
Figure 1. Pipe flow laws. In both panels, the grey dots are the data from the Oregon experiments (Swanson et al. Reference Swanson, Julian, Ihas and Donnelly2002), while the red open squares are the data of the Princeton pipe, discussed in McKeon et al. (Reference McKeon, Zagarola and Smits2005). These data can be used to test two types of law. (a) The Blasius versus Prandtl log-law. The blue line is the Blasius law  $\lambda = 0.3164 Re^{-1/4}$. The blue dashed line is the fit obtained by inverting the Prandtl-type formula 2.1, resulting in
$\lambda = 0.3164 Re^{-1/4}$. The blue dashed line is the fit obtained by inverting the Prandtl-type formula 2.1, resulting in  $\lambda =[0.8382 W(0.6287 Re)]^{-2}$, where
$\lambda =[0.8382 W(0.6287 Re)]^{-2}$, where  $W$ is the Lambert function; the black dotted line is the laminar
$W$ is the Lambert function; the black dotted line is the laminar  $1/Re$ law. (b) The algebraic laws with slowly varying exponent. The green line is the fit
$1/Re$ law. (b) The algebraic laws with slowly varying exponent. The green line is the fit  $\lambda =17.73 Re^{-\alpha }$, where
$\lambda =17.73 Re^{-\alpha }$, where  $\alpha =1.6405/(1+0.35\log _{10} Re)$; the black dotted line is the laminar
$\alpha =1.6405/(1+0.35\log _{10} Re)$; the black dotted line is the laminar  $1/Re$ law. In both cases, the inserts show the ratio of the data to the dashed-line fit, to evidence the quality of the correlation. The dotted line in the inserts marks the
$1/Re$ law. In both cases, the inserts show the ratio of the data to the dashed-line fit, to evidence the quality of the correlation. The dotted line in the inserts marks the  $1\pm 0.005$ limits, corresponding to an agreement within
$1\pm 0.005$ limits, corresponding to an agreement within  $0.5\,\%$.
$0.5\,\%$.
2. Overview
The friction law was estimated from velocity profiles obtained using Pitot probes of diameter  $0.9$ mm and
$0.9$ mm and  $0.3$ mm. Care was taken to correct for static pressure and Pitot displacements. The data used in the paper cover the range
$0.3$ mm. Care was taken to correct for static pressure and Pitot displacements. The data used in the paper cover the range  $31\times 10^3< Re<35\times 10^6$. This range of Reynolds number is sufficient to test various hypothesis with great accuracy. The first test concerns the validity of the Blasius or Prandtl correlations. For
$31\times 10^3< Re<35\times 10^6$. This range of Reynolds number is sufficient to test various hypothesis with great accuracy. The first test concerns the validity of the Blasius or Prandtl correlations. For  $Re<98\times 10^3$ the data lie within 1.4 % of the Blasius formula, see figure 1(a). For larger values of
$Re<98\times 10^3$ the data lie within 1.4 % of the Blasius formula, see figure 1(a). For larger values of  $Re$, the data are better described by a Prandtl type correlation, albeit with different constants corresponding to
$Re$, the data are better described by a Prandtl type correlation, albeit with different constants corresponding to  $\kappa =0.423$ and
$\kappa =0.423$ and  $B=-0.537$, see figure 1(a). With these values, the correlation coefficient between the friction law described by (1.3) and the data is better than
$B=-0.537$, see figure 1(a). With these values, the correlation coefficient between the friction law described by (1.3) and the data is better than  $0.995$ for
$0.995$ for  $31\times 10^3< Re<18\times 10^6$ , as shown in the insert of figure 1(a). A second test concerns the role of the offset constant,
$31\times 10^3< Re<18\times 10^6$ , as shown in the insert of figure 1(a). A second test concerns the role of the offset constant,  $a_+$, of the velocity profile. This offset is predicted by a Lie group analysis (Oberlack Reference Oberlack1999) but is ignored in classical correlation laws. Including the offset produces corrections to the friction law that decay like
$a_+$, of the velocity profile. This offset is predicted by a Lie group analysis (Oberlack Reference Oberlack1999) but is ignored in classical correlation laws. Including the offset produces corrections to the friction law that decay like  $1/Re$, and impacts estimates of the Kármán constant. The present data set is insufficient to determine an appropriate value of
$1/Re$, and impacts estimates of the Kármán constant. The present data set is insufficient to determine an appropriate value of  $a_+$ for pipe flows. However, even a conservative value of
$a_+$ for pipe flows. However, even a conservative value of  $a_+=5$ results in less than a 1 % change for
$a_+=5$ results in less than a 1 % change for  $\kappa$. Finally, the role of possible viscous corrections was investigated. They provide a power-law correction to the friction factor, that also impacts the value of
$\kappa$. Finally, the role of possible viscous corrections was investigated. They provide a power-law correction to the friction factor, that also impacts the value of  $B$ and
$B$ and  $\kappa$, increasing the latter by a factor
$\kappa$, increasing the latter by a factor  $0.002$. However, both the addition of the offset and of viscous corrections degrade the correlation with the data by at least 1 %, so that the final conclusion is that the best fit to the data at large Reynolds is given by the formula
$0.002$. However, both the addition of the offset and of viscous corrections degrade the correlation with the data by at least 1 %, so that the final conclusion is that the best fit to the data at large Reynolds is given by the formula
This is the main conclusion of McKeon et al. (Reference McKeon, Zagarola and Smits2005).
3. Impact
Nineteen years later, the impact of the paper can easily be measured quantitatively by its citation records (135), showing that it has reached the level of ‘reference paper’ in the field. This is a testament to the fact that McKeon et al. (Reference McKeon, Zagarola and Smits2005) have clearly demonstrated the effectiveness of a log-law to fit their data at large Reynolds number. Is the logarithmic versus algebraic controversy now over with these results? Clearly, the Blasius solution with fixed exponent has been excluded, but one cannot completely dismiss a more subtle algebraic decay, as advocated by Barenblatt, Chorin & Protokishin (Reference Barenblatt, Chorin and Protokishin1997). As an example, we show in figure 1(b) a fit of the data by a power law formula given by (1.2), with an exponent decaying very slowly with Reynolds number,  $\alpha \sim 1/[1+0.35\log _{10}(Re)]$. At large Reynolds number, the agreement with the data is as good, if not better, than with the Prandtl-log formula. The difference between the two laws is more than just a fitting exegesis. Indeed, they behave very differently in the infinite
$\alpha \sim 1/[1+0.35\log _{10}(Re)]$. At large Reynolds number, the agreement with the data is as good, if not better, than with the Prandtl-log formula. The difference between the two laws is more than just a fitting exegesis. Indeed, they behave very differently in the infinite  $Re$ limit, where the Prandtl-log law predicts a vanishing friction coefficient, while the algebraic formula predicts a finite value of the friction coefficient. As discussed in Eyink (Reference Eyink2024), this last case would correspond to an ‘anomalous’ friction law that may be connected to the existence of dissipative weak solution to inviscid Navier–Stokes equations, an outstanding mathematical puzzle that has recently attracted much attention in the mathematical community.
$Re$ limit, where the Prandtl-log law predicts a vanishing friction coefficient, while the algebraic formula predicts a finite value of the friction coefficient. As discussed in Eyink (Reference Eyink2024), this last case would correspond to an ‘anomalous’ friction law that may be connected to the existence of dissipative weak solution to inviscid Navier–Stokes equations, an outstanding mathematical puzzle that has recently attracted much attention in the mathematical community.
Is there any way the debate between the logarithmic and algebraic laws could be settled? Obviously, this is a difficult numerical challenge, since reaching Reynolds numbers of the order of  $10^6$ already requires resolutions that are at the border of what is possible over current supercomputers (Yao et al. Reference Yao, Rezaeiravesh, Schlatter and Hussain2023). On the other hand, going beyond the Princeton range of Reynolds numbers is difficult. Experimental friction is accessible via various techniques, including force-balance measurement, the use of the velocity profile, pressure measurements by surface Pitot tubes or around obstacles, and the use of analogies with heat transfer, mass transfer or surface oil-flow. The challenge with all these measurements is to reach sufficient precision to measure otherwise very small friction that becomes increasingly small as the Reynolds number is increased. In that sense, hot-wire or image velocimetry are presently not precise enough to determine the shear stress within the fluid. Besides this measurement problem, two additional challenges concern the experimental apparatus. First, it is difficult to reach the very large Reynolds number limit, which can only be achieved using either very large facilities (Baidya et al. Reference Baidya2019), or fluids with very low viscosity, such as helium at very low temperature (Swanson et al. Reference Swanson, Julian, Ihas and Donnelly2002) or pressurized fluid with variable density (Bodenschatz et al. Reference Bodenschatz, Bewley, Nobach, Sinhuber and Xu2014). Second, it is difficult to realize a ‘sufficiently smooth pipe’, as the boundary roughness significantly modifies the friction as soon as the size of the boundary layer becomes smaller than the typical height of the roughness (Nikuradse Reference Nikuradse1950). Since the boundary layer thickness decreases with increasing Reynolds number, sufficiently smooth pipes become more and more difficult to achieve as
$10^6$ already requires resolutions that are at the border of what is possible over current supercomputers (Yao et al. Reference Yao, Rezaeiravesh, Schlatter and Hussain2023). On the other hand, going beyond the Princeton range of Reynolds numbers is difficult. Experimental friction is accessible via various techniques, including force-balance measurement, the use of the velocity profile, pressure measurements by surface Pitot tubes or around obstacles, and the use of analogies with heat transfer, mass transfer or surface oil-flow. The challenge with all these measurements is to reach sufficient precision to measure otherwise very small friction that becomes increasingly small as the Reynolds number is increased. In that sense, hot-wire or image velocimetry are presently not precise enough to determine the shear stress within the fluid. Besides this measurement problem, two additional challenges concern the experimental apparatus. First, it is difficult to reach the very large Reynolds number limit, which can only be achieved using either very large facilities (Baidya et al. Reference Baidya2019), or fluids with very low viscosity, such as helium at very low temperature (Swanson et al. Reference Swanson, Julian, Ihas and Donnelly2002) or pressurized fluid with variable density (Bodenschatz et al. Reference Bodenschatz, Bewley, Nobach, Sinhuber and Xu2014). Second, it is difficult to realize a ‘sufficiently smooth pipe’, as the boundary roughness significantly modifies the friction as soon as the size of the boundary layer becomes smaller than the typical height of the roughness (Nikuradse Reference Nikuradse1950). Since the boundary layer thickness decreases with increasing Reynolds number, sufficiently smooth pipes become more and more difficult to achieve as  $Re$ is pushed even higher. All these difficulties explain why there are presently no better data than those discussed in McKeon et al. (Reference McKeon, Zagarola and Smits2005), which combine large Reynolds number, measurement precision and sufficient smoothness.
$Re$ is pushed even higher. All these difficulties explain why there are presently no better data than those discussed in McKeon et al. (Reference McKeon, Zagarola and Smits2005), which combine large Reynolds number, measurement precision and sufficient smoothness.
The friction law in a pipe may thus be ‘log at first sight’, but there is always the possibility of finding an algebraic law after second thoughts. Such a finding would open the possibility of an anomalous friction law, and open the possibility of the existence of dissipative singularities in pipe flows. This is a thrilling prospect for mathematicians and physicists, and we are all eagerly waiting for the next chapter of this exciting debate.

 $\lambda = 0.3164 Re^{-1/4}$. The blue dashed line is the fit obtained by inverting the Prandtl-type formula 2.1, resulting in
$\lambda = 0.3164 Re^{-1/4}$. The blue dashed line is the fit obtained by inverting the Prandtl-type formula 2.1, resulting in  $\lambda =[0.8382 W(0.6287 Re)]^{-2}$, where
$\lambda =[0.8382 W(0.6287 Re)]^{-2}$, where  $W$ is the Lambert function; the black dotted line is the laminar
$W$ is the Lambert function; the black dotted line is the laminar  $1/Re$ law. (b) The algebraic laws with slowly varying exponent. The green line is the fit
$1/Re$ law. (b) The algebraic laws with slowly varying exponent. The green line is the fit  $\lambda =17.73 Re^{-\alpha }$, where
$\lambda =17.73 Re^{-\alpha }$, where  $\alpha =1.6405/(1+0.35\log _{10} Re)$; the black dotted line is the laminar
$\alpha =1.6405/(1+0.35\log _{10} Re)$; the black dotted line is the laminar  $1/Re$ law. In both cases, the inserts show the ratio of the data to the dashed-line fit, to evidence the quality of the correlation. The dotted line in the inserts marks the
$1/Re$ law. In both cases, the inserts show the ratio of the data to the dashed-line fit, to evidence the quality of the correlation. The dotted line in the inserts marks the  $1\pm 0.005$ limits, corresponding to an agreement within
$1\pm 0.005$ limits, corresponding to an agreement within  $0.5\,\%$.
$0.5\,\%$.
1. Introduction
Many fluids of importance to human life or activity flow through canals or pipes, and so they attracted attention early in the development of the science. As early as 1775, Antoine de Chézy established a link between the mean velocity in a water channel, the hydraulic radius and the channel slope, and showed that this link could depend on the state of the surface via algae growth or decline, for example. This equation proved very robust, and was used to build many canals in the 19th century. While the Chézy equation can be obtained by simple balance arguments for linear momentum, it hides subtleties of the pipe or channel flow physics, some of which may be connected to a famous conjecture by Onsager (Eyink Reference Eyink2024).
The mean flow rate in parallel flows is obtained by a balance between the work done by the applied force (gravity or pressure gradient) and the energy loss due to friction against the surface. The frictional process is very subtle as it depends both on the state of the surface and of the fluid state itself, i.e. whether the flow is laminar or turbulent. In general, frictional losses are characterized by a skin friction coefficient which is proportional to the ratio of the applied shear stress at the surface, $\tau _w$, divided by the pressure in the free stream. In straight, smooth circular pipe flows, for which the pressure gradient balances the shear stress, the friction coefficient is simply given by the formula
$\tau _w$, divided by the pressure in the free stream. In straight, smooth circular pipe flows, for which the pressure gradient balances the shear stress, the friction coefficient is simply given by the formula
where $\partial _x P$ is the pressure drop per unit length,
$\partial _x P$ is the pressure drop per unit length,  $D$ is the pipe diameter,
$D$ is the pipe diameter,  $\rho$ is the fluid density,
$\rho$ is the fluid density,  $\bar {U}$ is the velocity averaged over the pipe cross-sectional area and
$\bar {U}$ is the velocity averaged over the pipe cross-sectional area and  $u_\tau =\sqrt {\tau _w/\rho }$ is the skin friction velocity. This formula shows that the friction depends on the velocity profile at the wall (via
$u_\tau =\sqrt {\tau _w/\rho }$ is the skin friction velocity. This formula shows that the friction depends on the velocity profile at the wall (via  $\bar {U}$) and on the viscosity
$\bar {U}$) and on the viscosity  $\nu$ (through
$\nu$ (through  $\tau_w$). Experimental measurements indicate in fact that they only depend on these two ingredients, provided one normalizes the viscosity by
$\tau_w$). Experimental measurements indicate in fact that they only depend on these two ingredients, provided one normalizes the viscosity by  $D \bar {U}$ to form the Reynolds number
$D \bar {U}$ to form the Reynolds number  $Re=D \bar {U}/\nu$.
$Re=D \bar {U}/\nu$.
In the laminar state, where $Re<10^3$, the velocity profile close to the wall (
$Re<10^3$, the velocity profile close to the wall ( $y=0$) is linear in the coordinate normal to the wall,
$y=0$) is linear in the coordinate normal to the wall,  $U(y)=Sy$, with
$U(y)=Sy$, with  $\tau _w=\rho \nu S$, so that
$\tau _w=\rho \nu S$, so that  $\bar {U}^2/u_\tau ^2\propto Re$, meaning that the friction coefficient simply decreases like
$\bar {U}^2/u_\tau ^2\propto Re$, meaning that the friction coefficient simply decreases like  $\lambda \sim 1/Re$. As soon as the flow becomes turbulent, however, the velocity profile displays a more complex behaviour, and the drag exhibits a transition towards a milder decrease with
$\lambda \sim 1/Re$. As soon as the flow becomes turbulent, however, the velocity profile displays a more complex behaviour, and the drag exhibits a transition towards a milder decrease with  $Re$. For economical and theoretical reasons, prediction of this decrease has been the topic of active research since 1945. A search using ‘Web of Science’ for papers including ‘skin friction’ in the title displays 1120 papers since 1945, cited 17 485 times, following an exponential curve.
$Re$. For economical and theoretical reasons, prediction of this decrease has been the topic of active research since 1945. A search using ‘Web of Science’ for papers including ‘skin friction’ in the title displays 1120 papers since 1945, cited 17 485 times, following an exponential curve.
From a theoretical point of view, two large categories of laws can be found, depending on whether one assumes that the turbulent velocity profile is logarithmic, $U(y)\sim \kappa ^{-1} u_\tau \log (y_++a_+)+B_*$, or algebraic,
$U(y)\sim \kappa ^{-1} u_\tau \log (y_++a_+)+B_*$, or algebraic,  $U(y)=A_* u_\tau (y_++a_+)^{\alpha }$, with
$U(y)=A_* u_\tau (y_++a_+)^{\alpha }$, with  $y_+=yu_\tau /\nu$;
$y_+=yu_\tau /\nu$;  $\kappa$ is the Kármán constant, and
$\kappa$ is the Kármán constant, and  $a_+$,
$a_+$,  $A_*$ and
$A_*$ and  $B_*$ are constants. By continuity of the velocity profile, we can write
$B_*$ are constants. By continuity of the velocity profile, we can write  $\bar {U}=U(\beta D)$, where
$\bar {U}=U(\beta D)$, where  $\beta \in [0, 1]$ is a constant that depends on the profile shape. Taking
$\beta \in [0, 1]$ is a constant that depends on the profile shape. Taking  $a_+=0$ for simplicity, we are thus led to implicit equations for the drag coefficient for the two cases
$a_+=0$ for simplicity, we are thus led to implicit equations for the drag coefficient for the two cases
respectively, where $A$ and
$A$ and  $B$ are new constants depending on the choice of
$B$ are new constants depending on the choice of  $\beta$. Equation (1.2) encompasses, for example, the Blasius formula (Blasius Reference Blasius1913) with
$\beta$. Equation (1.2) encompasses, for example, the Blasius formula (Blasius Reference Blasius1913) with  $\lambda _B\sim 0.3164 Re^{-1/4}$ corresponding to
$\lambda _B\sim 0.3164 Re^{-1/4}$ corresponding to  $\alpha =1/7$, while (1.3) corresponds to the Prandtl formula (Prandtl Reference Prandtl1932) with
$\alpha =1/7$, while (1.3) corresponds to the Prandtl formula (Prandtl Reference Prandtl1932) with  $\kappa =0.407$ and
$\kappa =0.407$ and  $B=-0.8$. In the limit
$B=-0.8$. In the limit  $Re\to \infty$, it is easy to solve the implicit equations to obtain the asymptotic decay of the drag as
$Re\to \infty$, it is easy to solve the implicit equations to obtain the asymptotic decay of the drag as  $\lambda _{alg}\sim Re^{-2\alpha /(1+\alpha )}$ and
$\lambda _{alg}\sim Re^{-2\alpha /(1+\alpha )}$ and  $\lambda _{log}\sim 1/\log (Re)^2$.
$\lambda _{log}\sim 1/\log (Re)^2$.
Blasius and Prandtl theories basically provide the same value of friction for $Re\in [10^3, 10^5]$, see figure 1. However, they markedly differ in the large Reynolds limit. Reaching this limit numerically or experimentally is challenging, as both the computational burden, or the inaccuracy of experimental measurements increase with Reynolds due to the thinning of the boundary layers at the wall. In this respect McKeon, Zagarola & Smits (Reference McKeon, Zagarola and Smits2005) set up a benchmark by analysing results obtained from high-performance measurement devices installed in a large Reynolds number facility, the Princeton SuperPipe.
$Re\in [10^3, 10^5]$, see figure 1. However, they markedly differ in the large Reynolds limit. Reaching this limit numerically or experimentally is challenging, as both the computational burden, or the inaccuracy of experimental measurements increase with Reynolds due to the thinning of the boundary layers at the wall. In this respect McKeon, Zagarola & Smits (Reference McKeon, Zagarola and Smits2005) set up a benchmark by analysing results obtained from high-performance measurement devices installed in a large Reynolds number facility, the Princeton SuperPipe.
Figure 1. Pipe flow laws. In both panels, the grey dots are the data from the Oregon experiments (Swanson et al. Reference Swanson, Julian, Ihas and Donnelly2002), while the red open squares are the data of the Princeton pipe, discussed in McKeon et al. (Reference McKeon, Zagarola and Smits2005). These data can be used to test two types of law. (a) The Blasius versus Prandtl log-law. The blue line is the Blasius law $\lambda = 0.3164 Re^{-1/4}$. The blue dashed line is the fit obtained by inverting the Prandtl-type formula 2.1, resulting in
$\lambda = 0.3164 Re^{-1/4}$. The blue dashed line is the fit obtained by inverting the Prandtl-type formula 2.1, resulting in  $\lambda =[0.8382 W(0.6287 Re)]^{-2}$, where
$\lambda =[0.8382 W(0.6287 Re)]^{-2}$, where  $W$ is the Lambert function; the black dotted line is the laminar
$W$ is the Lambert function; the black dotted line is the laminar  $1/Re$ law. (b) The algebraic laws with slowly varying exponent. The green line is the fit
$1/Re$ law. (b) The algebraic laws with slowly varying exponent. The green line is the fit  $\lambda =17.73 Re^{-\alpha }$, where
$\lambda =17.73 Re^{-\alpha }$, where  $\alpha =1.6405/(1+0.35\log _{10} Re)$; the black dotted line is the laminar
$\alpha =1.6405/(1+0.35\log _{10} Re)$; the black dotted line is the laminar  $1/Re$ law. In both cases, the inserts show the ratio of the data to the dashed-line fit, to evidence the quality of the correlation. The dotted line in the inserts marks the
$1/Re$ law. In both cases, the inserts show the ratio of the data to the dashed-line fit, to evidence the quality of the correlation. The dotted line in the inserts marks the  $1\pm 0.005$ limits, corresponding to an agreement within
$1\pm 0.005$ limits, corresponding to an agreement within  $0.5\,\%$.
$0.5\,\%$.
2. Overview
The friction law was estimated from velocity profiles obtained using Pitot probes of diameter $0.9$ mm and
$0.9$ mm and  $0.3$ mm. Care was taken to correct for static pressure and Pitot displacements. The data used in the paper cover the range
$0.3$ mm. Care was taken to correct for static pressure and Pitot displacements. The data used in the paper cover the range  $31\times 10^3< Re<35\times 10^6$. This range of Reynolds number is sufficient to test various hypothesis with great accuracy. The first test concerns the validity of the Blasius or Prandtl correlations. For
$31\times 10^3< Re<35\times 10^6$. This range of Reynolds number is sufficient to test various hypothesis with great accuracy. The first test concerns the validity of the Blasius or Prandtl correlations. For  $Re<98\times 10^3$ the data lie within 1.4 % of the Blasius formula, see figure 1(a). For larger values of
$Re<98\times 10^3$ the data lie within 1.4 % of the Blasius formula, see figure 1(a). For larger values of  $Re$, the data are better described by a Prandtl type correlation, albeit with different constants corresponding to
$Re$, the data are better described by a Prandtl type correlation, albeit with different constants corresponding to  $\kappa =0.423$ and
$\kappa =0.423$ and  $B=-0.537$, see figure 1(a). With these values, the correlation coefficient between the friction law described by (1.3) and the data is better than
$B=-0.537$, see figure 1(a). With these values, the correlation coefficient between the friction law described by (1.3) and the data is better than  $0.995$ for
$0.995$ for  $31\times 10^3< Re<18\times 10^6$ , as shown in the insert of figure 1(a). A second test concerns the role of the offset constant,
$31\times 10^3< Re<18\times 10^6$ , as shown in the insert of figure 1(a). A second test concerns the role of the offset constant,  $a_+$, of the velocity profile. This offset is predicted by a Lie group analysis (Oberlack Reference Oberlack1999) but is ignored in classical correlation laws. Including the offset produces corrections to the friction law that decay like
$a_+$, of the velocity profile. This offset is predicted by a Lie group analysis (Oberlack Reference Oberlack1999) but is ignored in classical correlation laws. Including the offset produces corrections to the friction law that decay like  $1/Re$, and impacts estimates of the Kármán constant. The present data set is insufficient to determine an appropriate value of
$1/Re$, and impacts estimates of the Kármán constant. The present data set is insufficient to determine an appropriate value of  $a_+$ for pipe flows. However, even a conservative value of
$a_+$ for pipe flows. However, even a conservative value of  $a_+=5$ results in less than a 1 % change for
$a_+=5$ results in less than a 1 % change for  $\kappa$. Finally, the role of possible viscous corrections was investigated. They provide a power-law correction to the friction factor, that also impacts the value of
$\kappa$. Finally, the role of possible viscous corrections was investigated. They provide a power-law correction to the friction factor, that also impacts the value of  $B$ and
$B$ and  $\kappa$, increasing the latter by a factor
$\kappa$, increasing the latter by a factor  $0.002$. However, both the addition of the offset and of viscous corrections degrade the correlation with the data by at least 1 %, so that the final conclusion is that the best fit to the data at large Reynolds is given by the formula
$0.002$. However, both the addition of the offset and of viscous corrections degrade the correlation with the data by at least 1 %, so that the final conclusion is that the best fit to the data at large Reynolds is given by the formula
This is the main conclusion of McKeon et al. (Reference McKeon, Zagarola and Smits2005).
3. Impact
Nineteen years later, the impact of the paper can easily be measured quantitatively by its citation records (135), showing that it has reached the level of ‘reference paper’ in the field. This is a testament to the fact that McKeon et al. (Reference McKeon, Zagarola and Smits2005) have clearly demonstrated the effectiveness of a log-law to fit their data at large Reynolds number. Is the logarithmic versus algebraic controversy now over with these results? Clearly, the Blasius solution with fixed exponent has been excluded, but one cannot completely dismiss a more subtle algebraic decay, as advocated by Barenblatt, Chorin & Protokishin (Reference Barenblatt, Chorin and Protokishin1997). As an example, we show in figure 1(b) a fit of the data by a power law formula given by (1.2), with an exponent decaying very slowly with Reynolds number, $\alpha \sim 1/[1+0.35\log _{10}(Re)]$. At large Reynolds number, the agreement with the data is as good, if not better, than with the Prandtl-log formula. The difference between the two laws is more than just a fitting exegesis. Indeed, they behave very differently in the infinite
$\alpha \sim 1/[1+0.35\log _{10}(Re)]$. At large Reynolds number, the agreement with the data is as good, if not better, than with the Prandtl-log formula. The difference between the two laws is more than just a fitting exegesis. Indeed, they behave very differently in the infinite  $Re$ limit, where the Prandtl-log law predicts a vanishing friction coefficient, while the algebraic formula predicts a finite value of the friction coefficient. As discussed in Eyink (Reference Eyink2024), this last case would correspond to an ‘anomalous’ friction law that may be connected to the existence of dissipative weak solution to inviscid Navier–Stokes equations, an outstanding mathematical puzzle that has recently attracted much attention in the mathematical community.
$Re$ limit, where the Prandtl-log law predicts a vanishing friction coefficient, while the algebraic formula predicts a finite value of the friction coefficient. As discussed in Eyink (Reference Eyink2024), this last case would correspond to an ‘anomalous’ friction law that may be connected to the existence of dissipative weak solution to inviscid Navier–Stokes equations, an outstanding mathematical puzzle that has recently attracted much attention in the mathematical community.
Is there any way the debate between the logarithmic and algebraic laws could be settled? Obviously, this is a difficult numerical challenge, since reaching Reynolds numbers of the order of $10^6$ already requires resolutions that are at the border of what is possible over current supercomputers (Yao et al. Reference Yao, Rezaeiravesh, Schlatter and Hussain2023). On the other hand, going beyond the Princeton range of Reynolds numbers is difficult. Experimental friction is accessible via various techniques, including force-balance measurement, the use of the velocity profile, pressure measurements by surface Pitot tubes or around obstacles, and the use of analogies with heat transfer, mass transfer or surface oil-flow. The challenge with all these measurements is to reach sufficient precision to measure otherwise very small friction that becomes increasingly small as the Reynolds number is increased. In that sense, hot-wire or image velocimetry are presently not precise enough to determine the shear stress within the fluid. Besides this measurement problem, two additional challenges concern the experimental apparatus. First, it is difficult to reach the very large Reynolds number limit, which can only be achieved using either very large facilities (Baidya et al. Reference Baidya2019), or fluids with very low viscosity, such as helium at very low temperature (Swanson et al. Reference Swanson, Julian, Ihas and Donnelly2002) or pressurized fluid with variable density (Bodenschatz et al. Reference Bodenschatz, Bewley, Nobach, Sinhuber and Xu2014). Second, it is difficult to realize a ‘sufficiently smooth pipe’, as the boundary roughness significantly modifies the friction as soon as the size of the boundary layer becomes smaller than the typical height of the roughness (Nikuradse Reference Nikuradse1950). Since the boundary layer thickness decreases with increasing Reynolds number, sufficiently smooth pipes become more and more difficult to achieve as
$10^6$ already requires resolutions that are at the border of what is possible over current supercomputers (Yao et al. Reference Yao, Rezaeiravesh, Schlatter and Hussain2023). On the other hand, going beyond the Princeton range of Reynolds numbers is difficult. Experimental friction is accessible via various techniques, including force-balance measurement, the use of the velocity profile, pressure measurements by surface Pitot tubes or around obstacles, and the use of analogies with heat transfer, mass transfer or surface oil-flow. The challenge with all these measurements is to reach sufficient precision to measure otherwise very small friction that becomes increasingly small as the Reynolds number is increased. In that sense, hot-wire or image velocimetry are presently not precise enough to determine the shear stress within the fluid. Besides this measurement problem, two additional challenges concern the experimental apparatus. First, it is difficult to reach the very large Reynolds number limit, which can only be achieved using either very large facilities (Baidya et al. Reference Baidya2019), or fluids with very low viscosity, such as helium at very low temperature (Swanson et al. Reference Swanson, Julian, Ihas and Donnelly2002) or pressurized fluid with variable density (Bodenschatz et al. Reference Bodenschatz, Bewley, Nobach, Sinhuber and Xu2014). Second, it is difficult to realize a ‘sufficiently smooth pipe’, as the boundary roughness significantly modifies the friction as soon as the size of the boundary layer becomes smaller than the typical height of the roughness (Nikuradse Reference Nikuradse1950). Since the boundary layer thickness decreases with increasing Reynolds number, sufficiently smooth pipes become more and more difficult to achieve as  $Re$ is pushed even higher. All these difficulties explain why there are presently no better data than those discussed in McKeon et al. (Reference McKeon, Zagarola and Smits2005), which combine large Reynolds number, measurement precision and sufficient smoothness.
$Re$ is pushed even higher. All these difficulties explain why there are presently no better data than those discussed in McKeon et al. (Reference McKeon, Zagarola and Smits2005), which combine large Reynolds number, measurement precision and sufficient smoothness.
The friction law in a pipe may thus be ‘log at first sight’, but there is always the possibility of finding an algebraic law after second thoughts. Such a finding would open the possibility of an anomalous friction law, and open the possibility of the existence of dissipative singularities in pipe flows. This is a thrilling prospect for mathematicians and physicists, and we are all eagerly waiting for the next chapter of this exciting debate.
Acknowledgements
I thank T. Drivas and G. Eyink for many discussions around these issues.
Funding
This work has been supported by the ANR TILT no. ANR-16-CE06-0006-01 and the ANR BANG no. ANR-16-CE06-0006-01.
Declaration of interests
The author reports no conflict of interest.