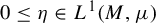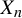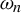1 Introduction
Consider a family of transformations
![]() $\mathcal F = \{f_\omega :E\to E\}_{\omega \in \Delta }$
, where E is a metric space. Given a subset
$\mathcal F = \{f_\omega :E\to E\}_{\omega \in \Delta }$
, where E is a metric space. Given a subset
![]() $M \subset E$
and endowing
$M \subset E$
and endowing
![]() $\mathcal F$
with a probability measure, we aim to understand the statistical behaviour of the random dynamical system
$\mathcal F$
with a probability measure, we aim to understand the statistical behaviour of the random dynamical system
conditioned upon remaining in M.
Such a problem can be naturally modelled via the Markov chain
![]() $X_n = f_n(X_{n-1})$
with
$X_n = f_n(X_{n-1})$
with
![]() $f_n\in \mathcal F$
absorbed at
$f_n\in \mathcal F$
absorbed at
![]() $\partial := E\setminus M$
, that is,
$\partial := E\setminus M$
, that is,
![]() $X_n\in \partial $
implies
$X_n\in \partial $
implies
![]() $X_{n+1} \in \partial $
. Statistical information for the above (conditioned) random dynamical system is then obtained by certain limiting distributions for the paths
$X_{n+1} \in \partial $
. Statistical information for the above (conditioned) random dynamical system is then obtained by certain limiting distributions for the paths
![]() $X_n$
. In the literature, such limiting distributions appear mainly in two forms. The first is the so-called Yaglom limit
$X_n$
. In the literature, such limiting distributions appear mainly in two forms. The first is the so-called Yaglom limit
where
![]() $x\in M$
,
$x\in M$
,
![]() $\tau =\min \{n\in \mathbb N\mid X_n\in \partial \}$
and A is a measurable subset of M. The second one is the so-called quasi-ergodic limit
$\tau =\min \{n\in \mathbb N\mid X_n\in \partial \}$
and A is a measurable subset of M. The second one is the so-called quasi-ergodic limit

There are several contexts in which the Yaglom limit converges to a quasi-stationary measure. We recall that a probability measure
![]() $\mu $
on M is called a quasi-stationary measure for
$\mu $
on M is called a quasi-stationary measure for
![]() $X_n$
on M if for every
$X_n$
on M if for every
![]() $n\in \mathbb N$
,
$n\in \mathbb N$
,
![]() $\mu (\mathrm {d} x) := {\mathbb P}[X_n \in \mathrm {d} x\mid X_0 \sim \mu , \tau>n].$
However, the limit in equation (1.2) is related to the existence of a quasi-ergodic measure for
$\mu (\mathrm {d} x) := {\mathbb P}[X_n \in \mathrm {d} x\mid X_0 \sim \mu , \tau>n].$
However, the limit in equation (1.2) is related to the existence of a quasi-ergodic measure for
![]() $X_n$
on M. A measure
$X_n$
on M. A measure
![]() $\nu $
on M is called a quasi-ergodic measure for
$\nu $
on M is called a quasi-ergodic measure for
![]() $X_n$
on M if for every measurable subset A of M, equation (1.2) converges to
$X_n$
on M if for every measurable subset A of M, equation (1.2) converges to
![]() $\nu (A)$
for
$\nu (A)$
for
![]() $\nu $
-almost every
$\nu $
-almost every
![]() $x\in M.$
$x\in M.$
In the literature [Reference Benaïm, Champagnat, Oçafrain and Villemonais3, Reference Breyer and Roberts4, Reference Castro, Lamb, Olicón-Méndez and Rasmussen7–Reference Darroch and Seneta9, Reference Zhang, Li and Song29], various sufficient conditions are presented for the existence and uniqueness of quasi-stationary measures
![]() $\mu $
and quasi-ergodic measures
$\mu $
and quasi-ergodic measures
![]() $\nu $
. These conditions imply that
$\nu $
. These conditions imply that
![]() $\nu \ll \mu $
and that the Radon–Nikodym derivative
$\nu \ll \mu $
and that the Radon–Nikodym derivative
![]() ${\eta (x) =\nu (\mathrm {d} x)/\mu (\mathrm {d} x)}$
is an eigenfunction of
${\eta (x) =\nu (\mathrm {d} x)/\mu (\mathrm {d} x)}$
is an eigenfunction of
![]() ${\mathcal P},$
where
${\mathcal P},$
where
![]() ${\mathcal P}$
is the transition kernel of
${\mathcal P}$
is the transition kernel of
![]() $X_n$
. The uniform convergence of the sequence
$X_n$
. The uniform convergence of the sequence
![]() $\{{\mathcal P}^n(\cdot ,M)/\unicode{x3bb} ^n\}_{n\in \mathbb N}$
, where
$\{{\mathcal P}^n(\cdot ,M)/\unicode{x3bb} ^n\}_{n\in \mathbb N}$
, where
![]() $\unicode{x3bb} := \int _M {\mathcal P}(y,M)\mu (\mathrm {d} y)$
, to the eigenfunction
$\unicode{x3bb} := \int _M {\mathcal P}(y,M)\mu (\mathrm {d} y)$
, to the eigenfunction
![]() $\eta $
plays a crucial role in the proofs.
$\eta $
plays a crucial role in the proofs.
In this paper, we take a different approach. We set out to derive a quasi-ergodic measure starting from a quasi-stationary measure. The existence of quasi-stationary measures is a well-established problem (see [Reference Pollett26] for a bibliography). Quasi-stationary measures arise as positive eigenmeasures of the operator
![]() $\mu \mapsto \int _M {\mathcal P}(x,\cdot )\mu (\mathrm {d} x)$
and extensive literature exists on how to solve such eigenvalue problems [Reference Meyer-Nieberg22, Reference Oikhberg and Troitsky24, Reference Pflug25]. Since quasi-ergodic measures do not admit such an approach, they are less well understood. Quasi-ergodic measures are important in the analysis of random dynamical systems, for instance, in the context of the recently established conditioned Lyapunov spectrum [Reference Castro, Chemnitz, Chu, Engel, Lamb and Rasmussen6, Reference Engel, Lamb and Rasmussen11].
$\mu \mapsto \int _M {\mathcal P}(x,\cdot )\mu (\mathrm {d} x)$
and extensive literature exists on how to solve such eigenvalue problems [Reference Meyer-Nieberg22, Reference Oikhberg and Troitsky24, Reference Pflug25]. Since quasi-ergodic measures do not admit such an approach, they are less well understood. Quasi-ergodic measures are important in the analysis of random dynamical systems, for instance, in the context of the recently established conditioned Lyapunov spectrum [Reference Castro, Chemnitz, Chu, Engel, Lamb and Rasmussen6, Reference Engel, Lamb and Rasmussen11].
Inspired by these results, where quasi-ergodic measures can be expressed as a density over the quasi-stationary measures, we obtain natural conditions on the transition kernel
![]() ${\mathcal P}$
such that the existence of a quasi-ergodic measure becomes equivalent to solving an eigenvalue problem for
${\mathcal P}$
such that the existence of a quasi-ergodic measure becomes equivalent to solving an eigenvalue problem for
![]() ${\mathcal P}$
in
${\mathcal P}$
in
![]() $L^1.$
As a result, we considerably simplify the procedure of finding a quasi-ergodic measure. Furthermore, we also obtain, under aperiodicity conditions, that the Yaglom limit in equation (1.1) converges to the quasi-stationary measure
$L^1.$
As a result, we considerably simplify the procedure of finding a quasi-ergodic measure. Furthermore, we also obtain, under aperiodicity conditions, that the Yaglom limit in equation (1.1) converges to the quasi-stationary measure
![]() $\mu $
-almost surely (a.s.)
$\mu $
-almost surely (a.s.)
As an application of our results, we characterize the limits in equations (1.1) and (1.2) for the random logistic map
![]() $Y_{n+1} = \omega _n Y_n(1-Y_n)$
absorbed at
$Y_{n+1} = \omega _n Y_n(1-Y_n)$
absorbed at
![]() ${\mathbb R} \setminus [0,1],$
with
${\mathbb R} \setminus [0,1],$
with
![]() $\{\omega _n\}_{n\in \mathbb N}$
an independent and identically distributed (i.i.d.) sequence of random variables such that
$\{\omega _n\}_{n\in \mathbb N}$
an independent and identically distributed (i.i.d.) sequence of random variables such that
![]() $\omega _0 \sim \mathrm {Unif}([a,b]),$
with
$\omega _0 \sim \mathrm {Unif}([a,b]),$
with
![]() $1\leq a <4$
and
$1\leq a <4$
and
![]() $b>4,$
where
$b>4,$
where
![]() $\mathrm {Unif}([a,b])$
denotes the continuous uniform distribution in
$\mathrm {Unif}([a,b])$
denotes the continuous uniform distribution in
![]() $[a,b]$
. The analysis of this system is challenging since its transition kernel presents a change of behaviour on the points
$[a,b]$
. The analysis of this system is challenging since its transition kernel presents a change of behaviour on the points
![]() $0$
and
$0$
and
![]() $1$
. In particular, for every
$1$
. In particular, for every
![]() $x\in (0,1)$
,
$x\in (0,1)$
,
while
![]() ${\mathcal P}(0,\mathrm {d} y ) = {\mathcal P}(1,\mathrm {d} y) = \delta _0(\mathrm {d} y).$
This implies that the transition densities
${\mathcal P}(0,\mathrm {d} y ) = {\mathcal P}(1,\mathrm {d} y) = \delta _0(\mathrm {d} y).$
This implies that the transition densities
![]() ${\mathcal P}(x,\mathrm {d} y)$
explode when x approaches the points
${\mathcal P}(x,\mathrm {d} y)$
explode when x approaches the points
![]() $0$
and
$0$
and
![]() $1$
. Consequently, the results in the literature [Reference Benaïm, Champagnat, Oçafrain and Villemonais3, Reference Breyer and Roberts4, Reference Castro, Lamb, Olicón-Méndez and Rasmussen7, Reference Champagnat and Villemonais8, Reference Zhang, Li and Song29] cannot be applied, since
$1$
. Consequently, the results in the literature [Reference Benaïm, Champagnat, Oçafrain and Villemonais3, Reference Breyer and Roberts4, Reference Castro, Lamb, Olicón-Méndez and Rasmussen7, Reference Champagnat and Villemonais8, Reference Zhang, Li and Song29] cannot be applied, since
![]() ${\mathcal P}$
does not act as a compact operator on
${\mathcal P}$
does not act as a compact operator on
![]() $\mathcal C^0(M)$
and
$\mathcal C^0(M)$
and
![]() $L^p(M)$
, with
$L^p(M)$
, with
![]() $p\geq 1$
. Hence, a more refined analysis is needed.
$p\geq 1$
. Hence, a more refined analysis is needed.
To overcome this issue, we consider
![]() $AM$
-compact operators (see [Reference Glück and Haase16, Appendix A]), a generalization of compact operators. Inspired by the novel results on positive integral operators in [Reference Gerlach and Glück14–Reference Glück and Haase16], we analyse the action of
$AM$
-compact operators (see [Reference Glück and Haase16, Appendix A]), a generalization of compact operators. Inspired by the novel results on positive integral operators in [Reference Gerlach and Glück14–Reference Glück and Haase16], we analyse the action of
![]() ${\mathcal P}$
on
${\mathcal P}$
on
![]() $L^1(M,\mu )$
. Since
$L^1(M,\mu )$
. Since
![]() ${\mathcal P}$
is an integral operator, it is
${\mathcal P}$
is an integral operator, it is
![]() $AM$
-compact, and we can establish its peripheral spectrum from which the asymptotic behaviour of
$AM$
-compact, and we can establish its peripheral spectrum from which the asymptotic behaviour of
![]() $Y_n$
follows.
$Y_n$
follows.
This paper is divided into six sections. In §2, the basic concepts of the theory of absorbing Markov chains are briefly recalled, the main underlying hypotheses of this paper are defined (Hypotheses H1 and H2) and the main results of this paper are stated (Theorems 2.1, 2.2, 2.3 and 2.4). In §3, it is shown that Hypothesis H1 implies that
![]() ${\mathcal P}/\unicode{x3bb} $
is a mean ergodic operator. Section 4 is dedicated to a brief presentation of Banach lattice theory, the definition of an
${\mathcal P}/\unicode{x3bb} $
is a mean ergodic operator. Section 4 is dedicated to a brief presentation of Banach lattice theory, the definition of an
![]() $AM$
-compact operator and the proof of Theorem 2.2. In §5, we combine the results of the previous sections to prove Theorems 2.3 and 2.4. Finally, in §6, we analyse the asymptotic behaviour of the random logistic map
$AM$
-compact operator and the proof of Theorem 2.2. In §5, we combine the results of the previous sections to prove Theorems 2.3 and 2.4. Finally, in §6, we analyse the asymptotic behaviour of the random logistic map
![]() $Y_n$
, introduced above, and prove Theorem 2.1.
$Y_n$
, introduced above, and prove Theorem 2.1.
2 Main results
Let E be a metric space and M a subspace of E. We aim to study Markov chains on E conditioned upon remaining in the set M. With this objective in mind, we denote as
![]() $E_M$
the topological space
$E_M$
the topological space
![]() $M \sqcup \partial $
generated by the topological basis
$M \sqcup \partial $
generated by the topological basis
where
![]() $\sqcup $
denotes disjoint union. In this paper, we assume that
$\sqcup $
denotes disjoint union. In this paper, we assume that
is a Markov chain with state space
![]() ${E_M}$
, in the sense of [Reference Rogers and Williams27, Definition III.1.1], that is, the pair
${E_M}$
, in the sense of [Reference Rogers and Williams27, Definition III.1.1], that is, the pair
![]() $(\Omega ,\{\mathcal F_n\}_{n\in \mathbb N})$
is a filtered space;
$(\Omega ,\{\mathcal F_n\}_{n\in \mathbb N})$
is a filtered space;
![]() $X_n$
is an
$X_n$
is an
![]() $\mathcal F_n$
-adapted process with state space
$\mathcal F_n$
-adapted process with state space
![]() ${E_M}$
;
${E_M}$
;
![]() ${\mathcal P}^n$
a time-homogeneous transition probability function of the process
${\mathcal P}^n$
a time-homogeneous transition probability function of the process
![]() $X_n$
satisfying the usual measurability assumptions and Chapman–Kolmogorov equation;
$X_n$
satisfying the usual measurability assumptions and Chapman–Kolmogorov equation;
![]() $\{{\mathbb P}_x\}_{x\in {E_M}}$
is a family of probability function satisfying
$\{{\mathbb P}_x\}_{x\in {E_M}}$
is a family of probability function satisfying
![]() ${\mathbb P}_x[X_0=x] = 1$
for every
${\mathbb P}_x[X_0=x] = 1$
for every
![]() $x\in {E_M}$
; and for all
$x\in {E_M}$
; and for all
![]() $m,n\in \mathbb N_0$
,
$m,n\in \mathbb N_0$
,
![]() $x\in E_M$
, and every bounded measurable function f on
$x\in E_M$
, and every bounded measurable function f on
![]() ${E_M}$
,
${E_M}$
,
We assume that
![]() $X_n$
is a Markov chain that is absorbed at
$X_n$
is a Markov chain that is absorbed at
![]() $\partial ,$
meaning that
$\partial ,$
meaning that
![]() ${{\mathcal P}}(\partial ,\partial ) = 1. $
In view of the above definitions, it is natural to define the stopping time
${{\mathcal P}}(\partial ,\partial ) = 1. $
In view of the above definitions, it is natural to define the stopping time
Throughout the paper, the following notation is used.
Notation 2.1. Given a probability measure
![]() $\mu $
on M and
$\mu $
on M and
![]() $p\in [1,\infty ], $
we denote
$p\in [1,\infty ], $
we denote
![]() ${L^p (M,{\mathscr B}(M),\mu )}$
as
${L^p (M,{\mathscr B}(M),\mu )}$
as
![]() $L^p(M,\mu )$
and
$L^p(M,\mu )$
and
![]() $\mathcal M(M)$
as the set of Borel signed-measures on
$\mathcal M(M)$
as the set of Borel signed-measures on
![]() $M.$
Moreover, we denote
$M.$
Moreover, we denote
![]() ${{\mathbb P}_\mu (\cdot ) := \int _{M} {\mathbb P}_x (\cdot ) \mu (\mathrm {d} x).}$
${{\mathbb P}_\mu (\cdot ) := \int _{M} {\mathbb P}_x (\cdot ) \mu (\mathrm {d} x).}$
We denote as
![]() $\mathcal C^0(M) :=\{f:M\to {\mathbb R}; \ f \text { is continuous}\}$
and
$\mathcal C^0(M) :=\{f:M\to {\mathbb R}; \ f \text { is continuous}\}$
and
![]() $\mathcal F_b(M)$
as the set of bounded Borel measurable functions on M. Given
$\mathcal F_b(M)$
as the set of bounded Borel measurable functions on M. Given
![]() $f\in {\mathcal F_b}(M)$
, write
$f\in {\mathcal F_b}(M)$
, write
and by abuse of notation, denote
 $$ \begin{align*} f\circ X_n := \begin{cases} f\circ X_n& \text{if } X_n\in M,\\ 0 & \text{if } X_n \notin M .\end{cases}\end{align*} $$
$$ \begin{align*} f\circ X_n := \begin{cases} f\circ X_n& \text{if } X_n\in M,\\ 0 & \text{if } X_n \notin M .\end{cases}\end{align*} $$
Given a sub
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathscr F$
of
$\mathscr F$
of
![]() $\mathscr B(M)$
and
$\mathscr B(M)$
and
![]() $f\in L^1(M,\mu ),$
we denote
$f\in L^1(M,\mu ),$
we denote
![]() $ {\mathbb E}_\mu [f\mid \mathscr F ] \in L^1(M,\mathcal F,\mu )$
as the conditioned conditional expectation of f given
$ {\mathbb E}_\mu [f\mid \mathscr F ] \in L^1(M,\mathcal F,\mu )$
as the conditioned conditional expectation of f given
![]() $\mathscr F$
, that is, the unique function in
$\mathscr F$
, that is, the unique function in
![]() $L^1(M,\mathscr F,\mu )$
such that
$L^1(M,\mathscr F,\mu )$
such that
We define the sets
and
Finally, given a Banach space
![]() $E,$
we say that the sequence
$E,$
we say that the sequence
![]() $\{x_n\}_{n\in \mathbb N}\subset E$
converges in the weak topology to
$\{x_n\}_{n\in \mathbb N}\subset E$
converges in the weak topology to
![]() $x\in E$
if for every bounded linear functional
$x\in E$
if for every bounded linear functional
![]() $\phi \in E^*$
,
$\phi \in E^*$
,
![]() $\lim _{n\to \infty } \phi (x_n) = \phi (x).$
Moreover, we say that the sequence
$\lim _{n\to \infty } \phi (x_n) = \phi (x).$
Moreover, we say that the sequence
![]() $\{\phi _n\}_{n\in \mathbb N}\subset E^*$
converges in the weak
$\{\phi _n\}_{n\in \mathbb N}\subset E^*$
converges in the weak
![]() $^*$
topology to
$^*$
topology to
![]() $\phi $
if
$\phi $
if
![]() $\lim _{n\to \infty }\phi _n(x) = \phi (x)$
for every
$\lim _{n\to \infty }\phi _n(x) = \phi (x)$
for every
![]() $x\in E.$
$x\in E.$
Since stationary measures do not capture the behaviour of
![]() $X_n$
before absorption, they become irrelevant when dealing with absorbing Markov chains. Due to this issue, it is necessary to extend the concept of stationary measures to quasi-stationary measures. Below, we recall the definition of a quasi-stationary measure.
$X_n$
before absorption, they become irrelevant when dealing with absorbing Markov chains. Due to this issue, it is necessary to extend the concept of stationary measures to quasi-stationary measures. Below, we recall the definition of a quasi-stationary measure.
Definition 2.2. A Borel measure
![]() $\mu $
on a metric space M is to be a quasi-stationary measure for the Markov chain
$\mu $
on a metric space M is to be a quasi-stationary measure for the Markov chain
![]() $X_n$
if
$X_n$
if
We call
![]() $\unicode{x3bb} = \int _M{\mathcal P}(x,M)\mu (\mathrm {d} x)$
the survival rate of
$\unicode{x3bb} = \int _M{\mathcal P}(x,M)\mu (\mathrm {d} x)$
the survival rate of
![]() $\mu $
.
$\mu $
.
Observe that if
![]() $X_n$
admits a quasi-stationary measure
$X_n$
admits a quasi-stationary measure
![]() $\mu $
on M with survival rate
$\mu $
on M with survival rate
![]() $\unicode{x3bb} $
, then
$\unicode{x3bb} $
, then
![]() ${\mathcal P}$
may be seen as a bounded linear operator in
${\mathcal P}$
may be seen as a bounded linear operator in
![]() $ L^\infty (M,\mu )$
. Moreover, since
$ L^\infty (M,\mu )$
. Moreover, since
and
![]() $L^\infty (M,\mu )$
is dense in
$L^\infty (M,\mu )$
is dense in
![]() $ L^1(M,\mu ),$
the operator
$ L^1(M,\mu ),$
the operator
![]() ${\mathcal P}$
can be naturally extended as a bounded linear operator in
${\mathcal P}$
can be naturally extended as a bounded linear operator in
![]() $L^1(M,\mu ).$
$L^1(M,\mu ).$
While we have that ergodic stationary measures can be described in terms of Birkhoff averages for classical Markov chains, this is not true any longer when dealing with absorbing Markov chains, meaning that quasi-stationary measures cannot be described in terms of conditioned Birkhoff averages. This obstruction motivates the definition of quasi-ergodic measures.
Definition 2.3. A measure
![]() $\nu $
on M is called a quasi-ergodic measure if for every
$\nu $
on M is called a quasi-ergodic measure if for every
![]() $f\in {\mathcal F_b}(M),$
$f\in {\mathcal F_b}(M),$
 $$ \begin{align*} \lim_{n\to\infty}{\mathbb E}_x\bigg[\frac{1}{n} \sum_{i=0}^{n-1} f\circ X_i \hspace{0.1cm}\bigg\vert \hspace{0.1cm} \tau>n\bigg] = \int_M f(y) \nu(\mathrm{d} y) \quad\mbox{for } \nu\mbox{-almost every } x\in M. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}{\mathbb E}_x\bigg[\frac{1}{n} \sum_{i=0}^{n-1} f\circ X_i \hspace{0.1cm}\bigg\vert \hspace{0.1cm} \tau>n\bigg] = \int_M f(y) \nu(\mathrm{d} y) \quad\mbox{for } \nu\mbox{-almost every } x\in M. \end{align*} $$
One of the main objectives of this paper is to study the statistical asymptotic behaviour of the Markov chain
![]() $Y_{n+1}^{a,b} := \omega _n Y_{n}^{a,b} (1-Y_n^{a,b})$
absorbed at
$Y_{n+1}^{a,b} := \omega _n Y_{n}^{a,b} (1-Y_n^{a,b})$
absorbed at
![]() ${\mathbb R}\setminus [0,1]$
, where
${\mathbb R}\setminus [0,1]$
, where
![]() $\{\omega _n\}_n$
is an i.i.d. sequence of random variables such that
$\{\omega _n\}_n$
is an i.i.d. sequence of random variables such that
![]() $\omega _0 \sim \mathrm {Unif}([a,b])$
with
$\omega _0 \sim \mathrm {Unif}([a,b])$
with
![]() $1\leq a<4$
and
$1\leq a<4$
and
![]() $b>4$
.
$b>4$
.
We mention that in the case where
![]() $Y_n^{a,b}$
does not escape from the interval
$Y_n^{a,b}$
does not escape from the interval
![]() $[0,1]$
, that is,
$[0,1]$
, that is,
![]() $1\leq a < b\leq 4$
, [Reference Athreya and Dai2, Theorem 2] and [Reference Zmarrou and Homburg30, Proposition 9.5] show that
$1\leq a < b\leq 4$
, [Reference Athreya and Dai2, Theorem 2] and [Reference Zmarrou and Homburg30, Proposition 9.5] show that
![]() $Y_n^{a,b}$
admits a unique stationary measure
$Y_n^{a,b}$
admits a unique stationary measure
![]() $\mu _{a,b}$
for
$\mu _{a,b}$
for
![]() $Y_n^{a,b}$
on
$Y_n^{a,b}$
on
![]() $[0,1]$
such that
$[0,1]$
such that
![]() $\mu _{a,b} ((0,1)) = 1.$
For dynamical considerations of random logistic maps and an analysis of the case were the sample space is finite, see [Reference Abbasi, Gharaei and Homburg1].
$\mu _{a,b} ((0,1)) = 1.$
For dynamical considerations of random logistic maps and an analysis of the case were the sample space is finite, see [Reference Abbasi, Gharaei and Homburg1].
The following theorem describes the asymptotic distribution of
![]() $Y_n^{a,b}$
conditioned upon survival when
$Y_n^{a,b}$
conditioned upon survival when
![]() $1\leq a < 4<b$
, also establishing the existence of quasi-stationary and quasi-ergodic measures for
$1\leq a < 4<b$
, also establishing the existence of quasi-stationary and quasi-ergodic measures for
![]() $Y_n^{a,b}$
on
$Y_n^{a,b}$
on
![]() $[0,1]$
.
$[0,1]$
.
Theorem 2.1. Consider
![]() $M=[0,1]$
,
$M=[0,1]$
,
![]() $1\leq a<4<b$
, the Markov chain
$1\leq a<4<b$
, the Markov chain
![]() $Y_n^{a,b}$
on
$Y_n^{a,b}$
on
![]() ${\mathbb R}_{M}$
absorbed at
${\mathbb R}_{M}$
absorbed at
![]() $\partial ={\mathbb R}\setminus M$
and
$\partial ={\mathbb R}\setminus M$
and
![]() $\tau ^{a,b}(\omega ) = \min \{n\in \mathbb N; Y_n^{a,b} \in {\mathbb R}\setminus [0,1]\}.$
Then we have the following.
$\tau ^{a,b}(\omega ) = \min \{n\in \mathbb N; Y_n^{a,b} \in {\mathbb R}\setminus [0,1]\}.$
Then we have the following.
-
(i)
 $Y_n^{a,b}$
admits a quasi-stationary measure
$Y_n^{a,b}$
admits a quasi-stationary measure
 $\mu _{a,b}$
with survival rate
$\mu _{a,b}$
with survival rate
 $\unicode{x3bb} _{a,b}$
such that
$\unicode{x3bb} _{a,b}$
such that
 $\mathrm {supp}(\mu _{a,b}) =[0,1]$
and
$\mathrm {supp}(\mu _{a,b}) =[0,1]$
and
 $\mu _{a,b} \ll \mathrm {Leb}$
, where
$\mu _{a,b} \ll \mathrm {Leb}$
, where
 $\mathrm {Leb}$
denotes the Lebesgue measure on
$\mathrm {Leb}$
denotes the Lebesgue measure on
 $[0,1].$
$[0,1].$
-
(ii) There exists
 $\eta _{a,b} \in L^1(M,\mu )$
such that
$\eta _{a,b} \in L^1(M,\mu )$
such that
 ${\mathcal P} \eta _{a,b} = \unicode{x3bb} _{a,b} \eta _{a,b} $
,
${\mathcal P} \eta _{a,b} = \unicode{x3bb} _{a,b} \eta _{a,b} $
,
 $\|\eta _{a,b}\|_{L^1(M,\mu )} =1$
and
$\|\eta _{a,b}\|_{L^1(M,\mu )} =1$
and
 $\eta _{a,b}>0 \ \mu _{a,b}$
-a.s.
$\eta _{a,b}>0 \ \mu _{a,b}$
-a.s. -
(iii) For every
 $h\in L^\infty (M,\mathrm {Leb})$
and
$h\in L^\infty (M,\mathrm {Leb})$
and
 $x\in (0,1)$
,
$x\in (0,1)$
,  $$ \begin{align*} \lim_{n\to\infty} {\mathbb E}_x \bigg[ \frac{1}{n}\sum_{i=0}^{n-1} h\circ Y_i^{a,b}\, \bigg|\, \tau^{a,b}>n\bigg] = \int_M h(y) \eta_{a,b}(y) \mu_{a,b}(\mathrm{d} y).\end{align*} $$
$$ \begin{align*} \lim_{n\to\infty} {\mathbb E}_x \bigg[ \frac{1}{n}\sum_{i=0}^{n-1} h\circ Y_i^{a,b}\, \bigg|\, \tau^{a,b}>n\bigg] = \int_M h(y) \eta_{a,b}(y) \mu_{a,b}(\mathrm{d} y).\end{align*} $$
-
(iv) For every
 $h\in L^\infty (M,\mathrm {Leb})$
and
$h\in L^\infty (M,\mathrm {Leb})$
and
 $x\in (0,1)$
,
$x\in (0,1)$
,  $$ \begin{align*}\lim_{n\to \infty} {\mathbb E}_x[ h \circ Y_i^{a,b}\mid \tau^{a,b}>n] = \int h(y) \mu_{a,b}(\mathrm{d} y). \end{align*} $$
$$ \begin{align*}\lim_{n\to \infty} {\mathbb E}_x[ h \circ Y_i^{a,b}\mid \tau^{a,b}>n] = \int h(y) \mu_{a,b}(\mathrm{d} y). \end{align*} $$
Theorem 2.1 is proved in §6.1. Later, we generalize the above result allowing values of a in the interval
![]() $(0,1)$
(see Theorem 6.15). However, this result relies on the technical assumption of
$(0,1)$
(see Theorem 6.15). However, this result relies on the technical assumption of
![]() $(a,b)$
being an admissible pair (see Definition 6.1). We were not able to show the existence of quasi-stationary and quasi-ergodic measures for all values of
$(a,b)$
being an admissible pair (see Definition 6.1). We were not able to show the existence of quasi-stationary and quasi-ergodic measures for all values of
![]() $a\in [0,1),$
which can be seen from technical details in the inequalities of Proposition 6.17 that is used in Step 2 of Lemma 6.7. This technical obstruction is explained in Remark 6.10.
$a\in [0,1),$
which can be seen from technical details in the inequalities of Proposition 6.17 that is used in Step 2 of Lemma 6.7. This technical obstruction is explained in Remark 6.10.
We use a more general setup for the proof of the above theorem. We present two incrementally restrictive hypotheses, Hypothesis H1 and H2, which are satisfied by
![]() $Y^{a,b}_n$
for every
$Y^{a,b}_n$
for every
![]() $(a,b) \in [1,4)\times (4,\infty ),$
and implies results similar to Theorem 2.1 in different modes of convergence (see Theorems 2.2, 2.3 and 2.4).
$(a,b) \in [1,4)\times (4,\infty ),$
and implies results similar to Theorem 2.1 in different modes of convergence (see Theorems 2.2, 2.3 and 2.4).
In the following, we recall the definition of an integral operator.
Definition 2.4. Let
![]() $p,q \in [1,\infty )$
and
$p,q \in [1,\infty )$
and
![]() $(\Omega _1,\mathcal F_1,\mu _1)$
,
$(\Omega _1,\mathcal F_1,\mu _1)$
,
![]() $(\Omega _2,\mathcal F_2,\mu _2)$
be measure spaces. We say that the bounded linear map
$(\Omega _2,\mathcal F_2,\mu _2)$
be measure spaces. We say that the bounded linear map
![]() $T:L^p(\Omega _1,\mathcal F_1,\mu _1)\to L^q(\Omega _2,\mathcal F_2,\mu _2)$
is an integral operator if there exists a measurable function
$T:L^p(\Omega _1,\mathcal F_1,\mu _1)\to L^q(\Omega _2,\mathcal F_2,\mu _2)$
is an integral operator if there exists a measurable function
![]() $\kappa :\Omega _2\times \Omega _1\to {\mathbb R}$
, called kernel function, such that for every
$\kappa :\Omega _2\times \Omega _1\to {\mathbb R}$
, called kernel function, such that for every
![]() $f\in L^p(\Omega _1,\mathcal F_1,\mu _1)$
,
$f\in L^p(\Omega _1,\mathcal F_1,\mu _1)$
,
and
 $$ \begin{align*} Tf(x)= \int_{\Omega_1} f(y) \kappa( x,y) \mu_1 (\mathrm{d} y)\quad\mbox{for } \mu_2\mbox{-almost every } x\in \Omega_2. \end{align*} $$
$$ \begin{align*} Tf(x)= \int_{\Omega_1} f(y) \kappa( x,y) \mu_1 (\mathrm{d} y)\quad\mbox{for } \mu_2\mbox{-almost every } x\in \Omega_2. \end{align*} $$
For a large class of Markov processes, it is common for the existence of a probability function
![]() $\rho $
on M such that
$\rho $
on M such that
In such systems, it is natural to seek quasi-stationary measures that are absolutely continuous with respect to
![]() $\rho $
. In this situation and assuming that
$\rho $
. In this situation and assuming that
![]() $\mu \ll \rho $
, we have from equation (2.1) that
$\mu \ll \rho $
, we have from equation (2.1) that
![]() ${\mathcal P}: L^1(M,\mu )\to L^1(M,\mu )$
is an integral operator.
${\mathcal P}: L^1(M,\mu )\to L^1(M,\mu )$
is an integral operator.
It is also natural to assume that the absorbing Markov chain
![]() $X_n$
is irreducible, that is, if there exists
$X_n$
is irreducible, that is, if there exists
![]() $A \in \mathscr B(M)$
such that
$A \in \mathscr B(M)$
such that
![]() $\mu (\{{\mathcal P}(\cdot ,A)>0\}\triangle A) =0,$
then either
$\mu (\{{\mathcal P}(\cdot ,A)>0\}\triangle A) =0,$
then either
![]() $\mu (A) = 0$
or
$\mu (A) = 0$
or
![]() $\mu (X\setminus A)=0,$
where
$\mu (X\setminus A)=0,$
where
![]() $\triangle $
denotes the symmetric difference of sets. In cases where
$\triangle $
denotes the symmetric difference of sets. In cases where
![]() $X_n$
is not irreducible, it is always possible to separate the state space into irreducible regions and analyse each region separately.
$X_n$
is not irreducible, it is always possible to separate the state space into irreducible regions and analyse each region separately.
The conditions discussed above are summarized in Hypothesis H1.
Hypothesis H1. Let
![]() $X_n$
be an absorbing Markov chain on
$X_n$
be an absorbing Markov chain on
![]() $E_M$
absorbed at
$E_M$
absorbed at
![]() $\partial $
. We say that
$\partial $
. We say that
![]() $X_n$
fulfils Hypothesis H1 if the following conditions are met.
$X_n$
fulfils Hypothesis H1 if the following conditions are met.
-
(H1a) There exists a quasi-stationary measure
 $\mu \in \mathcal M_+(M)$
for the Markov chain
$\mu \in \mathcal M_+(M)$
for the Markov chain
 $X_n$
with survival rate
$X_n$
with survival rate
 $\unicode{x3bb} $
.
$\unicode{x3bb} $
. -
(H1b) There exists
 $\eta \in L^1_+(M,\mu )$
such that
$\eta \in L^1_+(M,\mu )$
such that
 ${\mathcal P} \eta = \unicode{x3bb} \eta $
and
${\mathcal P} \eta = \unicode{x3bb} \eta $
and
 $\|\eta \|_{L^1(M,\mu )}=1$
.
$\|\eta \|_{L^1(M,\mu )}=1$
. -
(H1c) The transition kernel
 ${\mathcal P}:L^1(M,\mu ) \to L^1(M,\mu )$
is an integral operator with kernel function
${\mathcal P}:L^1(M,\mu ) \to L^1(M,\mu )$
is an integral operator with kernel function
 $\kappa :M\times M \to {\mathbb R}_+.$
$\kappa :M\times M \to {\mathbb R}_+.$
-
(H1d) For every
 $A \in \mathcal B(M)$
such that
$A \in \mathcal B(M)$
such that
 $0<\mu (A) < 1$
, that is, if there exists
$0<\mu (A) < 1$
, that is, if there exists $$ \begin{align*}\int_{M\setminus A} \int_A \kappa (x,y) \mu(\mathrm{d} y) \mu(\mathrm{d} x)> 0, \end{align*} $$
$$ \begin{align*}\int_{M\setminus A} \int_A \kappa (x,y) \mu(\mathrm{d} y) \mu(\mathrm{d} x)> 0, \end{align*} $$
 $A\in \mathscr B(M)$
such that then either
$A\in \mathscr B(M)$
such that then either
 $\mu (M\setminus A) = 0$
or
$\mu (M\setminus A) = 0$
or
 $\mu (A) = 0.$
$\mu (A) = 0.$
We mention that given an absorbing Markov chain
![]() $X_n$
satisfying Hypothesis H1, we obtain from [Reference Meyer-Nieberg22, Lemma 4.2.9 and Example (i) on p. 262] that
$X_n$
satisfying Hypothesis H1, we obtain from [Reference Meyer-Nieberg22, Lemma 4.2.9 and Example (i) on p. 262] that
![]() $\eta (x)>0$
for
$\eta (x)>0$
for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in M.$
$x\in M.$
The theorem below implies that under Hypothesis H1,
![]() $\eta (x) \mu (\mathrm {d} x)$
is the only candidate for the quasi-ergodic measure for
$\eta (x) \mu (\mathrm {d} x)$
is the only candidate for the quasi-ergodic measure for
![]() $X_n$
on
$X_n$
on
![]() $M.$
Moreover, it is also shown that such a hypothesis implies the existence of a maximal
$M.$
Moreover, it is also shown that such a hypothesis implies the existence of a maximal
![]() $m\in \mathbb N,$
with the following properties:
$m\in \mathbb N,$
with the following properties:
-
• there exists measurable sets
 $C_0,\ldots ,C_{m-1} \subset M$
such that
$C_0,\ldots ,C_{m-1} \subset M$
such that
 $M= C_0 \sqcup \cdots \sqcup C_{m-1};$
$M= C_0 \sqcup \cdots \sqcup C_{m-1};$
-
• for every
 $n\in \mathbb N$
,
$n\in \mathbb N$
,
 $X_n \in C_{k\ (\mathrm {mod}\ m)},$
then
$X_n \in C_{k\ (\mathrm {mod}\ m)},$
then
 $X_{n+1} \in C_{k+1\ (\mathrm {mod}\ m)}.$
$X_{n+1} \in C_{k+1\ (\mathrm {mod}\ m)}.$
Theorem 2.2. Let
![]() $X_n$
be an absorbing Markov chain fulfilling Hypothesis H1 then the following assertions hold.
$X_n$
be an absorbing Markov chain fulfilling Hypothesis H1 then the following assertions hold.
-
(i) There exist a natural number
 $m\in \mathbb N$
and sets
$m\in \mathbb N$
and sets
 $C_m:= C_0, C_1, \ldots , C_{m-1} \in \mathscr B(M)$
such that
$C_m:= C_0, C_1, \ldots , C_{m-1} \in \mathscr B(M)$
such that
 $\mu (C_i) = 1/m$
for every
$\mu (C_i) = 1/m$
for every
 $i\in \{0,1\ldots , m-1\}$
and
$i\in \{0,1\ldots , m-1\}$
and 
-
(ii) For every
 $f\in L^1(M,\mu )$
, in
$f\in L^1(M,\mu )$
, in $$ \begin{align*} \frac{1}{n} \sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^n}{\mathcal P}^n f \xrightarrow{n\to\infty} \eta \int_M f(y) \eta(y) \mu(\mathrm{d} y), \end{align*} $$
$$ \begin{align*} \frac{1}{n} \sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^n}{\mathcal P}^n f \xrightarrow{n\to\infty} \eta \int_M f(y) \eta(y) \mu(\mathrm{d} y), \end{align*} $$
 $L^1(M,\mu )$
and
$L^1(M,\mu )$
and
 $\mu $
-a.s.
$\mu $
-a.s.
-
(iii) The following limit holds
 $$ \begin{align*} \frac{1}{\unicode{x3bb}^n} {\mathcal P}^n (x, M) \xrightarrow{n\to\infty} \eta(x)\ \text{in }L^1(M,\mu).\end{align*} $$
$$ \begin{align*} \frac{1}{\unicode{x3bb}^n} {\mathcal P}^n (x, M) \xrightarrow{n\to\infty} \eta(x)\ \text{in }L^1(M,\mu).\end{align*} $$
-
(iv) If, in addition, we assume that M is a Polish space, then for every
 $h\in L^\infty (M,\mu )$
, (2.2)in the
$h\in L^\infty (M,\mu )$
, (2.2)in the $$ \begin{align} \bigg(x\mapsto {\mathbb E}_x \bigg[\frac{1}{n} \sum_{i=0}^{n-1}h\circ X_i \mid \tau> n\bigg]\bigg) \xrightarrow{n\to\infty} \int_M h(y) \eta(y) \mu(\mathrm{d} y) \end{align} $$
$$ \begin{align} \bigg(x\mapsto {\mathbb E}_x \bigg[\frac{1}{n} \sum_{i=0}^{n-1}h\circ X_i \mid \tau> n\bigg]\bigg) \xrightarrow{n\to\infty} \int_M h(y) \eta(y) \mu(\mathrm{d} y) \end{align} $$
 $L^\infty (M,\mu )$
-weak
$L^\infty (M,\mu )$
-weak
 ${}^*$
topology (see [Reference Brezis5, Ch. 3.4] for the definition and the main properties of the weak
${}^*$
topology (see [Reference Brezis5, Ch. 3.4] for the definition and the main properties of the weak
 $^{*}$
topology), in particular, we obtain that (2.2) also converges weakly in
$^{*}$
topology), in particular, we obtain that (2.2) also converges weakly in
 $L^1(M,\mu ).$
$L^1(M,\mu ).$
It is observed that Theorem 2.2(iv) gives us
![]() $L^\infty (M,\mu )$
-weak
$L^\infty (M,\mu )$
-weak
![]() $^{*}$
convergence of equation (2.2), and to guarantee such convergence in
$^{*}$
convergence of equation (2.2), and to guarantee such convergence in
![]() $L^\infty (M,\mu )$
, we require an additional regularity hypothesis (Hypothesis H2) on the kernel functions of the operator
$L^\infty (M,\mu )$
, we require an additional regularity hypothesis (Hypothesis H2) on the kernel functions of the operator
![]() ${\mathcal P}$
.
${\mathcal P}$
.
Hypothesis H2. Let
![]() $X_n$
be a Markov chain
$X_n$
be a Markov chain
![]() $X_n$
on
$X_n$
on
![]() $E_M$
absorbed at
$E_M$
absorbed at
![]() $\partial $
. We say that
$\partial $
. We say that
![]() $X_n$
fulfils Hypothesis H2 if:
$X_n$
fulfils Hypothesis H2 if:
-
(1)
 $X_n$
fulfils Hypothesis H1; and
$X_n$
fulfils Hypothesis H1; and -
(2) for
 $\mu $
-almost every point
$\mu $
-almost every point
 $x\in M$
,
$x\in M$
,
 $\kappa (x,\cdot )\in L^\infty (M,\mu )$
. Equivalently, since
$\kappa (x,\cdot )\in L^\infty (M,\mu )$
. Equivalently, since
 $\mu $
is an inner regular measure [Reference Viana and Oliveira28, Proposition A.3.2], there exists a sequence of nested compact sets
$\mu $
is an inner regular measure [Reference Viana and Oliveira28, Proposition A.3.2], there exists a sequence of nested compact sets
 $\{K_i\}_{i\in \mathbb N}$
such that
$\{K_i\}_{i\in \mathbb N}$
such that
 $\mu (\bigcup _{i\in \mathbb N} K_i ) = 1,$
and for every
$\mu (\bigcup _{i\in \mathbb N} K_i ) = 1,$
and for every
 $i\in \mathbb N,$
$i\in \mathbb N,$

We mention that, in practice, once
![]() $\mathrm {(H1a)}$
and
$\mathrm {(H1a)}$
and
![]() $\mathrm {(H1b)}$
are verified, then
$\mathrm {(H1b)}$
are verified, then
![]() $\mathrm {(H1c)}$
,
$\mathrm {(H1c)}$
,
![]() $\mathrm {(H1d)}$
and Hypothesis H2 can be readily verified. We exemplify this in §6 considering the absorbing Markov chain
$\mathrm {(H1d)}$
and Hypothesis H2 can be readily verified. We exemplify this in §6 considering the absorbing Markov chain
![]() $Y^{a,b}_n$
(see the proof Theorem 6.15).
$Y^{a,b}_n$
(see the proof Theorem 6.15).
In addition to quasi-stationary measures, the so-called Yaglom limit
provides an alternative perspective on the asymptotic behaviour of the paths
![]() $X_n$
conditioned on survival. Observe that for the Yaglom limit to exist, it is necessary that M does not exhibit a cyclic decomposition under
$X_n$
conditioned on survival. Observe that for the Yaglom limit to exist, it is necessary that M does not exhibit a cyclic decomposition under
![]() $X_n$
, that is, that
$X_n$
, that is, that
![]() $m=1$
on item (i) of Theorem 2.2.
$m=1$
on item (i) of Theorem 2.2.
The following two results provide conditions that ensure the existence of a quasi-ergodic measure for
![]() $X_n$
on M and the convergence of the Yaglom limit.
$X_n$
on M and the convergence of the Yaglom limit.
Theorem 2.3. Let
![]() $X_n$
be an absorbing Markov chain fulfilling Hypothesis H1. If any of the following items hold:
$X_n$
be an absorbing Markov chain fulfilling Hypothesis H1. If any of the following items hold:
-
(a) there exists
 $K>0$
such that
$K>0$
such that
 $\mu (\{K<\eta \}) =1$
a.s.;
$\mu (\{K<\eta \}) =1$
a.s.; -
(b) there exists
 $ g\in L^1(M,\mu )$
such that
$ g\in L^1(M,\mu )$
such that  $$ \begin{align*} \frac{1}{\unicode{x3bb}^n} {\mathcal P}^n(\cdot,M) \leq g \quad \text{for every }n\in \mathbb N; \end{align*} $$
$$ \begin{align*} \frac{1}{\unicode{x3bb}^n} {\mathcal P}^n(\cdot,M) \leq g \quad \text{for every }n\in \mathbb N; \end{align*} $$
-
(c) the absorbing Markov chain
 $X_n$
fulfils Hypothesis H2,
$X_n$
fulfils Hypothesis H2,
then for every
![]() $h\in L^\infty (M,\mu )$
,
$h\in L^\infty (M,\mu )$
,
 $$ \begin{align} \lim_{n\to\infty} {\mathbb E}_x\bigg[ \frac{1}{n}\sum_{i=0}^{n-1} h \circ X_i\, \bigg|\, \tau>n\bigg] = \int_M h(y) \eta(y) \mu(\mathrm{d} y) \mbox{ for } \mu\mbox{-almost every } x\in M. \end{align} $$
$$ \begin{align} \lim_{n\to\infty} {\mathbb E}_x\bigg[ \frac{1}{n}\sum_{i=0}^{n-1} h \circ X_i\, \bigg|\, \tau>n\bigg] = \int_M h(y) \eta(y) \mu(\mathrm{d} y) \mbox{ for } \mu\mbox{-almost every } x\in M. \end{align} $$
If, additionally,
![]() $m=1$
in Theorem 2.2(i), then
$m=1$
in Theorem 2.2(i), then
The following theorem is a refinement of the previous theorem, allowing us to characterize the set where the convergence of equations (2.3) and (2.4) hold.
Theorem 2.4. Let
![]() $X_n$
be an absorbing Markov chain fulfilling Hypothesis H2. Then, given
$X_n$
be an absorbing Markov chain fulfilling Hypothesis H2. Then, given
![]() $h\in L^\infty (M,\mu )$
, equation (2.3) holds for every
$h\in L^\infty (M,\mu )$
, equation (2.3) holds for every
![]() $x\in \bigcup _{i\in \mathbb N} K_i,$
where
$x\in \bigcup _{i\in \mathbb N} K_i,$
where
![]() $\{K_i\}_{i\in \mathbb N}$
is the nested sequence of compact sets given by the second part of Hypothesis H2.
$\{K_i\}_{i\in \mathbb N}$
is the nested sequence of compact sets given by the second part of Hypothesis H2.
In the case where
![]() $m=1$
in Theorem 2.2(i), equation (2.4) holds for every
$m=1$
in Theorem 2.2(i), equation (2.4) holds for every
![]() $x\in \bigcup _{i\in \mathbb N} K_i$
.
$x\in \bigcup _{i\in \mathbb N} K_i$
.
Remark 2.5. Notice that Theorems 2.3 and 2.4 also hold in a non-escape context. This means that if
![]() $X_n$
is a Markov chain on the metric space M without absorption, satisfying the following properties:
$X_n$
is a Markov chain on the metric space M without absorption, satisfying the following properties:
-
•
 $\mu $
is ergodic stationary measure for
$\mu $
is ergodic stationary measure for
 $X_n$
on
$X_n$
on
 $M;$
$M;$
-
• the transition kernel
 ${\mathcal P}:L^1(M,\mu )\to L^1(M,\mu )$
is an integral operator; and
${\mathcal P}:L^1(M,\mu )\to L^1(M,\mu )$
is an integral operator; and -
•
 $X_n$
is aperiodic, that is,
$X_n$
is aperiodic, that is,
 $m=1$
in Theorem 2.2(i),
$m=1$
in Theorem 2.2(i),
then for every
![]() $h \in L^\infty (M,\mu ), \lim _{n\to \infty } {\mathcal P}^n h = \int h \,\mathrm {d} \mu , \mu $
-a.s. In particular, from [Reference Lin20, Theorem 1(ii)], we obtain that
$h \in L^\infty (M,\mu ), \lim _{n\to \infty } {\mathcal P}^n h = \int h \,\mathrm {d} \mu , \mu $
-a.s. In particular, from [Reference Lin20, Theorem 1(ii)], we obtain that
![]() $X_n$
is a weak-mixing Markov chain.
$X_n$
is a weak-mixing Markov chain.
3 Mean-ergodic operators
For classical dynamical systems and Markov processes, mean-ergodic operators provide a vast array of tools and techniques for analysing their statistical properties [Reference Eisner, Farkas, Haase and Nagel10, Chs. 7, 8 and 10]. This section shows that this is also true for absorbing Markov chains.
In the following, we recall the definition of a mean ergodic operator.
Definition 3.1. Let
![]() $(E,\|\cdot \|)$
be a Banach space, we say that
$(E,\|\cdot \|)$
be a Banach space, we say that
![]() $T:E\to E$
is a mean-ergodic operator if there exists a projection
$T:E\to E$
is a mean-ergodic operator if there exists a projection
![]() $P:E\to E$
such that
$P:E\to E$
such that
 $$ \begin{align*}\lim_{n\to\infty}\bigg\|\frac{1}{n} \sum_{i=0}^{n-1} T^i x - Px\bigg\| =0\quad \text{for every }x\in E. \end{align*} $$
$$ \begin{align*}\lim_{n\to\infty}\bigg\|\frac{1}{n} \sum_{i=0}^{n-1} T^i x - Px\bigg\| =0\quad \text{for every }x\in E. \end{align*} $$
Let M be a metric space,
![]() $\rho $
a Borel probability measure on
$\rho $
a Borel probability measure on
![]() $X,$
and
$X,$
and
![]() $T:L^1(M,\rho )\to L^1(M,\rho ).$
We denote
$T:L^1(M,\rho )\to L^1(M,\rho ).$
We denote
where
![]() $T^*:L^\infty (M,\rho )\to L^\infty (M,\rho )$
is the dual operator of
$T^*:L^\infty (M,\rho )\to L^\infty (M,\rho )$
is the dual operator of
![]() $T,$
that is, the unique bounded automorphism on
$T,$
that is, the unique bounded automorphism on
![]() $L^\infty (M,\rho )$
such that
$L^\infty (M,\rho )$
such that
 $$ \begin{align*}&\int_M (Tf)(x) h(x)~\rho(\mathrm{d} x)\\ &\quad= \int f(x) (T^*h)(x)~\rho(\mathrm{d} x)\quad \mbox{for every } f\in L^1(M,\rho) \mbox{ and } h\in L^\infty(M,\rho). \end{align*} $$
$$ \begin{align*}&\int_M (Tf)(x) h(x)~\rho(\mathrm{d} x)\\ &\quad= \int f(x) (T^*h)(x)~\rho(\mathrm{d} x)\quad \mbox{for every } f\in L^1(M,\rho) \mbox{ and } h\in L^\infty(M,\rho). \end{align*} $$
Our results are highly dependent on the following two propositions.
Proposition 3.1. ([Reference Krengel18, Theorem 3.3.5] and [Reference Pflug25, Corollary V.8.1])
Let M be a metric space and
![]() $\rho $
be a probability measure on M, and
$\rho $
be a probability measure on M, and
![]() $T:L^1(M,\rho ) \to L^1(M,\rho )$
be a linear operator such that
$T:L^1(M,\rho ) \to L^1(M,\rho )$
be a linear operator such that
![]() $\|T\| = 1.$
Assume that there exists
$\|T\| = 1.$
Assume that there exists
![]() $\eta \in L^1(M,\rho )$
satisfying
$\eta \in L^1(M,\rho )$
satisfying
![]() $T\eta = \eta $
and
$T\eta = \eta $
and
![]() $\rho (\{\eta>0\}) = 1.$
Then, we have the following.
$\rho (\{\eta>0\}) = 1.$
Then, we have the following.
-
(i) For every
 $f\in L^1(M,\rho )$
,
$f\in L^1(M,\rho )$
,  $$ \begin{align*}\lim_{n\to \infty} \frac{1}{n} \sum_{i=0}^{n-1}T ^i f = \eta \frac{{\mathbb E}_\rho[f \eta \mid \mathcal I(T,\rho)]}{{\mathbb E}_\rho[ \eta \mid \mathcal I(T,\rho)]}\quad \mu\mbox{-a.s}. \end{align*} $$
$$ \begin{align*}\lim_{n\to \infty} \frac{1}{n} \sum_{i=0}^{n-1}T ^i f = \eta \frac{{\mathbb E}_\rho[f \eta \mid \mathcal I(T,\rho)]}{{\mathbb E}_\rho[ \eta \mid \mathcal I(T,\rho)]}\quad \mu\mbox{-a.s}. \end{align*} $$
-
(ii) The operator T is mean-ergodic.
While Hypothesis H1 does not imply that
![]() ${\mathcal P}$
is a compact operator, the proposition shows that given
${\mathcal P}$
is a compact operator, the proposition shows that given
![]() $f\in L^1(M,\mu )$
, the orbit
$f\in L^1(M,\mu )$
, the orbit
![]() $\{({1}/{\unicode{x3bb} ^n}){\mathcal P}^n f\}_{n\in \mathbb N}$
is weakly precompact.
$\{({1}/{\unicode{x3bb} ^n}){\mathcal P}^n f\}_{n\in \mathbb N}$
is weakly precompact.
Proposition 3.2. Suppose that the Markov process
![]() $X_n$
satisfies Hypothesis H1, then for every
$X_n$
satisfies Hypothesis H1, then for every
![]() $f\in L^1(M,\mu )$
the sequence
$f\in L^1(M,\mu )$
the sequence
 $$ \begin{align*}\bigg\{\frac{1}{\unicode{x3bb}^i}{\mathcal P}^i f\bigg\}_{i\in\mathbb N}\ \mbox{ is weakly-}L^1(M,\mu) \mbox{ precompact.} \end{align*} $$
$$ \begin{align*}\bigg\{\frac{1}{\unicode{x3bb}^i}{\mathcal P}^i f\bigg\}_{i\in\mathbb N}\ \mbox{ is weakly-}L^1(M,\mu) \mbox{ precompact.} \end{align*} $$
Proof. Let
![]() $f\in L^1_+(M,\mu )$
. Note that for every
$f\in L^1_+(M,\mu )$
. Note that for every
![]() $i,m\in \mathbb N,$
$i,m\in \mathbb N,$
where given two functions
![]() $f_1,f_2$
, we define
$f_1,f_2$
, we define
![]() $f_1\wedge f_2:= \min \{f_1,f_2\}$
. Since
$f_1\wedge f_2:= \min \{f_1,f_2\}$
. Since
![]() $\|({1}/{\unicode{x3bb} ^i}) {\mathcal P}^i f\|_{L^1(M,\mu )} = \|f\|_{L^1(M,\mu )}$
for every
$\|({1}/{\unicode{x3bb} ^i}) {\mathcal P}^i f\|_{L^1(M,\mu )} = \|f\|_{L^1(M,\mu )}$
for every
![]() $i\in \mathbb N$
and
$i\in \mathbb N$
and
![]() $ m \eta \wedge f \xrightarrow {m\to \infty } f$
in
$ m \eta \wedge f \xrightarrow {m\to \infty } f$
in
![]() $L^1(M,\mu )$
and
$L^1(M,\mu )$
and
![]() $\mu $
-a.s., we can obtain that for every
$\mu $
-a.s., we can obtain that for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\delta>0$
such that
$\delta>0$
such that
From [Reference Lasota and Mackey19, p. 87, item 3], we conclude that
![]() $\{({1}/{\unicode{x3bb} ^n}){\mathcal P}^n f\}_{n\in \mathbb N}$
is weakly
$\{({1}/{\unicode{x3bb} ^n}){\mathcal P}^n f\}_{n\in \mathbb N}$
is weakly
![]() $L^1(M,\mu )$
precompact.
$L^1(M,\mu )$
precompact.
4
 $AM$
-compact operators
$AM$
-compact operators
Observe that under Hypothesis H1, the operator
![]() $ ({1}/{\unicode{x3bb} }){\mathcal P} :L^1(M,\mu ) \to L^1(M,\mu )$
, is well behaved in a functional analytical point of view. Namely,
$ ({1}/{\unicode{x3bb} }){\mathcal P} :L^1(M,\mu ) \to L^1(M,\mu )$
, is well behaved in a functional analytical point of view. Namely,
![]() $\frac {1}{\unicode{x3bb} }{\mathcal P}$
is a positive integral operator whose orbits are weakly compact. The theory of Banach lattices provides powerful tools for studying the spectrum of such operators. In the following two paragraphs, we recall the definition of a Banach lattice (we follow the definitions provided in [Reference Meyer-Nieberg22, Ch. 2] and [Reference Pflug25, Ch. 2]).
$\frac {1}{\unicode{x3bb} }{\mathcal P}$
is a positive integral operator whose orbits are weakly compact. The theory of Banach lattices provides powerful tools for studying the spectrum of such operators. In the following two paragraphs, we recall the definition of a Banach lattice (we follow the definitions provided in [Reference Meyer-Nieberg22, Ch. 2] and [Reference Pflug25, Ch. 2]).
Given
![]() $(L,\leq )$
a partially ordered set and a set
$(L,\leq )$
a partially ordered set and a set
![]() $B\subset L,$
we define, if exists,
$B\subset L,$
we define, if exists,
and
With the above definitions, we say that L is a lattice if for every
![]() $f_1,f_2\in L,$
$f_1,f_2\in L,$
exists. Additionally, in the case where L is a vector space and the lattice
![]() $(L,\leq )$
satisfies
$(L,\leq )$
satisfies
then
![]() $(L,\leq )$
is called a vector lattice. Finally, if
$(L,\leq )$
is called a vector lattice. Finally, if
![]() $(L,\|\cdot \|)$
is a Banach space and the vector lattice
$(L,\|\cdot \|)$
is a Banach space and the vector lattice
![]() $(L,\leq )$
satisfies
$(L,\leq )$
satisfies
where
![]() $|f_1| := f_1\lor (-f_1),$
then the triple
$|f_1| := f_1\lor (-f_1),$
then the triple
![]() $(L,\leq ,\|\cdot \|)$
is called a Banach lattice. When the context is clear, we denote the Banach lattice
$(L,\leq ,\|\cdot \|)$
is called a Banach lattice. When the context is clear, we denote the Banach lattice
![]() $(L,\leq ,\|\cdot \|)$
simply by L.
$(L,\leq ,\|\cdot \|)$
simply by L.
In this paper, we use two fundamental notions from Banach lattice theory. The first one is that of an ideal of a Banach lattice and the second one is that of an irreducible operator on a Banach lattice. A vector subspace
![]() $I \subset L$
is called an ideal if for every
$I \subset L$
is called an ideal if for every
![]() $f_1,f_2\in L$
such that
$f_1,f_2\in L$
such that
![]() $f_2\in I$
and
$f_2\in I$
and
![]() $|f_1|\leq |f_2|,$
we have
$|f_1|\leq |f_2|,$
we have
![]() $f_1\in I$
. Finally, a positive linear operator
$f_1\in I$
. Finally, a positive linear operator
![]() $T:L\to L$
is called irreducible if
$T:L\to L$
is called irreducible if
![]() $\{0\}$
and L are the only T-invariant closed ideals of T.
$\{0\}$
and L are the only T-invariant closed ideals of T.
The theory of
![]() $AM$
-compact operators provides a generalization to the theory of compact operators.
$AM$
-compact operators provides a generalization to the theory of compact operators.
![]() $AM$
-compact operators are considerably more general than compact operators and possess a sufficient degree of regularity. In the following, we recall the definition of an
$AM$
-compact operators are considerably more general than compact operators and possess a sufficient degree of regularity. In the following, we recall the definition of an
![]() $AM$
-compact operator.
$AM$
-compact operator.
Definition 4.1. Let E be a Banach lattice and Y a Banach space. A linear operator
![]() $T:E \to Y$
is called
$T:E \to Y$
is called
![]() $AM$
-compact if for every
$AM$
-compact if for every
![]() $x_1,x_2\in E$
,
$x_1,x_2\in E$
,
![]() $T([x_1,x_2])$
is precompact in Y, where
$T([x_1,x_2])$
is precompact in Y, where
![]() ${[x_1,x_2] :=\{y\in E;\ x_1\leq y \leq x_2\}.}$
${[x_1,x_2] :=\{y\in E;\ x_1\leq y \leq x_2\}.}$
The following result shows us that all positive integral operators are
![]() $AM$
-compact.
$AM$
-compact.
Theorem 4.1. [Reference Gerlach and Glück14, Proposition A.5]
Let
![]() $(\Omega _1,\mu _1)$
and
$(\Omega _1,\mu _1)$
and
![]() $(\Omega _2,\mu _2)$
be the
$(\Omega _2,\mu _2)$
be the
![]() $\sigma $
-finite measure spaces and
$\sigma $
-finite measure spaces and
![]() $p,q\in [1,\infty )$
. Let
$p,q\in [1,\infty )$
. Let
![]() $T:L^p(\Omega _1,\mu _1) \to L^q (\Omega _2,\mu _2)$
be a positive bounded integral operator, then T is an
$T:L^p(\Omega _1,\mu _1) \to L^q (\Omega _2,\mu _2)$
be a positive bounded integral operator, then T is an
![]() $AM$
-compact operator.
$AM$
-compact operator.
Given
![]() $f\in L^1(M,\mu )$
, the key to our results is to understand the asymptotic behaviour of the sequence
$f\in L^1(M,\mu )$
, the key to our results is to understand the asymptotic behaviour of the sequence
![]() $\{({1}/{\unicode{x3bb} ^n}){\mathcal P}^n f\}_{n\in \mathbb N}$
. It turns out that the behaviour of this sequence has a strong connection with the peripheral spectrum of
$\{({1}/{\unicode{x3bb} ^n}){\mathcal P}^n f\}_{n\in \mathbb N}$
. It turns out that the behaviour of this sequence has a strong connection with the peripheral spectrum of
![]() ${\mathcal P}$
. In this way, we denote
${\mathcal P}$
. In this way, we denote
![]() $L^1(M,\mu ;\mathbb C) := L^1(M,\mu ) \oplus i L^1(M,\mu )$
and linearly extend the operator
$L^1(M,\mu ;\mathbb C) := L^1(M,\mu ) \oplus i L^1(M,\mu )$
and linearly extend the operator
![]() ${\mathcal P}$
to the Banach space
${\mathcal P}$
to the Banach space
![]() $L^1(M,\mu ;\mathbb C)$
.
$L^1(M,\mu ;\mathbb C)$
.
Here, we summarize the spectral properties implied by Hypothesis H1.
Proposition 4.2. Let
![]() $X_n$
be an absorbing Markov chain satisfying Hypothesis H1. Then:
$X_n$
be an absorbing Markov chain satisfying Hypothesis H1. Then:
-
(i) for every
 $f\in L^1(M,\mu ),$
in
$f\in L^1(M,\mu ),$
in $$ \begin{align*} \frac{1}{n}\sum_{i=0}^{n-1}\frac{1}{\unicode{x3bb}^i}{\mathcal P}^i f \xrightarrow{n\to\infty} \eta \int_M f(y)\eta(y)\mu(\mathrm{d} y), \end{align*} $$
$$ \begin{align*} \frac{1}{n}\sum_{i=0}^{n-1}\frac{1}{\unicode{x3bb}^i}{\mathcal P}^i f \xrightarrow{n\to\infty} \eta \int_M f(y)\eta(y)\mu(\mathrm{d} y), \end{align*} $$
 $L^1(M,\mu )$
and
$L^1(M,\mu )$
and
 $\mu $
-a.s.;
$\mu $
-a.s.;
-
(ii) there exists a decomposition
 ${L^1(M,\mu; \mathbb C)= E_{\mathrm {rev}} \oplus E_{\mathrm {aws}}},$
such that
${L^1(M,\mu; \mathbb C)= E_{\mathrm {rev}} \oplus E_{\mathrm {aws}}},$
such that
 $E_{\mathrm {rev}}$
and
$E_{\mathrm {rev}}$
and
 $E_{\mathrm {aws}}$
are
$E_{\mathrm {aws}}$
are
 ${\mathcal P}$
-invariant, and
${\mathcal P}$
-invariant, and $$ \begin{align*}E_{\mathrm{rev}}= \mathrm{span} \bigg\{f \in L^1(M,\mu;\mathbb C);\ \frac{1}{\unicode{x3bb}}{\mathcal P} f = e^{{2\pi j i}/{m} } f \text{ for some }j\in\{0,1,\ldots,m-1\} \bigg\},\end{align*} $$
$$ \begin{align*}E_{\mathrm{rev}}= \mathrm{span} \bigg\{f \in L^1(M,\mu;\mathbb C);\ \frac{1}{\unicode{x3bb}}{\mathcal P} f = e^{{2\pi j i}/{m} } f \text{ for some }j\in\{0,1,\ldots,m-1\} \bigg\},\end{align*} $$
 $$ \begin{align*}E_{\mathrm{aws}}= \bigg\{f \in L^1(M,\mu; \mathbb C); \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i f\xrightarrow{n\to \infty }0, \text{ in }L^1(M,\mu)\bigg\}.\end{align*} $$
$$ \begin{align*}E_{\mathrm{aws}}= \bigg\{f \in L^1(M,\mu; \mathbb C); \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i f\xrightarrow{n\to \infty }0, \text{ in }L^1(M,\mu)\bigg\}.\end{align*} $$
Moreover,
 $$ \begin{align*}\mathrm{dim}\ker\bigg(\frac{1}{\unicode{x3bb}}{\mathcal P} - e^{{2 \pi j i}/{m}}\mathrm{Id}\bigg) = 1 \quad \text{for every }j\in\{0,1,\ldots,m-1\}.\end{align*} $$
$$ \begin{align*}\mathrm{dim}\ker\bigg(\frac{1}{\unicode{x3bb}}{\mathcal P} - e^{{2 \pi j i}/{m}}\mathrm{Id}\bigg) = 1 \quad \text{for every }j\in\{0,1,\ldots,m-1\}.\end{align*} $$
Proof. (i) From Proposition 3.1, it is enough to show that if
![]() $A \in \mathcal I({\mathcal P}/\unicode{x3bb} , \mu )$
, then either
$A \in \mathcal I({\mathcal P}/\unicode{x3bb} , \mu )$
, then either
![]() ${\mu (A) = 0 }$
or
${\mu (A) = 0 }$
or
![]() $\mu (A) = 1.$
To see this, let
$\mu (A) = 1.$
To see this, let
![]() $A\in \mathscr B(M)$
such that
$A\in \mathscr B(M)$
such that
then

From Hypothesis H1, we obtain that either
![]() $\mu (A) = 1$
or
$\mu (A) = 1$
or
![]() $\mu (A)=0$
.
$\mu (A)=0$
.
(ii) From Propositions 3.2 and 4.1, we have that the semigroup
![]() $\{({1}/{\unicode{x3bb} ^n}) {\mathcal P}^n \}_{n\in \mathbb N}$
fulfils the standard assumptions of [Reference Glück and Haase16, §6]. Combining [Reference Glück and Haase16, Proposition 4.3, Theorem 2.2] and [Reference Eisner, Farkas, Haase and Nagel10, Proposition 16.27 and Corollary 16.32], we obtain that
$\{({1}/{\unicode{x3bb} ^n}) {\mathcal P}^n \}_{n\in \mathbb N}$
fulfils the standard assumptions of [Reference Glück and Haase16, §6]. Combining [Reference Glück and Haase16, Proposition 4.3, Theorem 2.2] and [Reference Eisner, Farkas, Haase and Nagel10, Proposition 16.27 and Corollary 16.32], we obtain that
 $$ \begin{align*}E_{\mathrm{rev}} = \overline{\bigg\{f \in L^1(M,\mu; C); \frac{1}{\unicode{x3bb}}{\mathcal P} f = e^{2 i \pi \theta} f \text{ for some }\theta\in {\mathbb R}\bigg\}},\end{align*} $$
$$ \begin{align*}E_{\mathrm{rev}} = \overline{\bigg\{f \in L^1(M,\mu; C); \frac{1}{\unicode{x3bb}}{\mathcal P} f = e^{2 i \pi \theta} f \text{ for some }\theta\in {\mathbb R}\bigg\}},\end{align*} $$
and
Applying [Reference Glück and Haase16, Theorem 6.1(a)], we obtain that if
![]() $ \unicode{x3bb} e^{2 i \pi \theta } \in \sigma _{\mathrm {pnt}}(\mathcal P)$
, then
$ \unicode{x3bb} e^{2 i \pi \theta } \in \sigma _{\mathrm {pnt}}(\mathcal P)$
, then
![]() $\theta \in {\mathbb Q}.$
Observe Hypothesis H1 implies that
$\theta \in {\mathbb Q}.$
Observe Hypothesis H1 implies that
![]() ${\mathcal P}/\unicode{x3bb} $
is an irreducible operator [Reference Meyer-Nieberg22, Example (i), p. 262]. From [Reference Glück and Haase16, Theorem 6.1(b)], we obtain that
${\mathcal P}/\unicode{x3bb} $
is an irreducible operator [Reference Meyer-Nieberg22, Example (i), p. 262]. From [Reference Glück and Haase16, Theorem 6.1(b)], we obtain that
![]() ${\mathcal P}/\unicode{x3bb} $
has only finitely many unimodular eigenvalues. Finally, from [Reference Meyer-Nieberg22, Theorem 4.2.13(iii)] (taking
${\mathcal P}/\unicode{x3bb} $
has only finitely many unimodular eigenvalues. Finally, from [Reference Meyer-Nieberg22, Theorem 4.2.13(iii)] (taking
![]() $x' = 1$
), the proof is finished.
$x' = 1$
), the proof is finished.
Let
![]() $\sigma _{\mathrm {pnt}}(({1}/{\unicode{x3bb} }){\mathcal P}) := \{ \widetilde {\unicode{x3bb} } \in {\mathbb C}; \mbox { there exists } h\in L^1(M), ({1}/{\unicode{x3bb} }){\mathcal P}h = \widetilde {\unicode{x3bb} } h\}$
be the point spectrum of the operator
$\sigma _{\mathrm {pnt}}(({1}/{\unicode{x3bb} }){\mathcal P}) := \{ \widetilde {\unicode{x3bb} } \in {\mathbb C}; \mbox { there exists } h\in L^1(M), ({1}/{\unicode{x3bb} }){\mathcal P}h = \widetilde {\unicode{x3bb} } h\}$
be the point spectrum of the operator
![]() $({1}/{\unicode{x3bb} }){\mathcal P}.$
In [Reference Castro, Lamb, Olicón-Méndez and Rasmussen7, Reference Oçafrain23], it is shown that the cardinality of
$({1}/{\unicode{x3bb} }){\mathcal P}.$
In [Reference Castro, Lamb, Olicón-Méndez and Rasmussen7, Reference Oçafrain23], it is shown that the cardinality of
![]() $\mathbb S^1 \cap \sigma _{\mathrm {pnt}}(({1}/{\unicode{x3bb} }){\mathcal P})$
is intrinsically connected with the existence a possible periodic behaviour of
$\mathbb S^1 \cap \sigma _{\mathrm {pnt}}(({1}/{\unicode{x3bb} }){\mathcal P})$
is intrinsically connected with the existence a possible periodic behaviour of
![]() $X_n$
in a suitable partition of M. This remains true under Hypothesis H1, and such periodic behaviour is established in Lemmas 4.3 and 4.4.
$X_n$
in a suitable partition of M. This remains true under Hypothesis H1, and such periodic behaviour is established in Lemmas 4.3 and 4.4.
Definition 4.2. Given an absorbing Markov chain
![]() $X_n$
that satisfies Hypothesis H1, we define
$X_n$
that satisfies Hypothesis H1, we define
![]() ${m(X_n) := \#( \mathbb S^1 \cap \sigma _{\mathrm {pnt}}(\frac {1}{\unicode{x3bb} }{\mathcal P}))},$
which is finite from Proposition 4.2.
${m(X_n) := \#( \mathbb S^1 \cap \sigma _{\mathrm {pnt}}(\frac {1}{\unicode{x3bb} }{\mathcal P}))},$
which is finite from Proposition 4.2.
From now on, we denote
![]() $m(X_n)$
simply as m.
$m(X_n)$
simply as m.
Lemma 4.3. Let
![]() $X_n$
be a Markov chain satisfying Hypothesis H1. Then there exist eigenfunctions
$X_n$
be a Markov chain satisfying Hypothesis H1. Then there exist eigenfunctions
![]() $g_1,\ldots ,g_{m-1} \in L^1_+(M,\mu )$
of
$g_1,\ldots ,g_{m-1} \in L^1_+(M,\mu )$
of
![]() ${\mathcal P}^m$
such that
${\mathcal P}^m$
such that
![]() $\|g_j\|_{L^1(M,\mu )} =1$
for every
$\|g_j\|_{L^1(M,\mu )} =1$
for every
![]() $j\in \{0,1,\ldots ,m-1\}$
, and
$j\in \{0,1,\ldots ,m-1\}$
, and
![]() $\mathrm {span}_{\mathbb C} (\{g_i\}_{i=0}^{m-1}) = \mathrm {ker}( {\mathcal P}^m - \unicode{x3bb} ^m \mathrm {Id}). $
$\mathrm {span}_{\mathbb C} (\{g_i\}_{i=0}^{m-1}) = \mathrm {ker}( {\mathcal P}^m - \unicode{x3bb} ^m \mathrm {Id}). $
Moreover, the eigenfunctions
![]() $g_0$
,
$g_0$
,
![]() $g_1$
,
$g_1$
,
![]() $\ldots $
,
$\ldots $
,
![]() $g_{m-1}$
can be chosen in a way such that they have disjoint support, that is, defining
$g_{m-1}$
can be chosen in a way such that they have disjoint support, that is, defining
![]() $C_i = \{g_i>0\}$
for all
$C_i = \{g_i>0\}$
for all
![]() $i\in \{0,\ldots ,m-1\}, $
then
$i\in \{0,\ldots ,m-1\}, $
then
![]() $ \mu ( C_i\cap C_j ) = 0\ {\ \text {for all}} \ i\neq j.$
$ \mu ( C_i\cap C_j ) = 0\ {\ \text {for all}} \ i\neq j.$
Furthermore, the family of sets
![]() $\{C_i\}_{i=0}^{m-1}$
satisfies
$\{C_i\}_{i=0}^{m-1}$
satisfies
Proof. The proof follows from similar arguments and computations laid out in [Reference Castro, Lamb, Olicón-Méndez and Rasmussen7, Proposition 6.9] with the following two adaptations:
-
(1) the space
 $\mathcal C^0(M)$
is replaced by
$\mathcal C^0(M)$
is replaced by
 $L^1(M,\mu );$
and
$L^1(M,\mu );$
and -
(2) the set equalities are replaced by the relation
 $\sim .$
Namely, the given
$\sim .$
Namely, the given
 $A,B \in \mathscr B(M)$
are said to be equivalent, that is,
$A,B \in \mathscr B(M)$
are said to be equivalent, that is,
 $A\sim B$
if
$A\sim B$
if
 $\mu (A\triangle B) = 0,$
where
$\mu (A\triangle B) = 0,$
where
 $A\triangle B := (A\setminus B) \cup (B\setminus A).$
$A\triangle B := (A\setminus B) \cup (B\setminus A).$
The proof of the following lemma is analogous to the proof [Reference Castro, Lamb, Olicón-Méndez and Rasmussen7, Lemma 6.15].
Lemma 4.4. Let
![]() $\{g_i\}_{i=0}^{m-1}\subset L^1_+(M,\mu )$
, as in Proposition 4.3. Then, there exists a cyclic permutation
$\{g_i\}_{i=0}^{m-1}\subset L^1_+(M,\mu )$
, as in Proposition 4.3. Then, there exists a cyclic permutation
![]() $\sigma :\{0,1,\ldots ,m-1\}\to \{0,1,\ldots ,m-1\}$
of order m such that for every
$\sigma :\{0,1,\ldots ,m-1\}\to \{0,1,\ldots ,m-1\}$
of order m such that for every
![]() $i\in \{0,1,\ldots ,m-1\}$
,
$i\in \{0,1,\ldots ,m-1\}$
,
![]() ${\mathcal P} g_i = \unicode{x3bb} g_{\sigma (i)}.$
In particular, this implies that
${\mathcal P} g_i = \unicode{x3bb} g_{\sigma (i)}.$
In particular, this implies that
The following two lemmas are the last ingredients needed for the proof of Theorem 2.2.
Lemma 4.5. Suppose the absorbing Markov chain
![]() $X_n$
satisfies Hypothesis H1. Then,
$X_n$
satisfies Hypothesis H1. Then,
Proof. We divide the proof into three steps.
Step 1. We show that
![]() $\mu (C_i) = 1/m$
for every
$\mu (C_i) = 1/m$
for every
![]() $i\in \{0,1\ldots ,m-1\}$
.
$i\in \{0,1\ldots ,m-1\}$
.
Observe that Proposition 3.1 implies that for every
![]() $i\in \mathbb N$
,
$i\in \mathbb N$
,

and

in
![]() $L^1(M,\mu )$
and
$L^1(M,\mu )$
and
![]() $\mu $
-a.s.
$\mu $
-a.s.
However, from [Reference Foguel12, Theorem E, p. 29], we obtain that for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in M$
,
$x\in M$
,
 $$ \begin{align*} \mu(C_i) &= \lim_{n\to\infty}\frac{\sum_{j=0}^{n} {\mathcal P}^j(x,C_i)}{\sum_{j=0}^{n} {\mathcal P}^j(x,M)} \leq \lim_{n\to\infty} \frac{\sum_{j=0}^{n} ({1}/{\unicode{x3bb}^{i+mj}}) {\mathcal P}^{i + m j }(x,M)}{ \sum_{j=0}^{nm} ({1}/{\unicode{x3bb}^j}) {\mathcal P}^j(x,M)}\\ &= \frac{ \lim_{n\to\infty} ({1}/{nm}) \sum_{j=0}^{n} ({1}/{\unicode{x3bb}^{i+mj}}) {\mathcal P}^{i + m j }(x,M)}{ \lim_{n\to\infty} ({1}/{mn}) \sum_{j=0}^{nm} ({1}/{\unicode{x3bb}^j}) {\mathcal P}^i(x,M)}\\ &= \frac{1}{m} \frac{{\mathbb E}_\mu[({1}/{\unicode{x3bb}^i}) {\mathcal P}^i(\cdot,M) \mid \mathcal I(({1}/{\unicode{x3bb}^m}) {\mathcal P}^i,\mu)]}{{\mathbb E}_\mu[\eta\mid \mathcal I(({1}/{\unicode{x3bb}^m}) {\mathcal P}^i,\mu)]}. \end{align*} $$
$$ \begin{align*} \mu(C_i) &= \lim_{n\to\infty}\frac{\sum_{j=0}^{n} {\mathcal P}^j(x,C_i)}{\sum_{j=0}^{n} {\mathcal P}^j(x,M)} \leq \lim_{n\to\infty} \frac{\sum_{j=0}^{n} ({1}/{\unicode{x3bb}^{i+mj}}) {\mathcal P}^{i + m j }(x,M)}{ \sum_{j=0}^{nm} ({1}/{\unicode{x3bb}^j}) {\mathcal P}^j(x,M)}\\ &= \frac{ \lim_{n\to\infty} ({1}/{nm}) \sum_{j=0}^{n} ({1}/{\unicode{x3bb}^{i+mj}}) {\mathcal P}^{i + m j }(x,M)}{ \lim_{n\to\infty} ({1}/{mn}) \sum_{j=0}^{nm} ({1}/{\unicode{x3bb}^j}) {\mathcal P}^i(x,M)}\\ &= \frac{1}{m} \frac{{\mathbb E}_\mu[({1}/{\unicode{x3bb}^i}) {\mathcal P}^i(\cdot,M) \mid \mathcal I(({1}/{\unicode{x3bb}^m}) {\mathcal P}^i,\mu)]}{{\mathbb E}_\mu[\eta\mid \mathcal I(({1}/{\unicode{x3bb}^m}) {\mathcal P}^i,\mu)]}. \end{align*} $$
Therefore,
 $$ \begin{align*} \mu(C_i) &= \mu(C_i) \int_M {{\mathbb E}_\mu\bigg[\eta\mid \mathcal I\bigg(\frac{1}{\unicode{x3bb}^m} {\mathcal P}^i,\mu\bigg)\bigg]}\mu(\mathrm{d} x)\\ &\leq \frac{1}{m} \int_M {\mathbb E}_\mu\bigg[\frac{1}{\unicode{x3bb}^i}{\mathcal P}^i(\cdot,M)\mid \mathcal I\bigg(\frac{1}{\unicode{x3bb}^m} {\mathcal P}^i,\mu\bigg)\bigg](x) \mu(\mathrm{d} x)\\ &\leq \frac{1}{m}\quad \text{for all }i\in\{0,1,\ldots,m-1\}. \end{align*} $$
$$ \begin{align*} \mu(C_i) &= \mu(C_i) \int_M {{\mathbb E}_\mu\bigg[\eta\mid \mathcal I\bigg(\frac{1}{\unicode{x3bb}^m} {\mathcal P}^i,\mu\bigg)\bigg]}\mu(\mathrm{d} x)\\ &\leq \frac{1}{m} \int_M {\mathbb E}_\mu\bigg[\frac{1}{\unicode{x3bb}^i}{\mathcal P}^i(\cdot,M)\mid \mathcal I\bigg(\frac{1}{\unicode{x3bb}^m} {\mathcal P}^i,\mu\bigg)\bigg](x) \mu(\mathrm{d} x)\\ &\leq \frac{1}{m}\quad \text{for all }i\in\{0,1,\ldots,m-1\}. \end{align*} $$
Since
we obtain that
Step 2. We show that for every
![]() $i \in \{0,1,\ldots ,m-1\}$
, there exists
$i \in \{0,1,\ldots ,m-1\}$
, there exists
![]() $f_i \in E_{\mathrm {aws}}$
such that
$f_i \in E_{\mathrm {aws}}$
such that
From the decomposition
![]() $L^1(M,\mu ) = E_{\mathrm {rev}}\oplus E_{\mathrm {aws}} $
(see Proposition 4.2(ii)), there exist
$L^1(M,\mu ) = E_{\mathrm {rev}}\oplus E_{\mathrm {aws}} $
(see Proposition 4.2(ii)), there exist
![]() $\alpha _1,\ldots ,\alpha _m \in {\mathbb R}$
and
$\alpha _1,\ldots ,\alpha _m \in {\mathbb R}$
and
![]() $f_i\in E_{\mathrm {aws}}$
such that
$f_i\in E_{\mathrm {aws}}$
such that

Since
![]() $f_i\in E_{\mathrm {aws}}$
, it follows that
$f_i\in E_{\mathrm {aws}}$
, it follows that
![]() $\int _M f_i(y) \mu (\mathrm {d} y) = 0.$
Therefore,
$\int _M f_i(y) \mu (\mathrm {d} y) = 0.$
Therefore,
![]() $\alpha _0,\ldots ,\alpha _{i-1},\alpha _{i+1},\ldots , \alpha _m = 0$
and
$\alpha _0,\ldots ,\alpha _{i-1},\alpha _{i+1},\ldots , \alpha _m = 0$
and
![]() Since
Since
![]() $\mu (C_i) =1/m$
, we obtain that
$\mu (C_i) =1/m$
, we obtain that
![]() $\alpha _i =1/m.$
$\alpha _i =1/m.$
Step 3. We conclude the proof of the proposition.
From Step 2, we obtain that

Since
![]() $f:=f_1 +\cdots + f_m \in E_{\mathrm {aws}}$
, this shows that
$f:=f_1 +\cdots + f_m \in E_{\mathrm {aws}}$
, this shows that
![]() $({1}/{\unicode{x3bb} ^n}){\mathcal P}^n(\cdot ,M) \xrightarrow []{n\to \infty } \eta $
in
$({1}/{\unicode{x3bb} ^n}){\mathcal P}^n(\cdot ,M) \xrightarrow []{n\to \infty } \eta $
in
![]() $L^1(M,\mu ).$
$L^1(M,\mu ).$
Lemma 4.6. Let
![]() $X_n$
be an absorbing Markov chain satisfying Hypothesis H1, then for every
$X_n$
be an absorbing Markov chain satisfying Hypothesis H1, then for every
![]() $h\in L^\infty (M,\mu )$
,
$h\in L^\infty (M,\mu )$
,
 $$ \begin{align} \frac{1}{n} \sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot) \frac{1}{\unicode{x3bb}^{n-i}}{\mathcal P}^{n-i}(\cdot,M)\bigg) \xrightarrow{n\to\infty} \eta \int_M h(y) \eta(y) \mu(\mathrm{d} y), \text{ in } L^1(M,\mu). \end{align} $$
$$ \begin{align} \frac{1}{n} \sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot) \frac{1}{\unicode{x3bb}^{n-i}}{\mathcal P}^{n-i}(\cdot,M)\bigg) \xrightarrow{n\to\infty} \eta \int_M h(y) \eta(y) \mu(\mathrm{d} y), \text{ in } L^1(M,\mu). \end{align} $$
Proof. Let
![]() $h \in L^\infty (M,\mu ),$
from a direct computation
$h \in L^\infty (M,\mu ),$
from a direct computation
 $$ \begin{align*} I_h^n&:=\bigg\| \frac{1}{n} \sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot) \frac{1}{\unicode{x3bb}^{n-i}}{\mathcal P}^{n-i}(\cdot,M)\bigg)- \frac{1}{n} \sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i(h\eta)\bigg\|_{L^1(M,\mu)}\\ &\leq \frac{1}{n} \sum_{i=0}^{n-1} \bigg\| \frac{1}{\unicode{x3bb}^i}{\mathcal P}^i\bigg(h\cdot \bigg( \frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{n-i}(\cdot, M) - \eta\bigg)\bigg)\bigg\|_{L^1(M,\mu)}\\ &\leq \frac{\|h\|_{\infty}}{n} \sum_{i=0}^{n-1} \bigg\| \frac{1}{\unicode{x3bb}^i}{\mathcal P}^i\bigg| \frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{n-i}(\cdot, M) - \eta\bigg|\bigg\|_{L^1(M,\mu)}\\ &\leq \frac{\|h\|_{\infty}}{n} \sum_{i=0}^{n-1} \bigg\| \frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{n-i}(\cdot, M) - \eta\bigg\|_{L^1(M,\mu)}\xrightarrow[\text{Lem } 4.5]{n\to\infty} 0. \end{align*} $$
$$ \begin{align*} I_h^n&:=\bigg\| \frac{1}{n} \sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot) \frac{1}{\unicode{x3bb}^{n-i}}{\mathcal P}^{n-i}(\cdot,M)\bigg)- \frac{1}{n} \sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i(h\eta)\bigg\|_{L^1(M,\mu)}\\ &\leq \frac{1}{n} \sum_{i=0}^{n-1} \bigg\| \frac{1}{\unicode{x3bb}^i}{\mathcal P}^i\bigg(h\cdot \bigg( \frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{n-i}(\cdot, M) - \eta\bigg)\bigg)\bigg\|_{L^1(M,\mu)}\\ &\leq \frac{\|h\|_{\infty}}{n} \sum_{i=0}^{n-1} \bigg\| \frac{1}{\unicode{x3bb}^i}{\mathcal P}^i\bigg| \frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{n-i}(\cdot, M) - \eta\bigg|\bigg\|_{L^1(M,\mu)}\\ &\leq \frac{\|h\|_{\infty}}{n} \sum_{i=0}^{n-1} \bigg\| \frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{n-i}(\cdot, M) - \eta\bigg\|_{L^1(M,\mu)}\xrightarrow[\text{Lem } 4.5]{n\to\infty} 0. \end{align*} $$
The theorem follows by combining the above equation with Proposition 4.2 (i).
Now, we prove Theorem 2.2.
Proof of Theorem 2.2
Items (i), (ii) and (iii) follows directly from respectively Propositions 4.4, 4.2(i) and Lemma 4.5.
In the following, we prove item (iv). Given
![]() $h\in L^\infty (M,\mu )$
, define
$h\in L^\infty (M,\mu )$
, define
 $$ \begin{align*} g_n(x) &:= {\mathbb E}_x\bigg[\frac{1}{n}\sum_{i=0}^{n-1} h\circ X_i \mid \tau>n\bigg]= \frac{\unicode{x3bb}^n}{{\mathcal P}^n(x,M)} \frac{1}{n}\sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot) \frac{1}{\unicode{x3bb}^{n-i}}{\mathcal P}^{n-i}(\cdot,M)\bigg)(x). \end{align*} $$
$$ \begin{align*} g_n(x) &:= {\mathbb E}_x\bigg[\frac{1}{n}\sum_{i=0}^{n-1} h\circ X_i \mid \tau>n\bigg]= \frac{\unicode{x3bb}^n}{{\mathcal P}^n(x,M)} \frac{1}{n}\sum_{i=0}^{n-1} \frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot) \frac{1}{\unicode{x3bb}^{n-i}}{\mathcal P}^{n-i}(\cdot,M)\bigg)(x). \end{align*} $$
It is clear that
![]() $\|g_n\|_{L^\infty (M,\mu )} \leq \|h\|_{L^\infty (M,\mu )}$
for every
$\|g_n\|_{L^\infty (M,\mu )} \leq \|h\|_{L^\infty (M,\mu )}$
for every
![]() $n\in \mathbb N$
. Since M is a Polish space, from the Banach–Alaoglu theorem, we obtain that the space
$n\in \mathbb N$
. Since M is a Polish space, from the Banach–Alaoglu theorem, we obtain that the space
is a compact metric space when endowed with the
![]() $L^\infty (M,\mu )$
-weak
$L^\infty (M,\mu )$
-weak
![]() ${}^*$
topology. Let
${}^*$
topology. Let
![]() $\{g_{n_k}\}_{n\in \mathbb N}$
be a
$\{g_{n_k}\}_{n\in \mathbb N}$
be a
![]() $L^\infty (M,\mu )$
-weak
$L^\infty (M,\mu )$
-weak
![]() ${}^*$
convergent subsequence of
${}^*$
convergent subsequence of
![]() $\{g_n\}_{n\in \mathbb N}$
, and denote its limit as g.
$\{g_n\}_{n\in \mathbb N}$
, and denote its limit as g.
We show that
![]() $g = \int _M h \eta \ \mathrm {d} \mu \ \mu $
-a.s., which implies item (iv). Observe that given
$g = \int _M h \eta \ \mathrm {d} \mu \ \mu $
-a.s., which implies item (iv). Observe that given
![]() $A\in \mathscr B(M),$
from Lemmas 4.5 and 4.6, we obtain that
$A\in \mathscr B(M),$
from Lemmas 4.5 and 4.6, we obtain that

Since
![]() $\mu (\{\eta>0\})=1$
, it follows that
$\mu (\{\eta>0\})=1$
, it follows that
![]() $g = \int _M h(x)\eta (x) \mu (\mathrm {d} x) \ \mu $
-a.s.
$g = \int _M h(x)\eta (x) \mu (\mathrm {d} x) \ \mu $
-a.s.
5 Almost-sure convergence
In this section, we strengthen the
![]() $L^\infty (M,\mu )$
-weak
$L^\infty (M,\mu )$
-weak
![]() ${}^*$
convergence given in Theorem 2.2 to
${}^*$
convergence given in Theorem 2.2 to
![]() $L^\infty (M,\mu )$
convergence.
$L^\infty (M,\mu )$
convergence.
Note that for every
![]() $n\in \mathbb N$
,
$n\in \mathbb N$
,
![]() $x\in M$
and
$x\in M$
and
![]() $A\in \mathscr B(M)$
,
$A\in \mathscr B(M)$
,

Therefore, to prove Theorem 2.3, it is enough to find conditions where equations (4.1) and (4.2) converge almost surely.
To prove Theorem 2.3, we need the following three propositions.
Proposition 5.1. [Reference Meyer-Nieberg22, Proposition 3.3.3]
Let
![]() $T:L^1(M,\mu )\to L^1(M,\mu )$
be a positive bounded integral operator. Then if
$T:L^1(M,\mu )\to L^1(M,\mu )$
be a positive bounded integral operator. Then if
![]() $\{f_n\}_{n\in \mathbb N}\subset L^1(M,\mu )$
is a
$\{f_n\}_{n\in \mathbb N}\subset L^1(M,\mu )$
is a
![]() $L^1(M,\mu )$
-order bounded sequence satisfying
$L^1(M,\mu )$
-order bounded sequence satisfying
![]() $f_n\to 0$
in
$f_n\to 0$
in
![]() $\mu $
-measure as
$\mu $
-measure as
![]() $n\to \infty $
, then
$n\to \infty $
, then
![]() $Tf_n \to 0$
as
$Tf_n \to 0$
as
![]() $n\to \infty \ \mu $
-almost everywhere.
$n\to \infty \ \mu $
-almost everywhere.
Proposition 5.2. Let
![]() $X_n$
be an absorbing Markov chain satisfying Hypothesis H1. Suppose that one of the following items holds:
$X_n$
be an absorbing Markov chain satisfying Hypothesis H1. Suppose that one of the following items holds:
-
(a) there exists
 $K>0$
such that
$K>0$
such that
 $\mu (\{K<\eta \}) =1$
almost surely;
$\mu (\{K<\eta \}) =1$
almost surely; -
(b) there exists
 $ g\in L^1(M,\mu )$
such that
$ g\in L^1(M,\mu )$
such that  $$ \begin{align*} \frac{1}{\unicode{x3bb}^n} {\mathcal P}^n(x,M) \leq g \quad \text{for every }n\in \mathbb N; \end{align*} $$
$$ \begin{align*} \frac{1}{\unicode{x3bb}^n} {\mathcal P}^n(x,M) \leq g \quad \text{for every }n\in \mathbb N; \end{align*} $$
-
(c) the absorbing Markov chain
 $X_n$
fulfils Hypothesis H2.
$X_n$
fulfils Hypothesis H2.
Then for every
![]() $h\in L^\infty (M,\mu )$
$h\in L^\infty (M,\mu )$
 $$ \begin{align} \lim_{n\to \infty} \frac{1}{n}\sum_{i=0}^{n-1}\frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot)\frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{(n-i)}(\cdot,M)\bigg)(x) \xrightarrow{n\to\infty} \eta(x)\int_M h(y)\eta(y)\mu(\mathrm{d} y)\quad \mu\text{-a.s}. \end{align} $$
$$ \begin{align} \lim_{n\to \infty} \frac{1}{n}\sum_{i=0}^{n-1}\frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot)\frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{(n-i)}(\cdot,M)\bigg)(x) \xrightarrow{n\to\infty} \eta(x)\int_M h(y)\eta(y)\mu(\mathrm{d} y)\quad \mu\text{-a.s}. \end{align} $$
In addition, if
then
![]() $({1}/{\unicode{x3bb} ^n}) {\mathcal P}^n h \xrightarrow {n\to \infty } \eta \int _M h(x)\mu (\mathrm {d} x) \ \mu $
-a.s.
$({1}/{\unicode{x3bb} ^n}) {\mathcal P}^n h \xrightarrow {n\to \infty } \eta \int _M h(x)\mu (\mathrm {d} x) \ \mu $
-a.s.
Proof. Observe that item (a) is a particular case of item (b). In fact, note that for every
![]() $x\in M,$
$x\in M,$
![]() $({1}/{\unicode{x3bb} ^n}){\mathcal P}(x,M)\leq {1}/{K}({1}/{\unicode{x3bb} ^n}){\mathcal P}^n\eta (x) = {\eta (x)}/{K}$
which correspond to item (b) when setting
$({1}/{\unicode{x3bb} ^n}){\mathcal P}(x,M)\leq {1}/{K}({1}/{\unicode{x3bb} ^n}){\mathcal P}^n\eta (x) = {\eta (x)}/{K}$
which correspond to item (b) when setting
![]() $g := \eta /K.$
Now, we assume item (b). From Lemmas 4.2 and 4.5, we obtain that equations (5.1) and (5.2) converge in probability. Moreover, item (b) implies that for every
$g := \eta /K.$
Now, we assume item (b). From Lemmas 4.2 and 4.5, we obtain that equations (5.1) and (5.2) converge in probability. Moreover, item (b) implies that for every
![]() $n\in \mathbb N$
and for
$n\in \mathbb N$
and for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x \in M$
,
$x \in M$
,
and
 $$ \begin{align*}-\|h\|_{L^\infty(M,\mu)} g(x) \leq \frac{1}{n}\sum_{i=0}^{n-1}\frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot)\frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{(n-i)}(\cdot,M)\bigg)(x) \leq \|h\|_\infty g(x).\end{align*} $$
$$ \begin{align*}-\|h\|_{L^\infty(M,\mu)} g(x) \leq \frac{1}{n}\sum_{i=0}^{n-1}\frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot)\frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{(n-i)}(\cdot,M)\bigg)(x) \leq \|h\|_\infty g(x).\end{align*} $$
Therefore, Proposition 5.1 implies the result.
Now, we assume item (c). Let us consider the set
It is clear that the

is a bounded linear operator. Therefore, we have for every
![]() $h\in L^\infty (M,\mu ),$
$h\in L^\infty (M,\mu ),$

and

Since Hypothesis H2 implies that
![]() $\mu (\bigcup _{m=1} K_m) = 1$
, we obtain the result.
$\mu (\bigcup _{m=1} K_m) = 1$
, we obtain the result.
Proposition 5.3. Let
![]() $X_n$
be an absorbing Markov chain satisfying Hypothesis H2 and
$X_n$
be an absorbing Markov chain satisfying Hypothesis H2 and
![]() $m=1$
in Theorem 2.2(i). Then for every
$m=1$
in Theorem 2.2(i). Then for every
![]() $h\in L^\infty (M,\mu )$
,
$h\in L^\infty (M,\mu )$
,
Proof. In the case where
![]() $m=1$
in Theorem 2.2(i), we obtain that
$m=1$
in Theorem 2.2(i), we obtain that
![]() $\mathrm {dim}(E_{\mathrm {rev}}) =1.$
Then, given
$\mathrm {dim}(E_{\mathrm {rev}}) =1.$
Then, given
![]() $f\in L^1(M,\mu )$
, there exists
$f\in L^1(M,\mu )$
, there exists
![]() $\alpha \in \mathbb C$
and
$\alpha \in \mathbb C$
and
![]() $g \in {\mathbb E}_{\mathrm {aws}}$
such that
$g \in {\mathbb E}_{\mathrm {aws}}$
such that
From Proposition 4.2, we obtain that
Finally, integrating over
![]() $\mu $
in the above limit, we obtain that
$\mu $
in the above limit, we obtain that
![]() $\alpha =\int _M f(x)\mu (\mathrm {d} x).$
$\alpha =\int _M f(x)\mu (\mathrm {d} x).$
Finally, we prove Theorems 2.3 and 2.4.
Proof of Theorem 2.3
Observe that given
![]() $h\in L^\infty (M,\mu )$
, for every
$h\in L^\infty (M,\mu )$
, for every
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $x\in M$
, we obtain
$x\in M$
, we obtain
 $$ \begin{align} {\mathbb E}_x\bigg[\frac{1}{n} \sum_{i=0}^{n-1}h\circ X_i \mid \tau> n\bigg] = \frac{ {1}/{n}\sum_{i=0}^{n-1} ({1}/{\unicode{x3bb}^i}){\mathcal P}^i(h(\cdot) ({1}/{\unicode{x3bb}^{n-i}}){\mathcal P}^{n-i}(\cdot,M) )(x)}{({1}/{\unicode{x3bb}^n}) {\mathcal P}^n(x,M)}. \end{align} $$
$$ \begin{align} {\mathbb E}_x\bigg[\frac{1}{n} \sum_{i=0}^{n-1}h\circ X_i \mid \tau> n\bigg] = \frac{ {1}/{n}\sum_{i=0}^{n-1} ({1}/{\unicode{x3bb}^i}){\mathcal P}^i(h(\cdot) ({1}/{\unicode{x3bb}^{n-i}}){\mathcal P}^{n-i}(\cdot,M) )(x)}{({1}/{\unicode{x3bb}^n}) {\mathcal P}^n(x,M)}. \end{align} $$
From Proposition 5.2, we obtain that for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in M$
,
$x\in M$
,
which proves the first part of the theorem.
In the case where
![]() $m=1$
in Theorem 2.2, then
$m=1$
in Theorem 2.2, then
![]() $\# (\sigma _{\mathrm {pnt}}({\mathcal P}/\unicode{x3bb} ) \cap \mathbb S^1) =1$
, then combining Propositions 5.2 and 5.3, we obtain that for
$\# (\sigma _{\mathrm {pnt}}({\mathcal P}/\unicode{x3bb} ) \cap \mathbb S^1) =1$
, then combining Propositions 5.2 and 5.3, we obtain that for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in M$
,
$x\in M$
,
Proof of Theorem 2.4
Observe that under the conditions of Theorem 2.4, we obtain that for every
![]() $i\in \mathbb N$
, the operators
$i\in \mathbb N$
, the operators

are bounded linear operators, since
 $$ \begin{align} \frac{1}{n}\sum_{i=0}^{n-1}\frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot)\frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{(n-i)}(\cdot,M)\bigg)(x) \xrightarrow[L^1(M,\mu)]{n\to\infty} \eta(x)\int_M h(y)\eta(y)\mu(\mathrm{d} y) \end{align} $$
$$ \begin{align} \frac{1}{n}\sum_{i=0}^{n-1}\frac{1}{\unicode{x3bb}^i} {\mathcal P}^i\bigg(h(\cdot)\frac{1}{\unicode{x3bb}^{n-i}} {\mathcal P}^{(n-i)}(\cdot,M)\bigg)(x) \xrightarrow[L^1(M,\mu)]{n\to\infty} \eta(x)\int_M h(y)\eta(y)\mu(\mathrm{d} y) \end{align} $$
and
Composing
![]() $\mathcal G^i$
on both sides, we obtain that equations (5.4) and (5.5) hold pointwise in
$\mathcal G^i$
on both sides, we obtain that equations (5.4) and (5.5) hold pointwise in
![]() $K^i$
for every
$K^i$
for every
![]() $i\in \mathbb N.$
From equation (5.3), we obtain that for every
$i\in \mathbb N.$
From equation (5.3), we obtain that for every
![]() $x\in \bigcup _{x\in \mathbb N} K_i$
and
$x\in \bigcup _{x\in \mathbb N} K_i$
and
![]() $h\in L^\infty (M,\mu )$
,
$h\in L^\infty (M,\mu )$
,
 $$ \begin{align*} \lim_{n\to\infty }{\mathbb E}_x\bigg[\frac{1}{n} \sum_{i=0}^{n-1}h\circ X_i \mid \tau> n\bigg] = \int_M h(y) \eta (y)\mu(\mathrm{d} y).\end{align*} $$
$$ \begin{align*} \lim_{n\to\infty }{\mathbb E}_x\bigg[\frac{1}{n} \sum_{i=0}^{n-1}h\circ X_i \mid \tau> n\bigg] = \int_M h(y) \eta (y)\mu(\mathrm{d} y).\end{align*} $$
Note that if
![]() $m=1$
in Theorem 2.2, we obtain that
$m=1$
in Theorem 2.2, we obtain that
![]() $\#(\sigma _{\mathrm {pnt} {\mathcal P}/\unicode{x3bb} }\cap \mathbb S^1) =1.$
Therefore,
$\#(\sigma _{\mathrm {pnt} {\mathcal P}/\unicode{x3bb} }\cap \mathbb S^1) =1.$
Therefore,
![]() $h\in L^\infty (M,\mu )$
$h\in L^\infty (M,\mu )$
 $$ \begin{align*} \lim_{n\to\infty} \frac{{\mathcal P}^n h}{{\mathcal P}^n(x,M)} = \int_M h(y) \mu(\mathrm{d} y)\quad \text{for every }x\in\bigcup_{m\in\mathbb N} K_m.\\[-40pt] \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty} \frac{{\mathcal P}^n h}{{\mathcal P}^n(x,M)} = \int_M h(y) \mu(\mathrm{d} y)\quad \text{for every }x\in\bigcup_{m\in\mathbb N} K_m.\\[-40pt] \end{align*} $$
6 Random logistic map with escape
In this section, we analyse the Markov chain
![]() $Y_{n+1}^{a,b} = \omega _n Y_{n}^{a,b} (1-Y_n^{a,b})$
absorbed at
$Y_{n+1}^{a,b} = \omega _n Y_{n}^{a,b} (1-Y_n^{a,b})$
absorbed at
![]() $\partial = {\mathbb R}\setminus M,$
where
$\partial = {\mathbb R}\setminus M,$
where
![]() $\{\omega _n\}_{n\in \mathbb N}$
is an i.i.d. sequence of random variables such that
$\{\omega _n\}_{n\in \mathbb N}$
is an i.i.d. sequence of random variables such that
![]() $\omega _n\sim \mathrm {Unif}([a,b])$
, where
$\omega _n\sim \mathrm {Unif}([a,b])$
, where
![]() $0<a<4<b$
and
$0<a<4<b$
and
![]() $M=[0,1].$
As before, for every
$M=[0,1].$
As before, for every
![]() $A\in \mathscr B(M)$
and
$A\in \mathscr B(M)$
and
![]() $x\in M$
, we denote
$x\in M$
, we denote
Clearly,
![]() $\delta _0$
is a stationary measure for
$\delta _0$
is a stationary measure for
![]() $Y_n^{a,b}$
on
$Y_n^{a,b}$
on
![]() $[0,1]$
. In the following, we provide conditions to show that
$[0,1]$
. In the following, we provide conditions to show that
![]() $Y_n^{a,b}$
admits a non-trivial quasi-stationary measure on
$Y_n^{a,b}$
admits a non-trivial quasi-stationary measure on
![]() $[0,1]$
, which we define as a quasi-stationary measure for
$[0,1]$
, which we define as a quasi-stationary measure for
![]() $Y_n^{a,b}$
different from
$Y_n^{a,b}$
different from
![]() $\delta _0.$
For the sake of simplicity and in the interest of readability, we denote
$\delta _0.$
For the sake of simplicity and in the interest of readability, we denote
![]() $Y^{a,b}_n$
simply as
$Y^{a,b}_n$
simply as
![]() $Y_n$
. Similarly, when the context is clear, we omit the
$Y_n$
. Similarly, when the context is clear, we omit the
![]() $a,b$
superscript from future objects that depend on a and b.
$a,b$
superscript from future objects that depend on a and b.
In the following proposition, we explicitly compute the transition functions of
![]() $Y_n.$
$Y_n.$
Proposition 6.1. Let
![]() $0\leq a \leq b $
, and consider the absorbing Markov chain
$0\leq a \leq b $
, and consider the absorbing Markov chain
![]() $Y_n^{a,b}$
. Moreover, given
$Y_n^{a,b}$
. Moreover, given
![]() $f\in L^1(M,\mathrm {Leb}),$
$f\in L^1(M,\mathrm {Leb}),$
 $$ \begin{align*} {{\mathcal P}} f(x) = \frac{1}{(b-a)x(1-x)}\int_{ax(1-x)}^{bx(1-x)\wedge 1} f (y) \mathrm{d} y. \end{align*} $$
$$ \begin{align*} {{\mathcal P}} f(x) = \frac{1}{(b-a)x(1-x)}\int_{ax(1-x)}^{bx(1-x)\wedge 1} f (y) \mathrm{d} y. \end{align*} $$
In the case where
![]() $f\in \mathcal C^0(M),$
then
$f\in \mathcal C^0(M),$
then
![]() ${\mathcal P} f \in \mathcal C^0(M)$
and
${\mathcal P} f \in \mathcal C^0(M)$
and
![]() ${\mathcal P} f (0) = {{\mathcal P}}f(1) = f(0). $
${\mathcal P} f (0) = {{\mathcal P}}f(1) = f(0). $
Proof. Let
![]() $f\in L^1(M,\mathrm {Leb})$
by a direct computation,
$f\in L^1(M,\mathrm {Leb})$
by a direct computation,

Now, consider
![]() $f\in \mathcal C^0(M).$
The above equation implies that
$f\in \mathcal C^0(M).$
The above equation implies that
![]() $\mathcal Pf$
is continuous in
$\mathcal Pf$
is continuous in
![]() $(0,1)$
. For every
$(0,1)$
. For every
![]() $x\in (0,1)$
, let us define the interval
$x\in (0,1)$
, let us define the interval
![]() $J_x := [ax(1-x), bx(1-x)\land 1].$
It follows that for every
$J_x := [ax(1-x), bx(1-x)\land 1].$
It follows that for every
![]() $x\in (0,1/b)$
,
$x\in (0,1/b)$
,
![]() $\min _{y\in J_x} f(y) \leq \mathcal Pf(x) \leq \max _{y\in J_x} f(y).$
From the continuity of f, we obtain that
$\min _{y\in J_x} f(y) \leq \mathcal Pf(x) \leq \max _{y\in J_x} f(y).$
From the continuity of f, we obtain that
![]() $\lim _{x\to 0} \mathcal Pf = f(0).$
Since
$\lim _{x\to 0} \mathcal Pf = f(0).$
Since
![]() ${\mathcal P}(x) = {\mathcal P} (1-x)$
for every
${\mathcal P}(x) = {\mathcal P} (1-x)$
for every
![]() $x\in (0,1/2)$
, it follows that
$x\in (0,1/2)$
, it follows that
![]() $\lim _{x\to 1}{\mathcal P}(x) = f(0),$
implying that
$\lim _{x\to 1}{\mathcal P}(x) = f(0),$
implying that
![]() ${\mathcal P} f\in \mathcal C^0(M)$
.
${\mathcal P} f\in \mathcal C^0(M)$
.
The first step to apply Theorem 2.4 to
![]() $Y_n$
on
$Y_n$
on
![]() $[0,1]$
is to show that
$[0,1]$
is to show that
![]() $Y_n$
admits a quasi-stationary measure different from
$Y_n$
admits a quasi-stationary measure different from
![]() $\delta _0$
on
$\delta _0$
on
![]() $[0,1]$
.
$[0,1]$
.
Consider a measure
![]() $\mu \in \mathcal M (M)$
such that
$\mu \in \mathcal M (M)$
such that
![]() $\mu \ll \mathrm {Leb}(\mathrm {d}x)$
and define
$\mu \ll \mathrm {Leb}(\mathrm {d}x)$
and define
![]() $ g:=\mu (\mathrm {d} x)/ \mathrm {Leb}(\mathrm {d} x).$
Note that
$ g:=\mu (\mathrm {d} x)/ \mathrm {Leb}(\mathrm {d} x).$
Note that

where
 $$ \begin{align*}\alpha_{\pm}(x) := \frac{1}{2} \pm \frac{1}{2}\sqrt{1 - \frac{4}{b}x}\quad \text{and}\quad \beta_{\pm}(x) := \frac{1}{2} \pm \frac{1}{2}\sqrt{1 - \frac{4}{a}x}.\end{align*} $$
$$ \begin{align*}\alpha_{\pm}(x) := \frac{1}{2} \pm \frac{1}{2}\sqrt{1 - \frac{4}{b}x}\quad \text{and}\quad \beta_{\pm}(x) := \frac{1}{2} \pm \frac{1}{2}\sqrt{1 - \frac{4}{a}x}.\end{align*} $$
The above observation motivates the definition of the stochastic transfer operator,
 $$ \begin{align} \mathcal L: L^1([0,1],\mathrm{Leb}) &\to L^1([0,1],\mathrm{Leb}), \\ g&\mapsto \bigg(x\mapsto \int_{\alpha_-(x)}^{\alpha_+(x)} \frac{ g(y)}{(b-a)y(1-y)} \ \mathrm{d} y\nonumber\\ &\quad- \int_{\beta_-(x\wedge a/4)}^{\beta_+(x\wedge a/4)} \frac{ g(y)}{(b-a)y(1-y)} \ \mathrm{d} y \bigg), \nonumber \end{align} $$
$$ \begin{align} \mathcal L: L^1([0,1],\mathrm{Leb}) &\to L^1([0,1],\mathrm{Leb}), \\ g&\mapsto \bigg(x\mapsto \int_{\alpha_-(x)}^{\alpha_+(x)} \frac{ g(y)}{(b-a)y(1-y)} \ \mathrm{d} y\nonumber\\ &\quad- \int_{\beta_-(x\wedge a/4)}^{\beta_+(x\wedge a/4)} \frac{ g(y)}{(b-a)y(1-y)} \ \mathrm{d} y \bigg), \nonumber \end{align} $$
note that
![]() $\mathcal L$
is a well-defined linear operator since for every
$\mathcal L$
is a well-defined linear operator since for every
![]() $g\in L^1([0,1],\mathrm {Leb})$
,
$g\in L^1([0,1],\mathrm {Leb})$
,
 $$ \begin{align*} \|\mathcal L (g)\|_{L^1(M,\mathrm{Leb})} := \int_0^1 |\mathcal L g(x)| \,\mathrm{d} x \leq \int_M {\mathcal P}(x,M) |g(y)| \mathrm{d} y \leq \|g\|_{L^1(M,\mathrm{Leb})}. \end{align*} $$
$$ \begin{align*} \|\mathcal L (g)\|_{L^1(M,\mathrm{Leb})} := \int_0^1 |\mathcal L g(x)| \,\mathrm{d} x \leq \int_M {\mathcal P}(x,M) |g(y)| \mathrm{d} y \leq \|g\|_{L^1(M,\mathrm{Leb})}. \end{align*} $$
The following two propositions summarize the above comments and show that
![]() $\mathcal L$
is well defined as an automorphism in
$\mathcal L$
is well defined as an automorphism in
![]() $L^p(M,\mathrm {Leb})$
for every
$L^p(M,\mathrm {Leb})$
for every
![]() $p\in [1,\infty ].$
For the following result, see for instance [Reference Zmarrou and Homburg30, §5].
$p\in [1,\infty ].$
For the following result, see for instance [Reference Zmarrou and Homburg30, §5].
Proposition 6.2. A probability measure
![]() $\mu \in \mathcal M_+(M)\setminus \{\delta _0\}$
on
$\mu \in \mathcal M_+(M)\setminus \{\delta _0\}$
on
![]() $[0,1]$
is a quasi- stationary measure for
$[0,1]$
is a quasi- stationary measure for
![]() $Y_n$
if and only if
$Y_n$
if and only if
![]() $\mu (\mathrm {d} x) \ll \mathrm {Leb}(\mathrm {d} x)$
and there exists
$\mu (\mathrm {d} x) \ll \mathrm {Leb}(\mathrm {d} x)$
and there exists
![]() $0<\unicode{x3bb} <1,$
such that
$0<\unicode{x3bb} <1,$
such that
Proposition 6.3. For every
![]() $p\in [1,\infty ]$
, the operators
$p\in [1,\infty ]$
, the operators
are well defined and bounded.
Proof. By a direct computation, one can check that

implying that
 $$ \begin{align*}\|\mathcal L\|_{L^\infty(M,\mathrm{Leb})} = \frac{4}{b-a} \tanh^{-1}\bigg(\sqrt{1-\frac{a}{b}}\bigg).\end{align*} $$
$$ \begin{align*}\|\mathcal L\|_{L^\infty(M,\mathrm{Leb})} = \frac{4}{b-a} \tanh^{-1}\bigg(\sqrt{1-\frac{a}{b}}\bigg).\end{align*} $$
Since
![]() $\|\mathcal L\|_{L^1(M,\mathrm {Leb})} \leq 1,$
by the Riesz–Thorin interpolation theorem [Reference Folland13, Theorem 6.27],
$\|\mathcal L\|_{L^1(M,\mathrm {Leb})} \leq 1,$
by the Riesz–Thorin interpolation theorem [Reference Folland13, Theorem 6.27],
For the operator
![]() ${\mathcal P},$
note that for every
${\mathcal P},$
note that for every
![]() $0\leq f \in L^1 ([0,1])$
(
$0\leq f \in L^1 ([0,1])$
(
![]() $1\leq p \leq \infty $
),
$1\leq p \leq \infty $
),

showing that
![]() $\|{\mathcal P}\|_{L^1(M,\mathrm {Leb})} \leq \|\mathcal L\|_{L^\infty (M,\mathrm {Leb})}<\infty .$
Using that
$\|{\mathcal P}\|_{L^1(M,\mathrm {Leb})} \leq \|\mathcal L\|_{L^\infty (M,\mathrm {Leb})}<\infty .$
Using that
![]() $\|{\mathcal P}\|_{L^\infty (M,\mathrm {Leb})} \leq 1$
, we have again by the Riesz–Thorin interpolation theorem that
$\|{\mathcal P}\|_{L^\infty (M,\mathrm {Leb})} \leq 1$
, we have again by the Riesz–Thorin interpolation theorem that
![]() $\|{\mathcal P}\|_{L^p(M,\mathrm {Leb})} <\infty \ \text {for all } \ p\in [1,\infty ]. $
$\|{\mathcal P}\|_{L^p(M,\mathrm {Leb})} <\infty \ \text {for all } \ p\in [1,\infty ]. $
For every
![]() $a\in (0,4)$
and
$a\in (0,4)$
and
![]() $0<\varepsilon <3/8$
, let us define
$0<\varepsilon <3/8$
, let us define
![]() $M_\varepsilon := [4\varepsilon (1-\varepsilon )^2,1-\varepsilon ]$
and the Markov chain
$M_\varepsilon := [4\varepsilon (1-\varepsilon )^2,1-\varepsilon ]$
and the Markov chain
![]() ${Y^{a,b,\varepsilon }_{n+1}:=Y^\varepsilon _{n+1} = \omega _n Y_n^\varepsilon (1 - Y^\varepsilon _n)}$
absorbed at
${Y^{a,b,\varepsilon }_{n+1}:=Y^\varepsilon _{n+1} = \omega _n Y_n^\varepsilon (1 - Y^\varepsilon _n)}$
absorbed at
![]() $\partial ^\varepsilon = {\mathbb R} \setminus M_\varepsilon $
, where
$\partial ^\varepsilon = {\mathbb R} \setminus M_\varepsilon $
, where
![]() $\{\omega _n\}_{n\in \mathbb N}$
is an i.i.d. sequence of random variables and
$\{\omega _n\}_{n\in \mathbb N}$
is an i.i.d. sequence of random variables and
![]() $\omega _n\sim \mathrm {Unif}([a,b])$
. Moreover, for every
$\omega _n\sim \mathrm {Unif}([a,b])$
. Moreover, for every
![]() $\varepsilon \in (0,3/8),$
we denote the transition kernels and transfer operator for the absorbing Markov chain
$\varepsilon \in (0,3/8),$
we denote the transition kernels and transfer operator for the absorbing Markov chain
![]() $Y_n^\varepsilon $
respectively as
$Y_n^\varepsilon $
respectively as
In the next proposition, we show the existence of a sequence of positive real numbers
![]() $\{\varepsilon _i\}_{i\in \mathbb N}$
converging to
$\{\varepsilon _i\}_{i\in \mathbb N}$
converging to
![]() $0$
, such that for every
$0$
, such that for every
![]() $i\in \mathbb N$
, the absorbing Markov chain
$i\in \mathbb N$
, the absorbing Markov chain
![]() $Y_n^{\varepsilon _i}$
admits a unique quasi-stationary measure
$Y_n^{\varepsilon _i}$
admits a unique quasi-stationary measure
![]() $\mu _{\varepsilon _i}$
supported on
$\mu _{\varepsilon _i}$
supported on
![]() $M_{\varepsilon _i}.$
Moreover, these measures will play an important role in constructing a non-trivial quasi-stationary measure for
$M_{\varepsilon _i}.$
Moreover, these measures will play an important role in constructing a non-trivial quasi-stationary measure for
![]() $Y_n$
on M.
$Y_n$
on M.
Proposition 6.4. Let
![]() $(a,b) \in [1,4) \times (4,\infty )$
and
$(a,b) \in [1,4) \times (4,\infty )$
and
![]() $Y_n^{a,b,\varepsilon }$
be the Markov chain absorbed at
$Y_n^{a,b,\varepsilon }$
be the Markov chain absorbed at
![]() $\partial ^{\varepsilon }$
defined above. Then, there exists a sequence of positive numbers
$\partial ^{\varepsilon }$
defined above. Then, there exists a sequence of positive numbers
![]() $\{\varepsilon _i\}_{i\in \mathbb N}$
converging to
$\{\varepsilon _i\}_{i\in \mathbb N}$
converging to
![]() $0$
such that, for every
$0$
such that, for every
![]() $i\in \mathbb N$
, the following items hold:
$i\in \mathbb N$
, the following items hold:
-
(a)
 $Y_n^{a,b,\varepsilon _i}$
admits a unique quasi-stationary measure
$Y_n^{a,b,\varepsilon _i}$
admits a unique quasi-stationary measure
 $\mu _{a,b,\varepsilon _i} := \mu _\varepsilon $
on
$\mu _{a,b,\varepsilon _i} := \mu _\varepsilon $
on
 $M_\varepsilon $
with survival rate
$M_\varepsilon $
with survival rate
 $\unicode{x3bb} _{\varepsilon _i}>0$
;
$\unicode{x3bb} _{\varepsilon _i}>0$
; -
(b) there exists a continuous function
 $g_\varepsilon ^{a,b}:= g_{\varepsilon _i} \in \mathcal C^0(M_{\varepsilon _i})$
such that
$g_\varepsilon ^{a,b}:= g_{\varepsilon _i} \in \mathcal C^0(M_{\varepsilon _i})$
such that
 $\mu _{\varepsilon _i}(\mathrm {d} x) = g_{\varepsilon _i}(x)\,\mathrm {d} x$
; and
$\mu _{\varepsilon _i}(\mathrm {d} x) = g_{\varepsilon _i}(x)\,\mathrm {d} x$
; and -
(c)
 $\mathrm {supp}(\mu _{\varepsilon _i}) = M_{\varepsilon _i}.$
$\mathrm {supp}(\mu _{\varepsilon _i}) = M_{\varepsilon _i}.$
Proof. From [Reference Jakobson17, Theorem B and Remark XIII/5], there exists a sequence
![]() $\{r_i\}_{i\in \mathbb N} \subset [a,4)$
converging to
$\{r_i\}_{i\in \mathbb N} \subset [a,4)$
converging to
![]() $4$
such that for every
$4$
such that for every
![]() $i\in \mathbb N$
, the logistic map
$i\in \mathbb N$
, the logistic map
![]() $f_{r_i} :[0,1]\to [0,1]$
,
$f_{r_i} :[0,1]\to [0,1]$
,
![]() $f_{r_i}(x)= r_i x(1-x)$
admits an invariant ergodic measure
$f_{r_i}(x)= r_i x(1-x)$
admits an invariant ergodic measure
![]() $\rho _{r_i} \ll \mathrm {Leb}$
and
$\rho _{r_i} \ll \mathrm {Leb}$
and
![]() $\mathrm {supp}(\rho _{r_i}) = [f_{r_i}^2(1/2), f_{r_i}(1/2)]$
.
$\mathrm {supp}(\rho _{r_i}) = [f_{r_i}^2(1/2), f_{r_i}(1/2)]$
.
Consider the sequence
![]() $\{\varepsilon _i = (4 - r_i)/4\}_{i\in \mathbb N}$
. Combining equation (6.2) and Proposition 6.1, we obtain that
$\{\varepsilon _i = (4 - r_i)/4\}_{i\in \mathbb N}$
. Combining equation (6.2) and Proposition 6.1, we obtain that

In the following, we show that for every
![]() $i\in \mathbb N,$
given
$i\in \mathbb N,$
given
![]() $x\in M_{\varepsilon _i}$
and open interval
$x\in M_{\varepsilon _i}$
and open interval
![]() $I \subset M_{\varepsilon _i} =[f_{r_i}^2(1/2), f_{r_i}(1/2)] ,$
there exists
$I \subset M_{\varepsilon _i} =[f_{r_i}^2(1/2), f_{r_i}(1/2)] ,$
there exists
![]() $n_0 = n_0(x,I) \in \mathbb N$
such that
$n_0 = n_0(x,I) \in \mathbb N$
such that
![]() ${\mathcal P}_{\varepsilon _i}^{n_0}(x, I)> 0.$
${\mathcal P}_{\varepsilon _i}^{n_0}(x, I)> 0.$
Consider the set
![]() $J := \{y\in M_{\varepsilon _i}; \omega x(1-x) =y\ \text {for some }\omega \in [a,b]\}.$
Since J has non-empty interior, we obtain that
$J := \{y\in M_{\varepsilon _i}; \omega x(1-x) =y\ \text {for some }\omega \in [a,b]\}.$
Since J has non-empty interior, we obtain that
![]() $\rho _{r_i}(J)>0.$
Since
$\rho _{r_i}(J)>0.$
Since
![]() $\rho _{r_i}$
is an invariant ergodic measure, there exists
$\rho _{r_i}$
is an invariant ergodic measure, there exists
![]() $\omega _0 \in [a,b]$
such that
$\omega _0 \in [a,b]$
such that
![]() $y:=\omega _0 x(1-x) \in J$
and
$y:=\omega _0 x(1-x) \in J$
and
![]() $n_1>0 \in \mathbb N$
such that
$n_1>0 \in \mathbb N$
such that
![]() $f^{n_1}_{r_i}(y)~\in ~I$
.
$f^{n_1}_{r_i}(y)~\in ~I$
.
Consider the natural number
![]() $n_0 \in \mathbb N$
and the continuous function
$n_0 \in \mathbb N$
and the continuous function
![]() ${F^{x,n_0}: [a,b]^{n_0} \to {\mathbb R},} F^{x,n_0}(c_1,\ldots , c_{n_0}) := f_{c_1} \circ f_{c_2} \circ \ldots f_{c_{n_0}}(x)$
. From the last paragraph, we obtain that
${F^{x,n_0}: [a,b]^{n_0} \to {\mathbb R},} F^{x,n_0}(c_1,\ldots , c_{n_0}) := f_{c_1} \circ f_{c_2} \circ \ldots f_{c_{n_0}}(x)$
. From the last paragraph, we obtain that
![]() $F^{x,n_0}(\omega _0,r_{\varepsilon _i},\ldots ,r_{\varepsilon _i}) \in I$
. Finally, since
$F^{x,n_0}(\omega _0,r_{\varepsilon _i},\ldots ,r_{\varepsilon _i}) \in I$
. Finally, since
![]() $F^{x,n_0}$
is a continuous function, we obtain that
$F^{x,n_0}$
is a continuous function, we obtain that
 $$ \begin{align} {\mathcal P}^{n_0}(x, I) &= {\mathbb P} [Y_{n_0}^{a,b,\varepsilon_i} \in I\mid X_0 = x]\nonumber\\&= \frac{1}{(b-a)^{n_0}}\mathrm{Leb}^{\otimes n_0}(\{p\in [a,b]^{n_0};\ F^{x,n_0}(p) \in I\})>0. \end{align} $$
$$ \begin{align} {\mathcal P}^{n_0}(x, I) &= {\mathbb P} [Y_{n_0}^{a,b,\varepsilon_i} \in I\mid X_0 = x]\nonumber\\&= \frac{1}{(b-a)^{n_0}}\mathrm{Leb}^{\otimes n_0}(\{p\in [a,b]^{n_0};\ F^{x,n_0}(p) \in I\})>0. \end{align} $$
From equations (6.2) and (6.4), we conclude that [Reference Castro, Lamb, Olicón-Méndez and Rasmussen7, Hypothesis (H)] is fulfilled and therefore items (a), (b) and (c) follows directly from [Reference Castro, Lamb, Olicón-Méndez and Rasmussen7, Theorem A].
Observe that the family of measures given by the previous proposition
![]() $\{\mu _{\varepsilon _i}\}_{i\in \mathbb N}$
can be naturally extended on
$\{\mu _{\varepsilon _i}\}_{i\in \mathbb N}$
can be naturally extended on
![]() $[0,1]$
by imposing that
$[0,1]$
by imposing that
![]() $\mu _{\varepsilon _i}([0,1]\setminus M_{\varepsilon _i}) =0$
for every
$\mu _{\varepsilon _i}([0,1]\setminus M_{\varepsilon _i}) =0$
for every
![]() $i\in \mathbb N.$
To construct a quasi-stationary measure for the Markov process
$i\in \mathbb N.$
To construct a quasi-stationary measure for the Markov process
![]() $Y_n$
on
$Y_n$
on
![]() $[0,1]$
, we use that
$[0,1]$
, we use that
![]() $\{\mu _{\varepsilon _i}\}_{i \in \mathbb N}$
is precompact in the weak
$\{\mu _{\varepsilon _i}\}_{i \in \mathbb N}$
is precompact in the weak
![]() $^*$
of
$^*$
of
![]() $\mathcal M([0,1]),$
that is,
$\mathcal M([0,1]),$
that is,
 $$ \begin{align} \bigcap_{i\in \mathbb N} \overline{ \{\mu_{\varepsilon_{k+i}}\}_{k\in\mathbb N}}^{\mathrm{w}^*\text{-}\mathcal M(M)} \neq \emptyset, \end{align} $$
$$ \begin{align} \bigcap_{i\in \mathbb N} \overline{ \{\mu_{\varepsilon_{k+i}}\}_{k\in\mathbb N}}^{\mathrm{w}^*\text{-}\mathcal M(M)} \neq \emptyset, \end{align} $$
where
![]() $\mathrm {w}^*\text {-}\mathcal M(M)$
denotes the weak
$\mathrm {w}^*\text {-}\mathcal M(M)$
denotes the weak
![]() ${}^*$
topology of
${}^*$
topology of
![]() $\mathcal M(M).$
$\mathcal M(M).$
The proposition below shows that the elements of equation (6.5) are natural candidates for quasi-stationary measures for
![]() $Y_n$
on
$Y_n$
on
![]() $[0,1]$
.
$[0,1]$
.
Proposition 6.5. Assume that there exists a probability measure
![]() $\mu _{a,b} :=\mu $
on M,
$\mu _{a,b} :=\mu $
on M,
![]() $\unicode{x3bb}>0,$
and subsequences
$\unicode{x3bb}>0,$
and subsequences
such that
Then
![]() $\mu $
is a quasi-stationary measure for
$\mu $
is a quasi-stationary measure for
![]() $Y_n$
on
$Y_n$
on
![]() $[0,1].$
$[0,1].$
Proof. Let
note that E is, at most, countable. Consider the set
It is clear that
![]() $\sigma (\mathcal A) = \mathcal B(M).$
Note that for every
$\sigma (\mathcal A) = \mathcal B(M).$
Note that for every
![]() $I \in \mathcal A,$
there exists
$I \in \mathcal A,$
there exists
![]() $n_0 = n_0(I)$
such that
$n_0 = n_0(I)$
such that
This implies that for every
![]() $n>n_0,$
$n>n_0,$
 $$ \begin{align*} \int_M {\mathcal P}(x,I) \mu_{\delta_n}(\mathrm{d} x) &= \int_{M_\varepsilon} {\mathcal P}(x,I) \mu_{\varepsilon_n}(\mathrm{d} x) = \unicode{x3bb}_{\delta_n} \mu_{\delta_n} (I). \end{align*} $$
$$ \begin{align*} \int_M {\mathcal P}(x,I) \mu_{\delta_n}(\mathrm{d} x) &= \int_{M_\varepsilon} {\mathcal P}(x,I) \mu_{\varepsilon_n}(\mathrm{d} x) = \unicode{x3bb}_{\delta_n} \mu_{\delta_n} (I). \end{align*} $$
Since
![]() ${\mathcal P}(x,I)$
is a continuous function, we obtain
${\mathcal P}(x,I)$
is a continuous function, we obtain
Since
![]() $({4-b})/({b-a}) \leq {\mathcal P}(x,M) \ \text {for all } \ x\in [0,1],$
it follows that
$({4-b})/({b-a}) \leq {\mathcal P}(x,M) \ \text {for all } \ x\in [0,1],$
it follows that
![]() $\unicode{x3bb}>0.$
$\unicode{x3bb}>0.$
Applying the monotone class theorem, we obtain that
![]() $\mu $
is a quasi-stationary measure for
$\mu $
is a quasi-stationary measure for
![]() $Y_n$
on
$Y_n$
on
![]() $[0,1]$
.
$[0,1]$
.
In light of Proposition 6.5, to construct a non-trivial quasi-stationary measure for
![]() $Y_n$
on
$Y_n$
on
![]() $[0,1]$
, it remains to show that
$[0,1]$
, it remains to show that
 $$ \begin{align} \bigcap_{i\in \mathbb N} \overline{ \{\mu_{\varepsilon_{i+k}}\}_{i\in \mathbb N}}^{\mathrm{w}^*\text{-}\mathcal M(M)} \setminus \{\delta_0\} \neq \emptyset. \end{align} $$
$$ \begin{align} \bigcap_{i\in \mathbb N} \overline{ \{\mu_{\varepsilon_{i+k}}\}_{i\in \mathbb N}}^{\mathrm{w}^*\text{-}\mathcal M(M)} \setminus \{\delta_0\} \neq \emptyset. \end{align} $$
Note that for every
![]() $i\in \mathbb N$
,
$i\in \mathbb N$
,
![]() $\mu _{\varepsilon _i}(\mathrm {d} x) \ll \mathrm {Leb}(\mathrm {d} x)$
. To show that equation (6.6) holds, we study the behaviour of the distributions of
$\mu _{\varepsilon _i}(\mathrm {d} x) \ll \mathrm {Leb}(\mathrm {d} x)$
. To show that equation (6.6) holds, we study the behaviour of the distributions of
![]() $\mu _{\varepsilon _i}$
with respect to the Lebesgue measure.
$\mu _{\varepsilon _i}$
with respect to the Lebesgue measure.
The definition below provides conditions on a and b, which implies that equation (6.6) holds (see Theorem 6.9).
Definition 6.1. A pair
![]() $(a,b)\in \mathbb (0,4)\times (4,\infty )$
is called an admissible pair if either
$(a,b)\in \mathbb (0,4)\times (4,\infty )$
is called an admissible pair if either
-
•
 $a\geq 2;$
or
$a\geq 2;$
or -
• for every
 $x\in [(4 a^2 - a^3)/16,a/4]$
, (6.7)and
$x\in [(4 a^2 - a^3)/16,a/4]$
, (6.7)and $$ \begin{align} 0\leq \frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{2}{b} \bigg(1- \sqrt{1-\frac{4 x}{a}}\bigg)} \leq \frac{a}{4} \end{align} $$
(6.8)
$$ \begin{align} 0\leq \frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{2}{b} \bigg(1- \sqrt{1-\frac{4 x}{a}}\bigg)} \leq \frac{a}{4} \end{align} $$
(6.8) $$ \begin{align} &\frac{2 \big(\tanh ^{-1}\big(\sqrt{{2 \sqrt{1-({4 x}/{b})}+b-2}/{b}}\big)-\tanh ^{-1}\big(\sqrt{{a+2 \sqrt{1-({4 x}/{b})}-2}/{a}}\big)\big)}{2 \tanh ^{-1}\big(\sqrt{{2 \sqrt{1-({4 x}/{a})}+b-2}/{b}}\big)+\log ({a}/{4-a})}\nonumber\\&\quad\leq \frac{\sqrt{1-{4 x}/{b}}}{\sqrt{1-{4 x}/{a}}}. \end{align} $$
$$ \begin{align} &\frac{2 \big(\tanh ^{-1}\big(\sqrt{{2 \sqrt{1-({4 x}/{b})}+b-2}/{b}}\big)-\tanh ^{-1}\big(\sqrt{{a+2 \sqrt{1-({4 x}/{b})}-2}/{a}}\big)\big)}{2 \tanh ^{-1}\big(\sqrt{{2 \sqrt{1-({4 x}/{a})}+b-2}/{b}}\big)+\log ({a}/{4-a})}\nonumber\\&\quad\leq \frac{\sqrt{1-{4 x}/{b}}}{\sqrt{1-{4 x}/{a}}}. \end{align} $$
In Theorem 6.18, we show that if
![]() $(a,b)\in [1,4)\times (4,\infty )$
, then
$(a,b)\in [1,4)\times (4,\infty )$
, then
![]() $(a,b)$
is an admissible pair. Assuming that
$(a,b)$
is an admissible pair. Assuming that
![]() $(a,b)$
is an admissible pair, it is possible to show that
$(a,b)$
is an admissible pair, it is possible to show that
![]() $Y_n^{a,b}$
admits a non-trivial quasi-stationary measure on
$Y_n^{a,b}$
admits a non-trivial quasi-stationary measure on
![]() $[0,1].$
To accomplish this goal, we need the following three technical lemmas.
$[0,1].$
To accomplish this goal, we need the following three technical lemmas.
Lemma 6.6. Let
![]() $(a,b)$
be an admissible pair, with
$(a,b)$
be an admissible pair, with
![]() $a <2$
, and
$a <2$
, and
![]() $f:[0,1]\to {\mathbb R}$
be a function continuous by parts with a finite number of discontinuities, such that:
$f:[0,1]\to {\mathbb R}$
be a function continuous by parts with a finite number of discontinuities, such that:
-
(1)
 $0\leq f(x)$
for every
$0\leq f(x)$
for every
 $x\in [0,1];$
$x\in [0,1];$
-
(2) f is non-decreasing in the interval
 $[0,a/4];$
and
$[0,a/4];$
and -
(3) f is non-increasing in the interval
 $[a/4,1].$
$[a/4,1].$
Then
![]() $\mathcal L f$
is a continuous function such that:
$\mathcal L f$
is a continuous function such that:
-
(1)
 $0\leq \mathcal L f(x)$
for every
$0\leq \mathcal L f(x)$
for every
 $x\in [0,1];$
$x\in [0,1];$
-
(2)
 $\mathcal L f$
is non-decreasing in the interval
$\mathcal L f$
is non-decreasing in the interval
 $[0,(4a^2 - a^3)/16];$
and
$[0,(4a^2 - a^3)/16];$
and -
(3)
 $\mathcal L f$
is non-increasing in the interval
$\mathcal L f$
is non-increasing in the interval
 $[a/4,1].$
$[a/4,1].$
Proof. Recall that
 $$ \begin{align} \mathcal L f(x) = \int_{\alpha_-(x)}^{\alpha_+(x)} \frac{f(y)}{(b-a)y(1-y)} \ \mathrm{d} y - \int_{\beta_-(x\wedge a/4)}^{\beta_+(x\wedge a/4)} \frac{ f(y)}{(b-a)y(1-y)} \ \mathrm{d} y , \end{align} $$
$$ \begin{align} \mathcal L f(x) = \int_{\alpha_-(x)}^{\alpha_+(x)} \frac{f(y)}{(b-a)y(1-y)} \ \mathrm{d} y - \int_{\beta_-(x\wedge a/4)}^{\beta_+(x\wedge a/4)} \frac{ f(y)}{(b-a)y(1-y)} \ \mathrm{d} y , \end{align} $$
where
 $$ \begin{align*} \alpha_{\pm}(x) = \frac{1}{2} \pm \frac{1}{2}\sqrt{1 - \frac{4}{b}x}\quad \text{and}\quad \beta_{\pm}(x) = \frac{1}{2} \pm \frac{1}{2}\sqrt{1 - \frac{4}{a}x}. \end{align*} $$
$$ \begin{align*} \alpha_{\pm}(x) = \frac{1}{2} \pm \frac{1}{2}\sqrt{1 - \frac{4}{b}x}\quad \text{and}\quad \beta_{\pm}(x) = \frac{1}{2} \pm \frac{1}{2}\sqrt{1 - \frac{4}{a}x}. \end{align*} $$
It is clear that
![]() $\mathcal L f$
is continuous and a non-negative function. Observe that
$\mathcal L f$
is continuous and a non-negative function. Observe that
![]() $\mathcal L f$
is differentiable except for finitely many points. In fact, the derivative of
$\mathcal L f$
is differentiable except for finitely many points. In fact, the derivative of
![]() $\mathcal L f$
on the points where the derivative exists is given by
$\mathcal L f$
on the points where the derivative exists is given by

Since for every
![]() $x\in [a/4,1],$
$x\in [a/4,1],$
 $$ \begin{align*} \frac{\mathrm{d} \mathcal L f}{\mathrm{d} x}(x) = - \frac{1}{b-a}\frac{ f(\alpha_+ (x)) + f(\alpha_-(x))}{ x\sqrt{1-{4}/{b}x} } \leq 0,\end{align*} $$
$$ \begin{align*} \frac{\mathrm{d} \mathcal L f}{\mathrm{d} x}(x) = - \frac{1}{b-a}\frac{ f(\alpha_+ (x)) + f(\alpha_-(x))}{ x\sqrt{1-{4}/{b}x} } \leq 0,\end{align*} $$
if follows that
![]() $\mathcal L f$
is non-increasing in
$\mathcal L f$
is non-increasing in
![]() $[a/4,1].$
$[a/4,1].$
Observe that for every
![]() $x\in [0,a/4]$
, we obtain
$x\in [0,a/4]$
, we obtain
 $$ \begin{align*}\frac{1}{(b-a) x\sqrt{1-{4}/{b}x} } < \frac{1}{(b-a) x\sqrt{1- {4}/{a}x}}\quad \text{and}\quad \frac{a}{4} \leq \beta_+(x)\leq \alpha_+(x).\end{align*} $$
$$ \begin{align*}\frac{1}{(b-a) x\sqrt{1-{4}/{b}x} } < \frac{1}{(b-a) x\sqrt{1- {4}/{a}x}}\quad \text{and}\quad \frac{a}{4} \leq \beta_+(x)\leq \alpha_+(x).\end{align*} $$
Since f is non-increasing in
![]() $[a/4,1],$
we conclude that
$[a/4,1],$
we conclude that
To finish the proof, it is enough to show that
![]() $f(\beta _-(x)) \geq f(\alpha _-(x))$
for every
$f(\beta _-(x)) \geq f(\alpha _-(x))$
for every
![]() $x\in [0,(4a^2 - a^3)/16].$
Observe that since f is non-decreasing on
$x\in [0,(4a^2 - a^3)/16].$
Observe that since f is non-decreasing on
![]() $[0,a/4]$
, we obtain that for every
$[0,a/4]$
, we obtain that for every
![]() $x\in [0,(4a^2 - a^3)/16]$
,
$x\in [0,(4a^2 - a^3)/16]$
,
implying that
Lemma 6.7. Let
![]() $(a,b)$
be an admissible pair and
$(a,b)$
be an admissible pair and
![]() $\varepsilon \in (0,3/8)$
such that
$\varepsilon \in (0,3/8)$
such that
![]() $[(4a^2 - a^3)/16, a/4]\subset {M_\varepsilon }$
. Consider that sequence of functions
$[(4a^2 - a^3)/16, a/4]\subset {M_\varepsilon }$
. Consider that sequence of functions
![]() , then for every
, then for every
![]() $n\in \mathbb N$
, the following assertions hold:
$n\in \mathbb N$
, the following assertions hold:
-
(1)
 for every
for every
 $x\in [0,1];$
$x\in [0,1];$
-
(2)
 is non-decreasing in the interval
is non-decreasing in the interval
 $[0,(4a^2-a^3)/16];$
and
$[0,(4a^2-a^3)/16];$
and -
(3)
 is non-increasing in the interval
is non-increasing in the interval
 $[a/4,1].$
$[a/4,1].$
Proof. Recall that for every
![]() $\varepsilon \in (0,3/8)$
and
$\varepsilon \in (0,3/8)$
and
![]() $f\in \mathcal C^0(M_{\varepsilon })$
,
$f\in \mathcal C^0(M_{\varepsilon })$
,
![]() We divide the proof into two steps.
We divide the proof into two steps.
Step 1. We show the result for the case where
![]() $a\geq 2.$
$a\geq 2.$
We show the above result by induction on n. The case
![]() $n=0$
is immediately verified. Suppose that items
$n=0$
is immediately verified. Suppose that items
![]() $(1)$
,
$(1)$
,
![]() $(2)$
and
$(2)$
and
![]() $(3)$
are true for
$(3)$
are true for
![]() We will show that the same is true for
We will show that the same is true for
![]()
Item
![]() $(1)$
is trivially fulfilled since
$(1)$
is trivially fulfilled since
![]() $\mathcal L_\varepsilon $
is a positive operator. Additionally items
$\mathcal L_\varepsilon $
is a positive operator. Additionally items
![]() $(2)$
and
$(2)$
and
![]() $(3)$
follow from equation (6.10) and realizing that for every
$(3)$
follow from equation (6.10) and realizing that for every
![]() $(a,b)\in [2,4)\times (4,\infty )$
,
$(a,b)\in [2,4)\times (4,\infty )$
,
 $$ \begin{align*}\alpha_-(x) \leq \beta_-(x) \leq \frac{4a^2 - a^3}{16} \leq \frac{a}{4}\leq \beta_+(x) \leq \alpha_+(x)\quad \text{for every }x\in\bigg[0,\frac{4 a^2 - a^3}{16}\bigg].\end{align*} $$
$$ \begin{align*}\alpha_-(x) \leq \beta_-(x) \leq \frac{4a^2 - a^3}{16} \leq \frac{a}{4}\leq \beta_+(x) \leq \alpha_+(x)\quad \text{for every }x\in\bigg[0,\frac{4 a^2 - a^3}{16}\bigg].\end{align*} $$
This proves Step 1.
Step 2. We show that if
![]() $(a,b)$
is an admissible pair and
$(a,b)$
is an admissible pair and
![]() $a\in (0,2)$
, then:
$a\in (0,2)$
, then:
-
(1)
 for every
for every
 $x\in [0,1];$
$x\in [0,1];$
-
(2)
 is non-decreasing in the interval
is non-decreasing in the interval
 $[0,a/4];$
and
$[0,a/4];$
and -
(3)
 is non-increasing in the interval
is non-increasing in the interval
 $[a/4,1]$
.
$[a/4,1]$
.
We will prove that the above items hold by strong induction on n. For the cases
![]() $n=0$
and
$n=0$
and
![]() $n = 1$
, the computations can explicitly be done and such a conclusion is achieved.
$n = 1$
, the computations can explicitly be done and such a conclusion is achieved.
Now, suppose that the conclusions of Step
![]() $2$
are true for
$2$
are true for
and we will show that it is also true for
From Lemma 6.6, it follows that:
-
(1)
 for every
for every
 $x\in [0,1];$
$x\in [0,1];$
-
(2)
 is non-decreasing in the interval
is non-decreasing in the interval
 $[0,(4a^2 - a^3)/16];$
and
$[0,(4a^2 - a^3)/16];$
and -
(3)
 is non-increasing in the interval
is non-increasing in the interval
 $[a/4,1].$
$[a/4,1].$
It remains to show that
![]() $\mathcal L^{n+1}_\varepsilon {M_{\varepsilon }} $
is non-decreasing in
$\mathcal L^{n+1}_\varepsilon {M_{\varepsilon }} $
is non-decreasing in
![]() $[(4a^2 - a^3)/16,a/4].$
From the proof of the previous theorem, it is enough to show that
$[(4a^2 - a^3)/16,a/4].$
From the proof of the previous theorem, it is enough to show that

Observe that
 $$ \begin{align*} \alpha_-(x) <\frac{a}{4} < \beta_-(x) \quad \text{for every } x\in \bigg[\frac{4a^2 - a^3}{16},\frac{a}{4}\bigg]. \end{align*} $$
$$ \begin{align*} \alpha_-(x) <\frac{a}{4} < \beta_-(x) \quad \text{for every } x\in \bigg[\frac{4a^2 - a^3}{16},\frac{a}{4}\bigg]. \end{align*} $$
Therefore,

and

Since
![]() $(a,b)$
is an admissible pair, equation (6.7) implies that for every
$(a,b)$
is an admissible pair, equation (6.7) implies that for every
![]() $x\in [(4a^2 - a^3)/16,a/4]$
,
$x\in [(4a^2 - a^3)/16,a/4]$
,
This implies that

where
However, from the induction hypothesis and equation (6.12),

where
 $$ \begin{align*}I_2^{(a,b)}(x) :=\bigg( 2\tanh ^{-1}\bigg(\sqrt{{2 \sqrt{1-{4 x}/{a}}+b-2}/{b}}\bigg)+\log \bigg(\frac{a}{4-a}\bigg)\bigg).\end{align*} $$
$$ \begin{align*}I_2^{(a,b)}(x) :=\bigg( 2\tanh ^{-1}\bigg(\sqrt{{2 \sqrt{1-{4 x}/{a}}+b-2}/{b}}\bigg)+\log \bigg(\frac{a}{4-a}\bigg)\bigg).\end{align*} $$
Combining the above three equations, equation (6.8) and using the definition of admissible pair, we obtain that equation (6.11) holds. This proves Step
![]() $2$
.
$2$
.
Observe the above two steps imply the proof of the lemma.
Recall from Proposition 6.4, for every
![]() $i\in \mathbb N$
,
$i\in \mathbb N$
,
where we set
![]() $g_{\varepsilon _i}(x) =0$
for every
$g_{\varepsilon _i}(x) =0$
for every
![]() $x\in M\setminus M_{\varepsilon _i}.$
$x\in M\setminus M_{\varepsilon _i}.$
Lemma 6.8. Let
![]() $(a,b)$
be an admissible pair. Then, for every
$(a,b)$
be an admissible pair. Then, for every
![]() $i\in \mathbb N$
:
$i\in \mathbb N$
:
-
(1)
 $0\leq g_{\varepsilon _i} (x)$
for every
$0\leq g_{\varepsilon _i} (x)$
for every
 $x\in [0,1];$
$x\in [0,1];$
-
(2)
 $ g_{\varepsilon _i}(x)$
is non-decreasing in the interval
$ g_{\varepsilon _i}(x)$
is non-decreasing in the interval
 $[0,(4a^2 - a^3)/16];$
and
$[0,(4a^2 - a^3)/16];$
and -
(3)
 $ g_{\varepsilon _i} (x)$
is non-increasing in the interval
$ g_{\varepsilon _i} (x)$
is non-increasing in the interval
 $[a/4,1].$
$[a/4,1].$
Proof. Recall that for every
![]() $i\in \mathbb N$
and
$i\in \mathbb N$
and
![]() $f\in \mathcal C^0(M_{\varepsilon _i})$
,
$f\in \mathcal C^0(M_{\varepsilon _i})$
,
Observe that if
![]() $(a,b)$
is an admissible pair and
$(a,b)$
is an admissible pair and
![]() $i\in \mathbb N$
, then
$i\in \mathbb N$
, then
![]() $\mathcal L_{\varepsilon _i} :\mathcal C^0(M_{\varepsilon _i} )\to \mathcal C^0(M_{\varepsilon _i} )$
is an irreducible compact operator. Moreover, it is readily verified that
$\mathcal L_{\varepsilon _i} :\mathcal C^0(M_{\varepsilon _i} )\to \mathcal C^0(M_{\varepsilon _i} )$
is an irreducible compact operator. Moreover, it is readily verified that
![]() $\mathcal L_{\varepsilon _i} $
admits a single eigenvalue in its peripheral spectrum, implying that
$\mathcal L_{\varepsilon _i} $
admits a single eigenvalue in its peripheral spectrum, implying that

for some
![]() $\alpha _{\varepsilon _i}>0.$
$\alpha _{\varepsilon _i}>0.$
The lemma follows directly from the above equation in combination with Lemma 6.7.
Combining Lemmas 6.6, 6.7 and 6.8, we obtain the following result.
Theorem 6.9. Let
![]() $(a,b)$
be an admissible pair. Then the absorbing Markov chain
$(a,b)$
be an admissible pair. Then the absorbing Markov chain
![]() $Y_n^{a,b}$
admits a quasi-stationary measure
$Y_n^{a,b}$
admits a quasi-stationary measure
![]() $\mu $
on
$\mu $
on
![]() $[0,1]$
different from
$[0,1]$
different from
![]() $\delta _0.$
$\delta _0.$
Proof. For every
![]() $i\in \mathbb N$
, let
$i\in \mathbb N$
, let
![]() $\mu _{\varepsilon _i}(\mathrm {d} x) = g_{\varepsilon _i} (x) \mathrm {d} x$
be the unique quasi-stationary measures for
$\mu _{\varepsilon _i}(\mathrm {d} x) = g_{\varepsilon _i} (x) \mathrm {d} x$
be the unique quasi-stationary measures for
![]() $Y_n^{\varepsilon _i}$
on
$Y_n^{\varepsilon _i}$
on
![]() $M_{\varepsilon _i}$
given by Proposition 6.4 and extend it to
$M_{\varepsilon _i}$
given by Proposition 6.4 and extend it to
![]() $[0,1]$
in a way that
$[0,1]$
in a way that
![]() $\mu _{\varepsilon _i}( M\setminus M_{\varepsilon _i} ) = 0. $
$\mu _{\varepsilon _i}( M\setminus M_{\varepsilon _i} ) = 0. $
Since
![]() $\mathcal M_1 ([0,1])$
is sequentially compact in the weak
$\mathcal M_1 ([0,1])$
is sequentially compact in the weak
![]() $^*$
topology, we can assume without loss of generality (passing to a subsequence if necessary) that the sequence of real numbers
$^*$
topology, we can assume without loss of generality (passing to a subsequence if necessary) that the sequence of real numbers
![]() $\{\varepsilon _i\}_{i\in \mathbb N}$
is such that
$\{\varepsilon _i\}_{i\in \mathbb N}$
is such that
![]() $\lim _{i\to \infty } \varepsilon _i = 0, \mu _{\varepsilon _i} \to \mu \ \text {in the weak}^{*}\ \text {topology}$
and
$\lim _{i\to \infty } \varepsilon _i = 0, \mu _{\varepsilon _i} \to \mu \ \text {in the weak}^{*}\ \text {topology}$
and
![]() $\lim _{i\to \infty } \unicode{x3bb} _{\varepsilon _i} = \unicode{x3bb} \geq ({4-a})/({b-a}).$
$\lim _{i\to \infty } \unicode{x3bb} _{\varepsilon _i} = \unicode{x3bb} \geq ({4-a})/({b-a}).$
From Proposition 6.5, the probability measure
![]() $\mu $
is a quasi-stationary measure of
$\mu $
is a quasi-stationary measure of
![]() ${\mathcal P}$
. It remains to show that
${\mathcal P}$
. It remains to show that
![]() $\mu \neq \delta _0.$
Suppose by contradiction that
$\mu \neq \delta _0.$
Suppose by contradiction that
![]() $\mu = \delta _0.$
Then,
$\mu = \delta _0.$
Then,
![]() $\lim _{i\to \infty } \mu _{\varepsilon _i}([0,(4a^2 -a^3)/32]) = 1. $
However, from Lemma 6.8, it follows that
$\lim _{i\to \infty } \mu _{\varepsilon _i}([0,(4a^2 -a^3)/32]) = 1. $
However, from Lemma 6.8, it follows that
Taking the limit as
![]() $i\to \infty $
, we obtain that
$i\to \infty $
, we obtain that
![]() $1 \leq \mu ([4a^2 -a^3)/32,(4a^2 -a^3)/16])$
, which is a contradiction, implying that
$1 \leq \mu ([4a^2 -a^3)/32,(4a^2 -a^3)/16])$
, which is a contradiction, implying that
![]() $\mu \neq \delta _0.$
$\mu \neq \delta _0.$
Remark 6.10. Observe that without assuming that
![]() $(a,b)$
is an admissible pair, the inductive step presented in Step 2 of Lemma 6.7 no longer holds. Without this lemma, the core argument in the proof of Theorem 6.9 cannot be applied, and the existence of a non-trivial quasi-stationary measure for
$(a,b)$
is an admissible pair, the inductive step presented in Step 2 of Lemma 6.7 no longer holds. Without this lemma, the core argument in the proof of Theorem 6.9 cannot be applied, and the existence of a non-trivial quasi-stationary measure for
![]() $Y_n^{a,b}$
becomes unclear.
$Y_n^{a,b}$
becomes unclear.
From now on, we define
![]() $\mu _{a,b} = \mu $
as a non-trivial quasi-stationary measure for
$\mu _{a,b} = \mu $
as a non-trivial quasi-stationary measure for
![]() $Y_n$
on
$Y_n$
on
![]() $[0,1]$
and
$[0,1]$
and
![]() $\unicode{x3bb} _{a,b} =\unicode{x3bb} $
its associated survival rate (given by Theorem 6.9). The next proposition shows that
$\unicode{x3bb} _{a,b} =\unicode{x3bb} $
its associated survival rate (given by Theorem 6.9). The next proposition shows that
![]() $\mu $
is absolutely continuous to the Lebesgue measure.
$\mu $
is absolutely continuous to the Lebesgue measure.
Proposition 6.11. Let
![]() $(a,b)$
be an admissible pair. Then,
$(a,b)$
be an admissible pair. Then,
![]() $\mu \ll \mathrm {Leb}(\mathrm {d} x)$
and
$\mu \ll \mathrm {Leb}(\mathrm {d} x)$
and
![]() $0<\unicode{x3bb} < 1.$
$0<\unicode{x3bb} < 1.$
Proof. We can decompose
![]() $\mu (\mathrm {d} x) = \mu (\{0\})\delta _0(\mathrm {d} x) + \mu '(\mathrm {d} x) + \mu (\{1\})\delta _1(\mathrm {d} x).$
$\mu (\mathrm {d} x) = \mu (\{0\})\delta _0(\mathrm {d} x) + \mu '(\mathrm {d} x) + \mu (\{1\})\delta _1(\mathrm {d} x).$
Since
![]() $\delta _0 \neq \mu $
, we obtain that
$\delta _0 \neq \mu $
, we obtain that
![]() $\mu (\{0\}) \neq 1.$
Observe that
$\mu (\{0\}) \neq 1.$
Observe that
 $$ \begin{align*} \unicode{x3bb} \mu(\{0\}) \delta_0(\mathrm{d} x) + \unicode{x3bb} \mu'(\mathrm{d} x) + \unicode{x3bb} \mu(\{1\}) \delta_1(\mathrm{d} x) &= \unicode{x3bb} \mu(\mathrm{d} x)\\ &= {\mathcal P}^*(\mu)(\mathrm{d} x)\\ &= (\mu(\{1\}) + \mu\{0\}) \delta_0(\mathrm{d} x) + {\mathcal P}^* (\mu'). \end{align*} $$
$$ \begin{align*} \unicode{x3bb} \mu(\{0\}) \delta_0(\mathrm{d} x) + \unicode{x3bb} \mu'(\mathrm{d} x) + \unicode{x3bb} \mu(\{1\}) \delta_1(\mathrm{d} x) &= \unicode{x3bb} \mu(\mathrm{d} x)\\ &= {\mathcal P}^*(\mu)(\mathrm{d} x)\\ &= (\mu(\{1\}) + \mu\{0\}) \delta_0(\mathrm{d} x) + {\mathcal P}^* (\mu'). \end{align*} $$
Since
![]() ${\mathcal P}^*(\mu ') \ll \mathrm {Leb}(\mathrm {d} x)$
, it follows that
${\mathcal P}^*(\mu ') \ll \mathrm {Leb}(\mathrm {d} x)$
, it follows that
![]() ${\mathcal P}^*(\mu ')(\{1\}) =0,$
implying that
${\mathcal P}^*(\mu ')(\{1\}) =0,$
implying that
and
We claim that
![]() $\unicode{x3bb} < 1.$
Suppose, by contradiction, the opposite that
$\unicode{x3bb} < 1.$
Suppose, by contradiction, the opposite that
![]() $\unicode{x3bb} =1$
, then
$\unicode{x3bb} =1$
, then
Since
![]() pointwise as
pointwise as
![]() $n\to \infty ,$
we have, by the Lebesgue dominated convergence theorem,
$n\to \infty ,$
we have, by the Lebesgue dominated convergence theorem,
which is contradiction since
![]() $\mu (\{0\}) \neq 1.$
$\mu (\{0\}) \neq 1.$
This implies that
![]() $\unicode{x3bb} < 1$
and therefore
$\unicode{x3bb} < 1$
and therefore
![]() $\mu (\{0\}) = 0.$
Therefore,
$\mu (\{0\}) = 0.$
Therefore,
![]() $\mu (\{0\}\cup \{1\}) = 0$
and
$\mu (\{0\}\cup \{1\}) = 0$
and
From now on, we define
The next result summarizes the properties of
![]() $g.$
$g.$
Proposition 6.12. Let
![]() $(a,b)$
be an admissible pair. Then the function g fulfils the following properties:
$(a,b)$
be an admissible pair. Then the function g fulfils the following properties:
-
(i)
 $g \in \mathcal C^0(M);$
$g \in \mathcal C^0(M);$
-
(ii) g is non-decreasing in the interval
 $[0,4a^2 -a^3)/16];$
$[0,4a^2 -a^3)/16];$
-
(iii) g is non-increasing in the interval
 $[a/4,1]$
;
$[a/4,1]$
; -
(iv) there exists
 $k>0$
such that
$k>0$
such that
 $k<g(x)$
for every
$k<g(x)$
for every
 $x\in M.$
$x\in M.$
Proof. We divide this proof into
![]() $3$
steps.
$3$
steps.
Step 1. We show that
![]() $g(x)>0$
for every
$g(x)>0$
for every
![]() $x\in (0,1].$
$x\in (0,1].$
Suppose that there exists
![]() $x \in (0,1]$
such that
$x \in (0,1]$
such that
![]() $g(x) = 0.$
Therefore,
$g(x) = 0.$
Therefore,
 $$ \begin{align*}0 = \unicode{x3bb} g(x) = \int_{\alpha_-(x)}^{\alpha_+(x)}\frac{g(y)}{(b-a)y(1-y)} \mathrm{d} y - \int_{\beta_-(x\wedge a/4)}^{\beta_+(x\wedge a/4)}\frac{g(y)}{(b-a)y(1-y)} \mathrm{d} y. \end{align*} $$
$$ \begin{align*}0 = \unicode{x3bb} g(x) = \int_{\alpha_-(x)}^{\alpha_+(x)}\frac{g(y)}{(b-a)y(1-y)} \mathrm{d} y - \int_{\beta_-(x\wedge a/4)}^{\beta_+(x\wedge a/4)}\frac{g(y)}{(b-a)y(1-y)} \mathrm{d} y. \end{align*} $$
This implies that
Let
![]() $x_0 \in \mathrm {supp}(\mu )\cap (0,1).$
By the same arguments presented in the proof of Proposition 6.4, we can show that there exist
$x_0 \in \mathrm {supp}(\mu )\cap (0,1).$
By the same arguments presented in the proof of Proposition 6.4, we can show that there exist
![]() $n_0 = n_0(x,I_1)$
such that
$n_0 = n_0(x,I_1)$
such that
![]() ${\mathcal P}^{n_0}(x_0, I_1)>0.$
Since
${\mathcal P}^{n_0}(x_0, I_1)>0.$
Since
![]() ${\mathcal P}^{n_0}(x_0,I_1)$
is a continuous function, there exists an open neighbourhood
${\mathcal P}^{n_0}(x_0,I_1)$
is a continuous function, there exists an open neighbourhood
![]() $B \subset (0,1)$
of x such that
$B \subset (0,1)$
of x such that
Therefore,
which is a contradiction. Therefore,
![]() $g(x)>0$
for every
$g(x)>0$
for every
![]() $x\in (0,1].$
$x\in (0,1].$
Step 2. We show
![]() $(i),(ii)$
and
$(i),(ii)$
and
![]() $(iii).$
$(iii).$
Recall that for every
![]() $i\in \mathbb N$
,
$i\in \mathbb N$
,
![]() This observation, combined with Theorem 6.8 and Lemma 6.6, implies that
This observation, combined with Theorem 6.8 and Lemma 6.6, implies that
Let
 $$ \begin{align*} J := \bigcup_{x\in[({4a^2 - a^3})/{16},{a}/{4}]} ( [\alpha_-(x),\beta_-(x) \land a/4 ]\cup [\beta_-(x) \land a/4, \alpha_+(x) \land a/4])\subset (0,1),\end{align*} $$
$$ \begin{align*} J := \bigcup_{x\in[({4a^2 - a^3})/{16},{a}/{4}]} ( [\alpha_-(x),\beta_-(x) \land a/4 ]\cup [\beta_-(x) \land a/4, \alpha_+(x) \land a/4])\subset (0,1),\end{align*} $$
and observe that J is a compact set. Finally,
 $$ \begin{align} 0&\leq g_{\varepsilon_i}(x) \leq \frac{1}{\unicode{x3bb}_{\varepsilon_i}} \mathcal{L} g_{\varepsilon_i}(x) \leq \frac{1}{\unicode{x3bb}_\varepsilon}\sup_{y\in [({4a^2 - a^3})/{16},{a}/{4}]}\mathcal{L} g_{\varepsilon_i}(y)\nonumber\leq \frac{1}{\unicode{x3bb}_{\varepsilon_i}}\!\int_{J}\frac{g_{\varepsilon_i} (y)}{(b-a)y(1-y)} \mathrm{d} y\\ &\leq \sup_{y\in J}\frac{1}{4 y (1-y)} \sup_{i\in\mathbb N} \frac{1}{\unicode{x3bb}_{\varepsilon_i}}=: C <\infty. \end{align} $$
$$ \begin{align} 0&\leq g_{\varepsilon_i}(x) \leq \frac{1}{\unicode{x3bb}_{\varepsilon_i}} \mathcal{L} g_{\varepsilon_i}(x) \leq \frac{1}{\unicode{x3bb}_\varepsilon}\sup_{y\in [({4a^2 - a^3})/{16},{a}/{4}]}\mathcal{L} g_{\varepsilon_i}(y)\nonumber\leq \frac{1}{\unicode{x3bb}_{\varepsilon_i}}\!\int_{J}\frac{g_{\varepsilon_i} (y)}{(b-a)y(1-y)} \mathrm{d} y\\ &\leq \sup_{y\in J}\frac{1}{4 y (1-y)} \sup_{i\in\mathbb N} \frac{1}{\unicode{x3bb}_{\varepsilon_i}}=: C <\infty. \end{align} $$
Therefore, we obtain a uniform bound for
![]() $\{ g_{\varepsilon _i}\}_{i\in \mathbb N}$
on
$\{ g_{\varepsilon _i}\}_{i\in \mathbb N}$
on
![]() $L^{\infty }(M)$
for n big enough. For every
$L^{\infty }(M)$
for n big enough. For every
![]() $\delta>0,$
consider the map
$\delta>0,$
consider the map

From the Arzelà–Ascoli theorem, it is readily verified that
![]() $T_\delta $
is a compact operator for every
$T_\delta $
is a compact operator for every
![]() $0 <\delta <1/2$
. From equation (6.13), we obtain that there exists a subsequence
$0 <\delta <1/2$
. From equation (6.13), we obtain that there exists a subsequence
![]() $\{\mathcal L g_{\varepsilon _{i_n}}\}_{n\in \mathbb N} \subset \{\mathcal L g_{\varepsilon _{i}}\}_{i\in \mathbb N} $
and
$\{\mathcal L g_{\varepsilon _{i_n}}\}_{n\in \mathbb N} \subset \{\mathcal L g_{\varepsilon _{i}}\}_{i\in \mathbb N} $
and
![]() $f_\delta \in \mathcal C^0([\delta ,1-\delta ])$
such that
$f_\delta \in \mathcal C^0([\delta ,1-\delta ])$
such that
Choosing an interval
![]() $I_\delta \subset [\delta ,1-\delta ]$
, observe that
$I_\delta \subset [\delta ,1-\delta ]$
, observe that
it follows that
 $$ \begin{align*} \int_{I_\delta} f_{\delta}(y) \,\mathrm{d} x = \lim_{n\to\infty } \int_{I_\delta} \mathcal L g_{\varepsilon_{i_n}}(x)\,\mathrm{d} x = \lim_{n\to\infty } \int_{0}^{1} {\mathcal P} (x,I_\delta) g_{\varepsilon_{i_n}}(x)\,\mathrm{d} x = \int_{I_\delta} \unicode{x3bb} g (x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} \int_{I_\delta} f_{\delta}(y) \,\mathrm{d} x = \lim_{n\to\infty } \int_{I_\delta} \mathcal L g_{\varepsilon_{i_n}}(x)\,\mathrm{d} x = \lim_{n\to\infty } \int_{0}^{1} {\mathcal P} (x,I_\delta) g_{\varepsilon_{i_n}}(x)\,\mathrm{d} x = \int_{I_\delta} \unicode{x3bb} g (x)\,\mathrm{d} x. \end{align*} $$
Since
![]() $I_\delta $
is an arbitrary interval subset of
$I_\delta $
is an arbitrary interval subset of
![]() $[\delta ,1-\delta ]$
, we obtain
$[\delta ,1-\delta ]$
, we obtain
![]() $f_\delta =\unicode{x3bb} g|_{[\delta ,1-\delta ]}$
. Using that for every subsequence of
$f_\delta =\unicode{x3bb} g|_{[\delta ,1-\delta ]}$
. Using that for every subsequence of
there exists subsubsequence converging to
, we obtain that
Since
![]() $\{g_{\varepsilon _i}\}_{i\in \mathbb N}$
is bounded
$\{g_{\varepsilon _i}\}_{i\in \mathbb N}$
is bounded
![]() $L^\infty (M,\mu )$
and g lies in
$L^\infty (M,\mu )$
and g lies in
![]() $L^1(M,\mu ),$
the above equation implies that
$L^1(M,\mu ),$
the above equation implies that
Thus, there exists a subsequence
![]() $\{g_{\varepsilon _{n_i}}\}_{i\in \mathbb N} \subset \{g_{\varepsilon _{n}}\}_{n\in \mathbb N} $
such that
$\{g_{\varepsilon _{n_i}}\}_{i\in \mathbb N} \subset \{g_{\varepsilon _{n}}\}_{n\in \mathbb N} $
such that
Therefore, for
![]() $\mu $
-almost every
$\mu $
-almost every
![]() $x\in M$
,
$x\in M$
,
which implies that g is
![]() $L^\infty ([0,1])$
. Since for every
$L^\infty ([0,1])$
. Since for every
![]() $i\in \mathbb N$
:
$i\in \mathbb N$
:
-
(1)
 $ \mathcal {L} g_{\varepsilon _{n_i}}$
is non-decreasing in the interval
$ \mathcal {L} g_{\varepsilon _{n_i}}$
is non-decreasing in the interval
 $[0,(4a^2 - a^3)/16];$
and
$[0,(4a^2 - a^3)/16];$
and -
(2)
 $ \mathcal {L} g_{\varepsilon _{n_i}}$
is non-increasing in the interval
$ \mathcal {L} g_{\varepsilon _{n_i}}$
is non-increasing in the interval
 $[a/4,1],$
$[a/4,1],$
from equation (6.14) and the continuity of g on
![]() $(0,1]$
, we obtain that:
$(0,1]$
, we obtain that:
-
(1) g is non-decreasing in the interval
 $[0,(4a^2 - a^3)/16];$
and
$[0,(4a^2 - a^3)/16];$
and -
(2) g is non-increasing in the interval
 $[a/4,1].$
$[a/4,1].$
The proof is finished observing that
![]() $g\in \mathcal C^0([0,1])$
when imposing
$g\in \mathcal C^0([0,1])$
when imposing
![]() $g(0) := \inf _{x\in (0,a/4)} g(x). $
$g(0) := \inf _{x\in (0,a/4)} g(x). $
Step 3. We show item (iv).
Observe that in virtue of Step 2, it is enough to show that
![]() $g(0)>0$
. Since g is continuous, it follows that
$g(0)>0$
. Since g is continuous, it follows that
 $$ \begin{align*}\lim_{\varepsilon \to 0} \frac{1}{\varepsilon}\int_0^\varepsilon g(y) \,\mathrm{d} y = g(0). \end{align*} $$
$$ \begin{align*}\lim_{\varepsilon \to 0} \frac{1}{\varepsilon}\int_0^\varepsilon g(y) \,\mathrm{d} y = g(0). \end{align*} $$
Since
![]() $g(x)\,\mathrm {d} x$
is a quasi-stationary measure of
$g(x)\,\mathrm {d} x$
is a quasi-stationary measure of
![]() $Y_n$
on
$Y_n$
on
![]() $[0,1]$
, we obtain that
$[0,1]$
, we obtain that
 $$ \begin{align*} \int_0^\varepsilon g(y)\mathrm{d} y = \frac{1}{\unicode{x3bb}} \int_0^1 {\mathcal P}(y,[0,\varepsilon]) g(y)\, \mathrm{d} y. \end{align*} $$
$$ \begin{align*} \int_0^\varepsilon g(y)\mathrm{d} y = \frac{1}{\unicode{x3bb}} \int_0^1 {\mathcal P}(y,[0,\varepsilon]) g(y)\, \mathrm{d} y. \end{align*} $$
It is clear that
Since g is decreasing in
![]() $[a/4,1]$
and
$[a/4,1]$
and
![]() $g(1)>0$
, it follows that
$g(1)>0$
, it follows that
 $$ \begin{align*} \int_0^\varepsilon g(y)\,\mathrm{d} y = \frac{1}{\unicode{x3bb}} \int_0^1 {\mathcal P}(y,[0,\varepsilon]) g(y) \mathrm{d} y \geq \frac{g(1)}{\unicode{x3bb}} \bigg(1- \alpha_+(\varepsilon)\bigg) = \frac{g(1)}{\unicode{x3bb}} \bigg(\frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{4 \varepsilon }{b}}\bigg).\end{align*} $$
$$ \begin{align*} \int_0^\varepsilon g(y)\,\mathrm{d} y = \frac{1}{\unicode{x3bb}} \int_0^1 {\mathcal P}(y,[0,\varepsilon]) g(y) \mathrm{d} y \geq \frac{g(1)}{\unicode{x3bb}} \bigg(1- \alpha_+(\varepsilon)\bigg) = \frac{g(1)}{\unicode{x3bb}} \bigg(\frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{4 \varepsilon }{b}}\bigg).\end{align*} $$
Finally,
 $$ \begin{align*} g(0) &= \lim_{\varepsilon \to 0} \frac{1}{\varepsilon} \int_0^\varepsilon g(y)\mathrm{d} y \geq \lim_{\varepsilon \to 0} \frac{1}{\varepsilon} \frac{g(1)}{\unicode{x3bb}} \bigg(\frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{4 \varepsilon }{b}}\bigg) = \frac{g(1)}{b\unicode{x3bb}}>0. \end{align*} $$
$$ \begin{align*} g(0) &= \lim_{\varepsilon \to 0} \frac{1}{\varepsilon} \int_0^\varepsilon g(y)\mathrm{d} y \geq \lim_{\varepsilon \to 0} \frac{1}{\varepsilon} \frac{g(1)}{\unicode{x3bb}} \bigg(\frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{4 \varepsilon }{b}}\bigg) = \frac{g(1)}{b\unicode{x3bb}}>0. \end{align*} $$
Combining Steps 1–3, we conclude the proof of the theorem.
To apply Theorem 2.4, we need to show that
![]() ${\mathcal P}$
admits an eigenfunction lying in
${\mathcal P}$
admits an eigenfunction lying in
![]() $L^1([0,1],\mathrm {Leb}).$
To do this, consider the operator
$L^1([0,1],\mathrm {Leb}).$
To do this, consider the operator
 $$ \begin{align*} T: \mathcal C^0([0,1])&\to \mathcal C^0([0,1]),\\ f&\mapsto \frac{\mathcal L(g f)}{\unicode{x3bb} g}. \end{align*} $$
$$ \begin{align*} T: \mathcal C^0([0,1])&\to \mathcal C^0([0,1]),\\ f&\mapsto \frac{\mathcal L(g f)}{\unicode{x3bb} g}. \end{align*} $$
It is clear that T is a Markov operator that is:
-
(1)
 $T: \mathcal C^0([0,1])\to \mathcal C^0([0,1])$
is a bounded positive linear operator;
$T: \mathcal C^0([0,1])\to \mathcal C^0([0,1])$
is a bounded positive linear operator; -
(2)
 $T1 =1.$
$T1 =1.$
Proposition 6.13. Let
![]() $(a,b)$
be an admissible pair. Then there exists a probability
$(a,b)$
be an admissible pair. Then there exists a probability
![]() $\nu \ll \mathrm {Leb}$
such that
$\nu \ll \mathrm {Leb}$
such that
![]() $\nu $
is a fixed point of the operator
$\nu $
is a fixed point of the operator
![]() $T^*: \mathcal M(M) \to \mathcal M(M)$
.
$T^*: \mathcal M(M) \to \mathcal M(M)$
.
Proof. Since T is a Markov operator, it is well known that there exists a probability measure
![]() $\nu $
such that
$\nu $
such that
![]() $T^*\nu = \nu $
(see [Reference Eisner, Farkas, Haase and Nagel10, Ch. 10]).
$T^*\nu = \nu $
(see [Reference Eisner, Farkas, Haase and Nagel10, Ch. 10]).
Let us decompose
![]() $\nu $
as
$\nu $
as
where
![]() $\nu \in \mathcal M_1(M)$
and
$\nu \in \mathcal M_1(M)$
and
![]() $\nu '(\{0\} \cup \{1\}) = 0.$
$\nu '(\{0\} \cup \{1\}) = 0.$
Since
 $$ \begin{align*} \mathcal L (fg)(0) &= \frac{1}{b-a}\lim_{x\to 0} \bigg(\int_{\alpha_-(x)}^{\beta_-(x)} \frac{f(y)g(y)}{ y(1-y)} \mathrm{d} y + \int_{\beta_+(x)}^{\alpha_+(x)} \frac{f(y)g(y)}{ y(1-y)} \mathrm{d} y \bigg) \\ &= \frac{\log(b/a)}{b-a}f(0)g(0) + \frac{\log(b/a)}{b-a}f(1)g(1), \end{align*} $$
$$ \begin{align*} \mathcal L (fg)(0) &= \frac{1}{b-a}\lim_{x\to 0} \bigg(\int_{\alpha_-(x)}^{\beta_-(x)} \frac{f(y)g(y)}{ y(1-y)} \mathrm{d} y + \int_{\beta_+(x)}^{\alpha_+(x)} \frac{f(y)g(y)}{ y(1-y)} \mathrm{d} y \bigg) \\ &= \frac{\log(b/a)}{b-a}f(0)g(0) + \frac{\log(b/a)}{b-a}f(1)g(1), \end{align*} $$
we obtain that
From a similar computation, we obtain that
 $$ \begin{align} Tf(1) = \frac{1}{ \unicode{x3bb} g(1)}\int_{\alpha_-(1)}^{\alpha_+(1)} f(x) g(x) \,\mathrm{d} x. \end{align} $$
$$ \begin{align} Tf(1) = \frac{1}{ \unicode{x3bb} g(1)}\int_{\alpha_-(1)}^{\alpha_+(1)} f(x) g(x) \,\mathrm{d} x. \end{align} $$
Note that given
![]() $A\in \mathscr B([0,1])$
such that
$A\in \mathscr B([0,1])$
such that
![]() $\mathrm {Leb}(A)= 0$
and
$\mathrm {Leb}(A)= 0$
and
![]() $A \subset [\delta , 1-\delta ]$
for some
$A \subset [\delta , 1-\delta ]$
for some
![]() $\delta>0,$
then
$\delta>0,$
then
This implies that

since
![]() $\nu '(\{0\} \cup \{1\}) = 0$
, we obtain
$\nu '(\{0\} \cup \{1\}) = 0$
, we obtain
Combining
![]() $T^*\nu = \nu $
, and equations (6.15), (6.16) and (6.17), we obtain that
$T^*\nu = \nu $
, and equations (6.15), (6.16) and (6.17), we obtain that
![]() $\nu ' \ll \mathrm {Leb}(\mathrm {d} x). $
$\nu ' \ll \mathrm {Leb}(\mathrm {d} x). $
Let
![]() $\{f_n\}_{n\in \mathbb N} \in \mathcal C^0(M)$
be a sequence of continuous functions such that:
$\{f_n\}_{n\in \mathbb N} \in \mathcal C^0(M)$
be a sequence of continuous functions such that:
-
(1)
 $0\leq f_n (x)\leq 1$
for every
$0\leq f_n (x)\leq 1$
for every
 $n\in \mathbb N$
and
$n\in \mathbb N$
and
 $x\in [0,1];$
$x\in [0,1];$
-
(2)
 $f_n (1) =1;$
and
$f_n (1) =1;$
and -
(3)
 $f_n(x) =0$
for every
$f_n(x) =0$
for every
 $x\in [0,1-1/n].$
$x\in [0,1-1/n].$
Since
![]() $T^*\nu = \nu $
and
$T^*\nu = \nu $
and
![]() $f_n$
is continuous, it follows that
$f_n$
is continuous, it follows that
The left-hand side of equation (6.18) is equal to
and the right-hand side of equation (6.18) is equal to
 $$ \begin{align*} &\int_M f_n(x) T^*\nu(\mathrm{d} x)\\ &\quad= \alpha_1\bigg( \frac{\log(b/a)}{(b-a)\unicode{x3bb} }f_n(0) + \frac{\log(b/a) g(1)}{(b-a) g(0)\unicode{x3bb}}f_n(1)\bigg) + \alpha_2 \int_0^1 f_n(x)T^*\nu(\mathrm{d} x) \\ &\qquad + \alpha_3 \frac{1}{\unicode{x3bb} g(1)}\int_{\alpha_-(1)}^{\alpha_+(1)} f_n(x) g(x) \,\mathrm{d} x\\ &\quad= \alpha_1 \frac{\log(b/a)}{b-a} \frac{ g(1)}{\unicode{x3bb} g(0)} + \alpha_2 \int_0^1 f_n(x)T^*\nu(\mathrm{d} x)+ \alpha_3 \frac{1}{\unicode{x3bb} g(1)}\int_{\alpha_-(1)}^{\alpha_+(1)} f_n(x) g(x) \,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\int_M f_n(x) T^*\nu(\mathrm{d} x)\\ &\quad= \alpha_1\bigg( \frac{\log(b/a)}{(b-a)\unicode{x3bb} }f_n(0) + \frac{\log(b/a) g(1)}{(b-a) g(0)\unicode{x3bb}}f_n(1)\bigg) + \alpha_2 \int_0^1 f_n(x)T^*\nu(\mathrm{d} x) \\ &\qquad + \alpha_3 \frac{1}{\unicode{x3bb} g(1)}\int_{\alpha_-(1)}^{\alpha_+(1)} f_n(x) g(x) \,\mathrm{d} x\\ &\quad= \alpha_1 \frac{\log(b/a)}{b-a} \frac{ g(1)}{\unicode{x3bb} g(0)} + \alpha_2 \int_0^1 f_n(x)T^*\nu(\mathrm{d} x)+ \alpha_3 \frac{1}{\unicode{x3bb} g(1)}\int_{\alpha_-(1)}^{\alpha_+(1)} f_n(x) g(x) \,\mathrm{d} x. \end{align*} $$
Taking the limit as
![]() $n\to \infty $
in equation (6.18), we obtain that
$n\to \infty $
in equation (6.18), we obtain that
Repeating the same argument with the sequence
![]() $\{f_n(1-x)\}_{n\in \mathbb N} \subset \mathcal C^0([0,1])$
, we obtain that
$\{f_n(1-x)\}_{n\in \mathbb N} \subset \mathcal C^0([0,1])$
, we obtain that
If
![]() $\alpha _1=0$
, then
$\alpha _1=0$
, then
![]() $\alpha _3 =0$
and the proof is finished. Suppose by contradiction that
$\alpha _3 =0$
and the proof is finished. Suppose by contradiction that
![]() $\alpha _1>0$
, the above equation shows that
$\alpha _1>0$
, the above equation shows that
![]() $ 1= \log (b/a)\unicode{x3bb} ^{-1}(b-a)^{-1}.$
However, we obtain that
$ 1= \log (b/a)\unicode{x3bb} ^{-1}(b-a)^{-1}.$
However, we obtain that
therefore,
![]() $g(1) =0,$
contradicting Proposition 6.12.
$g(1) =0,$
contradicting Proposition 6.12.
With the above results, we can prove the following two theorems.
Theorem 6.14. Let
![]() $(a,b)$
be an admissible pair. Then the operator
$(a,b)$
be an admissible pair. Then the operator
![]() ${\mathcal P}:L^1([0,1],\mu ) \to L^1([0,1],\mu )$
admits eigenvalue
${\mathcal P}:L^1([0,1],\mu ) \to L^1([0,1],\mu )$
admits eigenvalue
![]() $\eta $
with respect to eigenvalue
$\eta $
with respect to eigenvalue
![]() $\unicode{x3bb} $
such that
$\unicode{x3bb} $
such that
![]() $\mu (\{\eta>0\})=1$
and
$\mu (\{\eta>0\})=1$
and
![]() $\|\eta \|_{L^1(M,\mu )}=1.$
In particular,
$\|\eta \|_{L^1(M,\mu )}=1.$
In particular,
![]() $Y_n^{a,b}$
fulfils Hypothesis H1.
$Y_n^{a,b}$
fulfils Hypothesis H1.
Proof. From Proposition 6.13, there exists an eigenmeasure
![]() $\nu (\mathrm {d} x) = h (x) \,\mathrm {d} x$
of
$\nu (\mathrm {d} x) = h (x) \,\mathrm {d} x$
of
![]() $T^*$
with
$T^*$
with
![]() $h \in L^1([0,1],\mu ).$
This implies that for every
$h \in L^1([0,1],\mu ).$
This implies that for every
![]() $f\in \mathcal C^0(M)$
,
$f\in \mathcal C^0(M)$
,
 $$ \begin{align*} \int_0^1 T(f)(x) h(x) \,\mathrm{d} x = \int_0^1 f(x) h (x) \,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} \int_0^1 T(f)(x) h(x) \,\mathrm{d} x = \int_0^1 f(x) h (x) \,\mathrm{d} x. \end{align*} $$
However, since
![]() $f g\in L^\infty ([0,1])$
, we obtain that
$f g\in L^\infty ([0,1])$
, we obtain that
 $$ \begin{align*} \int_0^1 f(x) h (x) \,\mathrm{d} x &= \int_0^1 Tf (x) h(x) \,\mathrm{d} x = \int_0^1 \frac{\mathcal L (fg) (x)}{ \unicode{x3bb} g(x)} h(x) \,\mathrm{d} x\\&= \int_0^1 f(x) \frac{g(x)}{\unicode{x3bb}}{\mathcal P}\bigg( \frac{h}{g}\bigg) \,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} \int_0^1 f(x) h (x) \,\mathrm{d} x &= \int_0^1 Tf (x) h(x) \,\mathrm{d} x = \int_0^1 \frac{\mathcal L (fg) (x)}{ \unicode{x3bb} g(x)} h(x) \,\mathrm{d} x\\&= \int_0^1 f(x) \frac{g(x)}{\unicode{x3bb}}{\mathcal P}\bigg( \frac{h}{g}\bigg) \,\mathrm{d} x. \end{align*} $$
Finally, defining
![]() $\eta (x) = h(x)/g(x)$
, it follows that
$\eta (x) = h(x)/g(x)$
, it follows that
![]() ${\mathcal P}\eta = \unicode{x3bb} \eta .$
Since
${\mathcal P}\eta = \unicode{x3bb} \eta .$
Since
 $$ \begin{align*}\eta (x) = \frac{1}{\unicode{x3bb} (b-a) x(1-x)} \int_{a x(1-x)}^{b x(1-x)\land 1} \eta (y)\, \mathrm{d} y, \end{align*} $$
$$ \begin{align*}\eta (x) = \frac{1}{\unicode{x3bb} (b-a) x(1-x)} \int_{a x(1-x)}^{b x(1-x)\land 1} \eta (y)\, \mathrm{d} y, \end{align*} $$
we clearly have that
![]() $\eta \in \mathcal C^0( (0,1)).$
Moreover, it is easy to see that if there exists
$\eta \in \mathcal C^0( (0,1)).$
Moreover, it is easy to see that if there exists
![]() $x_0\in (0,1)$
such that
$x_0\in (0,1)$
such that
![]() $ \eta (x_0) = 0,$
then
$ \eta (x_0) = 0,$
then
![]() $\eta ( x) = 0 \ \mathrm {Leb}$
-a.s. in
$\eta ( x) = 0 \ \mathrm {Leb}$
-a.s. in
![]() $(0,1)$
, which is a contradiction.
$(0,1)$
, which is a contradiction.
Theorem 6.15. Let
![]() $(a,b)$
be an admissible pair. Consider
$(a,b)$
be an admissible pair. Consider
![]() $M=[0,1]$
and the Markov chain
$M=[0,1]$
and the Markov chain
![]() $Y_{n+1}^{(a,b)} = \omega _n Y_n^{(a,b)} (1-Y_n^{(a,b)})$
absorbed at
$Y_{n+1}^{(a,b)} = \omega _n Y_n^{(a,b)} (1-Y_n^{(a,b)})$
absorbed at
![]() $\partial = {\mathbb R} \setminus M,$
with
$\partial = {\mathbb R} \setminus M,$
with
![]() $\{\omega _n\}_{n\in \mathbb N}$
an i.i.d sequence of random variables such that
$\{\omega _n\}_{n\in \mathbb N}$
an i.i.d sequence of random variables such that
![]() $\omega _n\sim \mathrm {Unif}([a,b])$
on
$\omega _n\sim \mathrm {Unif}([a,b])$
on
![]() ${\mathbb R}_{M}$
with absorption
${\mathbb R}_{M}$
with absorption
![]() $\partial $
. Then we have the following.
$\partial $
. Then we have the following.
-
(i)
 $Y_n^{a,b}$
admits a quasi-stationary measure
$Y_n^{a,b}$
admits a quasi-stationary measure
 $\mu _{a,b}$
with survival rate
$\mu _{a,b}$
with survival rate
 $\unicode{x3bb} _{a,b}$
such that
$\unicode{x3bb} _{a,b}$
such that
 $\mathrm {supp}(\mu ) =[0,1]$
and
$\mathrm {supp}(\mu ) =[0,1]$
and
 $\mu \ll \mathrm {Leb}$
, where
$\mu \ll \mathrm {Leb}$
, where
 $\mathrm {Leb}$
denotes the Lebesgue measure on
$\mathrm {Leb}$
denotes the Lebesgue measure on
 $[0,1].$
$[0,1].$
-
(ii) There exists
 $\eta ^{a,b} \in L^1(M,\mu )$
such that
$\eta ^{a,b} \in L^1(M,\mu )$
such that
 ${\mathcal P} \eta ^{a,b} = \unicode{x3bb} _{a,b} \eta ^{a,b} $
,
${\mathcal P} \eta ^{a,b} = \unicode{x3bb} _{a,b} \eta ^{a,b} $
,
 $\|\eta ^{a,b}\|_{L^1(M,\mu )} =1$
and
$\|\eta ^{a,b}\|_{L^1(M,\mu )} =1$
and
 $\eta ^{a,b}>0 \ \mu _{a,b}$
-a.s.
$\eta ^{a,b}>0 \ \mu _{a,b}$
-a.s. -
(iii) For every
 $h\in L^\infty (M,\mathrm {Leb}),$
$h\in L^\infty (M,\mathrm {Leb}),$
 $$ \begin{align*} \lim_{n\to\infty} {\mathbb E}\bigg[ \frac{1}{n}\sum_{i=0}^{n-1} h\circ Y_n^{a,b} \mid \tau>n\bigg] = \int_M h(y) \eta^{a,b}(y) \mu_{a,b}(\mathrm{d} y)\quad \text{for every }x\in(0,1).\end{align*} $$
$$ \begin{align*} \lim_{n\to\infty} {\mathbb E}\bigg[ \frac{1}{n}\sum_{i=0}^{n-1} h\circ Y_n^{a,b} \mid \tau>n\bigg] = \int_M h(y) \eta^{a,b}(y) \mu_{a,b}(\mathrm{d} y)\quad \text{for every }x\in(0,1).\end{align*} $$
-
(iv) For every
 $h\in L^\infty (M,\mu )$
,
$h\in L^\infty (M,\mu )$
,  $$ \begin{align*}\lim_{n\to \infty} {\mathbb E}_x[ h \circ X_i\mid \tau>n] = \int h(y) \mu(\mathrm{d} y)\quad \mbox{for every } x\in (0,1). \end{align*} $$
$$ \begin{align*}\lim_{n\to \infty} {\mathbb E}_x[ h \circ X_i\mid \tau>n] = \int h(y) \mu(\mathrm{d} y)\quad \mbox{for every } x\in (0,1). \end{align*} $$
Proof. Note that Theorem 6.14 implies that
![]() $Y_n^{(a,b)}$
satisfies items
$Y_n^{(a,b)}$
satisfies items
![]() $\mathrm {(H1a)}$
and
$\mathrm {(H1a)}$
and
![]() $\mathrm {(H1b)}$
of Hypothesis H1, also items
$\mathrm {(H1b)}$
of Hypothesis H1, also items
![]() $\mathrm {(H1c)}$
and
$\mathrm {(H1c)}$
and
![]() $\mathrm {(H1d)}$
of Hypothesis H1 follow from Propositions 6.1 and 6.12.
$\mathrm {(H1d)}$
of Hypothesis H1 follow from Propositions 6.1 and 6.12.
Once again, from Propositions 6.1 and 6.12, we obtain that
![]() $Y_n^{a,b}$
satisfies Hypothesis H2 defining
$Y_n^{a,b}$
satisfies Hypothesis H2 defining
![]() $K_i := [1/i,1-1/i]$
for every
$K_i := [1/i,1-1/i]$
for every
![]() $i\in \mathbb N$
. Also, since the logistic map
$i\in \mathbb N$
. Also, since the logistic map
![]() $4 x(1-x)$
is chaotic in
$4 x(1-x)$
is chaotic in
![]() $[0,1]$
and
$[0,1]$
and
![]() $f:{\mathbb R}\times [a,b]\to {\mathbb R}$
,
$f:{\mathbb R}\times [a,b]\to {\mathbb R}$
,
![]() $f(x,\omega )=\omega x(1-x)$
is a continuous function, so we conclude that
$f(x,\omega )=\omega x(1-x)$
is a continuous function, so we conclude that
![]() $m=1$
in Theorem 2.2. Therefore, the conclusions of the theorem follow directly from Theorem 2.4.
$m=1$
in Theorem 2.2. Therefore, the conclusions of the theorem follow directly from Theorem 2.4.
6.1 Analysis of the admissible pairs
Fixing a pair
![]() $(a,b) \in (0,4)\times (4,\infty )$
, it is relatively easy to check if
$(a,b) \in (0,4)\times (4,\infty )$
, it is relatively easy to check if
![]() $(a,b)$
is an admissible pair or not. However, it is complicated to solve inequality equations (6.7) and (6.8) in terms of
$(a,b)$
is an admissible pair or not. However, it is complicated to solve inequality equations (6.7) and (6.8) in terms of
![]() $(a,b)$
. In this section, we prove that every
$(a,b)$
. In this section, we prove that every
![]() $(a,b)\in [1,4)\times (4,\infty )$
is an admissible pair.
$(a,b)\in [1,4)\times (4,\infty )$
is an admissible pair.
We start showing that for every
![]() $(a,b)\in [1,2)\times (4,\infty ),$
inequality equation (6.7) is fulfilled.
$(a,b)\in [1,2)\times (4,\infty ),$
inequality equation (6.7) is fulfilled.
Proposition 6.16. For every
![]() $(a,b)\in [1,2)\times (4,\infty )$
, we have that
$(a,b)\in [1,2)\times (4,\infty )$
, we have that
 $$ \begin{align*}0\leq \frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{2}{b}\bigg(1-\sqrt{1-\frac{4x}{a} }\bigg)} \leq \frac{a}{4}\quad \text{for every }x\in\bigg[\frac{4 a^2 - a^3}{16},\frac{a}{4}\bigg].\end{align*} $$
$$ \begin{align*}0\leq \frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{2}{b}\bigg(1-\sqrt{1-\frac{4x}{a} }\bigg)} \leq \frac{a}{4}\quad \text{for every }x\in\bigg[\frac{4 a^2 - a^3}{16},\frac{a}{4}\bigg].\end{align*} $$
Proof. Note that
![]() $\tfrac 12-\tfrac 12 \sqrt {1-{2}/{b}(1-\sqrt {1-{4x}/{a}})}$
is an increasing function in
$\tfrac 12-\tfrac 12 \sqrt {1-{2}/{b}(1-\sqrt {1-{4x}/{a}})}$
is an increasing function in
![]() $x.$
Therefore, for every
$x.$
Therefore, for every
![]() $x\in [(4a^2 - a^3)/16,a/4]$
, we obtain
$x\in [(4a^2 - a^3)/16,a/4]$
, we obtain
 $$ \begin{align*} 0\leq & \frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{2}{b}\bigg(1-\sqrt{1-\frac{4x}{a}}\bigg)} \leq \frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{2}{b}}\leq \frac{1}{4}\leq \frac{a}{4}.\\[-3.3pc] \end{align*} $$
$$ \begin{align*} 0\leq & \frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{2}{b}\bigg(1-\sqrt{1-\frac{4x}{a}}\bigg)} \leq \frac{1}{2}-\frac{1}{2} \sqrt{1-\frac{2}{b}}\leq \frac{1}{4}\leq \frac{a}{4}.\\[-3.3pc] \end{align*} $$
Proposition 6.17. For every
![]() $b>4$
, the following maps
$b>4$
, the following maps
 $$ \begin{align*} &F^{a,b}_1(x)\\ &\quad:= \frac{2\big( \tanh^{-1}\big(\sqrt{1 - {2}/{b} + {2}/{b} \sqrt{1-({4x}/{b})}}\big) - \tanh^{-1}\big(\sqrt{1 - {2}/{a} +{2}/{a}\sqrt{1-({4 x}/{b})}}\big)\big) }{\sqrt{1-({4x}/{b})}} \end{align*} $$
$$ \begin{align*} &F^{a,b}_1(x)\\ &\quad:= \frac{2\big( \tanh^{-1}\big(\sqrt{1 - {2}/{b} + {2}/{b} \sqrt{1-({4x}/{b})}}\big) - \tanh^{-1}\big(\sqrt{1 - {2}/{a} +{2}/{a}\sqrt{1-({4 x}/{b})}}\big)\big) }{\sqrt{1-({4x}/{b})}} \end{align*} $$
and
 $$ \begin{align*} F^{a,b}_2(x):= \frac{2 \tanh ^{-1}\big(\sqrt{{-2 +2 \sqrt{1-({4 x}/{a})}+b}/{b}}\big)+\log\big({a}/({4-a})\big)}{\sqrt{1-({4x}/{a})}} \end{align*} $$
$$ \begin{align*} F^{a,b}_2(x):= \frac{2 \tanh ^{-1}\big(\sqrt{{-2 +2 \sqrt{1-({4 x}/{a})}+b}/{b}}\big)+\log\big({a}/({4-a})\big)}{\sqrt{1-({4x}/{a})}} \end{align*} $$
are increasing in x in the interval
![]() $[(4a^2 -a^3)/16,a/4].$
$[(4a^2 -a^3)/16,a/4].$
Proof. It is readily verified that
 $$ \begin{align*}&{x\mapsto \tanh^{-1}\bigg(\sqrt{1 - \frac{2}{b} + \frac{2}{b} \sqrt{1-\frac{4x}{b}}}\bigg) - \tanh^{-1}\bigg(\sqrt{1 - \frac{2}{a} +\frac{2}{a}\sqrt{1-\frac{4 x}{b}}}\bigg) }\ \quad\text{and }\\&x \mapsto \sqrt{1-\frac{4x}{b}}\end{align*} $$
$$ \begin{align*}&{x\mapsto \tanh^{-1}\bigg(\sqrt{1 - \frac{2}{b} + \frac{2}{b} \sqrt{1-\frac{4x}{b}}}\bigg) - \tanh^{-1}\bigg(\sqrt{1 - \frac{2}{a} +\frac{2}{a}\sqrt{1-\frac{4 x}{b}}}\bigg) }\ \quad\text{and }\\&x \mapsto \sqrt{1-\frac{4x}{b}}\end{align*} $$
are respectively increasing and decreasing for
![]() $x\in [(4a^2 -a^3)/16,a/4],$
implying that
$x\in [(4a^2 -a^3)/16,a/4],$
implying that
![]() $F^{a,b}_1(x)$
is increasing in x in the interval
$F^{a,b}_1(x)$
is increasing in x in the interval
![]() $[(4a^2 -a^3)/16,a/4].$
$[(4a^2 -a^3)/16,a/4].$
In the following, we prove that
![]() $F^{a,b}_2$
is an increasing function in
$F^{a,b}_2$
is an increasing function in
![]() $[(4a^2 -a^3)/ 16,a/4].$
Through the change of coordinates
$[(4a^2 -a^3)/ 16,a/4].$
Through the change of coordinates
![]() $y =\sqrt {({-2 +2 \sqrt {1-4x/a}+b})/{b}},$
we obtain that to show that
$y =\sqrt {({-2 +2 \sqrt {1-4x/a}+b})/{b}},$
we obtain that to show that
![]() $F^{a,b}_2$
is an increasing function, it is enough to show that
$F^{a,b}_2$
is an increasing function, it is enough to show that
is decreasing in x in the interval
![]() $[\sqrt {(b-2)/b} ,\sqrt {(b-1)/b}]\supset [\sqrt {(-2+b)/b} , \sqrt {(b-a)/b}].$
Since
$[\sqrt {(b-2)/b} ,\sqrt {(b-1)/b}]\supset [\sqrt {(-2+b)/b} , \sqrt {(b-a)/b}].$
Since
 $$ \begin{align*}\frac{\mathrm{d} F^b_3}{\mathrm{d} y}(y) = \frac{2 (b (y^2-1) y (\log ({a}/({4-a}))+\log (({1+y})/({1-y})))+b y^2-b+2)}{(1-y^2) (b (y^2-1)+2)^2},\end{align*} $$
$$ \begin{align*}\frac{\mathrm{d} F^b_3}{\mathrm{d} y}(y) = \frac{2 (b (y^2-1) y (\log ({a}/({4-a}))+\log (({1+y})/({1-y})))+b y^2-b+2)}{(1-y^2) (b (y^2-1)+2)^2},\end{align*} $$
it is enough to show that
 $$ \begin{align*} b (y^2-1)\bigg( y \log \bigg(\frac{a}{4-a} \cdot \frac{1+y}{1-y}\bigg)+1\bigg)+2 &\leq b (y^2-1) \bigg(y\log \bigg( \frac{1+y}{3-3 y}\bigg)+ 1\bigg)+2 \\ &\leq 0\quad \text{for every }y\in\bigg[\sqrt{\frac{b-2}{b}} , \sqrt{\frac{b-1}{b}}\bigg]. \end{align*} $$
$$ \begin{align*} b (y^2-1)\bigg( y \log \bigg(\frac{a}{4-a} \cdot \frac{1+y}{1-y}\bigg)+1\bigg)+2 &\leq b (y^2-1) \bigg(y\log \bigg( \frac{1+y}{3-3 y}\bigg)+ 1\bigg)+2 \\ &\leq 0\quad \text{for every }y\in\bigg[\sqrt{\frac{b-2}{b}} , \sqrt{\frac{b-1}{b}}\bigg]. \end{align*} $$
Observe that given
![]() $y\in [\sqrt {(-2+b)/b} ,\sqrt {(-1+b)/b}]\subset [\sqrt {2}/2,1],$
we obtain that
$y\in [\sqrt {(-2+b)/b} ,\sqrt {(-1+b)/b}]\subset [\sqrt {2}/2,1],$
we obtain that
 $$ \begin{align*} b y (y^2-1) \log\bigg(\frac{1+ y}{3- 3y}\bigg) \leq 0\quad \text{and}\quad \frac{1+y}{3-3y} -1 \geq 0.\end{align*} $$
$$ \begin{align*} b y (y^2-1) \log\bigg(\frac{1+ y}{3- 3y}\bigg) \leq 0\quad \text{and}\quad \frac{1+y}{3-3y} -1 \geq 0.\end{align*} $$
From [Reference Love21, equation (2)], it follows that
![]() $\log (1+x)\geq x/(1+x/2)$
for every
$\log (1+x)\geq x/(1+x/2)$
for every
![]() $x\geq 0.$
Therefore,
$x\geq 0.$
Therefore,
 $$ \begin{align} &2+ b (y^2-1)+b y (y^2-1) \log \bigg(\frac{y+1}{3-3 y}\bigg)\nonumber\\ &\quad\leq 2+ b (y^2-1)+\frac{b y (({y+1})/(3-3 y)-1) (y^2-1)}{{1}/{2} (({y+1})/({3-3 y})-1)+1}\nonumber\\ &\quad=2-\frac{b (1-y^2) (4 y^2-3y+2)}{2-y}. \end{align} $$
$$ \begin{align} &2+ b (y^2-1)+b y (y^2-1) \log \bigg(\frac{y+1}{3-3 y}\bigg)\nonumber\\ &\quad\leq 2+ b (y^2-1)+\frac{b y (({y+1})/(3-3 y)-1) (y^2-1)}{{1}/{2} (({y+1})/({3-3 y})-1)+1}\nonumber\\ &\quad=2-\frac{b (1-y^2) (4 y^2-3y+2)}{2-y}. \end{align} $$
Using standard techniques, one can check that
![]() ${b>4}$
and
${b>4}$
and
![]() $y \in [\sqrt {(-2+b)/b} ,\sqrt {(-1+b/b}]$
then equation (6.19) is less than or equal to
$y \in [\sqrt {(-2+b)/b} ,\sqrt {(-1+b/b}]$
then equation (6.19) is less than or equal to
![]() $0$
, implying that
$0$
, implying that
![]() $F^{a,b}_3$
is decreasing in the interval
$F^{a,b}_3$
is decreasing in the interval
![]() $[\sqrt {(-2+b)/b} ,\sqrt {(-1+b)/b}]$
for every
$[\sqrt {(-2+b)/b} ,\sqrt {(-1+b)/b}]$
for every
![]() $(a,b) \in [1,2]\times (4,\infty )$
and therefore
$(a,b) \in [1,2]\times (4,\infty )$
and therefore
![]() $F^{a,b}_2$
is increasing in
$F^{a,b}_2$
is increasing in
![]() $[(4a^2 -a^3)/16,a/4]$
for every
$[(4a^2 -a^3)/16,a/4]$
for every
![]() $(a,b)\in [1,2]\times (4,\infty )$
.
$(a,b)\in [1,2]\times (4,\infty )$
.
Using the above proposition, we show that if
![]() $(a,b) \in [1,4)\times (4,\infty )$
, then
$(a,b) \in [1,4)\times (4,\infty )$
, then
![]() $(a,b)$
is an admissible pair.
$(a,b)$
is an admissible pair.
Theorem 6.18. If
![]() $(a,b) \in [1,4)\times (4,\infty )$
, then
$(a,b) \in [1,4)\times (4,\infty )$
, then
![]() $(a,b)$
is an admissible pair.
$(a,b)$
is an admissible pair.
Proof. From the definition of admissible pair, we just need to consider the case
![]() $(a,b) \in [1,2]\times (4,\infty ).$
From Proposition 6.16, we obtain that the pair
$(a,b) \in [1,2]\times (4,\infty ).$
From Proposition 6.16, we obtain that the pair
![]() $(1,b)$
satisfies equation (6.7).
$(1,b)$
satisfies equation (6.7).
In the following, we show that the pair
![]() $(1,b)$
satisfies equation (6.8). Observe that equation (6.8) is equivalent of showing that
$(1,b)$
satisfies equation (6.8). Observe that equation (6.8) is equivalent of showing that
![]() $F^{a,b}_1(x) \leq F^{a,b}_2(x)$
for every
$F^{a,b}_1(x) \leq F^{a,b}_2(x)$
for every
![]() $x\in [(4a^2 - a^3)/16,a/4]$
, where
$x\in [(4a^2 - a^3)/16,a/4]$
, where
![]() $F^{a,b}_1$
and
$F^{a,b}_1$
and
![]() $F^{a,b}_2$
are defined in Proposition 6.17. From Proposition 6.17, it is enough to show that
$F^{a,b}_2$
are defined in Proposition 6.17. From Proposition 6.17, it is enough to show that
 $$ \begin{align*}F_1^{a,b}\bigg(\frac{a}{4}\bigg) \leq F_2^b\bigg(\frac{4a^2 -a^3}{16}\bigg) \quad\text{for every }(a,b)\in [1,4)\times(4,\infty).\end{align*} $$
$$ \begin{align*}F_1^{a,b}\bigg(\frac{a}{4}\bigg) \leq F_2^b\bigg(\frac{4a^2 -a^3}{16}\bigg) \quad\text{for every }(a,b)\in [1,4)\times(4,\infty).\end{align*} $$
We divide the proof into two steps.
Step 1. 1 We show that for every
![]() $b>4$
,
$b>4$
,
![]() $(1,b)$
is an admissible pair.
$(1,b)$
is an admissible pair.
Note that for every
![]() $b>4,$
$b>4,$
 $$ \begin{align*} F_1^{1,b}\bigg(\frac{1}{4}\bigg) &=\frac{2 \big(\tanh ^{-1}\big(\sqrt{({b+2 \sqrt{1-{1}/{b}}-2})/{b}}\big)-\tanh ^{-1}\big(\sqrt{2 \sqrt{1-{1}/{b}}-1}\big)\big)}{\sqrt{1-{1}/{b}}}\\ &\leq 4 \tanh ^{-1}\bigg(\frac{\sqrt{2 \sqrt{({b-1})/{b}}-1}-\sqrt{({b+2 \sqrt{({b-1})/{b}}-2})/{b}}}{1- \sqrt{\big(2 \sqrt{({b-1})/{b}}-1\big)\big(({b+2 \sqrt{({b-1})/{b}}-2})/{b}\big)}}\bigg) \end{align*} $$
$$ \begin{align*} F_1^{1,b}\bigg(\frac{1}{4}\bigg) &=\frac{2 \big(\tanh ^{-1}\big(\sqrt{({b+2 \sqrt{1-{1}/{b}}-2})/{b}}\big)-\tanh ^{-1}\big(\sqrt{2 \sqrt{1-{1}/{b}}-1}\big)\big)}{\sqrt{1-{1}/{b}}}\\ &\leq 4 \tanh ^{-1}\bigg(\frac{\sqrt{2 \sqrt{({b-1})/{b}}-1}-\sqrt{({b+2 \sqrt{({b-1})/{b}}-2})/{b}}}{1- \sqrt{\big(2 \sqrt{({b-1})/{b}}-1\big)\big(({b+2 \sqrt{({b-1})/{b}}-2})/{b}\big)}}\bigg) \end{align*} $$
and
 $$ \begin{align*} F_2^{1,b}\bigg(\frac{3}{16}\bigg) = 4 \tanh ^{-1}\bigg(\frac{\sqrt{1-({1}/{b})}-{1}/{2}}{1-{1}/{2} \sqrt{1-({1}/{b})}}\bigg) = 4 \tanh^{-1}\bigg(\frac{3 \sqrt{b-1} \sqrt{b}-2}{3 b+1}\bigg).\end{align*} $$
$$ \begin{align*} F_2^{1,b}\bigg(\frac{3}{16}\bigg) = 4 \tanh ^{-1}\bigg(\frac{\sqrt{1-({1}/{b})}-{1}/{2}}{1-{1}/{2} \sqrt{1-({1}/{b})}}\bigg) = 4 \tanh^{-1}\bigg(\frac{3 \sqrt{b-1} \sqrt{b}-2}{3 b+1}\bigg).\end{align*} $$
Since the function
![]() $x\mapsto 4 \tanh ^{-1}(x)$
is increasing, to finish the proof of this step it is enough to show that
$x\mapsto 4 \tanh ^{-1}(x)$
is increasing, to finish the proof of this step it is enough to show that
 $$ \begin{align} &\frac{\sqrt{-1+2 \sqrt{({b-1})/{b}}}-\sqrt{({b+2 \sqrt{({b-1})/{b}}-2})/{b}}}{1- \sqrt{\big(-1+2 \sqrt{({b-1})/{b}}\big)\big(({b+2 \sqrt{({b-1})/{b}}-2})/{b}\big)}}\nonumber\\ &\quad\leq \frac{3 \sqrt{b-1} \sqrt{b}-2}{3 b+1}\quad \text{for every }b>4. \end{align} $$
$$ \begin{align} &\frac{\sqrt{-1+2 \sqrt{({b-1})/{b}}}-\sqrt{({b+2 \sqrt{({b-1})/{b}}-2})/{b}}}{1- \sqrt{\big(-1+2 \sqrt{({b-1})/{b}}\big)\big(({b+2 \sqrt{({b-1})/{b}}-2})/{b}\big)}}\nonumber\\ &\quad\leq \frac{3 \sqrt{b-1} \sqrt{b}-2}{3 b+1}\quad \text{for every }b>4. \end{align} $$
Using standard methods, one can show that the above equation simplifies in showing that
 $$ \begin{align*}p(b)&:=4239 b^6-23868 b^5+31482 b^4+8964 b^3\\ &\quad-40401 b^2+23424 b -4096 \geq 0\quad \text{for every }b>4.\end{align*} $$
$$ \begin{align*}p(b)&:=4239 b^6-23868 b^5+31482 b^4+8964 b^3\\ &\quad-40401 b^2+23424 b -4096 \geq 0\quad \text{for every }b>4.\end{align*} $$
However, since for every
![]() $\delta>0$
,
$\delta>0$
,
 $$ \begin{align*}p(4+\delta) &= 4239 \delta ^6+77868 \delta ^5+571482 \delta ^4\\ &\quad+2119716 \delta ^3+4091679 \delta ^2+3683256 \delta +998384>0, \end{align*} $$
$$ \begin{align*}p(4+\delta) &= 4239 \delta ^6+77868 \delta ^5+571482 \delta ^4\\ &\quad+2119716 \delta ^3+4091679 \delta ^2+3683256 \delta +998384>0, \end{align*} $$
we obtain that equation (6.20) holds. This completes Step 1.
Step 2. 2 We show that
![]() $(a,b)$
is an admissible pair for every
$(a,b)$
is an admissible pair for every
![]() $(a,b)\in [1,2)\times (4,\infty ).$
$(a,b)\in [1,2)\times (4,\infty ).$
Fixing
![]() $b>4,$
observe that
$b>4,$
observe that
 $$ \begin{align*}&(2-a) F_1^{a,b}\bigg(\frac{a}{4}\bigg)\\ &\quad= 2\frac{2-a}{\sqrt{1-({a}/{b})}} \bigg(\tanh ^{-1}\bigg(\sqrt{\frac{2 \sqrt{1-({a}/{b})}+b-2}{b}}\bigg)-\tanh ^{-1}\bigg(\sqrt{\frac{2 \sqrt{1-({a}/{b})}+a-2}{a}}\bigg)\bigg) \end{align*} $$
$$ \begin{align*}&(2-a) F_1^{a,b}\bigg(\frac{a}{4}\bigg)\\ &\quad= 2\frac{2-a}{\sqrt{1-({a}/{b})}} \bigg(\tanh ^{-1}\bigg(\sqrt{\frac{2 \sqrt{1-({a}/{b})}+b-2}{b}}\bigg)-\tanh ^{-1}\bigg(\sqrt{\frac{2 \sqrt{1-({a}/{b})}+a-2}{a}}\bigg)\bigg) \end{align*} $$
and
 $$ \begin{align*} (2-a) F_2^{a,b}\bigg(\frac{4a^2 - a^4}{16}\bigg) = 2 \bigg(2 \tanh ^{-1}\bigg(\sqrt{\frac{b-a}{b}}\bigg)+\log \bigg(\frac{a}{4-a}\bigg)\bigg).\end{align*} $$
$$ \begin{align*} (2-a) F_2^{a,b}\bigg(\frac{4a^2 - a^4}{16}\bigg) = 2 \bigg(2 \tanh ^{-1}\bigg(\sqrt{\frac{b-a}{b}}\bigg)+\log \bigg(\frac{a}{4-a}\bigg)\bigg).\end{align*} $$
It is readily verified that
 $$ \begin{align*}\frac{2-a}{\sqrt{1-({a}/{b})}}\quad \text{and}\quad\tanh ^{-1}\bigg(\sqrt{\frac{2 \sqrt{1-({a}/{b})}+b-2}{b}}\bigg)-\tanh ^{-1}\bigg(\sqrt{\frac{2 \sqrt{1-({a}/{b})}+a-2}{a}}\bigg) \end{align*} $$
$$ \begin{align*}\frac{2-a}{\sqrt{1-({a}/{b})}}\quad \text{and}\quad\tanh ^{-1}\bigg(\sqrt{\frac{2 \sqrt{1-({a}/{b})}+b-2}{b}}\bigg)-\tanh ^{-1}\bigg(\sqrt{\frac{2 \sqrt{1-({a}/{b})}+a-2}{a}}\bigg) \end{align*} $$
are decreasing functions in
![]() $a\in [1,2),$
implying that
$a\in [1,2),$
implying that
![]() $(2-a) F_1^{a,b}(a/4)$
is a decreasing function in
$(2-a) F_1^{a,b}(a/4)$
is a decreasing function in
![]() $a\in [0,1]$
and
$a\in [0,1]$
and
 $$ \begin{align*} (a-2) F_2^{a,b} ((4a^2 - a^3)/16) = 2 \bigg(2 \tanh ^{-1}\bigg(\sqrt{\frac{b-a}{b}}\bigg)+\log \bigg(\frac{a}{4-a}\bigg)\bigg)\end{align*} $$
$$ \begin{align*} (a-2) F_2^{a,b} ((4a^2 - a^3)/16) = 2 \bigg(2 \tanh ^{-1}\bigg(\sqrt{\frac{b-a}{b}}\bigg)+\log \bigg(\frac{a}{4-a}\bigg)\bigg)\end{align*} $$
is an increasing function in
![]() $a \in [1,2)$
. From Step
$a \in [1,2)$
. From Step
![]() $1$
, we obtain that for every
$1$
, we obtain that for every
![]() $a\in [1,2),$
$a\in [1,2),$
 $$ \begin{align*}F_1^{a,b}\bigg(\frac{a}{4}\bigg)=\frac{(2-a)F_1^{a,b}({a}/{4})}{2-a} \leq \frac{ F_1^{a,b}(1/4)}{2-a}\leq \frac{F_2^{a,b}(3/16)}{2-a} \leq F_2^{a,b}\bigg(\frac{4a^2-a^3}{16}\bigg).\end{align*} $$
$$ \begin{align*}F_1^{a,b}\bigg(\frac{a}{4}\bigg)=\frac{(2-a)F_1^{a,b}({a}/{4})}{2-a} \leq \frac{ F_1^{a,b}(1/4)}{2-a}\leq \frac{F_2^{a,b}(3/16)}{2-a} \leq F_2^{a,b}\bigg(\frac{4a^2-a^3}{16}\bigg).\end{align*} $$
This completes the proof of the theorem.
We finish the paper proving Theorem 2.1.
Acknowledgements
We are grateful to Jochen Glück for many useful discussions and valuable comments regarding the theory of positive integral operators. MC’s research has been supported by an Imperial College President’s PhD scholarship. MC, VG and JL are also supported by the EPSRC Centre for Doctoral Training in Mathematics of Random Systems: Analysis, Modelling and Simulation (EP/S023925/1). JL gratefully acknowledges research support from IRCN, University of Tokyo and CAMB, Gulf University of Science and Technology, as well as from the London Mathematical Laboratory.