1. Introduction
The genetic architecture of a character conditions its evolutionary properties (Hansen, Reference Hansen2006). However, being able to determine the number of genes and alleles involved in trait expression, their respective effects, their interactions and their frequencies in a specific population remains a challenge for evolutionary biologists.
A common approach consists in dissecting genetic architectures by identifying the genomic regions influencing phenotypic polymorphism (e.g. QTL mapping) and measuring both their individual effects and their interactions with other genes. Empirical work both in natural and artificial populations generally reports that the genetic architecture of most traits is polygenic. Often, few large factors and many small ones are identified, with a prevalence of non-additive interactions between them (Barton & Keightley, Reference Barton and Keightley2002; Carlborg & Haley, Reference Carlborg and Haley2004; Mackay, Reference Mackay2004). However, the statistical power of gene mapping remains unsatisfactory in terms of genetic architecture description, since most of the genetic variation, attributed to small genetic factors, typically remains unexplained (Gudbjartsson et al., Reference Gudbjartsson, Walters, Thorleifsson, Stefansson, Halldorsson, Zusmanovich, Sulem, Thorlacius, Gylfason, Steinberg, Helgadottir, Ingason, Steinthorsdottir, Olafsdottir, Olafsdottir, Jonsson, Borch-Johnsen, Hansen, Andersen, Jorgensen, Pedersen, Aben, Witjes, Swinkels, den Heijer, Franke, Verbeek, Becker, Yanek, Becker, Tryggvadottir, Rafnar, Gulcher, Kiemeney, Kong, Thorsteinsdottir and Stefansson2008; Manolio et al., Reference Manolio, Collins, Cox, Goldstein, Hindorff, Hunter, McCarthy, Ramos, Cardon, Chakravarti, Cho, Guttmacher, Kong, Kruglyak, Mardis, Rotimi, Slatkin, Valle, Whittemore, Boehnke, Clark, Eichler, Gibson, Haines, Mackay, McCarroll and Visscher2009). Except for very simple cases (e.g. Colosimo et al., Reference Colosimo, Peichel, Nereng, Blackman, Shapiro, Schluter and Kingsley2004), the contribution of unidentified factors remains essential to understand and quantify the evolutionary properties of a trait (Le Rouzic et al., Reference Le Rouzic, Siegel and Carlborg2007). Arguably, most traits might be too complex for such a reductionist approach to quantify evolutionary relevant parameters with satisfactory precision.
Alternatively, the general properties of the genetic architecture may be evaluated through quantitative genetics models from phenotypic measurements in controlled populations. Classical designs include line-cross analyses or parent–offspring studies (Lynch & Walsh, Reference Lynch and Walsh1998). Of particular interest are selective breeding experiments, which mimic the evolution of a character on a shorter timescale. Through a nonrandom selection of individuals that will be allowed to breed, it is possible to accumulate, generation after generation, an impressive amount of phenotypic change in a population (Falconer, Reference Falconer1992; Hill & Caballero, Reference Hill and Caballero1992).
It is well known that many phenomena like genetic drift (Weber & Diggins, Reference Weber and Diggins1990), epistasis (Carter et al., Reference Carter, Hermisson and Hansen2005), joint effect of natural selection (Zhang & Hill, Reference Zhang and Hill2002), pleiotropy and genetic correlations (Lande, Reference Lande1979; Hansen & Houle, Reference Hansen and Houle2008) and mutations (Hill, Reference Hill1982a; Zeng et al., Reference Zeng, Tachida and Cockerham1989), may affect selection response. Consequently, a careful statistical analysis of the time series, combining information about the dynamics of the mean and the phenotypic variance in the population, should be able to (i) sort out the different hypotheses and ground the interpretation of the data (e.g. through the rejection of some models) and (ii) quantify the value of parameters of interest. It is of particular interest to challenge the constant genetic-architecture models based on the ‘infinitesimal’ expectation (infinite number of loci with infinitesimal effect on the phenotype).
So far, few statistical tools are available to measure, survey and predict the changes in the genetic architecture of the trait under selection. From selection-response experiments, researchers generally estimate by regression the average rate at which the population responds to selection (often expressed as the realized heritability). A few other characteristics of interest, such as the selection limits (the extreme phenotypic values beyond which the population does not seem to respond to selection), are sometimes roughly estimated from direct observation of the selection-response time series (Eisen, Reference Eisen1972). Estimating non-constant genetic architecture features from the whole time series requires specific models (e.g. Sorensen et al., Reference Sorensen, Fernando and Gianola2001) or, more commonly, slicing the time series into parts on which a parameter of interest will be evaluated independently (e.g. Meyer & Hill, Reference Meyer and Hill1991; Martinez et al., Reference Martinez, Bunger and Hill2000; Holt et al., Reference Holt, Meuwissen and Vangen2005). As suggested in Le Rouzic et al. (Reference Le Rouzic, Skaug and Hansen2010), large Mendelian factors could also be detected from artificial-selection responses. However, this becomes difficult when the number of loci increases, and quantitative genetics models have to be considered when the trait is truly polygenic. An individual-based random-effect model (the ‘animal model’) is often used to analyse high-quality data sets reporting individual phenotypes and individual crossing schemes, i.e. full pedigrees (Gianola & Fernando, Reference Gianola and Fernando1986; Hill & Caballero, Reference Hill and Caballero1992; see Walsh & Lynch, Reference Lynch and Walsh1998). Such models, however, rely on strong hypotheses about the behaviour of the genetic architecture and the way characters are transmitted between parents and offspring. Well suited for the estimation of breeding values in complex pedigrees, they lack flexibility when applied to evolutionary issues, long time series (for which simple heredity assumptions may not hold) or mass-breeding selection experiments (in which the pedigree is not known).
Arguably, the dynamical properties of the selection responses (including changes in the phenotypic mean and the phenotypic variance) are often underexploited. In spite of the availability of many data sets accumulated for more than a century, and regardless of the scientific interest of comparative studies to address pending questions about the evolutionary properties of genetic architectures, there are few general tools to compare different models fitted to a data set, or to analyse and compare the dynamics of independent experiments on a quantitative basis.
With this paper, we provide a comprehensive and simple statistical framework to analyse the temporal pattern of polygenic artificial-selection time series. First, we propose purely descriptive (phenomenological) models, designed to catch the trends in population means and variances without assuming specific features of the genetic architecture (i.e. including patterns unexpected by classical models). The models can be fit to data by maximum likelihood, and models of different complexity can be compared according to model selection procedures. We then show how these simple models can be modified to account explicitly for mechanisms of biological interest, such as epistasis, canalization or linkage disequilibrium. Models are implemented in a documented software package for R named selection response analysis (sra), and the approach is illustrated by analysing the example of an artificial-selection procedure modifying the shape of the wing in Drosophila melanogaster.
2. Models
(i) General framework
Our aim is to describe general time-series models that can be used to analyse artificial-selection data, with a high degree of flexibility related to the dynamics of the process and its underlying genetic mechanisms. The genetic architecture of the trait of interest is assumed to be polygenic, and both genetic and environmental effects are normally distributed (the importance of scale will be addressed below). More complex models involving one or two major loci can be derived (Pong-Wong et al., Reference Pong-Wong, Haley and Woolliams1999; Le Rouzic et al., Reference Le Rouzic, Skaug and Hansen2010), but will be only briefly considered in this manuscript.
The mean of the trait at generation t is μt, and its dynamics are predicted by the breeder's equation, μt+1=μt+h 2 (μt*−μt), where μt* is the phenotypic average of the artificially selected individuals allowed to reproduce, and h 2 the narrow-sense heritability, i.e. the ratio between additive (σA2) and phenotypic (σP2) variances. Here, we will use Lande's reformulation of the breeder's equation: μt+1=μt+σA2β, where β is the selection gradient, and corresponds to the slope of the regression of fitness to the phenotype (Lande, Reference Lande1979; Lande & Arnold, Reference Lande1983); the larger |β|, the stronger the selection. In the context of truncation selection, the realized selection gradient β can be calculated as (μ*t−μt)/σP2.
Traditionally, the phenotypic variance is split into a genetic component σG2 and an environmental variance σE2, such as σP2=σG2+σE2, assuming that the genetic-by-environment interactions can be neglected. The genetic variance itself is split into σG2=σA2+σD2+σI2, where σD2 stands for the dominance variance and σI2 for the sum of all epistatic variance components. According to the approximation of the Lande equation, only the additive part of the variance, σA2, matters for the selection response, and in most of this manuscript, we will consider that σP2=σA2+σE2. This does not necessarily mean that the models we describe are purely additive, but rather that environmental variance includes the non-additive genetic variance components. In a few cases (e.g. directional epistasis), a part of the non-additive variance contributes to the general dynamics and will be considered explicitly.
(ii) Phenomenological models
Accounting for the dynamics of the variance components is achieved by modelling their change in the course of time. We will explore two families of models, corresponding to opposite approaches of statistical modelling. One possibility is to consider a set of models, based on accumulated knowledge in biology and population genetics, and to express the dynamics on the genetic architecture in terms of biologically meaningful parameters. Such models will be referred to as ‘mechanistic models’, and some simple examples will be detailed in the last part of this ‘Model’ section. The alternative possibility is to build flexible models designed to describe trends in the time series, without connecting these observations explicitly to underlying mechanisms. Such models, referred to as ‘phenomenological models’, are the focus of the current section.
Contrary to most situations encountered when analysing time series, neither the population mean nor the variance components are expected to be stationary. The models thus have to include the possibility that the parameters vary in a systematic way. The trends that will be considered for variance components include exponential and linear changes, as well as a combination of both. Such simple models are, however, unlikely to capture the whole complexity of the time series. Ideally, models growing in complexity should be straightforward to build, and extra parameters should provide significant flexibility to the new models. A satisfactory framework was derived by predicting the trend from the previous generations.
The two variance components (the additive genetic variance σA2 and the environmental variance σE2) are assumed to be algebraically independent. To a first approximation, their change can be exponential only, and the general dynamics can be written as:

This model involves five parameters (in vector Θ), three describing the state of the population at the first generation (μ1, ![]() and
and ![]() ), and two featuring the dynamics of the variances (k A for the additive variance and k E for the environmental variance).
), and two featuring the dynamics of the variances (k A for the additive variance and k E for the environmental variance).
The model may be expanded by considering linear terms in the variance dynamics:

Variances should remain positive or null, so that the previous setting has to be understood as e.g. ![]() , and 0 otherwise.
, and 0 otherwise.
Real time series are expected to show more complex patterns, and relatively good generality can be achieved by using a framework based on the previous generations. Because the time series are trended, the model is not equivalent to a classical auto-regressive setting; however, it relies on the same principles: by letting the variances depend on the generations t−2, …, t−n, n being as large as necessary, it is possible to add up new parameters. The general formulation becomes:

The parameters k n are purely descriptive, and they are not intended to be interpreted in terms of meaningful biological processes. In particular, non-Markov lags (n>1) should not be understood as a real impact of remote generations on the current dynamics of the variance components, but rather as hidden variables (including e.g. skew or kurtosis of the distribution of genetic effects, complex dominance or epistasis patterns, changes in frequency of large-effect alleles, etc) whose effects happens to be captured by this parameterization.
Allowing the k n to take negative values could lead to non-convergent series, which might indicate over-parameterization, but could also identify potentially relevant cyclic patterns in the data set. If considered as a nuisance, this behaviour can be avoided by forcing k n>0. Models have been explored up to n=3, with satisfactory results, as evidenced by the analysis of real data detailed later.
(iii) Alternative scales
In many cases, there is no particular reason to expect that the description of the genetic architecture from the scale on which the trait was measured is a priori meaningful. Models of similar complexity can thus be defined just by allowing the scale to change. Scale changes include common logarithm and power transformations, or more specific operations for traits expressed as frequencies or probabilities (e.g. logistic transformation).
In addition to general scale transformation, it is possible to consider scaling operations that are more specific to quantitative genetics. Most of the time, artificial-selection procedures target characters that are on ratio scales, such as weights or lengths. Consequently, phenotypic and genetic standard deviations should change along with the mean of the population, as suggested by Houle (Reference Houle1992) . Here, we use the ‘mean-scaled evolvability’, defined as I A=σA2/μ2, as a measurement of the adaptation potential of a population (see Hansen et al., Reference Hansen2003; Hansen & Houle, Reference Hansen and Houle2008 for justification). The environmental variance can also be affected, such that I E=σE2/μ2 is the quantity of interest. In this context, equation (1) can be expressed as:

Direct comparison of the parameters can be achieved by rewriting equation (4) in terms of σA2 and σE2, given that ![]() , e.g.:
, e.g.: ![]() .
.
Alternatively, it is possible to interpret the evolutionary properties of the population based on the narrow-sense heritability h 2, the ratio between additive and phenotypic variance. A model centred on heritability is

All the models described in this paper can be applied to any scale (e.g. log/power scale, evolvability or heritability scales). These combinations provide a large number of settings designed to catch major trends in the data, and to describe changes in the genetic architectures.
(iv) Mechanistic models
The quantitative-genetics literature focuses on mechanistic models, describing how selection response is expected to change assuming some specific genetic architectures. Model selection may rule out some of these, while leaving others can appear as plausible explanations for the trends seen in the phenomenological analysis. In this section, some of these models will be described as special cases of equation (2). This will allow us to estimate biologically relevant parameters directly.
(a) Constant additive variance
The simplest model assumes that the genetic architecture of the population stays constant. This model thus considers that ![]() and
and ![]() at any time t, so that the response to selection is linear (provided that selection does not vary). The ‘infinitesimal model’ of genetic architecture (Lande, Reference Lande1975) is generally cited as a justification for the constant variance model. By assuming an infinite number of loci, each of them having an infinitely small effect on the phenotype, the mean of the population can change without affecting allele frequencies (Bulmer, Reference Bulmer1980; Turelli, Reference Turelli and Weir1988). Neglecting migration, mutation, linkage disequilibrium and genetic drift, the additive variance can remain constant. The infinitesimal model is widely used in the literature, either explicitly or implicitly.
at any time t, so that the response to selection is linear (provided that selection does not vary). The ‘infinitesimal model’ of genetic architecture (Lande, Reference Lande1975) is generally cited as a justification for the constant variance model. By assuming an infinite number of loci, each of them having an infinitely small effect on the phenotype, the mean of the population can change without affecting allele frequencies (Bulmer, Reference Bulmer1980; Turelli, Reference Turelli and Weir1988). Neglecting migration, mutation, linkage disequilibrium and genetic drift, the additive variance can remain constant. The infinitesimal model is widely used in the literature, either explicitly or implicitly.
Only three parameters are necessary to estimate the expected dynamics, with

This is equivalent to equation (2) assuming ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
This model constitutes a basis on which more realistic models can be built. Such models may introduce the effects of finite population sizes (genetic drift), mutations or linkage disequilibrium. Although described separately for clarity, they can be combined in order to get a more realistic picture of the properties of a population under selection (Keightley & Hill, Reference Keightley and Hill1987).
(b) Genetic drift
The constant additive-variance prediction can be interpreted as the consequence of the assumption that individual allele frequencies do not change much. However, unless the population is virtually infinite, genetic drift will drive alleles to irreversible fixation, with a rate that is inversely proportional to the population size. Genetic drift thus has two major impacts, a stochastic effect that can be accounted for when calculating the likelihood (as detailed later in this manuscript or in e.g. Le Rouzic et al., Reference Le Rouzic, Skaug and Hansen2010) and a deterministic effect on the additive variance, which is the topic of the current paragraph. Drift in finite populations is indeed expected to decrease σA2 by a factor of 1/(2N e) in each generation (Robertson, Reference Robertson1960; Lande, Reference Lande1975), where N e is the effective population size. In small populations and long time series, this deterministic effect is cumulative over generations and can be strong enough to affect the population dynamics. It can be accounted for simply by considering the same model as in equation (6), but letting the additive variance σA2 decrease with time:
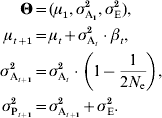
(c) Mutations
From mutation-accumulation experiments, it is known that spontaneous mutations tend to generate a small but significant amount of selectable additive variation, ranging from 0·01 to 1% of σP2 per generation, the mutational coefficient of variation being 0·1–4% of the trait mean (e.g. mutational evolvability I M=σM2/μ2 between 10−6 and 1·6×10−3) (Lynch, Reference Lynch1988; Houle et al., Reference Houle, Morikawa and Lynch1996; Keightley, Reference Keightley1998; Houle, Reference Houle1998; Lynch et al., Reference Lynch, Blanchard, Houle, Kibota, Schultz, Vassilieva and Willis1999; Keightley, Reference Keightley2004). The depletion in additive variance is thus rarely total and irreversible. Mutations can be accounted for, considering that a fixed (additive) mutational variance σM2 (a composite parameter featuring the appearance of new mutations and their change in frequency under selection) is generated in each generation:

Similar models can be defined according to the alternative scales detailed before. For instance, on the evolvability scale, the quantity of interest would be I M=σM2/μ2, and ![]() . Similarly, on the heritability scale, the logical parameter should be h m2=σM2/σP2; however, h m2=σM2/σE2 could also be used to correspond to a quantity that is often estimated empirically (e.g. Lynch, Reference Lynch1988).
. Similarly, on the heritability scale, the logical parameter should be h m2=σM2/σP2; however, h m2=σM2/σE2 could also be used to correspond to a quantity that is often estimated empirically (e.g. Lynch, Reference Lynch1988).
This model remains a rough approximation of what happens at mutation–selection–drift equilibrium. The actual probability for mutations to appear and to be fixed depend on the distribution of mutational effects, strength of selection and population size (Hill, Reference Hill1982b; Bürger & Ewens, Reference Bürger and Ewens1995; Otto & Whitlock, Reference Otto and Whitlock1997; Hermisson & Pennings, Reference Hermisson and Pennings2005; Engen et al., Reference Engen, Lande and Sæther2009).
(d) Linkage disequilibrium
In artificial selection, breeders are chosen according to some non-random selection rule, such that the group of breeders is a biased sample of the population. Most of the time, breeders tend be more similar to each other than the rest of the population: only big or small phenotypes are bred (directional selection), or rarely individuals close to the mean of the population are chosen (stabilizing selection). Exceptionally, the bias is towards dissimilar individuals (disruptive selection). In any case, the phenotypic variance among breeders is different from the phenotypic variance in the population, and so is the additive variance. Such a direct or indirect selection on the variance will generate some linkage disequilibrium, which will affect the selection response. This effect of linkage disequilibrium on selection response is known as the ‘Bulmer effect’ (Bulmer, Reference Bulmer1971).
A simple model consists in decomposing the additive variance: σA2=σa2+d; the ‘genic’ variance σa2 corresponding to the additive variance if all loci were at linkage equilibrium, the influence of linkage disequilibrium being d. According to Bulmer (Reference Bulmer1971), ![]() , where δt=(s t2*−s t2)/s t2 stands for the relative difference between the phenotypic variance of the breeders (s t2*) and the phenotypic variance of the rest of the population s t2. If the variance among breeders is unknown, there is no general formula to compute this effect in all situations, but it can be deduced from the properties of the normal distribution for specific selection regimes.
, where δt=(s t2*−s t2)/s t2 stands for the relative difference between the phenotypic variance of the breeders (s t2*) and the phenotypic variance of the rest of the population s t2. If the variance among breeders is unknown, there is no general formula to compute this effect in all situations, but it can be deduced from the properties of the normal distribution for specific selection regimes.
Assuming that the genic variance is constant, the change in additive variance between two generations can thus be written as ![]() , and since
, and since ![]() ,
,
If δt<0 (breeders are more similar to each other than in the whole population, which is expected for most selection regimes, including directional and stabilizing), the additive variance is reduced. If δt>0 (disruptive selection), the additive variance in the population is larger than in a non-selected population.
Combining linkage disequilibrium with e.g. genetic drift as described in equation (7), the following model can be derived:
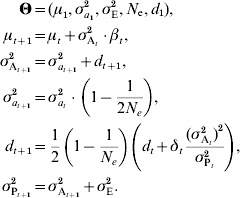
A similar result was derived by Dempfle (Reference Dempfle1975) using a different approach. While changes in μ depend on selection on trait value, changes in d occur because of selection on variance. It is thus possible to predict changes in additive variance even if β=0 (for instance, if selection is stabilizing or disruptive). If there is no selection on variance (δt=0) and loci are unlinked, the effect on linkage disequilibrium is halved each generation. If selection is constant, the disequilibrium rapidly stabilizes. This model considers that the initial linkage disequilibrium d 1 is unknown, but if the initial population is derived from several generations of random mating, it can be safely assumed that d 1=0.
(e) Finite number of loci
The infinitesimal model relies on the assumption that a large number of small-effect loci influence the trait. When this assumption is violated, the additive variance is expected to decrease faster than predicted in the models described above. Although precisely modelling the effect of individual loci is unrealistic, a general model was proposed by Chevalet (Reference Chevalet1994) . This model introduces an additional parameter, n, corresponding to the number of loci in the genetic architecture, provided that all loci have the same effect. The previous model, including drift and linkage disequilibrium, can then be rewritten as:
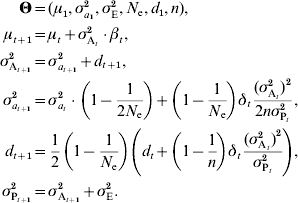
If loci actually have different effects, n can be interpreted as n e, an effective number of loci (Chevalet, Reference Chevalet1994). As a first approximation, when estimating the number of loci, n e can be considered as constant. However, this assumption is likely to be inaccurate for long time series, since n e is expected to change along with the allele frequencies.
(f) Directional epistasis
Epistasis refers to the situation in which the effect of an allele substitution at a given locus depends on the genotype at other loci. Originally defined for discrete Mendelian genes, the concept has been extended to quantitative genetics, and corresponds to genetic effects that cannot be attributed to single-locus (i.e. additive and dominance) effects (Cockerham, Reference Cockerham1954; Kempthorne, Reference Kempthorne1954; Phillips, Reference Phillips1998). Although often neglected in evolutionary models, epistasis (as well as dominance, the intra-locus equivalent to epistasis) has proved to be common for quantitative traits (Carlborg & Haley, Reference Carlborg and Haley2004), and their impact on the selection response may be important (Carter et al., Reference Carter, Hermisson and Hansen2005; Hallander & Waldmann, Reference Hallander and Waldmann2007; Hansen et al., Reference Hansen, Alvarez-Castro, Carter, Hermisson and Wagner2006; Le Rouzic et al., Reference Le Rouzic, Siegel and Carlborg2007; Reference Le Rouzic, Álvarez-Castro and Carlborg2008).
When there is epistasis, the effect of artificial or natural selection can still be predicted by the Lande equation over a single generation (i.e. only additive variance matters), but changes in the genetic background due to selection modify genetic effects, so that the additive variance can change (upwards or downwards according to the pattern of interactions) in the course of time. In addition, the dynamics of non-additive genetic variance terms (interaction variance) may lead to changes in what is considered as σE2 in the current setting.
One impact of epistasis on a selection-response time series can be summarized by a directional epistasis coefficient ε (Carter et al., Reference Carter, Hermisson and Hansen2005), featuring the average curvature of the genotype–phenotype map in the current population. If directionality is positive, epistasis tends to amplify the effects of alleles that have a positive effect on the trait, and the selection response accelerates when selecting for higher phenotypic values (decelerates when selecting for lower phenotypes). If ε<0, allelic effects tend to reduce each other, and ‘up’ selection becomes less and less effective, while ‘down’ selection becomes easier. If ε=0, the population will respond to selection in a similar way as if there was no epistasis.
If the genotype–phenotype map is multilinear (Hansen & Wagner, Reference Hansen and Wagner2001), the interaction between two loci i and j is quantified by an epistatic parameter ijε. Even if ijε is different between all pairs of loci (the variance of all pairwise ε can be noted σε2), the properties of the genotype–phenotype map can still be summarized by the composite parameter ε (Carter et al., Reference Carter, Hermisson and Hansen2005). Two predictions can be made: (i) the change in additive variance scales with ε and with the strength of selection, and (ii) the epistatic variance σAA2 scales with the square of the additive variance. More specifically:
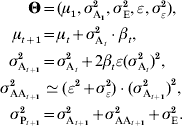
In practice, σε2 has very little impact on the overall time series, and can be ignored. The multilinear model remains a local approximation, and is probably less realistic when studying large phenotypic distances. In particular, long-term selection (directional or stabilizing) may lead to changes in ε (Hermisson et al., Reference Hermisson, Hansen and Wagner2003; Hansen et al., Reference Hansen, Alvarez-Castro, Carter, Hermisson and Wagner2006; Álvarez-Castro et al., Reference Álvarez-Castro, Kopp and Hermisson2009). Directional epistasis predicts an asymmetric response to selection, additive variance increasing when selecting in the direction of epistasis.
(g) Canalization
Directional epistasis is an operational tool to model and describe genetic architectures, and contrary to most architecture parameters (e.g. mutational variance, effective population size), it can be estimated from QTL data (Le Rouzic & Álvarez-Castro, Reference Le Rouzic, Álvarez-Castro and Carlborg2008; Pavlicev et al., Reference Pavlicev, Le Rouzic, Cheverud, Wagner and Hansen2010), and thus has the potential to help linking the results of reductionist genetic-architecture dissections and selection-response approaches. Yet, directional epistasis does not allow e.g. additive variance to decrease or increase in both selection directions, corresponding to what may be referred to as genetic canalization and decanalization.
A simple way to model genetic canalization is to consider that additive variance decreases or increases according to the distance ![]() between the mean of the population μt and a specific phenotypic value θ (the ‘canalization optimum’) at which the additive variance is maximum (or minimum). The distance might be linear (
between the mean of the population μt and a specific phenotypic value θ (the ‘canalization optimum’) at which the additive variance is maximum (or minimum). The distance might be linear (![]() ) or more elaborated (e.g.
) or more elaborated (e.g. ![]() (μt−θ)2). The model can be written as
(μt−θ)2). The model can be written as ![]() , and a recursive form, more similar to the previous models, can be easily derived since
, and a recursive form, more similar to the previous models, can be easily derived since ![]() . The strength of the genetic canalization is quantified by the parameter k g, if k g>0, σA2 increases with
. The strength of the genetic canalization is quantified by the parameter k g, if k g>0, σA2 increases with ![]() (decanalization), while k g<0 models some genetic canalization.
(decanalization), while k g<0 models some genetic canalization.
Environmental variance can also be affected by canalization or decanalization. Genotype-by-environment (G×E) interactions occur when genotypes react in a different way to the same environmental conditions. When selecting for extreme phenotypes, it is likely that the selected genotypes may differ in their ability to deal with stress, temperature changes, food-quality variation, etc. Modelling environmental canalization can be done in a very similar way as for genetic canalization, by considering that environmental variance may increase when the population gets farther from a specific phenotypic value θ. This model thus assumes that σE2 depends on a measure ![]() , defined in the same way as for genetic canalization. In this model, k c quantifies the strength of the canalization; if k c>0, σE2 increases when the population moves away from its initial state (the genotypes are less stable and more sensitive to micro-environmental effects); on the contrary, k c<0 indicates a canalizing effect when the mean is shifted.
, defined in the same way as for genetic canalization. In this model, k c quantifies the strength of the canalization; if k c>0, σE2 increases when the population moves away from its initial state (the genotypes are less stable and more sensitive to micro-environmental effects); on the contrary, k c<0 indicates a canalizing effect when the mean is shifted.
Considering both genetic and environmental canalization gives:
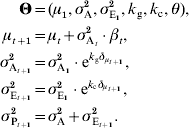
To simplify the model, as a first approximation, θ can be considered as identical to the initial population mean (θ=μ1).
(h) Effect of natural selection
Even in carefully controlled conditions in the lab, it is impossible to avoid the effects of natural selection. Indeed, selected traits are often correlated with fitness, either by influencing directly the survival or the fecundity of the organism, or by sharing some pleiotropic genes with fitness-related traits.
If natural selection tends to have a stabilizing effect, the efficiency of artificial selection will decrease when the mean of the population moves away from the optimal phenotype. As a consequence, selection response is expected to decrease as the mean changes, while a respectable amount of additive variance is still present in the population (e.g. Zhang & Hill, Reference Zhang and Hill2002). These ‘joint-effect’ models should be considered as alternative models to the framework proposed in equation (2), since the additive variance is not really reduced (e.g. when computing the phenotypic variance), but only partially available for artificial selection. A simple way to model this phenomenon is to consider a slightly modified version of Lande equation, such as:
in which the efficiency of artificial selection is decreased as μt gets further from the phenotypic optimum θ, s being the strength of natural selection (stabilizing when s<0, the larger |s|, the stronger the selection). If artificial selection is relaxed, βt=0, and the mean of the population will tend to stabilize at θ. Under a constant directional artificial-selection pressure, the population will eventually stabilize at a point where artificial and natural selection intensities are equal, but in opposite directions, so that no more phenotypic change occurs. The selection function presented in equation (14) is chosen for simplicity, and realistic alternatives (e.g. quadratic or exponential call-back terms) may be considered. More complex mechanistic models of joint-effect selection have been elaborated (Lande, Reference Lande1983; Zhang & Hill, Reference Zhang and Hill2002; Reference Zhang and Hill2005) and may be used under different assumptions on e.g. distribution of allele frequencies.
Another alternative is to consider that the focal trait is only correlated with characters constrained by stabilizing selection, without itself having a direct impact on fitness. These correlations slow down the selection response, but do not lead to a halt: the trait can evolve, but not as freely as if all other traits were free to change; the ability to evolve when all correlated characters are kept constant has been termed the conditional evolvability of the trait (Hansen, Reference Hansen2003; Hansen et al., Reference Hansen, Armbruster, Carlson and Pélabon2003a; Hansen & Houle, Reference Hansen and Houle2008). Deriving a precise mechanistic model would require some knowledge about the strength of stabilizing selection on the other traits as well as their correlation with the focus trait. Nevertheless, a simple model such as:
with 0<k a<1, is able to describe the expected effect of the correlation of the selected trait with one or other characters that is not allowed to vary. The factor k a can be interpreted as the part of the additive genetic variation in the trait of interest that is independent with traits under strong natural selection (Hansen et al., Reference Hansen, Armbruster, Carlson and Pélabon2003a). If k a=0, no change in the trait is possible, in spite of some genetic variation, because all genes underlying the trait also affect other characters that are strongly constrained.
3. Methods
(i) Maximum-likelihood estimates
(a) General setting
The models described in the previous section provide a way to predict the response to selection from a given set of parameters. They can also be used to estimate the dynamic properties of the genetic architecture, given an experimental data set. The next paragraph details the way to compute the likelihood of a specific model given some phenotypic time series Y, which can be used to estimate the parameters (![]() ) by maximizing the likelihood function L(Θ|Y).
) by maximizing the likelihood function L(Θ|Y).
A typical artificial-selection experiment is carried out on a population of size N, in which the phenotype of interest Y=(y 1, …, y i, …, y N) (i.e. the trait on which selection is performed) is measured for each individual i. A subset Y* of individuals is then chosen for breeding according to some selection rule. The process is then being repeated over T generations, and the full data set is Y=(Y 1, …, Y T).
It is common to report and archive only summary statistics of the population at each generation t: the average phenotype, ![]() t, the population variance of the phenotype, s yt2 and the mean phenotype of the breeders,
t, the population variance of the phenotype, s yt2 and the mean phenotype of the breeders, ![]() t*. The selection gradient at generation t can be computed as βt=(
t*. The selection gradient at generation t can be computed as βt=(![]() t*−
t*−![]() t)/s yt2 (i.e. the selection differential divided by the phenotypic variance). For convenience, the full data set, Y, will be split into
t)/s yt2 (i.e. the selection differential divided by the phenotypic variance). For convenience, the full data set, Y, will be split into ![]() , where
, where ![]() =(
=(![]() 1, …,
1, …, ![]() T), and st2=(s y12, …, s yT2). In addition, two vectors, β=(β1, …, βT), and N=(N 1, …, N T), describe the experimental setting (selection gradient and population size for each generation).
T), and st2=(s y12, …, s yT2). In addition, two vectors, β=(β1, …, βT), and N=(N 1, …, N T), describe the experimental setting (selection gradient and population size for each generation).
Deterministic models for the dynamics of the mean and the variance in the population provide the theoretical expectations μt and ![]() at generation t. However, even if the population is large and the underlying model is correct, the observed means and variances
at generation t. However, even if the population is large and the underlying model is correct, the observed means and variances ![]() t and s yt2 will be affected by sampling error: each individual phenotypic measurement y it is expected to follow a Gaussian distribution of mean μt and variance
t and s yt2 will be affected by sampling error: each individual phenotypic measurement y it is expected to follow a Gaussian distribution of mean μt and variance ![]() . The probability density for the whole population at this generation is thus:
. The probability density for the whole population at this generation is thus:
where φ(x|μ, σ2) is the Gaussian probability density with mean μ and variance σ2.
The polygenic models assume that the phenotypes in a population follow a normal distribution, so that the entire distribution can be described by its mean and its variance. For the whole time series (T generations), the total probability is
The models will predict the expected means and variances (μt and ![]() ) for all generations, based on a set of parameters describing the genetic architecture (Θ) and the strength of selection for all generations (β). The full likelihood function can thus be written as:
) for all generations, based on a set of parameters describing the genetic architecture (Θ) and the strength of selection for all generations (β). The full likelihood function can thus be written as:
The estimates of interest are the values ![]() maximizing this function.
maximizing this function.
(b) Combining time series
This framework is flexible, and can easily be adapted to particular experimental designs. A common feature in selection-response experiments is that several time series are often initiated from the same population, so that the data comprise several series of selection responses. Typically, at least two lines are selected, one for high values of the trait, the other one for low values; sometimes an unselected control line is used as a reference, and some selection treatments can be replicated. Considering all these series in a single genetic-architecture model would improve the precision and the meaning of the parameters, since differently selected lines will explore different parts of the genotype–phenotype map.
As discussed in Le Rouzic et al. (Reference Le Rouzic, Skaug and Hansen2010), if Y1, …, YR are R phenotypic series initiated from a unique population, it is possible to combine the likelihoods such that:
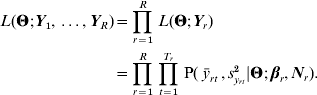
(c) Random-effect models
The likelihood function described above is based on the assumption that the sampling effect is the only source of stochasticity. In some cases, however, this assumption is unreasonable. Including additional sources of stochasticity can be achieved by considering nuisance parameters (e.g. generation-specific effects) that are not estimated individually, but rather considered as random effects. Two families of random effect models are briefly described below and detailed as supplementary material: (i) generation-specific macro-environmental effects and (ii) genetic drift.
The possibility to include generation-specific environmental effects is detailed in the Supplementary Methods section. The model considers that the influence of environment can be split into two components. The micro-environmental variance σE2, as described above, explains the non-genetic dispersion of the phenotypes among individuals of the same population, while the macro-environmental variance σme2 catches generation-specific environmental shifts. Macro-environmental effects are considered as random effects, and the likelihood can be computed analytically under the assumption that effects are not correlated between generations.
Another source of randomness is genetic drift. Although small when considering consecutive generations, deviations due to genetic drift accumulates over time and may impact the time series substantially, especially in small populations. The possibility to account for drift on the mean phenotype of the population was detailed in Le Rouzic et al. (Reference Le Rouzic, Skaug and Hansen2010), and is briefly described below.
The model is based on the assumption that the genetic mean μt and the additive variance σt2 at generation t are random effects, the source of stochasticity being genetic drift. Then, ![]() , where
, where ![]() is the expected mean at generation t (e.g.
is the expected mean at generation t (e.g. ![]() or any alternative model describing changes in the mean), and x 1 is drawn in a normal distribution of mean 0 and variance σA2/N, the sampling variance of the genetic mean. In a similar way,
or any alternative model describing changes in the mean), and x 1 is drawn in a normal distribution of mean 0 and variance σA2/N, the sampling variance of the genetic mean. In a similar way, ![]() , where x 2 follows a χ2 distribution with N−1 degrees of freedom, and
, where x 2 follows a χ2 distribution with N−1 degrees of freedom, and ![]() is the expected value of the variance at generation t, e.g.
is the expected value of the variance at generation t, e.g. ![]() or any alternative model. Assuming that drift affects genetic mean and genetic variance independently, equation (16) can be rewritten as:
or any alternative model. Assuming that drift affects genetic mean and genetic variance independently, equation (16) can be rewritten as:
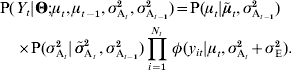
The vector of genetic means μ and the vector of additive variances σ A 2 being considered as random effects, the likelihood function has to be integrated over them:
![\eqalign{ L\lpar \bmTheta \vert {\bi Y}\rpar \equals \tab\!\!\! \int\limits_{\mu _{\setnum{1}} \comma \ldots \comma }\!\!\!\!\!\!\! { \cdots\!\!\! \int\limits_{_{{\mu_{ T}}} }\!\!\! {\int\limits_{\sigma _{{{\rm A}_{\setnum{1}} }}^{\setnum{2}} \comma \ldots \comma }\!\!\!\!\!\!\! \cdots } } \!\!\int\limits_{\sigma _{{{\rm A}_{T} }}^{\setnum{2}} } {} \cr \tab \left[ {\prod\limits_{t \equals \setnum{1}}^{T} \, {\rm P}\lpar Y_{t} \vert \rmTheta \semi \ \mu _{t} \comma \mu _{t \minus \setnum{1}} \comma \sigma _{{\rm A}_{t} }^{\setnum{2}} \comma \sigma _{{\rm A}_{{t \minus \setnum{1}}} }^{\setnum{2}} \semi \ \beta _{t} \comma N_{t} \rpar } \right] \cr \tab \times {\rm d}\mu _{\setnum{1}} \cdots {\rm \, d}\mu _{T} \, {\rm d}\sigma _{{\rm A}_{\setnum{1}} }^{\setnum{2}} \cdots \comma {\rm \, d}\sigma _{{\rm A}_{T} }^{\setnum{2}} . \cr}\hskip-32pt](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20160920235900076-0410:S0016672311000024:S0016672311000024_eqn21.gif?pub-status=live)
Contrary to macro-environmental variance (described in the Supplementary Results 1), genetic drift generates random deviations that are correlated between consecutive generations. The likelihood cannot be computed independently for each generation, and analytical development is complicated. Instead, likelihoods were calculated based on Laplace approximation, using the random-effect module of the software ADMB-RE (Skaug & Fournier, Reference Skaug and Fournier2006). Laplace approximation is exact when the posterior distribution of the random effects is normal, which is not exactly the case here (variances are χ2-distributed). For simplicity, when implementing the model, it was considered that (![]() was normally distributed with a mean of 0 and a variance of 2/(N t−1), which is a good approximation provided that 2/(N t−1)≪1.
was normally distributed with a mean of 0 and a variance of 2/(N t−1), which is a good approximation provided that 2/(N t−1)≪1.
(ii) Implementation
(a) Model fitting
Some of the models described in the previous section have been implemented as a fully documented free package for the statistical software R (R Development Core Team 2007). The package sra and its documentation can be downloaded on http://cran.r-project.org/web/packages/sra/. It provides a user-friendly wrapper for the optimum function of R, which performs the numerical maximization of the likelihood function.
In general, numerical convergence is not problematic when meaningful starting values are provided. Positive-only parameters (such as the variances or the population size) are log transformed before being fit in order to improve the efficiency of the convergence algorithm. The likelihood function of the highly nonlinear directional-epistasis model (equation (12)) was challenging for the gradient-based algorithms, and the package implements directional epistasis as two distinct models (positive and negative epistasis) that are discriminated based on their likelihood. Models were compared by calculating their Akaike Information Criteria (AIC) or Bayesian Information Criteria (BIC) (Akaike, Reference Akaike1973; Anderson et al., Reference Anderson, Burnham and Thompson2000; Burnham & Anderson, Reference Burnham and Anderson2002).
The most complex models, involving more than ten parameters, were challenging for simple hillclimbing algorithms. In particular, some phenomenological models (those in which more than one-generation lags were considered) often produced a complex likelihood function with several peaks. Maximum-likelihood estimates thus depend on the starting values, and the results reported in the next section are based on the best likelihood score out of C convergence attempts with randomized starting values, C varying from 1 to 30 depending on the complexity of the model. This procedure gave convincingly stable results, even if there is no certainty that the global maximum was reached. In any case, this does not raise interpretation issues, since different likelihood peaks generally correspond to similar patterns for the dynamics of the means and the variances. Conversely, convergence in mechanistic models was less problematic, and the few optimization errors that were encountered were easily solved by using the results of simpler models (e.g. the constant-variance model) as starting values for the more complex ones.
The likelihood function in the model including macro-environmental effects could be derived analytically, and convergence was achieved in R. The drift model is more complex and was implemented in the software AD Model Builder (http://admb-foundation.org), which offers a more sophisticated convergence algorithm (Skaug & Fournier, Reference Skaug and Fournier2006) based on Laplace approximation of the likelihood function. The corresponding code is available on request.
The framework proposed in the previous sections is flexible and can be easily extended. Possible improvements or alternatives include: (i) the definition of additional mechanistic models in order to test new biological hypotheses, and (ii) the adaptation of the statistical framework for philosophical or pragmatic reasons, e.g. by replacing the maximum-likelihood approach with a Bayesian framework (see e.g. O'Hara et al., Reference O'Hara, Cano, Ovaskainen, Teplitsky and Alho2008).
(b) Simulations
Simulated data sets were generated to assess the validity of the models and the accuracy of the parameter estimates. Two procedures have been used to generate simulated data: (i) stochastic simulation of the model and (ii) individual-based simulations.
The stochastic simulation procedure is based on deterministic times series generated from specific models (equations (6)–(15)) with known parameters. Theoretical means and variances are then randomly modified independently for each generation, according to μsim=μth+x 1+x 2 and ![]() , where x 1 is drawn from a normal distribution of mean 0 and variance
, where x 1 is drawn from a normal distribution of mean 0 and variance ![]() (sampling variance of the mean), x 2 is drawn from a normal distribution of mean 0 and variance σme2 (macro-environmental variation), and y is drawn in a χ2 distribution with N−1 degrees of freedom (sampling variance of the variance).
(sampling variance of the mean), x 2 is drawn from a normal distribution of mean 0 and variance σme2 (macro-environmental variation), and y is drawn in a χ2 distribution with N−1 degrees of freedom (sampling variance of the variance).
Individual-based simulations rely on the constant-variance model, considering a genetic value g i and a phenotypic value p i for each simulated individual i. At each generation, the N individuals are ranked according to their phenotype, and the N sel extreme individuals constitute the parental population. A pair of parents is then randomly drawn in this parental population for each offspring j, the genotypic value of which is g j=(g f+g m)/2+x j, where g f and g m are the genotypic value of the father and the mother, respectively, and x j is a random number drawn in a normal distribution of mean 0 and variance σA2/2. The phenotypic value of individual j is drawn in a normal distribution of mean g j and variance σE2.
4. Statistical properties
The accuracy of the likelihood equation as well as the software implementation of the models have been evaluated by simulation. Several properties of the statistical models have been explored: the ability for the model to converge on the expected estimates when the exact model is simulated, the power of model selection to discriminate among models depending on the quantity of the data, and the robustness of the parameter estimates when additional sources of noise that are not explicitly accounted for in the likelihood function (macro-environmental variance and stochastic genetic drift) are considered.
(i) Accuracy
First, the quality of the estimates provided by the model was checked in the constant-variance case, supposing that model assumptions are true (i.e. no stochastic effects apart from sampling). In order to simulate a realistic situation, parameter values were chosen close to the estimates obtained from the example detailed in example section below: μ0=0·04, σA2=0·0001, σE2=0·0004. The Supplementary Results 1 section reports the bias and the precision of parameter estimates for various population sizes and various lengths of the time series. Estimates appeared to be satisfactorily unbiased. Even poor data sets (e.g. 20 individuals selected for five generations) provide meaningful estimates.
The flexibility of phenomenological models was also confirmed by fitting arbitrary variance dynamics (Supplementary Results 2). The power of model selection was assessed by simulating the selection response expected from two different genetic architectures ((i) constant variance and (ii) directional epistasis) and running various mechanistic models on these time series. AIC and BIC were calculated for each model, and the differences between models are reported (Supplementary Results 3). For large data sets, model selection is satisfactory (the correct model is chosen most of the time). From the simulation results, it appears that two factors are important regarding the accuracy of model selection: (i) the length of the selection experiment and (ii) the number of selected lines. When the time series is short (ten generations in this example), the simplest model (the constant-variance model) seems to be favoured, which is an expected result. One selected line alone does contain enough information to reject the constant-variance model when the real genetic architecture is complex (here, directional epistasis), but not enough to discriminate among the complex ones (AIC and BIC scores remain very close). This points out the importance of maximizing the number of selection lines in order to maximize the amount of information available. In contrast, the impact of population size appears to be smaller. Indeed, with two lines selected for 30 generations, the right model (directional epistasis) has the lowest AIC in 95% of the simulations even with a population size as small as N=20.
(ii) Robustness
The simplest models (likelihood equation (18)) assume that the stochasticity of the time series can be completely attributed to sampling effects. However, it is not clear whether the models based on infinite-size populations behave when fit to ‘real’ data when both sampling variance and other sources of stochasticity affect the measurements of the means and variances. The impact of two independent sources of stochasticity, the stochastic effect of genetic drift and macro-environmental variations, have thus been checked by simulation.
Some of the models presented above do account for some properties of genetic drift, such as the deterministic loss of genetic variation due to inbreeding in small populations (equation (7)). However, genetic drift will also generate some departure from the expected dynamics, which is accounted for by more complex random-effect models (equation (21)). Although the magnitude of this departure is expected to be smaller than e.g. sampling effects in a given generation, deviations due to genetic drift are heritable, and may then accumulate over generations according to a Markov process. Therefore, it is expected that genetic drift may affect parameter estimates. Supplementary Results 4 report the mean parameter estimates obtained when running the model on individual-based simulated data, with various population sizes. Fixed-effect estimates of additive and environmental variance are slightly biased: additive variance is underestimated in small populations, while environmental variance tends to be overestimated. Confidence intervals are also less reliable, being too narrow for σA2, and too wide for σE2. Nevertheless, apart from very small populations, drift-related effects on parameter estimates remains limited, and are unlikely to affect significantly the conclusions of the analysis. Supplementary Results 5 illustrate how considering random-effect models improves the estimated standard error, and Supplementary Results 6 focus on the impact of considering replicated selection experiments on parameter estimates.
Finally, we investigated the impact of macro-environmental effects by adding a random deviate to the mean phenotype each generation in the simulated data, drawn from a normal distribution with variance parameter σme2 (Supplementary Results 7). It appears that macro-environmental variation affects the estimate of the environmental variance (and environmental variance related parameters, such as the k c in equation (13)), which reflects the residual variance when fitting the model, but other parameters (additive variance, initial population mean) remain unaffected, even when σme2>σE2. The statistical framework developed in this paper thus appears to be robust to macro-environmental effects. Computing the likelihood while accounting for macro-environmental effects efficiently removes the bias on σE2. However, the additional flexibility provided by macro-environmental effects may be misleading when fitting simple models on complex data (Supplementary Results 8). To avoid interpretation issues, the example detailed below will thus be analysed without macro-environmental effects.
5. Example: artificial selection on wing shape in fruit flies
The properties of the statistical procedure will be illustrated by analyses of data from an artificial-selection experiment on morphology in D. melanogaster. From an initial stock, four populations of N≃100 were selected in two directions (two ‘up’ and two ‘down’ lines). A picture of the wing of each individual fly was taken by the automatic system known as the Wingmachine (Houle et al., Reference Houle, Mezey, Galpern and Carter2003), and selection was performed on a composite, dimensionless index involving two relative distances (Fig. 1(a)), as described in Pélabon et al. (Reference Pélabon, Hansen, Carter and Houle2006) . Each generation, the most extreme 20 males and 20 females were bred randomly, and the selection procedure was carried on for 28 or 29 generations. At that point, the selected populations have accumulated easily recognizable wing-shape differences in the selected index (Fig. 1(b) and (c)), of a relative magnitude larger than what can be observed in the whole subgenus Sophophora.

Fig. 1. Drosophila melanogaster wing pictures taken with the Wingmachine system. (a) Individual from the initial population; the two measures used to build the selection index are indicated: ‘1’ is the the distance between veins III and IV and ‘2’ is the relative position of the posterior cross-vein. (b) Individual wing from generation 29 of the ‘up’ selection line (selection for increasing the two indexes). (c) Individual wing from generation 29 of the ‘down’ line (selection for decreasing both indexes).
The distribution of the selection index in males and females is virtually identical, and the sexes were merged for the analysis. All measured wings were considered except for three individuals from generation 20 of one of the the ‘up’ line, which were clear outliers. A summarized data set reporting: (i) the phenotypic mean in the population, (ii) the phenotypic variance, (iii) the mean of the selected breeders and (iv) the population size before selection, was computed for model fitting.
The analysis was performed in three steps: (i) the best scale for the data was determined by comparing the fit of basic models on different scales, (ii) the properties of the time series and the potential explanatory power of simple models were assessed by fitting phenomenological models of increasing complexity, and (iii) mechanistic models were fit and the corresponding biological parameters were estimated. For simplicity, the fixed-effect version of the model (infinite population size) was used in all cases.
The phenotypic measurement in this experiment is a complex variable. The selection index I is a combination of two traits (Pélabon et al., Reference Pélabon, Hansen, Carter and Houle2006). I 1 is the average distance between veins III and IV normalized by the square root of the wing area. I 2 is the relative position of the posterior cross-vein, i.e. the average of two distance ratios. The total index is a weighted sum of these two traits, the weights being chosen in order to compensate for the fact that the phenotypic variance of I 1 was 2·6 times smaller than the variance of I 2: I=2·6I 1+I 2. I is thus a dimensionless index; apart from the fact that it cannot be negative, its expected scaling properties are difficult to assess a priori. Table 1 reports the AIC of simple phenomenological models (exponential or linear changes in the variances) on four different scales (for the log scale, equation (16) was changed to a log-normal density function). For all models, the logarithmic scale outperformed other scales, and was thus retained for subsequent analysis. The main effect of the log scale here is to correct partially the asymmetry of selection responses, in a way that is very similar to the evolvability scale.
Table 1. AIC (expressed as the difference with the best model (AIC=0)) for simple phenomenological models fitted on the whole data set (both ‘up’ and ‘down’ lines) on four different scales: original scale, logarithm scale, evolvability scale, and heritability scale. Log-transformed means and variances were computed from the original means and variances assuming log–normality on the original scale. The four different models correspond to subsets of equation (2): the constant variances model forces ![]() ,
, ![]() ,
, ![]() ,
, ![]() . In the ‘exponential changes’ model,
. In the ‘exponential changes’ model, ![]() and
and ![]() can vary, in the linear change model,
can vary, in the linear change model, ![]() and
and ![]() can vary, and in the last model (linear and exponential change), all four parameters are active. The logarithmic scale appears to provide the best fit, whatever the model
can vary, and in the last model (linear and exponential change), all four parameters are active. The logarithmic scale appears to provide the best fit, whatever the model

Fitting phenomenological models on the variance trends is a convenient way to introduce additional explanatory variables in the models without making specific assumptions about the underlying genetic mechanisms. Table 2 summarizes the gain in explanatory power when introducing an increasing number of variables, and the fit differences across models are illustrated in Supplementary Figures 1 to 3. This phenomenological analysis brings three main results: (i) The models fitting the data the most convincingly without over-parameterization have more than nine parameters. This illustrates the potential number of hidden variables in the system. Such variables might involve macro-environmental factors, measurement errors, genetic factors (segregation of large-effect alleles, complex epistatic patterns) or other biological mechanisms (e.g. maternal or epigenetic effects). (ii) The AIC obtained when fitting independently the four lines (44 parameters) is much better (by >1850 units) than the models considering all at the same time: any model predicting symmetric selection responses is thus necessarily approximate. Although less important, this very significant gap still exists when comparing two identically selected lines (the ‘up’ lines considered independently (22 parameters) perform 380 AIC units better than when pooled together (11 parameters), and the difference is 420 AIC units for the ‘down’ lines). (iii) The predicted trends systematically show unexpected patterns in variance dynamics: the additive variance trend is ‘V-shaped’, with an initial decrease and a late increase after 15–20 generations, which does not correspond to classical quantitative genetics expectations; possible explanations include, e.g. new mutations arising in both lines, a specific pattern of epistasis, or close linkage between two loci in repulsion (Hospital & Chevalet, Reference Hospital and Chevalet1996). In a similar way, environmental variance also increases at the end of the time series, especially in the ‘up’ lines, which also does not fit with common assumptions.
Table 2. AIC score for phenomenological models of different complexity, expressed as the difference with the best model (AIC=0) for each data set. Seven data sets are considered, the two ‘up’ selected lines (independently and together, i.e. assuming an identical genetic architecture in both lines), the two ‘down’ selected lines (independently and together), and all four lines simultaneously. The first line corresponds to a model where the variance does not change, and is thus equivalent to the constant variance model of tables 1 and 3. The different models are described as in equation (2), i.e. the ‘lag 0’ model corresponds to a model in which only the constant parameters ![]() and
and ![]() are active, ‘lag 1’ to a model where both k 0 and k 1 parameters are estimated, etc. The simplest model (‘no change’) has three parameters, the most complex (‘lag 3’) has 11 parameters
are active, ‘lag 1’ to a model where both k 0 and k 1 parameters are estimated, etc. The simplest model (‘no change’) has three parameters, the most complex (‘lag 3’) has 11 parameters

Fitting mechanistic models made it possible to estimate some parameters of direct biological interest. Table 3 reports maximum-likelihood estimates for six simple models. The initial additive variance is estimated to be between 8×10−5 and 1·4×10−4 depending on the model. The variance of the log-transformed data is approximately equal to the evolvability (as defined in equation (4)) on the original scale (![]() ), so that the evolvability of the selection index (on the original scale) is
), so that the evolvability of the selection index (on the original scale) is ![]() : the index would evolve relatively slowly (0·01% change per generation) if selection on the wing index was as strong as selection on fitness (i.e. a change of 1% in the index represents 1% change in fitness). Consequently, this means that the genetic variation available on this wing-shape index was small, and that artificial-selection pressure had to be large in order to achieve a significant response (about 0·5%/generation). In other words, the evolvability of the wing shape is rather low, and rapid evolution is unlikely to occur unless the fitness function is particularly steep.
: the index would evolve relatively slowly (0·01% change per generation) if selection on the wing index was as strong as selection on fitness (i.e. a change of 1% in the index represents 1% change in fitness). Consequently, this means that the genetic variation available on this wing-shape index was small, and that artificial-selection pressure had to be large in order to achieve a significant response (about 0·5%/generation). In other words, the evolvability of the wing shape is rather low, and rapid evolution is unlikely to occur unless the fitness function is particularly steep.
Table 3. Maximum-likelihood estimates for six quantitative genetics models (log-transformed data): constant variances (model (6)), genetic drift (model (7)), finite number of loci (model (11)), mutations (along with drift) (model (8)), directional epistasis (model (12)) and stabilizing natural selection on the focus trait (equation (14), with the optimum θ=μ1). The mutation model and the finite number of locus model were fitted by fixing N e to 9·36, the estimate from the drift model, because N e could not be reliably estimated independently from mutational variance and the number of loci, respectively. Parameters that were fixed instead of being estimated are indicated by an asterisk. AIC values are compared with the constant variance model (reference model), the more negative the AIC, the better the fit. Variances are multiplied by 100 because this number can be directly interpreted in terms of percentage of evolvability (see text)

The estimate of the effective population size by the drift model (![]() , 95% confidence interval: 9·0–9·7) is compatible with the experimental procedure: 20 males and 20 females were mated, the ratio N e/N being typically around 0·2 in short-term experiments, and 0·1 on a longer time scale (Frankham, Reference Frankham1995). The mutation model was forced to consider N e=9·36 (the estimate from the drift model alone) to provide more realistic estimates of the mutational variance:
, 95% confidence interval: 9·0–9·7) is compatible with the experimental procedure: 20 males and 20 females were mated, the ratio N e/N being typically around 0·2 in short-term experiments, and 0·1 on a longer time scale (Frankham, Reference Frankham1995). The mutation model was forced to consider N e=9·36 (the estimate from the drift model alone) to provide more realistic estimates of the mutational variance: ![]() (confidence interval: 9·9×10−8 to 4·1×10−7), which is less than 0·1% of the phenotypic variance. This estimate, low but not unrealistic (alternatively, mutational heritability h m2=σM2/σE2≃0·0007), suggests that new mutations did not play an important part in the observed phenotypic change. The estimate of directional epistasis
(confidence interval: 9·9×10−8 to 4·1×10−7), which is less than 0·1% of the phenotypic variance. This estimate, low but not unrealistic (alternatively, mutational heritability h m2=σM2/σE2≃0·0007), suggests that new mutations did not play an important part in the observed phenotypic change. The estimate of directional epistasis ![]() (CI 95%: −0·43 to −0·32) suggests small but significant negative directional epistasis (this number means that a mutation that increases the phenotype by 0.2 (about one phenotypic standard deviation) would on average reduce the effect of other genes by around 1%). Selection response tends to slow down over the course of the experiment, which might also be due to natural (stabilizing) selection. In this case, the joint-effect model predicts stabilizing selection (ŝ=−264 is equivalent to a pull-back force of ≃β/2 when the population evolves by 0·1 phenotypic log unit). Important biological parameters can thus be estimated precisely through this procedure, some mechanisms can be ruled out while others are supported by model selection, and constitute interesting hypotheses to test with further experimental work.
(CI 95%: −0·43 to −0·32) suggests small but significant negative directional epistasis (this number means that a mutation that increases the phenotype by 0.2 (about one phenotypic standard deviation) would on average reduce the effect of other genes by around 1%). Selection response tends to slow down over the course of the experiment, which might also be due to natural (stabilizing) selection. In this case, the joint-effect model predicts stabilizing selection (ŝ=−264 is equivalent to a pull-back force of ≃β/2 when the population evolves by 0·1 phenotypic log unit). Important biological parameters can thus be estimated precisely through this procedure, some mechanisms can be ruled out while others are supported by model selection, and constitute interesting hypotheses to test with further experimental work.
The most convincing models are the ones in which environmental variance can evolve independently, as revealed by fitting six ‘canalization’ models (Table 4). The environmental variance increases in the course of selection, by about 17% when the mean changes by one (initial) phenotypic standard deviation (environmental decanalization: ![]() ). Conversely, additive variance barely decreases when the population is selected away from its original state, by only 3% per phenotypic standard deviation change in the mean (genetic canalization:
). Conversely, additive variance barely decreases when the population is selected away from its original state, by only 3% per phenotypic standard deviation change in the mean (genetic canalization: ![]() , in addition to the ≃5% decrease per generation due to inbreeding. The canalization optimum (the phenotype at which genetic variance is maximum and environmental variance is minimum) is
, in addition to the ≃5% decrease per generation due to inbreeding. The canalization optimum (the phenotype at which genetic variance is maximum and environmental variance is minimum) is ![]() in the largest model, close to the original mean of the population (
in the largest model, close to the original mean of the population (![]() ): models including a free canalization optimum only slightly outperform those in which the optimum is the original mean. Figure 2 illustrates the fit of the worst (constant variances) and the best (environmental canalization with a free optimum) models. Although the canalization model convincingly describes the trends in genetic and environmental variances, the fit remains far from the best phenomenological model. In particular, phenomenological models predict a late raise in additive variance (Supplementary figures 1 to 3), which cannot be explained with simple quantitative genetics models.
): models including a free canalization optimum only slightly outperform those in which the optimum is the original mean. Figure 2 illustrates the fit of the worst (constant variances) and the best (environmental canalization with a free optimum) models. Although the canalization model convincingly describes the trends in genetic and environmental variances, the fit remains far from the best phenomenological model. In particular, phenomenological models predict a late raise in additive variance (Supplementary figures 1 to 3), which cannot be explained with simple quantitative genetics models.

Fig. 2. Illustration of mechanistic model fitting on the Drosophila experiment (four lines). Symbols represent the data points (phenotypic mean on panels (a) and (c), phenotypic variance on panels (b) and (d)). Solid lines are model expectations for phenotypic means or variances, dashed lines are the expected additive variances. (a) and (b): Constant-variance model; (c) and (d): Environmental canalization with a free canalization optimum (one of the best mechanistic models). Predicted means and variances are not strictly identical across selected lines, because of slight differences in the realized selection gradients. In the decanalization model, the ‘up’ lines are closer to the canalization optimum, and so their predicted environmental variance is smaller than in the ‘down’ lines. The late raise in phenotypic variance in both ‘up’ lines can hardly be explained by genetic mechanisms, and affects the variance estimates for the whole time series, especially in the constant-variance model.
Table 4. Canalization and decanalization. Six genetic and environmental canalization models were fit independently and in combination, considering either a canalization optimum at the initial phenotypic mean (three first models) or independent (three last models). The effect of genetic drift is almost confounded with genetic canalization, and the effective population size was fixed in a similar way as explained in Table 3. The AIC score is displayed as the difference from the constant-variance model

Fitting both phenomenological and mechanistic models on the fly-wing selection data was thus succesful in quantifying the genetic architecture of this complex trait in an experimental population. By comparing the fit of classical quantitative-genetics models on different scales, we were able to identify the log scale as the most relevant for subsequent analysis. Phenomenological models revealed that the dynamics of the selection response is complex, and needs more parameters than are usually considered in quantitative genetics to be fully explained. There are strong indications that the change in both environmental and additive variances is non-monotonic, with a late increase after 15 generations in both selected lines. Mechanistic models showed that additive variance, if it were constant, would be around 8×10−5 in log units (I A=0·008% on the original scale). Nevertheless, more flexible models letting the variance decrease estimate a higher initial additive variance, around 1·5×10−4 (I A=0·015% on the original scale). This figure is rather low when scaled with the mean phenotype, and the trait is not very evolvable; selection pressure had to be strong for obtaining the observed changes. Genetic drift can be partly responsible for the early decrease in variance, with an effective population size estimated between seven and ten depending on the model. Mutational variance could not be reliably estimated, but new mutations do not appear to play a major role in this experimental selection. Interestingly, the best model predicts environmental decanalization (environmental variance increases with deviance from an optimum), and changes in the genetic architecture seem to be more related to the evolutionary distance rather than the elapsed time.
6. Discussion
(i) Scaling
The models and the likelihood functions described above assume that phenotypes are normally distributed, and departure from normality may affect parameter estimates and model selection. Most models in quantitative genetics rely on the assumption that effects tend to combine additively, and that both genetic and environmental effects are normally distributed. There are solid reasons, both experimental and theoretical, to question this hypothesis. Most measured traits cannot be negative (such as weight, size, yield, fertility, etc), so that the normal distribution is at best an approximation of the real phenotypic distribution. Gaussian distributions seem to be empirically supported, although often outperformed by log-normal (e.g. Powers, Reference Powers1950; Gingerich, Reference Gingerich2000). Knowledge about molecular, cellular and physiological mechanisms does not suggest that genetic factors should combine additively, since the expression of complex phenotypes relies on multiple gene networks featuring multiple loops of regulation, and the overall process is expected to generate statistical interactions (Omholt et al., Reference Omholt, Plahte, Oyehaug and Xiang2000; Gjuvsland et al., Reference Gjuvsland, Hayes, Omholt and Carlborg2007).
According to the measurement-theory concepts (Hand, Reference Hand2004; Hansen & Houle, Reference Hansen and Houle2008; Wagner, Reference Wagner2010; Houle et al., Reference Houle, Pelabon, Wagner and Hansen2011), many traits are on a ratio scale. They may result from the multiplication (rather than the addition) of multiple small factors, so that the resulting phenotypic distribution is not expected to be Gaussian. Since most models are not supposed to be applied to multiplicative traits, the easiest way to analyse them is to consider the logarithm of the measurements. Log transformation is common, but not universal.
Scaling issues are thus not only related to statistical problems, but they do affect biological conclusions. Directional epistasis or dominance on a linear scale might vanish on a different scale (Pavlicev et al., Reference Pavlicev, Le Rouzic, Cheverud, Wagner and Hansen2010), or, on the contrary, apparent additivity might hide interesting physiological interactions. Since the literature is not particularly consistent in the use of the log transformation on ratio-scale characters, general statements dealing with the symmetry or the linearity of selection responses are thus doubtful.
An ideal procedure would be to determine the scale on which the data are considered a priori, based on measurement theoretical considerations and the nature of the measured trait. A more pragmatic approach consists in estimating the best scale from the data itself. From the statistical framework previously defined, it is perfectly possible to fit the models on several scales. Model selection can be performed to compare them, and the procedure may constitute additional evidence towards the use of a particular scale.
(ii) Evolvability and selection
In the context of an artificial-selection experiment, in which the identity (and the phenotype) of the breeders is known, the between-generation expected change in the mean can be written R=σA2(μt*−μt)/σP2, where R is the selection response μt+1−μt and μt*−μt the selection differential (difference between selected individuals and the phenotypic mean of the population. We have chosen to write this equation as proposed by Lande & Arnold (Reference Lande and Arnold1983), as R=σA2β, calculating the selection gradient β=(μt*−μt)/σP2.
Another common way to write this equation is the ‘breeder's equation’, R=h 2(μt*−μt), in which h 2=σA2/σP2 is the narrow-sense heritability. This form is often used in experimental genetics, as the selection differential is known from the selection procedure, h 2 describing the (supposedly constant) capacity for the population to respond to selection. However, it has been argued that this parameterization is confusing, or even misleading (Houle, Reference Houle1992; Hansen et al., Reference Hansen, Pélabon, Armbruster and Carlson2003b; Wilson, Reference Wilson2008; Hansen & Houle, Reference Hansen and Houle2008). The additive variance σA2 is both in the numerator and in the denominator of h 2, and also influences the selection differential, so that changes in h 2 are harder to detect and interpret than changes in σA2. Understanding the dynamics of complex genetic architectures necessarily implies a clear separation between variation (σA2) and selection (β), which is the case when using the formulation of Lande & Arnold (Reference Lande1983) . This framework can easily be extended to multiple characters, replacing R and β by vectors, and σA2 by the additive genetic variance-covariance G matrix. Additionally, since β can also be defined as the regression coefficient of the fitness over the phenotype, the parameters of the equation remain meaningful when selection is not artificial, e.g. when there are fitness differences among breeders.
(iii) Conclusion
In this paper, we have proposed alternatives to the classical analysis of selection-response time series. Rather than assuming a constant genetic architecture, we propose to fit phenomenological models designed to describe the changes in genetic and environmental variances (the dynamics of the phenotypic mean being constrained by the additive variance and the selection gradient). In the selection experiment on fly wings used as an example, this phenomenological approach pointed out an unexpected pattern (late increase in additive variance in both lines), which could have easily remained unnoticed otherwise. Temporal trends, which are direct observations from the data, can then be interpreted in the light of more or less elaborated mechanistic models, and parameters of biological interest can be estimated.
The estimates obtained with the deterministic framework remain satisfactory, even when sources of stochasticity that were not accounted for explicitly are simulated. Nevertheless, in extreme cases, imprecise confidence intervals might affect the accuracy of the results. It is then possible to account for these different sources of randomness through random-effect models. By considering that genetic means and genetic variances are themselves random variables with known distributions, depending on the effective population size and their status at the previous generation, models in which the cumulative effect of genetic drift can be implemented to estimate the genetic architecture parameters through a more realistic population genetics framework. The resulting statistical tools are, however, more complex. Because models are non-linear, random effects have to be integrated out through specialized algorithms, numerical convergence can be problematic and takes more time and more computational power. Additionally, random effects may have side effects raising interpretation issues. A detailed description of such models, their benefits and their limitations is provided in Le Rouzic et al. (Reference Le Rouzic, Skaug and Hansen2010) and in supplementary results. Whether or not random-effect models have to be preferred depends on multiple factors, including the experimental setting itself and the precision of the estimates that is desired.
Meticulous analysis of artificial-selection time series is likely to deepen our understanding of how selection affects the phenotypic changes in a population, of the impact of genetic architecture differences, and of the importance of measurement issues, including scaling. The two approaches (phenomenological and mechanistic) described in this paper are complementary, and may highlight how far common quantitative genetic models actually are from experimental results. Overall, the definition of a solidstatistical framework for selection time-series analysis enables the extraction of meaningful parameters from existing data sets, and highlights the benefits and the limitations of this experimental approach. Perhaps one of the most crucial points to investigate is the rate at which the additive variance changes in a population and the consistency of this phenomenon. Indeed, the constancy (or at least the inertia) of the additive variance–covariance matrix is a key assumption when trying to bridge what has often been considered as a gap between intraspecific and interspecific evolution (Arnold et al., Reference Arnold, Pfrender and Jones2001; Gingerich, Reference Gingerich2001; McGuigan, Reference McGuigan2006; Blows, Reference Blows2007; Hohenlohe & Arnold, Reference Hohenlohe and Arnold2008; Arnold et al., Reference Arnold, Burger, Hohenlohe, Ajie and Jones2008). By empirically simulating large adaptive shifts, artificial-selection experiments provide valuable information to understand how genetic architectures behave when submitted to such directional selection pressures.
We thank H. J. Skaug, T. Reitan and T. Rouyer for helpful discussion, and A. J. R. Carter for helping assembling the data. The authors acknowledge W. G. Hill, B. Walsh, G. J. Geyer and two anonymous reviewers for their comments and suggestions on anearlier version of the manuscript. T. F. H. was supported by grant no 177857 from the Research Council of Norway and NSF grant DEB-0344417 to T. F. H. and D. H. A. L. R. was funded by the Marie Curie fellowships EIF-220558 and ERG-256507. D. H. was supported in this research by a visiting professorship at the Centre for Ecological and Evolutionary Synthesis at the University of Oslo, Norway.
7. Supplementary material
The online data can be found available at http://journals.cambridge.org/GRH








