1. INTRODUCTION
The technological process in mechanical engineering is a fundamental part of the production process that is directly related to changes in the shape, size, surface quality, and physicochemical properties of the workpiece. This definition determines the function of the technological process, which is to transform the workpiece from an initial state (semiproduct or raw material) to the final state (finished product).
The traditional approach to the planning of a technological process consists of an analysis of the drawing of the part and of the implementation methods, and of the identification and comparison of the technologies of parts with similar geometrical elements, and then of the development of the manufacturing process. The manufacturing process is most often developed based on knowledge of technological processes for similar parts (Feld, Reference Feld2003). The process then involves a long design time and a significant amount of routine and time-consuming work.
Planning of technological processes has lost its traditional character due to the possibility of using information technology in the technological preparation of production. Automation, typification rules, and group technology also have an impact on the development of methods for the design of technological processes (Feld, Reference Feld2003).
Over the years, approaches to the design of technological processes have changed. The use of databases of ready-made technological processes (systematic research of previous solutions, use of alternative solutions from group technology, use of data for modeling, and simulation of designed processes) and the use of computer-aided design, computer-aided process planning (CAPP), and their integration (through shared databases and knowledge bases) are now common.
The first artificial intelligence technology used in CAPP systems included expert systems with a knowledge base in the form of frameworks, decision rules, and semantic networks. Contemporary technologies utilize fuzzy logic, neural networks, genetic algorithms, and hybrid systems (Han & Kamber, Reference Han and Kamber2000; Hand et al., Reference Hand, Mannila and Smyth2001; Klosgen & Zytkow, Reference Klosgen and Zytkow2002; Larose, Reference Larose2005; Russell & Norvig, Reference Russell and Norvig2009; Tadeusiewicz et al., Reference Tadeusiewicz, Chaki and Chaki2014). There is a tendency to produce hybrid systems that include many combinations of the aforementioned artificial intelligence methods. Hybrid systems integrate artificial intelligence methods that have many complementary features and attributes. Such a hybrid allows the utilization of all the assets of the individual methods, and so these hybrids provide the possibility of creating better problem-solving methods.
The use of artificial intelligence in CAPP systems allows inclusion of the experience of process engineers in the form of knowledge included in knowledge bases and the making of inferences during the design process, akin to human reasoning.
Combination of artificial intelligence with a CAPP system results in an intelligent CAPP system. This is also emphasized in past studies (Koh & Gunasekaran, Reference Koh and Gunasekaran2006; Ming et al., Reference Ming, Yan, Wang, Li, Lu, Peng and Ma2008). Integration of artificial intelligence methods can lead to the creation of better and more accurate methods, which could be used in this area of expertise. The most important function of intelligent systems is drawing conclusions. Contemporary CAPP is an increasingly used artificial intelligence method.
The central objective of the present author's research is to develop a system supporting the design of a technological process (a CAPP system) that functions similarly to a human expert in the field in question. The use of neural networks makes the creation of such a system possible. Based on technological processes that have already been developed, it is possible to teach neural networks to carry out such a design process. The design of a technological process is a very complex task, requiring a process engineer's knowledge and experience. It can be divided into smaller tasks:
• creation of a technological process plan, in which the sequence of technological operations is defined; and
• for each operation in the technological process, the appropriate selection of machine, tools, and machining parameters is defined.
Such a CAPP system will be especially useful for process engineers who do not yet have sufficient experience in the design of technological processes, or who have only recently joined a particular manufacturing enterprise and are not fully familiar with its machines and other means of production (tools and instrumentation). It should be emphasized that such a system performs an advisory role, and it is always the process engineer who makes the final decision.
2. CAPP OVERVIEW
The planning of technological processes is carried out in different ways. In the traditional approach, the process engineer designs the technological process manually, without the assistance of a computer. There are also IT systems, including a technological database, supporting the work of the process engineer. Azab and ElMaraghy (Reference Azab and ElMaraghy2007) describe mathematical modeling for reconfigurable process planning on the background variant and generative process-planning systems. Reconfigurable process planning is an important enabler of changeability for evolving products and systems. The proposed reconfigurable process-planning mathematical scheme scales better with problem size compared with classical process-planning models. Another paper (Lee et al., Reference Lee, Lee, Kim, Heo and Kim2013) describes the construction of a practical CAPP system for hole making that satisfies the specific requirements of marine engine machining. The applied examples (engine block and cylinder header) described in the article are machined using the proposed system. The CAPP system consists of a hole manager, cutting sequence definition, and operation manager, which are derived from a conventional knowledge-based system.
There also exist solutions using neural networks for the planning of particular elements included in the technological process. An example is found in Al-Ghanim's article (Reference Al-Ghanim2002), describing the ART neural network that supports the selection of machining parameters for a milling process. In another example (Deb et al., Reference Deb, Ghosh and Paul2006), the selection of machining operations is assisted by neural networks. Other authors (Joshi et al., Reference Joshi, Kumar and Sharma2008) report setup planning and operation sequencing using a neural network and genetic algorithm. The operation-sequencing problem is converted into a traveling salesman problem in which the objective function is to reduce total cost. To solve such problems efficiently, a genetic algorithm technique is more suitable. The work describes results for prismatic parts. A further article (Rana et al., Reference Rana, Kumar, Singh and Kumar2013) presents an application of a neural network for the fast identification of optimal or near-optimal operation sequences for rotational parts. Other authors (Klancnik et al., Reference Klancnik, Balic and Cus2008) describe the use of a self-organizing map (SOM) neural network for the prediction of a tool-path strategy in milling to obtain the best possible quality of the machined surface. Another article (Markopoulos et al., Reference Markopoulos, Mandakos and Vaxevanidis2008) describes neural network models created for the prediction of surface roughness in electrical discharge machining.
These articles usually describe the application of computer techniques for solving single tasks, such as the prediction of surface roughness in electrical discharge machining, or the selection of machining parameters. Unfortunately, there is a visible lack of an integrated approach to technological process planning as a whole.
The author's earlier publications also include models of neural networks for tool selection in process planning (Rojek, Reference Rojek2008, Reference Rojek2010). Those papers present neural networks as models for classification in intelligent CAPP systems. For the construction of classification models, three types of neural networks were used: linear network, multilayer network with error backpropagation (MLP), and radial basis function network (RBF). The classification models were compared for their ability to produce the best classification. Classification models were constructed for tool selection for selected manufacturing operations: turning, milling, and grinding. The models for milling were presented in detail.
The present work concerns the development of a CAPP system whose functions include the design of essential elements of a technological process, and so it can be said to describe a method of technological process design in which neural networks are used in a comprehensive manner.
As well as the method of technological process design, a case study is presented involving the selection of appropriate machines, tools, and machining parameters for a milling operation at a real manufacturing enterprise. The goal of the research was to develop the best neural networks for selecting particular elements of the technological process.
Neural networks are used here for the selection of machines, tools, and machining parameters, namely, all elements that are chosen for each technological operation of the technological process. The set of operations creates a technological process. For each selection, models are constructed in the form of MLP, RBF, and Kohonen neural networks for different processes: milling, grinding, turning, and so on. The best neural networks were chosen based on the quality of the selections made.
A method was also developed for the elimination of defects occurring in the course of the manufacturing process. This method uses decision rules. When such a defect comes to light, the process engineer can use this method to determine how to adapt the technological process so that such a defect does not occur in the future. This method improves the quality of the technological process.
A support system based on intelligent models makes it possible to create scenarios for the selection of different components for technological operations. The models created are therefore able to improve the technological processes. The models were tested on real data from an enterprise.
3. METHODS
3.1. Theories of neural networks
Neural networks are selected as data-mining algorithms. Neural networks are very good tools for extracting patterns from databases. This property enables the performance and automation of tasks hitherto reserved for humans. MLPs are the most widespread and universal neural networks applied to solving a variety of problems. In these networks, the selection of the number of neurons in the input layer is conditioned by the dimension of the data vector x. The neural model consists of the sum of input signals x 1, x 2, . . . , x N multiplied by weight coefficients w i1, w i2, … , w iN and of an additional value w i0. The output signal of the model is the sum of the elements, and it is subsequently input into a nonlinear sigmoid activation function. The error backpropagation algorithm is the basic algorithm for supervised learning by many-layered one-way neural networks. It depends on a change in the weights of the input signals of every neuron in every layer so that the value of the error for the next learning couples contained in the learning file is minimized. For this purpose, it uses the gradient method, the fastest drop (Tadeusiewicz et al., Reference Tadeusiewicz, Chaki and Chaki2014).
RBF networks have several advantages compared with MLP-type networks. They can model any nonlinear function using their single hidden layer, which eliminates the need to decide on the number of layers during the design stage. For this reason, RBF networks can be trained quickly (the difference in training speed is around an order of magnitude; Tadeusiewicz et al., Reference Tadeusiewicz, Chaki and Chaki2014).
When calculating the MLP and RBF networks, the transition (activation) functions used for the neurons in the hidden layer are optionally hyperbolic tangent, linear, logarithmic, and exponential, and the functions used for the neurons in the output layer are hyperbolic tangent, linear, or softmax. The error functions used in the learning process are, optionally, the sum of squares function (SOS) and the cross entropy. The cross entropy function is given by Eq. (1):
 $$E_{{\rm CE}} = - \sum\limits_{i = 1}^N {t_i \,\hbox{ln} \Big(\displaystyle{{y_i} \over {t_i}} {\rm \Big)\comma}} $$
$$E_{{\rm CE}} = - \sum\limits_{i = 1}^N {t_i \,\hbox{ln} \Big(\displaystyle{{y_i} \over {t_i}} {\rm \Big)\comma}} $$where N is the number of examples used, y i is the calculated output value of the neural network, and t i is the real output value from the data file.
In the learning process of MLP neural networks, the iterative Broyden–Fletcher–Goldfarb–Shanno algorithm is used to perform the optimization computing (Neural Networks, 2015).
Kohonen networks are among the basic types of self-organizing nets. Thanks to their capacity for self-organization, they open up completely new possibilities, one of which is adaptation to previously unknown input data. SOMs, also referred to as Kohonen networks, are neural networks that are associated with coordinates defined on a straight line, in a plane, or in any n-dimensional space. The learning of this type of network consists in changing the coordinates of the neurons so that they strive to reach a pattern that conforms to the structure of the analyzed data. This means that the networks “stretch” around data sets and adapt their structure to them. Kohonen networks are usually one-way nets in which each neuron is connected to all components of the N-dimensional input vector x. The weight coefficients of neuron connections create the vector w i. The input signals are normalized at the start of the computation; that is, ||x|| = 1. After stimulation of the network by the input vector x, a kind of competition occurs between the neurons, the winner w w fulfilling the condition in Eq. (2):
where d(x, w i) denotes the distance between vector x and vector w i in Euclidean space.
Each neuron is enclosed within a topological neighborhood G(i, x), and in the classic Kohonen algorithm the function G(i, x) is defined as follows [Eq. (3)]:
where R denotes the neighborhood radius. When calculating a Kohonen network, the radius R approximates to 0.
Detailed descriptions of neural networks can be found in a number of publications (Larose, 2006; Haykin, Reference Haykin2008; Russell & Norvig, Reference Russell and Norvig2009; Tadeusiewicz et al., Reference Tadeusiewicz, Chaki and Chaki2014).
The following section describes trials conducted using models based on MLP, RBF, and Kohonen artificial neural networks.
3.2. Method of technological process planning using neural networks
The technological process planning method uses a system of three blocks of neural networks, and involves the creation of neural networks for the selection of machines, tools, and machining parameters. These networks are built for each process operation separately; that is, for each selection, a set of neural networks is created. For the construction of models, different types of neural networks (MLP, RBF, and Kohonen) with different structures were employed, and the networks that provided the best selections were identified.
A technological process can be defined as a sequence of individual technological operations; this forms the framework of the technological process. After defining the framework of the technological process for each process operation, a proper selection of machines, tools, and machining parameters is made using a system of three blocks of neural networks.
Following selection of the operational process, information about the technological operation is transferred to the input of the block for selection of the machine, tools, and machining parameters. On the basis of the supplied input parameters, the first neural network selects the machine and the second neural network selects the tool. The results of these two networks are transmitted together with the input parameters to the third neural network for the selection of machining parameters. The results of all three neural networks, consisting of the code of the machine, the code of the tool, and the machining parameters, are passed to a module that collects information about the whole technological process. The design of the technological process is completed when selections have been made for all of the technological operations in the process framework (Fig. 1).
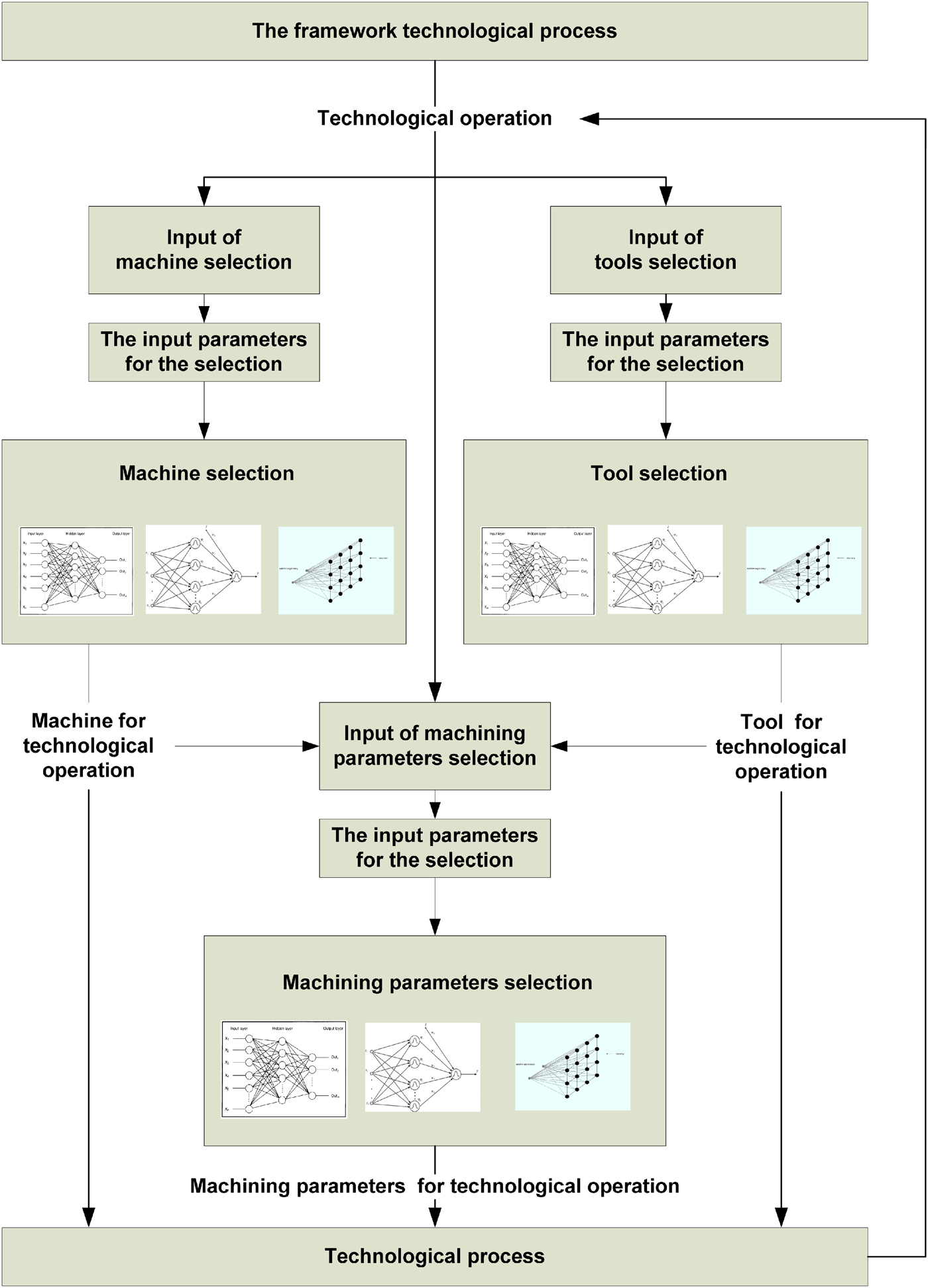
Fig. 1. Method of technological process planning using neural networks.
Trials were performed for selected technological operations. The models for the milling operation will be presented here in detail. Models were prepared in the form of different types of neural network: MLP, RBF, and Kohonen networks. For each type of network, the model parameters were varied appropriately.
The neural networks were created using Statsoft STATISTICA Data Miner, NeuralSolutions, and the author's own software.
4. CASE STUDY
4.1. Description of the Bohamet enterprise
Bohamet is a company offering a wide range of products. The main areas of its operations are the following:
• production of parts for ships (windows, illuminators, and wipers),
• production of industrial valves and fittings,
• production of glass,
• processing of metals, and
• products for the mining industry.
In its manufacturing operations, the company uses many domestic suppliers, as well as contractors from other European countries. The high quality of Bohamet's products is confirmed by the numerous certificates of conformity with standards and quality held by the company and its suppliers. In order to ensure the highest quality of its products and services, the company has obtained an ISO 9001:2000 certificate.
For the purposes of the present study, the processing of metals at Bohamet was analyzed. Some parts are made as single elements, while others can be classified as small- or medium-series production. During the manufacture of its products, basic technological operations are performed, including cutting, laser cutting, milling, rolling, grinding, threading, and so on. (Bohamet, 2015). The developed approach was tested in a real case scenario.
4.2. Production data
An analysis of the organizational structure of the company and its production process constitutes the first stage of data and knowledge acquisition for the intelligent CAPP system.
The method of designing the technological process and the scope of the information collected also depend on the type of manufacturing operations undertaken by the company. In this case, the types of operations are single-item and small-series production. These two types of manufacturing operations are characterized by the large number of variants of products made in small series or even as single elements. Their diversity results in a low level of standardization.
The manufacturing data of the company focuses on three basic groups of items (orders, products, and means of production). The orders item is associated with data on schedules and quantities of products to be manufactured. The products item includes all data that describe the products (i.e., structure, geometry, material, technological data, technological process, and product lifecycle). The means of production item is associated with data that describe the company's manufacturing capacity (i.e., machines, instruments, and tools). Data concerning orders, products, and means of production are used when designing the technological process. The process engineer uses information containing a large amount of data, which is constantly modified. Data searching is performed in accordance with specific criteria. Moreover, information takes different forms (text and drawings) and is present at different locations within the company. As a result, quick access to accurate and current data is important.
The initial stage of the design of the technological process after the engineering data is received is the preparation of the framework technological process. Next, the framework technological process is supplemented with additional data on technological operations. The next stages of designing the technological process involve the selection of machines, tools, and processing parameters for specific technological operations. The last stage is the generation of a technological process in the form of a process card and instructions for the machining stations.
Manufacturing knowledge comes from many sources. Data from catalogs and databases can be obtained easily. However, if one wishes to acquire the knowledge, preferences, and experience of the process engineer, simple information tools are not enough. It is necessary to create such models and tools that will enable that knowledge to be contained in a computer system. For this reason, in the present study, methods of machine learning (neural networks) were used.
In the past, a process engineer used tool catalogs, often in paper form. The computer system did not record parameters such as degree of wear of the machine, which often makes it necessary to choose other machining parameters than those indicated by the catalog. Then the process engineer applies his or her knowledge, experience, and preferences. In traditional computer systems the preferences and experience of the process engineer are not taken into account in CAPP. Use of the engineer's knowledge and experience is made possible by neural network models.
The content of the learning files for the neural networks was prepared in consultation with a process engineer.
4.3. Selection criteria
For the purpose of the selection models, the following criteria were determined:
• criteria for the selection of machines for technological operations include the following factors: type and scope of machining, dimensions of the workpiece, accuracy of machining, production efficiency, anticipated load, and hourly cost of operation of the machine;
• criteria for the selection of machining tools for technological operations include the following factors: method of machining, shape of the machined surfaces, type and accuracy of machining, production volume, material of the machined object, and type of machine used; and
• the criteria for selection of the machining parameters are significantly affected by the following factors: material of the machined object, material of the tool blade, the machine used, the type of machining, and requirements relating to the quality of the surface.
5. RESULTS AND DISCUSSION
5.1. Machine selection
5.1.1. Data preparation
In order to prepare the learning data for neural networks, an analysis of the machinery used at Bohamet was performed, in particular in relation to the CNC machines: mills, mill-drills, grinders, and turning lathes. The machine was selected separately for each technological operation.
Based on the machine data and the selection criteria, a learning file was prepared for the MLP and RBF neural networks. The following data are supplied at the input of the neural network: type of operation (e.g., rough and finishing); X product length (mm), Y product width/diameter (mm), Z product height/diameter (mm), X size of the working space (mm), Y size of the working space (mm), Z size of the working space (mm), maximum diameter of tool (mm), length of tool (mm), cost of operation of the machine (PLN/h), minimum rotational speed (rpm), maximum rotational speed (rpm), maximum working range f (mm/min), and machine power (power at the spindle motor = l kW). The machine code is obtained at the output of the neural network. In the case of the Kohonen network, the learning file contained both machine selection parameters and the machine code as input. Figure 2 shows the inputs and outputs of neural networks for machine selection. Table 1 contains example data for the selection of a milling machine.

Fig. 2. Inputs and output of multilayer network with error backpropagation (MLP) and radial basis function (RBF) neural networks for machine selection.
Table 1. Structure of the learning file for neural networks for machine selection (multilayer network with error backpropagation and radial basis function network)

All the cases of machine selection in the database (521 records) were divided into a learning file (75% of the records), a test file (15% of the records), and a validation file (10% of the records). The neural network was taught using the learning file and tested using the test file; in addition, its operation was verified using the validation file. The validation file is used to address the problem of overfitting of neural networks.
5.1.2. Neural networks supporting machine selection
For the MLP and RBF networks, the trials involved the creation of neural network models with one hidden layer and with two parameters: the number of neurons in the hidden layer and the number of learning epochs. The neurons in the hidden layer were selected experimentally. In the trial, the parameter defining the number of neurons in the hidden layer took values from 5 to 30 (for MLP) and from 10 to 60 (for RBF), while the second parameter, the number of learning epochs, took values from 5 to 100.
In the case of the Kohonen network (SOM network), the topology of the network (5 × 6, 10 × 10, and 15 × 15) and the number of learning epochs were varied.
Figure 3 shows the parameters of the learning process for MLP, RBF, and Kohonen neural networks. Among the parameters for the MLP and RBF networks, a determination was made of the range of the number of neurons in the hidden layer, the number of taught and retained neural networks, and an error function. For the Kohonen network, a determination was made of the network topology and learning parameters. In addition, using the example of that network, a learning and testing graph is shown.
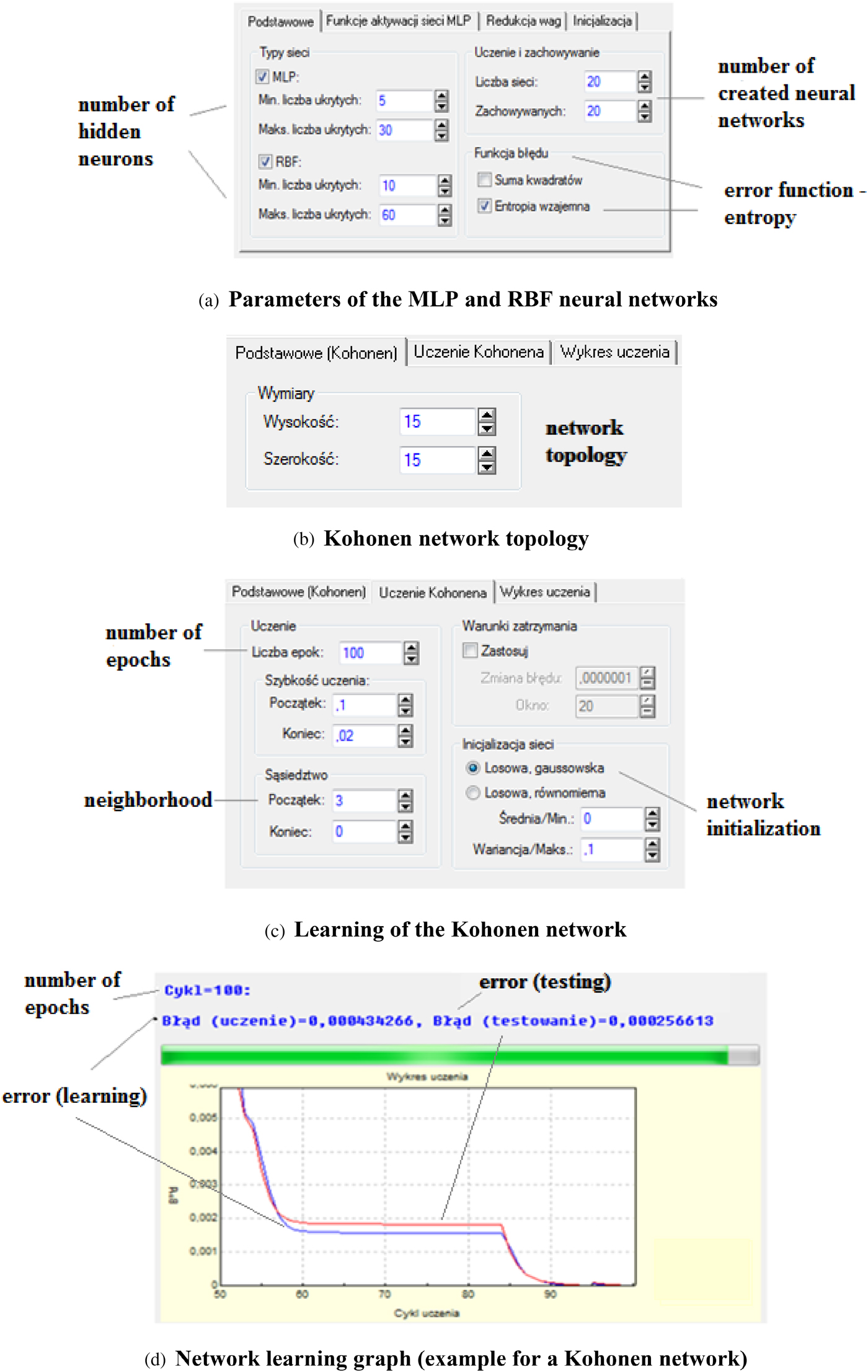
Fig. 3. Parameters of the learning process for multilayer network with error backpropagation (MLP), radial basis function (RBF), and Kohonen neural networks.
Neural network models were constructed with different stop conditions for the network learning process. The first of the conditions was the number of epochs, and the second was the attainment of a defined error value. Table 2 shows the epoch number condition (100) and the error value attained at that number of epochs.
Table 2. Parameters of the best multilayer network with error backpropagation (MLP), radial basis function network (RBF), and self-organizing map network (SOM) for machine selection

For each condition for the end of the learning process, an error function (entropy and SOS function) was verified. After the completion of each trial, tests were performed to provide information on incorrectly classified decisions. The quality of a network's operation and its root mean square (RMS) error were compared. In classifying networks, quality was calculated as the ratio of correctly classified cases to all cases in the set.
Table 2 contains a summary of the neural networks for milling machine selection. For the purpose of learning MLP networks, the Broyden–Fletcher–Goldfarb–Shanno algorithm was used. The RBF network was taught using the RBF training algorithm. The RBF network was taught in two stages. In the first stage, the radial functions, which use only input variables from the data, were distributed. In the second stage, the weights connecting the radial functions with the output neurons were determined. In the case of the Kohonen network, network learning was performed using the Kohonen method, which consists in assigning cluster centers to the radial neuron layer. The overall evaluation of a network was the classification quality measure given as a percentage. The table shows the RMS error in the teaching, testing, and validation phases, as well as the effectiveness of machine selection expressed in percentages.
When analyzing neural networks (MLP, RBF, and Kohonen), one must note that their effectiveness is influenced by the number of neurons in the hidden layer, the number of learning cycles, and the error function. In addition, the activation functions in the hidden and output layers have an impact in the case of MLP and RBF networks.
An analysis was also made of the outputs of the neural networks. Figure 4 shows a summary of the classification of selections of particular machines. The summary contains the total number of selections of each machine, the numbers of cases correctly and incorrectly classified, and the same numbers expressed as percentages. Following analysis of the various neural network models, the Kohonen network model (15-225) was chosen as the most effective for machine selection (effectiveness 99.96%).

Fig. 4. Summary of classification of machine selection. MLP, multilayer network with error backpropagation; RBF, radial basis function network; SOM, self-organizing map network.
The accuracy and the degree of certainty of the neural networks were also assessed. Accuracy refers to the operation of the network on new data, while the degree of certainty indicates the relationship of new input data to a particular class of patterns. Both parameters depend on the quality of classification of the neural network. The greater are the accuracy and degree of certainty, the better is the classification capability of the neural network. The same method was used to develop neural network models for the selection of tools and machining parameters.
5.2. Tool selection
5.2.1. Data preparation
In order to prepare the learning data for neural networks, an analysis was performed using Bohamet's tools, which were divided into drills, milling cutters, lathe tools, and grinding wheels. The tools were selected separately for each technological operation.
Based on the tool data and the selection criteria, a learning file was prepared for the MLP and RBF neural networks for milling. The following data were supplied at the input of the neural network: type of operation (e.g., rough, and finishing), type of machined surface (e.g., groove, outline, and surface), type of machined material (e.g., 316L), roughness (e.g., 20), type of tool (e.g., connected or monolithic), type of milling cutter mounting (e.g., top-mounted), diameter of milling cutter (mm), shape of milling cutter (cylindrical), number of blades (e.g., 10), total length of milling cutter (mm), milling speed vc (m/min), milling depth a p (mm), feed rate (mm/min), cost of operation of the tool (PLN/h), and milling width a e (mm). At the output of the neural network, the milling cutter code was obtained. In the case of the Kohonen network, the learning file contained both milling cutter selection parameters and the milling cutter code as input.
All of the cases of tool selection in the database (553 records) were divided into a learning file (75% of the records), a test file (15% of the records), and a validation file (10% of the records). The neural network was taught using the learning file and tested using the test file; in addition, its operation was verified using the validation file. The validation file is used to address the problem of overfitting of neural networks.
5.2.2. Neural networks supporting tool selection
For MLP and RBF networks, the trials involved the creation of neural network models with one hidden layer and with two parameters: the number of neurons in the hidden layer and the number of learning epochs. The neurons in the hidden layer were selected experimentally. In the trial, the parameter defining the number of neurons in the hidden layer took values from 5 to 30 (for MLP) and from 10 to 60 (for RBF), while the second parameter, the number of learning epochs, took values from 5 to 100.
In the case of the Kohonen network (SOM network), the topology of the network (5 × 6, 10 × 10, 15 × 15, and 20 × 20) and the number of learning epochs were varied.
For each condition for the end of the learning process, an error function (entropy and SOS function) was verified. After the completion of each trial, tests were performed to provide information on incorrectly classified decisions. The quality of a network's operation and its RMS error were compared. In classifying networks, quality was calculated as the ratio of correctly classified cases to all cases in the set.
Table 3 provides a summary of the neural networks for milling cutter selection. The overall evaluation of a network was the classification quality measure given as a percentage. The table shows the RMS error in the learning, testing, and validation phases, as well as the effectiveness of tool selection expressed in percentages. Following analysis of the various neural network models, Kohonen network model (16-400) was chosen as the most effective for tool selection (network effectiveness 100%).
Table 3. Parameters of the best multilayer network with error backpropagation (MLP), radial basis function network (RBF), and self-organizing map network (SOM) for tool selection

The accuracy and the degree of certainty of the neural networks were also assessed. Accuracy refers to the operation of the network on new data, while the degree of certainty indicates the relationship of new input data to a particular class of patterns. Both parameters depend on the quality of classification of the neural network. The greater are the accuracy and degree of certainty, the better is the classification capability of the neural network.
For example, Figure 5 shows the accuracy of MLP networks (15-18-1 and 15-26-1). The first network has 15 inputs, 18 neurons in the hidden layer and 1 output; the second has 15 inputs, 26 neurons in the hidden layer and 1 output. The first network (15-18-1) has a quality classification of 98.33%, and the second network (15-26-1) 92.35%. Hence, we conclude that there will be differences in accuracy. In the graph below, the accuracy is represented by the value “incorrect” or “correct.”
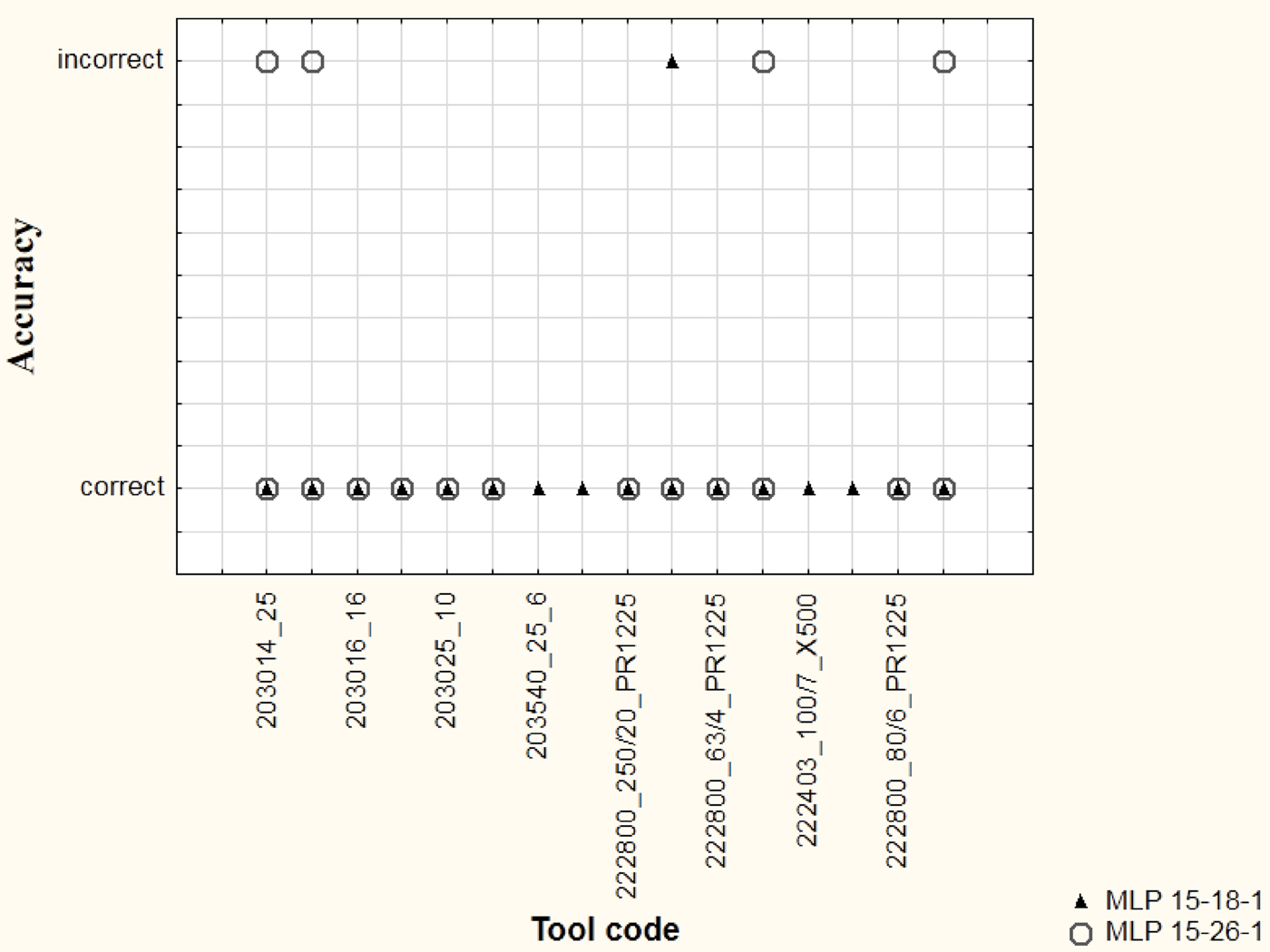
Fig. 5. Accuracy of multilayer network with error backpropagation neural networks (MLP).
In the case of MLP 15-18-1 (the better network), there is only one tool incorrectly classified, whereas with MLP 15-26-1 (the inferior network) there are four incorrectly classified tools for the same number of attempts to enter new data. The accuracy is greater when the neural network has a higher quality classification.
An analysis was also made of the output of neural networks. Figure 6 shows a summary of the classification of selections of particular tools. The summary includes the total number of selections of each tool, the numbers of cases classified as correct and incorrect, and the same numbers expressed as percentages. In view of the large number of tools, only a part of the analysis is shown.

Fig. 6. Summary of classification of tool selection. MLP, multilayer network with error backpropagation; RBF, radial basis function network; SOM, self-organizing map network.
5.3. Machining parameter selection
5.3.1. Data preparation
In order to prepare the learning data for the neural networks, an analysis was performed of the technological processes with regard to selection of the machining parameters for specific machines and tools at Bohamet. The machining parameters were selected separately for each technological operation.
Based on the machining parameter data and the selection criteria, a learning file was prepared for the MLP and RBF neural networks. The following data were supplied at the input of the neural network: type of operation (e.g., rough and finishing), type of machined material (e.g., 316L), selected tool code, roughness (e.g., 20), machining depth a p (mm), milling width a e (mm), target depth (mm), and machine code. At the output of the neural network, a set of parameters to be configured on the machine was obtained: feed rate (mm/min), machining speed (m/min), duration of the operation (min), and tool service life (min). In the case of the Kohonen network, the learning file contained all of the parameters as input.
All the cases of machining parameter selection in the database (617 records) were divided into a learning file (75% of the records), a test file (15% of the records), and a validation file (10% of the records). The neural network was taught using the learning file and tested using the test file; in addition, its operation was verified using the validation file. The validation file is used to address the problem of overfitting of neural networks.
5.3.2. Neural networks supporting machining parameter selection
For the MLP and RBF networks, the trials involved the creation of neural network models with one hidden layer and with two parameters: the number of neurons in the hidden layer and the number of learning epochs. The neurons in the hidden layer were selected experimentally. In the trial, the parameter defining the number of neurons in the hidden layer took values from 5 to 30 (for MLP) and from 10 to 60 (for RBF), while the second parameter, the number of learning epochs, took values from 5 to 100.
In the case of the Kohonen network (SOM network), the topology of the network (5 × 6, 10 × 10, 15 × 15, 20 × 20, 25 × 25, and 30 × 30) and the number of learning cycles were varied.
For each condition for the end of the learning process, an error function (entropy and SOS function) was verified. After the completion of each trial, tests were performed to provide information on incorrectly classified decisions. The quality of a network's operation and its RMS error were compared. In classifying networks, quality was calculated as the ratio of correctly classified cases to all cases in the set.
Table 4 shows a summary of the neural networks for milling parameter selection. The overall evaluation of a network was the classification quality measure given as a percentage. The table shows the RMS error in the teaching, testing, and validation phases, as well as the effectiveness of selection expressed in percentages.
Table 4. Parameters of the best multilayer network with error backpropagation (MLP), radial basis function network (RBF), and self-organizing map network (SOM) for machining parameter selection

Following analysis of the various neural network models, the Kohonen network model (8–900) was chosen as the most effective for machining parameter selection (effectiveness 100%), but it required a long learning time and a large number of neurons to build the neural structure. The accuracy and the degree of certainty of the neural networks were also assessed.
An analysis was also made of the outputs of the neural networks for machining parameter selection. The total effectiveness of the networks is given in Table 4.
Figure 7 shows the menu of the developed system based on neural networks for the selection of a milling machine, milling tool, and machining parameters (a) and the result produced by the system for the milling operation (b). The system was created using AITECH SPHINX.
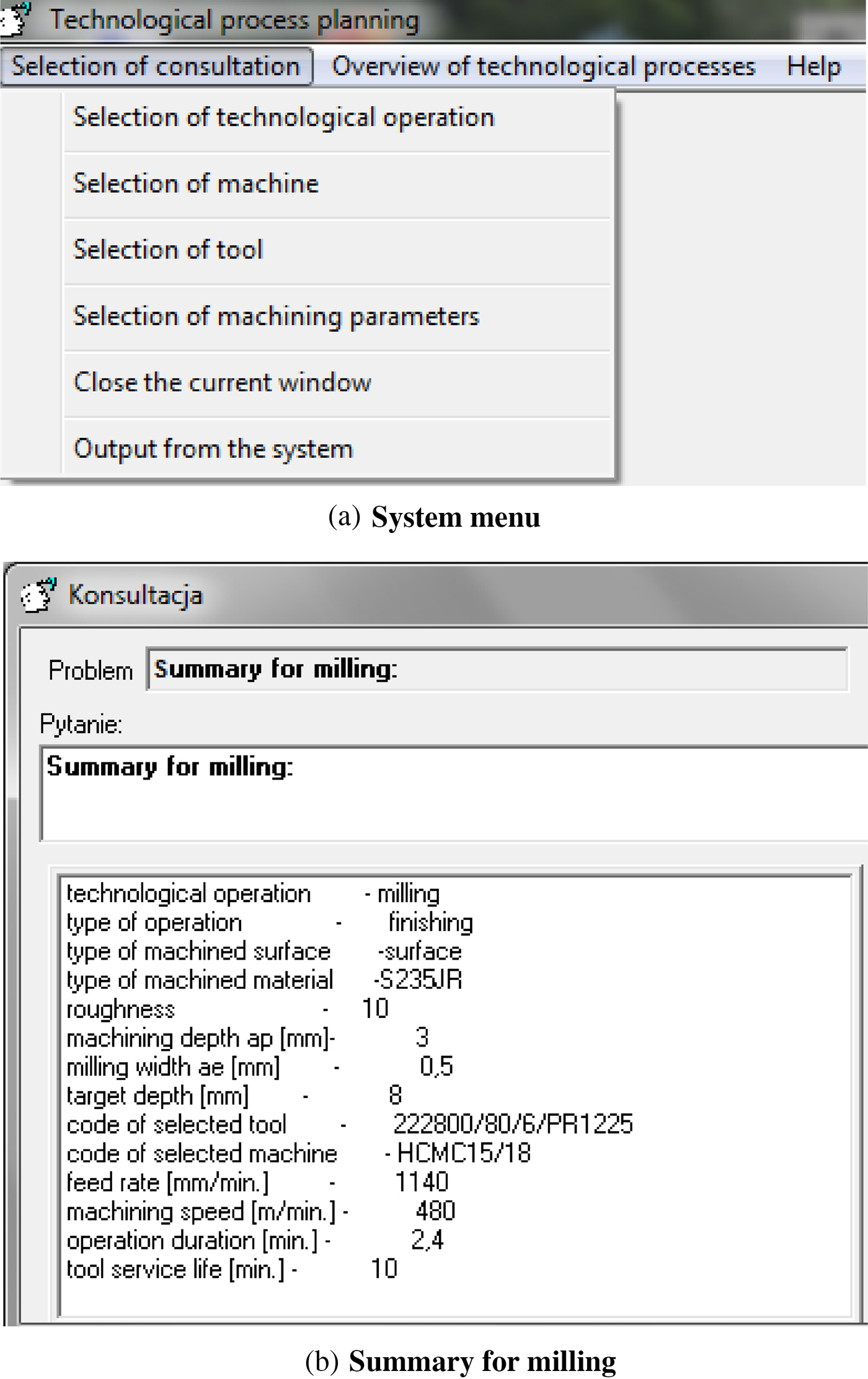
Fig. 7. Summary for the milling operation.
5.4. Advantages and disadvantages of neural networks
The application of neural networks to the design of a technological process has both advantages and disadvantages. A very significant advantage is the ability to acquire the technological knowledge and experience of process engineers from technological processes that have already been developed. This knowledge and experience, contained within a computer system, enables the design of technological processes by less experienced engineers, who in this way avoid errors and thus reduce losses to the enterprise.
A disadvantage of the use of neural networks is the complexity of the CAPP system. Models for the selection of a machine, tools, and machining parameters are developed for each technological operation separately (for milling, grinding, turning, etc.). Moreover, the learning files for the neural networks contain both quantitative and qualitative parameters. Qualitative parameters are also coded as zero-one sequences. For example, if for a type of operation we have two values, “rough” and “finishing,” this may be coded as follows:
• a rough operation by the sequence 01 and
• a finishing operation by the sequence 10.
In this case, one nominal value is replaced by two numerical values. This means that due to qualitative parameters, the number of inputs and outputs of the neural network is increased. The actual number of a network's inputs and outputs depends on the number of qualitative values considered. The neural networks also require additional learning periodically as new data are received. These data may include new machines and tools, as well as additional examples of developed technological processes.
Furthermore, the knowledge contained in the system is specific to a particular enterprise. This means that such a CAPP system is a universal tool because the technological process is designed in a defined way, and the same neural network structures can be used. In contrast, the neural networks have to go through a new learning process based on data and examples for each enterprise.
5.5. Elimination of defects in technological operations
A method was also developed for the elimination of defects occurring in the course of the manufacturing process. This method uses decision rules. When such a defect comes to light, the process engineer can use this method to determine how to adapt the technological process so that such a defect does not occur in the future. This method improves the quality of the technological process. The guidelines for the milling operation are presented in detail.
An analysis of tool catalogs can provide general guidelines for the elimination of defects in milling. However, the real knowledge and experience of a process engineer are very important here. Based on the engineer's knowledge, decision rules to assist the machine operator were prepared.
For example, the improper surface quality defect may be caused by wear of the cutting edges or by run-out of the milling cutter. This defect may be eliminated in several ways:
• selecting a harder grade of cutting plates,
• selecting an adhesion-proof grade of cutting plates,
• increasing the cutting speed,
• reducing the movement speed,
• reducing the cutting depth, or
• checking the use of a coolant–lubricant.
The priority level assigned to these methods of eliminating defects depends on the experience of the process engineer.
Examples of rules are shown below:
If improper_surface_quality then cutting_edges_are_worn;
If cutting_edges_are_worn then select_harder_grade_of_cutting_plates and priority = 0.5;
If cutting_edges_are_worn then increase_cutting_speed and priority = 1.
The rules were checked for accuracy in the knowledge base. Verification and validation of the rules were performed. Anomalies, such as conflicting, absorbing, repeated, and incomplete rules, were eliminated.
A CAPP system based on rules and neural network models enables the intelligent design of a technological process. An example of the use of rules is shown in Figure 8.
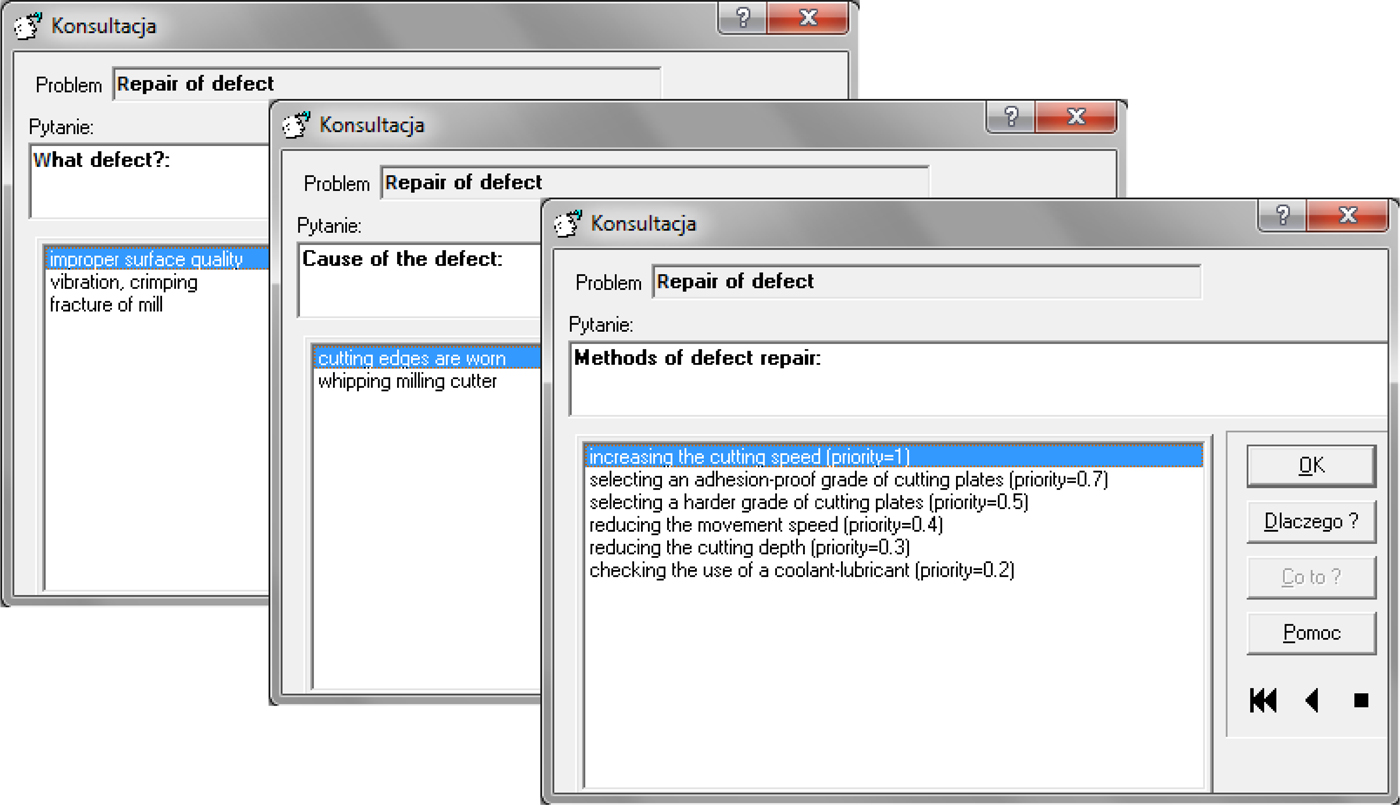
Fig. 8. Elimination of defects in milling operations.
6. CONCLUSIONS
The tests performed in this study have demonstrated the usefulness of neural networks and their high effectiveness in supporting the design of technological processes. Neural networks, being very good algorithms for data exploration, have provided wide opportunities for making use of the data contained in technological databases. The comparison of MLP, RBF, and Kohonen networks has resulted in interesting research conclusions. MLP networks are a very good universal tool for solving complex problems. RBF networks provide results faster. A comparison of RBF networks with Kohonen networks enabled verification of the behavior of networks using supervised and unsupervised learning. Moreover, it was possible to test the behavior of those networks when handling a real problem, such as the design of a technological process.
The outputs of neural network models can serve as suggestions for a process engineer. However, it is the process engineer who should be responsible for making the final decision.
The use of neural network models to aid process planning has introduced a new quality to CAPP systems and enables the creation of a support system that collects knowledge automatically and has the capacity for adaptation. This is particularly important when developing CAPP systems for complex real systems.
Izabela Rojek is an Assistant Professor in the Institute of Mechanics and Applied Computer Science at Kazimierz Wielki University. She was previously an Assistant Professor at the Institute of Mechanical Technology, Poznan University of Technology. She received an MS in computer science and a PhD in mechanical engineering and operation from Poznan University of Technology. Her main research interests are in the fields of knowledge management, artificial intelligence, and intelligent CAPP systems. Dr. Rojek is the author or coauthor of approximately 100 papers published in international and national journals and presented at conferences.














