1. Introduction
This article proposes a theoretical framework for how to organise complex system design and development activities in a way that actively considers both strategies for breaking up the technical work and the capabilities of potential solvers – both inside and outside the organisation. We call this approach the solver-aware system architecting (SASA) framework, where ‘solvers’ refer to the individuals and groups who will engage in design and development work and ‘architecting’ refers to the process of breaking up (decomposing) and coordinating that work. We suggest that through a joint consideration of technical decomposition and solving capacity, organisations can leverage and combine the relative strengths of domain-experts, crowds and specialists to improve complex system design and innovation. So far, system architecting theory has focused on optimally grouping tasks or subproblems based on attributes of the technical design space (Browning Reference Browning2001; Crawley, Cameron & Selva Reference De Stefano2015; Eppinger & Ulrich Reference Ethiraj and Levinthal2015), and strategies for hedging against changing operating environments, for example, through modularity (Ulrich Reference Vincenti1995), commonality (Boas, Cameron & Crawley Reference Boas, Cameron and Crawley2013), flexibility and changeability (Ulrich Reference Vincenti1995; Brusoni & Prencipe Reference Brusoni and Prencipe2001; Fricke & Schulz Reference Fu, Chan, Cagan, Kotovsky, Schunn and Wood2005; Brusoni et al. Reference Brusoni and Prencipe2007). Multiple powerful tools have been created to aid in that process (Sobieszczanski-Sobieski & Haftka Reference Suh and de Weck1997; Browning Reference Browning2001; Ross, Rhodes & Hastings Reference Sanchez and Mahoney2008; Martins & Lambe Reference McNerney, Farmer, Redner and Trancik2013; Neufville et al. Reference Nonaka2019). However, although uncertainty in the operating environment is core to systems engineering, the literature makes the implicit assumption that systems will be developed by traditional players using traditional practices. Here, traditional players are domain experts working in typical organisational contexts. We contend that this view ignores an important dimension regarding the players themselves. For example, even one-of-a-kind satellites are composed of expected subsystems including propulsion, command and data handling, power, and so on, interacting through traditional interfaces. Established prime contractors serve as the systems integrator, and let contracts to lower-tier suppliers. This concentrates potential novelty within the category of payload, or within-subsystem advances (Szajnfarber & Weigel Reference Terwiesch and Xu2013; Vrolijk & Szajnfarber Reference Wiggins and Crowston2015), even though there may be opportunities for architectural innovation (Henderson & Clark Reference Hoffman and Weiss1990) which remain unexplored.
While the assumption of dominant architectures has been valid historically, the recent rise of complex system innovations originating from outside of traditional firm structures (Baldwin & Von Hippel Reference Baldwin and Clark2011; Lakhani, Lifshitz-Assaf & Tushman Reference Larson, Kirkpatrick, Sellers, Thomas and Verma2013) may limit its validity in the future. There is increasing recognition that architectures developed to support traditional modes of engineering design may be less effective when solutions are incorporated from a wider range of stakeholders (Kittur et al. Reference Kittur, Yu, Hope, Chan, Lifshitz-Assaf, Gilon, Ng, Kraut and Shahaf2013; Vrolijk & Szajnfarber Reference Wiggins and Crowston2015). Specifically, ‘Joint’ programs and ‘Systems-of-Systems’ are increasingly popular and challenge traditional structures of authority, with multiple organisations collaborating as peers (Dwyer, Cameron & Szajnfarber Reference Eck, Mcadams and Vermaas2015). Similarly, the ‘gig’ economy and other forms of ad hoc work are taking off, with nontraditional players, including crowds of amateurs, increasingly being leveraged through nontraditional contracting mechanisms, such as open competitions (Poetz & Schreier Reference Raveendran, Puranam and Warglien2012; Franzoni & Sauermann Reference Fricke and Schulz2014; Gustetic et al. Reference Haskins, Forsberg, Michael Krueger and Hamelin2015; Suh & de Weck Reference Szajnfarber and Vrolijk2018; Lifshitz-Assaf, Lebovitz & Zalmanson Reference Logsdon2021). Successes in these areas call into question the notion that talent and expertise only reside within traditional organisations and professions (Chesbrough Reference Chubin2003; Baldwin & Von Hippel Reference Baldwin and Clark2011; Gambardella, Raasch & von Hippel Reference Garud and Kumaraswamy2016; Lifshitz-Assaf Reference Lifshitz-Assaf, Lebovitz and Zalmanson2018). From an architecture perspective, whether, and under what conditions, dominant forms are the best option to leverage these new kinds of contributions.
We contend that traditional architecting practices developed for complex systems engineering may be less effective when solutions are incorporated from a wider range of stakeholders from inside and outside traditional firms. To test and elaborate this idea, this article develops an abstract simulation model to study the relationship between problem architecture, solver characteristics, and how that interaction drives solution efficacy. We used this simulation framework to address three specific research questions: (a) How do characteristics of the solver (e.g., expert versus novice capabilities) affect which architectural form should be preferred? (b) Can ‘good’ architecting choices enable productive contributions from nontraditional solvers (e.g., crowds of amateurs)? and more generally (c) How should solver attributes be considered during the architecting process? With respect to the first two questions, the simulation enables us to investigate relative improvements due to decomposition decisions in conjunction with solver assignment. We find that indeed the best alternatives include contributions from nontraditional solvers working on architectures that would not have been selected through typical practices (i.e., if these solvers were not considered as part of the architecting process). Building on these observations, and in response to the third question, we synthesise preliminary heuristics for ‘good’ module-solver pairs and suggest strategies for SASA practices. We then discuss the relevance of these findings to real-world engineering systems design and management.
2. Related literature
Our suggested framework (SASA) draws on, and elaborates, two main lines of theory bringing together the management and systems engineering bodies of literatures. Within these bodies of literature, we focus on the increased availability of, and potential for, nontraditional sources of expertise to contribute to innovation, and the need for correspondence between technical and organisational structure. The below sections summarise these theoretical building blocks, starting from the more general to the more specific, and then synthesise the specific gap addressed by our work in the context of systems architecting.
2.1. The case for nontraditional expertise in the innovation process
Since Schumpeter’s (Reference Simon1934) seminal work on the process of innovation, researchers have theorised and analysed ways to organise for the production of scientific and technological innovation (cf., Baldwin & Von Hippel Reference Baldwin and Clark2011; Felin & Zenger Reference Fixson and Park2014; Benner & Tushman Reference Benner and Tushman2015). These theories usually assume that innovating on scientific and technological problems is the sole purview of domain professionals (i.e., experts). Indeed, as professionals gain experience and expertise, their ability to solve the typical problems of their domain improves. Solving problems requires high familiarity with the specific context in which they are situated (Vincenti Reference Von Hippel1990; Carlile Reference Cetina2004), as well as with the domain’s tacit knowledge (Nonaka Reference Pahl and Beitz1994; Argote & Miron-Spektor Reference Argote and Miron-Spektor2011). However, the innovation literature has also shown that professionals’ accumulated depth of knowledge is a double-edged sword. As professionals gain expertise and socialise within their professional ‘epistemic cultures’ (Cetina Reference Chaudhari, Sha and Panchal2009), they often become ‘locked in’ to their professional cognitive frames regarding a problem (Foster & Kaplan Reference Franzoni and Sauermann2011), creating an ‘innovation blindness’ (Leonardi Reference Lifshitz-Assaf2011). Moreover, expert time and the availability of expert labour is increasingly viewed as a scarce resource (Cappelli Reference Carlile2014), leading to many engineering organisations to consider alternative models, including contractors and in the extreme, just-in-time workforce (De Stefano Reference De Weck, Roos and Magee2015).
One way to overcome these challenges is by opening up problems to external, nondomain, nonexpert solvers. In the last two decades, technological progress in information and communication technologies has made many of the tools needed for the production of technological and scientific innovation widely accessible, enabling individuals who are not domain professionals to innovate (Baldwin & Von Hippel Reference Baldwin and Clark2011; Wiggins & Crowston Reference Zeigler, Muzy and Kofman2011; Altman, Nagle & Tushman Reference Altman, Nagle and Tushman2014). Multiple theories have been offered for how external solvers can contribute ‘extreme value solutions’ sampled from multiple solvers (Terwiesch & Xu Reference Topcu and Mesmer2008; Jeppesen & Lakhani Reference Kim, Michelena, Papalambros and Jiang2010) or by bringing novel perspectives to bear (Chubin Reference Colfer and Baldwin1976; Collins & Evans Reference Collopy and Hollingsworth2002; Acar & van den Ende Reference Acar and van den Ende2016; Szajnfarber & Vrolijk Reference Taylor2018; Szajnfarber et al. Reference Szajnfarber and Weigel2020. In addition to bringing outside perspectives, open innovation models can mitigate labour shortfalls by allowing experts to focus on the issues that most critically need their focus, and tapping into external sources of talent.
Open innovation approaches have been shown to be effective across multiple contexts, solving aspects of problems from aerospace (Lifshitz-Assaf Reference Lifshitz-Assaf, Lebovitz and Zalmanson2018; Szajnfarber & Vrolijk Reference Taylor2018), to medicine (Ben-David Reference Ben-David1960; Good & Su Reference Goucher-Lambert and Cagan2013; Lakhani et al. Reference Lakhani, Lifshitz-Assaf and Tushman2013; Küffner et al. Reference Kusiak and Wang2015), energy and sustainability (Fayard, Gkeredakis & Levina Reference Felin and Zenger2016), design (Panchal Reference Panchal, Fuge, Liu, Missoum and Tucker2015; Chaudhari, Sha & Panchal Reference Chen, Allen and Mistree2018; Goucher-Lambert & Cagan Reference Guan and Chen2019), evaluation of tasks (Welinder et al. Reference Yin2010; Budescu & Chen Reference Buede and Miller2015; Krishna et al. Reference Küffner, Zach, Norel, Hawe, Schoenfeld, Wang, Li, Fang, Mackey, Hardiman, Cudkowicz, Sherman, Ertaylan, Grosse-Wentrup, Hothorn, van Ligtenberg, Macke, Meyer, Schölkopf, Tran, Vaughan, Stolovitzky and Leitner2017), astronomy (Wiggins & Crowston Reference Zeigler, Muzy and Kofman2011), to software engineering (Mao et al. Reference Martins and Lambe2017) and robotics (Szajnfarber et al. Reference Szajnfarber and Weigel2020), among many other fields of science (Franzoni & Sauermann Reference Fricke and Schulz2014; Beck et al. Reference Beck, Bergenholtz, Bogers, Brasseur, Conradsen, Di Marco, Distel, Dobusch, Dörler, Effert, Fecher, Filiou, Frederiksen, Gillier, Grimpe, Gruber, Haeussler, Heigl, Hoisl, Hyslop, Kokshagina, LaFlamme, Lawson, Lifshitz-Assaf, Lukas, Nordberg, Norn, Poetz, Ponti, Pruschak, Pujol Priego, Radziwon, Rafner, Romanova, Ruser, Sauermann, Shah, Sherson, Suess-Reyes, Tucci, Tuertscher, Bjørn Vedel, Velden, Verganti, Wareham, Wiggins and Mosangzi Xu2020). Despite these successes, many sustain that open innovation only works well for certain types of problems that match the strengths of external solving (Boudreau & Lakhani Reference Boudreau and Lakhani2009). Even among strong proponents of open and distributed innovation, there is a notion that applying open innovation methods with crowds should be reserved for modular problems and not complex ones. Complex problems or systems are typically defined in terms of their high number of parts, the nontrivial dependencies among those parts, and the contributions they incorporate from multiple disciplines (De Weck, Roos & Magee Reference Du and Chen2011). These interdependencies – both among the technical parts and the deep contextual knowledge associated with them and their integration – have led scholars to suggest that it is unlikely for crowds to solve whole complex problems (Lakhani et al. Reference Larson, Kirkpatrick, Sellers, Thomas and Verma2013; Felin & Zenger Reference Fixson and Park2014).
2.2. Mirroring: correspondence of technical and organisational structures
Fundamental to the design of complex systems is the core organisational function of coordinating interdependent tasks (cf., Galbraith Reference Gambardella, Raasch and von Hippel1974; Thompson Reference Topcu, Mukherjee, Hennig and Szajnfarber2003). Interdependent tasks arise when complex systems are partitioned into lower complexity subproblems (Simon Reference Sinha, Christiaan, Liang and Khosla1962, Reference Sobieszczanski-Sobieski1996). However, since most complex problems are only partially decomposable (Simon Reference Sinha, Christiaan, Liang and Khosla1962), there remains a critical task of managing those interdependencies (Campagnolo & Camuffo Reference Camuffo and Wilhelm2010). This led organisational scholars to conceptualise design as an organisational problem-solving process where the goal is to place organisational links such that scarce cognitive resources are conserved (Baldwin & Clark Reference Baldwin and Von Hippel2000; Colfer & Baldwin Reference Collins and Evans2016) and to build theory around where such ties should be placed (Parnas Reference Pine1972; Hoffman & Weiss Reference Hölttä-Otto and de Weck2001; Thompson Reference Topcu, Mukherjee, Hennig and Szajnfarber2003).
Working across multiple disciplines and domains, researchers began noticing that ‘the formal structure of an organisation will (or should) “mirror” the design of the underlying technical system’ (Conway Reference Crawley, Cameron and Selva1968; Henderson & Clark Reference Hoffman and Weiss1990; Von Hippel Reference Welinder, Branson, Perona and Belongie1990; Sanchez & Mahoney Reference Schumpeter and Opie1996; Chesbrough & Teece Reference Chesbrough and Teece1998; Baldwin & Clark Reference Baldwin and Von Hippel2000; Cabigiosu & Camuffo Reference Campagnolo and Camuffo2012). Colfer & Baldwin (Reference Collins and Evans2016) formalised these ideas as the so-called Mirroring Hypothesis, which states that organisational ties are more likely to be present in places where technical interdependencies are present (or dense) and that ‘mirrored’ systems perform better.
An extension of this idea is that the relationship between technical and organisational dependencies can be intentionally designed to be better match (Ulrich Reference Vincenti1995; Hoffman & Weiss Reference Hölttä-Otto and de Weck2001; Camuffo & Wilhelm Reference Cappelli2016). Since coordinating across dependencies can be so costly, these scholars emphasise minimising across-module dependencies, managed instead through design rules (Baldwin & Clark Reference Baldwin and Von Hippel2000). Specifically, Parnas’s notion of modules as being “characterized by its knowledge of a design decision that it hides from all others” (Parnas Reference Pine1972, p. 1056) emphasises the role and value of information hiding in complex system design (Baldwin & Clark Reference Baldwin and Von Hippel2000). This is particularly important when nontraditional contributors are involved because it opens to door for lower-skilled contributions. Moreover, it opens the door to consider different modules depending on which decisions need to be hidden.
2.3. Current focus of system architecting: the technical system and its environment
At its core, systems engineering aims to architect complex systems such that subtasks can be completed efficiently in parallel, and later re-integrated to make a system that delivers value over long lifetimes (Haskins et al. Reference Hazelrigg2006). Upfront architecting choices are critical because they affect both the process of designing and later, the system’s ability to sustain value postdeployment over extended lifetimes. During design, the architecture defines the task units and the need for coordination among them (Parnas Reference Pine1972; Baldwin & Clark Reference Baldwin and Von Hippel2000; Brusoni & Prencipe Reference Budescu and Chen2006). Post deployment that same structure enables (or constrains) which subsystems can be easily replaced and or upgraded as emergent needs arise (Fricke & Schulz Reference Fu, Chan, Cagan, Kotovsky, Schunn and Wood2005; Hölttä-Otto & de Weck Reference Hong and Page2007).
Systems Architecting is a process of mapping function to form for a given design concept (Crawley et al. Reference De Stefano2015). It is recognised as both an art and a science (Maier Reference Maier and Rechtin1998; Maier & Rechtin Reference Malak, Aughenbaugh and Christiaan2009) because successful architecting requires a synergistic combination of both. The science facet describes the necessity to conform with the relevant engineering principles and the normative standards (e.g., laws, codes and regulations). Whereas, the art facet represents the informal skills that are needed for the comprehensive identification of the stakeholders and incorporation of their conflicting preferences into the design process, along with the heuristics for facilitating these counterbalancing objectives.
Architecting involves making trade-offs between performance, cost, and schedule, under ambiguity and uncertainty regarding both the characteristics of the system and its operational environment (Malak et al. Reference Mao, Capra, Harman and Jia2009; Blanchard & Fabrycky Reference Blanchard and Fabrycky2011). This incentivizes practicing system architects to adopt an uncertainty reducing approach, where the abstract concept is iteratively refined by articulating its inputs, outputs, and processes, along with the interfaces through which these interactions will occur (Kossiakoff & Sweet Reference Krishna, Zhu, Groth, Johnson, Hata, Kravitz, Chen, Kalantidis, Li, Shamma, Bernstein and Fei-Fei2003; Larson et al. Reference Leonardi2009; Buede & Miller Reference Cabigiosu and Camuffo2016). The concept development is followed by an exploration of the design space (Hazelrigg Reference Henderson and Clark1998; Du & Chen Reference Dwyer, Cameron and Szajnfarber2002; Ross et al. Reference Sanchez and Mahoney2008; Collopy & Hollingsworth Reference Colombo, Shougarian, Sinha, Cascini and de Weck2011; Topcu & Mesmer Reference Tribes, Dubé and Trépanier2018).
While earlier research focused on identifying and optimising feasible alternatives within the design space (Chen, Allen & Mistree Reference Chesbrough1997; Papalambros & Wilde Reference Parker and Van Alstyne2000; Brusoni & Prencipe Reference Brusoni and Prencipe2001), in the last decades the community has shifted its attention to decomposition. In the design literature, decomposition focuses on the technical problem space (Eck, Mcadams & Vermaas Reference Eisenhardt2007), whether it is at the conceptual design level or at the parametric level. The Pahl and Beitz systematic design method (Pahl & Beitz Reference Panchal2013), for example, prescribes hierarchical decomposition of the function structure as a core strategy for conceptual design. Within the multidisciplinary design and optimization (MDO) literature, the goal is to concurrently handle the interdependencies among coupled design variables, which may be shared across different disciplines, in pursuit of a preferred system-level solution (Martins & Lambe Reference McNerney, Farmer, Redner and Trancik2013). In MDO, often the complexity of finding an optimal solution is reduced by decomposing the parametric design space (Kusiak & Wang Reference Lakhani, Boudreau, Loh, Backstrom, Baldwin, Lonstein, Lydon, MacCormack, Arnaout and Guinan1993; Tribes, Dubé, & Trépanier Reference Ulrich2005). MDO techniques including concurrent subspace optimization (Sobieszczanski-Sobieski Reference Sobieszczanski-Sobieski and Haftka1988; Bloebaum, Hajela & Sobieszczanski-Sobieski Reference Bloebaum, Hajela and Sobieszczanski-Sobieski1992), collaborative optimization (Braun et al. Reference Braun, Gage, Kroo and Sobieski1996), bi-level integrated system synthesis (Sobieszczanski-Sobieski, Agte & Sandusky Reference Steward2000), and analytical target cascading (Kim et al. Reference Kittur, Nickerson, Bernstein, Gerber, Shaw, Zimmerman, Lease and Horton2003; Bayrak, Kang & Papalambros Reference Bayrak, Kang and Papalambros2016) use different forms of problem decomposition and coordination between the subproblems.
In the systems engineering literature, emphasis is placed on the interactions of the system with its uncertain operational environment and identifying decomposition strategies that sustain value over uncertain and extended lifecycles. These design strategies are generally referred to as the ‘-ilities,’ including, flexibility and changeability (Fricke & Schulz Reference Fu, Chan, Cagan, Kotovsky, Schunn and Wood2005; Ross et al. Reference Sanchez and Mahoney2008; Broniatowski Reference Broniatowski2017), survivability (Richards Reference Ross, Rhodes and Hastings2009), modularity (Sanchez & Mahoney Reference Schumpeter and Opie1996; Fixson & Park Reference Fogliatto, Da Silveira and Borenstein2008) and commonality (Boas & Crawley Reference Boas and Crawley2011). At their core is the insight that alternative decompositions sustain value in response to different environmental disruptions, including both threats and opportunities (e.g., changing markets) (Pine Reference Poetz and Schreier1993; Fogliatto, Da Silveira & Borenstein Reference Foster and Kaplan2012; Colombo et al. Reference Conway2020). These ideas have been applied to both integrated and distributed systems (Mosleh, Ludlow & Heydari Reference Neufville, Smet, Cardin and Ranjbar-Bourani2016; Mosleh, Dalili & Heydari Reference Mosleh, Ludlow and Heydari2018).
Overall, the literature recognises decomposition (through modularity or otherwise) as a key strategy in complexity reduction and management, and to enable sustained value across long uncertain lifetimes. However, there is also recognition that too much decomposition can be detrimental to system performance (Ethiraj & Levinthal Reference Fayard, Gkeredakis and Levina2004; Topcu et al. Reference Tushman and Nadler2021). The need to identify the right balance is particularly poignant when considering contributions from nonexpert solvers, as in open innovation. In that context, the desire to reduce scope and complexity to enable wider participation (Szajnfarber & Vrolijk Reference Taylor2018), while retaining the value that comes from jointly optimising shared variables (Sobieszczanski-Sobieski & Haftka Reference Suh and de Weck1997; Martins & Lambe Reference McNerney, Farmer, Redner and Trancik2013) emphasises the need for guidance on achieving the ‘right’ level and mode of decomposition.
2.4. Research gap: the need to assess solver capabilities early in the architecting process
So far, these perspectives all emphasise the need to consider downstream uncertainties during the design stage. Here, we introduce a new dimension in the design process, namely, solver capability. While the notion of decomposing problems to make solving more tractable is not new (Garud & Kumaraswamy Reference Good and Su1995; Baldwin & Clark Reference Baldwin and Von Hippel2000; Schilling Reference Shergadwala, Bilionis, Kannan and Panchal2000; Raveendran, Puranam & Warglien Reference Richards2016); for the first time, we systematically explore the interaction of architecting choices and how that enables solvers with different capabilities to contribute. Building on the mirroring hypothesis ideas that technical and organisational architectures must match, and wishing to leverage the increased capability and availability of nontraditional solvers, we explore how new ways of grouping and partitioning design variables can create new opportunities for nonexpert solving. The contribution is in both the formulation of a SASA process and specific insights about the relationship between solvers and decomposing. Fundamentally, we propose a rethinking of system architecting as a sociotechnical process, allowing for a joint consideration of problem formulation, organisational knowledge and external expertise to improve design process outcomes.
3. Model formulation
We wish to explore the relationship between design decomposition and solver assignment in the context of system architecting. More broadly the goal is to generate insight about when, under what conditions, nondomain, nonexperts can contribute high-quality solutions to difficult ‘expert-only’ problems. To do this, we examine alternative problem decompositions in combination with task assignment to solvers with differing capabilities, within an abstract simulation model (Kleijnen Reference Kossiakoff and Sweet2018). The overall model flow is illustrated in Figure 1. The simulation framework begins by instantiating a reference problem in context; this creates the baseline values against which every other simulation will be compared. Next, multiple alternative architectures, operationalised as task structures, for solving that problem, are defined. Third, alternative solver types are instantiated and assigned combinatorially to every task structure at the task level. Finally, problem solving is simulated for each combination, with solvers executing their assigned tasks in the context of the overall task structure. The model maintains an accounting of multiple relevant measures of merit: performance, cost and reliance on domain experts. As with any simplified model world, care must be taken to assess to scope of representativeness, which is discussed in Section 3.6.

Figure 1. An overview of the simulation model. Squares represent task structures and the colours represent assignment to a different solver archetype.
3.1. Instantiating a reference problem and context
Problem-solving processes are frequently represented as a sequence of interdependent tasks, where the output of taskn defines the input of taskn + 1 along with potential feedback from other processes (McNerney et al. Reference Meluso, Austin-Breneman and Shaw2011; Guan & Chen Reference Gustetic, Crusan, Rader and Ortega2018; Shergadwala et al. Reference Simon2018; Eletreby et al. Reference Enkel, Gassmann and Chesbrough2020). A cartoon of a two-task system of this form is illustrated in Figure 1. When modelling such task structures, it is also necessary to represent the underlying ‘physics’ of each task, since it drives the internal solving processes. Some authors represent the task model in general terms, typically combining the problem and solver as a solving process (see Terwiesch & Xu Reference Topcu and Mesmer2008; Meluso, Austin-Breneman & Shaw Reference Mosleh, Dalili and Heydari2020; Valencia-Romero & Grogan Reference Voelpel and Dous2020), whereas others adopt a reference system, model the interdependencies among its elements and use this platform to study the investigated trade-offs (Sobieszczanski-Sobieski & Haftka Reference Suh and de Weck1997; Hazelrigg Reference Henderson and Clark1998; Sinha et al. Reference Sobieszczanski-Sobieski, Agte and Sandusky2001; Topcu & Mesmer Reference Tribes, Dubé and Trépanier2018). We chose to adopt a reference system because it enables easier intuition about the opportunities for feasible alternative task structures and solver types. Specifically, we adopted the problem of playing a golf tournament as our reference problem.
Although golf may seem like an unusual choice for a reference problem, it meets the most relevant criteria, while also enabling intuitive interpretation of results. Golf is a game dominated by domain experts, even though amateurs and aspirational professionals abound. The tasks associated with playing golf follow the structure defined above. It includes feedforward dependencies in that the difficulty of every next stroke is defined by the result of the last. For example, a favourable green placement makes for an easy putt compared to an approach that lands in the rough. It also includes shared design variables across subfunctions, in that professional golfers prefer to ‘set up’ their next shots in accordance with their particular skills. For example, one golfer might prefer to approach the pin with a short chip off the fairway, whereas other might have more confidence in their long-putting. In either case, the subsequent preference influences choices made during the driving stage.
Additionally, there is variability in both the kinds of tasks associated with playing golf and the availability of amateurs who are qualified to perform them. Driving off the tee requires strength and form and is something that some people specialise in – the longest drivers in the world would not qualify for the Professional Golf Association (PGA) tour. In contrast, putting requires a lighter touch and an ability to ‘read’ the green. Every amateur can putt, but few can do so reliably. These attributes give us the space to define a model world with different decompositions and different task assignments. Finally, as the problem of golf is decomposed, each subsystem embodies different objectives, that in some cases are multivariate. For example, a good approach is defined both by the resulting green placement and the number of strokes to achieve it. This creates richness in interface choices (e.g., picking the closest ball is an easier handoff than weighting both figures of merit) that are representative of real-world module design challenges.
In the model, we represent the golf context as a nine-hole golf course where each identical hole measures 700 yards from tee to pin, along a straight line. Solving the ‘problem’ requires the player(s) to move the ball from the tee to the pin using a sequence of generic golf strokes. Most attempts result in the ball sinking in a reasonable number of strokes, through some runs never converge (we implement a ‘mercy rule’ after 15 strokes). The simulation implements three stroke types – driving off the tee, shots from the fairway and putting. Within each stroke type, we include variations that depend on the context of the ball placement. For example, on the fairway, golfers might aim for the pin if they are within range. These stroke types are reflective of the major differences in golf club options and techniques, without some of the subtle variation available in a modern golf set.
Figure 2a shows the flow of each model run for the whole problem: after the first drive, simulated players pick the stroke type that is most appropriate for the next shot based on the current ball position. When the model is executed for alternative decompositions and assignments to solver types, two key changes are made to the flow. First, the problem formulation changes the boundaries of which modules are solved and how they are coordinated (see Section 3.2). Second, when alternative solvers (Section 3.3) participate in a tournament structure, this means that for each assignment the model is run ‘K’ times, for the size of the tournament, then the outcomes are judged and only the best of K is retained. Each selection happens on a per module basis, so for a decomposed problem, there may be more than one tournament and associated selection.

Figure 2. (a) Flowchart of the simulation based on field position (Tee, Fairway and Green) and stroke types (Drive, Approach and Putt) and (b) simulation parameters for strokes per solver type. *‘d’ represents the remaining distance to the hole, ‘N’ denotes normal distribution and ‘U’ represents uniform distribution.
3.2. Alternative task structures
To define alternative task structures for solving the golf ‘problem’ we follow established principles from the systems engineering literature on the modularization of systems (Ulrich Reference Vincenti1995; Eppinger Reference Eppinger and Browning1997; Browning Reference Browning2001; Hölttä-Otto & de Weck Reference Hong and Page2007; Eppinger & Browning Reference Eppinger and Ulrich2012). The basic principle is to decompose the system such that tightly couple tasks with similar functions are grouped together in modules, and loosely couple tasks are separated (Parnas Reference Pine1972; Baldwin & Clark Reference Baldwin and Von Hippel2000; Parnas et al. Reference Parnas, Branch, Washington, Clements and Weiss2000; Schilling Reference Shergadwala, Bilionis, Kannan and Panchal2000). Since most practical systems can only be partially decoupled (Simon Reference Sinha, Christiaan, Liang and Khosla1962), once the basic structure has been defined, rules for how modules interact must be defined in advance. A given system can be modularized in multiple different ways (Crawley et al. Reference De Stefano2015). Importantly, the process of decomposing generates new subproblems that may rely on, and prioritise, different types of expertise than the original problem, potentially opening the door for external contributions.
In the context of the golf problem, we identified three reasonable modules based on functional similarity: Tee, where the primary functional objective is distance; Fairway, which combines a need for both distance and accuracy and Green, which is almost exclusively focused on accuracy. We then designed the interfaces and coordination rules that would enable combinations of these subfunctions to perform the overall golf function. To formally represent the alternatives, we adopt the widely used DSM N × N representation (Steward Reference Szajnfarber, Grogan, Panchal and Gralla1981; Schilling Reference Shergadwala, Bilionis, Kannan and Panchal2000; Browning Reference Browning2001; Browning Reference Brusoni, Marengo, Prencipe and Valente2016) to document the resultant alternative decompositions in terms of tasks and their interaction rules. In a DSM representation, each of the rows (and corresponding columns) relate to a predefined system element (in this case modules) and the off-diagonal x’s represent dependencies. Below the diagonal dependencies are feedforward, and above them are feedback.
When modules are decoupled for the purpose of solving, dependencies can be replaced with design rules (Baldwin & Clark Reference Baldwin and Von Hippel2000). This is shown by the R’s in the DSM representation. In golf, as in engineering, the choice of design rule can have an important impact on overall system performance. In most cases, there is a trade-off between ease of coordination and optimality of the rule. In the specific instance of golf, this manifests as two alternative rules for how to pick the best output from module n to pass to module n + 1: (a) pick the shortest remaining distance to the hole versus (b) of the attempts with the fewest strokes, pick the one with the shortest distance to the hole. In the first case, the judgement can be made easily on the whole population, but especially with large numbers of trials, there will be many instances where a slight improvement in the distance comes with a cost in stroke count. This can be detrimental to overall performance since, at the system level, strokes are what matters most. On the other hand, to make the more sophisticated evaluation that includes both features, the judgement can no longer be made at the population level. Rather each trial must be tracked to record the stroke count per ball. This will guarantee a better overall result, but comes at a high coordination cost. In future work, one could explore the complexities of this trade-off, but since our present focus is on decomposition, we will adopt the practical design rule (shortest distance) in the remainder of the discussion.
In the baseline problem per Figure 2, solvers begin at the Tee with the problem statement: sink the ball in the fewest strokes. In practice, when a single golf Pro is responsible for the whole problem, they can apply system-level strategy to their solution as desired. For example, one strategic element is a choice to either choke up on a drive to set up a more ‘favourable’ approach shot or take a (normal) long drive shot. Favourable here is a ‘sweet spot’ on the fairway: typically the ‘sweet spot’ is unique to each pro based on their specific style of play. To simplify, in the model we assumed Pros always prefer to approach from the (fixed) ‘sweet spot’ and that fairway shots taken from the ‘sweet spot’ are both more accurate and aim for a closer green position. As a result, they are more likely to result in a better green position, leading to fewer strokes on the green to sink. In the model, this strategy is only available to Pros and only when T and F reside in the same module (as in H and LG shown in Figure 3) because the Pro assigned to T would not be aware of the preferences of the solver assigned to F, a necessary condition for adopting a system-level strategy.

Figure 3. The baseline undecomposed expert-only problem H (a), LG decomposition (b), TFG decomposition (c) and TS decomposition (d).
Each of the panels in Figure 3 represents alternative solving architectures, breaking up the problem through different combinations of the three identified subtasks: Tee, Fairway and Green. When dependencies are contained within a subproblem, they are managed internally by the single solver. When decomposition breaks those dependencies, they are replaced by design rules (R1 and R2) or just removed, in the case of the feedback between T and F. Specifics of each architecture are as follows:
(i) H: Figure 3a shows the baseline H, which solves the problem: sink the ball in the fewest strokes, follows the solving process outlined above.
(ii) LG: Figure 3b breaks H into two tasks: the long game (L) where the task is presented as the following: starting from the Tee, reach the green in as few strokes as possible; and green (G) where the task is: starting from the green, sink the ball in the hole in as few strokes as possible. To combine L and G into the LG architecture a coordinator C is introduced to manage a handoff rule (R2). R2 defines which ball initiates the G module, that is: pick the ball that is closest to the hole.
(iii) TFG: Figure 3c breaks H into three tasks: Tee (T) where the task is: hit the ball as far as possible; the fairway (F), where the task is: from the fairway get as close to hole on the green as possible; and green (G) described above. T, F and G are combined into TFG through a coordinator C managing two handoff rules, R1 and R2. R1: pick the ball closest to the hole. R2 is as above.
(iv) TS: Figure 3d breaks H into two tasks: Tee (T), as above; and the short game (S), where the task is: from the Fairway, sink the ball in as few strokes as possible. T and S are combined into TS through the R1 handoff rule.
Even in this relatively simple problem, the act of decomposing creates multiple subproblems with different primary objectives (e.g., hit far versus traverse with fewest strokes). These different problem statements have the potential to attract and enable solvers with different skill sets.
3.3. Solver types
In defining alternative solver types, the goal was to reflect the novel sources of expertise identified in the open and distributed innovation literature. The open innovation literature suggests value from external contributions through three main mechanisms: (a) independent draws over a solution distribution whereby the value comes from our ability to select right-tailed solutions after the fact (Taylor Reference Thompson1995; Terwiesch & Xu Reference Topcu and Mesmer2008); independent draws over a talent distribution whereby the value comes from identifying talented solvers who have not had the opportunity to reveal their capabilities through normal labour markets (Fullerton et al. Reference Galbraith2002; Afuah & Tucci Reference Afuah and Tucci2012; Franzoni & Sauermann Reference Fricke and Schulz2014; Budescu & Chen Reference Buede and Miller2015; Szajnfarber et al. Reference Szajnfarber and Weigel2020); or (b) distant expert searches whereby the process of search identifies external disciplines that share similar underlying skills (Collins & Evans Reference Collopy and Hollingsworth2002; Szajnfarber & Vrolijk Reference Taylor2018). In the latter case, the solvers are experts in their own right, but they come from another discipline and therefore are unlikely to be experts in all aspects of the domain problem and may not be able to map all of their skills without help (Szajnfarber et al. Reference Szajnfarber and Weigel2020.
Here, we define three solver archetypes to cover the above mechanisms and also the traditional discipline-expert baseline. In the context of golf, these are Professional golfers (the baseline), Amateur golfers (who represent the random solution draws) and Specialist long-drivers (which combines the second and third category where the search is for out-of-discipline, or out-of-domain talent). These types have meaning in the context of golf, but also reflect the broader context of expertise in problem solving and innovation. Professionals are assumed to be good and reliable at all aspects of solving. Amateurs, exhibit both a lower average capability and much higher variability in their performance on any given stroke. Specialists represent experts from another domain that shares one common function. As such, they behave like amateurs in general but are excellent at the one overlapping task, on which they are specialists. In this case, we only introduce driving specialists, taking inspiration from the professional long driving association.
In the model, the different capabilities of these player types are represented as a function of their relative performance on each of the three facets of playing golf described above: driving, approach and putting. Each shot is simulated as a random variable, drawing from a distribution that reflects the function of that stroke in the game of golf. For example, driving draws from a normal distribution, putting strokes are represented with a coin flip between a good putt and a ‘flubbed’ putt. Good putts draw from a normal distribution, while flubbed putts draw from a uniform distribution to better represent the situation where a poor read of the green can result in a regression from the hole. Each of the distributions is parameterized differently to match the specific solver type. Therefore, while professionals and amateurs both use the same putting function, the former are much more likely to have a good putt, than the latter. Note that not all the differences between solver types persist across the different functions. This creates the opportunity for certain subproblems that do not rely on all the same golf functions to be more amenable to one type of solver than others.
3.4. Solver assignment
One of the core advantages of decomposition is that it enables tasks to be conducted independently (Eppinger et al. Reference Eppinger, Whitney, Smith and Gebala1994; Eppinger Reference Eppinger and Browning1997). Even when a sequential dependency is preserved (as is the case here) decomposition makes it possible to assign tasks to different solvers, which enables task specialisation (Tushman & Nadler Reference Valencia-Romero and Grogan1978; Nonaka Reference Pahl and Beitz1994). To explore the impact of assignment, our model enables every combination of solver assignments to be simulated for each decomposition. Figure 4 shows how task assignment works for the two module LG decomposition with the three types of solvers defined in Figure 2b.

Figure 4. Alternative assignment of solvers to tasks of an LG architecture. The boxes represent the tasks (L and G shown) where the colours (Blue, Red and Black) represent solver types.
While it is possible that all three solver types could engage through multiple different mechanisms (e.g., long-term employment, contracts, prize competitions) (Safarkhani, Bilionis & Panchal Reference Schilling2020), we focus on the most common mode for each of the three solver archetypes. Specifically, in the model:
(i) Professionals follow an employment contract, wherein a single pro is assigned the work and they are paid a wage (
 $ {w}_P $) for the work they do (i.e., for each stroke,
$ {w}_P $) for the work they do (i.e., for each stroke,  $ {S}_P $, they take), so
$ {S}_P $, they take), so  $ {c}_{WP} $=
$ {c}_{WP} $= $ {w}_P\times {S}_P $.
$ {w}_P\times {S}_P $.(ii) Amateurs are paid as if they are participating in a simple winner-takes-all Crowdsourcing Contest, which allows for an intuitive analogy with amateur golf tournaments. We assume that the seeker organisation poses a problem or a Task such as T, F, G, L or S, along with a prize purse
 $ (p) $. This attracts the amateur solvers who generate solutions to compete for the purse. Then, the seeker makes an ex-post selection based on the quality distribution of the solver solutions. Therefore, the only incurred cost of amateur tournaments is so from the firm’s perspective it is
$ (p) $. This attracts the amateur solvers who generate solutions to compete for the purse. Then, the seeker makes an ex-post selection based on the quality distribution of the solver solutions. Therefore, the only incurred cost of amateur tournaments is so from the firm’s perspective it is  $ {c}_{WA} $=
$ {c}_{WA} $=  $ p $. In the baseline model, we define a crowdsourcing tournament to include 100 participants, which is a moderate size tournament.
$ p $. In the baseline model, we define a crowdsourcing tournament to include 100 participants, which is a moderate size tournament.(iii) Specialists are represented as technical contractors. Here, we specify a bidding phase wherein n competing contractors demonstrate their capability and a work phase where a single contractor is selected to execute the task. The cost to the firm is, therefore,
 $ {c}_{WS}=b\times \left(m-1\right)+{w}_S\times {S}_S $. In the baseline model, the number of bidders (
$ {c}_{WS}=b\times \left(m-1\right)+{w}_S\times {S}_S $. In the baseline model, the number of bidders ( $ m $) is always three, and we assume the bidding cost (
$ m $) is always three, and we assume the bidding cost ( $ b $) to be one-tenth of the specialist wage (
$ b $) to be one-tenth of the specialist wage ( $ {w}_S $). To reflect differences in wages, Professionals are paid 10 cost units per stroke, amateurs are paid 1 and specialists are paid 12.
$ {w}_S $). To reflect differences in wages, Professionals are paid 10 cost units per stroke, amateurs are paid 1 and specialists are paid 12.
3.5. Model execution and accounting
To generate the data for our analysis, we ran a Monte Carlo simulation, with 1000 iterations.Footnote 1 A single run of the model simulates nine holes of golf played in each task structure (H, LG, TFG and TS) with all combinations of assignment (Pro, Am and Spec). Since assignment happens at the task level, that constitutes the baseline (H_Pro) and 47 alternative scenarios.
For each run, we recorded three measures of interest: performance, cost and expert reliance. We track these attributes separately since in many practical settings one might expect the seeking organisation to have different relative preferences among them. For example, if expert bandwidth is extremely scarce, an organisation might be willing to compromise on the cost to free up time (e.g., by hiring external specialists).
Performance
In typical problem-solving contexts, system performance considers one or both the performance of the artefact and schedule performance. For example, in the race for COVID-19 vaccine development, a key measure of merit was speed to FDA approval (subject to the threshold performance of adequate safety and effectiveness). In the context of golf, performance (![]() $ P $) is simply measured as the fewest strokes to achieve the threshold of completing the course. Schedule is rarely considered, though fewer strokes are highly correlated to quicker play. Thus, in the analysis, we adopt the single-dimensional measure of strokes to complete nine holes, where lower is better, and we compute it following Eq. (1):
$ P $) is simply measured as the fewest strokes to achieve the threshold of completing the course. Schedule is rarely considered, though fewer strokes are highly correlated to quicker play. Thus, in the analysis, we adopt the single-dimensional measure of strokes to complete nine holes, where lower is better, and we compute it following Eq. (1):
In Eq. (1), ![]() $ s $ is the number of strokes,
$ s $ is the number of strokes, ![]() $ j $ is tasks and
$ j $ is tasks and ![]() $ i $ is holes.
$ i $ is holes.
Cost
Product development processes incur costs (![]() $ C\Big) $ in three main activities, architecting, execution and integration (Eppinger & Ulrich Reference Ethiraj and Levinthal2015). Architecting activities typically involve planning the breakdown of tasks and associated requirements allocation. Execution is when the development work is done by assigned work groups. Integration is when the outputs of execution tasks are recombined. In our formulation of golf – where different player types can be assigned to subtasks with a hole – costs are incurred in the same generic categories. Therefore, we calculate costs following Eq. (2):
$ C\Big) $ in three main activities, architecting, execution and integration (Eppinger & Ulrich Reference Ethiraj and Levinthal2015). Architecting activities typically involve planning the breakdown of tasks and associated requirements allocation. Execution is when the development work is done by assigned work groups. Integration is when the outputs of execution tasks are recombined. In our formulation of golf – where different player types can be assigned to subtasks with a hole – costs are incurred in the same generic categories. Therefore, we calculate costs following Eq. (2):
Execution costs are a function of the solver assignment and the associated cost function. Architecting costs are assumed to be constant for modularized architectures and negligible for the undecomposed problem. Assuming that this work is done by knowledgeable experts, as is typical in the industry, we represent it in our model with ![]() $ {c}_{\mathrm{architecting}}={w}_P $. Integration in the context of golf involves coordinating the defined hand-off rules between modules. Since our rule requires the coordinators to know the number of strokes ‘taken’ by each ball, we assume one low-skilled ball tracker per participant.
$ {c}_{\mathrm{architecting}}={w}_P $. Integration in the context of golf involves coordinating the defined hand-off rules between modules. Since our rule requires the coordinators to know the number of strokes ‘taken’ by each ball, we assume one low-skilled ball tracker per participant. ![]() $ {c}_{\mathrm{integration}}=\mathrm{n}\times {w}_C $, where
$ {c}_{\mathrm{integration}}=\mathrm{n}\times {w}_C $, where ![]() $ n $ is the number of participants (e.g., 100 for an amateur tournament) and
$ n $ is the number of participants (e.g., 100 for an amateur tournament) and![]() $ {w}_C $ is the wage for each coordinator.
$ {w}_C $ is the wage for each coordinator.
Expert reliance
Experts are a scarce resource in most fields. Thus, while experts are often better at most of the specialised tasks in their field, if the goal is to speed up innovation, for example in the Space Race, the Manhattan project or the race to a COVID-19 vaccine, tracking expert reliance (![]() $ R $) can be a key measure of merit as well. If some tasks can be removed from the expert’s plate, it gives them more time to focus on the tasks on which they have the most comparative advantage. Therefore, we also tracked expert reliance following Eq. (3):
$ R $) can be a key measure of merit as well. If some tasks can be removed from the expert’s plate, it gives them more time to focus on the tasks on which they have the most comparative advantage. Therefore, we also tracked expert reliance following Eq. (3):
It is important to note that lower expert reliance does not necessarily indicate a good outcome. Among the three outcome measures, some level of performance must always be maintained. Cost and expert reliance are measures of merit too, but they are more to provide important balances in the tradespace. For example, depending on the context, freeing up 50% of the expert time for a 1% penalty in performance might be a preferable trade-off, since those experts (employees) could presumably put that freed up time to other valuable uses. These trade-offs will be explored in the model analysis below.
3.6. Verification, validation and calibration of baseline scenario
In an abstract simulation model, attempting to match model outputs to empirical data is of limited value. Instead, our verification efforts focused on ensuring that (a) the accounting was executed correctly through unit testing subfunctions (Zeigler, Muzy & Kofman Reference Zeigler, Muzy and Kofman2018) and (b) the decomposition and solver assignment processes are self-consistent. For item (b), Figure 5a confirms that the process of reformulating the model to satisfy the alternative decompositions was done correctly. Specifically, it shows the results for a single solver (Pro, Am or Spec) playing each of the alternative decompositions (H, TS, LG and TFG), where performance is measured as strokes to complete the nine holes (lower is better). We expect to see the following: (a) since decomposition hurts performance when the opportunity for strategic overview is removed – in this case, Pros lose the ability to plan their approach by aiming for the ‘sweet spot’ – in the Pro facet, H and LG should show better performance than TS and TFG. (b) Since decomposition improves performance by enabling specialisation, parallel work or multiple selections at the subproblem level, none of which are present when single players of a fixed archetype are simulated, all other variants should be constant within the same solver type. These results verify that the model is working as intended.

Figure 5. Consistency of solver efficacy for different decompositions (a) and comparison of amateur tournaments of increasing size (shown in blue confidence intervals) to the performance of a professional benchmark (shown in horizontal black line) (b). We multiplied confidence intervals with five for ease of readability.
In terms of model validation, the critical question is whether the simulation adequately represents the research question we wish to explore. We addressed this both practically and theoretically. Practically, Section 3.1 justified golf as a representative interdependent system design problem. The relationship between attributes of the problem structure of golf and other more typical system design problems are further elaborated in Appendix A, through comparison to the design of an autonomous robotic manipulator. We argue that golf provides a useful basis for analytical generalizability (Eisenhardt Reference Eletreby, Zhuang, Carley, Yağan and Poor1989; Yin Reference Yin2003) in terms of the focal impact on decomposition and solver capability. However, we recognise that the golf context is limited in terms of its representation of aspects like infusion costs. Moreover, while the specific golf formulation enables variation in both quality and approach to solving, in the end, most golf attempts result in game completion (albeit with very poor performance) where not all innovation attempts result in a functional product. This may lead to an overestimate of the potential for crowd contributions in the simulation results.
Theoretically, what is most important is that our baseline model replicates an ‘expert-only’ innovation problem at the system level – one where, no matter how large the crowd, experts still provide dominant solutions to H – so that our results cannot be attributed to the stochastic nature of generating results from a normal distribution. This is important because a potential criticism of relying on normal distributions is that it unrealistically advantages tournaments of amateurs, because (a) the formulation incorrectly assumes that amateur solutions will be correct and (b) it is over-optimistic about how good the best crowd-derived solutions will be.
With respect to concern (a), the model does not assume the correctness of all amateur solutions. In practice, to deal with a wide range of solutions types and qualities, a strong burden is placed on challenge evaluators to weed out inappropriate solutions (Gustetic et al. Reference Haskins, Forsberg, Michael Krueger and Hamelin2015; Acar Reference Acar2019). This feature is represented in the model through the choice of selection rules introduced in Section 3.1. The premise of a crowdsourcing tournament is that the seeker only needs one good solution (Taylor Reference Thompson1995) and is indifferent to whether many more inappropriate solutions are provided, as long as the types can be distinguished. In many of our model runs, some amateurs overshot substantially and ended up in a worse ball position at ![]() $ {s}_{n+1} $than they had been for
$ {s}_{n+1} $than they had been for ![]() $ {s}_n $. These runs do not show up in the final results because they were rarely the best of the 100 entries. In fact, a ‘mercy rule’ was introduced after 15 putts to handle cases where amateur runs were not making progress.
$ {s}_n $. These runs do not show up in the final results because they were rarely the best of the 100 entries. In fact, a ‘mercy rule’ was introduced after 15 putts to handle cases where amateur runs were not making progress.
With respect to criticism (b), the concern about right-tail sampling exaggerating the performance of crowd solutions is fair. To address this concern, the base distributions for each solver type were calibrated to be sufficiently different from each other that even with an inordinately large crowd, experts dominate in the H architecture. Further, since we are not aiming to predict absolute performance, and instead of comparing performance changes due to alternative decompositions, with the H baseline established, any improvements observed in LG, TFG or TS are due to the architecture not the sampling.
To demonstrate this condition, Figure 5b plots amateur performance on the H architecture in blue confidence intervals, as a function of tournament size. The horizontal black ruler line shows the average performance of a single Pro playing the undecomposed problem H. While increases in tournament size improve amateur performance, these improvements asymptotically approach a max crowd performance that is far worse than the Pro performance. Even with a tournament of 10,000 Ams (much larger than the number of solutions typically received through a tournament mechanism), the Pro is dominant, satisfying the condition of an ‘expert-only’ problem at the system levels. This means that any performance improvements (compared to the H_Pro baseline) presented in the results section can be attributable to the decomposition-assignment manipulations, and not the random results of the model due to increased tournament sizes.
4. Model analysis
This section summarises the results from our computer experiment. In all, 48 alternative decomposition-assignment pairs were simulated and evaluated in terms of their performance, cost and expert reliance defined formally in Section 3.4. In all cases for Pro assignments, a single Pro is retained through an employment mechanism for each relevant module; for Specs, assignment is made through a bidding process that picks the best of three attempts for each module; and for Ams, assignment initiates a crowdsourcing tournament, wherein the best of 100 attempts is selected after the fact. This section is organised around responses to each of our first two research questions. The third research question is addressed in Section 5, generalising beyond golf.
4.1. The ‘best’ architecture changes depending on who solves
We start the discussion of results with our first research question: how does the choice of solver archetype affect which architecture form is preferred? Figure 6 visualises the performance distribution by solver archetype (Pro, Am or Spec) playing each of the alternative decompositions (H, TS, LG and TFG). This means each of the modules would be assigned to the same solver type, but module solving would still proceed separately, with tournaments for amateurs and bidding for specialists. For instance, for the three-module decomposition TFG, Pro assignment represents TFG_ProProPro. In Figure 6, the y-axis shows relative architecture performance, plotted against the performance of that solver on the undecomposed problem H – the black line. For example, in the Pro facet, the reference line is for H_Pro, while in the Am facet, the reference line is for H_Am. The categorical x-axis is divided by solver type and then architecture. Each point is the mean result for that architecture-assignment pair, with error bars showing confidence intervals on the estimate.

Figure 6. Performance of alternative decompositions by solver type.
The overarching result is that the best architecture – the lowest value on a given facet – changes depending on which type of solver is assigned: for Pros, it’s H or LG (since LG crosses the ruler line), for amateurs, it’s TS and for specialists, it’s TFG (but not by much). To understand these results, consider the following intuitions: For Pros, representing the typical internal expert case, architectures that enable strategic oversight (H and LG) are better than ones that remove it. This is shown in Figure 6, with the confidence interval of LG_Pro_Pro spanning the reference H_Pro line, and both of DS_Pro_Pro and TFG_Pro_Pro_Pro above the line (and therefore worse).
In contrast, in the amateur assignment, the performance across architectures varies significantly. TS is by far the best because it balances two competing mechanisms: fine-grained selection and hand-off inefficiency. First, with amateurs who compete in relatively large tournaments, high performance comes from extremely valued solutions. While an individual amateur might have a lucky stroke once every 20 attempts, the odds of getting ‘lucky’ twice in a row are much smaller. Therefore, tournaments are more likely to produce excellent results when the selection is fine-grained. Decomposing the T module is a prime example of this because it reduces the scope to a single attempt at a long drive. This is in stark contrast to any of the modules that include multiple subfunctions. For example, an excellent L result would require approximately three excellent strokes in a row, which has a much lower likelihood than a single one. Second, the reason why the logic of ‘reduce the scope’ of each module does not extend from TS to TFG is because of inefficiencies inherent in interface design (or in this case handoff between modules). Because we chose to implement a low-cost practical interface rule (pick the closest ball), for larger tournaments, as in the case of amateurs, there is a performance penalty for decoupling F and G. A similar difference is also seen comparing H to LG in Figure 6.
For specialists, the relative performance is different again, but the magnitude of the differences is not as large. As with amateurs, specialists benefit from finer-grained selection and are also penalised by inefficiencies in the handoff. However, because bidding only involves three solvers (versus 100) neither effect is very large. For specialists, the main impact driving the preference for TFG (or nearly as good, TS) is the ability to isolate T, the particular function that specialists are best at. This is an instance where decomposition isolates a single function from the rest, making it possible to identity solvers that are systematically excellent at that one function.
4.2. The ‘best’ hybrid assignments dominate expert-only approaches
Our second research question asks whether decomposition makes it possible to improve expert performance through the use of nondomain and or nonexpert solvers. Recall we calibrated the model to ensure that experts dominate at the full problem level. Figure 7 summarises the results. In the plot, each dot represents a single scenario (e.g., LG_ProPro). The x-axis captures performance, measured as mean strokes to play nine holes. The y-axis records the cost to architect, execute and integrate the process for nine holes. The size of each dot is calibrated to the expert reliance, with the largest dots corresponding to Pro-only scenarios. The colours of the dots map to the architecture. The red dot at the centre of the crosshairs is the reference H_Pro scenario; therefore, everything to the left of the vertical line corresponds to improved performance, and everything below the horizontal ruler line is a lower cost.
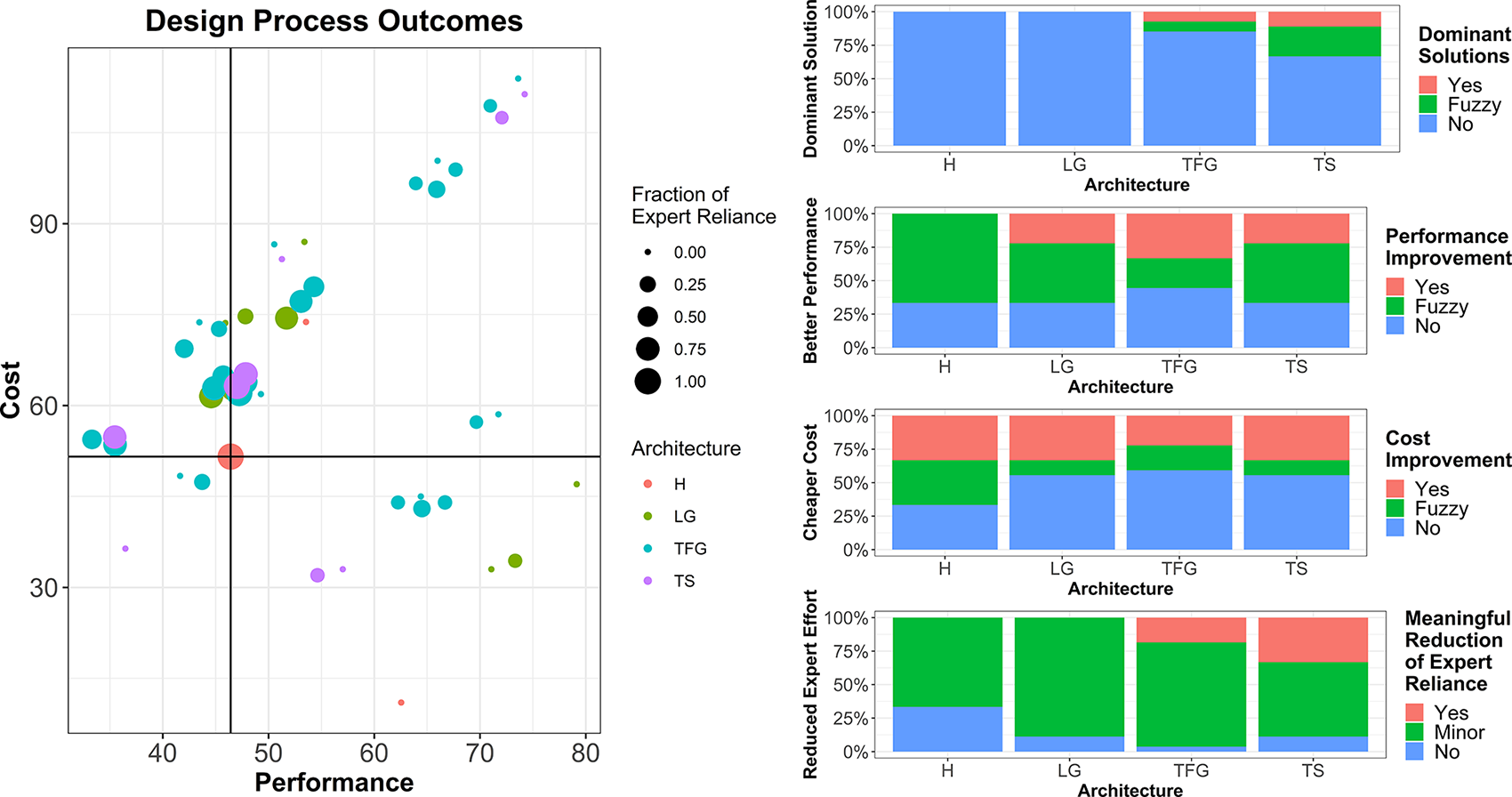
Figure 7. Design process outcomes with respect to the professional benchmark (a), comparison of innovation outcomes of performance, cost, meaningful reduction of expert reliance and dominance on all attributes, by problem decomposition (b).
Our results indicate that external solvers can indeed improve solving outcomes even on problems that are ‘expert-only’ at the system level. The bottom left quadrant of Figure 7a shows the three scenarios that fared better on all measures. They are TFG_SpecAmAm, TFG_SpecAmPro, and TS_SpecAm. If the standard of dominant solutions is relaxed to include solutions that are better on at least one measure and close on the two others, the list expands to seven, accounting for 15% of all scenarios. Here close means within 20% of the relevant measure. Importantly, not all decomposition-assignment pairs improve results – 51% are worse on all measures – and not all decompositions are equally good for all innovation goals (cost, performance and expert reliance).
Figure 7b shows how each of the decompositions fairs against each of the measures. The top facet breaks down the dominant and fuzzy dominant solutions by architecture. All of the best architectures come from TFG and TS, with the highest fraction coming from TS. This should not be a surprise given that it both isolates the specialist modules and minimises handoff costs.
When the focus is on performance, we see 27% of all scenarios yielding performance improvements. Each of the LP, TFG and TS architectures contributed to this result, and TS and LG were equally likely to generate high-performing alternatives with 22% compared to 33% of TFG. These were on average 15% more expensive than the benchmark. The solution offering the best performance overall, TS_SpecAm, offers 29% improvement over the benchmark.
A total of 27% of all scenarios reduced costs, though many of these did so with a high-performance penalty; on average 29% lower than the benchmark. A total of 33% of H, LG and TS architectures led to cost reductions compared to 22% of TFG decompositions.
As discussed earlier, relieving expert time is not an end in and of itself, so it is only helpful if it frees up significant time without overly compromising performance. Therefore, we focused on alternatives that freed up at least 25% of expert time (a reliance of <75%) and remain within 20% of expert performance and cost. Only 17% of all cases met this standard with no contribution from the LG decompositions. The TS decomposition has the highest fraction with 33% and the TFG has 19%. While few in numbers, these observations reduce the reliance on experts while offering an average of 12% performance improvement over the benchmark and cost 6% less.
4.3. Sensitivity analysis
The previous sections established our model-derived results responding to each of our first two research questions: (a) we demonstrated that the preferred architecture changes depending on which type of solver is assigned and (b) we identified multiple dominant and fuzzy dominant hybrid architecture-assignment pairs. However, since the results are all derived from an abstract simulation, which embodies multiple modelling assumptions, it is important to understand how robust the main findings are to these assumptions. Importantly, we are not looking at specific output values, rather the resultant insights related to the stated research questions.
Table 1 shows the results of the sensitivity analysis. The overall takeaway is that our two main results are robust to the alternative assumptions explored. With respect to RQ1, the architecture preference is consistent in all cases. With respect to RQ2, there is variation in how many architecture-solver pairs show up as dominant or fuzzy dominant, but for the most part, the best pairs are always best. As will be discussed below, there is one extreme condition where there are no dominant pairs, only fuzzy dominant ones.
Table 1. Results of the sensitivity analysis

To elaborate, we explored three categories of modelling assumptions, with multiple levels in each. First, since most of the high-performing results include a specialist driver, we wanted to ensure that we had not just made the Specs too capable. What is important is their relative capability compared to Pro driving, and each distribution is loosely based on the capability of Long Driving tournaments for specialists and PGA tournaments for Pros. We implemented two alternative specialists drives, one that halves the distance advantage compared to Pros, and a second that increases it by the same margin. This change had no impact on the main insights for either research question, but as expected better specialists yielded more dominant options, while worse specialists yielded fewer.
Second, since the use of Gaussian distributions (or any unbounded distribution) in a simulation can generate overly optimistic performance results, we replaced the amateur approach functions with matched triangular distributions. We chose the Am approach to focus on because it is the situation that sees the most advantage from a high upside and amateurs are the only solver type that employs a large enough tournament to take advantage of that upside. The results show no impact on RQ1 or RQ2, for an equivalent triangular distribution, supporting the argument that normal distributions are an acceptable simplification given the implementation. When instead of selecting a comparable triangular distribution, a highly skewed one, with a much lower mode (of 80 instead of 200) and a negative lower bound (−20) is used instead. In that extreme case, no dominant nonexpert solutions exist. This is likely an unrealistic representation, but it does confirm that the tournament set up does not by itself guarantee a winning crowd solution.
Third, in formulating the model we had the least basis for parameterizing the cost values associated with decomposing since it is not something that is commonly done in golf. Therefore, in this sensitivity analysis, we explored the widest variation of values for cost-contributors. Decomposition introduces ‘costs’ through the need to coordinate among modules and also the optimality (or lack thereof) in the handoff. In the baseline model, the costs are associated with the amount of work (a fixed unit per activity) and an implicit performance penalty due to our choice of a practical handoff rule. Here, we varied the scale of that cost ±100% and also reran the model with optimal handoff rules (and associated coordination costs). The results of changing the coordination costs show no impact on either main conclusion, but as expected, lower costs bring more options in the dominant category. Somewhat counterintuitively the optimal handoff produces less dominant solutions. This is because there is a significant cost penalty to implementing it, as discussed above.
5. Towards heuristics for including ‘solver-awareness’ in the architecting of complex engineering systems
Having offered an existence proof that the best architecture depends on who is solving (Section 4.1), shown that even for so-called expert-only problems, ‘good’ decompositions can enable hybrid architectures to perform better than professionals working alone (Section 4.2), and explored the robustness of these findings to alternative model choices (Section 4.3), we contend that there is value to developing architecting heuristics that are ‘solver-aware’. Specifically, we propose a SASA process that adds a new modelling step to a typical architecture screening process – the new step includes characterising a variety of archetypal solver capabilities with respect to different subfunctions – and screening architectures for performance under different solving configurations, as part of a broader analysis of alternatives.
Section 3 serves as a template for how that can be done. However, since these types of solver models may not exist for many problems, and if not, be difficult to create, it would be helpful to also develop heuristics guiding which architectures will advantage different types of solvers more generally. While a complete analysis of the decomposition-assignment performance space is outside the scope of this article, in this section, we take a first step towards the goal of useful heuristics, focusing on elaborating two potential guidelines that emerged from our analysis. Specifically, we elaborate two heuristics that could be applied beyond the context of golf: (a) Isolate subproblems that match an external specialty and (b) Leverage the benefits of tournaments to explore more of a highly uncertain (but low skill threshold) problem spaces. In the sections below, we begin by explaining how the strategy operates in the golf model and then relate it to more general design practice through analogy to the design of a robotic manipulator.
5.1. Isolate subproblems that match external expertise
Our results suggest that a powerful strategy for leveraging external solvers involves isolating a subproblem that can be matched to known external expertise. This requires both that a subproblem be isolate-able and that a source of external nondomain expertise be identifiable. Note that this heuristic goes beyond the idea that distant expertise exists (Collins & Evans Reference Collopy and Hollingsworth2002; Jeppesen & Lakhani Reference Kim, Michelena, Papalambros and Jiang2010; Afuah & Tucci Reference Afuah and Tucci2012) and can be leveraged, and focuses on how it can be leveraged through decomposition.
In the context of golf, only the T and L subproblems can be fully isolated, since all of F, S and G remain sequentially dependent on other problems. Of T and L, T only relies on golf function: driving, unlike L, which relies on both driving and approach. Since the specialist architype models’ external solvers who are excellent drivers (but quite poor at approach strokes) we would expect that any assignment that matches specialists to only the T module would dominate. Of course, anytime a specialist drives will yield a performance improvement, but since specialists are also more expensive source of labour we would expect other assignments to negatively impact the cost in some cases.
To understand the impact of just this heuristic, in Figure 8, we illustrate the scale of improvement when Pros are replaced with Specs for the T module, for otherwise equivalent architectures. The blue bars show the percentage improvement in performance, for example, XSA captures the difference between SpecSpecAm and ProSpecAm assignments to the TFG architecture. The red bars show the equivalent delta for cost. In reading this figure it is important to realise that the change in performance or cost does not necessarily correspond to the highest quality assignments. Recall that SA, SAP and SAA were dominant and both show up with very high-performance improvements due to the S-T assignment, but with cost penalties compared to their PX equivalent, but not the Pro-H baseline.

Figure 8. Performance impact of replacing solver drive assignment with a specialist on different decomposition solver assignment combinations.
Figure 8 shows that a Spec-T assignment yields performance benefits across the board. Although they vary depending on the rest of the decomposition, they are all positive and significant.Footnote 2 When all else is held constant, on average, replacing a Pro with a Spec improves performance by ~29% and the range of improvement is between ~20 and ~33%. In terms of cost, although Specs are more expensive to utilise than the Pros, on average, the Isolate heuristic results in an 8% reduction of cost, with results varying from ~14% more expensive to 24% less expensive. The variability in these results can be explained in terms of the sequential dependency of golf, and specifically the impact of a long drive on the remaining solving. Although Specs always yield a closer ball position than a Pro that assignment always comes with a higher cost, but does not always result in fewer remaining strokes. For example, if an amateur tournament can reliably reach the green in one stroke from anywhere less than 250 yards out, a ball position of 50 is functionally equivalent to 250. In contrast Specs (and their corresponding three bids) are less reliable in their approach, so benefit much more from the better fairway position, which is why the XSX/XS assignments see the most improvement in cost. This highlights some of the subtleties in the assignment problem that will enable a SASA approach more broadly.
Having demonstrated how the isolate heuristic can yield useful predictions for which golf assignments will perform well, we now apply it to seek guidance in the context of an autonomous robotic manipulator. First, we consider alternative subproblems, ranging from gripping mechanisms to modular joints, to surface features. For the most part, robotic arms are tightly coupled, but recent industry evolution has demonstrated that multiple subcomponents, particularly relating to gripping can be relatively isolated. Second, we consider potential sources of expertise outside of core robotics. We recognise that robotics is already highly interdisciplinary with many roboticists cross-training in, for example, mechatronics and software. Thus, while it is natural to imagine ‘distant experts’ coming from any of the mechanical, electrical or software domains, that is not the kind of distance this heuristic points to. Roboticists often cross-train in these disciplines because important insights arise at the intersection of these disciplines, for example, novel mechanism designs often leverage motion planning capabilities.
Here, we are looking for aspects of the robotics problems, that, when decomposed, look like the kind of problem that distant experts normally solve. One area that seems ripe for exploration is material science, and specifically experts in surface friction. The isolate heuristic could be applied by decoupling the surface friction aspect of the gripping function so that material scientists can bring their deep insight to a problem that is familiar to them, and only to that problem. In addition, their solution to the surface friction problem can be applied to any robotic manipulator tasked to grab and hold a surface. This reasoning path suggests that even a simple heuristic, like isolating and assigning to a distant expert, can inform a solver-aware architecting process in more realistic settings, like robotics.
5.2. Leverage the tournament mechanism to relieve expert reliance and broaden search
Our results suggest an opportunity to identify subproblems that embody high solution uncertainty and relatively few barriers to entry. In such cases, the tournament mechanism is particularly adept at accomplishing two important goals of reducing expert reliance (and freeing their time for the most productive pursuits) and also more fully exploring the solution space. The latter aspect has been discussed extensively in the open innovation literature (cf., Terwiesch & Xu Reference Topcu and Mesmer2008; Afuah & Tucci Reference Afuah and Tucci2012) but here we connect that idea to the need to adequately decompose most problems first. Moreover, the combination of expert reliance and tournaments is new here, building on insights about relative knowledge thresholds (Szajnfarber & Vrolijk Reference Taylor2018).
In the context of golf, all of F, G and S (as a combination of both) exhibit high uncertainty in the problem space. However, F also has a high skill threshold with Pros dominant in the associated approach subfunctions. Only G adequately isolates a subproblem that is both highly uncertain and accessible (within the capability of amateurs to perform well). However, since the difficulty of putting depends strongly on the putting distance, which is a function of the preceding module, we expect more variability in the performance of an amateur-green assignment, even within fixed architecture. Specifically, when the ball is relatively close to the pin, amateurs dominate, but when the initial lie is on the edge of the Green, Professionals are much better because of the need to string together multiple strokes. Since that is not a factor that can be controlled through decomposition and assignment there is a risk in this assignment. There is potential to mitigate this risk by controlling the preceding shot, for example, by assigning it to a professional. This is something that can be explored in future work. Nonetheless, we expect them to match or exceed Pro performance on average with the added benefit of significant reductions in expert reliance, as well as broader search (less apparent in our simple model).
To understand the impact of this heuristic in the context of our golf simulation, Figure 9 shows how the amateur-green assignment performs compared to their equivalent Pro-Green architectures. There is a small (~2–5%) but significant and consistent benefit in performance.Footnote 3 The impact on cost (not shown) is very small (~2.5% on average) and not significant.Footnote 4 There is a large reduction of expert reliance that varies by architecture, ranging from 15 to 26%, with an average of ~19%. Therefore Am-G assignment can provide significant benefit in cases where there is a need to relieve expert effort, with limited impact on cost and performance. As with the Spec-T assignment, there are more nuanced considerations that can be made to guide which Am-G assignments would be more broadly preferred.

Figure 9. Performance impact of replacing a solver green assignment with an amateur on different decomposition solver assignment combinations.
Having shown that the tournament heuristic can yield useful predictions about which assignments will reduce expert reliance without compromising on performance, we illustrate how it can be applied to provide guidance in the context of an autonomous robotic manipulator. As before we consider reasonably decouplable subproblems, but now, instead of thinking about external sources of expertise, we focus on the extent of expected solution variation and the skill threshold to contribute. In the robotics context, one example of a comparable solution space is the design of a gripper. While some of the most complex grippers mimic a human hand, the function can also be satisfied by a relatively simple passive clamp, implementable by a novice. Moreover, the gripping function is highly context-specific, and it is sometimes hard to know in advance which approach will be best, making it valuable to examine multiple options, generated by people coming from different perspectives. Thus, it is preferable to explore the entire design space. Given this context, the tendency of the expert designers to gravitate towards particular solutions could be balanced with an option to work with a ‘crowd’, to obtain a diverse set of independent attempts (Hong & Page Reference Hung and Chou2004; Fu et al. Reference Fullerton, Linster, McKee and Slate2013). This is reflected in practice, where grippers are often sold separately from manipulators because there are both values to application customization and there are many more unconventional approaches being explored (e.g., gecko grippers and electromagnets). We would therefore suggest focusing tournament competition on a gripping element, as NASA did in their GrabCad competition which yielded many variable results (Chaudhari et al. Reference Chen, Allen and Mistree2018).
6. Conclusion
The system architecting process is fundamental to ensuring value delivery over the lifetime of a system. It is the process that defines how needed functions map to elements of form. Despite significant prior work clarifying how alternative architectures perform in different operating contexts (e.g., subject to changing requirements or external disruptions) we identified a gap in prior consideration of how different solvers might (a) affect preferences among architectures and (b) serve as an underutilised source of innovative potential even in the context of ‘expert-only’ problems. To that end, we developed an abstract simulation to demonstrate the potential importance of ‘solver-awareness’ and then illustrated how these ideas can be implemented in this solving process.
Specifically, we outlined preliminary guidance for how to think about architecting in this new way – identifying opportunities to pair decomposition with favourable (or available) labour. SASA offers the potential to leverage the capabilities of a much wider range of contributors than typical systems architecting approaches afford. In most complex system domains, the community has long settled on a particular dominant architecture, which is now taken for granted. This results in established relationships with suppliers and traditional contractors. While efficient, this set up is not particularly agile. By forcing a direct consideration of alternative decompositions and (nontraditional) solver capabilities upfront we expect to find many new ways to approach traditional problems.
Our specific findings also contribute to the open innovation literature. Despite increasing interest and recognition of the potential power of open innovation methods in general, there is still a widely held expectation that many complex systems problems are the sole domain of experts (Lakhani et al. Reference Larson, Kirkpatrick, Sellers, Thomas and Verma2013; Szajnfarber et al. Reference Szajnfarber and Weigel2020). To that end, a core contribution of this article is to demonstrate that if problems are decomposed in a way that takes advantage of external resources – either specialised expertise or the sheer availability of human power – there is an underutilised opportunity to apply open tools to solve expert-only problems. A critical corollary to our findings is that not all decompositions and certainly not all decomposition-assignment pairs are equally effective for achieving desired outcomes. It is therefore important to understand the relationship between decomposition and solver assignment.
As an initial proof-of-concept, we demonstrated the potential of a SASA approach in the context of an abstract simulation of a distinctly nontechnology problem (golf). So, a relevant question is how this applies to other contexts. To illustrate why we believe the main concepts hold more generally, we outline how the ideas apply to a more representative robotics design problem. Overall, we found the findings to be highly relevant. Nonetheless, we also recognise the limitations of its generalizability and identified opportunities to extend this framework significantly. Future work should explore more complex architectures and a more diverse capacity for solvers. This will also provide a richer tradespace of potential decomposition and solver assignment combinations. We expect the mechanisms identified here to hold, but we also expect to identify new ones, for example, in terms of the sequence of solver assignments in a particular architecture. This analysis could be supported by ongoing innovation in mechanism design and learning methods (Panchal et al. Reference Papalambros and Wilde2019; Safarkhani et al. Reference Schilling2020).
As the world becomes more connected, the competitiveness of firms and the capacity for engineering organisations to innovate will rely on an ability to leverage talent where it resides (Chesbrough Reference Chubin2003; Enkel, Gassmann & Chesbrough Reference Eppinger2009; Hung & Chou Reference Jeppesen and Lakhani2013; Gambardella et al. Reference Garud and Kumaraswamy2016; Parker & Van Alstyne Reference Parnas2018). At the same time, many organisations are facing a workforce shortage as demand increases and many experienced engineers are retiring (Logsdon Reference Maier2006; Voelpel & Dous Reference Vrolijk and Szajnfarber2006). This makes it increasingly important to focus expertise where it is specifically needed and effectively leverage the capacity that exists outside one’s organisation. The proposed style of thinking asks: how do we decompose the problem to free up more expert time for the things only they can do, while leveraging external sources of effort for the parts they can do nearly as well? When you think about systems architecting with distributed, nontraditional, solvers in mind the ‘best’ architecture might look quite different than the dominant design. Moving forward, there is a need to theorise about how to formulate problems with an awareness of external capacity, be it crowds, specialists or even algorithms (Kittur et al. Reference Kleijnen, Pilz, Rasch, Melas and Moder2019). If we can do that well, there is an opportunity for huge efficiency gains across the economy.
Financial support
This study was supported by the NSF under Grant CMMI-1535539.
Appendix A. Is golf representative of complex systems design?
Although we made the case in Section 3.1 for why an abstract simulation inspired by the game of golf can provide insight into complex system architecture, we revisit that assertion here, analysing whether the features of how the simulation was formulated reflect key attributes of a more representative engineering system, and consequently whether specific results are likely to generalise (Szajnfarber et al. Reference Szajnfarber, Zhang, Mukherjee, Crusan, Hennig and Vrolijk2020). We chose a robotic arm as the reference system for this comparison because it a reasonably complex interdisciplinary system and also one that we have explored extensively in the context of decomposing for open innovation through a recent open innovation field experiment (Szajnfarber et al. Reference Szajnfarber, Zhang, Mukherjee, Crusan, Hennig and Vrolijk2020).
In the golf model, there are four key features of system representation: problem architecture(s), solver types and associated capabilities, innovative solving and coordination costs. Below we assess the extent to which each is representative of a robotic arm, and more generally, a complex system.
A.1. Problem architecture
In golf, the problem was conceptualised in terms of three subfunctions driving, approach and putting. Alternative architectures were considered in terms of alternative groupings of these functions. In golf, order matters, so three subfunctions translate to four alternative grouping structures. In the context of the robotic arm design problem, the core functions involved, positioning, gripping and orienting (a payload). Similar to golf, order matters since gripping of a perching handrail cannot precede posting the gripper near said handrail. In the same way, these three subfunctions translate to four alternative architectures. Of course, these subfunctions can be further decomposed into more elementary functions or could have been architected in a different way. Regardless, the overall representation of interdependent functions of golf closely mirrors the interdependence of a real-world system.
A.2. Solver types and their associated capabilities
In golf, we represented three canonical solver types: professional players, amateurs and driving specialists. We could have represented many other variants including gradients of amateurs, or specialists in different aspects of the game (e.g., putting). However, we chose these three to explore different mappings of solver capabilities to aspects of the game. Specifically, professionals were represented as similarly capable at all aspects of the game. Amateurs were less capable and also more variable in each aspect. Specialists were highly capable at one golf function – driving – and otherwise behaved like amateurs. In the context of the robotic arm, there is similarly a rich distribution of capabilities in different disciplines that are relevant to robotics, spanning across software, electrical engineering, mechanical engineering and design, among others. Nonetheless, the abstraction of a representative professional roboticist who is capable of each aspect of robotics is relevant. For example, most engineers with the title roboticist have some cross-training in multiple underlying disciplines and over the course of their careers have gained additional cross-capability. In the same way, there are many capable experts who specialise in specific functions relevant to robotics, but not others. For example, many of the exotic grippers being envisioned today rely on deep knowledge of material science, not typically possessed by traditional roboticists. Therefore, the representation of a specialist excellent at one function but otherwise a veritable amateur, tracks. Similarly, many engineering undergraduates take at least one course in industrial robotics, making it reasonable to expect that a large population of amateur roboticists exists. Thus, while it is certainly reasonable to consider much more nuanced representations of contrasting solver expertise, the simplified archetypes represented in the model are relevant to the real-world system.
A.3. Innovative solving
In golf ‘solving’ the whole involves moving a golf ball from the Tee to the hole, with the goal of minimising the number of strokes required to do so. Golf players develop their own techniques for, for example, driving long and straight, reading the green or how to set up their approach. In the simulation, this variation was represented by a generative model that drew each next stroke from normal or uniform distributions, parameterized to match the capabilities of the solver type on each stroke type. As a result, different solving types tended to take different paths through the hole, with specialists often reaching the green on the first stroke, and generally requiring more tries to sink, whereas professionals generally took two strokes to the green, but often sunk the ball in at most two putts. In the context of a robotic arm, there are many more design parameters in play. Here, solving means designing a robotic arm that meets all the requirements and minimises mass (per the challenge rules; Szajnfarber et al. Reference Szajnfarber, Zhang, Mukherjee, Crusan, Hennig and Vrolijk2020). Looking across the system, engineers can find many approaches to doing so. For example, a talented mechanism designer might find ways to traverse the workspace with fewer degrees of freedom. Reducing the actuators and the associated wiring and electronics required to drive them, saves mass. Other engineers might explore low power solutions or the potential for wireless power beaming to save wiring and the structure needed to support local electronics. While the full space of this solution and solving variety is not represented in a stochastic golf model, the same principles that enable different best solving paths as a function of solver capabilities and task structure constraints are highly relevant to understanding solving in the real-world context too.
A.4. Integration costs
In golf, we replaced two kinds of dependencies with coordination rules and applied a cost to implement each. First, to coordinate the handoff of ball placement of the best solution to module n to define the initial conditions of module n + 1, we defined selection rules. These involved balancing a desire for a closer ball placement and minimal total strokes. Therefore, for some of the handoffs evaluation required an assessment of each of the attempts individually, while others simply required a review of the aggregate result. We costed this coordination burden as a function of the number of evaluations (see Section 3.4). This reflects a difference in evaluation burden experienced by prime contractors who let subawards to different types of entities. They tend to include less oversight and shared testing for established suppliers (when the type of product is held constant). Second, to decouple shared variables, as in the choice of how far to drive to set up an easier approach, we transformed the objective into a decoupled one: drive as far down the fairway as possible. While this mode of decoupling does not introduce any additional integration costs, it does introduce a performance penalty (illustrated clearly in Figure 5a).
Both types of decoupling choices and their associated integration costs and performance penalties are relevant to robotic design as well. For example, if a gripping module and manipulator arm must share a power source, it is easier to write an allocated requirement that cleanly divides the budget. However, that tends to force both systems into a particular operating regime, which can prematurely close off parts of the design space. New gripping mechanisms that rely on electromagnetism would not be considered even though their functionality might make it worth developing a low-powered manipulator or choosing to sequence operations to share power over time versus across modules. Rather than a clean division of the power budget, a more sophisticated design rule might focus globally and create a coordination function that only picks pairs of solutions that meet the overall requirement. Therefore, while the specific coordination costs will be unique to each setting, golf is a sufficiently rich example to bring up the key tradeoffs that are relevant to practical settings.
Overall, while golf is simpler in several ways, it embodies all of the key structural features of the robotic arm problem as an example of other complex systems. We, therefore, believe that the insights gained here are analytically generalizable to other settings, relevant to the design community.













