The propagation saw test: slope scale validation and alternative test methods

Abstract

The propagation saw test (PST) is a recently developed snowpack test that enables assessment of the fracture propagation propensity of selected persistent weak-layer and slab combinations, which are known to release dry-slab avalanches. In this paper, we assess the slope- scale accuracy of the standard PST method at validated sites of observed weak-layer fracture initiation, with or without propagation. We also report on experiments with alternative test methods and varying saw thicknesses. Results show the standard PST method is comparably accurate to other common snowpack tests in predictive skill when predicting propagation propensity on the slope scale. Although a slight but significant dependence on saw thickness was found, it did not affect the interpretation in our validation study. Alternative methods such as scaling the test column length with weak-layer depth or leaving the upslope end of the column attached to the surrounding snowpack did not improve slope- scale accuracy and these tests were often more difficult to interpret.

1. Introduction

Dry slab avalanche release involves the consecutive processes of fracture initiation and fracture propagation within a weak layer or interface buried beneath a snow slab. Although fracture initiation is required prior to fracture propagation, the propensity for self-sustained propagation is thought to be independent of the ease of initiation (e.g. Schweizer and others, 2003). For this reason, alternative snowpack test methods have been sought that test the fracture propagation potential of slab and weak-layer combinations independently of, or in addition to, the ease with which fractures can be initiated. Such efforts include the recently developed extended column test (e.g. Simenhois and Birkeland, 2006, 2009), and recording the observed ‘release type’ or ‘fracture character’ in the rutsch- block test and compression test, respectively (Greene and others, 2009, p.42-47). In most common snowpack tests, including those just mentioned, weak-layer fractures are initiated via dynamic surface loading, and the ease with which and way in which fractures initiate are interpreted as an indication of overall slope stability. These test methods may miss favourable propagation propensity in deeply buried weak layers where initiation is difficult, or conversely may indicate instabilities in numerous near-surface weak layers that do not possess the characteristics required for extensive propagation and avalanche release.

In light of these limitations, the propagation saw test (PST) was recently developed to specifically test the propagation propensity of weak layers buried within the snowpack. Since Gauthier (2007), Gauthier and Jamieson (2007a) and Sigrist and Schweizer (2007) described the test method, research has aimed to validate its accuracy and efficiency in the field (e.g. Gauthier, 2007; Birkeland and Simenhois, 2008; Gauthier and Jamieson, 2007b; Gauthier and others, 2008; Ross, 2010). More recently, some research has questioned the influence of alternative equipment and methods on the test (e.g. McClung, 2009, 2011).

In this study, we further evaluate the PST by presenting the combined dataset from four winter seasons of validating the standard PST for the first time in its entirety (Section 4). Previously, Gauthier and Jamieson (2007b) presented early validation data that included results in test columns that exceeded the now-standard length, followed by updated validation results at sites of confirmed propagation only (Gauthier and others, 2008).

Also in this study, the effect of variable saw thickness is examined through numerous side-by-side comparisons (Section 5). Furthermore, two alternative test methods are evaluated: leaving the upslope column end attached to the surrounding snowpack when performing the test (Section 6), and shortening the column length below 1 m to match the depth of weak layers shallower than 1 m (Section 7).

2. Standard PST Procedure and Recording Convention

The standard PST (Fig. 1) involves a column 30 cm cross-slope by >100 cm upslope isolated to below the weak layer of interest on two sides by shovel and, typically, on the other two sides by cutting with a cord. The upslope length is the greater of 100 cm or equivalent to the vertical depth of the weak layer being tested (Greene and others, 2009, p. 53-55). Fracture initiation is simulated by steadily drawing the blunt edge of a snow saw, ~2mm thick, upslope within the weak layer until the onset of propagation, or until the entire column has been cut.

Fig. 1. PST in process. (a) The upslope and left side of the column has been cut from the snowpack by a cord or saw. (b) The operator begins drawing the blunt edge of a snow saw upwards through the weak layer, (c) stopping and marking the spot where the fracture propagates suddenly forward from the leading edge of the saw.

Three different results can be observed in the PST: the fracture propagates suddenly from the end of the saw-cut to the end of the column (denoted end); or the fracture propagates but stops within the column either at a slope- normal fracture through the overlying slab (denoted sf) or at a point of self-arrest along the layer (denoted arr). To interpret the PST results, propagation within the weak layer is considered likely on adjacent slopes (assumed to have similar snowpack conditions) only when fracture propagation initiates with a saw cut of <50% of the column length and continues uninterrupted to the end (Gauthier, 2007, p. 156).

When performing multiple PSTs in the same pit, sufficient snow (15 cm minimum) must be cut away laterally between each test column to ensure an undisturbed and intact slab and weak layer for the subsequent test. If multiple weak layers exist in a single test column they can be tested successively starting with the lowest and working up, ensuring that the overlying weak layers and associated slabs are not disturbed by the deeper tests.

PST results are recorded as: x/y (arr/sf/end) down z on yymmdd(or alternative layer ID) on a ψ slope, where x is the cut length, y is the column length, (arr/sf/end) indicates noting one of the three observable results, z is the weak- layer depth (measured vertically) in the snowpack, yymmdd refers to the date of burial (weak-layer ID) for the weak layer being tested, and ψ is the slope angle (°).

3. Fieldwork

Fieldwork for this study was conducted in the Columbia Mountains, British Columbia, Canada: primarily in the Selkirk Mountains within Glacier National Park and in the Monashee and Cariboo Mountains around Blue River. Some additional data were collected in the Purcell Mountains near Kicking Horse Mountain Resort in Golden, British Columbia, and in the Rocky Mountains at Chatter Creek Cat Skiing north of Donald, British Columbia.

Tests over the 4 years were performed mostly at or below tree line on all aspects and slopes ranging in inclination from 4° to 49° (mean = median = 29°, std dev. = 8.2°). (Note that Heierli and others (2011) use a model and field data to argue that triggering a fracture is relatively insensitive to slope angle.) Weak layers tested ranged in depth from 12 to 115 cm (mean = 52 cm, median = 48 cm, std dev. = 25 cm) below the surface and included primarily surface-hoar layers and layers of faceted crystals above or within melt-freeze crusts. Some shallow storm interfaces and wind slabs were also tested. At all test sites, standard weather and snow-pit observations were recorded including temperature, grain size and type, hand resistance and density in accordance with the guidelines for avalanche safety programs in North America (CAA, 2007;Greene and others, 2009).

4. Validating the Standard PST

4.1. Methods and data

To assess the predictive accuracy of the PST, pairs of tests were performed (1) beside observed instances of weak-layer fracture propagation in the field or (2) at instances of confirmed fracture initiation without propagation. Instances of observed propagation included natural (spontaneous) avalanches, or human-triggered avalanches or whumpfs (audible weak-layer collapse and propagation without avalanche release, typically on slopes inclined at <25°). Alternatively, where a researcher attempted but failed to release a small avalanche by ski-cutting (skiing across the top of a slope and down-weighting), a cross section through the resulting ski tracks was exposed to observe and confirm whether any weak layer(s) in the snowpack had been fractured during the event but had not propagated (after Gauthier, 2007, p. 91) (Fig. 2). Test sites were then carefully selected on undisturbed representative slopes nearby. Typically, two tests were performed side by side, although at some sites the number of valid tests ranged from one to four. At sites of confirmed propagation, slope angles ranged from 4° to 48° (mean = 30°, median = 29.5°, std dev. = 8.8) and weak-layer depths ranged from 12 to 114.5cm (mean = 56 cm, median = 52 cm, std dev. = 23.5 cm). At sites of confirmed initiation without propagation, slope angles ranged from 10° to 49° (mean = median = 31°, std dev. = 7.4) and weak-layer depths ranged from 15 to 65 cm (mean = median = 30 cm, std dev. =12.2 cm).

Fig. 2. Exposed tracks after skiing initiated but did not propagate a fracture. (a) Although the weak layer has been crushed beneath the skis, it remains intact both up- and downslope of the tracks, indicating fracture arrest as opposed to a propensity for propagation. This is analogous to the arr condition in a PST in which the fracture arrests but the arrest point may be indistinct. (b) Fracture arrest at a slab fracture, which is analogous to the sf condition in a PST.

In cases where no weak layer was disturbed during a ski cut (usually due to a depth beyond ski penetration), the site could not be used as part of this validation study since it gave no indication as to whether propagation would or would not have occurred if the weak layer had fractured. This method effectively isolated the propagation variable by ensuring fracture initiation had occurred at all event sites and explicitly allowed the validation of both PST results that suggested high propagation propensity (propL) and PST results that predicted low or no propagation propensity (propUL).

Test locations near validation events were judged to be representative of the event site in terms of snowpack properties and layering and to ensure the weak layer at the test location had not fractured or been disturbed during the event. Occasionally, PST and other measurements were not made because no undisturbed site could be found with confidence. Test locations were at least 1.5 m back from any crown or flank fracture and often further back (CAA, 2007, p. 25). This method of validating a snowpack test at sites that did not fracture or release an avalanche, and those that did, has been used in other studies (e.g. Föhn, 1987a,b; Van Herwijnen and Jamieson, 2007;Simenhois and Birkeland, 2009). In some cases where avalanches were reported by a third party, researchers were only able to access the site 1-3 days after the event. Any changes in snowpack or weather conditions since the avalanche were carefully noted.

In four seasons of the validation study (winters 2007-10), researchers performed 247 standard PSTs on 120 validation site-layers at 108 unique sites where an avalanche or whumpf occurred, or where weak-layer fracture initiated but did not propagate. Site-layers refer to the few instances of multiple weak layers that fractured during the same avalanche or ski cut event and could all be tested at the same site, often within the same test columns. Table 1 shows the cumulative validation dataset.

Table 1. Cumulative dataset for the validation study of the standard PST. In 4 years, 247 PSTs were validated, of which 172 were near 83 avalanches or whumpfs and 75 were next to 37 site-layers of confirmed initiation without propagation

4.2. Validation results

4.2.1 Predictive accuracy and comparison with other standard tests

Results of the validation study are presented in a contingency table (Table 2). PST results that indicated likely propagation (propL) next to an observed avalanche or whumpf were classified as correct predictions, for example, whereas false- propUL PST results were those that predicted unlikely propagation next to an avalanche or whumpf.

Table 2. PST validation results presented in a contingency table. Where propagation is both predicted and observed, the test result is classified as a correct-propL prediction. n = 247

Table 3 shows the seasonal breakdown of prediction-type frequencies, exemplifying the general seasonal consistency despite different snowpack conditions and different operators. Only the 2008 season showed a substantially larger number of false-propUL predictions overall, as discussed in Section 4.2.2. The prediction-type frequencies for the combined dataset are also shown. Correct predictions were made in 76% of tests in the validated dataset.

Table 3. Seasonal prediction-type frequencies indicating the overall accuracy of the PST in predicting propagation, along with the frequencies of incorrect predictions

The True Skill Statistic (TSS) method (e.g. Doswell and others, 1990) is frequently employed in the comparison of snowpack tests (e.g. Gauthier, 2007, p. 128;Gauthier and Jamieson, 2008b;Moner and others, 2008;Simenhois and Birkeland, 2009) as it compares the relative success of the data to a random forecast with a TSS of 0. A hypothetical perfect forecast has a TSS of 1 (no false predictions). For the current validated PST dataset the TSS is 0.61.

Table 4 compares the TSS of the PST with those of other commonly used standard snowpack tests. It is important to note that the values reported for the other test methods measure the success of predicting fracture initiation, or initiation and propagation together (‘stability), since they are typically compared to slopes that were skier-tested and either avalanched or not (i.e. any untriggered slope was classified as stable). In the case of PST, where initiation was confirmed in all validation cases, only the success of predicting propagation was inferred. TSS values for other tests were calculated from a sample-weighted average of multiple datasets summarized by Schweizer and Jamieson (2010). As evident in Table 4, the predictive strength of the PST based on TSS scores is comparable to and often exceeds alternative snowpack tests, albeit testing the propagation process of avalanche release only.

Table 4. Comparison of the TSS for the current PST dataset with other commonly used snowpack tests and assessment methods

4.2.2 False predictions of the PST

The goal for the PST, as with any predictive field test, is to maximize the TSS with the highest number of correct predictions possible in a balanced dataset where events with and without propagation are roughly equally represented. In four seasons, the frequency of false-propL predictions was consistently low and only 2% of the total. The higher- consequence and less desirable false-propUL prediction type comprised 22% of the dataset. Sources of these false- propUL predictions have previously been related to shallow, soft slabs (Gauthier and Jamieson, 2007a), which can also be attributed to four such results in 2009, all with soft slabs overlying layers <25 cm deep. In other seasons, with similar numbers of false-propUL results, no shallow-slab (<30cm) avalanche sites were tested.

Another primary source of false-stable test results was avalanche sites visited 1-3 days after the event (‘old’ avalanches). Between 2007 and 2010, 54 PSTs were performed at 24 sites of old avalanches, producing 25 correct-propL results (46%) and 29 false-propUL results. This includes 10 such sites in 2008 and 12 in 2010, which contributed to the lower accuracy observed in those seasons (Table 3).

The small fraction of false-propL results had no distinguishing characteristics other than that they were all in surface hoar layers and were accompanied by at least one correct prediction.

4.2.3 Adjusted validation without old avalanches

Omitting results from old avalanches, the validation analysis produced a contingency table (Table 5) and improved the overall accuracy of the PST from 76% to 84% and the TSS from 0.61 to 0.71.

Table 5. Adjusted validation results of the PST that omit tests performed at avalanche sites visited 1-3 days after the event. Both correctly and incorrectly predicted sites were removed, reducing the number of correct-propL results by 25 and false-propUL results by 29. n = 193

4.3. Discussion

The predictive skill of the PST has been shown to compare favourably to other commonly used snowpack tests. In fact, Gauthier and Jamieson (2008b) also showed that when only sites with confirmed fracture initiation were used, the compression test, rutschblock test and Threshold Sum (which do not require the weak layer to be preselected) all had substantially lower TSS scores (0.24, 0.35 and -0.12, respectively). Although the PST is relatively successful at predicting the propagation part of the slab release process, we note that most other snowpack tests are assessed based on whether or not the slab released. (For more on the comparison between tests, Schweizer and Jamieson (2010) report the specificity and sensitivity.) Despite this success, a high frequency of false-propUL predictions was observed each year, particularly in 2008. Shallow, soft slabs continued to be a source of false-propUL results such as Gauthier (2007, p. 135) had observed, and day-old avalanche sites produced a substantial number of false-propUL results in 2008, 2009 and 2010. Although day-old avalanche sites have been successfully used to validate other snowpack tests such as the rutschblock (Jamieson and Johnston, 1993) and compression test (Van Herwijnen and Jamieson, 2007), Birkeland and Chabot (2006) also discussed the possibility of the snowpack subsequently strengthening after a nearby avalanche and producing false-stable results in stability tests. Perhaps in some cases where fracture initiation is still possible within the undisturbed weak layer, the energy balance required for sustained propagation may no longer exist days after the nearby avalanche occurred. In other words, the ‘strength’ of the weak layer tested in the compression test and rutschblock test may remain low at old avalanches, so the layers still react at adjacent sites, whereas the propagation propensity nearby may dissipate over time after an avalanche if the fracture toughness of the weak layer (or slab and weak layer) increases.

Many of the sites where false predictions, particularly false-propUL, were observed also had correct predictions on the same layer in the same snow pit. These results are congruent with observations of slope-scale spatial variability affecting test results (e.g. Campbell and Jamieson, 2007; Hendrikx and Birkeland, 2008; Schweizer and others, 2008), and suggest that doing more than one PST can improve interpretation and reduce incorrect predictions, especially if the more conservative (propagation-likely) result is taken. The same has been shown to apply to other snowpack tests (Birkeland and Chabot, 2006; Winkler and Schweizer, 2009; Schweizer and Jamieson, 2010). It is also possible that the different test results on the same validation site-layer could be attributed to operator error, or the mechanics of the test itself, as discussed below. Overall, however, the PST showed consistent reproducibility of results between multiple tests in the same snow pit. In fact, Ross (2010, p.89) showed that only 15% of all validation sites produced disagreement between adjacent PSTs.

The results presented throughout Section 4.2 bring to light two important potential causes for incorrect predictions in the test: (1) spatial variability in the snowpack, and (2) physical differences between the mechanical process of the test and true propagation in a natural, three-dimensional (3-D), undisturbed snowpack. Spatial variability of snowpack layers and test results is beyond the scope of this paper; however, numerous studies have shown significant spatial variability in test results within a few metres of each other (e.g. Campbell and Jamieson, 2007; Hendrikx and others, 2009). Thus, the test may not always be inaccurately assessing propagation potential when a false prediction results, since it may be accurately sampling the spatial variability that exists both across the immediate test site and across the adjacent slope used to validate it. After all, a potential reason why the later-tested areas immediately surrounding an avalanche did not release with the avalanche is perhaps because those areas were stable and never had high propagation propensity. Spatial variation is one of the limitations to the validation method that we and other authors have used.

There is also the possibility that false predictions are the result of test geometry or mechanics inadequately replicating real propagation on natural, 3-D slopes;something which is addressed in part later in this study. For example, Heierli and others (2008) and Van Herwijnen and others (2008) chose to use longer columns to fully develop a propagating bending wave and demonstrate theoretical arguments. McClung (2009) proposed that test-column lengths be at least three to four times the slab thickness. He supported this with observations that critical cut lengths required for propagation are a significant fraction of slab thickness, so the column should be much longer and attached at the upslope end to observe a truly propagating fracture, free from the influence of boundary conditions. McClung (2011) more recently showed that the median critical cut length was a fraction of the standard 1 m column length (<0.65 m) in a similar dataset and thus argued that it was free from the influence of the upslope end condition (see Section 6). Gauthier (2007) observed similar variable relationships between critical cut length and slab thickness in some PSTs. However, the objective of the PST is not to measure the true critical length required for propagation in an undisturbed snowpack, but rather to test the general propensity for propagation to begin and the ability of the slab and weak layer to sustain propagation once it begins. In this sense, the standard PST method may not appropriately test natural initiation lengths or realistically replicate slab deformation required for self- propagating fractures (McClung, 2009, 2011), but allows users to target and identify most slab and weak-layer combinations in which a propagating fracture can easily begin and be sustained (Tables 2 and 3). The only consistent exception appears to be in shallow, soft slabs where perhaps the lateral support provided by the 3-D snowpack on a natural slope sustains the slab and weak-layer mechanical balance required for propagation, whereas in the test the soft slab breaks (sf results) more easily.

5. Assessing the Effect of Saw Thickness on PST Results

Many commercial snow saws are available and used by avalanche practitioners for which there is no standard length, thickness or serration pattern, etc. Length is dictated by the 30cm column width required for the PST, and serration pattern is not an influence since the dull edge of the saw is used for ‘cutting’. However, the thickness of the saw blade could influence test results. The thickness of the gap left in place of the weak layer while performing the PST arguably influences slab bending and potential weak-layer collapse height in the test column (McClung, 2011). It is conceivable that a thicker saw would increase both these variables and potentially lead to shorter cut lengths and increased propagation. Thus, practitioners using thin saws might observe a higher frequency of false-propUL results due to longer cut lengths or shorter propagation lengths. McClung (2011) also observed an increased frequency of slab fractures initiating at the surface and prior to slope- parallel fracture when thick saws were used, although he did not address the effect of saw thickness on cut length or propagation within the weak layer. In order to test the effect of saw thickness on PST results, pairs of tests using different saw thicknesses were compared for this study.

5.1. Methods and data

In the boreal winter of 2009/10, ‘thin-saw’ PSTs were performed using 1 mm thick saws as commonly used by avalanche fieldworkers, as opposed to the standard 2 mm thick saw used to validate the test as described above. Procedure and recorded results for the thin-saw test were otherwise identical to the standard PST. An objective field observation reported by researchers experimenting with the different saws was that it was occasionally difficult to tell if the thin saw deviated from the weak layer since the adjacent snow slabs provided little additional resistance compared to the weak layer. This was particularly true in weak layers less than a few millimetres thick. Any test in which the operator felt the saw might have deviated from within the weak layer was rejected.

Pairs of standard PSTs were performed for comparison besides alternating pairs of thin-saw PSTs at 39 sites in 2009-10, generating 140 comparable pairs (one-to-one). Of these, 27 comparisons were at 14 validation sites (seven avalanche/whumpf sites and seven sites with initiation without propagation) as described in Section 3.1.

5.2. Results and discussion

Using the Wilcoxon signed-rank tests for the 140 matched pairs of cut length proportions (as a percentage of column length) from tests with thin and thick saws, the difference (mean = 6, median = 2 percentage points) is significant (p = 2 × 10^-4), indicating that the cut length with the thin saw tended to be longer. The distributions of cut lengths for the two types of tests are shown in Figure 3, along with the distribution of differences in cut length.

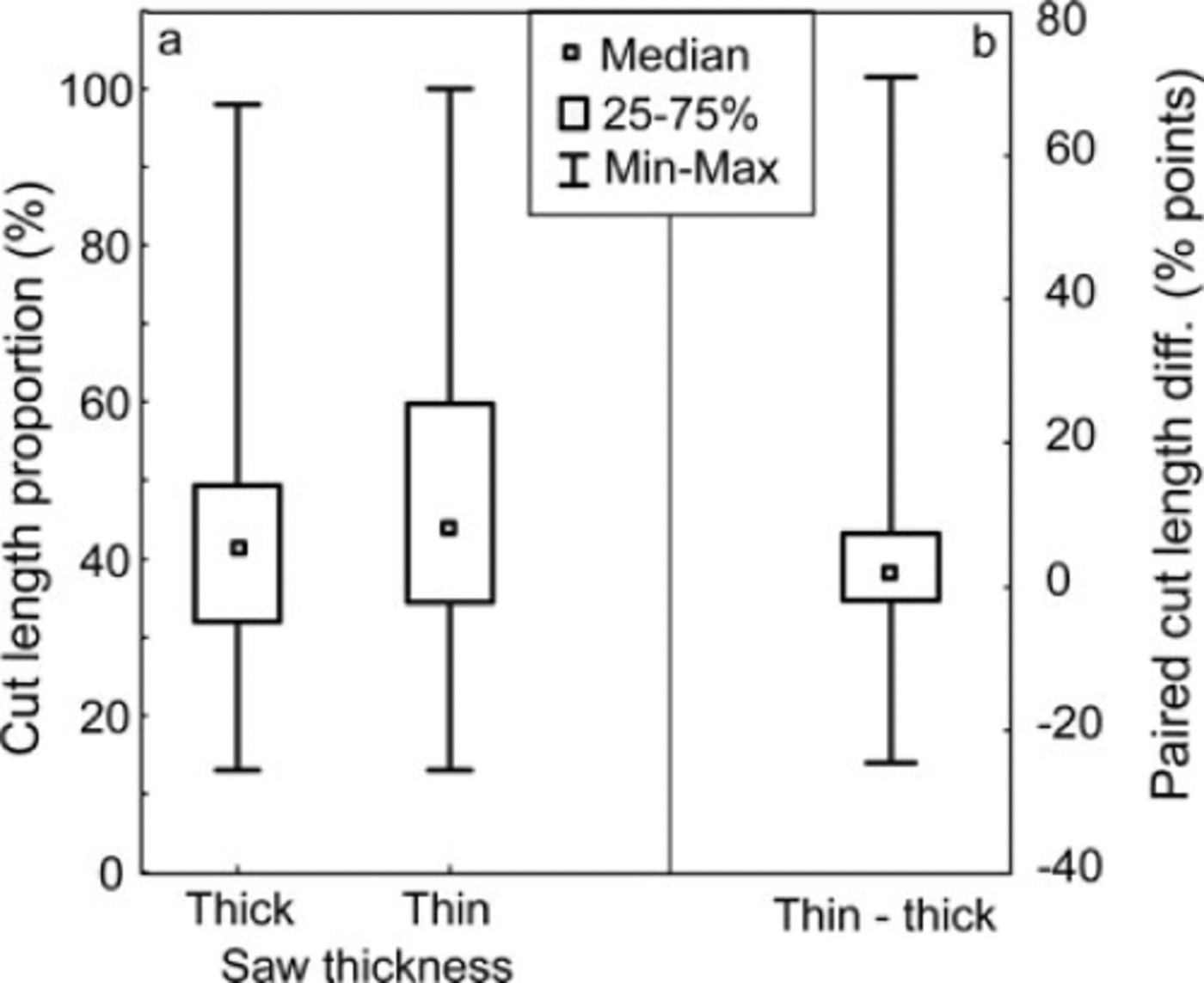
Fig. 3. (a) A box-and-whisker plot showing the distribution of cut length proportions for the standard thick-saw and thin-saw tests (n = 140 for both). The thin-saw tests show a great interquartile range and a mean cut length that is 6 percentage points longer than the standard thick-saw tests. (b) A plot of the difference in cut lengths between the tests with the thin and thick saws (thin – thick).

Compared predictions between the same set of thin-saw and standard PST pairs are presented in Table 6. In 126 comparisons (90%), both saw thicknesses generated the same result in terms of predicting propagation to be likely (propL) or unlikely (propUL). In 12 cases (9%), the thin-saw test predicted propUL while the standard PST predicted propL, which supports the hypothesis presented earlier. Many of these involved small increases in cut length within the thin-saw test (e.g. a 46%-cut with propagation result in the standard PST, compared to a 52%-cut with propagation result in the thin-saw PST). Figure 3 compares the distribution of results for the two saw thicknesses in a box-and-whisker plot. In only two cases (1%) did the standard thick-saw tests have a longer cut length than adjacent thin-saw tests.

Table 6. Predictions of the standard PST and adjacent thin-saw PST presented in a contingency table. The first standard PST was compared to the first thin-saw PST, the second to the second and so on. n = 140

On the 14 validated site-layers where thin-saw tests were performed, every standard thick-saw PST gave a correct prediction of propagation propensity, and only two thin-saw tests gave incorrect false-propUL predictions. Both were at the same site where a large whumpf was observed in a surface hoar layer buried 74 cm. At this site, thick-saw tests gave 25%- and 34%-cuts propagating to end, while thin-saw tests gave a 90%-cut to end and a 38%-cut that ended in arrest. Perhaps this is an example of increased slab bending generated by the thicker saw-cut favouring shorter cut lengths and/or increased propagation.

Although a slight but significant increase in cut length was observed with thin saws, it rarely affected the interpreted test outcome, generating only a 10% rate of disagreement between compared tests, which is comparable to other sources of uncertainty such as spatial variations. Therefore, tests with thinner saws tended to require slightly longer cut lengths, but this difference is small and did not substantially affect the interpretation at validated sites. Consequently, we do not adjust the interpretation of results for different saw thicknesses.

6. Assessing the Effect of Isolating the Upslope End of the Column

6.1. Methods and data

McClung (2009) proposed that for PST-like tests, the upslope end of the column should not be cut from the surrounding snowpack and the column should be substantially longer than the standard length of 1 m. However, with reference to a similar dataset, McClung (2011) noted that the 1 m column length should not affect the results since the maximum of the medians of cut length in the tests was <0.65 m. His arguments for not cutting the upslope end of the column derive from finite-element modeling that shows the maximum tensile force in the slab to be on the order of one slab depth’s length ahead of the progressing saw cut (personal communication from C. Borstad, 2011). This would suggest that once 35 cm of the weak layer has been cut beneath a 60 cm slab, for example, the tensile forces may be influenced by the column’s end condition. By leaving the upslope end attached and potentially extending the column length, it is argued that the critical cut length (independent of increasing column length as described by Gauthier, 2007, p. 81) can always be obtained and that a tensile fracture is allowed to develop through the slab that will interrupt fracture propagation if it is occurring. The critical cut length found in the standard PST represents approximately half the critical flaw/ deficit zone or fracture length required within the weak layer to initiate the propagation process in a two-dimensional (2D) model of the natural snowpack (McClung, 2011), although rate effects (McClung, 2009, 2011), 2-D test effects (Gauthier, 2007, p. 170) and potentially saw effects limit the accuracy of this relationship. Additionally, the cut end in the standard method may ‘attract’ a propagating crack since there is little resistance to rotational and tensile forces that develop in the slab ahead of the saw cut, particularly in conditions where the fracture process zone is a substantial fraction of the column length (McClung, 2009).

In 2010 we assessed the effect of isolating (or not) the upslope end of the column, but did not assess the effect of substantially longer columns. Forty alternative tests with the upslope column end attached to the surrounding snowpack (un-isolated columns) were performed next to 40 standard PSTs, all at 20 validated sites, to test the practicality of this change to the standard procedure, and to determine whether the same heuristic interpretation rule can be applied to predict propagation in the natural snowpack. The effect on critical cut length and on propagation length was also evaluated. A further ten matched pairs of isolated and unisolated columns, not from validation sites, were included in the analysis. Other than leaving the upslope end attached to the snowpack, the preparation procedure and test method were identical, including the standard method of determining column length.

6.2. Results

Critical cut lengths were compared with a Wilcoxon signed- rank test. Based on the difference in cut lengths between matched pairs, the distributions were not significantly different (p = 0.10). Box plots for the two distributions are shown in Figure 4, along with the distribution of differences (mean = 3, median = 2 percentage points).

Fig. 4. (a) Distribution of cut length proportions for isolated (cut) and un-isolated (uncut) columns (n = 50 for both). (b) Distribution of paired differences in cut lengths for isolated (cut) and un-isolated (uncut) columns (un-isolated – isolated).

Using the Wilcoxon signed-rank test for matched pairs, the propagation lengths for the same 50 matched pairs were compared. Based on the difference in propagation lengths between matched pairs (mean = -18cm, median = -9cm), the distributions were significantly different (p =10^-5). Box plots for the two distributions are shown in Figure 5, along with the distribution of differences in propagation lengths.

Fig. 5. (a) Distribution of propagation length for isolated and unisolated columns (n = 50 for both). (b) Distribution of paired differences in propagation lengths for isolated (cut) and un-isolated (uncut) columns (un-isolated – isolated).

At validated sites where both methods were performed, the standard PST gave correct predictions in 84% of tests. The other 16% were false-propUL results. The adjacent unisolated columns produced 58% correct predictions and 42% false-propUL predictions using the same interpretation rule (since an interpretation rule for un-isolated columns has not been proposed). Propagating fractures that continued beyond the end of the un-isolated column or ended with a slab fracture where the column met the upslope snowpack were considered indications of propagation-likely. At seven of the validation sites, the propagating fracture arrested or was interrupted by a slab fracture before the end of the unisolated columns next to standard PSTs that correctly predicted propagation- likely.

Table 7 shows that the test method had no effect on interpretation in 73% of comparisons. Since no false-propL standard PSTs existed in this dataset, for all 11 cases (28%) where the methods disagreed the un-isolated columns falsely predicted low or no propagation propensity next to correct standard PSTs. This can be attributed to the shorter propagation lengths in un-isolated columns as shown in Figure 5.

Table 7. Predictions of the standard PST next to PSTs with the upslope end of the column attached to the snowpack. The first standard PST was compared to the first alternative PST, the second to the second and so on. n = 40

6.3. Discussion

A variety of field observations while performing the test gave early insight into how the method performed as a predictive tool. Many results were similar to the standard PST method including propagating fractures arresting within the column or the slab fracturing before the column end. In many cases, cut lengths required to initiate propagation and propagation lengths themselves were consistent between test methods, while in some cases one or both differed. The distributions in Figures 4 and 5 show that both test methods gave comparable indications of the critical cut lengths required to initiate propagation, although un-isolated columns generally resulted in shorter propagation lengths.

Two new result types were observed when fracture propagation occurred and approached the column end. Either the slab vertically fractured at the point where the column met the attached snowpack, or the propagating fracture ‘disappeared’ into the undisturbed snowpack upslope of the column. The latter was considered to indicate propL provided that propagation started when <50% of the column had been cut. Slab fractures were not observed in every test as had been hypothesized, although longer-than- standard columns were not tested.

In terms of the free column end attracting a propagating fracture, two conditions can be considered. The first involves initiation of a propagating fracture and whether the free end has the potential to influence the critical cut length. This was shown not to be the case as critical cut length was not significantly different between the two methods. In fact, Ross (2010, p. 105) showed that standard PST results propagating to the free end had a higher frequency of cut lengths exceeding 80% than between 60% and 80%. This is likely due to the free upslope end of the column attracting the crack only once the saw is within 20% of the end. In other words, it could be expected that the entire column would be cut to the end when propagation propensity is low or nonexistent, which explains the lack of propagating fractures that started between 60%- and 80%-cut. However, numerous results did propagate a fracture to the end once 80100% of the column was cut, perhaps because the free end attracted the fracture.

The second condition involves a fracture that is propagating, and may be ‘drawn’ to the isolated end where it would otherwise arrest prior to the end if the column was attached. This condition was observed at seven validated sites as described in Section 6.2, although in all seven cases the standard PST gave the accurate prediction of propagation.

Although the un-isolated method arguably has research applications and may prove more successful in column lengths three to four times the slab thickness (e.g. McClung, 2009), it cannot be used to predict propagation with the same interpretation rule as the standard PST. In terms of practicality in the field, interpreting propagating fractures that disappear into the snowpack or are interrupted by a slab fracture where the column meets the snowpack adds complication to the current interpretation rules. In addition, since the PST often targets deep weak layers, long column lengths of three to four times the slab thickness become very time-consuming and hence less practical. The same applies to retaining the connection at the upslope column end, as it prevents cordcutting the back side of the column, requiring shoveling instead. The results here show that the upslope column-end condition does not significantly affect cut lengths, although it does affect propagation lengths, which can in turn affect the interpreted outcome.

7. Short-Scaled PSTS

In 2009, we experimented with PST columns that were scaled in length to match weak-layer depths shallower than 1 m (Fig. 6). Since numerous false-propUL results in standard PSTs occurred in shallow, soft slabs, and in longer-than- standard columns in 2007 (Gauthier and Jamieson, 2008a), it was considered that scaling the PST below 1 m in length to match layer depth could potentially reduce the frequency of false-propUL results.

Fig. 6. Standard and scaled PSTs were performed side by side in 2009 when weak layers were <1m deep.

When targeted weak layers were shallower than 1 m, pairs of scaled PSTs (of length equal to layer depth) were performed beside pairs of standard PSTs to compare their predictive accuracy at validation sites, and to test their practicality and consistency next to standard PSTs at nonvalidation sites. In total, 276 short-scaled PSTs were performed. Of these, 73 were recorded on 34 validation site-layers beside standard PSTs. The results are shown in Table 8. Although scaling the PST below 1 m was aimed at reducing false-propUL results in shallow, soft slabs in particular, a full range of weak-layer depths from 10 to 100cm were tested with scaled PSTs over the course of the winter. Thus, the full range of equivalent column lengths were also tested, in case results suggested a change to the standard test method.

Table 8. Validation results from 2009 for scaled PSTs with column length equivalent to weak-layer depth for layers shallower than 1 m

At two sites of confirmed propagation in 2009, each scaled PST (four tests) accurately predicted propagation where each standard PST failed, both in shallow layers <35 cm deep. Despite this small reduction in false-propUL results in a few shallow, soft-slab cases, scaling the PST below 1 m did not improve the predictive accuracy of the test overall. In fact it often became more challenging to perform, particularly in the shallow soft slabs where the test column was too fragile. In other words, the slab often tended to ‘move’ during operation or ‘pivot’ at the saw around midcut rather than propagate the fracture. In addition, a high percentage (18%) of scaled tests had near-50% cuts which are interpreted based on the 50% rule (Gauthier, 2007, p. 156), but with less practical confidence.

8. Conclusions

For four winters the PST has been shown to predict whether weak-layer fracture propagation is likely or unlikely within the natural snowpack in the majority of tests and under most conditions (TSS = 0.61, overall accuracy = 76%). Using a common measure of statistical skill, the PST was compared to numerous other standard snowpack tests and assessment methods and compared favourably. Although rarely overestimating propagation propensity, the PST produced more false predictions of low or no propagation propensity, particularly in thin, soft slabs and at avalanche sites tested in the days following the event. It was also shown to be consistent, producing conflicting test results at only 15% of sites. Understanding these limitations can improve site selection or lead to more cautious interpretation of results under such conditions. When day-old avalanche sites were removed from the analysis, the overall accuracy of the PST increased to 84% and the TSS increased to 0.71, which is arguably more realistic for avalanche forecasting.

Evaluation of the effect of alternative saw thicknesses on test results revealed that using a 1 mm thick saw instead of the standard 2 mm saw generated a small but significant increase in the cut lengths, although it rarely altered the interpreted outcome of the test. In fact, the same frequency of disagreement between alternative saw thicknesses was observed when side-by-side pairs of standard tests from the same dataset were compared (10%).

Theory had suggested that retaining a connection between the upslope end of the column and the surrounding snowpack could improve the PST’s replication of propagation and arrest in natural avalanche release. However, the same critical cut length was generally obtained in both methods, indicating that the free column end was not influencing the initiation of fracture propagation. Slab fractures did not occur in each test either, although 3-4 m columns were not tested. Furthermore, increased propagation lengths in standard PSTs show that the free end may be attracting a fracture that is already propagating, although this condition proves to be a more accurate predictor of propagation propensity in the field than the un-isolated method, at least under the standard interpretation rules. In addition to being less accurate, the un-isolated columns proved objectively more difficult to interpret. The same was concluded for the alternative method of scaling column lengths below 1 m to match weak-layer depths shallower than 1 m. Thus, our results support the standard PST method presented by Greene and others (2009, p. 53-55) for practical use in the field when evaluating the propensity for fracture propagation in user-selected, non-shallow (>30cm), persistent weak layers.