Swirl boundary layer and flow separation at the inlet of a rotating pipe

Abstract

When a fluid enters a rotating circular pipe, an angular momentum or swirl boundary layer appears at the wall and interacts with the axial momentum boundary layer. In the centre of the pipe, the fluid is free of swirl and is accelerated due to boundary layer growth. Below a critical flow number, defined as the ratio of average axial velocity to circumferential velocity of the pipe, there is flow separation, known in the turbomachinery context as part load recirculation. To describe this phenomenon analytically, we extended boundary layer theory to a swirl boundary layer interacting with the axial momentum boundary layer. The solution of the resulting generalized von Kármán momentum equation takes into account the influence of the Reynolds number and flow number. We show the impact of swirl on the axial boundary layer and conduct experiments in which we vary Reynolds number, flow number and surface roughness to validate the analytical results. The extended boundary layer theory predicts a critical flow number which is analytically derived and validated. Below this critical flow number, separation is expected.

1 Introduction

Turbomachines often operate at part load due to the claim of flexibility and not at the design point where the efficiency reaches its maximum. At part load for small flow numbers $\unicode[STIX]{x1D711}:=\tilde{\overline{U}}/\tilde{R}\tilde{\unicode[STIX]{x1D6FA}}$ , with the average axial velocity $\tilde{\overline{U}}$ and circumferential velocity of the pipe $\tilde{R}\tilde{\unicode[STIX]{x1D6FA}}$ , losses causing flow phenomena such as cavitation, rotating stall, part load recirculation and so on appear. These flow phenomena reduce the efficiency of a turbomachine compared to the efficiency at the design point.

This paper investigates the evolution of the swirl, the interdependence of centrifugal force and axial moment to predict part load recirculation, e.g. flow separation at the critical flow number $\unicode[STIX]{x1D711}_{c}$ , by a generic model. The generic model is a rotating pipe with radius $\tilde{R}$ as appears for example in a shrouded turbomachine or the secondary air flow in gas turbines. In the following, all symbols marked with a tilde ‘ ${\sim}$ ’ are dimensional quantities, whereas all symbols without a tilde are dimensionless. Thus, this paper non-dimensionalizes length with the pipe radius $\tilde{R}$ , velocities with the pipe circumferential velocity $\tilde{R}\tilde{\unicode[STIX]{x1D6FA}}$ , the typical velocity in rotating machinery, and stresses with the dynamic pressure $\tilde{\unicode[STIX]{x1D70C}}\tilde{R}^{2}\tilde{\unicode[STIX]{x1D6FA}}^{2}$ . Hence, the Reynolds number is $Re:=2\tilde{R}^{2}\tilde{\unicode[STIX]{x1D6FA}}/\tilde{\unicode[STIX]{x1D708}}$ with the kinematic viscosity $\tilde{\unicode[STIX]{x1D708}}$ . The axial Reynolds number is $Re_{ax}:=2\tilde{R}\tilde{\overline{U}}/\tilde{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D711}Re$ .

Figure 1. Inlet of a rotating pipe.

The incoming axial flow is constant over the cross-section $U(0)=\overline{U}=\unicode[STIX]{x1D711}$ and swirl-free; see figure 1. Following the idea of Ludwig Prandtl, a thin region close to a boundary, where viscous effects are significant, evolves, the boundary layer having a thickness of $\unicode[STIX]{x1D6FF}$ . Outside the boundary layer, the flow is irrotational; thus, the axial flow velocity $U$ is independent of the radial coordinate for $y\geqslant \unicode[STIX]{x1D6FF}$ and only a function of the axial coordinate $U=U(z)$ ; see figure 1. The swirl near the rotating wall is produced by viscosity in a similar manner to the axial momentum boundary layer. Hence, close to the wall there is a region with a circumferential velocity component. We call this region the swirl boundary layer, having a thickness of $\unicode[STIX]{x1D6FF}_{S}$ . Outside the swirl boundary layer the flow is swirl-free; see figure 1. The centrifugal force takes effect within the swirl boundary layer and interacts with the axial moment; thus $\unicode[STIX]{x1D6FF}$ and $\unicode[STIX]{x1D6FF}_{S}$ have an influence on each other due to the radial pressure distribution. The evolution of the boundary layers depends on flow number, Reynolds number and relative surface roughness $R_{z}=\tilde{R}_{z}/\tilde{R}$ . This paper derives a generalization of the von Kármán momentum equation taking into account the evolution and interdependence of the axial and swirl boundary layer in the developing inlet. Employing this integral method, this paper provides an axiomatic description of the developing boundary layers that represents the influence of the Reynolds number and the flow number. This approach is motivated by Schlichting, who extended the integral method of boundary layer theory established by von Kármán (1921) and Pohlhausen (1921). Schlichting (1953) generalized the von Kármán equation for laminar outer flow around a rotating body.

This paper is organized as follows. First, it gives a literature review concerning the influence of swirl on friction, velocity profiles and separation in the following section. In § 3 the generalized von Kármán equation together with the angular momentum balance is derived for an extended boundary layer theory. This approach is valid for laminar and turbulent flow and indeed validated by the experimental results also presented in the context of this paper. The radial pressure gradient is derived as a function of the swirl boundary layer thickness. For the integral method, an ansatz function for the velocity profiles, i.e. axial and swirl velocity, and for the wall shear stresses is needed. Appropriated profiles and wall shear stresses are discussed in § 4 and the solution of the axial boundary layer and swirl boundary layer thickness is given. Section 5 presents the experimental set-up together with the experimental results, which validate the theory. Thereby, the influence of roughness and flow separation is investigated. Applying Stratford’s criterion (Stratford 1959) to the presented extended boundary layer theory, the critical flow number is derived analytically for a turbulent flow in a rotating pipe. This result is validated by our experiment as well. Hence, this paper gives a physical insight to the impact of the centrifugal force on the axial momentum balance, which is discussed in the closing of this article in § 6.

2 Literature review

The interaction of the centrifugal force and axial momentum is less investigated at the inlet of a rotating pipe than in the fully developed region. At the inlet of a rotating pipe, the boundary layers develop and an axial gradient of the velocity field occurs. At the fully developed region, this gradient vanishes and the boundary layers reach the centreline of the pipe. For a turbulent flow, the boundary layers reach the centreline for $z>10^{2}$ depending on flow number and Reynolds number (Nishibori, Kikuyama & Murakami 1987). In the following, the influence of the swirl on friction, axial and circumferential velocity profile and flow separation is analysed depending on the flow, e.g. turbulent versus laminar, and region, e.g. fully developed region versus inlet of a rotating pipe.

In contrast to Blasius’ investigations of friction losses in non-rotating smooth pipes by a turbulent flow (Blasius 1913), the hydraulic losses decrease with decreasing flow number in a rotating pipe (Levy 1927; White 1964). This is due to the turbulence damping by the swirl, which stabilizes the flow. The damping has a stronger influence close to the wall than in the core. Consequently, more low-frequency than high-frequency vibrations are damped (Borisenko, Kostikov & Chumachenko 1973). At the inlet of the rotating pipe for $\unicode[STIX]{x1D711}>1$ the turbulence is stimulated due to a sudden increase of the swirl for $z<20$ , but further downstream the damping due to centrifugal force predominates (Nagib et al. 1973; Bissonnette & Mellor 1974). For a laminar flow with small Reynolds number, the swirl increases the friction coefficient and stimulates the turbulence. Thus, the transition point to a turbulence flow is further upstream than in a non-rotating pipe (White 1964).

At the inlet of a rotating pipe, a complex transformation of the axial velocity profile occurs due to the interaction of the increased centrifugal force and the stimulating turbulence burst. The transformation depends on the inlet condition: when a fully developed, turbulent flow enters the rotating pipe, the turbulent profile transforms continuously into a laminar profile in the axial direction (Kikuyama et al. 1983b ). This effect is called ‘laminarization’ (Nishibori et al. 1987; Weigand & Beer 1994; Imao, Itohi & Harada 1996). For higher flow number, the axial velocity profile is retransformed to a turbulent profile, being well described by Prandtl’s $1/7$ power law (Nishibori et al. 1987), and for small flow number the ‘laminarized’ profile reaches the fully developed region. Weigand & Beer (1992) model the transformation analytically and meet the experimental results qualitatively whereby the coupling effect between the swirl and axial flow is overestimated. Thus, the influence of the swirl on the axial momentum has so far not been sufficiently investigated at the inlet of a rotating pipe.

The evolution of the swirl is given by the swirl boundary layer with the circumferential velocity profile. At the fully developed region, the circumferential velocity profile is parabolic and follows $u_{\unicode[STIX]{x1D711}}=r^{2}$ when a turbulent flow enters a rotating pipe (Murakami & Kikuyama 1980; Kikuyama, Murakami & Nishibori 1983a ; Reich 1988; Imao et al. 1996), and for a laminar flow it follows solid-body rotation $u_{\unicode[STIX]{x1D711}}=r$ (Reich 1988). Both profiles are derived by Lie group analysis (Oberlack 1999). In the transition region between laminar and turbulent flow, the circumferential velocity profile is between the parabolic and linear profiles (Imao, Zhang & Yamada 1989). At the inlet of a rotating pipe, the circumferential velocity profile is less investigated. The experimental investigations with a thin laminar boundary layer at $\unicode[STIX]{x1D711}>0.71$ show a possible transformation of the circumferential velocity profile. Whether and where the transformation occurs depend on flow number and Reynolds number. The circumferential velocity profile transforms before an effect on the axial velocity can be perceived. After the transformation, both boundary layers become thicker (Nishibori et al. 1987). Kikuyama et al. (1983a ) give a circumferential velocity profile scaled with the momentum thickness $\unicode[STIX]{x1D6FF}_{2}$ for high flow numbers. However, considerable deviations exist for $z<40$ . Also the profile presented by Weigand & Beer (1992) is not sufficient because it is not independent of the axial coordinate with deviations for $z<20$ . Thus, there is a need to describe the circumferential velocity profile and the evolution of the swirl in more detail at the inlet of a rotating pipe.

For $\unicode[STIX]{x1D711}<\unicode[STIX]{x1D711}_{c}$ , flow separates and a recirculation bubble appears at the wall. The separation is caused by the sudden pressure increase due to swirl at the wall. At the inlet of a rotating pipe, the flow separation is analytically and numerically investigated by a laminar flow with $Re<10^{3}$ (Lavan, Nielsen & Fejer 1969; Crane & Burley 1976). For small Reynolds numbers $Re\ll 10^{3}$ , the critical flow number is a linear function of the Reynolds number (Lavan et al. 1969; Crane & Burley 1976), but for $Re>10^{2}$ , the linear relation loses its validity (Crane & Burley 1976). Experimental investigations by Imao et al. (1989) show flow separation for $\unicode[STIX]{x1D711}<\unicode[STIX]{x1D711}_{c}\approx 0.33$ at $Re=3000$ . Up to now, flow separation for a turbulent flow at the inlet of a rotating pipe has not been sufficiently analysed.

Najafi et al. (2005) investigate the complementary case in which a turbulent rotating flow enters a pipe at rest. Analysing this work, we find three limitations: first, the radial pressure gradient, which is the root cause of flow separation, is initially assumed to be constant and is later neglected in the analytic section; second, the governing equations are linearized, which is not justified in this paper; and finally, the results are ‘validated’ by Reynolds-averaged Navier–Stokes (RANS) simulations. The referenced RANS simulations, solved with a commercial solver, still do not predict turbulent rotating flows satisfyingly today. Thus, RANS simulations are not suitable to validate these kinds of flows.

3 Generalized von Kármán’s momentum equation

In the following we give an order-of-magnitude analysis of all relevant physical quantities. The order of magnitude of the time-averaged circumferential velocity $u_{\unicode[STIX]{x1D719}}$ is 1 and the order of magnitude of the time-averaged axial velocities $u,U$ follows $\unicode[STIX]{x1D711}$ . The order of magnitude of the wall coordinate $y$ follows $\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}_{S}$ . For thin boundary layers $\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}_{S}\ll 1$ , an order-of-magnitude analysis of the continuity equation within the boundary layer yields $u_{y}\sim \unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}$ ( ${\sim}$ represents ‘is of the order’) for the time-averaged radial velocity and $u_{y}^{\prime }\sim u^{\prime }\unicode[STIX]{x1D6FF}$ for the turbulent fluctuations since $z\sim 1$ . Here $u^{\prime }$ and $u_{y}^{\prime }$ are the fluctuations of the axial and radial velocity components, respectively. With the order-of-magnitude analysis given so far, the order of magnitude of $\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D719}}/\unicode[STIX]{x2202}y$ is $1/\unicode[STIX]{x1D6FF}$ and  $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y\sim \unicode[STIX]{x1D711}/\unicode[STIX]{x1D6FF}$ . For $\unicode[STIX]{x1D711}\sim \unicode[STIX]{x1D6FF}\ll 1$ , $\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D719}}/\unicode[STIX]{x2202}y$ dominates the time-averaged velocity gradient because all other components, especially $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$ , are at least one order of magnitude smaller than $\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D719}}/\unicode[STIX]{x2202}y$ . In contrast, for $\unicode[STIX]{x1D711}\sim 1/\unicode[STIX]{x1D6FF}\gg 1$ , $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$ is the dominating component of the velocity gradient.

In a non-rotating pipe, the mixing length $l$ equals $\unicode[STIX]{x1D705}y$ near the smooth wall with the von Kármán constant $\unicode[STIX]{x1D705}=0.4$ (Nikuradse 1932), whereas in a rotating pipe $l\leqslant \unicode[STIX]{x1D705}y$ (Kikuyama et al. 1983a , b ; Weigand & Beer 1994). For both cases, with $\unicode[STIX]{x1D705}=0.4$ and $y\sim \unicode[STIX]{x1D6FF}\sim 10^{-1}$ , the mixing length is of the order of magnitude $10^{-2}$ or equivalent to the order of magnitude $\unicode[STIX]{x1D6FF}^{2}$ . An order-of-magnitude analysis of the turbulence viscosity introduced by Smagorinsky (1963) yields

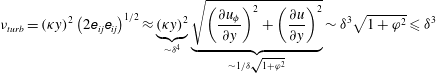(3.1) $$\begin{eqnarray}\unicode[STIX]{x1D708}_{turb}=(\unicode[STIX]{x1D705}y)^{2}\left(2\unicode[STIX]{x1D626}_{ij}\unicode[STIX]{x1D626}_{ij}\right)^{1/2}\approx \underbrace{(\unicode[STIX]{x1D705}y)^{2}}_{{\sim}\unicode[STIX]{x1D6FF}^{4}}\underbrace{\sqrt{\left(\frac{\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D719}}}{\unicode[STIX]{x2202}y}\right)^{2}+\left(\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right)^{2}}}_{{\sim}1/\unicode[STIX]{x1D6FF}\sqrt{1+\unicode[STIX]{x1D711}^{2}}}\sim \unicode[STIX]{x1D6FF}^{3}\sqrt{1+\unicode[STIX]{x1D711}^{2}}\leqslant \unicode[STIX]{x1D6FF}^{3}\end{eqnarray}$$

for the present flow. Even though it is unusual to have an order of magnitude as a sum, we prefer to use this presentation for the distinction of cases $\unicode[STIX]{x1D711}\ll 1$ and $\unicode[STIX]{x1D711}\sim 1$ in the following. By doing so, the order-of-magnitude analysis keeps the flow number general. For the generic set-up considered here, flow separation is expected for $\unicode[STIX]{x1D711}\ll 1$ and is the focus of this paper. Hence, there is no need to consider the case $\unicode[STIX]{x1D711}\gg 1$ . Applying Boussinesq’s eddy viscosity concept (Pope 2011), the Reynolds stress tensor is

(3.2) $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{ij,turb}=\overline{u_{i}^{\prime }u_{j}^{\prime }}={\textstyle \frac{1}{3}}\overline{u_{l}^{\prime }u_{l}^{\prime }}\unicode[STIX]{x1D6FF}_{ij}-\unicode[STIX]{x1D708}_{turb}\unicode[STIX]{x1D626}_{ij}.\end{eqnarray}$$

Here, $\unicode[STIX]{x1D6FF}_{ij}$ is the Kronecker tensor and $\unicode[STIX]{x1D626}_{ij}$ is the mean strain-rate tensor. In the following, (3.2) is exclusively applied to analyse the order of magnitude of the Reynolds stress tensor.

The normal components of the Reynolds stress tensor are implicit due to the turbulent kinetic energy $\overline{u_{i}^{\prime }u_{i}^{\prime }}/3$ . The order of magnitude of the normal components of the Reynolds stress tensor (3.2) is determined by eliminating the kinetic energy. Subtracting $\overline{u_{y}^{\prime }u_{y}^{\prime }}$ from $\overline{u^{\prime }u^{\prime }}$ yields

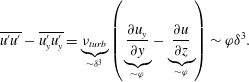(3.3) $$\begin{eqnarray}\overline{u^{\prime }u^{\prime }}-\overline{u_{y}^{\prime }u_{y}^{\prime }}=\underbrace{\unicode[STIX]{x1D708}_{turb}}_{{\sim}\unicode[STIX]{x1D6FF}^{3}}\left(\underbrace{\frac{\unicode[STIX]{x2202}u_{y}}{\unicode[STIX]{x2202}y}}_{{\sim}\unicode[STIX]{x1D711}}-\underbrace{\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}z}}_{{\sim}\unicode[STIX]{x1D711}}\right)\sim \unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}.\end{eqnarray}$$

With $u_{y}^{\prime }\sim u^{\prime }\unicode[STIX]{x1D6FF}$ it follows that $\overline{u_{y}^{\prime }u_{y}^{\prime }}\sim \overline{u^{\prime }u^{\prime }}\unicode[STIX]{x1D6FF}^{2}$ . Thus, $\overline{u^{\prime }u^{\prime }}$ is of the order of magnitude of $\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}$ . Hence, $\unicode[STIX]{x1D70F}_{zz,turb}=\overline{u^{\prime }u^{\prime }}\sim \unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}$ and $\unicode[STIX]{x1D70F}_{yy,turb}=\overline{u_{y}^{\prime }u_{y}^{\prime }}\sim \unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{5}$ . With this result, the order of magnitude of $\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D719}\unicode[STIX]{x1D719},turb}=\overline{u_{\unicode[STIX]{x1D719}}^{\prime }u_{\unicode[STIX]{x1D719}}^{\prime }}\sim \unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}$ is given.

The radial component of the momentum equation is

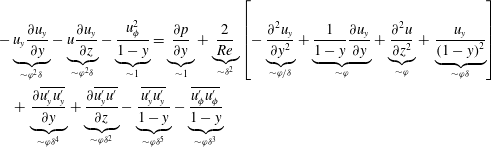(3.4) $$\begin{eqnarray}\displaystyle & & \displaystyle -\underbrace{u_{y}\frac{\unicode[STIX]{x2202}u_{y}}{\unicode[STIX]{x2202}y}}_{{\sim}\unicode[STIX]{x1D711}^{2}\unicode[STIX]{x1D6FF}}-\underbrace{u\frac{\unicode[STIX]{x2202}u_{y}}{\unicode[STIX]{x2202}z}}_{{\sim}\unicode[STIX]{x1D711}^{2}\unicode[STIX]{x1D6FF}}-\underbrace{\frac{u_{\unicode[STIX]{x1D719}}^{2}}{1-y}}_{{\sim}1}=\underbrace{\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}y}}_{{\sim}1}+\underbrace{\frac{2}{Re}}_{{\sim}\unicode[STIX]{x1D6FF}^{2}}\left[-\underbrace{\frac{\unicode[STIX]{x2202}^{2}u_{y}}{\unicode[STIX]{x2202}y^{2}}}_{{\sim}\unicode[STIX]{x1D711}/\unicode[STIX]{x1D6FF}}+\underbrace{\frac{1}{1-y}\frac{\unicode[STIX]{x2202}u_{y}}{\unicode[STIX]{x2202}y}}_{{\sim}\unicode[STIX]{x1D711}}+\underbrace{\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}z^{2}}}_{{\sim}\unicode[STIX]{x1D711}}+\,\underbrace{\frac{u_{y}}{\left(1-y\right)^{2}}}_{{\sim}\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\underbrace{\frac{\unicode[STIX]{x2202}\overline{u_{y}^{\prime }u_{y}^{\prime }}}{\unicode[STIX]{x2202}y}}_{{\sim}\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{4}}+\underbrace{\frac{\unicode[STIX]{x2202}\overline{u_{y}^{\prime }u^{\prime }}}{\unicode[STIX]{x2202}z}}_{{\sim}\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{2}}-\underbrace{\frac{\overline{u_{y}^{\prime }u_{y}^{\prime }}}{1-y}}_{{\sim}\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{5}}-\underbrace{\frac{\overline{u_{\unicode[STIX]{x1D719}}^{\prime }u_{\unicode[STIX]{x1D719}}^{\prime }}}{1-y}}_{{\sim}\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}}\end{eqnarray}$$

with the static pressure $p$ . An order-of-magnitude analysis of (3.4) yields that the viscous and Reynolds stresses are negligible for $\unicode[STIX]{x1D711}\ll 1$ , $\unicode[STIX]{x1D711}\sim 1$ and $\unicode[STIX]{x1D711}>1$ . The case $\unicode[STIX]{x1D711}>1$ is treated by Kikuyama et al. (1983a ), Kitoh (1991) and Imao et al. (1996). The order of magnitude of the centrifugal force, i.e. the third term on the left-hand side of (3.4), is 1. The momentum fluxes, i.e. the first and second terms on the left-hand side of (3.4), are of the order of magnitude $\unicode[STIX]{x1D711}^{2}\unicode[STIX]{x1D6FF}$ . The order of magnitude of the viscous stress, i.e. the terms in the square brackets on the right-hand side of (3.4), are smaller than or equal to $\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}$ since $Re\sim 1/\unicode[STIX]{x1D6FF}^{2}$ for a laminar flow (Schlichting 1970; Pope 2011). For a turbulent flow, the Reynolds number is much larger. Hence, $Re\sim 1/\unicode[STIX]{x1D6FF}^{2}$ serves as an upper bound on the order of magnitude of the viscous stress for the order-of-magnitude analysis. Indeed, our measurements indicate that $Re\sim 10^{4}\approx 1/\unicode[STIX]{x1D6FF}^{4}$ for a turbulent flow. The Reynolds stress, i.e. the last four terms on the right-hand side of (3.4), is of the order of magnitude smaller than or equal to $\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{2}$ . Thus, the viscous and the Reynolds stresses are at least one order of magnitude smaller than the centrifugal force and are negligible, especially for $\unicode[STIX]{x1D711}\ll 1$ . Consequently, the radial pressure gradient has to balance the centrifugal force, and this gradient is of the order of magnitude $1$ . The radial component of the momentum equation (3.4) yields

(3.5) $$\begin{eqnarray}-\frac{u_{\unicode[STIX]{x1D719}}^{2}}{1-y}=\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}y}+O(\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF})\end{eqnarray}$$

$\text{for}~y<\unicode[STIX]{x1D6FF}_{S}$ . For $y>\unicode[STIX]{x1D6FF}_{S}$ , the circumferential velocity vanishes ( $u_{\unicode[STIX]{x1D719}}=0$ ) by definition and the static pressure is a function only of the axial coordinate $P(z)$ , satisfying the axial component of Euler’s equation

(3.6) $$\begin{eqnarray}\frac{\text{d}P}{\text{d}z}=-U\frac{\text{d}U}{\text{d}z}\sim \unicode[STIX]{x1D711}^{2},\end{eqnarray}$$

where $U$ is the axial flow velocity in the core region. Hence, the pressure distribution within the swirl boundary layer $y<\unicode[STIX]{x1D6FF}_{S}$ is

(3.7) $$\begin{eqnarray}p(y,z)=\int _{y}^{\unicode[STIX]{x1D6FF}_{S}}\frac{u_{\unicode[STIX]{x1D719}}^{2}}{1-y^{\prime }}\,\text{d}y^{\prime }+P(z)\sim \unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D711}^{2}.\end{eqnarray}$$

For the sketched control volume in figure 1 (broken line), the axial momentum balance reads

(3.8) $$\begin{eqnarray}\displaystyle & & \displaystyle \underbrace{\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)u^{2}\,\text{d}y}_{{\sim}\unicode[STIX]{x1D711}^{2}\unicode[STIX]{x1D6FF}}-\underbrace{U\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)u\,\text{d}y}_{{\sim}\unicode[STIX]{x1D711}^{2}\unicode[STIX]{x1D6FF}}\nonumber\\ \displaystyle & & \displaystyle \quad =\underbrace{\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)\unicode[STIX]{x1D70F}_{zz}(y,z)\,\text{d}y}_{{\sim}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D711}^{2})+\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}+\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{4}}-\underbrace{(1-\unicode[STIX]{x1D6FF})\unicode[STIX]{x1D70F}_{zz}(\unicode[STIX]{x1D6FF},z)\frac{\text{d}\unicode[STIX]{x1D6FF}}{\text{d}z}}_{{\sim}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D711}^{2})+\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}+\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{4}}-\underbrace{\unicode[STIX]{x1D70F}_{yz,w}}_{{\sim}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D711}^{2})},\end{eqnarray}$$

where $u$ is the time-averaged axial velocity component inside the axial boundary layer, $\unicode[STIX]{x1D70F}_{yz,w}$ is the $yz$ shear-stress component at the wall and $\unicode[STIX]{x1D70F}_{zz}$ is the $zz$ shear-stress component. For a Newtonian fluid and a turbulent flow, $\unicode[STIX]{x1D70F}_{zz}=-p+\unicode[STIX]{x1D70F}_{zz,vis}+\unicode[STIX]{x1D70F}_{zz,turb}$ . Hereby, the order of magnitude of the viscous stress is

(3.9) $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{zz,vis}=\frac{4}{Re}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}z}\sim \unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{2},\end{eqnarray}$$

since employing the lower bound of the Reynolds number $Re\sim 1/\unicode[STIX]{x1D6FF}^{2}$ for a laminar flow yields an upper bound of the order of magnitude of the viscous stress. As stated earlier, with $Re\sim 1/\unicode[STIX]{x1D6FF}^{4}$ for a turbulent flow, this gives the lower bound for the viscous stress. As known from (3.3), $\unicode[STIX]{x1D70F}_{zz,turb}=\overline{u^{\prime }u^{\prime }}\sim \unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}$ . Thus, an order-of-magnitude analysis of the axial momentum balance (3.8) yields the following: the viscous and Reynolds stress of the $zz$ component are negligible. The axial momentum fluxes, i.e. the terms on the left-hand side of (3.8), are of the order of magnitude $\unicode[STIX]{x1D711}^{2}\unicode[STIX]{x1D6FF}$ . The order of magnitude of the pressure is $\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D711}^{2}$ as (3.6) and (3.7) indicate. Thus, the order of magnitude of the centrifugal force, i.e. the terms on the right-hand side of (3.8) including the pressure $p$ , is $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D711}^{2})$ . The wall shear stress, i.e. the third term on the right-hand side of (3.8), needs to balance the axial momentum fluxes and the centrifugal force. Thus, its order of magnitude is $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D711}^{2})$ . All terms with the viscous stress of the $zz$ component are of the order of magnitude $\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}$ and of the Reynolds stress are of the order of magnitude $\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{4}$ . The terms of the viscous and Reynolds stresses are at least one order of magnitude smaller than all other terms and are negligible. Hence, the axial momentum balance reads

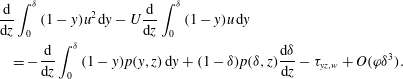(3.10) $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)u^{2}\,\text{d}y-U\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)u\,\text{d}y\nonumber\\ \displaystyle & & \displaystyle \quad =-\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)p(y,z)\,\text{d}y+(1-\unicode[STIX]{x1D6FF})p(\unicode[STIX]{x1D6FF},z)\frac{\text{d}\unicode[STIX]{x1D6FF}}{\text{d}z}-\unicode[STIX]{x1D70F}_{yz,w}+O(\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}^{3}).\end{eqnarray}$$

For $\unicode[STIX]{x1D711}\ll 1$ , the axial momentum fluxes are an order of magnitude smaller than the centrifugal force. Hence, the centrifugal force and the wall shear stress dominate the axial momentum balance. The pressure $p(y>\unicode[STIX]{x1D6FF}_{S},z)$ equals the pressure of the core flow $P(z)$ .

Using the displacement thickness $\unicode[STIX]{x1D6FF}_{1}$ , defined as usual (Piquet 1999) as

(3.11) $$\begin{eqnarray}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)u\,\text{d}y:=\frac{1}{2}U\left[(1-\unicode[STIX]{x1D6FF}_{1})^{2}-(1-\unicode[STIX]{x1D6FF})^{2}\right]\end{eqnarray}$$

and the momentum thickness $\unicode[STIX]{x1D6FF}_{2}$ defined by

(3.12) $$\begin{eqnarray}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)u^{2}\,\text{d}y:=\frac{1}{2}U^{2}\left[(1-\unicode[STIX]{x1D6FF}_{2})^{2}+(1-\unicode[STIX]{x1D6FF}_{1})^{2}-(1-\unicode[STIX]{x1D6FF})^{2}-1\right],\end{eqnarray}$$

the axial momentum balance yields

(3.13) $$\begin{eqnarray}(1-\unicode[STIX]{x1D6FF}_{2})\frac{\text{d}\unicode[STIX]{x1D6FF}_{2}}{\text{d}z}+\left(2\unicode[STIX]{x1D6FF}_{2}-\unicode[STIX]{x1D6FF}_{2}^{2}+\unicode[STIX]{x1D6FF}_{1}-\frac{1}{2}\unicode[STIX]{x1D6FF}_{1}^{2}\right)\frac{1}{U}\frac{\text{d}U}{\text{d}z}+\frac{G}{U^{2}}=\frac{\unicode[STIX]{x1D70F}_{yz,w}}{U^{2}}+O\left(\frac{\unicode[STIX]{x1D6FF}^{3}}{\unicode[STIX]{x1D711}}\right),\end{eqnarray}$$

with the coupling term

(3.14) $$\begin{eqnarray}G:=-\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)\int _{y}^{\unicode[STIX]{x1D6FF}_{S}}\frac{u_{\unicode[STIX]{x1D719}}^{2}}{1-y^{\prime }}\,\text{d}y^{\prime }\,\text{d}y+(1-\unicode[STIX]{x1D6FF})\frac{\text{d}\unicode[STIX]{x1D6FF}}{\text{d}z}\int _{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D6FF}_{S}}\frac{u_{\unicode[STIX]{x1D719}}^{2}}{1-y}\,\text{d}y.\end{eqnarray}$$

The second term on the right-hand side of (3.14) vanishes for $\unicode[STIX]{x1D6FF}>\unicode[STIX]{x1D6FF}_{S}$ because $u_{\unicode[STIX]{x1D719}}(y>\unicode[STIX]{x1D6FF}_{S})=0$ . For swirl-free flow, the coupling term vanishes ( $G=0$ ) and (3.13) reduces to the von Kármán momentum equation. Hence, (3.13) is a generalization of the von Kármán momentum equation and considers the radial pressure distribution due to swirl. The angular momentum equation

(3.15) $$\begin{eqnarray}\underbrace{\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)^{2}u_{\unicode[STIX]{x1D719}}u\,\text{d}y}_{{\sim}\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}}+\underbrace{\frac{\text{d}}{\text{d}z}\int _{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D6FF}_{S}}(1-y)^{2}u_{\unicode[STIX]{x1D719}}U\,\text{d}y}_{{\sim}\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}}=\underbrace{\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}_{S}}(1-y)^{2}\unicode[STIX]{x1D70F}_{z\unicode[STIX]{x1D719}}\,\text{d}y}_{{\sim}\unicode[STIX]{x1D6FF}^{3}+\unicode[STIX]{x1D6FF}^{4}}-\underbrace{\unicode[STIX]{x1D70F}_{y\unicode[STIX]{x1D719},w}}_{{\sim}\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}}\end{eqnarray}$$

is needed to determine $G$ . Here, $\unicode[STIX]{x1D70F}_{y\unicode[STIX]{x1D719},w}$ is the $y\unicode[STIX]{x1D719}$ shear-stress component at the wall and $\unicode[STIX]{x1D70F}_{z\unicode[STIX]{x1D719}}$ is the $z\unicode[STIX]{x1D719}$ shear-stress component. Equation (3.15) is valid for any case, either $\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D6FF}_{S}$ or $\unicode[STIX]{x1D6FF}>\unicode[STIX]{x1D6FF}_{S}$ . For $\unicode[STIX]{x1D6FF}>\unicode[STIX]{x1D6FF}_{S}$ , the second term on the left-hand side of (3.15) vanishes because $u_{\unicode[STIX]{x1D719}}(y>\unicode[STIX]{x1D6FF}_{S})=0$ . For $\unicode[STIX]{x1D6FF}<\unicode[STIX]{x1D6FF}_{S}$ , the axial velocity profile changes within the swirl boundary layer and this is considered by the second term on the left-hand side of (3.15). Furthermore, there is no convective angular momentum transport either into or out of the swirl boundary layer over $\unicode[STIX]{x1D6FF}_{S}$ , as there is with the convective axial momentum transport over $\unicode[STIX]{x1D6FF}$ (second term of the left-hand side of (3.8)). This is justified by the swirl-free flow outside the swirl boundary layer.

An order-of-magnitude analysis of the angular momentum balance (3.15) yields that the viscous and Reynolds stresses of the $z\unicode[STIX]{x1D719}$ component are negligible. The angular momentum flux, i.e. the left-hand side of (3.15), is of the order of magnitude $\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}$ . The wall shear stress needs to balance the angular momentum fluxes, thus its order of magnitude is $\unicode[STIX]{x1D711}\unicode[STIX]{x1D6FF}$ as well. The torque due to the shear stress of the $z\unicode[STIX]{x1D719}$ component at the inlet and outlet of the control volume, i.e. the first term on the right-hand side of (3.15), is of the order of magnitude $\unicode[STIX]{x1D6FF}^{3}$ . This is due to the order of magnitude of the stress component $\unicode[STIX]{x1D70F}_{z\unicode[STIX]{x1D719}}$ . The upper bound of the order of magnitude of the viscous stress of this component is given by

(3.16) $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{z\unicode[STIX]{x1D719},vis}=\frac{2}{Re}\frac{\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D719}}}{\unicode[STIX]{x2202}z}\sim \unicode[STIX]{x1D6FF}^{2}.\end{eqnarray}$$

We employ (3.2) to approximate the order of magnitude of the Reynolds stress

(3.17) $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{z\unicode[STIX]{x1D719},turb}=-\overline{u^{\prime }u_{\unicode[STIX]{x1D719}}^{\prime }}=\unicode[STIX]{x1D708}_{turb}\frac{\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D719}}}{\unicode[STIX]{x2202}z}\sim \unicode[STIX]{x1D6FF}^{3}.\end{eqnarray}$$

Hence, at the inlet and outlet of the control volume, the order of magnitude of the viscous and Reynolds stresses $\unicode[STIX]{x1D70F}_{z\unicode[STIX]{x1D719}}$ is smaller than or even of the same order of magnitude as $\unicode[STIX]{x1D6FF}^{2}$ . Thus, only the torque integral on the right-hand side of (3.15) is of the order of magnitude $\unicode[STIX]{x1D6FF}^{3}$ and for $\unicode[STIX]{x1D711}\sim 1$ it is two orders of magnitude smaller than all other terms and one order of magnitude smaller for $\unicode[STIX]{x1D711}\ll 1$ . Hence, for the boundary layer approximation, (3.15) reduces to

(3.18) $$\begin{eqnarray}\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}(1-y)^{2}u_{\unicode[STIX]{x1D719}}u\,\text{d}y+\frac{\text{d}}{\text{d}z}\int _{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D6FF}_{S}}(1-y)^{2}u_{\unicode[STIX]{x1D719}}U\,\text{d}y=-\unicode[STIX]{x1D70F}_{y\unicode[STIX]{x1D719},w}+O(\unicode[STIX]{x1D6FF}^{3}),\end{eqnarray}$$

and is valid for thin laminar and turbulent boundary layers. The system of equations (3.13) and (3.18) is completed by the continuity equation

(3.19) $$\begin{eqnarray}\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}}u(1-y)\,\text{d}y+\frac{\text{d}}{\text{d}z}\int _{\unicode[STIX]{x1D6FF}}^{1}U(1-y)\,\text{d}y=0,\end{eqnarray}$$

which describes the interdependence between the boundary layer and the core flow velocity. Substituting the first term on the left-hand side with the displacement thickness (3.11), the continuity equation yields

(3.20) $$\begin{eqnarray}\frac{1}{U}\frac{\text{d}U}{\text{d}z}=\frac{2}{1-\unicode[STIX]{x1D6FF}_{1}}\frac{\text{d}\unicode[STIX]{x1D6FF}_{1}}{\text{d}z}.\end{eqnarray}$$

By doing so, it becomes clear that the flow is accelerated due to the displacement thickness at the core region. Thus, the axial pressure gradient (3.6) must be negative at the core region, as (3.20) indicates.

To analyse the interdependence of the axial momentum balance and the angular momentum balance, (3.13), (3.18) and (3.20) have to be solved. All velocity profiles $u(y,z)$ and $u_{\unicode[STIX]{x1D719}}(y,z)$ must satisfy these conservation laws in integral form. In the following, we assume power laws for both axial and swirl velocity profiles with the corresponding wall shear stress and determine both boundary layer thicknesses $\unicode[STIX]{x1D6FF}$ and $\unicode[STIX]{x1D6FF}_{S}$ and their interaction.

4 Solution of the generalized von Kármán momentum equation

The well-recognized advantage of the integral method is that neither detailed knowledge of the velocity distribution within the boundary layers nor a turbulence model is needed. As will be shown, the velocity profiles can be modelled by power laws, logarithmic, harmonic functions (Schlichting 1970) or other functions that capture the asymptotic behaviour of the velocity profile. In other words, the method is robust with respect to the shape of the ansatz functions; the shape of the ansatz function has a very limited influence on the findings. This work employs power-law distributions as ansatz functions for the axial velocity profile

(4.1) $$\begin{eqnarray}\frac{u(y,z)}{U(z)}=\left(\frac{y}{\unicode[STIX]{x1D6FF}(z)}\right)^{n}\end{eqnarray}$$

and circumferential velocity profile

(4.2) $$\begin{eqnarray}u_{\unicode[STIX]{x1D719}}(y,z)=\left(1-\frac{y}{\unicode[STIX]{x1D6FF}_{S}(z)}\right)^{k}.\end{eqnarray}$$

Applying the integral method to flows with a turbulent boundary layer, it is known that the ansatz function like the chosen (4.1) has to be adjusted, since $\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y\rightarrow \infty$ for $y\rightarrow 0$ . To adjust the ansatz function, it is common to use an empirical ansatz function in treating the turbulent boundary layer by integral methods (Schubauer & Tchen 1961; Schlichting 1970). The integral method keeps the physical content of the flow even for seemingly crude assumptions. For a turbulent pipe flow, Schlichting (1970) models the wall shear stress with $\unicode[STIX]{x1D70F}_{yz,w}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D711}^{2}/8$ using the Blasius law $\unicode[STIX]{x1D706}=0.3164(\unicode[STIX]{x1D711}Re)^{-1/4}$ (Blasius 1913), as shown in appendix A. The ansatz function (4.1) in combination with the Blasius law reads

(4.3) $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{yz,w}(z)=c^{-2/(n+1)}U(z)^{2/(n+1)}\left(\frac{2}{\unicode[STIX]{x1D6FF}(z)Re}\right)^{2n/(n+1)}.\end{eqnarray}$$

For the Reynolds number interval $Re=10^{4}{-}10^{6}$ , the exponent $n$ is $1/7$ and $c=8.74$ (Schlichting 1970). Even the value of $c$ has a very limited influence on the findings, as shown in appendix A. This again shows the desired robustness of the chosen integral method.

In contrast to the axial velocity profile (4.1), the circumferential velocity profile (4.2) shows no singularity in the velocity gradient at the wall. Near the smooth wall, the Reynolds stress vanishes due to kinematic reasons. Hence, the viscous stress is

(4.4) $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{y\unicode[STIX]{x1D719},w}(z)=\frac{2a}{Re}\frac{\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D719}}}{\unicode[STIX]{x2202}y}\bigg|_{w}=-\frac{2ak}{\unicode[STIX]{x1D6FF}_{S}(z)Re},\end{eqnarray}$$

with $a=1$ . Our experiments indicate $a>1$ to predict the turbulent swirl boundary layer thickness properly. For $k=2$ and $a=1.53$ , being independent of Reynolds number and flow number, the swirl boundary layer thickness is well predicted. The influence of the constant $a$ on the boundary layer thicknesses is plotted in appendix A for $1\leqslant a\leqslant 2$ . It has become clear so far that the Blasius constant $c=8.74$ and $a=1.53$ are empirical constants, as is the von Kármán constant $\unicode[STIX]{x1D705}=0.4$ . Despite these empirical constants, the findings are robust, since these constants are independent of flow parameters like Reynolds number and flow number.

The constant $a$ is determined by solving the generalized von Kármán equations (3.13) and (3.18) and the continuity equation (3.20) with the ansatz functions (4.1)–(4.4) and calibrates the swirl boundary layer thickness with the experimental measurements at $z=2$ , $\unicode[STIX]{x1D711}=0.40$ and $\log (Re)=4.41$ .

For those who are not familiar with the power of the integral method of the boundary layer theory approach of using ansatz functions, it may seem like fitting, but it is not. At the very end, the conservation laws in integral form are fulfilled to a very good degree of approximation as our experimental validation shows. The method and the outcomes, i.e. the boundary layer thicknesses, are very robust with respect to the ansatz function (von Kármán 1921; Pohlhausen 1921; Schlichting 1970).

4.1 Axial and swirl boundary layer thickness

Solving the generalized von Kármán equation (3.13) and (3.18) and the continuity equation (3.20) with the velocity profiles (4.1) and (4.2) and the wall shear stresses (4.3) and (4.4) with $n=1/7$ and $k=2$ numerically, the swirl boundary layer thickness, depending on axial coordinate, Reynolds number and flow number, is given by the lines in figure 2. The solution of axial boundary layer thickness is shown in figure 3 and, due to swirl, the axial boundary layer is thickened. For $\unicode[STIX]{x1D711}>1$ , the swirl-free solution $\unicode[STIX]{x1D6FF}(G=0)$ (black lines in figure 3) is approached asymptotically. For $\unicode[STIX]{x1D711}<1$ , a clear influence of swirl is observed. As indicated by the order-of-magnitude analysis of (3.8), the centrifugal force balances the wall shear stress. A new asymptote appears and dominates the axial boundary layer thickness. The interdependence of the axial boundary layer and the swirl is represented by an increase of the axial boundary layer thickness $g:=\unicode[STIX]{x1D6FF}-\unicode[STIX]{x1D6FF}(G=0)$ .

Figure 2. Swirl boundary layer thickness versus axial coordinate, Reynolds number and flow number for $R_{z}=0.04\,\%$ . Experiments and solution of the boundary layer theory. Description of the experimental set-up is given by § 5.

Figure 3. Influence of Reynolds number and flow number on the axial boundary layer thickness. Solution of the boundary layer theory.

4.2 Power laws of the boundary layer thicknesses

Throughout this paper, only the empirical constants of von Kármán $\unicode[STIX]{x1D705}=0.4$ , Blasius constant $c=8.74$ and $a=1.53$ are the fundamental empirical constants. All other calibrations are employed only for a short representation of the solution of the generalized von Kármán momentum equation. Analysing the slope of the boundary layer solution in the double-logarithmic diagrams (figure 2) for each parameter far away from the singularity at $z=0$ , a power law for the swirl boundary layer thickness is given,

(4.5) $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{S}=C_{S}Re^{m_{1}}\unicode[STIX]{x1D711}^{m_{2}}z^{m_{3}},\end{eqnarray}$$

with $m_{1}=-0.487$ , $m_{2}=-0.492$ and $m_{3}=0.507$ . The outcome of a ‘power law’ for the swirl boundary layer thickness is obvious. We calibrate the constant $C_{S}$ to the achieved swirl boundary layer thickness from the generalized von Kármán momentum equations (3.13), (3.18) and (3.20) with the ansatz functions (4.1)–(4.4), yielding $C_{S}=6.39$ . This constant and the exponents $m_{1}\ldots m_{3}$ are independent of the Reynolds number, flow number and axial coordinate. Therefore, the exponents and the constant are very robust concerning changes of the ansatz functions, cf. appendix A and von Kármán (1921), Pohlhausen (1921) and Schlichting (1970). Applying equation (4.5) by (4.4), we get an approximation for the circumferential wall shear stress for a turbulent, hydraulic smooth flow,

(4.6) $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{y\unicode[STIX]{x1D719},w}=-\frac{2ak}{C_{S}}Re^{-(m_{1}+1)}\unicode[STIX]{x1D711}^{-m_{2}}z^{-m_{3}},\end{eqnarray}$$

and also the dimensionless hydraulic torque, which is equal to the shaft power and non-dimensionalized with $\tilde{\unicode[STIX]{x1D70C}}\tilde{R}^{3}\tilde{\unicode[STIX]{x1D6FA}}^{2}$ , depending on the length of the pipe $L$ (see figure 1),

(4.7) $$\begin{eqnarray}T=2\unicode[STIX]{x03C0}\int _{0}^{L}\unicode[STIX]{x1D70F}_{y\unicode[STIX]{x1D719},w}\,\text{d}z=-\frac{4\unicode[STIX]{x03C0}}{1-m_{3}}\frac{ak}{C_{S}}Re^{-(m_{1}+1)}\unicode[STIX]{x1D711}^{-m_{2}}L^{1-m_{3}}.\end{eqnarray}$$

Applying the method once again for the axial boundary layer thickness as was done for the swirl boundary layer thickness (4.5), the axial boundary layer thickness follows $g\propto \unicode[STIX]{x1D711}^{m_{7}}Re^{m_{8}}z^{m_{9}}$ and we obtain

(4.8) $$\begin{eqnarray}\unicode[STIX]{x1D6FF}=C_{1}Re^{m_{4}}\unicode[STIX]{x1D711}^{m_{5}}z^{m_{6}}+C_{2}Re^{m_{7}}\unicode[STIX]{x1D711}^{m_{8}}z^{m_{9}},\end{eqnarray}$$

with $m_{4}=-0.198$ , $m_{5}=-0.198$ , $m_{6}=0.790$ , $m_{7}=-0.969$ , $m_{8}=-2.94$ and $m_{9}=0.974$ . The values for the constants $C_{1}=0.414$ and $C_{2}=11.520$ are analogous to $C_{S}$ . The value of $\unicode[STIX]{x1D6FF}(G=0)$ , i.e. the first term on the right-hand side of (4.8), is close to the turbulent boundary layer on a flat plate. Again, the constants in (4.5) and (4.8) are to a large degree independent of the ansatz function. The relative accuracy of the power-law equations (4.5) and (4.8) to the numerical solution of the generalized von Kármán momentum equation (figures 2 and 3) is less than 10 %. The advantage of the power laws is that the differential equation system need not be solved to predict the boundary layer thicknesses.

This section presented the solution, i.e. the axial and swirl boundary layer thicknesses $\unicode[STIX]{x1D6FF}$ and $\unicode[STIX]{x1D6FF}_{S}$ , of the differential equation system, (3.13), (3.18) and (3.20), using (4.1) and (4.2) for the velocity profiles with $n=1/7$ and $k=2$ and (4.3) and (4.4) for the wall shear stresses. In addition, this section gave power laws for $\unicode[STIX]{x1D6FF}$ and  $\unicode[STIX]{x1D6FF}_{S}$ .

5 Experiments and discussion

An apparatus is designed for the experimental validation of the swirl boundary layer thickness; see figure 4. With this apparatus, the swirl velocity distribution, the swirl boundary layer thickness and the flow separation depending on flow number, Reynolds number, axial position and surface roughness are investigated. Thereby, only the circumferential velocity component is measured by laser Doppler anemometry (LDA).

5.1 Experimental set-up

The air flow at room temperature and ambient pressure is provided by a radial fan, which increases pressure in a large plenum chamber with a flow resistance. The outlet of this chamber is followed by the first flow straightener, shown in figure 4 on the left side. Using this set-up, possible forced pulsations by the fan are minimized. The volume flow is measured by an orifice plate. Hence, the average flow velocity is given and is controlled by changing the rotation speed of the fan. The apparatus allows axial velocity up to $13~\text{m}~\text{s}^{-1}$ , resulting in a Mach number smaller than 0.1.

Figure 4. Configuration test rig.

The orifice plate is followed by a diffuser, the second flow straightener, three turbulence screens and a so-called Börger nozzle (Börger 1973). Owing to the acceleration with the nozzle, the velocity profile is forced to be uniform across the inlet section of the rotating pipe. We measure the axial boundary layer of a thickness of $\tilde{\unicode[STIX]{x1D6FF}}/\tilde{R}=0.08{-}0.12\,\%$ at the inlet of the rotating pipe $(z=0)$ . For $\log (\unicode[STIX]{x1D711}Re)\geqslant 4.22$ the axial boundary layer is turbulent; the turbulence intensity has a value of approximately $Tu_{z}:=\tilde{u} _{rms}^{\prime }/\tilde{U} =1\,\%$ in the core region and $13\,\%$ in the boundary layer. The turbulence intensity slightly increases with increasing core velocity.

There is a small axial gap of $4\,\unicode[STIX]{x2030}\,\tilde{R}$ between the non-rotating and the rotating pipe. The rotating pipe with a diameter of 50 mm and a length of $5\tilde{R}$ is supported by sealed ball bearings and is driven by a belt. Thus, the gap is sealed as well. By doing so, a maximum angular speed of $\tilde{\unicode[STIX]{x1D6FA}}=1308~\text{s}^{-1}$ is reached and controlled. The rotating pipe is made of stainless steel with a surface roughness of $\tilde{R}_{z}/\tilde{R}=0.04\,\%$ . For the experiment we also coated the pipe with silicon carbide powder of different grain sizes to change the surface roughness. This resulted in three further relative roughnesses: $0.75\,\%$ , $1.24\,\%$ and $4.90\,\%$ . The air leaves the rotating pipe as a free jet. The advantage of this design is a convenient accessibility from downstream to the flow field within the rotating pipe.

This accessibility is used to measure the circumferential velocity component by one-dimensional LDA with frequency shift. The probe has a focus of $315$  mm and is located downstream of the rotating pipe at an angle of $12^{\circ }$ . By doing so, only the swirl component is measured and averaged over ${\geqslant}30$  s, weighted by the transit time and consisting of at least 500 velocity measurements. The measurement volume has a length of ${<}1.6\,\%\,\tilde{R}$ and a diameter of ${<}2\,\unicode[STIX]{x2030}\,\tilde{R}$ . The measurement volume can be moved in a two-dimensional plane by using a traverse table. The positioning accuracy of the measurement volume is approximated as $\pm 4\,\unicode[STIX]{x2030}\,\tilde{R}$ in the plane. With this LDA system, a measurement of the swirl velocity up to a wall distance of ${>}1.6\,\%\,\tilde{R}$ is possible. An aerosol of silicone oil as tracer particles is added to the air to enable LDA measurements; see figure 4.

Hence, all design and operation parameters are chosen so that typical Reynolds numbers $\log (Re)=4.1{-}5.1$ and flow numbers $\unicode[STIX]{x1D711}=0.05{-}1$ of the turbomachinery are met. The systematic error of the Reynolds number is less than $2\,\%$ and that of the flow number less than $3.6\,\%$ .

Figure 5. Measured self-similar swirl velocity profile versus axial coordinate, Reynolds number and flow number for attached flow for $R_{z}=0.04\,\%$ .

5.2 Swirl velocity profile

In the developing region for an attached turbulent flow, the swirl velocity profile is self-similar within the swirl boundary layer $u_{\unicode[STIX]{x1D719}}(y<\unicode[STIX]{x1D6FF}_{S},z)=(1-y/\unicode[STIX]{x1D6FF}_{S}(z))^{2}$ , as measurements indicate; see figure 5. This measurement result confirms that the incoming flow is turbulent; cf. the literature review. Below the critical flow number $\unicode[STIX]{x1D711}_{c}$ , the boundary layer separates and the swirl velocity distribution changes dramatically. For turbulent flow and Reynolds numbers up to $Re=10^{5.1}$ , the swirl velocity profile is unaffected by Reynolds number and flow number for attached flow.

To validate our results, we performed three series of independent parameter variations: Reynolds number (figure 2 b), flow number (figure 2 c) and surface roughness (figure 6). In the parameter field investigated, the measurement result of swirl boundary layer thickness is in accordance with the analytical solution for the smooth pipe. Only in figure 2(a) next to the entrance of the rotating pipe, $z<1$ , is a relative deviation of approximately $10\,\%$ observable. The dependence of the swirl boundary layer thickness on the axial coordinate, Reynolds number and flow number in the measurements agrees very well with the analytical solution. Hence, the derived generalized von Kármán equation (see § 3) describes the flow situation at the inlet of a rotating pipe. The agreement between the experimental data and the model is better by far than the agreement between experiment and computational fluid dynamics results; cf. the literature review.

5.3 Surface roughness

On the basis of Nikuradse’s and Prandtl’s work we know that, when the Reynolds number of a non-swirling flow reaches a critical value, depending on surface roughness, both the velocity profile and also wall shear stress become independent of viscous friction, i.e. Reynolds number. Because up to this point we assumed hydraulically smooth walls, we examined the swirl boundary layer thickness at constant flow number $\unicode[STIX]{x1D711}=0.35$ , varying Reynolds number $\log (Re)=4.1{-}5.1$ for different pipe roughnesses. Figure 6 shows the measured swirl boundary layer thickness at $z=2$ . What is known from the axial boundary layer is also true for the swirl boundary layer: for Reynolds numbers below the critical number, the swirl boundary layer thickness is independent of roughness. When the critical value is exceeded, the swirl boundary layer thickness increases and ultimately becomes independent of the Reynolds number.

Figure 6. Influence of surface roughness on swirl boundary layer thickness versus Reynolds number.

Thus, the given analytical solutions with the chosen assumption of swirl velocity distribution and wall shear stress only represent the turbulent flow in a hydraulically smooth pipe. The extension of the presented method to rough surfaces is within the current research focus.

For safe operation of turbomachinery it is desirable to predict part load recirculation. To do so, the critical flow number $\unicode[STIX]{x1D711}_{c}$ is needed. The method validated so far can easily serve for Stratford’s criterion (Stratford 1959) to predict the stability limit $\unicode[STIX]{x1D711}_{c}(Re)$ . This is done in § 5.4.

Figure 7. Experimentally measured $\unicode[STIX]{x1D711}_{c}$ for fully separated flow at the inlet of a rotating pipe for the hydraulically smooth case.

5.4 Flow separation

In the following, we restrict ourselves to turbulent flow in a hydraulically smooth pipe. From the velocity measurements, we derive the desired stability limit $\unicode[STIX]{x1D711}_{c}=\unicode[STIX]{x1D711}_{c}(Re)$ . In parallel with our experiments, we identify the critical flow number $\unicode[STIX]{x1D711}_{c}$ for the fully separated flow, e.g. part load recirculation at the inlet of the rotating pipe. The stability map is shown in figure 7. In the core region, the fluid is accelerated, hence $\text{d}P/\text{d}z<0$ , whereas at the wall, the axial component of the wall pressure gradient $\text{d}p_{w}/\text{d}z$ can be positive due to swirl. From (3.7) for $y=0$ with (3.6) and (3.20), we obtain

(5.1) $$\begin{eqnarray}\frac{\text{d}p_{w}}{\text{d}z}=\frac{\text{d}}{\text{d}z}\int _{0}^{\unicode[STIX]{x1D6FF}_{S}}\frac{u_{\unicode[STIX]{x1D711}}^{2}}{1-y^{\prime }}\,\text{d}y^{\prime }-\frac{2U^{2}}{1-\unicode[STIX]{x1D6FF}_{1}}\frac{\text{d}\unicode[STIX]{x1D6FF}_{1}}{\text{d}z}.\end{eqnarray}$$

Hence, the swirl can cause a positive pressure gradient at the wall and also aids the growth of the axial boundary layer. Both effects provoke a separation of the axial boundary layer when a critical flow number $\unicode[STIX]{x1D711}_{c}(Re)$ is reached. To indicate an incipient separation, we assume the swirl-induced pressure slope as a superimposed pressure field for an axial boundary layer in a non-rotating pipe $G(=0)$ . Then, we use the criterion of Stratford (1959) to determine the point of zero wall friction. Starting from equation (16)

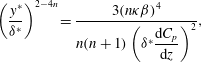(5.2) $$\begin{eqnarray}\left(\frac{y^{\ast }}{\unicode[STIX]{x1D6FF}^{\ast }}\right)^{2-4n}=\frac{3(n\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FD})^{4}}{n(n+1)\left(\unicode[STIX]{x1D6FF}^{\ast }{\displaystyle \frac{\text{d}C_{p}}{\text{d}z}}\right)^{2}},\end{eqnarray}$$

with equation (17)

(5.3) $$\begin{eqnarray}\left(\frac{u}{u^{\ast }}\right)^{2}=\frac{3n}{1+n},\end{eqnarray}$$

and equation (18) of Stratford (1959)

(5.4) $$\begin{eqnarray}C_{p}=\left[1-\left(\frac{u}{u^{\ast }}\right)^{2}\right]\left(\frac{y^{\ast }}{\unicode[STIX]{x1D6FF}^{\ast }}\right)^{2n},\end{eqnarray}$$

where $y^{\ast }=y$ , $\unicode[STIX]{x1D6FF}^{\ast }=\unicode[STIX]{x1D6FF}(G=0)$ and $C_{p}=2(p^{\ast }-p_{0}(G=0))/\unicode[STIX]{x1D711}^{2}$ with

(5.5) $$\begin{eqnarray}p^{\ast }=\frac{1}{\unicode[STIX]{x1D6FF}_{S}}\int _{0}^{\unicode[STIX]{x1D6FF}_{S}}p(y,z)\,\text{d}y,\end{eqnarray}$$

$p$ is given by (3.7) and $p_{0}(G=0)=\text{d}p_{0}(G=0)/\text{d}z=0$ . By doing so, an alternative, equivalent pressure distribution within the swirl boundary layer is defined by (5.5), which is independent of the wall coordinate as is necessary for using Stratford’s criterion. To avoid overestimating the influence of the centrifugal force, the pressure distribution is area averaged within the swirl boundary layer by (5.5). Here $p^{\ast }$ represents the pressure within the outer layer, and the pressure gradient in (5.2) represents the pressure distribution within the inner layer. Therefore, the wall pressure gradient (5.1) is used and not the pressure gradient of $p^{\ast }$ . To balance the omitted higher-order term, Stratford introduced the empirical parameter $\unicode[STIX]{x1D6FD}$ . The wall shear stress $\unicode[STIX]{x1D70F}_{yz,w}$ vanishes for

(5.6) $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6FF}(G=0)}{\unicode[STIX]{x1D711}^{2}}\frac{\text{d}p_{w}}{\text{d}z}\left(\frac{p^{\ast }}{\unicode[STIX]{x1D711}^{2}}\right)^{(1-2n)/2n}=\frac{1}{2}(n\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FD})^{2}\left(\frac{1-2n}{2+2n}\right)^{(1-2n)/2n}\sqrt{\frac{3}{n(n+1)}}.\end{eqnarray}$$

The von Kármán constant appears because Stratford describes the Reynolds stresses with Prandtl’s mixing model to consider the profile transformation within the inner layer due to the pressure rise; see (11) of Stratford (1959). With $\unicode[STIX]{x1D705}=0.4$ , $n=1/7$ and $\unicode[STIX]{x1D6FD}=0.66$ , this simplifies to

(5.7) $$\begin{eqnarray}\unicode[STIX]{x1D711}_{c}=3.442\left(\unicode[STIX]{x1D6FF}(G=0)\frac{\text{d}p_{w}}{\text{d}z}p^{\ast 5/2}\right)^{1/7}.\end{eqnarray}$$

With equation (4.2) and $k=2$ , $\text{d}p_{w}/\text{d}z$ is given by (5.1), $p^{\ast }$ is given by (5.5) and $\unicode[STIX]{x1D6FF}(G=0)$ . When the zero wall shear stress condition is fulfilled, an incipient separation is predicted. In figure 8, the isoline for zero wall shear stress (5.7) is plotted versus the axial coordinate at $\log (Re)=4.7$ .

Figure 8. Zero wall shear stress at $\unicode[STIX]{x1D711}_{c}$ and measured separation.

One must be aware that the criterion $\unicode[STIX]{x1D70F}_{yz,w}=0$ indicates the beginning of flow separation. Hence, the associated $\unicode[STIX]{x1D711}_{c}$ given by (5.7) indicates the incipient separation. For a validation of separation criterion (5.7), we observe the swirl velocity profile as an indicator of the beginning of flow separation. When separation occurs, the swirl velocity profile within the swirl boundary layer differs from the self-similar swirl velocity profile of an attached flow (broken lines in figure 9) and a new distribution develops. At different axial positions, the swirl velocity profile is measured by changing the flow number. Hence, we determine the separation with the swirl velocity profile as an indicator depending on the axial coordinate, as shown in figure 9. We define separation when the measured swirl velocity profile differs on average by more than $15\,\%$ from the attached swirl velocity profile.

Figure 9. Measured swirl velocity profile depending on axial coordinate and flow number to indicate separation.

By reducing the flow number, the measurements show a transformation of the swirl velocity profile beginning further downstream. This transformation moves upstream as the flow number is reduced, until the swirl reaches the non-rotating pipe and indicates the fully developed separation at the critical flow number. The comparison of the separation criterion (5.7) is in qualitative agreement with the experimental findings, as figure 8 indicates.

6 Conclusion

Applying the integral method of boundary layer theory, a generalization of the von Kármán momentum equation is derived to model the flow at the inlet of a rotating pipe. By doing so, the radial pressure distribution due to the centrifugal force is considered and yields a coupling term $G$ which is solved by using the angular momentum equation. Equations (3.13), (3.18) and (3.20) are solved, assuming an ansatz function, e.g. power laws, for the axial and circumferential velocity distribution and wall shear stresses. The solutions of the boundary layer thicknesses $\unicode[STIX]{x1D6FF}_{S}$ and $\unicode[STIX]{x1D6FF}$ , figures 2 and 3, take Reynolds number and flow number into account. The growth of the swirl boundary layer thickness is confirmed by experiments for the hydraulically smooth wall. Both boundary layers become thicker for small flow numbers due to swirl and this is in contrast to the results of Kikuyama et al. (1983a ). For $\unicode[STIX]{x1D711}\ll 1$ , the influence of the coupling term $G$ becomes of the same order of magnitude as the wall shear stress and dominates the axial boundary layer thickness. Hence, the radial pressure distribution should not be neglected for small flow numbers. Additionally, it is well known that the swirl deforms the axial velocity distribution and this could be quantified by the coupling term $G$ using the axial boundary layer thickness from measurements as an input to the differential equation system. The validation of the axial boundary layer is within the current research focus.

For a hydraulically rough wall, the experiments meet our expectation and the expansion of the given approach will be researched further. When the critical Reynolds number is exceeded, the swirl boundary layer becomes independent of viscous friction, i.e. the Reynolds number, but depends on the surface roughness and its thickness increases. Figure 6 is analogous to the well-known Nikuradse diagram (Nikuradse 1933) for the swirl boundary layer.

With decreasing Reynolds number and flow number, a critical flow number is reached and the wall shear stress vanishes. We call this point incipient separation. Applying Stratford’s criterion, we derived a critical flow number for this point and validated it with measurements. Incipient separation begins downstream and moves upstream for reduced flow numbers. Full separation is expected at a flow number below this critical value, as figure 7 shows. Closing, this prediction of part load recirculation in a rotating pipe is employable for the design of a turbomachine, especially a shrouded turbomachine and flow channels of secondary air flow of a gas turbine. Thus, part load recirculation does not require blades.