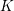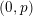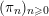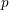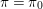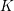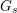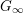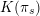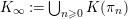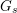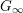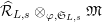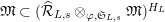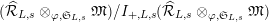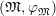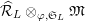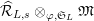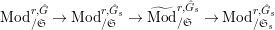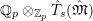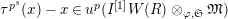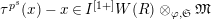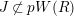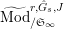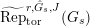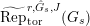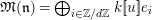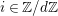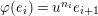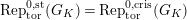1 Introduction
Let
![]() $p$
be a prime number and
$p$
be a prime number and
![]() $r\geqslant 0$
an integer. Let
$r\geqslant 0$
an integer. Let
![]() $K$
be a complete discrete valuation field of mixed characteristic
$K$
be a complete discrete valuation field of mixed characteristic
![]() $(0,p)$
with perfect residue field and absolute ramification index
$(0,p)$
with perfect residue field and absolute ramification index
![]() $e$
. Let
$e$
. Let
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{0}$
be a uniformizer of
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{0}$
be a uniformizer of
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D70B}_{n}$
a
$\unicode[STIX]{x1D70B}_{n}$
a
![]() $p^{n}$
th root of
$p^{n}$
th root of
![]() $\unicode[STIX]{x1D70B}$
such that
$\unicode[STIX]{x1D70B}$
such that
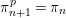 $\unicode[STIX]{x1D70B}_{n+1}^{p}=\unicode[STIX]{x1D70B}_{n}$
for all
$\unicode[STIX]{x1D70B}_{n+1}^{p}=\unicode[STIX]{x1D70B}_{n}$
for all
![]() $n\geqslant 0$
. For any integer
$n\geqslant 0$
. For any integer
![]() $s\geqslant 0$
, we put
$s\geqslant 0$
, we put
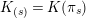 $K_{(s)}=K(\unicode[STIX]{x1D70B}_{s})$
. We also put
$K_{(s)}=K(\unicode[STIX]{x1D70B}_{s})$
. We also put
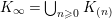 $K_{\infty }=\bigcup _{n\geqslant 0}K_{(n)}$
. We denote by
$K_{\infty }=\bigcup _{n\geqslant 0}K_{(n)}$
. We denote by
![]() $G_{K},G_{s}$
and
$G_{K},G_{s}$
and
![]() $G_{\infty }$
absolute Galois groups of
$G_{\infty }$
absolute Galois groups of
![]() $K$
,
$K$
,
![]() $K_{(s)}$
and
$K_{(s)}$
and
![]() $K_{\infty }$
, respectively. By definition we have the following decreasing sequence of Galois groups:
$K_{\infty }$
, respectively. By definition we have the following decreasing sequence of Galois groups:
 $$\begin{eqnarray}G_{K}=G_{0}\supset G_{1}\supset G_{2}\supset \cdots \supset G_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}G_{K}=G_{0}\supset G_{1}\supset G_{2}\supset \cdots \supset G_{\infty }.\end{eqnarray}$$
Since
![]() $K_{\infty }$
is a strict APF extension of
$K_{\infty }$
is a strict APF extension of
![]() $K$
, the theory of fields of norm implies that
$K$
, the theory of fields of norm implies that
![]() $G_{\infty }$
is isomorphic to the absolute Galois group of some field of characteristic
$G_{\infty }$
is isomorphic to the absolute Galois group of some field of characteristic
![]() $p$
. Therefore, representations of
$p$
. Therefore, representations of
![]() $G_{\infty }$
have easy interpretations via Fontaine’s étale
$G_{\infty }$
have easy interpretations via Fontaine’s étale
![]() $\unicode[STIX]{x1D711}$
-modules. Hence it seems natural to pose the following question:
$\unicode[STIX]{x1D711}$
-modules. Hence it seems natural to pose the following question:
Question 1.1. Let
![]() $T$
be a
$T$
be a
![]() $\mathbb{Z}_{p}$
- or
$\mathbb{Z}_{p}$
- or
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
. How small can we choose
$G_{K}$
. How small can we choose
![]() $s\geqslant 0$
to recover “enough” information of
$s\geqslant 0$
to recover “enough” information of
![]() $T|_{G_{s}}$
from that of
$T|_{G_{s}}$
from that of
![]() $T|_{G_{\infty }}$
?
$T|_{G_{\infty }}$
?
Nowadays there is an interesting insight of Breuil for this question; he showed that representations of
![]() $G_{K}$
arising from finite flat group schemes or
$G_{K}$
arising from finite flat group schemes or
![]() $p$
-divisible groups over the integer ring of
$p$
-divisible groups over the integer ring of
![]() $K$
are “determined” by their restriction to
$K$
are “determined” by their restriction to
![]() $G_{\infty }$
. Furthermore, for
$G_{\infty }$
. Furthermore, for
![]() $\mathbb{Q}_{p}$
-representations, Kisin proved the following theorem in [Reference KisinKis] (which was a conjecture of Breuil): the restriction functor from the category of crystalline
$\mathbb{Q}_{p}$
-representations, Kisin proved the following theorem in [Reference KisinKis] (which was a conjecture of Breuil): the restriction functor from the category of crystalline
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{K}$
into the category of
$G_{K}$
into the category of
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{\infty }$
is fully faithful.
$G_{\infty }$
is fully faithful.
In this paper, we give some partial answers to Question 1.1 for torsion crystalline representations. A torsion
![]() $\mathbb{Z}_{p}$
-representation
$\mathbb{Z}_{p}$
-representation
![]() $T$
of
$T$
of
![]() $G_{K}$
is torsion crystalline with Hodge–Tate weights in
$G_{K}$
is torsion crystalline with Hodge–Tate weights in
![]() $[0,r]$
if it can be written as the quotient of lattices in some crystalline
$[0,r]$
if it can be written as the quotient of lattices in some crystalline
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
with Hodge–Tate weights in
$G_{K}$
with Hodge–Tate weights in
![]() $[0,r]$
. Let
$[0,r]$
. Let
 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
be the category of them. In the case
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
be the category of them. In the case
![]() $r=1$
, such representations are equivalent to finite flat representations. (Here, a torsion
$r=1$
, such representations are equivalent to finite flat representations. (Here, a torsion
![]() $\mathbb{Z}_{p}$
-representation of
$\mathbb{Z}_{p}$
-representation of
![]() $G_{K}$
is finite flat if it arises from the generic fiber of some
$G_{K}$
is finite flat if it arises from the generic fiber of some
![]() $p$
-power order finite flat commutative group scheme over the integer ring of
$p$
-power order finite flat commutative group scheme over the integer ring of
![]() $K$
.) We denote by
$K$
.) We denote by
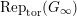 $\text{Rep}_{\text{tor}}(G_{\infty })$
the category of torsion
$\text{Rep}_{\text{tor}}(G_{\infty })$
the category of torsion
![]() $\mathbb{Z}_{p}$
-representations of
$\mathbb{Z}_{p}$
-representations of
![]() $G_{\infty }$
. The first main result in this paper is as follows.
$G_{\infty }$
. The first main result in this paper is as follows.
Theorem 1.2. (Full Faithfulness Theorem)
Suppose
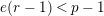 $e(r-1)<p-1$
. Then the restriction functor
$e(r-1)<p-1$
. Then the restriction functor
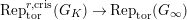 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is fully faithful.
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is fully faithful.
Before this work, some results were already known. First, the full faithfulness theorem was proved by Breuil for
![]() $e=1$
and
$e=1$
and
 $r<p-1$
via the Fontaine–Laffaille theory [Reference BreuilBr2, the proof of Théorèm 5.2]. He also proved the theorem under the assumptions
$r<p-1$
via the Fontaine–Laffaille theory [Reference BreuilBr2, the proof of Théorèm 5.2]. He also proved the theorem under the assumptions
![]() $p>2$
and
$p>2$
and
![]() $r\leqslant 1$
as a consequence of a study of the category of finite flat group schemes [Reference BreuilBr3, Theorem 3.4.3]. Later, his result was extended to the case
$r\leqslant 1$
as a consequence of a study of the category of finite flat group schemes [Reference BreuilBr3, Theorem 3.4.3]. Later, his result was extended to the case
![]() $p=2$
in [Reference KimKim], [Reference LauLa], [Reference LiuLi4] (proved independently). In particular, the case
$p=2$
in [Reference KimKim], [Reference LauLa], [Reference LiuLi4] (proved independently). In particular, the case
![]() $p=2$
of the full faithfulness theorem is a consequence of their works. On the other hand, Abrashkin proved the full faithfulness in the case where
$p=2$
of the full faithfulness theorem is a consequence of their works. On the other hand, Abrashkin proved the full faithfulness in the case where
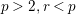 $p>2,r<p$
and
$p>2,r<p$
and
![]() $K$
is a finite unramified extension of
$K$
is a finite unramified extension of
![]() $\mathbb{Q}_{p}$
[Reference AbrashkinAb2, Section 8.3.3]. His proof is based on calculations of ramification bounds for torsion crystalline representations. In [Reference OzekiOz2], a proof of Theorem 1.2 under the assumption
$\mathbb{Q}_{p}$
[Reference AbrashkinAb2, Section 8.3.3]. His proof is based on calculations of ramification bounds for torsion crystalline representations. In [Reference OzekiOz2], a proof of Theorem 1.2 under the assumption
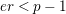 $er<p-1$
is given via
$er<p-1$
is given via
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules (which was introduced by Tong Liu [Reference LiuLi2] to classify lattices in semistable representations). We should remark that Abrashkin’s approach implies that calculations of ramification bounds induce full faithfulness results on restriction functors such as our theorems. However, known results on ramification bounds for torsion crystalline representations are not sufficient to obtain our results. Conversely, our results possibly help us to study ramification bounds for them.
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules (which was introduced by Tong Liu [Reference LiuLi2] to classify lattices in semistable representations). We should remark that Abrashkin’s approach implies that calculations of ramification bounds induce full faithfulness results on restriction functors such as our theorems. However, known results on ramification bounds for torsion crystalline representations are not sufficient to obtain our results. Conversely, our results possibly help us to study ramification bounds for them.
Our proof of Theorem 1.2 is similar to the proof for the main result of [Reference OzekiOz2], but we need more careful considerations for
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules. In fact, we prove a full faithfulness theorem for torsion representations arising from certain classes of
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules. In fact, we prove a full faithfulness theorem for torsion representations arising from certain classes of
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules (cf. Theorem 4.9), which immediately gives our main theorem. In addition, our study gives a result as below which is the second main result of this paper (here, we define
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules (cf. Theorem 4.9), which immediately gives our main theorem. In addition, our study gives a result as below which is the second main result of this paper (here, we define
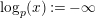 $\text{log}_{p}(x):=-\infty$
for any real number
$\text{log}_{p}(x):=-\infty$
for any real number
![]() $x\leqslant 0$
).
$x\leqslant 0$
).
Theorem 1.3. Suppose that
![]() $p$
is odd and
$p$
is odd and
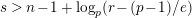 $s>n-1+\text{log}_{p}(r-(p-1)/e)$
. Let
$s>n-1+\text{log}_{p}(r-(p-1)/e)$
. Let
![]() $T$
and
$T$
and
![]() $T^{\prime }$
be objects of
$T^{\prime }$
be objects of
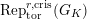 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
which are killed by
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
which are killed by
![]() $p^{n}$
. Then any
$p^{n}$
. Then any
![]() $G_{\infty }$
-equivariant homomorphism
$G_{\infty }$
-equivariant homomorphism
![]() $T\rightarrow T^{\prime }$
is
$T\rightarrow T^{\prime }$
is
![]() $G_{s}$
-equivariant.
$G_{s}$
-equivariant.
For torsion semistable representations, a similar result was shown in [Reference Caruso and LiuCL2, Theorem 3], which was a consequence of a study of ramification bounds. The bound appearing in their theorem was
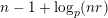 $n-1+\text{log}_{p}(nr)$
. By applying our arguments given in this paper, we can obtain a generalization of their result; our refined condition is
$n-1+\text{log}_{p}(nr)$
. By applying our arguments given in this paper, we can obtain a generalization of their result; our refined condition is
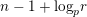 $n-1+\text{log}_{p}r$
(see Theorem 4.17). Some other consequences of our study are described in Section 4.7. Motivated by the full faithfulness theorem (= Theorem 1.2) and Theorem 1.3, we raise the following question.
$n-1+\text{log}_{p}r$
(see Theorem 4.17). Some other consequences of our study are described in Section 4.7. Motivated by the full faithfulness theorem (= Theorem 1.2) and Theorem 1.3, we raise the following question.
Question 1.4. Does there exist a constant
![]() $c$
depending on
$c$
depending on
![]() $e,r$
and
$e,r$
and
![]() $p$
so that any
$p$
so that any
![]() $G_{\infty }$
-equivariant homomorphism in the category
$G_{\infty }$
-equivariant homomorphism in the category
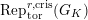 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
is
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
is
![]() $G_{s}$
-equivariant for
$G_{s}$
-equivariant for
![]() $s>c$
? Moreover, can we choose
$s>c$
? Moreover, can we choose
![]() $c$
to be
$c$
to be
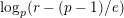 $\text{log}_{p}(r-(p-1)/e)$
?
$\text{log}_{p}(r-(p-1)/e)$
?
On the other hand, there exist counter examples of the full faithfulness theorem when we ignore the condition
 $e(r-1)<p-1$
. Let
$e(r-1)<p-1$
. Let
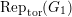 $\text{Rep}_{\text{tor}}(G_{1})$
be the category of torsion
$\text{Rep}_{\text{tor}}(G_{1})$
be the category of torsion
![]() $\mathbb{Z}_{p}$
-representations of
$\mathbb{Z}_{p}$
-representations of
![]() $G_{1}$
.
$G_{1}$
.
Theorem 1.5. (= Special case of Corollary 5.15)
Suppose that
![]() $K$
is a finite extension of
$K$
is a finite extension of
![]() $\mathbb{Q}_{p}$
, and also suppose
$\mathbb{Q}_{p}$
, and also suppose
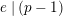 $e\mid (p-1)$
or
$e\mid (p-1)$
or
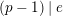 $(p-1)\mid e$
. If
$(p-1)\mid e$
. If
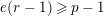 $e(r-1)\geqslant p-1$
, the restriction functor
$e(r-1)\geqslant p-1$
, the restriction functor
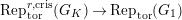 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{1})$
is not full (in particular, the restriction functor
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{1})$
is not full (in particular, the restriction functor
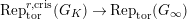 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is not full).
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is not full).
In particular, if
![]() $p=2$
, then the full faithfulness never hold for any finite extension
$p=2$
, then the full faithfulness never hold for any finite extension
![]() $K$
of
$K$
of
![]() $\mathbb{Q}_{2}$
and any
$\mathbb{Q}_{2}$
and any
![]() $r\geqslant 2$
. Theorem 1.5 implies that the condition “
$r\geqslant 2$
. Theorem 1.5 implies that the condition “
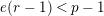 $e(r-1)<p-1$
” in Theorem 1.2 is optimal for many finite extensions
$e(r-1)<p-1$
” in Theorem 1.2 is optimal for many finite extensions
![]() $K$
of
$K$
of
![]() $\mathbb{Q}_{p}$
.
$\mathbb{Q}_{p}$
.
Now we describe the organization of this paper. In Section 2, we set up notations and summarize facts we need later. In Section 3, we define variant notions of
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules and give some basic properties. They are needed to study certain classes of potentially crystalline representations and restrictions of semistable representations. In Section 4, we study technical torsion
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules and give some basic properties. They are needed to study certain classes of potentially crystalline representations and restrictions of semistable representations. In Section 4, we study technical torsion
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules which are related with torsion (potentially) crystalline representations. The key result in this section is the full faithfulness result Theorem 4.9 on them, which allows us to prove our main results immediately. Finally, in Section 5, we calculate the smallest integer
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules which are related with torsion (potentially) crystalline representations. The key result in this section is the full faithfulness result Theorem 4.9 on them, which allows us to prove our main results immediately. Finally, in Section 5, we calculate the smallest integer
![]() $r$
for a given torsion representation
$r$
for a given torsion representation
![]() $T$
such that
$T$
such that
![]() $T$
admits a crystalline lift with Hodge–Tate weights in
$T$
admits a crystalline lift with Hodge–Tate weights in
![]() $[0,r]$
. We mainly study the rank two case. We use our full faithfulness theorem to assure the nonexistence of crystalline lifts with small Hodge–Tate weights. Theorem 1.5 is a consequence of studies of this section.
$[0,r]$
. We mainly study the rank two case. We use our full faithfulness theorem to assure the nonexistence of crystalline lifts with small Hodge–Tate weights. Theorem 1.5 is a consequence of studies of this section.
Notation and convention: Throughout this paper, we fix a prime number
![]() $p$
. Except in Section 5, we always assume that
$p$
. Except in Section 5, we always assume that
![]() $p$
is odd.
$p$
is odd.
For any topological group
![]() $H$
, we denote by
$H$
, we denote by
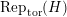 $\text{Rep}_{\text{tor}}(H)$
(resp.
$\text{Rep}_{\text{tor}}(H)$
(resp.
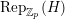 $\text{Rep}_{\mathbb{Z}_{p}}(H)$
, resp.
$\text{Rep}_{\mathbb{Z}_{p}}(H)$
, resp.
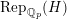 $\text{Rep}_{\mathbb{Q}_{p}}(H)$
) the category of torsion
$\text{Rep}_{\mathbb{Q}_{p}}(H)$
) the category of torsion
![]() $\mathbb{Z}_{p}$
-representations of
$\mathbb{Z}_{p}$
-representations of
![]() $H$
(resp. the category of free
$H$
(resp. the category of free
![]() $\mathbb{Z}_{p}$
-representations of
$\mathbb{Z}_{p}$
-representations of
![]() $H$
, resp. the category of
$H$
, resp. the category of
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $H$
). All
$H$
). All
![]() $\mathbb{Z}_{p}$
-representations (resp.
$\mathbb{Z}_{p}$
-representations (resp.
![]() $\mathbb{Q}_{p}$
-representations) in this paper are always assumed to be finitely generated over
$\mathbb{Q}_{p}$
-representations) in this paper are always assumed to be finitely generated over
![]() $\mathbb{Z}_{p}$
(resp.
$\mathbb{Z}_{p}$
(resp.
![]() $\mathbb{Q}_{p}$
) and continuous.
$\mathbb{Q}_{p}$
) and continuous.
For any field
![]() $F$
, we denote by
$F$
, we denote by
![]() $G_{F}$
the absolute Galois group of
$G_{F}$
the absolute Galois group of
![]() $F$
(for a fixed separable closure of
$F$
(for a fixed separable closure of
![]() $F$
).
$F$
).
2 Preliminaries
In this section, we recall definitions and basic properties for Kisin modules and
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules. Throughout Sections 2–4, we always assume that
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules. Throughout Sections 2–4, we always assume that
![]() $p$
is an odd prime.
$p$
is an odd prime.
2.1 Basic notations
Let
![]() $k$
be a perfect field of characteristic
$k$
be a perfect field of characteristic
![]() $p$
,
$p$
,
![]() $W(k)$
the ring of Witt vectors with coefficients in
$W(k)$
the ring of Witt vectors with coefficients in
![]() $k$
,
$k$
,
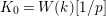 $K_{0}=W(k)[1/p]$
,
$K_{0}=W(k)[1/p]$
,
![]() $K$
a finite totally ramified extension of
$K$
a finite totally ramified extension of
![]() $K_{0}$
of degree
$K_{0}$
of degree
![]() $e$
,
$e$
,
![]() $\overline{K}$
a fixed algebraic closure of
$\overline{K}$
a fixed algebraic closure of
![]() $K$
. Throughout this paper, we fix a uniformizer
$K$
. Throughout this paper, we fix a uniformizer
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $K$
. Let
$K$
. Let
![]() $E(u)$
be the minimal polynomial of
$E(u)$
be the minimal polynomial of
![]() $\unicode[STIX]{x1D70B}$
over
$\unicode[STIX]{x1D70B}$
over
![]() $K_{0}$
. Then
$K_{0}$
. Then
![]() $E(u)$
is an Eisenstein polynomial. For any integer
$E(u)$
is an Eisenstein polynomial. For any integer
![]() $n\geqslant 0$
, we fix a system
$n\geqslant 0$
, we fix a system
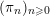 $(\unicode[STIX]{x1D70B}_{n})_{n\geqslant 0}$
of
$(\unicode[STIX]{x1D70B}_{n})_{n\geqslant 0}$
of
![]() $p^{n}$
th roots of
$p^{n}$
th roots of
![]() $\unicode[STIX]{x1D70B}$
in
$\unicode[STIX]{x1D70B}$
in
![]() $\overline{K}$
such that
$\overline{K}$
such that
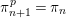 $\unicode[STIX]{x1D70B}_{n+1}^{p}=\unicode[STIX]{x1D70B}_{n}$
. Let
$\unicode[STIX]{x1D70B}_{n+1}^{p}=\unicode[STIX]{x1D70B}_{n}$
. Let
 $R=\varprojlim {\mathcal{O}}_{\overline{K}}/p$
, where
$R=\varprojlim {\mathcal{O}}_{\overline{K}}/p$
, where
![]() ${\mathcal{O}}_{\overline{K}}$
is the integer ring of
${\mathcal{O}}_{\overline{K}}$
is the integer ring of
![]() $\overline{K}$
and the transition maps are given by the
$\overline{K}$
and the transition maps are given by the
![]() $p$
th power map. For any integer
$p$
th power map. For any integer
![]() $s\geqslant 0$
, we write
$s\geqslant 0$
, we write
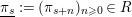 $\text{}\underline{\unicode[STIX]{x1D70B}_{s}}:=(\unicode[STIX]{x1D70B}_{s+n})_{n\geqslant 0}\in R$
and
$\text{}\underline{\unicode[STIX]{x1D70B}_{s}}:=(\unicode[STIX]{x1D70B}_{s+n})_{n\geqslant 0}\in R$
and
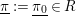 $\text{}\underline{\unicode[STIX]{x1D70B}}:=\text{}\underline{\unicode[STIX]{x1D70B}_{0}}\in R$
. Note that we have
$\text{}\underline{\unicode[STIX]{x1D70B}}:=\text{}\underline{\unicode[STIX]{x1D70B}_{0}}\in R$
. Note that we have
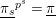 $\text{}\underline{\unicode[STIX]{x1D70B}_{s}}^{p^{s}}=\text{}\underline{\unicode[STIX]{x1D70B}}$
.
$\text{}\underline{\unicode[STIX]{x1D70B}_{s}}^{p^{s}}=\text{}\underline{\unicode[STIX]{x1D70B}}$
.
Let
![]() $L$
be the completion of an unramified algebraic extension of
$L$
be the completion of an unramified algebraic extension of
![]() $K$
with residue field
$K$
with residue field
![]() $k_{L}$
. Then
$k_{L}$
. Then
![]() $\unicode[STIX]{x1D70B}_{s}$
is a uniformizer of
$\unicode[STIX]{x1D70B}_{s}$
is a uniformizer of
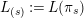 $L_{(s)}:=L(\unicode[STIX]{x1D70B}_{s})$
and
$L_{(s)}:=L(\unicode[STIX]{x1D70B}_{s})$
and
![]() $L_{(s)}$
is a totally ramified degree
$L_{(s)}$
is a totally ramified degree
![]() $ep^{s}$
extension of
$ep^{s}$
extension of
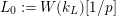 $L_{0}:=W(k_{L})[1/p]$
. We set
$L_{0}:=W(k_{L})[1/p]$
. We set
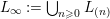 $L_{\infty }:=\bigcup _{n\geqslant 0}L_{(n)}$
. We put
$L_{\infty }:=\bigcup _{n\geqslant 0}L_{(n)}$
. We put
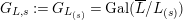 $G_{L,s}:=G_{L_{(s)}}=\text{Gal}(\overline{L}/L_{(s)})$
and
$G_{L,s}:=G_{L_{(s)}}=\text{Gal}(\overline{L}/L_{(s)})$
and
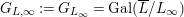 $G_{L,\infty }:=G_{L_{\infty }}=\text{Gal}(\overline{L}/L_{\infty })$
. By definitions, we have
$G_{L,\infty }:=G_{L_{\infty }}=\text{Gal}(\overline{L}/L_{\infty })$
. By definitions, we have
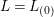 $L=L_{(0)}$
and
$L=L_{(0)}$
and
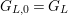 $G_{L,0}=G_{L}$
. Put
$G_{L,0}=G_{L}$
. Put
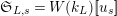 $\mathfrak{S}_{L,s}=W(k_{L})[\![u_{s}]\!]$
(resp.
$\mathfrak{S}_{L,s}=W(k_{L})[\![u_{s}]\!]$
(resp.
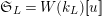 $\mathfrak{S}_{L}=W(k_{L})[\![u]\!]$
) with an indeterminate
$\mathfrak{S}_{L}=W(k_{L})[\![u]\!]$
) with an indeterminate
![]() $u_{s}$
(resp.
$u_{s}$
(resp.
![]() $u$
). We equip a Frobenius endomorphism
$u$
). We equip a Frobenius endomorphism
![]() $\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D711}$
of
![]() $\mathfrak{S}_{L,s}$
(resp.
$\mathfrak{S}_{L,s}$
(resp.
![]() $\mathfrak{S}_{L}$
) by
$\mathfrak{S}_{L}$
) by
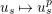 $u_{s}\mapsto u_{s}^{p}$
(resp.
$u_{s}\mapsto u_{s}^{p}$
(resp.
![]() $u\mapsto u^{p}$
) and the Frobenius on
$u\mapsto u^{p}$
) and the Frobenius on
![]() $W(k_{L})$
. We embed the
$W(k_{L})$
. We embed the
![]() $W(k_{L})$
-algebra
$W(k_{L})$
-algebra
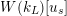 $W(k_{L})[u_{s}]$
(resp.
$W(k_{L})[u_{s}]$
(resp.
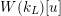 $W(k_{L})[u]$
) into
$W(k_{L})[u]$
) into
![]() $W(R)$
via the map
$W(R)$
via the map
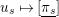 $u_{s}\mapsto [\text{}\underline{\unicode[STIX]{x1D70B}_{s}}]$
(resp.
$u_{s}\mapsto [\text{}\underline{\unicode[STIX]{x1D70B}_{s}}]$
(resp.
![]() $u\mapsto [\text{}\underline{\unicode[STIX]{x1D70B}}]$
), where
$u\mapsto [\text{}\underline{\unicode[STIX]{x1D70B}}]$
), where
![]() $[\ast ]$
stands for the Teichmüller representative. This embedding extends to an embedding
$[\ast ]$
stands for the Teichmüller representative. This embedding extends to an embedding
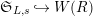 $\mathfrak{S}_{L,s}{\hookrightarrow}W(R)$
(resp.
$\mathfrak{S}_{L,s}{\hookrightarrow}W(R)$
(resp.
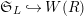 $\mathfrak{S}_{L}{\hookrightarrow}W(R)$
). By identifying
$\mathfrak{S}_{L}{\hookrightarrow}W(R)$
). By identifying
![]() $u$
with
$u$
with
![]() $u_{s}^{p^{s}}$
, we regard
$u_{s}^{p^{s}}$
, we regard
![]() $\mathfrak{S}_{L}$
as a subalgebra of
$\mathfrak{S}_{L}$
as a subalgebra of
![]() $\mathfrak{S}_{L,s}$
. It is readily seen that the embedding
$\mathfrak{S}_{L,s}$
. It is readily seen that the embedding
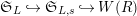 $\mathfrak{S}_{L}{\hookrightarrow}\mathfrak{S}_{L,s}{\hookrightarrow}W(R)$
is compatible with the Frobenius endomorphisms. If we denote by
$\mathfrak{S}_{L}{\hookrightarrow}\mathfrak{S}_{L,s}{\hookrightarrow}W(R)$
is compatible with the Frobenius endomorphisms. If we denote by
![]() $E_{s}(u_{s})$
the minimal polynomial of
$E_{s}(u_{s})$
the minimal polynomial of
![]() $\unicode[STIX]{x1D70B}_{s}$
over
$\unicode[STIX]{x1D70B}_{s}$
over
![]() $K_{0}$
, with indeterminate
$K_{0}$
, with indeterminate
![]() $u_{s}$
, then we have
$u_{s}$
, then we have
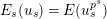 $E_{s}(u_{s})=E(u_{s}^{p^{s}})$
. Therefore, we have
$E_{s}(u_{s})=E(u_{s}^{p^{s}})$
. Therefore, we have
 $E_{s}(u_{s})=E(u)$
in
$E_{s}(u_{s})=E(u)$
in
![]() $\mathfrak{S}_{L,s}$
. We note that the minimal polynomial of
$\mathfrak{S}_{L,s}$
. We note that the minimal polynomial of
![]() $\unicode[STIX]{x1D70B}_{s}$
over
$\unicode[STIX]{x1D70B}_{s}$
over
![]() $L_{0}$
is
$L_{0}$
is
![]() $E_{s}(u_{s})$
.
$E_{s}(u_{s})$
.
Let
![]() $S_{L_{0},s}^{\text{int}}$
(resp.
$S_{L_{0},s}^{\text{int}}$
(resp.
![]() $S_{L_{0}}^{\text{int}}$
) be the
$S_{L_{0}}^{\text{int}}$
) be the
![]() $p$
-adic completion of the divided power envelope of
$p$
-adic completion of the divided power envelope of
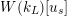 $W(k_{L})[u_{s}]$
(resp.
$W(k_{L})[u_{s}]$
(resp.
 $W(k_{L})[u]$
) with respect to the ideal generated by
$W(k_{L})[u]$
) with respect to the ideal generated by
![]() $E_{s}(u_{s})$
(resp.
$E_{s}(u_{s})$
(resp.
![]() $E(u)$
). There exist a unique Frobenius map
$E(u)$
). There exist a unique Frobenius map
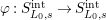 $\unicode[STIX]{x1D711}:S_{L_{0},s}^{\text{int}}\rightarrow S_{L_{0},s}^{\text{int}}$
(resp.
$\unicode[STIX]{x1D711}:S_{L_{0},s}^{\text{int}}\rightarrow S_{L_{0},s}^{\text{int}}$
(resp.
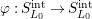 $\unicode[STIX]{x1D711}:S_{L_{0}}^{\text{int}}\rightarrow S_{L_{0}}^{\text{int}}$
) and monodromy
$\unicode[STIX]{x1D711}:S_{L_{0}}^{\text{int}}\rightarrow S_{L_{0}}^{\text{int}}$
) and monodromy
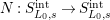 $N:S_{L_{0},s}^{\text{int}}\rightarrow S_{L_{0},s}^{\text{int}}$
defined by
$N:S_{L_{0},s}^{\text{int}}\rightarrow S_{L_{0},s}^{\text{int}}$
defined by
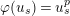 $\unicode[STIX]{x1D711}(u_{s})=u_{s}^{p}$
(resp.
$\unicode[STIX]{x1D711}(u_{s})=u_{s}^{p}$
(resp.
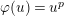 $\unicode[STIX]{x1D711}(u)=u^{p}$
) and
$\unicode[STIX]{x1D711}(u)=u^{p}$
) and
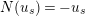 $N(u_{s})=-u_{s}$
(resp.
$N(u_{s})=-u_{s}$
(resp.
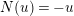 $N(u)=-u$
). Put
$N(u)=-u$
). Put
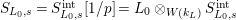 $S_{L_{0},s}=S_{L_{0},s}^{\text{int}}[1/p]=L_{0}\otimes _{W(k_{L})}S_{L_{0},s}^{\text{int}}$
(resp.
$S_{L_{0},s}=S_{L_{0},s}^{\text{int}}[1/p]=L_{0}\otimes _{W(k_{L})}S_{L_{0},s}^{\text{int}}$
(resp.
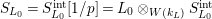 $S_{L_{0}}=S_{L_{0}}^{\text{int}}[1/p]=L_{0}\otimes _{W(k_{L})}S_{L_{0}}^{\text{int}}$
). We equip
$S_{L_{0}}=S_{L_{0}}^{\text{int}}[1/p]=L_{0}\otimes _{W(k_{L})}S_{L_{0}}^{\text{int}}$
). We equip
![]() $S_{L_{0},s}^{\text{int}}$
and
$S_{L_{0},s}^{\text{int}}$
and
![]() $S_{L_{0},s}$
(resp.
$S_{L_{0},s}$
(resp.
![]() $S_{L_{0}}^{\text{int}}$
and
$S_{L_{0}}^{\text{int}}$
and
![]() $S_{L_{0}}$
) with decreasing filtrations
$S_{L_{0}}$
) with decreasing filtrations
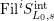 $\text{Fil}^{i}S_{L_{0},s}^{\text{int}}$
and
$\text{Fil}^{i}S_{L_{0},s}^{\text{int}}$
and
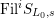 $\text{Fil}^{i}S_{L_{0},s}$
(resp.
$\text{Fil}^{i}S_{L_{0},s}$
(resp.
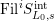 $\text{Fil}^{i}S_{L_{0},s}^{\text{int}}$
and
$\text{Fil}^{i}S_{L_{0},s}^{\text{int}}$
and
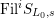 $\text{Fil}^{i}S_{L_{0},s}$
) by the
$\text{Fil}^{i}S_{L_{0},s}$
) by the
![]() $p$
-adic completion of the ideal generated by
$p$
-adic completion of the ideal generated by
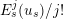 $E_{s}^{j}(u_{s})/j!$
(resp.
$E_{s}^{j}(u_{s})/j!$
(resp.
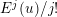 $E^{j}(u)/j!$
) for all
$E^{j}(u)/j!$
) for all
![]() $j\geqslant 0$
. The inclusion
$j\geqslant 0$
. The inclusion
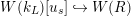 $W(k_{L})[u_{s}]{\hookrightarrow}W(R)$
(resp.
$W(k_{L})[u_{s}]{\hookrightarrow}W(R)$
(resp.
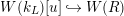 $W(k_{L})[u]{\hookrightarrow}W(R)$
) via the map
$W(k_{L})[u]{\hookrightarrow}W(R)$
) via the map
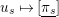 $u_{s}\mapsto [\text{}\underline{\unicode[STIX]{x1D70B}_{s}}]$
(resp.
$u_{s}\mapsto [\text{}\underline{\unicode[STIX]{x1D70B}_{s}}]$
(resp.
![]() $u\mapsto [\text{}\underline{\unicode[STIX]{x1D70B}}]$
) induces
$u\mapsto [\text{}\underline{\unicode[STIX]{x1D70B}}]$
) induces
![]() $\unicode[STIX]{x1D711}$
-compatible inclusions
$\unicode[STIX]{x1D711}$
-compatible inclusions
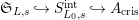 $\mathfrak{S}_{L,s}{\hookrightarrow}S_{L_{0},s}^{\text{int}}{\hookrightarrow}A_{\text{cris}}$
and
$\mathfrak{S}_{L,s}{\hookrightarrow}S_{L_{0},s}^{\text{int}}{\hookrightarrow}A_{\text{cris}}$
and
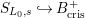 $S_{L_{0},s}{\hookrightarrow}B_{\text{cris}}^{+}$
(resp.
$S_{L_{0},s}{\hookrightarrow}B_{\text{cris}}^{+}$
(resp.
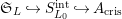 $\mathfrak{S}_{L}{\hookrightarrow}S_{L_{0}}^{\text{int}}{\hookrightarrow}A_{\text{cris}}$
and
$\mathfrak{S}_{L}{\hookrightarrow}S_{L_{0}}^{\text{int}}{\hookrightarrow}A_{\text{cris}}$
and
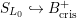 $S_{L_{0}}{\hookrightarrow}B_{\text{cris}}^{+}$
). By these inclusions, we often regard these rings as subrings of
$S_{L_{0}}{\hookrightarrow}B_{\text{cris}}^{+}$
). By these inclusions, we often regard these rings as subrings of
![]() $B_{\text{cris}}^{+}$
. By identifying
$B_{\text{cris}}^{+}$
. By identifying
![]() $u$
with
$u$
with
![]() $u_{s}^{p^{s}}$
as before, we regard
$u_{s}^{p^{s}}$
as before, we regard
![]() $S_{L_{0}}^{\text{int}}$
(resp.
$S_{L_{0}}^{\text{int}}$
(resp.
![]() $S_{L_{0}}$
) as a
$S_{L_{0}}$
) as a
![]() $\unicode[STIX]{x1D711}$
-stable (but not
$\unicode[STIX]{x1D711}$
-stable (but not
![]() $N$
-stable) subalgebra of
$N$
-stable) subalgebra of
![]() $S_{L_{0},s}^{\text{int}}$
(resp.
$S_{L_{0},s}^{\text{int}}$
(resp.
![]() $S_{L_{0},s}$
). By definitions, we have
$S_{L_{0},s}$
). By definitions, we have
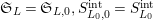 $\mathfrak{S}_{L}=\mathfrak{S}_{L,0},S_{L_{0},0}^{\text{int}}=S_{L_{0}}^{\text{int}}$
and
$\mathfrak{S}_{L}=\mathfrak{S}_{L,0},S_{L_{0},0}^{\text{int}}=S_{L_{0}}^{\text{int}}$
and
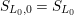 $S_{L_{0},0}=S_{L_{0}}$
(cf. Figure 1).
$S_{L_{0},0}=S_{L_{0}}$
(cf. Figure 1).
Convention: For simplicity, if
![]() $L=K$
, then we often omit the subscript “
$L=K$
, then we often omit the subscript “
![]() $L$
” from various notations (e.g.,
$L$
” from various notations (e.g.,
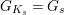 $G_{K_{s}}=G_{s}$
,
$G_{K_{s}}=G_{s}$
,
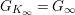 $G_{K_{\infty }}=G_{\infty }$
,
$G_{K_{\infty }}=G_{\infty }$
,
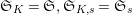 $\mathfrak{S}_{K}=\mathfrak{S},\mathfrak{S}_{K,s}=\mathfrak{S}_{s}$
).
$\mathfrak{S}_{K}=\mathfrak{S},\mathfrak{S}_{K,s}=\mathfrak{S}_{s}$
).

Figure 1. Ring extensions.
2.2 Kisin modules
Let
![]() $r,s\geqslant 0$
be integers. A
$r,s\geqslant 0$
be integers. A
![]() $\unicode[STIX]{x1D711}$
-module over
$\unicode[STIX]{x1D711}$
-module over
![]() $\mathfrak{S}_{L,s}$
is an
$\mathfrak{S}_{L,s}$
is an
![]() $\mathfrak{S}_{L,s}$
-module
$\mathfrak{S}_{L,s}$
-module
![]() $\mathfrak{M}$
equipped with a
$\mathfrak{M}$
equipped with a
![]() $\unicode[STIX]{x1D711}$
-semilinear map
$\unicode[STIX]{x1D711}$
-semilinear map
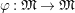 $\unicode[STIX]{x1D711}:\mathfrak{M}\rightarrow \mathfrak{M}$
. A morphism between two
$\unicode[STIX]{x1D711}:\mathfrak{M}\rightarrow \mathfrak{M}$
. A morphism between two
![]() $\unicode[STIX]{x1D711}$
-modules
$\unicode[STIX]{x1D711}$
-modules
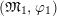 $(\mathfrak{M}_{1},\unicode[STIX]{x1D711}_{1})$
and
$(\mathfrak{M}_{1},\unicode[STIX]{x1D711}_{1})$
and
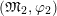 $(\mathfrak{M}_{2},\unicode[STIX]{x1D711}_{2})$
over
$(\mathfrak{M}_{2},\unicode[STIX]{x1D711}_{2})$
over
![]() $\mathfrak{S}_{L,s}$
is an
$\mathfrak{S}_{L,s}$
is an
![]() $\mathfrak{S}_{L,s}$
-linear map
$\mathfrak{S}_{L,s}$
-linear map
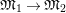 $\mathfrak{M}_{1}\rightarrow \mathfrak{M}_{2}$
compatible with
$\mathfrak{M}_{1}\rightarrow \mathfrak{M}_{2}$
compatible with
![]() $\unicode[STIX]{x1D711}_{1}$
and
$\unicode[STIX]{x1D711}_{1}$
and
![]() $\unicode[STIX]{x1D711}_{2}$
. Denote by
$\unicode[STIX]{x1D711}_{2}$
. Denote by
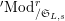 $^{\prime }\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
the category of
$^{\prime }\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
the category of
![]() $\unicode[STIX]{x1D711}$
-modules
$\unicode[STIX]{x1D711}$
-modules
![]() $(\mathfrak{M},\unicode[STIX]{x1D711})$
over
$(\mathfrak{M},\unicode[STIX]{x1D711})$
over
![]() $\mathfrak{S}_{L,s}$
of height
$\mathfrak{S}_{L,s}$
of height
![]() ${\leqslant}r$
in the sense that
${\leqslant}r$
in the sense that
![]() $\mathfrak{M}$
is of finite type over
$\mathfrak{M}$
is of finite type over
![]() $\mathfrak{S}_{L,s}$
and the cokernel of
$\mathfrak{S}_{L,s}$
and the cokernel of
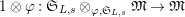 $1\otimes \unicode[STIX]{x1D711}:\mathfrak{S}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}\rightarrow \mathfrak{M}$
is killed by
$1\otimes \unicode[STIX]{x1D711}:\mathfrak{S}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}\rightarrow \mathfrak{M}$
is killed by
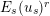 $E_{s}(u_{s})^{r}$
.
$E_{s}(u_{s})^{r}$
.
Let
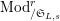 $\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
be the full subcategory of
$\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
be the full subcategory of
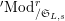 $^{\prime }\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
consisting of finite free
$^{\prime }\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
consisting of finite free
![]() $\mathfrak{S}_{L,s}$
-modules. We call an object of
$\mathfrak{S}_{L,s}$
-modules. We call an object of
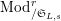 $\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
a free Kisin module
of height
$\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
a free Kisin module
of height
![]() ${\leqslant}r$
(over
${\leqslant}r$
(over
![]() $\mathfrak{S}_{L,s}$
).
$\mathfrak{S}_{L,s}$
).
Let
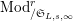 $\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r}$
be the full subcategory of
$\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r}$
be the full subcategory of
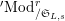 $^{\prime }\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
consisting of finite
$^{\prime }\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
consisting of finite
![]() $\mathfrak{S}_{L,s}$
-modules which are killed by some power of
$\mathfrak{S}_{L,s}$
-modules which are killed by some power of
![]() $p$
and have projective dimension
$p$
and have projective dimension
![]() $1$
in the sense that
$1$
in the sense that
![]() $\mathfrak{M}$
has a two term resolution by finite free
$\mathfrak{M}$
has a two term resolution by finite free
![]() $\mathfrak{S}_{L,s}$
-modules. We call an object of
$\mathfrak{S}_{L,s}$
-modules. We call an object of
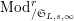 $\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r}$
a torsion Kisin module of height
$\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r}$
a torsion Kisin module of height
![]() ${\leqslant}r$
(over
${\leqslant}r$
(over
![]() $\mathfrak{S}_{L,s}$
).
$\mathfrak{S}_{L,s}$
).
For any free or torsion Kisin module
![]() $\mathfrak{M}$
over
$\mathfrak{M}$
over
![]() $\mathfrak{S}_{L,s}$
, we define a
$\mathfrak{S}_{L,s}$
, we define a
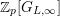 $\mathbb{Z}_{p}[G_{L,\infty }]$
-module
$\mathbb{Z}_{p}[G_{L,\infty }]$
-module
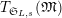 $T_{\mathfrak{S}_{L,s}}(\mathfrak{M})$
by
$T_{\mathfrak{S}_{L,s}}(\mathfrak{M})$
by
 $$\begin{eqnarray}T_{\mathfrak{S}_{L,s}}(\mathfrak{M}):=\left\{\begin{array}{@{}ll@{}}\text{Hom}_{\mathfrak{S}_{L,s},\unicode[STIX]{x1D711}}(\mathfrak{M},W(R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{free},\\ \text{Hom}_{\mathfrak{S}_{L,s},\unicode[STIX]{x1D711}}(\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{torsion}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}T_{\mathfrak{S}_{L,s}}(\mathfrak{M}):=\left\{\begin{array}{@{}ll@{}}\text{Hom}_{\mathfrak{S}_{L,s},\unicode[STIX]{x1D711}}(\mathfrak{M},W(R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{free},\\ \text{Hom}_{\mathfrak{S}_{L,s},\unicode[STIX]{x1D711}}(\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{torsion}.\end{array}\right.\end{eqnarray}$$
Here a
![]() $G_{L,\infty }$
-action on
$G_{L,\infty }$
-action on
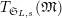 $T_{\mathfrak{S}_{L,s}}(\mathfrak{M})$
is given by
$T_{\mathfrak{S}_{L,s}}(\mathfrak{M})$
is given by
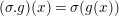 $(\unicode[STIX]{x1D70E}.g)(x)=\unicode[STIX]{x1D70E}(g(x))$
for
$(\unicode[STIX]{x1D70E}.g)(x)=\unicode[STIX]{x1D70E}(g(x))$
for
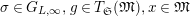 $\unicode[STIX]{x1D70E}\in G_{L,\infty },g\in T_{\mathfrak{S}}(\mathfrak{M}),x\in \mathfrak{M}$
.
$\unicode[STIX]{x1D70E}\in G_{L,\infty },g\in T_{\mathfrak{S}}(\mathfrak{M}),x\in \mathfrak{M}$
.
Convention: For simplicity, if
![]() $L=K$
, then we often omit the subscript “
$L=K$
, then we often omit the subscript “
![]() $L$
” from various notations (e.g.,
$L$
” from various notations (e.g.,
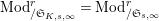 $\text{Mod}_{/\mathfrak{S}_{K,s,\infty }}^{r}=\text{Mod}_{/\mathfrak{S}_{s,\infty }}^{r}$
,
$\text{Mod}_{/\mathfrak{S}_{K,s,\infty }}^{r}=\text{Mod}_{/\mathfrak{S}_{s,\infty }}^{r}$
,
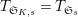 $T_{\mathfrak{S}_{K,s}}=T_{\mathfrak{S}_{s}}$
). Also, if
$T_{\mathfrak{S}_{K,s}}=T_{\mathfrak{S}_{s}}$
). Also, if
![]() $s=0$
, we often omit the subscript “
$s=0$
, we often omit the subscript “
![]() $s$
” from various notations (e.g.,
$s$
” from various notations (e.g.,
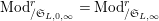 $\text{Mod}_{/\mathfrak{S}_{L,0,\infty }}^{r}=\text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r}$
,
$\text{Mod}_{/\mathfrak{S}_{L,0,\infty }}^{r}=\text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r}$
,
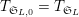 $T_{\mathfrak{S}_{L,0}}=T_{\mathfrak{S}_{L}}$
,
$T_{\mathfrak{S}_{L,0}}=T_{\mathfrak{S}_{L}}$
,
 $\text{Mod}_{/\mathfrak{S}_{K,0,\infty }}^{r}=\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
,
$\text{Mod}_{/\mathfrak{S}_{K,0,\infty }}^{r}=\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
,
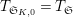 $T_{\mathfrak{S}_{K,0}}=T_{\mathfrak{S}}$
).
$T_{\mathfrak{S}_{K,0}}=T_{\mathfrak{S}}$
).
Proposition 2.1.
![]() $(1)$
[Reference KisinKis, Corollary 2.1.4 and Proposition 2.1.12] The functor
$(1)$
[Reference KisinKis, Corollary 2.1.4 and Proposition 2.1.12] The functor
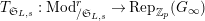 $T_{\mathfrak{S}_{L,s}}:\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}\rightarrow \text{Rep}_{\mathbb{Z}_{p}}(G_{\infty })$
is exact and fully faithful.
$T_{\mathfrak{S}_{L,s}}:\text{Mod}_{/\mathfrak{S}_{L,s}}^{r}\rightarrow \text{Rep}_{\mathbb{Z}_{p}}(G_{\infty })$
is exact and fully faithful.
![]() $(2)$
[Reference Caruso and LiuCL1, Corollaries 2.1.6, 3.3.10 and 3.3.15] The functor
$(2)$
[Reference Caruso and LiuCL1, Corollaries 2.1.6, 3.3.10 and 3.3.15] The functor
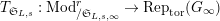 $T_{\mathfrak{S}_{L,s}}:\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r}\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is exact and faithful. Furthermore, it is full if
$T_{\mathfrak{S}_{L,s}}:\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r}\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is exact and faithful. Furthermore, it is full if
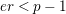 $er<p-1$
.
$er<p-1$
.
2.3
 $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules
The notion of
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules is introduced by Liu in [Reference LiuLi2] to classify lattices in semistable representations. We recall definitions and properties of them. We continue to use same notations as above.
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules is introduced by Liu in [Reference LiuLi2] to classify lattices in semistable representations. We recall definitions and properties of them. We continue to use same notations as above.
Let
![]() $L_{p^{\infty }}$
be the field obtained by adjoining all
$L_{p^{\infty }}$
be the field obtained by adjoining all
![]() $p$
-power roots of unity to
$p$
-power roots of unity to
![]() $L$
. We denote by
$L$
. We denote by
![]() $\hat{L}$
the composite field of
$\hat{L}$
the composite field of
![]() $L_{\infty }$
and
$L_{\infty }$
and
![]() $L_{p^{\infty }}$
. We define
$L_{p^{\infty }}$
. We define
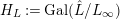 $H_{L}:=\text{Gal}(\hat{L}/L_{\infty })$
,
$H_{L}:=\text{Gal}(\hat{L}/L_{\infty })$
,
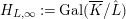 $H_{L,\infty }:=\text{Gal}(\overline{K}/\hat{L})$
$H_{L,\infty }:=\text{Gal}(\overline{K}/\hat{L})$
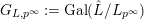 $G_{L,p^{\infty }}:=\text{Gal}(\hat{L}/L_{p^{\infty }})$
and
$G_{L,p^{\infty }}:=\text{Gal}(\hat{L}/L_{p^{\infty }})$
and
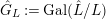 ${\hat{G}}_{L}:=\text{Gal}(\hat{L}/L)$
(cf. Figure 2). Furthermore, putting
${\hat{G}}_{L}:=\text{Gal}(\hat{L}/L)$
(cf. Figure 2). Furthermore, putting
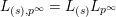 $L_{(s),p^{\infty }}=L_{(s)}L_{p^{\infty }\!}$
, we define
$L_{(s),p^{\infty }}=L_{(s)}L_{p^{\infty }\!}$
, we define
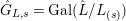 ${\hat{G}}_{L,s}=\text{Gal}(\hat{L}/L_{(s)})$
and
${\hat{G}}_{L,s}=\text{Gal}(\hat{L}/L_{(s)})$
and
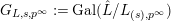 $G_{L,s,p^{\infty }}:=\text{Gal}(\hat{L}/L_{(s),p^{\infty }})$
.
$G_{L,s,p^{\infty }}:=\text{Gal}(\hat{L}/L_{(s),p^{\infty }})$
.

Figure 2. Galois groups of field extensions.
Since
![]() $p>2$
, it is known that
$p>2$
, it is known that
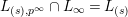 $L_{(s),p^{\infty }}\cap L_{\infty }=L_{(s)}$
and thus
$L_{(s),p^{\infty }}\cap L_{\infty }=L_{(s)}$
and thus
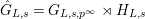 ${\hat{G}}_{L,s}=G_{L,s,p^{\infty }}\rtimes H_{L,s}$
(cf. [Reference LiuLi1, Lemma 5.1.2]). Furthermore,
${\hat{G}}_{L,s}=G_{L,s,p^{\infty }}\rtimes H_{L,s}$
(cf. [Reference LiuLi1, Lemma 5.1.2]). Furthermore,
![]() $G_{L,s,p^{\infty }}$
is topologically isomorphic to
$G_{L,s,p^{\infty }}$
is topologically isomorphic to
![]() $\mathbb{Z}_{p}$
.
$\mathbb{Z}_{p}$
.
Lemma 2.2. The natural map
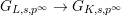 $G_{L,s,p^{\infty }}\rightarrow G_{K,s,p^{\infty }}$
defined by
$G_{L,s,p^{\infty }}\rightarrow G_{K,s,p^{\infty }}$
defined by
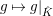 $g\mapsto g|_{\hat{K}}$
is bijective.
$g\mapsto g|_{\hat{K}}$
is bijective.
Proof. By replacing
![]() $L_{s}$
with
$L_{s}$
with
![]() $L$
, we may assume
$L$
, we may assume
![]() $s=0$
. It suffices to prove
$s=0$
. It suffices to prove
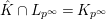 $\hat{K}\cap L_{p^{\infty }}=K_{p^{\infty }}$
. Since
$\hat{K}\cap L_{p^{\infty }}=K_{p^{\infty }}$
. Since
![]() $G_{K,p^{\infty }}$
is isomorphic to
$G_{K,p^{\infty }}$
is isomorphic to
![]() $\mathbb{Z}_{p}$
, we know that any finite subextension of
$\mathbb{Z}_{p}$
, we know that any finite subextension of
 $\hat{K}/K_{p^{\infty }}$
is of the form
$\hat{K}/K_{p^{\infty }}$
is of the form
![]() $K_{(s),p^{\infty }}$
for some
$K_{(s),p^{\infty }}$
for some
![]() $s\geqslant 0$
. Assume that we have
$s\geqslant 0$
. Assume that we have
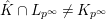 $\hat{K}\cap L_{p^{\infty }}\not =K_{p^{\infty }}$
. Then we have
$\hat{K}\cap L_{p^{\infty }}\not =K_{p^{\infty }}$
. Then we have
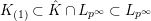 $K_{(1)}\subset \hat{K}\cap L_{p^{\infty }}\subset L_{p^{\infty }}$
. Thus
$K_{(1)}\subset \hat{K}\cap L_{p^{\infty }}\subset L_{p^{\infty }}$
. Thus
![]() $\unicode[STIX]{x1D70B}_{1}$
is contained in
$\unicode[STIX]{x1D70B}_{1}$
is contained in
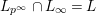 $L_{p^{\infty }}\cap L_{\infty }=L$
. However, since
$L_{p^{\infty }}\cap L_{\infty }=L$
. However, since
![]() $L$
is unramified over
$L$
is unramified over
![]() $K$
, this contradicts the fact that
$K$
, this contradicts the fact that
![]() $\unicode[STIX]{x1D70B}$
is a uniformizer of
$\unicode[STIX]{x1D70B}$
is a uniformizer of
![]() $L$
.◻
$L$
.◻
We fix a topological generator
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $G_{K,p^{\infty }}$
. We also denote by
$G_{K,p^{\infty }}$
. We also denote by
![]() $\unicode[STIX]{x1D70F}$
the preimage of
$\unicode[STIX]{x1D70F}$
the preimage of
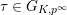 $\unicode[STIX]{x1D70F}\in G_{K,p^{\infty }}$
under the bijection
$\unicode[STIX]{x1D70F}\in G_{K,p^{\infty }}$
under the bijection
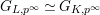 $G_{L,p^{\infty }}\simeq G_{K,p^{\infty }}$
of the above lemma. Note that
$G_{L,p^{\infty }}\simeq G_{K,p^{\infty }}$
of the above lemma. Note that
![]() $\unicode[STIX]{x1D70F}^{p^{s}}$
is a topological generator of
$\unicode[STIX]{x1D70F}^{p^{s}}$
is a topological generator of
![]() $G_{L,s,p^{\infty }}$
.
$G_{L,s,p^{\infty }}$
.
For any
![]() $g\in G_{K}$
, we put
$g\in G_{K}$
, we put
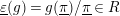 $\text{}\underline{\unicode[STIX]{x1D700}}(g)=g(\text{}\underline{\unicode[STIX]{x1D70B}})/\text{}\underline{\unicode[STIX]{x1D70B}}\in R$
, and define
$\text{}\underline{\unicode[STIX]{x1D700}}(g)=g(\text{}\underline{\unicode[STIX]{x1D70B}})/\text{}\underline{\unicode[STIX]{x1D70B}}\in R$
, and define
 $\text{}\underline{\unicode[STIX]{x1D700}}:=\text{}\underline{\unicode[STIX]{x1D700}}(\tilde{\unicode[STIX]{x1D70F}})$
. Here,
$\text{}\underline{\unicode[STIX]{x1D700}}:=\text{}\underline{\unicode[STIX]{x1D700}}(\tilde{\unicode[STIX]{x1D70F}})$
. Here,
![]() $\tilde{\unicode[STIX]{x1D70F}}\in G_{K}$
is any lift of
$\tilde{\unicode[STIX]{x1D70F}}\in G_{K}$
is any lift of
![]() $\unicode[STIX]{x1D70F}\in {\hat{G}}_{K}$
and then
$\unicode[STIX]{x1D70F}\in {\hat{G}}_{K}$
and then
![]() $\text{}\underline{\unicode[STIX]{x1D700}}(\tilde{\unicode[STIX]{x1D70F}})$
is independent of the choice of the lift of
$\text{}\underline{\unicode[STIX]{x1D700}}(\tilde{\unicode[STIX]{x1D70F}})$
is independent of the choice of the lift of
![]() $\unicode[STIX]{x1D70F}$
. With these notations, we also note that we have
$\unicode[STIX]{x1D70F}$
. With these notations, we also note that we have
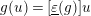 $g(u)=[\text{}\underline{\unicode[STIX]{x1D700}}(g)]u$
(recall that
$g(u)=[\text{}\underline{\unicode[STIX]{x1D700}}(g)]u$
(recall that
![]() $\mathfrak{S}$
is embedded in
$\mathfrak{S}$
is embedded in
![]() $W(R)$
). An easy computation shows that
$W(R)$
). An easy computation shows that
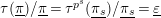 $\unicode[STIX]{x1D70F}(\text{}\underline{\unicode[STIX]{x1D70B}})/\text{}\underline{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D70F}^{p^{s}}(\text{}\underline{\unicode[STIX]{x1D70B}_{s}})/\text{}\underline{\unicode[STIX]{x1D70B}_{s}}=\text{}\underline{\unicode[STIX]{x1D700}}$
. Therefore, we have
$\unicode[STIX]{x1D70F}(\text{}\underline{\unicode[STIX]{x1D70B}})/\text{}\underline{\unicode[STIX]{x1D70B}}=\unicode[STIX]{x1D70F}^{p^{s}}(\text{}\underline{\unicode[STIX]{x1D70B}_{s}})/\text{}\underline{\unicode[STIX]{x1D70B}_{s}}=\text{}\underline{\unicode[STIX]{x1D700}}$
. Therefore, we have
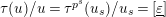 $\unicode[STIX]{x1D70F}(u)/u=\unicode[STIX]{x1D70F}^{p^{s}}(u_{s})/u_{s}=[\text{}\underline{\unicode[STIX]{x1D700}}]$
.
$\unicode[STIX]{x1D70F}(u)/u=\unicode[STIX]{x1D70F}^{p^{s}}(u_{s})/u_{s}=[\text{}\underline{\unicode[STIX]{x1D700}}]$
.
We put
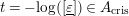 $t=-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}])\in A_{\text{cris}}$
. Denote by
$t=-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}])\in A_{\text{cris}}$
. Denote by
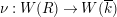 $\unicode[STIX]{x1D708}:W(R)\rightarrow W(\overline{k})$
the unique lift of the projection
$\unicode[STIX]{x1D708}:W(R)\rightarrow W(\overline{k})$
the unique lift of the projection
![]() $R\rightarrow \overline{k}$
, which extends to a map
$R\rightarrow \overline{k}$
, which extends to a map
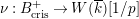 $\unicode[STIX]{x1D708}:B_{\text{cris}}^{+}\rightarrow W(\overline{k})[1/p]$
. For any subring
$\unicode[STIX]{x1D708}:B_{\text{cris}}^{+}\rightarrow W(\overline{k})[1/p]$
. For any subring
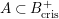 $A\subset B_{\text{cris}}^{+}$
, we put
$A\subset B_{\text{cris}}^{+}$
, we put
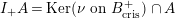 $I_{+}A=\text{Ker}(\unicode[STIX]{x1D708}~\text{on}~B_{\text{cris}}^{+})\cap A$
. For any integer
$I_{+}A=\text{Ker}(\unicode[STIX]{x1D708}~\text{on}~B_{\text{cris}}^{+})\cap A$
. For any integer
![]() $n\geqslant 0$
, let
$n\geqslant 0$
, let
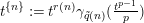 $t^{\{n\}}:=t^{r(n)}\unicode[STIX]{x1D6FE}_{\tilde{q}(n)}(\frac{t^{p-1}}{p})$
where
$t^{\{n\}}:=t^{r(n)}\unicode[STIX]{x1D6FE}_{\tilde{q}(n)}(\frac{t^{p-1}}{p})$
where
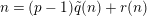 $n=(p-1)\tilde{q}(n)+r(n)$
with
$n=(p-1)\tilde{q}(n)+r(n)$
with
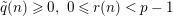 $\tilde{q}(n)\geqslant 0,~0\leqslant r(n)<p-1$
and
$\tilde{q}(n)\geqslant 0,~0\leqslant r(n)<p-1$
and
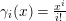 $\unicode[STIX]{x1D6FE}_{i}(x)=\frac{x^{i}}{i!}$
is the standard divided power. We define a subring
$\unicode[STIX]{x1D6FE}_{i}(x)=\frac{x^{i}}{i!}$
is the standard divided power. We define a subring
![]() ${\mathcal{R}}_{L_{0},s}$
(resp.
${\mathcal{R}}_{L_{0},s}$
(resp.
![]() ${\mathcal{R}}_{L_{0}}$
) of
${\mathcal{R}}_{L_{0}}$
) of
![]() $B_{\text{cris}}^{+}$
as below:
$B_{\text{cris}}^{+}$
as below:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{R}}_{L_{0},s}:=\Bigl\{\mathop{\sum }_{i=0}^{\infty }f_{i}t^{\{i\}}\mid f_{i}\in S_{L_{0},s}~\text{and}~f_{i}\rightarrow 0~\text{as}~i\rightarrow \infty \Bigr\} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Bigl(\text{resp}.\quad {\mathcal{R}}_{L_{0}}:=\Bigl\{\mathop{\sum }_{i=0}^{\infty }f_{i}t^{\{i\}}\mid f_{i}\in S_{L_{0}}~\text{and}~f_{i}\rightarrow 0~\text{as}~i\rightarrow \infty \Bigr\}\Bigr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{R}}_{L_{0},s}:=\Bigl\{\mathop{\sum }_{i=0}^{\infty }f_{i}t^{\{i\}}\mid f_{i}\in S_{L_{0},s}~\text{and}~f_{i}\rightarrow 0~\text{as}~i\rightarrow \infty \Bigr\} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Bigl(\text{resp}.\quad {\mathcal{R}}_{L_{0}}:=\Bigl\{\mathop{\sum }_{i=0}^{\infty }f_{i}t^{\{i\}}\mid f_{i}\in S_{L_{0}}~\text{and}~f_{i}\rightarrow 0~\text{as}~i\rightarrow \infty \Bigr\}\Bigr). & \displaystyle \nonumber\end{eqnarray}$$
Put
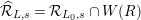 $\widehat{{\mathcal{R}}}_{L,s}={\mathcal{R}}_{L_{0},s}\cap W(R)$
(resp.
$\widehat{{\mathcal{R}}}_{L,s}={\mathcal{R}}_{L_{0},s}\cap W(R)$
(resp.
 $\widehat{{\mathcal{R}}}_{L}={\mathcal{R}}_{L_{0}}\cap W(R)$
) and
$\widehat{{\mathcal{R}}}_{L}={\mathcal{R}}_{L_{0}}\cap W(R)$
) and
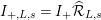 $I_{+,L,s}=I_{+}\widehat{{\mathcal{R}}}_{L,s}$
(resp.
$I_{+,L,s}=I_{+}\widehat{{\mathcal{R}}}_{L,s}$
(resp.
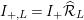 $I_{+,L}=I_{+}\widehat{{\mathcal{R}}}_{L}$
). By definitions, we have
$I_{+,L}=I_{+}\widehat{{\mathcal{R}}}_{L}$
). By definitions, we have
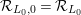 ${\mathcal{R}}_{L_{0},0}={\mathcal{R}}_{L_{0}}$
,
${\mathcal{R}}_{L_{0},0}={\mathcal{R}}_{L_{0}}$
,
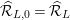 $\widehat{{\mathcal{R}}}_{L,0}=\widehat{{\mathcal{R}}}_{L}$
and
$\widehat{{\mathcal{R}}}_{L,0}=\widehat{{\mathcal{R}}}_{L}$
and
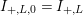 $I_{+,L,0}=I_{+,L}$
. Lemma 2.2.1 in [Reference LiuLi2] shows that
$I_{+,L,0}=I_{+,L}$
. Lemma 2.2.1 in [Reference LiuLi2] shows that
![]() $\widehat{{\mathcal{R}}}_{L,s}$
(resp.
$\widehat{{\mathcal{R}}}_{L,s}$
(resp.
![]() ${\mathcal{R}}_{L_{0},s}$
) is a
${\mathcal{R}}_{L_{0},s}$
) is a
![]() $\unicode[STIX]{x1D711}$
-stable
$\unicode[STIX]{x1D711}$
-stable
![]() $\mathfrak{S}_{L,s}$
-subalgebra of
$\mathfrak{S}_{L,s}$
-subalgebra of
![]() $W(R)$
(resp.
$W(R)$
(resp.
![]() $B_{\text{cris}}^{+}$
), and
$B_{\text{cris}}^{+}$
), and
![]() $\unicode[STIX]{x1D708}$
induces
$\unicode[STIX]{x1D708}$
induces
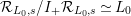 ${\mathcal{R}}_{L_{0},s}/I_{+}{\mathcal{R}}_{L_{0},s}\simeq L_{0}$
and
${\mathcal{R}}_{L_{0},s}/I_{+}{\mathcal{R}}_{L_{0},s}\simeq L_{0}$
and
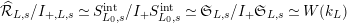 $\widehat{{\mathcal{R}}}_{L,s}/I_{+,L,s}\simeq S_{L_{0},s}^{\text{int}}/I_{+}S_{L_{0},s}^{\text{int}}\simeq \mathfrak{S}_{L,s}/I_{+}\mathfrak{S}_{L,s}\simeq W(k_{L})$
. Furthermore,
$\widehat{{\mathcal{R}}}_{L,s}/I_{+,L,s}\simeq S_{L_{0},s}^{\text{int}}/I_{+}S_{L_{0},s}^{\text{int}}\simeq \mathfrak{S}_{L,s}/I_{+}\mathfrak{S}_{L,s}\simeq W(k_{L})$
. Furthermore,
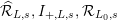 $\widehat{{\mathcal{R}}}_{L,s},I_{+,L,s},{\mathcal{R}}_{L_{0},s}$
and
$\widehat{{\mathcal{R}}}_{L,s},I_{+,L,s},{\mathcal{R}}_{L_{0},s}$
and
 $I_{+}{\mathcal{R}}_{L_{0},s}$
are
$I_{+}{\mathcal{R}}_{L_{0},s}$
are
![]() $G_{L,s}$
-stable, and
$G_{L,s}$
-stable, and
![]() $G_{L,s}$
-actions on them factors through
$G_{L,s}$
-actions on them factors through
![]() ${\hat{G}}_{L,s}$
. For any torsion Kisin module
${\hat{G}}_{L,s}$
. For any torsion Kisin module
![]() $\mathfrak{M}$
over
$\mathfrak{M}$
over
![]() $\mathfrak{S}_{L,s}$
, we equip
$\mathfrak{S}_{L,s}$
, we equip
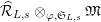 $\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
with a Frobenius by
$\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
with a Frobenius by
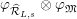 $\unicode[STIX]{x1D711}_{\widehat{{\mathcal{R}}}_{L,s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
. It is known that the natural map
$\unicode[STIX]{x1D711}_{\widehat{{\mathcal{R}}}_{L,s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
. It is known that the natural map
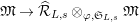 $\mathfrak{M}\rightarrow \widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
given by
$\mathfrak{M}\rightarrow \widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
given by
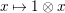 $x\mapsto 1\otimes x$
is an injection (cf. [Reference OzekiOz1, Corollary 2.12]). By this injection, we regard
$x\mapsto 1\otimes x$
is an injection (cf. [Reference OzekiOz1, Corollary 2.12]). By this injection, we regard
![]() $\mathfrak{M}$
as a
$\mathfrak{M}$
as a
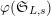 $\unicode[STIX]{x1D711}(\mathfrak{S}_{L,s})$
-stable submodule of
$\unicode[STIX]{x1D711}(\mathfrak{S}_{L,s})$
-stable submodule of
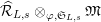 $\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
.
$\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
.
Definition 2.3. A free (resp. torsion)
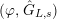 $(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-module of height
$(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-module of height
![]() ${\leqslant}r$
over
${\leqslant}r$
over
![]() $\mathfrak{S}_{L,s}$
is a triple
$\mathfrak{S}_{L,s}$
is a triple
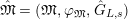 $\hat{\mathfrak{M}}=(\mathfrak{M},\unicode[STIX]{x1D711}_{\mathfrak{M}},{\hat{G}}_{L,s})$
where
$\hat{\mathfrak{M}}=(\mathfrak{M},\unicode[STIX]{x1D711}_{\mathfrak{M}},{\hat{G}}_{L,s})$
where
-
(1)
 $(\mathfrak{M},\unicode[STIX]{x1D711}_{\mathfrak{M}})$
is a free (resp. torsion) Kisin module of height
$(\mathfrak{M},\unicode[STIX]{x1D711}_{\mathfrak{M}})$
is a free (resp. torsion) Kisin module of height
 ${\leqslant}r$
over
${\leqslant}r$
over
 $\mathfrak{S}_{L,s}$
;
$\mathfrak{S}_{L,s}$
; -
(2)
 ${\hat{G}}_{L,s}$
is an
${\hat{G}}_{L,s}$
is an
 $\widehat{{\mathcal{R}}}_{L,s}$
-semilinear
$\widehat{{\mathcal{R}}}_{L,s}$
-semilinear
 ${\hat{G}}_{L,s}$
-action on
${\hat{G}}_{L,s}$
-action on
 $\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
which induces a continuous
$\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
which induces a continuous
 $G_{L,s}$
-action on
$G_{L,s}$
-action on
 $W(\text{Fr}R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
;
$W(\text{Fr}R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
; -
(3) the
 ${\hat{G}}_{L,s}$
-action commutes with
${\hat{G}}_{L,s}$
-action commutes with
 $\unicode[STIX]{x1D711}_{\widehat{{\mathcal{R}}}_{L,s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
;
$\unicode[STIX]{x1D711}_{\widehat{{\mathcal{R}}}_{L,s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
; -
(4)
 $\mathfrak{M}\subset (\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M})^{H_{L}}$
;
$\mathfrak{M}\subset (\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M})^{H_{L}}$
; -
(5)
 ${\hat{G}}_{L,s}$
acts on the
${\hat{G}}_{L,s}$
acts on the
 $W(k_{L})$
-module
$W(k_{L})$
-module
 $(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M})/I_{+,L,s}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M})$
trivially.
$(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M})/I_{+,L,s}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M})$
trivially.
A morphism between two
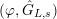 $(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-modules
$(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-modules
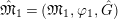 $\hat{\mathfrak{M}}_{1}=(\mathfrak{M}_{1},\unicode[STIX]{x1D711}_{1},{\hat{G}})$
and
$\hat{\mathfrak{M}}_{1}=(\mathfrak{M}_{1},\unicode[STIX]{x1D711}_{1},{\hat{G}})$
and
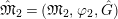 $\hat{\mathfrak{M}}_{2}=(\mathfrak{M}_{2},\unicode[STIX]{x1D711}_{2},{\hat{G}})$
is a morphism
$\hat{\mathfrak{M}}_{2}=(\mathfrak{M}_{2},\unicode[STIX]{x1D711}_{2},{\hat{G}})$
is a morphism
 $f:\mathfrak{M}_{1}\rightarrow \mathfrak{M}_{2}$
of
$f:\mathfrak{M}_{1}\rightarrow \mathfrak{M}_{2}$
of
![]() $\unicode[STIX]{x1D711}$
-modules over
$\unicode[STIX]{x1D711}$
-modules over
![]() $\mathfrak{S}_{L,s}$
such that
$\mathfrak{S}_{L,s}$
such that
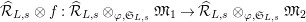 $\widehat{{\mathcal{R}}}_{L,s}\otimes f:\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}_{1}\rightarrow \widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}_{2}$
is
$\widehat{{\mathcal{R}}}_{L,s}\otimes f:\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}_{1}\rightarrow \widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}_{2}$
is
![]() ${\hat{G}}_{L,s}$
-equivariant. We denote by
${\hat{G}}_{L,s}$
-equivariant. We denote by
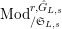 $\text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}$
(resp.
$\text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}$
(resp.
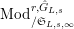 $\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r,{\hat{G}}_{L,s}}$
) the category of free (resp. torsion)
$\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r,{\hat{G}}_{L,s}}$
) the category of free (resp. torsion)
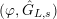 $(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-modules of height
$(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-modules of height
![]() ${\leqslant}r$
over
${\leqslant}r$
over
![]() $\mathfrak{S}_{L,s}$
. We often regard
$\mathfrak{S}_{L,s}$
. We often regard
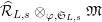 $\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
as a
$\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
as a
![]() $G_{L,s}$
-module via the projection
$G_{L,s}$
-module via the projection
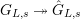 $G_{L,s}{\twoheadrightarrow}{\hat{G}}_{L,s}$
.
$G_{L,s}{\twoheadrightarrow}{\hat{G}}_{L,s}$
.
For any free or torsion
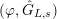 $(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-module
$(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-module
![]() $\hat{\mathfrak{M}}$
over
$\hat{\mathfrak{M}}$
over
![]() $\mathfrak{S}_{L,s}$
, we define a
$\mathfrak{S}_{L,s}$
, we define a
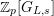 $\mathbb{Z}_{p}[G_{L,s}]$
-module
$\mathbb{Z}_{p}[G_{L,s}]$
-module
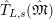 $\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
$\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
 $$\begin{eqnarray}\hat{T}_{L,s}(\hat{\mathfrak{M}})=\left\{\begin{array}{@{}ll@{}}\text{Hom}_{\widehat{{\mathcal{R}}}_{L,s},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M},W(\!R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{free},\\ \text{Hom}_{\widehat{{\mathcal{R}}}_{L,s},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}\!W(\!R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{torsion}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\hat{T}_{L,s}(\hat{\mathfrak{M}})=\left\{\begin{array}{@{}ll@{}}\text{Hom}_{\widehat{{\mathcal{R}}}_{L,s},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M},W(\!R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{free},\\ \text{Hom}_{\widehat{{\mathcal{R}}}_{L,s},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}\!W(\!R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{torsion}.\end{array}\right.\end{eqnarray}$$
Here,
![]() $G_{L,s}$
acts on
$G_{L,s}$
acts on
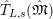 $\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
$\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
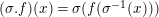 $(\unicode[STIX]{x1D70E}.f)(x)=\unicode[STIX]{x1D70E}(f(\unicode[STIX]{x1D70E}^{-1}(x)))$
for
$(\unicode[STIX]{x1D70E}.f)(x)=\unicode[STIX]{x1D70E}(f(\unicode[STIX]{x1D70E}^{-1}(x)))$
for
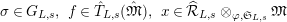 $\unicode[STIX]{x1D70E}\in G_{L,s},~f\in \hat{T}_{L,s}(\hat{\mathfrak{M}}),~x\in \widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
. Then, there exists a natural
$\unicode[STIX]{x1D70E}\in G_{L,s},~f\in \hat{T}_{L,s}(\hat{\mathfrak{M}}),~x\in \widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
. Then, there exists a natural
![]() $G_{L,\infty }$
-equivariant map
$G_{L,\infty }$
-equivariant map
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{L,s}:T_{\mathfrak{S}_{L,s}}(\mathfrak{M})\rightarrow \hat{T}_{L,s}(\hat{\mathfrak{M}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{L,s}:T_{\mathfrak{S}_{L,s}}(\mathfrak{M})\rightarrow \hat{T}_{L,s}(\hat{\mathfrak{M}})\end{eqnarray}$$
defined by
 $\unicode[STIX]{x1D703}(f)(a\otimes x)=a\unicode[STIX]{x1D711}(f(x))$
for
$\unicode[STIX]{x1D703}(f)(a\otimes x)=a\unicode[STIX]{x1D711}(f(x))$
for
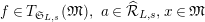 $f\in T_{\mathfrak{S}_{L,s}}(\mathfrak{M}),~a\in \widehat{{\mathcal{R}}}_{L,s},x\in \mathfrak{M}$
. We have the following theorem.
$f\in T_{\mathfrak{S}_{L,s}}(\mathfrak{M}),~a\in \widehat{{\mathcal{R}}}_{L,s},x\in \mathfrak{M}$
. We have the following theorem.
Theorem 2.4. [Reference LiuLi2, Theorem 2.3.1(1)] and [Reference Caruso and LiuCL2, Theorem 3.1.3(1)]
The map
![]() $\unicode[STIX]{x1D703}_{L,s}$
is an isomorphism of
$\unicode[STIX]{x1D703}_{L,s}$
is an isomorphism of
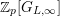 $\mathbb{Z}_{p}[G_{L,\infty }]$
-modules.
$\mathbb{Z}_{p}[G_{L,\infty }]$
-modules.
Convention: For simplicity, if
![]() $L=K$
, then we often omit the subscript “
$L=K$
, then we often omit the subscript “
![]() $L$
” from various notations (e.g., “a
$L$
” from various notations (e.g., “a
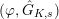 $(\unicode[STIX]{x1D711},{\hat{G}}_{K,s})$
-module” = “a
$(\unicode[STIX]{x1D711},{\hat{G}}_{K,s})$
-module” = “a
![]() $(\unicode[STIX]{x1D711},{\hat{G}}_{s})$
-module”,
$(\unicode[STIX]{x1D711},{\hat{G}}_{s})$
-module”,
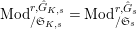 $\text{Mod}_{/\mathfrak{S}_{K,s}}^{r,{\hat{G}}_{K,s}}=\text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
,
$\text{Mod}_{/\mathfrak{S}_{K,s}}^{r,{\hat{G}}_{K,s}}=\text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
,
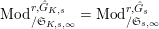 $\text{Mod}_{/\mathfrak{S}_{K,s,\infty }}^{r,{\hat{G}}_{K,s}}=\text{Mod}_{/\mathfrak{S}_{s,\infty }}^{r,{\hat{G}}_{s}}$
,
$\text{Mod}_{/\mathfrak{S}_{K,s,\infty }}^{r,{\hat{G}}_{K,s}}=\text{Mod}_{/\mathfrak{S}_{s,\infty }}^{r,{\hat{G}}_{s}}$
,
 $\hat{T}_{K,s}=\hat{T}_{s}$
,
$\hat{T}_{K,s}=\hat{T}_{s}$
,
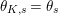 $\unicode[STIX]{x1D703}_{K,s}=\unicode[STIX]{x1D703}_{s}$
). Furthermore, if
$\unicode[STIX]{x1D703}_{K,s}=\unicode[STIX]{x1D703}_{s}$
). Furthermore, if
![]() $s=0$
, we often omit the subscript “
$s=0$
, we often omit the subscript “
![]() $s$
” from various notations (e.g.,
$s$
” from various notations (e.g.,
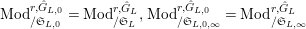 $\text{Mod}_{/\mathfrak{S}_{L,0}}^{r,{\hat{G}}_{L,0}}=\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}},\text{Mod}_{/\mathfrak{S}_{L,0,\infty }}^{r,{\hat{G}}_{L,0}}=\text{Mod}_{/\mathfrak{S}_{L,\infty }\!}^{r,{\hat{G}}_{L}}$
,
$\text{Mod}_{/\mathfrak{S}_{L,0}}^{r,{\hat{G}}_{L,0}}=\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}},\text{Mod}_{/\mathfrak{S}_{L,0,\infty }}^{r,{\hat{G}}_{L,0}}=\text{Mod}_{/\mathfrak{S}_{L,\infty }\!}^{r,{\hat{G}}_{L}}$
,
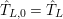 $\hat{T}_{L,0}=\hat{T}_{L}$
,
$\hat{T}_{L,0}=\hat{T}_{L}$
,
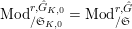 $\text{Mod}_{/\mathfrak{S}_{K,0}}^{r,{\hat{G}}_{K,0}}=\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}$
, “a
$\text{Mod}_{/\mathfrak{S}_{K,0}}^{r,{\hat{G}}_{K,0}}=\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}$
, “a
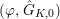 $(\unicode[STIX]{x1D711},{\hat{G}}_{K,0})$
-module” = “a
$(\unicode[STIX]{x1D711},{\hat{G}}_{K,0})$
-module” = “a
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-module”,
$(\unicode[STIX]{x1D711},{\hat{G}})$
-module”,
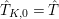 $\hat{T}_{K,0}=\hat{T}$
,
$\hat{T}_{K,0}=\hat{T}$
,
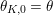 $\unicode[STIX]{x1D703}_{K,0}=\unicode[STIX]{x1D703}$
).
$\unicode[STIX]{x1D703}_{K,0}=\unicode[STIX]{x1D703}$
).
We denote by
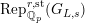 $\text{Rep}_{\mathbb{Q}_{p}}^{r,\text{st}}(G_{L,s})$
(resp.
$\text{Rep}_{\mathbb{Q}_{p}}^{r,\text{st}}(G_{L,s})$
(resp.
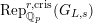 $\text{Rep}_{\mathbb{Q}_{p}}^{r,\text{cris}}(G_{L,s})$
, resp.
$\text{Rep}_{\mathbb{Q}_{p}}^{r,\text{cris}}(G_{L,s})$
, resp.
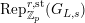 $\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{L,s})$
, resp.
$\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{L,s})$
, resp.
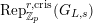 $\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{cris}}(G_{L,s})$
) the category of semistable
$\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{cris}}(G_{L,s})$
) the category of semistable
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{L,s}$
with Hodge–Tate weights in
$G_{L,s}$
with Hodge–Tate weights in
![]() $[0,r]$
(resp. the category of crystalline
$[0,r]$
(resp. the category of crystalline
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{L,s}$
with Hodge–Tate weights in
$G_{L,s}$
with Hodge–Tate weights in
![]() $[0,r]$
, resp. the category of lattices in semistable
$[0,r]$
, resp. the category of lattices in semistable
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{L,s}$
with Hodge–Tate weights in
$G_{L,s}$
with Hodge–Tate weights in
![]() $[0,r]$
, resp. the category of lattices in crystalline
$[0,r]$
, resp. the category of lattices in crystalline
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{L,s}$
with Hodge–Tate weights in
$G_{L,s}$
with Hodge–Tate weights in
![]() $[0,r]$
).
$[0,r]$
).
There exists
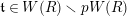 $\mathfrak{t}\in W(R)\smallsetminus pW(R)$
such that
$\mathfrak{t}\in W(R)\smallsetminus pW(R)$
such that
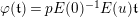 $\unicode[STIX]{x1D711}(\mathfrak{t})=pE(0)^{-1}E(u)\mathfrak{t}$
. Such
$\unicode[STIX]{x1D711}(\mathfrak{t})=pE(0)^{-1}E(u)\mathfrak{t}$
. Such
![]() $\mathfrak{t}$
is unique up to units of
$\mathfrak{t}$
is unique up to units of
![]() $\mathbb{Z}_{p}$
(cf. [Reference LiuLi2, Example 2.3.5]). Now we define the full subcategory
$\mathbb{Z}_{p}$
(cf. [Reference LiuLi2, Example 2.3.5]). Now we define the full subcategory
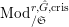 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}},\text{cris}}$
(resp.
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}},\text{cris}}$
(resp.
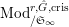 $\text{Mod}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}},\text{cris}}$
) of
$\text{Mod}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}},\text{cris}}$
) of
![]() $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}$
(resp.
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}$
(resp.
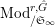 $\text{Mod}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}}$
) consisting of objects
$\text{Mod}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}}$
) consisting of objects
![]() $\hat{\mathfrak{M}}$
which satisfy the following condition;
$\hat{\mathfrak{M}}$
which satisfy the following condition;
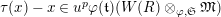 $\unicode[STIX]{x1D70F}(x)-x\in u^{p}\unicode[STIX]{x1D711}(\mathfrak{t})(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})$
for any
$\unicode[STIX]{x1D70F}(x)-x\in u^{p}\unicode[STIX]{x1D711}(\mathfrak{t})(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})$
for any
![]() $x\in \mathfrak{M}$
.
$x\in \mathfrak{M}$
.
The following results are important properties for the functor
![]() $\hat{T}_{L,s}$
.
$\hat{T}_{L,s}$
.
Theorem 2.5.
![]() $(1)$
[Reference LiuLi2, Theorem 2.3.1(2)] The functor
$(1)$
[Reference LiuLi2, Theorem 2.3.1(2)] The functor
![]() $\hat{T}$
induces an anti-equivalence of categories between
$\hat{T}$
induces an anti-equivalence of categories between
![]() $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}$
and
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}$
and
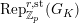 $\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{K})$
.
$\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{K})$
.
![]() $(2)$
[Reference Gee, Liu and SavittGLS, Proposition 5.9]
$(2)$
[Reference Gee, Liu and SavittGLS, Proposition 5.9]
![]() $\text{and}$
[Reference OzekiOz2, Theorem 19] The functor
$\text{and}$
[Reference OzekiOz2, Theorem 19] The functor
![]() $\hat{T}$
induces an anti-equivalence of categories between
$\hat{T}$
induces an anti-equivalence of categories between
 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}},\text{cris}}$
and
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}},\text{cris}}$
and
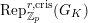 $\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{cris}}(G_{K})$
.
$\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{cris}}(G_{K})$
.
![]() $(3)$
[Reference OzekiOz1, Corollaries 2.8 and 5.34] The functor
$(3)$
[Reference OzekiOz1, Corollaries 2.8 and 5.34] The functor
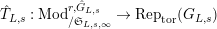 $\hat{T}_{L,s}:\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r,{\hat{G}}_{L,s}}\rightarrow \text{Rep}_{\text{tor}}(G_{L,s})$
is exact and faithful. Furthermore, it is full if
$\hat{T}_{L,s}:\text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r,{\hat{G}}_{L,s}}\rightarrow \text{Rep}_{\text{tor}}(G_{L,s})$
is exact and faithful. Furthermore, it is full if
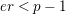 $er<p-1$
.
$er<p-1$
.
2.4
 $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules, Breuil modules and filtered
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules, Breuil modules and filtered
 $(\unicode[STIX]{x1D711},N)$
-modules
$(\unicode[STIX]{x1D711},N)$
-modules
We recall some relations between Breuil modules and
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules. Here we give a rough sketch only. For more precise information, see [Reference BreuilBr1, Section 6], [Reference LiuLi1, Section 5] and the proof of [Reference LiuLi2, Theorem 2.3.1(2)].
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules. Here we give a rough sketch only. For more precise information, see [Reference BreuilBr1, Section 6], [Reference LiuLi1, Section 5] and the proof of [Reference LiuLi2, Theorem 2.3.1(2)].
Let
![]() $\hat{\mathfrak{M}}$
be a free
$\hat{\mathfrak{M}}$
be a free
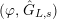 $(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-module over
$(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-module over
![]() $\mathfrak{S}_{L,s}$
. If we put
$\mathfrak{S}_{L,s}$
. If we put
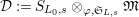 ${\mathcal{D}}:=S_{L_{0},s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
, then
${\mathcal{D}}:=S_{L_{0},s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
, then
![]() ${\mathcal{D}}$
has a structure of a Breuil module over
${\mathcal{D}}$
has a structure of a Breuil module over
![]() $S_{L_{0},s}$
which corresponds to the semistable representation
$S_{L_{0},s}$
which corresponds to the semistable representation
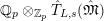 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{L,s}(\hat{\mathfrak{M}})$
of
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{L,s}(\hat{\mathfrak{M}})$
of
![]() $G_{L,s}$
(for the definition and properties of Breuil modules, see [Reference BreuilBr1]). Thus
$G_{L,s}$
(for the definition and properties of Breuil modules, see [Reference BreuilBr1]). Thus
![]() ${\mathcal{D}}$
is equipped with a Frobenius
${\mathcal{D}}$
is equipped with a Frobenius
 $\unicode[STIX]{x1D711}_{{\mathcal{D}}}(=\unicode[STIX]{x1D711}_{S_{L_{0},s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}})$
, a decreasing filtration
$\unicode[STIX]{x1D711}_{{\mathcal{D}}}(=\unicode[STIX]{x1D711}_{S_{L_{0},s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}})$
, a decreasing filtration
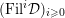 $(\text{Fil}^{i}{\mathcal{D}})_{i\geqslant 0}$
of
$(\text{Fil}^{i}{\mathcal{D}})_{i\geqslant 0}$
of
![]() $S_{L_{0},s}$
-submodules of
$S_{L_{0},s}$
-submodules of
![]() ${\mathcal{D}}$
and a
${\mathcal{D}}$
and a
![]() $L_{0}$
-linear monodromy operator
$L_{0}$
-linear monodromy operator
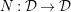 $N:{\mathcal{D}}\rightarrow {\mathcal{D}}$
which satisfy certain properties (for example, Griffiths transversality).
$N:{\mathcal{D}}\rightarrow {\mathcal{D}}$
which satisfy certain properties (for example, Griffiths transversality).
Putting
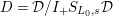 $D={\mathcal{D}}/I_{+}S_{L_{0},s}{\mathcal{D}}$
, we can associate a filtered
$D={\mathcal{D}}/I_{+}S_{L_{0},s}{\mathcal{D}}$
, we can associate a filtered
![]() $(\unicode[STIX]{x1D711},N)$
-module over
$(\unicode[STIX]{x1D711},N)$
-module over
![]() $L_{(s)}$
as following:
$L_{(s)}$
as following:
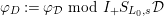 $\unicode[STIX]{x1D711}_{D}:=\unicode[STIX]{x1D711}_{{\mathcal{D}}}~\text{mod}~I_{+}S_{L_{0},s}{\mathcal{D}}$
,
$\unicode[STIX]{x1D711}_{D}:=\unicode[STIX]{x1D711}_{{\mathcal{D}}}~\text{mod}~I_{+}S_{L_{0},s}{\mathcal{D}}$
,
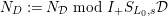 $N_{D}:=N_{{\mathcal{D}}}~\text{mod}~I_{+}S_{L_{0},s}{\mathcal{D}}$
and
$N_{D}:=N_{{\mathcal{D}}}~\text{mod}~I_{+}S_{L_{0},s}{\mathcal{D}}$
and
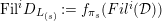 $\text{Fil}^{i}D_{L_{(s)}}:=f_{\unicode[STIX]{x1D70B}_{s}}(Fil^{i}({\mathcal{D}}))$
. Here,
$\text{Fil}^{i}D_{L_{(s)}}:=f_{\unicode[STIX]{x1D70B}_{s}}(Fil^{i}({\mathcal{D}}))$
. Here,
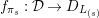 $f_{\unicode[STIX]{x1D70B}_{s}}:{\mathcal{D}}\rightarrow D_{L_{(s)}}$
is the projection defined by
$f_{\unicode[STIX]{x1D70B}_{s}}:{\mathcal{D}}\rightarrow D_{L_{(s)}}$
is the projection defined by
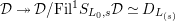 ${\mathcal{D}}{\twoheadrightarrow}{\mathcal{D}}/\text{Fil}^{1}S_{L_{0},s}{\mathcal{D}}\simeq D_{L_{(s)}}$
. Proposition 6.2.1.1 of [Reference BreuilBr1] implies that there exists a unique
${\mathcal{D}}{\twoheadrightarrow}{\mathcal{D}}/\text{Fil}^{1}S_{L_{0},s}{\mathcal{D}}\simeq D_{L_{(s)}}$
. Proposition 6.2.1.1 of [Reference BreuilBr1] implies that there exists a unique
![]() $\unicode[STIX]{x1D711}$
-compatible section
$\unicode[STIX]{x1D711}$
-compatible section
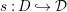 $s:D{\hookrightarrow}{\mathcal{D}}$
of
$s:D{\hookrightarrow}{\mathcal{D}}$
of
![]() ${\mathcal{D}}{\twoheadrightarrow}D$
. By this embedding, we regard
${\mathcal{D}}{\twoheadrightarrow}D$
. By this embedding, we regard
![]() $D$
as a submodule of
$D$
as a submodule of
![]() ${\mathcal{D}}$
. Then we have
${\mathcal{D}}$
. Then we have
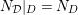 $N_{{\mathcal{D}}}|_{D}=N_{D}$
and
$N_{{\mathcal{D}}}|_{D}=N_{D}$
and
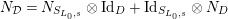 $N_{{\mathcal{D}}}=N_{S_{L_{0},s}}\otimes \text{Id}_{D}+\text{Id}_{S_{L_{0},s}}\otimes N_{D}$
under the identification
$N_{{\mathcal{D}}}=N_{S_{L_{0},s}}\otimes \text{Id}_{D}+\text{Id}_{S_{L_{0},s}}\otimes N_{D}$
under the identification
 ${\mathcal{D}}=S_{L_{0},s}\otimes _{L_{(s)}}D$
.
${\mathcal{D}}=S_{L_{0},s}\otimes _{L_{(s)}}D$
.
The
![]() $G_{L,s}$
-action on
$G_{L,s}$
-action on
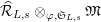 $\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
extends to
$\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}$
extends to
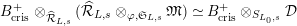 $B_{\text{cris}}^{+}\otimes _{\widehat{{\mathcal{R}}}_{L,s}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M})\simeq B_{\text{cris}}^{+}\otimes _{S_{L_{0},s}}{\mathcal{D}}$
. This action is in fact explicitly written as follows:
$B_{\text{cris}}^{+}\otimes _{\widehat{{\mathcal{R}}}_{L,s}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M})\simeq B_{\text{cris}}^{+}\otimes _{S_{L_{0},s}}{\mathcal{D}}$
. This action is in fact explicitly written as follows:
 $$\begin{eqnarray}\displaystyle g(a\otimes x) & = & \displaystyle \mathop{\sum }_{i=0}^{\infty }g(a)\unicode[STIX]{x1D6FE}_{i}\Bigl(-\text{log}\Bigl(\frac{g[\text{}\underline{\unicode[STIX]{x1D70B}_{s}}]}{[\text{}\underline{\unicode[STIX]{x1D70B}_{s}}]}\Bigr)\Bigr)\otimes N_{{\mathcal{D}}}^{i}(x)\nonumber\\ \displaystyle & & \displaystyle \quad \text{for}~g\in G_{L,s},a\in B_{\text{cris}}^{+},x\in {\mathcal{D}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g(a\otimes x) & = & \displaystyle \mathop{\sum }_{i=0}^{\infty }g(a)\unicode[STIX]{x1D6FE}_{i}\Bigl(-\text{log}\Bigl(\frac{g[\text{}\underline{\unicode[STIX]{x1D70B}_{s}}]}{[\text{}\underline{\unicode[STIX]{x1D70B}_{s}}]}\Bigr)\Bigr)\otimes N_{{\mathcal{D}}}^{i}(x)\nonumber\\ \displaystyle & & \displaystyle \quad \text{for}~g\in G_{L,s},a\in B_{\text{cris}}^{+},x\in {\mathcal{D}}.\end{eqnarray}$$
By this explicit formula, we can obtain an easy relation between
![]() $N_{{\mathcal{D}}}$
and
$N_{{\mathcal{D}}}$
and
![]() $\unicode[STIX]{x1D70F}^{p^{s}}$
-action on
$\unicode[STIX]{x1D70F}^{p^{s}}$
-action on
![]() $\hat{\mathfrak{M}}$
as follows: first we recall that
$\hat{\mathfrak{M}}$
as follows: first we recall that
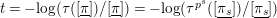 $t=-\text{log}(\unicode[STIX]{x1D70F}([\text{}\underline{\unicode[STIX]{x1D70B}}])/[\text{}\underline{\unicode[STIX]{x1D70B}}])=-\text{log}(\unicode[STIX]{x1D70F}^{p^{s}}([\text{}\underline{\unicode[STIX]{x1D70B}_{s}}])/[\text{}\underline{\unicode[STIX]{x1D70B}_{s}}])$
. By the formula, for any
$t=-\text{log}(\unicode[STIX]{x1D70F}([\text{}\underline{\unicode[STIX]{x1D70B}}])/[\text{}\underline{\unicode[STIX]{x1D70B}}])=-\text{log}(\unicode[STIX]{x1D70F}^{p^{s}}([\text{}\underline{\unicode[STIX]{x1D70B}_{s}}])/[\text{}\underline{\unicode[STIX]{x1D70B}_{s}}])$
. By the formula, for any
![]() $n\geqslant 0$
and
$n\geqslant 0$
and
![]() $x\in {\mathcal{D}}$
, an induction on
$x\in {\mathcal{D}}$
, an induction on
![]() $n$
shows that we have
$n$
shows that we have
 $$\begin{eqnarray}(\unicode[STIX]{x1D70F}^{p^{s}}-1)^{n}(x)=\mathop{\sum }_{m=n}^{\infty }\Bigl(\mathop{\sum }_{\substack{ i_{1}+\cdots i_{n}=m \\ i_{j}\geqslant 0}}\frac{m!}{i_{1}!\cdots i_{n}!}\Bigr)\unicode[STIX]{x1D6FE}_{m}(t)\otimes N_{{\mathcal{D}}}^{m}(x)\in B_{\text{cris}}^{+}\otimes _{S_{L_{0},s}}{\mathcal{D}}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}^{p^{s}}-1)^{n}(x)=\mathop{\sum }_{m=n}^{\infty }\Bigl(\mathop{\sum }_{\substack{ i_{1}+\cdots i_{n}=m \\ i_{j}\geqslant 0}}\frac{m!}{i_{1}!\cdots i_{n}!}\Bigr)\unicode[STIX]{x1D6FE}_{m}(t)\otimes N_{{\mathcal{D}}}^{m}(x)\in B_{\text{cris}}^{+}\otimes _{S_{L_{0},s}}{\mathcal{D}}\end{eqnarray}$$
and in particular we see
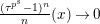 $\frac{(\unicode[STIX]{x1D70F}^{p^{s}}-1)^{n}}{n}(x)\rightarrow 0$
$\frac{(\unicode[STIX]{x1D70F}^{p^{s}}-1)^{n}}{n}(x)\rightarrow 0$
![]() $p$
-adically as
$p$
-adically as
![]() $n\rightarrow \infty$
. Hence we can define
$n\rightarrow \infty$
. Hence we can define
 $$\begin{eqnarray}\text{log}(\unicode[STIX]{x1D70F}^{p^{s}})(x):=\mathop{\sum }_{n=1}^{\infty }(-1)^{n-1}\frac{(\unicode[STIX]{x1D70F}^{p^{s}}-1)^{n}}{n}(x)\in B_{\text{cris}}^{+}\otimes _{S_{L_{0},s}}{\mathcal{D}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{log}(\unicode[STIX]{x1D70F}^{p^{s}})(x):=\mathop{\sum }_{n=1}^{\infty }(-1)^{n-1}\frac{(\unicode[STIX]{x1D70F}^{p^{s}}-1)^{n}}{n}(x)\in B_{\text{cris}}^{+}\otimes _{S_{L_{0},s}}{\mathcal{D}}.\end{eqnarray}$$
It is not difficult to check the equation
 $$\begin{eqnarray}\text{log}(\unicode[STIX]{x1D70F}^{p^{s}})(x)=t\otimes N_{{\mathcal{D}}}(x).\end{eqnarray}$$
$$\begin{eqnarray}\text{log}(\unicode[STIX]{x1D70F}^{p^{s}})(x)=t\otimes N_{{\mathcal{D}}}(x).\end{eqnarray}$$
2.5 Base changes for Kisin modules
Let
![]() $\mathfrak{M}$
be a free or torsion Kisin module of height
$\mathfrak{M}$
be a free or torsion Kisin module of height
![]() ${\leqslant}r$
over
${\leqslant}r$
over
![]() $\mathfrak{S}_{L}$
(resp. over
$\mathfrak{S}_{L}$
(resp. over
![]() $\mathfrak{S}$
). We put
$\mathfrak{S}$
). We put
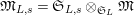 $\mathfrak{M}_{L,s}=\mathfrak{S}_{L,s}\otimes _{\mathfrak{S}_{L}}\mathfrak{M}$
(resp.
$\mathfrak{M}_{L,s}=\mathfrak{S}_{L,s}\otimes _{\mathfrak{S}_{L}}\mathfrak{M}$
(resp.
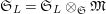 $\mathfrak{S}_{L}=\mathfrak{S}_{L}\otimes _{\mathfrak{S}}\mathfrak{M}$
) and equip
$\mathfrak{S}_{L}=\mathfrak{S}_{L}\otimes _{\mathfrak{S}}\mathfrak{M}$
) and equip
![]() $\mathfrak{M}_{L,s}$
(resp.
$\mathfrak{M}_{L,s}$
(resp.
![]() $\mathfrak{M}_{L}$
) with a Frobenius by
$\mathfrak{M}_{L}$
) with a Frobenius by
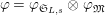 $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{\mathfrak{S}_{L,s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
(resp.
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{\mathfrak{S}_{L,s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
(resp.
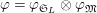 $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{\mathfrak{S}_{L}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
). Then it is not difficult to check that
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{\mathfrak{S}_{L}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
). Then it is not difficult to check that
![]() $\mathfrak{M}_{L,s}$
(resp.
$\mathfrak{M}_{L,s}$
(resp.
![]() $\mathfrak{M}_{L}$
) is a free or torsion Kisin module of height
$\mathfrak{M}_{L}$
) is a free or torsion Kisin module of height
![]() ${\leqslant}r$
over
${\leqslant}r$
over
![]() $\mathfrak{S}_{L,s}$
(resp. over
$\mathfrak{S}_{L,s}$
(resp. over
![]() $\mathfrak{S}_{L}$
) (here we recall that
$\mathfrak{S}_{L}$
) (here we recall that
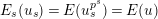 $E_{s}(u_{s})=E(u_{s}^{p^{s}})=E(u)$
). Hence we obtained natural functors
$E_{s}(u_{s})=E(u_{s}^{p^{s}})=E(u)$
). Hence we obtained natural functors
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{Mod}_{/\mathfrak{S}_{L}}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r}\qquad \text{and}\qquad \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Big(\text{resp.}~\text{Mod}_{/\mathfrak{S}}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L}}^{r}~\text{and}~\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r}\Big). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{Mod}_{/\mathfrak{S}_{L}}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r}\qquad \text{and}\qquad \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Big(\text{resp.}~\text{Mod}_{/\mathfrak{S}}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L}}^{r}~\text{and}~\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r}\Big). & \displaystyle \nonumber\end{eqnarray}$$
By definition, we immediately see that we have
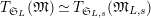 $T_{\mathfrak{S}_{L}}(\mathfrak{M})\simeq T_{\mathfrak{S}_{L,s}}(\mathfrak{M}_{L,s})$
(resp.
$T_{\mathfrak{S}_{L}}(\mathfrak{M})\simeq T_{\mathfrak{S}_{L,s}}(\mathfrak{M}_{L,s})$
(resp.
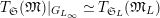 $T_{\mathfrak{S}}(\mathfrak{M})|_{G_{L_{\infty }}}\simeq T_{\mathfrak{S}_{L}}(\mathfrak{M}_{L})$
). In particular, it follows from Proposition 2.1(1) that the following holds:
$T_{\mathfrak{S}}(\mathfrak{M})|_{G_{L_{\infty }}}\simeq T_{\mathfrak{S}_{L}}(\mathfrak{M}_{L})$
). In particular, it follows from Proposition 2.1(1) that the following holds:
Proposition 2.6. The functor
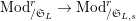 $\text{Mod}_{/\mathfrak{S}_{L}}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
is fully faithful.
$\text{Mod}_{/\mathfrak{S}_{L}}^{r}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r}$
is fully faithful.
2.6 Base changes for
 $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules
Let
![]() $\hat{\mathfrak{M}}$
be a free or torsion
$\hat{\mathfrak{M}}$
be a free or torsion
![]() $(\unicode[STIX]{x1D711},{\hat{G}}_{L})$
-module (resp.
$(\unicode[STIX]{x1D711},{\hat{G}}_{L})$
-module (resp.
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-module) of height
$(\unicode[STIX]{x1D711},{\hat{G}})$
-module) of height
![]() ${\leqslant}r$
over
${\leqslant}r$
over
![]() $\mathfrak{S}_{L}$
(resp. over
$\mathfrak{S}_{L}$
(resp. over
![]() $\mathfrak{S}$
). The
$\mathfrak{S}$
). The
![]() $G_{L,s}$
action on
$G_{L,s}$
action on
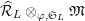 $\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
(resp. the
$\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
(resp. the
![]() $G_{L}$
action on
$G_{L}$
action on
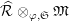 $\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
) extends to
$\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
) extends to
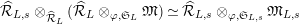 $\widehat{{\mathcal{R}}}_{L,s}\otimes _{\widehat{{\mathcal{R}}}_{L}}(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})\simeq \widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}_{L,s}$
(resp.
$\widehat{{\mathcal{R}}}_{L,s}\otimes _{\widehat{{\mathcal{R}}}_{L}}(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})\simeq \widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L,s}}\mathfrak{M}_{L,s}$
(resp.
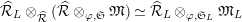 $\widehat{{\mathcal{R}}}_{L}\otimes _{\widehat{{\mathcal{R}}}}(\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})\simeq \widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
), which factors through
$\widehat{{\mathcal{R}}}_{L}\otimes _{\widehat{{\mathcal{R}}}}(\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})\simeq \widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
), which factors through
![]() ${\hat{G}}_{L,s}$
(resp.
${\hat{G}}_{L,s}$
(resp.
![]() ${\hat{G}}_{L}$
). Then it is not difficult to check that
${\hat{G}}_{L}$
). Then it is not difficult to check that
![]() $\mathfrak{M}_{L,s}$
(resp.
$\mathfrak{M}_{L,s}$
(resp.
![]() $\mathfrak{M}_{L}$
) has a structure of a
$\mathfrak{M}_{L}$
) has a structure of a
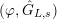 $(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-module (resp.
$(\unicode[STIX]{x1D711},{\hat{G}}_{L,s})$
-module (resp.
![]() $(\unicode[STIX]{x1D711},{\hat{G}}_{L})$
-module). Hence we obtained natural functors
$(\unicode[STIX]{x1D711},{\hat{G}}_{L})$
-module). Hence we obtained natural functors
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}\qquad \text{and}\qquad \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r,{\hat{G}}_{L,s}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Big(\text{resp.}~\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}~\text{and}~\text{Mod}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L}}\Big). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}\qquad \text{and}\qquad \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r,{\hat{G}}_{L,s}} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \Big(\text{resp.}~\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}~\text{and}~\text{Mod}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L}}\Big). & \displaystyle \nonumber\end{eqnarray}$$
By definition, we immediately see that we have
 $\hat{T}_{L}(\hat{\mathfrak{M}})|_{G_{L,s}}\simeq \hat{T}_{L,s}(\hat{\mathfrak{M}}_{L,s})$
(resp.
$\hat{T}_{L}(\hat{\mathfrak{M}})|_{G_{L,s}}\simeq \hat{T}_{L,s}(\hat{\mathfrak{M}}_{L,s})$
(resp.
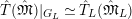 $\hat{T}(\hat{\mathfrak{M}})|_{G_{L}}\simeq \hat{T}_{L}(\hat{\mathfrak{M}}_{L})$
). Similar to Proposition 2.6, we can prove the following.
$\hat{T}(\hat{\mathfrak{M}})|_{G_{L}}\simeq \hat{T}_{L}(\hat{\mathfrak{M}}_{L})$
). Similar to Proposition 2.6, we can prove the following.
Proposition 2.7. The functor
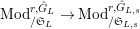 $\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}$
is fully faithful.
$\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}$
is fully faithful.
The proposition immediately follows from the full faithfulness property of Theorem 2.5(1) and the lemma below.
Lemma 2.8. Let
![]() $K^{\prime }$
be a finite totally ramified extension of
$K^{\prime }$
be a finite totally ramified extension of
![]() $K$
. Then the restriction functor from the category of semistable
$K$
. Then the restriction functor from the category of semistable
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{K}$
into the category of semistable
$G_{K}$
into the category of semistable
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{K^{\prime }}$
is fully faithful.
$G_{K^{\prime }}$
is fully faithful.
Proof. Let
![]() $V$
and
$V$
and
![]() $V^{\prime }$
be semistable
$V^{\prime }$
be semistable
![]() $\mathbb{Q}_{p}$
-representations of
$\mathbb{Q}_{p}$
-representations of
![]() $G_{K}$
and let
$G_{K}$
and let
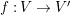 $f:V\rightarrow V^{\prime }$
be a
$f:V\rightarrow V^{\prime }$
be a
![]() $G_{K^{\prime }}$
-equivariant homomorphism. Considering the morphism of filtered
$G_{K^{\prime }}$
-equivariant homomorphism. Considering the morphism of filtered
![]() $(\unicode[STIX]{x1D711},N)$
-modules over
$(\unicode[STIX]{x1D711},N)$
-modules over
![]() $K^{\prime }$
corresponding to
$K^{\prime }$
corresponding to
![]() $f$
, we can check without difficulty that
$f$
, we can check without difficulty that
![]() $f$
is in fact a morphism of filtered
$f$
is in fact a morphism of filtered
![]() $(\unicode[STIX]{x1D711},N)$
-modules over
$(\unicode[STIX]{x1D711},N)$
-modules over
![]() $K$
. This is because
$K$
. This is because
![]() $K^{\prime }$
is totally ramified over
$K^{\prime }$
is totally ramified over
![]() $K_{0}$
as same as
$K_{0}$
as same as
![]() $K$
. This gives the desired result.◻
$K$
. This gives the desired result.◻
3 Variants of free
 $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules
In this section, we define some variant notions of
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules. We continue to use same notation as in the previous section. In particular,
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules. We continue to use same notation as in the previous section. In particular,
![]() $p$
is odd.
$p$
is odd.
3.1 Definitions
We start with some definitions which are our main concern in this and the next section.
Definition 3.1. We define the category
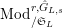 $\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
(resp.
$\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
(resp.
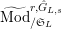 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
) as follows. An object is a triple
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
) as follows. An object is a triple
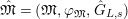 $\hat{\mathfrak{M}}=(\mathfrak{M},\unicode[STIX]{x1D711}_{\mathfrak{M}},{\hat{G}}_{L,s})$
where
$\hat{\mathfrak{M}}=(\mathfrak{M},\unicode[STIX]{x1D711}_{\mathfrak{M}},{\hat{G}}_{L,s})$
where
-
(1)
 $(\mathfrak{M},\unicode[STIX]{x1D711}_{\mathfrak{M}})$
is a free Kisin module of height
$(\mathfrak{M},\unicode[STIX]{x1D711}_{\mathfrak{M}})$
is a free Kisin module of height
 ${\leqslant}r$
over
${\leqslant}r$
over
 $\mathfrak{S}_{L}$
;
$\mathfrak{S}_{L}$
; -
(2)
 ${\hat{G}}_{L,s}$
is an
${\hat{G}}_{L,s}$
is an
 $\widehat{{\mathcal{R}}}_{L}$
-semilinear
$\widehat{{\mathcal{R}}}_{L}$
-semilinear
 ${\hat{G}}_{L,s}$
-action on
${\hat{G}}_{L,s}$
-action on
 $\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
(resp. an
$\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
(resp. an
 $\widehat{{\mathcal{R}}}_{L,s}$
-semilinear
$\widehat{{\mathcal{R}}}_{L,s}$
-semilinear
 ${\hat{G}}_{L,s}$
-action on
${\hat{G}}_{L,s}$
-action on
 $\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
) which induces a continuous
$\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
) which induces a continuous
 $G_{L,s}$
-action on
$G_{L,s}$
-action on
 $W(\text{Fr}R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
;
$W(\text{Fr}R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
; -
(3) the
 ${\hat{G}}_{L,s}$
-action commutes with
${\hat{G}}_{L,s}$
-action commutes with
 $\unicode[STIX]{x1D711}_{\widehat{{\mathcal{R}}}_{L}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
(resp.
$\unicode[STIX]{x1D711}_{\widehat{{\mathcal{R}}}_{L}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
(resp.
 $\unicode[STIX]{x1D711}_{\widehat{{\mathcal{R}}}_{L,s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
);
$\unicode[STIX]{x1D711}_{\widehat{{\mathcal{R}}}_{L,s}}\otimes \unicode[STIX]{x1D711}_{\mathfrak{M}}$
); -
(4)
 $\mathfrak{M}\subset (\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})^{H_{L}}$
(resp.
$\mathfrak{M}\subset (\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})^{H_{L}}$
(resp.
 $\mathfrak{M}\subset (\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})^{H_{L}}$
);
$\mathfrak{M}\subset (\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})^{H_{L}}$
); -
(5)
 ${\hat{G}}_{L,s}$
acts on the
${\hat{G}}_{L,s}$
acts on the
 $W(k_{L})$
-module
$W(k_{L})$
-module
 $(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})/I_{+,L}(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})$
(resp.
$(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})/I_{+,L}(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})$
(resp.
 $(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})/I_{+,L,s}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})$
) trivially.
$(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})/I_{+,L,s}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M})$
) trivially.
Morphisms are defined by the obvious way. By replacing “free” of (1) with “torsion”, we define the category
 $\text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
(resp.
$\text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
(resp.
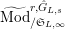 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
).
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
).
Remark 3.2. The category
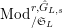 $\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
is very similar to the category
$\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
is very similar to the category
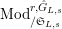 $\text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}$
from Definition 2.3, and so it may give the reader a little confusion. The differences between these categories are as follows.
$\text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}$
from Definition 2.3, and so it may give the reader a little confusion. The differences between these categories are as follows.

For any object
![]() $\hat{\mathfrak{M}}$
of
$\hat{\mathfrak{M}}$
of
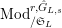 $\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
or
$\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
or
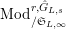 $\text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
, we define a
$\text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
, we define a
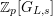 $\mathbb{Z}_{p}[G_{L,s}]$
-module
$\mathbb{Z}_{p}[G_{L,s}]$
-module
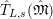 $\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
$\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
 $$\begin{eqnarray}\hat{T}_{L,s}(\hat{\mathfrak{M}})=\left\{\begin{array}{@{}ll@{}}\text{Hom}_{\widehat{{\mathcal{R}}}_{L},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M},W(R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{free},\\ \text{Hom}_{\widehat{{\mathcal{R}}}_{L},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{torsion}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\hat{T}_{L,s}(\hat{\mathfrak{M}})=\left\{\begin{array}{@{}ll@{}}\text{Hom}_{\widehat{{\mathcal{R}}}_{L},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M},W(R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{free},\\ \text{Hom}_{\widehat{{\mathcal{R}}}_{L},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\quad & \text{if}~\mathfrak{M}~\text{is}~\text{torsion}.\end{array}\right.\end{eqnarray}$$
Here,
![]() $G_{L,s}$
acts on
$G_{L,s}$
acts on
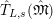 $\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
$\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
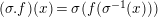 $(\unicode[STIX]{x1D70E}.f)(x)=\unicode[STIX]{x1D70E}(f(\unicode[STIX]{x1D70E}^{-1}(x)))$
for
$(\unicode[STIX]{x1D70E}.f)(x)=\unicode[STIX]{x1D70E}(f(\unicode[STIX]{x1D70E}^{-1}(x)))$
for
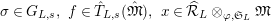 $\unicode[STIX]{x1D70E}\in G_{L,s},~f\in \hat{T}_{L,s}(\hat{\mathfrak{M}}),~x\in \widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
. Similar to the above, for any object
$\unicode[STIX]{x1D70E}\in G_{L,s},~f\in \hat{T}_{L,s}(\hat{\mathfrak{M}}),~x\in \widehat{{\mathcal{R}}}_{L}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}$
. Similar to the above, for any object
![]() $\hat{\mathfrak{M}}$
of
$\hat{\mathfrak{M}}$
of
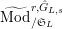 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
or
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
or
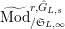 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
, we define a
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
, we define a
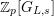 $\mathbb{Z}_{p}[G_{L,s}]$
-module
$\mathbb{Z}_{p}[G_{L,s}]$
-module
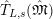 $\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
$\hat{T}_{L,s}(\hat{\mathfrak{M}})$
by
 $$\begin{eqnarray}\hat{T}_{L,s}(\hat{\mathfrak{M}})=\left\{\begin{array}{@{}l@{}}\text{Hom}_{\widehat{{\mathcal{R}}}_{L,s},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M},W(R))\hspace{59.75078pt}\text{if}~\mathfrak{M}~\text{is}~\text{free},\quad \\ \text{Hom}_{\widehat{{\mathcal{R}}}_{L,s},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\hspace{5.69054pt}\text{if}~\mathfrak{M}~\text{is}~\text{torsion}.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\hat{T}_{L,s}(\hat{\mathfrak{M}})=\left\{\begin{array}{@{}l@{}}\text{Hom}_{\widehat{{\mathcal{R}}}_{L,s},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M},W(R))\hspace{59.75078pt}\text{if}~\mathfrak{M}~\text{is}~\text{free},\quad \\ \text{Hom}_{\widehat{{\mathcal{R}}}_{L,s},\unicode[STIX]{x1D711}}(\widehat{{\mathcal{R}}}_{L,s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\hspace{5.69054pt}\text{if}~\mathfrak{M}~\text{is}~\text{torsion}.\quad \end{array}\right.\end{eqnarray}$$
On the other hand, we have natural functors
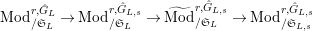 $\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}$
and
$\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}$
and
 $$\begin{eqnarray}\text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r,{\hat{G}}_{L,s}}\end{eqnarray}$$
$$\begin{eqnarray}\text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{L,s,\infty }}^{r,{\hat{G}}_{L,s}}\end{eqnarray}$$
and it is readily seen that these functors are compatible with
![]() $\hat{T}_{L}$
and
$\hat{T}_{L}$
and
![]() $\hat{T}_{L,s}$
. In particular, the functors
$\hat{T}_{L,s}$
. In particular, the functors
![]() $\hat{T}_{L,s}$
on
$\hat{T}_{L,s}$
on
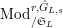 $\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
and
$\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
and
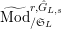 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
take their values in
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,s}}$
take their values in
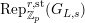 $\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{L,s})$
since we have an equivalence of categories
$\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{L,s})$
since we have an equivalence of categories
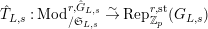 $\hat{T}_{L,s}:\text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}\overset{{\sim}}{\rightarrow }\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{L,s})$
by Theorem 2.5.
$\hat{T}_{L,s}:\text{Mod}_{/\mathfrak{S}_{L,s}}^{r,{\hat{G}}_{L,s}}\overset{{\sim}}{\rightarrow }\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{L,s})$
by Theorem 2.5.
In the rest of this section, we study free cases. We leave studies for torsion cases to the next section.
Convention: For simplicity, if
![]() $L=K$
, then we often omit the subscript “
$L=K$
, then we often omit the subscript “
![]() $L$
” from various notations (e.g.,
$L$
” from various notations (e.g.,
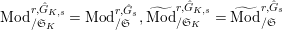 $\text{Mod}_{/\mathfrak{S}_{K}}^{r,{\hat{G}}_{K,s}}=\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}},\widetilde{\text{Mod}}_{/\mathfrak{S}_{K}}^{r,{\hat{G}}_{K,s}}=\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
). Furthermore, if
$\text{Mod}_{/\mathfrak{S}_{K}}^{r,{\hat{G}}_{K,s}}=\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}},\widetilde{\text{Mod}}_{/\mathfrak{S}_{K}}^{r,{\hat{G}}_{K,s}}=\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
). Furthermore, if
![]() $s=0$
, we often omit the subscript “
$s=0$
, we often omit the subscript “
![]() $s$
” from various notations (e.g.,
$s$
” from various notations (e.g.,
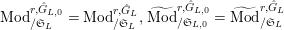 $\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,0}}=\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}},\widetilde{\text{Mod}}_{/\mathfrak{S}_{L,0}}^{r,{\hat{G}}_{L,0}}=\widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}$
).
$\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L,0}}=\text{Mod}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}},\widetilde{\text{Mod}}_{/\mathfrak{S}_{L,0}}^{r,{\hat{G}}_{L,0}}=\widetilde{\text{Mod}}_{/\mathfrak{S}_{L}}^{r,{\hat{G}}_{L}}$
).
3.2 The functors
 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
Now we consider the functors
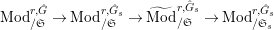 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
. At first, by Proposition 2.6, we see that the functor
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
. At first, by Proposition 2.6, we see that the functor
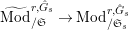 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
is fully faithful. It follows from this fact and Theorem 2.5(1) that the functor
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
is fully faithful. It follows from this fact and Theorem 2.5(1) that the functor
 $\hat{T}_{s}:\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{s})$
is fully faithful. It is clear that the functor
$\hat{T}_{s}:\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{s})$
is fully faithful. It is clear that the functor
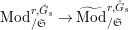 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
is fully faithful and thus so is
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
is fully faithful and thus so is
 $\hat{T}_{s}:\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{s})$
. Combining this with Theorem 2.5(1) and Lemma 2.8, we obtain that the functor
$\hat{T}_{s}:\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Rep}_{\mathbb{Z}_{p}}^{r,\text{st}}(G_{s})$
. Combining this with Theorem 2.5(1) and Lemma 2.8, we obtain that the functor
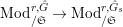 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
is also fully faithful. Furthermore, we prove the following.
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}}\rightarrow \text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
is also fully faithful. Furthermore, we prove the following.
Proposition 3.3. The functor
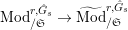 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
is an equivalence of categories.
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
is an equivalence of categories.
Summary, we obtained the following commutative diagram.

Remark 3.4. The functor
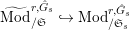 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}{\hookrightarrow}\text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
may not be possibly essentially surjective. In fact, under some conditions, there exists a representation of
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}{\hookrightarrow}\text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
may not be possibly essentially surjective. In fact, under some conditions, there exists a representation of
![]() $G_{K}$
which is crystalline over
$G_{K}$
which is crystalline over
![]() $K_{s}$
but not of finite height. For more precise information, see [Reference LiuLi2, Example 4.2.3].
$K_{s}$
but not of finite height. For more precise information, see [Reference LiuLi2, Example 4.2.3].
Before starting the proof of Proposition 3.3, we give an explicit formula such as (1) for an object of
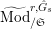 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. The argument below follows the method of [Reference LiuLi2]. Let
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. The argument below follows the method of [Reference LiuLi2]. Let
![]() $\hat{\mathfrak{M}}$
be an object of
$\hat{\mathfrak{M}}$
be an object of
 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. Let
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. Let
![]() $\hat{\mathfrak{M}}_{s}$
be the image of
$\hat{\mathfrak{M}}_{s}$
be the image of
![]() $\hat{\mathfrak{M}}$
for the functor
$\hat{\mathfrak{M}}$
for the functor
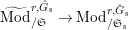 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
. Put
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
. Put
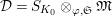 ${\mathcal{D}}=S_{K_{0}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
and also put
${\mathcal{D}}=S_{K_{0}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
and also put
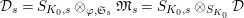 ${\mathcal{D}}_{s}=S_{K_{0},s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{s}}\mathfrak{M}_{s}=S_{K_{0},s}\otimes _{S_{K_{0}}}{\mathcal{D}}$
. Then
${\mathcal{D}}_{s}=S_{K_{0},s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{s}}\mathfrak{M}_{s}=S_{K_{0},s}\otimes _{S_{K_{0}}}{\mathcal{D}}$
. Then
![]() ${\mathcal{D}}_{s}$
has a structure of a Breuil module and also
${\mathcal{D}}_{s}$
has a structure of a Breuil module and also
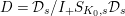 $D={\mathcal{D}}_{s}/I_{+}S_{K_{0},s}{\mathcal{D}}_{s}$
has a structure of a filtered
$D={\mathcal{D}}_{s}/I_{+}S_{K_{0},s}{\mathcal{D}}_{s}$
has a structure of a filtered
![]() $(\unicode[STIX]{x1D711},N)$
-module corresponding to
$(\unicode[STIX]{x1D711},N)$
-module corresponding to
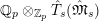 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}}_{s})$
(see Section 2.4), which is isomorphic to
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}}_{s})$
(see Section 2.4), which is isomorphic to
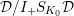 ${\mathcal{D}}/I_{+}S_{K_{0}}{\mathcal{D}}$
as a
${\mathcal{D}}/I_{+}S_{K_{0}}{\mathcal{D}}$
as a
![]() $\unicode[STIX]{x1D711}$
-module over
$\unicode[STIX]{x1D711}$
-module over
![]() $K_{0}$
. By [Reference LiuLi1, Lemma 7.3.1], we have a unique
$K_{0}$
. By [Reference LiuLi1, Lemma 7.3.1], we have a unique
![]() $\unicode[STIX]{x1D711}$
-compatible section
$\unicode[STIX]{x1D711}$
-compatible section
![]() $D{\hookrightarrow}{\mathcal{D}}$
and we regard
$D{\hookrightarrow}{\mathcal{D}}$
and we regard
![]() $D$
as a submodule of
$D$
as a submodule of
![]() ${\mathcal{D}}\subset {\mathcal{D}}_{s}$
by this section. Then we have
${\mathcal{D}}\subset {\mathcal{D}}_{s}$
by this section. Then we have
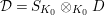 ${\mathcal{D}}=S_{K_{0}}\otimes _{K_{0}}D$
and
${\mathcal{D}}=S_{K_{0}}\otimes _{K_{0}}D$
and
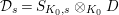 ${\mathcal{D}}_{s}=S_{K_{0},s}\otimes _{K_{0}}D$
. By the explicit formula (1) for
${\mathcal{D}}_{s}=S_{K_{0},s}\otimes _{K_{0}}D$
. By the explicit formula (1) for
![]() $\hat{\mathfrak{M}}_{s}$
, we know that
$\hat{\mathfrak{M}}_{s}$
, we know that
 $$\begin{eqnarray}{\hat{G}}_{s}(D)\subset (K_{0}[\![t]\!]\cap {\mathcal{R}}_{K_{0},s})\otimes _{K_{0}}D.\end{eqnarray}$$
$$\begin{eqnarray}{\hat{G}}_{s}(D)\subset (K_{0}[\![t]\!]\cap {\mathcal{R}}_{K_{0},s})\otimes _{K_{0}}D.\end{eqnarray}$$
(Note that
![]() ${\mathcal{R}}_{K_{0},s}$
can be regarded as a subring of
${\mathcal{R}}_{K_{0},s}$
can be regarded as a subring of
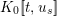 $K_{0}[\![t,u_{s}]\!]$
via [Reference LiuLi1, Lemma 7.1.2 ].) Hence, taking any
$K_{0}[\![t,u_{s}]\!]$
via [Reference LiuLi1, Lemma 7.1.2 ].) Hence, taking any
![]() $K_{0}$
-basis
$K_{0}$
-basis
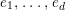 $e_{1},\ldots ,e_{d}$
of
$e_{1},\ldots ,e_{d}$
of
![]() $D$
, there exist
$D$
, there exist
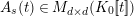 $A_{s}(t)\in M_{d\times d}(K_{0}[\![t]\!])$
such that
$A_{s}(t)\in M_{d\times d}(K_{0}[\![t]\!])$
such that
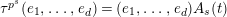 $\unicode[STIX]{x1D70F}^{p^{s}}(e_{1},\ldots ,e_{d})=(e_{1},\ldots ,e_{d})A_{s}(t)$
. Since
$\unicode[STIX]{x1D70F}^{p^{s}}(e_{1},\ldots ,e_{d})=(e_{1},\ldots ,e_{d})A_{s}(t)$
. Since
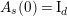 $A_{s}(0)=\text{I}_{d}$
, we see that
$A_{s}(0)=\text{I}_{d}$
, we see that
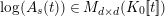 $\text{log}(A_{s}(t))\in M_{d\times d}(K_{0}[\![t]\!])$
is well defined. On the other hand, choose
$\text{log}(A_{s}(t))\in M_{d\times d}(K_{0}[\![t]\!])$
is well defined. On the other hand, choose
![]() $g_{0}\in G_{s}$
such that
$g_{0}\in G_{s}$
such that
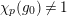 $\unicode[STIX]{x1D712}_{p}(g_{0})\not =1$
, where
$\unicode[STIX]{x1D712}_{p}(g_{0})\not =1$
, where
![]() $\unicode[STIX]{x1D712}_{p}$
is the
$\unicode[STIX]{x1D712}_{p}$
is the
![]() $p$
-adic cyclotomic character. Since
$p$
-adic cyclotomic character. Since
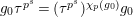 $g_{0}\unicode[STIX]{x1D70F}^{p^{s}}=(\unicode[STIX]{x1D70F}^{p^{s}})^{\unicode[STIX]{x1D712}_{p}(g_{0})}g_{0}$
, we have
$g_{0}\unicode[STIX]{x1D70F}^{p^{s}}=(\unicode[STIX]{x1D70F}^{p^{s}})^{\unicode[STIX]{x1D712}_{p}(g_{0})}g_{0}$
, we have
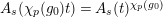 $A_{s}(\unicode[STIX]{x1D712}_{p}(g_{0})t)=A_{s}(t)^{\unicode[STIX]{x1D712}_{p}(g_{0})}$
and thus we also have
$A_{s}(\unicode[STIX]{x1D712}_{p}(g_{0})t)=A_{s}(t)^{\unicode[STIX]{x1D712}_{p}(g_{0})}$
and thus we also have
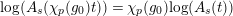 $\text{log}(A_{s}(\unicode[STIX]{x1D712}_{p}(g_{0})t))=\unicode[STIX]{x1D712}_{p}(g_{0})\text{log}(A_{s}(t))$
. Since
$\text{log}(A_{s}(\unicode[STIX]{x1D712}_{p}(g_{0})t))=\unicode[STIX]{x1D712}_{p}(g_{0})\text{log}(A_{s}(t))$
. Since
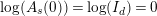 $\text{log}(A_{s}(0))=\text{log}(I_{d})=0$
, we can write
$\text{log}(A_{s}(0))=\text{log}(I_{d})=0$
, we can write
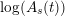 $\text{log}(A_{s}(t))$
as
$\text{log}(A_{s}(t))$
as
![]() $tB(t)$
for some
$tB(t)$
for some
 $B(t)\in M_{d\times d}(K_{0}[\![t]\!])$
. Then we have
$B(t)\in M_{d\times d}(K_{0}[\![t]\!])$
. Then we have
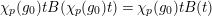 $\unicode[STIX]{x1D712}_{p}(g_{0})tB(\unicode[STIX]{x1D712}_{p}(g_{0})t)=\unicode[STIX]{x1D712}_{p}(g_{0})tB(t)$
, that is,
$\unicode[STIX]{x1D712}_{p}(g_{0})tB(\unicode[STIX]{x1D712}_{p}(g_{0})t)=\unicode[STIX]{x1D712}_{p}(g_{0})tB(t)$
, that is,
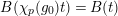 $B(\unicode[STIX]{x1D712}_{p}(g_{0})t)=B(t)$
. Hence the assumption
$B(\unicode[STIX]{x1D712}_{p}(g_{0})t)=B(t)$
. Hence the assumption
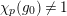 $\unicode[STIX]{x1D712}_{p}(g_{0})\not =1$
implies that
$\unicode[STIX]{x1D712}_{p}(g_{0})\not =1$
implies that
![]() $B(t)$
is a constant. Putting
$B(t)$
is a constant. Putting
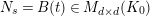 $N_{s}=B(t)\in M_{d\times d}(K_{0})$
, we obtain
$N_{s}=B(t)\in M_{d\times d}(K_{0})$
, we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}(e_{1},\ldots ,e_{d})=(e_{1},\ldots ,e_{d})\Bigl(\mathop{\sum }_{i=0}^{\infty }N_{s}^{i}\unicode[STIX]{x1D6FE}_{i}(t)\Bigr).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}(e_{1},\ldots ,e_{d})=(e_{1},\ldots ,e_{d})\Bigl(\mathop{\sum }_{i=0}^{\infty }N_{s}^{i}\unicode[STIX]{x1D6FE}_{i}(t)\Bigr).\end{eqnarray}$$
Now we define
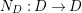 $N_{D}:D\rightarrow D$
by
$N_{D}:D\rightarrow D$
by
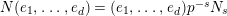 $N(e_{1},\ldots ,e_{d})=(e_{1},\ldots ,e_{d})p^{-s}N_{s}$
and also define
$N(e_{1},\ldots ,e_{d})=(e_{1},\ldots ,e_{d})p^{-s}N_{s}$
and also define
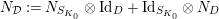 $N_{{\mathcal{D}}}:=N_{S_{K_{0}}}\otimes \text{Id}_{D}+\text{Id}_{S_{K_{0}}}\otimes N_{D}$
. (Note that we have
$N_{{\mathcal{D}}}:=N_{S_{K_{0}}}\otimes \text{Id}_{D}+\text{Id}_{S_{K_{0}}}\otimes N_{D}$
. (Note that we have
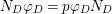 $N_{D}\unicode[STIX]{x1D711}_{D}=p\unicode[STIX]{x1D711}_{D}N_{D}$
and thus
$N_{D}\unicode[STIX]{x1D711}_{D}=p\unicode[STIX]{x1D711}_{D}N_{D}$
and thus
![]() $N_{D}$
is nilpotent.) It is a routine work to check the following:
$N_{D}$
is nilpotent.) It is a routine work to check the following:
 $$\begin{eqnarray}g(a\otimes x)=\mathop{\sum }_{i=0}^{\infty }g(a)\unicode[STIX]{x1D6FE}_{i}(-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}(g)]))\otimes N_{D}^{i}(x)\quad \text{for}~g\in G_{s},a\in B_{\text{cris}}^{+},x\in D.\end{eqnarray}$$
$$\begin{eqnarray}g(a\otimes x)=\mathop{\sum }_{i=0}^{\infty }g(a)\unicode[STIX]{x1D6FE}_{i}(-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}(g)]))\otimes N_{D}^{i}(x)\quad \text{for}~g\in G_{s},a\in B_{\text{cris}}^{+},x\in D.\end{eqnarray}$$
Since we have
 $$\begin{eqnarray}g(f)=\mathop{\sum }_{i=0}^{\infty }\unicode[STIX]{x1D6FE}_{i}(-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}(g)]))N_{S_{K_{0}}}^{i}(f)\end{eqnarray}$$
$$\begin{eqnarray}g(f)=\mathop{\sum }_{i=0}^{\infty }\unicode[STIX]{x1D6FE}_{i}(-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}(g)]))N_{S_{K_{0}}}^{i}(f)\end{eqnarray}$$
for any
![]() $g\in G_{K}$
and
$g\in G_{K}$
and
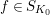 $f\in S_{K_{0}}$
, we obtain the following explicit formula:
$f\in S_{K_{0}}$
, we obtain the following explicit formula:
 $$\begin{eqnarray}g(a\otimes x)=\mathop{\sum }_{i=0}^{\infty }g(a)\unicode[STIX]{x1D6FE}_{i}(-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}(g)]))\otimes N_{{\mathcal{D}}}^{i}(x)\quad \text{for}~g\in G_{s},a\in B_{\text{cris}}^{+},x\in {\mathcal{D}}.\end{eqnarray}$$
$$\begin{eqnarray}g(a\otimes x)=\mathop{\sum }_{i=0}^{\infty }g(a)\unicode[STIX]{x1D6FE}_{i}(-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}(g)]))\otimes N_{{\mathcal{D}}}^{i}(x)\quad \text{for}~g\in G_{s},a\in B_{\text{cris}}^{+},x\in {\mathcal{D}}.\end{eqnarray}$$
In particular, as in Section 2.4, we can show that
 $$\begin{eqnarray}\text{log}(\unicode[STIX]{x1D70F}^{p^{s}})(x)=p^{s}t\otimes N_{{\mathcal{D}}}(x)\end{eqnarray}$$
$$\begin{eqnarray}\text{log}(\unicode[STIX]{x1D70F}^{p^{s}})(x)=p^{s}t\otimes N_{{\mathcal{D}}}(x)\end{eqnarray}$$
for any
![]() $x\in {\mathcal{D}}$
.
$x\in {\mathcal{D}}$
.
Proof of Proposition 3.3.
We continue to use the above notation. It suffices to prove that the
![]() $G_{s}$
-action on
$G_{s}$
-action on
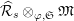 $\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
preserves
$\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
preserves
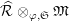 $\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
. Note that we have
$\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
. Note that we have
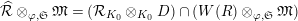 $\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}=({\mathcal{R}}_{K_{0}}\otimes _{K_{0}}D)\cap (W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})$
,
$\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}=({\mathcal{R}}_{K_{0}}\otimes _{K_{0}}D)\cap (W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})$
,
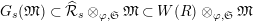 $G_{s}(\mathfrak{M})\subset \widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\subset W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
and
$G_{s}(\mathfrak{M})\subset \widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\subset W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
and
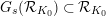 $G_{s}({\mathcal{R}}_{K_{0}})\subset {\mathcal{R}}_{K_{0}}$
. Thus it is enough to show
$G_{s}({\mathcal{R}}_{K_{0}})\subset {\mathcal{R}}_{K_{0}}$
. Thus it is enough to show
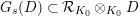 $G_{s}(D)\subset {\mathcal{R}}_{K_{0}}\otimes _{K_{0}}D$
. This quickly follows from (3). In fact, we have
$G_{s}(D)\subset {\mathcal{R}}_{K_{0}}\otimes _{K_{0}}D$
. This quickly follows from (3). In fact, we have
 $$\begin{eqnarray}g(x)=\mathop{\sum }_{i=0}^{\infty }\unicode[STIX]{x1D6FE}_{i}(-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}(g)]))\otimes N_{D}^{i}(x)\in {\mathcal{R}}_{K_{0}}\otimes _{K_{0}}D\quad \text{for}~x\in D,~g\in G_{s}.\square\end{eqnarray}$$
$$\begin{eqnarray}g(x)=\mathop{\sum }_{i=0}^{\infty }\unicode[STIX]{x1D6FE}_{i}(-\text{log}([\text{}\underline{\unicode[STIX]{x1D700}}(g)]))\otimes N_{D}^{i}(x)\in {\mathcal{R}}_{K_{0}}\otimes _{K_{0}}D\quad \text{for}~x\in D,~g\in G_{s}.\square\end{eqnarray}$$
3.3 Relations with crystalline representations
We know that
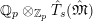 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is semistable over
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is semistable over
![]() $K_{s}$
for any object
$K_{s}$
for any object
![]() $\hat{\mathfrak{M}}$
of
$\hat{\mathfrak{M}}$
of
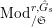 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
or
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
or
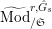 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. This subsection is devoted to prove a criterion, for
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. This subsection is devoted to prove a criterion, for
![]() $\hat{\mathfrak{M}}$
, that describes when
$\hat{\mathfrak{M}}$
, that describes when
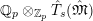 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
becomes crystalline.
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
becomes crystalline.
Following [Reference FontaineFo2, Section 5] we set
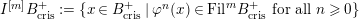 $I^{[m]}B_{\text{cris}}^{+}:=\{x\in B_{\text{cris}}^{+}\mid \unicode[STIX]{x1D711}^{n}(x)\in \text{Fil}^{m}B_{\text{cris}}^{+}~\text{for all}~n\geqslant 0\}$
. For any subring
$I^{[m]}B_{\text{cris}}^{+}:=\{x\in B_{\text{cris}}^{+}\mid \unicode[STIX]{x1D711}^{n}(x)\in \text{Fil}^{m}B_{\text{cris}}^{+}~\text{for all}~n\geqslant 0\}$
. For any subring
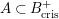 $A\subset B_{\text{cris}}^{+}$
, we put
$A\subset B_{\text{cris}}^{+}$
, we put
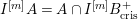 $I^{[m]}A=A\cap I^{[m]}B_{\text{cris}}^{+}$
. Furthermore, we also put
$I^{[m]}A=A\cap I^{[m]}B_{\text{cris}}^{+}$
. Furthermore, we also put
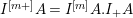 $I^{[m+]}A=I^{[m]}A.I_{+}A$
(here,
$I^{[m+]}A=I^{[m]}A.I_{+}A$
(here,
![]() $I_{+}A$
is defined in Section 2.3). By [Reference FontaineFo2, Proposition 5.1.3] and the proof of [Reference LiuLi2, Lemma 3.2.2], we know that
$I_{+}A$
is defined in Section 2.3). By [Reference FontaineFo2, Proposition 5.1.3] and the proof of [Reference LiuLi2, Lemma 3.2.2], we know that
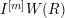 $I^{[m]}W(R)$
is a principal ideal which is generated by
$I^{[m]}W(R)$
is a principal ideal which is generated by
![]() $\unicode[STIX]{x1D711}(\mathfrak{t})^{m}$
.
$\unicode[STIX]{x1D711}(\mathfrak{t})^{m}$
.
Now we recall Theorem 2.5(2): if
![]() $\mathfrak{M}$
is an object of
$\mathfrak{M}$
is an object of
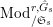 $\text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
, then
$\text{Mod}_{/\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
, then
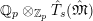 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is crystalline if and only if
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is crystalline if and only if
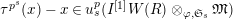 $\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in u_{s}^{p}(I^{[1]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{s}}\mathfrak{M})$
for any
$\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in u_{s}^{p}(I^{[1]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{s}}\mathfrak{M})$
for any
![]() $x\in \mathfrak{M}$
. However, if such
$x\in \mathfrak{M}$
. However, if such
![]() $\mathfrak{M}$
descends to a Kisin module over
$\mathfrak{M}$
descends to a Kisin module over
![]() $\mathfrak{S}$
, then we can show the following.
$\mathfrak{S}$
, then we can show the following.
Theorem 3.5. Let
![]() $\hat{\mathfrak{M}}$
be an object of
$\hat{\mathfrak{M}}$
be an object of
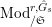 $\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
or
$\text{Mod}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
or
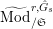 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. Then the following is equivalent:
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. Then the following is equivalent:
-
(1)
 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is crystalline;
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is crystalline; -
(2)
 $\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in u^{p}(I^{[1]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})$
for any
$\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in u^{p}(I^{[1]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})$
for any
 $x\in \mathfrak{M}$
;
$x\in \mathfrak{M}$
; -
(3)
 $\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in I^{[1+]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
for any
$\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in I^{[1+]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
for any
 $x\in \mathfrak{M}$
.
$x\in \mathfrak{M}$
.
Proof. (1)
![]() $\Rightarrow$
(2): The proof here mainly follows that of [Reference Gee, Liu and SavittGLS, Proposition 4.7]. We may suppose
$\Rightarrow$
(2): The proof here mainly follows that of [Reference Gee, Liu and SavittGLS, Proposition 4.7]. We may suppose
![]() $\hat{\mathfrak{M}}$
is an object of
$\hat{\mathfrak{M}}$
is an object of
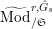 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. Put
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}$
. Put
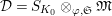 ${\mathcal{D}}=S_{K_{0}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
and
${\mathcal{D}}=S_{K_{0}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
and
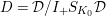 $D={\mathcal{D}}/I_{+}S_{K_{0}}{\mathcal{D}}$
as in the previous subsection. We fix a
$D={\mathcal{D}}/I_{+}S_{K_{0}}{\mathcal{D}}$
as in the previous subsection. We fix a
![]() $\unicode[STIX]{x1D711}(\mathfrak{S})$
-basis
$\unicode[STIX]{x1D711}(\mathfrak{S})$
-basis
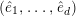 $(\hat{e}_{1},\ldots ,\hat{e}_{d})$
of
$(\hat{e}_{1},\ldots ,\hat{e}_{d})$
of
![]() $\mathfrak{M}\subset {\mathcal{D}}$
and denote by
$\mathfrak{M}\subset {\mathcal{D}}$
and denote by
 $(e_{1},\ldots ,e_{d})$
the image of
$(e_{1},\ldots ,e_{d})$
the image of
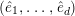 $(\hat{e}_{1},\ldots ,\hat{e}_{d})$
for the projection
$(\hat{e}_{1},\ldots ,\hat{e}_{d})$
for the projection
![]() ${\mathcal{D}}\rightarrow D$
. Then
${\mathcal{D}}\rightarrow D$
. Then
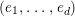 $(e_{1},\ldots ,e_{d})$
is a
$(e_{1},\ldots ,e_{d})$
is a
![]() $K_{0}$
-basis of
$K_{0}$
-basis of
![]() $D$
. As described before the proof of Proposition 3.3, we regard
$D$
. As described before the proof of Proposition 3.3, we regard
![]() $D$
as a
$D$
as a
![]() $\unicode[STIX]{x1D711}$
-stable submodule of
$\unicode[STIX]{x1D711}$
-stable submodule of
![]() ${\mathcal{D}}$
, and we have
${\mathcal{D}}$
, and we have
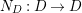 $N_{D}:D\rightarrow D$
and
$N_{D}:D\rightarrow D$
and
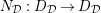 $N_{{\mathcal{D}}}:D_{{\mathcal{D}}}\rightarrow D_{{\mathcal{D}}}$
.
$N_{{\mathcal{D}}}:D_{{\mathcal{D}}}\rightarrow D_{{\mathcal{D}}}$
.
Now we consider a matrix
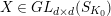 $X\in GL_{d\times d}(S_{K_{0}})$
such that
$X\in GL_{d\times d}(S_{K_{0}})$
such that
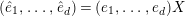 $(\hat{e}_{1},\ldots ,\hat{e}_{d})=(e_{1},\ldots ,e_{d})X$
. We define
$(\hat{e}_{1},\ldots ,\hat{e}_{d})=(e_{1},\ldots ,e_{d})X$
. We define
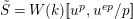 $\tilde{S}=W(k)[\![u^{p},u^{ep}/p]\!]$
as in [Reference Gee, Liu and SavittGLS, Section 4], which is a sub
$\tilde{S}=W(k)[\![u^{p},u^{ep}/p]\!]$
as in [Reference Gee, Liu and SavittGLS, Section 4], which is a sub
![]() $W(k)$
-algebra of
$W(k)$
-algebra of
![]() $S_{K_{0}}^{\text{int}}$
with the property
$S_{K_{0}}^{\text{int}}$
with the property
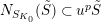 $N_{S_{K_{0}}}(\tilde{S})\subset u^{p}\tilde{S}$
. By an easy computation we have
$N_{S_{K_{0}}}(\tilde{S})\subset u^{p}\tilde{S}$
. By an easy computation we have
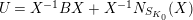 $U=X^{-1}BX+X^{-1}N_{S_{K_{0}}}(X)$
. Here,
$U=X^{-1}BX+X^{-1}N_{S_{K_{0}}}(X)$
. Here,
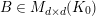 $B\in M_{d\times d}(K_{0})$
and
$B\in M_{d\times d}(K_{0})$
and
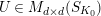 $U\in M_{d\times d}(S_{K_{0}})$
are defined by
$U\in M_{d\times d}(S_{K_{0}})$
are defined by
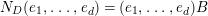 $N_{D}(e_{1},\ldots ,e_{d})=(e_{1},\ldots ,e_{d})B$
and
$N_{D}(e_{1},\ldots ,e_{d})=(e_{1},\ldots ,e_{d})B$
and
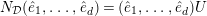 $N_{{\mathcal{D}}}(\hat{e}_{1},\ldots ,\hat{e}_{d})=(\hat{e}_{1},\ldots ,\hat{e}_{d})U$
. By the same proof as in the former half part of the proof of [Reference Gee, Liu and SavittGLS, Proposition 4.7], we obtain
$N_{{\mathcal{D}}}(\hat{e}_{1},\ldots ,\hat{e}_{d})=(\hat{e}_{1},\ldots ,\hat{e}_{d})U$
. By the same proof as in the former half part of the proof of [Reference Gee, Liu and SavittGLS, Proposition 4.7], we obtain
 $X,X^{-1}\in M_{d\times d}(\tilde{S}[1/p])$
. On the other hand, let
$X,X^{-1}\in M_{d\times d}(\tilde{S}[1/p])$
. On the other hand, let
![]() $\hat{\mathfrak{M}}_{s}$
be the image of
$\hat{\mathfrak{M}}_{s}$
be the image of
![]() $\hat{\mathfrak{M}}$
for the functor
$\hat{\mathfrak{M}}$
for the functor
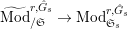 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
. Now we recall that
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
. Now we recall that
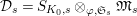 ${\mathcal{D}}_{s}=S_{K_{0},s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{s}}\mathfrak{M}_{s}$
has a structure of the Breuil module corresponding to
${\mathcal{D}}_{s}=S_{K_{0},s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{s}}\mathfrak{M}_{s}$
has a structure of the Breuil module corresponding to
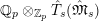 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}}_{s})$
Denote by
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}}_{s})$
Denote by
![]() $N_{{\mathcal{D}}_{s}}$
its monodromy operator. By the formula (2) for
$N_{{\mathcal{D}}_{s}}$
its monodromy operator. By the formula (2) for
![]() $\hat{\mathfrak{M}}_{s}$
and the formula (6) for
$\hat{\mathfrak{M}}_{s}$
and the formula (6) for
![]() $\hat{\mathfrak{M}}$
, we see that
$\hat{\mathfrak{M}}$
, we see that
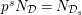 $p^{s}N_{{\mathcal{D}}}=N_{{\mathcal{D}}_{s}}$
on
$p^{s}N_{{\mathcal{D}}}=N_{{\mathcal{D}}_{s}}$
on
![]() ${\mathcal{D}}$
. Therefore,
${\mathcal{D}}$
. Therefore,
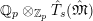 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is crystalline if and only if
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is crystalline if and only if
![]() $N_{{\mathcal{D}}_{s}}$
mod
$N_{{\mathcal{D}}_{s}}$
mod
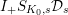 $I_{+}S_{K_{0},s}{\mathcal{D}}_{s}$
is zero, which is equivalent to say that
$I_{+}S_{K_{0},s}{\mathcal{D}}_{s}$
is zero, which is equivalent to say that
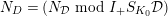 $N_{D}=(N_{{\mathcal{D}}}~\text{mod}~I_{+}S_{K_{0}}{\mathcal{D}})$
is zero, that is,
$N_{D}=(N_{{\mathcal{D}}}~\text{mod}~I_{+}S_{K_{0}}{\mathcal{D}})$
is zero, that is,
![]() $B=0$
. Therefore, the latter half part of the proof [Reference Gee, Liu and SavittGLS, Proposition 4.7] gives the assertion (2).
$B=0$
. Therefore, the latter half part of the proof [Reference Gee, Liu and SavittGLS, Proposition 4.7] gives the assertion (2).
(2)
![]() $\Rightarrow$
(3): This is clear.
$\Rightarrow$
(3): This is clear.
(3)
![]() $\Rightarrow$
(1): Suppose that (3) holds. We denote by
$\Rightarrow$
(1): Suppose that (3) holds. We denote by
![]() $\hat{\mathfrak{M}}_{s}$
the image of
$\hat{\mathfrak{M}}_{s}$
the image of
![]() $\hat{\mathfrak{M}}$
for the functor
$\hat{\mathfrak{M}}$
for the functor
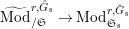 $\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
as above. We claim that, for any
$\widetilde{\text{Mod}}_{/\mathfrak{S}}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{\mathfrak{S}_{s}}^{r,{\hat{G}}_{s}}$
as above. We claim that, for any
![]() $x\in \mathfrak{M}_{s}$
, we have
$x\in \mathfrak{M}_{s}$
, we have
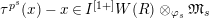 $\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in I^{[1+]}W(R)\otimes _{\unicode[STIX]{x1D711}_{s}}\mathfrak{M}_{s}$
. Let
$\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in I^{[1+]}W(R)\otimes _{\unicode[STIX]{x1D711}_{s}}\mathfrak{M}_{s}$
. Let
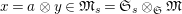 $x=a\otimes y\in \mathfrak{M}_{s}=\mathfrak{S}_{s}\otimes _{\mathfrak{S}}\mathfrak{M}$
where
$x=a\otimes y\in \mathfrak{M}_{s}=\mathfrak{S}_{s}\otimes _{\mathfrak{S}}\mathfrak{M}$
where
![]() $a\in \mathfrak{S}_{s}$
and
$a\in \mathfrak{S}_{s}$
and
![]() $y\in \mathfrak{M}$
. Then
$y\in \mathfrak{M}$
. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}(x)-x=\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))(\unicode[STIX]{x1D70F}^{p^{s}}(y)-y)+(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a))y\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}(x)-x=\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))(\unicode[STIX]{x1D70F}^{p^{s}}(y)-y)+(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a))y\end{eqnarray}$$
and thus it suffices to show
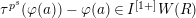 $\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a)\in I^{[1+]}W(R)$
. This follows from the lemma below and thus we obtained the claim. By the claim and [Reference OzekiOz2, Theorem 21], we know that
$\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a)\in I^{[1+]}W(R)$
. This follows from the lemma below and thus we obtained the claim. By the claim and [Reference OzekiOz2, Theorem 21], we know that
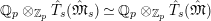 $\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}}_{s})\simeq \mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is crystalline.◻
$\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}}_{s})\simeq \mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}(\hat{\mathfrak{M}})$
is crystalline.◻
Lemma 3.6.
![]() $(1)$
We have
$(1)$
We have
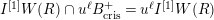 $I^{[1]}W(R)\cap u^{\ell }B_{\text{cris}}^{+}=u^{\ell }I^{[1]}W(R)$
for
$I^{[1]}W(R)\cap u^{\ell }B_{\text{cris}}^{+}=u^{\ell }I^{[1]}W(R)$
for
![]() $\ell \geqslant 0$
.
$\ell \geqslant 0$
.
![]() $(2)$
We have
$(2)$
We have
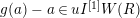 $g(a)-a\in uI^{[1]}W(R)$
for
$g(a)-a\in uI^{[1]}W(R)$
for
![]() $g\in G$
and
$g\in G$
and
![]() $a\in \mathfrak{S}$
.
$a\in \mathfrak{S}$
.
Proof. This is due to [Reference Gee, Liu and SavittGLS, the proof of Proposition 7] but we write a proof here.
(1) Take
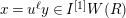 $x=u^{\ell }y\in I^{[1]}W(R)$
with
$x=u^{\ell }y\in I^{[1]}W(R)$
with
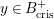 $y\in B_{\text{cris}}^{+}$
. By [Reference LiuLi4, Lemma 3.2.2] we have
$y\in B_{\text{cris}}^{+}$
. By [Reference LiuLi4, Lemma 3.2.2] we have
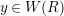 $y\in W(R)$
. Now we remark that
$y\in W(R)$
. Now we remark that
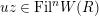 $uz\in \text{Fil}^{n}W(R)$
with
$uz\in \text{Fil}^{n}W(R)$
with
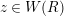 $z\in W(R)$
implies
$z\in W(R)$
implies
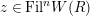 $z\in \text{Fil}^{n}W(R)$
since
$z\in \text{Fil}^{n}W(R)$
since
![]() $u$
is a unit of
$u$
is a unit of
![]() $B_{\text{dR}}^{+}$
. Hence
$B_{\text{dR}}^{+}$
. Hence
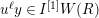 $u^{\ell }y\in I^{[1]}W(R)$
implies
$u^{\ell }y\in I^{[1]}W(R)$
implies
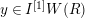 $y\in I^{[1]}W(R)$
.
$y\in I^{[1]}W(R)$
.
(2) By the relation (4), we see that
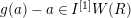 $g(a)-a\in I^{[1]}W(R)$
. On the other hand, if
$g(a)-a\in I^{[1]}W(R)$
. On the other hand, if
![]() $i>0$
, we can write
$i>0$
, we can write
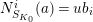 $N_{S_{K_{0}}}^{i}(a)=ub_{i}$
for some
$N_{S_{K_{0}}}^{i}(a)=ub_{i}$
for some
![]() $b_{i}\in \mathfrak{S}$
. Thus by the relation (4) again we obtain
$b_{i}\in \mathfrak{S}$
. Thus by the relation (4) again we obtain
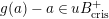 $g(a)-a\in uB_{\text{cris}}^{+}$
. Then the result follows from (1).◻
$g(a)-a\in uB_{\text{cris}}^{+}$
. Then the result follows from (1).◻
4 Variants of torsion
 $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules
In this section, we mainly study full subcategories of
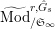 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
defined below and also study representations associated with them. As a consequence, we prove theorems in Introduction. We use same notation as in Sections 2 and 3. In particular,
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
defined below and also study representations associated with them. As a consequence, we prove theorems in Introduction. We use same notation as in Sections 2 and 3. In particular,
![]() $p$
is odd. In below, let
$p$
is odd. In below, let
![]() $v_{R}$
be the valuation of
$v_{R}$
be the valuation of
![]() $R$
normalized such that
$R$
normalized such that
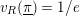 $v_{R}(\text{}\underline{\unicode[STIX]{x1D70B}})=1/e$
and, for any real number
$v_{R}(\text{}\underline{\unicode[STIX]{x1D70B}})=1/e$
and, for any real number
![]() $x\geqslant 0$
, we denote by
$x\geqslant 0$
, we denote by
![]() $\mathfrak{m}_{R}^{{\geqslant}x}$
the ideal of
$\mathfrak{m}_{R}^{{\geqslant}x}$
the ideal of
![]() $R$
consisting of elements
$R$
consisting of elements
![]() $a$
with
$a$
with
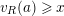 $v_{R}(a)\geqslant x$
.
$v_{R}(a)\geqslant x$
.
Let
![]() $J$
be an ideal of
$J$
be an ideal of
![]() $W(R)$
which satisfies the following conditions:
$W(R)$
which satisfies the following conditions:
-
∙
 $J\not \subset pW(R)$
;
$J\not \subset pW(R)$
; -
∙
 $J$
is a principal ideal;
$J$
is a principal ideal; -
∙
 $J$
is
$J$
is
 $\unicode[STIX]{x1D711}$
-stable and
$\unicode[STIX]{x1D711}$
-stable and
 $G_{s}$
-stable in
$G_{s}$
-stable in
 $W(R)$
.
$W(R)$
.
By the above first and second assumptions for
![]() $J$
, the image of
$J$
, the image of
![]() $J$
under the projection
$J$
under the projection
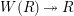 $W(R){\twoheadrightarrow}R$
is of the form
$W(R){\twoheadrightarrow}R$
is of the form
![]() $\mathfrak{m}_{R}^{{\geqslant}c_{J}}$
for some real number
$\mathfrak{m}_{R}^{{\geqslant}c_{J}}$
for some real number
![]() $c_{J}\geqslant 0$
.
$c_{J}\geqslant 0$
.
Definition 4.1. We denote by
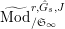 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
the full subcategory of
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
the full subcategory of
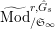 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
consisting of objects
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
consisting of objects
![]() $\hat{\mathfrak{M}}$
which satisfy the following condition:
$\hat{\mathfrak{M}}$
which satisfy the following condition:
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\quad \text{for any}~x\in \mathfrak{M}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\quad \text{for any}~x\in \mathfrak{M}.\end{eqnarray}$$
We denote by
 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
the essential image of the functor
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
the essential image of the functor
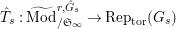 $\hat{T}_{s}:\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \text{Rep}_{\text{tor}}(G_{s})$
restricted to
$\hat{T}_{s}:\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \text{Rep}_{\text{tor}}(G_{s})$
restricted to
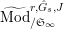 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
.
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
.
By definition, we have relations
 $$\begin{eqnarray}\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}\subset \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J^{\prime }}\qquad \text{and}\qquad \widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})\subset \widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J^{\prime }}(G_{s})\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}\subset \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J^{\prime }}\qquad \text{and}\qquad \widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})\subset \widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J^{\prime }}(G_{s})\end{eqnarray}$$
for
![]() $J\subset J^{\prime }$
.
$J\subset J^{\prime }$
.
4.1 Full faithfulness for
 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
For the beginning of a study of
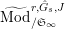 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
, we prove the following full faithfulness result.
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
, we prove the following full faithfulness result.
Proposition 4.2. Let
![]() $r$
and
$r$
and
![]() $r^{\prime }$
be nonnegative integers with
$r^{\prime }$
be nonnegative integers with
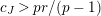 $c_{J}>pr/(p-1)$
. Let
$c_{J}>pr/(p-1)$
. Let
![]() $\hat{\mathfrak{M}}$
and
$\hat{\mathfrak{M}}$
and
![]() $\hat{\mathfrak{N}}$
be objects of
$\hat{\mathfrak{N}}$
be objects of
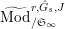 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
and
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
and
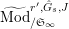 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s},J}$
, respectively. Then we have
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s},J}$
, respectively. Then we have
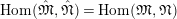 $\text{Hom}(\hat{\mathfrak{M}},\hat{\mathfrak{N}})=\text{Hom}(\mathfrak{M},\mathfrak{N})$
. (Here, two “
$\text{Hom}(\hat{\mathfrak{M}},\hat{\mathfrak{N}})=\text{Hom}(\mathfrak{M},\mathfrak{N})$
. (Here, two “
![]() $\text{Hom}$
”s are defined by obvious manners.)
$\text{Hom}$
”s are defined by obvious manners.)
In particular, if
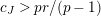 $c_{J}>pr/(p-1)$
, then the forgetful functor
$c_{J}>pr/(p-1)$
, then the forgetful functor
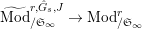 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}\rightarrow \text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
is fully faithful.
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}\rightarrow \text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
is fully faithful.
Proof. A very similar proof of [Reference OzekiOz2, Lemma 7] proceeds, and hence we only give a sketch here. Let
![]() $\hat{\mathfrak{M}}$
and
$\hat{\mathfrak{M}}$
and
![]() $\hat{\mathfrak{N}}$
be objects of
$\hat{\mathfrak{N}}$
be objects of
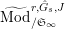 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
and
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
and
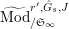 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s},J}$
, respectively. Let
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s},J}$
, respectively. Let
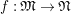 $f:\mathfrak{M}\rightarrow \mathfrak{N}$
be a morphism of Kisin modules over
$f:\mathfrak{M}\rightarrow \mathfrak{N}$
be a morphism of Kisin modules over
![]() $\mathfrak{S}$
. Put
$\mathfrak{S}$
. Put
 $\hat{f}=W(R)\otimes f:W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\rightarrow W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
. Choose any lift of
$\hat{f}=W(R)\otimes f:W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\rightarrow W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
. Choose any lift of
![]() $\unicode[STIX]{x1D70F}\in {\hat{G}}$
to
$\unicode[STIX]{x1D70F}\in {\hat{G}}$
to
![]() $G_{K}$
; we denote it also by
$G_{K}$
; we denote it also by
![]() $\unicode[STIX]{x1D70F}$
. Since the
$\unicode[STIX]{x1D70F}$
. Since the
![]() ${\hat{G}}_{s}$
-action for
${\hat{G}}_{s}$
-action for
![]() $\hat{\mathfrak{M}}$
is continuous, it suffices to prove that
$\hat{\mathfrak{M}}$
is continuous, it suffices to prove that
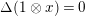 $\unicode[STIX]{x1D6E5}(1\otimes x)=0$
for any
$\unicode[STIX]{x1D6E5}(1\otimes x)=0$
for any
![]() $x\in \mathfrak{M}$
where
$x\in \mathfrak{M}$
where
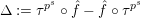 $\unicode[STIX]{x1D6E5}:=\unicode[STIX]{x1D70F}^{p^{s}}\circ \hat{f}-\hat{f}\circ \unicode[STIX]{x1D70F}^{p^{s}}$
. We use induction on
$\unicode[STIX]{x1D6E5}:=\unicode[STIX]{x1D70F}^{p^{s}}\circ \hat{f}-\hat{f}\circ \unicode[STIX]{x1D70F}^{p^{s}}$
. We use induction on
![]() $n$
such that
$n$
such that
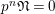 $p^{n}\mathfrak{N}=0$
.
$p^{n}\mathfrak{N}=0$
.
Suppose
![]() $n=1$
. Since
$n=1$
. Since
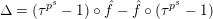 $\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D70F}^{p^{s}}-1)\circ \hat{f}-\hat{f}\circ (\unicode[STIX]{x1D70F}^{p^{s}}-1)$
, we obtain the following:
$\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D70F}^{p^{s}}-1)\circ \hat{f}-\hat{f}\circ (\unicode[STIX]{x1D70F}^{p^{s}}-1)$
, we obtain the following:
 $$\begin{eqnarray}(0):\quad \text{For any }x\in \mathfrak{M},\quad \unicode[STIX]{x1D6E5}(1\otimes x)\in \mathfrak{m}_{R}^{{\geqslant}c(0)}(R\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N})\end{eqnarray}$$
$$\begin{eqnarray}(0):\quad \text{For any }x\in \mathfrak{M},\quad \unicode[STIX]{x1D6E5}(1\otimes x)\in \mathfrak{m}_{R}^{{\geqslant}c(0)}(R\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N})\end{eqnarray}$$
where
 $c(0)=c_{J}$
. Since
$c(0)=c_{J}$
. Since
![]() $\mathfrak{M}$
is of height
$\mathfrak{M}$
is of height
![]() ${\leqslant}r$
, we further obtain the following for any
${\leqslant}r$
, we further obtain the following for any
![]() $i\geqslant 1$
inductively:
$i\geqslant 1$
inductively:
 $$\begin{eqnarray}(i):\quad \text{For any }x\in \mathfrak{M},\quad \unicode[STIX]{x1D6E5}(1\otimes x)\in \mathfrak{m}_{R}^{{\geqslant}c(i)}(R\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N})\end{eqnarray}$$
$$\begin{eqnarray}(i):\quad \text{For any }x\in \mathfrak{M},\quad \unicode[STIX]{x1D6E5}(1\otimes x)\in \mathfrak{m}_{R}^{{\geqslant}c(i)}(R\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N})\end{eqnarray}$$
where
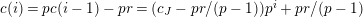 $c(i)=pc(i-1)-pr=(c_{J}-pr/(p-1))p^{i}+pr/(p-1)$
. The condition
$c(i)=pc(i-1)-pr=(c_{J}-pr/(p-1))p^{i}+pr/(p-1)$
. The condition
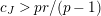 $c_{J}>pr/(p-1)$
implies that
$c_{J}>pr/(p-1)$
implies that
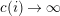 $c(i)\rightarrow \infty$
as
$c(i)\rightarrow \infty$
as
![]() $i\rightarrow \infty$
and thus
$i\rightarrow \infty$
and thus
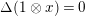 $\unicode[STIX]{x1D6E5}(1\otimes x)=0$
.
$\unicode[STIX]{x1D6E5}(1\otimes x)=0$
.
Suppose
![]() $n>1$
. Consider the exact sequence
$n>1$
. Consider the exact sequence
 $0\rightarrow \text{Ker}(p)\rightarrow \mathfrak{N}\overset{p}{\rightarrow }p\mathfrak{N}\rightarrow 0$
of
$0\rightarrow \text{Ker}(p)\rightarrow \mathfrak{N}\overset{p}{\rightarrow }p\mathfrak{N}\rightarrow 0$
of
![]() $\unicode[STIX]{x1D711}$
-modules over
$\unicode[STIX]{x1D711}$
-modules over
![]() $\mathfrak{S}$
. It is not difficult to check that
$\mathfrak{S}$
. It is not difficult to check that
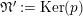 $\mathfrak{N}^{\prime }:=\text{Ker}(p)$
and
$\mathfrak{N}^{\prime }:=\text{Ker}(p)$
and
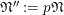 $\mathfrak{N}^{\prime \prime }:=p\mathfrak{N}$
are torsion Kisin modules of height
$\mathfrak{N}^{\prime \prime }:=p\mathfrak{N}$
are torsion Kisin modules of height
![]() ${\leqslant}r^{\prime }$
over
${\leqslant}r^{\prime }$
over
![]() $\mathfrak{S}$
(cf. [Reference LiuLi1, Lemma 2.3.1]). Moreover, we can check that
$\mathfrak{S}$
(cf. [Reference LiuLi1, Lemma 2.3.1]). Moreover, we can check that
![]() $\mathfrak{N}^{\prime }$
and
$\mathfrak{N}^{\prime }$
and
![]() $\mathfrak{N}^{\prime \prime }$
have natural structures of objects of
$\mathfrak{N}^{\prime \prime }$
have natural structures of objects of
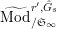 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s}}$
(which are denoted by
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s}}$
(which are denoted by
![]() $\hat{\mathfrak{N}}^{\prime }$
and
$\hat{\mathfrak{N}}^{\prime }$
and
![]() $\hat{\mathfrak{N}}^{\prime \prime }$
, respectively) such that the sequence
$\hat{\mathfrak{N}}^{\prime \prime }$
, respectively) such that the sequence
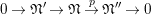 $0\rightarrow \mathfrak{N}^{\prime }\rightarrow \mathfrak{N}\overset{p}{\rightarrow }\mathfrak{N}^{\prime \prime }\rightarrow 0$
induces an exact sequence
$0\rightarrow \mathfrak{N}^{\prime }\rightarrow \mathfrak{N}\overset{p}{\rightarrow }\mathfrak{N}^{\prime \prime }\rightarrow 0$
induces an exact sequence
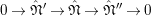 $0\rightarrow \hat{\mathfrak{N}}^{\prime }\rightarrow \hat{\mathfrak{N}}\rightarrow \hat{\mathfrak{N}}^{\prime \prime }\rightarrow 0$
. By the lemma below, we know that
$0\rightarrow \hat{\mathfrak{N}}^{\prime }\rightarrow \hat{\mathfrak{N}}\rightarrow \hat{\mathfrak{N}}^{\prime \prime }\rightarrow 0$
. By the lemma below, we know that
![]() $\hat{\mathfrak{N}}^{\prime }$
and
$\hat{\mathfrak{N}}^{\prime }$
and
![]() $\hat{\mathfrak{N}}^{\prime \prime }$
are in fact contained in
$\hat{\mathfrak{N}}^{\prime \prime }$
are in fact contained in
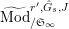 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s},J}$
. By the induction hypothesis, we see that
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s},J}$
. By the induction hypothesis, we see that
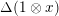 $\unicode[STIX]{x1D6E5}(1\otimes x)$
has values in
$\unicode[STIX]{x1D6E5}(1\otimes x)$
has values in
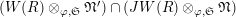 $(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N}^{\prime })\cap (JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N})$
. By [Reference OzekiOz2, Lemma 6] and the assumption that
$(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N}^{\prime })\cap (JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N})$
. By [Reference OzekiOz2, Lemma 6] and the assumption that
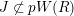 $J\not \subset pW(R)$
is principal, we obtain that
$J\not \subset pW(R)$
is principal, we obtain that
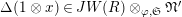 $\unicode[STIX]{x1D6E5}(1\otimes x)\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N}^{\prime }$
. Since
$\unicode[STIX]{x1D6E5}(1\otimes x)\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{N}^{\prime }$
. Since
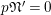 $p\mathfrak{N}^{\prime }=0$
, an analogous argument in the case
$p\mathfrak{N}^{\prime }=0$
, an analogous argument in the case
![]() $n=1$
proceeds and we have
$n=1$
proceeds and we have
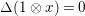 $\unicode[STIX]{x1D6E5}(1\otimes x)=0$
as desired.◻
$\unicode[STIX]{x1D6E5}(1\otimes x)=0$
as desired.◻
Lemma 4.3. Let
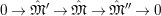 $0\rightarrow \hat{\mathfrak{M}}^{\prime }\rightarrow \hat{\mathfrak{M}}\rightarrow \hat{\mathfrak{M}}^{\prime \prime }\rightarrow 0$
be an exact sequence in
$0\rightarrow \hat{\mathfrak{M}}^{\prime }\rightarrow \hat{\mathfrak{M}}\rightarrow \hat{\mathfrak{M}}^{\prime \prime }\rightarrow 0$
be an exact sequence in
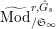 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
. Suppose that
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
. Suppose that
![]() $\hat{\mathfrak{M}}$
is an object of
$\hat{\mathfrak{M}}$
is an object of
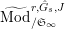 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
. Then
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
. Then
![]() $\hat{\mathfrak{M}}^{\prime }$
and
$\hat{\mathfrak{M}}^{\prime }$
and
![]() $\hat{\mathfrak{M}}^{\prime \prime }$
are also objects of
$\hat{\mathfrak{M}}^{\prime \prime }$
are also objects of
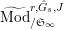 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
.
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
.
Proof. The fact
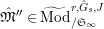 $\hat{\mathfrak{M}}^{\prime \prime }\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
is clear. Take any
$\hat{\mathfrak{M}}^{\prime \prime }\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
is clear. Take any
![]() $x\in \mathfrak{M}^{\prime }$
. Then we have
$x\in \mathfrak{M}^{\prime }$
. Then we have
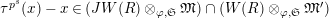 $\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in (JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})\cap (W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}^{\prime })$
. Since
$\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in (JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})\cap (W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}^{\prime })$
. Since
![]() $J$
is a principal ideal which is not contained in
$J$
is a principal ideal which is not contained in
![]() $pW(R)$
, we obtain
$pW(R)$
, we obtain
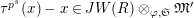 $\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}^{\prime }$
by [Reference OzekiOz2, Lemma 6]. This implies
$\unicode[STIX]{x1D70F}^{p^{s}}(x)-x\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}^{\prime }$
by [Reference OzekiOz2, Lemma 6]. This implies
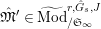 $\hat{\mathfrak{M}}^{\prime }\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
.◻
$\hat{\mathfrak{M}}^{\prime }\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
.◻
4.2 The category
 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
In this subsection, we study some categorical properties of
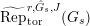 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
.
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
.
Let
![]() $\hat{\mathfrak{M}}$
be an object of
$\hat{\mathfrak{M}}$
be an object of
 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
. Following [Reference LiuLi2, Section 3.2] (note that arguments in [Reference LiuLi2] is the “free case”), we construct a map
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
. Following [Reference LiuLi2, Section 3.2] (note that arguments in [Reference LiuLi2] is the “free case”), we construct a map
![]() $\hat{\unicode[STIX]{x1D704}}_{s}$
which connects
$\hat{\unicode[STIX]{x1D704}}_{s}$
which connects
![]() $\hat{\mathfrak{M}}$
and
$\hat{\mathfrak{M}}$
and
![]() $\hat{T}_{s}(\hat{\mathfrak{M}})$
as follows. Observe that there exists a natural isomorphism of
$\hat{T}_{s}(\hat{\mathfrak{M}})$
as follows. Observe that there exists a natural isomorphism of
![]() $\mathbb{Z}_{p}[G_{s}]$
-modules
$\mathbb{Z}_{p}[G_{s}]$
-modules
 $$\begin{eqnarray}\hat{T}_{s}(\hat{\mathfrak{M}})\simeq \text{Hom}_{W(R),\unicode[STIX]{x1D711}}(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\end{eqnarray}$$
$$\begin{eqnarray}\hat{T}_{s}(\hat{\mathfrak{M}})\simeq \text{Hom}_{W(R),\unicode[STIX]{x1D711}}(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\end{eqnarray}$$
where
![]() $G_{s}$
acts on
$G_{s}$
acts on
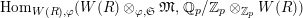 $\text{Hom}_{W(R),\unicode[STIX]{x1D711}}(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))$
by
$\text{Hom}_{W(R),\unicode[STIX]{x1D711}}(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))$
by
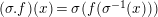 $(\unicode[STIX]{x1D70E}.f)(x)=\unicode[STIX]{x1D70E}(f(\unicode[STIX]{x1D70E}^{-1}(x)))$
for
$(\unicode[STIX]{x1D70E}.f)(x)=\unicode[STIX]{x1D70E}(f(\unicode[STIX]{x1D70E}^{-1}(x)))$
for
![]() $\unicode[STIX]{x1D70E}\in G_{s}$
,
$\unicode[STIX]{x1D70E}\in G_{s}$
,
 $$\begin{eqnarray}\displaystyle & \displaystyle f\in \text{Hom}_{W(R),\unicode[STIX]{x1D711}}(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R)), & \displaystyle \nonumber\\ \displaystyle & \displaystyle x\in W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}=W(R)\otimes _{\widehat{{\mathcal{R}}}_{s}}(\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f\in \text{Hom}_{W(R),\unicode[STIX]{x1D711}}(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R)), & \displaystyle \nonumber\\ \displaystyle & \displaystyle x\in W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}=W(R)\otimes _{\widehat{{\mathcal{R}}}_{s}}(\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}). & \displaystyle \nonumber\end{eqnarray}$$
Thus we can define a morphism
 $$\begin{eqnarray}\hat{\unicode[STIX]{x1D704}}_{s}^{\prime }:W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\rightarrow \text{Hom}_{\mathbb{Z}_{p}}(\hat{T}_{s}(\hat{\mathfrak{M}}),\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\end{eqnarray}$$
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D704}}_{s}^{\prime }:W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\rightarrow \text{Hom}_{\mathbb{Z}_{p}}(\hat{T}_{s}(\hat{\mathfrak{M}}),\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\end{eqnarray}$$
by
 $$\begin{eqnarray}x\mapsto (f\mapsto f(x)),\quad x\in W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M},f\in \hat{T}_{s}(\hat{\mathfrak{M}}).\end{eqnarray}$$
$$\begin{eqnarray}x\mapsto (f\mapsto f(x)),\quad x\in W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M},f\in \hat{T}_{s}(\hat{\mathfrak{M}}).\end{eqnarray}$$
Since
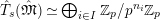 $\hat{T}_{s}(\hat{\mathfrak{M}})\simeq \bigoplus _{i\in I}\mathbb{Z}_{p}/p^{n_{i}}\mathbb{Z}_{p}$
as
$\hat{T}_{s}(\hat{\mathfrak{M}})\simeq \bigoplus _{i\in I}\mathbb{Z}_{p}/p^{n_{i}}\mathbb{Z}_{p}$
as
![]() $\mathbb{Z}_{p}$
-modules, we have a natural isomorphism
$\mathbb{Z}_{p}$
-modules, we have a natural isomorphism
 $\text{Hom}_{\mathbb{Z}_{p}}(\hat{T}_{s}(\hat{\mathfrak{M}}),\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\simeq W(R)\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}^{\vee }(\hat{\mathfrak{M}})$
where
$\text{Hom}_{\mathbb{Z}_{p}}(\hat{T}_{s}(\hat{\mathfrak{M}}),\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))\simeq W(R)\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}^{\vee }(\hat{\mathfrak{M}})$
where
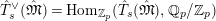 $\hat{T}_{s}^{\vee }(\hat{\mathfrak{M}})=\text{Hom}_{\mathbb{Z}_{p}}(\hat{T}_{s}(\hat{\mathfrak{M}}),\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is the dual representation of
$\hat{T}_{s}^{\vee }(\hat{\mathfrak{M}})=\text{Hom}_{\mathbb{Z}_{p}}(\hat{T}_{s}(\hat{\mathfrak{M}}),\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is the dual representation of
![]() $\hat{T}_{s}(\hat{\mathfrak{M}})$
. Composing this isomorphism with
$\hat{T}_{s}(\hat{\mathfrak{M}})$
. Composing this isomorphism with
![]() $\hat{\unicode[STIX]{x1D704}}_{s}^{\prime }$
, we obtain the desired map
$\hat{\unicode[STIX]{x1D704}}_{s}^{\prime }$
, we obtain the desired map
 $$\begin{eqnarray}\hat{\unicode[STIX]{x1D704}}_{s}:W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\rightarrow W(R)\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}^{\vee }(\hat{\mathfrak{M}}).\end{eqnarray}$$
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D704}}_{s}:W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\rightarrow W(R)\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}^{\vee }(\hat{\mathfrak{M}}).\end{eqnarray}$$
It follows from a direct calculation that
![]() $\hat{\unicode[STIX]{x1D704}}_{s}$
is
$\hat{\unicode[STIX]{x1D704}}_{s}$
is
![]() $\unicode[STIX]{x1D711}$
-equivariant and
$\unicode[STIX]{x1D711}$
-equivariant and
![]() $G_{s}$
-equivariant. If we denote by
$G_{s}$
-equivariant. If we denote by
![]() $\hat{\mathfrak{M}}_{s}$
the image of
$\hat{\mathfrak{M}}_{s}$
the image of
![]() $\hat{\mathfrak{M}}$
for the functor
$\hat{\mathfrak{M}}$
for the functor
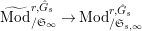 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s,\infty }}^{r,{\hat{G}}_{s}}$
(cf. Section 3.1), then the above
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \text{Mod}_{/\mathfrak{S}_{s,\infty }}^{r,{\hat{G}}_{s}}$
(cf. Section 3.1), then the above
![]() $\hat{\unicode[STIX]{x1D704}}_{s}$
is isomorphic to “
$\hat{\unicode[STIX]{x1D704}}_{s}$
is isomorphic to “
![]() $\hat{\unicode[STIX]{x1D704}}$
for
$\hat{\unicode[STIX]{x1D704}}$
for
![]() $\hat{\mathfrak{M}}_{s}$
in [Reference OzekiOz1, Section 4.1]”. Hence [Reference OzekiOz1, Lemma 4.2(4)] implies that
$\hat{\mathfrak{M}}_{s}$
in [Reference OzekiOz1, Section 4.1]”. Hence [Reference OzekiOz1, Lemma 4.2(4)] implies that
 $$\begin{eqnarray}\displaystyle & & \displaystyle W(\text{Fr}~R)\otimes \hat{\unicode[STIX]{x1D704}}_{s}:W(\text{Fr}~R)\otimes _{W(R)}(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow W(\text{Fr}~R)\otimes _{W(R)}(W(R)\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}^{\vee }(\hat{\mathfrak{M}}))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle W(\text{Fr}~R)\otimes \hat{\unicode[STIX]{x1D704}}_{s}:W(\text{Fr}~R)\otimes _{W(R)}(W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M})\nonumber\\ \displaystyle & & \displaystyle \quad \rightarrow W(\text{Fr}~R)\otimes _{W(R)}(W(R)\otimes _{\mathbb{Z}_{p}}\hat{T}_{s}^{\vee }(\hat{\mathfrak{M}}))\nonumber\end{eqnarray}$$
is bijective.
Proposition 4.4. Let
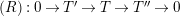 $(R):0\rightarrow T^{\prime }\rightarrow T\rightarrow T^{\prime \prime }\rightarrow 0$
be an exact sequence in
$(R):0\rightarrow T^{\prime }\rightarrow T\rightarrow T^{\prime \prime }\rightarrow 0$
be an exact sequence in
 $\text{Rep}_{\text{tor}}(G_{s})$
. Assume that there exists
$\text{Rep}_{\text{tor}}(G_{s})$
. Assume that there exists
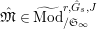 $\hat{\mathfrak{M}}\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
such that
$\hat{\mathfrak{M}}\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
such that
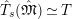 $\hat{T}_{s}(\hat{\mathfrak{M}})\simeq T$
. Then there exists an exact sequence
$\hat{T}_{s}(\hat{\mathfrak{M}})\simeq T$
. Then there exists an exact sequence
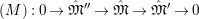 $(M):0\rightarrow \hat{\mathfrak{M}}^{\prime \prime }\rightarrow \hat{\mathfrak{M}}\rightarrow \hat{\mathfrak{M}}^{\prime }\rightarrow 0$
in
$(M):0\rightarrow \hat{\mathfrak{M}}^{\prime \prime }\rightarrow \hat{\mathfrak{M}}\rightarrow \hat{\mathfrak{M}}^{\prime }\rightarrow 0$
in
 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
such that
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
such that
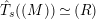 $\hat{T}_{s}((M))\simeq (R)$
.
$\hat{T}_{s}((M))\simeq (R)$
.
Proof. The same proof as [Reference OzekiOz1, Theorem 4.5], except using not
![]() $\hat{\unicode[STIX]{x1D704}}$
in the proof of [Reference OzekiOz1, Theorem 4.5] but
$\hat{\unicode[STIX]{x1D704}}$
in the proof of [Reference OzekiOz1, Theorem 4.5] but
![]() $\hat{\unicode[STIX]{x1D704}}_{s}$
as above, gives an exact sequence
$\hat{\unicode[STIX]{x1D704}}_{s}$
as above, gives an exact sequence
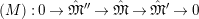 $(M):0\rightarrow \hat{\mathfrak{M}}^{\prime \prime }\rightarrow \hat{\mathfrak{M}}\rightarrow \hat{\mathfrak{M}}^{\prime }\rightarrow 0$
in
$(M):0\rightarrow \hat{\mathfrak{M}}^{\prime \prime }\rightarrow \hat{\mathfrak{M}}\rightarrow \hat{\mathfrak{M}}^{\prime }\rightarrow 0$
in
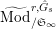 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
such that
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
such that
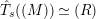 $\hat{T}_{s}((M))\simeq (R)$
. Therefore, Lemma 4.3, gives the desired result.◻
$\hat{T}_{s}((M))\simeq (R)$
. Therefore, Lemma 4.3, gives the desired result.◻
Corollary 4.5. The full subcategory
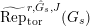 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
of
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
of
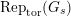 $\text{Rep}_{\text{tor}}(G_{s})$
is stable under subquotients.
$\text{Rep}_{\text{tor}}(G_{s})$
is stable under subquotients.
Let
![]() $L$
be as in Section 2, that is, the completion of an unramified algebraic extension of
$L$
be as in Section 2, that is, the completion of an unramified algebraic extension of
![]() $K$
with residue field
$K$
with residue field
![]() $k_{L}$
. We prove the following base change lemma.
$k_{L}$
. We prove the following base change lemma.
Lemma 4.6. Assume that
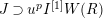 $J\supset u^{p}I^{[1]}W(R)$
or
$J\supset u^{p}I^{[1]}W(R)$
or
![]() $L$
is a finite unramified extension of
$L$
is a finite unramified extension of
![]() $K$
. If
$K$
. If
![]() $T$
is an object of
$T$
is an object of
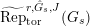 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
, then
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
, then
![]() $T|_{G_{L,s}}$
is an object of
$T|_{G_{L,s}}$
is an object of
 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{L,s},J}(G_{L,s})$
.
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{L,s},J}(G_{L,s})$
.
By an obvious way, we define a functor
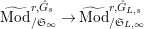 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
. The underlying Kisin module of the image of
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
. The underlying Kisin module of the image of
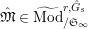 $\hat{\mathfrak{M}}\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
for this functor is
$\hat{\mathfrak{M}}\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
for this functor is
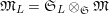 $\mathfrak{M}_{L}=\mathfrak{S}_{L}\otimes _{\mathfrak{S}}\mathfrak{M}$
. Lemma 4.6 immediately follows from the lemma below.
$\mathfrak{M}_{L}=\mathfrak{S}_{L}\otimes _{\mathfrak{S}}\mathfrak{M}$
. Lemma 4.6 immediately follows from the lemma below.
Lemma 4.7. Assume that
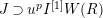 $J\supset u^{p}I^{[1]}W(R)$
or
$J\supset u^{p}I^{[1]}W(R)$
or
![]() $L$
is a finite unramified extension of
$L$
is a finite unramified extension of
![]() $K$
. Then the functor
$K$
. Then the functor
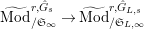 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
induces a functor
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
induces a functor
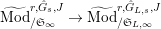 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s},J}$
.
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s},J}$
.
Proof. Let
![]() $\hat{\mathfrak{M}}$
be an object of
$\hat{\mathfrak{M}}$
be an object of
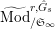 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
and let
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
and let
![]() $\hat{\mathfrak{M}}_{L}$
be the image of
$\hat{\mathfrak{M}}_{L}$
be the image of
![]() $\hat{\mathfrak{M}}$
for the functor
$\hat{\mathfrak{M}}$
for the functor
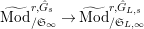 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
. In the rest of this proof, to avoid confusions, we denote the image of
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}\rightarrow \widetilde{\text{Mod}}_{/\mathfrak{S}_{L,\infty }}^{r,{\hat{G}}_{L,s}}$
. In the rest of this proof, to avoid confusions, we denote the image of
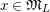 $x\in \mathfrak{M}_{L}$
in
$x\in \mathfrak{M}_{L}$
in
 $W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
by
$W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
by
![]() $1\otimes x$
. Recall that we abuse notations by writing
$1\otimes x$
. Recall that we abuse notations by writing
![]() $\unicode[STIX]{x1D70F}$
for the preimage of
$\unicode[STIX]{x1D70F}$
for the preimage of
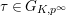 $\unicode[STIX]{x1D70F}\in G_{K,p^{\infty }}$
under the bijection
$\unicode[STIX]{x1D70F}\in G_{K,p^{\infty }}$
under the bijection
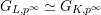 $G_{L,p^{\infty }}\simeq G_{K,p^{\infty }}$
of Lemma 2.2. Then
$G_{L,p^{\infty }}\simeq G_{K,p^{\infty }}$
of Lemma 2.2. Then
![]() $\unicode[STIX]{x1D70F}^{p^{s}}$
is a topological generator of
$\unicode[STIX]{x1D70F}^{p^{s}}$
is a topological generator of
![]() $G_{L,s,p^{\infty }}$
. It suffices to show the following: if
$G_{L,s,p^{\infty }}$
. It suffices to show the following: if
![]() $\hat{\mathfrak{M}}$
is an object of
$\hat{\mathfrak{M}}$
is an object of
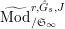 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
, then we have
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
, then we have
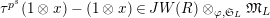 $\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes x)-(1\otimes x)\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
for any
$\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes x)-(1\otimes x)\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
for any
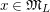 $x\in \mathfrak{M}_{L}$
. Now we suppose
$x\in \mathfrak{M}_{L}$
. Now we suppose
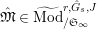 $\hat{\mathfrak{M}}\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
. Take any
$\hat{\mathfrak{M}}\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
. Take any
![]() $a\in \mathfrak{S}_{L}$
and
$a\in \mathfrak{S}_{L}$
and
![]() $x\in \mathfrak{M}$
. Note that we have
$x\in \mathfrak{M}$
. Note that we have
 $\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes ax)-(1\otimes ax)=\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes x)-(1\otimes x))+(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a))(1\otimes x)$
in
$\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes ax)-(1\otimes ax)=\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes x)-(1\otimes x))+(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a))(1\otimes x)$
in
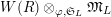 $W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
. Since
$W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
. Since
![]() $\hat{\mathfrak{M}}$
is an object of
$\hat{\mathfrak{M}}$
is an object of
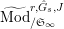 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
, we have
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
, we have
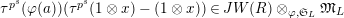 $\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes x)-(1\otimes x))\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
. Therefore, it is enough to show
$\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes x)-(1\otimes x))\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
. Therefore, it is enough to show
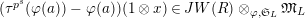 $(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a))(1\otimes x)\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
. This follows from Lemma 3.6 immediately in the case where
$(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a))(1\otimes x)\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
. This follows from Lemma 3.6 immediately in the case where
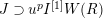 $J\supset u^{p}I^{[1]}W(R)$
. Next we consider the case where
$J\supset u^{p}I^{[1]}W(R)$
. Next we consider the case where
![]() $L$
is a finite unramified extension of
$L$
is a finite unramified extension of
![]() $K$
. Let
$K$
. Let
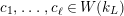 $c_{1},\ldots ,c_{\ell }\in W(k_{L})$
be generators of
$c_{1},\ldots ,c_{\ell }\in W(k_{L})$
be generators of
![]() $W(k_{L})$
as a
$W(k_{L})$
as a
![]() $W(k)$
-module. Then we have
$W(k)$
-module. Then we have
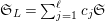 $\mathfrak{S}_{L}=\sum _{j=1}^{\ell }c_{j}\mathfrak{S}$
and thus we can write
$\mathfrak{S}_{L}=\sum _{j=1}^{\ell }c_{j}\mathfrak{S}$
and thus we can write
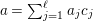 $a=\sum _{j=1}^{\ell }a_{j}c_{j}$
for some
$a=\sum _{j=1}^{\ell }a_{j}c_{j}$
for some
![]() $a_{j}\in \mathfrak{S}$
. Hence it suffices to show
$a_{j}\in \mathfrak{S}$
. Hence it suffices to show
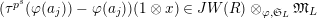 $(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a_{j}))-\unicode[STIX]{x1D711}(a_{j}))(1\otimes x)\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
but this in fact immediately follows from the equation
$(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a_{j}))-\unicode[STIX]{x1D711}(a_{j}))(1\otimes x)\in JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}_{L}}\mathfrak{M}_{L}$
but this in fact immediately follows from the equation
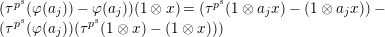 $(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a_{j}))-\unicode[STIX]{x1D711}(a_{j}))(1\otimes x)=(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes a_{j}x)-(1\otimes a_{j}x))-(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a_{j}))(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes x)-(1\otimes x)))$
.◻
$(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a_{j}))-\unicode[STIX]{x1D711}(a_{j}))(1\otimes x)=(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes a_{j}x)-(1\otimes a_{j}x))-(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a_{j}))(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes x)-(1\otimes x)))$
.◻
Remark 4.8. For a general
![]() $L$
, the author does not know whether the statement of the above lemma is true or not.
$L$
, the author does not know whether the statement of the above lemma is true or not.
4.3 Full faithfulness theorem for
 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
Our goal in this subsection is to prove the following full faithfulness theorem, which plays an important role in our proofs of main theorems.
Theorem 4.9. Assume that
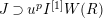 $J\supset u^{p}I^{[1]}W(R)$
or
$J\supset u^{p}I^{[1]}W(R)$
or
![]() $k$
is algebraically closed. If
$k$
is algebraically closed. If
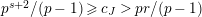 $p^{s+2}/(p-1)\geqslant c_{J}>pr/(p-1)$
, then the restriction functor
$p^{s+2}/(p-1)\geqslant c_{J}>pr/(p-1)$
, then the restriction functor
 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is fully faithful.
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is fully faithful.
First we give a very rough sketch of the theory of maximal models for Kisin modules (cf. [Reference Caruso and LiuCL1]). For any
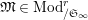 $\mathfrak{M}\in \text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
, put
$\mathfrak{M}\in \text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
, put
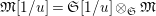 $\mathfrak{M}[1/u]=\mathfrak{S}[1/u]\otimes _{\mathfrak{S}}\mathfrak{M}$
and denote by
$\mathfrak{M}[1/u]=\mathfrak{S}[1/u]\otimes _{\mathfrak{S}}\mathfrak{M}$
and denote by
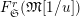 $F_{\mathfrak{S}}^{r}(\mathfrak{M}[1/u])$
the (partially) ordered set (by inclusion) of torsion Kisin modules
$F_{\mathfrak{S}}^{r}(\mathfrak{M}[1/u])$
the (partially) ordered set (by inclusion) of torsion Kisin modules
![]() $\mathfrak{N}$
of height
$\mathfrak{N}$
of height
![]() ${\leqslant}r$
which are contained in
${\leqslant}r$
which are contained in
![]() $\mathfrak{M}[1/u]$
and
$\mathfrak{M}[1/u]$
and
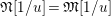 $\mathfrak{N}[1/u]=\mathfrak{M}[1/u]$
as
$\mathfrak{N}[1/u]=\mathfrak{M}[1/u]$
as
![]() $\unicode[STIX]{x1D711}$
-modules. The set
$\unicode[STIX]{x1D711}$
-modules. The set
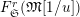 $F_{\mathfrak{S}}^{r}(\mathfrak{M}[1/u])$
has a greatest element (cf. [Reference Caruso and LiuCL1, Corollary 3.2.6]). We denote this element by
$F_{\mathfrak{S}}^{r}(\mathfrak{M}[1/u])$
has a greatest element (cf. [Reference Caruso and LiuCL1, Corollary 3.2.6]). We denote this element by
 $\text{Max}^{r}(\mathfrak{M})$
. We say that
$\text{Max}^{r}(\mathfrak{M})$
. We say that
![]() $\mathfrak{M}$
is maximal of height
$\mathfrak{M}$
is maximal of height
![]() ${\leqslant}r$
(or, maximal for simplicity) if it is the greatest element of
${\leqslant}r$
(or, maximal for simplicity) if it is the greatest element of
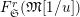 $F_{\mathfrak{S}}^{r}(\mathfrak{M}[1/u])$
. The association
$F_{\mathfrak{S}}^{r}(\mathfrak{M}[1/u])$
. The association
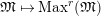 $\mathfrak{M}\mapsto \text{Max}^{r}(\mathfrak{M})$
defines a functor “
$\mathfrak{M}\mapsto \text{Max}^{r}(\mathfrak{M})$
defines a functor “
![]() $\text{Max}^{r}$
” from the category
$\text{Max}^{r}$
” from the category
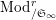 $\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
of torsion Kisin modules of height
$\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
of torsion Kisin modules of height
![]() ${\leqslant}r$
into the category
${\leqslant}r$
into the category
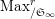 $\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
of maximal Kisin modules of height
$\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
of maximal Kisin modules of height
![]() ${\leqslant}r$
. The category
${\leqslant}r$
. The category
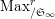 $\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
is abelian (cf. [Reference Caruso and LiuCL1, Theorem 3.3.8]). Furthermore, the functor
$\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
is abelian (cf. [Reference Caruso and LiuCL1, Theorem 3.3.8]). Furthermore, the functor
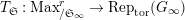 $T_{\mathfrak{S}}:\text{Max}_{/\mathfrak{S}_{\infty }}^{r}\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
, defined by
$T_{\mathfrak{S}}:\text{Max}_{/\mathfrak{S}_{\infty }}^{r}\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
, defined by
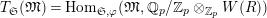 $T_{\mathfrak{S}}(\mathfrak{M})=\text{Hom}_{\mathfrak{S},\unicode[STIX]{x1D711}}(\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))$
, is exact and fully faithful (cf. [Reference Caruso and LiuCL1, Corollary 3.3.10]). It is not difficult to check that
$T_{\mathfrak{S}}(\mathfrak{M})=\text{Hom}_{\mathfrak{S},\unicode[STIX]{x1D711}}(\mathfrak{M},\mathbb{Q}_{p}/\mathbb{Z}_{p}\otimes _{\mathbb{Z}_{p}}W(R))$
, is exact and fully faithful (cf. [Reference Caruso and LiuCL1, Corollary 3.3.10]). It is not difficult to check that
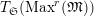 $T_{\mathfrak{S}}(\text{Max}^{r}(\mathfrak{M}))$
is canonically isomorphic to
$T_{\mathfrak{S}}(\text{Max}^{r}(\mathfrak{M}))$
is canonically isomorphic to
![]() $T_{\mathfrak{S}}(\mathfrak{M})$
as representations of
$T_{\mathfrak{S}}(\mathfrak{M})$
as representations of
![]() $G_{\infty }$
for any torsion Kisin module
$G_{\infty }$
for any torsion Kisin module
![]() $\mathfrak{M}$
of height
$\mathfrak{M}$
of height
![]() ${\leqslant}r$
.
${\leqslant}r$
.
Definition 4.10. [Reference Caruso and LiuCL1, Section 3.6.1]
Let
![]() $d$
be a positive integer. Let
$d$
be a positive integer. Let
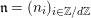 $\mathfrak{n}=(n_{i})_{i\in \mathbb{Z}/d\mathbb{Z}}$
be a sequence of nonnegative integers of smallest period
$\mathfrak{n}=(n_{i})_{i\in \mathbb{Z}/d\mathbb{Z}}$
be a sequence of nonnegative integers of smallest period
![]() $d$
. We define a torsion Kisin module
$d$
. We define a torsion Kisin module
![]() $\mathfrak{M}(\mathfrak{n})$
as below:
$\mathfrak{M}(\mathfrak{n})$
as below:
-
∙ as a
 $k[\![u]\!]$
-module,
$k[\![u]\!]$
-module,
 $\mathfrak{M}(\mathfrak{n})=\bigoplus _{i\in \mathbb{Z}/d\mathbb{Z}}k[\![u]\!]e_{i}$
;
$\mathfrak{M}(\mathfrak{n})=\bigoplus _{i\in \mathbb{Z}/d\mathbb{Z}}k[\![u]\!]e_{i}$
; -
∙ for all
 $i\in \mathbb{Z}/d\mathbb{Z}$
,
$i\in \mathbb{Z}/d\mathbb{Z}$
,
 $\unicode[STIX]{x1D711}(e_{i})=u^{n_{i}}e_{i+1}$
.
$\unicode[STIX]{x1D711}(e_{i})=u^{n_{i}}e_{i+1}$
.
We denote by
![]() ${\mathcal{S}}_{\text{max}}^{r}$
the set of sequences
${\mathcal{S}}_{\text{max}}^{r}$
the set of sequences
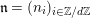 $\mathfrak{n}=(n_{i})_{i\in \mathbb{Z}/d\mathbb{Z}}$
of integers
$\mathfrak{n}=(n_{i})_{i\in \mathbb{Z}/d\mathbb{Z}}$
of integers
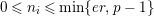 $0\leqslant n_{i}\leqslant \text{min}\{er,p-1\}$
with smallest period
$0\leqslant n_{i}\leqslant \text{min}\{er,p-1\}$
with smallest period
![]() $d$
for some integer
$d$
for some integer
![]() $d$
except the constant sequence with value
$d$
except the constant sequence with value
![]() $p-1$
(if necessary). By definition, we see that
$p-1$
(if necessary). By definition, we see that
![]() $\mathfrak{M}(\mathfrak{n})$
is of height
$\mathfrak{M}(\mathfrak{n})$
is of height
![]() ${\leqslant}r$
for any
${\leqslant}r$
for any
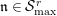 $\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
. Putting
$\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
. Putting
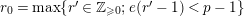 $r_{0}=\text{max}\{r^{\prime }\in \mathbb{Z}_{{\geqslant}0};e(r^{\prime }-1)<p-1\}$
, we also see that
$r_{0}=\text{max}\{r^{\prime }\in \mathbb{Z}_{{\geqslant}0};e(r^{\prime }-1)<p-1\}$
, we also see that
![]() $\mathfrak{M}(\mathfrak{n})$
is of height
$\mathfrak{M}(\mathfrak{n})$
is of height
![]() ${\leqslant}r_{0}$
for any
${\leqslant}r_{0}$
for any
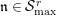 $\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
. It is known that
$\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
. It is known that
![]() $\mathfrak{M}(\mathfrak{n})$
is maximal for any
$\mathfrak{M}(\mathfrak{n})$
is maximal for any
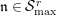 $\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
[Reference Caruso and LiuCL1, Proposition 3.6.7]. If
$\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
[Reference Caruso and LiuCL1, Proposition 3.6.7]. If
![]() $k$
is algebraically closed, then
$k$
is algebraically closed, then
![]() $\mathfrak{M}(\mathfrak{n})$
is simple in
$\mathfrak{M}(\mathfrak{n})$
is simple in
 $\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
for any
$\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
for any
 $\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
(cf. [Reference Caruso and LiuCL1, Propositions 3.6.7 and 3.6.12]) and furthermore, the converse holds; any simple object in
$\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
(cf. [Reference Caruso and LiuCL1, Propositions 3.6.7 and 3.6.12]) and furthermore, the converse holds; any simple object in
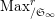 $\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
is of the form
$\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
is of the form
![]() $\mathfrak{M}(\mathfrak{n})$
for some
$\mathfrak{M}(\mathfrak{n})$
for some
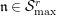 $\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
(cf. [Reference Caruso and LiuCL1, Propositions 3.6.8 and 3.6.12]).
$\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
(cf. [Reference Caruso and LiuCL1, Propositions 3.6.8 and 3.6.12]).
Lemma 4.11. Assume that
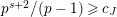 $p^{s+2}/(p-1)\geqslant c_{J}$
. Let
$p^{s+2}/(p-1)\geqslant c_{J}$
. Let
![]() $d$
be a positive integer. Let
$d$
be a positive integer. Let
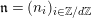 $\mathfrak{n}=(n_{i})_{i\in \mathbb{Z}/d\mathbb{Z}}$
be a sequence of nonnegative integers of smallest period
$\mathfrak{n}=(n_{i})_{i\in \mathbb{Z}/d\mathbb{Z}}$
be a sequence of nonnegative integers of smallest period
![]() $d$
. If
$d$
. If
![]() $\mathfrak{M}(\mathfrak{n})$
is of height
$\mathfrak{M}(\mathfrak{n})$
is of height
![]() ${\leqslant}r$
, then
${\leqslant}r$
, then
![]() $\mathfrak{M}(\mathfrak{n})$
has a structure of an object of
$\mathfrak{M}(\mathfrak{n})$
has a structure of an object of
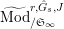 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
.
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
.
Proof. Choose any
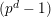 $(p^{d}-1)$
th root
$(p^{d}-1)$
th root
![]() $\unicode[STIX]{x1D702}\in R$
of
$\unicode[STIX]{x1D702}\in R$
of
![]() $\text{}\underline{\unicode[STIX]{x1D700}}$
. Since
$\text{}\underline{\unicode[STIX]{x1D700}}$
. Since
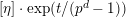 $[\unicode[STIX]{x1D702}]\cdot \text{exp}(t/(p^{d}-1))$
is a
$[\unicode[STIX]{x1D702}]\cdot \text{exp}(t/(p^{d}-1))$
is a
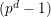 $(p^{d}-1)$
th root of unity, it is of the form
$(p^{d}-1)$
th root of unity, it is of the form
![]() $[a]$
for some
$[a]$
for some
![]() $a\in \mathbb{F}_{p^{d}}^{\times }$
. Replacing
$a\in \mathbb{F}_{p^{d}}^{\times }$
. Replacing
![]() $\unicode[STIX]{x1D702}a^{-1}$
with
$\unicode[STIX]{x1D702}a^{-1}$
with
![]() $\unicode[STIX]{x1D702}$
, we obtain
$\unicode[STIX]{x1D702}$
, we obtain
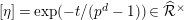 $[\unicode[STIX]{x1D702}]=\text{exp}(-t/(p^{d}-1))\in \widehat{{\mathcal{R}}}^{\times }$
. Put
$[\unicode[STIX]{x1D702}]=\text{exp}(-t/(p^{d}-1))\in \widehat{{\mathcal{R}}}^{\times }$
. Put
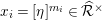 $x_{i}=[\unicode[STIX]{x1D702}]^{m_{i}}\in \widehat{{\mathcal{R}}}^{\times }$
and
$x_{i}=[\unicode[STIX]{x1D702}]^{m_{i}}\in \widehat{{\mathcal{R}}}^{\times }$
and
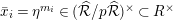 $\bar{x}_{i}=\unicode[STIX]{x1D702}^{m_{i}}\in (\widehat{{\mathcal{R}}}/p\widehat{{\mathcal{R}}})^{\times }\subset R^{\times }$
for any
$\bar{x}_{i}=\unicode[STIX]{x1D702}^{m_{i}}\in (\widehat{{\mathcal{R}}}/p\widehat{{\mathcal{R}}})^{\times }\subset R^{\times }$
for any
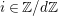 $i\in \mathbb{Z}/d\mathbb{Z}$
, where
$i\in \mathbb{Z}/d\mathbb{Z}$
, where
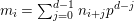 $m_{i}=\sum _{j=0}^{d-1}n_{i+j}p^{d-j}$
. We see that
$m_{i}=\sum _{j=0}^{d-1}n_{i+j}p^{d-j}$
. We see that
![]() $x_{i}-1$
is contained in
$x_{i}-1$
is contained in
![]() $I_{+}\widehat{{\mathcal{R}}}$
. In the rest of this proof, to avoid confusions, we denote the image of
$I_{+}\widehat{{\mathcal{R}}}$
. In the rest of this proof, to avoid confusions, we denote the image of
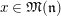 $x\in \mathfrak{M}(\mathfrak{n})$
in
$x\in \mathfrak{M}(\mathfrak{n})$
in
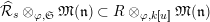 $\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}(\mathfrak{n})\subset R\otimes _{\unicode[STIX]{x1D711},k[\![u]\!]}\mathfrak{M}(\mathfrak{n})$
by
$\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}(\mathfrak{n})\subset R\otimes _{\unicode[STIX]{x1D711},k[\![u]\!]}\mathfrak{M}(\mathfrak{n})$
by
![]() $1\otimes x$
. Now we define a
$1\otimes x$
. Now we define a
![]() ${\hat{G}}_{s}$
-action on
${\hat{G}}_{s}$
-action on
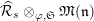 $\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}(\mathfrak{n})$
by
$\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}(\mathfrak{n})$
by
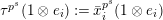 $\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i}):=\bar{x}_{i}^{p^{s}}(1\otimes e_{i})$
for the basis
$\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i}):=\bar{x}_{i}^{p^{s}}(1\otimes e_{i})$
for the basis
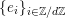 $\{e_{i}\}_{i\in \mathbb{Z}/d\mathbb{Z}}$
of
$\{e_{i}\}_{i\in \mathbb{Z}/d\mathbb{Z}}$
of
![]() $\mathfrak{M}(\mathfrak{n})$
as in Definition 4.10. We claim that
$\mathfrak{M}(\mathfrak{n})$
as in Definition 4.10. We claim that
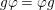 $g\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}g$
on
$g\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}g$
on
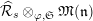 $\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}(\mathfrak{n})$
for any
$\widehat{{\mathcal{R}}}_{s}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}(\mathfrak{n})$
for any
![]() $g\in G_{s}$
. For this, it suffices to check that the equality
$g\in G_{s}$
. For this, it suffices to check that the equality
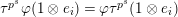 $\unicode[STIX]{x1D70F}^{p^{s}}\unicode[STIX]{x1D711}(1\otimes e_{i})=\unicode[STIX]{x1D711}\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i})$
holds for any
$\unicode[STIX]{x1D70F}^{p^{s}}\unicode[STIX]{x1D711}(1\otimes e_{i})=\unicode[STIX]{x1D711}\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i})$
holds for any
![]() $i$
. Note that we have
$i$
. Note that we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}\unicode[STIX]{x1D711}(1\otimes e_{i})=\unicode[STIX]{x1D70F}^{p^{s}}(u^{pn_{i}}(1\otimes e_{i+1}))=\bar{x}_{i+1}^{p^{s}}(\text{}\underline{\unicode[STIX]{x1D700}}^{p^{s}}u)^{pn_{i}}(1\otimes e_{i+1})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}\unicode[STIX]{x1D711}(1\otimes e_{i})=\unicode[STIX]{x1D70F}^{p^{s}}(u^{pn_{i}}(1\otimes e_{i+1}))=\bar{x}_{i+1}^{p^{s}}(\text{}\underline{\unicode[STIX]{x1D700}}^{p^{s}}u)^{pn_{i}}(1\otimes e_{i+1})\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D711}\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i})=\unicode[STIX]{x1D711}(\bar{x}_{i}^{p^{s}}(1\otimes e_{i}))=\bar{x}_{i}^{p^{s+1}}u^{pn_{i}}(1\otimes e_{i+1}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i})=\unicode[STIX]{x1D711}(\bar{x}_{i}^{p^{s}}(1\otimes e_{i}))=\bar{x}_{i}^{p^{s+1}}u^{pn_{i}}(1\otimes e_{i+1}).\end{eqnarray}$$
Hence it is enough to check
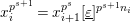 $x_{i}^{p^{s+1}}=x_{i+1}^{p^{s}}[\text{}\underline{\unicode[STIX]{x1D700}}]^{p^{s+1}n_{i}}$
but we can show this equality without difficulty. In fact, we have equivalences
$x_{i}^{p^{s+1}}=x_{i+1}^{p^{s}}[\text{}\underline{\unicode[STIX]{x1D700}}]^{p^{s+1}n_{i}}$
but we can show this equality without difficulty. In fact, we have equivalences
 $$\begin{eqnarray}\displaystyle x_{i}^{p^{s+1}} & = & \displaystyle x_{i+1}^{p^{s}}[\text{}\underline{\unicode[STIX]{x1D700}}]^{p^{s+1}n_{i}}\Leftrightarrow \text{exp}\Bigl(-p^{s+1}m_{i}\frac{t}{p^{d}-1}\Bigr)\nonumber\\ \displaystyle & = & \displaystyle \text{exp}\Bigl(-p^{s}m_{i+1}\frac{t}{p^{d}-1}-p^{s+1}n_{i}t\Bigr)\Leftrightarrow pm_{i}\nonumber\\ \displaystyle & = & \displaystyle m_{i+1}+(p^{d+1}-p)n_{i}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{i}^{p^{s+1}} & = & \displaystyle x_{i+1}^{p^{s}}[\text{}\underline{\unicode[STIX]{x1D700}}]^{p^{s+1}n_{i}}\Leftrightarrow \text{exp}\Bigl(-p^{s+1}m_{i}\frac{t}{p^{d}-1}\Bigr)\nonumber\\ \displaystyle & = & \displaystyle \text{exp}\Bigl(-p^{s}m_{i+1}\frac{t}{p^{d}-1}-p^{s+1}n_{i}t\Bigr)\Leftrightarrow pm_{i}\nonumber\\ \displaystyle & = & \displaystyle m_{i+1}+(p^{d+1}-p)n_{i}\nonumber\end{eqnarray}$$
and the last equality can be checked immediately by definition of
![]() $m_{i}$
.
$m_{i}$
.
By the claim above, we see that
![]() $\mathfrak{M}(\mathfrak{n})$
has a structure of an object of
$\mathfrak{M}(\mathfrak{n})$
has a structure of an object of
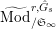 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
via this
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}$
via this
![]() ${\hat{G}}_{s}$
-action; we denote it by
${\hat{G}}_{s}$
-action; we denote it by
![]() $\hat{\mathfrak{M}}(\mathfrak{n})$
. It suffices to prove that
$\hat{\mathfrak{M}}(\mathfrak{n})$
. It suffices to prove that
![]() $\hat{\mathfrak{M}}(\mathfrak{n})$
is in fact an object of
$\hat{\mathfrak{M}}(\mathfrak{n})$
is in fact an object of
 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
. Recall that
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
. Recall that
![]() $v_{R}$
is the valuation of
$v_{R}$
is the valuation of
![]() $R$
normalized such that
$R$
normalized such that
 $v_{R}(\text{}\underline{\unicode[STIX]{x1D70B}})=1/e$
. Define
$v_{R}(\text{}\underline{\unicode[STIX]{x1D70B}})=1/e$
. Define
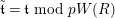 $\tilde{\mathfrak{t}}=\mathfrak{t}~\text{mod}~pW(R)$
an element of
$\tilde{\mathfrak{t}}=\mathfrak{t}~\text{mod}~pW(R)$
an element of
![]() $R$
. We denote by
$R$
. We denote by
![]() $v_{p}$
the usual
$v_{p}$
the usual
![]() $p$
-adic valuation normalized by
$p$
-adic valuation normalized by
 $v_{p}(p)=1$
. Note that we have
$v_{p}(p)=1$
. Note that we have
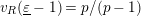 $v_{R}(\text{}\underline{\unicode[STIX]{x1D700}}-1)=p/(p-1)$
and
$v_{R}(\text{}\underline{\unicode[STIX]{x1D700}}-1)=p/(p-1)$
and
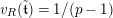 $v_{R}(\tilde{\mathfrak{t}})=1/(p-1)$
(here, the latter equation follows from the relation
$v_{R}(\tilde{\mathfrak{t}})=1/(p-1)$
(here, the latter equation follows from the relation
 $\unicode[STIX]{x1D711}(\mathfrak{t})=pE(0)^{-1}E(u)\mathfrak{t}$
). Moreover, we have
$\unicode[STIX]{x1D711}(\mathfrak{t})=pE(0)^{-1}E(u)\mathfrak{t}$
). Moreover, we have
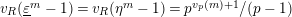 $v_{R}(\text{}\underline{\unicode[STIX]{x1D700}}^{m}-1)=v_{R}(\unicode[STIX]{x1D702}^{m}-1)=p^{v_{p}(m)+1}/(p-1)$
for any
$v_{R}(\text{}\underline{\unicode[STIX]{x1D700}}^{m}-1)=v_{R}(\unicode[STIX]{x1D702}^{m}-1)=p^{v_{p}(m)+1}/(p-1)$
for any
![]() $m\in \mathbb{Z}_{p}$
by [Reference Gee, Liu and SavittGLS, Lemma 6.6(1)]. Thus we have
$m\in \mathbb{Z}_{p}$
by [Reference Gee, Liu and SavittGLS, Lemma 6.6(1)]. Thus we have
 $$\begin{eqnarray}v_{R}(\bar{x}_{i}^{p^{s}}-1)=v_{R}(\unicode[STIX]{x1D702}^{p^{s}m_{i}}-1)=\frac{p^{s+v_{p}(m_{i})+1}}{p-1}\geqslant \frac{p^{s+2}}{p-1}.\end{eqnarray}$$
$$\begin{eqnarray}v_{R}(\bar{x}_{i}^{p^{s}}-1)=v_{R}(\unicode[STIX]{x1D702}^{p^{s}m_{i}}-1)=\frac{p^{s+v_{p}(m_{i})+1}}{p-1}\geqslant \frac{p^{s+2}}{p-1}.\end{eqnarray}$$
Since
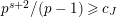 $p^{s+2}/(p-1)\geqslant c_{J}$
and the image of
$p^{s+2}/(p-1)\geqslant c_{J}$
and the image of
![]() $J$
in
$J$
in
![]() $R$
is
$R$
is
![]() $\mathfrak{m}_{R}^{{\geqslant}c_{J}}$
, we obtain
$\mathfrak{m}_{R}^{{\geqslant}c_{J}}$
, we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i})-(1\otimes e_{i})\in \mathfrak{m}_{R}^{{\geqslant}c_{J}}R\otimes _{\unicode[STIX]{x1D711},k[\![u]\!]}\mathfrak{M}(\mathfrak{n})\simeq JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}(\mathfrak{n}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i})-(1\otimes e_{i})\in \mathfrak{m}_{R}^{{\geqslant}c_{J}}R\otimes _{\unicode[STIX]{x1D711},k[\![u]\!]}\mathfrak{M}(\mathfrak{n})\simeq JW(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}(\mathfrak{n}).\end{eqnarray}$$
Finally we have to show that
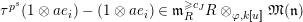 $\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes ae_{i})-(1\otimes ae_{i})\in \mathfrak{m}_{R}^{{\geqslant}c_{J}}R\otimes _{\unicode[STIX]{x1D711},k[\![u]\!]}\mathfrak{M}(\mathfrak{n})$
for any
$\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes ae_{i})-(1\otimes ae_{i})\in \mathfrak{m}_{R}^{{\geqslant}c_{J}}R\otimes _{\unicode[STIX]{x1D711},k[\![u]\!]}\mathfrak{M}(\mathfrak{n})$
for any
 $a\in k[\![u]\!]$
. Since
$a\in k[\![u]\!]$
. Since
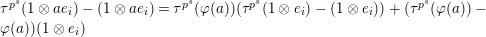 $\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes ae_{i})-(1\otimes ae_{i})=\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i})-(1\otimes e_{i}))+(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a))(1\otimes e_{i})$
, it suffices to show
$\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes ae_{i})-(1\otimes ae_{i})=\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))(\unicode[STIX]{x1D70F}^{p^{s}}(1\otimes e_{i})-(1\otimes e_{i}))+(\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a))(1\otimes e_{i})$
, it suffices to show
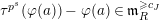 $\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a)\in \mathfrak{m}_{R}^{{\geqslant}c_{J}}$
. Write
$\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a)\in \mathfrak{m}_{R}^{{\geqslant}c_{J}}$
. Write
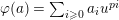 $\unicode[STIX]{x1D711}(a)=\sum _{i\geqslant 0}a_{i}u^{pi}$
for some
$\unicode[STIX]{x1D711}(a)=\sum _{i\geqslant 0}a_{i}u^{pi}$
for some
![]() $a_{i}\in k$
. Then we have
$a_{i}\in k$
. Then we have
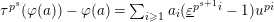 $\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a)=\sum _{i\geqslant 1}a_{i}(\text{}\underline{\unicode[STIX]{x1D700}}^{p^{s+1}i}-1)u^{pi}$
. Since we have
$\unicode[STIX]{x1D70F}^{p^{s}}(\unicode[STIX]{x1D711}(a))-\unicode[STIX]{x1D711}(a)=\sum _{i\geqslant 1}a_{i}(\text{}\underline{\unicode[STIX]{x1D700}}^{p^{s+1}i}-1)u^{pi}$
. Since we have
 $$\begin{eqnarray}v_{R}((\text{}\underline{\unicode[STIX]{x1D700}}^{p^{s+1}i}-1)u^{pi})=p^{s+1}v_{R}(\text{}\underline{\unicode[STIX]{x1D700}}^{i}-1)+v_{R}(u^{pi})>\frac{p^{s+2}}{p-1}\geqslant c_{J}\end{eqnarray}$$
$$\begin{eqnarray}v_{R}((\text{}\underline{\unicode[STIX]{x1D700}}^{p^{s+1}i}-1)u^{pi})=p^{s+1}v_{R}(\text{}\underline{\unicode[STIX]{x1D700}}^{i}-1)+v_{R}(u^{pi})>\frac{p^{s+2}}{p-1}\geqslant c_{J}\end{eqnarray}$$
for any
![]() $i\geqslant 1$
, we have done.◻
$i\geqslant 1$
, we have done.◻
Recall that
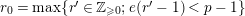 $r_{0}=\text{max}\{r^{\prime }\in \mathbb{Z}_{{\geqslant}0};e(r^{\prime }-1)<p-1\}$
. Put
$r_{0}=\text{max}\{r^{\prime }\in \mathbb{Z}_{{\geqslant}0};e(r^{\prime }-1)<p-1\}$
. Put
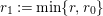 $r_{1}:=\text{min}\{r,r_{0}\}$
.
$r_{1}:=\text{min}\{r,r_{0}\}$
.
Corollary 4.12. Assume that
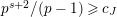 $p^{s+2}/(p-1)\geqslant c_{J}$
. If
$p^{s+2}/(p-1)\geqslant c_{J}$
. If
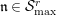 $\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
, then
$\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
, then
![]() $\mathfrak{M}(\mathfrak{n})$
has a structure of an object of
$\mathfrak{M}(\mathfrak{n})$
has a structure of an object of
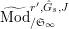 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s},J}$
for any
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r^{\prime },{\hat{G}}_{s},J}$
for any
![]() $r^{\prime }\geqslant r_{1}$
. Furthermore, if
$r^{\prime }\geqslant r_{1}$
. Furthermore, if
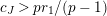 $c_{J}>pr_{1}/(p-1)$
, it is uniquely determined. We denote this object by
$c_{J}>pr_{1}/(p-1)$
, it is uniquely determined. We denote this object by
![]() $\hat{\mathfrak{M}}(\mathfrak{n})$
.
$\hat{\mathfrak{M}}(\mathfrak{n})$
.
Proof. We should remark that
![]() $\mathfrak{M}(\mathfrak{n})$
is of height
$\mathfrak{M}(\mathfrak{n})$
is of height
![]() ${\leqslant}r_{1}$
for any
${\leqslant}r_{1}$
for any
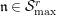 $\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
. The uniqueness assertion follows from Proposition 4.2.◻
$\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
. The uniqueness assertion follows from Proposition 4.2.◻
Before the lemma below, we remark that any semisimple
![]() $\mathbb{F}_{p}$
-representation of
$\mathbb{F}_{p}$
-representation of
![]() $G_{K}$
is automatically tame.
$G_{K}$
is automatically tame.
Lemma 4.13.
![]() $(1)$
The restriction functor from the category of tamely ramified torsion
$(1)$
The restriction functor from the category of tamely ramified torsion
![]() $\mathbb{Z}_{p}$
-representations of
$\mathbb{Z}_{p}$
-representations of
![]() $G_{K}$
to the category of torsion
$G_{K}$
to the category of torsion
![]() $\mathbb{Z}_{p}$
-representations of
$\mathbb{Z}_{p}$
-representations of
![]() $G_{\infty }$
is fully faithful.
$G_{\infty }$
is fully faithful.
![]() $(2)$
The restriction functor in
$(2)$
The restriction functor in
![]() $(1)$
induces an equivalence between the category of semisimple (resp. irreducible)
$(1)$
induces an equivalence between the category of semisimple (resp. irreducible)
![]() $\mathbb{F}_{p}$
-representations of
$\mathbb{F}_{p}$
-representations of
![]() $G_{K}$
and the category of semisimple (resp. irreducible)
$G_{K}$
and the category of semisimple (resp. irreducible)
![]() $\mathbb{F}_{p}$
-representations of
$\mathbb{F}_{p}$
-representations of
![]() $G_{\infty }$
.
$G_{\infty }$
.
Proof. (1) The result immediately follows from the fact that
![]() $G_{K}$
is topologically generated by
$G_{K}$
is topologically generated by
![]() $G_{\infty }$
and the wild inertia subgroup of
$G_{\infty }$
and the wild inertia subgroup of
![]() $G_{K}$
.
$G_{K}$
.
(2) It suffices to show the assertion for irreducible representations. Denote by
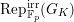 $\text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{K})$
and
$\text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{K})$
and
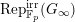 $\text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{\infty })$
the category of irreducible
$\text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{\infty })$
the category of irreducible
![]() $\mathbb{F}_{p}$
-representations of
$\mathbb{F}_{p}$
-representations of
![]() $G_{K}$
and
$G_{K}$
and
![]() $G_{\infty }$
, respectively. First we show that the restriction of the action of
$G_{\infty }$
, respectively. First we show that the restriction of the action of
![]() $G_{K}$
to
$G_{K}$
to
![]() $G_{\infty }$
induces a functor
$G_{\infty }$
induces a functor
 $\text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{K})\rightarrow \text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{\infty })$
. Let
$\text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{K})\rightarrow \text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{\infty })$
. Let
![]() $T$
be an irreducible
$T$
be an irreducible
![]() $\mathbb{F}_{p}$
-representation of
$\mathbb{F}_{p}$
-representation of
![]() $G_{K}$
. Take a
$G_{K}$
. Take a
![]() $G_{\infty }$
-stable submodule
$G_{\infty }$
-stable submodule
![]() $T^{\prime }$
of
$T^{\prime }$
of
![]() $T$
. Let
$T$
. Let
![]() $K^{\text{t}}$
be the maximal tamely ramified extension of
$K^{\text{t}}$
be the maximal tamely ramified extension of
![]() $K$
and
$K$
and
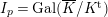 $I_{p}=\text{Gal}(\overline{K}/K^{\text{t}})$
the wild inertia subgroup of
$I_{p}=\text{Gal}(\overline{K}/K^{\text{t}})$
the wild inertia subgroup of
![]() $G_{K}$
. Then
$G_{K}$
. Then
![]() $I_{p}$
acts on
$I_{p}$
acts on
![]() $T$
trivially. In particular,
$T$
trivially. In particular,
![]() $T^{\prime }$
is stable under
$T^{\prime }$
is stable under
![]() $I_{p}$
-action. Since
$I_{p}$
-action. Since
![]() $G_{K}$
is topologically generated by
$G_{K}$
is topologically generated by
![]() $G_{\infty }$
and
$G_{\infty }$
and
![]() $I_{p}$
, we know that
$I_{p}$
, we know that
![]() $T^{\prime }$
is a
$T^{\prime }$
is a
![]() $G_{K}$
-stable submodule of
$G_{K}$
-stable submodule of
![]() $T$
. Hence
$T$
. Hence
![]() $T^{\prime }=0$
or
$T^{\prime }=0$
or
![]() $T$
and this implies that
$T$
and this implies that
![]() $T|_{G_{\infty }}$
is irreducible. Thus the restriction functor
$T|_{G_{\infty }}$
is irreducible. Thus the restriction functor
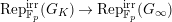 $\text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{K})\rightarrow \text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{\infty })$
is well defined. This is fully faithful by (1). It is enough to show that this functor is essentially surjective. Let
$\text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{K})\rightarrow \text{Rep}_{\mathbb{F}_{p}}^{\text{irr}}(G_{\infty })$
is well defined. This is fully faithful by (1). It is enough to show that this functor is essentially surjective. Let
![]() $T$
be an irreducible
$T$
be an irreducible
![]() $\mathbb{F}_{p}$
-representation of
$\mathbb{F}_{p}$
-representation of
![]() $G_{\infty }$
. Since
$G_{\infty }$
. Since
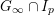 $G_{\infty }\cap I_{p}$
acts on
$G_{\infty }\cap I_{p}$
acts on
![]() $T$
trivially, the
$T$
trivially, the
![]() $G_{\infty }$
-action on
$G_{\infty }$
-action on
![]() $T$
factors through
$T$
factors through
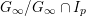 $G_{\infty }/G_{\infty }\cap I_{p}$
. We define a
$G_{\infty }/G_{\infty }\cap I_{p}$
. We define a
![]() $G_{K}$
-action on
$G_{K}$
-action on
![]() $T$
via natural maps
$T$
via natural maps
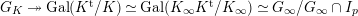 $G_{K}{\twoheadrightarrow}\text{Gal}(K^{\text{t}}/K)\simeq \text{Gal}(K_{\infty }K^{\text{t}}/K_{\infty })\simeq G_{\infty }/G_{\infty }\cap I_{p}$
. The restriction of this
$G_{K}{\twoheadrightarrow}\text{Gal}(K^{\text{t}}/K)\simeq \text{Gal}(K_{\infty }K^{\text{t}}/K_{\infty })\simeq G_{\infty }/G_{\infty }\cap I_{p}$
. The restriction of this
![]() $G_{K}$
-action on
$G_{K}$
-action on
![]() $T$
to
$T$
to
![]() $G_{\infty }$
coincides with the original
$G_{\infty }$
coincides with the original
![]() $G_{\infty }$
-action on
$G_{\infty }$
-action on
![]() $T$
and thus we finish a proof.◻
$T$
and thus we finish a proof.◻
Lemma 4.14. Assume that
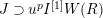 $J\supset u^{p}I^{[1]}W(R)$
or
$J\supset u^{p}I^{[1]}W(R)$
or
![]() $k$
is algebraically closed. Let
$k$
is algebraically closed. Let
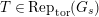 $T\in \text{Rep}_{\text{tor}}(G_{s})$
and
$T\in \text{Rep}_{\text{tor}}(G_{s})$
and
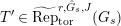 $T^{\prime }\in \widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
. Suppose that
$T^{\prime }\in \widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
. Suppose that
![]() $T$
is tame,
$T$
is tame,
![]() $pT=0$
and
$pT=0$
and
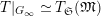 $T|_{G_{\infty }}\simeq T_{\mathfrak{S}}(\mathfrak{M})$
for some
$T|_{G_{\infty }}\simeq T_{\mathfrak{S}}(\mathfrak{M})$
for some
 $\mathfrak{M}\in \text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
. Furthermore, we suppose
$\mathfrak{M}\in \text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
. Furthermore, we suppose
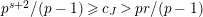 $p^{s+2}/(p-1)\geqslant c_{J}>pr/(p-1)$
. Then all
$p^{s+2}/(p-1)\geqslant c_{J}>pr/(p-1)$
. Then all
![]() $G_{\infty }$
-equivariant homomorphisms
$G_{\infty }$
-equivariant homomorphisms
![]() $T\rightarrow T^{\prime }$
are
$T\rightarrow T^{\prime }$
are
![]() $G_{s}$
-equivariant.
$G_{s}$
-equivariant.
Proof. Let
![]() $L$
be the completion of the maximal unramified extension
$L$
be the completion of the maximal unramified extension
![]() $K^{\text{ur}}$
of
$K^{\text{ur}}$
of
![]() $K$
. By identifying
$K$
. By identifying
![]() $G_{L}$
with
$G_{L}$
with
![]() $G_{K^{\text{ur}}}$
, we may regard
$G_{K^{\text{ur}}}$
, we may regard
![]() $G_{L}$
as a subgroup of
$G_{L}$
as a subgroup of
![]() $G_{K}$
. Note that
$G_{K}$
. Note that
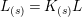 $L_{(s)}=K_{(s)}L$
is the completion of the maximal unramified extension of
$L_{(s)}=K_{(s)}L$
is the completion of the maximal unramified extension of
![]() $K_{(s)}$
, and
$K_{(s)}$
, and
![]() $G_{s}$
is topologically generated by
$G_{s}$
is topologically generated by
![]() $G_{L,s}$
and
$G_{L,s}$
and
![]() $G_{\infty }$
. Consider the following commutative diagram:
$G_{\infty }$
. Consider the following commutative diagram:

Since
![]() $T^{\prime }|_{G_{L,s}}$
is contained in
$T^{\prime }|_{G_{L,s}}$
is contained in
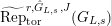 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{L,s},J}(G_{L,s})$
if
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{L,s},J}(G_{L,s})$
if
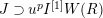 $J\supset u^{p}I^{[1]}W(R)$
(cf. Lemma 4.6), the above diagram allows us to reduce a proof to the case where
$J\supset u^{p}I^{[1]}W(R)$
(cf. Lemma 4.6), the above diagram allows us to reduce a proof to the case where
![]() $k$
is algebraically closed. In the rest of this proof, we assume that
$k$
is algebraically closed. In the rest of this proof, we assume that
![]() $k$
is algebraically closed. Under this assumption, an
$k$
is algebraically closed. Under this assumption, an
![]() $\mathbb{F}_{p}$
-representation of
$\mathbb{F}_{p}$
-representation of
![]() $G_{s}$
is tame if and only if it is semisimple by Maschke’s theorem. Thus we may also assume that
$G_{s}$
is tame if and only if it is semisimple by Maschke’s theorem. Thus we may also assume that
![]() $T$
is irreducible (here, we remark that any subquotient of
$T$
is irreducible (here, we remark that any subquotient of
![]() $T$
is tame and, also remark that the essential image of
$T$
is tame and, also remark that the essential image of
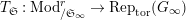 $T_{\mathfrak{S}}:\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is stable under subquotients in
$T_{\mathfrak{S}}:\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is stable under subquotients in
 $\text{Rep}_{\text{tor}}(G_{\infty })$
). By the assumption on
$\text{Rep}_{\text{tor}}(G_{\infty })$
). By the assumption on
![]() $T$
, we have
$T$
, we have
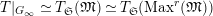 $T|_{G_{\infty }}\simeq T_{\mathfrak{S}}(\mathfrak{M})\simeq T_{\mathfrak{S}}(\text{Max}^{r}(\mathfrak{M}))$
for some
$T|_{G_{\infty }}\simeq T_{\mathfrak{S}}(\mathfrak{M})\simeq T_{\mathfrak{S}}(\text{Max}^{r}(\mathfrak{M}))$
for some
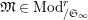 $\mathfrak{M}\in \text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
. Since
$\mathfrak{M}\in \text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
. Since
![]() $T|_{G_{\infty }}$
is irreducible (cf. By Lemma 4.13(2)) and
$T|_{G_{\infty }}$
is irreducible (cf. By Lemma 4.13(2)) and
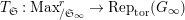 $T_{\mathfrak{S}}:\text{Max}_{/\mathfrak{S}_{\infty }}^{r}\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is exact and fully faithful, we know that
$T_{\mathfrak{S}}:\text{Max}_{/\mathfrak{S}_{\infty }}^{r}\rightarrow \text{Rep}_{\text{tor}}(G_{\infty })$
is exact and fully faithful, we know that
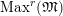 $\text{Max}^{r}(\mathfrak{M})$
is a simple object in the abelian category
$\text{Max}^{r}(\mathfrak{M})$
is a simple object in the abelian category
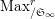 $\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
. Therefore, since
$\text{Max}_{/\mathfrak{S}_{\infty }}^{r}$
. Therefore, since
![]() $k$
is algebraically closed, we have
$k$
is algebraically closed, we have
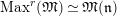 $\text{Max}^{r}(\mathfrak{M})\simeq \mathfrak{M}(\mathfrak{n})$
for some
$\text{Max}^{r}(\mathfrak{M})\simeq \mathfrak{M}(\mathfrak{n})$
for some
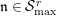 $\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
(cf. [Reference Caruso and LiuCL1, Propositions 3.6.8 and 3.6.12]). Let
$\mathfrak{n}\in {\mathcal{S}}_{\text{max}}^{r}$
(cf. [Reference Caruso and LiuCL1, Propositions 3.6.8 and 3.6.12]). Let
![]() $\hat{\mathfrak{M}}(\mathfrak{n})$
be the object of
$\hat{\mathfrak{M}}(\mathfrak{n})$
be the object of
 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
as in Corollary 4.12. We recall that
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
as in Corollary 4.12. We recall that
 $T_{\mathfrak{S}}(\mathfrak{M}(\mathfrak{n}))$
is isomorphic to
$T_{\mathfrak{S}}(\mathfrak{M}(\mathfrak{n}))$
is isomorphic to
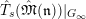 $\hat{T}_{s}(\hat{\mathfrak{M}}(\mathfrak{n}))|_{G_{\infty }}$
(see Theorem 2.5(1)), and hence we have an isomorphism
$\hat{T}_{s}(\hat{\mathfrak{M}}(\mathfrak{n}))|_{G_{\infty }}$
(see Theorem 2.5(1)), and hence we have an isomorphism
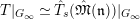 $T|_{G_{\infty }}\simeq \hat{T}_{s}(\hat{\mathfrak{M}}(\mathfrak{n}))|_{G_{\infty }}$
. Here, we note that
$T|_{G_{\infty }}\simeq \hat{T}_{s}(\hat{\mathfrak{M}}(\mathfrak{n}))|_{G_{\infty }}$
. Here, we note that
![]() $T$
and
$T$
and
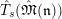 $\hat{T}_{s}(\hat{\mathfrak{M}}(\mathfrak{n}))$
are irreducible as representations of
$\hat{T}_{s}(\hat{\mathfrak{M}}(\mathfrak{n}))$
are irreducible as representations of
![]() $G_{s}$
(cf. [Reference Caruso and LiuCL1, Theorem 3.6.11]). Applying Lemma 4.13 again, we obtain an isomorphism
$G_{s}$
(cf. [Reference Caruso and LiuCL1, Theorem 3.6.11]). Applying Lemma 4.13 again, we obtain an isomorphism
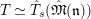 $T\simeq \hat{T}_{s}(\hat{\mathfrak{M}}(\mathfrak{n}))$
as representations of
$T\simeq \hat{T}_{s}(\hat{\mathfrak{M}}(\mathfrak{n}))$
as representations of
![]() $G_{s}$
. On the other hand, we can take
$G_{s}$
. On the other hand, we can take
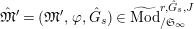 $\hat{\mathfrak{M}}^{\prime }=(\mathfrak{M}^{\prime },\unicode[STIX]{x1D711},{\hat{G}}_{s})\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
such that
$\hat{\mathfrak{M}}^{\prime }=(\mathfrak{M}^{\prime },\unicode[STIX]{x1D711},{\hat{G}}_{s})\in \widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
such that
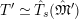 $T^{\prime }\simeq \hat{T}_{s}(\hat{\mathfrak{M}}^{\prime })$
. We consider the following commutative diagram:
$T^{\prime }\simeq \hat{T}_{s}(\hat{\mathfrak{M}}^{\prime })$
. We consider the following commutative diagram:

Here,
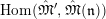 $\text{Hom}(\hat{\mathfrak{M}}^{\prime },\hat{\mathfrak{M}}(\mathfrak{n}))$
is the set of morphisms
$\text{Hom}(\hat{\mathfrak{M}}^{\prime },\hat{\mathfrak{M}}(\mathfrak{n}))$
is the set of morphisms
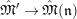 $\hat{\mathfrak{M}}^{\prime }\rightarrow \hat{\mathfrak{M}}(\mathfrak{n})$
in the category
$\hat{\mathfrak{M}}^{\prime }\rightarrow \hat{\mathfrak{M}}(\mathfrak{n})$
in the category
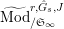 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
. The first arrow in the bottom line is bijective by Proposition 4.2 and so is the second (this follows from the fact that
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s},J}$
. The first arrow in the bottom line is bijective by Proposition 4.2 and so is the second (this follows from the fact that
![]() $\mathfrak{M}(\mathfrak{n})$
is maximal by [Reference Caruso and LiuCL1, Proposition 3.6.7]). Since the right vertical arrow is bijective, the top horizontal arrow must be bijective.◻
$\mathfrak{M}(\mathfrak{n})$
is maximal by [Reference Caruso and LiuCL1, Proposition 3.6.7]). Since the right vertical arrow is bijective, the top horizontal arrow must be bijective.◻
Now we are ready to prove Theorem 4.9.
Proof of Theorem 4.9.
At first, we note that the category
 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
is an exact category in the sense of Quillen [Reference QuillenQu, Section 2] by Corollary 4.5. Hence short exact sequences in
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
is an exact category in the sense of Quillen [Reference QuillenQu, Section 2] by Corollary 4.5. Hence short exact sequences in
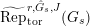 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
give rise to exact sequences of Hom’s and
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
give rise to exact sequences of Hom’s and
![]() $\text{Ext}^{1}$
’s in the usual way. (This property holds for any exact category.) Let
$\text{Ext}^{1}$
’s in the usual way. (This property holds for any exact category.) Let
![]() $T$
and
$T$
and
![]() $T^{\prime }$
be objects of
$T^{\prime }$
be objects of
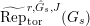 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
. Take any Jordan–Hölder sequence
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
. Take any Jordan–Hölder sequence
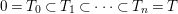 $0=T_{0}\subset T_{1}\subset \cdots \subset T_{n}=T$
of
$0=T_{0}\subset T_{1}\subset \cdots \subset T_{n}=T$
of
![]() $T$
in
$T$
in
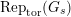 $\text{Rep}_{\text{tor}}(G_{s})$
. By Corollary 4.5 again, we know that
$\text{Rep}_{\text{tor}}(G_{s})$
. By Corollary 4.5 again, we know that
![]() $T_{i}$
and
$T_{i}$
and
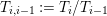 $T_{i,i-1}:=T_{i}/T_{i-1}$
are contained in
$T_{i,i-1}:=T_{i}/T_{i-1}$
are contained in
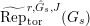 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
for any
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
for any
![]() $i$
. By Lemma 4.14, if an exact sequence
$i$
. By Lemma 4.14, if an exact sequence
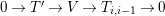 $0\rightarrow T^{\prime }\rightarrow V\rightarrow T_{i,i-1}\rightarrow 0$
in
$0\rightarrow T^{\prime }\rightarrow V\rightarrow T_{i,i-1}\rightarrow 0$
in
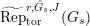 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
splits as representations of
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
splits as representations of
![]() $G_{\infty }$
, then it splits as a sequence of representations of
$G_{\infty }$
, then it splits as a sequence of representations of
![]() $G_{s}$
. This shows that the fourth column in the diagram below is injective:
$G_{s}$
. This shows that the fourth column in the diagram below is injective:

Here, the extension
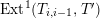 $\text{Ext}^{1}(T_{i,i-1},T^{\prime })$
in the above diagram is taken in the category
$\text{Ext}^{1}(T_{i,i-1},T^{\prime })$
in the above diagram is taken in the category
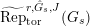 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
. In addition, it follows from Lemma 4.14 that the first column is an isomorphism. Therefore, we obtain an implication that, if the third column is an isomorphism, then the second one is an isomorphism. Hence a dévissage argument works and the desired full faithfulness follows. ◻
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
. In addition, it follows from Lemma 4.14 that the first column is an isomorphism. Therefore, we obtain an implication that, if the third column is an isomorphism, then the second one is an isomorphism. Hence a dévissage argument works and the desired full faithfulness follows. ◻
4.4 Proof of Theorem 1.2
Now we are ready to prove our main theorems. First we prove Theorem 1.2. Recall that a torsion
![]() $\mathbb{Z}_{p}$
-representation
$\mathbb{Z}_{p}$
-representation
![]() $T$
of
$T$
of
![]() $G_{K}$
is torsion crystalline with Hodge–Tate weights in
$G_{K}$
is torsion crystalline with Hodge–Tate weights in
![]() $[0,r]$
if it can be written as the quotient of lattices in some crystalline
$[0,r]$
if it can be written as the quotient of lattices in some crystalline
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
with Hodge–Tate weights in
$G_{K}$
with Hodge–Tate weights in
![]() $[0,r]$
. Let
$[0,r]$
. Let
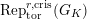 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
be the category of them. We apply our arguments given in previous subsections with the following
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
be the category of them. We apply our arguments given in previous subsections with the following
![]() $J$
:
$J$
:
 $$\begin{eqnarray}J=u^{p}I^{[1]}W(R)=u^{p}\unicode[STIX]{x1D711}(\mathfrak{t})W(R).\end{eqnarray}$$
$$\begin{eqnarray}J=u^{p}I^{[1]}W(R)=u^{p}\unicode[STIX]{x1D711}(\mathfrak{t})W(R).\end{eqnarray}$$
Then we have
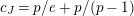 $c_{J}=p/e+p/(p-1)$
and thus the inequalities
$c_{J}=p/e+p/(p-1)$
and thus the inequalities
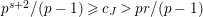 $p^{s+2}/(p-1)\geqslant c_{J}>pr/(p-1)$
are satisfied if
$p^{s+2}/(p-1)\geqslant c_{J}>pr/(p-1)$
are satisfied if
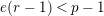 $e(r-1)<p-1$
. Therefore, Theorem 1.2 is an easy consequence of the following proposition and Theorem 4.9.
$e(r-1)<p-1$
. Therefore, Theorem 1.2 is an easy consequence of the following proposition and Theorem 4.9.
Proposition 4.15. The category
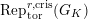 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
is a subcategory of the category
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
is a subcategory of the category
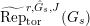 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
when
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
when
![]() $s=0$
.
$s=0$
.
Proof. In this proof, we put
![]() $s=0$
. So we omit subscript
$s=0$
. So we omit subscript
![]() $s$
in various notations (e.g.,
$s$
in various notations (e.g.,
![]() ${\hat{G}}_{s}={\hat{G}}$
,
${\hat{G}}_{s}={\hat{G}}$
,
 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}=\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}}$
). Let
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}_{s}}=\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}}$
). Let
![]() $T$
be an object of
$T$
be an object of
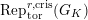 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
and let
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
and let
![]() $L\subset L^{\prime }$
be lattices in a crystalline
$L\subset L^{\prime }$
be lattices in a crystalline
![]() $\mathbb{Q}_{p}$
-representation with Hodge–Tate weights in
$\mathbb{Q}_{p}$
-representation with Hodge–Tate weights in
![]() $[0,r]$
such that
$[0,r]$
such that
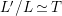 $L^{\prime }/L\simeq T$
. By Theorem 2.5(1), there exists an injection
$L^{\prime }/L\simeq T$
. By Theorem 2.5(1), there exists an injection
![]() $\hat{\mathfrak{L}}^{\prime }{\hookrightarrow}\hat{\mathfrak{L}}$
of
$\hat{\mathfrak{L}}^{\prime }{\hookrightarrow}\hat{\mathfrak{L}}$
of
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules over
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules over
![]() $\mathfrak{S}$
which corresponds to the injection
$\mathfrak{S}$
which corresponds to the injection
![]() $L{\hookrightarrow}L^{\prime }$
. Now we put
$L{\hookrightarrow}L^{\prime }$
. Now we put
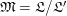 $\mathfrak{M}=\mathfrak{L}/\mathfrak{L}^{\prime }$
. Since
$\mathfrak{M}=\mathfrak{L}/\mathfrak{L}^{\prime }$
. Since
![]() $L^{\prime }/L$
is killed by a power of
$L^{\prime }/L$
is killed by a power of
![]() $p$
,
$p$
,
![]() $\mathfrak{M}$
is an object of
$\mathfrak{M}$
is an object of
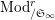 $\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
. We equip a
$\text{Mod}_{/\mathfrak{S}_{\infty }}^{r}$
. We equip a
![]() ${\hat{G}}$
-action with
${\hat{G}}$
-action with
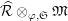 $\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
by a natural isomorphism
$\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}$
by a natural isomorphism
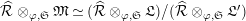 $\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\simeq (\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L})/(\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L}^{\prime })$
. Then we see that
$\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\simeq (\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L})/(\widehat{{\mathcal{R}}}\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L}^{\prime })$
. Then we see that
![]() $\mathfrak{M}$
has a structure of an object of
$\mathfrak{M}$
has a structure of an object of
 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}}$
; denote it by
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}}}$
; denote it by
![]() $\hat{\mathfrak{M}}$
. Moreover, Theorem 3.5 implies that
$\hat{\mathfrak{M}}$
. Moreover, Theorem 3.5 implies that
![]() $\hat{\mathfrak{M}}$
is in fact contained in
$\hat{\mathfrak{M}}$
is in fact contained in
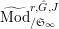 $\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}},J}$
. By a similar argument to the proof of [Reference Caruso and LiuCL2, Lemma 3.1.4], we have an exact sequence
$\widetilde{\text{Mod}}_{/\mathfrak{S}_{\infty }}^{r,{\hat{G}},J}$
. By a similar argument to the proof of [Reference Caruso and LiuCL2, Lemma 3.1.4], we have an exact sequence
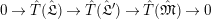 $0\rightarrow \hat{T}(\hat{\mathfrak{L}})\rightarrow \hat{T}(\hat{\mathfrak{L}}^{\prime })\rightarrow \hat{T}(\hat{\mathfrak{M}})\rightarrow 0$
of representations of
$0\rightarrow \hat{T}(\hat{\mathfrak{L}})\rightarrow \hat{T}(\hat{\mathfrak{L}}^{\prime })\rightarrow \hat{T}(\hat{\mathfrak{M}})\rightarrow 0$
of representations of
![]() $G_{K}$
which is isomorphic to
$G_{K}$
which is isomorphic to
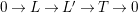 $0\rightarrow L\rightarrow L^{\prime }\rightarrow T\rightarrow 0$
. This finishes a proof.◻
$0\rightarrow L\rightarrow L^{\prime }\rightarrow T\rightarrow 0$
. This finishes a proof.◻
4.5 Proof of Theorem 1.3
We give a proof of Theorem 1.3. If
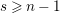 $s\geqslant n-1$
, then we put
$s\geqslant n-1$
, then we put
 $$\begin{eqnarray}J=u^{p}I^{[p^{s-n+1}]}W(R)=u^{p}\unicode[STIX]{x1D711}(\mathfrak{t})^{p^{s-n+1}}W(R).\end{eqnarray}$$
$$\begin{eqnarray}J=u^{p}I^{[p^{s-n+1}]}W(R)=u^{p}\unicode[STIX]{x1D711}(\mathfrak{t})^{p^{s-n+1}}W(R).\end{eqnarray}$$
Note that we have
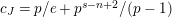 $c_{J}=p/e+p^{s-n+2}/(p-1)$
and thus the inequalities
$c_{J}=p/e+p^{s-n+2}/(p-1)$
and thus the inequalities
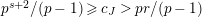 $p^{s+2}/(p-1)\geqslant c_{J}>pr/(p-1)$
are satisfied if
$p^{s+2}/(p-1)\geqslant c_{J}>pr/(p-1)$
are satisfied if
 $$\begin{eqnarray}s>n-1+\text{log}_{p}(r-(p-1)/e).\end{eqnarray}$$
$$\begin{eqnarray}s>n-1+\text{log}_{p}(r-(p-1)/e).\end{eqnarray}$$
Proposition 4.16. Suppose
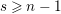 $s\geqslant n-1$
. If
$s\geqslant n-1$
. If
![]() $T$
is an object of
$T$
is an object of
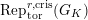 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
which is killed by
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
which is killed by
![]() $p^{n}$
, then
$p^{n}$
, then
![]() $T|_{G_{s}}$
is contained in
$T|_{G_{s}}$
is contained in
 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
.
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
.
Proof. Let
![]() $L$
be an object of
$L$
be an object of
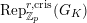 $\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{cris}}(G_{K})$
. Take a
$\text{Rep}_{\mathbb{Z}_{p}}^{r,\text{cris}}(G_{K})$
. Take a
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-module
$(\unicode[STIX]{x1D711},{\hat{G}})$
-module
![]() $\hat{\mathfrak{L}}$
over
$\hat{\mathfrak{L}}$
over
![]() $\mathfrak{S}$
such that
$\mathfrak{S}$
such that
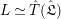 $L\simeq \hat{T}(\hat{\mathfrak{L}})$
. It is known that
$L\simeq \hat{T}(\hat{\mathfrak{L}})$
. It is known that
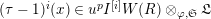 $(\unicode[STIX]{x1D70F}-1)^{i}(x)\in u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L}$
for any
$(\unicode[STIX]{x1D70F}-1)^{i}(x)\in u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L}$
for any
![]() $i\geqslant 1$
and any
$i\geqslant 1$
and any
![]() $x\in \mathfrak{L}$
(cf. the latter half part of the proof of [Reference Gee, Liu and SavittGLS, Proposition 4.7]). Take any
$x\in \mathfrak{L}$
(cf. the latter half part of the proof of [Reference Gee, Liu and SavittGLS, Proposition 4.7]). Take any
![]() $x\in \mathfrak{L}$
. Since
$x\in \mathfrak{L}$
. Since
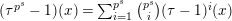 $(\unicode[STIX]{x1D70F}^{p^{s}}-1)(x)=\sum _{i=1}^{p^{s}}\binom{p^{s}}{i}(\unicode[STIX]{x1D70F}-1)^{i}(x)$
, we obtain that
$(\unicode[STIX]{x1D70F}^{p^{s}}-1)(x)=\sum _{i=1}^{p^{s}}\binom{p^{s}}{i}(\unicode[STIX]{x1D70F}-1)^{i}(x)$
, we obtain that
 $$\begin{eqnarray}(\unicode[STIX]{x1D70F}^{p^{s}}-1)(x)\in \mathop{\sum }_{i=1}^{p^{s}}p^{s-v_{p}(i)}u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}^{p^{s}}-1)(x)\in \mathop{\sum }_{i=1}^{p^{s}}p^{s-v_{p}(i)}u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L}.\end{eqnarray}$$
Now let
![]() $T$
be an object of
$T$
be an object of
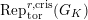 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
which is killed by
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
which is killed by
![]() $p^{n}$
. Take an exact sequence
$p^{n}$
. Take an exact sequence
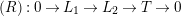 $(R):0\rightarrow L_{1}\rightarrow L_{2}\rightarrow T\rightarrow 0$
of
$(R):0\rightarrow L_{1}\rightarrow L_{2}\rightarrow T\rightarrow 0$
of
![]() $\mathbb{Z}_{p}$
-representations of
$\mathbb{Z}_{p}$
-representations of
![]() $G_{K}$
with
$G_{K}$
with
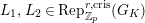 $L_{1},L_{2}\in \text{Rep}_{\mathbb{Z}_{p}}^{r,\text{cris}}(G_{K})$
. By [Reference Caruso and LiuCL2, Theorem 3.1.3 and Lemma 3.1.4], there exists an exact sequence
$L_{1},L_{2}\in \text{Rep}_{\mathbb{Z}_{p}}^{r,\text{cris}}(G_{K})$
. By [Reference Caruso and LiuCL2, Theorem 3.1.3 and Lemma 3.1.4], there exists an exact sequence
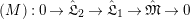 $(M):0\rightarrow \hat{\mathfrak{L}}_{2}\rightarrow \hat{\mathfrak{L}}_{1}\rightarrow \hat{\mathfrak{M}}\rightarrow 0$
of
$(M):0\rightarrow \hat{\mathfrak{L}}_{2}\rightarrow \hat{\mathfrak{L}}_{1}\rightarrow \hat{\mathfrak{M}}\rightarrow 0$
of
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-modules over
$(\unicode[STIX]{x1D711},{\hat{G}})$
-modules over
![]() $\mathfrak{S}$
such that
$\mathfrak{S}$
such that
 $\hat{T}((M))\simeq (R)$
. By (7), we see that
$\hat{T}((M))\simeq (R)$
. By (7), we see that
 $$\begin{eqnarray}(\unicode[STIX]{x1D70F}^{p^{s}}-1)(x)\in \mathop{\sum }_{i=1}^{p^{s}}p^{s-v_{p}(i)}u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}^{p^{s}}-1)(x)\in \mathop{\sum }_{i=1}^{p^{s}}p^{s-v_{p}(i)}u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\end{eqnarray}$$
for any
![]() $x\in \mathfrak{M}$
. Since
$x\in \mathfrak{M}$
. Since
![]() $\mathfrak{M}$
is killed by
$\mathfrak{M}$
is killed by
![]() $p^{n}$
and
$p^{n}$
and
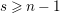 $s\geqslant n-1$
, we have
$s\geqslant n-1$
, we have
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=1}^{p^{s}}p^{s-v_{p}(i)}u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M} & = & \displaystyle \mathop{\sum }_{\substack{ i=1,\ldots ,p^{s} \\ s-v_{p}(i)<n}}p^{s-v_{p}(i)}u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\ell =0}^{n-1}p^{\ell }u^{p}I^{[p^{s-\ell }]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\nonumber\\ \displaystyle & \subset & \displaystyle u^{p}I^{[p^{s-n+1}]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i=1}^{p^{s}}p^{s-v_{p}(i)}u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M} & = & \displaystyle \mathop{\sum }_{\substack{ i=1,\ldots ,p^{s} \\ s-v_{p}(i)<n}}p^{s-v_{p}(i)}u^{p}I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\ell =0}^{n-1}p^{\ell }u^{p}I^{[p^{s-\ell }]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}\nonumber\\ \displaystyle & \subset & \displaystyle u^{p}I^{[p^{s-n+1}]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{M}.\nonumber\end{eqnarray}$$
Therefore, we obtained the desired result. ◻
Proof of Theorem 1.3.
By Theorem 1.2, we may suppose
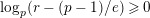 $\text{log}_{p}(r-(p-1)/e)\geqslant 0$
, that is,
$\text{log}_{p}(r-(p-1)/e)\geqslant 0$
, that is,
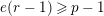 $e(r-1)\geqslant p-1$
. Suppose
$e(r-1)\geqslant p-1$
. Suppose
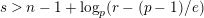 $s>n-1+\text{log}_{p}(r-(p-1)/e)$
. Note that the condition
$s>n-1+\text{log}_{p}(r-(p-1)/e)$
. Note that the condition
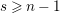 $s\geqslant n-1$
is now satisfied. Let
$s\geqslant n-1$
is now satisfied. Let
![]() $T$
and
$T$
and
![]() $T^{\prime }$
be as in the statement of Theorem 1.3. Let
$T^{\prime }$
be as in the statement of Theorem 1.3. Let
 $f:T\rightarrow T^{\prime }$
be a
$f:T\rightarrow T^{\prime }$
be a
![]() $G_{\infty }$
-equivariant homomorphism. Denote by
$G_{\infty }$
-equivariant homomorphism. Denote by
![]() $L$
the completion of
$L$
the completion of
![]() $K^{\text{ur}}$
and identify
$K^{\text{ur}}$
and identify
![]() $G_{L}$
with the inertia subgroup of
$G_{L}$
with the inertia subgroup of
![]() $G_{K}$
. We note that
$G_{K}$
. We note that
![]() $T|_{G_{L}}$
and
$T|_{G_{L}}$
and
![]() $T^{\prime }|_{G_{L}}$
are objects of
$T^{\prime }|_{G_{L}}$
are objects of
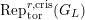 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{L})$
. By Proposition 4.16,
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{L})$
. By Proposition 4.16,
![]() $T|_{G_{L,s}}$
and
$T|_{G_{L,s}}$
and
![]() $T^{\prime }|_{G_{L,s}}$
are objects of
$T^{\prime }|_{G_{L,s}}$
are objects of
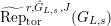 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{L,s},J}(G_{L,s})$
. Hence we have that
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{L,s},J}(G_{L,s})$
. Hence we have that
![]() $f$
is
$f$
is
![]() $G_{L,s}$
-equivariant by Theorem 4.9. Since
$G_{L,s}$
-equivariant by Theorem 4.9. Since
![]() $G_{s}$
is topologically generated by
$G_{s}$
is topologically generated by
![]() $G_{L,s}$
and
$G_{L,s}$
and
![]() $G_{\infty }$
, we see that
$G_{\infty }$
, we see that
![]() $f$
is
$f$
is
![]() $G_{s}$
-equivariant.◻
$G_{s}$
-equivariant.◻
4.6 Galois equivariance for torsion semistable representations
In this subsection, we prove a Galois equivariance theorem for torsion semistable representations. A torsion
![]() $\mathbb{Z}_{p}$
-representation
$\mathbb{Z}_{p}$
-representation
![]() $T$
of
$T$
of
![]() $G_{K}$
is torsion semistable with Hodge–Tate weights in
$G_{K}$
is torsion semistable with Hodge–Tate weights in
![]() $[0,r]$
if it can be written as the quotient of lattices in some semistable
$[0,r]$
if it can be written as the quotient of lattices in some semistable
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
with Hodge–Tate weights in
$G_{K}$
with Hodge–Tate weights in
![]() $[0,r]$
. We denote by
$[0,r]$
. We denote by
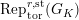 $\text{Rep}_{\text{tor}}^{r,\text{st}}(G_{K})$
the category of them. Note that
$\text{Rep}_{\text{tor}}^{r,\text{st}}(G_{K})$
the category of them. Note that
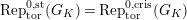 $\text{Rep}_{\text{tor}}^{0,\text{st}}(G_{K})=\text{Rep}_{\text{tor}}^{0,\text{cris}}(G_{K})$
. Similar to Theorem 1.3, we show the following, which is the main result of this subsection.
$\text{Rep}_{\text{tor}}^{0,\text{st}}(G_{K})=\text{Rep}_{\text{tor}}^{0,\text{cris}}(G_{K})$
. Similar to Theorem 1.3, we show the following, which is the main result of this subsection.
Theorem 4.17. Suppose that
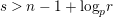 $s>n-1+\text{log}_{p}r$
. Let
$s>n-1+\text{log}_{p}r$
. Let
![]() $T$
and
$T$
and
![]() $T^{\prime }$
be objects of
$T^{\prime }$
be objects of
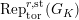 $\text{Rep}_{\text{tor}}^{r,\text{st}}(G_{K})$
which are killed by
$\text{Rep}_{\text{tor}}^{r,\text{st}}(G_{K})$
which are killed by
![]() $p^{n}$
. Then any
$p^{n}$
. Then any
![]() $G_{\infty }$
-equivariant homomorphism
$G_{\infty }$
-equivariant homomorphism
![]() $T\rightarrow T^{\prime }$
is
$T\rightarrow T^{\prime }$
is
![]() $G_{s}$
-equivariant.
$G_{s}$
-equivariant.
If
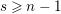 $s\geqslant n-1$
, then we put
$s\geqslant n-1$
, then we put
 $$\begin{eqnarray}J=I^{[p^{s-n+1}]}W(R)=\unicode[STIX]{x1D711}(\mathfrak{t})^{p^{s-n+1}}W(R).\end{eqnarray}$$
$$\begin{eqnarray}J=I^{[p^{s-n+1}]}W(R)=\unicode[STIX]{x1D711}(\mathfrak{t})^{p^{s-n+1}}W(R).\end{eqnarray}$$
Then we have
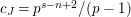 $c_{J}=p^{s-n+2}/(p-1)$
. To show Theorem 4.17, we use similar arguments to those in the proof of Theorem 1.3.
$c_{J}=p^{s-n+2}/(p-1)$
. To show Theorem 4.17, we use similar arguments to those in the proof of Theorem 1.3.
Proposition 4.18. Suppose
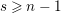 $s\geqslant n-1$
. If
$s\geqslant n-1$
. If
![]() $T$
is an object of
$T$
is an object of
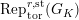 $\text{Rep}_{\text{tor}}^{r,\text{st}}(G_{K})$
which is killed by
$\text{Rep}_{\text{tor}}^{r,\text{st}}(G_{K})$
which is killed by
![]() $p^{n}$
, then
$p^{n}$
, then
![]() $T|_{G_{s}}$
is contained in
$T|_{G_{s}}$
is contained in
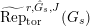 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
.
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
.
Proof. Let
![]() $L$
be a lattice in a semistable
$L$
be a lattice in a semistable
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
with Hodge–Tate weights in
$G_{K}$
with Hodge–Tate weights in
![]() $[0,r]$
. Take a
$[0,r]$
. Take a
![]() $(\unicode[STIX]{x1D711},{\hat{G}})$
-module
$(\unicode[STIX]{x1D711},{\hat{G}})$
-module
![]() $\hat{\mathfrak{L}}$
over
$\hat{\mathfrak{L}}$
over
![]() $\mathfrak{S}$
such that
$\mathfrak{S}$
such that
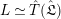 $L\simeq \hat{T}(\hat{\mathfrak{L}})$
. It is known that
$L\simeq \hat{T}(\hat{\mathfrak{L}})$
. It is known that
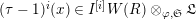 $(\unicode[STIX]{x1D70F}-1)^{i}(x)\in I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L}$
for any
$(\unicode[STIX]{x1D70F}-1)^{i}(x)\in I^{[i]}W(R)\otimes _{\unicode[STIX]{x1D711},\mathfrak{S}}\mathfrak{L}$
for any
![]() $i\geqslant 1$
and any
$i\geqslant 1$
and any
![]() $x\in \mathfrak{L}$
(cf. the proof of [Reference LiuLi3, Proposition 2.4.1]). Thus the same proof proceeds as that of Proposition 4.16.◻
$x\in \mathfrak{L}$
(cf. the proof of [Reference LiuLi3, Proposition 2.4.1]). Thus the same proof proceeds as that of Proposition 4.16.◻
4.7 Some consequences
In this subsection, we generalize some results proved in [Reference BreuilBr3, Section 3.4]. First of all, we show the following elementary lemma, which should be well known to experts, but we include a proof here for the sake of completeness.
Lemma 4.19. The full subcategories
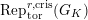 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
and
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
and
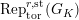 $\text{Rep}_{\text{tor}}^{r,\text{st}}(G_{K})$
of
$\text{Rep}_{\text{tor}}^{r,\text{st}}(G_{K})$
of
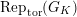 $\text{Rep}_{\text{tor}}(G_{K})$
are stable under formation of subquotients, direct sums and the association
$\text{Rep}_{\text{tor}}(G_{K})$
are stable under formation of subquotients, direct sums and the association
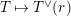 $T\mapsto T^{\vee }(r)$
. Here
$T\mapsto T^{\vee }(r)$
. Here
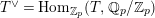 $T^{\vee }=\text{Hom}_{\mathbb{Z}_{p}}(T,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is the dual representation of
$T^{\vee }=\text{Hom}_{\mathbb{Z}_{p}}(T,\mathbb{Q}_{p}/\mathbb{Z}_{p})$
is the dual representation of
![]() $T$
.
$T$
.
Proof. We prove the statement only for the category
 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
. Let
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
. Let
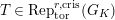 $T\in \text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
be killed by
$T\in \text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
be killed by
![]() $p^{n}$
for some
$p^{n}$
for some
![]() $n>0$
. Assertions for quotients and direct sums are clear. We prove that
$n>0$
. Assertions for quotients and direct sums are clear. We prove that
![]() $T^{\vee }(r)$
is contained in
$T^{\vee }(r)$
is contained in
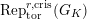 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
. There exist lattices
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
. There exist lattices
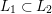 $L_{1}\subset L_{2}$
in some crystalline
$L_{1}\subset L_{2}$
in some crystalline
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
and an exact sequence
$G_{K}$
and an exact sequence
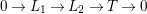 $0\rightarrow L_{1}\rightarrow L_{2}\rightarrow T\rightarrow 0$
of
$0\rightarrow L_{1}\rightarrow L_{2}\rightarrow T\rightarrow 0$
of
![]() $\mathbb{Z}_{p}[G_{K}]$
-modules. This exact sequence induces an exact sequence
$\mathbb{Z}_{p}[G_{K}]$
-modules. This exact sequence induces an exact sequence
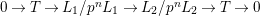 $0\rightarrow T\rightarrow L_{1}/p^{n}L_{1}\rightarrow L_{2}/p^{n}L_{2}\rightarrow T\rightarrow 0$
of finite
$0\rightarrow T\rightarrow L_{1}/p^{n}L_{1}\rightarrow L_{2}/p^{n}L_{2}\rightarrow T\rightarrow 0$
of finite
![]() $\mathbb{Z}_{p}[G_{K}]$
-modules. By duality, we obtain an exact sequence
$\mathbb{Z}_{p}[G_{K}]$
-modules. By duality, we obtain an exact sequence
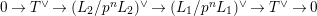 $0\rightarrow T^{\vee }\rightarrow (L_{2}/p^{n}L_{2})^{\vee }\rightarrow (L_{1}/p^{n}L_{1})^{\vee }\rightarrow T^{\vee }\rightarrow 0$
of finite
$0\rightarrow T^{\vee }\rightarrow (L_{2}/p^{n}L_{2})^{\vee }\rightarrow (L_{1}/p^{n}L_{1})^{\vee }\rightarrow T^{\vee }\rightarrow 0$
of finite
![]() $\mathbb{Z}_{p}[G_{K}]$
-modules. Then we obtain a
$\mathbb{Z}_{p}[G_{K}]$
-modules. Then we obtain a
![]() $G_{K}$
-equivariant surjection
$G_{K}$
-equivariant surjection
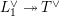 $L_{1}^{\vee }{\twoheadrightarrow}T^{\vee }$
by the composite
$L_{1}^{\vee }{\twoheadrightarrow}T^{\vee }$
by the composite
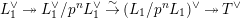 $L_{1}^{\vee }{\twoheadrightarrow}L_{1}^{\vee }/p^{n}L_{1}^{\vee }\overset{{\sim}}{\rightarrow }(L_{1}/p^{n}L_{1})^{\vee }{\twoheadrightarrow}T^{\vee }$
of natural maps (here, for any free
$L_{1}^{\vee }{\twoheadrightarrow}L_{1}^{\vee }/p^{n}L_{1}^{\vee }\overset{{\sim}}{\rightarrow }(L_{1}/p^{n}L_{1})^{\vee }{\twoheadrightarrow}T^{\vee }$
of natural maps (here, for any free
![]() $\mathbb{Z}_{p}$
-representation
$\mathbb{Z}_{p}$
-representation
![]() $L$
of
$L$
of
![]() $G_{K}$
,
$G_{K}$
,
 $L^{\vee }:=\text{Hom}_{\mathbb{Z}_{p}}(L,\mathbb{Z}_{p})$
stands for the dual of
$L^{\vee }:=\text{Hom}_{\mathbb{Z}_{p}}(L,\mathbb{Z}_{p})$
stands for the dual of
![]() $L$
). Therefore, we obtain
$L$
). Therefore, we obtain
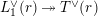 $L_{1}^{\vee }(r){\twoheadrightarrow}T^{\vee }(r)$
and thus
$L_{1}^{\vee }(r){\twoheadrightarrow}T^{\vee }(r)$
and thus
 $T^{\vee }(r)\in \text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
. Finally, we prove the stability assertion for subobjects. Let
$T^{\vee }(r)\in \text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
. Finally, we prove the stability assertion for subobjects. Let
![]() $T^{\prime }$
be a
$T^{\prime }$
be a
![]() $G_{K}$
-stable submodule of
$G_{K}$
-stable submodule of
![]() $T$
. We have a
$T$
. We have a
![]() $G_{K}$
-equivariant surjection
$G_{K}$
-equivariant surjection
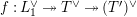 $f:L_{1}^{\vee }{\twoheadrightarrow}T^{\vee }{\twoheadrightarrow}(T^{\prime })^{\vee }$
. Let
$f:L_{1}^{\vee }{\twoheadrightarrow}T^{\vee }{\twoheadrightarrow}(T^{\prime })^{\vee }$
. Let
![]() $L_{2}^{\prime }$
be a free
$L_{2}^{\prime }$
be a free
![]() $\mathbb{Z}_{p}$
-representation of
$\mathbb{Z}_{p}$
-representation of
![]() $G_{K}$
such that its dual is the kernel of
$G_{K}$
such that its dual is the kernel of
![]() $f$
. We have an exact sequence
$f$
. We have an exact sequence
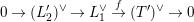 $0\rightarrow (L_{2}^{\prime })^{\vee }\rightarrow L_{1}^{\vee }\overset{f}{\rightarrow }(T^{\prime })^{\vee }\rightarrow 0$
of
$0\rightarrow (L_{2}^{\prime })^{\vee }\rightarrow L_{1}^{\vee }\overset{f}{\rightarrow }(T^{\prime })^{\vee }\rightarrow 0$
of
![]() $\mathbb{Z}_{p}[G_{K}]$
-modules. Repeating the construction of the surjection
$\mathbb{Z}_{p}[G_{K}]$
-modules. Repeating the construction of the surjection
 $L_{1}^{\vee }{\twoheadrightarrow}T^{\vee }$
, we obtain a
$L_{1}^{\vee }{\twoheadrightarrow}T^{\vee }$
, we obtain a
![]() $G_{K}$
-equivariant surjection
$G_{K}$
-equivariant surjection
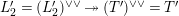 $L_{2}^{\prime }=(L_{2}^{\prime })^{\vee \vee }{\twoheadrightarrow}(T^{\prime })^{\vee \vee }=T^{\prime }$
and thus we have
$L_{2}^{\prime }=(L_{2}^{\prime })^{\vee \vee }{\twoheadrightarrow}(T^{\prime })^{\vee \vee }=T^{\prime }$
and thus we have
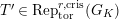 $T^{\prime }\in \text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
.◻
$T^{\prime }\in \text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
.◻
In the case where
![]() $r=1$
, the assertion (1) of the following corollary was shown in [Reference BreuilBr3, Theorem 3.4.3].
$r=1$
, the assertion (1) of the following corollary was shown in [Reference BreuilBr3, Theorem 3.4.3].
Corollary 4.20. Let
![]() $T$
be an object of
$T$
be an object of
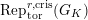 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
which is killed by
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
which is killed by
![]() $p^{n}$
for some
$p^{n}$
for some
![]() $n>0$
. Let
$n>0$
. Let
![]() $T^{\prime }$
be a
$T^{\prime }$
be a
![]() $G_{\infty }$
-stable subquotient of
$G_{\infty }$
-stable subquotient of
![]() $T$
.
$T$
.
![]() $(1)$
If
$(1)$
If
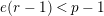 $e(r-1)<p-1$
, then
$e(r-1)<p-1$
, then
![]() $T^{\prime }$
is
$T^{\prime }$
is
![]() $G_{K}$
-stable (with respect to
$G_{K}$
-stable (with respect to
![]() $T$
).
$T$
).
![]() $(2)$
If
$(2)$
If
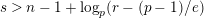 $s>n-1+\text{log}_{p}(r-(p-1)/e)$
, then
$s>n-1+\text{log}_{p}(r-(p-1)/e)$
, then
![]() $T^{\prime }$
is
$T^{\prime }$
is
![]() $G_{s}$
-stable (with respect to
$G_{s}$
-stable (with respect to
![]() $T$
).
$T$
).
Proof. By the duality assertion of Lemma 4.19, it is enough to show the case where
![]() $T^{\prime }$
is a
$T^{\prime }$
is a
![]() $G_{\infty }$
-stable submodule of
$G_{\infty }$
-stable submodule of
![]() $T$
. Take any sequence
$T$
. Take any sequence
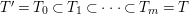 $T^{\prime }=T_{0}\subset T_{1}\subset \cdots \subset T_{m}=T$
of torsion
$T^{\prime }=T_{0}\subset T_{1}\subset \cdots \subset T_{m}=T$
of torsion
![]() $G_{\infty }$
-stable submodules of
$G_{\infty }$
-stable submodules of
![]() $T$
such that
$T$
such that
![]() $T_{i}/T_{i-1}$
is irreducible for any
$T_{i}/T_{i-1}$
is irreducible for any
![]() $i$
. As explained in the proof of Proposition 4.14, the
$i$
. As explained in the proof of Proposition 4.14, the
![]() $G_{\infty }$
-action on
$G_{\infty }$
-action on
![]() $T_{i}/T_{i-1}$
can be (uniquely) extended to
$T_{i}/T_{i-1}$
can be (uniquely) extended to
![]() $G_{K}$
. By Theorem 5.3 given in the next section, we know that
$G_{K}$
. By Theorem 5.3 given in the next section, we know that
![]() $T_{i}/T_{i-1}$
is an object of
$T_{i}/T_{i-1}$
is an object of
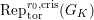 $\text{Rep}_{\text{tor}}^{r_{0},\text{cris}}(G_{K})$
where
$\text{Rep}_{\text{tor}}^{r_{0},\text{cris}}(G_{K})$
where
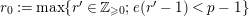 $r_{0}:=\text{max}\{r^{\prime }\in \mathbb{Z}_{{\geqslant}0};e(r^{\prime }-1)<p-1\}$
.
$r_{0}:=\text{max}\{r^{\prime }\in \mathbb{Z}_{{\geqslant}0};e(r^{\prime }-1)<p-1\}$
.
(1) We may suppose
![]() $r=r_{0}$
. The
$r=r_{0}$
. The
![]() $G_{\infty }$
-equivariant projection
$G_{\infty }$
-equivariant projection
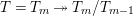 $T=T_{m}{\twoheadrightarrow}T_{m}/T_{m-1}$
is
$T=T_{m}{\twoheadrightarrow}T_{m}/T_{m-1}$
is
![]() $G_{K}$
-equivariant by the full faithfulness theorem (= Theorem 1.2). Thus we know that
$G_{K}$
-equivariant by the full faithfulness theorem (= Theorem 1.2). Thus we know that
![]() $T_{m-1}$
is
$T_{m-1}$
is
![]() $G_{K}$
-stable in
$G_{K}$
-stable in
![]() $T$
, and also know that
$T$
, and also know that
![]() $T_{m-1}$
is contained in
$T_{m-1}$
is contained in
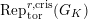 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
by Lemma 4.19. By the same argument for the
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
by Lemma 4.19. By the same argument for the
![]() $G_{\infty }$
-equivariant projection
$G_{\infty }$
-equivariant projection
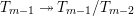 $T_{m-1}{\twoheadrightarrow}T_{m-1}/T_{m-2}$
, we know that
$T_{m-1}{\twoheadrightarrow}T_{m-1}/T_{m-2}$
, we know that
![]() $T_{m-2}$
is
$T_{m-2}$
is
![]() $G_{K}$
-stable in
$G_{K}$
-stable in
![]() $T$
, and also know that
$T$
, and also know that
![]() $T_{m-2}$
is contained in
$T_{m-2}$
is contained in
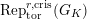 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
. Repeating this argument, we have that
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
. Repeating this argument, we have that
![]() $T^{\prime }=T_{0}$
is
$T^{\prime }=T_{0}$
is
![]() $G_{K}$
-stable in
$G_{K}$
-stable in
![]() $T$
.
$T$
.
(2) Put
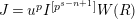 $J=u^{p}I^{[p^{s-n+1}]}W(R)$
. By (1) we may assume
$J=u^{p}I^{[p^{s-n+1}]}W(R)$
. By (1) we may assume
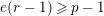 $e(r-1)\geqslant p-1$
. Under this assumption we have
$e(r-1)\geqslant p-1$
. Under this assumption we have
![]() $r\geqslant r_{0}$
and
$r\geqslant r_{0}$
and
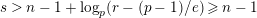 $s>n-1+\text{log}_{p}(r-(p-1)/e)\geqslant n-1$
. In particular,
$s>n-1+\text{log}_{p}(r-(p-1)/e)\geqslant n-1$
. In particular,
![]() $T|_{G_{s}}$
and
$T|_{G_{s}}$
and
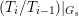 $(T_{i}/T_{i-1})|_{G_{s}}$
, for any
$(T_{i}/T_{i-1})|_{G_{s}}$
, for any
![]() $i$
, are contained in
$i$
, are contained in
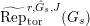 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
by Proposition 4.16. First we consider the case where
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
by Proposition 4.16. First we consider the case where
![]() $k$
is algebraically closed. By Theorem 4.9, the
$k$
is algebraically closed. By Theorem 4.9, the
![]() $G_{\infty }$
-equivariant projection
$G_{\infty }$
-equivariant projection
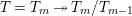 $T=T_{m}{\twoheadrightarrow}T_{m}/T_{m-1}$
is
$T=T_{m}{\twoheadrightarrow}T_{m}/T_{m-1}$
is
![]() $G_{s}$
-stable. Thus we know that
$G_{s}$
-stable. Thus we know that
![]() $T_{m-1}$
is
$T_{m-1}$
is
![]() $G_{s}$
-stable in
$G_{s}$
-stable in
![]() $T$
, and also know that
$T$
, and also know that
![]() $T_{m-1}$
is contained in
$T_{m-1}$
is contained in
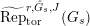 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
by Corollary 4.5. By the same argument for the
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
by Corollary 4.5. By the same argument for the
![]() $G_{\infty }$
-equivariant projection
$G_{\infty }$
-equivariant projection
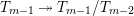 $T_{m-1}{\twoheadrightarrow}T_{m-1}/T_{m-2}$
, we know that
$T_{m-1}{\twoheadrightarrow}T_{m-1}/T_{m-2}$
, we know that
![]() $T_{m-2}$
is
$T_{m-2}$
is
![]() $G_{s}$
-stable in
$G_{s}$
-stable in
![]() $T$
, and also know that
$T$
, and also know that
![]() $T_{m-2}$
is contained in
$T_{m-2}$
is contained in
 $\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
. Repeating this argument, we have that
$\widetilde{\text{Rep}}_{\text{tor}}^{r,{\hat{G}}_{s},J}(G_{s})$
. Repeating this argument, we have that
![]() $T^{\prime }=T_{0}$
is
$T^{\prime }=T_{0}$
is
![]() $G_{s}$
-stable in
$G_{s}$
-stable in
![]() $T$
. Next we consider the case where
$T$
. Next we consider the case where
![]() $k$
is not necessary algebraically closed. Let
$k$
is not necessary algebraically closed. Let
![]() $L$
be the completion of the maximal unramified extension
$L$
be the completion of the maximal unramified extension
![]() $K^{\text{ur}}$
of
$K^{\text{ur}}$
of
![]() $K$
, and we identify
$K$
, and we identify
![]() $G_{L}$
with the inertia subgroup of
$G_{L}$
with the inertia subgroup of
![]() $G_{K}$
. Clearly
$G_{K}$
. Clearly
![]() $T|_{G_{L}}$
is contained in
$T|_{G_{L}}$
is contained in
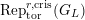 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{L})$
and
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{L})$
and
![]() $T^{\prime }$
is
$T^{\prime }$
is
![]() $G_{L_{\infty }}$
-stable submodule of
$G_{L_{\infty }}$
-stable submodule of
![]() $T$
. We have already shown that
$T$
. We have already shown that
![]() $T^{\prime }$
is
$T^{\prime }$
is
![]() $G_{L,s}$
-stable in
$G_{L,s}$
-stable in
![]() $T$
. Since
$T$
. Since
![]() $G_{s}$
is topologically generated by
$G_{s}$
is topologically generated by
![]() $G_{L,s}$
and
$G_{L,s}$
and
![]() $G_{\infty }$
, we conclude that
$G_{\infty }$
, we conclude that
![]() $T^{\prime }$
is
$T^{\prime }$
is
![]() $G_{s}$
-stable in
$G_{s}$
-stable in
![]() $T$
.◻
$T$
.◻
Now let
![]() $V$
be a
$V$
be a
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
and
$G_{K}$
and
![]() $T$
a
$T$
a
![]() $\mathbb{Z}_{p}$
-lattice of
$\mathbb{Z}_{p}$
-lattice of
![]() $V$
which is stable under
$V$
which is stable under
![]() $G_{\infty }$
. Then we know that
$G_{\infty }$
. Then we know that
![]() $T$
is automatically
$T$
is automatically
![]() $G_{s}$
-stable for some
$G_{s}$
-stable for some
![]() $s\geqslant 0$
. Indeed we can check this as follows. Take any
$s\geqslant 0$
. Indeed we can check this as follows. Take any
![]() $G_{K}$
-stable
$G_{K}$
-stable
![]() $\mathbb{Z}_{p}$
-lattice
$\mathbb{Z}_{p}$
-lattice
![]() $T^{\prime }$
of
$T^{\prime }$
of
![]() $V$
which contains
$V$
which contains
![]() $T$
, and take an integer
$T$
, and take an integer
![]() $n>0$
with the property that
$n>0$
with the property that
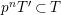 $p^{n}T^{\prime }\subset T$
. Furthermore, we take a finite extension
$p^{n}T^{\prime }\subset T$
. Furthermore, we take a finite extension
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $K$
such that
$K$
such that
![]() $G_{K^{\prime }}$
acts trivially on
$G_{K^{\prime }}$
acts trivially on
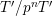 $T^{\prime }/p^{n}T^{\prime }$
. Then
$T^{\prime }/p^{n}T^{\prime }$
. Then
![]() $T/p^{n}T^{\prime }$
is
$T/p^{n}T^{\prime }$
is
![]() $G_{\infty }$
-stable and also
$G_{\infty }$
-stable and also
![]() $G_{K^{\prime }}$
-stable in
$G_{K^{\prime }}$
-stable in
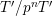 $T^{\prime }/p^{n}T^{\prime }$
. If we take any integer
$T^{\prime }/p^{n}T^{\prime }$
. If we take any integer
![]() $s\geqslant 0$
with the property
$s\geqslant 0$
with the property
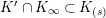 $K^{\prime }\cap K_{\infty }\subset K_{(s)}$
, we know that
$K^{\prime }\cap K_{\infty }\subset K_{(s)}$
, we know that
![]() $T/p^{n}T^{\prime }$
is
$T/p^{n}T^{\prime }$
is
![]() $G_{s}$
-stable. This implies that
$G_{s}$
-stable. This implies that
![]() $T$
is
$T$
is
![]() $G_{s}$
-stable in
$G_{s}$
-stable in
![]() $T^{\prime }$
.
$T^{\prime }$
.
The following corollary, which was shown in [Reference BreuilBr3, Corollary 3.4.4] in the case where
![]() $r=1$
, is related with the above property.
$r=1$
, is related with the above property.
Corollary 4.21. Let
![]() $V$
be a crystalline
$V$
be a crystalline
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
with Hodge–Tate weights in
$G_{K}$
with Hodge–Tate weights in
![]() $[0,r]$
and
$[0,r]$
and
![]() $T$
a
$T$
a
![]() $\mathbb{Z}_{p}$
-submodule of
$\mathbb{Z}_{p}$
-submodule of
![]() $V$
which is stable under
$V$
which is stable under
![]() $G_{\infty }$
. If
$G_{\infty }$
. If
 $e(r-1)<p-1$
, then
$e(r-1)<p-1$
, then
![]() $T$
is stable under
$T$
is stable under
![]() $G_{K}$
.
$G_{K}$
.
Proof. We follow the method of the proof of [Reference BreuilBr3, Corollary 3.4.4]. First we suppose that
![]() $T$
is finitely generated over
$T$
is finitely generated over
![]() $\mathbb{Z}_{p}$
. Take any
$\mathbb{Z}_{p}$
. Take any
![]() $G_{K}$
-stable
$G_{K}$
-stable
![]() $\mathbb{Z}_{p}$
-lattice
$\mathbb{Z}_{p}$
-lattice
![]() $T^{\prime }$
of
$T^{\prime }$
of
![]() $V$
which contains
$V$
which contains
![]() $T$
. Since
$T$
. Since
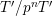 $T^{\prime }/p^{n}T^{\prime }$
is contained in
$T^{\prime }/p^{n}T^{\prime }$
is contained in
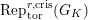 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
for any
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})$
for any
![]() $n>0$
, Corollary 4.20(1) implies that any
$n>0$
, Corollary 4.20(1) implies that any
![]() $G_{\infty }$
-stable submodule of
$G_{\infty }$
-stable submodule of
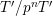 $T^{\prime }/p^{n}T^{\prime }$
is in fact
$T^{\prime }/p^{n}T^{\prime }$
is in fact
![]() $G_{K}$
-stable. Thus
$G_{K}$
-stable. Thus
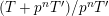 $(T+p^{n}T^{\prime })/p^{n}T^{\prime }$
is
$(T+p^{n}T^{\prime })/p^{n}T^{\prime }$
is
![]() $G_{K}$
-stable in
$G_{K}$
-stable in
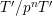 $T^{\prime }/p^{n}T^{\prime }$
. Therefore, we obtain
$T^{\prime }/p^{n}T^{\prime }$
. Therefore, we obtain
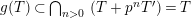 $g(T)\subset \bigcap _{n>0}~(T+p^{n}T^{\prime })=T$
for any
$g(T)\subset \bigcap _{n>0}~(T+p^{n}T^{\prime })=T$
for any
![]() $g\in G_{K}$
. Next we consider general case; so
$g\in G_{K}$
. Next we consider general case; so
![]() $T$
is not necessary finitely generated over
$T$
is not necessary finitely generated over
![]() $\mathbb{Z}_{p}$
. We may suppose
$\mathbb{Z}_{p}$
. We may suppose
![]() $T\not =0$
. Denote by
$T\not =0$
. Denote by
![]() $T_{x}$
the smallest
$T_{x}$
the smallest
![]() $\mathbb{Z}_{p}$
-submodule of
$\mathbb{Z}_{p}$
-submodule of
![]() $T$
which contains
$T$
which contains
![]() $x$
and is stable under
$x$
and is stable under
![]() $G_{\infty }$
. Since
$G_{\infty }$
. Since
![]() $T_{x}$
is contained in some (
$T_{x}$
is contained in some (
![]() $G_{K}$
-stable)
$G_{K}$
-stable)
![]() $\mathbb{Z}_{p}$
-lattice of
$\mathbb{Z}_{p}$
-lattice of
![]() $V$
, we see that
$V$
, we see that
![]() $T_{x}$
is finitely generated over
$T_{x}$
is finitely generated over
![]() $\mathbb{Z}_{p}$
, and hence it is stable under
$\mathbb{Z}_{p}$
, and hence it is stable under
![]() $G_{K}$
. Then the relation
$G_{K}$
. Then the relation
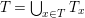 $T=\bigcup _{x\in T}T_{x}$
gives the desired result. ◻
$T=\bigcup _{x\in T}T_{x}$
gives the desired result. ◻
5 Crystalline lifts and c-weights
We continue to use the same notation except for that we may allow
![]() $p=2$
. We remark that a torsion
$p=2$
. We remark that a torsion
![]() $\mathbb{Z}_{p}$
-representation of
$\mathbb{Z}_{p}$
-representation of
![]() $G_{K}$
is torsion crystalline with Hodge–Tate weights in
$G_{K}$
is torsion crystalline with Hodge–Tate weights in
![]() $[0,r]$
if there exists a lattice
$[0,r]$
if there exists a lattice
![]() $L$
in some crystalline
$L$
in some crystalline
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
with Hodge–Tate weights in
$G_{K}$
with Hodge–Tate weights in
![]() $[0,r]$
and a
$[0,r]$
and a
![]() $G_{K}$
-equivariant surjection
$G_{K}$
-equivariant surjection
 $f:L{\twoheadrightarrow}T$
. We call
$f:L{\twoheadrightarrow}T$
. We call
![]() $f$
a crystalline lift (of
$f$
a crystalline lift (of
![]() $T$
) of weight
$T$
) of weight
![]() ${\leqslant}r$
. Our interest in this section is to determine the minimum integer
${\leqslant}r$
. Our interest in this section is to determine the minimum integer
![]() $r$
(if it exists) such that
$r$
(if it exists) such that
![]() $T$
admits crystalline lifts of weight
$T$
admits crystalline lifts of weight
![]() ${\leqslant}r$
. We call this minimum integer the c-weight of
${\leqslant}r$
. We call this minimum integer the c-weight of
![]() $T$
and denote it by
$T$
and denote it by
![]() $w_{c}(T)$
. If
$w_{c}(T)$
. If
![]() $T$
does not have crystalline lifts of weight
$T$
does not have crystalline lifts of weight
![]() ${\leqslant}r$
for any integer
${\leqslant}r$
for any integer
![]() $r$
, then we define the c-weight
$r$
, then we define the c-weight
![]() $w_{c}(T)$
of
$w_{c}(T)$
of
![]() $T$
to be
$T$
to be
![]() $\infty$
. For the existence of crystalline lifts of various torsion representations, for example, it is useful for the readers to refer the Muller’s PhD Thesis [Reference MullerMu]. Motivated by [Reference Caruso and LiuCL2, Question 5.5], we pose the following question.
$\infty$
. For the existence of crystalline lifts of various torsion representations, for example, it is useful for the readers to refer the Muller’s PhD Thesis [Reference MullerMu]. Motivated by [Reference Caruso and LiuCL2, Question 5.5], we pose the following question.
Question 5.1. For a torsion
![]() $\mathbb{Z}_{p}$
-representation
$\mathbb{Z}_{p}$
-representation
![]() $T$
of
$T$
of
![]() $G_{K}$
, is the c-weight
$G_{K}$
, is the c-weight
![]() $w_{c}(T)$
of
$w_{c}(T)$
of
![]() $T$
finite? Furthermore, can we calculate
$T$
finite? Furthermore, can we calculate
![]() $w_{c}(T)$
?
$w_{c}(T)$
?
This question strongly related to the weight part of Serre’s conjecture. It is dated to Serre, when raised Serre’s conjecture over
![]() $\mathbb{Q}$
, he had already considered the question to lift a
$\mathbb{Q}$
, he had already considered the question to lift a
![]() $2$
-dimensional mod
$2$
-dimensional mod
![]() $p$
representation of
$p$
representation of
![]() $G_{\mathbb{Q}_{p}}$
to a
$G_{\mathbb{Q}_{p}}$
to a
![]() $2$
-dimensional crystalline representation with “optimal” weights (which is very close to minimum weights considered here). He obtained some partial results that contained in Proposition 5.6 and Corollary 5.7. We do not go into details here but the recent developments of the weight part of Serre’s conjecture (e.g., [Reference Gee, Liu and SavittGLS]) also contribute (explicitly or implicitly) partial results in this section.
$2$
-dimensional crystalline representation with “optimal” weights (which is very close to minimum weights considered here). He obtained some partial results that contained in Proposition 5.6 and Corollary 5.7. We do not go into details here but the recent developments of the weight part of Serre’s conjecture (e.g., [Reference Gee, Liu and SavittGLS]) also contribute (explicitly or implicitly) partial results in this section.
5.1 General properties of c-weights
We study general properties of c-weights. At first, by ramification estimates, it is known that c-weights may have infinitely large values [Reference Caruso and LiuCL2, Theorem 5.4]; for any
![]() $c>0$
, there exists a torsion
$c>0$
, there exists a torsion
![]() $\mathbb{Z}_{p}$
-extension
$\mathbb{Z}_{p}$
-extension
![]() $T$
of
$T$
of
![]() $G_{K}$
with
$G_{K}$
with
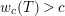 $w_{c}(T)>c$
. In this paper, we mainly consider representations with “small” c-weights. If c-weights are “small”, they are closely related with tame inertia weights. Now we recall the definition of tame inertia weights. Let
$w_{c}(T)>c$
. In this paper, we mainly consider representations with “small” c-weights. If c-weights are “small”, they are closely related with tame inertia weights. Now we recall the definition of tame inertia weights. Let
![]() $I_{K}$
be the inertia subgroup of
$I_{K}$
be the inertia subgroup of
![]() $G_{K}$
. Let
$G_{K}$
. Let
![]() $T$
be a
$T$
be a
![]() $d$
-dimensional irreducible
$d$
-dimensional irreducible
![]() $\mathbb{F}_{p}$
-representation of
$\mathbb{F}_{p}$
-representation of
![]() $I_{K}$
. Then
$I_{K}$
. Then
![]() $T$
is isomorphic to
$T$
is isomorphic to
 $$\begin{eqnarray}\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{n_{1}}\cdots \unicode[STIX]{x1D703}_{d,d}^{n_{d}})\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{n_{1}}\cdots \unicode[STIX]{x1D703}_{d,d}^{n_{d}})\end{eqnarray}$$
for one sequence of integers between
![]() $0$
and
$0$
and
![]() $p-1$
, periodic of period
$p-1$
, periodic of period
![]() $d$
. Here,
$d$
. Here,
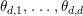 $\unicode[STIX]{x1D703}_{d,1},\ldots ,\unicode[STIX]{x1D703}_{d,d}$
are the fundamental characters of level
$\unicode[STIX]{x1D703}_{d,1},\ldots ,\unicode[STIX]{x1D703}_{d,d}$
are the fundamental characters of level
![]() $d$
. The integers
$d$
. The integers
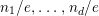 $n_{1}/e,\ldots ,n_{d}/e$
are called the tame inertia weights of
$n_{1}/e,\ldots ,n_{d}/e$
are called the tame inertia weights of
![]() $T$
. For any
$T$
. For any
![]() $\mathbb{F}_{p}$
-representation
$\mathbb{F}_{p}$
-representation
![]() $T$
of
$T$
of
![]() $G_{K}$
, the tame inertia weights of
$G_{K}$
, the tame inertia weights of
![]() $T$
are the tame inertia weights of the Jordan–Hölder quotients of
$T$
are the tame inertia weights of the Jordan–Hölder quotients of
![]() $T|_{I_{K}}$
.
$T|_{I_{K}}$
.
Let
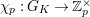 $\unicode[STIX]{x1D712}_{p}:G_{K}\rightarrow \mathbb{Z}_{p}^{\times }$
be the
$\unicode[STIX]{x1D712}_{p}:G_{K}\rightarrow \mathbb{Z}_{p}^{\times }$
be the
![]() $p$
-adic cyclotomic character and
$p$
-adic cyclotomic character and
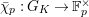 $\bar{\unicode[STIX]{x1D712}}_{p}:G_{K}\rightarrow \mathbb{F}_{p}^{\times }$
the mod
$\bar{\unicode[STIX]{x1D712}}_{p}:G_{K}\rightarrow \mathbb{F}_{p}^{\times }$
the mod
![]() $p$
cyclotomic character. It is well known that
$p$
cyclotomic character. It is well known that
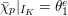 $\bar{\unicode[STIX]{x1D712}}_{p}|_{I_{K}}=\unicode[STIX]{x1D703}_{1}^{e}$
where
$\bar{\unicode[STIX]{x1D712}}_{p}|_{I_{K}}=\unicode[STIX]{x1D703}_{1}^{e}$
where
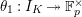 $\unicode[STIX]{x1D703}_{1}:I_{K}{\twoheadrightarrow}\mathbb{F}_{p}^{\times }$
is the fundamental character of level
$\unicode[STIX]{x1D703}_{1}:I_{K}{\twoheadrightarrow}\mathbb{F}_{p}^{\times }$
is the fundamental character of level
![]() $1$
. In particular, denoting by
$1$
. In particular, denoting by
![]() $K^{\text{ur}}$
the maximal unramified extension of
$K^{\text{ur}}$
the maximal unramified extension of
![]() $K$
, we have
$K$
, we have
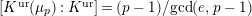 $[K^{\text{ur}}(\unicode[STIX]{x1D707}_{p}):K^{\text{ur}}]=(p-1)/\text{gcd}(e,p-1)$
.
$[K^{\text{ur}}(\unicode[STIX]{x1D707}_{p}):K^{\text{ur}}]=(p-1)/\text{gcd}(e,p-1)$
.
Proposition 5.2.
![]() $(1)$
Minimum c-weights are invariant under finite unramified extensions of the base field
$(1)$
Minimum c-weights are invariant under finite unramified extensions of the base field
![]() $K$
.
$K$
.
![]() $(2)$
The c-weight of an unramified torsion
$(2)$
The c-weight of an unramified torsion
![]() $\mathbb{Z}_{p}$
-representation of
$\mathbb{Z}_{p}$
-representation of
![]() $G_{K}$
is
$G_{K}$
is
![]() $0$
.
$0$
.
![]() $(3)$
Put
$(3)$
Put
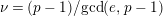 $\unicode[STIX]{x1D708}=(p-1)/\text{gcd}(e,p-1)$
. Let
$\unicode[STIX]{x1D708}=(p-1)/\text{gcd}(e,p-1)$
. Let
![]() $s$
be an integer such that
$s$
be an integer such that
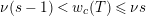 $\unicode[STIX]{x1D708}(s-1)<w_{c}(T)\leqslant \unicode[STIX]{x1D708}s$
. Then we have
$\unicode[STIX]{x1D708}(s-1)<w_{c}(T)\leqslant \unicode[STIX]{x1D708}s$
. Then we have
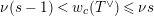 $\unicode[STIX]{x1D708}(s-1)<w_{c}(T^{\vee })\leqslant \unicode[STIX]{x1D708}s$
. In particular, if
$\unicode[STIX]{x1D708}(s-1)<w_{c}(T^{\vee })\leqslant \unicode[STIX]{x1D708}s$
. In particular, if
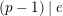 $(p-1)\mid e$
, then we have
$(p-1)\mid e$
, then we have
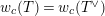 $w_{c}(T)=w_{c}(T^{\vee })$
.
$w_{c}(T)=w_{c}(T^{\vee })$
.
![]() $(4)$
Let
$(4)$
Let
![]() $T$
be an
$T$
be an
![]() $\mathbb{F}_{p}$
-representation of
$\mathbb{F}_{p}$
-representation of
![]() $G_{K}$
and
$G_{K}$
and
![]() $i$
the largest tame inertia weight of
$i$
the largest tame inertia weight of
![]() $T$
. Then we have
$T$
. Then we have
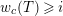 $w_{c}(T)\geqslant i$
.
$w_{c}(T)\geqslant i$
.
Proof. (1) Let
![]() $T$
be a torsion
$T$
be a torsion
![]() $\mathbb{Z}_{p}$
-representation of
$\mathbb{Z}_{p}$
-representation of
![]() $G_{K}$
. Let
$G_{K}$
. Let
![]() $K^{\prime }$
be a finite unramified extension of
$K^{\prime }$
be a finite unramified extension of
![]() $K$
. It suffices to prove that
$K$
. It suffices to prove that
![]() $T$
has crystalline lifts of weight
$T$
has crystalline lifts of weight
![]() ${\leqslant}r$
if and only if
${\leqslant}r$
if and only if
![]() $T|_{G_{K^{\prime }}}$
has crystalline lifts of weight
$T|_{G_{K^{\prime }}}$
has crystalline lifts of weight
![]() ${\leqslant}r$
. The “only if” assertion is clear and thus it is enough to prove the “if” assertion. Let
${\leqslant}r$
. The “only if” assertion is clear and thus it is enough to prove the “if” assertion. Let
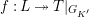 $f:L{\twoheadrightarrow}T|_{G_{K^{\prime }}}$
be a crystalline lift of
$f:L{\twoheadrightarrow}T|_{G_{K^{\prime }}}$
be a crystalline lift of
![]() $T|_{G_{K^{\prime }}}$
of weight
$T|_{G_{K^{\prime }}}$
of weight
![]() ${\leqslant}r$
. Since
${\leqslant}r$
. Since
![]() $K^{\prime }/K$
is unramified,
$K^{\prime }/K$
is unramified,
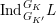 $\text{Ind}_{G_{K^{\prime }}}^{G_{K}}L$
is a lattice in some crystalline
$\text{Ind}_{G_{K^{\prime }}}^{G_{K}}L$
is a lattice in some crystalline
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K}$
with Hodge–Tate weights in
$G_{K}$
with Hodge–Tate weights in
![]() $[0,r]$
. Furthermore, the map
$[0,r]$
. Furthermore, the map
 $$\begin{eqnarray}\text{Ind}_{G_{K^{\prime }}}^{G_{K}}L=\mathbb{Z}_{p}[G_{K}]\otimes _{\mathbb{Z}_{p}[G_{K^{\prime }}]}L\rightarrow T,\quad \unicode[STIX]{x1D70E}\otimes x\mapsto \unicode[STIX]{x1D70E}(f(x))\end{eqnarray}$$
$$\begin{eqnarray}\text{Ind}_{G_{K^{\prime }}}^{G_{K}}L=\mathbb{Z}_{p}[G_{K}]\otimes _{\mathbb{Z}_{p}[G_{K^{\prime }}]}L\rightarrow T,\quad \unicode[STIX]{x1D70E}\otimes x\mapsto \unicode[STIX]{x1D70E}(f(x))\end{eqnarray}$$
is a
![]() $G_{K}$
-equivariant surjection and hence we have done.
$G_{K}$
-equivariant surjection and hence we have done.
(2) The result follows from (1) immediately.
(3) Taking a finite unramified extension
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $K$
with the property
$K$
with the property
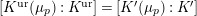 $[K^{\text{ur}}(\unicode[STIX]{x1D707}_{p}):K^{\text{ur}}]=[K^{\prime }(\unicode[STIX]{x1D707}_{p}):K^{\prime }]$
, it follows from Lemma 4.19 that we have
$[K^{\text{ur}}(\unicode[STIX]{x1D707}_{p}):K^{\text{ur}}]=[K^{\prime }(\unicode[STIX]{x1D707}_{p}):K^{\prime }]$
, it follows from Lemma 4.19 that we have
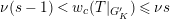 $\unicode[STIX]{x1D708}(s-1)<w_{c}(T|_{G_{K}^{\prime }})\leqslant \unicode[STIX]{x1D708}s$
if and only if we have
$\unicode[STIX]{x1D708}(s-1)<w_{c}(T|_{G_{K}^{\prime }})\leqslant \unicode[STIX]{x1D708}s$
if and only if we have
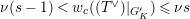 $\unicode[STIX]{x1D708}(s-1)<w_{c}((T^{\vee })|_{G_{K}^{\prime }})\leqslant \unicode[STIX]{x1D708}s$
. Thus the result follows from the assertion (1).
$\unicode[STIX]{x1D708}(s-1)<w_{c}((T^{\vee })|_{G_{K}^{\prime }})\leqslant \unicode[STIX]{x1D708}s$
. Thus the result follows from the assertion (1).
(4) If
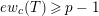 $ew_{c}(T)\geqslant p-1$
, then there is nothing to prove, and thus we may suppose that
$ew_{c}(T)\geqslant p-1$
, then there is nothing to prove, and thus we may suppose that
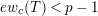 $ew_{c}(T)<p-1$
. Let
$ew_{c}(T)<p-1$
. Let
![]() $L{\twoheadrightarrow}T$
be a crystalline lift of
$L{\twoheadrightarrow}T$
be a crystalline lift of
![]() $T$
of weight
$T$
of weight
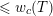 ${\leqslant}w_{c}(T)$
. Since the tame inertia polygon of
${\leqslant}w_{c}(T)$
. Since the tame inertia polygon of
![]() $L$
lies on the Hodge polygon of
$L$
lies on the Hodge polygon of
![]() $L$
[Reference Caruso and SavittCS, Théorème 1], the largest slope of the former polygon is less than or equal to that of the latter polygon. This implies
$L$
[Reference Caruso and SavittCS, Théorème 1], the largest slope of the former polygon is less than or equal to that of the latter polygon. This implies
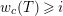 $w_{c}(T)\geqslant i$
.◻
$w_{c}(T)\geqslant i$
.◻
Theorem 5.3. Let
![]() $T$
be a tamely ramified
$T$
be a tamely ramified
![]() $\mathbb{F}_{p}$
-representation of
$\mathbb{F}_{p}$
-representation of
![]() $G_{K}$
. Let
$G_{K}$
. Let
![]() $i$
be the largest tame inertia weight of
$i$
be the largest tame inertia weight of
![]() $T$
. Then we have
$T$
. Then we have
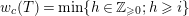 $w_{c}(T)=\text{min}\{h\in \mathbb{Z}_{{\geqslant}0};h\geqslant i\}$
.
$w_{c}(T)=\text{min}\{h\in \mathbb{Z}_{{\geqslant}0};h\geqslant i\}$
.
Proof. The proof below is essentially due to Caruso and Liu [Reference Caruso and LiuCL2, Theorem 5.7], but we give a proof here for the sake of completeness. Put
 $i_{0}=\text{min}\{h\in \mathbb{Z}_{{\geqslant}0};h\geqslant i\}$
. By Proposition 5.2(4), we have
$i_{0}=\text{min}\{h\in \mathbb{Z}_{{\geqslant}0};h\geqslant i\}$
. By Proposition 5.2(4), we have
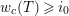 $w_{c}(T)\geqslant i_{0}$
. Thus it suffices to show
$w_{c}(T)\geqslant i_{0}$
. Thus it suffices to show
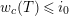 $w_{c}(T)\leqslant i_{0}$
. We note that
$w_{c}(T)\leqslant i_{0}$
. We note that
![]() $T|_{I_{K}}$
is semisimple. Any irreducible component
$T|_{I_{K}}$
is semisimple. Any irreducible component
![]() $T_{0}$
of
$T_{0}$
of
![]() $T|_{I_{K}}$
is of the form
$T|_{I_{K}}$
is of the form
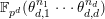 $\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{n_{1}}\cdots \unicode[STIX]{x1D703}_{d,d}^{n_{d}})$
for one sequence of integers between
$\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{n_{1}}\cdots \unicode[STIX]{x1D703}_{d,d}^{n_{d}})$
for one sequence of integers between
![]() $0$
and
$0$
and
![]() $p-1$
, periodic of period
$p-1$
, periodic of period
![]() $d$
. We decompose
$d$
. We decompose
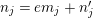 $n_{j}=em_{j}+n_{j}^{\prime }$
by integers
$n_{j}=em_{j}+n_{j}^{\prime }$
by integers
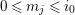 $0\leqslant m_{j}\leqslant i_{0}$
and
$0\leqslant m_{j}\leqslant i_{0}$
and
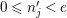 $0\leqslant n_{j}^{\prime }<e$
. Now we define an integer
$0\leqslant n_{j}^{\prime }<e$
. Now we define an integer
![]() $k_{j,\ell }$
by
$k_{j,\ell }$
by
 $$\begin{eqnarray}k_{j,\ell }:=\left\{\begin{array}{@{}ll@{}}e\quad & \text{if}~1\leqslant \ell \leqslant m_{j},\\ n_{j}^{\prime }\quad & \text{if}~\ell =m_{j}+1,\\ 0\quad & \text{if}~\ell >m_{j}+1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}k_{j,\ell }:=\left\{\begin{array}{@{}ll@{}}e\quad & \text{if}~1\leqslant \ell \leqslant m_{j},\\ n_{j}^{\prime }\quad & \text{if}~\ell =m_{j}+1,\\ 0\quad & \text{if}~\ell >m_{j}+1.\end{array}\right.\end{eqnarray}$$
Note that we have
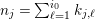 $n_{j}=\sum _{\ell =1}^{i_{0}}k_{j,\ell }$
, and also have an
$n_{j}=\sum _{\ell =1}^{i_{0}}k_{j,\ell }$
, and also have an
![]() $I_{K}$
-equivariant surjection
$I_{K}$
-equivariant surjection
 $$\begin{eqnarray}T_{0}\simeq \bigotimes _{\ell =1,\ldots ,i_{0},\mathbb{F}_{p^{d}}}\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{k_{1,\ell }}\cdots \unicode[STIX]{x1D703}_{d,d}^{k_{d,\ell }}){\twoheadleftarrow}\bigotimes _{\ell =1,\ldots ,i_{0},\mathbb{F}_{p}}\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{k_{1,\ell }}\cdots \unicode[STIX]{x1D703}_{d,d}^{k_{d,\ell }}).\end{eqnarray}$$
$$\begin{eqnarray}T_{0}\simeq \bigotimes _{\ell =1,\ldots ,i_{0},\mathbb{F}_{p^{d}}}\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{k_{1,\ell }}\cdots \unicode[STIX]{x1D703}_{d,d}^{k_{d,\ell }}){\twoheadleftarrow}\bigotimes _{\ell =1,\ldots ,i_{0},\mathbb{F}_{p}}\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{k_{1,\ell }}\cdots \unicode[STIX]{x1D703}_{d,d}^{k_{d,\ell }}).\end{eqnarray}$$
By a classical result of Raynaud, each
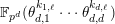 $\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{k_{1,\ell }}\cdots \unicode[STIX]{x1D703}_{d,d}^{k_{d,\ell }})$
comes from a finite flat group scheme defined over
$\mathbb{F}_{p^{d}}(\unicode[STIX]{x1D703}_{d,1}^{k_{1,\ell }}\cdots \unicode[STIX]{x1D703}_{d,d}^{k_{d,\ell }})$
comes from a finite flat group scheme defined over
![]() $K^{\text{ur}}$
. We should remark that such a finite flat group scheme is in fact defined over a finite unramified extension of
$K^{\text{ur}}$
. We should remark that such a finite flat group scheme is in fact defined over a finite unramified extension of
![]() $K$
. Since any finite flat group scheme can be embedded in a
$K$
. Since any finite flat group scheme can be embedded in a
![]() $p$
-divisible group, the above observation implies the following: there exist a finite unramified extension
$p$
-divisible group, the above observation implies the following: there exist a finite unramified extension
![]() $K^{\prime }$
over
$K^{\prime }$
over
![]() $K$
, a lattice
$K$
, a lattice
![]() $L$
in some crystalline
$L$
in some crystalline
![]() $\mathbb{Q}_{p}$
-representation of
$\mathbb{Q}_{p}$
-representation of
![]() $G_{K^{\prime }}$
with Hodge–Tate weights in
$G_{K^{\prime }}$
with Hodge–Tate weights in
![]() $[0,i_{0}]$
and an
$[0,i_{0}]$
and an
![]() $I_{K}$
-equivariant surjection
$I_{K}$
-equivariant surjection
 $f:L{\twoheadrightarrow}T$
. The map
$f:L{\twoheadrightarrow}T$
. The map
![]() $f$
induces an
$f$
induces an
![]() $I_{K}$
-equivariant surjection
$I_{K}$
-equivariant surjection
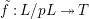 $\tilde{f}:L/pL{\twoheadrightarrow}T$
. Since
$\tilde{f}:L/pL{\twoheadrightarrow}T$
. Since
![]() $L/pL$
and
$L/pL$
and
![]() $T$
is finite, we see that
$T$
is finite, we see that
![]() $\tilde{f}$
is in fact
$\tilde{f}$
is in fact
![]() $G_{K^{\prime \prime }}$
-equivariant for some finite unramified extension
$G_{K^{\prime \prime }}$
-equivariant for some finite unramified extension
![]() $K^{\prime \prime }$
over
$K^{\prime \prime }$
over
![]() $K^{\prime }$
, and then so is
$K^{\prime }$
, and then so is
![]() $f$
. Therefore, we obtain
$f$
. Therefore, we obtain
 $w_{c}(T|_{G_{K^{\prime \prime }}})\leqslant i_{0}$
. By Proposition 5.2(1), we obtain
$w_{c}(T|_{G_{K^{\prime \prime }}})\leqslant i_{0}$
. By Proposition 5.2(1), we obtain
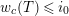 $w_{c}(T)\leqslant i_{0}$
.◻
$w_{c}(T)\leqslant i_{0}$
.◻
5.2 Rank
 $2$
cases
$2$
cases
We give some computations of c-weights related with torsion representations of rank
![]() $2$
. We prove the following lemma by an almost identical method with [Reference Gee, Liu and SavittGLS, Lemma 9.4].
$2$
. We prove the following lemma by an almost identical method with [Reference Gee, Liu and SavittGLS, Lemma 9.4].
Lemma 5.4. Let
![]() $K$
be a finite extension of
$K$
be a finite extension of
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
![]() $E$
be a finite extension of
$E$
be a finite extension of
![]() $\mathbb{Q}_{p}$
with residue field
$\mathbb{Q}_{p}$
with residue field
![]() $\mathbb{F}$
. Let
$\mathbb{F}$
. Let
![]() $i$
and
$i$
and
![]() $\unicode[STIX]{x1D708}$
be integers such that
$\unicode[STIX]{x1D708}$
be integers such that
![]() $\unicode[STIX]{x1D708}$
is divisible by
$\unicode[STIX]{x1D708}$
is divisible by
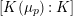 $[K(\unicode[STIX]{x1D707}_{p}):K]$
. Suppose that
$[K(\unicode[STIX]{x1D707}_{p}):K]$
. Suppose that
![]() $T$
is an
$T$
is an
![]() $\mathbb{F}$
-representation of
$\mathbb{F}$
-representation of
![]() $G_{K}$
which sits in an exact sequence
$G_{K}$
which sits in an exact sequence
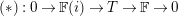 $(\ast ):0\rightarrow \mathbb{F}(i)\rightarrow T\rightarrow \mathbb{F}\rightarrow 0$
of
$(\ast ):0\rightarrow \mathbb{F}(i)\rightarrow T\rightarrow \mathbb{F}\rightarrow 0$
of
![]() $\mathbb{F}$
-representations of
$\mathbb{F}$
-representations of
![]() $G_{K}$
. Then there exist a ramified degree at most
$G_{K}$
. Then there exist a ramified degree at most
![]() $2$
extension
$2$
extension
![]() $E^{\prime }$
over
$E^{\prime }$
over
![]() $E$
, with integer ring
$E$
, with integer ring
![]() ${\mathcal{O}}_{E^{\prime }}$
, and an unramified continuous character
${\mathcal{O}}_{E^{\prime }}$
, and an unramified continuous character
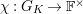 $\unicode[STIX]{x1D712}:G_{K}\rightarrow \mathbb{F}^{\times }$
with trivial reduction such that
$\unicode[STIX]{x1D712}:G_{K}\rightarrow \mathbb{F}^{\times }$
with trivial reduction such that
![]() $(\ast )$
is the reduction of some exact sequence
$(\ast )$
is the reduction of some exact sequence
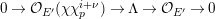 $0\rightarrow {\mathcal{O}}_{E^{\prime }}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}})\rightarrow \unicode[STIX]{x1D6EC}\rightarrow {\mathcal{O}}_{E^{\prime }}\rightarrow 0$
of free
$0\rightarrow {\mathcal{O}}_{E^{\prime }}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}})\rightarrow \unicode[STIX]{x1D6EC}\rightarrow {\mathcal{O}}_{E^{\prime }}\rightarrow 0$
of free
![]() ${\mathcal{O}}_{E^{\prime }}$
-representations of
${\mathcal{O}}_{E^{\prime }}$
-representations of
![]() $G_{K}$
. Furthermore, we have the followings:
$G_{K}$
. Furthermore, we have the followings:
![]() $(1)$
If
$(1)$
If
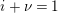 $i+\unicode[STIX]{x1D708}=1$
or
$i+\unicode[STIX]{x1D708}=1$
or
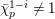 $\bar{\unicode[STIX]{x1D712}}_{p}^{1-i}\not =1$
, then we can take
$\bar{\unicode[STIX]{x1D712}}_{p}^{1-i}\not =1$
, then we can take
![]() $E^{\prime }=E$
and
$E^{\prime }=E$
and
![]() $\unicode[STIX]{x1D712}=1$
.
$\unicode[STIX]{x1D712}=1$
.
![]() $(2)$
If
$(2)$
If
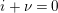 $i+\unicode[STIX]{x1D708}=0$
and
$i+\unicode[STIX]{x1D708}=0$
and
![]() $T$
is unramified, then we can take
$T$
is unramified, then we can take
![]() $E^{\prime }=E$
,
$E^{\prime }=E$
,
![]() $\unicode[STIX]{x1D712}=1$
and
$\unicode[STIX]{x1D712}=1$
and
![]() $\unicode[STIX]{x1D6EC}$
to be unramified.
$\unicode[STIX]{x1D6EC}$
to be unramified.
Proof. Suppose
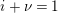 $i+\unicode[STIX]{x1D708}=1$
(resp.
$i+\unicode[STIX]{x1D708}=1$
(resp.
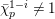 $\bar{\unicode[STIX]{x1D712}}_{p}^{1-i}\not =1$
). Then the map
$\bar{\unicode[STIX]{x1D712}}_{p}^{1-i}\not =1$
). Then the map
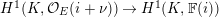 $H^{1}(K,{\mathcal{O}}_{E}(i+\unicode[STIX]{x1D708}))\rightarrow H^{1}(K,\mathbb{F}(i))$
arising from the exact sequence
$H^{1}(K,{\mathcal{O}}_{E}(i+\unicode[STIX]{x1D708}))\rightarrow H^{1}(K,\mathbb{F}(i))$
arising from the exact sequence
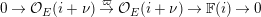 $0\rightarrow {\mathcal{O}}_{E}(i+\unicode[STIX]{x1D708})\overset{\unicode[STIX]{x1D71B}}{\rightarrow }{\mathcal{O}}_{E}(i+\unicode[STIX]{x1D708})\rightarrow \mathbb{F}(i)\rightarrow 0$
is surjective since
$0\rightarrow {\mathcal{O}}_{E}(i+\unicode[STIX]{x1D708})\overset{\unicode[STIX]{x1D71B}}{\rightarrow }{\mathcal{O}}_{E}(i+\unicode[STIX]{x1D708})\rightarrow \mathbb{F}(i)\rightarrow 0$
is surjective since
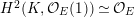 $H^{2}(K,{\mathcal{O}}_{E}(1))\simeq {\mathcal{O}}_{E}$
(resp.
$H^{2}(K,{\mathcal{O}}_{E}(1))\simeq {\mathcal{O}}_{E}$
(resp.
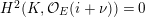 $H^{2}(K,{\mathcal{O}}_{E}(i+\unicode[STIX]{x1D708}))=0$
), where
$H^{2}(K,{\mathcal{O}}_{E}(i+\unicode[STIX]{x1D708}))=0$
), where
![]() $\unicode[STIX]{x1D71B}$
is a uniformizer of
$\unicode[STIX]{x1D71B}$
is a uniformizer of
![]() $E$
. Hence we obtained a proof of (1). The assertion (2) follows immediately from the fact that the natural map
$E$
. Hence we obtained a proof of (1). The assertion (2) follows immediately from the fact that the natural map
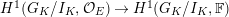 $H^{1}(G_{K}/I_{K},{\mathcal{O}}_{E})\rightarrow H^{1}(G_{K}/I_{K},\mathbb{F})$
is surjective.
$H^{1}(G_{K}/I_{K},{\mathcal{O}}_{E})\rightarrow H^{1}(G_{K}/I_{K},\mathbb{F})$
is surjective.
In the rest of this proof, we always assume that
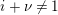 $i+\unicode[STIX]{x1D708}\not =1$
and
$i+\unicode[STIX]{x1D708}\not =1$
and
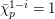 $\bar{\unicode[STIX]{x1D712}}_{p}^{1-i}=1$
. Let
$\bar{\unicode[STIX]{x1D712}}_{p}^{1-i}=1$
. Let
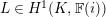 $L\in H^{1}(K,\mathbb{F}(i))$
be a
$L\in H^{1}(K,\mathbb{F}(i))$
be a
![]() $1$
-cocycle corresponding to
$1$
-cocycle corresponding to
![]() $(\ast )$
. We may suppose
$(\ast )$
. We may suppose
![]() $L\not =0$
. For any unramified continuous character
$L\not =0$
. For any unramified continuous character
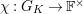 $\unicode[STIX]{x1D712}:G_{K}\rightarrow \mathbb{F}^{\times }$
with trivial reduction, we denote by
$\unicode[STIX]{x1D712}:G_{K}\rightarrow \mathbb{F}^{\times }$
with trivial reduction, we denote by
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}^{1}:H^{1}(K,\mathbb{F}(i))\rightarrow H^{2}(K,{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}})) & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\text{resp.}~\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}^{0}:H^{0}(K,E/{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}))\rightarrow H^{1}(K,\mathbb{F})) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}^{1}:H^{1}(K,\mathbb{F}(i))\rightarrow H^{2}(K,{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}})) & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\text{resp.}~\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}^{0}:H^{0}(K,E/{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}))\rightarrow H^{1}(K,\mathbb{F})) & \displaystyle \nonumber\end{eqnarray}$$
the connection map arising from the exact sequence
 $$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow {\mathcal{O}}_{E}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}})\overset{\unicode[STIX]{x1D71B}}{\rightarrow }{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}})\rightarrow \mathbb{F}(i)\rightarrow 0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\text{resp.}~0\rightarrow \mathbb{F}\rightarrow E/{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}})\overset{\unicode[STIX]{x1D71B}}{\rightarrow }E/{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}})\rightarrow 0) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow {\mathcal{O}}_{E}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}})\overset{\unicode[STIX]{x1D71B}}{\rightarrow }{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}})\rightarrow \mathbb{F}(i)\rightarrow 0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\text{resp.}~0\rightarrow \mathbb{F}\rightarrow E/{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}})\overset{\unicode[STIX]{x1D71B}}{\rightarrow }E/{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}})\rightarrow 0) & \displaystyle \nonumber\end{eqnarray}$$
of
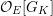 ${\mathcal{O}}_{E}[G_{K}]$
-modules. Consider the following commutative diagram:
${\mathcal{O}}_{E}[G_{K}]$
-modules. Consider the following commutative diagram:

Since we know that the above two pairings are perfect, we see that
![]() $L$
lifts to
$L$
lifts to
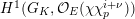 $H^{1}(G_{K},{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}}))$
if and only if
$H^{1}(G_{K},{\mathcal{O}}_{E}(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{i+\unicode[STIX]{x1D708}}))$
if and only if
![]() $H$
is contained in the image of
$H$
is contained in the image of
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}^{0}$
. Here,
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}^{0}$
. Here,
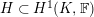 $H\subset H^{1}(K,\mathbb{F})$
is the annihilator of
$H\subset H^{1}(K,\mathbb{F})$
is the annihilator of
![]() $L$
under the local Tate pairing
$L$
under the local Tate pairing
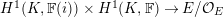 $H^{1}(K,\mathbb{F}(i))\times H^{1}(K,\mathbb{F})\rightarrow E/{\mathcal{O}}_{E}$
. Let
$H^{1}(K,\mathbb{F}(i))\times H^{1}(K,\mathbb{F})\rightarrow E/{\mathcal{O}}_{E}$
. Let
![]() $n\geqslant 1$
be the largest integer with the property that
$n\geqslant 1$
be the largest integer with the property that
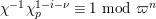 $\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}\equiv 1~\text{mod}~\unicode[STIX]{x1D71B}^{n}$
(such
$\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}\equiv 1~\text{mod}~\unicode[STIX]{x1D71B}^{n}$
(such
![]() $n$
exists since
$n$
exists since
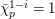 $\bar{\unicode[STIX]{x1D712}}_{p}^{1-i}=1$
and
$\bar{\unicode[STIX]{x1D712}}_{p}^{1-i}=1$
and
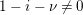 $1-i-\unicode[STIX]{x1D708}\not =0$
). We define
$1-i-\unicode[STIX]{x1D708}\not =0$
). We define
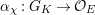 $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}:G_{K}\rightarrow {\mathcal{O}}_{E}$
by the relation
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}:G_{K}\rightarrow {\mathcal{O}}_{E}$
by the relation
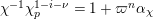 $\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}=1+\unicode[STIX]{x1D71B}^{n}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}$
, and denote
$\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}=1+\unicode[STIX]{x1D71B}^{n}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}$
, and denote
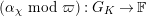 $(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}~\text{mod}~\unicode[STIX]{x1D71B}):G_{K}\rightarrow \mathbb{F}$
by
$(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}~\text{mod}~\unicode[STIX]{x1D71B}):G_{K}\rightarrow \mathbb{F}$
by
![]() $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
. By definition,
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
. By definition,
![]() $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
is a nonzero element of
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
is a nonzero element of
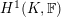 $H^{1}(K,\mathbb{F})$
, and it is not difficult to check that the image of
$H^{1}(K,\mathbb{F})$
, and it is not difficult to check that the image of
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}^{0}$
is generated by
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}}^{0}$
is generated by
![]() $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
. If
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
. If
![]() $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
is contained in
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
is contained in
![]() $H$
for some
$H$
for some
![]() $\unicode[STIX]{x1D712}$
, we are done. Suppose this is not the case.
$\unicode[STIX]{x1D712}$
, we are done. Suppose this is not the case.
Suppose that
![]() $H$
is not contained in the unramified line in
$H$
is not contained in the unramified line in
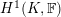 $H^{1}(K,\mathbb{F})$
. We claim that we can choose
$H^{1}(K,\mathbb{F})$
. We claim that we can choose
![]() $\unicode[STIX]{x1D712}$
such that
$\unicode[STIX]{x1D712}$
such that
![]() $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
is ramified. Let
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
is ramified. Let
![]() $m$
be the largest integer with the property that
$m$
be the largest integer with the property that
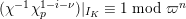 $(\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}})|_{I_{K}}\equiv 1~\text{mod}~\unicode[STIX]{x1D71B}^{n}$
. Clearly, we have
$(\unicode[STIX]{x1D712}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}})|_{I_{K}}\equiv 1~\text{mod}~\unicode[STIX]{x1D71B}^{n}$
. Clearly, we have
![]() $m\geqslant n$
. If
$m\geqslant n$
. If
![]() $m=n$
, then we are done and thus we may assume
$m=n$
, then we are done and thus we may assume
![]() $m>n$
. Fix a lift
$m>n$
. Fix a lift
![]() $g\in G_{K}$
of the Frobenius of
$g\in G_{K}$
of the Frobenius of
![]() $K$
. We see that
$K$
. We see that
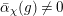 $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}(g)\not =0$
. Let
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}(g)\not =0$
. Let
![]() $\unicode[STIX]{x1D712}^{\prime }$
be the unramified character sending
$\unicode[STIX]{x1D712}^{\prime }$
be the unramified character sending
![]() $g$
to
$g$
to
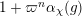 $1+\unicode[STIX]{x1D71B}^{n}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}(g)$
. Then
$1+\unicode[STIX]{x1D71B}^{n}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}(g)$
. Then
![]() $\unicode[STIX]{x1D712}^{\prime }$
has trivial reduction. After replacing
$\unicode[STIX]{x1D712}^{\prime }$
has trivial reduction. After replacing
![]() $\unicode[STIX]{x1D712}$
with
$\unicode[STIX]{x1D712}$
with
![]() $\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}^{\prime }$
, we reduce the case where
$\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}^{\prime }$
, we reduce the case where
![]() $m=n$
and thus the claim follows. Suppose
$m=n$
and thus the claim follows. Suppose
![]() $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
is ramified. Then there exists a unique
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}$
is ramified. Then there exists a unique
![]() $\bar{x}\in \mathbb{F}^{\times }$
such that
$\bar{x}\in \mathbb{F}^{\times }$
such that
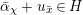 $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}+u_{\bar{x}}\in H$
where
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}}+u_{\bar{x}}\in H$
where
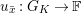 $u_{\bar{x}}:G_{K}\rightarrow \mathbb{F}$
is the unramified character sending
$u_{\bar{x}}:G_{K}\rightarrow \mathbb{F}$
is the unramified character sending
![]() $g$
to
$g$
to
![]() $\bar{x}$
. Denote by
$\bar{x}$
. Denote by
![]() $\unicode[STIX]{x1D712}^{\prime \prime }$
the unramified character sending
$\unicode[STIX]{x1D712}^{\prime \prime }$
the unramified character sending
![]() $g$
to
$g$
to
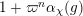 $1+\unicode[STIX]{x1D71B}^{n}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}(g)$
. Replacing
$1+\unicode[STIX]{x1D71B}^{n}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}}(g)$
. Replacing
![]() $\unicode[STIX]{x1D712}$
with
$\unicode[STIX]{x1D712}$
with
![]() $\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}^{\prime \prime }$
, we have done.
$\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}^{\prime \prime }$
, we have done.
Suppose that
![]() $H$
is contained in the unramified line in
$H$
is contained in the unramified line in
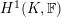 $H^{1}(K,\mathbb{F})$
(thus
$H^{1}(K,\mathbb{F})$
(thus
![]() $H$
and the unramified line coincide with each other). By replacing
$H$
and the unramified line coincide with each other). By replacing
![]() $E$
with
$E$
with
![]() $E(\sqrt{\unicode[STIX]{x1D71B}})$
, we may assume that
$E(\sqrt{\unicode[STIX]{x1D71B}})$
, we may assume that
![]() $n>1$
. Let
$n>1$
. Let
![]() $\unicode[STIX]{x1D712}_{0}$
be a character defined by
$\unicode[STIX]{x1D712}_{0}$
be a character defined by
![]() $\unicode[STIX]{x1D712}$
times the unramified character sending our fixed
$\unicode[STIX]{x1D712}$
times the unramified character sending our fixed
![]() $g$
to
$g$
to
![]() $1+\unicode[STIX]{x1D71B}$
. Since
$1+\unicode[STIX]{x1D71B}$
. Since
![]() $n>1$
, we see that
$n>1$
, we see that
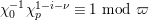 $\unicode[STIX]{x1D712}_{0}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}\equiv 1~\text{mod}~\unicode[STIX]{x1D71B}$
and
$\unicode[STIX]{x1D712}_{0}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}\equiv 1~\text{mod}~\unicode[STIX]{x1D71B}$
and
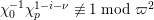 $\unicode[STIX]{x1D712}_{0}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}\not \equiv 1~\text{mod}~\unicode[STIX]{x1D71B}^{2}$
. We define
$\unicode[STIX]{x1D712}_{0}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}\not \equiv 1~\text{mod}~\unicode[STIX]{x1D71B}^{2}$
. We define
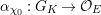 $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}_{0}}:G_{K}\rightarrow {\mathcal{O}}_{E}$
by the relation
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}_{0}}:G_{K}\rightarrow {\mathcal{O}}_{E}$
by the relation
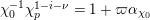 $\unicode[STIX]{x1D712}_{0}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}=1+\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}_{0}}$
, and denote
$\unicode[STIX]{x1D712}_{0}^{-1}\unicode[STIX]{x1D712}_{p}^{1-i-\unicode[STIX]{x1D708}}=1+\unicode[STIX]{x1D71B}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}_{0}}$
, and denote
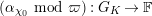 $(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}_{0}}~\text{mod}~\unicode[STIX]{x1D71B}):G_{K}\rightarrow \mathbb{F}$
by
$(\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D712}_{0}}~\text{mod}~\unicode[STIX]{x1D71B}):G_{K}\rightarrow \mathbb{F}$
by
![]() $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}_{0}}$
. By definition and the assumption
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}_{0}}$
. By definition and the assumption
![]() $n>1$
,
$n>1$
,
![]() $\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}_{0}}$
is a nonzero unramified element of
$\bar{\unicode[STIX]{x1D6FC}}_{\unicode[STIX]{x1D712}_{0}}$
is a nonzero unramified element of
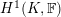 $H^{1}(K,\mathbb{F})$
, hence it is contained in
$H^{1}(K,\mathbb{F})$
, hence it is contained in
![]() $H$
. Therefore, we have done.◻
$H$
. Therefore, we have done.◻
Lemma 5.5. Let
![]() $K$
be a finite extension of
$K$
be a finite extension of
![]() $\mathbb{Q}_{p}$
,
$\mathbb{Q}_{p}$
,
![]() $n\geqslant 2$
an integer and
$n\geqslant 2$
an integer and
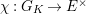 $\unicode[STIX]{x1D712}:G_{K}\rightarrow E^{\times }$
an unramified character. Then any
$\unicode[STIX]{x1D712}:G_{K}\rightarrow E^{\times }$
an unramified character. Then any
![]() $E$
-representation of
$E$
-representation of
![]() $G_{K}$
which is an extension of
$G_{K}$
which is an extension of
![]() $E$
by
$E$
by
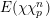 $E(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{n})$
is crystalline.
$E(\unicode[STIX]{x1D712}\unicode[STIX]{x1D712}_{p}^{n})$
is crystalline.
Proof. This is well known; for example, see the argument of [Reference Bloch and KatoBK, Section 3]. ◻
Proposition 5.6. Suppose
![]() $p>2$
. Let
$p>2$
. Let
![]() $K$
be a finite unramified extension of
$K$
be a finite unramified extension of
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
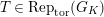 $T\in \text{Rep}_{\text{tor}}(G_{K})$
be killed by
$T\in \text{Rep}_{\text{tor}}(G_{K})$
be killed by
![]() $p$
and sit in an exact sequence
$p$
and sit in an exact sequence
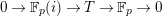 $0\rightarrow \mathbb{F}_{p}(i)\rightarrow T\rightarrow \mathbb{F}_{p}\rightarrow 0$
of
$0\rightarrow \mathbb{F}_{p}(i)\rightarrow T\rightarrow \mathbb{F}_{p}\rightarrow 0$
of
![]() $\mathbb{F}_{p}$
-representations of
$\mathbb{F}_{p}$
-representations of
![]() $G_{K}$
. Then we have the followings:
$G_{K}$
. Then we have the followings:
![]() $(1)$
If
$(1)$
If
![]() $i=0$
and
$i=0$
and
![]() $T$
is unramified, then we have
$T$
is unramified, then we have
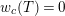 $w_{c}(T)=0$
.
$w_{c}(T)=0$
.
![]() $(2)$
If
$(2)$
If
![]() $i=0$
and
$i=0$
and
![]() $T$
is not unramified, then we have
$T$
is not unramified, then we have
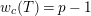 $w_{c}(T)=p-1$
.
$w_{c}(T)=p-1$
.
![]() $(3)$
If
$(3)$
If
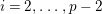 $i=2,\ldots ,p-2$
, then we have
$i=2,\ldots ,p-2$
, then we have
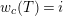 $w_{c}(T)=i$
.
$w_{c}(T)=i$
.
Proof. (1) By Lemma 5.4(2), we know that
![]() $T$
has unramified (and thus crystalline) lift, which implies
$T$
has unramified (and thus crystalline) lift, which implies
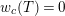 $w_{c}(T)=0$
.
$w_{c}(T)=0$
.
(2) By Lemmas 5.4 and 5.5, it suffices to prove that
![]() $T$
is not torsion crystalline with Hodge–Tate weights in
$T$
is not torsion crystalline with Hodge–Tate weights in
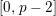 $[0,p-2]$
if
$[0,p-2]$
if
![]() $T$
is not unramified. Let
$T$
is not unramified. Let
![]() $K_{T}$
be the definition field of the representation
$K_{T}$
be the definition field of the representation
![]() $T$
of
$T$
of
![]() $G_{K}$
and put
$G_{K}$
and put
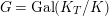 $G=\text{Gal}(K_{T}/K)$
. Let
$G=\text{Gal}(K_{T}/K)$
. Let
![]() $G^{j}$
be the upper numbering
$G^{j}$
be the upper numbering
![]() $j$
th ramification subgroup of
$j$
th ramification subgroup of
![]() $G$
(in the sense of [Reference SerreSe]). Since
$G$
(in the sense of [Reference SerreSe]). Since
![]() $T$
is not unramified and killed by
$T$
is not unramified and killed by
![]() $p$
, we see that
$p$
, we see that
![]() $K_{T}$
is a totally ramified degree
$K_{T}$
is a totally ramified degree
![]() $p$
extension over
$p$
extension over
![]() $K$
. Thus
$K$
. Thus
![]() $G^{1}$
is the wild inertia subgroup of
$G^{1}$
is the wild inertia subgroup of
![]() $G$
and
$G$
and
![]() $G^{1}=G$
, which does not act on
$G^{1}=G$
, which does not act on
![]() $T$
trivial by the definition of
$T$
trivial by the definition of
![]() $G$
. Thus we obtain the desired result by ramification estimates of [Reference FontaineFo1] (or [Reference AbrashkinAb1]) for torsion crystalline representations with Hodge–Tate weights in
$G$
. Thus we obtain the desired result by ramification estimates of [Reference FontaineFo1] (or [Reference AbrashkinAb1]) for torsion crystalline representations with Hodge–Tate weights in
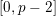 $[0,p-2]$
: if
$[0,p-2]$
: if
![]() $T$
is torsion crystalline with Hodge–Tate weights in
$T$
is torsion crystalline with Hodge–Tate weights in
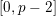 $[0,p-2]$
, then
$[0,p-2]$
, then
![]() $G^{j}$
acts on
$G^{j}$
acts on
![]() $T$
trivial for any
$T$
trivial for any
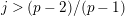 $j>(p-2)/(p-1)$
.
$j>(p-2)/(p-1)$
.
(3) The result follows immediately from Proposition 5.2(4), Lemmas 5.4 and 5.5. ◻
Corollary 5.7. Let
![]() $K$
be a finite unramified extension of
$K$
be a finite unramified extension of
![]() $\mathbb{Q}_{p}$
. Then any
$\mathbb{Q}_{p}$
. Then any
![]() $2$
-dimensional
$2$
-dimensional
![]() $\mathbb{F}_{p}$
-representation of
$\mathbb{F}_{p}$
-representation of
![]() $G_{K}$
is torsion crystalline with Hodge–Tate weights in
$G_{K}$
is torsion crystalline with Hodge–Tate weights in
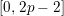 $[0,2p-2]$
.
$[0,2p-2]$
.
Proof. If
![]() $T$
is irreducible, the result follows from Theorem 5.3. Assume that
$T$
is irreducible, the result follows from Theorem 5.3. Assume that
![]() $T$
is reducible. Since
$T$
is reducible. Since
![]() $K$
is unramified over
$K$
is unramified over
![]() $\mathbb{Q}_{p}$
, any continuous character
$\mathbb{Q}_{p}$
, any continuous character
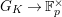 $G_{K}\rightarrow \mathbb{F}_{p}^{\times }$
is of the form
$G_{K}\rightarrow \mathbb{F}_{p}^{\times }$
is of the form
![]() $\unicode[STIX]{x1D712}\bar{\unicode[STIX]{x1D712}}_{p}^{i}$
for some unramified character
$\unicode[STIX]{x1D712}\bar{\unicode[STIX]{x1D712}}_{p}^{i}$
for some unramified character
![]() $\unicode[STIX]{x1D712}$
and some integer
$\unicode[STIX]{x1D712}$
and some integer
![]() $i$
. Replacing
$i$
. Replacing
![]() $K$
with its finite unramified extension, we may assume that
$K$
with its finite unramified extension, we may assume that
![]() $T$
sits in an exact sequence
$T$
sits in an exact sequence
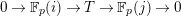 $0\rightarrow \mathbb{F}_{p}(i)\rightarrow T\rightarrow \mathbb{F}_{p}(j)\rightarrow 0$
of
$0\rightarrow \mathbb{F}_{p}(i)\rightarrow T\rightarrow \mathbb{F}_{p}(j)\rightarrow 0$
of
![]() $\mathbb{F}_{p}$
-representations of
$\mathbb{F}_{p}$
-representations of
![]() $G_{K}$
, where
$G_{K}$
, where
![]() $i$
and
$i$
and
![]() $j$
are integers in the range
$j$
are integers in the range
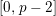 $[0,p-2]$
(we remark that
$[0,p-2]$
(we remark that
![]() $w_{c}(T)$
is invariant under unramified extensions of
$w_{c}(T)$
is invariant under unramified extensions of
![]() $K$
by Proposition 5.2(1)). It follows from Lemmas 5.4 and 5.5 that
$K$
by Proposition 5.2(1)). It follows from Lemmas 5.4 and 5.5 that
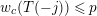 $w_{c}(T(-j))\leqslant p$
. Therefore, we obtain
$w_{c}(T(-j))\leqslant p$
. Therefore, we obtain
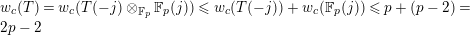 $w_{c}(T)=w_{c}(T(-j)\otimes _{\mathbb{F}_{p}}\mathbb{F}_{p}(j))\leqslant w_{c}(T(-j))+w_{c}(\mathbb{F}_{p}(j))\leqslant p+(p-2)=2p-2$
.◻
$w_{c}(T)=w_{c}(T(-j)\otimes _{\mathbb{F}_{p}}\mathbb{F}_{p}(j))\leqslant w_{c}(T(-j))+w_{c}(\mathbb{F}_{p}(j))\leqslant p+(p-2)=2p-2$
.◻
Remark 5.8. The author does not know whether
![]() $2p-2$
in the statement of Corollary 5.7 is optimal or not.
$2p-2$
in the statement of Corollary 5.7 is optimal or not.
5.3 Extensions of
 $\mathbb{F}_{p}$
by
$\mathbb{F}_{p}$
by
 $\mathbb{F}_{p}(1)$
and nonfullness theorems
$\mathbb{F}_{p}(1)$
and nonfullness theorems
By Lemma 5.4, we know that the c-weight
![]() $w_{c}(T)$
of an
$w_{c}(T)$
of an
![]() $\mathbb{F}_{p}$
-representation
$\mathbb{F}_{p}$
-representation
![]() $T$
of
$T$
of
![]() $G_{K}$
which sits in an exact sequence
$G_{K}$
which sits in an exact sequence
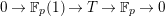 $0\rightarrow \mathbb{F}_{p}(1)\rightarrow T\rightarrow \mathbb{F}_{p}\rightarrow 0$
of
$0\rightarrow \mathbb{F}_{p}(1)\rightarrow T\rightarrow \mathbb{F}_{p}\rightarrow 0$
of
![]() $\mathbb{F}_{p}$
-representations of
$\mathbb{F}_{p}$
-representations of
![]() $G_{K}$
, is less than or equal to
$G_{K}$
, is less than or equal to
![]() $p$
. Let us calculate
$p$
. Let us calculate
![]() $w_{c}(T)$
for such
$w_{c}(T)$
for such
![]() $T$
more precisely. We should remark that such
$T$
more precisely. We should remark that such
![]() $T$
is written as
$T$
is written as
![]() $p$
-torsion points of a Tate curve. Hence we consider torsion representations coming from Tate curves.
$p$
-torsion points of a Tate curve. Hence we consider torsion representations coming from Tate curves.
Let
![]() $v_{K}$
be the valuation of
$v_{K}$
be the valuation of
![]() $K$
normalized such that
$K$
normalized such that
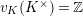 $v_{K}(K^{\times })=\mathbb{Z}$
, and take any
$v_{K}(K^{\times })=\mathbb{Z}$
, and take any
![]() $q\in K^{\times }$
with
$q\in K^{\times }$
with
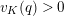 $v_{K}(q)>0$
. Let
$v_{K}(q)>0$
. Let
![]() $E_{q}$
be the Tate curve over
$E_{q}$
be the Tate curve over
![]() $K$
associated with
$K$
associated with
![]() $q$
and
$q$
and
![]() $E_{q}[p^{n}]$
the module of
$E_{q}[p^{n}]$
the module of
![]() $p^{n}$
-torsion points of
$p^{n}$
-torsion points of
![]() $E_{q}$
for any integer
$E_{q}$
for any integer
![]() $n>0$
. It is well known that there exists an exact sequence
$n>0$
. It is well known that there exists an exact sequence
 $$\begin{eqnarray}(\#)\quad 0\rightarrow \unicode[STIX]{x1D707}_{p^{n}}\rightarrow E_{q}[p^{n}]\rightarrow \mathbb{Z}/p^{n}\mathbb{Z}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}(\#)\quad 0\rightarrow \unicode[STIX]{x1D707}_{p^{n}}\rightarrow E_{q}[p^{n}]\rightarrow \mathbb{Z}/p^{n}\mathbb{Z}\rightarrow 0\end{eqnarray}$$
of
![]() $\mathbb{Z}_{p}[G_{K}]$
-modules. Here,
$\mathbb{Z}_{p}[G_{K}]$
-modules. Here,
![]() $\unicode[STIX]{x1D707}_{p^{n}}$
is the group of
$\unicode[STIX]{x1D707}_{p^{n}}$
is the group of
![]() $p^{n}$
th roots of unity in
$p^{n}$
th roots of unity in
![]() $\overline{K}$
. Let
$\overline{K}$
. Let
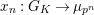 $x_{n}:G_{K}\rightarrow \unicode[STIX]{x1D707}_{p^{n}}$
be the
$x_{n}:G_{K}\rightarrow \unicode[STIX]{x1D707}_{p^{n}}$
be the
![]() $1$
-cocycle defined to be the image of
$1$
-cocycle defined to be the image of
![]() $1$
for the connection map
$1$
for the connection map
 $H^{0}(K,\mathbb{Z}/p^{n}\mathbb{Z})\rightarrow H^{1}(K,\unicode[STIX]{x1D707}_{p^{n}})$
arising from the exact sequence
$H^{0}(K,\mathbb{Z}/p^{n}\mathbb{Z})\rightarrow H^{1}(K,\unicode[STIX]{x1D707}_{p^{n}})$
arising from the exact sequence
![]() $(\#)$
. Then
$(\#)$
. Then
![]() $x_{n}$
corresponds to
$x_{n}$
corresponds to
![]() $q$
mod
$q$
mod
![]() $(K^{\times })^{p^{n}}$
via the isomorphism
$(K^{\times })^{p^{n}}$
via the isomorphism
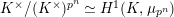 $K^{\times }/(K^{\times })^{p^{n}}\simeq H^{1}(K,\unicode[STIX]{x1D707}_{p^{n}})$
of Kummer theory. Thus the exact sequence
$K^{\times }/(K^{\times })^{p^{n}}\simeq H^{1}(K,\unicode[STIX]{x1D707}_{p^{n}})$
of Kummer theory. Thus the exact sequence
![]() $(\#)$
splits if and only if
$(\#)$
splits if and only if
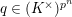 $q\in (K^{\times })^{p^{n}}$
.
$q\in (K^{\times })^{p^{n}}$
.
First we consider the case
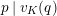 $p\mid v_{K}(q)$
(i.e., peu ramifié case).
$p\mid v_{K}(q)$
(i.e., peu ramifié case).
Lemma 5.9. Let
![]() $K$
be a finite extension of
$K$
be a finite extension of
![]() $\mathbb{Q}_{p}$
. If
$\mathbb{Q}_{p}$
. If
 $p\mid v_{K}(q)$
, then
$p\mid v_{K}(q)$
, then
![]() $E_{q}[p]$
is the reduction modulo
$E_{q}[p]$
is the reduction modulo
![]() $p$
of a lattice in some
$p$
of a lattice in some
![]() $2$
-dimensional crystalline
$2$
-dimensional crystalline
![]() $\mathbb{Q}_{p}$
-representation with Hodge–Tate weights in
$\mathbb{Q}_{p}$
-representation with Hodge–Tate weights in
![]() $[0,1]$
.
$[0,1]$
.
Proof. Since
 $p\mid v_{K}(q)$
, there exists
$p\mid v_{K}(q)$
, there exists
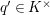 $q^{\prime }\in K^{\times }$
such that
$q^{\prime }\in K^{\times }$
such that
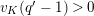 $v_{K}(q^{\prime }-1)>0$
and
$v_{K}(q^{\prime }-1)>0$
and
![]() $q\equiv q^{\prime }$
mod
$q\equiv q^{\prime }$
mod
![]() $(K^{\times })^{p}$
. Consider the exact sequence
$(K^{\times })^{p}$
. Consider the exact sequence
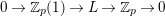 $0\rightarrow \mathbb{Z}_{p}(1)\rightarrow L\rightarrow \mathbb{Z}_{p}\rightarrow 0$
of
$0\rightarrow \mathbb{Z}_{p}(1)\rightarrow L\rightarrow \mathbb{Z}_{p}\rightarrow 0$
of
![]() $\mathbb{Z}_{p}$
-representations of
$\mathbb{Z}_{p}$
-representations of
![]() $G_{K}$
corresponding to
$G_{K}$
corresponding to
![]() $q^{\prime }$
via the isomorphism
$q^{\prime }$
via the isomorphism
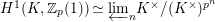 $H^{1}(K,\mathbb{Z}_{p}(1))\simeq \mathop{\varprojlim }\nolimits_{n}K^{\times }/(K^{\times })^{p^{n}}$
of Kummer theory. By the condition
$H^{1}(K,\mathbb{Z}_{p}(1))\simeq \mathop{\varprojlim }\nolimits_{n}K^{\times }/(K^{\times })^{p^{n}}$
of Kummer theory. By the condition
![]() $q\equiv q^{\prime }$
mod
$q\equiv q^{\prime }$
mod
![]() $(K^{\times })^{p}$
, the reduction modulo
$(K^{\times })^{p}$
, the reduction modulo
![]() $p$
of
$p$
of
![]() $L$
is
$L$
is
![]() $E_{q}[p]$
. Thus it suffices to show that
$E_{q}[p]$
. Thus it suffices to show that
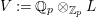 $V:=\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}L$
is crystalline. Take a system
$V:=\mathbb{Q}_{p}\otimes _{\mathbb{Z}_{p}}L$
is crystalline. Take a system
![]() $(q_{n}^{\prime })_{n\geqslant 0}$
of
$(q_{n}^{\prime })_{n\geqslant 0}$
of
![]() $p$
-power roots of
$p$
-power roots of
![]() $q^{\prime }$
in
$q^{\prime }$
in
![]() ${\mathcal{O}}_{\overline{K}}$
such that
${\mathcal{O}}_{\overline{K}}$
such that
![]() $q_{0}^{\prime }=q^{\prime }$
and
$q_{0}^{\prime }=q^{\prime }$
and
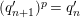 $(q_{n+1}^{\prime })^{p}=q_{n}^{\prime }$
for any
$(q_{n+1}^{\prime })^{p}=q_{n}^{\prime }$
for any
![]() $n\geqslant 0$
. We also take a system
$n\geqslant 0$
. We also take a system
![]() $(\unicode[STIX]{x1D700}_{n}^{\prime })_{n\geqslant 0}$
of
$(\unicode[STIX]{x1D700}_{n}^{\prime })_{n\geqslant 0}$
of
![]() $p$
-power roots of unity in
$p$
-power roots of unity in
![]() ${\mathcal{O}}_{\overline{K}}$
such that
${\mathcal{O}}_{\overline{K}}$
such that
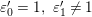 $\unicode[STIX]{x1D700}_{0}^{\prime }=1,~\unicode[STIX]{x1D700}_{1}^{\prime }\not =1$
and
$\unicode[STIX]{x1D700}_{0}^{\prime }=1,~\unicode[STIX]{x1D700}_{1}^{\prime }\not =1$
and
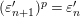 $(\unicode[STIX]{x1D700}_{n+1}^{\prime })^{p}=\unicode[STIX]{x1D700}_{n}^{\prime }$
for any
$(\unicode[STIX]{x1D700}_{n+1}^{\prime })^{p}=\unicode[STIX]{x1D700}_{n}^{\prime }$
for any
![]() $n\geqslant 0$
. We define a map
$n\geqslant 0$
. We define a map
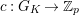 $c:G_{K}\rightarrow \mathbb{Z}_{p}$
by
$c:G_{K}\rightarrow \mathbb{Z}_{p}$
by
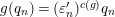 $g(q_{n})=(\unicode[STIX]{x1D700}_{n}^{\prime })^{c(g)}q_{n}$
for any
$g(q_{n})=(\unicode[STIX]{x1D700}_{n}^{\prime })^{c(g)}q_{n}$
for any
![]() $n\geqslant 0$
. Then we can choose a basis
$n\geqslant 0$
. Then we can choose a basis
![]() $\mathbf{e},\mathbf{f}$
of
$\mathbf{e},\mathbf{f}$
of
![]() $V$
such that
$V$
such that
 $g(\mathbf{e})=\unicode[STIX]{x1D712}_{p}(g)\mathbf{e}$
and
$g(\mathbf{e})=\unicode[STIX]{x1D712}_{p}(g)\mathbf{e}$
and
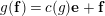 $g(\mathbf{f})=c(g)\mathbf{e}+\mathbf{f}$
for any
$g(\mathbf{f})=c(g)\mathbf{e}+\mathbf{f}$
for any
![]() $g\in G_{K}$
. Put
$g\in G_{K}$
. Put
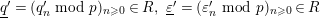 $\text{}\underline{q}^{\prime }=(q_{n}^{\prime }~\text{mod}~p)_{n\geqslant 0}\in R,~\text{}\underline{\unicode[STIX]{x1D700}}^{\prime }=(\unicode[STIX]{x1D700}_{n}^{\prime }~\text{mod}~p)_{n\geqslant 0}\in R$
and
$\text{}\underline{q}^{\prime }=(q_{n}^{\prime }~\text{mod}~p)_{n\geqslant 0}\in R,~\text{}\underline{\unicode[STIX]{x1D700}}^{\prime }=(\unicode[STIX]{x1D700}_{n}^{\prime }~\text{mod}~p)_{n\geqslant 0}\in R$
and
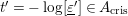 $t^{\prime }=-\log [\text{}\underline{\unicode[STIX]{x1D700}}^{\prime }]\in A_{\text{cris}}$
. By the condition
$t^{\prime }=-\log [\text{}\underline{\unicode[STIX]{x1D700}}^{\prime }]\in A_{\text{cris}}$
. By the condition
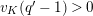 $v_{K}(q^{\prime }-1)>0$
, we see
$v_{K}(q^{\prime }-1)>0$
, we see
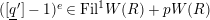 $([\text{}\underline{q}^{\prime }]-1)^{e}\in \text{Fil}^{1}W(R)+pW(R)$
and thus
$([\text{}\underline{q}^{\prime }]-1)^{e}\in \text{Fil}^{1}W(R)+pW(R)$
and thus
![]() $\log [\text{}\underline{q}^{\prime }]$
converges in
$\log [\text{}\underline{q}^{\prime }]$
converges in
![]() $B_{\text{cris}}^{+}$
. With these notations, we see that the
$B_{\text{cris}}^{+}$
. With these notations, we see that the
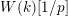 $W(k)[1/p]$
-vector space
$W(k)[1/p]$
-vector space
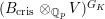 $(B_{\text{cris}}\otimes _{\mathbb{Q}_{p}}V)^{G_{K}}$
is of dimension
$(B_{\text{cris}}\otimes _{\mathbb{Q}_{p}}V)^{G_{K}}$
is of dimension
![]() $2$
with basis
$2$
with basis
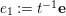 $e_{1}:=t^{-1}\mathbf{e}$
and
$e_{1}:=t^{-1}\mathbf{e}$
and
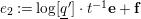 $e_{2}:=\text{log}[\text{}\underline{q}^{\prime }]\cdot t^{-1}\mathbf{e}+\mathbf{f}$
. Therefore,
$e_{2}:=\text{log}[\text{}\underline{q}^{\prime }]\cdot t^{-1}\mathbf{e}+\mathbf{f}$
. Therefore,
![]() $V$
is crystalline.◻
$V$
is crystalline.◻
Corollary 5.10. Suppose that
![]() $K$
is a finite extension of
$K$
is a finite extension of
![]() $\mathbb{Q}_{p}$
,
$\mathbb{Q}_{p}$
,
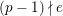 $(p-1)\nmid e$
and
$(p-1)\nmid e$
and
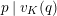 $p\mid v_{K}(q)$
. Then we have
$p\mid v_{K}(q)$
. Then we have
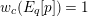 $w_{c}(E_{q}[p])=1$
.
$w_{c}(E_{q}[p])=1$
.
Proof. By the assumption
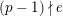 $(p-1)\nmid e$
, we know that the largest tame inertia weight of
$(p-1)\nmid e$
, we know that the largest tame inertia weight of
![]() $E_{q}[p]$
is positive. Thus Proposition 5.2(4) shows
$E_{q}[p]$
is positive. Thus Proposition 5.2(4) shows
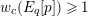 $w_{c}(E_{q}[p])\geqslant 1$
. The inequality
$w_{c}(E_{q}[p])\geqslant 1$
. The inequality
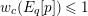 $w_{c}(E_{q}[p])\leqslant 1$
follows from Lemma 5.9.◻
$w_{c}(E_{q}[p])\leqslant 1$
follows from Lemma 5.9.◻
Next we consider the case
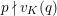 $p\nmid v_{K}(q)$
(i.e., très ramifié case).
$p\nmid v_{K}(q)$
(i.e., très ramifié case).
Proposition 5.11. If
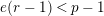 $e(r-1)<p-1$
and
$e(r-1)<p-1$
and
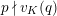 $p\nmid v_{K}(q)$
, then
$p\nmid v_{K}(q)$
, then
![]() $E_{q}[p^{n}]$
is not torsion crystalline with Hodge–Tate weights in
$E_{q}[p^{n}]$
is not torsion crystalline with Hodge–Tate weights in
![]() $[0,r]$
for any
$[0,r]$
for any
![]() $n>0$
.
$n>0$
.
Remark 5.12. If
![]() $e=1$
, the fact that
$e=1$
, the fact that
![]() $E_{\unicode[STIX]{x1D70B}}[p^{n}]$
is not torsion crystalline with Hodge–Tate weights in
$E_{\unicode[STIX]{x1D70B}}[p^{n}]$
is not torsion crystalline with Hodge–Tate weights in
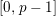 $[0,p-1]$
immediately follows from the theory of ramification bound as below. We may suppose
$[0,p-1]$
immediately follows from the theory of ramification bound as below. We may suppose
![]() $n=1$
. Suppose
$n=1$
. Suppose
![]() $E_{\unicode[STIX]{x1D70B}}[p]$
is torsion crystalline with Hodge–Tate weights in
$E_{\unicode[STIX]{x1D70B}}[p]$
is torsion crystalline with Hodge–Tate weights in
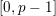 $[0,p-1]$
. Then the upper numbering
$[0,p-1]$
. Then the upper numbering
![]() $j$
th ramification subgroup
$j$
th ramification subgroup
![]() $G_{K}^{j}$
of
$G_{K}^{j}$
of
![]() $G_{K}$
(in the sense of [Reference SerreSe]) acts trivially on
$G_{K}$
(in the sense of [Reference SerreSe]) acts trivially on
![]() $E_{\unicode[STIX]{x1D70B}}[p]$
for any
$E_{\unicode[STIX]{x1D70B}}[p]$
for any
![]() $j>1$
[Reference AbrashkinAb1, Section 6, Theorem 3.1]. However, this contradicts the fact that the upper bound of the ramification of
$j>1$
[Reference AbrashkinAb1, Section 6, Theorem 3.1]. However, this contradicts the fact that the upper bound of the ramification of
![]() $E_{\unicode[STIX]{x1D70B}}[p]$
is
$E_{\unicode[STIX]{x1D70B}}[p]$
is
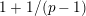 $1+1/(p-1)$
.
$1+1/(p-1)$
.
Proof of Proposition 5.11.
We may suppose
![]() $n=1$
. We choose any uniformizer
$n=1$
. We choose any uniformizer
![]() $\unicode[STIX]{x1D70B}^{\prime }$
of
$\unicode[STIX]{x1D70B}^{\prime }$
of
![]() $K$
. Putting
$K$
. Putting
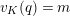 $v_{K}(q)=m$
, we can write
$v_{K}(q)=m$
, we can write
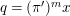 $q=(\unicode[STIX]{x1D70B}^{\prime })^{m}x$
with some unit
$q=(\unicode[STIX]{x1D70B}^{\prime })^{m}x$
with some unit
![]() $x$
of the integer ring of
$x$
of the integer ring of
![]() $K$
. Since
$K$
. Since
![]() $m$
is prime to
$m$
is prime to
![]() $p$
, we have a decomposition
$p$
, we have a decomposition
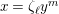 $x=\unicode[STIX]{x1D701}_{\ell }y^{m}$
in
$x=\unicode[STIX]{x1D701}_{\ell }y^{m}$
in
![]() $K^{\times }$
for some
$K^{\times }$
for some
![]() $\ell >0$
prime to
$\ell >0$
prime to
![]() $p$
and
$p$
and
![]() $y\in K$
with
$y\in K$
with
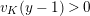 $v_{K}(y-1)>0$
. Here
$v_{K}(y-1)>0$
. Here
![]() $\unicode[STIX]{x1D701}_{\ell }$
is a (not necessary primitive)
$\unicode[STIX]{x1D701}_{\ell }$
is a (not necessary primitive)
![]() $\ell$
th root of unity. Since
$\ell$
th root of unity. Since
![]() $\ell$
is prime to
$\ell$
is prime to
![]() $p$
, we have
$p$
, we have
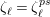 $\unicode[STIX]{x1D701}_{\ell }=\unicode[STIX]{x1D701}_{\ell }^{ps}$
for some integer
$\unicode[STIX]{x1D701}_{\ell }=\unicode[STIX]{x1D701}_{\ell }^{ps}$
for some integer
![]() $s$
. We put
$s$
. We put
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}^{\prime }y$
. This is a uniformizer of
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}^{\prime }y$
. This is a uniformizer of
![]() $K$
. Choose any
$K$
. Choose any
![]() $p$
th root
$p$
th root
![]() $\unicode[STIX]{x1D70B}_{1}$
of
$\unicode[STIX]{x1D70B}_{1}$
of
![]() $\unicode[STIX]{x1D70B}$
and put
$\unicode[STIX]{x1D70B}$
and put
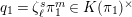 $q_{1}=\unicode[STIX]{x1D701}_{\ell }^{s}\unicode[STIX]{x1D70B}_{1}^{m}\in K(\unicode[STIX]{x1D70B}_{1})^{\times }$
. Then we have
$q_{1}=\unicode[STIX]{x1D701}_{\ell }^{s}\unicode[STIX]{x1D70B}_{1}^{m}\in K(\unicode[STIX]{x1D70B}_{1})^{\times }$
. Then we have
 $q=q_{1}^{p}\in (K(\unicode[STIX]{x1D70B}_{1})^{\times })^{p}$
and in particular, the exact sequence
$q=q_{1}^{p}\in (K(\unicode[STIX]{x1D70B}_{1})^{\times })^{p}$
and in particular, the exact sequence
![]() $(\#)$
(for
$(\#)$
(for
![]() $n=1$
) splits as representations of
$n=1$
) splits as representations of
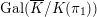 $\text{Gal}(\overline{K}/K(\unicode[STIX]{x1D70B}_{1}))$
. Now assume that
$\text{Gal}(\overline{K}/K(\unicode[STIX]{x1D70B}_{1}))$
. Now assume that
![]() $E_{q}[p]$
is torsion crystalline with Hodge–Tate weights in
$E_{q}[p]$
is torsion crystalline with Hodge–Tate weights in
![]() $[0,r]$
. Then
$[0,r]$
. Then
![]() $(\#)$
(for
$(\#)$
(for
![]() $n=1$
) splits as representations of
$n=1$
) splits as representations of
![]() $G_{K}$
by Theorem 1.2. This contradicts the assumption
$G_{K}$
by Theorem 1.2. This contradicts the assumption
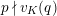 $p\nmid v_{K}(q)$
(and hence
$p\nmid v_{K}(q)$
(and hence
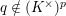 $q\notin (K^{\times })^{p}$
).◻
$q\notin (K^{\times })^{p}$
).◻
Now we put
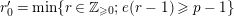 $r_{0}^{\prime }=\text{min}\{r\in \mathbb{Z}_{{\geqslant}0};e(r-1)\geqslant p-1\}$
. Recall that we have
$r_{0}^{\prime }=\text{min}\{r\in \mathbb{Z}_{{\geqslant}0};e(r-1)\geqslant p-1\}$
. Recall that we have
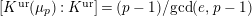 $[K^{\text{ur}}(\unicode[STIX]{x1D707}_{p}):K^{\text{ur}}]=(p-1)/\text{gcd}(e,p-1)$
.
$[K^{\text{ur}}(\unicode[STIX]{x1D707}_{p}):K^{\text{ur}}]=(p-1)/\text{gcd}(e,p-1)$
.
Lemma 5.13. Let
![]() $K$
be a finite extension of
$K$
be a finite extension of
![]() $\mathbb{Q}_{p}$
. Then
$\mathbb{Q}_{p}$
. Then
![]() $E_{q}[p]$
is torsion crystalline with Hodge–Tate weights in
$E_{q}[p]$
is torsion crystalline with Hodge–Tate weights in
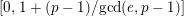 $[0,1+(p-1)/\text{gcd}(e,p-1)]$
.
$[0,1+(p-1)/\text{gcd}(e,p-1)]$
.
Proof. Taking a finite unramified extension
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $K$
such that
$K$
such that
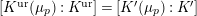 $[K^{\text{ur}}(\unicode[STIX]{x1D707}_{p}):K^{\text{ur}}]=[K^{\prime }(\unicode[STIX]{x1D707}_{p}):K^{\prime }]$
, we obtain
$[K^{\text{ur}}(\unicode[STIX]{x1D707}_{p}):K^{\text{ur}}]=[K^{\prime }(\unicode[STIX]{x1D707}_{p}):K^{\prime }]$
, we obtain
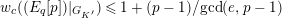 $w_{c}((E_{q}[p])|_{G_{K^{\prime }}})\leqslant 1+(p-1)/\text{gcd}(e,p-1)$
by Lemma 5.4. Thus we have
$w_{c}((E_{q}[p])|_{G_{K^{\prime }}})\leqslant 1+(p-1)/\text{gcd}(e,p-1)$
by Lemma 5.4. Thus we have
 $w_{c}(E_{q}[p])\leqslant 1+(p-1)/\text{gcd}(e,p-1)$
by Proposition 5.2(1).◻
$w_{c}(E_{q}[p])\leqslant 1+(p-1)/\text{gcd}(e,p-1)$
by Proposition 5.2(1).◻
Corollary 5.14. Suppose that
![]() $K$
is a finite extension of
$K$
is a finite extension of
![]() $\mathbb{Q}_{p}$
, and also suppose
$\mathbb{Q}_{p}$
, and also suppose
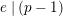 $e\mid (p-1)$
or
$e\mid (p-1)$
or
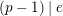 $(p-1)\mid e$
. We further suppose that
$(p-1)\mid e$
. We further suppose that
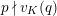 $p\nmid v_{K}(q)$
. Then we have
$p\nmid v_{K}(q)$
. Then we have
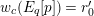 $w_{c}(E_{q}[p])=r_{0}^{\prime }$
.
$w_{c}(E_{q}[p])=r_{0}^{\prime }$
.
Proof. We have
 $w_{c}(E_{q}[p])\leqslant r_{0}^{\prime }$
by Lemma 5.13. In addition, we also have
$w_{c}(E_{q}[p])\leqslant r_{0}^{\prime }$
by Lemma 5.13. In addition, we also have
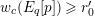 $w_{c}(E_{q}[p])\geqslant r_{0}^{\prime }$
by Proposition 5.11.◻
$w_{c}(E_{q}[p])\geqslant r_{0}^{\prime }$
by Proposition 5.11.◻
Lemma 5.13 gives some nonfullness results on torsion crystalline representations.
Corollary 5.15. Suppose that
![]() $K$
is a finite extension of
$K$
is a finite extension of
![]() $\mathbb{Q}_{p}$
. If
$\mathbb{Q}_{p}$
. If
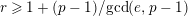 $r\geqslant 1+(p-1)/\text{gcd}(e,p-1)$
, then the restriction functor
$r\geqslant 1+(p-1)/\text{gcd}(e,p-1)$
, then the restriction functor
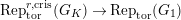 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{1})$
is not full.
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{1})$
is not full.
Proof. We consider two representations
![]() $E_{\unicode[STIX]{x1D70B}}[p]$
and
$E_{\unicode[STIX]{x1D70B}}[p]$
and
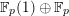 $\mathbb{F}_{p}(1)\oplus \mathbb{F}_{p}$
, which are objects of
$\mathbb{F}_{p}(1)\oplus \mathbb{F}_{p}$
, which are objects of
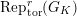 $\text{Rep}_{\text{tor}}^{r}(G_{K})$
by Lemma 5.13. They are not isomorphic as representations of
$\text{Rep}_{\text{tor}}^{r}(G_{K})$
by Lemma 5.13. They are not isomorphic as representations of
![]() $G_{K}$
but isomorphic as representations of
$G_{K}$
but isomorphic as representations of
![]() $G_{1}$
. Thus the desired nonfullness follows.◻
$G_{1}$
. Thus the desired nonfullness follows.◻
Corollary 5.16. Suppose that any one of the following holds:
-
∙
 $p=2$
and
$p=2$
and
 $K$
is a finite extension of
$K$
is a finite extension of
 $\mathbb{Q}_{2}$
(in this case
$\mathbb{Q}_{2}$
(in this case
 $r_{0}^{\prime }=2$
);
$r_{0}^{\prime }=2$
); -
∙
 $K$
is a finite unramified extension of
$K$
is a finite unramified extension of
 $\mathbb{Q}_{p}$
(in this case
$\mathbb{Q}_{p}$
(in this case
 $r_{0}^{\prime }=p$
);
$r_{0}^{\prime }=p$
); -
∙
 $K$
is a finite extension of
$K$
is a finite extension of
 $\mathbb{Q}_{p}(\unicode[STIX]{x1D707}_{p})$
(in this case
$\mathbb{Q}_{p}(\unicode[STIX]{x1D707}_{p})$
(in this case
 $r_{0}^{\prime }=2$
).
$r_{0}^{\prime }=2$
).
Then the restriction functor
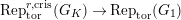 $\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{1})$
is not full.
$\text{Rep}_{\text{tor}}^{r,\text{cris}}(G_{K})\rightarrow \text{Rep}_{\text{tor}}(G_{1})$
is not full.
Acknowledgments
The author would like to thank Shin Hattori, Naoki Imai and Yuichiro Taguchi who gave him many valuable advice. The author is grateful to the anonymous referee for his/her comments. This work was supported by JSPS KAKENHI Grant Number 25
![]() $\cdot$
173.
$\cdot$
173.