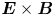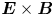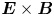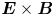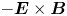Theory of gradient drift instabilities in low-temperature, partially magnetised plasmas

Abstract

A fluid dispersion theory in partially magnetised plasmas is analysed to examine the conditions under which large-wavelength modes develop in Penning-type configurations, that is, where an electric field is imposed perpendicular to a homogeneous magnetic field. The fluid dispersion relation assuming a slab geometry shows that two types of low-frequency, gradient drift instabilities occur in the direction of the $\boldsymbol {E} \times \boldsymbol {B}$ and diamagnetic drifts. One type of instability, observed when the equilibrium electric field and plasma density gradient are in the same direction, is similar to the classic modified Simon–Hoh instability. A second instability is found for conditions in which (i) the diamagnetic drift is in the direction opposite to the $\boldsymbol {E} \times \boldsymbol {B}$ drift and (ii) the magnitude of the diamagnetic drift is sufficiently larger than the electron thermal speed. The present fluid dispersion theory suggests that the rotating spokes driven by such fluid instabilities propagate in the same direction as the diamagnetic drift, which can be in the same direction as or opposite to the $\boldsymbol {E} \times \boldsymbol {B}$ drift, depending on the plasma conditions. This finding may account for the observation, in some plasma devices, of the rotation of large-scale structures in both the $\boldsymbol {E} \times \boldsymbol {B}$ and $-\boldsymbol {E} \times \boldsymbol {B}$ directions.

1. Introduction

Low-temperature magnetised plasmas can be found in a variety of applications and natural phenomena, including magnetron discharges (Keidar & Beilis 2006; Anders 2012; Ito, Young & Cappelli 2015; Hecimovic & von Keudell 2018), Penning discharges (Quraishi, Robertson & Walch 2002; Abolmasov 2012), Hall effect thrusters (HETs) and accelerators (Ellison, Raitses & Fisch 2012; Sekerak et al. 2015; Romadanov et al. 2016; Mazouffre et al. 2019), high-power microwaves (Lau 2001; Benford, Swegle & Schamiloglu 2015), dusty (complex) plasmas (Bal & Bose 2010) and interplanetary and interstellar environments (Breneman et al. 2013). An applied magnetic field traps the charged particles, thus increasing ionisation efficiency and reducing the diffusivity, serving as a critical path to control flows and chemistry in low-temperature plasmas.

Depending on the magnetic field strength and collision frequency, plasmas can be either partially magnetised (i.e. electrons are magnetised but ions are non-magnetised) or fully magnetised (i.e. both ions and electrons are magnetised). In low-temperature plasmas, the dynamics of the neutral gas also play an important role in the transport properties and time-dependent plasma behaviour. The multiscale nature of the plasma flow in such low-temperature magnetised plasmas leads to various oscillation modes from high frequency (of the order of gigahertz) to low frequency (of the order of kilohertz) (Hara 2019). Recent studies suggest that the anomalous electron transport across magnetic fields can be due to plasma–wall interaction (Kaganovich et al. 2007; Sydorenko et al. 2008), the plasma waves initiated by kinetic instabilities (Adam, Héron & Laval 2004; Héron & Adam 2013; Boeuf 2017; Janhunen et al. 2018) or a combination of these effects (Héron & Adam 2013; Villafana et al. 2021). A few examples of the kinetic instabilities in the high-frequency range include the electron cyclotron drift instability (Forslund, Morse & Nielson 1971), modified two-stream instability (McBride et al. 1972), and ion–ion two-stream instability (Gary 1991; Tsikata et al. 2014). On the other hand, low-frequency plasma oscillations include breathing mode oscillations (Boeuf & Garrigues 1998; Barral & Ahedo 2009; Hara et al. 2014a, b; Dale & Jorns 2019) and azimuthally rotating spokes (Ellison et al. 2012; Sekerak et al. 2015; Kawashima, Hara & Komurasaki 2018). The coupling between different instabilities in various spatial and temporal scales plays an important role in determining the transport coefficients and turbulent phenomena in such low-temperature magnetised plasmas.

In this paper, we derive the dispersion relation of low-frequency, large-wavelength gradient drift instabilities, which may lead to the self-organising patterns in the low-temperature magnetised plasmas. We consider a Penning-type configuration, where a homogeneous axial magnetic field is applied and an electric field and density gradient exist in the radial direction. Although the spokes are often observed in numerical simulations (Boeuf 2014; Powis et al. 2018; Boeuf & Takahashi 2020) and in experiments (Raitses, Kaganovich & Smolyakov 2015; Marcovati, Ito & Cappelli 2020), the mechanism of the spoke formation is still not well understood. One of the most accepted theories attributes the formation of rotating spokes in a Penning-type discharge to the class of Simon–Hoh instabilities (SHIs) (Simon 1963; Hoh 1963). This terminology was first used by Sakawa et al. (1993), who proposed the modified Simon–Hoh instability (MSHI), which comes from a dispersion relation for partially magnetised plasma, whereas the original work by Simon and Hoh individually focused on fully magnetised plasmas. In work by Simon (1963), the criterion for rotating spoke formation has been proposed to be $\boldsymbol {E}_0\boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$, where $\boldsymbol {E}_0$ is the applied electric field and $\boldsymbol {\nabla } n_0$ is the equilibrium plasma density gradient. Recent experimental studies in low-temperature magnetised plasma sources have shown, however, that the rotation direction and speed can depend on various plasma parameters, such as the current (Anders & Yang 2017), indicating that the instability criterion needs to be revisited.

The theory of gradient-drift instabilities in low-temperature magnetised plasmas is introduced in this paper. Section 2 discusses the linearised fluid equations for magnetised plasmas under an applied magnetic field, assuming that the gyroviscosity effects are negligible. Section 3 shows a low-frequency plasma dispersion relation of the partially magnetised plasma considering a slab geometry. The criteria for the large-wavelength, low-frequency, gradient drift instability under a homogeneous magnetic field are discussed. Section 4 illustrates the results of the dispersion relation for partially magnetised plasmas, showing results consistent with the instability criteria derived in § 3. The gradient drift instability theory is applied to various cross-field plasma devices in § 5.

2. Linearised plasma equations for low-temperature magnetised plasmas

Although the rotating spokes are observed in cylindrical (axisymmetric) systems, here we simplify the dispersion relation assuming a slab (Cartesian) geometry. A static, uniform magnetic field in $z$ direction $\boldsymbol {B} = B_0 \hat {\boldsymbol {z}}$ and an equilibrium electric field (applied electric field) are considered: $\boldsymbol {E}_0 = E_0 \hat {\boldsymbol {x}}$. It is assumed that the equilibrium plasma is quasineutral and a plasma density gradient exists locally in the $x$ direction: $E_{0} \neq 0$ and ${\rm d}n_0 /{{\rm d} x} \neq 0$, generating $\boldsymbol {E}\times \boldsymbol {B}$ and diamagnetic drifts in the ${\pm }y$ direction, for the equilibrium condition. In addition, the following assumptions are made: (i) although the temperature gradient may affect the instabilities, we assume that the temperature is uniform and constant, for simplicity; (ii) only ions and electrons are assumed for the species; (iii) the plasma is assumed to be partially magnetised (i.e. magnetised electrons and unmagnetised ions); (iv) collisions are assumed negligible; and (v) the plasma is electrostatic, that is, effects of the induced magnetic field are negligible compared with the applied magnetic field.

2.1. Governing equations

The fluid equations are used for both ions and electrons, i.e. when kinetic effects, such as the Bernstein modes (Bernstein 1958), can be neglected.

Conservation of mass can be constructed by taking the zeroth moment of the kinetic equation. Here, ionisation and recombination are neglected. Thus, the continuity equation can be written as

(2.1)\begin{equation} \frac{\partial n_s}{\partial t} + \boldsymbol{\nabla}\boldsymbol{\cdot}(n_s\boldsymbol{u}_s) = 0, \end{equation}

where $n_s$ is the number density and $\boldsymbol {u}_s$ is the bulk velocity for species $s$.

The equation for the fluid momentum can be formulated by taking the first moment of the kinetic equation, which can be written using conservative or primitive variables. Assuming that the plasma is collisionless and the distribution function is close to an isotropic Maxwellian distribution function, the conservation of momentum can be written as

(2.2)\begin{equation} \frac{\partial (m_sn_s\boldsymbol{u}_s)}{\partial t} + \boldsymbol{\nabla} \boldsymbol{\cdot}(m_sn_s\boldsymbol{u}_s\boldsymbol{u_s}) ={-}\boldsymbol{\nabla} p_s + q_s n_s(\boldsymbol{E} + \boldsymbol{u}_s\times\boldsymbol{B}), \end{equation}

where $m_s$ is the mass, $p_s$ is the pressure, $q_s$ is the charge, $\boldsymbol {E}$ is the electric field and $\boldsymbol {B}$ is the magnetic field. Using the source-less continuity equation, as shown in (2.1), the momentum equation can also be given, using the primitive variables, by

(2.3)\begin{equation} \frac{\partial \boldsymbol{u}_s}{\partial t} + (\boldsymbol{u}_s\boldsymbol{\cdot} \boldsymbol{\nabla})\boldsymbol{u}_s ={-}\frac{\boldsymbol{\nabla} p_s}{m_s n_s} + \frac{q_s}{m_s} (\boldsymbol{E} + \boldsymbol{u_s}\times \boldsymbol{B}). \end{equation}

Note that the pressure is a scalar term, which is valid when the velocity distribution function (VDF) is close to an isotropic Maxwellian distribution function, that is, the temperatures in three directions are equal. Under this condition, the pressure can be written using the ideal gas law: $p_s = n_s k_B T_s$, where $k_B$ is the Boltzmann constant and $T_s$ is the temperature for species $s$.

In the present model, the ideal gas law is assumed for the electron fluid model. It is to be noted that standard drift models account for gyroviscosity effects, which arise due to the non-Maxwellian distribution and lead to cancellation of the diamagnetic drift in the inertia term in the momentum equation (Ramos 2005; Schnack et al. 2006). Although the gyroviscosity effects may play an important role in low-temperature, partially magnetised plasmas (Smolyakov et al. 2016), the validity of the drift models and the necessity of including gyroviscosity effects in low-temperature magnetised plasmas needs to be investigated. In the state-of-the-art computational models for low-temperature plasmas, simplified fluid models such as the drift-diffusion model are known to represent the physical processes (Kushner 2009; Hara 2019). In this paper, a five-moment model that neglects the gyroviscosity effects is used, based on recent numerical simulations that show low-frequency rotating spokes (Mansour & Hara 2022). The inclusion of the gyroviscosity effects is reserved for future work.

2.2. Linear perturbation analysis for partially magnetised plasmas

We consider the growth of the instabilities in $y$ direction, that is, the direction in which the electrons drift. Under the linear perturbation analysis, a plasma property $Q$ can be described as a sum of the steady-state quantity and a linear perturbation, such that

(2.4)\begin{equation} Q = Q_0 + Q_1 \exp(-{\rm i}\omega t + {\rm i} k_y y), \end{equation}

where $Q_0$ and $Q_1$ are the equilibrium (steady-state) and first-order perturbation terms of a plasma property $Q$, respectively, $\omega$ is the frequency, $t$ is time and $k_y$ is the wave number in the $y$ direction. Here, $\omega = \omega _r + {\rm i}\gamma$, where $\omega _r$ is the real frequency and $\gamma$ is the imaginary part which corresponds to the growth rate.

2.3. Zeroth-order (equilibrium) equations for magnetised electrons

Inserting (2.4) into the governing equations and considering the zeroth-order terms leads to the equilibrium equations. For magnetised electrons, using (2.3) and considering the equilibrium bulk velocity $\boldsymbol {u}_{e0} = (u_{e0x}, u_{e0y}, u_{e0z})^\intercal$, where subscripts $x$, $y$ and $z$ denote the direction, the steady-state momentum equation in $x$ and $y$ directions can be written as

(2.5)\begin{gather} 0 ={-}\frac{k_B T_e}{m_e n_0}\frac{\partial n_0}{\partial x} -\frac{e}{m_e} (E_0 + u_{e0y}B_0) , \end{gather}

(2.6)\begin{gather}0 = \frac{e}{m_e} u_{e0x}B_0 , \end{gather}

where $e$ is the elementary charge, $T_e$ is the electron temperature, $m_e$ is the electron mass and $n_0$ is the equilibrium density, assuming quasineutrality for the equilibrium condition.

Recall that the equilibrium density gradient and electric field are considered to exist locally only in $x$ direction. Although (2.6) results in $u_{e0x}=0$, (2.5) yields the well-known drifts:

(2.7)\begin{equation} u_{e0y} ={-}\frac{E_0}{B_0} - \frac{k_B T_e}{e n_0} \frac{ n_0'}{B_0}, \end{equation}

where $n_0'={\rm d}n_0/{{\rm d} x}$ is the plasma density gradient. The first term in (2.7) is the $\boldsymbol {E} \times \boldsymbol {B}$ drift and the second term is the diamagnetic drift, which can be written as $u_E$ and $u_*$, respectively. The diamagnetic drift does not come from the single-particle trajectory analysis but appears as an equilibrium drift from the fluid theory, whereas the $\boldsymbol {E} \times \boldsymbol {B}$ drift can be derived from single particle trajectories. Nonetheless, the diamagnetic drift is a steady-state bulk velocity that can propagate in the same or opposite direction of the $\boldsymbol {E} \times \boldsymbol {B}$ drift.

As the density gradient is only considered in $x$ direction and using $u_{e0x} = 0$ obtained from (2.6), the steady-state conservation of mass can be written as

(2.8)\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{u}_{e0} = 0. \end{equation}

This relation shows that $u_{e0y}$ is constant in $y$ direction, i.e. homogeneous, which is consistent with the configuration considered.

2.4. First-order (linear perturbation) equations for magnetised electrons

Let us consider the perturbation terms of the electron bulk velocity to be $\boldsymbol {u}_{e1} = (u_{e1x}, u_{e1y}, 0)^\intercal$ for magnetised electrons. Using (2.8), the first-order conservation of mass can be derived from (2.1) as

(2.9)\begin{equation} \frac{ \partial n_{e1}}{\partial t} + n_0\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{u}_{e1} + \boldsymbol{u}_{e0}\boldsymbol{\cdot}\boldsymbol{\nabla} n_{e1} + \boldsymbol{u}_{e1}\boldsymbol{\cdot} \boldsymbol{\nabla} n_0 = 0. \end{equation}

Using the linear perturbation shown in (2.4), the perturbed electron density can be written as

(2.10)\begin{equation} n_{e1} = \frac{n_0k_yu_{e1y} -{\rm i} u_{e1x} n_0'}{\tilde{\omega}}, \end{equation}

where $\tilde {\omega }= \omega - k_yu_{e0y}$. Note that $u_{e0y}$ is given in (2.7).

The first-order momentum equation can be derived from (2.2). Note that pressure term leads to

(2.11)\begin{equation} \frac{k_B T_e \boldsymbol{\nabla}(n_0+n_{e1})}{m_e(n_0+n_{e1})} =\frac{k_B T_e}{m_e}\left[ \frac{\boldsymbol{\nabla} n_0}{n_0} \left( 1 - \frac{n_{e1}}{n_0} \right) + \frac{\boldsymbol{\nabla} n_{e1}}{n_0} \right], \end{equation}

which results in two contributions to the linearised momentum equation. Thus, using (2.11), the first-order momentum equation for magnetised electrons can be given by

(2.12)\begin{equation} -{\rm i}\tilde{\omega} \boldsymbol{u}_{e1} = v_{{\rm th}}^2 k_n \frac{n_{e1}}{n_0} \hat{\boldsymbol{x}} - v_{{\rm th}}^2 \frac{\boldsymbol{\nabla} n_{e1}}{n_0} - \frac{e}{m_e}(\boldsymbol{E}_1 + \boldsymbol{u}_{e1}\times\boldsymbol{B}_0), \end{equation}

where $v_{{\rm th}} = (k_B T_e/m_e)^{1/2}$ is the electron thermal speed and $k_n = n_0' / n_0$ is the inverse of the density gradient length scale, which is also defined similarly by Sakawa et al. (1993) and Smolyakov et al. (2016). Taking the perturbation terms in $y$ direction, e.g. $\phi _1 \exp (-{\rm i}\omega t +{\rm i} k_y y)$ for the electric field using the electrostatic assumption: $\boldsymbol {E}=-\boldsymbol {\nabla } \phi$, (2.12) can be written for $x$ and $y$ directions as

(2.13)\begin{equation} \begin{bmatrix} -{\rm i}\tilde{\omega} & \omega_{{\rm ce}}\\ -\omega_{{\rm ce}} & -{\rm i}\tilde{\omega} \end{bmatrix} \begin{bmatrix} u_{e1x}\\ u_{e1y} \end{bmatrix} =\begin{bmatrix} v_{{\rm th}}^2 k_n \frac{n_{e1}}{n_0}\\ -{\rm i} v_{{\rm th}}^2 k_y \frac{n_{e1}}{n_0} +{\rm i} \frac{e}{m_e}k_y\phi_1 \end{bmatrix}, \end{equation}

where $\omega _{{\rm ce}} = eB_0/m_e$ is the electron gyrofrequency. Solving for $u_{e1x}$ and $u_{e1y}$ in (2.13) gives

(2.14)\begin{gather} u_{e1x} = \frac{{\rm i}}{\tilde{\omega}^2-\omega_{{\rm ce}}^2} \left[ \tilde{\omega} k_n v_{{\rm th}}^2 \frac{n_{e1}}{n_0} - \omega_{{\rm ce}}k_y\left(v_{{\rm th}}^2 \frac{n_{e1}}{n_0} - \frac{e}{m_e} \phi_1 \right) \right], \end{gather}

(2.15)\begin{gather}u_{e1y} = \frac{1}{\tilde{\omega}^2-\omega_{{\rm ce}}^2} \left[- \omega_{{\rm ce}}k_n v_{{\rm th}}^2 \frac{n_1}{n_0} + \tilde{\omega}k_y\left( v_{{\rm th}}^2 \frac{n_{e1}}{n_0} - \frac{e}{m_e}\phi_1 \right) \right]. \end{gather}

Equations (2.14) and (2.15) are similarly derived in the Rayleigh–Taylor instability analysis (Chen 1984). If cold electrons are assumed (i.e. $v_{{\rm th}} = 0$) and one considers the low-frequency approximation (i.e. $\tilde {\omega }^2 \ll \omega _{{\rm ce}}^2$), (2.14) and (2.15) reduce to $u_{e1x} = E_{1y}/B_0$ and $u_{e1y}= {\rm i}\tilde {\omega } u_{e1x}/\omega _{{\rm ce}}$, which are equivalent to the perturbed $\boldsymbol {E} \times \boldsymbol {B}$ and polarisation drifts, respectively. However, it can be seen that the determinant of the matrix in (2.13) becomes negative if $\tilde {\omega }^2 \gg \omega _{{\rm ce}}^2$. In this case, $u_{e1x}$ moves in the opposite direction of the perturbed $\boldsymbol {E} \times \boldsymbol {B}$ drift, which seems to be non-physical (see Appendix A for some discussions). Therefore, assuming $\tilde {\omega }^2 \ll \omega _{{\rm ce}}^2$ and using (2.14) and (2.15), (2.10) can be written as

(2.16)\begin{equation} \frac{n_{e1}}{n_0} = \frac{e\phi_1 }{m_e} \frac{ k_y^2 \tilde{\omega}- k_nk_y \omega_{{\rm ce}}}{ \omega_{{\rm ce}}^2 \tilde{\omega} + \left( k_y^2 + k_n^2\right)v_{{\rm th}}^2 \tilde{\omega} - 2k_nk_y \omega_{{\rm ce}}v_{{\rm th}}^2}. \end{equation}

Note that this equation is similar to (10) in Sakawa et al. (1993), except for the coefficient of the last term in the denominator.

2.5. Dispersion function for unmagnetised ions

Let us derive the zeroth-order equations for unmagnetised ions. If restricting the argument to the cross-field direction ($x$ and $y$), that is, neglecting the plasma dynamics in $z$ direction (along the magnetic field), the steady-state continuity equation gives, $n_0 u_{i0x} ={\rm const}.$, where $u_{i0x}$ is the equilibrium ion bulk velocity in $x$ direction. Assuming that the ion bulk velocity is negligible in $y$ direction (i.e. $u_{i0y} = 0$), the linear perturbation of the ion number density, $n_{i1}$, can be derived from the linearised conservation of mass as

(2.17)\begin{equation} n_{i1} = \frac{n_0k_yu_{i1y} -{\rm i} u_{i1x} n_0'}{ \omega - {\rm i} k_n u_{i0x}}, \end{equation}

where ${\boldsymbol {u}}_{i1} = (u_{i1x}, u_{i1y},0)^\intercal$ is the linear perturbation of the ion bulk velocities.

Assuming cold ions ($T_i= 0$, where $T_i$ is the ion temperature) and only considering perturbation in $y$ direction, as shown in (2.4), the linearised momentum equation for unmagnetised ions can be written as

(2.18)\begin{gather} u_{1x} = 0, \end{gather}

(2.19)\begin{gather}u_{1y} = \frac{k_y}{{\omega}} \frac{e}{m_i}\phi_1, \end{gather}

where $m_i$ is the ion mass. If one further assumes that the effects of $k_n u_{i0x}$ to be small, (2.17) can be reduced to

(2.20)\begin{equation} \frac{n_{i1}}{n_0} = \frac{e k_y^2}{m_i \omega^2}\phi_1. \end{equation}

This is consistent with the dispersion function used for unmagnetised ions in Sakawa et al. (1993).

3. Gradient drift instability for partially magnetised plasmas

3.1. Fluid dispersion relation

Assuming quasineutrality and perturbations occur in the azimuthal direction, which are similar assumptions employed for the Rayleigh–Taylor instability theory (Chen 1984), and using (2.16) and (2.20), the dispersion relation for partially magnetised plasmas can be derived as

(3.1)\begin{equation} \frac{m_e k_y}{m_i \omega^2 } = \frac{ k_y \tilde{\omega}- k_n \omega_{{\rm ce}}}{ [\omega_{{\rm ce}}^2 + \left( k_y^2 + k_n^2\right)v_{{\rm th}}^2] \tilde{\omega} - 2k_nk_y \omega_{{\rm ce}}v_{{\rm th}}^2}, \end{equation}

where $\tilde {\omega } = \omega - k_y u_{e0y}$ is used throughout the derivation. Here, this drift-shifted frequency can be written as $\tilde {\omega } = \omega - \omega _E - \omega _*,$ where $\omega _E = k_y u_E$, $\omega _* = k_y u_*$, $u_E = - E_0 / B_0$ and $u_* = - k_n k_B T_e / (e B_0)$, as can be seen from (2.7). It can be seen that (3.1) yields a third-order equation for $\omega$, from which the damping and linear instability growth can be evaluated.

3.2. Instability criteria in the large-wavelength limit

In the limit of a large-wavelength mode, a simplified form of (3.1) can be obtained by neglecting the $k_y \tilde {\omega }$ term in the numerator of (3.1) compared with $k_n \omega _{{\rm ce}}$, that is, $k_y \tilde {\omega } \ll k_n \omega _{{\rm ce}}$. In addition, $u_* \omega _{{\rm ce}} = - k_n v_{{\rm th}}^2$ gives $k_n^2 v_{{\rm th}}^2 = \tilde {u}_*^2 \omega _{{\rm ce}}^2$, where $\tilde {u}_*=u_*/v_{{\rm th}}$. Therefore, in this limit, (3.1) can be written as

(3.2)\begin{equation} 0 ={-} \frac{k_n m_i }{m_e \omega_{{\rm ce}}} \omega^2 - k_y(1 + \tilde{u}_*^2) \omega + \tilde{u}_*^2 k_y^2 (u_E+u_*) + k_y^2 (u_E-u_*). \end{equation}

For the solution to have an unstable mode, that is, a root with a positive growth rate, the discriminant of (3.2) must be negative. The instability condition can therefore be given by

(3.3)\begin{equation} \frac{m_e }{m_i}(1+\tilde{u}_*^2)^2-4\tilde{u}_* \left[ (1+\tilde{u}_*^2) \tilde{u}_E - (1-\tilde{u}_*^2) \tilde{u}_* \right] < 0, \end{equation}

where $\tilde {u}_E = u_E / v_{{\rm th}}$. By rewriting (3.3) considering $m_e \ll m_i$, the condition for the partially magnetised plasma to have an unstable mode in the limit of large wavelength can be written as

(3.4)\begin{equation} \tilde{u}_* F(\tilde{u}_*, \tilde{u}_E) >0, \end{equation}

where

(3.5)\begin{equation} F(\tilde{u}_*, \tilde{u}_E) = \tilde{u}_*^3 + \tilde{u}_E \tilde{u}_*^2 - \tilde{u}_* + \tilde{u}_E . \end{equation}

As can be seen from (3.4), the two instability criteria can be obtained as (i) $\tilde {u}_*>0$ and $F(\tilde {u}_*, \tilde {u}_E) >0$ and (ii) $\tilde {u}_*<0$ and $F(\tilde {u}_*, \tilde {u}_E) <0$.

It can be seen that (3.3), in the limit of $|\tilde {u}_*| \rightarrow 0$ and considering $m_e \ll m_i$, reduces to $u_E u_* > 0$, which is the instability criterion for the MSHI (Sakawa et al. 1993). See Appendix B for further discussion about the comparison of the present dispersion relation and MSHI.

Figure 1 shows the shape of (3.5) for two values of $\tilde {u}_E$, that is, $\tilde {u}_E = -0.1$ and $-0.6$, to illustrate the range of unstable and stable roots in the limit of large wavelength and low frequency. Here, negative $u_E$ values are chosen, as the $\boldsymbol {E} \times \boldsymbol {B}$ drift occurs in $-y$ direction when considering $E_0$ in $x$ direction and $B_0$ in $z$ direction. Unlike the MSHI that predicts one region for unstable modes, that is, $\tilde {u}_* \tilde {u}_E > 0$, two unstable regions can be seen in figure 1(a), whereas three unstable regions can be seen in figure 1(b).

Figure 1. Cubic function, $F(\tilde {u}_*, \tilde {u}_E)$, shown in (3.5) for (a) $u_E = -0.6 v_{{\rm th}}$ and (b) $u_E = -0.1 v_{{\rm th}}$, resulting in two and three instability regions, respectively. Instabilities occur according to (3.4) in the regions where the product of the $u_*$ and the function $F(\tilde {u}_*, \tilde {u}_E)$ is positive. The red dashed line denotes $F=0$ and the unstable regions are indicated in blue.

Figure 2 shows the unstable and stable regions of the gradient drift instability in the large-wavelength limit, as a function of the diamagnetic drift and $\boldsymbol {E} \times \boldsymbol {B}$ drift. The unstable roots are obtained according to the instability condition shown in (3.4), and the results are consistent with figure 1, showing the two and three unstable regions depending on $u_*$ and $u_E$. A few observations about the instability criteria can be made as follows.

1. (i) When $|\tilde {u}_E| > 0.3$, there are two regions that satisfy the instability condition shown in (3.4). One is $u_E u_*>0$, leading to a condition that can be written as $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$, which is similar to the MSHI. In this regime, both $\boldsymbol {E} \times \boldsymbol {B}$ and diamagnetic drifts are in the same direction, leading to instability. The other region that results in instability can be found at $u_* > v_{{\rm th}}$ while $u_E < 0$, as shown in figures 1(a) and 2. It is interesting to note that $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0<0$ in this second region, which is a different instability criterion compared to the MSHI. This indicates that a strong diamagnetic drift (compared with the magnitude of the $\boldsymbol {E} \times \boldsymbol {B}$ drift and the electron thermal speed) can drive an instability at large wavelength whereas the diamagnetic drift is in the opposite direction to the $\boldsymbol {E} \times \boldsymbol {B}$ drift.

2. (ii) When $0< |\tilde {u}_E| \lessapprox 0.3$, there are three regions that result in linear instability. As can be seen from figure 1(b), $F$ becomes positive in a certain range within $u_*<0$, leading to a stable root because $u_* F < 0$. The appearance of a stable mode in the $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$ region can also be seen from figure 2. It can be shown from (3.5) that $F\approx (\tilde {u}_*-\tilde {u}_E)(\tilde {u}_*+ \tilde {u}_E - 1 ) (\tilde {u}_*+ \tilde {u}_E + 1 )$ when assuming $|\tilde {u}_E| \ll 1$. Hence, the three instability regions can be observed approximately at (i) $\tilde {u}_* < -1 - \tilde {u}_E$, (ii) $\tilde {u}_E<\tilde {u}_* < 0$ and (iii) $\tilde {u}_* > 1-\tilde {u}_E$ for $\tilde {u}_E<0$.

3. (iii) When $\tilde {u}_E=0$, there are two regions where the unstable roots exist. Equation (3.5) reduces to $F = \tilde {u}_* (\tilde {u}_* - 1 ) (\tilde {u}_* + 1 )$ when $\tilde {u}_E=0$. Hence, the instability regions can be observed at (i) $\tilde {u}_* < -1$, and (ii) $\tilde {u}_* > 1$, which can be seen from figure 2. The solutions indicate that a low-frequency, large-wavelength instability can occur with a strong diamagnetic drift in the absence of any electric field.

Figure 2. Unstable and stable regions of the gradient drift instability in the large-wavelength limit, as a function of $u_E$ and $u_*$. The blue region indicates where the unstable modes exist, whereas unstable modes do not exist in the stable region, shown in white.

Figure 3 shows the schematic of the instability criteria for the low-frequency rotating spokes. The first condition $u_E u_*>0$ is similar to the MSHI, in which it is predicted that the $\boldsymbol {E} \times \boldsymbol {B}$ and diamagnetic drifts must be in the same direction. Another instability condition observed from the derivations shown in this section (i.e. (3.4) and (3.5)) illustrates that the partially magnetised plasma can be unstable when the diamagnetic drift is sufficiently larger than the electron thermal speed, even if the electric field and the density gradient exist in the opposite direction.

Figure 3. Instability criteria for low-frequency rotating spokes. (a) The $\boldsymbol {E} \times \boldsymbol {B}$ drift and diamagnetic drift are in the same direction. (b) The $\boldsymbol {E} \times \boldsymbol {B}$ drift and diamagnetic drift are in the opposite direction and the diamagnetic drift must be larger than the electron thermal speed.

3.3. Direction of the wave propagation

When the instability condition is met in (3.3), the real part of the solution in (3.2) can be obtained as

(3.6)\begin{equation} \omega_r = \frac{(1+\tilde{u}_*^2) c_s }{2u_*} k_y c_s, \end{equation}

where $c_s=(k_B T_e /m_i)^{1/2}$ is the ion acoustic speed. The phase velocity of the wave can be obtained from $v_\phi = \omega _r / k_y$. It can therefore be seen from (3.6) that the wave propagates in the direction of the diamagnetic drift, which may lead to the rotating spokes to propagate in the direction of $\boldsymbol {E} \times \boldsymbol {B}$ drift or $-\boldsymbol {E} \times \boldsymbol {B}$ drift, depending on the instability criteria discussed in § 3.2.

3.4. Resonance

It can be seen from (2.14) and (2.15) that the linear perturbation of the electron bulk velocities shows resonance when $\tilde {\omega }^2 \approx \omega _{{\rm ce}}^2$. In other words, $\omega \approx \pm \omega _{{\rm ce}} + k_y u_{e0y}$, where $u_{e0y}$ is the sum of the $\boldsymbol {E} \times \boldsymbol {B}$ drift and diamagnetic drift, given in (2.7). If the real frequency is of the order of ion plasma frequency, $\omega _r \ll \omega _{{\rm ce}}$, as shown later in § 4, a resonance condition for the dispersion relation can be considered to be

(3.7)\begin{equation} k_y ={\mp} \frac{\omega_{{\rm ce}}}{u_{e0y}}. \end{equation}

It can be seen that the smaller (larger) the electron drift, the larger (smaller) $k_y$ at which resonance occurs. Equation (3.7) indicates that the electron drift is in resonance with the electron gyromotion, which is akin to the electrostatic two-stream instability where the electron drift is in resonance with the electron plasma frequency.

Equation (3.7) can also be written as $k_y \lambda _D = \tilde {u}_{e0y}^{-1}{\omega _{{\rm ce}}}/{\omega _{{\rm pe}}}$ or $k_y r_L = \tilde {u}_{e0y}^{-1}$, where $\omega _{{\rm pe}}=(e^2n_0 / m_e \epsilon _0)^{1/2}$ is the electron plasma frequency, $\lambda _D = (\epsilon _0 k_B T_e / e^2 n_0)^{1/2}$ is the Debye length, $\epsilon _0$ is the vacuum permittivity, $\tilde {u}_{e0y}=u_{e0y}/v_{{\rm th}}$ and $r_L = v_{{\rm th}}/\omega _{{\rm ce}}$ is the electron Larmor radius. Although the kinetic effects, such as the electron Bernstein mode leading to electron cyclotron drift instability (Cavalier et al. 2013; Hara & Tsikata 2020), may play an important role when $k_y r_L=O(1)$, the results in the present fluid theory are applicable for the smaller $k_y$ range, e.g. $k_y r_L<1$. Investigation of the coupling of the present fluid theory and the kinetic dispersion relation (Chang & Callen 1992) is reserved for future work.

4. Results

In this section, the results from the linear perturbation theory are discussed. Although the analytic discussions made in § 3.2 are applicable only in the large-wavelength, low-frequency limit, the dispersion relation introduced in (3.1) is valid for a wide range of $k_y$ under the assumption of the fluid approach and before the resonance condition as shown in (3.7). It is discussed in this section that the growth rate exhibits a broadband profile and the real frequency is of the order of the ion plasma frequency, which suggests that the wave propagation speed is of the order of the ion acoustic speed.

The following conditions are considered for two cases: $B_0= 200$ G, $n_0=10^{15}\ {\rm m}^{-3}$, the electron temperature is $4$ eV and $m_i=40$ amu (assuming singly charged argon ions). These plasma parameters are representative of low-temperature cross-field plasma sources. Here, the two cases considered are (I) $E_0 = 10\ {\rm kV}\ {\rm m}^{-1}$ and (II) $E_0 = 4\ {\rm kV}\ {\rm m}^{-1}$. Cases I and II result in $u_E \approx -0.6 v_{{\rm th}}$ and $u_E \approx -0.24 v_{{\rm th}}$, respectively, which correspond to the two and three instability region cases as shown in figure 1. The solution to (3.1) is evaluated for several representative values of $u_*$.

4.1. Case I: two instability regions, $u_E \approx -0.6 v_{{\rm th}}$

Figure 4 shows the real and imaginary parts of the solution of (3.1) for different $u_*$ values for $u_E \approx -0.6 v_{{\rm th}}$. This is consistent with the two instability region case, which occurs when $|u_E| > 0.3$, as shown in figure 1(a).

Figure 4. Case I: two instability regions at large wavelength, for different values of $u_*$ with $u_E$ fixed at $u_E = -0.6 v_{{\rm th}}$. This value of $u_E = -0.6 v_{{\rm th}}$ corresponds to the case illustrated in figure 1(a). The real frequency, $\omega _r$, and growth rate, $\gamma$, are shown in blue dashed and black solid lines, respectively, for each value of $u_*$.

In the limit of a large positive diamagnetic drift (e.g. $u_* = 1.67 v_{{\rm th}}$ as shown in figure 4a), a low-frequency mode is indeed observed in the limit of large wavelength. The real frequency, $\omega _r$, is positive, indicating that wave propagates in the direction of the diamagnetic drift as opposed to the $\boldsymbol {E} \times \boldsymbol {B}$ drift. This observation is consistent with the theoretical observation in § 3.2.

Figures 4(b) and 4(c) show that the dispersion relation yields roots with a positive growth rate at a finite $k_y\neq 0$ but yields stable solutions in the large-wavelength limit, as the magnitude of the diamagnetic drift decreases. Note that for these cases, $u_E u_*<0$, that is, the diamagnetic drift is in the direction opposite to the $\boldsymbol {E} \times \boldsymbol {B}$ drift. These results are consistent with the prediction from the analytic theory obtained in § 3.2. It is to be noted that the sign of the real frequency flips, which can be seen from figures 4(b) and 4(c), indicating that the resonance type phenomenon is driven by the diamagnetic drift in figure 4(b). However, the wave propagates in the direction of the $\boldsymbol {E} \times \boldsymbol {B}$ drift in figure 4(c) despite the fact that the magnitude of diamagnetic drift is larger than the $\boldsymbol {E} \times \boldsymbol {B}$ drift. As the diamagnetic drift approaches zero, the resonance condition shifts towards a larger $k_y \lambda _D$, as shown in (3.7), and the partially magnetised plasma is stable for a wide range of $k_y$.

When the diamagnetic drift is in the same direction as the $\boldsymbol {E} \times \boldsymbol {B}$ drift (i.e. $u_E u_*>0$), the results in figure 4(d–f) illustrate that the large-wavelength mode is indeed unstable. This is consistent with § 3.2, in which it is observed that $u_E u_*>0$ yields a root with a positive growth rate at the large-wavelength, low-frequency limit, if $|u_E|> 0.3 v_{{\rm th}}$. Another observation that can be made is that the real frequency is negative, illustrating that the wave propagates in the direction of both $\boldsymbol {E} \times \boldsymbol {B}$ drift and diamagnetic drift. The real frequency where the growth rate is maximum is approximately $(5\text {-}6)\omega _{{\rm pi}}$, suggesting that the wave propagation speed is of the order of the ion acoustic speed. The cutoff where $\gamma$ becomes zero at a finite $k_y$ in figure 4(d–f) occurs before the resonance condition discussed in § 3.4.

4.2. Case II: three instability regions, $u_E \approx -0.24 v_{{\rm th}}$

Figure 5 shows the real and imaginary parts of the solution of (3.1) for several representative $u_*$ values for $u_E \approx -0.24 v_{{\rm th}}$. As discussed in § 3.2 and shown in figure 1(b), three instability regions can be seen in the large-wavelength limit, when $|u_E| \lessapprox 0.3 v_{{\rm th}}$.

Figure 5. Case II: three instability regions at large wavelength, for different values of $u_*$ with $u_E$ fixed at $u_E = -0.24 v_{{\rm th}}$. The real frequency, $\omega _r$, and growth rate, $\gamma$, are shown in blue dashed and black solid lines, respectively, for each value of $u_*$. In figure 5(e), the growth rate is zero at $k_y \lambda _D \ll 1$, which corresponds to the region where $u_*<0$ and $F>0$, shown in figure 1(b).

Similar to Case I, there is a low-frequency mode at large wavelength when the diamagnetic drift is opposite to the $\boldsymbol {E} \times \boldsymbol {B}$ drift and the magnitude of the diamagnetic drift is sufficiently larger than the electron thermal speed, as shown in figure 5(a). Under this situation, the wave propagation occurs in the direction of the diamagnetic drift. As the magnitude of the diamagnetic drift is decreased, the partially magnetised plasma becomes stable in the large-wavelength limit but a resonance type mode appears, as shown in figures 5(b) and 5(c), similar to Case I. In addition, when the diamagnetic drift is in the same direction as the $\boldsymbol {E} \times \boldsymbol {B}$ drift, the partially magnetised plasma is unstable in the large-wavelength limit, which can be seen in figures 5(d) and 5( f). However, it is interesting to note that the growth rate becomes zero at $k_y \rightarrow 0$ for the cases with intermediate $u_*$ values, as shown in figure 5(e). This is consistent with the theoretical prediction in § 3.2 and figure 1(b): when $|u_E| \lessapprox 0.3 v_{{\rm th}}$, the partially magnetised plasma becomes stable at $k_y \rightarrow 0$ for a range of $u_*$ in which $u_* F<0$, as shown in figure 1(b).

In summary, the partially magnetised plasma dispersion relation using the fluid approach shows that the linear growth rate is positive in the large-wavelength limit not only (i) when $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 >0$ but also (ii) when $\boldsymbol {E}_0 \boldsymbol {\cdot } \boldsymbol {\nabla } n_0 <0$ and the diamagnetic drift is sufficiently larger than the electron thermal speed. Although the former is similar to the so-called MSHI, the latter suggests that a strong diamagnetic drift may excite large-wavelength, low-frequency plasma oscillations that propagate in the direction of the diamagnetic drift.

5. Application of the gradient drift instability to cross-field plasma sources

Now that we have established the theory of the gradient drift instability, in this section, the theory is applied to various cross-field plasma configurations. Although the theory discussed in the present paper assumes a slab geometry and the real systems are cylindrical, the slab approximation may provide first-order estimates for the local instabilities in cross-field plasma sources. Here, four configurations are considered: (a) Penning discharge, (b) cylindrical magnetron (e.g. for high-power microwave generation), (c) planar magnetron discharge (e.g. for plasma-assisted deposition) and (d) Hall effect thruster (HET), as shown in figure 6.

Figure 6. Application of the gradient drift instability theory to various cross-field plasma devices. Note that the geometries between top and bottom figures are rotated to keep the magnetic field direction consistent, that is, into the page. Blue arrows, that is, $u_{0r}$ in (a,b) or $u_{0z}$ in (c,d), indicate the cross-field electron flow, whereas the red arrows indicate the electron drift in the azimuthal direction.

5.1. Penning discharge

The Penning discharge, as shown in figure 6(a), operates using an outer cylinder as an anode with a cathode placed along the centreline, in addition to an applied axial magnetic field (Hoh 1963; Simon 1963). The plasma density is typically largest near the cathode, generating a radially inward plasma density gradient, $\boldsymbol {\nabla }_r n_0<0$. At the same time, the applied electric field is also radially inward, $E_r<0$. Penning discharge typically naturally satisfies the condition $\boldsymbol {E}_0 \boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$, that is, the $\boldsymbol {E} \times \boldsymbol {B}$ and diamagnetic drifts are in the same direction. Therefore, as shown in figure 3(a), the Penning-type discharge satisfies (3.4), generating a gradient drift instability at low frequency.

5.2. Cylindrical magnetron

The cylindrical magnetron, shown in figure 6(b), is used to study critical ionisation velocity (CIV) phenomena (Brenning et al. 2013). In addition, such a cross-field configuration is used in high-power microwave sources. For its use as a microwave generator, ion formation is to be avoided because the working principle is that the electrons from the cathode are trapped (i.e. insulated) by the applied or induced magnetic field to generate high-power microwaves (Benford et al. 2015). However, as the devices increase in power and become more compact, plasma generation is unavoidable as the current density in the system increases (Hadas et al. 2008). Although low-frequency plasma oscillations are not well-studied due to the short pulse operation, it can be seen from figure 6(b) that the partially magnetised plasma is unstable in such configurations, similar to the Penning discharge.

5.3. Planar magnetron discharge

Figure 6(c) shows a schematic of the planar magnetron, used for plasma-assisted sputtering and deposition (Waits 1978). An axial electric field and a radial magnetic field are applied close to the cathode surface. The crossed electric and magnetic fields generate electron drifts in the azimuthal direction.

Recent experimental observations in high-power impulse magnetron sputtering (HiPIMS) show that the rotating spoke direction may be a function of the current (Anders & Yang 2017) and can be reversed during a certain operation (Hecimovic et al. 2016). Similar reversal of the rotating spoke propagation is found in a micro-magnetron discharge (Ito et al. 2015; Marcovati et al. 2020). The global axial plasma profile, such as the location and amplitude of the density and potential gradients, can affect the characteristics of the gradient drift instability, leading to rotating spokes.

In addition, magnetron sputtering devices have a large magnetic field inhomogeneity in the region where the rotating spokes occur, leading to the possibility of gradient drift instabilities due to magnetic field gradients (Esipchuk & Tilinin 1976; Tilinin 1977; Frias et al. 2013) playing an important role in the formation of rotating spokes.

5.4. HET

The HET operates using a radial applied magnetic field and axial electric field, as shown in figure 6(d). In the plume of a HET, the $\boldsymbol {E} \times \boldsymbol {B}$ drift is much larger than the diamagnetic drift and the diamagnetic drift is in the opposite direction to the $\boldsymbol {E} \times \boldsymbol {B}$ drift, which is shown as region 2 in figure 6(d). Consequently, using the instability criteria discussed in (3.4), the partially magnetised plasma in the HET plume is stable against the Penning-type instability. The simulation results by Kawashima et al. (2018) were compared with a class of gradient drift instabilities in the presence of a magnetic field gradient (Esipchuk & Tilinin 1976; Tilinin 1977; Frias et al. 2013) and showed that the gradient drift instability due to the magnetic field gradient grows in the plume region, which leads to the excitation of rotating spokes.

However, if one considers the plasma inside the channel, shown as region 1 in figure 6(d), the cross-field electron transport is primarily driven by the pressure gradient near the anode. It can therefore be considered that the magnitude of the diamagnetic drift is larger than that of the $\boldsymbol {E} \times \boldsymbol {B}$ drift, while the two drifts may be in the opposite direction. Thus, this condition may lead to the gradient drift instability presented in this paper to be unstable. The spoke rotation will be in the direction of the diamagnetic drift driven by the plasma density gradient inside the channel, which turns out to be in the same direction as the $\boldsymbol {E} \times \boldsymbol {B}$ drift due to the applied electric field (set up by the anode and cathode) in the system.

In summary, there are two scenarios in which azimuthally rotating spokes can occur in HETs and in the planar magnetron discharge. One is due to the instabilities that are caused by the magnetic field gradient. The other possibility is the gradient drift instability, discussed in the present paper, which is caused by the diamagnetic drift in the absence of magnetic field gradients.

6. Conclusion

The present paper has reviewed the fluid dispersion relation of the partially magnetised plasmas. The dispersion relation derived in this paper shows that the partially magnetised plasmas are unstable (i) when $\boldsymbol {E}_0\boldsymbol {\cdot }\boldsymbol {\nabla } n_0 >0$ or (ii) in the presence of a large diamagnetic drift while $\boldsymbol {E}_0\boldsymbol {\cdot }\boldsymbol {\nabla } n_0 <0$. The former is consistent with the so-called MSHI where the $\boldsymbol {E} \times \boldsymbol {B}$ drift and the diamagnetic drift are in the same direction. The latter is an instability that occurs when the diamagnetic drift is sufficiently larger than the electron thermal speed while occurring in the direction against the $\boldsymbol {E} \times \boldsymbol {B}$ drift. One similarity between the two instability conditions is that the plasma wave in the large-wavelength limit propagates in the direction of the diamagnetic drift. This indicates that the low-frequency, large-wavelength, partially magnetised plasma oscillations can occur in either $\boldsymbol {E} \times \boldsymbol {B}$ or $-\boldsymbol {E} \times \boldsymbol {B}$ direction, depending on the plasma conditions.