The Renewable Fuel Standard (RFS) program introduced in the Energy Policy Act of 2005 mandated a minimum of 7.5 billion gallons of renewable fuels to be incorporated into the gasoline supply by 2012. This has sparked a dramatic growth of ethanol production in the United States. RFS was later extended in December 2007 under the Energy Independence and Security Act, mandating renewable fuels production of 12 billion gallons by 2012 and 36 billion gallons by 2022. The ethanol mandate, along with high oil prices, government subsidies, and tariff protections, have fueled ethanol production in the United States. In 2004, 3.4 billion gallons of ethanol were produced in the United States. This number has skyrocketed to 13.9 billion gallons in 2011, and 14.8 billion gallons in 2015.Footnote 1
Distiller's dried grains with solubles at 10 percent moisture, also known as DDGS, is a primary co-product of ethanol production during the dry mill process. About one third of the grain used in dry-mill ethanol production comes out as DDGS. Due to its high protein and fat content, DDGS is often considered a more cost-effective source of energy, amino acids, and phosphorus for animals than either corn, soybean meal, or canola meal (Skinner, Weersink, and deLange, Reference Skinner, Weersink and deLange2012). The expansion of DDGS production in the United States has largely tracked the dramatic increase in ethanol production. According to USDA's Economic Research Service, DDGS production for marketing year 2014/15 was about 36.7 million metric tons, compared to about 8.0 million metric tons in 2004/05—an increase of over 350 percent.Footnote 2 DDGS are increasingly popular among livestock and poultry producers as an alternative to corn and soybean meal that have experienced higher prices since 2006 (Hoffman and Baker Reference Hoffman and Baker2010). Geoff Cooper, the vice president of research and analysis of the Renewable Fuels Association (RFA), calls distiller's grains “the best kept secret” of ethanol production, and “one of the most economically competitive sources of energy and protein available on the world feed market.”Footnote 3 In the 2014/15 marketing year, about 26 million tons of DDGS were fed to livestock and poultry, compared to about 7 million tons ten years ago. Irwin and Good (Reference Irwin and Good2015) and Irwin (Reference Irwin2016) show that distiller's grains could also significantly affect ethanol producer's profit margin.
Given the important role DDGS now plays in feed markets, concerns arise regarding the price behavior of this relatively new and opaque market. For instance, how does the continued market expansion of DDGS affect the U.S. feed complex in light of the ethanol mandate? How can market participants better manage their price risks when buying and selling DDGS? To what degree have the volatile corn prices over the past decade affected the price and volatility of DDGS? How have the price and volatility interrelationships between major feedstuffs changed over time due to the ethanol boom? Since corn is the primary grain used in both wet- and dry-mill ethanol plants (accounting for about 98 percent of all ethanol feedstocks), and the main energy ingredient in livestock feed, the price of DDGS should be closely aligned with the price of corn, with the difference in prices mainly reflecting the products’ differing nutrient contents. On the other hand, given its rich protein content, DDGS prices should also be influenced by the prices of other competing protein feeds, such as soybean meal. Clearly, the surge in ethanol production poses a need to reassess the relationships between DDGS, corn, and soybean meal markets and how they have changed over time. Answering this question is of great interest to market participants who wish to manage the increasingly volatile DDGS price, including ethanol producers, grain merchandizers, livestock farmers, and grain producers. On a macro-scale, policymakers could use this information to not only assess the impact of biofuel policy on the feed industry, but also to understand how exogenous shocks such as export disruptions in one market could have ripple effects on other markets.
The purpose of this paper is to investigate the price and volatility transmission mechanisms between DDGS, corn, and soybean meal in the US and how these relationships have changed over time. A vector error correction model (VECM) is used to examine the short- and long-run price dynamics between the three markets, and how prices of each market respond to deviations from long-run equilibriums. We then use multivariate generalized autoregressive conditional heteroskedasticity (MGARCH) models to investigate the intermarket volatility spillovers and the dynamic correlations over time between the three markets. Using weekly data from January 2000 to May 2016, we find important price and volatility interplays between the three commodities. On the price transmission mechanism, a stable long-run equilibrium path is found between the three markets and in the long-run, DDGS prices are positively correlated with the prices of the other two commodities. In the short-run, DDGS prices appear to be significantly affected by both corn and soybean meal prices, while the latter two are largely independent from DDGS prices. We also find that the co-movement between corn and DDGS appears to have strengthened following the ethanol boom but has declined in recent years. On the volatility transmission mechanism, there exists strong volatility spillover from corn and soybean meal markets to the DDGS market, while shocks in the DDGS market play little role in the volatility dynamics of the other two markets. This volatility spillover pattern is robust to a specification using a shorter sample period that excludes the pre-ethanol boom episode.
To the best of our knowledge, our paper is the first attempt in the literature to quantitatively characterize the dynamic relationship of price and volatility interactions within the U.S. feed complex. At the same time, our work is part of a growing body of literature examining the co-movement and volatility transmissions between commodity markets. Examples of these types of studies include Ait Sidhoum and Serra (Reference Ait Sidhoum and Serra2016), Etienne, Trujillo-Barrera, and Wiggins (Reference Etienne, Trujillo-Barrera and Wiggins2016), Gardebroek and Hernandez (Reference Gardebroek and Hernandez2013), and Trujillo-Barrera, Mallory, and Garcia (Reference Trujillo-Barrera, Mallory and Garcia2012). Our study attempts to address i) whether there exists any long-run price relationship between these markets; ii) how the conditional correlation between the three feedstocks have changed over time; iii) how volatility in one market affects the volatility in another market, and iv) the impact of exogenous shocks on the volatility of these commodities.
The remainder of the paper is structured as follows. Section two discusses the background information of DDGS, soybean meal, and corn markets and reviews relevant literature. Econometric procedures are discussed in section three, followed by the data used for the analysis. Empirical results are presented in section five. The last section concludes the paper.
Background and Related Literature
DDGS are a co-product from dry-mill ethanol productions, high in both energy and protein content. Traditionally, DDGS were used in livestock feeds as a source of protein, often replacing soybean meal in the feed ration. However, the rapid rise in corn processing for ethanol since 2006 has altered this pattern (Silvestri Reference Silvestri2015). Tightening corn supplies and the increasingly volatile corn prices had led many livestock producers to replace corn in the feed ration with DDGS as an energy source. DDGS feeding rapidly expanded against this backdrop and is emerging as a mainstream animal feed in the United States. Though questions remain over the substitution rate of DDGS for energy (corn) and protein (soybean meal) in livestock and poultry rations (Hoffman and Baker Reference Hoffman and Baker2010), it is expected that both corn and soybean meal prices play a significant role in the price behavior of DDGS, with price differences reflecting their differing nutritional values. In a survey conducted by Stroade et al. (Reference Stroade, Martin, Conrad and Schroeder2010), 87 percent of the ethanol plants used corn futures prices to establish the benchmark prices of distiller's grains, while 43 percent of the respondents used soybean meal futures prices as a benchmark.
Despite its importance, studies regarding the price and volatility interactions between DDGS and other feed ingredients in the U.S. remain scant. The U.S. Grain Council (2007) highlights the role of corn and soybean meal prices on DDGS prices, but notes that DDGS prices should be most closely linked to corn prices because of similarities in their economic and nutritional values. This relationship is supported by Hoffman and Baker (Reference Hoffman and Baker2010), who find that corn and soybean meal prices explain over 95% of the variation in DDGS prices, and that corn prices play a much larger role than soybean meal prices after the expansion of ethanol production in 2006. Irwin and Good (Reference Irwin and Good2013) examine the factors affecting spot DDGS prices in Iowa from 2007 to 2013, finding that a $1/ton increase in soybean meal and corn prices would lead to $0.11/ton and 0.85/ton increases in DDGS prices, respectively. These numbers were slightly higher than the regression results reported in Hoffman and Baker (Reference Hoffman and Baker2010) using Central Illinois DDGS prices. In a follow-up study, Irwin and Good (Reference Irwin and Good2015) consider the relationship between the three markets during the period of high protein prices (2011–2014), finding that soybean meal prices to play a much more significant role on Iowa DDGS prices in 2011–2014 compared to the period prior. However, this impact is still significantly smaller than corn.
Other studies have examined the long-run or dynamic pricing relationship between corn, soybean meal, and DDGS. Anderson, Anderson and Sawyer (Reference Anderson, Anderson and Sawyer2008) examine the price of DDGS in Central Illinois and the price of corn received by producers in the Texas Triangle area, finding these two prices to be cointegrated. These authors also note that the relationship between the two prices appears to be weak prior to 1998 but has strengthened since then as the DDGS market matures. Tejeda (Reference Tejeda2012) reports that under a dynamic correlation framework, correlations exist between DDGS and other feed grains after the ethanol mandate but not prior. Johnson et al. (Reference Johnson, Yu, Griffith, Jensen and Cho2015) study the price relationship between DDGS, corn, soybean meal and livestock outputs at four locations associated with a predominant livestock sector. They show that regardless of the regions examined, the price of corn is the largest contributor to DDGS price variances, and that other factors only have limited effects on DDGS prices. Using DDGS spot prices in Iowa, Silvestri (Reference Silvestri2015) finds a stable long-run relationship between corn, soybean meal, and DDGS prices and that corn prices are the primary channel through which exogenous shocks are transmitted to the system. They attribute such findings to the higher storability of corn relative to DDGS and soybean meal.
However, not all studies agree with the significant price relationship found between the three commodities. In particular, Van Winkle and Schroeder (Reference Van Winkle and Schroeder2008) examine the pricing efficiency of local DDGS markets by investigating their price relationships with the corn and soybean meal futures markets. Out of the 11 markets examined, they find that DDGS prices of only one location to be cointegrated with corn and soybean meal prices. Schroeder (Reference Schroeder2009) finds significant price risks in the DDGS market that cannot be eliminated by hedging using corn futures contracts. Murguia and Lawrence (Reference Murguia and Lawrence2010) find that the effects of corn and soybean meal prices on DDGS are highly dependent on the empirical model specified, and that the effectiveness of using these two futures contracts to hedge against DDGS price risk varies with the period used and the model considered.
Our paper departs from the aforementioned papers in a number of ways. First, while most of the previous studies have focused on how DDGS prices can be affected by the prices of corn and soybean meal, little research has investigated the interrelationship between these three commodities and how DDGS prices can influence the price behavior of the other two feed ingredients. This reverse causality is likely as livestock and poultry farmers can reasonably change the feed ration between the three commodities based on their relative price ratios. Since DDGS prices can significantly affect the profitability of ethanol plants (Irwin, Reference Irwin2016, Irwin and Good, Reference Irwin and Good2015), the relative price of DDGS may also affect the demand of corn to be used in ethanol production and further affect corn prices. Second, previous studies have only focused on the price interactions between the three feed ingredients, without paying much attention to the volatility dynamics. Our study, by contrast, examines how volatility transmits between the three markets. As Gallagher and Twomey (Reference Gallagher and Twomey1998) point out, examining the conditional second moment could provide additional valuable insights to the interrelationships across different markets. In particular, we investigate how exogenous shocks in one market could affect the volatility in the three markets to shed light on the volatility transmission mechanism. Finally, in light of the changing dynamics between the three markets identified in previous studies, we seek to identify how the interrelations between corn, soybean meal, and DDGS prices have changed over time. We expect the DDGS market to be more correlated with corn, but less with soybean meal as the feed ration in livestock and poultry production changes. Such information is a critical input for many of the common tasks involved in risk management. If the correlations and volatilities of the three commodities are time-varying, hedgers who wish to effectively manage their price risks may find it useful to adjust the hedge ratio to account for the most recent information.
Econometric Model
Standard time series procedures are used to evaluate the price and volatility linkages between DDGS, corn, and soybean meal markets. We first investigate stationarity, co-movement, and volatility clustering properties of the three price series. As noted in the next section, there is no evidence against the unit root null hypothesis in any of the price series, and overwhelming evidence in favor of stationarity in every differenced price series. Individual series that are nonstationary, however, could be cointegrated such that each series reverts to common stochastic trends. Assuming there exists a long-run equilibrium, the following vector error correction (VEC) model is estimated to investigate the price linkages between the three price series:
 $$\eqalign{& \Delta {\bi P}_t = \; \mathop \sum \limits_{\,j = 1}^p {\bi \beta} _j \Delta {\bi P}_{t - j{\bi \;}} + {\bi \alpha} ECT_{t - 1} + {\bi \varepsilon} _t, \cr & {\bi \varepsilon} _t \; \vert \; {\bi I}_{t - 1} \; \sim \; \lpar {\bf 0},{\bi H}_t \rpar,}$$
$$\eqalign{& \Delta {\bi P}_t = \; \mathop \sum \limits_{\,j = 1}^p {\bi \beta} _j \Delta {\bi P}_{t - j{\bi \;}} + {\bi \alpha} ECT_{t - 1} + {\bi \varepsilon} _t, \cr & {\bi \varepsilon} _t \; \vert \; {\bi I}_{t - 1} \; \sim \; \lpar {\bf 0},{\bi H}_t \rpar,}$$
where P t is a three-component vector including prices of DDGS, corn, and soybean meal, Δ is the first difference operator such that Δ P t = P t − P t−1, β j are parameters that capture the short-run dynamics between the three price series, p is the lag length, ECT is the error correction term that characterizes the long-run relationships between the three variables, and α is a 3 × 1 vector that describes the speed of adjustment when deviations from the long-run relationship occur. Additionally, ε t is a three-component vector of disturbance term, the variance-covariance matrix of which is characterized by matrix H t conditional on past information I t−1.
It is not uncommon for time series data, in particular prices, to exhibit time-varying volatility clustering, i.e. periods of large swings interspersed with periods of relative tranquility. For this matter, we consider two different multivariate generalized autoregressive conditional heteroscedasticity (MGARCH) models to account for the error structure in the VEC model. In the first specification, we consider the conditional correlation (DCC) model that assumes the conditional correlation matrix ( R t ) between the three markets to be time-varying, as shown in equation (2):
 $$\eqalign{& {\bi H}_t = {\bi D}_t^{1/2} {\bi R}_t {\bi D}_t^{1/2}, \cr & {\bi R}_t = {\rm diag}\lpar {{\bi Q}_t} \rpar^{ - 1/2} {\bi Q}_t {\rm diag}\lpar {{\bi Q}_t} \rpar^{ - 1/2} \cr & {\bi Q}_t = \lpar {1 - \lambda _1 - \lambda _2} \rpar{\bi Q} + \lambda _1 \tilde \varepsilon _{t - 1} \tilde \varepsilon _{t - 1}^{\prime} + \lambda _2 {\bi Q}_{t - 1},} $$
$$\eqalign{& {\bi H}_t = {\bi D}_t^{1/2} {\bi R}_t {\bi D}_t^{1/2}, \cr & {\bi R}_t = {\rm diag}\lpar {{\bi Q}_t} \rpar^{ - 1/2} {\bi Q}_t {\rm diag}\lpar {{\bi Q}_t} \rpar^{ - 1/2} \cr & {\bi Q}_t = \lpar {1 - \lambda _1 - \lambda _2} \rpar{\bi Q} + \lambda _1 \tilde \varepsilon _{t - 1} \tilde \varepsilon _{t - 1}^{\prime} + \lambda _2 {\bi Q}_{t - 1},} $$
where
![]() ${\bi D}_t = {\rm diag}\left\{ {\sqrt {h_{it}} } \right\}$
is a 3 × 3 diagonal matrix of time-varying standard deviations that evolves according to a univariate GARCH(1,1) process,
R
t
is a time-varying symmetric matrix of conditional correlations between the three prices, λ
1 and λ
2 are non-negative adjustment parameters satisfying λ
1 + λ
2 < 1 such that the conditional correlations are mean-reverting,
${\bi D}_t = {\rm diag}\left\{ {\sqrt {h_{it}} } \right\}$
is a 3 × 3 diagonal matrix of time-varying standard deviations that evolves according to a univariate GARCH(1,1) process,
R
t
is a time-varying symmetric matrix of conditional correlations between the three prices, λ
1 and λ
2 are non-negative adjustment parameters satisfying λ
1 + λ
2 < 1 such that the conditional correlations are mean-reverting,
![]() $\tilde \varepsilon _t$
is the standardized residuals, and
Q
is the 3 × 3 uncondtional variance matrix of
$\tilde \varepsilon _t$
is the standardized residuals, and
Q
is the 3 × 3 uncondtional variance matrix of
![]() $\tilde \varepsilon _t$
. The DCC specification has the flexibility of a univariate GARCH but not the complexity of many conventional MGARCH models (Engle, Reference Engle2002). The DCC model allows us to estimate the time-varying conditional correlations between DDGS, corn, and soybean meal markets. Previous applications of the DCC model in agricultural commodity markets include Gardebroek and Hernandez (Reference Gardebroek and Hernandez2013), Mensi et al. (Reference Mensi, Beljid, Boubaker and Managi2013), among others.
$\tilde \varepsilon _t$
. The DCC specification has the flexibility of a univariate GARCH but not the complexity of many conventional MGARCH models (Engle, Reference Engle2002). The DCC model allows us to estimate the time-varying conditional correlations between DDGS, corn, and soybean meal markets. Previous applications of the DCC model in agricultural commodity markets include Gardebroek and Hernandez (Reference Gardebroek and Hernandez2013), Mensi et al. (Reference Mensi, Beljid, Boubaker and Managi2013), among others.
To examine the volatility spillover between the three markets, we consider an alternative model for the error structure. Specifically, the conditional covariance matrix H t is modeled using the Baba-Engle-Kraft-Kroner (BEKK) procedure with one lag, as shown in equation (3).
where
C
is a 3 × 3 lower triangular matrix that corresponds to the constant,
![]() ${\bi \varepsilon }_{t - 1}{\bi \varepsilon }^{\prime}_{t - 1}$
are the squared lagged errors,
A
is a 3 × 3 matrix of ARCH parameters containing elements measuring the degree of innovation from one market to another, and
B
is a 3 × 3 matrix of GARCH parameters that shows the persistence in conditional volatility between two markets. The BEKK specification in equation (3) not only provides a direct estimation of the conditional covariance matrix, but also significantly reduces the number of parameters to be estimated in
H
t
while ensuring positive definiteness of the conditional covariance matrix. This specification has been widely used in the literature to investigate own- and cross-volatility spillovers and persistence between multiple markets, including Ait Sidhoum and Serra (Reference Ait Sidhoum and Serra2016), Etienne, Trujillo-Barrera and Wiggins (Reference Etienne, Trujillo-Barrera and Wiggins2016), Gardebroek and Hernandez (Reference Gardebroek and Hernandez2013), Jin, Lin and Tamvakis (Reference Jin, Lin and Tamvakis2012), Serra, Zilberman and Gil (Reference Serra, Zilberman and Gil2011), Trujillo-Barrera, Mallory and Garcia (Reference Trujillo-Barrera, Mallory and Garcia2012), among others.
${\bi \varepsilon }_{t - 1}{\bi \varepsilon }^{\prime}_{t - 1}$
are the squared lagged errors,
A
is a 3 × 3 matrix of ARCH parameters containing elements measuring the degree of innovation from one market to another, and
B
is a 3 × 3 matrix of GARCH parameters that shows the persistence in conditional volatility between two markets. The BEKK specification in equation (3) not only provides a direct estimation of the conditional covariance matrix, but also significantly reduces the number of parameters to be estimated in
H
t
while ensuring positive definiteness of the conditional covariance matrix. This specification has been widely used in the literature to investigate own- and cross-volatility spillovers and persistence between multiple markets, including Ait Sidhoum and Serra (Reference Ait Sidhoum and Serra2016), Etienne, Trujillo-Barrera and Wiggins (Reference Etienne, Trujillo-Barrera and Wiggins2016), Gardebroek and Hernandez (Reference Gardebroek and Hernandez2013), Jin, Lin and Tamvakis (Reference Jin, Lin and Tamvakis2012), Serra, Zilberman and Gil (Reference Serra, Zilberman and Gil2011), Trujillo-Barrera, Mallory and Garcia (Reference Trujillo-Barrera, Mallory and Garcia2012), among others.
The conditional mean specified in equation (1) and conditional variance specified in equations (2) or (3) jointly defines the trivariate VECM-MGARCH model used in this analysis. In both models, we first estimate the cointegration factor, and then use the maximum likelihood procedure as outlined in Seo (Reference Seo2007) and Serra, Zilberman and Gil (Reference Serra, Zilberman and Gil2011) to jointly model the mean and error processes. Estimation results are used to assess i) the long-run and short-run price dynamics (VECM), ii) the time-varying correlations (DCC), and iii) the volatility transmission mechanisms between DDGS, corn, and soybean meal markets in the US (BEKK).
It should be noted that the DCC- and BEKK-MGARCH specifications are not competing models; rather, they complement each other. We use the BEKK specification because it allows the identification of volatility spillovers from one market to the other, as well as investigation of how an exogenous shock in one market affect volatility in its own and other markets. DCC complements BEKK by uncovering the time-varying conditional correlations of price volatility, which are critical inputs for many common risk management strategies. As such, the use of both models offer a more thorough description of price volatility. We expect the results from BEKK- and DCC-MGARCH models to be robust, but offering differing information on the volatility dynamics between the three markets.
Data
Weekly nearby prices of the No.2 Yellow Corn futures contracts and soybean meal futures contracts are obtained from the Chicago Board of Trade (CBOT). Prices are rolled into the next nearby contracts on the first business day of the delivery month. We use the DDGS price in Central IL as the benchmark price for DDGS, as it is close to the corn and soybean meal delivery locations. These prices are obtained from the US Department of Agriculture (USDA) Agricultural Marketing Service (AMS). The sample period considered runs from January 2000 to May 2016, resulting in 857 weekly observations. The selection of the sample period is motivated by data availability, as the DDGS price in Central IL is not available until January 2000.
Figure 1 plots weekly DDGS, corn, and soybean meal prices in cents per unit (ton for DDGS and soybean meal and bushel for corn). All three prices experienced dramatic rises and drops. Three peaks are observed in corn prices: one in mid-2008, one in mid-2011, and another in mid-2012, all with comparable price levels. By contrast, the highest price in DDGS market is observed in 2012, significantly higher than the peak prices observed in other periods. A dramatic decline occurred in DDGS prices during 2014, dropping its value from a maximum of 252.5 cents/ton in March 2014 to a minimum of 91 cents/ton in November 2014. While similar price patterns are observed in corn and soybean meal markets during the same timeframe, the percentage price drops in these two markets were of smaller magnitudes than DDGS. Additionally, while corn prices started their run-up in mid-2006, the price of DDGS did not rise significantly until the end of 2007. The relatively low DDGS prices in the early stages of ethanol expansion quickly attracted attention from livestock producers who are constantly searching for cheaper feed ingredients. DDGS soon emerged as a mainstream substitute in animal feed rations, which eventually led to the rapid spike in DDGS prices in 2008.
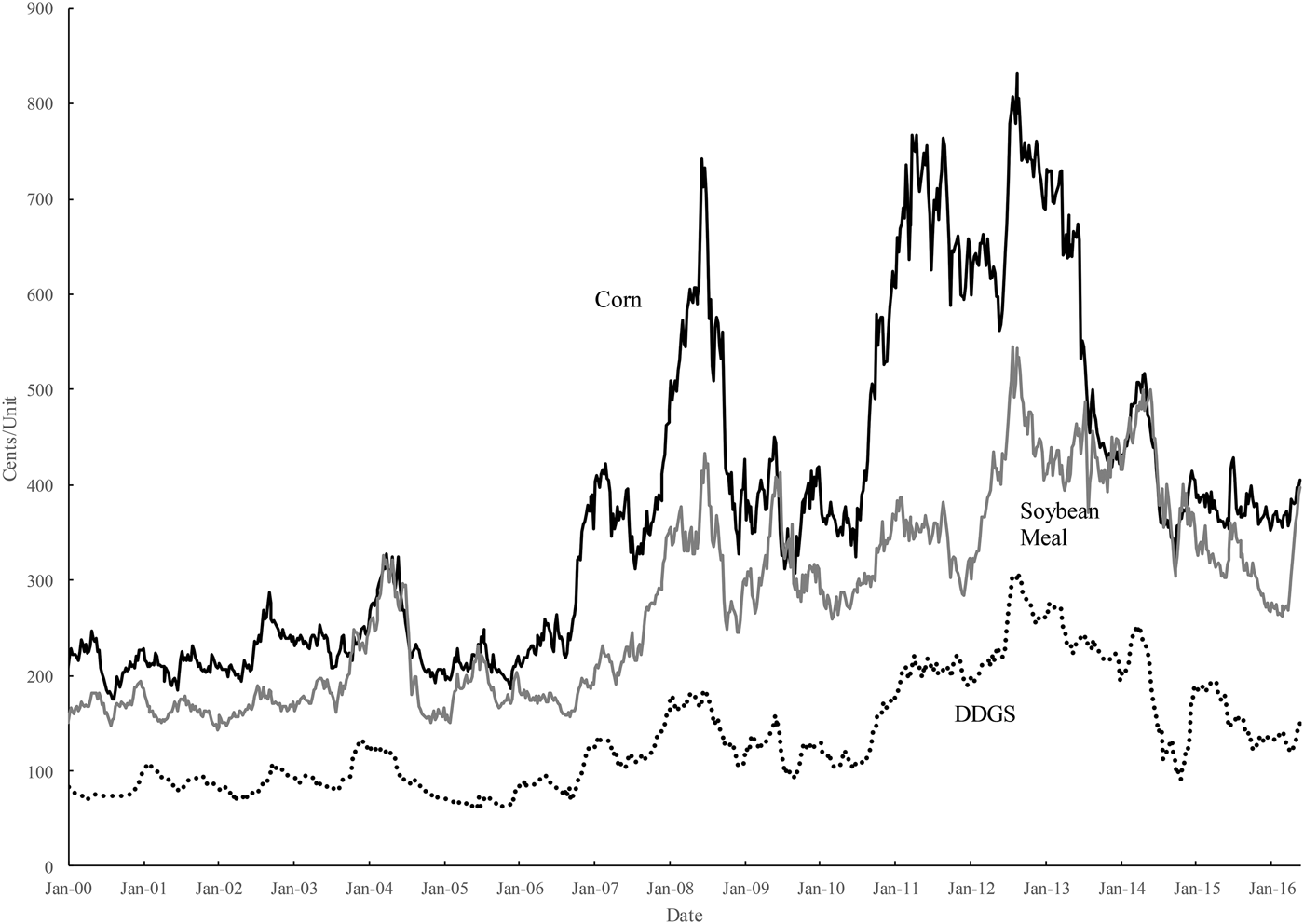
Figure 1. DDGS (in Cents/Short Ton), Corn (in Cents/Bushel), and Soybean Meal (in Cents/Short Ton) Prices in the U.S., (January 2000–May 2016)
Figure 2 plots the one-year rolling historical volatility (annualized standard deviation) for the three return series, along with their historical volatility for the whole sample period.Footnote 4 Several interesting patterns emerge. First, the three commodities experienced large volatility swings between mid-2008 and the end of 2010, a period that corresponds to the worldwide commodity price spike and financial crisis. Previous studies have detected considerable co-movement across various commodity prices during this period, an indication that commodity markets are increasingly “financialized” due to the participation of commodity index traders. Second, the overall volatility during the sample period appears to be comparable for the three markets. The corn market exhibits the highest annualized volatility (30.1%), followed by soybean meal (29.4%) and DDGS (27.8%). Third, despite the similarities, the volatility patterns of the three return series show a significant degree of heterogeneity. DDGS, for instance, has the highest annualized volatility in the first half of 2015, more than 25 percentage points higher than the average annualized volatility of the sample period. By contrast, both corn and soybean meal markets have the highest volatility in 2009. Soybean meal price volatility was also high between the end of 2004 and mid-2005. Finally, the three plots are indicative of volatility-clustering in the returns, as periods of high (low) volatilities are often followed by even higher (lower) volatilities. Accounting for time-varying volatility when modeling the interrelationships between the three markets appears to be an important task.
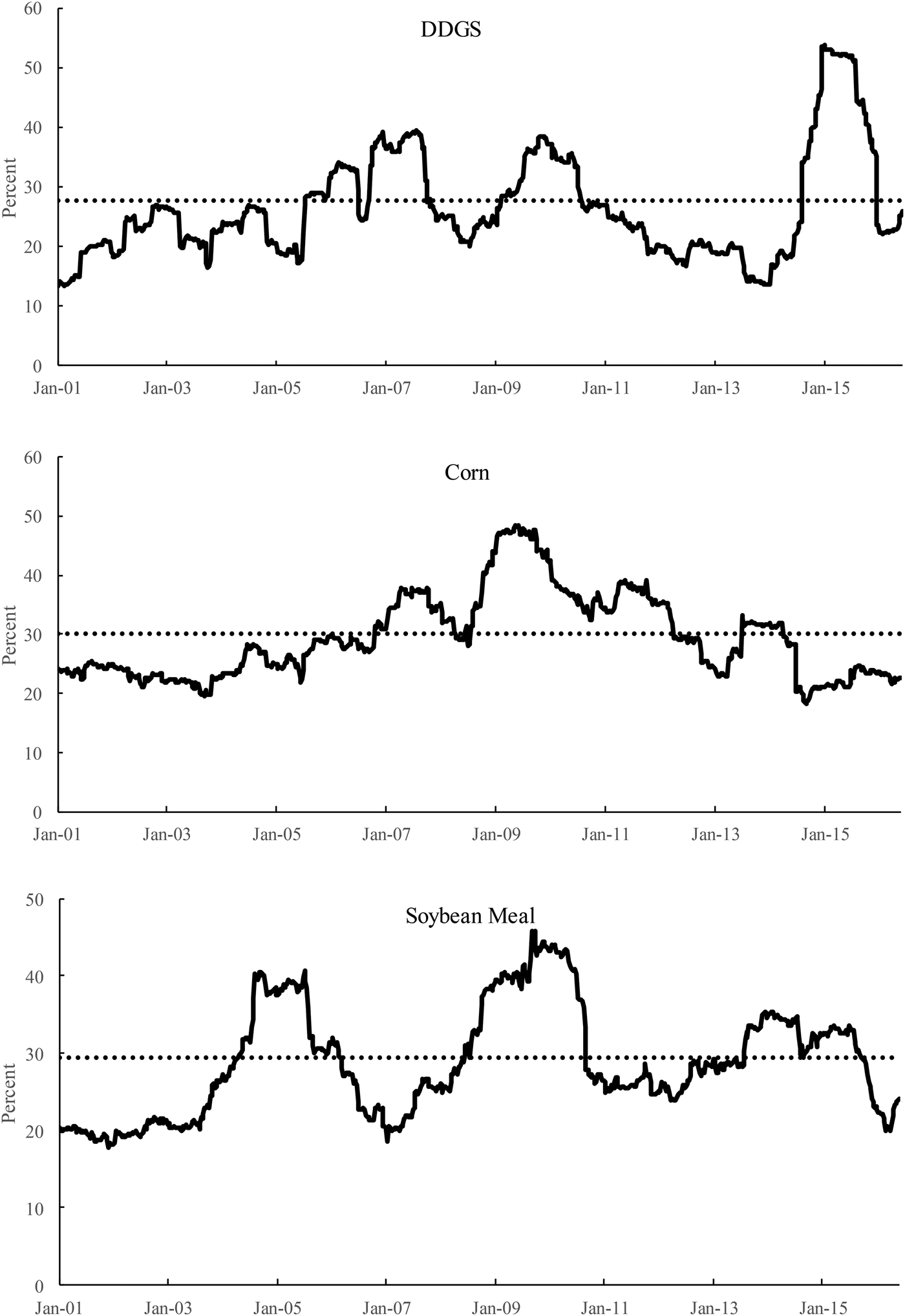
Figure 2. One-Year Rolling Historical Volatility (Solid Line) and Overall Historical Volatility (Dashed Line) for DDGS, Corn, and Soybean Meal Price Returns (January 2000– May 2016)
Summary statistics, unconditional correlations, and unit root test results for both log prices and returns (difference in log prices) are presented in table 1. Average returns are positive during the sample period for all three commodities, though none of them is statistically significant (panel A). All three return series appear to show a leptokurtic distribution, as the excess kurtosis is positive and statistically significant. Based on the Jarque-Bera test, the normality assumption is rejected for all three return series as well. Additionally, we find strong autocorrelation for the squared returns. For up to 3, 6 and 10 lags, the null hypothesis of no autocorrelation is uniformly rejected at the 1% significance level using the Ljung-Box test (Panel D), suggesting the existence of possible non-linear dependences in the returns.
Table 1. Summary Statistics, Contemporaneous Correlations, and Unit Root Test Results for DDGS, Corn, and Soybean Meal Prices (January 2000–May 2016)
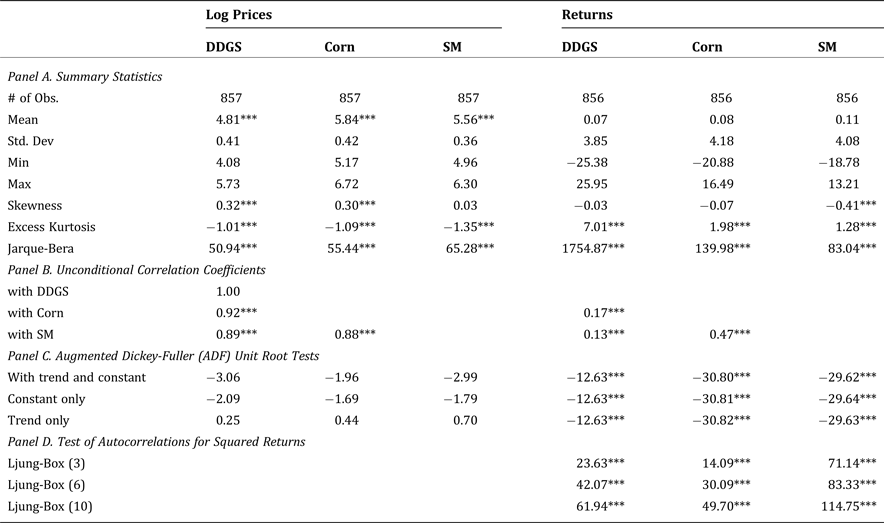
Note: One, two, and three asterisks represent statistical significance at 10, 5, and 1 percent, respectively.
Panel B of table 1 shows the unconditional contemporaneous correlations between the three log price and return series during the whole sample period. All correlation coefficients are statistically significant, and are of much higher magnitudes between log prices than between the three return series. Corn price returns are more correlated with soybean meal than DDGS price returns, with a correlation coefficient of 0.47. The correlation between DDGS returns and the other two commodities are much lower, both below 0.20.
We next examine the stationarity property of the price and return series using the augmented Dickey-Fuller (ADF) tests. Lag lengths are selected using the Bayesian information criterion (BIC). As panel (C) of table 1 suggests, regardless of the model (trend only, constant only, and both trend and constant) used, we fail to reject the null hypothesis of a unit root in all three log price series. By contrast, there is overwhelming evidence that all return series are stationary, supporting the use of returns instead of price levels in the regression analysis.
Since we find the prices of the three commodities to be non-stationary, we next investigate whether there exists stable long-run equilibriums between these prices using the Johansen maximum likelihood procedure, the results of which are presented in table 2. Two lags are selected based on BIC. At the 5% significance level, we reject the null hypothesis of at most zero cointegration relationship between the three prices, but fail to reject the null hypothesis of at most one cointegrating factor. We hence conclude that there is a stable long-run relationship between DDGS, corn, and soybean meal prices.
Table 2. Johansen Maximum Likelihood Tests for Cointegration between Log DDGS, Corn, and Soybean Meal Prices (January 2000–May 2016)
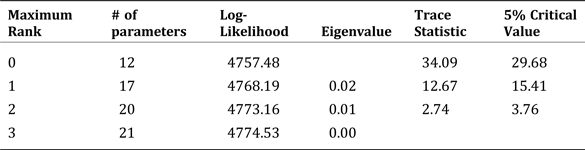
Note: The test starts with the null hypothesis of at most zero cointegrating equation (a maximum rank of zero), and accepts the null hypothesis of at most n cointegrating equations when it is first accepted.
Results
Given the presence of cointegration and time-varying volatility in the three price series, we consider two VECM-MGARCH models as outlined in equations (1)-(3). To account for seasonal variations commonly observed in grain prices, quarterly dummies are included in the VECM. The lag structure used in the model is again determined by the BIC. Additional lags are added to the model if autocorrelation or ARCH effects are detected in the residuals.
Estimation results using the DCC and BEKK specifications are presented in tables 3 and 4, respectively. Before delving into the specific estimation results, it is useful to first assess whether our two models fit the data well. Results of model adequacy tests are reported in the last panel of tables 3 and 4. For both models we fail to reject the null hypothesis of no residual autocorrelation at various lags using the multivariate Ljung-Box portmanteau test of Hosking (Reference Hosking1980). No ARCH effects are found in the residuals at various lags using the Lagrange Multiplier (LM) test as described in Hacker and Hatemi-J (Reference Hacker and Hatemi-J2005) in either model. The conditional covariance matrix is found to be stationary as all eigenvalues lie within the unit circle.
Table 3. VECM-MARGCH-DCC Model Estimation Results (January 2000–May 2016)
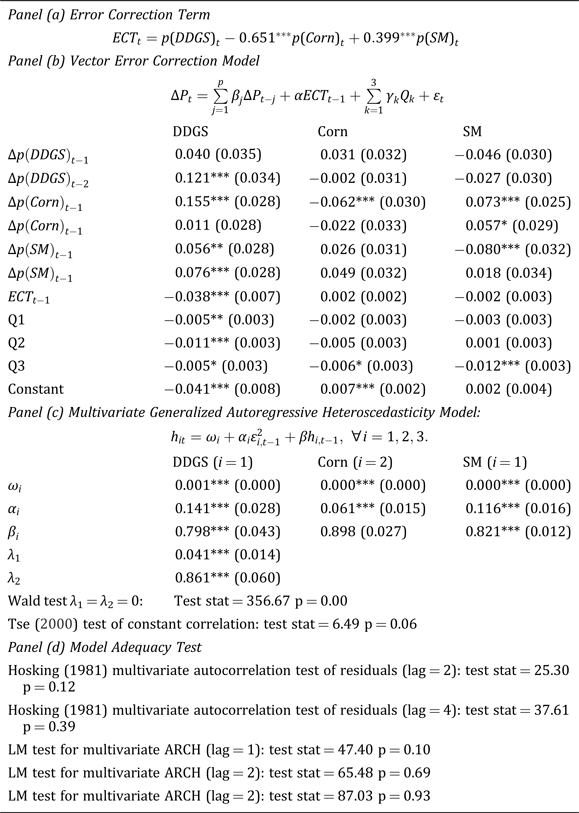
Notes: Prices are measured in logarithmic format. Standard deviation in parentheses. One, two, and three asterisks represent statistical significance at 10, 5, and 1 percent, respectively.
Table 4. VECM-MGARCH-BEKK Model Estimation Results (January 2000–May 2016)
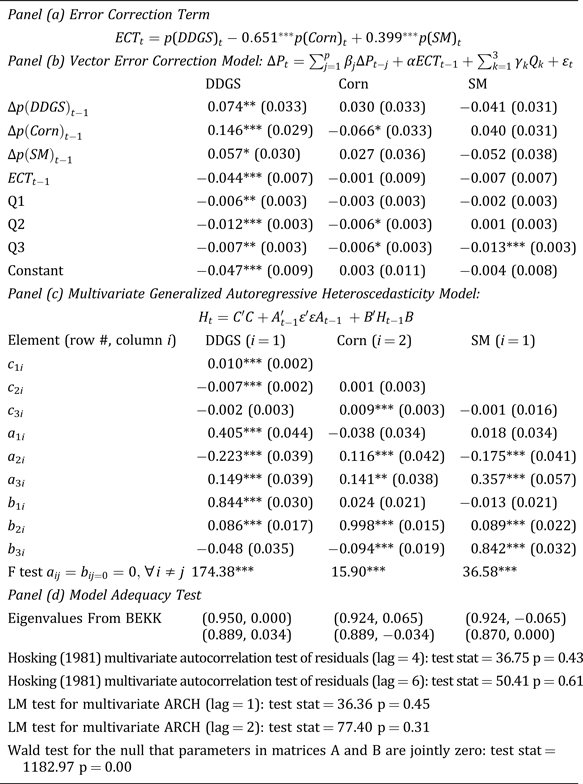
Notes: Prices are measured in logrithimic format. a ij and b ij represent the direct impact of lagged volatility and shocks originated in market i affect the conditional volatility in market j, respectively. Standard deviation in parentheses. One, two, and three asterisks represent statistical significance at 10, 5, and 1 percent, respectively.
Results from the Mean Equation
While we estimate a VECM-MGARCH-DCC and VECM-MGARCH-BEKK model separately, results for the mean equation obtained from these two estimations appear to be rather similar both in terms of statistical significances and coefficient estimates. We hence focus our discussion of the mean equation on the results obtained using the DCC specification in table 3.
Turning first to the error correction term, estimation results suggest that in the long-run, DDGS prices are positively linked to both corn and soybean meal prices, a conclusion consistent with the observation that animal feeders often view DDGS as a substitute for corn and soybean meal in feed rations. However, DDGS prices appear to be more highly correlated with corn than soybean meal in the long run. A 1% increase in corn and soybean meal prices is accompanied with a 0.65% and 0.39% increase in DDGS prices, respectively. The stronger link between DDGS and corn prices reflects, in part, the dominant role corn plays in the ethanol production process. It is also compatible with the observation that livestock producers, faced with tightening corn supplies and increasingly volatile corn prices, have turned to DDGS more as an energy source in animal feed rations than a protein source. Our finding is consistent with a number of recent studies that investigate the price dynamics between these three commodities. Irwin and Good (Reference Irwin and Good2015) and Hoffman and Baker (Reference Hoffman and Baker2010), for instance, both find that DDGS prices to be positively correlated with corn and soybean meal prices, and that an increase in corn prices would lead to a much larger increase in DDGS prices than an increase in soybean meal prices.
Short-run parameter estimates in the mean equation are reported in panel (b). Significant seasonal patterns are observed in all three markets. The adjustment coefficients (α i ) indicate that while DDGS prices respond negatively to deviations from the long-run relationship, soybean meal and corn prices are weakly exogenous in that neither prices adjust to departures from the equilibrium. To the extent that corn is a much larger market compared to DDGS, the lack of response from corn prices to deviations from the long-run equilibrium should not come as a surprise. Apart from being used as an animal feed and as a feedstock in ethanol production, a significant amount of the corn produced in the U.S. is exported, processed for human consumption and other industrial uses, or stored into the next marketing year. Previous studies have also found corn prices to be highly affected by a large number of exogenous factors linked to global economic growth (e.g., Abbott, Hurt and Tyner, Reference Abbott, Hurt and Tyner2009, Abbott, Hurt and Tyner, Reference Abbott, Hurt and Tyner2011). Similarly, results suggest that soybean meal does not respond to deviations from the long-run parity. The substitution effect between DDGS and soybean meal appears to play little role in the short-run price determination for soybean meal prices, a finding compatible with various previous studies suggesting that soybean meal market dynamics are primarily driven by the price of soybeans and the crushing spread (Pothidee, Allen and Hudson, Reference Pothidee, Allen and Hudson1999).
This lack of short-run responses in corn and soybean meal prices to DDGS price changes is further supported by the parameter estimates on the lagged return variables. Lagged DDGS price returns do not affect either corn or soybean meal returns. An increase in lagged corn and soybean meal returns, by contrast, leads to a significant increase in DDGS returns, with the magnitude of responses again higher for corn price increases. Again, these findings illustrate that soybean meal and corn prices are largely independent of DDGS prices in the short-run, while DDGS prices are highly affected by the other two commodities, a finding consistent with various previous studies (e.g., Hoffman and Baker, Reference Hoffman and Baker2010, Irwin and Good, Reference Irwin and Good2013, Silvestri, Reference Silvestri2015).
Results from the MGARCH-DCC Model
Table 3 displays estimation results from the DCC model in which the conditional variance of the residuals is modeled as a function of past realizations of both the volatility of the three variables and the correlations between them. Since h i is assumed to follow a univariate GARCH(1,1) process, the coefficient α i represents the ARCH effects, or how the lagged innovation affects the conditional volatility, while β i indicates the GARCH effects, or how conditional variance adjusts to past variances. All parameters associated with each GARCH process are statistically significant at the 10% level. High persistence is observed in the conditional volatility of all three markets as the sum of α i + β i is fairly close to 1 for all equations. In particular, the GARCH effect is large, as β i is above 0.80 for all three commodities.
Estimation results indicate significant time-varying co-movements between the three commodities. These effects are captured by the two adjustment coefficients, λ 1 and λ 2, both of which are highly statistically significant. The DCC model reduces to a constant conditional correlation (CCC) model if both adjustment coefficients are statistically non-significant. We conduct a Wald test to determine whether a CCC specification is preferred over the DCC model, finding strong evidence rejecting the null hypothesis of λ 1 = λ 2 = 0. We also conduct an LM test developed by Tse (Reference Tse2000) for parameter constancy, again showing evidence in favor of time-varying conditional correlations.
The dynamic conditional correlations between the standardized shocks for each pair of returns implied from the DCC model are plotted in figure 3. Consistent with the numbers reported for unconditional correlations, the dynamic conditional correlations between corn and soybean meal returns are much higher than the other two pairwise correlations. With a few exceptions, the conditional correlations between DDGS and corn or soybean meal are positive, though the overall magnitudes are not very large, at most 0.50. The correlation coefficient between DDGS and corn averaged at about 0.15 before 2005 but declined dramatically in mid-2005. This period represents the beginning of the run-up in corn prices while the price of DDGS remained low. From 2006 through 2012 when the ethanol production went through an explosive phase of expansion, the interdependence between the two markets significantly strengthened, with the correlation coefficient reaching as high as 0.50. Apart from increasing substitution between corn and DDGS in the feed rations due to larger availability of DDGS, the stronger linkage during this period may also reflect a growing number of market participants simultaneously taking part in both markets that facilitated price transmissions between the two commodities. We do, however, find that the relationship between corn and DDGS to be slightly weakened in recent years as corn prices plummeted and volatility declined.

Figure 3. Dynamic Conditional Correlations between DDGS, Corn, and Soybean Meal Markets (Dashed Line) Implied from the DCC-MGARCH Model (January 2000–May 2016)
The weakened price linkage between corn and DDGS over the past few years may be due in part to the increasing role of export markets in DDGS price dynamics. DDGS exports in 2014/15 marketing year skyrocketed to 11.5 million metric tons, as compared to 1 million in 2004/05. In 2014/15 over 30 percent of the domestic DDGS production was exported, of which almost 40 percent was exported to China.Footnote 5 Not surprisingly, any export disruptions or trade barriers could cause large price variations in the DDGS market. In late 2010 China launched an anti-dumping investigation into DDGS imports from the US, later extending the probe before dropping it in mid-2012. More recently, China contemplated a second anti-dumping investigation into US DDGS imports. Clearly, such trade barriers and export disruptions could significantly affect domestic DDGS prices in the US. In the meantime, corn prices were low in the US over the past few years, with high ending stocks (about 1800 million bushels, or 13% of the total use in the marketing year 2014/15) that can smooth out corn price variations due to exogenous shocks. As such, export disruptions and trade barriers in the DDGS market may have had little price impact on corn, causing the correlations between the two markets to be weakened in the later part of our sample.
The evolution of conditional correlation between DDGS and soybean meal markets have largely followed the same pattern as with the relationship between DDGS and corn, though magnitudes are considerably smaller. Similar to Irwin and Good (Reference Irwin and Good2015), we find the two markets to be more correlated during the period of high protein prices, January 2011 to September 2014. In particular, the correlation coefficient in mid-2014 is above 0.50, suggesting strong substitution effects between the two commodities. The correlations between corn and soybean meal have basically fluctuated with almost no trends. Though an important spike is observed in mid-2008 when both prices peaked, the average interdependence (or co-movement) during 2006–2012 only increased by approximately 5% between the two commodities, and the interrelationship has weakened by about the same percentage during the past few years.
Overall, empirical results based on the DCC-MGARCH model confirm that the overall returns of DDGS tend to move in the same direction as returns in the corn and soybean meal markets. With a few exceptions, the conditional correlations between DDGS and corn have increased since the ethanol boom in mid-2000s. However, the correlation coefficient has somewhat declined in recent years. Our results appear to be consistent with the previous findings suggesting increasing relationship between DDGS and corn after the ethanol mandate (e.g., Tejeda, Reference Tejeda2012). As anticipated, DDGS appears to be more correlated with corn than with soybean meal returns during the ethanol boom, though the magnitude of correlation may still appear to be low in light of the increasing use of DDGS in animal feeds. In light of the changing correlations, adjusting the hedge ratios appears to be an important task when cross hedging DDGS prices with corn and soybean meal futures prices.
Results from the MGARCH-BEKK model
The MGARCH-BEKK model allows us to assess volatility spillovers between markets. As seen in equation (3), Matrix A captures the innovation effects from shocks, while the B matrix captures the persistence of the conditional volatility. Table 4 displays the results of the estimation for the January 2000-May 2016 period. We also generate volatility impulse response functions (VIRFs) over the same period to a shock originated in another market that increases its conditional volatility by 1%, following the procedures of Gardebroek and Hernandez (Reference Gardebroek and Hernandez2013).
Similar to the DCC analysis, the a ji coefficients correspond to ARCH effects, and the b ji to the GARCH effects. Coefficients a 11, a 22, a 33, b 11.b 22.b 33 in table 4 are highly significant, indicating strong own-market effects from exogenous shocks, as well as strong persistence. Figure 4 shows strong responses on DDGS volatility from own market shocks that last around 15 weeks. Meanwhile the VIRF of soybean meal to own-market shocks last over 10 weeks, while for corn the impact is long-lived with positive responses for over 30 weeks.

Figure 4. Volatility Impulse Response Functions Based on the BEKK-MGARCH Model (January 2000–May 2016)
In terms of cross-market effects, strong volatility spillovers are observed from corn and soymeal prices into DDGS as a 21, a 31 and b 21 are all highly statistically significant. However, this relationship is unidirectional, since DDGS do not significantly influence volatility of the other two markets. The volatility of DDGS appears to be particularly affected by the volatility of corn. A shock that increases the volatility of corn markets by 1% would raise the conditional volatility of DDGS by about 5% in the first few weeks. Meanwhile, the volatility transmission from soybean meal to DDGS appears milder, and driven mainly by innovation, since coefficient b 31 suggests no volatility persistence flowing from soymeal to DDGS. Volatility spillovers between corn and soymeal exist and run in both directions, with a relatively stronger effect running from corn to soymeal than in the opposite direction.
Since the bulk of volatility has been observed since 2006, we also conduct an analysis over the May 2006—May 2016 period. Previous studies suggest a possible structural break in the grain market in mid-2006 driven primarily by corn-based ethanol production (e.g. Mallory, Irwin and Hayes Reference Mallory, Irwin and Hayes2012). Though there is no universal agreement on the specific date that the actual structural break occurred, May 2006 has been used in a number of studies to evaluate the effect of changing price dynamics in various agricultural commodity markets (e.g. Baumeister and Kilian, Reference Baumeister and Kilian2014, Wang, Wu and Yang, Reference Wang, Wu and Yang2014). Results on the volatility transmission pattern for this shorter sample period are summarized in the VIRFs shown in figure 5.Footnote 6

Figure 5. Volatility Impulse Response Functions Based on the BEKK-MGARCH Model (May 2006–May 2016)
The effect of DDGS market shocks on volatility is similar for the two time windows considered, with DDGS shocks only influencing its own volatility. Corn shocks in the 2006–2016 period also strongly contribute to DDGS volatility, though the magnitude of response appears to be smaller and the effect dies off faster compared to the results obtained from the whole sample period. This smaller and shorter-lived effect may suggest that the DDGS market is able to better absorb exogenous shocks as the market matures. Moreover, the effect of corn shocks on soybean meal volatility seems weaker during this period as well, and the own corn market shock effect becomes short-lived, dying off rapidly. Finally, the response to a soybean meal shock is strong for its own-market, and also for DDGS, however it appears weak for corn, even beyond two weeks.
In summary, for both the whole sample period and the period of 2006–2016 we observe strong volatility spillovers from corn and soybean meal going to DDGS, while DDGS does not affect the other two markets. Shocks originated from the corn market have a much larger impact on DDGS market volatility than those originated from the soybean meal market, supporting the argument of Silvestri (Reference Silvestri2015) that corn is the primary channel through which exogenous shocks are transmitted to the DDGS market. The important role corn plays in the system is also consistent with the observation that corn can be more easily stored than either DDGS or soybean meal. In light of exogenous shocks, inventory holders can release or expand existing inventory to meet changing market demand, thus reducing corn price volatility. The buffering function of inventory, however, is largely missing in the other two markets due to their low storability. Additionally, we find that volatility spillovers between corn and soybean meal become weaker when considering the shorter time period, suggesting a potential disconnection in volatility between these two markets even under a scenario of higher volatility.
Our results from the BEKK model can help to explain the findings from the DCC model that co-movements between corn and DDGS have weakened in the past few years. VIFs suggest that shocks in the corn and soybean meal markets have a large and significant impact on DDGS, whereas the reverse impact is almost nonexistent. Given the increasingly important role that export markets now play in DDGS price dynamics, exogenous shocks in the export market, such as the 2010–2012 Chinese anti-dumping investigation of US DDGS imports, apparently were not transmitted to the other two markets. A further implication is that while most of the price variations in the DDGS market prior to 2012 may have been associated with the volatility of corn—and to a lesser degree, soybean meal—export market variations now significantly affect DDGS prices, thus weakening the linkage between DDGS and the other two markets.
Conclusions
The dramatic rise of ethanol production in the U.S. has significantly increased the availability of DDGS. Despite the growing importance of DDGS, research on this relatively opaque, illiquid market remains scant. In this paper, we seek to fill in this literature gap by identifying the price and volatility transmission mechanisms between DDGS, corn, and soybean meal markets. Such an examination is needed as it provides useful information not only to market participants who wish to better manage their price risks in these three markets, but also to policymakers who wish to assess the impact of the ethanol mandate on the U.S. feed industry.
Using weekly data from January 2000 to May 2016, we find important interplays between the three markets in both price and volatility dynamics. We find a stable long-run equilibrium between the three prices, and that in the long-run, DDGS is viewed as a substitute for both corn and soybean meal. However, corn and soybean meal are weakly exogenous—as neither market responds to deviations from this long-run relationship. Short-run dynamics suggest that DDGS prices are affected by both corn and soybean meal prices, while the price of DDGS plays little role in the other two markets. We also find strong, time-varying dynamic conditional correlations between the three markets, with the correlation between DDGS and corn strengthening between 2006 and 2012, the period when ethanol production in the United States underwent massive expansion. However, the correlation between the two markets appeared to have weakened in recent years, possibly reflecting the increasingly important role that export markets play in the DDGS price dynamics.
Regarding the volatility transmission mechanisms, we identify significant volatility spillovers from both the corn and soybean meal markets to the DDGS market, with the impact of corn shocks much larger than soybean meal shocks. Corn appears to be the primary channel through which exogenous shocks are transmitted to the DDGS market, partly due to the high storability of corn compared to the other two commodities. Though Irwin and Good (Reference Irwin and Good2015) and Irwin (Reference Irwin2016) suggest that DDGS prices significantly affect the profit margin of ethanol plants, results in the present paper suggest that neither DDGS prices nor volatility are significant players in the corn and soybean meal markets.
As expressed by various market participants, managing DDGS price risks remains a challenging task as the market undergoes significant expansion and becomes increasingly involved in the international market. Though attempts have been made to create a DDGS futures contract in the United States, DDGS futures trading quickly became inactive only four months after its inception in early 2010. Participants in the DDGS market continue to face the question of how to better manage price risks. If risk management activities were carried out by cross-hedging using corn and soybean meal futures contracts, our paper clearly suggests that the hedge ratio needs to be adjusted periodically as correlations between DDGS, corn, and soybean meal appear to vary in time. Effective DDGS risk management strategies also require special attention be paid to the corn market, as shocks originating in the corn market can have a large, significant impact on the volatility of DDGS prices.











