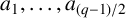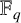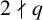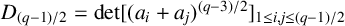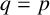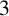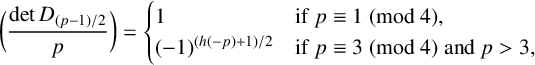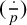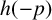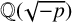ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS

Abstract

Motivated by the work initiated by Chapman [‘Determinants of Legendre symbol matrices’, Acta Arith. 115 (2004), 231–244], we investigate some arithmetical properties of generalised Legendre matrices over finite fields. For example, letting $a_1,\ldots ,a_{(q-1)/2}$ be all the nonzero squares in the finite field $\mathbb {F}_q$ containing q elements with $2\nmid q$, we give the explicit value of the determinant $D_{(q-1)/2}=\det [(a_i+a_j)^{(q-3)/2}]_{1\le i,j\le (q-1)/2}$. In particular, if $q=p$ is a prime greater than $3$, then

$$ \begin{align*}\bigg(\frac{\det D_{(p-1)/2}}{p}\bigg)= \begin{cases} 1 & \mbox{if}\ p\equiv1\pmod4,\\ (-1)^{(h(-p)+1)/2} & \mbox{if}\ p\equiv 3\pmod4\ \text{and}\ p>3, \end{cases}\end{align*} $$

where $(\frac {\cdot }{p})$ is the Legendre symbol and $h(-p)$ is the class number of $\mathbb {Q}(\sqrt {-p})$.

1 Introduction

1.1 Related work and motivations

Let p be an odd prime and let $(\frac {\cdot }{p})$ be the Legendre symbol. Chapman [1, 2] investigated determinants involving Legendre matrices

$$ \begin{align*}C_1=\bigg[\bigg(\frac{i+j-1}{p}\bigg)\bigg]_{1\le i,j\le (p-1)/2}\end{align*} $$

and

$$ \begin{align*}C_2=\bigg[\bigg(\frac{i+j-1}{p}\bigg)\bigg]_{1\le i,j\le (p+1)/2}.\end{align*} $$

Surprisingly, these determinants are closely related to quadratic fields. In fact, letting $\varepsilon _p>1$ and $h(p)$ be the fundamental unit and the class number of $\mathbb {Q}(\sqrt {p})$ , and writing $\varepsilon _p=a_p+b_p\sqrt {p}$ with $a_b,b_p\in \mathbb {Q}$ , Chapman [1] proved that

$$ \begin{align*}\det C_1= \begin{cases} (-1)^{(p-1)/4}2^{(p-1)/2}b_p & \mbox{if}\ p\equiv1\pmod4,\\ 0 & \mbox{otherwise,} \end{cases}\end{align*} $$

and

$$ \begin{align*}\det C_2= \begin{cases} (-1)^{(p+3)/4}2^{(p-1)/2}a_p & \mbox{if}\ p\equiv1\pmod4,\\ -2^{(p-1)/2} & \mbox{otherwise.} \end{cases}\end{align*} $$

Later, Chapman [2] posed the following conjecture.

Conjecture 1.1 (Chapman).

Let p be an odd prime and write $\varepsilon _p^{(2-(2/p))h(p)}= a_p^{\prime } +b_p^{\prime }\sqrt {p}$ with $a_p^{\prime },b_p^{\prime }\in \mathbb {Q}$ . Then

$$ \begin{align*}\det \bigg[\bigg(\frac{j-i}{p}\bigg)\bigg]_{1\le i,j\le (p+1)/2} =\begin{cases} -a_p^{\prime} & \mbox{if}\ p\equiv1\pmod 4,\\ 1 & \mbox{otherwise.} \end{cases}\end{align*} $$

Due to the difficulty of the conjecture, Chapman called this determinant ‘the evil determinant’. In 2012 and 2013, Vsemirnov [9, 10] confirmed the conjecture (the case $p\equiv 3\pmod 4$ in [9] and the case $p\equiv 1\pmod 4$ in [10]).

In 2019, Sun [8] studied some variants of Chapman’s determinants. For example, let

$$ \begin{align*} S(d,p)=\det\bigg[\bigg(\frac{i^2+dj^2}{p}\bigg)\bigg]_{1\le i,j\le (p-1)/2}.\end{align*} $$

Sun [8, Theorem 1.2] showed that $S(d,p)=0$ whenever $(d/p)=-1$ and that $(-S(d,p)/p)=1$ whenever $(d/p)=1$ . (See [3, 5, 11, 13] for recent progress on this topic.) Also, Sun [8, Theorem 1.4] proved that

(1.1) $$ \begin{align} \det\bigg[\frac{((i+j)/p)}{i+j}\bigg]_{1\le i,j\le (p-1)/2} \equiv\begin{cases} (2/p)\pmod p & \mbox{if}\ p\equiv1\pmod4,\\ ((p-1)/2)!\pmod p & \mbox{otherwise,} \end{cases} \end{align} $$

and that

$$ \begin{align*} \det\bigg[\frac{1}{i^2+j^2}\bigg]_{1\le i,j\le (p-1)/2}\equiv (-1)^{{(p+1)}/{4}}\pmod p \end{align*} $$

whenever $p\equiv 3\pmod 4$ . In 2022, the third author and Wang [14, Theorem 1.7] considered the determinant $\det [1/(\alpha _i+\alpha _j)]_{1\le i,j\le (p-1)/k}$ , where $0<\alpha _1,\ldots ,\alpha _{(p-1)/k}<p$ are all the kth power residues modulo p and showed that for any positive even integer k such that $k\mid p-1$ , if $-1$ is not a kth power modulo p, then

$$ \begin{align*} \det\bigg[\frac{1}{\alpha_i+\alpha_j}\bigg]_{1\le i,j\le m} \equiv \frac{(-1)^{(m+1)/2}}{(2k)^m}\pmod p, \end{align*} $$

where $m=(p-1)/k$ .

Now let $\mathbb {F}_q$ be the finite field of q elements with $\mathrm {char}(\mathbb {F}_q)=p>2$ . It is known that $\mathbb {F}_q^{\times }=\mathbb {F}_q\setminus \{0\}$ is a cyclic group of order $q-1$ and that the subgroups

$$ \begin{align*}U_k=\{x\in\mathbb{F}_q: x^k=1\}=\{a_1,\ldots,a_k\}\quad (k\ge 1, k\mid q-1)\end{align*} $$

are exactly all subgroups of $\mathbb {F}_q^{\times }$ . Let $\phi $ be the unique quadratic character of $\mathbb {F}_q$ , that is,

$$ \begin{align*}\phi(x)=\begin{cases} 1 & \mbox{if}\ x\ \text{is a nonzero square},\\ 0 & \mbox{if}\ x=0,\\ -1 & \mbox{otherwise.} \end{cases}\end{align*} $$

As $\mathrm {char}(\mathbb {F}_q)>2$ , the subset $\{\pm 1\}\subseteq \mathbb {Z}$ can be viewed as a subset of $\mathbb {F}_q$ . From now on, we always assume $\pm 1\in \mathbb {F}_q$ . Inspired by Sun’s determinant (1.1), it is natural to consider the matrix

$$ \begin{align*} \bigg[\frac{\phi(a_i+a_j)}{a_i+a_j}\bigg]_{1\le i,j\le k}. \end{align*} $$

However, if $k\mid q-1$ is even, then the denominator $a_i+a_j=0$ for some $i,j$ since ${-1\in U_k}$ in this case. To overcome this obstacle, note that for any $x\in \mathbb {F}_q$ , we have $\phi (x)=x^{(q-1)/2}$ . Hence, we first focus on the matrix

$$ \begin{align*} D_k:=[(a_i+a_j)^{(q-3)/2}]_{1\le i,j\le k}. \end{align*} $$

The main results involving $D_k$ will be given in Section 1.2.

We now consider another type of determinant. Sun [8, Remark 1.3] posed the following conjecture.

Conjecture 1.2 (Sun).

Let $p\equiv 2\pmod 3$ be an odd prime. Then

(1.2) $$ \begin{align} 2\det\bigg[\frac{1}{i^2-ij+j^2}\bigg]_{1\le i,j\le p-1} \end{align} $$

is a quadratic residue modulo p.

The third author, She and Ni [12] obtained the following generalised result.

Theorem 1.3 (Wu, She and Ni).

Let $q\equiv 2\pmod 3$ be an odd prime power. Let $\beta _1,\ldots ,\beta _{q-1}$ be all the nonzero elements of $\mathbb {F}_q$ . Then

$$ \begin{align*}\det\bigg[\frac{1}{\beta_i^2-\beta_i\beta_j+\beta_j^2}\bigg]_{1\le i,j\le q-1} =(-1)^{(q+1)/2}2^{(q-2)/3}\in\mathbb{F}_p, \end{align*} $$

where $p=\mathrm {char}(\mathbb {F}_q)$ .

Recently, Luo and Sun [6] investigated the determinant

(1.3) $$ \begin{align} \det S_p(c,d)=\det[(i^2+cij+dj^2)^{p-2}]_{1\le i,j\le p-1}. \end{align} $$

For $(c,d)=(1,1)$ or $(2,2)$ , they determined the explicit values of $({\det S_p(c,d)}/{p})$ .

Motivated by Sun’s determinants (1.1)–(1.3) and the above discussions, we also consider the matrix

$$ \begin{align*}T_k:=[(a_i^2+a_ia_j+a_j^2)^{(q-3)/2}]_{1\le i,j\le k}.\end{align*} $$

We will state our results concerning $T_k$ in Section 1.3.

1.2 The main results involving det $\,D_k$

Theorem 1.4. Let $\mathbb {F}_q$ be the finite field of q elements with $\mathrm {char}(\mathbb {F}_q)=p>2$ . Then for any integer $k\mid q-1$ with $1<k\le q-1$ ,

$$ \begin{align*}\det D_k=(-1)^{(k+1)(q-3)/2}\cdot w_k\cdot k^k\in\mathbb{F}_p,\end{align*} $$

where

$$ \begin{align*}w_k=\prod_{s=0}^{k-1}\sum_{r=0}^{\lfloor{(q-3-2s)}/{2k}\rfloor} \binom{(q-3)/2}{s+rk}\in\mathbb{F}_p.\end{align*} $$

Suppose now that $k=(q-1)/2$ , that is, $U_{(q-1)/2}$ is the set of all the nonzero squares over $\mathbb {F}_q$ . Then we can obtain the following simplified result which will be proved in Section 2.

Corollary 1.5. Let $\mathbb {F}_q$ be the finite field of q elements with $\mathrm {char}(\mathbb {F}_q)=p>2$ . Then

$$ \begin{align*}\det D_{(q-1)/2}= \begin{cases} (-1)^{({q+3})/{4}}u^2 & \mbox{if}\ q\equiv 1\pmod4,\\ (-1)^{({q+5})/{4}}\binom{(q-3)/2}{(q-3)/4}v^2 & \mbox{if}\ q\equiv 3\pmod4\ \text{and}\ q>3, \end{cases}\end{align*} $$

where $u,v\in \mathbb {F}_p$ are defined by

$$ \begin{align*}u=\prod_{s=0}^{(q-5)/4}\binom{(q-3)/2}{s}\quad \text{and}\quad v=\prod_{s=0}^{(q-7)/4}\binom{(q-3)/2}{s}.\end{align*} $$

In particular, if $q=p>3$ is an odd prime, then $D_{(p-1)/2}$ is nonsingular and

$$ \begin{align*}\bigg(\frac{\det D_{(p-1)/2}}{p}\bigg)= \begin{cases} 1 & \mbox{if}\ p\equiv1\pmod4,\\ (-1)^{(h(-p)+1)/2} & \mbox{if}\ p\equiv 3\pmod4\ \text{and}\ p>3, \end{cases}\end{align*} $$

where $h(-p)$ is the class number of $\mathbb {Q}(\sqrt {-p})$ .

From Theorem 1.4, we see that $\det D_k\in \mathbb {F}_p$ . The next result gives the explicit value of $({\det D_k}/{p})$ when k is odd.

Theorem 1.6. Let $\mathbb {F}_q$ be the finite field of q elements with $\mathrm {char}(\mathbb {F}_q)=p>2$ . Let ${1<k\le q-1}$ be an odd integer with $k\mid q-1$ . Suppose that $D_k$ is nonsingular. Then

$$ \begin{align*} \bigg(\frac{\det D_k}{p}\bigg)=\bigg(\frac{s_k}{p}\bigg), \end{align*} $$

where

$$ \begin{align*} s_k:=k\sum_{r=1}^{({q-1)}/{2k}}\binom{(q-3)/2}{((2r-1)k-1)/2}\in\mathbb{F}_p.\end{align*} $$

1.3 The main results involving $\mathrm{det}\ T_k$

To state the next results, we need to introduce some basic properties of trinomial coefficients. Let n be a positive integer. For any integer r, the trinomial coefficient $\binom {n}{r}_2$ is defined by

$$ \begin{align*}\bigg(x+\frac{1}{x}+1\bigg)^{n}= \sum_{r=-\infty}^{+\infty}\binom{n}{r}_2x^r.\end{align*} $$

This implies that $\binom {n}{r}_2=0$ whenever $|r|>n$ and that $\binom {n}{r}_2=\binom {n}{-r}_2$ for any integer r. In particular, $\binom {n}{0}_2$ is usually called the central trinomial coefficient because $\binom {n}{0}_2$ is exactly the coefficient of $x^n$ in the polynomial $(x^2+x+1)^n$ . For simplicity, $\binom {n}{0}_2$ is also denoted by $t_n$ .

Theorem 1.7. Let $\mathbb {F}_q$ be the finite field of q elements with $\mathrm {char}(\mathbb {F}_q)=p>2$ . Then for any integer $k\mid q-1$ with $1<k\le q-1$ ,

$$ \begin{align*}\det T_k=l_k\cdot k^k\in\mathbb{F}_p,\end{align*} $$

where

$$ \begin{align*}l_k=\prod_{s=0}^{k-1}\sum_{r=0}^{\lfloor{(q-3-s)}/{k}\rfloor} \binom{(q-3)/2}{(q-3)/2-s-kr}_2\in\mathbb{F}_p.\end{align*} $$

As a direct consequence of Theorem 1.7, we have the following result.

Corollary 1.8. Let $\mathbb {F}_q$ be the finite field of q elements with $\mathrm {char}(\mathbb {F}_q)=p>2$ . For any integer $k\mid q-1$ with $1<k\le q-1$ , the matrix $T_k$ is singular over $\mathbb {F}_q$ if and only if

$$ \begin{align*} \sum_{r=0}^{\lfloor{(q-3-s)}/{k}\rfloor} \binom{(q-3)/2}{(q-3)/2-s-kr}_2\equiv0\pmod p\end{align*} $$

for some s with $0\le s\le k-1$ . In particular, $T_{q-1}$ is a singular matrix over $\mathbb {F}_q$ .

In the case $k=(q-1)/2$ , similar to Corollary 1.5, by Theorem 1.7, we deduce the following simplified result.

Corollary 1.9. Let $\mathbb {F}_q$ be the finite field of q elements with $\mathrm {char}(\mathbb {F}_q)=p>2$ .

1. (i) If $q\equiv 1\pmod 4$ , then

   $$ \begin{align*}\det T_{(q-1)/2}= \prod_{s=0}^{(q-5)/4} \bigg(\binom{(q-3)/2}{(q-3)/2-s}_2+\binom{(q-3)/2}{1+s}_2\bigg)^2.\end{align*} $$

2. (ii) If $q\equiv 3\pmod 4$ and $q>3$ , then

   $$ \begin{align*}\det T_{(q-1)/2}= \binom{(q-3)/2}{0}_2\prod_{s=0}^{(q-7)/4} \Bigg(\binom{(q-3)/2}{(q-3)/2-s}_2+\binom{(q-3)/2}{1+s}_2\Bigg)^2.\end{align*} $$

In particular, if $T_{(q-1)/2}$ is nonsingular, then

$$ \begin{align*} \bigg(\frac{\det T_{(q-1)/2}}{p}\bigg)=\begin{cases} (-1)^{(q-1)/4} & \mbox{if}\ q\equiv1\pmod4,\\ \bigg(\dfrac{t_{(q-3)/2}}{p}\bigg)(-1)^{(q+5)/4} & \mbox{if}\ q\equiv3\pmod4\ \text{and}\ q>3. \end{cases} \end{align*} $$

2 Proofs of Theorem 1.4 and Corollary 1.5

We begin with the following result (see [4, Lemma 10]).

Lemma 2.1. Let R be a commutative ring. Let $P(t)=p_0+p_1t+\cdots +p_{n-1}t^{n-1}\in R[t]$ . Then

$$ \begin{align*}\det[P(X_iY_j)]_{1\le i,j\le n}=\prod_{i=0}^{n-1}p_i \cdot \prod_{1\le i<j\le n}(X_j-X_i)(Y_j-Y_i).\end{align*} $$

We also need the following result.

Lemma 2.2. Let $\mathbb {F}_q$ be the finite field of q elements with $\mathrm {char}(\mathbb {F}_q)=p$ . For any positive integer $k\mid q-1$ , if we set $U_k=\{a_1,\ldots ,a_k\}$ , then

$$ \begin{align*}\prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg)=k^k\in\mathbb{F}_p.\end{align*} $$

Proof. It is clear that

(2.1) $$ \begin{align} \prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg) =\prod_{1\le i<j\le k}\frac{(a_j-a_i)(a_i-a_j)}{a_ia_j} =\prod_{1\le i\neq j\le k}(a_j-a_i) \prod_{1\le i<j\le k}\frac{1}{a_ia_j}. \end{align} $$

Let $S_1=\prod _{1\le i\neq j\le k}(a_j-a_i)$ and let $S_2=\prod _{1\le i<j\le k}{1}/{(a_ia_j)}$ . We first consider $S_1$ . Let

$$ \begin{align*}G_k(t)=\prod_{i=1}^k(t-a_i)\in\mathbb{F}_q[t]\end{align*} $$

and let $G^{\prime }_k(t)$ be the formal derivative of $G_k(t)$ . Then by the definition of $U_k$ , we see that $G_k(t)=t^k-1$ . Thus, $G_k^{\prime }(t)=kt^{k-1}$ and $\prod _{1\le j\le k}a_j=(-1)^{k+1}$ . Now we can verify that

(2.2) $$ \begin{align} S_1 =\prod_{1\le i\neq j\le k}(a_j-a_i)=\prod_{1\le j\le k}G_k^{\prime}(a_j) =\prod_{1\le j\le k}ka_j^{k-1} =k^k(-1)^{k+1}. \end{align} $$

We turn to $S_2$ . It is clear that

(2.3) $$ \begin{align} S_2=\prod_{1\le i<j\le k}\frac{1}{a_ia_j}=\prod_{1\le j\le k}\frac{1}{a_j^{k-1}}=(-1)^{k+1}. \end{align} $$

Combining (2.1) with (2.2) and (2.3),

$$ \begin{align*} \prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg)=S_1S_2=k^k\in\mathbb{F}_p. \end{align*} $$

This completes the proof.

Proof of Theorem 1.4.

As $\mathrm {char}(\mathbb {F}_q)=p>2$ , the subset $\{1,-1\}\subseteq \mathbb {Z}$ can be naturally viewed as a subset of $\mathbb {F}_q$ . One can verify that

(2.4) $$ \begin{align} \det D_k =\det[(a_i+a_j)^{{(q-3)}/{2}}]_{1\le i,j\le k} &=\prod_{i=1}^ka_i^{{(q-3)}/{2}}\det\bigg[\bigg(1+\frac{a_j}{a_i}\bigg)^{{(q-3)}/{2}}\bigg]_{1\le i,j\le k}\nonumber\\ &=(-1)^{(k+1)(q-3)/2}\det\bigg[\bigg(1+\frac{a_j}{a_i}\bigg)^{{(q-3)}/{2}}\bigg]_{1\le i,j\le k}. \end{align} $$

The last equality follows from $\prod _{1\le j\le k}a_j=(-1)^{k+1}$ . Let

$$ \begin{align*}f_k(t) =\sum_{s=0}^{k-1} \Bigg(\sum_{r=0}^{\lfloor{(q-3-2s)}/{2k}\rfloor} \binom{(q-3)/2}{s+rk}\Bigg)t^s\in\mathbb{F}_p[t]\end{align*} $$

with $\deg (f_k)\le k-1$ . Noting that $(a_j/a_i)^{k+s}=(a_j/a_i)^s$ for any integer s, by (2.4),

$$ \begin{align*} \det D_k =(-1)^{(k+1)(q-3)/2} \cdot \det\bigg[f_k\bigg(\frac{a_j}{a_i}\bigg)\bigg]_{1\le i,j\le k}. \end{align*} $$

Let

$$ \begin{align*}w_k:=\prod_{s=0}^{k-1}\sum_{r=0}^{\lfloor{(q-3-2s)}/{2k}\rfloor} \binom{(q-3)/2}{s+rk}\in\mathbb{F}_p.\end{align*} $$

Then by Lemmas 2.1 and 2.2,

$$ \begin{align*}\det D_k=(-1)^{(k+1)(q-3)/2}\cdot w_k\cdot \prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg)=(-1)^{(k+1)(q-3)/2}\cdot w_k\cdot k^k\in\mathbb{F}_p.\end{align*} $$

This completes the proof.

Proof of Corollary 1.5.

By Theorem 1.4, if $k=(q-1)/2$ , then

(2.5) $$ \begin{align} \det D_{(q-1)/2} &=(-1)^{(q-3)/2}\cdot\prod_{s=0}^{(q-3)/2}\binom{(q-3)/2}{s}\cdot (-1)^{(q-1)/2}\bigg(\frac{1}{2}\bigg)^{(q-1)/2}\nonumber\\ &=-1\cdot\prod_{s=0}^{(q-3)/2}\binom{(q-3)/2}{s}\cdot\phi(2). \end{align} $$

The last equality follows from

$$ \begin{align*}(\tfrac{1}{2})^{(q-1)/2}=\phi(\tfrac{1}{2})=\phi(2).\end{align*} $$

We now divide the remaining part of the proof into two cases.

Case 1: $q\equiv 1\pmod 4$ .

In this case, we have $\sqrt {-1}\in \mathbb {F}_q$ , where $\sqrt {-1}$ is an element in the algebraic closure of $\mathbb {F}_q$ such that $(\sqrt {-1})^2=-1$ . Since $2=-\sqrt {-1}(1+\sqrt {-1})^2,$ we have $\phi (2)=\phi (-\sqrt {-1})$ and hence

(2.6) $$ \begin{align} \phi(2)=\phi(-\sqrt{-1})=(-\sqrt{-1})^{(q-1)/2}=(-1)^{(q-1)/4}. \end{align} $$

Combining (2.5) with (2.6) and noting that

$$ \begin{align*}\binom{(q-3)/2}{s}=\binom{(q-3)/2}{(q-3)/2-s},\end{align*} $$

we obtain

(2.7) $$ \begin{align} \det D_{(q-1)/2}=(-1)^{(q+3)/4}\prod_{s=0}^{(q-5)/4}\binom{(q-3)/2}{s}^2. \end{align} $$

This proves the case $q\equiv 1\pmod 4$ .

Case 2: $q\equiv 3\pmod 4$ and $q>3$ .

In this case, since $q\equiv 3\pmod 4$ , $(1+\sqrt {-1})^q=1+(\sqrt {-1})^q=1-\sqrt {-1}$ . This, together with $2=-\sqrt {-1}\big (1+\sqrt {-1}\big )^2$ , implies that

(2.8) $$ \begin{align} \phi(2) &=2^{(q-1)/2}=(-\sqrt{-1})^{(q-3)/2}(-\sqrt{-1})\big(1+\sqrt{-1}\big)^{q-1}\nonumber\\ &=(-1)^{(q-3)/4}(-\sqrt{-1})\frac{1-\sqrt{-1}}{1+\sqrt{-1}}\nonumber\\ &=(-1)^{(q+1)/4}. \end{align} $$

Combining (2.5) with (2.8),

(2.9) $$ \begin{align} \det D_{(q-1)/2}=(-1)^{(q+5)/4}\binom{(q-3)/2}{(q-3)/4}\prod_{s=0}^{(q-7)/4}\binom{(q-3)/2}{s}^2. \end{align} $$

This proves the case $q\equiv 3\pmod 4$ and $q>3$ .

Now we assume that $q=p$ is an odd prime. Suppose first $p\equiv 1\pmod 4$ . Then by (2.7), we see that $\det D_{(q-1)/2}$ is a nonzero square in $\mathbb {F}_p$ , that is, $({\det D_{(p-1)/2}}/{p})=1$ . In the case $p\equiv 3\pmod 4$ and $p>3$ , by (2.9) and $({-2}/{p})=({-\tfrac 12}/{p})=(-1)^{(p+5)/4}$ ,

$$ \begin{align*} \bigg(\frac{\det D_{(q-1)/2}}{p}\bigg)&=(-1)^{(p+5)/4}\Bigg(\frac{\tfrac{p-3}{2}!}{p}\Bigg) =(-1)^{(p+5)/4}\Bigg(\frac{\tfrac{p-1}{2}!}{p}\Bigg) \Bigg(\frac{\tfrac{-1}{2}}{p}\Bigg) =\Bigg(\frac{\tfrac{p-1}{2}!}{p}\Bigg) =(-1)^{(h(-p)+1)/2}. \end{align*} $$

The last equality follows from Mordell’s result [7] which states that

$$ \begin{align*}\frac{p-1}{2}!\equiv (-1)^{{(h(-p)+1)}/{2}}\pmod p\end{align*} $$

whenever $p\equiv 3\pmod 4$ and $p>3$ . This completes the proof.

3 Proof of Theorem 1.6

To prove Theorem 1.6, we first need the following well-known result.

Lemma 3.1. Let $\mathbb {F}_q$ be the finite field of q elements and let r be a positive integer. Then

$$ \begin{align*} \sum_{x\in\mathbb{F}_q}x^r=\begin{cases} 0 & \mbox{if}\ q-1\nmid r,\\ -1 & \mbox{if}\ q-1\mid r. \end{cases} \end{align*} $$

We will see later in the proof that $\det D_k$ has close relations with the determinant of a circulant matrix. Hence, we now introduce the definition of circulant matrices. Let R be a commutative ring. Let $b_0,b_1,\ldots ,b_{s-1}\in R$ . We define the circulant matrix $C(b_0,\ldots ,b_{s-1})$ to be an $s\times s$ matrix whose ( $i,j$ )-entry is $b_{j-i}$ where the indices are cyclic module s, that is, $b_i=b_j$ whenever $i\equiv j\pmod s$ . The third author [11, Lemma 3.4] obtained the following result.

Lemma 3.2. Let R be a commutative ring. Let s be a positive integer. Let $b_0,b_1,\ldots ,b_{s-1}\in R$ such that $b_i=b_{s-i}$ for $1\leqslant i\leqslant s-1$ .

If s is even, then there exists an element $u\in R$ such that

$$ \begin{align*} \det C(b_0,\ldots,b_{s-1})=\bigg(\sum_{i=0}^{s-1}b_i\bigg)\bigg(\sum_{i=0}^{s-1}(-1)^ib_i\bigg)\cdot u^2. \end{align*} $$

If s is odd, then there exists an element $v\in R$ such that

$$ \begin{align*} \det C(b_0,\ldots,b_{s-1})=\bigg(\sum_{i=0}^{s-1}b_i\bigg)\cdot v^2. \end{align*} $$

Proof of Theorem 1.6.

As k is odd, we have $2\mid (q-1)/k$ . For simplicity, we let $q-1=nk=2mk$ . Since $k\mid (q-1)/2$ in this case, $\phi (a_i)=a_i^{(q-1)/2}=1$ for each $a_i\in U_k$ . Let g be a generator of the cyclic group $\mathbb {F}_q^{\times }$ . By the above, one can verify that

$$ \begin{align*} \det D_k =\prod_{i=1}^ka_i^{(q-3)/2}\det\bigg[\bigg(1+\frac{a_j}{a_i}\bigg)^{(q-3)/2}\bigg]_{1\le i,j\le k} =\det[(1+g^{nj-ni})^{(q-3)/2}]_{0\le i,j\le k-1}. \end{align*} $$

The last equality follows from

$$ \begin{align*} \prod_{i=1}^ka_i=(-1)^{k+1}=1. \end{align*} $$

By the above and using the properties of determinants, one can verify that

(3.1) $$ \begin{align} \det D_k=\det[(1+g^{nj-ni})^{(q-3)/2}g^{mj-mi}(-1)^{j-i}]_{0\le i,j\le k-1}. \end{align} $$

For $0\le i\le k-1$ ,

$$ \begin{align*}b_i=(1+g^{ni})^{(q-3)/2}g^{mi}(-1)^i.\end{align*} $$

We claim that $b_i=b_{k-i}$ for $1\le i\le k-1$ . In fact, for $1\le i\le k-1$ , noting that

$$ \begin{align*}g^{km}=\phi(g)=-1,\quad g^{nk}=1,\ 2\nmid k \quad \text{and}\quad \bigg(\frac{1}{g^{ni}}\bigg)^{(q-3)/2}=g^{ni},\end{align*} $$

one can verify that

$$ \begin{align*} b_{k-i}&=(1+g^{nk-ni})^{(q-3)/2}g^{mk-mi}(-1)^{k-i}\\ &=\bigg(\frac{1+g^{ni}}{g^{ni}}\bigg)^{(q-3)/2}g^{-mi}(-1)^i\\ &=(1+g^{ni})^{(q-3)/2}g^{(n-m)i}(-1)^i\\ &=b_i. \end{align*} $$

Hence, by (3.1), $\det D_k=\det C(b_0,b_1,\ldots ,b_{k-1})$ . Now by Lemma 3.2 and (3.1),

(3.2) $$ \begin{align} \det D_k=\bigg(\sum_{i=0}^{k-1}b_i\bigg)v^2 \end{align} $$

for some $v\in \mathbb {F}_q$ . Now we consider the sum $\sum _{i=0}^{k-1}b_i$ . It is easy to verify that

(3.3) $$ \begin{align} \sum_{i=0}^{k-1}b_i &=\sum_{i=0}^{k-1}(1+g^{ni})^{(q-3)/2}g^{mi}(-1)^i =\sum_{i=0}^{k-1}(1+g^{ni})^{(q-3)/2}g^{mi}g^{mki}\nonumber\\ &=\frac{1}{n}\sum_{x\in\mathbb{F}_q}(1+x^n)^{(q-3)/2}x^{m+mk} =\frac{1}{n}\sum_{r=0}^{mk-1}\binom{(q-3)/2}{r}\sum_{x\in\mathbb{F}_q}x^{m+mk+2mr}. \end{align} $$

Now by Lemma 3.1, since $2\nmid k$ ,

$$ \begin{align*}\sum_{x\in\mathbb{F}_q}x^{m+mk+2mr}=\begin{cases} 0 & \mbox{if}\ k\nmid 1+2r,\\ -1 & \mbox{if}\ k\mid 1+2r. \end{cases} \end{align*} $$

Applying this and Lemma 3.1 to (3.3) and noting that $-1/n=k$ in $\mathbb {F}_p$ ,

(3.4) $$ \begin{align} s_k:=\sum_{i=0}^{k-1}b_i=k\sum_{r=1}^m\binom{(q-3)/2}{((2r-1)k-1)/2}. \end{align} $$

Suppose that $D_k$ is nonsingular. Then by Theorem 1.4, we have $\det D_k\in \mathbb {F}_p^{\times }$ . Hence, by (3.2) and (3.4),

$$ \begin{align*}\bigg(\frac{\det D_k}{p}\bigg)=\bigg(\frac{s_k}{p}\bigg).\end{align*} $$

This completes the proof.

4 Proof of Theorem 1.7

It is clear that

(4.1) $$ \begin{align} \det T_k &=\prod_{i=1}^{k}(a_i^2)^{(q-3)/2} \cdot \det\bigg[\bigg(1+\frac{a_j}{a_i}+\bigg(\frac{a_j}{a_i}\bigg)^2\bigg)^{(q-3)/2}\bigg]_{1\le i,j\le k}\nonumber\\ &=\det\bigg[\bigg(1+\frac{a_j}{a_i}+\bigg(\frac{a_j}{a_i}\bigg)^2\bigg)^{(q-3)/2}\bigg]_{1\le i,j\le k}. \end{align} $$

The last equality follows from

$$ \begin{align*}\prod_{i=1}^ka_i=(-1)^{k+1}.\end{align*} $$

Let

$$ \begin{align*}g_k(t)= \sum_{s=0}^{k-1} \Bigg(\sum_{r=0}^{\lfloor{(q-3-s)}/{k}\rfloor} \binom{(q-3)/2}{s+rk-(q-3)/2}_2\Bigg)t^s\in\mathbb{F}_p[t]\end{align*} $$

with $\deg (g_k)\le k-1$ . Then by (4.1), Lemma 2.1 and the definition of trinomial coefficients,

$$ \begin{align*} \det T_k &=\det\bigg[g_k\bigg(\frac{a_j}{a_i}\bigg)\bigg]_{1\le i,j\le k}\\ &=\prod_{1\le i<j\le k}(a_j-a_i)\bigg(\frac{1}{a_j}-\frac{1}{a_i}\bigg)\cdot \prod_{s=0}^{k-1}\sum_{r=0}^{\lfloor{(q-3-s)}/{k}\rfloor} \binom{(q-3)/2}{s+rk-(q-3)/2}_2\\ &=l_kk^k\in\mathbb{F}_p. \end{align*} $$

The last equality follows from Lemma 2.2. This completes the proof. $\Box $