Introduction
Due to the limited accessibility of the subglacial and englacial environment, the determination of subsurface ice velocities and components of the strain rate and stress is a technically difficult and expensive task. Such information is of crucial importance for understanding basal processes, such as variable basal sliding and its consequences for the near-basal strain field.
A number of methods and techniques, mostly in boreholes, have been applied to probe the englacial velocity and strain fields. An often used method is the observation of ice deformation in an open borehole with inclinometry (Reference Gerrard, Perutz and RochGerrard and others, 1952; Reference SharpSharp, 1953; Reference RaymondRaymond, 1971; Reference Hooke and HansonHooke and Hanson, 1986; Reference Hooke, Pohjola, Jansson and KohlerHooke and others, 1992). This method was used to determine longitudinal strain in a chain of boreholes (Reference Shreve and SharpShreve and Sharp, 1970), to identify extrusion flow type velocity profiles (Reference Hooke, Holmlund and IversonHooke and others, 1987), to determine local sliding velocities (Reference Copland, Harbor, Minner and SharpCopland and others, 1997) and to investigate the effect of a cold margin on ice flow (Reference Moore, Iverson, Brugger, Cohen, Hooyer and JanssonMoore and others, 2011). Reference Harper, Humphrey and PfefferHarper and others (1998, Reference Harper, Humphrey, Pfeffer, Huzurbazar, Bahr and Welch2001) used arrays of boreholes to determine three-dimensional flow and strain fields. Various methods were applied to measure vertical strain rates in open boreholes (Reference PatersonPaterson, 1976; Reference Raymond, Rogers, Taylor and KociRaymond and others, 1994; Reference GudmundssonGudmundsson, 2002; Reference Hawley, Waddington, Morse, Dunbar and ZielinskiHawley and others, 2002; Reference Sugiyama and GudmundssonSugiyama and Gudmundsson, 2003). Reference Schwerzmann, Funk and BlatterSchwerzmann and others (2006) used a combined inclinometer/caliper probe to measure the velocity profile together with the closure, cross-sectional deformation and vertical normal strain of a borehole.
The installation of continuously measuring inclinometers in boreholes allows us to perform measurements of high temporal resolution (Reference Gudmundsson, Bauder, Lüthi, Fischer and FunkGudmundsson and others, 1999; Reference Amundson, Truffer and LüthiAmundson and others, 2006). This method continuously observes the tilt and azimuth of the axes of instruments that are inserted into the ice. Modeled tilt curves that are calculated from assumed or modeled flow fields were fitted to the measured tilt curves to interpret the measurements.
An in situ measurement of the stress-strain-rate relation of glacier ice can only be performed if all stress components and strain components are measured simultaneously at the same location within the ice (Reference Pfeffer, Humphrey, Amadei, Harper and WegmannPfeffer and others, 2000; Reference Marshall, Harper, Pfeffer and HumphreyMarshall and others, 2002) without additional assumptions on the flow field or numerical modeling. In this work we propose and discuss a technique that allows us to meet these requirements for measurements of strain rates. The practical application of this technique may not be trivial, and in fact, the analysis was carried out as a result of difficulties in an experiment on Rhonegletscher, Switzerland. The coupling of the instruments to the ice in boreholes in temperate ice may take several months and seems to be unstable even then.
For the evaluation of the inclinometer data we assume that the instrument behaves as a Lagrangian unit vector attached to the ice, which leads to a time-evolution equation for the unit vector. This equation is (to lowest order in the time-step) identical to the one Reference Gudmundsson, Bauder, Lüthi, Fischer and FunkGudmundsson and others (1999) solved by an explicit Euler method. The evolution equation for the unit vector can be solved analytically with two restrictive assumptions: (1) the flow field is well represented with the plane-strain first-order approximation (Reference BlatterBlatter, 1995) and (2) the strain components are constant over the measurement period.
In the following sections, we give some technical information on the inclinometer/magnetometer probes and their calibration. The mathematical theory of strain measurements with inclinometer probes is outlined and discussed, and we present an analysis of time series of zenith and azimuth angles of probe axes to determine the strain components if only one sensor is available and show some examples of time series observed in Alpine glaciers. In the final section (Conclusions and prospects), we discuss the possibilities for strain measurements and propose experiments to further develop the method.
Inclinometer Probe
The inclinometer probe consists of a cylindrical aluminum casing of 46mm diameter and 63 mm length. A two-axis inclinometer of type SCA100T-D01 (VTI Technologies, http://www.vti.fi/en/products/inclinometers) with a nominal resolution of 0.044 mrad, and a three-axis magnetometer of type MicroMag3 (PNI Corporation, http://www.pnicorp.com/products/products) with a nominal resolution of 015 μT allow us to measure the absolute direction of the probe axis in space and, furthermore, to determine the absolute orientation of an orthogonal set of vectors that are fixed with respect to the casing. The limiting factor for the accuracy is given by the magnetometers and the large uncertainty in the orientation of the Earth's magnetic field at depth in the ice.
Calibration and processing of data
The combined inclinometer/magnetometer probes provide the strength of the magnetic field along three axes and the strength of the gravity field along two axes,
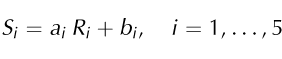
where Ri are the magnetic and gravity field strengths, Si are the readings of the sensor output, ai are the slopes of linear functions and bi are the offsets at zero field strength. The ten unknown parameters, ai and bi , must be determined by a calibration procedure.
Ideally, the calibration should be performed under laboratory conditions. If, however, the absolute value and the orientation of the magnetic field at the site of the measurement is not known, the problem can still be treated with the same number of unknown parameters. In this case, we simply assume the Ri to be normalized fields, and the parameters depend on the absolute field strengths. For the magnetic field this means that the calibration has to be repeated on site, as the geomagnetic field there may be different from that in the laboratory.
Given a parameterization of the pure rotations in three dimensions, three parameters completely describe the orientation of the instrument with respect to a fixed coordinate system at a given measurement. For N measurements, there are 3N unknown orientation parameters, i.e. a total of 10 + 3N unknowns (including instrument parameters). Every measurement results in five measured values of magnetic and gravity components along the corresponding axes. Thus, for N measurements, we obtain 5N readings. For N = 5 the problem is closed, for N > 5 measurements, the problem is overdetermined, and the solution can be optimized by a least-squares optimization procedure, yielding both ten instrument parameters and 3N orientation parameters of best fit. In detail, we need to minimize the sum
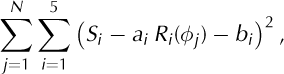
where ϕj is the set of orientation parameters at measurement j, and Ri(ϕj) are the normalized fields projected to the instrument’s coordinate system. The minimization with respect to ϕj, ai and bi is best done using the Gauss–Newton algorithm (e.g. Reference BjörkBjörk, 1996).
The calibration was done in several steps. First, a laboratory calibration measurement was used to determine the four gravimeter parameters. Once the instrument was at the field site, measurements close to the borehole were carried out to calibrate the magnetic sensors. The data processing of the sensors in the boreholes can be done using the same optimization procedure as for the calibration with the instrument parameters from the calibration kept constant and optimizing only the orientation parameters. This allows us to calculate for every measurement an orthogonal matrix, Q, that describes the orientation of the instrument with respect to a reference frame fixed in space, given by the gravity and geomagnetic fields. Q contains as rows three unit vectors each describing the orientation of one of three axes of the instrument with respect to the external reference frame. The angles θ and ϕ, that are used in the next sections, are the zenith (i.e. tilt from vertical) and azimuth angles of the row of Q which corresponds to the longitudinal axis of the instrument. It would be desirable to do a similar time-series analysis for the whole orthogonal system; however, it is not yet clear how similar theoretical evolution curves for the whole system can be obtained. Details of the underlying mathematics are given in Appendix A.
Mathematical Theory
A thin cylindrical probe inserted in the ice is assumed to move in the same way as a unit vector given by the direction of the image of a Lagrangian coordinate increment with respect to deformation. Using the notation of Reference HutterHutter (1983), we denote by dXA a vector increment in the reference (Lagrangian) configuration, and by dxi-(X A) the corresponding vector in the present (Eulerian) configuration. Using the Einstein summation convention, we define the unit vector through its components, ei , as
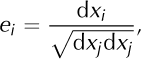
so it points in the direction of the vectorial quantity dx. The temporal evolution of the unit vector is given by
where

denotes the components of the velocity gradient. That is, the evolution of ei is given by the projection of Lijej on a plane perpendicular to the vector ei . A detailed derivation of Eqn (4) is given in Appendix B.
For practical purposes, we assume Cartesian coordinates with the base unit vectors n1, n2 and n3, such that the unit vector e = e1 n1 + e2 n2 + e3 n3. Furthermore, we use spherical coordinates with 0 ≤ θ < π, ≤ ϕ < 2π such that

Thus, the time derivative of the unit vector, e, has the form
where the vectors
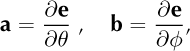
are orthogonal to vector e and orthogonal to each other,
Scalar multiplication of Eqn (4) with a and b, respectively, yields
and
The second part on the right-hand side of Eqn (4), ei(ejLjk ek), does not have any influence on ![]() and
and ![]() as it is colinear with e, and thus orthogonal to both vectors a and b. Equations (10) and (11) are two linear equations for the nine components Lij of the velocity gradient.
as it is colinear with e, and thus orthogonal to both vectors a and b. Equations (10) and (11) are two linear equations for the nine components Lij of the velocity gradient.
The analytical solution can be used for a regression with the measured time series of zenith angles. Interestingly, the azimuth angle does not occur in the solution for θ, except for its initial value, ϕ0, which can be used as a fitting parameter in the regression.
In principle it is possible to give an analytical solution including L12 ≠ 0 as well but this is much more complicated than Eqn (16), which makes it much less useful for purposes of field data analysis.
Analysis of time Series
One absolute mono-axial (linear) inclinometer/magnetometer yields one value for ![]() and
and ![]() at one time, and thus only two equations for the nine unknowns, Lij
. Three linear independent unit vectors, ek
k = 1, 2, 3 with measured angles θk
and ϕk
yield six equations. One additional spherical inclinometer/magnetometer, tracking the rigid rotation of the velocity field, would yield three more equations, and would thus allow one to close the system of equations.
at one time, and thus only two equations for the nine unknowns, Lij
. Three linear independent unit vectors, ek
k = 1, 2, 3 with measured angles θk
and ϕk
yield six equations. One additional spherical inclinometer/magnetometer, tracking the rigid rotation of the velocity field, would yield three more equations, and would thus allow one to close the system of equations.
However, in many situations interesting for glaciologists, fewer than nine components Lij are of interest. A suite of assumptions and approximations may reduce the number of unknowns. Some assumptions may not be trivial, though, and require careful testing to estimate the possibly imposed errors.
For a typical channel-like valley glacier it is reasonable to assume that in a coordinate system with x1-direction along the flow and x3 vertically (parallel to gravity), the transversal velocity component and its derivatives are comparably small, thus
Along a central flowline, where the transverse velocity vanishes and the along-flow velocity reaches its transversal maximum, the derivatives with respect to x 2 become small. Thus, the first-order plane-strain approximation for incompressible ice, L33 = −L11, with the only non-vanishing components L13 and L33 reduces Eqns (10) and (11) to
In principle, Eqns (13) and (14) are linear equations for L13 and L33, and thus could be used to calculate the temporal evolution of the velocity-gradient components. The analysis depends on the calculation of time derivatives of the measured angles, θ and ϕ. Depending on how noisy the data are, this procedure is more or less unstable and requires a smoothing of the data. Even then, the evaluation of Eqns (13) and (14) resulted in temporally drifting values for L13 and L33, that should result in a temporal drift of the surface velocity, which could not be observed. Apart from that, L13 and L33 depend explicitly on the evolution of ϕ. The measurement of this angle requires the use of magnetometers, which are much more susceptible to environmental perturbations and thus are less accurate than gravity-based inclinometry. Furthermore, Eqns (13) and (14) are only valid in a coordinate systemwith the x1-axis oriented parallel to the flowdirection. The azimuth angle measured by an instrument fixed to the ice is difficult to orient absolutely in space, and thus to align with respect to the ice flow direction.
With the assumption that L13 and L33 are constant over the period considered, Eqns (13) and (14) can be solved analytically for the time evolution of the zenith angle, θ = θ(t),
with
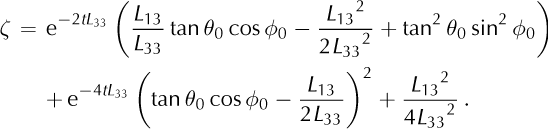
A detailed derivation of Eqns (15) and (16) is given in Appendix C. A numerical evaluation of this equation reproduces the same curves as the Euler scheme used by Reference Gudmundsson, Bauder, Lüthi, Fischer and FunkGudmundsson and others (1999) to a high accuracy (not shown here in detail).
In Figure 1, two examples for possible tilt curves according to solution Eqn (15) are given. There are always two asymptotic values, π/2 for L33 t < 0, and
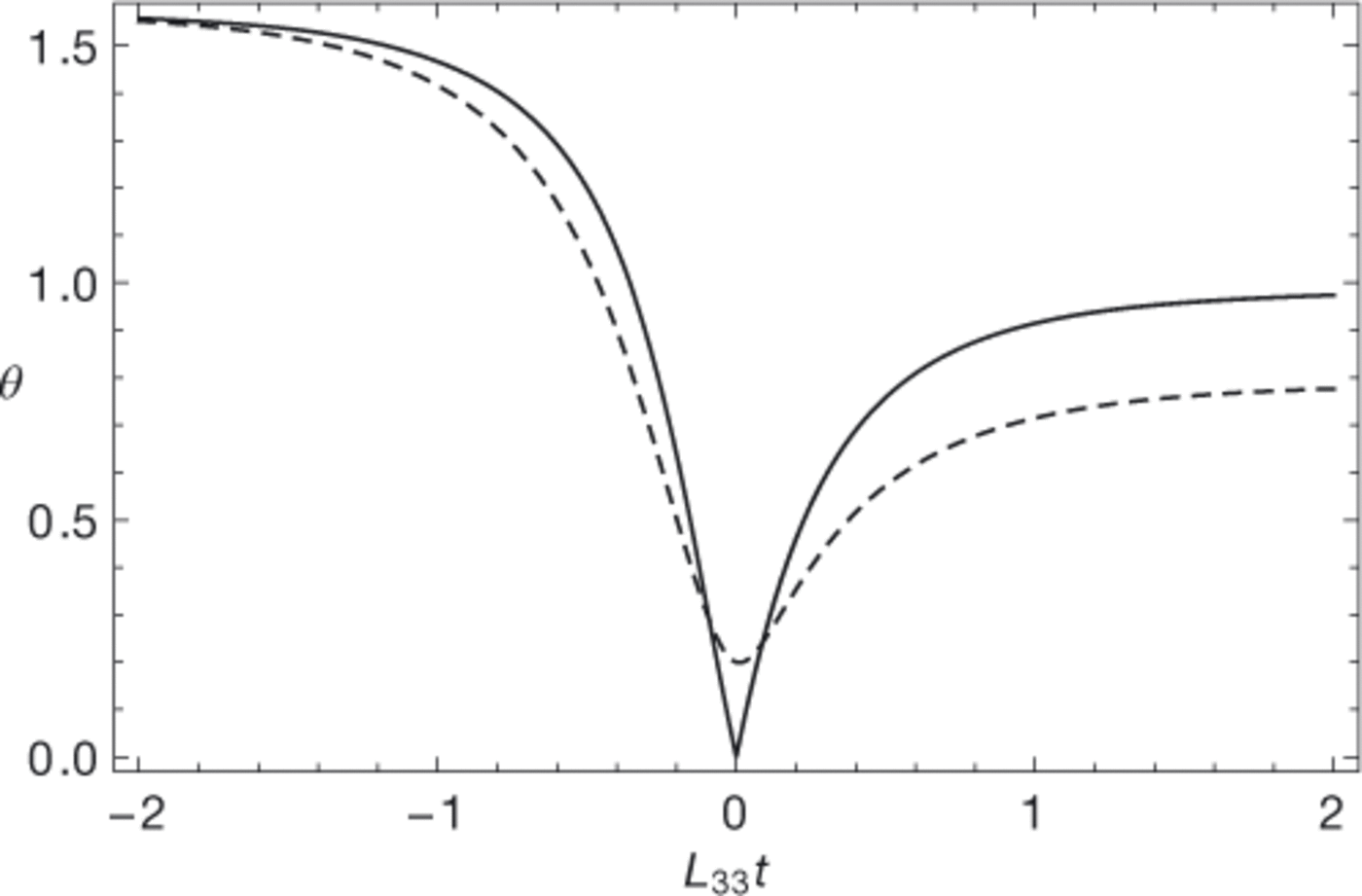
Fig. 1. Examples of possible tilt evolutions according to Eqn (15). Solid curve: L13 = 3L33, θ0 = 0. Dashed curve: L13 = 2L33, θ0 = 0.2, ϕ0 = π/2.

on the half-axis with L33t > 0. Thus, if the motion is dominated by shear, L13 » L13, both asymptotes are close to π/2, whereas for L13 ≈ L33 significantly lower asymptotes are possible. If ϕ0 = 0 or ϕ0 = π (depending on the sign of L33) or θ 0 = 0, the tilt reaches a minimum of θ = 0 and has a kink at the minimum (solid line in Fig. 1). In all other cases the minimum is greater than zero and is passed smoothly; in these cases e never reaches a vertical position.
Results
Field observations
Here we demonstrate the application of Eqns (15) and (16) to fit tilt data from field experiments. We consider field data from Rhonegletscher and Gornergletscher, both situated in the Swiss Alps. The Rhonegletscher data stem from a chain of five inclinometer/magnetometer probes that was installed in a borehole in summer 2009. The data were read every 5 min, except during winter2010/11, when the measurement interval was extended to 8 hours in order to cope with power supply problems. The instruments are labeled A, B, C, D and E, with corresponding approximate positions of 4, 23, 40, 58 and 75 m above the glacier bed (ice thickness 119 m). The borehole is situated in temperate ice, and was permanently water-filled during the experiment. The data measured by sensor E are extremely noisy, probably due to bad coupling of the sensor to the ice. Due to large shear rates, sensor A ran out of the measurement range of the instrument within 1 year. For comparison, we also show measurements obtained with the same type of instrument installed in summer 2006 in a borehole in Gornergletscher. InstrumentG1 is located 127 m above the bed (ice thickness 271 m) in cold ice of —1°C above a basal temperate layer of ~70m thickness, and can be assumed to be coupled tightly to the ice. Instrument G2 was inserted at 38 m above the bed in the temperate ice. In Figure 2 the measured tilt evolutions are displayed together with least-square fits obtained with Eqns (15) and (16).
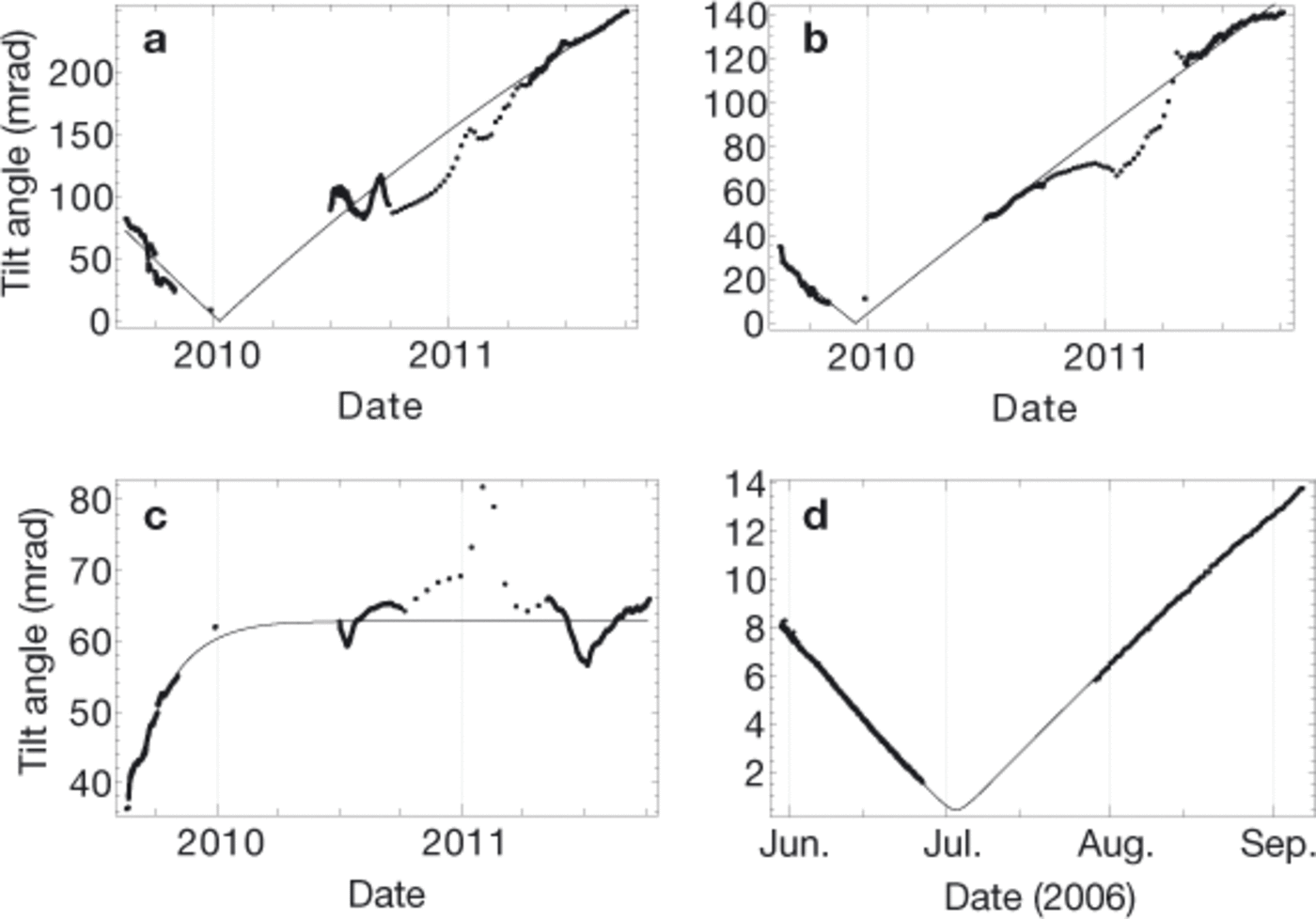
Fig. 2. Evolution of tilt angle, θ, on Rhonegletscher and Gornergletscher. The thin lines are the fitted curves according to Eqns (15) and (16). (a) Rhonegletscher, sensor B, L13 = 5.55 × 10-9 s-1, L33 = 3.40 × 10-9 s-1. (b) Rhonegletscher, sensor C, L13 = 2.73 × 10-9 s-1, L33 = 8.18 × 10-10 s-1. (c) Rhonegletscher, sensor D, L13 = 1.39 × 10-8 s-1, L33 = 1.10 × 10-7 s-1. (d) Gornergletscher, sensor G1, L13 = 2.69 × 10-9 s-1, L33 = 1.86 × 10-9 s-1.
Daily variations
At some times, the long-term evolution of the zenith angles is modulated by daily variations. These short-term variations cannot be captured by analytical tilt curves that are optimized for long periods of measurements with constant strain rates. The lowest (sensor A) and the second lowest (sensor B) instruments (Fig. 3a and b) show variations in shear strain in phase, whereas for the next highest instrument (sensor C) they are in antiphase (Fig. 3c). Interestingly, the shear rates change sign during one cycle. These variations may be caused by variations in basal sliding; however, due to possibly insufficient coupling of the instruments to the ice in the open and partially water-filled borehole, an influence of the daily variation in the water flux through the borehole cannot be excluded. Further interpretation of these patterns lies beyond the scope of this paper. Figure 3d demonstrates an example for diurnal variations in the tilt evolution inside a temperate basal layer in Gornergletscher.
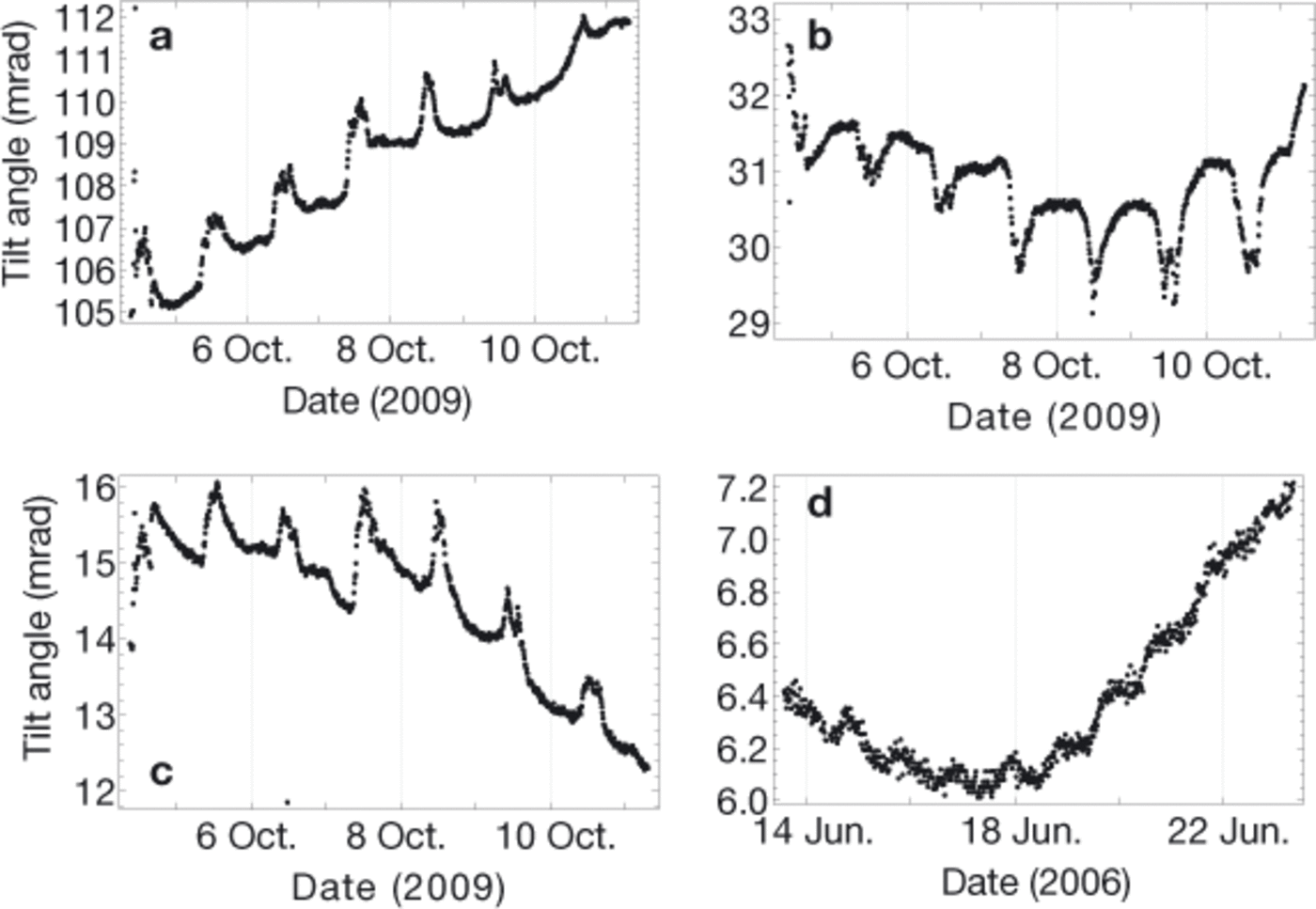
Fig. 3. Diurnal variations of tilt angles, θ, on Rhonegletscher and Gornergletscher. The scatter of the single points indicates the angular resolution of the sensor around 0.1mrad. (a) Rhonegletscher, sensor A. (b) Rhonegletscher, sensor B. (c) Rhonegletscher, sensor C. (d) Gornergletscher, sensor G2.
Conclusions and Prospects
The analysis of the tilt evolution observed with the inclinometer/magnetometer probes is based on the assumption that a thin cylindrical probe inserted into glacier ice follows the same movement as a unit vector, which is given as the direction of the image of a Lagrangian coordinate increment with respect to deformation. The time-evolution equation for this unit vector is defined by the flow field, or more precisely, by its spatial derivatives. For simple flow fields (simple shear with some vertical and horizontal stretching), explicit analytical solutions to the evolution equations in polar coordinates were used to fit field data.
The above findings allow us to calculate theoretical tilt curves, which should be recorded by an instrument sensitive to inclination that is fixed within the material, and can therefore be helpful for calibration/validation purposes or for the reconstruction of a local flow field from tilt measurements. Of course, one could try to avoid the mathematical difficulties of solving the evolution equations analytically and just rely on a numerical integration of the coupled system. The analytical solution has, however, the great advantage that we can write down the evolution of the tilt angle, θ, without simultaneously solving the equation for the azimuth angle; instead, the evolution of θ is parameterized by the initial azimuth angle, ϕ0.
The explicit time evolution, θ(t), has been used to fit data from inclinometer tilt experiments on Rhonegletscher and Gornergletscher, showing its ability to reproduce the measured curves. With the assumption of incompressible ice flow and the first-order plane-strain approximation, strain- rate measurements can be performed with much simpler instruments, only measuring the zenith angle of the probe axis.
Tilt measurements with high temporal resolution show examples of diurnal variations of strain rates. This phenomenon has been observed in different glaciers, such as the entirely temperate Rhonegletscher, the polythermal Gornergletscher and in the polythermal region of Jakobhavns Isbræ, Greenland ice sheet (Reference Marshall, Harper, Pfeffer and HumphreyLüthi and others, 2002). Reference Amundson, Truffer and LüthiAmundson and others (2006) measured similar features on Black Rapids Glacier, a large surge-type glacier in the central Alaska Range, USA. In these examples, the patterns in variations are similar in shape and magnitude. The mechanism causing these variations and the temporal coincidence with diurnal variations in englacial water pressure suggest that variations in sliding may explain the variations in the strain field. The partial reversibility of deformations perhaps indicates diurnal variations of normal strain (Reference GudmundssonGudmundsson, 2002) or elastic reactions of the ice base to variable basal water pressure (Reference Sugiyama, Bauder, Weiss and FunkSugiyama and others, 2007).
An unsolved question concerns the time evolution of an orthogonal system of unit vectors fixed to a rigid body inside the material. If all unit vectors evolve as described above, the orthonormality condition may be violated in the presence of a shear motion. One therefore has to define a way to couple the rigid body to the deforming material such that orthonormality of the coordinate system fixed to it is kept. This problem can probably be addressed by modeling the motion of a rigid or hard elastic body in a deforming viscous fluid, which, however, lies beyond the scope of this paper.
One suggestion that can be drawn from the above considerations is a possible in situ measurement of the local viscosity of glacier ice. A system of three thin cylindrical inclinometer/magnetometer probes with independent orientations and the same type probe with spherical shape to measure the rigid rotation components, allows us to close the system of equations for the nine velocity-gradient components. Combined with a probe with adequate pressure sensors to measure the stress components as suggested by Reference Pfeffer, Humphrey, Amadei, Harper and WegmannPfeffer and others (2000), this yields, in principle, the complete information to compute the ice viscosity
Acknowledgements
This work was funded by the Swiss National Science Foundation, grant No. 20021-119781/1. We thank Claudia Ryser, Martin Lüthi, Martin Funk, Jason Amundson and an anonymous reviewer for constructive input that helped improve the manuscript.
Appendix A: Parameterization of SO(3)
To describe the orientation of three linearly independent orthogonal vectors fixed to the probe with respect to a given coordinate system, a parameterization of the group of pure rotations in three dimensions, called the special orthogonal group in three dimensions, SO(3), can be applied. Although there is no global parameterization of this group (Reference StuelpnagelStuelpnagel, 1964), parameterizations of the whole group up to a finite number of singular points can be found, which is sufficient for our purpose. There are various ways to do this, such as with Euler angles. We use a matrix exponential representation of the group of special unitary transformations in two dimensions, SU(2), with Pauli matrices as generators, together with a homomorphism mapping SU(2) onto SO(3). This turned out to be computationally more convenient than using Euler angles. Independent of the parameterization, there are always three independent parameters describing the orientation of the instrument, reflecting the dimension of the group SO(3).
For every set of group parameters, we generate a unitary matrix, U ∈ SU(2), by the usual exponential representation with Pauli matrices as generators. Then, we calculate the corresponding orthogonal matrix, O ∊ SO(3), by
where τi , i ∈ {1, 2, 3} are Pauli matrices and U† denotes the Hermitian adjoint of U. Using the Fierz identity (Reference Borodulin, Rogalyov and SlabospitskyBorodulin and other, 1995),
Both the orthogonality of O,
And the homomorphism property
Can be proved.
Appendix B: Time Derivative of Unit Vector
The mapping of Lagrangian onto Eulerian coordinates (i.e. the time evolution of the material) yields
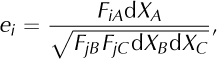
where

is the deformation gradient. The time evolution of e is given by
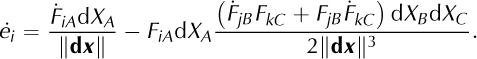
With the identity ϕ Ia = L ijF Ja(Reference HutterHutter, 1983), where
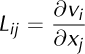
Denotes the velocity gradient, we obtain
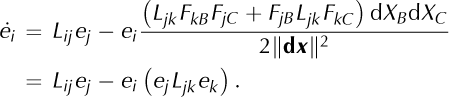
Appendix C: Temporal Evolution Of Zenith Angle
Depending on the initial conditions, solving Eqns (13) and (14) may require a number of case distinctions. In order to avoid most of them we will restrict our considerations to the case that is of interest for our application: initial conditions close to vertical, i.e. 0 ≤ θ0 < π/2. Now, we only have to take care if θ = 0, as this is a singular point of the spherical coordinates (Eqn (6)) where the angle ϕ is not well defined. This can be the case either initially, θ
0
= 0, or if ϕ0
∈ {0, π}; we consider these cases separately below and assume at first initial values 0 < θ0 < π/2 and ![]() we can use the bi-unique substitutions
we can use the bi-unique substitutions
in Eqns (13) and (14), yielding
The transformation partly decouples the system. The solution for ω is
where C1 is an integration constant. Substituting this solution in Eqn (C3) yields

with the solution

and a second integration constant, C2. The two integration constants can be determined from the initial conditions
and for ω(t) and ζ(t) we obtain
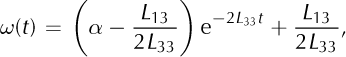
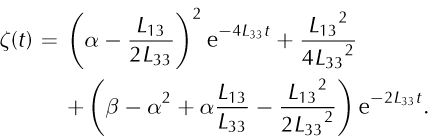
Finally, the solution for the zenith angle, θ, as a function of time is given in Eqns (15) and (16).
In the critical cases mentioned above, a critical situation only arises at the time when θ = 0 is reached (before this moment, Eqns (C9) and (C10) remain valid). As the evolution equations are of first order, we can simply assume that this is the case initially, and set θ0 = 0. In consequence, at t = 0 we may use neither the angle ϕ nor the substitutions (Eqn (C1)). However, at t = 0 the vector e is simply e = (0, 0, 1), and Eqn (4) yields
i.e. after a small time increment, Δt, we arrive at
This corresponds (to lowest order in Δt) to θ = L13 Δt and ϕ = 0 or ϕ = π (depending on the sign of L13), and from t = Δt onwards we may again use Eqns (C9) and (C10) with these initial conditions. As, furthermore, in the limit Δt → 0 we arrive at θ(0) = 0 = θ0, we may extend the validity of Eqns (C9) and (C10) to the critical case θ0 = 0 if we use the convention to set the initial condition for the (initially undefined) azimuth angle to ϕ0 = 0 or ϕ0 = π (depending on the sign of L13).





