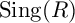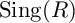1 Introduction
In continuing the studies of [Reference Negron and Pevtsova28], we introduce a notion of hypersurface support for infinite-dimensional modules over a noncommutative complete intersection. By a noncommutative complete intersection, we mean an algebra R which admits a smooth deformation
![]() $Q\to R$
by a Noetherian algebra Q which is of finite global dimension. In the sibling project [Reference Negron and Pevtsova27], we use hypersurface support for infinite-dimensional modules to classify thick ideals in certain tensor triangulated categories associated with finite-dimensional Hopf algebras.
$Q\to R$
by a Noetherian algebra Q which is of finite global dimension. In the sibling project [Reference Negron and Pevtsova27], we use hypersurface support for infinite-dimensional modules to classify thick ideals in certain tensor triangulated categories associated with finite-dimensional Hopf algebras.
This work began as a generalization of Avramov and Buchweitz’ theory of support for local (commutative) complete intersections, and the arguments employed in the text are often influenced by their commutative counterparts. One can compare with [Reference Avramov and Buchweitz1], [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3], [Reference Jorgensen24], in particular. We note, however, that while studies of hypersurface support for commutative complete intersections are often focused on finitely generated, or finite-dimensional modules, there is a precise synergy between supports of finite-dimensional and infinite-dimensional modules which is required by studies in tensor triangular geometry. So, in our present study, we focus on the relevant analysis of support for (generally) infinite-dimensional modules over a noncommutative complete intersection, and the manner in which our analysis reduces to the study of [Reference Negron and Pevtsova28] when we restrict to the class of finite-dimensional modules.
Dealing with infinite-dimensional modules brings an extra layer of complexity to the theory but also allows one to reap rewards as we demonstrate in [Reference Negron and Pevtsova27]. The utility of going beyond the finite-dimensional world in representation theory, even if one is ultimately interested in the category of finite-dimensional modules, was first demonstrated by Rickard [Reference Rickard31] building on the ideas from stable homotopy theory. The support theory for infinite-dimensional modules over finite groups in positive characteristic was developed in [Reference Benson, Carlson and Rickard5] and then applied in [Reference Benson, Carlson and Rickard6] to classify thick tensor ideals in the small stable module category of a finite group G. The technique of infinite-dimensional Rickard idempotent modules was employed again in [Reference Benson, Iyengar, Krause and Pevtsova7], [Reference Friedlander and Pevtsova19] to classify thick tensor ideals in the stable category of finite-dimensional modules of a finite group scheme. It is with an eye toward such applications that we develop the hypersurface support for infinite-dimensional modules in this work.
Let us now consider k an arbitrary field, and R a finite-dimensional algebra with prescribed smooth deformation
![]() $Q\to R$
, by a Noetherian algebra Q of finite global dimension. To be clear, by a deformation, we mean a choice of a flat Z-algebra Q equipped with a map
$Q\to R$
, by a Noetherian algebra Q of finite global dimension. To be clear, by a deformation, we mean a choice of a flat Z-algebra Q equipped with a map
![]() $Q\to R$
which reduces to an isomorphism
$Q\to R$
which reduces to an isomorphism
![]() $k\otimes _ZQ\cong R$
at a distinguished point for Z, and by smoothness we mean that the parameterizing algebra Z is smooth (commutative and augmented) over k. We denote by
$k\otimes _ZQ\cong R$
at a distinguished point for Z, and by smoothness we mean that the parameterizing algebra Z is smooth (commutative and augmented) over k. We denote by
![]() $m_Z \subset Z$
the augmentation ideal of Z.
$m_Z \subset Z$
the augmentation ideal of Z.
As a basic example, one can consider a skew polynomial ring
![]() $Q=\mathbb {C}_q[x_1,\dots , x_n]$
, with skew commutator relations
$Q=\mathbb {C}_q[x_1,\dots , x_n]$
, with skew commutator relations
![]() $x_ix_j-q^{a_{ij}}x_jx_i$
at q a root of unity of order l, Z the central algebra
$x_ix_j-q^{a_{ij}}x_jx_i$
at q a root of unity of order l, Z the central algebra
![]() $\mathbb {C}[x_1^l,\dots , x_n^l]$
, and the truncation
$\mathbb {C}[x_1^l,\dots , x_n^l]$
, and the truncation
(cf. [Reference Benson, Erdmann and Holloway10], [Reference Pevtsova and Witherspoon29], [Reference Pevtsova and Witherspoon30]). However, as noted in [Reference Negron and Pevtsova28, §2], there are various additional examples coming from studies in Hopf algebras. For example, we have the small quantum group
![]() $u_q(\mathfrak {g})$
along with its deformation provided by the De Concini–Kac algebra
$u_q(\mathfrak {g})$
along with its deformation provided by the De Concini–Kac algebra
![]() $U^{DK}_q(\mathfrak {g})\to u_q(\mathfrak {g})$
.
$U^{DK}_q(\mathfrak {g})\to u_q(\mathfrak {g})$
.
Given such
![]() $Q\to R$
as above, one can consider the projective space
$Q\to R$
as above, one can consider the projective space
![]() $\mathbb {P}(m_Z/m_Z^2)$
and assign to any point
$\mathbb {P}(m_Z/m_Z^2)$
and assign to any point
a (noncommutative) hypersurface algebra
![]() $Q_c=Q_K/(f)$
, where
$Q_c=Q_K/(f)$
, where
![]() $f \mod m^2_{Z_K}$
is a representative for the point c and K is an arbitrary extension of the base field k. For an R-module M, either finite-dimensional or infinite-dimensional, we say that M is supported at such a point c if the base change
$f \mod m^2_{Z_K}$
is a representative for the point c and K is an arbitrary extension of the base field k. For an R-module M, either finite-dimensional or infinite-dimensional, we say that M is supported at such a point c if the base change
![]() $M_K$
is of infinite projective dimension over
$M_K$
is of infinite projective dimension over
![]() $Q_c$
, and we define the hypersurface support of M as
$Q_c$
, and we define the hypersurface support of M as
 $$ \begin{align*} \operatorname{\mathrm{supp}}^{hyp}_{\mathbb{P}}(M):=\left\{ \begin{array}{c} \text{the image of all points }c:\operatorname{\mathrm{Spec}}(K)\to \mathbb{P}(m_Z/m_Z^2)\\ \text{at which}\ \operatorname{projdim}_{Q_c} M_K = \infty \end{array}\right\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{supp}}^{hyp}_{\mathbb{P}}(M):=\left\{ \begin{array}{c} \text{the image of all points }c:\operatorname{\mathrm{Spec}}(K)\to \mathbb{P}(m_Z/m_Z^2)\\ \text{at which}\ \operatorname{projdim}_{Q_c} M_K = \infty \end{array}\right\}. \end{align*} $$
To be clear, we restrict along the induced map
![]() $Q_c\to R_K$
to consider
$Q_c\to R_K$
to consider
![]() $M_K$
as a module over
$M_K$
as a module over
![]() $Q_c$
. Moreover, the subscript
$Q_c$
. Moreover, the subscript
![]() $\mathbb {P}$
in the notation
$\mathbb {P}$
in the notation
![]() $\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}$
indicates the projective space
$\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}$
indicates the projective space
![]() $\mathbb {P}(m_Z/m_Z^2)$
specifically. Our first result (in conjunction with Lemma 5.7 below) deals with the apparent ambiguity of this definition.
$\mathbb {P}(m_Z/m_Z^2)$
specifically. Our first result (in conjunction with Lemma 5.7 below) deals with the apparent ambiguity of this definition.
Theorem (Theorem 5.4)
Consider M any R-module (possibly infinite-dimensional), and
![]() $f,g\in m_Z$
with equivalent, nonzero, classes
$f,g\in m_Z$
with equivalent, nonzero, classes
![]() $\bar {f}=\bar {g}$
in
$\bar {f}=\bar {g}$
in
![]() $m_Z/m_Z^2$
. Then, M has finite projective dimension over
$m_Z/m_Z^2$
. Then, M has finite projective dimension over
![]() $Q/(f)$
if and only if M has finite projective dimension over
$Q/(f)$
if and only if M has finite projective dimension over
![]() $Q/(g)$
.
$Q/(g)$
.
To look at things from a different perspective, we can consider the singularity category
![]() $\operatorname {Sing}(R)$
, which is the quotient
$\operatorname {Sing}(R)$
, which is the quotient
![]() $D^b(R)/\langle \operatorname {\mathrm {Proj}}(R)\rangle $
of the bounded derived category by complexes of finite projective dimension. An R-module M is then supported at c if its image along the exact map of triangulated categories
$D^b(R)/\langle \operatorname {\mathrm {Proj}}(R)\rangle $
of the bounded derived category by complexes of finite projective dimension. An R-module M is then supported at c if its image along the exact map of triangulated categories
![]() $\operatorname {Sing}(R)\to \operatorname {Sing}(Q_c)$
(see §4.2) is nonzero.
$\operatorname {Sing}(R)\to \operatorname {Sing}(Q_c)$
(see §4.2) is nonzero.
From the singularity category perspective, it is clear that hypersurface support has the expected properties of a support theory for
![]() $\operatorname {Sing}(R)$
(see, e.g., [Reference Balmer and Favi4]). Namely, it is stable under shifting, splits over arbitrary sums
$\operatorname {Sing}(R)$
(see, e.g., [Reference Balmer and Favi4]). Namely, it is stable under shifting, splits over arbitrary sums
![]() $\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(\oplus _\lambda M_\lambda )=\cup _\lambda \operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M_\lambda )$
, and whenever there is an exact triangle
$\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(\oplus _\lambda M_\lambda )=\cup _\lambda \operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M_\lambda )$
, and whenever there is an exact triangle
![]() $N\to M\to N'$
, the support of M lies in the union of the supports of N and
$N\to M\to N'$
, the support of M lies in the union of the supports of N and
![]() $N'$
. We show furthermore that the supports of finite-dimensional R-modules are in fact closed subsets in
$N'$
. We show furthermore that the supports of finite-dimensional R-modules are in fact closed subsets in
![]() $\mathbb {P}(m_Z/m_Z^2)$
, as a byproduct of the following result.
$\mathbb {P}(m_Z/m_Z^2)$
, as a byproduct of the following result.
Theorem (Proposition 5.9)
For any finite-dimensional R-module V, there is an associated coherent sheaf
![]() $\mathcal {E}_V$
on
$\mathcal {E}_V$
on
![]() $\mathbb {P}(m_Z/m_Z^2)$
such that
$\mathbb {P}(m_Z/m_Z^2)$
such that
The sheaf
![]() $\mathcal {E}_V$
is constructed out of the extensions
$\mathcal {E}_V$
is constructed out of the extensions
![]() $\operatorname {\mathrm {Ext}}_R^*(V, \Lambda )$
where
$\operatorname {\mathrm {Ext}}_R^*(V, \Lambda )$
where
![]() $\Lambda $
is the maximal semisimple quotient of R. Hence, the right-hand side of the equality in the above theorem is a cohomological support. In proving Theorem 5.9, we also establish an identification between the hypersurface support of the present paper and the hypersurface support of [Reference Negron and Pevtsova28], which is certainly expected.
$\Lambda $
is the maximal semisimple quotient of R. Hence, the right-hand side of the equality in the above theorem is a cohomological support. In proving Theorem 5.9, we also establish an identification between the hypersurface support of the present paper and the hypersurface support of [Reference Negron and Pevtsova28], which is certainly expected.
As a final result, we prove a detection theorem for hypersurface support, which is an analog of Dade’s lemma [Reference Dade16, Lem. 11.8] in this context.
Theorem (Theorem 6.1)
For any R-module M (possibly infinite-dimensional), the support vanishes
![]() $\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)=\emptyset $
if and only if M has finite projective dimension over R.
$\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)=\emptyset $
if and only if M has finite projective dimension over R.
The proof of the independence of representatives (Theorem 5.4) is modeled upon the proof of Avramov–Iyengar of the same result for (commutative) complete intersections [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3]. The proof of the detection theorem, on the other hand, deviates from the proof of an analogous theorem in the commutative case: we apply our results on Koszul duality from [Reference Negron and Pevtsova28], whereas in [Reference Benson, Iyengar, Krause and Pevtsova8], the argument is inspired by [Reference Benson, Carlson and Rickard6] and uses the Kronecker quiver lemma. The Koszul duality approach yields a new proof of the infinite Dade’s lemma even in such a classical case as a group algebra of an elementary abelian p-group over a field of characteristic p.
In the sibling text [Reference Negron and Pevtsova27], hypersurface support is used explicitly to classify thick ideals, and compute the spectrum of prime ideals, in the stable categories
![]() $\operatorname {stab}(\mathsf {u})$
for
$\operatorname {stab}(\mathsf {u})$
for
![]() $\mathsf {u}$
among various classes of Hopf algebras. We consider, for example, rings of functions
$\mathsf {u}$
among various classes of Hopf algebras. We consider, for example, rings of functions
![]() $\mathscr {O}(\mathcal {G})$
on a finite group scheme
$\mathscr {O}(\mathcal {G})$
on a finite group scheme
![]() $\mathcal {G}$
, (bosonized) quantum complete intersections, Drinfeld doubles
$\mathcal {G}$
, (bosonized) quantum complete intersections, Drinfeld doubles
![]() $\mathcal {D}(B_{(1)})$
for Borel subgroups
$\mathcal {D}(B_{(1)})$
for Borel subgroups
![]() $B\subset \mathbb {G}$
in almost-simple algebraic groups, and quantum Borels
$B\subset \mathbb {G}$
in almost-simple algebraic groups, and quantum Borels
![]() $u_q(B)$
in type A.
$u_q(B)$
in type A.
2 Background and generic commentary
We work over a field k of arbitrary characteristic. All modules are left modules.
2.1 Smooth deformations
Recall that a deformation of an algebra R is a pair of a commutative augmented algebra Z and an algebra map
![]() $Q\to R$
from a flat Z-algebra Q which reduces to an isomorphism
$Q\to R$
from a flat Z-algebra Q which reduces to an isomorphism
![]() $k\otimes _ZQ\cong R$
. Note that, as part of this definition, we require that the structure map
$k\otimes _ZQ\cong R$
. Note that, as part of this definition, we require that the structure map
![]() $Z\to Q$
has central image.
$Z\to Q$
has central image.
By a (formally) smooth deformation of an algebra R, we mean a deformation
![]() $Q\to R$
parameterized by a (formally) smooth algebra Z over our base field k. In the formal setting, we require that Z is complete with finite-dimensional tangent space at its distinguished point. This implies an isomorphism of local algebras
$Q\to R$
parameterized by a (formally) smooth algebra Z over our base field k. In the formal setting, we require that Z is complete with finite-dimensional tangent space at its distinguished point. This implies an isomorphism of local algebras
![]() $Z\cong k[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
(see [Reference Negron and Pevtsova28, §3] for a more detailed account). Throughout we let
$Z\cong k[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
(see [Reference Negron and Pevtsova28, §3] for a more detailed account). Throughout we let
![]() $m_Z\subset Z$
denote the maximal ideal corresponding to the augmentation
$m_Z\subset Z$
denote the maximal ideal corresponding to the augmentation
![]() $1:Z\to k$
.
$1:Z\to k$
.
Note that a deformation parameterized by a smooth, that is, finite type, algebra Z can be completed to produce a formally smooth analog. This is technically convenient, because working with local rings is convenient.
2.2 The specific setup
Throughout this work, we consider specifically a deformation
![]() $Q\to R$
of a finite-dimensional algebra R parameterized by a formally smooth algebra Z, which is isomorphic to a power series algebra in finitely many variables. We assume additionally that Q is Noetherian and that the quotient
$Q\to R$
of a finite-dimensional algebra R parameterized by a formally smooth algebra Z, which is isomorphic to a power series algebra in finitely many variables. We assume additionally that Q is Noetherian and that the quotient
![]() $\Lambda =R/\operatorname {Jac}(R)$
is separable over k, so that all base changes
$\Lambda =R/\operatorname {Jac}(R)$
is separable over k, so that all base changes
![]() $\Lambda _K$
along arbitrary field extensions
$\Lambda _K$
along arbitrary field extensions
![]() $k\to K$
are also semisimple. One should always consider the deformation Q to be Gorenstein—although this assumption is not strictly necessary for many results.
$k\to K$
are also semisimple. One should always consider the deformation Q to be Gorenstein—although this assumption is not strictly necessary for many results.
We make a further assumption that the deformation
![]() $Q\to R$
admits an integral form, by which we mean that Q is obtained from a finite-type deformation of R via completion. The relevance of this assumption does not appear until §5, at which point we explain the notion in more detail.
$Q\to R$
admits an integral form, by which we mean that Q is obtained from a finite-type deformation of R via completion. The relevance of this assumption does not appear until §5, at which point we explain the notion in more detail.
2.3 New deformations from old
Given a deformation
![]() $Q\to R$
as in §2.2, and
$Q\to R$
as in §2.2, and
![]() $f\in m_Z$
with nonzero reduction
$f\in m_Z$
with nonzero reduction
![]() $\bar {f}\in m_Z/m_Z^2$
, we can produce another deformation
$\bar {f}\in m_Z/m_Z^2$
, we can produce another deformation
![]() $Q/(f)\to R$
parameterized by the algebra
$Q/(f)\to R$
parameterized by the algebra
![]() $Z/(f)$
. The algebra
$Z/(f)$
. The algebra
![]() $Z/(f)$
will still be a power series ring, so that
$Z/(f)$
will still be a power series ring, so that
![]() $Q/(f)\to R$
is still of the type demanded in §2.2.
$Q/(f)\to R$
is still of the type demanded in §2.2.
Remark 2.1. Existence of an integral form for
![]() $Q/(f)$
is subtle, but can be dealt with (see Remark 5.6 below).
$Q/(f)$
is subtle, but can be dealt with (see Remark 5.6 below).
In the early sections of this text, when we consider a deformation
![]() $Q\to R$
, we are considering either a deformation
$Q\to R$
, we are considering either a deformation
![]() $Q\to R$
with Q Noetherian and of finite global dimension, or some associated hypersurface
$Q\to R$
with Q Noetherian and of finite global dimension, or some associated hypersurface
![]() $Q/(f)\to R$
thereof. So we have these two flavors of deformation to consider: one of finite global dimension and one which is (generally) singular.
$Q/(f)\to R$
thereof. So we have these two flavors of deformation to consider: one of finite global dimension and one which is (generally) singular.
At the point at which we begin to discuss hypersurface support specifically, we fix Q to be of finite global dimension, and speak explicitly of the associated hypersurface deformations
![]() $Q/(f)\to R$
.
$Q/(f)\to R$
.
2.4 Smooth deformations and actions on categories
Given a (formally) smooth deformation
![]() $Q\to R$
, parameterized by a given (formally) smooth commutative algebra Z, we consider
$Q\to R$
, parameterized by a given (formally) smooth commutative algebra Z, we consider
![]() $A_Z$
the dg algebra
$A_Z$
the dg algebra
with vanishing differential. Bezrukavnikov and Ginzburg [Reference Bezrukavnikov and Ginzburg12] show that the deformation Q specifies an action of the algebra
![]() $A_Z$
on the derived category of R-modules
$A_Z$
on the derived category of R-modules
This action lifts to an action on a certain dg category
![]() $D_{coh}(R)$
[Reference Negron and Pevtsova28, §3.4], and manifests concretely as a collection of compatible algebra maps
$D_{coh}(R)$
[Reference Negron and Pevtsova28, §3.4], and manifests concretely as a collection of compatible algebra maps
at arbitrary M, where the image of
![]() $A_Z$
lands in the (graded) center of
$A_Z$
lands in the (graded) center of
![]() $\operatorname {\mathrm {REnd}}_R(M)$
.
$\operatorname {\mathrm {REnd}}_R(M)$
.
The algebra
![]() $A_Z$
, along with its action on
$A_Z$
, along with its action on
![]() $D(R)$
, can be seen as a generalization of the algebra of cohomological operators associated with a local complete intersection [Reference Avramov and Buchweitz1], [Reference Eisenbud17], [Reference Gulliksen21].
$D(R)$
, can be seen as a generalization of the algebra of cohomological operators associated with a local complete intersection [Reference Avramov and Buchweitz1], [Reference Eisenbud17], [Reference Gulliksen21].
2.5 Hypersurface support: a preliminary report
Consider
![]() $Q\to R$
a deformation as in §2.2, with Q additionally of finite global dimension. For a closed point
$Q\to R$
a deformation as in §2.2, with Q additionally of finite global dimension. For a closed point
![]() $c\in \mathbb {P}(m_Z/m_Z^2)$
, we consider an associated hypersurface algebra
$c\in \mathbb {P}(m_Z/m_Z^2)$
, we consider an associated hypersurface algebra
![]() $Q/(f)$
, with
$Q/(f)$
, with
![]() $f\in m_Z$
such that
$f\in m_Z$
such that
![]() $\bar {f}\in m_Z/m_Z^2$
is a (nonzero) representative for c. We speak of
$\bar {f}\in m_Z/m_Z^2$
is a (nonzero) representative for c. We speak of
![]() $f\in m_Z$
, specifically, as our representative for c. When the choice of representative is irrelevant, we write
$f\in m_Z$
, specifically, as our representative for c. When the choice of representative is irrelevant, we write
![]() $Q_c$
for an arbitrary expression
$Q_c$
for an arbitrary expression
![]() $Q_c=Q/(f)$
. We similarly define hypersurface algebras
$Q_c=Q/(f)$
. We similarly define hypersurface algebras
![]() $Q_c$
at nonclosed points in
$Q_c$
at nonclosed points in
![]() $\mathbb {P}(m_Z/m_Z^2)$
by employing base change (see §5).
$\mathbb {P}(m_Z/m_Z^2)$
by employing base change (see §5).
We would like to define the hypersurface support of R, relative to this deformation Q, as follows.
Proto-definition 2.2. For M an arbitrary R-module, we define the hypersurface support of M as
Here,
![]() $M_{k(c)}$
is simply the base change
$M_{k(c)}$
is simply the base change
![]() $M\otimes k(c)$
at the residue field for c. We would then like to prove that this hypersurface support satisfies many desirable properties. In pursuing this line of thinking, there are two primary issues which one has to deal with:
$M\otimes k(c)$
at the residue field for c. We would then like to prove that this hypersurface support satisfies many desirable properties. In pursuing this line of thinking, there are two primary issues which one has to deal with:
-
(a) One would like to show that this definition carries no ambiguity, in the sense that the projective dimension of
 $M_{k(c)}$
over
$M_{k(c)}$
over
 $Q_c$
is independent of the choice of representative f for c, and so independent of the specific choice of representing hypersurface algebra
$Q_c$
is independent of the choice of representative f for c, and so independent of the specific choice of representing hypersurface algebra
 $Q_c=Q/(f)$
.
$Q_c=Q/(f)$
. -
(b) One would like to understand that the projective dimension for M is encoded globally on
 $\mathbb {P}(m_Z/m_Z^2)$
.
$\mathbb {P}(m_Z/m_Z^2)$
.
For (b), we might mean, for example, that there is a sheaf
![]() $\mathcal {E}_M$
on
$\mathcal {E}_M$
on
![]() $\mathbb {P}(m_Z/m_Z^2)$
whose fibers contain information about the projective dimension of M at various
$\mathbb {P}(m_Z/m_Z^2)$
whose fibers contain information about the projective dimension of M at various
![]() $Q_c$
. In Proposition 3.1 and Theorem 5.4 below, we deal with these fundamental issues (see also Proposition 6.7). Having addressed these points, we formally define the hypersurface support in §5, and address some of its basic properties in §6.
$Q_c$
. In Proposition 3.1 and Theorem 5.4 below, we deal with these fundamental issues (see also Proposition 6.7). Having addressed these points, we formally define the hypersurface support in §5, and address some of its basic properties in §6.
3 Homological dimensions and derived functors
For this section,
![]() $Q\to R$
is a Noetherian deformation of a finite-dimensional algebra R which is parameterized by a formally smooth algebra
$Q\to R$
is a Noetherian deformation of a finite-dimensional algebra R which is parameterized by a formally smooth algebra
![]() $Z\cong k[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
, as in §2.2. As usual,
$Z\cong k[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
, as in §2.2. As usual,
![]() $\Lambda =Q/\operatorname {Jac}(Q)=R/\operatorname {Jac}(R)$
. In our analysis of hypersurface support, we need the following basic result.
$\Lambda =Q/\operatorname {Jac}(Q)=R/\operatorname {Jac}(R)$
. In our analysis of hypersurface support, we need the following basic result.
Proposition 3.1. Suppose that M is any
![]() $\operatorname {Jac}(Q)$
-torsion Q-module. Then, for any given integer d, M is of injective dimension
$\operatorname {Jac}(Q)$
-torsion Q-module. Then, for any given integer d, M is of injective dimension
![]() $\leq d$
if and only if
$\leq d$
if and only if
![]() $\operatorname {\mathrm {Ext}}^{>d}_Q(\Lambda ,M)=0$
. Similarly, M is of flat dimension
$\operatorname {\mathrm {Ext}}^{>d}_Q(\Lambda ,M)=0$
. Similarly, M is of flat dimension
![]() $\leq d$
if and only if
$\leq d$
if and only if
![]() $\operatorname {\mathrm {Tor}}^Q_{>d}(\Lambda ,M)=0$
.
$\operatorname {\mathrm {Tor}}^Q_{>d}(\Lambda ,M)=0$
.
By a torsion module, we mean that each element in M is annihilated by some power of the Jacobson radical. In this case, each Hom group
![]() $\operatorname {\mathrm {Hom}}_Q(L,M)$
from a finitely generated module L is
$\operatorname {\mathrm {Hom}}_Q(L,M)$
from a finitely generated module L is
![]() $m_Z$
-torsion, for
$m_Z$
-torsion, for
![]() $m_Z$
the maximal ideal in Z. By Noetherianity of Q, the extensions
$m_Z$
the maximal ideal in Z. By Noetherianity of Q, the extensions
![]() $\operatorname {\mathrm {Ext}}^\ast _Q(L,M)$
are
$\operatorname {\mathrm {Ext}}^\ast _Q(L,M)$
are
![]() $m_Z$
-torsion as well. Similarly,
$m_Z$
-torsion as well. Similarly,
![]() $\operatorname {\mathrm {Tor}}_\ast ^Q(L,M)$
is torsion for any finitely generated L. The proof of the proposition is postponed till §3.3.
$\operatorname {\mathrm {Tor}}_\ast ^Q(L,M)$
is torsion for any finitely generated L. The proof of the proposition is postponed till §3.3.
Of course, we are most interested in applying the above result in the case in which M is an (infinite-dimensional) R-module.
3.1 Application to Gorenstein deformations
As remarked previously, we generally consider Q to be a Gorenstein deformation of R. Recall that Q is called Gorenstein (resp. d-Gorenstein) if
![]() $\operatorname {injdim}_Q(Q)<\infty $
(resp.
$\operatorname {injdim}_Q(Q)<\infty $
(resp.
![]() $\operatorname {injdim}_Q(Q)\leq d$
). Specifically, Q should be of finite injective dimension over itself both on the left and the right. In this case, Proposition 3.1 proliferates as
$\operatorname {injdim}_Q(Q)\leq d$
). Specifically, Q should be of finite injective dimension over itself both on the left and the right. In this case, Proposition 3.1 proliferates as
Corollary 3.2. Suppose that Q is d-Gorenstein, and that M is a
![]() $\operatorname {Jac}(Q)$
-torsion module. Then the following are equivalent:
$\operatorname {Jac}(Q)$
-torsion module. Then the following are equivalent:
-
(a)
 $\operatorname {\mathrm {Ext}}^{\gg 0}_Q(\Lambda ,M)=0 \kern100pt (\mathrm{b})\ \operatorname {\mathrm {Ext}}^{>d}_Q(\Lambda ,M)=0$
.
$\operatorname {\mathrm {Ext}}^{\gg 0}_Q(\Lambda ,M)=0 \kern100pt (\mathrm{b})\ \operatorname {\mathrm {Ext}}^{>d}_Q(\Lambda ,M)=0$
. -
(c)
 $\operatorname {\mathrm {Tor}}^Q_{\gg 0}(\Lambda ,M)=0 \kern100.8pt (\mathrm{d})\ \operatorname {\mathrm {Tor}}^Q_{>d}(\Lambda ,M)=0$
.
$\operatorname {\mathrm {Tor}}^Q_{\gg 0}(\Lambda ,M)=0 \kern100.8pt (\mathrm{d})\ \operatorname {\mathrm {Tor}}^Q_{>d}(\Lambda ,M)=0$
. -
(e)
 $\operatorname {injdim}(M)<\infty \kern106.6pt (\mathrm{f})\ \operatorname {injdim}(M)\leq d$
.
$\operatorname {injdim}(M)<\infty \kern106.6pt (\mathrm{f})\ \operatorname {injdim}(M)\leq d$
. -
(g)
 $\operatorname {projdim}(M)<\infty \kern99.2pt (\mathrm{h})\ \operatorname {projdim}(M)\leq d$
.
$\operatorname {projdim}(M)<\infty \kern99.2pt (\mathrm{h})\ \operatorname {projdim}(M)\leq d$
. -
(i)
 $\operatorname {flatdim}(M)<\infty \kern103.2pt (\mathrm{j})\ \operatorname {flatdim}(M)\leq d$
.
$\operatorname {flatdim}(M)<\infty \kern103.2pt (\mathrm{j})\ \operatorname {flatdim}(M)\leq d$
.
Proof. The equivalences between (e)–(j) are implied by general results of Iwanaga [Reference Iwanaga22, Th. 2], [Reference Enochs and Jenda18, Prop. 9.1.7]. Proposition 3.1 provides the equivalence between (a) and (e), and (c) and (i). We therefore find (a)
![]() $\Leftrightarrow $
(b) and (c)
$\Leftrightarrow $
(b) and (c)
![]() $\Leftrightarrow $
(d) as well.
$\Leftrightarrow $
(d) as well.
3.2 Primes and associated primes
We recall that a prime ideal in Q is a (two-sided) proper ideal
![]() $\mathfrak {p}$
in Q such that the product of two ideals lies in
$\mathfrak {p}$
in Q such that the product of two ideals lies in
![]() $\mathfrak p$
,
$\mathfrak p$
,
![]() $IJ\subset \mathfrak p$
, if and only if I is contained in
$IJ\subset \mathfrak p$
, if and only if I is contained in
![]() $\mathfrak p$
or J is contained in
$\mathfrak p$
or J is contained in
![]() $\mathfrak p$
. By considering principal ideals, we see that primeness is equivalent to the implication
$\mathfrak p$
. By considering principal ideals, we see that primeness is equivalent to the implication
From this latter description, it is clear that prime ideals in commutative rings, in the above sense, are prime in the usual sense. This expression of primeness also implies
Lemma 3.3. Consider
![]() $f:Z\to Q$
any map from a commutative algebra which has central image. The preimage of a prime
$f:Z\to Q$
any map from a commutative algebra which has central image. The preimage of a prime
![]() $\mathfrak p\subset Q$
along f is a prime ideal in Z.
$\mathfrak p\subset Q$
along f is a prime ideal in Z.
Proof. Consider
![]() $\mathfrak p$
a prime ideal in Q. For central
$\mathfrak p$
a prime ideal in Q. For central
![]() $a,b\in Q$
, we have
$a,b\in Q$
, we have
![]() $aQb=abQ$
, so that
$aQb=abQ$
, so that
![]() $aQb\subset \mathfrak p$
if and only if
$aQb\subset \mathfrak p$
if and only if
![]() $ab\in \mathfrak p$
. Hence,
$ab\in \mathfrak p$
. Hence,
![]() $ab\in \mathfrak p$
implies
$ab\in \mathfrak p$
implies
![]() $a\in \mathfrak p$
or
$a\in \mathfrak p$
or
![]() $b\in \mathfrak p$
. Considering the case
$b\in \mathfrak p$
. Considering the case
![]() $a=f(x)$
and
$a=f(x)$
and
![]() $b=f(y)$
for
$b=f(y)$
for
![]() $x,y\in Z$
, we see that
$x,y\in Z$
, we see that
![]() $xy\in f^{-1}\mathfrak p$
implies
$xy\in f^{-1}\mathfrak p$
implies
![]() $x\in f^{-1}\mathfrak p$
or
$x\in f^{-1}\mathfrak p$
or
![]() $y\in f^{-1}\mathfrak p$
. Rather,
$y\in f^{-1}\mathfrak p$
. Rather,
![]() $f^{-1}\mathfrak p$
is prime ideal in Z.
$f^{-1}\mathfrak p$
is prime ideal in Z.
One also has the notion of a prime module over Q. This is a nonzero module N over Q such that any nonzero submodule
![]() $N'\subset N$
has
$N'\subset N$
has
![]() $\operatorname {ann}(N')=\operatorname {ann}(N)$
(see, e.g., [Reference Goodearl and Warfield20]). One can see that the annihilator of a prime module is prime, and by considering the quotient
$\operatorname {ann}(N')=\operatorname {ann}(N)$
(see, e.g., [Reference Goodearl and Warfield20]). One can see that the annihilator of a prime module is prime, and by considering the quotient
![]() $N=Q/\mathfrak p$
of Q by a prime ideal, we see also that all prime ideals appear as annihilators of prime modules.
$N=Q/\mathfrak p$
of Q by a prime ideal, we see also that all prime ideals appear as annihilators of prime modules.
Lemma 3.4. Suppose that N is a prime Q-module, and that x is a central element in
![]() $Q-\operatorname {ann}(N)$
. Then, the multiplication operation
$Q-\operatorname {ann}(N)$
. Then, the multiplication operation
![]() $x:N\to N$
is injective.
$x:N\to N$
is injective.
Proof. The kernel
![]() $N'$
of
$N'$
of
![]() $x\cdot -$
is a submodule in N, and hence is either
$x\cdot -$
is a submodule in N, and hence is either
![]() $0$
or has annihilator equal to that of N. The latter case cannot happen as
$0$
or has annihilator equal to that of N. The latter case cannot happen as
![]() $x\notin \operatorname {ann}(N)$
, while
$x\notin \operatorname {ann}(N)$
, while
![]() $x\in \operatorname {ann}(N')$
. So we must have
$x\in \operatorname {ann}(N')$
. So we must have
![]() $N'=0$
.
$N'=0$
.
Proposition 3.5 [Reference Goodearl and Warfield20, Prop. 3.12]
Any finitely generated, nonzero, module M over Q has a prime submodule.
By considering cyclic submodules of prime modules, and Noetherianity of Q, we have
Corollary 3.6. Any finitely generated Q-module M admits a finite filtration
![]() $F_0M\subset F_1M\subset \dots \subset F_rM=M$
such that each subquotient
$F_0M\subset F_1M\subset \dots \subset F_rM=M$
such that each subquotient
![]() $F_iM/F_{i-1}M$
is a cyclic prime Q-module.
$F_iM/F_{i-1}M$
is a cyclic prime Q-module.
3.3 Proof of Proposition 3.1
The following proof is adapted from [Reference Avramov and Foxby2, Prop. 5.5].
Proof of Proposition 3.1
We prove the statement for
![]() $\operatorname {\mathrm {Tor}}$
first. We have
$\operatorname {\mathrm {Tor}}$
first. We have
or
![]() $\operatorname {flatdim}(M)=\infty $
if no such d exists [Reference Weibel35, Prop. 3.2.4]. By Corollary 3.6, we find further that
$\operatorname {flatdim}(M)=\infty $
if no such d exists [Reference Weibel35, Prop. 3.2.4]. By Corollary 3.6, we find further that
or
![]() $\operatorname {flatdim}(M)=\infty $
if no such d exists.
$\operatorname {flatdim}(M)=\infty $
if no such d exists.
Now, let us assume that
![]() $\operatorname {\mathrm {Tor}}_{>d}^Q(\Lambda ,M)=0$
as in the statement of Proposition 3.1, and that d is the minimal nonnegative integer with this property. We want to show that
$\operatorname {\mathrm {Tor}}_{>d}^Q(\Lambda ,M)=0$
as in the statement of Proposition 3.1, and that d is the minimal nonnegative integer with this property. We want to show that
![]() $\operatorname {flatdim}(M) =d$
. Consider now the possibly empty collection of prime ideals in Q,
$\operatorname {flatdim}(M) =d$
. Consider now the possibly empty collection of prime ideals in Q,
We want to show that this collection is empty. Suppose this is not the case, and choose
![]() $\mathfrak p$
a maximal element in
$\mathfrak p$
a maximal element in
![]() $\mathscr {P}$
, which must exist by Noetherianity of Q. Let
$\mathscr {P}$
, which must exist by Noetherianity of Q. Let
![]() $N_{\mathfrak p}$
be its associated cyclic prime module. Note that we have a surjection
$N_{\mathfrak p}$
be its associated cyclic prime module. Note that we have a surjection
![]() $Q/\mathfrak p\to N_{\mathfrak p}$
, by cyclicity of
$Q/\mathfrak p\to N_{\mathfrak p}$
, by cyclicity of
![]() $N_{\mathfrak p}$
. We claim that the maximal ideal
$N_{\mathfrak p}$
. We claim that the maximal ideal
![]() $m_Z$
of Z must be contained in
$m_Z$
of Z must be contained in
![]() $\mathfrak p$
, in which case
$\mathfrak p$
, in which case
![]() $Q/\mathfrak p$
and
$Q/\mathfrak p$
and
![]() $N_{\mathfrak p}$
must be finite-dimensional.
$N_{\mathfrak p}$
must be finite-dimensional.
If
![]() $m_Z\nsubseteq \mathfrak p$
, then chose
$m_Z\nsubseteq \mathfrak p$
, then chose
![]() $x\in m_Z-\mathfrak p$
. Applying Lemma 3.4, we observe an exact sequence of modules
$x\in m_Z-\mathfrak p$
. Applying Lemma 3.4, we observe an exact sequence of modules
Note that
![]() $\mathfrak p\subsetneq xQ+\mathfrak p\subset \operatorname {ann}(N_{\mathfrak p}/xN_{\mathfrak p})$
. So now, by considering a filtration of
$\mathfrak p\subsetneq xQ+\mathfrak p\subset \operatorname {ann}(N_{\mathfrak p}/xN_{\mathfrak p})$
. So now, by considering a filtration of
![]() $N_{\mathfrak p}/xN_{\mathfrak p}$
as in Corollary 3.6 and maximality of
$N_{\mathfrak p}/xN_{\mathfrak p}$
as in Corollary 3.6 and maximality of
![]() $\mathfrak p$
in
$\mathfrak p$
in
![]() $\mathscr {P}$
, we conclude that
$\mathscr {P}$
, we conclude that
![]() $\operatorname {\mathrm {Tor}}_{>d}^Q(N_{\mathfrak p}/xN_{\mathfrak p},M)=0$
. The long exact sequence on cohomology obtained from (2) therefore implies that the action map
$\operatorname {\mathrm {Tor}}_{>d}^Q(N_{\mathfrak p}/xN_{\mathfrak p},M)=0$
. The long exact sequence on cohomology obtained from (2) therefore implies that the action map
is an isomorphism. But this cannot happen, as our torsion hypothesis implies that
![]() $\operatorname {\mathrm {Tor}}_\ast ^Q(N_{\mathfrak p},M)$
is
$\operatorname {\mathrm {Tor}}_\ast ^Q(N_{\mathfrak p},M)$
is
![]() $m_Z$
-torsion, and hence any
$m_Z$
-torsion, and hence any
![]() $x\in m_Z$
annihilates elements in each nonzero Tor group. So we conclude that
$x\in m_Z$
annihilates elements in each nonzero Tor group. So we conclude that
![]() $m_Z\subset \mathfrak p$
, and that
$m_Z\subset \mathfrak p$
, and that
![]() $N_{\mathfrak p}$
is finite-dimensional. In that case,
$N_{\mathfrak p}$
is finite-dimensional. In that case,
![]() $N_{\mathfrak p}$
has a finite composition series where the simple factors are direct summands of
$N_{\mathfrak p}$
has a finite composition series where the simple factors are direct summands of
![]() $\Lambda $
. Hence,
$\Lambda $
. Hence,
which contradicts our assumption that
![]() $\mathfrak p \in \mathscr {P}$
, and hence contradicts our assumption that
$\mathfrak p \in \mathscr {P}$
, and hence contradicts our assumption that
![]() $\mathscr {P}$
is nonempty. It follows that
$\mathscr {P}$
is nonempty. It follows that
![]() $\operatorname {flatdim}(M)=d$
.
$\operatorname {flatdim}(M)=d$
.
As for the injective dimension, by Baer’s criterion, we have
or
![]() $\operatorname {injdim}(M)=\infty $
if no such d exists. So we may proceed exactly as above, with
$\operatorname {injdim}(M)=\infty $
if no such d exists. So we may proceed exactly as above, with
![]() $\operatorname {\mathrm {Tor}}$
replaced by
$\operatorname {\mathrm {Tor}}$
replaced by
![]() $\operatorname {\mathrm {Ext}}$
, to obtain the desired result.
$\operatorname {\mathrm {Ext}}$
, to obtain the desired result.
4 Gorenstein rings and big singularity categories
A Gorenstein (resp. d-Gorenstein) ring R is a ring such that
![]() $\operatorname {injdim}_R(R)<\infty $
(resp.
$\operatorname {injdim}_R(R)<\infty $
(resp.
![]() $\operatorname {injdim}_R(R)\leq d$
). For such a ring, objects of finite projective dimension and finite injective dimension coincide [Reference Iwanaga22].
$\operatorname {injdim}_R(R)\leq d$
). For such a ring, objects of finite projective dimension and finite injective dimension coincide [Reference Iwanaga22].
All of the rings which are of interest in this work are Gorenstein (see Lemma 4.5 below). Singularity categories are employed in the formal definition of hypersurface support in §5. We now recall the construction of the singularity category for a Gorenstein ring.
4.1 Singularity categories
For R a Gorenstein ring, we define the big singularity category as
where R-Mod is the category of arbitrary R-modules. This is the Verdier quotient of the bounded derived category by the thick subcategory of objects of finite projective = finite injective dimension. We also have the small singularity category, which is the quotient of the derived category of finitely generated modules by the thick subcategory of perfect complexes
Although we do not explicitly use the following result, it clarifies the manner in which the theory of the present paper is an extension of that of [Reference Negron and Pevtsova28].
Lemma 4.1. The category
![]() $\operatorname {Sing}(R)$
is compactly generated, and the functor
$\operatorname {Sing}(R)$
is compactly generated, and the functor
![]() $\operatorname {sing}(R)\to \operatorname {Sing}(R)$
is an equivalence onto the subcategory of compacts
$\operatorname {sing}(R)\to \operatorname {Sing}(R)$
is an equivalence onto the subcategory of compacts
![]() $\operatorname {sing}(R)\cong \operatorname {Sing}(R)^c$
.
$\operatorname {sing}(R)\cong \operatorname {Sing}(R)^c$
.
Proof. The map
![]() $R\text {-Mod}\to \operatorname {Sing}(R)$
restricted to the subcategory
$R\text {-Mod}\to \operatorname {Sing}(R)$
restricted to the subcategory
![]() $\operatorname {GProj}(R)$
of Gorenstein projectives [Reference Enochs and Jenda18] induces an equivalence from the stable category
$\operatorname {GProj}(R)$
of Gorenstein projectives [Reference Enochs and Jenda18] induces an equivalence from the stable category
(see [Reference Iyengar and Krause23, Th. 5.6 and Cor. 6.6], [Reference Bergh, Oppermann and Jorgensen11, Th. 3.1]). Similarly, we have an equivalence between the stable category of finitely generated Gorenstein projectives and the small singularity category
![]() $\underline {\operatorname {Gproj}}(R)\cong \operatorname {sing}(R)$
[Reference Buchweitz13]. It is known now that
$\underline {\operatorname {Gproj}}(R)\cong \operatorname {sing}(R)$
[Reference Buchweitz13]. It is known now that
![]() $\underline {\operatorname {GProj}}(R)$
is compactly generated with compact objects identified with
$\underline {\operatorname {GProj}}(R)$
is compactly generated with compact objects identified with
![]() $\underline {\operatorname {Gproj}}(R)$
, via the functor induced by the inclusion
$\underline {\operatorname {Gproj}}(R)$
, via the functor induced by the inclusion
![]() $\operatorname {Gproj}(R)\to \operatorname {GProj}(R)$
[Reference Benson, Iyengar, Krause and Pevtsova9, Prop. 2.10]. So one considers the square connecting the two equivalences above to obtain the claimed result.
$\operatorname {Gproj}(R)\to \operatorname {GProj}(R)$
[Reference Benson, Iyengar, Krause and Pevtsova9, Prop. 2.10]. So one considers the square connecting the two equivalences above to obtain the claimed result.
As a more terrestrial comment, one can see by partially resolving bounded complexes that any object in
![]() $\operatorname {Sing}(R)$
is isomorphic to a shift
$\operatorname {Sing}(R)$
is isomorphic to a shift
![]() $\Sigma ^n M$
of some R-module M. Furthermore, by considering syzygies and cosyzygies, we see that the objects
$\Sigma ^n M$
of some R-module M. Furthermore, by considering syzygies and cosyzygies, we see that the objects
![]() $R\text {-Mod}\subset \operatorname {Sing}(R)$
are stable under shifting. So we see that the additive map
$R\text {-Mod}\subset \operatorname {Sing}(R)$
are stable under shifting. So we see that the additive map
is essentially surjective. The following is well known to experts and can be deduced, for example, by identifying the singularity category with the stable category of Gorenstein projectives and applying [Reference Enochs and Jenda18, Th. 10.2.14].
Lemma 4.2. The category
![]() $\operatorname {Sing}(R)$
admits arbitrary (set indexed) sums, and the functor
$\operatorname {Sing}(R)$
admits arbitrary (set indexed) sums, and the functor
![]() $R\text {-Mod}\to \operatorname {Sing}(R)$
commutes with sums.
$R\text {-Mod}\to \operatorname {Sing}(R)$
commutes with sums.
Remark 4.3. In the presentation above, we have used an identification between the singularity category of R and its stable category of Gorenstein projectives. One can also express the singularity category as the homotopy category of totally acyclic complexes of projectives (or injectives), as done in [Reference Krause25] for example.
Remark 4.4. In the case in which R is Frobenius, the functor
![]() $R\text {-mod}\to \operatorname {Sing}(R)$
induces an equivalence from the big stable category
$R\text {-mod}\to \operatorname {Sing}(R)$
induces an equivalence from the big stable category
![]() $\operatorname {Stab}(R)\cong \operatorname {Sing}(R)$
.
$\operatorname {Stab}(R)\cong \operatorname {Sing}(R)$
.
4.2 All of our algebras are Gorenstein
Lemma 4.5. Consider
![]() $Q\to R$
a deformation as in §2.2, and suppose that Q is of finite global dimension. Let
$Q\to R$
a deformation as in §2.2, and suppose that Q is of finite global dimension. Let
![]() $f_1,\dots , f_m$
be a regular sequence in the parameterizing algebra Z. Then, the quotient
$f_1,\dots , f_m$
be a regular sequence in the parameterizing algebra Z. Then, the quotient
![]() $Q/(f_1,\dots , f_m)$
is Gorenstein. In particular, all hypersurface algebras
$Q/(f_1,\dots , f_m)$
is Gorenstein. In particular, all hypersurface algebras
![]() $Q/(f)$
are Gorenstein, and R is Gorenstein.
$Q/(f)$
are Gorenstein, and R is Gorenstein.
Our proof is adapted from [Reference Cassidy, Conner, Kirkman and Moore14, Lem. 5.3].
Proof. Take I the ideal generated by the
![]() $f_i$
in Q, and take
$f_i$
in Q, and take
![]() $d=\operatorname {gldim}(Q)$
. Via the Koszul resolution
$d=\operatorname {gldim}(Q)$
. Via the Koszul resolution
![]() $Kos=Kos(f_1,\dots ,f_m)$
over Z, and the corresponding Koszul resolution
$Kos=Kos(f_1,\dots ,f_m)$
over Z, and the corresponding Koszul resolution
![]() $Kos_Q=Q\otimes _Z Kos$
of
$Kos_Q=Q\otimes _Z Kos$
of
![]() $Q/I$
over Q, we see that
$Q/I$
over Q, we see that
![]() $\operatorname {\mathrm {RHom}}_Q(Q/I,Q)\cong \Sigma ^{-m}Q/I$
. Hence,
$\operatorname {\mathrm {RHom}}_Q(Q/I,Q)\cong \Sigma ^{-m}Q/I$
. Hence,
 $$ \begin{align*} \begin{array}{rl} \operatorname{\mathrm{RHom}}_{Q/I}(-,Q/I)& \cong \Sigma^m\operatorname{\mathrm{RHom}}_{Q/I}(-,\operatorname{\mathrm{RHom}}^\ast_Q(Q/I,Q))\\[3pt] & \cong \Sigma^m\operatorname{\mathrm{RHom}}_Q(-,Q). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rl} \operatorname{\mathrm{RHom}}_{Q/I}(-,Q/I)& \cong \Sigma^m\operatorname{\mathrm{RHom}}_{Q/I}(-,\operatorname{\mathrm{RHom}}^\ast_Q(Q/I,Q))\\[3pt] & \cong \Sigma^m\operatorname{\mathrm{RHom}}_Q(-,Q). \end{array} \end{align*} $$
This functor has cohomology vanishing in degrees
![]() $>d$
, so that
$>d$
, so that
![]() $\operatorname {injdim}(Q/I)\leq d$
.
$\operatorname {injdim}(Q/I)\leq d$
.
Let us close the subsection with a remark about singularity categories. By considering the Koszul resolution for R over Q, we see that the restriction map
![]() $D^b(R)\to D^b(Q)$
sends the thick ideal
$D^b(R)\to D^b(Q)$
sends the thick ideal
![]() $\langle \operatorname {\mathrm {Proj}}(R)\rangle $
into
$\langle \operatorname {\mathrm {Proj}}(R)\rangle $
into
![]() $\langle \operatorname {\mathrm {Proj}}(Q)\rangle $
, and hence descends to a triangulated functor
$\langle \operatorname {\mathrm {Proj}}(Q)\rangle $
, and hence descends to a triangulated functor
5 Hypersurface support
We provide the promised definition of hypersurface support for arbitrary R-modules, when R comes equipped with the appropriate (formally) smooth deformation
![]() $Z \to Q \to R$
with Q of finite global dimension. We first elaborate on the integral form hypothesis of §2.2, then deal with some technical issues regarding base change in the formal setting.
$Z \to Q \to R$
with Q of finite global dimension. We first elaborate on the integral form hypothesis of §2.2, then deal with some technical issues regarding base change in the formal setting.
5.1 Integral forms
As mentioned in §2.2, we assume that our deformation
![]() $Q\to R$
admits an integral form
$Q\to R$
admits an integral form
![]() $\mathcal {Q}\to R$
. By this, we mean that R admits a deformation
$\mathcal {Q}\to R$
. By this, we mean that R admits a deformation
![]() $\mathcal {Q}\to R$
with
$\mathcal {Q}\to R$
with
![]() $\mathcal {Q}$
of finite global dimension for which the parameterizing algebra
$\mathcal {Q}$
of finite global dimension for which the parameterizing algebra
![]() $\mathcal {Z}$
is smooth, and in particular of finite type over k, and such that the completion at the distinguished point
$\mathcal {Z}$
is smooth, and in particular of finite type over k, and such that the completion at the distinguished point
![]() $1:\mathcal {Z}\to k$
recovers our original deformation. That is to say,
$1:\mathcal {Z}\to k$
recovers our original deformation. That is to say,
![]() $Z=\widehat {\mathcal {Z}}_1$
, the completion of
$Z=\widehat {\mathcal {Z}}_1$
, the completion of
![]() $\mathcal {Z}$
at the kernel of the augmentation map
$\mathcal {Z}$
at the kernel of the augmentation map
![]() $1: \mathcal {Z} \to k$
, and
$1: \mathcal {Z} \to k$
, and
![]() $Q\cong Z\otimes _{\mathcal {Z}}\mathcal {Q}$
.
$Q\cong Z\otimes _{\mathcal {Z}}\mathcal {Q}$
.
The point of this integral form is to pacify certain conflicts which arise when attempting to deal simultaneously with base change and completion.
Remark 5.1. One may ask at this point why we even work with complete local rings, rather than local rings which are essentially of finite type. The reason is that usual localization does not behave well with Hopf structures. For example, for
![]() $\mathbb {G}$
an algebraic group, the local ring at the identity
$\mathbb {G}$
an algebraic group, the local ring at the identity
![]() $\mathscr {O}_{\mathbb {G},1}$
does not have a Hopf structure, while the complete local ring
$\mathscr {O}_{\mathbb {G},1}$
does not have a Hopf structure, while the complete local ring
![]() $\widehat {\mathscr {O}}_{\mathbb {G},1}$
is a Hopf algebra in the symmetric monoidal category of pro-finite vector spaces.
$\widehat {\mathscr {O}}_{\mathbb {G},1}$
is a Hopf algebra in the symmetric monoidal category of pro-finite vector spaces.
5.2 Topological base change
Consider a deformation
![]() $Q\to R$
as in §2.2, with some integral form
$Q\to R$
as in §2.2, with some integral form
![]() $\mathcal {Q}\to R$
. For a field extension
$\mathcal {Q}\to R$
. For a field extension
![]() $k\to K$
, we let
$k\to K$
, we let
![]() $\mathcal {Z}_K$
,
$\mathcal {Z}_K$
,
![]() $\mathcal {Q}_K$
, and
$\mathcal {Q}_K$
, and
![]() $R_K$
denote the usual base change
$R_K$
denote the usual base change
![]() $-_K=K\otimes -$
, so that we have the base changed deformation
$-_K=K\otimes -$
, so that we have the base changed deformation
![]() $\mathcal {Q}_K\to R_K$
parameterized by
$\mathcal {Q}_K\to R_K$
parameterized by
![]() $\mathcal {Z}_K$
. We have the standard base change operation
$\mathcal {Z}_K$
. We have the standard base change operation
We complete at the distinguished point
![]() $1:\mathcal {Z}_K\to K$
to obtain the corresponding formal deformation
$1:\mathcal {Z}_K\to K$
to obtain the corresponding formal deformation
![]() $Q_K\to R_K$
parameterized by
$Q_K\to R_K$
parameterized by
![]() $Z_K=\widehat {(\mathcal {Z}_K)}_1$
. So, from another perspective, we obtain the formal deformation
$Z_K=\widehat {(\mathcal {Z}_K)}_1$
. So, from another perspective, we obtain the formal deformation
![]() $Q_K\to R_K$
via topological base change
$Q_K\to R_K$
via topological base change
![]() $Z_K=\varprojlim _n (Z/m_Z^n)\otimes K$
and
$Z_K=\varprojlim _n (Z/m_Z^n)\otimes K$
and
![]() $Q_K=\varprojlim _n (Q/m_Z^nQ)\otimes K$
. For
$Q_K=\varprojlim _n (Q/m_Z^nQ)\otimes K$
. For
![]() $Z=k[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
, we have
$Z=k[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
, we have
![]() $Z_K=K[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
.
$Z_K=K[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
.
Lemma 5.2. The base change
![]() $Q_K$
is Noetherian and of finite global dimension.
$Q_K$
is Noetherian and of finite global dimension.
Proof.
![]() $Q_K$
is Noetherian, as it is finite over the Noetherian algebra
$Q_K$
is Noetherian, as it is finite over the Noetherian algebra
![]() $Z_K$
. We have a finite projective resolution of
$Z_K$
. We have a finite projective resolution of
![]() $P\to \Lambda $
of
$P\to \Lambda $
of
![]() $\Lambda $
over the integral form
$\Lambda $
over the integral form
![]() $\mathcal {Q}$
, at least after localizing around
$\mathcal {Q}$
, at least after localizing around
![]() $1\in \operatorname {\mathrm {Spec}}(\mathcal {Z})$
. Apply base change to obtain a finite resolution
$1\in \operatorname {\mathrm {Spec}}(\mathcal {Z})$
. Apply base change to obtain a finite resolution
![]() $P_K\to \Lambda _K$
over
$P_K\to \Lambda _K$
over
![]() $\mathcal {Q}_K$
, then apply the exact functor
$\mathcal {Q}_K$
, then apply the exact functor
![]() $Z_K\otimes _{\mathcal {Z}_K}-$
to obtain a finite resolution
$Z_K\otimes _{\mathcal {Z}_K}-$
to obtain a finite resolution
![]() $\widehat {P}_K\to \Lambda _K$
over
$\widehat {P}_K\to \Lambda _K$
over
![]() $Q_K$
. So, for d the length of the resolution P, we have
$Q_K$
. So, for d the length of the resolution P, we have
![]() $\operatorname {\mathrm {Tor}}_{>d}^{Q_K}(\Lambda _K,-)=0$
. By considering minimal resolutions for finitely generated
$\operatorname {\mathrm {Tor}}_{>d}^{Q_K}(\Lambda _K,-)=0$
. By considering minimal resolutions for finitely generated
![]() $Q_K$
-modules, this vanishing of
$Q_K$
-modules, this vanishing of
![]() $\operatorname {\mathrm {Tor}}$
implies that
$\operatorname {\mathrm {Tor}}$
implies that
![]() $Q_K$
is of global dimension
$Q_K$
is of global dimension
![]() $\leq d$
.
$\leq d$
.
Lemma 5.3. Consider a field extension
![]() $k\to K$
. For any finite-dimensional R-module V, and arbitrary R-module M, the natural maps
$k\to K$
. For any finite-dimensional R-module V, and arbitrary R-module M, the natural maps
are isomorphisms.
Proof. As in the proof of Lemma 5.2, one employs the integral form
![]() $\mathcal {Q}$
, notes that
$\mathcal {Q}$
, notes that
![]() $\operatorname {\mathrm {Tor}}$
and
$\operatorname {\mathrm {Tor}}$
and
![]() $\operatorname {\mathrm {Ext}}$
over
$\operatorname {\mathrm {Ext}}$
over
![]() $\mathcal {Q}$
agree with those of Q (for R-modules), and recalls that such base change formulae are valid over
$\mathcal {Q}$
agree with those of Q (for R-modules), and recalls that such base change formulae are valid over
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
5.3 Representative independence over hypersurfaces
We have the following infinite analog of [Reference Negron and Pevtsova28, Cor. 5.3]. The proof is taken almost directly from [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3], and so is delayed until the appendix.
Theorem 5.4 (cf. [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3, Th. 2.1])
Let
![]() $Q\to R$
be a deformation as in §2.2, and assume that Q is of finite global dimension. Consider M any R-module, and
$Q\to R$
be a deformation as in §2.2, and assume that Q is of finite global dimension. Consider M any R-module, and
![]() $f,g\in m_Z$
with equivalent, nonzero, classes
$f,g\in m_Z$
with equivalent, nonzero, classes
![]() $\bar {f}=\bar {g}$
in
$\bar {f}=\bar {g}$
in
![]() $m_Z/m_Z^2$
. Then, there is an identification of graded vector space
$m_Z/m_Z^2$
. Then, there is an identification of graded vector space
Similarly, there is an identification
In particular, these (co)homology groups vanish in high degree over
![]() $Q/(f)$
if and only if they vanish in high degree over
$Q/(f)$
if and only if they vanish in high degree over
![]() $Q/(g)$
.
$Q/(g)$
.
Of course, the hypersurface algebra
![]() $Q/(f)$
depends on f only up to nonzero scaling,
$Q/(f)$
depends on f only up to nonzero scaling,
![]() $Q/(f)=Q/(\zeta f)$
for any
$Q/(f)=Q/(\zeta f)$
for any
![]() $\zeta \in k^\times $
. So, to phrase things slightly differently, the claimed identification of (co)homology groups holds whenever the reductions
$\zeta \in k^\times $
. So, to phrase things slightly differently, the claimed identification of (co)homology groups holds whenever the reductions
![]() $\bar {f}$
and
$\bar {f}$
and
![]() $\bar {g}$
represent the same point in projective space
$\bar {g}$
represent the same point in projective space
![]() $\mathbb {P}(m_Z/m_Z^2)$
.
$\mathbb {P}(m_Z/m_Z^2)$
.
5.4 Hypersurface support
Fix now R a finite-dimensional algebra with prescribed deformation
![]() $Q\to R$
as in §2.2, and suppose that Q is of finite global dimension.
$Q\to R$
as in §2.2, and suppose that Q is of finite global dimension.
Consider a point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
, which we may view as a map into the base change
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
, which we may view as a map into the base change
![]() $\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)_K=\mathbb {P}(m_{Z_K}/m_{Z_K}^2)$
. We say a hypersurface algebra
$\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)_K=\mathbb {P}(m_{Z_K}/m_{Z_K}^2)$
. We say a hypersurface algebra
![]() $Q_K/(f)$
is a hypersurface representative for c if the class of f in
$Q_K/(f)$
is a hypersurface representative for c if the class of f in
![]() $m_{Z_K}/m_{Z_K}^2$
lies in the punctured line defined by c. As a corollary to Theorem 5.4, we have
$m_{Z_K}/m_{Z_K}^2$
lies in the punctured line defined by c. As a corollary to Theorem 5.4, we have
Corollary 5.5. Consider
![]() $Q_K/(f)$
and
$Q_K/(f)$
and
![]() $Q_K/(g)$
two hypersurface representatives for a given point
$Q_K/(g)$
two hypersurface representatives for a given point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
. Then, for any R-module M, the base change
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
. Then, for any R-module M, the base change
![]() $M_K$
is of finite projective dimension over
$M_K$
is of finite projective dimension over
![]() $Q_K/(f)$
if and only if
$Q_K/(f)$
if and only if
![]() $M_K$
is of finite projective dimension over
$M_K$
is of finite projective dimension over
![]() $Q_K/(g)$
.
$Q_K/(g)$
.
Proof. After rescaling, if necessary, we may assume that f and g define the same class in
![]() $m_{Z_K}/m_{Z_K}^2$
. The result now follows by Corollary 3.2 and Theorem 5.4.
$m_{Z_K}/m_{Z_K}^2$
. The result now follows by Corollary 3.2 and Theorem 5.4.
Remark 5.6. A subtle point here is that Corollary 5.5 allows us to always assume that
![]() $f\in m_Z$
lies in the integral form
$f\in m_Z$
lies in the integral form
![]() $\mathcal {Z}$
, when desired, so that the hypersurface deformation
$\mathcal {Z}$
, when desired, so that the hypersurface deformation
![]() $Q/(f)$
can always be assumed to have an integral form
$Q/(f)$
can always be assumed to have an integral form
![]() $\mathcal {Q}/(f)$
.
$\mathcal {Q}/(f)$
.
When the distinction is unimportant, we take, for a given point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
,
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
,
By the above lemma, the kernel of the functor
defined as base change
![]() $(-)_K:\operatorname {Sing}(R)\to \operatorname {Sing}(R_K)$
composed with restriction (3), is independent of the choice of representative for the point c.
$(-)_K:\operatorname {Sing}(R)\to \operatorname {Sing}(R_K)$
composed with restriction (3), is independent of the choice of representative for the point c.
Lemma 5.7. Consider any field extension
![]() $K\to K'$
, and
$K\to K'$
, and
![]() $f\in m_{Z_K}$
with nontrivial reduction
$f\in m_{Z_K}$
with nontrivial reduction
![]() $\bar {f}\in (m_Z/m_Z^2)_K$
. Then, for any R-module M,
$\bar {f}\in (m_Z/m_Z^2)_K$
. Then, for any R-module M,
![]() $M_K$
is of finite projective dimension over
$M_K$
is of finite projective dimension over
![]() $Q_K/(f)$
if and only if
$Q_K/(f)$
if and only if
![]() $M_{K'}$
is of finite projective dimension over
$M_{K'}$
is of finite projective dimension over
![]() $Q_{K'}/(f)$
.
$Q_{K'}/(f)$
.
Lemma 5.7 says that if a given point
![]() $c':\operatorname {\mathrm {Spec}}(K')\to \mathbb {P}$
factors through some other point
$c':\operatorname {\mathrm {Spec}}(K')\to \mathbb {P}$
factors through some other point
then the kernels of the two functors
![]() $F_c:\operatorname {Sing}(R)\to \operatorname {Sing}(Q_c)$
and
$F_c:\operatorname {Sing}(R)\to \operatorname {Sing}(Q_c)$
and
![]() $F_{c'}:\operatorname {Sing}(R)\to \operatorname {Sing}(Q_{c'})$
agree.
$F_{c'}:\operatorname {Sing}(R)\to \operatorname {Sing}(Q_{c'})$
agree.
Definition 5.8. We say an R-module M is supported at a given point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
if M is not in
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
if M is not in
![]() $\ker \{F_c: \operatorname {Sing}(R)\to \operatorname {Sing}(Q_c)\}$
. Equivalently, M is supported at c if
$\ker \{F_c: \operatorname {Sing}(R)\to \operatorname {Sing}(Q_c)\}$
. Equivalently, M is supported at c if
![]() $M_K$
, considered as a
$M_K$
, considered as a
![]() $Q_c$
-module via the deformation
$Q_c$
-module via the deformation
![]() $Q_c\to R_K$
, is of infinite projective dimension over
$Q_c\to R_K$
, is of infinite projective dimension over
![]() $Q_c$
. We take
$Q_c$
. We take
 $$ \begin{align*} \operatorname{\mathrm{supp}}^{hyp}_{\mathbb{P}}(M):=\left\{ \begin{array}{c} \text{the image of all points }c:\operatorname{\mathrm{Spec}}(K)\to \mathbb{P}(m_Z/m_Z^2)\\ \text{at which }\operatorname{projdim}_{Q_c}(M_K)=\infty \end{array}\right\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{supp}}^{hyp}_{\mathbb{P}}(M):=\left\{ \begin{array}{c} \text{the image of all points }c:\operatorname{\mathrm{Spec}}(K)\to \mathbb{P}(m_Z/m_Z^2)\\ \text{at which }\operatorname{projdim}_{Q_c}(M_K)=\infty \end{array}\right\}. \end{align*} $$
Corollary 5.5 and Lemma 5.7 tell us that there are no ambiguities in the above definition. We note that the support
![]() $\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)$
is a subset in
$\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)$
is a subset in
![]() $\mathbb {P}(m_Z/m_Z^2)$
which is not necessarily closed. We see below that
$\mathbb {P}(m_Z/m_Z^2)$
which is not necessarily closed. We see below that
![]() $\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)$
is closed whenever M is finite-dimensional.
$\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)$
is closed whenever M is finite-dimensional.
5.5 Support for finite-dimensional modules
Recall our deformation algebra
![]() $A_Z=\operatorname {\mathrm {Sym}}(\Sigma ^{-2}(m_Z/m_Z^2)^\ast )$
, from §2.4, and its corresponding action on
$A_Z=\operatorname {\mathrm {Sym}}(\Sigma ^{-2}(m_Z/m_Z^2)^\ast )$
, from §2.4, and its corresponding action on
![]() $D^b(R)$
.
$D^b(R)$
.
We have
![]() $\operatorname {\mathrm {Proj}}(A_Z)=\mathbb {P}(m_Z/m_Z^2)$
and the natural
$\operatorname {\mathrm {Proj}}(A_Z)=\mathbb {P}(m_Z/m_Z^2)$
and the natural
![]() $A_Z$
-action on extensions provides, for any R-modules N and M, an associated quasicoherent sheaf
$A_Z$
-action on extensions provides, for any R-modules N and M, an associated quasicoherent sheaf
![]() $\operatorname {\mathrm {Ext}}^\ast _R(N,M)^\sim $
on
$\operatorname {\mathrm {Ext}}^\ast _R(N,M)^\sim $
on
![]() $\mathbb {P}(m_Z/m_Z^2)$
. By [Reference Negron and Pevtsova28, Cor. 4.7], these extension sheaves are coherent when N and M are finite-dimensional.
$\mathbb {P}(m_Z/m_Z^2)$
. By [Reference Negron and Pevtsova28, Cor. 4.7], these extension sheaves are coherent when N and M are finite-dimensional.
Proposition 5.9. For a finite-dimensional R-module V over R, we have
In particular, the support of a finite-dimensional R-module is closed in
![]() $\mathbb {P}(m_Z/m_Z^2)$
.
$\mathbb {P}(m_Z/m_Z^2)$
.
In the proof, we employ the following construction: to any point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
, we have an associated graded algebra map
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
, we have an associated graded algebra map
![]() $\phi _c:A_Z\to K[t]$
which is nonzero in degree
$\phi _c:A_Z\to K[t]$
which is nonzero in degree
![]() $2$
and annihilates the kernel of
$2$
and annihilates the kernel of
![]() $c:A_Z^2=(m_Z/m_Z^2)^\ast \to K$
. We also consider the base change
$c:A_Z^2=(m_Z/m_Z^2)^\ast \to K$
. We also consider the base change
![]() $\phi _{c,K}:(A_Z)_K\to K[t]$
, which is now a graded algebra surjection. Note that although the map c is really only defined up to scaling, its kernel is well defined and uniquely determined by the point c. Similarly, the map
$\phi _{c,K}:(A_Z)_K\to K[t]$
, which is now a graded algebra surjection. Note that although the map c is really only defined up to scaling, its kernel is well defined and uniquely determined by the point c. Similarly, the map
![]() $\phi _c$
is uniquely determined up to the
$\phi _c$
is uniquely determined up to the
![]() $K^\times $
-action on
$K^\times $
-action on
![]() $K[t]$
by graded automorphisms.
$K[t]$
by graded automorphisms.
Proof. Consider an arbitrary point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
. We want to show that V is supported at c if and only if the image
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
. We want to show that V is supported at c if and only if the image
![]() $c(pt)\in \mathbb {P}$
of c is in the support of the graded
$c(pt)\in \mathbb {P}$
of c is in the support of the graded
![]() $A_Z$
-module
$A_Z$
-module
![]() $\operatorname {\mathrm {Ext}}^\ast _R(V,\Lambda )$
. By Lemma 5.7, we are free to assume that c is a geometric point, that is, that
$\operatorname {\mathrm {Ext}}^\ast _R(V,\Lambda )$
. By Lemma 5.7, we are free to assume that c is a geometric point, that is, that
![]() $K=\overline {K}$
. (We make this assumption to conform to the setting of [Reference Negron and Pevtsova28].)
$K=\overline {K}$
. (We make this assumption to conform to the setting of [Reference Negron and Pevtsova28].)
By [Reference Negron and Pevtsova28, Lem. 6.8], we have
![]() $\operatorname {\mathrm {Ext}}^{\gg 0}_{Q_K/(f)}(V_K,\Lambda _K)=0$
if and only if the fiber of
$\operatorname {\mathrm {Ext}}^{\gg 0}_{Q_K/(f)}(V_K,\Lambda _K)=0$
if and only if the fiber of
along the localized map
![]() $\phi _{c,K}:K\otimes A_Z\to K[t,t^{-1}]$
vanishes. So, V is supported at the K-point c, in the sense of Definition 5.8, if and only if the pullback
$\phi _{c,K}:K\otimes A_Z\to K[t,t^{-1}]$
vanishes. So, V is supported at the K-point c, in the sense of Definition 5.8, if and only if the pullback
![]() $\pi ^\ast \operatorname {\mathrm {Ext}}^\ast _R(V,\Lambda )^\sim $
along the projection
$\pi ^\ast \operatorname {\mathrm {Ext}}^\ast _R(V,\Lambda )^\sim $
along the projection
![]() $\pi :\mathbb {P}_K\to \mathbb {P}$
is supported at c. Since, for any coherent sheaf
$\pi :\mathbb {P}_K\to \mathbb {P}$
is supported at c. Since, for any coherent sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
[Reference Tate34, Tag 056H], we see that V is supported at c if and only if
![]() $\operatorname {\mathrm {Ext}}^\ast _R(V,\Lambda )^\sim $
is supported at
$\operatorname {\mathrm {Ext}}^\ast _R(V,\Lambda )^\sim $
is supported at
![]() $c(pt)$
, as desired.
$c(pt)$
, as desired.
Remark 5.10. By Proposition 5.9 and [Reference Negron and Pevtsova28, Cor. 6.10], we see that the hypersurface support of the present paper agrees with that of its predecessor [Reference Negron and Pevtsova28, Def. 6.7].
6 The detection theorem
Fix for this section R is a finite-dimensional algebra which is equipped with a deformation
![]() $Q\to R$
as in §2.2, and we assume additionally that Q is of finite global dimension. We define the support
$Q\to R$
as in §2.2, and we assume additionally that Q is of finite global dimension. We define the support
![]() $\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)$
of R-modules via this given deformation (Definition 5.8). The point of this final section of the text is to prove the following detection theorem.
$\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)$
of R-modules via this given deformation (Definition 5.8). The point of this final section of the text is to prove the following detection theorem.
Theorem 6.1. For M any R-module,
![]() $\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)=\emptyset $
if and only if M has finite projective dimension over R. That is to say, hypersurface support for M vanishes if and only if M vanishes in the singularity category.
$\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)=\emptyset $
if and only if M has finite projective dimension over R. That is to say, hypersurface support for M vanishes if and only if M vanishes in the singularity category.
The proof is essentially an application of (dg) commutative algebra.
Remark 6.2. In the case of finite-dimensional M, Theorem 6.1 follows easily from the cohomological expression of Proposition 5.9.
6.1 Dg modules and sheaves on
 $\mathbb {P}$
$\mathbb {P}$
Fix
![]() $S=k[\xi _1,\dots , \xi _n]$
a polynomial ring in n variables, and
$S=k[\xi _1,\dots , \xi _n]$
a polynomial ring in n variables, and
![]() $\mathbb {P}=\operatorname {\mathrm {Proj}}(S)$
. We consider S as a dg algebra, with
$\mathbb {P}=\operatorname {\mathrm {Proj}}(S)$
. We consider S as a dg algebra, with
![]() $\deg (\xi _i)=2$
, for all i, and vanishing differential. Following standard notation, we take
$\deg (\xi _i)=2$
, for all i, and vanishing differential. Following standard notation, we take
![]() $S_{(f)}$
the degree
$S_{(f)}$
the degree
![]() $0$
portion of the localization
$0$
portion of the localization
![]() $S_f$
, for homogenous f, and
$S_f$
, for homogenous f, and
![]() $N_{(f)}=(N_f)^{0}$
for any graded S-module N. For a degree
$N_{(f)}=(N_f)^{0}$
for any graded S-module N. For a degree
![]() $2$
function
$2$
function
![]() $f\in S$
, let
$f\in S$
, let
![]() $U_f\subset \mathbb {P}$
denote the basic open
$U_f\subset \mathbb {P}$
denote the basic open
![]() $U_f=\operatorname {\mathrm {Spec}}(S_{(f)})$
.
$U_f=\operatorname {\mathrm {Spec}}(S_{(f)})$
.
For any dg S-module N, the differential
![]() $d:N\to N$
is a degree
$d:N\to N$
is a degree
![]() $1 S$
-linear homomorphism, and each localization
$1 S$
-linear homomorphism, and each localization
![]() $N_f$
is a dg module over
$N_f$
is a dg module over
![]() $S_f$
. We can consider each
$S_f$
. We can consider each
![]() $N_f$
as a dg module over the (non-dg) ring
$N_f$
as a dg module over the (non-dg) ring
![]() $S_{(f)}$
, in which case it becomes an unbounded complex of
$S_{(f)}$
, in which case it becomes an unbounded complex of
![]() $S_{(f)}$
-modules and we are in a classical (non-dg) situation. The dg modules
$S_{(f)}$
-modules and we are in a classical (non-dg) situation. The dg modules
![]() $N_f$
glue over the localizations
$N_f$
glue over the localizations
![]() $S_{(f)}$
,
$S_{(f)}$
,
![]() $\deg (f)=2$
, to produce a sheaf
$\deg (f)=2$
, to produce a sheaf
![]() $\mathcal {F}_N$
of quasi-coherent dg
$\mathcal {F}_N$
of quasi-coherent dg
![]() $\mathscr {O}_{\mathbb {P}}$
-modules on projective space
$\mathscr {O}_{\mathbb {P}}$
-modules on projective space
![]() $\mathbb {P}=\operatorname {\mathrm {Proj}}(S)$
. Indeed, as an
$\mathbb {P}=\operatorname {\mathrm {Proj}}(S)$
. Indeed, as an
![]() $\mathscr {O}_{\mathbb {P}}$
-module,
$\mathscr {O}_{\mathbb {P}}$
-module,
![]() $\mathcal {F}_N$
is assembled from the usual sheaves associated with
$\mathcal {F}_N$
is assembled from the usual sheaves associated with
![]() $N^{ev}$
,
$N^{ev}$
,
![]() $N^{odd}$
, and their shifts.
$N^{odd}$
, and their shifts.
The above construction is natural in N, so that in total we obtain an exact functor from dg S-modules to dg sheaves on projective space.
Definition 6.3. We let
![]() $\mathcal {F}_?:S\text {-dgmod}\to \operatorname {QCoh}_{dg}(\mathbb {P})$
denote the exact functor constructed above,
$\mathcal {F}_?:S\text {-dgmod}\to \operatorname {QCoh}_{dg}(\mathbb {P})$
denote the exact functor constructed above,
![]() $N\mapsto \mathcal {F}_N$
.
$N\mapsto \mathcal {F}_N$
.
Consider a geometric point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}$
, which determines (up to
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}$
, which determines (up to
![]() $K^\times $
-action) a graded surjection
$K^\times $
-action) a graded surjection
![]() $\phi _c:S_K\to K[t]$
,
$\phi _c:S_K\to K[t]$
,
![]() $\deg (t)=2$
. If this point lies in
$\deg (t)=2$
. If this point lies in
![]() $U_f\subset \mathbb {P}_K$
, then
$U_f\subset \mathbb {P}_K$
, then
![]() $f\in S_K^2$
maps to a nonzero scaling of t, and we may generally assume that this scalar is
$f\in S_K^2$
maps to a nonzero scaling of t, and we may generally assume that this scalar is
![]() $1$
.
$1$
.
Lemma 6.4. Consider a geometric point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}$
, and a standard open
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}$
, and a standard open
![]() $U_f\subset \mathbb {P}_K$
containing c. Then, there is a natural isomorphism
$U_f\subset \mathbb {P}_K$
containing c. Then, there is a natural isomorphism
in
![]() $D(K)$
, where we change base along the (localized) map
$D(K)$
, where we change base along the (localized) map
![]() $\phi _c:S_K\to K[t,t^{-1}]$
.
$\phi _c:S_K\to K[t,t^{-1}]$
.
Proof. By changing base initially, we may assume
![]() $K=k$
, so that c is a closed point, and by replacing N with a semiprojective resolution, we may assume that N is K-flat (see, e.g., [Reference Negron and Pevtsova28, §3.2] for a discussion of a semiprojective resolutions and [Reference Spaltenstein32, Def. 5.1] for the definition of K-flat). In this case, the derived fiber and derived product are identified with their underived counterparts. It suffices to provide an isomorphism
$K=k$
, so that c is a closed point, and by replacing N with a semiprojective resolution, we may assume that N is K-flat (see, e.g., [Reference Negron and Pevtsova28, §3.2] for a discussion of a semiprojective resolutions and [Reference Spaltenstein32, Def. 5.1] for the definition of K-flat). In this case, the derived fiber and derived product are identified with their underived counterparts. It suffices to provide an isomorphism
![]() $k\otimes _{S_{(f)}}N_f\cong k[t,t^{-1}]\otimes _{S}N$
. The latter space is isomorphic to
$k\otimes _{S_{(f)}}N_f\cong k[t,t^{-1}]\otimes _{S}N$
. The latter space is isomorphic to
![]() $k[t,t^{-1}]\otimes _{S_f}N_f$
, since f maps to a nonzero scaling of t,
$k[t,t^{-1}]\otimes _{S_f}N_f$
, since f maps to a nonzero scaling of t,
![]() $\phi (f)=\zeta t$
.
$\phi (f)=\zeta t$
.
We have the two maps
and
One observes directly that these maps are mutually inverse, and so provide the desired isomorphism.
Lemma 6.5. At all
![]() $f\in S^2$
,
$f\in S^2$
,
![]() $H^\ast (\mathcal {F}_N)|_{U_f}\cong H^\ast (N)_f$
.
$H^\ast (\mathcal {F}_N)|_{U_f}\cong H^\ast (N)_f$
.
Proof. We have
![]() $H^\ast (\mathcal {F}_N)|_{U_f}=H^\ast (\mathcal {F}_N|_{U_f})=H^\ast (N_f)$
. By exactness of localization, and the fact that the differential
$H^\ast (\mathcal {F}_N)|_{U_f}=H^\ast (\mathcal {F}_N|_{U_f})=H^\ast (N_f)$
. By exactness of localization, and the fact that the differential
![]() $d:N\to N$
is S-linear, we localize the exact sequences
$d:N\to N$
is S-linear, we localize the exact sequences
to get exact sequences
This gives
![]() $Z(N)_f\cong Z(N_f)$
,
$Z(N)_f\cong Z(N_f)$
,
![]() $B(N)_f\cong B(N_f)$
, and therefore
$B(N)_f\cong B(N_f)$
, and therefore
![]() $H^\ast (N_f)\cong H^\ast (N)_f$
.
$H^\ast (N_f)\cong H^\ast (N)_f$
.
6.2 A vanishing theorem
Theorem 6.6. Suppose that N is a bounded below dg S-module, and that at each geometric point
![]() $c:S\to K[t]$
, the fiber
$c:S\to K[t]$
, the fiber
![]() $K[t]\otimes ^{\textrm {L}}_S N$
has cohomology vanishing in degrees
$K[t]\otimes ^{\textrm {L}}_S N$
has cohomology vanishing in degrees
![]() $>d$
, for some (uniformly chosen) integer d. Then, N has bounded cohomology.
$>d$
, for some (uniformly chosen) integer d. Then, N has bounded cohomology.
To be clear, by a geometric point, we mean a graded algebra map
![]() $S\to K[t]$
, with
$S\to K[t]$
, with
![]() $\deg (t)=2$
and
$\deg (t)=2$
and
![]() $K=\bar {K}$
, such that the base change
$K=\bar {K}$
, such that the base change
![]() $S_K\to K[t]$
is surjective.
$S_K\to K[t]$
is surjective.
Proof. The proof is by induction on the number of generators of S. Before proceeding with the induction argument, we first claim that for N as in the statement of the theorem, all of the localizations of cohomology
![]() $H^\ast (N)_f$
,
$H^\ast (N)_f$
,
![]() $f\in S^2$
, vanish.
$f\in S^2$
, vanish.
Indeed, boundedness of the fibers
![]() $K[t]\otimes ^{\textrm {L}}_S N$
implies that all of the localizations
$K[t]\otimes ^{\textrm {L}}_S N$
implies that all of the localizations
![]() $K[t,t^{-1}]\otimes ^{\textrm {L}}_S N$
vanish, and by Lemma 6.4, we conclude that all of the derived fibers
$K[t,t^{-1}]\otimes ^{\textrm {L}}_S N$
vanish, and by Lemma 6.4, we conclude that all of the derived fibers
![]() $\mathrm {L}c^\ast \mathcal {F}_N$
of the associated sheaf vanish, at all geometric points
$\mathrm {L}c^\ast \mathcal {F}_N$
of the associated sheaf vanish, at all geometric points
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}$
. By Neeman [Reference Neeman and Bökstedt26, Lem. 2.12], this implies that
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}$
. By Neeman [Reference Neeman and Bökstedt26, Lem. 2.12], this implies that
![]() $H^\ast (\mathcal {F}_N)=0$
, and by Lemma 6.5, we conclude
$H^\ast (\mathcal {F}_N)=0$
, and by Lemma 6.5, we conclude
![]() $H^\ast (N)_f=0$
at all
$H^\ast (N)_f=0$
at all
![]() $f\in S^2$
.
$f\in S^2$
.
Now, let us proceed with our induction argument. Take
![]() $n=\dim (S^2)$
, and consider for the base case the algebra
$n=\dim (S^2)$
, and consider for the base case the algebra
![]() $k[t]$
,
$k[t]$
,
![]() $\deg (t)=2$
. If the base change
$\deg (t)=2$
. If the base change
![]() $\bar {k}[t]\otimes _{k[t]}N=N_{\overline {k}}$
of any dg
$\bar {k}[t]\otimes _{k[t]}N=N_{\overline {k}}$
of any dg
![]() $k[t]$
-module along the map
$k[t]$
-module along the map
![]() $k[t]\to \overline {k}[t]$
,
$k[t]\to \overline {k}[t]$
,
![]() $t\mapsto t$
, has bounded cohomology, then obviously N has bounded cohomology, as desired. Now, suppose that the claimed result holds for all polynomial rings
$t\mapsto t$
, has bounded cohomology, then obviously N has bounded cohomology, as desired. Now, suppose that the claimed result holds for all polynomial rings
![]() $S'$
in
$S'$
in
![]() $<n$
variables.
$<n$
variables.
Consider
![]() $S'=S/(f)$
for any nonzero
$S'=S/(f)$
for any nonzero
![]() $f\in S^2$
, and N as prescribed. Then, the derived fibers of
$f\in S^2$
, and N as prescribed. Then, the derived fibers of
![]() $S'\otimes ^{\textrm {L}}_S N$
have uniformly bounded cohomology, and thus
$S'\otimes ^{\textrm {L}}_S N$
have uniformly bounded cohomology, and thus
![]() $S'\otimes ^{\textrm {L}}_S N$
has bounded cohomology by our induction hypothesis. By replacing N with a semiprojective resolution, we may assume that f acts as a nonzero divisor on N, and that
$S'\otimes ^{\textrm {L}}_S N$
has bounded cohomology by our induction hypothesis. By replacing N with a semiprojective resolution, we may assume that f acts as a nonzero divisor on N, and that
![]() $N/fN=S'\otimes ^{\textrm {L}}_SN$
. We now have the exact sequence
$N/fN=S'\otimes ^{\textrm {L}}_SN$
. We now have the exact sequence
with
![]() $H^{>r-2}(N/fN)=H^{>r-2}(S\otimes ^{\textrm {L}}_SN)=0$
at some large r. By considering the long exact sequence on cohomology, the map
$H^{>r-2}(N/fN)=H^{>r-2}(S\otimes ^{\textrm {L}}_SN)=0$
at some large r. By considering the long exact sequence on cohomology, the map
is therefore seen to be an isomorphism for all
![]() $i>r$
. It follows that
$i>r$
. It follows that
![]() $H^{>r}(N)$
either vanishes or has no f-torsion. As the localization
$H^{>r}(N)$
either vanishes or has no f-torsion. As the localization
![]() $H^\ast (N)_f$
vanishes, the latter case is impossible. We conclude that
$H^\ast (N)_f$
vanishes, the latter case is impossible. We conclude that
![]() $H^{\gg 0}(N)=0$
.
$H^{\gg 0}(N)=0$
.
6.3 Proof of Theorem 6.1
As a final ingredient, we have the following result, which was essentially proved in [Reference Negron and Pevtsova28, §6.3]. In the statement, we employ the maps
![]() $\phi _c:A_Z\to K[t]$
discussed in §5.5.
$\phi _c:A_Z\to K[t]$
discussed in §5.5.
Proposition 6.7. At any geometric point
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
, with corresponding map
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}(m_Z/m_Z^2)$
, with corresponding map
![]() $\phi _c:A_Z\to K[t]$
from
$\phi _c:A_Z\to K[t]$
from
![]() $A_Z$
, we have
$A_Z$
, we have
Proof. Take
![]() $\phi _{c,K}:(A_Z)_K\to K[t]$
the base change of
$\phi _{c,K}:(A_Z)_K\to K[t]$
the base change of
![]() $\phi _c$
,
$\phi _c$
,
![]() $A=A_Z$
, and
$A=A_Z$
, and
![]() $A_c$
the corresponding algebra for the hypersurface deformation
$A_c$
the corresponding algebra for the hypersurface deformation
![]() $Q_c\to R_K$
. We have
$Q_c\to R_K$
. We have
in the derived category of dg
![]() $A_c$
-modules, with
$A_c$
-modules, with
![]() $A_c\otimes ^t\operatorname {\mathrm {RHom}}_{Q_c}(\Lambda _K,M_K)$
a K-flat dg module [Reference Negron and Pevtsova28, Lems. 4.1 and 4.2]. Recall that
$A_c\otimes ^t\operatorname {\mathrm {RHom}}_{Q_c}(\Lambda _K,M_K)$
a K-flat dg module [Reference Negron and Pevtsova28, Lems. 4.1 and 4.2]. Recall that
![]() $A_c^2=\ker (\phi _{c,K}^2)$
. Thus,
$A_c^2=\ker (\phi _{c,K}^2)$
. Thus,
 $$ \begin{align*} K[t]\otimes^{\textrm{L}}_{A}\operatorname{\mathrm{RHom}}_Q(\Lambda,M)&\cong K[t]\otimes^{\textrm{L}}_{A_K}K\otimes\operatorname{\mathrm{RHom}}_R(\Lambda,M)\\[6pt]&\cong K[t]\otimes^{\textrm{L}}_{A_K}\operatorname{\mathrm{RHom}}_{R_K}(\Lambda_K,M_K)\\[6pt]&\cong K\otimes^{\textrm{L}}_{A_c}\operatorname{\mathrm{RHom}}_{R_K}(\Lambda_K,M_K)\\[6pt]&\cong K\otimes_{A_c} (A_c\otimes^t\operatorname{\mathrm{RHom}}_{Q_c}(\Lambda_K,M_K))\cong \operatorname{\mathrm{RHom}}_{Q_c}(\Lambda_K,M_K).\end{align*} $$
$$ \begin{align*} K[t]\otimes^{\textrm{L}}_{A}\operatorname{\mathrm{RHom}}_Q(\Lambda,M)&\cong K[t]\otimes^{\textrm{L}}_{A_K}K\otimes\operatorname{\mathrm{RHom}}_R(\Lambda,M)\\[6pt]&\cong K[t]\otimes^{\textrm{L}}_{A_K}\operatorname{\mathrm{RHom}}_{R_K}(\Lambda_K,M_K)\\[6pt]&\cong K\otimes^{\textrm{L}}_{A_c}\operatorname{\mathrm{RHom}}_{R_K}(\Lambda_K,M_K)\\[6pt]&\cong K\otimes_{A_c} (A_c\otimes^t\operatorname{\mathrm{RHom}}_{Q_c}(\Lambda_K,M_K))\cong \operatorname{\mathrm{RHom}}_{Q_c}(\Lambda_K,M_K).\end{align*} $$
We now prove our theorem.
Proof of Theorem 6.1
Fix
![]() $d=\operatorname {gldim}(Q)$
. Recall that
$d=\operatorname {gldim}(Q)$
. Recall that
![]() $\operatorname {\mathrm {Ext}}^{\gg 0}_{Q_c}(\Lambda _K,M_K)=0$
if and only if
$\operatorname {\mathrm {Ext}}^{\gg 0}_{Q_c}(\Lambda _K,M_K)=0$
if and only if
![]() $\operatorname {\mathrm {Ext}}^{>d}_{Q_c}(\Lambda _K,M_K)=0$
, by Corollary 3.2. We have the formula
$\operatorname {\mathrm {Ext}}^{>d}_{Q_c}(\Lambda _K,M_K)=0$
, by Corollary 3.2. We have the formula
at arbitrary points
![]() $c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}$
. So, we apply Theorem 6.6, with
$c:\operatorname {\mathrm {Spec}}(K)\to \mathbb {P}$
. So, we apply Theorem 6.6, with
![]() $S=A_Z$
and N the dg
$S=A_Z$
and N the dg
![]() $A_Z$
-module
$A_Z$
-module
![]() $\operatorname {\mathrm {RHom}}_R(\Lambda ,M)$
, and Corollary 3.2, to find that the hypersurface support for M vanishes if and only if
$\operatorname {\mathrm {RHom}}_R(\Lambda ,M)$
, and Corollary 3.2, to find that the hypersurface support for M vanishes if and only if
![]() $H^\ast (\operatorname {\mathrm {RHom}}_R(\Lambda ,M))=\operatorname {\mathrm {Ext}}^\ast _R(\Lambda ,M)$
vanishes in high degree. Such vanishing of cohomology occurs if and only if M is of finite projective dimension over R, by Corollary 3.2. So, we have the desired relation,
$H^\ast (\operatorname {\mathrm {RHom}}_R(\Lambda ,M))=\operatorname {\mathrm {Ext}}^\ast _R(\Lambda ,M)$
vanishes in high degree. Such vanishing of cohomology occurs if and only if M is of finite projective dimension over R, by Corollary 3.2. So, we have the desired relation,
![]() $\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)=\emptyset $
, if and only if M vanishes in
$\operatorname {\mathrm {supp}}^{hyp}_{\mathbb {P}}(M)=\emptyset $
, if and only if M vanishes in
![]() $\operatorname {Sing}(R)$
.
$\operatorname {Sing}(R)$
.
Acknowledgments
Thanks to Lucho Avramov, Eric Friedlander, Henning Krause, and Mark Walker for helpful commentary. Special thanks to Srikanth Iyengar for offering myriad insights throughout the production of this work. Thanks to the referee for a thoughtful reading of the text.
Appendix A Proof of Theorem 5.4
We prove the representative independence result of Theorem 5.4. Fix a deformation
![]() $Q\to R$
as in §2.2, with Q of finite global dimension. Take as usual
$Q\to R$
as in §2.2, with Q of finite global dimension. Take as usual
![]() $\Lambda =R/\operatorname {Jac}(R)$
.
$\Lambda =R/\operatorname {Jac}(R)$
.
A.1 A dg resolution of the simples
We recall the Koszul resolutions
![]() $\mathcal {K}_Z\overset {\sim }\to k$
of k over Z, and corresponding resolution
$\mathcal {K}_Z\overset {\sim }\to k$
of k over Z, and corresponding resolution
![]() $\mathcal {K}_Q\overset {\sim }\to R$
of R over Q obtained via base change [Reference Bezrukavnikov and Ginzburg12]. In coordinates,
$\mathcal {K}_Q\overset {\sim }\to R$
of R over Q obtained via base change [Reference Bezrukavnikov and Ginzburg12]. In coordinates,
![]() $Z\cong k[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
, the Koszul resolution is explicitly the dg Z-algebra
$Z\cong k[\!\hspace {.1mm}[{y_1,\dots ,y_n}]\!\hspace {.1mm}]$
, the Koszul resolution is explicitly the dg Z-algebra
![]() $\mathcal {K}_Z=\wedge ^\ast _Z(\oplus _i Z\widetilde {y}_i)$
with the
$\mathcal {K}_Z=\wedge ^\ast _Z(\oplus _i Z\widetilde {y}_i)$
with the
![]() $\deg (\widetilde {y}_i)=-1$
and differential
$\deg (\widetilde {y}_i)=-1$
and differential
![]() $d(\widetilde {y}_i)=y_i\in Z$
. The dg algebra
$d(\widetilde {y}_i)=y_i\in Z$
. The dg algebra
![]() $\mathcal {K}_Q$
is then obtained via base change
$\mathcal {K}_Q$
is then obtained via base change
![]() $\mathcal {K}_Q=Q\otimes _Z \mathcal {K}_Z$
, and flatness of Q over Z implies that the induced map
$\mathcal {K}_Q=Q\otimes _Z \mathcal {K}_Z$
, and flatness of Q over Z implies that the induced map
![]() $\mathcal {K}_Q \to R=Q\otimes _Z k$
remains a quasi-isomorphism.
$\mathcal {K}_Q \to R=Q\otimes _Z k$
remains a quasi-isomorphism.
Lemma A.1. There is a dg algebra resolution
![]() $T_Q\overset {\sim }\to \Lambda $
of the simples over Q such that the following hold:
$T_Q\overset {\sim }\to \Lambda $
of the simples over Q such that the following hold:
-
(1)
 $T_Q$
comes equipped with a dg algebra inclusion
$T_Q$
comes equipped with a dg algebra inclusion
 $\mathcal {K}_Q\to T_Q$
, which restricts to a central inclusion
$\mathcal {K}_Q\to T_Q$
, which restricts to a central inclusion
 $\mathcal {K}_Z\to T_Q$
, and an isomorphism in degree zero
$\mathcal {K}_Z\to T_Q$
, and an isomorphism in degree zero
 $Q\cong T^0_Q$
.
$Q\cong T^0_Q$
. -
(2)
 $T_Q$
is bounded, nonpositively graded, and finite and projective over Q in each degree.
$T_Q$
is bounded, nonpositively graded, and finite and projective over Q in each degree.
Proof. Below, for an algebra T and a T-bimodule M, we let
![]() $Tens_T(M)$
denote the tensor algebra, over T, generated by the bimodule M. So, as a vector space,
$Tens_T(M)$
denote the tensor algebra, over T, generated by the bimodule M. So, as a vector space,
![]() $Tens_{T}(M)=\cdots \oplus (M\otimes _T M)\oplus M\oplus \mathcal {K}$
. The product is given by tensor concatenation. We construct
$Tens_{T}(M)=\cdots \oplus (M\otimes _T M)\oplus M\oplus \mathcal {K}$
. The product is given by tensor concatenation. We construct
![]() $T_Q$
in a series of steps, producing a tower of nonpositively graded dg-algebras
$T_Q$
in a series of steps, producing a tower of nonpositively graded dg-algebras
![]() $\mathcal {K}_Q = T_0 \to T_1 \to T_1 \to \cdots $
such that
$\mathcal {K}_Q = T_0 \to T_1 \to T_1 \to \cdots $
such that
![]() $T_i$
is quasi-isomorphic to
$T_i$
is quasi-isomorphic to
![]() $\Lambda $
is degrees
$\Lambda $
is degrees
![]() $> i$
. The construction follows [Reference Ciocan-Fontanine and Kapranov15], which in turn mimics the classical construction of the universal covering space in topology. As a last step of the construction, we truncate the tower utilizing the finiteness of the global dimension of Q.
$> i$
. The construction follows [Reference Ciocan-Fontanine and Kapranov15], which in turn mimics the classical construction of the universal covering space in topology. As a last step of the construction, we truncate the tower utilizing the finiteness of the global dimension of Q.
Take
![]() $T_0=\mathcal {K}_Q$
and consider degree
$T_0=\mathcal {K}_Q$
and consider degree
![]() $0$
cocycles
$0$
cocycles
![]() $v^0_1,\dots , v^0_{n_0}$
which generate the kernel of the augmentation
$v^0_1,\dots , v^0_{n_0}$
which generate the kernel of the augmentation
![]() $Q=\mathcal {K}_Q^0\to \Lambda $
, modulo boundaries
$Q=\mathcal {K}_Q^0\to \Lambda $
, modulo boundaries
![]() $B^0(\mathcal {K}_Q)$
. Consider
$B^0(\mathcal {K}_Q)$
. Consider
![]() $M_1'$
the free dg
$M_1'$
the free dg
![]() $T_0$
-bimodule with generators
$T_0$
-bimodule with generators
![]() $\widetilde {v}^0_i$
for each
$\widetilde {v}^0_i$
for each
![]() $v_i$
along with the dg bimodule map
$v_i$
along with the dg bimodule map
![]() $M_1'\to T_0$
,
$M_1'\to T_0$
,
![]() $\widetilde {v}_i\mapsto v_i$
. More specifically, we take
$\widetilde {v}_i\mapsto v_i$
. More specifically, we take
![]() $M_1'$
the
$M_1'$
the
![]() $\mathcal {K}_Z$
-central bimodule
$\mathcal {K}_Z$
-central bimodule
along with the proposed dg bimodule map
![]() $\xi _1:M^{\prime }_1\to T_0$
,
$\xi _1:M^{\prime }_1\to T_0$
,
![]() $\xi _1(\widetilde {v}_i^0)\mapsto v_i^0$
. Take
$\xi _1(\widetilde {v}_i^0)\mapsto v_i^0$
. Take
![]() $M_1$
the shifted dg bimodule
$M_1$
the shifted dg bimodule
![]() $\Sigma M^{\prime }_1$
, with generators now in degree
$\Sigma M^{\prime }_1$
, with generators now in degree
![]() $-1$
, and consider the dg
$-1$
, and consider the dg
![]() $\mathcal {K}_Z$
-algebra
$\mathcal {K}_Z$
-algebra
 $$ \begin{align*} T_1=Tens_{T_0}(M_1)\ \ \text{with differential}\ d_{T_1}|_{M_1^{\otimes n}}=d_{M_1^{\otimes n}}+\sum_{l=0}^{n-1} id^{\otimes l}\otimes \xi_1\otimes id^{\otimes n-l-1}. \end{align*} $$
$$ \begin{align*} T_1=Tens_{T_0}(M_1)\ \ \text{with differential}\ d_{T_1}|_{M_1^{\otimes n}}=d_{M_1^{\otimes n}}+\sum_{l=0}^{n-1} id^{\otimes l}\otimes \xi_1\otimes id^{\otimes n-l-1}. \end{align*} $$
The operation
![]() $d_{T_1}$
is a graded algebra derivation by construction, and we claim that it is in fact square
$d_{T_1}$
is a graded algebra derivation by construction, and we claim that it is in fact square
![]() $0$
. Since
$0$
. Since
![]() $d_{T_1}$
is a derivation, it suffices to check the formula
$d_{T_1}$
is a derivation, it suffices to check the formula
![]() $d_{T_1}^2=0$
on the generators
$d_{T_1}^2=0$
on the generators
![]() $M_1\oplus T_0$
. But
$M_1\oplus T_0$
. But
![]() $d_{T_1}|_{M_1\oplus T_0}$
is just the differential on the mapping cone,
$d_{T_1}|_{M_1\oplus T_0}$
is just the differential on the mapping cone,
![]() $\operatorname {cone}(\xi _1)=(M_1\oplus T_0, d_{M_1}+d_{T_0}+\xi _1)$
, so that the formula
$\operatorname {cone}(\xi _1)=(M_1\oplus T_0, d_{M_1}+d_{T_0}+\xi _1)$
, so that the formula
![]() $d^2_{T_1}=0$
is verified.
$d^2_{T_1}=0$
is verified.
We have now a dg algebra
![]() $T_1$
satisfying (1) such that
$T_1$
satisfying (1) such that
![]() $H^0(T_1)=\Lambda $
and which is finite and projective over Q in each degree. We repeat the above process to produce a dg algebra
$H^0(T_1)=\Lambda $
and which is finite and projective over Q in each degree. We repeat the above process to produce a dg algebra
![]() $T_2=Tens_{T_1}(M_2)$
which is
$T_2=Tens_{T_1}(M_2)$
which is
![]() $\mathcal {K}_Z$
-central, finite, and projective over Q in each degree, and which comes equipped with a projection
$\mathcal {K}_Z$
-central, finite, and projective over Q in each degree, and which comes equipped with a projection
![]() $T_2\to \Lambda $
which is a quasi-isomorphism in degrees
$T_2\to \Lambda $
which is a quasi-isomorphism in degrees
![]() $> -2$
. As the notation suggests,
$> -2$
. As the notation suggests,
![]() $T_2$
is produced by attaching a dg
$T_2$
is produced by attaching a dg
![]() $T_1$
-bimodule
$T_1$
-bimodule
![]() $M_2\to T_1$
, with
$M_2\to T_1$
, with
![]() $M_2$
in degree
$M_2$
in degree
![]() $\leq -2$
, which annihilates cohomology in degree
$\leq -2$
, which annihilates cohomology in degree
![]() $-1$
. Note that such
$-1$
. Note that such
![]() $T_2$
comes equipped with an inclusion
$T_2$
comes equipped with an inclusion
![]() $T_1\to T_2$
of dg algebras which is an equality in degrees
$T_1\to T_2$
of dg algebras which is an equality in degrees
![]() $>-2$
, and that the augmentation
$>-2$
, and that the augmentation
![]() $T_1\to \Lambda $
extends to a
$T_1\to \Lambda $
extends to a
![]() $\Lambda $
-augmentation on
$\Lambda $
-augmentation on
![]() $T_2$
which (necessarily) annihilates
$T_2$
which (necessarily) annihilates
![]() $M_2$
. We proceed recursively to produce such dg algebras and inclusions
$M_2$
. We proceed recursively to produce such dg algebras and inclusions
up to
![]() $N=\max \{\operatorname {gldim}(Q),\operatorname {gldim}(Z)\}$
. To be clear, we now have a nonpositively graded dg
$N=\max \{\operatorname {gldim}(Q),\operatorname {gldim}(Z)\}$
. To be clear, we now have a nonpositively graded dg
![]() $\mathcal {K}_Z$
-algebra
$\mathcal {K}_Z$
-algebra
![]() $T_{N+1}$
with an inclusion
$T_{N+1}$
with an inclusion
![]() $\mathcal {K}_Q\to T_{N+1}$
which is an equality in degree
$\mathcal {K}_Q\to T_{N+1}$
which is an equality in degree
![]() $0$
and a projection
$0$
and a projection
![]() $T_{N+1}\to \Lambda $
which is a quasi-isomorphism in degrees
$T_{N+1}\to \Lambda $
which is a quasi-isomorphism in degrees
![]() $\geq -N$
. We have also that
$\geq -N$
. We have also that
![]() $T_{N+1}$
is finite and projective over Q in each degree.
$T_{N+1}$
is finite and projective over Q in each degree.
We take finally
Since Q is of global dimension
![]() $\leq N$
,
$\leq N$
,
![]() $T_Q$
is projective over Q in degree
$T_Q$
is projective over Q in degree
![]() $-N$
, and by the properties of
$-N$
, and by the properties of
![]() $T_{N+1}$
, the induced projection
$T_{N+1}$
, the induced projection
![]() $T_Q\to \Lambda $
is in fact a quasi-isomorphism. Furthermore, since
$T_Q\to \Lambda $
is in fact a quasi-isomorphism. Furthermore, since
![]() $\operatorname {gldim}(Z)\leq N$
, and
$\operatorname {gldim}(Z)\leq N$
, and
![]() $K_Q$
is concentrated in nonpositive degrees
$K_Q$
is concentrated in nonpositive degrees
![]() $\geq -\operatorname {gldim}(Z)$
, the injective map
$\geq -\operatorname {gldim}(Z)$
, the injective map
![]() $K_Q\to T_{N+1}$
composed with the projection
$K_Q\to T_{N+1}$
composed with the projection
![]() $T_{N+1}\to T_Q$
remains injective.
$T_{N+1}\to T_Q$
remains injective.
A.2 Systems of divided powers
We recall some information, almost word for word, from [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3, §1.2]. For
![]() $\mathscr {T}$
a dg algebra, and an integer d, we call a collection of elements
$\mathscr {T}$
a dg algebra, and an integer d, we call a collection of elements
![]() $\{w^{(i)}\in \mathscr {T}^{2di}:i\geq 0\}$
a system of divided powers for
$\{w^{(i)}\in \mathscr {T}^{2di}:i\geq 0\}$
a system of divided powers for
![]() $w=w^{(1)}$
if all of the
$w=w^{(1)}$
if all of the
![]() $w^{(i)}$
are central,
$w^{(i)}$
are central,
![]() $w^{(0)}=1$
,
$w^{(0)}=1$
,
 $$ \begin{align*} w^{(i)}w^{(j)}={\left(\begin{matrix}i+j\ \\ i \end{matrix} \right)}w^{(i+j)},\ \ \text{and}\ \ d(w^{(i)})=d(w)w^{(i-1)}. \end{align*} $$
$$ \begin{align*} w^{(i)}w^{(j)}={\left(\begin{matrix}i+j\ \\ i \end{matrix} \right)}w^{(i+j)},\ \ \text{and}\ \ d(w^{(i)})=d(w)w^{(i-1)}. \end{align*} $$
In characteristic
![]() $0$
, any central element w of even degree admits a unique system of divided powers, given by
$0$
, any central element w of even degree admits a unique system of divided powers, given by
![]() $w^{(i)}=(i!)^{-1}w^i$
. In positive characteristic, this is not always the case.
$w^{(i)}=(i!)^{-1}w^i$
. In positive characteristic, this is not always the case.
Given an odd degree central cocycle
![]() $z\in \mathscr {T}$
, we let
$z\in \mathscr {T}$
, we let
denote the divided power algebra
![]() $\oplus _{\geq 0} \mathscr {T} y^{(i)}$
with each of the
$\oplus _{\geq 0} \mathscr {T} y^{(i)}$
with each of the
![]() $y^{(i)}$
central and extended differential
$y^{(i)}$
central and extended differential
![]() $d(y^{(i)})=zy^{(i-1)}$
. As the notation suggests, the
$d(y^{(i)})=zy^{(i-1)}$
. As the notation suggests, the
![]() $y^{(i)}$
form a system of divided powers in
$y^{(i)}$
form a system of divided powers in
![]() $\mathscr {T}\langle y:d(y)=z\rangle $
.
$\mathscr {T}\langle y:d(y)=z\rangle $
.
A.3 The Tate construction for noncommutative hypersurfaces
We provide a version of Tate’s construction [33], which is applicable to our noncommutative setting. Our presentation is adapted directly from [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3, §§1.4 and 2.2].
Take
![]() $f\in m_Z$
and
$f\in m_Z$
and
![]() $z_f\in K_{Z}^{-1}\subset T_Q^{-1}$
any degree
$z_f\in K_{Z}^{-1}\subset T_Q^{-1}$
any degree
![]() $-1$
element bounding f. Take
$-1$
element bounding f. Take
![]() $\overline {T}_Q=Z/(f)\otimes _Z T_Q$
and
$\overline {T}_Q=Z/(f)\otimes _Z T_Q$
and
Note that in the quotient
![]() $\overline {T}_Q=Z/(f)\otimes _Z T_Q$
, the degree
$\overline {T}_Q=Z/(f)\otimes _Z T_Q$
, the degree
![]() $-1$
element
$-1$
element
![]() $z_f$
is in fact a (central) cocycle, so that the definition of
$z_f$
is in fact a (central) cocycle, so that the definition of
![]() $\mathscr {T}_f$
makes sense. The projection
$\mathscr {T}_f$
makes sense. The projection
![]() $T_Q\to \Lambda $
induces a projection
$T_Q\to \Lambda $
induces a projection
which (necessarily) annihilates all the
![]() $y^{(i)}$
, for
$y^{(i)}$
, for
![]() $i>0$
. This map is a map of dg
$i>0$
. This map is a map of dg
![]() $\mathcal {K}_Z$
-algebras, and of dg
$\mathcal {K}_Z$
-algebras, and of dg
![]() $Q/(f)$
-bimodules.
$Q/(f)$
-bimodules.
Lemma A.2. The cohomology
![]() $H^{-1}(\overline {T}_Q)$
is generated by the class of
$H^{-1}(\overline {T}_Q)$
is generated by the class of
![]() $z_f$
, as a Q-module on the left or the right.
$z_f$
, as a Q-module on the left or the right.
Proof. Since
![]() $f\in Q$
is central, we have that
$f\in Q$
is central, we have that
![]() $Qf$
is the ideal in Q generated by f. By a direct analysis of the diagram
$Qf$
is the ideal in Q generated by f. By a direct analysis of the diagram

we see that
![]() $\ker (\bar {d}^{-1})$
is generated by the image of the submodule
$\ker (\bar {d}^{-1})$
is generated by the image of the submodule
![]() $B^{-1}(T_Q)+Qz_f$
in
$B^{-1}(T_Q)+Qz_f$
in
![]() $T^{-1}_Q$
. Consequently, the map
$T^{-1}_Q$
. Consequently, the map
![]() $Q z_f\to H^{-1}(\overline {T}_Q)$
is a surjective left module map. We similarly find that the map
$Q z_f\to H^{-1}(\overline {T}_Q)$
is a surjective left module map. We similarly find that the map
![]() $z_fQ\to H^{-1}(\overline {T}_Q)$
is surjective.
$z_fQ\to H^{-1}(\overline {T}_Q)$
is surjective.
Lemma A.3 [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3]
The dg map
![]() $\pi _f:\mathscr {T}_f\to \Lambda $
is a quasi-isomorphism of dg
$\pi _f:\mathscr {T}_f\to \Lambda $
is a quasi-isomorphism of dg
![]() $\mathcal {K}_Z$
-algebras, and dg
$\mathcal {K}_Z$
-algebras, and dg
![]() $Q/(f)$
-bimodules.
$Q/(f)$
-bimodules.
Proof. The proof is the same as [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3, Lem. 2.3]. We have
and the degree
![]() $-1$
cohomology is generated by the class of
$-1$
cohomology is generated by the class of
![]() $z_f$
, by Lemma A.2. The result now follows by Lemma A.2 and a straightforward spectral sequence argument [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3, Lem. 1.1(2)].
$z_f$
, by Lemma A.2. The result now follows by Lemma A.2 and a straightforward spectral sequence argument [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3, Lem. 1.1(2)].
We note that
![]() $\mathscr {T}_f$
is finite and projective over
$\mathscr {T}_f$
is finite and projective over
![]() $Q/(f)$
in each degree, so that the quasi-isomorphism
$Q/(f)$
in each degree, so that the quasi-isomorphism
![]() $\pi _f:\mathscr {T}_f\overset {\sim }\to \Lambda $
is in particular a projective resolution of
$\pi _f:\mathscr {T}_f\overset {\sim }\to \Lambda $
is in particular a projective resolution of
![]() $\Lambda $
over
$\Lambda $
over
![]() $Q/(f)$
.
$Q/(f)$
.
A.4 Representative independence
Proof of Theorem 5.4
Take
![]() $\overline {\mathscr {T}}_f=k\otimes _Z \mathscr {T}_f$
and
$\overline {\mathscr {T}}_f=k\otimes _Z \mathscr {T}_f$
and
![]() $\overline {\mathscr {T}}_g=k\otimes _Z \mathscr {T}_g$
. Explicitly,
$\overline {\mathscr {T}}_g=k\otimes _Z \mathscr {T}_g$
. Explicitly,
and we have a similar expression for
![]() $\overline {\mathscr {T}}_g$
. By [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3, Lem. 2.2], the (class of the) difference
$\overline {\mathscr {T}}_g$
. By [Reference Avramov, Iyengar, Carlson, Iyengar and Pevtsova3, Lem. 2.2], the (class of the) difference
![]() $z_f-z_g$
is bounded by an element w in the reduction
$z_f-z_g$
is bounded by an element w in the reduction
![]() $k\otimes _Z \mathcal {K}_Z$
. Since the differential on this complex vanishes, we see that in fact the images of
$k\otimes _Z \mathcal {K}_Z$
. Since the differential on this complex vanishes, we see that in fact the images of
![]() $z_f$
and
$z_f$
and
![]() $z_g$
agree in
$z_g$
agree in
![]() $k\otimes _Z\mathcal {K}_Z$
and hence in
$k\otimes _Z\mathcal {K}_Z$
and hence in
![]() $k\otimes _Z T_Q$
. So, actually,
$k\otimes _Z T_Q$
. So, actually,
![]() $\overline {\mathscr {T}}_f=\overline {\mathscr {T}}_g$
as dg
$\overline {\mathscr {T}}_f=\overline {\mathscr {T}}_g$
as dg
![]() $\mathcal {K}_Z$
-algebras and dg R-bimodules. Now, we have
$\mathcal {K}_Z$
-algebras and dg R-bimodules. Now, we have
and similarly,
![]() $\Lambda \otimes ^{\textrm {L}}_{Q/(g)}M=\overline {\mathscr {T}}_g\otimes _RM$
, so that
$\Lambda \otimes ^{\textrm {L}}_{Q/(g)}M=\overline {\mathscr {T}}_g\otimes _RM$
, so that
![]() $\Lambda \otimes ^{\textrm {L}}_{Q/(f)}M=\Lambda \otimes ^{\textrm {L}}_{Q/(g)}M$
. Taking homology provides the claimed identification of graded
$\Lambda \otimes ^{\textrm {L}}_{Q/(f)}M=\Lambda \otimes ^{\textrm {L}}_{Q/(g)}M$
. Taking homology provides the claimed identification of graded
![]() $\operatorname {\mathrm {Tor}}$
groups.
$\operatorname {\mathrm {Tor}}$
groups.
The result for
![]() $\operatorname {\mathrm {Ext}}$
is completely similar, as one calculates
$\operatorname {\mathrm {Ext}}$
is completely similar, as one calculates