Gridded temperature and accumulation distributions for Greenland for use in cryospheric models

Abstract

Gridded distributions of the annual mean temperature and annual total accumulation for Greenland are presented. They are objectively derived by deterministic and statistical interpolation from measurements at coastal stations and at locations on the ice sheet. They can be used not only for driving cryospheric models, but also for verifying atmospheric simulations.

1. Introduction

The distributions of the annual mean surface temperature and of the annual total accumulation are essential quantities for cryospheric modeling. They not only represent necessary boundary conditions but also provide reference states for the model validation. Moreover, these distributions are vital for the verification of climate simulations (Ohmura and others, 1996).

For the Greenland ice sheet, hand-drawn maps of these fields have been prepared in recent years at the Swiss Federal Institute of Technology (ETH) (Ohmura, 1987; Ohmura and Reeh, 1991; Ohmura and others, 1999), but these have not been available in digital form. The production of gridded distributions by objective methods is tackled in the present paper.

Objective procedures are superior to the simple translation of printed maps into digital form. They allow more flexible handling of the basic data (inclusion of new data, removal of erroneous entries), as well as straightforward recalculation of the final fields if more refined interpolation algorithms are implemented.

2. Climatic Data, Topographic Model and Grid Definition

The basic data used in the present work are identical to those described in Ohmura (1987), Ohmura and Reeh (1991) and Ohmura and others (1999).

Data of the monthly mean temperature at 27 regular meteorological stations along the coast and 22 short-term stations on the ice sheet were extracted from various sources. The length of the records varies significantly from location to location (for a detailed account, see appendix in Ohmura, 1987), with data collected by scientific expeditions often not extending beyond a few months. A reduction of all data to a standard period is therefore appropriate. For simplicity, the reference decade of 1951–60 proposed by Ohmura (1987) was maintained.

The annual total accumulation was inferred using data from pit and core studies carried out in the interior of the ice sheet. In addition, the monthly amount of solid precipitation was considered for the analysis. It was inferred for meteorological stations of the operational network from the measured precipitation, using an empirical relation between the percentage of solid precipitation and the monthly mean air temperature (Fig. 1). The amount of solid precipitation was subsequently corrected for the error induced by the deformation of the wind-field around the precipitation gauge (Sevruk, 1986). The correction can be quantified in the order of+20%.

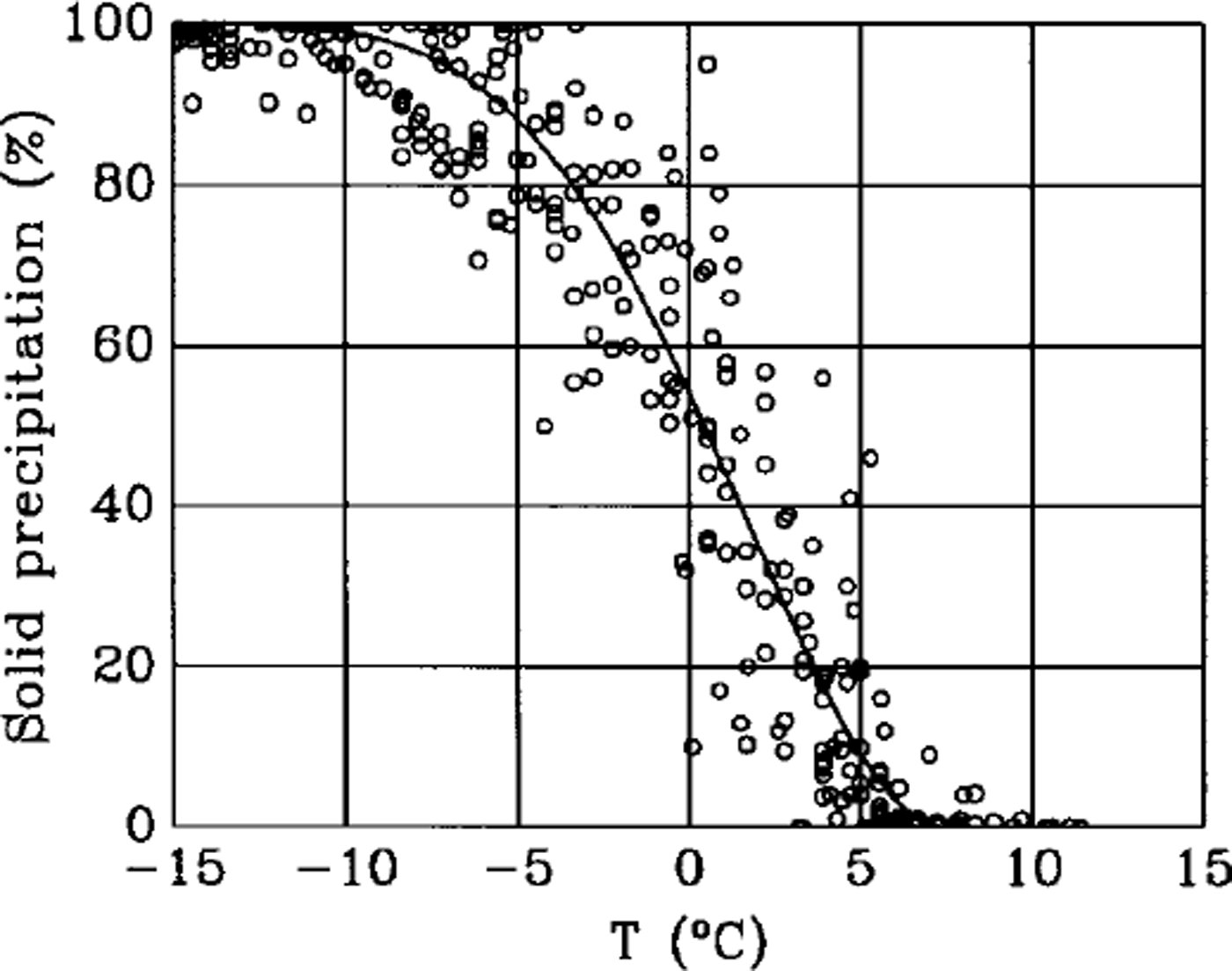
Fig. 1. Percentage of solid precipitation in the monthly total precipitation as a function of the monthly mean temperature.

No attempt was made to reduce the data of the total accumulation and of the solid precipitation to the same standard period as the temperature data (or tha data altogether to another reference decade). The task is not trivial, because the decadal variations caused by the North Atlantic Oscillation (Ohmura and others, 1999) should be considered.

Concerning the topography, the model of the National Survey and Cadastre of Denmark (KMS) (Ekholm and others, 1995; Ekholm, 1996) was chosen, as it is probably the best product available to date. Its accuracy ranges from about 30 m in areas covered by stereo ρτogτσmmεtτy to 300 m elsewhere. The model is given on a grid with horizontal resolution of 0.05° in the longitudinal direction and 0.02° in the latitudinal direction.

This choice automatically defines one possible spatial grid on which to project the temperature and accumulation distributions. We will refer to this as the KMS grid.

3. Interpolation of the Temperature Data

An essential property of the temperature field is the lapse rate. According to Ohmura (1987), there is an appreciable difference between the west and the east slopes with respect to the monthly mean lapse rate along the ice-sheet surface. This difference must be considered in preparing gridded distributions of the monthly and annual mean temperature.

In the present study a pragmatic approach was adopted. In practice, digital versions of the cross-sections prepared by Ohmura (1987), separately for the east and west slopes, were obtained by redefining each isotherm in terms of latitude and altitude, and by using local polynomials (Akima, 1978,1984) to calculate the monthly mean temperature on a latitude/altitude grid with a resolution of 0.2° and 0.05 km, respectively.

Starting from these gridded cross-sections, the temperature distribution with respect to the KMS grid was calculated by distance-weighted interpolation, firstly within each cross-section, secondly between the cross-sections.

The weights were chosen to be inversely proportional to the square of the distance, according to:

(1)

and

(2)

where × is the geometric coordinate of a given KMS gridpoint in zonal direction, y is the geometric coordinate in meridional direction, z is the altitude, and x_n, y_n and z_n are the geometric coordinates of each of the relevant nodes. Within a gridded longitudinal cross-section, four nodes were placed around the spot defined by the coordinate (y,z). On the other hand, the zonal coordinate of each longitudinal cross-section, x_n, was chosen to be equal to the coordinate of the coastal line at the corresponding latitude (or meridional coordinate y).

Distance-weighted interpolation, although of straightforward application, introduces a small residual noise. For this reason, the last step in the derivation of the gridded distributions of the monthly and annual surface temperature fields was the application of a spatial filter. The filter was defined with respect to the great-circle distance on the sphere as:

(3)

where a is the great-circle distance on the sphere and σ₀ = 0.2° is the great-circle radius of the smoothing domain.

For all months (not shown) and for the year as a whole (Fig. 2), the final results are very close to those subjectively obtained by Ohmura (1987).

Fig. 2. Interpolated annual mean surface air temperature (°C).

4. Interpolation of the Accumulation Data

For the interpolation of the accumulation data, a statistical procedure, specifically optimal interpolation, is preferable. Deterministic methods were also tested, but the results obtained were not satisfactory because many of the measurements are located on transects.

Optimal interpolation was carried out in the form of universal kriging, using the geostatistical software Gstat (Pebesma and Wesseling, 1998). Like most other geostatistical packages, Gstat only allows for Euclidean distances and has no options for calculating distances on the sphere. To circumvent this difficulty, the geographical system of coordinates (λ,–φ) was therefore projected onto a polar stereographic plane (x,y).

To yield a more symmetric distribution, the accumulation data were then subjected to a log transformation. This was followed by the definition of a linear model for the expectation (trend surface). The trend was calculated with respect to the base functions x, y, xy and xz. It accounts for 60% of the total variance. The inclusion of the additional base functions z,yz,x2y2z² did not increase the amount of variance explained by the trend.

After this, the trend was subtracted from the log-transformed data, and the variogram was estimated for all directions from the residuals, allowing for a maximum distance of 1000 coordinate units and a directional width of 50 units. The estimation of the trend and of the variogram was carried out iteratively using generalized least squares. The iteration was repeated until the estimated variogram became stable.

Given the variogram, interpolation of the logarithm of the accumulation to the KMS grid was carried out by universal kriging using all available data in a neighbourhood set by the range of the variogram (340 coordinate units). The gridded distribution of the accumulation proper was finally obtained by exponentiation.

Despite the intrinsic difference between accumulation (the results of several processes) and solid precipitation, at each stage of the interpolation procedure both types of data were considered. The amount of solid precipitation at the coastal stations had to be included to ensure a reasonable overall performance, as the accumulation data alone are too sparse in the marginal zones of the ice sheet. However, gridpoints not belonging to the ice sheet, together with those characterized by too large a prediction error, were excluded from the final product. The attribution of each gridpoint to one of the four categories ocean, land, small ice caps and ice sheet was based on the mask described in Ekholm (1996). The mask has the same horizontal resolution as the KMS digital elevation model.

In general, the results of universal kriging are well in line with the subjective maps of Ohmura and Reeh (1991) and Ohmura and others (1999) (Fig. 3). The validity of the present interpolation can be appreciated noting that the areally averaged, annual total accumulation amounts to 290 mm, very close to the value of 297 mm obtained by Ohmura and others (1999).

Fig. 3. Interpolated annual total accumulation (mmw.e.).

5. Conclusions

Gridded distributions of the annual mean temperature and annual total accumulation for Greenland were derived from direct observations by objective methods. The results compare favourably with subjective maps prepared by Ohmura (1987), Ohmura and Reeh (1991) and Ohmura and others (1999).

In the near future, a few actions will be needed to enhance the quality of the present products. We think of: the inclusion of more recent surface and upper air data, in particular those from automatic weather stations and the operational radiosonde network; the reduction of all input data to one and the same reference period; the recalculation of the longitudinal cross-sections of Ohmura (1987); and the improvement of the interpolation of the accumulation along the periphery of the ice sheet, paying more attention to the the intrinsic difference between the accumulation and the solid precipitation.

Despite their evident shortcomings, we believe that the digital products presented here can be useful for ongoing and future modelling efforts. For this reason, the fields of the annual mean temperature and of the annual total accumulation are made available on the Web at: http://www.geo.umnw.ethz.ch/ staff/homepages/calanca/download/ as two ASCII files: temp.-dat and acc.dat. A description of the data and of the file organization is provided separately at the same site as dscr.txt. Problems with the files, or questions concerning the fields should be addressed to one of the authors (PC.) sending an εmail to [email protected].

Whenever the data are used, reference to this paper and explicit acknowledgement of the Department of Climate Research, Swiss Federal Institute of Technology, Winterthurerstrasse 190, CH-8057 Zürich, Switzerland, are kindly appreciated.