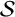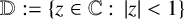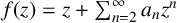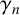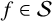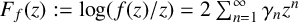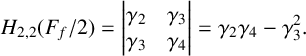1 Introduction
Let
![]() $\mathcal {H}$
denote the class of analytic functions in the unit disk
$\mathcal {H}$
denote the class of analytic functions in the unit disk
![]() $\mathbb {D}:=\{z\in \mathbb {C}:\, |z|<1\}$
. Here,
$\mathbb {D}:=\{z\in \mathbb {C}:\, |z|<1\}$
. Here,
![]() $\mathcal {H}$
is a locally convex topological vector space endowed with the topology of uniform convergence over compact subsets of
$\mathcal {H}$
is a locally convex topological vector space endowed with the topology of uniform convergence over compact subsets of
![]() $\mathbb {D}$
. Let
$\mathbb {D}$
. Let
![]() $\mathcal {A}$
denote the class of functions
$\mathcal {A}$
denote the class of functions
![]() $f\in \mathcal {H}$
such that
$f\in \mathcal {H}$
such that
![]() $f(0)=0$
and
$f(0)=0$
and
![]() $f'(0)=1$
. Let
$f'(0)=1$
. Let
![]() $\mathcal {S}$
denote the subclass of
$\mathcal {S}$
denote the subclass of
![]() $\mathcal {A}$
consisting of functions which are univalent (that is, one-to-one) in
$\mathcal {A}$
consisting of functions which are univalent (that is, one-to-one) in
![]() $\mathbb {D}$
. If
$\mathbb {D}$
. If
![]() $f\in \mathcal {S}$
, then it has the series representation
$f\in \mathcal {S}$
, then it has the series representation
 $$ \begin{align} f(z)= z+\sum_{n=2}^{\infty}a_n z^n,\quad z\in \mathbb{D}. \end{align} $$
$$ \begin{align} f(z)= z+\sum_{n=2}^{\infty}a_n z^n,\quad z\in \mathbb{D}. \end{align} $$
The logarithmic coefficients
![]() $\gamma _{n}$
of
$\gamma _{n}$
of
![]() $f\in \mathcal {S}$
are defined by
$f\in \mathcal {S}$
are defined by
 $$ \begin{align} F_{f}(z):= \log\frac{f(z)}{z}=2\sum\limits_{n=1}^{\infty}\gamma_{n}z^{n},\quad z \in \mathbb{D}. \end{align} $$
$$ \begin{align} F_{f}(z):= \log\frac{f(z)}{z}=2\sum\limits_{n=1}^{\infty}\gamma_{n}z^{n},\quad z \in \mathbb{D}. \end{align} $$
The logarithmic coefficients
![]() $\gamma _{n}$
play a central role in the theory of univalent functions. A very few exact upper bounds for
$\gamma _{n}$
play a central role in the theory of univalent functions. A very few exact upper bounds for
![]() $\gamma _{n}$
seem to have been established. Milin [Reference Milin17] highlighted the importance of the logarithmic coefficients within the framework of the Bieberbach conjecture. For
$\gamma _{n}$
seem to have been established. Milin [Reference Milin17] highlighted the importance of the logarithmic coefficients within the framework of the Bieberbach conjecture. For
![]() $f\in \mathcal {S}$
and
$f\in \mathcal {S}$
and
![]() $n\ge 2$
, Milin conjectured that
$n\ge 2$
, Milin conjectured that
 $$ \begin{align*} \sum\limits_{m=1}^{n}\sum\limits_{k=1}^{m}\bigg(k|\gamma_{k}|^{2}-\frac{1}{k}\bigg)\le 0. \end{align*} $$
$$ \begin{align*} \sum\limits_{m=1}^{n}\sum\limits_{k=1}^{m}\bigg(k|\gamma_{k}|^{2}-\frac{1}{k}\bigg)\le 0. \end{align*} $$
De Branges [Reference de Branges9] proved the Bieberbach conjecture by proving Milin’s conjecture. The logarithmic coefficients for the Koebe function
![]() $k(z)=z/(1-z)^{2}$
are
$k(z)=z/(1-z)^{2}$
are
![]() $\gamma _{n}=1/n$
. For many extremal problems in the class
$\gamma _{n}=1/n$
. For many extremal problems in the class
![]() $\mathcal {S}$
, the Koebe function
$\mathcal {S}$
, the Koebe function
![]() $k(z)$
serves as the extremal function; thus,
$k(z)$
serves as the extremal function; thus,
![]() $|\gamma _{n}|\le 1/n$
was predicted to hold for functions in
$|\gamma _{n}|\le 1/n$
was predicted to hold for functions in
![]() $\mathcal {S}$
. However, this is not always the case, not even in order of magnitude. Indeed, there exists a bounded function f in the class
$\mathcal {S}$
. However, this is not always the case, not even in order of magnitude. Indeed, there exists a bounded function f in the class
![]() $\mathcal {S}$
with logarithmic coefficients
$\mathcal {S}$
with logarithmic coefficients
![]() $\gamma _{n}\ne O(n^{-0.83})$
(see [Reference Duren10, Theorem 8.4]). By differentiating (1.2) and then equating coefficients,
$\gamma _{n}\ne O(n^{-0.83})$
(see [Reference Duren10, Theorem 8.4]). By differentiating (1.2) and then equating coefficients,
 $$ \begin{align} \begin{aligned} & \gamma_{1}=\tfrac{1}{2}a_{2}, \\ & \gamma_{2}=\tfrac{1}{2}(a_{3}-\tfrac{1}{2}a_{2}^{2}),\\ & \gamma_{3}=\tfrac{1}{2}(a_{4}-a_{2}a_{3}+\tfrac{1}{3}a_{2}^{3}),\\ & \gamma_4=\tfrac{1}{4}(a_5-a_2a_4+a_2^2a_3-\tfrac{1}{2}a_3^2-\tfrac{1}{4}a_2^2). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & \gamma_{1}=\tfrac{1}{2}a_{2}, \\ & \gamma_{2}=\tfrac{1}{2}(a_{3}-\tfrac{1}{2}a_{2}^{2}),\\ & \gamma_{3}=\tfrac{1}{2}(a_{4}-a_{2}a_{3}+\tfrac{1}{3}a_{2}^{3}),\\ & \gamma_4=\tfrac{1}{4}(a_5-a_2a_4+a_2^2a_3-\tfrac{1}{2}a_3^2-\tfrac{1}{4}a_2^2). \end{aligned} \end{align} $$
If
![]() $f\in \mathcal {S}$
, it is easy to see that
$f\in \mathcal {S}$
, it is easy to see that
![]() $|\gamma _{1}|\le 1$
, because
$|\gamma _{1}|\le 1$
, because
![]() $|a_2| \leq 2$
. Using the Fekete–Szegö inequality [Reference Duren10, Theorem 3.8] for functions in
$|a_2| \leq 2$
. Using the Fekete–Szegö inequality [Reference Duren10, Theorem 3.8] for functions in
![]() $\mathcal {S}$
in (1.3), we obtain the sharp estimate
$\mathcal {S}$
in (1.3), we obtain the sharp estimate
For
![]() $n\ge 3$
, the problem seems much harder, and no significant bounds for
$n\ge 3$
, the problem seems much harder, and no significant bounds for
![]() $|\gamma _{n}|$
when
$|\gamma _{n}|$
when
![]() $f\in \mathcal {S}$
appear to be known. In 2017, Ali and Allu [Reference Ali and Allu1] obtained bounds for the initial logarithmic coefficients for close-to-convex functions. The problem of computing bounds for the logarithmic coefficients is considered in [Reference Ali and Allu2, Reference Cho, Kowalczyk, Kwon, Lecko and Sim8, Reference Pranav Kumar and Vasudevarao20, Reference Thomas21] for several subclasses of close-to-convex functions.
$f\in \mathcal {S}$
appear to be known. In 2017, Ali and Allu [Reference Ali and Allu1] obtained bounds for the initial logarithmic coefficients for close-to-convex functions. The problem of computing bounds for the logarithmic coefficients is considered in [Reference Ali and Allu2, Reference Cho, Kowalczyk, Kwon, Lecko and Sim8, Reference Pranav Kumar and Vasudevarao20, Reference Thomas21] for several subclasses of close-to-convex functions.
Given
![]() $q,n \in \mathbb {N}$
, the Hankel determinant
$q,n \in \mathbb {N}$
, the Hankel determinant
![]() $H_{q,n}(f)$
of the Taylor coefficients of a function
$H_{q,n}(f)$
of the Taylor coefficients of a function
![]() $f \in \mathcal {A}$
of the form (1.1) is defined by
$f \in \mathcal {A}$
of the form (1.1) is defined by
 $$ \begin{align*} H_{q,n}(f) = \begin{vmatrix} a_n & a_{n+1} & \cdots & a_{n+q-1} \\ a_{n+1} & a_{n+2} & \cdots & a_{n+q} \\ \vdots & \vdots & \ddots &\vdots \\ a_{n+q-1} & a_{n+q} & \cdots & a_{n+2(q-1)} \end{vmatrix}. \end{align*} $$
$$ \begin{align*} H_{q,n}(f) = \begin{vmatrix} a_n & a_{n+1} & \cdots & a_{n+q-1} \\ a_{n+1} & a_{n+2} & \cdots & a_{n+q} \\ \vdots & \vdots & \ddots &\vdots \\ a_{n+q-1} & a_{n+q} & \cdots & a_{n+2(q-1)} \end{vmatrix}. \end{align*} $$
Hankel determinants of various order have been studied recently by several authors (see [Reference Allu, Lecko and Thomas5, Reference Pommerenke18, Reference Pommerenke19]). One can easily observe that the Fekete–Szegö functional is the second Hankel determinant
![]() $H_{2,1}(f)$
. Fekete and Szegö generalised the estimate to
$H_{2,1}(f)$
. Fekete and Szegö generalised the estimate to
![]() $|a_3 - \mu a_2 ^2|$
with
$|a_3 - \mu a_2 ^2|$
with
![]() $\mu $
real for f given by (1.1) (see [Reference Duren10, Theorem 3.8]).
$\mu $
real for f given by (1.1) (see [Reference Duren10, Theorem 3.8]).
Kowalczyk and Lecko [Reference Kowalczyk and Lecko13] studied the Hankel determinant whose entries are logarithmic coefficients of
![]() $f \in \mathcal {S}$
,
$f \in \mathcal {S}$
,
 $$ \begin{align*} H_{q,n}(F_f/2) = \begin{vmatrix} \gamma_n & \gamma_{n+1} & \cdots & \gamma_{n+q-1} \\ \gamma_{n+1} & \gamma_{n+2} & \cdots & \gamma_{n+q} \\ \vdots & \vdots & \ddots &\vdots \\ \gamma_{n+q-1} & \gamma_{n+q} & \cdots & \gamma_{n+2(q-1)} \end{vmatrix}. \end{align*} $$
$$ \begin{align*} H_{q,n}(F_f/2) = \begin{vmatrix} \gamma_n & \gamma_{n+1} & \cdots & \gamma_{n+q-1} \\ \gamma_{n+1} & \gamma_{n+2} & \cdots & \gamma_{n+q} \\ \vdots & \vdots & \ddots &\vdots \\ \gamma_{n+q-1} & \gamma_{n+q} & \cdots & \gamma_{n+2(q-1)} \end{vmatrix}. \end{align*} $$
They obtained sharp bounds for
![]() $|H_{2,1}(F_f/2)|$
for the classes of convex and starlike functions. In [Reference Kowalczyk and Lecko14], they gave sharp bounds for
$|H_{2,1}(F_f/2)|$
for the classes of convex and starlike functions. In [Reference Kowalczyk and Lecko14], they gave sharp bounds for
![]() $|H_{2,1}(F_f/2)|$
for the classes of starlike and convex functions of order
$|H_{2,1}(F_f/2)|$
for the classes of starlike and convex functions of order
![]() $\alpha \ (0 \leq \alpha < 1)$
and, in [Reference Kowalczyk and Lecko15], they gave sharp bounds for
$\alpha \ (0 \leq \alpha < 1)$
and, in [Reference Kowalczyk and Lecko15], they gave sharp bounds for
![]() $|H_{2,1}(F_f/2)|$
for the classes of strongly starlike and strongly convex functions. Allu and Arora [Reference Allu and Arora3] obtained sharp bounds for
$|H_{2,1}(F_f/2)|$
for the classes of strongly starlike and strongly convex functions. Allu and Arora [Reference Allu and Arora3] obtained sharp bounds for
![]() $|H_{2,1}(F_f/2)|$
for various subclasses of univalent functions. Allu et al. [Reference Allu, Arora and Shaji4] obtained sharp bounds for
$|H_{2,1}(F_f/2)|$
for various subclasses of univalent functions. Allu et al. [Reference Allu, Arora and Shaji4] obtained sharp bounds for
![]() $|H_{2,1}(F_f/2)|$
for the classes of starlike and convex functions with respect to symmetric points. Recently, Allu and Shaji [Reference Allu and Shaji6] obtained the sharp bound for the second Hankel determinant for inverse logarithmic coefficients for the classes of convex and starlike functions. Also, Eker et al. [Reference Eker, Lecko, Çekiç and Şeker12] obtained sharp bounds for
$|H_{2,1}(F_f/2)|$
for the classes of starlike and convex functions with respect to symmetric points. Recently, Allu and Shaji [Reference Allu and Shaji6] obtained the sharp bound for the second Hankel determinant for inverse logarithmic coefficients for the classes of convex and starlike functions. Also, Eker et al. [Reference Eker, Lecko, Çekiç and Şeker12] obtained sharp bounds for
![]() $|H_{2,1}(F_f/2)|$
for the classes of strongly Ozaki close-to-convex functions and their inverse functions.
$|H_{2,1}(F_f/2)|$
for the classes of strongly Ozaki close-to-convex functions and their inverse functions.
In this paper, we consider the second Hankel determinant for logarithmic coefficients of order 2, that is,
 $$ \begin{align*} H_{2,2}(F_f/2) = \begin{vmatrix} \gamma_2 & \gamma_3 \\ \gamma_3 & \gamma_4 \end{vmatrix} =\gamma_2\gamma_4 -\gamma_3^2. \end{align*} $$
$$ \begin{align*} H_{2,2}(F_f/2) = \begin{vmatrix} \gamma_2 & \gamma_3 \\ \gamma_3 & \gamma_4 \end{vmatrix} =\gamma_2\gamma_4 -\gamma_3^2. \end{align*} $$
From (1.3),
 $$ \begin{align} H_{2,2}(F_{f}/2) =\tfrac{1}{288}(a_2^6 & -6a_2^4a_3+18a_2^2a_3^2-36a_3^3-12a_2^3a_4+72 a_2 a_3 a_4\nonumber \\ & -72a_4^2-36a_2^2a_5+72 a_3 a_5). \end{align} $$
$$ \begin{align} H_{2,2}(F_{f}/2) =\tfrac{1}{288}(a_2^6 & -6a_2^4a_3+18a_2^2a_3^2-36a_3^3-12a_2^3a_4+72 a_2 a_3 a_4\nonumber \\ & -72a_4^2-36a_2^2a_5+72 a_3 a_5). \end{align} $$
It is now appropriate to remark that
![]() $|H_{2,2}(F_{f^{-1}}/2)|$
is invariant under rotation, since for
$|H_{2,2}(F_{f^{-1}}/2)|$
is invariant under rotation, since for
![]() $f_{\theta }(z):=e^{-i \theta } f(e^{i \theta } z), \theta \in \mathbb {R}$
and
$f_{\theta }(z):=e^{-i \theta } f(e^{i \theta } z), \theta \in \mathbb {R}$
and
![]() $f \in \mathcal {S}$
,
$f \in \mathcal {S}$
,
 $$ \begin{align*} \begin{aligned} H_{2,2}(F_{f_{\theta}}/2) =\frac{e^{i6 \theta}}{288}(a_2^6 & -6a_2^4a_3+18a_2^2a_3^2-36a_3^3-12a_2^3a_4+72 a_2 a_3 a_4 \\ & -72a_4^2-36a_2^2a_5+72 a_3 a_5)=e^{i6 \theta} H_{2,2}(F_{f}/2). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} H_{2,2}(F_{f_{\theta}}/2) =\frac{e^{i6 \theta}}{288}(a_2^6 & -6a_2^4a_3+18a_2^2a_3^2-36a_3^3-12a_2^3a_4+72 a_2 a_3 a_4 \\ & -72a_4^2-36a_2^2a_5+72 a_3 a_5)=e^{i6 \theta} H_{2,2}(F_{f}/2). \end{aligned} \end{align*} $$
The main aim of this paper is to a find sharp upper bound for
![]() $|H_{2,2}(F_{f}/2)| $
when f belongs to the class of starlike and convex functions. A domain
$|H_{2,2}(F_{f}/2)| $
when f belongs to the class of starlike and convex functions. A domain
![]() $\Omega \subseteq \mathbb {C}$
is said to be starlike with respect to a point
$\Omega \subseteq \mathbb {C}$
is said to be starlike with respect to a point
![]() $z_{0}\in \Omega $
if the line segment joining
$z_{0}\in \Omega $
if the line segment joining
![]() $z_{0}$
to any point in
$z_{0}$
to any point in
![]() $\Omega $
lies entirely in
$\Omega $
lies entirely in
![]() $\Omega $
. If
$\Omega $
. If
![]() $z_0$
is the origin, then we say that
$z_0$
is the origin, then we say that
![]() $\Omega $
is a starlike domain. A function
$\Omega $
is a starlike domain. A function
![]() $f \in \mathcal {A}$
is said to be starlike if
$f \in \mathcal {A}$
is said to be starlike if
![]() $f(\mathbb {D})$
is a starlike domain. We denote by
$f(\mathbb {D})$
is a starlike domain. We denote by
![]() $\mathcal {S}^*$
the class of starlike functions f in
$\mathcal {S}^*$
the class of starlike functions f in
![]() $\mathcal {S}$
. It is well known that a function
$\mathcal {S}$
. It is well known that a function
![]() $f \in \mathcal {A}$
is in
$f \in \mathcal {A}$
is in
![]() $\mathcal {S}^*$
if and only if
$\mathcal {S}^*$
if and only if
 $$ \begin{align} \mathrm{Re\,}\bigg( \frac{zf'(z)}{f(z)} \bigg)> 0 \quad \text{for}\,\, z \in \mathbb{D}. \end{align} $$
$$ \begin{align} \mathrm{Re\,}\bigg( \frac{zf'(z)}{f(z)} \bigg)> 0 \quad \text{for}\,\, z \in \mathbb{D}. \end{align} $$
Further, a domain
![]() $\Omega \subseteq \mathbb {C}$
is called convex if the line segment joining any two points of
$\Omega \subseteq \mathbb {C}$
is called convex if the line segment joining any two points of
![]() $\Omega $
lies entirely in
$\Omega $
lies entirely in
![]() $\Omega $
. A function
$\Omega $
. A function
![]() $f\in \mathcal {A}$
is called convex if
$f\in \mathcal {A}$
is called convex if
![]() $f(\mathbb {D})$
is a convex domain. We denote by
$f(\mathbb {D})$
is a convex domain. We denote by
![]() $\mathcal {C}$
the class of convex functions in
$\mathcal {C}$
the class of convex functions in
![]() $\mathcal {S}$
. A function
$\mathcal {S}$
. A function
![]() $f \in \mathcal {A}$
is in
$f \in \mathcal {A}$
is in
![]() $\mathcal {C}$
if and only if
$\mathcal {C}$
if and only if
 $$ \begin{align} \mathrm{Re\,}\bigg( 1+\frac{zf"(z)}{f'(z)} \bigg)> 0 \quad \text{for}\,\, z \in \mathbb{D}. \end{align} $$
$$ \begin{align} \mathrm{Re\,}\bigg( 1+\frac{zf"(z)}{f'(z)} \bigg)> 0 \quad \text{for}\,\, z \in \mathbb{D}. \end{align} $$
2 Preliminary results
In this section, we present the key lemmas which will be used to prove the main results of this paper. Let
![]() $\mathcal {P}$
denote the class of all analytic functions p having positive real part in
$\mathcal {P}$
denote the class of all analytic functions p having positive real part in
![]() $\mathbb {D}$
, with the form
$\mathbb {D}$
, with the form
Members of
![]() $\mathcal {P}$
are called Carathéodory functions. To prove our Theorem 3.1, we need the following lemmas.
$\mathcal {P}$
are called Carathéodory functions. To prove our Theorem 3.1, we need the following lemmas.
Lemma 2.1 [Reference Duren10].
For a function
![]() $p \in \mathcal {P}$
of the form (2.1), the sharp inequality
$p \in \mathcal {P}$
of the form (2.1), the sharp inequality
![]() $|p_n| \leq 2$
holds for each
$|p_n| \leq 2$
holds for each
![]() $n \geq 1$
. Equality holds for the function
$n \geq 1$
. Equality holds for the function
![]() $p(z) =(1+z)/(1-z)$
.
$p(z) =(1+z)/(1-z)$
.
Lemma 2.2 [Reference Livingston16].
For a function
![]() $p \in \mathcal {P}$
of the form (2.1), the sharp inequality
$p \in \mathcal {P}$
of the form (2.1), the sharp inequality
![]() ${|p_n-p_kp_{n-k}|\leq 2}$
holds for
${|p_n-p_kp_{n-k}|\leq 2}$
holds for
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $k\geq 1$
.
$k\geq 1$
.
In view of Lemma 2.2, it is easy to see that
![]() $|p_{n+1}p_{n-1}-p_n^2| \leq 4$
for a function
$|p_{n+1}p_{n-1}-p_n^2| \leq 4$
for a function
![]() $p \in \mathcal {P}$
of the form (2.1) and
$p \in \mathcal {P}$
of the form (2.1) and
![]() $n\geq 2$
. In particular, if
$n\geq 2$
. In particular, if
![]() $n=3$
,
$n=3$
,
Let
![]() $\mathcal {B}_{0}$
denote the class of analytic functions
$\mathcal {B}_{0}$
denote the class of analytic functions
![]() $w : \mathbb {D} \rightarrow \mathbb {D}$
such that
$w : \mathbb {D} \rightarrow \mathbb {D}$
such that
![]() $w(0)=0$
. Functions in
$w(0)=0$
. Functions in
![]() $\mathcal {B}_{0}$
are known as the Schwarz functions. A function
$\mathcal {B}_{0}$
are known as the Schwarz functions. A function
![]() $w \in \mathcal {B}_{0}$
can be written as a power series
$w \in \mathcal {B}_{0}$
can be written as a power series
 $$ \begin{align} w(z)=\sum_{n=1}^\infty c_nz^n. \end{align} $$
$$ \begin{align} w(z)=\sum_{n=1}^\infty c_nz^n. \end{align} $$
It is clear that if
then
![]() $p \in \mathcal {P}$
if and only if
$p \in \mathcal {P}$
if and only if
![]() $\omega \in \mathcal {B}_0$
.
$\omega \in \mathcal {B}_0$
.
Due to the evident connection between Carathéodory functions and Schwarz functions, the results applicable to the coefficients of Schwarz functions are useful in solving coefficient problems associated with starlike and convex functions. To prove Theorem 3.3, we need the following lemmas for the Schwarz functions.
Lemma 2.3 [Reference Carlson7].
Let
![]() $w(z)=c_1z+c_2z^2+ \cdots $
be a Schwarz function. Then,
$w(z)=c_1z+c_2z^2+ \cdots $
be a Schwarz function. Then,
 $$ \begin{align*} |c_1|\leq 1, \quad |c_2| \leq 1-|c_1|^2 \quad \mbox{and}\quad |c_3| \leq 1-|c_1|^2-\frac{|c_2|^2}{1+|c_1|}. \end{align*} $$
$$ \begin{align*} |c_1|\leq 1, \quad |c_2| \leq 1-|c_1|^2 \quad \mbox{and}\quad |c_3| \leq 1-|c_1|^2-\frac{|c_2|^2}{1+|c_1|}. \end{align*} $$
Lemma 2.4 [Reference Efraimidis11].
If
![]() $\omega \in \mathcal {B}_0$
of the form (2.3) and
$\omega \in \mathcal {B}_0$
of the form (2.3) and
![]() $\lambda \in \mathbb {C}$
, then
$\lambda \in \mathbb {C}$
, then
Lemma 2.5 [Reference Zaprawa22].
If
![]() $\omega \in \mathcal {B}_0$
of the form (2.3), then
$\omega \in \mathcal {B}_0$
of the form (2.3), then
3 Main results
Theorem 3.1. If
![]() $f \in \mathcal {S}^*,$
then
$f \in \mathcal {S}^*,$
then
The bound is sharp.
Proof. Let
![]() $f\in \mathcal {S}^*$
be of the form (1.1). By (1.5),
$f\in \mathcal {S}^*$
be of the form (1.1). By (1.5),
 $$ \begin{align} \frac{zf'(z)}{f(z)}=p(z) \end{align} $$
$$ \begin{align} \frac{zf'(z)}{f(z)}=p(z) \end{align} $$
for some
![]() $p \in \mathcal {P}$
of the form (2.1). By comparing the coefficients on both sides of (3.1),
$p \in \mathcal {P}$
of the form (2.1). By comparing the coefficients on both sides of (3.1),
 $$ \begin{align} \begin{aligned} & a_2=p_1, \\ & a_3=\tfrac{1}{2}(p_1^2+p_2), \\ & a_4=\tfrac{1}{6}(p_1^3+3p_1p_2+2p_3 ),\\ & a_5=\tfrac{1}{24}(p_1^4 + 6 p_1^2 p_2 + 3 p_2^2 + 8 p_1 p_3+ 6 p_4). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & a_2=p_1, \\ & a_3=\tfrac{1}{2}(p_1^2+p_2), \\ & a_4=\tfrac{1}{6}(p_1^3+3p_1p_2+2p_3 ),\\ & a_5=\tfrac{1}{24}(p_1^4 + 6 p_1^2 p_2 + 3 p_2^2 + 8 p_1 p_3+ 6 p_4). \end{aligned} \end{align} $$
Hence, by (1.4),
By taking the modulus on both sides and applying the triangle inequality,
Equality holds for the function
![]() $f\in \mathcal {A}$
given by (3.1), where
$f\in \mathcal {A}$
given by (3.1), where
 $$ \begin{align*} p(z)=\frac{1+z^2}{1-z^2}. \end{align*} $$
$$ \begin{align*} p(z)=\frac{1+z^2}{1-z^2}. \end{align*} $$
Then,
![]() $c_1=c_3=0$
and
$c_1=c_3=0$
and
![]() $c_2=c_4=2$
. So by (3.2),
$c_2=c_4=2$
. So by (3.2),
![]() $a_2=0,a_3=1,a_4=0$
and
$a_2=0,a_3=1,a_4=0$
and
![]() $a_5=1$
. Therefore, by (1.4),
$a_5=1$
. Therefore, by (1.4),
which completes the proof of the theorem.
Example 3.2. The Koebe function,
has logarithmic coefficients
![]() $\gamma _n=1/n$
and
$\gamma _n=1/n$
and
![]() $|\gamma _2\gamma _4-\gamma _3^2|= 1/72$
.
$|\gamma _2\gamma _4-\gamma _3^2|= 1/72$
.
Theorem 3.3. If
![]() $f \in \mathcal {C},$
then
$f \in \mathcal {C},$
then
The bound is sharp.
Proof. Let
![]() $f\in \mathcal {C}$
be of the form (1.1). By (1.6),
$f\in \mathcal {C}$
be of the form (1.1). By (1.6),
 $$ \begin{align} 1 + \frac{zf"(z)}{f'(z)}=\frac{1+\omega(z)}{1-\omega(z)} \end{align} $$
$$ \begin{align} 1 + \frac{zf"(z)}{f'(z)}=\frac{1+\omega(z)}{1-\omega(z)} \end{align} $$
for some
![]() $\omega \in \mathcal {B}_0$
of the form (2.3). By comparing the coefficients of powers of z on both sides of (3.4),
$\omega \in \mathcal {B}_0$
of the form (2.3). By comparing the coefficients of powers of z on both sides of (3.4),
 $$ \begin{align} \begin{aligned} & a_2=c_1, \\ & a_3=\tfrac{1}{3}(3c_1^2+c_2), \\ & a_4=\tfrac{1}{6}(6c_1^3+5c_1c_2+c_3 ),\\ & a_5=\tfrac{1}{30}(30c_1^4 +43c_1^2 c_2 + 6 c_2^2 + 14 c_1 c_3+ 3 c_4). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} & a_2=c_1, \\ & a_3=\tfrac{1}{3}(3c_1^2+c_2), \\ & a_4=\tfrac{1}{6}(6c_1^3+5c_1c_2+c_3 ),\\ & a_5=\tfrac{1}{30}(30c_1^4 +43c_1^2 c_2 + 6 c_2^2 + 14 c_1 c_3+ 3 c_4). \end{aligned} \end{align} $$
Hence, by (1.4),
 $$ \begin{align} H_{2,2}(F_{f}/2)=\tfrac{1}{4320}(15 c_1^6 & + 54 c_1^4 c_2 + 24 c_1^2 c_2^2 + 52 c_2^3 + 42 c_1^3 c_3\nonumber\\ & -72 c_1 c_2 c_3 - 30 c_3^2 + 54 c_1^2 c_4 + 36 c_2 c_4). \end{align} $$
$$ \begin{align} H_{2,2}(F_{f}/2)=\tfrac{1}{4320}(15 c_1^6 & + 54 c_1^4 c_2 + 24 c_1^2 c_2^2 + 52 c_2^3 + 42 c_1^3 c_3\nonumber\\ & -72 c_1 c_2 c_3 - 30 c_3^2 + 54 c_1^2 c_4 + 36 c_2 c_4). \end{align} $$
By rearranging the terms in (3.6), we can write the right-hand side as
 $$ \begin{align*} \begin{aligned} \tfrac{1}{ 4320}(36(c_2c_4 & -c_3^2+c_1^2c_4-2c_1c_2c_3+c_2^3)+16c_1^2(c_4+2c_1 c_3 + c_2^2+3c_1^2c_2+c_1^4)\\ & +3c_1^2(c_4+2c_1c_3+c_1^2c_2)+c_1^2(6c_1^2c_2+9c_2^2+6c_1c_3)+16c_2^2+6c_3^2).\\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \tfrac{1}{ 4320}(36(c_2c_4 & -c_3^2+c_1^2c_4-2c_1c_2c_3+c_2^3)+16c_1^2(c_4+2c_1 c_3 + c_2^2+3c_1^2c_2+c_1^4)\\ & +3c_1^2(c_4+2c_1c_3+c_1^2c_2)+c_1^2(6c_1^2c_2+9c_2^2+6c_1c_3)+16c_2^2+6c_3^2).\\ \end{aligned} \end{align*} $$
By applying the triangle inequality and using Lemmas 2.3, 2.4 and 2.5,
where
 $$ \begin{align*} \begin{aligned} g(x,y)&=18 x^2 + 36 (1 - x^2) + 6 x^4 y + 16 y^3 + 9 x^2 y^2 \\ &\quad + 6 x^3 \bigg(1 - x^2 - \frac{y^2}{1 + x}\bigg) + 6 \bigg(1 - x^2 - \frac{y^2}{1 + x}\bigg)^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} g(x,y)&=18 x^2 + 36 (1 - x^2) + 6 x^4 y + 16 y^3 + 9 x^2 y^2 \\ &\quad + 6 x^3 \bigg(1 - x^2 - \frac{y^2}{1 + x}\bigg) + 6 \bigg(1 - x^2 - \frac{y^2}{1 + x}\bigg)^2. \end{aligned} \end{align*} $$
Since the class
![]() $\mathcal {C}$
and the functional
$\mathcal {C}$
and the functional
![]() $|H_{2,2}(F_{f}/2)|$
are rotationally invariant, we can assume that
$|H_{2,2}(F_{f}/2)|$
are rotationally invariant, we can assume that
![]() $c \in [0,1]$
. Further, in view of Lemma 2.1, the region of variability of the pair
$c \in [0,1]$
. Further, in view of Lemma 2.1, the region of variability of the pair
![]() $(x,y)$
coincides with the set
$(x,y)$
coincides with the set
Since y varies between
![]() $0$
and
$0$
and
![]() $1$
, it is clear that
$1$
, it is clear that
where
 $$ \begin{align*} \begin{aligned} G(x,y)&=18 x^2 + 36 (1 - x^2) + 6 x^4 y + 16 y^2 + 9 x^2 y^2 \\[2mm] &\quad + 6 x^3 \bigg(1 - x^2 - \frac{y^2}{1 + x}\bigg) + 6 \bigg(1 - x^2 - \frac{y^2}{1 + x}\bigg)^2. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} G(x,y)&=18 x^2 + 36 (1 - x^2) + 6 x^4 y + 16 y^2 + 9 x^2 y^2 \\[2mm] &\quad + 6 x^3 \bigg(1 - x^2 - \frac{y^2}{1 + x}\bigg) + 6 \bigg(1 - x^2 - \frac{y^2}{1 + x}\bigg)^2. \end{aligned} \end{align*} $$
Therefore,
We need to find the maximum value of
![]() $G(x,y)$
over the region
$G(x,y)$
over the region
![]() $\Omega $
. The critical points of G satisfy the conditions
$\Omega $
. The critical points of G satisfy the conditions
 $$ \begin{align*} \begin{aligned} \frac{\partial G}{\partial x}&= \frac{6}{(1+x)^2} (10 x + 27 x^2 + 17 x^3 - 6 x^4 + 11 x^6 + 5 x^7- 4 x^3 y - 12 x^4 y \\[2mm] &\quad - 12 x^5 y - 4 x^6 y - 2 y^2 - 9 x y^2 - 12 x^2 y^2 - 6 x^3 y^2 - x^4 y^2 + 2 y^4)=0 \\[3mm] \frac{\partial G}{\partial y}& = \frac{12 x^5 + 6 x^6 + 40 x y + 74 x^2 y + 48 x^3 y + 6 x^4 (1 + y) + 8 (y + 3 y^3)}{(1+x)^2}=0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{\partial G}{\partial x}&= \frac{6}{(1+x)^2} (10 x + 27 x^2 + 17 x^3 - 6 x^4 + 11 x^6 + 5 x^7- 4 x^3 y - 12 x^4 y \\[2mm] &\quad - 12 x^5 y - 4 x^6 y - 2 y^2 - 9 x y^2 - 12 x^2 y^2 - 6 x^3 y^2 - x^4 y^2 + 2 y^4)=0 \\[3mm] \frac{\partial G}{\partial y}& = \frac{12 x^5 + 6 x^6 + 40 x y + 74 x^2 y + 48 x^3 y + 6 x^4 (1 + y) + 8 (y + 3 y^3)}{(1+x)^2}=0. \end{aligned} \end{align*} $$
It is clear that, in the interior of
![]() $\Omega $
,
$\Omega $
,
![]() ${\partial G}/{\partial y}>0$
. So the function
${\partial G}/{\partial y}>0$
. So the function
![]() $G(x,y)$
has no critical point in the interior of
$G(x,y)$
has no critical point in the interior of
![]() $\Omega $
and cannot have a maximum in the interior of
$\Omega $
and cannot have a maximum in the interior of
![]() $\Omega $
. Since G is continuous in the compact set
$\Omega $
. Since G is continuous in the compact set
![]() $\Omega $
, it attains its maximum on the boundary of
$\Omega $
, it attains its maximum on the boundary of
![]() $\Omega $
. Considering the boundary of
$\Omega $
. Considering the boundary of
![]() $\Omega $
leads to the following three cases.
$\Omega $
leads to the following three cases.
Case (i): if
![]() $x=0$
and
$x=0$
and
![]() $0\leq y \leq 1$
, then
$0\leq y \leq 1$
, then
![]() $G(0,y)=42+4y^2+6y^4 \leq 52$
.
$G(0,y)=42+4y^2+6y^4 \leq 52$
.
Case (ii): if
![]() $y=0$
and
$y=0$
and
![]() $0\leq x \leq 1$
, then
$0\leq x \leq 1$
, then
Since
![]() $h_1'(x)=-60x+18x^2+24x^3-30x^4 < 0$
for
$h_1'(x)=-60x+18x^2+24x^3-30x^4 < 0$
for
![]() $0 < x \leq 1$
, the function
$0 < x \leq 1$
, the function
![]() $h_1$
is decreasing. So
$h_1$
is decreasing. So
![]() $G(x,0)\leq h_1(0)=42$
.
$G(x,0)\leq h_1(0)=42$
.
Case (iii): if
![]() $y=1-x^2$
and
$y=1-x^2$
and
![]() $0\leq x\leq 1$
, then
$0\leq x\leq 1$
, then
Clearly,
![]() $ h_2'(x)=-70x-8x^3+18x^5 < 0 $
for
$ h_2'(x)=-70x-8x^3+18x^5 < 0 $
for
![]() $0< x < 1$
. Hence, the function
$0< x < 1$
. Hence, the function
![]() $h_2$
is decreasing and
$h_2$
is decreasing and
![]() $G(x,1-x^2)\leq h_2(0)=52$
.
$G(x,1-x^2)\leq h_2(0)=52$
.
Thus, combining the three cases,
and by (3.7),
To prove the equality in (3.8), we consider the function
 $$ \begin{align*} f(z)=\frac{1}{2}\log\bigg(\frac{1+z}{1-z}\bigg)=z+\frac{z^3}{3}+\frac{z^5}{5}+\cdots. \end{align*} $$
$$ \begin{align*} f(z)=\frac{1}{2}\log\bigg(\frac{1+z}{1-z}\bigg)=z+\frac{z^3}{3}+\frac{z^5}{5}+\cdots. \end{align*} $$
A simple computation shows that f belongs to the class
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $|H_{2,2}(F_{f}/2)|=13/1080$
. This completes the proof.
$|H_{2,2}(F_{f}/2)|=13/1080$
. This completes the proof.
Example 3.4. For an example illustrating Theorem 3.3, consider the function
It is easy to see that the function f belongs to the class
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\gamma _n(f)=1/2n$
. Hence,
$\gamma _n(f)=1/2n$
. Hence,