I. INTRODUCTION
Stabilizing nanocrystalline materials against grain growth is a critical bottleneck to their reliable use as bulk components. Pure nanocrystalline materials undergo rapid grain growth into micron-scale grain sizes at relatively low homologous temperatures, Reference Gertsman and Birringer1–Reference Ames, Markmann, Karos, Michels, Tschope and Birringer4 but with the addition of alloying elements grain growth can be greatly hindered. Reference Lücke and Detert5–Reference Darling, VanLeeuween, Koch and Scattergood13 Two mechanisms for suppressing grain growth by alloying have been proposed: alloying elements can either kinetically impede grain growth by increasing the activation energy for grain boundary motion (effectively decreasing grain boundary mobility) or decrease the grain boundary energy thermodynamically through grain boundary segregation (or both). The latter mechanism is particularly promising, as substantial decreases to the grain boundary energy from grain boundary segregation could stabilize nanoscale grain sizes to higher temperatures and for longer times. Reference Boylan, Ostrander, Erb, Palumbo and Aust8–Reference Darling, VanLeeuween, Koch and Scattergood13
There is an even more enticing prospect when alloying to reduce the grain boundary energy: if the excess energy of the grain boundary is eliminated by grain boundary segregation, grain growth can be entirely avoided and a thermodynamically stable grain size in the nanocrystalline regime could exist. This concept was put forth by Weissmüller, Reference Weissmüller14,Reference Weissmüller15 with an accompanying analytical model that revealed that a system with an enthalpy of grain boundary segregation large enough to offset the pure grain boundary energy should have such a stable nanocrystalline state. Further analytical models have been developed, for example improving on assumptions that only applied in the dilute limit by incorporating the energy of solute–solvent interactions both in the grain boundary and in the crystal using a regular solution model. Reference Trelewicz and Schuh16–Reference Abdeljawad, Lu, Argibay, Clark, Boyce and Foiles19 Such efforts have produced alloy design criteria for identifying potential alloy systems with thermodynamically stable nanocrystalline states formed through grain boundary segregation. Several of these alloy systems have shown considerable nanometer-scale grain size stability in experiments, including Ni–P, Ni–W, Fe–Zr, and W–Ti. Reference Boylan, Ostrander, Erb, Palumbo and Aust8–Reference Darling, VanLeeuween, Koch and Scattergood13
While these models are able to identify systems with potential stability through energetic considerations of grain boundary segregation, the accurate accounting of entropic effects has been limited by assumptions needed to make the analytical models tractable, i.e., dilute limit or regular solution assumptions. A number of analytical Reference Cahn20–Reference Tang, Carter and Cannon23 and atomistic models Reference Rittner and Seidman24,Reference Seidman25 have been developed for determining the change in free energy associated with grain boundary segregation under a variety of conditions, but typically do not allow the grain size to change during disordering. Thus the process of how a thermodynamically stable nanocrystalline state would disorder remains obscured; since the nanocrystalline state is stabilized by the enthalpic benefits of grain boundary segregation, it should still favor a higher entropy state at elevated temperatures (e.g., a solid solution phase). Understanding this process requires a different type of model capable of capturing both the enthalpic and entropic effects of grain boundary segregation and desegregation along with the accompanying changes to the equilibrium grain size that are key to this disordering process.
One potential approach was developed by Chookajorn and Schuh, Reference Chookajorn and Schuh26 where a Monte Carlo simulation is used to incorporate non-regular mixing effects. In their lattice-based simulation, each lattice site is prescribed two pieces of information: a grain allegiance and a chemical identity. Neighboring lattice sites with different grain allegiances have a grain boundary bond between them, which is energetically different than a bulk bond. The Monte Carlo simulation then identifies the minimum free energy configuration by performing atom swaps (swapping a solute and solvent atom) and grain swaps (locally moving a grain boundary or nucleating a new grain). Through these swapping events, both solute configuration space (i.e., the distribution of solute on the lattice) and grain boundary network configuration space (i.e., the configuration of the grain boundary network on the lattice, which determines the average grain size, grain size distribution, etc.) are surveyed in search of the minimum free energy configuration. Reference Kalidindi, Chookajorn and Schuh27 The equilibrium state from these simulations matches a bulk phase diagram when the enthalpy of grain boundary segregation is low, but when the enthalpy of grain boundary segregation is large enough to offset the pure solvent grain boundary energy, nanocrystalline configurations with solute decorated grain boundaries emerge as stable states.
These simulations have been useful for both identifying alloying systems that produce stable nanocrystalline states against grain growth, as well as understanding some of the unique configurational opportunities available when grain sizes are at nanometer length scales. Reference Chookajorn and Schuh12,Reference Polyakov, Chookajorn, Mecklenburg, Schuh and Hodge28–Reference Xing, Kalidindi and Schuh31 At the same time, the method has a limited temperature window in which it operates well. This is because the grain swaps are highly localized movements in configuration space; the simulation is not necessarily able to sample the grain boundary network configuration space ergodically and can become trapped in metastable states. In addition, at high temperatures, a non-physical structure often forms wherein grain boundaries are no longer formed as a network but rather as individual island grains that are but one atom in size. Reference Polyakov, Chookajorn, Mecklenburg, Schuh and Hodge28 This occurs because in strongly grain boundary-segregating systems, the solute–solvent interactions at the grain boundary are the most favored, and so forming a grain boundary around an individual site allows for a higher coordination of grain boundary solute–solvent bonds. The presence of this non-physical state in the configuration space, as well as the slow kinematics of grain swaps, has limited the exploration of temperature effects on stability and our understanding of the role of entropy in stabilizing the nanocrystalline state of alloys.
The above challenges to the Monte Carlo approach of simulating nanocrystalline alloys remain in need of further methodological developments. One preliminary suggestion of Chookajorn and Schuh was the use of (ergodic) atom swaps on fixed grain topologies, which avoids many of the challenges described above but samples only a limited region of grain boundary configuration space, reducing it to, e.g., a sweep over grain boundary areas. Nonetheless, their preliminary work further verified that the minimum in internal energy for the alloy is a segregated nanocrystalline state at a particular grain size. Reference Chookajorn and Schuh26 If instead of internal energy, a free energy were calculated for the different fixed grain topologies, not only could one decouple exploration of the grain boundary network configuration space and the solute configuration space, but one also could explicitly evaluate the role of entropy in nanocrystalline structures. Here, we develop a method for investigating the equilibrium behavior of stable nanocrystalline alloys with explicit consideration of entropic and enthalpic effects and employ it to observe the nature of phase transitions in stable nanocrystalline states.
II. METHOD
The advantage of the Chookajorn and Schuh model Reference Chookajorn and Schuh26 is that both grain boundary network configuration space and solute configuration space are sampled within the Monte Carlo simulation and as a result the equilibrium state produced by the simulation is one which minimizes the free energy with respect to both configuration spaces, simultaneously. However, as described above, due to the difficulty of exploring the grain boundary network configuration space well, it can be beneficial to decouple the free energy minimization onto each configuration space separately. The Monte Carlo simulation is relatively robust for sampling the solute configuration space. Reference Landau and Binder32 By performing these calculations over a set of grain boundary network configurations that cover (an appropriate swath of) the network configuration space we can determine the minimum free energy configuration with respect to both configuration spaces. Since the grain boundary network is not changed within each Monte Carlo simulation of solute configuration space, the lattice effects from performing grain swaps are entirely avoided. A schematic of this framework is shown in Fig. 1 for a simplified view of grain boundary network space that only changes the relative area of a single planar boundary.

FIG. 1. Schematic representation of the framework for identifying free energy minimizing nanocrystalline states by separately exploring solute and grain boundary network configuration spaces. The four configurations shown are all of the same volume (area), but have different relative proportions of grain boundary area (length); comparing across them at constant composition therefore speaks to the energetics of the boundary area and its interaction with the solute.
The grain boundary network configuration space can be surveyed with respect to any set of parameters describing the grain boundary network, such as the grain boundary area density, triple junction linear density, and the grain size distribution. In strongly grain boundary segregated systems, grain boundary area is expected to have the largest influence on the thermodynamic properties of a particular grain boundary network configuration space, Reference Weissmüller15,Reference Trelewicz and Schuh16,Reference Detor and Schuh33,Reference Liu and Kircheim34 and thus we focus on surveying the space with respect to grain boundary area. While this neglects many topological features, such as thickened grain boundaries and triple junctions which will be addressed in future work, it provides the simplest physical starting point for quantitative thermodynamic analysis of nanocrystalline systems.
To this end, we construct a number of bicrystal systems where the grain boundary volume fraction is varied by altering the dimensions of a bicrystal cell, each with a body-centered cubic (BCC) atomic lattice. For comparison we also simulate a single crystal cell without a grain boundary. Each cell has roughly 30,000 atoms (±10%) and the grain boundary ‘volume fractions’ in the bicrystals (i.e., the fraction of atoms at the boundary) range from 0.004 to 0.5. If the atoms are taken to be a BCC metal such as W, the resulting relative grain boundary areas corresponding to this range spans from 30 to 2500 nm2, which relates to grain sizes ranging from 1.4 to 175 nm. The bicrystal lattice has periodic boundary conditions in each direction, though in the dimension normal to the grain boundary where the periodic boundary conditions would normally form a second grain boundary the grain boundary bonds are replaced with crystalline bonds to limit the system to just a single grain boundary plane for more consistent results and finer control.
The internal energy of a particular solute configuration is determined by summing pairwise bonds within the lattice. There are solvent–solvent (AA), solvent–solute (AB), and solute–solute (BB) pairwise bonds, each of which can have different energies depending on whether it is a crystalline (c) or a grain boundary (gb) bond, where the latter is defined as a bond that crosses the plane of the grain boundary. The internal energy of the system is calculated by:
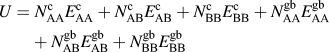 $$U = N_{{\rm{AA}}}^{\rm{c}}E_{{\rm{AA}}}^{\rm{c}} + N_{{\rm{AB}}}^{\rm{c}}E_{{\rm{AB}}}^{\rm{c}} + N_{{\rm{BB}}}^{\rm{c}}E_{{\rm{BB}}}^{\rm{c}} + N_{{\rm{AA}}}^{{\rm{gb}}}E_{{\rm{AA}}}^{{\rm{gb}}} + N_{{\rm{AB}}}^{{\rm{gb}}}E_{{\rm{AB}}}^{{\rm{gb}}} + N_{{\rm{BB}}}^{{\rm{gb}}}E_{{\rm{BB}}}^{{\rm{gb}}}$$
$$U = N_{{\rm{AA}}}^{\rm{c}}E_{{\rm{AA}}}^{\rm{c}} + N_{{\rm{AB}}}^{\rm{c}}E_{{\rm{AB}}}^{\rm{c}} + N_{{\rm{BB}}}^{\rm{c}}E_{{\rm{BB}}}^{\rm{c}} + N_{{\rm{AA}}}^{{\rm{gb}}}E_{{\rm{AA}}}^{{\rm{gb}}} + N_{{\rm{AB}}}^{{\rm{gb}}}E_{{\rm{AB}}}^{{\rm{gb}}} + N_{{\rm{BB}}}^{{\rm{gb}}}E_{{\rm{BB}}}^{{\rm{gb}}}$$
where N is the number of occurrences of a particular type of pairwise bond in the lattice and E is the energy of a single pairwise bond of that type.
The Monte Carlo simulation on a fixed bicrystal geometry is conducted by randomly swapping a solute and solvent atom within the lattice and accepting the swap with a probability of 1 if it lowers the internal energy of the system or with a probability
![]() ${{\rm{e}}^{{{ - \Delta U} \over {{k_{\rm{b}}}T}}}}$
if the internal energy of the system increases by ΔU, where T is the temperature and k
b is the Boltzmann constant. By performing millions of such swaps, the free energy minimizing configuration is produced. The simulation, however, does not directly provide the free energy of this configuration, which we require to compare the free energy of all the equilibrium systems with different grain boundary volume fractions. To extract the free energy from the Monte Carlo simulation of a particular bicrystal geometry with a fixed solute concentration at a temperature, T, we first calculate the specific heat, C, from the thermodynamic fluctuations of the internal energy for a number of temperatures from 0 K to T:
${{\rm{e}}^{{{ - \Delta U} \over {{k_{\rm{b}}}T}}}}$
if the internal energy of the system increases by ΔU, where T is the temperature and k
b is the Boltzmann constant. By performing millions of such swaps, the free energy minimizing configuration is produced. The simulation, however, does not directly provide the free energy of this configuration, which we require to compare the free energy of all the equilibrium systems with different grain boundary volume fractions. To extract the free energy from the Monte Carlo simulation of a particular bicrystal geometry with a fixed solute concentration at a temperature, T, we first calculate the specific heat, C, from the thermodynamic fluctuations of the internal energy for a number of temperatures from 0 K to T:
where
![]() $\sigma _{U(t)}^2$
is the variance of the internal energy at constant temperature, t. When calculating this variance, each of the samples of internal energy should ideally be uncorrelated from one another; defining a Monte Carlo step as occurring when the number of attempted swaps equals the number of lattice sites in the system, we use internal energy values after every 10 Monte Carlo steps to compute the variance. We then perform a thermodynamic integration of the specific heat to determine the entropy, S(T):
$\sigma _{U(t)}^2$
is the variance of the internal energy at constant temperature, t. When calculating this variance, each of the samples of internal energy should ideally be uncorrelated from one another; defining a Monte Carlo step as occurring when the number of attempted swaps equals the number of lattice sites in the system, we use internal energy values after every 10 Monte Carlo steps to compute the variance. We then perform a thermodynamic integration of the specific heat to determine the entropy, S(T):
where the residual entropy, S
res, is the entropy of the 0 K configuration. The residual entropy is zero when the grain boundary is fully saturated, i.e., when there are exactly enough solute atoms to fully occupy the grain boundary segregation sites. When the grain boundary volume fraction is changed, there can be ground state degeneracy, Ω, in some lattices (such as body-centered cubic) since a plane of N
t atoms that is partially filled with N
s solute atoms can be occupied in
![]() $\Omega = {{{N_{\rm{t}}}!} \over {{N_{\rm{s}}}!\left( {{N_{\rm{t}}} - {N_{\rm{s}}}} \right)!}}$
ways. This results in a residual entropy of
$\Omega = {{{N_{\rm{t}}}!} \over {{N_{\rm{s}}}!\left( {{N_{\rm{t}}} - {N_{\rm{s}}}} \right)!}}$
ways. This results in a residual entropy of
![]() ${S_{{\rm{res}}}} = {k_{\rm{b}}}\ln \left( \Omega \right)$
. From the entropy, the Helmholtz free energy, F, is simply:
${S_{{\rm{res}}}} = {k_{\rm{b}}}\ln \left( \Omega \right)$
. From the entropy, the Helmholtz free energy, F, is simply:
where U
avg(T) is the average internal energy at temperature, T (computed with the same sampling as the specific heat) and
![]() $T \cdot S\left( T \right)$
is the entropic component of the free energy, which we will refer to as the entropic energy.
$T \cdot S\left( T \right)$
is the entropic component of the free energy, which we will refer to as the entropic energy.
To attain such free energies, we begin the simulation at 0 K with a solute configuration that is known to be the ground state based on the set of pairwise bond energies provided. The temperature is then raised in increments of 10 K, performing 10,000 Monte Carlo steps at each temperature up to at least 2000 K. The first 3000 Monte Carlo steps at each temperature are excluded from the specific heat and average internal energy calculations to allow the system to equilibrate to the new temperature. As a model system, we choose an enthalpy of mixing of 20 kJ/mol and an enthalpy of grain boundary segregation of 65 kJ/mol, which matches the energies used by Chookajorn and Schuh (physically representing W alloyed with Ti).
Reference Chookajorn and Schuh26
We use a BCC lattice with a grain boundary along the (100) plane and assign pairwise bonds energies as
![]() $E_{{\rm{AA}}}^{\rm{c}} = E_{{\rm{BB}}}^{\rm{c}} = 0,\;E_{{\rm{AB}}}^{\rm{c}} = 25.9,E_{{\rm{AA}}}^{{\rm{gb}}} = E_{{\rm{BB}}}^{{\rm{gb}}} = 54.8{\rm{,\ and\ }}E_{{\rm{AB}}}^{{\rm{gb}}} = - 61.8$
meV/bond. We calculate minimum free energy configurations over the range of temperatures from 0 to 2000 K for solute concentrations from 1 to 10 at.%.
$E_{{\rm{AA}}}^{\rm{c}} = E_{{\rm{BB}}}^{\rm{c}} = 0,\;E_{{\rm{AB}}}^{\rm{c}} = 25.9,E_{{\rm{AA}}}^{{\rm{gb}}} = E_{{\rm{BB}}}^{{\rm{gb}}} = 54.8{\rm{,\ and\ }}E_{{\rm{AB}}}^{{\rm{gb}}} = - 61.8$
meV/bond. We calculate minimum free energy configurations over the range of temperatures from 0 to 2000 K for solute concentrations from 1 to 10 at.%.
III. ORDER–DISORDER TRANSITIONS AT FIXED GRAIN BOUNDARY AREA
We first study the order–disorder processes that occur from 0 to 2000 K on each bicrystal system separately. At fixed solute concentration, there are four configurational families that are easily distinguished at 0 K for the alloys studied here (i.e., with positive heat of mixing and enthalpically favored grain boundary segregation) based on the grain boundary area of the system:
-
(i) the single crystal (grain boundary area of zero) where solute precipitation is enthalpically favorable.
-
(ii) “oversaturated” systems where the grain boundary area is low, such that solute cannot be entirely accommodated at the grain boundary and excess solutes therefore form a second-phase precipitate (generally first along the boundary),
-
(iii) a “saturated” system in which the grain boundary area is precisely enough to fully accommodate all solute atoms,
-
(iv) “undersaturated” systems where the grain boundary area is higher than the saturated case and solute cannot occupy all of the available grain boundary sites.
Figure 2 shows the order–disorder behavior of each of these cases for a 1 at.% alloy. Two types of ordering emerge in these systems: bulk ordering in the form of phase separation and grain boundary segregation where solute and solvent atoms bond across the grain boundary. We can define order parameters for each of these forms of ordering: the crystalline precipitate order parameter (ηc) is the fraction of solute atoms only bonded to solute atoms (all bonds are crystalline), and the grain boundary order parameter (ηgb) is the fraction of solute atoms that have four solvent grain boundary bonds (which is the lowest energy configuration for grain boundary segregation in the model).

FIG. 2. Order–disorder transitions of 1 at.% alloys at fixed grain boundary volume fraction for each of the four cases. Heat capacities are presented in the first row, followed by crystalline and grain boundary order parameters in the second row, and total system energy in the form of entropic energy, internal energy, and free energy in the third row.
At an order–disorder transition, heat capacity exhibits a peak. The first row of Fig. 2 reveals two clearly distinct such order–disorder peaks when grain boundary area is fixed:
-
(i) The peak around 400 K corresponds to the dissolution (disordering) of the bulk solute precipitate as evidenced by the drop in the crystalline precipitate order parameter. Note that this transition occurs in the single crystal case as well as in the oversaturated case where the precipitate along the grain boundary also undergoes bulk disordering. The single crystal system has a much sharper peak in heat capacity, since all of the solute dissolves into solution at this transition point, as opposed to the oversaturated case where some solute atoms remain segregated at the grain boundary after the bulk disordering transition is completed. Nonetheless, the precipitate dissolution transition appears to occur at roughly the same temperature in this system whether the grain boundary is present or not.
-
(ii) In the oversaturated case, there is a second disordering temperature at around 1000 K, also defined by a peak in the heat capacity, and related to the disordering of the grain boundary segregation state (i.e., dissolution of solute off the grain boundary and into the bulk). All of the three different bicrystal cases exhibit this transition, with the sharpest peak occurring for the saturated case.
These two transitions both reflect entropic disordering, but exhibit some key differences. The bulk phase transition is completed in a relatively small temperature window of ∼100 K, while the grain boundary desegregation transition occurs over a much broader range of almost ∼1000 K. The more gradual nature of the grain boundary desegregation transition is also evidenced in how the characteristic system energies change as a function of temperature, as shown in the third row of Fig. 2. Whereas the free energy exhibits a change in slope at the critical temperature for bulk dissolution, emblematic of a first-order phase transition, that for the grain boundary desegregation reaction is broad and gradual, and thus more likely to be a second-order phase transition.
In Fig. 2, for this specific alloy, the bulk transition occurs at lower temperatures than the grain boundary one. We expect that this should be generally true for a nanocrystalline alloy that is stabilized by grain boundary segregation; the internal energy gained by grain boundary segregation must be sufficiently larger than the internal energy gained by forming the bulk phase in order for the nanostructure to be stable in the first place. When the bulk phase transition occurs, the oversaturated and single crystal states undergo an increase in entropy when the solute precipitate dissolves into a solid solution, which allows these states to lower their free energy significantly at temperatures lower than the saturated and undersaturated systems. This behavior may also explain the ‘nano-duplex’ behavior described in our earlier work, Reference Chookajorn, Park and Schuh30 where a system with second phase bulk precipitates can disorder into a grain boundary-segregated polycrystal; the stable nanocrystalline state is thus an activated state in such alloys.
Figure 3 shows in more depth the effect of decreasing the grain boundary area from the saturated (grain boundary volume fraction of 0.02) to the single crystal case. Figure 3(a) shows the heat capacity peaks for both the single crystal (which exhibits only the bulk dissolution peak), a saturated bicrystal (which exhibits only the grain boundary desegregation peak), and a variety of states in between these two. As grain boundary area (volume fraction) decreases, the peak in specific heat from the bulk phase transition increases in intensity, while the peak from the grain boundary desegregation transition shrinks, as fewer atoms participate in grain boundary desegregation. This corresponds, according to Eq. (3), to larger rises in entropy for more oversaturated bicrystals, as shown in Fig. 3(b). As the grain size rises, these entropy rises trend toward the maximum entropy jump possible, i.e., that for the single crystal, which reaches the neighborhood of the ideal solution entropy, 0.465 J/(mol K). However, the enthalpies follow a similar trend, which can be read from the free energy curves in Fig. 3(c) at low temperatures; the enthalpies increase with decreasing grain boundary area. This trade-off leads to the oversaturated bicrystals becoming equilibrium configurations first before the solid solution’s higher entropy fully dominates as temperature increases. This transition is discussed in more detail in Sec. IV.
IV. ORDER–DISORDER TRANSITIONS FOR STABLE NANOCRYSTALLINE STATES
The true equilibrium state at a given temperature and solute concentration is the state with the grain boundary area that attains the lowest free energy compared with any other at that temperature and concentration. Figure 4(a) shows how the free energy behaves as a function of grain boundary volume fraction at 0, 600, 840, and 1000 K for the same 1 at.% alloy. The grain boundary volume fraction that provides the lowest free energy at a given temperature is the equilibrium state. At 0 K, the saturated state has the lowest internal energy and therefore the lowest free energy as expected. The dependence of free energy on grain boundary volume fraction at 0 K is linear both in the oversaturated regime, where the precipitate is growing, and in the undersaturated regime, where the pure solvent grain boundary is increasing in volume fraction. Systems in the undersaturated regime are not observed to become the equilibrium state at any temperature as free energy increases with grain boundary volume fraction above the saturated state, even beyond the range of values shown in Fig. 4(a).

FIG. 4. (a) Free energy as a function of grain boundary volume fraction at three temperatures: 0 K, 600 K where the stable grain boundary volume fraction is lower, 840 K where the solid solution phase first becomes stable, and 1000 K. (b) The same free energies are also shown with respect to grain size.
At 600 K, the oversaturated cases have undergone their first disordering transition, and entropy plays a significant role in the free energy of the states with grain boundary volume fractions below 0.02, as evidenced by the reduction in free energy relative to the 0 K states. A grain boundary volume fraction of 0.016 is now the lowest free energy configuration, lower in free energy than the saturated state which has not been able to access as much entropy; entropy and the loss of some solute from the grain boundary favors grain growth by a small degree to a somewhat larger equilibrium grain size. The preference for a grain boundary area between the saturated state and the single crystalline state comes from the balance between the enthalpic advantage of grain boundary segregation, which benefits from a larger number of available grain boundary sites, and the entropic advantage of disordering into a solid solution, which benefits from a smaller grain boundary area where more solute atoms originally reside in a bulk precipitate and thus disorder during the first transition. At 840 K, the free energy of the single crystalline state becomes the lowest free energy state, marking a completed transition away from the stable nanocrystalline configuration. As temperature continues to increase, the solid solution state continues to be the lowest free energy state as it has the highest entropy.
As mentioned in the introduction, Chookajorn and Schuh Reference Chookajorn and Schuh26 calculated the internal energy as a function of grain size and found the minimum internal energy to be at a saturated nanocrystalline state; their internal energy dependence on grain size resembles the free energy dependence on grain size at 0 K in Fig. 4(b). The free energy, however, captures temperature effects and shows that as temperature increases, larger grain sizes become more energetically favorable. In addition, at a critical temperature grain growth to a single crystal is entirely downhill in free energy and the nanocrystalline state is no longer stable.
To determine the true equilibrium behavior of the alloy and attain useful relationships, such as equilibrium grain size as a function of temperature, we need to merge the decoupled sampling of the grain boundary network configuration space and the solute configuration space. This is accomplished by defining the properties of the equilibrium state (e.g., energy, configuration, grain boundary volume fraction) at a given temperature to be equal to the properties of the free energy minimizing bicrystal/single crystal at that temperature. Figure 5 shows the equilibrium behavior of the alloy system, now defined as the free energy minimizing configuration across both solute configuration space and grain boundary network configuration space. Overall, the observed behavior is much more similar to a bulk phase transition than the grain boundary desegregation transition. The free energy in Fig. 5(a) shows a more discontinuous change in slope at the transition temperature of 840 K. The corresponding enthalpies and entropies also have an increasing slope as the transition temperature is approached, as opposed to the more gradual increase in internal energy in the saturated bicrystal in Fig. 1. The order parameter in Fig. 5(b) also has an abrupt drop that is similar to the crystalline order parameter in Fig. 1 for the single crystal. This suggests that the transition marking the loss of nanocrystal stability is much like crossing a standard alloy solvus transition and is similarly a first-order transition.

FIG. 5. Order–disorder transitions for a 1 at.% stable nanocrystalline alloy. (a) The free energy, entropic energy, and internal energy, accompanied by (b) the grain boundary and crystalline order parameters, and (c) the grain boundary volume fraction are shown as a function of temperature from 0 K to 2000 K. (d) The equilibrium microstructures at 300, 500, 700, and 900 K.
As the crystalline order parameter decreases in the single crystal case, the volume fraction of the precipitate correspondingly decreases as more solid solution phase is formed. In the case where grain boundary segregation stabilizes a nanocrystalline state, as the grain boundary segregation order parameter decreases, the volume fraction of segregated grain boundary decreases as well, again to form more solid solution phase. This corresponds to a decrease in the grain boundary area as shown in Fig. 5(c), and in the equilibrium microstructures in Fig. 5(d). Effectively, this means that as temperature increases, the equilibrium grain size of a nanocrystalline state should rise. It is also important to note that in each of the microstructures in Fig. 5(d) the grain boundary remains relatively fully segregated, which is necessary in order for the nanocrystalline state to remain energetically favorable.
One of the difficulties with exploring grain boundary network configuration space by performing separate Monte Carlo simulations is that it relies on accurate measurement of free energy from these simulations, which requires fine sampling of temperature to numerically integrate the specific heat, and fine sampling of grain boundary network configuration space. Each of the curves in Fig. 5, particularly the entropic energy, internal energy, and grain boundary volume fraction, have several small jumps where in fact it is more likely that each of those parameters is actually continuous with temperature. The small jumps emerge because in actuality the grain boundary area should change continuously, and our sampling is not fine enough to fully capture the continuous curve. In addition, the calculation of entropy depends on how the specific heat is sampled when the numerical integration in Eq. (3) is conducted, and this leads to some error in the estimation of entropy and correspondingly in the free energy. Thus, even if grain boundary area is sampled more finely these equilibrium curves would likely still not be perfectly continuous due to the differences in the magnitude of the error in free energy in each simulation. Developing a way to overcome this resolution issue is an area for future work in improving the simulation framework. Nonetheless, this method is able to observe the thermodynamic disordering of a stable nanocrystalline state, which previous simulations could not, and is thus a useful tool for understanding how the equilibrium grain size changes during the disordering process.
V. FREE ENERGY AND PHASE DIAGRAMS FOR STABLE NANOCRYSTALLINE STATES
The equilibrium free energy was similarly determined for solute concentrations from 2 to 10 at.%; the general behavior is very similar to the 1 at.% alloy that has been described thus far. Figure 6 shows the free energy diagram that results from these calculations at three temperatures. At 2000 K, the equilibrium phase for all systems in this concentration range is a solid solution, and the free energy curve has a decreasing slope as the solute concentration increases, as is expected for a solid solution phase. At 1550 K, the 7 at.% alloy is at its critical temperature, and the free energy curve above and below this composition exhibits different behaviors. From 1 at.% to 7 at.% where the solid solution phase is stable, the free energy curve has the same decreasing slope behavior as the solid solution phase at 2000 K. From 7 to 10 at.%, the free energy curve becomes a straight line. This is even more evident at 1100 K, where the 3 at.% alloy is at its critical temperature and a straight line emerges from 3 to 10 at.%.

FIG. 6. The free energy diagram at 1100, 1550, and 2000 K for solute concentrations from 1 to 10 at.%, where the solid lines represent systems where the solid solution is stable and the dashed lines represent systems with stable grain boundaries in equilibrium with a solid solution.
The equilibrium state along these straight line regions is a stable bicrystal, resembling the bicrystal microstructures in Fig. 5(d). A straight line in a free energy diagram is indicative of a two-phase equilibrium state, with the free energy determined from the common tangent line between the two equilibrium phases. The two phases for the bicrystal state are the crystalline solid solution phase and the grain boundary “phase”, where the grain boundary “phase” in our model is best likened to a 2D compound. Just as in a standard alloy free energy diagram, the lever rule can be used to determine the volume fraction and concentrations of the two phases present at equilibrium. In the case of nanocrystalline stability, the grain boundary volume fraction is determined by the volume fraction of the grain boundary “phase” and the concentration of solute in the grains is determined by the concentration of the solid solution phase thus defining the configuration of the equilibrium bicrystal/nanocrystalline state.
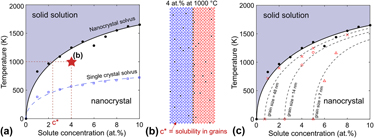
By collecting the group of critical temperatures for transitioning from the nanocrystalline state to the single crystal solid solution at each solute concentration, we construct a phase diagram for a stable nanocrystalline alloy as shown in Fig. 7(a). The solid black dots represent the critical temperatures above which the single crystal solid solution phase is stable and below which a nanocrystalline state is stable. The corresponding solid black line is the solvus for the grain boundary segregated state and it is important to note that this nanocrystal solvus is different than the single crystal solvus we would determine if only single crystalline states are considered [shown by the blue dashed line in Fig. 7(a)]. The single crystal solvus is the solvus traditionally read from a binary phase diagram, denoting the solubility limit with respect to the bulk solute precipitate phase. However, in this system the single crystal solvus has a lower temperature than the nanocrystal solvus at all concentrations as a consequence of the nanocrystalline state being stable in this system and the bulk solute precipitate phase being metastable. The single crystal solvus depends on the enthalpy of mixing; the nanocrystal solvus similarly depends on the enthalpic benefit of the segregated nanocrystal, which is equal to the enthalpy of grain boundary segregation minus the enthalpy of the pure solvent grain boundary.

FIG. 7. (a) The phase diagram for a stable nanocrystalline alloy, where the solid line and black dots represent the transition temperature for forming a solid solution from the nanocrystalline state (nanocrystal solvus). The blue squares represent the transition temperature for forming a solid solution from a bulk precipitate, which form the single crystal solvus for when nanocrystalline states are not considered. The white region is a two-phase region. (b) The equilibrium microstructure for a 4 at.% alloy at 1000 °C [denoted by a star in (a)] for which the concentration of solute in the crystalline region is that of the nanocrystal solvus when read from the phase diagram according to the lever rule. (c) The phase diagram with curves of constant grain size (dashed lines) where unfilled markers (red in color version) denote the temperature at which a particular grain size is stable for a given concentration.
The nanocrystal solvus can be used to determine the composition of the two-phase equilibrium state in the same manner as in a standard binary alloy phase diagram. To illustrate this, take as an example an alloy with 4 at.% solute at 1000 °C [marked by the star in Fig. 7(a), microstructure shown in Fig. 7(b)]. The solvus at 1000 °C corresponds to a solute concentration of 2.4 at.%, which is the concentration of solute in the crystalline regions of the stable nanocrystalline state at 1000 °C. The volume fractions of the crystalline and grain boundary phases are determined by the lever rule between the solvus and the grain boundary “phase”; in our model the grain boundary “phase” has an effective concentration of one-third (a plane of solute atoms is sandwiched between two planes of solvent to form the segregated grain boundary) and is expected to be essentially a line compound. Based on the volume fractions of each phase, the grain boundary volume fraction is determined, which dictates the grain size of the nanocrystalline state.
The nanocrystal solvus is essentially a curve where the grain boundary area goes to zero as a function of solute concentration. We can draw equivalent curves for when the grain boundary area equals a constant greater than zero. The dashed lines in Fig. 7(c) represent such curves for fixed grain boundary volume fractions of 0.015, 0.05 and 0.1, which correspond to grain sizes of 7, 14, and 48 nm. These are effectively curves of equal volume fraction of the second phase according to the lever rule, as all nanocrystals with the same volume fraction of the grain boundary phase have the same grain size. This is an interesting contrast from the phase diagram of Fe–Zr with a metastable nanocrystalline state calculated by Zhou and Luo, Reference Zhou and Luo18 where the constant grain size curves are constant functions of temperature and effectively vertical lines in the phase diagram. Vertical lines would imply a discontinuous change in grain size from the saturated grain boundary volume fraction to a solid solution state, whereas for the thermodynamically stable nanocrystalline states presented here, the phase transition occurs by passing through a two-phase region with increasing solubility and grain sizes decrease accordingly with temperature. While we chose a positive enthalpy of mixing system in this study, this approach can be generalized to include negative enthalpy of mixing systems with stable intermetallics and ordered compounds by using the compound unit approach. Reference Kalidindi and Schuh35
The ability to construct phase diagrams of this type should improve the selection of alloying candidates for stabilizing grain size, as not only can systems be designed to have stable nanocrystalline states at low temperature but also selected based on their ability to retain a fine grain size up to higher temperatures. In addition, the similarities and differences between the order–disorder transition of the nanocrystalline state and that of a standard two-phase alloy allow us to better understand the thermodynamic implications of having a nanocrystalline ground state.
VI. CONCLUSIONS
In this paper, we improve upon the lattice Monte Carlo method for studying the thermodynamics of nanocrystalline alloys stabilized by grain boundary segregation of solute. Specifically, with some algorithmic improvements we are able to explore the processes of disordering and destabilization of the nanocrystalline state as temperature is increased. This method uses Monte Carlo simulations to attain minimum free energy solute configurations on fixed bicrystals with different grain boundary areas. The free energies of these different bicrystals are then compared to determine which system is the equilibrium state at a given temperature.
The simulations show that a solute-stabilized nanocrystalline alloy undergoes a disordering transition that is very similar to a standard bulk phase transition. As temperature increases, solid solution forms at the expense of grain boundary area until a critical temperature where all solute atoms prefer the solid solution phase and thus a single crystal state becomes the equilibrium state. The nanocrystalline states appear to behave similarly to standard two-phase alloy states, even though the second “phase” is a grain boundary state (i.e., a 2D compound or complexion). From the simulations, we have determined how the equilibrium grain size changes for a single system as a function of temperature, providing a phase diagram for a thermodynamically stable nanocrystalline alloy.
ACKNOWLEDGMENTS
This work was supported by the U.S. Army Research office under Grant No. W911NF-14-1-0539. ARK thanks the support of a National Defense Science and Engineering Graduate Research Fellowship.