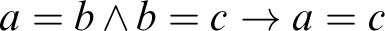WITTGENSTEIN’S ELIMINATION OF IDENTITY FOR QUANTIFIER-FREE LOGIC

Abstract

One of the central logical ideas in Wittgenstein’s Tractatus logico-philosophicus is the elimination of the identity sign in favor of the so-called “exclusive interpretation” of names and quantifiers requiring different names to refer to different objects and (roughly) different variables to take different values. In this paper, we examine a recent development of these ideas in papers by Kai Wehmeier. We diagnose two main problems of Wehmeier’s account, the first concerning the treatment of individual constants, the second concerning so-called “pseudo-propositions” (Scheinsätze) of classical logic such as $a=a$ or $a=b \wedge b=c \rightarrow a=c$ . We argue that overcoming these problems requires two fairly drastic departures from Wehmeier’s account: (1) Not every formula of classical first-order logic will be translatable into a single formula of Wittgenstein’s exclusive notation. Instead, there will often be a multiplicity of possible translations, revealing the original “inclusive” formulas to be ambiguous. (2) Certain formulas of first-order logic such as $a=a$ will not be translatable into Wittgenstein’s notation at all, being thereby revealed as nonsensical pseudo-propositions which should be excluded from a “correct” conceptual notation. We provide translation procedures from inclusive quantifier-free logic into the exclusive notation that take these modifications into account and define a notion of logical equivalence suitable for assessing these translations.

1 Introduction

One of the central logical ideas in Wittgenstein’s Tractatus logico-philosophicus is the elimination of the identity sign from logical notation. At the time, this idea was taken very seriously, for example by Bertrand Russell and Frank Ramsey. Russell considered Wittgenstein’s criticism of Principia’s definition of identity “a destructive criticism from which there seems no escape” (Wittgenstein, 1998, p. 274) and tried to make amends in Principia’s second edition. Frank Ramsey tried to incorporate “Wittgenstein’s discovery that the sign of identity is not a necessary constituent of logical notation” (Ramsey, 1990, p. 194) into his own revision of Principia’s version of the foundations of mathematics. Two other notable commentators were Kurt Grelling and Friedrich Waismann. ¹ But since then, interest has largely faded ² and first-order logic with identity has become standard. In recent years, however, discussion has picked up again and it could be argued that only with the work of authors like Juliet Floyd, Kai Wehmeier and Gregory Landini have we moved close to a full understanding of Wittgenstein’s proposal. In part, this delay seems due to a reluctance to engage not only with the philosophical aspects of the proposal but also with the details of its technical execution.

In this paper we examine what seems to us the most advanced recent development of Wittgenstein’s identity-free logic, which is given in a series of papers by Kai Wehmeier. We diagnose two main problems of Wehmeier’s account, the first concerning the treatment of individual constants (or names), the second concerning so-called “pseudo-propositions” (Scheinsätze) of classical logic ³ such as $a=a$ or $a=b \wedge b=c \rightarrow a=c$ . We argue that overcoming these problems requires two fairly drastic departures from Wehmeier’s account: (1) Not every formula of classical first-order logic will be translatable into a single formula of Wittgenstein’s “exclusive” notation. In many cases there will instead be a set of possible translations, revealing the original formulas to be ambiguous in a certain way. (2) Certain formulas of first-order logic such as $a=a$ will not be translatable into Wittgenstein’s notation at all. These formulas are thereby revealed as nonsensical pseudo-propositions which should be excluded from a “correct” conceptual notation. In order to keep the discussion focused on these two points, our alternative account of Wittgenstein’s exclusive notation in this paper will be restricted to the fragment of quantifier-free logic (i.e., first-order logic with names and identity, but without quantifiers).

2 Wittgenstein’s proposal for the elimination of identity

Wittgenstein’s main proposal concerning identity in the Tractatus is outlined in remarks 5.53 to 5.5352. The core of his proposal is stated right at the beginning: ⁴

5.53 Identity of object I express by identity of sign, and not by using a sign for identity. Difference of objects I express by difference of signs.

He illustrates this proposal with a couple of examples both for individual constants and quantifiers.

5.531 Thus I do not write ‘ $f(a,b).a=b$ ’, but ‘ $f(a,a)$ ’ (or ‘ $f(b,b)$ ’); and not ‘ $f(a,b).\sim a=b$ ’, but ‘ $f(a,b)$ ’.

5.532 And analogously I do not write ‘ $(\exists x,y).f(x,y).x=y$ ’, but ‘ $(\exists x).f(x,x)$ ’; and not ‘ $(\exists x,y).f(x,y).\sim x=y$ ’, but ‘ $(\exists x,y)\\ .f(x,y)$ ’. (So Russell’s ‘ $(\exists x,y).f(x,y)$ ’ becomes ‘ $(\exists x,y).f(x,y).\vee .(\exists x).f(x,x)$ ’.)

Wittgenstein’s convention for individual constants (names) therefore requires a one-to-one correspondence between individual constants and objects. The convention for quantifiers requires that under certain circumstances quantifiers are to be interpreted “exclusively,” i.e., different variables will take different objects as values. ⁵ If carried out, Wittgenstein’s twin conventions are intended to obviate the need for a sign for identity.

It may seem puzzling at first that in another cluster of remarks subordinate to 4.42 which deal with names as “simple symbols,” Wittgenstein seems to give the identity sign a role in logical notation:

4.241 When I use two signs with one and the same meaning, I express this by putting the sign ‘ $=$ ’ between them. So ‘ $a=b$ ’ means that the sign ‘b’ can be substituted for the sign ‘a’.

However, it is important to distinguish between identity as a relation between objects and identity of meaning as a relation between signs. Concerning the first, Wittgenstein clearly states that “identity is not a relation between objects” (5.5301) because “to say of two things that they are identical is nonsense, and to say of one thing that it is identical with itself is to say nothing” (5.5303). Statements expressing sameness of meaning, on the other hand, are merely “rules dealing with signs” (4.241) or “representational devices” (4.242). One crucial question for any account of Wittgenstein’s exclusive notation concerns the interpretation of the identity signs occurring in 5.531 and following. On our view, these remarks show how identity statements understood as rules governing the use of signs can be used for eliminating the identity sign from Russellian notation and it therefore remains true that “the identity sign is not an essential constituent of conceptual notation” (5.533).

As with many of Wittgenstein’s doctrines, he apparently wasn’t interested in working out his proposal for eliminating identity systematically. But there is a very early attempt to work it out by Frank Ramsey, who reported in his classical paper on the foundations of mathematics that “the convention is slightly ambiguous, but can be made definite, and is then workable, although generally inconvenient” (Ramsey, 1990, pp. 194–195). The details of his account were published in manuscripts edited from his Nachlass (Ramsey, 1991). In the meantime, Hintikka (1956) seems to have been the only serious attempt to spell out the proposal. After Hintikka’s canonical paper there has been little serious discussion of the exclusive interpretation of quantifiers until the issue was taken up in Floyd (2001), Wehmeier (2004) and Landini (2007).

3 Wehmeier’s account of the elimination of identity

Since Wittgenstein gives no explicit set of rules for handling his exclusive quantifiers and names, there is some leeway in interpreting the intended convention. As Wehmeier convincingly argues, the so-called “weakly exclusive” interpretation is best positioned both exegetically and systematically. For the weakly exclusive interpretation Ramsey set down the following two semantic rules:

Two different constants must not have the same meaning. An apparent variable cannot [have] the value of any letter occurring in its scope, unless the letter is a variable apparent in that scope. (Ramsey, 1991, p. 159)

The term “letter” here covers both constants (names) and variables. A variable “apparent in the scope” of a quantifier is a variable bound by some quantifier in that scope. So, in effect, the convention tells us that two different names cannot have the same referent and that the range of a bound variable excludes the values (or referents) of any free variable or name occurring in the scope of the binding quantifier. If we take the exclusive formula $\exists x\exists y Fxy$ from remark 5.532 as an example, the variables x and y cannot take the same value because in the subformula $\exists y Fxy$ , the variable x occurs freely within the scope of the quantifier binding the variable y. If names are present, their values are also excluded from the range of any bound variable in the scope of whose quantifier they occur. ⁶

Wehmeier’s procedure for translating classical inclusive formulas into the exclusive notation ⁷ has remained almost invariant throughout his papers and is given here in its latest version. Atomic formulas can be left unchanged. The translation of a conjunction is the conjunction of the translations of the conjuncts. The translation of a negated formula is the negation of the translation of the formula and so on for all other sentence connectives. So the issue boils down to (1) quantifier rules and (2) rules for identity. Statements of the form $\forall x \phi $ are translated by $\forall x \psi \wedge \psi (y_{1}/x) \wedge \psi (y_{2}/x) \cdots $ where $y_{1}, y_{2}, \ldots $ are the free variables (or names) in $\phi $ other than $x, \psi $ is the translation of $\phi $ into exclusive notation and $\psi (y_{1}/x)$ is the translation of $\phi $ into exclusive notation after replacing all free occurrences of x in $\phi $ by $y_{1}$ . Analogously, $\exists x \phi x$ is translated by $\exists x \psi \vee \psi (y_{1}/x) \vee \psi (y_{2}/x) \vee \cdots $ . Identity statements of form $x = y$ are translated by any contradiction in x and y (for example, $Rxy \wedge \neg Rxy)$ while identities of form $x = x$ are translated by any tautology in x (for example, $Px \vee \neg Px$ ). For the purpose of translation, names can be treated as free variables, so $x=y$ and $x=x$ here cover both variables and names. Translating back from Wittgenstein’s system to classical logic can be achieved by similar rules.

Prima facie, it would seem to be a minimal requirement for any attempted reconstruction of Wittgenstein’s account to handle the cases that are explicitly provided in the Tractatus. So it may come as a surprise that Wehmeier’s translation procedure fails this test. Table 1 contains the Russellian formulas of remarks 5.531 and 5.532 along with their translations according to Wittgenstein and Wehmeier. ⁸ We are not going to discuss the quantified cases in detail here. Concerning the quantifier-free cases, something is clearly wrong with case #1. Wittgenstein’s translation of the non-contradictory Russellian formula $Fab \wedge a=b$ is the equally noncontradictoy formula $Faa$ while Wehmeier’s translation $Fab \wedge (Rab \wedge \neg Rab)$ is contradictory, given one-to-one correlations between names and objects (cf. Rogers & Wehmeier, 2012, p. 12). In the next section we examine this and related cases involving individual constants more closely.

Table 1. Comparison of Wittgenstein’s and Wehmeier’s translations

4 The problem of individual constants

4.1 Wehmeier’s treatment of individual constants

The failure in case $Fab \wedge a=b$ is explicitly acknowledged in Rogers & Wehmeier (2012, pp. 11–12). Rogers and Wehmeier argue that no adequate translation is possible because exclusive logic cannot express what is classically expressed by $a=b$ . ⁹ On their view, Wittgenstein’s own translation $Faa$ (or $Fbb$ ) is inadequate, because it fails to have the same truth conditions as the original inclusive formula. However, both $Faa$ and $Fbb$ are implied by $Fab \wedge a=b$ , and so Rogers and Wehmeier speculate that Wittgenstein, faced with the impossibility of adequately translating the case, may have substituted an implication of the original formula for translation. On our view, this dismissal of Wittgenstein’s translation of case #1 reveals a crucial misunderstanding of Wittgenstein’s view of identity statements. Our intention in this paper is to develop an alternative account preserving Wittgenstein’s translation.

As a consequence of excluding case #1, Rogers and Wehmeier have restricted their translatability results in certain ways and argued for the exegetic or systematic adequacy of these restrictions. One remedy considered by them is to impose the so-called “satisfaction principle” on classical logic, i.e., to demand that there be a one-to-one correlation between names and objects. This move would certainly give Rogers’ and Wehmeier’s own translation $Fab \wedge (Rab \wedge \neg Rab)$ the right truth conditions. But while it is clear that Wittgenstein intends the satisfaction principle to obtain for Tractarian logic, he nowhere suggests that it should be imposed as a prerequisite on classical logic. In fact, it would hardly make sense for him to offer $Faa$ or $Fbb$ as translations of $Fab \wedge a=b$ if a and b couldn’t co-refer in the classical statement. Therefore, it is misleading to suggest that in imposing the satisfaction principle on classical logic we would be “[following] Wittgenstein”(Rogers & Wehmeier, 2012, p. 11).

Wehmeier states that, with respect to languages without any individual constants, “W-logic and FOL $^{=}$ are fully equivalent” (Wehmeier, 2008, p. 10). Consequently, another argument given by Rogers and Wehmeier for the adequacy of their presentation of “W-logic” is that, according to Wittgenstein, “names are not essential for a description of the world” (Rogers & Wehmeier, 2012, p. 10). Indeed, the following remark of the Tractatus can be quoted in support of this argument:

5.526 We can describe the world completely by means of fully generalized propositions, i.e., without first correlating any name with a particular object.

In a footnote, Rogers and Wehmeier equate this idea with the eliminability of names from first-order logic and point to a technical proof of this in Boolos, Burgess, & Jeffrey (2007, pp. 255–257). So, in effect, the problem of accounting for Wittgenstein’s translation of case #1 is simply rejected as irrelevant because names can be eliminated from first-order logic without loss of expressive power. One thing to note concerning this argument is that Wittgenstein is very explicit in his examples that individual constants are part of the language of Tractarian logic. So it seems strange to base an argument for the acceptability of a translation procedure on the eliminability of these names. Furthermore, the proof in Boolos merely shows that for each formula $\phi $ containing names there is a formula $\psi $ without names which is satisfiable iff $\phi $ is satisfiable. In our context, this standard of equisatisfiability seems too low to guarantee the expressive adequacy of exclusive translations.

Finally, Wehmeier suggests that the problem could be solved by adding a “co-denotation predicate” to the language of Tractarian logic (Wehmeier, 2008, pp. 12–14), which expresses not identity of object but identity of meaning as a relation between signs. This approach is based on remark 4.241ff (see above, §2). The fact that this is possible and renders Tractarian logic equivalent to classical logic is a significant result. Still, the question remains how this proposal relates to Wittgenstein’s main idea of eliminating the identity sign. Clearly, this idea is not restricted to a sign for “objectual identity”; his claim is straight and simple: there is no need for any kind of identity sign in logic. This point is made clearly in 5.533 and also, for example in Waismann’s “Thesen”(cf. Waismann, 1984, pp. 242–243). Another reason why this isn’t convincing is that it makes little sense as an account of the translations in 5.531. According to metalinguistic identity, the translation of $Fab \wedge a=b$ would not be $Faa$ (or $Fbb$ ) but $Fab \wedge a \equiv b$ with the triple bar representing metalinguistic identity.

So it seems that after considering Wehmeier’s arguments, the fact remains that his translation procedure cannot account for case #1. The arguments for why this isn’t a serious problem are unconvincing and so in the absence of further arguments we have to conclude that either Wittgenstein’s proposal is a failure unless first-order logic is restricted in artificial ways or there must be some other way of accounting for Wittgenstein’s case #1.

4.2 The missing case

Before we go on to discuss case #1 and its possible accommodation in a systematic account of Tractarian logic, we should point out a peculiar gap in Wittgenstein’s presentation of cases. The basic cases concerning names and quantifiers are presented in 5.531 and 5.532. Comparing these two remarks and the five cases presented there, reveals a certain symmetry which is broken at one point. In 5.532, Wittgenstein first presents the cases $\exists x \exists y (Fxy \wedge x=y)$ and $\exists x \exists y (Fxy \wedge \neg x=y)$ , which translate to $\exists x Fxx$ and $\exists x \exists y Fxy$ , respectively. In these two cases, the statement in exclusive notation (which is usually more cumbersome) is actually shorter than the inclusive statement, so let us call these two cases “contracting cases.” These two are followed by a parenthetical remark giving a case which we will (in analogy) call the “expanding case”: $\exists x \exists y Fxy$ , translated as $\exists x \exists y Fxy \vee \exists x Fxx$ . In 5.531, we see that Wittgenstein also first presents the two contracting cases: $Fab \wedge a=b$ , translated either as $Faa$ or $Fbb$ , and $Fab \wedge \neg a=b$ , translated as $Fab$ . What is missing in 5.531, however, is the parenthetical statement of the expanding case. This omission seems all the more striking because it is obvious that the inclusive statement using names, which would correspond to the inclusive $\exists x \exists y Fxy$ , is readily available: it is simply the statement $Fab$ . The symmetry between 5.531 and 5.532 is clearly intentional, so it couldn’t be lost on Wittgenstein that there was a missing case in 5.532. Why didn’t Wittgenstein provide a translation for this case?

The answer seems to be that the translation of the inclusive $Fab$ is even more problematic than the translation of $Fab \wedge a=b$ which has haunted Wehmeier’s account. What seems clear is that the translation of $Fab$ has to contain a disjunction of cases, $Fab$ being equivalent to $Fab \wedge a=b \vee Fab \wedge \neg a=b$ . This would also be in line with the translation of the expanding case $\exists x \exists y Fxy$ . Going on Wehmeier’s sensible rule of translating a disjunction by the disjunction of the translations of the disjuncts, this would seem to yield a disjunction with either $Faa$ or $Fbb$ as first disjunct and $Fab$ (exclusive) as second disjunct. Putting these together would yield either $Faa \vee Fab$ or $Fbb \vee Fab$ (exclusive) as translations of $Fab$ (inclusive). But this is intolerable, because $Faa \vee Fab$ and $Fbb \vee Fab$ are clearly not equivalent. This peculiarity reflects back on Wittgenstein’s translation of case #1 because it makes us wonder what exactly Wittgenstein meant by translating $Fab \wedge a=b$ as “ $Faa$ or $Fbb$ .” It seems clear that this “or” cannot be a disjunction in the object language, but taking it as the license to translate either way (which seems the most natural reading) is also problematic once we go beyond the simplest case. Certainly, the exclusive translations $Faa$ and $Fbb$ are, in a sense, equivalent. This is not logical equivalence in the ordinary sense, but given the co-reference expressed by the identity statement $a=b$ , there should be nothing to distinguish between $Faa$ and $Fbb$ because the names a and b are intersubstitutable throughout the formula. How to incorporate this view into a coherent translation of the “missing case,” however, will be one of the main challenges in this paper.

4.3 Criteria of success

As pointed out in 4.1, Wehmeier (2008, pp. 11–12) contains a proof that Wittgensteinian logic cannot express what is expressed by $a=b$ in classical first-order logic. What this proof boils down to is that there are certain first-order structures which can be distinguished by the formula $a=b$ but cannot be distinguished by any formula of Wittgensteinian logic. Given two structures $U_1$ and $U_2$ in which (1) all predicates apply universally and (2) the only difference between the structures is that in $U_1$ the constants a and b have the same interpretation, whereas in $U_2$ the interpretation $\Im (a)$ differs from $\Im (b)$ , the classical formula $a=b$ will be true in $U_1$ and false in $U_2$ . But there is no formula of exclusive logic for which this holds; all exclusive formulas will be either true in both structures or false in both structures. From the point of present-day model theory, the proof is impeccable. But one could argue that from Wittgenstein’s perspective the concept of “truth condition” used to state the result of the proof begs the question against Wittgenstein. Wittgenstein’s point may be that in the crucial case at the center of the proof there is nothing to distinguish. Adapting some of Wittgenstein’s terminology, the difference between these structures is a mere pseudo-difference.

Still, what the proof shows is that if one is serious about accommodating all of Wittgenstein’s cases, there is no way around facing the possibility that classical and Tractarian logic are not equivalent in the sense that certain things expressible in classical logic may be inexpressible in exclusive notation. Rogers and Wehmeier note that case #1 reveals an “incommensurability” of the two logics under investigation, but lay the blame on Wittgenstein for failing to provide an “adequate translation” (Rogers & Wehmeier, 2012, p. 12). It is clear that there is a strong desire on Wehmeier’s part to show the equivalence between classical and Tractarian logic. Motivating this desire is the idea that only by showing the equivalence between classical and Tractarian logic can we counter indispensability arguments for the identity relation (Wehmeier, 2012, cf.). On our view, we shouldn’t presuppose that strict equivalence to classical logic is necessary to prove the adequacy of the exclusive notation. It may well be that, according to Wittgenstein, certain things expressible only by means of identity are better left unexpressed.

This complicates the search for criteria for assessing the success of any solution. Obviously, the aim would still be to achieve some kind of equivalence between inclusive and exclusive notation, even though the scope of this equivalence will be limited by Wittgenstein’s philosophical arguments concerning identity. In contemporary logic, logical equivalence is usually spelled out by reference to a semantics of the language. Even apart from specific worries about identity, this is somewhat problematic in the context of Tractarian logic, because Wittgenstein was strongly critical of set theory as a tool in the foundations of mathematics and favored a purely syntactical approach to logic. ¹⁰ But we don’t want to restrict ourselves prematurely to this kind of approach. If there is anything wrong in using model theory in our context, this should emerge from our investigations and not be presupposed by fiat.

Because a semantics for the exclusive notation needs to be sensitive to our account of the identity sign, we won’t start until §4.7 to define a suitable concept of logical equivalence. In the meantime we will sometimes use simple classical models to point out certain problems. We might thus illustrate the problem of translating the “missing case” in the following way: If we assign different objects $o_{1}$ and $o_{2}$ to a and b respectively and the set containing only the pair $(o_{1},o_{1})$ to the predicate F, the missing case $Fab$ (inclusive) will turn out false but the hypothetical exclusive translation $Faa \vee Fab$ will turn out true. On the other hand, $Fbb \vee Fab$ (exclusive), which is supposed to be an alternative (and therefore equivalent) translation of $Fab$ (inclusive) turns out false.

4.4 The scope of names

Concerning the failure of equivalence between $Fab$ (inclusive) and $Faa \vee Fab$ (or $Fbb \vee Fab$ ) (exclusive), it is not too difficult to see what’s going wrong. As an intermediate step we have proposed to treat $Fab$ as equivalent to $Fab \wedge a=b \vee Fab \wedge \neg a=b$ . In translating the subformula $Fab \wedge a=b$ (inclusive) into $Faa$ (or $Fbb$ ) (exclusive) we have in effect assumed a and b to refer to the same object. In translating the subformula $Fab \wedge \neg a=b$ (inclusive) into $Fab$ (exclusive) we have in effect assumed a and b to refer to different objects. Therefore it may seem illegitimate to apply the model $\Im (a)=o_{1}$ , $\Im (b)=o_{2}$ , $\Im (F)=\{(o_{1},o_{1})\}$ to the whole formula $Faa \vee Fab$ (exclusive) because the model violates the assumption used for generating the exclusive subformula $Faa$ (or $Fbb$ ). Similarly, any model with $\Im (a)=\Im (b)$ would seem inapplicable to the exclusive subformula $Fab$ .

These observations reveal a certain predicament which may have lead Wehmeier to his treatment of names. If we really want to represent the content of the inclusive formula $Fab$ in one single formula of exclusive notation, we have to ensure that the models we use to evaluate our translations are in line with the identity statements that we used to manufacture the exclusive statements. This would require only models with $\Im (a)=\Im (b)$ to be applied to the first disjunct of $Faa \vee Fab$ and only models with $\Im (a) \neq \Im (b)$ to be applied to the second disjunct. Under such a modified semantics, we get exactly the right truth conditions for our exclusive test statements.

Approaching this as a technical problem, the main challenge then would be how to “remember” which identity statements were used to generate which part of the exclusive formula without making the account circular. As an example of an obviously circular “solution,” we could simply index every subformula in the exclusive statement with the identity statements that went into the translation. Such an account, however, would hardly prove identity to be an expendable part of logical notation. On the other hand, it seems clear that some kind of extra notation is needed to fix the class of applicable models for each subformula. It is not enough, for example, as a general rule, to restrict interpretation to single disjuncts. Just by looking at the exclusive formula, we cannot tell which models we should use to interpret the disjunct $Faa$ in $Faa \vee Fab$ (exclusive). $Faa \vee Fab$ could be the result of translating $Fab$ , but it could also be the result of translating $(Faa \vee Fab) \wedge \neg a=b$ . Only in the first, but not in the second case, would it be appropriate to use models with $\Im (a)=\Im (b)$ for interpreting the disjunct $Faa$ .

Interestingly enough, Wittgenstein himself seems to provide a blueprint for an appropriate notational device in the Notebooks. In the entry for December 2, 1916 he writes:

The similarity of the generality notation and the argument appears if we write $(ax)\phi x$ instead of $\phi a$ . (Wittgenstein, 1998, p. 90)

What Wittgenstein seems to mean is: Instead of using a name to fill the argument position of a predicate, we could leave the open sentence $\phi x$ and use $(ax)$ to indicate that the variable position x is “bound” by the name a. Let us term this device the “denotifier.” There is no indication that Wittgenstein intended to use it for any technical purpose. Nevertheless, we could recruit it for our purposes because the similarity to quantifiers makes it possible to draw a crucial distinction. For the translation of the “missing case,” we could now—quite similar to Wittgenstein’s translation of the expanding case $\exists x \exists y Fxy$ —write $(ax) (by) Fxy \vee (ax) Fxx$ while the translation of $(Fab \vee Faa) \wedge \neg a=b$ would become $(ax) (by) (Fxy \vee Fxx)$ . Similar to quantifiers, each name is thereby assigned a certain scope.

There would still remain the problem of how exactly to fix the class of applicable models. But even assuming any device such as the denotifier could be made to work, we think that there is an overwhelming reason not to pursue this approach, quite apart from the obvious fact that there is no indication whatsoever that Wittgenstein ever intended to introduce this kind of apparatus in order to deal with names in exclusive notation. The main problem is that Wittgenstein’s injunction to “express identity of object by identity of sign” is clearly violated if we use models assigning different referents to a certain name in different parts of the formula. According to Wittgenstein, one name should have the same meaning throughout a formula and different names should have different meanings throughout the formula. There is simply no way to do justice to this requirement while segmenting a formula into different scopes in which the same name may have different meanings or different names may have the same meaning. The “missing case” therefore faces us with a stark choice: Either we must give up Wittgenstein’s main principle concerning identity and invent a device such as the denotifier or we must give up the representability of the missing case (and similar cases) in a single exclusive formula. In the next section, we want to explore this second option.

4.5 Translation as disambiguation

So far, we have concluded that the inclusive formula $Fab$ seems to contain two possibilities of translation into exclusive notation: $Faa$ (or, equivalently, $Fbb$ ) and $Fab$ . The inclusive notation leaves these two possibilities open and it is this feature that cannot be represented in a single formula in the exclusive notation. The question may then be: Should it be possible to represent these possibilities or is there some way to show that, from Wittgenstein’s standpoint, all is well if we reject the representability of this feature in a single formula?

As an alternative approach, we could argue that the inclusive statement $Fab$ is ambiguous between the case $a=b$ , which can be expressed as $Faa$ or $Fbb$ and the case $\neg a=b$ , which can be expressed as $Fab$ . Because in the exclusive notation, the correlation between names and objects has to be one-to-one, the only way to represent this ambiguity is to say that $Fab$ (inclusive) becomes either $Faa / Fbb$ (exclusive) or $Fab$ (exclusive). A similar use of “metalinguistic disjunction” can be found explicitly in remark 5.531. The inclusive $Fab \wedge a=b$ , Wittgenstein proposes to translate by $Faa$ “or” $Fbb$ . It’s obvious that this is not a disjunction in the object language. It is a license to write either $Faa$ or $Fbb$ , not a license to write $Faa \vee Fbb$ .

We propose that a similar reading could be applied to the translation of the “missing case.” The analogy is this: In both cases there is a multiplicity of possible translations which cannot be expressed by a disjunction of cases in the object language. In translating $Fab$ (inclusive), we have to make up our minds whether to write $Faa$ or $Fab$ (both exclusive). From this viewpoint, translation becomes a form of disambiguation. Of course, there is also a disanalogy between the two cases. In the case of translating $Fab \wedge a=b$ (inclusive), the exclusive translations $Faa$ and $Fbb$ are, in a sense, equivalent. By this, we don’t mean that they are logically equivalent in the ordinary sense (they aren’t). But given the co-reference expressed by the identity statement $a=b$ , there is nothing to distinguish between $Faa$ and $Fbb$ because the names a and b are intersubstitutable throughout the formula. In the case of translating the missing case $Fab$ , the two possible translations are nonequivalent in that sense; they are different possibilities of disambiguation. So there are two distinct metalinguistic uses of “or” that cannot be translated by a disjunction in the object language. $Fab \wedge a=b$ (inclusive) can equivalently be translated as $Faa$ “or” $Fbb$ (both exclusive). $Fab$ (inclusive) can nonequivalently be disambiguated as $Faa$ “or” $Fab$ (both exclusive). ¹¹

There is some evidence in the text of the Tractatus that Wittgenstein may have thought that anyone who understands a certain sentence must already know whether the names occurring in that sentence have the same meaning or different meanings (see, for example, remarks 4.243 and 6.2322), so that all we have to do for translating a sentence like $Fab$ (inclusive) is to decide whether what we mean is $Faa$ (exclusive) or $Fab$ (exclusive). A good way to motivate this approach independently of a Tractarian perspective is by appeal to Etchemendy’s distinction between interpretational and representational semantics (cf. Etchemendy, 1999). According to Etchemendy, there are two ways to understand the models of a formal language. On the representational view, different models represent different possible configurations of the world. For example, a truth table may tell us, that the sentence “Snow is white and roses are red” would be false if snow was not white. On the interpretational view, the truth table would support a much different counterfactual, not about the world, but about language. For example, the sentence “Snow is white and roses are red” would have been false had “Snow is white” meant what “George Washington had a beard” means now.

When we look at the models of first-order logic through this lens, it seems obvious that the interpretation of names belongs to the interpretational paradigm, while the interpretation of predicates is much more naturally understood as representational. According to Etchemendy, a standard representational semantics for a language needs two things: “First we define a class of models that will represent all possible configurations of the world relevant to the truth values of our sentences”(Etchemendy, 1999, p. 21). The second is a recursive definition of truth, but let’s focus on the first step. What aspects of classical models can reasonably be understood as “representing possible configurations of the world”?

It seems clear that the representational reading is much more natural for the interpretation of predicates than for the interpretation of names. What really changes between $\Im (a)=\Im (b)$ and $\Im (a) \neq \Im (b)$ ? Only what the names a and b mean in the model. The change affects only the “Bezeichnungsweise” (“mode of signifying,” cf. 3.3421). On the other hand, the change from $\Im (F)=\{\}$ to $\Im (F)=\{(o_{1},o_{1})\}$ can readily be understood as the change from a world in which no objects stand in the relation F vs. a world in which at least one object $o_{1}$ has F to itself.

From Wittgenstein’s standpoint, logic should only represent facts, which are “the existence of states of affairs” (2), which are formed by “configurations of objects” (2.0272). Anything belonging only to the mode of signifying may be shown, but cannot be said. From this standpoint, it seems natural to insist that the interpretation of names in classical model theory doesn’t really belong there. Interpreting a name is just a way of fixing its meaning and finding out what a sentence means is a prerequisite for translating it. So as long as we don’t even know whether a and b refer to the same object or to different objects, there is no way to unambiguously represent $Fab$ (inclusive) as a single formula in the exclusive notation. If we insist on formulating an algorithm for providing exclusive translations of inclusive formulas including names, all we can do is offer possible translations. To repeat: $Fab$ (inclusive) considered by itself is ambiguous because it is unclear whether a and b refer to the same or to different objects. In exclusive notation, we can express this ambiguity by offering the set of two possible translations: $\{Faa, Fab\}$ .

This account of translating from inclusive to exclusive statements puts into effect the understanding of identity Wittgenstein expresses in remarks 4.241 and following (cf. §2). The statement $a=b$ is not an assertion that can be true or false, it is a rule for the use of the signs a and b, allowing a to be substituted for b and vice versa. Putting this understanding into effect dispels the problems concerning constants that have plagued Wehmeier’s account and preserves Wittgenstein’s translations offered in 5.531.

4.6 Translating prefix-matrix forms

Can we generalize the paradigm cases we have examined so far into a procedure for translating at least a fragment of quantifier-free classical logic into the exclusive dialect? The formulas $Fab \wedge a=b$ and $Fab \wedge \neg a=b$ exemplify a way of thinking about identity statements that has emerged in the context of the “denotifier”: There is a certain analogy between identity statements and quantifiers. Similar to the way a “prefix” of quantifiers governs the use of variables in a “matrix,” the statements $a=b$ and $\neg a=b$ can be seen as rules governing the use of names in the statement $Fab$ . To keep the analogy tight, we will at first extend this approach to formulas in “prefix-matrix form” (PMF), i.e., formulas consisting of an identity-free part (the “matrix”) connected by conjunction to a conjunction of identity statements (the “prefix”). We stipulate that (1) the prefix may be empty, but not the matrix, (2) prefixes should be consistent and nonredundant and (3) all names occurring in the prefix must occur in the matrix. ¹² The reasoning behind these stipulations will emerge more clearly in the next two sections; but for the moment we simply want to restrict ourselves to cases in which the prefix can clearly be interpreted as a set of rules governing the use of names occurring in the matrix.

The first challenge will be to define the notion of an unambiguous formula in prefix-matrix form. The number of possible interpretations of an ambiguous formula in PMF will depend on two factors: (1) the number of names used in the matrix and (2) the prefix. Mathematically, the most succinct way of expressing possibilities of disambiguation based on a set of names is by co-reference sets, which are partitions of the set of names into sets of co-referring names. For two names a and b there are only two possible partitions: $\{\{a,b\}\}$ , in which a and b co-refer and $\{\{a\},\{b\}\}$ , in which a and b have distinct reference. For three names there are five, for four names fifteen. In general, the number of possible disambiguations of a formula with n names will be equal to the nth Bell number. Let us call a conjunction of identity statements inducing a partition on a set of names a “canonical conjunction of identity statements” or “canonical conjunction” (CC) for short. A canonical conjunction expressing the co-reference set $\{\{a,b\}, \{c,d\}\}$ , for example, will be $a=b \wedge c=d \wedge \neg a=c$ . ¹³ A formula in prefix-matrix form will then be considered unambiguous if the prefix is “canonical” relative to the matrix.

If a given prefix-matrix form is ambiguous, it has to be expanded into a disjunction of unambiguous PMF. This can be achieved by considering the set of all co-reference sets consistent with the given prefix. The original formula will be equivalent to the disjunction of the conjunctions of the matrix with CCs expressing the elements of this set. Let us call this disjunction of unambiguous PMF, which is equivalent to the original PMF, the “disambiguating disjunction” (DD) for that PMF. Based on the DD of the formula, the set of possible translations into exclusive notation can then be generated by substituting in accordance with the prefixes of the individual disjuncts of the DD, each disjunct generating one possible translation. ¹⁴ For illustration, here are the steps for the missing case $Fab$ : Based on the set $\{a,b\}$ of names occurring in the matrix $Fab$ , there are two CC: $a=b$ and $\neg a=b$ , expressing the co-reference sets $\{\{a,b\}\}$ and $\{\{a\}, \{b\}\}$ , respectively. Since both CC are consistent with the (empty) prefix of $Fab$ , the disambiguating disjunction of unambiguous PMF is $Fab \wedge a=b \vee Fab \wedge \neg a=b$ . ¹⁵ Each disjunct of the DD yields a possible translation by substituting in accordance with the respective CC, yielding the set $\{Faa,Fab\}$ of possible translations.

4.7 Logical equivalence for prefix-matrix forms

At this point we return to the question posed in §4.2: Is there a sense in which a set of possible exclusive translations can be considered logically equivalent to an inclusive formula? There are two main difficulties for defining a suitable concept. First, we have to explain what it means for a single formula to be logically equivalent to a set of formulas. Second, there is the fact that, while classically understood, identity statements contribute to the truth conditions of a formula, exclusively understood they instead fix the meaning of the identity-free part of the formula. In order to do justice to the exclusive viewpoint, the definition of logical equivalence has to reflect this difference.

In the last section, we already defined the concept of a “disambiguating disjunction,” which is the disjunction of unambiguous PMF equivalent to some ambiguous PMF of inclusive logic. Since each disjunct of the DD generates one possible exclusive translation, we solve the first difficulty by defining an inclusive PMF $\phi $ to be logically equivalent to a set of possible exclusive translations iff for every disjunct of the disambiguating disjunction of $\phi $ there is a logically equivalent exclusive translation in the set of possible translations and vice versa. Logical equivalence between individual unambiguous inclusive formula (the “DD”) and individual exclusive translation can be defined by restricting the available models to those we may term “appropriate” to the prefix that goes into the translation. In the example of the missing case, we will thus only use models with $\Im (a)=\Im (b)$ for assessing the equivalence between $Fab \wedge a=b$ and $Faa$ and only models with $\Im (a)\neq \Im (b)$ for assessing the equivalence between $Fab \wedge \neg a=b$ and $Fab$ .

In general, an unambiguous inclusive formula in PMF $\phi $ is logically equivalent to an exclusive formula $\psi $ iff for all models M that are appropriate for $\phi $ , M satisfies $\phi $ iff it satisfies $\psi $ . A model M is considered appropriate for $\phi $ iff its interpretation of names is consistent with the prefix of $\phi $ . ¹⁶ An interpretation of names is consistent with a prefix iff it would classically be considered to make the prefix true. On this conception, $\{Faa, Fab\}$ indeed proves to be a logically equivalent exclusive translation of $Fab$ (inclusive).

5 The problem of pseudo-propositions

5.1 Wehmeier’s approach to pseudo-propositions

Next to the problem concerning names there is a second problem with Wehmeier’s account of Wittgenstein’s elimination of identity having to do with so-called “pseudo-propositions” (Scheinsätze) of classical logic. Following the outline of his proposal in remarks 5.53 to 5.533, Wittgensteins claims:

5.534 And now we see that in a correct conceptual notation pseudo-propositions like ‘ $a=a$ ’, ‘ $a=b.b=c.\supset .a=c$ ’, ‘ $(x).x=x$ ’, ‘ $(\exists x).x=a$ ’, etc. cannot even be written down.

From the standpoint of classical logic, all these formulas would be considered logical truths. Since we are dealing only with quantifier-free logic at the moment, we may restrict our attention to $a=a$ and $a=b \wedge b=c \rightarrow a=c$ (a.k.a. the law of transitivity). Based on our interpretation of Wittgenstein’s understanding of the identity sign so far, why would he consider these formulas to be “pseudo-propositions”? For one, it seems clear that neither of the two is interpretable as a substitution license or prohibition fixing the use of names in any way. Second, these formulas lack matrices, consisting purely of identity statements. Most interpreters have taken 5.534 to exclude formulas like $a=a$ from the “correct conceptual notation.” ¹⁷ Wehmeier, as we have seen, takes a different approach. He takes statements of the form $x=x$ to be translatable into a tautology involving x, and statements of the form $x=y$ to be translatable into a contradiction involving x and y.

The essential virtue of this approach, which was probably decisive for Wehmeier’s endorsement of it, is the fact that only by translating $a=a$ as a tautology is there any hope of getting equivalent exclusive translations for equivalent inclusive statements. In classical logic, $a=a$ is equivalent to $Fa \vee \neg Fa$ . So any translation procedure that would translate a truth-functional tautology into a truth-functional tautology, but would deny $a=a$ representation in the exclusive notation, would violate what we could call the “equivalence principle,” namely, that formulas which are classically equivalent should also have equivalent exclusive translations. In order to make this principle precise, let us call two exclusive formulas $\phi $ and $\psi $ logically equivalent iff for all models M that are 1-1 on the set of names M satisfies $\phi $ iff M satisfies $\psi $ . ¹⁸ We can then define two classical formulas $\phi $ and $\psi $ to have equivalent exclusive translations iff either (1) both are classified as pseudo-propositions from the exclusive standpoint, or (2) neither $\phi $ nor $\psi $ are classified as pseudo-propositions and their translations are equivalent.

The evidence that Wittgenstein didn’t intend the pseudo-propositions of 5.534 to be represented by tautologies or contradictions is very strong, however. In 5.531, the phrase Wittgenstein uses to give his translations is “Ich schreibe also nicht [ $\ldots $ ], sondern [ $\ldots $ ].” ¹⁹ So it seems obvious that there is an intended contrast, when in 5.534 he says, “dass Scheinsätze wie [ $\ldots $ ] sich in einer richtigen Begriffsschrift gar nicht hinschreiben lassen” (our emphasis). ²⁰ Wehmeier thinks we should interpret this phrase literally: Since the new notation doesn’t contain the identity sign, $a=a$ literally cannot be written down (Rogers & Wehmeier, 2012, p. 13). But given the context of the remark this seems artificial. If Wittgenstein had wanted to use a tautology as the exclusive transcription of $a=a$ , it would have been natural for him to write “Ich schreibe also nicht $a=a$ , sondern $Fa \vee \neg Fa$ ” (or any other tautologous formula). Also the expression “gar nicht” (“not at all”) seems to indicate that there is nothing to be written down. Finally, if Wittgenstein only meant to say that these pseudo-propositions cannot literally be written down, this would also exclude the sentences in 5.531 to 5.5321 from being written down since they also include the identity sign. But for these sentences Wittgenstein explicitly offers instructions on how to write them down. We also take issue with Wehmeier’s suggestion that pseudo-propositions like $a=a$ are conceptually in the same category as truth-functional tautologies. ²¹ It is widely agreed that there is a distinction to be made between non-sensical pseudo-propositions and merely senseless tautologies. ²² Tautologies are never marked as “Scheinsätze” in the Tractatus. ²³

An even stronger piece of evidence comes from an interesting letter by Wittgenstein addressed to Ramsey in 1927. In his “Foundations of Mathematics” Ramsey had acknowledged Wittgenstein’s criticism of identity, but instead of abandoning it, he defined a substitute for the identity relation. According to this definition, any formula of the form $x=y$ will be either tautologous or contradictory. Now, in the letter criticizing Ramsey’s definition, Wittgenstein writes, after summarizing Ramsey’s account:

I will try to show that this definition won’t do nor any other that tries to make $x=y$ a tautology or a contradiction. (Ramsey, 1991, p. 339, our emphasis)

From an exegetical point of view this seems to settle the issue. We may still reflect about why Wittgenstein didn’t want to “make $x=y$ a tautology or a contradiction”. One systematic reason seems to be Wittgenstein’s analysis of logical truth as truth-functional tautology. Logical truth is not a matter of the content of any statement but only of the form of truth-functional combination of atomic propositions. But this wouldn’t be true of identity statements because statements like $a=a$ or $\forall x \, x=x$ would emerge as logical truths which are not truth-functional tautologies. Also, since $a=a$ seems to be an atomic proposition and yet a logical truth, it would no longer be possible to think of the world as an assignment of truth-values to atomic propositions. ²⁴ According to Wittgenstein, all atomic propositions represented in the formalism should be bipolar, i.e., capable of being true or false, which certainly isn’t the case for $a=a$ .

5.2 Excluding pseudo-propositions

As a next step, we should wonder how comprehensive is this class of nonsensical pseudo-propositions? Concerning instances of the “law of identity,” i.e., formulas like $a=a$ or $b=b$ , the reasoning seems clear. Applying the understanding of identity statements we ascribe to Wittgenstein, we argue that, since any name is always substitutable for itself, $a=a$ represents an empty substitution rule. Analogously, we argue that $\neg a=a$ , which is not explicitly treated in 5.534 (or anywhere else in the Tractatus), must be considered a nonsensical substitution rule prohibiting the substitution of a name for itself. This difference between empty and nonsensical rules becomes important when we consider $a=a$ and $\neg a=a$ as possible prefixes. In $Fab \wedge a=a$ the prefix is redundant; since nothing is prescribed it can be eliminated without loss. So in our view $Fab \wedge a=a$ is equivalent to $Fab$ and can be disambiguated as $Faa$ or $Fab$ (exclusive). In $Fab \wedge \neg a=a$ , however, the prefix is nonsensical, prescribing something impossible. On our interpretation, this vitiates any translation into exclusive notation. What about $a=b$ ? This is neither a redundant nor a nonsensical substitution rule, but occurring in isolation, it is unclear what the rule is supposed to be applied to. Exploiting the prefix-matrix analogy, $a=b$ by itself may be considered similar to a quantifier occurring by itself. But $\forall x$ or $\exists x$ by itself would usually not be considered a well-formed formula. Our conclusion is that $a=b$ by itself should similarly be considered ill-formed and therefore denied translation. ²⁵ In summary:

• • Any prefix not governing any matrix must be considered nonsensical because there is no proposition the substitution rules are applied to.

• • Identity-logical “truths” such as $a=a$ or the law of transitivity occurring in a prefix governing a matrix must be considered redundant because they don’t fix the use of names in any way.

• • Identity-logical “falsehoods” such as $\neg a=a$ occurring in a prefix governing a matrix must be considered nonsensical because there is no coherent way to prescribe different meanings for one and the same name.

In §5.1 we introduced the “equivalence principle” stating that formulas which are classically equivalent should also have equivalent exclusive translations. It is clear that this principle is violated if we deny formulas like $a=a$ , $a=b$ or $\neg a=a$ representation in the exclusive notation. For example, $Fa \vee \neg Fa$ is classically equivalent to $a=a$ . However, since the first formula is in prefix-matrix form (with an empty prefix) it can be translated into $Fa \vee \neg Fa$ while $a=a$ by itself has no exclusive translation. Thus, classically equivalent formulas receive translations into exclusive notation which are non-equivalent in the sense that one is translated as a tautology while the other is denied representation. As we see it, this strange feature of the exclusive notation is a consequence of Wittgenstein’s critique of the classical understanding of identity. Conceptualizing identity as a relation between objects can be seen as the kind of “misunderstanding of language” to be cleared up by philosophical analysis. From Wittgenstein’s perspective, classical quantifier-free logic falls short of constituting a proper logic. This defect shows up in the way the proper understanding of identity (as a rule governing the use of signs) invalidates certain classical formulas and principles of inference. However, in the cases we have dealt with so far, this violation of the equivalence principle is merely a “local” violation in the sense that it only affects the distinction between nonsensical pseudo-propositions on the one hand and merely senseless tautologies and contradictions on the other hand. In other words, there aren’t any cases in which the equivalence principle is violated unless the translation of equivalent formulas yields a tautology or contradiction in one case and is rejected as a pseudo-proposition in the other case.

6 Towards a generalized translation procedure

6.1 Disjunctive prefix-matrix forms

We are now in possession of (1) a positive criterion defining a class of formulas whose translation into exclusive notation seems clear (“prefix-matrix form”) and (2) a negative criterion defining a class of formulas which must be considered untranslatable (“pseudo-propositions”). In between these classes, there is still a large gray area of formulas whose translatability is doubtful. In this and the next section we attempt to generalize both of our criteria into an account covering this area.

In §4.6, we only considered formulas consisting of a single matrix and a single prefix. We now consider disjunctive prefix-matrix forms (DPMF), which we define as disjunctions (which may be of length one) of subformulas in prefix-matrix form as defined in §4.6. Since a DPMF will typically have multiple matrices and multiple prefixes, we have to adjust condition (3) for prefixes (cf. §4.6): names in prefixes should occur in some matrix of the DPMF (not necessarily the matrix governed by the prefix). To generate the DD for a DPMF we proceed as follows:

1. 1. Generate the set of canonical conjunctions expressing all possible partitions of the set of names occurring in any matrix.

2. 2. For each CC in the set that is consistent with at least one prefix in the DPMF, we generate one disjunct of the DD by:

   1. (a) Forming the disjunction of all matrices of the DPMF whose prefix is consistent with the CC.

   2. (b) Conjoining the CC as prefix to this disjunction.

Let us illustrate this procedure with an example. For the formula $(Fab \vee Gab) \wedge a=b \vee Fac \wedge a=b \wedge \neg a=c$ , which is in disjunctive prefix-matrix form, there are two CCs expressing different partitions of the set of names compatible with at least one of the prefixes: $\{a=b \wedge a=c, a=b \wedge \neg a=c\}$ . To generate the disambiguating conjunction, we take each CC in turn and conjoin it to the disjunction of all matrices whose prefixes are consistent with the CC. This yields the DD $(Fab \vee Gab) \wedge a=b \wedge a=c \vee\\ (Fab \vee Gab \vee Fac) \wedge a=b \wedge \neg a=c$ . Each disjunct of the DD is an unambiguous PMF and can be used to generate one possible exclusive translation by substitution, yielding the set of possible translations $\{Faa \vee Gaa, Faa \vee Gaa \vee Fac\}$ . Since a DPMF generates a disambiguating disjunction just like the more restrictive PMF, the definition of logical equivalence given in 4.7 applies equally to DPMF.

6.2 Disjunctive normal forms

Disjunctive prefix-matrix forms are still a fairly narrow class of formulas. For further generalization we take a second look at the stipulations for prefix-matrix form in §4.6. There we required (1) that the matrix not be empty, (2) that the prefix be consistent and nonredundant and (3) that all names occurring in prefixes also occur in the matrix. Stipulations (1) and (2) were partly borne out by our analysis in Section 5.2, since identity statements occurring in isolation, as well as inconsistent prefixes, were ruled out as nonsensical. Concerning prefixes like $a=a$ , we argued that they were not strictly nonsensical but merely redundant. “Allowing” the substitution of a name for itself seems to be compatible with any “mode of signifying” whatsoever, so that $Fab \wedge a=a$ should have the same translation as $Fab$ . We now also argue that an inconsistent prefix governing a single disjunct, as for example in $Fab \vee Gab \wedge \neg a=a$ , doesn’t affect other disjuncts and should be treated as a disjunct incompatible with any CC, leading to the elimination of the disjunct. Finally, concerning (1), we argue that a formula containing a disjunct with empty matrix such as $Fab \vee a=b$ is not nonsensical per se, but only relative to a given CC consistent with the matrix-less prefix. Disambiguating the formula according to the CC $\neg a=b$ we simply eliminate the second disjunct on the ground of its prefix being inconsistent with the CC. On this view, $Fab \vee a=b$ would receive the same translation as the formula $Fab \wedge \neg a=b$ .

Concerning condition (3), we see that formulas like $Fab \wedge c=d$ have both a matrix and a consistent prefix, but matrix and prefix bypass each other. We argue that $Fab \wedge c=d$ is analogous to $\exists x \phi $ where x has no free occurrence in $\phi $ . Depending on the way the syntax is set up, such cases may either be rejected as ill-formed or else the semantics should make clear that the quantifier contributes nothing to the truth-conditions of the formula and could be eliminated without loss. In fact, we can convince ourselves that something like the latter is the case for $Fab \wedge c=d$ by the following consideration: In what way could the identity $c=d$ become relevant for the translation of the matrix $Fab$ ? For each of the names c and d there are two possibilities: Either it co-refers with one or both names in the matrix—then it could be substituted for that name, but we could also express the same meaning by leaving the original name in place; or its reference is different from both names in the matrix—then the name doesn’t occur in any matrix and is irrelevant for translating the formula. The same reasoning can be applied to convince ourselves that $c=d$ is irrelevant for translating the first disjunct in $Fab \vee c=d$ , but here the additional question arises whether this formula should count as a pseudo-proposition. Relative to a hypothetical CC in which c and d co-refer, it should indeed. But for any such CC there is another CC differing from the first one only with respect to c and d having different reference. Disambiguation according to this second CC will eliminate the deviant disjunct, leaving only the first disjunct $Fab$ for translation. We therefore propose to eliminate all prefixes containing names not occurring in any matrix. In the case of $Fab \vee c=d$ this leads to the elimination of the second disjunct. Thus, according to this argument, $Fab \wedge c=d$ and $Fab \vee c=d$ are equivalent to $Fab$ with respect to their translation into exclusive notation.

As it turns out, there is little to distinguish DPMFs in which conditions (1)–(3) are relaxed in the way just described from ordinary disjunctive normal forms of quantifier-free logic. One major conceptual difference between DPMFs and disjunctive normal forms (DNFs) is that the former are guaranteed to have at least one possible translation into exclusive notation, while DNFs may also be pseudo-propositions not translatable at all. Here is the algorithm for generating the DD for a DNF:

1. 1. Eliminate all prefixes or elements of prefixes containing names not occurring in any matrix.

2. 2. If any disjuncts remain, generate the set of canonical conjunctions expressing all possible partitions of the set of names occurring in any matrix.

3. 3. For each CC in the set that is consistent with the prefix of at least one disjunct in the DNF:

   1. (a) if any of these disjuncts with a prefix consistent with the CC has no matrix, there is no possible translation according to this CC;

   2. (b) if all prefixes consistent with the CC have matrices we generate one disjunct of the DD by:

      1. (i) Forming the disjunction of all matrices of the DNF whose prefix is consistent with the CC.

      2. (ii) Conjoining the CC as prefix to this disjunction.

If no DD is generated, the formula is a nonsensical pseudo-proposition. A disjunct consisting only of a redundant prefix by itself, for example, will be consistent with any CC and therefore any formula containing it will not yield any translations. A disjunct containing a contradictory prefix will be inconsistent with any CC and not yield any translation for that disjunct. If a disjunct consists only of identities containing names not occurring in any matrix, elimination of the prefix will eliminate the whole disjunct.

Concerning the definition of logical equivalence given in §4.7 we may wonder whether it is extendable to pseudo-propositions. A simple consideration shows that it is. We have to distinguish two cases: If the algorithm generates a DD, the definition clearly applies. If the algorithm generates no DD, thus revealing the formula to be a pseudo-proposition, the definition also applies because for every disjunct of the DD (namely, none) there is an equivalent translation (and vice versa). The algorithm for disjunctive normal forms therefore performs a double function: it disambiguates a formula insofar it is meaningful (i.e., not nonsensical), but it may also reveal a formula itself or aspects of it (as in $Fab \vee a=b$ ) to be nonsensical.

Given a translation procedure for disjunctive normal forms, extending the account to arbitrary formulas of quantifier-free logic may seem easy. After all, any formula of quantifier-free logic has an equivalent disjunctive normal form. However, as we have seen in §5, equivalence transformations considered valid in classical logic are put in doubt by Wittgenstein’s account of the role of identity statements. Tautology introduction, for example, is an equivalence transformation of classical logic that allows us to go from $a=b$ to $(Fab \vee \neg Fab) \wedge a=b$ . But the first formula is considered nonsensical by our account while the second is translated as a tautology. Therefore, tautology introduction is not an equivalence transformation from the standpoint of exclusive logic. Before extending our account to arbitrary formulas of quantifier-free logic we would have to make sure that none of the equivalence transformations needed to transform an arbitrary formula into disjunctive normal form changes the exclusive translation of the formula. These are: definition of operators in terms of disjunction, conjunction and negation, De Morgan’s laws and distributive laws. If we assume these to be unproblematic, full generality of the algorithm could be achieved by transforming any formula into disjunctive normal form and then applying the algorithm. ²⁶

This concludes our treatment of Wittgenstein’s elimination of identity for quantifier-free logic. The next step in the development of exclusive logic would be to extend our treatment to quantified logic, but since this leads to a host of further difficult problems, we reserve this step for a different occasion.