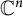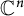1 Introduction
Studying Dirichlet-type spaces in the unit ball of
![]() ${\mathbb C}^n$
, we can draw conclusions for classical Hilbert spaces of holomorphic functions such as the Hardy, Bergman, and Dirichlet spaces. General introduction to this theory can be found in [Reference Rudin18, Reference Zhu22].
${\mathbb C}^n$
, we can draw conclusions for classical Hilbert spaces of holomorphic functions such as the Hardy, Bergman, and Dirichlet spaces. General introduction to this theory can be found in [Reference Rudin18, Reference Zhu22].
The purpose of this note is to characterize model polynomials and to study special families of functions that are cyclic for the shift operators on these spaces. Moreover, we give a sufficient capacity condition in order to identify noncyclic functions. Norm comparisons, sharp decay of norms for special subspaces, capacity conditions studied in [Reference Bénéteau, Condori, Liaw, Seco and Sola3, Reference Bénéteau, Condori, Liaw, Seco and Sola4, Reference Bergqvist6, Reference Sola21] are the main motivation for this work. The cyclicity of a function f in a space of holomorphic functions is connected also with the problem of approximating
![]() $1/f$
(see [Reference Sargent and Sola19, Reference Sargent and Sola20] for the study of this subject).
$1/f$
(see [Reference Sargent and Sola19, Reference Sargent and Sola20] for the study of this subject).
Full characterization of polynomials in more than two variables looks like a hard problem either in the unit ball or the polydisk. The cyclicity problem of polynomials for the bidisk was solved in [Reference Bénéteau, Knese, Kosiński, Liaw, Seco and Sola5] and shortly after extended in [Reference Knese, Kosiński, Ransford and Sola13]. The corresponding problem in the setting of the unit ball of
![]() ${\mathbb C}^2$
was solved in [Reference Kosiński and Vavitsas14].
${\mathbb C}^2$
was solved in [Reference Kosiński and Vavitsas14].
1.1 Dirichlet-type spaces in the unit ball
Denote the unit ball by
and its boundary, the unit sphere by
where
![]() $||z||=\sqrt {|z_1|^2+\cdots +|z_n|^2}$
is the associated norm of the usual Euclidean inner product
$||z||=\sqrt {|z_1|^2+\cdots +|z_n|^2}$
is the associated norm of the usual Euclidean inner product
![]() $\langle z,w \rangle =z_1\bar {w}_1+\cdots +z_n\bar {w}_n$
. Denote the class of holomorphic functions in
$\langle z,w \rangle =z_1\bar {w}_1+\cdots +z_n\bar {w}_n$
. Denote the class of holomorphic functions in
![]() ${\mathbb B_n}$
by
${\mathbb B_n}$
by
![]() $\textrm {Hol}({\mathbb B_n})$
. Any function
$\textrm {Hol}({\mathbb B_n})$
. Any function
![]() $f\in \textrm {Hol}({\mathbb B_n})$
has a power series expansion
$f\in \textrm {Hol}({\mathbb B_n})$
has a power series expansion
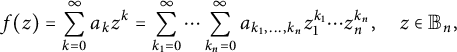 $$ \begin{align} f(z)=\sum_{k=0}^{\infty}a_kz^k=\sum_{k_1=0}^{\infty}\cdots \sum_{k_n=0}^{\infty}a_{k_1,\ldots,k_n}z_1^{k_1}\cdots z_n^{k_n}, \quad z\in {\mathbb B_n}, \end{align} $$
$$ \begin{align} f(z)=\sum_{k=0}^{\infty}a_kz^k=\sum_{k_1=0}^{\infty}\cdots \sum_{k_n=0}^{\infty}a_{k_1,\ldots,k_n}z_1^{k_1}\cdots z_n^{k_n}, \quad z\in {\mathbb B_n}, \end{align} $$
where
![]() $k=(k_1,\ldots ,k_n)$
is an n-tuple index of nonnegative integers,
$k=(k_1,\ldots ,k_n)$
is an n-tuple index of nonnegative integers,
![]() $k!=k_1!\cdots k_n!$
and
$k!=k_1!\cdots k_n!$
and
![]() $z^k=z_1^{k_1}\cdots z_n^{k_n}$
. The power series in (1) exist, converges normal in
$z^k=z_1^{k_1}\cdots z_n^{k_n}$
. The power series in (1) exist, converges normal in
![]() ${\mathbb B_n}$
and it is unique since the unit ball is a connected Reinhardt domain containing the origin, i.e.,
${\mathbb B_n}$
and it is unique since the unit ball is a connected Reinhardt domain containing the origin, i.e.,
![]() $(z_1,\ldots ,z_n)\in {\mathbb B_n}$
implies
$(z_1,\ldots ,z_n)\in {\mathbb B_n}$
implies
![]() $(e^{i\theta _1}z_1,\ldots ,e^{i\theta _n}z_n)\in {\mathbb B_n}$
for arbitrary real
$(e^{i\theta _1}z_1,\ldots ,e^{i\theta _n}z_n)\in {\mathbb B_n}$
for arbitrary real
![]() $\theta _1,\ldots ,\theta _n$
(see [Reference Hörmander12]).
$\theta _1,\ldots ,\theta _n$
(see [Reference Hörmander12]).
To simplify the notation, we may write (1) as follows:
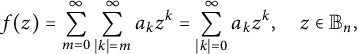 $$ \begin{align} f(z)=\sum_{m=0}^{\infty}\sum_{|k|=m}^{\infty}a_kz^k=\sum_{|k|=0}^{\infty}a_kz^k, \quad z\in {\mathbb B_n}, \end{align} $$
$$ \begin{align} f(z)=\sum_{m=0}^{\infty}\sum_{|k|=m}^{\infty}a_kz^k=\sum_{|k|=0}^{\infty}a_kz^k, \quad z\in {\mathbb B_n}, \end{align} $$
where
![]() $|k|=k_1+\cdots +k_n$
.
$|k|=k_1+\cdots +k_n$
.
Let
![]() $f\in \mathrm {Hol}({\mathbb B_n})$
. We say that f belongs to the Dirichlet-type space
$f\in \mathrm {Hol}({\mathbb B_n})$
. We say that f belongs to the Dirichlet-type space
![]() $D_{\alpha }({\mathbb B_n})$
, where
$D_{\alpha }({\mathbb B_n})$
, where
![]() $\alpha \in \mathbb {R}$
is a fixed parameter, if
$\alpha \in \mathbb {R}$
is a fixed parameter, if
 $$ \begin{align} ||f||^2_{\alpha}:=\sum_{|k|=0}^{\infty}(n+|k|)^{\alpha}\frac{(n-1)!k!}{(n-1+|k|)!}|a_{k}|^2<\infty. \end{align} $$
$$ \begin{align} ||f||^2_{\alpha}:=\sum_{|k|=0}^{\infty}(n+|k|)^{\alpha}\frac{(n-1)!k!}{(n-1+|k|)!}|a_{k}|^2<\infty. \end{align} $$
General introduction to the theory of Dirichlet-type spaces in the unit ball of
![]() ${\mathbb C}^n$
can be found in [Reference Ahern and Cohn1, Reference Beatrous and Burbea2, Reference Li15, Reference Michalska16, Reference Sargent and Sola20–Reference Zhu22]. One variable Dirichlet-type spaces are discussed in the textbook [Reference El-Fallah, Kellay, Mashreghi and Ransford11]. The weights in the norm in (3) are chosen in such a way that
${\mathbb C}^n$
can be found in [Reference Ahern and Cohn1, Reference Beatrous and Burbea2, Reference Li15, Reference Michalska16, Reference Sargent and Sola20–Reference Zhu22]. One variable Dirichlet-type spaces are discussed in the textbook [Reference El-Fallah, Kellay, Mashreghi and Ransford11]. The weights in the norm in (3) are chosen in such a way that
![]() $D_0({\mathbb B_n})$
and
$D_0({\mathbb B_n})$
and
![]() $D_{-1}({\mathbb B_n})$
coincide with the Hardy and Bergman spaces of the ball, respectively. The Dirichlet space having Möbius invariant norm corresponds to the parameter choice
$D_{-1}({\mathbb B_n})$
coincide with the Hardy and Bergman spaces of the ball, respectively. The Dirichlet space having Möbius invariant norm corresponds to the parameter choice
![]() $\alpha =n$
.
$\alpha =n$
.
By the definition,
![]() $D_{\alpha }({\mathbb B_n})\subset D_{\beta }({\mathbb B_n})$
, when
$D_{\alpha }({\mathbb B_n})\subset D_{\beta }({\mathbb B_n})$
, when
![]() $\alpha \geq \beta $
. Polynomials are dense in the spaces
$\alpha \geq \beta $
. Polynomials are dense in the spaces
![]() $D_{\alpha }({\mathbb B_n})$
,
$D_{\alpha }({\mathbb B_n})$
,
![]() $\alpha \in {\mathbb R}$
, and
$\alpha \in {\mathbb R}$
, and
![]() $z_i\cdot f\in D_{\alpha }({\mathbb B_n})$
,
$z_i\cdot f\in D_{\alpha }({\mathbb B_n})$
,
![]() $i=1,\ldots ,n$
whenever
$i=1,\ldots ,n$
whenever
![]() $f\in D_{\alpha }({\mathbb B_n})$
.
$f\in D_{\alpha }({\mathbb B_n})$
.
A multiplier in
![]() $D_{\alpha }({\mathbb B_n})$
is a holomorphic function
$D_{\alpha }({\mathbb B_n})$
is a holomorphic function
![]() $\phi :{\mathbb B_n}\rightarrow {\mathbb C}$
that satisfies
$\phi :{\mathbb B_n}\rightarrow {\mathbb C}$
that satisfies
![]() $\phi \cdot f\in D_{\alpha }({\mathbb B_n})$
for all
$\phi \cdot f\in D_{\alpha }({\mathbb B_n})$
for all
![]() $f\in D_{\alpha }({\mathbb B_n})$
. Polynomials, as well as holomorphic functions in a neighbourhood of the closed unit ball, are multipliers in every space
$f\in D_{\alpha }({\mathbb B_n})$
. Polynomials, as well as holomorphic functions in a neighbourhood of the closed unit ball, are multipliers in every space
![]() $D_{\alpha }({\mathbb B_n})$
.
$D_{\alpha }({\mathbb B_n})$
.
1.2 Shift operators and cyclic vectors
Consider the bounded linear operators
![]() $S_1,\ldots ,S_n:D_{\alpha }({\mathbb B_n})\rightarrow D_{\alpha }({\mathbb B_n})$
defined by
$S_1,\ldots ,S_n:D_{\alpha }({\mathbb B_n})\rightarrow D_{\alpha }({\mathbb B_n})$
defined by
![]() $S_i:f\mapsto z_i\cdot f$
. We say that
$S_i:f\mapsto z_i\cdot f$
. We say that
![]() $f\in D_{\alpha }({\mathbb B_n})$
is a cyclic vector if the closed invariant subspace, i.e.,
$f\in D_{\alpha }({\mathbb B_n})$
is a cyclic vector if the closed invariant subspace, i.e.,
coincides with
![]() $D_{\alpha }({\mathbb B_n})$
(the closure is taken with respect to the
$D_{\alpha }({\mathbb B_n})$
(the closure is taken with respect to the
![]() $D_{\alpha }({\mathbb B_n})$
norm). An equivalent definition is that f is cyclic if and only if
$D_{\alpha }({\mathbb B_n})$
norm). An equivalent definition is that f is cyclic if and only if
![]() $1\in [f]$
.
$1\in [f]$
.
Since
![]() $D_{\alpha }({\mathbb B_n})$
enjoys the bounded point evaluation property a function that is cyclic cannot vanish inside the unit ball. Thus, we focus on functions nonvanishing in the domain. Also, nonzero constant functions are cyclic in every space
$D_{\alpha }({\mathbb B_n})$
enjoys the bounded point evaluation property a function that is cyclic cannot vanish inside the unit ball. Thus, we focus on functions nonvanishing in the domain. Also, nonzero constant functions are cyclic in every space
![]() $D_{\alpha }({\mathbb B_n})$
. More information regarding cyclic vectors in Dirichlet-type spaces over the disk, the polydisk and the unit ball can be found in [Reference Bénéteau, Condori, Liaw, Seco and Sola3–Reference Bergqvist6, Reference Brown and Shields8, Reference El-Fallah, Kellay, Mashreghi and Ransford11, Reference Knese, Kosiński, Ransford and Sola13, Reference Kosiński and Vavitsas14, Reference Sargent and Sola19, Reference Sola21].
$D_{\alpha }({\mathbb B_n})$
. More information regarding cyclic vectors in Dirichlet-type spaces over the disk, the polydisk and the unit ball can be found in [Reference Bénéteau, Condori, Liaw, Seco and Sola3–Reference Bergqvist6, Reference Brown and Shields8, Reference El-Fallah, Kellay, Mashreghi and Ransford11, Reference Knese, Kosiński, Ransford and Sola13, Reference Kosiński and Vavitsas14, Reference Sargent and Sola19, Reference Sola21].
Just as in the settings of the bidisk and the unit ball of two variables, the cyclicity of a function
![]() $f\in D_{\alpha }({\mathbb B_n})$
is inextricably linked with its zero set
$f\in D_{\alpha }({\mathbb B_n})$
is inextricably linked with its zero set
The zeros of a function lying on the sphere are called the boundary zeros.
1.3 Plan of the paper
Section 3 studies Dirichlet-type spaces. In particular, we give a crucial relation among them. Using fractional radial derivatives and the Cauchy formula of functions lying in the ball algebra
![]() $A({\mathbb B_n})$
which contains functions that are continuous on the closed unit ball and holomorphic in its interior, we give an equivalent characterization of Dirichlet-type spaces for a wide range of parameters
$A({\mathbb B_n})$
which contains functions that are continuous on the closed unit ball and holomorphic in its interior, we give an equivalent characterization of Dirichlet-type spaces for a wide range of parameters
![]() $\alpha $
.
$\alpha $
.
Section 4 studies diagonal subspaces. In particular, we extend result from [Reference Sola21]. It makes sense to define functions
![]() $f\in \mathrm {Hol}({\mathbb B_n})$
using functions
$f\in \mathrm {Hol}({\mathbb B_n})$
using functions
![]() $\tilde {f}\in \mathrm {Hol}({\mathbb D}(\mu ))$
for a proper
$\tilde {f}\in \mathrm {Hol}({\mathbb D}(\mu ))$
for a proper
![]() $\mu>0$
. Geometrically speaking, we are looking at a disk embedded in the ball but not in a coordinate plane. Thus, we may switch the problem of cyclicity from the ball to spaces of holomorphic functions of one variable that are well known. Then we use optimal approximants in order to identify cyclicity.
$\mu>0$
. Geometrically speaking, we are looking at a disk embedded in the ball but not in a coordinate plane. Thus, we may switch the problem of cyclicity from the ball to spaces of holomorphic functions of one variable that are well known. Then we use optimal approximants in order to identify cyclicity.
Moreover, we prove cyclicity for model polynomials for proper parameters. In the setting of the unit ball of two variables (see [Reference Sola21]), the model polynomials are the following:
![]() $1-z_1$
which vanishes in the closed unit ball on a singleton, i.e.,
$1-z_1$
which vanishes in the closed unit ball on a singleton, i.e.,
![]() $\mathcal {Z}(1-z_1)\cap \mathbb S_2=\{(1,0)\}$
, and
$\mathcal {Z}(1-z_1)\cap \mathbb S_2=\{(1,0)\}$
, and
![]() $1-2z_1z_2$
which vanishes along an analytic curve, i.e.,
$1-2z_1z_2$
which vanishes along an analytic curve, i.e.,
![]() $\mathcal {Z}(1-2z_1z_2)\cap \mathbb S_2=\{(e^{i\theta }/\sqrt {2},e^{-i\theta }/\sqrt {2}):\theta \in {\mathbb R}\}$
. In our case, the corresponding candidates are the following:
$\mathcal {Z}(1-2z_1z_2)\cap \mathbb S_2=\{(e^{i\theta }/\sqrt {2},e^{-i\theta }/\sqrt {2}):\theta \in {\mathbb R}\}$
. In our case, the corresponding candidates are the following:
They vanish in the closed unit ball along the following analytic sets:
These polynomials are also studied with respect to the Drury–Arveson space in [Reference Sargent and Sola20].
In two variables,
![]() $1-z_1$
is cyclic in
$1-z_1$
is cyclic in
![]() $D_{\alpha }(\mathbb B_2)$
precisely when
$D_{\alpha }(\mathbb B_2)$
precisely when
![]() $\alpha \leq 2$
, and
$\alpha \leq 2$
, and
![]() $1-2z_1z_2$
is cyclic in
$1-2z_1z_2$
is cyclic in
![]() $D_{\alpha }(\mathbb B_2)$
precisely when
$D_{\alpha }(\mathbb B_2)$
precisely when
![]() $\alpha \leq 3/2$
. Here, there are more than two fixed parameters. The characterization of cyclicity of these two polynomials was crucial in [Reference Kosiński and Vavitsas14].
$\alpha \leq 3/2$
. Here, there are more than two fixed parameters. The characterization of cyclicity of these two polynomials was crucial in [Reference Kosiński and Vavitsas14].
Section 5 studies the radial dilation of a polynomial. Using the equivalent characterization of Section 3, we identify cyclicity for the model polynomials via the powerful radial dilation method. In particular, we show that if
![]() $p/p_r\rightarrow 1$
weakly, where
$p/p_r\rightarrow 1$
weakly, where
![]() $p_r(z)=p(rz)$
is a radial dilation of p, then p is cyclic (see [Reference Knese, Kosiński, Ransford and Sola13] for the bidisk settings and [Reference Kosiński and Vavitsas14] for the unit ball in two variables). This method is quite interesting since it can be applied to an arbitrary polynomial. Note that in [Reference Knese, Kosiński, Ransford and Sola13, Reference Kosiński and Vavitsas14], the radial dilation method is one of the main tools of solving cyclicity problem for polynomials. The main result of this section verifies the arguments made about polynomials in Section 4.
$p_r(z)=p(rz)$
is a radial dilation of p, then p is cyclic (see [Reference Knese, Kosiński, Ransford and Sola13] for the bidisk settings and [Reference Kosiński and Vavitsas14] for the unit ball in two variables). This method is quite interesting since it can be applied to an arbitrary polynomial. Note that in [Reference Knese, Kosiński, Ransford and Sola13, Reference Kosiński and Vavitsas14], the radial dilation method is one of the main tools of solving cyclicity problem for polynomials. The main result of this section verifies the arguments made about polynomials in Section 4.
Section 6 studies noncyclic vectors. We use the notion of Riesz
![]() $\alpha $
-capacity in order to identify noncyclic functions. Moreover, we study Cauchy transforms of Borel measures supported on zero sets of the radial limits of a given function
$\alpha $
-capacity in order to identify noncyclic functions. Moreover, we study Cauchy transforms of Borel measures supported on zero sets of the radial limits of a given function
![]() $f\in D_{\alpha }({\mathbb B_n})$
and we give asymptotic expansions of their norms. Then employing a standard scheme due to Brown and Shields [Reference Brown and Shields8], we prove the main result. Note that this sufficient capacity condition for noncyclicity in Dirichlet-type spaces in the unit ball of two variables was proved by Sola in [Reference Sola21].
$f\in D_{\alpha }({\mathbb B_n})$
and we give asymptotic expansions of their norms. Then employing a standard scheme due to Brown and Shields [Reference Brown and Shields8], we prove the main result. Note that this sufficient capacity condition for noncyclicity in Dirichlet-type spaces in the unit ball of two variables was proved by Sola in [Reference Sola21].
2 Standard tools
Let us give some standard tools which will be useful in the sequel.
The binomial series
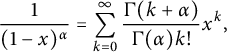 $$ \begin{align*}\frac{1}{(1-x)^{\alpha}}=\sum_{k=0}^{\infty}\frac{\Gamma(k+\alpha)}{\Gamma(\alpha)k!}x^k,\end{align*} $$
$$ \begin{align*}\frac{1}{(1-x)^{\alpha}}=\sum_{k=0}^{\infty}\frac{\Gamma(k+\alpha)}{\Gamma(\alpha)k!}x^k,\end{align*} $$
where
![]() $|x|<1$
is a complex number and
$|x|<1$
is a complex number and
![]() $\alpha $
is a nonnegative real number. The asymptotic behavior of the
$\alpha $
is a nonnegative real number. The asymptotic behavior of the
![]() $\Gamma $
-function is the following:
$\Gamma $
-function is the following:
![]() $\Gamma (k+\alpha )\asymp (k-1)!k^{\alpha }$
, where the symbol
$\Gamma (k+\alpha )\asymp (k-1)!k^{\alpha }$
, where the symbol
![]() $\asymp $
denotes that the ratio of the two quantities either tends to a constant as k tends to infinity or it is rather two sides bound by constants.
$\asymp $
denotes that the ratio of the two quantities either tends to a constant as k tends to infinity or it is rather two sides bound by constants.
The multinomial formula
 $$ \begin{align*}(x_1+\cdots+x_n)^k=\sum_{|j|=k}\frac{k!}{j!}x_1^{j_1}\cdots x_n^{j_n},\end{align*} $$
$$ \begin{align*}(x_1+\cdots+x_n)^k=\sum_{|j|=k}\frac{k!}{j!}x_1^{j_1}\cdots x_n^{j_n},\end{align*} $$
where
![]() $j=(j_1,\ldots ,j_n)$
is an n-tuple index of nonnegative integers and
$j=(j_1,\ldots ,j_n)$
is an n-tuple index of nonnegative integers and
![]() $x_i$
are complex numbers.
$x_i$
are complex numbers.
The Stirling formula that describes the asymptotic behavior of the gamma function
Denote the normalized area measure on
![]() ${\mathbb C}^n={\mathbb R}^{2n}$
by
${\mathbb C}^n={\mathbb R}^{2n}$
by
![]() $du(z)$
and the normalized rotation-invariant positive Borel measure on
$du(z)$
and the normalized rotation-invariant positive Borel measure on
![]() $\mathbb S_n$
by
$\mathbb S_n$
by
![]() $d\sigma (\zeta )$
(see [Reference Rudin18, Reference Zhu22]). The measures
$d\sigma (\zeta )$
(see [Reference Rudin18, Reference Zhu22]). The measures
![]() $du(z)$
and
$du(z)$
and
![]() $d\sigma (\zeta )$
are related by the formula
$d\sigma (\zeta )$
are related by the formula
The holomorphic monomials are orthogonal to each other in
![]() $L^2(\sigma )$
, that is, if k and l are multiindices such that
$L^2(\sigma )$
, that is, if k and l are multiindices such that
![]() $k\neq l$
, then
$k\neq l$
, then
Moreover,
3 Relation among Dirichlet-type spaces and an equivalent characterization
We study the structure of Dirichlet-type spaces. Note that
is the radial derivative of a function f. The radial derivative plays a key role in the function theory of the unit ball. A crucial relation among these spaces is the following.
Proposition 1 Let
![]() $f\in \mathrm {Hol}({\mathbb B_n})$
and
$f\in \mathrm {Hol}({\mathbb B_n})$
and
![]() $\alpha \in {\mathbb R}$
be fixed. Then
$\alpha \in {\mathbb R}$
be fixed. Then
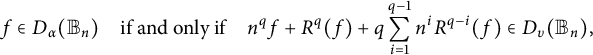 $$ \begin{align*} f\in D_{\alpha}({\mathbb B_n})\quad \text{if and only if} \quad n^q f+R^q (f)+q\sum_{i=1}^{q-1}n^iR^{q-i}(f)\in D_{\upsilon}({\mathbb B_n}), \end{align*} $$
$$ \begin{align*} f\in D_{\alpha}({\mathbb B_n})\quad \text{if and only if} \quad n^q f+R^q (f)+q\sum_{i=1}^{q-1}n^iR^{q-i}(f)\in D_{\upsilon}({\mathbb B_n}), \end{align*} $$
where
![]() $\alpha =2q+\upsilon $
,
$\alpha =2q+\upsilon $
,
![]() $q\in \mathbb N$
, and
$q\in \mathbb N$
, and
![]() $R^q$
is the q-image of the operator R.
$R^q$
is the q-image of the operator R.
Proof Indeed, it is enough to check that
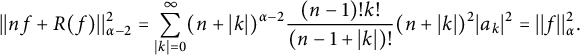 $$ \begin{align*}||nf+R(f)||^2_{\alpha-2}=\sum_{|k|=0}^{\infty}(n+|k|)^{\alpha-2}\frac{(n-1)!k!}{(n-1+|k|)!}(n+|k|)^2|a_{k}|^2=||f||_{\alpha}^2.\\[-40pt]\end{align*} $$
$$ \begin{align*}||nf+R(f)||^2_{\alpha-2}=\sum_{|k|=0}^{\infty}(n+|k|)^{\alpha-2}\frac{(n-1)!k!}{(n-1+|k|)!}(n+|k|)^2|a_{k}|^2=||f||_{\alpha}^2.\\[-40pt]\end{align*} $$
We continue by giving an equivalent characterization of Dirichlet-type spaces. In Dirichlet-type spaces in the unit ball, one of the Dirichlet-type integrals is achieved in a limited range of parameters.
Lemma 2 (See [Reference Michalska16])
If
![]() $\alpha \in (-1,1)$
, then
$\alpha \in (-1,1)$
, then
![]() $f\in D_\alpha(\mathbb B_n)$
if and only if
$f\in D_\alpha(\mathbb B_n)$
if and only if
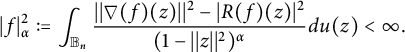 $$\begin{align*}|f|^2_{\alpha}:=\int_{{\mathbb B_n}} \frac{||\nabla(f)(z)||^2 - |R(f)(z)|^2}{ (1-||z||^2)^{\alpha}} du(z)<\infty.\end{align*}$$
$$\begin{align*}|f|^2_{\alpha}:=\int_{{\mathbb B_n}} \frac{||\nabla(f)(z)||^2 - |R(f)(z)|^2}{ (1-||z||^2)^{\alpha}} du(z)<\infty.\end{align*}$$
Above,
![]() $\nabla (f)(z)=(\partial _{z_1}f(z),\ldots ,\partial _{z_n}f(z))$
denotes the holomorphic gradient of a holomorphic function f. Note that Proposition 1 allows us to use Lemma 2 whenever
$\nabla (f)(z)=(\partial _{z_1}f(z),\ldots ,\partial _{z_n}f(z))$
denotes the holomorphic gradient of a holomorphic function f. Note that Proposition 1 allows us to use Lemma 2 whenever
![]() $\upsilon \in (-1,1)$
. Let
$\upsilon \in (-1,1)$
. Let
![]() $\gamma ,t\in {\mathbb R}$
be such that neither
$\gamma ,t\in {\mathbb R}$
be such that neither
![]() $n+\gamma $
nor
$n+\gamma $
nor
![]() $n+\gamma +t$
is a negative integer. If
$n+\gamma +t$
is a negative integer. If
![]() $f=\sum _{|k|=0}^{\infty }a_kz^k$
is the homogeneous expansion of a function
$f=\sum _{|k|=0}^{\infty }a_kz^k$
is the homogeneous expansion of a function
![]() $f\in \textrm {Hol}({\mathbb B_n})$
, then we may define an invertible continuous linear operator with respect to the topology of uniform convergence on compact subsets of
$f\in \textrm {Hol}({\mathbb B_n})$
, then we may define an invertible continuous linear operator with respect to the topology of uniform convergence on compact subsets of
![]() ${\mathbb B_n}$
, denoted by
${\mathbb B_n}$
, denoted by
![]() $R^{\gamma ,t}: \textrm {Hol}({\mathbb B_n})\rightarrow \textrm {Hol}({\mathbb B_n})$
and having expression
$R^{\gamma ,t}: \textrm {Hol}({\mathbb B_n})\rightarrow \textrm {Hol}({\mathbb B_n})$
and having expression
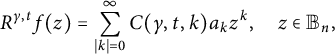 $$ \begin{align*} R^{\gamma,t}f(z)=\sum_{|k|=0}^{\infty}C(\gamma,t,k)a_kz^k, \quad z\in {\mathbb B_n}, \end{align*} $$
$$ \begin{align*} R^{\gamma,t}f(z)=\sum_{|k|=0}^{\infty}C(\gamma,t,k)a_kz^k, \quad z\in {\mathbb B_n}, \end{align*} $$
where
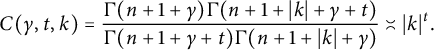 $$ \begin{align} C(\gamma,t,k)=\frac{\Gamma(n+1+\gamma)\Gamma(n+1+|k|+\gamma+t)}{\Gamma(n+1+\gamma+t)\Gamma(n+1+|k|+\gamma)}\asymp |k|^t. \end{align} $$
$$ \begin{align} C(\gamma,t,k)=\frac{\Gamma(n+1+\gamma)\Gamma(n+1+|k|+\gamma+t)}{\Gamma(n+1+\gamma+t)\Gamma(n+1+|k|+\gamma)}\asymp |k|^t. \end{align} $$
See [Reference Zhu22] for more information regarding these fractional radial derivatives.
Lemma 3 Let
![]() $t\in {\mathbb R}$
be such that
$t\in {\mathbb R}$
be such that
![]() $n-1+t \geq 0$
. If
$n-1+t \geq 0$
. If
![]() $f\in A({\mathbb B_n})$
, then
$f\in A({\mathbb B_n})$
, then
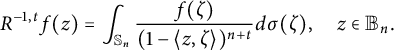 $$ \begin{align*}R^{-1,t}f(z)=\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\zeta \rangle)^{n+t}}d\sigma(\zeta), \quad z\in {\mathbb B_n}.\end{align*} $$
$$ \begin{align*}R^{-1,t}f(z)=\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\zeta \rangle)^{n+t}}d\sigma(\zeta), \quad z\in {\mathbb B_n}.\end{align*} $$
Proof The continuous linear operator
![]() $R^{\gamma ,t}$
(see [Reference Zhu22]) satisfies
$R^{\gamma ,t}$
(see [Reference Zhu22]) satisfies
for all
![]() $w\in {\mathbb B_n}$
. Next, define
$w\in {\mathbb B_n}$
. Next, define
![]() $f_{\epsilon }$
for
$f_{\epsilon }$
for
![]() $\epsilon \in (0,1)$
by
$\epsilon \in (0,1)$
by
 $$ \begin{align*}f_{\epsilon}(z)=\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\epsilon\zeta \rangle)^n}d\sigma(\zeta), \quad z\in {\mathbb B_n}.\end{align*} $$
$$ \begin{align*}f_{\epsilon}(z)=\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\epsilon\zeta \rangle)^n}d\sigma(\zeta), \quad z\in {\mathbb B_n}.\end{align*} $$
The Cauchy formula holds for
![]() $f\in A({\mathbb B_n})$
and hence
$f\in A({\mathbb B_n})$
and hence
![]() $f=\lim _{\epsilon \rightarrow 1^{-}}f_{\epsilon }$
. It follows that
$f=\lim _{\epsilon \rightarrow 1^{-}}f_{\epsilon }$
. It follows that
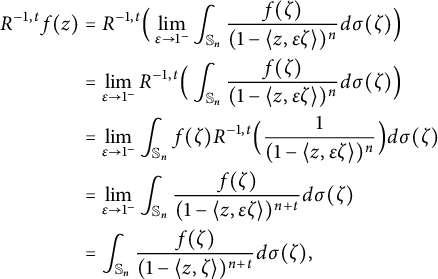 $$ \begin{align*} R^{-1,t}f(z)&=R^{-1,t}\Big(\lim_{\epsilon\rightarrow 1^{-}}\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\epsilon\zeta \rangle)^n}d\sigma(\zeta) \Big)\\ &=\lim_{\epsilon\rightarrow 1^{-}}R^{-1,t}\Big(\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\epsilon\zeta \rangle)^n}d\sigma(\zeta) \Big)\\ &=\lim_{\epsilon\rightarrow 1^{-}}\int_{\mathbb S_n}f(\zeta)R^{-1,t}\Big(\frac{1}{(1-\langle z,\epsilon\zeta \rangle)^{n}}\Big)d\sigma(\zeta)\\ &=\lim_{\epsilon\rightarrow 1^{-}}\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\epsilon\zeta \rangle)^{n+t}}d\sigma(\zeta)\\ &=\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\zeta \rangle)^{n+t}}d\sigma(\zeta), \end{align*} $$
$$ \begin{align*} R^{-1,t}f(z)&=R^{-1,t}\Big(\lim_{\epsilon\rightarrow 1^{-}}\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\epsilon\zeta \rangle)^n}d\sigma(\zeta) \Big)\\ &=\lim_{\epsilon\rightarrow 1^{-}}R^{-1,t}\Big(\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\epsilon\zeta \rangle)^n}d\sigma(\zeta) \Big)\\ &=\lim_{\epsilon\rightarrow 1^{-}}\int_{\mathbb S_n}f(\zeta)R^{-1,t}\Big(\frac{1}{(1-\langle z,\epsilon\zeta \rangle)^{n}}\Big)d\sigma(\zeta)\\ &=\lim_{\epsilon\rightarrow 1^{-}}\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\epsilon\zeta \rangle)^{n+t}}d\sigma(\zeta)\\ &=\int_{\mathbb S_n}\frac{f(\zeta)}{(1-\langle z,\zeta \rangle)^{n+t}}d\sigma(\zeta), \end{align*} $$
and the assertion follows.
Theorem 4 Let
![]() $\alpha \in {\mathbb R}$
be such that
$\alpha \in {\mathbb R}$
be such that
![]() $n-1+\alpha /2\geq 0$
and
$n-1+\alpha /2\geq 0$
and
![]() $f\in A({\mathbb B_n})$
. Then
$f\in A({\mathbb B_n})$
. Then
![]() $f\in D_{\alpha }({\mathbb B_n})$
if and only if
$f\in D_{\alpha }({\mathbb B_n})$
if and only if
 $$ \begin{align*}\int_{{\mathbb B_n}}(1-||z||^2)\Big|\int_{\mathbb S_n}\frac{f(\zeta)\bar{\zeta}_p}{(1-\langle z,\zeta \rangle)^{n+\alpha/2+1}}d\sigma(\zeta)\Big|^2du(z)<\infty\end{align*} $$
$$ \begin{align*}\int_{{\mathbb B_n}}(1-||z||^2)\Big|\int_{\mathbb S_n}\frac{f(\zeta)\bar{\zeta}_p}{(1-\langle z,\zeta \rangle)^{n+\alpha/2+1}}d\sigma(\zeta)\Big|^2du(z)<\infty\end{align*} $$
and
 $$ \begin{align*}\int_{{\mathbb B_n}}\Big|\int_{\mathbb S_n}\frac{(\overline{z_p\zeta_q-z_q\zeta_p})f(\zeta)}{(1-\langle z,\zeta \rangle)^{n+\alpha/2+1}}d\sigma(\zeta)\Big|^2du(z)<\infty,\end{align*} $$
$$ \begin{align*}\int_{{\mathbb B_n}}\Big|\int_{\mathbb S_n}\frac{(\overline{z_p\zeta_q-z_q\zeta_p})f(\zeta)}{(1-\langle z,\zeta \rangle)^{n+\alpha/2+1}}d\sigma(\zeta)\Big|^2du(z)<\infty,\end{align*} $$
where
![]() $p,q=1,\ldots ,n$
.
$p,q=1,\ldots ,n$
.
Proof Choose t so that
![]() $\alpha =2t$
. Note that
$\alpha =2t$
. Note that
![]() $n,t$
are fixed and hence
$n,t$
are fixed and hence
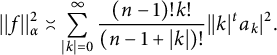 $$ \begin{align*} ||f||^2_{\alpha}\asymp\sum_{|k|=0}^{\infty}\frac{(n-1)!k!}{(n-1+|k|)!}||k|^ta_{k}|^2. \end{align*} $$
$$ \begin{align*} ||f||^2_{\alpha}\asymp\sum_{|k|=0}^{\infty}\frac{(n-1)!k!}{(n-1+|k|)!}||k|^ta_{k}|^2. \end{align*} $$
Thus, (4) implies that
![]() $||R^{-1,t}f||_{0}\asymp ||f||_{\alpha }$
. One can apply then the equivalent integral representation of Dirichlet-type norms to
$||R^{-1,t}f||_{0}\asymp ||f||_{\alpha }$
. One can apply then the equivalent integral representation of Dirichlet-type norms to
![]() $R^{-1,t}f\in \textrm {Hol}({\mathbb B_n})$
, i.e.,
$R^{-1,t}f\in \textrm {Hol}({\mathbb B_n})$
, i.e.,
![]() $R^{-1,t}f\in D_0(\mathbb B_n)$
if and only if
$R^{-1,t}f\in D_0(\mathbb B_n)$
if and only if
![]() $|R^{-1,t}f|_{0}<\infty$
. According to Lemma 3, we get that
$|R^{-1,t}f|_{0}<\infty$
. According to Lemma 3, we get that
 $$ \begin{align*}\partial_{z_p}(R^{-1,t}f)(z)=\int_{\mathbb S_n}\frac{f(\zeta)\bar{\zeta}_p}{(1-\langle z,\zeta \rangle)^{n+t+1}}d\sigma(\zeta), \quad z\in {\mathbb B_n},\end{align*} $$
$$ \begin{align*}\partial_{z_p}(R^{-1,t}f)(z)=\int_{\mathbb S_n}\frac{f(\zeta)\bar{\zeta}_p}{(1-\langle z,\zeta \rangle)^{n+t+1}}d\sigma(\zeta), \quad z\in {\mathbb B_n},\end{align*} $$
where
![]() $p=1,\ldots ,n$
. Expand the term
$p=1,\ldots ,n$
. Expand the term
![]() $||\nabla (f)||^2-|R(f)|^2$
as follows:
$||\nabla (f)||^2-|R(f)|^2$
as follows:
The assertion follows by Lemma 2.
4 Diagonal subspaces
In [Reference Bénéteau, Condori, Liaw, Seco and Sola3], a method of construction of optimal approximants via determinants in Dirichlet-type spaces in the unit disk is provided. Similarly, we may define optimal approximants in several variables (see [Reference Sargent and Sola20]).
Fix
![]() $N\in \mathbb N$
. We define the space of polynomials
$N\in \mathbb N$
. We define the space of polynomials
![]() $p\in {\mathbb C}[z_1,\ldots ,z_n]$
with degree at most
$p\in {\mathbb C}[z_1,\ldots ,z_n]$
with degree at most
![]() $nN$
as follows:
$nN$
as follows:
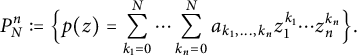 $$ \begin{align*}P_N^n:=\Big\{p(z)=\sum_{k_1=0}^{N}\cdots \sum_{k_n=0}^{N}a_{k_1,\ldots,k_n}z_1^{k_1}\cdots z_n^{k_n}\Big\}.\end{align*} $$
$$ \begin{align*}P_N^n:=\Big\{p(z)=\sum_{k_1=0}^{N}\cdots \sum_{k_n=0}^{N}a_{k_1,\ldots,k_n}z_1^{k_1}\cdots z_n^{k_n}\Big\}.\end{align*} $$
Remark 5 Let
![]() $(X,||\cdot ||)$
be a normed space and fix
$(X,||\cdot ||)$
be a normed space and fix
![]() $x\in X$
,
$x\in X$
,
![]() $C\subset X$
. The distance between x and the set C is the following:
$C\subset X$
. The distance between x and the set C is the following:
It is well known that if X is a Hilbert space and
![]() $C\subset X$
a convex closed subset, then for any
$C\subset X$
a convex closed subset, then for any
![]() $x\in X$
, there exists a unique
$x\in X$
, there exists a unique
![]() $y\in C$
such that
$y\in C$
such that
![]() $||x-y||=\mathrm {dist}_X(x,C)$
. Let
$||x-y||=\mathrm {dist}_X(x,C)$
. Let
![]() $f\in D_{\alpha }({\mathbb B_n})$
be nonzero constant. We deduce that for any
$f\in D_{\alpha }({\mathbb B_n})$
be nonzero constant. We deduce that for any
![]() $N\in \mathbb N$
, there exists exactly one
$N\in \mathbb N$
, there exists exactly one
![]() $p_N\in P_N^n$
satisfying
$p_N\in P_N^n$
satisfying
Let
![]() $f\in D_{\alpha }({\mathbb B_n})$
. We say that a polynomial
$f\in D_{\alpha }({\mathbb B_n})$
. We say that a polynomial
![]() $p_N\in P^n_N$
is an optimal approximant of order N to
$p_N\in P^n_N$
is an optimal approximant of order N to
![]() $1/f$
if
$1/f$
if
![]() $p_N$
minimizes
$p_N$
minimizes
![]() $||pf-1||_{\alpha }$
among all polynomials
$||pf-1||_{\alpha }$
among all polynomials
![]() $p\in P_N^n$
. We call
$p\in P_N^n$
. We call
![]() $||p_Nf-1||_{\alpha }$
the optimal norm of order N associated with f.
$||p_Nf-1||_{\alpha }$
the optimal norm of order N associated with f.
Let
![]() $M=(M_1,\ldots ,M_n)$
be a multiindex, where
$M=(M_1,\ldots ,M_n)$
be a multiindex, where
![]() $M_i$
are nonnegative integers, and
$M_i$
are nonnegative integers, and
![]() $m\in \{1,\ldots ,n\}$
. Setting
$m\in \{1,\ldots ,n\}$
. Setting
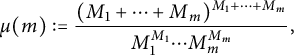 $$ \begin{align*}\mu(m):=\frac{(M_1+\cdots+M_m)^{M_1+\cdots+M_m}}{M_1^{M_1}\cdots M_m^{M_m}},\end{align*} $$
$$ \begin{align*}\mu(m):=\frac{(M_1+\cdots+M_m)^{M_1+\cdots+M_m}}{M_1^{M_1}\cdots M_m^{M_m}},\end{align*} $$
we see that
Using (5), we may construct polynomials that vanish in the closed unit ball along analytic subsets of the unit sphere.
Remark 6 Let
![]() $\tilde {f}\in \mathrm {Hol}({\mathbb D}(\mu (m)^{-1/4}))$
, where
$\tilde {f}\in \mathrm {Hol}({\mathbb D}(\mu (m)^{-1/4}))$
, where
According to (5), we define the following function:
Then
![]() $f\in \mathrm {Hol}({\mathbb B_n})$
and it depends on m variables. Note that we may change the variables
$f\in \mathrm {Hol}({\mathbb B_n})$
and it depends on m variables. Note that we may change the variables
![]() $z_1,\ldots ,z_m$
by any other m variables. For convenience, we choose the m first variables. The power
$z_1,\ldots ,z_m$
by any other m variables. For convenience, we choose the m first variables. The power
![]() $1/4$
will be convenient in the sequel.
$1/4$
will be convenient in the sequel.
Thus, the question that arises out is if we may define closed subspaces of
![]() $D_{\alpha }({\mathbb B_n})$
passing through one variable functions. We shall see that these subspaces are called diagonal subspaces due to the nature of the power series expansion of their elements.
$D_{\alpha }({\mathbb B_n})$
passing through one variable functions. We shall see that these subspaces are called diagonal subspaces due to the nature of the power series expansion of their elements.
Instead of the classical one variable Dirichlet-type spaces of the unit disk, we may consider spaces
![]() $d_{\beta }$
,
$d_{\beta }$
,
![]() $\beta \in {\mathbb R}$
, consisting of holomorphic functions
$\beta \in {\mathbb R}$
, consisting of holomorphic functions
![]() $\tilde {f}\in \mathrm {Hol}({\mathbb D}(\mu ^{-1/4}))$
. Moreover, such functions with power series expansion
$\tilde {f}\in \mathrm {Hol}({\mathbb D}(\mu ^{-1/4}))$
. Moreover, such functions with power series expansion
![]() $\tilde {f}(z)=\sum _{l=0}^{\infty }a_lz^l$
are said to belong to
$\tilde {f}(z)=\sum _{l=0}^{\infty }a_lz^l$
are said to belong to
![]() $d_{\beta }$
if
$d_{\beta }$
if
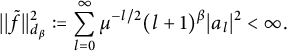 $$ \begin{align*} ||\tilde{f}||^2_{d_{\beta}}:= \sum_{l=0}^{\infty}\mu^{-l/2}(l+1)^{\beta}|a_l|^2<\infty. \end{align*} $$
$$ \begin{align*} ||\tilde{f}||^2_{d_{\beta}}:= \sum_{l=0}^{\infty}\mu^{-l/2}(l+1)^{\beta}|a_l|^2<\infty. \end{align*} $$
There is a natural identification between the function theories of
![]() $D_{\beta }({\mathbb D})$
: one variable Dirichlet-type spaces of the unit disk, and
$D_{\beta }({\mathbb D})$
: one variable Dirichlet-type spaces of the unit disk, and
![]() $d_{\beta }$
, and one verifies that the results in [Reference Bénéteau, Condori, Liaw, Seco and Sola3] are valid for
$d_{\beta }$
, and one verifies that the results in [Reference Bénéteau, Condori, Liaw, Seco and Sola3] are valid for
![]() $d_{\beta }$
.
$d_{\beta }$
.
We are ready to define diagonal closed subspaces. Set
Let
![]() $\alpha $
, M, m be as above. The diagonal closed subspace of
$\alpha $
, M, m be as above. The diagonal closed subspace of
![]() $D_{\alpha }({\mathbb B_n})$
is the following:
$D_{\alpha }({\mathbb B_n})$
is the following:
The existence of a holomorphic function
![]() $\tilde {f}$
is unique by identity principle, and hence there is no any amiss in the definition. Any function
$\tilde {f}$
is unique by identity principle, and hence there is no any amiss in the definition. Any function
![]() $f\in J_{\alpha ,M,m}$
has an expansion of the form
$f\in J_{\alpha ,M,m}$
has an expansion of the form
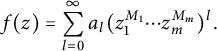 $$ \begin{align*} f(z)=\sum_{l=0}^{\infty}a_l(z_1^{M_1}\cdots z_m^{M_m})^l. \end{align*} $$
$$ \begin{align*} f(z)=\sum_{l=0}^{\infty}a_l(z_1^{M_1}\cdots z_m^{M_m})^l. \end{align*} $$
The relation of norms between one variable and diagonal subspaces follows.
Proposition 7 If
![]() $f\in J_{\alpha ,M,m}$
, then
$f\in J_{\alpha ,M,m}$
, then
![]() $||f||_{\alpha }\asymp ||\tilde {f}||_{d_{\beta (\alpha )}}$
.
$||f||_{\alpha }\asymp ||\tilde {f}||_{d_{\beta (\alpha )}}$
.
Proof If
![]() $f\in J_{\alpha ,M,m}$
, then
$f\in J_{\alpha ,M,m}$
, then
 $$ \begin{align*}||f||^2_{\alpha} \asymp \sum_{l=0}^{\infty}(l+1)^{\alpha}\frac{(M_1l)!\cdots (M_ml)!}{(n-1+(M_1+\cdots M_m)l)!}|a_l|^2.\end{align*} $$
$$ \begin{align*}||f||^2_{\alpha} \asymp \sum_{l=0}^{\infty}(l+1)^{\alpha}\frac{(M_1l)!\cdots (M_ml)!}{(n-1+(M_1+\cdots M_m)l)!}|a_l|^2.\end{align*} $$
By Stirling’s formula, we obtain
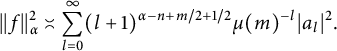 $$ \begin{align*}||f||^2_{\alpha} \asymp \sum_{l=0}^{\infty}(l+1)^{\alpha-n+m/2+1/2}\mu(m)^{-l}|a_l|^2.\end{align*} $$
$$ \begin{align*}||f||^2_{\alpha} \asymp \sum_{l=0}^{\infty}(l+1)^{\alpha-n+m/2+1/2}\mu(m)^{-l}|a_l|^2.\end{align*} $$
On the other hand, define the function
![]() $f'(z)=\sum _{l=0}^{\infty }\mu (m)^{-l/4}a_lz^l$
. Then
$f'(z)=\sum _{l=0}^{\infty }\mu (m)^{-l/4}a_lz^l$
. Then
![]() $f'(\mu (m)^{1/4} z_1^{M_1}\cdots z_m^{M_m})=f(z_1,\ldots ,z_n)$
and
$f'(\mu (m)^{1/4} z_1^{M_1}\cdots z_m^{M_m})=f(z_1,\ldots ,z_n)$
and
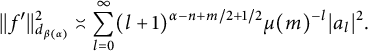 $$\begin{align*}||f'||^2_{d_{\beta(\alpha)}}\asymp \sum_{l=0}^{\infty}(l+1)^{\alpha-n+m/2+1/2}\mu(m)^{-l}|a_l|^2.\end{align*}$$
$$\begin{align*}||f'||^2_{d_{\beta(\alpha)}}\asymp \sum_{l=0}^{\infty}(l+1)^{\alpha-n+m/2+1/2}\mu(m)^{-l}|a_l|^2.\end{align*}$$
The assertion follows since
![]() $f'$
coincides with
$f'$
coincides with
![]() $\tilde {f}$
.
$\tilde {f}$
.
The corresponding Lemma 3.4 of [Reference Bénéteau, Condori, Liaw, Seco and Sola4] in our case is the following.
Lemma 8 Let
![]() $f\in J_{\alpha ,M,m}$
, where
$f\in J_{\alpha ,M,m}$
, where
![]() $\alpha ,M,m$
be as above. Let
$\alpha ,M,m$
be as above. Let
![]() $r_N\in P_N^n$
with expansion
$r_N\in P_N^n$
with expansion
 $$ \begin{align*}r_N(z)=\sum_{k_1=0}^{N}\cdots \sum_{k_n=0}^{N}a_{k_1,\ldots,k_n}z_1^{k_1}\ldots z_n^{k_n},\end{align*} $$
$$ \begin{align*}r_N(z)=\sum_{k_1=0}^{N}\cdots \sum_{k_n=0}^{N}a_{k_1,\ldots,k_n}z_1^{k_1}\ldots z_n^{k_n},\end{align*} $$
and consider its projection onto
![]() $J_{\alpha ,M,m}$
$J_{\alpha ,M,m}$
Then
Moreover, just as in Proposition 7, there is a relation of optimal approximants between one variable and diagonal subspaces.
Proposition 9 If
![]() $f\in J_{\alpha ,M,m}$
, then
$f\in J_{\alpha ,M,m}$
, then
Proof Let
![]() $r_N$
,
$r_N$
,
![]() $\pi (r_N)$
be as in Lemma 8. Then
$\pi (r_N)$
be as in Lemma 8. Then
![]() $\pi (r_N)f-1\in J_{\alpha ,M,m}$
. It follows that
$\pi (r_N)f-1\in J_{\alpha ,M,m}$
. It follows that
since
![]() $\tilde {\pi }(r_N)\in P^1_N$
. On the other hand, let
$\tilde {\pi }(r_N)\in P^1_N$
. On the other hand, let
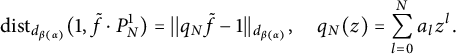 $$ \begin{align*}\mathrm{dist}_{d_{\beta(\alpha)}}(1,\tilde{f}\cdot P^1_N)=||q_N\tilde{f}-1||_{d_{\beta(\alpha)}}, \quad q_N(z)=\sum_{l=0}^{N}a_lz^l.\end{align*} $$
$$ \begin{align*}\mathrm{dist}_{d_{\beta(\alpha)}}(1,\tilde{f}\cdot P^1_N)=||q_N\tilde{f}-1||_{d_{\beta(\alpha)}}, \quad q_N(z)=\sum_{l=0}^{N}a_lz^l.\end{align*} $$
Then, the polynomial
 $$ \begin{align*}q^{\prime}_N(z_1,\ldots,z_n)=\sum_{l=0}^{N}\mu(m)^{-l/4}a_lz_1^{M_1l}\cdots z_m^{M_ml}\end{align*} $$
$$ \begin{align*}q^{\prime}_N(z_1,\ldots,z_n)=\sum_{l=0}^{N}\mu(m)^{-l/4}a_lz_1^{M_1l}\cdots z_m^{M_ml}\end{align*} $$
satisfies
![]() $q_N^{\prime }\in J_{\alpha ,M,m}\cap P_N^n$
and
$q_N^{\prime }\in J_{\alpha ,M,m}\cap P_N^n$
and
![]() $q_N^{\prime }f-1\in J_{\alpha ,M,m}$
. Thus,
$q_N^{\prime }f-1\in J_{\alpha ,M,m}$
. Thus,
and the assertion follows.
Define the function
![]() $\phi _{\beta }:[0,\infty )\rightarrow [0,\infty )$
by
$\phi _{\beta }:[0,\infty )\rightarrow [0,\infty )$
by
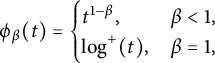 $$ \begin{align*}\phi_{\beta}(t)= \begin{cases} t^{1-\beta}, & \beta<1, \\ \log^+(t), & \beta=1, \end{cases} \end{align*} $$
$$ \begin{align*}\phi_{\beta}(t)= \begin{cases} t^{1-\beta}, & \beta<1, \\ \log^+(t), & \beta=1, \end{cases} \end{align*} $$
where
![]() $\log ^+(t):=\max \{\log t,0\}$
. We have the following.
$\log ^+(t):=\max \{\log t,0\}$
. We have the following.
Theorem 10 Let
![]() $\alpha \in {\mathbb R}$
be such that
$\alpha \in {\mathbb R}$
be such that
![]() $\beta (\alpha )\leq 1$
. Let
$\beta (\alpha )\leq 1$
. Let
![]() $f\in J_{\alpha ,M,m}$
be as above, and suppose that the corresponding
$f\in J_{\alpha ,M,m}$
be as above, and suppose that the corresponding
![]() $\tilde {f}$
has no zeros inside its domain, has at least one zero on the boundary, and admits an analytic continuation to a strictly bigger domain. Then f is cyclic in
$\tilde {f}$
has no zeros inside its domain, has at least one zero on the boundary, and admits an analytic continuation to a strictly bigger domain. Then f is cyclic in
![]() $D_{\alpha }({\mathbb B_n})$
whenever
$D_{\alpha }({\mathbb B_n})$
whenever
![]() $\alpha \leq \frac {2n-m+1}{2}$
and
$\alpha \leq \frac {2n-m+1}{2}$
and
Proof It is an immediate consequence of the identification between
![]() $D_{\beta }({\mathbb D})$
and
$D_{\beta }({\mathbb D})$
and
![]() $d_{\beta }$
and previous lemmas and propositions.
$d_{\beta }$
and previous lemmas and propositions.
If we focus on polynomials, then the following is true.
Theorem 11 Consider the polynomial
![]() $p(z)=1-m^{m/2} z_1\cdots z_m$
, where
$p(z)=1-m^{m/2} z_1\cdots z_m$
, where
![]() $1\leq m\leq n$
. Then p is cyclic in
$1\leq m\leq n$
. Then p is cyclic in
![]() $D_{\alpha }({\mathbb B_n})$
whenever
$D_{\alpha }({\mathbb B_n})$
whenever
![]() $\alpha \leq \frac {2n+1-m}{2}$
.
$\alpha \leq \frac {2n+1-m}{2}$
.
Note that the Theorem 11 is not a characterization. We shall study the case
![]() $\alpha>\frac {2n+1-m}{2}$
.
$\alpha>\frac {2n+1-m}{2}$
.
5 Cyclicity for model polynomials via radial dilation
The radial dilation of a function
![]() $f:{\mathbb B_n}\rightarrow {\mathbb C}$
is defined for
$f:{\mathbb B_n}\rightarrow {\mathbb C}$
is defined for
![]() $r\in (0,1)$
by
$r\in (0,1)$
by
![]() $f_r(z)=f(rz)$
. To prove Theorem 11, it is enough to prove the following lemma.
$f_r(z)=f(rz)$
. To prove Theorem 11, it is enough to prove the following lemma.
Lemma 12 Consider the polynomial
![]() $p(z)=1-m^{m/2} z_1\cdots z_m$
, where
$p(z)=1-m^{m/2} z_1\cdots z_m$
, where
![]() $1\leq m\leq n$
. Then
$1\leq m\leq n$
. Then
![]() $||p/p_r||_{\alpha }<\infty $
as
$||p/p_r||_{\alpha }<\infty $
as
![]() $r\rightarrow 1^{-}$
whenever
$r\rightarrow 1^{-}$
whenever
![]() $\alpha \leq \frac {2n+1-m}{2}$
.
$\alpha \leq \frac {2n+1-m}{2}$
.
We follow the arguments of [Reference Knese, Kosiński, Ransford and Sola13, Reference Kosiński and Vavitsas14]. Indeed, if Lemma 12 holds, then
![]() $\phi _r\cdot p\rightarrow 1$
weakly, where
$\phi _r\cdot p\rightarrow 1$
weakly, where
![]() $\phi _r:=1/p_r$
. This is a consequence of a crucial property of Dirichlet-type spaces: if
$\phi _r:=1/p_r$
. This is a consequence of a crucial property of Dirichlet-type spaces: if
![]() $\{f_n\}\subset D_{\alpha }({\mathbb B_n})$
, then
$\{f_n\}\subset D_{\alpha }({\mathbb B_n})$
, then
![]() $f_n\rightarrow 0$
weakly if and only if
$f_n\rightarrow 0$
weakly if and only if
![]() $f_n\rightarrow 0$
pointwise and
$f_n\rightarrow 0$
pointwise and
![]() $\sup _{n}\{||f_n||_{\alpha }\}<\infty $
. Since
$\sup _{n}\{||f_n||_{\alpha }\}<\infty $
. Since
![]() $\phi _r$
extends holomorphically past the closed unit ball,
$\phi _r$
extends holomorphically past the closed unit ball,
![]() $\phi _r$
are multipliers, and hence,
$\phi _r$
are multipliers, and hence,
![]() $\phi _r\cdot p\in [p]$
. Finally,
$\phi _r\cdot p\in [p]$
. Finally,
![]() $1$
is weak limit of
$1$
is weak limit of
![]() $\phi _r\cdot p$
and
$\phi _r\cdot p$
and
![]() $[p]$
is closed and convex or, equivalently, weakly closed. It is clear that
$[p]$
is closed and convex or, equivalently, weakly closed. It is clear that
![]() $1\in [p]$
, and hence p is cyclic.
$1\in [p]$
, and hence p is cyclic.
Moreover, it is enough to prove that
![]() $||p/p_r||_{\alpha }<\infty $
, as
$||p/p_r||_{\alpha }<\infty $
, as
![]() $r\rightarrow 1^{-}$
, for
$r\rightarrow 1^{-}$
, for
![]() $\alpha _0=\frac {2n+1-m}{2}$
. Then the case
$\alpha _0=\frac {2n+1-m}{2}$
. Then the case
![]() $\alpha <\alpha _0$
follows since the inclusion
$\alpha <\alpha _0$
follows since the inclusion
![]() $D_{\alpha _0}({\mathbb B_n})\hookrightarrow D_{\alpha }({\mathbb B_n})$
is a compact linear map and weak convergence in
$D_{\alpha _0}({\mathbb B_n})\hookrightarrow D_{\alpha }({\mathbb B_n})$
is a compact linear map and weak convergence in
![]() $D_{\alpha _0}({\mathbb B_n})$
gives weak convergence in
$D_{\alpha _0}({\mathbb B_n})$
gives weak convergence in
![]() $D_{\alpha }({\mathbb B_n})$
.
$D_{\alpha }({\mathbb B_n})$
.
Proof of Lemma 12
By Theorem 4, it is enough to show the following:
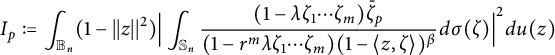 $$ \begin{align*}I_p:=\int_{{\mathbb B_n}}(1-||z||^2)\Big|\int_{\mathbb S_n}\frac{(1-\lambda \zeta_1\cdots \zeta_m)\bar{\zeta}_p}{(1-r^m\lambda \zeta_1\cdots \zeta_m)(1-\langle z,\zeta \rangle)^{\beta}}d\sigma(\zeta)\Big|^2du(z)\end{align*} $$
$$ \begin{align*}I_p:=\int_{{\mathbb B_n}}(1-||z||^2)\Big|\int_{\mathbb S_n}\frac{(1-\lambda \zeta_1\cdots \zeta_m)\bar{\zeta}_p}{(1-r^m\lambda \zeta_1\cdots \zeta_m)(1-\langle z,\zeta \rangle)^{\beta}}d\sigma(\zeta)\Big|^2du(z)\end{align*} $$
and
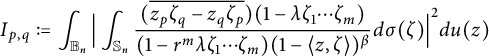 $$ \begin{align*}I_{p,q}:=\int_{{\mathbb B_n}}\Big|\int_{\mathbb S_n}\frac{(\overline{z_p\zeta_q-z_q\zeta_p})(1-\lambda \zeta_1\cdots \zeta_m)}{(1-r^m\lambda \zeta_1\cdots \zeta_m)(1-\langle z,\zeta \rangle)^{\beta}}d\sigma(\zeta)\Big|^2du(z)\end{align*} $$
$$ \begin{align*}I_{p,q}:=\int_{{\mathbb B_n}}\Big|\int_{\mathbb S_n}\frac{(\overline{z_p\zeta_q-z_q\zeta_p})(1-\lambda \zeta_1\cdots \zeta_m)}{(1-r^m\lambda \zeta_1\cdots \zeta_m)(1-\langle z,\zeta \rangle)^{\beta}}d\sigma(\zeta)\Big|^2du(z)\end{align*} $$
are finite, as
![]() $r\rightarrow 1^{-}$
, where
$r\rightarrow 1^{-}$
, where
![]() $\beta =n+t+1$
,
$\beta =n+t+1$
,
![]() $t=\frac {2n+1-m}{4}$
, and
$t=\frac {2n+1-m}{4}$
, and
![]() $\lambda =m^{m/2}$
.
$\lambda =m^{m/2}$
.
Denote
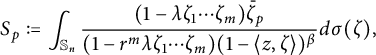 $$ \begin{align*}S_p:=\int_{\mathbb S_n}\frac{(1-\lambda \zeta_1\cdots \zeta_m)\bar{\zeta}_p}{(1-r^m\lambda \zeta_1\cdots \zeta_m)(1-\langle z,\zeta \rangle)^{\beta}}d\sigma(\zeta),\end{align*} $$
$$ \begin{align*}S_p:=\int_{\mathbb S_n}\frac{(1-\lambda \zeta_1\cdots \zeta_m)\bar{\zeta}_p}{(1-r^m\lambda \zeta_1\cdots \zeta_m)(1-\langle z,\zeta \rangle)^{\beta}}d\sigma(\zeta),\end{align*} $$
where the last integral is equal to
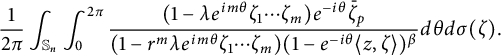 $$ \begin{align*}\frac{1}{2\pi}\int_{\mathbb S_n}\int_{0}^{2\pi}\frac{(1-\lambda e^{im\theta}\zeta_1\cdots \zeta_m)e^{-i\theta}\bar{\zeta}_p}{(1-r^m\lambda e^{im\theta}\zeta_1\cdots \zeta_m)(1-e^{-i\theta}\langle z,\zeta \rangle)^{\beta}}d\theta d\sigma(\zeta).\end{align*} $$
$$ \begin{align*}\frac{1}{2\pi}\int_{\mathbb S_n}\int_{0}^{2\pi}\frac{(1-\lambda e^{im\theta}\zeta_1\cdots \zeta_m)e^{-i\theta}\bar{\zeta}_p}{(1-r^m\lambda e^{im\theta}\zeta_1\cdots \zeta_m)(1-e^{-i\theta}\langle z,\zeta \rangle)^{\beta}}d\theta d\sigma(\zeta).\end{align*} $$
Let
![]() $z,\zeta $
be fixed. Then
$z,\zeta $
be fixed. Then
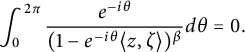 $$ \begin{align*}\int_{0}^{2\pi}\frac{e^{-i\theta}}{(1-e^{-i\theta}\langle z,\zeta \rangle)^{\beta}}d\theta=0.\end{align*} $$
$$ \begin{align*}\int_{0}^{2\pi}\frac{e^{-i\theta}}{(1-e^{-i\theta}\langle z,\zeta \rangle)^{\beta}}d\theta=0.\end{align*} $$
Thus, replacing
![]() $p(e^{i\theta }\zeta )/p(re^{i\theta }\zeta )$
by
$p(e^{i\theta }\zeta )/p(re^{i\theta }\zeta )$
by
![]() $p(e^{i\theta }\zeta )/p(re^{i\theta }\zeta )-1$
, we obtain
$p(e^{i\theta }\zeta )/p(re^{i\theta }\zeta )-1$
, we obtain
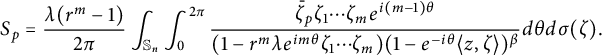 $$ \begin{align*}S_p=\frac{\lambda(r^m-1)}{2\pi}\int_{\mathbb S_n}\int_{0}^{2\pi}\frac{ \bar{\zeta}_p\zeta_1\cdots\zeta_me^{i(m-1)\theta}}{(1-r^m\lambda e^{im\theta}\zeta_1\cdots \zeta_m)(1-e^{-i\theta}\langle z,\zeta \rangle)^{\beta}}d\theta d\sigma(\zeta).\end{align*} $$
$$ \begin{align*}S_p=\frac{\lambda(r^m-1)}{2\pi}\int_{\mathbb S_n}\int_{0}^{2\pi}\frac{ \bar{\zeta}_p\zeta_1\cdots\zeta_me^{i(m-1)\theta}}{(1-r^m\lambda e^{im\theta}\zeta_1\cdots \zeta_m)(1-e^{-i\theta}\langle z,\zeta \rangle)^{\beta}}d\theta d\sigma(\zeta).\end{align*} $$
Next, expand the binomials
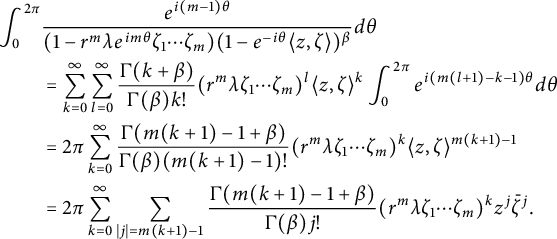 $$ \begin{align*} \int_{0}^{2\pi}&\frac{e^{i(m-1)\theta}}{(1-r^m\lambda e^{im\theta}\zeta_1\cdots \zeta_m)(1-e^{-i\theta}\langle z,\zeta \rangle)^{\beta}}d\theta\\ &=\sum_{k=0}^{\infty}\sum_{l=0}^{\infty}\frac{\Gamma(k+\beta)}{\Gamma(\beta)k!}(r^m\lambda\zeta_1\cdots \zeta_m)^l\langle z,\zeta \rangle^k\int_{0}^{2\pi}e^{i(m(l+1)-k-1)\theta}d\theta\\ &=2\pi\sum_{k=0}^{\infty}\frac{\Gamma(m(k+1)-1+\beta)}{\Gamma(\beta)(m(k+1)-1)!}(r^m\lambda\zeta_1\cdots \zeta_m)^k\langle z,\zeta \rangle^{m(k+1)-1}\\ &=2\pi \sum_{k=0}^{\infty}\sum_{|j|=m(k+1)-1}\frac{\Gamma(m(k+1)-1+\beta)}{\Gamma(\beta)j!}(r^m\lambda\zeta_1\cdots \zeta_m)^kz^j\bar{\zeta}^j. \end{align*} $$
$$ \begin{align*} \int_{0}^{2\pi}&\frac{e^{i(m-1)\theta}}{(1-r^m\lambda e^{im\theta}\zeta_1\cdots \zeta_m)(1-e^{-i\theta}\langle z,\zeta \rangle)^{\beta}}d\theta\\ &=\sum_{k=0}^{\infty}\sum_{l=0}^{\infty}\frac{\Gamma(k+\beta)}{\Gamma(\beta)k!}(r^m\lambda\zeta_1\cdots \zeta_m)^l\langle z,\zeta \rangle^k\int_{0}^{2\pi}e^{i(m(l+1)-k-1)\theta}d\theta\\ &=2\pi\sum_{k=0}^{\infty}\frac{\Gamma(m(k+1)-1+\beta)}{\Gamma(\beta)(m(k+1)-1)!}(r^m\lambda\zeta_1\cdots \zeta_m)^k\langle z,\zeta \rangle^{m(k+1)-1}\\ &=2\pi \sum_{k=0}^{\infty}\sum_{|j|=m(k+1)-1}\frac{\Gamma(m(k+1)-1+\beta)}{\Gamma(\beta)j!}(r^m\lambda\zeta_1\cdots \zeta_m)^kz^j\bar{\zeta}^j. \end{align*} $$
Therefore,
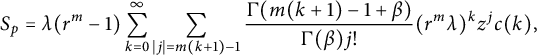 $$ \begin{align*}S_p=\lambda(r^m-1)\sum_{k=0}^{\infty}\sum_{|j|=m(k+1)-1}\frac{\Gamma(m(k+1)-1+\beta)}{\Gamma(\beta)j!}(r^m\lambda)^kz^jc(k),\end{align*} $$
$$ \begin{align*}S_p=\lambda(r^m-1)\sum_{k=0}^{\infty}\sum_{|j|=m(k+1)-1}\frac{\Gamma(m(k+1)-1+\beta)}{\Gamma(\beta)j!}(r^m\lambda)^kz^jc(k),\end{align*} $$
where
![]() $c(k)=\int _{\mathbb {S}_n}\zeta ^{\alpha (k)}\bar {\zeta }^{b(k)}d\sigma (\zeta )$
,
$c(k)=\int _{\mathbb {S}_n}\zeta ^{\alpha (k)}\bar {\zeta }^{b(k)}d\sigma (\zeta )$
,
![]() $\alpha (k)=(k+1,\ldots ,k+1\text {(m-comp.)},0,\ldots ,0)$
and
$\alpha (k)=(k+1,\ldots ,k+1\text {(m-comp.)},0,\ldots ,0)$
and
![]() $b(k)=(j_1,\ldots ,j_{p-1},j_p+1,j_{p+1},\ldots ,j_n)$
. Whence,
$b(k)=(j_1,\ldots ,j_{p-1},j_p+1,j_{p+1},\ldots ,j_n)$
. Whence,
![]() $1\leq p\leq m$
. Since the holomorphic monomials are orthogonal to each other in
$1\leq p\leq m$
. Since the holomorphic monomials are orthogonal to each other in
![]() $L^2(\sigma )$
, we get that
$L^2(\sigma )$
, we get that
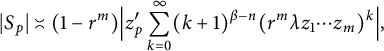 $$ \begin{align*}|S_p|\asymp(1-r^m)\Big|z^{\prime}_p\sum_{k=0}^{\infty}(k+1)^{\beta-n}(r^m\lambda z_1\cdots z_m)^k\Big|,\end{align*} $$
$$ \begin{align*}|S_p|\asymp(1-r^m)\Big|z^{\prime}_p\sum_{k=0}^{\infty}(k+1)^{\beta-n}(r^m\lambda z_1\cdots z_m)^k\Big|,\end{align*} $$
where
![]() $z^{\prime }_p=z_1\cdots z_{p-1}z_{p+1}\cdots z_m$
. Hence, we obtain
$z^{\prime }_p=z_1\cdots z_{p-1}z_{p+1}\cdots z_m$
. Hence, we obtain
 $$ \begin{align*}I_p\asymp(1-r^m)^2\sum_{k=0}^{\infty}(k+1)^{2(\beta-n)}(r^m\lambda)^{2k}\int_{{\mathbb B_n}}(1-||z||^2)|z^{\prime}_p|^2|z_1\cdots z_m|^{2k}du(z),\end{align*} $$
$$ \begin{align*}I_p\asymp(1-r^m)^2\sum_{k=0}^{\infty}(k+1)^{2(\beta-n)}(r^m\lambda)^{2k}\int_{{\mathbb B_n}}(1-||z||^2)|z^{\prime}_p|^2|z_1\cdots z_m|^{2k}du(z),\end{align*} $$
where has been used again the orthogonality of the holomorphic monomials in
![]() $L^2(\sigma )$
. To handle the integral above, we use polar coordinates
$L^2(\sigma )$
. To handle the integral above, we use polar coordinates
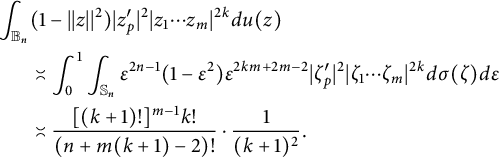 $$ \begin{align*} \int_{{\mathbb B_n}}&(1-||z||^2)|z^{\prime}_p|^2|z_1\cdots z_m|^{2k}du(z)\\ &\asymp \int_{0}^{1}\int_{\mathbb S_n}\epsilon^{2n-1}(1-\epsilon^2)\epsilon^{2km+2m-2}|\zeta_p^{\prime}|^2|\zeta_1\cdots \zeta_m|^{2k}d\sigma(\zeta)d\epsilon\\ &\asymp \frac{[(k+1)!]^{m-1}k!}{(n+m(k+1)-2)!}\cdot\frac{1}{(k+1)^2}. \end{align*} $$
$$ \begin{align*} \int_{{\mathbb B_n}}&(1-||z||^2)|z^{\prime}_p|^2|z_1\cdots z_m|^{2k}du(z)\\ &\asymp \int_{0}^{1}\int_{\mathbb S_n}\epsilon^{2n-1}(1-\epsilon^2)\epsilon^{2km+2m-2}|\zeta_p^{\prime}|^2|\zeta_1\cdots \zeta_m|^{2k}d\sigma(\zeta)d\epsilon\\ &\asymp \frac{[(k+1)!]^{m-1}k!}{(n+m(k+1)-2)!}\cdot\frac{1}{(k+1)^2}. \end{align*} $$
If we recall that
![]() $\beta =n+t+1$
,
$\beta =n+t+1$
,
![]() $t=\frac {2n+1-m}{4}$
and
$t=\frac {2n+1-m}{4}$
and
![]() $\lambda ^{2k}=m^{mk}$
, then applying the Stirling formula more than one time, we see that
$\lambda ^{2k}=m^{mk}$
, then applying the Stirling formula more than one time, we see that
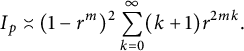 $$ \begin{align*}I_p\asymp(1-r^m)^2 \sum_{k=0}^{\infty}(k+1)r^{2mk}.\end{align*} $$
$$ \begin{align*}I_p\asymp(1-r^m)^2 \sum_{k=0}^{\infty}(k+1)r^{2mk}.\end{align*} $$
This proves the assertion made about
![]() $I_p$
.
$I_p$
.
It remains to estimate the following term:
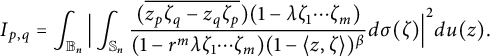 $$ \begin{align*}I_{p,q}=\int_{{\mathbb B_n}}\Big|\int_{\mathbb S_n}\frac{(\overline{z_p\zeta_q-z_q\zeta_p})(1-\lambda \zeta_1\cdots \zeta_m)}{(1-r^m\lambda \zeta_1\cdots \zeta_m)(1-\langle z,\zeta \rangle)^{\beta}}d\sigma(\zeta)\Big|^2du(z).\end{align*} $$
$$ \begin{align*}I_{p,q}=\int_{{\mathbb B_n}}\Big|\int_{\mathbb S_n}\frac{(\overline{z_p\zeta_q-z_q\zeta_p})(1-\lambda \zeta_1\cdots \zeta_m)}{(1-r^m\lambda \zeta_1\cdots \zeta_m)(1-\langle z,\zeta \rangle)^{\beta}}d\sigma(\zeta)\Big|^2du(z).\end{align*} $$
We shall show that
![]() $I_{p,q}\asymp I_p$
. Denote again the inner integral by
$I_{p,q}\asymp I_p$
. Denote again the inner integral by
![]() $S_{p,q}$
which is convenient to expand it as
$S_{p,q}$
which is convenient to expand it as
![]() $S_{p,q}=\bar {z}_pS_q-\bar {z}_qS_p$
. Recall that
$S_{p,q}=\bar {z}_pS_q-\bar {z}_qS_p$
. Recall that
![]() $z_p^{\prime }=z_1\cdots z_{p-1}z_{p+1}\cdots z_m$
. Similar calculations to the one above lead to
$z_p^{\prime }=z_1\cdots z_{p-1}z_{p+1}\cdots z_m$
. Similar calculations to the one above lead to
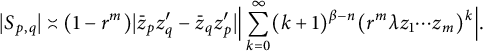 $$ \begin{align*}|S_{p,q}|\asymp(1-r^m)|\bar{z}_pz_q^{\prime}-\bar{z}_qz_p^{\prime}|\Big|\sum_{k=0}^{\infty}(k+1)^{\beta-n}(r^m\lambda z_1\cdots z_m)^k\Big|.\end{align*} $$
$$ \begin{align*}|S_{p,q}|\asymp(1-r^m)|\bar{z}_pz_q^{\prime}-\bar{z}_qz_p^{\prime}|\Big|\sum_{k=0}^{\infty}(k+1)^{\beta-n}(r^m\lambda z_1\cdots z_m)^k\Big|.\end{align*} $$
Moreover, the orthogonality of the holomorphic monomials in
![]() $L^2(\sigma )$
gives the following estimation:
$L^2(\sigma )$
gives the following estimation:
 $$ \begin{align*}I_{p,q}\asymp (1-r^m)^2\sum_{k=0}^{\infty}(k+1)^{2\beta-2n}(r^m\lambda)^{2k}\int_{{\mathbb B_n}}|\bar{z}_pz_q^{\prime}-\bar{z}_qz_p^{\prime}|^2|z_1\cdots z_m|^{2k}du(z).\end{align*} $$
$$ \begin{align*}I_{p,q}\asymp (1-r^m)^2\sum_{k=0}^{\infty}(k+1)^{2\beta-2n}(r^m\lambda)^{2k}\int_{{\mathbb B_n}}|\bar{z}_pz_q^{\prime}-\bar{z}_qz_p^{\prime}|^2|z_1\cdots z_m|^{2k}du(z).\end{align*} $$
It is easy to see that
![]() $|\bar {z}_pz_q^{\prime }-\bar {z}_qz_p^{\prime }|^2=|z_p|^2|z^{\prime }_q|^2+|z_q|^2|z^{\prime }_p|^2-2|z_1\cdots z_m|^2$
. Let us estimate the integral
$|\bar {z}_pz_q^{\prime }-\bar {z}_qz_p^{\prime }|^2=|z_p|^2|z^{\prime }_q|^2+|z_q|^2|z^{\prime }_p|^2-2|z_1\cdots z_m|^2$
. Let us estimate the integral
Passing through polar coordinates, we get, for
![]() $p\neq q$
, that
$p\neq q$
, that
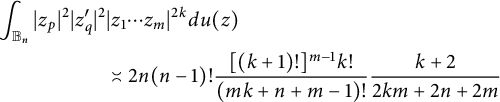 $$ \begin{align*} \int_{{\mathbb B_n}}|z_p|^2|z_q^{\prime}|^2&|z_1\cdots z_m|^{2k}du(z)\\ &\asymp 2n(n-1)!\frac{[(k+1)!]^{m-1}k!}{(mk+n+m-1)!}\frac{k+2}{2km+2n+2m} \end{align*} $$
$$ \begin{align*} \int_{{\mathbb B_n}}|z_p|^2|z_q^{\prime}|^2&|z_1\cdots z_m|^{2k}du(z)\\ &\asymp 2n(n-1)!\frac{[(k+1)!]^{m-1}k!}{(mk+n+m-1)!}\frac{k+2}{2km+2n+2m} \end{align*} $$
and
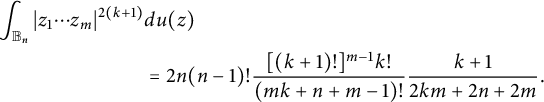 $$ \begin{align*} \int_{{\mathbb B_n}}|z_1\cdots z_m|^{2(k+1)}&du(z)\\ &=2n(n-1)!\frac{[(k+1)!]^{m-1}k!}{(mk+n+m-1)!}\frac{k+1}{2km+2n+2m}. \end{align*} $$
$$ \begin{align*} \int_{{\mathbb B_n}}|z_1\cdots z_m|^{2(k+1)}&du(z)\\ &=2n(n-1)!\frac{[(k+1)!]^{m-1}k!}{(mk+n+m-1)!}\frac{k+1}{2km+2n+2m}. \end{align*} $$
Hence, we obtain
 $$ \begin{align*} \int_{{\mathbb B_n}}(|z_p|^2|z_q^{\prime}|^2-|z_1 \cdots z_m|^2)&|z_1\cdots z_m|^{2k}du(z)\\ &\asymp \frac{[(k+1)!]^{m-1}k!}{(mk+n+m-2)!(k+1)^2}. \end{align*} $$
$$ \begin{align*} \int_{{\mathbb B_n}}(|z_p|^2|z_q^{\prime}|^2-|z_1 \cdots z_m|^2)&|z_1\cdots z_m|^{2k}du(z)\\ &\asymp \frac{[(k+1)!]^{m-1}k!}{(mk+n+m-2)!(k+1)^2}. \end{align*} $$
Again, applying the Stirling formula to the one above estimates, we obtain
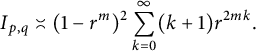 $$ \begin{align*}I_{p,q}\asymp(1-r^m)^2 \sum_{k=0}^{\infty}(k+1)r^{2mk}.\end{align*} $$
$$ \begin{align*}I_{p,q}\asymp(1-r^m)^2 \sum_{k=0}^{\infty}(k+1)r^{2mk}.\end{align*} $$
This proves the assertion made about
![]() $I_{p,q}$
.
$I_{p,q}$
.
6 Sufficient conditions for noncyclicity via Cauchy transforms and
 $\alpha $
-capacities
$\alpha $
-capacities
We consider the Cauchy transform of a complex Borel measure
![]() $\mu $
on the unit sphere by
$\mu $
on the unit sphere by
Note that this definition differs from the classical one.
Let
![]() $f\in D_{\alpha }({\mathbb B_n})$
and put a measure
$f\in D_{\alpha }({\mathbb B_n})$
and put a measure
![]() $\mu $
on
$\mu $
on
![]() $\mathcal {Z}(f^*)$
: the zero set in the sphere of the radial limits of f. The results in [Reference Sola21] about Cauchy transforms and noncyclicity are valid in our settings. We deduce that
$\mathcal {Z}(f^*)$
: the zero set in the sphere of the radial limits of f. The results in [Reference Sola21] about Cauchy transforms and noncyclicity are valid in our settings. We deduce that
![]() $[f] \neq D_{\alpha }({\mathbb B_n})$
, and hence noncyclicity, whenever
$[f] \neq D_{\alpha }({\mathbb B_n})$
, and hence noncyclicity, whenever
![]() $C_{[\mu ]}\in D_{-\alpha }({\mathbb B_n})$
. Thus, it is important to compute the Dirichlet-type norm of the Cauchy transform.
$C_{[\mu ]}\in D_{-\alpha }({\mathbb B_n})$
. Thus, it is important to compute the Dirichlet-type norm of the Cauchy transform.
Let
![]() $\mu $
be a Borel measure on
$\mu $
be a Borel measure on
![]() $\mathbb {S}_n$
and set
$\mathbb {S}_n$
and set
![]() $\mu ^*(j)=\int _{\mathbb S_n}\zeta ^jd\mu (\zeta )$
,
$\mu ^*(j)=\int _{\mathbb S_n}\zeta ^jd\mu (\zeta )$
,
![]() $\bar {\mu }^*(j)=\int _{\mathbb S_n}\bar {\zeta }^jd\mu (\zeta )$
. We have the following.
$\bar {\mu }^*(j)=\int _{\mathbb S_n}\bar {\zeta }^jd\mu (\zeta )$
. We have the following.
Lemma 13 Let
![]() $\mu $
be a Borel measure on
$\mu $
be a Borel measure on
![]() $\mathbb {S}_n$
. Then
$\mathbb {S}_n$
. Then
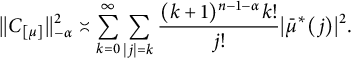 $$ \begin{align*}||C_{[\mu]}||_{-\alpha}^2\asymp \sum_{k=0}^{\infty}\sum_{|j|=k}\frac{(k+1)^{n-1-\alpha}k!}{j!}|\bar{\mu}^*(j)|^2.\end{align*} $$
$$ \begin{align*}||C_{[\mu]}||_{-\alpha}^2\asymp \sum_{k=0}^{\infty}\sum_{|j|=k}\frac{(k+1)^{n-1-\alpha}k!}{j!}|\bar{\mu}^*(j)|^2.\end{align*} $$
Proof Our Cauchy integral of
![]() $\mu $
on
$\mu $
on
![]() ${\mathbb B_n}$
has the following expansion:
${\mathbb B_n}$
has the following expansion:
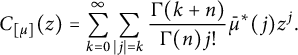 $$ \begin{align*}C_{[\mu]}(z)=\sum_{k=0}^{\infty}\sum_{|j|=k}\frac{\Gamma(k+n)}{\Gamma(n)j!}\bar{\mu}^*(j)z^j.\end{align*} $$
$$ \begin{align*}C_{[\mu]}(z)=\sum_{k=0}^{\infty}\sum_{|j|=k}\frac{\Gamma(k+n)}{\Gamma(n)j!}\bar{\mu}^*(j)z^j.\end{align*} $$
Therefore, one can compute the norm of
![]() $C_{[\mu ]}$
in the space
$C_{[\mu ]}$
in the space
![]() $D_{-\alpha }({\mathbb B_n})$
. The assertion follows.
$D_{-\alpha }({\mathbb B_n})$
. The assertion follows.
The following lemma is crucial in the sequel. It is probably known, but we were not able to locate it in the literature, and hence we include its proof.
Lemma 14 Let
![]() $j_1,\ldots ,j_n,k$
be nonnegative integers satisfying
$j_1,\ldots ,j_n,k$
be nonnegative integers satisfying
![]() $j_1+\cdots +j_n=nk$
. Then
$j_1+\cdots +j_n=nk$
. Then
Proof The
![]() $\Gamma $
-function is logarithmically convex, and hence we may apply the Jensen inequality to it:
$\Gamma $
-function is logarithmically convex, and hence we may apply the Jensen inequality to it:
Set
![]() $x_i:=j_i+1$
,
$x_i:=j_i+1$
,
![]() $i=1,\ldots ,n$
. Since
$i=1,\ldots ,n$
. Since
![]() $j_1+\cdots +j_n=nk$
, the assertion follows.
$j_1+\cdots +j_n=nk$
, the assertion follows.
We may identify noncyclicity for model polynomials via Cauchy transforms.
Lemma 15 Consider the polynomial
![]() $p(z)=1-m^{m/2} z_1\cdots z_m$
, where
$p(z)=1-m^{m/2} z_1\cdots z_m$
, where
![]() $1\leq m\leq n$
. Then p is not cyclic in
$1\leq m\leq n$
. Then p is not cyclic in
![]() $D_{\alpha }({\mathbb B_n})$
whenever
$D_{\alpha }({\mathbb B_n})$
whenever
![]() $\alpha>\frac {2n+1-m}{2}$
.
$\alpha>\frac {2n+1-m}{2}$
.
Proof Recall that the model polynomials vanish in the closed unit ball along analytic sets of the form:
It is easy to see that for a proper measure
![]() $\mu $
,
$\mu $
,
![]() $\mu ^*(j)$
is nonzero, when
$\mu ^*(j)$
is nonzero, when
![]() $mj_m=k$
and
$mj_m=k$
and
![]() $\mu ^*(j)\asymp m^{-k/2}$
. By Stirling’s formula and Lemma 14, we get that
$\mu ^*(j)\asymp m^{-k/2}$
. By Stirling’s formula and Lemma 14, we get that
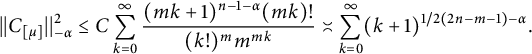 $$ \begin{align*} ||C_{[\mu]}||_{-\alpha}^2&\leq C \sum_{k=0}^{\infty}\frac{(mk+1)^{n-1-\alpha}(mk)!}{(k!)^mm^{mk}}\asymp \sum_{k=0}^{\infty}(k+1)^{1/2(2n-m-1)-\alpha}. \end{align*} $$
$$ \begin{align*} ||C_{[\mu]}||_{-\alpha}^2&\leq C \sum_{k=0}^{\infty}\frac{(mk+1)^{n-1-\alpha}(mk)!}{(k!)^mm^{mk}}\asymp \sum_{k=0}^{\infty}(k+1)^{1/2(2n-m-1)-\alpha}. \end{align*} $$
Thus, p is not cyclic in
![]() $D_{\alpha }({\mathbb B_n})$
for
$D_{\alpha }({\mathbb B_n})$
for
![]() $\alpha>\frac {2n+1-m}{2}$
.
$\alpha>\frac {2n+1-m}{2}$
.
We consider Riesz
![]() $\alpha $
-capacity for a fixed parameter
$\alpha $
-capacity for a fixed parameter
![]() $\alpha \in (0,n)$
with respect to the anisotropic distance in
$\alpha \in (0,n)$
with respect to the anisotropic distance in
![]() $\mathbb S_n$
given by
$\mathbb S_n$
given by
and the nonnegative kernel
![]() $K_{\alpha }:(0,\infty )\rightarrow [0,\infty )$
given by
$K_{\alpha }:(0,\infty )\rightarrow [0,\infty )$
given by
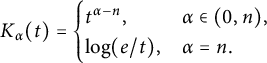 $$ \begin{align*}K_{\alpha}(t)= \begin{cases} t^{\alpha-n}, & \alpha\in(0,n), \\ \log(e/t), & \alpha=n. \end{cases} \end{align*} $$
$$ \begin{align*}K_{\alpha}(t)= \begin{cases} t^{\alpha-n}, & \alpha\in(0,n), \\ \log(e/t), & \alpha=n. \end{cases} \end{align*} $$
Note that we may extend the definition of K to
![]() $0$
by defining
$0$
by defining
![]() $K(0):=\lim _{t\rightarrow 0^+}K(t)$
.
$K(0):=\lim _{t\rightarrow 0^+}K(t)$
.
Let
![]() $\mu $
be any Borel probability measure supported on some Borel set
$\mu $
be any Borel probability measure supported on some Borel set
![]() $E\subset \mathbb {S}_n$
. Then the Riesz
$E\subset \mathbb {S}_n$
. Then the Riesz
![]() $\alpha $
-energy of
$\alpha $
-energy of
![]() $\mu $
is given by
$\mu $
is given by
and the Riesz
![]() $\alpha $
-capacity of E by
$\alpha $
-capacity of E by
where
![]() $\mathcal {P}(E)$
is the set of all Borel probability measures supported on E. Note that if
$\mathcal {P}(E)$
is the set of all Borel probability measures supported on E. Note that if
![]() $\text {cap}_{\alpha }(E)>0$
, then there exist at least one probability measure supported on E having finite Riesz
$\text {cap}_{\alpha }(E)>0$
, then there exist at least one probability measure supported on E having finite Riesz
![]() $\alpha $
-energy. Moreover, any
$\alpha $
-energy. Moreover, any
![]() $f\in D_{\alpha }({\mathbb B_n})$
has finite radial limits
$f\in D_{\alpha }({\mathbb B_n})$
has finite radial limits
![]() $f^*$
on
$f^*$
on
![]() $\mathbb {S}_n$
, except possibly, on a set E having
$\mathbb {S}_n$
, except possibly, on a set E having
![]() $\text {cap}_{\alpha }(E)=0$
. Theory regarding to the above standard construction in potential theory can be found in [Reference Ahern and Cohn1, Reference Cohn and Verbitsky9, Reference El-Fallah, Kellay, Mashreghi and Ransford11, Reference Pestana and Rodríguez17].
$\text {cap}_{\alpha }(E)=0$
. Theory regarding to the above standard construction in potential theory can be found in [Reference Ahern and Cohn1, Reference Cohn and Verbitsky9, Reference El-Fallah, Kellay, Mashreghi and Ransford11, Reference Pestana and Rodríguez17].
The relation between noncyclicity of a function and the Riesz
![]() $\alpha $
-capacity of the zeros of its radial limits follows.
$\alpha $
-capacity of the zeros of its radial limits follows.
Theorem 16 Fix
![]() $\alpha \in (0,n]$
and let
$\alpha \in (0,n]$
and let
![]() $f\in D_{\alpha }({\mathbb B_n})$
. If
$f\in D_{\alpha }({\mathbb B_n})$
. If
![]() $\mathrm {cap}_{\alpha }(\mathcal {Z}(f^*))>0$
, then f is not cyclic in
$\mathrm {cap}_{\alpha }(\mathcal {Z}(f^*))>0$
, then f is not cyclic in
![]() $D_{\alpha }({\mathbb B_n})$
.
$D_{\alpha }({\mathbb B_n})$
.
Proof Let
![]() $\mu $
be a probability measure supported in
$\mu $
be a probability measure supported in
![]() $\mathcal {Z}(f^*)$
, with finite Riesz n-energy. If
$\mathcal {Z}(f^*)$
, with finite Riesz n-energy. If
![]() $r\in (0,1)$
, then
$r\in (0,1)$
, then
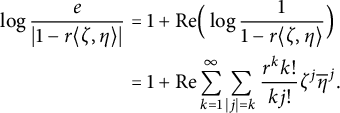 $$ \begin{align*} \log\frac{e}{|1-r\langle \zeta,\eta\rangle|}&=1+\textrm{Re}\Big(\log\frac{1}{1-r\langle \zeta,\eta\rangle}\Big)\\ &=1+\textrm{Re} \sum_{k=1}^{\infty}\sum_{|j|=k}\frac{r^kk!}{kj!}\zeta^j\overline{\eta}^j. \end{align*} $$
$$ \begin{align*} \log\frac{e}{|1-r\langle \zeta,\eta\rangle|}&=1+\textrm{Re}\Big(\log\frac{1}{1-r\langle \zeta,\eta\rangle}\Big)\\ &=1+\textrm{Re} \sum_{k=1}^{\infty}\sum_{|j|=k}\frac{r^kk!}{kj!}\zeta^j\overline{\eta}^j. \end{align*} $$
Note that
![]() $\mu $
is a probability measure, and hence
$\mu $
is a probability measure, and hence
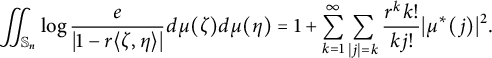 $$ \begin{align*} \iint_{\mathbb S_n}\log\frac{e}{|1-r\langle \zeta,\eta\rangle|}d\mu(\zeta)d\mu(\eta) =1+ \sum_{k=1}^{\infty}\sum_{|j|=k}\frac{r^kk!}{kj!}|\mu^*(j)|^2. \end{align*} $$
$$ \begin{align*} \iint_{\mathbb S_n}\log\frac{e}{|1-r\langle \zeta,\eta\rangle|}d\mu(\zeta)d\mu(\eta) =1+ \sum_{k=1}^{\infty}\sum_{|j|=k}\frac{r^kk!}{kj!}|\mu^*(j)|^2. \end{align*} $$
Since
![]() $|1-w|/|1-rw|\leq 2$
for
$|1-w|/|1-rw|\leq 2$
for
![]() $r\in (0,1)$
and
$r\in (0,1)$
and
![]() $w\in \overline {{\mathbb D}}$
, the dominated convergence theorem and Lemma 13 give
$w\in \overline {{\mathbb D}}$
, the dominated convergence theorem and Lemma 13 give
 $$ \begin{align*}||C_{[\mu]}||^2_{-n}\asymp\sum_{k=1}^{\infty}\sum_{|j|=k}\frac{k!}{kj!}|\mu^*(j)|^2<\infty.\end{align*} $$
$$ \begin{align*}||C_{[\mu]}||^2_{-n}\asymp\sum_{k=1}^{\infty}\sum_{|j|=k}\frac{k!}{kj!}|\mu^*(j)|^2<\infty.\end{align*} $$
The assertion follows.
We continue setting a probability measure
![]() $\mu $
, supported in
$\mu $
, supported in
![]() $\mathcal {Z}(f^*)$
, with finite Riesz
$\mathcal {Z}(f^*)$
, with finite Riesz
![]() $\alpha $
-energy, where
$\alpha $
-energy, where
![]() $\alpha \in (0,n)$
. If
$\alpha \in (0,n)$
. If
![]() $r\in (0,1)$
, then
$r\in (0,1)$
, then
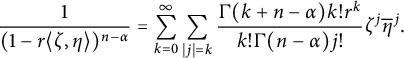 $$ \begin{align*} \frac{1}{(1-r\langle \zeta,\eta\rangle)^{n-\alpha}}&=\sum_{k=0}^{\infty}\sum_{|j|=k} \frac{\Gamma(k+n-\alpha)k!r^k}{k!\Gamma(n-\alpha)j!}\zeta^j\overline{\eta}^j. \end{align*} $$
$$ \begin{align*} \frac{1}{(1-r\langle \zeta,\eta\rangle)^{n-\alpha}}&=\sum_{k=0}^{\infty}\sum_{|j|=k} \frac{\Gamma(k+n-\alpha)k!r^k}{k!\Gamma(n-\alpha)j!}\zeta^j\overline{\eta}^j. \end{align*} $$
Similar arguments to the one above show that
 $$ \begin{align*} I_{\alpha}[\mu]&\geq\Big|\iint_{\mathbb S_n}\textrm{Re}\Big(\frac{1}{(1-r\langle \zeta,\eta\rangle)^{n-\alpha}}\Big)d\mu(\zeta)d\mu(\eta)\Big|\\ &=\Big|\sum_{k=0}^{\infty}\sum_{|j|=k} \frac{\Gamma(k+n-\alpha)k!r^k}{k!\Gamma(n-\alpha)j!}\iint_{\mathbb S_n}\zeta^j\overline{\eta}^jd\mu(\zeta)d\mu(\eta)\Big|\\ &\asymp \sum_{k=0}^{\infty}\sum_{|j|=k}\frac{(k+1)^{n-1-\alpha}k!}{j!}r^k|\mu^*(j)|^2. \end{align*} $$
$$ \begin{align*} I_{\alpha}[\mu]&\geq\Big|\iint_{\mathbb S_n}\textrm{Re}\Big(\frac{1}{(1-r\langle \zeta,\eta\rangle)^{n-\alpha}}\Big)d\mu(\zeta)d\mu(\eta)\Big|\\ &=\Big|\sum_{k=0}^{\infty}\sum_{|j|=k} \frac{\Gamma(k+n-\alpha)k!r^k}{k!\Gamma(n-\alpha)j!}\iint_{\mathbb S_n}\zeta^j\overline{\eta}^jd\mu(\zeta)d\mu(\eta)\Big|\\ &\asymp \sum_{k=0}^{\infty}\sum_{|j|=k}\frac{(k+1)^{n-1-\alpha}k!}{j!}r^k|\mu^*(j)|^2. \end{align*} $$
Again, letting
![]() $r\rightarrow 1^{-}$
by Lemma 13, we obtain that
$r\rightarrow 1^{-}$
by Lemma 13, we obtain that
![]() $C_{[\mu ]}\in D_{-\alpha }({\mathbb B_n})$
. The assertion follows.
$C_{[\mu ]}\in D_{-\alpha }({\mathbb B_n})$
. The assertion follows.
Remark 17 According to [Reference Kosiński and Vavitsas14], one can expect that the cyclicity problem of polynomials in the unit ball of
![]() ${\mathbb C}^n$
depends on the real dimension of their zero set restricted on the unit sphere:
${\mathbb C}^n$
depends on the real dimension of their zero set restricted on the unit sphere:
![]() $\text {dim}_{{\mathbb R}}(\mathcal {Z}(p)\cap \mathbb S_n)$
.
$\text {dim}_{{\mathbb R}}(\mathcal {Z}(p)\cap \mathbb S_n)$
.
Let us point out the nature of the boundary zeros of a polynomial nonvanishing in the ball. See [Reference Kosiński and Vavitsas14] for the two-dimensional case where had been used the Curve Selection Lemma of [Reference Denkowska and Denkowski10].
Let
![]() $p\in {\mathbb C}[z_1,\ldots ,z_n]$
be a polynomial nonvanishing in the ball. Looking at
$p\in {\mathbb C}[z_1,\ldots ,z_n]$
be a polynomial nonvanishing in the ball. Looking at
![]() $\mathcal {Z}(p)\cap \mathbb S_n$
as at a semi-algebraic set, we conclude that it is the disjoint union of a finite number of Nash manifolds
$\mathcal {Z}(p)\cap \mathbb S_n$
as at a semi-algebraic set, we conclude that it is the disjoint union of a finite number of Nash manifolds
![]() $M_i$
, each Nash diffeomorphic to an open hypercube
$M_i$
, each Nash diffeomorphic to an open hypercube
![]() $(0,1)^{\textrm {dim}(M_i)}$
. Note that the Nash diffeomorphisms over the closed field of the real numbers satisfy some additional properties (see [Reference Bochnak, Coste and Roy7, Proposition 2.9.10]).
$(0,1)^{\textrm {dim}(M_i)}$
. Note that the Nash diffeomorphisms over the closed field of the real numbers satisfy some additional properties (see [Reference Bochnak, Coste and Roy7, Proposition 2.9.10]).
One can expect then that the characterization of cyclicity and the nature of the boundary zeros of the model polynomials, as well as, the unitary invariance of the Dirichlet norm and the sufficient capacity condition, will be crucial in the characterization of cyclic polynomials in arbitrary dimension.
Acknowledgment
I would like to thank Ł. Kosiński for the helpful conversations during the preparation of the present work. I would also like to thank the anonymous referee for numerous remarks that substantially improved the shape of the paper.