Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T10:51:29.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Bouncing behaviour of a particle settling through a density transition layer

Published online by Cambridge University Press:  16 October 2024

Shuhong Wang ,
Prabal Kandel ,
Jian Deng Open the ORCID record for Jian Deng [Opens in a new window] ,
C.P. Caulfield Open the ORCID record for C.P. Caulfield [Opens in a new window]  and
Stuart B. Dalziel
Shuhong Wang
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems, Department of Mechanics, Zhejiang University, Hangzhou 310027, PR China Huanjiang Laboratory, Zhuji 311816, PR China
Prabal Kandel
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems, Department of Mechanics, Zhejiang University, Hangzhou 310027, PR China Huanjiang Laboratory, Zhuji 311816, PR China
Jian Deng*
Affiliation:
State Key Laboratory of Fluid Power and Mechatronic Systems, Department of Mechanics, Zhejiang University, Hangzhou 310027, PR China
C.P. Caulfield
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
Stuart B. Dalziel
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

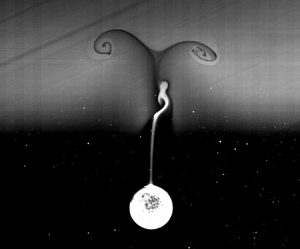
The present work focuses on a specific bouncing behaviour as a spherical particle settles through a density interface in the absence of a neutral buoyant position. This behaviour was initially discovered by Abaid et al. (Phys. Fluids, vol. 16, issue 5, 2004, pp. 1567–1580) in salinity-induced stratification. Both experimental and numerical investigations are conducted to understand this phenomenon. In our experiments, we employ particle image velocimetry (PIV) to measure the velocity distribution around the particle and to capture the transient wake structure. Our findings reveal that the bouncing process begins after the wake detaches from the particle. The PIV results indicate that an upward jet forms at the central axis behind the particle following wake detachment. By performing a force decomposition procedure, we quantify the contributions from the buoyancy of the wake ($F_{sb}$) and the flow structure ($F_{sj}$) to the enhanced drag. It is observed that $F_{sb}$ contributes primarily to the enhanced drag at the early stage, whereas $F_{sj}$ plays a critical role in reversing the particle's motion. Furthermore, our results indicate that the jet is a necessary condition for the occurrence of the bouncing motion. We also explore the minimum velocities (where negative values denote the occurrence of bouncing) of the particle, while varying the lower Reynolds number $Re_l$, the Froude number $Fr$, and the upper Reynolds number $Re_u$, within the ranges $1 \leqslant Re_l\leqslant 125$, $115 \leqslant Re_u\leqslant 356$ and $2 \leqslant Fr\leqslant 7$. Our findings suggest that the bouncing behaviour is influenced primarily by $Re_l$. Specifically, we observe that the bouncing motion occurs below a critical lower Reynolds number $Re^\ast _{l}=30$ in our experiments. In the numerical simulations, the highest value for this critical number is $Re^\ast _{l}=46.2$, which is limited to the parametric ranges studied in this work.

JFM classification

Geophysical and Geological Flows: Stratified flows Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 997 , 25 October 2024 , A49
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abaid, N., Adalsteinsson, D., Agyapong, A. & McLaughlin, R.M. 2004 An internal splash: levitation of falling spheres in stratified fluids. Phys. Fluids 16 (5), 1567–1580.CrossRefGoogle Scholar
Ahmerkamp, S., Liu, B., Kindler, K., Maerz, J., Stocker, R., Kuypers, M.M.M. & Khalili, A. 2022 Settling of highly porous and impermeable particles in linear stratification: implications for marine aggregates. J. Fluid Mech. 931, A9.CrossRefGoogle Scholar
Ardekani, A.M. & Stocker, R. 2010 Stratlets: low Reynolds number point-force solutions in a stratified fluid. Phys. Rev. Lett. 105 (8), 084502.CrossRefGoogle Scholar
Bayareh, M., Doostmohammadi, A., Dabiri, S. & Ardekani, A.M. 2013 On the rising motion of a drop in stratified fluids. Phys. Fluids 25 (10), 023029.CrossRefGoogle Scholar
Blanchette, F. & Shapiro, A.M. 2012 Drops settling in sharp stratification with and without Marangoni effects. Phys. Fluids 24 (4), 042104.CrossRefGoogle Scholar
Camassa, R., Ding, L., McLaughlin, R.M., Overman, R., Parker, R. & Vaidya, A. 2022 Critical density triplets for the arrestment of a sphere falling in a sharply stratified fluid. In Recent Advances in Mechanics and Fluid–Structure Interaction with Applications: The Bong Jae Chung Memorial Volume (ed. F. Carapau & A. Vaidya), pp. 69–91. Springer.CrossRefGoogle Scholar
Camassa, R., Falcon, C., Lin, J., McLaughlin, R.M. & Mykins, N. 2010 A first-principle predictive theory for a sphere falling through sharply stratified fluid at low Reynolds number. J. Fluid Mech. 664, 436–465.CrossRefGoogle Scholar
Camassa, R., Falcon, C., Lin, J., McLaughlin, R.M. & Parker, R. 2009 Prolonged residence times for particles settling through stratified miscible fluids in the Stokes regime. Phys. Fluids 21 (3), 031702.CrossRefGoogle Scholar
Camassa, R., McLaughlin, R.M., Moore, M.N.J. & Vaidya, A. 2008 Brachistochrones in potential flow and the connection to Darwin's theorem. Phys. Lett. A 372 (45), 6742–6749.CrossRefGoogle Scholar
Deng, J. & Caulfield, C.P. 2016 Dependence on aspect ratio of symmetry breaking for oscillating foils: implications for flapping flight. J. Fluid Mech. 787, 16–49.CrossRefGoogle Scholar
Diercks, A., Ziervogel, K., Sibert, R., Joye, S.B., Asper, V. & Montoya, J.P. 2019 Vertical marine snow distribution in the stratified, hypersaline, and anoxic Orca Basin (Gulf of Mexico). Elementa: Sci. Anthropocene 7, 10.Google Scholar
Doostmohammadi, A. & Ardekani, A.M. 2014 a Reorientation of elongated particles at density interfaces. Phys. Rev. E 90 (3), 033013.CrossRefGoogle ScholarPubMed
Doostmohammadi, A., Dabiri, S. & Ardekani, A.M. 2014 b A numerical study of the dynamics of a particle settling at moderate Reynolds numbers in a linearly stratified fluid. J. Fluid Mech. 750, 5–32.CrossRefGoogle Scholar
Economidou, M. & Hunt, G.R. 2009 Density stratified environments: the double-tank method. Exp. Fluids 46, 453–466.CrossRefGoogle Scholar
Epps, B.P. 2010 An impulse framework for hydrodynamic force analysis: fish propulsion, water entry of spheres, and marine propellers. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Ferziger, J.H. & Perić, M. 2002 Computational Methods for Fluid Dynamics. Springer.CrossRefGoogle Scholar
Hanazaki, H., Kashimoto, K. & Okamura, T. 2009 Jets generated by a sphere moving vertically in a stratified fluid. J. Fluid Mech. 638, 173.CrossRefGoogle Scholar
Higginson, R.C., Dalziel, S.B. & Linden, P.F. 2003 The drag on a vertically moving grid of bars in a linearly stratified fluid. Exp. Fluids 34 (6), 678–686.CrossRefGoogle Scholar
Jasak, H. 2009 Dynamic mesh handling in OpenFOAM. In 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA. AIAA Paper 2009-341. AIAA.CrossRefGoogle Scholar
Magnaudet, J. & Mercier, M.J. 2020 Particles, drops, and bubbles moving across sharp interfaces and stratified layers. Annu. Rev. Fluid Mech. 52, 61–91.CrossRefGoogle Scholar
Mandel, T.L., Waldrop, L., Theillard, M., Kleckner, D. & Khatri, S. 2020 Retention of rising droplets in density stratification. Phys. Rev. Fluids 5 (12), 124803.CrossRefGoogle Scholar
Mordant, N. & Pinton, J.F. 2000 Velocity measurement of a settling sphere. Eur. Phys. J. B 18 (2), 343–352.CrossRefGoogle Scholar
More, R.V. & Ardekani, A.M. 2023 Motion in stratified fluids. Annu. Rev. Fluid Mech. 55, 157–192.CrossRefGoogle Scholar
More, R.V., Ardekani, M.N., Brandt, L. & Ardekani, A.M. 2021 Orientation instability of settling spheroids in a linearly density-stratified fluid. J. Fluid Mech. 929, A7.CrossRefGoogle Scholar
Mrokowska, M.M. 2018 Stratification-induced reorientation of disk settling through ambient density transition. Sci. Rep. 8 (1), 1–12.CrossRefGoogle ScholarPubMed
Mrokowska, M.M. 2020 Influence of pycnocline on settling behaviour of non-spherical particle and wake evolution. Sci. Rep. 10 (1), 20595.CrossRefGoogle ScholarPubMed
Okino, S., Akiyama, S. & Hanazaki, H. 2017 Velocity distribution around a sphere descending in a linearly stratified fluid. J. Fluid Mech. 826, 759–780.CrossRefGoogle Scholar
Okino, S., Akiyama, S., Takagi, K. & Hanazaki, H. 2021 Density distribution in the flow past a sphere descending in a salt-stratified fluid. J. Fluid Mech. 927, A15.CrossRefGoogle Scholar
Prairie, J.C. & White, B.L. 2017 A model for thin layer formation by delayed particle settling at sharp density gradients. Cont. Shelf Res. 133, 37–46.CrossRefGoogle Scholar
Schlichting, H. & Klaus, J. 2003 Boundary-Layer Theory. Springer Science & Business Media.Google Scholar
Sharqawy, M.H., Lienhard, J.H. & Zubair, S.M. 2010 Thermophysical properties of seawater: a review of existing correlations and data. Desalination Water Treatment 16 (1–3), 354–380.CrossRefGoogle Scholar
Srdić-Mitrović, A.N., Mohamed, N.A. & Fernando, H.J.S. 1999 Gravitational settling of particles through density interfaces. J. Fluid Mech. 381, 175–198.CrossRefGoogle Scholar
Torres, C.R., Hanazaki, H., Ochoa, J., Castillo, J. & Van Woert, M. 2000 Flow past a sphere moving vertically in a stratified diffusive fluid. J. Fluid Mech. 417, 211–236.CrossRefGoogle Scholar
Truscott, T.T., Epps, B.P. & Techet, A.H. 2012 Unsteady forces on spheres during free-surface water entry. J. Fluid Mech. 704, 173–210.CrossRefGoogle Scholar
Verso, L., van Reeuwijk, M. & Liberzon, A. 2019 Transient stratification force on particles crossing a density interface. Intl J. Multiphase Flow 121, 103109.CrossRefGoogle Scholar
Wang, S., Wang, J. & Deng, J. 2023 Effect of layer thickness for the bounce of a particle settling through a density transition layer. Phys. Rev. E 108 (6), 065108.CrossRefGoogle ScholarPubMed
White, F.M. & Majdalani, J. 2006 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Yick, K.Y., Torres, C.R., Peacock, T. & Stocker, R. 2009 Enhanced drag of a sphere settling in a stratified fluid at small Reynolds numbers. J. Fluid Mech. 632, 49–68.CrossRefGoogle Scholar
Zhang, J., Mercier, M.J. & Magnaudet, J. 2019 Core mechanisms of drag enhancement on bodies settling in a stratified fluid. J. Fluid Mech. 875, 622–656.CrossRefGoogle Scholar