Discovery of the Sub-second Linearly Polarized Spikes of Synchrotron Origin in the UV Ceti Giant Optical Flare

Abstract

During our optical monitoring of UV Ceti, iconic late-type flaring star, with high temporal resolution using the Russian 6-m telescope in 2008, we detected a giant flare with the amplitude of about 3 magnitudes in U band. Near flare maximum, more than a dozen of spike bursts have been discovered with triangular shapes and durations from 0.6 to 1.2 s and maximal luminosities in the range (1.5–8) × 10²⁷ erg s⁻¹. For the half of these events, the linear polarization exceeds 35% with significance better than 5σ. We argue that these events are synchrotron emission of electron streams with the energies of several hundred MeV moving in the magnetic field of about 1.4 kG. Emission from such ultra-relativistic (with energies far exceeding 10 MeV) particles is being routinely observed in solar flares, but has never been detected from UV Ceti-type stars. This is the first ever detection of linearly polarized optical light from the UV Ceti-type stars which indicates that at least some fraction of the flaring events on these stars is powered by a non-thermal synchrotron emission mechanism.

1 INTRODUCTION

Presently, there are no doubts that the flaring activity of the Sun and flaring stars, particularly those of UV Ceti-type, is of a common origin (Gershberg 2015). Flaring events are caused by the release of energy stored in coronal magnetic fields. Therewith up to 10–50% of the magnetic energy is converted to the kinetic energy of accelerated electrons and ions in solar flares (Lin & Hudson 1976; Miller et al. 1997; Holman et al. 2003). They are partly ejected away from the star and partly move along coronal magnetic loops, heating dense regions of the stellar atmosphere and generating the flare-like emission in a wide range of frequencies, from radio to gamma-rays (Priest & Forbes 2000; Benz & Güdel 2010).

On the Sun, these initial electrons are accelerated up to hundreds of MeV to 1 GeV, as observations of gamma-ray emission of flares suggest (see, for example, Kanbach et al. 1993; Ramaty & Mandzhavidze 1994; Aschwanden 2005). Flaring stars also display some manifestations of energetic non-thermal particles with Lorentz factors 1 < γ ⩽ 10 in the form of bursts of gyrosynchrotron radio emission (Bastian 1990; Güdel et al. 1996; Güdel 2002) correlated with variations of soft X-ray emission of the chromospheric and photospheric plasma heated by these particles (Güdel 2002; Smith, Güdel, & Audard 2005; Benz & Güdel 2010), but the presence of ultra-relativistic electrons with γ > 10 has never been revealed in these studies. On the other hand, the detection of such particles has been reported as a result of radio observations of T Tau stars in binary systems (Massi et al. 2006; Salter et al. 2010).

If such energetic particles exists in UV Ceti-type stars too, they may produce optical synchrotron emission while moving in the magnetic fields of coronal loops (Gordon 1954). Due to the discrete nature of particle acceleration driven by the magnetic field reconnection in a stellar corona, this emission may be in the form of separate sub-second spikes. Similar events, seen on the Sun in X-ray and gamma-ray bands, are generated by the bremsstrahlung emission of electron beams in the chromosphere, and have typical durations of 0.05–1 s (Kiplinger et al. 1983; Aschwanden, Schwartz, & Alt 1995; Cheng et al. 2012). ¹ On the other hand, optical spike bursts with sub-second durations in quiet states of flaring stars have been detected only in a few cases – a bit more than dozen of flashes seen in different years and with different instruments while observing EV Lac, BY Dra, V577 Mon and CN Leo (Zhilyaev & Verlyuk 1995; Robinson et al. 1995; Tovmassian et al. 1997; Zhilyaev et al. 1998) and lacking proper interpretations. A number of small amplitude flares with durations of a few seconds have recently been reported in UV Ceti (Schmitt et al. 2016).

As the timescale of synchrotron spikes is close to the one of thermal emission mechanism for optical flashes, which may be down to 0.1–1 s (Katsova & Livshits 1986; Shvartsman et al. 1988; Katsova & Livshits 2001), an additional criterion is necessary to distinguish between these mechanisms – the presence of linear polarization, which is a characteristic feature of synchrotron emission (Ginzburg & Syrovatskii 1965; Rybicki & Lightman 1979). Therefore, in order to confidently detect such synchrotron emission from a flaring star, one has to perform its regular photo-polarimetric monitoring with high temporal resolution using a large telescope.

Numerous attempts to detect the polarization in flares of YZ CMi, AD Leo, EV Lac and YY Gem, observed with various telescopes (Karpen et al. 1977; Eritsian 1978; Tuominen et al. 1989), were also unsuccessful. Most reliable data have been acquired during EV Lac study using 1.25-m telescope of the Crimean Astrophysical Observatory (Alekseev et al. 1994). The upper limits for polarization degree in strong flares have been placed on 2% level on 10-s timescale, and 1% level – on a 50 s one.

In 1982–1985, we performed a regular photometric monitoring of UV Ceti, CN Leo, V 577 Mon and Wolf 424 flaring stars using the Russian 6-m telescope with 1-μs temporal resolution. More than hundred flashes have been detected in U band, and the upper limits on the amplitude of intensity variations, both during the flares and outside them, on time scales from 1 μs to 1 s have been placed on the level of 20–0.5% (Beskin et al. 1988a, 1988b), correspondingly. The shortest details detected were the rising fronts of four flares of these stars with durations from 0.3 to 0.8 s; decay times of these flares were 1–3 s (Shvartsman et al. 1988). These data, along with the statistical properties of all temporal characteristics, have led to conclusion that the flares, even the shortest ones, may be explained by the gas-dynamic model (Beskin et al. 1988b; Katsova & Livshits 2001; Gershberg 2015).

In order to reliably detect the polarized non-thermal emission from UV Ceti-type stars, since 2008 we started the new set of observations of these objects with the Russian 6-m telescope using a panoramic photo-polarimeter. In this study, we report the detection of a giant, with amplitude of nearly 3 magnitudes, flare of dMe-dwarf UV Ceti during this monitoring. Near its maximum, we discovered more than a dozen of spike bursts with the duration of 0.6–1.2 s, with linear polarization exceeding 35–40% for the majority of them. We argue that these events were generated by synchrotron emission of electrons with the energies of several hundred MeV moving in magnetic fields with the strength of about 1.4 kG, and therefore are the first ever evidence for the presence of ultra-relativistic electrons in the flares of UV Ceti-type stars.

The paper is organized as follows. Section 2 describes the equipment and methods used for the high temporal resolution photopolarimetric observations of flaring stars with the Russian 6-m telescope. In Section 3, the observational characteristics of detected spike bursts are described, and in Section 4 the physical conditions necessary for their generation are analysed. Section 4 also contains the discussion of ultra-relativistic electrons production mechanisms in UV Ceti-type stars. Section 5 presents the brief summary of our results.

2 OBSERVATIONS AND DATA REDUCTION

Systematic monitoring of flaring stars with 1-μs temporal resolution with the Russian 6-m telescope is ongoing since 2008, using the panoramic photospectropolarimeter in its various configurations (Plokhotnichenko et al. 2009a). The detector is the microchannel plate-based position-sensitive photon counter with four-electrode cathode (Debur et al. 2003), and the high speed data acquisition is performed with the dedicated ‘Quantochron 4–48’ card plugged into the PC, which encodes and stores the coordinates and times of arrival of detected photons with 1-μs accuracy (Plokhotnichenko, Solin, & Tikhonov 2009b). The data acquired are the photon lists, which may be later arbitrarily binned for light curve and image analysis on various time scales.

In 2008, the monitoring has been performed in U photometric band using the Wollaston prism as a polarizer. Field of view of the instrument was about 20 arcsec and angular resolution was about 2 arcsec, with no stars except for inseparable UV/BL Ceti pair seen. On the photocathode of the detector, the Wollaston prism formed two images of an object with orthogonal orientations of polarization plane. The intensities of these two images are as follows (Shurkliff 1962; Snik & Keller 2013):

(1) $$\begin{equation} I_0 & =& \frac{1}{2} (I + Q), \\ \end{equation}$$

(2) $$\begin{equation} I_{90} & =& \frac{1}{2} (I - Q). \end{equation}$$

These quantities allow one to determine two of the four Stokes parameters:

(3) $$\begin{equation} I & =& I_0 + I_{90}, \\ \end{equation}$$

(4) $$\begin{equation} Q & =& I_0 - I_{90}. \end{equation}$$

The degree of linear polarization is a combination of I, Q and U Stokes parameters (Snik & Keller 2013):

(5) $$\begin{equation} P = \frac{1}{I}\sqrt{Q^2 + U^2}. \end{equation}$$

We know only the first two, and may therefore place the lower limit on the degree of linear polarization, as P ⩾ |Q|/I for all U values.

That is, if we detect any significant deviation of Q/I from zero, then the lower limit on the degree of linear polarization is

(6) $$\begin{equation} P_{\rm low} = |Q|/I = \frac{|I_0-I_{90}|}{I_0+I_{90}}. \end{equation}$$

The giant flare of UV Ceti, with nearly 3^m amplitude and fast (~10 s, as compared to 30 min overall duration) initial rise, has been detected on 2008 December 28 at 15:27:02 UT.

The light curve, computed as a sum of background subtracted intensities in two images, is shown in Figure 1. As we did not have any other star in the field of view, to calibrate the flux, we associated the average pre-flare flux (−100 to 0 s) level with m_U = 14.86 magnitude of UV/BL Ceti pair (Eason et al. 1992), and assumed the distance d = 2.68 pc. The inset of Figure 1 also shows the 2-min interval of maximal intensity with 0.1-s temporal resolution. During this interval, more than a dozen of spike bursts with 6–50% relative amplitudes and durations not exceeding (except for two cases) 1.2 s are clearly seen. Their analysis will be performed in the next section.

Figure 1. Light curve of UV Ceti flare in U band with 0.1-s temporal resolution, obtained with the Russian 6-m telescope on 2008 December 28. The inlet shows the region marked with dashed lines in the main plot. In turn, the region marked with vertical dashed lines in the inlet, containing all the spike bursts, is shown in Figure 3.

As we are interested in polarization variations during the flare, and to accommodate for the instrumental, atmospheric and interstellar polarization, we computed the mean value of k = I ₀/I ₉₀ over the 100-s long pre-flare interval, < k > =1.23, and scaled the I ₉₀ using this coefficient. This way normalized Stokes Q/I parameter has zero mean over that interval.

Figure 2 shows the Stokes Q/I over the pre-flare and the main part of the flare interval (the gap from 240 to 250 s corresponds to the restart of data acquisition system where the information has been lost). No significant deviations from zero may be seen, except for the short events coinciding with the spike bursts detected in the light curve.

Figure 2. The behaviour of normalized Stokes Q/I parameter during the pre-flare and flare main part intervals. Levels of σ and 3σ, estimated assuming Poissonian statistics, are shown. Vertical lines mark the interval where spike bursts are detected. Some of them show significant polarization, whereas all other intervals of the light curve (upper panel) do not.

3 ANALYSIS OF SPIKES PROPERTIES

3.1 Durations and shapes

Figure 3 shows the region of the light curve with clearly seen flaring activity, where 14 spike bursts have been detected. Their rise times are 0.2–0.5 s, and the shapes are nearly symmetric (see upper panel in Figure 3).

Figure 3. The fragment of UV Ceti flare light curve containing 14 spike bursts, whose shapes are approximated with split Gaussian profiles (upper panel), approximated with the smooth spline for the background flare and split Gaussians for the spikes. Lower panel shows the normalized residuals, normally distributed everywhere except for the 10-s region around complex peak No. 12.

We approximated the slowly changing flare background with manually adjusted smooth spline, and the spike shapes with split Gaussians, having different rising and fading characteristic times:

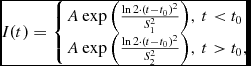(7) $$\begin{equation} I(t) = \left\lbrace \begin{array}{rl}A \exp {\left(\frac{\ln {2} \cdot (t-t_0)^2}{S_1^2}\right)} , & t < t_0 \\ A \exp {\left(\frac{\ln {2} \cdot (t-t_0)^2}{S_2^2}\right)} , & t > t_0, \end{array} \right. \end{equation}$$

where A is the peak intensity, t ₀ is the peak time and S is the half-width at half maximum – the characteristic time of a two-fold change of the intensity. The approximation is shown in Figure 3, and the fit parameters are listed in Table 1. The residuals, shown in lower panel of Figure 3, are distributed normally – Shapiro–Wilk normality test cannot reject their normality with p-value better than 0.3 (except for 10-s long interval around spike No. 12, which has very complex shape, and most probably consists of several blended sub-spikes, which cannot be easily separated), and therefore the approximation is quite optimal.

Table 1. Parameters of the light curve spikes. The spikes have been fitted with split Gaussian profiles. Here, t ₀ – peak time, A – peak amplitude, FWHM – peak full width at half -maximum, S ₁ and S ₂ – half-widths at half-maximum of the rising and fading fronts, respectively, L – peak luminosity in U-band. Also, A ₀ and A ₉₀ represent the amplitudes of the split Gaussian profiles fitted to I ₀(t) and I ₉₀(t) intensities, correspondingly, and < P _{low, int} > is the mean intrinsic polarization of the spikes computed according to Equation (11).

^a To account for instrumental polarization, I ₉₀ has been scaled by a constant coefficient < k > =1.23, and therefore the sum of A ₀ and A ₉₀ is not equal to A.

To test the randomness of spikes’ peak times we performed the Kolmogorov–Smirnov test on t ₀ values from Table 1, which gave p-value of 0.7, which confirms that the distribution of spikes in time is uniform.

Figure 4 displays the spikes’ rise and fading times with corresponding fit errors. If we exclude complex spikes Nos. 12 and 13, then the rise and fading times are uncorrelated (with Pearson correlation coefficient r = 0.08) and follow the same distribution (with Kolmogorov–Smirnov test p-value p = 0.26). Their mean values are < S1 > =(0.24 ± 0.04) s, < S2 > =(0.38 ± 0.06) s. Therefore, the spikes are nearly symmetric and have triangular form.

Figure 4. Comparison of the spikes’ rise and fall times. Total durations of 12 events are less than 1 s; for six events rise and fall times are nearly equal, whereas for six others – the latters are 2–2.5 times greater. Durations of two spikes (Nos. 12 and 13) are 2–3 s – most probably, they consist of several overlapping events.

3.2 Polarization of spikes

Figure 2 shows the temporal behaviour of Q/I normalized Stokes parameter, i.e., the ‘projection’ of linear polarization onto the Wollaston prism axis, over the 10 min of pre-flare and flare peak intervals. There are no signs of any significant deviation from zero level (p-value of Shapiro–Wilk normality test is p = 0.4) except for the moments coinciding with the spikes seen in the light curve. Figure 5 shows the close-up of the interval containing these spikes with polarization fitted with the same split Gaussian profiles with all the parameters fixed to values listed in Table 1 except for the amplitudes. It is clear that the positional and morphological coincidence of spikes in intensity and normalized Stokes Q/I parameter is perfect, whereas the amplitudes of the latter ones are in most cases exceeding 2.5σ (spikes Nos. 1, 2, 4, 5, 7, 10, 11, 12 and 14). For a more evident picture of their significances, the lower panel of Figure 5 shows the same quantity as the middle one, but constructed from the light curves rebinned to 0.5-s temporal resolution, so that the spikes fall into 1–3 bins, and the RMS decreases by 2.23 times. Then, the significance of polarized spikes is better than 10⁻⁴, and the probability of overall effect to be random is definitely lower than 10⁻²⁰.

Figure 5. The region of UV Ceti flare near its maximum (see Figure 3) with 0.1-s resolution (upper panel) and the normalized Stokes Q/I parameter with the same resolution (middle panel). Red lines are approximations of spikes with all parameters except amplitudes fixed to values listed in Table 1. The lower panel is the same quantity rebinned to 0.5-s resolution and normalized to its Poissonian errors.

The polarization is absent anywhere except the spikes; therefore, we may suggest that the spikes represent an additional, polarized emission component superimposed with the overall unpolarised giant flare. Then, the observed intensities may be represented as a sum of ‘flare’ and ‘spike’ components as

(8) $$\begin{equation} I_{0}(t) & =& I_{0}^{\rm flare}(t) + I_{0}^{\rm spike}(t), \\ \end{equation}$$

(9) $$\begin{equation} I_{90}(t) & =& I_{90}^{\rm flare}(t) + I_{90}^{\rm spike}(t). \end{equation}$$

Next, we may introduce an intrinsic spike polarization, analogous to Equation (6), but corresponding to the polarization of a spike emission alone, excluding the background flare emission:

(10) $$\begin{equation} P_{\rm low,int}(t) = |Q^{\rm spike}(t)|/I^{\rm spike}(t) = \frac{|I_{0}^{\rm spike}(t)-I_{90}^{\rm spike}(t)|}{I_{0}^{\rm spike}(t)+I_{90}^{\rm spike}(t)}. \end{equation}$$

Figure 6 shows the I ₀ and I ₉₀ components over the spikes interval. The shapes in both components are quite similar, and nearly the same as spike shapes in total intensity, which may suggest that the polarization of every spike is more or less constant over time. Therefore, we may characterize the mean intrinsic polarization of every spike by independently fitting the I ₀ and I ₉₀ intensity profiles with split Gaussians described by Equation (7) with all parameters except for the amplitude A fixed to ones from Table 1 (see Figure 6) and substitute the corresponding amplitudes A ₀ and A ₉₀ into Equation (10) as mean intensities:

(11) $$\begin{equation} \left<P_{\rm low,int}\right> = \frac{|A_0-A_{90}|}{A_0+A_{90}} \ \ {\rm .} \end{equation}$$

Figure 6. Independent fits of I ₀ and I ₉₀ polarized emission components of the region shown in Figure 5 with split Gaussians with all parameters except amplitudes fixed to values listed in Table 1.

Table 1 and Figure 7 show these values along with corresponding errors. For six spikes (Nos. 3, 6, 7, 8, 9 and 13) the polarization lower limits do not differ significantly from zero, exceeding it for less than 1σ (in three cases) and for 1.5–2σ (three more cases). The polarization of eight other spikes is significant and quite high – it peaks at 20% (No. 4), 30% (Nos. 5 and 11), 40% (Nos. 1, 12 and 14) and 45% (Nos. 2 and 10) and is not correlated with either spike intensity or its duration.

Figure 7. Lower limits on the degree of mean intrinsic linear polarization of the spikes, computed according to Equation (11), versus the peak fluxes. Spikes with low significance polarization (less than 3σ) are in grey, whereas spikes with significant polarization (with significance levels 10⁻³–10⁻⁵) are in red.

4 DISCUSSION

4.1 Large linear polarization of spikes – the evidence of their synchrotron origin

In our observations of a giant UV Ceti flare on 2012 December 28, we discovered 14 spike bursts near its maximum, and clearly detected their polarization. Their short durations, sufficiently high intensities and comparable scales of rise and fading phases – and most importantly their high intrinsic polarization exceeding 30–45% – suggest that these events may only be caused by the synchrotron emission of ultra-relativistic electron streams moving in the magnetic fields of the corona.

Indeed, no other mechanism of emission generation and/or transformation in astrophysical conditions can produce such level of linear polarization. For Thompson scattering, its degree cannot exceed 10–20% (Angel 1969; Brown & McLean 1977). Linear polarization of bremsstrahlung radiation is typically in 5–25% range (Brown 1972; Emslie, Bradsher, & McConnell 2008). Inverse Compton scattering on the electron beam does not change the state of unpolarised emission, whereas for the intrinsic synchrotron (synchrotron self-Compton mechanism) emission it lowers the original polarization degree by several times – its maximal degree is lower than 30–35% (Bonometto & Saggion 1973; Krawczynski 2012). Therefore, the linear polarization exceeding 35–45% that we detected in sub-second spikes is a direct proof of their synchrotron origin.

The synchrotron mechanism for optical flaring emission from red dwarfs had been initially proposed by Gordon (1954), who noted that the detection of polarized flares might be the proof for it. However, the sparse and irregular (see Section 1) polarimetric observations of UV Ceti-type stars have been fruitless until now (Karpen et al. 1977; Eritsian 1978; Tuominen et al. 1989; Alekseev et al. 1994). It seems that the majority of flares, especially the longer ones studied in these works, are dominated by thermal emission. Shorter ones are, however, still may be at least partially driven by synchrotron emission, as our observations strongly suggest.

Below, we will discuss possible origin of accelerated electrons, estimate their energies and number densities and show that they may indeed be naturally formed in UV Ceti corona.

4.2 On possible origin of ultra-relativistic electrons

The multi-wavelength observations of the Sun and solar flares, as well as active stars, which have analogous nature of flaring activity (Gershberg 2015), theoretical analysis and numerical simulations have recently made it clear that the structure of magnetic fields here is a complex system of small-scale magnetic knots, multiple organized thin loops and regular thread-like structures with minimal scales about 10⁸–10⁹ cm or even smaller, and with the magnetic field strength nearly constant along the threads from corona to photosphere (Shibata & Yokoyama 2002; López Fuentes, Démoulin, & Klimchuk 2008; Meyer et al. 2013; Klimchuk 2015).

During the magnetic reconnection in the corona, the collisionless Hall current sheets, which may spontaneously form in a critical self-organizing state and trigger the flaring energy release (Cassak, Mullan, & Shay 2008), are being fragmented to separate filaments due to tearing instabilities, and the particles are being accelerated in these small-scale filaments or between them on a short time scales (Drake et al. 2006; Che, Drake, & Swisdak 2011).

Possible mechanisms of electron acceleration up to 300–400 MeV energy include super-Dreicer electric fields in magnetic reconnection regions what may form the streams of ultra-relativistic electrons (Craig & Litvinenko 2002; Gordovskyy, Browning, & Vekstein 2010). Gordovskyy et al. (2010) demonstrated by an illustrative estimation that in the conditions of solar corona (B ≈ 100 Gauss) the electrons may accelerate up to energies of several tens of MeV, while having quite flat (δ ≈ 1.5) energetic spectrum. As the strength of accelerating electric field E∝B ², for typical UV Ceti coronal magnetic field of 300–1 500 G (Mullan et al. 2006), the electrons may reach the energies of hundreds of MeV. At the same time, Craig & Litvinenko (2002) and Litvinenko (2006) demonstrated that during the magnetic reconnections the super-Dreicer electric field also forms and may accelerate the electrons up to few hundred MeV – several GeV with similar flat energetic spectrum. The same electron energies may result from interaction of electrons with fast magneto-hydrodynamical modes during the acceleration (Yan, Lazarian, & Petrosian 2008).

The streams of ultra-relativistic electrons, formed due to acceleration of background thermal particles, subsequently lose their energy radiatively during the motion in slowly changing magnetic fields of separate threads, producing the spike bursts we observed in UV Ceti flare. Due to the stochastic nature of particle acceleration, the pitch-angle distribution of ejected electrons is isotropic (Dalla & Browning 2005; Minoshima & Yokoyama 2008), and their emission is therefore omnidirectional. Pitch-angle diffusion due to elastic scattering on whistlers (Stepanov et al. 2007) or other fast MHD modes (Yan et al. 2008) keeps it isotropic and prevents the particles from streaming rapidly along the field lines, keeping them close to the acceleration region during the cool-down. Moreover, if the particle source is powerful enough, the strong pitch-angle diffusion regime is realized and a the turbulent ‘wall’ is formed when a cloud of high-energy particles propagates along the magnetic field with the velocity of about the phase velocity of waves that is much less than particle velocity (Bespalov, Zaitsev, & Stepanov 1991; Trakhtengerts & Rycroft 2008). Therefore, the geometric effects of emission beaming and finite propagation time may be neglected in the analysis of the spikes.

Note that the giant flare itself (which seems to be purely thermal) and spike bursts are produced at different regions – the former at a loop footpoint in chromosphere (see Gershberg 2015 and references therein), whereas the latter in the corona itself. Moreover, these phenomena may in principle be produced on two different stars (as both UV Ceti and BL Ceti are flaring stars). Of course, the probability of latter case is quite small, but it cannot be completely ignored.

4.3 What are the parameters of magnetic fields and electrons responsible for the spikes?

If the spike bursts are indeed caused by synchrotron radiation, we may estimate the range of magnetic field strengths, Lorentz factors and numbers of accelerated electrons necessary to provide their observed peak luminosities and fading durations, while keeping the emission in U band. For simplicity, and following the arguments presented earlier, we will assume the isotropic distribution of electron pitch angles, and will use corresponding angle-averaged formulae for their synchrotron emission.

For a single electron, the peak frequency of its synchrotron emission is (Ginzburg & Syrovatskii 1965; Rybicki & Lightman 1979)

(12) $$\begin{equation} \nu _s \approx 1.2\times 10^6 B \gamma ^2 \ \ \mbox{Hz,} \end{equation}$$

where γ = E_s/mc ² is the Lorentz factor, E_s is the electron energy and B is the magnetic field strength, whereas the characteristic timescale of its energy loss is (Ginzburg & Syrovatskii 1965)

(13) $$\begin{equation} \tau _s \approx 5\times 10^8 B^{-2} \gamma ^{-1} \ \ \mbox{s.} \end{equation}$$

By combining Equations (12) and (13), for the effective frequency of U band ν _s = 8 × 10¹⁴ Hz, we may get

(14) $$\begin{equation} \gamma \approx 700 \left(\frac{\tau _s}{0.38\ \mbox{s}}\right)^{1/3} \end{equation}$$

and

(15) $$\begin{equation} B \approx 1.4\times 10^3\left(\frac{\tau _s}{0.38\ \mbox{s}}\right)^{-2/3} \ \ \mbox{G.} \end{equation}$$

For the average fading time of spikes (see Table 1 and Section 3.1) τ _s = 0.38 s, from Equations (14) and (15), we get γ ≈ 700, which corresponds to the electron energy E_s = γmc ² ≈ 360 MeV and B ≈ 1.4 × 10³ G. The latter value is in good agreement with the magnetic field strength derived from observations of UV Ceti flares (Mullan et al. 2006; Zaitsev & Stepanov 2008).

The number of ultra-relativistic electrons N responsible for the synchrotron emission of the spike burst may then be estimated as

(16) $$\begin{equation} N \approx \frac{W}{L}\mbox{,} \end{equation}$$

where W is the observed luminosity in U band and the luminosity of a single electron is (Ginzburg & Syrovatskii 1965)

(17) $$\begin{equation} L \approx 1.6\times 10^{-15} B^2 \gamma ^2 \ \ \mbox{erg~s$^{-1}$.} \end{equation}$$

Using the average luminosity of spikes W = 4.6 × 10²⁷ erg s⁻¹ (see Table 1), B = 1400 G and γ = 700, we get for the number of emitting particles N = 3 × 10³⁰.

The scatter of actual spikes’ fading times from 0.11 to 0.7 s (excluding two longer ones, see Table 1), as well as their luminosities, gives the ranges of γ = 460–860, B = 900–2300 G, E_s = 235–440 MeV and N = 4 × 10²⁹–8 × 10³⁰.

4.4 The spectrum of accelerated electrons

Now, we may estimate the slope δ of electron energy distribution which is necessary to have $N \approx 4\times 10^{29}\text{&#x2013;}8\times 10^{30}$ particles accelerated up to energies exceeding E_s ≈ 440 MeV to generate observed spike bursts.

For simplicity, we may assume that the accelerated electrons follow the same power law, dN = N(E)dE∝E ^−δ dE, in the wide range of energies from tens of keV up to hundreds of MeVs, which is consistent with observations of solar (see, for example, Ramaty & Mandzhavidze 1994; Kanbach et al. 1993; Lin 2011) and stellar flares (Smith et al. 2005).

The lower energy cutoff E ₀ for different solar flares have been found to be 10–50 keV (Sui, Holman, & Dennis 2007; Kontar, Dickson, & Kašparová 2008; Caspi & Lin 2010). For the analysis of synchronous radio and X-ray observations of flaring stars, the value of 10 keV has been used (Smith et al. 2005). The maximal energy E_m of accelerated electrons may be as high as 0.5–1 GeV, as both observations of solar flares (Ramaty & Mandzhavidze 1994; Kanbach et al. 1993; Lin 2011) and theoretical models (Craig & Litvinenko 2002; Litvinenko 2006; Yan et al. 2008) suggest.

Then, the total number of accelerated particles is

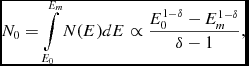(18) $$\begin{equation} N_0 = \int \limits _{E_0}^{E_m}N(E)dE \propto \frac{E_0^{1-\delta }-E_{m}^{1-\delta }}{\delta -1} \mbox{,} \end{equation}$$

and the mean energy of accelerated particle is

(19) $$\begin{equation} \left<E\right> = \frac{1}{N_0} \int \limits _{E_0}^{E_m} E N(E) dE = \frac{\delta -1}{\delta -2} \frac{E_0^{2-\delta }-E_{m}^{2-\delta }}{E_0^{1-\delta }-E_{m}^{1-\delta }} \mbox{.} \end{equation}$$

All the particles with energies exceeding E_s sooner or later contribute to U band emission during the spike burst (as for the higher energy electrons cooling time is shorter, according to Equation (13)); therefore. the number of electrons responsible for the synchrotron emission of the spike burst is

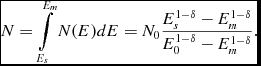(20) $$\begin{equation} N = \int \limits _{E_s}^{E_m}N(E)dE = N_0 \frac{E_s^{1-\delta }-E_{m}^{1-\delta }}{E_0^{1-\delta }-E_{m}^{1-\delta }} \mbox{.} \end{equation}$$

The number of accelerated electrons may also be written as

(21) $$\begin{equation} N_0 = k n_t V \mbox{,} \end{equation}$$

where k is the fraction of thermal electrons with density n_t being accelerated during the magnetic reconnection in the filament zone with characteristic size l and volume V = πl ³/6 (assuming spherical shape). As an upper estimate of l, we will use the minimal scale of inhomogeneities in solar (or stellar) corona of 10⁸–10⁹ cm (Shibata & Yokoyama 2002; Meyer et al. 2013). The efficiency of thermal particles acceleration k in solar flares may reach 10–100% (see, for example, Lin 2011). On the other hand, for flares on UV Ceti-type stars, it is not determined yet, and we will consider below the interval k = 10⁻⁷ − 1. Finally, for the thermal density n_t on UV Ceti, we will assume the interval from 10¹⁰ cm⁻³ in a quiet state (Güdel & Nazé 2009) to 10¹² cm⁻³ during the flares (Mullan et al. 2006).

As the energy for particle acceleration is originating from the magnetic field, we may write the (probably over-conservative) energy budget condition as

(22) $$\begin{equation} \frac{\left<E\right> N_0}{V} = \left<E\right> n_t k < \frac{B^2}{8\pi } \mbox{.} \end{equation}$$

Then, we may solve Equations (19)–(22) for possible values of δ on k allowed for the aforementioned set of parameters: E ₀ = 10–50 keV, E_m = 0.5–1 GeV, N = 4 × 10²⁹–8 × 10³⁰, n_t = 10¹⁰–10¹² cm⁻³ and l = 10⁸–10⁹ cm. The result is shown as a filled region in Figure 8 bounded by the lines with parameters marked there. One can readily see that even for the lowest fraction of accelerated electrons k = 10⁻⁷, there are always parameters of coronal plasma that may explain the generation of observed spike bursts, if the electron spectral slope is steeper than δ = 1.7. On the other hand, to have spectral slope flatter than δ = 2 and δ = 3, one have to accelerate more than 10⁻⁴% and 1% thermal particles, correspondingly. The former case is valid for any combination of E ₀, l and N, whereas the latter is just for some subset of it. The upper limit on δ ≲ 3.4 is placed by the energy density condition of Equation (22).

Figure 8. Allowed power law slopes δ of electron distribution and fractions k of thermal electrons being accelerated, necessary to generate the observed spike bursts for different parameter values.

It is clear that the observed spike bursts may be generated for any combination of possible parameters of the corona if one have 1 < δ < 3.4 and k > 10⁻⁷. The larger luminosities and/or smaller sizes of active regions correspond to the harder spectra with smaller slopes, to get the necessary amount of electrons with sufficiently large energies. Such values of δ differ from typical slopes of energy spectrum of electrons in solar flares, typically greater than 3 and reaching values of 4–6 (Aschwanden 2005). On the other hand, there are evidences for the detection of quite flat spectra of electrons with slopes of 2–3 in the flares of UV Ceti-type stars (Smith et al. 2005).

Therefore, we may conclude that the conditions for the synchrotron origin of the detected highly polarized spike bursts may naturally occur in the corona of UV Ceti, with no additional assumptions except for the contemporary views on coronal activity of the Sun and flaring stars.

5 CONCLUSIONS

In our observations of a giant flare of UV Ceti on 2012 December 28, we discovered 14 spike bursts near its maximum, and clearly detected their linear polarization, in which intrinsic value exceeds 35–40%. These events in such numbers, and the polarization of the flare emission in general, have never been seen before from any UV Ceti-type star. We argue that their short durations, sufficiently high intensities and comparable scales of rise and fading phases, and most importantly the polarization, suggest that these events may only be caused by the synchrotron emission of ultra-relativistic electrons moving in the magnetic fields of the corona. As we demonstrated in Section 4, the UV Ceti corona may indeed possess the conditions – densities and magnetic field strengths – necessary to accelerate significant amount of particles up to the energies of hundreds of MeV, producing the emission in U band with the durations about fractions of a second. Therefore, our result is the first ever evidence for the generation of ultra-relativistic electrons with such energies in the coronae of UV Ceti-type stars.

As a side note, let us also mention that the presence of very energetic particles in flares of UV Ceti-type stars may have significant impact on the planets orbiting them. Indeed, the fraction of such particles may be ejected away from the star and may significantly worsen the conditions for the appearance and development of life on the planets formally inside the habitable zones around the red dwarfs (Kasting, Whitmire, & Reynolds 1993; Tarter et al. 2007). It is important as such stars are easier targets for exoplanet detection, as the recent observations suggest (Guinan et al. 2014; Gillon et al. 2014).