Relative contribution of surface mass-balance and ice-flux changes to the accelerated thinning of Mer de Glace, French Alps, over1979-2008

Abstract

By subtracting surface topographies from 1979, 1994, 2000 and 2008, we measured icethinning rates increasing from 1 ma^-1 (1979-94) to >4 ma^-1 (2000-08) on the tongue of Mer de Glace, French Alps. The relative contributions of changes in surface mass balance and ice fluxes to this acceleration in the thinning are estimated using field and remote-sensing measurements. Between 1979-94 and 2000-08, surface mass balance diminished by 1.2mw.e.a^-1, mainly because of atmospheric warming. Mass-balance changes induced by the growing debris-covered area and the evolving glacier hypsometry compensated each other. Meanwhile, Mer de Glace slowed down and the ice fluxes through two cross sections at 2200 and 2050ma.s.l. decreased by 60%. Between 1979-94 and 2000-08, two-thirds of the increase in the thinning rates was caused by reduced ice fluxes and one- third by rising surface ablation. However, these numbers need to be interpreted cautiously given our inability to respect mass conservation below our upper cross section. An important implication is that large errors would occur if one term of the continuity equation (e.g. surface mass balance) were deduced from the two others (e.g. elevation and ice-flux changes).

1. Introduction

The sensitivity of glacier mass balance to climate change is widely recognized (Dyurgerov and Meier, 1999;Oerlemans, 2001;Vincent, 2002;Ohmura, 2006;Lemke and others, 2007). In a warming climate, a consequence of this sensitivity is a rapid thinning of most glaciers, particularly at their lowest elevations (Schwitter and Raymond, 1993). Over the past few decades, this thinning has been observed for most mountain glacier tongues using either field measurements (e.g. Vincent and others, 2009) or various remote-sensing techniques (e.g. Rignot and others, 2003;Magnusson and others, 2005; Surazakov and Aizen, 2006;Kohler and others, 2007;Paul and Haeberli, 2008;Soruco and others, 2009;Berthier and others, 2010;Nuth and others, 2010).

The continuity equation, applied to a glacier tongue, indicates that two main processes potentially drive this recent low-elevation thinning (Cuffey and Paterson, 2010; Nuth and others, 2012): (1) a warmer climate leads to enhanced ablation at the glacier surface (Vincent and others, 2004);(2) decreasing ice fluxes from upstream regions can also play a role. For mountain glaciers, a contribution of ice dynamics to their recent low-elevation thinning is often suggested (Rignot and others, 2003;Lambrecht and Kuhn, 2007;Paul and others, 2007), but is quantified in only a few studies (Hagen and others, 2005;Huss and others, 2007; Vincent and others, 2009). In particular, Huss and others (2007) showed that present-day ice fluxes from the upper part of Unteraargletscher, Swiss Alps, are insufficient to counteract the high ablation rates on the glacier tongue, and in their effort to model a future retreat scenario they highlighted the importance of taking into account an evolving ice dynamics. On Glacier d’Argentiere, French Alps, Vincent and others (2009) also showed that the elevation changes below 1800 m are mainly dynamically driven. Located close to Glacier d’Argentiere, the tongue of Mer de Glace has also experienced accelerated thinning in the late 20th and early 21st centuries (Berthier and others, 2004). The first goal of the present paper is to quantify the relative contribution of changes in surface mass balance and changes in glacier dynamics (ice fluxes) to this accelerated thinning.

Additionally, an important question in modern glaciology is to determine whether it is reasonable to infer area- averaged surface mass-balance changes of a glacier tongue from observations of the thinning rates and the ice fluxes only. This question deserves attention given that surface mass balance (and its temporal variations) is the glacier variable most closely related to climate change (e.g. Vincent and others, 2004). The spatial pattern of surface mass balance of a limited number of glacier tongues can be determined directly from field measurements using ablation stakes but cannot be directly measured regionally by remote-sensing methods (photogrammetry, laser scan or satellite images). Thus, deriving this variable for large, remote, numerous and/or debris-covered glacier tongues remains problematic.

In the past, there have been various attempts to infer the spatial distribution of mountain glacier surface mass balance from (1) the principle of mass conservation combined with remotely sensed elevation changes and a well- constrained high-resolution ice-flow model (Hubbard and others, 2000) or (2) the kinematic boundary condition applied to a glacier tongue and constrained using remotely sensed surface elevation changes and velocities (Gud-mundsson and Bauder, 1999;Kaab and Funk, 1999;Kaab, 2000). In both cases, comprehensive bedrock topographies were required. Hubbard and others (2000) succeeded in modeling the annual mass balances measured at ablation stakes at Haut Glacier d’Arolla, Swiss Alps, but the obvious drawback of their method is the difficult transferability to other glaciers that may not present a simple geometry and/or not be as extensively monitored as Haut Glacier d’Arolla. An alternative to these complex and data-demanding approaches is to infer the average surface mass balance below (or between) selected cross sections where the bedrock topography is known (Reynaud and others, 1986). The latter approach does not provide the complete spatial distribution of glacier mass balance, but it is simpler and less data-demanding, and thus easier to apply to remote or larger glaciers. This cross-sectional approach has received renewed attention recently to derive tongue-wide average mass balance and its change with time, in particular for Himalayan/Tibetan partly debris-covered glaciers (Sakai and others, 2006;Zhang and others, 2010;Nuimura and others, 2011). However, the reliability of mass-balance changes inferred from this cross-sectional method has not been assessed using observed values at ablation stakes.

2. Thinning of Lower Mer De Glace Between 1979 And 2008

Mer de Glace, the largest glacier in the French Alps, with an area of ~30km² (Zumbuhl and others, 2008), is located in the Mont Blanc massif (Fig. 1). It is composed of an upper basin the maximum elevation of which reaches about 4300 m. From this accumulation region, the ice flows rapidly (maximum surface velocities of 900 m a^-1 were measured by Reynaud (1973) and 700 m a^-1 by Berthier and others (2005)) through a narrow, steep portion (the Geant icefall, between 2700 and 2400 m) before feeding the lower 7 km of the glacier down to a front located at about 1500m. During the last 15years, the equilibrium-line altitude (ELA) has been located above the Geant icefall at an altitude of about 2800 m (Rabatel and others, 2005). The lower part of the glacier tongue is covered with debris. The extent of the debris-covered area has grown since the end of the Little Ice Age (Deline, 2005).

Fig. 1. (a) Mer de Glace (solid triangle) in the Mont Blanc area of the French Alps, close to the border between France, Switzerland and Italy. (b) Orthorectified SPOT5 (Satellite Pour l’Observation de la Terre) image acquired in August 2003 (©CNES 2003/Distribution Spot Image). The main glacier features are named (gl. stands for glacier). The portion of Mer de Glace studied here (outlined) is located downstream of two flux gates labeled FG_TAC (TAC stands for Tacul) and FG_TRE (TRE stands for Trelaporte).

Thus, the second goal of this paper is to test, for the relatively well-observed Mer de Glace tongue, whether it is reasonable to infer temporal variations in surface mass balance from changes in geometric variables (surface elevation and ice fluxes) only.

In a previous study, we adjusted and compared a 1979 map from the French mapping agency (Institut Geographique National) and satellite-derived digital elevation models (DEMs) to determine the changes in surface elevation of Mer de Glace between 1979-94, 1994-2000 and 2000-03 (Berthier and others, 2004). The comparison with elevation profiles surveyed in the field each year showed that, after Gaussian filtering and averaging by altitude range, the DEM- derived elevation changes were accurate within ±1-2 m in the ablation area. One conclusion of our work was that the lower part of Mer de Glace had recently been thinning at an increasing rate. Here, we have extended our time series by using an additional DEM derived from a SPOT5 2.5 m stereopair acquired on 26 August and 2 September 2008 (Fig. 2). This 2008 DEM is used in place of the 2003 DEM that had a short (3 year) time separation from the previous DEM (2000), resulting in larger uncertainties on the thinning rates.

Fig. 2. Rate of surface elevation change as a function of altitude on the Mer de Glace tongue for three different epochs. The upper histogram shows the ice hypsometry below the Tacul flux gate in 1979.

Between a flux gate (noted as FG_TRE; Fig. 1b) at about 2050 m in 1979 and the glacier front (a glacierized area of about 2 km²), the average ice-thinning rate has evolved from (a glacier zed area of about 2 km²), the average ice-thinning rate has evolved from 6 ± 0.1 m a^-1 in 1979-94 (referred to as epoch I in the following) to 3.0± 0.3 ma^-1 in 1994-2000 (epoch II) and 4.0 ± 0.2 m a^-1 in 2000-08 (epoch III). In other words, the ice-thinning rate has increased by 2.4 ±0.4 m a^-1 (from epoch I to II) and then by 1.0±0.4m a^-1 (from epoch II to III). Between another flux gate (noted as FG_TAC; Fig. 1b) at higher altitude (about 2225 m in 1979) and the glacier front, the ice-thinning rate has increased by 1.7 ± 0.4 m a^-1 (from epoch I to II) and 1.0±0.4ma^-1 (from epoch II to III). The main goal of the present study is to understand what has driven this acceleration of the thinning of lower Mer de Glace during recent years.

For the portion of Mer de Glace downstream of a flux gate (FG), the equation of mass conservation (Reynaud and others, 1986;Cuffey and Paterson, 2010) states that the change in surface elevation (h) with time (t) between year 1 (yr1) and year 2 (yr2) is the sum of the area-average surface mass balance (B) and the flux term (all terms in m ice a^-1):

(1)

where ρ is the density of ice (900 kg m^-3), Ф_FG is the ice flux through FG, Ф_front is the flux at the glacier front (Ф_front = 0) and A is the glacier area below FG. indicates an average between year 1 and year 2. is the average emergence velocity below FG (noted V”) between year 1 and year 2.

Consequently, to understand the increase in the thinning rate of lower Mer de Glace from one epoch to another (left- hand term in Eqn (1)), we computed the surface mass balance (Section 3) and the emergence velocity (Section 4) of the glacier tongue for each epoch (I, II and III).

The choice of the flux gates, FG_TAC and FG_TRE, was constrained by data availability and glaciological reasons. They correspond to two of the five transverse profiles where the surface topography is measured yearly in the field with an accuracy of ±0.5 m (Vincent and others, 2009). The upstream flux gate, FG_tac, has the advantage of feeding a larger area (about 4 km² compared with 2 km² for Trélaporte) but it is located above the confluence of Mer de Glace with Glacier de Leschaux (Fig. 1b) and we lack thickness and velocity measurements to estimate the ice fluxes coming from this tributary glacier. The three other flux gates, downstream of Trelaporte, are not considered here because they feed a much smaller part (<0.7km²) of the glacier tongue where only two ablation stakes are surveyed each year.

3. Changes in Surface Mass Balance

3.1. Field measurements at ablation stakes

Each year in late September, the annual surface mass balance on Mer de Glace is determined below 2300 m using an ablation stake network mainly located along the glacier center line. The annual mass balance varies from about -4 m w.e. a^-1 at 2300 m to -9 m w.e. a^-1 at the lowest ablation stake (1750m). All annual mass-balance measurements available on clean ice between hydrological years 1979/80 and 2007/08 are processed using the linear mass- balance model (Lliboutry, 1974) and are corrected for local elevation changes. This model consists of the linear decomposition of time and space variability of surface mass balance. The surface mass balance at each stake (b_i,_t) is modeled as the sum of its spatial pattern (α_i), its temporal anomalies (β_t) and a residual (ε_i,t).

(2)

Details of the method can be found elsewhere (Thibert and Vincent, 2009).

Over the three time periods considered here (Fig. 3a), the mass balance on clean ice has decreased first by 0.28 m w.e. a^-1 (epoch I to II) and then by 0.96 m w.e. a^-1 (epoch II to III). From epoch I to III, the total change in mass balance was -1.23 m w.e. a^-1. These results are consistent with previous observations on glaciers in the European Alps (Vincent, 2002;Vincent and others, 2004;Huss and others, 2008): the surface mass balance has increased between 1960 and 1981, an increase related to low ablation values. For the more recent period (1982-2008), a sharp mass-balance decline is observed and connected to an ablation rise.

Fig. 3. Output of the linear mass-balance model (Lliboutry, 1974) applied to all mass-balance measurements in the debris-free part of the ablation area of Mer de Glace between September 1979 and September 2008 (29 hydrological years). (a) Annual mass-balance anomaly (β_t ). The grey boxes show the mass-balance anomalies averaged over epochs I, II and III. (b) Relationship between the 1979–2008 average mass balances (α_i ) and altitude (z). The regression lines used on clean and debris-covered ice to compute the mass balance of the whole glacier tongue are also shown.

3.2. Mass balance for the whole glacier tongue

We now estimate the tongue-averaged mass balance for each epoch, taking into account the evolving hypsometry of the ice-covered area and the reduction of ablation on the debris-covered parts. Lliboutry’s (1974) linear model provides the mass balances at the location of stakes and thus they must be extrapolated to the whole ice tongue. For all stakes (on clean ice), 91% of the mass-balance spatial variance is explained by altitude (Fig. 3b). For each epoch, this linear mass-balance-altitude relationship is combined with the evolving hypsometry of the debris-free areas to estimate their area-weighted mass balances. For debris- covered areas, the same mass-balance gradient with altitude is used but the curve is shifted upward by 3 mw.e. to account for the reduction in ablation due to the insulating effect of debris (Fig. 3b). This constant ablation reduction factor under debris (noted f _d) has been estimated from field measurements during 5 years at five locations on Mer de Glace and neighboring Glacier d’Argentiere where ablation was systematically compared between stakes anchored at the same altitude on clean and debris-covered ice (Vincent, unpublished information). Area-weighted mass balances for the debris-free and debris-covered parts are then summed to obtain the mass balance of the whole glacier tongue. In a final step, we added the mass-balance temporal anomaly (β_t) for each epoch. Melt at the base of the glacier was assumed to be negligible.

The hypsometry on the debris-free and debris-covered parts of the glacier is calculated for each year when a DEM is available (1979, 1994, 2000 and 2008). Because we did not have any imagery accompanying the DEM from 1979, we used instead a Satellite Pour l’Observation de la Terre (SPOT) image from 1988 and assumed no change in ice extent between 1979 and 1988, an assumption supported by the limited length variations (only a small advance) during the same time period (Vincent and others, 2007). Between 1988 and 2008, the ice-covered area diminished by 0.4 km², mainly close to the glacier front. From visual inspection of the satellite images, the percentage of the glacier tongue covered with debris was digitized and below FG_TRE was found to increase from 45% in 1988 to 65% in 2008 (31% to 45% below FG_tac). Increased ablation due to dust (Oerle-mans and others, 2009) and changes in solar radiation due to evolving shading on a lowering glacier surface (Arnold and others, 2006) are not estimated since they should already be accounted for in the mass-balance observations at stakes.

During 1979-2008, the average surface mass balance was -6.4mw.e. a^-1 below FG_TRE and -5.4mw.e. a^-1 below FG_tac. Surface mass balances (converted to ice equivalent using a density of 900 kgm^-3) for epochs I-III are listed in Tables 1 (FG_TAC) and 2 (FG_TRE). Interestingly, the mass- balance changes between the different periods for the whole tongue are close to the mass-balance temporal anomaly (β_t) determined at ablation stakes located on clean ice only. This indicates that the main driver of mass-balance change on the Mer de Glace tongue is climate change, whereas other feedbacks potentially influencing the mass balance (growing debris coverage, thinning of the tongue and area loss close to the glacier front) nearly compensate each other. Between epochs I and III, the glacier front retreated to higher elevations such that ice-covered areas at the lowermost elevations, where ablation is high, disappeared. Meanwhile, the glacier tongue thinned and thus was immerged in a warmer atmosphere due to the adiabatic decrease of temperature with altitude. These two feedbacks have opposite effects on ablation (Elsberg and others, 2001), and the net effect is quantified by an average altitude below FG_tre that decreased by 35 m (from 1873 m to 1838 m). This net lowering of the Mer de Glace tongue indicates that, in term of ablation feedbacks, thinning dominates over the retreat of the front. This 35 m area-average lowering corresponds to an enhanced ablation of about 0.35 mw.e. a^-1 (using the mass-balance gradient with altitude from Fig. 3b). This increase in ice ablation was counterbalanced by the growth in debris-covered areas (+20% below FG_TRE) that lowered the ablation by 0.51 mw.e.a^-1.

Table 1. Mean annual thinning rate (Sh), emergence velocity (V”) and surface mass balances (B) below FG_TRE for each epoch and (bottom column) average values during 1979-2008. The changes from one epoch to another are indicated in bold. The last row contains the sum of the emergence velocity and the surface mass balance. All data are in m ice a^-1

3.3. Uncertainties on the mass balance

Sources of uncertainties on the total mass balance are as follows:

1. 1. The residual, ε_i,t , of the linear mass-balance model, ±0.5 m w.e. a^-1, that is divided by the square root of the number of years during each period.

2. 2. The standard deviation, ±0.4 m w.e. a^-1, of the residual to the linear fit between mass balance and altitude (Fig. 3b). Given the lack of ablation stakes below 1750 m, an extrapolation of the mass-balance gradient is needed for the lowermost part of the glacier (dashed line in Fig. 3b) where we double the uncertainty to ±0.8 m w.e. a^-1.

3. 3. The average altitude of each altitude band is known within ±2 m, translating into a negligible ±0.02 m w.e. a^-1 mass- balance uncertainty.

4. 4. A ±1 mw.e. a^-1 uncertainty (33%) was assumed for f_d. This error should account for the unknown spatial variability in debris thickness and only applies to the glacier area covered with debris.

5. 5. A 10% uncertainty was estimated for our ability to delimitate the debris-covered area, and after multiplying by f _d this leads to a ±0.3 m w.e. a^-1 mass-balance uncertainty.

These individual error components are summed quad- ratically, leading to total uncertainties of ±0.8 and ±0.7 m w.e. a^-1, respectively, for the area-average surface mass balance below FG_TRE and FG_TAC (Tables 1 and 2).

Table 2. Same as Table 1 but for FG^TAC

Lower uncertainties, ±0.4 to ±0.5 m w.e. a^-1, are calculated for the mass-balance changes from one period to another (Tables 1 and 2). This is because the large uncertainty on f_d, ±1 mw.e.a^-1, is applied to areas where debris coverage changed (and not to the total debris-covered area). Also, uncertainties associated with the linear fit of mass balance with altitude (±0.4 m w.e. a^-1) are restricted to changing glacier areas (and not to the whole glacier tongue).

4. Changes in Ice Fluxes and Emergence Velocities

We now estimate the ice fluxes through both cross sections for the three different epochs:

(3)

where S represents the area of the cross section, U is the component of the ice velocity perpendicular to the cross section and (U) is the depth and width average (= crosssectional average) of this velocity component.

4.1. Cross-sectional areas

The bedrock topography of Mer de Glace has been measured by various authors (Susstrunk, 1951;Vallon, 1961;Gluck, 1967) and compiled in a comprehensive map (Lliboutry and Reynaud, 1981). We digitized the elevation contours from this map, interpolated them and then extracted a profile of the subglacial topography at FG_TRE and FG_TAC (Fig. 4). To compute the evolving cross section, the surface elevation is updated using topographic surveys performed yearly (Vincent and others, 2007).

Fig. 4. Bedrock (black), 1985 surface (blue) and 2008 surface (red) elevations at (a) FGTAC and (b) FGTRE. Between 1979 and 1985 (not shown), the glacier thickened by 5m at FGTAC and 10m at FGTRE before thinning by 50m at FGTAC and 61m at FGTRE between 1985 and 2008.

4.2. Surface velocities and their temporal evolution

Velocities are available from two data sources. Spatially sparse, but accurate and temporally regular, annual velocities are calculated from annual positioning of stakes anchored in the glacier. About 10-15 velocity measurement are available each year since 1979 along a longitudinal profile of Mer de Glace with an accuracy of ±0.2 m a^-1 (Vincent and others, 2009). The September 1987 survey was not performed, so velocity data are lacking for hydrological years 1986/87 and 1987/88.

Velocity fields have also been computed by orthorectifying and tracking surface features on 10m resolution SPOT satellite images. Annual velocity fields are available for hydrological years 1993/94 and 2000/01 (Berthier, 2007). The comparison with simultaneous field-derived velocities shows that their precision (1 σ) is ±2-3 m a^-1, or one-quarter of the satellite image pixel size. Two velocity fields, derived from 2.5 m SPOT5 imagery, are also available during summer 2003 with a precision of ±10 m a^-1 (Berthier and others, 2005).

All velocity measurements are compared along a longitudinal profile (Fig. 5). Between 1965 and 1980, interannual variations in speed were small, within ±20 m a^-1, and these fluctuations were in phase all along the longitudinal profile (Lliboutry and Reynaud, 1981). This period was followed first by a small acceleration that peaked in 1985 and then by a strong slowdown.

Fig. 5. (a) Location of surface velocity measurements along a longitudinal profile of Mer de Glace (©CNES 2003/Distribution Spot Image). (b) Changes in annual velocity along the profile. Solid symbols (blue triangles and red dots) correspond to satellite measurements. Other velocities (open red and blue squares and grey envelope) were measured in the field.

Annual velocities are not available every year at each flux gate exactly, but one velocity measurement is generally available up- and downstream of the flux gate. Thus, we obtained the velocity at each flux gate by linear interpolation of the surrounding velocities (Fig. 6). At FGTRE, the glacier flow has decreased by 52% from a peak velocity of 124 m a^-1 (hydrological year 1984/85) to a minimum of 59 m a^-1 (hydrological year 2007/08). At FGTAC, the annual velocity decreased by 49% from a maximum of 180 m a^-1 in 1980/81 down to 92 m a^-1 in 2007/08. Since 1984/85, the decrease is nearly linear at FGTRE, whereas at FGTAC there is an 11 year plateau between 1991/92 and 2002/03 when velocities remained stable at about 120 m a^-1. These nonmonotonic variations in velocity imply that it is important to have continuous annual velocity measurements to infer realistic multi-year averaged ice fluxes.

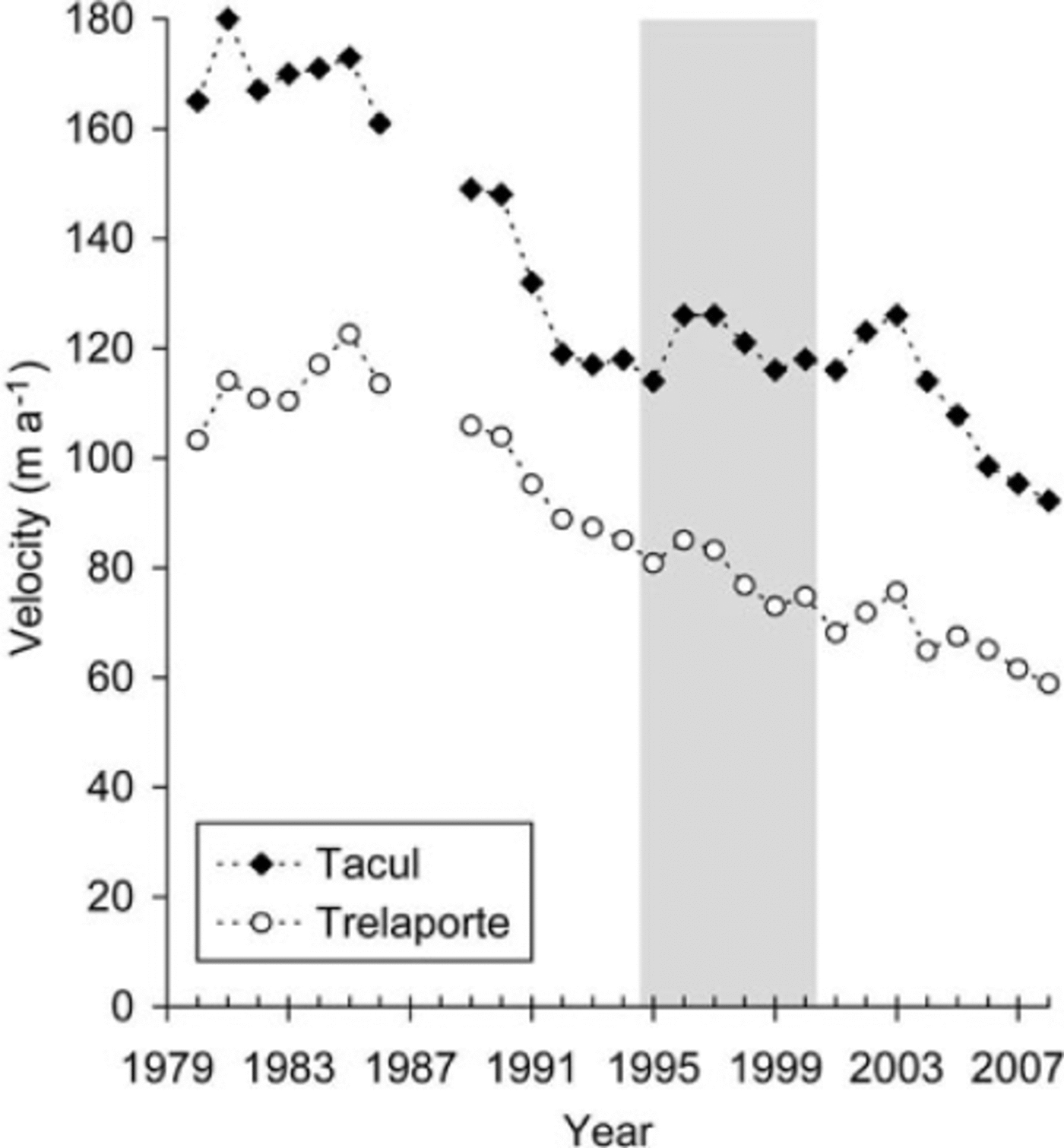
Fig. 6. Annual center-line surface velocity at FGTRE (open circles) and FGTAC (solid diamonds) between 1979 and 2008. Epoch II (1994–2000) is identified with grey shading. Data are missing for hydrological years 1986/87 and 1987/88. To estimate the ice fluxes,the velocities for these years were calculated by linear interpolation using the 1985/86 and 1988/89 velocities.

4.3. Changes in ice fluxes

Mean cross-sectional velocity (U) is required to compute the ice fluxes through the flux gates, but only center-line surface velocity (U_s,_c) is available from yearly field measurements. A correcting factor is needed to convert all centerline velocities to mean cross-sectional velocities.

First, we calculate the ratio between the mean surface velocity for each flux gate (U_s) and the center-line surface velocity U_s,c . The ratio is estimated from satellite-derived velocity fields. Preferably, this ratio should be evaluated on annual velocities to limit the influence of seasonal variations in basal sliding (Willis, 1995). The 1993/94 and 2000/01 annual velocity fields do not entirely sample the transverse profile because the tracking of surface features on sequential satellite imagery failed close to the glacier margins, where too much shear occurred within 1 year. Thus, the velocity at the shear margins was filled using linear interpolation between the glacier boundary (where the velocity is zero) and the closest available velocity measurement. At FG_TRE, the ratio equals 0.68 in 1993/94 and 0.71 in 2000/01. Additionally, we estimated the ratio on the 2003 summer velocity fields derived from SPOT5 images acquired during 19 July to 19 August and 23 August to 18 September (Berthier and others, 2005). These summer velocity fields have the advantage of providing a complete transverse profile because after a few weeks surface features are still trackable even at the shear margins (Fig. 7). The ratio equals 0.69 for the August-September velocity field and 0.74 for the July-August velocity field. The average of these four values, 0.70 (±0.02), was used to convert all annual centerline velocities to mean surface velocities at FG_TRE. At FG_TAC (Fig. 7c), and using the same procedure, a ratio of 0.8 was calculated between the width-average surface velocity and the center-line surface velocity.

Fig. 7. (a) Surface velocity of Mer de Glace obtained by correlating 2.5m SPOT5 images acquired on 23 August and 18 September 2003. The thick white lines locate the FGTAC and FGTRE cross sections for which the respective surface velocities are shown on the right (b, c).

The next step is the conversion from mean surface to depth-averaged velocity. Without basal sliding, theoretical calculations suggest that the depth-averaged velocity is 80% of the surface velocity (for n = 3 in Glen’s law;Cuffey and Paterson, 2010, p. 310). With basal sliding, this percentage increases, and for example in the case of Athabasca Glacier, Canada, the mean cross-sectional velocity equals the mean surface velocity (Raymond, 1971). Here we used an intermediate value assuming that the depth-averaged velocity is 90% of the surface velocity.

Mean cross-sectional velocities and cross-sectional areas are multiplied to compute annual ice fluxes. The 1979-2008 mean ice flux was 0.0105 km³ ice a^-1 at FG_TRE. These fluxes, once distributed over a mean downstream glacier area of 1.85 km², correspond to an emergence ice velocity of 5.4 m a^-1. Between 1979 and 2008, there is a strong reduction in the annual ice fluxes at FGTRE. The minimum ice flux in 2007/08 is only 38% of the maximum recorded during hydrological year 1984/85. Consequently, the emergence ice velocities have decreased from 6.6 (epoch I) to 4.7 (epoch II) to 3.8 m a^-1 (epoch III).

At FG_tac, the 1979-2008 mean ice flux was 0.0230 km³ ice a^-1 and also decreased with time: the ice flux in 2007/08 was 43% of the maximum flux measured during hydrological year 1980/81. Below FG_TAC (feeding an ice-covered area of 4.0 km²), the emergence ice velocities averaged over 1979-2008 are 5.7 ma^-1 evolving from 6.7 (epoch I) to 5.0 (epoch II) to 4.5 m a^-1 (epoch III).

4.4. Uncertainties on the ice fluxes

At both cross sections, the surface topography is known within ±0.5 m (Vincent and others, 2009) and the basal topography within ±10 m (~5% of the mean cross-sectional thickness). This uncertainty on the bedrock topography was conservatively adapted from Susstrunk (1951) who proposed a 3% error for the seismic refraction method. Our findings (see Section 5.1) suggest that these ±10 m uncertainties may be too small. The center-line annual velocities are measured in the field with a precision of ±0.2 ma^-1. We assumed a ±5ma^-1 error (~5%) for the conversion of center-line velocities to mean cross-sectional velocities. After standard propagation of these errors in the ice flux equation (Berthier and others, 2003), the uncertainties vary between ±0.0012 and ±0.0015 km³ a^-1 at FG_TRE, 11-16% of the total ice fluxes. At FGTAC, they vary between ±0.0016 and ±0.0020 km³ a^-1, 10-13% of the total ice fluxes.

The uncertainties on the changes in emergence ice velocity from one period to another are ±0.9-1.0 m a^-1 below FG_tre and are slightly smaller at ±0.6ma^-1 below FG_tac, mainly because the downstream area is twice as large below FG_TAC.

5. Discussion

Tables 1 and 2 list, for the two flux gates, the annual thinning rates, emergence velocities and surface mass balances for the different epochs and also their changes from one epoch to another. Based on these data, we can discuss: (1) our ability to close the budget of the thinning and see if the law of mass conservation is respected below each flux gate; (2) the cause of the accelerated thinning on the Mer de Glace tongue;and (3) whether reliable changes in surface mass balance could be inferred from changes in geometric variables (ice fluxes and thinning rates) only.

5.1. Is the law of mass conservation respected?

If the law of mass conservation is respected, the sum of the emergence velocity and the surface mass balance should equal the thinning rate for each epoch (Tables 1 and 2; Fig. 8). This is the case within error bars below FG_TRE where, if the whole study period (1979-2008) is considered, the mean icethinning rate is-2.0 m a^-1, whereas the sum of emergence ice velocity (5.5 m a^-1) and mass balance (-7.1 m icea^-1) equals -1.6 m a^-1. At this cross section, the law of mass conservation is respected well within error bars for each time period (Fig. 8a).

Fig. 8. Observed annual thinning rate (thin solid line), emergence velocity (V”, dotted line) and surface mass balance (B, thick solid line) below (a) FG_TRE and (b) FG_TAC for each epoch. The dashed line represents the sum of the emergence velocity and the surface mass balance (B + V”) and, if mass conservation is respected, will equal the observed thinning rates.

There is a different story at FG_TAC, where the sums of the emergence ice velocities and the surface mass balances are systematically larger than the observed ice-thinning rates (by 1.7 m a^-1 in epoch I, 1.6 m a^-1 in epoch II, 1.1 m a^-1 in epoch III and 1.6 m a^-1 overall). These differences, larger than our uncertainties and similar for the different time periods, indicate that a systematic error affects at least one term of the mass conservation equation. This non-closure of the budget of thinning below FG_TAC implies that we would make large errors if one term of the mass conservation equation were unknown and inferred from the two others (see Section 5.3).

Given the small uncertainties on the thinning rates, this non-closure of the mass budget may be explained either by emergence velocities (ultimately ice fluxes at FG_TAC) that are too high or by surface mass balances that are not negative enough (or a combination of both). Uncertainties on the tongue-average surface mass balances are large (about ±0.8 mice a^-1), but to explain the mass budget discrepancy we need a process that decreases the mass balances between FG_TAC and FG_TRE but not below FG_TRE, otherwise we would lose mass conservation below FG_TRE. A systematic bias of the mass balance on clean ice (concentrated mainly between FG_TAC and FG_TRE) could arise from our network of center-line ablation stakes that would not capture some transverse variations in surface mass balance. However, ablations at seven stakes across the Tacul section were measured between 19 June and 4 September 2007 and suggest little transverse variation. The 3.5 month mean ablation was 3.55 m w.e. with a standard deviation of only 0.2mw.e. Ablations at the two stakes close to the glacier margins did not differ from other measurements. Thus, ablations measured along the center line are indeed representative of the whole debris-free part of the glacier tongue. Another possibility is that we overestimated the debris-covered area between FG_TAC and FG_TRE or that the ablation reduction factor under debris (f _d, assumed to be constant) may be lower between FG_TAC and FG_TRE than below FG_tre. These potential sources of systematic error on the tongue-average mass balance deserve more attention in the future, for example using the thermal resistance derived from Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) imagery (Zhang and others, 2011).

Although the non-closure of the mass budget could be explained partly by a systematic error in surface mass balance, an overestimation of the ice fluxes at FG_TAC is our preferred hypothesis. If data were available to take into account the ice fluxes from tributary Glacier de Leschaux, the total incoming ice fluxes would be increased and the law of mass conservation would be violated even more below FG_tac. The ice fluxes at FG_TAC could be lowered (and mass conservation approached but not reached) by decreasing (from 0.9 to 0.8) the factor used to convert surface velocities to mean cross-sectional velocities. However, a value of 0.8 implies no sliding, whereas sliding was found to account for a significant part of the ice flow at this location (Vallon, 1967). Furthermore, we did not find any justification for using a different factor at FG_TAC and FG_TRE. Thus, our most likely explanation is an overestimated ice thickness at FG_tac. Mass conservation is reached if the ice thickness is reduced by 27%. When this ice-thickness correction is applied, the differences between on one hand the sum of the ice emergence velocities and the surface mass balances and on the other hand the observed ice-thinning rates are reduced to 0.0ma^-1 in epoch I, 0.2ma^-1 in epoch II and -0.1m a^-1 in epoch III. Ice-penetrating radar campaigns should be organized in the future to verify the bedrock topography at FGTAC and validate this hypothesis.

5.2. Budget of the increase in the thinning rate

Within error bars, the budget of the increase in the thinning rate is closed below both cross sections (Tables 1 and 2; Fig. 9), i.e. the change in thinning rate from one period to another equals the sum of the changes in surface mass balances and the changes in emergence velocities. The closure is especially good between epochs I and II, partly because the changes in ice-thinning rates are large (~2ma^_1). The agreement is not as satisfactory between epochs II and III, with the sum of the changes in surface mass balances and emergence velocities higher than the observed thinning by 83% below FG_TRE and 47% below FG_TAC. When epochs I and III are compared, these percentages are reduced to 14% and 23%, respectively, suggesting that the changes of ice fluxes and/or ice ablation are slightly overestimated. Below FG_tac, this 23% discrepancy is reduced to only 2% when the ice thickness is diminished by 27%, as proposed in Section 5.1, to reach overall mass conservation.

Fig. 9. Ice-thinning rate (black), its evolution from one period to another (white) and the relative contribution of changes in surface mass balance (light grey) and changes in emergence velocity (dark grey) to the increase in the thinning rate. (a, b) Average values below FGTRE; (c, d) average values below FGTAC. Numbers close to the histograms correspond to percentage of the change in ice-thinning rate.

This relatively good closure of the budget of the increase in the thinning rate at both flux gates gives confidence to our estimates of the relative role played by changes in surface mass balance and ice dynamics. Overall, surface mass- balance changes only explained about one-third of the increase in the thinning rate. Mass-balance changes are very small between epochs I and II but larger between epochs II and III where they explain approximately half of the change in thinning rate (and even two-thirds at FG_TAC). Decreasing ice fluxes from the upper part of the glacier toward the tongue are responsible for the remaining two-thirds of the increase in the thinning rate.

This dynamic response of Mer de Glace is not an exception given that recent multi-decadal deceleration of glacier tongues seems to be a widespread feature in the Alps (Vincent and others, 2000, 2009; Span and Kuhn, 2003) and elsewhere (Kirkbride and Warren, 1999;Zhang and others, 2010;Heid and Kaab, 2011;Nuimura and others, 2011). A reduction in the ice fluxes exerts a strong control on the geometry of glaciers by starving their lowest elevations and preserving their upper reaches. The prevalence of this geometric response is confirmed by the observation of limited thinning in the accumulation zone for a large number of glaciers in the European Alps during the past two to three decades (Span and Kuhn, 2003; Berthier and others, 2006;Bauder and others, 2007;Lambrecht and Kuhn, 2007; Paul and Haeberli, 2008).

5.3. Can we infer temporal changes in mass balance from changes in thinning rates and ice fluxes?

Given our ability to close the budget of increase in the thinning rate, it seems possible to infer the changes in surface mass balance from the changes in geometric terms (thinning rate and ice flux) only. More surface mass-balance observations are eagerly desired because changes in surface mass balance are directly related to climate fluctuations but are only observed on selected generally small glaciers, whereas, if bedrock topography had been measured at least once for selected cross sections, geometric terms (thinning rate and ice flux) potentially could then be derived regularly for large glacier tongues using remote-sensing techniques. This strategy would be particularly relevant to deriving tongue-average surface mass-balance changes for debris- covered glaciers (e.g. in the Himalaya), which are difficult to sample comprehensively in the field due to a rough surface. Indeed, ablation is known to be highly variable on a debris- covered surface and the representativeness of a few ablation stakes is highly questionable (Mihalcea and others, 2006). Furthermore, ablation stakes cannot capture the enhanced ablation taking place at supraglacial lakes and ice cliffs (Sakai and others, 2000, 2002). This continuity-equation method has already been applied to glaciers in China (Sakai and others, 2006;Zhang and others, 2010) and recently to Khumbu Glacier, Nepal (Nuimura and others, 2011).

Our field-observed and calculated changes in surface mass balance for the tongue of Mer de Glace are given in Table 3. For both cross sections, they differ on average by 0.3 m w.e. a^-1 (N = 4) and up to 0.8 m w.e. a^-1. These differences are expected as they remain within our calculated uncertainties. In the case of FG_TAC, a better agreement is reached when the cross-sectional ice thickness is reduced by 27% to respect mass conservation (Section 5.1), but still the sharp increase in ablation between epochs II and III is not fully reproduced. These discrepancies have the same magnitude as the current climatic signal of mass-balance changes, so higher accuracy on geometric terms (in particular on the ice fluxes) is required if useful estimates of the changes in mass balance are to be computed on glacier tongues not observed using ablation stakes. We also stress here the importance of a comprehensive error analysis to determine the reliability of the calculated mass-balance changes using this continuity-equation method.

Table 3. Comparison of the observed (ΔBobs) and calculated (ΔB _cal) surface mass-balance changes below FG_TRE and FG_TAC between the different epochs: I (1979-94), II (1994-2000) and III (2000-08). For FG_TAC, we also calculated (bottom row) the changes in mass balances when the cross-sectional ice thickness is reduced by 27% to respect mass conservation (see Section 5.1). All values are in m w.e. a^-1

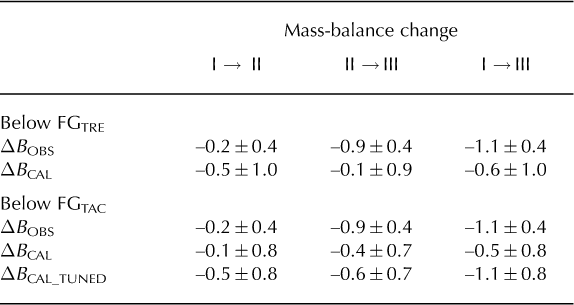
6. Conclusions

We have quantified the geometric and dynamic evolution of the tongue of Mer de Glace between 1979 and 2008 using an extensive dataset of field and remote-sensing observations. Thinning rates were measured by comparing remotely sensed DEMs calibrated against topographic field surveys. Ice fluxes through two cross sections were estimated using field-measured annual center-line velocities complemented with satellite-derived velocity fields. Mass balances were observed yearly using ablation stakes and processed using Lliboutry’s linear mass-balance model to separate their spatial pattern and temporal fluctuations. These point-wise mass balances were extrapolated to the whole glacier tongue by taking into account the insulating effect of debris, the changes in debris coverage with time and the evolving glacier hypsometry.

Between 1985 and 2008, the whole tongue of Mer de Glace slowed down (by 51% at FG_TAC and 53% at FG_tre) and thinned (by 17% at FG_TAC and 23% at FG_tre) so that the annual ice fluxes were reduced by ~60%. Meanwhile, area- average ablation increased by 1.2 m w.e. a^-1. Positive (lowering of the glacier surface) and negative (loss of low-lying areas close to the front and growth of debris-covered areas) ablation feedbacks nearly cancelled out.

Because all three terms of the continuity equation were estimated independently we could verify the correct closure of the mass budget for the glacier tongue below FG_TRE. Conversely, its non-closure below FG_TAC suggests that the ice fluxes through this gate may be overestimated, possibly due to errors on the bedrock topography. Future field campaigns should aim at verifying the ice thickness at this location. However, we cannot rule out a systematic error in the surface mass balance between FG_TAC and FG_TRE due to the unknown thickness of the evolving debris cover.

Our analysis reveals that more than two-thirds of the increase in the thinning rate for lower Mer de Glace is due to decreasing ice fluxes from the upper parts of the glacier and only one-third is due to rising ice ablation. Thus, we quantitatively confirm here the need to take into account ice dynamics and its continuous change with time to understand the reaction of mountain glacier tongues to climate change.

Our extensive dataset also allows evaluation of the continuity-equation method of determining the temporal evolution of the surface mass balance for a whole glacier tongue. Errors on the geometric terms (ice fluxes and thinning rates) in the continuity equation indicate some uncertainties of 0.8-1.0 m w.e. a^-1 for the changes in mass balance for the tongue of Mer de Glace. These large a priori errors are confirmed by the comparison of the calculated values with field-observed mass-balance changes that indicate errors up to 0.8 m w.e. a^-1. These errors have the same magnitude as the recent mass-balance response to climate change, severely limiting the current usefulness of this continuity- equation method. Nearly an order of magnitude needs to be gained in our ability to measure the geometric terms (in particular the ice fluxes) from space before this method can be usefully applied to remote and large mountain glaciers. Thus, although remote-sensing techniques have reached a certain level of maturity to observe velocity fields or glacierwide averaged mass balances, dense networks of ablation stakes on selected glaciers seem to remain the best means to assess the spatial pattern and temporal changes in their mass balance and thus the influence of climate change.