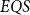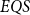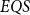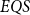1. Background, motivations, and challenges
We provide a quick overview of this work from its background to challenging open questions to tackle.
1.1 Recursion schematic definitions that capture quantum computability
Over the four decades, the study of quantum computing has made significant progress in both theory and practice. Quantum computing is one of the most anticipated nature-inspired computing paradigms today because it relies on the principle of quantum mechanics, which is assumed to govern nature. The core of quantum computing is an exquisite handling of superpositions, which are linear combinations of basic quantum states expressing classical strings, and entanglement, which binds multiple quantum bits (or qubits, for short) with no direct contact, of quantum states. Early models of quantum computation were proposed by Benioff (Reference Benioff1980), Deutsch (Reference Deutsch1985, Reference Deutsch1989Reference Deutsch), and Yao (Reference Yao1993) as quantum analogs of Turing machines and Boolean circuits. Those models have been used in a theoretical study of quantum computing within the area of computational complexity theory since their introduction. The quantum Turing machine (QTM) model is a natural quantum extension of the classical Turing machine (TM) model, which has successfully served for decades as a basis to theoretical aspects of computer science. The basic formulation of the QTM modelFootnote 1 used today attributes to Bernstein and Vazirani (Reference Bernstein and Vazirani1997). QTMs provide a blueprint of algorithmic procedures by describing how to transform each superposition of configurations of the machines. There have been other computational models proposed to capture different aspects of quantum computing, including a (black-box) query model.
A recursion schematic approach has been a recent incentive for the full characterization of the notion of quantum polynomial-time computability (Yamakami, Reference Yamakami2020), which can be seen as a quantum extension of deterministic polynomial-time computability. The primary purpose of taking such an exceptional approach toward quantum computability stems from a successful development of recursion theory (or recursive function theory) for classical computability. Earlier, Peano, Herbrand, Gödel, and Kleene (Reference Kleene1936, Reference Kleene1943) all made significant contributions to paving a straight road to a coherent study of computability and decidability from a purely logical aspect (see, e.g., (Soare, Reference Soare1996) for further references therein). In this theory, recursive functions are formulated in the following simple “schematic” way. (i) We begin with a few initial functions. (ii) We sequentially build more complicated functions by applying a small set of construction schemes to the already-built functions. The description of how to construct a recursive function actually serves as a blueprint of the function, which resembles like a “computer program” of the modern times in such a way that each construction scheme is a command line of a computer program. Hence, a schematic definition itself may be viewed as a high-level programming language by which we can render a computer program that describes the movement of any recursive function. As the benefit of the use of such a schematic definition, when we express a target function as a series of schemes, the “size” of this series can serve as a “descriptional complexity measure” of the function. This has lead to a fully enriched study of the descriptive complexity of functions. This schematic approach sharply contrasts the ones based on Turing machines as well as Boolean circuit families to formulate the recursive functions. A similar approach taken by Yamakami (Reference Yamakami2020) aims at capturing the polynomial-time computability of quantum functions,Footnote 2 each of which maps a finite-dimensional Hilbert space to itself, in place of the aforementioned recursive functions. Unlike quantum transitions of QTMs, the recursion schemes can provide a clear view of how quantum transforms act on target quantum states in the Hilbert space.
Two important classes of quantum functions, denoted ![]() $\Box ^{\mathrm{QP}}_{1}$ and
$\Box ^{\mathrm{QP}}_{1}$ and ![]() $\widehat{\Box ^{\mathrm{QP}}_{1}}$, were formulated by Yamakami (Reference Yamakami2020) from six initial quantum functions and three basic construction schemes. The major difference between
$\widehat{\Box ^{\mathrm{QP}}_{1}}$, were formulated by Yamakami (Reference Yamakami2020) from six initial quantum functions and three basic construction schemes. The major difference between ![]() $\Box ^{\mathrm{QP}}_{1}$ and
$\Box ^{\mathrm{QP}}_{1}$ and ![]() $\widehat{\Box ^{\mathrm{QP}}_{1}}$ is the permitted use of quantum measurement operations, which make quantum states collapse to classical states with incurred probabilities. Unfortunately, this is a non-reversible operation. Shown by Yamakami (Reference Yamakami2020) are a precise characterization of quantum polynomial-time computability and a quantum analog of the normal form theorem. A key in his recursion schematic definition is an introduction of the multi-qubit quantum recursion scheme, which looks quite different in its formulation from the corresponding classical recursion scheme. We will give its formal definition in Section 3.1 as Scheme T. This quantum recursion scheme turns out to be so powerful that it has helped us capture the notion of quantum polynomial-time computability.
$\widehat{\Box ^{\mathrm{QP}}_{1}}$ is the permitted use of quantum measurement operations, which make quantum states collapse to classical states with incurred probabilities. Unfortunately, this is a non-reversible operation. Shown by Yamakami (Reference Yamakami2020) are a precise characterization of quantum polynomial-time computability and a quantum analog of the normal form theorem. A key in his recursion schematic definition is an introduction of the multi-qubit quantum recursion scheme, which looks quite different in its formulation from the corresponding classical recursion scheme. We will give its formal definition in Section 3.1 as Scheme T. This quantum recursion scheme turns out to be so powerful that it has helped us capture the notion of quantum polynomial-time computability.
There are a few but important advantages of using recursion schematic definitions to introduce the notion of quantum computation over other quantum computational models, such as QTMs and quantum circuits. The most significant advantage is in fact that there is no use of the well-formedness requirement of QTMs and the uniformity requirement of quantum circuit families. These natural but cumbersome requirements are necessary to guarantee the unitary nature of QTMs and the algorithmic construction of quantum circuit families. Recursion schematic definitions, on the contrary, avoid such extra requirements and make it much simpler to design a quantum algorithm in the form of a quantum function for solving a target combinatorial problem. This is because each basic scheme naturally embodies “well-formedness” and “uniformity” in its formulation. More accurately, the scheme produces only “well-formed” and “uniform” quantum functions by way of applying the scheme directly to the existing quantum functions. In fact, the schematic definition of Yamakami (Reference Yamakami2020) constitutes only six initial quantum functions together with three basic construction schemes and this fact helps us render a short procedural sequence of how to construct each target quantum function. A descriptional aspect of the recursion schematic definition of Yamakami (Reference Yamakami2020) has become a helpful guide to develop even a suitable form of quantum programming language (Hainry et al., Reference Hainry and Péchoux2023). It is worth mentioning that such a recursion schematic definition has been made possible because of an extensional use of the bra and ket notations. See Section 2.3 for detailed explanations.
A schematic approach of Yamakami (Reference Yamakami2020) to quantum computing has exhibited a great possibility of treating quantum computable functions in such a way that is quite different from the traditional ways with QTMs and quantum circuit families. Recursion schemes further lead us to the descriptional complexity of quantum functions. Concerning such recursion schematic definitions, numerous questions still remain unanswered. It is important and also imperative to expand the scope of our research to various resource-bounded quantum computing. In this work, we particularly wish to turn our attention to a “limited” form of quantum computing, which can be naturally implemented by small runtime-restricted QTMs as well as families of small depth-bounded quantum circuits, and we further wish to examine how the schematic approach of Yamakami (Reference Yamakami2020) copes with such restricted quantum computing.
Of practical importance, resource-bounded computability has been studied in the classical setting based on various computational models, including families of Boolean circuits and time-bounded (classical) Turing machines (or TMs, for short). Among all reasonable resource bounds, we are particularly keen to (poly)logarithmic time. The logarithmic-time (abbreviated as logtime) computability may be one of the most restricted but meaningful, practical resource-bounded computabilities and it was discussed earlier by Buss (Reference Buss1987) and Barrington et al. (Reference Barrington, Immerman and Straubing1990) in terms of TMs equipped with index tapes to access particular locations of input symbols. Hereafter, we denote by ![]() $\mathrm{DLOGTIME}$ (resp.,
$\mathrm{DLOGTIME}$ (resp., ![]() $\mathrm{NLOGTIME}$) the class of decision problems solvable by logtime deterministic (resp., nondeterministic) TMs. The logtime computability has played a central role in characterizing a uniform notion of constant-depth Boolean circuit families. As shown by Barrington et al. (Reference Barrington, Immerman and Straubing1990), logtime computability is also closely related to the first-order logic with the special predicate
$\mathrm{NLOGTIME}$) the class of decision problems solvable by logtime deterministic (resp., nondeterministic) TMs. The logtime computability has played a central role in characterizing a uniform notion of constant-depth Boolean circuit families. As shown by Barrington et al. (Reference Barrington, Immerman and Straubing1990), logtime computability is also closely related to the first-order logic with the special predicate ![]() $BIT$. As slightly more general resource-bounded computability, polylogarithmic-time (abbreviated as polylogtime) computability has been widely studied in the literature. Numerous polylogtime algorithms were developed to solve, for example, the matrix chain ordering problem (Bradford et al., Reference Bradford, Rawlins and Shannon1994) and deterministic graph construction (Holm et al., Reference Holm, de Lichtenberg and Thorup2001). There were also studies on data structures that support polylog operations (Munro, Reference Munro1984) and probabilistic checking of polylog bits of proofs (Babai et al., Reference Babai, Fortnow, Levin and Szegedy1991). We denote by
$BIT$. As slightly more general resource-bounded computability, polylogarithmic-time (abbreviated as polylogtime) computability has been widely studied in the literature. Numerous polylogtime algorithms were developed to solve, for example, the matrix chain ordering problem (Bradford et al., Reference Bradford, Rawlins and Shannon1994) and deterministic graph construction (Holm et al., Reference Holm, de Lichtenberg and Thorup2001). There were also studies on data structures that support polylog operations (Munro, Reference Munro1984) and probabilistic checking of polylog bits of proofs (Babai et al., Reference Babai, Fortnow, Levin and Szegedy1991). We denote by ![]() $\mathrm{PPOLYLOGTIME}$ the complexity class of decision problems solvable by polylogtime probabilistic TMs with unbounded-error probability.
$\mathrm{PPOLYLOGTIME}$ the complexity class of decision problems solvable by polylogtime probabilistic TMs with unbounded-error probability.
In the setting of quantum computing, nevertheless, we are able to take a similar approach using resource-bounded QTMs. A quantum analog of ![]() $\mathrm{DLOGTIME}$, called
$\mathrm{DLOGTIME}$, called ![]() $\mathrm{BQLOGTIME}$, was lately discussed in connection to an oracle separation between
$\mathrm{BQLOGTIME}$, was lately discussed in connection to an oracle separation between ![]() $\mathrm{BQP}$ and the polynomial hierarchy in (Raz and Tal, Reference Raz and Tal2022). In this work, however, we are interested in polylogtime-bounded quantum computations, and thus we wish to look into the characteristics of quantum polylogtime computability. Later in Section 5.1, we formally describe the fundamental model of polylogtime QTMs as a quantum analog of classical polylogtime TMs. These polylogtime QTMs naturally induce the corresponding bounded-error complexity class
$\mathrm{BQP}$ and the polynomial hierarchy in (Raz and Tal, Reference Raz and Tal2022). In this work, however, we are interested in polylogtime-bounded quantum computations, and thus we wish to look into the characteristics of quantum polylogtime computability. Later in Section 5.1, we formally describe the fundamental model of polylogtime QTMs as a quantum analog of classical polylogtime TMs. These polylogtime QTMs naturally induce the corresponding bounded-error complexity class ![]() $\mathrm{BQPOLYLOGTIME}$. In Section 5.2,
$\mathrm{BQPOLYLOGTIME}$. In Section 5.2, ![]() $\mathrm{BQPOLYLOGTIME}$ is shown to differ in computational power from
$\mathrm{BQPOLYLOGTIME}$ is shown to differ in computational power from ![]() $\mathrm{NLOGTIME}$ as well as
$\mathrm{NLOGTIME}$ as well as ![]() $\mathrm{PPOLYLOGTIME}$.
$\mathrm{PPOLYLOGTIME}$.
1.2 Our challenges in this work
We intend to extend the scope of the existing research on resource-bounded quantum computability by way of an introduction of a small set of recursion schemes defining runtime-restricted quantum computability. In particular, we look into quantum polylogtime computability and seek out an appropriate recursion schematic definition to exactly capture such computability. Since ![]() $\Box ^{\mathrm{QP}}_{1}$ and
$\Box ^{\mathrm{QP}}_{1}$ and ![]() $\widehat{\Box ^{\mathrm{QP}}_{1}}$ precisely capture quantum polynomial-time computability, it is natural to raise a question of how we can capture quantum polylogtime computability in a similar fashion.
$\widehat{\Box ^{\mathrm{QP}}_{1}}$ precisely capture quantum polynomial-time computability, it is natural to raise a question of how we can capture quantum polylogtime computability in a similar fashion.
As noted earlier, the multi-qubit quantum recursion scheme of Yamakami (Reference Yamakami2020) is capable of precisely capturing quantum polynomial-time computability. A basic idea of this quantum recursion scheme is, starting with ![]() $n$ qubits, to modify at each round of recursion the first
$n$ qubits, to modify at each round of recursion the first ![]() $k$ qubits and continue to the next round with the rest of the qubits after discarding the first
$k$ qubits and continue to the next round with the rest of the qubits after discarding the first ![]() $k$ qubits. This recursive process slowly consumes the entire
$k$ qubits. This recursive process slowly consumes the entire ![]() $n$ qubits and finally grinds to halt after linearly-many recursive rounds. To describe limited quantum computability, in contrast, how can we weaken the quantum recursion scheme? Our attempt in this work is to speed up this recursive process significantly by discarding a bundle of
$n$ qubits and finally grinds to halt after linearly-many recursive rounds. To describe limited quantum computability, in contrast, how can we weaken the quantum recursion scheme? Our attempt in this work is to speed up this recursive process significantly by discarding a bundle of ![]() $\lceil n/2 \rceil$(or
$\lceil n/2 \rceil$(or ![]() $\lfloor n/2 \rfloor$) qubits from the entire
$\lfloor n/2 \rfloor$) qubits from the entire ![]() $n$ qubits at each round. Such a way of halving the number of qubits at each recursive round makes the recursive process terminate significantly faster; in fact, ending in at most
$n$ qubits at each round. Such a way of halving the number of qubits at each recursive round makes the recursive process terminate significantly faster; in fact, ending in at most ![]() $\lceil \log{n} \rceil$ recursive rounds. For this very reason, we intend to call this weakened recursive process the (code-controlled) fast quantum recursion scheme.
$\lceil \log{n} \rceil$ recursive rounds. For this very reason, we intend to call this weakened recursive process the (code-controlled) fast quantum recursion scheme.
Although the fast quantum recursion scheme is significantly weaker in power than the quantum recursion scheme of Yamakami (Reference Yamakami2020), the scheme still generates numerous interesting and useful quantum functions, as listed in Lemmas 4–8 and 15–22. More importantly, it is possible to implement the binary search strategy, which has been a widely used key programming technique. We call the set of all quantum functions generated from six initial quantum functions and three construction schemes together with the fast quantum recursion scheme by ![]() $EQS$ (elementary quantum schemes) in Section 3. This class
$EQS$ (elementary quantum schemes) in Section 3. This class ![]() $EQS$ turns out to precisely characterize quantum polylogtime computability (Theorems 33–34).
$EQS$ turns out to precisely characterize quantum polylogtime computability (Theorems 33–34).
To cope with polylogtime computability, we need an appropriate encoding of various types of “objects” (such as numbers, graphs, matrices, and tape symbols) into qubits of an equal length and also another efficient way of decoding the original “objects” from those encoded qubits. For this purpose, we introduce in Section 3.2 a code-skipping scheme, which recognizes encoded segments to skip them one by one. This scheme in fact plays a key role in performing the fast recursion scheme.
Throughout this work, we try to promote much better understandings of resource-bounded quantum computing in theory and in practice.
New Materials after the Preliminary Conference Report. The current work corrects and significantly alters the preliminary conference report (Yamakami, Reference Yamakami2022b), particularly in the following points. Five schemes, which constitute ![]() $EQS$, in the preliminary report have been modified and reorganized, and thus they look slightly different in their formulations. In particular, Scheme V is introduced to establish a precise characterization of quantum functions computable by polylogtime QTMs.
$EQS$, in the preliminary report have been modified and reorganized, and thus they look slightly different in their formulations. In particular, Scheme V is introduced to establish a precise characterization of quantum functions computable by polylogtime QTMs.
Beyond the scope of the preliminary report (Yamakami, Reference Yamakami2022b), this work further looks into another restricted quantum algorithmic procedure, known as the divide-and-conquer strategy in Section 6. A key idea behind this strategy is to inductively split an given instance into small pieces and then inductively assemble them piece by piece after an appropriate modification. This new scheme helps us capture the parity function, which requires more than polylogtime quantum computation. This fact implies that this new procedure is not “realized” in the framework of ![]() $EQS$.
$EQS$.
2. Preparation: notions and notation
We will briefly explain basic notions and notation used throughout this work.
2.1 Numbers, strings, and languages
The notations ![]() $\mathbb{Z}$,
$\mathbb{Z}$, ![]() $\mathbb{Q}$, and
$\mathbb{Q}$, and ![]() $\mathbb{R}$ respectively denote the sets of all integers, of all rational numbers, and of all real numbers. In particular, we set
$\mathbb{R}$ respectively denote the sets of all integers, of all rational numbers, and of all real numbers. In particular, we set ![]() $\bar{\mathbb{Q}}=\mathbb{Q}\cap [0,1]$. The natural numbers are nonnegative integers and the notation
$\bar{\mathbb{Q}}=\mathbb{Q}\cap [0,1]$. The natural numbers are nonnegative integers and the notation ![]() $\mathbb{N}$ expresses the set of those numbers. We further write
$\mathbb{N}$ expresses the set of those numbers. We further write ![]() $\mathbb{N}^{+}$ to denote the set
$\mathbb{N}^{+}$ to denote the set ![]() $\mathbb{N}-\{0\}$. For two integers
$\mathbb{N}-\{0\}$. For two integers ![]() $m,n$ with
$m,n$ with ![]() $m\leq n$,
$m\leq n$, ![]() $[m,n]_{\mathbb{Z}}$ indicates the integer interval
$[m,n]_{\mathbb{Z}}$ indicates the integer interval ![]() $\{m,m+1,m+2,\ldots, n\}$. In particular, we abbreviate
$\{m,m+1,m+2,\ldots, n\}$. In particular, we abbreviate ![]() $[1,n]_{\mathbb{Z}}$ as
$[1,n]_{\mathbb{Z}}$ as ![]() $[n]$ when
$[n]$ when ![]() $n\geq 1$. In addition,
$n\geq 1$. In addition, ![]() $\mathbb{C}$ denotes the set of all complex numbers. We use the notations
$\mathbb{C}$ denotes the set of all complex numbers. We use the notations ![]() $\lceil \cdot \rceil$ and
$\lceil \cdot \rceil$ and ![]() $\lfloor \cdot \rfloor$ for the ceiling function and the floor function, respectively. In this work, all polynomials have nonnegative integer coefficients and all logarithms are taken to the base
$\lfloor \cdot \rfloor$ for the ceiling function and the floor function, respectively. In this work, all polynomials have nonnegative integer coefficients and all logarithms are taken to the base ![]() $2$. We further define
$2$. We further define ![]() $\mathrm{ilog}(n)$ and
$\mathrm{ilog}(n)$ and ![]() $\mathrm{iloglog}(n)$ to be
$\mathrm{iloglog}(n)$ to be ![]() $\lceil \log{n} \rceil$ and
$\lceil \log{n} \rceil$ and ![]() $\lceil \log \log{n} \rceil$ for any
$\lceil \log \log{n} \rceil$ for any ![]() $n\in \mathbb{N}$, respectively. To circumvent any cumbersome description to avoid the special case of
$n\in \mathbb{N}$, respectively. To circumvent any cumbersome description to avoid the special case of ![]() $n=0$, we intentionally set
$n=0$, we intentionally set ![]() $\mathrm{ilog}(0)=\mathrm{iloglog}(0)=0$. The notation
$\mathrm{ilog}(0)=\mathrm{iloglog}(0)=0$. The notation ![]() $\imath$ denotes
$\imath$ denotes ![]() $\sqrt{-1}$ and
$\sqrt{-1}$ and ![]() $e$ does the base of natural logarithms. Given a complex number
$e$ does the base of natural logarithms. Given a complex number ![]() $\alpha$,
$\alpha$, ![]() $\alpha ^*$ denotes the complex conjugate of
$\alpha ^*$ denotes the complex conjugate of ![]() $\alpha$. As for a nonempty set of quantum amplitudes, which is a subset of
$\alpha$. As for a nonempty set of quantum amplitudes, which is a subset of ![]() $\mathbb{C}$, we use the notation
$\mathbb{C}$, we use the notation ![]() $K$.
$K$.
A nonempty finite set of “symbols” (or “letters”) is called an alphabet and a sequence of such symbols from a fixed alphabet ![]() $\Sigma$ is called a string over
$\Sigma$ is called a string over ![]() $\Sigma$. The total number of occurrences of symbols in a given string
$\Sigma$. The total number of occurrences of symbols in a given string ![]() $x$ is the length of
$x$ is the length of ![]() $x$ and is denoted
$x$ and is denoted ![]() $|x|$. The empty string
$|x|$. The empty string ![]() $\lambda$ is a unique string of length
$\lambda$ is a unique string of length ![]() $0$. A collection of those strings over
$0$. A collection of those strings over ![]() $\Sigma$ is a language over
$\Sigma$ is a language over ![]() $\Sigma$. Throughout this work, we deal only with binary strings, which are sequences of 0s and 1s. Given a number
$\Sigma$. Throughout this work, we deal only with binary strings, which are sequences of 0s and 1s. Given a number ![]() $n\in \mathbb{N}$,
$n\in \mathbb{N}$, ![]() $\Sigma ^{n}$ (resp.,
$\Sigma ^{n}$ (resp., ![]() $\Sigma ^{\leq n}$) denotes the set of all strings of length exactly
$\Sigma ^{\leq n}$) denotes the set of all strings of length exactly ![]() $n$ (resp., at most
$n$ (resp., at most ![]() $n$). Let
$n$). Let ![]() $\Sigma ^* = \bigcup _{n\in \mathbb{N}}\Sigma ^n$ and
$\Sigma ^* = \bigcup _{n\in \mathbb{N}}\Sigma ^n$ and ![]() $\Sigma ^{+} = \Sigma ^*-\{\lambda \}$. Given a string
$\Sigma ^{+} = \Sigma ^*-\{\lambda \}$. Given a string ![]() $x$ and a bit
$x$ and a bit ![]() $b\in \{0,1\}$, the notation
$b\in \{0,1\}$, the notation ![]() $\#_b(x)$ denotes the total number of occurrences of the symbol
$\#_b(x)$ denotes the total number of occurrences of the symbol ![]() $b$ in
$b$ in ![]() $x$. Due to the nature of quantum computation, we also discuss “promise” decision problems. A pair
$x$. Due to the nature of quantum computation, we also discuss “promise” decision problems. A pair ![]() $(A,R)$ of subsets of
$(A,R)$ of subsets of ![]() $\Sigma ^*$ is said to be a promise (decision) problem over
$\Sigma ^*$ is said to be a promise (decision) problem over ![]() $\Sigma$ if
$\Sigma$ if ![]() $A\cup R \subseteq \Sigma ^*$ and
$A\cup R \subseteq \Sigma ^*$ and ![]() $A\cap R =\varnothing$. Intuitively,
$A\cap R =\varnothing$. Intuitively, ![]() $A$ and
$A$ and ![]() $R$ are, respectively, composed of accepted strings and rejected strings. When
$R$ are, respectively, composed of accepted strings and rejected strings. When ![]() $A\cup R=\Sigma ^*$,
$A\cup R=\Sigma ^*$, ![]() $(A,R)$ becomes
$(A,R)$ becomes ![]() $(A,\Sigma ^*-A)$, and this can be identified with the language
$(A,\Sigma ^*-A)$, and this can be identified with the language ![]() $A$.
$A$.
Given a number ![]() $n\in \mathbb{N}$, we need to partition it into two halves. To describe the “left half” and the “right half” of
$n\in \mathbb{N}$, we need to partition it into two halves. To describe the “left half” and the “right half” of ![]() $n$, we introduce two special functions:
$n$, we introduce two special functions: ![]() $LH(n) = \lceil n/2 \rceil$ and
$LH(n) = \lceil n/2 \rceil$ and ![]() $RH(n) = \lfloor n/2 \rfloor$.
$RH(n) = \lfloor n/2 \rfloor$.
For a function ![]() $f$ and a number
$f$ and a number ![]() $k\in \mathbb{N}^{+}$, we write
$k\in \mathbb{N}^{+}$, we write ![]() $f^k$ for the
$f^k$ for the ![]() $k$ consecutive applications of
$k$ consecutive applications of ![]() $f$ to an input. For example,
$f$ to an input. For example, ![]() $f^{2}(x) = f\circ f(x)=f(f(x))$ and
$f^{2}(x) = f\circ f(x)=f(f(x))$ and ![]() $f^{3}(x) = f\circ f \circ f(x) = f( f ( f(x)))$. The functions
$f^{3}(x) = f\circ f \circ f(x) = f( f ( f(x)))$. The functions ![]() $LH$ and
$LH$ and ![]() $RH$ satisfy the following property.
$RH$ satisfy the following property.
Lemma 1. Let ![]() $k,n\in \mathbb{N}^{+}$ be any two numbers. (1) If
$k,n\in \mathbb{N}^{+}$ be any two numbers. (1) If ![]() $n$ is in
$n$ is in ![]() $[2^{k-1}+1,2^k]_{\mathbb{Z}}$ (i.e.,
$[2^{k-1}+1,2^k]_{\mathbb{Z}}$ (i.e., ![]() $\lceil \log{n} \rceil =k$), then
$\lceil \log{n} \rceil =k$), then ![]() $LH^{k}(n)=1$ holds. Moreover, if
$LH^{k}(n)=1$ holds. Moreover, if ![]() $k\geq 2$, then
$k\geq 2$, then ![]() $LH^{k-1}(n) =2$. (2) If
$LH^{k-1}(n) =2$. (2) If ![]() $n$ is in
$n$ is in ![]() $[2^{k},2^{k+1}-1]_{\mathbb{Z}}$ (i.e.,
$[2^{k},2^{k+1}-1]_{\mathbb{Z}}$ (i.e., ![]() $\lfloor \log{n} \rfloor =k$), then
$\lfloor \log{n} \rfloor =k$), then ![]() $RH^{k}(n)=1$ holds. Moreover, if
$RH^{k}(n)=1$ holds. Moreover, if ![]() $k\geq 2$, then
$k\geq 2$, then ![]() $RH^{k-1}(n)\in \{2,3\}$.
$RH^{k-1}(n)\in \{2,3\}$.
Proof. (1) Consider a series: ![]() $n$,
$n$, ![]() $LH(n)$,
$LH(n)$, ![]() $LH^2(n)$,
$LH^2(n)$, ![]() $\cdots$,
$\cdots$, ![]() $LH^k(n)$. It follows that, for any number
$LH^k(n)$. It follows that, for any number ![]() $n \gt 2$,
$n \gt 2$, ![]() $n\in [2^{k-1}+1,2^k]_{\mathbb{Z}}$ iff
$n\in [2^{k-1}+1,2^k]_{\mathbb{Z}}$ iff ![]() $LH(n) \in [2^{k-2}+1,2^{k-1}]_{\mathbb{Z}}$. Thus, we obtain
$LH(n) \in [2^{k-2}+1,2^{k-1}]_{\mathbb{Z}}$. Thus, we obtain ![]() $LH^{k-1}(n)\in \{2\}$ and
$LH^{k-1}(n)\in \{2\}$ and ![]() $LH^{k}(n)\in \{1\}$. When
$LH^{k}(n)\in \{1\}$. When ![]() $n\geq 3$, the last two numbers of the above series must be
$n\geq 3$, the last two numbers of the above series must be ![]() $2$ and
$2$ and ![]() $1$.
$1$.
(2) In a similar fashion to (1), let us consider a series: ![]() $n$,
$n$, ![]() $RH(n)$,
$RH(n)$, ![]() $RH^2(n)$,
$RH^2(n)$, ![]() $\ldots$,
$\ldots$, ![]() $RH^k(n)$. It then follows that
$RH^k(n)$. It then follows that ![]() $n\in [2^k,2^{k+1}-1]_{\mathbb{Z}}$ iff
$n\in [2^k,2^{k+1}-1]_{\mathbb{Z}}$ iff ![]() $RH(n)\in [2^{k-1},2^k-1]_{\mathbb{Z}}$. We then obtain
$RH(n)\in [2^{k-1},2^k-1]_{\mathbb{Z}}$. We then obtain ![]() $RH^{k-1}(n)\in \{2,3\}$ and
$RH^{k-1}(n)\in \{2,3\}$ and ![]() $RH^{k}(n)\in \{1\}$.
$RH^{k}(n)\in \{1\}$.
We assume the standard lexicographical order on ![]() $\{0,1\}^*$:
$\{0,1\}^*$: ![]() $\lambda, 0,1,00,01,10,11,000,\cdots$ and, based on this ordering, we assign natural numbers to binary strings as
$\lambda, 0,1,00,01,10,11,000,\cdots$ and, based on this ordering, we assign natural numbers to binary strings as ![]() $bin(0)=\lambda$,
$bin(0)=\lambda$, ![]() $bin(1)=0$,
$bin(1)=0$, ![]() $bin(2)=1$,
$bin(2)=1$, ![]() $bin(3)=00$,
$bin(3)=00$, ![]() $bin(4)=01$,
$bin(4)=01$, ![]() $bin(5)=10$,
$bin(5)=10$, ![]() $bin(6)=11$,
$bin(6)=11$, ![]() $bin(7)=000$, etc. In contrast, for a fixed number
$bin(7)=000$, etc. In contrast, for a fixed number ![]() $k\in \mathbb{N}^{+}$,
$k\in \mathbb{N}^{+}$, ![]() $bin_k(n)$ denotes lexicographically the
$bin_k(n)$ denotes lexicographically the ![]() $n$th string in
$n$th string in ![]() $\{0,1\}^k$ as long as
$\{0,1\}^k$ as long as ![]() $n\in [2^k]$. For instance, we obtain
$n\in [2^k]$. For instance, we obtain ![]() $bin_3(1)=000$,
$bin_3(1)=000$, ![]() $bin_3(2)=001$,
$bin_3(2)=001$, ![]() $bin_3(3)=010$,
$bin_3(3)=010$, ![]() $bin_3(4)=011$, etc. Remember that
$bin_3(4)=011$, etc. Remember that ![]() $bin_k(0)$ is not defined whereas
$bin_k(0)$ is not defined whereas ![]() $bin(0)$ means
$bin(0)$ means ![]() $\lambda$.
$\lambda$.
2.2 Quantum States and Hilbert spaces
We assume the reader’s familiarity with basic quantum information and computation (see, e.g., textbooks (Kitaev et al., Reference Kitaev, Shen and Vyalyi2002; Neilsen and Chuang, Reference Nielsen and Chuang2016). A basic concept in quantum computing is a Hilbert space and unitary transformations over it. The ket notation ![]() $| \phi \rangle$ expresses a (column) vector in a Hilbert space and its transposed conjugate is expressed as a (row) vector of the dual space and is denoted by the bra notation
$| \phi \rangle$ expresses a (column) vector in a Hilbert space and its transposed conjugate is expressed as a (row) vector of the dual space and is denoted by the bra notation ![]() $\langle{\phi } |$. The notation
$\langle{\phi } |$. The notation ![]() $\langle \psi | \phi \rangle$ denotes the inner product of two vectors
$\langle \psi | \phi \rangle$ denotes the inner product of two vectors ![]() $| \psi \rangle$ and
$| \psi \rangle$ and ![]() $| \phi \rangle$. We use the generic notation
$| \phi \rangle$. We use the generic notation ![]() $I$ to denote the identity matrix of an arbitrary dimension. A square complex matrix
$I$ to denote the identity matrix of an arbitrary dimension. A square complex matrix ![]() $U$ is called unitary if
$U$ is called unitary if ![]() $U$ satisfies
$U$ satisfies ![]() $UU^{\dagger } = U^{\dagger }U = I$, where
$UU^{\dagger } = U^{\dagger }U = I$, where ![]() $U^{\dagger }$ is the transposed conjugate of
$U^{\dagger }$ is the transposed conjugate of ![]() $U$.
$U$.
The generic notation ![]() $\boldsymbol{0}$ is used to denote the null vector of an arbitrary dimension. A quantum bit (or a qubit, for short) is a linear combination of two basis vectors
$\boldsymbol{0}$ is used to denote the null vector of an arbitrary dimension. A quantum bit (or a qubit, for short) is a linear combination of two basis vectors ![]() $| 0 \rangle$ and
$| 0 \rangle$ and ![]() $| 1 \rangle$. The notation
$| 1 \rangle$. The notation ![]() $\mathscr{H}_2$ indicates the Hilbert space spanned by
$\mathscr{H}_2$ indicates the Hilbert space spanned by ![]() $| 0 \rangle$ and
$| 0 \rangle$ and ![]() $| 1 \rangle$. More generally,
$| 1 \rangle$. More generally, ![]() $\mathscr{H}_{2^n}$ refers to the Hilbert space spanned by the computational basis
$\mathscr{H}_{2^n}$ refers to the Hilbert space spanned by the computational basis ![]() $B_n=\{| s \rangle \mid s\in \{0,1\}^n\}$. For convenience, we write
$B_n=\{| s \rangle \mid s\in \{0,1\}^n\}$. For convenience, we write ![]() $\mathscr{H}_{\infty }$ for the collection of all quantum states in
$\mathscr{H}_{\infty }$ for the collection of all quantum states in ![]() $\mathscr{H}_{2^n}$ for any
$\mathscr{H}_{2^n}$ for any ![]() $n\in \mathbb{N}^{+}$. Remember that
$n\in \mathbb{N}^{+}$. Remember that ![]() $\mathscr{H}_{\infty }$ does not form a Hilbert space. Given a non-zero quantum state
$\mathscr{H}_{\infty }$ does not form a Hilbert space. Given a non-zero quantum state ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$, its length
$| \phi \rangle \in \mathscr{H}_{\infty }$, its length ![]() $\ell (| \phi \rangle )$ denotes a unique number
$\ell (| \phi \rangle )$ denotes a unique number ![]() $n\in \mathbb{N}$ for which
$n\in \mathbb{N}$ for which ![]() $| \phi \rangle \in \mathscr{H}_{2^n}$. We stress that the length of
$| \phi \rangle \in \mathscr{H}_{2^n}$. We stress that the length of ![]() $| \phi \rangle$ is defined only for a quantum state residing in
$| \phi \rangle$ is defined only for a quantum state residing in ![]() $\mathscr{H}_{\infty }$. As a special case, we set
$\mathscr{H}_{\infty }$. As a special case, we set ![]() $\ell (\boldsymbol{0})=0$ for the null vector
$\ell (\boldsymbol{0})=0$ for the null vector ![]() $\boldsymbol{0}$ (although
$\boldsymbol{0}$ (although ![]() $\boldsymbol{0}$ belongs to
$\boldsymbol{0}$ belongs to ![]() $\mathscr{H}_k$ for any
$\mathscr{H}_k$ for any ![]() $k\in \mathbb{N}^{+}$). For convenience, we also set
$k\in \mathbb{N}^{+}$). For convenience, we also set ![]() $\ell (\alpha )=0$ for any scalar
$\ell (\alpha )=0$ for any scalar ![]() $\alpha \in \mathbb{C}$. For a quantum state
$\alpha \in \mathbb{C}$. For a quantum state ![]() $| \phi \rangle$, if we make a measurement in the computational basis, then each binary string
$| \phi \rangle$, if we make a measurement in the computational basis, then each binary string ![]() $x$ of length
$x$ of length ![]() $\ell (| \phi \rangle )$ is observed with probability
$\ell (| \phi \rangle )$ is observed with probability ![]() $|\langle x | \phi \rangle |^2$. Thus,
$|\langle x | \phi \rangle |^2$. Thus, ![]() $| \phi \rangle$ can be expressed as
$| \phi \rangle$ can be expressed as ![]() $| 0 \rangle \langle 0 | \phi \rangle + | 1 \rangle \langle 1 | \phi \rangle$ and also as
$| 0 \rangle \langle 0 | \phi \rangle + | 1 \rangle \langle 1 | \phi \rangle$ and also as ![]() $\sum _{x\in \{0,1\}^n} | x \rangle \otimes \langle x | \phi \rangle$, where
$\sum _{x\in \{0,1\}^n} | x \rangle \otimes \langle x | \phi \rangle$, where ![]() $| \phi \rangle \otimes | \psi \rangle$ is the tensor product of
$| \phi \rangle \otimes | \psi \rangle$ is the tensor product of ![]() $| \phi \rangle$ and
$| \phi \rangle$ and ![]() $| \psi \rangle$. The norm of
$| \psi \rangle$. The norm of ![]() $| \phi \rangle$ is defined as
$| \phi \rangle$ is defined as ![]() $\sqrt{\langle \phi | \phi \rangle }$ and is denoted
$\sqrt{\langle \phi | \phi \rangle }$ and is denoted ![]() $\|| \phi \rangle \|$.
$\|| \phi \rangle \|$.
A qustring of length ![]() $n$ is a unit-norm quantum state in
$n$ is a unit-norm quantum state in ![]() $\mathscr{H}_{2^n}$. As a special case, the null vector is treated as the qustring of length
$\mathscr{H}_{2^n}$. As a special case, the null vector is treated as the qustring of length ![]() $0$ (although its norm is
$0$ (although its norm is ![]() $0$). Let
$0$). Let ![]() $\Phi _{n}$ denote the set of all qustrings of length
$\Phi _{n}$ denote the set of all qustrings of length ![]() $n$. Clearly,
$n$. Clearly, ![]() $\Phi _{n}\subseteq \mathscr{H}_{2^n}$ holds for all
$\Phi _{n}\subseteq \mathscr{H}_{2^n}$ holds for all ![]() $n\in \mathbb{N}^{+}$. We then set
$n\in \mathbb{N}^{+}$. We then set ![]() $\Phi _{\infty }$ to be the collection of all qustrings of length
$\Phi _{\infty }$ to be the collection of all qustrings of length ![]() $n$ for any
$n$ for any ![]() $n\in \mathbb{N}$.
$n\in \mathbb{N}$.
Abusing the aforementioned notations of ![]() $LH(n)$ and
$LH(n)$ and ![]() $RH(n)$, we set
$RH(n)$, we set ![]() $LH(| \phi \rangle ) = \lceil \ell (| \phi \rangle )/2 \rceil$ and
$LH(| \phi \rangle ) = \lceil \ell (| \phi \rangle )/2 \rceil$ and ![]() $RH(| \phi \rangle )=\lfloor \ell (| \phi \rangle /2 \rfloor$ for any quantum state
$RH(| \phi \rangle )=\lfloor \ell (| \phi \rangle /2 \rfloor$ for any quantum state ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$. It then follows that
$| \phi \rangle \in \mathscr{H}_{\infty }$. It then follows that ![]() $\ell (| \phi \rangle )=LH(| \phi \rangle )+RH(| \phi \rangle )$.
$\ell (| \phi \rangle )=LH(| \phi \rangle )+RH(| \phi \rangle )$.
We are interested only in functions mapping ![]() $\mathscr{H}_{\infty }$ to
$\mathscr{H}_{\infty }$ to ![]() $\mathscr{H}_{\infty }$, and these functions are generally referred to as quantum functions on
$\mathscr{H}_{\infty }$, and these functions are generally referred to as quantum functions on ![]() $\mathscr{H}_{\infty }$ to differentiate from “functions” working with natural numbers or strings. Such a quantum function
$\mathscr{H}_{\infty }$ to differentiate from “functions” working with natural numbers or strings. Such a quantum function ![]() $f$ is said to be dimension-preserving (resp., norm-preserving) if
$f$ is said to be dimension-preserving (resp., norm-preserving) if ![]() $\ell (| \phi \rangle ) = \ell (f(| \phi \rangle ))$ (resp.,
$\ell (| \phi \rangle ) = \ell (f(| \phi \rangle ))$ (resp., ![]() $\|| \phi \rangle \|=\|f(| \phi \rangle )\|$) holds for any quantum state
$\|| \phi \rangle \|=\|f(| \phi \rangle )\|$) holds for any quantum state ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$.
$| \phi \rangle \in \mathscr{H}_{\infty }$.
2.3 Conventions on the bra and the ket notations
To calculate the outcomes of quantum functions on ![]() $\mathscr{H}_{\infty }$, we must take advantage of making a purely symbolic treatment of the bra and the ket notations together with the tensor product notation
$\mathscr{H}_{\infty }$, we must take advantage of making a purely symbolic treatment of the bra and the ket notations together with the tensor product notation ![]() $\otimes$. We generally follow (Yamakami, Reference Yamakami2020) for the conventions on the specific usage of these notations. These notational conventions in fact help us simplify the description of various qubit operations in later sections. Since we greatly deviate from the standard usage of those notations, hereafter, we explain how to use them throughout this work.
$\otimes$. We generally follow (Yamakami, Reference Yamakami2020) for the conventions on the specific usage of these notations. These notational conventions in fact help us simplify the description of various qubit operations in later sections. Since we greatly deviate from the standard usage of those notations, hereafter, we explain how to use them throughout this work.
It is important to distinguish between the number ![]() $0$ and the null vector
$0$ and the null vector ![]() $\boldsymbol{0}$. To deal with the null vector, we conveniently take the following specific conventions concerning the operator “
$\boldsymbol{0}$. To deal with the null vector, we conveniently take the following specific conventions concerning the operator “![]() $\otimes$”. For any
$\otimes$”. For any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$, (i)
$| \phi \rangle \in \mathscr{H}_{\infty }$, (i) ![]() $0\otimes | \phi \rangle = | \phi \rangle \otimes 0 =\boldsymbol{0}$ (scalar case), (ii)
$0\otimes | \phi \rangle = | \phi \rangle \otimes 0 =\boldsymbol{0}$ (scalar case), (ii) ![]() $| \phi \rangle \otimes \boldsymbol{0} = \boldsymbol{0}\otimes | \phi \rangle =\boldsymbol{0}$, and (iii) if
$| \phi \rangle \otimes \boldsymbol{0} = \boldsymbol{0}\otimes | \phi \rangle =\boldsymbol{0}$, and (iii) if ![]() $| \psi \rangle$ is the null vector, then
$| \psi \rangle$ is the null vector, then ![]() $\langle \phi | \psi \rangle = \langle \psi | \phi \rangle =\boldsymbol{0}$. In the case of (i), we here extend the standard usage of
$\langle \phi | \psi \rangle = \langle \psi | \phi \rangle =\boldsymbol{0}$. In the case of (i), we here extend the standard usage of ![]() $\otimes$ to even cover “scalar multiplication” to simplify later calculations. Given two binary strings
$\otimes$ to even cover “scalar multiplication” to simplify later calculations. Given two binary strings ![]() $u,s\in \{0,1\}^+$, if
$u,s\in \{0,1\}^+$, if ![]() $|s|=|u|$, then
$|s|=|u|$, then ![]() $\langle u | s \rangle =1$ if
$\langle u | s \rangle =1$ if ![]() $u=s$, and
$u=s$, and ![]() $\langle u | s \rangle =0$ otherwise. On the contrary, when
$\langle u | s \rangle =0$ otherwise. On the contrary, when ![]() $|u|\lt |s|$,
$|u|\lt |s|$, ![]() $\langle u | s \rangle$ expresses the quantum state
$\langle u | s \rangle$ expresses the quantum state ![]() $| z \rangle$ if
$| z \rangle$ if ![]() $s=uz$ for a certain string
$s=uz$ for a certain string ![]() $z$, and
$z$, and ![]() $0$ otherwise. By sharp contrast, if
$0$ otherwise. By sharp contrast, if ![]() $|u|\gt |s|$, then
$|u|\gt |s|$, then ![]() $\langle u | s \rangle$ always denotes
$\langle u | s \rangle$ always denotes ![]() $\boldsymbol{0}$. More generally, if
$\boldsymbol{0}$. More generally, if ![]() $| \phi \rangle =\sum _{u\in \{0,1\}^n}\sum _{s\in \{0,1\}^m} \alpha _{u,s}| u \rangle \otimes | s \rangle$ and
$| \phi \rangle =\sum _{u\in \{0,1\}^n}\sum _{s\in \{0,1\}^m} \alpha _{u,s}| u \rangle \otimes | s \rangle$ and ![]() $u_0\in \{0,1\}^n$, then
$u_0\in \{0,1\}^n$, then ![]() $\langle u_0 | \phi \rangle$ expresses the quantum state
$\langle u_0 | \phi \rangle$ expresses the quantum state ![]() $\sum _{s\in \{0,1\}^m}\alpha _{u_0,s}| s \rangle$. For instance, if
$\sum _{s\in \{0,1\}^m}\alpha _{u_0,s}| s \rangle$. For instance, if ![]() $| \phi \rangle =\frac{1}{\sqrt{2}}(| 00 \rangle +| 11 \rangle )$, then
$| \phi \rangle =\frac{1}{\sqrt{2}}(| 00 \rangle +| 11 \rangle )$, then ![]() $\langle 0 | \phi \rangle$ equals
$\langle 0 | \phi \rangle$ equals ![]() $\frac{1}{\sqrt{2}}| 0 \rangle$ and
$\frac{1}{\sqrt{2}}| 0 \rangle$ and ![]() $\langle 1 | \phi \rangle$ does
$\langle 1 | \phi \rangle$ does ![]() $\frac{1}{\sqrt{2}}| 1 \rangle$. These notations
$\frac{1}{\sqrt{2}}| 1 \rangle$. These notations ![]() $\langle 0 | \phi \rangle$ and
$\langle 0 | \phi \rangle$ and ![]() $\langle 1 | \phi \rangle$ together make it possible to express any qustring
$\langle 1 | \phi \rangle$ together make it possible to express any qustring ![]() $| \phi \rangle$ as
$| \phi \rangle$ as ![]() $| 0 \rangle \otimes \langle 0 | \phi \rangle + | 1 \rangle \otimes \langle 1 | \phi \rangle$. In a more general case with
$| 0 \rangle \otimes \langle 0 | \phi \rangle + | 1 \rangle \otimes \langle 1 | \phi \rangle$. In a more general case with ![]() $| \xi \rangle =\sum _{u\in \{0,1\}^n} \beta _u| u \rangle$,
$| \xi \rangle =\sum _{u\in \{0,1\}^n} \beta _u| u \rangle$, ![]() $\langle \xi | \phi \rangle$ means
$\langle \xi | \phi \rangle$ means ![]() $\sum _{u\in \{0,1\}^n} \beta _u^{*} \langle u | \phi \rangle$, which equals
$\sum _{u\in \{0,1\}^n} \beta _u^{*} \langle u | \phi \rangle$, which equals ![]() $\sum _{u\in \{0,1\}^n} \sum _{s\in \{0,1\}^m} \alpha _{u,s}\beta _u^{*}| s \rangle$. Moreover,
$\sum _{u\in \{0,1\}^n} \sum _{s\in \{0,1\}^m} \alpha _{u,s}\beta _u^{*}| s \rangle$. Moreover, ![]() $| \phi \rangle$ can be expressed as
$| \phi \rangle$ can be expressed as ![]() $\sum _{u\in \{0,1\}^n} \beta _u | u \rangle \otimes \langle u | \phi \rangle$. We often abbreviate
$\sum _{u\in \{0,1\}^n} \beta _u | u \rangle \otimes \langle u | \phi \rangle$. We often abbreviate ![]() $| \phi \rangle \otimes | \psi \rangle$ as
$| \phi \rangle \otimes | \psi \rangle$ as ![]() $| \phi \rangle | \psi \rangle$. In particular, for strings
$| \phi \rangle | \psi \rangle$. In particular, for strings ![]() $s$ and
$s$ and ![]() $u$,
$u$, ![]() $| s \rangle \otimes | u \rangle$ is further abbreviated as
$| s \rangle \otimes | u \rangle$ is further abbreviated as ![]() $| s,u \rangle$ or even
$| s,u \rangle$ or even ![]() $| su \rangle$. When
$| su \rangle$. When ![]() $\langle s | \phi \rangle$ is just a scalar, say,
$\langle s | \phi \rangle$ is just a scalar, say, ![]() $\alpha \in \mathbb{C}$, the notation
$\alpha \in \mathbb{C}$, the notation ![]() $| s \rangle \otimes \langle s | \phi \rangle$ (or equivalently,
$| s \rangle \otimes \langle s | \phi \rangle$ (or equivalently, ![]() $| s \rangle \langle s | \phi \rangle$) is equal to
$| s \rangle \langle s | \phi \rangle$) is equal to ![]() $\alpha | s \rangle$.
$\alpha | s \rangle$.
We also expand the norm notation ![]() $\|\cdot \|$ for vectors to scalars in the following way. For any quantum states
$\|\cdot \|$ for vectors to scalars in the following way. For any quantum states ![]() $| \phi \rangle$ and
$| \phi \rangle$ and ![]() $| \psi \rangle$ with
$| \psi \rangle$ with ![]() $\ell (| \phi \rangle ) = \ell (| \psi \rangle )\gt 0$, the notation
$\ell (| \phi \rangle ) = \ell (| \psi \rangle )\gt 0$, the notation ![]() $\|\langle \phi | \psi \rangle \|$ is used to express the absolute value
$\|\langle \phi | \psi \rangle \|$ is used to express the absolute value ![]() $|\langle \phi | \psi \rangle |$. In general, for any scalar
$|\langle \phi | \psi \rangle |$. In general, for any scalar ![]() $\alpha \in \mathbb{C}$,
$\alpha \in \mathbb{C}$, ![]() $\|\alpha \|$ denotes
$\|\alpha \|$ denotes ![]() $|\alpha |$. This notational convention is quite useful in handling the value obtained after making a measurement without worrying about whether the resulting object is a quantum state or a scalar.
$|\alpha |$. This notational convention is quite useful in handling the value obtained after making a measurement without worrying about whether the resulting object is a quantum state or a scalar.
Later, we will need to encode (or translate) a series of symbols into an appropriate qustring. In such an encoding, the empty string ![]() $\lambda$ is treated quite differently. Notably, we tend to automatically translate
$\lambda$ is treated quite differently. Notably, we tend to automatically translate ![]() $| \lambda \rangle$ into the null vector
$| \lambda \rangle$ into the null vector ![]() $\boldsymbol{0}$ unless otherwise stated.
$\boldsymbol{0}$ unless otherwise stated.
3. A recursion schematic definition of EQS
We will present a recursion schematic definition to formulate a class of special quantum functions on ![]() $\mathscr{H}_{\infty }$ (i.e., from
$\mathscr{H}_{\infty }$ (i.e., from ![]() $\mathscr{H}_{\infty }$ to
$\mathscr{H}_{\infty }$ to ![]() $\mathscr{H}_{\infty }$), later called
$\mathscr{H}_{\infty }$), later called ![]() $EQS$. To improve the readability, we first provide a skeleton system of
$EQS$. To improve the readability, we first provide a skeleton system of ![]() $EQS$ and later we expand it to the full-fledged system.
$EQS$ and later we expand it to the full-fledged system.
3.1 Skeleton EQS
As a starter, we discuss a “skeleton” of our recursion schematic definition for “elementary” quantum functions, which are collectively called ![]() $EQS$ (elementary quantum schemes) in Definition20, involving six initial quantum functions and two construction schemes. All initial quantum functions were already presented when defining
$EQS$ (elementary quantum schemes) in Definition20, involving six initial quantum functions and two construction schemes. All initial quantum functions were already presented when defining ![]() $\Box ^{\mathrm{QP}}_{1}$ and
$\Box ^{\mathrm{QP}}_{1}$ and ![]() $\widehat{\Box ^{\mathrm{QP}}_{1}}$ in (Yamakami, Reference Yamakami2020).
$\widehat{\Box ^{\mathrm{QP}}_{1}}$ in (Yamakami, Reference Yamakami2020).
Throughout the rest of this work, we fix a nonempty amplitude set ![]() $K$, and we often omit the clear reference to
$K$, and we often omit the clear reference to ![]() $K$ as long as the choice of
$K$ as long as the choice of ![]() $K$ is not important in our discussion.
$K$ is not important in our discussion.
Definition 2. The skeleton class ![]() $EQS_0$ is composed of all quantum functions constructed by selecting the initial quantum functions of Scheme I and then inductively applying Schemes II–III a finite number of times. In what follows,
$EQS_0$ is composed of all quantum functions constructed by selecting the initial quantum functions of Scheme I and then inductively applying Schemes II–III a finite number of times. In what follows, ![]() $| \phi \rangle$ denotes an arbitrary quantum state in
$| \phi \rangle$ denotes an arbitrary quantum state in ![]() $\mathscr{H}_{\infty }$. When the item 6) of Scheme I is not used, we denote the resulting class by
$\mathscr{H}_{\infty }$. When the item 6) of Scheme I is not used, we denote the resulting class by ![]() $\widehat{EQS}_0$.
$\widehat{EQS}_0$.
I. The initial quantum functions. Let
 $\theta \in [0,2\pi )\cap K$ and
$\theta \in [0,2\pi )\cap K$ and  $a\in \{0,1\}$.
$a\in \{0,1\}$.
1)
 $I(| \phi \rangle ) = | \phi \rangle$. (identity)
$I(| \phi \rangle ) = | \phi \rangle$. (identity)2)
 $PHASE_{\theta }(| \phi \rangle ) = | 0 \rangle \!\langle 0 | \phi \rangle + e^{\imath \theta }| 1 \rangle \!\langle 1 | \phi \rangle$. (phase shift)
$PHASE_{\theta }(| \phi \rangle ) = | 0 \rangle \!\langle 0 | \phi \rangle + e^{\imath \theta }| 1 \rangle \!\langle 1 | \phi \rangle$. (phase shift)3)
 $ROT_{\theta }(| \phi \rangle ) = \cos \theta | \phi \rangle + \sin \theta (| 1 \rangle \!\langle 0 | \phi \rangle - | 0 \rangle \!\langle 1 | \phi \rangle )$. (rotation around
$ROT_{\theta }(| \phi \rangle ) = \cos \theta | \phi \rangle + \sin \theta (| 1 \rangle \!\langle 0 | \phi \rangle - | 0 \rangle \!\langle 1 | \phi \rangle )$. (rotation around  $xy$-axis at angle
$xy$-axis at angle  $\theta$)
$\theta$)4)
 $NOT(| \phi \rangle ) = | 0 \rangle \!\langle 1 | \phi \rangle + | 1 \rangle \!\langle 0 | \phi \rangle$. (negation)
$NOT(| \phi \rangle ) = | 0 \rangle \!\langle 1 | \phi \rangle + | 1 \rangle \!\langle 0 | \phi \rangle$. (negation)5)
 $SWAP(| \phi \rangle ) = \left \{ \begin{array}{ll} | \phi \rangle & if \mbox{$\ell (| \phi \rangle )\leq 1$,} \\ \sum _{a,b\in \{0,1\}} | ab \rangle \!\langle ba | \phi \rangle & {otherwise.} \end{array}\right .$ (swapping of 2 qubits)
$SWAP(| \phi \rangle ) = \left \{ \begin{array}{ll} | \phi \rangle & if \mbox{$\ell (| \phi \rangle )\leq 1$,} \\ \sum _{a,b\in \{0,1\}} | ab \rangle \!\langle ba | \phi \rangle & {otherwise.} \end{array}\right .$ (swapping of 2 qubits)6)
 $MEAS[a](| \phi \rangle ) = | a \rangle \!\langle a | \phi \rangle$. (partial projective measurement)
$MEAS[a](| \phi \rangle ) = | a \rangle \!\langle a | \phi \rangle$. (partial projective measurement)
II. The composition scheme. From
 $g$ and
$g$ and  $h$, we define
$h$, we define  $Compo[g,h]$ as follows:
$Compo[g,h]$ as follows:  $Compo[g,h](| \phi \rangle ) = g\circ h(| \phi \rangle )$ (
$Compo[g,h](| \phi \rangle ) = g\circ h(| \phi \rangle )$ (  $=g(h(| \phi \rangle ))$).
$=g(h(| \phi \rangle ))$).III. The branching scheme. Footnote 3 From
 $g$ and
$g$ and  $h$, we define
$h$, we define  $Branch[g,h]$ as:
$Branch[g,h]$ as:
(i)
 $Branch[g,h](| \phi \rangle ) = | \phi \rangle\qquad\qquad\qquad\qquad\qquad\qquad$ if
$Branch[g,h](| \phi \rangle ) = | \phi \rangle\qquad\qquad\qquad\qquad\qquad\qquad$ if  $\ell (| \phi \rangle )\leq 1$,
$\ell (| \phi \rangle )\leq 1$,(ii)
 $Branch[g,h](| \phi \rangle ) = | 0 \rangle \otimes g(\langle 0 | \phi \rangle ) + | 1 \rangle \otimes h(\langle 1 | \phi \rangle )\quad$ otherwise.
$Branch[g,h](| \phi \rangle ) = | 0 \rangle \otimes g(\langle 0 | \phi \rangle ) + | 1 \rangle \otimes h(\langle 1 | \phi \rangle )\quad$ otherwise.
We remark that all quantum functions in Items 1)–4) and 6) in Scheme I directly manipulate only the first qubit of ![]() $| \phi \rangle$ and that
$| \phi \rangle$ and that ![]() $SWAP$ manipulates the first two qubits of
$SWAP$ manipulates the first two qubits of ![]() $| \phi \rangle$. All other qubits of
$| \phi \rangle$. All other qubits of ![]() $| \phi \rangle$ are intact. Notice that the length function
$| \phi \rangle$ are intact. Notice that the length function ![]() $\ell (| \phi \rangle )$ is not included as part of
$\ell (| \phi \rangle )$ is not included as part of ![]() $EQS_0$. Since
$EQS_0$. Since ![]() $| \phi \rangle$ is always taken from
$| \phi \rangle$ is always taken from ![]() $\mathscr{H}_{\infty }$, the value
$\mathscr{H}_{\infty }$, the value ![]() $\ell (| \phi \rangle )$ is uniquely determined from
$\ell (| \phi \rangle )$ is uniquely determined from ![]() $| \phi \rangle$. It is also important to remark that, for any
$| \phi \rangle$. It is also important to remark that, for any ![]() $| \phi \rangle$ and
$| \phi \rangle$ and ![]() $a\in \{0,1\}$,
$a\in \{0,1\}$, ![]() $\ell (MEAS[a](| \phi \rangle )) = \ell (| \phi \rangle )$.
$\ell (MEAS[a](| \phi \rangle )) = \ell (| \phi \rangle )$.
In Schemes II and III, the constructions of ![]() $Compo[g,h]$ and
$Compo[g,h]$ and ![]() $Branch[g,h]$ need two quantum functions,
$Branch[g,h]$ need two quantum functions, ![]() $g$ and
$g$ and ![]() $h$, which are assumed to have been already constructed in their own construction processes. To refer to these supporting quantum functions used in the scheme, we call them the ground (quantum) functions of
$h$, which are assumed to have been already constructed in their own construction processes. To refer to these supporting quantum functions used in the scheme, we call them the ground (quantum) functions of ![]() $Compo[g,h]$ and
$Compo[g,h]$ and ![]() $Branch[g,h]$. In the case of a special need to emphasize
$Branch[g,h]$. In the case of a special need to emphasize ![]() $K$, we write
$K$, we write ![]() $EQS_{K,0}$ and
$EQS_{K,0}$ and ![]() $\widehat{EQS}_{K,0}$ with a clear reference to
$\widehat{EQS}_{K,0}$ with a clear reference to ![]() $K$.
$K$.
We quickly provide simple examples of how to compute the quantum functions induced by appropriate applications of Schemes I–III.
Example 3. It follows that ![]() $PHASE_{\pi }(| 1 \rangle ) = - | 1 \rangle$ and
$PHASE_{\pi }(| 1 \rangle ) = - | 1 \rangle$ and ![]() $PHASE_{\pi /2}(\frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )= \frac{1}{\sqrt{2}}(| 0 \rangle +\imath | 1 \rangle )$,
$PHASE_{\pi /2}(\frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )= \frac{1}{\sqrt{2}}(| 0 \rangle +\imath | 1 \rangle )$, ![]() $ROT_{\pi /4}(| 0 \rangle ) = \frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )$ and
$ROT_{\pi /4}(| 0 \rangle ) = \frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )$ and ![]() $ROT_{\pi /4}(| 1 \rangle ) = \frac{1}{\sqrt{2}}(| 0 \rangle -| 1 \rangle )$,
$ROT_{\pi /4}(| 1 \rangle ) = \frac{1}{\sqrt{2}}(| 0 \rangle -| 1 \rangle )$, ![]() $NOT(| a \rangle )=| 1-a \rangle$, and
$NOT(| a \rangle )=| 1-a \rangle$, and ![]() $SWAP(| abc \rangle )=| bac \rangle$ for three bits
$SWAP(| abc \rangle )=| bac \rangle$ for three bits ![]() $a,b,c\in \{0,1\}$. We also obtain
$a,b,c\in \{0,1\}$. We also obtain ![]() $MEAS[0](ROT_{\pi /4}(| 00 \rangle )) = MEAS[0](\frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )\otimes | 0 \rangle ) = \frac{1}{\sqrt{2}}| 00 \rangle$. As for Scheme III, it is important to note that
$MEAS[0](ROT_{\pi /4}(| 00 \rangle )) = MEAS[0](\frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )\otimes | 0 \rangle ) = \frac{1}{\sqrt{2}}| 00 \rangle$. As for Scheme III, it is important to note that ![]() $Branch[g,g]$ is not the same as
$Branch[g,g]$ is not the same as ![]() $g$ itself. For example,
$g$ itself. For example, ![]() $Branch[NOT,NOT](| b \rangle | \phi \rangle )$ equals
$Branch[NOT,NOT](| b \rangle | \phi \rangle )$ equals ![]() $| b \rangle \otimes NOT(| \phi \rangle )$ by Scheme III(ii) whereas
$| b \rangle \otimes NOT(| \phi \rangle )$ by Scheme III(ii) whereas ![]() $NOT(| b \rangle | \phi \rangle )$ is just
$NOT(| b \rangle | \phi \rangle )$ is just ![]() $| 1-b \rangle | \phi \rangle$, where
$| 1-b \rangle | \phi \rangle$, where ![]() $b$ denotes any bit. The EPR pair
$b$ denotes any bit. The EPR pair ![]() $\frac{1}{\sqrt{2}}(| 00 \rangle +| 11 \rangle )$ is obtainable from
$\frac{1}{\sqrt{2}}(| 00 \rangle +| 11 \rangle )$ is obtainable from ![]() $| 0 \rangle | 0 \rangle$ as follows. By first applying
$| 0 \rangle | 0 \rangle$ as follows. By first applying ![]() $ROT_{\pi /4}$ to
$ROT_{\pi /4}$ to ![]() $| 0 \rangle | 0 \rangle$, we obtain
$| 0 \rangle | 0 \rangle$, we obtain ![]() $| \phi \rangle = ROT_{\pi /4}(| 0 \rangle | 0 \rangle )$. We then apply
$| \phi \rangle = ROT_{\pi /4}(| 0 \rangle | 0 \rangle )$. We then apply ![]() $Branch[I,NOT]$ and obtain
$Branch[I,NOT]$ and obtain  $Branch[I,NOT](| \phi \rangle ) = Branch[I,NOT](\frac{1}{\sqrt{2}}(| 00 \rangle +| 10 \rangle )) = | 0 \rangle \otimes I(\frac{1}{\sqrt{2}}| 0 \rangle ) + | 1 \rangle \otimes NOT(\frac{1}{\sqrt{2}}| 0 \rangle ) = \frac{1}{\sqrt{2}}(| 00 \rangle +| 11 \rangle )$.
$Branch[I,NOT](| \phi \rangle ) = Branch[I,NOT](\frac{1}{\sqrt{2}}(| 00 \rangle +| 10 \rangle )) = | 0 \rangle \otimes I(\frac{1}{\sqrt{2}}| 0 \rangle ) + | 1 \rangle \otimes NOT(\frac{1}{\sqrt{2}}| 0 \rangle ) = \frac{1}{\sqrt{2}}(| 00 \rangle +| 11 \rangle )$.
For later reference, let us review from Yamakami (Reference Yamakami2020) the multi-qubit quantum recursion scheme, which is a centerpiece of schematically characterizing quantum polynomial-time computability. In this work, this special scheme is referred to as Scheme T.
(T) The multi-qubit quantum recursion scheme (Yamakami, Reference Yamakami2020). Let
 $g$,
$g$,  $h$,
$h$,  $p$ be quantum functions and let
$p$ be quantum functions and let  $k,t\in \mathbb{N}^{+}$ be numbers. Assume that
$k,t\in \mathbb{N}^{+}$ be numbers. Assume that  $p$ is dimension-preserving. For
$p$ is dimension-preserving. For  $\mathscr{F}_k=\{f_u\}_{u\in \{0,1\}^k}$, we define
$\mathscr{F}_k=\{f_u\}_{u\in \{0,1\}^k}$, we define  $F\equiv kQRec_t[g,h,p|\mathscr{F}_k]$ as follows:
$F\equiv kQRec_t[g,h,p|\mathscr{F}_k]$ as follows:
(i)
 $F(| \phi \rangle ) = g(| \phi \rangle )\qquad\qquad\qquad\qquad\qquad\qquad$ if
$F(| \phi \rangle ) = g(| \phi \rangle )\qquad\qquad\qquad\qquad\qquad\qquad$ if  $\ell (| \phi \rangle )\leq t$,
$\ell (| \phi \rangle )\leq t$,(ii)
 $F(| \phi \rangle ) = h( \sum _{u:|u|=k} | u \rangle \otimes f_u ( \langle u | \psi _{p,\phi } \rangle ))\qquad$ otherwise,
$F(| \phi \rangle ) = h( \sum _{u:|u|=k} | u \rangle \otimes f_u ( \langle u | \psi _{p,\phi } \rangle ))\qquad$ otherwise,
where
 $| \psi _{p,\phi } \rangle = p(| \phi \rangle )$ and
$| \psi _{p,\phi } \rangle = p(| \phi \rangle )$ and  $f_u\in \{F,I\}$ for any
$f_u\in \{F,I\}$ for any  $u\in \{0,1\}^k$.
$u\in \{0,1\}^k$.
This quantum recursion scheme together with Schemes I–III given above and another quantum function called ![]() $REMOVE$ (removal) defines the function class
$REMOVE$ (removal) defines the function class ![]() $\Box ^{\mathrm{QP}}_{1}$, which constitutes all polynomial-time computable quantum functions (Yamakami, Reference Yamakami2020). Although we do not consider
$\Box ^{\mathrm{QP}}_{1}$, which constitutes all polynomial-time computable quantum functions (Yamakami, Reference Yamakami2020). Although we do not consider ![]() $REMOVE$ here, its restricted form, called
$REMOVE$ here, its restricted form, called ![]() $CodeREMOVE[\cdot ]$, will be introduced in Section 3.2.
$CodeREMOVE[\cdot ]$, will be introduced in Section 3.2.
Let us present a short list of typical quantum functions “definable” within ![]() $EQS_0$; that is, those quantum functions are actually constructed from Items 1)–5) of Scheme I and by finitely many applications of Schemes II–III. As the first simple application of Scheme I–III, we demonstrate how to construct the special quantum function called
$EQS_0$; that is, those quantum functions are actually constructed from Items 1)–5) of Scheme I and by finitely many applications of Schemes II–III. As the first simple application of Scheme I–III, we demonstrate how to construct the special quantum function called ![]() $Skip_k[\cdot ]$.
$Skip_k[\cdot ]$.
Lemma 4. Let ![]() $g$ denote any quantum function in
$g$ denote any quantum function in ![]() $EQS_0$ and let
$EQS_0$ and let ![]() $k\in \mathbb{N}^{+}$. The quantum function
$k\in \mathbb{N}^{+}$. The quantum function ![]() $Skip_k[g]$ is defined by
$Skip_k[g]$ is defined by ![]() $Skip_k[g](| \phi \rangle ) = | \phi \rangle$ if
$Skip_k[g](| \phi \rangle ) = | \phi \rangle$ if ![]() $\ell (| \phi \rangle )\leq k$, and
$\ell (| \phi \rangle )\leq k$, and ![]() $\sum _{u:|u|=k} | u \rangle \otimes g(\langle u | \phi \rangle )$ otherwise. This
$\sum _{u:|u|=k} | u \rangle \otimes g(\langle u | \phi \rangle )$ otherwise. This ![]() $Skip_k[g]$ is definable within
$Skip_k[g]$ is definable within ![]() $EQS_0$.
$EQS_0$.
Proof. We construct the desired quantum function ![]() $Skip_k[g]$ inductively for any
$Skip_k[g]$ inductively for any ![]() $k\in \mathbb{N}^{+}$. When
$k\in \mathbb{N}^{+}$. When ![]() $k=1$, we set
$k=1$, we set ![]() $Skip_1[g] \equiv Branch[g,g]$. Clearly, when
$Skip_1[g] \equiv Branch[g,g]$. Clearly, when ![]() $\ell (| \phi \rangle )\gt 1$, we obtain
$\ell (| \phi \rangle )\gt 1$, we obtain ![]() $Skip_1[g](| \phi \rangle ) = $
$Skip_1[g](| \phi \rangle ) = $ ![]() $Branch[g,g](| \phi \rangle ) = \sum _{a\in \{0,1\}} | a \rangle \otimes g(\langle a | \phi \rangle )$. For any index
$Branch[g,g](| \phi \rangle ) = \sum _{a\in \{0,1\}} | a \rangle \otimes g(\langle a | \phi \rangle )$. For any index ![]() $k\geq 2$, we define
$k\geq 2$, we define ![]() $Skip_{k+1}[g]$ as
$Skip_{k+1}[g]$ as ![]() $Branch[Skip_k[g],Skip_k[g]]$. It then follows that, if
$Branch[Skip_k[g],Skip_k[g]]$. It then follows that, if ![]() $\ell (| \phi \rangle )\gt k+1$, then
$\ell (| \phi \rangle )\gt k+1$, then ![]() $Skip_{k+1}[g](| x \rangle | \phi \rangle ) = \sum _{a\in \{0,1\}} | a \rangle \otimes Skip_k[g](\langle a | \phi \rangle ) = \sum _{a\in \{0,1\}} \sum _{s:|s|=k} | a \rangle | s \rangle \otimes g(\langle s | \psi _{Skip_k[g],\langle a | \phi \rangle } \rangle ) = \sum _{s':|s'|=k+1} | s' \rangle$
$Skip_{k+1}[g](| x \rangle | \phi \rangle ) = \sum _{a\in \{0,1\}} | a \rangle \otimes Skip_k[g](\langle a | \phi \rangle ) = \sum _{a\in \{0,1\}} \sum _{s:|s|=k} | a \rangle | s \rangle \otimes g(\langle s | \psi _{Skip_k[g],\langle a | \phi \rangle } \rangle ) = \sum _{s':|s'|=k+1} | s' \rangle$ ![]() $\otimes g(\langle s' | \phi \rangle )$, as requested.
$\otimes g(\langle s' | \phi \rangle )$, as requested.
Lemma 5. Fix ![]() $\theta \in [0,2\pi )\cap K$ and
$\theta \in [0,2\pi )\cap K$ and ![]() $i,j,k\in \mathbb{N}^{+}$ and
$i,j,k\in \mathbb{N}^{+}$ and ![]() $i\lt j$. Let
$i\lt j$. Let ![]() $| \phi \rangle$ be any quantum state in
$| \phi \rangle$ be any quantum state in ![]() $\mathscr{H}_{\infty }$, let
$\mathscr{H}_{\infty }$, let ![]() $a$,
$a$, ![]() $b$, and
$b$, and ![]() $c$ be any bits. The following quantum functions are definable by Schemes I–III and thus in
$c$ be any bits. The following quantum functions are definable by Schemes I–III and thus in ![]() $EQS_0$.
$EQS_0$.
1.
 $CNOT(| \phi \rangle ) = | \phi \rangle$ if
$CNOT(| \phi \rangle ) = | \phi \rangle$ if  $\ell (| \phi \rangle )\leq 1$ and
$\ell (| \phi \rangle )\leq 1$ and  $CNOT(| \phi \rangle ) = | 0 \rangle \langle 0 | \phi \rangle + | 1 \rangle \otimes NOT(\langle 1 | \phi \rangle )$ otherwise. (controlled NOT)
$CNOT(| \phi \rangle ) = | 0 \rangle \langle 0 | \phi \rangle + | 1 \rangle \otimes NOT(\langle 1 | \phi \rangle )$ otherwise. (controlled NOT)2.
 $GPS_{\theta }(| \phi \rangle ) = e^{\imath \theta }| \phi \rangle$. (global phase shift)
$GPS_{\theta }(| \phi \rangle ) = e^{\imath \theta }| \phi \rangle$. (global phase shift)3.
 $WH(| \phi \rangle ) = \frac{1}{\sqrt{2}}| 0 \rangle \otimes (\langle 0 | \phi \rangle +\langle 1 | \phi \rangle ) + \frac{1}{\sqrt{2}}| 1 \rangle \otimes (\langle 0 | \phi \rangle -\langle 1 | \phi \rangle )$. (Walsh-Hadamard transform)
$WH(| \phi \rangle ) = \frac{1}{\sqrt{2}}| 0 \rangle \otimes (\langle 0 | \phi \rangle +\langle 1 | \phi \rangle ) + \frac{1}{\sqrt{2}}| 1 \rangle \otimes (\langle 0 | \phi \rangle -\langle 1 | \phi \rangle )$. (Walsh-Hadamard transform)4.
 $Z_{1,\theta }(| \phi \rangle ) = e^{\imath \theta }| 0 \rangle \langle 0 | \phi \rangle + | 1 \rangle \langle 1 | \phi \rangle$.
$Z_{1,\theta }(| \phi \rangle ) = e^{\imath \theta }| 0 \rangle \langle 0 | \phi \rangle + | 1 \rangle \langle 1 | \phi \rangle$.5.
 $zROT_{\theta }(| \phi \rangle ) = e^{\imath \theta }| 0 \rangle \langle 0 | \phi \rangle + e^{-\imath \theta } | 1 \rangle \langle 1 | \phi \rangle$. (rotation around the
$zROT_{\theta }(| \phi \rangle ) = e^{\imath \theta }| 0 \rangle \langle 0 | \phi \rangle + e^{-\imath \theta } | 1 \rangle \langle 1 | \phi \rangle$. (rotation around the  $z$-axis)
$z$-axis)6.
 $C_{\theta }(| \phi \rangle ) = | \phi \rangle$ if
$C_{\theta }(| \phi \rangle ) = | \phi \rangle$ if  $\ell (| \phi \rangle )\leq 1$ and
$\ell (| \phi \rangle )\leq 1$ and  $C_{\theta }(| \phi \rangle ) = | 0 \rangle \langle 0 | \phi \rangle + | 1 \rangle \otimes ROT_{\theta }(\langle 1 | \phi \rangle )$ otherwise. (controlled ROT
$C_{\theta }(| \phi \rangle ) = | 0 \rangle \langle 0 | \phi \rangle + | 1 \rangle \otimes ROT_{\theta }(\langle 1 | \phi \rangle )$ otherwise. (controlled ROT  $_{\theta }$)
$_{\theta }$)7.
 $CPHASE_{\theta } (| \phi \rangle ) = | \phi \rangle$ if
$CPHASE_{\theta } (| \phi \rangle ) = | \phi \rangle$ if  $\ell (| \phi \rangle )\leq 1$, and
$\ell (| \phi \rangle )\leq 1$, and  $CPHASE_{\theta } (| \phi \rangle ) = \frac{1}{\sqrt{2}}\sum _{b\in \{0,1\}} (| 0 \rangle \langle b | \phi \rangle + e^{\imath \theta b}| 1 \rangle \langle b | \phi \rangle )$ otherwise. (controlled PHASE)
$CPHASE_{\theta } (| \phi \rangle ) = \frac{1}{\sqrt{2}}\sum _{b\in \{0,1\}} (| 0 \rangle \langle b | \phi \rangle + e^{\imath \theta b}| 1 \rangle \langle b | \phi \rangle )$ otherwise. (controlled PHASE)8.
 $CSWAP(| a \rangle | \phi \rangle ) = | 0 \rangle \otimes \langle 0 | a \rangle | \phi \rangle + | 1 \rangle \otimes SWAP( \langle 1 | a \rangle | \phi \rangle )$ (controlled SWAP)
$CSWAP(| a \rangle | \phi \rangle ) = | 0 \rangle \otimes \langle 0 | a \rangle | \phi \rangle + | 1 \rangle \otimes SWAP( \langle 1 | a \rangle | \phi \rangle )$ (controlled SWAP)9.
 $LengthQ_k(| b \rangle | \phi \rangle ) = | b \rangle | \phi \rangle$ if
$LengthQ_k(| b \rangle | \phi \rangle ) = | b \rangle | \phi \rangle$ if  $\ell (| \phi \rangle )\lt k$ and
$\ell (| \phi \rangle )\lt k$ and  $LengthQ_k(| b \rangle | \phi \rangle ) = | 1-b \rangle | \phi \rangle$ otherwise. (length query)
$LengthQ_k(| b \rangle | \phi \rangle ) = | 1-b \rangle | \phi \rangle$ otherwise. (length query)10.
 $SWAP_{i,j}(| \phi \rangle ) = \sum _{a_1\cdots a_j\in \{0,1\}} | a_1\cdots a_{i-1}a_{j}a_{i+1} \cdots a_{j-1}a_{i} a_{j+1}\cdots a_n \rangle \otimes \langle a_1\cdots a_{i-1} a_i a_{i+1}\cdots a_{j-1} a_j a_{j+1}\cdots a_n | \phi \rangle$ if
$SWAP_{i,j}(| \phi \rangle ) = \sum _{a_1\cdots a_j\in \{0,1\}} | a_1\cdots a_{i-1}a_{j}a_{i+1} \cdots a_{j-1}a_{i} a_{j+1}\cdots a_n \rangle \otimes \langle a_1\cdots a_{i-1} a_i a_{i+1}\cdots a_{j-1} a_j a_{j+1}\cdots a_n | \phi \rangle$ if  $\ell (| \phi \rangle )\geq j$ and
$\ell (| \phi \rangle )\geq j$ and  $SWAP_{i,j}(| \phi \rangle ) =| \phi \rangle$ otherwise, where
$SWAP_{i,j}(| \phi \rangle ) =| \phi \rangle$ otherwise, where  $n=\ell (| \phi \rangle )$.
$n=\ell (| \phi \rangle )$.
Proof. (1)–(5) These quantum functions are constructed in (Yamakami, Reference Yamakami2020, Lemma 3.3). (6) We set ![]() $C_{\theta } \equiv Branch[I,ROT_{\theta }]$. (7) This was shown in (Yamakami, Reference Yamakami2020, Lemma 3.6). (8) We set
$C_{\theta } \equiv Branch[I,ROT_{\theta }]$. (7) This was shown in (Yamakami, Reference Yamakami2020, Lemma 3.6). (8) We set ![]() $CSWAP$ to be
$CSWAP$ to be ![]() $Branch[I,SWAP]$. This gives the equation
$Branch[I,SWAP]$. This gives the equation ![]() $CSWAP(| a \rangle | \phi \rangle ) = | 0 \rangle \otimes I(\langle 0 | a \rangle | \phi \rangle ) + | 1 \rangle \otimes SWAP(\langle 1 | a \rangle | \phi \rangle )$.
$CSWAP(| a \rangle | \phi \rangle ) = | 0 \rangle \otimes I(\langle 0 | a \rangle | \phi \rangle ) + | 1 \rangle \otimes SWAP(\langle 1 | a \rangle | \phi \rangle )$.
(9) For simplicity, we write ![]() $g\circ f$ in place of
$g\circ f$ in place of ![]() $Compo[g,f]$. Let
$Compo[g,f]$. Let ![]() $h\equiv Branch[NOT,NOT]\circ SWAP$. We construct
$h\equiv Branch[NOT,NOT]\circ SWAP$. We construct ![]() $LengthQ_k$ inductively for any
$LengthQ_k$ inductively for any ![]() $k\geq 1$ as follows. Firstly, when
$k\geq 1$ as follows. Firstly, when ![]() $k=1$,
$k=1$, ![]() $LengthQ_1$ is set to be
$LengthQ_1$ is set to be ![]() $SWAP\circ Skip_1[SWAP] \circ Skip_1[h]\circ SWAP$. It then follows that
$SWAP\circ Skip_1[SWAP] \circ Skip_1[h]\circ SWAP$. It then follows that ![]() $LengthQ_1(| b \rangle ) = | b \rangle$ and
$LengthQ_1(| b \rangle ) = | b \rangle$ and ![]() $LengthQ_1(| b \rangle | \phi \rangle ) = | 1-b \rangle | \phi \rangle$. Letting
$LengthQ_1(| b \rangle | \phi \rangle ) = | 1-b \rangle | \phi \rangle$. Letting ![]() $k\geq 2$, assume that
$k\geq 2$, assume that ![]() $LengthQ_{k-1}$ has been already defined. We then define
$LengthQ_{k-1}$ has been already defined. We then define ![]() $LengthQ_{k}$ as
$LengthQ_{k}$ as ![]() $SWAP \circ Skip_1[Branch[LengthQ_{k-1},LengthQ_{k-1}]] \circ SWAP$.
$SWAP \circ Skip_1[Branch[LengthQ_{k-1},LengthQ_{k-1}]] \circ SWAP$.
(10) Notice that ![]() $SWAP_{1,2}$ coincides with
$SWAP_{1,2}$ coincides with ![]() $SWAP$ of Scheme I. For any fixed constant
$SWAP$ of Scheme I. For any fixed constant ![]() $k\geq 1$, we first define
$k\geq 1$, we first define ![]() $SWAP_{k,k+1}$ to be
$SWAP_{k,k+1}$ to be ![]() $Skip_{k-1}[SWAP]$. For any indices
$Skip_{k-1}[SWAP]$. For any indices ![]() $i,j\geq 1$ with
$i,j\geq 1$ with ![]() $i\lt j$, we further define
$i\lt j$, we further define ![]() $MOVE_{i,j}$ to be
$MOVE_{i,j}$ to be ![]() $SWAP_{i,i+1}\circ SWAP_{i+1,i+2}\circ \cdots \circ SWAP_{j-1,j}$. Note that
$SWAP_{i,i+1}\circ SWAP_{i+1,i+2}\circ \cdots \circ SWAP_{j-1,j}$. Note that ![]() $MOVE_{1,j-1}^{-1}$ equals
$MOVE_{1,j-1}^{-1}$ equals ![]() $SWAP_{j-2,j-1}\circ SWAP_{j-3,j-2} \circ \cdots \circ SWAP_{1,2}$. With the use of
$SWAP_{j-2,j-1}\circ SWAP_{j-3,j-2} \circ \cdots \circ SWAP_{1,2}$. With the use of ![]() $MOVE_{1,j}$, we define
$MOVE_{1,j}$, we define ![]() $SWAP_{1,j}$ as
$SWAP_{1,j}$ as ![]() $MOVE_{1,j}\circ MOVE_{1,j-1}^{-1}$. The target quantum function
$MOVE_{1,j}\circ MOVE_{1,j-1}^{-1}$. The target quantum function ![]() $SWAP_{i,j}$ is finally set to be
$SWAP_{i,j}$ is finally set to be ![]() $Skip_{i-1}[SWAP_{1,j-i}]$.
$Skip_{i-1}[SWAP_{1,j-i}]$.
Lemma 6. Fix ![]() $i,j,k\in \mathbb{N}^{+}$ with
$i,j,k\in \mathbb{N}^{+}$ with ![]() $k\geq 2$ and
$k\geq 2$ and ![]() $i\lt j$, and let
$i\lt j$, and let ![]() $| \phi \rangle$ denote any quantum state in
$| \phi \rangle$ denote any quantum state in ![]() $\mathscr{H}_{\infty }$. The following quantum functions are definable using Schemes I–III and thus in
$\mathscr{H}_{\infty }$. The following quantum functions are definable using Schemes I–III and thus in ![]() $EQS_0$.
$EQS_0$.
1.
 $SecSWAP^{(k)}_{i,j}(| x_1 \rangle | x_2 \rangle \cdots | x_{i-1} \rangle | x_i \rangle | x_{i+1} \rangle \cdots | x_{j-1} \rangle | x_j \rangle | \phi \rangle ) = | x_1 \rangle | x_2 \rangle \cdots | x_{i-1} \rangle | x_j \rangle | x_{i+1} \rangle$
$SecSWAP^{(k)}_{i,j}(| x_1 \rangle | x_2 \rangle \cdots | x_{i-1} \rangle | x_i \rangle | x_{i+1} \rangle \cdots | x_{j-1} \rangle | x_j \rangle | \phi \rangle ) = | x_1 \rangle | x_2 \rangle \cdots | x_{i-1} \rangle | x_j \rangle | x_{i+1} \rangle$  $\cdots | x_{j-1} \rangle | x_i \rangle | \phi \rangle$ for any
$\cdots | x_{j-1} \rangle | x_i \rangle | \phi \rangle$ for any  $k$-bit strings
$k$-bit strings  $x_1,x_2,\ldots, x_i,\ldots, x_j\in \{0,1\}^k$. (section SWAP)
$x_1,x_2,\ldots, x_i,\ldots, x_j\in \{0,1\}^k$. (section SWAP)2.
 $SecMOVE^{(k)}_{i,j}(| x_1 \rangle | x_2 \rangle \cdots | x_{i-1} \rangle | x_i \rangle | x_{i+1} \rangle \cdots | x_j \rangle | \phi \rangle ) = | x_1 \rangle | x_2 \rangle \cdots | x_{i-1} \rangle | x_{i+1} \rangle \cdots | x_j \rangle | x_i \rangle | \phi \rangle$ for any
$SecMOVE^{(k)}_{i,j}(| x_1 \rangle | x_2 \rangle \cdots | x_{i-1} \rangle | x_i \rangle | x_{i+1} \rangle \cdots | x_j \rangle | \phi \rangle ) = | x_1 \rangle | x_2 \rangle \cdots | x_{i-1} \rangle | x_{i+1} \rangle \cdots | x_j \rangle | x_i \rangle | \phi \rangle$ for any  $k$-bit strings
$k$-bit strings  $x_1,x_2,\ldots, x_i,\ldots, x_j\in \{0,1\}^k$. (section MOVE)
$x_1,x_2,\ldots, x_i,\ldots, x_j\in \{0,1\}^k$. (section MOVE)
Proof. (1) Since ![]() $x_1,x_2,\ldots, x_i,\ldots, x_j$ are
$x_1,x_2,\ldots, x_i,\ldots, x_j$ are ![]() $k$-bit strings, we obtain
$k$-bit strings, we obtain ![]() $|x_1x_2\cdots x_{i-1}|=(i-1)k$ and
$|x_1x_2\cdots x_{i-1}|=(i-1)k$ and ![]() $|x_1x_2\cdots x_{j-1}|=(j-1)k$. For convenience, we write
$|x_1x_2\cdots x_{j-1}|=(j-1)k$. For convenience, we write ![]() $i_k$ for
$i_k$ for ![]() $(i-1)k$ and
$(i-1)k$ and ![]() $j_k$ for
$j_k$ for ![]() $(j-1)k$. We then define the desired quantum function
$(j-1)k$. We then define the desired quantum function ![]() $SecSWAP^{(k)}_{i,j}$ to be
$SecSWAP^{(k)}_{i,j}$ to be ![]() $SWAP_{i_k+1,j_k+1} \circ SWAP_{i_k+2,j_k+2}\circ \cdots \circ SWAP_{i_k+k,j_k+k}$.
$SWAP_{i_k+1,j_k+1} \circ SWAP_{i_k+2,j_k+2}\circ \cdots \circ SWAP_{i_k+k,j_k+k}$.
(2) The quantum function ![]() $SecMOVE^{(k)}_{i,j}$ is set to be
$SecMOVE^{(k)}_{i,j}$ is set to be ![]() $SecSWAP^{(k)}_{j-1,j}\circ \cdots \circ SecSWAP^{(k)}_{i+1,i+2}\circ SecSWAP^{(k)}_{i,i+1}$.
$SecSWAP^{(k)}_{j-1,j}\circ \cdots \circ SecSWAP^{(k)}_{i+1,i+2}\circ SecSWAP^{(k)}_{i,i+1}$.
Hereafter, let us construct more quantum functions in ![]() $EQS_0$.
$EQS_0$.
Lemma 7. Consider ![]() $COPY_1$ that satisfies
$COPY_1$ that satisfies ![]() $COPY_1(| a \rangle | \phi \rangle ) = \sum _{s\in \{0,1\}} | a\oplus s \rangle | s \rangle \langle s | \phi \rangle$ for any quantum state
$COPY_1(| a \rangle | \phi \rangle ) = \sum _{s\in \{0,1\}} | a\oplus s \rangle | s \rangle \langle s | \phi \rangle$ for any quantum state ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$ and any bit
$| \phi \rangle \in \mathscr{H}_{\infty }$ and any bit ![]() $a$, where
$a$, where ![]() $\oplus$ denotes the bitwise XOR. More generally, for each fixed constant
$\oplus$ denotes the bitwise XOR. More generally, for each fixed constant ![]() $k\geq 2$, let
$k\geq 2$, let ![]() $COPY_k(| x \rangle | \phi \rangle ) = \sum _{z\in \{0,1\}^k} | x\oplus z \rangle | z \rangle \langle z | \phi \rangle$ for any quantum state
$COPY_k(| x \rangle | \phi \rangle ) = \sum _{z\in \{0,1\}^k} | x\oplus z \rangle | z \rangle \langle z | \phi \rangle$ for any quantum state ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$ and any
$| \phi \rangle \in \mathscr{H}_{\infty }$ and any ![]() $k$-bit string
$k$-bit string ![]() $x$. These quantum functions are all definable using Schemes I–III.
$x$. These quantum functions are all definable using Schemes I–III.
Proof. We inductively define ![]() $COPY_k$ for any index
$COPY_k$ for any index ![]() $k\geq 1$. In the case of
$k\geq 1$. In the case of ![]() $k=1$, we set
$k=1$, we set ![]() $COPY_1$ to be
$COPY_1$ to be ![]() $SWAP\circ CNOT\circ SWAP$. It then follows that
$SWAP\circ CNOT\circ SWAP$. It then follows that ![]() $COPY_1(| a \rangle | \phi \rangle ) = SWAP\circ CNOT\circ SWAP (| a \rangle | \phi \rangle ) = SWAP\circ CNOT (\sum _{s\in \{0,1\}} | s \rangle | a \rangle \otimes \langle s | \phi \rangle ) = \sum _{s\in \{0,1\}} SWAP(| s \rangle | a\oplus s \rangle \otimes \langle s | \phi \rangle ) = \sum _{s\in \{0,1\}} | a\oplus s \rangle \langle s | \phi \rangle$.
$COPY_1(| a \rangle | \phi \rangle ) = SWAP\circ CNOT\circ SWAP (| a \rangle | \phi \rangle ) = SWAP\circ CNOT (\sum _{s\in \{0,1\}} | s \rangle | a \rangle \otimes \langle s | \phi \rangle ) = \sum _{s\in \{0,1\}} SWAP(| s \rangle | a\oplus s \rangle \otimes \langle s | \phi \rangle ) = \sum _{s\in \{0,1\}} | a\oplus s \rangle \langle s | \phi \rangle$.
Let ![]() $k\geq 2$. Assume by induction hypothesis that
$k\geq 2$. Assume by induction hypothesis that ![]() $COPY_{k-1}$ has been already defined. The quantum function
$COPY_{k-1}$ has been already defined. The quantum function ![]() $COPY_k(| x \rangle | \phi \rangle )$ is obtained by taking the following process. To
$COPY_k(| x \rangle | \phi \rangle )$ is obtained by taking the following process. To ![]() $| x \rangle | \phi \rangle$, we first apply
$| x \rangle | \phi \rangle$, we first apply ![]() $SWAP_{[2,k]} \equiv SWAP_{2,3}\circ SWAP_{3,4}\circ \cdots \circ SWAP_{k-1,k}$. Next, we apply
$SWAP_{[2,k]} \equiv SWAP_{2,3}\circ SWAP_{3,4}\circ \cdots \circ SWAP_{k-1,k}$. Next, we apply ![]() $COPY_1$ and then
$COPY_1$ and then ![]() $Skip_2[COPY_{k-1}]$. Finally, we apply
$Skip_2[COPY_{k-1}]$. Finally, we apply ![]() $SWAP_{[2,k]}^{-1}$. It is not difficult to check that the obtained quantum function matches
$SWAP_{[2,k]}^{-1}$. It is not difficult to check that the obtained quantum function matches ![]() $COPY_k$.
$COPY_k$.
Let us construct the basic quantum functions ![]() $g_{AND}$ and
$g_{AND}$ and ![]() $g_{OR}$, which “mimic” the behaviors of the two-bit operations
$g_{OR}$, which “mimic” the behaviors of the two-bit operations ![]() $AND$ and
$AND$ and ![]() $OR$, using only Schemes I–III.
$OR$, using only Schemes I–III.
Lemma 8. There exist two quantum functions ![]() $g_{AND}$ and
$g_{AND}$ and ![]() $g_{OR}$ that satisfy the following. Let
$g_{OR}$ that satisfy the following. Let ![]() $x,y\in \{0,1\}$ and
$x,y\in \{0,1\}$ and ![]() $b\in \{0,1\}$. (1)
$b\in \{0,1\}$. (1) ![]() $AND(x,y)=b$ iff
$AND(x,y)=b$ iff ![]() $\|\langle b | \psi _{0xy}^{(AND)} \rangle \| =1$, where
$\|\langle b | \psi _{0xy}^{(AND)} \rangle \| =1$, where ![]() $| \psi _{0xy}^{(AND)} \rangle = g_{AND}(| 0 \rangle | x \rangle | y \rangle )$. (2)
$| \psi _{0xy}^{(AND)} \rangle = g_{AND}(| 0 \rangle | x \rangle | y \rangle )$. (2) ![]() $OR(x,y)=b$ iff
$OR(x,y)=b$ iff ![]() $\|\langle b | \psi _{0xy}^{(OR)} \rangle \| =1$, where
$\|\langle b | \psi _{0xy}^{(OR)} \rangle \| =1$, where ![]() $| \psi _{0xy}^{(OR)} \rangle = g_{OR}(| 0 \rangle | x \rangle | y \rangle )$. These quantum functions are defined by Schemes I–III.
$| \psi _{0xy}^{(OR)} \rangle = g_{OR}(| 0 \rangle | x \rangle | y \rangle )$. These quantum functions are defined by Schemes I–III.
Proof. Recall the quantum functions ![]() $SWAP_{i,j}$ and
$SWAP_{i,j}$ and ![]() $COPY_1$, respectively, from Lemmas5 and 7. We first define
$COPY_1$, respectively, from Lemmas5 and 7. We first define ![]() $g_{OR}$ to be
$g_{OR}$ to be ![]() $SWAP_{1,3}\circ CSWAP\circ COPY_1$. From this definition, for any
$SWAP_{1,3}\circ CSWAP\circ COPY_1$. From this definition, for any ![]() $x,y\in \{0,1\}$, it follows that
$x,y\in \{0,1\}$, it follows that ![]() $g_{OR}(| 0 \rangle | x \rangle | y \rangle ) = \langle 0 | x \rangle | y \rangle | x \rangle | 0 \rangle + \langle 1 | x \rangle | x \rangle | y \rangle | 1 \rangle$. Thus, we obtain
$g_{OR}(| 0 \rangle | x \rangle | y \rangle ) = \langle 0 | x \rangle | y \rangle | x \rangle | 0 \rangle + \langle 1 | x \rangle | x \rangle | y \rangle | 1 \rangle$. Thus, we obtain ![]() $g_{OR}(| 0 \rangle | 0 \rangle | y \rangle ) = | y \rangle | 0 \rangle | 0 \rangle$ and
$g_{OR}(| 0 \rangle | 0 \rangle | y \rangle ) = | y \rangle | 0 \rangle | 0 \rangle$ and ![]() $g_{OR}(| 0 \rangle | 1 \rangle | y \rangle )=| 1 \rangle | y \rangle | 1 \rangle$.
$g_{OR}(| 0 \rangle | 1 \rangle | y \rangle )=| 1 \rangle | y \rangle | 1 \rangle$.
We next define ![]() $g_{AND}$ to be
$g_{AND}$ to be ![]() $SWAP_{1,3}\circ SWAP_{2,3}\circ CSWAP\circ COPY_1$. It then follows that
$SWAP_{1,3}\circ SWAP_{2,3}\circ CSWAP\circ COPY_1$. It then follows that ![]() $g_{AND}(| 0 \rangle | x \rangle | y \rangle ) = \langle 0 | x \rangle | x \rangle | y \rangle | 0 \rangle + \langle 1 | x \rangle | y \rangle | x \rangle | 1 \rangle$. From this equality, we obtain
$g_{AND}(| 0 \rangle | x \rangle | y \rangle ) = \langle 0 | x \rangle | x \rangle | y \rangle | 0 \rangle + \langle 1 | x \rangle | y \rangle | x \rangle | 1 \rangle$. From this equality, we obtain ![]() $g_{AND}(| 0 \rangle | 0 \rangle | y \rangle )= | 0 \rangle | y \rangle | 0 \rangle$ and
$g_{AND}(| 0 \rangle | 0 \rangle | y \rangle )= | 0 \rangle | y \rangle | 0 \rangle$ and ![]() $g_{AND}(| 0 \rangle | 1 \rangle | y \rangle ) = | y \rangle | 1 \rangle | 1 \rangle$.
$g_{AND}(| 0 \rangle | 1 \rangle | y \rangle ) = | y \rangle | 1 \rangle | 1 \rangle$.
For later use, we define another quantum function, which splits the entire input qubits into two halves and then swaps them. We do not intend to include this quantum function to our system, but it will be used to support the description of a new scheme given in Section 3.2. We remark that, to construct this quantum function, we need Schemes I–III together with the quantum recursion Scheme T. By recalling the left-half function ![]() $LH$ and the right-half function
$LH$ and the right-half function ![]() $RH$ from Section 2.1, let us introduce
$RH$ from Section 2.1, let us introduce ![]() $HalfSWAP$ as
$HalfSWAP$ as
*)
 $HalfSWAP(| \phi \rangle ) = \left \{ \begin{array}{ll} | \phi \rangle & \quad if \mbox{$\ell (| \phi \rangle )\leq 1$,} \\ \sum _{s:|s|=LH(| \phi \rangle )} \langle s | \phi \rangle \otimes | s \rangle & \quad {otherwise.} \end{array}\right .$
$HalfSWAP(| \phi \rangle ) = \left \{ \begin{array}{ll} | \phi \rangle & \quad if \mbox{$\ell (| \phi \rangle )\leq 1$,} \\ \sum _{s:|s|=LH(| \phi \rangle )} \langle s | \phi \rangle \otimes | s \rangle & \quad {otherwise.} \end{array}\right .$
The inverse of ![]() $HalfSWAP$, denoted
$HalfSWAP$, denoted ![]() $HalfSWAP^{-1}$, matches the quantum function obtained from
$HalfSWAP^{-1}$, matches the quantum function obtained from ![]() $HalfSWAP$ by replacing
$HalfSWAP$ by replacing ![]() $LH(| \phi \rangle )$ in its definition with
$LH(| \phi \rangle )$ in its definition with ![]() $RH(| \phi \rangle )$. In the special case where
$RH(| \phi \rangle )$. In the special case where ![]() $\ell (| \phi \rangle )$ is even,
$\ell (| \phi \rangle )$ is even, ![]() $HalfSWAP\circ HalfSWAP(| \phi \rangle )$ equals
$HalfSWAP\circ HalfSWAP(| \phi \rangle )$ equals ![]() $| \phi \rangle$ since
$| \phi \rangle$ since ![]() $LH(| \phi \rangle )=RH(| \phi \rangle )$.
$LH(| \phi \rangle )=RH(| \phi \rangle )$.
Example 9. Consider a quantum state ![]() $| \phi \rangle = \sum _{u:|u|=3}\alpha _u | u \rangle$, which is
$| \phi \rangle = \sum _{u:|u|=3}\alpha _u | u \rangle$, which is ![]() $\alpha _{000}| 000 \rangle + \alpha _{001}| 001 \rangle + \alpha _{010}| 010 \rangle + \alpha _{011}| 011 \rangle + \cdots + \alpha _{111}| 111 \rangle$. Notice that
$\alpha _{000}| 000 \rangle + \alpha _{001}| 001 \rangle + \alpha _{010}| 010 \rangle + \alpha _{011}| 011 \rangle + \cdots + \alpha _{111}| 111 \rangle$. Notice that ![]() $LH(| \phi \rangle )= \lceil \ell (| \phi \rangle )/2 \rceil = 2$ and
$LH(| \phi \rangle )= \lceil \ell (| \phi \rangle )/2 \rceil = 2$ and ![]() $RH(\ell (| \phi \rangle ))=\lfloor \ell (| \phi \rangle )/2 \rfloor = 1$. Since
$RH(\ell (| \phi \rangle ))=\lfloor \ell (| \phi \rangle )/2 \rfloor = 1$. Since ![]() $\langle s | \phi \rangle = \sum _{u:|u|=3} \alpha _u \langle s | u \rangle$, it then follows that
$\langle s | \phi \rangle = \sum _{u:|u|=3} \alpha _u \langle s | u \rangle$, it then follows that ![]() $HalfSWAP(| \phi \rangle ) = \sum _{s:|s|=2}\sum _{u:|u|=3} \alpha _u \langle s | u \rangle \otimes | s \rangle$, which equals
$HalfSWAP(| \phi \rangle ) = \sum _{s:|s|=2}\sum _{u:|u|=3} \alpha _u \langle s | u \rangle \otimes | s \rangle$, which equals ![]() $\alpha _{000}| 000 \rangle + \alpha _{001}| 100 \rangle + \alpha _{010}| 001 \rangle + \alpha _{011}| 101 \rangle + \cdots + \alpha _{111}| 111 \rangle$.
$\alpha _{000}| 000 \rangle + \alpha _{001}| 100 \rangle + \alpha _{010}| 001 \rangle + \alpha _{011}| 101 \rangle + \cdots + \alpha _{111}| 111 \rangle$.
3.2 Binary encoding of various types of objects
All quantum functions discussed in Section 3.1 take only “single” quantum states in ![]() $\mathscr{H}_{\infty }$ as their inputs. For practical applications of these quantum functions, we need to further deal with a problem that consists of various types of “objects,” such as numbers, graphs, matrices, and tape symbols. Since each QTM uses multiple tapes with their associated tape heads, these tapes hold possibly different qubits and their tape heads move separately. This is an advantage of the QTM model over quantum functions. For our purpose, nevertheless, it is imperative to set up an appropriate binary encoding to transform multiple objects into a single quantum state with an appropriate use of designated “separators”. In the polynomial-time setting (Yamakami, Reference Yamakami2020), the scheme of quantum recursion (Scheme T) is powerful enough to handle several inputs altogether as a single encoded quantum state in a way similar to a multiple-tape QTM being simulated by a single-tape QTM with only polynomial overhead. However, since we aim at capturing quantum polylogtime computability instead, we cannot take the same approach to cope with multiple inputs. We thus need to ponder how to circumvent this difficulty to expand the scope of our quantum functions. As a feasible solution to this problem, we introduce “extra” schemes that help us handle intended binary encodings.
$\mathscr{H}_{\infty }$ as their inputs. For practical applications of these quantum functions, we need to further deal with a problem that consists of various types of “objects,” such as numbers, graphs, matrices, and tape symbols. Since each QTM uses multiple tapes with their associated tape heads, these tapes hold possibly different qubits and their tape heads move separately. This is an advantage of the QTM model over quantum functions. For our purpose, nevertheless, it is imperative to set up an appropriate binary encoding to transform multiple objects into a single quantum state with an appropriate use of designated “separators”. In the polynomial-time setting (Yamakami, Reference Yamakami2020), the scheme of quantum recursion (Scheme T) is powerful enough to handle several inputs altogether as a single encoded quantum state in a way similar to a multiple-tape QTM being simulated by a single-tape QTM with only polynomial overhead. However, since we aim at capturing quantum polylogtime computability instead, we cannot take the same approach to cope with multiple inputs. We thus need to ponder how to circumvent this difficulty to expand the scope of our quantum functions. As a feasible solution to this problem, we introduce “extra” schemes that help us handle intended binary encodings.
In what follows, we attempt to design an encoding (or a translation) of various types of objects into binary strings of the same fixed length so that a series of these encoded objects forms a larger-dimensional quantum state. Each “segment” of such a quantum state representing one encoded object is referred to as a section, and this fixed-length encoding makes it possible to work with each section separately.
Let us describe our encoding scheme for eight symbols in ![]() $\{0, 1, 2,{\dashv }, B, H, S, T\}$, where
$\{0, 1, 2,{\dashv }, B, H, S, T\}$, where ![]() $\dashv$,
$\dashv$, ![]() $B$,
$B$, ![]() $H$,
$H$, ![]() $S$, and
$S$, and ![]() $T$, respectively, stand for an “ending,” a “blank,” a “head,” a “separator,” and a “time”. With the use of three bits, we take the following abbreviations:
$T$, respectively, stand for an “ending,” a “blank,” a “head,” a “separator,” and a “time”. With the use of three bits, we take the following abbreviations: ![]() $\hat{0}=000$,
$\hat{0}=000$, ![]() $\hat{1}=001$,
$\hat{1}=001$, ![]() $\hat{B}=010$,
$\hat{B}=010$, ![]() $\hat{\dashv }=011$,
$\hat{\dashv }=011$, ![]() $\hat{2}=111$,
$\hat{2}=111$, ![]() $\hat{H}= 100$,
$\hat{H}= 100$, ![]() $\hat{S}=110$, and
$\hat{S}=110$, and ![]() $\hat{T}=101$. Given a binary string
$\hat{T}=101$. Given a binary string ![]() $s=s_1s_2\cdots s_k$, the notation
$s=s_1s_2\cdots s_k$, the notation ![]() $\tilde{s}^{(-)}$ denotes
$\tilde{s}^{(-)}$ denotes ![]() $\hat{s}_1\hat{s}_2\cdots \hat{s}_k$, and
$\hat{s}_1\hat{s}_2\cdots \hat{s}_k$, and ![]() $\widetilde{s}$ denotes
$\widetilde{s}$ denotes ![]() $\tilde{s}^{(-)}\hat{\dashv }$. For convenience, we also define
$\tilde{s}^{(-)}\hat{\dashv }$. For convenience, we also define ![]() $\widetilde{\lambda }$ to be
$\widetilde{\lambda }$ to be ![]() $\hat{\dashv }$. This makes us encode, for example, the number
$\hat{\dashv }$. This makes us encode, for example, the number ![]() $8$ into
$8$ into ![]() $\widetilde{bin(8)} = \widetilde{001} = \hat{0}\hat{0}\hat{1}\hat{\dashv }$, while
$\widetilde{bin(8)} = \widetilde{001} = \hat{0}\hat{0}\hat{1}\hat{\dashv }$, while ![]() $\widetilde{bin_3(2)}$ also equals
$\widetilde{bin_3(2)}$ also equals ![]() $\widetilde{001}$. Given an arbitrary quantum state
$\widetilde{001}$. Given an arbitrary quantum state ![]() $| \phi \rangle$ in
$| \phi \rangle$ in ![]() $\mathscr{H}_{\infty }$, we finally define its encoding
$\mathscr{H}_{\infty }$, we finally define its encoding ![]() $| \tilde{\phi } \rangle$ as
$| \tilde{\phi } \rangle$ as ![]() $\sum _{s:|s|=\ell (| \phi \rangle )} | \tilde{s} \rangle \langle s | \phi \rangle$. Notice that
$\sum _{s:|s|=\ell (| \phi \rangle )} | \tilde{s} \rangle \langle s | \phi \rangle$. Notice that ![]() $\ell (| \tilde{\phi } \rangle ) = 3\ell (| \phi \rangle )+3$.
$\ell (| \tilde{\phi } \rangle ) = 3\ell (| \phi \rangle )+3$.
To mark the end of a series of encoded objects, we use a designated separator, say, ![]() $r_0$ in
$r_0$ in ![]() $\{0,1\}^+$. We fix such
$\{0,1\}^+$. We fix such ![]() $r_0$ in the following discussion. We make each series of encoded objects have length proportional to the section size
$r_0$ in the following discussion. We make each series of encoded objects have length proportional to the section size ![]() $|r_0|$, and thus any encoding
$|r_0|$, and thus any encoding ![]() $x$ satisfies
$x$ satisfies ![]() $|x|=k|r_0|$ for an appropriate, fixed number
$|x|=k|r_0|$ for an appropriate, fixed number ![]() $k\in \mathbb{N}^{+}$. This helps us partition
$k\in \mathbb{N}^{+}$. This helps us partition ![]() $x$ section-wise as
$x$ section-wise as ![]() $x_1x_2\cdots x_k$ with
$x_1x_2\cdots x_k$ with ![]() $|x_i|=|r_0|$ for all indices
$|x_i|=|r_0|$ for all indices ![]() $i\in [k]$. We also demand that no
$i\in [k]$. We also demand that no ![]() $x_i$ should match
$x_i$ should match ![]() $r_0$. Here, we say that
$r_0$. Here, we say that ![]() $x$ section-wise contains no
$x$ section-wise contains no ![]() $r_0$ if
$r_0$ if ![]() $x_i\neq r_0$ holds for all indices
$x_i\neq r_0$ holds for all indices ![]() $i\in [k]$. Let
$i\in [k]$. Let ![]() $NON_{r_0} =\{x\in \{0,1\}^+\mid |x|\equiv 0 \:(\mathrm{mod}\:|r_0|), \text{ $x$ section-wise contains no $r_0$ }\}$. Similarly, we set
$NON_{r_0} =\{x\in \{0,1\}^+\mid |x|\equiv 0 \:(\mathrm{mod}\:|r_0|), \text{ $x$ section-wise contains no $r_0$ }\}$. Similarly, we set ![]() $NON_{r_0}(| \phi \rangle ) =\{x\in NON_{r_0} \mid \langle xr_0 | \phi \rangle \neq 0 \}$. For convenience, when
$NON_{r_0}(| \phi \rangle ) =\{x\in NON_{r_0} \mid \langle xr_0 | \phi \rangle \neq 0 \}$. For convenience, when ![]() $r_0=\hat{2}$, we tend to omit
$r_0=\hat{2}$, we tend to omit ![]() $r_0$ from
$r_0$ from ![]() $NON_{r_0}$ and
$NON_{r_0}$ and ![]() $NON_{r_0}(| \phi \rangle )$.
$NON_{r_0}(| \phi \rangle )$.
Example 10. Fix ![]() $r_0\in \{0,1\}^+$. Choose three strings
$r_0\in \{0,1\}^+$. Choose three strings ![]() $x_1,x_2,x_3\in \{0,1\}^{|r_0|}$ satisfying
$x_1,x_2,x_3\in \{0,1\}^{|r_0|}$ satisfying ![]() $x_i\neq r_0$ for all
$x_i\neq r_0$ for all ![]() $i\in [3]$, and consider three quantum states
$i\in [3]$, and consider three quantum states ![]() $| \psi \rangle = | x_1x_2x_3 \rangle | r_0 \rangle | \phi \rangle$,
$| \psi \rangle = | x_1x_2x_3 \rangle | r_0 \rangle | \phi \rangle$, ![]() $| \psi ' \rangle = | x_1x_2 r_0 x_3 \rangle | \phi \rangle$, and
$| \psi ' \rangle = | x_1x_2 r_0 x_3 \rangle | \phi \rangle$, and ![]() $| \psi '' \rangle =| x_1r_0x_2x_3 \rangle | \phi \rangle$ for any
$| \psi '' \rangle =| x_1r_0x_2x_3 \rangle | \phi \rangle$ for any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$. We then obtain
$| \phi \rangle \in \mathscr{H}_{\infty }$. We then obtain ![]() $NON_{r_0}(| \psi \rangle ) = \{x_1x_2x_3\}$,
$NON_{r_0}(| \psi \rangle ) = \{x_1x_2x_3\}$, ![]() $NON_{r_0}(| \psi ' \rangle ) = \{x_1x_2\}$, and
$NON_{r_0}(| \psi ' \rangle ) = \{x_1x_2\}$, and ![]() $NON_{r_0}(| \psi '' \rangle ) = \{x_1\}$. By contrast, when
$NON_{r_0}(| \psi '' \rangle ) = \{x_1\}$. By contrast, when ![]() $| \psi \rangle$ has the form
$| \psi \rangle$ has the form ![]() $(\alpha | x_1 \rangle | r_0 \rangle + \beta | x_2 \rangle | r_0 \rangle )| \phi \rangle$,
$(\alpha | x_1 \rangle | r_0 \rangle + \beta | x_2 \rangle | r_0 \rangle )| \phi \rangle$, ![]() $NON_{r_0}(| \psi \rangle )$ equals
$NON_{r_0}(| \psi \rangle )$ equals ![]() $\{x_1,x_2\}$.
$\{x_1,x_2\}$.
As another example, if ![]() $x=0111$ and
$x=0111$ and ![]() $r_0=\hat{2}$, then
$r_0=\hat{2}$, then ![]() $\widetilde{x}$ equals
$\widetilde{x}$ equals ![]() $\widetilde{x}^{(-)}\hat{\dashv } = \hat{0}\hat{1}\hat{1}\hat{1}\hat{\dashv }$. Notice that
$\widetilde{x}^{(-)}\hat{\dashv } = \hat{0}\hat{1}\hat{1}\hat{1}\hat{\dashv }$. Notice that ![]() $|\widetilde{x}|\equiv 0\:(\mathrm{mod}\:|r_0|)$. Thus, we obtain
$|\widetilde{x}|\equiv 0\:(\mathrm{mod}\:|r_0|)$. Thus, we obtain ![]() $NON_{r_0}(| \widetilde{x} \rangle | r_0 \rangle | \phi \rangle ) = \{\widetilde{x}\}$.
$NON_{r_0}(| \widetilde{x} \rangle | r_0 \rangle | \phi \rangle ) = \{\widetilde{x}\}$.
We then need a quantum function that splits an input into sections and apply “section-wise” two predetermined quantum operations. We actually introduce two slightly different code skipping schemes described below. We do not unconditionally include them to ![]() $EQS$, but we use them in a certain restricted situation, which will be discussed later. Such a restriction is in fact necessary because these schemes are too powerful to use for quantum polylogtime computability.
$EQS$, but we use them in a certain restricted situation, which will be discussed later. Such a restriction is in fact necessary because these schemes are too powerful to use for quantum polylogtime computability.
*) The code skipping schemes. From
 $g$,
$g$,  $h$ and
$h$ and  $r_0\in \{0,1\}^+$, we define
$r_0\in \{0,1\}^+$, we define  $CodeSKIP_{+}[r_0,g,h]$ and
$CodeSKIP_{+}[r_0,g,h]$ and  $CodeSKIP_{-}[r_0,g,h]$ as follows:
$CodeSKIP_{-}[r_0,g,h]$ as follows:(i)
 $CodeSKIP_{+}[r_0,g,h](| \phi \rangle ) = \left \{ \begin{array}{l@{\quad}r} | \phi \rangle & if \mbox{$NON_{r_0}(| \phi \rangle ) = \varnothing $,} \\
\sum _{x\in NON_{r_0}(| \phi \rangle )} ( g( | xr_0 \rangle ) \otimes h( \langle xr_0 | \phi \rangle )) & {otherwise.} \end{array}\right .$
$CodeSKIP_{+}[r_0,g,h](| \phi \rangle ) = \left \{ \begin{array}{l@{\quad}r} | \phi \rangle & if \mbox{$NON_{r_0}(| \phi \rangle ) = \varnothing $,} \\
\sum _{x\in NON_{r_0}(| \phi \rangle )} ( g( | xr_0 \rangle ) \otimes h( \langle xr_0 | \phi \rangle )) & {otherwise.} \end{array}\right .$(ii)
 $CodeSKIP_{-}[r_0,g,h](| \phi \rangle ) = \left \{ \begin{array}{l@{\quad}r} | \phi \rangle & if \mbox{$NON_{r_0}(| \phi \rangle ) = \varnothing $,} \\
\sum _{x\in NON_{r_0}(| \phi \rangle )} ( g( | x \rangle ) \otimes h( \langle x | \phi \rangle )) & {otherwise.} \end{array}\right .$
$CodeSKIP_{-}[r_0,g,h](| \phi \rangle ) = \left \{ \begin{array}{l@{\quad}r} | \phi \rangle & if \mbox{$NON_{r_0}(| \phi \rangle ) = \varnothing $,} \\
\sum _{x\in NON_{r_0}(| \phi \rangle )} ( g( | x \rangle ) \otimes h( \langle x | \phi \rangle )) & {otherwise.} \end{array}\right .$
The difference between ![]() $CodeSKIP_{+}[r_0,g,h]$ and
$CodeSKIP_{+}[r_0,g,h]$ and ![]() $CodeSKIP_{-}[r_0,g,h]$ looks subtle but becomes clear in the following example. When
$CodeSKIP_{-}[r_0,g,h]$ looks subtle but becomes clear in the following example. When ![]() $| \phi \rangle =| x \rangle | r_0 \rangle | y \rangle$ with
$| \phi \rangle =| x \rangle | r_0 \rangle | y \rangle$ with ![]() $|x|=|r_0|$ and
$|x|=|r_0|$ and ![]() $x\neq r_0$, it follows that
$x\neq r_0$, it follows that ![]() $CodeSKIP_{+}[r_0,g,h](| \phi \rangle ) = g(| xr_0 \rangle )\otimes h(| y \rangle )$ but
$CodeSKIP_{+}[r_0,g,h](| \phi \rangle ) = g(| xr_0 \rangle )\otimes h(| y \rangle )$ but ![]() $CodeSKIP_{-}[r_0,g,h](| \phi \rangle ) = g(| x \rangle )\otimes h(| r_0y \rangle )$. These schemes are not interchangeable in most applications.
$CodeSKIP_{-}[r_0,g,h](| \phi \rangle ) = g(| x \rangle )\otimes h(| r_0y \rangle )$. These schemes are not interchangeable in most applications.
A quantum function ![]() $g$ is said to be query-independent if, in the process of constructing
$g$ is said to be query-independent if, in the process of constructing ![]() $g$, for any input of the form
$g$, for any input of the form ![]() $| xr_0 \rangle | \phi \rangle$, any quantum function that appears in this construction process does not directly access
$| xr_0 \rangle | \phi \rangle$, any quantum function that appears in this construction process does not directly access ![]() $| \phi \rangle$ and thus it does not depend on
$| \phi \rangle$ and thus it does not depend on ![]() $| \phi \rangle$. This instantly implies that
$| \phi \rangle$. This instantly implies that ![]() $g(| xr_0 \rangle | \phi \rangle ) = g(| xr_0 \rangle )\otimes | \phi \rangle$ for any
$g(| xr_0 \rangle | \phi \rangle ) = g(| xr_0 \rangle )\otimes | \phi \rangle$ for any ![]() $x$ and
$x$ and ![]() $| \phi \rangle$. Using this terminology, when
$| \phi \rangle$. Using this terminology, when ![]() $h=I$ in the code skipping schemes,
$h=I$ in the code skipping schemes, ![]() $CodeSKIP_{+}[r_0,g,I]$ and
$CodeSKIP_{+}[r_0,g,I]$ and ![]() $CodeSKIP_{-}[r_0,g,I]$ are query-independent.
$CodeSKIP_{-}[r_0,g,I]$ are query-independent.
Here, we present a few more examples of ![]() $CodeSKIP_{+}$.
$CodeSKIP_{+}$.
Example 11. Let ![]() $g=ROT_{\pi /4}$ and
$g=ROT_{\pi /4}$ and ![]() $h=NOT$. Let
$h=NOT$. Let ![]() $r_0=0^5$ and let
$r_0=0^5$ and let ![]() $| \phi \rangle = | x_1x_2 \rangle | r_0 \rangle | x_3x_4 \rangle | r_0 \rangle | \psi \rangle$ with binary strings
$| \phi \rangle = | x_1x_2 \rangle | r_0 \rangle | x_3x_4 \rangle | r_0 \rangle | \psi \rangle$ with binary strings ![]() $x_i=bin_5(i)$ for any
$x_i=bin_5(i)$ for any ![]() $i\in [4]$ and a qustring
$i\in [4]$ and a qustring ![]() $| \psi \rangle$. Since
$| \psi \rangle$. Since ![]() $NON_{r_0}(| \phi \rangle ) = \{x_1x_2\}$, we obtain
$NON_{r_0}(| \phi \rangle ) = \{x_1x_2\}$, we obtain ![]() $CodeSKIP_{+}[r_0,g,h](| \phi \rangle ) = ROT_{\pi /4}(| x_1x_2r_0 \rangle )\otimes NOT(| x_3x_4r_0 \rangle | \psi \rangle )$.
$CodeSKIP_{+}[r_0,g,h](| \phi \rangle ) = ROT_{\pi /4}(| x_1x_2r_0 \rangle )\otimes NOT(| x_3x_4r_0 \rangle | \psi \rangle )$.
Let ![]() $| \phi ' \rangle = \alpha | y_1r_0 \rangle | \psi _1 \rangle + \beta | y_2r_0 \rangle | \psi _2 \rangle$ with
$| \phi ' \rangle = \alpha | y_1r_0 \rangle | \psi _1 \rangle + \beta | y_2r_0 \rangle | \psi _2 \rangle$ with ![]() $|y_1|=|y_2|=|r_0|$ and
$|y_1|=|y_2|=|r_0|$ and ![]() $y_1,y_2\notin \{r_0\}$. In this case,
$y_1,y_2\notin \{r_0\}$. In this case, ![]() $NON_{r_0}$ is the set
$NON_{r_0}$ is the set ![]() $\{y_1,y_2\}$. It then follows that
$\{y_1,y_2\}$. It then follows that ![]() $CodeSKIP_{+}[r_0,g,h](| \psi ' \rangle ) = \alpha g(| y_1r_0 \rangle )\otimes h(| \psi _1 \rangle ) + \beta g(| y_2r_0 \rangle )\otimes h(| \psi _2 \rangle )$.
$CodeSKIP_{+}[r_0,g,h](| \psi ' \rangle ) = \alpha g(| y_1r_0 \rangle )\otimes h(| \psi _1 \rangle ) + \beta g(| y_2r_0 \rangle )\otimes h(| \psi _2 \rangle )$.
We wish to recall the two useful quantum functions ![]() $REMOVE$ (removal) and
$REMOVE$ (removal) and ![]() $REP$ (replacement) introduced by Yamakami (Reference Yamakami2020). We introduce the “code-controlled” versions of them. Let
$REP$ (replacement) introduced by Yamakami (Reference Yamakami2020). We introduce the “code-controlled” versions of them. Let ![]() $r_0\in \{0,1\}^{+}$ be a separator.
$r_0\in \{0,1\}^{+}$ be a separator.
(i)
 $CodeREMOVE[r_0](| \phi \rangle ) = \left \{ \begin{array}{l} | \phi \rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\ \ if \mbox{$NON_{r_0}(| \phi \rangle ) = \varnothing $,} \\
\sum _{x\in NON_{r_0}(| \phi \rangle )} \sum _{a\in \{0,1\}} ( \langle a | x \rangle \otimes | ar_0 \rangle \otimes \langle xr_0 | \phi \rangle ) \quad {otherwise.} \end{array}\right .$
$CodeREMOVE[r_0](| \phi \rangle ) = \left \{ \begin{array}{l} | \phi \rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\ \ if \mbox{$NON_{r_0}(| \phi \rangle ) = \varnothing $,} \\
\sum _{x\in NON_{r_0}(| \phi \rangle )} \sum _{a\in \{0,1\}} ( \langle a | x \rangle \otimes | ar_0 \rangle \otimes \langle xr_0 | \phi \rangle ) \quad {otherwise.} \end{array}\right .$(ii)
 $CodeREP[r_0](| \phi \rangle ) = \left \{ \begin{array}{l} | \phi \rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\ if \mbox{$NON_{r_0}(| \phi \rangle ) = \varnothing $,} \\
\sum _{x\in NON_{r_0}(| \phi \rangle )} \sum _{u:|u|=|x|-1} ( \langle u | x \rangle \otimes | ur_0 \rangle \otimes \langle xr_0 | \phi \rangle ) \quad {otherwise.} \end{array}\right .$
$CodeREP[r_0](| \phi \rangle ) = \left \{ \begin{array}{l} | \phi \rangle \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\ if \mbox{$NON_{r_0}(| \phi \rangle ) = \varnothing $,} \\
\sum _{x\in NON_{r_0}(| \phi \rangle )} \sum _{u:|u|=|x|-1} ( \langle u | x \rangle \otimes | ur_0 \rangle \otimes \langle xr_0 | \phi \rangle ) \quad {otherwise.} \end{array}\right .$
Notice that the quantum functions ![]() $CodeREMOVE[r_0]$ and
$CodeREMOVE[r_0]$ and ![]() $CodeREP[r_0]$ are query-independent.
$CodeREP[r_0]$ are query-independent.
We wish to include a simple example of ![]() $CodeREMOVE$ and
$CodeREMOVE$ and ![]() $CodeREP$.
$CodeREP$.
Example 12. Let ![]() $| \phi \rangle =\alpha | x_1r_0 \rangle | \psi _1 \rangle + \beta | x_2r_0 \rangle | \psi _2 \rangle + \gamma | r_0 \rangle | \psi _3 \rangle$ with
$| \phi \rangle =\alpha | x_1r_0 \rangle | \psi _1 \rangle + \beta | x_2r_0 \rangle | \psi _2 \rangle + \gamma | r_0 \rangle | \psi _3 \rangle$ with ![]() $\ell (| x_1r_0 \rangle | \psi _1 \rangle ) = \ell (| x_2r_0 \rangle | \psi _2 \rangle ) $
$\ell (| x_1r_0 \rangle | \psi _1 \rangle ) = \ell (| x_2r_0 \rangle | \psi _2 \rangle ) $ ![]() $=\ell (| r_0 \rangle | \psi _3 \rangle )$,
$=\ell (| r_0 \rangle | \psi _3 \rangle )$, ![]() $NON_{r_0}(| \psi \rangle ) =\{x_1,x_2\}$,
$NON_{r_0}(| \psi \rangle ) =\{x_1,x_2\}$, ![]() $|\alpha |^2+|\beta |^2+|\gamma |^2=1$, and
$|\alpha |^2+|\beta |^2+|\gamma |^2=1$, and ![]() $\alpha \beta \gamma \neq 0$. If
$\alpha \beta \gamma \neq 0$. If ![]() $x_1=0y_1$ and
$x_1=0y_1$ and ![]() $x_2=1y_2$ for two strings
$x_2=1y_2$ for two strings ![]() $y_1$ and
$y_1$ and ![]() $y_2$, then
$y_2$, then ![]() $CodeREMOVE[r_0](| \psi \rangle )$ equals
$CodeREMOVE[r_0](| \psi \rangle )$ equals ![]() $\alpha | y_10r_0 \rangle | \psi _1 \rangle + \beta | y_21r_0 \rangle | \psi _2 \rangle + \gamma | r_0 \rangle | \psi _3 \rangle$. If
$\alpha | y_10r_0 \rangle | \psi _1 \rangle + \beta | y_21r_0 \rangle | \psi _2 \rangle + \gamma | r_0 \rangle | \psi _3 \rangle$. If ![]() $x_1=z_10$ and
$x_1=z_10$ and ![]() $x_2=z_21$, then we obtain
$x_2=z_21$, then we obtain ![]() $CodeREP[r_0](| \phi \rangle ) = \alpha | 0z_1r_0 \rangle | \psi _1 \rangle + \beta | 1z_2r_0 \rangle | \psi _2 \rangle + \gamma | r_0 \rangle | \psi _3 \rangle$.
$CodeREP[r_0](| \phi \rangle ) = \alpha | 0z_1r_0 \rangle | \psi _1 \rangle + \beta | 1z_2r_0 \rangle | \psi _2 \rangle + \gamma | r_0 \rangle | \psi _3 \rangle$.
3.3 Code-controlled fast quantum recursion scheme
Let us introduce a new scheme, called Scheme IV, which is a variant of the multi-qubit quantum recursion scheme (Scheme T) geared up with the code skipping schemes in Section 3.2. Recall that, in Scheme T, we inductively discard ![]() $k$ qubits from an input quantum state
$k$ qubits from an input quantum state ![]() $| \phi \rangle$ until we consume all qubits except for the last (at most)
$| \phi \rangle$ until we consume all qubits except for the last (at most) ![]() $t$ qubits. Unlike Scheme T, since our access to input qubits is quite limited, we need to split the whole input into two separate parts, which play quite different roles as we will see.
$t$ qubits. Unlike Scheme T, since our access to input qubits is quite limited, we need to split the whole input into two separate parts, which play quite different roles as we will see.
Before formally introducing the complexity class ![]() $EQS$, for each quantum function
$EQS$, for each quantum function ![]() $f$ in
$f$ in ![]() $EQS_0$, we define its “code-controlled” version
$EQS_0$, we define its “code-controlled” version ![]() $f^*$ by setting
$f^*$ by setting ![]() $f^*(| xr_0 \rangle | \phi \rangle ) = | xr_0 \rangle | \phi \rangle$ if
$f^*(| xr_0 \rangle | \phi \rangle ) = | xr_0 \rangle | \phi \rangle$ if ![]() $|x|\leq 2$,
$|x|\leq 2$, ![]() $\ell (| \phi \rangle )\leq 1$, or
$\ell (| \phi \rangle )\leq 1$, or ![]() $|x|\gt |r_0|\mathrm{ilog}(\ell (| \phi \rangle ))$, and
$|x|\gt |r_0|\mathrm{ilog}(\ell (| \phi \rangle ))$, and ![]() $f^*(| xr_0 \rangle | \phi \rangle ) = f(| xr_0 \rangle )\otimes | \phi \rangle$ otherwise, for any
$f^*(| xr_0 \rangle | \phi \rangle ) = f(| xr_0 \rangle )\otimes | \phi \rangle$ otherwise, for any ![]() $x\in \{0,1\}^*$ and any
$x\in \{0,1\}^*$ and any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$. In the rest of this work, it is convenient to identify
$| \phi \rangle \in \mathscr{H}_{\infty }$. In the rest of this work, it is convenient to identify ![]() $f$ with
$f$ with ![]() $f^*$. It is important to note that
$f^*$. It is important to note that ![]() $f^*$ does not access
$f^*$ does not access ![]() $| \phi \rangle$ in
$| \phi \rangle$ in ![]() $| xr_0 \rangle | \phi \rangle$ by its definition.
$| xr_0 \rangle | \phi \rangle$ by its definition.
In the fast quantum recursion, on the contrary, we discard a half of the second part of input quantum state ![]() $| xr_0 \rangle \otimes | \phi \rangle$. By halving the input at each step, this recursive process quickly terminates.
$| xr_0 \rangle \otimes | \phi \rangle$. By halving the input at each step, this recursive process quickly terminates.
Definition 13. We introduce the following scheme.
IV. The code-controlled fast quantum recursion scheme. Assume that we are given quantum functions
 $d$,
$d$,  $g$,
$g$,  $h$, a number
$h$, a number  $t\in \mathbb{N}^{+}$, and a string
$t\in \mathbb{N}^{+}$, and a string  $r_0\in \{0,1\}^+$ (where
$r_0\in \{0,1\}^+$ (where  $d$ is not defined using
$d$ is not defined using  $MEAS[\cdot ]$ but
$MEAS[\cdot ]$ but  $d$ and
$d$ and  $h$ may be defined using
$h$ may be defined using  $CodeSKIP_{+}[\cdot ]$ and
$CodeSKIP_{+}[\cdot ]$ and  $CodeSKIP_{-}[\cdot ]$). We then define
$CodeSKIP_{-}[\cdot ]$). We then define  $F\equiv CFQRec_t[r_0,d,g,h| \mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ for
$F\equiv CFQRec_t[r_0,d,g,h| \mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ for  $\mathscr{P}_{|r_0|}=\{p_u\}_{u\in \{0,1\}^{|r_0|}}$ with
$\mathscr{P}_{|r_0|}=\{p_u\}_{u\in \{0,1\}^{|r_0|}}$ with  $p_u\in \{I,HalfSWAP\}$ and
$p_u\in \{I,HalfSWAP\}$ and  $\mathscr{F}_{|r_0|}=\{f_u\}_{u\in \{0,1\}^{|r_0|}}$ with
$\mathscr{F}_{|r_0|}=\{f_u\}_{u\in \{0,1\}^{|r_0|}}$ with  $f_u\in \{I,F\}$ as follows. For any
$f_u\in \{I,F\}$ as follows. For any  $x\in \{0,1\}^*$ and any
$x\in \{0,1\}^*$ and any  $| \phi \rangle \in \mathscr{H}_{\infty }$, let
$| \phi \rangle \in \mathscr{H}_{\infty }$, let
(i)
 $F(| xr_0 \rangle | \phi \rangle ) = g(| xr_0 \rangle | \phi \rangle )\qquad\qquad\qquad\qquad\quad\qquad\ \ $ if
$F(| xr_0 \rangle | \phi \rangle ) = g(| xr_0 \rangle | \phi \rangle )\qquad\qquad\qquad\qquad\quad\qquad\ \ $ if  $x=\lambda$,
$x=\lambda$,  $\ell (| \phi \rangle )\leq t$, or
$\ell (| \phi \rangle )\leq t$, or  $|x|\gt |r_0|k$,
$|x|\gt |r_0|k$,(ii)
 $F(| xr_0 \rangle | \phi \rangle ) = \sum _{u:|u|=|r_0|} \sum _{v:|v|= \ell (\langle u | xr_0 \rangle )} ( h( | u \rangle | v \rangle ) \otimes p_u^{-1} ( \langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) )\qquad\quad$ otherwise,
$F(| xr_0 \rangle | \phi \rangle ) = \sum _{u:|u|=|r_0|} \sum _{v:|v|= \ell (\langle u | xr_0 \rangle )} ( h( | u \rangle | v \rangle ) \otimes p_u^{-1} ( \langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) )\qquad\quad$ otherwise,
where
 $k=\mathrm{ilog}(\ell (| \phi \rangle ))$,
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$,  $x\in NON_{r_0}$,
$x\in NON_{r_0}$,  $| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle = \sum _{s:|s|= m_u(| \phi \rangle )} ( f_u( \langle u | x'r_0 \rangle \otimes | s \rangle ) \otimes \langle s | \psi _{p_u,\phi } \rangle )$,
$| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle = \sum _{s:|s|= m_u(| \phi \rangle )} ( f_u( \langle u | x'r_0 \rangle \otimes | s \rangle ) \otimes \langle s | \psi _{p_u,\phi } \rangle )$,  $d(| xr_0 \rangle ) = | x'r_0 \rangle$ with
$d(| xr_0 \rangle ) = | x'r_0 \rangle$ with  $x'\in NON_{r_0}$,
$x'\in NON_{r_0}$,  $| \psi _{p_u,\phi } \rangle = p_{u}(| \phi \rangle )$. Moreover,
$| \psi _{p_u,\phi } \rangle = p_{u}(| \phi \rangle )$. Moreover,  $m_u(\cdot )$ is determined to be
$m_u(\cdot )$ is determined to be  $LH$ if
$LH$ if  $p_u=I$ and
$p_u=I$ and  $RH$ if
$RH$ if  $p_u=HalfSWAP$. Notice that
$p_u=HalfSWAP$. Notice that  $u\neq r_0$ follows from
$u\neq r_0$ follows from  $x'\in NON_{r_0}$. In the other case where an input, say,
$x'\in NON_{r_0}$. In the other case where an input, say,  $| y \rangle$ to
$| y \rangle$ to  $F$ satisfies
$F$ satisfies  $NON_{r_0}(| y \rangle )=\varnothing$, we automatically set
$NON_{r_0}(| y \rangle )=\varnothing$, we automatically set  $F(| y \rangle ) =| y \rangle$. For readability, the prefix term “code-controlled” is often dropped and
$F(| y \rangle ) =| y \rangle$. For readability, the prefix term “code-controlled” is often dropped and  $| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle$ is expressed briefly as
$| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle$ is expressed briefly as  $| \zeta _{u,p_u,\phi } \rangle$ as long as
$| \zeta _{u,p_u,\phi } \rangle$ as long as  $x'r_0$ is clear from the context.
$x'r_0$ is clear from the context.
The quantum functions ![]() $d,g,h$ in the above definition are called ground (quantum) functions of
$d,g,h$ in the above definition are called ground (quantum) functions of ![]() $F$. If
$F$. If ![]() $g$ is query-independent, Scheme IV is said to be query-independent.
$g$ is query-independent, Scheme IV is said to be query-independent.
Although the description of Items (i)–(ii) in Scheme IV concerns only with a classical string ![]() $xr_0$, whenever any quantum state
$xr_0$, whenever any quantum state ![]() $| \psi \rangle =\sum _{x}\alpha _x| xr_0 \rangle \otimes | \phi _x \rangle$ is plugged in to
$| \psi \rangle =\sum _{x}\alpha _x| xr_0 \rangle \otimes | \phi _x \rangle$ is plugged in to ![]() $F$, we obtain the result
$F$, we obtain the result ![]() $\sum _{x}\alpha _x F(| xr_0 \rangle | \phi _x \rangle )$.
$\sum _{x}\alpha _x F(| xr_0 \rangle | \phi _x \rangle )$.
Since ![]() $p_u\in \{I,HalfSWAP\}$ and
$p_u\in \{I,HalfSWAP\}$ and ![]() $|x'|=|x|$, it follows that
$|x'|=|x|$, it follows that ![]() $\ell (| \psi _{u,p_u,\phi } \rangle ) = \ell (| \phi \rangle )$,
$\ell (| \psi _{u,p_u,\phi } \rangle ) = \ell (| \phi \rangle )$, ![]() $\ell (| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) = \ell (\langle u | x'r_0 \rangle ) + \ell (| \phi \rangle )$, and
$\ell (| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) = \ell (\langle u | x'r_0 \rangle ) + \ell (| \phi \rangle )$, and ![]() $\ell (\langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) = \ell (| \phi \rangle )$. In Item (ii), since the size
$\ell (\langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) = \ell (| \phi \rangle )$. In Item (ii), since the size ![]() $|s|$ is exactly
$|s|$ is exactly ![]() $LH(| \phi \rangle )$ (or
$LH(| \phi \rangle )$ (or ![]() $RH(| \phi \rangle )$),
$RH(| \phi \rangle )$), ![]() $f_u$ takes inputs of length
$f_u$ takes inputs of length ![]() $(\ell (| x'r_0 \rangle )-|r_0|)+\lceil \ell (| \phi \rangle )/2 \rceil$ (or
$(\ell (| x'r_0 \rangle )-|r_0|)+\lceil \ell (| \phi \rangle )/2 \rceil$ (or ![]() $(\ell (| x'r_0 \rangle )-|r_0|)+\lfloor \ell (| \phi \rangle )/2 \rfloor$). Hence, within
$(\ell (| x'r_0 \rangle )-|r_0|)+\lfloor \ell (| \phi \rangle )/2 \rfloor$). Hence, within ![]() $\lceil \log{\ell (| \phi \rangle )} \rceil$ recursive steps, the whole process terminates.
$\lceil \log{\ell (| \phi \rangle )} \rceil$ recursive steps, the whole process terminates.
As a special case of Scheme IV, when ![]() $r_0=1$, Item (ii) has the following simple form:
$r_0=1$, Item (ii) has the following simple form:
(ii![]() $'$)
$'$) ![]() $F(| 0^n1 \rangle | \phi \rangle ) = \sum _{v:|v|=n} ( h( | 0 \rangle \otimes | v \rangle ) \otimes p_0^{-1} ( \langle v | \zeta _{0,p_0,\phi }^{(0^n1)} \rangle ))$,
$F(| 0^n1 \rangle | \phi \rangle ) = \sum _{v:|v|=n} ( h( | 0 \rangle \otimes | v \rangle ) \otimes p_0^{-1} ( \langle v | \zeta _{0,p_0,\phi }^{(0^n1)} \rangle ))$,
where ![]() $| \zeta _{0,p_0,\phi }^{(0^n1)} \rangle = \sum _{s:|s|= m(| \phi \rangle )} ( f_0( | 0^{n-1}1 \rangle \otimes | s \rangle ) \otimes \langle s | \psi _{p_0,\phi } \rangle )$.
$| \zeta _{0,p_0,\phi }^{(0^n1)} \rangle = \sum _{s:|s|= m(| \phi \rangle )} ( f_0( | 0^{n-1}1 \rangle \otimes | s \rangle ) \otimes \langle s | \psi _{p_0,\phi } \rangle )$.
At this moment, it is worth remarking the usage of the length function ![]() $\ell (\cdot )$. In Scheme IV, the input quantum state
$\ell (\cdot )$. In Scheme IV, the input quantum state ![]() $| xr_0 \rangle | \phi \rangle$ is reduced to
$| xr_0 \rangle | \phi \rangle$ is reduced to ![]() $\langle u | x'r_0 \rangle | s \rangle$ (with
$\langle u | x'r_0 \rangle | s \rangle$ (with ![]() $|s|=m_u(| \phi \rangle )$ and
$|s|=m_u(| \phi \rangle )$ and ![]() $|u|=|r_0|$) so that we can inductively apply
$|u|=|r_0|$) so that we can inductively apply ![]() $F$ (when
$F$ (when ![]() $f_u=F$) to it. The length
$f_u=F$) to it. The length ![]() $\ell (| \phi \rangle )$ then becomes
$\ell (| \phi \rangle )$ then becomes ![]() $\ell (| s \rangle )$, and thus the conditional execution of Item (i) depends on the value
$\ell (| s \rangle )$, and thus the conditional execution of Item (i) depends on the value ![]() $\ell (| s \rangle )$.
$\ell (| s \rangle )$.
To understand Scheme IV better, we provide in Example14 a simple example of how to calculate the quantum function ![]() $F\equiv CFQRec_t[r_0,d,g,h | \mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ step by step.
$F\equiv CFQRec_t[r_0,d,g,h | \mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ step by step.
Example 14. In this example, we wish to show how to calculate the quantum function ![]() $F\equiv CFQRec_t[r_0,d,g,h | \mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ defined with the parameters
$F\equiv CFQRec_t[r_0,d,g,h | \mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ defined with the parameters ![]() $t=1$,
$t=1$, ![]() $r_0=1$,
$r_0=1$, ![]() $d=I$, and
$d=I$, and ![]() $g\equiv I$. Furthermore,
$g\equiv I$. Furthermore, ![]() $h$ is defined as
$h$ is defined as ![]() $h(| 01 \rangle )=| 11 \rangle$ and
$h(| 01 \rangle )=| 11 \rangle$ and ![]() $h(| 010^m1 \rangle )=| 10^{m+1}1 \rangle$ for any
$h(| 010^m1 \rangle )=| 10^{m+1}1 \rangle$ for any ![]() $m\in \mathbb{N}$. We also set
$m\in \mathbb{N}$. We also set ![]() $p_0=HalfSWAP$,
$p_0=HalfSWAP$, ![]() $p_1=I$,
$p_1=I$, ![]() $f_0=F$, and
$f_0=F$, and ![]() $f_1=I$. Let
$f_1=I$. Let ![]() $x\in \{0\}^*$ and
$x\in \{0\}^*$ and ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$. In what follows, we will calculate
$| \phi \rangle \in \mathscr{H}_{\infty }$. In what follows, we will calculate ![]() $F(| x1 \rangle | \phi \rangle )$ in a “bottom-up” fashion.
$F(| x1 \rangle | \phi \rangle )$ in a “bottom-up” fashion.
(1) We start with the base case. If ![]() $x=\lambda$, then
$x=\lambda$, then ![]() $F(| 1 \rangle | \phi \rangle )=g(| 1 \rangle | \phi \rangle ) = | 1 \rangle | \phi \rangle$. If
$F(| 1 \rangle | \phi \rangle )=g(| 1 \rangle | \phi \rangle ) = | 1 \rangle | \phi \rangle$. If ![]() $x=0^m1$ with
$x=0^m1$ with ![]() $m\geq 1$ and
$m\geq 1$ and ![]() $\ell (| \phi \rangle )\leq 1$, then
$\ell (| \phi \rangle )\leq 1$, then ![]() $F(| 0^m1 \rangle | \phi \rangle ) = g(| 0^m1 \rangle | \phi \rangle ) = | 0^{m}1 \rangle | \phi \rangle$.
$F(| 0^m1 \rangle | \phi \rangle ) = g(| 0^m1 \rangle | \phi \rangle ) = | 0^{m}1 \rangle | \phi \rangle$.
(2) Hereafter, we assume that ![]() $x\neq \lambda$ and
$x\neq \lambda$ and ![]() $\ell (| \phi \rangle )\geq 2$. For simplicity, let
$\ell (| \phi \rangle )\geq 2$. For simplicity, let ![]() $| \phi \rangle$ denote
$| \phi \rangle$ denote ![]() $| u \rangle$ for a certain string
$| u \rangle$ for a certain string ![]() $u\in \{0,1\}^*$. When
$u\in \{0,1\}^*$. When ![]() $u=u_1u_2\cdots u_n$ and
$u=u_1u_2\cdots u_n$ and ![]() $1\leq i\lt j\leq n$, we use the succinct notation
$1\leq i\lt j\leq n$, we use the succinct notation ![]() $u_{[i,j]}$ to express the string
$u_{[i,j]}$ to express the string ![]() $u_{i}u_{i+1}\cdots u_{j}$.
$u_{i}u_{i+1}\cdots u_{j}$.
(a) We first calculate ![]() $F(| 01 \rangle | u \rangle )$ for
$F(| 01 \rangle | u \rangle )$ for ![]() $u=u_1u_2u_3u_4$. Since
$u=u_1u_2u_3u_4$. Since ![]() $| u \rangle =| u_{[1,2]} \rangle | u_{[3,4]} \rangle$, we obtain
$| u \rangle =| u_{[1,2]} \rangle | u_{[3,4]} \rangle$, we obtain ![]() $p_0(| u \rangle )=| u_{[3,4]} \rangle | u_{[1,2]} \rangle$. We also obtain
$p_0(| u \rangle )=| u_{[3,4]} \rangle | u_{[1,2]} \rangle$. We also obtain ![]() $| \zeta _{0,p_0,u} \rangle = F(| 1 \rangle | u_{[3,4]} \rangle )\otimes | u_{[1,2]} \rangle = | 1 \rangle \otimes | u_{[3,4]} \rangle | u_{[1,2]} \rangle$ by (1), and thus
$| \zeta _{0,p_0,u} \rangle = F(| 1 \rangle | u_{[3,4]} \rangle )\otimes | u_{[1,2]} \rangle = | 1 \rangle \otimes | u_{[3,4]} \rangle | u_{[1,2]} \rangle$ by (1), and thus ![]() $F(| 01 \rangle | u \rangle )$ equals
$F(| 01 \rangle | u \rangle )$ equals ![]() $h(| 0 \rangle \otimes | 1 \rangle ) \otimes p_0^{-1}( | u_{[3,4]} \rangle | u_{[1,2]} \rangle )$, which is
$h(| 0 \rangle \otimes | 1 \rangle ) \otimes p_0^{-1}( | u_{[3,4]} \rangle | u_{[1,2]} \rangle )$, which is ![]() $| 11 \rangle | u_{[1,2]} \rangle | u_{3,4]} \rangle = | 11 \rangle | u \rangle$.
$| 11 \rangle | u_{[1,2]} \rangle | u_{3,4]} \rangle = | 11 \rangle | u \rangle$.
(b) Next, we calculate ![]() $F(| 001 \rangle | u' \rangle )$ for
$F(| 001 \rangle | u' \rangle )$ for ![]() $u'=u_1u_2\cdots u_8$. Note that
$u'=u_1u_2\cdots u_8$. Note that ![]() $| \zeta _{0,p_0,u'} \rangle = F(| 01 \rangle | u^{\prime}_{[5,8]} \rangle )\otimes | u^{\prime}_{[1,4]} \rangle = | 11 \rangle \otimes | u^{\prime}_{[5,8]} \rangle | u^{\prime}_{[1,4]} \rangle$ by (a). From this, we obtain
$| \zeta _{0,p_0,u'} \rangle = F(| 01 \rangle | u^{\prime}_{[5,8]} \rangle )\otimes | u^{\prime}_{[1,4]} \rangle = | 11 \rangle \otimes | u^{\prime}_{[5,8]} \rangle | u^{\prime}_{[1,4]} \rangle$ by (a). From this, we obtain ![]() $F(| 001 \rangle | u' \rangle ) = h(| 0 \rangle \otimes | 11 \rangle ) \otimes p_0^{-1}(| u^{\prime}_{[5,8]} \rangle | u^{\prime}_{[1,4]} \rangle ) = | 101 \rangle | u' \rangle$.
$F(| 001 \rangle | u' \rangle ) = h(| 0 \rangle \otimes | 11 \rangle ) \otimes p_0^{-1}(| u^{\prime}_{[5,8]} \rangle | u^{\prime}_{[1,4]} \rangle ) = | 101 \rangle | u' \rangle$.
3.4 Power of Scheme IV
In what follows, we intend to show the usefulness of Scheme IV by applying it to construct a quantum function, which calculates the logarithmic value of (part of) input size. Formally, for any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$ and
$| \phi \rangle \in \mathscr{H}_{\infty }$ and ![]() $m\in \mathbb{N}^{+}$, we define
$m\in \mathbb{N}^{+}$, we define ![]() $SIZE_1$ as
$SIZE_1$ as ![]() $SIZE_1(| 0^m1 \rangle | \phi \rangle ) = | 0^k1 \rangle | 0^{m-k-1}1 \rangle | \phi \rangle$ if
$SIZE_1(| 0^m1 \rangle | \phi \rangle ) = | 0^k1 \rangle | 0^{m-k-1}1 \rangle | \phi \rangle$ if ![]() $\ell (| \phi \rangle )\leq 2^{m-1}$, where
$\ell (| \phi \rangle )\leq 2^{m-1}$, where ![]() $k=\mathrm{ilog}(\ell (| \phi \rangle ))$, and
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$, and ![]() $SIZE_1(| 0^m1 \rangle | \phi \rangle ) = | 0^m1 \rangle | \phi \rangle$ otherwise. More generally, for any
$SIZE_1(| 0^m1 \rangle | \phi \rangle ) = | 0^m1 \rangle | \phi \rangle$ otherwise. More generally, for any ![]() $r_0\notin \{0\}^*$ with
$r_0\notin \{0\}^*$ with ![]() $|r_0|\geq 1$, we define
$|r_0|\geq 1$, we define ![]() $SIZE_{r_0}$ as
$SIZE_{r_0}$ as ![]() $SIZE_{r_0}(| 0^{m|r_0|}r_0 \rangle | \phi \rangle ) = | 0^{k|r_0|}r_0 \rangle | 0^{(m-k-1)|r_0|}r_0 \rangle | \phi \rangle$. The choice of
$SIZE_{r_0}(| 0^{m|r_0|}r_0 \rangle | \phi \rangle ) = | 0^{k|r_0|}r_0 \rangle | 0^{(m-k-1)|r_0|}r_0 \rangle | \phi \rangle$. The choice of ![]() $0^{m|r_0|}$ here is only for simplicity.
$0^{m|r_0|}$ here is only for simplicity.
For brevity, we intend to use the notation ![]() $EQS_0+IV$ to express the set of quantum functions constructed by applying Schemes I–IV.
$EQS_0+IV$ to express the set of quantum functions constructed by applying Schemes I–IV.
Lemma 15. Let ![]() $r_0\notin \{0\}^*$ with
$r_0\notin \{0\}^*$ with ![]() $|r_0|\geq 1$. The above quantum function
$|r_0|\geq 1$. The above quantum function ![]() $SIZE_{r_0}$ can be definable within
$SIZE_{r_0}$ can be definable within ![]() $EQS_0+IV$.
$EQS_0+IV$.
Proof. We prove the lemma only for the simple case of ![]() $r_0=1$. Given
$r_0=1$. Given ![]() $m\in \mathbb{N}^{+}$ and
$m\in \mathbb{N}^{+}$ and ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$, let
$| \phi \rangle \in \mathscr{H}_{\infty }$, let ![]() $| \xi \rangle =| 0^{m}1 \rangle | \phi \rangle$. Recall the quantum function
$| \xi \rangle =| 0^{m}1 \rangle | \phi \rangle$. Recall the quantum function ![]() $LengthQ_1$ from Lemma5(9) and, for simplicity, write
$LengthQ_1$ from Lemma5(9) and, for simplicity, write ![]() $g$ for
$g$ for ![]() $LengthQ_1$. It then follows that
$LengthQ_1$. It then follows that ![]() $g(| 1 \rangle ) = | 1 \rangle$ and
$g(| 1 \rangle ) = | 1 \rangle$ and ![]() $g(| 0^{m}1 \rangle ) = | 10^{m-1}1 \rangle$ if
$g(| 0^{m}1 \rangle ) = | 10^{m-1}1 \rangle$ if ![]() $m\geq 1$. We denote by
$m\geq 1$. We denote by ![]() $F$ the quantum function
$F$ the quantum function ![]() $CFQRec_1[1,I,g,I | \{p_0,p_1\},\{f_0,f_1\}]$ with the parameters
$CFQRec_1[1,I,g,I | \{p_0,p_1\},\{f_0,f_1\}]$ with the parameters ![]() $f_{0}=F$,
$f_{0}=F$, ![]() $f_{1}=I$, and
$f_{1}=I$, and ![]() $p_0=p_1=I$.
$p_0=p_1=I$.
If either ![]() $m=0$ or
$m=0$ or ![]() $\ell (| \phi \rangle ) \leq 1$, then
$\ell (| \phi \rangle ) \leq 1$, then ![]() $F(| 1 \rangle | \phi \rangle )$ equals
$F(| 1 \rangle | \phi \rangle )$ equals ![]() $g(| 1 \rangle )\otimes | \phi \rangle = | 1 \rangle | \phi \rangle$. Hereafter, we assume that
$g(| 1 \rangle )\otimes | \phi \rangle = | 1 \rangle | \phi \rangle$. Hereafter, we assume that ![]() $m\geq 1$ and
$m\geq 1$ and ![]() $\ell (| \phi \rangle )\geq 2$. By induction hypothesis, we obtain
$\ell (| \phi \rangle )\geq 2$. By induction hypothesis, we obtain ![]() $F(| 0^{m-1}1 \rangle \otimes | s \rangle ) = | 0^{k-1}1 \rangle | 0^{m-k-1}1 \rangle | \phi \rangle$ if
$F(| 0^{m-1}1 \rangle \otimes | s \rangle ) = | 0^{k-1}1 \rangle | 0^{m-k-1}1 \rangle | \phi \rangle$ if ![]() $\ell (| s \rangle )\leq 2^{m-2}$ and
$\ell (| s \rangle )\leq 2^{m-2}$ and ![]() $k-1=\mathrm{ilog}(\ell (| s \rangle ))$. Starting with
$k-1=\mathrm{ilog}(\ell (| s \rangle ))$. Starting with ![]() $| \xi \rangle = | 0^m1 \rangle | \phi \rangle$,
$| \xi \rangle = | 0^m1 \rangle | \phi \rangle$, ![]() $F(| \xi \rangle )$ equals
$F(| \xi \rangle )$ equals ![]() $| 0 \rangle \otimes \sum _{s:|s|=LH(| \phi \rangle )} F( | 0^{m-1}1 \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle = | 0 \rangle \otimes | 0^{k-1}1 \rangle | 0^{m-k-1}1 \rangle | \phi \rangle = | 0^k1 \rangle | 0^{m-k-1}1 \rangle | \phi \rangle$.
$| 0 \rangle \otimes \sum _{s:|s|=LH(| \phi \rangle )} F( | 0^{m-1}1 \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle = | 0 \rangle \otimes | 0^{k-1}1 \rangle | 0^{m-k-1}1 \rangle | \phi \rangle = | 0^k1 \rangle | 0^{m-k-1}1 \rangle | \phi \rangle$.
The general case of ![]() $r_0\neq 1$ is similarly handled. The desired quantum function
$r_0\neq 1$ is similarly handled. The desired quantum function ![]() $SIZE_1$ is therefore set to be
$SIZE_1$ is therefore set to be ![]() $F$.
$F$.
Given an input of the form ![]() $| xr_0 \rangle | \phi \rangle$, it is possible to apply any quantum function
$| xr_0 \rangle | \phi \rangle$, it is possible to apply any quantum function ![]() $g$ in
$g$ in ![]() $EQS_0$ to the first segment
$EQS_0$ to the first segment ![]() $| xr_0 \rangle$ with keeping the second segment
$| xr_0 \rangle$ with keeping the second segment ![]() $| \phi \rangle$ intact. This can be done by the use of Scheme IV in the following way.
$| \phi \rangle$ intact. This can be done by the use of Scheme IV in the following way.
Lemma 16. For any string ![]() $r_0\in \{0,1\}^+$ and any quantum function
$r_0\in \{0,1\}^+$ and any quantum function ![]() $g\in \widehat{EQS}_0$ satisfying
$g\in \widehat{EQS}_0$ satisfying ![]() $g(| r_0 \rangle \otimes | \phi \rangle ) = g(| r_0 \rangle )\otimes | \phi \rangle$, there exists another quantum function
$g(| r_0 \rangle \otimes | \phi \rangle ) = g(| r_0 \rangle )\otimes | \phi \rangle$, there exists another quantum function ![]() $F$ definable within
$F$ definable within ![]() $EQS_0+IV$ such that
$EQS_0+IV$ such that ![]() $F(| xr_0 \rangle | \phi \rangle ) = g(| xr_0 \rangle )\otimes | \phi \rangle$ for any
$F(| xr_0 \rangle | \phi \rangle ) = g(| xr_0 \rangle )\otimes | \phi \rangle$ for any ![]() $x\in NON_{r_0}$ and any
$x\in NON_{r_0}$ and any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$.
$| \phi \rangle \in \mathscr{H}_{\infty }$.
Proof. Let us recall the quantum function ![]() $Skip_k[g]$ from Lemma4. For a given
$Skip_k[g]$ from Lemma4. For a given ![]() $g\in \widehat{EQS}_0$, we set
$g\in \widehat{EQS}_0$, we set ![]() $h\equiv g\circ Skip_{|r_0|}[g^{-1}]$. Notice that
$h\equiv g\circ Skip_{|r_0|}[g^{-1}]$. Notice that ![]() $h$ belongs to
$h$ belongs to ![]() $\widehat{EQS}_0$ because
$\widehat{EQS}_0$ because ![]() $g^{-1}$ exists within
$g^{-1}$ exists within ![]() $\widehat{EQS}_0$ (as shown in Lemma23). The desired quantum function
$\widehat{EQS}_0$ (as shown in Lemma23). The desired quantum function ![]() $F$ is defined by Scheme IV as
$F$ is defined by Scheme IV as ![]() $F\equiv CFQRec_{1}[r_0,I,g,h|\mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$, where
$F\equiv CFQRec_{1}[r_0,I,g,h|\mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$, where ![]() $\mathscr{P}_{|r_0|} =\{p_u\}_{u\in \{0,1\}^{|r_0|}}$ with
$\mathscr{P}_{|r_0|} =\{p_u\}_{u\in \{0,1\}^{|r_0|}}$ with ![]() $p_u=I$ for all
$p_u=I$ for all ![]() $u$’s and
$u$’s and ![]() $\mathscr{F}_{|r_0|} =\{f_u\}_{u\in \{0,1\}^{|r_0|}}$ with
$\mathscr{F}_{|r_0|} =\{f_u\}_{u\in \{0,1\}^{|r_0|}}$ with ![]() $f_u = F$ for all
$f_u = F$ for all ![]() $u$’s. As a special case, we then obtain
$u$’s. As a special case, we then obtain ![]() $F(| r_0 \rangle | \phi \rangle ) = g(| r_0 \rangle | \phi \rangle ) = g(| r_0 \rangle )\otimes | \phi \rangle$.
$F(| r_0 \rangle | \phi \rangle ) = g(| r_0 \rangle | \phi \rangle ) = g(| r_0 \rangle )\otimes | \phi \rangle$.
Assume by induction hypothesis that ![]() $F(| xr_0 \rangle | \phi \rangle ) = g(| xr_0 \rangle )\otimes | \phi \rangle$. Let us consider
$F(| xr_0 \rangle | \phi \rangle ) = g(| xr_0 \rangle )\otimes | \phi \rangle$. Let us consider ![]() $F(| axr_0 \rangle | \phi \rangle )$ for an arbitrary string
$F(| axr_0 \rangle | \phi \rangle )$ for an arbitrary string ![]() $a\in \{0,1\}^{|r_0|}\cap NON_{r_0}$. It then follows that
$a\in \{0,1\}^{|r_0|}\cap NON_{r_0}$. It then follows that ![]() $| \zeta _{a,I,\phi }^{(xr_0)} \rangle = \sum _{s:|s|=LH(| \phi \rangle )} ( F(| xr_0 \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} ( g(| xr_0 \rangle )\otimes | s \rangle \langle s | \phi \rangle ) = g(| xr_0 \rangle )\otimes | \phi \rangle$. We therefore conclude that
$| \zeta _{a,I,\phi }^{(xr_0)} \rangle = \sum _{s:|s|=LH(| \phi \rangle )} ( F(| xr_0 \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} ( g(| xr_0 \rangle )\otimes | s \rangle \langle s | \phi \rangle ) = g(| xr_0 \rangle )\otimes | \phi \rangle$. We therefore conclude that ![]() $F(| axr_0 \rangle | \phi \rangle ) = \sum _{v:|v|=|xr_0|} ( h(| a \rangle | v \rangle ) \otimes \langle v | \zeta _{a,I,\phi }^{(xr_0)} \rangle ) = \sum _{v:|v|=|xr_0|} ( h(| a \rangle | v \rangle ) \otimes \langle v | \psi _{g,xr_0} \rangle \otimes | \phi \rangle ) = h(| a \rangle | \psi _{g,xr_0} \rangle )\otimes | \phi \rangle = h(| a \rangle \otimes g(| xr_0 \rangle ))\otimes | \phi \rangle$ since
$F(| axr_0 \rangle | \phi \rangle ) = \sum _{v:|v|=|xr_0|} ( h(| a \rangle | v \rangle ) \otimes \langle v | \zeta _{a,I,\phi }^{(xr_0)} \rangle ) = \sum _{v:|v|=|xr_0|} ( h(| a \rangle | v \rangle ) \otimes \langle v | \psi _{g,xr_0} \rangle \otimes | \phi \rangle ) = h(| a \rangle | \psi _{g,xr_0} \rangle )\otimes | \phi \rangle = h(| a \rangle \otimes g(| xr_0 \rangle ))\otimes | \phi \rangle$ since ![]() $|v|=|xr_0|$, where
$|v|=|xr_0|$, where ![]() $| \psi _{g,xr_0} \rangle = g(| xr_0 \rangle )$. Because
$| \psi _{g,xr_0} \rangle = g(| xr_0 \rangle )$. Because ![]() $h(| a \rangle \otimes g(| xr_0 \rangle ))$ equals
$h(| a \rangle \otimes g(| xr_0 \rangle ))$ equals ![]() $g(| a \rangle \otimes g^{-1}(g(| xr_0 \rangle )) = g(| axr_0 \rangle )$, it follows that
$g(| a \rangle \otimes g^{-1}(g(| xr_0 \rangle )) = g(| axr_0 \rangle )$, it follows that ![]() $F(| 0xr_0 \rangle | \phi \rangle ) = g(| axr_0 \rangle )\otimes | \phi \rangle$, as requested.
$F(| 0xr_0 \rangle | \phi \rangle ) = g(| axr_0 \rangle )\otimes | \phi \rangle$, as requested.
As shown in Proposition18, Scheme IV turns out to be so powerful that it generates quantum functions, which can modify the first segment, ![]() $| xr_0 \rangle$,
$| xr_0 \rangle$, ![]() $\mathrm{ilog}(\ell (| \phi \rangle ))$ times for any given input of the form
$\mathrm{ilog}(\ell (| \phi \rangle ))$ times for any given input of the form ![]() $| xr_0 \rangle | \phi \rangle$.
$| xr_0 \rangle | \phi \rangle$.
Let ![]() $h$ be any quantum function defined by Schemes I–III. Consider a quantum function
$h$ be any quantum function defined by Schemes I–III. Consider a quantum function ![]() $\hat{h}$ defined inductively as
$\hat{h}$ defined inductively as
for any ![]() $x\in NON_{r_0}$ with
$x\in NON_{r_0}$ with ![]() $x\neq \lambda$. This recursive construction scheme (*) looks similar to Scheme T but it is not supported in our system
$x\neq \lambda$. This recursive construction scheme (*) looks similar to Scheme T but it is not supported in our system ![]() $EQS_0+IV$. Nevertheless, as shown in Proposition18, whenever the length of an input qustring
$EQS_0+IV$. Nevertheless, as shown in Proposition18, whenever the length of an input qustring ![]() $| xr_0 \rangle$ is “short” enough compared to another supplemental input qustring
$| xr_0 \rangle$ is “short” enough compared to another supplemental input qustring ![]() $| \phi \rangle$, it may be possible to “realize” this scheme within
$| \phi \rangle$, it may be possible to “realize” this scheme within ![]() $EQS_0+IV$.
$EQS_0+IV$.
Example 17. As a concrete example of the above function ![]() $\hat{h}$, we consider
$\hat{h}$, we consider ![]() $CodeSKIP_{+}[r_0,g,I]$ (as well as
$CodeSKIP_{+}[r_0,g,I]$ (as well as ![]() $CodeSKIP_{-}[r_0,g,I]$) for a norm-preserving quantum function
$CodeSKIP_{-}[r_0,g,I]$) for a norm-preserving quantum function ![]() $g$. To see this, we set
$g$. To see this, we set ![]() $h$ to be
$h$ to be ![]() $g\circ Skip_{|r_0|}[g^{-1}]$ and define
$g\circ Skip_{|r_0|}[g^{-1}]$ and define ![]() $\hat{h}$ from
$\hat{h}$ from ![]() $h$ by applying the above scheme (*). Here, we wish to claim that this quantum function
$h$ by applying the above scheme (*). Here, we wish to claim that this quantum function ![]() $\hat{h}$ coincides with
$\hat{h}$ coincides with ![]() $CodeSKIP_{+}[r_0,g,I]$. Initially, we obtain
$CodeSKIP_{+}[r_0,g,I]$. Initially, we obtain ![]() $CodeSKIP_{+}[r_0,g,I](| r_0 \rangle ) = | r_0 \rangle = \hat{h}(| r_0 \rangle )$ by (*). For any two strings
$CodeSKIP_{+}[r_0,g,I](| r_0 \rangle ) = | r_0 \rangle = \hat{h}(| r_0 \rangle )$ by (*). For any two strings ![]() $a,x\in NON_{r_0}\cap \{0,1\}^{+}$ with
$a,x\in NON_{r_0}\cap \{0,1\}^{+}$ with ![]() $|a|=|r_0|$, it follows from (*) that
$|a|=|r_0|$, it follows from (*) that ![]() $\hat{h}(| axr_0 \rangle ) = \sum _{u:|u|=|r_0|} h(| u \rangle \otimes \hat{h}(\langle u | axr_0 \rangle )) = h(| a \rangle \otimes CodeSKIP_{+}[r_0,g,I](| xr_0 \rangle )) = h(| a \rangle \otimes g(| xr_0 \rangle )) = g\circ Skip_{|r_0|}[g^{-1}](| a \rangle \otimes g(| xr_0 \rangle )) = g(| axr_0 \rangle )$.
$\hat{h}(| axr_0 \rangle ) = \sum _{u:|u|=|r_0|} h(| u \rangle \otimes \hat{h}(\langle u | axr_0 \rangle )) = h(| a \rangle \otimes CodeSKIP_{+}[r_0,g,I](| xr_0 \rangle )) = h(| a \rangle \otimes g(| xr_0 \rangle )) = g\circ Skip_{|r_0|}[g^{-1}](| a \rangle \otimes g(| xr_0 \rangle )) = g(| axr_0 \rangle )$.
The quantum function ![]() $\hat{h}$ given by the recursive scheme (*) may not be constructed by the only use of Schemes I–IV since the
$\hat{h}$ given by the recursive scheme (*) may not be constructed by the only use of Schemes I–IV since the ![]() $k$-qubit quantum recursion scheme is required. For relatively “short” inputs, however, it is possible to compute the value of
$k$-qubit quantum recursion scheme is required. For relatively “short” inputs, however, it is possible to compute the value of ![]() $\hat{h}$ within the existing system
$\hat{h}$ within the existing system ![]() $EQS_0+IV$.
$EQS_0+IV$.
Proposition 18. For a quantum function ![]() $h$ in
$h$ in ![]() $EQS_0$, let
$EQS_0$, let ![]() $\hat{h}$ satisfy the conditions of the aforementioned recursive scheme (*). There exists a quantum function
$\hat{h}$ satisfy the conditions of the aforementioned recursive scheme (*). There exists a quantum function ![]() $F$ definable within
$F$ definable within ![]() $EQS_0+IV$ such that, for any
$EQS_0+IV$ such that, for any ![]() $(x,| \phi \rangle )$ with
$(x,| \phi \rangle )$ with ![]() $x\in NON_{r_0}$ and
$x\in NON_{r_0}$ and ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$, if
$| \phi \rangle \in \mathscr{H}_{\infty }$, if ![]() $|x|\leq |r_0|\log{\ell (| \phi \rangle )}$, then
$|x|\leq |r_0|\log{\ell (| \phi \rangle )}$, then ![]() $F(| xr_0 \rangle | \phi \rangle ) = \hat{h}( | xr_0 \rangle ) \otimes | \phi \rangle$ holds. However, there is no guarantee that
$F(| xr_0 \rangle | \phi \rangle ) = \hat{h}( | xr_0 \rangle ) \otimes | \phi \rangle$ holds. However, there is no guarantee that ![]() $F(| xr_0 \rangle | \phi \rangle )$ matches
$F(| xr_0 \rangle | \phi \rangle )$ matches ![]() $\hat{h}(| xr_0 \rangle )\otimes | \phi \rangle$ when
$\hat{h}(| xr_0 \rangle )\otimes | \phi \rangle$ when ![]() $|x|\gt |r_0|\log \ell (| \phi \rangle )$.
$|x|\gt |r_0|\log \ell (| \phi \rangle )$.
Proof. Assume that ![]() $|x|\leq |r_0|\log{\ell (| \phi \rangle )}$. Consider the quantum function
$|x|\leq |r_0|\log{\ell (| \phi \rangle )}$. Consider the quantum function ![]() $F \equiv CFQRec_{|r_0|-1}[r_0,I,g,h |\mathscr{P}_{|r_0|}, \mathscr{F}_{|r_0|}]$, where
$F \equiv CFQRec_{|r_0|-1}[r_0,I,g,h |\mathscr{P}_{|r_0|}, \mathscr{F}_{|r_0|}]$, where ![]() $\mathscr{P}_{|r_0|}=\{p_u\}_{u\in \{0,1\}^{|r_0|}}$ and
$\mathscr{P}_{|r_0|}=\{p_u\}_{u\in \{0,1\}^{|r_0|}}$ and ![]() $\mathscr{F}_{|r_0|} =\{f_u\}_{u\in \{0,1\}^{|r_0|}}$ with
$\mathscr{F}_{|r_0|} =\{f_u\}_{u\in \{0,1\}^{|r_0|}}$ with ![]() $p_u\equiv I$ and
$p_u\equiv I$ and ![]() $f_u\equiv F$ for all
$f_u\equiv F$ for all ![]() $u\in \{0,1\}^{|r_0|}$. We verify the proposition by induction on the number of applications of
$u\in \{0,1\}^{|r_0|}$. We verify the proposition by induction on the number of applications of ![]() $F$. In the base case, we obtain
$F$. In the base case, we obtain ![]() $F(| r_0 \rangle | \phi \rangle ) = | r_0 \rangle | \phi \rangle = \hat{h}(| r_0 \rangle )\otimes | \phi \rangle$ since
$F(| r_0 \rangle | \phi \rangle ) = | r_0 \rangle | \phi \rangle = \hat{h}(| r_0 \rangle )\otimes | \phi \rangle$ since ![]() $\hat{h}(| r_0 \rangle ) = | r_0 \rangle$ by (*). Next, we consider any string
$\hat{h}(| r_0 \rangle ) = | r_0 \rangle$ by (*). Next, we consider any string ![]() $ax$ with
$ax$ with ![]() $a\in \{0,1\}^{|r_0|}\cap NON_{r_0}$ and
$a\in \{0,1\}^{|r_0|}\cap NON_{r_0}$ and ![]() $x\in NON_{r_0}$. We obtain
$x\in NON_{r_0}$. We obtain ![]() $F(| xr_0 \rangle | \phi \rangle ) = \hat{h}(| xr_0 \rangle )\otimes | \phi \rangle$ by induction hypothesis. It then follows that
$F(| xr_0 \rangle | \phi \rangle ) = \hat{h}(| xr_0 \rangle )\otimes | \phi \rangle$ by induction hypothesis. It then follows that ![]() $F(| axr_0 \rangle | \phi \rangle ) = \sum _{v:|v|=|xr_0|} ( h( | a \rangle \otimes | v \rangle ) \otimes \langle v | \zeta _{a,I,\phi }^{(xr_0)} \rangle )$, where
$F(| axr_0 \rangle | \phi \rangle ) = \sum _{v:|v|=|xr_0|} ( h( | a \rangle \otimes | v \rangle ) \otimes \langle v | \zeta _{a,I,\phi }^{(xr_0)} \rangle )$, where ![]() $| \zeta _{a,I,\phi }^{(xr_0)} \rangle = \sum _{s:|s|=LH(| \phi \rangle )}$
$| \zeta _{a,I,\phi }^{(xr_0)} \rangle = \sum _{s:|s|=LH(| \phi \rangle )}$ ![]() $(F(| xr_0 \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle )$. Since
$(F(| xr_0 \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle )$. Since ![]() $F(| xr_0 \rangle | \phi \rangle ) = \hat{h}(| xr_0 \rangle )\otimes | \phi \rangle$,
$F(| xr_0 \rangle | \phi \rangle ) = \hat{h}(| xr_0 \rangle )\otimes | \phi \rangle$, ![]() $| \zeta _{a,I,\phi }^{(xr_0)} \rangle$ equals
$| \zeta _{a,I,\phi }^{(xr_0)} \rangle$ equals ![]() $\sum _{s:|s|=LH(| \phi \rangle )}$
$\sum _{s:|s|=LH(| \phi \rangle )}$ ![]() $(\hat{h}(| xr_0 \rangle )\otimes | s \rangle \otimes \langle s | \phi \rangle ) = \hat{h}(| xr_0 \rangle ) \otimes | \phi \rangle$. We briefly write
$(\hat{h}(| xr_0 \rangle )\otimes | s \rangle \otimes \langle s | \phi \rangle ) = \hat{h}(| xr_0 \rangle ) \otimes | \phi \rangle$. We briefly write ![]() $| \psi _{\hat{h},xr_0} \rangle$ for
$| \psi _{\hat{h},xr_0} \rangle$ for ![]() $\hat{h}(| xr_0 \rangle )$. We then obtain
$\hat{h}(| xr_0 \rangle )$. We then obtain ![]() $F(| axr_0 \rangle | \phi \rangle ) = \sum _{v:|v|=|xr_0|} ( h(| a \rangle \otimes | v \rangle ) \otimes \langle v | \psi _{\hat{h},xr_0} \rangle ) \otimes | \phi \rangle$. This implies that
$F(| axr_0 \rangle | \phi \rangle ) = \sum _{v:|v|=|xr_0|} ( h(| a \rangle \otimes | v \rangle ) \otimes \langle v | \psi _{\hat{h},xr_0} \rangle ) \otimes | \phi \rangle$. This implies that ![]() $F(| axr_0 \rangle | \phi \rangle ) = h(| a \rangle \otimes \hat{h}(| xr_0 \rangle )) \otimes | \phi \rangle = \hat{h}(| axr_0 \rangle )\otimes | \phi \rangle$ by the definition of
$F(| axr_0 \rangle | \phi \rangle ) = h(| a \rangle \otimes \hat{h}(| xr_0 \rangle )) \otimes | \phi \rangle = \hat{h}(| axr_0 \rangle )\otimes | \phi \rangle$ by the definition of ![]() $\hat{h}$.
$\hat{h}$.
Since ![]() $CodeSKIP_{+}[\cdot ]$ can be realized by the recursive construction scheme (*), Proposition18 allows us to use
$CodeSKIP_{+}[\cdot ]$ can be realized by the recursive construction scheme (*), Proposition18 allows us to use ![]() $CodeSKIP_{+}[\cdot ]$ freely as if it is a quantum function in
$CodeSKIP_{+}[\cdot ]$ freely as if it is a quantum function in ![]() $EQS_0+IV$.
$EQS_0+IV$.
Corollary 1. There exists a quantum function ![]() $F$ definable within
$F$ definable within ![]() $EQS_0+IV$ such that
$EQS_0+IV$ such that ![]() $F(| xr_0 \rangle | \phi \rangle ) = CodeSKIP_{+}[r_0,g,I](| xr_0 \rangle | \phi \rangle )$ if
$F(| xr_0 \rangle | \phi \rangle ) = CodeSKIP_{+}[r_0,g,I](| xr_0 \rangle | \phi \rangle )$ if ![]() $|x|\leq |r_0|\log{\ell (| \phi \rangle )}$.
$|x|\leq |r_0|\log{\ell (| \phi \rangle )}$.
3.5 Elementary quantum schemes
Formally, let us introduce ![]() $\widehat{EQS}$ and
$\widehat{EQS}$ and ![]() $EQS$. We have already explained Schemes I–IV. Now, we wish to add the final piece of construction schemes, called Scheme V, which intuitively supports successive
$EQS$. We have already explained Schemes I–IV. Now, we wish to add the final piece of construction schemes, called Scheme V, which intuitively supports successive ![]() $\mathrm{ilog}(\ell (| \phi \rangle ))$ applications of
$\mathrm{ilog}(\ell (| \phi \rangle ))$ applications of ![]() $Compo[g,g]$ for a given quantum function
$Compo[g,g]$ for a given quantum function ![]() $g$ taking
$g$ taking ![]() $| xr_0 \rangle | \phi \rangle$ as an input.
$| xr_0 \rangle | \phi \rangle$ as an input.
Definition 19. We introduce the following scheme.
V. The logarithmically many composition scheme. From
 $g$, we define
$g$, we define  $LCompo[g]$ as follows:
$LCompo[g]$ as follows:
(i)
 $LCompo[g](| xr_0 \rangle | \phi \rangle ) = | xr_0 \rangle \otimes | \phi \rangle\qquad\qquad$ if
$LCompo[g](| xr_0 \rangle | \phi \rangle ) = | xr_0 \rangle \otimes | \phi \rangle\qquad\qquad$ if  $x=\lambda$,
$x=\lambda$,  $\ell (| \phi \rangle )\leq 1$, or
$\ell (| \phi \rangle )\leq 1$, or  $|x|\gt |r_0|k$,
$|x|\gt |r_0|k$,(ii)
 $LCompo[g](| xr_0 \rangle | \phi \rangle ) = g^{k}(| xr_0 \rangle | \phi \rangle )\qquad\quad\ \ \ $ otherwise,
$LCompo[g](| xr_0 \rangle | \phi \rangle ) = g^{k}(| xr_0 \rangle | \phi \rangle )\qquad\quad\ \ \ $ otherwise,
where
 $x\in NON_{r_0}$ and
$x\in NON_{r_0}$ and  $k=\mathrm{ilog}(\ell (| \phi \rangle ))$.
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$.
When ![]() $g$ is query-independent, we say that Scheme V is query-independent. We remark that query-independent Scheme V is actually redundant because Proposition18 helps us realize
$g$ is query-independent, we say that Scheme V is query-independent. We remark that query-independent Scheme V is actually redundant because Proposition18 helps us realize ![]() $LCompo[g]$ by an application of Scheme IV.
$LCompo[g]$ by an application of Scheme IV.
Definition 20. The class ![]() $EQS$ is the smallest set of (code-controlled) quantum functions that contains the quantum functions of Scheme I and is closed under Schemes II–V. Similarly,
$EQS$ is the smallest set of (code-controlled) quantum functions that contains the quantum functions of Scheme I and is closed under Schemes II–V. Similarly, ![]() $\widehat{EQS}$ is defined with no use of Item 6) of Scheme I.
$\widehat{EQS}$ is defined with no use of Item 6) of Scheme I.
Note that any quantum function ![]() $F$ in
$F$ in ![]() $EQS$ is constructed by sequential applications of Schemes I–V. Such a finite series is referred to as a construction history of
$EQS$ is constructed by sequential applications of Schemes I–V. Such a finite series is referred to as a construction history of ![]() $F$. The length of this construction history serves as a descriptive complexity measure of
$F$. The length of this construction history serves as a descriptive complexity measure of ![]() $F$. Refer to (Yamakami, Reference Yamakami2020) for more discussions.
$F$. Refer to (Yamakami, Reference Yamakami2020) for more discussions.
4. Quantum functions definable within EQS
In Section 3.5, we have introduced the system ![]() $\widehat{EQS}$ as well as
$\widehat{EQS}$ as well as ![]() $EQS$. In this section, we will study the basic properties of all quantum functions in
$EQS$. In this section, we will study the basic properties of all quantum functions in ![]() $\widehat{EQS}$ and
$\widehat{EQS}$ and ![]() $EQS$ by introducing several useful quantum functions and extra schemes, which are also definable within
$EQS$ by introducing several useful quantum functions and extra schemes, which are also definable within ![]() $EQS$. One of the most important properties we can show is an implementation of a simple “binary search strategy” in
$EQS$. One of the most important properties we can show is an implementation of a simple “binary search strategy” in ![]() $EQS$.
$EQS$.
4.1 Basic properties of  $\widehat{EQS}$
$\widehat{EQS}$
The only difference between ![]() $\widehat{EQS}$ and
$\widehat{EQS}$ and ![]() $EQS$ is the free use of Item 6) (quantum measurement) of Scheme I. Since
$EQS$ is the free use of Item 6) (quantum measurement) of Scheme I. Since ![]() $\widehat{EQS}$ does not involve quantum measurement, we naturally expect that
$\widehat{EQS}$ does not involve quantum measurement, we naturally expect that ![]() $\widehat{EQS}$ enjoys the unitary nature of quantum computation described in the following three lemmas, Lemmas 21–23.
$\widehat{EQS}$ enjoys the unitary nature of quantum computation described in the following three lemmas, Lemmas 21–23.
Lemma 21. Any quantum function in ![]() $\widehat{EQS}$ is dimension-preserving and norm-preserving.
$\widehat{EQS}$ is dimension-preserving and norm-preserving.
Proof. Let us check Schemes I–V separately to verify the lemma. Note that Items 1)–5) of Scheme I are clearly dimension-preserving and norm-preserving. The lemma was already shown for Schemes II–III by Yamakami (Reference Yamakami2020). Therefore, it suffices to check Schemes IV and V. Let ![]() $F\equiv CFQRec_t[r_0,g,h| \mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ be any quantum function defined by Scheme IV. It is easy to verify that
$F\equiv CFQRec_t[r_0,g,h| \mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ be any quantum function defined by Scheme IV. It is easy to verify that ![]() $HalfSWAP$ is dimension-preserving and norm-preserving. Thus, so are all quantum functions in
$HalfSWAP$ is dimension-preserving and norm-preserving. Thus, so are all quantum functions in ![]() $\mathscr{P}_{|r_0|}$. By induction hypothesis, we assume that
$\mathscr{P}_{|r_0|}$. By induction hypothesis, we assume that ![]() $g$ and
$g$ and ![]() $h$ are dimension-preserving and norm-preserving. In what follows, we argue by way of induction on the input length of
$h$ are dimension-preserving and norm-preserving. In what follows, we argue by way of induction on the input length of ![]() $F$ that
$F$ that ![]() $F$ is dimension-preserving and norm-preserving. If either
$F$ is dimension-preserving and norm-preserving. If either ![]() $x=\lambda$ or
$x=\lambda$ or ![]() $\ell (| \phi \rangle )\leq t$, then we obtain
$\ell (| \phi \rangle )\leq t$, then we obtain ![]() $\ell (F(| xr_0 \rangle | \phi \rangle )) = \ell (g(| xr_0 \rangle | \phi \rangle )) = \ell (| xr_0 \rangle | \phi \rangle )$ and
$\ell (F(| xr_0 \rangle | \phi \rangle )) = \ell (g(| xr_0 \rangle | \phi \rangle )) = \ell (| xr_0 \rangle | \phi \rangle )$ and ![]() $\|F(| xr_0 \rangle | \phi \rangle )\| = \|g(| xr_0 \rangle | \phi \rangle )\| = \|| xr_0 \rangle | \phi \rangle \|$.
$\|F(| xr_0 \rangle | \phi \rangle )\| = \|g(| xr_0 \rangle | \phi \rangle )\| = \|| xr_0 \rangle | \phi \rangle \|$.
Let us consider the case where ![]() $x\neq \lambda$ and
$x\neq \lambda$ and ![]() $\ell (| \phi \rangle )\gt t$. We then obtain
$\ell (| \phi \rangle )\gt t$. We then obtain ![]() $\ell (h(| u \rangle | v \rangle ) \otimes p_u^{-1}(\langle v | \zeta _{u,p_u,\phi } \rangle )) = \ell (| u \rangle )+\ell (| v \rangle \langle v | \zeta _{u,p_u,\phi } \rangle ) = \ell (| xr_0 \rangle )-|r_0| + \ell (| \zeta _{u,p_u,\phi } \rangle )$. By induction hypothesis, we obtain
$\ell (h(| u \rangle | v \rangle ) \otimes p_u^{-1}(\langle v | \zeta _{u,p_u,\phi } \rangle )) = \ell (| u \rangle )+\ell (| v \rangle \langle v | \zeta _{u,p_u,\phi } \rangle ) = \ell (| xr_0 \rangle )-|r_0| + \ell (| \zeta _{u,p_u,\phi } \rangle )$. By induction hypothesis, we obtain ![]() $\ell (F(\langle u | xr_0 \rangle | s \rangle )) = \ell (\langle u | xr_0 \rangle | s \rangle )$. This implies that
$\ell (F(\langle u | xr_0 \rangle | s \rangle )) = \ell (\langle u | xr_0 \rangle | s \rangle )$. This implies that ![]() $\ell (| \zeta _{u,p_u,\phi } \rangle ) = \ell (\sum _{s}F(\langle u | xr_0 \rangle | s \rangle )\otimes \langle s | \psi _{p_u,\phi } \rangle ) =\ell (\langle u | xr_0 \rangle | \phi \rangle )$. It then follows that
$\ell (| \zeta _{u,p_u,\phi } \rangle ) = \ell (\sum _{s}F(\langle u | xr_0 \rangle | s \rangle )\otimes \langle s | \psi _{p_u,\phi } \rangle ) =\ell (\langle u | xr_0 \rangle | \phi \rangle )$. It then follows that ![]() $\ell (F(| xr_0 \rangle | \phi \rangle )) = \ell ( \sum _{u}\sum _{v} h(| u \rangle | v \rangle ) \otimes p_u^{-1}(\langle v | \zeta _{u,p_u,\phi } \rangle )) = \ell (| xr_0 \rangle | \phi \rangle )$. The property of norm-preserving is similarly proven.
$\ell (F(| xr_0 \rangle | \phi \rangle )) = \ell ( \sum _{u}\sum _{v} h(| u \rangle | v \rangle ) \otimes p_u^{-1}(\langle v | \zeta _{u,p_u,\phi } \rangle )) = \ell (| xr_0 \rangle | \phi \rangle )$. The property of norm-preserving is similarly proven.
For Scheme V, it is obvious that, if ![]() $g$ is dimension-preserving and norm-preserving, then so is
$g$ is dimension-preserving and norm-preserving, then so is ![]() $g^k$ for any number
$g^k$ for any number ![]() $k\in \mathbb{N}^{+}$. Thus,
$k\in \mathbb{N}^{+}$. Thus, ![]() $LCompo[g]$ satisfies the lemma.
$LCompo[g]$ satisfies the lemma.
We further discuss two useful construction schemes, which are definable within ![]() $\widehat{EQS}$.
$\widehat{EQS}$.
Lemma 22. Let ![]() $k\in \mathbb{N}^{+}$ and let
$k\in \mathbb{N}^{+}$ and let ![]() $\mathscr{G}_k=\{g_u\}_{u\in \{0,1\}^k}$ be a series of
$\mathscr{G}_k=\{g_u\}_{u\in \{0,1\}^k}$ be a series of ![]() $\widehat{EQS}$-functions. The following quantum functions all belong to
$\widehat{EQS}$-functions. The following quantum functions all belong to ![]() $\widehat{EQS}$. The lemma also holds even if
$\widehat{EQS}$. The lemma also holds even if ![]() $\widehat{EQS}$ is replaced by
$\widehat{EQS}$ is replaced by ![]() $EQS$. Let
$EQS$. Let ![]() $| \phi \rangle$ be any quantum state in
$| \phi \rangle$ be any quantum state in ![]() $\mathscr{H}_{\infty }$ and let
$\mathscr{H}_{\infty }$ and let ![]() $x\in \{0,1\}^k$.
$x\in \{0,1\}^k$.
1.
 $Compo[\mathscr{G}_k](| \phi \rangle ) = g_{s_1}\circ g_{s_2}\circ \cdots \circ g_{s_{2^k}}(| \phi \rangle )$. (multiple composition)
$Compo[\mathscr{G}_k](| \phi \rangle ) = g_{s_1}\circ g_{s_2}\circ \cdots \circ g_{s_{2^k}}(| \phi \rangle )$. (multiple composition)-
2.
 $Branch_k[\mathscr{G}_k](| \phi \rangle )= | \phi \rangle$ if
$Branch_k[\mathscr{G}_k](| \phi \rangle )= | \phi \rangle$ if  $\ell (| \phi \rangle )\lt k$ and
$\ell (| \phi \rangle )\lt k$ and  $Branch_k[\mathscr{G}_k](| \phi \rangle )= \sum _{s:|s|=k}| s \rangle \otimes g_s(\langle s | \phi \rangle )$ otherwise.
$Branch_k[\mathscr{G}_k](| \phi \rangle )= \sum _{s:|s|=k}| s \rangle \otimes g_s(\langle s | \phi \rangle )$ otherwise.
Proof. (1)–(2) The above schemes were shown in (Yamakami, Reference Yamakami2020, Lemma 3.6) to be valid for ![]() $\Box ^{\mathrm{QP}}_{1}$ and
$\Box ^{\mathrm{QP}}_{1}$ and ![]() $\widehat{\Box ^{\mathrm{QP}}_{1}}$, and their argument also work for
$\widehat{\Box ^{\mathrm{QP}}_{1}}$, and their argument also work for ![]() $EQS$ and
$EQS$ and ![]() $\widehat{EQS}$.
$\widehat{EQS}$.
As a quick example of ![]() $Branch_k[\mathscr{G}_k]$, let us recall the quantum function
$Branch_k[\mathscr{G}_k]$, let us recall the quantum function ![]() $Skip_k[g]$ from Lemma4. It is obvious that
$Skip_k[g]$ from Lemma4. It is obvious that ![]() $Skip_k[g]$ is simply defined to be
$Skip_k[g]$ is simply defined to be ![]() $Branch_k[\{g_u\}_{u\in \{0,1\}^k}]$ with
$Branch_k[\{g_u\}_{u\in \{0,1\}^k}]$ with ![]() $g_u=g$ for all
$g_u=g$ for all ![]() $u\in \{0,1\}^k$.
$u\in \{0,1\}^k$.
For any given quantum function, when there exists another quantum function ![]() $g$ satisfying
$g$ satisfying ![]() $f\circ g(| \phi \rangle ) = g\circ f(| \phi \rangle ) = | \phi \rangle$ for any
$f\circ g(| \phi \rangle ) = g\circ f(| \phi \rangle ) = | \phi \rangle$ for any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$, we express this
$| \phi \rangle \in \mathscr{H}_{\infty }$, we express this ![]() $g$ as
$g$ as ![]() $f^{-1}$ (or sometimes
$f^{-1}$ (or sometimes ![]() $f^{\dagger }$) and call it the inverse (function) of
$f^{\dagger }$) and call it the inverse (function) of ![]() $f$.
$f$.
Lemma 23. For any quantum function ![]() $g$ in
$g$ in ![]() $\widehat{EQS}$, its inverse function
$\widehat{EQS}$, its inverse function ![]() $g^{-1}$ exists in
$g^{-1}$ exists in ![]() $\widehat{EQS}$. Moreover, if
$\widehat{EQS}$. Moreover, if ![]() $g$ is in
$g$ is in ![]() $\widehat{EQS}_0$, then
$\widehat{EQS}_0$, then ![]() $g^{-1}$ is also in
$g^{-1}$ is also in ![]() $\widehat{EQS}_0$.
$\widehat{EQS}_0$.
Proof. For Scheme I, it is obvious that ![]() $PHASE_{\theta }^{-1}=PHASE_{-\theta }$,
$PHASE_{\theta }^{-1}=PHASE_{-\theta }$, ![]() $ROT_{\theta }^{-1} = ROT_{-\theta }$,
$ROT_{\theta }^{-1} = ROT_{-\theta }$, ![]() $NOT^{-1}=NOT$, and
$NOT^{-1}=NOT$, and ![]() $SWAP^{-1}=SWAP$. For Scheme II,
$SWAP^{-1}=SWAP$. For Scheme II, ![]() $Compo[g,h]^{-1}$ equals
$Compo[g,h]^{-1}$ equals ![]() $Compo[h^{-1},g^{-1}]$. For Scheme III, it suffices to set
$Compo[h^{-1},g^{-1}]$. For Scheme III, it suffices to set ![]() $Branch[g,h]^{-1}$ to be
$Branch[g,h]^{-1}$ to be ![]() $Branch[g^{-1},h^{-1}]$. For Scheme IV, let
$Branch[g^{-1},h^{-1}]$. For Scheme IV, let ![]() $F\equiv CFQRec_t[r_0,d,g,h | \mathscr{P}_{|r_0|}, \mathscr{F}_{|r_0|}]$. If
$F\equiv CFQRec_t[r_0,d,g,h | \mathscr{P}_{|r_0|}, \mathscr{F}_{|r_0|}]$. If ![]() $x=\lambda$,
$x=\lambda$, ![]() $\ell (| \phi \rangle )\leq t$, or
$\ell (| \phi \rangle )\leq t$, or ![]() $|x|\gt |r_0|k$ with
$|x|\gt |r_0|k$ with ![]() $k=\mathrm{ilog}(\ell (| \phi \rangle ))$, then we set
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$, then we set ![]() $F^{-1}\equiv g^{-1}$. In this case, we obtain
$F^{-1}\equiv g^{-1}$. In this case, we obtain ![]() $F^{-1}\circ F(| xr_0 \rangle | \phi \rangle ) = F^{-1}(g(| xr_0 \rangle | \phi \rangle )) = g^{-1}\circ g(| xr_0 \rangle | \phi \rangle )=| xr_0 \rangle | \phi \rangle$. Assuming otherwise, we define
$F^{-1}\circ F(| xr_0 \rangle | \phi \rangle ) = F^{-1}(g(| xr_0 \rangle | \phi \rangle )) = g^{-1}\circ g(| xr_0 \rangle | \phi \rangle )=| xr_0 \rangle | \phi \rangle$. Assuming otherwise, we define ![]() $F^{-1}$ to be the consecutive applications of two quantum functions:
$F^{-1}$ to be the consecutive applications of two quantum functions: ![]() $h^{-1}$ and
$h^{-1}$ and ![]() $G\equiv CFQRec_t[r_0,d^{-1},g^{-1},I |\mathscr{P}_{|r_0|}, \mathscr{F}^{-1}_{|r_0|}]$, where
$G\equiv CFQRec_t[r_0,d^{-1},g^{-1},I |\mathscr{P}_{|r_0|}, \mathscr{F}^{-1}_{|r_0|}]$, where ![]() $\mathscr{F}^{-1}_{|r_0|} = \{f_u^{-1}\}_{u\in \{0,1\}^{|r_0|}}$. It is important to note that we do not use
$\mathscr{F}^{-1}_{|r_0|} = \{f_u^{-1}\}_{u\in \{0,1\}^{|r_0|}}$. It is important to note that we do not use ![]() $\mathscr{P}_{|r_0|}^{-1} = \{p_u^{-1}\}_{u\in \{0,1\}^{|r_0|}}$ in place of
$\mathscr{P}_{|r_0|}^{-1} = \{p_u^{-1}\}_{u\in \{0,1\}^{|r_0|}}$ in place of ![]() $\mathscr{P}_{|r_0|}$ in the definition of
$\mathscr{P}_{|r_0|}$ in the definition of ![]() $G$. Let us show that
$G$. Let us show that ![]() $F^{-1}\circ F(| xr_0 \rangle | \phi \rangle ) = | xr_0 \rangle | \phi \rangle$. Assume that
$F^{-1}\circ F(| xr_0 \rangle | \phi \rangle ) = | xr_0 \rangle | \phi \rangle$. Assume that ![]() $F(| xr_0 \rangle | \phi \rangle )$ has the form
$F(| xr_0 \rangle | \phi \rangle )$ has the form ![]() $\sum _{u:|u|=|r_0|} \sum _{v:|v|= \ell (\langle u | xr_0 \rangle )} ( h( | u \rangle | v \rangle ) \otimes p_u^{-1} ( \langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) )$. We first apply
$\sum _{u:|u|=|r_0|} \sum _{v:|v|= \ell (\langle u | xr_0 \rangle )} ( h( | u \rangle | v \rangle ) \otimes p_u^{-1} ( \langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) )$. We first apply ![]() $h^{-1}$ to the first
$h^{-1}$ to the first ![]() $|xr_0|$ qubits and then obtain
$|xr_0|$ qubits and then obtain ![]() $\sum _{u:|u|=|r_0|} \sum _{v:|v|= \ell (\langle u | xr_0 \rangle )} ( | u \rangle | v \rangle \otimes p_u^{-1} ( \langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) )$. To this quantum state, we further apply
$\sum _{u:|u|=|r_0|} \sum _{v:|v|= \ell (\langle u | xr_0 \rangle )} ( | u \rangle | v \rangle \otimes p_u^{-1} ( \langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle ) )$. To this quantum state, we further apply ![]() $G$. By an application of
$G$. By an application of ![]() $p_u$ to
$p_u$ to ![]() $p_u^{-1}(\langle v | \zeta ^{(x'r_0)}_{u,p_u,\phi } \rangle )$, we obtain
$p_u^{-1}(\langle v | \zeta ^{(x'r_0)}_{u,p_u,\phi } \rangle )$, we obtain ![]() $\sum _{u:|u|=|r_0|} \sum _{v:|v|= \ell (\langle u | xr_0 \rangle )} | u \rangle | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle$. Notice that
$\sum _{u:|u|=|r_0|} \sum _{v:|v|= \ell (\langle u | xr_0 \rangle )} | u \rangle | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle$. Notice that ![]() $| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle$ equals
$| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle$ equals ![]() $\sum _{s:|s|=m_u(| \phi \rangle )} ( f_u(\langle u | x'r_0 \rangle \otimes | s \rangle )\otimes \langle s | \psi _{p_u,\phi } \rangle )$. An application of
$\sum _{s:|s|=m_u(| \phi \rangle )} ( f_u(\langle u | x'r_0 \rangle \otimes | s \rangle )\otimes \langle s | \psi _{p_u,\phi } \rangle )$. An application of ![]() $f_u^{-1}$ to
$f_u^{-1}$ to ![]() $f_u(\langle u | x'r_0 \rangle \otimes | s \rangle )$ leads to
$f_u(\langle u | x'r_0 \rangle \otimes | s \rangle )$ leads to ![]() $\sum _{u:|u|=|r_0|} \langle u | x'r_0 \rangle \otimes | \psi _{p_u,\phi } \rangle$. Since
$\sum _{u:|u|=|r_0|} \langle u | x'r_0 \rangle \otimes | \psi _{p_u,\phi } \rangle$. Since ![]() $| x'r_0 \rangle = d(| xr_0 \rangle )$, by applying
$| x'r_0 \rangle = d(| xr_0 \rangle )$, by applying ![]() $d^{-1}$ and
$d^{-1}$ and ![]() $p_u^{-1}$ (which come from the definition of
$p_u^{-1}$ (which come from the definition of ![]() $G$), we finally obtain
$G$), we finally obtain ![]() $| xr_0 \rangle \otimes | \phi \rangle$. For Scheme V, it suffices to set
$| xr_0 \rangle \otimes | \phi \rangle$. For Scheme V, it suffices to set ![]() $LCompo[g]^{-1}$ to be
$LCompo[g]^{-1}$ to be ![]() $LCompo[g^{-1}]$.
$LCompo[g^{-1}]$.
The above argument also proves the second part of the lemma.
4.2 Section-wise handling of binary encoding
We have discussed in Section 3.2 the binary encodings of various objects usable as part of inputs. We further explore the characteristics of quantum functions that can handle these binary encodings.
Given ![]() $k$ encoded strings
$k$ encoded strings ![]() $\widetilde{x_1},\widetilde{x_2},\ldots, \widetilde{x_k}$, we merge them into a single string of the form
$\widetilde{x_1},\widetilde{x_2},\ldots, \widetilde{x_k}$, we merge them into a single string of the form ![]() $\widetilde{x_1} \widetilde{x_2} \cdots \widetilde{x_k}\hat{2}$, where
$\widetilde{x_1} \widetilde{x_2} \cdots \widetilde{x_k}\hat{2}$, where ![]() $\hat{2}$ serves as an endmarker. Let
$\hat{2}$ serves as an endmarker. Let ![]() $k\geq 2$ and let
$k\geq 2$ and let ![]() $\mathscr{G}=\{g_i\}_{i\in [k]}$ denote a series of
$\mathscr{G}=\{g_i\}_{i\in [k]}$ denote a series of ![]() $k$ quantum functions. We then consider a simultaneous application of all quantum functions in
$k$ quantum functions. We then consider a simultaneous application of all quantum functions in ![]() $\mathscr{G}$,
$\mathscr{G}$, ![]() $MultiApp_k[\mathscr{G}]$, given as
$MultiApp_k[\mathscr{G}]$, given as
Lemma 24. For any ![]() $k\geq 2$ and any series
$k\geq 2$ and any series ![]() $\mathscr{G}=\{g_i\}_{i\in [k]}$ of
$\mathscr{G}=\{g_i\}_{i\in [k]}$ of ![]() $k$ quantum functions, the quantum function
$k$ quantum functions, the quantum function ![]() $MultiApp_k[\hat{2},\mathscr{G}]$ is definable from
$MultiApp_k[\hat{2},\mathscr{G}]$ is definable from ![]() $\mathscr{G}$ and the code skipping scheme.
$\mathscr{G}$ and the code skipping scheme.
Proof. Let ![]() $\mathscr{G}=\{g_i\}_{i\in [k]}$ denote any series of
$\mathscr{G}=\{g_i\}_{i\in [k]}$ denote any series of ![]() $k$ quantum functions, not necessarily in
$k$ quantum functions, not necessarily in ![]() $EQS$. For brevity, we set
$EQS$. For brevity, we set ![]() $\bar{r}_0=\hat{\dashv }$ and
$\bar{r}_0=\hat{\dashv }$ and ![]() $r_0 = \hat{2}$. The quantum function
$r_0 = \hat{2}$. The quantum function ![]() $MultiApp_k[\hat{2},\mathscr{G}]$ is constructed from
$MultiApp_k[\hat{2},\mathscr{G}]$ is constructed from ![]() $\mathscr{G}$ by applying
$\mathscr{G}$ by applying ![]() $CodeSKIP_{+}[\cdot ]$ in the following inductive way. Initially, we set
$CodeSKIP_{+}[\cdot ]$ in the following inductive way. Initially, we set ![]() $G_{[k,k]}\equiv CodeSKIP_{+}[r_0,g_k,I]$. Let
$G_{[k,k]}\equiv CodeSKIP_{+}[r_0,g_k,I]$. Let ![]() $X_k = \widetilde{x_k}$ (
$X_k = \widetilde{x_k}$ (![]() $= \widehat{x_k}\hat{\dashv }$). Since
$= \widehat{x_k}\hat{\dashv }$). Since ![]() $NON_{r_0}(| X_k \rangle | r_0 \rangle | \phi \rangle ) = \{X_k\}$, we obtain
$NON_{r_0}(| X_k \rangle | r_0 \rangle | \phi \rangle ) = \{X_k\}$, we obtain ![]() $G_{[k,k]}(| X_k \rangle | r_0 \rangle | \phi \rangle ) = g_k(| X_k \rangle | r_0 \rangle ) \otimes | \phi \rangle$. Let
$G_{[k,k]}(| X_k \rangle | r_0 \rangle | \phi \rangle ) = g_k(| X_k \rangle | r_0 \rangle ) \otimes | \phi \rangle$. Let ![]() $i$ be any index in
$i$ be any index in ![]() $[k-1]$ and set
$[k-1]$ and set ![]() $X_{i+1} = \widetilde{x_{i+1}}\widetilde{x_{i+2}}\cdots \widetilde{x_k}$. We assume by induction hypothesis that
$X_{i+1} = \widetilde{x_{i+1}}\widetilde{x_{i+2}}\cdots \widetilde{x_k}$. We assume by induction hypothesis that ![]() $G_{[i+1,k]}(| X_{i+1} \rangle | r_0 \rangle | \phi \rangle ) = g_{i+1}(| \widetilde{x_{i+1}} \rangle )\otimes g_{i+2}(| \widetilde{x_{i+2}} \rangle ) \otimes \cdots \otimes g_k(| \widetilde{x_k} \rangle | r_0 \rangle )\otimes | \phi \rangle$. We then define
$G_{[i+1,k]}(| X_{i+1} \rangle | r_0 \rangle | \phi \rangle ) = g_{i+1}(| \widetilde{x_{i+1}} \rangle )\otimes g_{i+2}(| \widetilde{x_{i+2}} \rangle ) \otimes \cdots \otimes g_k(| \widetilde{x_k} \rangle | r_0 \rangle )\otimes | \phi \rangle$. We then define ![]() $G_{[i,k]}\equiv CodeSKIP_{+}[\bar{r}_0,g_i,G_{[i+1,k]}]$. Since
$G_{[i,k]}\equiv CodeSKIP_{+}[\bar{r}_0,g_i,G_{[i+1,k]}]$. Since ![]() $NON_{\bar{r}_0}(| X_{i} \rangle | r_0 \rangle | \phi \rangle ) = \{\widehat{x_i}\}$, it follows that
$NON_{\bar{r}_0}(| X_{i} \rangle | r_0 \rangle | \phi \rangle ) = \{\widehat{x_i}\}$, it follows that ![]() $G_{[i,k]}(| X_{i} \rangle | r_0 \rangle | \phi \rangle ) = g_i(| \widehat{x_i}\bar{r}_0 \rangle ) \otimes G_{[i+1,k]}(| X_{i+1} \rangle | r_0 \rangle | \phi \rangle ) = g_i(| \widetilde{x_i} \rangle ) \otimes g_{i+1}(| \widetilde{x_{i+1}} \rangle )\otimes \cdots \otimes g_k(| \widetilde{x_k} \rangle | r_0 \rangle )\otimes | \phi \rangle$.
$G_{[i,k]}(| X_{i} \rangle | r_0 \rangle | \phi \rangle ) = g_i(| \widehat{x_i}\bar{r}_0 \rangle ) \otimes G_{[i+1,k]}(| X_{i+1} \rangle | r_0 \rangle | \phi \rangle ) = g_i(| \widetilde{x_i} \rangle ) \otimes g_{i+1}(| \widetilde{x_{i+1}} \rangle )\otimes \cdots \otimes g_k(| \widetilde{x_k} \rangle | r_0 \rangle )\otimes | \phi \rangle$.
The desired quantum function ![]() $MultiApp_k[r_0,\mathscr{G}]$ therefore equals
$MultiApp_k[r_0,\mathscr{G}]$ therefore equals ![]() $G_{[1,k]}$, which is
$G_{[1,k]}$, which is ![]() $g_1(| \widetilde{x_1} \rangle ) \otimes g_2(| \widetilde{x_2} \rangle ) \otimes \cdots \otimes g_k(| \widetilde{x_k} \hat{2} \rangle ) \otimes | \phi \rangle$.
$g_1(| \widetilde{x_1} \rangle ) \otimes g_2(| \widetilde{x_2} \rangle ) \otimes \cdots \otimes g_k(| \widetilde{x_k} \hat{2} \rangle ) \otimes | \phi \rangle$.
By Lemma24, we can construct ![]() $MultiApp_k[\hat{2},\mathscr{G}]$ from
$MultiApp_k[\hat{2},\mathscr{G}]$ from ![]() $\mathscr{G} = \{g_i\}_{i\in [k]}$ and
$\mathscr{G} = \{g_i\}_{i\in [k]}$ and ![]() $CodeSKIP_{+}[r_0,g,h]$. Since
$CodeSKIP_{+}[r_0,g,h]$. Since ![]() $CodeSKIP_{+}[r_0,g,h]$ stays outside of
$CodeSKIP_{+}[r_0,g,h]$ stays outside of ![]() $EQS$,
$EQS$, ![]() $MultiApp_k[\hat{2},\mathscr{G}]$ in general does not belong to
$MultiApp_k[\hat{2},\mathscr{G}]$ in general does not belong to ![]() $EQS$. However, as the next lemma ensures, we can use
$EQS$. However, as the next lemma ensures, we can use ![]() $MultiApp_k[\hat{2},\mathscr{G}]$ as if it is an
$MultiApp_k[\hat{2},\mathscr{G}]$ as if it is an ![]() $EQS$ function under certain circumstances.
$EQS$ function under certain circumstances.
To describe our result, let us recall the 3-bit encoding of ![]() $\hat{S}$, which indicates “separator”.
$\hat{S}$, which indicates “separator”.
Lemma 25. Let ![]() $k\in \mathbb{N}^{+}$ and let
$k\in \mathbb{N}^{+}$ and let ![]() $\mathscr{G}=\{g_i\}_{i\in [k]}$ be any series of
$\mathscr{G}=\{g_i\}_{i\in [k]}$ be any series of ![]() $k$ quantum functions in
$k$ quantum functions in ![]() $EQS$. There exists a quantum function
$EQS$. There exists a quantum function ![]() $F$ in
$F$ in ![]() $EQS$ such that
$EQS$ such that ![]() $F(| \hat{S} \widetilde{x}_1 \widetilde{x}_2\cdots \widetilde{x}_k \hat{2} \rangle | \phi \rangle ) = MultiApp_{k}[\hat{2},\mathscr{G}](| \hat{S} \widetilde{x}_1 \widetilde{x}_2 \cdots \widetilde{x}_k \hat{2} \rangle | \phi \rangle )$ as long as
$F(| \hat{S} \widetilde{x}_1 \widetilde{x}_2\cdots \widetilde{x}_k \hat{2} \rangle | \phi \rangle ) = MultiApp_{k}[\hat{2},\mathscr{G}](| \hat{S} \widetilde{x}_1 \widetilde{x}_2 \cdots \widetilde{x}_k \hat{2} \rangle | \phi \rangle )$ as long as ![]() $|\hat{S} \widetilde{x}_1\widetilde{x}_2\cdots \widetilde{x}_k \hat{2}|\leq |\hat{2}|\log{\ell (| \phi \rangle )}$. However, the equality may not hold if
$|\hat{S} \widetilde{x}_1\widetilde{x}_2\cdots \widetilde{x}_k \hat{2}|\leq |\hat{2}|\log{\ell (| \phi \rangle )}$. However, the equality may not hold if ![]() $|\hat{S} \widetilde{x}_1\widetilde{x}_2\cdots \widetilde{x}_k \hat{2}| \gt |\hat{2}|\log{\ell (| \phi \rangle )}$.
$|\hat{S} \widetilde{x}_1\widetilde{x}_2\cdots \widetilde{x}_k \hat{2}| \gt |\hat{2}|\log{\ell (| \phi \rangle )}$.
Proof. Let ![]() $k\in \mathbb{N}^{+}$ and let
$k\in \mathbb{N}^{+}$ and let ![]() $\mathscr{G}= \{g_i\}_{i\in [k]}$ be given as in the premise of the lemma. Since
$\mathscr{G}= \{g_i\}_{i\in [k]}$ be given as in the premise of the lemma. Since ![]() $|\hat{2}|=3$, we set
$|\hat{2}|=3$, we set ![]() $h$ to be
$h$ to be ![]() $Branch_3[\{h_u\}_{u\in \{0,1\}^3}]$ with
$Branch_3[\{h_u\}_{u\in \{0,1\}^3}]$ with ![]() $h_{\hat{S}} \equiv MultiApp_{k}[\hat{2},\mathscr{G}]$ and
$h_{\hat{S}} \equiv MultiApp_{k}[\hat{2},\mathscr{G}]$ and ![]() $h_u \equiv I$ for any
$h_u \equiv I$ for any ![]() $u\neq \hat{S}$. The desired quantum function
$u\neq \hat{S}$. The desired quantum function ![]() $F$ is defined to be
$F$ is defined to be ![]() $CFQRec_1[\hat{2},I,I,h|\mathscr{P}_{3},\mathscr{F}_{3}]$, where
$CFQRec_1[\hat{2},I,I,h|\mathscr{P}_{3},\mathscr{F}_{3}]$, where ![]() $\mathscr{P}_3=\{p_u\}_{u\in \{0,1\}^3}$ with
$\mathscr{P}_3=\{p_u\}_{u\in \{0,1\}^3}$ with ![]() $p_u=I$ for all
$p_u=I$ for all ![]() $u\in \{0,1\}^3$ and
$u\in \{0,1\}^3$ and ![]() $\mathscr{F}_3=\{f_u\}_{u\in \{0,1\}^3}$ with
$\mathscr{F}_3=\{f_u\}_{u\in \{0,1\}^3}$ with ![]() $f_u = F$ for all
$f_u = F$ for all ![]() $u\in \{0,1\}^3$. Because of
$u\in \{0,1\}^3$. Because of ![]() $|\hat{S} \widetilde{x}_1\widetilde{x}_2\cdots \widetilde{x}_k \hat{2}| \leq |\hat{2}|\log{\ell (| \phi \rangle )}$, in the following recursive process of computing
$|\hat{S} \widetilde{x}_1\widetilde{x}_2\cdots \widetilde{x}_k \hat{2}| \leq |\hat{2}|\log{\ell (| \phi \rangle )}$, in the following recursive process of computing ![]() $F$, it suffices to start with
$F$, it suffices to start with ![]() $F(| \hat{2} \rangle | \phi ' \rangle )$ with
$F(| \hat{2} \rangle | \phi ' \rangle )$ with ![]() $\ell (| \phi ' \rangle )\geq 1$.
$\ell (| \phi ' \rangle )\geq 1$.
For each index ![]() $i\in [k]$, we abbreviate
$i\in [k]$, we abbreviate ![]() $\widetilde{x_i}\widetilde{x_{i+1}}\cdots \widetilde{x_k}$ as
$\widetilde{x_i}\widetilde{x_{i+1}}\cdots \widetilde{x_k}$ as ![]() $X_i$. In what follows, we fix
$X_i$. In what follows, we fix ![]() $i\in [k]$ arbitrarily and assume that
$i\in [k]$ arbitrarily and assume that ![]() $F(| X_i\hat{2} \rangle | \phi \rangle ) = | X_i\hat{2} \rangle | \phi \rangle$. Note that
$F(| X_i\hat{2} \rangle | \phi \rangle ) = | X_i\hat{2} \rangle | \phi \rangle$. Note that ![]() $| \zeta _{u,I,\phi } \rangle = \sum _{s:|s|=LH(| \phi \rangle )} (F(\langle u | X_{i-1}\hat{2} \rangle | s \rangle ) \otimes \langle s | \phi \rangle )$. If
$| \zeta _{u,I,\phi } \rangle = \sum _{s:|s|=LH(| \phi \rangle )} (F(\langle u | X_{i-1}\hat{2} \rangle | s \rangle ) \otimes \langle s | \phi \rangle )$. If ![]() $u=\widetilde{x_{i-1}}$, then
$u=\widetilde{x_{i-1}}$, then ![]() $| \zeta _{u,I,\phi } \rangle = \sum _{s:|s|=LH(| \phi \rangle )} ( F(| X_i\hat{2} \rangle | s \rangle ) \otimes \langle s | \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} (| X_i\hat{2} \rangle | s \rangle \otimes \langle s | \phi \rangle ) = | X_i\hat{2} \rangle | \phi \rangle$. From this, it follows that
$| \zeta _{u,I,\phi } \rangle = \sum _{s:|s|=LH(| \phi \rangle )} ( F(| X_i\hat{2} \rangle | s \rangle ) \otimes \langle s | \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} (| X_i\hat{2} \rangle | s \rangle \otimes \langle s | \phi \rangle ) = | X_i\hat{2} \rangle | \phi \rangle$. From this, it follows that ![]() $F(| X_i\hat{2} \rangle | \phi \rangle ) = h(| \widetilde{x_{i-1}} \rangle | X_i\hat{2} \rangle ) \otimes \langle X_i\hat{2} | \zeta _{\widetilde{x_{i-1}},I,\phi } \rangle = | X_{i-1}\hat{2} \rangle | \phi \rangle$. Finally, we consider the case of
$F(| X_i\hat{2} \rangle | \phi \rangle ) = h(| \widetilde{x_{i-1}} \rangle | X_i\hat{2} \rangle ) \otimes \langle X_i\hat{2} | \zeta _{\widetilde{x_{i-1}},I,\phi } \rangle = | X_{i-1}\hat{2} \rangle | \phi \rangle$. Finally, we consider the case of ![]() $| \hat{S} \rangle | X_1\hat{2} \rangle | \phi \rangle$. We then obtain
$| \hat{S} \rangle | X_1\hat{2} \rangle | \phi \rangle$. We then obtain ![]() $F(| \hat{S} \rangle | X_1\hat{2} \rangle | \phi \rangle ) = h(| \hat{S} \rangle | X_1\hat{2} \rangle ) \otimes \langle X_1\hat{2} | \zeta _{\hat{S},I,\phi } \rangle$. Since
$F(| \hat{S} \rangle | X_1\hat{2} \rangle | \phi \rangle ) = h(| \hat{S} \rangle | X_1\hat{2} \rangle ) \otimes \langle X_1\hat{2} | \zeta _{\hat{S},I,\phi } \rangle$. Since ![]() $| \zeta _{\hat{S},I,\phi } \rangle = | X_1\hat{2} \rangle \otimes | \phi \rangle$, it follows that
$| \zeta _{\hat{S},I,\phi } \rangle = | X_1\hat{2} \rangle \otimes | \phi \rangle$, it follows that ![]() $F(| \hat{S} \rangle | X_1\hat{2} \rangle | \phi \rangle ) = h(| \hat{S} \rangle | X_1\hat{2} \rangle ) \otimes \langle X_1\hat{2} | X_1\hat{2} \rangle | \phi \rangle = h(| \hat{S} \rangle | X_1\hat{2} \rangle )\otimes | \phi \rangle = Branch_3[\{h_u\}_{u\in \{0,1\}^3}](| \hat{S} \rangle | X_1\hat{2} \rangle )\otimes | \phi \rangle = MultiApp_k[\hat{2},\mathscr{G}](| \hat{S} \rangle | X_1\hat{2} \rangle ) \otimes | \phi \rangle$.
$F(| \hat{S} \rangle | X_1\hat{2} \rangle | \phi \rangle ) = h(| \hat{S} \rangle | X_1\hat{2} \rangle ) \otimes \langle X_1\hat{2} | X_1\hat{2} \rangle | \phi \rangle = h(| \hat{S} \rangle | X_1\hat{2} \rangle )\otimes | \phi \rangle = Branch_3[\{h_u\}_{u\in \{0,1\}^3}](| \hat{S} \rangle | X_1\hat{2} \rangle )\otimes | \phi \rangle = MultiApp_k[\hat{2},\mathscr{G}](| \hat{S} \rangle | X_1\hat{2} \rangle ) \otimes | \phi \rangle$.
In a certain limited case, Lemma25 makes possible a repeated application of any quantum function within ![]() $EQS_0+IV$ (as well as
$EQS_0+IV$ (as well as ![]() $EQS$). Let us recall the notation
$EQS$). Let us recall the notation ![]() $\hat{T}$, which indicates “time”.
$\hat{T}$, which indicates “time”.
Proposition 26. Let ![]() $r_0\in \{0,1\}^+$ and let
$r_0\in \{0,1\}^+$ and let ![]() $g$ be any quantum function definable within
$g$ be any quantum function definable within ![]() $EQS_0+IV$ (resp.,
$EQS_0+IV$ (resp., ![]() $EQS$). There exists a quantum function
$EQS$). There exists a quantum function ![]() $F$ definable within
$F$ definable within ![]() $EQS_0+IV$ (resp.,
$EQS_0+IV$ (resp., ![]() $EQS$) such that, for any
$EQS$) such that, for any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$ and
$| \phi \rangle \in \mathscr{H}_{\infty }$ and ![]() $x\in \{0,1\}^*$, if
$x\in \{0,1\}^*$, if ![]() $\ell (| \phi \rangle )\leq 1$, then
$\ell (| \phi \rangle )\leq 1$, then ![]() $F(| \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle$, and otherwise,
$F(| \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle$, and otherwise, ![]() $F(| \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle \otimes g^{m(| \phi \rangle )}(| x\hat{2} \rangle ) \otimes | \phi \rangle$, where
$F(| \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle \otimes g^{m(| \phi \rangle )}(| x\hat{2} \rangle ) \otimes | \phi \rangle$, where ![]() $m(| \phi \rangle ) = \mathrm{ilog}(\ell (| \phi \rangle ))$.
$m(| \phi \rangle ) = \mathrm{ilog}(\ell (| \phi \rangle ))$.
Proof. Let ![]() $F$ denote the desired quantum function. Remember that
$F$ denote the desired quantum function. Remember that ![]() $|\hat{2}|=|\hat{T}|=|\hat{S}|=3$. We set
$|\hat{2}|=|\hat{T}|=|\hat{S}|=3$. We set ![]() $\mathscr{P}_3=\{p_u\}_{u\in \{0,1\}^3}$ with
$\mathscr{P}_3=\{p_u\}_{u\in \{0,1\}^3}$ with ![]() $p_u=I$ for all
$p_u=I$ for all ![]() $u\in \{0,1\}^3$ and set
$u\in \{0,1\}^3$ and set ![]() $\mathscr{G}=\{g_u\}_{u\in \{0,1\}^3}$ with
$\mathscr{G}=\{g_u\}_{u\in \{0,1\}^3}$ with ![]() $g_{\hat{T}}=CodeSKIP_{+}[\hat{S},I,g]$, and
$g_{\hat{T}}=CodeSKIP_{+}[\hat{S},I,g]$, and ![]() $g_u=I$ for all other indices
$g_u=I$ for all other indices ![]() $u\in \{0,1\}^3-\{\hat{T}\}$. We then define
$u\in \{0,1\}^3-\{\hat{T}\}$. We then define ![]() $h$ to be
$h$ to be ![]() $Branch_3[\mathscr{G}]$. Finally,
$Branch_3[\mathscr{G}]$. Finally, ![]() $F$ is defined as
$F$ is defined as ![]() $F\equiv CFQRec_1[\hat{2},I,I,h|\mathscr{P}_3,\mathscr{F}_3]$, where
$F\equiv CFQRec_1[\hat{2},I,I,h|\mathscr{P}_3,\mathscr{F}_3]$, where ![]() $\mathscr{F}_3=\{f_u\}_{u\in \{0,1\}^3}$ with
$\mathscr{F}_3=\{f_u\}_{u\in \{0,1\}^3}$ with ![]() $f_u=F$ for all
$f_u=F$ for all ![]() $u\in \{0,1\}^3$.
$u\in \{0,1\}^3$.
For any index ![]() $i\in [0,m(| \phi \rangle )]_{\mathbb{Z}}$, we set
$i\in [0,m(| \phi \rangle )]_{\mathbb{Z}}$, we set ![]() $z_i=\hat{T}^{m(| \phi \rangle )-i}$. If
$z_i=\hat{T}^{m(| \phi \rangle )-i}$. If ![]() $\ell (| \phi \rangle )\leq 1$, then we obtain
$\ell (| \phi \rangle )\leq 1$, then we obtain ![]() $F(| z_i \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | z_i \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle$ for any
$F(| z_i \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | z_i \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle$ for any ![]() $i\in [0,m(| \phi \rangle )]_{\mathbb{Z}}$. Next, we assume that
$i\in [0,m(| \phi \rangle )]_{\mathbb{Z}}$. Next, we assume that ![]() $\ell (| \phi \rangle )\geq 2$. Let
$\ell (| \phi \rangle )\geq 2$. Let ![]() $i\in [0,m(| \phi \rangle )]_{\mathbb{Z}}$ and set
$i\in [0,m(| \phi \rangle )]_{\mathbb{Z}}$ and set ![]() $y=z_i\hat{S}x$. By induction hypothesis,
$y=z_i\hat{S}x$. By induction hypothesis, ![]() $F(| z_{i+1} \hat{S} \rangle | x\hat{2} \rangle | s \rangle = | z_{i+1} \hat{S} \rangle \otimes g^{m(| \phi \rangle )-i-1}(| x\hat{2} \rangle )\otimes | \phi \rangle$ holds. Let us consider the value
$F(| z_{i+1} \hat{S} \rangle | x\hat{2} \rangle | s \rangle = | z_{i+1} \hat{S} \rangle \otimes g^{m(| \phi \rangle )-i-1}(| x\hat{2} \rangle )\otimes | \phi \rangle$ holds. Let us consider the value ![]() $F(| z_i \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle$. Note that
$F(| z_i \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle$. Note that ![]() $h(| z_i\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i}(| x\hat{2} \rangle ) ) = CodeSKIP_{+}[\hat{S},I,g](| z_i\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i}(| x\hat{2} \rangle )) = | z_i\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i-1}(| x\hat{2} \rangle )$. It thus follows that
$h(| z_i\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i}(| x\hat{2} \rangle ) ) = CodeSKIP_{+}[\hat{S},I,g](| z_i\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i}(| x\hat{2} \rangle )) = | z_i\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i-1}(| x\hat{2} \rangle )$. It thus follows that ![]() $F(| z_i \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle = \sum _{u:|u|=|\hat{2}|} \sum _{v:|v|=\ell (\langle u | y\hat{2} \rangle )} (h(| u \rangle \otimes | v \rangle ) \otimes \langle v | \zeta _{u,I,\phi } \rangle )$, where
$F(| z_i \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle = \sum _{u:|u|=|\hat{2}|} \sum _{v:|v|=\ell (\langle u | y\hat{2} \rangle )} (h(| u \rangle \otimes | v \rangle ) \otimes \langle v | \zeta _{u,I,\phi } \rangle )$, where ![]() $| \zeta _{u,I,\phi } \rangle$ is calculated as follows. If
$| \zeta _{u,I,\phi } \rangle$ is calculated as follows. If ![]() $u\neq \hat{T}$, then
$u\neq \hat{T}$, then ![]() $| \zeta _{u,I,\phi } \rangle = \boldsymbol{0}$ holds. Otherwise,
$| \zeta _{u,I,\phi } \rangle = \boldsymbol{0}$ holds. Otherwise, ![]() $| \zeta _{u,I,\phi } \rangle$ is equal to
$| \zeta _{u,I,\phi } \rangle$ is equal to  $\sum _{s:|s|=LH(| \phi \rangle )} (F(\langle u | z_i\hat{S} \rangle | x\hat{2} \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} (F(| z_{i+1}\hat{S} \rangle | x\hat{2} \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} h(| z_{i+1}\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i-1}( | x\hat{2} \rangle ) \otimes | s \rangle \langle s | \phi \rangle ) = | z_{i+1}\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i-1}(| x\hat{2} \rangle )\otimes | \phi \rangle$. Thus, we obtain
$\sum _{s:|s|=LH(| \phi \rangle )} (F(\langle u | z_i\hat{S} \rangle | x\hat{2} \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} (F(| z_{i+1}\hat{S} \rangle | x\hat{2} \rangle \otimes | s \rangle ) \otimes \langle s | \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} h(| z_{i+1}\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i-1}( | x\hat{2} \rangle ) \otimes | s \rangle \langle s | \phi \rangle ) = | z_{i+1}\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i-1}(| x\hat{2} \rangle )\otimes | \phi \rangle$. Thus, we obtain ![]() $F(| z_i\hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | z_i\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i} (| x\hat{2} \rangle )\otimes | \phi \rangle$. In particular, when
$F(| z_i\hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | z_i\hat{S} \rangle \otimes g^{m(| \phi \rangle )-i} (| x\hat{2} \rangle )\otimes | \phi \rangle$. In particular, when ![]() $i=0$, we conclude that
$i=0$, we conclude that ![]() $F(| \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle \otimes g^{m(| \phi \rangle )}(| x\hat{2} \rangle ) \otimes | \phi \rangle$.
$F(| \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle | x\hat{2} \rangle | \phi \rangle ) = | \hat{T}^{\:m(| \phi \rangle )} \hat{S} \rangle \otimes g^{m(| \phi \rangle )}(| x\hat{2} \rangle ) \otimes | \phi \rangle$.
4.3 Implementing the binary search strategy
The strength of Scheme IV is further exemplified by an implementation of a simple binary search algorithm. Given any string ![]() $x\in \{0,1\}^k$ with
$x\in \{0,1\}^k$ with ![]() $k\geq 1$, assume that
$k\geq 1$, assume that ![]() $x$ equals
$x$ equals ![]() $bin_k(m)$ for a certain number
$bin_k(m)$ for a certain number ![]() $m\in [2^k]$. For any
$m\in [2^k]$. For any ![]() $s$ with
$s$ with ![]() $|s|=2^k$ and
$|s|=2^k$ and ![]() $b\in \{0,1\}$, the quantum function
$b\in \{0,1\}$, the quantum function ![]() $BinSearch$ satisfies the following equality:
$BinSearch$ satisfies the following equality: ![]() $BinSearch(| \widetilde{x} \rangle | \hat{b} \rangle | \hat{2} \rangle | s \rangle ) = | \widetilde{x} \rangle | \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | s \rangle$, where
$BinSearch(| \widetilde{x} \rangle | \hat{b} \rangle | \hat{2} \rangle | s \rangle ) = | \widetilde{x} \rangle | \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | s \rangle$, where ![]() $s_{(m)}$ is the
$s_{(m)}$ is the ![]() $m$th bit of
$m$th bit of ![]() $s$. This quantum function finds the
$s$. This quantum function finds the ![]() $m$th bit of
$m$th bit of ![]() $s$ and extracts its bit
$s$ and extracts its bit ![]() $s_{(m)}$ from
$s_{(m)}$ from ![]() $s$ by way of modifying
$s$ by way of modifying ![]() $| \hat{b} \rangle$ to
$| \hat{b} \rangle$ to ![]() $| \widehat{b\oplus s_{(m)}} \rangle$.
$| \widehat{b\oplus s_{(m)}} \rangle$.
Theorem 27. The above quantum function ![]() $BinSearch$ is definable within
$BinSearch$ is definable within ![]() $EQS_0+IV$.
$EQS_0+IV$.
Proof. We remark that the length of ![]() $s$ given to
$s$ given to ![]() $BinSearch(| \widetilde{x} \rangle | \hat{b} \rangle | \hat{2} \rangle | s \rangle )$ is a power of
$BinSearch(| \widetilde{x} \rangle | \hat{b} \rangle | \hat{2} \rangle | s \rangle )$ is a power of ![]() $2$. In this proof, we intend to use the quantum functions
$2$. In this proof, we intend to use the quantum functions ![]() $SecSWAP^{(3)}_{i,j}$ and
$SecSWAP^{(3)}_{i,j}$ and ![]() $COPY_1$ introduced in Lemmas6(1) and 7, respectively. Given any strings
$COPY_1$ introduced in Lemmas6(1) and 7, respectively. Given any strings ![]() $x=x_1x_2\cdots x_k$,
$x=x_1x_2\cdots x_k$, ![]() $s=s_1s_2\cdots s_{2^k}$, and
$s=s_1s_2\cdots s_{2^k}$, and ![]() $b\in \{0,1\}$ associated with the number
$b\in \{0,1\}$ associated with the number ![]() $m\in [2^k]$ satisfying
$m\in [2^k]$ satisfying ![]() $x=bin_k(m)$, we define the quantum function
$x=bin_k(m)$, we define the quantum function ![]() $g$ by setting
$g$ by setting ![]() $g(|{\hat{\dashv }} \rangle | \hat{b} \rangle | \hat{2} \rangle | s_m \rangle ) = |{\hat{\dashv }} \rangle | \widehat{b\oplus s_m} \rangle | \hat{2} \rangle | s_m \rangle$. Notice that
$g(|{\hat{\dashv }} \rangle | \hat{b} \rangle | \hat{2} \rangle | s_m \rangle ) = |{\hat{\dashv }} \rangle | \widehat{b\oplus s_m} \rangle | \hat{2} \rangle | s_m \rangle$. Notice that ![]() $\hat{b}=00b$ and
$\hat{b}=00b$ and ![]() $\widehat{b\oplus s_m} = 00b'$ with
$\widehat{b\oplus s_m} = 00b'$ with ![]() $b'=b\oplus s_m$. It is possible to realize
$b'=b\oplus s_m$. It is possible to realize ![]() $g$ by simply setting
$g$ by simply setting ![]() $g\equiv SWAP_{7,10} \circ Skip_5[COPY_1]\circ SWAP_{7,10}$ since
$g\equiv SWAP_{7,10} \circ Skip_5[COPY_1]\circ SWAP_{7,10}$ since ![]() $COPY_1(| b \rangle | s_m \rangle | w \rangle ) = | b\oplus s_m \rangle | s_m \rangle | w \rangle$ for any
$COPY_1(| b \rangle | s_m \rangle | w \rangle ) = | b\oplus s_m \rangle | s_m \rangle | w \rangle$ for any ![]() $w$. Let
$w$. Let ![]() $p_{\hat{0}} \equiv I$,
$p_{\hat{0}} \equiv I$, ![]() $p_{\hat{1}}\equiv HalfSWAP$, and
$p_{\hat{1}}\equiv HalfSWAP$, and ![]() $p_u=I$ for all indices
$p_u=I$ for all indices ![]() $u\in \{0,1\}^3-\{\hat{0},\hat{1}\}$. We then define
$u\in \{0,1\}^3-\{\hat{0},\hat{1}\}$. We then define ![]() $F$ to be
$F$ to be ![]() $CFQRec_1[\hat{2},I,g,I| \mathscr{P}_3,\mathscr{F}_3]$, where
$CFQRec_1[\hat{2},I,g,I| \mathscr{P}_3,\mathscr{F}_3]$, where ![]() $\mathscr{P}_3=\{p_u\}_{u\in \{0,1\}^3}$ and
$\mathscr{P}_3=\{p_u\}_{u\in \{0,1\}^3}$ and ![]() $\mathscr{F}_3=\{f_u\}_{u\in \{0,1\}^3}$ with
$\mathscr{F}_3=\{f_u\}_{u\in \{0,1\}^3}$ with ![]() $f_u=F$ for all
$f_u=F$ for all ![]() $u\in \{0,1\}^3$. Now, our goal is to verify that
$u\in \{0,1\}^3$. Now, our goal is to verify that ![]() $F$ indeed matches
$F$ indeed matches ![]() $BinSearch$.
$BinSearch$.
For any string ![]() $s\in \{0,1\}^{+}$ whose length is a power of
$s\in \{0,1\}^{+}$ whose length is a power of ![]() $2$ and for any number
$2$ and for any number ![]() $m\in [|s|]$, we explain how to find the
$m\in [|s|]$, we explain how to find the ![]() $m$th bit
$m$th bit ![]() $s_m$ of
$s_m$ of ![]() $s$. We first split
$s$. We first split ![]() $s$ into the left part and the right part of
$s$ into the left part and the right part of ![]() $s$ whose lengths are
$s$ whose lengths are ![]() $LH(|s|)$ and
$LH(|s|)$ and ![]() $RH(|s|)$, respectively. We assign
$RH(|s|)$, respectively. We assign ![]() $0$ to the left part and
$0$ to the left part and ![]() $1$ to the right part and we call the left part by
$1$ to the right part and we call the left part by ![]() $s_0$ and the right part by
$s_0$ and the right part by ![]() $s_1$. Starting
$s_1$. Starting ![]() $s_0$ (resp.,
$s_0$ (resp., ![]() $s_1$), we further split it into its left part, called
$s_1$), we further split it into its left part, called ![]() $s_{00}$ (resp.,
$s_{00}$ (resp., ![]() $s_{10}$), and its right part, called
$s_{10}$), and its right part, called ![]() $s_{01}$ (resp.,
$s_{01}$ (resp., ![]() $s_{11}$). Inductively, we repeat this process until the target strings become single symbols. In the end, a string
$s_{11}$). Inductively, we repeat this process until the target strings become single symbols. In the end, a string ![]() $x\in \{0,1\}^{\mathrm{ilog}(|s|)}$ is assigned to the single symbol obtained by the series of the above-described processes. We denote this unique symbol by
$x\in \{0,1\}^{\mathrm{ilog}(|s|)}$ is assigned to the single symbol obtained by the series of the above-described processes. We denote this unique symbol by ![]() $s_x$. If
$s_x$. If ![]() $x=bin_{\mathrm{ilog}(|s|)}(m)$, then
$x=bin_{\mathrm{ilog}(|s|)}(m)$, then ![]() $s_x$ coincides with the desired bit
$s_x$ coincides with the desired bit ![]() $s_m$. We then treat
$s_m$. We then treat ![]() $x$ as the binary representation of an index of the symbol
$x$ as the binary representation of an index of the symbol ![]() $s_{x}$ in
$s_{x}$ in ![]() $s$.
$s$.
Let ![]() $X_{k+1}=\hat{\dashv }$ and let
$X_{k+1}=\hat{\dashv }$ and let ![]() $X_i=\widehat{x_i} \widehat{x_{i+1}} \cdots \widehat{x_k} \hat{\dashv }$ for any index
$X_i=\widehat{x_i} \widehat{x_{i+1}} \cdots \widehat{x_k} \hat{\dashv }$ for any index ![]() $i\in [k]$. We split
$i\in [k]$. We split ![]() $s$ into two parts as
$s$ into two parts as ![]() $s=s^{(l)}s^{(r)}$ with
$s=s^{(l)}s^{(r)}$ with ![]() $|s^{(l)}|=LH(|s|)$ and
$|s^{(l)}|=LH(|s|)$ and ![]() $|s^{(r)}|=RH(|s|)$. We set
$|s^{(r)}|=RH(|s|)$. We set ![]() $m_1=m$ and, for each index
$m_1=m$ and, for each index ![]() $i\in [2,k]_{\mathbb{Z}}$, we take the number
$i\in [2,k]_{\mathbb{Z}}$, we take the number ![]() $m_i$ satisfying
$m_i$ satisfying ![]() $bin_{k-i+1}(m_i)=x_ix_{i+1}\cdots x_k$. Note that
$bin_{k-i+1}(m_i)=x_ix_{i+1}\cdots x_k$. Note that ![]() $s_{m_i} = s^{(r)}_{m_{i+1}}$ if
$s_{m_i} = s^{(r)}_{m_{i+1}}$ if ![]() $x_i=1$, and
$x_i=1$, and ![]() $s_{m_i} = s^{(l)}_{m_{i+1}}$ otherwise. When
$s_{m_i} = s^{(l)}_{m_{i+1}}$ otherwise. When ![]() $\ell (| s \rangle )=1$, we conclude that
$\ell (| s \rangle )=1$, we conclude that ![]() $F(| X_{k+1} \rangle | \hat{b}\hat{2} \rangle | s \rangle ) = g(| X_{k+1} \rangle | \hat{b}\hat{2} \rangle | s \rangle ) = g(| \hat{\dashv } \rangle | \hat{b} \rangle | \hat{2} \rangle | s \rangle ) = | \hat{\dashv } \rangle | \widehat{b\oplus s} \rangle | \hat{2} \rangle | s \rangle = BinSearch(| X_{k+1} \rangle | \hat{b}\hat{2} \rangle | s \rangle )$. Next, we assume that
$F(| X_{k+1} \rangle | \hat{b}\hat{2} \rangle | s \rangle ) = g(| X_{k+1} \rangle | \hat{b}\hat{2} \rangle | s \rangle ) = g(| \hat{\dashv } \rangle | \hat{b} \rangle | \hat{2} \rangle | s \rangle ) = | \hat{\dashv } \rangle | \widehat{b\oplus s} \rangle | \hat{2} \rangle | s \rangle = BinSearch(| X_{k+1} \rangle | \hat{b}\hat{2} \rangle | s \rangle )$. Next, we assume that ![]() $\ell (| s \rangle )=i\geq 2$. It follows by induction hypothesis that
$\ell (| s \rangle )=i\geq 2$. It follows by induction hypothesis that ![]() $F(| X_{i+1} \rangle | \hat{b}\hat{2} \rangle | s^{(r)} \rangle ) = | X_{i+1} \rangle | \hat{u} \rangle | \hat{2} \rangle | s^{(r)} \rangle$ with
$F(| X_{i+1} \rangle | \hat{b}\hat{2} \rangle | s^{(r)} \rangle ) = | X_{i+1} \rangle | \hat{u} \rangle | \hat{2} \rangle | s^{(r)} \rangle$ with ![]() $u= b\oplus s^{(r)}_{m_{i+1}}$ if
$u= b\oplus s^{(r)}_{m_{i+1}}$ if ![]() $x_i=1$, and
$x_i=1$, and ![]() $F(| X_{i+1} \rangle | \hat{b}\hat{2} \rangle | s^{(l)} \rangle ) = | X_{i+1} \rangle | \hat{v} \rangle | \hat{2} \rangle | s^{(l)} \rangle$ with
$F(| X_{i+1} \rangle | \hat{b}\hat{2} \rangle | s^{(l)} \rangle ) = | X_{i+1} \rangle | \hat{v} \rangle | \hat{2} \rangle | s^{(l)} \rangle$ with ![]() $v= b\oplus s^{(l)}_{m_{i+1}}$ otherwise. In the case of
$v= b\oplus s^{(l)}_{m_{i+1}}$ otherwise. In the case of ![]() $u=1$, since
$u=1$, since ![]() $| \psi _{p_{\hat{u}},s} \rangle = HalfSWAP(| s \rangle )$, it follows that
$| \psi _{p_{\hat{u}},s} \rangle = HalfSWAP(| s \rangle )$, it follows that ![]() $| \zeta _{\hat{u},p_{\hat{u}},s} \rangle = \sum _{t:|t|=RH(|s|)} ( F(| X_{i+1} \rangle | \hat{b}\hat{2} \rangle | t \rangle ) \otimes \langle t | s^{(r)}s^{(l)} \rangle ) = | X_{i+1} \rangle | \hat{u} \rangle | \hat{2} \rangle | s^{(l)} \rangle$. Therefore, when
$| \zeta _{\hat{u},p_{\hat{u}},s} \rangle = \sum _{t:|t|=RH(|s|)} ( F(| X_{i+1} \rangle | \hat{b}\hat{2} \rangle | t \rangle ) \otimes \langle t | s^{(r)}s^{(l)} \rangle ) = | X_{i+1} \rangle | \hat{u} \rangle | \hat{2} \rangle | s^{(l)} \rangle$. Therefore, when ![]() $x_i=1$, we obtain
$x_i=1$, we obtain ![]() $F(| X_i \rangle | \hat{b}\hat{2} \rangle | s \rangle ) = | x_i \rangle | X_{i+1} \rangle | \hat{u} \rangle | \hat{2} \rangle | s \rangle = BinSearch(| X_i \rangle | \hat{b}\hat{2} \rangle | s \rangle )$. When
$F(| X_i \rangle | \hat{b}\hat{2} \rangle | s \rangle ) = | x_i \rangle | X_{i+1} \rangle | \hat{u} \rangle | \hat{2} \rangle | s \rangle = BinSearch(| X_i \rangle | \hat{b}\hat{2} \rangle | s \rangle )$. When ![]() $x_i=0$, in contrast, we obtain
$x_i=0$, in contrast, we obtain ![]() $F(| X_i \rangle | \hat{b}\hat{2} \rangle | s \rangle ) = | x_i \rangle | X_{i+1} \rangle | \hat{v} \rangle | \hat{2} \rangle | s \rangle = BinSearch(| X_i \rangle | \hat{b}\hat{2} \rangle | s \rangle )$.
$F(| X_i \rangle | \hat{b}\hat{2} \rangle | s \rangle ) = | x_i \rangle | X_{i+1} \rangle | \hat{v} \rangle | \hat{2} \rangle | s \rangle = BinSearch(| X_i \rangle | \hat{b}\hat{2} \rangle | s \rangle )$.
As a result, we conclude that ![]() $F = BinSearch$, as requested.
$F = BinSearch$, as requested.
Hereafter, we demonstrate how to use the quantum function ![]() $BinSearch$. For this purpose, we first show the following statement.
$BinSearch$. For this purpose, we first show the following statement.
Corollary 2. Given ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$ and
$| \phi \rangle \in \mathscr{H}_{\infty }$ and ![]() $x=bin_k(m)$ for
$x=bin_k(m)$ for ![]() $k\in \mathbb{N}^{+}$ and
$k\in \mathbb{N}^{+}$ and ![]() $m\in [2^k]$, if
$m\in [2^k]$, if ![]() $| \phi \rangle$ is of the form
$| \phi \rangle$ is of the form ![]() $\sum _{s:|s|=2^k}\alpha _s | s \rangle$, then we set
$\sum _{s:|s|=2^k}\alpha _s | s \rangle$, then we set ![]() $Bit(| 0^5 \rangle | b \rangle | \widetilde{x} \rangle | \phi \rangle ) = \sum _{s:|s|=2^k}\alpha _s | 0^5 \rangle | b\oplus s_{(m)} \rangle | \widetilde{x} \rangle | s \rangle$, where
$Bit(| 0^5 \rangle | b \rangle | \widetilde{x} \rangle | \phi \rangle ) = \sum _{s:|s|=2^k}\alpha _s | 0^5 \rangle | b\oplus s_{(m)} \rangle | \widetilde{x} \rangle | s \rangle$, where ![]() $s_{(m)}$ is the
$s_{(m)}$ is the ![]() $m$th bit of
$m$th bit of ![]() $s$. This quantum function
$s$. This quantum function ![]() $Bit$ is definable within
$Bit$ is definable within ![]() $EQS_0+IV$.
$EQS_0+IV$.
Proof. Recall the quantum function ![]() $Skip_k[g]$ from Lemma4. We first change the quantum state
$Skip_k[g]$ from Lemma4. We first change the quantum state ![]() $| 0^5 \rangle | b \rangle | \widetilde{x} \rangle | \phi \rangle$ into
$| 0^5 \rangle | b \rangle | \widetilde{x} \rangle | \phi \rangle$ into ![]() $| \hat{b} \rangle | \hat{2} \rangle | \widetilde{x} \rangle | \phi \rangle$ by applying
$| \hat{b} \rangle | \hat{2} \rangle | \widetilde{x} \rangle | \phi \rangle$ by applying ![]() $h\equiv SWAP_{1,4}\circ SWAP_{2,5}\circ SWAP_{3,6} \circ Skip_2[NOT]\circ Skip_1[NOT]\circ NOT$.
$h\equiv SWAP_{1,4}\circ SWAP_{2,5}\circ SWAP_{3,6} \circ Skip_2[NOT]\circ Skip_1[NOT]\circ NOT$.
Consider the quantum function ![]() $f$ defined by
$f$ defined by ![]() $f(| \phi \rangle ) = \sum _{z:|z|=6} \langle z | \phi \rangle \otimes | z \rangle$ for all
$f(| \phi \rangle ) = \sum _{z:|z|=6} \langle z | \phi \rangle \otimes | z \rangle$ for all ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$. This
$| \phi \rangle \in \mathscr{H}_{\infty }$. This ![]() $f$ satisfies the following recursive property:
$f$ satisfies the following recursive property: ![]() $f(| x \rangle | \hat{\dashv } \rangle ) = SecSWAP^{(3)}_{1,3} \circ SecSWAP^{(3)}_{2,4} ( | u_1u_2 \rangle \otimes f(\langle u_1u_2 | x{\hat{\dashv }} \rangle ))$, where
$f(| x \rangle | \hat{\dashv } \rangle ) = SecSWAP^{(3)}_{1,3} \circ SecSWAP^{(3)}_{2,4} ( | u_1u_2 \rangle \otimes f(\langle u_1u_2 | x{\hat{\dashv }} \rangle ))$, where ![]() $x=u_1u_2x'$ with
$x=u_1u_2x'$ with ![]() $|u_1|=|u_2|=3$.
$|u_1|=|u_2|=3$.
Proposition18 makes it possible to realize the quantum function ![]() $F$ that satisfies
$F$ that satisfies ![]() $F(| \hat{b} \rangle | \hat{2} \rangle | \widetilde{x} \rangle \otimes | \phi \rangle ) = f(| \hat{b} \rangle | \hat{2} \rangle | \widetilde{x} \rangle )\otimes | \phi \rangle$. The last term actually equals
$F(| \hat{b} \rangle | \hat{2} \rangle | \widetilde{x} \rangle \otimes | \phi \rangle ) = f(| \hat{b} \rangle | \hat{2} \rangle | \widetilde{x} \rangle )\otimes | \phi \rangle$. The last term actually equals ![]() $| \widetilde{x} \rangle | \hat{b} \rangle | \hat{2} \rangle | \phi \rangle$. We apply
$| \widetilde{x} \rangle | \hat{b} \rangle | \hat{2} \rangle | \phi \rangle$. We apply ![]() $BinSearch$ to
$BinSearch$ to ![]() $| \widetilde{x} \rangle | \hat{b} \rangle | \hat{2} \rangle | s \rangle$ and obtain
$| \widetilde{x} \rangle | \hat{b} \rangle | \hat{2} \rangle | s \rangle$ and obtain ![]() $| \widetilde{x} \rangle | \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | s \rangle$. We further apply
$| \widetilde{x} \rangle | \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | s \rangle$. We further apply ![]() $f^{-1}$ to obtain
$f^{-1}$ to obtain ![]() $f^{-1}( | \widetilde{x} \rangle | \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | s \rangle ) = | \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | \widetilde{x} \rangle | s \rangle$. Finally, we apply
$f^{-1}( | \widetilde{x} \rangle | \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | s \rangle ) = | \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | \widetilde{x} \rangle | s \rangle$. Finally, we apply ![]() $h^{-1}$ to
$h^{-1}$ to ![]() $| \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | \widetilde{x} \rangle | s \rangle$ and obtain
$| \widehat{b\oplus s_{(m)}} \rangle | \hat{2} \rangle | \widetilde{x} \rangle | s \rangle$ and obtain ![]() $| 0^5 \rangle | b\oplus s_{(m)} \rangle | \widetilde{x} \rangle | s \rangle$. Therefore,
$| 0^5 \rangle | b\oplus s_{(m)} \rangle | \widetilde{x} \rangle | s \rangle$. Therefore, ![]() $Bit$ can be defined by a finite series of applications of Scheme I–IV.
$Bit$ can be defined by a finite series of applications of Scheme I–IV.
As the second application of ![]() $BinSearch$, we wish to “count” the number of 0s and 1s in an input string in a quantum-mechanical fashion. It is impossible to do so deterministically in polylogarithmic time. Fix a constant
$BinSearch$, we wish to “count” the number of 0s and 1s in an input string in a quantum-mechanical fashion. It is impossible to do so deterministically in polylogarithmic time. Fix a constant ![]() $\varepsilon \in [0,3/4)$ and consider the promise decision problem
$\varepsilon \in [0,3/4)$ and consider the promise decision problem ![]() $MAJPDP_{\varepsilon }$ in which we determine whether the total number of
$MAJPDP_{\varepsilon }$ in which we determine whether the total number of ![]() $0$s in
$0$s in ![]() $x$ is at least
$x$ is at least ![]() $\sqrt{1-\varepsilon }|x|$ or the total number of
$\sqrt{1-\varepsilon }|x|$ or the total number of ![]() $1$s is at least
$1$s is at least ![]() $\sqrt{1-\varepsilon }|x|$. Formally,
$\sqrt{1-\varepsilon }|x|$. Formally, ![]() $MAJPDP_{\varepsilon }$ is expressed as
$MAJPDP_{\varepsilon }$ is expressed as ![]() $(A_{\varepsilon },B_{\varepsilon })$, where
$(A_{\varepsilon },B_{\varepsilon })$, where ![]() $A_{\varepsilon } =\{x\in \{0,1\}^*\mid \#_1(x)\geq \sqrt{1-\varepsilon }|x|\}$ and
$A_{\varepsilon } =\{x\in \{0,1\}^*\mid \#_1(x)\geq \sqrt{1-\varepsilon }|x|\}$ and ![]() $B_{\varepsilon } =\{x\in \{0,1\}^*\mid \#_0(x)\geq \sqrt{1-\varepsilon }|x|\}$. We intend to prove the existence of a quantum function in
$B_{\varepsilon } =\{x\in \{0,1\}^*\mid \#_0(x)\geq \sqrt{1-\varepsilon }|x|\}$. We intend to prove the existence of a quantum function in ![]() $EQS_0+IV$ that “solves” this promise problem
$EQS_0+IV$ that “solves” this promise problem ![]() $MAJPDP_{\varepsilon }$ in the following sense.
$MAJPDP_{\varepsilon }$ in the following sense.
Proposition 28. Let ![]() $\varepsilon$ be any constant in
$\varepsilon$ be any constant in ![]() $[0,3/4)$. There exists a quantum function
$[0,3/4)$. There exists a quantum function ![]() $F$ in
$F$ in ![]() $EQS_0+IV$ such that, for any
$EQS_0+IV$ such that, for any ![]() $x\in \{0,1\}^*$, (1) if
$x\in \{0,1\}^*$, (1) if ![]() $x\in A_{\varepsilon }$, then
$x\in A_{\varepsilon }$, then ![]() $\|\langle 1 | \psi _{F,x} \rangle \|^2\geq 1-\varepsilon$ and (2) if
$\|\langle 1 | \psi _{F,x} \rangle \|^2\geq 1-\varepsilon$ and (2) if ![]() $x\in B_{\varepsilon }$, then
$x\in B_{\varepsilon }$, then ![]() $\|\langle 0 | \psi _{F,x} \rangle \|^2\geq 1-\varepsilon$, where
$\|\langle 0 | \psi _{F,x} \rangle \|^2\geq 1-\varepsilon$, where ![]() $| \psi _{F,x} \rangle = F(| 0^{3k} \rangle | \hat{\dashv } \rangle | x \rangle )$ with
$| \psi _{F,x} \rangle = F(| 0^{3k} \rangle | \hat{\dashv } \rangle | x \rangle )$ with ![]() $k=\mathrm{ilog}(|x|)$.
$k=\mathrm{ilog}(|x|)$.
To prove this proposition, we first demonstrate how to produce a superposition of all “indices” of a given input. This can be done by recursively applying ![]() $WH$ to
$WH$ to ![]() $| 0^{3k} \rangle | \hat{\dashv } \rangle$ as shown below.
$| 0^{3k} \rangle | \hat{\dashv } \rangle$ as shown below.
Lemma 29. There exists a quantum function ![]() $G$ in
$G$ in ![]() $EQS_0+IV$ satisfying
$EQS_0+IV$ satisfying ![]() $G(| 0^{3k} \rangle | \hat{\dashv } \rangle \otimes | \phi \rangle ) = \frac{1}{\sqrt{2^k}} \sum _{x:|x|=k}| \widetilde{x} \rangle | \phi \rangle$ for any
$G(| 0^{3k} \rangle | \hat{\dashv } \rangle \otimes | \phi \rangle ) = \frac{1}{\sqrt{2^k}} \sum _{x:|x|=k}| \widetilde{x} \rangle | \phi \rangle$ for any ![]() $n\in \mathbb{N}^{+}$ and any
$n\in \mathbb{N}^{+}$ and any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$, provided that
$| \phi \rangle \in \mathscr{H}_{\infty }$, provided that ![]() $k= \mathrm{ilog}(\ell (| \phi \rangle ))$.
$k= \mathrm{ilog}(\ell (| \phi \rangle ))$.
Proof. Consider the quantum function ![]() $\hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ) = \frac{1}{\sqrt{2^k}} \sum _{x:|x|=k}| \widetilde{x} \rangle$. This function
$\hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ) = \frac{1}{\sqrt{2^k}} \sum _{x:|x|=k}| \widetilde{x} \rangle$. This function ![]() $\hat{h}$ satisfies the following recursive property:
$\hat{h}$ satisfies the following recursive property: ![]() $\hat{h}(| \hat{\dashv } \rangle ) = | \hat{\dashv } \rangle$ and
$\hat{h}(| \hat{\dashv } \rangle ) = | \hat{\dashv } \rangle$ and ![]() $\hat{h}(| 0^3 \rangle | w\hat{\dashv } \rangle ) = h(| 0^3 \rangle \otimes \hat{h}(| w\hat{\dashv } \rangle ))$ for any string
$\hat{h}(| 0^3 \rangle | w\hat{\dashv } \rangle ) = h(| 0^3 \rangle \otimes \hat{h}(| w\hat{\dashv } \rangle ))$ for any string ![]() $w$, where
$w$, where ![]() $h\equiv Branch_2[\{g_u\}_{u\in \{0,1\}^2}]$ with
$h\equiv Branch_2[\{g_u\}_{u\in \{0,1\}^2}]$ with ![]() $g_{00}=WH$ and
$g_{00}=WH$ and ![]() $g_u=I$ for all indices
$g_u=I$ for all indices ![]() $u\in \{0,1\}^2-\{00\}$. Let us prove this property. Assume that
$u\in \{0,1\}^2-\{00\}$. Let us prove this property. Assume that ![]() $\hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ) = \frac{1}{\sqrt{2^k}}\sum _{x:|x|=k}| \widetilde{x} \rangle$. For the value
$\hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ) = \frac{1}{\sqrt{2^k}}\sum _{x:|x|=k}| \widetilde{x} \rangle$. For the value ![]() $\hat{h}(| 0^{3k+3} \rangle | \hat{\dashv } \rangle )$, we calculate
$\hat{h}(| 0^{3k+3} \rangle | \hat{\dashv } \rangle )$, we calculate ![]() $h(| 0^3 \rangle \otimes \hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ))$ as
$h(| 0^3 \rangle \otimes \hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ))$ as  $| 00 \rangle \otimes g(| 0 \rangle \otimes \hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle )) = | 00 \rangle \otimes \frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )\otimes \hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ) = \frac{1}{\sqrt{2}}(| \hat{0} \rangle +| \hat{1} \rangle )\otimes \frac{1}{\sqrt{2^k}}\sum _{x:|x|=3k}| \widetilde{x} \rangle = \frac{1}{\sqrt{2^{k+1}}}\sum _{y:|y|=k+1}| \widetilde{y} \rangle$. The last term clearly equals
$| 00 \rangle \otimes g(| 0 \rangle \otimes \hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle )) = | 00 \rangle \otimes \frac{1}{\sqrt{2}}(| 0 \rangle +| 1 \rangle )\otimes \hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ) = \frac{1}{\sqrt{2}}(| \hat{0} \rangle +| \hat{1} \rangle )\otimes \frac{1}{\sqrt{2^k}}\sum _{x:|x|=3k}| \widetilde{x} \rangle = \frac{1}{\sqrt{2^{k+1}}}\sum _{y:|y|=k+1}| \widetilde{y} \rangle$. The last term clearly equals ![]() $\hat{h}(| 0^{3k+3} \rangle | \hat{\dashv } \rangle )$.
$\hat{h}(| 0^{3k+3} \rangle | \hat{\dashv } \rangle )$.
By Proposition18, there exists a quantum function ![]() $G$ in
$G$ in ![]() $EQS_0+IV$ for which
$EQS_0+IV$ for which ![]() $G(| 0^{3k} \rangle | \hat{\dashv } \rangle \otimes | \phi \rangle ) = \hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ) \otimes | \phi \rangle$, where
$G(| 0^{3k} \rangle | \hat{\dashv } \rangle \otimes | \phi \rangle ) = \hat{h}(| 0^{3k} \rangle | \hat{\dashv } \rangle ) \otimes | \phi \rangle$, where ![]() $k= \mathrm{ilog}(\ell (| \phi \rangle ))$. This completes the lemma’s proof.
$k= \mathrm{ilog}(\ell (| \phi \rangle ))$. This completes the lemma’s proof.
With the help of Lemma29, the proof of Proposition28 easily follows.
Proof of Proposition 28. Consider ![]() $MAJPDP_{\varepsilon } = (A_{\varepsilon },B_{\varepsilon })$ defined above. We wish to construct a quantum function, say,
$MAJPDP_{\varepsilon } = (A_{\varepsilon },B_{\varepsilon })$ defined above. We wish to construct a quantum function, say, ![]() $F$ in
$F$ in ![]() $EQS_0+IV$ that “solves”
$EQS_0+IV$ that “solves” ![]() $MAJPDP_{\varepsilon }$ in the proposition’s sense. Recall the quantum function
$MAJPDP_{\varepsilon }$ in the proposition’s sense. Recall the quantum function ![]() $G$ of Lemma29. Since
$G$ of Lemma29. Since ![]() $G$ is norm-preserving and thus in
$G$ is norm-preserving and thus in ![]() $\widehat{EQS}$, Lemma23 ensures that
$\widehat{EQS}$, Lemma23 ensures that ![]() $G^{-1}$ exists.
$G^{-1}$ exists.
Let ![]() $x$ denote any string. We then set
$x$ denote any string. We then set ![]() $b_x=1$ if
$b_x=1$ if ![]() $x\in A_{\varepsilon }$ and
$x\in A_{\varepsilon }$ and ![]() $b_x=0$ if
$b_x=0$ if ![]() $x\in B_{\varepsilon }$. We start the desired computation with the quantum state
$x\in B_{\varepsilon }$. We start the desired computation with the quantum state ![]() $| \phi _x \rangle = | 0^6 \rangle | 0^{3k} \rangle | \hat{\dashv } \rangle | x \rangle$, where
$| \phi _x \rangle = | 0^6 \rangle | 0^{3k} \rangle | \hat{\dashv } \rangle | x \rangle$, where ![]() $k=\mathrm{ilog}(|x|)$, and apply
$k=\mathrm{ilog}(|x|)$, and apply ![]() $Skip_6[G]$ to generate
$Skip_6[G]$ to generate ![]() $\frac{1}{\sqrt{2^k}}\sum _{u:|u|=k}| \widetilde{u} \rangle | x \rangle | 0^6 \rangle$. We then move
$\frac{1}{\sqrt{2^k}}\sum _{u:|u|=k}| \widetilde{u} \rangle | x \rangle | 0^6 \rangle$. We then move ![]() $| 0^6 \rangle$ to the front and obtain
$| 0^6 \rangle$ to the front and obtain ![]() $\frac{1}{\sqrt{2^k}}\sum _{u:|u|=k}| 0^6 \rangle | \widetilde{u} \rangle | x \rangle$. We further apply
$\frac{1}{\sqrt{2^k}}\sum _{u:|u|=k}| 0^6 \rangle | \widetilde{u} \rangle | x \rangle$. We further apply ![]() $Bit$ to the resulting quantum state and generate
$Bit$ to the resulting quantum state and generate ![]() $\frac{1}{\sqrt{2^k}}\sum _{u:|u|=k} | 0^5 \rangle | x_{(m(u))} \rangle | \widetilde{u} \rangle | x \rangle$, where
$\frac{1}{\sqrt{2^k}}\sum _{u:|u|=k} | 0^5 \rangle | x_{(m(u))} \rangle | \widetilde{u} \rangle | x \rangle$, where ![]() $m(u)$ denotes a unique number satisfying that
$m(u)$ denotes a unique number satisfying that ![]() $u=bin_k(m(u))$ and
$u=bin_k(m(u))$ and ![]() $x_{(m(u))}$ is the
$x_{(m(u))}$ is the ![]() $m(u)$-th bit of
$m(u)$-th bit of ![]() $x$. We change it to
$x$. We change it to ![]() $| \gamma _x \rangle = \frac{1}{\sqrt{2^k}}\sum _{u:|u|=k} | \widetilde{u} \rangle | x \rangle | 0^5 \rangle | x_{(m(u))} \rangle$ and then apply
$| \gamma _x \rangle = \frac{1}{\sqrt{2^k}}\sum _{u:|u|=k} | \widetilde{u} \rangle | x \rangle | 0^5 \rangle | x_{(m(u))} \rangle$ and then apply ![]() $G^{-1}$. We denote the resulting quantum state by
$G^{-1}$. We denote the resulting quantum state by ![]() $| \beta _x \rangle$. Letting
$| \beta _x \rangle$. Letting ![]() $| \xi \rangle = | 0^{3k} \rangle | \hat{\dashv } \rangle$, we wish to calculate
$| \xi \rangle = | 0^{3k} \rangle | \hat{\dashv } \rangle$, we wish to calculate ![]() $\langle \xi | \beta _x \rangle$. Note that
$\langle \xi | \beta _x \rangle$. Note that ![]() $| \beta _x \rangle = G^{-1}(| \gamma _x \rangle )$ is equivalent to
$| \beta _x \rangle = G^{-1}(| \gamma _x \rangle )$ is equivalent to ![]() $G(| \beta _x \rangle ) = | \gamma _x \rangle$. It thus follows that
$G(| \beta _x \rangle ) = | \gamma _x \rangle$. It thus follows that ![]() $\langle \xi | \beta _x \rangle$ equals
$\langle \xi | \beta _x \rangle$ equals ![]() $\langle \psi _{G,\xi } | \gamma _x \rangle$, which is further calculated to
$\langle \psi _{G,\xi } | \gamma _x \rangle$, which is further calculated to ![]() $(\frac{1}{\sqrt{2^k}}\sum _{v:|v|=k}\langle{\widetilde{v}} |)\cdot (\frac{1}{\sqrt{2^k}}\sum _{u:|u|=k} | \widetilde{u} \rangle | x \rangle | 0^5 \rangle | x_{(m(u))} \rangle ) = \frac{1}{2^k}| x \rangle | 0^5 \rangle | x_{(m(u))} \rangle$, where
$(\frac{1}{\sqrt{2^k}}\sum _{v:|v|=k}\langle{\widetilde{v}} |)\cdot (\frac{1}{\sqrt{2^k}}\sum _{u:|u|=k} | \widetilde{u} \rangle | x \rangle | 0^5 \rangle | x_{(m(u))} \rangle ) = \frac{1}{2^k}| x \rangle | 0^5 \rangle | x_{(m(u))} \rangle$, where ![]() $| \psi _{G,\xi } \rangle =G(| \xi \rangle )$.
$| \psi _{G,\xi } \rangle =G(| \xi \rangle )$.
After removing the last qubit to the front, we obtain a unique quantum state, say, ![]() $| \eta _x \rangle$. Finally, we measure the first qubit of
$| \eta _x \rangle$. Finally, we measure the first qubit of ![]() $| \eta _x \rangle$ in the computational basis. If
$| \eta _x \rangle$ in the computational basis. If ![]() $x\in A_{\varepsilon }\cup B_{\varepsilon }$, then
$x\in A_{\varepsilon }\cup B_{\varepsilon }$, then ![]() $b_x$ satisfies that
$b_x$ satisfies that ![]() $\|\langle b_x | \eta _x \rangle \|^2 \geq (\frac{1}{2^{k}}\sum _{u}\langle b_x | x_{(m(u))} \rangle )^2 = (\frac{\#_{b_x}(x)}{2^k})^2 \geq (\sqrt{1-\varepsilon })^2 = 1-\varepsilon$ because of the promise given by
$\|\langle b_x | \eta _x \rangle \|^2 \geq (\frac{1}{2^{k}}\sum _{u}\langle b_x | x_{(m(u))} \rangle )^2 = (\frac{\#_{b_x}(x)}{2^k})^2 \geq (\sqrt{1-\varepsilon })^2 = 1-\varepsilon$ because of the promise given by ![]() $(A_{\varepsilon },B_{\varepsilon })$.
$(A_{\varepsilon },B_{\varepsilon })$.
5. Relationships to quantum computability
Throughout Section 3, we have studied basic properties of quantum functions in ![]() $EQS$. In this section, we will look into relationships of these quantum functions to other platforms of limited computability, in particular, a model of polylogarithmic-time (or polylogtime) Turing machine.
$EQS$. In this section, we will look into relationships of these quantum functions to other platforms of limited computability, in particular, a model of polylogarithmic-time (or polylogtime) Turing machine.
5.1 Runtime-restricted quantum Turing machines
We wish to describe a computational model of quantum Turing machine (or QTM, for short) that runs particularly in polylogarithmic time. For this purpose, we need to modify a standard model of QTM defined in (Bernstein and Vazirani, Reference Bernstein and Vazirani1997; Ozawa and Nishimura, Reference Ozawa and Nishimura2000; Yamakami, Reference Yamakami1999) structurally and behaviorally. This new model also expands the classical model of (poly)logtime Turing machine (TM) discussed in (Barrington et al., Reference Barrington, Immerman and Straubing1990). Notice that quantum polylogtime computability was already discussed by, for example, Raz and Tal (Reference Raz and Tal2022) based on uniform quantum circuit families. For more information, refer to (Raz and Tal, Reference Raz and Tal2022) and references therein.
A (random-access) QTM Footnote 4 (or just a QTM in this work) is equipped with a random-access read-only input tape, multiple rewritable work tapes of ![]() $O(\log ^k{n})$ cells, and a rewritable index tape of exactly
$O(\log ^k{n})$ cells, and a rewritable index tape of exactly ![]() $\mathrm{ilog}(n)+1$ cells, where
$\mathrm{ilog}(n)+1$ cells, where ![]() $k$ is a constant in
$k$ is a constant in ![]() $\mathbb{N}^{+}$ and
$\mathbb{N}^{+}$ and ![]() $n$ refers to the length of an input. The index tape indicates the cell location (or address) of the input tape, specifying which qubit of a given input we wish to access. This QTM
$n$ refers to the length of an input. The index tape indicates the cell location (or address) of the input tape, specifying which qubit of a given input we wish to access. This QTM ![]() $M$ is formally expressed as
$M$ is formally expressed as ![]() $(Q,\Sigma, \{\rhd, \lhd \},\delta, q_0,Q_{acc},Q_{rej})$, where
$(Q,\Sigma, \{\rhd, \lhd \},\delta, q_0,Q_{acc},Q_{rej})$, where ![]() $Q$ is a finite set of inner states,
$Q$ is a finite set of inner states, ![]() $\Sigma =\{0,1\}$ is an alphabet,
$\Sigma =\{0,1\}$ is an alphabet, ![]() $\rhd$ and
$\rhd$ and ![]() $\lhd$ are endmarkers,
$\lhd$ are endmarkers, ![]() $\delta$ is a quantum transition function,
$\delta$ is a quantum transition function, ![]() $q_0$ (
$q_0$ (![]() $\in Q)$ is the initial (inner) state, and
$\in Q)$ is the initial (inner) state, and ![]() $Q_{acc}$ (resp.,
$Q_{acc}$ (resp., ![]() $Q_{rej}$) (
$Q_{rej}$) (![]() $\subseteq Q$) is a set of accepting (resp., rejecting) states. We use an additional convention that the input tape, the index tape, and all the work tapes have two endmarkers to mark the usable areas of these tapes. This in fact helps the machine understand the “size” of a given input. The QTM
$\subseteq Q$) is a set of accepting (resp., rejecting) states. We use an additional convention that the input tape, the index tape, and all the work tapes have two endmarkers to mark the usable areas of these tapes. This in fact helps the machine understand the “size” of a given input. The QTM ![]() $M$ begins with an input qustring
$M$ begins with an input qustring ![]() $| \phi \rangle$ given on the input tape marked by the endmarkers. Let
$| \phi \rangle$ given on the input tape marked by the endmarkers. Let ![]() $| \phi \rangle = \sum _{x\in \Sigma ^n}\alpha _x| x \rangle$ with
$| \phi \rangle = \sum _{x\in \Sigma ^n}\alpha _x| x \rangle$ with ![]() $n\in \mathbb{N}^{+}$ and
$n\in \mathbb{N}^{+}$ and ![]() $\alpha _x\in \mathbb{C}$ for all
$\alpha _x\in \mathbb{C}$ for all ![]() $x$’s.
$x$’s.
Recall from Section 2.1 the binary encoding of natural numbers. Let ![]() $k_n=\mathrm{ilog}(n)$. To access the tape cell indexed by
$k_n=\mathrm{ilog}(n)$. To access the tape cell indexed by ![]() $m$,
$m$, ![]() $M$ first produces the binary string
$M$ first produces the binary string ![]() $bin_{k_n}(m)$ on the index tape with an auxiliary bit
$bin_{k_n}(m)$ on the index tape with an auxiliary bit ![]() $b$ and then enters a designated query state, say,
$b$ and then enters a designated query state, say, ![]() $q_{query}$ in
$q_{query}$ in ![]() $Q$. If the index tape contains
$Q$. If the index tape contains ![]() $| bin_{k_n}(m) \rangle | b \rangle$, then this quantum state becomes
$| bin_{k_n}(m) \rangle | b \rangle$, then this quantum state becomes ![]() $| bin_{k_n}(m) \rangle | b\oplus x_{(m)} \rangle$ as the immediate consequence of the query, where
$| bin_{k_n}(m) \rangle | b\oplus x_{(m)} \rangle$ as the immediate consequence of the query, where ![]() $x_{(m)}$ is the
$x_{(m)}$ is the ![]() $m$th input symbol of an input
$m$th input symbol of an input ![]() $x\in \Sigma ^+$. With the proper use of work tapes, we assume that, while writing
$x\in \Sigma ^+$. With the proper use of work tapes, we assume that, while writing ![]() $| bin_{k_n}(m) \rangle | b \rangle$ until entering a query state, the tape head never moves to the left and, whenever it writes a non-blank symbol, it must move to the right. We remark that the number of queries and their timings may vary on all computation paths of
$| bin_{k_n}(m) \rangle | b \rangle$ until entering a query state, the tape head never moves to the left and, whenever it writes a non-blank symbol, it must move to the right. We remark that the number of queries and their timings may vary on all computation paths of ![]() $M$ on
$M$ on ![]() $| \phi \rangle$.
$| \phi \rangle$.
Concerning a random access to an input, a classical polylogtime TM takes the following convention (Barrington et al., Reference Barrington, Immerman and Straubing1990; Vollmer, Reference Vollmer1999). When the machine enters a query state with index-tape content ![]() $bin_{k_n}(m)$, an input-tape head instantly jumps to the target bit
$bin_{k_n}(m)$, an input-tape head instantly jumps to the target bit ![]() $x_{(m)}$ of an input
$x_{(m)}$ of an input ![]() $x$ and reads it. After this query process, the index tape remains unerased and the corresponding tape head does not automatically return to the start cell. Therefore, for the next query, the machine can save time to rewrite the same query word, but it must overwrite a different query word over the previous query word on the index tape.
$x$ and reads it. After this query process, the index tape remains unerased and the corresponding tape head does not automatically return to the start cell. Therefore, for the next query, the machine can save time to rewrite the same query word, but it must overwrite a different query word over the previous query word on the index tape.
The quantum transition function ![]() $\delta$ takes a quantum transition of the form
$\delta$ takes a quantum transition of the form ![]() $\delta (q,\sigma, $
$\delta (q,\sigma, $ ![]() $\tau _1,\tau _2,\ldots, \tau _c) = \sum _{r}\alpha _r | p,\xi, \eta _1,\eta _2,\ldots, \eta _c, d,d^{\prime}_1,d^{\prime}_2,\ldots, d^{\prime}_c \rangle$, where
$\tau _1,\tau _2,\ldots, \tau _c) = \sum _{r}\alpha _r | p,\xi, \eta _1,\eta _2,\ldots, \eta _c, d,d^{\prime}_1,d^{\prime}_2,\ldots, d^{\prime}_c \rangle$, where ![]() $r=(p,\xi, \eta _1,\eta _2,\ldots, $
$r=(p,\xi, \eta _1,\eta _2,\ldots, $ ![]() $\eta _c, d,d^{\prime}_1,d^{\prime}_2,\ldots, d^{\prime}_c)$, which indicates that, if
$\eta _c, d,d^{\prime}_1,d^{\prime}_2,\ldots, d^{\prime}_c)$, which indicates that, if ![]() $M$ is in inner state
$M$ is in inner state ![]() $q$ reading
$q$ reading ![]() $\sigma$ on the index tape and
$\sigma$ on the index tape and ![]() $(\tau _1,\tau _2,\ldots, \tau _c)$ on the
$(\tau _1,\tau _2,\ldots, \tau _c)$ on the ![]() $c$ work tapes, then, in a single step, with transition amplitude
$c$ work tapes, then, in a single step, with transition amplitude ![]() $\alpha _r$,
$\alpha _r$, ![]() $M$ changes
$M$ changes ![]() $q$ to
$q$ to ![]() $p$, writes
$p$, writes ![]() $\xi$ over
$\xi$ over ![]() $\sigma$ by moving the input-tape head in direction
$\sigma$ by moving the input-tape head in direction ![]() $d\in \{-1,+1\}$, and writes
$d\in \{-1,+1\}$, and writes ![]() $\eta _i$ over
$\eta _i$ over ![]() $\tau _i$ by moving the
$\tau _i$ by moving the ![]() $i$th work-tape head in direction
$i$th work-tape head in direction ![]() $d^{\prime}_i\in \{-1,+1\}$. For practicality, we can limit the scope of transition amplitudes of QTMs. In this work, we allow only the following two forms of quantum transitions:
$d^{\prime}_i\in \{-1,+1\}$. For practicality, we can limit the scope of transition amplitudes of QTMs. In this work, we allow only the following two forms of quantum transitions: ![]() $\delta (q,\sigma, \tau _1,\tau _2,\ldots, \tau _c) = \cos \theta | p_1,\xi _1,\eta _{11},\eta _{12},\ldots, \eta _{1c}, d_1,d^{\prime}_{11},d^{\prime}_{12},\ldots, d^{\prime}_{1c} \rangle + \sin \theta | p_2,\xi _2,\eta _{21},\eta _{22},\ldots, \eta _{2c}, d_2,d^{\prime}_{21},d^{\prime}_{22},\ldots, d^{\prime}_{2c} \rangle$ and
$\delta (q,\sigma, \tau _1,\tau _2,\ldots, \tau _c) = \cos \theta | p_1,\xi _1,\eta _{11},\eta _{12},\ldots, \eta _{1c}, d_1,d^{\prime}_{11},d^{\prime}_{12},\ldots, d^{\prime}_{1c} \rangle + \sin \theta | p_2,\xi _2,\eta _{21},\eta _{22},\ldots, \eta _{2c}, d_2,d^{\prime}_{21},d^{\prime}_{22},\ldots, d^{\prime}_{2c} \rangle$ and ![]() $\delta (q,\sigma, \tau _1,\tau _2,\ldots, \tau _c) = e^{\imath \theta } | p,\xi, \eta _1,$
$\delta (q,\sigma, \tau _1,\tau _2,\ldots, \tau _c) = e^{\imath \theta } | p,\xi, \eta _1,$ ![]() $\eta _2,\ldots, \eta _c, d,d^{\prime}_1,d^{\prime}_2, \ldots, d^{\prime}_c \rangle$, based on the universality of a set of quantum gates of Barenco et al. (Reference Barenco, Bennett, Cleve, DiVicenzo, Margolus, Shor, Sleator, Smolin and Weinfurter1995).
$\eta _2,\ldots, \eta _c, d,d^{\prime}_1,d^{\prime}_2, \ldots, d^{\prime}_c \rangle$, based on the universality of a set of quantum gates of Barenco et al. (Reference Barenco, Bennett, Cleve, DiVicenzo, Margolus, Shor, Sleator, Smolin and Weinfurter1995).
A QTM is required to satisfy the so-called “well-formedness condition” (see, e.g., Yamakami, Reference Yamakami1999, Reference Yamakami2003) to guarantee that the behaviors of the QTM obeys the laws of quantum physics. A surface configuration of ![]() $M$ on an input
$M$ on an input ![]() $x$ of length
$x$ of length ![]() $n$ is an element
$n$ is an element ![]() $(q,u,r,w_1,s_1,w_2,s_2,\ldots, w_c,s_c)$ of the surface-configuration set
$(q,u,r,w_1,s_1,w_2,s_2,\ldots, w_c,s_c)$ of the surface-configuration set ![]() $Q\times \{\triangleright u\triangleleft \mid u\in \{0,1,B\}^{k_n+1}\} \times [0,k_n+2]_{\mathbb{Z}} \times ( \{\triangleright w\triangleleft \mid w\in \{0,1,B\}^{k_n}\} \times [0,k_n+1]_{\mathbb{Z}})^c$, which depicts the circumstance where
$Q\times \{\triangleright u\triangleleft \mid u\in \{0,1,B\}^{k_n+1}\} \times [0,k_n+2]_{\mathbb{Z}} \times ( \{\triangleright w\triangleleft \mid w\in \{0,1,B\}^{k_n}\} \times [0,k_n+1]_{\mathbb{Z}})^c$, which depicts the circumstance where ![]() $M$ is in inner state
$M$ is in inner state ![]() $q$, scanning the
$q$, scanning the ![]() $r$th bit of the index tape content
$r$th bit of the index tape content ![]() $u$, and the
$u$, and the ![]() $s_i$th bit of the
$s_i$th bit of the ![]() $i$th work tape content
$i$th work tape content ![]() $w_i$. We call the space spanned by this set of surface configurations the surface configuration space of
$w_i$. We call the space spanned by this set of surface configurations the surface configuration space of ![]() $M$ on
$M$ on ![]() $x$. The time-evolution operator of
$x$. The time-evolution operator of ![]() $M$ on the input
$M$ on the input ![]() $x$ is a map from superpositions of surface configurations of
$x$ is a map from superpositions of surface configurations of ![]() $M$ on
$M$ on ![]() $x$ to other superpositions of surface configurations resulting from a single application of
$x$ to other superpositions of surface configurations resulting from a single application of ![]() $\delta$ of
$\delta$ of ![]() $M$. A QTM
$M$. A QTM ![]() $M$ is said to be well-formed if its time-evolution operator of
$M$ is said to be well-formed if its time-evolution operator of ![]() $M$ preserves the
$M$ preserves the ![]() $\ell _2$-norm in the surface configuration space of
$\ell _2$-norm in the surface configuration space of ![]() $M$ on all inputs.
$M$ on all inputs.
At every step, we first apply ![]() $\delta$ to a superposition of surface configurations and then perform a measurement in the halting inner states (i.e., either accepting states or rejecting states). If
$\delta$ to a superposition of surface configurations and then perform a measurement in the halting inner states (i.e., either accepting states or rejecting states). If ![]() $M$ is not in a halting state, we move to the next step with the quantum state obtained by tracing out all halting surface configurations. Generally, QTMs can “recognize” not only sets of classical strings but also sets of qustrings.
$M$ is not in a halting state, we move to the next step with the quantum state obtained by tracing out all halting surface configurations. Generally, QTMs can “recognize” not only sets of classical strings but also sets of qustrings.
For convenience, we modify ![]() $M$ slightly so that
$M$ slightly so that ![]() $M$ produces
$M$ produces ![]() $1$ (resp.,
$1$ (resp., ![]() $0$) in the first cell of the first work tape when
$0$) in the first cell of the first work tape when ![]() $M$ enters a designated final state (in place of accepting/rejecting states). We say that
$M$ enters a designated final state (in place of accepting/rejecting states). We say that ![]() $M$ produces
$M$ produces ![]() $b$ with probability
$b$ with probability ![]() $\gamma$ if, after
$\gamma$ if, after ![]() $M$ halts, we observe
$M$ halts, we observe ![]() $b$ as an outcome of
$b$ as an outcome of ![]() $M$ with probability
$M$ with probability ![]() $\gamma$.
$\gamma$.
We call ![]() $M$ polylogarithmic time (or polylogtime) if we force
$M$ polylogarithmic time (or polylogtime) if we force ![]() $M$ to stop its application of
$M$ to stop its application of ![]() $\delta$ after
$\delta$ after ![]() $O(\log ^k{n})$ steps for a certain fixed constant
$O(\log ^k{n})$ steps for a certain fixed constant ![]() $k\in \mathbb{N}^{+}$, not depending on the choice of inputs. We do not require all computation paths to terminate within the specified time.
$k\in \mathbb{N}^{+}$, not depending on the choice of inputs. We do not require all computation paths to terminate within the specified time.
Let us consider a language ![]() $L$ over
$L$ over ![]() $\{0,1\}$ that satisfies the following condition: there are a constant
$\{0,1\}$ that satisfies the following condition: there are a constant ![]() $\varepsilon \in [0,1/2)$ and a polylogtime QTM
$\varepsilon \in [0,1/2)$ and a polylogtime QTM ![]() $M$ whose amplitude set is
$M$ whose amplitude set is ![]() $K$ such that (i) for any input
$K$ such that (i) for any input ![]() $x\in L$,
$x\in L$, ![]() $M$ accepts
$M$ accepts ![]() $x$ with probability at least
$x$ with probability at least ![]() $1-\varepsilon$ and (ii) for any
$1-\varepsilon$ and (ii) for any ![]() $x\notin L$,
$x\notin L$, ![]() $M$ rejects
$M$ rejects ![]() $x$ with probability at least
$x$ with probability at least ![]() $1-\varepsilon$. These conditions are referred to as bounded-error probability. The notation
$1-\varepsilon$. These conditions are referred to as bounded-error probability. The notation ![]() $\mathrm{BQPOLYLOGTIME}_{K}$ denotes the collection of all such languages
$\mathrm{BQPOLYLOGTIME}_{K}$ denotes the collection of all such languages ![]() $L$.
$L$.
5.2 Computational complexity of polylogtime QTMs
We begin with a discussion on the computational complexity of polylogtime QTMs. Remember that input tapes of these machines are read-only and accessed by way of writing cell locations onto index tapes.
In the classical setting, the notation ![]() $\mathrm{DLOGTIME}$ was used by Barrington et al. (1990) to express the family of all languages recognized by logtime deterministic TMs (or succinctly, DTMs). Similarly, we denote the nondeterministic variant of
$\mathrm{DLOGTIME}$ was used by Barrington et al. (1990) to express the family of all languages recognized by logtime deterministic TMs (or succinctly, DTMs). Similarly, we denote the nondeterministic variant of ![]() $\mathrm{DLOGTIME}$ by
$\mathrm{DLOGTIME}$ by ![]() $\mathrm{NLOGTIME}$. With the use of classical probabilistic TMs (or PTMs) in place of DTMs, we say that a PTM
$\mathrm{NLOGTIME}$. With the use of classical probabilistic TMs (or PTMs) in place of DTMs, we say that a PTM ![]() $M$ recognizes a language
$M$ recognizes a language ![]() $L$ with unbounded-error probability if, for any
$L$ with unbounded-error probability if, for any ![]() $x\in L$,
$x\in L$, ![]() $M$ accepts it with probability more than
$M$ accepts it with probability more than ![]() $1/2$ and, for any
$1/2$ and, for any ![]() $x\notin L$,
$x\notin L$, ![]() $M$ rejects with probability at least
$M$ rejects with probability at least ![]() $1/2$. We further define
$1/2$. We further define ![]() $\mathrm{PPOLYLOGTIME}$ using unbounded-error polylogtime PTMs.
$\mathrm{PPOLYLOGTIME}$ using unbounded-error polylogtime PTMs.
Theorem 30. ![]() $\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}} \subsetneqq \mathrm{PPOLYLOGTIME}$ and
$\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}} \subsetneqq \mathrm{PPOLYLOGTIME}$ and ![]() $\mathrm{NLOGTIME}\nsubseteq \mathrm{BQPOLYLOGT}$
$\mathrm{NLOGTIME}\nsubseteq \mathrm{BQPOLYLOGT}$ ![]() $\mathrm{IME}_{\mathbb{C}}$.
$\mathrm{IME}_{\mathbb{C}}$.
For the proof of Theorem 30, nevertheless, we first verify the following impossibility result of the parity function and the OR function by polylogtime QTMs, where the parity function, ![]() $Parity$, is defined by
$Parity$, is defined by ![]() $Parity(x) = \bigoplus _{i=1}^{n}x_i$ and the OR function,
$Parity(x) = \bigoplus _{i=1}^{n}x_i$ and the OR function, ![]() $OR$, is defined by
$OR$, is defined by ![]() $OR(x)=\max \{x_i\mid i\in [n]\}$ for any number
$OR(x)=\max \{x_i\mid i\in [n]\}$ for any number ![]() $n\in \mathbb{N}^{+}$ and any
$n\in \mathbb{N}^{+}$ and any ![]() $n$-bit string
$n$-bit string ![]() $x=x_1x_2\ldots x_n$.
$x=x_1x_2\ldots x_n$.
Lemma 31. The parity function and the OR function cannot be computed by any polylogtime QTM with bounded-error probability.
Proof. This proof comes from a result on the quantum query complexity gap between quantum and deterministic query complexities of the parity function. Assume that a polylogtime QTM, say, ![]() $M$ computes the parity function with bounded-error probability.
$M$ computes the parity function with bounded-error probability.
We encode ![]() $M$’s surface configuration
$M$’s surface configuration ![]() $conf$ into a “single” quantum state
$conf$ into a “single” quantum state ![]() $| \phi \rangle$. As done in Lemma29, it is possible to produce in polylog time a superposition of all locations of the input-tape cells by repeatedly applying
$| \phi \rangle$. As done in Lemma29, it is possible to produce in polylog time a superposition of all locations of the input-tape cells by repeatedly applying ![]() $WH$ to
$WH$ to ![]() $| 0^{\mathrm{ilog}(n)} \rangle$. This helps us access all input bits quantumly at once with the equal probability. Since the input tape is read-only, this type of input access can be realized as a (black-box) quantum query model Footnote 5 used in the study of quantum query complexity. Refer to, for example, (Ambainis, Reference Ambainis2002; Beals et al., Reference Beals, Buhrman, Cleve, Mosca and de Wolf2001; Nishimura and Yamakami, Reference Nishimura and Yamakami2004).
$| 0^{\mathrm{ilog}(n)} \rangle$. This helps us access all input bits quantumly at once with the equal probability. Since the input tape is read-only, this type of input access can be realized as a (black-box) quantum query model Footnote 5 used in the study of quantum query complexity. Refer to, for example, (Ambainis, Reference Ambainis2002; Beals et al., Reference Beals, Buhrman, Cleve, Mosca and de Wolf2001; Nishimura and Yamakami, Reference Nishimura and Yamakami2004).
In such a (black-box) quantum query model, we run the following quantum algorithm on a binary input ![]() $x$ of length
$x$ of length ![]() $n$. We prepare a series of unitary transformations
$n$. We prepare a series of unitary transformations ![]() $U_0,U_1,\ldots, U_{t-1},U_t$ and a special oracle transformationFootnote 6
$U_0,U_1,\ldots, U_{t-1},U_t$ and a special oracle transformationFootnote 6 ![]() $Q_x$ that changes
$Q_x$ that changes ![]() $| bin_{k_n}(m) \rangle | b \rangle | \phi \rangle$ to
$| bin_{k_n}(m) \rangle | b \rangle | \phi \rangle$ to ![]() $| bin_{k_n}(m) \rangle | b\oplus x_{(m)} \rangle | \phi \rangle$, where
$| bin_{k_n}(m) \rangle | b\oplus x_{(m)} \rangle | \phi \rangle$, where ![]() $k_n=\mathrm{ilog}(n)$ and
$k_n=\mathrm{ilog}(n)$ and ![]() $x_{(m)}$ is the
$x_{(m)}$ is the ![]() $m$th bit of
$m$th bit of ![]() $x$. We start with the initial quantum state
$x$. We start with the initial quantum state ![]() $| \psi _0 \rangle = | 0^m \rangle$. We then compute
$| \psi _0 \rangle = | 0^m \rangle$. We then compute ![]() $U_tQ_xU_{t-1}Q_x\cdots U_1Q_xU_0| \psi _0 \rangle$. Finally, we measure the resulting quantum state in the computational basis. The number
$U_tQ_xU_{t-1}Q_x\cdots U_1Q_xU_0| \psi _0 \rangle$. Finally, we measure the resulting quantum state in the computational basis. The number ![]() $t$ indicates the total number of queries made by this algorithm on each computation path.
$t$ indicates the total number of queries made by this algorithm on each computation path.
Claim 32. Each polylogtime QTM can be simulated by a (black-box) quantum query model with ![]() $O(\log ^k{n})$ queries for an appropriate constant
$O(\log ^k{n})$ queries for an appropriate constant ![]() $k\in \mathbb{N}^{+}$.
$k\in \mathbb{N}^{+}$.
Proof. Recall that a QTM has an read-only input tape, which holds an input string. Whenever a QTM makes a query on the ![]() $i$th position by entering a unique query state
$i$th position by entering a unique query state ![]() $q_{query}$, the machine instantly receives the information on the
$q_{query}$, the machine instantly receives the information on the ![]() $i$th bit of a given input string written on the input tape. We view this input tape as an oracle of a (black-box) quantum query model and we further view this entire query process of the QTM as a procedure of forming a superposition of query words indicating input-bit positions and receiving their answers from the oracle.
$i$th bit of a given input string written on the input tape. We view this input tape as an oracle of a (black-box) quantum query model and we further view this entire query process of the QTM as a procedure of forming a superposition of query words indicating input-bit positions and receiving their answers from the oracle.
We first construct a unitary transformation to simulate a single non-query transition of ![]() $M$. Recall that, when
$M$. Recall that, when ![]() $M$ enters
$M$ enters ![]() $q_{query}$, it changes
$q_{query}$, it changes ![]() $| bin_{k_n}(m) \rangle | b \rangle | \phi \rangle$ to
$| bin_{k_n}(m) \rangle | b \rangle | \phi \rangle$ to ![]() $| bin_{k_n}(m) \rangle | b\oplus x_{(m)} \rangle | \phi \rangle$ in a single step. To translate
$| bin_{k_n}(m) \rangle | b\oplus x_{(m)} \rangle | \phi \rangle$ in a single step. To translate ![]() $M$’s query process, we generate
$M$’s query process, we generate ![]() $| bin_{k_n}(1) \rangle | 0 \rangle$ in an extra register. If
$| bin_{k_n}(1) \rangle | 0 \rangle$ in an extra register. If ![]() $M$ is in the inner state
$M$ is in the inner state ![]() $q_{query}$, then we swap between this register and the register containing the content of
$q_{query}$, then we swap between this register and the register containing the content of ![]() $M$’s index tape. Otherwise, we do nothing. We then apply
$M$’s index tape. Otherwise, we do nothing. We then apply ![]() $Q_x$ to change
$Q_x$ to change ![]() $| bin_{k_n}(m) \rangle | b \rangle | \phi \rangle$ to
$| bin_{k_n}(m) \rangle | b \rangle | \phi \rangle$ to ![]() $| bin_{k_n}(m) \rangle | b\oplus x_{(m)} \rangle | \phi \rangle$. Notice that this process does not alter the inner state of
$| bin_{k_n}(m) \rangle | b\oplus x_{(m)} \rangle | \phi \rangle$. Notice that this process does not alter the inner state of ![]() $M$. After applying
$M$. After applying ![]() $Q_x$, we swap back the two registers exactly when
$Q_x$, we swap back the two registers exactly when ![]() $M$’s inner state is
$M$’s inner state is ![]() $q_{query}$ and then we follow the transition of
$q_{query}$ and then we follow the transition of ![]() $M$’s inner state.
$M$’s inner state.
Note that the given QTM makes only ![]() $O(\log ^k{n})$ queries because it runs in
$O(\log ^k{n})$ queries because it runs in ![]() $O(\log ^k{n})$ time. Therefore, we can transform this QTM to a query model of
$O(\log ^k{n})$ time. Therefore, we can transform this QTM to a query model of ![]() $O(\log ^k{n})$ queries.
$O(\log ^k{n})$ queries.
By Claim32, the parity function requires only ![]() $O(\log{n})$ queries in the (black box) quantum query model. However, it is shown by Beals et al. (Reference Beals, Buhrman, Cleve, Mosca and de Wolf2001) that, for the parity function of
$O(\log{n})$ queries in the (black box) quantum query model. However, it is shown by Beals et al. (Reference Beals, Buhrman, Cleve, Mosca and de Wolf2001) that, for the parity function of ![]() $n$ Boolean variables,
$n$ Boolean variables, ![]() $n/2$ queries are necessary in the bounded-error quantum query model (while
$n/2$ queries are necessary in the bounded-error quantum query model (while ![]() $n$ queries are necessary in the deterministic query model). This is obviously a contradiction. The case of the OR function can be similarly handled.
$n$ queries are necessary in the deterministic query model). This is obviously a contradiction. The case of the OR function can be similarly handled.
Let us return to Theorem 30. Using Lemma31, we can prove the theorem as described below. The core of its proof is founded on a simulation result of one-tape linear-time QTMs in (Tadaki et al., Reference Tadaki, Yamakami and Lin2010, Section 8).
Shown in (Tadaki et al., Reference Tadaki, Yamakami and Lin2010, Lemma 8) is how to simulate a one-tape well-formed stationary QTM running in linear time on an appropriate one-tape probabilistic Turing machine (or a PTM) in linear time. In a similar vein, we can simulate polylogtime QTMs on polylogtime PTMs.
Proof of Theorem 30. Let us take an arbitrary language ![]() $L$ in
$L$ in ![]() $\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}}$ and consider a polylogtime QTM
$\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}}$ and consider a polylogtime QTM ![]() $M$ that recognizes
$M$ that recognizes ![]() $L$ with bounded-error probability. We intend to show that
$L$ with bounded-error probability. We intend to show that ![]() $L$ falls in
$L$ falls in ![]() $\mathrm{PPOLYLOGTIME}$. We first modify
$\mathrm{PPOLYLOGTIME}$. We first modify ![]() $M$ in the following way. We prepare two extra work tapes. One of them is used as an internal clock by moving a tape head always to the right. To avoid any unwanted interference after a computation halts prematurely, we use the other extra tape as a “garbage tape”, to which
$M$ in the following way. We prepare two extra work tapes. One of them is used as an internal clock by moving a tape head always to the right. To avoid any unwanted interference after a computation halts prematurely, we use the other extra tape as a “garbage tape”, to which ![]() $M$ dumps all information produced at the time of entering halting states, so that
$M$ dumps all information produced at the time of entering halting states, so that ![]() $M$ continues its operation without actually halting. Lemma 8 of Tadaki et al. (2010) shows the existence of a constant
$M$ continues its operation without actually halting. Lemma 8 of Tadaki et al. (2010) shows the existence of a constant ![]() $d\in \mathbb{N}^{+}$ and an NTM
$d\in \mathbb{N}^{+}$ and an NTM ![]() $N$ such that
$N$ such that ![]() $d^{\mathrm{Time}_{M}(x)}\cdot p_{M}(x) = \# N(x) - \#\overline{N}(x)$ for every
$d^{\mathrm{Time}_{M}(x)}\cdot p_{M}(x) = \# N(x) - \#\overline{N}(x)$ for every ![]() $x$, where
$x$, where ![]() $\#N(x)$ (resp.,
$\#N(x)$ (resp., ![]() $\#\overline{N}(x)$) denotes the total number of accepting (resp., rejecting) computation paths of
$\#\overline{N}(x)$) denotes the total number of accepting (resp., rejecting) computation paths of ![]() $N$ on input
$N$ on input ![]() $x$. This equality holds for polylogtime machines. The desired polylogtime PTM is obtained from
$x$. This equality holds for polylogtime machines. The desired polylogtime PTM is obtained from ![]() $N$ by assigning an equal probability to all nondeterministic transitions.
$N$ by assigning an equal probability to all nondeterministic transitions.
The OR function can be computed by the polylogtime NTM that nondeterministically writes a number, say ![]() $i$ on an index tape, makes a query for the
$i$ on an index tape, makes a query for the ![]() $i$th bit
$i$th bit ![]() $x_{(i)}$ of an input
$x_{(i)}$ of an input ![]() $x$, and accepts exactly when
$x$, and accepts exactly when ![]() $x_{(i)}$ is
$x_{(i)}$ is ![]() $1$. Thus, the OR function belongs to
$1$. Thus, the OR function belongs to ![]() $\mathrm{NLOGTIME}$. The separation between
$\mathrm{NLOGTIME}$. The separation between ![]() $\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}}$ and
$\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}}$ and ![]() $\mathrm{NLOGTIME}$ comes from Lemma31. Since
$\mathrm{NLOGTIME}$ comes from Lemma31. Since ![]() $\mathrm{PPOLYLOGTIME}$ includes
$\mathrm{PPOLYLOGTIME}$ includes ![]() $\mathrm{NLOGTIME}$, we obtain the desired separation between
$\mathrm{NLOGTIME}$, we obtain the desired separation between ![]() $\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}}$ and
$\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}}$ and ![]() $\mathrm{PPOLYLOGTIME}$.
$\mathrm{PPOLYLOGTIME}$.
5.3 Comparison between EQS and BQPOLYLOGTIME
In what follows, we discuss a close relationship between quantum functions definable within ![]() $EQS$ and quantum functions computable by polylogtime QTMs despite numerous differences between
$EQS$ and quantum functions computable by polylogtime QTMs despite numerous differences between ![]() $EQS$ and polylogtime QTMs. One such difference is that input tapes of QTMs are read-only and thus inputs are not changeable, whereas quantum functions in
$EQS$ and polylogtime QTMs. One such difference is that input tapes of QTMs are read-only and thus inputs are not changeable, whereas quantum functions in ![]() $EQS$ can freely modify their inputs. In the following two theorems (Theorems 33 and 34); however, we can establish the “computational” equivalence between polylogtime QTMs and quantum functions in
$EQS$ can freely modify their inputs. In the following two theorems (Theorems 33 and 34); however, we can establish the “computational” equivalence between polylogtime QTMs and quantum functions in ![]() $EQS$.
$EQS$.
To make the later simulation process simpler, we first modify a polylogtime QTM so that it uses the binary alphabet on an index tape as well as all work tapes by way of encoding each non-binary tape symbol into a binary one using an appropriately chosen encoding scheme. This modification makes it possible to assume that the QTM should hold superpositions ![]() $| \phi \rangle$ of binary strings on its input tape and its work tapes. For convenience, a QTM that satisfies these conditions is called normalized.
$| \phi \rangle$ of binary strings on its input tape and its work tapes. For convenience, a QTM that satisfies these conditions is called normalized.
Theorem 33. Any normalized polylogtime QTM ![]() $M$ with
$M$ with ![]() $c$ work tapes can be simulated by an appropriate quantum function
$c$ work tapes can be simulated by an appropriate quantum function ![]() $F$ in
$F$ in ![]() $EQS$ in the sense that, for any
$EQS$ in the sense that, for any ![]() $b\in \{0,1\}$,
$b\in \{0,1\}$, ![]() $\alpha \in [0,1]$, and
$\alpha \in [0,1]$, and ![]() $| \phi \rangle \in \Phi _{\infty }$,
$| \phi \rangle \in \Phi _{\infty }$, ![]() $M$ takes
$M$ takes ![]() $| \phi \rangle$ as an input and finally produces
$| \phi \rangle$ as an input and finally produces ![]() $b$ with probability
$b$ with probability ![]() $\alpha$ exactly when
$\alpha$ exactly when ![]() $\|\langle b | \psi _{F,\xi _{\phi }} \rangle \|^2=\alpha$ holds, where
$\|\langle b | \psi _{F,\xi _{\phi }} \rangle \|^2=\alpha$ holds, where ![]() $| \xi _{\phi } \rangle = | \hat{S} \rangle | \widetilde{B^k} \rangle ^{\otimes (c+1)} | \hat{2} \rangle \otimes | \phi \rangle$ with
$| \xi _{\phi } \rangle = | \hat{S} \rangle | \widetilde{B^k} \rangle ^{\otimes (c+1)} | \hat{2} \rangle \otimes | \phi \rangle$ with ![]() $k=\mathrm{ilog}(\ell (| \phi \rangle ))$ and
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$ and ![]() $| \psi _{F,\xi _{\phi }} \rangle = F(| \xi _{\phi } \rangle )$.
$| \psi _{F,\xi _{\phi }} \rangle = F(| \xi _{\phi } \rangle )$.
Proof. Let ![]() $M$ denote any polylogtime QTM equipped with a read-only input tape, a rewritable index tape, and multiple rewritable work tapes. We further assume that
$M$ denote any polylogtime QTM equipped with a read-only input tape, a rewritable index tape, and multiple rewritable work tapes. We further assume that ![]() $M$ is normalized. For readability, we hereafter deal with the special case where
$M$ is normalized. For readability, we hereafter deal with the special case where ![]() $M$ has a single work tape. A general case of
$M$ has a single work tape. A general case of ![]() $c$ work tapes can be handled in a similar but naturally extended way. Assume that
$c$ work tapes can be handled in a similar but naturally extended way. Assume that ![]() $M$’s input tape holds a superposition
$M$’s input tape holds a superposition ![]() $| \phi \rangle$ of binary inputs with
$| \phi \rangle$ of binary inputs with ![]() $\ell (| \phi \rangle ) \geq 4$ and that
$\ell (| \phi \rangle ) \geq 4$ and that ![]() $M$ runs in time at most
$M$ runs in time at most ![]() $\mathrm{ilog}(\ell (| \phi \rangle ))^{e}$ for a fixed constant
$\mathrm{ilog}(\ell (| \phi \rangle ))^{e}$ for a fixed constant ![]() $e\geq 1$. For convenience, let
$e\geq 1$. For convenience, let ![]() $k=\mathrm{ilog}(\ell (| \phi \rangle ))$. We denote by
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$. We denote by ![]() $Q$ the set of all inner states of
$Q$ the set of all inner states of ![]() $M$. Since
$M$. Since ![]() $Q$ is finite, without loss of generality,
$Q$ is finite, without loss of generality, ![]() $Q$ assumed to have the form
$Q$ assumed to have the form ![]() $\{bin_{3t'}(i)\mid i\in [2^{3t'}]\}$ for an appropriate constant
$\{bin_{3t'}(i)\mid i\in [2^{3t'}]\}$ for an appropriate constant ![]() $t'\in \mathbb{N}^{+}$. We set the initial inner state
$t'\in \mathbb{N}^{+}$. We set the initial inner state ![]() $q_0$ to be
$q_0$ to be ![]() $bin_{3t'}(1)$. For each inner state
$bin_{3t'}(1)$. For each inner state ![]() $q\in Q$, since
$q\in Q$, since ![]() $q$ is expressed as a binary string, we can encode it into the string
$q$ is expressed as a binary string, we can encode it into the string ![]() $\widetilde{q}^{(-)}$ defined in Section 3.2.
$\widetilde{q}^{(-)}$ defined in Section 3.2.
We treat the content of each tape (except for the input tape) as a code block of the desired quantum function ![]() $F$. We maintain the contents of the index tape and of the work tape as a part of two appropriate qustrings. We intend to simulate each move of
$F$. We maintain the contents of the index tape and of the work tape as a part of two appropriate qustrings. We intend to simulate each move of ![]() $M$ on
$M$ on ![]() $| \phi \rangle$ by applying an adequately defined quantum function.
$| \phi \rangle$ by applying an adequately defined quantum function.
Since ![]() $M$’s computation is a series of surface configurations of
$M$’s computation is a series of surface configurations of ![]() $M$, we thus need to “express” such a surface configuration using a single quantum state. Initially,
$M$, we thus need to “express” such a surface configuration using a single quantum state. Initially, ![]() $M$’s index tape holds
$M$’s index tape holds ![]() $B^{k}{\lhd }$ and
$B^{k}{\lhd }$ and ![]() $M$’s single work tape holds
$M$’s single work tape holds ![]() $B^{kt}{\lhd }$ for a fixed constant
$B^{kt}{\lhd }$ for a fixed constant ![]() $t\in \mathbb{N}^{+}$. Let
$t\in \mathbb{N}^{+}$. Let ![]() $w$ and
$w$ and ![]() $z$, respectively, denote the contents of the index tape and of the work tape without the right endmarker
$z$, respectively, denote the contents of the index tape and of the work tape without the right endmarker ![]() $\lhd$ and let
$\lhd$ and let ![]() $q$ be any inner state of
$q$ be any inner state of ![]() $M$. Associated with
$M$. Associated with ![]() $(q,w,z)$, we describe
$(q,w,z)$, we describe ![]() $M$’s current surface configuration as
$M$’s current surface configuration as ![]() $q\# w_1H w_2\# z_1 H z_2$ with
$q\# w_1H w_2\# z_1 H z_2$ with ![]() $w=w_1w_2$ and
$w=w_1w_2$ and ![]() $z=z_1z_2$ by including a designated symbol
$z=z_1z_2$ by including a designated symbol ![]() $H$ and
$H$ and ![]() $M$’s inner state
$M$’s inner state ![]() $q$, where
$q$, where ![]() $H$ is used to indicate the locations of the index-tape head and of the work-tape head, which are scanning the leftmost symbols of
$H$ is used to indicate the locations of the index-tape head and of the work-tape head, which are scanning the leftmost symbols of ![]() $w_2$ and
$w_2$ and ![]() $z_2$, respectively. Assume that these two tape heads are, respectively, scanning tape symbols
$z_2$, respectively. Assume that these two tape heads are, respectively, scanning tape symbols ![]() $\eta$ and
$\eta$ and ![]() $\sigma$ on the index tape and the work tape, that is,
$\sigma$ on the index tape and the work tape, that is, ![]() $w_2=\eta x_2$ and
$w_2=\eta x_2$ and ![]() $z_2=\sigma y_2$. For technical reason, we slightly modify the above description of a surface configuration and express it as
$z_2=\sigma y_2$. For technical reason, we slightly modify the above description of a surface configuration and express it as ![]() $w_1H B x_2\# z_1 H B y_2\# q\eta \sigma$ by inserting the extra symbol
$w_1H B x_2\# z_1 H B y_2\# q\eta \sigma$ by inserting the extra symbol ![]() $B$. To refer to this special form, we call it a modified (surface) configuration. In particular, the suffix
$B$. To refer to this special form, we call it a modified (surface) configuration. In particular, the suffix ![]() $q\eta \sigma$ is called a transition status.
$q\eta \sigma$ is called a transition status.
By Lemma25, it suffices for us to focus on each block of encoded tape content. The modified configuration ![]() $w_1H B x_2\# z_1 H B y_2\# q\eta \sigma$ is encoded into the quantum state
$w_1H B x_2\# z_1 H B y_2\# q\eta \sigma$ is encoded into the quantum state ![]() $| \widetilde{w_1}^{(-)} \hat{H} \hat{B} \widetilde{x} \rangle | \widetilde{z_1}^{(-)} \hat{H} \hat{B} \widetilde{y} \rangle | \widetilde{q}^{(-)} \hat{\eta }\hat{\sigma } \rangle | \hat{\dashv } \rangle$. We conveniently refer to it as the encoded (surface) configuration. Note that
$| \widetilde{w_1}^{(-)} \hat{H} \hat{B} \widetilde{x} \rangle | \widetilde{z_1}^{(-)} \hat{H} \hat{B} \widetilde{y} \rangle | \widetilde{q}^{(-)} \hat{\eta }\hat{\sigma } \rangle | \hat{\dashv } \rangle$. We conveniently refer to it as the encoded (surface) configuration. Note that ![]() $|\widetilde{q}^{(-)}\hat{\eta }\hat{\sigma }|=6t'+6=6(t'+1)$. In fact, the modified initial configuration is of the form
$|\widetilde{q}^{(-)}\hat{\eta }\hat{\sigma }|=6t'+6=6(t'+1)$. In fact, the modified initial configuration is of the form ![]() $H B^k\# H B^{kt} \# q_0BB$ and its encoding is of the form
$H B^k\# H B^{kt} \# q_0BB$ and its encoding is of the form ![]() $| \hat{H}\widetilde{B^k} \rangle | \hat{H} \widetilde{B^{kt}} \rangle | \widetilde{q_0}^{(-)} \hat{B}\hat{B} \rangle | \hat{\dashv } \rangle$.
$| \hat{H}\widetilde{B^k} \rangle | \hat{H} \widetilde{B^{kt}} \rangle | \widetilde{q_0}^{(-)} \hat{B}\hat{B} \rangle | \hat{\dashv } \rangle$.
A run of ![]() $M$, which covers from the initial surface configuration to certain halting surface configurations, can be simulated using the fast quantum recursion. To explain this simulation, for convenience, we split each move of
$M$, which covers from the initial surface configuration to certain halting surface configurations, can be simulated using the fast quantum recursion. To explain this simulation, for convenience, we split each move of ![]() $M$ into three separate “phases”: (1) a tape content change, (2) an input access by a query, and (4) an output production. We consider these three different phases of
$M$ into three separate “phases”: (1) a tape content change, (2) an input access by a query, and (4) an output production. We consider these three different phases of ![]() $M$ separately. In Phase (3), in particular, we will use Scheme V to repeat Phases (1) and (2)
$M$ separately. In Phase (3), in particular, we will use Scheme V to repeat Phases (1) and (2) ![]() $\mathrm{ilog}(\ell (| \phi \rangle ))$ times. In the end, we will combine Phases (1)–(4) into a single quantum function.
$\mathrm{ilog}(\ell (| \phi \rangle ))$ times. In the end, we will combine Phases (1)–(4) into a single quantum function.
(1) The first case to consider is that ![]() $M$ modifies multiple tapes (except for the input tape) by a single move. We begin with paying our attention to the modification of the index-tape symbol and describe how to simulate this tape-symbol modification. In a single step, as our convention, a tape head firstly changes a tape symbol and secondly moves to an adjacent cell. In other words,
$M$ modifies multiple tapes (except for the input tape) by a single move. We begin with paying our attention to the modification of the index-tape symbol and describe how to simulate this tape-symbol modification. In a single step, as our convention, a tape head firstly changes a tape symbol and secondly moves to an adjacent cell. In other words, ![]() $M$ locally changes
$M$ locally changes ![]() $w_1 H w_2\# z_1H z_2 \# q\eta \sigma$ to its successor
$w_1 H w_2\# z_1H z_2 \# q\eta \sigma$ to its successor ![]() $w^{\prime}_1Hw^{\prime}_2 \# z^{\prime}_1H z^{\prime}_2 \# q'\eta '\sigma '$ by applying
$w^{\prime}_1Hw^{\prime}_2 \# z^{\prime}_1H z^{\prime}_2 \# q'\eta '\sigma '$ by applying ![]() $\delta$. This process can be expressed by a single quantum function defined as follows.
$\delta$. This process can be expressed by a single quantum function defined as follows.
Let us consider ![]() $M$’s single transition of the form
$M$’s single transition of the form ![]() $\delta (q,\eta _2,\sigma _2) = \sum _{r}\alpha _r | p,\xi _2,\tau _2,d,d' \rangle$, where
$\delta (q,\eta _2,\sigma _2) = \sum _{r}\alpha _r | p,\xi _2,\tau _2,d,d' \rangle$, where ![]() $r$ refers to
$r$ refers to ![]() $(q,\eta _2,\sigma _2,p,\xi _2,\tau _2,d,d')$. This transition means that the index-tape head changes
$(q,\eta _2,\sigma _2,p,\xi _2,\tau _2,d,d')$. This transition means that the index-tape head changes ![]() $\eta _2$ to
$\eta _2$ to ![]() $\xi _2$ and moves in direction
$\xi _2$ and moves in direction ![]() $d$ and that the work-tape head changes
$d$ and that the work-tape head changes ![]() $\sigma _2$ to
$\sigma _2$ to ![]() $\tau _2$ and moves in direction
$\tau _2$ and moves in direction ![]() $d'$. To simulate this transition, it suffices to focus on four consecutive cells whose second cell is being scanned by the tape head. For simplicity, we call such a series an
$d'$. To simulate this transition, it suffices to focus on four consecutive cells whose second cell is being scanned by the tape head. For simplicity, we call such a series an ![]() $H$-block. Let
$H$-block. Let ![]() $\eta _1H B\eta _3$ and
$\eta _1H B\eta _3$ and ![]() $\sigma _1H B\sigma _3$ denote two
$\sigma _1H B\sigma _3$ denote two ![]() $H$-blocks, and let
$H$-blocks, and let ![]() $q\eta _2\sigma _2$ denote the current transition status of
$q\eta _2\sigma _2$ denote the current transition status of ![]() $\delta$.
$\delta$.
(a) We make an application of Scheme IV in the following fashion. Let ![]() $v=(q,\eta _2,\sigma _2,p,\xi _2,\tau _2,d,d')$. We first change
$v=(q,\eta _2,\sigma _2,p,\xi _2,\tau _2,d,d')$. We first change ![]() $| \widetilde{q}^{(-)}\hat{\eta _2}\hat{\sigma _2} \rangle$ to
$| \widetilde{q}^{(-)}\hat{\eta _2}\hat{\sigma _2} \rangle$ to ![]() $| \widetilde{p}^{(-)}\hat{B}\hat{B} \rangle$ by remembering
$| \widetilde{p}^{(-)}\hat{B}\hat{B} \rangle$ by remembering ![]() $(\xi _2,\tau _2,d,d')$ in the form of different quantum functions
$(\xi _2,\tau _2,d,d')$ in the form of different quantum functions ![]() $g_u$, which are controlled by
$g_u$, which are controlled by ![]() $Branch[\{g_u\}_{u}]$. We then search for an
$Branch[\{g_u\}_{u}]$. We then search for an ![]() $H$-block of the form
$H$-block of the form ![]() $| \hat{\eta _1}\hat{H}\hat{B}\hat{\eta _3} \rangle$ and change it to
$| \hat{\eta _1}\hat{H}\hat{B}\hat{\eta _3} \rangle$ and change it to ![]() $| \hat{H}\hat{\eta _1}\hat{\xi _2}\hat{\eta _3} \rangle$ if
$| \hat{H}\hat{\eta _1}\hat{\xi _2}\hat{\eta _3} \rangle$ if ![]() $d=-1$ and to
$d=-1$ and to ![]() $| \hat{\eta _1}\hat{\xi _2}\hat{H}\hat{\eta _3} \rangle$ if
$| \hat{\eta _1}\hat{\xi _2}\hat{H}\hat{\eta _3} \rangle$ if ![]() $d=+1$. Similarly, we change
$d=+1$. Similarly, we change ![]() $| \hat{\sigma _1}\hat{H}\hat{B}\hat{\sigma _3} \rangle$ according to the value of
$| \hat{\sigma _1}\hat{H}\hat{B}\hat{\sigma _3} \rangle$ according to the value of ![]() $d'$. These changes can be made by an appropriate quantum function, say,
$d'$. These changes can be made by an appropriate quantum function, say, ![]() $F_{v,d}$. This quantum function
$F_{v,d}$. This quantum function ![]() $F_{v,d}$ is realized as follows.
$F_{v,d}$ is realized as follows.
In the case of ![]() $\tau _2\in \{0,1\}$, we introduce
$\tau _2\in \{0,1\}$, we introduce ![]() $f_{B,\tau _2}$ that satisfies
$f_{B,\tau _2}$ that satisfies ![]() $f_{B,\tau _2}(| \hat{B} \rangle | \hat{H} \rangle ) = | \hat{\tau _2} \rangle | \hat{H} \rangle$. This quantum function
$f_{B,\tau _2}(| \hat{B} \rangle | \hat{H} \rangle ) = | \hat{\tau _2} \rangle | \hat{H} \rangle$. This quantum function ![]() $f_{B,\tau _2}$ is constructed as
$f_{B,\tau _2}$ is constructed as ![]() $f_{B,\tau _2}\equiv Branch_3[\{g^{\prime}_u\}_{u\in \{0,1\}^3}]\circ SecSWAP^{(3)}_{1,2} \circ Branch_3[\{g_u\}_{u\in \{0,1\}^3}]$, where
$f_{B,\tau _2}\equiv Branch_3[\{g^{\prime}_u\}_{u\in \{0,1\}^3}]\circ SecSWAP^{(3)}_{1,2} \circ Branch_3[\{g_u\}_{u\in \{0,1\}^3}]$, where ![]() $g_{010}(| 100 \rangle )=| 00\tau _2 \rangle$,
$g_{010}(| 100 \rangle )=| 00\tau _2 \rangle$, ![]() $g_u=I$ for all other
$g_u=I$ for all other ![]() $u$’s,
$u$’s, ![]() $g^{\prime}_{000}=g^{\prime}_{001}$,
$g^{\prime}_{000}=g^{\prime}_{001}$, ![]() $g^{\prime}_{00}(| 010 \rangle )=| 100 \rangle$,
$g^{\prime}_{00}(| 010 \rangle )=| 100 \rangle$, ![]() $g^{\prime}_{000}(| 100 \rangle )=| 010 \rangle$,
$g^{\prime}_{000}(| 100 \rangle )=| 010 \rangle$, ![]() $g^{\prime}_{000}(| x \rangle )=| x \rangle$ for all other
$g^{\prime}_{000}(| x \rangle )=| x \rangle$ for all other ![]() $x$’s, and
$x$’s, and ![]() $g^{\prime}_u=I$ for all other
$g^{\prime}_u=I$ for all other ![]() $u$’s. The remaining cases are similarly handled. Now, let us define
$u$’s. The remaining cases are similarly handled. Now, let us define ![]() $\hat{G}$ to be
$\hat{G}$ to be ![]() $SecSWAP^{(3)}_{1,3}$, which transforms
$SecSWAP^{(3)}_{1,3}$, which transforms ![]() $| \alpha \rangle | \hat{H} \rangle | \beta \rangle$ to
$| \alpha \rangle | \hat{H} \rangle | \beta \rangle$ to ![]() $| \beta \rangle | \hat{H} \rangle | \alpha \rangle$ for any
$| \beta \rangle | \hat{H} \rangle | \alpha \rangle$ for any ![]() $\alpha, \beta \in \{0,1\}^3$. Finally, when
$\alpha, \beta \in \{0,1\}^3$. Finally, when ![]() $d=-1$, we define
$d=-1$, we define ![]() $F_{v,d}$ to be
$F_{v,d}$ to be ![]() $SecSWAP^{(3)}_{2,3} \circ SecSWAP^{(3)}_{1,2} \circ f_{B,\tau _2} \circ \hat{G}$, which satisfies
$SecSWAP^{(3)}_{2,3} \circ SecSWAP^{(3)}_{1,2} \circ f_{B,\tau _2} \circ \hat{G}$, which satisfies ![]() $F_{v,d}(| \hat{\sigma }_1 \rangle | \hat{H} \rangle | \hat{B} \rangle | \hat{\sigma }_3 \rangle ) = | \hat{H} \rangle | \hat{\sigma }_1 \rangle | \hat{\tau }_2 \rangle | \hat{\sigma _3} \rangle$. In a similar way, when
$F_{v,d}(| \hat{\sigma }_1 \rangle | \hat{H} \rangle | \hat{B} \rangle | \hat{\sigma }_3 \rangle ) = | \hat{H} \rangle | \hat{\sigma }_1 \rangle | \hat{\tau }_2 \rangle | \hat{\sigma _3} \rangle$. In a similar way, when ![]() $d=+1$, we define
$d=+1$, we define ![]() $F_{v,d} \equiv SecSWAP^{(3)}_{1,2} \circ SecSWAP^{(3)}_{2,3}\circ f_{B,\tau _2} \circ \hat{G}$, which transforms
$F_{v,d} \equiv SecSWAP^{(3)}_{1,2} \circ SecSWAP^{(3)}_{2,3}\circ f_{B,\tau _2} \circ \hat{G}$, which transforms ![]() $| \hat{\sigma }_1 \rangle | \hat{H} \rangle | \hat{B} \rangle | \hat{\sigma }_3 \rangle$ to
$| \hat{\sigma }_1 \rangle | \hat{H} \rangle | \hat{B} \rangle | \hat{\sigma }_3 \rangle$ to ![]() $| \hat{\sigma }_1 \rangle | \hat{\tau }_2 \rangle | \hat{H} \rangle | \hat{\sigma _3} \rangle$. A similar treatment works for the simulation of the work-tape head.
$| \hat{\sigma }_1 \rangle | \hat{\tau }_2 \rangle | \hat{H} \rangle | \hat{\sigma _3} \rangle$. A similar treatment works for the simulation of the work-tape head.
Notice that ![]() $M$ uses only two forms of quantum transitions. These transitions can be correctly simulated by Items 1)–3) of Scheme I. Let
$M$ uses only two forms of quantum transitions. These transitions can be correctly simulated by Items 1)–3) of Scheme I. Let ![]() $r_0=\hat{\dashv }$. Proposition18 makes it possible, under a certain condition, to make a quantum function definable in a recursive fashion. We first define a quantum function
$r_0=\hat{\dashv }$. Proposition18 makes it possible, under a certain condition, to make a quantum function definable in a recursive fashion. We first define a quantum function ![]() $K$ by setting
$K$ by setting ![]() $K(| r_0 \rangle ) = | r_0 \rangle$ and
$K(| r_0 \rangle ) = | r_0 \rangle$ and ![]() $K(| xr_0 \rangle ) = \sum _{u:|u|=9} h(| u \rangle \otimes K(\langle u | xr_0 \rangle ))$, where
$K(| xr_0 \rangle ) = \sum _{u:|u|=9} h(| u \rangle \otimes K(\langle u | xr_0 \rangle ))$, where ![]() $h(| u \rangle | wr_0 \rangle ) = \sum _{v,d}\alpha _{v,d} F_{v,d}(| u \rangle | wr_0 \rangle )$ if
$h(| u \rangle | wr_0 \rangle ) = \sum _{v,d}\alpha _{v,d} F_{v,d}(| u \rangle | wr_0 \rangle )$ if ![]() $u=\hat{\sigma }_1\hat{H}\hat{\sigma }_2$, and
$u=\hat{\sigma }_1\hat{H}\hat{\sigma }_2$, and ![]() $h(| u \rangle | wr_0 \rangle ) = | u \rangle | wr_0 \rangle$ otherwise. The proposition then guarantees the existence of a quantum function that mimics
$h(| u \rangle | wr_0 \rangle ) = | u \rangle | wr_0 \rangle$ otherwise. The proposition then guarantees the existence of a quantum function that mimics ![]() $K$ in the presence of the large-size qustring
$K$ in the presence of the large-size qustring ![]() $| \phi \rangle$. In the proof of the proposition, such a quantum function is constructed with the use of Scheme IV. It is important to note that, its ground (quantum) functions are all query-independent. Thus, Scheme IV used here is also query-independent.
$| \phi \rangle$. In the proof of the proposition, such a quantum function is constructed with the use of Scheme IV. It is important to note that, its ground (quantum) functions are all query-independent. Thus, Scheme IV used here is also query-independent.
(b) Secondly, we apply ![]() $CodeREP^6$ to move the last six qubits
$CodeREP^6$ to move the last six qubits ![]() $| \hat{B}\hat{B} \rangle$ obtained by (a) to the front.
$| \hat{B}\hat{B} \rangle$ obtained by (a) to the front.
(c) We then make the second application of Scheme IV. We change ![]() $| \hat{H}\hat{\eta _1}\hat{\xi _2}\hat{\eta _3} \rangle$ (resp.,
$| \hat{H}\hat{\eta _1}\hat{\xi _2}\hat{\eta _3} \rangle$ (resp., ![]() $| \hat{\eta _1}\hat{\xi _2}\hat{H}\hat{\eta _3} \rangle$) to
$| \hat{\eta _1}\hat{\xi _2}\hat{H}\hat{\eta _3} \rangle$) to ![]() $| \hat{H}\hat{B} \hat{\xi _2} \hat{\eta _3} \rangle$ (resp.,
$| \hat{H}\hat{B} \hat{\xi _2} \hat{\eta _3} \rangle$ (resp., ![]() $| \hat{\eta _1}\hat{\xi _2}\hat{H} \hat{B} \rangle$) by remembering
$| \hat{\eta _1}\hat{\xi _2}\hat{H} \hat{B} \rangle$) by remembering ![]() $\eta _1$ (resp.,
$\eta _1$ (resp., ![]() $\eta _3$). This change is handled in essence similarly to (a). Moreover, a similar construction deals with the case of
$\eta _3$). This change is handled in essence similarly to (a). Moreover, a similar construction deals with the case of ![]() $| \hat{H}\hat{\sigma _1}\hat{\tau _2}\hat{\sigma _3} \rangle$ (resp.,
$| \hat{H}\hat{\sigma _1}\hat{\tau _2}\hat{\sigma _3} \rangle$ (resp., ![]() $| \hat{\sigma _1}\hat{\tau _2}\hat{H}\hat{\sigma _3} \rangle$).
$| \hat{\sigma _1}\hat{\tau _2}\hat{H}\hat{\sigma _3} \rangle$).
Toward the end, we change the first six qubits ![]() $| \hat{B}\hat{B} \rangle$ to
$| \hat{B}\hat{B} \rangle$ to ![]() $| \hat{\xi }\hat{\tau } \rangle$ for symbols
$| \hat{\xi }\hat{\tau } \rangle$ for symbols ![]() $\xi \in \{\xi _2,\eta _3\}$ and
$\xi \in \{\xi _2,\eta _3\}$ and ![]() $\tau \in \{\tau _2,\sigma _3\}$.
$\tau \in \{\tau _2,\sigma _3\}$.
(d) Finally, we apply ![]() $CodeREMOVE^6$ to move
$CodeREMOVE^6$ to move ![]() $| \hat{\xi }\hat{\tau } \rangle$ back to the end.
$| \hat{\xi }\hat{\tau } \rangle$ back to the end.
(2) Next, we simulate ![]() $M$’s query access to its input qubits. Assume that the current encoded surface configuration contains
$M$’s query access to its input qubits. Assume that the current encoded surface configuration contains ![]() $| \widetilde{q_{query}}^{(-)} \hat{\eta _2}\hat{\sigma _2} \rangle$. Assume that
$| \widetilde{q_{query}}^{(-)} \hat{\eta _2}\hat{\sigma _2} \rangle$. Assume that ![]() $| \phi \rangle = \sum _{s:|s|=2^k}\alpha _s| s \rangle$ is written on the input tape and that the index tape contains
$| \phi \rangle = \sum _{s:|s|=2^k}\alpha _s| s \rangle$ is written on the input tape and that the index tape contains ![]() $| bin_k(m) \rangle | a \rangle$, where
$| bin_k(m) \rangle | a \rangle$, where ![]() $a$ is an auxiliary bit. When entering the query state
$a$ is an auxiliary bit. When entering the query state ![]() $q_{query}$,
$q_{query}$, ![]() $M$ changes
$M$ changes ![]() $q_{query}$ to another inner state, say,
$q_{query}$ to another inner state, say, ![]() $p$ and
$p$ and ![]() $| bin_k(m) \rangle | a \rangle$ to
$| bin_k(m) \rangle | a \rangle$ to ![]() $| bin_k(m) \rangle | a\oplus s_{(m)} \rangle$, where
$| bin_k(m) \rangle | a\oplus s_{(m)} \rangle$, where ![]() $s_{(m)}$ is the
$s_{(m)}$ is the ![]() $m$th bit of
$m$th bit of ![]() $s$. We need to build a quantum function that simulates this entire query process. As the first step, we change
$s$. We need to build a quantum function that simulates this entire query process. As the first step, we change ![]() $| \widetilde{q_{query}}^{(-)} \rangle$ to
$| \widetilde{q_{query}}^{(-)} \rangle$ to ![]() $| \widetilde{p}^{(-)} \rangle$. Since
$| \widetilde{p}^{(-)} \rangle$. Since ![]() $| bin_k(m) \rangle | a \rangle$ is encoded into
$| bin_k(m) \rangle | a \rangle$ is encoded into ![]() $| \widetilde{bin_k(m)} \rangle | \widetilde{a} \rangle$, we can transform it to
$| \widetilde{bin_k(m)} \rangle | \widetilde{a} \rangle$, we can transform it to ![]() $| \widetilde{a} \rangle | \widetilde{bin_k(m)} \rangle$ and then to
$| \widetilde{a} \rangle | \widetilde{bin_k(m)} \rangle$ and then to ![]() $| 0^5 \rangle | a \rangle | \widetilde{bin_k(m)} \rangle$. Finally, we apply
$| 0^5 \rangle | a \rangle | \widetilde{bin_k(m)} \rangle$. Finally, we apply ![]() $Bit$ (defined in Corollary2) to
$Bit$ (defined in Corollary2) to ![]() $| 0^5 \rangle | a \rangle | \widetilde{bin_k(m)} \rangle$ and obtain
$| 0^5 \rangle | a \rangle | \widetilde{bin_k(m)} \rangle$ and obtain ![]() $\sum _{s}\alpha _s| 0^5 \rangle | a\otimes s_{(m)} \rangle | \widetilde{bin_k(m)} \rangle | s \rangle$. Since
$\sum _{s}\alpha _s| 0^5 \rangle | a\otimes s_{(m)} \rangle | \widetilde{bin_k(m)} \rangle | s \rangle$. Since ![]() $Bit$ is query-dependent, Scheme IV used here is also query-dependent.
$Bit$ is query-dependent, Scheme IV used here is also query-dependent.
(3) We then combine the above two types of moves into one and express it by a single application of an appropriate quantum function. Note that ![]() $M$ accesses only the first
$M$ accesses only the first ![]() $O(\log{\ell (| \phi \rangle )})$ cells of the work tape. We compose (1)–(2) by applying
$O(\log{\ell (| \phi \rangle )})$ cells of the work tape. We compose (1)–(2) by applying ![]() $Compo[\cdot, \cdot ]$. We call by
$Compo[\cdot, \cdot ]$. We call by ![]() $F'$ the obtained quantum function. We repeatedly apply it
$F'$ the obtained quantum function. We repeatedly apply it ![]() $\mathrm{ilog}(\ell (| \phi \rangle ))^{e}$ times to complete the simulation of the entire computation of
$\mathrm{ilog}(\ell (| \phi \rangle ))^{e}$ times to complete the simulation of the entire computation of ![]() $M$ until
$M$ until ![]() $M$ enters a halting (either accepting or rejecting) inner state. This repetition procedure is realized by the
$M$ enters a halting (either accepting or rejecting) inner state. This repetition procedure is realized by the ![]() $e$ applications of
$e$ applications of ![]() $LCompo[\cdot ]$ to
$LCompo[\cdot ]$ to ![]() $F'$.
$F'$.
(4) When ![]() $M$ finally enters a halting inner state,
$M$ finally enters a halting inner state, ![]() $M$ produces an output bit, say,
$M$ produces an output bit, say, ![]() $b$ on the first cell of the first work tape. By (1)–(2) described above, the encoded configuration has the form
$b$ on the first cell of the first work tape. By (1)–(2) described above, the encoded configuration has the form ![]() $| \hat{b}\widetilde{w_1}^{(-)}\hat{H} \widetilde{w_2} \rangle | \widetilde{z_1}^{(-)}\hat{H} \widetilde{z_2} \rangle | \widetilde{q_{halt}}\hat{\eta }\hat{\sigma } \rangle | \hat{\dashv } \rangle$. We then change
$| \hat{b}\widetilde{w_1}^{(-)}\hat{H} \widetilde{w_2} \rangle | \widetilde{z_1}^{(-)}\hat{H} \widetilde{z_2} \rangle | \widetilde{q_{halt}}\hat{\eta }\hat{\sigma } \rangle | \hat{\dashv } \rangle$. We then change ![]() $\hat{b}$ (
$\hat{b}$ (![]() $=00b$) to
$=00b$) to ![]() $b00$ by applying
$b00$ by applying ![]() $SWAP_{1,3}$ to prepare the “correct” output qubit. We combine this quantum function with
$SWAP_{1,3}$ to prepare the “correct” output qubit. We combine this quantum function with ![]() $F'$ to obtain the desired quantum function
$F'$ to obtain the desired quantum function ![]() $F$.
$F$.
This completes the entire simulation of ![]() $M$.
$M$.
The converse of Theorem 33 is stated as Theorem 34, which is given below. Recall that, at the start of a QTM ![]() $M$, its index tape and all work tapes hold the blank symbol
$M$, its index tape and all work tapes hold the blank symbol ![]() $B$ (except for the right endmarker) in their tape cells. From this fact, we assume that inputs of quantum functions must be of the form
$B$ (except for the right endmarker) in their tape cells. From this fact, we assume that inputs of quantum functions must be of the form ![]() $| \gamma _{\phi } \rangle = | \widetilde{B^k} \rangle | r_0 \rangle \otimes | \phi \rangle$ with the designated separator
$| \gamma _{\phi } \rangle = | \widetilde{B^k} \rangle | r_0 \rangle \otimes | \phi \rangle$ with the designated separator ![]() $r_0 =\hat{2}$ and
$r_0 =\hat{2}$ and ![]() $k=\mathrm{ilog}(\ell (| \phi \rangle ))$ for any qustring
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$ for any qustring ![]() $| \phi \rangle \in \Phi _{\infty }$.
$| \phi \rangle \in \Phi _{\infty }$.
Theorem 34. For any quantum function ![]() $F$ defined by Schemes I–V,
$F$ defined by Schemes I–V, ![]() $F$ is computed by a certain polylogtime QTM
$F$ is computed by a certain polylogtime QTM ![]() $M$ in the following sense: for any
$M$ in the following sense: for any ![]() $b\in \{0,1\}$, for any
$b\in \{0,1\}$, for any ![]() $\alpha \in [0,1]$, and
$\alpha \in [0,1]$, and ![]() $| \phi \rangle \in \Phi _{\infty }$, if
$| \phi \rangle \in \Phi _{\infty }$, if ![]() $\ell (| \phi \rangle )$ is sufficiently large, then
$\ell (| \phi \rangle )$ is sufficiently large, then ![]() $M$ on input
$M$ on input ![]() $| \phi \rangle$ produces
$| \phi \rangle$ produces ![]() $b$ with probability
$b$ with probability ![]() $\alpha$ iff
$\alpha$ iff ![]() $\|\langle b | \psi _{F,\gamma _{\phi }} \rangle \|=\alpha$ holds, where
$\|\langle b | \psi _{F,\gamma _{\phi }} \rangle \|=\alpha$ holds, where ![]() $| \psi _{F,\gamma _{\phi }} \rangle = F(| \gamma _{\phi } \rangle )$.
$| \psi _{F,\gamma _{\phi }} \rangle = F(| \gamma _{\phi } \rangle )$.
In the description of the above theorem, we need to use the norm ![]() $\|\cdot \|$ instead of
$\|\cdot \|$ instead of ![]() $|\cdot |$ because the superposition of
$|\cdot |$ because the superposition of ![]() $M$’s final configurations may contain not only the value
$M$’s final configurations may contain not only the value ![]() $F(| \gamma _{\phi } \rangle )$ but also additional “garbage” information, which might possibly be a quantum state of large dimension, and we may need to ignore it when making a measurement.
$F(| \gamma _{\phi } \rangle )$ but also additional “garbage” information, which might possibly be a quantum state of large dimension, and we may need to ignore it when making a measurement.
We wish to prove Theorem 34 by induction on the construction process of ![]() $F$. To make this induction work, we slightly modify the theorem into the following key lemma.
$F$. To make this induction work, we slightly modify the theorem into the following key lemma.
Lemma 35. For any quantum function ![]() $F$ defined by Schemes I–V,
$F$ defined by Schemes I–V, ![]() $F$ is computed by a certain polylogtime QTM
$F$ is computed by a certain polylogtime QTM ![]() $M$ in the following sense: for any
$M$ in the following sense: for any ![]() $b\in \{0,1\}$, any
$b\in \{0,1\}$, any ![]() $| \phi \rangle \in \Phi _{\infty }$, and any
$| \phi \rangle \in \Phi _{\infty }$, and any ![]() $x$ in
$x$ in ![]() $NON_{r_0}(| \phi \rangle ) \cap \{0,1\}^{|r_0|k}$, if
$NON_{r_0}(| \phi \rangle ) \cap \{0,1\}^{|r_0|k}$, if ![]() $\ell (| \phi \rangle )$ is sufficiently large, then
$\ell (| \phi \rangle )$ is sufficiently large, then ![]() $\|\langle \psi _{F,\overline{\gamma }_{\phi, x}} | {\xi _{M,\overline{\gamma }_{\phi, x}}}\rangle\|=1$ holds, where
$\|\langle \psi _{F,\overline{\gamma }_{\phi, x}} | {\xi _{M,\overline{\gamma }_{\phi, x}}}\rangle\|=1$ holds, where ![]() $| \overline{\gamma }_{\phi, x} \rangle = | xr_0 \rangle | \phi \rangle$,
$| \overline{\gamma }_{\phi, x} \rangle = | xr_0 \rangle | \phi \rangle$, ![]() $k=\mathrm{ilog}(\ell (| \phi \rangle ))$,
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$, ![]() $| \psi _{F,\overline{\gamma }_{\phi, x}} \rangle = F(| \overline{\gamma }_{\phi, x} \rangle )$, and
$| \psi _{F,\overline{\gamma }_{\phi, x}} \rangle = F(| \overline{\gamma }_{\phi, x} \rangle )$, and ![]() $| \xi _{M,\overline{\gamma }_{\phi, x}} \rangle$ is the superposition of final configurations of
$| \xi _{M,\overline{\gamma }_{\phi, x}} \rangle$ is the superposition of final configurations of ![]() $M$ that starts with
$M$ that starts with ![]() $| \phi \rangle$ on the input tape and
$| \phi \rangle$ on the input tape and ![]() $| xr_0 \rangle$ on the first work tape.
$| xr_0 \rangle$ on the first work tape.
Theorem 34 follows immediately from Lemma35 by setting ![]() $xr_0$ in the lemma to be
$xr_0$ in the lemma to be ![]() $\widetilde{B^k}$. The remaining task is to verify the lemma.
$\widetilde{B^k}$. The remaining task is to verify the lemma.
Proof of Lemma 35. Let ![]() $F$ denote any quantum function in
$F$ denote any quantum function in ![]() $EQS$. For any qustring
$EQS$. For any qustring ![]() $| \phi \rangle \in \Phi _{\infty }$ and any string
$| \phi \rangle \in \Phi _{\infty }$ and any string ![]() $x\in NON_{r_0}(| \phi \rangle ) \cap \{0,1\}^{|r_0|k}$ with
$x\in NON_{r_0}(| \phi \rangle ) \cap \{0,1\}^{|r_0|k}$ with ![]() $k=\mathrm{ilog}(\ell (| \phi \rangle ))$, let
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$, let ![]() $| \overline{\gamma }_{\phi, x} \rangle = | xr_0 \rangle | \phi \rangle$ denote a qustring given as an input to
$| \overline{\gamma }_{\phi, x} \rangle = | xr_0 \rangle | \phi \rangle$ denote a qustring given as an input to ![]() $F$. Assuming that
$F$. Assuming that ![]() $\ell (| \phi \rangle )$ is sufficiently large, we first focus on
$\ell (| \phi \rangle )$ is sufficiently large, we first focus on ![]() $F$ and simulate the outcome of
$F$ and simulate the outcome of ![]() $F$ by an appropriate QTM that takes an input of the form
$F$ by an appropriate QTM that takes an input of the form ![]() $| \overline{\gamma }_{\phi, x} \rangle$. The desired polylogtime QTM
$| \overline{\gamma }_{\phi, x} \rangle$. The desired polylogtime QTM ![]() $M$ reads
$M$ reads ![]() $| \phi \rangle$ on its input tape and
$| \phi \rangle$ on its input tape and ![]() $| xr_0 \rangle$ on its first work tape.
$| xr_0 \rangle$ on its first work tape.
As seen later in (3) of this proof, Scheme IV may allow ![]() $F$ to access at most a constant number of locations of the input
$F$ to access at most a constant number of locations of the input ![]() $| \phi \rangle$, whereas
$| \phi \rangle$, whereas ![]() $M$ does not. To circumvent this difficulty in simulating
$M$ does not. To circumvent this difficulty in simulating ![]() $F$ on the QTM, whenever
$F$ on the QTM, whenever ![]() $F$ modifies any qubit of
$F$ modifies any qubit of ![]() $| \phi \rangle$,
$| \phi \rangle$, ![]() $M$ remembers this qubit modification using its work tape as a reference to the future access to it since
$M$ remembers this qubit modification using its work tape as a reference to the future access to it since ![]() $M$ cannot alter any qubit of
$M$ cannot alter any qubit of ![]() $| \phi \rangle$.
$| \phi \rangle$.
We intend to prove the lemma by induction on the descriptive complexity of ![]() $F$. We assume that the work-tape head is scanning the cell that contains the first qubit on the first work tape before each series of applications of the schemes of
$F$. We assume that the work-tape head is scanning the cell that contains the first qubit on the first work tape before each series of applications of the schemes of ![]() $EQS$.
$EQS$.
(1) We first assert that all quantum functions ![]() $F$ defined by Items 1)–6) of Scheme I are computable by appropriate polylogtime QTMs, say,
$F$ defined by Items 1)–6) of Scheme I are computable by appropriate polylogtime QTMs, say, ![]() $M$ because the target qubits of these items lie in
$M$ because the target qubits of these items lie in ![]() $xr_0$, which are written on the work tape, not on the input tape. To verify this assertion, let us consider
$xr_0$, which are written on the work tape, not on the input tape. To verify this assertion, let us consider ![]() $PHASE_{\theta }$ of Item 2). Starting with
$PHASE_{\theta }$ of Item 2). Starting with ![]() $| \phi \rangle$ as well as
$| \phi \rangle$ as well as ![]() $| xr_0 \rangle$, if the first bit of
$| xr_0 \rangle$, if the first bit of ![]() $xr_0$ is
$xr_0$ is ![]() $1$, then we use the QTM’s quantum transition function
$1$, then we use the QTM’s quantum transition function ![]() $\delta$ to make a phase shift of
$\delta$ to make a phase shift of ![]() $e^{\imath \theta }$. Otherwise, we do nothing. A similar treatment works for Items 3)–4). For
$e^{\imath \theta }$. Otherwise, we do nothing. A similar treatment works for Items 3)–4). For ![]() $SWAP$ of Item 5), we simply swap between the content of the cell currently scanned by
$SWAP$ of Item 5), we simply swap between the content of the cell currently scanned by ![]() $M$’s work-tape head and the content of its right adjacent cell. For Item 6), it suffices to “observe” the first qubit on the first work tape in the computational basis
$M$’s work-tape head and the content of its right adjacent cell. For Item 6), it suffices to “observe” the first qubit on the first work tape in the computational basis ![]() $| a \rangle$.
$| a \rangle$.
(2) We next show by way of induction on the construction process of the target quantum function ![]() $F$ by Scheme II. Let us consider the quantum function
$F$ by Scheme II. Let us consider the quantum function ![]() $F$ of the form
$F$ of the form ![]() $Compo[g,h]$ for two ground (quantum) functions
$Compo[g,h]$ for two ground (quantum) functions ![]() $g$ and
$g$ and ![]() $h$. By induction hypothesis, there are two polylogtime QTMs
$h$. By induction hypothesis, there are two polylogtime QTMs ![]() $M_g$ and
$M_g$ and ![]() $M_h$ that respectively compute
$M_h$ that respectively compute ![]() $g$ and
$g$ and ![]() $h$ in the lemma’s sense. The desired QTM
$h$ in the lemma’s sense. The desired QTM ![]() $M$ first checks whether
$M$ first checks whether ![]() $\ell (| \phi \rangle )\leq 1$. This part is called the first phase, and it can be done by searching for the location of the right endmarker on the index tape. We then run
$\ell (| \phi \rangle )\leq 1$. This part is called the first phase, and it can be done by searching for the location of the right endmarker on the index tape. We then run ![]() $M_h$ on
$M_h$ on ![]() $| \phi \rangle$ as well as
$| \phi \rangle$ as well as ![]() $| xr_0 \rangle$. After
$| xr_0 \rangle$. After ![]() $M_h$ halts, we wish to run
$M_h$ halts, we wish to run ![]() $M_g$ in the second phase.
$M_g$ in the second phase.
Now, there are two issues to deal with. Unlike the classical case of “composing” two TMs, we need to distinguish work tapes of ![]() $M_g$ and those of
$M_g$ and those of ![]() $M_h$ since we may not be able to erase the contents of
$M_h$ since we may not be able to erase the contents of ![]() $M_g$’s work tapes freely at the start of the simulation of
$M_g$’s work tapes freely at the start of the simulation of ![]() $M_h$ in the second phase. Since we want to use
$M_h$ in the second phase. Since we want to use ![]() $M_h$’s index tape as the index tape of
$M_h$’s index tape as the index tape of ![]() $M$, we need to rename
$M$, we need to rename ![]() $M_g$’s index tape to one of the work tapes of
$M_g$’s index tape to one of the work tapes of ![]() $M$. Since the original input of
$M$. Since the original input of ![]() $M_g$ is the qustring
$M_g$ is the qustring ![]() $h(| \phi \rangle )$, we also need to mimic
$h(| \phi \rangle )$, we also need to mimic ![]() $M_g$’s access to
$M_g$’s access to ![]() $h(| \phi \rangle )$ using only
$h(| \phi \rangle )$ using only ![]() $| \phi \rangle$. For this purpose, we need to remember the “history” of how we have modified qubits of
$| \phi \rangle$. For this purpose, we need to remember the “history” of how we have modified qubits of ![]() $| \phi \rangle$ so far and, whenever
$| \phi \rangle$ so far and, whenever ![]() $M_g$ accesses its input, we first consult this history log to check whether or not the accessed qubit has already been modified.
$M_g$ accesses its input, we first consult this history log to check whether or not the accessed qubit has already been modified.
(3) To simulate Scheme III, let ![]() $F\equiv Branch[g,h]$ for two ground functions
$F\equiv Branch[g,h]$ for two ground functions ![]() $g$ and
$g$ and ![]() $h$. By induction hypothesis, we take two polylogtime QTMs
$h$. By induction hypothesis, we take two polylogtime QTMs ![]() $M_g$ and
$M_g$ and ![]() $M_h$, respectively, for
$M_h$, respectively, for ![]() $g$ and
$g$ and ![]() $h$ working with
$h$ working with ![]() $| \phi \rangle$ written on their input tapes and
$| \phi \rangle$ written on their input tapes and ![]() $| zr_0 \rangle$ written on their first work tapes. Let us design the desired QTM
$| zr_0 \rangle$ written on their first work tapes. Let us design the desired QTM ![]() $M$ to simulate
$M$ to simulate ![]() $F$ on
$F$ on ![]() $| \phi \rangle$ and
$| \phi \rangle$ and ![]() $| xr_0 \rangle$ as follows. We first check if
$| xr_0 \rangle$ as follows. We first check if ![]() $\ell (| \phi \rangle )\leq 1$. If so, we do nothing. Hereafter, we assume otherwise. Since
$\ell (| \phi \rangle )\leq 1$. If so, we do nothing. Hereafter, we assume otherwise. Since ![]() $Branch[g,h](| xr_0 \rangle | \phi \rangle ) = | 0 \rangle \otimes g(\langle 0 | xr_0 \rangle \otimes | \phi \rangle ) + | 1 \rangle \otimes h(\langle 1 | xr_0 \rangle \otimes | \phi \rangle )$, we scan the first qubit of
$Branch[g,h](| xr_0 \rangle | \phi \rangle ) = | 0 \rangle \otimes g(\langle 0 | xr_0 \rangle \otimes | \phi \rangle ) + | 1 \rangle \otimes h(\langle 1 | xr_0 \rangle \otimes | \phi \rangle )$, we scan the first qubit of ![]() $| xr_0 \rangle$ by a tape head and determine which machine (either
$| xr_0 \rangle$ by a tape head and determine which machine (either ![]() $M_g$ or
$M_g$ or ![]() $M_h$) to run with the rest of the input. Since
$M_h$) to run with the rest of the input. Since ![]() $M_g$ and
$M_g$ and ![]() $M_h$ correctly simulate
$M_h$ correctly simulate ![]() $g$ and
$g$ and ![]() $h$, respectively, this new machine
$h$, respectively, this new machine ![]() $M$ correctly simulates
$M$ correctly simulates ![]() $F$.
$F$.
(4) Concerning Scheme IV, let ![]() $F\equiv CFQRec_t[r_0,d,g,h|\mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ and assume that
$F\equiv CFQRec_t[r_0,d,g,h|\mathscr{P}_{|r_0|},\mathscr{F}_{|r_0|}]$ and assume that ![]() $M$’s input tape holds
$M$’s input tape holds ![]() $| \phi \rangle$ and its first work tape holds
$| \phi \rangle$ and its first work tape holds ![]() $| xr_0 \rangle$. We first calculate the length
$| xr_0 \rangle$. We first calculate the length ![]() $\ell (| \phi \rangle )$ by checking the size of the available area of the index tape in logarithmic time. If either
$\ell (| \phi \rangle )$ by checking the size of the available area of the index tape in logarithmic time. If either ![]() $\ell (| \phi \rangle )\lt t$ or
$\ell (| \phi \rangle )\lt t$ or ![]() $x=\lambda$, then we run
$x=\lambda$, then we run ![]() $M_g$ on
$M_g$ on ![]() $| \phi \rangle$ as well as
$| \phi \rangle$ as well as ![]() $| xr_0 \rangle$ until it eventually halts. Now, we assume that
$| xr_0 \rangle$ until it eventually halts. Now, we assume that ![]() $\ell (| \phi \rangle )\geq t$ and
$\ell (| \phi \rangle )\geq t$ and ![]() $x\neq \lambda$.
$x\neq \lambda$.
If ![]() $h$ is defined using none of
$h$ is defined using none of ![]() $CodeSKIP_{+}$ and
$CodeSKIP_{+}$ and ![]() $CodeSKIP_{-}$, then the induction hypothesis guarantees the existence of a polylogtime QTM
$CodeSKIP_{-}$, then the induction hypothesis guarantees the existence of a polylogtime QTM ![]() $M_h$ for
$M_h$ for ![]() $h$. In the case where
$h$. In the case where ![]() $h$ is constructed using
$h$ is constructed using ![]() $CodeSKIP_{\tau }$ for a certain sign
$CodeSKIP_{\tau }$ for a certain sign ![]() $\tau \in \{+,-\}$, we first build a QTM that simulates
$\tau \in \{+,-\}$, we first build a QTM that simulates ![]() $CodeSKIP_{\tau }[r_0,g',h']$ for certain ground functions
$CodeSKIP_{\tau }[r_0,g',h']$ for certain ground functions ![]() $g'$ and
$g'$ and ![]() $h'$ without requiring “polylogarithmic” runtime. It is important to note that such a QTM reads target qubits written on the work tape, not on the input tape. The QTM
$h'$ without requiring “polylogarithmic” runtime. It is important to note that such a QTM reads target qubits written on the work tape, not on the input tape. The QTM ![]() $M$ searches for the first appearance of
$M$ searches for the first appearance of ![]() $r_0$ and then runs the corresponding QTMs
$r_0$ and then runs the corresponding QTMs ![]() $M_{g'}$ and
$M_{g'}$ and ![]() $M_{h'}$ in parallel. Since the input length is
$M_{h'}$ in parallel. Since the input length is ![]() $\ell (| \phi \rangle )$, the QTM halts within
$\ell (| \phi \rangle )$, the QTM halts within ![]() $O(\log{\ell (| \phi \rangle )})$ steps.
$O(\log{\ell (| \phi \rangle )})$ steps.
Similarly, we can handle ![]() $CodeREMOVE$ and
$CodeREMOVE$ and ![]() $CodeREP$.
$CodeREP$.
Since ![]() $x\neq \lambda$,
$x\neq \lambda$, ![]() $F(| xr_0 \rangle | \phi \rangle )$ is calculated as
$F(| xr_0 \rangle | \phi \rangle )$ is calculated as ![]() $\sum _{u:|u|=|r_0|} \sum _{v:|v|=\ell (\langle u | xr_0 \rangle )} (h(| u \rangle | v \rangle )\otimes p^{-1}_u(\langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle )$, where
$\sum _{u:|u|=|r_0|} \sum _{v:|v|=\ell (\langle u | xr_0 \rangle )} (h(| u \rangle | v \rangle )\otimes p^{-1}_u(\langle v | \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle )$, where ![]() $| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle = \sum _{s:|s|=H(| \phi \rangle )} (f_u(\langle u | x'r_0 \rangle | s \rangle ) \otimes \langle s | \psi _{p_u,\phi } \rangle )$ and
$| \zeta _{u,p_u,\phi }^{(x'r_0)} \rangle = \sum _{s:|s|=H(| \phi \rangle )} (f_u(\langle u | x'r_0 \rangle | s \rangle ) \otimes \langle s | \psi _{p_u,\phi } \rangle )$ and ![]() $d(| xr_0 \rangle )=| x'r_0 \rangle$. Starting with
$d(| xr_0 \rangle )=| x'r_0 \rangle$. Starting with ![]() $| \phi \rangle$ as well as
$| \phi \rangle$ as well as ![]() $| xr_0 \rangle$, we first move a work-tape head, passing through at most
$| xr_0 \rangle$, we first move a work-tape head, passing through at most ![]() $\mathrm{ilog}(\ell (| \phi \rangle ))$ blocks of size
$\mathrm{ilog}(\ell (| \phi \rangle ))$ blocks of size ![]() $|r_0|$. Recursively, we move back the tape head to the start cell (i.e., cell
$|r_0|$. Recursively, we move back the tape head to the start cell (i.e., cell ![]() $0$) and run
$0$) and run ![]() $M_h$. For this purpose, we write
$M_h$. For this purpose, we write ![]() $0$ and
$0$ and ![]() $1$ on an index tape whenever we choose
$1$ on an index tape whenever we choose ![]() $p_u=I$ and
$p_u=I$ and ![]() $p_u=HalfSWAP$, respectively, because we need to trace the location of the start of each recursively halved input until we reach
$p_u=HalfSWAP$, respectively, because we need to trace the location of the start of each recursively halved input until we reach ![]() $x=\lambda$ or
$x=\lambda$ or ![]() $|x|\gt |r_0|k$. The entire algorithm thus requires
$|x|\gt |r_0|k$. The entire algorithm thus requires ![]() $O(\log{\ell (| \phi \rangle )})$ steps.
$O(\log{\ell (| \phi \rangle )})$ steps.
By the definition of Scheme IV, the quantum function ![]() $F$ can make a direct access to
$F$ can make a direct access to ![]() $| \phi \rangle$ when
$| \phi \rangle$ when ![]() $g$ is finally called to compute the value of
$g$ is finally called to compute the value of ![]() $F$. Notice that
$F$. Notice that ![]() $g$ accesses at most
$g$ accesses at most ![]() $t$ locations of
$t$ locations of ![]() $| \phi \rangle$. Therefore, during the simulation of
$| \phi \rangle$. Therefore, during the simulation of ![]() $F$,
$F$, ![]() $M$ makes the same number of queries to its input
$M$ makes the same number of queries to its input ![]() $| \phi \rangle$.
$| \phi \rangle$.
(5) Finally, let us consider Scheme V. Assume that ![]() $F$ is defined to be
$F$ is defined to be ![]() $LCompo[g]$ for a ground function
$LCompo[g]$ for a ground function ![]() $g$. By induction hypothesis, we take a polylogtime QTM
$g$. By induction hypothesis, we take a polylogtime QTM ![]() $M_g$ that simulates
$M_g$ that simulates ![]() $g$. Assume further that, for a fixed constant
$g$. Assume further that, for a fixed constant ![]() $t\in \mathbb{N}^{+}$,
$t\in \mathbb{N}^{+}$, ![]() $M_g$ runs in
$M_g$ runs in ![]() $O(\log ^t{\ell (| \phi \rangle )})$ time for any input
$O(\log ^t{\ell (| \phi \rangle )})$ time for any input ![]() $| \phi \rangle$. Let
$| \phi \rangle$. Let ![]() $k=\mathrm{ilog}(\ell (| \phi \rangle ))$. To simulate
$k=\mathrm{ilog}(\ell (| \phi \rangle ))$. To simulate ![]() $F$,
$F$, ![]() $M$ repeats a run of
$M$ repeats a run of ![]() $M_g$
$M_g$ ![]() $k$ times since
$k$ times since ![]() $F(| xr_0 \rangle | \phi \rangle ) = g^k(| xr_0 \rangle | \phi \rangle )$. The total runtime of
$F(| xr_0 \rangle | \phi \rangle ) = g^k(| xr_0 \rangle | \phi \rangle )$. The total runtime of ![]() $M$ is at most
$M$ is at most ![]() $k\cdot O(\log ^t{\ell (| \phi \rangle )})$, which equals
$k\cdot O(\log ^t{\ell (| \phi \rangle )})$, which equals ![]() $O(\log ^{t+1}{\ell (| \phi \rangle )})$.
$O(\log ^{t+1}{\ell (| \phi \rangle )})$.
We have shown in Section 5.2 that the parity function, ![]() $Parity$, cannot be computed by polylogtime QTMs. It is possible to generalize
$Parity$, cannot be computed by polylogtime QTMs. It is possible to generalize ![]() $Parity$ and treat it as a quantum function defined on
$Parity$ and treat it as a quantum function defined on ![]() $\mathscr{H}_{\infty }$. Lemma31 together with Lemma35 then leads to the following conclusion.
$\mathscr{H}_{\infty }$. Lemma31 together with Lemma35 then leads to the following conclusion.
Proposition 36. The parity function is not definable within ![]() $EQS$.
$EQS$.
6. The divide-and-conquer scheme and EQS
We have formulated the system ![]() $EQS$ in Section 3 by the use of recursion schematic definition and discussed in Section 5.1 the
$EQS$ in Section 3 by the use of recursion schematic definition and discussed in Section 5.1 the ![]() $EQS$-characterization of quantum polylogtime computing. In what follows, we intend to strengthen the system
$EQS$-characterization of quantum polylogtime computing. In what follows, we intend to strengthen the system ![]() $EQS$ by appending an extra scheme. As such a scheme, we particularly consider the divide-and-conquer strategy, which is one of the most useful algorithmic strategies in solving many practical problems. We further show that the divide-and-conquer strategy cannot be “realized” within
$EQS$ by appending an extra scheme. As such a scheme, we particularly consider the divide-and-conquer strategy, which is one of the most useful algorithmic strategies in solving many practical problems. We further show that the divide-and-conquer strategy cannot be “realized” within ![]() $EQS$. This implies that the addition of this strategy as a new scheme truly strengthens the expressing power of
$EQS$. This implies that the addition of this strategy as a new scheme truly strengthens the expressing power of ![]() $EQS$.
$EQS$.
6.1 Multi-qubit divide-and-conquer scheme
A basic idea of the divide-and-conquer strategy is to continue splitting an input of a given combinatorial problem into two (or more) smaller parts until each part is small enough to handle separately and efficiently and then to combine all the small parts in order to solve the entire problem on the given input.
To define the scheme that expresses this divide-and-conquer strategy, we first introduce a useful scheme called the half division scheme. Given two quantum functions ![]() $g$ and
$g$ and ![]() $h$ and any input quantum state
$h$ and any input quantum state ![]() $| \phi \rangle$ in
$| \phi \rangle$ in ![]() $\mathscr{H}_{\infty }$, we simultaneously apply
$\mathscr{H}_{\infty }$, we simultaneously apply ![]() $g$ to the left half of
$g$ to the left half of ![]() $| \phi \rangle$ and
$| \phi \rangle$ and ![]() $h$ to the right half of
$h$ to the right half of ![]() $| \phi \rangle$ and then obtain the new quantum function denoted by
$| \phi \rangle$ and then obtain the new quantum function denoted by ![]() $HalfD[g,h]$.
$HalfD[g,h]$.
*) The half division scheme. From
 $g$ and
$g$ and  $h$, we define
$h$, we define  $HalfD[g,h]$ as follows:
$HalfD[g,h]$ as follows:
(i)
 $HalfD[g,h](| \phi \rangle ) = | \phi \rangle\qquad\qquad\qquad\qquad\qquad\qquad\quad\ \ $ if
$HalfD[g,h](| \phi \rangle ) = | \phi \rangle\qquad\qquad\qquad\qquad\qquad\qquad\quad\ \ $ if  $\ell (| \phi \rangle )\leq 1$,
$\ell (| \phi \rangle )\leq 1$,(ii)
 $HalfD[g,h](| \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} ( g(| s \rangle ) \otimes h(\langle s | \phi \rangle ) )\qquad$ otherwise.
$HalfD[g,h](| \phi \rangle ) = \sum _{s:|s|=LH(| \phi \rangle )} ( g(| s \rangle ) \otimes h(\langle s | \phi \rangle ) )\qquad$ otherwise.
Here is a quick example of how this scheme works.
Example 37. Let us consider ![]() $F_1\equiv HalfD[g,h]$ with
$F_1\equiv HalfD[g,h]$ with ![]() $g=NOT$ and
$g=NOT$ and ![]() $h=WH$. Given an input
$h=WH$. Given an input ![]() $| 0^n \rangle | 0^n \rangle$, we obtain
$| 0^n \rangle | 0^n \rangle$, we obtain ![]() $F_{1}(| 0^n \rangle | 0^n \rangle ) = g(| 0^n \rangle ) \otimes h(| 0^n \rangle ) = \frac{1}{\sqrt{2}} | 10^{n-1} \rangle \otimes (| 0^n \rangle +| 10^{n-1} \rangle )$. Similarly, consider
$F_{1}(| 0^n \rangle | 0^n \rangle ) = g(| 0^n \rangle ) \otimes h(| 0^n \rangle ) = \frac{1}{\sqrt{2}} | 10^{n-1} \rangle \otimes (| 0^n \rangle +| 10^{n-1} \rangle )$. Similarly, consider ![]() $F_2\equiv HalfD[I,h]$. We then obtain
$F_2\equiv HalfD[I,h]$. We then obtain ![]() $F_2(| 0^n \rangle | 0^n \rangle ) = \frac{1}{\sqrt{2}}| 0^n \rangle \otimes (| 0^n \rangle +| 10^{n-1} \rangle )$. For the quantum function
$F_2(| 0^n \rangle | 0^n \rangle ) = \frac{1}{\sqrt{2}}| 0^n \rangle \otimes (| 0^n \rangle +| 10^{n-1} \rangle )$. For the quantum function ![]() $F'\equiv HalfD[F_1,F_2]$, if
$F'\equiv HalfD[F_1,F_2]$, if ![]() $| 0^{2n} \rangle | 0^{2n} \rangle$ is an input to
$| 0^{2n} \rangle | 0^{2n} \rangle$ is an input to ![]() $F'$, then we obtain
$F'$, then we obtain ![]() $F'(| 0^{2n} \rangle | 0^{2n} \rangle ) = \frac{1}{2} (| 10^{2n-1} \rangle + | 10^{n-1}10^{n-1} \rangle ) \otimes (| 0^{2n} \rangle +| 0^n10^{n-1} \rangle )$.
$F'(| 0^{2n} \rangle | 0^{2n} \rangle ) = \frac{1}{2} (| 10^{2n-1} \rangle + | 10^{n-1}10^{n-1} \rangle ) \otimes (| 0^{2n} \rangle +| 0^n10^{n-1} \rangle )$.
We intend to formulate the multi-qubit divide-and-conquer scheme (Scheme DC) using ![]() $HalfD[g,h]$. Recall the quantum function
$HalfD[g,h]$. Recall the quantum function ![]() $SWAP_{i,j}$ given in Lemma5(10). We expand it by allowing its parameter
$SWAP_{i,j}$ given in Lemma5(10). We expand it by allowing its parameter ![]() $j$ to take a non-constant value. In particular, we intend to take
$j$ to take a non-constant value. In particular, we intend to take ![]() $LH(\ell (| \phi \rangle ))+1$ for
$LH(\ell (| \phi \rangle ))+1$ for ![]() $j$ and then define
$j$ and then define ![]() $midSWAP_1(| \phi \rangle )$ to be
$midSWAP_1(| \phi \rangle )$ to be ![]() $SWAP_{2,LH(\ell (| \phi \rangle ))+1}(| \phi \rangle )$ for any
$SWAP_{2,LH(\ell (| \phi \rangle ))+1}(| \phi \rangle )$ for any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$. More generally, for a constant
$| \phi \rangle \in \mathscr{H}_{\infty }$. More generally, for a constant ![]() $k\in \mathbb{N}^{+}$, we set
$k\in \mathbb{N}^{+}$, we set ![]() $midSWAP_k(| \phi \rangle )$ to be
$midSWAP_k(| \phi \rangle )$ to be ![]() $SWAP_{2k,m+k}\circ SWAP_{2k-1,m+k-1}\circ \cdots \circ SWAP_{k+2,m+2}\circ SWAP_{k+1,m+1}$, where
$SWAP_{2k,m+k}\circ SWAP_{2k-1,m+k-1}\circ \cdots \circ SWAP_{k+2,m+2}\circ SWAP_{k+1,m+1}$, where ![]() $m=LH(\ell (| \phi \rangle ))$. With the use of
$m=LH(\ell (| \phi \rangle ))$. With the use of ![]() $midSWAP_k$, for any given quantum function
$midSWAP_k$, for any given quantum function ![]() $h$, we introduce another scheme
$h$, we introduce another scheme ![]() $MidApp_k[h]$ by setting
$MidApp_k[h]$ by setting ![]() $MidApp_k[h]\equiv midSWAP_k^{-1}\circ h \circ midSWAP_k$.
$MidApp_k[h]\equiv midSWAP_k^{-1}\circ h \circ midSWAP_k$.
Let us quickly examine the behavior of ![]() $MidApp_k[\cdot ]$ with a concrete example.
$MidApp_k[\cdot ]$ with a concrete example.
Example 38. For a later argument, we consider the case of quantum function ![]() $h_0 \equiv SWAP^{-1}\circ CNOT\circ SWAP$, which obviously belongs to
$h_0 \equiv SWAP^{-1}\circ CNOT\circ SWAP$, which obviously belongs to ![]() $EQS_0$. Let
$EQS_0$. Let ![]() $| \phi \rangle$ denote
$| \phi \rangle$ denote ![]() $| x_1x_2\cdots x_n \rangle$ for
$| x_1x_2\cdots x_n \rangle$ for ![]() $n\in \mathbb{N}^{+}$ and
$n\in \mathbb{N}^{+}$ and ![]() $x_1,x_2,\ldots, x_n\in \{0,1\}$. The quantum function
$x_1,x_2,\ldots, x_n\in \{0,1\}$. The quantum function ![]() $MidApp_1[h_0]$ satisfies that
$MidApp_1[h_0]$ satisfies that ![]() $MidApp_1[h_0](| \phi \rangle ) = | x_1 \rangle$ if
$MidApp_1[h_0](| \phi \rangle ) = | x_1 \rangle$ if ![]() $n=1$, and
$n=1$, and ![]() $MidApp_1[h_0](| \phi \rangle ) = | x_1\oplus x_{LH(n)+1} \rangle | x_2x_3\cdots x_n \rangle$ if
$MidApp_1[h_0](| \phi \rangle ) = | x_1\oplus x_{LH(n)+1} \rangle | x_2x_3\cdots x_n \rangle$ if ![]() $n\geq 2$. If we are allowed to use extra qubits, then
$n\geq 2$. If we are allowed to use extra qubits, then ![]() $MidApp_1[h_0]$ can be realized by an appropriate quantum function, say,
$MidApp_1[h_0]$ can be realized by an appropriate quantum function, say, ![]() $K$ in
$K$ in ![]() $EQS$ obtained with
$EQS$ obtained with ![]() $Bit$ given in Corollary 2 in the following sense:
$Bit$ given in Corollary 2 in the following sense: ![]() $K(| 0^{3k+8} \rangle | x_1x_2\cdots x_n \rangle ) = | 0^{3k+8} \rangle \otimes MidApp_1[h_0](| x_1x_2\cdots x_n \rangle )$ if
$K(| 0^{3k+8} \rangle | x_1x_2\cdots x_n \rangle ) = | 0^{3k+8} \rangle \otimes MidApp_1[h_0](| x_1x_2\cdots x_n \rangle )$ if ![]() $k\in \mathbb{N}^{+}$ satisfies
$k\in \mathbb{N}^{+}$ satisfies ![]() $n=2^k$.
$n=2^k$.
Now, we formally introduce Scheme DC, which “expresses” the divide-and-conquer strategy.
Definition 39. We express as ![]() $DC$ the following scheme.
$DC$ the following scheme.
(DC) The multi-qubit divide-and-conquer scheme. From
 $g$,
$g$,  $h$, and
$h$, and  $p$, and
$p$, and  $k\in \mathbb{N}^{+}$, (where
$k\in \mathbb{N}^{+}$, (where  $p$ is not defined using
$p$ is not defined using  $MEAS[\cdot ]$ and
$MEAS[\cdot ]$ and  $g$,
$g$,  $h$, and
$h$, and  $p$ are not defined using Scheme DC), we define
$p$ are not defined using Scheme DC), we define  $F\equiv DivConq_k[g,h,p|f_1,f_2]$ as:
$F\equiv DivConq_k[g,h,p|f_1,f_2]$ as:
(i)
 $F(| \phi \rangle ) = g(| \phi \rangle )\qquad\qquad\qquad\qquad\qquad\qquad\quad$ if
$F(| \phi \rangle ) = g(| \phi \rangle )\qquad\qquad\qquad\qquad\qquad\qquad\quad$ if  $\ell (| \phi \rangle )\leq k$,
$\ell (| \phi \rangle )\leq k$,(ii)
 $F(| \phi \rangle ) = MidApp_k[h]( HalfD[ f_1,f_2] ( p(| \phi \rangle ) ))\qquad$ otherwise,
$F(| \phi \rangle ) = MidApp_k[h]( HalfD[ f_1,f_2] ( p(| \phi \rangle ) ))\qquad$ otherwise,
where
 $f_1,f_2 \in \{F,I\}$.
$f_1,f_2 \in \{F,I\}$.
The notation ![]() $EQS+DC$ denotes the smallest set including the quantum functions of Scheme I and being closed under Schemes II–V and DC.
$EQS+DC$ denotes the smallest set including the quantum functions of Scheme I and being closed under Schemes II–V and DC.
Hereafter, we discuss the usefulness of Scheme DC. Recall the parity function ![]() $Parity$ from Section 5.2. We have shown in Corollary36 that
$Parity$ from Section 5.2. We have shown in Corollary36 that ![]() $EQS$ is not powerful enough to include
$EQS$ is not powerful enough to include ![]() $Parity$. In sharp contrast, we argue that
$Parity$. In sharp contrast, we argue that ![]() $Parity$ is in fact definable by applying Schemes I–V and DC.
$Parity$ is in fact definable by applying Schemes I–V and DC.
Proposition 40. There exists a quantum function ![]() $f$ in
$f$ in ![]() $EQS+DC$ that simulates
$EQS+DC$ that simulates ![]() $Parity$ in the following sense: for any
$Parity$ in the following sense: for any ![]() $x\in \{0,1\}^*$ and any
$x\in \{0,1\}^*$ and any ![]() $b\in \{0,1\}$,
$b\in \{0,1\}$, ![]() $Parity(x)=b$ iff
$Parity(x)=b$ iff ![]() $\|\langle b | \psi _{f,x} \rangle \|^2=1$, where
$\|\langle b | \psi _{f,x} \rangle \|^2=1$, where ![]() $| \psi _{f,x} \rangle = f(| x \rangle )$.
$| \psi _{f,x} \rangle = f(| x \rangle )$.
Proof. Let us recall the quantum function ![]() $h_0$ described in Example38 and define
$h_0$ described in Example38 and define ![]() $F$ to be
$F$ to be ![]() $DivConq_1[g,h,p|f_1,f_2]$ with
$DivConq_1[g,h,p|f_1,f_2]$ with ![]() $g=p=I$ and
$g=p=I$ and ![]() $f_1=f_2=F$. For any
$f_1=f_2=F$. For any ![]() $n$-bit string
$n$-bit string ![]() $x=x_1x_2\cdots x_n$, we want to show by induction on
$x=x_1x_2\cdots x_n$, we want to show by induction on ![]() $n\in \mathbb{N}^{+}$ that (*) there exist
$n\in \mathbb{N}^{+}$ that (*) there exist ![]() $y_2,y_3,\ldots, y_n\in \{0,1\}$ for which
$y_2,y_3,\ldots, y_n\in \{0,1\}$ for which ![]() $F(| x \rangle ) = | \bigoplus _{i=1}^{n}x_i \rangle | y_2 \rangle \cdots | y_n \rangle$.
$F(| x \rangle ) = | \bigoplus _{i=1}^{n}x_i \rangle | y_2 \rangle \cdots | y_n \rangle$.
If ![]() $n=1$, then we instantly obtain
$n=1$, then we instantly obtain ![]() $F(| \phi \rangle )=| \phi \rangle$. Assume that
$F(| \phi \rangle )=| \phi \rangle$. Assume that ![]() $n=2$. Since
$n=2$. Since ![]() $HalfD[f_1,f_2](| x_1x_2 \rangle ) = f_1(| x_1 \rangle )\otimes f_2(| x_2 \rangle )$, it follows that
$HalfD[f_1,f_2](| x_1x_2 \rangle ) = f_1(| x_1 \rangle )\otimes f_2(| x_2 \rangle )$, it follows that ![]() $F(| x_1x_2 \rangle ) = MidApp_1[h_0](F(| x_1 \rangle )\otimes F(| x_2 \rangle )) = MidApp_1[h_0](| x_1x_2 \rangle ) = | x_1\oplus x_2 \rangle | x_2 \rangle$. Let
$F(| x_1x_2 \rangle ) = MidApp_1[h_0](F(| x_1 \rangle )\otimes F(| x_2 \rangle )) = MidApp_1[h_0](| x_1x_2 \rangle ) = | x_1\oplus x_2 \rangle | x_2 \rangle$. Let ![]() $n\geq 3$ and assume by induction hypothesis that (*) is true for all indices
$n\geq 3$ and assume by induction hypothesis that (*) is true for all indices ![]() $k\in [n-1]$; namely,
$k\in [n-1]$; namely, ![]() $F(| x_1x_2\cdots x_k \rangle ) = | \bigoplus _{i=1}^{k}x_i \rangle | y_2 \rangle \cdots | y_k \rangle$ for certain suitable bits
$F(| x_1x_2\cdots x_k \rangle ) = | \bigoplus _{i=1}^{k}x_i \rangle | y_2 \rangle \cdots | y_k \rangle$ for certain suitable bits ![]() $y_2,y_3,\ldots, y_k\in \{0,1\}$. Let us concentrate on the case of
$y_2,y_3,\ldots, y_k\in \{0,1\}$. Let us concentrate on the case of ![]() $x\in \{0,1\}^{n}$ with
$x\in \{0,1\}^{n}$ with ![]() $x=x_1x_2\cdots x_n$. For simplicity, we write
$x=x_1x_2\cdots x_n$. For simplicity, we write ![]() $m$ in place of
$m$ in place of ![]() $LH(n)$. Let
$LH(n)$. Let ![]() $x'=x_1x_2\cdots x_{m}$ and
$x'=x_1x_2\cdots x_{m}$ and ![]() $x''=x_{m+1}\cdots x_n$ so that
$x''=x_{m+1}\cdots x_n$ so that ![]() $x=x'x''$. It thus follows that
$x=x'x''$. It thus follows that ![]() $HalfD[f_1,f_2](| x \rangle ) = f_1(| x' \rangle )\otimes f_2(| x'' \rangle )$. Since
$HalfD[f_1,f_2](| x \rangle ) = f_1(| x' \rangle )\otimes f_2(| x'' \rangle )$. Since ![]() $F(| x' \rangle ) = | \bigoplus _{i=1}^{m}x_i \rangle | y_2\cdots y_{m} \rangle$ and
$F(| x' \rangle ) = | \bigoplus _{i=1}^{m}x_i \rangle | y_2\cdots y_{m} \rangle$ and ![]() $F(| x'' \rangle ) = | \bigoplus _{i=m+1}^{n}x_i \rangle | y_{m+2}\cdots y_n \rangle$ by induction hypothesis, we conclude that
$F(| x'' \rangle ) = | \bigoplus _{i=m+1}^{n}x_i \rangle | y_{m+2}\cdots y_n \rangle$ by induction hypothesis, we conclude that ![]() $MidApp_1[h_0](F(| x' \rangle )\otimes F(| x'' \rangle )) = MidApp_1[h_0]( | \bigoplus _{i=1}^{m}x_i \rangle | y_2\cdots y_{m} \rangle \otimes | \bigoplus _{i=m+1}^{n}x_i \rangle | y_{m+2}\cdots y_n \rangle ) = | \bigoplus _{i=1}^{n}x_i \rangle | y_2\cdots y_n \rangle$. This implies that (*) holds for all
$MidApp_1[h_0](F(| x' \rangle )\otimes F(| x'' \rangle )) = MidApp_1[h_0]( | \bigoplus _{i=1}^{m}x_i \rangle | y_2\cdots y_{m} \rangle \otimes | \bigoplus _{i=m+1}^{n}x_i \rangle | y_{m+2}\cdots y_n \rangle ) = | \bigoplus _{i=1}^{n}x_i \rangle | y_2\cdots y_n \rangle$. This implies that (*) holds for all ![]() $n\in \mathbb{N}^{+}$.
$n\in \mathbb{N}^{+}$.
6.2 Approximately admitting
By Proposition40, we may anticipate that the multi-qubit divide-and-conquer scheme (Scheme DC) cannot be “realized” or even “approximated” within the system ![]() $EQS$. We formalize this latter notion under the new terminology of “approximately admitting”.
$EQS$. We formalize this latter notion under the new terminology of “approximately admitting”.
Let us consider an arbitrary scheme (such as composition and fast quantum recursion) whose construction requires a series of quantum functions. Recall the notion of ground (quantum) functions from Section 3.1. Let ![]() $\mathscr{S}$ denote a class of quantum functions and assume that
$\mathscr{S}$ denote a class of quantum functions and assume that ![]() $\mathscr{R}$ is a scheme requiring a series of
$\mathscr{R}$ is a scheme requiring a series of ![]() $k$ ground functions taken from
$k$ ground functions taken from ![]() $\mathscr{S}$. We say that
$\mathscr{S}$. We say that ![]() $\mathscr{S}$ approximately admits
$\mathscr{S}$ approximately admits ![]() $\mathscr{R}$ if, for any series
$\mathscr{R}$ if, for any series ![]() $\mathscr{G}=(g_1,g_2,\ldots, g_k)$ with
$\mathscr{G}=(g_1,g_2,\ldots, g_k)$ with ![]() $g_1,g_2,\ldots, g_k\in \mathscr{S}$, there exists a quantum function
$g_1,g_2,\ldots, g_k\in \mathscr{S}$, there exists a quantum function ![]() $f\in \mathscr{S}$ and a constant
$f\in \mathscr{S}$ and a constant ![]() $\varepsilon \in [0,1/2)$ such that, for any
$\varepsilon \in [0,1/2)$ such that, for any ![]() $| \phi \rangle \in \mathscr{H}_{\infty }$,
$| \phi \rangle \in \mathscr{H}_{\infty }$, ![]() $\|\langle \psi _{f,\phi } | \xi _{\mathscr{R},\mathscr{G},\phi } \rangle \|^2\geq 1-\varepsilon$ holds, where
$\|\langle \psi _{f,\phi } | \xi _{\mathscr{R},\mathscr{G},\phi } \rangle \|^2\geq 1-\varepsilon$ holds, where ![]() $| \psi _{f,\phi } \rangle = f(| \phi \rangle )$ and
$| \psi _{f,\phi } \rangle = f(| \phi \rangle )$ and ![]() $| \xi _{\mathscr{R},\mathscr{G},\phi } \rangle = \mathscr{R}(g_1,g_2,\ldots, g_k)(| \phi \rangle )$. With this new terminology, we can claim that all schemes listed in Lemma22, for example, are indeed approximately admitted by
$| \xi _{\mathscr{R},\mathscr{G},\phi } \rangle = \mathscr{R}(g_1,g_2,\ldots, g_k)(| \phi \rangle )$. With this new terminology, we can claim that all schemes listed in Lemma22, for example, are indeed approximately admitted by ![]() $EQS$.
$EQS$.
Theorem 41. ![]() $EQS$ does not approximately admit the multi-qubit divide-and-conquer scheme.
$EQS$ does not approximately admit the multi-qubit divide-and-conquer scheme.
Proof. Assume that ![]() $EQS$ approximately admits Scheme DC. Since the parity function is realized in
$EQS$ approximately admits Scheme DC. Since the parity function is realized in ![]() $EQS+DC$ (Proposition40), there exists a polylogtime QTM that computes
$EQS+DC$ (Proposition40), there exists a polylogtime QTM that computes ![]() $Parity$ due to the characterization theorem (Theorem 33) of
$Parity$ due to the characterization theorem (Theorem 33) of ![]() $EQS$ in terms of polylogtime QTMs. This clearly contradicts the fact that no polylogtime QTM can compute the parity function (Lemma31).
$EQS$ in terms of polylogtime QTMs. This clearly contradicts the fact that no polylogtime QTM can compute the parity function (Lemma31).
7. Further discussion and future directions
The schematic approach toward quantum computability was initiated by Yamakami (Reference Yamakami2020) and made a great success to precisely capture quantum polynomial-time computability using the exquisite scheme of multi-qubit quantum recursion. The use of such recursion schemes to characterize quantum computability further leads us to a study on the expressibility of the schemes for quantum computations rather than the more popular algorithmic complexity of quantum computations. In this work, we have made an additional step toward an introduction of a more elementary form of the recursion schematic definition than the one in (Yamakami, Reference Yamakami2020). In particular, we have investigated the scheme of (code-controlled) fast quantum recursion in Section 3.2 as a basis to the class ![]() $EQS$ of “elementary” quantum functions, and we have demonstrated the usefulness of various quantum functions based on this new scheme in connection to “parallel” computability in Section 5. An additional scheme, multi-qubit divide-and-conquer, has been examined and shown not to be approximately admitted within the framework of
$EQS$ of “elementary” quantum functions, and we have demonstrated the usefulness of various quantum functions based on this new scheme in connection to “parallel” computability in Section 5. An additional scheme, multi-qubit divide-and-conquer, has been examined and shown not to be approximately admitted within the framework of ![]() $EQS$ in Section 6.
$EQS$ in Section 6.
To promote the future research on the schematic definability of quantum computations, we wish to list seven natural open questions that have been left unanswered throughout this work. We expect that fruitful research toward the answers to these questions would make significant progress in the near future on the descriptional aspects of quantum computing.
1. It is quite important to discuss what recursion schemes must be chosen as a basis of
 $EQS$. In our formulation, Scheme IV in particular looks rather complicated compared to other schemes. Therefore, we still need to find more “natural” and “simpler” schemes needed to define
$EQS$. In our formulation, Scheme IV in particular looks rather complicated compared to other schemes. Therefore, we still need to find more “natural” and “simpler” schemes needed to define  $EQS$ precisely.
$EQS$ precisely.2. Scheme V looks quite different from the other schemes. For instance, the recursive application of
 $f_u$ to compute
$f_u$ to compute  $F$ in Scheme IV is controlled by “internal” conditions, whereas the repeated application of
$F$ in Scheme IV is controlled by “internal” conditions, whereas the repeated application of  $g$ to compute
$g$ to compute  $F$ in Scheme V is controlled by an “external” condition. It is thus desirable to remove Scheme V from the definition of
$F$ in Scheme V is controlled by an “external” condition. It is thus desirable to remove Scheme V from the definition of  $EQS$ by simply modifying the definitions of Schemes I–IV. How can we modify them to achieve this goal?
$EQS$ by simply modifying the definitions of Schemes I–IV. How can we modify them to achieve this goal?3. We have shown in Theorem 41 that
 $EQS+DC$ has more expressing power than
$EQS+DC$ has more expressing power than  $EQS$ alone. However, we do not know the exact computational complexity of
$EQS$ alone. However, we do not know the exact computational complexity of  $EQS+DC$. It is of great importance to determine its exact complexity.
$EQS+DC$. It is of great importance to determine its exact complexity.4. Concerning recursion-schematic characterizations of quantum computing, we have focussed our attention only on “runtime-restricted” quantum computations. Any discussion on “space-restricted” quantum computing has eluded from our attention so far. How can we characterize such computations in terms of recursion schemes?
5. We have discussed the relative complexity of
 $\mathrm{BQPOLYLOGTIME}$ in Section 5.2 in comparison to
$\mathrm{BQPOLYLOGTIME}$ in Section 5.2 in comparison to  $\mathrm{NLOGTIME}$ and
$\mathrm{NLOGTIME}$ and  $\mathrm{PPOLYLOGTIME}$. On the contrary, we still do not know whether
$\mathrm{PPOLYLOGTIME}$. On the contrary, we still do not know whether  $\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}}$ differs from
$\mathrm{BQPOLYLOGTIME}_{\bar{\mathbb{Q}}}$ differs from  $\mathrm{BPPOLYLOGTIME}$, which is the bounded-error analog of
$\mathrm{BPPOLYLOGTIME}$, which is the bounded-error analog of  $\mathrm{PPOLYLOGTIME}$. Are they truly different?
$\mathrm{PPOLYLOGTIME}$. Are they truly different?6. It is well known that the choice of (quantum) amplitudes of QTMs affects their computational complexity. In the polynomial-time setting, for example, the bounded-error quantum polynomial-time class
 $\mathrm{BQP}_{\mathbb{C}}$ differs from
$\mathrm{BQP}_{\mathbb{C}}$ differs from  $\mathrm{BQP}_{\tilde{\mathbb{C}}}$, where
$\mathrm{BQP}_{\tilde{\mathbb{C}}}$, where  $\tilde{\mathbb{C}}$ is the set of polynomial-time approximable complex numbers. On the contrary, the nondeterministic variant
$\tilde{\mathbb{C}}$ is the set of polynomial-time approximable complex numbers. On the contrary, the nondeterministic variant  $\mathrm{NQP}_{\mathbb{C}}$ collapses to
$\mathrm{NQP}_{\mathbb{C}}$ collapses to  $\mathrm{NQP}_{\tilde{\mathbb{C}}}$ (Yamakami and Yao, Reference Yamakami and Yao1999). In the polylogtime setting, is it true that
$\mathrm{NQP}_{\tilde{\mathbb{C}}}$ (Yamakami and Yao, Reference Yamakami and Yao1999). In the polylogtime setting, is it true that  $\mathrm{BQPOLYLOGTIME}_{\mathbb{C}} \neq \mathrm{BQPOLYLOGTIME}_{\tilde{\mathbb{C}}}$?
$\mathrm{BQPOLYLOGTIME}_{\mathbb{C}} \neq \mathrm{BQPOLYLOGTIME}_{\tilde{\mathbb{C}}}$?7. It is desirable to develop a general theory of descriptional complexity based on recursion schematic definitions of quantum functions for a better understanding of quantum computability and beyond. For a further extension of quantum computability by quantum quantifiers, for example, see (Yamakami, Reference Yamakami2002)