Hostname: page-component-6587cd75c8-4pd2k Total loading time: 0 Render date: 2025-04-24T02:39:47.064Z Has data issue: false hasContentIssue false
  • English
  • Français

Essential covers of the hypercube require many hyperplanes

Part of: Extremal combinatorics

Published online by Cambridge University Press:  16 December 2024

Lisa Sauermann  and
Zixuan Xu
Lisa Sauermann
Affiliation:
University of Bonn, Bonn, Germany
Zixuan Xu*
Affiliation:
Massachusetts Institute of Technology, Cambridge, USA
*
Corresponding author: Zixuan Xu; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a new lower bound for the almost 20-year-old problem of determining the smallest possible size of an essential cover of the $n$-dimensional hypercube 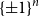$\{\pm 1\}^n$, that is, the smallest possible size of a collection of hyperplanes that forms a minimal cover of $\{\pm 1\}^n$ and such that, furthermore, every variable appears with a non-zero coefficient in at least one of the hyperplane equations. We show that such an essential cover must consist of at least 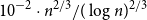$10^{-2}\cdot n^{2/3}/(\log n)^{2/3}$ hyperplanes, improving previous lower bounds of Linial–Radhakrishnan, of Yehuda–Yehudayoff, and of Araujo–Balogh–Mattos.

Keywords

Essential covershypercube

MSC classification

Primary: 05D40: Probabilistic methods
Type
Paper
Information
Combinatorics, Probability and Computing , First View , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

*

Research supported in part by NSF Award DMS-2100157 and a Sloan Research Fellowship.

References

Alon, N. (1999) Combinatorial Nullstellensatz. Comb. Probab. Comp. 8(1-2) 7–29. DOI: 10.1017/S0963548398003411.CrossRefGoogle Scholar
Alon, N. and Füredi, Z. (1993) Covering the cube by affine hyperplanes. European J. Combin. 14(2) 79–83. DOI: 10.1006/eujc.1993.1011.CrossRefGoogle Scholar
Araujo, I., Balogh, J. and Mattos, L. (2022) New lower bounds for essential covers of the cube, arXiv:2209.00140.Google Scholar
Ball, K. (1991) The plank problem for symmetric bodies. Invent. Math. 104(3) 535–543. DOI: 10.1007/BF01245089.CrossRefGoogle Scholar
Bang, T. (1951) A solution of the “plank problem. Proc. Amer. Math. Soc. 2(6) 990–993. DOI: 10.2307/2031721.Google Scholar
Clifton, A. and Huang, H. (2020) On almost k-covers of hypercubes. Combinatorica 40(4) 511–526. DOI: 10.1007/s00493-019-4221-y.CrossRefGoogle Scholar
Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58(301) 13–30. DOI: 10.2307/2282952.CrossRefGoogle Scholar
Ivanisvili, P., Klein, O. and Vershynin, R. (2023) Covering the hypercube, the uncertainty principle, and an interpolation formula, arXiv:2310.13277.Google Scholar
Klein, O. (2023) Slicing all Edges of an n-cube Requires n 2/3 Hyperplanes, pp. 1931–1936. In: 2023 IEEE 64th Annual Symposium on Foundations of Computer Science (FOCS), DOI: 10.1109/FOCS57990.2023.00117.CrossRefGoogle Scholar
Linial, N. and Radhakrishnan, J. (2005) Essential covers of the cube by hyperplanes. J. Comb. Theory Ser. A 109(2) 331–338. DOI: 10.1016/j.jcta.2004.07.012.CrossRefGoogle Scholar
Saxton, D. (2013) Essential positive covers of the cube. J. Comb. Theory Ser. A 120(5) 971–975. DOI: 10.1016/j.jcta.2013.02.002.CrossRefGoogle Scholar
Yehuda, G. and Yehudayoff, A. (2024) A lower bound for essential covers of the cube. Combinatorica 44(4) 801–815. DOI: 10.1007/s00493-024-00093-4.CrossRefGoogle Scholar
Yehuda, G. and Yehudayoff, A. (2021) Slicing the hypercube is not easy, arXiv:2102.05536.Google Scholar