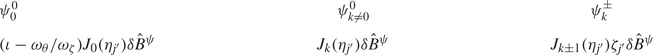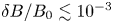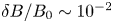1. Introduction
Energetic particles have historically been challenging to confine in stellarator configurations due to the possibility of unconfined orbits and resonances exposed at low collisionality. These difficulties must be overcome to develop a stellarator reactor concept, as excessive alpha losses before thermalization can impact power balance and impart damage to plasma-facing components. In recent years, significant progress has been made in designing stellarator magnetic fields that can confine the orbits of fusion-born alpha particles without perturbations (Bader et al. Reference Bader, Drevlak, Anderson, Faber, Hegna, Likin, Schmitt and Talmadge2019; Landreman, Buller & Drevlak Reference Landreman, Buller and Drevlak2022; Landreman & Paul Reference Landreman and Paul2022). However, reducing the guiding-centre orbit loss mechanisms may make mode–particle interactions relatively significant.
The interaction of Alfvén eigenmodes (AEs) with energetic particles has been shown to drive substantial flattening of the fast-ion profile in tokamak experiments (Heidbrink et al. Reference Heidbrink, Van Zeeland, Austin, Burrell, Gorelenkov, Kramer, Luo, Makowski, McKee and Muscatello2008). Alvénic activity has also been observed on several stellarator configurations, including HSX (Deng et al. Reference Deng, Brower, Breizman, Spong, Almagri, Anderson, Anderson, Ding, Guttenfelder and Likin2009), CHS (Takechi et al. Reference Takechi, Matsunaga, Toi, Isobe, Minami, Tanaka, Nishimura, Takahashi, Okamura and Matsuoka2002), LHD (Toi et al. Reference Toi, Ogawa, Isobe, Osakabe, Spong and Todo2011), W7-AS (Weller et al. Reference Weller, Spong, Jaenicke, Lazaros, Penningsfeld and Sattler1994), TJ-II (Melnikov et al. Reference Melnikov, Ochando, Ascasibar, Castejon, Cappa, Eliseev, Hidalgo, Krupnik, Lopez-Fraguas and Liniers2014), W7-X (Rahbarnia et al. Reference Rahbarnia, Thomsen, Schilling, Vaz Mendes, Endler, Kleiber, Könies, Borchardt, Slaby and Bluhm2020) and Heliotron-J (Yamamoto et al. Reference Yamamoto, Nagasaki, Suzuki, Mizuuchi, Okada, Kobayashi, Blackwell, Kondo, Motojima and Nakajima2007). Alfvénic instabilities have been thought to be potentially benign in a stellarator reactor due to their ability to operate at high density (Helander et al. Reference Helander, Beidler, Bird, Drevlak, Feng, Hatzky, Jenko, Kleiber, Proll and Turkin2012). However, fast-ion-driven modes may still be destabilized at high density: LHD modelling indicates that Alfvénic activity remains present even at a fast-ion beta of ${\approx }0.05\,\%$![]() (Varela, Spong & Garcia Reference Varela, Spong and Garcia2017). For comparison, using the profiles from the ARIES-CS stellarator reactor study with density ${\approx }5 \times 10^{20}$
(Varela, Spong & Garcia Reference Varela, Spong and Garcia2017). For comparison, using the profiles from the ARIES-CS stellarator reactor study with density ${\approx }5 \times 10^{20}$![]() m$^{-3}$
m$^{-3}$![]() (Ku et al. Reference Ku, Garabedian, Lyon, Turnbull, Grossman, Mau and Zarnstorff2008), the fast-ion beta is ${\approx }0.2\,\%$
(Ku et al. Reference Ku, Garabedian, Lyon, Turnbull, Grossman, Mau and Zarnstorff2008), the fast-ion beta is ${\approx }0.2\,\%$![]() . It remains to be seen to what extent Alfvénic activity can be controlled in a stellarator reactor by manipulating the density profile or optimizing the magnetic field.
. It remains to be seen to what extent Alfvénic activity can be controlled in a stellarator reactor by manipulating the density profile or optimizing the magnetic field.
Significant recent work has focused on energetic particle physics in quasisymmetric configurations based on properties of guiding-centre orbits (Bader et al. Reference Bader, Anderson, Drevlak, Faber, Hegna, Henneberg, Landreman, Schmitt, Suzuki and Ware2021; LeViness et al. Reference LeViness, Schmitt, Lazerson, Bader, Faber, Hammond and Gates2022; Paul et al. Reference Paul, Bhattacharjee, Landreman, Alex, Velasco and Nies2022), but relatively little has been studied with respect to AE-driven transport. The AE stability of the Chinese First Quasisymmetric Stellarator (CFQS) configuration has been evaluated using the linear gyrofluid FAR3D code (Varela et al. Reference Varela, Shimizu, Spong, Garcia and Ghai2021). However, a systematic study of the AE-driven transport in quasisymmetric configurations has not yet been performed. For equilibria sufficiently close to quasisymmetry (QS), phenomena previously observed on tokamaks are anticipated. Monte Carlo simulations indicate that a resonant perturbation induces some rapid convective transport due to phase-space islands near the boundaries. Island overlap occurs for larger perturbation amplitudes, $\delta B^r/B_0 \sim 10^{-3}$![]() , where $\delta B^r$
, where $\delta B^r$![]() is the radial perturbed magnetic field and $B_0$
is the radial perturbed magnetic field and $B_0$![]() is the equilibrium field strength, causing diffusive losses (Hsu & Sigmar Reference Hsu and Sigmar1992; Sigmar et al. Reference Sigmar, Hsu, White and Cheng1992). Because of the coupling of a single AE to the poloidal variation of the magnetic drifts, sideband resonances arise and can lead to island overlap even in the presence of a single AE (Hsu & Sigmar Reference Hsu and Sigmar1992; Mynick Reference Mynick1993a,Reference Mynickb). In perfect symmetry with the addition of a single perturbation harmonic, kinetic Poincaré plots (White Reference White2011, Reference White2012) can be employed to observe the formation of phase-space islands, island overlap and chaos.
is the equilibrium field strength, causing diffusive losses (Hsu & Sigmar Reference Hsu and Sigmar1992; Sigmar et al. Reference Sigmar, Hsu, White and Cheng1992). Because of the coupling of a single AE to the poloidal variation of the magnetic drifts, sideband resonances arise and can lead to island overlap even in the presence of a single AE (Hsu & Sigmar Reference Hsu and Sigmar1992; Mynick Reference Mynick1993a,Reference Mynickb). In perfect symmetry with the addition of a single perturbation harmonic, kinetic Poincaré plots (White Reference White2011, Reference White2012) can be employed to observe the formation of phase-space islands, island overlap and chaos.
We aim to address unresolved questions in this area, including how the QS helicity and deviations from QS impact transport. Recent simulations (White, Bierwage & Ethier Reference White, Bierwage and Ethier2022; White & Duarte Reference White and Duarte2023) of resonant AEs in W7-X and the precise QH equilibrium (Landreman & Paul Reference Landreman and Paul2022) have indicated that even a small-amplitude Alfvénic perturbation, $\delta B/B \sim 10^{-6}$![]() , can lead to global flattening of the distribution function. This extreme sensitivity to perturbations is postulated to arise because the low magnetic shear of the equilibrium implies low transit frequency shear for passing particles. Here, we study the impact of magnetic shear in more detail by evaluating the island width and drift-harmonic overlap conditions for quasisymmetric configurations. As discussed later, our conclusions do not quantitatively agree with these recent studies, which predict substantive diffusive losses for low AE perturbation amplitudes for equilibria very close to QS.
, can lead to global flattening of the distribution function. This extreme sensitivity to perturbations is postulated to arise because the low magnetic shear of the equilibrium implies low transit frequency shear for passing particles. Here, we study the impact of magnetic shear in more detail by evaluating the island width and drift-harmonic overlap conditions for quasisymmetric configurations. As discussed later, our conclusions do not quantitatively agree with these recent studies, which predict substantive diffusive losses for low AE perturbation amplitudes for equilibria very close to QS.
The impact of AEs on the fast-ion transport in a stellarator reactor is challenging to compute in practice, requiring knowledge of the saturated mode amplitude. The nonlinear saturation can be obtained from high-fidelity modelling (Fehér Reference Fehér2014; Spong et al. Reference Spong, Holod, Todo and Osakabe2017; Todo et al. Reference Todo, Seki, Spong, Wang, Suzuki, Yamamoto, Nakajima and Osakabe2017), which depends on the details of the thermal and fast-ion profiles. Rather than attempt such calculations here, we consider the potential impact of a single Alfvénic perturbation on the phase-space integrability and resulting transport in reactor-scale equilibria designed to be close to QS. We employ a ‘worst-case scenario’ approach, in which an Alfvénic perturbation is chosen to strongly resonate with rational periodic passing orbits in the core for several quasisymmetric configurations. We consider several mode amplitudes consistent with experimental measurements and high-fidelity modelling. While physically, such a perturbation should correspond to an AE of the background plasma, we instead let the perturbation be a radially global mode with prescribed mode numbers, frequency and perturbation amplitude. We assess the impact of the perturbation mode number, amplitude and residual QS error on the resulting transport. Phase-space Poincaré plots are used to guide the analysis and assess the transition to chaos. While Poincaré plots have been used to study the structure of phase space for energetic passing particles in the absence of time-dependent perturbations for some stellarators (White et al. Reference White, Bierwage and Ethier2022), this technique has not yet been applied to assess the impact of AEs on the transport. We evaluate the extent to which this technique provides insight into the transport in configurations with varying deviations from QS.
In § 2, we outline the guiding-centre equations of motion with Alfvénic perturbations. In § 3, we describe the theory for resonance, island width and island overlap in QS configurations. Resonance analysis is performed for several equilibria designed to be close to QS in § 4, and resonant perturbations are identified. Kinetic Poincaré plots are employed in § 5 to assess the formation of phase-space islands and chaos in the presence of the resonant perturbations. A Monte Carlo guiding-centre transport analysis is performed in § 6. We conclude in § 7.
2. Guiding-centre motion in the presence of an Alfvénic perturbation
The guiding-centre motion, $\boldsymbol {R}(t)$![]() , is described by the Lagrangian (Littlejohn Reference Littlejohn1983)
, is described by the Lagrangian (Littlejohn Reference Littlejohn1983)

where $q$![]() is the charge, $M$
is the charge, $M$![]() is the mass, $v_{\|}$
is the mass, $v_{\|}$![]() is the velocity in the direction of the magnetic field, $\mu$
is the velocity in the direction of the magnetic field, $\mu$![]() is the magnetic moment, $\varPhi$
is the magnetic moment, $\varPhi$![]() is the electrostatic potential, and $\boldsymbol{A}$
is the electrostatic potential, and $\boldsymbol{A}$![]() is the vector potential. We assume the magnetic field is comprised of an equilibrium field, $\boldsymbol {B}_0$
is the vector potential. We assume the magnetic field is comprised of an equilibrium field, $\boldsymbol {B}_0$![]() , and a shear Alfvénic perturbation (White et al. Reference White, Goldston, McGuire, Boozer, Monticello and Park1983),
, and a shear Alfvénic perturbation (White et al. Reference White, Goldston, McGuire, Boozer, Monticello and Park1983),
for parameter $\alpha $![]() while the scalar potential vanishes in the equilibrium, $\varPhi = \delta \varPhi$
while the scalar potential vanishes in the equilibrium, $\varPhi = \delta \varPhi$![]() . With the reduced magnetohydrodynamic (MHD) assumption (Kruger, Hegna & Callen Reference Kruger, Hegna and Callen1998) – $k_{\|}/k_{\perp } \ll 1$
. With the reduced magnetohydrodynamic (MHD) assumption (Kruger, Hegna & Callen Reference Kruger, Hegna and Callen1998) – $k_{\|}/k_{\perp } \ll 1$![]() , where $k_{\|}$
, where $k_{\|}$![]() is the characteristic parallel wavenumber and $k_{\perp }$
is the characteristic parallel wavenumber and $k_{\perp }$![]() is the characteristic perpendicular wavenumber associated with perturbed quantities – the form of the perturbed field (2.2) implies that the linear perturbation to the field strength vanishes, $\delta B = 0$
is the characteristic perpendicular wavenumber associated with perturbed quantities – the form of the perturbed field (2.2) implies that the linear perturbation to the field strength vanishes, $\delta B = 0$![]() . Under the ideal MHD assumption, the corresponding scalar potential must satisfy $\boldsymbol {B}_0 \boldsymbol {\cdot }\delta \boldsymbol {E} =0$
. Under the ideal MHD assumption, the corresponding scalar potential must satisfy $\boldsymbol {B}_0 \boldsymbol {\cdot }\delta \boldsymbol {E} =0$![]() , which implies
, which implies
The perturbed fields could be computed from a global AE solver such as AE3D (Spong, D'azevedo & Todo Reference Spong, D'azevedo and Todo2010). For the fundamental studies here, we instead assume a single harmonic perturbation of the form
where $(\psi,\theta,\zeta )$![]() are Boozer coordinates such that the unperturbed magnetic field is expressed as
are Boozer coordinates such that the unperturbed magnetic field is expressed as
where $m$![]() is the poloidal mode number, $n$
is the poloidal mode number, $n$![]() is the toroidal mode number and $\omega$
is the toroidal mode number and $\omega$![]() is the frequency. We define the phase variable $\eta = \omega t + m \theta - n \zeta$
is the frequency. We define the phase variable $\eta = \omega t + m \theta - n \zeta$![]() . The corresponding expression for $\alpha$
. The corresponding expression for $\alpha$![]() is then obtained from (2.3), which we write schematically as
is then obtained from (2.3), which we write schematically as
We impose $\hat {\varPhi }$![]() and compute $\hat {\alpha }$
and compute $\hat {\alpha }$![]() so that a magnetic differential equation need not be inverted, which can give rise to singular solutions on rational surfaces.
so that a magnetic differential equation need not be inverted, which can give rise to singular solutions on rational surfaces.
Since $M v_{\|}/(qB_0)$![]() is small in comparison with the characteristic length scale of the equilibrium and $\delta B=0$
is small in comparison with the characteristic length scale of the equilibrium and $\delta B=0$![]() , the perturbed Lagrangian reads (Littlejohn Reference Littlejohn1985)
, the perturbed Lagrangian reads (Littlejohn Reference Littlejohn1985)

The resulting equations of motion are integrated in Boozer coordinates using the SIMSOPT stellarator optimization and modelling package (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021).
To compare Alfvénic perturbations across configurations with different mode numbers, we will express the strength of the perturbation in terms of its normalized radial magnetic field
Here, we have assumed that the gradient scale length of the perturbed field is larger than that of the equilibrium. Since $G \gg I$![]() for stellarator equilibria, we define the parameter $\delta \hat {B}^{\psi } = m \hat {\alpha }/r \sim \delta \boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\nabla } \psi /(B_0 |\boldsymbol {\nabla } \psi |)$
for stellarator equilibria, we define the parameter $\delta \hat {B}^{\psi } = m \hat {\alpha }/r \sim \delta \boldsymbol {B} \boldsymbol {\cdot } \boldsymbol {\nabla } \psi /(B_0 |\boldsymbol {\nabla } \psi |)$![]() to compare equilibria with respect to the strength of the perturbed radial field.
to compare equilibria with respect to the strength of the perturbed radial field.
3. Resonance theory
We assume a quasisymmetric equilibrium for which the unperturbed field strength can be expressed as $B_0(\psi,\chi )$![]() , where $\chi = \theta - N \zeta$
, where $\chi = \theta - N \zeta$![]() is the symmetry angle and $N$
is the symmetry angle and $N$![]() is an integer representing the symmetry helicity ($N = 0$
is an integer representing the symmetry helicity ($N = 0$![]() for quasiaxisymmetry and $N \ne 0$
for quasiaxisymmetry and $N \ne 0$![]() for quasihelical symmetry). Each equilibrium we consider in § 4 is sufficiently close to QS that such an assumption provides valuable insight into the resulting dynamics.
for quasihelical symmetry). Each equilibrium we consider in § 4 is sufficiently close to QS that such an assumption provides valuable insight into the resulting dynamics.
The radial drift over the unperturbed trajectories is analysed in the presence of an Alfvénic perturbation in Appendix A, generalizing the theory of Mynick (Reference Mynick1993b) to quasisymmetric configurations and moderate frequency perturbations. At moderate frequencies, the electrostatic potential enters the guiding-centre equations of motion. Because $\boldsymbol {B}_0 \boldsymbol {\cdot } \delta \boldsymbol {E} = 0$![]() , particles continue to follow perturbed field lines to lowest order in the gyroradius but experience an additional $\boldsymbol {E} \times \boldsymbol {B}$
, particles continue to follow perturbed field lines to lowest order in the gyroradius but experience an additional $\boldsymbol {E} \times \boldsymbol {B}$![]() drift. Under the assumption of QS and stellarator symmetry, the unperturbed equations of motion can be written schematically as
drift. Under the assumption of QS and stellarator symmetry, the unperturbed equations of motion can be written schematically as

where $\omega _{\chi } = \langle \dot {\chi } \rangle$![]() and $\omega _{\zeta } = \langle \dot {\zeta } \rangle$
and $\omega _{\zeta } = \langle \dot {\zeta } \rangle$![]() are the averaged drifts in the $\chi$
are the averaged drifts in the $\chi$![]() and $\zeta$
and $\zeta$![]() directions. The overdot represents a time derivative, and the average is performed over many toroidal transits, $\langle A \rangle = \int _0^T \, \textrm {d} t A /T$
directions. The overdot represents a time derivative, and the average is performed over many toroidal transits, $\langle A \rangle = \int _0^T \, \textrm {d} t A /T$![]() . The summations represent the periodic contributions from the drifts.
. The summations represent the periodic contributions from the drifts.
For an Alfvénic perturbation of the form (2.4) to provide a net radial drift, a resonance condition must be satisfied
As discussed in Appendix A, the integer $l$![]() arises due to coupling through the $\chi$
arises due to coupling through the $\chi$![]() dependence of the magnetic drifts. If the drift dynamics (3.1) is dominated by a particular cosine harmonic with integer $j'$
dependence of the magnetic drifts. If the drift dynamics (3.1) is dominated by a particular cosine harmonic with integer $j'$![]() , then $l$
, then $l$![]() is assumed to be an integer multiple of $j'$
is assumed to be an integer multiple of $j'$![]() . To simplify the analysis, the $j' = 1$
. To simplify the analysis, the $j' = 1$![]() harmonic of the field strength is assumed to be dominant, which holds near the magnetic axis (Garren & Boozer Reference Garren and Boozer1991) and for the equilibria of interest. More general expressions are provided in Appendix A. Under the assumption that the characteristic frequencies are approximately flux functions, the full island width associated with a given resonance is given by
harmonic of the field strength is assumed to be dominant, which holds near the magnetic axis (Garren & Boozer Reference Garren and Boozer1991) and for the equilibria of interest. More general expressions are provided in Appendix A. Under the assumption that the characteristic frequencies are approximately flux functions, the full island width associated with a given resonance is given by

where $\psi _l$![]() is a cosine harmonic of the radial perturbed drift and we have made the approximation $h'(\psi )\approx \omega _{\theta }'(\psi )/\omega _{\zeta }$
is a cosine harmonic of the radial perturbed drift and we have made the approximation $h'(\psi )\approx \omega _{\theta }'(\psi )/\omega _{\zeta }$![]() . The perturbed radial drift, $\delta \dot {\psi }$
. The perturbed radial drift, $\delta \dot {\psi }$![]() , can be evaluated along the unperturbed trajectory and expressed as a cosine series in $\cos (\varOmega _l t + \eta ^0)$
, can be evaluated along the unperturbed trajectory and expressed as a cosine series in $\cos (\varOmega _l t + \eta ^0)$![]() and $\cos (\varOmega _l t + \eta ^0 \mp \chi ^0)$
and $\cos (\varOmega _l t + \eta ^0 \mp \chi ^0)$![]() with coefficients given by $\psi _l^0$
with coefficients given by $\psi _l^0$![]() and $\psi _l^{\pm }$
and $\psi _l^{\pm }$![]() ; see (A5). Here, $\eta ^0 = m \theta ^0 - n \zeta ^0$
; see (A5). Here, $\eta ^0 = m \theta ^0 - n \zeta ^0$![]() is the initial phase. The scaling of these coefficients with the magnitude of the magnetic drifts, mode numbers and perturbed radial field is summarized as
is the initial phase. The scaling of these coefficients with the magnitude of the magnetic drifts, mode numbers and perturbed radial field is summarized as

where $J_l$![]() are the Bessel functions of the first kind, $\eta _{1} = (m\chi _{1}- (n-Nm)\zeta _{1})/\omega _{\chi }$
are the Bessel functions of the first kind, $\eta _{1} = (m\chi _{1}- (n-Nm)\zeta _{1})/\omega _{\chi }$![]() with $\chi _1$
with $\chi _1$![]() and $\zeta _1$
and $\zeta _1$![]() defined through (3.1), and $\omega _{\theta } = \langle \dot {\theta } \rangle$
defined through (3.1), and $\omega _{\theta } = \langle \dot {\theta } \rangle$![]() . The full expressions for general $j'$
. The full expressions for general $j'$![]() are provided in Appendix A.
are provided in Appendix A.
When considering the dependence of the island width on the magnetic drifts in the small argument limit of the Bessel functions, the most significant radial transport will arise from $\psi _0^0$![]() , $\psi _{\pm 1}^0$
, $\psi _{\pm 1}^0$![]() or $\psi _{\mp 1}^{\pm }$
or $\psi _{\mp 1}^{\pm }$![]() . In the limit of large mode numbers, $\psi _{\pm 1}^0$
. In the limit of large mode numbers, $\psi _{\pm 1}^0$![]() will dominate due to its dependence on $\eta _1$
will dominate due to its dependence on $\eta _1$![]() . Considering the small argument limit of the Bessel function, the island width scales with $\sqrt {\eta _1^{|l|}/(m+1)}$
. Considering the small argument limit of the Bessel function, the island width scales with $\sqrt {\eta _1^{|l|}/(m+1)}$![]() for fixed $\delta \hat {B}^{\psi }$
for fixed $\delta \hat {B}^{\psi }$![]() , thus increasing the island width for quasihelical configurations due to the dependence of $\eta _1$
, thus increasing the island width for quasihelical configurations due to the dependence of $\eta _1$![]() on the helicity $N$
on the helicity $N$![]() . Given the scaling of $\eta _1$
. Given the scaling of $\eta _1$![]() with the mode numbers, the island width will roughly scale independently of $m$
with the mode numbers, the island width will roughly scale independently of $m$![]() for $|l| =1$
for $|l| =1$![]() but will scale with $m^{(|l|-1)/2}$
but will scale with $m^{(|l|-1)/2}$![]() for $|l|>1$
for $|l|>1$![]() . Finally, the island width decreases strongly with increasing $|l|$
. Finally, the island width decreases strongly with increasing $|l|$![]() .
.
Defining the passing orbital helicity as $h = \omega _{\theta }/\omega _{\zeta }$![]() , resonances occur where
, resonances occur where
For a given primary resonance $l$![]() at $h = h_0$
at $h = h_0$![]() , additional sideband resonances may be excited for other drift harmonics $l'$
, additional sideband resonances may be excited for other drift harmonics $l'$![]() corresponding to neighbouring periodic orbits. The spacing between the $l$
corresponding to neighbouring periodic orbits. The spacing between the $l$![]() and $l+1$
and $l+1$![]() resonances is given by
resonances is given by
The ratio between the island width and the resonance spacing

provides a conservative estimate for the island overlap criterion, $w_l^{\psi }/(\Delta \psi )_l \gtrsim 1$![]() . Given the scaling of $\psi _l$
. Given the scaling of $\psi _l$![]() (3.4), the potential for island overlap increases with $m$
(3.4), the potential for island overlap increases with $m$![]() and decreases with $N$
and decreases with $N$![]() for fixed $\delta \hat {B}^{\psi }$
for fixed $\delta \hat {B}^{\psi }$![]() . In this way, quasihelical configurations are advantageous for preventing the transition to phase-space chaos. Finally, while shear in the transit frequency, $\omega _{\theta }'(\psi )$
. In this way, quasihelical configurations are advantageous for preventing the transition to phase-space chaos. Finally, while shear in the transit frequency, $\omega _{\theta }'(\psi )$![]() , reduces individual island widths, it promotes island overlap if multiple resonances are present.
, reduces individual island widths, it promotes island overlap if multiple resonances are present.
4. Resonance analysis
We consider four equilibria optimized to be close to QS: $\beta = 2.5\,\%$![]() quasihelical (QH) and quasiaxisymmetric (QA) equilibria with self-consistent bootstrap current (Landreman et al. Reference Landreman, Buller and Drevlak2022), a vacuum equilibrium with precise levels of quasiaxisymmetry (Landreman & Paul Reference Landreman and Paul2022) and the QA NCSX li383 equilibrium (Mynick, Pomphrey & Ethier Reference Mynick, Pomphrey and Ethier2002; Koniges et al. Reference Koniges, Grossman, Fenstermacher, Kisslinger, Mioduszewski, Rognlien, Strumberger and Umansky2003). Each equilibrium considered is scaled to the minor radius (1.70 m) and the field strength (5.86 T) of ARIES-CS (Najmabadi et al. Reference Najmabadi, Raffray, Abdel-Khalik, Bromberg, Crosatti, El-Guebaly, Garabedian, Grossman, Henderson and Ibrahim2008). The rotational transform profiles and QS error
quasihelical (QH) and quasiaxisymmetric (QA) equilibria with self-consistent bootstrap current (Landreman et al. Reference Landreman, Buller and Drevlak2022), a vacuum equilibrium with precise levels of quasiaxisymmetry (Landreman & Paul Reference Landreman and Paul2022) and the QA NCSX li383 equilibrium (Mynick, Pomphrey & Ethier Reference Mynick, Pomphrey and Ethier2002; Koniges et al. Reference Koniges, Grossman, Fenstermacher, Kisslinger, Mioduszewski, Rognlien, Strumberger and Umansky2003). Each equilibrium considered is scaled to the minor radius (1.70 m) and the field strength (5.86 T) of ARIES-CS (Najmabadi et al. Reference Najmabadi, Raffray, Abdel-Khalik, Bromberg, Crosatti, El-Guebaly, Garabedian, Grossman, Henderson and Ibrahim2008). The rotational transform profiles and QS error

are shown in figure 1, where the unperturbed field strength in Boozer coordinates is $B_0(s,\theta,\zeta ) = \sum _{m,n}B_{m,n}^c(s) \cos (m \theta - n \zeta )$![]() .
.

Figure 1. (a) Rotational transform and (b) QS error (4.1) profiles for the four equilibria under consideration.
We first identify the low-order periodic passing orbits present in the equilibrium to determine the impact of a potential resonant perturbation on the guiding-centre losses. Fusion-born alpha particles are initialized with equally spaced pitch angle and radius values and followed for 500 toroidal transits. The net change in the poloidal angle, $\Delta \theta$![]() , and transit time, $\Delta t$
, and transit time, $\Delta t$![]() , are computed for each toroidal transit. In the integrable case, the average of the characteristic frequencies over many transits, denoted $\omega _{\zeta } = 2{\rm \pi} / \langle \Delta t \rangle$
, are computed for each toroidal transit. In the integrable case, the average of the characteristic frequencies over many transits, denoted $\omega _{\zeta } = 2{\rm \pi} / \langle \Delta t \rangle$![]() , and $\omega _{\theta } = \langle \Delta \theta \rangle /\langle \Delta t \rangle$
, and $\omega _{\theta } = \langle \Delta \theta \rangle /\langle \Delta t \rangle$![]() , converges quickly with respect to the number of toroidal transits (Das et al. Reference Das, Saiki, Sander and Yorke2016). In this way, we obtain $\omega _{\zeta }$
, converges quickly with respect to the number of toroidal transits (Das et al. Reference Das, Saiki, Sander and Yorke2016). In this way, we obtain $\omega _{\zeta }$![]() and $\omega _{\theta }$
and $\omega _{\theta }$![]() in the two-dimensional space $(s,\mu )$
in the two-dimensional space $(s,\mu )$![]() , where $s = \psi /\psi _0$
, where $s = \psi /\psi _0$![]() is the normalized toroidal flux and $\psi _0$
is the normalized toroidal flux and $\psi _0$![]() is the value of the toroidal flux on the boundary. All non-symmetric modes are artificially suppressed for this frequency analysis so that all trajectories lie on Kolmogorov-Arnold-Moser (KAM) surfaces.
is the value of the toroidal flux on the boundary. All non-symmetric modes are artificially suppressed for this frequency analysis so that all trajectories lie on Kolmogorov-Arnold-Moser (KAM) surfaces.
For the subsequent analysis, resonant perturbations are intentionally imposed, satisfying the condition (3.2) for a resonant surface near mid-radius. As many potential Alfvénic perturbations exist that resonate with a given periodic orbit, a comparison is made between $m = 1$![]() , 15 and 30 perturbations. The perturbation with the highest mode number is chosen such that $m \approx a/\rho _{EP}$
, 15 and 30 perturbations. The perturbation with the highest mode number is chosen such that $m \approx a/\rho _{EP}$![]() for the ARIES-CS reactor parameters, where $a$
for the ARIES-CS reactor parameters, where $a$![]() is the effective minor radius and $\rho _{EP}$
is the effective minor radius and $\rho _{EP}$![]() is the energetic particle orbit width. With this choice, the radial width of the AE eigenstructure is predicted to be comparable to the EP orbit width, and the growth rate is maximized (Gorelenkov, Pinches & Toi Reference Gorelenkov, Pinches and Toi2014). The smaller values of $m$
is the energetic particle orbit width. With this choice, the radial width of the AE eigenstructure is predicted to be comparable to the EP orbit width, and the growth rate is maximized (Gorelenkov, Pinches & Toi Reference Gorelenkov, Pinches and Toi2014). The smaller values of $m$![]() are more typical for current experiments such as LHD (Varela et al. Reference Varela, Spong and Garcia2017). We choose perturbation amplitudes in the range $\delta \hat {B}^{\psi } \sim 10^{-4}\unicode{x2013} 10^{-3}$
are more typical for current experiments such as LHD (Varela et al. Reference Varela, Spong and Garcia2017). We choose perturbation amplitudes in the range $\delta \hat {B}^{\psi } \sim 10^{-4}\unicode{x2013} 10^{-3}$![]() , consistent with LHD modelling (Nishimura et al. Reference Nishimura, Todo, Spong, Suzuki and Nakajima2013) and experimental measurements from TFTR and (Nazikian et al. Reference Nazikian, Fu, Batha, Bell, Bell, Budny, Bush, Chang, Chen and Cheng1997) and NSTX (Crocker et al. Reference Crocker, Fredrickson, Gorelenkov, Peebles, Kubota, Bell, Diallo, LeBlanc, Menard and Podesta2013). In analysis of the impact of toroidal Alfvén eigenmodes (TAEs) on guiding-centre confinement in tokamaks, alpha orbit stochasticity is typically present for $\delta \hat {B}^{\psi } \sim 10^{-3}$
, consistent with LHD modelling (Nishimura et al. Reference Nishimura, Todo, Spong, Suzuki and Nakajima2013) and experimental measurements from TFTR and (Nazikian et al. Reference Nazikian, Fu, Batha, Bell, Bell, Budny, Bush, Chang, Chen and Cheng1997) and NSTX (Crocker et al. Reference Crocker, Fredrickson, Gorelenkov, Peebles, Kubota, Bell, Diallo, LeBlanc, Menard and Podesta2013). In analysis of the impact of toroidal Alfvén eigenmodes (TAEs) on guiding-centre confinement in tokamaks, alpha orbit stochasticity is typically present for $\delta \hat {B}^{\psi } \sim 10^{-3}$![]() , while for $\delta \hat {B}^{\psi } < 10^{-4}$
, while for $\delta \hat {B}^{\psi } < 10^{-4}$![]() the losses are insignificant (Sigmar et al. Reference Sigmar, Hsu, White and Cheng1992). Although the eigenfunction typically depends on the mode number, we choose a radially uniform mode structure for a conservative analysis.
the losses are insignificant (Sigmar et al. Reference Sigmar, Hsu, White and Cheng1992). Although the eigenfunction typically depends on the mode number, we choose a radially uniform mode structure for a conservative analysis.
Given a $\omega _{\theta }/\omega _{\zeta } = p/q$![]() periodic orbit and poloidal mode number $m$
periodic orbit and poloidal mode number $m$![]() , the resonant wave frequency satisfying (3.2) can be expressed as $\omega /\omega _{\zeta } = p'/q$
, the resonant wave frequency satisfying (3.2) can be expressed as $\omega /\omega _{\zeta } = p'/q$![]() for some integer $p'$
for some integer $p'$![]() . The toroidal mode number $n$
. The toroidal mode number $n$![]() and the frequency parameter $p'$
and the frequency parameter $p'$![]() are chosen to satisfy the $l = 1$
are chosen to satisfy the $l = 1$![]() resonance condition (3.2), given that the $l = \pm 1$
resonance condition (3.2), given that the $l = \pm 1$![]() resonance is predicted to give rise to the most substantial radial transport as described in § 3. The value of $n$
resonance is predicted to give rise to the most substantial radial transport as described in § 3. The value of $n$![]() is chosen to yield small magnitudes of $|p'|$
is chosen to yield small magnitudes of $|p'|$![]() , corresponding with lower-frequency perturbations. The mode parameters are summarized in table 1.
, corresponding with lower-frequency perturbations. The mode parameters are summarized in table 1.
Table 1. Alfvénic perturbation mode parameters chosen to satisfy the resonance condition (3.2).

For each configuration, the profile of the effective orbit helicity $h$![]() (3.5) is shown in figure 2 for co- and counter-passing orbits (blue and orange, respectively). While the helicity profile does not change substantially between co- and counter-passing orbits, the resonance condition (3.5) is modified since the sign and magnitude of $\omega _{\zeta }$
(3.5) is shown in figure 2 for co- and counter-passing orbits (blue and orange, respectively). While the helicity profile does not change substantially between co- and counter-passing orbits, the resonance condition (3.5) is modified since the sign and magnitude of $\omega _{\zeta }$![]() differs. Although the choice of pitch angle will impact the resonance condition, for the following calculations, we focus on co-passing orbits, $v_{\|}/v_0 = +1$
differs. Although the choice of pitch angle will impact the resonance condition, for the following calculations, we focus on co-passing orbits, $v_{\|}/v_0 = +1$![]() . The horizontal black lines in the figures indicate the chosen resonant surface for the co-passing orbits. For the $\beta = 2.5\,\%$
. The horizontal black lines in the figures indicate the chosen resonant surface for the co-passing orbits. For the $\beta = 2.5\,\%$![]() QA and NCSX equilibria, the nearby resonant surfaces corresponding to other values of $l$
QA and NCSX equilibria, the nearby resonant surfaces corresponding to other values of $l$![]() are indicated by the coloured horizontal lines. As $m$
are indicated by the coloured horizontal lines. As $m$![]() increases, the resonance spacing decreases according to (3.6). For the vacuum QA equilibrium, the magnetic shear is very low, see figure 1, and no sideband resonances exist. Although the shear is moderate for the $\beta = 2.5\,\%$
increases, the resonance spacing decreases according to (3.6). For the vacuum QA equilibrium, the magnetic shear is very low, see figure 1, and no sideband resonances exist. Although the shear is moderate for the $\beta = 2.5\,\%$![]() QH equilibrium, sideband resonances are not present due to the factor of $N$
QH equilibrium, sideband resonances are not present due to the factor of $N$![]() in the resonance spacing expression.
in the resonance spacing expression.
Figure 2. The characteristic orbit helicity, $h = \omega _{\theta }/\omega _{\zeta }$![]() , is computed for co-passing ($v_{\|}/v_0 = +1$
, is computed for co-passing ($v_{\|}/v_0 = +1$![]() , blue) and counter-passing orbits ($v_{\|}/v_0 = -1$
, blue) and counter-passing orbits ($v_{\|}/v_0 = -1$![]() , orange). A low-order periodic orbit is selected near the mid-radius, denoted by the horizontal dashed black line. Alfvénic perturbations with several mode numbers $m$
, orange). A low-order periodic orbit is selected near the mid-radius, denoted by the horizontal dashed black line. Alfvénic perturbations with several mode numbers $m$![]() are chosen to resonate with this orbit periodicity. Sideband resonances are excited in the $\beta = 2.5\,\%$
are chosen to resonate with this orbit periodicity. Sideband resonances are excited in the $\beta = 2.5\,\%$![]() QA and NCSX equilibria due to the angular dependence of the drifts, denoted by the coloured horizontal lines. Because of the increased distance between resonances, no sidebands are excited for in the vacuum QA or $\beta = 2.5\,\%$
QA and NCSX equilibria due to the angular dependence of the drifts, denoted by the coloured horizontal lines. Because of the increased distance between resonances, no sidebands are excited for in the vacuum QA or $\beta = 2.5\,\%$![]() QH equilibria for the mode numbers chosen; (a) $\beta = 2.5\,\%$
QH equilibria for the mode numbers chosen; (a) $\beta = 2.5\,\%$![]() QA, (b) $\beta = 2.5\,\%$
QA, (b) $\beta = 2.5\,\%$![]() QH, (c) vacuum QA and (d) NCSX.
QH, (c) vacuum QA and (d) NCSX.
5. Kinetic Poincaré plots
Given a magnetic field with exact QS, a kinetic Poincaré plot can be constructed analogously to the case of axisymmetric magnetic fields (Sigmar et al. Reference Sigmar, Hsu, White and Cheng1992). Given a quasisymmetric field $B_0(\psi,\chi =\theta -N\zeta )$![]() in the absence of a perturbation, the canonical angular momentum
in the absence of a perturbation, the canonical angular momentum
and energy
are conserved. When an Alfvénic perturbation is applied with single mode numbers $n$![]() and $m$
and $m$![]() , neither $P_{\zeta }$
, neither $P_{\zeta }$![]() nor $E$
nor $E$![]() are conserved, but a conserved quantity is obtained by moving with the wave frame
are conserved, but a conserved quantity is obtained by moving with the wave frame
Given the velocity-space parameters – $\mu$![]() , $\bar {E}_n$
, $\bar {E}_n$![]() , and $\textrm {sign}(v_{\|})$
, and $\textrm {sign}(v_{\|})$![]() – and specification of the position in space and time – $t$
– and specification of the position in space and time – $t$![]() , $s$
, $s$![]() , $\theta$
, $\theta$![]() and $\zeta$
and $\zeta$![]() – (5.3) provides a nonlinear equation for $v_{\|}$
– (5.3) provides a nonlinear equation for $v_{\|}$![]() (Hsu & Sigmar Reference Hsu and Sigmar1992).
(Hsu & Sigmar Reference Hsu and Sigmar1992).
Given the form for the phase factor of the perturbation (2.4), the resulting equations of motion depend on $(s,\chi,\zeta - \bar {\omega }_n t, v_{\|})$![]() , where $\bar {\omega }_n = \omega /(n - N m)$
, where $\bar {\omega }_n = \omega /(n - N m)$![]() . The resulting motion is generally four-dimensional. If purely passing particles are considered, then ${sign}(v_{\|})$
. The resulting motion is generally four-dimensional. If purely passing particles are considered, then ${sign}(v_{\|})$![]() is fixed, $v_{\|}$
is fixed, $v_{\|}$![]() can be computed from the other coordinates as described above, and the resulting motion becomes three-dimensional. For a fixed value of $\bar {E}_n$
can be computed from the other coordinates as described above, and the resulting motion becomes three-dimensional. For a fixed value of $\bar {E}_n$![]() and $\mu$
and $\mu$![]() , a kinetic Poincaré map $M(s,\chi ) \rightarrow (s',\chi ')$
, a kinetic Poincaré map $M(s,\chi ) \rightarrow (s',\chi ')$![]() is constructed by moving with the wave frame to eliminate the time dependence. Guiding-centre trajectories are followed until they intersect a plane of constant $\zeta - \bar {\omega }_nt$
is constructed by moving with the wave frame to eliminate the time dependence. Guiding-centre trajectories are followed until they intersect a plane of constant $\zeta - \bar {\omega }_nt$![]() . Therefore, the resulting Poincaré section is two-dimensional.
. Therefore, the resulting Poincaré section is two-dimensional.
When QS is broken in the equilibrium, $\bar {E}_n$![]() is no longer precisely conserved. Nonetheless, if the QS errors are sufficiently small, the kinetic Poincaré analysis provides insight into the resulting transport. The non-quasisymmetric modes are artificially suppressed when constructing the kinetic Poincaré plots to aid the analysis. The impact of QS-breaking modes will be assessed in the following section.
is no longer precisely conserved. Nonetheless, if the QS errors are sufficiently small, the kinetic Poincaré analysis provides insight into the resulting transport. The non-quasisymmetric modes are artificially suppressed when constructing the kinetic Poincaré plots to aid the analysis. The impact of QS-breaking modes will be assessed in the following section.
In figure 3, kinetic Poincaré plots are displayed for particles with $\textrm {sign}(v_{\|}) = +1$![]() , $\mu = 0$
, $\mu = 0$![]() , $E = 3.52$
, $E = 3.52$![]() MeV and Alfvénic perturbations with parameters given in table 1. The amplitude $\hat {\varPhi }$
MeV and Alfvénic perturbations with parameters given in table 1. The amplitude $\hat {\varPhi }$![]() is chosen such that $\delta \hat {B}^{\psi } = 10^{-3}$
is chosen such that $\delta \hat {B}^{\psi } = 10^{-3}$![]() on the $s = 1$
on the $s = 1$![]() surface. Periodic orbits that satisfy the resonance condition $\varOmega _l = 0$
surface. Periodic orbits that satisfy the resonance condition $\varOmega _l = 0$![]() appear as $n/(m+l)$
appear as $n/(m+l)$![]() periodic orbits in the kinetic Poincaré plots.
periodic orbits in the kinetic Poincaré plots.
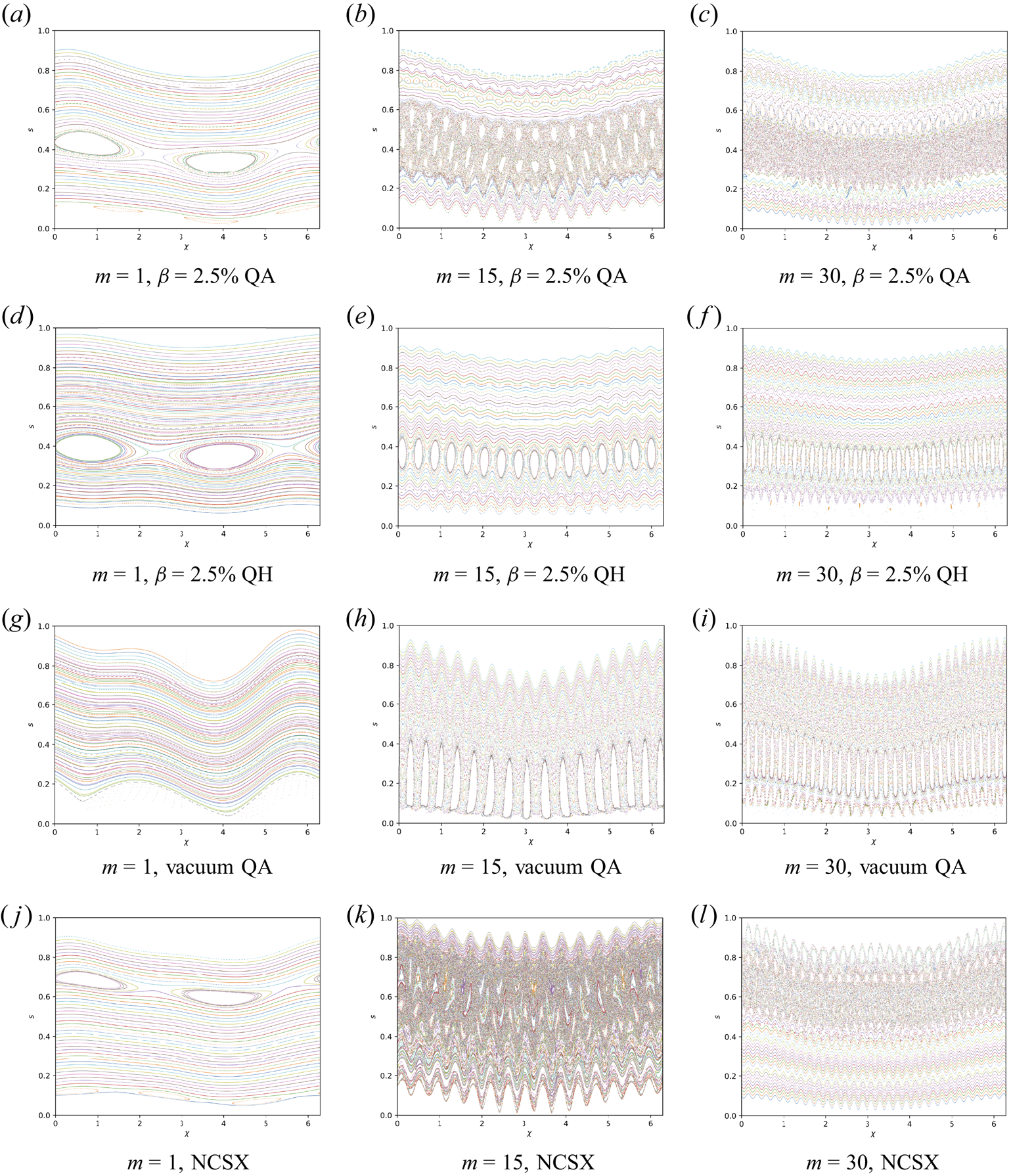
Figure 3. Kinetic Poincaré plots are constructed using the mode parameters in table 1 with the perturbation amplitude $\delta \hat {B}^{\psi }= 10^{-3}$![]() . All QS-breaking harmonics of the equilibrium field are artificially suppressed for this analysis; (a) $m = 1$
. All QS-breaking harmonics of the equilibrium field are artificially suppressed for this analysis; (a) $m = 1$![]() , $\beta = 2.5\,\%$
, $\beta = 2.5\,\%$![]() QA, (b) $m = 15$
QA, (b) $m = 15$![]() , $\beta = 2.5\,\%$
, $\beta = 2.5\,\%$![]() QA, (c) $m = 30$
QA, (c) $m = 30$![]() , $\beta = 2.5\,\%$
, $\beta = 2.5\,\%$![]() QA, (d) $m = 1$
QA, (d) $m = 1$![]() , $\beta = 2.5\,\%$
, $\beta = 2.5\,\%$![]() QH, (e) $m = 15$
QH, (e) $m = 15$![]() , $\beta = 2.5\,\%$
, $\beta = 2.5\,\%$![]() QH, ( f) $m = 30$
QH, ( f) $m = 30$![]() , $\beta = 2.5\,\%$
, $\beta = 2.5\,\%$![]() QH, (g) $m = 1$
QH, (g) $m = 1$![]() , vacuum QA, (h) $m = 15$
, vacuum QA, (h) $m = 15$![]() , vacuum QA, (i) $m = 30$
, vacuum QA, (i) $m = 30$![]() , vacuum QA, (j) $m = 1$
, vacuum QA, (j) $m = 1$![]() , NCSX, (k) $m = 15$
, NCSX, (k) $m = 15$![]() , NCSX and (l) $m = 30$
, NCSX and (l) $m = 30$![]() , NCSX.
, NCSX.
For the NCSX and $\beta = 2.5\,\%$![]() QA configurations, a clear $l = 1$
QA configurations, a clear $l = 1$![]() island chain is apparent in the presence of the $m = 1$
island chain is apparent in the presence of the $m = 1$![]() perturbation. For the vacuum QA equilibrium, the perturbation shifts the orbit helicity slightly, moving the resonance outside the equilibrium due to the low magnetic shear. The resonance reappears by increasing the perturbation frequency by 8 %, see figure 4. In the $\beta = 2.5\,\%$
perturbation. For the vacuum QA equilibrium, the perturbation shifts the orbit helicity slightly, moving the resonance outside the equilibrium due to the low magnetic shear. The resonance reappears by increasing the perturbation frequency by 8 %, see figure 4. In the $\beta = 2.5\,\%$![]() QA equilibria, in addition to the primary $l = 1$
QA equilibria, in addition to the primary $l = 1$![]() resonance, the $l = 2$
resonance, the $l = 2$![]() resonance is apparent near $s = 0.1$
resonance is apparent near $s = 0.1$![]() . However, the island width is small due to the reduced magnitude of the $J_2(\eta _1)$
. However, the island width is small due to the reduced magnitude of the $J_2(\eta _1)$![]() coupling parameter. As indicated by the resonance plots, figure 2, none of the other equilibria contain the $m=1$
coupling parameter. As indicated by the resonance plots, figure 2, none of the other equilibria contain the $m=1$![]() , $l =2$
, $l =2$![]() resonance.
resonance.

Figure 4. (a) In the presence of the resonant perturbation of amplitude $\delta \hat {B}^{\psi } = 10^{-4}$![]() , the characteristic frequencies $\omega _{\theta }$
, the characteristic frequencies $\omega _{\theta }$![]() and $\omega _{\zeta }$
and $\omega _{\zeta }$![]() shift, causing the resonance defined by $\varOmega _l = 0$
shift, causing the resonance defined by $\varOmega _l = 0$![]() to move outside the equilibrium due to the low shear, see figure 3(g). By increasing the mode frequency by 8 %, the resonance re-enters. (b) The kinetic Poincaré plot of amplitude $\delta \hat {B}^{\psi } = 10^{-4}$
to move outside the equilibrium due to the low shear, see figure 3(g). By increasing the mode frequency by 8 %, the resonance re-enters. (b) The kinetic Poincaré plot of amplitude $\delta \hat {B}^{\psi } = 10^{-4}$![]() with the shifted frequency ($\omega = 2.15$
with the shifted frequency ($\omega = 2.15$![]() kHz) reveals the corresponding $l = 1$
kHz) reveals the corresponding $l = 1$![]() island on the shifted resonant surface.
island on the shifted resonant surface.
As the mode number increases from $m = 15$![]() to $m = 30$
to $m = 30$![]() , the $l = 1$
, the $l = 1$![]() island width stays roughly the same for the $\beta = 2.5\,\%$
island width stays roughly the same for the $\beta = 2.5\,\%$![]() QH configuration, as indicated by the scaling of the island width formula (3.3) and (3.4) for fixed $\delta \hat {B}^{\psi }$
QH configuration, as indicated by the scaling of the island width formula (3.3) and (3.4) for fixed $\delta \hat {B}^{\psi }$![]() . For the vacuum QA configuration, the $l = 1$
. For the vacuum QA configuration, the $l = 1$![]() resonance reappears for the $m = 15$
resonance reappears for the $m = 15$![]() and $m = 30$
and $m = 30$![]() perturbations, its width being especially wide due to the low magnetic shear of the configuration. For both the vacuum QA and $\beta = 2.5\,\%$
perturbations, its width being especially wide due to the low magnetic shear of the configuration. For both the vacuum QA and $\beta = 2.5\,\%$![]() QH configurations with the $m = 15$
QH configurations with the $m = 15$![]() and $m = 30$
and $m = 30$![]() perturbations, the island chain is wide enough to lead to visible destruction of nearby KAM surfaces and the formation of secondary island chains.
perturbations, the island chain is wide enough to lead to visible destruction of nearby KAM surfaces and the formation of secondary island chains.
In the $\beta = 2.5\,\%$![]() QA equilibrium, overlap between the $l = 0$
QA equilibrium, overlap between the $l = 0$![]() , 1, 2 and 3 resonances is observed with the $m = 15$
, 1, 2 and 3 resonances is observed with the $m = 15$![]() perturbation. Substantial island overlap is also observed in the NCSX equilibrium with the $m = 15$
perturbation. Substantial island overlap is also observed in the NCSX equilibrium with the $m = 15$![]() perturbation. In the presence of the $m = 30$
perturbation. In the presence of the $m = 30$![]() perturbation, strong island overlap is observed in the $\beta = 2.5\,\%$
perturbation, strong island overlap is observed in the $\beta = 2.5\,\%$![]() QA and NCSX equilibria. However, the phase-space volume over which island overlap occurs is narrowed. As seen in figure 2, the resonances become more closely spaced for the $m = 30$
QA and NCSX equilibria. However, the phase-space volume over which island overlap occurs is narrowed. As seen in figure 2, the resonances become more closely spaced for the $m = 30$![]() perturbation compared with the $m = 15$
perturbation compared with the $m = 15$![]() perturbation. However, because the island width scales as $\sqrt {\eta _1^{|l|}}$
perturbation. However, because the island width scales as $\sqrt {\eta _1^{|l|}}$![]() with $\eta _1 \ll 1$
with $\eta _1 \ll 1$![]() , island overlap does not occur for the large $|l|$
, island overlap does not occur for the large $|l|$![]() resonant surfaces. This island width scaling effectively reduces the non-integrable volume as $m$
resonant surfaces. This island width scaling effectively reduces the non-integrable volume as $m$![]() increases.
increases.
The impact of these phase-space features on the resulting transport will be discussed in § 6.
5.1. Impact of QS deviations
We now investigate the impact of the finite QS deviations, quantified in figure 1, on the kinetic Poincaré analysis. When QS deviations are present, the motion of passing particles becomes four-dimensional $(s,\chi,\zeta,t)$![]() , and the Poincaré section becomes three-dimensional, $M(s,\chi,\zeta ) \rightarrow (s',\chi ',\zeta ')$
, and the Poincaré section becomes three-dimensional, $M(s,\chi,\zeta ) \rightarrow (s',\chi ',\zeta ')$![]() . Nonetheless, we can still visualize the Poincaré map in the $(s,\chi )$
. Nonetheless, we can still visualize the Poincaré map in the $(s,\chi )$![]() plane to assess the structure of phase space.
plane to assess the structure of phase space.
In figures 5 and 6, we show a selection of the kinetic Poincaré plots constructed with the same parameters as those in figure 3, but without the suppression of the QS-breaking modes. For the case of the $\beta = 2.5\,\%$![]() QH equilibrium, the phase-space structure remains mostly unchanged, with the addition of small-scale mixing. In the case of the NCSX equilibrium, the amplitude of the phase-space mixing is amplified due to the enhanced symmetry breaking. The gross phase-space structure remains mostly unchanged in the presence of the $m = 1$
QH equilibrium, the phase-space structure remains mostly unchanged, with the addition of small-scale mixing. In the case of the NCSX equilibrium, the amplitude of the phase-space mixing is amplified due to the enhanced symmetry breaking. The gross phase-space structure remains mostly unchanged in the presence of the $m = 1$![]() perturbation. In the presence of the $m = 15$
perturbation. In the presence of the $m = 15$![]() perturbation, the effective diffusion due to the non-integrability of the orbits destroys many of the remaining KAM surfaces and island chains, leading to a wide region of phase-space chaos. We conclude that most large-scale phase space structure is preserved by adding QS deviations, especially for equilibria close to QS, $f_\textrm {QS} \sim 10^{-3}$
perturbation, the effective diffusion due to the non-integrability of the orbits destroys many of the remaining KAM surfaces and island chains, leading to a wide region of phase-space chaos. We conclude that most large-scale phase space structure is preserved by adding QS deviations, especially for equilibria close to QS, $f_\textrm {QS} \sim 10^{-3}$![]() . This finding does not quantitatively agree with recent results (White & Duarte Reference White and Duarte2023), indicating substantial diffusive losses in an equilibrium very close to QH ($f_\textrm {QS} \sim 10^{-4}$
. This finding does not quantitatively agree with recent results (White & Duarte Reference White and Duarte2023), indicating substantial diffusive losses in an equilibrium very close to QH ($f_\textrm {QS} \sim 10^{-4}$![]() ) with an Alfvénic perturbation as small as $\delta \hat {B}^{\psi } \sim 10^{-6}$
) with an Alfvénic perturbation as small as $\delta \hat {B}^{\psi } \sim 10^{-6}$![]() .
.
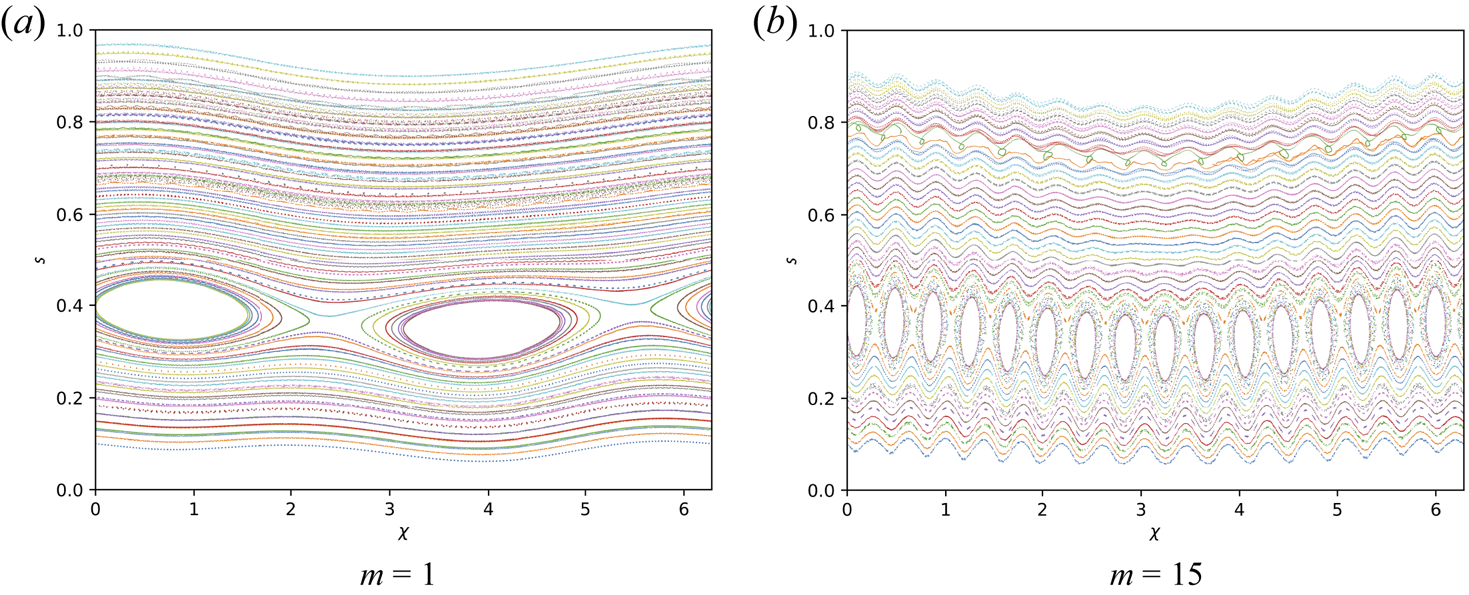
Figure 5. The $\beta = 2.5\,\%$![]() QH kinetic Poincaré plots with the same parameters as figure 3, but without the suppression of the QS-breaking modes; (a) $m = 1$
QH kinetic Poincaré plots with the same parameters as figure 3, but without the suppression of the QS-breaking modes; (a) $m = 1$![]() and (b) $m = 15$
and (b) $m = 15$![]() .
.
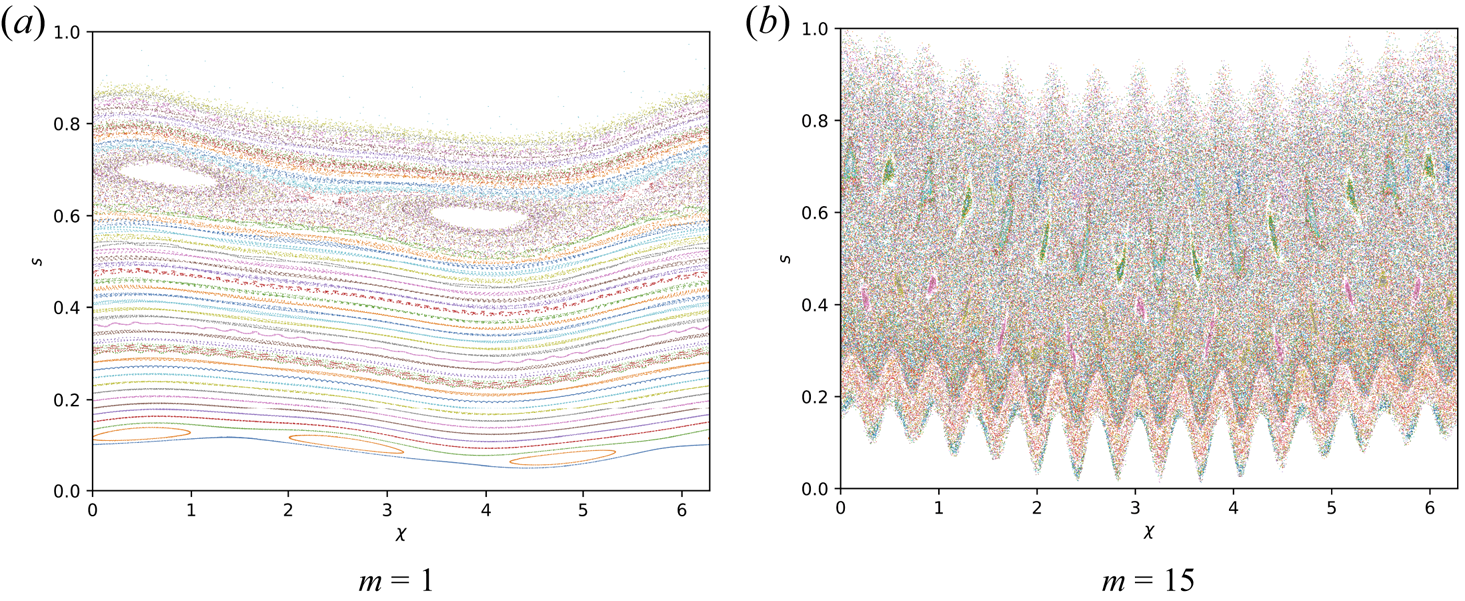
Figure 6. The NCSX kinetic Poincaré plots with the same parameters as figure 3, but without the suppression of the QS-breaking modes; (a) $m = 1$![]() and (b) $m = 15$
and (b) $m = 15$![]() .
.
6. Monte Carlo analysis
To assess the impact of the phase-space structure on the resulting transport, we perform Monte Carlo collisionless guiding-centre tracing simulations. We initialize 5000 particles uniformly in pitch angle and volume for $s \in [0.25, 0.75]$![]() . This initial spatial distribution was chosen to avoid effects related to the coordinate singularity. Particles are followed for $10^{-3}$
. This initial spatial distribution was chosen to avoid effects related to the coordinate singularity. Particles are followed for $10^{-3}$![]() seconds or until they are considered lost when they cross through $s = 0$
seconds or until they are considered lost when they cross through $s = 0$![]() or $s= 1$
or $s= 1$![]() .Footnote 1 Figures 7 and 8 display results of tracing performed with the true equilibria (solid curves, ‘equilibrium’) as well as with the QS-breaking modes artificially filtered out (dashed curves, ‘perfect QS’). Calculations are carried out without Alfvénic perturbations ($\hat {\alpha } = 0$
.Footnote 1 Figures 7 and 8 display results of tracing performed with the true equilibria (solid curves, ‘equilibrium’) as well as with the QS-breaking modes artificially filtered out (dashed curves, ‘perfect QS’). Calculations are carried out without Alfvénic perturbations ($\hat {\alpha } = 0$![]() ) and for the $m = 1$
) and for the $m = 1$![]() , 15 and 30 perturbations indicated in table 1.
, 15 and 30 perturbations indicated in table 1.

Figure 7. The loss fraction as a function of time is shown. Monte Carlo tracing is performed in the presence of a $\delta \hat {B}^{\psi } = 10^{-3}$![]() perturbation with parameters described in table 1. Guiding-centre trajectories of fusion-born alpha particles are followed for $10^{-3}$
perturbation with parameters described in table 1. Guiding-centre trajectories of fusion-born alpha particles are followed for $10^{-3}$![]() seconds or until they cross through $s=0$
seconds or until they cross through $s=0$![]() or $s=1$
or $s=1$![]() . A comparison is made between the actual equilibrium and the equilibrium for which the QS-breaking modes are suppressed, ‘perfect QS’; (a) $\beta = 2.5\,\%$
. A comparison is made between the actual equilibrium and the equilibrium for which the QS-breaking modes are suppressed, ‘perfect QS’; (a) $\beta = 2.5\,\%$![]() QA, (b) $\beta = 2.5\,\%$
QA, (b) $\beta = 2.5\,\%$![]() QH, (c) vacuum QA and (d) NCSX.
QH, (c) vacuum QA and (d) NCSX.
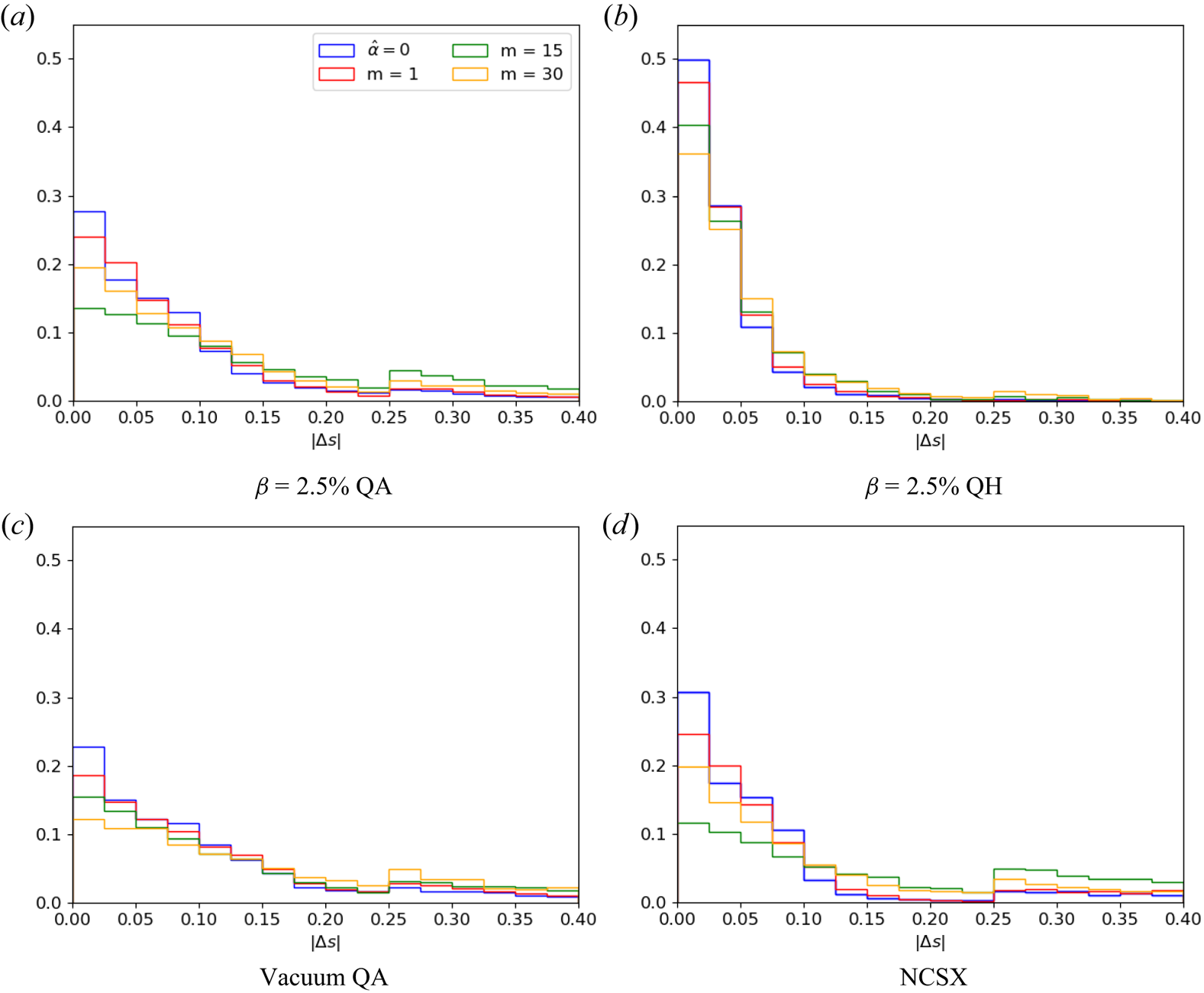
Figure 8. Distribution of radial displacement, $|\Delta s|$![]() , between $t=0$
, between $t=0$![]() and the final recorded time among Monte Carlo samples for the same calculation presented in figure 7; (a) $\beta = 2.5\,\%$
and the final recorded time among Monte Carlo samples for the same calculation presented in figure 7; (a) $\beta = 2.5\,\%$![]() QA, (b) $\beta = 2.5\,\%$
QA, (b) $\beta = 2.5\,\%$![]() QH, (c) vacuum QA and (d) NCSX.
QH, (c) vacuum QA and (d) NCSX.
In figure 8, the effective transport is quantified by the distribution of the radial displacement, $|\Delta s|$![]() , between $t = 0$
, between $t = 0$![]() and the final recorded time (after $10^{-3}$
and the final recorded time (after $10^{-3}$![]() or when a particle is considered lost). By initializing with a uniform distribution over $s$
or when a particle is considered lost). By initializing with a uniform distribution over $s$![]() in a fixed interval, flattening of the distribution function is not as apparent. On the other hand, the distribution of $|\Delta s|$
in a fixed interval, flattening of the distribution function is not as apparent. On the other hand, the distribution of $|\Delta s|$![]() allows us to identify the net displacement of trajectories due to phase-space islands or chaos. The double maximum structure reflects the confined trajectories, centred around $|\Delta s| = 0$
allows us to identify the net displacement of trajectories due to phase-space islands or chaos. The double maximum structure reflects the confined trajectories, centred around $|\Delta s| = 0$![]() , and lost trajectories, for which $|\Delta s| \ge 0.25$
, and lost trajectories, for which $|\Delta s| \ge 0.25$![]() . The loss fraction as a function of time is also shown in figure 7. A summary of the results is presented in table 2. When comparing the equilibrium and perfect QS cases, we see slight transport enhancement due to QS-breaking modes in the $\beta = 2.5\,\%$
. The loss fraction as a function of time is also shown in figure 7. A summary of the results is presented in table 2. When comparing the equilibrium and perfect QS cases, we see slight transport enhancement due to QS-breaking modes in the $\beta = 2.5\,\%$![]() QA and QH and vacuum QA equilibria. The enhancement of transport becomes much more pronounced in the NCSX equilibrium, given its more substantial deviations from QS; see figure 1.
QA and QH and vacuum QA equilibria. The enhancement of transport becomes much more pronounced in the NCSX equilibrium, given its more substantial deviations from QS; see figure 1.
Table 2. Summary of transport properties for Monte Carlo calculations in the presence of Alfvénic perturbations with mode parameters described in table 1 and amplitude $\delta \hat {B}^{\psi } = 10^{-3}$![]() . The mean radial displacement along a trajectory, $\textrm {mean}|\Delta s|$
. The mean radial displacement along a trajectory, $\textrm {mean}|\Delta s|$![]() , and total loss fraction after $10^{-3}$
, and total loss fraction after $10^{-3}$![]() s are compared between the actual equilibrium, ‘equil’, and the equilibrium for which the QS-breaking modes are suppressed, ‘perfect QS’.
s are compared between the actual equilibrium, ‘equil’, and the equilibrium for which the QS-breaking modes are suppressed, ‘perfect QS’.

In the equilibria that do not exhibit island overlap in figure 3, the vacuum QA and $\beta = 2.5\,\%$![]() QH equilibria, the total loss fraction increases monotonically with $m$
QH equilibria, the total loss fraction increases monotonically with $m$![]() . This result matches the observations in figure 3, which indicate that although the island width remains roughly the same, the destruction of nearby KAM surfaces increases with increasing mode number. On the other hand, in equilibria that exhibit strong resonance overlap in figure 3, NCSX and $\beta = 2.5\,\%$
. This result matches the observations in figure 3, which indicate that although the island width remains roughly the same, the destruction of nearby KAM surfaces increases with increasing mode number. On the other hand, in equilibria that exhibit strong resonance overlap in figure 3, NCSX and $\beta = 2.5\,\%$![]() QA, the transport increases monotonically with $m$
QA, the transport increases monotonically with $m$![]() until $m = 15$
until $m = 15$![]() , then decreases for $m = 30$
, then decreases for $m = 30$![]() . This characteristic is explained in terms of the kinetic Poincaré plots in figure 3, which indicate that the effective volume of non-integrability is decreased for $m = 30$
. This characteristic is explained in terms of the kinetic Poincaré plots in figure 3, which indicate that the effective volume of non-integrability is decreased for $m = 30$![]() compared with $m = 15$
compared with $m = 15$![]() due to the reduction in island width for large $l$
due to the reduction in island width for large $l$![]() perturbations.
perturbations.
Overall, the total induced transport is the lowest for the $\beta = 2.5\,\%$![]() QH configuration, for which the total losses remain less than $10\,\%$
QH configuration, for which the total losses remain less than $10\,\%$![]() in the presence of the Alfvénic perturbations. The losses are also less prompt for this configuration, with most beginning around $10^{-4}$
in the presence of the Alfvénic perturbations. The losses are also less prompt for this configuration, with most beginning around $10^{-4}$![]() seconds, rather than around $10^{-5}$
seconds, rather than around $10^{-5}$![]() seconds for the other configurations. This reduction in transport is due to the increased resonance spacing of QH configurations and its increased magnetic shear compared with the vacuum QA equilibria, see figure 1.
seconds for the other configurations. This reduction in transport is due to the increased resonance spacing of QH configurations and its increased magnetic shear compared with the vacuum QA equilibria, see figure 1.
6.1. Transition to phase-space chaos
We now study the transition to phase-space chaos and global transport with increasing perturbation amplitude in the $\beta = 2.5\,\%$![]() QA equilibria. We focus on the $m = 30$
QA equilibria. We focus on the $m = 30$![]() perturbation, given that this is the expected mode number at reactor scales. Kinetic Poincaré plots for co-passing particles resonant with the Alfvénic perturbation are shown in figure 9. The $l = -1$
perturbation, given that this is the expected mode number at reactor scales. Kinetic Poincaré plots for co-passing particles resonant with the Alfvénic perturbation are shown in figure 9. The $l = -1$![]() , 0, 1, 2 and 3 islands are visible at the smallest perturbation amplitude, corresponding to $\delta \hat {B}^{\psi } = 3.14 \times 10^{-4}$
, 0, 1, 2 and 3 islands are visible at the smallest perturbation amplitude, corresponding to $\delta \hat {B}^{\psi } = 3.14 \times 10^{-4}$![]() . As the amplitude is increased to $\delta \hat {B}^{\psi } = 5.58 \times 10^{-4}$
. As the amplitude is increased to $\delta \hat {B}^{\psi } = 5.58 \times 10^{-4}$![]() , a band of island overlap appears near the resonant surface. The region of destroyed KAM surfaces increases with increasing perturbation amplitude, with only a few remnant islands present at $\delta \hat {B}^{\psi } = 1.76 \times 10^{-3}$
, a band of island overlap appears near the resonant surface. The region of destroyed KAM surfaces increases with increasing perturbation amplitude, with only a few remnant islands present at $\delta \hat {B}^{\psi } = 1.76 \times 10^{-3}$![]() .
.

Figure 9. Kinetic Poincaré plots for co-passing orbits in the $\beta = 2.5\,\%$![]() QA in the presence of an $m = 30$
QA in the presence of an $m = 30$![]() perturbation with parameters described in table 1.
perturbation with parameters described in table 1.
Monte Carlo calculations, as described above, are performed for the same Alfvénic perturbations to distinguish the impact of the phase-space structure on transport. The loss fraction as a function of time, initial and final distribution function, and net radial displacement $|\Delta s|$![]() are shown in figure 10. We note a sudden increase in the loss fraction above $\delta \hat {B}^{\psi } = 5.58\times 10^{-4}$
are shown in figure 10. We note a sudden increase in the loss fraction above $\delta \hat {B}^{\psi } = 5.58\times 10^{-4}$![]() , the value for which island overlap is seen to occur in figure 9. This behaviour is analogous to the observation of critical gradient behaviour on DIII-D, for which the fast-ion transport suddenly becomes stiff above a critical gradient threshold. Similar to our results, the critical gradient behaviour on DIII-D arises due to phase-space stochastization (Collins et al. Reference Collins, Heidbrink, Podestà, White, Kramer, Pace, Petty, Stagner, Van Zeeland and Zhu2017). The initial losses scale approximately as $t^2$
, the value for which island overlap is seen to occur in figure 9. This behaviour is analogous to the observation of critical gradient behaviour on DIII-D, for which the fast-ion transport suddenly becomes stiff above a critical gradient threshold. Similar to our results, the critical gradient behaviour on DIII-D arises due to phase-space stochastization (Collins et al. Reference Collins, Heidbrink, Podestà, White, Kramer, Pace, Petty, Stagner, Van Zeeland and Zhu2017). The initial losses scale approximately as $t^2$![]() , as expected for quasilinear diffusion. As the radial distribution of particles evolves, we see enhanced flattening near the primary resonance surface with increasing perturbation amplitude.
, as expected for quasilinear diffusion. As the radial distribution of particles evolves, we see enhanced flattening near the primary resonance surface with increasing perturbation amplitude.
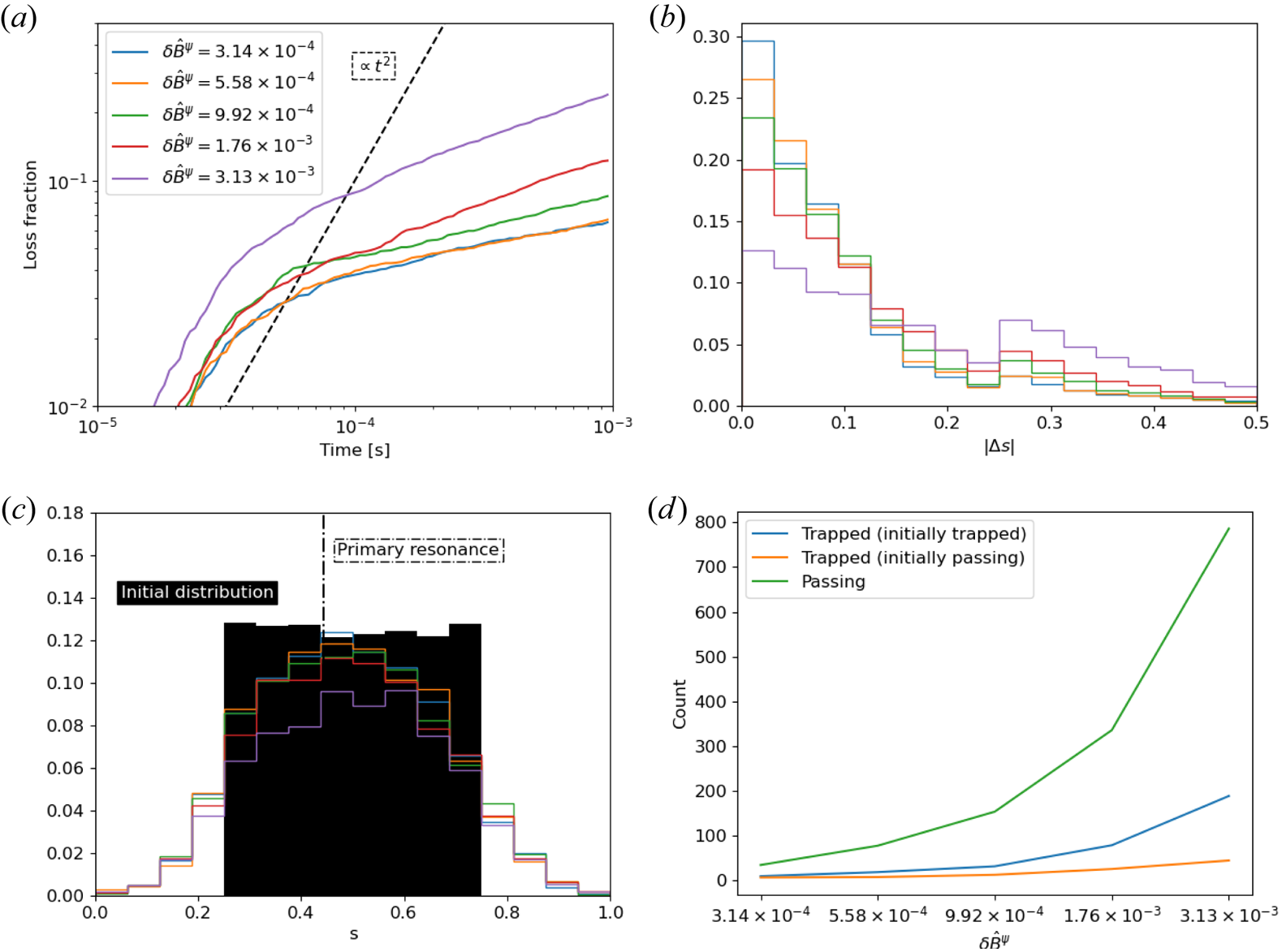
Figure 10. Monte Carlo guiding-centre tracing calculations are performed for the $\beta = 2.5\,\%$![]() QA configuration in the presence of an $m = 30$
QA configuration in the presence of an $m = 30$![]() perturbation with parameters described in table 1. The perturbation amplitude is increased to study the impact of island overlap, as illustrated in figure 9, on transport. (a) The loss fraction as a function of time. (b) The distribution of the total radial displacement, $|\Delta s|$
perturbation with parameters described in table 1. The perturbation amplitude is increased to study the impact of island overlap, as illustrated in figure 9, on transport. (a) The loss fraction as a function of time. (b) The distribution of the total radial displacement, $|\Delta s|$![]() , between the initial time and final recorded time. (c) The initial and final radial distribution of particles. (d) The increase in losses of different trajectory classes is plotted as a function of the perturbation amplitudes. The trapped and passing categorization is based on a comparison of the trapping parameter $\lambda = v_{\perp }^2/(v^2B)$
, between the initial time and final recorded time. (c) The initial and final radial distribution of particles. (d) The increase in losses of different trajectory classes is plotted as a function of the perturbation amplitudes. The trapped and passing categorization is based on a comparison of the trapping parameter $\lambda = v_{\perp }^2/(v^2B)$![]() with the maximum field strength on the magnetic surface where a given trajectory is initialized or lost.
with the maximum field strength on the magnetic surface where a given trajectory is initialized or lost.
Figure 10(d) displays the trapping state of lost trajectories as a function of the perturbation amplitude. The trapped and passing status at $t = 0$![]() and the time of loss are assessed by comparing the trapping parameter $\lambda = v_{\perp }^2/(v^2B)$
and the time of loss are assessed by comparing the trapping parameter $\lambda = v_{\perp }^2/(v^2B)$![]() with the maximum field strength on the initial and final magnetic surfaces. In order to focus on the losses due to the Alfvénic perturbation rather than symmetry-breaking or wide banana orbits, we subtract the count in each category from the losses without an Alfvénic perturbation. As expected, the majority of the loss increase is due to passing orbits. There are additional losses of initially passing orbits that transition to trapped orbits. This loss type can arise from diffusion in the constant of motion space, leading to transformation from a passing orbit to a barely trapped banana orbit with a large radial width (Hsu & Sigmar Reference Hsu and Sigmar1992; Sigmar et al. Reference Sigmar, Hsu, White and Cheng1992). Finally, there are losses of trapped particles that do not originate as passing. Further analysis is needed to understand the responsible loss mechanisms. Overall, we conclude that the kinetic Poincaré analysis provides insight into transport characteristics, even for these configurations with finite deviations from QS.
with the maximum field strength on the initial and final magnetic surfaces. In order to focus on the losses due to the Alfvénic perturbation rather than symmetry-breaking or wide banana orbits, we subtract the count in each category from the losses without an Alfvénic perturbation. As expected, the majority of the loss increase is due to passing orbits. There are additional losses of initially passing orbits that transition to trapped orbits. This loss type can arise from diffusion in the constant of motion space, leading to transformation from a passing orbit to a barely trapped banana orbit with a large radial width (Hsu & Sigmar Reference Hsu and Sigmar1992; Sigmar et al. Reference Sigmar, Hsu, White and Cheng1992). Finally, there are losses of trapped particles that do not originate as passing. Further analysis is needed to understand the responsible loss mechanisms. Overall, we conclude that the kinetic Poincaré analysis provides insight into transport characteristics, even for these configurations with finite deviations from QS.
7. Conclusions
We have developed the theory for guiding-centre transport in quasisymmetric equilibria with Alfvénic perturbations. Even if the perturbation is restricted to a single $m$![]() and $n$
and $n$![]() , additional resonances may be excited due to the coupling of the perturbation to the magnetic drifts, as discussed in § 3. The resonance condition, phase-space island width and island overlap conditions are discussed for several equilibria of interest. Quasihelical configurations have a reduced propensity for island overlap due to their increased resonance spacing. While the potential for island overlap increases with the poloidal mode number $m$
, additional resonances may be excited due to the coupling of the perturbation to the magnetic drifts, as discussed in § 3. The resonance condition, phase-space island width and island overlap conditions are discussed for several equilibria of interest. Quasihelical configurations have a reduced propensity for island overlap due to their increased resonance spacing. While the potential for island overlap increases with the poloidal mode number $m$![]() , the effective volume of phase-space non-integrability decreases when $m$
, the effective volume of phase-space non-integrability decreases when $m$![]() is large enough due to the reduced drift-island width for higher-order drift couplings. These features are visualized using kinetic Poincaré plots in § 5. Although the kinetic Poincaré section is only two-dimensional for a perfectly quasisymmetric equilibrium, this analysis still provides insight into the transport with finite QS-breaking errors. The QS-breakingerrors enhance the transport, especially in configurations with significant unconfined guiding-centre trajectories such as NCSX.
is large enough due to the reduced drift-island width for higher-order drift couplings. These features are visualized using kinetic Poincaré plots in § 5. Although the kinetic Poincaré section is only two-dimensional for a perfectly quasisymmetric equilibrium, this analysis still provides insight into the transport with finite QS-breaking errors. The QS-breakingerrors enhance the transport, especially in configurations with significant unconfined guiding-centre trajectories such as NCSX.
We evaluate the transport in several configurations close to QS for low ($m = 1$![]() ), moderate ($m = 15$
), moderate ($m = 15$![]() ) and high ($m = 30$
) and high ($m = 30$![]() ) mode number perturbations, with the highest mode number being that expected for reactor conditions. The toroidal mode number and frequency are chosen to resonate with a drift surface in the equilibrium. We fix the perturbation amplitude to an appropriate amplitude based on experimental measurements and modelling, $\delta B^{r}/B_0 \sim 10^{-3}$
) mode number perturbations, with the highest mode number being that expected for reactor conditions. The toroidal mode number and frequency are chosen to resonate with a drift surface in the equilibrium. We fix the perturbation amplitude to an appropriate amplitude based on experimental measurements and modelling, $\delta B^{r}/B_0 \sim 10^{-3}$![]() , finding that substantial island overlap can be present for moderate and high mode number perturbations. No island overlap occurs for a QH equilibrium or an equilibrium with very low magnetic shear, such as the recently obtained vacuum equilibria with precise QS (Landreman & Paul Reference Landreman and Paul2022). For the low-shear equilibrium, an enhancement of the loss fraction to ${\approx }20\,\%$
, finding that substantial island overlap can be present for moderate and high mode number perturbations. No island overlap occurs for a QH equilibrium or an equilibrium with very low magnetic shear, such as the recently obtained vacuum equilibria with precise QS (Landreman & Paul Reference Landreman and Paul2022). For the low-shear equilibrium, an enhancement of the loss fraction to ${\approx }20\,\%$![]() occurs due to the wide orbit width. For the QH configuration, the losses remain less than $7\,\%$
occurs due to the wide orbit width. For the QH configuration, the losses remain less than $7\,\%$![]() for all perturbations considered. For configurations with substantial island overlap, the losses increase to $10\unicode{x2013} 20\,\%$
for all perturbations considered. For configurations with substantial island overlap, the losses increase to $10\unicode{x2013} 20\,\%$![]() due to AE-driven transport.
due to AE-driven transport.
Our results are consistent with similar modelling for tokamak configurations (Hsu & Sigmar Reference Hsu and Sigmar1992; Sigmar et al. Reference Sigmar, Hsu, White and Cheng1992), which indicated resonant overlap and enhanced transport for $\delta B^r/B_0 \sim 10^{-3}$![]() . More recent work has highlighted the impact of symmetry-breaking on AE-driven transport in a QH configuration (White & Duarte Reference White and Duarte2023). Our results agree qualitatively with their conclusion that unconfined particle orbits enhance diffusive losses. However, our results are not in quantitative agreement with their findings of substantial diffusive losses for AE perturbation amplitudes $\delta B^r/B_0 \sim 10^{-6}$
. More recent work has highlighted the impact of symmetry-breaking on AE-driven transport in a QH configuration (White & Duarte Reference White and Duarte2023). Our results agree qualitatively with their conclusion that unconfined particle orbits enhance diffusive losses. However, our results are not in quantitative agreement with their findings of substantial diffusive losses for AE perturbation amplitudes $\delta B^r/B_0 \sim 10^{-6}$![]() for a QH equilibrium with precise levels of QS (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021). Further work is necessary in order to resolve this discrepancy.
for a QH equilibrium with precise levels of QS (Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021). Further work is necessary in order to resolve this discrepancy.
As the amplitude of the perturbation is increased, island overlap is observed, leading to a rapid transition to stiff fast-ion transport. This result is similar to observations of critical gradient transport in DIII-D (Collins et al. Reference Collins, Heidbrink, Austin, Kramer, Pace, Petty, Stagner, Van Zeeland, White and Zhu2016, Reference Collins, Heidbrink, Podestà, White, Kramer, Pace, Petty, Stagner, Van Zeeland and Zhu2017) and indicates the potential applicability of quasilinear models (Duarte et al. Reference Duarte, Berk, Gorelenkov, Heidbrink, Kramer, Nazikian, Pace, Podesta, Tobias and Van Zeeland2017; Gorelenkov et al. Reference Gorelenkov, Duarte, Podesta and Berk2018; Duarte et al. Reference Duarte, Gorelenkov, White and Berk2019) to predict the saturated AE amplitude in stellarators. Since the phase-space island width grows with the amplitude of the magnetic drifts, island overlap is more likely to occur at larger energies.
Our results suggest several avenues to reduce AE-driven transport in quasisymmetric configurations:
(i) Development of QH configurations, which avoid drift-island overlap due to increased resonance spacing.
(ii) Avoiding low magnetic shear, which manifests as wide drift-island widths for passing particles.
(iii) Evaluating metrics from the unperturbed equilibrium (e.g. the Bessel coupling parameters $J_l(\eta _1)$
 ) as a proxy for drift island width within a stellarator optimization loop.
) as a proxy for drift island width within a stellarator optimization loop.
Finally, we remark that many aspects of AEs were not considered in this study and will affect the transport. To gain a basic understanding of transport, a resonant AE was chosen to have a uniform radial structure. While the radial perturbation amplitude was assumed to be held fixed when comparing across configurations, in practice, the mode structure and amplitude will also depend on the mode numbers and other physical parameters through the AE's nonlinear evolution. In the future, we plan to build on this work to obtain a more complete picture of the evolution of AEs in stellarator reactor scenarios. For example, the analysis tools described here, such as kinetic Poincaré plots, could be used to study the nonlinear evolution of phase-space structures such as hole–clump pairs (Bierwage, White & Duarte Reference Bierwage, White and Duarte2021) and zonal structures (Zonca et al. Reference Zonca, Chen, Briguglio, Fogaccia, Vlad and Wang2015) in quasisymmetric configurations.
Acknowledgements
The authors would like to acknowledge discussions with V. Duarte and R. White.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
We acknowledge funding through the U. S. Department of Energy, under contract No. DE-SC0016268 and through the Simons Foundation collaboration ‘Hidden Symmetries and Fusion Energy’, Grant No. 601958.
Appendix A. Analysis of the resonance condition
Under the assumption of a vacuum magnetic field, the perturbed radial equation of motion reads
where subscript commas denote partial derivatives. The toroidal motion, $\dot {\zeta } = B_0v_{\|}/G$![]() , is not modified by the perturbation. The first term accounts for the perturbed $\boldsymbol {E} \times \boldsymbol {B}$
, is not modified by the perturbation. The first term accounts for the perturbed $\boldsymbol {E} \times \boldsymbol {B}$![]() drift, while the second term accounts for streaming along the perturbed magnetic field. Given the form for the perturbed potential (2.4), the perturbed radial drift is proportional to $\cos (\eta )$
drift, while the second term accounts for streaming along the perturbed magnetic field. Given the form for the perturbed potential (2.4), the perturbed radial drift is proportional to $\cos (\eta )$![]() . We begin our analysis by expressing $\cos (\eta )$
. We begin our analysis by expressing $\cos (\eta )$![]() along the unperturbed trajectory in terms of Bessel functions (A4). This expression is used to evaluate the perturbed radial drift in (A5) and (A6) and the resulting phase-space island width (A7).
along the unperturbed trajectory in terms of Bessel functions (A4). This expression is used to evaluate the perturbed radial drift in (A5) and (A6) and the resulting phase-space island width (A7).
We begin with the expressions for the unperturbed trajectories (3.1). Due to the relatively small magnitude of the periodic contributions, $\chi _j$![]() and $\zeta _j$
and $\zeta _j$![]() , in comparison with the secular terms, $\omega _{\chi }$
, in comparison with the secular terms, $\omega _{\chi }$![]() and $\omega _{\zeta }$
and $\omega _{\zeta }$![]() , the trajectories can be approximated as
, the trajectories can be approximated as

where $\chi ^0 = \chi (t = 0)$![]() and $\zeta ^0 = \zeta (t = 0)$
and $\zeta ^0 = \zeta (t = 0)$![]() .
.
To evaluate the radial drift due to the perturbation (A1), we evaluate the phase along the unperturbed trajectory

where $\eta ^0 = m \theta ^0 - n \zeta ^0$![]() is the initial phase. Under the assumption that one term, $j = j'$
is the initial phase. Under the assumption that one term, $j = j'$![]() , is dominant in the expression for the drifts (3.1), the phase factor $\cos (\eta )$
, is dominant in the expression for the drifts (3.1), the phase factor $\cos (\eta )$![]() can be expressed in terms of Bessel functions of the first kind
can be expressed in terms of Bessel functions of the first kind
where $\eta _{j'} = (m\chi _{j'}- (n-Nm)\zeta _{j'})/(j'\omega _{\chi })$![]() and $\varOmega _{kj'} = (m+kj')\omega _{\chi } - (n - Nm)\omega _{\zeta } + \omega$
and $\varOmega _{kj'} = (m+kj')\omega _{\chi } - (n - Nm)\omega _{\zeta } + \omega$![]() .
.
By expressing the instantaneous perturbed radial drift (A1) in terms of $\cos (\eta )$![]() along the unperturbed trajectory (A4) we obtain the expression
along the unperturbed trajectory (A4) we obtain the expression

with amplitudes given by

For a net drift to occur, a resonance condition $\varOmega _{kj'} = 0$![]() must be satisfied. The Fourier amplitudes $\psi _{kj'}^0$
must be satisfied. The Fourier amplitudes $\psi _{kj'}^0$![]() and $\psi _{kj'}^{\pm }$
and $\psi _{kj'}^{\pm }$![]() then determine the amplitude of the radial transport. The associated full island width is given by
then determine the amplitude of the radial transport. The associated full island width is given by

where $\psi _{kj'}$![]() is taken to be $\psi _{kj'}^0$
is taken to be $\psi _{kj'}^0$![]() or $\psi _{kj'}^{\pm }$
or $\psi _{kj'}^{\pm }$![]() .
.
We now consider the scaling of the cosine amplitudes (A6) with respect to the radial perturbed magnetic field amplitude and magnetic drifts. If a resonance condition $\varOmega _{kj'} = 0$![]() is satisfied, the corresponding radial perturbed field scales with the perturbation amplitude and mode numbers as $\delta \hat {B}^{\psi } \sim m (\iota m - n) \hat {\varPhi }$
is satisfied, the corresponding radial perturbed field scales with the perturbation amplitude and mode numbers as $\delta \hat {B}^{\psi } \sim m (\iota m - n) \hat {\varPhi }$![]() . Using the resonance condition, the factor appearing in $\psi _{kj'}^0$
. Using the resonance condition, the factor appearing in $\psi _{kj'}^0$![]() can be expressed as $1 + (\iota m -n )\omega _{\zeta }/\omega = (-kj' \omega _{\chi } + m (\iota \omega _{\zeta }-\omega _{\theta }))/\omega$
can be expressed as $1 + (\iota m -n )\omega _{\zeta }/\omega = (-kj' \omega _{\chi } + m (\iota \omega _{\zeta }-\omega _{\theta }))/\omega$![]() . Since the quantity $\iota - \omega _{\theta }/\omega _{\zeta }$
. Since the quantity $\iota - \omega _{\theta }/\omega _{\zeta }$![]() scales with the magnitude of the magnetic drifts, at low energy, this factor approaches $kj' \omega _{\chi }/\omega$
scales with the magnitude of the magnetic drifts, at low energy, this factor approaches $kj' \omega _{\chi }/\omega$![]() . Thus, $\psi _0^0 \sim (\iota - \omega _{\theta }/\omega _{\zeta }) J_0(\eta _{j'}) \delta \hat {B}^{\psi }$
. Thus, $\psi _0^0 \sim (\iota - \omega _{\theta }/\omega _{\zeta }) J_0(\eta _{j'}) \delta \hat {B}^{\psi }$![]() . The scaling of each harmonic is summarized in table 3. Considering the small argument limit of $\psi _0^{\pm }$
. The scaling of each harmonic is summarized in table 3. Considering the small argument limit of $\psi _0^{\pm }$![]() , this harmonic will scale with two factors of the magnetic drifts through both $\eta _{j'}$
, this harmonic will scale with two factors of the magnetic drifts through both $\eta _{j'}$![]() and $\zeta _{j'}$
and $\zeta _{j'}$![]() . Thus $\psi _0^0$
. Thus $\psi _0^0$![]() will dominate over $\psi _0^{\pm }$
will dominate over $\psi _0^{\pm }$![]() for $k = 0$
for $k = 0$![]() . Considering $k \ne 0$
. Considering $k \ne 0$![]() , $\psi _{k}^0$
, $\psi _{k}^0$![]() will have the same scaling with the magnetic drifts as $\psi _k^{-}$
will have the same scaling with the magnetic drifts as $\psi _k^{-}$![]() for $k > 0$
for $k > 0$![]() , while $\psi _k^+$
, while $\psi _k^+$![]() will be smaller in magnitude by a factor of the magnetic drifts. The magnitude of the harmonics decreases strongly with $|k|$
will be smaller in magnitude by a factor of the magnetic drifts. The magnitude of the harmonics decreases strongly with $|k|$![]() due to the Bessel coupling parameter. When considering the dependence on the magnetic drifts, the most significant radial transport will arise from $\psi _0^0$
due to the Bessel coupling parameter. When considering the dependence on the magnetic drifts, the most significant radial transport will arise from $\psi _0^0$![]() , $\psi _{\pm j'}^0$
, $\psi _{\pm j'}^0$![]() , and $\psi _{\mp j'}^{\pm }$
, and $\psi _{\mp j'}^{\pm }$![]() . Considering the limit of large mode number perturbations, $\psi _{\pm j'}^0$
. Considering the limit of large mode number perturbations, $\psi _{\pm j'}^0$![]() will dominate due to its dependence on $\eta _{j'}$
will dominate due to its dependence on $\eta _{j'}$![]() .
.
Table 3. Scaling of cosine harmonic amplitudes of the perturbed radial drift (A6) with the radial perturbed magnetic field, magnetic drifts and mode numbers. The quantities $(\iota - \omega _{\theta }/\omega _{\zeta })$![]() and $\zeta _{j'}$
and $\zeta _{j'}$![]() scale with the drift amplitude. The quantity $\eta _{j'}$
scale with the drift amplitude. The quantity $\eta _{j'}$![]() scales with both the drift amplitude and the mode numbers.
scales with both the drift amplitude and the mode numbers.