Published online by Cambridge University Press: 30 April 2024
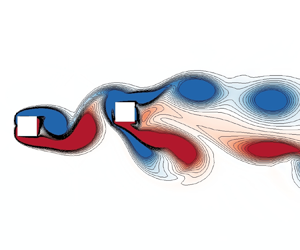
The flow-induced vibrations (FIVs) of two identical tandem square cylinders with mass ratio m* = 3.5 at Reynolds number Re = 150 are investigated through two-dimensional direct numerical simulation (DNS) and linear stability analysis over a parameter range of spacing ratio 1.5 ≤ L* ≤ 5 and reduced velocity 3 ≤ Ur ≤ 34. Three kinds of FIV responses, namely vortex-induced vibration (VIV), biased oscillation (BO) and galloping (GA), are identified. The FIVs are then further classified into the branches of initial VIV (IV), resonant VIV (RV and RV′), flutter-induced VIV (FV), desynchronized VIV (DV), VIV developing from GA (GV), transitional state between VIV and GA (TR), BO and GA based on the characteristics of the vibration responses. The transitions among different FIV branches are examined by combining the DNS with linear stability analysis, where the transition boundaries among the VIV, BO and GA branches over the concerned parameters are identified on the branch maps. The transition from IV to RV or RV′ is found to be related to the unstable wake mode, while the FV, transiting from RV or RV′, is induced by the unstable structural factor in the wake-structure mode. The structural instability is considered as the physical origin of GA, whereas the mode competition between unstable wake and structure leads to DV, GV and TR, and thus delays the appearance of GA. The transition from DV to BO with biased equilibrium position, accompanied by the even-order harmonic frequencies, is essentially induced by the symmetry breaking bifurcation.